1. A kvantummechanika alapjai
|
|
|
- Bence Vass
- 9 évvel ezelőtt
- Látták:
Átírás
1 1. A kvantummechanika alapjai 1.1. A klasszikus fizika tudományos világképe 1) Vannak anyagok vagy testek, amelyek tömeggel és impulzussal rendelkeznek. A mikrorészecskék közül ilyenek pl. az elektronok Vannak hullámok, amelyekre jellemző az elhajlás és az interferencia. Ilyen a fény, amely elektromágneses sugárzás. Ezek mereven elkülönülő jelenségek. ) Bármely mozgás energiája bármekkora értéket fölvehet. Energiafelvétel és energialeadás is tetszőleges lehet. 3) Ismerve a részecske helyzetét és impulzusát egy kezdeti pillanatban, abból pontosan megjósolható, hogy egy tetszőleges t időpillanatban mi lesz a részecske helyzetvektora és impulzusa. A XIX. sz. végén és a XX. sz. elején az elemi részecskék, atomok és molekulák energialeadásával és fölvételével, valamint a fény természetével és az anyaggal való kölcsönhatásaival kapcsolatban számos olyan kísérleti tény merült föl, amely ellentétben áll ezzel a világképpel. Magyarázatukra született meg a kvantummechanika.
2 1.. A klasszikus fizika korlátai az atomi szintű jelenségek leírásában. A kvantummechanika születése A feketetest-sugárzás Abszolút fekete test: bármilyen frekvenciájú sugárzást elnyel. Adott hőmérsékleten bármely más testnél nagyobb a fénykibocsátó képessége. Modellje: belülről bekormozott doboz, amelyen egy apró lyuk van (az itt kibocsátott sugárzás energiáját mérik, amelyet számszerűen a sugárzás energiasűrűségével, azaz az egységnyi térfogatra és hullámhosszra jutó energiával jellemeznek; egysége J/m4). A sugárzást a doboz falának hevítésével idézik elő. Klasszikus fizika alapján A frekvenciájú fényt sajátfrekvenciájú oszcillátorok bocsátják ki. Ezeket a hőmozgás gerjeszti, amelynek energiája egyenletesen oszlik meg az oszcillátorok között. Tehát valamennyi oszcillátor gerjesztődik és sugároz, a kis- és nagyfrekvenciájúak egyaránt.
3 Kísérleti tapasztalat Rayleigh Jeans-törvény csak kis frekvenciáknál érvényes Miért nem sugároznak a nagy frekvenciájú oszcillátorok? Planck-féle kvantumhipotézis A frekvenciájú oszcillátorok energiája nem lehet akármekkora, csakis n h, ahol n egész szám. Max Planck A nagy frekvenciájú oszcillátorok gerjesztéséhez ugyan a hőmérséklet növelésekor több termikus energia jut (lásd a görbék eltolódását a nagyobb frekvenciák felé a T növelésekor vörös izzásból fehér izzásba mennek át a sugárzó testek). Egy frekvencia határon túl azonban megszűnik az oszcillátorok gerjeszthetősége és így sugárzása is.
4 1... Szilárd testek hőkapacitásának hőmérsékletfüggése Klasszikus fizika: ekvipartíció tétele Termikus egyensúlyban lévő részecskerendszer teljes energiakifejezésében minden négyzetes tag egy részecskére jutó átlagértéke kt/, ahol k a Boltzmann-állandó, T a termodinamikai hőmérséklet Egydimenziós oszcillátor teljes energiája px 1 négyzetes tagot tartalmaz, H k x ezért energiája kt m 3 dimenziós oszcillátor energiája 3kT (x, y, z irányú elmozdulás és az impulzusvektor x, y, z irányú komponensei miatt). 1 mól oszcillátor belső energiája Um = NA 3 k T = 3 RT U CV-nek állandónak kellene lennie! C v m 3R T V A csökkenés a Planck-hipotézis alapján magyarázható: alacsony hőmérsékleten nem elegendő a termikus energia az oszcillátorok gerjesztéséhez, így energiát sem fölvenni, sem leadni nem képesek.
5 1..3. Fényelektromos hatás A jelenség: ultraibolya fény hatására a fémek felületéről elektronok lépnek ki. Klasszikus fizika: A sugárzás elektromos tere a fény haladási irányára merőlegesen oszcillál. A fény intenzitása az amplitúdó négyzetével arányos. Ha nő a fény intenzitása, nő az amplitúdó. Ezzel együtt a fém felületén az elektron is növekvő amplitúdóval oszcillál, mígnem leszakad a fém felületéről, annál nagyobb kinetikus energiára téve szert, minél nagyobb volt a fény intenzitása. Tehát az várható, hogy bármekkora frekvenciájú fény kiváltja az elektronok kilépését, ha elég nagy az intenzitása, és az elektronok kinetikus energiája a fényintenzitással együtt nő. Kísérleti tények: Elektronok csak akkor lépnek ki, ha a sugárzás frekvenciája meghalad egy küszöbértéket. Ha > 0, akármilyen kis intenzitású fény hatására azonnal elektronok lépnek ki. Az elektronok kinetikus energiája nem függ a fény intenzitásától, hanem annak frekvenciájával arányos. A kilépő elektronok száma arányos a fényintenzitással.
6 Einstein: Továbbfejlesztette Planck kvantumhipotézisét azzal, hogy nemcsak az atomi oszcillátorok adják le a sugárzási energiát h adagokban, hanem a kisugárzott fény is h energiaadagokból (fotonokból) áll. (A fény részecskejellege) Az elektron kinetikus energiája a foton energiájának és a kilépési munkának a különbsége: 1 me v e hν φ hν hν Compton-effektus A jelenség: a röntgensugarak elektronokon szóródnak, ami a sugárzás hullámhosszának csökkenésével jár. A csökkenés a szórási szögtől függ. Magyarázat: a fotonok impulzussal rendelkező részecskék. Más részecskékkel (az elektronokkal) ütközve az impulzus- és energiamegmaradás törvénye érvényesül. A fotonok impulzusa (Einstein): p h λ
7 1..5. Dualizmus a mikrovilágban Louis de Broglie de Broglie anyaghullámai: Feltételezte, hogy az anyagi világ egységes: amint a fény kettős természetű (bizonyos körülmények között hullámként, más körülmények között részecskék áramaként viselkedik), ugyanúgy az impulzussal rendelkező részecskékhez, pl. az elektronhoz vagy más testhez rendelhető egy hullám. Ennek hullámhossza és a test impulzusa között ugyanaz az összefüggés érvényes: λ h p Kísérleti bizonyíték Diffrakció alumínium fólián Röntgensugárzás Elektronnyaláb
8 1..6. A H-atom vonalas színképe A hidrogénatomokkal nagy energiát közöltek, majd a kisugárzott fényt hullámhossza szerint felbontották és fényérzékeny lemezen mutatták ki. Következtetés: Ultraibolya Látható Infravörös A színkép vonalas, vagyis a H-atom nem ad le akármekkora energiát, tehát meghatározott diszkrét energiaszintjei kell legyenek. Bohr, fölhasználva de Broglie anyaghullám-föltételezését, ki tudta mutatni, hogy csak bizonyos energiák megengedettek a H-atom számára, és ezek stacionárius állapotok (az elektron nem zuhan be az atommagba, amint azt a klasszikus fizika alapján várhatnánk). Alapföltételezés: az elektron olyan körpályán mozog, amelynek kerülete az elektronhullám hullámhosszának egész számú többszöröse. Ellenkező esetben a hullám amplitúdója csökken, majd kioltódik. Niels Bohr
9 1.3. A kvantummechanika néhány fontos alapelve A hullámfüggvény Egy kvantummechanikai rendszer állapotát tökéletesen jellemzi egy Ψ(x) függvény, amelyben x a részecske koordinátája. A rendszerre vonatkozó minden lehetséges információ levezethető a Ψ(x) hullámfüggvényből, amelynek valószínűségi tartalma van (Born-féle értelmezés). d d V az ún. valószínűségi sűrűségfüggvény. a tér egy pontjában megadja annak a valószínűségét, hogy a részecskét ezen pont egy kicsiny =dxdydz környezetében találjuk a véges V térfogatban való tartózkodás valószínűsége Ez d =dxdydz esetén pl. egy hármas integrál, amelynek értéke 0 és 1 közé esik. d 1 a teljes térre vett integrál pedig megadja annak a valószínűségét, hogy a részecske valahol a térben van (ez biztos esemény, amelynek valószínűsége 1).
10 Mindez akkor igaz, ha a hullámfüggvény normált. Egy függvény normált, ha abszolút értékének a teljes térre vett négyzetintegrálja 1, azaz egyváltozós függvény esetén f ( x ) f ( x )dx 1 Ha ez nem áll fönn, de a négyzetintegrál értéke véges, akkor a függvényt normálhatjuk. Normálás: a függvény normálttá tétele. Megkeressük azt az N konstansot, az ún. normálási tényezőt, amellyel a függvényt megszorozva, az új függvényre teljesül a normálási feltétel. A(z egyváltozós hullám)függvény normálása: ( N ( x )) N ( x ) dx N N ( x ) ( x )dx 1 1 ( x ) ( x)dx
11 A valószínűségi értelmezés bizonyos követelményeket ró a hullámfüggvényre: - folytonos legyen - folytonos első deriváltja legyen - egyértékű legyen - majdnem mindenütt véges legyen (azaz ne legyen véges intervallumon végtelen) - négyzetesen integrálható legyen (azaz a négyzetintegrálja ne legyen végtelen). Rossz hullámfüggvények: Nem folytonos. Első deriváltja nem folytonos. Többértékű. Véges intervallumon végtelen.
12 1.3.. Fizikai mennyiségek és operátorok. A Schrödinger-egyenlet. A kvantummechanika másik alapelve, hogy 1) a fizikai mennyiségeket operátorokkal reprezentálja, vagyis a fizikai mennyiségekhez operátorokat rendel; ) ezen operátorok sajátértékei az illető fizikai mennyiség mérhető értékeit adják meg. Operátor műveleti utasítás, amely egy függvényhez egy másik függvényt rendel, vagyis függvénytranszformáció: f g Dˆ x n n x n 1 pl. a differenciálás operátor, az xn függvényhez az nxn-1 függvényt rendeli Lineáris operátor (a kvantummechanikában ilyeneket alkalmaznak) ˆ ( f g) ˆ f ˆ g minden f-re és g-re teljesül ˆ (cf ) c ˆ f ahol c valós vagy komplex szám, és f tetszőleges
13 Operátorok egyenlősége ˆ ˆ 1 ha minden f-re teljesül, hogy ˆ f ˆ f 1 Operátorok összege és különbsége ˆ ˆ )f ˆ f ˆ f ( 1 1 Operátorok szorzata és felcserélhetősége ˆ ˆ ˆ ˆ ( 1 ) f 1 ( f ) először hajtjuk végre a második operátor által kijelölt transzformációt, majd az új függvényt az első operátor szerint transzformáljuk. Ha ˆ ˆ ˆ ˆ az operátorok nem felcserélhetők 1 1 ˆ ˆ ˆ ˆ 1 1 az operátorok felcserélhetők A kvantummechanikai operátorok értelmezési tartománya mindazon függvények összessége, amelyek a, intervallumon vannak értelmezve valós változójúak és komplex értékűek abszolút értékük négyzetintegrálja véges, azaz f ( x ) f ( x)dx
14 A kvantummechanikában alkalmazott legfontosabb operátorok x x,y y,z z p x, p y, p z i x i y i z helykoordináták impulzuskomponensek p,, i x y z i impulzus p x y z impulzusnégyzet T m x y z m kinetikus energia V V potenciális energia H T V összes energia Operátorok sajátfüggvényei és sajátértékei, sajátérték-egyenlet f f az operátor által kijelölt függvénytranszformáció az eredeti függvény konstansszorosát eredményezi
15 Az olyan függvényeket, amelyekre ez teljesül, az operátor sajátfüggvényeinek, a megfelelő konstansokat az operátor sajátértékeinek nevezzük. Ez utóbbiak adják meg az operátor által reprezentált fizikai mennyiség mérhető értékeit. Az operátort, sajátfüggvényét és sajátértékét tartalmazó, fentebbi típusú egyenlet az operátor sajátérték-egyenlete. Schrödinger-egyenlet az összes energia operátorának, a ún. Hamilton-operátornak a sajátérték-egyenlete a Schrödinger-egyenlet: H E Erwin Schrödinger Ennek megoldásával kaphatjuk meg a rendszer hullámfüggvényeit, valamint az ezeknek megfelelő E energia-sajátértékeket (a rendszer lehetséges, méréssel meghatározható energia-értékeit a legalacsonyabb energiájú, ún. alapállapotban, valamint a magasabb energiájú, ún. gerjesztett állapotokban). A várható érték A fizikai mennyiségek ún. várható értékének nevezik azt az átlagértéket, amely nagy számú mérés eredményeként adódik. A hullámfüggvény ismeretében ez is kiszámítható a következő, teljes térre vett integrál segítségével
16 ˆ d teljes tér az fizikai mennyiség várható értéke a fizikai mennyiséget reprezentáló operátor A Heisenberg-féle határozatlansági elv A kvantummechanika következő fontos alapelve: vannak olyan fizikai mennyiség-párok, ún. komplementer fizikai mennyiségek, amelyek egyidejűleg nem határozhatók meg tetszőleges pontossággal. A legfontosabb ilyen mennyiség-párok a hely és az impulzus, illetve az energia és az idő. Ha rendre p-vel, q-val, E-vel, ill. t-vel jelöljük az impulzus, a hely, az energia, ill. az idő bizonytalanságát, a közöttük lévő relációkat a következőképpen adhatjuk meg E t p q Werner Heisenberg
17 Felcserélhető-e a helyoperátor és az impulzusoperátor? xˆ pˆ f x pˆ xˆ f d df f x i dx i dx d df ( x f ) f x i dx i i dx NEM! A komplementer fizikai mennyiségek azok, amelyeknek az operátorai nem felcserélhetők. hely és impulzus energia és idő impulzusmomentum z- és x-, ill. z- és y-irányú komponense
18 Egyenes mentén való mozgás kvantummechanikai tárgyalása Egy m tömegű részecske egy egyenes mentén, akadálytalanul mozog, potenciális energiája zérus. Ennek megfelelően a Hamilton-operátor megegyezik a kinetikus energia-operátorral. Így a mozgásra vonatkozó Schrödinger-egyenlet: E m x Az ennek megoldásaként nyert hullámfüggvény: Az energia sajátértékek: k E m Aeikx Be ikx (A és B konstans) k konstans, értéke tetszőleges Ellenőrizzük, hogy a fentebbi függvény valóban sajátfüggvénye-e a Hamilton-operátornak! d d ikx ikx ikx ikx Hˆ ( Tˆ ) A e B e Aik e B ( ik ) e m dx m dx k ikx ikx Ai k e Bi k e Ae ikx Be ikx E m m Valóban visszakaptuk az eredeti függvény konstansszorosát, tehát a függvény a szabad haladó mozgást végző részecske Hamilton-operátorának sajátfüggvénye, a részecske hullámfüggvénye. A hullámfüggvény szorzója a részecske összes energiáját adja meg.
19 Vizsgáljuk meg, hogy a részecske hullámfüggvénye az impulzusoperátornak sajátfüggvénye-e! Először azonban alakítsuk át a függvényt az ei = cos + i sin Euler-egyenlet felhasználásával! (Itt = kx) Legyen A=B! = A(eikx + e-ikx) = A[cos kx + i sin kx + cos (-kx) + i sin (-kx)] = A cos kx, ugyanis pˆ cos (-kx) = cos kx sin (-kx) = - sin kx d ( Acoskx) Ak sinkx konst Acoskx i dx i A haladó mozgást végző részecske hullámfüggvénye nem sajátfüggvénye az impulzusoperátornak: a fenti egyenletből nem tudjuk megállapítani a részecske lehetséges impulzusát. Nézzük meg most, hogy a hullámfüggvény eikx és e-ikx összetevői sajátfüggvényei-e az impulzusoperátornak! pˆ e ikx d ikx e ik eikx k eikx i dx i pˆ e ikx d ikx e ik e ikx k e ikx i dx i IGEN!
20 Az impulzusoperátornak tehát az eikx és e-ikx függvények sajátfüggvényei. A sajátértékek: k k a részecske balról jobbra halad a részecske jobbról balra halad Jelen esetben a hullámfüggvény az impulzusperátor sajátfüggvényeinek lineáris szuperpozíciója. (Lineáris szuperpozíció: olyan függvény, amelyet úgy kapunk, hogy bizonyos függvényeket egy-egy konstanssal megszorzunk, majd ezeket összeadjuk.) Ha mérjük az impulzust, a mérés eredménye a szuperpozíciót alkotó sajátfüggvények valamelyikéhez tartozó sajátérték. Hogy az illető sajátértéket mekkora valószínűséggel mérjük, azt normált hullámfüggvény esetén a megfelelő sajátfüggvény együtthatója abszolút értékének négyzete adja meg, a jelen esetben A*A, ill. B*B. (Kézenfekvő feltételezés, hogy a szabad haladó mozgást végző részecske ugyanakkora valószínűséggel halad balról jobbra, illetve jobbról balra, vagyis A=B.)
Részecskék hullámtermészete
 Részecskék ullámtermészete Bevezetés A sugárzás és az anyag egyaránt mutat részecskejellegű és ullámjellegű tulajdonságokat. Atommodellek A Tomson modell J.J. Tomson 1898 A negatív töltésű elektronok pozitív
Részecskék ullámtermészete Bevezetés A sugárzás és az anyag egyaránt mutat részecskejellegű és ullámjellegű tulajdonságokat. Atommodellek A Tomson modell J.J. Tomson 1898 A negatív töltésű elektronok pozitív
OPTIKA. Fénykibocsátás mechanizmusa fényforrás típusok. Dr. Seres István
 OPTIKA Fénykibocsátás mechanizmusa Dr. Seres István Történeti áttekintés Ernest Rutherford (1911) Rutherford alfa részecskéket tanulmányozott 1898-tól (ő fedezte fel őket). 1909-ben egy kísérlet során
OPTIKA Fénykibocsátás mechanizmusa Dr. Seres István Történeti áttekintés Ernest Rutherford (1911) Rutherford alfa részecskéket tanulmányozott 1898-tól (ő fedezte fel őket). 1909-ben egy kísérlet során
Atomfizika I. Az anyagszerkezetről alkotott kép változása Ókori görög filozófusok régi kérdése: Miből vannak a testek? Meddig osztható az anyag?
 Atomfizika I. Az anyagszerkezetről alkotott kép változása Ókori görög filozófusok régi kérdése: Miből vannak a testek? Meddig osztható az anyag? Platón (i.e. 427-347), Arisztotelész (=i.e. 387-322): Végtelenségig
Atomfizika I. Az anyagszerkezetről alkotott kép változása Ókori görög filozófusok régi kérdése: Miből vannak a testek? Meddig osztható az anyag? Platón (i.e. 427-347), Arisztotelész (=i.e. 387-322): Végtelenségig
A jelenség magyarázata. Fényszórás mérése. A dipólus keletkezése. Oszcilláló dipólusok. A megfigyelhető jelenségek. A fény elektromágneses hullám.
 Fényszórás mérése A jelenség magyarázata A megfigyelhető jelenségek A fény elektromágneses hullám. Az elektromos tér töltésekre erőhatást fejt ki. A dipólus keletkezése Dipólusok: a pozitív és a negatív
Fényszórás mérése A jelenség magyarázata A megfigyelhető jelenségek A fény elektromágneses hullám. Az elektromos tér töltésekre erőhatást fejt ki. A dipólus keletkezése Dipólusok: a pozitív és a negatív
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria
 005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
paradoxonok a modern fizikában Dr. Héjjas István
 paradoxonok a modern fizikában Dr. Héjjas István 1 A modern fizika voltaképpen ezoterikus tudomány!!! miért? 1. Olyan jelenségekkel (is) foglalkozik, amelyeket képtelenségeknek tartunk, mivel ellentmondanak
paradoxonok a modern fizikában Dr. Héjjas István 1 A modern fizika voltaképpen ezoterikus tudomány!!! miért? 1. Olyan jelenségekkel (is) foglalkozik, amelyeket képtelenségeknek tartunk, mivel ellentmondanak
A nyugalomban levő levegő fizikai jellemzői. Dr. Lakotár Katalin
 A nyugalomban levő levegő fizikai jellemzői Dr. Lakotár Katalin Száraz, nyugalomban levő levegő légköri jellemzői egyszerűsített légkör modell állapotjelzői: sűrűség vagy fajlagos térfogat térfogategységben
A nyugalomban levő levegő fizikai jellemzői Dr. Lakotár Katalin Száraz, nyugalomban levő levegő légköri jellemzői egyszerűsített légkör modell állapotjelzői: sűrűség vagy fajlagos térfogat térfogategységben
AZ ELEKTROMÁGNESES SUGÁRZÁS KETTŐS TERMÉSZETE
 AZ ELEKTROMÁGNESES SUGÁRZÁS KETTŐS TERMÉSZETE Alapfogalmak 1. A hőmérsékleti sugárzás Értelmezés (hőmérsékleti sugárzás): A testek hőmérsékletével kapcsolatos, a teljes elektromágneses spektrumra kiterjedő
AZ ELEKTROMÁGNESES SUGÁRZÁS KETTŐS TERMÉSZETE Alapfogalmak 1. A hőmérsékleti sugárzás Értelmezés (hőmérsékleti sugárzás): A testek hőmérsékletével kapcsolatos, a teljes elektromágneses spektrumra kiterjedő
1. Prefix jelentések. 2. Mi alapján definiáljuk az 1 másodpercet? 3. Mi alapján definiáljuk az 1 métert? 4. Mi a tömegegység definíciója?
 1. Prefix jelentések. 10 1 deka 10-1 deci 10 2 hektó 10-2 centi 10 3 kiló 10-3 milli 10 6 mega 10-6 mikró 10 9 giga 10-9 nano 10 12 tera 10-12 piko 10 15 peta 10-15 fento 10 18 exa 10-18 atto 2. Mi alapján
1. Prefix jelentések. 10 1 deka 10-1 deci 10 2 hektó 10-2 centi 10 3 kiló 10-3 milli 10 6 mega 10-6 mikró 10 9 giga 10-9 nano 10 12 tera 10-12 piko 10 15 peta 10-15 fento 10 18 exa 10-18 atto 2. Mi alapján
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
5. Mérés. Fényelektromos jelenség vizsgálata Fotocella mérése 2014.02.15.
 1. Elméleti áttekintés: 5. Mérés Fényelektromos jelenség vizsgálata Fotocella mérése 2014.02.15. Fény hatására a fémekből elektronok lépnek ki. Ezt a jelenséget nevezzük fényelektromos jelenségnek (fotoeffektus).
1. Elméleti áttekintés: 5. Mérés Fényelektromos jelenség vizsgálata Fotocella mérése 2014.02.15. Fény hatására a fémekből elektronok lépnek ki. Ezt a jelenséget nevezzük fényelektromos jelenségnek (fotoeffektus).
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
2. AZ ATOM. 6.1. Az elektron felfedezése
 2. AZ ATOM Atom: atommag + elektronfelhő = proton, neutron, elektron Elemi részecskék 6.. Az elektron felfedezése 82. Henry Davy (-) katód (+) anód Az üveggel érintkező katódsugár zöldes luminesszenciát
2. AZ ATOM Atom: atommag + elektronfelhő = proton, neutron, elektron Elemi részecskék 6.. Az elektron felfedezése 82. Henry Davy (-) katód (+) anód Az üveggel érintkező katódsugár zöldes luminesszenciát
Mágneses szuszceptibilitás vizsgálata
 Mágneses szuszceptibilitás vizsgálata Mérést végezte: Gál Veronika I. A mérés elmélete Az anyagok külső mágnesen tér hatására polarizálódnak. Általában az anyagok mágnesezhetőségét az M mágnesezettség
Mágneses szuszceptibilitás vizsgálata Mérést végezte: Gál Veronika I. A mérés elmélete Az anyagok külső mágnesen tér hatására polarizálódnak. Általában az anyagok mágnesezhetőségét az M mágnesezettség
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI
 SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 12 KRISTÁLYkÉMIA XII. KÖTÉsTÍPUsOK A KRIsTÁLYOKBAN 1. KÉMIAI KÖTÉsEK Valamennyi kötéstípus az atommag és az elektronok, illetve az elektronok egymás közötti
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 12 KRISTÁLYkÉMIA XII. KÖTÉsTÍPUsOK A KRIsTÁLYOKBAN 1. KÉMIAI KÖTÉsEK Valamennyi kötéstípus az atommag és az elektronok, illetve az elektronok egymás közötti
Az atom felépítése, fénykibocsátás (tankönyv 68.o.- 86.o.)
 Az atom felépítése, fénykibocsátás (tankönyv 68.o.- 86.o.) Atomok, atommodellek (tankönyv 82.o.-84.o.) Már az ókorban Démokritosz (i. e. 500) úgy gondolta, hogy minden anyag tovább nem osztható alapegységekből,
Az atom felépítése, fénykibocsátás (tankönyv 68.o.- 86.o.) Atomok, atommodellek (tankönyv 82.o.-84.o.) Már az ókorban Démokritosz (i. e. 500) úgy gondolta, hogy minden anyag tovább nem osztható alapegységekből,
Biofizika tesztkérdések
 Biofizika tesztkérdések Egyszerű választás E kérdéstípusban A, B,...-vel jelölt lehetőségek szerepelnek, melyek közül az egyetlen megfelelőt kell kiválasztani. A választ írja a kérdés előtt lévő kockába!
Biofizika tesztkérdések Egyszerű választás E kérdéstípusban A, B,...-vel jelölt lehetőségek szerepelnek, melyek közül az egyetlen megfelelőt kell kiválasztani. A választ írja a kérdés előtt lévő kockába!
Analízis elo adások. Vajda István. 2012. október 3. Neumann János Informatika Kar Óbudai Egyetem. Vajda István (Óbudai Egyetem)
 Vajda István Neumann János Informatika Kar Óbudai Egyetem / 40 Fogalmak A függvények értelmezése Definíció: Az (A, B ; R ) bináris relációt függvénynek nevezzük, ha bármely a A -hoz pontosan egy olyan
Vajda István Neumann János Informatika Kar Óbudai Egyetem / 40 Fogalmak A függvények értelmezése Definíció: Az (A, B ; R ) bináris relációt függvénynek nevezzük, ha bármely a A -hoz pontosan egy olyan
1. Ha két közeg határfelületén nem folyik vezetési áram, a mágneses térerősség vektorának a(z). komponense folytonos.
 Az alábbi kiskérdéseket a korábbi Pacher-féle vizsgasorokból és zh-kból gyűjtöttük ki. A többségnek a lefényképezett hivatalos megoldás volt a forrása (néha még ezt is óvatosan kellett kezelni, mert egy
Az alábbi kiskérdéseket a korábbi Pacher-féle vizsgasorokból és zh-kból gyűjtöttük ki. A többségnek a lefényképezett hivatalos megoldás volt a forrása (néha még ezt is óvatosan kellett kezelni, mert egy
Reológia 2. Bányai István DE Kolloid- és Környezetkémiai Tanszék
 Reológia 2 Bányai István DE Kolloid- és Környezetkémiai Tanszék Mérése nyomásesés áramlásra p 1 p 2 v=0 folyás csőben z r p 1 p 2 v max I V 1 p p t 8 l 1 2 r 2 x Höppler-típusú viszkoziméter v 2g 9 2 testgömb
Reológia 2 Bányai István DE Kolloid- és Környezetkémiai Tanszék Mérése nyomásesés áramlásra p 1 p 2 v=0 folyás csőben z r p 1 p 2 v max I V 1 p p t 8 l 1 2 r 2 x Höppler-típusú viszkoziméter v 2g 9 2 testgömb
A döntő feladatai. valós számok!
 OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
3. alkalom, gyakorlat
 Vegyület-félvezető struktúrák technológiája és alkalmazásaik: III-V és II-VI típusú vegyület-félvezetők; direkt és indirekt sávszerkezet; optikai tulajdonságok és alkalmazásuk 3. alkalom, gyakorlat A GYAKORLAT
Vegyület-félvezető struktúrák technológiája és alkalmazásaik: III-V és II-VI típusú vegyület-félvezetők; direkt és indirekt sávszerkezet; optikai tulajdonságok és alkalmazásuk 3. alkalom, gyakorlat A GYAKORLAT
Jelek tanulmányozása
 Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
Ultrahangos mérőfej XRS-5. Használati utasítás SITRANS. XRS-5 mérőfej Használati utasítás
 Ultrahangos mérőfej XRS-5 Használati utasítás SITRANS 1 Tartalom Ismertető... 3 Áttekintés... 3 Külső méretek... 4 Telepítés... 5 Elektromos bekötések... 7 Közvetlen csatlakoztatás... 7 Kábel toldás...
Ultrahangos mérőfej XRS-5 Használati utasítás SITRANS 1 Tartalom Ismertető... 3 Áttekintés... 3 Külső méretek... 4 Telepítés... 5 Elektromos bekötések... 7 Közvetlen csatlakoztatás... 7 Kábel toldás...
Azonosító jel: Matematika emelt szint
 I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
Természettudomány. 1-2. témakör: Atomok, atommodellek Anyagok, gázok
 Természettudomány 1-2. témakör: Atomok, atommodellek Anyagok, gázok Atommodellek viták, elképzelések, tények I. i.e. 600. körül: Thálész: a víz az ősanyag i.e. IV-V. század: Démokritosz: az anyagot parányi
Természettudomány 1-2. témakör: Atomok, atommodellek Anyagok, gázok Atommodellek viták, elképzelések, tények I. i.e. 600. körül: Thálész: a víz az ősanyag i.e. IV-V. század: Démokritosz: az anyagot parányi
Az időtől független Schrödinger-egyenlet (energia sajátértékegyenlet), A Laplace operátor derékszögű koordinátarendszerben
 Atomfizika ψ ψ ψ ψ ψ E z y x U z y x m = + + + ),, ( h ) ( ) ( ) ( ) ( r r r r ψ ψ ψ E U m = + Δ h z y x + + = Δ ),, ( ) ( z y x ψ =ψ r Az időtől független Schrödinger-egyenlet (energia sajátértékegyenlet),
Atomfizika ψ ψ ψ ψ ψ E z y x U z y x m = + + + ),, ( h ) ( ) ( ) ( ) ( r r r r ψ ψ ψ E U m = + Δ h z y x + + = Δ ),, ( ) ( z y x ψ =ψ r Az időtől független Schrödinger-egyenlet (energia sajátértékegyenlet),
Analízis elo adások. Vajda István. 2012. szeptember 24. Neumann János Informatika Kar Óbudai Egyetem. Vajda István (Óbudai Egyetem)
 Vajda István Neumann János Informatika Kar Óbudai Egyetem 1/8 A halmaz alapfogalom, tehát nem definiáljuk. Jelölés: A halmazokat általában nyomtatott nagybetu vel jelöljük Egy H halmazt akkor tekintünk
Vajda István Neumann János Informatika Kar Óbudai Egyetem 1/8 A halmaz alapfogalom, tehát nem definiáljuk. Jelölés: A halmazokat általában nyomtatott nagybetu vel jelöljük Egy H halmazt akkor tekintünk
86 MAM112M előadásjegyzet, 2008/2009
 86 MAM11M előadásjegyzet, 8/9 5. Fourier-elmélet 5.1. Komplex trigonometrikus Fourier-sorok Tekintsük az [,], C Hilbert-teret, azaz azoknak a komplex értékű f : [,] C függvényeknek a halmazát, amelyek
86 MAM11M előadásjegyzet, 8/9 5. Fourier-elmélet 5.1. Komplex trigonometrikus Fourier-sorok Tekintsük az [,], C Hilbert-teret, azaz azoknak a komplex értékű f : [,] C függvényeknek a halmazát, amelyek
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 12 XII. STATIsZTIKA ellenőrző feladatsorok 1. FELADATsOR Megoldások: láthatók nem láthatók 1. minta: 6.10, 0.01, 6.97, 6.03, 3.85, 1.11,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 12 XII. STATIsZTIKA ellenőrző feladatsorok 1. FELADATsOR Megoldások: láthatók nem láthatók 1. minta: 6.10, 0.01, 6.97, 6.03, 3.85, 1.11,
tetszőleges időpillanatban értelmezhető végtelen sok időpont értéke egy véges tartományban bármilyen értéket felvehet végtelen sok érték
 Elektronika 2 tetszőleges időpillanatban értelmezhető végtelen sok időpont értéke egy véges tartományban bármilyen értéket felvehet végtelen sok érték Diszkrét időpillanatokban értelmezhető (időszakaszos)
Elektronika 2 tetszőleges időpillanatban értelmezhető végtelen sok időpont értéke egy véges tartományban bármilyen értéket felvehet végtelen sok érték Diszkrét időpillanatokban értelmezhető (időszakaszos)
Kooperáció és intelligencia
 Kooperáció és intelligencia Tanulás többágenses szervezetekben/2 Tanulás több ágensből álló környezetben -a mozgó cél tanulás problémája (alapvetően megerősítéses tanulás) Legyen az ágens közösség formalizált
Kooperáció és intelligencia Tanulás többágenses szervezetekben/2 Tanulás több ágensből álló környezetben -a mozgó cél tanulás problémája (alapvetően megerősítéses tanulás) Legyen az ágens közösség formalizált
Debreceni Egyetem Orvos- és Egészségtudományi Centrum (DE OEC) Biofizikai és Sejtbiológiai Intézet, igazgató: Szöllősi János, egyetemi tanár
 Debreceni Egyetem Orvos- és Egészségtudományi Centrum (DE OEC) Biofizikai és Sejtbiológiai Intézet, igazgató: Szöllősi János, egyetemi tanár Biofizikai Tanszék (1. félév) vezető: Panyi György, egyetemi
Debreceni Egyetem Orvos- és Egészségtudományi Centrum (DE OEC) Biofizikai és Sejtbiológiai Intézet, igazgató: Szöllősi János, egyetemi tanár Biofizikai Tanszék (1. félév) vezető: Panyi György, egyetemi
Arany Dániel Matematikai Tanulóverseny 2011/2012-es tanév első (iskolai) forduló haladók I. kategória
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 011/01-es tanév első (iskolai) forduló haladók I. kategória Megoldások és javítási útmutató 1. Az ábrán látható ABC derékszögű háromszög
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 011/01-es tanév első (iskolai) forduló haladók I. kategória Megoldások és javítási útmutató 1. Az ábrán látható ABC derékszögű háromszög
A Tömegspektrométer elve AZ ATOMMAG FIZIKÁJA. Az atommag szerkezete (40-44 oldal) A tömegspektrométer elve. Az atommag komponensei:
 AZ ATOMMAG FIZIKÁJA Az atommag szerkezete (40-44 oldal) A tömegspektrométer elve Az atommag komponensei izotópok Tömeghiány, kötési energia, stabilitás Magerők Magmodellek Az atommag stabilitásának tényezői
AZ ATOMMAG FIZIKÁJA Az atommag szerkezete (40-44 oldal) A tömegspektrométer elve Az atommag komponensei izotópok Tömeghiány, kötési energia, stabilitás Magerők Magmodellek Az atommag stabilitásának tényezői
Lineáris algebra jegyzet
 Lineáris algebra jegyzet Készítette: Jezsoviczki Ádám Forrás: Az előadások és a gyakorlatok anyaga Legutóbbi módosítás dátuma: 2011-12-04 A jegyzet nyomokban hibát tartalmazhat, így fentartásokkal olvasandó!
Lineáris algebra jegyzet Készítette: Jezsoviczki Ádám Forrás: Az előadások és a gyakorlatok anyaga Legutóbbi módosítás dátuma: 2011-12-04 A jegyzet nyomokban hibát tartalmazhat, így fentartásokkal olvasandó!
A Hozzárendelési feladat megoldása Magyar-módszerrel
 A Hozzárendelési feladat megoldása Magyar-módszerrel Virtuális vállalat 2013-2014/1. félév 3. gyakorlat Dr. Kulcsár Gyula A Hozzárendelési feladat Adott meghatározott számú gép és ugyanannyi független
A Hozzárendelési feladat megoldása Magyar-módszerrel Virtuális vállalat 2013-2014/1. félév 3. gyakorlat Dr. Kulcsár Gyula A Hozzárendelési feladat Adott meghatározott számú gép és ugyanannyi független
A fény. Abszorpciós fotometria Fluoreszcencia spektroszkópia. A fény. A spektrumok megjelenési formái. A fény kettıs természete: Huber Tamás
 A fény Abszorpciós fotometria Fluoreszcencia spektroszkópia. 2010. október 19. Huber Tamás PTE ÁOK Biofizikai Intézet E A fény elektromos térerısségvektor hullámhossz A fény kettıs természete: Hullám (terjedéskor)
A fény Abszorpciós fotometria Fluoreszcencia spektroszkópia. 2010. október 19. Huber Tamás PTE ÁOK Biofizikai Intézet E A fény elektromos térerısségvektor hullámhossz A fény kettıs természete: Hullám (terjedéskor)
xdsl Optika Kábelnet Mért érték (2012. II. félév): SL24: 79,12% SL72: 98,78%
 Minőségi mutatók Kiskereskedelmi mutatók (Internet) Megnevezés: Új hozzáférés létesítési idő Meghatározás: A szolgáltatáshoz létesített új hozzáféréseknek, az esetek 80%ban teljesített határideje. Mérési
Minőségi mutatók Kiskereskedelmi mutatók (Internet) Megnevezés: Új hozzáférés létesítési idő Meghatározás: A szolgáltatáshoz létesített új hozzáféréseknek, az esetek 80%ban teljesített határideje. Mérési
MINTA. Fizetendô összeg: 62 136,00 HUF. Telefonon: 06 40 / 20 99 20 ben: Interneten:
 Részszámla Számla. eredeti példány / oldal Elszámolási idôszak: 00.0. - 00.09.. Partnerszám: 000009 Fizetési határidô: 00.09.0. Vevô neve, címe: Minta út. Fizetendô összeg:, Minta út. Szerzôdéses folyószámla
Részszámla Számla. eredeti példány / oldal Elszámolási idôszak: 00.0. - 00.09.. Partnerszám: 000009 Fizetési határidô: 00.09.0. Vevô neve, címe: Minta út. Fizetendô összeg:, Minta út. Szerzôdéses folyószámla
Készítette: Bujnóczki Tibor Lezárva: 2005. 01. 01.
 VILÁGÍTÁSTECHNIKA Készítette: Bujnóczki Tibor Lezárva: 2005. 01. 01. ANYAGOK FELÉPÍTÉSE Az atomok felépítése: elektronhéjak: K L M N O P Q elektronok atommag W(wolfram) (Atommag = proton+neutron protonok
VILÁGÍTÁSTECHNIKA Készítette: Bujnóczki Tibor Lezárva: 2005. 01. 01. ANYAGOK FELÉPÍTÉSE Az atomok felépítése: elektronhéjak: K L M N O P Q elektronok atommag W(wolfram) (Atommag = proton+neutron protonok
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 10 X DETERmINÁNSOk 1 DETERmINÁNS ÉRTELmEZÉSE, TULAJdONSÁGAI A másodrendű determináns értelmezése: A harmadrendű determináns értelmezése és annak első sor szerinti kifejtése: A
KOVÁCS BÉLA, MATEmATIkA I 10 X DETERmINÁNSOk 1 DETERmINÁNS ÉRTELmEZÉSE, TULAJdONSÁGAI A másodrendű determináns értelmezése: A harmadrendű determináns értelmezése és annak első sor szerinti kifejtése: A
Sz ekelyhidi L aszl o Val osz ın us egsz am ıt as es matematikai statisztika *************** Budapest, 1998
 Székelyhidi László Valószínűségszámítás és matematikai statisztika *************** Budapest, 1998 Előszó Ez a jegyzet a valószínűségszámításnak és a matematikai statisztikának azokat a fejezeteit tárgyalja,
Székelyhidi László Valószínűségszámítás és matematikai statisztika *************** Budapest, 1998 Előszó Ez a jegyzet a valószínűségszámításnak és a matematikai statisztikának azokat a fejezeteit tárgyalja,
2011. március 9. Dr. Vincze Szilvia
 . márius 9. Dr. Vinze Szilvia Tartalomjegyzék.) Elemi bázistranszformáió.) Elemi bázistranszformáió alkalmazásai.) Lineáris függőség/függetlenség meghatározása.) Kompatibilitás vizsgálata.) Mátri/vektorrendszer
. márius 9. Dr. Vinze Szilvia Tartalomjegyzék.) Elemi bázistranszformáió.) Elemi bázistranszformáió alkalmazásai.) Lineáris függőség/függetlenség meghatározása.) Kompatibilitás vizsgálata.) Mátri/vektorrendszer
rezegnek, mások pedig nyugalomban maradnak. Ezek a csomópontok. Ha mindkét végén L = nλ n
 Állóhullám kötélen 1. Elméleti háttér A hullámok alapvető tulajdonságai egyszerűen tanulmányozhatók kötélen kialakult állóhullámok segítségével. A hullámoknak ez a típusa gyakran megfigyelhető mindennapi
Állóhullám kötélen 1. Elméleti háttér A hullámok alapvető tulajdonságai egyszerűen tanulmányozhatók kötélen kialakult állóhullámok segítségével. A hullámoknak ez a típusa gyakran megfigyelhető mindennapi
XXV. ELEKTROMOS VEZETÉS SZILÁRD TESTEKBEN
 2007. február 6. 1 Pálinkás József: Fizika 2. XXV. ELEKTROMOS VEZETÉS SZILÁRD TESTEKBEN Bevezetés: Az előző fejezetekben megismertük, hogy a kvantumelmélet milyen jól leírja az atomok és a molekulák felépítését.
2007. február 6. 1 Pálinkás József: Fizika 2. XXV. ELEKTROMOS VEZETÉS SZILÁRD TESTEKBEN Bevezetés: Az előző fejezetekben megismertük, hogy a kvantumelmélet milyen jól leírja az atomok és a molekulák felépítését.
Programozás I. - 9. gyakorlat
 Programozás I. - 9. gyakorlat Mutatók, dinamikus memóriakezelés Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Rendszer- és Számítástudományi Tanszék Utolsó frissítés: November 9, 2009 1 tar@dcs.vein.hu
Programozás I. - 9. gyakorlat Mutatók, dinamikus memóriakezelés Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Rendszer- és Számítástudományi Tanszék Utolsó frissítés: November 9, 2009 1 tar@dcs.vein.hu
Rutherford-féle atommodell
 Rutherfordféle atommodell Manchesteri Egyetem 1909 1911 Hans Geiger, Ernest Marsden Ernest Rutherford vezetésével Az arany szerkezetének felderítésére irányuló szóráskísérletek Alfarészecskékkel bombáztak
Rutherfordféle atommodell Manchesteri Egyetem 1909 1911 Hans Geiger, Ernest Marsden Ernest Rutherford vezetésével Az arany szerkezetének felderítésére irányuló szóráskísérletek Alfarészecskékkel bombáztak
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 5 V. BECsLÉsELMÉLET 1. STATIsZTIKAI becslés A becsléselméletben gyakran feltesszük, hogy a megfigyelt mennyiségek független valószínűségi
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 5 V. BECsLÉsELMÉLET 1. STATIsZTIKAI becslés A becsléselméletben gyakran feltesszük, hogy a megfigyelt mennyiségek független valószínűségi
Statisztika 2016. március 11. A csoport Neptun kód
 Statisztika 2016. március 11. A csoport Név Neptun kód 1. Egy közösségben az élelmiszerre fordított kiadások az alábbiak szerint alakultak: osszeg (ezer Ft) csalad(db) 20 7 20:1 30 12 30:1 40 20 40:1 50
Statisztika 2016. március 11. A csoport Név Neptun kód 1. Egy közösségben az élelmiszerre fordított kiadások az alábbiak szerint alakultak: osszeg (ezer Ft) csalad(db) 20 7 20:1 30 12 30:1 40 20 40:1 50
Optika és Relativitáselmélet II. BsC fizikus hallgatóknak
 Optika és Relativitáselmélet II. BsC fizikus hallgatóknak 10. Elektrooptika, nemlineáris optika, kvantumoptika, lézerek Cserti József, jegyzet, ELTE, 2007. Az elektrooptika, a nemlineáris optikai és az
Optika és Relativitáselmélet II. BsC fizikus hallgatóknak 10. Elektrooptika, nemlineáris optika, kvantumoptika, lézerek Cserti József, jegyzet, ELTE, 2007. Az elektrooptika, a nemlineáris optikai és az
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN
 GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten RACIONÁLIS TÖRTFÜGGVÉNYEK INTEGRÁLJA Készítette: Gábor Szakmai felel s: Gábor Vázlat
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten RACIONÁLIS TÖRTFÜGGVÉNYEK INTEGRÁLJA Készítette: Gábor Szakmai felel s: Gábor Vázlat
Pozitron-emissziós tomográf (PET) mire való és hogyan működik?
 Pozitron-emissziós tomográf (PET) mire való és hogyan működik? Major Péter Atomoktól csillagokig, 2011. nov. 10. Vázlat Mi az hogy Tomográf? (fajták, képek) Milyen tomográfok vannak, miért van ennyi? Milyen
Pozitron-emissziós tomográf (PET) mire való és hogyan működik? Major Péter Atomoktól csillagokig, 2011. nov. 10. Vázlat Mi az hogy Tomográf? (fajták, képek) Milyen tomográfok vannak, miért van ennyi? Milyen
Radioaktivitás. 9.2 fejezet
 Radioaktivitás 9.2 fejezet A bomlási törvény Bomlási folyamat alapjai: Értelmezés (bomlás): Azt a magfizikai folyamatot, amely során nagy tömegszámú atommagok spontán módon, azaz véletlenszerűen (statisztikailag)
Radioaktivitás 9.2 fejezet A bomlási törvény Bomlási folyamat alapjai: Értelmezés (bomlás): Azt a magfizikai folyamatot, amely során nagy tömegszámú atommagok spontán módon, azaz véletlenszerűen (statisztikailag)
Fizika 2 (Modern fizika szemlélete) feladatsor
 Fizika 2 (Modern fizika szemlélete) feladatsor 1. Speciális relativitáselmélet 1. A Majmok bolygója című mozifilm és könyv szerint hibernált asztronauták a Föld távoli jövőjébe utaznak, amikorra az emberi
Fizika 2 (Modern fizika szemlélete) feladatsor 1. Speciális relativitáselmélet 1. A Majmok bolygója című mozifilm és könyv szerint hibernált asztronauták a Föld távoli jövőjébe utaznak, amikorra az emberi
A mérések eredményeit az 1. számú táblázatban tüntettük fel.
 Oktatási Hivatal A Mérések függőleges, vastag falú alumínium csőben eső mágnesekkel 2011/2012. tanévi Fizika Országos Középiskolai Tanulmányi Verseny döntő feladatának M E G O L D Á S A I. kategória. A
Oktatási Hivatal A Mérések függőleges, vastag falú alumínium csőben eső mágnesekkel 2011/2012. tanévi Fizika Országos Középiskolai Tanulmányi Verseny döntő feladatának M E G O L D Á S A I. kategória. A
Fluxus. A G vektormező V egyszeresen összefüggő, zárt felületre vett fluxusa:
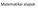 Matematikai alapok Fluxus A G vektormező V egyszeresen összefüggő, zárt felületre vett fluxusa: GF d V Divergencia Koordinátaredszertől független definíció: div G lim V Descartes-féle koordináták esetén:
Matematikai alapok Fluxus A G vektormező V egyszeresen összefüggő, zárt felületre vett fluxusa: GF d V Divergencia Koordinátaredszertől független definíció: div G lim V Descartes-féle koordináták esetén:
Mit mond ki a Huygens elv, és miben több ehhez képest a Huygens Fresnel-elv?
 Ismertesse az optika fejlődésének legjelentősebb mérföldköveit! - Ókor: korai megfigyelések - Euklidész (i.e. 280) A fény homogén közegben egyenes vonalban terjed. Legrövidebb út elve (!) Tulajdonképpen
Ismertesse az optika fejlődésének legjelentősebb mérföldköveit! - Ókor: korai megfigyelések - Euklidész (i.e. 280) A fény homogén közegben egyenes vonalban terjed. Legrövidebb út elve (!) Tulajdonképpen
Pár szó az Optikáról
 Pár szó az Optikáról Hullámok: Tekintsünk egy haladó hullámot, pl. vízhullámot, a hullám forrásától elég távol. Ha egy konkrét időpillanatban lefényképeznénk, azt látnánk, hogy térben (megközelítőleg)
Pár szó az Optikáról Hullámok: Tekintsünk egy haladó hullámot, pl. vízhullámot, a hullám forrásától elég távol. Ha egy konkrét időpillanatban lefényképeznénk, azt látnánk, hogy térben (megközelítőleg)
MATEMATIKA ÍRÁSBELI VIZSGA 2011. május 3.
 MATEMATIKA ÍRÁSBELI VIZSGA I. rész Fontos tudnivalók A megoldások sorrendje tetszőleges. A feladatok megoldásához szöveges adatok tárolására és megjelenítésére nem alkalmas zsebszámológépet és bármelyik
MATEMATIKA ÍRÁSBELI VIZSGA I. rész Fontos tudnivalók A megoldások sorrendje tetszőleges. A feladatok megoldásához szöveges adatok tárolására és megjelenítésére nem alkalmas zsebszámológépet és bármelyik
A FIZIKA KÖZÉPSZINTŰ SZÓBELI ÉRETTSÉGI VIZSGA TÉTELEINEK TÉMAKÖREI 2015. MÁJUSI VIZSGAIDŐSZAK
 - 1 - A FIZIKA KÖZÉPSZINTŰ SZÓBELI ÉRETTSÉGI VIZSGA TÉTELEINEK TÉMAKÖREI 2015. MÁJUSI VIZSGAIDŐSZAK 1. Newton törvényei Newton I. törvénye Kölcsönhatás, mozgásállapot, mozgásállapot-változás, tehetetlenség,
- 1 - A FIZIKA KÖZÉPSZINTŰ SZÓBELI ÉRETTSÉGI VIZSGA TÉTELEINEK TÉMAKÖREI 2015. MÁJUSI VIZSGAIDŐSZAK 1. Newton törvényei Newton I. törvénye Kölcsönhatás, mozgásállapot, mozgásállapot-változás, tehetetlenség,
OSZTÁLYOZÓ VIZSGA TÉMAKÖREI
 OSZTÁLYOZÓ VIZSGA TÉMAKÖREI Az anyag néhány tulajdonsága, kölcsönhatások Fizika - 7. évfolyam 1. Az anyag belső szerkezete légnemű, folyékony és szilárd halmazállapotban 2. A testek mérhető tulajdonságai
OSZTÁLYOZÓ VIZSGA TÉMAKÖREI Az anyag néhány tulajdonsága, kölcsönhatások Fizika - 7. évfolyam 1. Az anyag belső szerkezete légnemű, folyékony és szilárd halmazállapotban 2. A testek mérhető tulajdonságai
VASÚTI PÁLYA DINAMIKÁJA
 VASÚTI PÁLYA DINAMIKÁJA Dynamics of the railway track Liegner Nándor BME Út és Vasútépítési Tanszék A vasúti felépítmény szerkezeti elemeiben ébredő igénybevételek A Zimmermann Eisenmann elmélet alapján
VASÚTI PÁLYA DINAMIKÁJA Dynamics of the railway track Liegner Nándor BME Út és Vasútépítési Tanszék A vasúti felépítmény szerkezeti elemeiben ébredő igénybevételek A Zimmermann Eisenmann elmélet alapján
KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA
 ÉRETTSÉGI VIZSGA 2016. május 17. FIZIKA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2016. május 17. 8:00 Az írásbeli vizsga időtartama: 120 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fizika
ÉRETTSÉGI VIZSGA 2016. május 17. FIZIKA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2016. május 17. 8:00 Az írásbeli vizsga időtartama: 120 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fizika
 Felépítettünk egy modellt, amely dinamikus, megfelel a Lucas kritikának képes reprodukálni bizonyos makro aggregátumok alakulásában megfigyelhető szabályszerűségeket (üzleti ciklus, a fogyasztás simítottab
Felépítettünk egy modellt, amely dinamikus, megfelel a Lucas kritikának képes reprodukálni bizonyos makro aggregátumok alakulásában megfigyelhető szabályszerűségeket (üzleti ciklus, a fogyasztás simítottab
[MECHANIKA- HAJLÍTÁS]
![[MECHANIKA- HAJLÍTÁS] [MECHANIKA- HAJLÍTÁS]](/thumbs/39/20428431.jpg) 2010. Eötvös Loránd Szakközép és Szakiskola Molnár István [MECHANIKA- HAJLÍTÁS] 1 A hajlításra való méretezést sok helyen lehet használni, sok mechanikai probléma modelljét vissza lehet vezetni a hajlítás
2010. Eötvös Loránd Szakközép és Szakiskola Molnár István [MECHANIKA- HAJLÍTÁS] 1 A hajlításra való méretezést sok helyen lehet használni, sok mechanikai probléma modelljét vissza lehet vezetni a hajlítás
Analízis előadások. Vajda István. 2013. február 10. Neumann János Informatika Kar Óbudai Egyetem
 Analízis előadások Vajda István Neumann János Informatika Kar Óbudai Egyetem 013. február 10. Vajda István (Óbudai Egyetem) Analízis előadások 013. február 10. 1 / 3 Az elemi függvények csoportosítása
Analízis előadások Vajda István Neumann János Informatika Kar Óbudai Egyetem 013. február 10. Vajda István (Óbudai Egyetem) Analízis előadások 013. február 10. 1 / 3 Az elemi függvények csoportosítása
A mechanika alapjai. A pontszerű testek dinamikája. Horváth András SZE, Fizika és Kémia Tsz. 2006. szeptember 29.
 A mechanika alapjai A pontszerű testek dinamikája Horváth András SZE, Fizika és Kémia Tsz. 2006. szeptember 29. Bevezetés Newton I. Newton II. Newton III. Newton IV. 2 / 27 Bevezetés Bevezetés Newton I.
A mechanika alapjai A pontszerű testek dinamikája Horváth András SZE, Fizika és Kémia Tsz. 2006. szeptember 29. Bevezetés Newton I. Newton II. Newton III. Newton IV. 2 / 27 Bevezetés Bevezetés Newton I.
Forgómozgás alapjai. Forgómozgás alapjai
 Forgómozgás alapjai Kiterjedt test általános mozgása Kísérlet a forgómozgásra Forgómozgás és haladó mozgás analógiája Merev test általános mozgása Gondolkodtató kérdés Összetett mozgások Egy test általános
Forgómozgás alapjai Kiterjedt test általános mozgása Kísérlet a forgómozgásra Forgómozgás és haladó mozgás analógiája Merev test általános mozgása Gondolkodtató kérdés Összetett mozgások Egy test általános
FIZIKA I. RÉSZLETES VIZSGAKÖVETELMÉNYEK
 FIZIKA KOMPETENCIÁK A vizsgázónak a követelményrendszerben és a vizsgaleírásban meghatározott módon az alábbi kompetenciák meglétét kell bizonyítania: - ismeretei összekapcsolása a mindennapokban tapasztalt
FIZIKA KOMPETENCIÁK A vizsgázónak a követelményrendszerben és a vizsgaleírásban meghatározott módon az alábbi kompetenciák meglétét kell bizonyítania: - ismeretei összekapcsolása a mindennapokban tapasztalt
Kombinatorika. 9. előadás. Farkas István. DE ATC Gazdaságelemzési és Statisztikai Tanszék. Kombinatorika p. 1/
 Kombinatorika 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Kombinatorika p. 1/ Permutáció Definíció. Adott n különböző elem. Az elemek egy meghatározott sorrendjét az adott
Kombinatorika 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Kombinatorika p. 1/ Permutáció Definíció. Adott n különböző elem. Az elemek egy meghatározott sorrendjét az adott
1. forduló. MEGOLDÁSOK Pontszerző Matematikaverseny 2015/2016-os tanév
 MEGOLDÁSOK Pontszerző Matematikaverseny 2015/2016-os tanév 1. forduló 1. feladat: Jancsi és Juliska Matematikai Memory-t játszik. A játék lényege, hogy négyzet alakú kártyákra vagy műveletsorokat írnak
MEGOLDÁSOK Pontszerző Matematikaverseny 2015/2016-os tanév 1. forduló 1. feladat: Jancsi és Juliska Matematikai Memory-t játszik. A játék lényege, hogy négyzet alakú kártyákra vagy műveletsorokat írnak
L Ph 1. Az Egyenlítő fölötti közelítőleg homogén földi mágneses térben a proton (a mágneses indukció
 A 2008-as bajor fizika érettségi feladatok (Leistungskurs) Munkaidő: 240 perc (A vizsgázónak két, a szakbizottság által kiválasztott feladatsort kell kidolgoznia) L Ph 1 1. Kozmikus részecskék mozgása
A 2008-as bajor fizika érettségi feladatok (Leistungskurs) Munkaidő: 240 perc (A vizsgázónak két, a szakbizottság által kiválasztott feladatsort kell kidolgoznia) L Ph 1 1. Kozmikus részecskék mozgása
Szem. (látás, térlátás, közelre-távolra ill. sötétben-világosban éleslátás)
 Szem (látás, térlátás, közelre-távolra ill. sötétben-világosban éleslátás) Légköri fényjelenségek diffúz nappali fény kék égbolt vöröslő naplemente délibáb légköri sugártörés sarki fény szivárvány holdudvar
Szem (látás, térlátás, közelre-távolra ill. sötétben-világosban éleslátás) Légköri fényjelenségek diffúz nappali fény kék égbolt vöröslő naplemente délibáb légköri sugártörés sarki fény szivárvány holdudvar
ATOMOSZ = OSZTHATATLAN
 AZ ATOMOK SZERKEZETE/KVANTUMSZÁMOK 2014 szeptember 15-16-17. PTE ÁOK Biofizikai Intézet ATOMOSZ = OSZTHATATLAN Semmi más nem létezik, csak atomok és üres tér. Minden egyéb puszta vélekedés. Démokritosz,
AZ ATOMOK SZERKEZETE/KVANTUMSZÁMOK 2014 szeptember 15-16-17. PTE ÁOK Biofizikai Intézet ATOMOSZ = OSZTHATATLAN Semmi más nem létezik, csak atomok és üres tér. Minden egyéb puszta vélekedés. Démokritosz,
Házi dolgozat. Minta a házi dolgozat formai és tartalmi követelményeihez. Készítette: (név+osztály) Iskola: (az iskola teljes neve)
 Házi dolgozat Minta a házi dolgozat formai és tartalmi követelményeihez Készítette: (név+osztály) Iskola: (az iskola teljes neve) Dátum: (aktuális dátum) Tartalom Itt kezdődik a címbeli anyag érdemi kifejtése...
Házi dolgozat Minta a házi dolgozat formai és tartalmi követelményeihez Készítette: (név+osztály) Iskola: (az iskola teljes neve) Dátum: (aktuális dátum) Tartalom Itt kezdődik a címbeli anyag érdemi kifejtése...
AZ ATOM. Atom: atommag + elektronfelhő = proton, neutron, elektron. Elemi részecskék
 AZ ATOM Atom: atommag + elektronfelhő = proton, neutron, elektron Elemi részecskék Atomok Dalton elmélete (1805): John DALTON 1766-1844 1. Az elemek apró részecskékből, atomokból állnak. Atom: görög szó
AZ ATOM Atom: atommag + elektronfelhő = proton, neutron, elektron Elemi részecskék Atomok Dalton elmélete (1805): John DALTON 1766-1844 1. Az elemek apró részecskékből, atomokból állnak. Atom: görög szó
Feladatok megoldásokkal a negyedik gyakorlathoz (Függvényvizsgálat) f(x) = 2x 2 x 4. 2x 2 x 4 = 0, x 2 (2 x 2 ) = 0.
 Feladatok megoldásokkal a negyedik gyakorlathoz (Függvényvizsgálat). Feladat. Végezzük el az f(x) = x x 4 ) Értelmezési tartomány: x R. ) A zérushelyet az f(x) = 0 egyenlet megoldásával kapjuk: amiből
Feladatok megoldásokkal a negyedik gyakorlathoz (Függvényvizsgálat). Feladat. Végezzük el az f(x) = x x 4 ) Értelmezési tartomány: x R. ) A zérushelyet az f(x) = 0 egyenlet megoldásával kapjuk: amiből
Az aktiválódásoknak azonban itt még nincs vége, ugyanis az aktiválódások 30 évenként ismétlődnek!
 1 Mindannyiunk életében előfordulnak jelentős évek, amikor is egy-egy esemény hatására a sorsunk új irányt vesz. Bár ezen események többségének ott és akkor kevésbé tulajdonítunk jelentőséget, csak idővel,
1 Mindannyiunk életében előfordulnak jelentős évek, amikor is egy-egy esemény hatására a sorsunk új irányt vesz. Bár ezen események többségének ott és akkor kevésbé tulajdonítunk jelentőséget, csak idővel,
Ph 11 1. 2. Mozgás mágneses térben
 Bajor fizika érettségi feladatok (Tervezet G8 2011-től) Munkaidő: 180 perc (A vizsgázónak két, a szakbizottság által kiválasztott feladatsort kell kidolgoznia. A két feladatsor nem származhat azonos témakörből.)
Bajor fizika érettségi feladatok (Tervezet G8 2011-től) Munkaidő: 180 perc (A vizsgázónak két, a szakbizottság által kiválasztott feladatsort kell kidolgoznia. A két feladatsor nem származhat azonos témakörből.)
BOLYAI MATEMATIKA CSAPATVERSENY FŐVÁROSI DÖNTŐ SZÓBELI (2005. NOVEMBER 26.) 5. osztály
 5. osztály Írd be az ábrán látható hat üres körbe a 10, 30, 40, 60, 70 és 90 számokat úgy, hogy a háromszög mindhárom oldala mentén a számok összege 200 legyen! 50 20 80 Egy dobozban háromféle színű: piros,
5. osztály Írd be az ábrán látható hat üres körbe a 10, 30, 40, 60, 70 és 90 számokat úgy, hogy a háromszög mindhárom oldala mentén a számok összege 200 legyen! 50 20 80 Egy dobozban háromféle színű: piros,
Zitterbewegung. általános elmélete. Grafén Téli Iskola 2011. 02. 04. Dávid Gyula ELTE TTK Atomfizikai Tanszék
 A Zitterbewegung általános elmélete Grafén Téli Iskola 2011. 02. 04. Dávid Gyula ELTE TTK Atomfizikai Tanszék 1. Mi a Zitterbewegung? A Zitterbewegung általános elmélete 2. Kvantumdinamika Heisenberg-képben
A Zitterbewegung általános elmélete Grafén Téli Iskola 2011. 02. 04. Dávid Gyula ELTE TTK Atomfizikai Tanszék 1. Mi a Zitterbewegung? A Zitterbewegung általános elmélete 2. Kvantumdinamika Heisenberg-képben
Az elektron felfedezése
 Az elektron felfedezése A katódsugárcső végét foszforeszkáló anyaggal vonják be. Ha ezt eltalálja a katódsugár, akkor ezen a helyen zöldesen világít. feszültségforrás katód anód kis rés vákuum foszforeszkáló
Az elektron felfedezése A katódsugárcső végét foszforeszkáló anyaggal vonják be. Ha ezt eltalálja a katódsugár, akkor ezen a helyen zöldesen világít. feszültségforrás katód anód kis rés vákuum foszforeszkáló
MBLK12: Relációk és műveletek (levelező) (előadásvázlat) Maróti Miklós, Kátai-Urbán Kamilla
 MBLK12: Relációk és műveletek (levelező) (előadásvázlat) Maróti Miklós, Kátai-Urbán Kamilla Jelölje Z az egész számok halmazát, N a pozitív egészek halmazát, N 0 a nem negatív egészek halmazát, Q a racionális
MBLK12: Relációk és műveletek (levelező) (előadásvázlat) Maróti Miklós, Kátai-Urbán Kamilla Jelölje Z az egész számok halmazát, N a pozitív egészek halmazát, N 0 a nem negatív egészek halmazát, Q a racionális
B2. A FÉNY FOGALMA, FÉNYJELENSÉGEK ISMERTETÉSE,
 B2. A FÉNY FOGALMA, FÉNYJELENSÉGEK ISMERTETÉSE, FÉNYVISSZAVERŐDÉS, FÉNYTÖRÉS, FÉNYINTERFERENCIA, FÉNYPOLARIZÁCIÓ, FÉNYELHAJLÁS Fény: elektromágneses sugárzás (Einstein meghatározása, hogy idesorolta a
B2. A FÉNY FOGALMA, FÉNYJELENSÉGEK ISMERTETÉSE, FÉNYVISSZAVERŐDÉS, FÉNYTÖRÉS, FÉNYINTERFERENCIA, FÉNYPOLARIZÁCIÓ, FÉNYELHAJLÁS Fény: elektromágneses sugárzás (Einstein meghatározása, hogy idesorolta a
Elektromágneses hullámok, a fény
 Elektromágneses hullámok, a fény Az elektromos töltéssel rendelkező testeknek a töltésük miatt fellépő kölcsönhatását az elektromos és mágneses tér segítségével írhatjuk le. A kölcsönhatás úgy működik,
Elektromágneses hullámok, a fény Az elektromos töltéssel rendelkező testeknek a töltésük miatt fellépő kölcsönhatását az elektromos és mágneses tér segítségével írhatjuk le. A kölcsönhatás úgy működik,
Robottechnika. Differenciális kinematika és dinamika. Magyar Attila
 Robottechnika Differenciális kinematika és dinamika Magyar Attila Pannon Egyetem Műszaki Informatika Kar Villamosmérnöki és Információs Rendszerek Tanszék amagyar@almos.vein.hu 2009 október 8. Áttekintés
Robottechnika Differenciális kinematika és dinamika Magyar Attila Pannon Egyetem Műszaki Informatika Kar Villamosmérnöki és Információs Rendszerek Tanszék amagyar@almos.vein.hu 2009 október 8. Áttekintés
Fordítóprogramok Készítette: Nagy Krisztián
 Fordítóprogramok Készítette: Nagy Krisztián Reguláris kifejezések (FLEX) Alapelemek kiválasztása az x karakter. tetszőleges karakter (kivéve újsor) [xyz] karakterhalmaz; vagy egy x, vagy egy y vagy egy
Fordítóprogramok Készítette: Nagy Krisztián Reguláris kifejezések (FLEX) Alapelemek kiválasztása az x karakter. tetszőleges karakter (kivéve újsor) [xyz] karakterhalmaz; vagy egy x, vagy egy y vagy egy
A TételWiki wikiből. Tekintsük a következő Hamilton-operátorral jellemezhető rendszert:
 1 / 12 A TételWiki wikiből 1 Ritka gázok állapotegyenlete 2 Viriál sorfejtés 3 Van der Waals gázok 4 Ising-modell 4.1 Az Ising-modell megoldása 1 dimenzióban(*) 4.2 Az Ising-modell átlagtérelmélete 2 dimenzióban(**)
1 / 12 A TételWiki wikiből 1 Ritka gázok állapotegyenlete 2 Viriál sorfejtés 3 Van der Waals gázok 4 Ising-modell 4.1 Az Ising-modell megoldása 1 dimenzióban(*) 4.2 Az Ising-modell átlagtérelmélete 2 dimenzióban(**)
A mérés célkitűzései: Kaloriméter segítségével az étolaj fajhőjének kísérleti meghatározása a Joule-féle hő segítségével.
 A mérés célkitűzései: Kaloriméter segítségével az étolaj fajhőjének kísérleti meghatározása a Joule-féle hő segítségével. Eszközszükséglet: kaloriméter fűtőszállal digitális mérleg tanulói tápegység vezetékek
A mérés célkitűzései: Kaloriméter segítségével az étolaj fajhőjének kísérleti meghatározása a Joule-féle hő segítségével. Eszközszükséglet: kaloriméter fűtőszállal digitális mérleg tanulói tápegység vezetékek
Sugárzási alapismeretek
 Sugárzási alapismeretek Energia 10 20 J Évi bejövő sugárzásmennyiség 54 385 1976-os kínai földrengés 5006 Föld széntartalékának energiája 1952 Föld olajtartalékának energiája 179 Föld gáztartalékának energiája
Sugárzási alapismeretek Energia 10 20 J Évi bejövő sugárzásmennyiség 54 385 1976-os kínai földrengés 5006 Föld széntartalékának energiája 1952 Föld olajtartalékának energiája 179 Föld gáztartalékának energiája
F1404 ATOMMAG- és RÉSZECSKEFIZIKA
 F1404 ATOMMAG- és RÉSZECSKEFIZIKA Dr. Raics Péter DE TTK Kísérleti Fizikai Tanszék, Debrecen, Bem tér 18/A RAICS@TIGRIS.KLTE.HU Ajánlott irodalom Raics P.: Atommag- és részecskefizika. Jegyzet. DE Kísérleti
F1404 ATOMMAG- és RÉSZECSKEFIZIKA Dr. Raics Péter DE TTK Kísérleti Fizikai Tanszék, Debrecen, Bem tér 18/A RAICS@TIGRIS.KLTE.HU Ajánlott irodalom Raics P.: Atommag- és részecskefizika. Jegyzet. DE Kísérleti
Fizikai kémia és radiokémia labor II, Laboratóriumi gyakorlat: Spektroszkópia mérés
 Fizikai kémia és radiokémia labor II, Laboratóriumi gyakorlat: Spektroszkópia mérés A gyakorlatra vigyenek magukkal pendrive-ot, amire a mérési adatokat átvehetik. Ajánlott irodalom: P. W. Atkins: Fizikai
Fizikai kémia és radiokémia labor II, Laboratóriumi gyakorlat: Spektroszkópia mérés A gyakorlatra vigyenek magukkal pendrive-ot, amire a mérési adatokat átvehetik. Ajánlott irodalom: P. W. Atkins: Fizikai
Vektorok összeadása, kivonása, szorzás számmal, koordináták, lineáris függetlenség
 Vektoralgebra Vektorok összeadása, kivonása, szorzás számmal, koordináták, lineáris függetlenség Feladatok: 1) A koordinátarendszerben úgy helyezzük el az egységkockát, hogy az origó az egyik csúcsba essék,
Vektoralgebra Vektorok összeadása, kivonása, szorzás számmal, koordináták, lineáris függetlenség Feladatok: 1) A koordinátarendszerben úgy helyezzük el az egységkockát, hogy az origó az egyik csúcsba essék,
- mit, hogyan, miért?
 - mit, hogyan, miért? Dr. Bélavári Csilla VITUKI Nonprofit Kft., Minőségbiztosítási és Ellenőrzési Csoport c.belavari@vituki.hu 2011.02.10. 2010. évi záróértekezlet - VITUKI, MECS 1 I. Elfogadott érték
- mit, hogyan, miért? Dr. Bélavári Csilla VITUKI Nonprofit Kft., Minőségbiztosítási és Ellenőrzési Csoport c.belavari@vituki.hu 2011.02.10. 2010. évi záróértekezlet - VITUKI, MECS 1 I. Elfogadott érték
1. A gyorsulás Kísérlet: Eszközök Számítsa ki
 1. A gyorsulás Gyakorlati példákra alapozva ismertesse a változó és az egyenletesen változó mozgást! Általánosítsa a sebesség fogalmát úgy, hogy azzal a változó mozgásokat is jellemezni lehessen! Ismertesse
1. A gyorsulás Gyakorlati példákra alapozva ismertesse a változó és az egyenletesen változó mozgást! Általánosítsa a sebesség fogalmát úgy, hogy azzal a változó mozgásokat is jellemezni lehessen! Ismertesse
Játékok (domináns stratégia, alkalmazása. 2016.03.30.
 Játékok (domináns stratégia, Nash-egyensúly). A Nashegyensúly koncepciójának alkalmazása. 2016.03.30. Játékelmélet és közgazdaságtan 1914: Zermelo (sakk) 1944. Neumann-Morgenstern: Game Theory and Economic
Játékok (domináns stratégia, Nash-egyensúly). A Nashegyensúly koncepciójának alkalmazása. 2016.03.30. Játékelmélet és közgazdaságtan 1914: Zermelo (sakk) 1944. Neumann-Morgenstern: Game Theory and Economic
Lumineszcencia (fluoreszcencia, foszforeszcencia)
 Lumineszcencia (fluoreszcencia, foszforeszcencia) Lumineszcencia Bizonyos anyagok fény (látható fény, röntgen sugárzás, vagy radioaktív sugárzás) hatására látható fényt sugároznak ki. A hőmérsékleti sugárzással
Lumineszcencia (fluoreszcencia, foszforeszcencia) Lumineszcencia Bizonyos anyagok fény (látható fény, röntgen sugárzás, vagy radioaktív sugárzás) hatására látható fényt sugároznak ki. A hőmérsékleti sugárzással
Fizika 1i (keresztfélév) vizsgakérdések kidolgozása
 Fizika 1i (keresztfélév) vizsgakérdések kidolgozása Készítette: Hornich Gergely, 2013.12.31. Kiegészítette: Mosonyi Máté (10., 32. feladatok), 2015.01.21. (Talapa Viktor 2013.01.15.-i feladatgyűjteménye
Fizika 1i (keresztfélév) vizsgakérdések kidolgozása Készítette: Hornich Gergely, 2013.12.31. Kiegészítette: Mosonyi Máté (10., 32. feladatok), 2015.01.21. (Talapa Viktor 2013.01.15.-i feladatgyűjteménye
B1: a tej pufferkapacitását B2: a tej fehérjéinek enzimatikus lebontását B3: a tej kalciumtartalmának meghatározását. B.Q1.A a víz ph-ja = [0,25 pont]
![B1: a tej pufferkapacitását B2: a tej fehérjéinek enzimatikus lebontását B3: a tej kalciumtartalmának meghatározását. B.Q1.A a víz ph-ja = [0,25 pont] B1: a tej pufferkapacitását B2: a tej fehérjéinek enzimatikus lebontását B3: a tej kalciumtartalmának meghatározását. B.Q1.A a víz ph-ja = [0,25 pont]](/thumbs/41/22606346.jpg) B feladat : Ebben a kísérleti részben vizsgáljuk, Összpontszám: 20 B1: a tej pufferkapacitását B2: a tej fehérjéinek enzimatikus lebontását B3: a tej kalciumtartalmának meghatározását B1 A tej pufferkapacitása
B feladat : Ebben a kísérleti részben vizsgáljuk, Összpontszám: 20 B1: a tej pufferkapacitását B2: a tej fehérjéinek enzimatikus lebontását B3: a tej kalciumtartalmának meghatározását B1 A tej pufferkapacitása
