sztochasztikus módszerekkel
|
|
|
- Gréta Törökné
- 8 évvel ezelőtt
- Látták:
Átírás
1 Épületek és változásaik detekciója sztochasztikus módszerekkel Benedek Csaba 12, Xavier Descombes 2, Josiane Zerubia 2 1 Elosztott Események Elemzése Kutatócsoport, MTA SZTAKI, 1111 Budapest, Kende utca bcsaba@sztaki.hu 2 Ariana Project Team (INRIA/CNRS/UNSA), 2004 route des Lucioles, BP 93, SOPHIA ANTIPOLIS Cedex - FRANCE firstname.lastname@sophia.inria.fr Absztrakt. Cikkünkben légi- és műholdképek feldolgozását végző valószínűségi módszert mutatunk be. A modell együttesen célozza meg épületek kinyerését és változásaik detektálását többidejű, jelentős időkülönbséggel készült képi bemeneteteket feltételezve. Globális optimalizációs folyamat találja meg az épületek megfelelő konfigurációját, figyelembe véve a megfigyelt képi adatot, prior információt és a szomszédos épületszegmensek közötti interakciót. A módszer pontosságát Bayesi verifikációs folyamat biztosítja, míg a számítási idő jelentősen lerövidül egy új sztochasztikus objektum születési folyamat segítségével, mely alacsony képi jellemzők alapján nagy valószínűséggel javasol releváns objektumokat. 1. Bevezetés Beépített területek változásainak monitorozása központi feladat nagy felbontású légi- és műholdképek vizsgálatakor. Számos módszer végez épületdetekciót különálló képeken [5, 7, 9]. Ez a folyamat jelentősen megkönnyíthető DEM/DSM adat-bemenetek felhasználásával [3, 7], melyek sztereo képpárokból vagy speciális szenzoradatokból nyerhetők ki: ekkor a házak elkülöníthetők a földfelszíntől a becsült magassági adatok alapján. Több nézeti információ hiányában azonban az épületek azonosítása komoly kihívássá válik [8]. Az épületváltozások észlelését végző számos korábbi módszer [3] feltételezi, hogy a korábbi időpontról topografikus épület adatbázis áll rendelkezésre, így a folyamat szétválasztható két részre: a korábbi épületek ellenőrzésére és az új épületek felderítésére. Ugyanakkor sok képi adatbázis nem tartalmaz kiegészítő adatokat, ezért szükségessé válik mindkét időrétegen az automatikus épületkinyerés. A távérzékelésben korábban számos alacsonyszintű változásdetekciós módszert ismertettek [2], melyek statisztikailag kiugró különbségeket keresnek a képeken konkrét A cikk eredményei az alábbi publikációban jelentek meg: C. Benedek, X. Descombes, and J. Zerubia. Building extraction and change detection in multitemporal remotely sensed images with multiple birth and death dynamics. In IEEE Workshop on Applications of Computer Vision (WACV), pages , 2009.
2 Épületek és változásaik detekciója 15 objektum modellek használata nélkül. Bár ezeket a módszereket általában csak előfeldolgozó lépéseknek tekintik a szakirodalomban, viszonylag kevés olyan kutatási eredményt tettek közzé, amely felhasználhatóságukat bizonyítaná objektum szintű vizsgálatokban. Ezt a hiányosságot pótolva, módszerünk kombinálja az objektumfelismerést lokális alacsonyszintű hasonlóság vizsgálattal, melyek egy egyesített valószínűségi modellben működnek. Bemutatjuk, hogy különböző alapvető tényezők együttesen használhatók ki, úgy mint épületváltozások a textúra szinten is megváltozott területeken találhatók, míg a változatlan objektumokról rendelkezésünkre álló több nézetű információ pontosítja a felismerést. A módszerek másik fontos csoportosítási szempontja az objektumok modellezésén alapul. A direkt módszerek [5] az épületeket primitív elemekből építik fel; a leggyakrabban használt primitívek a tető blokkok, él részletek vagy sarokpontok. Bár ezek az eljárások általában gyorsak, hibáznak, ha a képeken a primitíveket nem sikerül megbízhatóan kinyerni. Egy másik jelentős módszertani csoportba tartoznak az inverz modellek [4], melyek fitnesz értéket rendelnek a különböző lehetséges objektumkonfigurációkhoz, és egy optimalizációs folyamattal keresik a legvalószínűbb populációt. így rugalmas objektummodellek építhetők, és könnyen vehetünk figyelembe prior alaki információkat és objektum interakciókat. Ugyanakkor, nagy számítási igény szükséges a magas dimenziójú populációtérben történő kereséshez, mialatt a fitnesz függvény lokális maximumai félrevezethetik az optimalizációt. Módszerünkben egyaránt kihasználjuk az alacsony és az objektumszintű megközelítések előnyeit. Az felhasznált többszörös születés és halál (Multiple Birth and Death, MBD) optimalizáció [4] az épületek populációját objektumgenerálás (születés) és eldobás (halál) lépések iterációival fejleszti lépésről lépésre, szimulált lehűtés keretrendszerbe ágyazva. A felderítés fázist alacsony szintű képi leírók vezérlik, míg az objektum verifikáció a robosztus inverz megközelítést követi. 2. Probléma definíció A bemutatásra kerülő módszer bemenete két egymáshoz regisztrált légi- vagy műholdkép, melyeket ugyanarról a földrajzi területről készítettek több hónapos vagy éves időkülönbséggel. Bár figyelembe vesszük, hogy az eltérő nézetekből adódóan képregisztrációs hibák lehetnek jelen, feltételezzük, hogy ezek csak néhány pixelnyi torzítást okoznak. Az épületeket felülnézetből téglalap alakú szegmensek együttesének tekintjük, így a következőkben csak ezekre a szegmensekre koncentrálunk. JelöljükS-sel a képek közös pixelrácsát, éss S-sel egy adott pixelt. Legyenu egy téglalap alakú épület szegmens jelölt. Azért hogy együtt kezelhessünk két időréteget, u-hoz egy képindex attribútumot is rendelünk ξ(u) {1, 2, }, ahol változatlan épületet jelöl, míg 1 illetve 2 olyan szegmensekhez tartozik, melyek csak az első illetve második képen szerepelnek. LegyenR u S azu-hoz tartozó a pixelek halmaza. R u -t öt téglalap-paraméter írja le:c x ésc y középponti koordináták,e L,e l oldal hosszak ésθ [ 90,+90 ] orientációs szög (1. ábra).
3 16 Benedek Csaba, Xavier Descombes, Josiane Zerubia 3. Jellemzőválasztás Módszerünkben alacsonyszintű és objektumszintű jellemzőket használunk együttesen. Az alacsony szintű jellemzőket a pixelek környezetéből nyerjük ki, ilyenek lehetnek tipikus színek, textúrák és lokális hasonlóság a rétegek között. E jellemzőket a felderítés folyamat használja fel annak becslésére, hogy az épületek hol helyezkednek el nagy valószínűséggel, illetve milyen lehet a geometriai megjelenésük: a születés lépés az objektumokat a becsült beépített területeken nagyobb valószínűséggel generálja. Másfelől, az objektum szintű jellemzők egy adott u épületjelöltet írnak le, és felhasználhatók a generált téglalapok fitnesz értékének meghatározásához. Mivel az épületek verifikációja ez utóbbi jellemzőkön alapul, a pontosságuk kritikus. Mivel a hasonlóság leírón kívül a következő jellemzők számítása a két képen függetlenül történik, gyakran nem hangsúlyozzuk ki az aktuális képindexet ebben a fejezetben. 1. ábra: A téglalap geometriai paraméterei 3.1. Alacsony szintű jellemzők a beépítések felismeréséhez Az első jellemző azt a tényt használja ki, hogy az épületeket tartalmazó képrészletek hangsúlyos és egymásra merőleges éleket tartalmaznak. Ezt a tulajdonságot robosztusan jellemezhetjük lokális gradiens orientációs hisztogramokkal [6]. Jelölje g s azspixelhez tartozó intenzitás gradiens vektort, g s abszolút értékkel ésϑ s szöggel. Legyen W l (s) a négyzet alakú l l méretű ablak s körül, ahol l-t úgy választjuk, hogy W l (s) szűken lefedjen egy átlagos épületet. Mindens pixelw l (s) környezetében kiszámítjuk a súlyozottϑ s sűrűséget: λ s (ϑ) = 1 N s r W l (s) ( ) 1 h g ϑ ϑr r k h aholn s = r W l (s) g r éshakernel sávszélessége. A gyors számításhoz uniform kerneleket használtunk. Ha W l (s) lefed egy épületet, a λ s (ϑ) függvény két jellemző csúccsal rendelkezik, melyek 90 távolságban találhatók a ϑ-térben (2. ábra). Ezt a tulajdonságot mérhetjük a λ s (ϑ) függvény és egy megfelelően illesztett kétmódusú Gaussi keverék függvény korrelációjával: α(s,m) = λ s (ϑ)η 2 (ϑ,m,d λ )dϑ
4 Épületek és változásaik detekciója 17 W l(r) W(s) l s r λ s (ϑ) 90 λ r (ϑ) 90 Gradient orient. KDEs λ s (ϑ), λ r (ϑ) Bimodal MGM estimate ϑ (degree) ϑ (degree) 2. ábra: Két választott pixel környezetéhez tartozó lokális gradiens orientációs hisztogramok: s épület középpont, r üres terület része. aholη 2 (.) két Gauss függvény keverékemilletvem+90 várható értékkel és azonosd λ szórással (d λ a folyamat paramétere). A maximális korrelációhoz tartozó eltolás (m s ) korrelációs érték (α s ) így megkapható a következőképpen: { } m s = argmax m [ 90,0] α(s,m) α s = α(s,m s ) Nagy α s értékkel rendelkező pixelek nagyobb valószínűséggel lehetnek épület középpontok, amit az α-születés-térképen kódolhatunk: P α b (s) = α s/ r S α r. Az elnevezés onnan ered, hogy az s pixelben a lokális P b (s) születési értékkel arányos frekvenciával fogunk generálni objektumokat az eljárás során. Másrészről az m s eltolás értéke becslést ad a domináns gradiens irányra W l (s)- ben. Ezért ha s középponttal generálunk egy u objektumot, az orientációját θ(u) = m s + η s -ként modellezzük, ahol η s zéró várható értékű Gaussi valószínűségi változó kisσ θ szórás paraméterrel. Kísérleteinkben megfigyeltük, hogy az α s -gradiens jellemző általában képes a beépített területek durva becslésére. Ugyanakkor, számos esetben a detekció finomítható további jellemzők figyelembevételével, például tetőszín és árnyékok modellezésével [9]. A tetőszínek egy része jól elkülöníthető megvilágítás invariáns színreprezentációkban, mint a HSV színtér hue csatornája. Tegyük fel, hogy ki tudunk nyerni egy µ c (s) {0,1} indikátor maszkot, aholµ c (s) = 1 tartozik a tetőszínűspixelhez. Ekkor s színleíróját a következőképpen számoljuk: Γ s = r W l (s) µ c(r) és a szín alapú születés térképet szintén meghatározzuk:p c b (s) = Γ s/ r S Γ r. Jegyezzük meg, hogy ez a jellemző nyilvánvalóan nem használható szürkeárnyalatú képekre, illetve színes felvételek esetén is általában csak a tetők egy részét azonosítja, melyek például tipikus piros színűek ([9] és 5(b) ábra). Az épületek jelenlétére vetett árnyékaikon keresztül is tehetünk becslést [5, 9]. Kihasználva, hogy az árnyékok sötétsége és iránya globális képi jellemzők, gyakran kinyerhetünk egy (zajos)µ sh (s) árnyék maszkot, például a sötét-kék színtartományba eső pixelek kiszűrésével [9]. Ezután az épületeket tartalmazó területek azonosíthatók azon
5 18 Benedek Csaba, Xavier Descombes, Josiane Zerubia képrészletekként, amelyek az árnyék foltok mellett nap irányban fekszenek (6. ábra). Konstans Pb sh (s) = psh 0 születési értéket használtunk a kinyert beépített területeken belül, míg lényegesen kisebbǫ sh 0 konstanst kívül. Mivel a kombinált születéstérkép célja az, hogy valamennyi lehetséges beépített területre ráirányítsa a figyelmet, a jellemző térképekből a maximum operátorral származtatjuk: P b (s) = max { P α b (s),pc b (s),psh b (s)} s S. Olyan képi bemenetekre, melyek nem tartalmaznak szín- vagy árnyékinformációt, egyszerűen el kell hagyni a megfelelő komponenst. Ismét megjegyezzük, hogy a születési és orientációs térképeket mindkét képre külön generáljuk, szükség esetén az időfüggést az alábbi módon jelöljük: P (i) b (s),m (i) s,i {1,2}. W s(s) l r W (r) l W (s) l r W (r) l s s λ 1 s (ϑ) λ 2 s (ϑ) λ 1 r (ϑ) λ 2 r (ϑ) ϑ ϑ 3. ábra: A λ(.) függvények összehasonlítása a két különböző idejű képen két választott pixel környezetében. Az s pixel változatlan régió eleme, míg r pixel körül egy új megjelenő épület figyelhető meg Alacsony szintű hasonlóságvizsgálat A gradiens orientációs statisztika hatékony eszközt biztosít régiók alacsony szintű összevetésére is. A λ 1 s (.) és λ2 s (.) függvények illesztése felfogható az s körüli területek összehasonlításaként, épületspecifikus textúra jellemzők alapján (3. ábra). Mi több, ezek a leírók függetlenek a megvilágítástól és fehéregyensúlytól, valamint robosztusak a parallaxis és regisztrációs hibákra. A textúrális különbségeket az eloszlások Bhattacharyya távolságával mérjük: b(s) = log λ 1 s(ϑ) λ 2 s(ϑ)dϑ A bináris hasonlóságtérkép B a következő módon számítható: B(s) = 1 akkor és csak akkor hab(s) < b 0, egyébkéntb(s) = 0.
6 Épületek és változásaik detekciója 19 (a) Objektum jelölt (b) Gradiens térkép (c) Maszkolt grad. térkép 4. ábra: A gradiens jellemző bemutatása (a) Piros tető (b) Szín maszk 5. ábra: A tetőszín jellemző bemutatása 3.3. Objektum szintű jellemzők Ebben a fejezetben különböző objektum szintű jellemzőket mutatunk be. Felhasználva ezeket, ϕ (i) (u) energia tagokat definiálunk, melyek kiértékelik az u épület-hipotézist az i-edik képen (később ismét elhagyjuk az i indexet). ϕ(u) negatív fitnesz értékként értelmezhető, míg egy téglalapot ϕ(u) < 0 értékkel attraktív objektumnak hívunk. Mivel a populáció bővítése attraktív objektumokkal csökkentheti a globális konfigurációs energiát [4], ezek az alakzatok hatékony épület-jelöltek. A vizsgálatokat a gradienstérkép analízisével kezdjük ismét. Egy releváns téglalapjelölt R u határai alatt elvárhatjuk, hogy a képen a gradiens értékek magasak legyenek, és a gradiens irány legyen merőleges az R u legközelebbi oldalára (4. ábra). A Λ u jellemzőt a következőképpen számítjuk: Λ u = 1 q u s R u g s cos ( ϑs Θ s u) ahol R u az R u dilatált él maszkja, Θ s u {θ(u),θ(u) + 90 } az R u él orientációja s R u körül, és q u a R u pixeleinek száma. Az adat-energia tagot az alábbi módon számítjuk:ϕ Λ (u) = Q(Λ u,d Λ,D Λ ) ahol a következő nemlineárisq átviteli függvényt használjuk [4]: Q(x,d 0,D) = ) {(1 xd0 ha x < d 0 exp ( ) x d0 D 1 ha x d0
7 20 Benedek Csaba, Xavier Descombes, Josiane Zerubia A tetőszín jellemző számítását az 5. ábra szemlélteti. Definiáljuk a T u objektum környezetet és kiszámítjuk a C R (u) = 1 #R u s R u µ c (s) belső és C o (u) = 1 #T u [ s T 1 µc u (s) ] külső kitöltési tényezőket (# pixelekben mért területet jelöl). Végül származtatjuk az energiatagot:ϕ C (u) = max [ Q(C R (u),d C R,DC R ),Q(C o(u),d C o,dc o )] 6. ábra: Az árnyék jellemző bemutatása Az árnyék tényezőt a színével analóg módon definiáljuk, de a vizsgált objektum környezetet, Tu sh -t az árnyék irányban helyezzük el (6. ábra). [ Ezután a belső illetve külső kitöltési tényezőket számítjuk χ R (u) = 1 #R u s R u 1 µsh (s) ] és χ o (u) = µ sh (s), míg a ϕ χ (u) energiatag meghatározása azonos módon történik, 1 #T sh u s T sh u mint a ϕ C (u) esetén. Megjegyezzük, hogy kísérleteinkben a ϕ χ (u) tag akkor is robosztusnak bizonyult, amikor az árnyékos területek mérete erősen különböző volt az épületek magasságainak változatosságából adódóan. T d T r object candidate estimated symmetry dark side histogram bright side histogram 7. ábra: A tető homogenitás jellemző bemutatása Szürkeárnyalatos műhold képeken a tető homogenitása szintén hasznos jellemzőt ad. A 7. ábra bemutat egy példát két komponensű homogén tetők leírására. Miután kinyertük az u objektum jelölt fő szimmetria tengelyét, a világos és sötét tetőrészlet hisztogramjainak csúcsosságát a κ d (u) illetve κ b (u) kurtózisukkal jellemezzük. Vegyük észre azonban (8. ábra), hogy a kurtózis maximuma alapján gyakran töredék-tetőkhöz juthatunk (homogén tető része is homogén), ezért a tető teljességét is mérni kell egyidejűleg. Ezért létrehozzuk u elárasztás-maszkját (floodfill mask), F u -t, ami az R u
8 Épületek és változásaik detekciója ábra: Elárasztás alapú tető teljesség jellemző belsejéből a bemeneti képen elárasztás művelettel elérhető pixeleket tartalmazza. Ha a homogén tető jelölt teljes, F u alacsony átlapolódási értékkel rendelkezik az R u horizontális (NH u ) valamint vertikális (NV u ) szomszédossági területeivel (8. ábra). Végül, a ϕ κ (u) energiatagot a kurtózis és teljesség jellemzőkből az előzőkben ismertetett módon hozzuk létre. A keretrendszer lehetővé teszi a jellemzők rugalmas integrációját a bemeneti képek tulajdonságaitól függően. Minden épület prototípushoz előírhatunk egy vagy több jellemző kényszert, melyek ϕ energiatagjait a max operátorral csatoljuk össze a prototípus összesített energiatagjában (logikai és művelet a negatív fitnesz értékek terében). Egy adott képpáron több prototípust detektálhatunk párhuzamosan, ha a különböző prototípusok energiatagjait a min (logikai vagy) operátorral csatoljuk. Például, a Budapest képpáron (11. ábra) két prototípus használunk: az első előírja az élekre és az árnyékokra vonatkozó kényszert, míg a másik kizárólag a tető színre vonatkozót. így a teljes energiatag az alábbi módon számítható: ϕ(u) = min { max{ϕ Λ (u),ϕ χ (u)},ϕ c (u) }. 4. Jelölt pontfolyamat modell JelöljükH-val az u objektumok terét. Definiáljunk egyh H Borel halmazt, és az Ω konfigurációs teret az alábbi módon határozzuk meg [4]: Ω = Ω n, Ω n = { {u 1,...,u n } H n} n=0 Jelöljönω egy tetszőleges objektum konfigurációt{u 1,...,u n } Ω. Definiáljuk ezenfelül a szomszédossági relációt H-ban: u v ha a téglalapjaik, R u és R v metszik egymást. Bevezetünk egy nem stacionárius adatfüggő Gibbs eloszlást a konfigurációs téren: P D (ω) = 1/Z exp[ Φ D (ω)], aholz normalizáló konstans, és Φ D (ω) = u ωa D (u)+γ u,v ω u v I(u,v) (1)
9 22 Benedek Csaba, Xavier Descombes, Josiane Zerubia A D (u) és I(u,v) az adatfüggő szingleton, illetve a prior interakciós potenciálok és γ súlyozó tényező a két energiatag között. A legvalószínűbb, Maximum Likelihood (ML) konfigurációp D (ω) alapján becsülhető: ω ML = argmin ω Ω [ ΦD (ω) ] A szingleton potenciálok egy adottu = {c x,c y,e L,e l,θ,ξ} épület szegmens jelöltet jellemeznek a környezetbeli képi adat függvényében, azonban függetlenül a populáció többi objektumától: A D (u) = I [ξ(u) {1, }] ϕ (1) (u)+i [ξ(u) {2, }] ϕ (2) (u)+ { } + γ ξ ( ) I [ξ(u)= ] 1 B(s) +I[ξ(u) {1,2}] B(s) #R u s R u s R u ahol I [E] {0,1} az E esemény indikátor függvénye, és ahogy korábban definiáltuk, ϕ (1) (u) és ϕ (2) (u) épület illeszkedési energiák az első, illetve második képen (3.3. fejezet). B(.) az alacsony szintű hasonlósági maszk a két időréteg között (3.2. fejezet). Az utolsó tag bünteti a populációban található változatlannak jelölt objektumokat (ξ(u) = ) melyek nagy textúraváltozást jelző területeken helyezkednek el, illetve újnak/leromboltnak jelzett épületeket (ξ(u) {1, 2}) a változatlan területeken. Az interakciós potenciálok prior geometriai kényszereket írnak le: büntetik az azonos időréteget osztó objektum téglalapok nagy mértékű átlapolódását (4.. ábra): I(u,v) = I [ξ(u) ξ(v)] #(R u R v ) #(R u R v ) aholξ(u) ξ(v) fennáll, ha ξ(u) = ξ(v), vagyξ(u) =, orξ(v) =. 9. ábra: Interakciós jellemző 5. Optimalizáció Az optimális objektum konfigurációt a többszörös születés és halál (Multiple Birth and Death) algoritmussal [4] becsüljük, mely a következő lépéseket tartalmazza:
10 Épületek és változásaik detekciója 23 Inicializáció: határozzuk meg ap (i) b (s) ésm (i) s (i {1, 2}) születési térképeket, és induljunk ki üres populációból ω =. Fő program: állítsuk be a kezdeti inverz hőmérséklet paramétertβ = β 0 és a diszkretizációs lépcsőtδ = δ 0, ezután alternáljuk a születés és halál lépéseket. 1. Születés: sorban vizsgáljuk meg azs S pixeleket, és ha nincssközéppontú objektum a jelenlegi ω konfigurációban, vegyünk fel véletlenszerűen egy ξ {1, 2, } értéket, legyen P b = P (ξ) b (s) ha ξ {1,2}, Pb = max{p (1) b (s),p (2) b (s)} ha ξ = ; és futtassuk a születés folyamatots-benδ P b valószínűséggel. Születés folyamat s-ben: generáljunk egy új u objektumot s középponttal, ξ időindexszel, állítsuk be a e L (u), e l (u) oldalhossz értékeket véletlenszerűen előre meghatározott maximális és minimális oldalhosszak között, és állítsuk be a θ(u) orientációtη(.,m (ξ) s,σ θ ) Gaussi sűrűségfüggvényű véletlen változó alapján, ahogy azt a 3.1. fejezetben leírtuk. Végül, adjuku-t az aktuálisω konfigurációhoz. 2. Halál: tekintsük az aktuális ω = {u 1,...,u n } objektum konfigurációt és rendezzük az objektumokata D (u) alapján, csökkenő irányban. Az objektumokat vizsgáljunk meg ebben a sorrendben, és minden egyes u-ra számítsuk ki az alábbi értéket Φ ω (u) = Φ D (ω/{u}) Φ D (ω), amely az u törlésével létrejövő potenciális energia változást határozza meg. A halálozási arány így: d ω (u) = δa ω(u) 1+δa ω (u), ahol a ω(u) = e β Φω(u) Ezután töröljüku-tω-bóld ω (u) valószínűséggel. Konvergencia teszt: amíg a folyamat nem konvergál, növeljük a β inverz hőmérsékletet, csökkentsük a diszkretizációs lépcsőt δ geometriai sémával, és lépjünk vissza a születés lépésre. A konvergencia tényét akkor állapíthatjuk meg, ha minden olyan objektum, melyet az aktuális születés lépés generált, és csak azok tűnnek el a következő halál lépésben. 1. táblázat: A tesztadatok fő jellemzői. Adathalmaz Típus Szín árnyék Gradiens Kurtózis BUDAPEST légi igen igen jó részben BEIJING QBird nem igen gyenge részben SZADA légi igen nem gyenge nem ABIDJAN Ikonos nem nem éles igen 6. Kísérletek Módszerünket négy jelentősen különböző adathalmazon értékeltük ki 1, melyek fő jellemzőit az 1. táblázat tartalmazza. Kvalitatív eredmények a ábrákon láthatók. 1 A szerzők köszönetet mondanak az adatszolgáltatóknak: Görög András, Budapest, Francia Védelmi Hivatal (DGA) és Liama Laboratórium, Kína
11 24 Benedek Csaba, Xavier Descombes, Josiane Zerubia Azért, hogy alátámasszuk az objetumdetekció és a változásfelismerés együttes kezelésének előnyeit, a javasolt modellt (együttes detekció, ED) összehasonlítottuk egy konvencionális megoldással, ahol az épületeket külön nyerjük ki az egyes képeken, a változásinformációt pedig utólag becsüljük a kinyert objektumok elhelyezkedésének és geometriai paramétereinek összevetésével (szekvenciális detekció, SD). A 12. ábrán látható, hogy a SD módszer hamis riasztásokat okoz, mivel alacsony kontrasztú területeken egy-egy objektum hiányozhat valamelyik időrétegen, valamint zaj miatt hamis találatok is gyakrabban megjelennek a kevésbé robosztus egynézetű információra való hagyatkozással. A több jellemzőt együttesen kihasználó épületleíró modell hatékonyságát összehasonlítjuk egy főként éleken alapuló módszerrel (Él Verifikáció, ÉV). Az ÉV módszerben hasonlóan [9]-hez, az árnyék és tetőszín információt csak a beépített területek hozzávetőleges becsléséhez használjuk, míg az objektum verifikáció kizárólag az élkép illesztésén alapul. Kvantitatív tesztjeinkben a hiányzó (HO) és hamisan (FO) detektált objektumainkat valamint a hiányzó (HV) és hamis (FV) változásokat számoltuk meg, ezenfelül a detekció pixel szintű pontosságát (DP) is megadtuk. A DP számításához összehasonlítottuk az eredményül kapott épület alaprajz maszkjainkat a kézzel készített referencia (ground truth) maszkhoz, és meghatároztuk a detekció F-mértékét (a precizitás és visszahívási arány harmonikus közepe). A 2. táblázatban található eredmények megerősítik a javasolt ED modell általánosságát és előnyeit az SD és év módszerekhez képest (alacsonyabb objektum szintű hibák, magasabb DP tényező). A kiértékelés további részletei a szerzők kutatási riportjában olvashatók [1]. 10. ábra: Eredmények két képrészleten a SZADA adathalmazból. A kék téglalapok változatlan objektumokat jelölnek, a piros téglalapok változottakat (új, lerombolt vagy átépített).
12 Épületek és változásaik detekciója ábra: Az ismertetett módszer eredményei két képpáron. Fenn: BUDAPEST képrészlet (forrás: Görög András c ). Lenn: BEIJING (Liama Laboratórium CAS c Kína). A változatlan (kék) és a megváltozott (piros) épületeket megkülönböztetjük. 12. ábra: Eredmények az ABIDJAN képeken (DGA c Franciaország). Fenn: szekvenciális detekció (SD), valamennyi jelzett változás hamis riasztás. Lenn: az ismertetett együttes detekciós (ED) modell.
13 26 Benedek Csaba, Xavier Descombes, Josiane Zerubia 2. táblázat: Kvantitatív eredmények. #VT and #VN a változatlan és változott épületek számát jelöli az adott teszthalmazban. ED a saját módszer, míg az SD és ÉV referenciamódszerek valamint a HO, FO, HV, FV és DP kiértékelési tényezők a 6. fejezetben kerülnek részletes bemutatásra. HO FO HV FV DP Adathalmaz #VT #VN ÉV SD ED ÉV SD ED ÉV SD RD ÉV SD ED ÉV SD ED BUDAPEST BEIJING SZADA ABIDJAN Irodalom 1. C. Benedek, X. Descombes, and J. Zerubia. Building extraction and change detection in multitemporal aerial and satellite images in a joint stochastic approach. Research Report 7143, INRIA, Sophia Antipolis, December F. Bovolo. A multilevel parcel-based approach to change detection in very high resolution multitemporal images. IEEE GRS Letters, 6(1):33 37, Nicolas Champion, Leena Matikainen, Xinlian Liang, Juha Hyyppa, and Franz Rottensteiner. A test of 2D building change detection methods: Comparison, evaluation and perspectives. In ISPRS Congress, pages , Beijing, China, X. Descombes, R. Minlos, and E. Zhizhina. Object extraction using a stochastic birth-anddeath dynamics in continuum. J. of Math. Imaging and Vision, 33(3): , A. Katartzis and H. Sahli. A stochastic framework for the identification of building rooftops using a single remote sensing image. IEEE Trans. GRS, 46(1): , Sanjiv Kumar and Martial Hebert. Man-made structure detection in natural images using a causal multiscale random field. In CVPR, volume 1, pages , F. Lafarge, X. Descombes, J. Zerubia, and M. Pierrot-Deseilligny. Structural approach for building reconstruction from a single DSM. IEEE Trans. PAMI, in press. 8. J.A. Shufelt. Performance evaluation and analysis of monocular building extraction from aerial imagery. IEEE Trans. PAMI, 21(4): , B. Sirmacek and C. Unsalan. Building detection from aerial imagery using invariant color features and shadow information. In IEEE ISCIS, Istanbul, Turkey, 2008.
Városi forgalomfelügyelet kétszintű jelölt pontfolyamat modellel légi LiDAR felvételeken
 Városi forgalomfelügyelet kétszintű jelölt pontfolyamat modellel légi LiDAR felvételeken Börcs Attila 1,2, Benedek Csaba 1 1 Elosztott Események Elemzése Kutatólaboratórium, Magyar Tudományos Akadémia,
Városi forgalomfelügyelet kétszintű jelölt pontfolyamat modellel légi LiDAR felvételeken Börcs Attila 1,2, Benedek Csaba 1 1 Elosztott Események Elemzése Kutatólaboratórium, Magyar Tudományos Akadémia,
8. Pontmegfeleltetések
 8. Pontmegfeleltetések Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Példa: panoráma kép készítés 1. Jellemzőpontok detektálása mindkét
8. Pontmegfeleltetések Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Példa: panoráma kép készítés 1. Jellemzőpontok detektálása mindkét
Kevert Markov modell alapú változásdetekció nagy
 Kevert Markov modell alapú változásdetekció nagy időkülönbséggel készült légi fotókon Benedek Csaba 1,2 és Szirányi Tamás 1 1 Elosztott Események Elemzése Kutatócsoport, MTA Számítástechnikai és Automatizálási
Kevert Markov modell alapú változásdetekció nagy időkülönbséggel készült légi fotókon Benedek Csaba 1,2 és Szirányi Tamás 1 1 Elosztott Események Elemzése Kutatócsoport, MTA Számítástechnikai és Automatizálási
Hierarchikus jelölt pontfolyamat modell
 Hierarchikus jelölt pontfolyamat modell objektumpopulációk többszintű elemzéséhez Benedek Csaba Elosztott Események Elemzése Kutatólaboratórium, MTA SZTAKI 1111, Budapest, Kende utca 13-17benedek.csaba@sztaki.mta.hu
Hierarchikus jelölt pontfolyamat modell objektumpopulációk többszintű elemzéséhez Benedek Csaba Elosztott Események Elemzése Kutatólaboratórium, MTA SZTAKI 1111, Budapest, Kende utca 13-17benedek.csaba@sztaki.mta.hu
egyenletesen, és c olyan színű golyót teszünk az urnába, amilyen színűt húztunk. Bizonyítsuk
 Valószínűségszámítás 8. feladatsor 2015. november 26. 1. Bizonyítsuk be, hogy az alábbi folyamatok mindegyike martingál. a S n, Sn 2 n, Y n = t n 1+ 1 t 2 Sn, t Fn = σ S 1,..., S n, 0 < t < 1 rögzített,
Valószínűségszámítás 8. feladatsor 2015. november 26. 1. Bizonyítsuk be, hogy az alábbi folyamatok mindegyike martingál. a S n, Sn 2 n, Y n = t n 1+ 1 t 2 Sn, t Fn = σ S 1,..., S n, 0 < t < 1 rögzített,
c adatpontok és az ismeretlen pont közötti kovariancia vektora
 1. MELLÉKLET: Alkalmazott jelölések A mintaterület kiterjedése, területe c adatpontok és az ismeretlen pont közötti kovariancia vektora C(0) reziduális komponens varianciája C R (h) C R Cov{} d( u, X )
1. MELLÉKLET: Alkalmazott jelölések A mintaterület kiterjedése, területe c adatpontok és az ismeretlen pont közötti kovariancia vektora C(0) reziduális komponens varianciája C R (h) C R Cov{} d( u, X )
Sergyán Szabolcs szeptember 21.
 Éldetektálás Sergyán Szabolcs Budapesti Műszaki Főiskola Neumann János Informatikai Kar 2009. szeptember 21. Sergyán Sz. (BMF NIK) Éldetektálás 2009. szeptember 21. 1 / 28 Mit nevezünk élnek? Intuitív
Éldetektálás Sergyán Szabolcs Budapesti Műszaki Főiskola Neumann János Informatikai Kar 2009. szeptember 21. Sergyán Sz. (BMF NIK) Éldetektálás 2009. szeptember 21. 1 / 28 Mit nevezünk élnek? Intuitív
Statisztika elméleti összefoglaló
 1 Statisztika elméleti összefoglaló Tel.: 0/453-91-78 1. Tartalomjegyzék 1. Tartalomjegyzék.... Becsléselmélet... 3 3. Intervallumbecslések... 5 4. Hipotézisvizsgálat... 8 5. Regresszió-számítás... 11
1 Statisztika elméleti összefoglaló Tel.: 0/453-91-78 1. Tartalomjegyzék 1. Tartalomjegyzék.... Becsléselmélet... 3 3. Intervallumbecslések... 5 4. Hipotézisvizsgálat... 8 5. Regresszió-számítás... 11
Számítógépes döntéstámogatás. Genetikus algoritmusok
 BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
Robotika. Kinematika. Magyar Attila
 Robotika Kinematika Magyar Attila amagyar@almos.vein.hu Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
Robotika Kinematika Magyar Attila amagyar@almos.vein.hu Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
Pontműveletek. Sergyán Szabolcs Óbudai Egyetem Neumann János Informatikai Kar február 20.
 Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
Termelés- és szolgáltatásmenedzsment
 Termelés- és szolgáltatásmenedzsment egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék Termelés- és szolgáltatásmenedzsment 13. Előrejelzési módszerek 14. Az előrejelzési modellek felépítése
Termelés- és szolgáltatásmenedzsment egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék Termelés- és szolgáltatásmenedzsment 13. Előrejelzési módszerek 14. Az előrejelzési modellek felépítése
Infobionika ROBOTIKA. X. Előadás. Robot manipulátorok II. Direkt és inverz kinematika. Készült a HEFOP P /1.0 projekt keretében
 Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Statisztika - bevezetés Méréselmélet PE MIK MI_BSc VI_BSc 1
 Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Általánosan, bármilyen mérés annyit jelent, mint meghatározni, hányszor van meg
 LMeasurement.tex, March, 00 Mérés Általánosan, bármilyen mérés annyit jelent, mint meghatározni, hányszor van meg a mérendő mennyiségben egy másik, a mérendővel egynemű, önkényesen egységnek választott
LMeasurement.tex, March, 00 Mérés Általánosan, bármilyen mérés annyit jelent, mint meghatározni, hányszor van meg a mérendő mennyiségben egy másik, a mérendővel egynemű, önkényesen egységnek választott
Kör alakú objektumok szegmentálása Markov mez segítségével
 Kör alakú objektumok szegmentálása Markov mez segítségével Blaskovics Tamás 1, Kató Zoltán 1 és Ian Jermyn 1 Szegedi Tudományegyetem, Informatikai Tanszékcsoport, Szeged, Magyarország Ariana (joint INRIA/I3S
Kör alakú objektumok szegmentálása Markov mez segítségével Blaskovics Tamás 1, Kató Zoltán 1 és Ian Jermyn 1 Szegedi Tudományegyetem, Informatikai Tanszékcsoport, Szeged, Magyarország Ariana (joint INRIA/I3S
Regresszió. Csorba János. Nagyméretű adathalmazok kezelése március 31.
 Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
A médiatechnológia alapjai
 A médiatechnológia alapjai Úgy döntöttem, hogy a Szirányi oktatta előadások számonkérhetőnek tűnő lényegét kiemelem, az alapján, amit a ZH-ról mondott: rövid kérdések. A rész és az egész: összefüggések
A médiatechnológia alapjai Úgy döntöttem, hogy a Szirányi oktatta előadások számonkérhetőnek tűnő lényegét kiemelem, az alapján, amit a ZH-ról mondott: rövid kérdések. A rész és az egész: összefüggések
Képrekonstrukció 9. előadás
 Képrekonstrukció 9. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem hv-konvex összefüggő halmazok Mag-burok-szerű rekonstrukció: S. Brunetti, A. Del Lungo, F.
Képrekonstrukció 9. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem hv-konvex összefüggő halmazok Mag-burok-szerű rekonstrukció: S. Brunetti, A. Del Lungo, F.
7. Régió alapú szegmentálás
 Digitális képek szegmentálása 7. Régió alapú szegmentálás Kató Zoltán http://www.cab.u-szeged.hu/~kato/segmentation/ Szegmentálási kritériumok Particionáljuk a képet az alábbi kritériumokat kielégítő régiókba
Digitális képek szegmentálása 7. Régió alapú szegmentálás Kató Zoltán http://www.cab.u-szeged.hu/~kato/segmentation/ Szegmentálási kritériumok Particionáljuk a képet az alábbi kritériumokat kielégítő régiókba
A gradiens törésmutatójú közeg I.
 10. Előadás A gradiens törésmutatójú közeg I. Az ugrásszerű törésmutató változással szemben a TracePro-ban lehetőség van folytonosan változó törésmutatójú közeg definiálására. Ilyen érdekes típusú közegek
10. Előadás A gradiens törésmutatójú közeg I. Az ugrásszerű törésmutató változással szemben a TracePro-ban lehetőség van folytonosan változó törésmutatójú közeg definiálására. Ilyen érdekes típusú közegek
Segítség az outputok értelmezéséhez
 Tanulni: 10.1-10.3, 10.5, 11.10. Hf: A honlapra feltett falco_exp.zip-ben lévő exploratív elemzések áttanulmányozása, érdekességek, észrevételek kigyűjtése. Segítség az outputok értelmezéséhez Leiro: Leíró
Tanulni: 10.1-10.3, 10.5, 11.10. Hf: A honlapra feltett falco_exp.zip-ben lévő exploratív elemzések áttanulmányozása, érdekességek, észrevételek kigyűjtése. Segítség az outputok értelmezéséhez Leiro: Leíró
Keresés képi jellemzők alapján. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
1. ábra Egy terület DTM-je (balra) és ugyanazon terület DSM-je (jobbra)
 Bevezetés A digitális terepmodell (DTM) a Föld felszínének digitális, 3D-ós reprezentációja. Az automatikus DTM előállítás folyamata jelenti egyrészt távérzékelt felvételekből a magassági adatok kinyerését,
Bevezetés A digitális terepmodell (DTM) a Föld felszínének digitális, 3D-ós reprezentációja. Az automatikus DTM előállítás folyamata jelenti egyrészt távérzékelt felvételekből a magassági adatok kinyerését,
Mérési struktúrák
 Mérési struktúrák 2007.02.19. 1 Mérési struktúrák A mérés művelete: a mérendő jellemző és a szimbólum halmaz közötti leképezés megvalósítása jel- és rendszerelméleti aspektus mérési folyamat: a leképezést
Mérési struktúrák 2007.02.19. 1 Mérési struktúrák A mérés művelete: a mérendő jellemző és a szimbólum halmaz közötti leképezés megvalósítása jel- és rendszerelméleti aspektus mérési folyamat: a leképezést
környezetben 1. Bevezetés Utasi Ákos, Benedek Csaba Személyek detektálása, valamint lokalizálása a legtöbb megfigyelő alkalmazásban kulcsprobléma,
 Személyek lokalizálása és magasságuk becslése többszörös születés és halál dinamikával többkamerás környezetben Utasi Ákos, Benedek Csaba Magyar Tudományos Akadémia Számítástechnikai és Automatizálási
Személyek lokalizálása és magasságuk becslése többszörös születés és halál dinamikával többkamerás környezetben Utasi Ákos, Benedek Csaba Magyar Tudományos Akadémia Számítástechnikai és Automatizálási
Compton-effektus. Zsigmond Anna. jegyzıkönyv. Fizika BSc III.
 Compton-effektus jegyzıkönyv Zsigmond Anna Fizika BSc III. Mérés vezetıje: Csanád Máté Mérés dátuma: 010. április. Leadás dátuma: 010. május 5. Mérés célja A kvantumelmélet egyik bizonyítékának a Compton-effektusnak
Compton-effektus jegyzıkönyv Zsigmond Anna Fizika BSc III. Mérés vezetıje: Csanád Máté Mérés dátuma: 010. április. Leadás dátuma: 010. május 5. Mérés célja A kvantumelmélet egyik bizonyítékának a Compton-effektusnak
Számítógépes képelemzés 7. előadás. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Loss Distribution Approach
 Modeling operational risk using the Loss Distribution Approach Tartalom»Szabályozói környezet»modellezési struktúra»eseményszám eloszlás»káreloszlás»aggregált veszteségek»további problémák 2 Szabályozói
Modeling operational risk using the Loss Distribution Approach Tartalom»Szabályozói környezet»modellezési struktúra»eseményszám eloszlás»káreloszlás»aggregált veszteségek»további problémák 2 Szabályozói
Osztott jáva programok automatikus tesztelése. Matkó Imre BBTE, Kolozsvár Informatika szak, IV. Év 2007 január
 Osztott jáva programok automatikus tesztelése Matkó Imre BBTE, Kolozsvár Informatika szak, IV. Év 2007 január Osztott alkalmazások Automatikus tesztelés Tesztelés heurisztikus zaj keltés Tesztelés genetikus
Osztott jáva programok automatikus tesztelése Matkó Imre BBTE, Kolozsvár Informatika szak, IV. Év 2007 január Osztott alkalmazások Automatikus tesztelés Tesztelés heurisztikus zaj keltés Tesztelés genetikus
Grafikonok automatikus elemzése
 Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
Új markovi változásdetekciós modellek a képfeldolgozásban
 Új markovi változásdetekciós modellek a képfeldolgozásban Ph.D. disszertáció tézisei Benedek Csaba mérnök-informatikus Tudományos vezető: Dr. Szirányi Tamás az MTA doktora Pázmány Péter Katolikus Egyetem
Új markovi változásdetekciós modellek a képfeldolgozásban Ph.D. disszertáció tézisei Benedek Csaba mérnök-informatikus Tudományos vezető: Dr. Szirányi Tamás az MTA doktora Pázmány Péter Katolikus Egyetem
Gauss-Seidel iteráció
 Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Geofizikai kutatómódszerek I.
 Geofizikai kutatómódszerek I. A gravitációs és mágneses kutatómódszer Dr. Szabó Norbert Péter egyetemi docens Miskolci Egyetem Geofizikai Intézeti Tanszék e-mail: norbert.szabo.phd@gmail.com 1. A gravitációs
Geofizikai kutatómódszerek I. A gravitációs és mágneses kutatómódszer Dr. Szabó Norbert Péter egyetemi docens Miskolci Egyetem Geofizikai Intézeti Tanszék e-mail: norbert.szabo.phd@gmail.com 1. A gravitációs
Babeş Bolyai Tudományegyetem, Kolozsvár Matematika és Informatika Kar Magyar Matematika és Informatika Intézet
 / Babeş Bolyai Tudományegyetem, Kolozsvár Matematika és Informatika Kar Magyar Matematika és Informatika Intézet / Tartalom 3/ kernelek segítségével Felügyelt és félig-felügyelt tanulás felügyelt: D =
/ Babeş Bolyai Tudományegyetem, Kolozsvár Matematika és Informatika Kar Magyar Matematika és Informatika Intézet / Tartalom 3/ kernelek segítségével Felügyelt és félig-felügyelt tanulás felügyelt: D =
A maximum likelihood becslésről
 A maximum likelihood becslésről Definíció Parametrikus becsléssel foglalkozunk. Adott egy modell, mellyel elképzeléseink szerint jól leírható a meghatározni kívánt rendszer. (A modell típusának és rendszámának
A maximum likelihood becslésről Definíció Parametrikus becsléssel foglalkozunk. Adott egy modell, mellyel elképzeléseink szerint jól leírható a meghatározni kívánt rendszer. (A modell típusának és rendszámának
ACM Snake. Orvosi képdiagnosztika 11. előadás első fele
 ACM Snake Orvosi képdiagnosztika 11. előadás első fele ACM Snake (ismétlés) A szegmentáló kontúr egy paraméteres görbe: x Zs s X s, Y s,, s A szegmentáció energia funkcionál minimalizálása: E x Eint x
ACM Snake Orvosi képdiagnosztika 11. előadás első fele ACM Snake (ismétlés) A szegmentáló kontúr egy paraméteres görbe: x Zs s X s, Y s,, s A szegmentáció energia funkcionál minimalizálása: E x Eint x
Felügyelt önálló tanulás - Analízis III.
 Felügyelt önálló tanulás - Analízis III Kormos Máté Differenciálható sokaságok Sokaságok Röviden, sokaságoknak nevezzük azokat az objektumokat, amelyek egy n dimenziós térben lokálisan k dimenziósak Definíció:
Felügyelt önálló tanulás - Analízis III Kormos Máté Differenciálható sokaságok Sokaságok Röviden, sokaságoknak nevezzük azokat az objektumokat, amelyek egy n dimenziós térben lokálisan k dimenziósak Definíció:
Követelmény a 6. évfolyamon félévkor matematikából
 Követelmény a 6. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Halmazba rendezés adott tulajdonság alapján, részhalmaz felírása, felismerése. Két véges halmaz közös részének,
Követelmény a 6. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Halmazba rendezés adott tulajdonság alapján, részhalmaz felírása, felismerése. Két véges halmaz közös részének,
Mérési hibák 2006.10.04. 1
 Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
Digitális képek feldolgozása Előfeldolgozás Radiometriai korrekció Geometriai korrekció Képjavítás Szűrők Sávok közötti műveletek Képosztályozás Utófe
 Távérzékelés Digitális felvételek előfeldolgozása (EENAFOTOTV, ETNATAVERV) Erdőmérnöki szak, Környezettudós szak Király Géza NyME, Erdőmérnöki Kar Geomatikai, Erdőfeltárási és Vízgazdálkodási Intézet Földmérési
Távérzékelés Digitális felvételek előfeldolgozása (EENAFOTOTV, ETNATAVERV) Erdőmérnöki szak, Környezettudós szak Király Géza NyME, Erdőmérnöki Kar Geomatikai, Erdőfeltárási és Vízgazdálkodási Intézet Földmérési
Statisztikai módszerek a skálafüggetlen hálózatok
 Statisztikai módszerek a skálafüggetlen hálózatok vizsgálatára Gyenge Ádám1 1 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Számítástudományi és Információelméleti
Statisztikai módszerek a skálafüggetlen hálózatok vizsgálatára Gyenge Ádám1 1 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Számítástudományi és Információelméleti
STATISZTIKA ELŐADÁS ÁTTEKINTÉSE. Matematikai statisztika. Mi a modell? Binomiális eloszlás sűrűségfüggvény. Binomiális eloszlás
 ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
Követelmény az 5. évfolyamon félévkor matematikából
 Követelmény az 5. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Néhány elem kiválasztása adott szempont szerint. Néhány elem sorba rendezése, az összes lehetséges sorrend felsorolása.
Követelmény az 5. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Néhány elem kiválasztása adott szempont szerint. Néhány elem sorba rendezése, az összes lehetséges sorrend felsorolása.
Matematikai geodéziai számítások 10.
 Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Számítástechnikai és Automatizálási Kutatóintézet (MTA SZTAKI), 1111, Budapest, Kende utca 13 17, email:{vezetéknév.keresztnév}@sztaki.mta.
 Mozgó személyek követése és 4D vizualizációja Lidar-alapú járáselemzéssel Nagy Balázs 1, Benedek Csaba 1 és Jankó Zsolt 2 1 Elosztott Események Elemzése Kutatólaboratórium, Magyar Tudományos Akadémia,
Mozgó személyek követése és 4D vizualizációja Lidar-alapú járáselemzéssel Nagy Balázs 1, Benedek Csaba 1 és Jankó Zsolt 2 1 Elosztott Események Elemzése Kutatólaboratórium, Magyar Tudományos Akadémia,
Vektorgeometria (1) First Prev Next Last Go Back Full Screen Close Quit
 Vektorgeometria (1) First Prev Next Last Go Back Full Screen Close Quit 1. A térbeli irányított szakaszokat vektoroknak hívjuk. Két vektort egyenlőnek tekintünk, ha párhuzamos eltolással fedésbe hozhatók.
Vektorgeometria (1) First Prev Next Last Go Back Full Screen Close Quit 1. A térbeli irányított szakaszokat vektoroknak hívjuk. Két vektort egyenlőnek tekintünk, ha párhuzamos eltolással fedésbe hozhatók.
Gépi tanulás a gyakorlatban. Lineáris regresszió
 Gépi tanulás a gyakorlatban Lineáris regresszió Lineáris Regresszió Legyen adott egy tanuló adatbázis: Rendelkezésünkre áll egy olyan előfeldolgozott adathalmaz, aminek sorai az egyes ingatlanokat írják
Gépi tanulás a gyakorlatban Lineáris regresszió Lineáris Regresszió Legyen adott egy tanuló adatbázis: Rendelkezésünkre áll egy olyan előfeldolgozott adathalmaz, aminek sorai az egyes ingatlanokat írják
Digitális képek szegmentálása. 5. Textúra. Kató Zoltán.
 Digitális képek szegmentálása 5. Textúra Kató Zoltán http://www.cab.u-szeged.hu/~kato/segmentation/ Textúra fogalma Sklansky: Egy képen egy területnek állandó textúrája van ha a lokális statisztikák vagy
Digitális képek szegmentálása 5. Textúra Kató Zoltán http://www.cab.u-szeged.hu/~kato/segmentation/ Textúra fogalma Sklansky: Egy képen egy területnek állandó textúrája van ha a lokális statisztikák vagy
Minták automatikus osztályba sorolása a mintát leíró jellemzők alapján. Típusok: felügyelt és felügyelet nélküli tanuló eljárások
 Minták automatikus osztályba sorolása a mintát leíró jellemzők alapján Típusok: felügyelt és felügyelet nélküli tanuló eljárások Különbség: előbbinél szükséges egy olyan tanulóhalmaz, ahol ismert a minták
Minták automatikus osztályba sorolása a mintát leíró jellemzők alapján Típusok: felügyelt és felügyelet nélküli tanuló eljárások Különbség: előbbinél szükséges egy olyan tanulóhalmaz, ahol ismert a minták
Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea
 Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea Geometrikus deformálható modellek Görbe evolúció Level set módszer A görbe evolúció parametrizálástól független mindössze geometriai
Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea Geometrikus deformálható modellek Görbe evolúció Level set módszer A görbe evolúció parametrizálástól független mindössze geometriai
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások
 Megoldások 1. Határozd meg a szakasz hosszát, ha a végpontok koordinátái: A ( 1; ) és B (5; )! A szakasz hosszához számítsuk ki a két pont távolságát: d AB = AB = (5 ( 1)) + ( ) = 6 + 1 = 7 6,08.. Határozd
Megoldások 1. Határozd meg a szakasz hosszát, ha a végpontok koordinátái: A ( 1; ) és B (5; )! A szakasz hosszához számítsuk ki a két pont távolságát: d AB = AB = (5 ( 1)) + ( ) = 6 + 1 = 7 6,08.. Határozd
Új típusú döntési fa építés és annak alkalmazása többtényezős döntés területén
 Új típusú döntési fa építés és annak alkalmazása többtényezős döntés területén Dombi József Szegedi Tudományegyetem Bevezetés - ID3 (Iterative Dichotomiser 3) Az ID algoritmusok egy elemhalmaz felhasználásával
Új típusú döntési fa építés és annak alkalmazása többtényezős döntés területén Dombi József Szegedi Tudományegyetem Bevezetés - ID3 (Iterative Dichotomiser 3) Az ID algoritmusok egy elemhalmaz felhasználásával
Folyadékszcintillációs spektroszkópia jegyz könyv
 Folyadékszcintillációs spektroszkópia jegyz könyv Zsigmond Anna Julia Fizika MSc I. Mérés vezet je: Horváth Ákos Mérés dátuma: 2010. október 21. Leadás dátuma: 2010. november 8. 1 1. Bevezetés A mérés
Folyadékszcintillációs spektroszkópia jegyz könyv Zsigmond Anna Julia Fizika MSc I. Mérés vezet je: Horváth Ákos Mérés dátuma: 2010. október 21. Leadás dátuma: 2010. november 8. 1 1. Bevezetés A mérés
Közösség detektálás gráfokban
 Közösség detektálás gráfokban Önszervező rendszerek Hegedűs István Célkitűzés: valamilyen objektumok halmaza felett minták, csoportok detektálása csakis az egyedek közötti kapcsolatok struktúrájának a
Közösség detektálás gráfokban Önszervező rendszerek Hegedűs István Célkitűzés: valamilyen objektumok halmaza felett minták, csoportok detektálása csakis az egyedek közötti kapcsolatok struktúrájának a
Adaptív dinamikus szegmentálás idősorok indexeléséhez
 Adaptív dinamikus szegmentálás idősorok indexeléséhez IPM-08irAREAE kurzus cikkfeldolgozás Balassi Márton 1 Englert Péter 1 Tömösy Péter 1 1 Eötvös Loránd Tudományegyetem Informatikai Kar 2013. november
Adaptív dinamikus szegmentálás idősorok indexeléséhez IPM-08irAREAE kurzus cikkfeldolgozás Balassi Márton 1 Englert Péter 1 Tömösy Péter 1 1 Eötvös Loránd Tudományegyetem Informatikai Kar 2013. november
Least Squares becslés
 Least Squares becslés A négyzetes hibafüggvény: i d i ( ) φx i A négyzetes hibafüggvény mellett a minimumot biztosító megoldás W=( d LS becslés A gradiens számítása és nullává tétele eredményeképp A megoldás
Least Squares becslés A négyzetes hibafüggvény: i d i ( ) φx i A négyzetes hibafüggvény mellett a minimumot biztosító megoldás W=( d LS becslés A gradiens számítása és nullává tétele eredményeképp A megoldás
Gépi tanulás a gyakorlatban. Bevezetés
 Gépi tanulás a gyakorlatban Bevezetés Motiváció Nagyon gyakran találkozunk gépi tanuló alkalmazásokkal Spam detekció Karakter felismerés Fotó címkézés Szociális háló elemzés Piaci szegmentáció analízis
Gépi tanulás a gyakorlatban Bevezetés Motiváció Nagyon gyakran találkozunk gépi tanuló alkalmazásokkal Spam detekció Karakter felismerés Fotó címkézés Szociális háló elemzés Piaci szegmentáció analízis
Információ megjelenítés Számítógépes ábrázolás. Dr. Iványi Péter
 Információ megjelenítés Számítógépes ábrázolás Dr. Iványi Péter Raszterizáció OpenGL Mely pixelek vannak a primitíven belül fragment generálása minden ilyen pixelre Attribútumok (pl., szín) hozzárendelése
Információ megjelenítés Számítógépes ábrázolás Dr. Iványi Péter Raszterizáció OpenGL Mely pixelek vannak a primitíven belül fragment generálása minden ilyen pixelre Attribútumok (pl., szín) hozzárendelése
Adatok statisztikai értékelésének főbb lehetőségei
 Adatok statisztikai értékelésének főbb lehetőségei 1. a. Egy- vagy kétváltozós eset b. Többváltozós eset 2. a. Becslési problémák, hipotézis vizsgálat b. Mintázatelemzés 3. Szint: a. Egyedi b. Populáció
Adatok statisztikai értékelésének főbb lehetőségei 1. a. Egy- vagy kétváltozós eset b. Többváltozós eset 2. a. Becslési problémák, hipotézis vizsgálat b. Mintázatelemzés 3. Szint: a. Egyedi b. Populáció
Amortizációs költségelemzés
 Amortizációs költségelemzés Amennyiben műveleteknek egy M 1,...,M m sorozatának a futási idejét akarjuk meghatározni, akkor egy lehetőség, hogy külön-külön minden egyes művelet futási idejét kifejezzük
Amortizációs költségelemzés Amennyiben műveleteknek egy M 1,...,M m sorozatának a futási idejét akarjuk meghatározni, akkor egy lehetőség, hogy külön-külön minden egyes művelet futási idejét kifejezzük
Monte Carlo módszerek a statisztikus fizikában. Az Ising modell. 8. előadás
 Monte Carlo módszerek a statisztikus fizikában. Az Ising modell. 8. előadás Démon algoritmus az ideális gázra időátlag fizikai mennyiségek átlagértéke sokaságátlag E, V, N pl. molekuláris dinamika Monte
Monte Carlo módszerek a statisztikus fizikában. Az Ising modell. 8. előadás Démon algoritmus az ideális gázra időátlag fizikai mennyiségek átlagértéke sokaságátlag E, V, N pl. molekuláris dinamika Monte
BME MOGI Gépészeti informatika 1.
 BME MOGI Gépészeti informatika 1. 1. feladat Végezze el a következő feladatokat! Olvassa be a nevét és írjon üdvözlő szöveget a képernyőre! Generáljon két 1-100 közötti egész számot, és írassa ki a hányadosukat
BME MOGI Gépészeti informatika 1. 1. feladat Végezze el a következő feladatokat! Olvassa be a nevét és írjon üdvözlő szöveget a képernyőre! Generáljon két 1-100 közötti egész számot, és írassa ki a hányadosukat
Modern műszeres analitika szeminárium Néhány egyszerű statisztikai teszt
 Modern műszeres analitika szeminárium Néhány egyszerű statisztikai teszt Galbács Gábor KIUGRÓ ADATOK KISZŰRÉSE STATISZTIKAI TESZTEKKEL Dixon Q-tesztje Gyakori feladat az analitikai kémiában, hogy kiugrónak
Modern műszeres analitika szeminárium Néhány egyszerű statisztikai teszt Galbács Gábor KIUGRÓ ADATOK KISZŰRÉSE STATISZTIKAI TESZTEKKEL Dixon Q-tesztje Gyakori feladat az analitikai kémiában, hogy kiugrónak
egyetemi jegyzet Meskó Balázs
 egyetemi jegyzet 2011 Előszó 2. oldal Tartalomjegyzék 1. Bevezetés 4 1.1. A matematikai statisztika céljai.............................. 4 1.2. Alapfogalmak......................................... 4 2.
egyetemi jegyzet 2011 Előszó 2. oldal Tartalomjegyzék 1. Bevezetés 4 1.1. A matematikai statisztika céljai.............................. 4 1.2. Alapfogalmak......................................... 4 2.
Hipotézis STATISZTIKA. Kétmintás hipotézisek. Munkahipotézis (H a ) Tematika. Tudományos hipotézis. 1. Előadás. Hipotézisvizsgálatok
 STATISZTIKA 1. Előadás Hipotézisvizsgálatok Tematika 1. Hipotézis vizsgálatok 2. t-próbák 3. Variancia-analízis 4. A variancia-analízis validálása, erőfüggvény 5. Korreláció számítás 6. Kétváltozós lineáris
STATISZTIKA 1. Előadás Hipotézisvizsgálatok Tematika 1. Hipotézis vizsgálatok 2. t-próbák 3. Variancia-analízis 4. A variancia-analízis validálása, erőfüggvény 5. Korreláció számítás 6. Kétváltozós lineáris
Kvantummechanika gyakorlat Beadandó feladatsor Határid : 4. heti gyakorlatok eleje
 Kvantummechanika gyakorlat 015 1. Beadandó feladatsor Határid : 4. heti gyakorlatok eleje 1. Mutassuk meg, hogy A és B tetsz leges operátorokra igaz, hogy e B A e B = A + [B, A] + 1![ B, [B, A] ] +....
Kvantummechanika gyakorlat 015 1. Beadandó feladatsor Határid : 4. heti gyakorlatok eleje 1. Mutassuk meg, hogy A és B tetsz leges operátorokra igaz, hogy e B A e B = A + [B, A] + 1![ B, [B, A] ] +....
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Vektorok II.
 Vektorok II. DEFINÍCIÓ: (Vektorok hajlásszöge) Két vektor hajlásszögének azt a φ (0 φ 180 ) szöget nevezzük, amelyet a vektorok egy közös pontból felmért reprezentánsai által meghatározott félegyenesek
Vektorok II. DEFINÍCIÓ: (Vektorok hajlásszöge) Két vektor hajlásszögének azt a φ (0 φ 180 ) szöget nevezzük, amelyet a vektorok egy közös pontból felmért reprezentánsai által meghatározott félegyenesek
Számítógép és programozás 2
 Számítógép és programozás 2 11. Előadás Halmazkeresések, dinamikus programozás http://digitus.itk.ppke.hu/~flugi/ A keresési feladat megoldása Legyen a lehetséges megoldások halmaza M ciklus { X legyen
Számítógép és programozás 2 11. Előadás Halmazkeresések, dinamikus programozás http://digitus.itk.ppke.hu/~flugi/ A keresési feladat megoldása Legyen a lehetséges megoldások halmaza M ciklus { X legyen
Képrekonstrukció 6. előadás
 Képrekonstrukció 6. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Diszkrét tomográfia (DT) A CT-hez több száz vetület szükséges időigényes költséges károsíthatja
Képrekonstrukció 6. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Diszkrét tomográfia (DT) A CT-hez több száz vetület szükséges időigényes költséges károsíthatja
Funkcionális konnektivitás vizsgálata fmri adatok alapján
 Funkcionális konnektivitás vizsgálata fmri adatok alapján Képalkotási technikák 4 Log Resolution (mm) 3 Brain EEG & MEG fmri TMS PET Lesions 2 Column 1 0 Lamina -1 Neuron -2 Dendrite -3 Synapse -4 Mikrolesions
Funkcionális konnektivitás vizsgálata fmri adatok alapján Képalkotási technikák 4 Log Resolution (mm) 3 Brain EEG & MEG fmri TMS PET Lesions 2 Column 1 0 Lamina -1 Neuron -2 Dendrite -3 Synapse -4 Mikrolesions
Mátrixhatvány-vektor szorzatok hatékony számítása
 Mátrixhatvány-vektor szorzatok hatékony számítása Izsák Ferenc ELTE TTK, Alkalmazott Analízis és Számításmatematikai Tanszék & ELTE-MTA NumNet Kutatócsoport munkatárs: Szekeres Béla János Alkalmazott Analízis
Mátrixhatvány-vektor szorzatok hatékony számítása Izsák Ferenc ELTE TTK, Alkalmazott Analízis és Számításmatematikai Tanszék & ELTE-MTA NumNet Kutatócsoport munkatárs: Szekeres Béla János Alkalmazott Analízis
5. előadás - Regressziószámítás
 5. előadás - Regressziószámítás 2016. október 3. 5. előadás 1 / 18 Kétváltozós eset A modell: Y i = α + βx i + u i, i = 1,..., T, ahol X i független u i -től minden i esetén, (u i ) pedig i.i.d. sorozat
5. előadás - Regressziószámítás 2016. október 3. 5. előadás 1 / 18 Kétváltozós eset A modell: Y i = α + βx i + u i, i = 1,..., T, ahol X i független u i -től minden i esetén, (u i ) pedig i.i.d. sorozat
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
Optika gyakorlat 6. Interferencia. I = u 2 = u 1 + u I 2 cos( Φ)
 Optika gyakorlat 6. Interferencia Interferencia Az interferencia az a jelenség, amikor kett vagy több hullám fázishelyes szuperpozíciója révén a térben állóhullám kép alakul ki. Ez elektromágneses hullámok
Optika gyakorlat 6. Interferencia Interferencia Az interferencia az a jelenség, amikor kett vagy több hullám fázishelyes szuperpozíciója révén a térben állóhullám kép alakul ki. Ez elektromágneses hullámok
λ 1 u 1 + λ 2 v 1 + λ 3 w 1 = 0 λ 1 u 2 + λ 2 v 2 + λ 3 w 2 = 0 λ 1 u 3 + λ 2 v 3 + λ 3 w 3 = 0
 Vektorok a térben Egy (v 1,v 2,v 3 ) valós számokból álló hármast vektornak nevezzünk a térben (R 3 -ban). Használni fogjuk a v = (v 1,v 2,v 3 ) jelölést. A v 1,v 2,v 3 -at a v vektor komponenseinek nevezzük.
Vektorok a térben Egy (v 1,v 2,v 3 ) valós számokból álló hármast vektornak nevezzünk a térben (R 3 -ban). Használni fogjuk a v = (v 1,v 2,v 3 ) jelölést. A v 1,v 2,v 3 -at a v vektor komponenseinek nevezzük.
Véletlenszám generátorok és tesztelésük HORVÁTH BÁLINT
 Véletlenszám generátorok és tesztelésük HORVÁTH BÁLINT Mi a véletlen? Determinisztikus vs. Véletlen esemény? Véletlenszám: számok sorozata, ahol véletlenszerűen követik egymást az elemek Pszeudo-véletlenszám
Véletlenszám generátorok és tesztelésük HORVÁTH BÁLINT Mi a véletlen? Determinisztikus vs. Véletlen esemény? Véletlenszám: számok sorozata, ahol véletlenszerűen követik egymást az elemek Pszeudo-véletlenszám
Minősítéses mérőrendszerek képességvizsgálata
 Mnősítéses mérőrendszerek képességvzsgálata Vágó Emese, Dr. Kemény Sándor Budapest Műszak és Gazdaságtudomány Egyetem Kéma és Környezet Folyamatmérnök Tanszék Az előadás vázlata 1. Mnősítéses mérőrendszerek
Mnősítéses mérőrendszerek képességvzsgálata Vágó Emese, Dr. Kemény Sándor Budapest Műszak és Gazdaságtudomány Egyetem Kéma és Környezet Folyamatmérnök Tanszék Az előadás vázlata 1. Mnősítéses mérőrendszerek
Gépi tanulás a gyakorlatban. Kiértékelés és Klaszterezés
 Gépi tanulás a gyakorlatban Kiértékelés és Klaszterezés Hogyan alkalmazzuk sikeresen a gépi tanuló módszereket? Hogyan válasszuk az algoritmusokat? Hogyan hangoljuk a paramétereiket? Precízebben: Tegyük
Gépi tanulás a gyakorlatban Kiértékelés és Klaszterezés Hogyan alkalmazzuk sikeresen a gépi tanuló módszereket? Hogyan válasszuk az algoritmusokat? Hogyan hangoljuk a paramétereiket? Precízebben: Tegyük
Matematikai geodéziai számítások 6.
 Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
9. Írjuk fel annak a síknak az egyenletét, amely átmegy az M 0(1, 2, 3) ponton és. egyenessel;
 Síkok és egyenesek FELADATLAP Írjuk fel annak az egyenesnek az egyenletét, amely átmegy az M 0(,, ) ponton és a) az M(,, 0) ponton; b) párhuzamos a d(,, 5) vektorral; c) merőleges a x y + z 0 = 0 síkra;
Síkok és egyenesek FELADATLAP Írjuk fel annak az egyenesnek az egyenletét, amely átmegy az M 0(,, ) ponton és a) az M(,, 0) ponton; b) párhuzamos a d(,, 5) vektorral; c) merőleges a x y + z 0 = 0 síkra;
Loványi István vizsgakérdései kidolgozva (béta)
 Loványi István vizsgakérdései kidolgozva (béta) 1. Morfológiai képfeldolgozás elmélete 1. Alapvető halmazműveletek, tulajdonságaik Műveletek: egyesítés (unió) metszet negált összetett műveletek... Tulajdonságok:
Loványi István vizsgakérdései kidolgozva (béta) 1. Morfológiai képfeldolgozás elmélete 1. Alapvető halmazműveletek, tulajdonságaik Műveletek: egyesítés (unió) metszet negált összetett műveletek... Tulajdonságok:
GROVER-algoritmus. Sinkovicz Péter. ELTE, MSc II dec.15.
 ELTE, MSc II. 2011.dec.15. Áttekintés Feladat Algoritmus Kvantum keresési algoritmus áttekintése Input: N = 2 n elemű tömb, Ψ 1 = 0 1 kezdőállapot, f x0 (x) orákulum függvény. Output: x 0 keresett elem
ELTE, MSc II. 2011.dec.15. Áttekintés Feladat Algoritmus Kvantum keresési algoritmus áttekintése Input: N = 2 n elemű tömb, Ψ 1 = 0 1 kezdőállapot, f x0 (x) orákulum függvény. Output: x 0 keresett elem
EEE Kutatólaboratórium MTA-SZTAKI Magyar Tudományos Akadémia
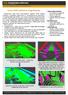 DElosztott I S T R I B U T EEsemények D EV E N T S A NElemzé A L Y S I S se R E SKutatólaboratór E A R C H L A B O R A T Oium R Y L I D A R B a s e d S u r v e i l l a n c e Városi LIDAR adathalmaz szegmentációja
DElosztott I S T R I B U T EEsemények D EV E N T S A NElemzé A L Y S I S se R E SKutatólaboratór E A R C H L A B O R A T Oium R Y L I D A R B a s e d S u r v e i l l a n c e Városi LIDAR adathalmaz szegmentációja
VI. Magyar Földrajzi Konferencia 524-529
 Van Leeuwen Boudewijn Tobak Zalán Szatmári József 1 BELVÍZ OSZTÁLYOZÁS HAGYOMÁNYOS MÓDSZERREL ÉS MESTERSÉGES NEURÁLIS HÁLÓVAL BEVEZETÉS Magyarország, különösen pedig az Alföld váltakozva szenved aszályos
Van Leeuwen Boudewijn Tobak Zalán Szatmári József 1 BELVÍZ OSZTÁLYOZÁS HAGYOMÁNYOS MÓDSZERREL ÉS MESTERSÉGES NEURÁLIS HÁLÓVAL BEVEZETÉS Magyarország, különösen pedig az Alföld váltakozva szenved aszályos
GCF 1.1 Gas Consumption Forecast
 GCF 1.1 Gas Consumption Forecast A szabadpiaci gáz-kereskedelem alapja a forrás- és a fogyasztói oldali menetrendek tervezése, operatív levezénylése és elszámolása. Az energia kereskedelem a jövõre vonatkozik,
GCF 1.1 Gas Consumption Forecast A szabadpiaci gáz-kereskedelem alapja a forrás- és a fogyasztói oldali menetrendek tervezése, operatív levezénylése és elszámolása. Az energia kereskedelem a jövõre vonatkozik,
1. Generátorrendszer. Házi feladat (fizikából tudjuk) Ha v és w nem párhuzamos síkvektorok, akkor generátorrendszert alkotnak a sík vektorainak
 1. Generátorrendszer Generátorrendszer. Tétel (Freud, 4.3.4. Tétel) Legyen V vektortér a T test fölött és v 1,v 2,...,v m V. Ekkor a λ 1 v 1 + λ 2 v 2 +... + λ m v m alakú vektorok, ahol λ 1,λ 2,...,λ
1. Generátorrendszer Generátorrendszer. Tétel (Freud, 4.3.4. Tétel) Legyen V vektortér a T test fölött és v 1,v 2,...,v m V. Ekkor a λ 1 v 1 + λ 2 v 2 +... + λ m v m alakú vektorok, ahol λ 1,λ 2,...,λ
Követelmény a 7. évfolyamon félévkor matematikából
 Követelmény a 7. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Elemek halmazba rendezése több szempont alapján. Halmazok ábrázolása. A nyelv logikai elemeinek helyes használata.
Követelmény a 7. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Elemek halmazba rendezése több szempont alapján. Halmazok ábrázolása. A nyelv logikai elemeinek helyes használata.
EGY ABLAK - GEOMETRIAI PROBLÉMA
 EGY ABLAK - GEOMETRIAI PROBLÉMA Írta: Hajdu Endre A számítógépemhez tartozó két hangfal egy-egy négyzet keresztmetszetű hasáb hely - szűke miatt az ablakpárkányon van elhelyezve (. ábra).. ábra Hogy az
EGY ABLAK - GEOMETRIAI PROBLÉMA Írta: Hajdu Endre A számítógépemhez tartozó két hangfal egy-egy négyzet keresztmetszetű hasáb hely - szűke miatt az ablakpárkányon van elhelyezve (. ábra).. ábra Hogy az
Miért fontos számunkra az előző gyakorlaton tárgyalt lineáris algebrai ismeretek
 Az november 23-i szeminárium témája Rövid összefoglaló Miért fontos számunkra az előző gyakorlaton tárgyalt lineáris algebrai ismeretek felfrissítése? Tekintsünk ξ 1,..., ξ k valószínűségi változókat,
Az november 23-i szeminárium témája Rövid összefoglaló Miért fontos számunkra az előző gyakorlaton tárgyalt lineáris algebrai ismeretek felfrissítése? Tekintsünk ξ 1,..., ξ k valószínűségi változókat,
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/54/33134304.jpg) [Biomatematika 2] Orvosi biometria 2016.02.29. A statisztika típusai Leíró jellegű statisztika: összegzi egy adathalmaz jellemzőit. A középértéket jelemzi (medián, módus, átlag) Az adatok változékonyságát
[Biomatematika 2] Orvosi biometria 2016.02.29. A statisztika típusai Leíró jellegű statisztika: összegzi egy adathalmaz jellemzőit. A középértéket jelemzi (medián, módus, átlag) Az adatok változékonyságát
Önálló labor beszámoló Képek szegmentálása textúra analízis segítségével. MAJF21 Eisenberger András május 22. Konzulens: Dr.
 Önálló labor beszámoló Képek szegmentálása textúra analízis segítségével 2011. május 22. Konzulens: Dr. Pataki Béla Tartalomjegyzék 1. Bevezetés 2 2. Források 2 3. Kiértékelő szoftver 3 4. A képek feldolgozása
Önálló labor beszámoló Képek szegmentálása textúra analízis segítségével 2011. május 22. Konzulens: Dr. Pataki Béla Tartalomjegyzék 1. Bevezetés 2 2. Források 2 3. Kiértékelő szoftver 3 4. A képek feldolgozása
Matematikai geodéziai számítások 6.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Q 1 D Q 2 (D x) 2 (1.1)
 . Gyakorlat 4B-9 Két pontszerű töltés az x tengelyen a következőképpen helyezkedik el: egy 3 µc töltés az origóban, és egy + µc töltés az x =, 5 m koordinátájú pontban van. Keressük meg azt a helyet, ahol
. Gyakorlat 4B-9 Két pontszerű töltés az x tengelyen a következőképpen helyezkedik el: egy 3 µc töltés az origóban, és egy + µc töltés az x =, 5 m koordinátájú pontban van. Keressük meg azt a helyet, ahol
x, x R, x rögzített esetén esemény. : ( ) x Valószínűségi Változó: Feltételes valószínűség: Teljes valószínűség Tétele: Bayes Tétel:
 Feltételes valószínűség: Teljes valószínűség Tétele: Bayes Tétel: Valószínűségi változó általános fogalma: A : R leképezést valószínűségi változónak nevezzük, ha : ( ) x, x R, x rögzített esetén esemény.
Feltételes valószínűség: Teljes valószínűség Tétele: Bayes Tétel: Valószínűségi változó általános fogalma: A : R leképezést valószínűségi változónak nevezzük, ha : ( ) x, x R, x rögzített esetén esemény.
Keresztmetszet másodrendű nyomatékainak meghatározása
 BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
Generátor differenciálvédelmi funkció blokk leírása
 Generátor differenciálvédelmi funkció blokk leírása Dokumentum azonosító: V1.2 Budapest, 2015. május A leírás verzió-információja Verzió Dátum Változás Szerkesztette 1.1 2015-05-25 Első verzió, angolból
Generátor differenciálvédelmi funkció blokk leírása Dokumentum azonosító: V1.2 Budapest, 2015. május A leírás verzió-információja Verzió Dátum Változás Szerkesztette 1.1 2015-05-25 Első verzió, angolból
Markov-láncok stacionárius eloszlása
 Markov-láncok stacionárius eloszlása Adatbányászat és Keresés Csoport, MTA SZTAKI dms.sztaki.hu Kiss Tamás 2013. április 11. Tartalom Markov láncok definíciója, jellemzése Visszatérési idők Stacionárius
Markov-láncok stacionárius eloszlása Adatbányászat és Keresés Csoport, MTA SZTAKI dms.sztaki.hu Kiss Tamás 2013. április 11. Tartalom Markov láncok definíciója, jellemzése Visszatérési idők Stacionárius
STATISZTIKA. A maradék független a kezelés és blokk hatástól. Maradékok leíró statisztikája. 4. A modell érvényességének ellenőrzése
 4. A modell érvényességének ellenőrzése STATISZTIKA 4. Előadás Variancia-analízis Lineáris modellek 1. Függetlenség 2. Normális eloszlás 3. Azonos varianciák A maradék független a kezelés és blokk hatástól
4. A modell érvényességének ellenőrzése STATISZTIKA 4. Előadás Variancia-analízis Lineáris modellek 1. Függetlenség 2. Normális eloszlás 3. Azonos varianciák A maradék független a kezelés és blokk hatástól
f(x) vagy f(x) a (x x 0 )-t használjuk. lim melyekre Mivel itt ɛ > 0 tetszőlegesen kicsi, így a a = 0, a = a, ami ellentmondás, bizonyítva
 6. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 6.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
6. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 6.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
