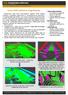
1. ábra Egy terület DTM-je (balra) és ugyanazon terület DSM-je (jobbra)

HTML
DOWNLOAD

Méret: px

Mutatás kezdődik a ... oldaltól:

Download "1. ábra Egy terület DTM-je (balra) és ugyanazon terület DSM-je (jobbra)"

Imre Rácz
9 évvel ezelőtt
Látták:

1 Bevezetés A digitális terepmodell (DTM) a Föld felszínének digitális, 3D-ós reprezentációja. Az automatikus DTM előállítás folyamata jelenti egyrészt távérzékelt felvételekből a magassági adatok kinyerését, másrészt a felszín térmodelljének előállítását. A DTM megjeleníti a felszíni topográfiát és nem tartalmazza a mesterséges (pl. épületek), valamint természetes (pl. fák) tereptárgyakat. A digitális felületmodell (DSM) megjeleníti a Föld felszínét a rajta található összes természetes és mesterséges objektummal együtt (1. ábra). 1. ábra Egy terület DTM-je (balra) és ugyanazon terület DSM-je (jobbra) A távérzékelt felvételek az elsődleges adatforrásai a DTM/DSM-ek előállításának. A modellek abban az esetben hozhatók létre, ha rendelkezésre áll az adott területről két, vagy több átfedő felvétel. Továbbá ismernünk kell a szenzor modellt (belső adatok), és a külső GPS/INS adatokat. DTM extrakció lépései 1. lépés: digitális kép-hozzárendelés a DTM mass pontok meghatározásához 2. lépés: ground pontkoordináták számítása 3. lépés: DTM felépítése 1. Lépés Közös képterülettel rendelkező (átfedő) digitális felvételek megegyező területeinek/pontjainak megtalálására gyakran alkalmazott eljárás a távérzékelésben és GIS-ben a korreláció. Az automatikus DTM generálást a korrelációs számításokon és képillesztési eljárásokon keresztül valóstják meg a digitális fotogrammetriai programok. Érdeklődési pont meghatározás Érdeklődési operátor alkalmazásával a légifotó-tömb felvételein érdeklődési pontok (feature points) sorozatát határozzuk meg. Az érdeklődési pont a középpontja egy kereső/minta ablaknak (mátrix), amely megfelelő szürkeségi intenzitással és kontraszttal rendelkezik. Az

A DTM megjeleníti a felszíni topográfiát és nem tartalmazza a mesterséges (pl. épületek), valamint természetes (pl. fák) tereptárgyakat.

2 érdeklődési pont ugyanakkor egy képpont is természetesen, egy jól felismerhető felszíni objektum jellemző pontja, pl. útkereszteződés, ház sarka, stb. Érdeklődési pont illesztése Amennyiben a tömb egy felvételén az érdeklődési pont meghatározása sikeresen megtörtént, a program az átfedő további felvételeken is megkeresi az adott pontot, így a vele azonosítható felszíni jellegzetességet is. A korrelációs ablak és a kereső ablak között keresztkorrelációs együttható kiszámítása a következő lépés. A korrelációs ablak a referencia képhez tartozik, a keresőablak a szomszédos átfedő kép(ek)hez. Az érdeklődési pontnak a szomszédos kép(ek)en több lehetséges illesztő-pont is megfelelhet. Minden lehetséges illeszkedő képponthalmazra kiszámítja a program a korrelációs koefficienst. A korrelációs együttható mutatja meg a hasonlóság mértékét az átfedő képterület ponthalmazai között. A magasabb érték (0.8-1) statisztikailag a hasonlóság nagyobb fokát jelenti értelemszerűen, mint az alacsonyabb érték (0.5 alatt). Startégiai paraméterek A startégiai paraméterek az illesztési eljárás sikerességét és pontosságát befolyásolják. A paraméterek közül a keresőablak és a korrelációs ablak méretének és a korrelációs együttható határértékének van legnagyobb hatása. Keresőablak mérete Miután egy érdeklődési pont meghatározásra került az első képen, a program megbecsüli a megközelítő helyét ugyanennek a pontnak a második képen. A közelítő érték alapján azután egy négyzetes keresőablakon belül határozza meg az egyező pont helyét. A keresőablak X értéke jelenti a keresési terület hosszát az epipoláris egyenes mentén; a keresőablak Y értéke jelenti a keresési terület szélességét az epipoláris egyenesen keresztül. A keresőablak X értékének nagysága függ az adott domborzat magassági változatosságától, minél élénkebb a domborzat, annál nagyobb az X érték. Az epipoláris egyenes pontosan megadható jó légiháromszögelési eredménnyel rendelkező légi keretkamerás felvételek esetén, így 1-3 pixeles Y érték a keresőablakra általában elegendő. A pushbroom technikával készült műholdfelvételeknél az epipoláris egyenes kevésbé pontos, így 3-5 pixeles Y érték ajánlott. Amennyiben a légiháromszögelés eredménye kevéssé megfelelő, az ablak méretének további növelésére lehet szükség. Ábra: kereső ablak ideális esete

azonosítható felszíni jellegzetességet is. A korrelációs ablak és a kereső ablak között keresztkorrelációs együttható kiszámítása a következő lépés.

3 Ebben az esetben keresőablak X értéke a következő formula alapján becsülhető: Sx = B*f/Ho*(Zmax-Zmin)/Ho Az Imagine OBPro legkisebb piramis rétege 250x250 pixeles, így itt Sx a következő összefüggés alapján számítható, ha a tömb felvételei között az átfedés értéke p: Sx = 250(Zmax-Zmin)/Ho*(1-p) Például: ha az átfedés 60%, a repülési magasság 4500 m, a magasságkülönbség 300 m, akkor a keresőablak becsült optimális X értéke: 7 pixel. Miután a gyakorlatban a felvételek egymáshoz képest elforgatott helyzetben vannak, nem ugyanabból a magasságból készülnek, az átfedés értéke is páronként változik a tömbön belül, így ajánlott a formulából kapott, kissé alábecsült értéket körüli értékkel beszorozni, tehát az előbbi példában az Sx értékének pixelt kell megadni. A korrelációs ablak mérete

keresőablak becsült optimális X értéke: 7 pixel.

4 A korrelációs ablak mérete a korrelációs koefficiens számításánál figyelembe vett ablak értékeinek számát határozza meg. Alapértéke 7x7-es, de alacsony relatív relieffel és színintenzitás-változással rendelkező felszín (mezőgazdasági parcella, gyep, homogén talaj, stb.) esetén az ablak mérete növelhető (9x9, vagy nagyobb). Amennyiben változatos a modellezett terület az ablak mérete csökkenthető (5x5). Az ablak alakja (nem szabályos) téglalap is lehet (pl. 7x9), mivel a domborzat okozta változás az epipoláris egyenes mentén (X irány) általában nagyobb, mint arra merőlegesen (Y irány). Korrelációs koefficiens határértéke A korrelációs koefficiens határértéke megadja azt a küszöbértéket, amely alapján meghatározzuk, hogy két kiválasztott pont megfeleltethető-e egymásnak, vagy sem. Amikor két felvétel két pontja között a korreláció értéke kiszámításra került, a program összehasonlítja ezt az értéket a határértékkel és amennyiben kisebbnek adódik, a két pont illesztése nem valósul meg. Nagyobb határérték pontosabb illesztést jelent, viszont kevesebb a kiválasztott pontok száma. Ha kisebbnek vesszük a küszöbértéket, akkor több illesztett pontot kapunk, viszont a figyelembe vett esetlegesen rossz pontok száma is növekedhet. Ajánlott a 0.7-es érték, viszont ha radiometrikusan jó minőségű, kis relatív reliefű felvételekkel dolgozunk, akkor a 0.8-as határérték lehet a megfelelő. Illeszkedési kikötések A képpárok geometriai és radiometrikus jellemzői meghatározzák a pontillesztési eljárások pontosságát és megbízhatóságát. A sztereopárok epipoláris geometriai tulajdonságait használjuk fel az illeszkedő pontpárok lehetséges elhelyezkedési környezeteinek megtalálásához. A 4-4. ábrán a referencia kép egy pontjának az átfedő kép epipoláris egyenesén megfeleltethető pontjait mutatja. A 4-5 ábra az epipoláris geometria alkalmazását mutatja be a pontillesztésben. Az L1PL2 az epipoláris sík és a képsíkok metszetét jelöli. A P felszíni pont, melynek koordinátái: Xp, Yp, Zp. Az epipoláris egyenes ismeretével, amelyen az összetartozó pontok elhelyezkednek, a keresési terület és a számítási idő is csökkenthető.

) esetén az ablak mérete növelhető (9x9, vagy nagyobb). Amennyiben változatos a modellezett terület az ablak mérete csökkenthető (5x5). Az ablak alakja (nem szabályos) téglalap is lehet (pl.

5 Az epipoláris geometria a komplanaritási feltételeket adja meg: a sztereopár felvételeinek vetítési centrumai, bármely felszíni pont és a neki megfelelő képpontok egy közös síkra kell, hogy illeszkedjenek. Ez a közös sík az epipoláris sík, vagy magsík. Az epipoláris sík metszi a jobb és a bal képet is, a metszésvonalat epipoláris egyenesenek (vagy magsugárnak) nevezzük. A földi pont képe az epipoláris egyenesre kell, hogy essen. A keresési és illesztési/egyeztetési eljárást így egy egyenes mentén kell végrehajtania a programnak, evvel egyszerűsítve az egyeztetési eljárást. Az epipoláris egyszerűsítések/kikötések csak tájékozott felvételek és ismert felvételi pozíciók esetén alkalmazhatók nyilvánvalóan. 2. lépés Amikor a korrelációs együttható meghatározásra került minden lehetséges illeszkedő ponthalmazra, statisztikai tesztek alapján választódik ki a földi pontnak leginkább megfelelő képi pont. A megoldáshalmaz pontjainak pixelkoordinátái tárolódnak, amelynek eredményeként a sztereopár által lefedett felszíni területet reprezentáló képpontok sor- és oszlopkoordinátáit kapjuk a jobb és a bal képre egyenként. Ezután kiszámításra kerülnek a képi pontok 3D koordinátái. Az eredmény-koordináták alkotják a DTM mass pontokat. A mass pont egy, legalább egy sztereoátfedésen megjelenő, diszkrét pont, melynek a a 3D koordinátái ismertek. A térbeli előremetszés/irányzás eljárása használatos a mass pont 3D koordinátáinak számításához. Ábra: DTM mass pontok 3D shape fájlban 3. lépés

A földi pont képe az epipoláris egyenesre kell, hogy essen.

6 Utolsó lépésként a kimeneti formátum meghatározása a feladat. Az OB PRO négyféle fájlformátumban állítja elő a DTM-et: DEM, Terramodel TIN, ESRI 3D shape, ASCII. A DEM és a Terramodell TIN a felszín mass pontokból interpolált folytonos modellje, míg a másik két formátum a 3D koordinátákkal rendelkező diszkrét mass pontokat tartalmazza. Irodalom Geoinformatika - elektronikus jegyzet Czimber Kornél, 2001 Imagine OrthoBase User s Guide

A DEM és a Terramodell TIN a felszín mass pontokból interpolált folytonos modellje, míg a másik két formátum

Hasonló dokumentumok

A fotogrammetria ismeretek és a szakmai tudás fontossága

Óbudai Egyetem Alba Regia Műszaki Kar Geoinformatikai Intézet A fotogrammetria ismeretek és a szakmai tudás fontossága 3. Légifotó Nap, Székesfehérvár, 2018. február 7. A fotogrammetria fogalma A fotogrammetria