Pontműveletek. Sergyán Szabolcs Óbudai Egyetem Neumann János Informatikai Kar február 20.
|
|
|
- Bálint Gál
- 6 évvel ezelőtt
- Látták:
Átírás
1 Pontműveletek Sergyán Szabolcs Óbudai Egyetem Neumann János Informatikai Kar február 20. Sergyán (OE NIK) Pontműveletek február / 40
2 Felhasznált irodalom Érdemes elolvasni: Gonzalez, Woods könyv 3. fejezetéből a 75. és 116. oldal közötti részt A diákon látható képek a Gonzalez, Woodz könyből származnak Sergyán (OE NIK) Pontműveletek február / 40
3 Képen található információk kiemelése A képfeldolgozási feladatok megvalósítása érdekében első lépésként a képet úgy kell átalakítani, hogy az aktuális feladat szempontjából releváns információkat kihangsúlyozzuk rajtuk Ezt a lépést előfeldolgozási lépésnek nevezzük Az előfeldolgozás történhet: térbeli tartományban ebben az esetben az eljárások direktben a pixel intenzitásokon történnek meg frekvencia tartományban ilyenkor a kép Fourier transzformáltján végzünk műveleteket Sergyán (OE NIK) Pontműveletek február / 40
4 Műveletek a térbeli tartományban A térbeli tartományban elvégzett műveletek az egyes pixelek intenzitás értékeit módosítják az alábbi képlet szerint: g(x, y) = T [f (x, y)], ahol f (x, y) a bemeneti, g(x, y) pedig az eredmény kép intenzitása az (x, y) helyen. Ha T csak f adott pontjának intenzitásából számítja ki g megfelelő pontjának intenzitását, akkor pontműveletről beszélünk. Ha T az (x, y), hely egy környezetét is figyelembe veszi, akkor ablakműveletről beszélünk. Sergyán (OE NIK) Pontműveletek február / 40
5 Egyszerűsített jelölési mód Az egyszerűség kedvéért pontműveletek esetén a transzformációt az s = T (r) formulával jelöljük, ahol r = f (x, y) és s = g(x, y). Sergyán (OE NIK) Pontműveletek február / 40
6 Kontraszt széthúzás (contrast stretching) Az alábbi típusú T esetén az eredmény képen feketék lesznek azok a pixelek, amelyek intenzitása alacsony volt a bemeneti képen fehérek lesznek azok a pixelek, amelyek intenzitása magas volt a bemeneti képen a transzformáció hatására a kép konrasztosabbá válik Sergyán (OE NIK) Pontműveletek február / 40
7 Küszöbölés Ha T az ábrán látható típusú, akkor a bemeneti kép m-nél kisebb intenzitású pixelei feketék lesznek az eredmény képen, a többi pixel pedig fehér. Így m mint egy küszöbérték binarizálja az eredeti képet. Sergyán (OE NIK) Pontműveletek február / 40
8 Alapvető szürkeségi transzformációk Az ábrán néhány alapvető szürkeségi transzformáció függvénye látható. Identitás Negatív transzformáció n-edik hatvány n-edik gyök Logaritmus Inverz logaritmus L jelöli a lehetséges szürkeségi értékek számát Sergyán (OE NIK) Pontműveletek február / 40
9 Negatív transzformáció A transzformáció képlete: s = L 1 r A negatív transzformáció hatására az eredeti képen sötét pixelek világossá válnak, így a kialakuló világos környezetben a részletek jobban érzékelhetők. Sergyán (OE NIK) Pontműveletek február / 40
10 Logaritmus transzformációk A logaritmus transzformáció általános alakja s = c log(1 + r), ahol c konstans, r pedig természetesen nem negatív. A transzformáció akkor alkalmazható, ha szűk sötét tartományban értékes információk vannak, amelyeket szeretnénk érzékelhetővé tenni. (Ilyen például a képek Fourier transzformáltjánál fordul elő.) Sergyán (OE NIK) Pontműveletek február / 40
11 Hatvány transzformációk A hatvány transzformációk általános alakja: s = cr γ, ahol c és γ pozitív konstansok. A gyakorlatban érdemes inkább s = c (r + ε) γ alakot használni, ahol ε egy kicsi pozitív érték. c = 1 Sergyán (OE NIK) Pontműveletek február / 40
12 Gamma korrekció A hatvány transzformáció más elnevezése a gamma korrekció A CRT monitorok a megjelenítés során módosítják a képet, ezért a pontos megjelenítés érdekében ajánlott korrigálni az előálló hibát. Sergyán (OE NIK) Pontműveletek február / 40
13 Pe lda hatva ny transzforma cio ra Sergya n (OE NIK) Pontmu veletek februa r / 40
14 Példa hatvány transzformációra Sergyán (OE NIK) Pontműveletek február / 40
15 Szakaszonként lineáris transzformációk A szakaszonként lineáris transzformációk olyan szürkeségi transzformációk, ahol a transzformációs függvény a bemeneti [0, L 1] intervallum egyes részintervallumain különböző lineáris függvényként adható meg. Néhány példa az alábbi ábrákon látható. Sergyán (OE NIK) Pontműveletek február / 40
16 Kontraszt széthúzás T (r) = Ha r 1 = s 1 és r 2 = s 2, akkor az identitás transzformációt kapjuk. Ha r 1 = r 2, s 1 = 0 és s 2 = L 1, akkor küszöbölésről van szó. Általános esetben r 1 r 2 és s 1 s 2, azaz mindegyik részintervallumon monoton növekvő a függvény. Ilyenkor az értékek helyes választásával a számunkra fontos részt emelhetjük ki. s 1 r1 r, ha r [0, r 1 ] s 1 + s 2 s 1 r 2 r 1 (r r 1 ), ha r [r 1, r 2 ] s 2 + L 1 s 2 L 1 r 2 (r r 2 ), ha r [r 2, L 1] Sergyán (OE NIK) Pontműveletek február / 40
17 Kontraszt széthúzás Gyakran használt beálĺıtás az (r 1, s 1 ) = (r min, 0), (r 2, s 2 ) = (r max, L 1), ahol r min az eredeti kép minimális, r max pedig a maximális intenzitás értéke. Sergyán (OE NIK) Pontműveletek február / 40
18 Küszöbölés Ha r 1 = r 2 = m, ahol m a pixel intenzitások középértéke (pontosabban várható értéke), valamint s 1 = 0 és s 2 = L 1, akkor az alábbi eredményt kapjuk. Sergyán (OE NIK) Pontműveletek február / 40
19 Szürkeségi szint vágás Ha egy bizonyos intervallumba eső intenzitású pixeleket szeretnénk kiemelni, akkor alkalmazhatjuk a szürkeségi szint vágást. A bal oldali transzformációs függvény a számunkra érdekes intervallumba eső pixelek intenzitását megnöveli egy konstans értékre, minden más pixel intenzitását pedig egy konstans alacsony szintre csökkenti. A jobb oldali transzformációs függvény hatására az eredeti szürkeárnyalatos értékek megmaradnak, viszont a releváns tartomány intenzitás értékei egy kiugró konstans szintre növekednek. Sergyán (OE NIK) Pontműveletek február / 40
20 Szürkeségi szint vágás (példa) Sergyán (OE NIK) Pontműveletek február / 40
21 Bit sík vágás Ha feltételezzük, hogy az egyes pixelek 8 biten vannak ábrázolva, akkor az egyes bitsíkok vizsgálatával is lehetőségünk van kiemelésre. A 0. bitréteg az alacsony rendű, a 7. réteg pedig a magas rendű információkat tartalmazza. Sergyán (OE NIK) Pontműveletek február / 40
22 Bit sík vágás példa Nyolc bites fraktál kép Sergyán (OE NIK) Pontműveletek február / 40
23 Hisztogram feldolgozás A h(r k ) = n k diszkrét függvény egy szürkeárnyalatos kép hisztogramja, ahol r k a k-adik szürkeségi szint a képen, n k pedig azon pixelek száma, amelyek szürkeségi értéke r k. A p(r k ) = n k n érték a normalizált hisztogram, ahol n a pixelek száma. Vegyük észre, hogy az összes lehetséges k-ra összegezve p(r k )-t 1-et kapunk eredményül. Sergyán (OE NIK) Pontműveletek február / 40
24 Hisztogram kiegyenĺıtés Tegyük fel, hogy a kép szürkeárnyalatos intenzitásai folytonos függvénnyel írhatók le, oly módon, hogy az intenzitás értékek a [0, 1] intervallumból kerülnek ki. Ebben az esetben r = 0 jelenti a fekete, r = 1 pedig a fehér intenzitás értéket. Tekintsük az s = T (r) (0 r 1) (1) transzformációs függvényt. Tegyük fel, hogy T (r) teljesíti az alábbi feltételeket: 1 T (r) injektív és monoton növekvő a [0, 1] intervallumon; 2 0 T (r) 1, ha 1 r 1. Ebben az esetben létezik a transzformáció inverze is: r = T 1 (s) (0 s 1) (2) Sergyán (OE NIK) Pontműveletek február / 40
25 Hisztogram kiegyenĺıtés A T transzformációs függvény például ilyen lehet: Sergyán (OE NIK) Pontműveletek február / 40
26 Hisztogram kiegyenĺıtés Egy kép szürkeségi értékeire tekinthetünk úgy is, mint valószínűségi változókra a [0, 1] intervallumban. Ebben az esetben az r valószínűségi változónak létezik sűrűség függvénye, amelyet p r (r)-rel jelölünk. Hasonlóan van az s valószínűségi változónak is sűrűség függvénye, amelyet pedig p s (s) jelöl. Valószínűségszámításból tudjuk, hogy p s (s) = p r (r) dr ds, (3) azaz az s sűrűségfüggvényét meghatározza az r sűrűségfüggvénye és a két valószínűségi változó közötti transzformáció. Sergyán (OE NIK) Pontműveletek február / 40
27 Hisztogram kiegyenĺıtés Tekintsük azt a transzformációs függvényt, amely az alábbiakat teljesíti: s = T (r) = r 0 p r (ω)dω, (4) ahol ω az integrálási változó. Vegyük észre, hogy a jobb oldalon álló integrál pont az r valószínűségi változó (kumulatív) eloszlásfüggvénye. Könnyen belátható, hogy az így definiált T (r) teljesíti a két korábban megfogalmazott feltételt. Sergyán (OE NIK) Pontműveletek február / 40
28 Hisztogram kiegyenĺıtés Vizsgáljuk az előbb definiált T (r)-t. ds dt (r) = = d dr dr dr r 0 p r (ω)dω = p r (r), (5) a Newton-Leibniz szabály miatt. Ebből viszont már következik: p s (s) = p r (r) dr ds = p r (r) 1 p r (r) = 1, (6) ha 0 s 0. Tehát azt kaptuk, hogy a választott T (r)-t használva az s valószínűségi változó egyenletes eloszlású függetlenül attól, hogy milyen volt r eloszlása. Sergyán (OE NIK) Pontműveletek február / 40
29 Hisztogram kiegyenĺıtés Előzőek alapján felmerül a kérdés, hogy milyen módon lehet egy diszkrét intenzitás értékekkel rendelkező kép intenzitás értékeit úgy transzformálni, hogy a transzformált kép intenzitás eloszlása (közel) egyenletes eloszlású legyen. A folytonos esetben vizsgált sűrűség függvénynek diszkrét esetben a normalizált hisztogram felel meg: p r (r k ) = n k n (k = 0, 1, 2,..., L 1) (7) Alkalmazzuk a (kumulatív) eloszlásfüggvény diszkrét változatát: s k = T (r k ) = ahol k = 0, 1, 2,..., L 1. k p r (r j ) = j=0 k j=0 n j n, (8) Sergyán (OE NIK) Pontműveletek február / 40
30 Hisztogram kiegyenĺıtés eredménye Sergyán (OE NIK) Pontműveletek február / 40
31 Az egyes alkalmazott transzformációk Sergyán (OE NIK) Pontműveletek február / 40
32 Hisztogram illesztés (histogram matching) Hisztogram illesztés esetén az a célunk, hogy az eredeti kép szürkeárnyalatos intenzitás értékeit úgy transzformáljuk, hogy a transzformált képen lévő intenzitások (valószínűségi) eloszlása egy előre meghatározott eloszlást kövessen. Sergyán (OE NIK) Pontműveletek február / 40
33 Hisztogram illesztés Kezdetben tekintsük megint a folytonos esetet. A bemeneti képen az egyes intenzitásokat jelölő valószínűségi változó legyen r (0 r 1), ennek sűrűségfüggvénye pedig p r (r). A transzformált képen z jelölje az intenzitás értékeket, sűrűségfüggvénye legyen p z (z). A korábbi levezetésből tudjuk, hogy s = T (r) = r 0 p r (ω)dω (9) egyenletes eloszlású. Mivel ez bármilyen valószínűségi változó esetén igaz, így G(z) = z 0 p z (t)dt = s (10) is egyenletes eloszlású. Ebből viszont G(z) = T (r) következik, azaz z = G 1 (s) = G 1 [T (r)] (11) Sergyán (OE NIK) Pontműveletek február / 40
34 Hisztogram illesztés Vizsgáljuk most a (valós) diszkrét esetet. Tudjuk, hogy Hasonlóan: Ebből pedig: s k = T (r k ) = k p r (r j ) = j=0 v k = G(z k ) = Nem biztos, hogy v k = s k teljesül! k j=0 n j n. (12) k p z (z i ) = s k (13) i=0 z k = G 1 [T (r k )] (14) Sergyán (OE NIK) Pontműveletek február / 40
35 Hisztogram illesztés Sergyán (OE NIK) Pontműveletek február / 40
36 Hisztogram illesztés Hogyan találhatjuk meg az s k -hoz tartozó z k -t? Egyáltalán nem biztos, hogy van olyan z k, melyre G(z k ) s k = 0 (15) teljesül. Keressük ezért az ideális z k -hoz közeli létező ẑ-t, mely teljesíti a G(ẑ) s k 0 (16) feltételt. Ezt úgy tehetjük meg, ha ẑ = 0-tól indulva, addig növeljük egyesével ẑ értékét, amíg igazzá nem válik a fenti feltétel. Javíthatunk az eljáráson, ha az s k -hoz tartozó ẑ-t a megtalált z k 1 -től növeljük csak. Sergyán (OE NIK) Pontműveletek február / 40
37 Hisztogram illesztés Az algorimus: 1 Határozzuk meg az eredeti kép hisztogramját. 2 Minden r k értékhez előre számítsuk ki a megfelelő s k értéket: s k = 3 Határozzuk meg a G transzformációs függvényt az adott p z (z)-ből: G(z k ) = k j=0 n j n (17) k p z (z i ) (18) i=0 4 Előre számítsuk ki z k -t az összes előforduló s k -hoz a összefüggést használva. G(ẑ) s k 0 (19) 5 Az eredeti kép minden r k pixeléhez rendeljük hozzá az előre meghatározott s k -t, illetve z k -t. Sergyán (OE NIK) Pontműveletek február / 40
38 Példa hisztogram operációra Bemeneti kép és a hisztogramja Sergyán (OE NIK) Pontműveletek február / 40
39 Példa hisztogram operációra Hisztogram kiegyenĺıtés eredménye Sergyán (OE NIK) Pontműveletek február / 40
40 Példa hisztogram operációra Hisztogram illesztés eredménye Sergyán (OE NIK) Pontműveletek február / 40
Gazdasági matematika II. vizsgadolgozat megoldása A csoport
 Gazdasági matematika II. vizsgadolgozat megoldása A csoport Definiálja az alábbi fogalmakat!. Egy eseménynek egy másik eseményre vonatkozó feltételes valószínűsége. ( pont) Az A esemény feltételes valószínűsége
Gazdasági matematika II. vizsgadolgozat megoldása A csoport Definiálja az alábbi fogalmakat!. Egy eseménynek egy másik eseményre vonatkozó feltételes valószínűsége. ( pont) Az A esemény feltételes valószínűsége
Morfológia. Sergyán Szabolcs Óbudai Egyetem Neumann János Informatikai Kar Szoftvertechnológia Intézet
 Morfológia Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Szoftvertechnológia Intézet 2012. október 9. Sergyán (OE NIK) Morfológia 2012. október 9. 1 /
Morfológia Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Szoftvertechnológia Intézet 2012. október 9. Sergyán (OE NIK) Morfológia 2012. október 9. 1 /
e (t µ) 2 f (t) = 1 F (t) = 1 Normális eloszlás negyedik centrális momentuma:
 Normális eloszlás ξ valószínűségi változó normális eloszlású. ξ N ( µ, σ 2) Paraméterei: µ: várható érték, σ 2 : szórásnégyzet (µ tetszőleges, σ 2 tetszőleges pozitív valós szám) Normális eloszlás sűrűségfüggvénye:
Normális eloszlás ξ valószínűségi változó normális eloszlású. ξ N ( µ, σ 2) Paraméterei: µ: várható érték, σ 2 : szórásnégyzet (µ tetszőleges, σ 2 tetszőleges pozitív valós szám) Normális eloszlás sűrűségfüggvénye:
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 3 III. VÉLETLEN VEKTOROK 1. A KÉTDIMENZIÓs VÉLETLEN VEKTOR Definíció: Az leképezést (kétdimenziós) véletlen vektornak nevezzük, ha Definíció:
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 3 III. VÉLETLEN VEKTOROK 1. A KÉTDIMENZIÓs VÉLETLEN VEKTOR Definíció: Az leképezést (kétdimenziós) véletlen vektornak nevezzük, ha Definíció:
Sergyán Szabolcs szeptember 21.
 Éldetektálás Sergyán Szabolcs Budapesti Műszaki Főiskola Neumann János Informatikai Kar 2009. szeptember 21. Sergyán Sz. (BMF NIK) Éldetektálás 2009. szeptember 21. 1 / 28 Mit nevezünk élnek? Intuitív
Éldetektálás Sergyán Szabolcs Budapesti Műszaki Főiskola Neumann János Informatikai Kar 2009. szeptember 21. Sergyán Sz. (BMF NIK) Éldetektálás 2009. szeptember 21. 1 / 28 Mit nevezünk élnek? Intuitív
2. Pont operációk. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 2. Pont operációk Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Kép transzformációk típusai Kép értékkészletének (radiometriai információ)
2. Pont operációk Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Kép transzformációk típusai Kép értékkészletének (radiometriai információ)
Matematika A3 Valószínűségszámítás, 5. gyakorlat 2013/14. tavaszi félév
 Matematika A3 Valószínűségszámítás, 5. gyakorlat 013/14. tavaszi félév 1. Folytonos eloszlások Eloszlásfüggvény és sűrűségfüggvény Egy valószínűségi változó, illetve egy eloszlás eloszlásfüggvényének egy
Matematika A3 Valószínűségszámítás, 5. gyakorlat 013/14. tavaszi félév 1. Folytonos eloszlások Eloszlásfüggvény és sűrűségfüggvény Egy valószínűségi változó, illetve egy eloszlás eloszlásfüggvényének egy
Fourier transzformáció
 a Matematika mérnököknek II. című tárgyhoz Fourier transzformáció Fourier transzformáció, heurisztika Tekintsük egy 2L szerint periodikus függvény Fourier sorát: f (x) = a 0 2 + ( ( nπ ) ( nπ )) a n cos
a Matematika mérnököknek II. című tárgyhoz Fourier transzformáció Fourier transzformáció, heurisztika Tekintsük egy 2L szerint periodikus függvény Fourier sorát: f (x) = a 0 2 + ( ( nπ ) ( nπ )) a n cos
Képfeldolgozás. 1. el adás. A képfeldolgozás m veletei. Mechatronikai mérnök szak BME, 2008
 Képfeldolgozás 1. el adás. A képfeldolgozás m veletei Mechatronikai mérnök szak BME, 2008 1 / 61 Alapfogalmak transzformációk Deníció Deníció Geometriai korrekciókra akkor van szükség, ha a képr l valódi
Képfeldolgozás 1. el adás. A képfeldolgozás m veletei Mechatronikai mérnök szak BME, 2008 1 / 61 Alapfogalmak transzformációk Deníció Deníció Geometriai korrekciókra akkor van szükség, ha a képr l valódi
Valószínűségi változók. Várható érték és szórás
 Matematikai statisztika gyakorlat Valószínűségi változók. Várható érték és szórás Valószínűségi változók 2016. március 7-11. 1 / 13 Valószínűségi változók Legyen a (Ω, A, P) valószínűségi mező. Egy X :
Matematikai statisztika gyakorlat Valószínűségi változók. Várható érték és szórás Valószínűségi változók 2016. március 7-11. 1 / 13 Valószínűségi változók Legyen a (Ω, A, P) valószínűségi mező. Egy X :
Valószínűségszámítás összefoglaló
 Statisztikai módszerek BMEGEVGAT Készítette: Halász Gábor Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel:
Statisztikai módszerek BMEGEVGAT Készítette: Halász Gábor Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel:
Készítette: Fegyverneki Sándor
 VALÓSZÍNŰSÉGSZÁMÍTÁS Összefoglaló segédlet Készítette: Fegyverneki Sándor Miskolci Egyetem, 2001. i JELÖLÉSEK: N a természetes számok halmaza (pozitív egészek) R a valós számok halmaza R 2 {(x, y) x, y
VALÓSZÍNŰSÉGSZÁMÍTÁS Összefoglaló segédlet Készítette: Fegyverneki Sándor Miskolci Egyetem, 2001. i JELÖLÉSEK: N a természetes számok halmaza (pozitív egészek) R a valós számok halmaza R 2 {(x, y) x, y
Abszolút folytonos valószín ségi változó (4. el adás)
 Abszolút folytonos valószín ségi változó (4. el adás) Deníció (Abszolút folytonosság és s r ségfüggvény) Az X valószín ségi változó abszolút folytonos, ha van olyan f : R R függvény, melyre P(X t) = t
Abszolút folytonos valószín ségi változó (4. el adás) Deníció (Abszolút folytonosság és s r ségfüggvény) Az X valószín ségi változó abszolút folytonos, ha van olyan f : R R függvény, melyre P(X t) = t
egyenletesen, és c olyan színű golyót teszünk az urnába, amilyen színűt húztunk. Bizonyítsuk
 Valószínűségszámítás 8. feladatsor 2015. november 26. 1. Bizonyítsuk be, hogy az alábbi folyamatok mindegyike martingál. a S n, Sn 2 n, Y n = t n 1+ 1 t 2 Sn, t Fn = σ S 1,..., S n, 0 < t < 1 rögzített,
Valószínűségszámítás 8. feladatsor 2015. november 26. 1. Bizonyítsuk be, hogy az alábbi folyamatok mindegyike martingál. a S n, Sn 2 n, Y n = t n 1+ 1 t 2 Sn, t Fn = σ S 1,..., S n, 0 < t < 1 rögzített,
4. Laplace transzformáció és alkalmazása
 4. Laplace transzformáció és alkalmazása 4.1. Laplace transzformált és tulajdonságai Differenciálegyenletek egy csoportja algebrai egyenletté alakítható. Ennek egyik eszköze a Laplace transzformáció. Definíció:
4. Laplace transzformáció és alkalmazása 4.1. Laplace transzformált és tulajdonságai Differenciálegyenletek egy csoportja algebrai egyenletté alakítható. Ennek egyik eszköze a Laplace transzformáció. Definíció:
6. Függvények. Legyen függvény és nem üreshalmaz. A függvényt az f K-ra való kiterjesztésének
 6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
1. Példa. A gamma függvény és a Fubini-tétel.
 . Példa. A gamma függvény és a Fubini-tétel.. Az x exp x + t )) függvény az x, t tartományon folytonos, és nem negatív, ezért alkalmazható rá a Fubini-tétel. I x exp x + t )) dxdt + t dt π 4. [ exp x +
. Példa. A gamma függvény és a Fubini-tétel.. Az x exp x + t )) függvény az x, t tartományon folytonos, és nem negatív, ezért alkalmazható rá a Fubini-tétel. I x exp x + t )) dxdt + t dt π 4. [ exp x +
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/54/34131233.jpg) [Biomatematika 2] Orvosi biometria 2016.02.22. Valószínűségi változó Véletlentől függő számértékeket (értékek sokasága) felvevő változókat valószínűségi változóknak nevezzük(jelölés: ξ, η, x). (pl. x =
[Biomatematika 2] Orvosi biometria 2016.02.22. Valószínűségi változó Véletlentől függő számértékeket (értékek sokasága) felvevő változókat valószínűségi változóknak nevezzük(jelölés: ξ, η, x). (pl. x =
Véletlen jelenség: okok rendszere hozza létre - nem ismerhetjük mind, ezért sztochasztikus.
 Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
Egyszerű programozási tételek
 Egyszerű programozási tételek 2. előadás Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2011. szeptember 15. Sergyán (OE NIK) AAO 02 2011. szeptember 15.
Egyszerű programozási tételek 2. előadás Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2011. szeptember 15. Sergyán (OE NIK) AAO 02 2011. szeptember 15.
Digitális jelfeldolgozás
 Digitális jelfeldolgozás Kvantálás Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2010. szeptember 15. Áttekintés
Digitális jelfeldolgozás Kvantálás Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2010. szeptember 15. Áttekintés
Matematika A1a Analízis
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika Aa Analízis BMETE90AX00 Az exp és ln függvények H607, EIC 209-04-24 Wettl
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika Aa Analízis BMETE90AX00 Az exp és ln függvények H607, EIC 209-04-24 Wettl
1.9. B - SPLINEOK B - SPLINEOK EGZISZTENCIÁJA. numerikus analízis ii. 34. [ a, b] - n legfeljebb n darab gyöke lehet. = r (m 1) n = r m + n 1
![1.9. B - SPLINEOK B - SPLINEOK EGZISZTENCIÁJA. numerikus analízis ii. 34. [ a, b] - n legfeljebb n darab gyöke lehet. = r (m 1) n = r m + n 1 1.9. B - SPLINEOK B - SPLINEOK EGZISZTENCIÁJA. numerikus analízis ii. 34. [ a, b] - n legfeljebb n darab gyöke lehet. = r (m 1) n = r m + n 1](/thumbs/88/116339870.jpg) numerikus analízis ii 34 Ezért [ a, b] - n legfeljebb n darab gyöke lehet = r (m 1) n = r m + n 1 19 B - SPLINEOK VOLT: Ω n véges felosztás S n (Ω n ) véges dimenziós altér A bázis az úgynevezett egyoldalú
numerikus analízis ii 34 Ezért [ a, b] - n legfeljebb n darab gyöke lehet = r (m 1) n = r m + n 1 19 B - SPLINEOK VOLT: Ω n véges felosztás S n (Ω n ) véges dimenziós altér A bázis az úgynevezett egyoldalú
Differenciálegyenletek numerikus megoldása
 a Matematika mérnököknek II. című tárgyhoz Differenciálegyenletek numerikus megoldása Fokozatos közeĺıtés módszere (1) (2) x (t) = f (t, x(t)), x I, x(ξ) = η. Az (1)-(2) kezdeti érték probléma ekvivalens
a Matematika mérnököknek II. című tárgyhoz Differenciálegyenletek numerikus megoldása Fokozatos közeĺıtés módszere (1) (2) x (t) = f (t, x(t)), x I, x(ξ) = η. Az (1)-(2) kezdeti érték probléma ekvivalens
MATE-INFO UBB verseny, március 25. MATEMATIKA írásbeli vizsga
 BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR MATE-INFO UBB verseny, 218. március 25. MATEMATIKA írásbeli vizsga FONTOS TUDNIVALÓK: 1 A feleletválasztós feladatok,,a rész esetén
BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR MATE-INFO UBB verseny, 218. március 25. MATEMATIKA írásbeli vizsga FONTOS TUDNIVALÓK: 1 A feleletválasztós feladatok,,a rész esetén
Integrálszámítás. a Matematika A1a-Analízis nevű tárgyhoz november
 Integrálszámítás a Matematika Aa-Analízis nevű tárgyhoz 009. november Tartalomjegyzék I. Feladatok 5. A határozatlan integrál (primitív függvények........... 7.. A definíciók egyszerű következményei..................
Integrálszámítás a Matematika Aa-Analízis nevű tárgyhoz 009. november Tartalomjegyzék I. Feladatok 5. A határozatlan integrál (primitív függvények........... 7.. A definíciók egyszerű következményei..................
f(x) vagy f(x) a (x x 0 )-t használjuk. lim melyekre Mivel itt ɛ > 0 tetszőlegesen kicsi, így a a = 0, a = a, ami ellentmondás, bizonyítva
 6. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 6.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
6. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 6.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
A következő feladat célja az, hogy egyszerű módon konstruáljunk Poisson folyamatokat.
 Poisson folyamatok, exponenciális eloszlások Azt mondjuk, hogy a ξ valószínűségi változó Poisson eloszlású λ, 0 < λ
Poisson folyamatok, exponenciális eloszlások Azt mondjuk, hogy a ξ valószínűségi változó Poisson eloszlású λ, 0 < λ
Jelek és rendszerek 1. 10/9/2011 Dr. Buchman Attila Informatikai Rendszerek és Hálózatok Tanszék
 Jelek és rendszerek 1 10/9/2011 Dr. Buchman Attila Informatikai Rendszerek és Hálózatok Tanszék 1 Ajánlott irodalom: FODOR GYÖRGY : JELEK ÉS RENDSZEREK EGYETEMI TANKÖNYV Műegyetemi Kiadó, Budapest, 2006
Jelek és rendszerek 1 10/9/2011 Dr. Buchman Attila Informatikai Rendszerek és Hálózatok Tanszék 1 Ajánlott irodalom: FODOR GYÖRGY : JELEK ÉS RENDSZEREK EGYETEMI TANKÖNYV Műegyetemi Kiadó, Budapest, 2006
Feladatok megoldásokkal a 9. gyakorlathoz (Newton-Leibniz formula, közelítő integrálás, az integrálszámítás alkalmazásai 1.
 Feladatok megoldásokkal a 9. gyakorlathoz (Newton-Leibniz formula, közelítő integrálás, az integrálszámítás alkalmazásai.). Feladat. Határozzuk meg az alábbi integrálokat: a) x x + dx d) xe x dx b) c)
Feladatok megoldásokkal a 9. gyakorlathoz (Newton-Leibniz formula, közelítő integrálás, az integrálszámítás alkalmazásai.). Feladat. Határozzuk meg az alábbi integrálokat: a) x x + dx d) xe x dx b) c)
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 2 II. A valószínűségi VÁLTOZÓ És JELLEMZÉsE 1. Valószínűségi VÁLTOZÓ Definíció: Az leképezést valószínűségi változónak nevezzük, ha
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 2 II. A valószínűségi VÁLTOZÓ És JELLEMZÉsE 1. Valószínűségi VÁLTOZÓ Definíció: Az leképezést valószínűségi változónak nevezzük, ha
A sorozat fogalma. függvényeket sorozatoknak nevezzük. Amennyiben az értékkészlet. az értékkészlet a komplex számok halmaza, akkor komplex
 A sorozat fogalma Definíció. A természetes számok N halmazán értelmezett függvényeket sorozatoknak nevezzük. Amennyiben az értékkészlet a valós számok halmaza, valós számsorozatról beszélünk, mígha az
A sorozat fogalma Definíció. A természetes számok N halmazán értelmezett függvényeket sorozatoknak nevezzük. Amennyiben az értékkészlet a valós számok halmaza, valós számsorozatról beszélünk, mígha az
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 5. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 5. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Gazdasági matematika II. vizsgadolgozat, megoldással,
 Gazdasági matematika II. vizsgadolgozat, megoldással, levelező képzés Definiálja az alábbi fogalmakat! 1. Kvadratikus mátrix invertálhatósága és inverze. (4 pont) Egy A kvadratikus mátrixot invertálhatónak
Gazdasági matematika II. vizsgadolgozat, megoldással, levelező képzés Definiálja az alábbi fogalmakat! 1. Kvadratikus mátrix invertálhatósága és inverze. (4 pont) Egy A kvadratikus mátrixot invertálhatónak
Tanulási cél Szorzatfüggvényekre vonatkozó integrálási technikák megismerése és különböző típusokra való alkalmazása. 5), akkor
 Integrálszámítás Integrálási szabályok Tanulási cél Szorzatfüggvényekre vonatkozó integrálási technikák megismerése és különböző típusokra való alkalmazása Motivációs feladat Valószínűség-számításnál találkozhatunk
Integrálszámítás Integrálási szabályok Tanulási cél Szorzatfüggvényekre vonatkozó integrálási technikák megismerése és különböző típusokra való alkalmazása Motivációs feladat Valószínűség-számításnál találkozhatunk
Matematika A3 Valószínűségszámítás, 6. gyakorlat 2013/14. tavaszi félév
 Matematika A3 Valószínűségszámítás, 6. gyakorlat 2013/14. tavaszi félév 1. A várható érték és a szórás transzformációja 1. Ha egy valószínűségi változóhoz hozzáadunk ötöt, mínusz ötöt, egy b konstanst,
Matematika A3 Valószínűségszámítás, 6. gyakorlat 2013/14. tavaszi félév 1. A várható érték és a szórás transzformációja 1. Ha egy valószínűségi változóhoz hozzáadunk ötöt, mínusz ötöt, egy b konstanst,
Fraktálok. Kontrakciók Affin leképezések. Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék. TARTALOMJEGYZÉK Kontrakciók Affin transzformációk
 Fraktálok Kontrakciók Affin leképezések Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék TARTALOMJEGYZÉK 1 of 71 A Lipschitz tulajdonság ÁTMÉRŐ, PONT ÉS HALMAZ TÁVOLSÁGA Definíció Az (S, ρ) metrikus tér
Fraktálok Kontrakciók Affin leképezések Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék TARTALOMJEGYZÉK 1 of 71 A Lipschitz tulajdonság ÁTMÉRŐ, PONT ÉS HALMAZ TÁVOLSÁGA Definíció Az (S, ρ) metrikus tér
4. Az A és B események egymást kizáró eseményeknek vagy idegen (diszjunkt)eseményeknek nevezzük, ha AB=O
 1. Mit nevezünk elemi eseménynek és eseménytérnek? A kísérlet lehetséges kimeneteleit elemi eseményeknek nevezzük. Az adott kísélethez tartozó elemi események halmazát eseménytérnek nevezzük, jele: X 2.
1. Mit nevezünk elemi eseménynek és eseménytérnek? A kísérlet lehetséges kimeneteleit elemi eseményeknek nevezzük. Az adott kísélethez tartozó elemi események halmazát eseménytérnek nevezzük, jele: X 2.
Matematika A2 vizsga mgeoldása június 4.
 Matematika A vizsga mgeoldása 03. június.. (a (3 pont Definiálja az f(x, y függvény határértékét az (x 0, y 0 helyen! Megoldás: Legyen D R, f : D R. Legyen az f(x, y függvény értelmezve az (x 0, y 0 pont
Matematika A vizsga mgeoldása 03. június.. (a (3 pont Definiálja az f(x, y függvény határértékét az (x 0, y 0 helyen! Megoldás: Legyen D R, f : D R. Legyen az f(x, y függvény értelmezve az (x 0, y 0 pont
Való szí nű sé gi va ltózó, sű rű sé gfű ggvé ny, élószla sfű ggvé ny
 Való szí nű sé gi va ltózó, sű rű sé gfű ggvé ny, élószla sfű ggvé ny Szűk elméleti összefoglaló Valószínűségi változó: egy függvény, ami az eseményteret a valós számok halmazára tudja vetíteni. A val.
Való szí nű sé gi va ltózó, sű rű sé gfű ggvé ny, élószla sfű ggvé ny Szűk elméleti összefoglaló Valószínűségi változó: egy függvény, ami az eseményteret a valós számok halmazára tudja vetíteni. A val.
Nem roncsoló tesztelés diszkrét tomográfiával
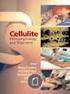 Nem roncsoló tesztelés diszkrét tomográfiával Dr. Balázs Péter, adjunktus Képfeldolgozás és Számítógépes Grafika Tanszék SZTE TTIK, Informatikai Tanszékcsoport A teszteléshez használt CT berendezés lapdetektor
Nem roncsoló tesztelés diszkrét tomográfiával Dr. Balázs Péter, adjunktus Képfeldolgozás és Számítógépes Grafika Tanszék SZTE TTIK, Informatikai Tanszékcsoport A teszteléshez használt CT berendezés lapdetektor
6. Folytonosság. pontbeli folytonosság, intervallumon való folytonosság, folytonos függvények
 6. Folytonosság pontbeli folytonosság, intervallumon való folytonosság, folytonos függvények Egy függvény egy intervallumon folytonos, ha annak miden pontjában folytonos. folytonos függvények tulajdonságai
6. Folytonosság pontbeli folytonosság, intervallumon való folytonosság, folytonos függvények Egy függvény egy intervallumon folytonos, ha annak miden pontjában folytonos. folytonos függvények tulajdonságai
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
MÉRÉSI EREDMÉNYEK PONTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI
 MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
Megoldott feladatok november 30. n+3 szigorúan monoton csökken, 5. n+3. lim a n = lim. n+3 = 2n+3 n+4 2n+1
 Megoldott feladatok 00. november 0.. Feladat: Vizsgáljuk az a n = n+ n+ sorozat monotonitását, korlátosságát és konvergenciáját. Konvergencia esetén számítsuk ki a határértéket! : a n = n+ n+ = n+ n+ =
Megoldott feladatok 00. november 0.. Feladat: Vizsgáljuk az a n = n+ n+ sorozat monotonitását, korlátosságát és konvergenciáját. Konvergencia esetén számítsuk ki a határértéket! : a n = n+ n+ = n+ n+ =
Numerikus integrálás
 Közelítő és szimbolikus számítások 11. gyakorlat Numerikus integrálás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján 1. Határozatlan integrál
Közelítő és szimbolikus számítások 11. gyakorlat Numerikus integrálás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján 1. Határozatlan integrál
Centrális határeloszlás-tétel
 13. fejezet Centrális határeloszlás-tétel A valószínűségszámítás legfontosabb állításai azok, amelyek független valószínűségi változók normalizált összegeire vonatkoznak. A legfontosabb ilyen tételek a
13. fejezet Centrális határeloszlás-tétel A valószínűségszámítás legfontosabb állításai azok, amelyek független valószínűségi változók normalizált összegeire vonatkoznak. A legfontosabb ilyen tételek a
Matematika A1a Analízis
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Folytonosság H607, EIC 2019-03-07 Wettl Ferenc
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Folytonosság H607, EIC 2019-03-07 Wettl Ferenc
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Logaritmus
 Logaritmus DEFINÍCIÓ: (Logaritmus) Ha egy pozitív valós számot adott, - től különböző pozitív alapú hatvány alakban írunk fel, akkor ennek a hatványnak a kitevőjét logaritmusnak nevezzük. Bármely pozitív
Logaritmus DEFINÍCIÓ: (Logaritmus) Ha egy pozitív valós számot adott, - től különböző pozitív alapú hatvány alakban írunk fel, akkor ennek a hatványnak a kitevőjét logaritmusnak nevezzük. Bármely pozitív
minden x D esetén, akkor x 0 -at a függvény maximumhelyének mondjuk, f(x 0 )-at pedig az (abszolút) maximumértékének.
 Függvények határértéke és folytonossága Egy f: D R R függvényt korlátosnak nevezünk, ha a függvényértékek halmaza korlátos. Ha f(x) f(x 0 ) teljesül minden x D esetén, akkor x 0 -at a függvény maximumhelyének
Függvények határértéke és folytonossága Egy f: D R R függvényt korlátosnak nevezünk, ha a függvényértékek halmaza korlátos. Ha f(x) f(x 0 ) teljesül minden x D esetén, akkor x 0 -at a függvény maximumhelyének
Statisztika - bevezetés Méréselmélet PE MIK MI_BSc VI_BSc 1
 Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Digitális képek szegmentálása. 5. Textúra. Kató Zoltán.
 Digitális képek szegmentálása 5. Textúra Kató Zoltán http://www.cab.u-szeged.hu/~kato/segmentation/ Textúra fogalma Sklansky: Egy képen egy területnek állandó textúrája van ha a lokális statisztikák vagy
Digitális képek szegmentálása 5. Textúra Kató Zoltán http://www.cab.u-szeged.hu/~kato/segmentation/ Textúra fogalma Sklansky: Egy képen egy területnek állandó textúrája van ha a lokális statisztikák vagy
A gyakorlat célja a fehér és a színes zaj bemutatása.
 A gyakorlat célja a fehér és a színes zaj bemutatása. 1.@. FFT begyakorlása n = [:9]; % Harminc minta x = cos(*pi*n/1); % 1 mintát veszünk periodusonként N1 = 64; % Három módon számoljuk az FFT-t N = 18;
A gyakorlat célja a fehér és a színes zaj bemutatása. 1.@. FFT begyakorlása n = [:9]; % Harminc minta x = cos(*pi*n/1); % 1 mintát veszünk periodusonként N1 = 64; % Három módon számoljuk az FFT-t N = 18;
Matematika III. 4. A valószínűségi változó és jellemzői Prof. Dr. Závoti, József
 Matematika III. 4. A valószínűségi változó és jellemzői Prof. Dr. Závoti, József Matematika III. 4. : A valószínűségi változó és jellemzői Prof. Dr. Závoti, József Lektor : Bischof, Annamária Ez a modul
Matematika III. 4. A valószínűségi változó és jellemzői Prof. Dr. Závoti, József Matematika III. 4. : A valószínűségi változó és jellemzői Prof. Dr. Závoti, József Lektor : Bischof, Annamária Ez a modul
RENDSZERTECHNIKA 8. GYAKORLAT
 RENDSZERTECHNIKA 8. GYAKORLAT ÜTEMTERV VÁLTOZÁS Gyakorlat Hét Dátum Témakör Házi feladat Egyéb 1 1. hét 02.09 Ismétlés, bevezetés Differenciálegyenletek mérnöki 2 2. hét 02.16 szemmel 1. Hf kiadás 3 3.
RENDSZERTECHNIKA 8. GYAKORLAT ÜTEMTERV VÁLTOZÁS Gyakorlat Hét Dátum Témakör Házi feladat Egyéb 1 1. hét 02.09 Ismétlés, bevezetés Differenciálegyenletek mérnöki 2 2. hét 02.16 szemmel 1. Hf kiadás 3 3.
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Exponenciális és Logaritmikus kifejezések
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Eponenciális és Logaritmikus kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szoálhatnak fontos információval
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Eponenciális és Logaritmikus kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szoálhatnak fontos információval
Határozatlan integrál (2) First Prev Next Last Go Back Full Screen Close Quit
 Határozatlan integrál () First Prev Next Last Go Back Full Screen Close Quit 1. Az összetett függvények integrálására szolgáló egyik módszer a helyettesítéssel való integrálás. Az idevonatkozó tétel pontos
Határozatlan integrál () First Prev Next Last Go Back Full Screen Close Quit 1. Az összetett függvények integrálására szolgáló egyik módszer a helyettesítéssel való integrálás. Az idevonatkozó tétel pontos
A L Hospital-szabály, elaszticitás, monotonitás, konvexitás
 A L Hospital-szabály, elaszticitás, monotonitás, konvexitás 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék A L Hospital-szabály, elaszticitás, monotonitás, konvexitás p. / A L
A L Hospital-szabály, elaszticitás, monotonitás, konvexitás 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék A L Hospital-szabály, elaszticitás, monotonitás, konvexitás p. / A L
Híradástechikai jelfeldolgozás
 Híradástechikai jelfeldolgozás 13. Előadás 015. 04. 4. Jeldigitalizálás és rekonstrukció 015. április 7. Budapest Dr. Gaál József docens BME Hálózati Rendszerek és SzolgáltatásokTanszék gaal@hit.bme.hu
Híradástechikai jelfeldolgozás 13. Előadás 015. 04. 4. Jeldigitalizálás és rekonstrukció 015. április 7. Budapest Dr. Gaál József docens BME Hálózati Rendszerek és SzolgáltatásokTanszék gaal@hit.bme.hu
Egyváltozós függvények 1.
 Egyváltozós függvények 1. Filip Ferdinánd filip.ferdinand@bgk.uni-obuda.hu siva.banki.hu/jegyzetek 015 szeptember 1. Filip Ferdinánd 015 szeptember 1. Egyváltozós függvények 1. 1 / 5 Az el adás vázlata
Egyváltozós függvények 1. Filip Ferdinánd filip.ferdinand@bgk.uni-obuda.hu siva.banki.hu/jegyzetek 015 szeptember 1. Filip Ferdinánd 015 szeptember 1. Egyváltozós függvények 1. 1 / 5 Az el adás vázlata
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
Határozott integrál és alkalmazásai
 Határozott integrál és alkalmazásai 5. május 5.. Alapfeladatok. Feladat: + d = Megoldás: Egy határozott integrál kiszámolása a feladat. Ilyenkor a Newton-Leibniz-tételt használhatjuk, mely azt mondja ki,
Határozott integrál és alkalmazásai 5. május 5.. Alapfeladatok. Feladat: + d = Megoldás: Egy határozott integrál kiszámolása a feladat. Ilyenkor a Newton-Leibniz-tételt használhatjuk, mely azt mondja ki,
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Exponenciális és Logaritmikus kifejezések
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Eponenciális és Logaritmikus kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Eponenciális és Logaritmikus kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos
A fontosabb definíciók
 A legfontosabb definíciókat jelöli. A fontosabb definíciók [Descartes szorzat] Az A és B halmazok Descartes szorzatán az A és B elemeiből képezett összes (a, b) a A, b B rendezett párok halmazát értjük,
A legfontosabb definíciókat jelöli. A fontosabb definíciók [Descartes szorzat] Az A és B halmazok Descartes szorzatán az A és B elemeiből képezett összes (a, b) a A, b B rendezett párok halmazát értjük,
Adaptív dinamikus szegmentálás idősorok indexeléséhez
 Adaptív dinamikus szegmentálás idősorok indexeléséhez IPM-08irAREAE kurzus cikkfeldolgozás Balassi Márton 1 Englert Péter 1 Tömösy Péter 1 1 Eötvös Loránd Tudományegyetem Informatikai Kar 2013. november
Adaptív dinamikus szegmentálás idősorok indexeléséhez IPM-08irAREAE kurzus cikkfeldolgozás Balassi Márton 1 Englert Péter 1 Tömösy Péter 1 1 Eötvös Loránd Tudományegyetem Informatikai Kar 2013. november
0-49 pont: elégtelen, pont: elégséges, pont: közepes, pont: jó, pont: jeles
 Matematika szigorlat, Mérnök informatikus szak I. 2013. jan. 10. Név: Neptun kód: Idő: 180 perc Elm.: 1. f. 2. f. 3. f. 4. f. 5. f. Fel. össz.: Össz.: Oszt.: Az elérhető pontszám 40 (elmélet) + 60 (feladatok)
Matematika szigorlat, Mérnök informatikus szak I. 2013. jan. 10. Név: Neptun kód: Idő: 180 perc Elm.: 1. f. 2. f. 3. f. 4. f. 5. f. Fel. össz.: Össz.: Oszt.: Az elérhető pontszám 40 (elmélet) + 60 (feladatok)
Matematika 11. osztály
 ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Humán tagozat Matematika 11. osztály I. rész: Hatvány, gyök, logaritmus Készítette: Balázs Ádám Budapest, 018 . Tartalomjegyzék Tartalomjegyzék
ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Humán tagozat Matematika 11. osztály I. rész: Hatvány, gyök, logaritmus Készítette: Balázs Ádám Budapest, 018 . Tartalomjegyzék Tartalomjegyzék
Kalkulus I. gyakorlat Fizika BSc I/1.
 . Ábrázoljuk a következő halmazokat a síkon! {, y) R 2 : + y < }, b) {, y) R 2 : 2 + y 2 < 4}, c) {, y) R 2 : 2 + y 2 < 4, + y < }, {, y) R 2 : + y < }. Kalkulus I. gyakorlat Fizika BSc I/.. gyakorlat
. Ábrázoljuk a következő halmazokat a síkon! {, y) R 2 : + y < }, b) {, y) R 2 : 2 + y 2 < 4}, c) {, y) R 2 : 2 + y 2 < 4, + y < }, {, y) R 2 : + y < }. Kalkulus I. gyakorlat Fizika BSc I/.. gyakorlat
A mérési eredmény megadása
 A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
BIOMATEMATIKA ELŐADÁS
 BIOMATEMATIKA ELŐADÁS 9. Együttes eloszlás, kovarianca, nevezetes eloszlások Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Bevezetés, definíciók Együttes eloszlás Függetlenség
BIOMATEMATIKA ELŐADÁS 9. Együttes eloszlás, kovarianca, nevezetes eloszlások Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Bevezetés, definíciók Együttes eloszlás Függetlenség
Függvény határérték összefoglalás
 Függvény határérték összefoglalás Függvény határértéke: Def: Függvény: egyértékű reláció. (Vagyis minden értelmezési tartománybeli elemhez, egyértelműen rendelünk hozzá egy elemet az értékkészletből. Vagyis
Függvény határérték összefoglalás Függvény határértéke: Def: Függvény: egyértékű reláció. (Vagyis minden értelmezési tartománybeli elemhez, egyértelműen rendelünk hozzá egy elemet az értékkészletből. Vagyis
(Independence, dependence, random variables)
 Két valószínűségi változó együttes vizsgálata Feltételes eloszlások Két diszkrét változó együttes eloszlása a lehetséges értékpárok és a hozzájuk tartozó valószínűségek (táblázat) Példa: Egy urna 3 fehér,
Két valószínűségi változó együttes vizsgálata Feltételes eloszlások Két diszkrét változó együttes eloszlása a lehetséges értékpárok és a hozzájuk tartozó valószínűségek (táblázat) Példa: Egy urna 3 fehér,
biometria II. foglalkozás előadó: Prof. Dr. Rajkó Róbert Matematikai-statisztikai adatfeldolgozás
 Kísérlettervezés - biometria II. foglalkozás előadó: Prof. Dr. Rajkó Róbert Matematikai-statisztikai adatfeldolgozás A matematikai-statisztika feladata tapasztalati adatok feldolgozásával segítséget nyújtani
Kísérlettervezés - biometria II. foglalkozás előadó: Prof. Dr. Rajkó Róbert Matematikai-statisztikai adatfeldolgozás A matematikai-statisztika feladata tapasztalati adatok feldolgozásával segítséget nyújtani
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x
Numerikus matematika. Irodalom: Stoyan Gisbert, Numerikus matematika mérnököknek és programozóknak, Typotex, Lebegőpontos számok
 Numerikus matematika Irodalom: Stoyan Gisbert, Numerikus matematika mérnököknek és programozóknak, Typotex, 2007 Lebegőpontos számok Normák, kondíciószámok Lineáris egyenletrendszerek Legkisebb négyzetes
Numerikus matematika Irodalom: Stoyan Gisbert, Numerikus matematika mérnököknek és programozóknak, Typotex, 2007 Lebegőpontos számok Normák, kondíciószámok Lineáris egyenletrendszerek Legkisebb négyzetes
Least Squares becslés
 Least Squares becslés A négyzetes hibafüggvény: i d i ( ) φx i A négyzetes hibafüggvény mellett a minimumot biztosító megoldás W=( d LS becslés A gradiens számítása és nullává tétele eredményeképp A megoldás
Least Squares becslés A négyzetes hibafüggvény: i d i ( ) φx i A négyzetes hibafüggvény mellett a minimumot biztosító megoldás W=( d LS becslés A gradiens számítása és nullává tétele eredményeképp A megoldás
Morfológia. Sergyán Szabolcs Óbudai Egyetem Neumann János Informatikai Kar Szoftvertechnológia Intézet
 Morfológia Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Szoftvertechnológia Intézet 2013. szeptember 15. Sergyán (OE NIK) Morfológia 2013. szeptember
Morfológia Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Szoftvertechnológia Intézet 2013. szeptember 15. Sergyán (OE NIK) Morfológia 2013. szeptember
Logaritmikus erősítő tanulmányozása
 13. fejezet A műveleti erősítők Logaritmikus erősítő tanulmányozása A műveleti erősítő olyan elektronikus áramkör, amely a két bemenete közötti potenciálkülönbséget igen nagy mértékben fölerősíti. A műveleti
13. fejezet A műveleti erősítők Logaritmikus erősítő tanulmányozása A műveleti erősítő olyan elektronikus áramkör, amely a két bemenete közötti potenciálkülönbséget igen nagy mértékben fölerősíti. A műveleti
Szili László. Integrálszámítás (Gyakorló feladatok) Analízis 3. Programtervező informatikus szak BSc, B és C szakirány
 Szili László Integrálszámítás (Gyakorló feladatok Analízis. Programtervező informatikus szak BSc, B és C szakirány. február Tartalomjegyzék I. Feladatok 5. A határozatlan integrál (primitív függvények...........
Szili László Integrálszámítás (Gyakorló feladatok Analízis. Programtervező informatikus szak BSc, B és C szakirány. február Tartalomjegyzék I. Feladatok 5. A határozatlan integrál (primitív függvények...........
Gyakorló feladatok. Agbeko Kwami Nutefe és Nagy Noémi
 Gyakorló feladatok Agbeko Kwami Nutefe és Nagy Noémi 25 Tartalomjegyzék. Klasszikus hibaszámítás 3 2. Lineáris egyenletrendszerek 3 3. Interpoláció 4 4. Sajátérték, sajátvektor 6 5. Lineáris és nemlineáris
Gyakorló feladatok Agbeko Kwami Nutefe és Nagy Noémi 25 Tartalomjegyzék. Klasszikus hibaszámítás 3 2. Lineáris egyenletrendszerek 3 3. Interpoláció 4 4. Sajátérték, sajátvektor 6 5. Lineáris és nemlineáris
Diszkréten mintavételezett függvények
 Diszkréten mintavételezett függvények A függvény (jel) értéke csak rögzített pontokban ismert, de köztes pontokban is meg akarjuk becsülni időben mintavételezett jel pixelekből álló műholdkép rácson futtatott
Diszkréten mintavételezett függvények A függvény (jel) értéke csak rögzített pontokban ismert, de köztes pontokban is meg akarjuk becsülni időben mintavételezett jel pixelekből álló műholdkép rácson futtatott
Nagy András. Feladatok a logaritmus témaköréhez 11. osztály 2010.
 Nagy András Feladatok a logaritmus témaköréhez. osztály 00. Feladatok a logaritmus témaköréhez. osztály ) Írd fel a következő egyenlőségeket hatványalakban! a) log 9 = b) log 4 = - c) log 7 = d) lg 0 =
Nagy András Feladatok a logaritmus témaköréhez. osztály 00. Feladatok a logaritmus témaköréhez. osztály ) Írd fel a következő egyenlőségeket hatványalakban! a) log 9 = b) log 4 = - c) log 7 = d) lg 0 =
Leképezések. Leképezések tulajdonságai. Számosságok.
 Leképezések Leképezések tulajdonságai. Számosságok. 1. Leképezések tulajdonságai A továbbiakban legyen A és B két tetszőleges halmaz. Idézzünk fel néhány definíciót. 1. Definíció (Emlékeztető). Relációknak
Leképezések Leképezések tulajdonságai. Számosságok. 1. Leképezések tulajdonságai A továbbiakban legyen A és B két tetszőleges halmaz. Idézzünk fel néhány definíciót. 1. Definíció (Emlékeztető). Relációknak
f(x) a (x x 0 )-t használjuk.
 5. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 5.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
5. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 5.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
1/1. Házi feladat. 1. Legyen p és q igaz vagy hamis matematikai kifejezés. Mutassuk meg, hogy
 /. Házi feladat. Legyen p és q igaz vagy hamis matematikai kifejezés. Mutassuk meg, hogy mindig igaz. (p (( p) q)) (( p) ( q)). Igazoljuk, hogy minden A, B és C halmazra A \ (B C) = (A \ B) (A \ C) teljesül.
/. Házi feladat. Legyen p és q igaz vagy hamis matematikai kifejezés. Mutassuk meg, hogy mindig igaz. (p (( p) q)) (( p) ( q)). Igazoljuk, hogy minden A, B és C halmazra A \ (B C) = (A \ B) (A \ C) teljesül.
Eseményalgebra. Esemény: minden amirl a kísérlet elvégzése során eldönthet egyértelmen hogy a kísérlet során bekövetkezett-e vagy sem.
 Eseményalgebra. Esemény: minden amirl a kísérlet elvégzése során eldönthet egyértelmen hogy a kísérlet során bekövetkezett-e vagy sem. Elemi esemény: a kísérlet egyes lehetséges egyes lehetséges kimenetelei.
Eseményalgebra. Esemény: minden amirl a kísérlet elvégzése során eldönthet egyértelmen hogy a kísérlet során bekövetkezett-e vagy sem. Elemi esemény: a kísérlet egyes lehetséges egyes lehetséges kimenetelei.
Nyugat-magyarországi Egyetem Geoinformatikai Kara. Prof. Dr. Závoti József. Matematika III. 4. MA3-4 modul. A valószínűségi változó és jellemzői
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Prof. Dr. Závoti József Matematika III. 4. MA3-4 modul A valószínűségi változó és jellemzői SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról
Nyugat-magyarországi Egyetem Geoinformatikai Kara Prof. Dr. Závoti József Matematika III. 4. MA3-4 modul A valószínűségi változó és jellemzői SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról
Véletlenszám generátorok és tesztelésük. Tossenberger Tamás
 Véletlenszám generátorok és tesztelésük Tossenberger Tamás Érdekességek Pénzérme feldobó gép: $0,25-os érme 1/6000 valószínűséggel esik az élére 51% eséllyel érkezik a felfelé mutató oldalára Pörgetésnél
Véletlenszám generátorok és tesztelésük Tossenberger Tamás Érdekességek Pénzérme feldobó gép: $0,25-os érme 1/6000 valószínűséggel esik az élére 51% eséllyel érkezik a felfelé mutató oldalára Pörgetésnél
Programozás I. 1. előadás: Algoritmusok alapjai. Sergyán Szabolcs
 Programozás I. 1. előadás: Algoritmusok alapjai Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Alkalmazott Informatikai Intézet 2015. szeptember 7. Sergyán
Programozás I. 1. előadás: Algoritmusok alapjai Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Alkalmazott Informatikai Intézet 2015. szeptember 7. Sergyán
Exponenciális, logaritmikus függvények
 Exponenciális, logaritmikus függvények DEFINÍCIÓ: (Összetett függvény) Ha az értékkészlet elemeihez, mint értelmezési tartományhoz egy újabb egyértelmű hozzárendelést adunk meg, akkor összetett (közvetett)
Exponenciális, logaritmikus függvények DEFINÍCIÓ: (Összetett függvény) Ha az értékkészlet elemeihez, mint értelmezési tartományhoz egy újabb egyértelmű hozzárendelést adunk meg, akkor összetett (közvetett)
Numerikus matematika vizsga
 1. Az a = 2, t = 4, k = 3, k + = 2 számábrázolási jellemzők mellett hány pozitív, normalizált lebegőpontos szám ábrázolható? Adja meg a legnagyobb ábrázolható számot! Mi lesz a 0.8-hoz rendelt lebegőpontos
1. Az a = 2, t = 4, k = 3, k + = 2 számábrázolási jellemzők mellett hány pozitív, normalizált lebegőpontos szám ábrázolható? Adja meg a legnagyobb ábrázolható számot! Mi lesz a 0.8-hoz rendelt lebegőpontos
Sarokba a bástyát! = nim
 Nim-összeadás, játékok összege Sarokba a bástyát! = nim Nim (két csomóval) Két kupac kaviccsal játszunk. Egy lépésben valamelyikből (de csak az egyikből!) elvehetünk bármennyit. Az nyer, aki az utolsó
Nim-összeadás, játékok összege Sarokba a bástyát! = nim Nim (két csomóval) Két kupac kaviccsal játszunk. Egy lépésben valamelyikből (de csak az egyikből!) elvehetünk bármennyit. Az nyer, aki az utolsó
Az egyenlőtlenség mindkét oldalát szorozzuk meg 4 16-al:
 Bevezető matematika kémikusoknak., 04. ősz. feladatlap. Ábrázoljuk számegyenesen a következő egyenlőtlenségek megoldáshalmazát! (a) x 5 < 3 5 x < 3 x 5 < (d) 5 x
Bevezető matematika kémikusoknak., 04. ősz. feladatlap. Ábrázoljuk számegyenesen a következő egyenlőtlenségek megoldáshalmazát! (a) x 5 < 3 5 x < 3 x 5 < (d) 5 x
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATLAB. 5. gyakorlat. Polinomok, deriválás, integrálás
 MATLAB 5. gyakorlat Polinomok, deriválás, integrálás Menetrend Kis ZH Polinomok Numerikus deriválás Numerikus integrálás (+ anonim függvények) pdf Kis ZH Polinomok Sok függvény és valós folyamat leírható
MATLAB 5. gyakorlat Polinomok, deriválás, integrálás Menetrend Kis ZH Polinomok Numerikus deriválás Numerikus integrálás (+ anonim függvények) pdf Kis ZH Polinomok Sok függvény és valós folyamat leírható
Matematika B4 VIII. gyakorlat megoldása
 Matematika B4 VIII. gyakorlat megoldása 5.április 7.. Eloszlás- és sűrűségfüggvény Ha az X egy folytonos valószínűségi változó, akkor X-et jól jellemzi az eloszlás illetve a sűrűségfüggvénye. Az eloszlásfüggvény
Matematika B4 VIII. gyakorlat megoldása 5.április 7.. Eloszlás- és sűrűségfüggvény Ha az X egy folytonos valószínűségi változó, akkor X-et jól jellemzi az eloszlás illetve a sűrűségfüggvénye. Az eloszlásfüggvény
A valószínűségszámítás elemei
 A valószínűségszámítás elemei Kísérletsorozatban az esemény relatív gyakorisága: k/n, ahol k az esemény bekövetkezésének abszolút gyakorisága, n a kísérletek száma. Pl. Jelenség: kockadobás Megfigyelés:
A valószínűségszámítás elemei Kísérletsorozatban az esemény relatív gyakorisága: k/n, ahol k az esemény bekövetkezésének abszolút gyakorisága, n a kísérletek száma. Pl. Jelenség: kockadobás Megfigyelés:
