Nanoszerkezetű anyagok vizsgálata diffrakcióval. Lábár János
|
|
|
- Léna Gáspárné
- 8 évvel ezelőtt
- Látták:
Átírás
1 Nanoszerkezetű anyagok vizsgálata diffrakcióval TEM-ben Lábár János
2 Sugarak elhajlása, diffrakció ( k ) r K r k 0 Ewald-gömb SAED-nél Ewald-gömb XRD-nél A Laue-egyenletek, A Bragg-egyenlet vagy az Ewald-szerkesztés a diffrakciós intenzitások maximumainak irányait adják meg egyszeres (kinematikus) szórást feltételezve. Maximumok iránya Szerkezet Az irányok megfigyeléséhez nem kell lencse (XRD, neutron, függöny )
3 Kinematikus szórás Ha a j. szórási centrum szórási amplitúdója f j, akkor a szórási centrumok rendszerére a szórási amplitúdók koherens összege: Ha a minta kristályos, az összegzés csoportosítható: az elemi cellán belüli, és az elemi cellákat összegző rész: H F(K) a kapcsos zárójelen belüli összeget jelenti, akkor az intenzitás: I(K) akkor maximális, amikor az összeg maximális, ami akkor következik be, ha a KR n skalár szorzat egész szám. Minthogy bármely vektor tetszőleges bázison kifejthető, a fenti feltétel akkor vizsgálható legegyszerűbben, ha K t olyan b j, bázison fejtjük ki, amelyet az alábbiakkal definiálunk: A fenti tulajdonságokkal rendelkező, b j, bázist kapunk pl. az alábbi definícióval: b = 1 a 1 a 2 xa ( a xa ) I A A i2π K r j ( K ) f = j je i2π K r p i2π K Rn ( K ) = f e e n 2 ( K ) = A( K ) = F( K ) a i p b j ( a xa ) p = δ ij 2 = 3 n 1 0 e 3 i2π K R if if 1 i i n = ( a xa ) A b j vektorok végpontjai pontrácsot alkotnak, ez az ú.n. reciprok-rács. Valahányszor a szórási vektor, K egy reciprok-rács pontba mutat, a szórt sugárzás intenzitása maximális. b = 2 a 2 a 3 xa b = a a xa j j
4 Leképezés gyűjtőlencsével: optika TEM A transzmissziós elektronmikroszkóp (TEM) objektív lencséje is egy gyűjtőlencse A lencse a diffraktált nyalábokat képszerűen összehozza a fókuszsíkban. Ez a diffrakciós ábra. A diffrakciós ábra a reciprok rács egy sík szelete Szerkezet. A TEM lehetővé teszi a valós térbeli kép és a reciprok térbeli diffrakció korrelált vizsgálatát. Rések használata Képi üzemmódban a fókuszsíkban kontraszt Diffrakciónál a képsíkban terület körülhatárolás Képen egy adott irányba szóró tartományok megjelenítése (BF) Kizárólag a képen kijelölt tartomány szórásából származó diffrakció rögzítése (SAED)
5 SAED felvételek alapvető fajtái Mindig 2D Ultramicroscopy, 103 (2005) Véletlenszerűen orientált nanokristályos por minta Koncentrikus gyűrűk: ilyenekkel foglalkozunk Egytengelyű textúrát mutató nanokristályos por minta a textúra tengely felől nézve
6 ProcessDiffraction: Körkörös átlagolás + elliptikus torzítás korrekciója
7 Minőségi fázis azonosítás: Marker Továbblépés: mennyiségi analízis kell nanoszemcsés anyagokon
8 Motiváció: A Rietveld módszer jól működik röntgen diffrakciós vizsgálatoknál Kristályos fázisok feltételezett szerkezetéből indul ki A teljes diffrakciós profilhoz illeszt Egyfázisú anyagok esetében a legjobb illeszkedésből szerkezeti paramétereket határoz meg Többfázisú mintáknál az illeszkedésből a fázisok mennyiségét határozza meg Illesztési paraméterek: Skálázó tényezők Elemi cella paraméterei Atomi koordináták Hőmérsékleti tényezők Csúcsalakok paraméterei (készülék minta) Háttér empirikus alakja Hasonló módszerre van szükség SAED esetén is
9 Miért nem volt korábban ilyen elektron diffrakciós módszer? Erős dinamikus szórás az erős kölcsönhatás miatt (szemcsemérettől függ) nanokristályos / Blackmann Széles dinamikus tartományban kell mérni az intenzitást IP, CCD Készülék hatások erősebbek és nem állandók mérési protokoll Rugalmatlan szórás hatása is jelentős minta vastagság, energia szűrés Amorf összetevők hatása (hordozó, mintán belüli amorf) empirikus háttér részeként közelíthetjük Nem dolgoztak ki módszert SAED-re A ProcessDiffraction módszer e problémákra ad közelítő megoldást
10 ProcessDiffraction Mit oldott meg ProcessDiffraction: Geometriai torzítás Minőségi fázis azonosítás Kristályos fázisok egymáshoz viszonyított relatív mennyisége A textúra tengely irányából vizsgált, egytengelyű textúrájú fázisok relatív mennyisége Különbségek a Rietveld-módszer és ProcessDiffraction között ProcessDiffraction elektron szórási tényezőkkel számol (2 alternatív készlet) Minimum kereső eljárás (lokális a Rietveldmódszerben és semi-globális a ProcessDiffraction-ban) A hátér számítása (polinom a Rietveldmódszerben, a ProcessDiffraction-ban több választás: az ED sajátságaihoz jobban illeszkedik a Spline) Szemcseméret becslése (csúcsszélességből Rietveld-módszerben, dinamikus szórás erősségéből ProcessDiffraction-ban) Lokális deformáció (még nincs beépítve ProcessDiffraction-ba)
11 Mérési protokoll Lencseáram normálás / fix objektív áram / minta magasság Fix kondenzor áram (reprodukálhatóság!): kamera hossz + konvergencia szög csúcs-szélesség Tömbi szórás (rácsbot, vastag ék, stb.) elkerülni Minta döntés hatása (kiküszöbölhetetlen, de fel kell ismerni) Gömbi hiba hatása (SAA mérete csúcs-szélesség) Képrögzítő hatása (kamera hossz csúcs-szélesség) Dinamikus tartományt meghaladó intenzitás Merge
12 Profil elemekre bontás: ProcessDiffraction Csúcs intenzitások elkülönítéséhez: Háttér (+ amorf) Normal, log-normal Polinom, Spline Csúcs alakok Gauss, Lorentz Pseudo-Voigt Globális minimum Downhill SIMPLEX Kézi vezérlés Példa: Al + Ge réteg: SAED Nagyobb kristályok Al: Gauss Kisebb kristályok Ge: Lorentz A háttér kölcsönhat a csúcsokkal A példából látható, hogy még egy mintán belül is lehet különböző csúcsalakra szükség a különböző összetevő fázisok modellezéséhez
13 1. példa: szilárd oldat képződés miatti rács paraméter változás mérése Polikristályos arannyal kalibrálunk. A kalibrálás reprodukálhatósága: 0.3% fcc-crn-ben oldunk 70% AlN-t Névleges: a=4.14 Å Mért: a=4.07 Å Változás: 1.6%
14 2. példa: fázisok mennyisége: egymás után párologtatott Cu és Ag kettősréteg Párologtatva 10-6 mbar-on Rezgő kvarc: 10 nm Cu 10 nm Ag Az Ag és Cu nem képez vegyület-fázist. Az egymás után párologtatott rétegek között nincs kölcsönhatás. A diffrakciót nem befolyásolja, hogy a vizsgált nano-térfogaton belül hogyan oszlanak el a nano-szemcsék (kettős réteg, vagy kevert fázis). ProcessDiffraction 49 Vol% Cu 51 Vol% Ag
15 3. példa: fázisok relatív mennyisége: Egymás után párologtatott Ag és Cr EDS: 77 Vol% Cr ProcessDiffraction: 70 Vol% Cr 23 Vol% Ag 30 Vol% Ag A Cr 57%-a <100> textúrát mutat. A rácsparaméter változás a módszer kimutatási határa körül van.
16 4. példa: Fázisok mennyisége + textúra + rácsparaméter + szemcseméret: együtt párologtatott Cu-Ag réteg Vastagság monitor: 66 Vol% Cu XRD: az Ag és Cu csúcsai közeledtek XRD Cu <111> pólusábra: ProcessDifraction: Vol% Cu Mind az Ag mind a Cu <111> textúrát mutat térfogatuk ~80%-ában Ha egy fő összetevő rács állandóját állandónak tekinthetjük, a másik relatív változása mérhető. A rács paraméter relatív változása 2,3%. Szemcseméret a Blackman-korrekcióból Ag: t=340 [Angstrom] Cu: t=570 [Angstrom]
17 Összefoglalás Vékony nanokristályos minták lokális fázisösszetételét 10-15% relatív hibával mérjük A detektálási határ 5% (térfogat) körül van. Egytengelyű textúrát mutató mintákról megfelelően felvett difrakcióból a textúrált komponens mennyisége is meghatározható. A rácsparaméter %-os változása mérhető A gyenge spektrális felbontás miatt, feltehetően, csak viszonylag egyszerű (magas szimmetriájú) fázisokra (pl. köbös, hexagonális, tetragonális) alkalmazható megbízhatóan Külön előny, hogy a TEM-ben képen választjuk ki vizsgálandó térfogatot látjuk a szemcseméretet kicsi térfogat vizsgálható Gyors a diffrakció rögzítése lassan változó folyamatok követése
18 További információ Lábár JL: Electron Diffraction Based Analysis of Phase Fractions and Texture in Nanocrystalline Thin Films, Part I: Principles, Microsc. Microanal. 14 (4) (2008), Lábár JL: Electron Diffraction Based Analysis of Phase Fractions and Texture in Nanocrystalline Thin Films, Part II : Implementation, Microsc. Microanal. 15 (1) (2009) Lábár JL et al.: Electron Diffraction Based Analysis of Phase Fractions and Texture in Nanocrystalline Thin Films, Part III: ApplicationExamples, Microsc. Microanal. 18 (2012) Lábár J: Nanokristályos anyagok elektrondiffrakciós vizsgálata (ProcessDiffraction), könyv-fejezet Bevezetés a nanoszerkezetű anyagok világába, Csanády A, Kálmán E, Konczos G, szerk., (ISBN ) MTA Kémiai Kutatóközpont, ELTE Eötvös Kiadó, (2009) Lábár JL, Consistent indexing of a (set of) SAED pattern(s) with the ProcessDiffraction program, Ultramicroscopy, 103 (2005) Kovács Kis V, Pósfai M, Lábár JL: Nanostructure of atmospheric soot particles, Atmospheric Environment 40 (2006) Viktória Kovács Kis, István Dódony János L. Lábár: Amorphous and partly ordered structures in SiO2 rich volcanic glasses. An ED study, Eur. J. Miner. 18. (2006) Lábár JL: Phase identification by combining local composition from EDX with information from diffraction database, in ELECTRON CRYSTALLOGRAPHY Novel Approaches for Structure Determination of Nanosized Materials (Ed: Thomas E. Weirich, János L. Lábár and Xiaodong Zou) (2006) Springer, Dordrecht, NATO ASI Lábár JL, Kovács A, Barna BP, Hanada T, Ishimaru M, Hirotsu Y, Bae IT, Variation of the short range order with the composition in an amorphous Al-Pt alloy, existing in a wide compositional range, Proc. 6th Multinational Congress on Electron Microscopy, Pula, 2003, Lábár JL: "A tool to help phase identification from electron diffraction powder patterns", Microscopy and Analysis, Issue 75 (2002 ) 9-11 Lábár JL: ProcessDiffraction: A computer program to process electron diffraction patterns from polycrystalline or amorphous samples, Proc. EUREM 12, Brno (Frank L and F Ciampor, eds.) (2000), Vol III., I
19 Köszönetet mondok kollégáimnak a közös munkáért, amiből a példákat merítettem: Barna B. Péter Geszti Olga Misják Fanni Radnóczi György Sáfrán György
20 Köszönöm m a figyelmet
Milyen simaságú legyen a minta felülete jó minőségű EBSD mérésekhez
 1 Milyen simaságú legyen a minta felülete jó minőségű EBSD mérésekhez Havancsák Károly Dankházi Zoltán Ratter Kitti Varga Gábor Visegrád 2012. január Elektron diffrakció 2 Diffrakció - kinematikus elmélet
1 Milyen simaságú legyen a minta felülete jó minőségű EBSD mérésekhez Havancsák Károly Dankházi Zoltán Ratter Kitti Varga Gábor Visegrád 2012. január Elektron diffrakció 2 Diffrakció - kinematikus elmélet
Célkitűzés kifejlesztjük nanofázisú anyagok kvantitatív elektrondiffrakciós (ED) fázisanalízisét
 Célkitűzés (a szerződés ide vonatkozó részének szó szerinti másolata): A transzmissziós elektronmikroszkópia (TEM) két fő területének: a diffrakciónak és a kép-értelmezésnek a fejlődését szándékozunk előrevinni.
Célkitűzés (a szerződés ide vonatkozó részének szó szerinti másolata): A transzmissziós elektronmikroszkópia (TEM) két fő területének: a diffrakciónak és a kép-értelmezésnek a fejlődését szándékozunk előrevinni.
Vázlat a transzmissziós elektronmikroszkópiához (TEM) dr. Dódony István
 Dódony István: TEM, vázlat vegyészeknek, 1996 1 Vázlat a transzmissziós elektronmikroszkópiához (TEM) dr. Dódony István A TEM a szilárd anyagok kémiai és szerkezeti jellemzésére alkalmas vizsgálati módszer.
Dódony István: TEM, vázlat vegyészeknek, 1996 1 Vázlat a transzmissziós elektronmikroszkópiához (TEM) dr. Dódony István A TEM a szilárd anyagok kémiai és szerkezeti jellemzésére alkalmas vizsgálati módszer.
Szemcsehatárok geometriai jellemzése a TEM-ben. Lábár János
 Szemcsehatárok geometriai jellemzése a TEM-ben Lábár János Szemcsehatárok geometriai jellemzése Rácsok relatív orientációja Coincidence Site Lattice (CSL) O-lattice Határ közelítése síkkal Határsík orientációja
Szemcsehatárok geometriai jellemzése a TEM-ben Lábár János Szemcsehatárok geometriai jellemzése Rácsok relatív orientációja Coincidence Site Lattice (CSL) O-lattice Határ közelítése síkkal Határsík orientációja
Mikroszerkezeti vizsgálatok
 Mikroszerkezeti vizsgálatok Dr. Szabó Péter BME Anyagtudomány és Technológia Tanszék 463-2954 szpj@eik.bme.hu www.att.bme.hu Tematika Optikai mikroszkópos vizsgálatok, klasszikus metallográfia. Kristálytan,
Mikroszerkezeti vizsgálatok Dr. Szabó Péter BME Anyagtudomány és Technológia Tanszék 463-2954 szpj@eik.bme.hu www.att.bme.hu Tematika Optikai mikroszkópos vizsgálatok, klasszikus metallográfia. Kristálytan,
Vázlatos tartalom. Szerkezet jellemzése és vizsgálata Szilárdtestek elektronszerkezete Rácsdinamika Transzportjelenségek Mágneses tulajdonságok
 Szilárdtestfizika Kondenzált Anyagok Fizikája Vázlatos tartalom Szerkezet jellemzése és vizsgálata Szilárdtestek elektronszerkezete Rácsdinamika Transzportjelenségek Mágneses tulajdonságok 2 Szerkezet
Szilárdtestfizika Kondenzált Anyagok Fizikája Vázlatos tartalom Szerkezet jellemzése és vizsgálata Szilárdtestek elektronszerkezete Rácsdinamika Transzportjelenségek Mágneses tulajdonságok 2 Szerkezet
Röntgendiffrakció. Orbán József PTE, ÁOK, Biofizikai Intézet november
 Röntgendiffrakció Orbán József PTE, ÁOK, Biofizikai Intézet 2013. november Előadás vázlata Röntgen sugárzás Interferencia, diffrakció (elektromágneses hullámok) Kristályok szerkezete Röntgendiffrakció
Röntgendiffrakció Orbán József PTE, ÁOK, Biofizikai Intézet 2013. november Előadás vázlata Röntgen sugárzás Interferencia, diffrakció (elektromágneses hullámok) Kristályok szerkezete Röntgendiffrakció
Nagynyomású csavarással tömörített réz - szén nanocső kompozit mikroszerkezete és termikus stabilitása
 Nagynyomású csavarással tömörített réz - szén nanocső kompozit mikroszerkezete és termikus stabilitása P. Jenei a, E.Y. Yoon b, J. Gubicza a, H.S. Kim b, J.L. Lábár a,c, T. Ungár a a Anyagfizikai Tanszék,
Nagynyomású csavarással tömörített réz - szén nanocső kompozit mikroszerkezete és termikus stabilitása P. Jenei a, E.Y. Yoon b, J. Gubicza a, H.S. Kim b, J.L. Lábár a,c, T. Ungár a a Anyagfizikai Tanszék,
Bevezetés az anyagtudományba III. előadás
 Bevezetés az anyagtudományba III. előadás 2010. február 18. Kristályos és s nem-krist kristályos anyagok A kristályos anyag atomjainak elrendeződése sok atomnyi távolságig, a tér mindhárom irányában periodikusan
Bevezetés az anyagtudományba III. előadás 2010. február 18. Kristályos és s nem-krist kristályos anyagok A kristályos anyag atomjainak elrendeződése sok atomnyi távolságig, a tér mindhárom irányában periodikusan
Fizikai kémia Diffrakciós módszerek. Bevezetés. Történeti áttekintés
 06.08.. Fizikai kémia. 6. Diffrakciós módszerek Dr. Berkesi Ottó SZTE Fizikai Kémiai és Anyagtudományi Tanszéke 05 Bevezetés A kémiai szerkezet vizsgálatához használatos módszerek közül eddig a különöző
06.08.. Fizikai kémia. 6. Diffrakciós módszerek Dr. Berkesi Ottó SZTE Fizikai Kémiai és Anyagtudományi Tanszéke 05 Bevezetés A kémiai szerkezet vizsgálatához használatos módszerek közül eddig a különöző
Optika és Relativitáselmélet II. BsC fizikus hallgatóknak
 Optika és Relativitáselmélet II. BsC fizikus hallgatóknak 3. Fényelhajlás (Diffrakció) Cserti József, jegyzet, ELTE, 2007. Akadályok között elhaladó hullámok továbbterjedése nem azonos a geometriai árnyékkal.
Optika és Relativitáselmélet II. BsC fizikus hallgatóknak 3. Fényelhajlás (Diffrakció) Cserti József, jegyzet, ELTE, 2007. Akadályok között elhaladó hullámok továbbterjedése nem azonos a geometriai árnyékkal.
Röntgenanalitika. Röntgenradiológia, Komputertomográfia (CT) Röntgenfluoreszcencia (XRF) Röntgenkrisztallográfia Röntgendiffrakció (XRD)
 Röntgenanalitika Röntgenradiológia, Komputertomográfia (CT) Röntgenfluoreszcencia (XRF) Röntgenkrisztallográfia Röntgendiffrakció (XRD) A röntgensugárzás Felfedezése (1895, W. K. Röntgen, katódsugárcső,
Röntgenanalitika Röntgenradiológia, Komputertomográfia (CT) Röntgenfluoreszcencia (XRF) Röntgenkrisztallográfia Röntgendiffrakció (XRD) A röntgensugárzás Felfedezése (1895, W. K. Röntgen, katódsugárcső,
Havancsák Károly Nagyfelbontású kétsugaras pásztázó elektronmikroszkóp az ELTÉ-n: lehetőségek, eddigi eredmények
 Havancsák Károly Nagyfelbontású kétsugaras pásztázó elektronmikroszkóp az ELTÉ-n: lehetőségek, eddigi eredmények Nanoanyagok és nanotechnológiák Albizottság ELTE TTK 2013. Havancsák Károly Nagyfelbontású
Havancsák Károly Nagyfelbontású kétsugaras pásztázó elektronmikroszkóp az ELTÉ-n: lehetőségek, eddigi eredmények Nanoanyagok és nanotechnológiák Albizottság ELTE TTK 2013. Havancsák Károly Nagyfelbontású
A röntgen-pordiffrakció lehetőségei és korlátai a kerámia vizsgálatokban
 Szakmány György ARCHEOMETRIA 2009/2010 I.félév ELTE A röntgen-pordiffrakció lehetőségei és korlátai a kerámia vizsgálatokban Tóth Mária MTA Geokémiai Kutatóintézet totyi@geochem.hu 1 Diagenezis ÜLEDÉKES
Szakmány György ARCHEOMETRIA 2009/2010 I.félév ELTE A röntgen-pordiffrakció lehetőségei és korlátai a kerámia vizsgálatokban Tóth Mária MTA Geokémiai Kutatóintézet totyi@geochem.hu 1 Diagenezis ÜLEDÉKES
Diffrakciós szerkezetvizsgálati módszerek
 Diffrakciós szerkezetvizsgálati módszerek Röntgendiffrakció Angler Gábor ELTE TTK Fizika BSc hallgató 2009. december 3. Kondenzált anyagok fizikája szeminárium Az előadás vázlata Bevezetés, motiváció,
Diffrakciós szerkezetvizsgálati módszerek Röntgendiffrakció Angler Gábor ELTE TTK Fizika BSc hallgató 2009. december 3. Kondenzált anyagok fizikája szeminárium Az előadás vázlata Bevezetés, motiváció,
Opakásványok kristályorientáció vizsgálata a lahócai Cu-Au ércesedésben
 Opakásványok kristályorientáció vizsgálata a lahócai Cu-Au ércesedésben Takács Ágnes & Molnár Ferenc Ásványtani Tanszék Visegrád, 2012. január 18-20. Kutatási téma Infravörös fluidzárvány vizsgálathoz
Opakásványok kristályorientáció vizsgálata a lahócai Cu-Au ércesedésben Takács Ágnes & Molnár Ferenc Ásványtani Tanszék Visegrád, 2012. január 18-20. Kutatási téma Infravörös fluidzárvány vizsgálathoz
ELTE Fizikai Intézet. FEI Quanta 3D FEG kétsugaras pásztázó elektronmikroszkóp
 ELTE Fizikai Intézet FEI Quanta 3D FEG kétsugaras pásztázó elektronmikroszkóp mintatartó mikroszkóp nyitott ajtóval Fő egységek 1. Elektron forrás 10-7 Pa 2. Mágneses lencsék 10-5 Pa 3. Pásztázó mágnesek
ELTE Fizikai Intézet FEI Quanta 3D FEG kétsugaras pásztázó elektronmikroszkóp mintatartó mikroszkóp nyitott ajtóval Fő egységek 1. Elektron forrás 10-7 Pa 2. Mágneses lencsék 10-5 Pa 3. Pásztázó mágnesek
Akusztikai tervezés a geometriai akusztika módszereivel
 Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék)
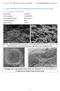 7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék) 7.1.1. SPS: 1150 C; 5 (1312 K1) Mért sűrűség: 3,795 g/cm 3 3,62 0,14 GPa Három pontos törés teszt: 105 4,2 GPa Súrlódási együttható:
7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék) 7.1.1. SPS: 1150 C; 5 (1312 K1) Mért sűrűség: 3,795 g/cm 3 3,62 0,14 GPa Három pontos törés teszt: 105 4,2 GPa Súrlódási együttható:
Röntgen sugárzás. Wilhelm Röntgen. Röntgen feleségének keze
 Röntgendiffrakció Kardos Roland 2010.03.08. Előadás vázlata Röntgen sugárzás Interferencia Huygens teória Diffrakció Diffrakciós eljárások Alkalmazás Röntgen sugárzás 1895 röntgen sugárzás felfedezés (1901
Röntgendiffrakció Kardos Roland 2010.03.08. Előadás vázlata Röntgen sugárzás Interferencia Huygens teória Diffrakció Diffrakciós eljárások Alkalmazás Röntgen sugárzás 1895 röntgen sugárzás felfedezés (1901
Dankházi Z., Kalácska Sz., Baris A., Varga G., Ratter K., Radi Zs.*, Havancsák K.
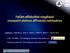 Dankházi Z., Kalácska Sz., Baris A., Varga G., Ratter K., Radi Zs.*, Havancsák K. ELTE, TTK KKMC, 1117 Budapest, Pázmány Péter sétány 1/A. * Technoorg Linda Kft., 1044 Budapest, Ipari Park utca 10. Műszer:
Dankházi Z., Kalácska Sz., Baris A., Varga G., Ratter K., Radi Zs.*, Havancsák K. ELTE, TTK KKMC, 1117 Budapest, Pázmány Péter sétány 1/A. * Technoorg Linda Kft., 1044 Budapest, Ipari Park utca 10. Műszer:
Optika gyakorlat 6. Interferencia. I = u 2 = u 1 + u I 2 cos( Φ)
 Optika gyakorlat 6. Interferencia Interferencia Az interferencia az a jelenség, amikor kett vagy több hullám fázishelyes szuperpozíciója révén a térben állóhullám kép alakul ki. Ez elektromágneses hullámok
Optika gyakorlat 6. Interferencia Interferencia Az interferencia az a jelenség, amikor kett vagy több hullám fázishelyes szuperpozíciója révén a térben állóhullám kép alakul ki. Ez elektromágneses hullámok
Az ipari komputer tomográfia vizsgálati lehetőségei
 Az ipari komputer tomográfia vizsgálati lehetőségei Dr. Czinege Imre, Kozma István Széchenyi István Egyetem 6. ANYAGVIZSGÁLAT A GYAKORLATBAN KONFERENCIA Cegléd, 2012. június 7-8. Tartalom A CT technika
Az ipari komputer tomográfia vizsgálati lehetőségei Dr. Czinege Imre, Kozma István Széchenyi István Egyetem 6. ANYAGVIZSGÁLAT A GYAKORLATBAN KONFERENCIA Cegléd, 2012. június 7-8. Tartalom A CT technika
Kristályorientáció-térképezés (SEM-EBSD) opakásványok és fluidzárványaik infravörös mikroszkópos vizsgálatához
 Kristályorientáció-térképezés (SEM-EBSD) opakásványok és fluidzárványaik infravörös mikroszkópos vizsgálatához Takács Ágnes, Molnár Ferenc & Dankházi Zoltán Ásványtani Tanszék & Anyagfizikai Tanszék Centrumban
Kristályorientáció-térképezés (SEM-EBSD) opakásványok és fluidzárványaik infravörös mikroszkópos vizsgálatához Takács Ágnes, Molnár Ferenc & Dankházi Zoltán Ásványtani Tanszék & Anyagfizikai Tanszék Centrumban
41. ábra A NaCl rács elemi cellája
 41. ábra A NaCl rács elemi cellája Mindkét rácsra jellemző, hogy egy tetszés szerint kiválasztott pozitív vagy negatív töltésű iont ellentétes töltésű ionok vesznek körül. Különbség a közvetlen szomszédok
41. ábra A NaCl rács elemi cellája Mindkét rácsra jellemző, hogy egy tetszés szerint kiválasztott pozitív vagy negatív töltésű iont ellentétes töltésű ionok vesznek körül. Különbség a közvetlen szomszédok
Kondenzált anyagok csoportosítása
 Szilárdtestfizika Kondenzált anyagok csoportosítása 1. Üvegek Nagy viszkozitású olvadék állapotú anyagok, amelyek nagyon lassan szilárd állapotba mennek át. Folyékony állapotból gyors hűtéssel állíthatók
Szilárdtestfizika Kondenzált anyagok csoportosítása 1. Üvegek Nagy viszkozitású olvadék állapotú anyagok, amelyek nagyon lassan szilárd állapotba mennek át. Folyékony állapotból gyors hűtéssel állíthatók
Réz - szén nanocső kompozit mikroszerkezete és mechanikai viselkedése
 Réz - szén nanocső kompozit mikroszerkezete és mechanikai viselkedése P. Jenei a, E.Y. Yoon b, J. Gubicza a, H.S. Kim b, J.L. Lábár a,c, T. Ungár a a Department of Materials Physics, Eötvös Loránd University,
Réz - szén nanocső kompozit mikroszerkezete és mechanikai viselkedése P. Jenei a, E.Y. Yoon b, J. Gubicza a, H.S. Kim b, J.L. Lábár a,c, T. Ungár a a Department of Materials Physics, Eötvös Loránd University,
Zárthelyi dolgozat I. /A.
 Zárthelyi dolgozat I. /A. 1. Az FCC rács és reciprokrácsa (és tudjuk, hogy: V W.S. * V B.z. /() 3 = 1 / mindig!/) a 1 = ½ a (0,1,1) ; a = ½ a (1,0,1) ; a 3 = ½ a (1,1,0) b 1 = (/a) (-1,1,1); b = (/a) (1,-1,1);
Zárthelyi dolgozat I. /A. 1. Az FCC rács és reciprokrácsa (és tudjuk, hogy: V W.S. * V B.z. /() 3 = 1 / mindig!/) a 1 = ½ a (0,1,1) ; a = ½ a (1,0,1) ; a 3 = ½ a (1,1,0) b 1 = (/a) (-1,1,1); b = (/a) (1,-1,1);
Havancsák Károly Az ELTE TTK kétsugaras pásztázó elektronmikroszkópja. Archeometriai műhely ELTE TTK 2013.
 Havancsák Károly Az ELTE TTK kétsugaras pásztázó elektronmikroszkópja Archeometriai műhely ELTE TTK 2013. Elektronmikroszkópok TEM SEM Transzmissziós elektronmikroszkóp Átvilágítós vékony minta < 100
Havancsák Károly Az ELTE TTK kétsugaras pásztázó elektronmikroszkópja Archeometriai műhely ELTE TTK 2013. Elektronmikroszkópok TEM SEM Transzmissziós elektronmikroszkóp Átvilágítós vékony minta < 100
Szerkezetvizsgálat ANYAGMÉRNÖK ALAPKÉPZÉS (BSc)
 Szerkezetvizsgálat ANYAGMÉRNÖK ALAPKÉPZÉS (BSc) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR ANYAGTUDOMÁNYI INTÉZET Miskolc, 2008. 1. Tantárgyleírás Szerkezetvizsgálat kommunikációs
Szerkezetvizsgálat ANYAGMÉRNÖK ALAPKÉPZÉS (BSc) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR ANYAGTUDOMÁNYI INTÉZET Miskolc, 2008. 1. Tantárgyleírás Szerkezetvizsgálat kommunikációs
Nanokeménység mérések
 Cirkónium Anyagtudományi Kutatások ek Nguyen Quang Chinh, Ugi Dávid ELTE Anyagfizikai Tanszék Kutatási jelentés a Nemzeti Kutatási, Fejlesztési és Innovációs Hivatal támogatásával az NKFI Alapból létrejött
Cirkónium Anyagtudományi Kutatások ek Nguyen Quang Chinh, Ugi Dávid ELTE Anyagfizikai Tanszék Kutatási jelentés a Nemzeti Kutatási, Fejlesztési és Innovációs Hivatal támogatásával az NKFI Alapból létrejött
EDX EBSD. Elméleti háttér Spektrumok alakja Gyakorlati alkalmazása
 EDX Elméleti háttér Spektrumok alakja Gyakorlati alkalmazása EBSD Elméleti háttér Felület előkészítése Orientálás Hough-transzformáció IPF, IQ Felület minősége 2 Elektron besugárzás Röntgen foton kisugárzás
EDX Elméleti háttér Spektrumok alakja Gyakorlati alkalmazása EBSD Elméleti háttér Felület előkészítése Orientálás Hough-transzformáció IPF, IQ Felület minősége 2 Elektron besugárzás Röntgen foton kisugárzás
Mikroszkóp vizsgálata Folyadék törésmutatójának mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 8. MÉRÉS Mikroszkóp vizsgálata Folyadék törésmutatójának mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 12. Szerda délelőtti csoport
KLASSZIKUS FIZIKA LABORATÓRIUM 8. MÉRÉS Mikroszkóp vizsgálata Folyadék törésmutatójának mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 12. Szerda délelőtti csoport
Amorf fényérzékeny rétegstruktúrák fotonikai alkalmazásokra. Csarnovics István
 Az Eötvös Loránd Fizikai Társulat Anyagtudományi és Diffrakciós Szakcsoportjának Őszi Iskolája 2012.10.03. Mátrafüred Amorf fényérzékeny rétegstruktúrák fotonikai alkalmazásokra Csarnovics István Debreceni
Az Eötvös Loránd Fizikai Társulat Anyagtudományi és Diffrakciós Szakcsoportjának Őszi Iskolája 2012.10.03. Mátrafüred Amorf fényérzékeny rétegstruktúrák fotonikai alkalmazásokra Csarnovics István Debreceni
TÉMA ÉRTÉKELÉS TÁMOP-4.2.1/B-09/1/KMR (minden téma külön lapra) június május 31
 1. A téma megnevezése TÉMA ÉRTÉKELÉS TÁMOP-4.2.1/B-09/1/KMR-2010-0003 (minden téma külön lapra) 2010. június 1 2012. május 31 Nanostruktúrák szerkezeti jellemzése 2. A témavezető (neve, intézet, tanszék)
1. A téma megnevezése TÉMA ÉRTÉKELÉS TÁMOP-4.2.1/B-09/1/KMR-2010-0003 (minden téma külön lapra) 2010. június 1 2012. május 31 Nanostruktúrák szerkezeti jellemzése 2. A témavezető (neve, intézet, tanszék)
A nanotechnológia mikroszkópja
 1 Havancsák Károly, ELTE Fizikai Intézet A nanotechnológia mikroszkópja EGIS 2011. június 1. FEI Quanta 3D SEM/FIB 2 Havancsák Károly, ELTE Fizikai Intézet A nanotechnológia mikroszkópja EGIS 2011. június
1 Havancsák Károly, ELTE Fizikai Intézet A nanotechnológia mikroszkópja EGIS 2011. június 1. FEI Quanta 3D SEM/FIB 2 Havancsák Károly, ELTE Fizikai Intézet A nanotechnológia mikroszkópja EGIS 2011. június
Fotoindukált változások vizsgálata amorf félvezető kalkogenid arany nanorészecskéket tartalmazó rendszerekben
 Az Eötvös Loránd Fizikai Társulat Anyagtudományi és Diffrakciós Szakcsoportjának Őszi Iskolája 2011.10.05 Visegrád Fotoindukált változások vizsgálata amorf félvezető kalkogenid arany nanorészecskéket tartalmazó
Az Eötvös Loránd Fizikai Társulat Anyagtudományi és Diffrakciós Szakcsoportjának Őszi Iskolája 2011.10.05 Visegrád Fotoindukált változások vizsgálata amorf félvezető kalkogenid arany nanorészecskéket tartalmazó
Gamma-röntgen spektrométer és eljárás kifejlesztése anyagok elemi összetétele és izotópszelektív radioaktivitása egyidejű elemzésére
 Gamma-röntgen spektrométer és eljárás kifejlesztése anyagok elemi összetétele és izotópszelektív radioaktivitása egyidejű elemzésére OAH-ABA-16/14-M Dr. Szalóki Imre, egyetemi docens Radócz Gábor, PhD
Gamma-röntgen spektrométer és eljárás kifejlesztése anyagok elemi összetétele és izotópszelektív radioaktivitása egyidejű elemzésére OAH-ABA-16/14-M Dr. Szalóki Imre, egyetemi docens Radócz Gábor, PhD
Mikrohullámú abszorbensek vizsgálata 4. félév
 Óbudai Egyetem Anyagtudományok és Technológiák Doktori Iskola Mikrohullámú abszorbensek vizsgálata 4. félév Balla Andrea Témavezetők: Dr. Klébert Szilvia, Dr. Károly Zoltán MTA Természettudományi Kutatóközpont
Óbudai Egyetem Anyagtudományok és Technológiák Doktori Iskola Mikrohullámú abszorbensek vizsgálata 4. félév Balla Andrea Témavezetők: Dr. Klébert Szilvia, Dr. Károly Zoltán MTA Természettudományi Kutatóközpont
Spektrográf elvi felépítése. B: maszk. A: távcső. Ø maszk. Rés Itt lencse, de általában komplex tükörrendszer
 Spektrográf elvi felépítése A: távcső Itt lencse, de általában komplex tükörrendszer Kis kromatikus aberráció fontos Leképezés a fókuszsíkban: sugarak itt metszik egymást B: maszk Fókuszsíkba kerül (kamera
Spektrográf elvi felépítése A: távcső Itt lencse, de általában komplex tükörrendszer Kis kromatikus aberráció fontos Leképezés a fókuszsíkban: sugarak itt metszik egymást B: maszk Fókuszsíkba kerül (kamera
ELTE II. Fizikus 2005/2006 I. félév KISÉRLETI FIZIKA Optika 8. (X. 5)
 N j=1 d ELTE II. Fizikus 005/006 I. félév KISÉRLETI FIZIKA Optika 8. (X. 5) Interferencia II. Többsugaras interferencia Diffrakciós rács, elhajlás rácson Hullámfront osztás d sinα α A e = A j e i(π/λo)
N j=1 d ELTE II. Fizikus 005/006 I. félév KISÉRLETI FIZIKA Optika 8. (X. 5) Interferencia II. Többsugaras interferencia Diffrakciós rács, elhajlás rácson Hullámfront osztás d sinα α A e = A j e i(π/λo)
Fényérzékeny amorf nanokompozitok: technológia és alkalmazásuk a fotonikában. Csarnovics István
 Új irányok és eredményak A mikro- és nanotechnológiák területén 2013.05.15. Budapest Fényérzékeny amorf nanokompozitok: technológia és alkalmazásuk a fotonikában Csarnovics István Debreceni Egyetem, Fizika
Új irányok és eredményak A mikro- és nanotechnológiák területén 2013.05.15. Budapest Fényérzékeny amorf nanokompozitok: technológia és alkalmazásuk a fotonikában Csarnovics István Debreceni Egyetem, Fizika
Pásztázó elektronmikroszkóp. Alapelv. Szinkron pásztázás
 Pásztázó elektronmikroszkóp Scanning Electron Microscope (SEM) Rasterelektronenmikroskope (REM) Alapelv Egy elektronágyúval vékony elektronnyalábot állítunk elő. Ezzel pásztázzuk (eltérítő tekercsek segítségével)
Pásztázó elektronmikroszkóp Scanning Electron Microscope (SEM) Rasterelektronenmikroskope (REM) Alapelv Egy elektronágyúval vékony elektronnyalábot állítunk elő. Ezzel pásztázzuk (eltérítő tekercsek segítségével)
Elektromágneses hullámok - Interferencia
 Bevezetés a modern fizika fejezeteibe 2. (d) Elektromágneses hullámok - Interferencia Utolsó módosítás: 2012 október 18. 1 Interferencia (1) Mi történik két elektromágneses hullám találkozásakor? Az elektromágneses
Bevezetés a modern fizika fejezeteibe 2. (d) Elektromágneses hullámok - Interferencia Utolsó módosítás: 2012 október 18. 1 Interferencia (1) Mi történik két elektromágneses hullám találkozásakor? Az elektromágneses
Anyagvizsgálati módszerek Elemanalitika. Anyagvizsgálati módszerek
 Anyagvizsgálati módszerek Elemanalitika Anyagvizsgálati módszerek Pannon Egyetem Mérnöki Kar Anyagvizsgálati módszerek Kémiai szenzorok 1/ 18 Elemanalitika Elemek minőségi és mennyiségi meghatározására
Anyagvizsgálati módszerek Elemanalitika Anyagvizsgálati módszerek Pannon Egyetem Mérnöki Kar Anyagvizsgálati módszerek Kémiai szenzorok 1/ 18 Elemanalitika Elemek minőségi és mennyiségi meghatározására
Fényhullámhossz és diszperzió mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 9. MÉRÉS Fényhullámhossz és diszperzió mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 19. Szerda délelőtti csoport 1. A mérés célja
KLASSZIKUS FIZIKA LABORATÓRIUM 9. MÉRÉS Fényhullámhossz és diszperzió mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 19. Szerda délelőtti csoport 1. A mérés célja
Zeolitos tufa alapú nanodiszperz rendszer tápelem hordozó mátrixnak
 Zeolitos tufa alapú nanodiszperz rendszer tápelem hordozó mátrixnak Mucsi Gábor, Bohács Katalin, Kristály Ferenc (Miskolci Egyetem), Dallos Zsolt (Eötvös Loránd Tudományegyetem) Bevezető Zeolitos savanyú
Zeolitos tufa alapú nanodiszperz rendszer tápelem hordozó mátrixnak Mucsi Gábor, Bohács Katalin, Kristály Ferenc (Miskolci Egyetem), Dallos Zsolt (Eötvös Loránd Tudományegyetem) Bevezető Zeolitos savanyú
IMFP meghatározása Co, Cu, Ge, Si és Au mintákban 56
 3.1.2. IMFP meghatározása Co, Cu, Ge, Si és Au mintákban 56 3.1.2. Elektronok rugalmatlan szórási közepes szabad úthosszának meghatározása Co, Cu, Ge, Si és Au mintákban, a 2-10 kev elektron energia tartományban
3.1.2. IMFP meghatározása Co, Cu, Ge, Si és Au mintákban 56 3.1.2. Elektronok rugalmatlan szórási közepes szabad úthosszának meghatározása Co, Cu, Ge, Si és Au mintákban, a 2-10 kev elektron energia tartományban
Mérés és modellezés 1
 Mérés és modellezés 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni kell
Mérés és modellezés 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni kell
Röntgen-gamma spektrometria
 Röntgen-gamma spektrométer fejlesztése radioaktív anyagok elemi összetétele és izotópszelektív radioaktivitása egyidejű meghatározására Szalóki Imre, Gerényi Anita, Radócz Gábor Nukleáris Technikai Intézet
Röntgen-gamma spektrométer fejlesztése radioaktív anyagok elemi összetétele és izotópszelektív radioaktivitása egyidejű meghatározására Szalóki Imre, Gerényi Anita, Radócz Gábor Nukleáris Technikai Intézet
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI
 SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 30 Műszeres ÁSVÁNYHATÁROZÁS XXX. Műszeres ÁsVÁNYHATÁROZÁs 1. BEVEZETÉs Az ásványok természetes úton, a kémiai elemek kombinálódásával keletkezett (és ma is keletkező),
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 30 Műszeres ÁSVÁNYHATÁROZÁS XXX. Műszeres ÁsVÁNYHATÁROZÁs 1. BEVEZETÉs Az ásványok természetes úton, a kémiai elemek kombinálódásával keletkezett (és ma is keletkező),
EBSD vizsgálatok alkalmazása a geológiában: Enargit és luzonit kristályok orientációs vizsgálata
 ELTE TTK, Ásványtani Tanszék EBSD vizsgálatok alkalmazása a geológiában: Enargit és luzonit kristályok orientációs vizsgálata Takács Ágnes & Molnár Ferenc TÁMOP-4.2.1/B-09/1/KMR-2010-0003 Szubmikroszkópos
ELTE TTK, Ásványtani Tanszék EBSD vizsgálatok alkalmazása a geológiában: Enargit és luzonit kristályok orientációs vizsgálata Takács Ágnes & Molnár Ferenc TÁMOP-4.2.1/B-09/1/KMR-2010-0003 Szubmikroszkópos
Modern Fizika Labor Fizika BSC
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. május 4. A mérés száma és címe: 9. Röntgen-fluoreszencia analízis Értékelés: A beadás dátuma: 2009. május 13. A mérést végezte: Márton Krisztina Zsigmond
Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. május 4. A mérés száma és címe: 9. Röntgen-fluoreszencia analízis Értékelés: A beadás dátuma: 2009. május 13. A mérést végezte: Márton Krisztina Zsigmond
Sugárzás és anyag kölcsönhatásán alapuló módszerek
 Sugárzás és anyag kölcsönhatásán alapuló módszerek Elektronmikroszkópok A leképzendő mintára elektronsugarakat bocsátunk. Mivel az elektronsugár (mint hullám) hullámhossza kb. 5 nagyságrenddel kisebb a
Sugárzás és anyag kölcsönhatásán alapuló módszerek Elektronmikroszkópok A leképzendő mintára elektronsugarakat bocsátunk. Mivel az elektronsugár (mint hullám) hullámhossza kb. 5 nagyságrenddel kisebb a
Kvalitatív fázisanalízis
 MISKOLCI EGYETEM ANYAG ÉS KOHÓMÉRNÖKI KAR FÉMTANI TANSZÉK GYAKORLATI ÚTMUTATÓ PHARE HU 9705000006 ÖSSZEÁLLÍTOTTA: NAGY ERZSÉBET LEKTORÁLTA: DR. MERTINGER VALÉRIA Kvalitatív fázisanalízis. A gyakorlat célja
MISKOLCI EGYETEM ANYAG ÉS KOHÓMÉRNÖKI KAR FÉMTANI TANSZÉK GYAKORLATI ÚTMUTATÓ PHARE HU 9705000006 ÖSSZEÁLLÍTOTTA: NAGY ERZSÉBET LEKTORÁLTA: DR. MERTINGER VALÉRIA Kvalitatív fázisanalízis. A gyakorlat célja
American Society of Materials. Szilárdtestek. Fullerének (C atomok, sokszögek) zárt gömb, tojás cső (egy és többrétegű)
 Szilárdtestek Fullerének (C atomok, sokszögek) zárt gömb, tojás cső (egy és többrétegű) csavart alakzatok (spirál, tórusz, stb.) egyatomos vastagságú sík, grafén (0001) Amorf (atomok geometriai rend nélkül)
Szilárdtestek Fullerének (C atomok, sokszögek) zárt gömb, tojás cső (egy és többrétegű) csavart alakzatok (spirál, tórusz, stb.) egyatomos vastagságú sík, grafén (0001) Amorf (atomok geometriai rend nélkül)
Kondenzált anyagok fizikája
 Kondenzált anyagok fizikája Rácsszerkezetek Groma István ELTE September 13, 2018 Groma István, ELTE Kondenzált anyagok fizikája, Rácsszerkezetek 1/22 Periódikus rendszerek Elemi rácsvektorok a 1, a 2,
Kondenzált anyagok fizikája Rácsszerkezetek Groma István ELTE September 13, 2018 Groma István, ELTE Kondenzált anyagok fizikája, Rácsszerkezetek 1/22 Periódikus rendszerek Elemi rácsvektorok a 1, a 2,
Az elektromágneses sugárzás kölcsönhatása az anyaggal
 Az elektromágneses sugárzás kölcsönhatása az anyaggal Radiometriai alapfogalmak Kisugárzott felületi teljesítmény Besugárzott felületi teljesítmény A fény kölcsönhatása az anyaggal 1. M ΔP W ΔA m 2 E be
Az elektromágneses sugárzás kölcsönhatása az anyaggal Radiometriai alapfogalmak Kisugárzott felületi teljesítmény Besugárzott felületi teljesítmény A fény kölcsönhatása az anyaggal 1. M ΔP W ΔA m 2 E be
Méréselmélet MI BSc 1
 Mérés és s modellezés 2008.02.15. 1 Méréselmélet - bevezetés a mérnöki problémamegoldás menete 1. A probléma kitűzése 2. A hipotézis felállítása 3. Kísérlettervezés 4. Megfigyelések elvégzése 5. Adatok
Mérés és s modellezés 2008.02.15. 1 Méréselmélet - bevezetés a mérnöki problémamegoldás menete 1. A probléma kitűzése 2. A hipotézis felállítása 3. Kísérlettervezés 4. Megfigyelések elvégzése 5. Adatok
Lövedékálló védőmellényekben alkalmazott ballisztikai kerámia azonosítása az atomsíkok közti rácssíktávolságok alapján
 Lövedékálló védőmellényekben alkalmazott ballisztikai kerámia azonosítása az atomsíkok közti rácssíktávolságok alapján Eur.Ing. Frank György c. docens SzVMSzK mérnök szakértő (B5, B6) Személy-, Vagyonvédelmi
Lövedékálló védőmellényekben alkalmazott ballisztikai kerámia azonosítása az atomsíkok közti rácssíktávolságok alapján Eur.Ing. Frank György c. docens SzVMSzK mérnök szakértő (B5, B6) Személy-, Vagyonvédelmi
Modern Fizika Labor. 11. Spektroszkópia. Fizika BSc. A mérés dátuma: dec. 16. A mérés száma és címe: Értékelés: A beadás dátuma: dec. 21.
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. dec. 16. A mérés száma és címe: 11. Spektroszkópia Értékelés: A beadás dátuma: 2011. dec. 21. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. dec. 16. A mérés száma és címe: 11. Spektroszkópia Értékelés: A beadás dátuma: 2011. dec. 21. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Elektronmikroszkópia
 Elektronmikroszkópia Tóth Bence fizikus, 3. évfolyam 006.05.04. csütörtök beadva: 006.05.4. . Ismertesse röviden a transzmissziós elektronmikroszkóp működési elveit, főbb üzemmódjait!. Vázolja fel az elektronmikroszkóp
Elektronmikroszkópia Tóth Bence fizikus, 3. évfolyam 006.05.04. csütörtök beadva: 006.05.4. . Ismertesse röviden a transzmissziós elektronmikroszkóp működési elveit, főbb üzemmódjait!. Vázolja fel az elektronmikroszkóp
A diplomaterv keretében megvalósítandó feladatok összefoglalása
 A diplomaterv keretében megvalósítandó feladatok összefoglalása Diplomaterv céljai: 1 Sclieren résoptikai módszer numerikus szimulációk validálására való felhasználhatóságának vizsgálata 2 Lamináris előkevert
A diplomaterv keretében megvalósítandó feladatok összefoglalása Diplomaterv céljai: 1 Sclieren résoptikai módszer numerikus szimulációk validálására való felhasználhatóságának vizsgálata 2 Lamináris előkevert
Az elektron hullámtermészete. Készítette Kiss László
 Az elektron hullámtermészete Készítette Kiss László Az elektron részecske jellemzői Az elektront Joseph John Thomson fedezte fel 1897-ben. 1906-ban Nobel díj! Az elektronoknak, az elektromos és mágneses
Az elektron hullámtermészete Készítette Kiss László Az elektron részecske jellemzői Az elektront Joseph John Thomson fedezte fel 1897-ben. 1906-ban Nobel díj! Az elektronoknak, az elektromos és mágneses
A diffúz reflektancia spektroszkópia (DRS) módszerének alkalmazhatósága talajok ásványos fázisának rutinvizsgálatában
 A diffúz reflektancia spektroszkópia (DRS) módszerének alkalmazhatósága talajok ásványos fázisának rutinvizsgálatában Készítette: Ringer Marianna Témavezető: Szalai Zoltán 2015.06.16. Bevezetés Kutatási
A diffúz reflektancia spektroszkópia (DRS) módszerének alkalmazhatósága talajok ásványos fázisának rutinvizsgálatában Készítette: Ringer Marianna Témavezető: Szalai Zoltán 2015.06.16. Bevezetés Kutatási
Matematika A1a Analízis
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
EBSD-alkalmazások. Minta-elôkészítés, felületkezelés
 VISSZASZÓRTELEKTRON-DIFFRAKCIÓS VIZSGÁLATOK AZ EÖTVÖS LORÁND TUDOMÁNYEGYETEMEN 2. RÉSZ Havancsák Károly, Kalácska Szilvia, Baris Adrienn, Dankházi Zoltán, Varga Gábor Eötvös Loránd Tudományegyetem, Természettudományi
VISSZASZÓRTELEKTRON-DIFFRAKCIÓS VIZSGÁLATOK AZ EÖTVÖS LORÁND TUDOMÁNYEGYETEMEN 2. RÉSZ Havancsák Károly, Kalácska Szilvia, Baris Adrienn, Dankházi Zoltán, Varga Gábor Eötvös Loránd Tudományegyetem, Természettudományi
Nagyműszeres vegyész laboratórium programja. 8:15-8:25 Rövid vizuális ismerkedés a SEM laborral. (Havancsák Károly)
 Nagyműszeres vegyész laboratórium programja 8:15-8:25 Rövid vizuális ismerkedés a SEM laborral. (Havancsák Károly) 8:30-9:15 A pásztázó elektronmikroszkópia (SEM) alapjai. (Havancsák Károly) 9:30-10:15
Nagyműszeres vegyész laboratórium programja 8:15-8:25 Rövid vizuális ismerkedés a SEM laborral. (Havancsák Károly) 8:30-9:15 A pásztázó elektronmikroszkópia (SEM) alapjai. (Havancsák Károly) 9:30-10:15
Modern mikroszkópiai módszerek 1 2011 2012
 MIKROSZKÓPIA AZ ORVOS GYÓGYSZERÉSZ GYAKORLATBAN - DIAGOSZTIKA -TERÁPIA például: szemészet nőgyógyászat szövettan bakteriológia patológia gyógyszerek fejlesztése, tesztelése Modern mikroszkópiai módszerek
MIKROSZKÓPIA AZ ORVOS GYÓGYSZERÉSZ GYAKORLATBAN - DIAGOSZTIKA -TERÁPIA például: szemészet nőgyógyászat szövettan bakteriológia patológia gyógyszerek fejlesztése, tesztelése Modern mikroszkópiai módszerek
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI
 SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 6 KRISTÁLYTAN VI. A KRIsTÁLYOs ANYAG belső RENDEZETTsÉGE 1. A KRIsTÁLYOs ÁLLAPOT A szilárd ANYAG jellemzője Az ásványok néhány kivételtől eltekintve kristályos
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 6 KRISTÁLYTAN VI. A KRIsTÁLYOs ANYAG belső RENDEZETTsÉGE 1. A KRIsTÁLYOs ÁLLAPOT A szilárd ANYAG jellemzője Az ásványok néhány kivételtől eltekintve kristályos
Mérés és modellezés Méréstechnika VM, GM, MM 1
 Mérés és modellezés 2008.02.04. 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni
Mérés és modellezés 2008.02.04. 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni
Hangfrekvenciás mechanikai rezgések vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea
 Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea Geometrikus deformálható modellek Görbe evolúció Level set módszer A görbe evolúció parametrizálástól független mindössze geometriai
Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea Geometrikus deformálható modellek Görbe evolúció Level set módszer A görbe evolúció parametrizálástól független mindössze geometriai
Mikroszerkezet Krisztallitonként Tömbi Polikristályos Mintában
 Mikroszerkezet Krisztallitonként Tömbi Polikristályos Mintában Ribárik Gábor, Zilahi Gyula és Ungár Tamás Anyagfizikai Tanszék TAMOP Szeminárium, Visegrád 2012, január 18-20. Diffrakciós vonalak kiszélesedése
Mikroszerkezet Krisztallitonként Tömbi Polikristályos Mintában Ribárik Gábor, Zilahi Gyula és Ungár Tamás Anyagfizikai Tanszék TAMOP Szeminárium, Visegrád 2012, január 18-20. Diffrakciós vonalak kiszélesedése
Quanta 3D SEM/FIB Kétsugaras pásztázó elektronmikroszkóp. Havancsák Károly
 Quanta 3D SEM/FIB Kétsugaras pásztázó elektronmikroszkóp Havancsák Károly http://sem.elte.hu 1 FEI Quanta 3D SEM/FIB Anton van Leeuwenhoek (1632-1723, Delft) FEI (Philips) Eindhoven 2 A Képképzés fajtái
Quanta 3D SEM/FIB Kétsugaras pásztázó elektronmikroszkóp Havancsák Károly http://sem.elte.hu 1 FEI Quanta 3D SEM/FIB Anton van Leeuwenhoek (1632-1723, Delft) FEI (Philips) Eindhoven 2 A Képképzés fajtái
Automatikus irányzás digitális képek. feldolgozásával TURÁK BENCE DR. ÉGETŐ CSABA
 Automatikus irányzás digitális képek feldolgozásával TURÁK BENCE DR. ÉGETŐ CSABA Koncepció Robotmérőállomásra távcsővére rögzített kamera Képek alapján a cél automatikus detektálása És az irányzás elvégzése
Automatikus irányzás digitális képek feldolgozásával TURÁK BENCE DR. ÉGETŐ CSABA Koncepció Robotmérőállomásra távcsővére rögzített kamera Képek alapján a cél automatikus detektálása És az irányzás elvégzése
Modern Fizika Labor. 5. ESR (Elektronspin rezonancia) Fizika BSc. A mérés dátuma: okt. 25. A mérés száma és címe: Értékelés:
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 25. A mérés száma és címe: 5. ESR (Elektronspin rezonancia) Értékelés: A beadás dátuma: 2011. nov. 16. A mérést végezte: Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 25. A mérés száma és címe: 5. ESR (Elektronspin rezonancia) Értékelés: A beadás dátuma: 2011. nov. 16. A mérést végezte: Szőke Kálmán Benjamin
Az alacsony rétegződési hibaenergia hatása az ultrafinom szemcseszerkezet kialakulására és stabilitására
 Az alacsony rétegződési hibaenergia hatása az ultrafinom szemcseszerkezet kialakulására és stabilitására Z. Hegedűs, J. Gubicza, M. Kawasaki, N.Q. Chinh, Zs. Fogarassy and T.G. Langdon Eötvös Loránd Tudományegyetem
Az alacsony rétegződési hibaenergia hatása az ultrafinom szemcseszerkezet kialakulására és stabilitására Z. Hegedűs, J. Gubicza, M. Kawasaki, N.Q. Chinh, Zs. Fogarassy and T.G. Langdon Eötvös Loránd Tudományegyetem
ÚJ CSALÁDTAG A KLÍMAMODELLEZÉSBEN: a felszíni modellek, mint a városi éghajlati hatásvizsgálatok eszközei
 ÚJ CSALÁDTAG A KLÍMAMODELLEZÉSBEN: a felszíni modellek, mint a városi éghajlati hatásvizsgálatok eszközei Zsebeházi Gabriella és Szépszó Gabriella 43. Meteorológiai Tudományos Napok 2017. 11. 23. Tartalom
ÚJ CSALÁDTAG A KLÍMAMODELLEZÉSBEN: a felszíni modellek, mint a városi éghajlati hatásvizsgálatok eszközei Zsebeházi Gabriella és Szépszó Gabriella 43. Meteorológiai Tudományos Napok 2017. 11. 23. Tartalom
A TERMÉSZETES RADIOAKTIVITÁS VIZSGÁLATA A RUDAS-FÜRDŐ TÖRÖK- FORRÁSÁBAN
 A TERMÉSZETES RADIOAKTIVITÁS VIZSGÁLATA A RUDAS-FÜRDŐ TÖRÖK- FORRÁSÁBAN Készítette: Freiler Ágnes II. Környezettudomány MSc. szak Témavezetők: Horváth Ákos Atomfizikai Tanszék Erőss Anita Általános és
A TERMÉSZETES RADIOAKTIVITÁS VIZSGÁLATA A RUDAS-FÜRDŐ TÖRÖK- FORRÁSÁBAN Készítette: Freiler Ágnes II. Környezettudomány MSc. szak Témavezetők: Horváth Ákos Atomfizikai Tanszék Erőss Anita Általános és
IX. Alkalmazott Informatikai Konferencia Kaposvári Egyetem február 25.
 Kaposvári Egyetem 2011. február 25. Egedy Attila, Varga Tamás, Chován Tibor Pannon Egyetem, Mérnöki Kar, Folyamatmérnöki Intézeti Tanszék Veszprém, 8200 Egyetem utca 10. Bevezetés Cellás modellezés Kvalitatív
Kaposvári Egyetem 2011. február 25. Egedy Attila, Varga Tamás, Chován Tibor Pannon Egyetem, Mérnöki Kar, Folyamatmérnöki Intézeti Tanszék Veszprém, 8200 Egyetem utca 10. Bevezetés Cellás modellezés Kvalitatív
17. előadás: Vektorok a térben
 17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
Amorf/nanoszerkezetű felületi réteg létrehozása lézersugaras felületkezeléssel
 Amorf/nanoszerkezetű felületi réteg létrehozása lézersugaras felületkezeléssel Svéda Mária és Roósz András MTA-ME Anyagtudományi Kutatócsoport 3515-Miskolc-Egyetemváros femmaria@uni-miskolc.hu Absztrakt
Amorf/nanoszerkezetű felületi réteg létrehozása lézersugaras felületkezeléssel Svéda Mária és Roósz András MTA-ME Anyagtudományi Kutatócsoport 3515-Miskolc-Egyetemváros femmaria@uni-miskolc.hu Absztrakt
Alap-ötlet: Karl Friedrich Gauss ( ) valószínűségszámítási háttér: Andrej Markov ( )
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
A mechanika alapjai. A pontszerű testek dinamikája
 A mechanika alapjai A pontszerű testek dinamikája Horváth András SZE, Fizika Tsz. v 0.6 1 / 26 alapi Bevezetés Newton I. Newton II. Newton III. Newton IV. alapi 2 / 26 Bevezetés alapi Bevezetés Newton
A mechanika alapjai A pontszerű testek dinamikája Horváth András SZE, Fizika Tsz. v 0.6 1 / 26 alapi Bevezetés Newton I. Newton II. Newton III. Newton IV. alapi 2 / 26 Bevezetés alapi Bevezetés Newton
MŰHOLDAKRÓL TÖRTÉNŐ LEVEGŐKÉMIAI MÉRÉSEK
 MŰHOLDAKRÓL TÖRTÉNŐ LEVEGŐKÉMIAI MÉRÉSEK Kocsis Zsófia, Országos Meteorológiai Szolgálat 35. Meteorológiai Tudományos Napok Budapest, 2009. november 19-20. VÁZLAT Bevezetés Légköri gázok és a műholdak
MŰHOLDAKRÓL TÖRTÉNŐ LEVEGŐKÉMIAI MÉRÉSEK Kocsis Zsófia, Országos Meteorológiai Szolgálat 35. Meteorológiai Tudományos Napok Budapest, 2009. november 19-20. VÁZLAT Bevezetés Légköri gázok és a műholdak
Typotex Kiadó. Tartalomjegyzék
 Tartalomjegyzék Előszó 1 1. Az alapok 3 1.1. A pásztázó elektronmikroszkópia helye a korszerű tudományban 3 Irodalom 6 1.2. Elektron anyag kölcsönhatás 7 1.2.1. Rugalmas szórás 12 1.2.2. Rugalmatlan szórás
Tartalomjegyzék Előszó 1 1. Az alapok 3 1.1. A pásztázó elektronmikroszkópia helye a korszerű tudományban 3 Irodalom 6 1.2. Elektron anyag kölcsönhatás 7 1.2.1. Rugalmas szórás 12 1.2.2. Rugalmatlan szórás
Az Ampère-Maxwell-féle gerjesztési törvény
 Az Ampère-Maxwell-féle gerjesztési törvény Maxwell elméleti meggondolások alapján feltételezte, hogy a változó elektromos tér örvényes mágneses teret kelt (hasonlóan ahhoz ahogy a változó mágneses tér
Az Ampère-Maxwell-féle gerjesztési törvény Maxwell elméleti meggondolások alapján feltételezte, hogy a változó elektromos tér örvényes mágneses teret kelt (hasonlóan ahhoz ahogy a változó mágneses tér
Az éghajlati modellek eredményeinek alkalmazhatósága hatásvizsgálatokban
 Az éghajlati modellek eredményeinek alkalmazhatósága hatásvizsgálatokban Szépszó Gabriella Országos Meteorológiai Szolgálat, szepszo.g@met.hu RCMTéR hatásvizsgálói konzultációs workshop 2015. június 23.
Az éghajlati modellek eredményeinek alkalmazhatósága hatásvizsgálatokban Szépszó Gabriella Országos Meteorológiai Szolgálat, szepszo.g@met.hu RCMTéR hatásvizsgálói konzultációs workshop 2015. június 23.
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011.
 BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
Projektfeladatok 2014, tavaszi félév
 Projektfeladatok 2014, tavaszi félév Gyakorlatok Félév menete: 1. gyakorlat: feladat kiválasztása 2-12. gyakorlat: konzultációs rendszeres beszámoló a munka aktuális állásáról (kötelező) 13-14. gyakorlat:
Projektfeladatok 2014, tavaszi félév Gyakorlatok Félév menete: 1. gyakorlat: feladat kiválasztása 2-12. gyakorlat: konzultációs rendszeres beszámoló a munka aktuális állásáról (kötelező) 13-14. gyakorlat:
A napenergia magyarországi hasznosítását támogató új fejlesztések az Országos Meteorológiai Szolgálatnál
 A napenergia magyarországi hasznosítását támogató új fejlesztések az Országos Meteorológiai Szolgálatnál Nagy Zoltán, Tóth Zoltán, Morvai Krisztián, Szintai Balázs Országos Meteorológiai Szolgálat A globálsugárzás
A napenergia magyarországi hasznosítását támogató új fejlesztések az Országos Meteorológiai Szolgálatnál Nagy Zoltán, Tóth Zoltán, Morvai Krisztián, Szintai Balázs Országos Meteorológiai Szolgálat A globálsugárzás
Fókuszált ionsugaras megmunkálás
 FEI Quanta 3D SEM/FIB Dankházi Zoltán 2016. március 1 FIB = Focused Ion Beam (Fókuszált ionnyaláb) Miből áll egy SEM/FIB berendezés? elektron oszlop ion oszlop gáz injektorok detektor CDEM (SE, SI) 2 Dual-Beam
FEI Quanta 3D SEM/FIB Dankházi Zoltán 2016. március 1 FIB = Focused Ion Beam (Fókuszált ionnyaláb) Miből áll egy SEM/FIB berendezés? elektron oszlop ion oszlop gáz injektorok detektor CDEM (SE, SI) 2 Dual-Beam
Rövid ismertető. Modern mikroszkópiai módszerek. A mikroszkóp. A mikroszkóp. Az optikai mikroszkópia áttekintése
 Rövid ismertető Modern mikroszkópiai módszerek Nyitrai Miklós 2010. március 16. A mikroszkópok csoportosítása Alapok, ismeretek A működési elvek Speciális módszerek A mikroszkópia története ld. Pdf. Minél
Rövid ismertető Modern mikroszkópiai módszerek Nyitrai Miklós 2010. március 16. A mikroszkópok csoportosítása Alapok, ismeretek A működési elvek Speciális módszerek A mikroszkópia története ld. Pdf. Minél
Vektorok. Wettl Ferenc október 20. Wettl Ferenc Vektorok október / 36
 Vektorok Wettl Ferenc 2014. október 20. Wettl Ferenc Vektorok 2014. október 20. 1 / 36 Tartalom 1 Vektorok a 2- és 3-dimenziós térben 2 Távolság, szög, orientáció 3 Vektorok koordinátás alakban 4 Összefoglalás
Vektorok Wettl Ferenc 2014. október 20. Wettl Ferenc Vektorok 2014. október 20. 1 / 36 Tartalom 1 Vektorok a 2- és 3-dimenziós térben 2 Távolság, szög, orientáció 3 Vektorok koordinátás alakban 4 Összefoglalás
időpont? ütemterv számonkérés segédanyagok
 időpont? ütemterv számonkérés segédanyagok 1. Bevezetés Végeselem-módszer Számítógépek alkalmazása a szerkezettervezésben: 1. a geometria megadása, tervkészítés, 2. műszaki számítások: - analitikus számítások
időpont? ütemterv számonkérés segédanyagok 1. Bevezetés Végeselem-módszer Számítógépek alkalmazása a szerkezettervezésben: 1. a geometria megadása, tervkészítés, 2. műszaki számítások: - analitikus számítások
7. Koordináta méréstechnika
 7. Koordináta méréstechnika Coordinate Measuring Machine: CMM, 3D-s mérőgép Egyiptomi piramis kövek mérése i.e. 1440 Egyiptomi mérővonalzó, Amenphotep fáraó (i.e. 1550) alkarjának hossza: 524mm A koordináta
7. Koordináta méréstechnika Coordinate Measuring Machine: CMM, 3D-s mérőgép Egyiptomi piramis kövek mérése i.e. 1440 Egyiptomi mérővonalzó, Amenphotep fáraó (i.e. 1550) alkarjának hossza: 524mm A koordináta
A mikroszkóp vizsgálata Lencse görbületi sugarának mérése Newton-gyűrűkkel Folyadék törésmutatójának mérése Abbe-féle refraktométerrel
 A mikroszkóp vizsgálata Lencse görbületi sugarának mérése Newton-gyűrűkkel Folyadék törésmutatójának mérése Abbe-féle refraktométerrel Mérő neve: Márkus Bence Gábor Mérőpár neve: Székely Anna Krisztina
A mikroszkóp vizsgálata Lencse görbületi sugarának mérése Newton-gyűrűkkel Folyadék törésmutatójának mérése Abbe-féle refraktométerrel Mérő neve: Márkus Bence Gábor Mérőpár neve: Székely Anna Krisztina
KRISTÁLYOK GEOMETRIAI LEÍRÁSA
 KRISTÁLYOK GEOMETRIAI LEÍRÁSA Kristály Bázis Pontrács Ideális Kristály: hosszútávúan rendezett hibamentes, végtelen szilárd test Kristály Bázis: a kristály legkisebb, ismétlœdœ atomcsoportja Rácspont:
KRISTÁLYOK GEOMETRIAI LEÍRÁSA Kristály Bázis Pontrács Ideális Kristály: hosszútávúan rendezett hibamentes, végtelen szilárd test Kristály Bázis: a kristály legkisebb, ismétlœdœ atomcsoportja Rácspont:
Digitális Domborzat Modellek (DTM)
 Digitális Domborzat Modellek (DTM) Digitális Domborzat Modellek (DTM) Digitális Domborzat Modellek (DTM) DTM fogalma A földfelszín számítógéppel kezelhető topográfiai modellje Cél: tetszőleges pontban
Digitális Domborzat Modellek (DTM) Digitális Domborzat Modellek (DTM) Digitális Domborzat Modellek (DTM) DTM fogalma A földfelszín számítógéppel kezelhető topográfiai modellje Cél: tetszőleges pontban
