Komputeralgebra rendszerek
|
|
|
- János Somogyi
- 6 évvel ezelőtt
- Látták:
Átírás
1 Komputeralgebra rendszerek P L O T Czirbusz Sándor czirbusz@gmail.com Komputeralgebra Tanszék ELTE Informatika Kar október 12.
2 Index I 1 Az alapok plot és plot3d Késleltetett megjelenítés Egyszerűbb opciók Szinezés,skálázás Stílus és nézőpont A koordináták testreszabása 2 Nem Descartes-féle koordináták Polár koordináták Henger koordináták 3 Egyszerű animációk Egyváltozós függvények Kétváltozós függvények Animáció frame-szekvenciával 4 Szöveg a grafikonokon 5 Vektorok Alapok
3 Index II Vektorok szorzása Az arrow opciói 6 Térgörbék spacecurve tubeplot 7 Tarnszformációk
4 plot és plot3d plot és plot3d Egyváltozós függvény plot( f(x), x=a..b, opts ) Több függvény rajzolása egyszerre : függvényhalmaz (3D-ben csak ez), vagy -lista megadásával.
5 plot és plot3d plot és plot3d Egyváltozós függvény plot( f(x), x=a..b, opts ) Több függvény rajzolása egyszerre : függvényhalmaz (3D-ben csak ez), vagy -lista megadásával. Kétváltozós függvény plot3d( f(x,y), x=a..b, y=c..d, opts)
6 plot és plot3d plot és plot3d Egyváltozós függvény plot( f(x), x=a..b, opts ) Több függvény rajzolása egyszerre : függvényhalmaz (3D-ben csak ez), vagy -lista megadásával. Kétváltozós függvény plot3d( f(x,y), x=a..b, y=c..d, opts) Paraméteres ábrázolás
7 plot és plot3d plot és plot3d Egyváltozós függvény plot( f(x), x=a..b, opts ) Több függvény rajzolása egyszerre : függvényhalmaz (3D-ben csak ez), vagy -lista megadásával. Kétváltozós függvény plot3d( f(x,y), x=a..b, y=c..d, opts) Paraméteres ábrázolás plot( [(f(t), g(t), t=a..b], opts )
8 plot és plot3d plot és plot3d Egyváltozós függvény plot( f(x), x=a..b, opts ) Több függvény rajzolása egyszerre : függvényhalmaz (3D-ben csak ez), vagy -lista megadásával. Kétváltozós függvény plot3d( f(x,y), x=a..b, y=c..d, opts) Paraméteres ábrázolás plot( [(f(t), g(t), t=a..b], opts ) plot3d( [f(s,t), g(s,t), h(s,t)], s=a..b, t=c..d, opts)
9 plot és plot3d plot és plot3d Egyváltozós függvény plot( f(x), x=a..b, opts ) Több függvény rajzolása egyszerre : függvényhalmaz (3D-ben csak ez), vagy -lista megadásával. Kétváltozós függvény plot3d( f(x,y), x=a..b, y=c..d, opts) Paraméteres ábrázolás plot( [(f(t), g(t), t=a..b], opts ) plot3d( [f(s,t), g(s,t), h(s,t)], s=a..b, t=c..d, opts) Pontok ábrázolása
10 plot és plot3d plot és plot3d Egyváltozós függvény plot( f(x), x=a..b, opts ) Több függvény rajzolása egyszerre : függvényhalmaz (3D-ben csak ez), vagy -lista megadásával. Kétváltozós függvény plot3d( f(x,y), x=a..b, y=c..d, opts) Paraméteres ábrázolás plot( [(f(t), g(t), t=a..b], opts ) plot3d( [f(s,t), g(s,t), h(s,t)], s=a..b, t=c..d, opts) Pontok ábrázolása style=point opcióval.(még 1 ponthoz is kell a halmaz-zárójel!)
11 plot és plot3d plot és plot3d Egyváltozós függvény plot( f(x), x=a..b, opts ) Több függvény rajzolása egyszerre : függvényhalmaz (3D-ben csak ez), vagy -lista megadásával. Kétváltozós függvény plot3d( f(x,y), x=a..b, y=c..d, opts) Paraméteres ábrázolás plot( [(f(t), g(t), t=a..b], opts ) plot3d( [f(s,t), g(s,t), h(s,t)], s=a..b, t=c..d, opts) Pontok ábrázolása style=point opcióval.(még 1 ponthoz is kell a halmaz-zárójel!) A pointplot 3d procedúra. A plots csomag tartalmazza.
12 Késleltetett megjelenítés Késleltetett megjelenítés display A plot utasítást : -al lezárva eltárolódik csak a a memóriában tárolódik a grafikon, a képernyőn nem jelenik meg. Megjelenítés : display
13 Egyszerűbb opciók Egyszerűbb opciók
14 Egyszerűbb opciók Egyszerűbb opciók Vonalvastagság: thickness=0..15 (egész szám)
15 Egyszerűbb opciók Egyszerűbb opciók Vonalvastagság: thickness=0..15 (egész szám) Simábbá tétel 3D-ben:
16 Egyszerűbb opciók Egyszerűbb opciók Vonalvastagság: thickness=0..15 (egész szám) Simábbá tétel 3D-ben: numpoints=n, Az x és y intervallumát n részre osztja Default : 625
17 Egyszerűbb opciók Egyszerűbb opciók Vonalvastagság: thickness=0..15 (egész szám) Simábbá tétel 3D-ben: numpoints=n, Az x és y intervallumát n részre osztja Default : 625 grid=[n,m] Változónként adjuk meg a felbontást Default : 25 X 25
18 Egyszerűbb opciók Egyszerűbb opciók Vonalvastagság: thickness=0..15 (egész szám) Simábbá tétel 3D-ben: numpoints=n, Az x és y intervallumát n részre osztja Default : 625 grid=[n,m] Változónként adjuk meg a felbontást Default : 25 X 25 A numpoints működik 2D-ben, default 50. A pontosságot a plot automatikusan tudja növelni. Ennek letiltása : adaptive=false
19 Szinezés,skálázás Szinezés, skálázás color.
20 Szinezés,skálázás Szinezés, skálázás color. Előredefiniált nevek, illetve RGB.
21 Szinezés,skálázás Szinezés, skálázás color. Előredefiniált nevek, illetve RGB. Változó színek 3D-ben : például 4D szimulálására
22 Szinezés,skálázás Szinezés, skálázás color. Előredefiniált nevek, illetve RGB. Változó színek 3D-ben : például 4D szimulálására Árnyékolás :shading=x, X {xyz, xy, z, zgrayscale, zhue, none}. Default a none
23 Szinezés,skálázás Szinezés, skálázás color. Előredefiniált nevek, illetve RGB. Változó színek 3D-ben : például 4D szimulálására Árnyékolás :shading=x, X {xyz, xy, z, zgrayscale, zhue, none}. Default a none scaling Értéke constrained vagy unconstrained lehet
24 Stílus és nézőpont Stílus és nézőpont style 2D-ben
25 Stílus és nézőpont Stílus és nézőpont style 2D-ben style= point line patch patchnogrid point
26 Stílus és nézőpont Stílus és nézőpont style 2D-ben style= point line patch patchnogrid point linestyle=solid DOT DASH DASHDOT
27 Stílus és nézőpont Stílus és nézőpont style 2D-ben style= point line patch patchnogrid point linestyle=solid DOT DASH DASHDOT style 3D-ben style=point hidden patch wireframe contour patchnogrid patchcontour line
28 Stílus és nézőpont Stílus és nézőpont style 2D-ben style= point line patch patchnogrid point linestyle=solid DOT DASH DASHDOT style 3D-ben style=point hidden patch wireframe contour patchnogrid patchcontour line viewpoint
29 Stílus és nézőpont Stílus és nézőpont style 2D-ben style= point line patch patchnogrid point linestyle=solid DOT DASH DASHDOT style 3D-ben style=point hidden patch wireframe contour patchnogrid patchcontour line viewpoint orientation=[α, β] A szögek fokban, az x és a z tengelyen pozitív irányból nézve, óramutató járásával ellentétesen.
30 Stílus és nézőpont Stílus és nézőpont style 2D-ben style= point line patch patchnogrid point linestyle=solid DOT DASH DASHDOT style 3D-ben style=point hidden patch wireframe contour patchnogrid patchcontour line viewpoint orientation=[α, β] A szögek fokban, az x és a z tengelyen pozitív irányból nézve, óramutató járásával ellentétesen. view=[xmin..xmax] view=[xmin..xmax,ymin..ymax,zmin..zmax ] view=zmin..zmax
31 A koordináták testreszabása A koordináták testreszabása
32 A koordináták testreszabása A koordináták testreszabása axes=normal boxed framed none. 2D-ben a normal default, 3D-ben a none
33 A koordináták testreszabása A koordináták testreszabása axes=normal boxed framed none. 2D-ben a normal default, 3D-ben a none tickmarks=[xticks,yticks] [xticks,yticks,zticks] Az elemek is listák. xticks=... yticks=..., zticks=...
34 A koordináták testreszabása A koordináták testreszabása axes=normal boxed framed none. 2D-ben a normal default, 3D-ben a none tickmarks=[xticks,yticks] [xticks,yticks,zticks] Az elemek is listák. xticks=... yticks=..., zticks=... labels=[string1,string2 ] [string1,string2,string3 ]
35 A koordináták testreszabása A koordináták testreszabása axes=normal boxed framed none. 2D-ben a normal default, 3D-ben a none tickmarks=[xticks,yticks] [xticks,yticks,zticks] Az elemek is listák. xticks=... yticks=..., zticks=... labels=[string1,string2 ] [string1,string2,string3 ] labeldirections=[d1,d2] Az d1 2=vertical horizontal
36 A koordináták testreszabása A koordináták testreszabása axes=normal boxed framed none. 2D-ben a normal default, 3D-ben a none tickmarks=[xticks,yticks] [xticks,yticks,zticks] Az elemek is listák. xticks=... yticks=..., zticks=... labels=[string1,string2 ] [string1,string2,string3 ] labeldirections=[d1,d2] Az d1 2=vertical horizontal labelfont axesfont font - [family,style,size] formájúak
37 A koordináták testreszabása A koordináták testreszabása axes=normal boxed framed none. 2D-ben a normal default, 3D-ben a none tickmarks=[xticks,yticks] [xticks,yticks,zticks] Az elemek is listák. xticks=... yticks=..., zticks=... labels=[string1,string2 ] [string1,string2,string3 ] labeldirections=[d1,d2] Az d1 2=vertical horizontal labelfont axesfont font - [family,style,size] formájúak setoption Ha sokszor használunk azonos paramétereket...(csak egy-értékű opció lehet, tehát lista, szekvencia nem :( )
38 Polár koordináták Polár koordináták
39 Polár koordináták Polár koordináták plot3d(r(θ),θ = α... β, coords=polat, opts)
40 Polár koordináták Polár koordináták plot3d(r(θ),θ = α... β, coords=polat, opts) plot([r(t),θ(t),t=a..b],coords=polar, opts) paraméteresen
41 Polár koordináták Polár koordináták plot3d(r(θ),θ = α... β, coords=polat, opts) plot([r(t),θ(t),t=a..b],coords=polar, opts) paraméteresen A plots csomaggal polarplot(r(θ),θ = α... β, opts) polarplot([r(t),θ(t),t=a..b],opts) paraméteresen
42 Henger koordináták Henger koordináták
43 Henger koordináták Henger koordináták plot3d(r(θ,z),θ = α... β,z=a..b coords=cylindric, opts)
44 Henger koordináták Henger koordináták plot3d(r(θ,z),θ = α... β,z=a..b coords=cylindric, opts) plot([r(s,t),θ(s,t),z(s,t)),s=a..b,t=c..d],coords=cylindric, opts) paraméteresen
45 Henger koordináták Henger koordináták plot3d(r(θ,z),θ = α... β,z=a..b coords=cylindric, opts) plot([r(s,t),θ(s,t),z(s,t)),s=a..b,t=c..d],coords=cylindric, opts) paraméteresen A plots csomaggal cylinderplot(r(θ,z),θ = α... β,z=a..b, opts) cylinderplot([r(s,t),θ(s,t),z(s,t)),s=a..b,t=c..d],opts) paraméteresen
46 Egyváltozós függvények Egyváltozós függvények Függvény és görbe animálása
47 Egyváltozós függvények Egyváltozós függvények Függvény és görbe animálása animate( F (x, t), x=a..b, t=p..q, opts)
48 Egyváltozós függvények Egyváltozós függvények Függvény és görbe animálása animate( F (x, t), x=a..b, t=p..q, opts) animatecurve( f (x), x=a..b, opts )
49 Egyváltozós függvények Egyváltozós függvények Függvény és görbe animálása animate( F (x, t), x=a..b, t=p..q, opts) animatecurve( f (x), x=a..b, opts ) x a független változó
50 Egyváltozós függvények Egyváltozós függvények Függvény és görbe animálása animate( F (x, t), x=a..b, t=p..q, opts) animatecurve( f (x), x=a..b, opts ) x a független változó t a frame-változó
51 Egyváltozós függvények Egyváltozós függvények Függvény és görbe animálása animate( F (x, t), x=a..b, t=p..q, opts) animatecurve( f (x), x=a..b, opts ) x a független változó t a frame-változó A végrehajtás interaktív
52 Kétváltozós függvények Kétváltozós függvények animate3d
53 Kétváltozós függvények Kétváltozós függvények animate3d animate3d( F (x, y, t), x=a..b, y=c..d, t=p..q, opts)
54 Kétváltozós függvények Kétváltozós függvények animate3d animate3d( F (x, y, t), x=a..b, y=c..d, t=p..q, opts) Új opció : frames
55 Animáció frame-szekvenciával Animáció frame-szekvenciával display(seq,insequence=true)
56 Szöveg a grafikonokon Cím : title="..."
57 Szöveg a grafikonokon Cím : title="..." textplot( [x,y,[z],"text"], ops ) Új opció : align=above BELOW LEFT RIGHT Megvalósítható a mozgó szöveg
58 Szöveg a grafikonokon Cím : title="..." textplot( [x,y,[z],"text"], ops ) Új opció : align=above BELOW LEFT RIGHT Megvalósítható a mozgó szöveg Számított érték a szövegben : a sprintf függvénnyel
59 Alapok Alapok A plots és a plottools csomagnak is van array procedúrája, a plots-é a korszerűbb. arrow( start, vektor, opts ) kezdőpont + vektor start elhagyható, a kezdőpont arrow( start, end, difference=true,opts) kezdőpont + végpont
60 Alapok Alapok A plots és a plottools csomagnak is van array procedúrája, a plots-é a korszerűbb. arrow( start, vektor, opts ) kezdőpont + vektor start elhagyható, a kezdőpont start, vektor : két vagy háromelemű lista, a vektor lehet <...> alakú oszlopvektor arrow( start, end, difference=true,opts) kezdőpont + végpont
61 Alapok Alapok A plots és a plottools csomagnak is van array procedúrája, a plots-é a korszerűbb. arrow( start, vektor, opts ) kezdőpont + vektor start elhagyható, a kezdőpont start, vektor : két vagy háromelemű lista, a vektor lehet <...> alakú oszlopvektor lehet összeadni őket arrow( start, end, difference=true,opts) kezdőpont + végpont
62 Alapok Alapok A plots és a plottools csomagnak is van array procedúrája, a plots-é a korszerűbb. arrow( start, vektor, opts ) kezdőpont + vektor start elhagyható, a kezdőpont start, vektor : két vagy háromelemű lista, a vektor lehet <...> alakú oszlopvektor lehet összeadni őket A 3D kiemeléséhez a ligthmodel opció használható, vagy light=[ϕ, θ,r,g,b]. arrow( start, end, difference=true,opts) kezdőpont + végpont
63 Vektorok szorzása Vektorok szorzása Belső szorzat :. vagy a LinearAlgebra csomag DotProduct
64 Vektorok szorzása Vektorok szorzása Belső szorzat :. vagy a LinearAlgebra csomag DotProduct Vektori szorzat : a LinearAlgebra csomag CrossProduct
65 Az arrow opciói Az arrow opciói shape=double_arrow cylindrical_arrow arrow harpoon
66 Az arrow opciói Az arrow opciói shape=double_arrow cylindrical_arrow arrow harpoon length=n [n,relative=true].az első a tényleges hossz, a második konstanssal szorzott
67 Az arrow opciói Az arrow opciói shape=double_arrow cylindrical_arrow arrow harpoon length=n [n,relative=true].az első a tényleges hossz, a második konstanssal szorzott width=n [n,relative=true] Abszolút ill. a hossz arányában
68 Az arrow opciói Az arrow opciói shape=double_arrow cylindrical_arrow arrow harpoon length=n [n,relative=true].az első a tényleges hossz, a második konstanssal szorzott width=n [n,relative=true] Abszolút ill. a hossz arányában head_width=n [n,relative=true]
69 Az arrow opciói Az arrow opciói shape=double_arrow cylindrical_arrow arrow harpoon length=n [n,relative=true].az első a tényleges hossz, a második konstanssal szorzott width=n [n,relative=true] Abszolút ill. a hossz arányában head_width=n [n,relative=true] head_length=n [n,relative=true]
70 Az arrow opciói Az arrow opciói shape=double_arrow cylindrical_arrow arrow harpoon length=n [n,relative=true].az első a tényleges hossz, a második konstanssal szorzott width=n [n,relative=true] Abszolút ill. a hossz arányában head_width=n [n,relative=true] head_length=n [n,relative=true] plane
71 spacecurve spacecurve Térgörbe grafikonka : spacecurve([f(t),g(t),h(t)], t=a..b, ops ) A paramétertartomány a listán belül is megadható.
72 tubeplot tubeplot A hernyó tubeplot([f(t),g(t),h(t)], t=a..b, ops ) Opciók tubepoints=n, default 10
73 tubeplot tubeplot A hernyó tubeplot([f(t),g(t),h(t)], t=a..b, ops ) Opciók tubepoints=n, default 10 radius=n, deafult=1, lehet változtatható is!
74 Tarnszformációk a plottools csomag : circle, line, polygon, icosahedron, stb.
75 Tarnszformációk a plottools csomag : circle, line, polygon, icosahedron, stb. rotate : rotate( P, α, [x0,y0 ] )
76 Tarnszformációk a plottools csomag : circle, line, polygon, icosahedron, stb. rotate : rotate( P, α, [x0,y0 ] ) transform( rendezett pár vagy hármas -> 2 vagy 3 elem listája )
Komputeralgebra rendszerek
XVII. A Maple grafikus képeségei Czirbusz Sándor czirbusz@gmail.com Komputeralgebra Tanszék ELTE Informatika Kar 2010-2011 ősz Index I 1 Az alapok A plot és plot3d Implicit függvény ábrázolása Késleltetett
Felületábrázolás és alkalmazásai Maple-ben
Debreceni Egyetem Informatikai Kar Felületábrázolás és alkalmazásai Maple-ben Témavezető: Dr. Hoffmann Miklós egyetemi docens Készítette: Szlahorek András informatikatanár Debrecen 2009 Tartalomjegyzék
Grafika. Egyváltozós függvény grafikonja
Grafika Egyváltozós függvény grafikonja Egyváltozós függvény grafikonját a plot paranccsal tudjuk kirajzolni. Elsı paraméter egy függvény képlete, a második paraméter változónév=intervallum alakú: plot(x^3-16*x+2,x=-6..6);
Maple: Grafikonok rajzolása
Maple: Grafikonok rajzolása A Maple számos lehetőséget kínál adatok és matematikai relációk grafikus megjelenítésére a plots függvény különböző formái által. Számtalan rajzoló függvényei között olyan függvényeket
TikZ, a L A T E X grakája
TikZ, a L A T E X grakája Informatika 1. L A TEX Móra Péter, Wettl Ferenc BME Algebra Tanszék, http://www.math.bme.hu/~wettl 2013-12-04 Móra Péter, Wettl Ferenc (BME) TikZ, a LATEX grakája 2013-12-04 1
17. előadás: Vektorok a térben
17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
Lengyelné Dr. Szilágyi Szilvia április 7.
ME, Anaĺızis Tanszék 2010. április 7. , alapfogalmak 2.1. Definíció A H 1, H 2,..., H n R (ahol n 2 egész szám) nemüres valós számhalmazok H 1 H 2... H n Descartes-szorzatán a következő halmazt értjük:
MATLAB alapismeretek IV. Eredmények grafikus megjelenítése: vonalgrafikonok
Alkalmazott Informatikai Intézeti Tanszék MŰSZAKI INFORMATIKA Dr.Dudás László 0. MATLAB alapismeretek IV. Eredmények grafikus megjelenítése: vonalgrafikonok Forrás: İ.Yücel Özbek: Introduction to Matlab
Számítógéppel támogatott geometriai kutatás és oktatás Debrecen 2009.
Debreceni Egyetem Informatikai Kar Számítógéppel támogatott geometriai kutatás és oktatás Témavezetı: Dr. Bácsó Sándor tanszékvezetı Készítette: Boda Judit informatikatanári-matematika Debrecen 2009. Köszönetnyilvánítás
Komputeralgebra Rendszerek
Komputeralgebra Rendszerek A szimbolikus megoldó a MAPLE -ben Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2014. március 4. TARTALOMJEGYZÉK 1 of 41 TARTALOMJEGYZÉK I 1 TARTALOMJEGYZÉK 2 Funkció és
Informatika 1. Informatika el adás. Kovács Kristóf, Pálovics Róbert. Budapesti M szaki Egyetem november 13.
Informatika 1 9. el adás Kovács Kristóf, Pálovics Róbert Budapesti M szaki Egyetem 2013. november 13. CSS HTML formázasára, elhelyezésére szolgál Cél az újrafelhasználhatóság és könny módosítás CSS kód
Matematika II. 1 sin xdx =, 1 cos xdx =, 1 + x 2 dx =
Matematika előadás elméleti kérdéseinél kérdezhető képletek Matematika II Határozatlan Integrálszámítás d) Adja meg az alábbi alapintegrálokat! x n 1 dx =, sin 2 x dx = d) Adja meg az alábbi alapintegrálokat!
sin x = cos x =? sin x = dx =? dx = cos x =? g) Adja meg a helyettesítéses integrálás szabályát határozott integrálokra vonatkozóan!
Matematika előadás elméleti kérdéseinél kérdezhető képletek Analízis II Határozatlan integrálszámítás g) t = tg x 2 helyettesítés esetén mivel egyenlő sin x = cos x =? g) t = tg x 2 helyettesítés esetén
Matematika II képletek. 1 sin xdx =, cos 2 x dx = sh 2 x dx = 1 + x 2 dx = 1 x. cos xdx =,
Matematika II előadás elméleti kérdéseinél kérdezhető képletek Matematika II képletek Határozatlan Integrálszámítás x n dx =, sin 2 x dx = sin xdx =, ch 2 x dx = sin xdx =, sh 2 x dx = cos xdx =, + x 2
Descartes-féle, derékszögű koordináta-rendszer
Descartes-féle, derékszögű koordináta-rendszer A derékszögű koordináta-rendszerben a sík minden pontjához egy rendezett valós számpár rendelhető. A számpár első tagja (abszcissza) a pont y tengelytől mért
Eredmények, objektumok grafikus megjelenítése 3D felületek rajzoló függvényei
Alkalmazott Informatikai Intézeti Tanszék MŰSZAKI INFORMATIKA Dr.Dudás László 0. MATLAB alapismeretek VII. Eredmények, objektumok grafikus megjelenítése 3D felületek rajzoló függvényei Alkalmazott Informatikai
Geometriai modellezés. Szécsi László
Geometriai modellezés Szécsi László Adatáramlás vezérlés Animáció világleírás Modellezés kamera Virtuális világ kép Képszintézis A modellezés részfeladatai Geometria megadása [1. előadás] pont, görbe,
Széchenyi István Egyetem. Informatika II. Számítási módszerek. 5. előadás. Függvények ábrázolása. Dr. Szörényi Miklós, Dr.
5. előadás Függvények ábrázolása Dr. Szörényi Miklós, Dr. Kallós Gábor 2013 2014 1 Tartalom Az elkészítés lépései, áttekintés Példa: egy ismert matematikai függvény és integráljának ábrázolása Technikai
MATLAB alapismeretek III.
Alkalmazott Informatikai Intézeti Tanszék MŰSZAKI INFORMATIKA Dr.Dudás László 0. MATLAB alapismeretek III. Z= F(x,y) alakú kétváltozós függvények rajzolása Több objektum rajzolása egy ábrába Kombináljuk
Matematika I. Vektorok, egyenesek, síkok
Matematika előadás elméleti kérdéseinél kérdezhető képletek Matematika I Vektorok, egyenesek, síkok a) Hogyan számítjuk ki az a = (a 1, a 2, a 3 ) és b = (b 1, b 2, b 3 ) vektorok szögét? a) Hogyan számítjuk
Informatika 1 CSS. Kovács Kristóf, Pálovics Róbert, Wettl Ferenc november 4. Budapesti M szaki Egyetem
Informatika 1 CSS Kovács Kristóf, Pálovics Róbert, Wettl Ferenc Budapesti M szaki Egyetem 2014. november 4. CSS CSS: Cascading Style Sheets CSS CSS: Cascading Style Sheets Cél: a tartalom és a megjelenítés
KOVÁCS BÉLA, MATEMATIKA II.
KOVÁCS BÉLA MATEmATIkA II 6 VI TÉRGÖRbÉk 1 Alapvető ÖSSZEFÜGGÉSEk A térgörbe (1) alakú egyenletével írható le Ez a vektoregyenlet egyenértékű az (2) skaláris egyenletrendszerrel A térgörbe három nevezetes
Kétváltozós függvények differenciálszámítása
Kétváltozós függvények differenciálszámítása 13. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Kétváltozós függvények p. 1/1 Definíció, szemléltetés Definíció. Az f : R R R függvényt
MATLAB alapismeretek V. Eredmények grafikus megjelenítése: oszlopdiagramok, hisztogramok, tortadiagramok
Alkalmazott Informatikai Intézeti Tanszék MŰSZAKI INFORMATIKA Dr.Dudás László 0. MATLAB alapismeretek V. Eredmények grafikus megjelenítése: oszlopdiagramok, hisztogramok, tortadiagramok Alkalmazott Informatikai
SCILAB programcsomag segítségével
Felhasználói függvények de niálása és függvények 3D ábrázolása SCILAB programcsomag segítségével 1. Felhasználói függvények de niálása A Scilab programcsomag rengeteg matematikai függvényt biztosít a számítások
Számítógépes geometria (mester kurzus) III
2010 sz, Debreceni Egyetem Felületek A felület megadása implicit: F : R 3 R, F (x, y, z) = 0 Euler-Monge: f : [a, b] [c, d] R, z = f (x, y) paraméteres: r : [a, b] [c, d] R 3 trianguláris háló direkt megadása
Komputeralgebra rendszerek
Komputeralgebra rendszerek Összetett adatszerkezetek Czirbusz Sándor czirbusz@gmail.com Komputeralgebra Tanszék ELTE Informatika Kar 2009-2010 ősz Index 1 Sorozatok 2 Halmazok 3 Listák 4 Vermek, sorok
Láthatósági kérdések
Láthatósági kérdések Láthatósági algoritmusok Adott térbeli objektum és adott nézőpont esetén el kell döntenünk, hogy mi látható az adott alakzatból a nézőpontból, vagy irányából nézve. Az algoritmusok
MATLAB OKTATÁS 5. ELŐADÁS FELTÉTEL NÉLKÜLI ÉS FELTÉTELES OPTIMALIZÁLÁS. Dr. Bécsi Tamás Hegedüs Ferenc
MATLAB OKTATÁS 5. ELŐADÁS FELTÉTEL NÉLKÜLI ÉS FELTÉTELES OPTIMALIZÁLÁS Dr. Bécsi Tamás Hegedüs Ferenc FELTÉTEL NÉLKÜLI OPTIMALIZÁLÁS (FMINSEARCH) Feltétel nélküli optimalizálásra a MATLAB az fminsearch
MATE-INFO UBB verseny, március 25. MATEMATIKA írásbeli vizsga
BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR MATE-INFO UBB verseny, 218. március 25. MATEMATIKA írásbeli vizsga FONTOS TUDNIVALÓK: 1 A feleletválasztós feladatok,,a rész esetén
2. Logika gyakorlat Függvények és a teljes indukció
2. Logika gyakorlat Függvények és a teljes indukció Folláth János Debreceni Egyetem - Informatika Kar 2012/13. I. félév Áttekintés 1 Függvények Relációk Halmazok 2 Természetes számok Formulák Definíció
E-tananyag Matematika 9. évfolyam 2014. Függvények
Függvények Függvények értelmezése Legyen adott az A és B két nem üres halmaz. Az A halmaz minden egyes eleméhez rendeljük hozzá a B halmaz egy-egy elemét. Ez a hozzárendelés egyértelmű, és ezt a hozzárendelést
Fraktálok. Klasszikus fraktálpéldák I. Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék
Fraktálok Klasszikus fraktálpéldák I Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék TARTALOMJEGYZÉK 1 of 86 Bevezetés. 2 of 86 TARTALOMJEGYZÉK Bevezetés. Az önhasonlóságról intuitív módon Klasszikus
Az elliptikus hengerre írt csavarvonalról
1 Az elliptikus hengerre írt csavarvonalról Erről viszonylag ritkán olvashatunk, ezért most erről lesz szó. Az [ 1 ] munkában találtuk az alábbi részt 1. ábra. 1. ábra Itt a ( c ) feladat és annak megoldása
Matematika 10 Másodfokú egyenletek. matematika és fizika szakos középiskolai tanár. > o < 2015. szeptember 27.
Matematika 10 Másodfokú egyenletek Juhász László matematika és fizika szakos középiskolai tanár > o < 2015. szeptember 27. copyright: c Juhász László Ennek a könyvnek a használatát szerzői jog védi. A
x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs mátrixa 3D-ben?
. Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a
a Matematika mérnököknek I. című tárgyhoz Függvények. Függvények A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a szabadon eső test sebessége az idő függvénye. Konstans hőmérsékleten
Komputeralgebra Rendszerek
Komputeralgebra Rendszerek Polinomok Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2015. február 24. TARTALOMJEGYZÉK 1 of 80 TARTALOMJEGYZÉK I 1 TARTALOMJEGYZÉK 2 Egyváltozós polinomok Alapfogalmak
Négycsuklós mechanizmus modelljének. Adams. elkészítése, kinematikai vizsgálata,
A példa megnevezése: A példa száma: A példa szintje: Modellezõ rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: Négycsuklós mechanizmus modellezése SZIE-K2 alap közepes - haladó Adams
HÁZI FELADATOK. 1. félév. 1. konferencia A lineáris algebra alapjai
HÁZI FELADATOK. félév. konferencia A lineáris algebra alapjai Értékelés:. egység: önálló feladatmegoldás.8. Döntse el, párhuzamosak-e a következő vektorpárok: a) a( ; ; 7) b(; 5; ) b) c(; 9; 5) d(8; 6;
Koordinátarendszerek
Koordinátarendszerek KO 1 Koordinátarendszerek Ponthalmazok előállításai Koordinátarendszerek KO Két gyakran alkalmazott síkbeli koordinátarendszer Derékszögű (Descartes féle) koordinátarendszer Síkbeli
First Prev Next Last Go Back Full Screen Close Quit
Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
Függvények ábrázolása
Függvények ábrázolása Matematikai függvényeket analitikusan nem tudunk a matlabban megadni (tudunk, de ilyet még nem tanulunk). Ahhoz, hogy egy függvényt ábrázoljuk, hasonlóan kell eljárni, mint a házi
GÉPÉSZETI ALKALMAZOTT SZÁMÍTÁSTECHNIKA f iskolai mérnökhallgatók számára. A 4. gyakorlat anyaga. Adott: Geometriai méretek:
SZÉCHENYI ISTVÁN EGYETEM KÖZLEKEDÉSI ÉS GÉPÉSZMÉRNÖKI INTÉZET ÁLTALÁNOS GÉPÉSZETI TANSZÉK GÉPÉSZETI ALKALMAZOTT SZÁMÍTÁSTECHNIKA f iskolai mérnökhallgatók számára A 4. gyakorlat anyaga Feladat: Saját síkjában
2012. október 2 és 4. Dr. Vincze Szilvia
2012. október 2 és 4. Dr. Vincze Szilvia Tartalomjegyzék 1.) Az egyváltozós valós függvény fogalma, műveletek 2.) Zérushely, polinomok zérushelye 3.) Korlátosság 4.) Monotonitás 5.) Szélsőérték 6.) Konvex
Csima Judit március 9. és 16.
Grafika Csima Judit BME, VIK, Számítástudományi és Információelméleti Tanszék 2017. március 9. és 16. Csima Judit Grafika 1 / 18 Grafika általában Grafika az R-ben Van néhány alapvető package az ábrázolásra:
1. Oldja meg a z 3 (5 + 3j) (8 + 2j) 2. Adottak az A(1,4,3), B(3,1, 1), C( 5,2,4) pontok a térben.
Szak: Műszaki menedzser I. Dátum: 006. június. MEGOLDÓKULCS Tárgy: Matematika szigorlat Idő: 0 perc Neptun kód: Előadó: Berta Gábor szig 06 06 0 Pontszám: /00p. Oldja meg a z (5 + j (8 + j + = (+5j (7
RE 1. Relációk Függvények. A diákon megjelenő szövegek és képek csak a szerző (Kocsis Imre, DE MFK) engedélyével használhatók fel!
RE 1 Relációk Függvények RE 2 Definíció: Ha A, B és ρ A B, akkor azt mondjuk, hogy ρ reláció A és B között, vagy azt, hogy ρ leképezés A-ból B-be. Ha speciálisan A=B, azaz ρ A A, akkor azt mondjuk, hogy
Számítógépek alkalmazása 2
1 BME Építészmérnöki kar Építészeti Ábrázolás Tanszék Háromdimenziós szerkesztés alapjai BMEEPAG2203 Számítógépek alkalmazása 2 2. előadás 2006. március 14. Strommer László 2 Tulajdonságok szín, vonaltípus
Összeállította: dr. Leitold Adrien egyetemi docens
Az R 3 tér geometriája Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. 1 Vektorok Vektor: irányított szakasz Jel.: a, a, a, AB, Jellemzői: irány, hosszúság, (abszolút érték) jel.: a Speciális
FRAKTÁLGEOMETRIA. Példák fraktálokra I. Czirbusz Sándor február 1. Komputeralgebra Tanszék ELTE Informatika Kar
Példák fraktálokra I Czirbusz Sándor czirbusz@gmail.com Komputeralgebra Tanszék ELTE Informatika Kar 2010. február 1. Vázlat 1 Mi a fraktál? 2 A konstrukció Egyszerű tulajdonságok Triadikus ábrázolás Transzlációk
Tamás Ferenc: CSS táblázatok 2.
Tamás Ferenc: CSS táblázatok 2. Ez az írás azoknak készült, akik már értik a HTML és a CSS nyelveket, csak használat közben kellene egy adott tulajdonság vagy érték. Kérem, hogy senki se ezzel kezdje a
Információ megjelenítés Számítógépes ábrázolás. Dr. Iványi Péter
Információ megjelenítés Számítógépes ábrázolás Dr. Iványi Péter (adat szerkezet) float x,y,z,w; float r,g,b,a; } vertex; glcolor3f(0, 0.5, 0); glvertex2i(11, 31); glvertex2i(37, 71); glcolor3f(0.5, 0,
Komputeralgebra rendszerek
Komputeralgebra rendszerek III. Változók Czirbusz Sándor czirbusz@gmail.com Komputeralgebra Tanszék ELTE Informatika Kar 2009-2010 ősz Index I 1 Szimbolikus konstansok kezelés A konstansok Nevek levédése
1. dolgozat Számítógéppel segített matematikai modellezés "A" változat 2009 október 20, kedd
Név:. dolgozat Számítógéppel segített matematikai modellezés "A" változat 9 október, kedd Oldd meg a következ: feladatokat. Készíts szép notebook-ot, figyelj a korrekt strukturált megoldásokra.. feladat
Komputeralgebra rendszerek
Komputeralgebra rendszerek III. Változók Czirbusz Sándor czirbusz@gmail.com Komputeralgebra Tanszék ELTE Informatika Kar 2009-2010 ősz Index I 1 Szimbolikus konstansok kezelés A konstansok Nevek levédése
ArcGIS 8.3 segédlet 5. Dr. Iványi Péter
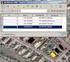ArcGIS 8.3 segédlet 5. Dr. Iványi Péter Térképek prezentálása Tartalomjegyzék Az elkészített analízis eredményeit, vagy egyszerűen magát a térképet prezentálni is kell. Ez azt jelenti, hogy össze kell
ANALÍZIS II. Példatár
ANALÍZIS II. Példatár Többszörös integrálok 3. április 8. . fejezet Feladatok 3 4.. Kett s integrálok Számítsa ki az alábbi integrálokat:...3. π 4 sinx.. (x + y) dx dy (x + y) dy dx.4. 5 3 y (5x y y 3
Feladatsor A differenciálgeometria alapja c. kurzus gyakorlatához
Feladatsor A differenciálgeometria alapja c. kurzus gyakorlatához Dr. Nagy Gábor, Geometria Tanszék 2010. szeptember 16. Görbék paraméterezése 1. feladat. (A) Bizonyítsuk be a vektoriális szorzatra vonatkozó
Hozzárendelés, lineáris függvény
Hozzárendelés, lineáris függvény Feladat 1 A ménesben a lovak száma és a lábaik száma közötti összefüggést vizsgáljuk. Hány lába van 0; 1; 2; 3; 5; 7... lónak? Készíts értéktáblázatot, és ábrázold derékszögű
PTE PMMFK Levelező-távoktatás, villamosmérnök szak
PTE PMMFK Levelező-távoktatás, villamosmérnök szak MATEMATIKA (A tantárgy tartalma és a tananyag elsajátításának időterve.) Összeállította: Kis Miklós adjunktus Tankönyvek (mindhárom félévre): 1. Scharnitzky
2012. október 9 és 11. Dr. Vincze Szilvia
2012. október 9 és 11. Dr. Vincze Szilvia Egyváltozós valós függvények nevezetes osztályai I. Algebrai függvények Racionális egész függvények (polinomok) Racionális törtfüggvények Irracionális függvények
3D koordináta-rendszerek
3D koordináta-rendszerek z z y x y x y balkezes bal-sodrású x jobbkezes jobb-sodrású z 3D transzformációk - homogén koordináták (x, y, z) megadása homogén koordinátákkal: (x, y, z, 1) (x, y, z, w) = (x,
Henger és kúp metsződő tengelyekkel
Henger és kúp metsződő tengelyekkel Ebben a dolgozatban egy forgáshenger és egy forgáskúp áthatását tanulmányozzuk abban az egyszerűbb esetben, amikor a két test tengelye egyazon síkban fekszik, vagyis
Mátrixok 2017 Mátrixok
2017 számtáblázatok" : számok rendezett halmaza, melyben a számok helye két paraméterrel van meghatározva. Például lineáris egyenletrendszer együtthatómátrixa 2 x 1 + 4 x 2 = 8 1 x 1 + 3 x 2 = 1 ( 2 4
Matematika szigorlat június 17. Neptun kód:
Név Matematika szigorlat 014. június 17. Neptun kód: 1.. 3. 4. 5. Elm. Fel. Össz. Oszt. Az eredményes szigorlat feltétele elméletből legalább 0 pont, feladatokból pedig legalább 30 pont elérése. A szigorlat
Diszkrét matematika 1. estis képzés
Diszkrét matematika 1. estis képzés 2019. tavasz 1. Diszkrét matematika 1. estis képzés 5. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
(Solid modeling, Geometric modeling) Testmodell: egy létező vagy elképzelt objektum digitális reprezentációja.
Testmodellezés Testmodellezés (Solid modeling, Geometric modeling) Testmodell: egy létező vagy elképzelt objektum digitális reprezentációja. A tervezés (modellezés) során megadjuk a objektum geometria
Számítógépes Grafika mintafeladatok
Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
9. Trigonometria. I. Nulladik ZH-ban láttuk: 1. Tegye nagyság szerint növekvő sorrendbe az alábbi értékeket! Megoldás:
9. Trigonometria I. Nulladik ZH-ban láttuk: 1. Tegye nagyság szerint növekvő sorrendbe az alábbi értékeket! x = cos 150 ; y = sin 5 ; z = tg ( 60 ) (A) z < x < y (B) x < y < z (C) y < x < z (D) z < y
Numerikus matematika
Numerikus matematika Baran Ágnes Gyakorlat Numerikus integrálás Matlab-bal Baran Ágnes Numerikus matematika 8. Gyakorlat 1 / 20 Anoním függvények, function handle Függvényeket definiálhatunk parancssorban
Relációk Függvények. A diákon megjelenő szövegek és képek csak a szerző (Kocsis Imre, DE MFK) engedélyével használhatók fel!
függvények RE 1 Relációk Függvények függvények RE 2 Definíció Ha A, B és ρ A B, akkor azt mondjuk, hogy ρ reláció A és B között, vagy azt, hogy ρ leképezés A-ból B-be. Ha speciálisan A=B, azaz ρ A A, akkor
Síkgörbék. 1. Készítsünk elfogadható ábrát a G: t frac(1/t) leképezés gráfjáról. (frac a törtrész függvény, ez a Maple függvénynév is.
Síkgörbék 1. Készítsünk elfogadható ábrát a G: t frac(1/t) leképezés gráfjáról. (frac a törtrész függvény, ez a Maple függvénynév is.) 2. (n szirmú virág.) Legyen r(t) = sin(nt), (0 t 2π). Ábrázoljuk polár
KOVÁCS BÉLA, MATEMATIKA II.
KOVÁCS BÉLA, MATEmATIkA II 7 VII VEkTORANALÍZIS 1 ELmÉLETI ALAPOk Az u függvényt skalár-vektor függvénynek nevezzük, ha értelmezési tartománya a háromdimenziós tér vektorainak halmaza, a függvényértékek
Bevezetés az algebrába 1
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Bevezetés az algebrába 1 BMETE92AX23 Egyenletrendszerek H406 2016-10-03 Wettl Ferenc
FELVÉTELI VIZSGA, szeptember 12.
BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR FELVÉTELI VIZSGA, 08. szeptember. Írásbeli vizsga MATEMATIKÁBÓL FONTOS TUDNIVALÓK: A feleletválasztós feladatok,,a rész esetén egy
I. feladatsor. 9x x x 2 6x x 9x. 12x 9x2 3. 9x 2 + x. x(x + 3) 50 (d) f(x) = 8x + 4 x(x 2 25)
I. feladatsor () Határozza meg az alábbi függvények határozatlan integrálját: (a) f(x) = (b) f(x) = x + 4 9x + (c) f(x) = (d) f(x) = 6x + 5 5x + f(x) = (f) f(x) = x + x + 5 x 6x + (g) f(x) = (h) f(x) =
2. GYAKORLAT THONET-ASZTAL
2. GYAKORLAT THONET-ASZTAL Asztallap Create Shapes Splines - Circle Modify Rendering: Sides=20 Interpolation: Steps=10 Parameters: Radius=40 Világkoordináta-rendszer középpontjába való mozgatásra nézzünk
Összeállította: dr. Leitold Adrien egyetemi docens
Skaláris szorzat az R n vektortérben Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. 1 Vektorok skaláris szorzata Két R n -beli vektor skaláris szorzata: Legyen a = (a 1,a 2,,a n ) és b
Feladatok a Gazdasági matematika II. tárgy gyakorlataihoz
Debreceni Egyetem Közgazdaságtudományi Kar Feladatok a Gazdasági matematika II tárgy gyakorlataihoz a megoldásra ajánlott feladatokat jelöli e feladatokat a félév végére megoldottnak tekintjük a nehezebb
PovRay. Oktatási segédlet
PovRay Oktatási segédlet PovRay A Povray segítségével egy speciális programozási nyelven nyelven a modelltérben (3D lebegőpontos világkordinátarendszer) definiált 3D objektumokról fotorealisztikus képeket
Nevezetes függvények
Nevezetes függvények Függvények értelmezése Legyen adott az A és B két nem üres halmaz. Az A halmaz minden egyes eleméhez rendeljük hozzá a B halmaz egy-egy elemét. Ez a hozzárendelés egyértelmű, és ezt
Görbe- és felületmodellezés. Szplájnok Felületmodellezés
Görbe- és felületmodellezés Szplájnok Felületmodellezés Spline (szplájn) Spline: Szakaszosan, parametrikus polinomokkal leírt görbe A spline nevét arról a rugalmasan hajlítható vonalzóról kapta, melyet
Robotika. Kinematika. Magyar Attila
Robotika Kinematika Magyar Attila amagyar@almos.vein.hu Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
Diszkrét matematika 1. estis képzés 2017. ősz 1. Diszkrét matematika 1. estis képzés 2. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
Eredmények, objektumok grafikus megjelenítése 3D felületek rajzoló függvényei.. Beépített 3D felületek rajzoló függvényei
Alkalmazott Informatikai Intézeti Tanszék MŰSZAKI INFORMATIKA Dr.Dudás László 0. MATLAB alapismeretek VIII. Eredmények, objektumok grafikus megjelenítése 3D felületek rajzoló függvényei.. Beépített 3D
anal2_03_szelsoertek_demo.nb 1
anal szelsoertek_demo.nb parciális deriválás f x^ y^; f Sin x Cos y ; g D f, x ; h D f, y ; Show GraphicsArray PlotD f, x,,, y,,, AxesLabel StringForm "f ``", f, None, None, DisplayFunction Identity, PlotD
HÁZI FELADATOK. 2. félév. 1. konferencia Komplex számok
Figyelem! A feladatok megoldása legyen áttekinthet és részletes, de férjen el az arra szánt helyen! Ha valamelyik HÁZI FELADATOK. félév. konferencia Komple számok Értékelés:. egység: önálló feladatmegoldás
Programozási környezetek
KOVÁSZNAI GERGELY ÉS BIRÓ CSABA EKF TTK Információtechnológia Tanszék Programozási környezetek Alkalmazható természettudományok oktatása a tudásalapú társadalomban TÁMOP-4.1.2.A/1-11/1-2011-0038 WPF Bevezetés
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
Diszkrét matematika 1. középszint 016. ősz 1. Diszkrét matematika 1. középszint 1. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
O ( 0, 0, 0 ) A ( 4, 0, 0 ) B ( 4, 3, 0 ) C ( 0, 3, 0 ) D ( 4, 0, 5 ) E ( 4, 3, 5 ) F ( 0, 3, 5 ) G ( 0, 0, 5 )
1. feladat Írjuk föl a következő vektorokat! AC, BF, BG, DF, BD, AG, GB Írjuk föl ezen vektorok egységvektorát is! a=3 m b= 4 m c= m Írjuk föl az egyes pontok koordinátáit: O ( 0, 0, 0 ) A ( 4, 0, 0 )
MÁTRIXFÜGGVÉNYEK, SAJÁT FÜGGVÉNYEK, GRAFIKA
1 4. GYAKORLAT MÁTRIXFÜGGVÉNYEK, SAJÁT FÜGGVÉNYEK, GRAFIKA SÁVMÁTRIXOK, ALSÓ- ÉS FELSŐHÁROMSZÖG MÁTRIXOK A diag parancs felhasználásával kiemelhetjük egy mátrix főátlóját vagy valamelyik mellékátlóját,
Objektumok és osztályok. Az objektumorientált programozás alapjai. Rajzolás tollal, festés ecsettel. A koordinátarendszer
Objektumok és osztályok Az objektumorientált programozás alapjai Rajzolás tollal, festés ecsettel A koordinátarendszer A vektorgrafikában az egyes grafikus elemeket (pontokat, szakaszokat, köröket, stb.)
Forgattyús mechanizmus modelljének. Adams. elkészítése, kinematikai vizsgálata,
A példa megnevezése: A példa száma: A példa szintje: Modellezõ rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: Forgattyús mechanizmus modellezése SZIE-K1 alap közepes - haladó Adams
10. modul: FÜGGVÉNYEK, FÜGGVÉNYTULAJDONSÁGOK
MATEMATIK A 9. évfolyam 10. modul: FÜGGVÉNYEK, FÜGGVÉNYTULAJDONSÁGOK KÉSZÍTETTE: CSÁKVÁRI ÁGNES Matematika A 9. évfolyam. 10. modul: FÜGGVÉNYEK, FÜGGVÉNYTULAJDONSÁGOK Tanári útmutató 2 MODULLEÍRÁS A modul
Nagy Gábor compalg.inf.elte.hu/ nagy
Diszkrét matematika 1. estis képzés 2017. ősz 1. Diszkrét matematika 1. estis képzés 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
1. Jelgenerálás, megjelenítés, jelfeldolgozás alapfunkciói
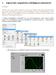1. Jelgenerálás, megjelenítés, jelfeldolgozás alapfunkciói FELADAT Készítsen egy olyan tömböt, amelynek az elemeit egy START gomb megnyomásakor feltölt a program 1 periódusnyi szinuszosan változó értékekkel.
Hajder Levente 2017/2018. II. félév
Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév Tartalom 1 2 3 Geometriai modellezés feladata A világunkat modellezni kell a térben. Valamilyen koordinátarendszer
1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás)
Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
Matematika III előadás
Matematika III. - 2. előadás Vinczéné Varga Adrienn Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Előadáskövető fóliák Vinczéné Varga Adrienn (DE-MK) Matematika III. 2016/2017/I 1 / 30 Egy