objektum-rekonstrukció gyenge perspektíva esetén
|
|
|
- Laura Balázsné
- 6 évvel ezelőtt
- Látták:
Átírás
1 Mozgásalapú háromdimenziós objektum-rekonstrukció gyenge perspektíva esetén Hajder Levente PhD értekezés Témavezetők: Dr. Csetverikov Dmitrij (MTA SZTAKI) Dr. Vajk István (BME AAIT) Magyar Tudományos Akadémia Számítástechnikai és Automatizálási Kutató Intézet Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Automatizálási és Alkalmazott Informatikai Tanszék Budapest 2007.
2 Ajánlom ezt a dolgozatot elsősorban édesapámnak, aki figyelmemet már akkor a számítástechnika területére irányította, amikor a legtöbben a számítógépet létezéséről még csak a híradásokból tudtak. Köszönöm szűkebb és tágabb családomnak a szerető támogatást, amellyel a disszertáció elkészítését lehetővé tették. Külön köszönet konzulenseimnek: prof. Csetverikov Dmirijnek és dr. Vajk Istvánnak a dolgozat elkészítésében nyújtott sok segítségéért. Hasonlóan köszönet illeti azokat az egyetemi és főiskolai hallgatókat, akiknek önálló laboratórium vagy diplomamunka készítése során a konzulense lehettem, és akiktől sok ötletet, problémafelvetést és sokszor a magaménál jobb ötleteket kaphattam: Belcsik Andrásnak, Borsa Ivánnak, Gévai Lőrincnek, Kardos Istvánnak, Kazó Csabának, Nagy-Varga Krisztiánnak, Pernek Ákosnak, Pethő Balázsnak és Újváry Gergelynek. Végül, de nem utolsósorban, köszönöm SZTAKI-s kollégáimnak, dr. Renner Gábornak, Jankó Zsoltnak és Megyesi Zoltánnak az együtt eltöltött szép pillanatokat, a közös projektekben végzett tanulságos munkákat.
3 Tartalomjegyzék 1. Bevezetés 1 2. Vetítési modellek A perspektív kameramodell Elforgatás és eltolás Vetítés Kameramodell gyenge perspektívára A modell-rekonstrukciós módszerek áttekintése Általános áttekintés Jellegzetes pontok detektálása Pontkövetés Háromdimenziós pontszámítás Általános rekonstrukciós módszerek Sztereó-rekonstrukció Rekonstrukció több képből Robusztus módszerek Pontszámítás hiányzó koordinátákkal Kamera-kalibrálás Rektifikáció és sűrű illesztés Háromszögelt felület létrehozása (felületképzés) Textúra rekonstrukció Esettanulmányok Háromdimenziós objektum rekonstrukció
4 TARTALOMJEGYZÉK Animációs trükkök: virtuális tárgyak beillesztése valós színtérbe Egyéb rekonstrukciós módszerek Összefoglaló Mozgásalapú objektum-rekonstrukció gyenge perspektíva esetén Bevezetés A Tomasi-Kanade faktorizáció Rangcsökkentés Megkötések alkalmazása merőleges vetítés esetén Megkötések gyenge perspektíva esetén A Tomasi-Kanade faktorizáció javítása Visszavetítési hiba Kiegészítő lépés S-lépés M-lépés Vizsgálati eredmények Vizsgálat szintetikus adatokon Eredmények valós képsorozaton Összefoglaló Objektum-rekonstrukció robusztus módszerei gyenge perspektíva esetén Irodalmi áttekintés Robusztus módszerek A Trajković-Kurata-féle robusztus eljárás RANSAC alapú robusztus eljárás A robusztus módszerek javítása LMedS cseréje LTS-re Affin mozgásmátrix helyett valós mozgásmátrix használata A robusztusmódszerekösszehasonlításaszintetikusadatokon Kísérletek valódi felvételeken Régió alapú mozgásszegmentálás
5 TARTALOMJEGYZÉK Irodalmi áttekintés A javasolt módszer Vizsgálati eredmények Összefoglaló Tagolt objektumok rekonstrukciója Nemmerev mozgások áttekintése Szakirodalmi áttekintés Pontszerűen kapcsolt tagolt objektumok csoportosítása A kapcsolódásipont optimális becslése legkisebbnégyzetes érelemben Vizsgálati eredmények: pontszerű illeszkedés Vizsgálat szintetikus adatokon Kísérlet valós adatokon Pontszerűen kapcsolt mozgó objektumok csoportosítása Tengellyel csatlakozó tagolt objektumok csoportosítása Két mozgó merev objektum relatív mozgásának meghatározása Vizsgálati eredmények: tengelyes csatlakozás Vizsgálatok szintetikus adatokon Vizsgálat valós adatokon Összefoglaló Összefoglalás További munkák Hivatkozások 109 A. Skálázottan ortonormált mátrix 2 3-mas részmátrixának paraméterezése 125 B. Hibafüggvény Jacobi mátrixa 127 C. A Tomasi-Kanade faktorizáció többértelműsége 129 5
6 TARTALOMJEGYZÉK D. Egy ortonormált és egy általános mátrix szorzatának pszeudoinverze 131 E. A faktorizáció változása eltolás esetén 133 F. Kötegelt behangolás (Bundle Adjustment) 135 F.1. Levenberg-Marquardt minimalizálás F.2. A Levenberg-Marquard módszer alkalmazása az objektumrekonstrukciós feladatra G. Ponthalmazok regisztrációja 139 G.1. A t eltolásvektor számítása G.2. Optimális forgatás számítása G.3. Optimális skálázás számítása H. Közös tengelyű körök illesztése háromdimenziós pontokra 143 6
7 Ábrák jegyzéke 2.1. Általános kameramodell Perspektív vetítés Gyengén perspektív vetítés Merőleges vetítés Vetítési példa. Baloldal: közeli kocka. Jobboldal: távoli kocka. Felül: perpektív vetítés. Középen: gyengén perspektív vetítés. Alul: merőleges vetítés Objektum-rekonstrukció blokkdiagramja Kalibrációs objektum Az eredeti és a rektifikált képpár Két képkocka a rekonstrukció bemeneti felvételei közül A 3D-s rekonstruált macska háromszöghálóval A 3D-s rekonstruált macska Három képkocka az arcrekonstrukció bemeneti felvételei közül A 3D-s rekonstruált arc A felvétel négy képkockája A kijelölt pontok Együtt a valós és a virtuális zsalukő A nemlineáris optimalizálás hatása. Bal: optimalizálás nélkül. Jobb: optimalizálással A felvételre renderelt mozgó fogaskerék négy képkockán Régiónöveléses algoritmus alkalmazása MR felvételeken Háromdimenziós csontfelület (aktív porcok kiemelésével)
8 ÁBRÁK JEGYZÉKE 4.1. Pontok (merőleges) vetítése Pontok (merőleges) vetítése, ha a koordinátarendszer középpontját két- és háromdimenzióban megfeleltetjük egymásnak Struktúra- és mozgáshiba a zajszint függvényében Visszavetítési hiba és az algoritmusok időigénye a zajszint függvényében Struktúra- és mozgáshiba a képkockák számának függvényében Visszavetítési hiba és az algoritmusok időigénye a képkockák számának függvényében Struktúra- és mozgáshiba a pontok számának függvényében Visszavetítési hiba és az algoritmusok időigénye a pontok számának függvényében Struktúra- és mozgáshiba a pontok számának függvényében Visszavetítési hiba és az algoritmusok időigénye a pontok számának függvényében Egy kép a sorozatból és a rekonstruált 3D-s modell A d paraméter optimális megválasztása Két pont távolsága a félkörön Bázisvektorok hibái a 2D zaj függvényében A valós és az affin metrika hibái A hibás ( x ) és a jó pontok R-RSC módszerrel a Hotel sorozaton. A helyes modellhez a pontok 93% tartozik A hibás ( x ) és a jó pontok R-LTS módszerrel a Hotel sorozaton. A helyes modellhez a pontok 85% tartozik A hibás ( x ) és a jó pontok R-LTS módszerrel saját felvételen. A helyes modellhez a pontok 42% tartozik Videósorozat két szomszédos képkockája Szintetikus szekvencia első és az utolsó képkockája Négyzet alapú régiók Szintetikus szekvencia első és az utolsó képkockája A szintetikus sorozat régióinak mozgáshibái
9 ÁBRÁK JEGYZÉKE Két domináns mozgás inkoherencia képe. Bal: kocka mozgásához képest. Jobb: gömb mozgásához képest Szegmentáció az inkoherencia képen A kocka (bal) és a gömb (jobb) szegmentált régióinak középpontjai A mackó sorozat első és utolsó képe A műanyag mackó szegmentált régióinak középpontjai Az autó sorozat első és utolsó képe Az autó szegmentált régióinak középpontjai D és 3D hiba a zaj függvényében. Balra: 2D-s hiba. Jobbra: 3D-s hiba D és 3D hiba a pontok számának függvényében. Balra: 2D-s hiba. Jobbra: 3D-s hiba D és 3D hiba a képkockák számának függvényében. Balra: 2D-s hiba. Jobbra: 3D-s hiba A kísérleti szekvencia három képkockája Az objektumok szegmentált jellegzetes pontjai Csatlakozási pont becsült helye. O : optimális módszer x :Tresadern-Reid módszer Illeszkedési hiba a zaj függvényében Illeszkedési hiba a pontok számának függvényében Illeszkedési hiba a képkockák számának függvényében Példa hibás körillesztésre A mackó és a CD doboz relatív mozgására illesztett közös tengelyű körök F.1. A normálegyenletstruktúrájaaz objektum-rekonstrukciósfeladatnál.137 F.2. A Jacobi-mátrix struktúrája az objektum-rekonstrukciós feladatnál
10 ÁBRÁK JEGYZÉKE 10
11 1. fejezet Bevezetés Amikor2001tájékán, atéli hónapokbanelhatároztam, hogydiplomámmegvédése után kutató mérnökként szeretnék dolgozni, nem volt más hátra, mint témát választani. Addig a pillanatig tanuló rendszerekkel foglalkoztam (ahogyan az villamoskari TDK dolgozataimból [45, 46] ki is derül), ám diplomamunkám konzulense alapos átgondolástjavasolt. Azttanácsolta, olyantémátválasszak, amelyek az elkövetkező évben kifogyhatatlan munícióval lát el, biztos lehetek abban, hogy csaknem fél évszázad elteltével is lehet válogatni a meg nem oldott feladatok közül. A különböző tudományterületek alapos elemzése után megszületett a döntés: a számítógépes látás, azon belül is a háromdimenziós gépi látás az a terület, amelyen hosszútávonis érdemes dolgozni. Doktorikutatásaim alatttovábbspecializálódtam: a háromdimenziós objektum-rekonstrukció és kamerarekalibráció területén kötöttem ki. Joggal vetődik fel a kérdés az Olvasóban: miért éppen gépi látás? Ha pedig gépi látás, miért háromdimenziós? A számítógépes látás nem véletlenül új tudományterület: egy folyamatos, de gyengefelbontású ( ) színes videokamerais =2, 764, 800 byte/sec sebességgel szolgáltatja a képi információt, amelyet a számítógépnek fel kell dolgoznia. Mindez sok feladatnál még a mai technika mellett is elképzelhetetlen valós-időben. Évtizedekkel ezelőtt, a khz-es processzorfrekvenciákesetében pedigteljesen reménytelen voltafeladat: éppen ezértbonyolultabb, számításigényes algoritmusokatnemvoltakképesek futtatnia kutatók. Ti- 1
12 1. BEVEZETÉS pikusanakétdimenziós, egyszerűmódszereketdolgoztakki,mintamilyen például az élkeresés, zajszűrés, képi statisztika készítése. A 80-as években a technológiai forradalomtól hajtva egyre gyorsabb és gyorsabb számítógépek jelentek meg, lehetővé téve a képfeldolgozásban a bonyolultabbalgoritmusok kifejlesztését és futtatását. Elérkezett azidő aháromdimenziós alkalmazások fejlesztésére, melyek között sok volt a más területekről (elsősorban a fotogrammetriából [117]) áthozott elméletek gyakorlati megvalósítása. A harmadik dimenzió megjelenése új perspektívát nyitott meg a gépi látásban: már nemcsak a kétdimenziós vetületet lehet feldolgozni (és a hozzájuk tartozó kontúrokat, jellegzetes textúrákatelemezni), hanem több képen látatóvetületéből háromdimenziós struktúrákat, felületeket is lehet számolni, majd vizsgálni és összehasonlítani. A 90-es években robbanásszerűen elterjedtek a háromdimenziós módszerek, amelyekelőszörkét, majdegyretöbbkép alapjánrekonstruáltakháromdimenziós objektumokat. Megjelentek az első alkalmazások is: a CAD rendszerektől a filmiparig számos helyen hasznosították a tudományos eredményeket. A módszerek többsége azonban még gyerekcipőben jár, több szempontból is: 1. Optimalitás: a módszerek rendszerint nem optimálisak (jobb esetben optimális részmegoldásokból állnak. melyek a feladat egészére már nem adnak optimális megoldást); 2. Sebesség: ipari alkalmazásoknál sokszor alapkövetelmény, hogy valósidőben működjenek; alétezőalkalmazásokazonbansokesetben mégnagyon messze vannak a valósidejű működéstől. 3. Beavatkozás: a jó működéshez legtöbbször emberi ellenőrzés szükséges, a kifejlesztett rendszerek nem annyira megbízhatóak, hogy magukra lehetne hagyni őket. Kutatómunkám során elsősorban mozgásalapú háromdimenziós objektumrekonstrukcióval foglalkoztam. A disszertációban először ismertetem a leggyakrabban alkalmazott vetítési modelleket, és megmutatom, hogy mikor lehet alkalmazni a gyenge perspektív vetítést, hiszen - mint az a későbbiekben ki fog derülni - téziseimetgyenge perspektívesetrefogalmaztammeg. Ezek utánleírom 2
13 a rekonstrukciós folyamat fontosabb módszereit, majd bemutatom azokat a tudományoseredményeket, amelyekkelreményeim szerintsikerülthozzájárulnoma terület fejlődéséhez. A dolgozat felépítése A dolgozat alapvetően két részre bontható. A kutatómunkám során kidolgozott három tézist a dolgozat második részében (negyedik, ötödik és hatodik fejezet) ismertetem, az első rész (második és harmadik fejezet) segíti a témaválasztás és a matematikai részletek megértését. A téziseimet a háromdimenziós mozgásalapú objektum-rekonstrukció területén fogalmaztam meg, mely feladatkörnek a célja videófelvételek alapján előállítani valamely tárgy valósághű háromdimenziós modelljét. A rekonstrukció folyamatáról a 2. fejezet ad részletes leírást. Ennek alapján el lehet helyezni a későbbiekben bemutatott új eredményeket a rekonstrukciós folyamatban. Az első tézisben egy újszerű faktorizációs eljárást mutatok be (amely a kétdimenziós pontokból számolja ki a háromdimenziós koordinátákat, illetve a kamera pozícióját). A második tézis első altézise egy újszerű robusztus faktorizációs módszerről szól, a második altézis pedig egy új régió alapú szegmentáló eljárást ismertet. Végezetül a harmadik tézis két módszert mutat be, amellyel pontszerűen, illetve tengely segítségével csatolt merev objektumokat lehet ún. tagolt objektumokká csoportosítani. Mivel az összes tézisemet gyenge perspektív vetítési modell feltételezésével mondtam ki, szükségesnek láttam egy külön fejezetet (3. fejezet) szentelni a vetítési modellek bemutatásának. 3
14 1. BEVEZETÉS 4
15 2. fejezet Vetítési modellek Ebbenafejezetbenrövidenáttekintjükakameramodelleket: előszöraz általános (perspektív) kameramodellel ismerkedünkmeg, majd egyszerűsítések segítségével megkapjuk a gyengén perspektív kameramodellt. R,T Z Π u v Z R,T X p(u,v) P(X,Y,Z ) P(X,Y,Z) Y X Y 2.1. ábra. Általános kameramodell 5
16 2. VETÍTÉSI MODELLEK 2.1. A perspektív kameramodell Ennek a szakasznak a célja megmutatni, hogy egy megadott P = [X, Y, Z] T pontból hogyan lehet kiszámítani a Π képsíkon levő p = [u, v] T képpontot (lásd a 2.1. ábrát). Mivel mozgó objektumok rekonstrukciójával foglalkozunk, a vetítési feladatot megelőzően egy transzformáció (elforgatás és eltolás együttese) leírása is szükséges Elforgatás és eltolás Első lépésben határozzuk meg, hogyan befolyásolja a mozgás a megadott P = [X, Y, Z] T pont pozícióját. A mozgást leírhatjuk egy R elforgatásmátrix és egy T eltolásvektor segítségével: P = R(P T) (2.1) Homogén koordinátákkal [84] tömörebb formában is felírhatjuk a transzformációt: [ P P = R[E T] 1 ahol E az egységmátrix (magyar terminológia szerint). ] (2.2) Vetítés Második lépésben le kell vetítenünk a P = [X, Y, Z ] T pontot a Π képsíkra. Így kapjuk a p = [u, v] T pontot. A vetítést az alábbi összefüggések segítségével lehet leírni: u = fk u Z X + u o (2.3) v = fk v Z Y + v o (2.4) ahol k u és k v a képek felbontását (pixelméret) adják meg (mértékegység pixel/hossz), f afókusztávolság (azazafókuszpontés akamerasíkközöttitávolság), (u o, v 0 ) pedig az úgynevezett döféspont (az a pont a képen, ahol az optikai tengely, azaz a fókuszpontból a képsíkra bocsátott egyenes metszi a képsíkot). 6
17 2.2 Kameramodell gyenge perspektívára Homogén koordináták segítségével mátrixos formában is kifejezhetjük: u v KP (2.5) 1 ahol jelöli a homogén osztás okozta skálázási többértelműséget, K pedig az ún. kalibraciós mátrix, amely így fejthető ki: fk u 0 u 0 K = 0 fk v v 0 (2.6) A transzformációt és a vetítést közös rendszerbe is össze lehet foglalni, és egy C projekciós mátrixszal lehet leírni: u [ v P KR[E T] 1 1 ] = C [ P 1 Ezzel megkaptuk az általános perspektív kameramodellt. ] (2.7) 2.2. Kameramodell gyenge perspektívára Ahhoz, hogyazáltalánosperspektívmodellrőláttérjünkagyenge perspektívára, több megszorítást kell tennünk. A legegyszerűbb megkötés szerint melyet perspektív vetítésre is szokás alkalmazni az u és v irányú felbontás egyezzen meg: k u = k v, azaz egy pixel mindkét dimenziójában ugyanakkora távolságot fogjon át. Jelöljük egyszerűen k-val ezt a felbontást meghatározó paramétert. Ez valós kameráknál elvárható, máskülönben a kamerák nagyon torzítanának. A második feltétel, hogy a mélységet az objektum egészére általánosnak tekintjük. A közös mélységet Z-vel jelöljük. Így a 2.3. és a 2.4. projekciós egyenletek átalakulnak: u = fk Z X + u o (2.8) v = fk Z Y + v o (2.9) 7
18 2. VETÍTÉSI MODELLEK Ha bevezetjük a q = fk Z -t, az elforgatási/eltolási transzformációval kiegészített összefüggés az alábbi módon írható le: u = qr1 T (P T) + u o (2.10) v = qr2 T (P T) + v o (2.11) ahol r1 T [ és r2 T ] az R elforgatásmátrix első [ és] második [ sorát ] jelenti. Bevezetve az r T M = q 1 u0 qr T r2 T mozgásmátrixot és t = 1 T v 0 qr2 T eltolásvektort, a gyenge T perspektív leképezés az alábbi egyszerű alakra hozható: [ ] [ ] u P = [M t] (2.12) v 1 A gyenge perspektív vetítés használata. E dolgozat olyan módszereket mutat be, amelyek során gyenge perspektívát feltételezünk. Gyenge perspektíva pedig csak bizonyos esetekben alkalmazható. A 2.2. ábrán láthatjuk néhány pont perspektív vetítését a képsíkra. Az elv egyszerű: a pontotösszekötjükafókuszponttal, és ott lesz azadottpont a képen, ahol ez az egyenes metszi a képsíkot. Gyenge perspektíva esetén (a 2.3. ábra) a pontokat először leképezzük a képsíkra merőleges egyenessel a súlyponton átmenő, a képsíkra merőleges síkra, majd erről a síkról valódi perspektíva segítségével vetítünk a képsíkra. A vetítések egy speciális esete a merőleges vetítés (a 2.4. ábra). Ebben az esetben a képsíkra merőleges egyenesekkel rögtön magára a képsíkra vetítjük le a pontokat. A 2.5. ábrán láthatjuk, hogy egy kocka közeli és távoli képét hogyan képzik le a különböző projekciós modellek. Meggyőződhetünk róla, hogy merőleges vetítés esetén a távolodás nem befolyásolja a méretet, ezért ez a modell csak akkor alkalmazható, ha az objektum viszonylag messze van a kamerától, és mélységben alig mozog az objektum. A gyengén perspektív és a merőleges vetítésre egyaránt igaz, hogy ami a térben párhuzamos, az a képsíkon is párhuzamos lesz. Ennek oka, hogy a tárgysíkra vetítésnél a párhuzamosság megmarad, ahogyan a projektív vetítés is megtartja a párhuzamosságot, mivel a képsíkra párhuzamos sík pontjait vetítjük le. 8
19 2.2 Kameramodell gyenge perspektívára Perspektív vetítés esetén a párhuzamosság sem igaz: a térben párhuzamos egyenesek vetületének a speciális eseteket kivéve van metszéspontja a képsíkon. A párhuzamosság alapján megállapíthajuk, hogy a gyengén perspektív vetítési modellnek akkor van létjogosultsága, ha a vetítendő tárgy mélysége (precízen fogalmazva: aképsíkhoz legközelebb és legtávolabb lévőpontok közötti mélységkülönbség) jóval kisebb, mint a képsík-tárgy távolság. 9
20 2. VETÍTÉSI MODELLEK A gyenge perspektíva előnyei. A gyenge perspektív vetítés alapvetően kétfajta előnnyel rendelkezik: Kevesebb paraméterrel tudjuk leírni a kamerát, ezért kevesebb paramétert kell megbecsülnünk; ezáltal a becslés minősége javulhat. A kevesebb paraméternek köszönhetően képesek vagyunk olyan problémákra is zárt alakú megoldást adni, ahol ismereteink szerint projektív vetítéssel zárt alakú megoldás még nem létezik. képsík fókuszpont x x x 2.2. ábra. Perspektív vetítés 10
21 2.2 Kameramodell gyenge perspektívára képsík tárgysík x x x 2.3. ábra. Gyengén perspektív vetítés képsík x x x x 2.4. ábra. Merőleges vetítés 11
22 2. VETÍTÉSI MODELLEK 2.5. ábra. Vetítési példa. Baloldal: közeli kocka. Jobboldal: távoli kocka. Felül: perpektív vetítés. Középen: gyengén perspektív vetítés. Alul: merőleges vetítés. 12
23 3. fejezet A modell-rekonstrukciós módszerek áttekintése Ebben a fejezetben röviden áttekintjük a modell-rekonstrukció egy lehetséges megvalósítását és a kapcsolódó szakirodalmat. A későbbi fejezetek csak egyegy speciális részproblémával foglalkoznak a későbbiekben, az Olvasó ebből a fejezetből alkothat átfogó képet a rekonstrukció folyamatáról Általános áttekintés A modell-rekonstrukció áttekintése a 3.1. ábrán látható. A módszer alapvetően három részre bontható: 1. Kétdimenziós rész: jellegzetes pontok meghatározása és követése. A videófelvétel első képsorozatán meg kell határozni pontokat, majd a következőkockákonkövetnikell azokat. Hapéldáulegyemberiarcotszeretnénk rekonstruálni, akkor jellegzetes pontként elképzelhető például a szem vagy az orrcsúcs. Ezeket a pontokat minél több képkockán meg kell határozni. 2. Térbeli számítás: a rekonstrukció lelke a képeken megfeleltetett pontok kétdimenziós koordinátáiból a pontok háromdimenziós koordinátáinak számítása. A kalkuláció alattszámtalanrészproblémávalszembesülhetünk, ahogyan azt a 3.4. szakaszban részletezni fogjuk. 13
24 3. A MODELL-REKONSTRUKCIÓS MÓDSZEREK ÁTTEKINTÉSE 3. Valósághű rekonstrukció: a háromdimenziós rekonstrukció akkor válik teljessé, ha háromszögeléssel, textúrával is ellátjuk a modelljeinket. Ezentúlszámtalanegyéb problémais van, amelyetnemlehet afenti kategóriákba beosztani, mint például a rektifikáció vagy a sűrű illesztés. Ebben a fejezetben ezeket a problémákat is röviden áttekintjük Jellegzetes pontok detektálása A modell-rekonstrukció első feladata a jellegzetességek detektálása. Jellegzetesség alatt elsősorban jellegzetes pontokat értünk, mert pontokat lehet a legjobban meghatározni és követni. Jól követhető pontok detektálására a Harrisdetektálót [58] kezdték alkalmazni, majd 1994-ben Tomasi és Shi módosította az eljárást [125], amelyik így - bizonyos szempontból - optimális megoldást ad. (A módszer megértéséhez érdemes Birchfield kiegészítését [16] is elolvasni.) A módszerek központi eleme az ún. lokális struktúra mátrix, amely egy adott pont körül a kép másodrendű parciális deriváltjainak lokális környezeti átlagából áll: C str = [ ] fxx fxy f yx fyy (3.1) Harris [58] heurisztikus módon jutott arra a következtetésre, hogy sarok esetén a Det(C Str ) 2 k Trace(C Str ) kifejezés nagyobb, mint élek és homogén területek esetében. k egy paraméter, amelyet 0, 04-nek szoktak a leggyakrabban választani. Tomasi és Shi [125] megmutatta, hogy minél nagyobb a C str mátrix kisebbik sajátértéke, annál jobban követhető az adott pont. Bár valóban pontokat lehet legegyszerűbben követni és rekonstrukciós feladatra alkalmazni, lehetőség van éleket [12] és régiókat [74] is felhasználni. Lehetséges optikai áramlások [68, 21, 11] használata is: ekkor a pontok minősége gyengébb lesz, viszont sokpontotkapunk, amelyeketazösszes képkockákrakövetnek az optikai áramlásokat 1 meghatározó módszerek. 1 angolul: optical flow 14
25 3.2 Jellegzetes pontok detektálása kalibrációs képsorozat Kamera kalibráció Fundamentális mátrix számítása Rektifikáció Textúrázás textúrázott 3D s modell Faktorizáció alapú számítása Sûrû illesztés Felület képzés Egyéb módszerek háromdimenziõs pontok kamera Háromdimenziós pontszámítás mozgás bemeneti képsorozat Jellegzetes pont generálás Pontkövetés 3.1. ábra. Objektum-rekonstrukció blokkdiagramja. 15
26 3. A MODELL-REKONSTRUKCIÓS MÓDSZEREK ÁTTEKINTÉSE 3.3. Pontkövetés A pontdetektáláshoz szorosan kapcsolódik a pontkövetés: például a Tomasi-Shi detektáló [125] a Kanade-Lucas-Tomasi (röviden: KLT) pontkövetőből [91, 123] alakult ki, amely a képminták elsőrendű közelítésének felhasználásával iteratív eljárással találja meg a minta helyét a következő képkockán. A KLT követő algoritmus mára a gyorsítási lehetőségekkel és a torzítási lehetőségekkel egy algoritmus-családdá nőtte ki magát, melyről a Carnegie Mellon Egyetem honlapjánrészletes összefoglalótalálható [8, 7, 5, 6, 10], illetve egykiválófolyóiratcikk is megjelent a témában [9]. A pontkövetés leírására mi is publikáltunk (magyar nyelven) egy KLT alapú megoldási javaslatot [85] Háromdimenziós pontszámítás Ha követtük a pontokat a képeken, a kétdimenziós koordináták alapján a követett pontok háromdimenziós koordinátáit ki lehet számítani. A rekonstrukció során számtalan problémávalkell megküzdenünkatakarásban levőpontoktólkezelésétől a rosszul követett pontok eldobásáig Általános rekonstrukciós módszerek Az általánosrekonstrukciósmódszerekfeltételezik, hogymindenegyes pontminden képkockán látszik. A módszerek két csoportba oszthatók aszerint, hogy két vagy több képkocka alapján becsüljük a pontok háromdimenziós koordinátáit Sztereó-rekonstrukció A szakirodalomban először a kétképes módszerek terjedtek el. Kalibrált kamera esetén már két kép alapján is lehet pontos háromdimenziós rekonstrukciót végezni. Az úttörő munkát a Nature folyóiratban publikálta Longuet- Higgins [89]. Sztereó látás esetén az epipoláris geometriát kell felhasználni, amelynek segítségével az egyik képen levő tetszőleges ponthoz meg lehet határozni a másik 16
27 3.4 Háromdimenziós pontszámítás képen egy egyenest, amelyiken a 3D-s pont vetülete elhelyezkedik. Kalibrált kamera esetén a két kamera relatív pozícióját és orientációját ki lehet számítani, ennek ismeretében pedig a Hartley-Sturm módszerrel [65] a 3D-s koordináták is számíthatók. Hartley azt is megmutatta [62], hogy a kétdimenziós koordináták normálása javítja a becslés pontosságát. Fontos fogalom a sztereó látás szempontjából az epipoláris geometriát leíró ún. fundamentális mátrix. Ennek becslésére több módszer is van: két irányzat terjedt el, attól függően, hogy nyolc pontból [62, 93] vagy hét pontból [93] végzik a fundamentális mátrix becslését. A kamera-kalibráció segítségével a fundamentális mátrixból az ún. esszenciális mátrixot lehet kiszámolni, azt pedig fel lehet bontani a T vektorral megadott pozícióra és az R orientációra [67, 61], ahogyan azt a 2 fejezetben a kameramodelleknél megmutattuk. Végezetül (mint általában a rekonstrukciós és a kalibrációs feladatoknál) az összes paramétert egy lépésben szokták optimalizálni valamilyen numerikus optimalizálási módszerrel [107, 88, 96, 73]. Erre azért van szükség, mert a becslő módszerek nem adnak optimális eredményt, a becsléseken lehet még javítani Rekonstrukció több képből Ha két képből a háromdimenziós mozgást ki lehet számolni, akkor logikus, hogy három képből is lehet. A fundamentális mátrixot ebben az esetben a trifokális tenzor váltja fel [60, 116, 33]. A trifokális tenzor nemcsak pontok, hanem egyenesek segítségével is becsülhető. Azt is megmutatták [63], hogy négy képre is lehet definiálni egy tenzort, az úgynevezett quadrifokális tenzort, amely a 4 kép közötti transzformációkat írja le. Ennek azonban már kisebb a jelentősége, mert a tetszőleges számú képre alkalmazott módszerek jobban használhatónak bizonyultak. A többképes módszerek egyszerűbb változatai a 90-es évek elején jelentek meg. E munkában a Carnegie Mellon egyetem kutatócsoportja úttörő szerepet vállalt. Először merőleges vetítésre [124] dolgozták ki a kisebb-nagyobb módosításokkalazótais használatos módszerüket. Hamarosanmegjelentagyenge 17
28 3. A MODELL-REKONSTRUKCIÓS MÓDSZEREK ÁTTEKINTÉSE perspektíva [136] és a paraperspektív [104] kiterjesztés. A Tomasi-Kanade faktorizáció javítására mi is publikáltunk újszerű eredményt [86, 49], amelyet a 4. fejezetben ismertetni is fogunk. A valódi perspektívára a feladatot a Triggs-Sturm kutatópáros oldotta meg először [121]. A megoldás viszonylag kézenfekvő: visszavezetik a perspektív problémát az eredeti, merőleges vetítés esetére úgy, hogy a sztereó módszer segítségével megbecsülik a pontok mélységét, majd azokkal visszaszorozva a kétdimenziós koordinátákat el lehet végezni a faktorizációt is, amely nagyon hasonlít az eredeti Tomasi-Kanade módszerre [124]. Ezek a módszerek kiválóan alkalmasak arra, hogy zajmentes esetben kiszámítsák a pontos eredményt, és zajos esetben is elfogadható rekonstrukciót adnak. A megoldás azonban nem pontos, mivel általában egy absztrakt térben levő hibát minimalizál, és nem a képtérben levő hibát. Ezért utolsó lépéskéntáltalábanegy képtérbeli numerikusoptimalizálással [107] pontosítjákaz eredményeket. Bebizonyították [117, 15, 90], hogy iteratív numerikus módszerrel (pl. A Levenberg-Marquardt algoritmus [88, 96, 73] segítségével) egyszerre lehet optimalizálni a kameraparamétereket és a háromdimenziós koordinátákat. Ez sokszor több ezer paramétert jelent. Az optimalizálás azért lehetséges, mert a Jacobi mátrix nagyon ritka. A módszert magyarul kötegelt beállításnak lehet nevezni az angol bundle adjustment kifejezés szószerinti fordításával. A köteg szó a beállítandó paraméterek magas számára utal Robusztus módszerek Nagyon fontos a rekonstrukciós folyamat során a robusztusság kérdése: mivel nem tudjuk garantálni, hogy minden egyes, kétdimenzióban követett pont jól lett meghatározva, a modellünket pedig csak a jó pontok alapján szabad elkészíteni, a rosszul követett pontokat el kell dobni. Szerencsére a robusztus regressziókhoz kifejlesztett módszerek [110] egy része átültethető a rekonstrukciós feladatokhoz is. A legnépszerűbb módszer a RANSAC [34], amelyet alkalmaztak sztereó látás [127, 128] és trifokális tenzor [126] alapú módszerek robusztussá tételéhez egyaránt. 18
29 3.5 Kamera-kalibrálás A faktorizációs módszerek esetében általánosan elterjedt megoldás, hogy Monte-Carlo módszerek segítségével keresnek domináns kameramozgást, és ennek segítségével különítik el a jó és a rossz adatokat egymástól [130, 82, 109]. A robusztus módszerek sorában az új hullámot a konvex (és kvázi-konvex) optimalizáláson alapuló módszerek jelentik [76, 75, 80], amelyek Frobenius-norma helyett más robusztus normákat optimalizálnak. Robusztus pontbecslésre mi is javasoltunk módszereket [55, 86, 53], amelyet az 5. fejezetben ismertetni fogunk Pontszámítás hiányzó koordinátákkal Sok kép esetén majdnem lehetetlen, hogy egyes jellegzetes pontok minden egyes képen jelen legyenek, hiszentakarás, átfordulás miatt tűnnek el a pontok, jelennek meg újabb részek. Érdekes, hogy a problémával már az eredeti Tomasi-Kanade faktorizációs cikk [124] is foglalkozott, azonban igazán jól működő módszereket csak az ezredforduló környékén kezdtek publikálni. A probléma kezelésére alapvetően két megközelítés létezik: 1. Az első megoldás [13, 35, 81] szerint két-három képből előállítunk egy kezdeti rekonstrukciót, majd ezt inkrementális elven pontosítjuk a többi kép figyelembevételével. Fontos megjegyeznünk, hogy a folyamat végén nemlineáris optimalizálással hiányzó adatok esetén is lehet az eredményt pontosítani. 2. A másik megoldási lehetőség szerint [42, 134, 23] egyben kezelik az összes pontot, és különböző faktorizációs (matematikai) módszerek segítségével oldják meg a problémát Kamera-kalibrálás Ahogyan azt már a 2. fejezetben leírtuk, a kameraparaméterek nélkül nem lehet a projekciót kiszámítani valódi perspektíva esetén. A gyenge perspektíva előnye, hogy csupán a külső paraméterek (elforgatási és eltolási mátrixok) és 19
30 3. A MODELL-REKONSTRUKCIÓS MÓDSZEREK ÁTTEKINTÉSE egyskálázásiparaméterbecslésére vanszükség, egyéb kameraparamétereketnem szükséges kiszámítanunk. A kalibrációs technikákat alapvetően két csoportba lehet sorolni: 1. Fotogrammetrikus kalibráció: mint az elnevezés is mutatja, már a fotogrammetriában is használták [20, 30]. A számítógépes látás kutatási eredményei további lendületetadottamódszerek fejlesztésének [32, 38, 41, 138, 135]. A fotogrammetrikus kalibrációhoz szükséges egy háromdimenziós kalibrációs objektum, melyet fényképezőgéppel felveszünk. A vetítési hibát a kameraparaméterek szerint minimalizálni tudjuk. A kalibrációs objektumra egy egyszerű példát láthatunk a 3.2. ábrán. A vetítési hiba minimalizálása általában két lépésben történik: először egy ún. algebrai hibát minimalizálunk optimálisan, majd az így megkapott paraméterértékeket nemlineáris optimalizálás segítségével [88, 96, 73] a képtérben minimalizálunk. A fotogrammetrikus kalibráció előnye az autókalibrációhoz képest, hogy a kiszámított értékek pontosabbak lesznek. Hátránya, hogy a paramétereket csak a referenciaképen képes meghatározni. Videofelvétel esetén elképzelhető, hogy az egyes képkockákon megváltoznak a paraméterek értékei: tipikus példa a fókuszpont, amelyet például gumioptika (zoom) használata esetén nem tekinthetünk változatlannak. 2. Autokalibráció: nincsen szükség kalibrációs objektumra, a kalibrációs adatok a rekonstrukció folyamán a kamera- és struktúra-információval 1 párhuzamosankerülnekkiszámításra. A módszerek alapjaa3.4. szakaszban említett kötegelt beállítás (bundle adjustment) algoritmus. Az eredmény ugyan pontatlanabb lesz a fotogrammetrikus rekonstrukcióhoz képest, de a megoldás minden esetben kiszámítható [59, 108, 72]. 20
31 3.6 Rektifikáció és sűrű illesztés 3.2. ábra. Kalibrációs objektum ábra. Az eredeti és a rektifikált képpár. 21
32 3. A MODELL-REKONSTRUKCIÓS MÓDSZEREK ÁTTEKINTÉSE 3.6. Rektifikáció és sűrű illesztés Eddig hagyományos mintaillesztő eljárásokkal feleltettük meg egymásnak a pontokat az egyes képeken. A mintaillesztő eljárások kétdimenzióban keresnek, és ezért csak viszonylag ritka megfeleltetést tudnak elérni. A sűrű illesztéshez először is rektifikálni szokták a képeket [64, 105, 61, 132]. A rektifikáció eredményeképpen igaz lesz, hogy ha egymás mellé tesszük a két rektifikáltképet, akkor az elsőkép egytetszőleges pontjánakpárja amásikképen ugyanabban a sorban lesz. Rektifikációra a 3.3. ábrán láthatunk egy példát. A már rektifikált képeket ezek után a sűrű illesztő eljárások segítségével kell feldolgozni. Sűrű illesztésre több módszer létezik a szakirodalomban. Régebben sűrű illesztést általában keskeny bázistávolságú sztereóra 1 alkalmaztak. Keskeny bázistávolságú sztereónak azt az esetet nevezzük, amikor a két képet elkészítő kamerák távolsága az objektum méreteihez viszonyítva kicsi (tipikus példa a keskeny bázistávolságú sztereóra az emberi szem). Nagy távolság esetén széles bázistávolságú sztereóról 2 beszélünk. Keskenybázistávolságúsztereóesetén globálisenergiaminimalizálásonalapuló módszereket szokás alkalmazni [113, 144], bár létezik hasonló módszer a széles bázistávolságú esetre is [120, 119]. A módszer lényege, hogy energiafüggvényt ír fel az epipoláris kényszerek és a színinformáció alapján, melyekben a felület simaságát jutalmazzák és takarást is megengednek. Másik elterjedt megoldás a régió alapú szegmentálás [99, 37], ahol magpontokból kiindulva régiónöveléses technikát alkalmaznak a megfeleltetés elkészítésére. A régiónöveléshez feltételezik, hogy a megfeleltetett régiók között affin [99], bonyolultabbesetbenperspektív [37] sík-síkmegfeleltetések írhatókfel. 1 A szakirodalomban struktúrának a háromdimenziós koordináták együttesét szokták nevezni. 1 angolul: short baseline stereo 2 angolul: wide baseline stereo 22
33 3.7 Háromszögelt felület létrehozása (felületképzés) 3.7. Háromszögelt felület létrehozása (felületképzés) A kapott (minél sűrűbb) háromdimenziós ponthalmazra háromszögeket kell illeszteni, amelyek a tárgy felületét reprezentálják. A legtöbb háromszögelő algoritmus alapja az ún. Dealunay-háromszögelés [4]. Ez az algoritmus kétdimenziós háromszögeléssel foglalkozik, de azon belül optimális megoldást ad (az optimalitás kritériuma, hogy a legkisebb szög maximális legyen a háromszögelésben). Számtalan kiterjesztés létezik, amelyek vagy a Delaunay-háromszögelést terjesztik ki magasabb háromdimenzióba [25, 18, 44, 83] vagy az ún. masírozó kockák 1 algoritmust alkalmazzák [66, 26] Textúra rekonstrukció Miután megkaptuk a háromszögelt modellt, utolsó feladatunk textúrázni a háromszögeket. A feladat nem egyszerű, mert az apró illesztési hibák miatt a háromszögekillesztése nem pontos. Ennek megoldására többféle stratégialétezik: 1. Egy képről kell venni az összes információt. Ebben az esetben az illesztés tökéletes lesz, de ha egy háromszög az adott kamerapozícióból kicsi szög alatt látszik, akkor a rekonstruált textúra nagyon durva lesz [81]. 2. Minden egyes háromszöghöz arról a képről vesszük a textúrainformációt, amelyiken a legjobban látszik. Ezáltal részletes lesz a modell, viszont a textúrák határán illesztési hibák lépnek fel. 3. Valamilyen eljárással súlyozzuk a képeken a háromszögeket, és a súlyozásnak megfelelően állítjuk elő a textúrákat [143, 27, 98] vagy egyszerűen elsimítjuk a kapott textúrákat [94, 24, 29]. 1 angolul: marching cube 23
34 3. A MODELL-REKONSTRUKCIÓS MÓDSZEREK ÁTTEKINTÉSE 3.9. Esettanulmányok A modellrekonstrukciókra egyetemi hallgatók segédletével már jó néhány megoldást készítettünk, melyek folyományaként diplomamunkák és TDK dolgozatok is születtek [14, 147, 43, 79, 102, 103]. Ebben a szakaszban megmutatjuk néhány konkrét feladat megoldásán keresztül, hogyan lehet a fejezetben ismertetett módszereket alkalmazni Háromdimenziós objektum rekonstrukció Két példát is nézünk objektum-rekonstrukcióra: először egy macskát ábrázoló, 360 fokban megforgatott szobor háromdimenziós rekonstrukciójátvégezzük el perspektívvetítéstfeltételező módszerek felhasználásával, majd gyenge perspektívfaktorizációsegítségévelrekonstruálunkegyemberi arcot. Szobor rekonstrukciója: A macska-szoborról összesen 80 képet készítettünk (lásd. a 3.4. ábrát): letettük a macskát az asztalra, és manuálisan forgattuk, minden pozícióban készítettünk egy képet. A 80 kép alapján végeztük el a rekonstrukciót. A rekonstrukciós munkát Belcsik András diplomamunkájában részletesen leírta [14], itt csak röviden ismertetjük közös munkánk eredményét. A rekonstrukció során a pontokat két dimenzióban az elterjedt KLT algoritmus [91, 123] segítségével detektáltuk, majd korreláció alapú mintaillesztés segítségével [28] követtük. Háromdimenziós pontszámításra és kamerakalibrálásra sztereó módszereket használtunk [89, 61, 65]. A robusztusságot egyszerű sztereó RANSAC eljárás segítségével [34, 105] biztosítottuk. A kapott háromdimenziós pontokat a masírozó kockák algoritmus [26] segítségével háromszögeltük, a textúrákat pedig mindig arról a képről vettük, ahol az a legjobban látszik [79]. A rekonstruált objektumot a 3.6 ábrán lehet megtekinteni, a 3.5 ábrán a háromszögelést kiemeltük, hogy jobban látszódjon. Emberi arc rekonstrukciója. 24
35 3.9 Esettanulmányok 3.4. ábra. Két képkocka a rekonstrukció bemeneti felvételei közül. Három képet készítettünk (3.7. ábra), mindegyiken manuálisan kijelöltünk 65 pontot. Az 1. tézisben (4. fejezet) bemutatott algoritmus segítségével háromdimenzióban rekonstruáltuk az arcot, a háromszögelést az optimális síkba történő vetítés után Delaunay-háromszögelő eljárással [4] valósítottuk meg. A textúrázást pedig a három képből egyidejűleg, súlyozással [79] valósítottuk meg. A rekonstruált objektumot a 3.8. ábrán tekinthetjük meg. A munka részleteit egyetemista hallgatók segítségével TDK dolgozatokban is publikáltuk [102, 79] Animációs trükkök: virtuális tárgyak beillesztése valós színtérbe Másik feladattípus, amelyből bemutatunk néhány eredményt, az animációs trükkök világába vezet bennünket: adott egy valós felvétel, amelyre úgy szeretnénk mesterséges objektumokat felvinni, hogy azok kövessék a kamera mozgását. A mi példánkon néhány zsalukőről készítettünk videófelvételt (3.9. ábra). Célunk volt egy egyenletes sebességgel mozgó objektumot esetünkben egy 25
36 3. A MODELL-REKONSTRUKCIÓS MÓDSZEREK ÁTTEKINTÉSE 3.5. ábra. A 3D-s rekonstruált macska háromszöghálóval. függőlegesen haladó fogaskereket renderelni a felvételre. (Végső célunk futkározó bogarak animálása, de ehhez a műszaki érzéken túl egyéb képességekre is szükség van, amelyekkel mi nem rendelkezünk. A feladatot már kiadtuk egyetemistáknak, ám jelen dolgozat elkészültéig még nem készült el az eredmény.) Bár a feladat bonyolultnak tűnik, a megoldás a hagyományos rekonstrukciós feladatoknál jóval egyszerűbb, és az alábbi lépésekben foglalható össze: 1. Háromdimenziós modell manuális felépítése. Az egyik zsalukőről 3D-s modellt kellett készítenünk. Szerencsére az építőipar szögletes sablonokkal dolgozik, ezért az oldalak lemérésével és egy háromdimenziós modellezőszoftverrel a feladat könnyen teljesíthető volt. 2. Pontok azonosítása. Összesen 100 képkockára rendereltünk animációt, ezért mind a 100 képen ki kell jelölni a látszó pontokat. Ez a rész volt a munka legunalmasabb része: kb. 60 pontot kellett 100 képkockán kijelölni, azaz nagyságrendileg 6000 klikkelésre volt szükség, amely 4-5 óra munkát jelentett. 26
37 3.10 Egyéb rekonstrukciós módszerek 3. Kamera kalibráció. Ahogyan azt már a 3.5 szakaszban leírtuk, a kamera kalibrálása segítségével meg tudjuk határozni a projekciót a háromdimenziós objektum és a képek között. A kamera kalibrálását két lépcsőben valósítottuk meg: Először a projekciós mátrix segítségével megfogalmaztunk egy algebrai hibát [61], amelysegítségével becsléstkaptunkakameraparamétereire. Második lépésben a képtérben levő illesztési hibát minimalizáltuk nemlineáris optimalizálás segítségével, ahol a paraméterek kiindulási pontját az első lépcső eredménye adja. A második lépcső (nemlineáris optimalizálás) hatékonyságát a 3.12 ábra szemlélteti. Jól látható, hogy a zsalukő orientációján csak picit finomít a módszer, a pozíción annál többet. Ennek oka, hogy tapasztalataink szerint az analitikus optimalizálás során a kamera döféspontja (ahol a fókuszpontból húzott, a képsíkra merőleges egyenes metszi a képsíkot) nagyon hibaérzékeny. 4. Renderelés. Végezetül a kamera paramétereket át kellett számolni a renderelelő-szoftverünk [2] rendszerébe, és ennek megfelelően a mesterséges, mozgó objektumot rá lehetett renderelni az eredeti képekre. A végeredmény néhány képkockáját a képen láthatjuk. A módszer leírására szintén született egy TDK dolgozat [103] Egyéb rekonstrukciós módszerek Háromdimenziós objektum-rekonstrukcióra egyéb módszerek is léteznek. Például a háromdimenziós pontok kiszámítása nem csak kétdimenzióban követett jellegzetes pontok, hanem kontúrok alapján is lehet rekonstruálni [87, 97]. Jelen dolgozatnaknem céljaaz összes lehetséges eljárást bemutatni, mindössze egy rövid példát mutatnánk az orvosi alkalmazásokról, lévén saját eredményeket is publikáltunk a témában [56, 78]. Célunk volt anatómiai struktúrák háromdimenziós rekonstrukcióját elvégezni MR felvételek alapján. Az MR 27
38 3. A MODELL-REKONSTRUKCIÓS MÓDSZEREK ÁTTEKINTÉSE felvétel kimenete tipikusan százas nagyságrendbe eső kép, amelyeken a csont és a környező szövetek jól elkülöníthetőek az intenzitásértékek alapján. Mi az ún. Fast Marchning eljárást alkalmaztuk [114, 115, 31]. Ennek segítségével háromdimenzióban rekonstruálni tudtuk a csontfelületet (3.15. ábra) Összefoglaló Ebben a fejezetben a modellrekonstrukció egy lehetséges folyamatát ismertettük blokk-diagrammon, majdnagyonrövidenbemutattukaz egyes részfeladatokmegoldására publikált, általunk leghasznosabbnak tartott módszereket. Ezek után konkrét példákon keresztül is bemutattuk, hogy a leírásra került módszerek segítségével valóban lehet háromdimenziós objektum-rekonstrukciót készíteni képekből, illetve egy felvételen azt is megmutattok, hogy 3D-s animációs trükköket is tudunk készíteni. 28
39 3.11 Összefoglaló 3.6. ábra. A 3D-s rekonstruált macska. 29
40 3. A MODELL-REKONSTRUKCIÓS MÓDSZEREK ÁTTEKINTÉSE 3.7. ábra. Három képkocka az arcrekonstrukció bemeneti felvételei közül ábra. A 3D-s rekonstruált arc. 30
41 3.11 Összefoglaló 3.9. ábra. A felvétel négy képkockája ábra. A kijelölt pontok. 31
42 3. A MODELL-REKONSTRUKCIÓS MÓDSZEREK ÁTTEKINTÉSE ábra. Együtt a valós és a virtuális zsalukő. 32
43 3.11 Összefoglaló ábra. A nemlineáris optimalizálás hatása. Bal: optimalizálás nélkül. Jobb: optimalizálással. 33
44 3. A MODELL-REKONSTRUKCIÓS MÓDSZEREK ÁTTEKINTÉSE ábra. A felvételre renderelt mozgó fogaskerék négy képkockán ábra. Régiónöveléses algoritmus alkalmazása MR felvételeken. 34
45 3.11 Összefoglaló ábra. Háromdimenziós csontfelület (aktív porcok kiemelésével). 35
46 3. A MODELL-REKONSTRUKCIÓS MÓDSZEREK ÁTTEKINTÉSE 36
47 4. fejezet Mozgásalapú objektum-rekonstrukció gyenge perspektíva esetén Ebbenafejezetben rátérünk arekonstrukciósfeladattalánlegfontosabbrészének megoldására: a háromdimenziós pontok koordinátáinak becslésére. A fejezet elején a Tomasi-Kanade [124] faktorizációs módszer részletes ismertetése szerepel, amely gyenge perspektíva alatt a leggyakrabban alkalmazott térbeli pontbecslésnek számít, mivel két, egyenként zárt alakú megoldás segítségével gyorsan képes a becslési feladatot megoldani. A fejezet második felében egy új algoritmust mutatunk be, amelyet ben dolgoztunk ki és publikáltunk [47, 49, 86, 57,?]. Ezután szintetikus adatokon mutatjuk meg, hogy a módszeraz alapalgoritmusnál [124] jobbbecsléstadazobjektumháromdimenziós koordinátáira. A módszert összehasonlítjuk a kötegelt behangolás [15, 90] gyenge perspektív változatával Bevezetés A háromdimenziós mozgásalapú objektum- és kamerarekonstrukció (angolul Structure from Motion vagy rövidítve SfM) problémája két évtizede foglalkoztatja intenzíven a számítógépes látás kutatóit. A kifejlesztett módszerek között a legismertebb, máig alkalmazott módszer a Tomasi-Kanade faktorizáció [124], amely 37
48 4. MOZGÁSALAPÚ OBJEKTUM-REKONSTRUKCIÓ GYENGE PERSPEKTÍVA ESETÉN a kétdimenzióban követett pontokból becsüli meg a pontok háromdimenziós koordinátáit, és a kamera pozícióját minden egyes képkockán. Az eredeti módszer [124] egy mozgó, merev objektumnak számítja ki a térbeli koordinátáit. A módszer merőleges vetítést feltételez, melyet a későbbiekben kiterjesztettek gyenge perspektívára [136], majd a paraperspektív esetre [104]. A valódi perspektív faktorizáció 1996-ban jelent meg [121], de ez nem adott végleges megoldást, hiszen az eredmény nem pontos, hanem egy lineáris torzítás erejéig bizonytalan. Az eredeti Tomasi-Kanade faktorizáció [124] két lépésből áll, melyet a következő szakaszokban részletesen is ismertetünk: 1. SVD-lépés. Ha a kétdimenzióban követett pályák koordinátáit belehelyezzük egy ún. mérési mátrixba, akkor megmutatható, hogy súlypontra centrálás 1 esetén ennek a mátrixnak a rangja három. Mindez csak zajmentes esetben igaz. Mivel a pontok helyét kétdimenzióban határozzuk meg, de a módszerek pontatlanok, a valódi adatokat tartalmazó mérési mátrix rangját 3-ra kell csökkenteni. Ehhez a PCA algoritmust 2 érdemes használni (praktikusan SVD, szinguláris értékek szerinti felbontás segítségével számítva), amely optimális rangcsökkentést végez azáltal, hogy megadja azt a 3- dimenziós alteret, amelybe a mátrix eredeti sorai a legkisebb négyzetes hibával vetíthetők [17]. 2. Transzformációs lépés. Az optimálisaltérben egytetszőleges lineáristranszformáció elvégezhető anélkül, hogy az eredmény hibája változna. A lehetséges transzformációk közül azt kell kiválasztani, amelyikre a kameraparaméterek leginkább megfelelnek a követelményeknek, ahogyan azt majd azt a és szakaszban formulák segítségével fel fogjuk írni. A fő ok, amely miatt a Tomasi-Kanade faktorizációt javítani lehet, az SVD lépés: ez meghatároz egyalteret, amely ugyanoptimális avetítés szempontjából, de nem optimális megoldás a feladat szemszögéből. A transzformációs lépés már 1 Súlypontra centráltnak nevezzük azt a mérési mátrixot, amely az eredeti mérési mátrixból úgyszámítható, hogymindensorpárbólkivonjuka kétdimenziós pontoksúlypontját. Részletek a [124]-ban olvashatóak. 2 A PCA elnevezés a Principal Component Analysis (magyarul: főkomponens analízis) rövidítéséből származik. 38
49 4.2 A Tomasi-Kanade faktorizáció nem tudja az eredményt kimozdítani ebből az altérből. Erre a problémára javasoltunk egy javított módszert [49, 86], amelyet a 4.3. szakaszban ismertetünk. A módszerünk az eredeti Tomasi-Kanade faktorizáció eredményét két független lépésben finomítja: a kamera paramétereit és a háromdimenziós pontokat különkülön. A fejezet felépítése a következő: A Tomasi-Kanade faktorizációt [124] a gyenge perspektív kiegészítéssel [136] tekintjük át először. Ezután a javasolt módszer ismertetésére kerül sor a 4.3. szakaszban. Majd kvantitatív vizsgálatokat mutatunk be szintetikus adatokon, és módszerünket összehasonlítjuk az eredeti [124, 136] és a kötegelt behangolásos módszerrel [15, 90] javított algoritmusokkal A Tomasi-Kanade faktorizáció Ha adott valamely merev mozgó objektum P darab (jellegzetes) pontja, amelyeket F számú képkockán keresztül követtünk, és a p-edik követett pont koordinátáit az f-edik képen x fp = (u fp, v fp ) T jelöli, akkor merőleges vetítés esetén a pont helye a következő módon számítható (lásd a 4.1. ábrát): x fp = R f s p + t f, (4.1) ahol R f = [r f1, r f2 ] T ortonormált mátrix első két sora, s p a jellegzetes pont háromdimenziós koordinátája, t f pedig az objektum-koordinátarendszere vetületének helye a képsík origójához képest. Gyenge perspektíva esetén az összefüggés kiegészül a gyenge perspektíva q f (nem nulla) skalárszorzójával (mindez a kamera modelleknél levezetett, gyenge perspektív vetítést leíró összefüggéssel egyezik meg): x fp = q f R f s p + t f, (4.2) A t f eltolás kiküszöbölhető, ha az objektum saját koordinátarendszerében a középpontját úgy választjuk meg, hogy az origó vetületét minden képen ismerjük (lásd a 4.2. ábrát). Praktikus és numerikus számítási megfontolásból a pontok átlagát, azaz a súlypontot szokták origónak választani, hiszen merőleges 39
50 4. MOZGÁSALAPÚ OBJEKTUM-REKONSTRUKCIÓ GYENGE PERSPEKTÍVA ESETÉN si s j r f1 x fi r f2 x fj t f 4.1. ábra. Pontok (merőleges) vetítése. s i s j x fi r f2 x fj t f rf1 4.2.ábra. Pontok (merőleges)vetítése, haakoordinátarendszer középpontjátkétés háromdimenzióban megfeleltetjük egymásnak. 40
51 4.2 A Tomasi-Kanade faktorizáció vetítés esetén kétdimenzióban és háromdimenzióban is a koordináták egyszerű átlagolásával meghatározható a súlypont. Ebben az esetben felírhatjuk, hogy x fp = q f R f s p. (4.3) Ha az összes pontot figyelembe vesszük az adott képen, a fenti egyenletből mátrixegyenletet készíthetünk: W f }{{} 2 P = (x f1...x fp ) = M }{{} f 2 3 S }{{} 3 P (4.4) ahol M f neve mozgásmátrix, S = (s 1,...,s P ) pedig a struktúramátrix. Merőleges vetítés esetén M f = R f, míg gyenge perspektíva alatt M f = q f R f. Havesszükaz összes képkockát, a 4.4. összefüggés alapjánamérési mátrixot is kifejezhetjük: W }{{} 2F P = M }{{} 2F 3 }{{}, (4.5) 3 P S ahol W T = [W T 1, W T 2,...,W T F ] és MT = [M T 1, M T 2,...,M T F ]. A feladat a W mérési mátrix szorzattá bontása (faktorizálása), és az M mozgási, valamint az S struktúramátrix becslése. Ahogyan azt a bevezetőben olvashattuk, a Tomasi-Kanade faktorizációs módszer két lépésben végzi el a feladatot: először egy rangcsökkentéssel zajszűrést hajt végre, majd a kapott altérben elvégzi azt a transzformációt, amely végén megkapjuk a kívánt mátrixokat Rangcsökkentés A W mérési mátrix SVD segítségével felbontható három mátrix szorzatára. Mivel a 4.5. egyenlet alapján a W mátrix rangja zajmentes esetben 3, meg kell találni azt a 3-dimenziós alteret, amelybe a W mátrix oszlopai optimálisan vetíthetők. A főkomponens analízis 1 [17] legkisebb négyzetes hiba szerint optimális megoldást ad. Mindez szinguláris értékek szerinti felbontással kiszámítható: Legyen W felbontása: W = UΣV T, ahol Σ diagonális (téglalap alakú) mátrix tartalmazza a nemnegatív szinguláris értékeket. Ha ennek a Σ mátrixnak vesszük az első három elemét (a többit elhagyjuk), U és V mátrixoknak pedig az első három 1 angolul principal component analysis - röviden PCA 41
52 4. MOZGÁSALAPÚ OBJEKTUM-REKONSTRUKCIÓ GYENGE PERSPEKTÍVA ESETÉN sorát ill. oszlopát hagyjuk el, az így kapott csonka mátrixokat Σ -vel, U -vel és V -vel jelöljük, akkor a mozgás és a struktúramátrixokra affin becslés 1 adható: ˆM = U Σ és Ŝ = V T. Az ˆM mátrixot a továbbiakban affin mozgás-, a Ŝ mátrixot pedig affin struktúramátrixnak nevezzük. Esetünkben ˆM tartalmazza a kamerasíkok bázisvektorainak torzított változatát, ahol a torzítás egy lineáris (azaz affin) transzformáció segítségével történik. Maga a faktorizáció a Ŵ = ˆMŜ összefüggéssel írható le. Triviális, hogyha beillesztjük a 3 3-mas nemszinguláris Q mátrixot és inverzét az összefüggésbe, akkor a becslés pontossága nem változik: ˆMŜ = ( ˆMQ)(Q 1 Ŝ). A kérdés csak az, hogyan lehet a Q transzformációt meghatározni. Legyen R = ˆMQ, ahol R = [r 11, r 12,...,r F1, r F2 ] T tartalmazza a kamerasíkok bázisvektorait. Tudjuk, hogy ezek a vektorok nem lehetnek tetszőlegesek: egyazon sík két bázisvektorának merőlegesnek kell lennie, hosszuknak egységnyinek (merőleges vetítés esetén), vagy azonosnak (gyenge perspektíva esetén). A további fejezetekben az M = ˆMQ és az S = Q 1 Ŝ mátrixokat valós mozgásés struktúramátrixoknak fogjuk nevezni Megkötések alkalmazása merőleges vetítés esetén Ha az összes képkockára felírjuk a fenti megkötéseket, Q T Q-ra túlhatározott lineáris egyenletrendszert kapunk, ezért Q-ra zárt alakú megoldás adható, amelyet először Morita és Kanade publikált [100] 1994-ben. Merőleges vetítés esetén a bázisvektorok ortonormáltak. Mindez képkockánként három megkötést eredményez: r T f1r f1 = ˆm T f1 QT Q ˆm f1 = 1, r T f2r f2 = ˆm T f2 QT Q ˆm f2 = 1, r T f1r f2 = ˆm T f1 QT Q ˆm f2 = 0 Vezessük be a szimmetrikus L mátrixot: L = Q T Q = l 1 l 2 l 3 l 2 l 4 l 5 l 3 l 5 l 6 (4.6) 1 Azért nevezzük affin becslésnek, mert a pontos (metrikus) becslés affint transzformáltját kapjuk meg. 42
53 4.2 A Tomasi-Kanade faktorizáció A megkötések alapján L mátrix optimálisan meghatározható a kapott túlhatározott lineáris egyenletrendszer segítségével: l 1 l 2 l 3 l 4 l 5 l 6 = vagy egyszerűen l = G c, ahol G g T ( ˆm 11, ˆm 11 ) g T ( ˆm 12, ˆm 12 ) g T ( ˆm 11, ˆm 12 ) g T ( ˆm F1, ˆm F1 ) g T ( ˆm F2, ˆm F2 ) g T ( ˆm F1, ˆm F2 ) , (4.7) a G mátrix Moore-Penrose-féle pszeudoinverze [101], és g(a, b) az alábbi vektor egyszerűsített jelölése: g T (a, b) = [a 1 b 1, a 1 b 2 + a 2 b 1, a 1 b 3 + a 3 b 1, a 2 b 2, a 2 b 3 + a 3 b 2, a 3 b 3 ], Q mátrix pedig mindezek után L sajátérték-felbontása alapján könnyen meghatározható Megkötések gyenge perspektíva esetén Gyenge perspektíva esetén szintén a fenti gondolat szerint szintén meghatározhatjuk a Q mátrixot, ahogyan azt Weinshall és Tomasi [136] 1995-ben meg is mutatta. A megkötéseket gyengeperspektíva esetén módosítanikell. Eszerint azazonos képkockához tartozó r f1 és r f2 bázisvektorok hosszának egyenlőnek, irányuknak egymásra merőlegesnek kell lennie: r T f1r f1 = r T f2 r f2 r T f1r f2 = 0 A 4.7. egyenlet a következőképpen módosul: g( ˆm 11, ˆm 11 ) g( ˆm 12, ˆm 12 ) g( ˆm 11, ˆm 12 ) G weak = g( ˆm F1, ˆm F1 ) g( ˆm F2, ˆm F2 ) = c weak (4.8) g( ˆm F1, ˆm F2 ) 43
54 4. MOZGÁSALAPÚ OBJEKTUM-REKONSTRUKCIÓ GYENGE PERSPEKTÍVA ESETÉN és c weak = [0, 0,...,0, 0] T. G weak l = c weak -re optimális megoldás l = 0, amely számunkra nem megfelelő. Ezért szükséges még egy megkötést tenni: keressük azt a megoldás, amely esetében l vektor hossza egységnyi, azaz l T l = 1. A lineáris algebrából jól ismert tény [17], hogy az optimális megoldást a G T weak G weak mátrix legkisebb sajátértékéhez tartozó sajátvektor adja meg A Tomasi-Kanade faktorizáció javítása Ebben a szakaszban a Tomasi-Kanade faktorizáció javított változatait mutatjuk be: az alapötletet először 2005-ben publikáltunk [49], majd jelentősen felgyorsítottuk [57]. Ahogyan azt a korábbiakban leírtuk, az eredeti módszer gyengéje a rangcsökkentés: a szinguláris érték felbontás után a mérési mátrixunk rangját 3- racsökkentjük, amiegyfajtakorlátotis jelent: arangcsökkentés utánaz eredmény már nem tud kilépni a 3-dimenziós altérből. Az általunk javasolt algoritmus iteratív alapon működő hibaminimalizálás. Első lépésben a paramétereknek kell kezdőértéket találni, majd megkezdődhet az iteráció, amely során a mozgás- és a struktúramátrixot egymástól függetlenül finomítani lehet. A szakirodalomban a módszert alternációnak 1 hívják. Az újdonság, hogy a mozgásmátrixok számításánál nem affin, hanem valós mozgásmátrixszal dolgozunk. Első cikkünkben [49] nemlineáris optimalizálást javasoltunk a mozgásmátrix számítására, majd 2007-ben zárt alakú megoldásra [57] tettünk javaslatot. Az értekezésben az utóbbit közöljük le, a teszteredmények mind a két módszert tartalmazzák Visszavetítési hiba A későbbiekben szükség lesz egy hibamértékre, amely azt mutatja meg, hogy a faktorizáció milyen pontosságú. Erre a mátrixszorzat és az eredeti mérési mátrix különbségmátrixának Frobenius-normája, azaz a különbségmátrix elemeinek a négyzetösszege alkalmas: ǫ = W MS 2 F (4.9) 1 angolul: alternation 44
55 4.3 A Tomasi-Kanade faktorizáció javítása Célunk ennek a költségfüggvénynek a minimalizálása M f Mf T = q f E, f megkötéssel, ahol E a magyar terminológia szerint az egységmátrixot (esetünkben 2 2-est) jelöl, q pedig valós szám. A javasolt módszer megadott kiindulási pontból megkeresi a visszavetítési hiba legközelebbi lokális minimumát. A globális minimum elérését sajnos nem tudjuk garantálni, de így is sokat tud az eredmény minőségén javítani, ahogyan azt a vizsgálati eredményeknél látni fogjuk. Kiindulási értéknek a Tomasi-Kanade faktorizáció eredményéül kapott mozgás- és struktúramátrixokat választjuk, és M 0 -val, illetve S 0 -val jelöljük. A hibafüggvény minimumát a szakirodalomban is ismertetett alternációs módszer [22] adja. Eszerint a hibafüggvényt két lépésben érdemes csökkenteni: előszörrögzítettmozgásmátrixesetén astruktúramátrixotfinomítjuk, majd rögzített struktúramátrix mellett optimalizáljuk a mozgásmátrixot. A lépéseket S- és M-lépésnek hívjuk. Emellettbevezetünkegykiegészítőlépéstis, amelyikaz M-lépést segíti elő. A jelenlegi módszerek hátránya, hogy nem veszik figyelembe az M mozgásmátrix megkötéseit, hanem a 2F 3 méretű mátrix tetszőleges értékeket vehet fel. A mi módszerünk figyelembe veszi, hogy minden egyes képkockára a kamerasík bázisvektorainak skálázottan ortonormáltnak kell lennie, azaz M f Mf T = q f E, f. Kétféle módszert is javasolunk: az első módszer a mozgásmátrixokat 4 F paraméterrel írjuk le, és Levenberg-Marquardt-féle nemlineáris optimalizálással hangoljuk be a paramétereket. Ezt a módszert 2005-ben dolgoztuk ki [49, 86]. A módszert itt nem részletezzük, az A és abafuggveny JACOBI MATRI- XAAAPTER*.21AB függelékekbenaparamétereketés deriváltjaikatlevezettük, a megadott publikáció alapján [49] a módszer reprodukálható. Itt csak a tesztekben közöljük a futtatási eredményeket. Jelen értekezésben amódszergyorsítottváltozatátismertetjük, melyetangolul Fast Alternation-nak hívunk. Az elnevezés utal arra, hogy az újítás lényegesen gyorsabb az eredeti verziónál. A gyorsaságot az adja, hogy az M-lépésre a szögek szerintinemlineárisoptimalizálás helyettzártalakú megoldást adtunk, amelyegy lépésben megadja az optimális megoldást. 45
56 4. MOZGÁSALAPÚ OBJEKTUM-REKONSTRUKCIÓ GYENGE PERSPEKTÍVA ESETÉN Mielőtt ismertetnénk az M- és az S-lépéseket, be kell vezetnünk egy harmadik lépéstis, amelyetkiegészítőlépésnek hívunk. Az algoritmus véges időben befejezi a futását, ha megadunk egy ǫ küszöböt, aminél kisebb hibacsökkenés esetén az algoritmus befejezi az M és S mátrixok értékeinek optimalizálását. A gyakorlatbanaziterációs számotfixreis vehetjük, mivel tapasztalatainkszerintnéhány lépésben nagyon közel kerülünk a lokális optimumhoz Kiegészítő lépés A kiegészítő lépés csupán egy segédlépés, amely az M-lépés működését segíti elő. Eredetileg egy képkockához két sor tartozik a W mérési és M mozgásmátrixban, a kiegészítő lépés segítségével ezt háromra növeljük, így az M-lépésnél háromdimenziós regisztrációs technikát alkalmazhatunk az optimális mozgásmátrix kiszámítására. A mozgásmátrix f-edik képkockájához tartozó M f almátrix két sorvektorból áll: M f = [m T f,1 mt f,2 ]T. Ezt a mátrixot kiegészíthetjük egy harmadik sorral: M f = [m T f,1 mt f,2 mt f,3 ]T, ahol m f,3 iránya megegyezik az első két vektor (m f,1 és m f,2 ) vektoriális szorzatának irányával, hossza pedig az első két vektor hosszának átlaga legyen. Nemcsak a mozgásmátrix, hanem a W f mérési részmátrix is kiegészíthető egy harmadik sorral: a harmadik sorvektor legyen m T f,3s, a kiegészített mérési mátrixot pedig jelöljük W-vel S-lépés A S-lépés célja az S (k) struktúramátrix kiszámítása a mérési és a mozgásmátrixból. Mivel az S struktúramátrix elemei tetszőleges valós értékeket vehetnek fel, a hiba a Moore-Penrose féle pszeudoinverz segítségével legkisebb négyzetes értelemben optimálisan számolható: S (k) = M (k 1) W (k 1) f (4.10) ahol M (k 1) jelöli a Moore-Penrose-féle pszeudoinverzét a M (k 1) mátrixnak. 46
57 4.3 A Tomasi-Kanade faktorizáció javítása M-lépés Az M lépés célja M (k) meghatározása W (k) -ból és S (k) -ból. Triviális, hogy M i paramétereinek az értéke teljesen független M j paramétereitől, feltéve, hogy i j. Tehát képkockánként külön lehet számítani a mozgás paramétereit. A feladat tehát a háromdimenziós pontokat tartalmazó S mátrix vetítését meghatározni az M f = q f S (k ) mozgásmátrixszal. A vetítés eredménye optimális esetben a mérési mátrix W f. Ha a W f mérési mátrix három sort tartalmazna, a feladatot visszavezethetnénk háromdimenizós pontfelhők regisztrációjára, mely feladatot legkisebb négyzetes értelemben optimálisan meg tudunk oldani, ahogyan azt anthalmazok REGISZTRACIOJAAUATION.F.3A G függelékben leírtuk. Ennek érdekében kell elvégezni a szakaszban bemutatott kiegészítést. A kiegészítést úgy kell megoldani, hogy a lehető legkisebb hibát vigyük be a rendszerbe. A javasolt kiegészítő lépés a hiba értékét nem növeli, hiszen a harmadiksorralafrobenius-normaértéke nemváltozik. Ugyanakkoraregisztrációt természetszerűleg rontja, hiszen a harmadik sor próbálja az eredeti állapotban tartani regisztrációs mátrixot, míg az első két sor az új megoldás felé viszi. Emiattakonvergenciasebességetcsökkenti. Ezzel együttis gyors amódszer, ahogyan azt a vizsgálatok során majd látni is fogjuk. A függelékben ismertetett módszer szerint az optimális R f elforgatás a következő összefüggéssel számítható: R f = V f Uf T, ha H f = U f Λ f Vf T szinguláris érték szerinti felbontásából adódik: az alábbi mátrix H f = P s p w fp, T (4.11) p=1 ahol s p az S struktúramátrix p-edik oszlopa, w fp pedig a kiegészített mátrix megfelelő koordinátahármasa. Az optimális skálázás pedig így számítható: q f = P p=1 wt fp R fs p P p=1 st p s p. (4.12) 47
58 4. MOZGÁSALAPÚ OBJEKTUM-REKONSTRUKCIÓ GYENGE PERSPEKTÍVA ESETÉN Algorithm 1 Gyors alternáció M (0),S (0) Tomasi-Kanade(W) W (0), M(0) Kiegészítés(W,M (0),S (0) ) k 0 repeat k k + 1 S (k) S-lépés( W (k 1), M (k 1) ) W (k) Kiegészítés(W, M (k 1),S (k) ) M (k) M-lépés( W (k),s (k) ) W (k) ( Kiegészítés(W, M (k),s (k) ) until W (k 1) M (k 1) S (k 1) 2 W ) (k) M (k) S (k) 2 < ǫ M M (k) S S (k) 4.4. Vizsgálati eredmények Vizsgálat szintetikus adatokon F A módszerek jellemzőinek összehasonlítására szintetikus adatokon végeztünk vizsgálatokat. A tesztekben arra törekedtünk, hogy a háromdimenziós struktúraés mozgásmátrixok pontosságát számszerűsítsük. A faktorizációs módszerünket összehasonlítottuk a szakirodalomban legjobbnak tartott eljárással, amelyik esetünkben a kötegelt behangolás (bundle adjusment) alkalmazását jelenti. (A kötegelt behangolás alapelvét ategelt BEHANGOLAS (BUNDLE ADJUST- MENT)AAPTER*.21A F függelékben ismertetjük). A tesztelési adatokat (mozgó pontok trajektóriáit) a következőképpen állítottuk elő: 1. σ 3D szórásnégyzetű, nulla várható értékű normális eloszlást produkáló véletlenszámgenerátorsegítségével háromdimenzióspontfelhőt állítunkelő. Mindegyik koordinátát egymástól függetlenül ugyanúgy generáltuk. 2. A háromdimenziós ponthalmazt véletlen szögek segítségével elforgattuk. 3. Majd gyenge perspektíva segítségével levetítettünk. F 48
59 4.4 Vizsgálati eredmények 4. Zajt adtunk hozzá a vetített koordinátákhoz. A zajgenerátor nulla várható értékű, σ 2D szórásnégyzetű, normális eloszlású véletlenszámot ad. 5. A generált trajektóriákból összeállítottunk a W mérési mátrixot. Minden egyes futtatást többször (esetünkben pontosan húsz-szor) végeztünk el, hogy az eredmények pontosabban kiértékelhetőek legyenek: a véletlen okozta kilengéseket átlagolással mossuk el. Ahogy említettük, számszerűsíteni kell a kameramozgás és a háromdimenziós pontfelhő rekonstrukciós hibáját. Szintetikus adatok esetében mind a kamera-, mind a háromdimenziós struktúra ismert, és anthalmazok REGISZTRA- CIOJAAUATION.F.3A G függelékben levő regisztrációs módszerrel össze lehet vetni a rekonstruált háromdimenziós pontfelhővel, illetve kameramozgással. A regisztrációs módszer pontfelhők regisztrációjával foglalkozik: a mozgásmátrixok esetén mátrix sorait kell a háromdimenziós pontoknak tekinteni. A regisztráció hibáját (a regisztrált pontok közötti eltérésvektorok normáinak átlagát) használjuk rekonstrukciós hibának. A regisztrációs hibán túl az algoritmusok futási ideje is fontos. Minden eljárást, még a kötegelt behangolást is implementáltuk Octave alatt 1. A futtatásokat egy 2.4Ghz-es, 512 Mbájtos Linux alapú Pc-n végeztük. A futási eredményeket csak a módosított algoritmusokra adjuk meg. A Tomasi-Kanade faktorizáció minden esetben gyorsabb, hiszen az összes módosításkor el kell végezni az eredeti faktorizációs módszert, és az algoritmusok a kapott mozgás- és struktúramátrixokat finomítják. A vizsgálati eredményeket a ábrákon láthatjuk. Jól látszik, hogy a görbék karakterisztikái (a futási időt kivéve) hasonlóak egymáshoz, különbség elsősorban a minőség terén van. A tesztjeinkben négy módszert hasonlítottunk össze: az eredeti Tomasi- Kanade faktorizációs eljárást (jele az ábrákon TK), a kötegelt behangolást (BA - Bundle Adjustment), a 2005-ben általunk publikált [49, 86] módosított alternáló eljárást (MA - Modified Alternation) és végül az itt ismertetett gyors módszert (FA Fast Alternation). 1 Az Octave egy Matlab-kompatibilis interpreter (ld. 49
60 4. MOZGÁSALAPÚ OBJEKTUM-REKONSTRUKCIÓ GYENGE PERSPEKTÍVA ESETÉN A harmadikmódszert ( MA ) a tesztelési eredményeken összevontuka a gyors eljárással ( FA ). Ennek oka, hogy arekonstrukcióshibáikaz összes esetben megegyeztek. Ezért csak a futási időnél jelöltük külön a két módszert. Általános megjegyzések. Jól látszik, hogy az eredeti Tomasi-Kanade faktorizációnál minden módszer jobb eredményt ad, ahogyan az el is várható. Kivételt ez alól egyedül a visszavetítési hiba jelent: ennek oka, hogy a W MS 2 F mértéket a Tomasi-Kanade faktorizáció (pontosabban a szinguláris érték szerinti felbontás) úgy minimalizálja, hogy nem veszi figyelembe a M f Mf T = q fi, f megkötéseket. Márpedig a szinguláris érték szerinti felbontással optimális altérbe vetítés valósítható meg, tehát a Tomasi-Kanade faktorizáció optimális megoldást ad a visszavetítési hibára. Sebességalapjánmegállapíthatjuk, hogyagyorseljárás valóbanaleggyorsabb a javító algoritmusok között, míg a kötegelt behangolás és a módosított alternáció felváltva előzik meg egymást. Eredmények a zajszint függvényében ( ábrák) A vizsgálat során egyenletes növeltük a zajgenerátor σ 2D szórásnégyzetét. A képkockák számát 5-re, a pontok számát 10-re állítottuk be. A zajszintet a 100 σ 2D /σ 3D hányados alapján számoltuk ki: ez a hányados a zaj/jel viszonyt érzékelteti. Megállapítható, hogy a módszerek az elvárásnak megfelelően működnek: a zajszint növekedésével körülbelül lineárisan nő a rekonstrukciós hiba is a struktúra- és a mozgásmátrix kiszámítása során egyaránt. A legjobb eredményt egyértelműen a gyors eljárás adta, a legrosszabbat a kötegelt behangolás. Futási időben a gyors módszer fölénye megkérdőjelezhetetlen, egy nagyságrenddel gyorsabb, mint a kötegelt behangolás. Eredmények a képkockák számának függvényében ( ábrák. A vizsgálatot 5%-os zajszint mellett, 10 pontot tartalmazó adattal végeztük el. Ahogyan az elvárható, a képkockák növelésével a rekonstrukciós hiba csökken, és egy konstans értékhez tart. A gyors módszer és a kötegelt behangolás között minőségi különbséget nem tapasztaltunk, a mozgáshibát mindkettő körülbelül egyforma arányban csökkenti. A javítás a struktúrahibánál nem jelentős. Sebességben a gyors módszer ebben a tesztben sem talált legyőzőre. 50
61 4.4 Vizsgálati eredmények Eredmények a zajszint függvényében ( ábrák). Két tesztet is végeztünk, mindkettőben 5%-ra állítottuk a zajszintet, és tíz képkockányi adatot generáltunk le. Az első teszt során a pontok számát 4 és 10 között változtattuk, míg a második esetben 10-től 300-ig. Jól látszik, hogy alacsony pontszám esetén a javító módszerek használata indokolt: mind a mozgáshibán, mind a struktúrahibán sokat lehet javítani. Nagy pontszám esetén a struktúramátrix hibáján már nem nagyon lehet javítani, a mozgáshiba viszont még ebben az esetben is érzékelhetően javítható. A gyors módszer és a kötegelt behangolás körülbelül ugyanolyan minőségű eredményt produkál, azelőbbi árnyalatnyivalazértmegelőziaz utóbbit (akülönbségszemmel is látható például a 4 pontot tartalmazó vizsgálatnál a 4.7. ábrán). Futási időben a gyors módszer továbbra is a legkevesebb idő alatt számítja ki az eredmény. A sebességkülönbség a pontok számának növelésével fordítottan arányos, a gyors módszer előnye itt is körülbelül egy nagyságrend ábra. Struktúra- és mozgáshiba a zajszint függvényében Eredmények valós képsorozaton A javasoltalgoritmusunkatvalósképekenis teszteltük, ahogyanaztmár a3.9.1fejezetben is megmutattuk. A ábrán láthatjuk a már korábban is bemutatott 51
62 4. MOZGÁSALAPÚ OBJEKTUM-REKONSTRUKCIÓ GYENGE PERSPEKTÍVA ESETÉN 4.4. ábra. Visszavetítési hiba és az algoritmusok időigénye a zajszint függvényében ábra. Struktúra- és mozgáshiba a képkockák számának függvényében. 52
63 4.4 Vizsgálati eredmények 4.6. ábra. Visszavetítési hiba és az algoritmusok időigénye a képkockák számának függvényében ábra. Struktúra- és mozgáshiba a pontok számának függvényében. 53
64 4. MOZGÁSALAPÚ OBJEKTUM-REKONSTRUKCIÓ GYENGE PERSPEKTÍVA ESETÉN 4.8. ábra. Visszavetítési hiba és az algoritmusok időigénye a pontok számának függvényében ábra. Struktúra- és mozgáshiba a pontok számának függvényében. 54
65 4.4 Vizsgálati eredmények ábra. Visszavetítési hiba és az algoritmusok időigénye a pontok számának függvényében. arcrekonstrukciós példát. A javasolt algoritmus a kézzel kijelölt pontokból sikeresen rekonstruálta az arc háromdimenziós modelljét. Jól látható, hogy például az orr vagy a szemgödör a valósághoz hasonlóan emelkedik ki, illetve süllyed be az arc többi részéhez képest ábra. Egy kép a sorozatból és a rekonstruált 3D-s modell. 55
66 4. MOZGÁSALAPÚ OBJEKTUM-REKONSTRUKCIÓ GYENGE PERSPEKTÍVA ESETÉN 4.5. Összefoglaló 1. tézis Tomasi-Kanade faktorizáció javítása Kidolgoztam egy új módszert, amely a Tomasi-Kanade faktorizációs módszer javítása. Az új eljárás iteratív, futását a megadott leállási feltétel miatt véges időben befejezi. Az iteráció minden egyes ciklusa két lépést tartalmaz: (1) az S- lépést, amely a háromdimenziós pontokat tartalmazó struktúramátrixot optimálisan kiszámítja; (2) az M-lépést, amely nemlineáris optimalizálás segítségévelképkockánként4paraméterbehangolásátvégzi zártalakúmegoldás segítségével. Szintetikus adatokon megmutattam, hogy a javított módszer jobb eredményt ad az eredeti faktorizációnál. Összehasonlítottam módszeremet a kötegelt behangolással, és megmutattam, hogy a javasolt algoritmus árnyalatnyival jobb becslést ad sokkal kevesebb számítási idő alatt. Azt is megmutattam, hogy a javítás elsősorban alacsony pontszám esetén jelentős. A módszert valós képsorozatokon is sikerrel alkalmaztam. 56
67 5. fejezet Objektum-rekonstrukció robusztus módszerei gyenge perspektíva esetén 5.1. Irodalmi áttekintés A robusztus módszerekről egy rövid áttekintést a szakaszban adtunk, itt csak a gyenge perspektív megközelítéseket mutatjuk be. Kutatásainkat a gyenge perspektív módszerek kiforratlansága motiválta. A területen eddig elsősorban matematikusok publikáltak jelentősebb eredményeket, akikrangcsökkentési technikákravezettékvisszaaproblémát. Miis láttuka4.2.1 szakaszban, hogy a mérési mátrix rangja 3 (ha nem végezzük el a súlypont kivonását, akkor 4), ezért könnyen belátható, hogy abban az esetben, ha a mérési mátrixok többmozgó objektumkövetettjellegzetes pontjaittartalmazzák, akkor apontokszegmentálásánakproblémájavisszavezethetőaltérkeresési problémára. Számtalan gyenge perspektív megoldást találunk a szakirodalomban [40, 77, 133, 142]. Sajnos mindegyik nagy hátránya, hogy első lépésként a mérési mátrix rangjának becslésével kezdik. A rangbecslés pedig egy nagyon nehéz feladat, mert a mozgó objektumok és a rosszul követett pontok (outlier-ek) számának növekedésével a rang meghatározása nagyon hamar lehetetlenné válik. Ezértmiegymásikmegközelítést választottunk: véletlen (Monte-Carlo) mintavételezéssel próbálunkdomináns mozgásttalálni, és azehhez amozgáshoztar- 57
68 5. OBJEKTUM-REKONSTRUKCIÓ ROBUSZTUS MÓDSZEREI GYENGE PERSPEKTÍVA ESETÉN tozó pontokat szegmentáljuk. A szakirodalomban létezik ilyen megközelítés, a Trajković-Kurata módszer [130, 82], amelyet a névadó kutatók egymástól függetlenül dolgoztak ki és publikáltak a kilencvenes évek végén. Ebben a fejezetben előbb ismertetjük a Trajković-Kurata módszert, majd a lehetséges továbbfejlesztéseit mutatjuk be, melyeket a szakirodalomban publikáltunk [55, 86, 48]. Végezetülafejezet másodikfelébenegyúj, régióalapúszegmentáló módszert ismertetjük, melyet szintén mi dolgoztunk ki és publikáltunk [53, 54] először 2005-ben Robusztus módszerek A Trajković-Kurata-féle robusztus eljárás A legtöbb mintavételezésen alapuló robusztus módszer két lépést szokott tartalmazni: Először egy korrekt háromdimenziós modellt szoktak megbecsülni az adat részhalmazai alapján. Majd ezt a modellt illeszteni szokták a követett jellegzetes pontokra, és megszoktákvizsgálni, hogymelyikpontilleszkedik, melyiknem illeszkedik a megadott modellre. Ebben a szakaszban bemutatjuk a Trajković-Kurata módszert [130, 82], amely a fenti gondolatmenetet követi. Az algoritmust az alábbiakban foglaljuk össze: 1. Válasszunk ki véletlenszerűen négy pontot a követett jellegzetes pontok közül. (Legalább 4 pont szükséges ahhoz, hogy faktorizáció segítségével a mérési mátrixot felbontsuk a mozgásmátrix és a struktúramátrix szorzatára). A pontok koordinátáiból vonjuk ki a kétdimenziós súlypontokat, amivel a négy pontból álló mérési mátrix rangját háromra csökkentjük. Ezt a négy pontot tartalmazó mérési mátrixot jelöljük W-vel. Bontsuk fel az SVD algoritmus segítségével: W = UΣV T. Vezessük be az affin mozgásés struktúramátrixokat (a méretüket is jelöljük az egyszerűbb érthetőség miatt): M aff = U 2F 3 és S aff = Σ 3 3 V T 3 P. 58
69 5.2 Robusztus módszerek 2. Számítsuk ki a visszavetítési hibát: ǫ p = (E 2F 2F M aff M T aff)w p, (5.1) ahol w p a W mátrix p-edik oszlopa, és E a megadott méretű egységmátrix. Ha feltételezzük, hogy a követett pontok koordinátái a követés miatt normális eloszlású zajt tartalmaznak, akkor választhatjuk az ún. LMedS (Least Median of Squares) módszert [110]. Ez esetben kezdeti robusztus becslést kell a szórásra nézve számolnunk az alábbiak szerint: ( σ 0 = 1, ) medián{ǫ p }. (5.2) p 4 Az összefüggést elméleti és tapasztalati megfontolásokból vezette be Rousseeuw és Leroy [110]. Belátható, hogy ha az ǫ p hibákról feltételezzük, hogy nulla várható értékű, σ szórású véletlen eloszlást követ, akkor a szórásra a medián{ǫ p } 1/Φ 1 (0, 75) összefüggés aszimptotikusan konzisztens becslést ad. ( 1/Φ 1 (0, 75) = 1, 4826, ahol Φ a standard normális eloszlásfüggvény jele) 3. Az 1 2. lépéseket ismételni kell. Az ismétlések számát jelöljük N s -sel. Ha tudjuk, hogy egy követett pont κ valószínűséggel lesz jól követett pont 1, és ν jelöli annak a valószínűségét, hogy mind a négy véletlenszerűen kiválasztottpontjólkövetett, akkorν-t akövetkezőösszefüggés segítségével lehet kiszámítani [110]: ν = 1 {1 (1 κ) 4 } Ns. (5.3) 4. Válasszuk ki a legkisebb σ 0 -hoz tartozó pontokat. 5. Számoljuk ki a robusztus szórást: P σ = p=1 (w pǫ p2 ) P p=1 w p 4, (5.4) ahol w p = 1, ha ǫ p < 2.5σ 0, egyébként w p = 0. A 2.5-ös értéket empirikus megfontolásból ajánlja Rousseeuw és Leroy [110]. 1 Az angol terminológia inlier-nek hívja ezeket a pontokat, outlier-nek pedig a téves pontokat nevezi. 59
70 5. OBJEKTUM-REKONSTRUKCIÓ ROBUSZTUS MÓDSZEREI GYENGE PERSPEKTÍVA ESETÉN 6. Töröljükaponthalmazbólazokataz elemeket, amelyeka2.5σ-valmegadott konfidencia intervallumon kívül esnek. Az algoritmust lépéseit logikailag két csoportba lehet osztani: az 1 4. lépések a korrekt modell megtalálásában segítenek, az 5 7. lépések pedig elkülönítik a modellhez tartozó pontokat a rosszul követett (vagy másik merev mozgó objektumhoz tartozó) pontoktól. Ez a felosztás általában igaz a Monte-Carlo elvet követő robusztus algoritmusok esetében. A módszer legnagyobb hátránya, hogy κ nem lehet nagyobb 0, 5-nél, azaz a pontoklegalábbfelénekjólkövetettnekkell lennie, ellenkezőesetbena2. lépésben a medián rossz eredményt ad. A Trajković-Kurata módszert [130, 82] a továbbiakban az A-MED rövidítést használjuk, ahol A az affin, MED pedig a medián rövidítéséből származik RANSAC alapú robusztus eljárás Ebben a szakaszban egy újszerű algoritmust mutatunk be, amely a jól ismert RANSAC algoritmust [34, 61] alkalmazza objektum rekonstrukcióra gyenge perspektíva esetén. A robusztus algoritmus az alábbiakban foglalható össze: 1. Véletlenszerűen válasszunk ki 4 pontot, és számoljuk ki az M aff mozgásmátrixot. 2. Számoljuk ki a visszavetítési hibát. (Az 5.1. összefüggést kell alkalmazni minden egyes pontra.) 3. Számoljuk meg az adott M aff mozgásmátrixhoz tartozó pontokat. Ha w p a p. jellegzetes ponthoz tartozó oszlop a mozgásmátrixban, akkor a visszavetítési hiba a korábban leírtak szerint 1 (E M F aff Maff T )w p összefüggésből számítható. A modellhez akkor tartozik a mozgásmátrix, ha a visszavetítési hiba egy megadott t RSC küszöbnél kisebb. A küszöb mértékegységepixel-négyzet, hiszen azeredetiméréstőlvaló átlagoseltérés négyzetének maximumát adja meg. 60
71 5.2 Robusztus módszerek 4. Ismételjük az 1 3. lépéseket N s -szer. Annak a valószínűsége, hogy legalább egy esetben úgy választjuk meg mind a 4 pontot, hogy egyazon objektumhoz tartoznak, megegyezik a Trajković-Kurata módszerben megadott valószínűséggel (lásd az 5.3. összefüggést). 5. Válasszuk ki azt a modellt, ahol a legtöbb pontot kaptuk az aktuális mozgásmátrixhoz. A RANSAC alapú módszernek a legnagyobb hátránya, hogy a t RSC küszöböt be kell állítani. A jó beállítás igen nehéz feladat: ha t RSC nagyon kicsiny, szinte az összes pontot kidobjuk, ha t RSC nagy, sok hibás (nem az objektumhoz tartozó) pontot hagyunk bent. Tapasztalataink szerint a küszöböt nehéz megválasztani, szűk az az intervallum, ahol a módszer jó eredményt ad. A továbbiakban a módszert A-RSC-nak nevezzük, mely elnevezés az affin+ransac rövidítéséből jön A robusztus módszerek javítása LMedS cseréje LTS-re Az LTS (Least Trimmed Squares) algortimus [110] egy igen hatásos robusztus algoritmus, amelyiket az LMedS (Least Median of Squares) módszernél jobb eredményt szokott adni, mivel a célfüggvény simább, a lokális hatásokra kevésbé érzékeny [111]. A statisztikai hatékonysága a pontosság szempontjából szintén jobb. Éppen ezért módosítottuk a Trajković-Kurata algoritmust [130, 82], és az LMeDS-nek megfelelő részt kicseréltük LTS-re. Az eredeti módszer mindössze a másodiklépésben változottmeg, ahibaszámolásalapjamediánhelyettaddarab legkisebb hiba összege. Ezért az 5.2 összefüggést meg kell változtatni: ( σ 0 = ) d ǫ p 4 p, (5.5) p=1 ahol ǫ p a p-dik eleme az e p -k növekvő sorrendbe rendezésével kapott sorozatnak. A d paramétert pedig a modellhez tartozó pontok megbecsülésével kell 61
72 5. OBJEKTUM-REKONSTRUKCIÓ ROBUSZTUS MÓDSZEREI GYENGE PERSPEKTÍVA ESETÉN beállítani: ha például a pontoknak csak a 25%-a tartozik a mozgó objektumhoz, akkor d = 0, 25P. A d paraméter becslése Ha a mozgó objektumhoz tartozó pontok aránya nem ismert, a d paramétert az alábbi heurisztikus algoritmus segítségével lehet megbecsülni: Futtassuk le az LTS algoritmust különböző d értékek mellett. Minden beállítás egy feltételezés: a pontok hány százaléka tartozik a modellünkhöz. Ezt a feltételezést nevezhetjük a priori becslésnek, és jelölhetjük d prior -nak. A lefuttatás után megszámoljuk az eredményben a modellhez tartozónak kapott pontokat (d post ) vonjuk ki d prior -ból. Minél kisebb a különbség, annál jobb volt a becslés. Azt a d post -ot választjuk, ahol a különbség a legkisebb, és a hozzá tartozó pontszeparálást vesszük végeredménynek. Az 5.1. ábrán láthatunk példát d becslésére. A pontok az a poszteriori és az a priori arányokat tartalmazzák. Ideális esetben a megrajzolt vonalra esnek a pontok. Az is jól látszik, hogy a 0.0 és az 1.0 közelében nem érdemes nézni, a módszer csak a belső intervallumban működik jól. Tapasztalataink szerint a [ ] intervallumban jól használható a módszer. A fenti eljárás lassú, azonban egy apró trükk segítségével jelentős gyorsítás érhető el: ha nem a teljes algoritmust futtatjuk le, hanem csak egyszer négy pontotválasztunkki, és azabbólkapottmozgásmodellbőlszeparáljukapontokat. Ezekből ki lehet számolni az a poszteriori értékeket, és a d post d prior különbséget eltárolni különböző d post értékek mellett. Addig futtatjuk az algoritmust, amíg a minimális különbség egy megadott d thr küszöbnél kisebb nem lesz: ebben az esetben az iteráció leáll, és a legjobb modellt (továbbá a hozzá tartozó szeparálást) vesszük végeredménynek. Ez a trükk sokat gyorsít, hiszen nem kell az egész A-LTS algoritmust lefuttatni, hanem d variálása minden egyes 4 pontból számított mozgásmátrixra megtörténik. A sebességet befolyásolja d thr megválasztása: ha túl kicsi, sokkal később áll le az algoritmus viszont nagy valószínűséggel pontosabb lesz az eredmény. Futtatásaink során d thr = 0, 025P volt. 62
73 5.2 Robusztus módszerek Prior Optimális egyenes Poszterior 5.1. ábra. A d paraméter optimális megválasztása Affin mozgásmátrix helyett valós mozgásmátrix használata A második javítás az affin mozgásmátrixszal számított visszavetítési hiba ( 5.1. összefüggés) kicserélése valós mozgásmátrixra. A valós és az affin mozgás (és struktúra) definíciója a 4.2. szakaszban található meg, itt csak röviden tekintjük át a fogalmakat. A faktorizáció első lépése során a W mérési mátrix első lépésben szinguláris érték szerinti felbontás segítségével affin mozgás- és struktúramátrix szorzatára bontható: S = M T aff W. A p. pont visszavetítési hibája affin esetben: w p = M aff s p = M aff Maffw T p. (5.6) A valós mozgás- és struktúramátrix a Q transzformáció segítségével kapható meg: M = M aff Q és S = Q 1 S aff. A visszavetítési hiba így módosul: ǫ p = (E 2F 2F MM )w p. (5.7) Haaz eredeti, affinvisszavetítési hibátkicseréljükaza-med,a-lts, A-RSC módszerekben, akkor megkapjuk a valós módszereket, melyekre R-MED, R-LTS, R-RSC rövidítésekkel hivatkozunk a továbbiakban. (Az R rövidítés az angol real, azaz valós szóból jön.) A valós mozgás szimulációs vizsgálata 63
74 5. OBJEKTUM-REKONSTRUKCIÓ ROBUSZTUS MÓDSZEREI GYENGE PERSPEKTÍVA ESETÉN Ebbenaszakaszbanmegvizsgáljukavalósés az affinvisszavetítési hibaviselkedését a zaj függvényében, és összehasonlítjuk őket. A vizsgálatokhoz szintetikus adatokatgenerálunka következő módon: veszünk egy véletlenszerűen előállított háromdimenziós pontfelhőt, amelynek a pontjait normális eloszlás segítségével állítottuk elő (minden koordinátát egymástól független, nulla várható értékű és R szórású véletlenszámgenerátor állítja elő). Ezek után elforgattuk a pontokat, az elforgatás három szögét az α = 0, β = 0, γ = 0 értékektől α = 1.0, β = 1.0, γ = 1.0 értékekig lineárisan változtattuk, összesen 30 lépésben. Miutánapontokatlevetítettük (merőlegesvetítés segítségével), és megkaptuk a kétdimenziós koordinátákat, a következő eljárást futtattuk le: 1. A 2D koordinátákhoz adjunk nulla várható értékű, r szórású Gauss-zajt. 2. Válasszunk ki 4 pontot. 3. Számoljuk ki a faktorizáció segítségével a valós mozgás és struktúramátrixokat. 4. Normáljuk le a mozgásmátrix sorait (melyeket bázisvektoroknak is hívhatunk): minden egyes sorvektor legyen egységnyi hosszú, és a vektorok harmadik elemének vegyük az abszolútértékét Forgassuk el az összes bázisvektort úgy, hogyaz elsőkétbázisvektorlegyen egyenlő a [1, 0, 0] vektorral, a második pedig a z = 0 síkban legyen, és pozitív y irányba mutasson Fűzzük össze a vektorokat úgy, hogy az első sor az elejére, az utolsó sor a végére kerüljön. 7. Ismételjük meg a 2 5. lépéseket. Így az 2 6. lépések két 2F hosszúságú vektort eredményeznek. 8. Vegyük a két vektor különbségének a hossznégyzetét. 1 Az abszolútérték segítségével kiküszöböljük a tükrözésből adódó többértelműséget. 2 Ezzel a lépéssel pedig az elforgatásból adódó többértelműséget lehet kiküszöbölni. 64
75 5.2 Robusztus módszerek 9. A 2 7. lépéseket ismételjük meg többször (mi a vizsgálatainkban 20-szor ismételtünk). 10. Átlagoljuk a kapott normákat, hogy elsimítsuk a véletlen adatokból származó szórást. Ezt a vizsgálatot különböző r értékekre (zajértékekre) elvégeztük. Az eredmény az 5.3. ábrán látható. A vízszintes tengely a százalékos zajszintet (100r/R) adja, a függőleges tengelyen pedig a számított normaátlagokat rajzoltuk fel. Jól látszik, hogy a zaj növekedésével a norma is nő. Az is jól látszik, hogy nagy zaj esetén a hiba 1,5 körül szór. Az is megállapítható a grafikon alapján, hogy néhány százalékos zajszint mellett (amely reálisan előfordul) a hiba értéke bőven 0, 75 alatt van, tehát a hibamérték alkalmas arra, hogy eldöntsük: két mozgásmátrix ugyanahhoz a mozgó háromdimenziós objektumhoz tartozik-e. A végtelen zaj esetén kapott 1,5-ös várható értéket be is lehet bizonyítani: Tudjuk, hogy a bázisvektorok egységnyi hosszúak, és a harmadik koordinátájuk pozitív. Ez azt jelenti, hogy mindegyik bázisvektor egységnyi sugarú félkörön helyezkedik el. Ha nagyon nagy zajt adunk a koordinátákhoz, a faktorizáció gyakorlatilag véletlen elemeket eredményez. Ezért a kapott bázisvektorok a félgömbön véletlenszerűen lesznek elszórva. Egységsugarú félgömbön elhelyezkedő két pont távolságának várható értéke pedig 1,5, ahogyan azt a következő segédtétel segítségével ki lehet számítani: Lemma: r sugarú félgömbön véletlenszerűen elhelyezkedő két pont távolságának várható értéke 1, 5r 2. Bizonyítás: Amennyiben két pontot véletlenszerűen kiválasztunk egy r sugarú félgömbön, a két pont közötti távolság várható értéke az alábbiak szerint számolható ki: Válasszunk ki egy tetszőleges p pontot a felületen, ennek legyenek a koordinátái p = [r cos(α) cos(β), r sin(α) cos(β), r sin(β)] T polárkoordinátás alakban, ahol α [0...2π) és β [0... π) 2 Vegyünk fel egy másik pontot ugyanezen a félgömbön. Ez helyezkedjen el egy olyan metszetkörön, amelynek sugara r cos(δ). Ennek a körnek tetszőleges c pontját a polárkoordinátás felírás és egy γ paraméter segítségével fel lehet írni: c = [r cos(γ) cos(δ), r sin(γ) cos(δ), r sin(δ)] T, ahol γ [0...2π) és δ [0... π). 2 65
76 5. OBJEKTUM-REKONSTRUKCIÓ ROBUSZTUS MÓDSZEREI GYENGE PERSPEKTÍVA ESETÉN Az 5.2. ábrán láthatjuk a két pont elhelyezkedését (a szögeket, illetve a metszetkört a túlzsúfoltság elkerülése miatt csak a c ponthoz rajzoltuk be). p X p c X c γ δ ábra. Két pont távolsága a félkörön. A p pont átlagos távolsága a kör pontjaitól az alábbi összefüggés segítségével számítható: d 1 = 1 2π = 1 2π 2π 0 2π 0 (p c) T (p c) dγ { (r cos(α) cos(β) r cos(γ) cos(δ)) 2 + (r cos(α) cos(β) r cos(γ) cos(δ)) (r cos(α) cos(β) r cos(γ) cos(δ)) 2} dγ = 1 2π 2π 0 { 2r 2 2r 2 cos(α) cos(β) cos(γ) cos(δ) 2r 2 sin(α) cos(β) sin(γ) cos(δ) 2 sin(β) sin(δ) } dγ = 2r 2 2r 2 sin(β) sin(δ) (5.8) Most számoljuk ki az átlagos távolságot a pont és az összes kör között. Az egyes körökre számolt résztávolságokat természetesen a megfelelő kerülettel súlyozni 66
77 5.2 Robusztus módszerek kell: d 2 = 1 2πr π 2 0 d 1 2πr cos(γ)r dγ = 1 2πr = 2r 2 [ sin(δ) sin(β) sin2 (δ) 2 ] π 2 0 π 2 0 ( 2r 2 2r 2 sin(β) sin(δ) ) 2πr cos(δ)rdγ ( = 2r 2 1 sin(β) ) 2 (5.9) Most a kiválasztott p pontot kezdjük el mozgatni teljesen hasonlóan. Először egy rcos(α) sugarú kör mentén mozgatjuk, és az átlagos távolságot kiszámítjuk. Azt tapasztaljuk, hogy a kör minden egyes pontján azonosak a távolságértékek, ezért az átlagolás valójában felesleges: d 3 = 1 2π 2π 0 ( d 2 dα = 2r 2 1 sin(β) ) 2 (5.10) Végezetül az összes kör mentén kiszámítjuk az átlagot (a köröket most is a kerülettel súlyozva), és ez megadja a várható értéket: d 4 = 1 2πr = 2r 2 π 2 0 π 2 0 d 3 2πr cos(β)r dβ = 1 2πr ( cos(β) π 2 0 ( 2r 2 1 sin(β) ) 2πr cos(β)r dβ 2 ) [ ] π cos(β) sin(β) 2πr cos(β)r dβ = 2r 2 sin(β) sin2 2 (β) = 3 2 r2 (5.11) Ezzel a tételt bebizonyítottuk. Összességében tehát megállapíthatjuk, hogy egy r sugarú gömbön két véletlenszerűen kiválasztott pont távolságának várható értéke a sugár négyzetének másfélszerese. Az affin és a valós mozgás összehasonlítása Az összehasonlítóelemzés céljamegállapítani, hogyérdemes-e avalós mozgást használni affin mozgás helyett. A vizsgálathoz generáltunk két egymáshoz 67
78 5. OBJEKTUM-REKONSTRUKCIÓ ROBUSZTUS MÓDSZEREI GYENGE PERSPEKTÍVA ESETÉN hiba zajszint 5.3. ábra. Bázisvektorok hibái a 2D zaj függvényében. képest függetlenül mozgó háromdimenziós pontfelhőt, melyet gyenge perspektíva segítségével levetítettünk a képsíkra, majd a szokott módon zajt adtunk hozzá. A háromdimenziós objektumot most is nulla várható értékű, R szórású Gausseloszlást adó véletlenszámgenerátor állította elő, akárcsak a kétdimenziós zajt, amely esetében a szórást r-rel jelöljük. Az szakaszban ismertetett módon az elforgatást a megadott intervallumok között lineáris szöginterpoláció segítségével végeztük el. A első objektum pontkészletéből ezután kiválasztottunk három pontot, és hozzáraktunk egy új pontot a másik mozgó objektum pontkészletéből. Majd kiválasztunk másik négy pontot, ezúttal minden egyes pontot az első készletből. Így kétszer 4 pontot választottunk ki. Ezek után a faktorizációt elvégezzük, és az affin és a valós mozgást, továbbá a hozzájuk tartozó affin és valós visszavetítési hibát kiszámítjuk. A 4 pontra számított visszavetítési hibákat ezek után átlagoljuk. Ezen a ponton van egy-egy affin és egy-egy valós hibánk két esetre: első esetben minda4pontegyobjektumhoztartozik, másikesetben kétobjektumpontjainak 1 : 3-mas keveréke. Megnézzük, hogy a kapcsolódó affin hibák esetén a helyes modell (amelyik 4 jó pontot tartalmaz) hibája kisebb-e, mint a keverté (a kevert egy rossz pontot és három jó pontot tartalmaz). Ha nem, a hibaszámlálónkat megnöveljük. Ugyanígy a valós esetre is bevezetünk egy hibaszámlálót. 68
79 5.2 Robusztus módszerek Az egész eljárást ismételtük (most konkrétan 100-szor), és a hibákat grafikonon ábrázoltuk. A 100-as futtatást különböző zajszintekre végeztük el. Az eredmény az 5.4. ábrán látható. A következőmegállapítástehetőavizsgálatalapján: atévedések számavalós esetben szignifikánsan kisebb, mint affin esetben. A megállapítás a megvizsgált összes zajszintre igaz ábra. A valós és az affin metrika hibái A robusztus módszerek összehasonlítása szintetikus adatokon A következőkben a fejezetben ismertetett hat módszert vizsgáljuk A-MED, A-LTS, A-RSC, R-MED, R-LTS és R-RSC viselkedését szintetikus adatokon. Célunk az eredeti [130, 82] (A-MED) eljárás összehasonlítása az újakkal. A vizsgálatok számára az adatokat az első tézis vizsgálatakor is ismertetett módon ( szakasz) generáltuk, majd véletlenszerűen generált koordináták segítségével új pontokat adtunk az adatainkhoz. Végül kétdimenziós zajt is kevertünk a koordinátákhoz. (A zajok definíciója az szakaszban található meg.) Ezekutánminda hat robusztus eljárástlefuttattuk, és amozgóobjektumhoz tartozó pontokat elkülönítettük. Mivel mi állítottuk elő a ponthalmazt, tudjuk, 69
80 5. OBJEKTUM-REKONSTRUKCIÓ ROBUSZTUS MÓDSZEREI GYENGE PERSPEKTÍVA ESETÉN hogy melyik pont tartozik valójában az objektumhoz, és melyik nem. Ennek az ismeretnekabirtokábankétféle tévedést definiálhatunk: az álnegatívés álpozitív eseteket. Álnegatív esetnek mondjuk, ha egy pontot eldobunk, pedig valójában a modellhez tartozik, álpozitívnak, amikor eldobandó pontot választunk be a modell pontjainak a halmazába. A táblázatainkban ennek a két tévedésnek a számát soroljuk fel, N fn : N fp alakban, ahol N fp jelöli az álpozitív tévedést, N fn pedig az álnegatívat. Az is könnyen belátható, hogy a álnegatív tévedést jobban lehet tolerálni: inkább kevesebb pontból álljon a mozgó objektumunk modellje, de ne legyen hibás adat a ponthalmazban. Egy nagyon fontos probléma a paraméter helyes beállítása. Az LMedS algoritmusoknak nincsen beállítandó paraméterük, ezért itt nem merül fel ez a probléma. Az LTS algoritmusoknál a d paramétert kell beállítani, ezt a feladatot már megoldottuk, és egy módszert javasoltunk az szakaszban. A RANSAC alapú módszerek esetében is van egy kritikus paraméter, amit t RSC - vel jelöltünk. Ezt a paraméter a RANSAC-kel foglalkozó módszereket alkalmazó szakemberek manuálisan szokták beállítani. Az itt ismertetett vizsgálatokban különböző értékekkel próbáltuk ki a RANSAC-ot tartalmazó módszereket, és mindig a legjobb eredményt választottuk ki. Sok értéket nem kellett kipróbálni, mert a t RSC mértékegysége pixel, és pixelben mért eltérést jelent. Hibának pedig maximum néhány pixel engedhető meg: ezért szűk intervallumban kellett próbálkoznunk. Az első vizsgálat (5.1. és 5.1. táblázatok ) során egy objektumot vettünk, a szokásos generátor segítségével. Majd az eddig megszokott módon forgatjuk, gyenge perspektíva segítségével vetítjük és 2D-s Gauss-zajt adunk a koordinátákhoz. Ezek után véletlen zajt tartalmazó pontokat adunk az adatokhoz. A pontok70%-avéletlen adat. (Ez azeset nagyonsúlyosszennyezettségetszimulál.) A véletlen adatokat R szórású Gauss-generátor segítségével állítottuk elő. A vizsgálatban a70% véletlen adataztjelenti, hogy300pont tartozika mozgó objektumhoz, 700 pedig véletlenül generált pont. Az eredmények alapján egyértelmű, hogy az LMedS módszerek teljesen rossz eredményt adnak, hiszen kivétel nélkül minden esetben az összes pontot a modellhez tartozónak vették. Mindez nem meglepő, hiszen a medián csak abban az esetben működik, amikor legalább a pontok fele a modellhez tartozik. 70
81 5.2 Robusztus módszerek Az R-RSC módszer adta a legjobb (tökéletes) eredményt. Az R-LTS közel van a hibátlan eredményhez, mindössze 12 pozitív tévedést produkált 6%-os zajszint mellett, egyéb esetekben az R-RSC-hoz hasonlóan hibátlanul működött. Az A- RSC szintén szép eredményt adott: 4%-os zajszint mellett 4 álnegatív hiba az eredmény. A többi módszer alkalmazását erre a feladatra nem javasoljuk. Megjegyzés: Az A-RSC és az R-RSC esetén ugyanazt a t RNS küszöböt állítottuk be. Zaj A-MED 0:700 0:700 0:700 0:700 0:700 0:700 1:700 A-LTS 0:0 0:700 0:0 0:700 0:105 0:17 0:118 A-RSC 0:0 0:0 0:0 0:0 4:0 0:0 0: táblázat. Affin módszerek hibája (pozitív tévedés: negatív tévedés) egy mozgó objektum esetén, 70 % véletlen adattal. Zaj R-MED 0:700 0:700 0:700 0:700 0:700 0:700 1:700 R-LTS 0:0 0:1 0:0 0:0 0:0 0:0 0:12 R-RSC 0:0 0:0 0:0 0:0 0:0 0:0 0: táblázat. Valós módszerek hibája (pozitív tévedés: negatív tévedés) egy mozgó objektum esetén, 70 % véletlen adattal. A második vizsgálatban (5.3. és 5.3. táblázat) két mozgó objektumot generáltunk. Véletlen adatot nem adtunk hozzá. Az első objektum 700 ponttal, a második 300 ponttal rendelkezik, azaz összesen most is 1000 pontot tartalmaz az adathalmaz. A robusztus módszer feladata a két objektum pontjainak szegmentálása: a korábbi elnevezéseket használva az első (több pontot tartalmazó) objektum pontjait vesszük modellhez tartozó pontoknak, a második objektum pontjait pedig idegen pontoknak. A modellhez nem tartozó pontok aránya így 30% lett. 71
82 5. OBJEKTUM-REKONSTRUKCIÓ ROBUSZTUS MÓDSZEREI GYENGE PERSPEKTÍVA ESETÉN A vizsgálat során a RANSAC módszerekhez a t RNS küszöböt úgy állítottuk be, hogy a legjobb eredményt adja. Mindegyik módszer elfogadható eredményt produkált, az R-RSCegykicsiveljobbat (kevesebbnegatívtévedés), mintatöbbiek. Zaj A-MED 0:0 0:1 0:52 0:82 0:97 0:133 1:300 A-LTS 0:0 0:1 0:43 0:56 0:51 0:102 0:293 A-RSC 0:0 0:1 2:1 4:3 2:2 3:43 6: táblázat. Affin módszerek hibája (pozitív tévedés: negatív tévedés) két mozgó objektum esetén, véletlen adat nélkül. Zaj R-MED 0:0 0:1 0:23 0:19 0:21 0:122 0:279 R-LTS 0:0 0:1 0:22 0:19 0:15 0:118 0:227 R-RSC 0:0 0:22 1:18 0:34 0:29 0:41 0: táblázat. Affin módszerek hibája (pozitív tévedés: negatív tévedés) két mozgó objektum esetén, véletlen adat nélkül. Végezetül a harmadik vizsgálat (5.5. és 5.6. táblázatok) során két mozgó objektumhoz véletlen adatot is kevertünk. A két mozgó tárgyat a korábbiakhoz hasonlóan állítottuk elő, az első most 600 pontot tartalmaz, a második pedig 100-at. Véletlen adatot 300-at generáltunk. A RANSAC módszereknél a t RSC küszöb ugyanannyi, mint a második vizsgálatnál volt. Kipróbáltunk más küszöbértékeket, de a legjobb megoldást az eredeti beállítással értük el. Az eredmények alapján megállapíthatjuk, hogy a módszerek megbirkóznak a feladattal. Az A-RSC magas zajszint mellett már kudarcot vall, hiszen N fn elég nagy. Szerencsére a valós változat (R-RSC) korrigálja ezt a hibát. Az LMedS alapú megoldások az affin RANSAC-hoz hasonlóak: nagy zaj esetén megengedhetetlenül sokat tévednek. 72
83 5.2 Robusztus módszerek Összességében jó eredményt az R-RSC, az A-LTS és az R-LTS adott, de az utóbbi közülük is kiemelkedik. Zaj A-MED 0:0 0:0 0:5 0:161 0:395 0:397 1:392 A-LTS 0:0 0:3 0:0 0:5 0:47 0:58 0:70 A-RSC 0:0 0:3 0:2 0:5 7:105 21:303 3: táblázat. Affin módszerek hibája (pozitív tévedés: negatív tévedés) két mozgó objektum esetén, 30% véletlen adattal. Zaj R-MED 0:0 0:0 0:2 0:26 0:63 0:264 0:302 R-LTS 0:0 0:0 0:0 0:4 0:2 0:4 0:12 R-RSC 0:0 0:0 0:27 0:15 0:17 0:7 1: táblázat. Valós módszerek hibája (pozitív tévedés: negatív tévedés) két mozgó objektum esetén, 30% véletlen adattal. A kísérlet tanulságai az alábbiakban foglalható össze: A RANSAC és az LTS alapú módszerek akkor is működnek, ha az adathalmazunkban sok idegen pont szerepel. Az LMedS módszerek nem adnak jó eredményt. Az R-RSC és R-LTS módszerek adják a legmegbízhatóbb eredményt. Sajnos a RANSAC módszereknél a t RSC paramétert kézzel kell beállítani, amely sok esetben nem könnyű feladat, mivel az eredmény eléggé érzékeny erre a beállításra. Az affin mozgásmátrix lecserélése valós mátrixra sokat javít a módszerek megbízhatóságán. Ez különösen igaz a RANSAC alapú módszerekre. 73
84 5. OBJEKTUM-REKONSTRUKCIÓ ROBUSZTUS MÓDSZEREI GYENGE PERSPEKTÍVA ESETÉN Kísérletek valódi felvételeken Az algoritmusokat valódi felvételeken is teszteltük: a szakirodalomból jól ismert Hotel képsorozaton és saját felvételen végeztünk vizsgálatokat. Az 5.5. és az 5.6. képeken láthatjuk a Hotel szekvencia R-RSC és R-LTS módszerekkel számított eredményeit. Mindegyik módszernél a népszerű KLT követő alapján fejlesztett sarokdetektálóalgoritmust [91, 16] használtuk, majdakövetést normáltkeresztkorreláció alapútechnikávalvégeztük. Az ésszerűséghatárainbelülalehetőlegtöbbpontot követtük, hogy a módszereknek elegendő számú bemeneti pontjuk legyen. A kapott eredmény igazolja, hogy az ismertetett módszerek alkalmasak háromdimenziós mozgó objektumok követett pontjainak a szegmentálására, hiszenjóllátszik,hogyapontokkaljelzett megfeleltetések valóbanhelyesek, afőleg a tetőn előforduló helytelen megfeleltetések az algoritmus megtalálta. Az 5.7. ábra egy digitális fényképezőgéppel készített sorozaton kapott eredményt mutatja meg, melyet az R-LTS algoritmus használatával állítottuk elő. A felvételen egy rajzokkaldíszítettpapírkocka látható. A robusztusmódszer akockáhoztartozópontokatsikeresen megtalálta, és elkülönítetteaháttérrosszul mozgó pontjait ábra. A hibás ( x ) és a jó pontok R-RSC módszerrel a Hotel sorozaton. A helyes modellhez a pontok 93% tartozik. 74
85 5.3 Régió alapú mozgásszegmentálás 5.6. ábra. A hibás ( x ) és a jó pontok R-LTS módszerrel a Hotel sorozaton. A helyes modellhez a pontok 85% tartozik ábra. A hibás ( x ) és a jó pontok R-LTS módszerrel saját felvételen. A helyes modellhez a pontok 42% tartozik Régió alapú mozgásszegmentálás Irodalmi áttekintés A 3. fejezetben (3.4.2szakasz) már áttekintettük aháromdimenziós mozgásalapú objektum-rekonstrukció robusztus módszereit. Kitértünk rá, hogy a legtöbb módszer a W mérési mátrixban meglévő adatok alapján különíti el a mozgó objektumokhoztartozótrajektóriákat. Kétféle stratégialétezik: vagy (gyenge pers- 75
86 5. OBJEKTUM-REKONSTRUKCIÓ ROBUSZTUS MÓDSZEREI GYENGE PERSPEKTÍVA ESETÉN pektívát feltételezve) három rangú almátrixokat keresnek a mérési mátrixban [40, 77, 133, 142], vagy Monte-Carlo elven néhány pontból kezdeti modellt előállítva olyan pontokat keresnek, amelyik a kiszámított modellnek megfelelő mozgást végez [130, 82]. A jelen fejezet első részében javasolt módszer is ez utóbbi elvet követi. A meglévő módszerek nagy hátránya, hogy egy nagy adathalmazként tekintenek az összes kétdimenzióban követett jellegzetes pontra, és az egész adathalmazon próbálnak szegmentálni. Ezért egy újszerű módszerre teszünk javaslatot, amelyik régiókra bontás segítségével javít a szegmentáció hatásfokán. A régió alapú szegmentálás nem új ötlet a számítógépes képfeldolgozásban. Optikai áramlásokra azaz kétdimenziós elmozdulásra alapuló számtalan módszer létezik már a szakirodalomban [112, 137, 145, 71]. Egy tömör, de igen hasznos összefoglaló az Interneten is olvasható [95]. Az alapfeladat szerint egy képsorozat egyik képkockáját régiókra kell bontani, és a következő képhez képest elmozdulást kell számítani minden egyes régióra. Ugyanazon objektum szomszédos régióin hasonló elmozdulás található, míg az objektumok határán nagy valószínűséggel éles váltás észlelhető. Sajnos kétdimenziós mozgás esetén az éles váltást nem lehetgarantálni,csak reménykedni lehet benne, hiszenforgás esetén az elmozdulásvektorok kétdimenziós vetületei egy adott pillanatban szerencsétlen esetben meg is egyezhetnek két különbözőképpen mozgó objektum szomszédos régióiban. A szegmentálás működésére egy példát az 5.8. és az 5.9. ábrán láthatunk (a képet [95]-ból másoltuk ki). Éppen ezért a régió alapú szegmentálást ismereteink szerint eddig elsősorban olyan mozgó tárgyak szegmentálására használták, amelyek forgó mozgást alig végeznek, inkább csak az orientációjukat megtartva vagy alig változtatva mozognak a képen. A régió alapú módszerek működéséhez egyrész szükség van elmozduláskép meghatározásához, amelyre az optikai áramlások használatát javasoljuk [11, 68], de egyéb mintaillesztési algoritmusok [28, 91, 8] alkalmazására is lehetőség van. Ha a régiókra meghatározták az elmozdulásokat, egy hasonlósági mérték alapján össze kell az azonos régiókat vonni. Ez régió növelési és megosztási statégiával [118, 28] egyaránt szokás végezni. A mozgásalapú szegmentálást intenzitásinformációval is ki lehet egészíteni. A problémát számtalan módon próbálták 76
87 5.3 Régió alapú mozgásszegmentálás 5.8. ábra. Videósorozat két szomszédos képkockája ábra. Szintetikus szekvencia első és az utolsó képkockája. megoldani: például M-becslés [112], EM-algoritmus [137] vagy MDL 1 [145] segítségével. A következőkben javasolt megközelítésünk leginkább Irani és munkatársai módszeréhez [71] hasonlít. Az alapelvük, hogy először keressünk a régiókban domináns kétdimenziós mozgást, majd keressük meg azokat a régiókat, amelyek hasonló mozgást végeznek. Mi is ezt az elvet követjük. Az újdonság a mi megközelítésünkben az, hogy kétdimenzió helyett háromdimenziós mozgásra alapozzuk a szegmentálást. 1 Minimal Description Length 77
88 5. OBJEKTUM-REKONSTRUKCIÓ ROBUSZTUS MÓDSZEREI GYENGE PERSPEKTÍVA ESETÉN A javasolt módszer ábra. Négyzet alapú régiók. A mozgásszegmentáló módszerünk két fontos megkötés mellett működik: mindegyik szegmentálandó test merev; kompakt alakzatot alkot, azaz összefüggő területen helyezkedik el a képen (vagyis nem takarják ki más objektumok úgy, hogy részekre esik) és gyenge perspektívát feltételezhetünk. A szegmentálás menete a következő: miután követjük a lehető legtöbb jellegzetes pontot a képeken, a pontokat az első kép alapján régiókba osztjuk. Ezek a régiók melyeket tipikusan kör vagy téglalap alakúaknak szokás az egyszerűségkedvéért választani átfedőek is lehetnek, sőt javasolt, hogy azok legyenek. Az 5.10 ábrán látható példa egy lehetséges felosztást átfedő, négyzet alakú régiókra. (Csak az átlós régiókat jelöltük be, a szaggatott és az összekötött vonal nem jelent semmi különbséget, csupán a jobb láthatóságot szolgálja.) Egy jellegzetes pont abba a régióba tartozik, amelyikben az első képkockán van. Ezek után minden egyes régióra (pontosabban: azok pontjaira) lefuttatunk egy robusztus szegmentáló algoritmust, és az adott régióban domináns háromdimenziós mozgást keresünk. Mi az R-LTS módszert szoktuk alkalmaznia feladatra. 78
89 5.3 Régió alapú mozgásszegmentálás Azt a régiót választjuk ki, amelyikben a legkisebb hibával találtunk domináns mozgást. A domináns mozgást megpróbáljuk a szomszédokra is kiterjeszteni egészen addig haladva, amíg újabb összefüggő régiót nem találunk. Ezek után a domináns mozgáshoz tartozó régiókat kivonjuk, és újabb domináns mozgást keresünk a maradék területen. Ezt addig ismételjük, amíg domináns mozgást találunk. A legkisebb hibával rendelkező mozgásmátrix kiválasztása Először ki kell választanunk azt a régiót, ahol domináns mozgást találunk. Miutánakövetettjellegzetes pontokatrégiókraosztottuk, mindenegyes régió pontjaira le kell futtatni valamelyik robusztus algoritmust: mi az R-LTS módszert választottuk erre a feladatra. A maradék adat (amit a robusztus módszer kiválogatott) potenciális 3D-s mozgást tartalmaz, de nem lehet garantálni, hogy valóban korrekt háromdimenziós mozgást találtunk az adott régióban. Ezért ezt az adathalmazt meg kell vizsgálni. Ehhez az szakaszban ismertetett módszer alapján kell a valós mozgás hibáját megvizsgálni. Tudjuk, hogy a mozgáshiba pozitív, és 2,0-nál nem nagyobb, hiszen az egységsugarú félkörön levő két legmesszebbi pont távolsága 2,0. Azt is megvizsgáltuk, hogy 0,5 környékén lehet az a határ, ami felett nem szabad háromdimenziós mozgást elfogadni. Ha a mozgáshiba minden egyes régióban meghaladja a 0,5-et, akkor nem találtunk 3D mozgást: ebben az esetben a módszer leáll. Ha vannak 0,5 alatti mozgáshibával rendelkező régiók, akkor kiválasztjuk a legkisebb hibát, a régióhoz tartozó pontokra alkalmazzuk a faktorizációs módszert, és a mozgásmátrix ismeretével továbblépünk a következő lépésre. Ismert mozgáshoz tartozó pontok kiválasztása Adott tehát egy mozgásmátrix, szeretnénk olyan hibafüggvényt definiálni, amelyik kicsi akkor, ha a pont körülbelül a mozgásmátrix szerint mozog; nagy, ha teljesen másképpen. Ez a feladat nem triviális, hiszen a C. függelékben beláthatjuk, hogyafaktorizációnem egyértelmű: olyanhibamértéket kell tehát meghatározni, amely a lehető legkevésbé érzékeny a faktorizáció többértelműségére. A W mérési mátrixot a faktorizáció egy mozgás- és egy 79
90 5. OBJEKTUM-REKONSTRUKCIÓ ROBUSZTUS MÓDSZEREI GYENGE PERSPEKTÍVA ESETÉN struktúramátrix szorzatára bontja: W = ( ˆMQ)(Q 1 Ŝ), (5.12) ahol M = ( ˆMQ) a mozgás-, S = (Q 1 Ŝ) a struktúramátrix. A faktorizáció a C. függelék szerint egy ortonormált transzformáció erejéig többértelmű: ha ( ˆMQ) egy kiszámolt korrekt mozgásmátrix, akkor ˆMQA akkor és csak akkor az, ha A ortonormált (és a hozzá tartozó struktúramátrix A T Q 1 Ŝ). Ahhoz, hogy megtudjuk, egy pont a megadott M mozgásmátrix szerint mozog vagy sem, a következő hibát definiáljuk: ǫ p = (E MM )w p (5.13) ahol w p a p-edig oszlopa a mérési mátrixnak (azaz a p-edik ponthoz tartozó mérési adat). Ezt a hibát az adott pont M mátrixhoz viszonyított inkoherencia értékének neveztük el. Ennek a metrikának nagy előnye, hogy teljesen érzéketlen az ortonormált transzformációval való szorzásra. Ezt a következők alapján láthatjuk be: Tudjuk, hogy ha M pszeudoinverze M, akkor MA pszeudoinverze A T M, lásd a D. függeléket. Az inkoherencia érték pedig az alábbiak szerint módosul: ǫ p = (E MA(MA) )w p = (E MAA T (M) )w p = (E MM )w p (5.14) azaz az eredeti, és az A ortonormált mátrixszal szorzott mozgásmátrix pontosan ugyanakkora hibát ad. Az inkoherencia érték gyakorlatilag megegyezik a visszavetítési hibával, az egyetlen különbségabbanvan, hogya szakaszbanismertetettvisszavetítési hibánálamozgásmátrixotateljes adathalmazbólvettpontokalapjánbecsültük, itt pedig valamelyik régiók adataiból számoljuk. A javasolt algoritmus összefoglalója A javasolt háromdimenziós szegmentáló algoritmus főbb lépéseit az alábbiakban foglalhatjuk össze: 1. Követés és felosztás. Detektáljunk és kövessünk lehetőleg minél sűrűbben jellegzetes pontokat. Osszuk fel a jellegzetes pontokat régiók szerint. (Minden egyes jellegzetes pont ahhoz a régióhoz tartozik, amelyiken az első képkockán elhelyezkedik.) 80
91 5.3 Régió alapú mozgásszegmentálás 2. Mozgáshiba számítása. Minden egyes régióra (a) Futtassunk le egy robusztus algoritmust (pl. R-LTS) és a domináns modellhez tartozó pontokat tartsuk meg, a többi pontot dobjuk el. (b) Számítsuk ki a korábban (az szakasz) meghatározott mozgáshibát, melyet a valós és affin hiba összehasonlításához használtunk. Azaz válasszunk ki kétszer 4 pontot, számítsuk ki a mozgásmátrixot, a mozgásmátrixot fűzzük fel vektorrá, és a vektorok közötti különbség normáját számoljuk, és osszuk el a mozgásmátrix sorai számával a normát. Ismételjük meg sokszor (esetünkben: húszszor) a kiválasztást, és átlagoljuk a normaértékeket. 3. Magpont választása. Válasszuk ki azt a régiót, amelyikben a mozgáshiba a legkisebb. Ha ez a hiba nagyobb egy megadott küszöbnél (vizsgálatainkban T err = 0, 5), akkor az algoritmus jelenti, hogy nem talált több mozgó objektumot az adatokban, majd leáll. Ha nem haladja meg a hiba a megadott küszöböt, a régió megtartott pontjai alapján le kell futtatni a faktorizációs algoritmust: most az M mozgásmátrix számítása a lényeges. 4. Inkoherencia értékek számítása. Minden régióra (a) Futtassunk le egy robusztus algoritmust (mi R-LTS-t használtuk), vagy ha eltároltuk az előző lépés eredményét, akkor azt vegyük elő. (b) Minden egyes pontra számoljuk ki az M mozgásmátrixhoz viszonyított inkoherencia értéket. (c) A régió inkoherencia értékét a pontok inkoherenciájának átlaga adja meg. (d) Készítsünkegy inkoherenciaképet, aholminden egyes pixelegyrégiót ad, a szín pedig az inkoherencia érték a megfelelő szürkeségi intervallumba normálva. Az 5.13 ábrán láthatjuk az 5.11 képen bemutatott sorozat két mozgó objektumához tartozó inkoherencia képet. 81
92 5. OBJEKTUM-REKONSTRUKCIÓ ROBUSZTUS MÓDSZEREI GYENGE PERSPEKTÍVA ESETÉN ábra. Szintetikus szekvencia első és az utolsó képkockája. 5. A magpont terjesztése. Az inkoherencia képen induljunk ki a magpontból, és régió-növesztésieljárással [118] keressükmegaz összekapcsolódó régiókat. Mi a GIMP [1] szoftver kitöltő algoritmusát alkalmaztuk a feladatra. A régió-növelés lényege, hogy a szomszédos régiók között hasonlósági (ún. homogenitási) kritériumokat fogalmazunk meg, és a magpontból kiinduló terjeszkedés odáig tart, ameddig a szomszédos régiók teljesítik a kritériumot. 6. Iteráció. A szegmentált régiókat töröljük, és a maradékra újra le kell futtatni az algoritmust, a 2-es lepéstől kezdődően Vizsgálati eredmények A javasolt háromdimenziós módszer szintetikus (renderelt) és valódi adatokon egyaránt megvizsgáltuk. Minden esetben ugyanazt a pontdetektáló és -követő módszert futtattuk: a jellegzetes pontokat a Lucas-Kanade pontkövető algoritmusból [91] kifejlesztett Shi-féle sarokdetektáló [125, 16] határozta meg az első képen, és egyszerű mintaillesztő eljárást (shift-corrected SSD [28]) alkalmaztunk a pontkövetésre. A pontkövetőt úgy állítottuk be, hogy a lehető legtöbb pontot adja: inkább legyen több rosszul követett pont, mivel bízunk a robusztus módszereink hatékonyságában. Vizsgálati eredmények szintetikus (renderelt) képsorozaton. Az első vizsgálandó sorozat egy forgó kockát és egy forgó gömböt tartalmaz. A textúrázott háttér szintén dinamikus, mivel a kamera pozíciója és orientációja is 82
93 5.3 Régió alapú mozgásszegmentálás ábra. A szintetikus sorozat régióinak mozgáshibái ábra. Két domináns mozgás inkoherencia képe. Bal: kocka mozgásához képest. Jobb: gömb mozgásához képest. változik. A sorozat első és utolsó képe az ábrán tekinthető meg. A sorozat 10 képkockából áll, a képek felbontása pixel, a renderelő program az ingyenes hozzáférhető POVRay [2] volt. Érdekesség, hogy a mozgó kockát eltakarja a gömb minden egyes képkockán. Az ábra mutatja a régiók mozgáshibáit, melyet az algoritmus 2. lépése állít elő. Ha egy pixel világos, ott nagy a hiba, ha sötét, akkor kicsi. A fehér pixelek olyan régiókat jelentenek, ahol nem volt annyi jellegzetes pont, hogy értelme legyen a robusztus eljárást lefuttatni. Az ábrán jól látszik a kocka és a gömb régióinak a helye. A határon nagyobb a hiba, hiszen ebben az esetben határrégiókon belül keverednek a kocka és a gömb mozgását követő pontok. 83
94 5. OBJEKTUM-REKONSTRUKCIÓ ROBUSZTUS MÓDSZEREI GYENGE PERSPEKTÍVA ESETÉN ábra. Szegmentáció az inkoherencia képen ábra. A kocka (bal) és a gömb (jobb) szegmentált régióinak középpontjai ábra. A mackó sorozat első és utolsó képe 84
95 5.3 Régió alapú mozgásszegmentálás ábra. A műanyag mackó szegmentált régióinak középpontjai A mozgáshiba önmagában nem alkalmas szegmentálásra, de ennek alapján ki lehet választani első iterációban a gömbhöz, majd második iterációban a kockához tartozó domináns mozgást. A domináns mozgások alapján meg lehet határozni a régiók mozgáshoz tartozó inkoherencia értékét, az ábra szerint. Az inkoherencia kép alapján már jól lehet szegmentálni, lásd az és ábrákat. Vizsgálatieredmények valóssorozaton. A szegmentálóalgoritmustvalós sorozatokon is teszteltük. A mackó sorozat egy 2MPixeles digitális kamerával készült, a képeket felbontásra konvertáltuk. A sorozat első és utolsó képe az ábrán látható. A példa 15 képkockát tartalmaz, a mackó és a kamera egyaránt mozog. A szegmentált régiók az ábrán tekinthetők meg. Másik valós példánk az autó sorozat (5.19. ábra): felbontása (gyenge minőségű sorozat), 40 kockán keresztül. A kis felbontás és a keveset mozgó autó ellenére az algoritmusunk meglepően szép eredményt produkált ( ábra), azautójellegzetes pontjaitjólsikerültelválasztaniaszintén mozgó háttértől. Az algoritmusok időigénye. A módszerek időigényének meghatározására nem végeztünk részletes vizsgálatokat sem a fejezet első felében bemutatott robusztus módszerekre (A/R-MED, A/R-LTS, A/R-RANSAC), sem a második részben ismertetett régió alapú szegmentálásra. Röviden annyit mondhatunk, hogy robusztus módszerek időigényének nagyságrendje perc, a régió alapú szegmentálásé elérheti az egy órát is. 85
96 5. OBJEKTUM-REKONSTRUKCIÓ ROBUSZTUS MÓDSZEREI GYENGE PERSPEKTÍVA ESETÉN ábra. Az autó sorozat első és utolsó képe ábra. Az autó szegmentált régióinak középpontjai 86
97 5.4 Összefoglaló 5.4. Összefoglaló 2. tézis Mozgó objektumok pontjainak szegmentálása gyenge perspektíva esetén Megoldásokat kínáltam mozgó objektumok pontjainak szegmentálására, azaz olyan módszereket dolgoztam ki, fejlesztettem tovább, amelyek képesek mozgó objektumok kétdimenzióban követett pontjait különválasztani, a mozgó objektumokhoz nem tartozó (például rosszul követett) pontokat pedig elkülöníteni. 2.a. Hibás pontok kiszűrése Monte-Carlo módszerrel Továbbfejlesztettem a Trajković-Kurata módszert, amely a követett pontokból elkülöníti azokat a pontokat, amelyek nem tartoznak a domináns mozgó objektumhoz. A továbbfejlesztés két területen történt: (1) az LMedS robusztus statisztikát LTS-re cseréltem, (2) az affin mozgásmátrix helyett a valós mozgás felhasználását javasoltam. Az új módszerek pontosabb eredménytadnak, és LTSeseténmagasabbhibáspont-aránytengednek meg, mint az eredeti algoritmus. KidolgoztamegyRANSAC alapúeljárástis, amelyaszakmábanelterjedt RANdom SAmpling Consensus robusztus algoritmus alkalmazása a konkrétproblémára. Affin és valósmátrixokraegyaránt kiterjesztettem a módszert. A domináns mozgás meghatározásához egy mértéket vezettem be, amelyről bebizonyítottam, hogy korlátos, és ennek következtében küszöböléssel el lehet dönteni, hogy valamely domináns mozgás korrekt-e. 87
98 5. OBJEKTUM-REKONSTRUKCIÓ ROBUSZTUS MÓDSZEREI GYENGE PERSPEKTÍVA ESETÉN Ezeket az algoritmusokat szintetikus teszteken összehasonlítottam, és az eredményekkel igazoltam, hogy a medián alapú módszerek esetén a hibás pontok számának aránya maximum 50% lehet, LTS esetében ezt meghaladhatja. Azt is igazoltam, hogy a valós mátrixokat használó módszerek pontosabb eredményeket szolgáltatnak az affin mozgást használóknál. Az algoritmusokatvalósfelvételekbőlszármazótesztadatokonis sikerrel futtattam. 2.b. Régió alapú szegmentálás Kidolgoztam az 2.a. altézisben megfogalmazott módszerre alapozva egy új, régió alapú szegmentáló módszert, amely a pontok szegmentálását tovább javítja a kompakt és merev mozgó objektumok sajátosságainak figyelembevételével. A régió alapú megközelítés tudomásom szerint újítás a mozgásalapú, háromdimenziós objektumszegmentálás területén. Azt is bebizonyítottam, hogy a szegmentálás alapját képező ún. visszavetítési hiba a koordináta-transzformáció többértelműségére érzéketlen. Az algoritmus valós képekből származó tesztadatokon vizsgáltam meg, és meggyőző eredményeken kaptam: a szegmentálás még akkor is sikerült, ha a mozgó objektum lassú szögsebességgel forgott. 88
99 6. fejezet Tagolt objektumok rekonstrukciója Az előzőfejezetben merevobjektumokszegmentációjávalfoglalkoztunk, ittmost azt mutatjuk meg, hogy hogyan lehet két merev objektumról megállapítani, hogy tagolt objektumot alkotnak-e. A három ismertetett altézist konferenciákon publikáltuk [50, 51, 52,?], folyóiratpublikáció készítésén jelenleg is dolgozunk Nemmerev mozgások áttekintése A nemmerev objektumok háromdimenziós rekonstrukciójával a kutatók csak az elmúlt években kezdtek el foglalkozni (lásd [19, 129, 139, 140, 131, 141] hivatkozásokat). Alapvető problémát okoz a nemmerev testek mozgására megkötést tenni. A szakirodalomban kétféle megkötés használatos: Objektumok mozgásának leírása úgynevezett kulcsobjektumok [19, 129, 139, 140] súlyozott összegével: S f = K l i S i (6.1) i=1 ahol S f az f. képkockához tartozó struktúramátrix, S i az i. kulcsobjektum pontjait leíró mátrix (mérete az S struktúramátrixszal megegyező, azaz 89
100 6. TAGOLT OBJEKTUMOK REKONSTRUKCIÓJA 3 P, ahol P az objektum pontjainak a száma), l f i az i. kulcshoz tartozó súly. Ennek a leírásnak egy nagy hátránya van: nem tudjuk pontosan, hogy milyen objektumokatlehetilyen módonleírni. Aztérezzük, hogy kellően sok kulcsobjektum bevezetésével közelíthetjük az igazi objektumokat, azonban a kulcsobjektumok száma nem növelhető korlátlanul: a kulcsobjektumokat és ahozzájuktartozósúlyokatugyanismegkell becsülni, és sokbecsülendő paraméter esetén a becslés minősége nagymértékben romlik. Objektumok leírása merev objektumok csatolása segítségével [131, 141]. Ezeket az objektumokat hívjuk tagolt objektumoknak 1. Ebbenafejezetben amásodikmódszerrel, azazatagoltobjektumokkalfoglalkozunk, azon belül is a következő kérdésnek megválaszolására teszünk kísérletet: hogyan lehet két merev, mozgó objektumról megállapítani, hogy tagolt objektumot alkotnak Szakirodalmi áttekintés Az eddig megjelent, tagolt objektumok rekonstrukciójával foglalkozó cikkekben [131, 141] kétféle tagoltobjektumrólesik szó, bárelvilegújabbalkategóriákat lehetne bevezetni: 1. Két objektum legalább egy ponton kapcsolódik egymáshoz. 2. Két objektum egy tengelyen keresztül kapcsolódik egymáshoz. Ez utóbbi értelemszerűen az első típus alesete, hiszen a közös tengely minden pontja felfogható csatlakozási pontnak. További alesetek is elképzelhetőek, gondoljunkcsak az emberi testkülönböző szabadságfokokkal rendelkező ízületeire, azonban a dolgozatban mi is a két alapesettel foglalkozunk. A szakirodalomban ismereteink szerint az első munka 2003-ban jelent meg [146]. Ebben a publikációban egy összetett tagolt objektum mozgásával 1 angol szakirodalomban: articulated objects 90
101 6.3 Pontszerűen kapcsolt tagolt objektumok csoportosítása foglalkoznak, a szegmentációt elvégzettnek tekintik. Ezzel szemben Tresadern és Reid [131], illetve Yan és Pollefeys [141] dolgozatában a szegmentálással és a közös pont (illetve közös tengely) meghatározásával egyaránt foglalkoznak. A szegmentálást rangcsökkentés segítségével végzik el, ami az előző fejezet eredményeinek tükrében nem mindig célravezető. Éppen ezért ebben a fejezetben más koncepciót követünk: először szegmentáljuk a 2. tézisben (5. fejezet) ismertetett módszerrel a mozgó objektumokat, majd megpróbáljuk azokat összerakni (csoportosítani) tagolt objektumokká. Ebben a fejezetben két csoportosító algoritmust mutatunk be Pontszerűen kapcsolt tagolt objektumok csoportosítása A kapcsolódási pont optimális becslése legkisebb négyzetes érelemben Ebben a szakaszban megmutatjuk, hogyan lehet a kapcsolódási pontot gyenge perspektíva esetén optimálisan megbecsülni. Ez a becslés segít a későbbiekben a csoportosítási feladat megoldásában. Feltételezzük, hogy a két merev objektum szegmentálása megtörtént, a mozgás- és struktúramátrixokat a 4. fejezetben leírt módszerrel kiszámítottuk. Az f. képkockára a faktorizációs egyenlet az eltolást is figyelembe véve az alábbi összefüggéseket adja: W 1 = [ M 1 t 1 ] [ S 1 1 T 1 W 2 = [ M 2 t 2 ] [ S 2 1 T 2 ], (6.2) ]. (6.3) ahol az első objektumhoz tartozó mozgás- és struktúramátrixot és eltolásvektort M 1, S 1 és t 1 jelöli. A második objektumhoz tartozó megfelelő mátrixok/vektorok jele értelemszerűen M 2, S 2 és t 2. Amennyiben a két objektum legalább egy ponton keresztül csatlakozik, t 1 és t 2 eltolásvektorok helyett be lehet vezetni egy 91
102 6. TAGOLT OBJEKTUMOK REKONSTRUKCIÓJA közös t eltolásvektort. Ekkor a a fenti egyenletek átírhatóak a következő módon: W 1 = [ M 1 t ][ ] S 1 1 T, (6.4) 1 W 2 = [ M 2 t ][ S 2 1 T 2 ]. (6.5) ahol S 1 és S 2 mátrixok jelölik a csatlakozási ponttal eltolt háromdimenziós koordinátákat, a csatlakozási pontot magát pedig o 1 és o 2 jelöli. A közös kétdimenziós eltolásvektor kifejezhető a mozgásmátrixok és az offsetvektorok segítségével: t = t 1 M 1 o 1, (6.6) t = t 2 M 2 o 2. (6.7) (Az eltolás és a faktorizáció kapcsolatát az E. függelék ismerteti.) Ha fel akarjuk írni a rendszerünket, és meg akarjuk becsülni a csatlakozási pontot, egy költségfüggvényt kell meghatározni. Ezek alapján akkor kapjuk a legjobb megoldást, ha a mintavételi térben (esetünkben: képtérben) vesszük fel a hibát: azaz a követett pontok értékeinek és a becsült értékeknek a különbségét minimalizáljuk legkisebb négyzetes értelemben. A gondolatmenet alapján az alábbi költségfüggvényt lehet felírni: J = W 1 [ M 1 t ][ ] S W 2 [ M 2 t ][ ] S 2 2, (6.8) 1 T 1 ahol. 2 F a Frobenius-féle norma négyzetét jelöli ( A 2 F = trace(at A)). A feladat tehát megtalálni a költségfüggvény minimumát. F 1 T 2 F Mivel a költségfüggvény (a négyzettől eltekintve) az ismeretlen paramétereket adó o 1, o 2, t vektoroktól lineáris módon függ, a fenti költségfüggvény globális optimumát könnyen meg tudjuk határozni. Az ismeretlenek száma összesen 6 + 2F, ahol F a képkockák száma. A Frobenius-norma miatt az egyenletek száma összesen 2F(P 1 + P 2 ), ahol P 1 és P 2 az első és a második merev objektum pontjainak száma, de a gyenge perspektíva miatt az egyenletekben redundancia van. Ennek belátására először válasszuk ki az első objektum p-edik pontját. A költségfüggvény megfelelő része: w p 1 M 1 s p 1 t 2 F, (6.9) 92
103 6.3 Pontszerűen kapcsolt tagolt objektumok csoportosítása ahol w p 1 a W 1 mérési mátrix p-edik oszlopa, és s p 1 az első objektum struktúramátrixának a megfelelő oszlopa. Tudjuk, hogy az eredeti faktorizáció szerint w p 1 = M 1 s p 1+t 1 (lásd a 6.4. összefüggést), továbbá s p 1 = s p 1+o 1 a lehetséges eltolás miatt. A két összefüggés miatt az s p és a s p 1 vektorokat eliminálni lehet, és az alábbi összefüggést lehet kapni: t 1 = t M 1 o 1. (6.10) Teljesen analóg módon a második objektumra is fel tudjuk írni: t 2 = t M 2 o 2. (6.11) Jól látható, hogy ezek az összefüggések függetlenek a pontoktól, csak a faktorizáció során kiszámított M 1, M 2 mozgásvektoroktól és t 1, t 2 eltolásvektoroktól függenek. Az is jól látható, hogy így visszakaptuk a 6.6 és a 6.7 alapegyenleteket. További egyszerűsítést végezhetünk, ha a és a kifejezésekből t-t kifejezzük. A végső, megoldandó költségfüggvény az alábbi módon írható le: J = M 1 o 1 + t 1 M 2 o 2 + t 2 2 F (6.12) A megoldás a lineáris algebrából [17] jól ismert Moore-Penrose-féle pszeudoinverz használatávalkaphatómeg (inhomogén, túlhatározottegyenletrendszermegoldása): [ ô1 ô 2 ] = [M 1 M 2 ] [t 2 t 1 ], (6.13) ahol A az A a mátrix pszeudoinverze. A t eltolásvektor pedig a és a összefüggésekből egyszerű átlagolással kapható meg: ˆt = 1 2 (M 1ô 1 + t 1 + M 2 ô 2 + t 2 ) (6.14) Megjegyzés. Ez a megoldás nem meglepő: az o 1 és az o 2 vektorok adják meg a csatlakozási pontot az objektumok saját háromdimenziós rendszerében. A egyenlet azt mondja ki, hogy a csatlakozási pontok pozícióinak a képsíkon meg kell egyezniük, hiszen azok valójában a közös pont helyei a két objektum rendszerében. A fő eredmény, hogy ez a megoldás a 6.8. költségfüggvénynek optimális megoldása. A költségfüggvény pedig két ismert mozgás- és struktúramátrixszal rendelkező, pontszerűen tagolt objektum összes lehetséges kapcsolódását leírja. 93
104 6. TAGOLT OBJEKTUMOK REKONSTRUKCIÓJA 6.4. Vizsgálati eredmények: pontszerű illeszkedés Az előzőszakaszbanbemutatottmódszertszintetikusés valós adatokon egyaránt megvizsgáljuk. Mindkét esetben összehasonlítottuk módszerünket Tresadern és Reid [131] algoritmusával. Azért ezt a módszert választottuk, mert ismereteink szerint ez az egyetlen módszer, amely ugyanazokat a feltételezéseket használja, mint a mi módszerünk: azaz hogy a merev objektumokat előzőleg szegmentáltuk Vizsgálat szintetikus adatokon A szintetikus adatokon végzett vizsgálat célja, hogy a pontbecslés precizitását megvizsgáljuk három tényező függvényében: hogyan változik a becslés hibája zajnövelés, képkockaszám-növelés és pontszámnövelés esetén. Az eredményeket minden esetben összehasonlítjuk a Tresadern-Reid [131] módszerrel. A szintetikus adatokat a 2.a. tézisnél használt módszerhez nagyon hasonlóan állítottuk elő: a kapcsolódási pontot vettük az origónak. (Ezt az általánosság sérelme nélkülmegtehetjük.) A kétmerevenmozgópontfelhőkoordinátáitegyenletes eloszlás segítségével generáltuk, az első objektum összes koordinátája a [0, 1], a második objektumé a [ 1, 0] intervallumba esik. Ezek után véletlenül kiválasztott szögekkel minden egyes képen elforgattuk a két objektumot a közös pont, azaz az origó körül. (A két háromdimenziós mozgás egymástól teljesen független.) Végül gyenge perspektíva segítségével levetítettük a pontokat a képsíkokra, és zajt adtunk a kétdimenziós koordinátákhoz. Ezután lefuttattuk a javasolt pontbecslő módszert, majd a Tresadern-Reid módszert [131]. (A módszer eredeti forráskódját az oxfordi kutatóktól megkaptuk.) A kapott eredményeket két metrika szerint is összehasonlítottuk. Mivel tudjuk, hogy az origóban kell lennie a közös pontnak, a kétdimenziós hibát az alábbiak szerint számoljuk: ǫ 2D = 1 F ˆt 2 F (6.15) Ezt a hibát visszavetítési hibának nevezzük, mivel a közös pont képsíkra történő visszavetítésének a hibáját adja. 94
105 6.4 Vizsgálati eredmények: pontszerű illeszkedés A másikhibátegyszerűen háromdimenziós hibánaknevezzük. Mivel azobjektumok pontjait mi állítottuk elő, a rekonstruált és az eredeti pontokat össze tudjuk regisztrálni. Számtalan háromdimenziós pontregisztrációs [3, 69, 70] módszer létezik a szakirodalomban, mi Arun eljárását [3] választottuk. A regisztrálás után az eredeti csatlakozási pontokat és a becsülteket (ez utóbbiakat az o 1 és o 2 vektorok adják) össze tudjuk hasonlítani: a hibának a megfelelő pontok közötti távolságot vettük. Általános megjegyzések. Egyértelműen látszik, hogy a javasolt módszerünk minden esetben felülmúlja a Tresadern-Reid módszert, A különbség a visszavetítési hiba esetén rendkívül nagy, a háromdimenziós hiba esetén azonban kevésbé jelentős. A a 6.1, 6.2. és 6.3. ábrákon a regressziós egyeneseket is fel kellett tüntetni, hogy a javulás egyértelműen érzékelhető legyen. Hibák a zaj függvényében (6.1. ábra). A vizsgálat soránakétdimenziós pontok zaját egyenletesen növeltük. A visszavetítési és a háromdimenziós hiba szemmel láthatóan lineárisan növekszik a zaj növelésével. Hiba nulla zajszint esetén nincsen, ami pozitív fejlemény, hiszen egy becslő eljárással szemben alapvető elvárás, hogy zajmentes esetben tökéletes eredményt adjon. Ezt az elvárást nemcsak a saját módszerünk teljesíti, hanem a Tresadern-Reid algoritmus is. Hibák a pontok számának függvényében (6.2. ábra). A grafikon azt mutatja, hogy a hibák csökkennek, ahogyan a merev objektumok követett pontjainak a számát növeljük. Ez azért van, mert az M 1 és az M 2 mozgásmátrixok becslése pontosabbá válik a pontok számának növekedésével. Pontosabb mozgásmátrixokból az illeszkedés helyét is pontosabban meg lehet határozni. Hibák a képkockák számának függvényében (6.3. ábra). Ez a vizsgálati esetek közül az egyetlen, amikor a két módszer különbözően viselkedik: A Tresadern-Reid módszer kétdimenziós visszavetítési hibája növekszik a képkockák számának növelésével. Az optimális módszerünknél ezzel szemben csökken a hiba két- és háromdimenzióban egyaránt. A Tresadern-Reid algoritmus 3D-s hibája szintén csökken, de a regressziós egyenes minden esetben az optimális módszer regressziós egyenese felett helyezkedik el. 95
106 6. TAGOLT OBJEKTUMOK REKONSTRUKCIÓJA 6.1. ábra. 2D és 3D hiba a zaj függvényében. Balra: 2D-s hiba. Jobbra: 3D-s hiba Kísérlet valós adatokon A javasolt módszert egy 11 képkockát tartalmazó videószekvencián vizsgáltuk. Három kockát (1., 6. és 11. képek) láthatunk a 6.4. ábrán. Három mozgó objektumot tartalmaz a videó: egy CD dobozt, egy üdítő dobozát és egy műanyag (mézes) mackót. A mackót tengely segítségével rögzítettük a CD dobozhoz. A narancsos üdítő doboza szabadon mozog az asztalon. Magát a képeket készítő kamerát is mozgattuk a felvétel alatt. A képen követtük a jellegzetes pontokat, és a 2.b. tézisben (5.3. szakasz) bemutatott módszerrel szegmentáltuk a mozgó objektumokat. Ezek után az 1. tézisben (4. fejezet) megadott módon a struktúra- és a mozgásmátrixokat kiszámítottuk. A három objektum szegmentált pontjait a 6.5. ábrán láthatjuk. Ezek után meghatároztuk a kapcsolódási pontot a módszerünkkel és a Tresadern-Reid módszerrel egyaránt. (Mivel a mackó és a doboz egy tengellyel kapcsolódnak, a tengelyösszes pontja lehetséges kapcsolódási pontot ad.) A 6.6. ábrán látható a pontok becsült helye az 1., 6. és 11. képkockán. 96
107 6.5 Pontszerűen kapcsolt mozgó objektumok csoportosítása 6.2. ábra. 2D és 3D hiba a pontok számának függvényében. Balra: 2D-s hiba. Jobbra: 3D-s hiba Pontszerűen kapcsolt mozgó objektumok csoportosítása A tagolt objektumok szegmentálása igen nehéz feladat. A már sokszor hivatkozott módszerek [131, 141] rangbecslés alapján határozzák meg, hogy hány mozgó objektumot tartalmaz egy megadott mérési mátrix. Ahogyan azt a 2.b. tézisnél már megbeszéltük, a rangbecslés zajmentes esetben kiválóan működik, azonban teljesen kiszámíthatatlan lesz a működés, amikor zaj kerül a mérésekre, különösen akkor, ha a bemeneti mérési mátrixok idegen adatot tartalmaznak. Ezért mi a 2.b. tézisben bemutatott régió alapú megközelítést javasoljuk. A szakaszban már megvizsgáltuk a visszavetítési hibát, és megállapíthattuk, hogyzajmentes esetben 0 avisszavetítési hiba, azaj növelésével pedig lineárisan növekszik. A visszavetítési hibának van még egy igen jó tulajdonsága: a képtérben határozzuk meg, és a mértékegysége pixel. Ezzel a kapott eredmény kézzelfogható, és józan paraszti ésszel egy küszöbértéket beállíthatunk (tapasztalataink alapján a küszöböt 1 pixel környékére javasoljuk). A 6.1. ábrán jól látszik, hogy realisztikus zaj (pár százalék) esetén a visszavetítési hiba 1 pixel alatt marad. A szegmentálás helyett tehát javaslatunk a következő: a 2.b. tézisben ismertetett módszerrel szegmentáljuk a mozgó, merev objektumok pontjait, majd 97
108 6. TAGOLT OBJEKTUMOK REKONSTRUKCIÓJA 6.3. ábra. 2Dés 3Dhibaa képkockák számának függvényében. Balra: 2D-s hiba. Jobbra: 3D-s hiba ábra. A kísérleti szekvencia három képkockája párosítsuk az egymás mellett levő objektumokat, és határozzuk meg a közös pontot és ennek segítségével a visszavetítési hibát. Ha a visszavetítési hiba a küszöbnél kisebb, a két pontot tagolt objektummá csoportosíthatjuk. Módszerünk igazolására a három mozgó objektumunkat tartalmazó videofelvételt vettük szemügyre. Az objektumok közötti visszavetítési hibát kiszámítottuk, a 6.1. táblázatban az értékek megtekinthetőek. Jól látszik, hogy a mackó és a CD doboz között szignifikánsan kisebb a hiba, mint a másik két esetben. 98
109 6.6 Tengellyel csatlakozó tagolt objektumok csoportosítása 6.5. ábra. Az objektumok szegmentált jellegzetes pontjai 6.6. ábra. Csatlakozási pont becsült helye. O : optimális módszer x :Tresadern- Reid módszer Tengellyel csatlakozó tagolt objektumok csoportosítása Ebben a szakaszban bemutatunk egy módszert, amely két mozgó merev objektumról megállapítja, hogy tengelyesen csatoltak-e Két mozgó merev objektum relatív mozgásának meghatározása Az algoritmusunk első részében előállítjuk a két mozgó merev objektum relatív mozgását. Az elsőmódszerhez hasonlóantovábbrais feltételezzük, hogyamerev 99
110 6. TAGOLT OBJEKTUMOK REKONSTRUKCIÓJA Objektum pár CD doboz Mackó Üdítős doboz Mackó CD doboz Üdítős doboz Visszavetítési hiba táblázat. Az objektum párok visszavetítési hibái mozgó objektumok szegmentálása megtörtént. Emlékeztetőnek tekintsünk először az eredeti faktorizációs egyenletekre: W1 i = M1S i 1 + t i 1 és W2 i = M2S i 2 + t i 2. A relatív mozgás a mozgásmátrixok ismeretében könnyen számítható: M12 i = M 1 1 i M2 i vagy M21 i = M 2 1 i M1, i attól függően, hogy az első vagy a második objektumot rögzítettük. M1 i és M2 i az i. képkockához tartozó részmozgásmátrixot jelöli. Ez a két mátrix nem invertálható, csak abban azesetben, amennyiben kiegészítjük arészmátrixokat aharmadiksorral,amelyik az első kettőre merőleges, és a hossza az első kettő átlaga (gyenge perspektíva esetén) vagy egységnyi (merőleges vetítés során). Ahogyan azt megmutattuk a C. függelékben, a faktorizáció többértelmű: egy ortonormált mátrixszal való szorzásig szabadsága van a faktorizációnak. Tehát ha W1 i = M1S i 1 + t i 1 és W2 i = M2S i 2 + t i 2 érvényes felbontás, akkor W1 i = (M1A i 1 )(A T 1 S 1 ) + t i 1 és W2 i = (M2A i 2 )(A T 2 S 2 ) + t i 2 is érvényes, feltéve, hogy A T 1 A 1 = E és A T 2 A 2 = E. A relatív mozgás a faktorizáció többértelműsége miatt az alábbiak szerint módosul: M12 i = A T 1 M 1 1 i M2A i 2 = A T 1 M12A i 2 (6.16) M21 i = A T 2 M 2 1 i M1A i 1 = A T 2 M21A i 1 (6.17) Az A 1 és az A 2 mátrixok ortonormáltak, tehát egy forgatást (esetlegesen tükrözéssel) valósítanak meg: az eredeti relatív mozgás sorait (melyek háromdimenziós pontként is értelmezhetők) forgatják el. Nem nehéz belátni azt sem, hogy ha a mozgásmátrixok sorait háromdimenziós pontoknak képzeljük el, akkor ezek a pontok két, közös tengelyű körön helyezkednek el. (A páros és a páratlan sorok alkotnak külön kört, ez a két kör közös tengellyel rendelkezik.) Ezt a következő megfontolás szerint bizonyíthatjuk be: 100
111 6.7 Vizsgálati eredmények: tengelyes csatlakozás Az általánosság sérelme nélkül feltételezhetjük, hogy a közös tengely párhuzamos az [1, 0, 0] vektorral (így vesszük fel a koordinátarendszert). A második objektum a tengely közül forog, tehát ha a második objektum egy bázisvektora az első képkockán [x y, y 1, z 1 ], akkor az i. kockán ez a bázisvektor 1 a [x 1, y 1 cos(α i ) + z 1 sin(α i ), z 1 cos(α i ) y 1 sin(α i )] T koordinátákkal írható le, ha α i szöggel fordult el az objektum a közös tengely körül. A másik bázisvektor felírása teljesen hasonlóan kapható: [x 2, y 2 cos(α i )+z 2 sin(α i ), z 2 cos(α i ) y 2 sin(α i )] T, ha az első képkockán ez a második bázisvektor a [x 2, y 2, z 2 ] T koordinátákkal írható le. A felírásból látszik (és a tengelyes forgásból logikusan következik), hogy a bázisvektorok végpontjai köríveket rajzolnak le, amelyek a tengelye közös. A összefüggés szerint a faktorizáció többértelműsége miatt ezeket a pontokat elforgatva kapjuk meg, de ez nem befolyásolja a tényt, hogy a pontokra közös tengelyű köröket lehet illeszteni. A feladat tehát közös tengelyű körök illesztése, és az illesztési hiba segít eldönteni, hogy két mozgó tárgy vajon tengelyesen csatolt tagolt objektumot alkot-e. Bárkörillesztésre számospublikációtlehettalálni (például [106, 39, 122, 36, 92]), a közös tengelyű pontillesztéssel legjobb ismereteink szerint eddig nem foglalkoztak. Ezért saját módszert készítettünk, amelyet azos TENGELYU KOROK IL- LESZTESE HAROMDIMENZIOS PONTOKRAACTION*.23A H függelékben részletesen ismertetünk. Miutánaz illesztést elkészítettük, az illesztésihibátis ki kell számítani, amelyiknek a definíciója a függelékben szintén megtalálható Vizsgálati eredmények: tengelyes csatlakozás Vizsgálatok szintetikus adatokon A vizsgálatok megvalósításai teljesen hasonlóak a szakaszban ismertetett módszerhez, azzalakülönbséggel,hogyittcsaktengelyes mozgástengedünkmeg 1 Itt most bázisvektornak a relatív mozgás i. képkockájának két bázisvektorát nevezzük. 101
112 6. TAGOLT OBJEKTUMOK REKONSTRUKCIÓJA (atengelymentielforgástminden kockán véletlenszerűen forgatjukel). Ugyanazt a három esetet vizsgáltuk meg: 6.7. ábra. Illeszkedési hiba a zaj függvényében ábra. Illeszkedési hiba a pontok számának függvényében. Illesztési hiba a zaj függvényében. A 6.7. ábrán láthatjuk, hogy a hiba a tengelyes kapcsolódás esetén is nagyjából lineárisan függ a zajtól. Az ábra alapján látható, hogy körülbelül 7 8% zajszintig tart a linearitás, ami körülbelül 0,02-es illesztési hibának felel meg. 102
113 6.7 Vizsgálati eredmények: tengelyes csatlakozás 6.9. ábra. Illeszkedési hiba a képkockák számának függvényében. Illesztési hiba a képkockák számának függvényében. A 6.9. ábra mutatja az eredményeket. Látható, hogy a hiba a képkockák számának növekedésével fordítottan arányos. Ennek oka, hogy a mozgásmátrix több pontot tartalmaz, ha növekedik a képek száma, több pontból pedig pontosabb becslés adható a képekre. El kell azonban azt is ismerni, hogy a körillesztési algoritmuson még lehet javítani: a ábrán látszik, hogy időnként kiugró hibaértékeket produkál a módszer. Ennek oka, hogy elsősorban nagy hibaszint esetén a párhuzamos síkokat meghatározó rész nem az. Illesztési hiba a pontok számának függvényében. A grafikon a 6.8. ábrán szépen megmutatja, hogy a pontok számának növelésével hasonlóan a képkockák növeléséhez a hiba csökken, hiszen több ponttal a mozgásmátrix becslése javul; pontosabb mozgásmátrixokból pontosabb relatív mozgás becsülhető; pontosabb relatív mozgás esetén pedig a körillesztés is pontosabb lesz Vizsgálat valós adatokon A ábrán a szakaszban már vizsgált képsorozatból származó eredmény látható: meghatároztuk a mackó és a CD doboz relatív mozgását, és kiszámítottuk a relatív mozgás pontjaira illeszthető közös tengelyű köröket. Jól látszik a ábrán, hogy a relatív mozgást reprezentáló pontok szépen illeszkednek 103
114 6. TAGOLT OBJEKTUMOK REKONSTRUKCIÓJA ábra. Példa hibás körillesztésre. a párhuzamos körökre, az illeszkedési hiba kicsi, ezért a mackót és a CD dobozt vehetjük tengelyes kapcsolt tagolt objektumnak. Az algoritmusok futásigénye. A bemutatott két új módszer időigényének meghatározása nem végeztünk részletes vizsgálatokat, mivel mindkét módszer a másodperc törtrésze alattelvégzi a szükséges számításokat. A módszer feltételezi a szegmentáció meglétét, a szegmentáló algoritmusok pedig nagyságrendekkel lassabban futnak, mint a itt ismertetett csoportosítási módszerek, ahogyan ezt az szakaszban már leírtuk ábra. A mackó és a CD doboz relatív mozgására illesztett közös tengelyű körök. 104
115 6.8 Összefoglaló 6.8. Összefoglaló 3. tézis Nemmerev objektumok csatolása Kidolgoztam két új módszert, melynek segítségével el lehet dönteni két merev, mozgó objektumról, hogy tagolt objektumot alkot-e. Az első módszer pontszerűen kapcsolt, a második tengelyesen rögzített tagolt objektumok kapcsolódásának eldöntésével foglalkozik. Az első módszer esetén a kapcsolódás helyének becslését is megoldottam. Mindegyik módszer feltételezi, hogy a merev mozgó objektumok szegmentálása megtörtént és a struktúra- és mozgásmátrixokat kiszámítottuk. 3.a. Kapcsolódási pont becslése. A kapcsolódási pontra a megadott költségfüggvény esetében (6.8 összefüggés) optimális, zárt alakú megoldást adtam (ld és 6.14 összefüggéseket). 3.b. Pontszerűen kapcsolt tagolt objektumok csoportosítása. A csoportosításifeladatmegoldásáraa 3.a. altézis sorándefiniáltbecslés hibáját alkalmaztam. A csoportosítás eldöntésére egy küszöböt kell a hibára meghatározni. A megadott hiba mértékegysége pixel, ami a szükséges küszöb meghatározását megkönnyíti. 3.c. Tengelyesen kapcsolt tagolt objektumok csoportosítása. Megmutattam, hogy a közös tengelyű tagolt objektumok esetén a tengellyel összekötött két objektum relatív mozgását leíró mátrix sorai közös tengelyű köríveket írnak le. A közöstengelyűkörívekmeghatározásárakétrészbőlállóalgoritmust adtam: a módszer először párhuzamos síkokat illeszt az adathalmazokra, majd ezeken asíkokonközöstengelyű, azorigónátmenőköröket határoz meg. A döntést itt is küszöbölés segítségével lehet elvégezni, a szükséges hibát a körillesztés pontatlansága adja. Valamennyi altézist szintetikus és valós adatokon is megvizsgáltam, és a működőképességüket bemutattam. 105
116 6. TAGOLT OBJEKTUMOK REKONSTRUKCIÓJA 106
117 7. fejezet Összefoglalás A dolgozatbanaszámítógépes látásegyikalapvetőterületével, aháromdimenziós objektum-rekonstrukcióval foglalkoztam. A téma a nyolcvanas évek óta dinamikus fejlődik, a legfontosabb eredményeket a 3. fejezetben áttekintettük. Ahogyanazta2. fejezetben láthattuk, a gyakorlatbanhasznált, avalóságban nemlineáris leképzést megvalósító kamerák egyszerűsített leírására többféle kameramodell létezik. A perspektivitást a projektív kamera írja le, de bizonyos feltételek eseténgyenge perspektivitás is jó közelítéssel leírja avetítést. A gyengén perspektívrekonstrukciósegítségéveljómodelleketlehetalkotni, illetve ezeknek a modelleknek a paraméterit valós perspektivitás kezdeti értékeinek is lehet venni. A disszertációban a rekonstrukciós problémakörből három feladatnak a megoldására vállalkoztam: az első tézisben a Tomasi-Kanade faktorizáció pontosítását valósítottam meg, a második tézis robusztus algoritmusok továbbfejlesztését és egy újszerű szegmentáló algoritmust tartalmazott, a harmadiktézisben pedigtagoltobjektumokrekonstrukciójában elérteredményeimet mutattam meg További munkák A munka előrehaladtával újabb és újabb ötletek merültek fel a rekonstrukciós folyamat javítására. Ezért ez a dolgozat nem tekinthető egy folyamat lezárásának, hanem éppen ellenkezőleg, a munka java még csak most kezdődik el. A tudományterület állása szerint a rekonstrukciós folyamat minden egyes részproblémáján van bőven javítani- és csiszolnivaló. Kézenfekvő, hogy a 107
118 7. ÖSSZEFOGLALÁS tézisekben is megfogalmazott eredményeket terjesszük ki gyenge perspektíváról valódi perspektívára, illetve a már meglévő módszerek pontosságán tovább javítsunk. Legfontosabb cél, hogy olyan programkönyvtárat állítsunk elő, amely tartalmazza az objektum rekonstrukció legfontosabb algoritmusait, és amelynek segítségével új részmódszereket gyorsan ki lehet próbálni. Ennek a programkönyvtárnak a készítése elkezdődött tehetséges műegyetemi hallgatók segítségével, és a közös munkának gyümölcseként eddig is jó néhány diplomamunkaés TDK dolgozatis született. Reményeim szerintadisszertációmegvédése után még több energiát tudok arra szánni, és ezáltal segíteni tudok abban, hogy ez a rendkívül érdekes és korszerű téma elfoglalja megérdemelt helyét a magyar mérnökképzésben. 108
119 Hivatkozások [1] GIMP - GNU Image Manipulation Toolkit. [2] POVRay - Persistence of Vision Raytracer. [3] K. S. Arun, T. S. Huang, and S. D. Blostein. Least-squares fitting of two 3-D point sets. IEEE Trans. on PAMI, 9(5): , [4] Delaunay B. Sur la sphere vide. Izvestia Akademii Nauk SSSR, Otdelenie Matematicheskikh i Estestvennykh Nauk, 7: , [5] Simon Baker, Ralph Gross, and Iain Matthews. Lucas-Kanade 20 Years On: A Unifying Framework: Part 3. Technical Report CMU-RI-TR-03-35, Robotics Institute, Carnegie Mellon University, Pittsburgh, PA, November [6] Simon Baker, Ralph Gross, and Iain Matthews. Lucas-Kanade 20 Years On: A Unifying Framework: Part 4. Technical Report CMU-RI-TR-04-14, Robotics Institute, Carnegie Mellon University, Pittsburgh, PA, February [7] Simon Baker, Ralph Gross, Iain Matthews, and Takahiro Ishikawa. Lucas- Kanade 20 Years On: A Unifying Framework: Part 2. Technical Report CMU-RI-TR-03-01, Robotics Institute, Carnegie Mellon University, Pittsburgh, PA, February [8] Simon Baker and Iain Matthews. Lucas-Kanade 20 Years On: A Unifying Framework: Part 1. Technical Report CMU-RI-TR-02-16, Robotics Institute, Carnegie Mellon University, Pittsburgh, PA, July
120 HIVATKOZÁSOK [9] Simon Baker and Iain Matthews. Lucas-Kanade 20 Years On: A Unifying Framework. International Journal of Computer Vision, 56(3): , March [10] Simon Baker, Raju Patil, Kong Man Cheung, and Iain Matthews. Lucas- Kanade 20 Years On: Part 5. Technical Report CMU-RI-TR-04-64, Robotics Institute, CarnegieMellonUniversity, Pittsburgh, PA, November2004. [11] J.L. Barron and N.A. Thacker. Tutorial: Computing 2D and 3D Optical Flow [12] A. Bartoli. Structure-From-Motion Using Lines: Representation, Triangulation and Bundle Adjustment. Computer Vision and Image Understanding, 100: , [13] P. A. Beardsley, A P Zisserman, and D. W. Murray. Sequential Updating of Projective and Affine Structure from Motion. International Journal of Computer Vision, 23(3): , [14] A. Belcsik. Háromdimenziós modell előállítása videofelvétel alapján. Master s thesis, Budapesti Műszaki Egyetem, Villamosmérnöki és Informatikai Kar, Konzulens: Hajder Levente. [15] Bill Triggs and Philip McLauchlan and Richard Hartley and Andrew Fitzgibbon. Bundle Adjustment A Modern Synthesis. In W. Triggs, A. Zisserman, and R. Szeliski, editors, Vision Algorithms: Theory and Practice, LNCS, pages Springer Verlag, [16] S. Birchfield. Derivation of Kanade-Lucas-Tomasi Tracking Equation. stb/klt/birchfield-klt-derivation.pdf, [17] Åke Björck. Numerical Methods for Least Squares Problems. Siam, [18] Jean-Daniel Boissonnat. Geometric structures for three-dimensional shape representation. ACM Transactions on Graphics, 3(4): ,
121 HIVATKOZÁSOK [19] M. Brand and R. Bhotika. Flexible Flow for 3D Nonrigid Tracking and Shape Recovery. In IEEE Conf. on Computer Vision and Pattern Recognition, volume 1, pages , [20] D. C. Brown. Close-range camera calibration. Photogrammetric Engineering, 37: , [21] T. Brox, A. Bruhn, N. Papenberg, and J. Weickert. High accuracy optical flow estimation based on a theory for warping. In ECCV, volume 3024 of Springer LNCS, pages 25 36, [22] A.M. Buchanan. Investigationintomatrixfactorizationwhen elements are unknown. Technical report, University of Oxford, University of Oxford, [23] A. M. Buchanan and A. W. Fitzgibbon. Damped Newton Algorithms for Matrix Factorization with Missing Data. In CVPR 05: Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 05) - Volume 2, pages , [24] Yisong Chen and Horace Ho-Shing Ip. Texture evolution: 3D texture synthesis from single 2D growable texture pattern. The Visual Computer, 20(10): , [25] B. K. Choi, H. Y. Shin, Y. I. Yoon, and J. W. Lee. Triangulation of scattered data in 3D space. Computer Aided Design, 20(5): , [26] Brian Curless and Marc Levoy. A volumetric method for building complex models from range images. In SIGGRAPH 96: Proceedings of the 23rd annual conference on Computer graphics and interactive techniques, pages ACM Press, [27] Paul E. Debevec, Camillo J.Taylor, and Jitendra Malik. Modeling and rendering architecture from photographs: a hybrid geometry- and image-based approach. In SIGGRAPH 96: Proceedings of the 23rd annual conference on Computer graphics and interactive techniques, pages 11 20,
122 HIVATKOZÁSOK [28] Csetverikov Dimitrij. A digitális képelemzés alapvető algoritmusai, ELTE előadás jegyzet ftp://aramis.ipan.sztaki.hu/pub/kepelemzes/version2006/. [29] Junyu Dong and Mike Chantler. Capture and Synthesis of 3D Surface Texture. Int. J. Comput. Vision, 62(1-2): , [30] W. Faig. Calibration of close-range photogrammetry systems: Mathematical formulation. Photogrammetric Engineering and Remote Sensing, 41: , [31] Fast Marching tutorial. apeixoto/fastmarching.htm1. [32] O.D. Faugeras and G. Toscani. The calibration problem for stereo. In CVPR, pages 15 20, [33] Olivier D. Faugeras and Theodore Papadopoulo. A Nonlinear Method for Estimating the Projective Geometry of Three Views. In ICCV, pages , [34] M. Fischler and R.Bolles. RANdom SAmpling Consensus: a paradigm for model fitting with application to image analysis and automated cartography. Commun. Assoc. Comp. Mach., 24: , [35] A. W. Fitzgibbon and A. Zisserman. Automatic Camera Recovery for Closed or Open Image Sequences. In ECCV, pages , [36] A.W.Fitzgibbon, M. Pilu, and R.B.Fisher. Direct Least Square Fitting of Ellipses. IEEE Trans. on PAMI, 21(5): , [37] FriedrichFraundorfer, KonradSchindler, andhorstbischof. Piecewise planar scene reconstruction from sparse correspondences. Image and Vision Computing, 24(4): , April [38] S. Ganapathy. DecompositionofTransformationMatrices forrobotvision. In IEEE International Conference on Robotics and Automation, pages ,
123 HIVATKOZÁSOK [39] W. Gander, G. H. Golub, and R. Strebel. Least-Squares Fitting of Circles and Ellipses. In Numerical analysis (in honour of Jean Meinguet), pages 63 84, [40] C.W. Gear. Mutibody Grouping from Motion Images. Int. Journal of Computer Vision, 29: , [41] D. B. Gennery. Decomposition of Transformation Matrices for Robot Vision. In Image Understanding Workshop, pages , [42] Rui F. C. Guerreiro and Pedro M. Q. Aguiar. Factorization with missing data for 3D structure recovery. In IEEE Workshop on Multimedia Signal Processing, pages , [43] L. Gévai. Objektumok háromdimenziós rekonstrukciója képsorozatokból. Master sthesis, Budapesti MűszakiEgyetem, Villamosmérnöki és Informatikai Kar, Konzulens: Hajder Levente. [44] Edelsbrunner H. Weighted alpha shapes. ACM Transaction on Graphics, 13(1):43 72, [45] L. Hajder. Idősorokvizsgálataasszociatívmódszer segítségével, BME VIK TDK-konferenciaKonzulens: dr. CharafHassan, dr. VágóZsuzsanna. [46] L. Hajder. Tanuló rendszerek tesztelő környezete, BME VIK TDKkonferencia Konzulens: dr. Horváth Gábor. [47] L. Hajder. Shape and Motion from Video. In Second Hungarion Conference on Computer Graphics and Geometrics, pages , [48] L. Hajder. Robust Structure from Motion by Outlier Rejection. In Képfeldolgozók és Alakfelismerők Konferenciája, pages 30 36, [49] L. Hajder. An Iterative Improvement of the Tomasi Kanade Factorization. In Third Hungarion Conference on Computer Graphics and Geometrics, pages 30 36,
124 HIVATKOZÁSOK [50] L.Hajder. 3DMotionGroupingof ArticulatedObjects. InComputer Vision Winter Workshop, Oral presentation after double blinded review. [51] L. Hajder. 3D Motion Grouping of Articulated Objects. In Automation and Applied Computer Science Workshop, pages , [52] L. Hajder. Tagolt objektumok rekonstrukciója videó alapján. In Intelligens Rendszerek Fiatal Kutatók Szimpóziuma, [53] L. Hajder andd. Chetverikov. Robust3DSegmentationofMultipleMoving Objects Under WeakPerspective. In ICCV Workshop on Dynamical Vision, CD ROM. [54] L. Hajder andd. Chetverikov. Robust3DSegmentationofMultipleMoving Objects UnderWeakPerspective. Lecture Notes in Computer Science, 4358, Accepted for publication. [55] L. Hajder, D. Chetverikov, and I. Vajk. Robust Structure from Motion under Weak Perspective. In 2nd Symposium on 3D Data Processing, Visualization and Transmission (3DPVT), CD ROM. [56] L. Hajder, D. Chetverikov I. Kardos, and G. Renner. Aktív kontúrok és Fast Marching eljárás alkalmazása az orvosi képfeldolgozásban. Képfeldolgozók és Alakfelismerők Konferenciája, pages 90 96, [57] L. Hajder, Á. Pernek, and Cs. Kazó. Structure from Motion by Fast Alternation. In Workshop of the Austrian Assosiation for Pattern Recognition (ÖAGM), [58] Harris, C. and Stephens, M. A combined corner and edge detector. In Fourth Alvey Vision Conference, pages , [59] R. Hartley. An algorithm for self calibrationfrom severalviews. In CVPR, pages , [60] R. Hartley. Lines and Points in Three Views: A Unified Approach. In ARPA94, volume II, pages , In 114
125 HIVATKOZÁSOK [61] R. I. Hartley and A. Zisserman. Multiple View Geometry in Computer Vision. Cambridge University Press, [62] R.I. Hartley. In defence of the 8-point algorithm. International Conference on Computer Vision, pages , [63] Richard I. Hartley. Computation of the Quadrifocal Tensor. In European Conference on Computer Vision, volume II, pages 20 35, London, UK, Springer-Verlag. [64] Richard I. Hartley. Theory and Practice of Projective Rectification. Int. J. Comput. Vision, 35(2): , [65] Richard I. Hartley and Peter Sturm. Triangulation. Computer Vision and Image Understanding: CVIU, 68(2): , [66] Hugues Hoppe, Tony DeRose, Tom Duchamp,John McDonald,and Werner Stuetzle. Surface reconstruction from unorganized points. In SIGGRAPH 92: Proceedings of the 19th annual conference on Computer graphics and interactive techniques, pages 71 78, [67] B. Horn. RecoveringBaseline andorientationfromessentialmatrix, [68] B. Horn and B. Schunck. Determining optical flow. Artificial Intelligence, 17: , [69] B.K.P. Horn. Closed-form Solution of Absolute Orientation using Unit Quaternions. Journal of the Optical Society of America, 4: , [70] B.K.P. Horn, H.M. Hilden, and S. Negahdaripourt. Closed-form Solution of Absolute Orientation Using Orthonormal Matrices. Journal of the Optical Society of America, 5(7): , [71] Michal Irani, Benny Rousso, and Shmuel Peleg. Detecting and tracking multiple moving objects using temporal integration. In ECCV 92: Proceedings of the Second European Conference on Computer Vision, pages , London, UK, Springer-Verlag. 115
126 HIVATKOZÁSOK [72] Maybank S. J. and Faugeras O. A theory of self-calibration of a moving camera. International Journal of Computer Vision, 8(2): , [73] More J. The Levenberg-Marquardt algorithm, implementation and theory. In G. A. Watson, editor, Numerical Analysis, Lecture Notes in Mathematics 630, pages , [74] Ma Jianbo and N Ahuya. Dense shape and motion from region correspondences by factorization. In CVPR, pages , [75] Fredrik Kahl. Multiple View Geometry and the L inf -norm. In ICCV 05: Proceedings of the Tenth IEEE International Conference on Computer Vision, pages , [76] FredrikKahlandDidierHenrion. GloballyOptimalEstimates forgeometricreconstructionproblems. In ICCV 05: Proceedings of the Tenth IEEE International Conference on Computer Vision, pages , [77] K. Kanatani. Motion Segmentation by Subspace Separation and Model Selection. In ICCV, pages , [78] I. Kardos, L. Hajder, and D. Chetverikov. Bone Surface Reconstruction from MR/CT Images using Fast Marching and Level Set Methods. In Joint Hungarian-Austrian Conference on Image Processing and Pattern Recognition, pages 41 48, [79] Cs. Kazó. Háromdimenziós objektumok textúrázása videó alapján. BME Villamosmérnöki és Informatikai Kar, TDK konferencia, Konzulens: Hajder Levente. [80] Qifa Ke and Takeo Kanade. Quasiconvex Optimization for Robust Geometric Reconstruction. In ICCV 05: Proceedings of the Tenth IEEE International Conference on Computer Vision, pages , [81] Reinhard Koch, Marc Pollefeys, Benno Heigl, Luc J. Van Gool, and Heinrich Niemann. Calibration of Hand-Held Camera Sequences for Plenoptic Modeling. In ICCV (1), pages ,
127 HIVATKOZÁSOK [82] Kurata, T. and Fujiki, J. and Kourogi, M. and Sakaue, K. A Robust Recursive Factorization Method for Recovering Structure and Motion from Live Video Frames. In IEEE ICCV Frame-Rate Workshop, [83] GézaKós. AnAlgorithmtoTriangulateSurfaces in3dusingunorganised Point Clouds. In Geometric Modelling, pages Springer-Verlag, [84] Szirmay-Kalos L., Antal Gy., and Csonka Ferenc. Háromdimenziós grafika, animáció és játékfejlesztés. ComputerBooks, Budapest, [85] L. Hajder. Mozgásérzékelés webkamerával. Elektrotechnika, 98: , [86] L. HajderandD. Chetverikov. Weak-perspective structurefrommotionfor strongly contaminated data. Pattern Recognition Letters, 27: , [87] A. Laurentini. The visual hull concept for silhouette-based image understanding. IEEE Transactions on Pattern Analysis and Machine Intelligence, 16(2): , [88] K. Levenberg. A method for the solution of certain problems in least squares. Quart. Appl. Math., 2: , [89] H.C. Longuet-Higgins. A Computer Algorithm for Reconstructing a Scene from Two Projections. Nature, 293: , September [90] Manolis I. A. Lourakis and Antonis A. Argyros. Is Levenberg-Marquardt the Most Efficient Optimization Algorithm for Implementing Bundle Adjustment? In ICCV 05: Proceedings of the Tenth IEEE International Conference on Computer Vision, pages , [91] B.D. Lucas and T. Kanade. An Iterative Image Registration Technique with an Application to Stereo Vision. In International Joint Conference on Artificial Intelligence, pages ,
128 HIVATKOZÁSOK [92] Gabor Lukács, Ralph Martin, and Dave Marshall. Faithful least-squares fittingof spheres, cylinders, cones and tori forreliable segmentation. In ECCV 98: Proceedings of the 5th European Conference on Computer Vision- Volume I, pages , London, UK, Springer-Verlag. [93] Yi Ma, Stefano Soatto, Jana Kosecka, and S. Shankar Sastry. An Invitation to 3-D Vision: From Images to Geometric Models. SpringerVerlag, [94] SebastianMagdaandDavidKriegman. Fasttexturesynthesis onarbitrary meshes. In SIGGRAPH 03: Proceedings of the SIGGRAPH 2003 conference on Sketches & applications, pages 82 89, [95] Marc Gelgon. Motion-based Segmentation, Available at COPIES/GELGON/cvsegm.html. [96] D. Marquardt. An algorithm for least-squares estimation of nonlinear parameters. SIAM J. Appl. Math., 11: , [97] Wojciech Matusik, Chris Buehler, and Leonard McMillan. Polyhedral visual hulls for real-time rendering. In Proceedings of the 12th Eurographics Workshop on Rendering Techniques, pages , London, UK, Springer-Verlag. [98] Heinz Mayer, Franz Leberl, AlexanderBornik, Joachim Bauer, andkonrad Karner. Multiresolution Texture for Photorealistic Rendering. In SCCG 01: Proceedings of the 17th Spring conference on Computer graphics, pages , [99] Z. Megyesi, G. Kós, and D. Chetverikov. Dense 3D Reconstruction from Images by Normal Aided Matching. Machine Graphics & Vision, 15:3 28, [100] T. Morita and T. Kanade. A Sequential Factorization Method for Recovering Shape and Motion from Image Streams. In ARPA Image Understanding Workshops, volume II, pages ,
129 HIVATKOZÁSOK [101] RózsaP. Lineáris algebra és alkalmazásai. Nemzeti Tankönyvkiadó, Budapest, [102] Á. Pernek. Hibaminimalizáló algoritmusok összehasonlítása és alkalmazhatósága a számítógépes struktúra-rekonstrukció területén. BME Villamosmérnökiés InformatikaiKar, TDK konferencia, Konzulens: Hajder Levente. [103] Á. Pernek and Cs. Kazó. Valós és virtuális mozgások egyesítése. BME Villamosmérnöki és Informatikai Kar, TDK konferencia, Konzulens: Hajder Levente. [104] C. J. Poelman and T. Kanade. A Paraperspective Factorization Method for Shape and Motion Recovery. IEEE Trans. on PAMI, 19(3): , [105] Marc Pollefeys. Visual 3D Modeling from Images, Tutorial. [106] Vaughan Pratt. Direct least-squares fitting of algebraic surfaces. In SIG- GRAPH 87: Proceedings ofthe14thannualconferenceoncomputergraphics and interactive techniques, pages , New York, NY, USA, ACM Press. [107] William H. Press, Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery. Numerical Recipes in C: The Art of Scientific Computing. Cambridge University Press, New York, NY, USA, [108] Luong Q.-T. and Faugeras O. Self-calibration of a moving camera from point correspondences and fundamental matrices. International Journal of Computer Vision, 22(3): , [109] Gang Qian and Rama Chellappa. Structure from Motion Using Sequential Monte Carlo Methods. Int. J. Comput. Vision, 59(1):5 31, [110] P.J. Rousseeuw and A.M. Leroy. Robust Regression and Outlier Detection. John Wiley & Sons, NY, [111] P.J. Rousseeuw and S. Van Aelst. Positive-Breakdown Robust Methods in Computer Vision. Computing Science and Statistics, 31: ,
130 HIVATKOZÁSOK [112] Harpreet S. Sawhney and Serge Ayer. Compact representations of videos through dominant and multiple motion estimation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 18(8): , [113] D. Scharstein and R. Szeliski. A Taxonomy and Evaluation of Dense Two- Frame Stereo Correspondence Algorithms. International Journal of Computer Vision, 47:7 42, [114] J.A. Sethian. Fast Marching Methods. SIAM Review, 41(2): , [115] J.A. Sethian. Level Set Methods and Fast Marching Methods: Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision and Material Science. Cambridge University Press, Cambridge, UK, [116] A. Shashua and M. Werman. On the trilinear tensor of three perspective views and its underlying geomtry. In ICCV, [117] C.C. Slama. Manual of Photogrammetry. Book, [118] Sonka M., Hlavac V. and Boyle R. Image Processing, Analysis, and Machine Vision. Chapman & Hall, London, [119] C. Strecha, R. Fransens, and L. Van Gool. Wide-baseline Stereo from Multiple Views: a Probabilistic Account. In Proc. IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), volume 2, pages , [120] C. Strecha, T. Tuytelaars, and L. Van Gool. Dense Matching of Multiple Wide Baseline Views. In Proc. Int. Conf. on Computer Vision, volume 2, pages , [121] P. SturmandB. Triggs. A FactorizationBased AlgorithmforMulti-Image Projective Structure and Motion. In ECCV, volume 2, pages , [122] G. Taubin. Estimation of Planar Curves, Surfaces, and Nonplanar Space Curves Defined by Implicit Equations with Applications to Edge and Range Image Segmentation. IEEE Trans. on PAMI, 13(11): ,
131 HIVATKOZÁSOK [123] C. Tomasi andt. Kanade. DetectionandTrackingof PointFeatures. Technical Report CMU-CS , Robotics Institute, Carnegie Mellon University, [124] Tomasi, C. and Kanade, T. Shape and Motion from Image Streams under orthography: A factorization approach. Intl. Journal Computer Vision, 9: , [125] Tomasi, C. and Shi, J. Good Features to Track. In IEEE Conf. Computer Vision and Pattern Recognition, pages , [126] P. Torr and A. Zisserman. Robust parameterization and computation of the trifocal tensor, [127] P. H. Torr and D. W. Murray. Outlier detection and motion segmentation. In Proc. SPIE Vol. 2059, p , Sensor Fusion VI, Paul S. Schenker; Ed., pages , [128] P.H.S. Torr. Outlier Detection and Motion Segmentation. PhD thesis, University of Oxford, Engineering Dept., [129] L. Torresani, D.B. Yang, E.J. Alexander, and C. Bregler. Tracking and Modelling Nonrigid Objects with Rank Constraints. In IEEE Conf. on Computer Vision and Patter Recognition, [130] Trajković, M. and Hedley, M. Robust Recursive Structure and Motion RecoveryunderAffine Projection. InProc. British Machine Vision Conference, [131] P. Tresadern and I. Reid. Articulated Structure from Motion by Factorization. In IEEE Conf. Computer Vision and Pattern Recognition, volume 2, pages , [132] E. Trucco and A. Verrio. Introductory Techniques for 3-D Computer Vision. Prentice Hall,
132 HIVATKOZÁSOK [133] R. Vidal. Segmentation of Dynamic Scenes from the Multibody Fundamental Matrix. In ECCV Workshop on Vision and Modeling of Dynamic Scenes, [134] R. Vidal and R. Hartley. Motion segmentation with missing data using PowerFactorization and GPCA, [135] G.Q. Wei and S.D. Ma. Implicit and Explicit Camera Calibration: Theory and Experiments. IEEE Transactions on Pattern Analysis and Machine Intelligence, 16(5): , [136] D. Weinshall and C. Tomasi. Linear and Incremental Acquisition of Invariant Shape Models From Image Sequences. IEEE Trans. on PAMI, 17(5): , [137] Yair Weiss. Smoothness in layers: Motion segmentation using nonparametric mixture estimation. In CVPR 97: Proceedings of the 1997 Conference on Computer Vision and Pattern Recognition (CVPR 97), page 520, Washington, DC, USA, IEEE Computer Society. [138] C. G. Wie and S.D. Ma. A Complete Two-Plane Camera Calibration Method and Experimental Comparisons. In IEEE International Conference on Robotics and Automation, pages , [139] J. Xiao, J.-X. Chai, and T. Kanade. A Closed-Form Solution to Non-rigid Shape and Motion Recovery. In ECCV (4), pages , [140] X. Xladó, A. Del Bue, and L. Agapito. Non-rigid Factorization for Projective Reconstruction. In British Machine Vision Conference, pages , [141] J. Yan and M. Pollefeys. A Factorization-based Approach to Articulated Motion Recovery. In IEEE Conf. Computer Vision and Pattern Recognition, volume 2, pages , [142] J. Yan and M. Pollefeys. A General Framework for Motion Segmentation: Independent, Articulated, Rigid, Non-rigid, Degenerate and Nondegenerate. In ECCV06, pages ,
133 HIVATKOZÁSOK [143] Yücel Yemez and Francis Schmitt. 3D reconstruction of real objects with high resolution shape and texture. Image and Vision Computing, 22: , [144] G. Zeng, S. Paris, L. Quan, and M. Lhuillier. Surface Reconstruction by Propagating 3D Stereo Data in Multiple 2D Images. In Proc. European Conf. on Computer Vision, pages , [145] Heyun Zheng and Steven D. Blostein. Motion-based object segmentation and estimation using the MDL principle. IEEE Transactions on Image Processing, 4(9): , [146] H.Zhou and T.S. Huang. Recovering Articulated Motion with a Hierarchical Factorization Method. In Proc. of 5th Intl. Workshop on Gesture and Sign Language based Human-Computer Interaction, pages , [147] G. Újváry. Háromdimenziós objektum-rekonstrukció képszekvenciák alapján. Master s thesis, Budapesti Műszaki Egyetem, Villamosmérnöki és Informatikai Kar, Konzulens: Hajder Levente. 123
134 HIVATKOZÁSOK 124
135 A. Függelék Skálázottan ortonormált mátrix 2 3-mas részmátrixának paraméterezése Amennyiben az A mátrix egy 3 3-mas skálázott ortonormált mátrix első két sora (azért skálázott, mert a sorok hossza egymással megegyezik, azaz A T A = AA T = qe), a mátrix elemei felírhatók 4 paraméter (egy skálázás- és három eltolásparaméter) segítségével. Jelöljük a mátrix elemeit a következő módon: [ ] a11 a A = 22 a 13 a 21 a 22 a 23 Jelöljük a három elforgatás paramétert α-val, β-val és γ-val, a skálázást pedig q-val. α az x, β az y, γ pedig a z tengely mentén adja meg az elforgatást. Ha összeszorozzuk a három elforgatásmátrixot, és skalárisan megszorzunk q-val, megkapjuk az A mátrix elemeit a paraméterekkel kifejezve: a 11 = q cos α cos β a 12 = q(sinαcos γ cos α sin β sin γ) a 13 = q(sinαsin γ + cosαsin β cos γ) a 21 = q sin α cos β a 22 = q(cosαcos γ + sin α sin β sin γ) a 23 = q(cosαsin γ sin α sin β cos γ) ahol α, β, γ a tengelyek körüli forgás szögét, q pedig a skálázást jelöli. 125
136 A. SKÁLÁZOTTAN ORTONORMÁLT MÁTRIX 2 3-MAS RÉSZMÁTRIXÁNAK PARAMÉTEREZÉSE 126
137 B. Függelék Hibafüggvény Jacobi mátrixa Adott az ǫ hibafüggvény: ǫ = W MS 2 F ahol W egy mérési mátrix (azaz W f mérete 2F P), ha F darab képkockát tartalmaz az adathalmaz. M egy 2F 3- mas mozgásmátrix, S pedig egy 3 P méretű struktúramátrix. A hibafüggvény f-edik képkockáján a Jacobi mátrix definíció szerint: J f = [ E2f 1 α f E 2f α f E 2f 1 β f E 2f β f E 2f 1 γ f E 2f γ f E 2f 1 q f E 2f q f ] ahol E i az i-dik sora az E = W MS hibamátrixnak. A Jacobi mátrix kifejthető az alábbi módon: A páratlan sorokra a deriválás után a következő kifejezéseket kapjuk ( az A. 127
138 B. HIBAFÜGGVÉNY JACOBI MÁTRIXA függelék alapján): E 2 f 1 α f = P p=1 q f[( sin α f cos β f )s p1 + (cosα f cos γ f + sin α f sin β f sin γ f )s p2 + ( sin α f sin β f cos γ f + cosα f sin γ f )s p3 ] E 2 f 1 = P p=1 β q f[( cos α f sin β f )s p1 f (cosα f cos β f sin γ f )s p2 + (cos α f cos β f cos γ f )s p3 ] E 2 f 1 = P p=1 γ q f[0 s p1 f (sinα f sin γ f + cosα f sin β f cos γ f )s p2 + ( cos α f sin β f sin γ f + sin α f cos γ f )s p3 ] E 2 f 1 = P p=1 q [(cosα f cos β f )s p1 f + (sinα f cos γ f cos α f sin β f sin γ f )s p2 + (cosα f sin β f cos γ f + sin α f sin γ f )s p3 ], A páros sorok meghatározása hasonló módon: E 2 f α f = P p=1 q f[( cos α f cos β f )s p1 + ( sin α f cos γ f + cosα f sin β f sin γ f )s p2 (sin α f sin γ f + cosα f sin β f cos γ f )s p3 ] E 2 f = P p=1 β q f[(sinα f sin β f )s p1 f + (sin α f cos β f sin γ f )s p2 (sinα f cos β f cos γ f )s p3 ] E 2 f = P p=1 γ q f[0 s p1 f + ( cos α f sin γ f + sin α f sin β f cos γ f )s p2 + (cosα f cos γ f + sin α f sin β f sin γ f )s p3 ] E 2 f = P p=1 q [( sin α f cos β f )s p1 f + (cosα f cos γ f + sin α f sin β f sin γ f )s p2 + (cosα f sin γ f sin α f sin β f cos γ f )s p3 ]. 128
139 C. Függelék A Tomasi-Kanade faktorizáció többértelműsége A Tomasi-Kanade faktorizáció a W mérési mátrixot M mozgás- és S struktúramátrix szorzatává alakítja: W = MS, ahol M = [M T 1 M T 2...M T F ]T mozgásmátrix tartalmazza a kamerasíkok bázisvektorait minden egyes f képkockán: Ml T = [i T l,jt l ]; S pedig az objektum háromdimenziós koordinátáit. Állítás: A faktorizáció többértelmű: ha W = MS érvényes felbontás, akkor az összes érvényes felbontás felírható W = (MA)(A T S) alakban, ahol A egy tetszőleges ortonormált mátrix. Bizonyítás: Először is egészítsük ki az f-edik képkockához tartozó M f 2 3-mas mátrixot a megfelelő harmadik vektorral (sorral), amely az első két sor alkotta vektorra merőleges, hossza pedig megegyezik a másik két vektor hosszával. A kiegészítés egyértelmű, ha a harmadik vektort a balkézszabály alapján határozzuk meg. A kiegészített mátrixot nevezzük M f -nek. Tudjuk, hogy a kiegészítés után ortogonális mátrixot kapunk: M f M T f = MT f M f = q f E, ahol q f pozitív valós szám (merőleges vetítés esetén q f = 1). Mivel tudjuk, hogy W = MS, az is igaz, hogy az összes faktorizációs megoldás W = (MA)(A 1 S) alakban állítható elő. Feltétel, hogy az új MA mozgásmátrixnak teljesítenie kell a mozgás kényszereit: a bázisvektoroknak merőlegeseknek kell lenniük egymásra, hosszuknak egységnyinek (merőleges vetítés) vagy azonosnak (gyenge perspektíva) kell lenniük. Nevezzük el, és bontsuk fel a képkockák szerint az MA mátrixot: N = MA = [N T 1 N T 2...N T F ]T ahol N f az f-edik képkockához tartozó mozgásmátrix. N f -et tovább lehet bontani két 129
140 C. A TOMASI-KANADE FAKTORIZÁCIÓ TÖBBÉRTELMŰSÉGE bázisvektorra, és ki lehet egészíteni az M f mátrixokhoz hasonlóan: Ñ f = M f A. Ñ f konstrukciójából adódóan skálázottan ortonormált, ezért írhatjuk: Ñ T f Ñf = ÑfÑT f = M T f M f = M f MT f = q f E (C.1) Mivel Ñf TÑf = A T MT f A ortonormált. Mf A = q f A T A. Ez pedig akkor és csak akkor igaz, ha 130
141 D. Függelék Egy ortonormált és egy általános mátrix szorzatának pszeudoinverze Tétel: Adott egy M mátrix Moore-Penrose-féle pszeudoinverze M és egy ortonormált A mátrix. MA mátrix pszeudoinverze, ebben az esetben (MA) = A T M. Bizonyítás: Tudjuk [101], hogy egy mátrix felírható ún. minimális diadikus szorzatként: M = UV T, ahol M egy tetszőleges m n-es mátrix, U és V pedig m r, illetve n r méretű mátrixok, ha az M mátrix rangja r. A diadikus felbontástöbbértelmű, ennekellenére azegyértelműmoore-penrose-féle pszeudoinverzetegytetszőleges diadikusfelbontásbólpontosankilehetszámítani (részletes levezetés [101]-ben olvasható): M = V (V T V ) 1 (U T U) 1 V T, (D.1) MA diadikus dekompozíciója M dekompozíciójából egyszerűen felírható: MA = U(V T A). A pszeudoinverz pedig mivel AA T = E: (MA) = A T V (V T AA T V ) 1 (U T U) 1 V T = A T M. (D.2) 131
142 D. EGY ORTONORMÁLT ÉS EGY ÁLTALÁNOS MÁTRIX SZORZATÁNAK PSZEUDOINVERZE 132
143 E. Függelék A faktorizáció változása eltolás esetén Tétel: Ha W egymérési mátrix, amely a követettjellegzetes pontok trajektóriáit tartalmazza, és S = [s 1, s 2,...,s P ] egy struktúramátrix, akkor az eredeti faktorizációnak megfelelően a mérésmátrix így bontható fel: W = [ M t ][ S 1 T ], (E.1) Ezek után, ha az eredeti S struktúramátrix összes oszlopához hozzáadjuk az o eltolásvektort, A faktorizáció az alábbi módon változik: W = [ M t Mo ][ ] S, (E.2) ahol S = [s 1, s 2,...,s N] és s i = s i + o minden i-re. Bizonyítás: Az eredeti faktorizáció szerint az i. pontra fel lehet írni, hogy w i = Ms i + t, ahol w i a W mérési mátrix i. oszlopa. Mivel s i = s i + o, az i. pontra az egyenlőség így módosul: w i = M(s i + o) + t Mo. Vagyis a mozgásmátrix marad M, az új eltolásvektor pedig t Mo lesz. 1 T 133
144 E. A FAKTORIZÁCIÓ VÁLTOZÁSA ELTOLÁS ESETÉN 134
145 F. Függelék Kötegelt behangolás (Bundle Adjustment) A W = MS faktorizációs feladat megoldásának finomítására a legelterjedtebb módszer az ún. kötegelt behangolás. Akárcsak a 4. fejezetben ismertetett új algoritmus, feltételezi hogy mind a kamera-. mind a struktúramátrixra kezdeti becslés létezik. A módszera Levenberg-Marquardtminimalizálásieljárásonalapszik, amelyet itt röviden áttekintünk. F.1. Levenberg-Marquardt minimalizálás Adott egy y = f(x) költségfüggvény, ahol y egy skalár, x pedig egy tetszőles dimenziójú vektor. A cél x függvényében a költségfüggvény minimumának a megtalálása. A Levenberg-Marquardt módszer a Gauss-Newton és a gradiens módszerek keveréke. Az eredeti Newton módszer feltételezi, hogy a hibafüggvény kvadratikus, és az első és másodrendű parciális deriváltakból a kvadratikus hibafelület minimumhelyétegy lépésben kilehet számítani. A Gauss-Newtonmódszerabban különbözik az eredeti Newton módszertől, hogy a második parciális deriváltakat sem számolja ki. A hibafüggvény általános esetben nem kvadratikus, ahogyan ezt a Gauss- Newton eljárás feltételezi, ezért szükség van egy másik tagra is, amely a nagyon nem kvadratikus esetekben átveszi a minimumkeresést, és a legmeredekebb lejtő irányába tereli a paraméterek változtatását. 135
146 F. KÖTEGELT BEHANGOLÁS (BUNDLE ADJUSTMENT) Maga a módszer iteratív, minden egyes lépésben az alábbi szabály alapján változtatja az optimalizálandó paramétereket az eljárás: x = (J T J + λi) 1 J T ǫ p, (F.1) ahol J a Jacobi mátrix, λ pedig egy paraméter, amely a két tag közötti súlyozást végzi el. A paraméterek értékét az x i+1 = x i + x összefüggés adja meg. A hangoló λ paraméter értékét folyamatosan változtatni kell. Abban az esetben, ha az y f(x) hiba értéke növekszik, a paramétert nem szabad változtatni, λ értékét pedig csökkenteni kell. Ha csökken a hibafüggvény, a paraméter változtatható, λ-t pedig növelni kell. A Levenberg-Marquardt algoritmusról az Olvasó részletesen olvashat az eredeti publikációkban [88, 96, 90]. F.2. A Levenberg-Marquard módszer alkalmazása az objektum-rekonstrukciós feladatra A Levenberg-Marquardt algoritmus minden olyan esetben jól alkalmazható, amikor a hibafüggvényt fel tudjuk írni a a beállítandó paraméterek függvényében. Az objektum-rekonstrukciós módszer esetében a vetítési egyenletek felírhatóak, és a parciális deriváltak könnyen kiszámíthatóak. Mégsem lehet alkalmazni a módszert, mert a nemlineáris optimalizálási eljárások nem képesek, csak viszonylag kevés (tipikusan néhányszor tíz) paraméter beállítására, hiszen a hangolási szabály alapján a (J T J +λi) mátrixot kell invertálni, amely mátrix sorainakés oszlopainakszámaaparaméterekszámávallineárisannő. Az objektumrekonstrukciós feladatnál ez a szám nagy lehet, hiszen például 500 pontot és 10 képkockátfeltételezve =1540paraméterbeállításátkell megoldani. Ezt a problémát a kötegelt behangolás [15, 90] segítségével oldották meg. A Gauss-Newton módszer alapját képező J T J x = J T ǫ p ún. normálegyenlet a F.1. ábrának megfelelően ritka struktúrájú lesz, köszönhetően annak, hogy a Jacobi-mátrix szintél ritka (lásd az F.2. ábrát). A normálegyenlet így írható fel: 136
147 F.2 A Levenberg-Marquard módszer alkalmazása az objektum-rekonstrukciós feladatra U X X T V F.1. ábra. A normálegyenlet struktúrája az objektum-rekonstrukciós feladatnál. F.2. ábra. A Jacobi-mátrix struktúrája az objektum-rekonstrukciós feladatnál. [ U X X T V ][ s m ] = [ ǫs ǫ m ] (F.2) ahol s a struktúraparaméterekből, m a mozgásparaméterből előállított vektorok, ǫ s és ǫ m pedig a hozzájuk tartozó becsléshiba. Ha balról megszorozzuk a 137
Számítógépes látás alapjai
 Számítógépes látás alapjai Csetverikov Dmitrij, Hajder Levente Eötvös Lóránd Egyetem, Informatikai Kar Csetverikov, Hajder (ELTE Informatikai Kar) Számítógépes látás 1 / 44 Többkamerás 3D-s rekonstrukció
Számítógépes látás alapjai Csetverikov Dmitrij, Hajder Levente Eötvös Lóránd Egyetem, Informatikai Kar Csetverikov, Hajder (ELTE Informatikai Kar) Számítógépes látás 1 / 44 Többkamerás 3D-s rekonstrukció
A KLT (Kanade Lucas Tomasi) Feature Tracker Működése (jellegzetes pontok választása és követése)
 A KL (Kanade Lucas omasi) Feature racker Működése (jellegzetes pontok választása és követése) Készítette: Hajder Levente 008.11.18. 1. Feladat A rendelkezésre álló videó egy adott képkockájából minél több
A KL (Kanade Lucas omasi) Feature racker Működése (jellegzetes pontok választása és követése) Készítette: Hajder Levente 008.11.18. 1. Feladat A rendelkezésre álló videó egy adott képkockájából minél több
Tárgy. Forgóasztal. Lézer. Kamera 3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL
 3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL. Bevezetés A lézeres letapogatás a ma elérhet legpontosabb 3D-s rekonstrukciót teszi lehet vé. Alapelve roppant egyszer : egy lézeres csíkkal megvilágítjuk a tárgyat.
3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL. Bevezetés A lézeres letapogatás a ma elérhet legpontosabb 3D-s rekonstrukciót teszi lehet vé. Alapelve roppant egyszer : egy lézeres csíkkal megvilágítjuk a tárgyat.
Számítógépes látás alapjai
 Számítógépes látás alapjai Csetverikov Dmitrij, Hajder Levente Eötvös Lóránd Egyetem, Informatikai Kar Csetverikov, Hajder (ELTE Informatikai Kar) Számítógépes látás 1 / 23 Rekonstrukció speciális hardverekkel
Számítógépes látás alapjai Csetverikov Dmitrij, Hajder Levente Eötvös Lóránd Egyetem, Informatikai Kar Csetverikov, Hajder (ELTE Informatikai Kar) Számítógépes látás 1 / 23 Rekonstrukció speciális hardverekkel
Térbeli transzformációk, a tér leképezése síkra
 Térbeli transzformációk, a tér leképezése síkra Homogén koordináták bevezetése térben A tér minden P pontjához kölcsönösen egyértelműen egy valós (x, y, z) számhármast rendeltünk hozzá. (Descartes-féle
Térbeli transzformációk, a tér leképezése síkra Homogén koordináták bevezetése térben A tér minden P pontjához kölcsönösen egyértelműen egy valós (x, y, z) számhármast rendeltünk hozzá. (Descartes-féle
3D számítógépes geometria és alakzatrekonstrukció
 3D számítógépes geometria és alakzatrekonstrukció 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01
3D számítógépes geometria és alakzatrekonstrukció 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01
Kamerakalibráció és pozícióbecslés érzékenységi analízissel, sík mintázatokból. Dabóczi Tamás (BME MIT), Fazekas Zoltán (MTA SZTAKI)
 , 2008 feb. 4-5 Kamerakalibráció és pozícióbecslés érzékenységi Bódis-Szomorú András Dabóczi Tamás (BME MIT), Fazekas Zoltán (MTA SZTAKI) Méréstechnika- és Információs Rendszerek Tanszék BME Rendszer-
, 2008 feb. 4-5 Kamerakalibráció és pozícióbecslés érzékenységi Bódis-Szomorú András Dabóczi Tamás (BME MIT), Fazekas Zoltán (MTA SZTAKI) Méréstechnika- és Információs Rendszerek Tanszék BME Rendszer-
x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs mátrixa 3D-ben?
 . Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
. Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
Panorámakép készítése
 Panorámakép készítése Képregisztráció, 2009. Hantos Norbert Blaskovics Viktor Összefoglalás Panoráma (image stitching, planar mosaicing): átfedő képek összeillesztése Lépések: Előfeldolgozás (pl. intenzitáskorrekciók)
Panorámakép készítése Képregisztráció, 2009. Hantos Norbert Blaskovics Viktor Összefoglalás Panoráma (image stitching, planar mosaicing): átfedő képek összeillesztése Lépések: Előfeldolgozás (pl. intenzitáskorrekciók)
3D számítógépes geometria és alakzatrekonstrukció
 3D számítógépes geometria és alakzatrekonstrukció 14. Digitális Alakzatrekonstrukció - Bevezetés http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01 Dr. Várady Tamás, Dr.
3D számítógépes geometria és alakzatrekonstrukció 14. Digitális Alakzatrekonstrukció - Bevezetés http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01 Dr. Várady Tamás, Dr.
3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás
 3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav54
3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav54
Transzformációk síkon, térben
 Transzformációk síkon, térben Leképezés, transzformáció Leképezés: Ha egy A ponttér pontjaihoz egy másik B ponttér pontjait kölcsönösen egyértelműen rendeljük hozzá, akkor ezt a hozzárendelést leképezésnek
Transzformációk síkon, térben Leképezés, transzformáció Leképezés: Ha egy A ponttér pontjaihoz egy másik B ponttér pontjait kölcsönösen egyértelműen rendeljük hozzá, akkor ezt a hozzárendelést leképezésnek
Transzformációk. Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform
 Transzformációk Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform Koordinátarendszerek: modelltér Koordinátarendszerek: világtér Koordinátarendszerek: kameratér up right z eye ahead
Transzformációk Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform Koordinátarendszerek: modelltér Koordinátarendszerek: világtér Koordinátarendszerek: kameratér up right z eye ahead
3D-s számítógépes geometria és alakzatrekonstrukció
 3D-s számítógépes geometria és alakzatrekonstrukció 14. Digitális Alakzatrekonstrukció - Bevezetés http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav08 Dr. Várady Tamás,
3D-s számítógépes geometria és alakzatrekonstrukció 14. Digitális Alakzatrekonstrukció - Bevezetés http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav08 Dr. Várady Tamás,
2. Omnidirekcionális kamera
 2. Omnidirekcionális kamera Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Omnidirekcionális kamerák típusai Omnidirekcionális, körbelátó,
2. Omnidirekcionális kamera Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Omnidirekcionális kamerák típusai Omnidirekcionális, körbelátó,
Képfeldolgozás Szegmentálás Osztályozás Képfelismerés Térbeli rekonstrukció
 Mesterséges látás Miről lesz szó? objektumok Bevezetés objektumok A mesterséges látás jelenlegi, technikai eszközökön alapuló világunkban gyakorlatilag azonos a számítógépes képfeldolgozással. Számítógépes
Mesterséges látás Miről lesz szó? objektumok Bevezetés objektumok A mesterséges látás jelenlegi, technikai eszközökön alapuló világunkban gyakorlatilag azonos a számítógépes képfeldolgozással. Számítógépes
6. gyakorlat. Gelle Kitti. Csendes Tibor Somogyi Viktor. London András. jegyzetei alapján
 Közelítő és szimbolikus számítások 6. gyakorlat Sajátérték, Gersgorin körök Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján . Mátrixok sajátértékei
Közelítő és szimbolikus számítások 6. gyakorlat Sajátérték, Gersgorin körök Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján . Mátrixok sajátértékei
Számítógépes Grafika mintafeladatok
 Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
3D Számítógépes Geometria II.
 3D Számítógépes Geometria II. 1. Bevezetés http://cg.iit.bme.hu/portal/3dgeo2 https://www.vik.bme.hu/kepzes/targyak/viiiav16 Dr. Várady Tamás, Dr. Salvi Péter BME, Villamosmérnöki és Informatikai Kar Irányítástechnika
3D Számítógépes Geometria II. 1. Bevezetés http://cg.iit.bme.hu/portal/3dgeo2 https://www.vik.bme.hu/kepzes/targyak/viiiav16 Dr. Várady Tamás, Dr. Salvi Péter BME, Villamosmérnöki és Informatikai Kar Irányítástechnika
Transzformációk. Szécsi László
 Transzformációk Szécsi László A feladat Adott a 3D modell háromszögek csúcspontjai [modellezési koordináták] Háromszögkitöltő algoritmus pixeleket színez be [viewport koordináták] A feladat: számítsuk
Transzformációk Szécsi László A feladat Adott a 3D modell háromszögek csúcspontjai [modellezési koordináták] Háromszögkitöltő algoritmus pixeleket színez be [viewport koordináták] A feladat: számítsuk
A tér lineáris leképezései síkra
 A tér lineáris leképezései síkra Az ábrázoló geometria célja: A háromdimenziós térben elhelyezkedő alakzatok helyzeti és metrikus viszonyainak egyértelmű és egyértelműen rekonstruálható módon történő ábrázolása
A tér lineáris leképezései síkra Az ábrázoló geometria célja: A háromdimenziós térben elhelyezkedő alakzatok helyzeti és metrikus viszonyainak egyértelmű és egyértelműen rekonstruálható módon történő ábrázolása
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
Infobionika ROBOTIKA. X. Előadás. Robot manipulátorok II. Direkt és inverz kinematika. Készült a HEFOP P /1.0 projekt keretében
 Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Regresszió számítás. Tartalomjegyzék: GeoEasy V2.05+ Geodéziai Kommunikációs Program
 Regresszió számítás GeoEasy V2.05+ Geodéziai Kommunikációs Program DigiKom Kft. 2006-2010 Tartalomjegyzék: Egyenes x változik Egyenes y változik Egyenes y és x változik Kör Sík z változik Sík y, x és z
Regresszió számítás GeoEasy V2.05+ Geodéziai Kommunikációs Program DigiKom Kft. 2006-2010 Tartalomjegyzék: Egyenes x változik Egyenes y változik Egyenes y és x változik Kör Sík z változik Sík y, x és z
Sajátértékek és sajátvektorok. mf1n1a06- mf1n2a06 Csabai István
 Sajátértékek és sajátvektorok A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris transzformáció Vektorok lineáris transzformációja: általános esetben az x vektor iránya és nagysága
Sajátértékek és sajátvektorok A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris transzformáció Vektorok lineáris transzformációja: általános esetben az x vektor iránya és nagysága
Hajder Levente 2017/2018. II. félév
 Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév Tartalom 1 2 3 Geometriai modellezés feladata A világunkat modellezni kell a térben. Valamilyen koordinátarendszer
Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév Tartalom 1 2 3 Geometriai modellezés feladata A világunkat modellezni kell a térben. Valamilyen koordinátarendszer
2014/2015. tavaszi félév
 Hajder L. és Valasek G. hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom Geometria modellezés 1 Geometria modellezés 2 Geometria modellezés
Hajder L. és Valasek G. hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom Geometria modellezés 1 Geometria modellezés 2 Geometria modellezés
Mátrixhatvány-vektor szorzatok hatékony számítása
 Mátrixhatvány-vektor szorzatok hatékony számítása Izsák Ferenc ELTE TTK, Alkalmazott Analízis és Számításmatematikai Tanszék & ELTE-MTA NumNet Kutatócsoport munkatárs: Szekeres Béla János Alkalmazott Analízis
Mátrixhatvány-vektor szorzatok hatékony számítása Izsák Ferenc ELTE TTK, Alkalmazott Analízis és Számításmatematikai Tanszék & ELTE-MTA NumNet Kutatócsoport munkatárs: Szekeres Béla János Alkalmazott Analízis
Segédlet: Főfeszültségek meghatározása Mohr-féle feszültségi körök alkalmazásával
 Segédlet: Főfeszültségek meghatározása Mohr-féle feszültségi körök alkalmazásával Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 212. október 16. Frissítve: 215. január
Segédlet: Főfeszültségek meghatározása Mohr-féle feszültségi körök alkalmazásával Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 212. október 16. Frissítve: 215. január
Láthatósági kérdések
 Láthatósági kérdések Láthatósági algoritmusok Adott térbeli objektum és adott nézőpont esetén el kell döntenünk, hogy mi látható az adott alakzatból a nézőpontból, vagy irányából nézve. Az algoritmusok
Láthatósági kérdések Láthatósági algoritmusok Adott térbeli objektum és adott nézőpont esetén el kell döntenünk, hogy mi látható az adott alakzatból a nézőpontból, vagy irányából nézve. Az algoritmusok
Grafikonok automatikus elemzése
 Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
Akusztikai tervezés a geometriai akusztika módszereivel
 Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Számítási feladatok a Számítógépi geometria órához
 Számítási feladatok a Számítógépi geometria órához Kovács Zoltán Copyright c 2012 Last Revision Date: 2012. október 15. kovacsz@nyf.hu Technikai útmutató a jegyzet használatához A jegyzet képernyőbarát
Számítási feladatok a Számítógépi geometria órához Kovács Zoltán Copyright c 2012 Last Revision Date: 2012. október 15. kovacsz@nyf.hu Technikai útmutató a jegyzet használatához A jegyzet képernyőbarát
5. 3D rekonstrukció. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 5. 3D rekonstrukció Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 PASSZÍV SZTEREÓ 3 Passzív sztereó 3D rekonstrukció egy sztereó kamera
5. 3D rekonstrukció Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 PASSZÍV SZTEREÓ 3 Passzív sztereó 3D rekonstrukció egy sztereó kamera
VIK A2 Matematika - BOSCH, Hatvan, 3. Gyakorlati anyag. Mátrix rangja
 VIK A2 Matematika - BOSCH, Hatvan, 3. Gyakorlati anyag 2019. március 21. Mátrix rangja 1. Számítsuk ki az alábbi mátrixok rangját! (d) 1 1 2 2 4 5 1 1 1 1 1 1 1 1 2 1 2 1 1 0 1 1 2 1 0 1 1 1 1 2 3 1 3
VIK A2 Matematika - BOSCH, Hatvan, 3. Gyakorlati anyag 2019. március 21. Mátrix rangja 1. Számítsuk ki az alábbi mátrixok rangját! (d) 1 1 2 2 4 5 1 1 1 1 1 1 1 1 2 1 2 1 1 0 1 1 2 1 0 1 1 1 1 2 3 1 3
Denavit-Hartenberg konvenció alkalmazása térbeli 3DoF nyílt kinematikai láncú hengerkoordinátás és gömbi koordinátás robotra
 Budapesti M szaki És Gazdaságtudományi Egyetem Gépészmérnöki Kar M szaki Mechanikai Tanszék Denavit-Hartenberg konvenció alkalmazása térbeli 3DoF nyílt kinematikai láncú hengerkoordinátás és gömbi koordinátás
Budapesti M szaki És Gazdaságtudományi Egyetem Gépészmérnöki Kar M szaki Mechanikai Tanszék Denavit-Hartenberg konvenció alkalmazása térbeli 3DoF nyílt kinematikai láncú hengerkoordinátás és gömbi koordinátás
Példa: Háromszög síkidom másodrendű nyomatékainak számítása
 Példa: Háromszög síkidom másodrendű nyomatékainak számítása Készítette: Dr. Kossa Attila kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék. február 6. Határozzuk meg az alábbi ábrán látható derékszögű háromszög
Példa: Háromszög síkidom másodrendű nyomatékainak számítása Készítette: Dr. Kossa Attila kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék. február 6. Határozzuk meg az alábbi ábrán látható derékszögű háromszög
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011.
 BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
Alap-ötlet: Karl Friedrich Gauss ( ) valószínűségszámítási háttér: Andrej Markov ( )
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
Önálló labor beszámoló Képek szegmentálása textúra analízis segítségével. MAJF21 Eisenberger András május 22. Konzulens: Dr.
 Önálló labor beszámoló Képek szegmentálása textúra analízis segítségével 2011. május 22. Konzulens: Dr. Pataki Béla Tartalomjegyzék 1. Bevezetés 2 2. Források 2 3. Kiértékelő szoftver 3 4. A képek feldolgozása
Önálló labor beszámoló Képek szegmentálása textúra analízis segítségével 2011. május 22. Konzulens: Dr. Pataki Béla Tartalomjegyzék 1. Bevezetés 2 2. Források 2 3. Kiértékelő szoftver 3 4. A képek feldolgozása
A 3D-2D leképezés alatt melyek maradnak robusztus képjellemzők?
 A 3D-2D leképezés alatt melyek maradnak robusztus képjellemzők? Vagyis mely képjellemzőket érdemes a vetületképekből kihámozni? Az attól függ Térbeli viszonyok egyenes méret párh. / szög alak síkok helyzete
A 3D-2D leképezés alatt melyek maradnak robusztus képjellemzők? Vagyis mely képjellemzőket érdemes a vetületképekből kihámozni? Az attól függ Térbeli viszonyok egyenes méret párh. / szög alak síkok helyzete
Matematika (mesterképzés)
 Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
3. tétel Térelemek távolsága és szöge. Nevezetes ponthalmazok a síkon és a térben.
 3. tétel Térelemek távolsága és szöge. Nevezetes ponthalmazok a síkon és a térben. TÁVOLSÁG Általános definíció: két alakzat távolsága a két alakzat pontjai között húzható legrövidebb szakasz hosszaa távolság
3. tétel Térelemek távolsága és szöge. Nevezetes ponthalmazok a síkon és a térben. TÁVOLSÁG Általános definíció: két alakzat távolsága a két alakzat pontjai között húzható legrövidebb szakasz hosszaa távolság
Regresszió. Csorba János. Nagyméretű adathalmazok kezelése március 31.
 Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Vektorgeometria (2) First Prev Next Last Go Back Full Screen Close Quit
 Vektorgeometria (2) First Prev Next Last Go Back Full Screen Close Quit 1. Tekintsünk a térben egy P (p 1, p 2, p 3 ) pontot és egy v = (v 1, v 2, v 3 ) = 0 vektort. Ekkor pontosan egy egyenes létezik,
Vektorgeometria (2) First Prev Next Last Go Back Full Screen Close Quit 1. Tekintsünk a térben egy P (p 1, p 2, p 3 ) pontot és egy v = (v 1, v 2, v 3 ) = 0 vektort. Ekkor pontosan egy egyenes létezik,
3D számítógépes geometria és alakzatrekonstrukció
 3D számítógépes geometria és alakzatrekonstrukció 2a. Háromszöghálók http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01 Dr. Várady Tamás, Dr. Salvi Péter BME, Villamosmérnöki
3D számítógépes geometria és alakzatrekonstrukció 2a. Háromszöghálók http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01 Dr. Várady Tamás, Dr. Salvi Péter BME, Villamosmérnöki
Konjugált gradiens módszer
 Közelítő és szimbolikus számítások 12. gyakorlat Konjugált gradiens módszer Készítette: Gelle Kitti Csendes Tibor Vinkó Tamás Faragó István Horváth Róbert jegyzetei alapján 1 LINEÁRIS EGYENLETRENDSZEREK
Közelítő és szimbolikus számítások 12. gyakorlat Konjugált gradiens módszer Készítette: Gelle Kitti Csendes Tibor Vinkó Tamás Faragó István Horváth Róbert jegyzetei alapján 1 LINEÁRIS EGYENLETRENDSZEREK
Robotika. Kinematika. Magyar Attila
 Robotika Kinematika Magyar Attila amagyar@almos.vein.hu Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
Robotika Kinematika Magyar Attila amagyar@almos.vein.hu Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
Koordináta-geometria feladatok (emelt szint)
 Koordináta-geometria feladatok (emelt szint) 1. (ESZÉV Minta (2) 2004.05/7) Egy ABC háromszögben CAB = 30, az ACB = 45. A háromszög két csúcsának koordinátái: A(2; 2) és C(4; 2). Határozza meg a harmadik
Koordináta-geometria feladatok (emelt szint) 1. (ESZÉV Minta (2) 2004.05/7) Egy ABC háromszögben CAB = 30, az ACB = 45. A háromszög két csúcsának koordinátái: A(2; 2) és C(4; 2). Határozza meg a harmadik
3. Sztereó kamera. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 3. Sztereó kamera Kató Zoltá Képfeldolgozás és Számítógépes Grafika taszék SZTE (http://www.if.u-szeged.hu/~kato/teachig/) Sztereó kamerák Az emberi látást utáozza 3 Sztereó kamera pár Két, ugaazo 3D látvát
3. Sztereó kamera Kató Zoltá Képfeldolgozás és Számítógépes Grafika taszék SZTE (http://www.if.u-szeged.hu/~kato/teachig/) Sztereó kamerák Az emberi látást utáozza 3 Sztereó kamera pár Két, ugaazo 3D látvát
Kinematika szeptember Vonatkoztatási rendszerek, koordinátarendszerek
 Kinematika 2014. szeptember 28. 1. Vonatkoztatási rendszerek, koordinátarendszerek 1.1. Vonatkoztatási rendszerek A test mozgásának leírása kezdetén ki kell választani azt a viszonyítási rendszert, amelyből
Kinematika 2014. szeptember 28. 1. Vonatkoztatási rendszerek, koordinátarendszerek 1.1. Vonatkoztatási rendszerek A test mozgásának leírása kezdetén ki kell választani azt a viszonyítási rendszert, amelyből
PONTFELHŐ REGISZTRÁCIÓ
 PONTFELHŐ REGISZTRÁCIÓ ITERATIVE CLOSEST POINT Cserteg Tamás, URLGNI, 2018.11.22. TARTALOM Röviden Alakzatrekonstrukció áttekintés ICP algoritmusok Projektfeladat Demó FORRÁSOK Cikkek Efficient Variants
PONTFELHŐ REGISZTRÁCIÓ ITERATIVE CLOSEST POINT Cserteg Tamás, URLGNI, 2018.11.22. TARTALOM Röviden Alakzatrekonstrukció áttekintés ICP algoritmusok Projektfeladat Demó FORRÁSOK Cikkek Efficient Variants
Papp Ferenc Barlangkutató Csoport. Barlangtérképezés. Fotómodellezés. Holl Balázs 2014. negyedik változat hatodik kiegészítés 4.6
 Papp Ferenc Barlangkutató Csoport Barlangtérképezés Fotómodellezés Holl Balázs 2014 negyedik változat hatodik kiegészítés 4.6 (első változat 2011) A felszíni térképezés már egy évszázada a légifotókon
Papp Ferenc Barlangkutató Csoport Barlangtérképezés Fotómodellezés Holl Balázs 2014 negyedik változat hatodik kiegészítés 4.6 (első változat 2011) A felszíni térképezés már egy évszázada a légifotókon
Principal Component Analysis
 Principal Component Analysis Principal Component Analysis Principal Component Analysis Definíció Ortogonális transzformáció, amely az adatokat egy új koordinátarendszerbe transzformálja úgy, hogy a koordináták
Principal Component Analysis Principal Component Analysis Principal Component Analysis Definíció Ortogonális transzformáció, amely az adatokat egy új koordinátarendszerbe transzformálja úgy, hogy a koordináták
7. Régió alapú szegmentálás
 Digitális képek szegmentálása 7. Régió alapú szegmentálás Kató Zoltán http://www.cab.u-szeged.hu/~kato/segmentation/ Szegmentálási kritériumok Particionáljuk a képet az alábbi kritériumokat kielégítő régiókba
Digitális képek szegmentálása 7. Régió alapú szegmentálás Kató Zoltán http://www.cab.u-szeged.hu/~kato/segmentation/ Szegmentálási kritériumok Particionáljuk a képet az alábbi kritériumokat kielégítő régiókba
Felügyelt önálló tanulás - Analízis III.
 Felügyelt önálló tanulás - Analízis III Kormos Máté Differenciálható sokaságok Sokaságok Röviden, sokaságoknak nevezzük azokat az objektumokat, amelyek egy n dimenziós térben lokálisan k dimenziósak Definíció:
Felügyelt önálló tanulás - Analízis III Kormos Máté Differenciálható sokaságok Sokaságok Röviden, sokaságoknak nevezzük azokat az objektumokat, amelyek egy n dimenziós térben lokálisan k dimenziósak Definíció:
SZE, Doktori Iskola. Számítógépes grafikai algoritmusok. Összeállította: Dr. Gáspár Csaba. Felületmegjelenítés
 Felületmegjelenítés Megjelenítés paramétervonalakkal Drótvázas megjelenítés Megjelenítés takarással Triviális hátsólap eldobás A z-puffer algoritmus Megvilágítás és árnyalás Megjelenítés paramétervonalakkal
Felületmegjelenítés Megjelenítés paramétervonalakkal Drótvázas megjelenítés Megjelenítés takarással Triviális hátsólap eldobás A z-puffer algoritmus Megvilágítás és árnyalás Megjelenítés paramétervonalakkal
Diszkréten mintavételezett függvények
 Diszkréten mintavételezett függvények A függvény (jel) értéke csak rögzített pontokban ismert, de köztes pontokban is meg akarjuk becsülni időben mintavételezett jel pixelekből álló műholdkép rácson futtatott
Diszkréten mintavételezett függvények A függvény (jel) értéke csak rögzített pontokban ismert, de köztes pontokban is meg akarjuk becsülni időben mintavételezett jel pixelekből álló műholdkép rácson futtatott
Intelligens adatelemzés
 Antal Péter, Antos András, Horváth Gábor, Hullám Gábor, Kocsis Imre, Marx Péter, Millinghoffer András, Pataricza András, Salánki Ágnes Intelligens adatelemzés Szerkesztette: Antal Péter A jegyzetben az
Antal Péter, Antos András, Horváth Gábor, Hullám Gábor, Kocsis Imre, Marx Péter, Millinghoffer András, Pataricza András, Salánki Ágnes Intelligens adatelemzés Szerkesztette: Antal Péter A jegyzetben az
Matematika A1a Analízis
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
HÁROMDIMENZIÓS SZÁMÍTÓGÉPES LÁTÁS HAJDER LEVENTE
 HÁROMDIMENZIÓS SZÁMÍTÓGÉPES LÁTÁS HAJDER LEVENTE BEMUTATKOZÁS Hajder Levente (1975-?) Tanulmányok: BME első kísérlet 1993-1995 Kandó Kálmán Műszaki Főiskola (Ma: Óbudai Egyetem) 1995-1998 BME második,
HÁROMDIMENZIÓS SZÁMÍTÓGÉPES LÁTÁS HAJDER LEVENTE BEMUTATKOZÁS Hajder Levente (1975-?) Tanulmányok: BME első kísérlet 1993-1995 Kandó Kálmán Műszaki Főiskola (Ma: Óbudai Egyetem) 1995-1998 BME második,
Nagy pontosságú 3D szkenner
 Tartalom T-model Komponensek Előzmények Know-how Fejlesztés Pilot projektek Felhasználási lehetőségek 1 T-model: nagy pontosságú aktív triangulációs 3D lézerszkenner A 3D szkennert valóságos tárgyak 3D
Tartalom T-model Komponensek Előzmények Know-how Fejlesztés Pilot projektek Felhasználási lehetőségek 1 T-model: nagy pontosságú aktív triangulációs 3D lézerszkenner A 3D szkennert valóságos tárgyak 3D
Minimum követelmények matematika tantárgyból 11. évfolyamon
 Minimum követelmények matematika tantárgyból. évfolyamon A hatványozás általánosítása pozitív alap esetén racionális kitevőre. Műveletek hatványokkal. A, a 0 függvény. Az eponenciális függvény. Vizsgálata
Minimum követelmények matematika tantárgyból. évfolyamon A hatványozás általánosítása pozitív alap esetén racionális kitevőre. Műveletek hatványokkal. A, a 0 függvény. Az eponenciális függvény. Vizsgálata
Transzformációk, amelyek n-dimenziós objektumokat kisebb dimenziós terekbe visznek át. Pl. 3D 2D
 Vetítések Transzformációk, amelyek n-dimenziós objektumokat kisebb dimenziós terekbe visznek át. Pl. 3D 2D Vetítések fajtái - 1 perspektívikus A párhuzamos A A' B A' B A vetítés középpontja B' Vetítési
Vetítések Transzformációk, amelyek n-dimenziós objektumokat kisebb dimenziós terekbe visznek át. Pl. 3D 2D Vetítések fajtái - 1 perspektívikus A párhuzamos A A' B A' B A vetítés középpontja B' Vetítési
 MISKEI VENDEL TIPPEK ÉS TRÜKKÖK GÖMBPANORÁMA KÉSZÍTÉSÉHEZ I. 2007 Panorámakép készítése tükörtechnikával Nagyon érdekesnek tartom a gömbpanorámákat, ezért kerestem egy olyan egyszerű módszert, amivel viszonylag
MISKEI VENDEL TIPPEK ÉS TRÜKKÖK GÖMBPANORÁMA KÉSZÍTÉSÉHEZ I. 2007 Panorámakép készítése tükörtechnikával Nagyon érdekesnek tartom a gömbpanorámákat, ezért kerestem egy olyan egyszerű módszert, amivel viszonylag
FÉLMEREV KAPCSOLATOK NUMERIKUS SZIMULÁCIÓJA
 FÉLMEREV KAPCSOLATOK NUMERIKUS SZIMULÁCIÓJA Vértes Katalin * - Iványi Miklós ** RÖVID KIVONAT Acélszerkezeti kapcsolatok jellemzőinek (szilárdság, merevség, elfordulási képesség) meghatározása lehetséges
FÉLMEREV KAPCSOLATOK NUMERIKUS SZIMULÁCIÓJA Vértes Katalin * - Iványi Miklós ** RÖVID KIVONAT Acélszerkezeti kapcsolatok jellemzőinek (szilárdság, merevség, elfordulási képesség) meghatározása lehetséges
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Geometria III.
 Geometria III. DEFINÍCIÓ: (Vektor) Az egyenlő hosszúságú és egyirányú irányított szakaszoknak a halmazát vektornak nevezzük. Jele: v. DEFINÍCIÓ: (Geometriai transzformáció) Geometriai transzformációnak
Geometria III. DEFINÍCIÓ: (Vektor) Az egyenlő hosszúságú és egyirányú irányított szakaszoknak a halmazát vektornak nevezzük. Jele: v. DEFINÍCIÓ: (Geometriai transzformáció) Geometriai transzformációnak
Számítógépes Grafika SZIE YMÉK
 Számítógépes Grafika SZIE YMÉK Analóg - digitális Analóg: a jel értelmezési tartománya (idő), és az értékkészletes is folytonos (pl. hang, fény) Diszkrét idejű: az értelmezési tartomány diszkrét (pl. a
Számítógépes Grafika SZIE YMÉK Analóg - digitális Analóg: a jel értelmezési tartománya (idő), és az értékkészletes is folytonos (pl. hang, fény) Diszkrét idejű: az értelmezési tartomány diszkrét (pl. a
Haladó lineáris algebra
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Haladó lineáris algebra BMETE90MX54 Lineáris leképezések 2017-02-21 IB026 Wettl Ferenc
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Haladó lineáris algebra BMETE90MX54 Lineáris leképezések 2017-02-21 IB026 Wettl Ferenc
Lineáris leképezések. Wettl Ferenc március 9. Wettl Ferenc Lineáris leképezések március 9. 1 / 31
 Lineáris leképezések Wettl Ferenc 2015. március 9. Wettl Ferenc Lineáris leképezések 2015. március 9. 1 / 31 Tartalom 1 Mátrixleképezés, lineáris leképezés 2 Alkalmazás: dierenciálhatóság 3 2- és 3-dimenziós
Lineáris leképezések Wettl Ferenc 2015. március 9. Wettl Ferenc Lineáris leképezések 2015. március 9. 1 / 31 Tartalom 1 Mátrixleképezés, lineáris leképezés 2 Alkalmazás: dierenciálhatóság 3 2- és 3-dimenziós
Többnézetes geometria
 Vizuális helymeghatározás Többnézetes geometria Plósz Sándor 1 1 Budapesti Műszaki és Gazdaságtudományi Egyetem Távközlési és Médiainformatikai Tanszék 2015 Plósz Sándor (BME TMIT) Navigációs szolgáltatások
Vizuális helymeghatározás Többnézetes geometria Plósz Sándor 1 1 Budapesti Műszaki és Gazdaságtudományi Egyetem Távközlési és Médiainformatikai Tanszék 2015 Plósz Sándor (BME TMIT) Navigációs szolgáltatások
Számítógépes képelemzés 7. előadás. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Mechatronika segédlet 3. gyakorlat
 Mechatronika segédlet 3. gyakorlat 2017. február 20. Tartalom Vadai Gergely, Faragó Dénes Feladatleírás... 2 Fogaskerék... 2 Nézetváltás 3D modellezéshez... 2 Könnyítés megvalósítása... 2 A fogaskerék
Mechatronika segédlet 3. gyakorlat 2017. február 20. Tartalom Vadai Gergely, Faragó Dénes Feladatleírás... 2 Fogaskerék... 2 Nézetváltás 3D modellezéshez... 2 Könnyítés megvalósítása... 2 A fogaskerék
Gauss-Seidel iteráció
 Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2013. szeptember 23. Javítva: 2013.10.09.
Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2013. szeptember 23. Javítva: 2013.10.09.
Kocka perspektivikus ábrázolása. Bevezetés
 1 Kocka perspektivikus ábrázolása Bevezetés Előző három dolgozatunkban ~ melyek címe: 1. Sínpár perspektivikus ábrázolása, 2. Sínpár perspektivikus ábrázolása másként, 3. Sínpár perspektivikus ábrázolása
1 Kocka perspektivikus ábrázolása Bevezetés Előző három dolgozatunkban ~ melyek címe: 1. Sínpár perspektivikus ábrázolása, 2. Sínpár perspektivikus ábrázolása másként, 3. Sínpár perspektivikus ábrázolása
EEE Kutatólaboratórium MTA-SZTAKI Magyar Tudományos Akadémia
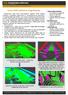 DElosztott I S T R I B U T EEsemények D EV E N T S A NElemzé A L Y S I S se R E SKutatólaboratór E A R C H L A B O R A T Oium R Y L I D A R B a s e d S u r v e i l l a n c e Városi LIDAR adathalmaz szegmentációja
DElosztott I S T R I B U T EEsemények D EV E N T S A NElemzé A L Y S I S se R E SKutatólaboratór E A R C H L A B O R A T Oium R Y L I D A R B a s e d S u r v e i l l a n c e Városi LIDAR adathalmaz szegmentációja
Keresztmetszet másodrendű nyomatékainak meghatározása
 BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
A dinamikus geometriai rendszerek használatának egy lehetséges területe
 Fejezetek a matematika tanításából A dinamikus geometriai rendszerek használatának egy lehetséges területe Készítette: Harsányi Sándor V. matematika-informatika szakos hallgató Porcsalma, 2004. december
Fejezetek a matematika tanításából A dinamikus geometriai rendszerek használatának egy lehetséges területe Készítette: Harsányi Sándor V. matematika-informatika szakos hallgató Porcsalma, 2004. december
Automatikus irányzás digitális képek. feldolgozásával TURÁK BENCE DR. ÉGETŐ CSABA
 Automatikus irányzás digitális képek feldolgozásával TURÁK BENCE DR. ÉGETŐ CSABA Koncepció Robotmérőállomásra távcsővére rögzített kamera Képek alapján a cél automatikus detektálása És az irányzás elvégzése
Automatikus irányzás digitális képek feldolgozásával TURÁK BENCE DR. ÉGETŐ CSABA Koncepció Robotmérőállomásra távcsővére rögzített kamera Képek alapján a cél automatikus detektálása És az irányzás elvégzése
Keresés képi jellemzők alapján. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
Termék modell. Definíció:
 Definíció: Termék modell Összetett, többfunkciós, integrált modell (számítógépes reprezentáció) amely leír egy műszaki objektumot annak különböző életfázis szakaszaiban: tervezés, gyártás, szerelés, szervízelés,
Definíció: Termék modell Összetett, többfunkciós, integrált modell (számítógépes reprezentáció) amely leír egy műszaki objektumot annak különböző életfázis szakaszaiban: tervezés, gyártás, szerelés, szervízelés,
Sztereó képfeldolgozás mobilrobot platform tájékozódásához Önálló laboratórium 2007/2008. tavaszi félév
 Sztereó képfeldolgozás mobilrobot platform tájékozódásához Önálló laboratórium 007/008. tavaszi félév Józsa Csongor Konzulens: Dr. Vajda Ferenc 1/1 1. A probléma ismertetése Mobilis robotok ismeretlen
Sztereó képfeldolgozás mobilrobot platform tájékozódásához Önálló laboratórium 007/008. tavaszi félév Józsa Csongor Konzulens: Dr. Vajda Ferenc 1/1 1. A probléma ismertetése Mobilis robotok ismeretlen
Matematikai geodéziai számítások 5.
 Matematikai geodéziai számítások 5 Hibaterjedési feladatok Dr Bácsatyai László Matematikai geodéziai számítások 5: Hibaterjedési feladatok Dr Bácsatyai László Lektor: Dr Benedek Judit Ez a modul a TÁMOP
Matematikai geodéziai számítások 5 Hibaterjedési feladatok Dr Bácsatyai László Matematikai geodéziai számítások 5: Hibaterjedési feladatok Dr Bácsatyai László Lektor: Dr Benedek Judit Ez a modul a TÁMOP
Differenciálegyenletek numerikus integrálása április 9.
 Differenciálegyenletek numerikus integrálása 2018. április 9. Differenciálegyenletek Olyan egyenletek, ahol a megoldást függvény alakjában keressük az egyenletben a függvény és deriváltjai szerepelnek
Differenciálegyenletek numerikus integrálása 2018. április 9. Differenciálegyenletek Olyan egyenletek, ahol a megoldást függvény alakjában keressük az egyenletben a függvény és deriváltjai szerepelnek
Mérési adatok illesztése, korreláció, regresszió
 Mérési adatok illesztése, korreláció, regresszió Korreláció, regresszió Két változó mennyiség közötti kapcsolatot vizsgálunk. Kérdés: van-e kapcsolat két, ugyanabban az egyénben, állatban, kísérleti mintában,
Mérési adatok illesztése, korreláció, regresszió Korreláció, regresszió Két változó mennyiség közötti kapcsolatot vizsgálunk. Kérdés: van-e kapcsolat két, ugyanabban az egyénben, állatban, kísérleti mintában,
További programozási esetek Hiperbolikus, kvadratikus, integer, bináris, többcélú programozás
 További programozási esetek Hiperbolikus, kvadratikus, integer, bináris, többcélú programozás Készítette: Dr. Ábrahám István Hiperbolikus programozás Gazdasági problémák optimalizálásakor gyakori, hogy
További programozási esetek Hiperbolikus, kvadratikus, integer, bináris, többcélú programozás Készítette: Dr. Ábrahám István Hiperbolikus programozás Gazdasági problémák optimalizálásakor gyakori, hogy
Diplomamunkám felépítése
 Üregek távolhatása gránitos kőzetkörnyezetben Tóth Szilvia Konzulensek: Dr. Török Ákos, BME Építőanyagok és Mérnökgeológia Tanszék Poromb Péter, Mott MacDonald Magyarország Kft. Diplomamunkám felépítése
Üregek távolhatása gránitos kőzetkörnyezetben Tóth Szilvia Konzulensek: Dr. Török Ákos, BME Építőanyagok és Mérnökgeológia Tanszék Poromb Péter, Mott MacDonald Magyarország Kft. Diplomamunkám felépítése
Követelmény a 7. évfolyamon félévkor matematikából
 Követelmény a 7. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Elemek halmazba rendezése több szempont alapján. Halmazok ábrázolása. A nyelv logikai elemeinek helyes használata.
Követelmény a 7. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Elemek halmazba rendezése több szempont alapján. Halmazok ábrázolása. A nyelv logikai elemeinek helyes használata.
Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea
 Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea Geometrikus deformálható modellek Görbe evolúció Level set módszer A görbe evolúció parametrizálástól független mindössze geometriai
Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea Geometrikus deformálható modellek Görbe evolúció Level set módszer A görbe evolúció parametrizálástól független mindössze geometriai
8. Pontmegfeleltetések
 8. Pontmegfeleltetések Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Példa: panoráma kép készítés 1. Jellemzőpontok detektálása mindkét
8. Pontmegfeleltetések Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Példa: panoráma kép készítés 1. Jellemzőpontok detektálása mindkét
Irányításelmélet és technika II.
 Irányításelmélet és technika II. Legkisebb négyzetek módszere Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék amagyar@almos.vein.hu 200 november
Irányításelmélet és technika II. Legkisebb négyzetek módszere Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék amagyar@almos.vein.hu 200 november
Compton-effektus. Zsigmond Anna. jegyzıkönyv. Fizika BSc III.
 Compton-effektus jegyzıkönyv Zsigmond Anna Fizika BSc III. Mérés vezetıje: Csanád Máté Mérés dátuma: 010. április. Leadás dátuma: 010. május 5. Mérés célja A kvantumelmélet egyik bizonyítékának a Compton-effektusnak
Compton-effektus jegyzıkönyv Zsigmond Anna Fizika BSc III. Mérés vezetıje: Csanád Máté Mérés dátuma: 010. április. Leadás dátuma: 010. május 5. Mérés célja A kvantumelmélet egyik bizonyítékának a Compton-effektusnak
Arany Dániel Matematikai Tanulóverseny 2010/2011-es tanév 1. forduló haladók III. kategória
 Bolyai János Matematikai Társulat Oktatásért Közalapítvány támogatásával Arany Dániel Matematikai Tanulóverseny 2010/2011-es tanév 1. forduló haladók III. kategória Megoldások és javítási útmutató 1. Határozzuk
Bolyai János Matematikai Társulat Oktatásért Közalapítvány támogatásával Arany Dániel Matematikai Tanulóverseny 2010/2011-es tanév 1. forduló haladók III. kategória Megoldások és javítási útmutató 1. Határozzuk
1. Generátorrendszer. Házi feladat (fizikából tudjuk) Ha v és w nem párhuzamos síkvektorok, akkor generátorrendszert alkotnak a sík vektorainak
 1. Generátorrendszer Generátorrendszer. Tétel (Freud, 4.3.4. Tétel) Legyen V vektortér a T test fölött és v 1,v 2,...,v m V. Ekkor a λ 1 v 1 + λ 2 v 2 +... + λ m v m alakú vektorok, ahol λ 1,λ 2,...,λ
1. Generátorrendszer Generátorrendszer. Tétel (Freud, 4.3.4. Tétel) Legyen V vektortér a T test fölött és v 1,v 2,...,v m V. Ekkor a λ 1 v 1 + λ 2 v 2 +... + λ m v m alakú vektorok, ahol λ 1,λ 2,...,λ
Képrekonstrukció 3. előadás
 Képrekonstrukció 3. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Computed Tomography (CT) Elv: Röntgen-sugarak áthatolása 3D objektum 3D térfogati kép Mérések
Képrekonstrukció 3. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Computed Tomography (CT) Elv: Röntgen-sugarak áthatolása 3D objektum 3D térfogati kép Mérések
Normák, kondíciószám
 Normák, kondíciószám A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris egyenletrendszerek Nagyon sok probléma közvetlenül lineáris egyenletrendszer megoldásával kezelhetı Sok numerikus
Normák, kondíciószám A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris egyenletrendszerek Nagyon sok probléma közvetlenül lineáris egyenletrendszer megoldásával kezelhetı Sok numerikus
Robotok inverz geometriája
 Robotok inverz geometriája. A gyakorlat célja Inverz geometriai feladatot megvalósító függvények implementálása. A megvalósított függvénycsomag tesztelése egy kétszabadságfokú kar előírt végberendezés
Robotok inverz geometriája. A gyakorlat célja Inverz geometriai feladatot megvalósító függvények implementálása. A megvalósított függvénycsomag tesztelése egy kétszabadságfokú kar előírt végberendezés
Lin.Alg.Zh.1 feladatok
 Lin.Alg.Zh. feladatok 0.. d vektorok Adott három vektor ā (0 b ( c (0 az R Euklideszi vektortérben egy ortonormált bázisban.. Mennyi az ā b skalárszorzat? ā b 0 + + 8. Mennyi az n ā b vektoriális szorzat?
Lin.Alg.Zh. feladatok 0.. d vektorok Adott három vektor ā (0 b ( c (0 az R Euklideszi vektortérben egy ortonormált bázisban.. Mennyi az ā b skalárszorzat? ā b 0 + + 8. Mennyi az n ā b vektoriális szorzat?
