- Levelek: operandusok - Csomópontok: operátorok. Fenti kifejezés: (x+ (y 10)) * (6 / z) Bináris Keresőfa (BST) Példa bináris keresőfára.
|
|
|
- Dénes Bognár
- 8 évvel ezelőtt
- Látták:
Átírás
1 Fák Fa definíciója Fa(Tree): csomópontok(nodes) halmaza, amelyeket élek(edges) kötnek össze, és teljesülnek az alábbi feltételek: - létezik egy kitűntetett csomópont: a gyökér (root) - a gyökértől különböző minden más C csomópont egy éllel van összekötve szülőjéhez - a fa összefüggő: bármely nem-gyökér csomóponttól kiindulva a szülőkön keresztül a gyökérhez eljutunk A gráfelmélet alapján fa definíciója: olyan gráf, amelyik - összefüggő - nem tartalmaz kört Alapfogalmak - Ha (v,w) ε E, akkor v-t a w szülőjének nevezzük - Ha u-ból vezető út w-be, akkor u a w őse, w az u leszármazottja - Ha u w, akkor valódi ős illetve leszármazott - Valódi leszármazottal nem rendelkező csomó-pont a fa levele - Egy s csomópont az összes leszármazottjával együtt F részfáját alkotja Ennek gyökere s - Erdő: fák együtteséből álló irányított gráf F=(V,E) U V S W Y Z Fa jellemzői - Csomópont mélysége: a gyökértől a hozzá elvezető út hossza - Csomópont magassága: annak az innen kiinduló útnak a hossza, amelyik a leghosszabb a levelekig vezető utak közül - Fa magassága: a gyökér magassága - Csomópont szintje: a fa magassága csomópont mélysége Rekurzív adattípusok - Az adatszerkezet egy része jól leírható egy rekurzív szerkezettel is, ami fizikailag hasonló tárolást, de egészen más algoritmusokat eredményezhet - TLista = Struktúra (tartalom, következő) A lista rekurzív értelmezése szerint minden eleme felfogható egy tartalom résszel, és egy másik ( a következő mutató által mutatott elemmel kezdődő) listával rendelkező szerkezetként - TFa = Struktúra ( tartalom, fák ) Egy fa egy eleme elképzelhető egy tartalom résszel, és további részfákkal rendelkező struktúrával - TBinárisFa = Struktúra (tartalom, balfa, jobbfa) Bináris a hasonló mint egy fa, csak definíció szerint legfeljebb két másik fát tartalmazhat Bináris Fa eleme - Bináris fa egy elemének a definíciója: TBinFaElem = Struktúra (tartalom, balgyerek, jobbgyerek) - Tartalom (példában: tart): tárolandó adat o Egyszer vagy összetett típus, objektum-referencia - Balgyerek, jobbgyerek: a csomópont baloldali illetve jobboldali részfáinak a gyökerére hivatkozik (bal, jobb) - A listához hasonlóan a gyerek mezőkben egy kitűntetett érték jelzi, ha hiányzik (példában: ø) - Általában egy külső változó tartalmaz egy hivatkozást a fa gyökérelemére (gyökér) - A csomóponton belül egyéb mezők is lehetnek, pl gyakran tároljuk a szülő címét is
2 Példa bináris fára Aritmetikai kifejezés fa: gyökér * - Levelek: operandusok - Csomópontok: operátorok + / Fenti kifejezés: (x+ (y 10)) * (6 / z) - 6 Z Y 10 Bináris Keresőfa (BST) - Rendezett Fa, emiatt pontosítjuk a struktúrát - TBSTElem = Struktúra (kulcs, tartalom, balgyerek, jobbgyerek) - Kulcs alapján rendezett: a fa minden r csomópontjára igaz, hogy r baloldali részfája legfeljebb rkulcs nagyságú, r jobboldali részfája pedig legalább rkulcs nagyságú kulcsokat tartalmaz - A rendezés természetesen lehet fordított is - A kulcs lehetséges megvalósításai o Különálló kulcs mező o A kulcs a tartalom része o A kulcs a tartalomból számítható érték Példa bináris keresőfára gyökér Megjegyzések: - a későbbiekben a záró ø eket nem jelöljük, az algoritmusokban azonban számítunk ezekre - Üres fa esetén: gyökér = ø ø ø ø ø ø ø ø ø ø ø ø ø
3 Bejárás - Bejárás: az adatszerkezet valamennyi elemének egyszeri elérése (feldolgozása) - A láncolt listához hasonlóan a bejárás algoritmusa független a végrehajtandó tevékenységtől, ezért az algoritmuson belül csak utalást teszünk erre - Mivel a láncolt listával ellentétben egy elemből több irányban is tovább lehet lépni, többféle bejárás is elképzelhető - A csomópontokban található adatok (tartaom, bal, jobb) feldolgozásának sorrendje alapján három fő változat különböztethető meg (ezen belül bal és jobb megcserélhető): o PreOrder bejárás: tartalom, bal, jobb o InOrder bejárás: bal, tartalom, jobb o PostOrder: bal, jobb, tartalom PreOrder bejárás Rekurzió Eljárás PreOrder(p) Ha p ø akkor Feldolgozás(p) PreOrder(pbal) PreOrder(pjobb) Eljárás Vége Bejárás indítása PreOrder(gyökér) # teljes fa bejárása PreOrder(p) # részfa bejárása (Gyakorlati alkalmazás: fa elmentése) PostOrder bejárás Rekurzió Eljárás PostOrder(p) Ha p= ø akkor PostOrder(pbal) PostOrder(pjobb) Feldolgozás(p) Eljárás Vége Bejárás indítása PostOrder(gyökér) # teljes fa bejárása PostOrder(p) # részfa bejárása (Gyakorlati alkalmazás: fa felszabadítása) InOrder bejárás Rekurzió Eljárás InOrder(p) Ha p= ø akkor InOrder(pbal) Feldolgozás(p) InOrder(pjobb) Eljárás Vége Bejárás indítása InOrder(gyökér) # teljes fa bejárása InOrder(p) # részfa bejárása (Gyakorlati alkalmazás: elemek elérése rendezés szerinti sorrendben, növekvő vagy csökkenő)
4 Keresés BST-ben - Alapelv: a fa gyökérelemének kulcsa vagy egyenlő a keresett kulccsal, vagy egyértelműen meghatározza, hogy melyik részfában kell keresést folytatni - Ez ugyanúgy igaz a teljes bináris fa gyökérelemére, illetve bármelyik (a keresés során elért) részfájának gyökerére - A keresés menete (keresendő kulcs: x) o Bázis Ha T üres, akkor nincs x benne Ha T gyökerének cimkéje x, akkor talált o Indukció (legyen T gyökerének kulcsa y) Ha x < y akkor x-et a bal részfában Ha x > y akkor a jobb részfában keressük Keresés algoritmusa Kulcs alapján keresés Függvény Keresés(p, mitkeres) Ha p ø akkor Ha pkulcs = mitkeres akkor Keresés! p Ha pkulcs > mitkeres akkor Keresés! Keresés (pbal, mitkeres) Keresés! Keresés(pjobb, mitkeres) Keresés! ø Függvény Vége * átlagos lépésszám (kiegyensúlyozott fában): Ordo(log 2 n) Beszúrás BST-be - A beszúrás során az elem beláncolásán kívül ügyelnünk kell a keresőfa tulajdonság fenntartására is - Ugyanazok az elemek többféleképpen is elhelyezkedhetnek egy bináris keresőfában, beszúráskor ez alapján több stratégiánk is lehet o Minél kisebb erőforrásigény legyen a beszúrás o Minél kiegyensúlyozottabb legyen a fa a beszúrások után - A beszúrás menete (beszúrandó kulcs: x) o Bázis Ha T üres, akkor új csomópontot készítünk x kulccsal és visszatérünk a csomópont címével Ha T gyökerének kulcsa x, akkor visszatérünk a csomópont címével o Indukció (legyen T gyökerének kulcsa y) Ha x < y, akkor x-t bal részfában Ha x > y, akkor a jobb részfába szúrjuk be
5 Beszúrás algoritmusa Új elem beszúrása Függvény Beszúrás(címszerin p, újkulcs) Ha p= ø akkor ElemLétrehozás(p) pkulcs! újkulcs; pbal! ø; pjobb! ø Beszúrás!p Ha pkulcs > újkulcs akkor Beszúrás!Beszúrás(pbal, újkulcs) Ha pkulcs < újkulcs akkor Beszúrás! Beszúrás(pjobb, újkulcs) Beszúrás!p Függvény Vége Törlés BST-ből 1 lépés - A törlés során az elem kiláncolásán kívül ügyelnünk kell a keresőfa tulajdonság fenntartására is - Törlés során az alábbi problémák merülhetnek fel: o Két gyerekkel rendelkező elem mindkét gyerekét nem tudjuk az ő szülőjének egy mutatójára rákapcsolni o Gyökérelem törlése - Törlés 1 lépése (beszúrandó kulcs: x) o Bázis Ha T üres, akkor nincs ilyen elem Ha T gyökerének kulcsa x, akkor töröljük, majd tovább 2 lépésre: BST tulajdonság visszaállítása Indukció Ha x < y akkor x-t a bal részfából Ha x > y akkor a jobb részfából töröljük Törlés BST-ből 2 lépés A) eset: a törlendő csúcspont egy levél, tehét nincsenek gyerek elemei a Pl töröljük a 70-et
6 Törlés BST-ből 2 lépés B) eset: törlendő csúcspontnak csak egy bal vagy csak egy jobb oldali gyereke van a Pl töröljük a 60-et Törlés BST-ből 2 lépés C) eset: a törlendő csúcspontnak bal és jobb oldali gyereke is van a Pl töröljük a -et
7 Törlés algoritmusa Eljárás Törlése(címszerint p, törlendő) Ha p=ø akkor Nincse ilyen elem Külünben Ha pkulcs > törlendő akkor Törlés(pbal, törlendő) Ha pkulcs < törlendő akkor Törlés(pjobb, törlendő) Ha pbal = ø akkor q=p; p!pjobb; ElemFelszabadítás(q) Ha pjobb = ø akkor q=p; p!pbal; ElemFelszabadítás(q) TörlésEset(p, pbal) Eljárás Vége Eljárás TörlésEset(p, címszerint r) Ha rjobb ø TörlésEset(p, rjobb) pkulcs! rkulcs ptart! rtart q! r r! rbal ElemFelszabadítás(q) ELjárás Vége - Baloldali részfa legjobboldalibb elemének megkeresése, és ennek tartalmával felülírjuk a törlendő elemet - Ezt megtehetjük, hiszen ez - Biztosan nagyobb, mint a baloldali elemek és - Biztosan kisebb, mint a jobboldali elemek Miért használjuk A bináris fa előnyei - Rendezett - Ebből adódóan gyors keresés - Relatív gyors elem felvétel - Relatív gyors elem törlés, legrosszabb esetben sincs szükség a fa nagy részének átalakítására - A csomópontok tartalma gyakran egy más adatszerkezet elemére mutat: ideális indexelésre kiegészítő adatszerkezetként A bináris fa hátrányai - bonyolult, lásd bejárások - rekurzióval a műveletek költségesek, illetve maga a rekurzió az OOP nyelvekben gyakran életidegen módon jelenik meg - elemek nem érhetőek el közvetlenül (sőt, maga az indexelés sem egyértelmű, csak a bejárás módjával együtt) - gyors keresés nem garantált, csak kiegyensúlyozott fákban valósul meg - két gyerek címe miatt még nagyobb egy elem helyfoglalása
8 Probléma felvetése - Vizsgáljuk meg az alábbi kettő, adattartalom szempontjából azonos, de szerkezetileg más fákat keresés szempontjából A jobboldali (elfajult) fa keresési szempontból nem ideális, láncolt listához hasonló lépésszámot igényel Kiegyensúlyozott fa - Kiegyensúlyozott fa: legfeljebb egy szintnyi (mélység) eltérés van az egyes (azonos szinten található részfái között) - Teljesen kiegyensúlyozott fa: minden csúcsából leágazó bal- és jobboldali részfa csúcsainak száma legfeljebb egyel különbözik egymáshoz képest - Teljes fa: Minden csúcsból leágazó bal-és jobboldali részfa csúcsainak száma azonos - Célunk: a módosító algoritmusok kiegészítése, hogy minél inkább kiegyensúlyozott (az előző oldalon látható baloldalihoz hasonló) fák építésére törekedjenek - Ennek lehetséges megoldásai: beszúrás s törlés után a fa szerkezetét megváltoztatjuk, például forgatással Forgatás - Forgatás: olyan lokális művelet, amely megváltoztatja a fa szerkezetét, de megőrzi a rendezettséget - Megkülönböztetjük balra- illetve jobbra forgatás műveletét Eljárás Balra-Forgat(x) y! xjobb xjobb! ybal Ha ybal ø akkor ybalszülő! x yszülő! xszülő Ha xszülő = ø akkor gyökér! y Ha xszülőbal = x akkor xszülőbal = y xszülőjobb = y ybal! x xszülő! y Eljárás Vége
9 Piros-Fekete Fa - Piros-Fekete fa: Olyan bináris keresőfa, amely rendelkezik az alábbi tulajdonságokkal o Minden csúcs színe piros vagy fekete o Minden levél színe fekete o Minden piros csúcsnak mindkét gyereke fekete o Bármely két, azonos csúcsból kiinduló és levélig vezető úton ugyanannyi fekete csúcs van (fekete magasság) - Megvalósítással kapcsolatos megjegyzések: o A BST struktúrát kiegészítjük egy új attribútummal, ami jelzi a színt (értéke vagy piros vagy fekete lehet) o Az egyszerűbb algoritmusok miatt tároljuk a csomópontok szüleit is (a gyökérpontok esetén ezt ø-el jelöljük) o Az egyszerűbb algoritmusok miatt tartalommal külön nem foglalkozunk, feltételezzük, hogy amennyiben a kulcsot átmásoljuk, az mindig a kulccsal együtt mozog Megjegyzés: - levélnek a nem ábrázolt ø értékeket tekintjük (ezek kötelezően feketék) - megközelítőleg kiegyensúlyozott: biztosítható, hogy bármely, a gyökértől levélig vezető út hossza nem nagyobb, mint a legrövidebb ilyen út hosszának a kétszerese Piros-Fekete fába beszúrás Eljárás PF-Fába-Beszúrás(x) BinárisFábaBeszúrás(gyökér, x); xszín! PIROS Ciklus amíg x gyökér és xszülőszülőszín = PIROS Ha xszülő = xszülőszülőbal akkor y! xszülőszülőjobb Ha y ø és yszín = PIROS akkor xszülőszín! FEKETE; yszín! FEKETE xszülőszülőszín! PIROS; x!xszülőszülő Ha x=xszülőjobb akkor x!xszülő; Balra-Forgat(x) xszülőszín! FEKETE; xszülőszülőszín! PIROS Jobbra-Forgat(xszülőszülő) Ciklus Vége Gyökérszín! FEKETE Eljárás Vége
10 Piros-Fekete fába beszúrás A eset Y Piros-Fekete fába beszúrás B eset Y Piros-Fekete fába beszúrás C eset Y
11 Piros-Fekete Fa további műveletei - Bejárás o Azonos az egyszerű bináris keresőfánál megismerttel o Piros-fekete tulajdonságoknak nincs szerepe - Keresés o Azonos az egyszerű bináris keresőfánál megismerttel o A piros-fekete tulajdonságnak nincs szerepe - Törlés o Alapja az egyszerű bináris keresőfánál megismert törlés o Kiegészítve egy piros-fekete tulajdonságot biztosító karbantartó eljárással o A beszúráshoz hasonlóan ezt átszínezésekkel és forgatásokkal oldja meg o Nem tárgyaljuk B-Fa - B-Fa: Olyan kiegyensúlyozott keresőfa, amelyet úgy terveztek, hogy hatákonyan lehessen alkalmazni háttértárolón tárolt adatok esetén is - Gyakorlati szempontból a futási időt két összetevőre bontjuk fel o Lemezhozzáférések száma o Központi egység műveleteinek száma - Napjainkban alkalmazott háttértárolók általában nagyságrendekkel nagyobb sebességet tudnak elérni blokkok írása/olvasása során, mintha ugyanezt az adatmennyiséget elemi adatokként írnánk/olvasnánk - A keresés során tehát egy optimalizálási lehetőség, ha a lemezhozzáférések számát blokkonkénti kezeléssel próbáljuk csökkenteni B-Fa további jellemzői: - Ha k i egy kulcs c i gyökerű részfában, akkor: k 1 kulcs 1 k 2 kulcs 2 k n kulcs n k n+1 - Minden levél mélysége azonos: h (fa magassága) - A csúcsokban található kulcsok darabszáma alulról és felülről is korlátos, ezt egy rögzített t számmal lehet kifejezni (B-fa minimális fokszáma): o Minden nemgyökér csúcsnak legalább t-1 kulcsa van, tehát minden belső csúcsnak legalább t gyereke o Minden csúcsnak legfeljebb 2t-1 kulcsa lehet, tehát minden belső csúcsnak legfeljebb 2t gyereke - A kulcsok darabszámára más módon is adhatunk korlátot, mi mindig ezt a definíciót használjuk (egyes szakirodalmak azonban ettől eltérhetnek) B-Fa példa N C F I Q T AB DE DE GH JK OP RS W
12 B-Fa csúcsának szétvágása (t=4) A szétvágás lépései: 1 Új z csúcs létrehozása 2 Az y utolsó t-1 db kulcsának (és ha van, gyerek mutatójának) átmásolása z-be 3 Az y így maradt legnagyobb kulcsának felvitele x-be 4 A z csúcs legyen x gyereke a 3 pontban felvitt kulcs után Megjegyzés: y telített, x nem telített Speciális eset: gyökér szétvágása A I U A E I U Y B C D E F G H Y B C D F G H Z T1 T2 T3 T4 T5 T6 T7 T8 T1 T2 T3 T4 T5 T6 T7 T8 B-Fába új elem beszúrása - Feladat: x csúcsba egy új K kulcs beszúrása - Megkülönböztetett esetek: o x egy levélelem o x egy nem-levélelem o x a gyökérelem és teltett - Minden esetben feltételezzük, hogy az x elem nem telített A) Ha x egy levélelem a a K kulcs helyének megkeresése az xkulcs i k alapján b ez mögötti xkulcs i k hátra léptetése c a K elhelyezése az üres helyre d az xn növelése B) Ha x nem levél a a K kulcsnak megfelelő gyerek meghatározása az xkulcs i k alapján b az így meghatározott gyerek betöltése x-be c ha ez a gyerek telített, szétvágás; vágás esetén ha szükséges (a keresést a létrejött új elemben kell folytatni), x aktualizálása d a beszúrást végző rekurzió folytatása az új csúcson C) Ha x a gyökér és telített a az x szétvágása egy új gyökérelem létrehozásával b a beszúrás rekurzió indítása a megfelelő gyerek csúcsban i A gyökércsúcs kettévágása az egyetlen művelet, amely a B-fa magasságát növeli ii A bináris keresőfával ellentétben tehát a B-fa a gyökerénél nő, és nem a fa alján iii Ennek köszönhetően a B-fa mindig kiegyensúlyozott
13 B-Fába új elem beszúrása 1 A O U A O U B C D E H I B C D E F H I B-Fába új elem beszúrása 2 A O U A F O U B C D E F H I B C D E G H I B-Fába új elem beszúrása 3 E B C D E F G H B C D F G H B-Fából elem törlése Egy x kulcsból K kulcs törlése: A) Ha K az x-ben van és x levél, akkor K kulcs törlése x-ből B) Ha K az x-ben van, és x belső csúcs a Ha van x-nek olyan y gyereke, amelyik tartalmaz egy K-t megelőző kulcsot és legalább t kulcsa van: a K-t közvetlenül megelőző K kulcs felhozatala x-be, majd a törlés folytatása K -re b Hasonló, mint az a, csak K-t közvetlenül követő kulcsot keressük meg c Ha a, b, -ben vizsgált mindkét szomszédos gyereknek csak t-1 kulcsa van, akkor egyesítjük a két gyereket és a törlendő K-t egy közös csúcsban, majd rekurzívan folytatjuk a törlést innen (feltételezzük, hogy x kulcsszáma mindig legalább t!) Feltételezzük, hogy x kulcsszáma mindig legalább t, a k-t tartalmazó csúcs keresése során ezt mindig garantálnunk kell a rekurzió újabb meghívása előtt Lehetőségek: - Ha a következő vizsgálandó y csúcsnak csak t-1 kulcsa van, de valamelyik testvérének t, akkor a testvérből vigyünk fel egy kulcsot a szülőbe, onnan pedig egyet le az y-ba - Ha a következő csúcsnak és testvéreinek is t-1 kulcsuk van, akkor egyesítsük valamelyik testvérével és vigyünk le az így feleslegessé vált kulcsot a szülőből (ha ez a gyökér és az utolsó kulcs, akkor csökken a fa magassága egyel) - További műveletek: Bejárás, keresés (alapelve hasonló a bináris fáknál megismerttel, kibővítve azzal, hogy egy csúcsnak több tartalma és gyereke lehet ( A fa minden szempontból kiegyensúlyozott, tehét keresés szempontjából hatékony) Mivel egy csúcs több kulcsot tartalmaz, így kevesebb csúcsbetöltést igényel
Fák 2009.04.06. Témakörök. Fa definíciója. Rekurzív típusok, fa adatszerkezet Bináris keresőfa, bejárások Bináris keresőfa, módosítás B-fa
 Fák szenasi.sandor@nik.bmf.hu PPT 2007/2008 tavasz http://nik.bmf.hu/ppt 1 Rekurzív típusok, fa adatszerkezet Bináris keresőfa, bejárások Bináris keresőfa, módosítás B-fa Témakörök 2 Fa (Tree): csomópontok
Fák szenasi.sandor@nik.bmf.hu PPT 2007/2008 tavasz http://nik.bmf.hu/ppt 1 Rekurzív típusok, fa adatszerkezet Bináris keresőfa, bejárások Bináris keresőfa, módosítás B-fa Témakörök 2 Fa (Tree): csomópontok
Fa (Tree): csomópontok (nodes) halmaza, amelyeket élek (edges) kötnek össze, és teljesülnek az alábbi feltételek:
 Fák szenasi.sandor@nik.bmf.hu PPT 2007/2008 tavasz http://nik.bmf.hu/ppt 1 Témakörök Rekurzív típusok, fa adatszerkezet Bináris keresőfa, bejárások Bináris keresőfa, módosítás Piros-fekete fa B-fa 2 Fa
Fák szenasi.sandor@nik.bmf.hu PPT 2007/2008 tavasz http://nik.bmf.hu/ppt 1 Témakörök Rekurzív típusok, fa adatszerkezet Bináris keresőfa, bejárások Bináris keresőfa, módosítás Piros-fekete fa B-fa 2 Fa
Bináris keresőfa. Felépítés, alapvető műveletek. Programozás II. előadás. Szénási Sándor
 Bináris keresőfa Felépítés, alapvető műveletek előadás http://nik.uni-obuda.hu/prog2 Szénási Sándor szenasi.sandor@nik.uni-obuda.hu Óbudai Egyetem,Neumann János Informatikai Kar Bináris keresőfa Rekurzív
Bináris keresőfa Felépítés, alapvető műveletek előadás http://nik.uni-obuda.hu/prog2 Szénási Sándor szenasi.sandor@nik.uni-obuda.hu Óbudai Egyetem,Neumann János Informatikai Kar Bináris keresőfa Rekurzív
Gyakorló feladatok ZH-ra
 Algoritmuselmélet Schlotter Ildi 2011. április 6. ildi@cs.bme.hu Gyakorló feladatok ZH-ra Nagyságrendek 1. Egy algoritmusról tudjuk, hogy a lépésszáma O(n 2 ). Lehetséges-e, hogy (a) minden páros n-re
Algoritmuselmélet Schlotter Ildi 2011. április 6. ildi@cs.bme.hu Gyakorló feladatok ZH-ra Nagyságrendek 1. Egy algoritmusról tudjuk, hogy a lépésszáma O(n 2 ). Lehetséges-e, hogy (a) minden páros n-re
B-fa. Felépítés, alapvető műveletek. Programozás II. előadás. Szénási Sándor.
 B-fa Felépítés, alapvető műveletek előadás http://nik.uni-obuda.hu/prog2 Szénási Sándor szenasi.sandor@nik.uni-obuda.hu Óbudai Egyetem,Neumann János Informatikai Kar B-fa Felépítése Beszúrás művelete Törlés
B-fa Felépítés, alapvető műveletek előadás http://nik.uni-obuda.hu/prog2 Szénási Sándor szenasi.sandor@nik.uni-obuda.hu Óbudai Egyetem,Neumann János Informatikai Kar B-fa Felépítése Beszúrás művelete Törlés
Bináris keres fák kiegyensúlyozásai. Egyed Boglárka
 Eötvös Loránd Tudományegyetem Természettudományi Kar Bináris keres fák kiegyensúlyozásai BSc szakdolgozat Egyed Boglárka Matematika BSc, Alkalmazott matematikus szakirány Témavezet : Fekete István, egyetemi
Eötvös Loránd Tudományegyetem Természettudományi Kar Bináris keres fák kiegyensúlyozásai BSc szakdolgozat Egyed Boglárka Matematika BSc, Alkalmazott matematikus szakirány Témavezet : Fekete István, egyetemi
3. gyakorlat Dinamikus programozás
 3. gyakorlat Dinamikus programozás 1. Az 1,2,...,n számoknak adott két permutációja, x 1,...,x n és y 1,...,y n. A két sorozat egy közös részsorozata egy 1 i 1 < < i k n, és egy 1 j 1
3. gyakorlat Dinamikus programozás 1. Az 1,2,...,n számoknak adott két permutációja, x 1,...,x n és y 1,...,y n. A két sorozat egy közös részsorozata egy 1 i 1 < < i k n, és egy 1 j 1
Adatszerkezetek és algoritmusok
 2010. január 8. Bevezet El z órák anyagainak áttekintése Ismétlés Adatszerkezetek osztályozása Sor, Verem, Lengyelforma Statikus, tömbös reprezentáció Dinamikus, láncolt reprezentáció Láncolt lista Lassú
2010. január 8. Bevezet El z órák anyagainak áttekintése Ismétlés Adatszerkezetek osztályozása Sor, Verem, Lengyelforma Statikus, tömbös reprezentáció Dinamikus, láncolt reprezentáció Láncolt lista Lassú
10. előadás Speciális többágú fák
 10. előadás Adatszerkezetek és algoritmusok előadás 2018. április 17., és Debreceni Egyetem Informatikai Kar 10.1 A többágú fák kezelésére nincsenek általános elvek, implementációjuk elsősorban alkalmazásfüggő.
10. előadás Adatszerkezetek és algoritmusok előadás 2018. április 17., és Debreceni Egyetem Informatikai Kar 10.1 A többágú fák kezelésére nincsenek általános elvek, implementációjuk elsősorban alkalmazásfüggő.
44. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY. Országos döntő, 1. nap - 2015. május 29.
 44. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY Országos döntő, 1. nap - 015. május 9. ÖTÖDIK OSZTÁLY - ok 1. Egy háromjegyű szám középső számjegyét elhagyva egy kétjegyű számot kaptunk. A két szám összege
44. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY Országos döntő, 1. nap - 015. május 9. ÖTÖDIK OSZTÁLY - ok 1. Egy háromjegyű szám középső számjegyét elhagyva egy kétjegyű számot kaptunk. A két szám összege
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Gráfelmélet II. Gráfok végigjárása
 Gráfelmélet II. Gráfok végigjárása DEFINÍCIÓ: (Séta) A G gráf egy olyan élsorozatát, amelyben a csúcsok és élek többször is szerepelhetnek, sétának nevezzük. Egy lehetséges séta: A; 1; B; 2; C; 3; D; 4;
Gráfelmélet II. Gráfok végigjárása DEFINÍCIÓ: (Séta) A G gráf egy olyan élsorozatát, amelyben a csúcsok és élek többször is szerepelhetnek, sétának nevezzük. Egy lehetséges séta: A; 1; B; 2; C; 3; D; 4;
Gráfokkal megoldható hétköznapi problémák
 Eötvös Loránd Tudományegyetem Természettudományi Kar Gráfokkal megoldható hétköznapi problémák Szakdolgozat Készítette Vincze Ágnes Melitta Konzulens Héger Tamás Budapest, 2015 Tartalomjegyzék Bevezetés
Eötvös Loránd Tudományegyetem Természettudományi Kar Gráfokkal megoldható hétköznapi problémák Szakdolgozat Készítette Vincze Ágnes Melitta Konzulens Héger Tamás Budapest, 2015 Tartalomjegyzék Bevezetés
Algoritmusok és adatszerkezetek II.
 Algoritmusok és adatszerkezetek II. Horváth Gyula Szegedi Tudományegyetem Természettudományi és Informatikai Kar horvath@inf.u-szeged.hu 3. Kiegyensúlyozott keresőfák A T tulajdonság magasság-egyensúlyozó
Algoritmusok és adatszerkezetek II. Horváth Gyula Szegedi Tudományegyetem Természettudományi és Informatikai Kar horvath@inf.u-szeged.hu 3. Kiegyensúlyozott keresőfák A T tulajdonság magasság-egyensúlyozó
A számítástudomány alapjai. Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem
 A számítástudomány alapjai Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem Bináris keresőfa, kupac Katona Gyula Y. (BME SZIT) A számítástudomány
A számítástudomány alapjai Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem Bináris keresőfa, kupac Katona Gyula Y. (BME SZIT) A számítástudomány
Programozás I. Metódusok C#-ban Egyszerű programozási tételek. Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu
 Programozás I. 3. előadás Tömbök a C#-ban Metódusok C#-ban Egyszerű programozási tételek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Szoftvertechnológia
Programozás I. 3. előadás Tömbök a C#-ban Metódusok C#-ban Egyszerű programozási tételek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Szoftvertechnológia
Miskolci Egyetem. Diszkrét matek I. Vizsga-jegyzet. Hegedűs Ádám Imre 2010.12.28.
 Miskolci Egyetem Diszkrét matek I. Vizsga-jegyzet Hegedűs Ádám Imre 2010.12.28. KOMBINATORIKA Permutáció Ismétlés nélküli permutáció alatt néhány különböző dolognak a sorba rendezését értjük. Az "ismétlés
Miskolci Egyetem Diszkrét matek I. Vizsga-jegyzet Hegedűs Ádám Imre 2010.12.28. KOMBINATORIKA Permutáció Ismétlés nélküli permutáció alatt néhány különböző dolognak a sorba rendezését értjük. Az "ismétlés
9. előadás Környezetfüggetlen nyelvek
 9. előadás Környezetfüggetlen nyelvek Dr. Kallós Gábor 2015 2016 1 Tartalom Bevezetés CF nyelv példák Nyelvek és nyelvtanok egy- és többértelműsége Bal- és jobboldali levezetések A fák magassága és határa
9. előadás Környezetfüggetlen nyelvek Dr. Kallós Gábor 2015 2016 1 Tartalom Bevezetés CF nyelv példák Nyelvek és nyelvtanok egy- és többértelműsége Bal- és jobboldali levezetések A fák magassága és határa
Relációs algebra áttekintés és egy táblára vonatkozó lekérdezések
 Relációs algebra áttekintés és egy táblára vonatkozó lekérdezések Tankönyv: Ullman-Widom: Adatbázisrendszerek Alapvetés Második, átdolgozott kiadás, Panem, 2009 2.4. Relációs algebra (áttekintés) 5.1.
Relációs algebra áttekintés és egy táblára vonatkozó lekérdezések Tankönyv: Ullman-Widom: Adatbázisrendszerek Alapvetés Második, átdolgozott kiadás, Panem, 2009 2.4. Relációs algebra (áttekintés) 5.1.
Készítette: niethammer@freemail.hu
 VLogo VRML generáló program Készítette: Niethammer Zoltán niethammer@freemail.hu 2008 Bevezetés A VLogo az általános iskolákban használt Comenius Logo logikájára épülő programozási nyelv. A végeredmény
VLogo VRML generáló program Készítette: Niethammer Zoltán niethammer@freemail.hu 2008 Bevezetés A VLogo az általános iskolákban használt Comenius Logo logikájára épülő programozási nyelv. A végeredmény
ADATBÁZISKEZELÉS ADATBÁZIS
 ADATBÁZISKEZELÉS 1 ADATBÁZIS Az adatbázis adott (meghatározott) témakörre vagy célra vonatkozó adatok gyűjteménye. - Pl. A megrendelések nyomon követése kereskedelemben. Könyvek nyilvántartása egy könyvtárban.
ADATBÁZISKEZELÉS 1 ADATBÁZIS Az adatbázis adott (meghatározott) témakörre vagy célra vonatkozó adatok gyűjteménye. - Pl. A megrendelések nyomon követése kereskedelemben. Könyvek nyilvántartása egy könyvtárban.
Analízisfeladat-gyűjtemény IV.
 Oktatási segédanyag a Programtervező matematikus szak Analízis. című tantárgyához (003 004. tanév tavaszi félév) Analízisfeladat-gyűjtemény IV. (Függvények határértéke és folytonossága) Összeállította
Oktatási segédanyag a Programtervező matematikus szak Analízis. című tantárgyához (003 004. tanév tavaszi félév) Analízisfeladat-gyűjtemény IV. (Függvények határértéke és folytonossága) Összeállította
Relációs algebra 1.rész
 Relációs algebra 1.rész Tankönyv: Ullman-Widom: Adatbázisrendszerek Alapvetés Második, átdolgozott kiadás, Panem, 2009 Lekérdezések a relációs modellben 2.4. Egy algebrai lekérdező nyelv -- 01B_RelAlg1alap:
Relációs algebra 1.rész Tankönyv: Ullman-Widom: Adatbázisrendszerek Alapvetés Második, átdolgozott kiadás, Panem, 2009 Lekérdezések a relációs modellben 2.4. Egy algebrai lekérdező nyelv -- 01B_RelAlg1alap:
Hierarchikus adatszerkezetek
 5. előadás Hierarchikus adatszerkezetek A hierarchikus adatszerkezet olyan < A, R > rendezett pár, amelynél van egy kitüntetett r A gyökérelem úgy, hogy: 1. r nem lehet végpont, azaz a A esetén R(a,r)
5. előadás Hierarchikus adatszerkezetek A hierarchikus adatszerkezet olyan < A, R > rendezett pár, amelynél van egy kitüntetett r A gyökérelem úgy, hogy: 1. r nem lehet végpont, azaz a A esetén R(a,r)
Kötegelt nyomtatványok kezelése a java-s nyomtatványkitöltő programban (pl.: 1044 kötegelt nyomtatvány - HIPA; 10ELEKAFA - Elekáfa)
 Kötegelt nyomtatványok kezelése a java-s nyomtatványkitöltő programban (pl.: 1044 kötegelt nyomtatvány - HIPA; 10ELEKAFA - Elekáfa) Kötegelt nyomtatványok általános jellemzői Minden nyomtatványköteg áll
Kötegelt nyomtatványok kezelése a java-s nyomtatványkitöltő programban (pl.: 1044 kötegelt nyomtatvány - HIPA; 10ELEKAFA - Elekáfa) Kötegelt nyomtatványok általános jellemzői Minden nyomtatványköteg áll
23. Kombinatorika, gráfok
 I Elméleti összefoglaló Leszámlálási alapfeladatok 23 Kombinatorika, gráfok A kombinatorikai alapfeladatok esetek, lehetőségek összeszámlálásával foglalkoznak Általában n jelöli a rendelkezésre álló különbözőfajta
I Elméleti összefoglaló Leszámlálási alapfeladatok 23 Kombinatorika, gráfok A kombinatorikai alapfeladatok esetek, lehetőségek összeszámlálásával foglalkoznak Általában n jelöli a rendelkezésre álló különbözőfajta
Elemi adatszerkezetek
 2017/12/16 17:22 1/18 Elemi adatszerkezetek < Programozás Elemi adatszerkezetek Szerző: Sallai András Copyright Sallai András, 2011, 2014 Licenc: GNU Free Documentation License 1.3 Web: http://szit.hu
2017/12/16 17:22 1/18 Elemi adatszerkezetek < Programozás Elemi adatszerkezetek Szerző: Sallai András Copyright Sallai András, 2011, 2014 Licenc: GNU Free Documentation License 1.3 Web: http://szit.hu
ÍRÁSBELI KIVONÁS. 31. modul. Készítette: KONRÁD ÁGNES
 Matematika A 3. évfolyam ÍRÁSBELI KIVONÁS 31. modul Készítette: KONRÁD ÁGNES matematika A 3. ÉVFOLYAM 31. modul ÍRÁSBELI KIVONÁS MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
Matematika A 3. évfolyam ÍRÁSBELI KIVONÁS 31. modul Készítette: KONRÁD ÁGNES matematika A 3. ÉVFOLYAM 31. modul ÍRÁSBELI KIVONÁS MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
Karbantartás. Az ESZR Karbantartás menüjébentudjuk elvégezni az alábbiakat:
 Karbantartás Az ESZR Karbantartás menüjébentudjuk elvégezni az alábbiakat: Jelszó módosítása: A felhasználói jelszavunkat módosíthatjuk ebben a menüpontban, a régi jelszavunk megadása után. Általánosan
Karbantartás Az ESZR Karbantartás menüjébentudjuk elvégezni az alábbiakat: Jelszó módosítása: A felhasználói jelszavunkat módosíthatjuk ebben a menüpontban, a régi jelszavunk megadása után. Általánosan
10. tétel. Adatszerkezetek és algoritmusok vizsga Frissült: 2013. január 28.
 10. tétel Adatszerkezetek és algoritmusok vizsga Frissült: 2013. január 28. 2-3 fák Hatékony keresőfa-konstrukció. Ez is fa, de a binárisnál annyival bonyolultabb hogy egy nem-levél csúcsnak 2 vagy 3 fia
10. tétel Adatszerkezetek és algoritmusok vizsga Frissült: 2013. január 28. 2-3 fák Hatékony keresőfa-konstrukció. Ez is fa, de a binárisnál annyival bonyolultabb hogy egy nem-levél csúcsnak 2 vagy 3 fia
Egyszerű programozási tételek
 Egyszerű programozási tételek Sorozatszámítás tétele Például az X tömbben kövek súlyát tároljuk. Ha ki kellene számolni az összsúlyt, akkor az S = f(s, X(i)) helyére S = S + X(i) kell írni. Az f0 tartalmazza
Egyszerű programozási tételek Sorozatszámítás tétele Például az X tömbben kövek súlyát tároljuk. Ha ki kellene számolni az összsúlyt, akkor az S = f(s, X(i)) helyére S = S + X(i) kell írni. Az f0 tartalmazza
K Ü L Ö N L E G E S T R A N S Z F O R M Á T O R O K
 VILLANYSZERELŐ KÉPZÉS 0 5 K Ü L Ö N L E G E S T R A N S Z F O R M Á T O R O K ÖSSZEÁLLÍTOTTA NAGY LÁSZLÓ MÉRNÖKTANÁR - - Tartalomjegyzék Különleges transzformátorok fogalma...3 Biztonsági és elválasztó
VILLANYSZERELŐ KÉPZÉS 0 5 K Ü L Ö N L E G E S T R A N S Z F O R M Á T O R O K ÖSSZEÁLLÍTOTTA NAGY LÁSZLÓ MÉRNÖKTANÁR - - Tartalomjegyzék Különleges transzformátorok fogalma...3 Biztonsági és elválasztó
EMMI kerettanterv 51/2012. (XII. 21.) EMMI rendelet 1. sz. melléklet 1.2.3. Matematika az általános iskolák 1 4. évfolyama számára
 EMMI kerettanterv 51/2012. (XII. 21.) EMMI rendelet 1. sz. melléklet 1.2.3 Matematika az általános iskolák 1 4. évfolyama számára Célok és feladatok Az iskolai matematikatanítás célja, hogy hiteles képet
EMMI kerettanterv 51/2012. (XII. 21.) EMMI rendelet 1. sz. melléklet 1.2.3 Matematika az általános iskolák 1 4. évfolyama számára Célok és feladatok Az iskolai matematikatanítás célja, hogy hiteles képet
Adatszerkezetek 7a. Dr. IványiPéter
 Adatszerkezetek 7a. Dr. IványiPéter 1 Fák Fákat akkor használunk, ha az adatok között valamilyen alá- és fölérendeltség van. Pl. könyvtárszerkezet gyökér () Nincsennek hurkok!!! 2 Bináris fák Azokat a
Adatszerkezetek 7a. Dr. IványiPéter 1 Fák Fákat akkor használunk, ha az adatok között valamilyen alá- és fölérendeltség van. Pl. könyvtárszerkezet gyökér () Nincsennek hurkok!!! 2 Bináris fák Azokat a
8. Mohó algoritmusok. 8.1. Egy esemény-kiválasztási probléma. Az esemény-kiválasztási probléma optimális részproblémák szerkezete
 8. Mohó algoritmusok Optimalizálási probléma megoldására szolgáló algoritmus gyakran olyan lépések sorozatából áll, ahol minden lépésben adott halmazból választhatunk. Sok optimalizálási probléma esetén
8. Mohó algoritmusok Optimalizálási probléma megoldására szolgáló algoritmus gyakran olyan lépések sorozatából áll, ahol minden lépésben adott halmazból választhatunk. Sok optimalizálási probléma esetén
Informatikai tehetséggondozás:
 Ég és Föld vonzásában a természet titkai Informatikai tehetséggondozás: Rendezések TÁMOP-4.2.3.-12/1/KONV-2012-0018 Az alapfeladat egy N elemű sorozat nagyság szerinti sorba rendezése. A sorozat elemei
Ég és Föld vonzásában a természet titkai Informatikai tehetséggondozás: Rendezések TÁMOP-4.2.3.-12/1/KONV-2012-0018 Az alapfeladat egy N elemű sorozat nagyság szerinti sorba rendezése. A sorozat elemei
Árvainé Libor Ildikó Murátiné Szél Edit. Tanítói kézikönyv. tanmenetjavaslattal. Sokszínû matematika. 4
 Árvainé Libor Ildikó Murátiné Szél Edit Tanítói kézikönyv tanmenetjavaslattal Sokszínû matematika. 4 Mozaik Kiadó - Szeged, 2007 Készítette: ÁRVAINÉ LIBOR ILDIKÓ szakvezetõ tanító MURÁTINÉ SZÉL EDIT szakvezetõ
Árvainé Libor Ildikó Murátiné Szél Edit Tanítói kézikönyv tanmenetjavaslattal Sokszínû matematika. 4 Mozaik Kiadó - Szeged, 2007 Készítette: ÁRVAINÉ LIBOR ILDIKÓ szakvezetõ tanító MURÁTINÉ SZÉL EDIT szakvezetõ
Karbantartás. Az ESZR Karbantartás menüjébentudjuk elvégezni az alábbiakat:
 Karbantartás Az ESZR Karbantartás menüjébentudjuk elvégezni az alábbiakat: Jelszó módosítása: A felhasználói jelszavunkat módosíthatjuk ebben a menüpontban, a régi jelszavunk megadása után. Általánosan
Karbantartás Az ESZR Karbantartás menüjébentudjuk elvégezni az alábbiakat: Jelszó módosítása: A felhasználói jelszavunkat módosíthatjuk ebben a menüpontban, a régi jelszavunk megadása után. Általánosan
MATEMATIKA C 6. évfolyam 6. modul CSUPA TALÁNY
 MATEMATIKA C 6. évfolyam 6. modul CSUPA TALÁNY Készítette: Köves Gabriella MATEMATIKA C 6. ÉVFOLYAM 6. MODUL: TALÁNY TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott korosztály A képességfejlesztés fókuszai
MATEMATIKA C 6. évfolyam 6. modul CSUPA TALÁNY Készítette: Köves Gabriella MATEMATIKA C 6. ÉVFOLYAM 6. MODUL: TALÁNY TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott korosztály A képességfejlesztés fókuszai
TERMELÉSMENEDZSMENT. Gyakorlati segédlet a műszaki menedzser szak hallgatói számára. Összeállította: Dr. Vermes Pál főiskolai tanár 2006.
 Szolnoki Főiskola Műszaki és Mezőgazdasági Fakultás Mezőtúr TERMELÉSMENEDZSMENT Gyakorlati segédlet a műszaki menedzser szak hallgatói számára Összeállította: Dr. Vermes Pál főiskolai tanár Mezőtúr 6.
Szolnoki Főiskola Műszaki és Mezőgazdasági Fakultás Mezőtúr TERMELÉSMENEDZSMENT Gyakorlati segédlet a műszaki menedzser szak hallgatói számára Összeállította: Dr. Vermes Pál főiskolai tanár Mezőtúr 6.
2. Hatványozás, gyökvonás
 2. Hatványozás, gyökvonás I. Elméleti összefoglaló Egész kitevőjű hatvány értelmezése: a 1, ha a R; a 0; a a, ha a R. Ha a R és n N; n > 1, akkor a olyan n tényezős szorzatot jelöl, aminek minden tényezője
2. Hatványozás, gyökvonás I. Elméleti összefoglaló Egész kitevőjű hatvány értelmezése: a 1, ha a R; a 0; a a, ha a R. Ha a R és n N; n > 1, akkor a olyan n tényezős szorzatot jelöl, aminek minden tényezője
reális tájékozódást. Mindehhez elengedhetetlen egyszerű matematikai szövegek értelmezése, elemzése. A tanulóktól megkívánjuk a szaknyelv életkornak
 MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
GAZDASÁGI STATISZTIKA
 GAZDASÁGI STATISZTIKA Dr. Kun István GÁBOR DÉNES FŐISKOLA Tantárgy: Gazdasági statisztika Kódszám: 224 Lapszám: 1 TÉMAKÖRÖK A STATISZTIKA ALAPFOGALMAI STATISZTIKAI SOROK STATISZTIKAI TÁBLÁK ÖSSZETETT VISZONYSZÁMOK
GAZDASÁGI STATISZTIKA Dr. Kun István GÁBOR DÉNES FŐISKOLA Tantárgy: Gazdasági statisztika Kódszám: 224 Lapszám: 1 TÉMAKÖRÖK A STATISZTIKA ALAPFOGALMAI STATISZTIKAI SOROK STATISZTIKAI TÁBLÁK ÖSSZETETT VISZONYSZÁMOK
II. Halmazok. Relációk. II.1. Rövid halmazelmélet. A halmaz megadása. { } { } { } { }
 II. Halmazok. Relációk II.1. Rövid halmazelmélet A halmaz (sokaság) jól meghatározott, megkülönböztetett dolgok (tárgyak, fogalmak, stb.) összessége. A halmaz alapfogalom. Ez azt jelenti, hogy csak példákon
II. Halmazok. Relációk II.1. Rövid halmazelmélet A halmaz (sokaság) jól meghatározott, megkülönböztetett dolgok (tárgyak, fogalmak, stb.) összessége. A halmaz alapfogalom. Ez azt jelenti, hogy csak példákon
Bevezetés. A WebAccess használatának bemutatása előtt néhány új funkció felsorolása következik:
 Bevezetés Leveleink, naptárunk, stb. megtekintése bármely gépen egy egyszerű webböngésző (Mozilla, Explorer) segítésével is lehetséges. GroupWise rendszernek ezt a megjelenési formáját GroupWise WebAccessnek
Bevezetés Leveleink, naptárunk, stb. megtekintése bármely gépen egy egyszerű webböngésző (Mozilla, Explorer) segítésével is lehetséges. GroupWise rendszernek ezt a megjelenési formáját GroupWise WebAccessnek
Valószínűségszámítás
 Eszterházy Károly Főiskola Matematikai és Informatikai Intézet Tómács Tibor Valószínűségszámítás programtervező informatikusok részére Eger, 010. szeptember 0. Tartalomjegyzék 1. Véletlen események...............................
Eszterházy Károly Főiskola Matematikai és Informatikai Intézet Tómács Tibor Valószínűségszámítás programtervező informatikusok részére Eger, 010. szeptember 0. Tartalomjegyzék 1. Véletlen események...............................
Soukup Dániel, Matematikus Bsc III. év Email cím: dsoukup123@gmail.com Témavezető: Szentmiklóssy Zoltán, egyetemi adjunktus
 Síktopológiák a Sorgenfrey-egyenes ötletével Soukup Dániel, Matematikus Bsc III. év Email cím: dsoukup123@gmail.com Témavezető: Szentmiklóssy Zoltán, egyetemi adjunktus 1. Bevezetés A Sorgenfrey-egyenes
Síktopológiák a Sorgenfrey-egyenes ötletével Soukup Dániel, Matematikus Bsc III. év Email cím: dsoukup123@gmail.com Témavezető: Szentmiklóssy Zoltán, egyetemi adjunktus 1. Bevezetés A Sorgenfrey-egyenes
Buborékrendezés: Hanoi Tornyai: Asszimptótikus fv.ek: Láncolt ábrázolás: For ciklussal:
 Buborékrendezés: For ciklussal: Hanoi Tornyai: Asszimptótikus fv.ek: Láncolt ábr.: ha p egy mutató típusú változó akkor p^ az általa mutatott adatelem, p^.adat;p^.mut. A semmibe mutató ponter a NIL.Szabad
Buborékrendezés: For ciklussal: Hanoi Tornyai: Asszimptótikus fv.ek: Láncolt ábr.: ha p egy mutató típusú változó akkor p^ az általa mutatott adatelem, p^.adat;p^.mut. A semmibe mutató ponter a NIL.Szabad
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 5 V ELEmI ALGEbRA 1 BINÁRIS műveletek Definíció Az halmazon definiált bináris művelet egy olyan függvény, amely -ből képez -be Ha akkor az elempár képét jelöljük -vel, a művelet
KOVÁCS BÉLA, MATEmATIkA I 5 V ELEmI ALGEbRA 1 BINÁRIS műveletek Definíció Az halmazon definiált bináris művelet egy olyan függvény, amely -ből képez -be Ha akkor az elempár képét jelöljük -vel, a művelet
... fi. ... fk. 6. Fabejáró algoritmusok Rekurzív preorder bejárás (elsőfiú-testvér ábrázolásra)
 6. Fabejáró algoritmusok Fa bejárásán olyan algoritmust értünk, amelynek bemenete egy F fa és egy M művelet, és az algoritmus adott sorrendben pontosan egyszer végrehajtja az M műveletet a fa pontjaiban
6. Fabejáró algoritmusok Fa bejárásán olyan algoritmust értünk, amelynek bemenete egy F fa és egy M művelet, és az algoritmus adott sorrendben pontosan egyszer végrehajtja az M műveletet a fa pontjaiban
Tárgyi eszközök felhasználói leírás
 Tárgyi eszközök felhasználói leírás Könyvelés modul 1149 Budapest, Egressy út 17-21. Telefon: +36 1 469 4021; fax: +36 1 469 4029 1/23 Tartalomjegyzék 1. Tárgyi eszköz kezelés a programban... 3 1.1. Beállítások...
Tárgyi eszközök felhasználói leírás Könyvelés modul 1149 Budapest, Egressy út 17-21. Telefon: +36 1 469 4021; fax: +36 1 469 4029 1/23 Tartalomjegyzék 1. Tárgyi eszköz kezelés a programban... 3 1.1. Beállítások...
különösen a média közleményeiben való reális tájékozódást. Mindehhez elengedhetetlen egyszerű matematikai szövegek értelmezése, elemzése.
 MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
különösen a média közleményeiben való reális tájékozódást. Mindehhez elengedhetetlen egyszerű matematikai szövegek értelmezése, elemzése.
 MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson amatematikáról, mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson amatematikáról, mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
Algoritmusok és adatszerkezetek II.
 Algoritmusok és adatszerkezetek II. Horváth Gyula Szegedi Tudományegyetem Természettudományi és Informatikai Kar horvath@inf.u-szeged.hu 5. Vágható-egyesíthető Halmaz adattípus megvalósítása önszervező
Algoritmusok és adatszerkezetek II. Horváth Gyula Szegedi Tudományegyetem Természettudományi és Informatikai Kar horvath@inf.u-szeged.hu 5. Vágható-egyesíthető Halmaz adattípus megvalósítása önszervező
Apor Vilmos Katolikus Iskolaközpont. Helyi tanterv. Matematika. készült. a 51/2012. (XII. 21.) EMMI rendelet 1. sz. melléklet 1-4./1.2.3.
 1 Apor Vilmos Katolikus Iskolaközpont Helyi tanterv Matematika készült a 51/2012. (XII. 21.) EMMI rendelet 1. sz. melléklet 1-4./1.2.3. alapján 1-4. évfolyam 2 MATEMATIKA Az iskolai matematikatanítás célja,
1 Apor Vilmos Katolikus Iskolaközpont Helyi tanterv Matematika készült a 51/2012. (XII. 21.) EMMI rendelet 1. sz. melléklet 1-4./1.2.3. alapján 1-4. évfolyam 2 MATEMATIKA Az iskolai matematikatanítás célja,
Budapest, 2009. 1. oldal
 e-m@il:vibastile@monornet.hu, web:www.vibastile.hu Budapest, 2009 1. oldal e-m@il:vibastile@monornet.hu, web:www.vibastile.hu TARTALOM 1. A PROGRAM INDÍTÁSA... 3 2. A PROGRAM FUNKCIÓI... 3 3. FIZETÉSI
e-m@il:vibastile@monornet.hu, web:www.vibastile.hu Budapest, 2009 1. oldal e-m@il:vibastile@monornet.hu, web:www.vibastile.hu TARTALOM 1. A PROGRAM INDÍTÁSA... 3 2. A PROGRAM FUNKCIÓI... 3 3. FIZETÉSI
2013. PÉNZBELI ÉS TERMÉSZETBENI ELLÁTÁSOK EGYSÉGES NYILVÁNTARTÁSI RENDSZERÉNEK KEZDETI ADATFELTÖLTÉSE 2013. 11. 07.
 2013. PÉNZBELI ÉS TERMÉSZETBENI ELLÁTÁSOK EGYSÉGES NYILVÁNTARTÁSI RENDSZERÉNEK KEZDETI ADATFELTÖLTÉSE 2013. 11. 07. Tartalom 1 Bevezetés... 3 2 Az adatrögzítés módja és határideje... 3 2.1 Kezdeti adatfeltöltés...
2013. PÉNZBELI ÉS TERMÉSZETBENI ELLÁTÁSOK EGYSÉGES NYILVÁNTARTÁSI RENDSZERÉNEK KEZDETI ADATFELTÖLTÉSE 2013. 11. 07. Tartalom 1 Bevezetés... 3 2 Az adatrögzítés módja és határideje... 3 2.1 Kezdeti adatfeltöltés...
Táblás játékok 2. 1. modul
 Táblás játékok 2 1. modul Készítette: KÖVES GABRIELLA 2 Táblás játékok 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A tudatos észlelés, a megfigyelés és a figyelem fejlesztése
Táblás játékok 2 1. modul Készítette: KÖVES GABRIELLA 2 Táblás játékok 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A tudatos észlelés, a megfigyelés és a figyelem fejlesztése
választással azaz ha c 0 -t választjuk sebesség-egységnek: c 0 :=1, akkor a Topa-féle sebességkör teljes hossza 4 (sebesség-)egységnyi.
 Egy kis számmisztika Az elmúlt másfél-két évben elért kutatási eredményeim szerint a fizikai téridő geometriai jellege szerint háromosztatú egységet alkot: egymáshoz (a lokális éterhez mért v sebesség
Egy kis számmisztika Az elmúlt másfél-két évben elért kutatási eredményeim szerint a fizikai téridő geometriai jellege szerint háromosztatú egységet alkot: egymáshoz (a lokális éterhez mért v sebesség
Scherlein Márta Dr. Hajdu Sándor Köves Gabriella Novák Lászlóné MATEMATIKA 1. MÓDSZERTANI AJÁNLÁSOK MÁSODIK FÉLÉV
 Scherlein Márta Dr. Hajdu Sándor Köves Gabriella Novák Lászlóné MATEMATIKA. MÓDSZERTANI AJÁNLÁSOK MÁSODIK FÉLÉV Tankönyv második kötet Számok és műveletek 0-től 0-ig Kompetenciák, fejlesztési feladatok:
Scherlein Márta Dr. Hajdu Sándor Köves Gabriella Novák Lászlóné MATEMATIKA. MÓDSZERTANI AJÁNLÁSOK MÁSODIK FÉLÉV Tankönyv második kötet Számok és műveletek 0-től 0-ig Kompetenciák, fejlesztési feladatok:
Középszintű érettségi feladatsorok és megoldásaik Összeállította: Pataki János; dátum: 2005. november. I. rész
 Pataki János, 005. november Középszintű érettségi feladatsorok és megoldásaik Összeállította: Pataki János; dátum: 005. november I. rész. feladat Egy liter 0%-os alkoholhoz / liter 40%-os alkoholt keverünk.
Pataki János, 005. november Középszintű érettségi feladatsorok és megoldásaik Összeállította: Pataki János; dátum: 005. november I. rész. feladat Egy liter 0%-os alkoholhoz / liter 40%-os alkoholt keverünk.
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Geometria I.
 Geometria I. Alapfogalmak: Az olyan fogalmakat, amelyeket nem tudunk egyszerűbb fogalmakra visszavezetni, alapfogalmaknak nevezzük, s ezeket nem definiáljuk. Pl.: pont, egyenes, sík, tér, illeszkedés.
Geometria I. Alapfogalmak: Az olyan fogalmakat, amelyeket nem tudunk egyszerűbb fogalmakra visszavezetni, alapfogalmaknak nevezzük, s ezeket nem definiáljuk. Pl.: pont, egyenes, sík, tér, illeszkedés.
Béres Mária TANÍTÓI KÉZIKÖNYV. Színes matematika tankönyvsorozat 2. osztályos elemeihez
 Béres Mária TANÍTÓI KÉZIKÖNYV a Színes matematika tankönyvsorozat 2. osztályos elemeihez Béres Mária, Nemzeti Tankönyvkiadó Zrt., 2009 Nemzeti Tankönyvkiadó Zrt. www.ntk.hu Vevőszolgálat: info@ntk.hu Telefon:
Béres Mária TANÍTÓI KÉZIKÖNYV a Színes matematika tankönyvsorozat 2. osztályos elemeihez Béres Mária, Nemzeti Tankönyvkiadó Zrt., 2009 Nemzeti Tankönyvkiadó Zrt. www.ntk.hu Vevőszolgálat: info@ntk.hu Telefon:
MS Access Feladatgyűjtemény
 SZENT ISTVÁN EGYETEM GAZDASÁG- ÉS TÁRSADALOMTUDOMÁNYI KAR MS Access Feladatgyűjtemény Klárné Barta Éva 2014.01.01. Microsoft Access - Feladatok 1 Feladatok 1. Hozzon létre egy új adatbázist SZÁMÍTÓGÉPEK
SZENT ISTVÁN EGYETEM GAZDASÁG- ÉS TÁRSADALOMTUDOMÁNYI KAR MS Access Feladatgyűjtemény Klárné Barta Éva 2014.01.01. Microsoft Access - Feladatok 1 Feladatok 1. Hozzon létre egy új adatbázist SZÁMÍTÓGÉPEK
REKURZIÓ. Rekurzív: önmagát ismétlő valami (tevékenység, adatszerkezet stb.) Rekurzív függvény: függvény, amely meghívja saját magát.
 1. A REKURZIÓ FOGALMA REKURZIÓ Rekurzív: önmagát ismétlő valami (tevékenység, adatszerkezet stb.) Rekurzív függvény: függvény, amely meghívja saját magát. 1.1 Bevezető példák: 1.1.1 Faktoriális Nemrekurzív
1. A REKURZIÓ FOGALMA REKURZIÓ Rekurzív: önmagát ismétlő valami (tevékenység, adatszerkezet stb.) Rekurzív függvény: függvény, amely meghívja saját magát. 1.1 Bevezető példák: 1.1.1 Faktoriális Nemrekurzív
Adósságrendezési eljárás - Ügyfél alkalmazás FELHASZNÁLÓI LEÍRÁS
 Adósságrendezési eljárás - Ügyfél alkalmazás FELHASZNÁLÓI LEÍRÁS Tartalom 1 BEVEZETÉS... 3 2 ÜGYFÉL ALKALMAZÁS SZOFTVERKÖVELEMÉNYEI... 3 3 ÜGYFÉL ALKALMAZÁS ÁLTALÁNOS JELLEGŰ FUNKCIÓI... 3 3.1 Be- és kijelentkezés...
Adósságrendezési eljárás - Ügyfél alkalmazás FELHASZNÁLÓI LEÍRÁS Tartalom 1 BEVEZETÉS... 3 2 ÜGYFÉL ALKALMAZÁS SZOFTVERKÖVELEMÉNYEI... 3 3 ÜGYFÉL ALKALMAZÁS ÁLTALÁNOS JELLEGŰ FUNKCIÓI... 3 3.1 Be- és kijelentkezés...
19. Hasításos technikák (hash-elés)
 19. Hasításos technikák (hash-elés) Példák: 1. Ha egy telefon előfizetőket a telefonszámaikkal azonosítjuk, mint kulcsokkal, akkor egy ritkán kitöltött kulcstartományhoz jutunk. A telefonszám tehát nem
19. Hasításos technikák (hash-elés) Példák: 1. Ha egy telefon előfizetőket a telefonszámaikkal azonosítjuk, mint kulcsokkal, akkor egy ritkán kitöltött kulcstartományhoz jutunk. A telefonszám tehát nem
KETTŐS KÖNYVELÉS PROGRAM
 KETTŐS KÖNYVELÉS PROGRAM Kezelési leírás 1993-2015 Program azonosító: UJEGYKE Fejlesztő: B a l o g h y S z o f t v e r K f t. Keszthely, Vak Bottyán utca 41. 8360 Tel: 83/515-080 Fax: 83/515-082 E-mail:
KETTŐS KÖNYVELÉS PROGRAM Kezelési leírás 1993-2015 Program azonosító: UJEGYKE Fejlesztő: B a l o g h y S z o f t v e r K f t. Keszthely, Vak Bottyán utca 41. 8360 Tel: 83/515-080 Fax: 83/515-082 E-mail:
Jövedelem-Kiegésztési Rendszer - JKR
 Jövedelem-Kiegésztési Rendszer - JKR Felhasználói kézikönyv Verzió: 1.0 Tartalomjegyzék I. Intézményi regisztráció... 4 I.1 Intézményi adatok... 4 II. Bejelentkezés... 6 III. Adatkezelés... 7 III.1 Munkavállalók...
Jövedelem-Kiegésztési Rendszer - JKR Felhasználói kézikönyv Verzió: 1.0 Tartalomjegyzék I. Intézményi regisztráció... 4 I.1 Intézményi adatok... 4 II. Bejelentkezés... 6 III. Adatkezelés... 7 III.1 Munkavállalók...
Ugrólisták. RSL Insert Example. insert(22) with 3 flips. Runtime?
 Ugrólisták Ugrólisták Ugrólisták Ugrólisták RSL Insert Example insert(22) with 3 flips 13 8 29 20 10 23 19 11 2 13 22 8 29 20 10 23 19 11 2 Runtime? Ugrólisták Empirical analysis http://www.inf.u-szeged.hu/~tnemeth/alga2/eloadasok/skiplists.pdf
Ugrólisták Ugrólisták Ugrólisták Ugrólisták RSL Insert Example insert(22) with 3 flips 13 8 29 20 10 23 19 11 2 13 22 8 29 20 10 23 19 11 2 Runtime? Ugrólisták Empirical analysis http://www.inf.u-szeged.hu/~tnemeth/alga2/eloadasok/skiplists.pdf
Objektum Orientált Szoftverfejlesztés (jegyzet)
 Objektum Orientált Szoftverfejlesztés (jegyzet) 1. Kialakulás Kísérletek a szoftverkrízisből való kilábalásra: 1.1 Strukturált programozás Ötlet (E. W. Dijkstra): 1. Elkészítendő programot elgondolhatjuk
Objektum Orientált Szoftverfejlesztés (jegyzet) 1. Kialakulás Kísérletek a szoftverkrízisből való kilábalásra: 1.1 Strukturált programozás Ötlet (E. W. Dijkstra): 1. Elkészítendő programot elgondolhatjuk
Feladatok és megoldások a 4. hétre
 Feladatok és megoldások a. hétre Építőkari Matematika A3. Pisti nem tanult semmit a vizsgára, ahol 0 darab eldöntendő kérdésre kell válaszolnia. Az anyagból valami kicsi dereng, ezért kicsit több, mint
Feladatok és megoldások a. hétre Építőkari Matematika A3. Pisti nem tanult semmit a vizsgára, ahol 0 darab eldöntendő kérdésre kell válaszolnia. Az anyagból valami kicsi dereng, ezért kicsit több, mint
5 HOZZÁFÉRÉS-VÉDELEM. A fejezet VIDEOTON fejlesztési dokumentációk felhasználásával készült
 5 HOZZÁFÉRÉS-VÉDELEM A rejtjelezésben az adatvédelem hatékony és az adathálózat védelmében nélkülözhetetlen eszközét ismertük meg. Természetesen annak sincs semmilyen elvi akadálya, hogy a rejtjelezést
5 HOZZÁFÉRÉS-VÉDELEM A rejtjelezésben az adatvédelem hatékony és az adathálózat védelmében nélkülözhetetlen eszközét ismertük meg. Természetesen annak sincs semmilyen elvi akadálya, hogy a rejtjelezést
MATEMATIKA 1-2.osztály
 MATEMATIKA 1-2.osztály A matematikatanítás feladata a matematika különböző arculatainak bemutatása. A tanulók matematikai gondolkodásának fejlesztése során alapvető cél, hogy mind inkább ki tudják választani
MATEMATIKA 1-2.osztály A matematikatanítás feladata a matematika különböző arculatainak bemutatása. A tanulók matematikai gondolkodásának fejlesztése során alapvető cél, hogy mind inkább ki tudják választani
OPTEN Online használati útmutató
 OPTEN Online használati útmutató www.opten.hu opten@opten.hu 2016. április - 1 - Tartalomjegyzék Bevezetés... - 4 - CÉGTÁR ALAP és KIEGÉSZÍTŐ szolgáltatások... - 7-1. Keresés / Leválogatás... - 8 - a)
OPTEN Online használati útmutató www.opten.hu opten@opten.hu 2016. április - 1 - Tartalomjegyzék Bevezetés... - 4 - CÉGTÁR ALAP és KIEGÉSZÍTŐ szolgáltatások... - 7-1. Keresés / Leválogatás... - 8 - a)
Matematikai alapismeretek. Huszti Andrea
 Tartalom 1 Matematikai alapismeretek Algebrai struktúrák Oszthatóság Kongruenciák Algebrai struktúrák Az S = {x, y, z,... } halmazban definiálva van egy művelet, ha az S-nek minden x, y elempárjához hozzá
Tartalom 1 Matematikai alapismeretek Algebrai struktúrák Oszthatóság Kongruenciák Algebrai struktúrák Az S = {x, y, z,... } halmazban definiálva van egy művelet, ha az S-nek minden x, y elempárjához hozzá
Blonde. Szépségszalon, Szolárium, Spa, Fitness. Ügyviteli Rendszer. Funkcionális Specifikáció. Verzió 1.1
 Blonde Szépségszalon, Szolárium, Spa, Fitness Ügyviteli Rendszer Funkcionális Specifikáció Verzió 1.1 Blonde Funkcionális Specifikáció v1.1 2012.01.12 1 Tartalomjegyzék 1. Bevezetés 3 1.1. A dokumentum
Blonde Szépségszalon, Szolárium, Spa, Fitness Ügyviteli Rendszer Funkcionális Specifikáció Verzió 1.1 Blonde Funkcionális Specifikáció v1.1 2012.01.12 1 Tartalomjegyzék 1. Bevezetés 3 1.1. A dokumentum
1. BEVEZETÉS... 5 2. A RENDSZER ELEMEI, ARCHITEKTÚRÁJA... 5
 EntryProx Beléptető Rendszer FELHASZNÁLÓI KÉZIKÖNYV v.1.0.7. EntryProx Beléptető Rendszer TARTALOM 1. BEVEZETÉS... 5 2. A RENDSZER ELEMEI, ARCHITEKTÚRÁJA... 5 3. A RENDSZER ÜZEMBE HELYEZÉSE... 7 3.1. Az
EntryProx Beléptető Rendszer FELHASZNÁLÓI KÉZIKÖNYV v.1.0.7. EntryProx Beléptető Rendszer TARTALOM 1. BEVEZETÉS... 5 2. A RENDSZER ELEMEI, ARCHITEKTÚRÁJA... 5 3. A RENDSZER ÜZEMBE HELYEZÉSE... 7 3.1. Az
NAV nyomtatványok xml szerkezete. (v6.7)
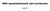 NAV nyomtatványok xml szerkezete (v6.7) BEVEZETŐ... 3 1.1 FOGALOMMAGYARÁZAT... 3 2 A NYOMTATVÁNYOK XML FORMÁTUMA... 4 2.1 AZ XML MODELL... 4 2.2 A NYOMTATVÁNYOK XML FELÉPÍTÉSE... 4 2.2.1 Megkötések...
NAV nyomtatványok xml szerkezete (v6.7) BEVEZETŐ... 3 1.1 FOGALOMMAGYARÁZAT... 3 2 A NYOMTATVÁNYOK XML FORMÁTUMA... 4 2.1 AZ XML MODELL... 4 2.2 A NYOMTATVÁNYOK XML FELÉPÍTÉSE... 4 2.2.1 Megkötések...
Algoritmuselmélet ZH 2015. április 8.
 Algoritmuselmélet ZH 2015. április 8. 1. Tekintsük az f(n) = 10n 2 log n + 7n n + 2000 log n + 1000 függvényt. Adjon olyan c konstanst és olyan n 0 küszöbértéket, ami a definíció szerint mutatja, hogy
Algoritmuselmélet ZH 2015. április 8. 1. Tekintsük az f(n) = 10n 2 log n + 7n n + 2000 log n + 1000 függvényt. Adjon olyan c konstanst és olyan n 0 küszöbértéket, ami a definíció szerint mutatja, hogy
Mesterséges Intelligencia I. (I602, IB602)
 Dr. Jelasity Márk Mesterséges Intelligencia I. (I602, IB602) harmadik (2008. szeptember 15-i) előadásának jegyzete Készítette: Papp Tamás PATLACT.SZE KPM V. HEURISZTIKUS FÜGGVÉNYEK ELŐÁLLÍTÁSA Nagyon fontos
Dr. Jelasity Márk Mesterséges Intelligencia I. (I602, IB602) harmadik (2008. szeptember 15-i) előadásának jegyzete Készítette: Papp Tamás PATLACT.SZE KPM V. HEURISZTIKUS FÜGGVÉNYEK ELŐÁLLÍTÁSA Nagyon fontos
Valószínűségszámítás
 1. Kombinatorika Valószínűségszámítás 2004.03.01. Készítette: Dr. Toledo Rodolfo 1.1. Tétel. Ha n darab különböző elemet az összes lehetséges módon sorba rendezünk, akkor ezt n! := n (n 1) (n 2) 2 1-féle
1. Kombinatorika Valószínűségszámítás 2004.03.01. Készítette: Dr. Toledo Rodolfo 1.1. Tétel. Ha n darab különböző elemet az összes lehetséges módon sorba rendezünk, akkor ezt n! := n (n 1) (n 2) 2 1-féle
Matematika C 3. évfolyam. Melyikhez tartozom? 4. modul. Készítette: Abonyi Tünde
 Matematika C 3. évfolyam Melyikhez tartozom? 4. modul Készítette: Abonyi Tünde Matematika C 3. évfolyam 4. modul Melyikhez tartozom? MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
Matematika C 3. évfolyam Melyikhez tartozom? 4. modul Készítette: Abonyi Tünde Matematika C 3. évfolyam 4. modul Melyikhez tartozom? MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
FELADATOK ÉS MEGOLDÁSOK
 3. osztály Az első oldalon 1-gyel kezdve egyesével beszámozták egy könyv összes oldalát. Hány oldalas ez a könyv, ha ehhez 55 számjegyet használtak fel? Az első 9 oldalhoz 9 számjegyet használtak, a további
3. osztály Az első oldalon 1-gyel kezdve egyesével beszámozták egy könyv összes oldalát. Hány oldalas ez a könyv, ha ehhez 55 számjegyet használtak fel? Az első 9 oldalhoz 9 számjegyet használtak, a további
KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA
 ÉRETTSÉGI VIZSGA 2007. október 25. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2007. október 25. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Matematika
ÉRETTSÉGI VIZSGA 2007. október 25. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2007. október 25. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Matematika
Adatbázisok* tulajdonságai
 Gazdasági folyamatok térbeli elemzése 4. előadás 2010. 10. 05. Adatbázisok* tulajdonságai Rendezett, logikailag összefüggő és meghatározott szempont szerint tárolt adatok és/vagy információk halmaza Az
Gazdasági folyamatok térbeli elemzése 4. előadás 2010. 10. 05. Adatbázisok* tulajdonságai Rendezett, logikailag összefüggő és meghatározott szempont szerint tárolt adatok és/vagy információk halmaza Az
Tájékozódás számvonalon, számtáblázatokon
 Matematika A 2. évfolyam Tájékozódás számvonalon, számtáblázatokon 12. modul Készítette: Bóta Mária Kőkúti Ágnes matematika A 2. évfolyam 12 modul Tájékozódás számvonalon, számtáblázatokon modulleírás
Matematika A 2. évfolyam Tájékozódás számvonalon, számtáblázatokon 12. modul Készítette: Bóta Mária Kőkúti Ágnes matematika A 2. évfolyam 12 modul Tájékozódás számvonalon, számtáblázatokon modulleírás
I. Egységtörtek. Ha az egységet nyolc egyenlő részre vágjuk, akkor ebből egy rész 1-nyolcadot ér.
 Tudnivaló I. Egységtörtek Ha az egységet nyolc egyenlő részre vágjuk, akkor ebből egy rész 1-nyolcadot ér. Ezt röviden így írhatjuk: A nevező megmutatja, hogy az egységet hány egyenlő részre vágjuk. A
Tudnivaló I. Egységtörtek Ha az egységet nyolc egyenlő részre vágjuk, akkor ebből egy rész 1-nyolcadot ér. Ezt röviden így írhatjuk: A nevező megmutatja, hogy az egységet hány egyenlő részre vágjuk. A
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Matematika emelt szint 05 ÉRETTSÉGI VIZSGA 006. május 9. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI MINISZTÉRIUM Formai előírások: Fontos tudnivalók A dolgozatot
Matematika emelt szint 05 ÉRETTSÉGI VIZSGA 006. május 9. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI MINISZTÉRIUM Formai előírások: Fontos tudnivalók A dolgozatot
Alkalmazott modul: Programozás
 Eötvös Loránd Tudományegyetem Informatikai Kar Alkalmazott modul: Programozás Feladatgyűjtemény Összeállította: Giachetta Roberto groberto@inf.elte.hu http://people.inf.elte.hu/groberto Frissítve: 2015.
Eötvös Loránd Tudományegyetem Informatikai Kar Alkalmazott modul: Programozás Feladatgyűjtemény Összeállította: Giachetta Roberto groberto@inf.elte.hu http://people.inf.elte.hu/groberto Frissítve: 2015.
Adatok szűrése, rendezése
 Adatok szűrése, rendezése Célkitűzések Szűrést kifejező lekérdezések végrehajtása A lekérdezés eredményének rendezése &változó használata isql*plus-ban futási időben megadható feltételek céljából A lista
Adatok szűrése, rendezése Célkitűzések Szűrést kifejező lekérdezések végrehajtása A lekérdezés eredményének rendezése &változó használata isql*plus-ban futási időben megadható feltételek céljából A lista
MATEMATIKA ÉRETTSÉGI 2006. május 9. EMELT SZINT
 ) A PQRS négyszög csúcsai: MATEMATIKA ÉRETTSÉGI 006. május 9. EMELT SZINT P 3; I., Q ;3, R 6; és S 5; 5 Döntse el, hogy az alábbi három állítás közül melyik igaz és melyik hamis! Tegyen * jelet a táblázat
) A PQRS négyszög csúcsai: MATEMATIKA ÉRETTSÉGI 006. május 9. EMELT SZINT P 3; I., Q ;3, R 6; és S 5; 5 Döntse el, hogy az alábbi három állítás közül melyik igaz és melyik hamis! Tegyen * jelet a táblázat
FELHASZNÁLÓI LEÍRÁS a DIMSQL Integrált Számviteli Rendszer Készlet moduljának használatához
 FELHASZNÁLÓI LEÍRÁS a DIMSQL Integrált Számviteli Rendszer Készlet moduljának használatához - 1 - www.dimenzio-kft.hu Tartalomjegyzék A. BEVEZETÉS... 4 I. BEÁLLÍTÁSOK, PARAMÉTEREK, NAPLÓFORMÁTUMOK... 4
FELHASZNÁLÓI LEÍRÁS a DIMSQL Integrált Számviteli Rendszer Készlet moduljának használatához - 1 - www.dimenzio-kft.hu Tartalomjegyzék A. BEVEZETÉS... 4 I. BEÁLLÍTÁSOK, PARAMÉTEREK, NAPLÓFORMÁTUMOK... 4
különösen a média közleményeiben való reális tájékozódást. Mindehhez elengedhetetlen egyszerű matematikai szövegek értelmezése, elemzése.
 MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról, mint tudásrendszerről, és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról, mint tudásrendszerről, és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
Reiczigel Jenő, 2006 1
 Reiczigel Jenő, 2006 1 Egytényezős (egyszempontos) varianciaelemzés k független minta (k kezelés vagy k csoport), a célváltozó minden csoportban normális eloszlású, a szórások azonosak, az átlagok vagy
Reiczigel Jenő, 2006 1 Egytényezős (egyszempontos) varianciaelemzés k független minta (k kezelés vagy k csoport), a célváltozó minden csoportban normális eloszlású, a szórások azonosak, az átlagok vagy
A 2008/2009. tanévi FIZIKA Országos Középiskolai Tanulmányi Verseny első fordulójának. feladatai és megoldásai fizikából. I.
 Oktatási Hivatal A 8/9. tanévi FIZIKA Országos Közéiskolai Tanulmányi Verseny első fordulójának feladatai és megoldásai fizikából I. kategória A dolgozatok elkészítéséhez minden segédeszköz használható.
Oktatási Hivatal A 8/9. tanévi FIZIKA Országos Közéiskolai Tanulmányi Verseny első fordulójának feladatai és megoldásai fizikából I. kategória A dolgozatok elkészítéséhez minden segédeszköz használható.
Algoritmusok és adatszerkezetek gyakorlat 07
 Algoritmusok és adatszerkezetek gyakorlat 0 Keresőfák Fák Fa: összefüggő, körmentes gráf, melyre igaz, hogy: - (Általában) egy gyökér csúcsa van, melynek 0 vagy több részfája van - Pontosan egy út vezet
Algoritmusok és adatszerkezetek gyakorlat 0 Keresőfák Fák Fa: összefüggő, körmentes gráf, melyre igaz, hogy: - (Általában) egy gyökér csúcsa van, melynek 0 vagy több részfája van - Pontosan egy út vezet
BAUSFT. Pécsvárad Kft. 7720 Pécsvárad, Pécsi út 49. Tel/Fax: 72/465-266 http://www.bausoft.hu. ISO-bau. Szigetelés kiválasztó. 1.02 verzió.
 BAUSFT Pécsvárad Kft. 7720 Pécsvárad, Pécsi út 49. Tel/Fax: 72/465-266 http://www.bausoft.hu ISO-bau Szigetelés kiválasztó 1.02 verzió Szerzők: dr. Baumann József okl. villamosmérnök 1188 Budapest, Fenyőfa
BAUSFT Pécsvárad Kft. 7720 Pécsvárad, Pécsi út 49. Tel/Fax: 72/465-266 http://www.bausoft.hu ISO-bau Szigetelés kiválasztó 1.02 verzió Szerzők: dr. Baumann József okl. villamosmérnök 1188 Budapest, Fenyőfa
NEPTUN_TÖRZS. (Funkcionális leírás)
 #+$k NEPTUN_TÖRZS NEPTUN_TÖRZS (Funkcionális leírás) S Budapest, 2002 #+ $k NEPTUN_TORZS NEPTUN_TÖRZS Tartalom TARTALOM... 2 1. BEVEZETÉS... 5 2. BELÉPÉS A RENDSZERBE... 6 3. ÚJ EGYÉN FELVÉTELE... 9 3.1
#+$k NEPTUN_TÖRZS NEPTUN_TÖRZS (Funkcionális leírás) S Budapest, 2002 #+ $k NEPTUN_TORZS NEPTUN_TÖRZS Tartalom TARTALOM... 2 1. BEVEZETÉS... 5 2. BELÉPÉS A RENDSZERBE... 6 3. ÚJ EGYÉN FELVÉTELE... 9 3.1
Programozási módszertan. Dinamikus programozás: Nyomtatási feladat A leghosszabb közös részsorozat
 PM-04 p. 1/18 Programozási módszertan Dinamikus programozás: Nyomtatási feladat A leghosszabb közös részsorozat Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu
PM-04 p. 1/18 Programozási módszertan Dinamikus programozás: Nyomtatási feladat A leghosszabb közös részsorozat Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu
Algoritmuselmélet. 2-3 fák. Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem. 8.
 Algoritmuselmélet 2-3 fák Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem 8. előadás Katona Gyula Y. (BME SZIT) Algoritmuselmélet 8. előadás
Algoritmuselmélet 2-3 fák Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem 8. előadás Katona Gyula Y. (BME SZIT) Algoritmuselmélet 8. előadás
