Optika Gröller BMF Kandó MTI. Optikai alapfogalmak. Fény: transzverzális elektromágneses hullám. n = c vákuum /c közeg. Optika Gröller BMF Kandó MTI
|
|
|
- Lóránd Orosz
- 9 évvel ezelőtt
- Látták:
Átírás
1 Optikai alapfogalmak Fény: transzverzális elektromágneses hullám n = c vákuum /c közeg 1
2 Az elektromágneses spektrum 2
3 Az anyag és s a fény f kölcsk lcsönhatása Visszaverődés, reflexió Törés, kettőstörés, polarizáció Elnyelés, abszorpció, szórás Fénykibocsátás, fotoeffektus Fotokémiai reakciók Elektrooptikai, magnetooptikai hatás Visszaverődés Fresnel törvény merőleges beesésnél: (minden közeg határfelületén, iránytól független) Szögfüggés: (n 1 n 2 ) 2 R= (n 1 + n 2 ) 2 Brewster szög: polarizációs sík szerinti szétválás: a párhuzamos megtörik (R párh =0), a merőleges visszaverődik 3
4 Reflexió módosítása sa dielektrikum-rétegekkel tegekkel Antireflexiós (AR) bevonat: Átlagos üvegfelületről (n = 1,5), R 4% Rétegvastagság: n 1 d = λ/4 Két visszavert sugár gyengítő interferencia Teljes kioltás, ha: Függ: hullámhossz beesési szög Egyrétegű bevonat: R 1% Többrétegű bevonatok Szélesebb λ-tartomány Szabályozható áteresztés, visszaverés, pl: interferenciaszűrő Dielektrikum tükrt krök: k: visszaverés irányában erősítő interferencia Felváltva nagy és kis törésmutatójú rétegrendszer, λ/2, λ/4 rétegek, Fehér fényre: R 99%, csak egy λ -ra: R 99,999% pl. lézerek, rétegszám:
5 Alkalmazások: Interferenciaszűrők Hidegtükrök (infrát nem veri vissza) pl. vetítőlámpa Lencsék tükrözésmentes bevonata Egyirányú tükrök Kirakatüveg Réteganyagok: Kis n: MgF 2, kriolit Nagy n: ZrO 2, TiO 2, ZnS A legjobban tükröző fémek reflexiós spektruma Fénytörés Schnellius-Descartestörvény: n =sinα /sinβ =c 1 /c 2 A törésmutató függ a hullámhossztól Diszperzió Fény felbontása hullámhossz szerint, spektroszkópia, ékszerek csillogása Optikai adatátvitelben a jelsebesség függ a λ -tól, a jel kiszélesedik, csökken az átviteli kapacitás Anyagdiszperzió [ps/nm/km] 5
6 Lencsék, lencserendszerek kromatikus hiba: fehér fényt használva minden hullámhosszra máshol van az éles kép Korrekció: kétféle optikai üvegcsalád: korona és flint ν: Abbe-szám Kettőst störés, s, polarizáci ció Anizotrópia: az anyagi tulajdonságok pl. n, ρ, D függenek a vizsgálati iránytól Izotróp anyagok: gázok, folyadékok, polikristályos anyagok, szimmetrikus rácsú egykristályos anyagok Anizotróp: nem szabályos rendszerű egykristályos anyagok, folyadékkristályok Anizotróp anyagokban kristálytani tengelyek irányában más más törésmutató n o (rendes, ordinárius), n eo (rendellenes, extraordinárius) SiO 2, kvarc: 1,544 1,553 TiO 2, rutil: 2,616 2,903 6
7 Két megtört fénysugár polarizációja egymásra merőleges A polarizáció síkja megegyezik a főtengelyek irányával. Kettőstörést / anizotrópiát okozhat: Mechanikai feszültség Makromolekulák rendeződése Elektromos, mágneses tér Polisztirol láncmolekulák rendeződése a fröccsöntő szerszámban Alkalmazás: Anyagvizsgálat, fényerő-szabályozás, reflexiócsökkentés (pl foto), LCD kijelző, optikai jelmodulálás Egy meteorit kőzetszemcse polarizációs mikroszkópi képe 7
8 Fényelnyelés Foton energiája megfelel egy elektron energia-átmenetnek Fekete, fehér, átlátszó, színes anyagok: a látható spektrumból mást-mást nyelnek el Mágneses tulajdonságok 8
9 Alapfogalmak B = µ 0 µ rel H B: Indukció (T) H: Térerősség (A/m) µ 0 : vákuum permeabilitása = Vs/Am µ rel : relatív permeabilitás, anyagi jellemző B = µ 0 H + M, ill. M = χ H M: mágnesezettség χ: mágn. szuszceptibilitás, anyagi jellemző µ rel = 1 + χ Alaptípusok: Paramágneses: µ rel > 1 χ > 0 Diamágneses: µ rel < 1 χ < 0 Ferromágneses: µ rel >> 1 χ >> 0 (µ rel ~ χ ) 9
10 Atomi szintű értelmezés Elektron mágneses momentuma: Pályamenti mozgás, Spin Bohr-magneton: a mágneses dipólmomentum egysége: µ B = eh/4πm e = 9, Am 2 Pálymenti mozgás hozzájárulása: m µ B, ahol m az elektron mágneses kvantumszáma ( 0, ±1, ±2..) Spin hozzájárulása: ± µ B Eredő mágneses momentum: az elektronok momentumainak vektori eredője. Telített héjon, párosított spínű elektronok egymás hatását kioltják. Csak a külső pályán levő, párosítatlan spinű számít. Az atommag hozzájárulása elhanyagolható Diamágneses anyagok: χ ~ -10-5, Alkalmazás ritka Szupravezetők: ideális diamágneses viselkedés: χ = -1 Paramágneses anyagok: χ ~ Alkalmazás: mágneses szétválasztás, mérés (pl O 2 ) Ferromágneses anyagok: Fe, Co, Ni, Gd, Fe 2 O 3, CrO 2, ötvözetek, stb. Szerkezeti tulajdonság is: elemi dipólusok erősek, egymást is irányítják Rendezett tartományok, A domének átfordulása ferromágneses domének anyagok első mágnesezése során 10
11 Ferromágneses jellemzők Hiszterézis Domén szerkezet cm Weiss 1907, kimutatás Bitter 1931 Curie-hőmérséklet Magnetostrikció: a doménszerkezet átalakulásával méretváltozás (+ -), mechanikai feszültség Jellegzetes mágnesezési görbe A doménfalak mozgása Fe egykristályban, növekvő térerősség hatására Lágy és kemény mágnes ideális mágnesezési görbéje 11
12 Lágymágnesekgnesek Nagy telítési indukció Kis hiszterézis Kis H c (< 300A/m), nagy fajlagos ellenállás Alkalmazás: Elektromágneses indukción alapuló: transzformátor, motor, generátor Elektromechanikus eszközök: emelők, relék, mágneskapcsolók Mágneses árnyékolók Anyagok: Fe: nagy hiszterézis és örvényáram veszteség Fe-Si (1 4%) C és O szennyezés káros Erősáramú alk Ni Fe (80 : 20) permalloy, Ni,Fe, Mn,Mo: supermalloy Fémüvegek, nanokristályos ötvözetek Ferritek: MnFe 2 O 4 -ZnFe 2 O 4, NiFe 2 O 4 - ZnFe 2 O 4 Gránátok: 3M 2 O 3 5Fe 2 O 3 M: Y, Sm, Eu, Gd 12
13 Állandó mágnesek Nagy H c, B r, nagy energiaszorzat (BH max ) W = 1/2H B V Nagy hiszterézis Kicsi krisztallitok, benne már nincs doménfal, átmágnesezés nehezebb Anyagok: acél ötvözetek (Cr, Ni, Co, W, Ti, Al) Ferritek: MOFe 2 O 3, MO6Fe 2 O 3 M: Ba, Sr, Co Ritkaföldfém-Co ötvözetek: RCo 5, R 2 Co 17 R: Sm, Pr, Nd, La,Ce, Tb, Eu, Gd Alkalmazások Mágneses információ tárolás: merevlemez, floppy, magnó, videó Híradástechnika: hangszóró, mikrofon Mérőműszerek, galvanométer 13
Optikai alapfogalmak. Az elektromágneses spektrum. n = c vákuum /c közeg. Fény: transzverzális elektromágneses hullám. (n 1 n 2 ) 2 R= (n 1 + n 2 ) 2
 Optikai alapfogalmak Az anyag és s a fény f kölcsk lcsönhatása Fény: transzverzális elektromágneses hullám n = c vákuum /c közeg Visszaverődés, reflexió Törés, kettőstörés, polarizáció Elnyelés, abszorpció,
Optikai alapfogalmak Az anyag és s a fény f kölcsk lcsönhatása Fény: transzverzális elektromágneses hullám n = c vákuum /c közeg Visszaverődés, reflexió Törés, kettőstörés, polarizáció Elnyelés, abszorpció,
Az anyagok mágneses tulajdonságai
 BME, Anyagtudomány és Technológia Tanszék Dr. Mészáros István Mágneses tulajdonságok, mágneses anyagok Előadásvázlat 2013. 1 Az anyagok mágneses tulajdonságai Alkalmazási területek Jelentőségük (lágy:
BME, Anyagtudomány és Technológia Tanszék Dr. Mészáros István Mágneses tulajdonságok, mágneses anyagok Előadásvázlat 2013. 1 Az anyagok mágneses tulajdonságai Alkalmazási területek Jelentőségük (lágy:
Optika Gröller BMF Kandó MTI
 Optika Gröller BMF Kandó MTI Optikai alapfogalmak Fény: transzverzális elektromágneses hullám n = c vákuum /c közeg Optika Gröller BMF Kandó MTI Az elektromágneses spektrum Az anyag és a fény kölcsönhatása
Optika Gröller BMF Kandó MTI Optikai alapfogalmak Fény: transzverzális elektromágneses hullám n = c vákuum /c közeg Optika Gröller BMF Kandó MTI Az elektromágneses spektrum Az anyag és a fény kölcsönhatása
Optika Gröller BMF Kandó MTI
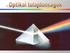 Optikai alapfogalmak Fény: transzverzális elektromágneses hullám n = c vákuum /c közeg Az elektromágneses spektrum Az anyag és a fény kölcsönhatása Visszaverődés, reflexió Törés, kettőstörés, polarizáció
Optikai alapfogalmak Fény: transzverzális elektromágneses hullám n = c vákuum /c közeg Az elektromágneses spektrum Az anyag és a fény kölcsönhatása Visszaverődés, reflexió Törés, kettőstörés, polarizáció
Visszaverődés. Optikai alapfogalmak. Az elektromágneses spektrum. Az anyag és a fény kölcsönhatása. n = c vákuum /c közeg
 Optikai alapfogalmak Fény: transzverzális elektromágneses hullám n = c vákuum /c közeg Az elektromágneses spektrum Az anyag és a fény kölcsönhatása Visszaverődés Visszaverődés, reflexió Törés, kettőstörés,
Optikai alapfogalmak Fény: transzverzális elektromágneses hullám n = c vákuum /c közeg Az elektromágneses spektrum Az anyag és a fény kölcsönhatása Visszaverődés Visszaverődés, reflexió Törés, kettőstörés,
Optikai alapfogalmak. Az elektromágneses spektrum. n = c vákuum /c közeg. Fény: transzverzális elektromágneses hullám. (n 1 n 2 ) 2 R= (n 1 + n 2 ) 2
 Optikai alapfogalmak Fény: transzverzális elektromágneses hullám n = c vákuum /c közeg Az elektromágneses spektrum Az anyag és s a fény f kölcsk lcsönhatása Visszaverıdés Visszaverıdés, reflexió Törés,
Optikai alapfogalmak Fény: transzverzális elektromágneses hullám n = c vákuum /c közeg Az elektromágneses spektrum Az anyag és s a fény f kölcsk lcsönhatása Visszaverıdés Visszaverıdés, reflexió Törés,
Elektronspinrezonancia (ESR) - spektroszkópia
 E m S Elektronspinrezonancia (ESR) - spektroszkópia Paramágneses anyagok vizsgáló módszere. A mágneses momentum iránykvantáltságán alapul. A mágneses momentum energiája B indukciójú mágneses térben = µ
E m S Elektronspinrezonancia (ESR) - spektroszkópia Paramágneses anyagok vizsgáló módszere. A mágneses momentum iránykvantáltságán alapul. A mágneses momentum energiája B indukciójú mágneses térben = µ
X. Fénypolarizáció. X.1. A polarizáció jelenségének magyarázata
 X. Fénypolarizáció X.1. A polarizáció jelenségének magyarázata A polarizáció a fény hullámtermészetét bizonyító jelenség, amely csak a transzverzális rezgések esetén észlelhető. Köztudott, hogy csak a
X. Fénypolarizáció X.1. A polarizáció jelenségének magyarázata A polarizáció a fény hullámtermészetét bizonyító jelenség, amely csak a transzverzális rezgések esetén észlelhető. Köztudott, hogy csak a
2. OPTIKA 2.1. Elmélet 2.1.1. Geometriai optika
 2. OPTIKA 2.1. Elmélet Az optika tudománya a látás élményéből fejlődött ki. A tárgyakat azért látjuk, mert fényt bocsátanak ki, vagy a rájuk eső fényt visszaverik, és ezt a fényt a szemünk érzékeli. A
2. OPTIKA 2.1. Elmélet Az optika tudománya a látás élményéből fejlődött ki. A tárgyakat azért látjuk, mert fényt bocsátanak ki, vagy a rájuk eső fényt visszaverik, és ezt a fényt a szemünk érzékeli. A
Az optikai jelátvitel alapjai. A fény két természete, terjedése
 Az optikai jelátvitel alapjai A fény két természete, terjedése A fény kettős természete 1. A fény: - Elektromágneses hullám (EMH) - Optikai jelenség Egyes dolgokat a hullám természettel könnyű magyarázni,
Az optikai jelátvitel alapjai A fény két természete, terjedése A fény kettős természete 1. A fény: - Elektromágneses hullám (EMH) - Optikai jelenség Egyes dolgokat a hullám természettel könnyű magyarázni,
Villamos tulajdonságok
 Villamos tulajdonságok A vezetés s magyarázata Elektron függıleges falú potenciálgödörben: állóhullámok alap és gerjesztett állapotok Több elektron: Pauli-elv Sok elektron: Energia sávok Sávelméletlet
Villamos tulajdonságok A vezetés s magyarázata Elektron függıleges falú potenciálgödörben: állóhullámok alap és gerjesztett állapotok Több elektron: Pauli-elv Sok elektron: Energia sávok Sávelméletlet
A fény. Abszorpciós fotometria Fluoreszcencia spektroszkópia. A fény. A spektrumok megjelenési formái. A fény kettıs természete: Huber Tamás
 A fény Abszorpciós fotometria Fluoreszcencia spektroszkópia. 2010. október 19. Huber Tamás PTE ÁOK Biofizikai Intézet E A fény elektromos térerısségvektor hullámhossz A fény kettıs természete: Hullám (terjedéskor)
A fény Abszorpciós fotometria Fluoreszcencia spektroszkópia. 2010. október 19. Huber Tamás PTE ÁOK Biofizikai Intézet E A fény elektromos térerısségvektor hullámhossz A fény kettıs természete: Hullám (terjedéskor)
ESR színképek értékelése és molekulaszerkezeti értelmezése
 ESR színképek értékelése és molekulaszerkezeti értelmezése Elméleti alap: Atkins: Fizikai Kémia II, 187-188, 146, 1410, 152 158 fejezetek A gyakorlat során egy párosítatlan elektronnal rendelkező benzoszemikinon
ESR színképek értékelése és molekulaszerkezeti értelmezése Elméleti alap: Atkins: Fizikai Kémia II, 187-188, 146, 1410, 152 158 fejezetek A gyakorlat során egy párosítatlan elektronnal rendelkező benzoszemikinon
Rutherford-féle atommodell
 Rutherfordféle atommodell Manchesteri Egyetem 1909 1911 Hans Geiger, Ernest Marsden Ernest Rutherford vezetésével Az arany szerkezetének felderítésére irányuló szóráskísérletek Alfarészecskékkel bombáztak
Rutherfordféle atommodell Manchesteri Egyetem 1909 1911 Hans Geiger, Ernest Marsden Ernest Rutherford vezetésével Az arany szerkezetének felderítésére irányuló szóráskísérletek Alfarészecskékkel bombáztak
Optoelektronikai Kommunikáció. Optikai alapismeretek
 Optoelektronikai Kommunikáció Optikai alapismeretek (OK-4) Budapesti Mûszaki Fõiskola Kandó Kálmán Villamosmérnöki Fõiskolai Kar Számítógéptechnikai Intézete Székesfehérvár 2002. Budapesti Mûszaki Fõiskola
Optoelektronikai Kommunikáció Optikai alapismeretek (OK-4) Budapesti Mûszaki Fõiskola Kandó Kálmán Villamosmérnöki Fõiskolai Kar Számítógéptechnikai Intézete Székesfehérvár 2002. Budapesti Mûszaki Fõiskola
Árnyék. Félárnyék. 3. A fény keletkezése
 OPTIKA 1. Az optika tárgya 2. Az optikában használt alapfogalmak Elsődleges fényforrás Másodlagos fényforrás Pontszerű fényforrás Kiterjedt fényforrás Fénysugár Árnyék Félárnyék 3. A fény keletkezése 1685.
OPTIKA 1. Az optika tárgya 2. Az optikában használt alapfogalmak Elsődleges fényforrás Másodlagos fényforrás Pontszerű fényforrás Kiterjedt fényforrás Fénysugár Árnyék Félárnyék 3. A fény keletkezése 1685.
Mágneses tér anyag kölcsönhatás leírása
 Anyagszerkezettan és anyagvizsgálat 2012/13 Mágneses anyagok Dr. Szabó Péter János szpj@eik.bme.hu Mágneses tér anyag kölcsönhatás leírása B = µ H B = µ µ H = µ H + M ) 0 r 0 ( 1 1 M = κh = Pi = P V V
Anyagszerkezettan és anyagvizsgálat 2012/13 Mágneses anyagok Dr. Szabó Péter János szpj@eik.bme.hu Mágneses tér anyag kölcsönhatás leírása B = µ H B = µ µ H = µ H + M ) 0 r 0 ( 1 1 M = κh = Pi = P V V
a fizikai (hullám) optika
 A fény f hullám m természete a fizikai (hullám) optika Geometriai optika Optika Fizikai optika Fény-anyag kölcsönhatás Összeállította: CSISZÁR IMRE SZTE, Ságvári E. Gyakorló Gimnázium SZEGED, 006. szeptember
A fény f hullám m természete a fizikai (hullám) optika Geometriai optika Optika Fizikai optika Fény-anyag kölcsönhatás Összeállította: CSISZÁR IMRE SZTE, Ságvári E. Gyakorló Gimnázium SZEGED, 006. szeptember
Gömbtükrök, leképezési hibák, OPTIKA. Dr. Seres István
 Gömbtükrök, leképezési hibák, OPTIKA Dr. Seres István Tükrök http://www.mozaik.info.hu/mozaweb/feny/fy_ft11.htm Seres István 2 http://fft.szie.hu Gömbtükrök Domború tükör képalkotása Jellegzetes sugármenetek
Gömbtükrök, leképezési hibák, OPTIKA Dr. Seres István Tükrök http://www.mozaik.info.hu/mozaweb/feny/fy_ft11.htm Seres István 2 http://fft.szie.hu Gömbtükrök Domború tükör képalkotása Jellegzetes sugármenetek
KOVÁCS ENDRe, PARIpÁS BÉLA, FIZIkA II.
 KOVÁCS ENDRe, PARIpÁS BÉLA, FIZIkA II. 4 ELeKTROMOSSÁG, MÁGNeSeSSÉG IV. MÁGNeSeSSÉG AZ ANYAGbAN 1. AZ alapvető mágneses mennyiségek A mágneses polarizáció, a mágnesezettség vektora A nukleonok (proton,
KOVÁCS ENDRe, PARIpÁS BÉLA, FIZIkA II. 4 ELeKTROMOSSÁG, MÁGNeSeSSÉG IV. MÁGNeSeSSÉG AZ ANYAGbAN 1. AZ alapvető mágneses mennyiségek A mágneses polarizáció, a mágnesezettség vektora A nukleonok (proton,
Képalkotás a pásztázó elektronmikroszkóppal
 1 Képalkotás a pásztázó elektronmikroszkóppal Anton van Leeuwenhoek (1632-1723, Delft) Havancsák Károly, 2011. január FEI Quanta 3D SEM/FIB 2 A TÁMOP pályázat eddigi történései 3 Időrend A helyiség kialakítás
1 Képalkotás a pásztázó elektronmikroszkóppal Anton van Leeuwenhoek (1632-1723, Delft) Havancsák Károly, 2011. január FEI Quanta 3D SEM/FIB 2 A TÁMOP pályázat eddigi történései 3 Időrend A helyiség kialakítás
Fénytechnika. A fény. Dr. Wenzel Klára. egyetemi magántanár Budapesti Műszaki és Gazdaságtudományi Egyetem. Budapest, 2013.
 Fénytechnika A fény Dr. Wenzel Klára egyetemi magántanár Budapesti Műszaki és Gazdaságtudományi Egyetem Budapest, 2013. A fénnyel kapcsolatos szabványok Az elektromágnenes MSZ 9620 spektrum: Fénytechnikai
Fénytechnika A fény Dr. Wenzel Klára egyetemi magántanár Budapesti Műszaki és Gazdaságtudományi Egyetem Budapest, 2013. A fénnyel kapcsolatos szabványok Az elektromágnenes MSZ 9620 spektrum: Fénytechnikai
Az időtől független Schrödinger-egyenlet (energia sajátértékegyenlet), A Laplace operátor derékszögű koordinátarendszerben
 Atomfizika ψ ψ ψ ψ ψ E z y x U z y x m = + + + ),, ( h ) ( ) ( ) ( ) ( r r r r ψ ψ ψ E U m = + Δ h z y x + + = Δ ),, ( ) ( z y x ψ =ψ r Az időtől független Schrödinger-egyenlet (energia sajátértékegyenlet),
Atomfizika ψ ψ ψ ψ ψ E z y x U z y x m = + + + ),, ( h ) ( ) ( ) ( ) ( r r r r ψ ψ ψ E U m = + Δ h z y x + + = Δ ),, ( ) ( z y x ψ =ψ r Az időtől független Schrödinger-egyenlet (energia sajátértékegyenlet),
Készítette: Bujnóczki Tibor Lezárva: 2005. 01. 01.
 VILÁGÍTÁSTECHNIKA Készítette: Bujnóczki Tibor Lezárva: 2005. 01. 01. ANYAGOK FELÉPÍTÉSE Az atomok felépítése: elektronhéjak: K L M N O P Q elektronok atommag W(wolfram) (Atommag = proton+neutron protonok
VILÁGÍTÁSTECHNIKA Készítette: Bujnóczki Tibor Lezárva: 2005. 01. 01. ANYAGOK FELÉPÍTÉSE Az atomok felépítése: elektronhéjak: K L M N O P Q elektronok atommag W(wolfram) (Atommag = proton+neutron protonok
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI
 SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 17 KRISTÁLYFIZIkA XVII. Hőtani, MÁGNEsEs, ELEKTROMOs, RADIOAKTÍV TULAJDONsÁGOK 1. Hőtani TULAJDONsÁGOK A hősugarak a színkép vörös színén túl lépnek fel (infravörös
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 17 KRISTÁLYFIZIkA XVII. Hőtani, MÁGNEsEs, ELEKTROMOs, RADIOAKTÍV TULAJDONsÁGOK 1. Hőtani TULAJDONsÁGOK A hősugarak a színkép vörös színén túl lépnek fel (infravörös
4. elıadás A KRISTÁLYFIZIKA ALAPJAI
 4. elıadás A KRISTÁLYFIZIKA ALAPJAI KRISTÁLYFIZIKA ANIZOTRÓPIA IZOTRÓPIA JELENSÉGE Izotrópia (irányok szerint egyenlı): ha a fizikai sajátságok függetlenek az iránytól. Ide tartoznak a köbös rendszerbe
4. elıadás A KRISTÁLYFIZIKA ALAPJAI KRISTÁLYFIZIKA ANIZOTRÓPIA IZOTRÓPIA JELENSÉGE Izotrópia (irányok szerint egyenlı): ha a fizikai sajátságok függetlenek az iránytól. Ide tartoznak a köbös rendszerbe
Mágneses alapjelenségek
 Mágneses alapjelenségek Bizonyos vasércek képesek apró vasdarabokat magukhoz vonzani: permanens mágnes Az acélrúd felmágnesezhető ilyen ércek segítségével. Rúd két vége: pólusok (a vasreszelék csak ide
Mágneses alapjelenségek Bizonyos vasércek képesek apró vasdarabokat magukhoz vonzani: permanens mágnes Az acélrúd felmágnesezhető ilyen ércek segítségével. Rúd két vége: pólusok (a vasreszelék csak ide
Fizika belépő kérdések /Földtudományi alapszak I. Évfolyam II. félév/
 Fizika belépő kérdések /Földtudományi alapszak I. Évfolyam II. félév/. Coulomb törvény: a pontszerű töltések között ható erő (F) egyenesen arányos a töltések (Q,Q ) szorzatával és fordítottan arányos a
Fizika belépő kérdések /Földtudományi alapszak I. Évfolyam II. félév/. Coulomb törvény: a pontszerű töltések között ható erő (F) egyenesen arányos a töltések (Q,Q ) szorzatával és fordítottan arányos a
Mágneses alapjelenségek
 Mágneses alapjelenségek Bizonyos vasércek képesek apró vasdarabokat magukhoz vonzani: permanens mágnes Az acélrúd felmágnesezhető ilyen ércek segítségével. Rúd két vége: pólusok (a vasreszelék csak ide
Mágneses alapjelenségek Bizonyos vasércek képesek apró vasdarabokat magukhoz vonzani: permanens mágnes Az acélrúd felmágnesezhető ilyen ércek segítségével. Rúd két vége: pólusok (a vasreszelék csak ide
lásd: enantiotóp, diasztereotóp
 anizokrón anisochronous árnyékolási állandó shielding constant árnyékolási járulékok és empirikus értelmezésük shielding contributions diamágneses és paramágneses árnyékolás diamagnetic and paramagnetic
anizokrón anisochronous árnyékolási állandó shielding constant árnyékolási járulékok és empirikus értelmezésük shielding contributions diamágneses és paramágneses árnyékolás diamagnetic and paramagnetic
Anyagtudomány MÁGNESES ANYAGOK GERZSON MIKLÓS
 Anyagtudomány MÁGNESES ANYAGOK GERZSON MIKLÓS 1 mágneses pólusok (Föld, állandó mágnesek) pólusok nem szétválaszthatók történetük: Magnetosz Kréta Ókori Kína iránytű Gilbert: On the Magnet (1600) Oersted:
Anyagtudomány MÁGNESES ANYAGOK GERZSON MIKLÓS 1 mágneses pólusok (Föld, állandó mágnesek) pólusok nem szétválaszthatók történetük: Magnetosz Kréta Ókori Kína iránytű Gilbert: On the Magnet (1600) Oersted:
Mágneses tér anyag kölcsönhatás leírása
 Anyagszerkezettan és anyagvizsgálat 2014/15 Mágneses anyagok Dr. Szabó Péter János szpj@eik.bme.hu Mágneses tér anyag kölcsönhatás leírása B H B H H M ) 0 1 M H V 1 r r 0 ( 1 Pi P V H : az anyagra ható
Anyagszerkezettan és anyagvizsgálat 2014/15 Mágneses anyagok Dr. Szabó Péter János szpj@eik.bme.hu Mágneses tér anyag kölcsönhatás leírása B H B H H M ) 0 1 M H V 1 r r 0 ( 1 Pi P V H : az anyagra ható
Mössbauer Spektroszkópia
 Mössbauer Spektroszkópia Homa Gábor, Markó Gergely Mérés dátuma: 2008. 10. 15., 2008. 10. 22., 2008. 11. 05. Leadás dátuma: 2008. 11. 23. Figure 1: Rezonancia-abszorpció és szórás 1 Elméleti összefoglaló
Mössbauer Spektroszkópia Homa Gábor, Markó Gergely Mérés dátuma: 2008. 10. 15., 2008. 10. 22., 2008. 11. 05. Leadás dátuma: 2008. 11. 23. Figure 1: Rezonancia-abszorpció és szórás 1 Elméleti összefoglaló
F1404 ATOMMAG- és RÉSZECSKEFIZIKA
 F1404 ATOMMAG- és RÉSZECSKEFIZIKA Dr. Raics Péter DE TTK Kísérleti Fizikai Tanszék, Debrecen, Bem tér 18/A RAICS@TIGRIS.KLTE.HU Ajánlott irodalom Raics P.: Atommag- és részecskefizika. Jegyzet. DE Kísérleti
F1404 ATOMMAG- és RÉSZECSKEFIZIKA Dr. Raics Péter DE TTK Kísérleti Fizikai Tanszék, Debrecen, Bem tér 18/A RAICS@TIGRIS.KLTE.HU Ajánlott irodalom Raics P.: Atommag- és részecskefizika. Jegyzet. DE Kísérleti
I. Atomszerkezeti ismeretek (9. Mozaik Tankönyv:10-30. oldal) 1. Részletezze az atom felépítését!
 I. Atomszerkezeti ismeretek (9. Mozaik Tankönyv:10-30. oldal) 1. Részletezze az atom felépítését! Az atom az anyagok legkisebb, kémiai módszerekkel tovább már nem bontható része. Az atomok atommagból és
I. Atomszerkezeti ismeretek (9. Mozaik Tankönyv:10-30. oldal) 1. Részletezze az atom felépítését! Az atom az anyagok legkisebb, kémiai módszerekkel tovább már nem bontható része. Az atomok atommagból és
Fizikai kémia és radiokémia labor II, Laboratóriumi gyakorlat: Spektroszkópia mérés
 Fizikai kémia és radiokémia labor II, Laboratóriumi gyakorlat: Spektroszkópia mérés A gyakorlatra vigyenek magukkal pendrive-ot, amire a mérési adatokat átvehetik. Ajánlott irodalom: P. W. Atkins: Fizikai
Fizikai kémia és radiokémia labor II, Laboratóriumi gyakorlat: Spektroszkópia mérés A gyakorlatra vigyenek magukkal pendrive-ot, amire a mérési adatokat átvehetik. Ajánlott irodalom: P. W. Atkins: Fizikai
Mit mond ki a Huygens elv, és miben több ehhez képest a Huygens Fresnel-elv?
 Ismertesse az optika fejlődésének legjelentősebb mérföldköveit! - Ókor: korai megfigyelések - Euklidész (i.e. 280) A fény homogén közegben egyenes vonalban terjed. Legrövidebb út elve (!) Tulajdonképpen
Ismertesse az optika fejlődésének legjelentősebb mérföldköveit! - Ókor: korai megfigyelések - Euklidész (i.e. 280) A fény homogén közegben egyenes vonalban terjed. Legrövidebb út elve (!) Tulajdonképpen
MŰSZAKI ISMERETEK. Az Agrármérnöki MSc szak tananyagfejlesztése TÁMOP-4.1.2-08/1/A-2009-0010
 MŰSZAKI ISMERETEK Az Agrármérnöki MSc szak tananyagfejlesztése TÁMOP-4.1.2-08/1/A-2009-0010 Az előadás áttekintése Méret meghatározás Alaki jellemzők Felületmérés Tömeg, térfogat, sűrűség meghatározása
MŰSZAKI ISMERETEK Az Agrármérnöki MSc szak tananyagfejlesztése TÁMOP-4.1.2-08/1/A-2009-0010 Az előadás áttekintése Méret meghatározás Alaki jellemzők Felületmérés Tömeg, térfogat, sűrűség meghatározása
Hibrid Integrált k, HIC
 Hordozók Hibrid Integrált Áramkörök, k, HIC Az alábbi bemutató egyes ábráit a Dr. Illyefalvi Vitéz Zsolt Dr. Ripka Gábor Dr. Harsányi Gábor: Elektronikai technológia, ill. Dr Ripka Gábor: Hordozók, alkatrészek
Hordozók Hibrid Integrált Áramkörök, k, HIC Az alábbi bemutató egyes ábráit a Dr. Illyefalvi Vitéz Zsolt Dr. Ripka Gábor Dr. Harsányi Gábor: Elektronikai technológia, ill. Dr Ripka Gábor: Hordozók, alkatrészek
Abszorpciós fotometria
 A fény Abszorpciós fotometria Barkó Szilvia PTE ÁOK Biofizikai ntézet 2011. február E A fény elektromos térerősségvektor hullámhossz A fény kettős termzete: Hullám (terjedkor) Rzecske (kölcsönhatáskor)
A fény Abszorpciós fotometria Barkó Szilvia PTE ÁOK Biofizikai ntézet 2011. február E A fény elektromos térerősségvektor hullámhossz A fény kettős termzete: Hullám (terjedkor) Rzecske (kölcsönhatáskor)
Könnyűfém és szuperötvözetek
 Könnyűfém és szuperötvözetek Anyagismeret a gyakorlatban Dr. Orbulov Imre Norbert Anyagtudomány és Technológia Tanszék Az előadás fő pontjai A könnyűfémek definíciója Alumínium és ötvözetei Magnézium és
Könnyűfém és szuperötvözetek Anyagismeret a gyakorlatban Dr. Orbulov Imre Norbert Anyagtudomány és Technológia Tanszék Az előadás fő pontjai A könnyűfémek definíciója Alumínium és ötvözetei Magnézium és
MAGYAR RÉZPIACI KÖZPONT. 1241 Budapest, Pf. 62 Telefon 317-2421, Fax 266-6794 e-mail: hcpc.bp@euroweb.hu
 MAGYAR RÉZPIACI KÖZPONT 1241 Budapest, Pf. 62 Telefon 317-2421, Fax 266-6794 e-mail: hcpc.bp@euroweb.hu Tartalom 1. A villamos csatlakozások és érintkezôk fajtái............................5 2. Az érintkezések
MAGYAR RÉZPIACI KÖZPONT 1241 Budapest, Pf. 62 Telefon 317-2421, Fax 266-6794 e-mail: hcpc.bp@euroweb.hu Tartalom 1. A villamos csatlakozások és érintkezôk fajtái............................5 2. Az érintkezések
Szilárdtestek mágnessége. Mágnesesen rendezett szilárdtestek
 Szilárdtestek mágnessége Mágnesesen rendezett szilárdtestek 2 Mágneses anyagok Permanens atomi mágneses momentumok: irány A kétféle spin-beállású elektronok betöltöttsége különbözik (spin-polarizáció)
Szilárdtestek mágnessége Mágnesesen rendezett szilárdtestek 2 Mágneses anyagok Permanens atomi mágneses momentumok: irány A kétféle spin-beállású elektronok betöltöttsége különbözik (spin-polarizáció)
A TételWiki wikiből. Tekintsük a következő Hamilton-operátorral jellemezhető rendszert:
 1 / 12 A TételWiki wikiből 1 Ritka gázok állapotegyenlete 2 Viriál sorfejtés 3 Van der Waals gázok 4 Ising-modell 4.1 Az Ising-modell megoldása 1 dimenzióban(*) 4.2 Az Ising-modell átlagtérelmélete 2 dimenzióban(**)
1 / 12 A TételWiki wikiből 1 Ritka gázok állapotegyenlete 2 Viriál sorfejtés 3 Van der Waals gázok 4 Ising-modell 4.1 Az Ising-modell megoldása 1 dimenzióban(*) 4.2 Az Ising-modell átlagtérelmélete 2 dimenzióban(**)
MÓDOSÍTOTT RÉSZLETEZÕ OKIRAT (1)
 Nemzeti Akkreditáló Testület MÓDOSÍTOTT RÉSZLETEZÕ OKIRAT (1) a NAT-1-1173/2011 nyilvántartási számú akkreditált státuszhoz A BM OKF Katasztrófavédelmi Kutatóintézet 1 (1033 Budapest, Laktanya u. 33.)
Nemzeti Akkreditáló Testület MÓDOSÍTOTT RÉSZLETEZÕ OKIRAT (1) a NAT-1-1173/2011 nyilvántartási számú akkreditált státuszhoz A BM OKF Katasztrófavédelmi Kutatóintézet 1 (1033 Budapest, Laktanya u. 33.)
töltéssel rendelkező vagy semleges részecskék kinetikus energiája és (vagy) impulzusa a kondenzált közegek atomjaival ütközve megváltozhat.
 Néhány szó a neutronról Különböző részecskék, úgymint fotonok, neutronok, elektronok és más, töltéssel rendelkező vagy semleges részecskék kinetikus energiája és (vagy) impulzusa a kondenzált közegek atomjaival
Néhány szó a neutronról Különböző részecskék, úgymint fotonok, neutronok, elektronok és más, töltéssel rendelkező vagy semleges részecskék kinetikus energiája és (vagy) impulzusa a kondenzált közegek atomjaival
1. Prefix jelentések. 2. Mi alapján definiáljuk az 1 másodpercet? 3. Mi alapján definiáljuk az 1 métert? 4. Mi a tömegegység definíciója?
 1. Prefix jelentések. 10 1 deka 10-1 deci 10 2 hektó 10-2 centi 10 3 kiló 10-3 milli 10 6 mega 10-6 mikró 10 9 giga 10-9 nano 10 12 tera 10-12 piko 10 15 peta 10-15 fento 10 18 exa 10-18 atto 2. Mi alapján
1. Prefix jelentések. 10 1 deka 10-1 deci 10 2 hektó 10-2 centi 10 3 kiló 10-3 milli 10 6 mega 10-6 mikró 10 9 giga 10-9 nano 10 12 tera 10-12 piko 10 15 peta 10-15 fento 10 18 exa 10-18 atto 2. Mi alapján
Az elektromágneses spektrum
 IR Az elektromágneses spektrum V Hamis színes felvételek Elektromágnes hullámok Jellemzők: Amplitúdó Hullámhossz E ~ A 2 / λ 2 Információ ~ 1/λ UV Összeállította: Juhász Tibor 2008 Függ a közegtől Légüres
IR Az elektromágneses spektrum V Hamis színes felvételek Elektromágnes hullámok Jellemzők: Amplitúdó Hullámhossz E ~ A 2 / λ 2 Információ ~ 1/λ UV Összeállította: Juhász Tibor 2008 Függ a közegtől Légüres
Javító és felrakó hegesztés
 Budapesti Műszaki és Gazdaságtudományi Egyetem Javító és felrakó hegesztés Dr. Palotás Béla Mechanikai Technológia és Anyagszerkezettani Tanszék Szerző: dr. Palotás Béla 1 Felületi rétegek tulajdonságainak
Budapesti Műszaki és Gazdaságtudományi Egyetem Javító és felrakó hegesztés Dr. Palotás Béla Mechanikai Technológia és Anyagszerkezettani Tanszék Szerző: dr. Palotás Béla 1 Felületi rétegek tulajdonságainak
Száloptika, endoszkópok
 Száloptika, endoszkópok Optikai mikroszkópok a diagnosztikában Elektronmikroszkópia, fluorescens és konfokális mikroszkópia PTE-ÁOK Biofizikai ntézet Czimbalek Lívia 2009.03.16. Száloptika, endoszkópok
Száloptika, endoszkópok Optikai mikroszkópok a diagnosztikában Elektronmikroszkópia, fluorescens és konfokális mikroszkópia PTE-ÁOK Biofizikai ntézet Czimbalek Lívia 2009.03.16. Száloptika, endoszkópok
7. elıadás KRISTÁLYFIZIKAI ALAPOK
 7. elıadás KRISTÁLYFIZIKAI ALAPOK ANIZOTRÓPIA IZOTRÓPIA FOGALMA Izotrópia (irányok szerint egyenlı): a fizikai sajátságok függetlenek az iránytól. Ide tartoznak a köbös rendszerben kristályosodó kristályok.
7. elıadás KRISTÁLYFIZIKAI ALAPOK ANIZOTRÓPIA IZOTRÓPIA FOGALMA Izotrópia (irányok szerint egyenlı): a fizikai sajátságok függetlenek az iránytól. Ide tartoznak a köbös rendszerben kristályosodó kristályok.
2. Melyik az, az elem, amelynek harmadik leggyakoribb izotópjában kétszer annyi neutron van, mint proton?
 GYAKORLÓ FELADATOK 1. Számítsd ki egyetlen szénatom tömegét! 2. Melyik az, az elem, amelynek harmadik leggyakoribb izotópjában kétszer annyi neutron van, mint proton? 3. Mi történik, ha megváltozik egy
GYAKORLÓ FELADATOK 1. Számítsd ki egyetlen szénatom tömegét! 2. Melyik az, az elem, amelynek harmadik leggyakoribb izotópjában kétszer annyi neutron van, mint proton? 3. Mi történik, ha megváltozik egy
BŐVÍTETT TEMATIKA a Kondenzált anyagok fizikája c. tárgyhoz
 BŐVÍTETT TEMATIKA a Kondenzált anyagok fizikája c. tárgyhoz Az anyag szerveződési formái Ebben a részben bemutatjuk az anyag elemi építőköveinek sokszerű kapcsolódási formáit, amelyek makroszkopikusan
BŐVÍTETT TEMATIKA a Kondenzált anyagok fizikája c. tárgyhoz Az anyag szerveződési formái Ebben a részben bemutatjuk az anyag elemi építőköveinek sokszerű kapcsolódási formáit, amelyek makroszkopikusan
Mikrohullámok vizsgálata. x o
 Mikrohullámok vizsgálata Elméleti alapok: Hullámjelenségen valamilyen rezgésállapot (zavar) térbeli tovaterjedését értjük. A hullám c terjedési sebességét a hullámhossz és a T rezgésido, illetve az f frekvencia
Mikrohullámok vizsgálata Elméleti alapok: Hullámjelenségen valamilyen rezgésállapot (zavar) térbeli tovaterjedését értjük. A hullám c terjedési sebességét a hullámhossz és a T rezgésido, illetve az f frekvencia
Anyagszerkezettan és anyagvizsgálat (BMEGEMTAGK1)
 Segédlet az Anyagszerkezettan és anyagvizsgálat (BMEGEMTAGK1) tárgy hallgatói számára Készítette a BME Anyagtudomány és Technológia Tanszék Munkaközössége Összeállította: dr. Orbulov Imre Norbert 1 Laborgyakorlatok
Segédlet az Anyagszerkezettan és anyagvizsgálat (BMEGEMTAGK1) tárgy hallgatói számára Készítette a BME Anyagtudomány és Technológia Tanszék Munkaközössége Összeállította: dr. Orbulov Imre Norbert 1 Laborgyakorlatok
Hősugárzás Hővédő fóliák
 Hősugárzás Hővédő fóliák Szikra Csaba Épületenergetikai és Épületgépészeti Tanszék Építészmérnöki Kar Budapesti Műszaki és Gazdaságtudományi Egyetem A sugárzás alaptörvényei A az érkező energia E=A+T+R
Hősugárzás Hővédő fóliák Szikra Csaba Épületenergetikai és Épületgépészeti Tanszék Építészmérnöki Kar Budapesti Műszaki és Gazdaságtudományi Egyetem A sugárzás alaptörvényei A az érkező energia E=A+T+R
Elektromágneses hullámok, a fény
 Elektromágneses hullámok, a fény Az elektromos töltéssel rendelkező testeknek a töltésük miatt fellépő kölcsönhatását az elektromos és mágneses tér segítségével írhatjuk le. A kölcsönhatás úgy működik,
Elektromágneses hullámok, a fény Az elektromos töltéssel rendelkező testeknek a töltésük miatt fellépő kölcsönhatását az elektromos és mágneses tér segítségével írhatjuk le. A kölcsönhatás úgy működik,
1. Atomspektroszkópia
 1. Atomspektroszkópia 1.1. Bevezetés Az atomspektroszkópia az optikai spektroszkópiai módszerek csoportjába tartozó olyan analitikai eljárás, mellyel az anyagok elemi összetételét határozhatjuk meg. Az
1. Atomspektroszkópia 1.1. Bevezetés Az atomspektroszkópia az optikai spektroszkópiai módszerek csoportjába tartozó olyan analitikai eljárás, mellyel az anyagok elemi összetételét határozhatjuk meg. Az
Model AX-7531. Használati útmutató A B C. FIGYELEM: Ez a használati útmutató három különféle modellt ismertet, a modellek jelölései A, B és C.
 Model AX-7531 FIGYELEM: Ez a használati útmutató három különféle modellt ismertet, a modellek jelölései A, B és C. A B C Szabályozható emisszióérték Hőmérséklet riasztás Használati útmutató Tartalomjegyzék
Model AX-7531 FIGYELEM: Ez a használati útmutató három különféle modellt ismertet, a modellek jelölései A, B és C. A B C Szabályozható emisszióérték Hőmérséklet riasztás Használati útmutató Tartalomjegyzék
Modern Fizika Labor. Értékelés: A mérés dátuma: A mérés száma és címe: 2005.10.05. A Zeeman-effektus. A beadás dátuma: A mérést végezte:
 Modern Fizika Labor A mérés dátuma: 005.10.05. A mérés száma és címe: 6. A Zeeman-effektus Értékelés: A beadás dátuma: 005.10.1. A mérést végezte: Orosz Katalin Tóth Bence 1 Az atomok mágneses momentuma
Modern Fizika Labor A mérés dátuma: 005.10.05. A mérés száma és címe: 6. A Zeeman-effektus Értékelés: A beadás dátuma: 005.10.1. A mérést végezte: Orosz Katalin Tóth Bence 1 Az atomok mágneses momentuma
BIOFIZIKA. Metodika- 4. Liliom Károly. MTA TTK Enzimológiai Intézet liliom@enzim.hu
 BIOFIZIKA 2012 11 26 Metodika- 4 Liliom Károly MTA TTK Enzimológiai Intézet liliom@enzim.hu A biofizika előadások temamkája 1. 09-03 Biofizika: fizikai szemlélet, modellalkotás, biometria 2. 09-10 SZÜNET
BIOFIZIKA 2012 11 26 Metodika- 4 Liliom Károly MTA TTK Enzimológiai Intézet liliom@enzim.hu A biofizika előadások temamkája 1. 09-03 Biofizika: fizikai szemlélet, modellalkotás, biometria 2. 09-10 SZÜNET
Elektromágneses hullámok - Hullámoptika
 Bevezetés a modern fizika fejezeteibe 2. (c) Elektromágneses hullámok - Hullámoptika Utolsó módosítás: 2015. január 17. 1 Az elektromágneses hullámok visszaverődési és törési törvényei (1) Kérdés: Mi történik
Bevezetés a modern fizika fejezeteibe 2. (c) Elektromágneses hullámok - Hullámoptika Utolsó módosítás: 2015. január 17. 1 Az elektromágneses hullámok visszaverődési és törési törvényei (1) Kérdés: Mi történik
Téma: A szerkezeti acélanyagok fajtái, jelölésük. Mechanikai tulajdonságok. Acélszerkezeti termékek. Keresztmetszeti jellemzők számítása
 1. gakorlat: Téma: A szerkezeti acélanagok fajtái, jelölésük. echanikai tulajdonságok. Acélszerkezeti termékek. Keresztmetszeti jellemzők számítása A szerkezeti acélanagok fajtái, jelölésük: Ádán Dulácska-Dunai-Fernezeli-Horváth:
1. gakorlat: Téma: A szerkezeti acélanagok fajtái, jelölésük. echanikai tulajdonságok. Acélszerkezeti termékek. Keresztmetszeti jellemzők számítása A szerkezeti acélanagok fajtái, jelölésük: Ádán Dulácska-Dunai-Fernezeli-Horváth:
B2. A FÉNY FOGALMA, FÉNYJELENSÉGEK ISMERTETÉSE,
 B2. A FÉNY FOGALMA, FÉNYJELENSÉGEK ISMERTETÉSE, FÉNYVISSZAVERŐDÉS, FÉNYTÖRÉS, FÉNYINTERFERENCIA, FÉNYPOLARIZÁCIÓ, FÉNYELHAJLÁS Fény: elektromágneses sugárzás (Einstein meghatározása, hogy idesorolta a
B2. A FÉNY FOGALMA, FÉNYJELENSÉGEK ISMERTETÉSE, FÉNYVISSZAVERŐDÉS, FÉNYTÖRÉS, FÉNYINTERFERENCIA, FÉNYPOLARIZÁCIÓ, FÉNYELHAJLÁS Fény: elektromágneses sugárzás (Einstein meghatározása, hogy idesorolta a
Az elemeket 3 csoportba osztjuk: Félfémek vagy átmeneti fémek nemfémek. fémek
 Kémiai kötések Az elemeket 3 csoportba osztjuk: Félfémek vagy átmeneti fémek nemfémek fémek Fémek Szürke színűek, kivétel a színesfémek: arany,réz. Szilárd halmazállapotúak, kivétel a higany. Vezetik az
Kémiai kötések Az elemeket 3 csoportba osztjuk: Félfémek vagy átmeneti fémek nemfémek fémek Fémek Szürke színűek, kivétel a színesfémek: arany,réz. Szilárd halmazállapotúak, kivétel a higany. Vezetik az
SPEKTROFOTOMETRIAI MÉRÉSEK
 SPEKTROFOTOMETRIAI MÉRÉSEK Elméleti bevezetés Ha egy anyagot a kezünkbe veszünk (valamilyen technológiai céllal alkalmazni szeretnénk), elsı kérdésünk valószínőleg az lesz, hogy mi ez az anyag, milyen
SPEKTROFOTOMETRIAI MÉRÉSEK Elméleti bevezetés Ha egy anyagot a kezünkbe veszünk (valamilyen technológiai céllal alkalmazni szeretnénk), elsı kérdésünk valószínőleg az lesz, hogy mi ez az anyag, milyen
DIPLOMAMUNKA. Óriás mágneses ellenállás Ni-Cu/Cu multirétegekben. Becsei Tamás V. fizikushallgató (ELTE TTK)
 DIPLOMAMUNKA Óriás mágneses ellenállás Ni-Cu/Cu multirétegekben Becsei Tamás V. fizikushallgató (ELTE TTK) Témavezető: Dr.Bakonyi Imre tud. osztályvezető Hely: MTA SZFKI Fémkutatási Osztály Budapest, 1996.
DIPLOMAMUNKA Óriás mágneses ellenállás Ni-Cu/Cu multirétegekben Becsei Tamás V. fizikushallgató (ELTE TTK) Témavezető: Dr.Bakonyi Imre tud. osztályvezető Hely: MTA SZFKI Fémkutatási Osztály Budapest, 1996.
Fény kölcsönhatása az anyaggal:
 Fény kölcsönhatása az Fény kölcsönhatása az : szórás, abszorpció, emisszió Kellermayer Miklós Fényszórás A fényszórás mérése, orvosi alkalmazásai Lord Rayleigh (1842-1919) J 0 Light Fényforrás source Rayleigh
Fény kölcsönhatása az Fény kölcsönhatása az : szórás, abszorpció, emisszió Kellermayer Miklós Fényszórás A fényszórás mérése, orvosi alkalmazásai Lord Rayleigh (1842-1919) J 0 Light Fényforrás source Rayleigh
Gerhátné Udvary Eszter
 Az optikai hálózatok alapjai (BMEVIHVJV71) Moduláció 2014.02.25. Gerhátné Udvary Eszter udvary@mht.bme.hu Budapest University of Technology and Economics Department of Broadband Infocommunication Systems
Az optikai hálózatok alapjai (BMEVIHVJV71) Moduláció 2014.02.25. Gerhátné Udvary Eszter udvary@mht.bme.hu Budapest University of Technology and Economics Department of Broadband Infocommunication Systems
NEUTRON-DETEKTOROK VIZSGÁLATA. Mérési útmutató BME NTI 1997
 NEUTRON-DETEKTOROK VIZSGÁLATA Mérési útmutató Gyurkócza Csaba, Balázs László BME NTI 1997 Tartalomjegyzék 1. Bevezetés 3. 2. Elméleti összefoglalás 3. 2.1. A neutrondetektoroknál alkalmazható legfontosabb
NEUTRON-DETEKTOROK VIZSGÁLATA Mérési útmutató Gyurkócza Csaba, Balázs László BME NTI 1997 Tartalomjegyzék 1. Bevezetés 3. 2. Elméleti összefoglalás 3. 2.1. A neutrondetektoroknál alkalmazható legfontosabb
Kondenzátorok. Fizikai alapok
 Kondenzátorok Fizikai alapok A kapacitás A kondenzátorok a kapacitás áramköri elemet megvalósító alkatrészek. Ha a kondenzátorra feszültséget kapcsolunk, feltöltődik. Egyenfeszültség esetén a lemezeken
Kondenzátorok Fizikai alapok A kapacitás A kondenzátorok a kapacitás áramköri elemet megvalósító alkatrészek. Ha a kondenzátorra feszültséget kapcsolunk, feltöltődik. Egyenfeszültség esetén a lemezeken
FORGÁCSOLÓ SZERSZÁMOK, SZERSZÁM- ÉS SEGÉDANYAGOK
 GYÁRTÁSTECHNOLÓGIA NGB_AJ008_1 Műszaki menedzser (BSc) szak, Mechatronikai mérnöki (BSc) szak, SZERSZÁM- ÉS SEGÉDANYAGOK Előadás Összeállította: , SZERSZÁM- ÉS SEGÉDANYAGOK 1. Szerszámok osztályozása 2.
GYÁRTÁSTECHNOLÓGIA NGB_AJ008_1 Műszaki menedzser (BSc) szak, Mechatronikai mérnöki (BSc) szak, SZERSZÁM- ÉS SEGÉDANYAGOK Előadás Összeállította: , SZERSZÁM- ÉS SEGÉDANYAGOK 1. Szerszámok osztályozása 2.
Kötő- és rögzítőtechnológiák
 Kötő- és rögzítőtechnológiák Szilárd anyagok illeszkedő felületük mentén külső (fizikai eredetű) vagy belső (kémiai eredetű) erővel köthetők össze. Külső erőnek az anyagok darabjait összefogó, összeszorító
Kötő- és rögzítőtechnológiák Szilárd anyagok illeszkedő felületük mentén külső (fizikai eredetű) vagy belső (kémiai eredetű) erővel köthetők össze. Külső erőnek az anyagok darabjait összefogó, összeszorító
OSZTÁLYOZÓ VIZSGA TÉMAKÖREI
 OSZTÁLYOZÓ VIZSGA TÉMAKÖREI Az anyag néhány tulajdonsága, kölcsönhatások Fizika - 7. évfolyam 1. Az anyag belső szerkezete légnemű, folyékony és szilárd halmazállapotban 2. A testek mérhető tulajdonságai
OSZTÁLYOZÓ VIZSGA TÉMAKÖREI Az anyag néhány tulajdonsága, kölcsönhatások Fizika - 7. évfolyam 1. Az anyag belső szerkezete légnemű, folyékony és szilárd halmazállapotban 2. A testek mérhető tulajdonságai
FIZIKA Tananyag a tehetséges gyerekek oktatásához
 HURO/1001/138/.3.1 THNB FIZIKA Tananyag a tehetséges gyerekek oktatásához Készült A tehetség nem ismer határokat HURO/1001/138/.3.1 című projekt keretén belül, melynek finanszírozása a Magyarország-Románia
HURO/1001/138/.3.1 THNB FIZIKA Tananyag a tehetséges gyerekek oktatásához Készült A tehetség nem ismer határokat HURO/1001/138/.3.1 című projekt keretén belül, melynek finanszírozása a Magyarország-Románia
Geometriai optika. A fénytan (optika) a fényjelenségekkel és a fény terjedési törvényeivel foglalkozik.
 Geometriai optika A fénytan (optika) a fényjelenségekkel és a fény terjedési törvényeivel foglalkozik. A geometriai optika egyszerű modell, amely a fény terjedését a fényforrásból minden irányba kilépő
Geometriai optika A fénytan (optika) a fényjelenségekkel és a fény terjedési törvényeivel foglalkozik. A geometriai optika egyszerű modell, amely a fény terjedését a fényforrásból minden irányba kilépő
2. tétel. 1. Nemfémes szerkezeti anyagok: szerves ( polimer ) szervetlen ( kerámiák ) természetes, mesterséges ( műanyag )
 2. tétel - A nemfémes szerkezeti anyagok tulajdonságai, felhasználásuk. - Vasfémek és ötvözeteik, tulajdonságaik, alkalmazásuk. - A könnyűfémek fajtái és jellemzői, ötvözése, alkalmazása. - A színesfémek
2. tétel - A nemfémes szerkezeti anyagok tulajdonságai, felhasználásuk. - Vasfémek és ötvözeteik, tulajdonságaik, alkalmazásuk. - A könnyűfémek fajtái és jellemzői, ötvözése, alkalmazása. - A színesfémek
Fémes szerkezeti anyagok
 Fémek felosztása: Fémes szerkezeti anyagok periódusos rendszerben elfoglalt helyük alapján, sűrűségük alapján: - könnyű fémek, ha ρ 4,5 kg/ dm 3. olvadáspont alapján:
Fémek felosztása: Fémes szerkezeti anyagok periódusos rendszerben elfoglalt helyük alapján, sűrűségük alapján: - könnyű fémek, ha ρ 4,5 kg/ dm 3. olvadáspont alapján:
Modern műszeres analitika számolási gyakorlat Galbács Gábor
 Modern műszeres analitika számolási gyakorlat Galbács Gábor Feladatok a mintavétel, spektroszkópia és automatikus tik analizátorok témakörökből ökből AZ EXTRAKCIÓS MÓDSZEREK Alapfogalmak megoszlási állandó:
Modern műszeres analitika számolási gyakorlat Galbács Gábor Feladatok a mintavétel, spektroszkópia és automatikus tik analizátorok témakörökből ökből AZ EXTRAKCIÓS MÓDSZEREK Alapfogalmak megoszlási állandó:
Kémiai fizikai alapok I. Vízminőség, vízvédelem 2009-2010. tavasz
 Kémiai fizikai alapok I. Vízminőség, vízvédelem 2009-2010. tavasz 1. A vízmolekula szerkezete Elektronegativitás, polaritás, másodlagos kötések 2. Fizikai tulajdonságok a) Szerkezetből adódó különleges
Kémiai fizikai alapok I. Vízminőség, vízvédelem 2009-2010. tavasz 1. A vízmolekula szerkezete Elektronegativitás, polaritás, másodlagos kötések 2. Fizikai tulajdonságok a) Szerkezetből adódó különleges
Részecskék hullámtermészete
 Részecskék ullámtermészete Bevezetés A sugárzás és az anyag egyaránt mutat részecskejellegű és ullámjellegű tulajdonságokat. Atommodellek A Tomson modell J.J. Tomson 1898 A negatív töltésű elektronok pozitív
Részecskék ullámtermészete Bevezetés A sugárzás és az anyag egyaránt mutat részecskejellegű és ullámjellegű tulajdonságokat. Atommodellek A Tomson modell J.J. Tomson 1898 A negatív töltésű elektronok pozitív
Környezetvédelmi mérések fotoakusztikus FTIR műszerrel
 Környezetvédelmi mérések fotoakusztikus FTIR műszerrel A légszennyezés mérése nem könnyű méréstechnikai feladat. Az eszközök széles skáláját fejlesztették ki, hagyományosan az emissziómérésre, ezen belül
Környezetvédelmi mérések fotoakusztikus FTIR műszerrel A légszennyezés mérése nem könnyű méréstechnikai feladat. Az eszközök széles skáláját fejlesztették ki, hagyományosan az emissziómérésre, ezen belül
1. táblázat. Szórt bevonatokhoz használható fémek és kerámiaanyagok jellemzői
 5.3.1. Termikus szórási eljárások általános jellemzése Termikus szóráskor a por, granulátum, pálca vagy huzal formájában adagolt hozag (1 és 2. táblázatok) részleges vagy teljes megolvasztásával és így
5.3.1. Termikus szórási eljárások általános jellemzése Termikus szóráskor a por, granulátum, pálca vagy huzal formájában adagolt hozag (1 és 2. táblázatok) részleges vagy teljes megolvasztásával és így
Magnetorezisztív jelenségek vizsgálata mágneses nanoszerkezetekben
 Magnetorezisztív jelenségek vizsgálata mágneses nanoszerkezetekben Jól ismert, hogy az elektronok az elektromos töltés mellett spinnel is rendelkeznek, mely számos érdekes jelenséget, többek között bizonyos
Magnetorezisztív jelenségek vizsgálata mágneses nanoszerkezetekben Jól ismert, hogy az elektronok az elektromos töltés mellett spinnel is rendelkeznek, mely számos érdekes jelenséget, többek között bizonyos
VILLAMOS ÉS MÁGNESES TÉR
 ELEKTRONIKI TECHNIKUS KÉPZÉS 3 VILLMOS ÉS MÁGNESES TÉR ÖSSZEÁLLÍTOTT NGY LÁSZLÓ MÉRNÖKTNÁR - - Tartalomjegyzék villamos tér...3 kondenzátor...6 Kondenzátorok fontosabb típusai és felépítésük...7 Kondenzátorok
ELEKTRONIKI TECHNIKUS KÉPZÉS 3 VILLMOS ÉS MÁGNESES TÉR ÖSSZEÁLLÍTOTT NGY LÁSZLÓ MÉRNÖKTNÁR - - Tartalomjegyzék villamos tér...3 kondenzátor...6 Kondenzátorok fontosabb típusai és felépítésük...7 Kondenzátorok
INTERFERENCIA - ÓRAI JEGYZET
 FZKA BSc,. évfolya /. félév, Optika tárgy TERFERECA - ÓRA JEGYZET (Erdei Gábor, Ph.D., 8. AJÁLOTT SZAKRODALOM: ALAPFOGALMAK Klei-Furtak, Optics Richter, Bevezetés a oder optikába Bor-Wolf, Priciples of
FZKA BSc,. évfolya /. félév, Optika tárgy TERFERECA - ÓRA JEGYZET (Erdei Gábor, Ph.D., 8. AJÁLOTT SZAKRODALOM: ALAPFOGALMAK Klei-Furtak, Optics Richter, Bevezetés a oder optikába Bor-Wolf, Priciples of
1. Ha két közeg határfelületén nem folyik vezetési áram, a mágneses térerősség vektorának a(z). komponense folytonos.
 Az alábbi kiskérdéseket a korábbi Pacher-féle vizsgasorokból és zh-kból gyűjtöttük ki. A többségnek a lefényképezett hivatalos megoldás volt a forrása (néha még ezt is óvatosan kellett kezelni, mert egy
Az alábbi kiskérdéseket a korábbi Pacher-féle vizsgasorokból és zh-kból gyűjtöttük ki. A többségnek a lefényképezett hivatalos megoldás volt a forrása (néha még ezt is óvatosan kellett kezelni, mert egy
9. Radioaktív sugárzás mérése Geiger-Müller-csővel. Preparátum helyének meghatározása. Aktivitás mérés.
 9. Radioaktív sugárzás mérése Geiger-Müller-csővel. Preparátum helyének meghatározása. ktivitás mérés. MÉRÉS CÉLJ: Megismerkedni a radioaktív sugárzás jellemzésére szolgáló mértékegységekkel, és a sugárzás
9. Radioaktív sugárzás mérése Geiger-Müller-csővel. Preparátum helyének meghatározása. ktivitás mérés. MÉRÉS CÉLJ: Megismerkedni a radioaktív sugárzás jellemzésére szolgáló mértékegységekkel, és a sugárzás
 Név:............................ Helység / iskola:............................ Beküldési határidő: Kémia tanár neve:........................... 2013.feb.18. TAKÁCS CSABA KÉMIA EMLÉKVERSENY, IX. osztály,
Név:............................ Helység / iskola:............................ Beküldési határidő: Kémia tanár neve:........................... 2013.feb.18. TAKÁCS CSABA KÉMIA EMLÉKVERSENY, IX. osztály,
Atomfizikai összefoglaló: radioaktív bomlás. Varga József. Debreceni Egyetem OEC Nukleáris Medicina Intézet 2010. 2. Kötési energia (MeV) Tömegszám
 Egy nukleonra jutó kötési energia Atomfizikai összefoglaló: radioaktív bomlás Varga József Debreceni Egyetem OEC Nukleáris Medicina Intézet Kötési energia (MeV) Tömegszám 1. 1. Áttekintés: atomfizika Varga
Egy nukleonra jutó kötési energia Atomfizikai összefoglaló: radioaktív bomlás Varga József Debreceni Egyetem OEC Nukleáris Medicina Intézet Kötési energia (MeV) Tömegszám 1. 1. Áttekintés: atomfizika Varga
Hibrid mágneses szerkezetek
 Zárójelentés Hibrid mágneses szerkezetek OTKA T046267 Négy és fél év időtartamú pályázatunkban két fő témakörben végeztünk intenzív elméleti kutatásokat: (A) Mágneses nanostruktúrák ab initio szintű vizsgálata
Zárójelentés Hibrid mágneses szerkezetek OTKA T046267 Négy és fél év időtartamú pályázatunkban két fő témakörben végeztünk intenzív elméleti kutatásokat: (A) Mágneses nanostruktúrák ab initio szintű vizsgálata
RÖNTGEN-FLUORESZCENCIA ANALÍZIS
 RÖNTGEN-FLUORESZCENCIA ANALÍZIS 1. Mire jó a röntgen-fluoreszcencia analízis? A röntgen-fluoreszcencia analízis (RFA vagy angolul XRF) roncsolás-mentes atomfizikai anyagvizsgálati módszer. Rövid idõ alatt
RÖNTGEN-FLUORESZCENCIA ANALÍZIS 1. Mire jó a röntgen-fluoreszcencia analízis? A röntgen-fluoreszcencia analízis (RFA vagy angolul XRF) roncsolás-mentes atomfizikai anyagvizsgálati módszer. Rövid idõ alatt
A HÚZÓSOK NYOMTASSÁK KI ÉS HOZZÁK MAGUKKAL A RÁJUK VONATKOZÓ TÉTELEKET. A KIHÚZOTT TÉTELT (CSAK AZT) MAGUKNÁL TARTHATJÁK A FELKÉSZÜLÉS ALATT.
 T&T tematika & tételek A magkémia alapjai, kv1n1mg1 (A) A magkémia alapjai tárgykiegészítés, kv1n1mgx (X) című, ill. kódú integrált előadáshoz http://www.chem.elte.hu/sandor.nagy/okt/amka/index.html Bevezető
T&T tematika & tételek A magkémia alapjai, kv1n1mg1 (A) A magkémia alapjai tárgykiegészítés, kv1n1mgx (X) című, ill. kódú integrált előadáshoz http://www.chem.elte.hu/sandor.nagy/okt/amka/index.html Bevezető
Biofizika tesztkérdések
 Biofizika tesztkérdések Egyszerű választás E kérdéstípusban A, B,...-vel jelölt lehetőségek szerepelnek, melyek közül az egyetlen megfelelőt kell kiválasztani. A választ írja a kérdés előtt lévő kockába!
Biofizika tesztkérdések Egyszerű választás E kérdéstípusban A, B,...-vel jelölt lehetőségek szerepelnek, melyek közül az egyetlen megfelelőt kell kiválasztani. A választ írja a kérdés előtt lévő kockába!
NE FELEJTSÉTEK EL BEÍRNI AZ EREDMÉNYEKET A KIJELÖLT HELYEKRE! A feladatok megoldásához szükséges kerekített értékek a következők:
 A Szerb Köztársaság Oktatási Minisztériuma Szerbiai Kémikusok Egyesülete Köztársasági verseny kémiából Kragujevac, 2008. 05. 24.. Teszt a középiskolák I. osztálya számára Név és utónév Helység és iskola
A Szerb Köztársaság Oktatási Minisztériuma Szerbiai Kémikusok Egyesülete Köztársasági verseny kémiából Kragujevac, 2008. 05. 24.. Teszt a középiskolák I. osztálya számára Név és utónév Helység és iskola
mágnes mágnesesség irányt Föld északi déli pólus mágneses megosztás influencia mágneses töltés
 MÁGNESESSÉG A mágneses sajátságok, az elektromossághoz hasonlóan, régóta megfigyelt tapasztalatok voltak, a két jelenségkör szoros kapcsolatának felismerése azonban csak mintegy két évszázaddal ezelőtt
MÁGNESESSÉG A mágneses sajátságok, az elektromossághoz hasonlóan, régóta megfigyelt tapasztalatok voltak, a két jelenségkör szoros kapcsolatának felismerése azonban csak mintegy két évszázaddal ezelőtt
Mérnöki anyagismeret. Szerkezeti anyagok
 Mérnöki anyagismeret Szerkezeti anyagok 1 Szerkezeti anyagok Fémek Vas, acél, réz és ötvözetei, könnyűfémek és ötvözeteik Műanyagok Hőre lágyuló és hőre keményedő műanyagok, elasztomerek Kerámiák Kristályos,
Mérnöki anyagismeret Szerkezeti anyagok 1 Szerkezeti anyagok Fémek Vas, acél, réz és ötvözetei, könnyűfémek és ötvözeteik Műanyagok Hőre lágyuló és hőre keményedő műanyagok, elasztomerek Kerámiák Kristályos,
Atomfizika I. Az anyagszerkezetről alkotott kép változása Ókori görög filozófusok régi kérdése: Miből vannak a testek? Meddig osztható az anyag?
 Atomfizika I. Az anyagszerkezetről alkotott kép változása Ókori görög filozófusok régi kérdése: Miből vannak a testek? Meddig osztható az anyag? Platón (i.e. 427-347), Arisztotelész (=i.e. 387-322): Végtelenségig
Atomfizika I. Az anyagszerkezetről alkotott kép változása Ókori görög filozófusok régi kérdése: Miből vannak a testek? Meddig osztható az anyag? Platón (i.e. 427-347), Arisztotelész (=i.e. 387-322): Végtelenségig
Röntgendiffrakció, tömegspektrometria, infravörös spektrometria.
 A biomolekuláris szerkezet és dinamika vizsgálómódszerei: Röntgendiffrakció, tömegspektrometria, infravörös spektrometria. Smeller László A molekuláris szerkezet és dinamika vizsgáló módszereinek áttekintése
A biomolekuláris szerkezet és dinamika vizsgálómódszerei: Röntgendiffrakció, tömegspektrometria, infravörös spektrometria. Smeller László A molekuláris szerkezet és dinamika vizsgáló módszereinek áttekintése
Energetikai minőségtanúsítvány összesítő
 Földvár Terv Kft Energetikai minőségtanúsítvány 1 Energetikai minőségtanúsítvány összesítő Épület: Megrendelő: Tanúsító: 5 lakásos társasház Paks, Kossuth Lajos utca 4. Hrsz.: 864. Viczai János GT/17-0469
Földvár Terv Kft Energetikai minőségtanúsítvány 1 Energetikai minőségtanúsítvány összesítő Épület: Megrendelő: Tanúsító: 5 lakásos társasház Paks, Kossuth Lajos utca 4. Hrsz.: 864. Viczai János GT/17-0469
