A xenonkoncentráció változásának vizsgálata homogén reaktor esetében
|
|
|
- Gusztáv Deák
- 5 évvel ezelőtt
- Látták:
Átírás
1 Tóth Zsófia A xenonkoncentráció változásának vizsgálata homogén reaktor esetében A xenonlengés a nagy beépített teljesítményű atomreaktorok egyik fontos folyamata, amely során a xenon térbeli és időbeli koncentrációja jelentős mértékben és folyamatosan változik az üzem közben. Ez a jelenség nagyban befolyásolja a reaktorok szabályozhatóságát és indíthatóságát is, így vizsgálata kiemelten fontos. A kutatás célja a reaktorüzem során kialakuló xenonkoncentráció térbeli és időbeli változásának minél pontosabb szimulációja. A probléma leírására alkalmazott modellkörnyezet az egydimenziós, időfüggő diffúzióegyenlet és a hozzá csatolt xenonmérlegegyenletből álló nemlineáris egyenletrendszer. Fő célkitűzés ennek numerikus megoldása és az általános tulajdonságainak vizsgálata. In the research work the phenomenon of xenon oscillation was examined. A coupled equation system containing the one-group, one-dimensional diffusion equation and the equations concerning the production of Xe-135 and I-135 was solved with finite difference method. The code was developed in Matlab. Kulcsszavak: Xenonlengés, atomreaktor, reaktorméreg, hatáskeresztmetszet, diffúzióegyenlet, véges differenciák 1. BEVEZETÉS, MOTIVÁCIÓ Napjainkban a világ számos országában alkalmaznak és tervezetten építenek atomerőműveket az egyre növekvő energiaigények kielégítésére. A jelenleg tervezett és beruházás alatt álló atomerőművek nagy részének beépített teljesítménye meghaladja az 1000 MW-ot. Az ilyen atomreaktor típusok egyik meghatározó folyamata a xenonlengés. A folyamat lényege, hogy a hasadás során a térben nem egyenletes eloszlással keletkező xenon izotóp (a láncreakció szempontjából erős reaktorméregnek (a maghasadás során keletkező olyan izotóp, amely befogási hatáskeresztmetszete sokkal nagyobb a fűtőanyagénál) tekinthető hasadási termék) a teljesítményszabályzás során erős instabilitásokat eredményezhet, melynek nem megfelelő kezelése a reaktor normál üzemének tekinthető állandósult (kritikus) állapot fenntartását nem biztosítja [1]. Erre jó példa a Paks II. projekt keretében tervezett új VVER-1200 blokkok esete [2], ahol a nagy teljesítményhez szükséges megnövekedett reaktorméret, ezen belül is az axiálisan nagyméretű zóna tipikusan érzékeny a nagy mennyiségben nem egyenletesen keletkező xenonkoncentráció változására. Mindezek alapján a nukleáris biztonság garantálása érdekében elengedhetetlen a xenonkoncentráció változásának nyomon követése és leírása, valamint a teljesítményre gyakorolt hatásának kompenzálása. A kutatás célja a reaktorüzem során kialakuló xenonkoncentráció térbeli és időbeli változásának minél pontosabb szimulációja. A jelenség vizsgálatához először az egydimenziós, időfüggő diffúzióegyenletet megoldó kódot, majd az ehhez csatolt xenonmérlegegyenletből álló nemlineáris egyenletrendszert megoldó programot fejlesztettem. Fő célkitűzés a jelenséget leíró differenciálegyenlet-rendszer numerikus megoldása, és a xenonlengés tulajdonságainak vizsgálata. 2. SZTATIKUS DIFFÚZIÓEGYENLET MEGOLDÁSA A kutatásom során a diffúzióegyenletet alkalmazom a probléma leírására. Ebben a fejezetben a sztatikus diffúzióegyenlet megoldását mutatom be végesdifferencia-módszerrel. 2.1 A végesdifferencia-módszer [3] A véges differenciák módszerét első lépésben az egycsoport diffúzióegyenletre alkalmazom, amely alakja homogén reaktorban az alábbi: ahol D a diffúziós állandó, a helyfüggő csoportfluxus, az átlagos neutronhozam, makroszkópikus hasadási hatáskeresztmetszet, a makroszkópikus abszorpciós hatáskeresztmetszet, a pedig az effektív sokszorozási tényező. Az egycsoport közelítésben a neutronok energiáját egyenlőnek tekintjük. A véges differenciák módszerének alkalmazásánál a vizsgált tartományt az x változó szerint tetszőleges sok kis részre osztom fel, amelyeken belül az anyagi paramétereket homogénnek tekintem, valamint az osztópontok között a fluxust is állandónak veszem. Az x koordináta szerinti első határpont indexe 1, az utolsóé n, illetve az intervallumokat a tartomány végpontájnak indexével jelelök. Ezen felosztásra példa az (i-1) és (i+1) tartományon az 1.ábrán található. (1) a
2 1. Ábra. Az (i-1)-(i+1) tartomány felosztása a véges differenciák módszerénél Az első egyenletet a tartományon integrálva az egyenletben szereplő tagok véges differenciákkal közelített alakjai az alábbiak szerint írhatóak fel: (2), (3). (4) Az átlagos neutronhozamot állandónak tekintem minden tartományban, mert változása olyan kismértékű, hogy ez megtehető. Így a stacioner diffúzióegyenlet véges differenciákkal közelített alakja az i-edik osztópontra:,. (11) A kapott egyenlet megoldásához iterációt kell alkalmazni, amelyet külső- vagy forrásiterációnak nevezünk. 2.2 Forrásiteráció direkt inverz számítással [4] A forrásiteráció során először a forrástagot állandónak véve számítom ki a fluxust, amit egy speciális egyes norma segítségével normálok (amely az iteráció során tart az effektív sokszorozási tényezőhöz), hogy biztosítva legyen az iteráció konvergenciája. A forráiteráció során számítódik így ki az effektív sokszorozási tényező is. Az iteráció akkor ér véget, hogyha két egymás utáni iterációban kapott effektív sokszorozási tényezők relatív különbsége egy megadott hiba alá csökken. Az iteráció folyamatábrája a 2. ábrán látható. A megoldás egyszerűsítése érdekében érdemes vektor, illetve mátrix alakban felírni az osztópontokban értelmezett fluxust, illetve szorzótényezőit, így az (5)-ös egyenlet az alábbi alakra egyszerűsödik: ahol (5) (6), (7), és (8) (9). A (6)-os egyenletet mátrix alakba rendezve a fluxusvektor az alábbi összefüggéssel számítható ki: Ahol az A mátrix: (10) 2. Ábra. A forrásiteráció folyamatábrája A módszerrel könnyen lehet megoldani az egyenletet, viszont nagyobb méretű mátrixok alkalmazása esetén megnő a numerikus hiba értéke a mátrixinverzió pontatlansága miatt. Bár a Matlab a mátrixinverziót iterálással oldja meg, megkíséreltem egy új iterációs eljárással megoldani az egyenletet a mátrixinverzió helyett, hogy növeljem a számítások pontosságát. Ezt a metódust a következő pontban mutatom be.
3 2.3 Forrásiteráció belső iterációval [4] A belső iteráció alkalmazásához definiálom a B mátrixot, amelynek értéke:. (12). Ezzel a fluxusvektor mátrixegyenlettel felírva és véges differenciákat alkalmazva az alábbi egyenletet kapom: ahol (14)., (13), Így a belső iteráció folyamatábrája a 3. ábrán látható. 1. Táblázat. Az effektív sokszorozási tényezők értékei és relatív eltérésük a kétféle módszert alkalmazva Osztópontok száma Forrásiteráció Belső iteráció Relatív eltérés (pcm) 10 1, , ,11E , , ,77E , , ,51E , , ,22E , , ,26E , , ,50E-01 A vizsgálatot 100 osztópontig végeztem el, mivel az effektív sokszorozási tényező ezen osztásköz felett már csak elenyészően kis mértékben változik egy osztásközön belül. Mindkét esetben 100 osztópont esetében az effektív sokszorozási tényező eltérése az analitikusan számítotthoz képest 0,34%-on belül tér el, így mindkét programot helyesnek ítélem meg. 3. AZ IDŐFÜGGŐ DIFFÚZIÓEGYENLET MEGOLDÁSA A következő lépésben az instacioner diffúzióegyenlet megoldására készítettem egy programot. 3.1 Az időfüggő megoldás bemutatása [1] A vizsgált egyenlet ebben az esetben: (15) A megoldási módszer az instacioner esetben is a végesdifferenciák módszerével történik. Az egyenlet bal oldali véges differenciákkal az alábbiak szerint írható fel: (16) Ha a jobb oldalra alkalmazva az (5)-ös egyenletet, a (14)-es egyenlet véges differenciákkal felírt alakja az alábbi: 3. Ábra. A belső iteráció folyamatábrája 2.4 Numerikus tesztelés A kódom pontosságát egy kritikus, egydimenziós reaktor adataival teszteltem le Szatmári Zoltán Reaktorfizikai számítások című könyvében található példa alapján. Erre az esetre a kétféle megoldási módszerrel kapott effektív sokszorozási tényezők értékeit különböző osztópontszámokra az első táblázat tartalmazza. (17) A hely szerint a fluxus komponenseit vektorba tudom rendezni, így egy mátrixegyenletté egyszerűsödik a kifejezés: (18)
4 ahol amelynek paramétereit az alábbiak szerint határozom meg: (24) (19). Ezek után időbeli diszkretizációt is végrehajtok és kicsiny időintervallumokra osztom fel a teljes időtartományt. Az osztópontokat ekkor p indexszel jelölöm. A megoldást előremutató (implicit) sémát használva tudom megkapni az alábbi egyenleteket használva: 4.2 A késő neutronok hatása a fluxusra (25) A késő neutronok hatásának tanulmányozására megvizsgáltam egy enyhén szuperkritikus rendszer fluxusának időfüggését késő neutronokat elhanyagoló és figyelembe vevő esetben, amit a következő grafikonon ábrázoltam. (20) (21). 4. KÉSŐ NEUTRONOKKAL KIEGÉSZÍTETT RENDSZER VIZSGÁLATA Az előző fejezetekben bemutatott rendszerek csupán a prompt neutronokat írják le, ám a reaktor szabályozása és üzemvitele szempontjából kiemelten fontos szerepe van a késő neutronoknak is [1]. Ezek a neutronok nem a hasadás pillanatában keletkeznek, hanem hasadványokmagok negatív béta-bomlása után. Emiatt nagy mértékben befolyásolják az időfüggés jellegét is, mivel keletkezési idejük sok nagyságrenddel nagyobb a prompt neutronokénál. Ugyanez teszi lehetővé a reaktor szabályozhatóságát is. 4.1 A késő neutronokra alkalmazott egyenletek bemutatása [3] A hasadványmagok bomlása következtében keletkező neutronok rendszerbe való építésénél egy újabb forrástag jelenik meg a diffúzióegyenletben, az eddigiekhez képest időben eltolva: (22), ahol a későneutron hányad, az i jelű anyamag bomlási állandója, pedig az i jelű anyamag koncentrációja. Utóbbi változását az alábbi egyenlettel tudjuk leírni: (23) A számítások gyorsítása érdekében egy átlagos késő neutron csoporttal számolok a 6 csoport helyett, 4. Ábra. A fluxus változása késő neutronok elhanyagolásával és figyelembevételével Látható, hogy a késő neutronok figyelembevételével a fluxus változása sokkal kisebb mértékű lesz a késő neutronok hosszabb megjelenési ideje miatt. 5. XENON 5.1 A xenonmérgezés és a xenonlengés folyamatának bemutatása A xenon 135-ös izotópjának befogási hatáskeresztmetszete 2,72*10 6 barn, ami négyezerszer nagyobb az urán 235-ös izotópjának ugyanezen értékénél [5]. A xenon-135 keletkezési gyakorisága is igen jelentős, 6,4% [5]. Ezen két tulajdonsága az izotópnak jelentős reaktivitáscsökkenést eredményez a zónában, így hatásával számolni kell a reaktor teljes élettartama során. A xenon a hasadás során közvetlenül is keletkezhet, illetve a tellúr-135-ből (hasadási termék) a jód-135-ön keresztül béta bomlással. A tellúr felezési ideje nagyon rövid, így azzal a feltételezéssel szoktak élni, hogy a hasadás során a jód közvetlenül keletkezik. A xenon béta negatív bomlással és neutronbefogással fogy a reaktorban. A xenon-135 egyszerűsített keletkezési és bomlási sémáját a 4. ábra mutatja. [1]
5 5.2 Az alkalmazott modell bemutatása A xenonmérgezettség leírására a diffúzióegyenletet megoldó kódhoz csatoltam a jód és xenon magok koncentrációját leíró egyenleteket, amelyek az alábbiak [7]: 5. Ábra. A xenon-135 keletkezési és bomlási sémája Amennyiben kisméretű reaktort vizsgálunk, a xenon koncentrációját tekinthetjük helytől függetlennek, csupán kis térbeli egyenlőtlenségek vannak a fluxust vizsgálva. Ugyanez nem mondható el nagyteljesítményű reaktorok esetén, ahol a neutronfluxus térbeli eloszlása széles határok között mozoghat. A xenon magok koncentrációja a fluxus változása esetében az idő függvényében az alábbiak szerint változik: (27), (26) ahol N a magsűrűséget, y a keletkezési gyakoriságot, lamba a felezési időt jelöli, míg a Xe és I indexek a xenon-135, illetve a jód-135 magokra utalnak. Ezeket az egyenleteket ugyancsak a véges differenciák módszerét alkalmazva építettem bele a megoldókódba. A xenon megjelenése miatt változik az abszorpciót leíró tag az eredeti diffúzióegyenletben, így az alábbiak szerint módosítottam azt: (28), 5. Ábra. A xenon-135 koncentrációjának változása teljesítménycsökkenés (bal) és teljesítménynövekedés (jobb) hatására [6] A xenonlengés kiváltó oka a reaktoron belüli teljesítményeloszlás inhomogenitása. Példaként, ha egy szabályozórúd elmozdítása következtében a reaktor egy részében a fluxus nő, a másik részében csökkenni fog a teljesítmény állandósága miatt. Így a reaktor két különböző részében a xenon magok koncentrációja különbözőképpen fog változni az 5. ábrán látható módon. Ennek következtében a reaktivitás a reaktor egyik felében nőni, a másikban csökkenni fog. A folyamat viszont a xenonmérgezettség szempontjából megfordul, míg a teljesítményváltozás iránya még egy darabig marad a korábbi. Amint a teljesítményváltozás iránya megváltozik, a reaktor folyamatosan visszatér az eredeti állapotába, így játszódik le egy periódusa a lengésnek. A folyamat periódusideje 30 óra körül változik. A periódusidó eltelte után a lengés kezdődik elölről, azaz a teljesítmény és a fluxus időben és térben is lengést fog végezni. Így a xenonmérgezettség vizsgálata kiemelten fontos nagyteljesítményű reaktorok esetén. ahol σ c Xe a xenon-135 mikroszkópikus befogási hatáskeresztmetszete. A megoldás során, ahogy változik a xenonkoncentráció, úgy folyamatosan felülíródik így az abszorpciót leíró tag. Kis mértékben a kifolyási tag is változik a xenon megjelenése miatt a diffúzióegyenletben, de ez elhanyagolható mértékű a kód szempontjából. Az egyenletek térbeli és időbeli diszkretizációját a 2. és 3. pontban írtak szerint végeztem el, és ezen numerikus egyenletek megoldására készítettem egy iterációs megoldó kódot. 5.3 Homogén, szimmetrikus reaktor vizsgálata a modellel A xenonkoncentráció vizsgálatánál a zóna középpontjára nézve koszinuszos eloszlást vártam. Ennek oka, hogy a sztatikus xenon mérlegegyenletet megoldva megoldásként koszinusz függvényt kapunk. A kódot lefuttatva a 6. Ábrán látható eloszlást kaptam meg, ami megfelel a várakozásainknak.
6 [2] Internetes forrás: [3] Dr. Szathmáry Zoltán: Reaktorfizikai számítások, Budapest, 2012 [4] Csengeri Eszter: A xenonlengés elméleti vizsgálata- BSc Szakdolgozat, Budapest, 2016 [5] Exfor adatbázis: [6] Dr. Czifrus Szabolcs: Atomreaktorok üzemtana előadás diasor [7] Dr. Szathmáry Zoltán: Reaktorfizika mérnököknek, Budapest, Ábra A xenon-135 koncentrációjának változása a hely függvényében különböző időpillanatokban Jól látható, hogy a xenonkoncentráció az idő előrehaladtával folyamatosan nő, ami ugyancsak megfelel az elvárásainknak. Ezekből az első futtatásokból a kódot továbbfejlesztve a jövőben lehetőség lesz nemcsak a xenonkoncentráció, de a xenonlengés vizsgálatára is homogén, illetve inhomogn reaktorokban. 6. ÖSSZEFOGALÁS, JÖVŐBENI TERVEK A munkám során sikerült felépítenem az alapoktól kezdve egy olyan diffúziós kódot, amely stacioner és instacioner esetben is képes kiszámítani a fluxust a reaktorban véges differenciák módszerének segítségével. Ehhez csatoltam a xenon és a jód magok koncentrációjának változását leíró differenciálegyenleteket megoldó kódot, amellyel vizsgálni tudtam a magok térbeli és időbeli eloszlását ugyancsak a véges differenciák módszerét alkalmazva. A jövőbeni fejlesztésekre nagyon sok lehetőség van. Célom, hogy a numerikus megoldások pontosságát növeljem a Runge-Kutta módszer alkalmazásával. Emellett szeretném vizsgálni átfogóbban a xenonmérgezettség és a xenonlengés reaktorteljesítményre gyakorolt hatását, térbeli és időbeli jellegzetességeit, illetve a befolyásoló paramétereket, ami a kód további fejlesztését is igényelni fogja. További fejlesztési lehetőségként felmerül a kódkiterjesztése egycsoportról több csoportra, ami által még pontosabban meg tudnám vizsgálni a problémakört. Emellett nagy lehetőséget rejt magában heterogén rendszerek vizsgálata is a kóddal, ami ugyancsak egy újabb területet nyitna meg a kutatási folyamatban. 7. IRODALOMJEGYZÉK [1] Dr. Csom Gyula: Atomreaktorok üzemtana, Budapest, 2005
ODE SOLVER-ek használata a MATLAB-ban
 ODE SOLVER-ek használata a MATLAB-ban Mi az az ODE? ordinary differential equation Milyen ODE megoldók vannak a MATLAB-ban? ode45, ode23, ode113, ode15s, ode23s, ode23t, ode23tb, stb. A részletes leírásuk
ODE SOLVER-ek használata a MATLAB-ban Mi az az ODE? ordinary differential equation Milyen ODE megoldók vannak a MATLAB-ban? ode45, ode23, ode113, ode15s, ode23s, ode23t, ode23tb, stb. A részletes leírásuk
Xe- és Sm-mérgezettség üzemviteli vonatkozásai
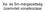 Xe- és Sm-mérgezettség üzemviteli vonatkozásai 9.1. ábra. A 135Xe abszorpciós hatáskeresztmetszetének energiafüggése 9.1. táblázat. A 135I és a 135Xe hasadásonkénti keletkezési gyakorisága különbözı hasadó
Xe- és Sm-mérgezettség üzemviteli vonatkozásai 9.1. ábra. A 135Xe abszorpciós hatáskeresztmetszetének energiafüggése 9.1. táblázat. A 135I és a 135Xe hasadásonkénti keletkezési gyakorisága különbözı hasadó
Annak a function-nak a neve, amiben letároltuk az egyenletünket.
 Function-ok a MATLAB-ban Előző óra 4. Feladata. Amikor mi egy function-t írunk, akkor azt eltárolhatjuk egy.m fileban. Ebben az esetben ha egy másik programunkból szeretnénk meghívni ezt a függvényt (pl
Function-ok a MATLAB-ban Előző óra 4. Feladata. Amikor mi egy function-t írunk, akkor azt eltárolhatjuk egy.m fileban. Ebben az esetben ha egy másik programunkból szeretnénk meghívni ezt a függvényt (pl
Perturbációk elméleti és kísérleti vizsgálata a BME Oktatóreaktorán
 Perturbációk elméleti és kísérleti vizsgálata a BME Oktatóreaktorán Horváth András, Kis Dániel Péter, Szatmáry Zoltán XV. Nukleáris Technikai Szimpózium 2016. december 8-9. Paks, Erzsébet Nagyszálloda
Perturbációk elméleti és kísérleti vizsgálata a BME Oktatóreaktorán Horváth András, Kis Dániel Péter, Szatmáry Zoltán XV. Nukleáris Technikai Szimpózium 2016. december 8-9. Paks, Erzsébet Nagyszálloda
Atomenergetikai alapismeretek
 Atomenergetikai alapismeretek 5/2. előadás: Atomreaktorok Prof. Dr. Aszódi Attila Egyetemi tanár, BME Nukleáris Technikai Intézet Budapest, 2019. március 5. Hasadás, láncreakció U-235: termikus neutronok
Atomenergetikai alapismeretek 5/2. előadás: Atomreaktorok Prof. Dr. Aszódi Attila Egyetemi tanár, BME Nukleáris Technikai Intézet Budapest, 2019. március 5. Hasadás, láncreakció U-235: termikus neutronok
Baran Ágnes, Burai Pál, Noszály Csaba. Gyakorlat Differenciálegyenletek numerikus megoldása
 Matematika Mérnököknek 2. Baran Ágnes, Burai Pál, Noszály Csaba Gyakorlat Differenciálegyenletek numerikus megoldása Baran Ágnes, Burai Pál, Noszály Csaba Matematika Mérnököknek 2. Gyakorlat 1 / 18 Fokozatos
Matematika Mérnököknek 2. Baran Ágnes, Burai Pál, Noszály Csaba Gyakorlat Differenciálegyenletek numerikus megoldása Baran Ágnes, Burai Pál, Noszály Csaba Matematika Mérnököknek 2. Gyakorlat 1 / 18 Fokozatos
Maghasadás (fisszió)
 http://www.etsy.com Maghasadás (fisszió) 1939. Hahn, Strassmann, Meitner neutronbesugárzásos kísérletei U magon új reakciótípus (maghasadás) Azóta U, Th, Pu (7 izotópja) hasadási sajátságait vizsgálták
http://www.etsy.com Maghasadás (fisszió) 1939. Hahn, Strassmann, Meitner neutronbesugárzásos kísérletei U magon új reakciótípus (maghasadás) Azóta U, Th, Pu (7 izotópja) hasadási sajátságait vizsgálták
Neutronabszorbens minták reaktivitás-értékességének meghatározása
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Nukleáris Technikai Intézet Neutronabszorbens minták reaktivitás-értékességének meghatározása Dr. Zsolnay Éva Hallgatói gyakorlat mérési útmutatója Budapest,
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Nukleáris Technikai Intézet Neutronabszorbens minták reaktivitás-értékességének meghatározása Dr. Zsolnay Éva Hallgatói gyakorlat mérési útmutatója Budapest,
Atomreaktorok üzemtana. Az üzemelő és leállított reaktor, mint sugárforrás
 Atomreaktorok üzemtana Az üzemelő és leállított reaktor, mint sugárforrás Atomreaktorban és környezetében keletkező sugárzástípusok és azok forrásai Milyen típusú sugárzások keletkeznek? Melyik ellen milyen
Atomreaktorok üzemtana Az üzemelő és leállított reaktor, mint sugárforrás Atomreaktorban és környezetében keletkező sugárzástípusok és azok forrásai Milyen típusú sugárzások keletkeznek? Melyik ellen milyen
egyenlőtlenségnek kell teljesülnie.
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Abszolútértékes és gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Abszolútértékes és gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
BIOMATEMATIKA ELŐADÁS
 BIOMATEMATIKA ELŐADÁS 6. Differenciálegyenletekről röviden Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Bevezetés 2 Elsőrendű differenciálegyenletek Definíciók Kezdetiérték-probléma
BIOMATEMATIKA ELŐADÁS 6. Differenciálegyenletekről röviden Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Bevezetés 2 Elsőrendű differenciálegyenletek Definíciók Kezdetiérték-probléma
17. Diffúzió vizsgálata
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.11.24. A beadás dátuma: 2011.12.04. A mérés száma és címe: 17. Diffúzió vizsgálata A mérést végezte: Németh Gergely Értékelés: Elméleti háttér Mi is
Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.11.24. A beadás dátuma: 2011.12.04. A mérés száma és címe: 17. Diffúzió vizsgálata A mérést végezte: Németh Gergely Értékelés: Elméleti háttér Mi is
Energetikai mérnökasszisztens Mérnökasszisztens
 A 10/07 (II. 27.) SzMM rendelettel módosított 1/06 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
A 10/07 (II. 27.) SzMM rendelettel módosított 1/06 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
Robotok inverz geometriája
 Robotok inverz geometriája. A gyakorlat célja Inverz geometriai feladatot megvalósító függvények implementálása. A megvalósított függvénycsomag tesztelése egy kétszabadságfokú kar előírt végberendezés
Robotok inverz geometriája. A gyakorlat célja Inverz geometriai feladatot megvalósító függvények implementálása. A megvalósított függvénycsomag tesztelése egy kétszabadságfokú kar előírt végberendezés
Magszintézis neutronbefogással
 Magszintézis neutronbefogással Kiss Miklós, Berze Nagy János Gimnázium Gyöngyös Magyar Fizikus Vándorgyűlés Debrecen, 2013. augusztus 21-24. Tartalom 1. A magok táblája 2. Elemgyakoriság 3. Neutrontermelés
Magszintézis neutronbefogással Kiss Miklós, Berze Nagy János Gimnázium Gyöngyös Magyar Fizikus Vándorgyűlés Debrecen, 2013. augusztus 21-24. Tartalom 1. A magok táblája 2. Elemgyakoriság 3. Neutrontermelés
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Exponenciális és Logaritmikus kifejezések
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Eponenciális és Logaritmikus kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szoálhatnak fontos információval
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Eponenciális és Logaritmikus kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szoálhatnak fontos információval
TOL A MEGYEI SZILÁRD LEÓ FIZIKAVERSE Y Szekszárd, március óra 11. osztály
 TOL A MEGYEI SZILÁRD LEÓ FIZIKAVERSE Y Szekszárd, 2002 március 13 9-12 óra 11 osztály 1 Egyatomos ideális gáz az ábrán látható folyamatot végzi A folyamat elsõ szakasza izobár folyamat, a második szakasz
TOL A MEGYEI SZILÁRD LEÓ FIZIKAVERSE Y Szekszárd, 2002 március 13 9-12 óra 11 osztály 1 Egyatomos ideális gáz az ábrán látható folyamatot végzi A folyamat elsõ szakasza izobár folyamat, a második szakasz
Numerikus módszerek I. zárthelyi dolgozat (2017/18. I., A. csoport) Megoldások
 Numerikus módszerek I. zárthelyi dolgozat (2017/18. I., A. csoport) Megoldások 1. Feladat. (6p) Jelöljön. egy tetszőleges vektornormát, ill. a hozzá tartozó indukált mátrixnormát! Igazoljuk, hogy ha A
Numerikus módszerek I. zárthelyi dolgozat (2017/18. I., A. csoport) Megoldások 1. Feladat. (6p) Jelöljön. egy tetszőleges vektornormát, ill. a hozzá tartozó indukált mátrixnormát! Igazoljuk, hogy ha A
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Exponenciális és Logaritmikus kifejezések
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Eponenciális és Logaritmikus kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Eponenciális és Logaritmikus kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos
Runge-Kutta módszerek
 Runge-Kutta módszerek A Runge-Kutta módszerek az Euler módszer továbbfejlesztésének, javításának tekinthetők, kezdeti értékkel definiált differenciál egyenletek megoldására. Előnye hogy a megoldás során
Runge-Kutta módszerek A Runge-Kutta módszerek az Euler módszer továbbfejlesztésének, javításának tekinthetők, kezdeti értékkel definiált differenciál egyenletek megoldására. Előnye hogy a megoldás során
Exponenciális és logaritmikus kifejezések Megoldások
 Eponenciális és logaritmikus kifejezések - megoldások Eponenciális és logaritmikus kifejezések Megoldások ) Igazolja, hogy az alábbi négy egyenlet közül az a) és jelű egyenletnek pontosan egy megoldása
Eponenciális és logaritmikus kifejezések - megoldások Eponenciális és logaritmikus kifejezések Megoldások ) Igazolja, hogy az alábbi négy egyenlet közül az a) és jelű egyenletnek pontosan egy megoldása
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Abszolútértékes és gyökös kifejezések
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Abszolútértékes és gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Abszolútértékes és gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzék módosításának eljárásrendjéről szóló 133/2010. (IV. 22.) Korm.
 Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzék módosításának eljárásrendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján: Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzék módosításának eljárásrendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján: Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
A teljesítménysűrűség térbeli eloszlása
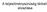 A teljesítménysűrűség térbeli eloszlása Primer és szekunder korlátok Primer korlátok Nem vagy nem feltétlenül mérhető mennyiségek Közvetlenül megadják, hogy egy feltétel teljesül-e Szekunder korlátok Mérhető
A teljesítménysűrűség térbeli eloszlása Primer és szekunder korlátok Primer korlátok Nem vagy nem feltétlenül mérhető mennyiségek Közvetlenül megadják, hogy egy feltétel teljesül-e Szekunder korlátok Mérhető
Parciális differenciálegyenletek numerikus módszerei számítógépes alkalmazásokkal Karátson, János Horváth, Róbert Izsák, Ferenc
 Karátson, János Horváth, Róbert Izsák, Ferenc numerikus módszerei számítógépes írta Karátson, János, Horváth, Róbert, és Izsák, Ferenc Publication date 2013 Szerzői jog 2013 Karátson János, Horváth Róbert,
Karátson, János Horváth, Róbert Izsák, Ferenc numerikus módszerei számítógépes írta Karátson, János, Horváth, Róbert, és Izsák, Ferenc Publication date 2013 Szerzői jog 2013 Karátson János, Horváth Róbert,
Abszolútértékes és gyökös kifejezések Megoldások
 Abszolútértékes és gyökös kifejezések Megoldások ) Igazolja, hogy az alábbi négy egyenlet közül az a) és b) jelű egyenletnek pontosan egy megoldása van, a c) és d) jelű egyenletnek viszont nincs megoldása
Abszolútértékes és gyökös kifejezések Megoldások ) Igazolja, hogy az alábbi négy egyenlet közül az a) és b) jelű egyenletnek pontosan egy megoldása van, a c) és d) jelű egyenletnek viszont nincs megoldása
MATEMATIKA HETI 5 ÓRA. IDŐPONT: 2009. június 8.
 EURÓPAI ÉRETTSÉGI 2009 MATEMATIKA HETI 5 ÓRA IDŐPONT: 2009. június 8. A VIZSGA IDŐTARTAMA: 4 óra (240 perc) ENGEDÉLYEZETT SEGÉDESZKÖZÖK : Európai képletgyűjtemény Nem programozható, nem grafikus kalkulátor
EURÓPAI ÉRETTSÉGI 2009 MATEMATIKA HETI 5 ÓRA IDŐPONT: 2009. június 8. A VIZSGA IDŐTARTAMA: 4 óra (240 perc) ENGEDÉLYEZETT SEGÉDESZKÖZÖK : Európai képletgyűjtemény Nem programozható, nem grafikus kalkulátor
Differenciálegyenletek numerikus integrálása április 9.
 Differenciálegyenletek numerikus integrálása 2018. április 9. Differenciálegyenletek Olyan egyenletek, ahol a megoldást függvény alakjában keressük az egyenletben a függvény és deriváltjai szerepelnek
Differenciálegyenletek numerikus integrálása 2018. április 9. Differenciálegyenletek Olyan egyenletek, ahol a megoldást függvény alakjában keressük az egyenletben a függvény és deriváltjai szerepelnek
Gauss-Seidel iteráció
 Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
(2) A tényezők jelentése a következő:
 REAKTOR ÜZEMELTETÉSI GYAKORLAT 1. Bevezetés Az üzemeltetési gyakorlat célja az atomreaktorban lejátszódó fizikai folyamatoknak, a reaktor felépítésének, nukleáris és technológiai berendezéseinek, valamint
REAKTOR ÜZEMELTETÉSI GYAKORLAT 1. Bevezetés Az üzemeltetési gyakorlat célja az atomreaktorban lejátszódó fizikai folyamatoknak, a reaktor felépítésének, nukleáris és technológiai berendezéseinek, valamint
DIFFERENCIAEGYENLETEK, MINT A MODELLEZÉS ESZKÖZEI AZ ISKOLAI MATEMATIKÁBAN
 DIFFERENCIAEGYENLETEK, MINT A MODELLEZÉS ESZKÖZEI AZ ISKOLAI MATEMATIKÁBAN KOVÁCS ZOLTÁN 1. Bevezetés A természeti jelenségeket sokszor differenciálegyenletekkel lehet leírni: a vizsgált mennyiség például
DIFFERENCIAEGYENLETEK, MINT A MODELLEZÉS ESZKÖZEI AZ ISKOLAI MATEMATIKÁBAN KOVÁCS ZOLTÁN 1. Bevezetés A természeti jelenségeket sokszor differenciálegyenletekkel lehet leírni: a vizsgált mennyiség például
Az egyenes egyenlete: 2 pont. Az összevont alak: 1 pont. Melyik ábrán látható e függvény grafikonjának egy részlete?
 1. Írja fel annak az egyenesnek az egyenletét, amely áthalad az (1; 3) ponton, és egyik normálvektora a (8; 1) vektor! Az egyenes egyenlete: 2. Végezze el a következő műveleteket, és vonja össze az egynemű
1. Írja fel annak az egyenesnek az egyenletét, amely áthalad az (1; 3) ponton, és egyik normálvektora a (8; 1) vektor! Az egyenes egyenlete: 2. Végezze el a következő műveleteket, és vonja össze az egynemű
A Richardson-extrapoláció és alkalmazása a Dániai Euleri Modellben
 A Richardson-extrapoláció és alkalmazása a Dániai Euleri Modellben Faragó István 1, Havasi Ágnes 1, Zahari Zlatev 2 1 ELTE Alkalmazott Analízis és Számításmatematikai Tanszék és MTA-ELTE Numerikus Analízis
A Richardson-extrapoláció és alkalmazása a Dániai Euleri Modellben Faragó István 1, Havasi Ágnes 1, Zahari Zlatev 2 1 ELTE Alkalmazott Analízis és Számításmatematikai Tanszék és MTA-ELTE Numerikus Analízis
Magfizika tesztek. 1. Melyik részecske nem tartozik a nukleonok közé? a) elektron b) proton c) neutron d) egyik sem
 1. Melyik részecske nem tartozik a nukleonok közé? a) elektron b) proton c) neutron d) egyik sem 2. Mit nevezünk az atom tömegszámának? a) a protonok számát b) a neutronok számát c) a protonok és neutronok
1. Melyik részecske nem tartozik a nukleonok közé? a) elektron b) proton c) neutron d) egyik sem 2. Mit nevezünk az atom tömegszámának? a) a protonok számát b) a neutronok számát c) a protonok és neutronok
Keresztmetszet másodrendű nyomatékainak meghatározása
 BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
Közönséges differenciál egyenletek megoldása numerikus módszerekkel: egylépéses numerikus eljárások
 Közönséges differenciál egyenletek megoldása numerikus módszerekkel: egylépéses numerikus eljárások Bevezetés Ebben a cikkben megmutatjuk, hogyan használhatóak a Mathematica egylépéses numerikus eljárásai,
Közönséges differenciál egyenletek megoldása numerikus módszerekkel: egylépéses numerikus eljárások Bevezetés Ebben a cikkben megmutatjuk, hogyan használhatóak a Mathematica egylépéses numerikus eljárásai,
Differenciálegyenletek numerikus megoldása
 a Matematika mérnököknek II. című tárgyhoz Differenciálegyenletek numerikus megoldása Fokozatos közeĺıtés módszere (1) (2) x (t) = f (t, x(t)), x I, x(ξ) = η. Az (1)-(2) kezdeti érték probléma ekvivalens
a Matematika mérnököknek II. című tárgyhoz Differenciálegyenletek numerikus megoldása Fokozatos közeĺıtés módszere (1) (2) x (t) = f (t, x(t)), x I, x(ξ) = η. Az (1)-(2) kezdeti érték probléma ekvivalens
Tartalomjegyzék. Typotex Kiadó, 2010
 Tartalomjegyzék 15. Elliptikus egyenletek 7 15.1. Bevezetés: Elliptikus egyenletek alkalmazott feladatokban... 7 15.2. Elméleti háttér.......................... 9 15.3. Véges dierencia eljárások II...................
Tartalomjegyzék 15. Elliptikus egyenletek 7 15.1. Bevezetés: Elliptikus egyenletek alkalmazott feladatokban... 7 15.2. Elméleti háttér.......................... 9 15.3. Véges dierencia eljárások II...................
Reakciókinetika és katalízis
 Reakciókinetika és katalízis 5. előadás: /22 : Elemi reakciók kapcsolódása. : Egy reaktánsból két külön folyamatban más végtermékek keletkeznek. Legyenek A k b A kc B C Írjuk fel az A fogyására vonatkozó
Reakciókinetika és katalízis 5. előadás: /22 : Elemi reakciók kapcsolódása. : Egy reaktánsból két külön folyamatban más végtermékek keletkeznek. Legyenek A k b A kc B C Írjuk fel az A fogyására vonatkozó
Gyakorló feladatok. Agbeko Kwami Nutefe és Nagy Noémi
 Gyakorló feladatok Agbeko Kwami Nutefe és Nagy Noémi 25 Tartalomjegyzék. Klasszikus hibaszámítás 3 2. Lineáris egyenletrendszerek 3 3. Interpoláció 4 4. Sajátérték, sajátvektor 6 5. Lineáris és nemlineáris
Gyakorló feladatok Agbeko Kwami Nutefe és Nagy Noémi 25 Tartalomjegyzék. Klasszikus hibaszámítás 3 2. Lineáris egyenletrendszerek 3 3. Interpoláció 4 4. Sajátérték, sajátvektor 6 5. Lineáris és nemlineáris
Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2013. szeptember 23. Javítva: 2013.10.09.
Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2013. szeptember 23. Javítva: 2013.10.09.
Szennyezőanyagok terjedésének numerikus szimulációja, MISKAM célszoftver
 Szennyezőanyagok terjedésének numerikus szimulációja, MISKAM célszoftver 1. A numerikus szimulációról általában A szennyeződés-terjedési modellek numerikus megoldása A szennyeződés-terjedési modellek transzportegyenletei
Szennyezőanyagok terjedésének numerikus szimulációja, MISKAM célszoftver 1. A numerikus szimulációról általában A szennyeződés-terjedési modellek numerikus megoldása A szennyeződés-terjedési modellek transzportegyenletei
Sorozatok I. Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma)
 Sorozatok I. DEFINÍCIÓ: (Számsorozat) A számsorozat olyan függvény, amelynek értelmezési tartománya a pozitív egész számok halmaza, értékkészlete a valós számok egy részhalmaza. Jelölés: (a n ), {a n }.
Sorozatok I. DEFINÍCIÓ: (Számsorozat) A számsorozat olyan függvény, amelynek értelmezési tartománya a pozitív egész számok halmaza, értékkészlete a valós számok egy részhalmaza. Jelölés: (a n ), {a n }.
a) A logaritmus értelmezése alapján: x 8 0 ( x 2 2 vagy x 2 2) (1 pont) Egy szorzat értéke pontosan akkor 0, ha valamelyik szorzótényező 0.
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Abszolútértékes és Gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Abszolútértékes és Gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
TDK dolgozat. A remanens-hő reaktor-tranziensek során történő változásának számítására szolgáló modell fejlesztése. Bucz Gábor.
 TDK dolgozat A remanens-hő reaktor-tranziensek során történő változásának számítására szolgáló modell fejlesztése Bucz Gábor Témavezető: Dr. Fehér Sándor egyetemi docens Nukleáris Technika Tanszék BME
TDK dolgozat A remanens-hő reaktor-tranziensek során történő változásának számítására szolgáló modell fejlesztése Bucz Gábor Témavezető: Dr. Fehér Sándor egyetemi docens Nukleáris Technika Tanszék BME
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Abszolútértékes és Gyökös kifejezések
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Abszolútértékes és Gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Abszolútértékes és Gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
0-49 pont: elégtelen, pont: elégséges, pont: közepes, pont: jó, pont: jeles
 Matematika szigorlat, Mérnök informatikus szak I. 2013. jan. 10. Név: Neptun kód: Idő: 180 perc Elm.: 1. f. 2. f. 3. f. 4. f. 5. f. Fel. össz.: Össz.: Oszt.: Az elérhető pontszám 40 (elmélet) + 60 (feladatok)
Matematika szigorlat, Mérnök informatikus szak I. 2013. jan. 10. Név: Neptun kód: Idő: 180 perc Elm.: 1. f. 2. f. 3. f. 4. f. 5. f. Fel. össz.: Össz.: Oszt.: Az elérhető pontszám 40 (elmélet) + 60 (feladatok)
10. Koordinátageometria
 I. Nulladik ZH-ban láttuk: 0. Koordinátageometria. Melyek azok a P x; y pontok, amelyek koordinátái kielégítik az Ábrázolja a megoldáshalmazt a koordináta-síkon! x y x 0 egyenlőtlenséget? ELTE 00. szeptember
I. Nulladik ZH-ban láttuk: 0. Koordinátageometria. Melyek azok a P x; y pontok, amelyek koordinátái kielégítik az Ábrázolja a megoldáshalmazt a koordináta-síkon! x y x 0 egyenlőtlenséget? ELTE 00. szeptember
Trigonometria Megoldások. 1) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( )
 Trigonometria Megoldások Trigonometria - megoldások ) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( ) akkor a háromszög egyenlő szárú vagy derékszögű!
Trigonometria Megoldások Trigonometria - megoldások ) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( ) akkor a háromszög egyenlő szárú vagy derékszögű!
Akusztikai tervezés a geometriai akusztika módszereivel
 Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
1 Lebegőpontos számábrázolás
 Tartalom 1 Lebegőpontos számábrázolás... 2 2 Vektornormák... 4 3 Indukált mátrixnormák és tulajdonságaik... 5 4 A lineáris rendszer jobboldala hibás... 6 5 A kondíciószám és tulajdonságai... 7 6 Perturbációs
Tartalom 1 Lebegőpontos számábrázolás... 2 2 Vektornormák... 4 3 Indukált mátrixnormák és tulajdonságaik... 5 4 A lineáris rendszer jobboldala hibás... 6 5 A kondíciószám és tulajdonságai... 7 6 Perturbációs
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások
 Megoldások 1. Oldd meg a következő egyenleteket! (Alaphalmaz: Z) a) (x 1) (x + 1) 7x + 1 = x (4 + x) + 2 b) 1 2 [5 (x 1) (1 + 2x) 2 4x] = (7 x) x c) 2 (x + 5) (x 2) 2 + (x + 1) 2 = 6 (2x + 1) d) 6 (x 8)
Megoldások 1. Oldd meg a következő egyenleteket! (Alaphalmaz: Z) a) (x 1) (x + 1) 7x + 1 = x (4 + x) + 2 b) 1 2 [5 (x 1) (1 + 2x) 2 4x] = (7 x) x c) 2 (x + 5) (x 2) 2 + (x + 1) 2 = 6 (2x + 1) d) 6 (x 8)
Numerikus matematika vizsga
 1. Az a = 2, t = 4, k = 3, k + = 2 számábrázolási jellemzők mellett hány pozitív, normalizált lebegőpontos szám ábrázolható? Adja meg a legnagyobb ábrázolható számot! Mi lesz a 0.8-hoz rendelt lebegőpontos
1. Az a = 2, t = 4, k = 3, k + = 2 számábrázolási jellemzők mellett hány pozitív, normalizált lebegőpontos szám ábrázolható? Adja meg a legnagyobb ábrázolható számot! Mi lesz a 0.8-hoz rendelt lebegőpontos
(kidolgozta: Dr. Nagy Zoltán egyetemi adjunktus)
 Széchenyi István Egyetem Műszaki Tudományi Kar Alkalmazott Mechanika Tanszék GÉPEK DINAMIKÁJA 2.gyak.hét 1. és 2. Feladat (kidolgozta: Dr. Nagy Zoltán egyetemi adjunktus) Gépek dinamikája - 2. gyakorlat
Széchenyi István Egyetem Műszaki Tudományi Kar Alkalmazott Mechanika Tanszék GÉPEK DINAMIKÁJA 2.gyak.hét 1. és 2. Feladat (kidolgozta: Dr. Nagy Zoltán egyetemi adjunktus) Gépek dinamikája - 2. gyakorlat
Forrócsatorna számítások a csatolt KIKO3D- COBRA kóddal az új blokkok biztonsági elemzéseihez
 Forrócsatorna számítások a csatolt KIKO3D- COBRA kóddal az új blokkok biztonsági elemzéseihez Panka István, Keresztúri András, Maráczy Csaba, Temesvári Emese TSO Szeminárium OAH, 2017. május 31. Tartalom
Forrócsatorna számítások a csatolt KIKO3D- COBRA kóddal az új blokkok biztonsági elemzéseihez Panka István, Keresztúri András, Maráczy Csaba, Temesvári Emese TSO Szeminárium OAH, 2017. május 31. Tartalom
25/1. Stacionárius és tranziens megoldás. Kezdeti és végérték tétel.
 25/1. Stacionárius és tranziens megoldás. Kezdeti és végérték tétel. A gerjesztı jelek hálózatba történı be- vagy kikapcsolása után átmeneti (tranziens) jelenség játszódik le. Az állandósult (stacionárius)
25/1. Stacionárius és tranziens megoldás. Kezdeti és végérték tétel. A gerjesztı jelek hálózatba történı be- vagy kikapcsolása után átmeneti (tranziens) jelenség játszódik le. Az állandósult (stacionárius)
A mikroskálájú modellek turbulencia peremfeltételeiről
 A mikroskálájú modellek turbulencia peremfeltételeiről Adjunktus Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Áramlástan Tanszék 27..23. 27..23. / 7 Általános célú CFD megoldók alkalmazása
A mikroskálájú modellek turbulencia peremfeltételeiről Adjunktus Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Áramlástan Tanszék 27..23. 27..23. / 7 Általános célú CFD megoldók alkalmazása
Trigonometria Megoldások. 1) Oldja meg a következő egyenletet a valós számok halmazán! (12 pont) Megoldás:
 Trigonometria Megoldások ) Oldja meg a következő egyenletet a valós számok halmazán! cos + cos = sin ( pont) sin cos + = + = ( ) cos cos cos (+ pont) cos + cos = 0 A másodfokú egyenlet megoldóképletével
Trigonometria Megoldások ) Oldja meg a következő egyenletet a valós számok halmazán! cos + cos = sin ( pont) sin cos + = + = ( ) cos cos cos (+ pont) cos + cos = 0 A másodfokú egyenlet megoldóképletével
Dinamikus modellek felállítása mérnöki alapelvek segítségével
 IgyR - 3/1 p. 1/20 Integrált Gyártórendszerek - MSc Dinamikus modellek felállítása mérnöki alapelvek segítségével Hangos Katalin PE Villamosmérnöki és Információs Rendszerek Tanszék IgyR - 3/1 p. 2/20
IgyR - 3/1 p. 1/20 Integrált Gyártórendszerek - MSc Dinamikus modellek felállítása mérnöki alapelvek segítségével Hangos Katalin PE Villamosmérnöki és Információs Rendszerek Tanszék IgyR - 3/1 p. 2/20
Hódmezővásárhelyi Városi Matematikaverseny április 14. A osztályosok feladatainak javítókulcsa
 Hódmezővásárhelyi Városi Matematikaverseny 2003. április 14. A 11-12. osztályosok feladatainak javítókulcsa 1. feladat Egy számtani sorozatot az első eleme és különbsége egyértelműen meghatározza, azt
Hódmezővásárhelyi Városi Matematikaverseny 2003. április 14. A 11-12. osztályosok feladatainak javítókulcsa 1. feladat Egy számtani sorozatot az első eleme és különbsége egyértelműen meghatározza, azt
Mag- és neutronfizika 9. elıadás
 Mag- és neutronfizika 9. elıadás 9. elıadás mlékeztetı: Atommagok kötési energiája (Weizs( Weizsäcker) Z ( Z ) B bv A bf A bc b + b A A P δ A A B ε (egy nukleon átlagos energiája) A A (energia kötési energia)
Mag- és neutronfizika 9. elıadás 9. elıadás mlékeztetı: Atommagok kötési energiája (Weizs( Weizsäcker) Z ( Z ) B bv A bf A bc b + b A A P δ A A B ε (egy nukleon átlagos energiája) A A (energia kötési energia)
Matematika (mesterképzés)
 Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel
 Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel Segédlet az A végeselem módszer alapjai tárgy 4. laborgyakorlatához http://www.mm.bme.hu/~kossa/vemalap4.pdf Kossa Attila (kossa@mm.bme.hu)
Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel Segédlet az A végeselem módszer alapjai tárgy 4. laborgyakorlatához http://www.mm.bme.hu/~kossa/vemalap4.pdf Kossa Attila (kossa@mm.bme.hu)
Egyenletek, egyenlőtlenségek grafikus megoldása TK. II. kötet 25. old. 3. feladat
 Egyenletek, egyenlőtlenségek grafikus megoldása TK. II. kötet. old.. feladat a. lépés: Az egyenlet bal oldalának ábrázolása függvényként.. lépés: Az egyenlet bal oldalának ábrázolása függvényként.. lépés:
Egyenletek, egyenlőtlenségek grafikus megoldása TK. II. kötet. old.. feladat a. lépés: Az egyenlet bal oldalának ábrázolása függvényként.. lépés: Az egyenlet bal oldalának ábrázolása függvényként.. lépés:
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Trigonometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
Egyenletek, egyenletrendszerek, egyenlőtlenségek Megoldások
 ) Egyenletek, egyenletrendszerek, egyenlőtlenségek - megoldások Egyenletek, egyenletrendszerek, egyenlőtlenségek Megoldások a) Oldja meg a valós számok halmazán az alábbi egyenletet! = 6 (5 pont) b) Oldja
) Egyenletek, egyenletrendszerek, egyenlőtlenségek - megoldások Egyenletek, egyenletrendszerek, egyenlőtlenségek Megoldások a) Oldja meg a valós számok halmazán az alábbi egyenletet! = 6 (5 pont) b) Oldja
Konjugált gradiens módszer
 Közelítő és szimbolikus számítások 12. gyakorlat Konjugált gradiens módszer Készítette: Gelle Kitti Csendes Tibor Vinkó Tamás Faragó István Horváth Róbert jegyzetei alapján 1 LINEÁRIS EGYENLETRENDSZEREK
Közelítő és szimbolikus számítások 12. gyakorlat Konjugált gradiens módszer Készítette: Gelle Kitti Csendes Tibor Vinkó Tamás Faragó István Horváth Róbert jegyzetei alapján 1 LINEÁRIS EGYENLETRENDSZEREK
Első magreakciók. Targetmag
 Magreakciók 7 N 14 17 8 7 N(, p) 14 O 17 8 O Első magreakciók p Targetmag 30 Al n P 27 13, 15. Megmaradási elvek: 1. a nukleonszám 2. a töltés megmaradását. 3. a spin, 4. a paritás, 5. az impulzus, 6.
Magreakciók 7 N 14 17 8 7 N(, p) 14 O 17 8 O Első magreakciók p Targetmag 30 Al n P 27 13, 15. Megmaradási elvek: 1. a nukleonszám 2. a töltés megmaradását. 3. a spin, 4. a paritás, 5. az impulzus, 6.
9. Előadás. Megyesi László: Lineáris algebra, oldal. 9. előadás Mátrix inverze, mátrixegyenlet
 9. Előadás Megyesi László: Lineáris algebra, 75. 84. oldal. Gondolkodnivalók Mátrix rangja 1. Gondolkodnivaló Határozzuk meg a p valós paraméter értékétől függően a következő mátrix rangját: p 3 1 2 2
9. Előadás Megyesi László: Lineáris algebra, 75. 84. oldal. Gondolkodnivalók Mátrix rangja 1. Gondolkodnivaló Határozzuk meg a p valós paraméter értékétől függően a következő mátrix rangját: p 3 1 2 2
Szakdolgozat. Reaktor remanens hőteljesítményének számítására szolgáló eljárás és program fejlesztése. Bucz Gábor. Témavezető:
 Szakdolgozat Reaktor remanens hőteljesítményének számítására szolgáló eljárás és program fejlesztése Bucz Gábor Témavezető: Dr. Fehér Sándor egyetemi docens Nukleáris Technika Tanszék BME 2012 Tartalomjegyzék
Szakdolgozat Reaktor remanens hőteljesítményének számítására szolgáló eljárás és program fejlesztése Bucz Gábor Témavezető: Dr. Fehér Sándor egyetemi docens Nukleáris Technika Tanszék BME 2012 Tartalomjegyzék
Monte Carlo módszerek fejlesztése reaktorfizikai szimulációkhoz
 Monte Carlo módszerek fejlesztése reaktorfizikai szimulációkhoz Légrády Dávid BME NTI Molnár Balázs, Takács Hajna, Tolnai Gábor 016.1.07 A munka a Nemzeti Kutatási, Fejlesztési és Innovációs Alap által
Monte Carlo módszerek fejlesztése reaktorfizikai szimulációkhoz Légrády Dávid BME NTI Molnár Balázs, Takács Hajna, Tolnai Gábor 016.1.07 A munka a Nemzeti Kutatási, Fejlesztési és Innovációs Alap által
Maghasadás, láncreakció, magfúzió
 Maghasadás, láncreakció, magfúzió Maghasadás 1938-ban hoztak létre először maghasadást úgy, hogy urán atommagokat bombáztak neutronokkal. Ekkor az urán két közepes méretű atommagra bomlott el, és újabb
Maghasadás, láncreakció, magfúzió Maghasadás 1938-ban hoztak létre először maghasadást úgy, hogy urán atommagokat bombáztak neutronokkal. Ekkor az urán két közepes méretű atommagra bomlott el, és újabb
Matematika III. harmadik előadás
 Matematika III. harmadik előadás Kézi Csaba Debreceni Egyetem, Műszaki Kar Debrecen, 2013/14 tanév, I. félév Kézi Csaba (DE) Matematika III. harmadik előadás 2013/14 tanév, I. félév 1 / 13 tétel Az y (x)
Matematika III. harmadik előadás Kézi Csaba Debreceni Egyetem, Műszaki Kar Debrecen, 2013/14 tanév, I. félév Kézi Csaba (DE) Matematika III. harmadik előadás 2013/14 tanév, I. félév 1 / 13 tétel Az y (x)
Az egyenlőtlenség mindkét oldalát szorozzuk meg 4 16-al:
 Bevezető matematika kémikusoknak., 04. ősz. feladatlap. Ábrázoljuk számegyenesen a következő egyenlőtlenségek megoldáshalmazát! (a) x 5 < 3 5 x < 3 x 5 < (d) 5 x
Bevezető matematika kémikusoknak., 04. ősz. feladatlap. Ábrázoljuk számegyenesen a következő egyenlőtlenségek megoldáshalmazát! (a) x 5 < 3 5 x < 3 x 5 < (d) 5 x
STATISZTIKA ELŐADÁS ÁTTEKINTÉSE. Matematikai statisztika. Mi a modell? Binomiális eloszlás sűrűségfüggvény. Binomiális eloszlás
 ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
Másodfokú egyenletek, egyenlőtlenségek
 Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x 1x 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x 1x 16 =. 1. lépés:
Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x 1x 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x 1x 16 =. 1. lépés:
Numerikus matematika. Irodalom: Stoyan Gisbert, Numerikus matematika mérnököknek és programozóknak, Typotex, Lebegőpontos számok
 Numerikus matematika Irodalom: Stoyan Gisbert, Numerikus matematika mérnököknek és programozóknak, Typotex, 2007 Lebegőpontos számok Normák, kondíciószámok Lineáris egyenletrendszerek Legkisebb négyzetes
Numerikus matematika Irodalom: Stoyan Gisbert, Numerikus matematika mérnököknek és programozóknak, Typotex, 2007 Lebegőpontos számok Normák, kondíciószámok Lineáris egyenletrendszerek Legkisebb négyzetes
Mátrixhatvány-vektor szorzatok hatékony számítása
 Mátrixhatvány-vektor szorzatok hatékony számítása Izsák Ferenc ELTE TTK, Alkalmazott Analízis és Számításmatematikai Tanszék & ELTE-MTA NumNet Kutatócsoport munkatárs: Szekeres Béla János Alkalmazott Analízis
Mátrixhatvány-vektor szorzatok hatékony számítása Izsák Ferenc ELTE TTK, Alkalmazott Analízis és Számításmatematikai Tanszék & ELTE-MTA NumNet Kutatócsoport munkatárs: Szekeres Béla János Alkalmazott Analízis
Matematikai háttér. 3. Fejezet. A matematika hozzászoktatja a szemünket ahhoz, hogy tisztán és világosan lássa az igazságot.
 3. Fejezet Matematikai háttér A matematika hozzászoktatja a szemünket ahhoz, hogy tisztán és világosan lássa az igazságot René Descartes Számtalan kiváló szakirodalom foglalkozik a különféle differenciálegyenletek
3. Fejezet Matematikai háttér A matematika hozzászoktatja a szemünket ahhoz, hogy tisztán és világosan lássa az igazságot René Descartes Számtalan kiváló szakirodalom foglalkozik a különféle differenciálegyenletek
Matematika 11. osztály
 ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Humán tagozat Matematika 11. osztály I. rész: Hatvány, gyök, logaritmus Készítette: Balázs Ádám Budapest, 018 . Tartalomjegyzék Tartalomjegyzék
ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Humán tagozat Matematika 11. osztály I. rész: Hatvány, gyök, logaritmus Készítette: Balázs Ádám Budapest, 018 . Tartalomjegyzék Tartalomjegyzék
Áramlástan feladatgyűjtemény. 6. gyakorlat Bernoulli-egyenlet instacionárius esetben
 Áramlástan feladatgyűjtemény Az energetikai mérnöki BSc és gépészmérnöki BSc képzések Áramlástan című tárgyához 6. gyakorlat Bernoulli-egyenlet instacionárius esetben Összeállította: Lukács Eszter Dr.
Áramlástan feladatgyűjtemény Az energetikai mérnöki BSc és gépészmérnöki BSc képzések Áramlástan című tárgyához 6. gyakorlat Bernoulli-egyenlet instacionárius esetben Összeállította: Lukács Eszter Dr.
A PAE 1-4. BLOKK HERMETIKUS TÉR SZIVÁRGÁS-KORLÁT CSÖKKENTÉS LEHETŐSÉGÉNEK VIZSGÁLATA. Az OAH-ABA-03/16-M1 kutatási jelentés rövid bemutatása
 A PAE 1-4. BLOKK HERMETIKUS TÉR SZIVÁRGÁS-KORLÁT CSÖKKENTÉS LEHETŐSÉGÉNEK VIZSGÁLATA. Az OAH-ABA-03/16-M1 kutatási jelentés rövid bemutatása Készítette: Kapocs György PM Kft TSO szeminárium, 2017.május
A PAE 1-4. BLOKK HERMETIKUS TÉR SZIVÁRGÁS-KORLÁT CSÖKKENTÉS LEHETŐSÉGÉNEK VIZSGÁLATA. Az OAH-ABA-03/16-M1 kutatási jelentés rövid bemutatása Készítette: Kapocs György PM Kft TSO szeminárium, 2017.május
Az R forgató mátrix [ 1 ] - beli képleteinek levezetése: I. rész
![Az R forgató mátrix [ 1 ] - beli képleteinek levezetése: I. rész Az R forgató mátrix [ 1 ] - beli képleteinek levezetése: I. rész](/thumbs/57/40130324.jpg) Az R forgató mátri [ ] - beli képleteinek levezetése: I rész Az [ ] forrás kötetében a ( 49 ), ( 50 ) képletek nyilván mint közismertek nem lettek levezetve Minthogy az ottani további számítások miatt
Az R forgató mátri [ ] - beli képleteinek levezetése: I rész Az [ ] forrás kötetében a ( 49 ), ( 50 ) képletek nyilván mint közismertek nem lettek levezetve Minthogy az ottani további számítások miatt
Egyenletek, egyenlőtlenségek VII.
 Egyenletek, egyenlőtlenségek VII. Magasabbfokú egyenletek: A 3, vagy annál nagyobb fokú egyenleteket magasabb fokú egyenleteknek nevezzük. Megjegyzés: Egy n - ed fokú egyenletnek legfeljebb n darab valós
Egyenletek, egyenlőtlenségek VII. Magasabbfokú egyenletek: A 3, vagy annál nagyobb fokú egyenleteket magasabb fokú egyenleteknek nevezzük. Megjegyzés: Egy n - ed fokú egyenletnek legfeljebb n darab valós
3. Egyenletek, egyenletrendszerek, egyenlőtlenségek
 . Egyenletek, egyenletrendszerek, egyenlőtlenségek I. Nulladik ZH-ban láttuk: 1. Mennyi a 2x 2 8x 5 = 0 egyenlet gyökeinek a szorzata? (A) 10 (B) 2 (C) 2,5 (D) 4 (E) ezek egyike sem Megoldás I.: BME 2011.
. Egyenletek, egyenletrendszerek, egyenlőtlenségek I. Nulladik ZH-ban láttuk: 1. Mennyi a 2x 2 8x 5 = 0 egyenlet gyökeinek a szorzata? (A) 10 (B) 2 (C) 2,5 (D) 4 (E) ezek egyike sem Megoldás I.: BME 2011.
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Megoldott feladatok november 30. n+3 szigorúan monoton csökken, 5. n+3. lim a n = lim. n+3 = 2n+3 n+4 2n+1
 Megoldott feladatok 00. november 0.. Feladat: Vizsgáljuk az a n = n+ n+ sorozat monotonitását, korlátosságát és konvergenciáját. Konvergencia esetén számítsuk ki a határértéket! : a n = n+ n+ = n+ n+ =
Megoldott feladatok 00. november 0.. Feladat: Vizsgáljuk az a n = n+ n+ sorozat monotonitását, korlátosságát és konvergenciáját. Konvergencia esetén számítsuk ki a határértéket! : a n = n+ n+ = n+ n+ =
A KLT (Kanade Lucas Tomasi) Feature Tracker Működése (jellegzetes pontok választása és követése)
 A KL (Kanade Lucas omasi) Feature racker Működése (jellegzetes pontok választása és követése) Készítette: Hajder Levente 008.11.18. 1. Feladat A rendelkezésre álló videó egy adott képkockájából minél több
A KL (Kanade Lucas omasi) Feature racker Működése (jellegzetes pontok választása és követése) Készítette: Hajder Levente 008.11.18. 1. Feladat A rendelkezésre álló videó egy adott képkockájából minél több
Szerkezetek numerikus modellezése az építőmérnöki gyakorlatban
 Szerkezetek numerikus modellezése az építőmérnöki gyakorlatban tanszékvezető, főiskolai docens a Magyar Építész Kamara tagja a Magyar Mérnöki Kamara tagja a fib Magyar Tagozatának tagja az ÉTE Debreceni
Szerkezetek numerikus modellezése az építőmérnöki gyakorlatban tanszékvezető, főiskolai docens a Magyar Építész Kamara tagja a Magyar Mérnöki Kamara tagja a fib Magyar Tagozatának tagja az ÉTE Debreceni
FENNTARTHATÓ FEJLİDÉS ÉS ATOMENERGIA
 FENNTARTHATÓ FEJLİDÉS ÉS ATOMENERGIA 4. elıadás AZ ATOMREAKTOROK FIZIKAI ÉS TECHNIKAI ALAPJAI, ATOMERİMŐVEK 2009/2010. tanév ıszi féléve Dr. Csom Gyula professor emeritus TARTALOM 1. Magfizikai alapok
FENNTARTHATÓ FEJLİDÉS ÉS ATOMENERGIA 4. elıadás AZ ATOMREAKTOROK FIZIKAI ÉS TECHNIKAI ALAPJAI, ATOMERİMŐVEK 2009/2010. tanév ıszi féléve Dr. Csom Gyula professor emeritus TARTALOM 1. Magfizikai alapok
1. tétel. 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója 7 cm. Mekkora a háromszög átfogója? (4 pont)
 1. tétel 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója cm. Mekkora a háromszög átfogója? (4 pont). Adott az ábrán két vektor. Rajzolja meg a b, a b és az a b vektorokat! (6 pont)
1. tétel 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója cm. Mekkora a háromszög átfogója? (4 pont). Adott az ábrán két vektor. Rajzolja meg a b, a b és az a b vektorokat! (6 pont)
Gauss elimináció, LU felbontás
 Közelítő és szimbolikus számítások 3. gyakorlat Gauss elimináció, LU felbontás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 EGYENLETRENDSZEREK 1. Egyenletrendszerek
Közelítő és szimbolikus számítások 3. gyakorlat Gauss elimináció, LU felbontás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 EGYENLETRENDSZEREK 1. Egyenletrendszerek
5. Laboratóriumi gyakorlat
 5. Laboratóriumi gyakorlat HETEROGÉN KÉMIAI REAKCIÓ SEBESSÉGÉNEK VIZSGÁLATA A CO 2 -nak vízben történő oldódása és az azt követő egyensúlyra vezető kémiai reakció az alábbi reakcióegyenlettel írható le:
5. Laboratóriumi gyakorlat HETEROGÉN KÉMIAI REAKCIÓ SEBESSÉGÉNEK VIZSGÁLATA A CO 2 -nak vízben történő oldódása és az azt követő egyensúlyra vezető kémiai reakció az alábbi reakcióegyenlettel írható le:
1. Egy lineáris hálózatot mikor nevezhetünk rezisztív hálózatnak és mikor dinamikus hálózatnak?
 Ellenörző kérdések: 1. előadás 1/5 1. előadás 1. Egy lineáris hálózatot mikor nevezhetünk rezisztív hálózatnak és mikor dinamikus hálózatnak? 2. Mit jelent a föld csomópont, egy áramkörben hány lehet belőle,
Ellenörző kérdések: 1. előadás 1/5 1. előadás 1. Egy lineáris hálózatot mikor nevezhetünk rezisztív hálózatnak és mikor dinamikus hálózatnak? 2. Mit jelent a föld csomópont, egy áramkörben hány lehet belőle,
Matematikai geodéziai számítások 5.
 Matematikai geodéziai számítások 5 Hibaterjedési feladatok Dr Bácsatyai László Matematikai geodéziai számítások 5: Hibaterjedési feladatok Dr Bácsatyai László Lektor: Dr Benedek Judit Ez a modul a TÁMOP
Matematikai geodéziai számítások 5 Hibaterjedési feladatok Dr Bácsatyai László Matematikai geodéziai számítások 5: Hibaterjedési feladatok Dr Bácsatyai László Lektor: Dr Benedek Judit Ez a modul a TÁMOP
Reaktorfizikai feladatok
 Budapesti Műszaki és Gazdaságtudományi Egyetem Természettudományi Kar Szatmáry Zoltán Reaktorfizikai feladatok Egyetemi jegyzet Budapest, 2007 2 3 Tartalomjegyzék Általános tudnivalók... 4 Köszönetnyilvánítás...
Budapesti Műszaki és Gazdaságtudományi Egyetem Természettudományi Kar Szatmáry Zoltán Reaktorfizikai feladatok Egyetemi jegyzet Budapest, 2007 2 3 Tartalomjegyzék Általános tudnivalók... 4 Köszönetnyilvánítás...
Másodfokú egyenletek, egyenlőtlenségek
 Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x + 1x + 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x + 1x + 16 = 0.
Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x + 1x + 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x + 1x + 16 = 0.
Markov-láncok stacionárius eloszlása
 Markov-láncok stacionárius eloszlása Adatbányászat és Keresés Csoport, MTA SZTAKI dms.sztaki.hu Kiss Tamás 2013. április 11. Tartalom Markov láncok definíciója, jellemzése Visszatérési idők Stacionárius
Markov-láncok stacionárius eloszlása Adatbányászat és Keresés Csoport, MTA SZTAKI dms.sztaki.hu Kiss Tamás 2013. április 11. Tartalom Markov láncok definíciója, jellemzése Visszatérési idők Stacionárius
