MINDEN FELADATOT A FELADATOT TARTALMAZÓ LAPON OLD- JONMEG!
|
|
|
- Elvira Csonka
- 6 évvel ezelőtt
- Látták:
Átírás
1 NÉV: ERA kód: évf.: gyak. vez.: MINDEN FELADATOT A FELADATOT TARTALMAZÓ LAPON OLD- JONMEG! Al. (a) Definiálja a mo ment um és a centrális momentum fogalmát (általában) (4 pont)! Egy megyében egy vizsgált hónapban az élveszületésekről és a születési súlyokról az alábbiak ismertek. súly (g) születések száma (b) szórását (3 pont), Cc) mediánját (3 pont)! Cd) Egy alkalmas mutatóval jellemezze a súlyak elaszlásának ferdeségét és értelmezze azt (3 pont)!
2 Fajta Arbevétel 2006-ban Eladási ár változása Volumenváltozás (millió Ft) (2005=100%) (2005=100%) Világos Barna Alkoholmentes (a) Határozza meg a Laspayres- és a Paasche-féle árindexeket! Cb) Számítsa ki az értékindexet és a Fischer-féle volumenindexet! Cc) 2005-ös eladott mennyiségekkel számolva mennyi az árak változása miatti többlet bevétel (vagy bevéte1csökkenés)? Minden eredményt szövegesen is értékeljen!
3 A3. (11 pont) Egy színház prózai és zenés darabokat játszik. A darabok nézettségéről az alábbi adatokat ismerjük: Előadások száma Az átlagos nézőszám különbsége Előadás típusa 2005-ben (db) (néző/előadás) Próza Zenés Összesen (a) Elemezze az előadások átlagos nézőszámának változását és az arra ható tényezőket! (b) Mit mondhatunk 2006-ra a zenés darabok számának változásáról, ha tudjuk, hogy a magyar lakosság a zenés darabokat kedveli jobban? A kapott eredményeket szövegesen is értékelje!
4 A4. Ca) (7 pont) Definiálja a lineáris korrelációs együttható fogalmát! Fogalmazza meg, hogy milyen esetben és mire használható hogyan értelmezhető annak értéke? pontosan a mutató és Cb) (3 pont) Írjon fel egy árindexet átlag-formában! Miért nevezzük ezt átlagformának?
5 A5. (a) Definiálja a külső szórás és a teljes négyzetösszeg fogalmát és értelmezze azokat (4 pont)! A Lerablosz biztosító, mielőtt összeállította volna a jövő évi gépjármű felelősségbiztosítási tarifáit, meg akarta vizsgálni, van-e összefüggés az ügyfelei életkora, és az általuk az elmúlt egy évben okozott balesetek száma között. (b) Töltse ki a táblázatok hiányzó értékeit (5 darab, 5 pont)! (c) Hány éves volt a legidősebb és a legfiatalabb balesetmentesen vezető ügyf-él? Mennyi volt a legbalesetveszélyesebb ügyfelek átlagéletkora (2 pont)? (d) Számítsa ki az életkor és az okozott balesetek száma közötti összefüggés mérésére szolgálő H 2 mutatót és értelmezze azt (2 pont)! N Mean Std. Deviation Minimum Maximum O baleset ,84 9, baleset ,90 9, baleset ,51 9,089 22??? 3 baleset 63 41,06 9, baleset??? 41,93 9, Total 500??? 9, Sum of Squares df Mean Square F Sig. Between Groups??? 4 10,214,118,976 Within Groups 42801, ,468 Total??? 499
6 NÉV: EHA kód: évf.: gyak. vez.: MINDEN FELADATOT A FELADATOT TARTALMAZÓ LAPON OLD- JON MEG! Bl. (11 pont) Egy kalapgyár két űzemből áll. Az egyikben női, a másikban férfi kalapokat készítenek. Az alábbi termelési adatok ismertek: Az alkalmazottak számának Az átlagtermés különbsége Üzemek megoszlása 2005-ben (%) (kalapszámjfő) Női Férfi Összesen (a) Határozza meg az átlagos termelés (az egy alkalmazottra jutó termelés) változását 2000-ről 2005-re és határozza meg a különbséget magyarázó tényezőketl (b) Hogyan változhatott a női kalapokat gyártó üzemben az alkalmazottak száma, ha tudjuk, hogy a másik üzem létszáma nem változott? A kapott eredményeket szövegesen is értékelje!
7 B2. (a) Definiálja a moment um és a centrális momentum fogalmát (általában) (4 pont)! Egy megyében egy vizsgált hónapban az eladott lakásokról és azok alapterületéről az alábbiak ismertek. alapterület (m 2 ) eladott lakások száma Határozza meg és értelmezze az eladott lakások alapterületének (b) felső kvartilisét (3 pont), (c) szórását (3 pont)! (d) Egy alkalmas mutatóval jellemezze az alapterületek eloszlás ának ferdeségét és értelmezze azt (3 pont)!
8 B3. (a) (7 pont) Definiálja a lineáris korrelációs együttható fogalmát! Fogalmazza meg, hogy milyen esetben és mire használható pontosan a mutató és hogyan értelmezhető annak értéke? (b) (3 pont) Írjon fel egy volumeninclexet átlag-formában! Miért nevezzük ezt átlagformának?
9 B4. (14 pont) Egy cipőbolt forgalmát vizsgáljuk 2000 és 2005 között. A következő adatokat ismerjük: Kínálat A bázisév árbevétele Eladási ár változása Volumenváltozás (millió Ft) (bázisév= 100%) (bázisév= 100%) Női cipő Férfi cipő Gyermek cipő (a) Határozza meg a Fischer-féle árindexet! Cb) Számítsa ki az értékindexet és mindkét súlyozású volumenindexet! Cc) Hány forint a bolt többletbevétele (vagy bevéte1csökkenése) az árváltozás miatt, ha 2005-ös eladott mennyiségekkel számolunk? Minden eredményt szövegesen is értékeljen!
10 B5. Ca) Definiálja a részátlag valamint a belső négyzetösszeg fogalmát és értelmezze e mennyiségeket (4 pont)! A Fapad Airlines hétfői, szerdai és pénteki napokon indít járatokat az Úperencián túlra. Egy adott héten e három járat összesen 399 utast szállított, akik jegyeiket az Interneten fogalták. A légitársaság a honlapján azt hirdeti, hogy nincsen összefüggés a jegyek ára (Euro) és az utazás napja között. Cb) Töltse ki a táblázatok hiányzó értékeit (5 darab, 5 pont)! Cc) Mennyibe került a legolcsóbb és a legdrágább jegy? Mennyi volt a hétfői átlagár (2 pont)? Cd) A H 2 mutató segítségével vizsgálja meg, igaz-e a légitársaság állítása a jegyár és az utazás napjának független voltáról (2 pont)! e~lyar N Mean Std. Deviation Minimum Maximum hétfő??? 78,87 15,130??? 115 szerda ,84 14, péntek ,13 27, Total 399??? 38, Jeqyár Sum of Squares df Mean Square F Siq, 8etween Groups??? , ,944,000 Within Groups??? ,264 Total ,
Helyzetmutatók, szóródási mutatók, alakmutatók
 Helyzetmutatók, szóródási mutatók, alakmutatók 1. A következ táblázat 48 darab 70 nm körüli budapesti lakás áráról 1995-ben összegy jtött információkat foglalja össze. Egészítse ki a táblázatot az alábbi
Helyzetmutatók, szóródási mutatók, alakmutatók 1. A következ táblázat 48 darab 70 nm körüli budapesti lakás áráról 1995-ben összegy jtött információkat foglalja össze. Egészítse ki a táblázatot az alábbi
[GVMGS11MNC] Gazdaságstatisztika
![[GVMGS11MNC] Gazdaságstatisztika [GVMGS11MNC] Gazdaságstatisztika](/thumbs/17/143095.jpg) [GVMGS11MNC] Gazdaságstatisztika 5. előadás Érték-, ár-, és volumenindexek http://uni-obuda.hu/users/koczyl/gazdasagstatisztika.htm Kóczy Á. László KGK-VMI Az indexszám fogalma Gazdasági elemzésben fontos
[GVMGS11MNC] Gazdaságstatisztika 5. előadás Érték-, ár-, és volumenindexek http://uni-obuda.hu/users/koczyl/gazdasagstatisztika.htm Kóczy Á. László KGK-VMI Az indexszám fogalma Gazdasági elemzésben fontos
STATISZTIKA 1. alapfogalmak egy ismérv szerinti elemzés két ismérv szerinti elemzés standardizálás indexszámítás idősorok PÉLDATÁR
 STATISZTIKA 1. PÉLDATÁR alapfogalmak egy ismérv szerinti elemzés két ismérv szerinti elemzés standardizálás indexszámítás idősorok A FELADATOK MEGOLDÁSAIT A www.mateking.hu OLDALON A STATISZTIKA 1 MENÜPONTBAN
STATISZTIKA 1. PÉLDATÁR alapfogalmak egy ismérv szerinti elemzés két ismérv szerinti elemzés standardizálás indexszámítás idősorok A FELADATOK MEGOLDÁSAIT A www.mateking.hu OLDALON A STATISZTIKA 1 MENÜPONTBAN
STATISZTIKA. Gyakorló feladatok az első zh-ra
 STATISZTIKA Gyakorló feladatok az első zh-ra A változás átlagos üteme év Kenyér Ft/ kg bázisindex % 2002 151 100,0 2003 156 103,3 2004 178 117,9 2005 173 114,6 2006 179 118,5 2007 215 142,4 I = n 1 l i
STATISZTIKA Gyakorló feladatok az első zh-ra A változás átlagos üteme év Kenyér Ft/ kg bázisindex % 2002 151 100,0 2003 156 103,3 2004 178 117,9 2005 173 114,6 2006 179 118,5 2007 215 142,4 I = n 1 l i
KÖZPONTI STATISZTIKAI HIVATAL. Szóbeli vizsgatevékenység
 KÖZPONTI STATISZTIKAI HIVATAL A vizsgarészhez rendelt követelménymodul azonosító száma, megnevezése: 2144-06 Statisztikai szervezői és elemzési feladatok A vizsgarészhez rendelt vizsgafeladat megnevezése:
KÖZPONTI STATISZTIKAI HIVATAL A vizsgarészhez rendelt követelménymodul azonosító száma, megnevezése: 2144-06 Statisztikai szervezői és elemzési feladatok A vizsgarészhez rendelt vizsgafeladat megnevezése:
Határozza meg és jellemezze az ár-, érték- és volumenváltozást %-ban és forintban!
 1. Egy fúvós hangszereket forgalmazó cégről a következő adatok ismertek: Termékcsoportok Forgalom 2003-ban A volumen változása Fafúvós 50 +50 Rézfúvós 30 +30 Egyéb +10 Összesen: Továbbá ismert, hogy a
1. Egy fúvós hangszereket forgalmazó cégről a következő adatok ismertek: Termékcsoportok Forgalom 2003-ban A volumen változása Fafúvós 50 +50 Rézfúvós 30 +30 Egyéb +10 Összesen: Továbbá ismert, hogy a
MINTAFELADATOK. 1. Az alábbi diagram egy kiskereskedelmi lánc boltjainak forgalomkoncentrációját szemlélteti:
 1. Az alábbi diagram egy kiskereskedelmi lánc boltjainak forgalomkoncentrációját szemlélteti: 100% 90% 80% 70% 60% 50% 2010 2011 40% 30% 20% 10% 0% 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% a) Nevezze
1. Az alábbi diagram egy kiskereskedelmi lánc boltjainak forgalomkoncentrációját szemlélteti: 100% 90% 80% 70% 60% 50% 2010 2011 40% 30% 20% 10% 0% 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% a) Nevezze
Sztochasztikus kapcsolatok
 Sztochasztikus kapcsolatok Petrovics Petra PhD Hallgató Ismérvek közötti kapcsolat (1) Függvényszerű az egyik ismérv szerinti hovatartozás egyértelműen meghatározza a másik ismérv szerinti hovatartozást.
Sztochasztikus kapcsolatok Petrovics Petra PhD Hallgató Ismérvek közötti kapcsolat (1) Függvényszerű az egyik ismérv szerinti hovatartozás egyértelműen meghatározza a másik ismérv szerinti hovatartozást.
Gazdasági elemzés 1. 4 alkalom. Budaházy György
 Gazdasági elemzés 1. Termelés és értékesítés 4 alkalom Budaházy György A termelı és szolgáltató tevékenység elemzése 1. A tevékenység besorolása (TEAOR) 2. A termelés mérése 3. A termelési érték elemzése
Gazdasági elemzés 1. Termelés és értékesítés 4 alkalom Budaházy György A termelı és szolgáltató tevékenység elemzése 1. A tevékenység besorolása (TEAOR) 2. A termelés mérése 3. A termelési érték elemzése
STATISZTIKA I. Centrális mutatók. Helyzeti középértékek. Középértékek. Bimodális eloszlás, U. Módusz, Mo. 4. Előadás.
 Centrális mutatók STATISZTIKA I. 4. Előadás Centrális mutatók 1/51 2/51 Középértékek Helyzeti középértékek A meghatározása gyakoriság vagy sorszám alapján Számítás nélkül Az elemek nagyság szerint rendezett
Centrális mutatók STATISZTIKA I. 4. Előadás Centrális mutatók 1/51 2/51 Középértékek Helyzeti középértékek A meghatározása gyakoriság vagy sorszám alapján Számítás nélkül Az elemek nagyság szerint rendezett
7, 6, 0, 4, 0, 1, 5, 2, 2, 16, 1, 0, 2, 3, 9, 2, 4, 10, 3, 1, 2, 12, 4, 1
 52. feladat Stat Jenő egyetemi hallgató autóbusszal jár az egyetemre. Néhány napon át megmérte, hogy mennyit kell várnia az első egyetem felé közlekedő autóbuszra. A következő időket tapasztalta (percben):
52. feladat Stat Jenő egyetemi hallgató autóbusszal jár az egyetemre. Néhány napon át megmérte, hogy mennyit kell várnia az első egyetem felé közlekedő autóbuszra. A következő időket tapasztalta (percben):
Gyakorló feladatok a Vezetõi számvitel tárgyhoz Témakör: Utólagos eredményelemzés
 1. feladat Egy ipari tevékenységet folytató vállalkozás termékeirõl az alábbi információkat ismeri: Termék Mennyiség db) Egységár Ft/db) Önköltség Ft/db) Terv Tény Terv Tény Terv Tény A 16 15 82 81 54
1. feladat Egy ipari tevékenységet folytató vállalkozás termékeirõl az alábbi információkat ismeri: Termék Mennyiség db) Egységár Ft/db) Önköltség Ft/db) Terv Tény Terv Tény Terv Tény A 16 15 82 81 54
STATISZTIKA I. 3. rész. T.Nagy Judit
 STATSZTKA. 3. rész T.Nagy Judit tnagy.judit@hjf.hu Standardizálás és standardizáláson alauló indexszámítás nhomogén (heterogén) sokaságokra vonatkozó átlagok; intenzitási viszonyszámok (átlagbérek, átlagos
STATSZTKA. 3. rész T.Nagy Judit tnagy.judit@hjf.hu Standardizálás és standardizáláson alauló indexszámítás nhomogén (heterogén) sokaságokra vonatkozó átlagok; intenzitási viszonyszámok (átlagbérek, átlagos
Módszertani Intézeti Tanszéki Osztály
 BGF KKK Módszertani Intézeti Tanszéki Osztály Budapest, 2012. Név:... Kód:...... Eredmény:..... STATISZTIKA I. VIZSGA; NG KM ÉS KG TQM SZAKOKON MINTAVIZSGA Feladatok 1. 2. 3. 4. 5. 6. Összesen Szerezhető
BGF KKK Módszertani Intézeti Tanszéki Osztály Budapest, 2012. Név:... Kód:...... Eredmény:..... STATISZTIKA I. VIZSGA; NG KM ÉS KG TQM SZAKOKON MINTAVIZSGA Feladatok 1. 2. 3. 4. 5. 6. Összesen Szerezhető
Korreláció számítás az SPSSben
 Korreláció számítás az SPSSben Kvantitatív statisztikai módszerek Petrovics Petra Statisztikai kapcsolatok Asszociáció 2 minőségi/területi ismérv között Vegyes kapcsolat minőségi/területi és egy mennyiségi
Korreláció számítás az SPSSben Kvantitatív statisztikai módszerek Petrovics Petra Statisztikai kapcsolatok Asszociáció 2 minőségi/területi ismérv között Vegyes kapcsolat minőségi/területi és egy mennyiségi
Gyakorló feladatok a Kontrolling alapjai tárgyhoz Témakör: Mérés és elemzés (Költség- és eredményelemzés)
 Gyakorló feladatok a Kontrolling alajai tárgyhoz. feladat Egy vállalkozás termeléséről az alábbi adatokat ismeri: Termelési érték Termelés (db) Közvetlen anyagköltség előző év tárgy év előző év tárgy év
Gyakorló feladatok a Kontrolling alajai tárgyhoz. feladat Egy vállalkozás termeléséről az alábbi adatokat ismeri: Termelési érték Termelés (db) Közvetlen anyagköltség előző év tárgy év előző év tárgy év
Gyakorló feladatok a Komplex elemzés tárgyhoz Témakör: Minőség
 Gyakorló feladatok a Komlex elemzés tárgyhoz. feladat Egy vállalkozás termelőfolyamatának minősége a következőkéen alakult: Megnevezés Termelés vezértermékben (db Selejt (db terv tény terv tény I. sz.
Gyakorló feladatok a Komlex elemzés tárgyhoz. feladat Egy vállalkozás termelőfolyamatának minősége a következőkéen alakult: Megnevezés Termelés vezértermékben (db Selejt (db terv tény terv tény I. sz.
Statisztika II. feladatok
 Statisztika II. feladatok 1. Egy női ruhákat és kiegészítőket forgalmazó üzletlánc 118 egységénél felmérést végzett arról, milyen tényezők befolyásolják a havi összbevételüket (EUR). a) Pótolja ki a táblázatok
Statisztika II. feladatok 1. Egy női ruhákat és kiegészítőket forgalmazó üzletlánc 118 egységénél felmérést végzett arról, milyen tényezők befolyásolják a havi összbevételüket (EUR). a) Pótolja ki a táblázatok
KERESKEDELMI ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA MINTAFELADATOK FELADATLAP
 KERESKEDELMI ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA MINTAFELADATOK FELADATLAP Jövedelmezőség 1. Jövedelmezőség tervezése 19 pont Egy papír-írószerbolt 2018. évi árbevétele 85 000 ezer Ft. Az üzlet 24%-os
KERESKEDELMI ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA MINTAFELADATOK FELADATLAP Jövedelmezőség 1. Jövedelmezőség tervezése 19 pont Egy papír-írószerbolt 2018. évi árbevétele 85 000 ezer Ft. Az üzlet 24%-os
Kvantitatív statisztikai módszerek
 Kvantitatív statisztikai módszerek 1. konzultáció tárgyjegyző Dr. Szilágyi Roland Mérési skálák Számok meghatározott szabályok szerinti hozzárendelése jelenségekhez, bizonyos tulajdonságokhoz. 4 féle szabály
Kvantitatív statisztikai módszerek 1. konzultáció tárgyjegyző Dr. Szilágyi Roland Mérési skálák Számok meghatározott szabályok szerinti hozzárendelése jelenségekhez, bizonyos tulajdonságokhoz. 4 féle szabály
Mátrixok február Feladat: Legyen A = ( ( B =
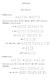 Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
KERESKEDELEMI ISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA MINTAFELADATOK FELADATLAP
 KERESKEDELEMI ISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA MINTAFELADATOK FELADATLAP Jövedelmezőség 1. Jövedelmezőség tervezése 21 pont Egy kereskedő vállalkozó 2018-ban 308 600 ezer Ft forgalmat ért el 28%-os
KERESKEDELEMI ISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA MINTAFELADATOK FELADATLAP Jövedelmezőség 1. Jövedelmezőség tervezése 21 pont Egy kereskedő vállalkozó 2018-ban 308 600 ezer Ft forgalmat ért el 28%-os
Bevezetés a Korreláció &
 Bevezetés a Korreláció & Regressziószámításba Petrovics Petra Doktorandusz Statisztikai kapcsolatok Asszociáció 2 minőségi/területi ismérv között Vegyes kapcsolat minőségi/területi és egy mennyiségi ismérv
Bevezetés a Korreláció & Regressziószámításba Petrovics Petra Doktorandusz Statisztikai kapcsolatok Asszociáció 2 minőségi/területi ismérv között Vegyes kapcsolat minőségi/területi és egy mennyiségi ismérv
A javítási-értékelési útmutatótól eltérő, de szakmailag helyes megoldásokat is el kell fogadni.
 A 29/2016. (VIII. 26.) NGM rendelet szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 54 341 02 Kereskedelmi képviselő Értékelési skála: 81 100 pont 5 (jeles) 71 80 pont
A 29/2016. (VIII. 26.) NGM rendelet szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 54 341 02 Kereskedelmi képviselő Értékelési skála: 81 100 pont 5 (jeles) 71 80 pont
Gyakorló feladatok a Komplex elemzés tárgyhoz Témakör: Minõség
 Gyakorló feladatok a Komlex elemzés tárgyhoz. feladat Egy vállalkozás termelõfolyamatának minõsége a következõkéen alakult: Megnevezés Termelés vezértermékben (db Selejt (db terv tény terv tény I. sz.
Gyakorló feladatok a Komlex elemzés tárgyhoz. feladat Egy vállalkozás termelõfolyamatának minõsége a következõkéen alakult: Megnevezés Termelés vezértermékben (db Selejt (db terv tény terv tény I. sz.
1.1: Egy felmérés során a BGF-ről frissen kikerült diplomások jövedelmét vizsgálták.
 1.1: Egy felmérés során a BGF-ről frissen kikerült diplomások jövedelmét vizsgálták. a) Hozzon létre osztályközös gyakoriságot az alábbi osztályközökkel: - 100.000 100.000-150.000 150.000-200.000 200.000-250.000
1.1: Egy felmérés során a BGF-ről frissen kikerült diplomások jövedelmét vizsgálták. a) Hozzon létre osztályközös gyakoriságot az alábbi osztályközökkel: - 100.000 100.000-150.000 150.000-200.000 200.000-250.000
Indexszámítási módszerek; Simpson-paradoxon
 Indexszámítási módszerek; Simpson-paradoxon Vida Balázs 2018. március 7. Vida Balázs Indexszám; SP 2018. március 7. 1 / 22 Bevezetés Mir l lesz szó? 1 Index(szám) fogalma, példák 2 Érték-, ár- és volumenindexek
Indexszámítási módszerek; Simpson-paradoxon Vida Balázs 2018. március 7. Vida Balázs Indexszám; SP 2018. március 7. 1 / 22 Bevezetés Mir l lesz szó? 1 Index(szám) fogalma, példák 2 Érték-, ár- és volumenindexek
Módszertani Intézeti Tanszéki Osztály. A megoldás részletes mellékszámítások hiányában nem értékelhető!
 BGF KKK Módszertani Intézeti Tanszéki Osztály Budapest, 2012.. Név:... Neptun kód:... Érdemjegy:..... STATISZTIKA II. VIZSGADOLGOZAT Feladatok 1. 2. 3. 4. 5. 6. Összesen Szerezhető pontszám 21 20 7 22
BGF KKK Módszertani Intézeti Tanszéki Osztály Budapest, 2012.. Név:... Neptun kód:... Érdemjegy:..... STATISZTIKA II. VIZSGADOLGOZAT Feladatok 1. 2. 3. 4. 5. 6. Összesen Szerezhető pontszám 21 20 7 22
Esetelemzés az SPSS használatával
 Esetelemzés az SPSS használatával A gepj.sav fileban négy különböző típusú, összesen 80 db gépkocsi üzemanyag fogyasztási adatai találhatók. Vizsgálja meg, hogy befolyásolja-e az üzemanyag fogyasztás mértékét
Esetelemzés az SPSS használatával A gepj.sav fileban négy különböző típusú, összesen 80 db gépkocsi üzemanyag fogyasztási adatai találhatók. Vizsgálja meg, hogy befolyásolja-e az üzemanyag fogyasztás mértékét
Varianciaanalízis 4/24/12
 1. Feladat Egy póker kártya keverő gép a kártyákat random módon választja ki. A vizsgálatban 1600 választott kártya színei az alábbi gyakorisággal fordultak elő. Vizsgáljuk meg, hogy a kártyák kiválasztása
1. Feladat Egy póker kártya keverő gép a kártyákat random módon választja ki. A vizsgálatban 1600 választott kártya színei az alábbi gyakorisággal fordultak elő. Vizsgáljuk meg, hogy a kártyák kiválasztása
Q1 = 1575 eft Me = 2027,7778 eft Q3 = 2526,3158 eft
 Gyak1: b) Mo = 1857,143 eft A kocsma tipikus (leggyakoribb) havi bevétele 1.857.143 Ft. c) Q1 = 1575 eft Me = 2027,7778 eft Q3 = 2526,3158 eft Gyak2: b) X átlag = 35 Mo = 33,33 σ = 11,2909 A = 0,16 Az
Gyak1: b) Mo = 1857,143 eft A kocsma tipikus (leggyakoribb) havi bevétele 1.857.143 Ft. c) Q1 = 1575 eft Me = 2027,7778 eft Q3 = 2526,3158 eft Gyak2: b) X átlag = 35 Mo = 33,33 σ = 11,2909 A = 0,16 Az
Easy PDF Creator is professional software to create PDF. If you wish to remove this line, buy it now.
 070421/1. példa Termékek Termelési érték (eft) Árindex Közvetlen bérköltség (eft) Terv Tény % Terv Tény A 60 000 84 000 105 9 000 11 760 B 18 000 15 000 100 1 800 1 800 C 40 000 35 280 98 4 800 5 292 Az
070421/1. példa Termékek Termelési érték (eft) Árindex Közvetlen bérköltség (eft) Terv Tény % Terv Tény A 60 000 84 000 105 9 000 11 760 B 18 000 15 000 100 1 800 1 800 C 40 000 35 280 98 4 800 5 292 Az
Legfontosabb tervezési feladatok. Milyen a jó terv? Terv teljesítési viszonyszám Vtt% Terv feladat viszonyszám Vtf%
 Tervezéssel kapcsolatos viszonyszámok Miért van szükség tervezésre? Eredményes gazdálkodás miatt minden vállalkozásnak szükséges tervezni. Mit kell megtervezni? Szinte mindent! Miben jobbak a külföldi
Tervezéssel kapcsolatos viszonyszámok Miért van szükség tervezésre? Eredményes gazdálkodás miatt minden vállalkozásnak szükséges tervezni. Mit kell megtervezni? Szinte mindent! Miben jobbak a külföldi
1. Egy Kft dolgozóit a havi bruttó kereseteik alapján csoportosítottuk: Havi bruttó bér, ezer Ft/fő
 Figyelem! A példasor nem tartalmazza valamennyi típuspéldát. A dolgozatban az órán leadott feladatok közül bármely típusú előfordulhat. A példasor már a második dolgozat anyagát gyakorló feladatokat is
Figyelem! A példasor nem tartalmazza valamennyi típuspéldát. A dolgozatban az órán leadott feladatok közül bármely típusú előfordulhat. A példasor már a második dolgozat anyagát gyakorló feladatokat is
STATISZTIKA 1. PÉLDATÁR. alapfogalmak egy ismérv szerinti elemzés két ismérv szerinti elemzés standardizálás indexszámítás idősorok
 STATISZTIKA 1. PÉLDATÁR alapfogalmak egy ismérv szerinti elemzés két ismérv szerinti elemzés standardizálás indexszámítás idősorok 1. ALAPFOGALMAK 1.1. Egy iskolai büfé napi vevőszámának alakulása az elmúlt
STATISZTIKA 1. PÉLDATÁR alapfogalmak egy ismérv szerinti elemzés két ismérv szerinti elemzés standardizálás indexszámítás idősorok 1. ALAPFOGALMAK 1.1. Egy iskolai büfé napi vevőszámának alakulása az elmúlt
Easy PDF Creator is professional software to create PDF. If you wish to remove this line, buy it now.
 . feladat Egy vállalkozás termelésérõl az alábbi adatokat ismeri: Termelési érték Termelés (db) Közvetlen anyagköltség elõzõ év tárgy év elõzõ év tárgy év elõzõ év tárgy év "A" termék 5 96 4 8 "B" termék
. feladat Egy vállalkozás termelésérõl az alábbi adatokat ismeri: Termelési érték Termelés (db) Közvetlen anyagköltség elõzõ év tárgy év elõzõ év tárgy év elõzõ év tárgy év "A" termék 5 96 4 8 "B" termék
Viszonyszám A B. Viszonyszám: két, egymással kapcsolatban álló statisztikai adat hányadosa, ahol A: a. viszonyítadóadat
 Viszonyszámok Viszonyszám Viszonyszám: két, egymással kapcsolatban álló statisztikai adat hányadosa, ahol A: a viszonyítandó adat Viszonyítás tárgya (viszonyítandó adat) B: a viszonyítás alapja V viszonyítadóadat
Viszonyszámok Viszonyszám Viszonyszám: két, egymással kapcsolatban álló statisztikai adat hányadosa, ahol A: a viszonyítandó adat Viszonyítás tárgya (viszonyítandó adat) B: a viszonyítás alapja V viszonyítadóadat
 Statisztika 3. Dr Gősi Zsuzsanna Egyetemi adjunktus Koncentráció mérése Koncentráció általában a jelenségek tömörülését, összpontosulását értjük. Koncentráció meglétéről gyorsan tájékozódhatunk, ha sokaságot
Statisztika 3. Dr Gősi Zsuzsanna Egyetemi adjunktus Koncentráció mérése Koncentráció általában a jelenségek tömörülését, összpontosulását értjük. Koncentráció meglétéről gyorsan tájékozódhatunk, ha sokaságot
Esettanulmányok és modellek 3
 Esettanulmányok és modellek 3 Pénzügyek Idegenforgalom Készítette: Dr. Ábrahám István 1 Pénzügyi feladatok 1. (Kocsis Péter: Opt. döntések lin.pr. (3. oldal) nyomán): Adott négy részvény jelenlegi árfolyama
Esettanulmányok és modellek 3 Pénzügyek Idegenforgalom Készítette: Dr. Ábrahám István 1 Pénzügyi feladatok 1. (Kocsis Péter: Opt. döntések lin.pr. (3. oldal) nyomán): Adott négy részvény jelenlegi árfolyama
55 345 01 0010 55 01 Európai Uniós üzleti
 A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
Feladatok. Az adatokat tartalmazó munkafüzetet mentsük le saját számítógépünkre, majd onnan nyissuk meg az Excel programmal!
 1. Feladat A táblázatunk négy légitársaság jegyeladását tartalmazza, negyedéves bontásban. Válaszoljunk a táblázat alatt lévő kérdésekre! Az eredmény IGAZ, vagy HAMIS legyen. Készítette: SZÁMALK Zrt, Szakképzési
1. Feladat A táblázatunk négy légitársaság jegyeladását tartalmazza, negyedéves bontásban. Válaszoljunk a táblázat alatt lévő kérdésekre! Az eredmény IGAZ, vagy HAMIS legyen. Készítette: SZÁMALK Zrt, Szakképzési
Korrelációs kapcsolatok elemzése
 Korrelációs kapcsolatok elemzése 1. előadás Kvantitatív statisztikai módszerek Két változó közötti kapcsolat Független: Az X ismérv szerinti hovatartozás ismerete nem ad semmilyen többletinformációt az
Korrelációs kapcsolatok elemzése 1. előadás Kvantitatív statisztikai módszerek Két változó közötti kapcsolat Független: Az X ismérv szerinti hovatartozás ismerete nem ad semmilyen többletinformációt az
Statisztikai alapfogalmak
 Statisztika I. KÉPLETEK 2011-2012-es tanév I. félév Statisztikai alapfogalmak Adatok pontossága Mért adat Abszolút hibakorlát Relatív hibakorlát Statisztikai elemzések viszonyszámokkal : a legutolsó kiírt
Statisztika I. KÉPLETEK 2011-2012-es tanév I. félév Statisztikai alapfogalmak Adatok pontossága Mért adat Abszolút hibakorlát Relatív hibakorlát Statisztikai elemzések viszonyszámokkal : a legutolsó kiírt
Erdélyi Magyar Adatbank Biró A. Zoltán Zsigmond Csilla: Székelyföld számokban. Család és háztartás
 Család és háztartás Hány személy lakik a háztartásban? 1 személy 7 2 22.9 3 24.7 4 30.2 5 9 6 4 7 8 személy 0.7 1.5 0 5 10 15 20 25 30 35 260. ábra. Hány személy lakik a háztartásban? Statisztikák Személyek
Család és háztartás Hány személy lakik a háztartásban? 1 személy 7 2 22.9 3 24.7 4 30.2 5 9 6 4 7 8 személy 0.7 1.5 0 5 10 15 20 25 30 35 260. ábra. Hány személy lakik a háztartásban? Statisztikák Személyek
7. A létszám- és bérgazdálkodás
 636. Egy áruház február havi létszáma: 7. A létszám- és bérgazdálkodás Nap Felvétel Kilépés Állományi tétszám Szabadság Betegállomány Dolgozói létszám 1 - - 342 2 3 337 2 1-343 2 3 338 3-2 341 4 2 335
636. Egy áruház február havi létszáma: 7. A létszám- és bérgazdálkodás Nap Felvétel Kilépés Állományi tétszám Szabadság Betegállomány Dolgozói létszám 1 - - 342 2 3 337 2 1-343 2 3 338 3-2 341 4 2 335
Gyakorló feladatok a kétváltozós regresszióhoz 2. Nemlineáris regresszió
 Gyakorló feladatok a kétváltozós regresszióhoz 2. Nemlineáris regresszió 1. A fizetés (Y, órabér dollárban) és iskolázottság (X, elvégzett iskolai év) közti kapcsolatot vizsgáljuk az Y t α + β X 2 t +
Gyakorló feladatok a kétváltozós regresszióhoz 2. Nemlineáris regresszió 1. A fizetés (Y, órabér dollárban) és iskolázottság (X, elvégzett iskolai év) közti kapcsolatot vizsgáljuk az Y t α + β X 2 t +
Érettségi feladatok: Statisztika
 Érettségi feladatok: Statisztika 2003. Próba 14. Bergengóciában az elmúlt 3 évben a kormány jelentése szerint kiemelt beruházás volt a bérlakások építése. Ezt az állítást az alábbi statisztikával támasztották
Érettségi feladatok: Statisztika 2003. Próba 14. Bergengóciában az elmúlt 3 évben a kormány jelentése szerint kiemelt beruházás volt a bérlakások építése. Ezt az állítást az alábbi statisztikával támasztották
Statisztikai szoftverek esszé
 Statisztikai szoftverek esszé Dávid Nikolett Szeged 2011 1 1. Helyzetfelmérés Adott egy kölcsön.txt nevű adatfájl, amely információkkal rendelkezik az ügyfelek életkoráról, családi állapotáról, munkaviszonyáról,
Statisztikai szoftverek esszé Dávid Nikolett Szeged 2011 1 1. Helyzetfelmérés Adott egy kölcsön.txt nevű adatfájl, amely információkkal rendelkezik az ügyfelek életkoráról, családi állapotáról, munkaviszonyáról,
Statisztika példatár
 Statisztika példatár v0.02 A példatár folyamatosan b vül, keresd a frissebb verziót a http://matstat.fw.hu honlapon a letölthet példatárak közt. Országh Tamás Budapest, 2006 Mottó: Ki kéne vágni minden
Statisztika példatár v0.02 A példatár folyamatosan b vül, keresd a frissebb verziót a http://matstat.fw.hu honlapon a letölthet példatárak közt. Országh Tamás Budapest, 2006 Mottó: Ki kéne vágni minden
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
Szöveges feladatok a mátrixaritmetika alkalmazására
 Szöveges feladatok a mátrixaritmetika alkalmazására Bevezetés: Tekintsük az alábbi -es mátrixot: A. Szorozzuk meg ezt jobbról egy alkalmas méretű (azaz -es) oszlopvektorral, amely az R tér kanonikus bázisának
Szöveges feladatok a mátrixaritmetika alkalmazására Bevezetés: Tekintsük az alábbi -es mátrixot: A. Szorozzuk meg ezt jobbról egy alkalmas méretű (azaz -es) oszlopvektorral, amely az R tér kanonikus bázisának
Statisztikai következtetések Nemlineáris regresszió Feladatok Vége
 [GVMGS11MNC] Gazdaságstatisztika 10. előadás: 9. Regressziószámítás II. Kóczy Á. László koczy.laszlo@kgk.uni-obuda.hu Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet A standard lineáris modell
[GVMGS11MNC] Gazdaságstatisztika 10. előadás: 9. Regressziószámítás II. Kóczy Á. László koczy.laszlo@kgk.uni-obuda.hu Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet A standard lineáris modell
AZ ÖSSZEHASONLÍTÁST TORZÍTÓ TÉNYEZŐK ÉS KISZŰRÉSÜK
 BUDAPESTI GAZDASÁGI FŐISKOLA PÉNZÜGYI ÉS SZÁMVITELI KAR KONTROLLING-ELLENŐRZÉS INTÉZETI TANSZÉK ÖSSZEÁLLÍTOTTA: BLUMNÉ BÁN ERIKA ADJUNKTUS ELEMZÉS-ELLENŐRZÉS MÓDSZERTANA ÉS RENDSZERE 2. ELŐADÁS MUNKAVEZÉRLŐ
BUDAPESTI GAZDASÁGI FŐISKOLA PÉNZÜGYI ÉS SZÁMVITELI KAR KONTROLLING-ELLENŐRZÉS INTÉZETI TANSZÉK ÖSSZEÁLLÍTOTTA: BLUMNÉ BÁN ERIKA ADJUNKTUS ELEMZÉS-ELLENŐRZÉS MÓDSZERTANA ÉS RENDSZERE 2. ELŐADÁS MUNKAVEZÉRLŐ
A konfidencia intervallum képlete: x± t( α /2, df )
 1. feladat. Egy erdőben az egy fészekben levő tojásszámokat vizsgáltuk egy madárfajnál. A következő tojásszámokat találtuk: 1, 1, 1,,,,,,, 3, 3, 3, 3, 3, 4, 4, 5, 6, 7. Mi a mintának a minimuma, maximuma,
1. feladat. Egy erdőben az egy fészekben levő tojásszámokat vizsgáltuk egy madárfajnál. A következő tojásszámokat találtuk: 1, 1, 1,,,,,,, 3, 3, 3, 3, 3, 4, 4, 5, 6, 7. Mi a mintának a minimuma, maximuma,
Idősorok elemzése [leíró statisztikai eszközök] I
![Idősorok elemzése [leíró statisztikai eszközök] I Idősorok elemzése [leíró statisztikai eszközök] I](/thumbs/96/128657832.jpg) Leíró és matematikai statisztika Matematika alapszak, matematikai elemző szakirány Zempléni András Valószínűségelméleti és Statisztika Tanszék Matematikai Intézet Természettudományi Kar Eötvös Loránd Tudományegyetem
Leíró és matematikai statisztika Matematika alapszak, matematikai elemző szakirány Zempléni András Valószínűségelméleti és Statisztika Tanszék Matematikai Intézet Természettudományi Kar Eötvös Loránd Tudományegyetem
Biometria gyakorló feladatok BsC hallgatók számára
 Biometria gyakorló feladatok BsC hallgatók számára 1. Egy üzem alkalmazottainak megoszlása az elért teljesítmény %-a szerint a következı: Norma teljesítmény % Dolgozók száma 60-80 30 81-90 70 91-100 90
Biometria gyakorló feladatok BsC hallgatók számára 1. Egy üzem alkalmazottainak megoszlása az elért teljesítmény %-a szerint a következı: Norma teljesítmény % Dolgozók száma 60-80 30 81-90 70 91-100 90
Statisztika II előadáslapok. 2003/4. tanév, II. félév
 Statisztika II előadáslapok 3/4 tanév, II félév BECSLÉS ÉS HIPOTÉZISVIZSGÁLAT Egyik konzervgyár vágott zöldbabot exportál A szabvány szerint az üvegek nettó töltősúlyának az átlaga 3 g, a szórása 5 g Az
Statisztika II előadáslapok 3/4 tanév, II félév BECSLÉS ÉS HIPOTÉZISVIZSGÁLAT Egyik konzervgyár vágott zöldbabot exportál A szabvány szerint az üvegek nettó töltősúlyának az átlaga 3 g, a szórása 5 g Az
Statisztika I. 7. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 7. előadás Előadó: Dr. Ertsey Imre STATISZTIKAI INDEXEK STATISZTIKAI INDEXEK Index: latin eredetű szó, egyszerűen mutatót jelent A statisztikai indexszám: - komplexebb tartalmú, - többet
Statisztika I. 7. előadás Előadó: Dr. Ertsey Imre STATISZTIKAI INDEXEK STATISZTIKAI INDEXEK Index: latin eredetű szó, egyszerűen mutatót jelent A statisztikai indexszám: - komplexebb tartalmú, - többet
A 4.m osztálynak gyakorlásra a statisztika felmérőre
 A 4.m osztálynak gyakorlásra a statisztika felmérőre 4. 2005. május, 8. feladat a), b) és c) része Az alábbi táblázat egy ország munkaképes lakosságának foglalkoztatottság szerinti megoszlását mutatja.
A 4.m osztálynak gyakorlásra a statisztika felmérőre 4. 2005. május, 8. feladat a), b) és c) része Az alábbi táblázat egy ország munkaképes lakosságának foglalkoztatottság szerinti megoszlását mutatja.
Statisztika 2. Dr Gősi Zsuzsanna Egyetemi adjunktus
 Statisztika 2. Dr Gősi Zsuzsanna Egyetemi adjunktus Gyakorisági sorok Mennyiségi ismérv jellemző rangsor készítünk. (pl. napi jegyeladások száma) A gyakorisági sor képzése igazából tömörítést jelent Nagyszámú
Statisztika 2. Dr Gősi Zsuzsanna Egyetemi adjunktus Gyakorisági sorok Mennyiségi ismérv jellemző rangsor készítünk. (pl. napi jegyeladások száma) A gyakorisági sor képzése igazából tömörítést jelent Nagyszámú
b) Ábrázolja ugyanabban a koordinátarendszerben a g függvényt! (2 pont) c) Oldja meg az ( x ) 2
 1) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) b) c) ( ) ) Határozza meg az 1. feladatban megadott, ; intervallumon
1) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) b) c) ( ) ) Határozza meg az 1. feladatban megadott, ; intervallumon
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
X PMS 2007 adatgyűjtés eredményeinek bemutatása X PMS ADATGYŰJTÉS
 X PMS ADATGYŰJTÉS 2007 1 Tartalom Összefoglalás...3 A kutatásba beválasztott betegek életkora... 4 A kutatásba bevont betegek nem szerinti megoszlása... 5 Az adatgyűjtés során feltárt diagnózisok megoszlása...
X PMS ADATGYŰJTÉS 2007 1 Tartalom Összefoglalás...3 A kutatásba beválasztott betegek életkora... 4 A kutatásba bevont betegek nem szerinti megoszlása... 5 Az adatgyűjtés során feltárt diagnózisok megoszlása...
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások
 Megoldások 1. A fős osztály dolgozatot írt matematikából és a következő jegyek születtek: 6 darab jeles, 9 darab jó, 8 darab közepes, darab elégséges és darab elégtelen. Készíts gyakorisági táblázatot,
Megoldások 1. A fős osztály dolgozatot írt matematikából és a következő jegyek születtek: 6 darab jeles, 9 darab jó, 8 darab közepes, darab elégséges és darab elégtelen. Készíts gyakorisági táblázatot,
A lánc viszonyszám: A lánc viszonyszám számítási képlete:
 A lánc viszonyszám: Az idősor minden egyes tagját a közvetlenül megelőzővel osztjuk, vagyis az idősor első évének, vagy időszakának láncviszonyszáma nem számítható. A lánc viszonyszám számítási képlete:
A lánc viszonyszám: Az idősor minden egyes tagját a közvetlenül megelőzővel osztjuk, vagyis az idősor első évének, vagy időszakának láncviszonyszáma nem számítható. A lánc viszonyszám számítási képlete:
[Biomatematika 2] Orvosi biometria. Visegrády Balázs
![[Biomatematika 2] Orvosi biometria. Visegrády Balázs [Biomatematika 2] Orvosi biometria. Visegrády Balázs](/thumbs/93/112272424.jpg) [Biomatematika 2] Orvosi biometria Visegrády Balázs 2016. 03. 27. Probléma: Klinikai vizsgálatban három különböző antiaritmiás gyógyszert (ß-blokkoló) alkalmaznak, hogy kipróbálják hatásukat a szívműködés
[Biomatematika 2] Orvosi biometria Visegrády Balázs 2016. 03. 27. Probléma: Klinikai vizsgálatban három különböző antiaritmiás gyógyszert (ß-blokkoló) alkalmaznak, hogy kipróbálják hatásukat a szívműködés
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x
TERMÉK ÖSSZEHASONLÍTÓ TÁBLÁZAT - GB661 JELŰ UTAZÁSI GARANCIA BIZTOSÍTÁS
 Termék neve GB661 jelű Utazási Garancia Biztosítás Termék besorolása Alapbiztosítási csomagok Prémium Komfort Bázis Biztosítható kockázatok Sürgősségi orvosi ellátás x x x Asszisztencia x x x Jogvédelem
Termék neve GB661 jelű Utazási Garancia Biztosítás Termék besorolása Alapbiztosítási csomagok Prémium Komfort Bázis Biztosítható kockázatok Sürgősségi orvosi ellátás x x x Asszisztencia x x x Jogvédelem
Lineáris algebra. (közgazdászoknak) T C T = ( 1 ) ; , D T D =
 Lineáris algebra (közgazdászoknak) 10A103 FELADATOK A GYAKORLATRA (1.) 2018/2019. tavaszi félév Mátrixok 1.1. Feladat. Legyen A = 1 2 1, B = 1 2 3 1 2 1 1, C = ( 1 2 0 ), D = 1 3 1 1 2 1 ( ) 10/2 0.6 1
Lineáris algebra (közgazdászoknak) 10A103 FELADATOK A GYAKORLATRA (1.) 2018/2019. tavaszi félév Mátrixok 1.1. Feladat. Legyen A = 1 2 1, B = 1 2 3 1 2 1 1, C = ( 1 2 0 ), D = 1 3 1 1 2 1 ( ) 10/2 0.6 1
Erdélyi Magyar Adatbank Biró A. Zoltán Zsigmond Csilla: Székelyföld számokban. Lakáskörülmények
 Lakáskörülmények Ön jelenleg hol lakik? önálló lakása van szüleinél 19.3 71.9 házastársa szüleinél rokonoknál ismerősöknél lakást bérel szobát bérel egyéb 4.3 0.5 0.3 2 0.5 1.3 0 10 20 30 40 50 60 70 80
Lakáskörülmények Ön jelenleg hol lakik? önálló lakása van szüleinél 19.3 71.9 házastársa szüleinél rokonoknál ismerősöknél lakást bérel szobát bérel egyéb 4.3 0.5 0.3 2 0.5 1.3 0 10 20 30 40 50 60 70 80
20 PONT Aláírás:... A megoldások csak szöveges válaszokkal teljes értékőek!
 SPEC 2009-2010. II. félév Statsztka II HÁZI dolgozat Név:... Neptun kód: 20 PONT Aláírás:... A megoldások csak szöveges válaszokkal teljes értékőek! 1. példa Egy üzemben tejport csomagolnak zacskókba,
SPEC 2009-2010. II. félév Statsztka II HÁZI dolgozat Név:... Neptun kód: 20 PONT Aláírás:... A megoldások csak szöveges válaszokkal teljes értékőek! 1. példa Egy üzemben tejport csomagolnak zacskókba,
Gyakorló feladatok a Kontrolling alapjai tárgyhoz Témakör: Mérés és elemzés (Tényezőkre bontás) 1. feladat
 . feladat Egy vállalkozás termeléséről az alábbi adatokat ismeri: Megnevezés mennyiségi egység terv tény Termelés db 2 Fajlagos anyagfelhasználás kg/db 8, 9, Anyag egységár Ft/kg 25,, Fajlagos munkaórafelhasználás
. feladat Egy vállalkozás termeléséről az alábbi adatokat ismeri: Megnevezés mennyiségi egység terv tény Termelés db 2 Fajlagos anyagfelhasználás kg/db 8, 9, Anyag egységár Ft/kg 25,, Fajlagos munkaórafelhasználás
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
STATISZTIKA. András hármas. Éva ötös. Nóri négyes. 5 4,5 4 3,5 3 2,5 2 1,5 ANNA BÉLA CILI 0,5 MAGY. MAT. TÖRT. KÉM.
 STATISZTIKA 5 4,5 4 3,5 3 2,5 2 1,5 1 0,5 0 MAGY. MAT. TÖRT. KÉM. ANNA BÉLA CILI András hármas. Béla Az átlag 3,5! kettes. Éva ötös. Nóri négyes. 1 mérés: dolgokhoz valamely szabály alapján szám rendelése
STATISZTIKA 5 4,5 4 3,5 3 2,5 2 1,5 1 0,5 0 MAGY. MAT. TÖRT. KÉM. ANNA BÉLA CILI András hármas. Béla Az átlag 3,5! kettes. Éva ötös. Nóri négyes. 1 mérés: dolgokhoz valamely szabály alapján szám rendelése
Gazdasági informatikus Informatikus
 A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
Segítség az outputok értelmezéséhez
 Tanulni: 10.1-10.3, 10.5, 11.10. Hf: A honlapra feltett falco_exp.zip-ben lévő exploratív elemzések áttanulmányozása, érdekességek, észrevételek kigyűjtése. Segítség az outputok értelmezéséhez Leiro: Leíró
Tanulni: 10.1-10.3, 10.5, 11.10. Hf: A honlapra feltett falco_exp.zip-ben lévő exploratív elemzések áttanulmányozása, érdekességek, észrevételek kigyűjtése. Segítség az outputok értelmezéséhez Leiro: Leíró
Diszkriminancia-analízis
 Diszkriminancia-analízis az SPSS-ben Petrovics Petra Doktorandusz Diszkriminancia-analízis folyamata Feladat Megnyitás: Employee_data.sav Milyen tényezőktől függ a dolgozók beosztása? Nem metrikus Független
Diszkriminancia-analízis az SPSS-ben Petrovics Petra Doktorandusz Diszkriminancia-analízis folyamata Feladat Megnyitás: Employee_data.sav Milyen tényezőktől függ a dolgozók beosztása? Nem metrikus Független
Biomatematika 15. Szent István Egyetem Állatorvos-tudományi Kar. Fodor János
 Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 15. Nemparaméteres próbák Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision Date: November
Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 15. Nemparaméteres próbák Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision Date: November
Stratégiai pénzügyi elemzés (A)
 Stratégiai pénzügyi elemzés (A) 1. ÜGYFÉL 2. ÜGYFÉL Személyes adatok Ügyfél neve Ügyfél neme férfi / nő férfi / nő Állandó lakcím Levelezési cím Születési idő Mobiltelefonszám E-mail cím Családi állapot
Stratégiai pénzügyi elemzés (A) 1. ÜGYFÉL 2. ÜGYFÉL Személyes adatok Ügyfél neve Ügyfél neme férfi / nő férfi / nő Állandó lakcím Levelezési cím Születési idő Mobiltelefonszám E-mail cím Családi állapot
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
operációkutatás példatár
 operációkutatás példatár . MŰVELETEK MÁTIXOKKAL. (Megoldás a.-es gyakorló ideóban.) Itt annak ezek a mátriok illete ektorok: A c B d * E f * Végezzük el a köetkező műeleteket: A B B E B c B A A E B d..
operációkutatás példatár . MŰVELETEK MÁTIXOKKAL. (Megoldás a.-es gyakorló ideóban.) Itt annak ezek a mátriok illete ektorok: A c B d * E f * Végezzük el a köetkező műeleteket: A B B E B c B A A E B d..
Kísérleti Szöveges Értékelés 2016.
 Kísérleti Szöveges Értékelés 2016. Gazda neve: Zsemberi Gábor, Ópusztaszer. Termesztés: -előnövény; saláta, -főnövény; berakó uborka Fajta: Triology F1 Genezis Kísérlet (GK): 350 m² 780 tő Üzemi Kísérlet
Kísérleti Szöveges Értékelés 2016. Gazda neve: Zsemberi Gábor, Ópusztaszer. Termesztés: -előnövény; saláta, -főnövény; berakó uborka Fajta: Triology F1 Genezis Kísérlet (GK): 350 m² 780 tő Üzemi Kísérlet
Makroökonómia (G-Kar és HR) gyakorló feladatok az 1. és 2. szemináriumra
 Makroökonómia (G-Kar és HR) gyakorló feladatok az 1. és 2. szemináriumra 1. Feladat Az általunk vizsgált gazdaságban 2018-ban és 2019-ben csupán két terméket állítanak el : X-et és Y-t. Az ezekre vonatkozó
Makroökonómia (G-Kar és HR) gyakorló feladatok az 1. és 2. szemináriumra 1. Feladat Az általunk vizsgált gazdaságban 2018-ban és 2019-ben csupán két terméket állítanak el : X-et és Y-t. Az ezekre vonatkozó
A 27/2012 (VIII. 27.) NGM rendelet szakmai és vizsgakövetelménye alapján.
 A 27/2012 (VIII. 27.) NGM rendelet szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 35 811 02 Vendéglátó-üzletvezető Tájékoztató A vizsgázó az első lapra írja fel a
A 27/2012 (VIII. 27.) NGM rendelet szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 35 811 02 Vendéglátó-üzletvezető Tájékoztató A vizsgázó az első lapra írja fel a
Statisztika I. 12. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 1. előadás Előadó: Dr. Ertsey Imre Regresszió analízis A korrelációs együttható megmutatja a kapcsolat irányát és szorosságát. A kapcsolat vizsgálata során a gyakorlatban ennél messzebb
Statisztika I. 1. előadás Előadó: Dr. Ertsey Imre Regresszió analízis A korrelációs együttható megmutatja a kapcsolat irányát és szorosságát. A kapcsolat vizsgálata során a gyakorlatban ennél messzebb
A leíró statisztikák
 A leíró statisztikák A leíró statisztikák fogalma, haszna Gyakori igény az, hogy egy adathalmazt elemei egyenkénti felsorolása helyett néhány jellemző tulajdonságának megadásával jellemezzünk. Ezeket az
A leíró statisztikák A leíró statisztikák fogalma, haszna Gyakori igény az, hogy egy adathalmazt elemei egyenkénti felsorolása helyett néhány jellemző tulajdonságának megadásával jellemezzünk. Ezeket az
A 27/2012 (VIII. 27.) NGM rendelet szakmai és vizsgakövetelménye alapján.
 A 27/2012 (VIII. 27.) NGM rendelet szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 35 811 02 Vendéglátó-üzletvezető Tájékoztató A vizsgázó az első lapra írja fel a
A 27/2012 (VIII. 27.) NGM rendelet szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 35 811 02 Vendéglátó-üzletvezető Tájékoztató A vizsgázó az első lapra írja fel a
Gazdasági informatikus Informatikus
 A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Próbaérettségi feladatsor_b NÉV: osztály Elért pont:
 Próbaérettségi feladatsor_b NÉV: osztály Elért pont: I. rész A feladatsor 12 példából áll, a megoldásokkal maimum 30 pont szerezhető. A kidolgozásra 45 perc fordítható. 1. feladat Egy derékszögű háromszög
Próbaérettségi feladatsor_b NÉV: osztály Elért pont: I. rész A feladatsor 12 példából áll, a megoldásokkal maimum 30 pont szerezhető. A kidolgozásra 45 perc fordítható. 1. feladat Egy derékszögű háromszög
Mikroökonómia. Vizsgafeladatok
 Mikroökonómia Vizsgafeladatok Bacsi, Mikro feladatok 1 1, Marshall- kereszt, piaci egyensúly Mennyi a savanyúcukorka egyensúlyi mennyisége, ha a cukorka iránti kereslet és kínálat függvénye a következı:
Mikroökonómia Vizsgafeladatok Bacsi, Mikro feladatok 1 1, Marshall- kereszt, piaci egyensúly Mennyi a savanyúcukorka egyensúlyi mennyisége, ha a cukorka iránti kereslet és kínálat függvénye a következı:
KOMPETENCIA MÉRÉS ÉVFOLYAM
 KOMPETENCIA MÉRÉS 2015. 6. ÉVFOLYAM MATEMATIKA A tanulók átlageredménye: Telephely: 1464 Országos: 1497 Városi ált. isk.: 1480 Megyeszékh. ált. isk.: 1530 Iskolánk átlageredménye rosszabb, mint az országos,
KOMPETENCIA MÉRÉS 2015. 6. ÉVFOLYAM MATEMATIKA A tanulók átlageredménye: Telephely: 1464 Országos: 1497 Városi ált. isk.: 1480 Megyeszékh. ált. isk.: 1530 Iskolánk átlageredménye rosszabb, mint az országos,
54 481 04 0010 54 01 Gazdasági informatikus Informatikus
 A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
Biostatisztika VIII. Mátyus László. 19 October
 Biostatisztika VIII Mátyus László 19 October 2010 1 Ha σ nem ismert A gyakorlatban ritkán ismerjük σ-t. Ha kiszámítjuk s-t a minta alapján, akkor becsülhetjük σ-t. Ez további bizonytalanságot okoz a becslésben.
Biostatisztika VIII Mátyus László 19 October 2010 1 Ha σ nem ismert A gyakorlatban ritkán ismerjük σ-t. Ha kiszámítjuk s-t a minta alapján, akkor becsülhetjük σ-t. Ez további bizonytalanságot okoz a becslésben.
A légzésszabályozás vizsgálata patkányon. A mérési adatok elemzése és értékelése
 A légzésszabályozás vizsgálata patkányon A mérési adatok elemzése és értékelése Biológia BSc. B gyakorlat A mérést és kiértékelést végezték:... [pont] 500 400 a n. vagus ingerlése... 300 200 idő Gyakorlatvezető:
A légzésszabályozás vizsgálata patkányon A mérési adatok elemzése és értékelése Biológia BSc. B gyakorlat A mérést és kiértékelést végezték:... [pont] 500 400 a n. vagus ingerlése... 300 200 idő Gyakorlatvezető:
SZIA 2000 Bt. BESZÁMOLÓ
 SZIA 2000 Bt. BESZÁMOLÓ a 2017. évi Püspökladány város közigazgatási határán belül autóbusszal végzett menetrendszerinti helyi személyszállítási tevékenységről Készült: Püspökladány Város Önkormányzatának
SZIA 2000 Bt. BESZÁMOLÓ a 2017. évi Püspökladány város közigazgatási határán belül autóbusszal végzett menetrendszerinti helyi személyszállítási tevékenységről Készült: Püspökladány Város Önkormányzatának
1. a. Vegye fel az alábbi táblázatban szereplő adatokat! Ügyeljen a táblázatban szereplő
 1. 1. a. Vegye fel az alábbi táblázatban szereplő adatokat! Ügyeljen a táblázatban szereplő formátumokra is! Sorszám Betét napja Kamatláb Bet. össz. (Ft) Kamat (Ft) Kifiz (Ft) 1. 1997. 08. 14. 12% 100
1. 1. a. Vegye fel az alábbi táblázatban szereplő adatokat! Ügyeljen a táblázatban szereplő formátumokra is! Sorszám Betét napja Kamatláb Bet. össz. (Ft) Kamat (Ft) Kifiz (Ft) 1. 1997. 08. 14. 12% 100
KORLÁTOZOTT TERJESZTÉSŰ. Cenzori. Írásbeli vizsgatevékenység
 NEMZETGAZDASÁGI MINISZTÉRIUM TÜK szám: 04 / 155 /2012. MK/HU KORLÁTOZOTT TERJESZTÉSŰ Érvényességi idő: 2012. május 15. 8.00. óra Minősítő neve: Pankucsi Zoltán Beosztása: főosztályvezető Készült: 1 eredeti
NEMZETGAZDASÁGI MINISZTÉRIUM TÜK szám: 04 / 155 /2012. MK/HU KORLÁTOZOTT TERJESZTÉSŰ Érvényességi idő: 2012. május 15. 8.00. óra Minősítő neve: Pankucsi Zoltán Beosztása: főosztályvezető Készült: 1 eredeti
A sokaság/minta eloszlásának jellemzése
 3. előadás A sokaság/mnta eloszlásának jellemzése tpkus értékek meghatározása; az adatok különbözőségének vzsgálata, a sokaság/mnta eloszlásgörbéjének elemzése. Eloszlásjellemzők Középértékek helyzet (Me,
3. előadás A sokaság/mnta eloszlásának jellemzése tpkus értékek meghatározása; az adatok különbözőségének vzsgálata, a sokaság/mnta eloszlásgörbéjének elemzése. Eloszlásjellemzők Középértékek helyzet (Me,
A gazdasági növekedés mérése
 A gazdasági növekedés mérése Érték-, volumen- és árindexek 25.) Az alábbi táblázat két egymást követő év termelési mennyiségeit és egységárait mutatja egy olyan gazdaságban, ahol csupán három terméket
A gazdasági növekedés mérése Érték-, volumen- és árindexek 25.) Az alábbi táblázat két egymást követő év termelési mennyiségeit és egységárait mutatja egy olyan gazdaságban, ahol csupán három terméket
