I9 Teleoperáció és távérzékelés virtuális cellában
|
|
|
- Ádám Dobos
- 6 évvel ezelőtt
- Látták:
Átírás
1 I9 Teleoperáció és távérzékelés Mérési útmutató az Irányítástechnika és Képfeldolgozás Laboratóriumhoz: 9. mérés Dr. Vajda Ferenc 3D érzékelés és Mobilrobotika kutatócsoport Irányítástechnika és Informatika Tanszék október 7.
2 Jelen dokumentum a Budapesti Műszaki és Gazdaságtudományi egyetem Irányítástechnika és képfeldolgozás laboratórium 1. c. tárgyához kapcsolódó mérési útmutató. A mérés és az útmutató a laboratórium 9. méréséhez készült a tanszék 3D érzékelés és mobilrobotika kutatócsoportjában. A mérések és a mérési útmutató kidolgozásában részt vettek a kutatócsoport tagjai: Vajda Ferenc Takács Tibor Srp Ágoston Mihály Helfenbein Tamás Tóth András A dokumentum szabadon letölthető, és átadható a tartalom módosítása nélkül. A dokumentumból történő idézések esetén a forrás megjelölendő. Verziók: Dátum Verzió Módosította Leírás 10/14/09 V0.1 Vajda Ferenc Első kész változat 11/25/14 V0.2 Szemenyei Márton Második változat 09/02/15 V0.3 Szemenyei Márton Harmadik kész változat
3 Tartalomjegyzék 1. Teleoperáció és távérzékelés Objektumfelismerés, pozíciómeghatározás Objektumtulajdonságok meghatározása Objektumtulajdonságok nyomatékok alapján Kétdimenziós pozíciómeghatározás a perspektív torzítású képen Teleoperáció bemerüléses virtuális valóság segítségével Célkitűzések A mérés során alkalmazott eszközök Feladatok OpenCV referencia Példa-programrészletek Kép létrehozása Megjelenítése Bináris kép előállítása Színtérkonverzió, szétválasztás komponensekre Műveletek objektumokkal Műveletek képrészletekkel Perspektív transzformáció Ellenőrző kérdések szeptember 2. 1
4 1. Teleoperáció és távérzékelés A valós életben számos olyan problémával taláhatjuk szemben magunkat, ahol a feladat elvégzését megnehezíti, hogy a munkavégzés környezete (a munkatér) az ember számára megközelíthetetlen, vagy éppenséggel veszélyes. Ilyen esetekben elterjedt megoldás az iparban a teleoperáció, vagyis távoli, biztonságos környezetből irányított robotok használata az adott feladat megoldásának érdekében. Az ilyen esetekben alkalmazott robotok gyakran rendelkeznek a környezetük feltérképezését, vagy egyéb információgyűjtést szolgáló szenzorokkal is, melyek adatai a robotot kezelő irányító döntéseit segítik. Ezt a folyamatot nevezzük távérzékelésnek. Gyakori probléma azonban a távérzékelés és a teleoperáció használata során, hogy a munkatér és az irányítóközpont közti nagy fizikai távolság, vagy egyéb technológiai korlátok az ember számára is érzékelhető és a kezelőket zavaró mértékű késleltetést okoznak. További problémaforrás lehet, ha a robot és a vezérlőközpont közti kommunikációs megoldás limitációi korlátozzák az átvihető adatmennyiséget, így nincs lehetőségünk az összes szenzoradat továbbítására az irányító felé. A fenti problémák miatt indokolt lehet a rendszer munkatérbeli, illetve a kezelőtérben található részegységében is egy visszacsatolás segítségével helyi irányítóhurkokat létrehozni. A helyi hurkok segítségével mindkét oldalon lehetőség nyílik a másik résztvevő által szolgáltatott jelek becslésére, szimulációjára késleltetés nélkül, az esetleges hibák korrigálására pedig a valódi adatok beérkezésekor lehetőség nyílik. A távérzékelés és teleoperáció modelljét a helyi visszacsatolásokkal kiegészítve kapjuk a Sheridan-modellt (1. ábra) szeptember 2. 2
5 1. ábra: A Sheridan-modell A távoli számítógép oldalán lévő helyi hurok esetén az irányítás, döntéshozás, valamint a jelfeldolgozás megvalósítása szükséges, így a robot képes váratlan helyzetekben az irányító beavatkozása (és így késlekedés) nélkül reagálni. A távoli hurokban lehetőség nyílik az irányító jövőbeli döntéseinek becslésére is, a használt módszerek megbízhatósága azonban sok esetben nem megfelelő. A kezelői oldalon található hurok feladata a robotnak, illetve a környezetének szimulációja, így azonnali visszajelzést képes szolgáltatni a kezelőnek a robot feltételezett reakciójáról a kiadott vezérlésre. Ezt a feladatot gyakorta végezzük el virtuális valóság környezetek segítségével, melyben mind a robot, mind a környezet modelljét elhelyezzük. A kezelői oldalon található vezérlési hurok fontos feladata, hogy a szimuláció eredményét a beérkező adatok alapján pontosítsa, nagy mértékben javítva a kezelhetőséget szeptember 2. 3
6 2. Objektumfelismerés, pozíciómeghatározás A kamerarendszerek egyik legfontosabb felhasználási célja a környezetben található objektumok szétválasztása és a lényeges elemek kiemelése, más szóval szegmentálás. Tekintettel a fontosságára, illetve a feladat meglehetősen nem egzakt jellegére, számos jó és kevésbé jó algoritmust alkalmazhatunk. Legtöbbjük csak különleges körülmények között használható, vagy olyan mértékű futásidőigénye, hogy a legtöbb alkalmazásban szóba se kerülhet. Emiatt az alkalmazások nagy részénél valamilyen módon egyszerűsítenünk kell a környezetet, és olyan módon kell átalakítanunk, hogy az algoritmus számára könnyedén feldolgozható legyen. Erre megoldás, ha a megkeresendő objektum színét megváltoztatjuk olyan módon, hogy a környezettől elüssön. A szegmentált objektumok megtalálása után annak releváns tulajdonságait is meg kell határoznunk. Szinte minden esetben szükséges a pozíció és/vagy orientáció, de gyakran van szükség méretre stb. A lényeges tulajdonságok kiemelése általában egyszerűbb feladat, mint a szegmentálás, de sokszor ezek meghatározása is szinte lehetetlennek tűnik. Az alábbiakban ismertetünk néhány fontosabb algoritmust, amely segítségével a mérésben szükséges képfeldolgozási feladatok elvégezhetők. Ez természetesen nem jelenti, hogy a hallgató nem használhat szofisztikáltabb megoldást. 2.1 Objektumtulajdonságok meghatározása A szegmentálás során megtalált objektumok azonosításához meg kell határoznunk az objektumok paramétereit. Ezek közé tartoznak az objektum mérete, elhelyezkedése, alakja, mintázata, színe stb. Az alábbiakban a mérés szempontjából fontosabb tulajdonságokra összpontosítunk Objektumtulajdonságok nyomatékok alapján Az objektumok területének, pozíciójának és orientációjának meghatározásához szeptember 2. 4
7 felhasználhatjuk a különféle geometriai nyomatékokat. Ehhez szükséges, hogy az adott képen csak az objektum legyen látható. A megoldás működik bináris, és szürkeárnyalatos képeken is. A hallgatók által is használt OpenCV rendszerben az egyes nyomatékok elnevezései m ij formában jelennek meg, így ezek is megtalálhatók az alábbiakban. Tekintettel arra, hogy a harmad, vagy magasabb rendű nyomatékok használata igen ritka, ezekkel a továbbiakban nem foglalkozunk. Nulladrendű nyomaték A nulladrendű nyomaték a megtalált objektum területét adja meg. A= I x, y =m 00 (1) x y Elsőrendű nyomaték Az elsőrendű nyomaték az objektum statikai nyomatékát adja meg. Az elsőrendű és a nulladrendű nyomaték hányadosából megkaphatjuk az objektum súlypontjának x, illetve y koordinátáját. Ebből Másodrendű nyomaték S x = y I x, y =m 01 x y (2) S y = x I x, y =m 10 x y (3) x c = S y A = x x y c = S x A = x x y y y y x I x, y I x, y y I x, y I x, y A másodrendű nyomatékok az objektum x és y tengely körüli tehetetlenségi (4) (5) szeptember 2. 5
8 nyomatékát adja meg. Orientációként többnyire a legkisebb másodrendű nyomatékhoz tartozó tengely irányát szoktuk választani. J x = x y y 2 I x, y =m 02 (6) J y = x 2 I x, y =m 20 (7) x y Illetve a Centrifugális másodrendű nyomaték: J xy = x y xy I x, y =m 11 (8) A nyomatékok alapján a súlyponton átmenő legkisebb nyomatékú tengely iránya (a részletes magyarázatra itt nem térünk ki): Amelyből: a=j y S 2 y (9) A b=2 J xy S x S y A (10) c=j x S 2 x A (11) tan 2 = b a c (12) b sin 2 =± b 2 a c 2 (13) a c cos 2 =± b 2 a c 2 (14) Azt a szöget kell megkeresnünk, amelyre mindhárom egyenlet teljesül. Tekintettel arra, hogy a tengely elfordulási szögét keressük, ennek értéke közé eshet. Érdemes még megemlíteni a középpontra vett másodrendű nyomatékot J 0 = x 2 y 2 I x, y =J x J y (15) x y amely alakinformációkat hordoz. Ez is abban az esetben a leghasznosabb, ha a középpont nem a kép (0,0) pozíciója, hanem az objektum súlypontja: szeptember 2. 6
9 J 0,c = J 0 S 2 2 x S y A (16) 2.2 Kétdimenziós pozíciómeghatározás a perspektív torzítású képen Amennyiben egy kamera nem pontosan felülről látja a munkateret, a munkatér a képen torzítva jelenik meg. Igaz azonban az, hogy amennyiben a munkatérben vizsgált összes objektum egy síkban helyezkedik el, a képernyőn található pontok egyértelműen összefüggenek a valós pontokkal. Az összefüggést a perspektív transzformáció adja meg. z x y f O 2. ábra Perspektív transzformáció két dimenzióban A transzformáció homogén koordináták segítségével az alábbi módon fogalmazható meg: [x w y w w ]=T persp [ u 1] v (17) Ahol u és v a képkoordináták, a 3 3 T persp pedig a kamera és a viszonyítási koordinátarendszer közötti forgatást és eltolást, illetve az egy ponton keresztüli síkra történő vetítés transzformációs együtthatóit tartalmazza. Ebből a világkoordináták az szeptember 2. 7
10 alábbi módon származtathatók. x= x w w, ill. y= y w w (18) Az ellenkező irányú transzformációt is elvégezhetjük a perspektív operátorral: illetve [u s v s s ]=T W C persp [ 1] x y (19) u= u s s, és v= v s s (20) Mivel nekünk a kamerakép áll rendelkezésünkre, a továbbiakban a (17)-(18) egyenleteket használjuk. A perspektív transzformációs mátrix meghatározásához fel kell vennünk pontokat, amelyeknek ismerjük a pontos pozícióját a valós térben és a kameraképen is. Tekintettel arra, hogy w értéke tetszőleges lehet (nyilvánvalóan leszámítva a 0 értéket) a mátrix determinánsa is tetszőlegesen megválasztható, vagyis a kilenc érték nem független egymástól, egyet tetszőlegesen megválaszthatunk. Az egyszerűség kedvéért válasszuk t 33 =1 értéket. A többi paraméter azonban meghatározható. Mivel nyolc paraméter értékére vagyunk kíváncsiak, nyolc független összerendelésre van szükségünk. Mivel minden pont két független értéket tartalmaz (x, y) (u, v), négy ismert pontra van szükségünk. Minden pontra igaz (17) alapján, hogy Vagyis [x ]=[t11 t12 t13 w, ] [u y w, t 21 t 22 t 23 v w t 31 t 32 1 ] (21) 1 x = t 11u t 12 v t 13 t 31 u t 32 v 1, ill. y = t 21u t 22 v t 23 t 31 u t 32 v 1 (22) Amelyből u t 11 v t 12 1 t 13 u x t 31 v x t 32 =x u t 21 v t 22 1 t 23 u y t 31 v y t 32 = y (23) szeptember 2. 8
11 Az összes pontra lineáris formában felírva v0 1 u0 x0 v0 x0 11 u 0 v 0 1 u 0 y 0 v 0 y 0 t 12 u 1 v 1 1 u 1 x 1 v 1 x 1 t 13 u 1 v 1 1 u 1 y 1 v 1 y 1 t A t=[u0 21 u 2 v 2 1 u 2 x 2 v 2 x 2 t 22 u 2 v 2 1 u 2 y 2 v 2 y 2 t 23 u 3 v 3 1 u 3 x 3 v 3 x 3 t 31 u 3 v 3 1 u 3 y 3 v 3 y 3] [t Így megkaphatjuk a transzformációs paramétereket: y 0 x 1 y 1 x 2 y 2 x 3 t 32]=[x0 y 3]=b (24) t=a 1 b (25) szeptember 2. 9
12 3. Teleoperáció bemerüléses virtuális valóság segítségével A mérés során a hallgatók megismerkednek az objektumfelismerés és a pozíciómeghatározás alapjaival, illetve betekintést nyernek a virtuális valóság rendszerekben való alkalmazásaiba. 3.1 Célkitűzések A mérés során a hallgatók egy sík munkaterületen dolgoznak, melyben egy távirányítású jármű, valamint egységes kinézetű akadályok helyezkednek el (3. ábra). Ezt a munkaterületet egy kamera figyelmi meg felülről/oldalról, így a vizuális távérzékelés használatához először a perspektív transzformáció meghatározása szükséges. (-0,2 ; 184,3) (189,9 ; 178,5) (0,0 ; 0,0) (162,2 ; 0,0) 13. ábra Munkaterület Ennek a transzformációnak a meghatározásához a hallgatók egy előre elkészített programot alkalmaznak, mely a munkatér négy kijelölt sarkába elhelyezett akadályok szeptember 2. 10
13 segítségével végzi el a számításokat. Ehhez a hallgatók két felvételt készítenek a munkatérről: Egy referenciaképet, melyen akadályok nem szerepelnek, valamint egy kalibrációs képet, melyen a négy akadály a munkatér négy kijelölt pozíciójában helyezkedik el. A kalibráció elvégzése után a hallgatók az akadályokat a munkatéren belül tetszőleges pozícióba helyezhetik, majd a program segítségével ezek pozícióit meghatározzák. Ezt követően az akadályokat statikusnak tekintjük. A mérés következő részében a hallgatók egy saját algoritmusot fejlesztenek, amely a kamera képén a jármű pozícióját és orientációját képes meghatározni a munkatér koordiántarendszerében. Definíció szerint a jármű középpontja a rajta található kék, illetve piros színű köröket összekötő szakasz felezőpontja, az orientációja pedig a prios körből a kékbe mutató vektor x tengellyel bezárt szöge. Az algoritmust az OpenCV nyílt forráskódú képfeldolgozó függvénykönyvtár segítségével valósítják meg. Ebben a feladatban segítséget nyújtanak a 4. fejezetben található minta kódrészletek, amelyek az OpenCV alapvető funkcióit demonstrálják. A hallgatók által előállított adatok (a jármű, illetve az akadályok pozíciója) egy virtuális valóság alkalmazás (4. ábra) bemeneti adataként szolgálnak, mely lehetővé teszi, hogy a hallgatók a távirányítású robotot mesterséges környezetben vezérelhessék egy távoli számítógépről. A környezet használata során a hallgatók megismerkedhetnek a virtuális környezetek használatának előnyeivel, illetve hátrányaival szeptember 2. 11
14 4. ábra: A virtuális környezet 3.2 A mérés során alkalmazott eszközök Eszköz Típus Paraméterek Kamera Canon Felbontás: 640x480 VC-C1 MK II Típus: 3 csatornás, RGB Akadályok Saját Alapterület: Átmérő: Kör 15,6 cm Robot Saját Alapterület: Markerek: cm Kék, piros kör, Ø5cm Munkatér Saját Terület: cm (l. 1. ábra) kamera által látott terület szeptember 2. 12
15 3.3 Feladatok a) A méréshez tartozó kamera segítségével készítse el a kalibrációhoz szükséges képeket a munkatérről. b) A mérésvezető által szolgáltatott program segítségével határozza meg az objektumok középpontjai által a kamera és a sík közötti perspektív transzformáció paramétereit. c) Írjon rutint, amely a kamera képén megtalálja a robotot, meghatározza annak valós pozícióját és orientációját. Használja az a, pontban előállított paramétereket a Valós értékek meghatározásához. d) Írjon automata vezérlő rutint, mely megállítja a robotot, ha az akadálynak ütközne. e) Vizsgálja meg az algoritmus gyorsítására szolgáló lehetséges eljárásokat. f) Tesztelje az eljárást a mérésvezető által biztosított rendszerrel szeptember 2. 13
16 4. OpenCV referencia Az alábbiakban egy nagyon rövid összefoglalást adunk a legfontosabb OpenCV típusokról és függvényekről. Részletesebb információ az OpenCV dokumentációjában található. 4.1 Példa-programrészletek Kép létrehozása, manipulálása // szürkeárnyalatos, egycsatornás kép ( a kép alapvetően cv::mat ) cv::mat image( cv::size( width, height ), CV_8UC1 ); // színes, háromcsatornás kép cv::mat image( cv::size( width, height ), CV_8UC3 ); // másik képpel megegyező méretű és típusú kép cv::mat image( other.size(), other.type() ); // betöltés fájlból cv::mat image = cv::imread( "filename.ext" ); // skálázás fix métetre cv::resize( original, scaled, cv::size( newwidth, newheight ) ); //skálázás arányosan cv::resize( original, scaled, cv::size( 0, 0 ), xratio, yratio ); // képrészlet kivágása cv::mat roi = image( cv::rect( x, y, width, height ) ); Megjelenítése // kép megjelenítése cv::imshow( "Ablak neve és egyben fejléce", image ); // várás billentyűzetre int key = cv::waitkey( 0 ); // várás ideje ms-ban. Ha 0, akkor végtelen // waitkey LEGALÁBB EGYSZER KELL!!! Bináris kép előállítása // szürkeárnyalatos kép előállítása színes képből cv::mat gray, binary; szeptember 2. 14
17 cv::cvtcolor( image, gray, CV_BGR2GRAY ); // BGR és nem RGB formátum az alapértelmezett!!! cv::threshold( gray, bin, thresholdvalue, 255, cv::thresh_binary ); // 255 a küszörbértéket meghaladó pixelek új értéke Színtérkonverzió, szétválasztás komponensekre // váltás színterek között cv::mat hsvimage; cv::cvtcolor( rgbimage, hsvimage, CV_BGR2HSV ); // más konverziók is lehetnek // színterek: RGB, BGR, RGBA, BGR555, BGR565, GRAY, YCrCb, HSV, HLS, Luv, Lab // XYZ, BayerBG, BayerGB, BayerRG, BayerGR // komponensek szétválasztása std::vector< cv::mat > hsv( 3 ); cv::split( hsvimage, hsv ); Műveletek objektumokkal //objektumok keresése cv::findcontours( binimg, contours, CV_RETR_EXTERNAL, CV_CHAIN_APPROX_SIMPLE ); // momentum kiszámolása for( int i( 0 ); i < contours.size(); i++ ) { cv::moments moments = cv::moments( cv::mat( contours[ i ] ); float zerothordermoment = moments.m00; } Műveletek képrészletekkel // kép feltöltése 0-val cv::mat maskimage( size, type, cv::scalar( 0, 0, 0 ) ); // kontúrok segítségével maszk kép készítése for( int i( 0 ); i < contours.size(); i++ ) { cv::drawcontrous( maskimage, contours, i, cv::scalar( 255, 255, 255 ), thickness ); // thickness a vonal vastagsága, ha -1, akkor kitölti a kontúr belsejét } // kép maszkolása a maskimage segítségével cv::mat roiimage; originalimage.copyto( roiimage, maskimage ); szeptember 2. 15
18 4.1.7 Perspektív transzformáció // kiinduló pontok megadása std::vector< cv::point2f > imagepointvector; imagepoints.push_back( p1 ); imagepoints.push_back( p2 ); // képek előállítása cv::mat ipoints( imagepointvector ), wpoints; // perspektív transzformáció cv::perspectivetransform( ipoints, wpoints, projmatrix ); // pontok előállítása cv::point2f P1( wpoints.at< float >( 0, 0 ), wpoints.at< float >( 0, 1 ) ); cv::point2f P2( wpoints.at< float >( 1, 0 ), wpoints.at< float >( 1, 1 ) ); szeptember 2. 16
19 5. Ellenőrző kérdések 1. Rajzolja le a távérzékelés és a teleoperáció Sheridan-féle modelljét. Mi a helyi hurkok feladata? 2. Mit jelent egy objektum nullad- és elsőrendű momentuma, illetve milyen összefüggésben áll az objektum középpontjával? 3. Mit ad meg a perspektív transzformáció? Milyen módon határozható meg? 4. Foglalja össze 2-3 mondatban a mérés célját és feladatait! 5. Írja le egy színes kép bináris képpé torténő konverziójának lépéseit! (csak műveletek, kód nem kell) 6. Milyen műveleteket végezne el, ha egy bináris képen lévő objektumok méretét szeretné meghatározni? (kód nem kell) 7. Milyen lehetőséget biztosít az OpenCV a perspektív transzformáció elvégzésére? szeptember 2. 17
Szenzorcsatolt robot: A szenzorcsatolás lépései:
 1. Mi a szenzorcsatolt robot, hogyan épül fel? Ismertesse a szenzorcsatolás lépéseit röviden az Egységes szenzorplatform architektúra segítségével. Mikor beszélünk szenzorfúzióról? Milyen módszereket használhatunk?
1. Mi a szenzorcsatolt robot, hogyan épül fel? Ismertesse a szenzorcsatolás lépéseit röviden az Egységes szenzorplatform architektúra segítségével. Mikor beszélünk szenzorfúzióról? Milyen módszereket használhatunk?
I8 - Környezeti tér feltérképezése sztereo kamerakép alapján
 I8 - Környezeti tér feltérképezése sztereo kamerakép alapján Mérési útmutató az Irányítástechnika és Képfeldolgozás Laboratóriumhoz: 8. mérés Dr. Vajda Ferenc 3D érzékelés és Mobilrobotika kutatócsoport
I8 - Környezeti tér feltérképezése sztereo kamerakép alapján Mérési útmutató az Irányítástechnika és Képfeldolgozás Laboratóriumhoz: 8. mérés Dr. Vajda Ferenc 3D érzékelés és Mobilrobotika kutatócsoport
Térbeli transzformációk, a tér leképezése síkra
 Térbeli transzformációk, a tér leképezése síkra Homogén koordináták bevezetése térben A tér minden P pontjához kölcsönösen egyértelműen egy valós (x, y, z) számhármast rendeltünk hozzá. (Descartes-féle
Térbeli transzformációk, a tér leképezése síkra Homogén koordináták bevezetése térben A tér minden P pontjához kölcsönösen egyértelműen egy valós (x, y, z) számhármast rendeltünk hozzá. (Descartes-féle
I7 - Objektumkövetés. Mérési útmutató az Irányítástechnika és Képfeldolgozás Laboratóriumhoz: 7. mérés
 I7 - Mérési útmutató az Irányítástechnika és Képfeldolgozás Laboratóriumhoz: 7. mérés Dr. Vajda Ferenc 3D érzékelés és Mobilrobotika kutatócsoport Irányítástechnika és Informatika Tanszék 2015. október
I7 - Mérési útmutató az Irányítástechnika és Képfeldolgozás Laboratóriumhoz: 7. mérés Dr. Vajda Ferenc 3D érzékelés és Mobilrobotika kutatócsoport Irányítástechnika és Informatika Tanszék 2015. október
Minták automatikus osztályba sorolása a mintát leíró jellemzők alapján. Típusok: felügyelt és felügyelet nélküli tanuló eljárások
 Minták automatikus osztályba sorolása a mintát leíró jellemzők alapján Típusok: felügyelt és felügyelet nélküli tanuló eljárások Különbség: előbbinél szükséges egy olyan tanulóhalmaz, ahol ismert a minták
Minták automatikus osztályba sorolása a mintát leíró jellemzők alapján Típusok: felügyelt és felügyelet nélküli tanuló eljárások Különbség: előbbinél szükséges egy olyan tanulóhalmaz, ahol ismert a minták
Szürke árnyalat: R=G=B. OPENCV: BGR Mátrix típus: CV_8UC3 Pont típus: img.at<vec3b>(i, j) Tartomány: R, G, B [0, 255]
![Szürke árnyalat: R=G=B. OPENCV: BGR Mátrix típus: CV_8UC3 Pont típus: img.at<vec3b>(i, j) Tartomány: R, G, B [0, 255] Szürke árnyalat: R=G=B. OPENCV: BGR Mátrix típus: CV_8UC3 Pont típus: img.at<vec3b>(i, j) Tartomány: R, G, B [0, 255]](/thumbs/92/108290996.jpg) Additív színmodell: piros, zöld, kék keverése RGB hullámhossz:700nm, 546nm, 435nm Elektronikai eszközök alkalmazzák: kijelzők, kamerák 16 millió szín kódolható Szürke árnyalat: R=G=B OPENCV: BGR Mátrix
Additív színmodell: piros, zöld, kék keverése RGB hullámhossz:700nm, 546nm, 435nm Elektronikai eszközök alkalmazzák: kijelzők, kamerák 16 millió szín kódolható Szürke árnyalat: R=G=B OPENCV: BGR Mátrix
Szürke árnyalat: R=G=B. OPENCV: BGR Mátrix típus: CV_8UC3 Pont típus: img.at<vec3b>(i, j) Tartomány: R, G, B [0, 255]
![Szürke árnyalat: R=G=B. OPENCV: BGR Mátrix típus: CV_8UC3 Pont típus: img.at<vec3b>(i, j) Tartomány: R, G, B [0, 255] Szürke árnyalat: R=G=B. OPENCV: BGR Mátrix típus: CV_8UC3 Pont típus: img.at<vec3b>(i, j) Tartomány: R, G, B [0, 255]](/thumbs/92/108587263.jpg) Additív színmodell: piros, zöld, kék keverése RGB hullámhossz:700nm, 546nm, 435nm Elektronikai eszközök alkalmazzák: kijelzők, kamerák 16 millió szín kódolható Szürke árnyalat: R=G=B OPENCV: BGR Mátrix
Additív színmodell: piros, zöld, kék keverése RGB hullámhossz:700nm, 546nm, 435nm Elektronikai eszközök alkalmazzák: kijelzők, kamerák 16 millió szín kódolható Szürke árnyalat: R=G=B OPENCV: BGR Mátrix
Transzformációk. Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform
 Transzformációk Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform Koordinátarendszerek: modelltér Koordinátarendszerek: világtér Koordinátarendszerek: kameratér up right z eye ahead
Transzformációk Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform Koordinátarendszerek: modelltér Koordinátarendszerek: világtér Koordinátarendszerek: kameratér up right z eye ahead
Infobionika ROBOTIKA. X. Előadás. Robot manipulátorok II. Direkt és inverz kinematika. Készült a HEFOP P /1.0 projekt keretében
 Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Kamerakalibráció és pozícióbecslés érzékenységi analízissel, sík mintázatokból. Dabóczi Tamás (BME MIT), Fazekas Zoltán (MTA SZTAKI)
 , 2008 feb. 4-5 Kamerakalibráció és pozícióbecslés érzékenységi Bódis-Szomorú András Dabóczi Tamás (BME MIT), Fazekas Zoltán (MTA SZTAKI) Méréstechnika- és Információs Rendszerek Tanszék BME Rendszer-
, 2008 feb. 4-5 Kamerakalibráció és pozícióbecslés érzékenységi Bódis-Szomorú András Dabóczi Tamás (BME MIT), Fazekas Zoltán (MTA SZTAKI) Méréstechnika- és Információs Rendszerek Tanszék BME Rendszer-
Robotok inverz geometriája
 Robotok inverz geometriája. A gyakorlat célja Inverz geometriai feladatot megvalósító függvények implementálása. A megvalósított függvénycsomag tesztelése egy kétszabadságfokú kar előírt végberendezés
Robotok inverz geometriája. A gyakorlat célja Inverz geometriai feladatot megvalósító függvények implementálása. A megvalósított függvénycsomag tesztelése egy kétszabadságfokú kar előírt végberendezés
Keresztmetszet másodrendű nyomatékainak meghatározása
 BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
Hajder Levente 2017/2018. II. félév
 Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév Tartalom 1 2 3 Geometriai modellezés feladata A világunkat modellezni kell a térben. Valamilyen koordinátarendszer
Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév Tartalom 1 2 3 Geometriai modellezés feladata A világunkat modellezni kell a térben. Valamilyen koordinátarendszer
Transzformációk síkon, térben
 Transzformációk síkon, térben Leképezés, transzformáció Leképezés: Ha egy A ponttér pontjaihoz egy másik B ponttér pontjait kölcsönösen egyértelműen rendeljük hozzá, akkor ezt a hozzárendelést leképezésnek
Transzformációk síkon, térben Leképezés, transzformáció Leképezés: Ha egy A ponttér pontjaihoz egy másik B ponttér pontjait kölcsönösen egyértelműen rendeljük hozzá, akkor ezt a hozzárendelést leképezésnek
Digitális képek feldolgozása Előfeldolgozás Radiometriai korrekció Geometriai korrekció Képjavítás Szűrők Sávok közötti műveletek Képosztályozás Utófe
 Távérzékelés Digitális felvételek előfeldolgozása (EENAFOTOTV, ETNATAVERV) Erdőmérnöki szak, Környezettudós szak Király Géza NyME, Erdőmérnöki Kar Geomatikai, Erdőfeltárási és Vízgazdálkodási Intézet Földmérési
Távérzékelés Digitális felvételek előfeldolgozása (EENAFOTOTV, ETNATAVERV) Erdőmérnöki szak, Környezettudós szak Király Géza NyME, Erdőmérnöki Kar Geomatikai, Erdőfeltárási és Vízgazdálkodási Intézet Földmérési
EGY ABLAK - GEOMETRIAI PROBLÉMA
 EGY ABLAK - GEOMETRIAI PROBLÉMA Írta: Hajdu Endre A számítógépemhez tartozó két hangfal egy-egy négyzet keresztmetszetű hasáb hely - szűke miatt az ablakpárkányon van elhelyezve (. ábra).. ábra Hogy az
EGY ABLAK - GEOMETRIAI PROBLÉMA Írta: Hajdu Endre A számítógépemhez tartozó két hangfal egy-egy négyzet keresztmetszetű hasáb hely - szűke miatt az ablakpárkányon van elhelyezve (. ábra).. ábra Hogy az
3D koordináta-rendszerek
 3D koordináta-rendszerek z z y x y x y balkezes bal-sodrású x jobbkezes jobb-sodrású z 3D transzformációk - homogén koordináták (x, y, z) megadása homogén koordinátákkal: (x, y, z, 1) (x, y, z, w) = (x,
3D koordináta-rendszerek z z y x y x y balkezes bal-sodrású x jobbkezes jobb-sodrású z 3D transzformációk - homogén koordináták (x, y, z) megadása homogén koordinátákkal: (x, y, z, 1) (x, y, z, w) = (x,
Transzformációk. Szécsi László
 Transzformációk Szécsi László A feladat Adott a 3D modell háromszögek csúcspontjai [modellezési koordináták] Háromszögkitöltő algoritmus pixeleket színez be [viewport koordináták] A feladat: számítsuk
Transzformációk Szécsi László A feladat Adott a 3D modell háromszögek csúcspontjai [modellezési koordináták] Háromszögkitöltő algoritmus pixeleket színez be [viewport koordináták] A feladat: számítsuk
Példák jellemzőkre: - minden pixelérték egy jellemző pl. neurális hálózat esetében csak kis képekre, nem invariáns sem a megvilágításra, sem a geom.
 Lépések 1. tanító és teszt halmaz összeállítása / megszerzése 2. jellemzők kinyerése 3. tanító eljárás választása Sok vagy kevés adat áll-e rendelkezésünkre? Mennyi tanítási idő/memória áll rendelkezésre?
Lépések 1. tanító és teszt halmaz összeállítása / megszerzése 2. jellemzők kinyerése 3. tanító eljárás választása Sok vagy kevés adat áll-e rendelkezésünkre? Mennyi tanítási idő/memória áll rendelkezésre?
Panorámakép készítése
 Panorámakép készítése Képregisztráció, 2009. Hantos Norbert Blaskovics Viktor Összefoglalás Panoráma (image stitching, planar mosaicing): átfedő képek összeillesztése Lépések: Előfeldolgozás (pl. intenzitáskorrekciók)
Panorámakép készítése Képregisztráció, 2009. Hantos Norbert Blaskovics Viktor Összefoglalás Panoráma (image stitching, planar mosaicing): átfedő képek összeillesztése Lépések: Előfeldolgozás (pl. intenzitáskorrekciók)
x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs mátrixa 3D-ben?
 . Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
. Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
Robotika. Kinematika. Magyar Attila
 Robotika Kinematika Magyar Attila amagyar@almos.vein.hu Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
Robotika Kinematika Magyar Attila amagyar@almos.vein.hu Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
Sajátértékek és sajátvektorok. mf1n1a06- mf1n2a06 Csabai István
 Sajátértékek és sajátvektorok A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris transzformáció Vektorok lineáris transzformációja: általános esetben az x vektor iránya és nagysága
Sajátértékek és sajátvektorok A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris transzformáció Vektorok lineáris transzformációja: általános esetben az x vektor iránya és nagysága
Robotika. Relatív helymeghatározás Odometria
 Robotika Relatív helymeghatározás Odometria Differenciális hajtás c m =πd n /nc e c m D n C e n = hány mm-t tesz meg a robot egy jeladó impulzusra = névleges kerék átmérő = jeladó fölbontása (impulzus/ford.)
Robotika Relatív helymeghatározás Odometria Differenciális hajtás c m =πd n /nc e c m D n C e n = hány mm-t tesz meg a robot egy jeladó impulzusra = névleges kerék átmérő = jeladó fölbontása (impulzus/ford.)
Képfeldolgozás Szegmentálás Osztályozás Képfelismerés Térbeli rekonstrukció
 Mesterséges látás Miről lesz szó? objektumok Bevezetés objektumok A mesterséges látás jelenlegi, technikai eszközökön alapuló világunkban gyakorlatilag azonos a számítógépes képfeldolgozással. Számítógépes
Mesterséges látás Miről lesz szó? objektumok Bevezetés objektumok A mesterséges látás jelenlegi, technikai eszközökön alapuló világunkban gyakorlatilag azonos a számítógépes képfeldolgozással. Számítógépes
TikZ, a L A T E X grakája
 TikZ, a L A T E X grakája Informatika 1. L A TEX Móra Péter, Wettl Ferenc BME Algebra Tanszék, http://www.math.bme.hu/~wettl 2013-12-04 Móra Péter, Wettl Ferenc (BME) TikZ, a LATEX grakája 2013-12-04 1
TikZ, a L A T E X grakája Informatika 1. L A TEX Móra Péter, Wettl Ferenc BME Algebra Tanszék, http://www.math.bme.hu/~wettl 2013-12-04 Móra Péter, Wettl Ferenc (BME) TikZ, a LATEX grakája 2013-12-04 1
Példa keresztmetszet másodrendű nyomatékainak számítására
 Példa keresztmetszet másodrendű nyomatékainak számítására Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. február 22. Tekintsük az alábbi keresztmetszetet. 1. ábra. A vizsgált
Példa keresztmetszet másodrendű nyomatékainak számítására Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. február 22. Tekintsük az alábbi keresztmetszetet. 1. ábra. A vizsgált
Mechatronika segédlet 3. gyakorlat
 Mechatronika segédlet 3. gyakorlat 2017. február 20. Tartalom Vadai Gergely, Faragó Dénes Feladatleírás... 2 Fogaskerék... 2 Nézetváltás 3D modellezéshez... 2 Könnyítés megvalósítása... 2 A fogaskerék
Mechatronika segédlet 3. gyakorlat 2017. február 20. Tartalom Vadai Gergely, Faragó Dénes Feladatleírás... 2 Fogaskerék... 2 Nézetváltás 3D modellezéshez... 2 Könnyítés megvalósítása... 2 A fogaskerék
Segédlet: Főfeszültségek meghatározása Mohr-féle feszültségi körök alkalmazásával
 Segédlet: Főfeszültségek meghatározása Mohr-féle feszültségi körök alkalmazásával Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 212. október 16. Frissítve: 215. január
Segédlet: Főfeszültségek meghatározása Mohr-féle feszültségi körök alkalmazásával Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 212. október 16. Frissítve: 215. január
Számítási feladatok a Számítógépi geometria órához
 Számítási feladatok a Számítógépi geometria órához Kovács Zoltán Copyright c 2012 Last Revision Date: 2012. október 15. kovacsz@nyf.hu Technikai útmutató a jegyzet használatához A jegyzet képernyőbarát
Számítási feladatok a Számítógépi geometria órához Kovács Zoltán Copyright c 2012 Last Revision Date: 2012. október 15. kovacsz@nyf.hu Technikai útmutató a jegyzet használatához A jegyzet képernyőbarát
Transzformációk, amelyek n-dimenziós objektumokat kisebb dimenziós terekbe visznek át. Pl. 3D 2D
 Vetítések Transzformációk, amelyek n-dimenziós objektumokat kisebb dimenziós terekbe visznek át. Pl. 3D 2D Vetítések fajtái - 1 perspektívikus A párhuzamos A A' B A' B A vetítés középpontja B' Vetítési
Vetítések Transzformációk, amelyek n-dimenziós objektumokat kisebb dimenziós terekbe visznek át. Pl. 3D 2D Vetítések fajtái - 1 perspektívikus A párhuzamos A A' B A' B A vetítés középpontja B' Vetítési
NGB_IN040_1 SZIMULÁCIÓS TECHNIKÁK dr. Pozna Claudio Radu, Horváth Ernő
 SZÉCHENYI ISTVÁN EGYETEM Műszaki Tudományi Kar Informatika Tanszék BSC FOKOZATÚ MÉRNÖK INFORMATIKUS SZAK NGB_IN040_1 SZIMULÁCIÓS TECHNIKÁK dr. Pozna Claudio Radu, Horváth Ernő Fejlesztői dokumentáció GROUP#6
SZÉCHENYI ISTVÁN EGYETEM Műszaki Tudományi Kar Informatika Tanszék BSC FOKOZATÚ MÉRNÖK INFORMATIKUS SZAK NGB_IN040_1 SZIMULÁCIÓS TECHNIKÁK dr. Pozna Claudio Radu, Horváth Ernő Fejlesztői dokumentáció GROUP#6
Matematikai geodéziai számítások 10.
 Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Regresszió számítás. Tartalomjegyzék: GeoEasy V2.05+ Geodéziai Kommunikációs Program
 Regresszió számítás GeoEasy V2.05+ Geodéziai Kommunikációs Program DigiKom Kft. 2006-2010 Tartalomjegyzék: Egyenes x változik Egyenes y változik Egyenes y és x változik Kör Sík z változik Sík y, x és z
Regresszió számítás GeoEasy V2.05+ Geodéziai Kommunikációs Program DigiKom Kft. 2006-2010 Tartalomjegyzék: Egyenes x változik Egyenes y változik Egyenes y és x változik Kör Sík z változik Sík y, x és z
Az objektum leírására szolgálnak. Mire jók? Sokszor maga a jellemző az érdekes: Tömörítés. Objektumok csoportosítására
 Az objektum leírására szolgálnak Mire jók? Sokszor maga a jellemző az érdekes: pl.: átlagosan mekkora egy szitakötő szárnyfesztávolsága? Tömörítés pl.: ha körszerű objektumokat tartalmaz a kép, elegendő
Az objektum leírására szolgálnak Mire jók? Sokszor maga a jellemző az érdekes: pl.: átlagosan mekkora egy szitakötő szárnyfesztávolsága? Tömörítés pl.: ha körszerű objektumokat tartalmaz a kép, elegendő
CARE. Biztonságos. otthonok idős embereknek CARE. Biztonságos otthonok idős embereknek 2010-09-02. Dr. Vajda Ferenc Egyetemi docens
 CARE Biztonságos CARE Biztonságos otthonok idős embereknek otthonok idős embereknek 2010-09-02 Dr. Vajda Ferenc Egyetemi docens 3D Érzékelés és Mobilrobotika kutatócsoport Budapesti Műszaki és Gazdaságtudományi
CARE Biztonságos CARE Biztonságos otthonok idős embereknek otthonok idős embereknek 2010-09-02 Dr. Vajda Ferenc Egyetemi docens 3D Érzékelés és Mobilrobotika kutatócsoport Budapesti Műszaki és Gazdaságtudományi
3D számítógépes geometria és alakzatrekonstrukció
 3D számítógépes geometria és alakzatrekonstrukció 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01
3D számítógépes geometria és alakzatrekonstrukció 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01
Lényege: valamilyen szempont szerint homogén csoportok képzése a pixelekből. Amit már ismerünk:
 Lényege: valamilyen szempont szerint homogén csoportok képzése a pixelekből. Amit már ismerünk: Küszöbölés, vágás, sávkijelölés hátránya: az azonos csoportba sorolt pixelek nem feltétlenül alkotnak összefüggő
Lényege: valamilyen szempont szerint homogén csoportok képzése a pixelekből. Amit már ismerünk: Küszöbölés, vágás, sávkijelölés hátránya: az azonos csoportba sorolt pixelek nem feltétlenül alkotnak összefüggő
8. előadás. Kúpszeletek
 8. előadás Kúpszeletek Kör A k kört egyértelműen meghatározza C(a,b) középpontja és r sugara. A P pont pontosan akkor van k-n, ha CP=r. Vektoregyenlet: p-c = r. Koordinátás egyenlet: (X-a)2 + (Y-b)2 =
8. előadás Kúpszeletek Kör A k kört egyértelműen meghatározza C(a,b) középpontja és r sugara. A P pont pontosan akkor van k-n, ha CP=r. Vektoregyenlet: p-c = r. Koordinátás egyenlet: (X-a)2 + (Y-b)2 =
Tartalom. Nevezetes affin transzformációk. Valasek Gábor 2016/2017. tavaszi félév
 Tartalom Motiváció Számítógépes Grafika Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2016/2017. tavaszi félév Transzformációk Transzformációk általában Nevezetes affin
Tartalom Motiváció Számítógépes Grafika Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2016/2017. tavaszi félév Transzformációk Transzformációk általában Nevezetes affin
2014/2015. tavaszi félév
 Hajder L. és Valasek G. hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom Geometria modellezés 1 Geometria modellezés 2 Geometria modellezés
Hajder L. és Valasek G. hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom Geometria modellezés 1 Geometria modellezés 2 Geometria modellezés
Valasek Gábor Informatikai Kar. 2016/2017. tavaszi félév
 Számítógépes Grafika Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2016/2017. tavaszi félév Tartalom 1 Motiváció 2 Transzformációk Transzformációk általában 3 Nevezetes
Számítógépes Grafika Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2016/2017. tavaszi félév Tartalom 1 Motiváció 2 Transzformációk Transzformációk általában 3 Nevezetes
Egybevágósági transzformációk. A geometriai transzformációk olyan függvények, amelyek ponthoz pontot rendelnek hozzá.
 Egybevágósági transzformációk A geometriai transzformációk olyan függvények, amelyek ponthoz pontot rendelnek hozzá. Egybevágósági transzformációk azok a geometriai transzformációk, amelyeknél bármely
Egybevágósági transzformációk A geometriai transzformációk olyan függvények, amelyek ponthoz pontot rendelnek hozzá. Egybevágósági transzformációk azok a geometriai transzformációk, amelyeknél bármely
Beltéri autonóm négyrotoros helikopter szabályozó rendszerének kifejlesztése és hardware-in-the-loop tesztelése
 Beltéri autonóm négyrotoros helikopter szabályozó rendszerének kifejlesztése és hardware-in-the-loop tesztelése Regula Gergely, Lantos Béla BME Villamosmérnöki és Informatikai Kar Irányítástechnika és
Beltéri autonóm négyrotoros helikopter szabályozó rendszerének kifejlesztése és hardware-in-the-loop tesztelése Regula Gergely, Lantos Béla BME Villamosmérnöki és Informatikai Kar Irányítástechnika és
Számítógépes Grafika mintafeladatok
 Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Matematika A1a Analízis
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
Érettségi feladatok Koordinátageometria_rendszerezve / 5
 Érettségi feladatok Koordinátageometria_rendszerezve 2005-2013 1/ 5 Vektorok 2005. május 28./12. Adottak az a (4; 3) és b ( 2; 1) vektorok. a) Adja meg az a hosszát! b) Számítsa ki az a + b koordinátáit!
Érettségi feladatok Koordinátageometria_rendszerezve 2005-2013 1/ 5 Vektorok 2005. május 28./12. Adottak az a (4; 3) és b ( 2; 1) vektorok. a) Adja meg az a hosszát! b) Számítsa ki az a + b koordinátáit!
Ember és robot együttműködése a gyártásban Ipar 4.0
 Helyszín: MTA Székház, Felolvasóterem Időpont: 2017. November 7. Ember és robot együttműködése a gyártásban Ipar 4.0 Dr. Erdős Ferenc Gábor MTA SZTAKI Fejlett robotika ígérete A fejlett robotika és az
Helyszín: MTA Székház, Felolvasóterem Időpont: 2017. November 7. Ember és robot együttműködése a gyártásban Ipar 4.0 Dr. Erdős Ferenc Gábor MTA SZTAKI Fejlett robotika ígérete A fejlett robotika és az
A PiFast program használata. Nagy Lajos
 A PiFast program használata Nagy Lajos Tartalomjegyzék 1. Bevezetés 3 2. Bináris kimenet létrehozása. 3 2.1. Beépített konstans esete.............................. 3 2.2. Felhasználói konstans esete............................
A PiFast program használata Nagy Lajos Tartalomjegyzék 1. Bevezetés 3 2. Bináris kimenet létrehozása. 3 2.1. Beépített konstans esete.............................. 3 2.2. Felhasználói konstans esete............................
Koordináta-geometria feladatgyűjtemény (A feladatok megoldásai a dokumentum végén találhatók)
 Koordináta-geometria feladatgyűjtemény (A feladatok megoldásai a dokumentum végén találhatók) Vektorok 1. Egy négyzet két szemközti csúcsának koordinátái: A( ; 7) és C(4 ; 1). Határozd meg a másik két
Koordináta-geometria feladatgyűjtemény (A feladatok megoldásai a dokumentum végén találhatók) Vektorok 1. Egy négyzet két szemközti csúcsának koordinátái: A( ; 7) és C(4 ; 1). Határozd meg a másik két
Kérdés Lista. A Magyarországon alkalmazott rajzlapoknál mekkora az oldalak aránya?
 Kérdés Lista információ megjelenítés :: műszaki rajz T A darabjegyzék előállítása során milyen sorrendben számozzuk a tételeket? Adjon meg legalább két módszert! T A Magyarországon alkalmazott rajzlapoknál
Kérdés Lista információ megjelenítés :: műszaki rajz T A darabjegyzék előállítása során milyen sorrendben számozzuk a tételeket? Adjon meg legalább két módszert! T A Magyarországon alkalmazott rajzlapoknál
6. gyakorlat. Gelle Kitti. Csendes Tibor Somogyi Viktor. London András. jegyzetei alapján
 Közelítő és szimbolikus számítások 6. gyakorlat Sajátérték, Gersgorin körök Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján . Mátrixok sajátértékei
Közelítő és szimbolikus számítások 6. gyakorlat Sajátérték, Gersgorin körök Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján . Mátrixok sajátértékei
Érettségi feladatok: Koordináta-geometria 1/5
 Érettségi feladatok: Koordináta-geometria 1/5 2003. Próba/ 13. Adott egy háromszög három csúcspontja a koordinátáival: A( 4; 4), B(4; 4) és C( 4; 8). Számítsa ki a C csúcsból induló súlyvonal és az A csúcsból
Érettségi feladatok: Koordináta-geometria 1/5 2003. Próba/ 13. Adott egy háromszög három csúcspontja a koordinátáival: A( 4; 4), B(4; 4) és C( 4; 8). Számítsa ki a C csúcsból induló súlyvonal és az A csúcsból
A KLT (Kanade Lucas Tomasi) Feature Tracker Működése (jellegzetes pontok választása és követése)
 A KL (Kanade Lucas omasi) Feature racker Működése (jellegzetes pontok választása és követése) Készítette: Hajder Levente 008.11.18. 1. Feladat A rendelkezésre álló videó egy adott képkockájából minél több
A KL (Kanade Lucas omasi) Feature racker Működése (jellegzetes pontok választása és követése) Készítette: Hajder Levente 008.11.18. 1. Feladat A rendelkezésre álló videó egy adott képkockájából minél több
Programozási környezetek
 KOVÁSZNAI GERGELY ÉS BIRÓ CSABA EKF TTK Információtechnológia Tanszék Programozási környezetek Alkalmazható természettudományok oktatása a tudásalapú társadalomban TÁMOP-4.1.2.A/1-11/1-2011-0038 WPF Bevezetés
KOVÁSZNAI GERGELY ÉS BIRÓ CSABA EKF TTK Információtechnológia Tanszék Programozási környezetek Alkalmazható természettudományok oktatása a tudásalapú társadalomban TÁMOP-4.1.2.A/1-11/1-2011-0038 WPF Bevezetés
Infobionika ROBOTIKA. IX. Előadás. Robot manipulátorok I. Alapfogalmak. Készült a HEFOP P /1.0 projekt keretében
 Infobionika ROBOTIKA IX. Előadás Robot manipulátorok I. Alapfogalmak Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Robot manipulátorok definíciója és alkalmazásai Manipulátorok szerkezete
Infobionika ROBOTIKA IX. Előadás Robot manipulátorok I. Alapfogalmak Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Robot manipulátorok definíciója és alkalmazásai Manipulátorok szerkezete
Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017.
 Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017. Vizuális feldolgozórendszerek feladatai Mesterséges intelligencia és idegtudomány Mesterséges intelligencia és idegtudomány Párhuzamos problémák
Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017. Vizuális feldolgozórendszerek feladatai Mesterséges intelligencia és idegtudomány Mesterséges intelligencia és idegtudomány Párhuzamos problémák
Skaláris szorzat: a b cos, ahol α a két vektor által bezárt szög.
 1 Összeadás: Legyen a (7; 3) és b (- 2; 4), akkor az összegük a + b (7 + (-2); 3 + 4) = (5; 7) Kivonás: Legyen a (7; 3) és b (- 2; 4), akkor a különbségük a b (7 - (-2); 3-4)=(9; - 1) Valós számmal való
1 Összeadás: Legyen a (7; 3) és b (- 2; 4), akkor az összegük a + b (7 + (-2); 3 + 4) = (5; 7) Kivonás: Legyen a (7; 3) és b (- 2; 4), akkor a különbségük a b (7 - (-2); 3-4)=(9; - 1) Valós számmal való
OpenGL és a mátrixok
 OpenGL és a mátrixok Róth Gergő 2013. március 4. Róth Gergő 1/20 A rajzoláskor a videókártya minden csúcson végrehajt egy transzformációt. Mire jó? Kamera helyének beállítása Egy objektum több pozícióra
OpenGL és a mátrixok Róth Gergő 2013. március 4. Róth Gergő 1/20 A rajzoláskor a videókártya minden csúcson végrehajt egy transzformációt. Mire jó? Kamera helyének beállítása Egy objektum több pozícióra
Koordináta-geometria feladatgyűjtemény
 Koordináta-geometria feladatgyűjtemény A feladatok megoldásai a dokumentum végén találhatók Vektorok 1. Egy négyzet két szemközti csúcsának koordinátái: A( ; 7) és C(4 ; 1). Határozd meg a másik két csúcs
Koordináta-geometria feladatgyűjtemény A feladatok megoldásai a dokumentum végén találhatók Vektorok 1. Egy négyzet két szemközti csúcsának koordinátái: A( ; 7) és C(4 ; 1). Határozd meg a másik két csúcs
Koordináta-geometria feladatok (középszint)
 Koordináta-geometria feladatok (középszint) 1. (KSZÉV Minta (1) 2004.05/I/4) Adott az A(2; 5) és B(1; 3) pont. Adja meg az AB szakasz felezőpontjának koordinátáit! 2. (KSZÉV Minta (2) 2004.05/I/7) Egy
Koordináta-geometria feladatok (középszint) 1. (KSZÉV Minta (1) 2004.05/I/4) Adott az A(2; 5) és B(1; 3) pont. Adja meg az AB szakasz felezőpontjának koordinátáit! 2. (KSZÉV Minta (2) 2004.05/I/7) Egy
Példa: Háromszög síkidom másodrendű nyomatékainak számítása
 Példa: Háromszög síkidom másodrendű nyomatékainak számítása Készítette: Dr. Kossa Attila kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék. február 6. Határozzuk meg az alábbi ábrán látható derékszögű háromszög
Példa: Háromszög síkidom másodrendű nyomatékainak számítása Készítette: Dr. Kossa Attila kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék. február 6. Határozzuk meg az alábbi ábrán látható derékszögű háromszög
λ 1 u 1 + λ 2 v 1 + λ 3 w 1 = 0 λ 1 u 2 + λ 2 v 2 + λ 3 w 2 = 0 λ 1 u 3 + λ 2 v 3 + λ 3 w 3 = 0
 Vektorok a térben Egy (v 1,v 2,v 3 ) valós számokból álló hármast vektornak nevezzünk a térben (R 3 -ban). Használni fogjuk a v = (v 1,v 2,v 3 ) jelölést. A v 1,v 2,v 3 -at a v vektor komponenseinek nevezzük.
Vektorok a térben Egy (v 1,v 2,v 3 ) valós számokból álló hármast vektornak nevezzünk a térben (R 3 -ban). Használni fogjuk a v = (v 1,v 2,v 3 ) jelölést. A v 1,v 2,v 3 -at a v vektor komponenseinek nevezzük.
Automatikus irányzás digitális képek. feldolgozásával TURÁK BENCE DR. ÉGETŐ CSABA
 Automatikus irányzás digitális képek feldolgozásával TURÁK BENCE DR. ÉGETŐ CSABA Koncepció Robotmérőállomásra távcsővére rögzített kamera Képek alapján a cél automatikus detektálása És az irányzás elvégzése
Automatikus irányzás digitális képek feldolgozásával TURÁK BENCE DR. ÉGETŐ CSABA Koncepció Robotmérőállomásra távcsővére rögzített kamera Képek alapján a cél automatikus detektálása És az irányzás elvégzése
Matematika (mesterképzés)
 Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás
 3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav54
3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav54
Denavit-Hartenberg konvenció alkalmazása térbeli 3DoF nyílt kinematikai láncú hengerkoordinátás és gömbi koordinátás robotra
 Budapesti M szaki És Gazdaságtudományi Egyetem Gépészmérnöki Kar M szaki Mechanikai Tanszék Denavit-Hartenberg konvenció alkalmazása térbeli 3DoF nyílt kinematikai láncú hengerkoordinátás és gömbi koordinátás
Budapesti M szaki És Gazdaságtudományi Egyetem Gépészmérnöki Kar M szaki Mechanikai Tanszék Denavit-Hartenberg konvenció alkalmazása térbeli 3DoF nyílt kinematikai láncú hengerkoordinátás és gömbi koordinátás
1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás)
 Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
Miről lesz szó? Videó tartalom elemzés (VCA) leegyszerűsített működése Kültéri védelem Közúthálózat megfigyelés Emberszámlálás
 Videóanalitikát mindenhova! Princz Adorján Miről lesz szó? Videó tartalom elemzés (VCA) leegyszerűsített működése Kültéri védelem Közúthálózat megfigyelés Emberszámlálás VCA alapú detektorok Videótartalom
Videóanalitikát mindenhova! Princz Adorján Miről lesz szó? Videó tartalom elemzés (VCA) leegyszerűsített működése Kültéri védelem Közúthálózat megfigyelés Emberszámlálás VCA alapú detektorok Videótartalom
Grafikonok automatikus elemzése
 Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
Matematika A2 vizsga mgeoldása június 4.
 Matematika A vizsga mgeoldása 03. június.. (a (3 pont Definiálja az f(x, y függvény határértékét az (x 0, y 0 helyen! Megoldás: Legyen D R, f : D R. Legyen az f(x, y függvény értelmezve az (x 0, y 0 pont
Matematika A vizsga mgeoldása 03. június.. (a (3 pont Definiálja az f(x, y függvény határértékét az (x 0, y 0 helyen! Megoldás: Legyen D R, f : D R. Legyen az f(x, y függvény értelmezve az (x 0, y 0 pont
Vektorgeometria (1) First Prev Next Last Go Back Full Screen Close Quit
 Vektorgeometria (1) First Prev Next Last Go Back Full Screen Close Quit 1. A térbeli irányított szakaszokat vektoroknak hívjuk. Két vektort egyenlőnek tekintünk, ha párhuzamos eltolással fedésbe hozhatók.
Vektorgeometria (1) First Prev Next Last Go Back Full Screen Close Quit 1. A térbeli irányított szakaszokat vektoroknak hívjuk. Két vektort egyenlőnek tekintünk, ha párhuzamos eltolással fedésbe hozhatók.
Pontfelhő létrehozás és használat Regard3D és CloudCompare nyílt forráskódú szoftverekkel. dr. Siki Zoltán
 Pontfelhő létrehozás és használat Regard3D és CloudCompare nyílt forráskódú szoftverekkel dr. Siki Zoltán siki.zoltan@epito.bme.hu Regard3D Nyílt forráskódú SfM (Structure from Motion) Fényképekből 3D
Pontfelhő létrehozás és használat Regard3D és CloudCompare nyílt forráskódú szoftverekkel dr. Siki Zoltán siki.zoltan@epito.bme.hu Regard3D Nyílt forráskódú SfM (Structure from Motion) Fényképekből 3D
Termék modell. Definíció:
 Definíció: Termék modell Összetett, többfunkciós, integrált modell (számítógépes reprezentáció) amely leír egy műszaki objektumot annak különböző életfázis szakaszaiban: tervezés, gyártás, szerelés, szervízelés,
Definíció: Termék modell Összetett, többfunkciós, integrált modell (számítógépes reprezentáció) amely leír egy műszaki objektumot annak különböző életfázis szakaszaiban: tervezés, gyártás, szerelés, szervízelés,
Láthatósági kérdések
 Láthatósági kérdések Láthatósági algoritmusok Adott térbeli objektum és adott nézőpont esetén el kell döntenünk, hogy mi látható az adott alakzatból a nézőpontból, vagy irányából nézve. Az algoritmusok
Láthatósági kérdések Láthatósági algoritmusok Adott térbeli objektum és adott nézőpont esetén el kell döntenünk, hogy mi látható az adott alakzatból a nézőpontból, vagy irányából nézve. Az algoritmusok
Rendszámfelismerő rendszerek
 Problémamegoldó szeminárium Témavezető: Pataki Péter ARH Zrt. ELTE-TTK 2013 Tartalomjegyzék 1 Bevezetés 2 Út a megoldás felé 3 Felmerült problémák 4 Alkalmazott matematika 5 További lehetőségek Motiváció
Problémamegoldó szeminárium Témavezető: Pataki Péter ARH Zrt. ELTE-TTK 2013 Tartalomjegyzék 1 Bevezetés 2 Út a megoldás felé 3 Felmerült problémák 4 Alkalmazott matematika 5 További lehetőségek Motiváció
Képfeldolgozás. 1. el adás. A képfeldolgozás m veletei. Mechatronikai mérnök szak BME, 2008
 Képfeldolgozás 1. el adás. A képfeldolgozás m veletei Mechatronikai mérnök szak BME, 2008 1 / 61 Alapfogalmak transzformációk Deníció Deníció Geometriai korrekciókra akkor van szükség, ha a képr l valódi
Képfeldolgozás 1. el adás. A képfeldolgozás m veletei Mechatronikai mérnök szak BME, 2008 1 / 61 Alapfogalmak transzformációk Deníció Deníció Geometriai korrekciókra akkor van szükség, ha a képr l valódi
Számítógépes geometria
 2011 sz A grakus szállítószalag terv a geometriai (matematikai) modell megalkotása modelltranszformáció (3D 3D) vetítés (3D 2D) képtranszformáció (2D 2D)... raszterizáció A grakus szállítószalag: koncepció
2011 sz A grakus szállítószalag terv a geometriai (matematikai) modell megalkotása modelltranszformáció (3D 3D) vetítés (3D 2D) képtranszformáció (2D 2D)... raszterizáció A grakus szállítószalag: koncepció
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT. Koordináta-geometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT 1) Adott két pont: A 4; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. Koordináta-geometria és B 3 1; Írja fel az AB szakasz 1 3 4
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT 1) Adott két pont: A 4; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. Koordináta-geometria és B 3 1; Írja fel az AB szakasz 1 3 4
1. A komplex számok ábrázolása
 1. komplex számok ábrázolása Vektorok és helyvektorok. Ismétlés sík vektorai irányított szakaszok, de két vektor egyenlő, ha párhuzamosak, egyenlő hosszúak és irányúak. Így minden vektor kezdőpontja az
1. komplex számok ábrázolása Vektorok és helyvektorok. Ismétlés sík vektorai irányított szakaszok, de két vektor egyenlő, ha párhuzamosak, egyenlő hosszúak és irányúak. Így minden vektor kezdőpontja az
12. előadás. Egyenletrendszerek, mátrixok. Dr. Szörényi Miklós, Dr. Kallós Gábor
 12. előadás Egyenletrendszerek, mátrixok Dr. Szörényi Miklós, Dr. Kallós Gábor 2015 2016 1 Tartalom Matematikai alapok Vektorok és mátrixok megadása Tömbkonstansok Lineáris műveletek Mátrixok szorzása
12. előadás Egyenletrendszerek, mátrixok Dr. Szörényi Miklós, Dr. Kallós Gábor 2015 2016 1 Tartalom Matematikai alapok Vektorok és mátrixok megadása Tömbkonstansok Lineáris műveletek Mátrixok szorzása
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások
 Megoldások 1. Tekintsük az alábbi szabályos hatszögben a következő vektorokat: a = AB és b = AF. Add meg az FO, DC, AO, AC, BE, FB, CE, DF vektorok koordinátáit az (a ; b ) koordinátarendszerben! Alkalmazzuk
Megoldások 1. Tekintsük az alábbi szabályos hatszögben a következő vektorokat: a = AB és b = AF. Add meg az FO, DC, AO, AC, BE, FB, CE, DF vektorok koordinátáit az (a ; b ) koordinátarendszerben! Alkalmazzuk
SZENZORFÚZIÓS ELJÁRÁSOK KIDOLGOZÁSA AUTONÓM JÁRMŰVEK PÁLYAKÖVETÉSÉRE ÉS IRÁNYÍTÁSÁRA
 infokommunikációs technológiák SZENZORFÚZIÓS ELJÁRÁSOK KIDOLGOZÁSA AUTONÓM JÁRMŰVEK PÁLYAKÖVETÉSÉRE ÉS IRÁNYÍTÁSÁRA BEVEZETŐ A KUTATÁS CÉLJA Autonóm járművek és robotok esetén elsődleges feladat a robotok
infokommunikációs technológiák SZENZORFÚZIÓS ELJÁRÁSOK KIDOLGOZÁSA AUTONÓM JÁRMŰVEK PÁLYAKÖVETÉSÉRE ÉS IRÁNYÍTÁSÁRA BEVEZETŐ A KUTATÁS CÉLJA Autonóm járművek és robotok esetén elsődleges feladat a robotok
Tárgy. Forgóasztal. Lézer. Kamera 3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL
 3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL. Bevezetés A lézeres letapogatás a ma elérhet legpontosabb 3D-s rekonstrukciót teszi lehet vé. Alapelve roppant egyszer : egy lézeres csíkkal megvilágítjuk a tárgyat.
3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL. Bevezetés A lézeres letapogatás a ma elérhet legpontosabb 3D-s rekonstrukciót teszi lehet vé. Alapelve roppant egyszer : egy lézeres csíkkal megvilágítjuk a tárgyat.
Matematikai geodéziai számítások 9.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr Bácsatyai László Matematikai geodéziai számítások 9 MGS9 modul Szabad álláspont kiegyenlítése SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr Bácsatyai László Matematikai geodéziai számítások 9 MGS9 modul Szabad álláspont kiegyenlítése SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői
Vektorok és koordinátageometria
 Vektorok és koordinátageometria Vektorral kapcsolatos alapfogalmak http://zanza.tv/matematika/geometria/vektorok-bevezetese Definíció: Ha egy szakasz két végpontját megkülönböztetjük egymástól oly módon,
Vektorok és koordinátageometria Vektorral kapcsolatos alapfogalmak http://zanza.tv/matematika/geometria/vektorok-bevezetese Definíció: Ha egy szakasz két végpontját megkülönböztetjük egymástól oly módon,
I. Vektorok. Adott A (2; 5) és B ( - 3; 4) pontok. (ld. ábra) A két pont által meghatározott vektor:
 I. Vektorok 1. Vektorok összege Általánosan: Az ábra alapján Adott: a(4; 1) és b(; 3) a + b (4 + ; 1 + 3) = (6; ) a(a 1 ; a ) és b(b 1 ; b ) a + b(a 1 + b 1 ; a + b ). Vektorok különbsége Általánosan:
I. Vektorok 1. Vektorok összege Általánosan: Az ábra alapján Adott: a(4; 1) és b(; 3) a + b (4 + ; 1 + 3) = (6; ) a(a 1 ; a ) és b(b 1 ; b ) a + b(a 1 + b 1 ; a + b ). Vektorok különbsége Általánosan:
A Hamilton-Jacobi-egyenlet
 A Hamilton-Jacobi-egyenlet Ha sikerül olyan kanonikus transzformációt találnunk, amely a Hamilton-függvényt zérusra transzformálja akkor valamennyi új koordináta és impulzus állandó lesz: H 0 Q k = H P
A Hamilton-Jacobi-egyenlet Ha sikerül olyan kanonikus transzformációt találnunk, amely a Hamilton-függvényt zérusra transzformálja akkor valamennyi új koordináta és impulzus állandó lesz: H 0 Q k = H P
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
Autonóm jármű forgalomszimulátorba illesztése
 Autonóm jármű forgalomszimulátorba illesztése Szalai Mátyás 2018 Konzulens: Dr. Tettamanti Tamás A szimulációs feladat Miért hasznos? Biztonságos környezetben nyújt lehetőséget az autonóm járművek forgalmi
Autonóm jármű forgalomszimulátorba illesztése Szalai Mátyás 2018 Konzulens: Dr. Tettamanti Tamás A szimulációs feladat Miért hasznos? Biztonságos környezetben nyújt lehetőséget az autonóm járművek forgalmi
Gépi tanulás és Mintafelismerés
 Gépi tanulás és Mintafelismerés jegyzet Csató Lehel Matematika-Informatika Tanszék BabesBolyai Tudományegyetem, Kolozsvár 2007 Aug. 20 2 1. fejezet Bevezet A mesterséges intelligencia azon módszereit,
Gépi tanulás és Mintafelismerés jegyzet Csató Lehel Matematika-Informatika Tanszék BabesBolyai Tudományegyetem, Kolozsvár 2007 Aug. 20 2 1. fejezet Bevezet A mesterséges intelligencia azon módszereit,
Méréselmélet és mérőrendszerek
 Méréselmélet és mérőrendszerek 6. ELŐADÁS KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba eredete o
Méréselmélet és mérőrendszerek 6. ELŐADÁS KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba eredete o
INFORMATIKA ÁGAZATI ALKALMAZÁSAI. Az Agrármérnöki MSc szak tananyagfejlesztése TÁMOP-4.1.2-08/1/A-2009-0010
 INFORMATIKA ÁGAZATI ALKALMAZÁSAI Az Agrármérnöki MSc szak tananyagfejlesztése TÁMOP-4.1.2-08/1/A-2009-0010 7. Digitális térképezés, georeferálás, vektorizálás Digitális térkép Fogalma Jellemzői Georeferálás
INFORMATIKA ÁGAZATI ALKALMAZÁSAI Az Agrármérnöki MSc szak tananyagfejlesztése TÁMOP-4.1.2-08/1/A-2009-0010 7. Digitális térképezés, georeferálás, vektorizálás Digitális térkép Fogalma Jellemzői Georeferálás
2. Omnidirekcionális kamera
 2. Omnidirekcionális kamera Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Omnidirekcionális kamerák típusai Omnidirekcionális, körbelátó,
2. Omnidirekcionális kamera Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Omnidirekcionális kamerák típusai Omnidirekcionális, körbelátó,
Kalkulus. Komplex számok
 Komplex számok Komplex számsík A komplex számok a valós számok természetes kiterjesztése, annak érdekében, hogy a gyökvonás művelete elvégezhető legyen a negatív számok körében is. Vegyük tehát hozzá az
Komplex számok Komplex számsík A komplex számok a valós számok természetes kiterjesztése, annak érdekében, hogy a gyökvonás művelete elvégezhető legyen a negatív számok körében is. Vegyük tehát hozzá az
Mechatronika segédlet 10. gyakorlat
 Mechatronika segédlet 10. gyakorlat 2017. április 21. Tartalom Vadai Gergely, Faragó Dénes Feladatleírás... 1 simrobot... 2 Paraméterei... 2 Visszatérési értéke... 2 Kód... 2 simrobotmdl... 3 robotsen.mdl...
Mechatronika segédlet 10. gyakorlat 2017. április 21. Tartalom Vadai Gergely, Faragó Dénes Feladatleírás... 1 simrobot... 2 Paraméterei... 2 Visszatérési értéke... 2 Kód... 2 simrobotmdl... 3 robotsen.mdl...
1. Generátorrendszer. Házi feladat (fizikából tudjuk) Ha v és w nem párhuzamos síkvektorok, akkor generátorrendszert alkotnak a sík vektorainak
 1. Generátorrendszer Generátorrendszer. Tétel (Freud, 4.3.4. Tétel) Legyen V vektortér a T test fölött és v 1,v 2,...,v m V. Ekkor a λ 1 v 1 + λ 2 v 2 +... + λ m v m alakú vektorok, ahol λ 1,λ 2,...,λ
1. Generátorrendszer Generátorrendszer. Tétel (Freud, 4.3.4. Tétel) Legyen V vektortér a T test fölött és v 1,v 2,...,v m V. Ekkor a λ 1 v 1 + λ 2 v 2 +... + λ m v m alakú vektorok, ahol λ 1,λ 2,...,λ
EEE Kutatólaboratórium MTA-SZTAKI Magyar Tudományos Akadémia
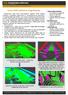 DElosztott I S T R I B U T EEsemények D EV E N T S A NElemzé A L Y S I S se R E SKutatólaboratór E A R C H L A B O R A T Oium R Y L I D A R B a s e d S u r v e i l l a n c e Városi LIDAR adathalmaz szegmentációja
DElosztott I S T R I B U T EEsemények D EV E N T S A NElemzé A L Y S I S se R E SKutatólaboratór E A R C H L A B O R A T Oium R Y L I D A R B a s e d S u r v e i l l a n c e Városi LIDAR adathalmaz szegmentációja
Párhuzamos programozási feladatok
 Párhuzamos programozási feladatok BMF NIK 2008. tavasz B. Wilkinson és M. Allen oktatási anyaga alapján készült Gravitációs N-test probléma Fizikai törvények alapján testek helyzetének, mozgásjellemzőinek
Párhuzamos programozási feladatok BMF NIK 2008. tavasz B. Wilkinson és M. Allen oktatási anyaga alapján készült Gravitációs N-test probléma Fizikai törvények alapján testek helyzetének, mozgásjellemzőinek
Mechatronika segédlet 2. gyakorlat
 Mechatronika segédlet 2. gyakorlat 2017. február 13. Tartalom Vadai Gergely, Faragó Dénes Feladatleírás... 3 Y-forma kialakítása... 3 Nagyítás... 3 Y forma kialakítása abszolút koordinátákkal... 4 Dinamikus
Mechatronika segédlet 2. gyakorlat 2017. február 13. Tartalom Vadai Gergely, Faragó Dénes Feladatleírás... 3 Y-forma kialakítása... 3 Nagyítás... 3 Y forma kialakítása abszolút koordinátákkal... 4 Dinamikus
