MIKROELEKTRONIKAI ANYAGVIZSGÁLAT KISENERGIÁJÚ MAGREAKCIÓS REZONANCIÁKKAL
|
|
|
- Norbert Jónás
- 6 évvel ezelőtt
- Látták:
Átírás
1 . MIKROELEKTRONIKAI ANYAGVIZSGÁLAT KISENERGIÁJÚ MAGREAKCIÓS REZONANCIÁKKAL Ph.D. értekezés Battistig Gábor MTA - Műszaki Fizikai és Anyagtudományi Kutatóintézet Budapest 2001.
2 Tartalomjegyzék 1 1. Bevezetés Elméleti összefoglalás Ion-anyag kölcsönhatás Fékeződés Straggling Doppler-szélesedés Magreakciók A magreakciós kölcsönhatás fizikai leírása Kinematika Magreakciók hatáskeresztmetszete Rezonancia-hatáskeresztmetszet Magreakciós mérések megvalósítása, méréstechnikai követelmények Gyorsítóberendezés, mérőnyaláb, mérőkamra Detektor, detektálás Felületi szennyezés Magreakciók alkalmazásának bemutatása az irodalom alapján Koncentrációprofilok mérése magreakciós rezonanciákkal A gerjesztési görbe elméleti leírása Magreakciós és rezonanciás módszerek jellemző tulajdonságai Oxigénrezonanciák A kisenergiás 18 O(p,α) 15 N magreakciós rezonancia Kísérleti feltételek A szükséges 18 O izotóppal dúsított oxidminták előállítása Kísérleti berendezés A rezonanciaszélesség meghatározása Mélységfelbontóképesség meghatározása, korlátok A minták elforgatásának hatása Felületi felbontóképesség Többszörös szórás hatása A 152 kev-es rezonancia összehasonlítás a nagyobb energiájú mérésekkel A kisenergiás oxigén rezonancia alkalmazása szilícium oxidációjának tanulmányozására Az oxidáció kinetikájának meghatározása nagyon vékony oxidok esetében A felületi tisztítás hatása a szilícium felületén kialakuló oxidrétegre...61
3 A gate oxid károsodása ionimplantáció hatására Nitrogénrezonancia alkalmazása pórusos szilícium rétegek vizsgálatára A 15 N(p,αγ) 12 C magreakció 429 kev energián A mérési elrendezés N izotóppal dúsított PS minták készítése Az izotópos jelölés és a magreakciós mérés alkalmazása pórusos szilícium minták morfológiájának vizsgálatára A PS rétegeken mért gerjesztési görbék A PS réteg anizotrópiája A hőkezelés hatása a PS struktúrára Az energiaveszteség fluktuáció vastagságfüggése Szivacsos szerkezetű PS rétegek mérése Összefoglalás Köszönetnyilvánítás Irodalomjegyzék...91
4 3 1. Bevezetés A mai mikroelektronikai technológiák megkívánják az anyagmérnöktől, hogy ismerje az egyes technológiai lépések közben lezajló atomi folyamatokat. A gyorsított, töltött részecskékkel végzett nukleáris analitika a félvezető kutatásokban elterjedten alkalmazott felületközeli anyagvizsgálati módszer. Legfőbb előnyei: roncsolásmentes, jó mélységi és abszolút összetételi információt szolgáltat néhány µm-es mélységig és alkalmazásával a minta kristálystruktúrája, valamint annak változásai is tanulmányozhatók. Könnyű atomsúlyú összetevők, illetve szennyezők mélységi eloszlásának meghatározására az egyik legalkalmasabb ionsugaras mérési módszer az izotópos jelöléssel kombinált magreakciós rezonancia módszer. Ha lehetséges alacsony energiákon végezni ilyen vizsgálatokat, igen jó mélységi felbontóképesség érhető el, még kis koncentrációk mérésekor is. Disszertációmban összefoglalom mindazokat az eredményeket, amelyeket oxigén és nitrogén atomok, illetve izotópok ionsugaras meghatározása területén értem el. Bemutatom, hogyan alkalmazhatók ezek a módszerek a félvezető technológia problémáinak vizsgálatára. Célom nem az, hogy az alacsonyenergiájú magrezonanciákat magukat tárgyaljam, hanem hogy a módszer bemutatása során felhívjam az olvasó figyelmét azokra a fontos kérdésekre, amelyeket figyelembe kell venni hasonló kísérletek tervezésénél. Az alapvető ionsugaras analitikai méréseket a Részecske és Magfizikai Kutató Intézet (RMKI) és a Műszaki Fizikai és Anyagtudományi Kutatóintézet (MFA) (előzőleg Anyagtudományi Kutató Intézet) által közösen üzemeltetett 5 MV-os Van de Graaff gyorsítójánál ismertem meg és végeztem el. Az alacsonyenergiás méréseket és az izotópkicseréléses kísérleteket a párizsi Denis Diderot Egyetem Szilárdtestfizikai csoportjánál tudtam elvégezni. Az egész munkának alapját jelentette az 1985-ben megvédett egyetemi doktori munkám, melyben ionimplantált mágneses egykristályos szigetelő rétegek tulajdonságait vizsgáltam, többek között ionsugaras és magrezonanciás módszerekkel [Bat86]. Azóta is fő kutatási területem a különféle anyagok, vékonyrétegek tanulmányozása ion visszaszórásos (RBS), csatornahatás (channeling), rugalmas meglökés (ERDA), magreakciós (NRA), összefoglalóan, ionsugaras analitikai módszerekkel.
5 4 A dolgozat öt, a témát mélységében taglaló, megjelent cikkem köré épül [Bat91, Bat92, Bat94b, Gan93, Ams97]. Természetesen az egyéb megjelent, a témához szorosan kötődő publikációimat is megemlítem a szükséges helyeken. A dolgozatot az irodalmi összefoglalóval kezdem, ebben leírom azokat az alapvető fizikai folyamatokat, amelyek az ionsugár-anyag kölcsönhatásban az ionsugaras analitika szempontjából szerepet játszanak. Fő hangsúlyt a magreakciós módszerek kapnak, mert munkám is ezekhez kapcsolódott. Röviden foglalkozom az iosugaras vizsgálatokban alkalmazott berendezésekkel, detektorokkal és a mintakészítés egyes kérdéseivel. Összehasonlítom az egyes ionsugaras anyagvizsgálati módszereket, tárgyalom előnyeiket és hátrányaikat. A következő fejezetben a 152 kev-es 18 O(p,α) 15 N magreakciós rezonanciával foglalkozom. Ennek az anyagvizsgálati szempontból nagyon fontos rezonanciának meghatároztam a rezonancia félszélességét, amelyet az irodalomban korábban található 500 ev helyett 50 ev-ben adtam meg. Irodalmi példákkal hasonlítom össze ezt a rezonanciát és bemutatok néhány anyagvizsgálati célokra általam végzett alkalmazást. Foglalkozom a módszerrel elérhető mélységfelbontóképesség meghatározásával is. Bemutatom, hogy a 152 kev-es rezonancia esetében a mélységfelbontóképesség a felületen 10 Å, de a rétegben a mélységgel a felbontóképesség rohamosan csökken, elsősorban a többszörös szórás hatása miatt. Alacsony energiájú magreakciós rezonanciával, a 429 kev-es 15 N(p,αγ) 12 C rezonanciával vizsgáltam pórusos szilícium vékonyrétegeket. Az elért eredmények közül kiemelkedik, hogy ezzel a módszerrel sikerült elsőként bebizonyítanom, hogy az oszlopos pórusos struktúra esetében a pórusok átlagos iránya egybeesik a Si hordozó (100) kristálytani irányával. Bemutatom, hogy hogyan követhető ezzel a módszerrel a pórusos struktúra megváltozása különböző kezelések hatására. Végül egy rövid összefoglalásban összegzem a keskeny magreakciós rezonancia módszer fejlesztésében és a módszer alkalmazásában elért eredményeimet.
6 5 2. Elméleti összefoglalás Szilárd anyagok felületközeli rétegeinek tanulmányozására az ionsugaras analitika széles körben alkalmazott anyagvizsgálati módszer. Segítségével nemcsak anyagösszetételi, de mélységi információt is kaphatunk a vizsgált mintáról 1.Alapvetően roncsolásmentes ez az anyagvizsgálati módszer, de speciális esetekben figyelembe kell venni a bombázó ionok által okozott sugárkárosodást. Az ion-atom kölcsönhatásról, ezen belül is az ionsugaras vizsgálati módszerekről több összefoglaló munka jelent meg, a legáltalánosabbak Bird, Chu, Deconninck, Mayer és Tesmer [Bir89, Chu78, Dec78, May77, Tes95] könyvei. Rövid összefoglalót adok az ion-atom kölcsönhatásról, de részletesen csak a dolgozat tárgyához tartozó magreakciókat tárgyalom. 2.1 Ion-anyag kölcsönhatás Az ion-anyag kölcsönhatást sok paraméter határozza meg, így az ion sebessége, energiája, a target atom és az ion mérete, rendszáma és tömege. A kölcsönhatás leírásánál figyelembe kell venni a résztvevő részecskék nagy sebességét valamint azokat az erőket, amelyek a kölcsönhatásban résztvevő részecskékre hatnak. A kölcsönhatásban meghatározó paraméter az, hogy a bombázó ion mennyire közelíti meg a céltárgy atomját, illetve milyen erők hatnak közöttük. Az ütközési, vagy impakt paraméter, ami az ion és az atom az ion irányára merőleges távolsága, írja le azt, hogy a két részecske mennyire kerül közel egymáshoz. A lezajló kölcsönhatásokat csoportosíthatjuk egyre csökkenő impakt paraméterrel a következő módon: - atomok rugalmas ütközése: a résztvevő atomokelektronfelhője között van Coulomb kölcsönhatás. Ez a folyamat csak kis ionenergiákon következik be. - atomok rugalmatlan szórása: gerjesztődik az atom, ionizáció történik, külső majd belső elektronoklökődhetnek ki. Nagy valószínűséggel ez a kölcsönhatás következik be, ha az ion sebessége megközelíti az elektronsebességet az elektronhéjban. Könnyű ionokra ez a kev-mev energiatartományt jelenti. Hatására az ion kis energiaveszteséget szenved, sebességének iránya kissé eltér a szóródás előttihez képest. - atommagok rugalmas ütközése: ez a klasszikus Rutherford szórás esete. Az impakt paraméter nagyon kicsi, vagy nulla is lehet. Az ütközés hatására az ion energiája és 1 Az ionsugaras analitikában bevett gyakorlat szerint a következőkben a felgyorsított, a céltárgyba ütköző részecskét, függetlenül a töltésállapotától, ionnak fogom nevezni. A céltárgy általános elnevezése target.
7 6 sebességének iránya is jelentősen megváltozik. A target atom magja is jelentős kinetikus energiát kaphat a kölcsönhatás következtében. - atommagok rugalmatlan ütközése vagy magreakció: ebben az esetben két mag egymáshoz cm-nél közelebb kerül, intenzív nukleáris kölcsönhatás lép fel közöttük, ami a magok átalakulásához is vezethet. Ez utóbbi, összefoglalóan magreakciónak nevezett kölcsönhatás néhány speciális esete, illetve azok anyagvizsgálati alkalmazása a dolgozatom tárgya. A 2.1 ábrán összefoglalom, hogy milyen kölcsönhatások játszódhatnak le, amikor egy nagy energiájú ion bombáz egy céltárgyat. Másodlagos elektronok Magreakció ionok, γ-fotonok, neutronok Látható, UV fotonok Ion Sugár Visszaszórt ion Vákuum Auger elektronok Szilárd anyag Röntgen sugárzás Kilökött atom 2.1 ábra Amikor egy felgyorsított részecske az anyagba ütközik többféle kölcsönhatás játszódhat le. A bekövetkező kölcsönhatásokat jellemzi a mintát elhagyó valamilyen részecske és/vagy sugárzás. Az ion-anyag kölcsönhatásokat a gyakorlatban anyagvizsgálatra, illetve anyagmódosításra alkalmazzuk. Az egyes módszereket a bombázó ionok energiája szerint is osztályozhatjuk. Akis 2 és közepes 3 energiájú szórások esetében a könnyű bombázó ionok energiája általában kisebb 10 kev-nél illetve 100 kev-nél. ionokat detektáljuk. Ezekben az esetekben a szóródott Szintén kis energiájú, de nehezebb ionok hatására ionos porlódás is bekövetkezhet, ekkor a céltárgy atomjai az ütközések során akkora energiát kapnak és sebességük iránya olyan lehet, hogy elhagyják az anyagot. Jellemzően például a 10 kev energiájú Ar ionok mindegyike 1-10 atomot tud kilökni az anyagból. Anyagvizsgálatra 2 Low Energy Ion Scattering, LEIS 3 Medium Energy Ion Scattering, MEIS
8 7 a kilökött atomokat detektálva 4 kaphatunk információt az anyag összetételéről. A porlasztott felület szintén vizsgálható elektron vagy foton besugárzással 5. A közepes energiájú besugárzásokat általában ionsugaras anyagmódosításra használjuk: az anyag besugárzása pár száz kev energiájú, főleg nehezebb ionokkal, megváltoztatja az anyag összetételét és szerkezetét a kezelt tartományban. Az ionimplantáció a félvezető technológiákban egy alapvető adalékolási eljárás, melynek során adalékatomokat jutattunk az anyagba az energia által meghatározott mélységbe. A besugárzó ionok a kristályos anyag szerkezetében rácskárosodást is okoznak, a bombázó ionok energiát adnak át az anyag atomjainak, a meghatározott poziciókban lévő atomok kilökődnek a rácspontból és további ütközésekben vesznek részt. Magasabb energiájú kölcsönhatásokat, jellemzően a száz kev - többszáz MeV energiatartományban, széles körben használunk anyagvizsgálatra. - Visszaszórás 6 : Általában könnyű (H vagy He) részecskékkel sugározzuk be az anyagot és ugyanazokat a visszaszóródott ionokat detektáljuk. A visszaszóródó ionok számából és energiájából következtethetünk a target összetételére és az összetevők mélység szerinti eloszlására. Amikor a bombázó részecske és a céltárgy atomjai között a Coulomb kölcsönhatás a meghatározó, akkor a szórás bekövetkezésének valószínűségét, azaz a hatáskeresztmetszetét az ú.n. Rutherford hatáskeresztmetszet adja meg 7. - Rugalmas meglökés 8 : Ebben az esetben a céltárgyunkban található könnyű atomokról kapunk felvilágosítást. A besugárzó nehezebb ionok kilökik a náluk könnyebb atomokat a targetből. Ebben az anyagvizsgálati módszerben nem a besugárzó, hanem a kilökött atomokat detektáljuk. - Részecske keltette röntgensugárzás 9 : Könnyü részecskékkel történő besugárzás hatására a target atomjainak belső elektronhéjairól egy vagy több elektron kilökődik, ionizáció történik. Az üres elektronpályák betöltésekor a kölcsönhatásban résztvevő atomrajellemző karakterisztikus 4 Secondary Ion Mass Spectroscopy, SIMS 5 Auger Electron Spectrometry, AES; X-ray Photoelectron Spectrometry, XPS 6 Rutherford Backscattering Spectroscopy, RBS 7 Az RBS általánosan elfogadott elnevezés, olyan esetekben is használják, amikor a hatáskeresztmetszet nem is Rutherford. 8 Elastric Recoil Detection Analysis, ERDA 9 Particle Induced X-ray Emission, PIXE
9 röntgensugárzás hagyja el a mintát. 8 Detektálva a kisugárzott energiákat szintén az anyagösszetételt állapíthatjuk meg. A besugárzó részecske leggyakrabban H vagy He. - Magreakciók 10 : A magreakció során a bombázó ion és a target atom energiája és impulzusa átrendeződik, amit néhány más részecske keletkezése kísérhet, melyek kirepülnek a kölcsönhatási tartományból. Ezeknek a részecskéknek vagy sugárzásnak a detektálásával kapunk információt a lejátszódott magreakcióról, ezáltal az anyag összetételéről. Az ionsugaras mérési módszerek kombinálhatók az ú.n. csatornahatással 11. Ez a jelenség akkor lép fel, ha egykristályos anyagot bombázunk úgy, hogy a beeső ionok iránya párhuzamos az egykristályos céltárgy egyik fő kristálytani tengelyével. Ekkor a target atomjainak rendezett elhelyezkedése az ionok útját befolyásolja. Ilyen mérésekből pontos információt kaphatunk a kristályos anyag szerkezetéről, kristályhibák, idegen atomok rácstérben való elhelyezkedésének maghatározására alkalmas. Ionsugaras anyagvizsgálatokban a most felsorolt kölcsönhatások az elsődleges jelenségek, vannak azonban ú.n. méréseket Fékeződés másodlagos folyamatok is, amelyek befolyásolják a A fékeződés az a folyamat, amikor felgyorsított ionok bombázzák anyagot és az anyagban haladva folyamatosan veszítik el az energiájukat a teljes megállásig. A részecske kinetikus energiája a közeg atomjainak gerjesztésére és ionizációjára fordítódik. fékeződést az ionok energiája szerint két független folyamatra lehet osztani. A Nagyobb energiákon az ú.n. elektronos fékeződés 12 dominál, amely a rugalmatlan ion-atom ütközések következménye. Ekkor az ion és a target atom elektronfelhője lép egymással kölcsönhatásba, ionizáció, töltésállapot változás következhet be. a magfékezés 13 Kisebb energiákon a jellemző folyamat, amelyet a rugalmas ion-atom ütközések hoznak létre. Az elektronos és magfékezés nagysága jellemző a vizsgált rendszert alkotó ionokra és atomokra. Például, ha szilíciumot bombázunk protonokkal, az elektronos fékezés maximuma 100 kev bombázó energia közelében van. tényező csökken. Nagyobb energiákon a fékezési Kisebb energiákon a magfékezés dominál, ennek maximuma 10 kev körül van. A fékeződés az ionok energiájával, azaz sebességével van összefüggésben. Nagy 10 Nuclear Reaction Analysis, NRA 11 Channeling 12 Electronic stopping 13 Nuclear stopping
10 9 sebességeknél a Bethe egyenlet írja le a fékeződést, kisebb sebsségeknél az ú.n. Lindhart- Scharff egyenlet alkalmazható [Bir89]. Az energiafüggő fékeződést 14, S(E), az egységnyi úthosszra eső átlagos energiaveszteséggel írhatjuk le S(E) = de dx. (1) A gyakorlatban használjuk az ε fékeződési hatáskeresztmetszetet 15 is: ε = de dρ, (2) ahol ρ az anyag felületi sűrűsége atom/cm 2 egységben. A Bragg-szabály szerint, összetett anyagokban a fékeződés az egyes összetevők által okozott fékeződés súlyozott összege. Ha az összetett anyag A m B n formában írható le, akkor a fékeződési hatáskeresztmetszet az összetett anyagra: ε AmBn = mε A + nε B. (3) Az ionsugaras analitikában alkalmazott energiákra, különféle ionokra és anyagokra táblázatok tartalmazzák a kísérleti eredményekből kapott fékeződési tényező értékeket. Többféle közelítés is létezik a fékezési tényező energiafüggésének leírására, ilyen a Ziegler, Biersack és Littmark-féle leírás (ZBL), amely magasabbrendű polinómokkal közelíti a kísérleti eredményeket. A munkámban én is általában a ZBL leírást használtam a fékeződési tényező meghatározására a SRIM programcsomag [Sri00] segítségével Straggling A nagy energiával az anyagba érkező ionok fékeződése véletlenszerű statisztikai folyamat, az ionnyalábot alkotó ionok ütközések sorozatán át vesztik el az energiájukat, míg teljesen meg nem állnak az anyagban. Egy adott fizikai mélységben az ugyanolyan energiával beérkező ionokoknak az energiája már nem lesz azonos: minden egyes ion különböző ütközések sorozatán át jutott az adott mélységbe. folyamatból származó energiaszórását hívják stragglingnek 16. Az ionnyaláb ebből a Kis energiaveszteségeknél, de amikor már elég nagyszámú ütközés játszódott le, egy adott mélységben az energiaelmosódást a Bohr-elmélet szerint, ami a dobozba zárt 14 stopping power 15 stopping cross section 16 Megfelelõ magyar kifejezés hiányában a jelenség angol nevét használom.
11 10 elektronok modeljén alapul, egy Gauss-függvény írja le [Tes95], aminek a szórása (σ s ) : σ 2 s =4π(Z 1 e 2 ) 2 Z 2 N 2 t, (4) ahol e az elemi töltés, N 2 t pedig az az anyagmennyiség, amelyen áthaladtak az ionok (Z 1 és Z 2 a bombázó és a target atom rendszáma). A gyakorlatban az x anyagvastagságban bekövetkező straggling kiszámítására a r Z2 p σ s [MeV]=0, 395Z 1 x[gcm 2 ]=B p x[gcm A 2 ] (5) 2 kifejezést használjuk, B az anyagtól és bombázó részecskétől függő úgynevezett straggling konstans. A Bohr elmélet szerint a straggling konstans értéke nem függ a bombázó részecske energiájától, meghatározó a részecske és a target atom elektronsűrűsége. Bonderup és Chu pontosította az energia straggling számítását figyelembe véve a minta atomjainak elektronszerkezetét is [Bon71, Chu76, Szi95]. Nagyon kis energiaveszteségre, azaz kis mélységekre, Vavilov számította ki ezt az energiaelmosódást [Dec78]. Ekkor egy aszimmetrikus, a magasabb energiák felé lassan eső függvény írja le a stagglinget. Ha egy adott elem mélységprofilját a felület közelében nagy pontossággal akarjuk meghatározni, akkor nem elég a szimmetrikus Bohr-stragglinggel számolnunk, figyelembe kell venni az aszimmetriát is. Több elemű minták esetében a straggling számítására a Bragg-szabályt alkalmazzuk (hasonlóan, mint (3) egyenletben) Doppler-szélesedés A minta atomjai hőmozgást végeznek melynek sebessége összemérhető lehet a bombázó részecske sebességével. A két sebességvektor irányától függően a bejövő részecske vagy nagyobb, vagy kisebb energiával ütközik a target atomjához, mintha az nem mozogna. Ez a jelenség is egyfajta energiaelmosódásban jelenik meg. Ezt az ú.n. Dopplerszélesedést Gauss-függvény írja le, amelynek szórása: σ 2 D = 2M 1E 1 kt, (6) M 2 ahol k a Boltzmann-állandó, T ahőmérséklet. 2.2 Magreakciók Magreakció során a céltárgyba ütköző ion nem a céltárgy atomjának elektronfelhőjével, hanem az atommagjával lép kölcsönhatásba. A mag felé haladó ionra a magot körülvevő
12 11 Coulomb-térben fellépő taszítóerő hat. Ha az ion energiája elegendően nagy ahhoz, hogy legyőzze a taszítást, akkor az ion behatol az atommagba és ott a magerőkön keresztül kölcsönhatásba lép a nukleonokkal, magreakciót idéz elő. A magreakció ideje alatt a két részecske energiája és impulzusa átrendeződik, amit néhány más részecske keletkezése kísér, melyek kirepülnek a kölcsönhatási tartományból. A magreakció általában nem vezet egyértelműen meghatározott végeredményhez (2.2 ábra). Egy adott magreakcióban a különböző végeredményhez vezető folyamatokat reakciócsatornáknak szokás nevezni. Az egyes reakciócsatornákat a részecskék típusa, belső állapotuk, spinjük és pályaimpulzusmomentumuk iránya különbözteti meg. a + A B + b C + c... A + a A + a 2.2ábraHaarészecskével bombázzuk A magot többféle magreakció is lejátszódhat, b vagy c emittálása után visszamarad B vagy C mag. Más reakciócsatornák is lehetségesek. Az utolsó két reakciócsatorna az ábrán a rugalmatlan és rugalmas szórás. Ezekben a speciális esetekben a reakciótermékek megegyeznek a reakcióba lépő részecskékkel. Rugalmas szórás esetében a mag belső állapota sem változik meg (Q =0), míg rugalmatlan szórás esetében a mag belső állapota megváltozik, gerjesztett állapotba kerül. A töltött részecskék a maggal való Coulomb kölcsönhatását a B c magassága, jellemzi: B c = Z 1Z 2 e 2 R Coulomb-gát Z 1 Z 2 A [MeV], (7) ahol Z 1 a bombázó részecske rendszáma, Z 2, A 2 pedig a mag rendszáma illetve atomsúlya; e az elektron töltése, R pedigamagsugara(r = r 0 A 1 3,r 0 = (1, 2 1, 4) cm). A B c -nél nagyobb kinetikus energiájú részecskék behatolnak a magba, magreakció jöhet létre. A B c -nél kisebb kinetikus energiájú részecskék a klasszikus mechanika szerint nem tudnak behatolni az atommagba. A kvantummechanika szerint azomban ezek a kis energiájú részecskék is véges valószínűséggel kölcsönhatásba léphetnek a maggal a kvantummechanikai alagúteffektus révén. Így következnek be kis energiákon is magreakciók. A magreakciókban a kibocsátott részecske lehet ion, γ-foton, vagy neutron. emittált részecskének az energiája, és az iránya jellemző a bekövetkezett magreakcióra. Az
13 12 A magreakció talán legfontosabb tulajdonsága, hogy izotópérzékeny, tehát egy adott magreakció csak egy elem egyetlen meghatározott izotópjával jöhet létre. Az első mesterségesen létrehozott magreakciót Rutherford figyelte meg 1919-ben. A magreakciók anyagvizsgálati alkalmazására 1957-ben jelent meg Rubin és társai cikke [Rub57], Chemical analysis of surfaces by nuclear methods címmel, ez a születése a modern magreakciós analitikának. A 60-as évektől gyorsan fejlődik ez a technika és egyre szélesebb körben alkalmazzák anyagvizsgálati célokra. A módszer meglehetősen összetett, mivel egy izotópon egyszerre több reakciócsatorna is megengedett lehet és a mintában lévő különböző izotópokkal egyidejűleg különböző magreakciók is történhetnek. A magreakciók négy alapvető kategóriáját különböztetjük meg a reakciótermék fajtája szerint: ion-ion, ion-gamma, ion-neutron reakciók és aktiváció. A módszer főelőnyei; - nagy érzékenység az adott könnyű, más ionsugaras technikával nehezen kimutatható izotóp detektálásában; - nagy szelektivitás a különböző izotópok között; - roncsolásmentes 17 vizsgálati módszer; - a mintában sok könnyű izotóp pontos és abszolút mennyisége meghatározható; Az irodalomból már sokféle magreakció ismert, de még napjainkban is újabb és újabb részleteket fedeznek fel a kutatók, főleg a nehezebb ionok által indukált reakciók területén. A dolgozatomban csak az ion-ion és ion-gamma típusú magreakciók közül néhánnyal foglalkozom. Anyagvizsgálatra szinte kizárólag az exotermikus magreakciók alkalmasak. Ekkor a reakcióban résztvevő izotópok milyenségéről, mennyiségéről és mélységi eloszlásáról a reakciótermékek detektálásával nyerhetünk információt. A reakció során a résztvevő atomok atomszáma és rendszáma a következők szerint változik: A A + A a A b = A B és Z A + Z a = Z b + Z B, 17 Az ionsugaras vizsgálatok során ionokkal bombázzuk a targetet, ezek az ionok lefékeződve megállnak az anyagban, útjuk során meglökik a céltárgy atomjait, amelyek kimozdulhatnak a helyükből. A vizsgálatokban a target atomjainak számához képest kevés iont lövünk a mintába, tehát ezek hatása elenyésző. Viszont a bombázó ionok a nagyon érzékeny atomi struktúrákat, az egykristályos anyag rendezettségét meg tudják változtatni. Ilyen értelemben természetesen destruktív a módszer. Az ionsugaras mérések tervezésénél és kiértékelésénél mindig gondolni kell arra, hogy megváltoztatja-e a mintát a mérés. Egy amorf, vagy polikristályos tömbi anyag vizsgálatánál az ionbombázásnak valószínűleg nem lesz mérhető hatása, de egy nagyon vékony rétegekből álló, egykristályos struktúra már megváltozhat az ionsugár hatására.
14 13 ahol A A és Z A atargetizotóp,a a és Z a a beeső részecske, A b és Z b areakciótermék részecske és A B és Z B a keletkező izotóp atomszáma és rendszáma. Az anyagvizsgálati célokra leggyakrabban alkalmazott magreakciók adatait a 2.1 táblázat tartalmazza. Egy tipikus példa: 18 O(p,α) 15 N Q =3, 9804 MeV Ebben az esetben az oxigén 18-as tömegszámú izotópját (a természetben 0,204%-os gyakoriságban fordul elő), amelynek az atommagja 8 protont és 10 db neutront tartalmaz, bombázzuk protonokkal. A bombázó proton befogódik a magba és egy α-részecske emittálódik. Közben az energiamegmaradás törvénye alapján, Q-nak megfelelő energia szabadul fel, amit a reakciótermékek visznek el a magtól. A visszamaradó magban a nukleonok száma a következő módonváltozik:protonok: = 7;neutronok: 10-2 = 8; tehát a keletkező elem rendszáma 7, atomsúlya pedig 15, a nitrogén 15-ös izotópja rendelkezik ilyen atommaggal, ez az elem keletkezett a reakció során. Proton-reakciók reakció Q [MeV] 6 Li(p,α) 3 He 4,02 Deuteron-reakciók reakció Q [MeV] 2 H(d,p) 3 He 4,03 3 He-reakciók reakció Q [MeV] 2 H( 3 He,p) 4 He 18,35 4 He-reakciók reakció Q [MeV] 10 B(α,p) 13 C 4,06 7 Li(p,α) 4 He 17,35 3 He(d,α) 1 H 18,35 6 Li( 3 He,p) 8 Be 16,79 11 B(α,p) 14 C 0,78 9 Be(p,α) 6 Li 2,13 12 C(d,p) 13 C 2,72 9 Be( 3 He,p) 11 B 10,32 14 N(α,p) 17 O -1,19 10 B(p,α) 7 Be 1,15 13 C(d,p) 14 C 5,95 9 Be( 3 He,α) 8 Be 18,91 19 F(α,p) 22 Ne 1,67 11 B(p,α) 8 Be 8,58 14 N(d,p) 15 N 8,61 12 C( 3 He,p) 14 N 4,78 31 P(α,p) 34 S 0,63 15 N(p,αγ) 12 C 4,97 14 N(d,α) 12 C 13,57 12 C( 3 He,α) 11 C 1,86 18 O(p,α) 15 N 3,98 16 O(d,p) 17 O 1,92 18 O( 3 He,p) 20 F 6,87 19 F(p,αγ) 16 O 8,11 16 O(d,α) 14 N 3,11 18 O( 3 He,d) 19 F 2,50 23 Na(p,γ) 24 Mg 11,69 19 F(d,α) 17 O 10,03 18 O( 3 He,α) 19 O 12,51 27 Al(p,γ) 28 Si 11,59 29 Si(p,γ) 30 P 5,59 52 Cr(p,γ) 53 Mn 7, táblázat: Gyakorlati szempontból legfontosabb magreakciók és Q-értékeik. 2.3 A magreakciós kölcsönhatás fizikai leírása Kinematika Ha a target A atommagját bombázzuk az a gyorsított, általában könnyű részecskével és az A(a, b)b magreakció következik be, akkor B atom és b könnyű reakciótermék keletkezik. Ebben az esetben is igaz az energiamegmaradás törvénye. E a + E A = E b + E B + Q, (8)
15 14 ahol E a a bombázó részecske energiája, E A a target atom kinetikus energiája (szilárd céltárgy esetében általában nulla, de pl. gáz target esetében figyelembe kell venni), E B és E b a keletkező mag és részecske energiája (laboratóriumi rendszerben számítva). Az energiaváltozást kifejező Q értéket meg lehet adni a reakcióban résztvevő részecskék tömegével is: Q =(M a + M A M b M B ) c 2. (9) Ebben a számításban az egyes tömegeket atomi tömegegységben kell megadni, figyelembe véve a magokhoz tartozó elektronok tömegét is. Itt c a fénysebesség. 1 a.m.u = 931,478 MeV/c 2. Ha Q értéke pozitív, akkor exoterm a folyamat, energia szabadul fel a reakció során, ha negatív akkor endoterm reakcióról beszélünk és többlet energiát kell befektetni ahhoz, hogy létrejöjjön a reakció. Ha Q negatív, akkor a reakció energetikailag mindaddig nem jöhet létre, amig a bombázó részecske energiája nem haladja meg az E th küszöbenergiát: E a E th = Q M B + M b M B + M b M a. (10) Q < 0 Q > 0 E a E th a + A b 2 b 1 b 0 Q B γ a + A Q b 2 b 1 b 0 B γ ábra: Az A(a, b)b magreakció energiadiagramja negatív és pozitív Q-érték esetében. Az energetikai folyamatot ábrázolhatjuk az energiadiagramon is (2.3 ábra). többféle reakciócsatornának megfelelően, az ábrán, az emittált részecske lehet b 0 vagy b 1 vagy b 2.Ab 1 vagy b 2 részecske kibocsátása által még nem kerül alapállapotba a mag. Ezekben az esetekben megfelelőenergiájúγ-fotont emittálva kerül a mag egy, az eredetitől A
16 15 Q val eltérő energiájú alapállapotba. Az energiadiagramból kiolvashatjuk a detektálni kívánt reakciótermék energiáját. 2.4 ábra Az E a energiájú M a tömegű ion bombázza a vizsgált anyag M A tömegű atomját. A magreakció hatására megváltozik mind a bombázó ion, mind a target atom energiája (E b,e B ), tömege (M b,m B ), illetve rendszáma (Z b,z B ). A magreakciók során is érvényes az energia- és impulzusmegmaradás törvénye. Ezekből kiszámíthatjuk az atommag és a reakciótermék könnyű ion energiáját (E b )a reakció után: p Eb = (M am b E a ) 1/2 cos φ M b + M B ± (M am b E a cos 2 φ +(M B + M b )(M B Q +(M B M a )E a )) 1/2 M b + M B, E B = E a + Q E b, (12) ahol φ a reakciótermék részecske iránya a bejövő részecske irányához képest. képletben a négyzetgyök alatt szereplő kifejezésnek mindig pozitívnak kell lennie. Ebből következően a reakcióban résztvevő tömegek arányai szerint lehet olyan elrendezés, amikor a reakciótermék tetszőleges irányba haladhat, de lehet olyan is, amikor csak egy szűk szögben térhetnek el a bejövő részecske irányától Magreakciók hatáskeresztmetszete A magreakciókat is jellemzi a hatáskeresztmetszet, ami a reakció bekövetkezési valószínűségét adja meg a bombázó ion energiája és a geometriai elrendezés függvényében (lsd. pl. 2.5 ábra). A valószínűséget a φ szög körüli Ω térszögben emittált részecskékre a következő formában írhatjuk le: dσ(φ) dω = N b N A N a Ω, dσ(φ) ahol dω a differenciális hatáskeresztmetszet, N b a detektált részecskék, N A a target magok, N a pedig az E a energiával beeső részecskék száma cm 2 egységekben. (11) A
17 16 A hatáskeresztmet praktikus egysége a barn, 1 barn = cm 2. Miután a hatáskeresztmetszet irányfüggő, az irodalomban különböző detektálási szögekhez tartozó hatáskeresztmetszet-energia értékek találhatók. A mérésben törekedni kell az optimális detektálási szög alkalmazására [Szi95]. A gyakorlatban a hatáskeresztmetszet és a beeső ionok száma ismert, a mérésből a targetben lévő A atomok mennyiségére vagyunk kiváncsiak. Így: N A =. (13) dσ(φ) dω N a Ω Az NRA mérést egy olyan jól megválasztott energián kell végezni, - figyelembe véve a fékeződést is a rétegben - ahol a hatáskeresztmetszet állandónak tekinthető. Ha ez nem lehetséges, pl. vastag rétegben, vagy tömbi anyagban, az adott izotóp mennyiségének meghatározásakor figyelembe kell venni a hatáskeresztmetszet energiafüggését is. N b 2.5. ábra: A 16 O(d,p) 17 Oésa 16 O(d,α) 14 N magreakció hatáskeresztmetszete látható az ábrán a 700 kev kev bombázóenergia-tartományban 165 detektorszögnél felvéve. ([Ams67] és [Nam92] alapján) Rezonancia-hatáskeresztmetszet A hatáskeresztmetszet sok esetben nem egy lassan változó függvény, a menetében bizonyos jól definiált energiaértékeknél lehetnek éles kiugrások, ú.n. rezonanciák. Rezonanciában, a környező értékhez képest, több nagyságrenddel megnövekedhet a hatáskeresztmetszet. A 2.6 ábrán a 18 O(p,α) 15 N magreakció hatáskeresztmetszete látható kev energiatartományban. Egy viszonylag keskeny rezonancia látható 629 kev energiánál.
18 17 A rezonancia σ R (E) hatáskeresztmetszet energiafüggését egy Breit-Wigner függvény (más néven Lorenz-görbe) írja le: σ R (E) =K, (14) (E E R ) 2 + Γ2 4 ahol K konstans, Γ a hatáskeresztmetszetben lévő rezonancia félszélessége 18. Γ areakció során létrejövő gerjesztett összetett mag energianívóival és azok élettartamával van összefüggésben. Növekvő bombázó energiával általában Γ értéke is nő, mert az egyes nívók átlapolódnak. Nagyobb energiákon az összetett mag alapállapotba kerülése több lépésben, különböző folyamatok által is végbemehet, ezért kiszélesedhet a rezonanciagörbe. Igazán keskeny rezonanciákat (Γ ev) csak kis bombázó energiákon találhatunk. Γ ábra A 18 O(p,α) 15 N magreakció hatáskeresztmetszete az energia függvényében. 629 kev proton energia környékén található egy intenzív rezonancia 2,9 kev szélességgel. Nagyobb energia felé a hatáskeresztmetszet növekedik, de éles rezonanciát nem látunk [Ams67]. 2.4 Magreakciós mérések megvalósítása, méréstechnikai követelmények Gyorsítóberendezés, mérőnyaláb, mérőkamra Magreakciós méréseket általában 10 kv MV feszültségű iongyorsító berendezéseknél végeznek. A gyorsító berendezésben van tömegszeparátor, amely után a nyaláb csak meghatározott tömegszámú ionokból áll. Alapvető követelmény,hogya nyaláb jól vezetett, lehetőleg minél párhuzamosabb, jól kollimált, energiában, helyben és áramban stabil legyen. Az áram nagysága legtöbbször na között váltakozik, de ionimplanter típusú gyorsítók esetében az alkalmazott ionáram sokkal nagyobb is lehet. Az ionáram megválasztásakor figyelembe kell venni a minta tulajdonságait. 18 Ahol egy függvény szélességéről beszélek, akkor a görbe a maximuma felénél felvett teljes szélességét értem (FWHM - full width at half maximum).
19 18 Mérés alatt a mérőnyaláb lehetőleg ne változtassa meg a minta rétegszerkezetéet és/vagy összetételét (a nyaláb ne okozzon ionos keverést), illetve ne növekedjék a minta hőmérséklete a megengedhető mértéknél jobban (magasabb hőmérsékleten nemvárt folyamatok játszódhatnak le a mintában) és a minta vastagsága se változzék (ne lépjen fel porlódás). Fontos az is, hogy a nyaláb hatására minél kevesebb szénhidrogén szennyezés rakodjék le a minta felületén, ezért jó vákuumban, folyékony nitrogénnel hűtött csapdák használata mellett kell a méréseket végezni. Keskeny rezonanciás méréseknél fontos követelmény, hogy a nyaláb energiaszórása minél kisebb legyen. Ez az energiaszórás egyrészt statisztikusan keletkezik az ionforrásban, másrészt a nagyfeszültségű terminál feszültségingadozásaiból áll. Az energiaszórás általában Gauss-függvény alakú, a magreakciós mérések kiértékelése alkalmával figyelembe kell venni. Ezért a nyaláb energiaeloszlását lehetőleg mindig meg kell mérni, folytonosan monitorozni kell. Főleg keskeny magrezonanciák alkalmazásánál jelenthet gondot a nagy nyaláb-energiaszórás. Az erre a célra alkalmas gyorsítók energiaszórása általában ev tartományba kell, hogy essen. 2.7 ábra Tipikus NRA mérési elrendezés, amikor a nyaláb merőlegesen esik be a mintára. A vákuum jobb, mint 10 5 Pa. A szennyeződések elkerülése érdekében folyékony nitrogénnel hűtött csapda használata szükséges.
20 19 Vákuumkamra LN 2 hűtött csapda Ion Sugár Minta Félvezető detektor Szűrő fólia BGO vagy NaI γ detektor 2.8 ábra Hasonló mérési elrendezés, mint amely az 2.7 ábrán: itt az ionsugár nem merőlegesen, hanem nagy szög alatt esik be a mintára. A magreakciós méréseket általában ugyanabban a mérőkamrában lehet végezni, mint amelyet az egyéb ionsugaras mérésekhez használunk. Fontos, hogy a mintatartó a nyaláb irányához képest forgatható legyen, hogy, ha szükséges, elforgatott mintán is lehessen méréseket végezni. Szintén fontos a detektor elhelyezése a kamrában. Ha a magreakció nem izotróp, akkor a detektálási szöget és detektor térszögét a hatáskeresztmetszet szögfüggésének figyelembevételével kell megválasztani. Illusztrációként bemutatok két jellemző elrendezést(2.7és2.8ábra) Detektor, detektálás Magreakciós vizsgálatokban a reakcióterméket detektáljuk, ennek mennyiségéből, energiájából tudunk a vizsgált anyag összetételére, tulajdonságaira következtetni. A mérés során természetesen rugalmas visszaszórás is történik. A visszaszórt ionok energiája, ahogy az RBS esetben megszokott, a target atomra jellemző kinematikai faktorral és a fékeződéssel kisebb, mint a bombázási energia. A reakciótermék energiája általában jóval nagyobb, mint a visszaszórt ionok energiája, tehát a visszaszórt ionokat a reakciótermék ionoktól energiájuk szerint szét lehet választani.
21 ábra Néhány proton és deuteron keltette magreakció esetében a bombázó és visszaszórt ionok, valamint a reakciótermék energiája látható az ábrán a bombázó ion energiájának függvényében. A satírozott rész a visszaszórt ionokat mutatja. Alkalmasan megválasztott szűrőfóliával ezt az energiatartományt teljesen ki tudjuk szűrni a mért spektrumokból, hogy csak a reakcióterméket detektáljuk. Zárójelben a reakcióban keletkező energia szerepel MeV egységekben 19 [Fel77]. A 2.9 ábrán néhány proton és deuteron keltette magreakció esetében bemutatom a reakcióban keletkező és a visszaszórt ionok energiáját a bombázó energia függvényében. Ahhoz, hogy energiájuk szerint szétválasszuk a részecskéket, legtöbbször egy szűrő fóliát helyezünk el a detektor előtt, aminek a vastagságát úgy választjuk meg, hogy a visszaszórt részecskék teljesen lefékeződjenek a fóliában, a reakciótermék részecskék viszont némi fékeződés után a fólián keresztül eljussanak a detektorba. Leggyakrabban különböző vastagságú fémezett Mylar fóliát használunk. (A Mylar fólia használatakor figyelni kell, nehogy lyukak legyenek a fólián, mert az ezeken keresztüljutó visszaszórt ionok teljesen meghamisíthatják a méréseket.) Más szeparálás is lehetséges a visszaszórt és a reakciótermék ionok szétválasztására, pl. a sebességkülönbségen alapuló mágneses energiaszétválasztás. A szükséges szűrőfólia vastagságok megállapításához ökölszabályként alkalmazhatjuk a következő összefüggéseket: ha a Mylar fólia fékezése protonokra S p (E), akkor deuteronokra, alfa- és 3 He részecskékre: S d (E) = S p (E/2), S α (E) = 4S p (E/4), S3 He(E) = 4S p (E/3). 19 Az irodalomból átvett ábrákat mindig a forrás megjelölésével, eredeti formájukban közlöm.
22 21 Előfordulhat, hogy a reakciótermék energiája nem elég nagy, így a visszaszórt ionok megállításához szükséges szűrőfólia ezt a részecskét is megállítja. Ilyenkor a méréseket szűrőfólia nélkül kell végezni. Viszont a visszaszórt részecskék száma nagyságrenddekkel nagyobb lehet, mint a magreakcióban keletkező reakciótermék ionok száma. Ebben az esetben ügyelni kell arra, hogy kellően gyors elektronika álljon rendelkezésre, nehogy a túl gyorsan egymás után beérkező ionok számlálási hibákat okozzanak a jelek feldolgozásakor. A reakciók során keletkező p, d, α részecske csoportok azonosítására és szétválasztására a félvezető detektor érzékeny rétegének, a tértöltési tartománynak a szélességét lehet az előfeszítés változtatásával beállítani [Ams92]. A detektor a tértöltési tartományban leadott energiát méri, ez a detektor érzékeny rétege. A detektor előfeszítésének változtatásával elérhető, hogy a különböző energiájú részecskék a detektorban a fékeződésnek megfelelően más és más energiát adjanak le, ha a részecskék behatolási mélysége nagyobb, mint a tértöltési tartomány vastagsága (pl. az azonos energiájú α részecske és proton közül az α részecske már megáll az érzékeny rétegben, akkor teljes energiáját ott adja le. A proton ugyanakkor nem fékeződik le teljesen a rétegben, energiájának csak kis egy részét adjá le a detektor érzékeny rétegében.). A helyzet egyszerűbbé válik, ha a reakciótermék γ-foton. Ennek detektálása nagy hatásfokú γ-detektorokkal történik. Miután nincs szükség a mérésben a fotonok energiájának pontos mérésére, kevésbé jó energiafelbontású NaI (nátrium-jodid) vagy BGO (bizmut-germanát) detektor is alkalmazható. Ezek a detektorok általában a vákuumtérbe benyúló zsebben a mintához minél közelebb vannak elhelyezve. A visszaszórt ionok el sem érik a detektort, így az csak a nagyenergiájú γ-fotonokat fogja detektálni. A detektor érzékeli a kozmikus vagy háttérsugárzást is. Ezért ajánlatos megmérni nyaláb nélkül az adott idő alatt detektált γ-fotonok számát és ezt a mérés kiértékelése során figyelembe kell venni Felületi szennyezés Ionsugaras méréseknél általában mindig van valamilyen felületi szennyező réteg a mintán. Tiszta, szennyezőmentes felületet előállítani is nehéz, de fenntartani még nehezebb. Ha nem ultranagy-vákuumban tartjuk a mintát, akkor levegő, vízgőz, stb. adszorbeálódik a felületen. Mikor ionsugárral bombázzuk a mintát, akkor a vákuumkamra maradékgázából az ionsugár hatására polimerjellegű, átlagosan CH 2 összetételű szénhidrogén réteg is lerakódik a felületre, pár tíz Å vastag rétegben. A mérés során a lerakódás és a visszaporlasztás dinamikus egyensúlyaként beáll egy állandó
23 22 vastagság. Ha nagyon érzékeny, felületközeli mérést végzünk, az ionnyaláb fékeződését és energiaszóródását mindenképpen figyelembe kell venni a felületi szennyező rétegbenis. 2.5 Magreakciók alkalmazásának bemutatása az irodalom alapján Magreakciós méréseket könnyű izotópok mennyiségi és mélységi meghatározására alkalmazunk. Azt használjuk ki a mérésben, hogy az adott izotóp résztvesz egy magreakcióban és ennek hatáskeresztmetszete elegendően nagy ábra Ezen az ábrán bemutatok egy SiO 2 rétegen felvett magreakciós spektrumot. A mérésben a 150 -ra elhelyezett detektor előtt 13 µm Mylar fólia volt. A bombázó deuteron nyaláb energiája 850 kev [Viz90]. Illusztrációképpen bemutatok egy deuteronos mérést. Nagyon vékony SiO 2 réteg vastagságának meghatározása volt a cél. Ha meg tudjuk mérni a rétegben levő oxigén atomok számát, akkor ebből ki tudjuk számolni az oxidréteg vastagságát feltételezve, hogy a szilíciumon a termikus oxidáció hatására sztöchiometrikus oxid keletkezik. A 16 O(d,p) 17 O magreakció lehetővé teszi kis mennyiségű oxigénmeghatározásátis. A reakciónak a hatáskeresztmetszete megtalálható a 2.5 ábrán. Ha a mintában a teljes 16 O mennyiségét akarjuk meghatározni, akkor olyan energiatartományokban érdemes mérni, ahol a hatáskeresztmetszet nem függ nagyon az energiától. A ábrán látható spektrumot [Viz90] úgy mérték, hogy 850 kev-os deuteron nyalábbal bombáztak egy SiO 2 vékonyréteg mintát. A reakciótermék protonokat felületi záróréteges félvezető detektorral detektálták. A rugalmasan szóródott deuteronokat, illetve a más reakcióból jövő ionokat egy, a detektor elé helyezett szűrőfólia megállította. (Jelen esetben 13 µm vastag Mylar fólia volt a detektor előtt.)
24 23 Láthatók a különböző izotópokon lejátszódó magreakciók termékei, ennek megfelelően különböző energiákon kapunk csúcsokat. A 16 O(d,p) 17 O reakcióból két protoncsoportot kapunk két külön energián (E 1180 kev és 2080 kev energián). Szintén megtaláljuk a 12 C(d,p) 13 C reakcióból származó protoncsúcsot is (E 2710 kev). A szén a mindig jelenlévő felületi szénhidrogén rétegben van. A mérés során a vizsgáló nyaláb deuteron ionokat implantál a minta felületi rétegébe, az ezután érkező deuteron ionok magreakciót okozhatnak a beimplantált deuteronokal. Ezért kapunk protonokat a 2 D(d,p) 3 Treakcióból is (E 1620 kev). Egy proton-csúcs alatti terület A, (tehát az összes ebben a reakcióban keletkezett proton száma) arányos a mintában levő oxigén abszolút mennyiségével: A = Q c Ω σ φ (E) Nt (15) ahol Q c az összegyűjtött összes töltés, tehát a bombázó ionok száma a spektrum felvétele közben, Ω a detektor térszöge, σ φ (E) a reakció hatáskeresztmetszete φ szögben E energián és Nt a reakció szempontjából érdekes magok száma a targetben cm 2 egységben. Ha az összes mennyiség pontosan ismert volna, akkor a magok száma is nagy pontossággal megadható lenne. A gyakorlatban azonban a szükséges mennyiségeket nem ismerjük eléggé, a mérési elrendezés, tehát a detektor térszöge is gyakran változhat. Ezt a problémát jól ismert referencia-minták mérésével küszöbölhetjük ki. Ugyanazzal a mérési elrendezéssel lemérünk egy olyan mintát, amiben ismert a minket érdeklő atom mennyisége, majd megmérjük az ismeretlen mintát. A csúcsterületek összehasonlításából megkaphatjuk az ismeretlen mintában levő magok számát: A Nt = Nt ref. Ekkor a pontosságot csak az határozza meg, hogy milyen A ref pontosan ismerjük a referencia target összetételét, illetve milyen pontossággal tudjuk a csúcsterületet meghatározni. További információk nyerhetők ugyanarról a mintáról, ugyanazzal a bombázó részecskével vizsgálva, ha nem teszünk szűrőfóliát a detektor elé. Ilyenkor olyan más magreakcióból származó reakcióterméket is detektálhatunk, amit az előző esetben kiszürt a fólia. A [Tur73]-ben bemutatott esetben a 16 O(d,α) 14 N magreakcióban keletkező α- részecskéket is detektálták. E reakció hatáskeresztmetszete is szerepelt a 2.5. ábrán.
25 ábra Hasonló mérés 600 nm vastag SiO 2 rétegen, mint a 2.10 ábrán. Most nincs a detektor előtt szűrőfólia. A bombázó nyaláb energiája 900 kev, a detektor 145 -ban helyezkedett el. [Tur73] Ebben az esetben a visszaszórt protonok jelét ki lehet vágni a spektrumból, mert kisebb energiával érik el a detektort, mint a reakciótermékek (visszaszórt protonok maximális energiája E Det 0,79 MeV, protonok a 12 C(d,p) 13 Creakcióból: E Det 2,96 MeV, protonok a 16 O(d,p) 17 O reakcióból: E Det 2,37 MeV és E Det 1,59 MeV, α-részecske a 16 O(d,α) 14 NreakcióbólE Det 2,63 MeV). A protonok fékeződése az anyagban kicsi, ezért közel azonos energiával erik el a detektort. Az α- részecskék fékeződése viszont nagy. A különböző mélységekben keletkező α-részecskék más és más energiát veszítenek az anyagban kifelé jövet, így más és más energiával érik el a detektort. Tehát az α-részecskék esetében egy energiaspektrumot lehet rögzíteni. Az energiaspektrum a target anyagának mélységi összetételéről is információt hordoz. A jelen mérésben egy közel lépcsőalakú α-spektrumot látunk, Ez azt mutatja, hogy az 16 O elosztása homogén a mintában. Az α-lépcső szélessége arányos a SiO 2 réteg vastagságával. Ez jó példa arra, hogy magreakciós méréssel egyidejűleg nemcsak mennyiségi, de mélységi, összetételi információt is kaphatunk a céltárgyról. Végül még egy példa magreakciós mérésre [Cac78] alapján (2.12 ábra). Ez egy bonyolultabb esetet mutat, amikor még több magreakció játszódik le ugyanazzal a bombázó részecskével és a spektrumban sok különböző reakciótermék csúcsa jelenik meg. Az egyes csúcsok területéből, referenciaminták használatával, meghatározható a vizsgált AlN minta összetétele. Kiértékelve a spektrumot nemcsak a réteg összetételét tudjuk megállapítani, hanem a szennyező oxigén és szén mennyisége is meghatározható.
26 ábra 170 nm vastag alumínium-nitrid réteg vizsgálata 1,7 MeV energiájú deuteronnyalábbal. Az energiaspektrumban láthatók az 27 Al(d,p) 28 Al, a 14 N(d,p) 15 N, a 16 O(d,p) 17 O és a 12 C(d,p) 13 C magreakciókban keletkező protoncsoportok. [Cac78] 2.6 Koncentrációprofilok mérése magreakciós rezonanciákkal A magreakciós rezonancia módszer a hatáskeresztmetszetben elkülönülten található ugrást, rezonanciát használja ki. A gyakorlatban a magreakció hatáskeresztmetszete a rezonanciában többszörös, esetenként több nagyságrenddel nagyobb, mint a rezonancián kívül. A mérés elvi menete a következő: ha a rezonancia-energiánál (E R ) nagyobb energiával bombázzuk a mintát, bejövő részecskék fékeződnek az anyagban és egy meghatározott mélységben lesz az energiájuk E R, azaz a rezonancia-feltétel egy adott mélységben teljesül. mélységből kapunk információt. energiáját, A magreakcióban résztvevő izotóp koncentrációjáról ebből a Ha E R -től folyamatosan növeljük a bejövő részecske akkor feltérképezhetjük az adott mag mélységi eloszlását (2.13 ábra). Ábrázolva az egyes energia-értékeknél kapott beütést a bombázó energia függvényében, megkapjuk a gerjesztési görbét, amely tartalmazza az adott izotóp koncentráció-profilját. Példaképpen a 2.14 ábrán bemutatok egy Ta hordozón elektronsugaras párologtatással készített vékony Al 2 O 3 rétegen felvett gerjesztési görbét.
27 ábra A rezonanciával történő mélységprofilozás elvi ábrázolása. Változtatva a bombázó részecskék energiáját mindig máshol következik be a rezonancia, így a mintán áttolva a rezonanciát a felvett gerjesztési görbe tükrözni fogja az adott elem koncentrációprofilját. Ebben az esetben a keskeny rezonancia-hatáskeresztmetszetet úgy használjuk, mint egy keskeny energiaszűrőt, hiszen csak abból a mintamélységből kapunk információt, ahol a nyaláb energiája pontosan megegyezik a rezonancia energiájával (E R ). A mintában a magreakcióban résztvevő izotóp koncentrációja nem feltétlenül állandó, a mélységgel változhat, C(x). A gerjesztési görbe magasságának energiafüggése leírható az alábbi alakban: N(E 0 )=σ R (E 0 ) D(E 0 ) h(e 0 ) C c (E 0 ) Z 0 g(e 0,x)C(x)dx, (16) ahol a akonvolúció 20 műveletét jelenti, E 0 anyalábenergiája,σ R (E 0 ) a rezonancia hatáskeresztmetszetet leíró Breit-Wigner függvény, D(E 0 ) a Doppler energiaszélesedés, h(e 0 ) a bombázó ionnyaláb energiaeloszlása, C c (E 0 ) a felületi szennyezés miatti R energiaszórás, g(e 0 0,x)C(x)dx pedig a koncentráció C(x) mélységi eloszlásának úgynevezett straggling transzformációja. A következő fejezetben ennek a leírásnak az elméleti alapjait mutatom be. R 20 A konvolúció definició szerint: a(x) b(x) = R a(x η)b(η)dη a(η)b(x η)dη
28 ábra Gerjesztési görbe 2000Å vastag Al 2 O 3 targeten, a 27 Al(p,γ) 28 Si magreakcióban 992 kev-nél lévő keskeny rezonanciát használva [Ams98]. A bombázó proton energiáját kev között változtattam. A reakciótermék γ-részecskéket a 3,5-12 MeV-es energiaablakban detektáltam. Semmiféle korrekció a görbén nem történt. Folytonos vonallal a szimuláció eredményét tüntettem fel A gerjesztési görbe elméleti leírása A keresett koncentrációprofil meghatározható a rezonanciamérésekben kapott gerjesztési görbéből, amelyet matematikailag le lehet írni az ionok fékeződésének sztochasztikus elméletét és a kis energiaveszteség közelítést alkalmazva [Mau82]. kis energiaveszteség közelítés azt jelenti, hogy abban az energiatartományban, ahol a gerjesztési görbét felvettük a de fékeződés állandó. Ezek alapján a gerjesztési görbe: dx Z N(Ē) = C(x)q 0 (x; Ē0)dx, (17) 0 ahol N(Ē) Ē energiánál a gerjesztési görbe magassága, a beütésszám, C(x) a target izotóp mélységfüggő koncentrációja, q 0 (x; Ē 0 ) pedig annak a valószínüsége, hogy egy Ē 0 energiával bejövő részecske egy detektálható kölcsönhatásban vesz részt x mélység dx környezetében. Az integrálban a felső integrálási határ azt a maximális mélységet jelzi, ahol már C(x) =0. Hogy q 0 (x; Ē0) -t megkapjuk, a σ θ (E) hatáskeresztmetszetet integrálni kell azzal a g 0 valószínűséggel súlyozva, amely megadja, hogy egy x mélységben lévő részecske energiája beleesik-e egy de energaablakba,: Z q 0 (x; Ē 0 )=n 0 Ωζ σ θ (η)g 0 (η; Ē 0 ; x)dη, (18) 0 A
29 28 ahol n 0 abejövő részecskék száma, Ω detektálás térszöge, ζ pedigadetektáláshatásfoka, g 0 (η; Ē0; x) pedig a bombázó nyaláb energiaeloszlása x mélységben. Ez az energiaeloszlás független Ē0 -től, szimmetrikus Ē 0 körül. Ha a σ θ (E) hatáskeresztmetszetnek E R energiánál csúcsa van, akkor gerjesztési görbe hozama csak ennek az energiának a közelében lesz nagy. Tehát de Ē 0 E R = x 0 dx. (19) Az energia straggling növekszik növekvő mélységekkel, ezért g 0 (η; Ē 0 ; x) és ezen keresztül q 0 (x; Ē0) is szélesedik növekvő mélységekkel. növekvő vastagságokkal. Ezért a mélység felbontóképesség romlik Ezek alapján megállapíthatjuk, hogy a gerjesztési görbe alakja, ahogy a (16) egyenletben megadtam, csak a rezonancia Γ szélességétől, a nyaláb energiaszórásától és a fékeződési folyamattól függ. Megjegyzem, hogy nagyon keskeny rezonanciáknál a Doppler szélesedést is figyelembe kell venni. Abban az egyszerűbb esetben, ha E E, tehát a kis energiaveszteség közelítést alkalmazva a gerjesztési görbe hozama leírható Z N(Ē) =n 0 Ωζσ θ (Ē 0 ) h(ē 0 ) C(x)ĝ(u; x)dx (20) formában. h(ē0 ) a nyaláb energiaszórása, ĝ(u; x) pedig annak a valószinűségi sűrűségfüggvénye, hogy egy részecske pontosan u energiát veszít, míg elér x mélységbe. Az integrál határozza meg, hogy milyen pontosan tudjuk megmérni C(x)-et, a Z S hc(x)i = W (u) = C(x)ĝ(u; x)dx (21) integrált C(x) straggling transzformáltjának is szokás nevezni. Ebben a kifejezésben az u változó az energiaveszteség. W (u) kauzális függvény, tehát W (u) =0, ha u 0, miután energiaveszteség csak akkor van, ha a részecske lassul az útja során. az ideális gerjesztési görbe. 0 0 W (u) egyébként Ezt akkor kapnánk, ha egy ideálisan monoenergetikus nyalábbal bombáznánk a targetet és a vizsgált reakcióban E R keskeny rezonancia lenne. energiánál végtelenül Ezek után a straggling transzformáltat vizsgáljuk, ennek ismerete szükséges a gerjesztési görbe leírásához. Előszőr is a bombázó ionok az útjuk során a homogén anyagban áthaladnak egy adott vastagságon és ebben véletlenszerűen bekövetkező ütközések sorozatán át veszítenek energiát. A fékeződésnek a statisztikai természetéből
30 29 következik, hogy egy x 1 vastagságban bekövetkező ütközések száma és az ezek során elvesztett energia u 1 nagysága teljesen független egy másik x 2 rétegben bekövetkező ütközések számától és az azokban elveszített u 2 energia nagyságától. Az x = x 1 + x 2 vastagságú rétegben az energiaveszteség tehát u = u 1 + u 2. A függetlenségből következik, hogy az u 1 illetve u 2 energiaveszteséget leíró ĝ(u; x 1 ) és ĝ(u; x 2 ) valószínűségi sűrűségfüggvény konvolúciója adja meg az x vastagságban vesztett u energia valószínűségi eloszlást. ĝ(u; x 1 + x 2 )=ĝ(u; x 1 ) ĝ(u; x 2 ). (22) Ezek alapján megmutatható [Mau82, Vic90a, Vic90b], hogy X (mx) n ĝ(u; x) = exp( mx)f(u) n n!, (23) n=0 ahol az együttható az a Poisson-valószínűség, hogy az ütközés N(x) száma, míg a részecske áthalad x vastagságon, pontosan n. Az átlagérték N(x) =mx. f(u) annak a valószínűségi sűrűségfüggvénye, hogy egy ütközésben u energiaveszteség következik be. f(u) n jelentése: f(u) konvolúciója önmagával (n 1)-szer (f(u) 2 = f(u) f(u), f(u) 0 = δ, az egység u =0-nál). Behelyettesítve (23)-t (21)-ba kapjuk a straggling transzformáltat X S hc(x)i = K n f(u) n. (24) n=0 Ebben a kifejezésben K n koefficiensek a koncentrációt írják le. Z K n = mn x n exp( mx)c(x)dx (25) n! 0 Mint a straggling transzformált legutóbbi kifejezésében, (24)-ban megmutattam, egy megadott anyagra az energiaveszteséget leíró valószínűségi sűrűségfüggvényt és konvolúcióit önmagával elég egyszer kiszámítani és a különféle koncentrációkhoz tartozó K n koefficienseket behelyettesítve megkaphatjuk a különböző S hc(x)i-ket. Az egymás utáni rétegekben bekövetkező energiaveszteség függetlenségéből az is következik, hogy, ha egy réteget felosztok alrétegekre, akkor az alrétegekre kiszámított gerjesztési görbék összeadhatóak. Miután K n értékeit analitikusan csak egy-két jól meghatározható koncentrációprofilra tudjuk kiszámítani, ezeknek a koncentrációprofiloknak a jól megválasztott összegével megadható egy gerjesztési görbe. A gyakorlatban a mintát
31 30 olyan alrétegekre szoktuk osztani, amelyekben már homogén a koncentráció, az ezekre kiszámított gerjesztési görbe darabok összege adja a teljes rétegre a gerjesztési görbét. A SPACES programcsomag [Vic90a, Vic90b] az itt vázlatosan megadott elméletet alkalmazva kiszámítja egy adott bombázó ionra, anyagra és energiára a gerjesztési görbét. Dolgozatomban a gerjesztési görbék szimulációjára ezt a programcsomot használtam. 2.7 Magreakciós és rezonanciás módszerek jellemző tulajdonságai A fenti példák alapján is összefoglalhatjuk a magreakciós ionsugaras mérések előnyeit és hátrányait. Előny, hogy a magreakciók izotóp-specifikusak. Nincs a targetben található más elemektől, izotópoktól származó beütés. Izotóp jelölési kísérletek végzésére kiválóan alkalmas. Már az adott izotóp kis mennyisége is meghatározható a mintában (magreakciótól függően ppm a legkisebb mérhető mennyiség). Hátrány viszont, hogy: Más magreakciók is lejátszódhatnak a minta többi izotópján, nehézzé tehetik a kiértékelést. Ez a probléma sokszor a detektálási szög vagy a szűrőfólia vastagságának a helyes megválasztásával kezelhető. A target összetétele általában egy mérésből nem határozható meg, más módszerekkel végzett mérések is szükségesek. Előny, hogy a reakciótermék energiája általában nagyobb mint a bombázó nyaláb energiája. A detektor előtt alkalmasan választott anyagú és vastagságú szűrőfólia alkalmazásával kiszűrhetjük a visszaszórt részecskéket, így csak a reakciótermék részecskéket detektáljuk. Hátrány, hogy a magreakciók hatáskeresztmetszete általában sokkal kisebb, mint a rugalmas szórás hatáskeresztmetszete. Ezért: Sokkal nagyobb beeső töltésigkellabegyűjtést végezni, hogy a spektrumban a szokásos RBS mérésekhez hasonló mennyiségben, statisztikával jelenjék meg a magreakciók spektruma. Haaz előbb említett okokból a méréseket sokkal nagyobb ionárammal végezzük, akkor viszont felléphet a jeltorlódás (pileup) jelensége. Ez azt jelenti, hogy a detektorba olyan gyakran, időben egymáshoz olyan közel érkeznek a részecskék,
32 31 hogy az elektronika már nem tudja az egyes jeleket szétválasztani. Két egymást gyorsan követő detektorjelet az elektronika úgy fog értelmezni, mint egy jelet, de olyan energiával, mint a két jel energiáinak összege. Az energia spektrum tehát torzulni fog, olyan energiákon is kapunk beütést, amelyekkel a valóságban nem is érkezik részecske a detektorhoz. Nagy ionáramoknál a minta is sérülhet, ionos keverés vagy porlódás léphet fel. A magreakciók hatáskeresztmetszete rendszerint kísérletileg nem eléggé ismert. Ezért: Hátrány, hogy A hatáskeresztmetszet-adatok sokszor pontatlanok, analitikai célokra nem alkalmazhatók. Ilyen esetben meg kell határozni a hatáskeresztmetszetet a feladat szempontjából fontos szögeken. Előny, hogy Jól definiált összetételű és vastagságú referencia mintákat lehet alkalmazni egyrészt a hatáskeresztmetszet méréséhez, másrészt a referencia mintáról és az ismeretlen mintáról kapott spektrumok összehasonlítására. Magreakciós rezonanciák alkalmazásával az adott izotóp mélységi eloszlása nagy pontossággal megállapítható. Előny, hogy Keskeny rezonancia alkalmazása esetén a rezonancia egy jó energia-szűrőként szerepel, a bombázó energia változtatásával a mintában lévő adott izotóp mélységi profilja letapogatható. A rezonancia az adott magreakció hatáskeresztmetszetében jelenik meg, ezért más elemek, izotópok nem járulnak hozzá a felvett gerjesztési görbéhez. Ha a magreakció hatáskeresztmetszete a keskeny rezonancia környezetében nagy, de a rezonancián kívül nagyon kicsiny (a két érték aránya nagy) a gerjesztési görbe alacsony háttérrel vehető fel. Kisenergiájú keskeny magreakciót használva, nagy mélységi felbontóképesség érhető el,mertabombázóionokfékeződése a mintában nagy. Ebben az esetben fontos paraméter az elektronos fékeződés maximuma, amely a target anyagától függően, protonokra 100 kev környékén van.
33 32 3. Oxigénrezonanciák A félvezető technológiában és általában az anyagtudományban központi helyet foglalnak el az oxidok és ezek vizsgálata. Az oxidációs folyamatok tanulmányozása elengedhetetlenül szükséges a félvezetők szigetelő oxidjánakelőállításához, de nagyon fontos például a különböző korróziós folyamatok megértéséhez is. A szilícium alapú integrált áramkörök elemsűrűsége növekszik, az elemeket alkotó rétegek, így a kapu elektród oxidrétegének vastagsága arányosan csökken. A nagyon vékony, néhány nm vastag oxidok tanulmányozása a jó mélységfelbontóképességgel rendelkező anyagvizsgálati technikákat igényel. Ebben a fejezetben az oxigén detektálásának általam is fejlesztett magreakciós rezonanciás módszeréről fogok beszámolni. Először a 152 kev bombázóenergiánál található rezonancia tulajdonságait, majd a módszernek a mélységfelbontóképességét tárgyalom. Röviden összehasonlítom a kisenergiás rezonanciát a magasabb energiákon bekövetkező rezonanciákkal, majd a kis energiás mérési módszer néhány alkalmazásáról számolok be. Az elmúlt években különböző problémák vizsgálatában használtam a 152 kev-es 18 O(p,α) 15 N rezonanciát, az elért eredményekről több publikáció is megjelent [Bat91, Bat92, Bat94a, Bat94b, Bau95, Gan93, Sch93, Ste94]. Az ionsugaras vizsgálatok szempontjából egyedi előnyt jelent, ha ritka oxigén izotóppal tudunk dolgozni. Az oxigénnek három stabil izotópja van a természetben, az 16 O 99,758%-os, az 17 O - 0,037%-osésaz 18 O - 0,204%-os relatív gyakorisággal fordul elő. Kémiai szempontból nincs különbség az izotópok között, ezért az oxidációs vizsgálatokban bármelyik izotópot használhatjuk. Kihasználva azonban a magreakciók izotóp érzékenységét, külön-külön lehet mérni az egyes izotópok mennyiségét és mélységi eloszlását. A magreakciókkal kombinált ionsugaras analitika egy erre a célra nagyon alkalmas és viszonylag könnyen használható méréstechnika. Az izotópjelöléses 21 módszer alkalmazásánál ellenőrzött módon juttatjuk a mintába ugyanazon elem különböző izotópjait. Ezek mennyiségét illetve eloszlását meghatározva képet kaphatunk a mintában lejátszódott atomos mozgásokról. Esetünkben, ha az oxidációt 18 O izotóppal (közel 100%-ban) dúsított gázban és felváltva 16 O gázban végezzük, akkor könnyű meghatározni, hogy hogyan épül be az 18 O a mintába a kísérlet folyamán, így ezzel a módszerrel alapvető információt nyerhetünk az oxidációs 21 Isotopic tracing
34 33 folyamatokról. (Érdekességként megemlítem, hogy az élő szervezet oxigén anyagcseréjét is kiterjedten vizsgálják 18 O izotóp segítségével, így követni tudják a szervezetbe bekerülő oxigén útját, a különböző szerves oxidációs folyamatokat és az oxigén beépülését az élő sejtekbe.) 3.1 A kisenergiás 18 O(p,α) 15 N magreakciós rezonancia Az izotóp-jelöléses kísérletekben a stabil oxigén izotópok közül az 18 O-t használják leggyakrabban. Ez az izotóp az 18 O(p,α) 15 N magreakció segítségével jól mérhető. A reakció hatáskeresztmetszetének energiafüggésében több energián is találhatunk rezonanciákat, ahol jól meghatározott, nagyon keskeny energiatartományban a hatáskeresztmetszet lényegesen nagyobb, mint a környezetében. Az 18 O izotópon lejátszódó magreakciókat először Amsel [Ams64] vizsgálta a közepes protonenergia tartományban, majd többen is pontosították a reakciók hatáskeresztmetszetét [Alk88, Ams67, Car61], (3.1 ábra). Egy átfogó munkában H. Lorenz-Wirzba és társai es cikkükben [Lor79] az 18 O(p,α) 15 N magreakció hatáskeresztmetszetét kev bombázó proton energiatartományban 135 szórási szögre adják meg (3.2 ábra). 3.1 ábra: Az 18 O(p,α) 15 N magreakció hatáskeresztmetszete a kev energiatartományban különböző szerzők munkáiból [Alk88, Ams64, Ams67, Car61] A cikkben tárgyalják az egyes rezonanciák tulajdonságait, rezonanciaszélességüket, erősségüket, szögfüggésüket és alkalmazhatóságukat. Megállapítják, hogy a 152 kev energia közelében lévő rezonanciában a hatáskeresztmetszet több, mint három nagyságrenddel nagyobb, mint a rezonancián kívül, valamint, hogy a rezonancia
35 34 izotróp, tehát a hatáskeresztmetszet minden detektálási irányban azonos. A rezonancia szélességére felső korlátként Γ =500eV-t adják meg. Differenciális Hatáskeresztmetszet [µb/sr] kev 334 kev 216 kev 629 kev 18 O(p,α) 15 N Q = MeV φ = Proton Energia [kev] 3.2. ábra: A 18 O(p,α) 15 N magreakció hatáskeresztmetszete, 135 -os szórási szögnél felvéve. A rezonanciák jelölve vannak. [Lor79] Ez a kisenergiás rezonancia anyagvizsgálatra különösen alkalmas lehet, mert: viszonylag nagy a hatáskeresztmetszet a rezonanciában; a rezonancián kívül nagyon kicsi a hatáskeresztmetszet, ezért várhatóan háttérmentes mérés végezhető; a rezonancia jól elkülönül a többi rezonanciától, a következő rezonancia 216 kev energiánál van, ami SiO 2 esetében kb Å tanulmányozható mélységet jelent; a rezonancia szélessége kicsi (Γ 500eV), azaz jó mélység felbontás érhető el; az 16 O(p,α) 13 N magreakció Q-értéke negatív ( 5.28 MeV), ez kizárja az interferencia lehetőségét a mintában lévő 16 Oizotóppal(az 17 O izotóp aránya olyan kicsi, hogy az azon esetlegesen fellépő 17 O(p,a) 14 N reakció hatása teljességgel elhanyagolható); azelérhető felületi mélységfelbontóképesség nagy, mivel ezen az energián a de/dx fékeződés nagyobb, mint magasabb energiákon. (A fékeződési tényező maximumaa legtöbb anyagra ebbe az energiatartományba esik); mivelareakcióq-értéke nagy, Q = MeV, a reakciótermék, az alfa részecske könnyen elválasztható a besugárzó és visszaszóródó protonoktól; Ennek a rezonanciának természetesen van néhány hátránya is, amikor alkalmazásával az 18 O 2 mélységi eloszlását határozzuk meg: a hatáskeresztmetszet abszolút értéke még a rezonanciában is kicsiny, ezért a
36 gyakorlatban csak 18 O izotópban mesterségesen dúsított minta vizsgálható; 35 kevés ion-gyorsító berendezés képes ilyen kis energiájú protonsugarat a szükséges energia-stabilitással előállítani; a nagy fékeződésből következően már nagyon vékony felületi szennyező réteg is leronthatja a felületközeli mélységfelbontóképességet; Miután ez a rezonancia nagyon ígéretesnek tűnt az 18 O mélységi eloszlásának meghatározására, jóllehet eddig még senki nem használta erre a célra, elkezdtem a 152 kev közelében lévő rezonancia szisztematikus vizsgálatát. Eredményeimet két cikkben jelentettem meg [Bat91 és Bat92], az első a rezonancia széleségének meghatározásával, a második a rezonancia méréstechnikai alkalmazásával foglalkozik. A bemutatott két legfontosabb eredmény az, hogy demonstráltam i) a 152 kev-es 18 O(p,α) 15 N keskeny rezonancia kiválóan alkalmas 18 O mélységeloszlásának nagyérzékenységű meghatározására, mivel ii) a rezonancia szélességére a legvalószínűbb érték a Γ =50eV [Bat91, Bat92]. Illusztrációként álljon itt két gerjesztési görbe, amelyeket Ta 2 18 O 5 vékonyrétegeken ennek a rezonanciának az alkalmazásával vettem fel (3.3 ábra). Felhívom az olvasó figyelmét a görbe felfutó élének meredekségére, valamint arra, hogy az egyes energiákon kapott összes α beütést ábrázoltam, semmilyen utólagos korrekciót, pl. háttérkivonást nem alkalmaztam. 3.3 ábra: Gerjesztési görbék Ta 2 O 5 mintán felvéve. A 170 Å és 595 Å vastagságú rétegek anódos oxidálással készültek Ta hordozóra, 97%-ban 18 O-ban dúsított vízben. 20 µc összegyüjtött töltés pontonként, E 1/2 energia gerjesztési görbék felfutó élének félmagasságához tartozó energiával egyenlő.
37 Kísérleti feltételek Ahhoz hogy a magreakciós rezonancia jellemzőit pontosan meg tudjuk mérni, olyan mintákat kell előállítanunk, amelyeknek az összetételét, vastagságát, egyéb jellemző tulajonságát jól ismerjük. ionsugaras mérések közben ne változzanak. Fontos az is, hogy a vizsgálandó minták tulajdonságai az A szükséges 18 O izotóppal dúsított oxidminták előállítása A nagypontosságú izotóp-jelöléses kísérleteknél mintaelőállításra alapvetően kétféle oxidációs eljárást alkalmazunk, a termikus és az anódos oxidációt. Ezek a módszerek meglehetősen jól ismertek, a mikroelektronikában széles körben alkalmazott rétegelőállítási módszerek. Különleges figyelmet kíván azonban az izotópban dúsított gáz vagy oldat kezelése. Mindkét mintaelőállítási módszernél biztosítható az izotóppal közel 100%-ra dúsított közeg gazdaságos alkalmazása. Ez azért fontos, mert az izotóppal dúsított gázok, illetve oldatok nagyon drágák, ezért kell azokat visszvezetni az oxid növesztése után a tároló edénybe. Így kismennyiségű anyag elégséges lehet sok réteg készítésére. (Megjegyzem, hogy a kereskedelemben mind 18 O-val dúsított víz, mind 18 O 2 gáz kapható, de meglehetősen drága anyagok. Az 18 O izotóp dúsítása súlykülönbségi elven alapul. A H2 18 O-t sokszoros desztillációval, az 18 O 2 gázt pedig a dúsított víz elektrolízisével állítják elő.) A mintaelőállításkor biztosítani kell, hogy mintáról mintára ne változzék az izotópösszetétel. Ez a kritérium nagyon tiszta, ellenőrzött körülményeket követel meg, az oxidáció csak zárt rendszerben valósítható meg. Szilícium oxidálására az egyik, jól ellenőrizhető módszer a termikus oxidáció száraz oxigén közegben. A termikus oxidációt diffúziós kályhában végeztem. A speciálisan 18 O izotópos oxidok előállítására épült összeállítás fő eleme egy kvarccső, amelyben létrehozható legalább 10 7 Pa vákuum. Ebbe a csőbe engedjük be egy üvegtartályból a 97%-ra dúsított 18 O gázt, úgy, hogy a nyomását oxidáció közben jellemzően a 10 mbar mbar tartományban szabályozzuk. Az oxidáció alatt a kvarccső szívás nélküli, statikus nyomáson van. Oxidáció után a 18 O gáz egy zeolitos molekulaszivattyú segítségével visszaszívható a tartályába, így teljes mértékben visszanyerhető. Termikus oxidációban a víz fontos szerepet játszik, mert megváltoztatja az oxidáció kinetikáját. Azért, hogy még mintacserekor se lásson a kvarccső belseje levegőt, illetve
38 37 vízgőzt, egy előkészítő vákuumkamra helyezkedik el a kályha előtt. Mintacserekor ebbe tesszük a mintákat, majd leszívjuk nagyvákuumra, csak utána nyitjuk a kvarccső felé a szelepet. Ezzel a megoldással biztosítható, hogy a száraz oxidáció feltételeit fenn tudjuk tartani. Szilícium termikus oxidációját Deal és Grove írta le [Dea65]. A szilícium termikus oxidációjának kinetikája egy ún. lineáris-parabolikus törvényt követ akár száraz O 2,akár vízgőz közegben. Az atomi transzport folyamat e mögött az, hogy az O 2 vagy H 2 O molekula bediffundál a már megnövekedett oxidrétegen keresztül és az oxidáció a Si/SiO 2 határfelületen játszódik le. Az oxidáció kezdeti szakaszában a határfelület határozza meg a sebességet, ez a lineáris szakasz. A továbbiakban kialakuló oxid növekedésének sebességét alapvetően az O 2 vagy H 2 O molekula diffúziója fogja meghatározni [Rig86, Tri89], ekkor a kinetika parabolikus törvényt követ. Az oxidációt leggyakrabban C hőmérséklet tartományban, atmoszférikus nyomáson végeznek. Ha vízgőz is van jelen az oxidáló közegben, akkor a növekedési sebesség jelentősen nagyobb, mintha teljesen száraz atmoszférában oxidálunk. A kialakuló oxid minősége elektromos szempontból ebben az esetben rosszabb, mint a száraz oxidé. Ezért a nagyon vékony oxidokat (elsősorban gateoxidokat) száraz közegben szokták előállítani. A másik mintaelőállításimódszer,amelypl.al,ta,nb,zr,ti,si,stb.oxidációjára alkalmas, az anódos oxidáció. Ekkor a minta egy elektrolizáló cellában vizes oldatba merül. A felépülő oxidréteg vastagsága az átfolyó töltéssel arányos (Faraday-törvény). A művelet során nagyon homogén, egyenletes vastagságú oxidréteg alakul ki. Ha növekedés közben vastagságkülönbség adódik, akkor az oxidációs sebességet meghatározó lokális elektromos tér az egyenetlenségek kisímítására törekszik. Első kísérleteimben a rezonancia szélességének megméréséhez anódos oxidációval készítettem Ta 2 O 5 mintákat. 18 O izotópos minták előállításához 98%-ra dúsított H2 18O vizet használtam. A víz vezetőképességének növelésére KCN sót adagoltam az oldathoz. Azért ezt az anyagot alkalmaztam, mert nem tartalmaz oxigént, tehát nem jutnak az oldatba 16 Oatomok. A 99.95%-os tisztaságú 0,2 mm vastag, 10 mm x 20 mm nagyságú Ta mintákat (Goodfellow) előszőr zsírtalanítottam, majd 5 rész 95%-os H 2 SO rész 53%-os HNO rész 45%-os HF oldatban 15 s-ig kémiailag políroztam. Az anódos oxidáció a cellában Pt katóddal történt. Az anodizáló áramsűrűség 0,5 ma/cm 2. A kezelés közben mértem
39 38 a mintán eső feszültséget. A [Sie71, Pri73] referenciák alapján ilyen körülmények között voltonként 9, /cm 2 oxigén atom épül be az oxidba. Figyelembe véve a Ta 2 O 5 réteg 8 g/cm 3 sűrűségét, 1 Å Ta 2 O 5 0, /cm 2 oxigén atomot tartalmaz. Így jól ismert vastagságú mintákat sikerült előállítani. Ellenőrizni kellett a minták oxigénizotóp összetételét is, mert a tantál felületén is kialakul egy natív oxid réteg, amely befolyásolhatja mérésünket. Ismeretes, hogy a tantál oxidációja az oldat/fém határfelületen zajlik le [Pri73]. Ezért a natív Ta 2 16O 5 réteg az anódizálás során eltemetődik, a felületen tehát Ta 2 18 O 5 réteg lesz. Az 16 O(d,p) 17 O magreakcióval 975 kev-en valamint az 18 O(p,α) 15 N magreakcióval 725 kev-en pontosan megmértem a mintákban levő 16 O, ill. 18 O atomok számát, majd ebből megállapítottam a minták vastagságát. A natív oxid vastagsága a mérések alapján 35 Å. Az így előállított és mind vastagságra, mind összetételre ellenőrzött mintákat használtam a rezonancia szélességének megméréséhez Kísérleti berendezés A hatékony és pontos mérés érdekében a mérési elrendezést is nagyon gondosan kell megtervezni: Van de Graaff ion-gyorsítóberendezés, 200 na proton nyaláb 2 mm nyalábátmérővel; A gyorsító hosszú és rövididejű energiastabilitása kétféle, egy kapacitív elven működő energiamérésre alapozott és egy résáram minimalizáláson alapuló visszacsatolással van szabályozva. nyalábenergia környezetében jobb, mint 80 ev. A nyalábenergia stabilitás a 150 kev Automatikus, elektrosztatikus nyalábenergia változtató rendszer, amely segítségével a nyaláb energiáját hiszterézismentesen, 150 kev körül ± 8%-on belül lehet változatni. A lényeg nem csak az automatikusság, hanem a hiszterézismentesség is. A rendszer azon alapul, hogy megváltoztatva a nyalábenergiát, az ionok pályája is megváltozik. Ahhoz, hogy a nyaláb a pályáján helyben maradjon, változtatni kell az ionnyaláb eltérítésén is. Ha mágnesesen változtatunk az eltérítésen, akkor az elektromágnesek remanens mágneses tere miatt azonos mágnesáramhoz nem azonos mágneses tér tartozik. Ha elektrosztatikusan térítjük el a nyalábot, akkor azonos eltérítéshez mindig azonos elektromos teret kell alkalmazni, tehát azonos beállításhoz azonos nyalábenergia tartozik. Az automatikusság pedig azt jelenti, hogy nem a gyorsító terminálfeszültségét kell vezérelni a nyalábenergia változtatáshoz, hanem az elektrosztatikus eltérítést kell kismértékben módosítani. Ezzel a nyaláb pályáját
40 39 változtatjuk meg kismértékben. Az előbb említett, résáram minimalizáláson alapuló energiastabilizáló rendszer megpróbálja a nyalábot helyben tartani. Ez csak a gyorsító terminálfeszültségének változtatásával lehetséges [Ams83]. Ezzel a módszerrel, amely tulajdonképpen az energiastabilizáció becsapásán alapul, lehet egyszerűen, hiszterézismentesen és megfelelő mértékben változtatni az ionnyaláb energiáját a gerjesztési görbe felvételéhez. Gyűrű alakú szilícium záróréteges detektor, 300 mm 2 aktív felülettel, 15 mmre elhelyezve a minta előtt, így a detektor térszöge 0,93 sr (3.4 ábra). Mivel a vizsgálandó rezonancia hatáskeresztmetszete meglehetősen kicsi, nagy térszögű detektálásra van szükség, azért, hogy az összegyűjtött beütésszám ne legyen nagyon kevés, illetve ne kelljen a spektrum felvételekor túl nagy begyüjtött töltésig végezni amérést. 3.4 ábra: A nagy térszögűgyűrűs detektor és fékező fólia szerelési elrendezése. A minta távolsága 15 mm a detektor felületétől így az elérhető térszög 1sr. A detektor aktív felülete 360 mm 2. (A detektorban a műanyag házon kialakított furatokon keresztül biztosítható vákuumra leszívás.) 3 µm Mylar fólia a detektor előtt, ami megállítja a visszaszóródott protonokat, de rajta keresztül a nagyobb energiájú α részecskék (E α 3, 9 MeV) a detektorba tudnak kerülni. Szokványos gyors elektronika az α részecskék detektálására. Vákuumkamrában folyékony nitrogénes kifagyasztó alkalmazásával a nyomás 10 6 mbar. A kifagyasztóra azért van szükség, hogy minimalizáljuk a mérés közben a
41 40 szénhidrogén lerakódást a minta felületére. A rezonanciaszélesség méréseket az Université Paris 7, Groupe de Physique des Solides által üzemeltetett gyorsítóberendezésen végeztem. 3.3 A rezonanciaszélesség meghatározása Az előbbi feltételek kellenek ahhoz, hogy meg tudjuk határozni a rezonancia egyik legfontosabb paraméterét, a félértékszélességét. Minden rezonancia kísérletnél fontos, hogy a mérőnyaláb energiaszórása ne legyen lényegesen nagyobb, mint az alkalmazott rezonancia szélessége. A lehető legtisztább körülmények között, jó vákuumban kell a méréseket végezni azért, hogy ne lépjen fel felületi szennyezés, amely lerontja a mérés érzékenységét. Ha a rezonanciaszélesség nagyon kicsi ( 50 ev), akkor hűtött mintán kell mérni, hogy a Doppler-energiaszórást minimalizáljuk. A jelen esetben szobahőmérsékletű mintákon végeztem a méréseket. A rezonancia energiájának pontos meghatározása szintén fontos feladat, de az ionsugaras méréseknél nincs abszolút energiaskála, ezért ez egy kényes kérdés. Csak az jöhet számításba, hogy több jól ismert energiájú rezonancia segítségével kalibráljuk a gyorsító energiaskáláját, majd ezekhez a rezonancia-energiákhoz viszonyítva kisebbnagyobb pontossággal lehet megadni a kérdéses rezonancia energiaértékét. Végeztünk ilyen méréseket az energiaskála kalibrációjához és az eredményeket a [Ams98] cikkben mutattuk be. energiája E R =152± 0.5 kev. Kísérleteink azt mutatják, hogy a kisenergiájú 18 O(p,α) 15 N rezonancia Első feladatom a 152 kev közelében lévő rezonancia félszélességének megállapítása volt. Ehhez különböző vastagságú Ta 2 18 O 5 mintákat használtam. A 3.5 ábrán megismétlem a 3.3 ábrán már bemutatott gerjesztési görbéke, amelyeket 170 Å és 595 Å vastag rétegeken vettem fel. Pontonként 20 µc töltést gyűjtöttem be, majd az egyes energiákon kapott α-részecskék számát ábrázoltam az energia függvényében. detektor érzékeny felülete előtti Mylar fólia kiszűri az összes visszaszóródó protont, csak a reakciótermék α-részecskét detektáljuk. A mérés során minden energialépésben összegezni lehet az összes beütést. Megjegyzem, azért, hogy a mérés közben a minta felületére lerakódó szénhidrogén réteg hatását minimalizáljuk, minden energialépésben a minta egy friss, előtte még nem használt pontját mértem (energiaváltáskor a mintát is mozgattam, hogy egy nem használt pontra essen a nyaláb). A
42 ábra: Gerjesztési görbék Ta 2 O 5 mintán felvéve. A 170 Å és 595 Å vastagságú rétegek anódos oxidálással készültek Ta hordozóra, 97%-ban 18 O-ban dúsított vízben. 20 µc összegyüjtött töltés pontonként, E 1/2 energia gerjesztési görbék felfutó élének félmagasságához tartozó energiával egyenlő. Látható, hogy a vastagabb mintán mért gerjesztési görbének van egy lapos platója, míg a vékony minta esetében a görbe éppen csak eléri ezt a telítési szintet. A görbék felfutó éléből lehet meghatározni a rezonancia szélességét. A felfutó él szélessége, tehát az az energiatartomány, ahol a beütésszám 12% -ról 88% -ra nő, mindkét esetben 520 ev. Mint már a fejezetben megmutattam, a felfutó él szélessége alapvetően három tényező, a rezonanciaszélesség, a nyaláb energiaszórás és a mintában lévő 18 O atomok hőmozgásából adódó Doppler-kiszélesedés konvolúciója. Esetünkben a nyaláb energiaszórásának félértékszélessége, amit kapacitív módon folyamatosan monitoroztunk, ezen az energián σ B 80 ev, alakja Gauss-görbe. A szintén Gauss-görbe alakú Dopplerszélesedés félértékszélessége szobahőmérsékleten σ D 50 ev. Ennek a két összetevőnek a félértékszélességét négyzetesen adhatjuk össze, tehát a nyaláb energiaszórása és a Dopplerszélesedés együttes félértékszélessége σ 100 ev. A rezonancia szélességének megállapítására a 16 számú kifejezés alapján konvolváltam egy σ = 100 ev FWHM-ú Gauss-görbét és változó szélességű Breit-Wigner görbéket. Az eredmény integrálja írja le a mérési görbe felfutó élét. A különböző rezonanciaszélességekkel kapott görbéket rajzoltam fel a 3.6 ábrán, ahol a mérési pontokat szintén feltüntettem. Az ábrán láthatjuk, hogy a rezonancia szélessége nem lehet nagyobb, mint Γ = 200 ev, de a kisenergiás részen a mérési pontok a Γ =100eV-s görbe alatt vannak.
43 ábra A mért gerjesztési görbe felfutó éle és szimulációk különböző rezonancia félértékszélességekkel. A szimulációkban a nyaláb energiaszórását és a Dopplerszélesedést 100 ev félszélességű Gauss-görbével vettem figyelembe. A mérés során lerakodó szénhidrogén réteget általában CH 2 formában lehet leírni. A SPACES program [Vic90a, Vic90b] segítségével kiszámítottam, hogy különböző vastagságú CH 2 rétegekben mennyi és milyen jellegű a proton nyaláb energiavesztesége. Ezt rajzoltam fel a 3.7 ábrán. Látható, hogy az energiaelmosódás kis rétegvastagságok esetében nagyon aszimmetrikus. Tetszoleges " egység 0.2 µg/cm µg/cm µg/cm µg/cm µg/cm kev-os protonok stragglingje CH 2 -ben 1 µg/cm Energia veszteség [kev] 3.7 ábra Az energia straggling különböző vastagságú szénhidrogén rétegen keresztül. A szénhidrogén lerakódást CH 2 összetételünek tételeztem fel a számításoknál. A proton nyaláb energiavesztesége a felületi szénhidrogén rétegben a gerjesztési görbe eltolódását fogja okozni a magasabb energiák irányába. Az aszimmetria miatt torzulni fog a felfutó él is, ugyanolyan gyorsan indul, de a plató közelében a hozam növekedése lelassul.
44 ábra: Mérési pontok Ta 2 O 5 mintán felvéve. A folytonos vonallal rajzolt görbék a SPACES szimulációk eredményei, 100 ev-os Gauss-komponens, 0,4 µg/cm 2 szénhidrogén felületi szennyező réteg esetén különböző rezonanciaszélességek esetében. A csúcsos görbe a felső ábrarészen a straggling transzformáció konvolúciója a Gausskomponenssel. A 3.8 ábrán részletesebben is bemutatom a mérési pontokat a számított gerjesztési görbével, amikor már 0,4 µg/cm 2 CH 2 szennyezést (a réteg sűrűségének függvényében ez kb Å) is figyelembe vettem. Most még jobban látszik, hogy a mért pontok a Γ =50eV és a Γ =100eV rezonanciaszélességű görbék közé esnek, a számított görbe az egész felfutási tartományban jól leírja a mérési pontokat.
45 44 Ha a kisenergiájú tartományt tekintem (E E R < 4 kev alatt), a mérési pontok mindenhol a számított görbe alatt helyezkednek el. Ez még keskenyebb rezonancia szélességet jelenthet. Meg kell jegyeznem, hogy ez a mérés igazán a rezonancia-energia előtti tartományokban nagyon érzékeny a rezonancia szélességére. A felületi szennyező rétegnek itt nincs hatása, a Gauss-görbe alakú nyaláb energiaszórás pedig csak egy kis eltolást jelenthet az energiaskálán. Ami befolyásolja a mért beütésszámot, az a rezonanciát leíró Breit - Wigner görbe nagyon lassan csökkenő értékei, a függvény értéke még a maximumnál több félértékszélességgel kisebb vagy nagyobb energián is jelentős Breit-Wigner Gauss ábra: Gauss és Breit-Wigner függvény integrálja (erfc és arctg függvények), a félszélesség 10 egység mindkét esetben. Ezt illusztrálja a 3.9 ábra, ahol egy azonos félszélességű Gauss-görbe és egy Breit-Wignergörbe integráljainak összehasonlítása látható. A Breit-Wigner-görbe lassan csökkenő függvény, ezért az integrálgörbe értéke is nagyon lassan változik. A fenti mérési erdményekből megállapíthatjuk, hogy a rezonancia félszélességére a Γ = 50 ev érték a legvalószínűbb. A legfontosabb eredmény azonban az, hogy a 18 O(p,α) 15 N reakció 152 kev közelében lévő rezonanciája keskeny, de mérhető erősségű, így kiválóan alkalmas felületközeli mélységprofilok meghatározására. A gerjesztési görbe kisenergiájú tartományában a mért pontok mindenhol az 50 ev rezonanciaszélességgel számított görbe alatt helyezkednek el, míg a rezonanca energiája kozelében a pontok a 100 ev-os görbe fölé esnek (3.6 ábra). Ezért a rezonancia félszélességére a pl. Γ =30eV vagy Γ =100eV érték sincs kizárva.
46 ábra: Gerjesztési görbék 595 Å, 170 Å és 50 Å vastag Ta 2 O 5 mintákon felvéve. A vonallal ábrázolt görbék SPACES szimulációk. Bemutatom újra a mért gerjesztési görbéket (3.10 ábra), de most már az 50 ev rezonanciaszélesség, 100 ev nyalábenergiastabilitás + Doppler-szélesedés, 0,4 µg/cm 2 felületi szénhidrogén szennyezőréteg figyelembevételével számított gerjesztési görbékkel kiegészítve. gerjesztési görbe. pontokkal. Szintén látható az ábrán egy nagyon keskeny, 50 Å vastag mintán mért Látható, hogy a számított görbék nagyon jó egyeznek a mérési A két vastagabb mintán mért gerjesztési görbe eléri a telítési értéket. A görbék lefutó éle arra jellemző, hogy mekkora szórást okoz a rétegen való áthaladás a protonok energiájában. A gerjesztési görbék szélességéből, tehát a felfutó és a lefutó él félértéke közötti energiakülönbségből, a rétegek vastagságát lehet meghatározni a de/dx fékeződési tényező ismeretében. A görbék alatti terület a mintában található 18 O atomok mennyiségével arányos. ( 18 O-ban fele ennyire dúsított minta esetében hasonló alakú és szélességű gerjesztési görbéket kapnánk, csak a mért beütésszám, így a görbék alatti terület fele akkora lenne.) A legvékonyabb minta esetében a gerjesztési görbe még nem érte el a telítési értéket, így csak szimulációval lehet a görbéből a mintavastagságot megállapítani. Megvizsgáltam szendvics-szerkezetűta 2 O 5 mintákat is. A minták anódos oxidálással készültek először H2 16 O, majd H2 18 O vizes elektrolitban ábrán tulajdonképpen két mintán külön mért görbét mutatok be. Az első mintáth2 18 O-ban anodizáltam, 50 Å vastag oxidot növesztettem. A 35 Å vastag natív oxid ott maradt az 18 O-
47 nal jelölt réteg alatt. 46 Ehhez a mintához az ábrán az -szel jelölt mérési pontok tartoznak. A másik mintán először 260 Å Ta 2 18 O 5 réteget, majd 170 Å Ta 2 16 O 5 réteget készítettem. A mintához tartozó pontok -rel jelöltek. Az első mintánálaz 18 Oatomok a minta felületén találhatók, következésképpen a hozzájuk tartozó gerjesztési görbe a rezonancia-energiánál (E R ) indul. A másodiknál az 18 O atomok el vannak temetve egy izotóppal nem jelölt réteg alá, ezért ezek gerjesztési görbéjét magasabb energiákon találjuk. Az energiaeltolódás értéke a felső rétegen keresztüli energiaveszteségnek felel meg. Figyeljük azonban meg, hogy az eltolódás mellett a felfutás meredeksége is csökken, kiszélesedik a görbe. Ez a felső rétegen keresztülhaladó protonok energiaszóródásának következménye. Egy három rétegből (és az eltemetett natív oxidból) összetett mintán mérhető gerjesztési görbe megfelelne a két bemutatott gerjesztési görbe összegének. Az ábra felső részében bejelöltem az egyes mintákat és rétegvastagságokat, valamint az összetett mintát, amelynek a gerjesztési görbéje a mutatott két görbe összege ábra: Szendvicsszerkezetű Ta 2 O 5 mintákon regisztrált gerjesztési görbék. 3.4 Mélységfelbontóképesség meghatározása, korlátok A minták elforgatásának hatása Az előző példákból már látható, hogy ez a keskeny, kisenergiás rezonancia kíválóan alkalmas vékony oxidrétegek tanulmányozására. Hogyan tehetjük még érzékenyebbé ezt a módszert? Egy megoldás lehet az, amikor a mintát a beeső nyaláb irányához képest elforgatjuk, pl. a nyalábot ψ =70 -os szögben ejtjük a mintára, tehát a nyaláb 70 -os szöget zár be
48 47 a minta felületi normálisával. Ekkor a nyaláb irányából a réteg látszólagos vastagsága 1/ cos(ψ) 3 faktorral megnő ábra: Gerjesztési görbék egy 50 Å vastag Ta 2 O 5 rétegről felvéve úgy, hogy az ionnyaláb ψ =0, illetve ψ =70 alatt esik a mintára. A vonalakkal ábrázolt görbék elméleti számítások. Látható a 3.12 ábrán, hogy a látszólag vastagabb rétegnek egy szélesebb gerjesztési görbe felel meg. Vegyük azt is észre, hogy a ψ =70 -os görbe nemcsak szélesebb, hanem kisebb lett a felfutó él meredeksége, valamint a görbe a magasabb energiák felé tolódott. A magyarázat egyszerű: az elforgatással a felületi szénhidrogén réteg látszólagos vastagsága is megnövekedett. A látszólag vastagabb felületi réteg miatt változott meg a felfutó él helyzete és meredeksége, ami a megnövekedett felületi mélységfelbontóképességet tükrözi. A 3.13 ábrán egy 18 O/ 16 O/ 18 O rétegszerkezetű mintán felvett gerjesztési görbét látunk. Ha nem forgatjuk el a mintát a nyalábhoz képest (ψ =0 ), akkor ugyan szétválnak akét 18 O-t tartalmazó rétegből származó jelek, de teljesen nem különülnek el egymástól. Ha elforgatjuk a mintát (ψ =70 ), akkor a rétegek látszólagos vastagsága megnő, ezért szélesebb gerjesztési görbét kapunk. A két 18 O-t tartalmazó rétegből származó jelek most már teljesen elkülönülnek, így nyilvánvaló, hogy a két réteg között olyan réteg helyezkedik el, ami nem tartalmaz 18 O-t.
49 ábra: Gerjesztési görbék egy SiO 2 szendvicsszerkezetű termikusan oxidált szilícium mintán mérve a 152 kev-es 18 O(p,α) 15 N rezonanciával. A minta sematikus szerkezete az ábra tetején látható. A folytonos vonal csak vezeti a szemet Felületi felbontóképesség Γ A felületi mélységfelbontóképesség legegyszerűbb definíciója: de/dx, tehát a rezonancia félértékszélességének és az adott anyagra jellemző fékezési tényezőnek a hányadosa. Eszerint a definíció szerint például a Ta 2 O 5 rétegben, ahol a fékezési tényező 150 kev-es protonokra de 10 ev/å, a Γ =50eVfélszélességű 152 kev-es rezonanciával dx 5 Å-ös felületi mélységfelbontás érhető el. A valóságban nem ilyen egyszerű ahelyzet, mert figyelembe kell venni a nyaláb energiaszórását, a Doppler-szélesedést valamint a felületi szennyezések hatását is. Sokkal realisztikusabb az a mélységfelbontóképesség meghatározás, amely egy felületi és egy x mélységben lévő δ vastagságú réteg vizsgálatán alapul. Eszerint azt a x távolságot nevezem felületi mélységfelbontóképességnek, amikor már szét lehet választani a gerjesztési görbében az egyes rétegekről kapott jeleket. Ez a definíció analóg az optikai felbontóképesség meghatározásához: mikor látok két pontot már különálló két pontnak. A mi esetünkben, ha a gerjesztési görbe deriváltja nulla lesz, vagy pozitívvá válik az
50 49 első csúcs után, akkor már szétválaszthatónak tekintem a két rétegről kapott gerjesztési görbéket. Ezek alapján, a SPACES szimulációk szerint (3.14 ábra), egy felületi és egy x =30Å mélyen lévő réteg jele már biztosan szétválasztható ábra: SPACES szimulációk SiO 2 rétrgre. A két δ vastagságú 18 Otartalmúréteg, az egyik a felületen, a másik x = 10Å, 20Å, 30Å, 40Å mélységben. Γ = 50eV G B =100 ev. (Felületi szennyezés nélkül) Ezt a felbontóképességet még javítani lehet a minta elforgatásával. Ha az ionnyaláb ψ =60 -os szögben (a felületi normálishoz képest) érkezik a mintához, akkor látszólagosan megduplázódik a minta vastagsága. Háromszoros, illetve négyszeres vastagságnövekedést érünk el ψ =70.5 illetve ψ =75.5 elforgatással. Visszatérve az 3.14 ábrához, ha a 10 Å-ös mintát elforgatjuk úgy, hogy a vastagsága látszólagosan megnégyszereződjön, akkor már felbontható a két réteg jele, a mélységfelbontóképesség 10 Å. Tehát a kisenergiájú 18 O(p,α) 15 N keskeny rezonancia felületi mélységfelbontóképessége a mérési paraméterek jó megválasztása esetén elérheti a10å-öt Többszörös szórás hatása Mint a 2. fejezetben említettem, az ionok sokszoros kisszögű szórás 22 révén fékeződnek, vesztik el az energiájukat. Minden egyes szórás esetében megváltozik az ion sebességvektora, annak nagysága, illetve iránya. Kisszögűnek tekintjük a szórást, ha az irányváltozás 5. A sok egymásutáni, egymástól független szórás eredménye vektorosan adódik össze. Egy adott út megtétele után az ion az anyagban nem feltétlenül ott lesz, ahol az eredeti iránya szerint várnánk, hanem laterálisan eltérhet az eredeti irány által meghatározott pozíciótól. Miután az irányeltérés kicsi, a megtett út az ionok eredeti 22 Multiple Scattering, MS
51 50 iránya által meghatározottól jelentősen nem különbözik. Az így mért spektrumokban a többszörös szórás hatása nem jelentkezik. Az olyan méréseknél azonban, ahol a minta erősen el van fordítva a nyalábhoz képest, a többszörös szórás hatása már nem elhanyagolható. Vegyük például azt az esetet, amikor az x vastagságú minta ψ =70 -ravanelfordítvaanyalábirányáhozképest. Ekkora minta látszólagos vastagsága t = x =2, 9 x lesz. Ha a többszörös szórás hatására cos ψ az ionok iránya ±5 -ot tér el az eredeti iránytól, akkor az x mélység eléréséig az ionok x közül lesz, amelyik t 1 = cos(70 +5 ) =3, 9 x és lesz amelyik t x 2 = cos(70 5 ) =2, 4 x utat fog megtenni. Statisztikailag teljesen véletlenszerű, hogy az egyes ionok mennyire térnek el az eredeti iránytól, a mérésben ez egy úthossz-fluktuációban jelentkezik. keskeny rezonanciáknál maradva ez azt jelenti, hogy a gerjesztési görbe felvételekor egy adott energián az ionok más és más valódi mélységben érik el a rezonanciaenergiát. Mikroszkópikusan úgy is leírhatjuk ezt a jelenséget, hogy minden egyes ion a fékeződése során más és más vastagságú réteget észlel. A gerjesztési görbében a többszörös szórás egy, a stragglinghez hasonló energiaelmosódásként jelentkezik a görbe lefutó élénél. Példaként bemutatok a 3.15 ábrán Si 18 O 2 rétegeken a 152 kev-es rezonanciával mért gerjesztési görbéket. A rétegek vastagságát úgy választottam meg, hogy azonos vastagságú minták legyenek elforgatás nélkül és elforgatva. (Elforgatás nélkül az 1700Å-ös, illetve 3200Å-ös mintán felvett gerjesztési görbe szélessége közel azonos a ψ =78, 5 -ra elforgatott 360 Å-ös és 700 Å- ös rétegen felvett gerjesztési görbéjével.) Így össze tudom hasonlítani az elforgatott és nem elforgatott esetben felvett gerjesztési görbéket. A Az ionok az elforgatás nélküli és elforgatott minta esetében is ugyanannyi utat tesznek meg az anyagban, az elforgatott minta esetében azonban az úthosszfluktuáció hatása nagyobb lesz. A vékonyabb minták esetében (1700 Å, ψ =0,illetve360Å,ψ =78, 5 ) a gerjesztési görbék lefutó élének meredeksége nem nagyon különbözik, a döntött minta esetében kicsit lelassul a görbe lefutása. A többszörös szórás hatása nem számottevő. A vastagabb minták esetében (3200 Å, ψ =0, illetve 700 Å, ψ =78, 5 )azonban az úthosszfluktuációból adódó hatás már nagyobb lesz. Az ábrán jól látszik, hogy ψ = 0 -on regisztrált gerjesztési görbe lefutó éle meredek, csak az energiastraggling hatása érvényesül. A ψ =78, 5 -on mért görbe lefutása kevésbé meredek, a stragglinghez hozzáadódik a többszörös szórásból adódó energiaszórás is.
52 ábra 152 kev-es 18 O(p,α) 15 N magreakciós rezonancia mérések különböző vastagságú SiO 2 mintákon különböző döntési szögeknél. Akisszögű szórás elméletét részleteiben tárgyalta Scott [Sco63], majd az elméletet Sigmund és Winterbon [Sig74] fejlesztette tovább. Folytatásképpen Marwick és Sigmund [Mar75] egy viszonylag egyszerű módot dolgozott ki a többszörös szórásból adódó energiaelmosódás kiszámítására. A fenti szerzők az összes számításukat a térben mozgó ionra adták meg. A magrezonanciás méréseknél az általunk alkalmazott geometriai elrendezések esetében viszont mérésünket csak az energiaelmosódásnak a beeső nyaláb és a minta felületi normálisa által meghatározott síkon vett vetülete befolyasolja. Ezért elegendő az erre a síkra vetített kétdimenziós MS eloszlást kiszámítani és a mérés kiértékelésében figyelembevenni. A [Bat94b] cikkben részletesen tárgyalom a többszörös szórás hatását magreakciós rezonancia mérések felbontóképességére. Az ionok fékeződésének sztochasztikus elméletén alapuló számítási módszerrel megadom statisztikai számítások alapján a kétdimenziós MS eloszlást a rétegvastagság függvényében. Az összes MS eloszlást redukált vastagságokra és szögekre határozom meg. Ez azért hasznos, mert a [Sco63, Sig74] által bevezetett redukált paraméterek függetlenek az anyagi minőségtől, így olyan általános eloszlásokat lehet meghatározni, amelyek alkalmazhatók más kísérleti feltételek mellett is. Disszertációmban a magreakciós rezonanciákhoz szorosan nem kapcsolódó többszörös szórás elméletét részletesen nem tárgyalom, csupán szeretném megmutatni annak hatását elforgatott minták mérése esetén. A 3.15 ábrán bemutatott gerjesztési görbék
53 52 szimulációjakor (folytonos vonallal ábrázoltam a szimulációk eredményét) alkalmaztam a többszörös szórás meghatározására kidolgozott számítási módszert. A számítási eljárásom helyességét mutatja, hogy a szimulált görbék jól egyeznek a mért görbékkel. A fejezetben megadott mélységfelbontóképesség definíció csak a felületi felbontóképesség megbecsülésére alkalmas. Ha nagyobb mélységben is meg akarjuk határozni a felbontóképességet, már figyelembe kell vennünk a nyaláb energiaszórását és a stragglinget is. Ha elforgatott mintán mérünk, akkor a többszörös szórás hatását is számítani kell. A mélységfelbontóképességet tehát a mélység, x, függvényében az alábbi módon határozhatjuk meg: x FWHM G(u) W(u) g MS (u, x) g s (u, cos ψ ) R x (x) = M de, (26) dx ahol a számlálóban a mérő ionnyaláb energiaeloszlásának, G(u), a rezonancia x alakjának, W (u), a többszörös szórás, g MS (u, x), és a straggling, g s (u, ), eloszlások cos ψ 1 konvolúciójának félértékszélessége, a nevezőben pedig M =, illetve a fékezési cos ψ tényező található. A 3.16 ábrán bemutatom a Ta 2 O 5 -re és SiO 2 -re számított mélységfüggő mélységfelbontóképesség görbéket két, ψ =60 és ψ =75, 5, elforgatási szög esetében. Ha csak az energia stragglinget vesszük figyelembe (folytonos vonallal rajzolva a 3.16 ábrán), akkor érdemes minél nagyobb döntési szögeknél végezni a mérést, hiszen a straggling a rétegvastagságtól négyzetgyökösen függ, ahogy a (5) egyenletben látható. Emiatt a hatása, adott mélységben, nagyobb elforgatási szögeknél viszonylagosan kisebb lesz. Figyelembe kell vennünk viszont a többszörös szórás hatását is, ami növekvő elforgatási szögek esetében rohamosan rontja a mélységfelbontóképességet. A 3.16 ábrán a o és + szimbólumokkal jelölt görbék mutatják a két hatást együttesen. Megállapíthatjuk, hogy egy, az anyagtól függő mélységig, a felbontóképesség tényleg kisebb nagyobb elforgatási szögek esetében, de nagyobb mélységekben a többszörös szórás hatásának nagyobb szögeknél való erősödése miatt a felbontóképesség romlik. Pl. SiO 2 esetében, 600 Å mélységben a mélységfelbontóképesség egyenlővé válik ψ = 60 és ψ = 75, 5 elforgatási szögeknél, nagyobb mélységekben pedig már a kisebb szöghöz tartozik nagyobb felbontóképesség. Ezért a mérések megtervezésénél mindenképpen figyelembe kell venni a többszörös szórás hatását és aszerint kell megválasztani az elforgatási szöget, hogy optimális mélységfelbontóképességet érjünk el.
54 ábra A mélységfelbontóképesség mélységfüggése (a) Ta 2 O 5 és (b) SiO 2 minta esetén. A ψ =60 és ψ =75.5 elforgatási szög M =2ill. M =4látszólagos rétegvastagodásnak felel meg. A folytonos vonallal ábrázolt görbe a straggling, a o és a + szimbólumok pedig a straggling és a többszörös szórás együttes hatását jelölik különböző elforgatási szögeknél. 3.5 A 152 kev-es rezonancia összehasonlítás a nagyobb energiájú mérésekkel Az 18 O(p,α) 15 N magreakció 629 kev-es Γ =2.1 kev félszélességű és a 1165 keves Γ = 50 ev félszélességű rezonanciáit már korábban is használták 18 O mélységi eloszlásának mérésére. A nagyobb energiás rezonanciának azonban több hátránya is van, ami korlátozza az alkalmazhatóságát. Hátrányt jelent, hogy a hatáskeresztmetszet a rezonancián kívül is nagy, így csak nagy háttérbeütéssel mérhető a gerjesztési görbe. Az 3.17 ábrán bemutatok különböző vastagságú Ta 2 18 O 5 rétegeken a 629 kev-es rezonanciával felvett gerjesztési görbéket [Mau82]. Ebben az esetben a rezonancia nagy félszélessége szintén rontja a felbontóképességet. Azonnal szembetűnik, hogy a görbék alakja nem szögletes, mint pl. a vastag mintához tartozó görbe a 3.10 ábrán. Ez még a kb. háromszor ilyen vastag réteg esetében is igaz, a görbe nem éri el a telítési értéket. A görbéken a rezonanciánál kisebb és jóval nagyobb energiákon is háttér látható, miután a hatáskeresztmetszet értéke a rezonancián kívül is nagy. A görbék kiértékelésében problémát okoz a háttér levonása. A magasabb ionenergia miatt kisebb a fékeződés is, ez is rosszabb felbontóképességet eredményez.
55 ábra Különböző vastagságú anódos oxidációval előállított Ta 18 2 O 5 rétegeken a 629 kev-es rezonanciával mért gerjesztési görbék [Mau82] 3.18 ábra Szintén Ta 18 2 O 5 rétegeken mért gerjesztési görbék, csak most a 1167 keves rezonanciával felvéve. Az ábrázolt görbékből a rezonancián kívüli nagy hatáskeresztmetszetből adódó háttér ki lett vonva. [Mau82] A3.18ábránTa2 18 O 5 rétegeken az E R =1167keV energiánál lévő Γ =50eV nagyon keskeny rezonanciával felvett gerjesztési görbék láthatók [Mau82]. Ebben az esetben a 18 O(p,αγ) 15 Nreakcióbólaγ-fotonokat detektálták. A megfelelő háttér levonása után hasonló szögletes gerjesztési görbéket láthatunk, mint a 152 kev-es rezonancia esetén (3.10 ábra). A görbék felfutó élén megjelenő túllövés az ún. Lewis-effektus [Mau82]. Ez annak következménye hogy a bombázó ionok csak véges, meghatározott adagokban veszítenek energiát. Az effektus csak ritkán, nagyon keskeny rezonanciák esetében, igen jó energiafelbontású mérési elrendezés használatánál lép fel, nagysága függ az anyag-ion
56 55 párosítástól is. Gyakorlati szempontból elhanyagolható, mert a Lewis-effektus legtöbbször már a felületi szennyező réteg hatására teljesen eltűnik. A fékeződési tényező ebben az energiatartományban kisebb, mint kis energián, ezért gerjesztési görbe a telítési értéket csak az 580 Å vastag minta esetében éri el, míg a kisenergiájú rezonanciánál már a 170 Å-ös mintán is elérte a telítést. Az előbbiekben látott gerjesztési görbék ugyanolyan koncentrációprofilhoz tartoznak, mindegyiket 18 O 2 -t tartalmazó homogén vékonyrétegen mérték. A gerjesztési görbe alakja hasonlít a mintában levő 18 O 2 mélységi eloszlására. Ezek alapján meghatározhatunk egy, a réteg vastagságától független m jósági tényezőt, amely arra utal, hogy egy gerjesztési görbe mennyire hasonlít a tényleges koncentrációprofilhoz. Ez a jósági tényező jellemzi egy adott rezonancia mélységfelbontóképességét. Az adott rezonanciával egy homogén réteget mérve egy szögletes, a telítési értéket elérő gerjesztési görbét kapunk, ahol E, a gerjesztési görbe félszélessége, a lefutó él meredeksége (a magasságának 12% - 88%-a közötti energiakülönbség) pedig L 1/2. E a réteg x vastagságától függ, L 1/2 pedig a rétegen áthaladó ionok energia-straggling eloszlásának félértékszélessége. Egy gerjesztési görbe annál jobb minél meredekebb a lefutó éle a szélességéhez képest ( szögletes a gerjesztési görbe). Adott vastagságú rétegre de E = de dx x, L 1/2 = B E x, = dx x L 1/2 B x = m x. Ebből megadhatjuk a vastagságfüggetlen jósági tényezőt: de m = dx (27) B A három fontos 18 O(p,α) 15 N rezonanciára a mért görbékből kiszámított de fékeződés és dx B starggling állandó (lsd. (5) egyenlet) adatokat és a belőlük származtatott m jósági tényezőt a 3.1 táblázatban tüntettem fel. A 152 kev-es rezonanciához tartozó jósági tényező lényegesen nagyobb, ez is mutatja a kisenergiájú rezonancia alkalmazásának előnyét vékonyrétegek mérésekor. de Energy [kev] dx [kev/mgcm 2 ] B [kev(mgcm 2 ) 1/2 ] m , 7 36, , 8 6, 6 18, , 6 6, 8 12, táblázat A 18 O(p,α) 15 N magreakció hatáskeresztmetszetében 152 kev-en, 629 kev-en és 1167 kev-en található rezonanciákhoz tartozó de fékeződés, B starggling dx állandó és m jósági tényező Ta2 18 O 5 minta esetében.
57 56 Összehasonlításképpen álljon itt két közel azonos szerkezetű mintán mért gerjesztési görbe, az elsőt (3.19 ábra) a 152 kev-es rezonanciával vettem fel, a másodikat a 629 kev-es (3.20 ábra) rezonanciával mérték [Roc84]. A minta mindkét mérés esetében a nyalábhoz képest el volt fordítva ψ 70 -ra ábra Szilícium termikus oxidációjával előállított szendvics szerkezetűmintánmért gerjesztési görbe. A minta a méréskor a nyalábhoz képest ψ =70 -ra el volt fordítva. Az egyes rétegek vastagságát az ábra felső felén megadtam ábra A 3.17 ábrán mutatotthoz hasonló szerkezetű mintán a 629 kev-es rezonanciával felvett gerjesztési görbe [Roc84]. A két gerjesztési görbe közötti különbség szembetűnő: A kisenergiájú rezonancia esetében a bombázó ionok fékeződése nagyobb a céltárgy anyagában, ezért jobban szétválik a szendvics-szerkezetű mintakét 18 O-t tartalmazó rétege. Jelen esetben a szétválás teljes, a két csúcs között (159 kev kev
58 57 tartományban) nem mértem beütéseket. A keskeny rezonancia hatáskeresztmetszet-alakja miatt a görbe fel- és lefutó éle is meredekebb. A 629 kev-es rezonancia esetében a hatáskeresztmetszet a rezonancián kívül is viszonylag nagy, ezért van háttere a mért görbének. Ebben az esetben a szeparáció nem olyan jó, a felületi 18 O alig látható. A 3.21 ábrán bemutatom egy hasonló szendvicsszerkezet gerjesztési görbéjét [Mau82], mint amilyet már mutattam a kisenergiájú rezonanciánál a 3.11 ábrán, csak most a 18 O(p,γ) 19 F reakció 1167 kev-es rezonanciájával felvéve. Miután a rezonancia nagyon keskeny, az egyes 18 O rétegeknek megfelelő görbék élesek, de mivel a fékeződés ezen az energián kicsiny, nem igazán választható el a két görbe egymástól. Ebben az esetben is nagy a hatáskeresztmetszet a rezonancián kívül, az innen származó jelentős háttérbeütést a gerjesztési görbékből kivonták ábra Az 1167 kev-es rezonanciával 50 Å vastag Ta 18 2 O 5 rétegeken mért gerjesztési görbék, az élesebb görbe esetében a réteg a minta felületén helyezkedett el, a laposabb görbét pedig egy 150 Å vastag, 18 O-t nem tartalmazó fedőréteg alatti rétegen mérték [Mau82]. Ebben az esetben is alkalmaztak háttérlevonást. Ezeken a példákon is jól látható, hogy a a 152 kev-es rezonanciának felületközeli mélységfelbontóképessége nagyon jó. Szintén előny, hogy a gerjesztési görbéket háttérmentesen lehet felvenni. Nagy felbontást igénylő esetekben mindenképpen érdemes a kisenergiájú rezonanciát alkalmazni, amennyiben a kísérleti berendezés azt lehetővé teszi. 3.6 A kisenergiás oxigén rezonancia alkalmazása szilícium oxidációjának
59 58 tanulmányozására Az oxidáció kinetikájának meghatározása nagyon vékony oxidok esetében A MOS eszközök kapu elektródja alatti oxidréteg meghatározó az eszköz működésében. Az arányos méretcsökkenéssel a gate-oxid vastagsága manapság jóval 100 Å alatt van. Ahhoz, hogy megfelelő elektromos és mechanikai tulajdonságokkal rendelkező réteget tudjunk készíteni, elengedhetetlen a vékony szilíciumdioxid réteg növekedésének alapos ismerete. Mint már a fejezetben jeleztem, az oxidációs mechanizmust két alapfolyamat alkotja, az oxigén atomok intersticiális diffúziója a már kialakult SiO 2 rétegen keresztül, valamint a kémiai reakció a Si/SiO 2 határfelületen. A Si oxidáció kinetikáját Deal és Grove által leírt elméletben [Dea65] ezt a két folyamatot az alábbi egyenlet adja meg: dt dx = 2X + 1, ahol K p = 2DC és K l = k rc, (28) K p K l N i N i K p és K l a parabolikus illetve a lineáris konstans; C az oldékonyság, N i a térfogategységnyi oxid előállításához szükséges atomok száma, D adiffúziós állandó és k r a reakciósebesség a Si/SiO 2 határfelületen. A szabad térfogat modellben az oldékonyság arányos az oxidáló közeg nyomásával. Azonban nagyon vékony ( 10 nm) oxidrétegek növesztésekor a fenti elmélettől eltérő viselkedést tapasztalhatunk. Az atomi transzport folyamatok tisztázása érdekében vizsgáltuk a SiO 2 réteg növekedésének kinetikáját. Ehhez az 18 O izotópos jelölés módszerét és a vékony 18 O(p,α) 15 N rezonanciát alkalmaztuk. Az oxidációs kísérleteket gyors hőkezelő berendezésben 23 végeztük nagytisztaságú, vízmentes, 40 mbar és 84 mbar nyomású oxigén atmoszférában. A minták előállításához természetes összetételű és 18 O-ban 96%-ra dúsított O 2 gázt is használtunk. A részletes kísérleti paramétereket és eredményeket a [Gan93] cikkben írtuk le. Mértem a mintákban az 16 O és 18 O izotópok összmennyiségét különböző idejű oxidáció esetében. A mintában lévő összes oxigénmennyiség meghatározására a 16 O(d,p) 17 O magreakciót 810 kev-en valamint a 18 O(p,α) 15 N magreakciót 730 kev energián használtam. A teljes oxigén mennyiségből ρ = 2.21 g/cm 3 oxidsűrűséggel a különböző oxidációs időkhöz tartozó rétegvastagságot ki tudtuk számítani, tehát meghatároztuk az oxid növekedési sebességét. Megállapítottuk, hogy az oxidáció 23 RTO - Rapid Thermal Oxidation
60 59 kezdeti, lineáris szakaszában az elfogadott irodalmi értéknél nagyobb a növekedési sebesség. A3.22ábraakétkülönböző oxigénnyomáson végzett RTO oxidáció esetében kapott oxid növekedési sebességeket mutatja. Látható, hogy az oxidálás első 20 s-ában a növekedési sebesség 3, 5-szerese a hosszabb idejű kezeléseknél mért értéknek ábra Si gyors hőkezelős oxidációjának kinetikája. Az ábrán az 1050 C-os oxidáció által létrehozott oxidréteg vastagságok láthatók az oxidálási idő függvényében 40 mbar és 84 mbar oxidáló közeg nyomás esetében. A Si minta tisztítása oxidáció előtt nagyon fontos és kényes lépés. Ennél a kísérletsorozatnál a gyors hőkezelőben végzett tisztítást 24 alkalmaztuk: a Si mintát rövid ideig hőkezeltünk vakuumban (1150 C, 5s, 10 7 mbar ), így kaptunk oxidmentes felületet. Az oxidáció mechanizmusának megállapítására izotópos jelöléses kísérleteket is végeztünk. Egymás után oxidálva 16 O 2 -ban és 18 O 2 -ban, az egyes izotópok mélységi elhelyezkedéséből megállapítható, hogy milyen transzportfolyamatok játszódnak le az oxidáció során. Mint írtam a fejezetben, a Si oxidációja során a mozgó részecske az oxigénmolekula, amely a már megnőtt SiO 2 rétegen keresztül diffundál és a reakció a SiO 2 /Si határfelületén játszódik le. Ha előszőr 16 O 2 -ban, majd 18 O 2 -ban folytatva végzem az oxidálást, a 3.13 ábrán bemutatott 18 O eloszláshoz hasonló profilt kell mérnem. A 30 s 16 O 2 és 150 s 18 O 2 oxidáció 1050 C-on, 84 mbar nyomáson kb. 100 Å vastag SiO 2 réteget hoz létre. Ebben az esetben a 3.22 ábra alapján már a parabolikus növekedési modell érvényes. A rétegben az 18 Oeloszlásahasonlóa3.13ábránbemutatotthoz,ahogy 24 RTC (Rapid Thermal Cleaning)
61 60 az elméleti megfontolásokból vártuk. A kb. 50 Å vastag SiO 2 réteget létrehozó 10 sec 16 O 2 és 20 sec 18 O 2 oxidáció azonos hőmérsékleten és nyomáson a 3.23 ábrán bemutatott 18 Oprofilt hozza létre. Ebben az esetben még a 3.22 ábrán mutatott nagyon gyors kezdeti növekedési szakaszban vagyunk ábra A 152 kev-es 18 O(p,α) 15 N magreakciós rezonanciával mért gerjesztési görbe és a számított 18 O eloszlás a mintában. Az 18 O koncentráció ábrán a távolság az oxid-hordozó határfelületetől a felület felé növekszik. Az oxidálás RTO-val történt 1050 C-on 84 mbar nyomású gázban, először 10 s-ig 16 O 2 majd 20 s-ig 18 O 2 gázban. A folytonos vonal a gerjesztési görbe SPACES szimulációját mutatja. A mintában lévő 18 O eloszlását a mélység függvényében szintén bemutatom. Itt tehát a teljes oxidrétegben található 18 O izotóp, nem csak a SiO 2 /Si határfelületére kerül 18 O az oxidáció során. A mérési eredmények alapján felállított modell szerint a Si oxidációjának kezdetén az oxidáció nem egyenletes, a felület egyes pontjain gyorsabb, míg más pontokon el sem indul. Fontos szerepet játszik ebben a jelenségben a Si felületének tisztasága, illetve a felületi érdesség. Az érdesség különféle kristálytani orientációjú Si felületeket jelent, amelyeken az oxidációs sebesség különböző. Így a réteg vastagodása során oxidálatlan Si zárványok maradnak az oxidrétegben. Tovább folytatva az oxidálást a reakció mind a zárványok felületén, mind a hordozó felé eső határfelületen létrejön. Ebben a szakaszban a Si/SiO 2 határfelület effektív mérete lényegesen nagyobb, mint a zárványokat nem tartalmazó esetben. A növekedés kinetikája itt lineáris, mert a reakciót a határfelületen lejátszódó reakció korlátozza és gyorsabb, mert az effektív határfelület is nagyobb. Később a zárványok teljesen eloxidálódnak, homogén oxid jön létre, így a további oxidáció már valóban a geometriai Si/SiO 2 határfelületen játszódik le. Itt a növekedés a Deal és Grove elmélettel megadott parabolikus modellt követi, mert a reakció sebességét korlátozó
62 61 folyamat már az oxigénmolekulák diffúziója a határfelületre, az oxidrétegen keresztül. A 3.24 ábrán sematikusan ábrázolom a növekedés egyes fázisait ábra A Si oxidációjának kezdeti szakaszát leíró modell egyes fázisai: a- a Si felülete magashőmérsékletű vákuum tisztítás után, b-a kialakuló réteg nagyon rövid ideig tartó oxidáció után, c-továbbfolytatva az oxidációt már homogén SiO 2 réteget kapunk. Az oxidációk 84 mbar nyomású gázban 1050 C-on történtek különböző ideig. A felállított model érvényességét néhány korábbi munka is igazolja, amelyek a Si zárványok létét bizonyítják nagyon vékony oxidrétegekben pl. elektronmikroszkópiai módszerekkel [Gib89]. Összefoglalva, a Si oxidációjának kezdeti szakaszát többek között a kisenergiás 18 O magrezonanciás és izotópjelöléses módszerrel vizsgáltam. A tényleges 18 O profil meghatározását a mintákban a kisenergiájú oxigénreakció érzékenysége és jó felületi mélységfelbontóképessége tette lehetővé A felületi tisztítás hatása a szilícium felületén kialakuló oxidrétegre Az előző fejezetekben leírt kisenergiájú oxigénrezonanciával vizsgáltuk az oxidáció előtti felületi tisztítás a kialakuló oxidrétegre gyakorolt hatását [Ste94]. Háromféle tisztítási eljárást alkalmaztunk: - 48%-os HF vizes oldatában marás 30 s-ig, majd kétszer desztillált vizes öblítés 30 s-ig, - marás 4% HF-es etanol oldatban 30 s-ig, majd öblítés etanolban 30 s-ig, -amintafelfűtése vákuumban (P < Pa) 1150 C-ra5s-ig(RTC-RapidThermal Cleaning).
63 62 Az első két esetben a mintákat száraz nitrogénnel leszárítottuk és azonnal vákuumba helyeztük. Az RTC tisztítás esetében a minták vákuumban maradtak az oxidációig. Az oxidációkat egy speciális gyorshőkezelőben végeztük. A hőkezelő kamrábana mintákat nagyvákuumban tartottuk, majd kisnyomású 16 Ovagy 18 O gázt töltöttünk a kamrába. A gyors oxidáció után a kamrát ismét nagyvákuumra szívtuk le. Az oxidáció paraméterei a következők voltak: -1)először 140 mbar 16 O gáz 1200 C2s-ig,majd84mbar 18 O gáz 1050 C50s-ig, -2)először 84 mbar 16 O gáz 1050 C 10 s-ig, majd 84 mbar 18 O gáz 1050 C20s-ig, -3)először 84 mbar 16 O gáz 1050 C 60 s-ig, majd 84 mbar 18 O gáz 1050 C150s-ig. Az alkalmazott 16 Oés 18 O gáz nagytisztaságú és nagyon száraz gáz volt. Az 16 Ogáza természetes izotópösszetételnek megfelelően 0,204% 18 O-t tartalmazott. Az 18 O gázban az 18 O izotóp koncentrációja 97% volt ábra A kisenergiájú 18 O(p,α) 15 N rezonanciával felvett gerjesztési görbe, az oxidáció 16 O 1050 C84mbar60sés 18 O 1050 C 84 mbar 150 s paraméterekkel történt. A mintát HF-ben tisztítottuk és etanollal öblítettük. Folytonos vonallal a betétábrában mutatott 18 O koncentrációprofilnak megfelelő szimulált gerjesztési görbe és az egyes alrétegeknek megfelelő összetevői láthatók. A mérés során a minta ψ =72 - ra el volt forgatva a beeső ionnyalábhoz képest. A kialakuló oxidrétegek vastagságát és összetételét 1,8 MeV-es RBS mérésekkel (a jobb felbontás érdekében 95 -os detektálási szöget alkalmaztunk) és magreakciós mérésekkel ( 18 O(p,α) 15 N 730 kev-en és 16 O(d,p) 17 O 810 kev-en) ellenőriztük. Megállapítottuk, hogy mindegyik oxidációs eljárást alkalmazva, 5 nm-nél vastagabb rétegek esetében a kialakuló SiO 2 réteg összetétele sztöchiometrikus, a beépülő oxigénmennyiség elegendő a réteg teljes oxidálásához.
64 63 A 3.25 ábrán látható egy a 3-as oxidációs eljárással készített rétegen felvett gerjesztési görbe, valamint a szimulációk alapján megállapított 18 O koncentráció profil. A 8,5 nm vastag rétegben hasonló az 18 O koncentrációja, mint amilyen látható a 3.13 ábrán. A felületen a fizikai kicserélődésből származó 18 O, majd a SiO 2 /Si határfelületnél a közel 100% 18 O-t tartalmazó SiO 2 található. Gyakorlatilag hasonló gerjesztési görbe, azaz 18 O koncentráció profil látható a 3.26 ábrán. Ebben az esetben a vizes tisztítást alkalmaztuk. A kb. 6,5 nm vastag réteg esetében a kialakuló szerkezet azonos, mint az előző esetben ábra Hasonló gerjesztési görbe, mint a 3.25 ábrán, itt az oxidáció paraméterei a következők voltak: 16 O 1200 C 140 mbar 2 s és. 18 O1050 C84mbar50s. Az oxidáció elötti tisztítás HF és vizes öblítés volt. Ha vékonyabb réteget növesztünk, akkor már lényegesen eltér a mért 18 O koncentráció profil. Ahogy az előző fejezetben megmutattam, nagyon vékony oxidok esetében az oxidáció során el nem oxidált Si szigetek maradnak a rétegben. További oxidáció során ezek a szigetek eloxidálódnak. A 3.27 ábrán bemutatott kb. 3,5 nm vékony oxid esetében még nem oxidált Si szigetek is vannak az oxidrétegben, egy 16 Oés 18 O kevert oxid található asio 2 /Si határfelületen. Az RTC-vel tisztított minta esetében is (3.28 ábra) az első oxidáció során el nem oxidált Si szigetek maradtak a rétegben, majd a második, 18 O-ban történő oxidáció ezeket a szigeteket is oxidálta. Ezért található 18 OazegészSiO 2 rétegben és nem csak a határfelületnél.
65 ábra Hasonló gerjesztési görbe, mint a 3.25 ábrán, 16 O 1050 C84mbar10s és 18 O 1050 C 84 mbar 20 s oxidált mintán felvéve. A minta oxidáció elött HF-es tisztítást és vizes öblítést kapott ábra Hasonló gerjesztési görbe, mint a 3.25 ábrán, az oxidáció 16 O 1200 C140 mbar 2 s és 18 O1050 C 84 mbar 50 s paraméterekkel történt. A mintát RTC tisztítás után oxidáltuk. Az itt bemutatott oxidációs kísérletsorozatban az első, 16 O-ban történőoxidálássorán kialakuló oxidréteg tulajdonságai befolyásolják a második, 18 O-ban történőoxidációsorán kialakuló réteg vastagságát, tulajdonságait. A kísérletekben több oxidációs paraméter is változott. Egyrészt különféle felületi tisztítási eljárásokat alkalmaztunk az oxidáció előtt, másrészt változott az első oxidációs lépés hőmérséklete és az alkalmazott 16 O gáz nyomása is. A gáz nyomása az adott hőmérsékeleten és idő alatt kialakuló oxid réteg vastagságára, relatív kis nyomások és kis vastagságok esetében, elhanyagolható [Rig86]. Az oxidáció
66 65 hőmérséklete és ideje az oxidáció meghatározó paraméterei. rövidebb idő alatt alakul ki adott vastagságú oxidréteg. Magasabb hőmérsékleten A 3.25 ábrán bemutatott esetben az első, alacsonyabb hőmérsékletű éshosszúidejű oxidációs lépés során kialakul egy homogén oxidréteg. A második oxidáció a SiO 2 /Si határfelületen játszódik le, ahogy a Deal és Grove oxidációs modell megjósolja. Ha növeljük az első oxidációhőmérsékletét, jóval kevesebb idő iselegendő egy homogén oxidréteg kialakulásához (3.26 ábra). Az első esethez hasonló alacsonyabb hőmérsékleten rövid ideig végezve az első oxidációt, a kialakuló vékony oxidréteg nem lesz összefüggő és homogén, el nem oxidált Si szigetek és mozgóképes oxidhibák maradnak a rétegben. A 18 O-ban történő második oxidációs lépés során ezek a Si zárványok is oxidálódnak, ezért találunk 18 O-t az egész rétegben. Ha a második oxidáció ideje nagyon kicsi, nincs elég idő homogén, csak 18 O-t tartalmazó SiO 2 réteg kialakulására a SiO 2 /Si határfelületen, hanem egy kevert, 16 O-t és 18 O-ttartalmazóoxidalakulki. Eztmutatjaa3.27ábránacsakkb. 50%-otelérő 18 O koncentráció a határfelületnél. RTC tisztítást követően az első oxidáció során még kevésbé formálódik homogén oxid, nagyobb Si szigetek maradnak az oxidban. Egy hosszabb idejű második oxidáció is csak egy nagyrészt kevert oxidot eredményez (3.28 ábra). Összefoglalva, a fenti kísérletsorozat alapján megállapíthatjuk, hogy a két kémiai felületi tisztítási eljárás után nagyjából azonos oxidnövekedési mechanizmust és kinetikát kapunk. Az RTC tisztítás azonban csak vastagabb oxidrétegek növesztése esetén megfelelő. Vékony rétegek esetében RTC tisztítás után egy nagyon szigetes, oxidhibákkal teli réteg kapható. Ha vékony oxidrétegre van szükségünk, jobb alacsonyabb hőmérsékleten hosszabb ideig oxidálni a Si mintát, mert ez az eljárás eredményez jó minőségű összefüggő vékony oxidréteget A gate oxid károsodása ionimplantáció hatására A mai nagyintegráltságú MOS eszközök előállítása során a technológiai lépések között szerepel ionimplantálás is a gate-oxidon keresztül, amely a csatorna adalékoltságát állítja be. A nagyon vékony (50-100Å) oxid tulajdonságai megváltoznak az implantáció hatására, nő a szivárgási áram és lecsökken a letörési feszültség a rétegen keresztül. Ennek okait az implantáció közben lejátszódó mellékhatások között kereshetjük.
67 66 Ismert, hogy ionimplantáció közben a beütköző ionok atomokat löknek ki a felületből, azaz porlódik a felület, meglökik a target atomokat, amelyek kimozdulnak a helyükből, beljebb lökődnek a felülettől, ún. ütközéses implantáció játszódhat le, keveredhetnek a mélyebben levő atomokkal és mechanikai feszültség is kialakulhat. A nehezebb implantált adalékatomok (As, Sb) nagyobb hatást váltanak ki, míg a könnyebbek (B, P) kisebbet. Izotóp jelöléssel és nagy mélységfelbontóképességű kisenergiás rezonanciával jól tanulmányozhatók az ionimplantáció közben lejátszódó atomi transzport folyamatok. Munkánkban [Bau95] az ionimplantációnak nagyon vékony SiO 2 rétegre, illetve a közvetlenül alatta lévő Si-ra gyakorolt hatását vizsgáltuk ábra A 49 Å vastag Si 18 O 2 rétegen felvett gerjesztési görbék, -implantáció előtt,? As/cm 2, 100 kev és Sb/cm 2, 140 kev implantáció után. Amintaψ =70 -ra el volt forgatva a nyaláb beesési irányától. A felülettől indulva jelöltem a közelítő mélységskálát. A Å vastag oxid réteget Si (100) egykristály mbar nyomású O 2 -ben (98% 18 O 2 illetve 16 O 2 ) 1050 Chőmérsékleten s ideig történő gyorshőkezelésével állítottuk elő. Ezután cm 2 dózisú As és Sb ionokat implantáltunk a mintába kev energiával. Ezen az energián az ionok áthaladnak az oxidrétegen és kb. 700 Å mélységig behatolnak a szilíciumba. Implantáció után vákuumban vagy oxigén atmoszférában Chőmérsékleten, percig hőkezelést alkalmaztunk az implantáció okozta kristályhibák kikezelésére. Visszaszórásos és csatornahatás mérések szerint a hőkezelés során az implantáció közben amorffá váló réteg szilárdfázisú epitaxiával visszanő, visszakapjuk az eredeti kristálystruktúrát. A mintaelőállítás körülményei és az ionsugaras vizsgálatok a [Bau95] referenciában pontosan megtalálhatók.
68 67 Az ionimplantáció előtt és után mértük a felületen lévő Si 18 O 2 rétegben az 18 O atomok mennyiségét és mélységi eloszlását. A 3.29 ábrán a kisenergiás 18 O(p,α) 15 N magreakcióval felvett gerjesztési görbék láthatók. A nem implantált minta esetében egy sztöchiometrikus SiO 2 réteg van a felületen, ennek gerjesztési görbéje szintén látható. A legszembeötlőbb, hogy az implantált mintákban kevesebb oxigén van, ez az implantáció közbeni porlódás hatása. A rétegnek kb. 15%-a porlódott le implantálás közben. Szintén látható, hogy az implantált mintákhoz tartozó görbék hátsó éle kisebb meredekségű, mint a nem implantálté. Ez mutatja, hogy a SiO 2 /Si határfelületen keveredtek az ott lévő atomok, oxigén atomok lökődtek be a hordozóba. Annak megállapítására, hogy hol történik a porlódás, tehát a réteg hogyan fogy implantáció közben, készítettünk egy 16 O/ 18 O szendvics szerkezetű oxidotis. Először 75 Å Si 16 O 2 -t majd 40 Å Si 18 O 2 -réteget növesztettünk. Az implantáció előtt a mintán a 3.30 ábra (a) ábrarészében látható gerjesztési görbét mértük. A betétképen a gerjesztési görbéből kiszámított 18 O koncentráció látható a vastagság függvényében. A felületen egy nagyon vékony, 10 Å-ös rétegben szintén található 18 O az izotópok második oxidáció közbeni kicserélődése miatt. A (b) ábrarészen a mért gerjesztési görbékből jól látszik, hogy a növekvő implantációs dózissal nő arétegporlódásais.először a felületközeli 16 O réteg fogy el, az 18 Oatomokat egyre inkább a felület közelében találjuk. Szintén szembetűnő, hogy az implantáció hatására a gerjesztési görbék lefutó éle egyre inkább elnyúlik a nagyobb energiák, azaz a nagyobb mélységek felé. Ez egyértelmű jele az implantácó közben lejátszódó ütközéses implantációnak. A határfelület az oxid és a Si között elmosódik.
69 ábra Egy 115 Å vastag SiO 2 rétegen a 152 kev-es 18 O(p,α) 15 N rezonanciával felvett gerjesztési görbék. A minta ψ =70 -ra volt elforgatva a mérés közben. Az oxidréteg külső felén 75 Å Si 16 O 2, míg belső részén 40 Å Si 18 O 2 helyezkedik el. A felületen a izotópkicserélődés miatt szintén található 18 O. (a) mutatja a kezeletlen mintán rögzített görbét és folytonos vonallal a szimulált rész- és összeg gerjesztési görbéket. A kis ábrarészben az 18 O koncentrációprofilt ábrázoltam. (b)-n láthatók az ugyanezen mintán, de 140 kev-es ionimplantáció után felvett görbék: pontok - ugyanaz, mint (a)-n, szaggatot vonal As/cm 2,pont-vonal As/cm 2, folytonos vonal As/cm 2. SIMS mérések, ugyanezeken a mintákon, szintén érdekes eredményt mutatnak (3.31 ábra). A mintákat implantáció, hőkezelés és az oxidréteg eltávolítása után ezzel a módszerrel vizsgálva, az 18 O eloszlása a felülettől exponenciálisan csökken. A profilban két helyen találhatók nagyobb koncentrációra utaló csúcsok, először ott, ahol a beimplantált As ionok megálltak az anyagban, másodszor pedig a korábbi amorfkristályos határfelületnél. Természetesen ezekben a mélységekben az 18 O koncentrációja nagyon kicsi, a magreakciós rezonancia módszer érzékenysége már nem elegendő ezekneka koncentrációknak a kimutatására. A SIMS módszer érzékeny ugyan, de a felület közelében nagyon rosszul adja meg a vizsgált atomok mennyiségét és a mélységskálát. Kombinálva az érzékeny, jó felületi mélységfelbontóképességű magreakciós rezonanciát a SIMS méréssel, pontosabb mennyiségi és mélységi információt kaphatunk a vizsgált mintáról.
70 ábra A 100 kev As/cm 2 implantált mintában az 18 O mélységi eloszlás mérése SIMS-szel. Az implantáció után az oxidréteget lemartuk, majd 700 C on nagyvákuumban 1 órát hőkezeltük a mintát. Az ábrán szintén látható a beimplantált 75 As mélységeloszlása is. A fent leírt vizsgálatok fontos információt adnak a technológusnak az adott paraméterekkel rendelkező MOS Si struktúra technológiájának megtervezéséhez.
71 70 4. Nitrogénrezonancia alkalmazása pórusos szilícium rétegek vizsgálatára A 15 N(p,αγ) 12 C magreakcióban 429 kev energiánál található rezonancia anyagvizsgálati célokra szintén nagyon alkalmas, kisenergiájú, keskeny rezonancia. Ennek a rezonanciának is hasonlóak az előnyei és hátrányai, mint a kisenergiájú 18 O magreakciós rezonanciának. A következőkben bemutatom, hogy milyen eredményeket értünk el ennek a rezonanciának a használatával a pórusos szilícium rétegek tanulmányozásában [Ams97]. Az elmúlt időszakban csoportunk intenzíven foglalkozott pórusos anyagok ionsugaras módosításával és vizsgálatával [Bat96, Haj96, Man97, Szi99, Pas00, Ram00]. Ezeknek a munkáknak a keretében, a különféle módon kezelt PS rétegeket, más ionsugaras módszerrekkel is vizsgáltuk. Jelentős eredményeket értünk el az implantált PS rétegek csatornahatással kombinált RBS mérésével és a 3.05 MeV-es 16 O(α, α) 16 O elasztikus rezonancia alkalmazásával. A pórusos Si (PS) elektrokémiai eljárással előállított réteg, amely üregeket, pórusokat tartalmaz. Ilyen módszerrel akár a P =90%-os pórusosság is elérhető, tehát a réteg térfogatának akár 90%-a is üregekből állhat. A PS rétegeknek igen jelentős szabad felületük van, az ilyen rétegek belső felülete akár a m 2 /cm 3 -t is elérheti. Az előállításból, az elektrokémiai oldásból következően a belső felület a külső térrel összeköttetésben áll. A PS rétegek alkalmazása elsősorban az optoelektronikában az elektro- és fotolumineszcenciához kapcsolódik. Fontos alkalmazások azok is, amikor a hatalmas belső felületet használjuk ki: katalizátorok vagy gázérzékelő elemek hordozója lehet. rétegeket alkalmazni lehet pl. molekulaszűrőként vagy antireflexiós rétegként is. A PS A kiinduló Si szelet adalékoltságától függően alapvetően kétféle pórusos struktúra alakitható ki: az oszlopos és a szivacsos szerkezetű PSréteg. Azerősen adalékolt n + vagy p + alapszeleten előállított PS szerkezete oszlopos, a Si <100> kristálytani irányával párhuzamos, nm átmérőjű üregek futnak egymással párhuzamosan, akár több tíz µm mélységig 25. Az üregek között nm vastag egykristályos Si falak maradnak. A falak kristályosságát elektrondiffrakcióval és csatornahatás mérésekkel is ellenőriztük. A pórusosság növekedésével a Si falak vastagsága általában nem csökken, hanem az 25 Készült olyan PS réteg is, amelynél az üregek végigfutnak a Si szelet teljes vastagságán, tehát kb. 0,3 mm mélyek.
72 71 üregek lesznek nagyobbak. A 4.1 ábrán oszlopos szerkezetű PSrétegről felvett pásztázó elektronmikroszkópos a) felületi, b) keresztmetszeti kép látható. Az enyhén adalékolt n vagy p Si alapszeleten szivacsos szerkezetű PSrétegalakítható ki, ebben az esetben a PS réteg 5-15 nm átmérőjű, véletlenszerűen, egyenletesen elosztott üregekből és körülöttük 5-15 nm vastag Si falakból áll. a) b) 4.1 ábra 66% pórusosságú, 1,6 µm vastag oszlopos pórusos szilícium rétegről készített pásztázó elektronmikroszkópos képek. Az a) képen felületi kép látható a pórusokkal és a közöttük maradó Si falakkal. A keresztmetszeti fotón (b) jól megfigyelhetők a hosszú, egymással közel párhuzamos, az <100> Si felületre merőleges pórusok. A PS réteg és a Si hordozó közötti határfelület nagyon egyenes, jól meghatározott (az ábra alsó felén a sötét tartomány az egykristályos Si hordozó). [Gro95] A dolgozatban nem foglalkozom a PS rétegek előállításával, vagy fizikai tulajdonságaival, csak a rétegek ionsugaras, ezen belül magrezonanciás vizsgálatát tárgyalom. Ionsugaras szempontból azért érdekesek az ilyen pórusos rétegek, mert elméletileg a pórusok az ionsugarak számára nem láthatók. A pórusban, tehát az azt kitöltő vákuumban haladó ionok semmivel sem ütköznek, nem szóródnak és sebességük iránya és nagysága sem változik meg. kölcsönhatásba, az üregekkel nem. A vizsgáló ionok tehát csak a pórusfalakkal léphetnek Az egyes ionok azonban más és más utat tesznek meg a pórusos anyagban, mint az a 4.2 ábrán is látható. Ha ugyanabban a fizikai mélységben nézzük az ionokat, mindegyik másutattettmeg(l i ), az útja során más energiát, U i = de dx L i vesztett. Ahhoz, hogy minden ion ugyanannyi energiát veszítsen, ugyanannyi utat kell megtenniuk az anyagban, tehát a pórusfalban. Miután eltérő mennyiségű üreget kereszteztek az ionok ugyanazt az energiaveszteséget eltérő mélységben érik el. Ha valahogy meg tudjuk határozni, hogy egy ion mennyi energiát veszített, míg elért egy adott fizikai mélységbe, akkor információt
73 72 kaphatunk a pórusos szerkezet milyenségéről is. Erre ad lehetőséget a magrezonanciák alkalmazása, hiszen a magrezonanciák egy jól definiált energiánál következnek be. Mivel a gerjesztési görbe lefutó éle a 15 N-t tartalmazó réteg és a hordozó határfelületének mélységét jelzi, ha minden ion más mennyiségű anyagot keresztezett, míg elérte ezt a határfelületet, a mért görbében energiaelmosódás fog emiatt jelentkezni. A lefutó él meredeksége tehát jellemző lesz a PS réteg szerkezetére. 4.2 ábra A pórusos réteg sematikus ábrázolása. A kör alakúnak ábrázolt pórusok belső felülete más szürkével jelölt. A bombázó ionok Ψ beesési szögben érkeznek a felülethez. Érdemes megjegyezni, hogy az egyes ionok az útjuk során mikroszkópikus, atomi méretekben érzékelik az anyagot. A mérést egy viszonylag nagy kiterjedésű (0,5-1 mm átmérőjű) ionnyalábbal, nagyon sok ionnal végezve egy makroszkópikus statisztikai átlagot tudunk mérni a nyaláb méretének megfelelő felületen. Ez az átlag tartalmazza a réteg szerkezetére jellemző információt. Ennek némileg ellentéte az elektronmikroszkópos mérés: ott egy nagyon kis térrészt vizsgálunk nagy helyi felbontással, de nem kapunk statisztikus információt az egész rétegről. Ezekből a megfontolásokból határoztam el, hogy pórusos szilícium réteget fogok vizsgálni magreakciós rezonancia módszerrel. A szóbajöhető magreakciók közül a 15 N(p,αγ) 12 C reakciót választottam, mert a PS minták belső felületének bevonása 15 N izotóppal viszonylag egyszerűen megvalósítható. A hatalmas belső felület eredményeként a rétegben lévő atomok 10%-a a felületen helyezkedik el. Ha sikerül akár egyetlen 15 N-t tartalmazó monoréteget létrehoznom a PS belső felületén, akkor a rétegben lévőösszes 15 N mennyisége elegendően nagy lesz, amit a rezonanciás mérés érzékenységével is detektálni lehet.
74 73 Aritka 15 N izotóp használatát az is idokolja, hogy ezáltal az egyéb szennyezők mérése elkerülhető. A mérhető 15 N izotóp csak szigorúan ellenőrzött körülmények között került amintába. 4.1 A 15 N(p,αγ) 12 C magreakció 429 kev energián A429keV-es 15 N(p,αγ) 12 C rezonancia tulajdonságait részletesen B. Maurel [Mau83, Ams86] vizsgálta, ők mérték meg nagy pontossággal a rezonancia félszélességét: Γ =120± 30 ev. Ebben az energiatartományban a rezonanciában a reakció hatáskeresztmetszete legalább 4 nagyságrenddel nagyobb, mint a rezonancián kívül. Ebben az esetben a γ- fotonokat detektáljuk. A magreakció során 4,43 MeV energiájú γ-fotonok keletkeznek, ezeket kell detektálni. Ezzel egyszerűsödik is a mérési összeállítás, mert a nagy térszög elérése érdekében nem kell speciális félvezető detektort használni. A legjobb egy nagy hatásfokú, nagy térfogatú γ-detektort alkalmazni. A bombázó és visszaszórt protonok szintén nem zavarnak, mert a γ-detektor ezekre a részecskékre érzéketlen. Érdekes megjegyeznem, hogy ennek a magreakciónak a fordítottját gyakran alkalmazzák hidrogénprofilok mérésére (lsd. Lanford [Tes95]-ben). Ekkor a reakció 1 H( 15 N,αγ) 12 C formában írható le, a rezonancia szélessége Γ =1, 8 ± 0, 45 kev és az energiája 6,435 MeV-nek adódik (az energia- és impulzusmegmaradás törvénye miatt: M a M A 0, 429 MeV =6, 435 MeV) [Dam83]. 4.2 A mérési elrendezés A 15 N(p,αγ) 12 C magreakciós rezonancia alkalmazásánál hasonló mérési elrendezés használható, mint az 18 O(p,α) 15 N magrezonanciás mérések esetében. Az egyetlen különbség, hogy most a reakcióterméket, a γ-fotont szcintillációs részecskedetektorral detektáljuk. Miután esetünkben nem a detektor nagy felbontóképességére, hanem a nagy detektálási hatásfokára van szükség, legelőnyösebb BGO detektort használni. detektort közel helyezzük el a mintához, hogy nagy térszögben érzékelje a detektálandó részecskéket. Előny az is, hogy mivel a γ-fotonok áthatolóképessége nagyon nagy, a detektort a mintatartó mögé is helyezhetjük. Ezt a mérési elrendezést is bemutattam vázlatosan a 2.7 és 2.8 ábrákon. használtam. Méréseimben 4 4 effektív felületű BGO detektort Ebben az esetben is nagyon lényeges a jó vákuum és a kifagyasztás a mérőkamrában, mert ez a módszer is nagyon érzékeny a felületi szennyezőkre. A mérés közben lerakódó A
75 74 szénhidrogén szennyeződések hatásának elkerülésére gyakran váltottam a mintán mérési pontot, lehetőleg mindig friss ponton mértem N izotóppal dúsított PS minták készítése A kísérletekhez oszlopos és szivacsos szerkezetű 66% pórusosságú, 0,8µm - 1,6µm vastagságú PS rétegeket készítettünk. A kiinduló Si szelet orientációja mindkét esetben <100> volt. Oszlopos mintákat bórral adalékolt 10 3 Ω cm ellenállású szelet HF-etanolvíz arányú oldatában 50 ma / cm 2 áramsűrűséggel s ideig történő elektrokémiai oldásával állítottuk elő. Szivacsos minták esetében ugyanilyen kezelésnek a paraméterei a következők voltak: 10 Ω cm ellenállású szelet, HF-etanol-víz arányú oldat, 10 ma / cm 2 áramsűrűség, s elektrokémiai oldás. A kapott rétegek pórusosságát súlyméréssel, vastagságát mikroszkópos méréssel, belső felületének nagyságát pedig gázadszorbciós ú.n. BET [Gre91] módszerekkel ellenőriztük. A PS rétegek szerkezete közvetlenül az elkészítésük után nem stabil. Hosszúidejű megfigyelések mutatják, hogy egyrészt lassan natív oxid alakul ki a belső felületen szobahőmérsékleten is, másrészt a belső felület nagysága is csökken. Annak érdekében, hogy a PS réteg lassú degradációs folyamatát megakadályozzuk, illetve a felület jól ellenőrzött körülmények között jöjjön létre, a PS réteg előállítása után 300 C-os, 12 mbar oxigénben történő 1 órás oxidációt alkalmaztam. Az irodalom szerint ennek a kezelésnek a célja a PS réteg szerkezetének stabilizálása [Gro95]. Ezután PS rétegek belső felületén termikus nitridálással Si3 15N 4 réteget alakítottam ki: a mintákat 12 mbar nyomású 99.1%-ban 15 N izotóppal dúsított ammónia ( 15 NH 3 ) gázban 850 C-1000 C hőmérsékleten 5-30 percig hőkezeltem. Ez a nitridálás tiszta Si felületen Å vastag Si 3 N 4 réteget eredményez [Ste95]. Az alábbi mintákat készítettem: A minta - 0,8 µm vastag oszlopos szerkezetű minta, nitridálva 1000 C-on 5 percig; B minta - 0,8 µm vastag oszlopos szerkezetű minta, nitridálva 850 C-on 15 percig; C minta - 1,6 µm vastag oszlopos szerkezetű minta, nitridálva 850 C-on 15 percig; D minta - 0,8 µm vastag oszlopos szerkezetű minta, nitridálva 1000 C-on 30 percig; E minta - 1,6 µm vastag oszlopos szerkezetű minta, nitridálva 1000 C-on 5 percig; F minta - 0,8 µm vastag szivacsos szerkezetű minta, nitridálva 1000 C-on 30 percig;
76 75 G minta - 1,6 µm vastag szivacsos szerkezetű minta, nitridálva 1000 C-on 30 percig. Előkísérleteink Si minták esetében azt mutatták, hogy a Si 3 N 4 réteg nagyon gyorsan kialakul a felületen, a kezelést hosszabb ideig végezve sem növekszik tovább a kialakuló réteg vastagsága. Ez annál is inkább így van, mert az ammónia ilyen magas hőmérsékleteken gyorsan elbomlik, a nitrogén gáz pedig önmagában már nem lép reakcióba a szilíciummal. Ezzel a kezeléssel egyrészt sikerült bevonni a PS rétegek belső felületét Si 15 3 N 4 réteggel, másrészt a magas hőmérséklet miatt szerkezeti változást is vártunk a PS rétegekben. Aminták 12 C, 14 Nés 16 O tartalmát a megfelelő magreakciókkal ellenőriztem ( 12 C: 12 C(d,p) 13 C 950 kev-en; 14 N: 14 N(d,α 0 ) 12 C1450keV-en; 16 O: 16 O(d,p 1 ) 17 O850keV-en;). A mért összetételből [Wil66] alapján meghatároztam a protonok fékeződését a rétegben, ez de dx =318keV/mgcm 2 értékre adódott. 4.4 Az izotópos jelölés és a magreakciós mérés alkalmazása pórusos szilícium minták morfológiájának vizsgálatára Referenciamintaként egy CVD 26 módszerrelsihordozónelőállított at/cm 2 15 N atomot tartalmazó Si3 15N 4 réteget mértem (4.3 ábra). A gerjesztési görbét pontonként 5 µ C töltést összegyűjtve, az automatikus elektrosztatikus nyalábenergia változtató rendszer segítségével vettem fel. A rezonancia-energia környékén az energialépés 200 ev, míg távolabb nagyobb. A felfutó él a rezonanciaenergiánál nagyon meredek, éles. Ez azt bizonyítja, hogy a rezonancia keskeny, így nagy felületi felbontóképességet érhető el alkalmaásával. A görbén látható plató magassága arányos a mintában levő 15 N/Si aránnyal. A plató magassága a görbén állandó, tehát a minta homogén összetételű. Amint már írtam a és a fejezetekben, a nagyobb energiáknál, a lefutó élnél az energiaelmosódás a straggling következménye. A mérésből a straggling félszélessége 3 kev-nek adódott, ami jó egyezésben van az elméleti értékkel (2, 7 kev). 26 CVD: Chemical Vapor Deposition, Kémiai gõzfázisú leválasztás
77 Γ=120 ev G B =135 ev Si 3 15 N 4 ref. target 15 N(p,αγ) 12 C E R = 429 kev Beütésszám E P -E R [kev] 4.3 ábra A magrezonanció gerjesztési görbéje amit a Si3 15 N 4 referenciamintán az E R =429keV-es 15 N(p, αγ) 12 C magreakciós rezonanciával mértem. Minden pontban 5 µc töltést gyüjtöttem össze. A folytonos vonal SPACES szimulációt jelent Γ = 120eV rezonanciaszélességgel és G B = 135eV nyaláb- és Doppler energiaszórással, illetve 3 kev félszélességű stragglinggel A PS rétegeken mért gerjesztési görbék A 4.4 ábrán oszlopos PS rétegen különböző beesési szögnél felvett gerjesztési görbéket mutatok be. Ebben az esetben a 0,8µm vastag 66 % pórusosságú PS réteget 850 C hőmérsékleten 15 percig 12 mbar nyomású 15 NH 3 gázban kezeltem. A rezonanciás mérés előtt csatornahatás méréssel megállapítottam a minta pontos kristálytani orientációját, így a 0 beesési szög megfelel az <100> kristálytani iránynak. A mért gerjesztési görbéken a felfutó él nagyon meredek, hasonlóan a kompakt Si 3 N 4 réteghez. A görbék egy jól meghatározott telítési értéket is mutatnak. Ezekből megállapítható, hogy a PS réteg pórusossága, illetve szerkezete és belső felülete sem változik a mélységgel. A nitridálás során mind mélységben, mind összetételben nagyon homogén Six 15 N y réteg alakult ki. Ezzel ellentétben a lefutó él meredeksége nagyon változik a nyaláb beesési szögének változásával, ψ =0 -nál nagyon lapos, majd a beesési szög növelésével egyre meredekebb. Ennek a viselkedésnek az okait egyértelműen a PS réteg szerkezetében kell keresnünk.
78 Ψ = 0º; 1º; 2º; 4º; 8º; 16º; 30º 2000 Beütésszám 1000 E R kev E R +38 kev E P -E R [kev] 4.4 ábra 15 N(p,αγ) 12 C magreakciós rezonancia gerjesztési görbék oszlopos PS rétegen felvéve (B minta). A réteg pórusossága P 66%. A legmeredekebben lefutó görbe tartozik a 30 -os tiltszöghöz, míg a leglaposabb a merőleges (0 ) beeséshez tartozik. A 30 -os görbe azért szélesebb, mert a nagyobb beesési szög miatt a minta nyalábirányú vastagsága megnövekszik az 1/ cos Ψ faktorral. A két nyíl két energiát jelöl, 18keV -vel és 38keV -vel a rezonanciaenergia fölött, a 4.6 ábrán látható görbéket mértem a jelölt energiákon. Kompakt anyagban minden ion közel azonos vastag anyagon áthaladva veszít E E R energiát, adott mélységben az ionok energiaeloszlását a straggling fogja meghatározni. Az L vastagságú anyagban fékeződő protonok straggling-energiaszórását σ S = B L alapján, ((5) egyenlet) számíthatjuk ki Ψ=8º Beütésszám Ψ=0º Bohr Straggling E P -E R [kev] 4.5 ábra Oszlopos PS rétegen ψ =0 -n és ψ =8 -n mért gerjesztési görbék (4.3 ábrából kivett két görbe). Az azonos vastagságú tömör rétegre Bohr-stragglinggel számított gerjesztési görbét is feltüntettem. (B minta)
79 78 A 4.5 ábrán látható oszlopos szerkezetű PS rétegen két különböző beesési szögön mért gerjesztési görbe. Szintén berajzoltam az ábrába az azonos vastagságú kompakt réteg számított gerjesztési görbéjét is. Ebben az esetben a Bohr-straggling konstanssal számítottam az energiaszórást. A mért görbék lefutó élének meredekségéből számítható egy energiaszórás. A pórusos minta esetében egy ideális oszlopos szerkezetet feltételezve (4.6 ábra), a felületre közel merőlegesen E energiával beeső vizsgálóionokvéletlenszerűen hol egy pórusba, hol a pórusok körüli falba érkeznek be. Fékeződésük során, ami csak a falban következhet be, különféle tényleges geometriai mélységig juthatnak a rétegben addig, míg elérik az E R rezonanciaenergiát. Ráadásul ez a jelenség a bombázó ionok beesési szögétől is nagyon függ. Ha a pórusokkal párhuzamosan érkeznek az ionok, akkor lesz olyan ion, ami pont a pórusba érkezik, ez fékeződés nélkül tud továbbrepülni egész nagy geometriai mélységekig is. Egy másik ion pont a pórusfalba ütközik, ez rögtön fékeződik és csak nagyon kis utat tesz meg a mintában. Az úthosszkülönbségből adódó energiaszórás tehát nagyon nagy lesz. 4.6 ábra Oszlopos PS réteg sematikus ábrázolása. A mintára E P energiával érkező ionok különféle geometriai mélységbe jutnak, míg elérik az E R rezonanciaenergiát. Minden ionnak azonos utat kell megtenni a pórusfalakban. Ψ az ionok beesési szöge a pórusirányhoz képest. A pórusfalakon szürkével jelöltem a Si3 15 N 4 bevonatot. Egy közbülső állapotot mutat a a 4.6 ábra, ekkor eléggé különböző utat tesznek meg az ionok, még mindig nagy lesz egy adott mélységben az energiaszórásuk, de már kisebb, mint a ψ =0 -os beesés esetében. Ha nagy szög alatt érik az ionok az oszlopos mintát, akkor keresztezve a pórusfalakat minden ion hasonló utat fog megtenni, kicsi lesz az úthosszkülönbségből adódó energiaszórás. A ψ =0 -os és ψ =8 -os beeséshez tartozó mért és hibafüggvénnyel illesztett görbéket is feltüntettem a 4.5 ábrán.
Sugárzások és anyag kölcsönhatása
 Sugárzások és anyag kölcsönhatása Az anyaggal kölcsönhatásba lépő részecskék Töltött részecskék Semleges részecskék Nehéz Könnyű Nehéz Könnyű T D p - + n Radioaktív sugárzás + anyag energia- szóródás abszorpció
Sugárzások és anyag kölcsönhatása Az anyaggal kölcsönhatásba lépő részecskék Töltött részecskék Semleges részecskék Nehéz Könnyű Nehéz Könnyű T D p - + n Radioaktív sugárzás + anyag energia- szóródás abszorpció
Compton-effektus. Zsigmond Anna. jegyzıkönyv. Fizika BSc III.
 Compton-effektus jegyzıkönyv Zsigmond Anna Fizika BSc III. Mérés vezetıje: Csanád Máté Mérés dátuma: 010. április. Leadás dátuma: 010. május 5. Mérés célja A kvantumelmélet egyik bizonyítékának a Compton-effektusnak
Compton-effektus jegyzıkönyv Zsigmond Anna Fizika BSc III. Mérés vezetıje: Csanád Máté Mérés dátuma: 010. április. Leadás dátuma: 010. május 5. Mérés célja A kvantumelmélet egyik bizonyítékának a Compton-effektusnak
A sugárzás és az anyag kölcsönhatása. A béta-sugárzás és anyag kölcsönhatása
 A sugárzás és az anyag kölcsönhatása A béta-sugárzás és anyag kölcsönhatása Cserenkov-sugárzás v>c/n, n törésmutató cos c nv Cserenkov-sugárzás Pl. vízre (n=1,337): 0,26 MeV c 8 m / s 2. 2* 10 A sugárzás
A sugárzás és az anyag kölcsönhatása A béta-sugárzás és anyag kölcsönhatása Cserenkov-sugárzás v>c/n, n törésmutató cos c nv Cserenkov-sugárzás Pl. vízre (n=1,337): 0,26 MeV c 8 m / s 2. 2* 10 A sugárzás
 http://www.nature.com 1) Magerő-sugár: a magközéppontból mért távolság, ameddig a magerők hatótávolsága terjed. Rutherford-szórásból határozható meg. R=1,4 x 10-13 A 1/3 cm Az atommag terének potenciálja
http://www.nature.com 1) Magerő-sugár: a magközéppontból mért távolság, ameddig a magerők hatótávolsága terjed. Rutherford-szórásból határozható meg. R=1,4 x 10-13 A 1/3 cm Az atommag terének potenciálja
Modern fizika laboratórium
 Modern fizika laboratórium Röntgen-fluoreszcencia analízis Készítette: Básti József és Hagymási Imre 1. Bevezetés A röntgen-fluoreszcencia analízis (RFA) egy roncsolásmentes anyagvizsgálati módszer. Rövid
Modern fizika laboratórium Röntgen-fluoreszcencia analízis Készítette: Básti József és Hagymási Imre 1. Bevezetés A röntgen-fluoreszcencia analízis (RFA) egy roncsolásmentes anyagvizsgálati módszer. Rövid
Theory hungarian (Hungary)
 Q3-1 A Nagy Hadronütköztető (10 pont) Mielőtt elkezded a feladat megoldását, olvasd el a külön borítékban lévő általános utasításokat! Ez a feladat a CERN-ben működő részecskegyorsító, a Nagy Hadronütköztető
Q3-1 A Nagy Hadronütköztető (10 pont) Mielőtt elkezded a feladat megoldását, olvasd el a külön borítékban lévő általános utasításokat! Ez a feladat a CERN-ben működő részecskegyorsító, a Nagy Hadronütköztető
A kvantummechanika kísérleti előzményei A részecske hullám kettősségről
 A kvantummechanika kísérleti előzményei A részecske hullám kettősségről Utolsó módosítás: 2016. május 4. 1 Előzmények Franck-Hertz-kísérlet (1) A Franck-Hertz-kísérlet vázlatos elrendezése: http://hyperphysics.phy-astr.gsu.edu/hbase/frhz.html
A kvantummechanika kísérleti előzményei A részecske hullám kettősségről Utolsó módosítás: 2016. május 4. 1 Előzmények Franck-Hertz-kísérlet (1) A Franck-Hertz-kísérlet vázlatos elrendezése: http://hyperphysics.phy-astr.gsu.edu/hbase/frhz.html
Modern Fizika Labor Fizika BSC
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. május 4. A mérés száma és címe: 9. Röntgen-fluoreszencia analízis Értékelés: A beadás dátuma: 2009. május 13. A mérést végezte: Márton Krisztina Zsigmond
Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. május 4. A mérés száma és címe: 9. Röntgen-fluoreszencia analízis Értékelés: A beadás dátuma: 2009. május 13. A mérést végezte: Márton Krisztina Zsigmond
Röntgensugárzás. Röntgensugárzás
 Röntgensugárzás 2012.11.21. Röntgensugárzás Elektromágneses sugárzás (f=10 16 10 19 Hz, E=120eV 120keV (1.9*10-17 10-14 J), λ
Röntgensugárzás 2012.11.21. Röntgensugárzás Elektromágneses sugárzás (f=10 16 10 19 Hz, E=120eV 120keV (1.9*10-17 10-14 J), λ
Sugárzások kölcsönhatása az anyaggal
 Radioaktivitás Biofizika előadások 2013 december Sugárzások kölcsönhatása az anyaggal PTE ÁOK Biofizikai Intézet, Orbán József Összefoglaló radioaktivitás alapok Nukleononkénti kötési energia (MeV) Egy
Radioaktivitás Biofizika előadások 2013 december Sugárzások kölcsönhatása az anyaggal PTE ÁOK Biofizikai Intézet, Orbán József Összefoglaló radioaktivitás alapok Nukleononkénti kötési energia (MeV) Egy
Abszolút és relatív aktivitás mérése
 Korszerű vizsgálati módszerek labor 8. mérés Abszolút és relatív aktivitás mérése Mérést végezte: Ugi Dávid B4VBAA Szak: Fizika Mérésvezető: Lökös Sándor Mérőtársak: Musza Alexandra Török Mátyás Mérés
Korszerű vizsgálati módszerek labor 8. mérés Abszolút és relatív aktivitás mérése Mérést végezte: Ugi Dávid B4VBAA Szak: Fizika Mérésvezető: Lökös Sándor Mérőtársak: Musza Alexandra Török Mátyás Mérés
Methods to measure low cross sections for nuclear astrophysics
 Methods to measure low cross sections for nuclear astrophysics Mérési módszerek asztrofizikailag jelentős alacsony magfizikai hatáskeresztmetszetek meghatározására Szücs Tamás Nukleáris asztrofizikai csoport
Methods to measure low cross sections for nuclear astrophysics Mérési módszerek asztrofizikailag jelentős alacsony magfizikai hatáskeresztmetszetek meghatározására Szücs Tamás Nukleáris asztrofizikai csoport
Az asztrofizikai p-folyamat kísérleti vizsgálata befogási reakciókban
 Az asztrofizikai p-folyamat kísérleti vizsgálata befogási reakciókban Zárójelentés az F 043408 ifjúsági OTKA pályázatról Témavezető: Gyürky György A vasnál nehezebb elemek izotópjai a csillagfejlődés előrehaladott
Az asztrofizikai p-folyamat kísérleti vizsgálata befogási reakciókban Zárójelentés az F 043408 ifjúsági OTKA pályázatról Témavezető: Gyürky György A vasnál nehezebb elemek izotópjai a csillagfejlődés előrehaladott
Az atommag összetétele, radioaktivitás
 Az atommag összetétele, radioaktivitás Az atommag alkotórészei proton: pozitív töltésű részecske, töltése egyenlő az elektron töltésével, csak nem negatív, hanem pozitív: 1,6 10-19 C tömege az elektron
Az atommag összetétele, radioaktivitás Az atommag alkotórészei proton: pozitív töltésű részecske, töltése egyenlő az elektron töltésével, csak nem negatív, hanem pozitív: 1,6 10-19 C tömege az elektron
PROMPT- ÉS KÉSŐ-GAMMA NEUTRONAKTIVÁCIÓS ANALÍZIS A GEOKÉMIÁBAN I. rész
 PROMPT- ÉS KÉSŐ-GAMMA NEUTRONAKTIVÁCIÓS ANALÍZIS A GEOKÉMIÁBAN I. rész MTA Izotópkutató Intézet Gméling Katalin, 2009. november 16. gmeling@iki.kfki.hu Isle of Skye, UK 1 MAGSPEKTROSZKÓPIAI MÓDSZEREK Gerjesztés:
PROMPT- ÉS KÉSŐ-GAMMA NEUTRONAKTIVÁCIÓS ANALÍZIS A GEOKÉMIÁBAN I. rész MTA Izotópkutató Intézet Gméling Katalin, 2009. november 16. gmeling@iki.kfki.hu Isle of Skye, UK 1 MAGSPEKTROSZKÓPIAI MÓDSZEREK Gerjesztés:
Folyadékszcintillációs spektroszkópia jegyz könyv
 Folyadékszcintillációs spektroszkópia jegyz könyv Zsigmond Anna Julia Fizika MSc I. Mérés vezet je: Horváth Ákos Mérés dátuma: 2010. október 21. Leadás dátuma: 2010. november 8. 1 1. Bevezetés A mérés
Folyadékszcintillációs spektroszkópia jegyz könyv Zsigmond Anna Julia Fizika MSc I. Mérés vezet je: Horváth Ákos Mérés dátuma: 2010. október 21. Leadás dátuma: 2010. november 8. 1 1. Bevezetés A mérés
 http://www.nucleonica.net Az atommag tömege A hidrogénre vonatkoztatott relatív atomtömeg (=atommag tömegével, ha az e - tömegét elhanyagoljuk) a hidrogénnek nem egész számú többszöröse. Az elemek különböző
http://www.nucleonica.net Az atommag tömege A hidrogénre vonatkoztatott relatív atomtömeg (=atommag tömegével, ha az e - tömegét elhanyagoljuk) a hidrogénnek nem egész számú többszöröse. Az elemek különböző
Atomfizika. A hidrogén lámpa színképei. Elektronok H atom. Fényképlemez. emisszió H 2. gáz
 Atomfizika A hidrogén lámpa színképei - Elektronok H atom emisszió Fényképlemez V + H 2 gáz Az atom és kvantumfizika fejlődésének fontos szakasza volt a hidrogén lámpa színképeinek leírása, és a vonalas
Atomfizika A hidrogén lámpa színképei - Elektronok H atom emisszió Fényképlemez V + H 2 gáz Az atom és kvantumfizika fejlődésének fontos szakasza volt a hidrogén lámpa színképeinek leírása, és a vonalas
8. AZ ATOMMAG FIZIKÁJA
 8. AZ ATOMMAG FIZIKÁJA Az atommag szerkezete (40-44 oldal) A tömegspektrométer elve Az atommag komponensei Izotópok Tömeghiány, kötési energia, stabilitás Magerők Magmodellek Az atommag stabilitásának
8. AZ ATOMMAG FIZIKÁJA Az atommag szerkezete (40-44 oldal) A tömegspektrométer elve Az atommag komponensei Izotópok Tömeghiány, kötési energia, stabilitás Magerők Magmodellek Az atommag stabilitásának
NEUTRON-DETEKTOROK VIZSGÁLATA. Mérési útmutató BME NTI 1997
 NEUTRON-DETEKTOROK VIZSGÁLATA Mérési útmutató Gyurkócza Csaba, Balázs László BME NTI 1997 Tartalomjegyzék 1. Bevezetés 3. 2. Elméleti összefoglalás 3. 2.1. A neutrondetektoroknál alkalmazható legfontosabb
NEUTRON-DETEKTOROK VIZSGÁLATA Mérési útmutató Gyurkócza Csaba, Balázs László BME NTI 1997 Tartalomjegyzék 1. Bevezetés 3. 2. Elméleti összefoglalás 3. 2.1. A neutrondetektoroknál alkalmazható legfontosabb
Radiokémia vegyész MSc radiokémia szakirány Kónya József, M. Nagy Noémi: Izotópia I és II. Debreceni Egyetemi Kiadó, 2007, 2008.
 Radiokémia vegyész MSc radiokémia szakirány Kónya József, M. Nagy Noémi: Izotópia I és II. Debreceni Egyetemi Kiadó, 2007, 2008. Kiss István,Vértes Attila: Magkémia (Akadémiai Kiadó) Nagy Lajos György,
Radiokémia vegyész MSc radiokémia szakirány Kónya József, M. Nagy Noémi: Izotópia I és II. Debreceni Egyetemi Kiadó, 2007, 2008. Kiss István,Vértes Attila: Magkémia (Akadémiai Kiadó) Nagy Lajos György,
Röntgensugárzás az orvostudományban. Röntgen kép és Komputer tomográf (CT)
 Röntgensugárzás az orvostudományban Röntgen kép és Komputer tomográf (CT) Orbán József, Biofizikai Intézet, 2008 Hand mit Ringen: print of Wilhelm Röntgen's first "medical" x-ray, of his wife's hand, taken
Röntgensugárzás az orvostudományban Röntgen kép és Komputer tomográf (CT) Orbán József, Biofizikai Intézet, 2008 Hand mit Ringen: print of Wilhelm Röntgen's first "medical" x-ray, of his wife's hand, taken
Radioaktív sugárzások tulajdonságai és kölcsönhatásuk az elnyelő közeggel. A radioaktív sugárzások detektálása.
 Radioaktív sugárzások tulajdonságai és kölcsönhatásuk az elnyelő közeggel. A radioaktív sugárzások detektálása. Magsugárzások (α, β, γ) kölcsönhatása atomi rendszerekkel (170-174, 540-545 o.) Direkt és
Radioaktív sugárzások tulajdonságai és kölcsönhatásuk az elnyelő közeggel. A radioaktív sugárzások detektálása. Magsugárzások (α, β, γ) kölcsönhatása atomi rendszerekkel (170-174, 540-545 o.) Direkt és
Atomenergetikai alapismeretek
 Atomenergetikai alapismeretek 2. előadás Dr. Szieberth Máté Dr. Sükösd Csaba előadásanyagának felhasználásával Négyfaktor formula (végtelen kiterjedésű n-sokszorozó közeg) n Maghasadás (gyors neutronok)
Atomenergetikai alapismeretek 2. előadás Dr. Szieberth Máté Dr. Sükösd Csaba előadásanyagának felhasználásával Négyfaktor formula (végtelen kiterjedésű n-sokszorozó közeg) n Maghasadás (gyors neutronok)
Az ionizáló sugárzások fajtái, forrásai
 Az ionizáló sugárzások fajtái, forrásai magsugárzás Magsugárzások Röntgensugárzás Függelék. Intenzitás 2. Spektrum 3. Atom Repetitio est mater studiorum. Röntgen Ionizációnak nevezzük azt a folyamatot,
Az ionizáló sugárzások fajtái, forrásai magsugárzás Magsugárzások Röntgensugárzás Függelék. Intenzitás 2. Spektrum 3. Atom Repetitio est mater studiorum. Röntgen Ionizációnak nevezzük azt a folyamatot,
Adatgyőjtés, mérési alapok, a környezetgazdálkodás fontosabb mőszerei
 GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Adatgyőjtés, mérési
GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Adatgyőjtés, mérési
Sugárterápia. Ionizáló sugárzások elnyelődésének következményei. Konzultáció: minden hétfőn 15 órakor. 1. Fizikai történések
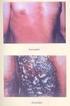 Sugárterápia 40% 35% 30% 25% 20% 15% % 5% 0% 2014/2015. tanév FOK biofizika kollokvium jegyspektruma 5 4,5 4 3,5 3 2,5 2 1,5 1 Konzultáció: minden hétfőn 15 órakor Ionizáló sugárzások elnyelődésének következményei
Sugárterápia 40% 35% 30% 25% 20% 15% % 5% 0% 2014/2015. tanév FOK biofizika kollokvium jegyspektruma 5 4,5 4 3,5 3 2,5 2 1,5 1 Konzultáció: minden hétfőn 15 órakor Ionizáló sugárzások elnyelődésének következményei
IBA: 5 MV Van de Graaff gyorsító
 Nanostruktúrák vizsgálata ionnyalábokkal Szilágyi Edit MTA Wigner FK, RMI Az előadás vázlata Ionnyalábos analitika (IBA) Lehet-e e információt szerezni nanoszerkezetekről IBA- val? Példák: Pórusos szerkezetek
Nanostruktúrák vizsgálata ionnyalábokkal Szilágyi Edit MTA Wigner FK, RMI Az előadás vázlata Ionnyalábos analitika (IBA) Lehet-e e információt szerezni nanoszerkezetekről IBA- val? Példák: Pórusos szerkezetek
Atommodellek de Broglie hullámhossz Davisson-Germer-kísérlet
 Atommodellek de Broglie hullámhossz Davisson-Germer-kísérlet Utolsó módosítás: 2016. május 4. 1 Előzmények Az atomok színképe (1) A fehér fény komponensekre bontható: http://en.wikipedia.org/wiki/spectrum
Atommodellek de Broglie hullámhossz Davisson-Germer-kísérlet Utolsó módosítás: 2016. május 4. 1 Előzmények Az atomok színképe (1) A fehér fény komponensekre bontható: http://en.wikipedia.org/wiki/spectrum
Modern Fizika Labor. Fizika BSc. Értékelés: A mérés dátuma: A mérés száma és címe: 5. mérés: Elektronspin rezonancia. 2008. március 18.
 Modern Fizika Labor Fizika BSc A mérés dátuma: 28. március 18. A mérés száma és címe: 5. mérés: Elektronspin rezonancia Értékelés: A beadás dátuma: 28. március 26. A mérést végezte: 1/7 A mérés leírása:
Modern Fizika Labor Fizika BSc A mérés dátuma: 28. március 18. A mérés száma és címe: 5. mérés: Elektronspin rezonancia Értékelés: A beadás dátuma: 28. március 26. A mérést végezte: 1/7 A mérés leírása:
Thomson-modell (puding-modell)
 Atommodellek Thomson-modell (puding-modell) A XX. század elejére világossá vált, hogy az atomban található elektronok ugyanazok, mint a katódsugárzás részecskéi. Magyarázatra várt azonban, hogy mi tartja
Atommodellek Thomson-modell (puding-modell) A XX. század elejére világossá vált, hogy az atomban található elektronok ugyanazok, mint a katódsugárzás részecskéi. Magyarázatra várt azonban, hogy mi tartja
Atomfizika. Az atommag szerkezete. Radioaktivitás Biofizika, Nyitrai Miklós
 Atomfizika. Az atommag szerkezete. Radioaktivitás. 2010. 10. 13. Biofizika, Nyitrai Miklós Összefoglalás Atommag alkotói, szerkezete; Erős vagy magkölcsönhatás; Tömegdefektus. A kölcsönhatások világképe
Atomfizika. Az atommag szerkezete. Radioaktivitás. 2010. 10. 13. Biofizika, Nyitrai Miklós Összefoglalás Atommag alkotói, szerkezete; Erős vagy magkölcsönhatás; Tömegdefektus. A kölcsönhatások világképe
3. GAMMA-SUGÁRZÁS ENERGIÁJÁNAK MÉRÉSE GAMMA-SPEKTROMETRIAI MÓDSZERREL
 3. GAMMA-SUGÁRZÁS ENERGIÁJÁNAK MÉRÉSE GAMMA-SPEKTROMETRIAI MÓDSZERREL A gamma-sugárzás elektromágneses sugárzás, amely vákuumban fénysebességgel terjed. Anyagba ütközve kölcsönhatásba lép az anyag alkotóelemeivel,
3. GAMMA-SUGÁRZÁS ENERGIÁJÁNAK MÉRÉSE GAMMA-SPEKTROMETRIAI MÓDSZERREL A gamma-sugárzás elektromágneses sugárzás, amely vákuumban fénysebességgel terjed. Anyagba ütközve kölcsönhatásba lép az anyag alkotóelemeivel,
Pásztázó elektronmikroszkóp. Alapelv. Szinkron pásztázás
 Pásztázó elektronmikroszkóp Scanning Electron Microscope (SEM) Rasterelektronenmikroskope (REM) Alapelv Egy elektronágyúval vékony elektronnyalábot állítunk elő. Ezzel pásztázzuk (eltérítő tekercsek segítségével)
Pásztázó elektronmikroszkóp Scanning Electron Microscope (SEM) Rasterelektronenmikroskope (REM) Alapelv Egy elektronágyúval vékony elektronnyalábot állítunk elő. Ezzel pásztázzuk (eltérítő tekercsek segítségével)
Alkalmazás a makrókanónikus sokaságra: A fotongáz
 Alkalmazás a makrókanónikus sokaságra: A fotongáz A fotonok az elektromágneses sugárzás hordozó részecskéi. Spinkvantumszámuk S=, tehát kvantumstatisztikai szempontból bozonok. Fotonoknak habár a spinkvantumszámuk,
Alkalmazás a makrókanónikus sokaságra: A fotongáz A fotonok az elektromágneses sugárzás hordozó részecskéi. Spinkvantumszámuk S=, tehát kvantumstatisztikai szempontból bozonok. Fotonoknak habár a spinkvantumszámuk,
Energia-diszperzív röntgen elemanalízis
 Fókuszált ionsugaras megmunkálás Energia-diszperzív röntgen elemanalízis FEI Quanta 3D SEM/FIB Dankházi Zoltán 2016. március 1 EDS = Energy Dispersive Spectroscopy Hol található a SEM/FIB berendezésen?
Fókuszált ionsugaras megmunkálás Energia-diszperzív röntgen elemanalízis FEI Quanta 3D SEM/FIB Dankházi Zoltán 2016. március 1 EDS = Energy Dispersive Spectroscopy Hol található a SEM/FIB berendezésen?
 http://www.flickr.com Az atommag állapotait kvantummechanikai állapotfüggvénnyel írjuk le. A mag paritását ezen fv. paritása adja meg. Paritás: egy állapot tértükrözéssel szemben mutatott viselkedését
http://www.flickr.com Az atommag állapotait kvantummechanikai állapotfüggvénnyel írjuk le. A mag paritását ezen fv. paritása adja meg. Paritás: egy állapot tértükrözéssel szemben mutatott viselkedését
Részecske azonosítás kísérleti módszerei
 Részecske azonosítás kísérleti módszerei Galgóczi Gábor Előadás vázlata A részecske azonosítás létjogosultsága Részecske azonosítás: Módszerek Detektorok ALICE-ból példa A részecskeazonosítás létjogosultsága
Részecske azonosítás kísérleti módszerei Galgóczi Gábor Előadás vázlata A részecske azonosítás létjogosultsága Részecske azonosítás: Módszerek Detektorok ALICE-ból példa A részecskeazonosítás létjogosultsága
Jegyzet. Kémia, BMEVEAAAMM1 Műszaki menedzser hallgatók számára Dr Csonka Gábor, egyetemi tanár Dr Madarász János, egyetemi docens.
 Kémia, BMEVEAAAMM Műszaki menedzser hallgatók számára Dr Csonka Gábor, egyetemi tanár Dr Madarász János, egyetemi docens Jegyzet dr. Horváth Viola, KÉMIA I. http://oktatas.ch.bme.hu/oktatas/konyvek/anal/
Kémia, BMEVEAAAMM Műszaki menedzser hallgatók számára Dr Csonka Gábor, egyetemi tanár Dr Madarász János, egyetemi docens Jegyzet dr. Horváth Viola, KÉMIA I. http://oktatas.ch.bme.hu/oktatas/konyvek/anal/
Radioaktív sugárzások tulajdonságai és kölcsönhatásuk az elnyelő közeggel. A radioaktív sugárzások detektálása.
 Különböző sugárzások tulajdonságai Típus töltés Energia hordozó E spektrum Radioaktí sugárzások tulajdonságai és kölcsönhatásuk az elnyelő közeggel. A radioaktí sugárzások detektálása. α-sugárzás pozití
Különböző sugárzások tulajdonságai Típus töltés Energia hordozó E spektrum Radioaktí sugárzások tulajdonságai és kölcsönhatásuk az elnyelő közeggel. A radioaktí sugárzások detektálása. α-sugárzás pozití
Sugárterápia. Ionizáló sugárzások elnyelődésének következményei
 Sugárterápia Sugárterápia: ionizáló sugárzások klinikai alkalmazása malignus daganatok eltávolításában. A sugárkezelés során célunk az ionizáló sugárzás terápiás dózisának elérése a kezelt daganatban a
Sugárterápia Sugárterápia: ionizáló sugárzások klinikai alkalmazása malignus daganatok eltávolításában. A sugárkezelés során célunk az ionizáló sugárzás terápiás dózisának elérése a kezelt daganatban a
Atommagok alapvető tulajdonságai
 Atommagok alapvető tulajdonságai Mag és részecskefizika 5. előadás 017. március 17. Áttekintés Atommagok szerkezete a kvarkképben proton szerkezete, atommagok szerkezete, magerő Atommagok összetétele izotópok,
Atommagok alapvető tulajdonságai Mag és részecskefizika 5. előadás 017. március 17. Áttekintés Atommagok szerkezete a kvarkképben proton szerkezete, atommagok szerkezete, magerő Atommagok összetétele izotópok,
A sugárzások és az anyag fizikai kölcsönhatásai
 A sugárzások és az anyag fizikai kölcsönhatásai A kölcsönhatásban résztvevő partner 1. Atommag 2. Az atommag erőtere 3. Elektron (szabad, kötött) 4. Elektromos erőtér 5. Molekulák 6. Makroszkopikus rendszerek
A sugárzások és az anyag fizikai kölcsönhatásai A kölcsönhatásban résztvevő partner 1. Atommag 2. Az atommag erőtere 3. Elektron (szabad, kötött) 4. Elektromos erőtér 5. Molekulák 6. Makroszkopikus rendszerek
Atomfizika. Fizika kurzus Dr. Seres István
 Atomfizika Fizika kurzus Dr. Seres István Történeti áttekintés J.J. Thomson (1897) Katódsugárcsővel végzett kísérleteket az elektron fajlagos töltésének (e/m) meghatározására. A katódsugarat alkotó részecskét
Atomfizika Fizika kurzus Dr. Seres István Történeti áttekintés J.J. Thomson (1897) Katódsugárcsővel végzett kísérleteket az elektron fajlagos töltésének (e/m) meghatározására. A katódsugarat alkotó részecskét
Termodinamika (Hőtan)
 Termodinamika (Hőtan) Termodinamika A hőtan nagyszámú részecskéből (pl. gázmolekulából) álló makroszkópikus rendszerekkel foglalkozik. A nagy számok miatt érdemes a mólt bevezetni, ami egy Avogadro-számnyi
Termodinamika (Hőtan) Termodinamika A hőtan nagyszámú részecskéből (pl. gázmolekulából) álló makroszkópikus rendszerekkel foglalkozik. A nagy számok miatt érdemes a mólt bevezetni, ami egy Avogadro-számnyi
Sugárzások kölcsönhatása az anyaggal
 Sugárzások kölcsönhatása az anyaggal Dr. Vincze Árpád vincze@oah.hu Mitől függ a kölcsönhatás? VÁLASZ: Az anyag felépítése A sugárzások típusai, forrásai és főbb tulajdonságai A sugárzások és az anyag
Sugárzások kölcsönhatása az anyaggal Dr. Vincze Árpád vincze@oah.hu Mitől függ a kölcsönhatás? VÁLASZ: Az anyag felépítése A sugárzások típusai, forrásai és főbb tulajdonságai A sugárzások és az anyag
OPTIKA. Fénykibocsátás mechanizmusa fényforrás típusok. Dr. Seres István
 OPTIKA Fénykibocsátás mechanizmusa Dr. Seres István Bohr modell Niels Bohr (19) Rutherford felfedezte az atommagot, és igazolta, hogy negatív töltésű elektronok keringenek körülötte. Niels Bohr Bohr ezt
OPTIKA Fénykibocsátás mechanizmusa Dr. Seres István Bohr modell Niels Bohr (19) Rutherford felfedezte az atommagot, és igazolta, hogy negatív töltésű elektronok keringenek körülötte. Niels Bohr Bohr ezt
Sugárvédelem kurzus fogorvostanhallgatók számra. Töltött részecskék elnyelődése. Sugárzások és anyag kölcsönhatása. A sugárzások elnyelődése
 Sugárvédelem kurzus fogorvostanhallgatók számra 2. Az ionizáló sugárzás és az anyag kölcsönhatása. Fizikai dózisfogalmak és az ionizáló sugárzás mérése Sugárzások és anyag kölcsönhatása. A sugárzások elnyelődése
Sugárvédelem kurzus fogorvostanhallgatók számra 2. Az ionizáló sugárzás és az anyag kölcsönhatása. Fizikai dózisfogalmak és az ionizáló sugárzás mérése Sugárzások és anyag kölcsönhatása. A sugárzások elnyelődése
A nanotechnológia mikroszkópja
 1 Havancsák Károly, ELTE Fizikai Intézet A nanotechnológia mikroszkópja EGIS 2011. június 1. FEI Quanta 3D SEM/FIB 2 Havancsák Károly, ELTE Fizikai Intézet A nanotechnológia mikroszkópja EGIS 2011. június
1 Havancsák Károly, ELTE Fizikai Intézet A nanotechnológia mikroszkópja EGIS 2011. június 1. FEI Quanta 3D SEM/FIB 2 Havancsák Károly, ELTE Fizikai Intézet A nanotechnológia mikroszkópja EGIS 2011. június
Az atom felépítése Alapfogalmak
 Anyagszerkezeti vizsgálatok 2017/2018. 1. félév Az atom felépítése Alapfogalmak Csordás Anita E-mail: csordasani@almos.uni-pannon.hu Tel:+36-88/624-924 Pannon Egyetem Radiokémiai és Radioökológiai Intézet
Anyagszerkezeti vizsgálatok 2017/2018. 1. félév Az atom felépítése Alapfogalmak Csordás Anita E-mail: csordasani@almos.uni-pannon.hu Tel:+36-88/624-924 Pannon Egyetem Radiokémiai és Radioökológiai Intézet
Izotóp geológia: Elemek izotópjainak használata geológiai folyamatok értelmezéséhez.
 Radioaktív izotópok Izotópok Egy elem különböző tömegű (tömegszámú - A) formái; Egy elem izotópjainak a magjai azonos számú protont (rendszám - Z) és különböző számú neutront (N) tartalmaznak; Egy elem
Radioaktív izotópok Izotópok Egy elem különböző tömegű (tömegszámú - A) formái; Egy elem izotópjainak a magjai azonos számú protont (rendszám - Z) és különböző számú neutront (N) tartalmaznak; Egy elem
A gamma-sugárzás kölcsönhatásai
 Ref. [3] A gamma-sugárzás kölcsönhatásai Az anyaggal való kölcsönhatás kis valószínűségű hatótávolság nagy A sugárzás gyengülését 3 féle kölcsönhatás okozza. fotoeffektus Compton-szórás párkeltés A gamma-fotonok
Ref. [3] A gamma-sugárzás kölcsönhatásai Az anyaggal való kölcsönhatás kis valószínűségű hatótávolság nagy A sugárzás gyengülését 3 féle kölcsönhatás okozza. fotoeffektus Compton-szórás párkeltés A gamma-fotonok
2, = 5221 K (7.2)
 7. Gyakorlat 4A-7 Az emberi szem kb. 555 nm hullámhossznál a Iegnagyobb érzékenységű. Adjuk meg annak a fekete testnek a hőmérsékletét, amely sugárzásának a spektrális teljesitménye ezen a hullámhosszon
7. Gyakorlat 4A-7 Az emberi szem kb. 555 nm hullámhossznál a Iegnagyobb érzékenységű. Adjuk meg annak a fekete testnek a hőmérsékletét, amely sugárzásának a spektrális teljesitménye ezen a hullámhosszon
Modern fizika vegyes tesztek
 Modern fizika vegyes tesztek 1. Egy fotonnak és egy elektronnak ugyanakkora a hullámhossza. Melyik a helyes állítás? a) A foton lendülete (impulzusa) kisebb, mint az elektroné. b) A fotonnak és az elektronnak
Modern fizika vegyes tesztek 1. Egy fotonnak és egy elektronnak ugyanakkora a hullámhossza. Melyik a helyes állítás? a) A foton lendülete (impulzusa) kisebb, mint az elektroné. b) A fotonnak és az elektronnak
A Tycho-szupernova. 1572ben Tycho Brahe megfigyelt egy felrobbanó csillagot. 400 évvel később egy többmillió fokos buborék látható (zöld és kék a
 A plazmaállapot + és tötésekből álló semleges gáz A részecskék közötti kcshatás jelentős A Debye-sugáron belül sok részecske található A Debye-sugár kicsi a plazma méreteihez képest Az elektron-kcsh erősebb,
A plazmaállapot + és tötésekből álló semleges gáz A részecskék közötti kcshatás jelentős A Debye-sugáron belül sok részecske található A Debye-sugár kicsi a plazma méreteihez képest Az elektron-kcsh erősebb,
Török Zsófia, Huszánk Róbert, Csedreki László, Kertész Zsófia és Dani János. Fizikus Doktoranduszok Konferenciája Balatonfenyves,
 Török Zsófia, Huszánk Róbert, Csedreki László, Kertész Zsófia és Dani János Fizikus Doktoranduszok Konferenciája Balatonfenyves, 2013.06.21-23 PIXE Particle Induced X-ray Emission Részecske indukált röntgenemissziós
Török Zsófia, Huszánk Róbert, Csedreki László, Kertész Zsófia és Dani János Fizikus Doktoranduszok Konferenciája Balatonfenyves, 2013.06.21-23 PIXE Particle Induced X-ray Emission Részecske indukált röntgenemissziós
Szilárd Leó Fizikaverseny Számítógépes feladat
 Szilárd Leó Fizikaverseny 2006. Számítógépes feladat A feladat során 10 B atommagok gerjesztett állapotának (rövid) élettartamát fogjuk megmérni. Egy gyorsító-berendezéssel 10 B ionokat (atommagokat) gyorsítunk,
Szilárd Leó Fizikaverseny 2006. Számítógépes feladat A feladat során 10 B atommagok gerjesztett állapotának (rövid) élettartamát fogjuk megmérni. Egy gyorsító-berendezéssel 10 B ionokat (atommagokat) gyorsítunk,
Sugárzás kölcsönhatása az anyaggal 1. Fény kölcsönhatása az anyaggal. 2. Ionizáló sugárzás kölcsönhatása az anyaggal KAD
 Sugárzás kölcsönhatása az anyaggal 1. Fény kölcsönhatása az anyaggal 2. Ionizáló sugárzás kölcsönhatása az anyaggal KAD 2012.10.03 1976 2 1. 3 4 n 1 >n 2 5 6 7 8 9 10 11 12 13 14 2. Az ionizáló sugárzások
Sugárzás kölcsönhatása az anyaggal 1. Fény kölcsönhatása az anyaggal 2. Ionizáló sugárzás kölcsönhatása az anyaggal KAD 2012.10.03 1976 2 1. 3 4 n 1 >n 2 5 6 7 8 9 10 11 12 13 14 2. Az ionizáló sugárzások
Általános Kémia, BMEVESAA101 Dr Csonka Gábor, egyetemi tanár. Az anyag Készítette: Dr. Csonka Gábor egyetemi tanár,
 Általános Kémia, BMEVESAA101 Dr Csonka Gábor, egyetemi tanár Az anyag Készítette: Dr. Csonka Gábor egyetemi tanár, csonkagi@gmail.com 1 Jegyzet Dr. Csonka Gábor http://web.inc.bme.hu/csonka/ Facebook,
Általános Kémia, BMEVESAA101 Dr Csonka Gábor, egyetemi tanár Az anyag Készítette: Dr. Csonka Gábor egyetemi tanár, csonkagi@gmail.com 1 Jegyzet Dr. Csonka Gábor http://web.inc.bme.hu/csonka/ Facebook,
Bevezetés a modern fizika fejezeteibe. 4. (a) Kvantummechanika. Utolsó módosítás: november 15. Dr. Márkus Ferenc BME Fizika Tanszék
 Bevezetés a modern fizika fejezeteibe 4. (a) Kvantummechanika Utolsó módosítás: 2015. november 15. 1 Előzmények Az atomok színképe (1) A fehér fény komponensekre bontható: http://en.wikipedia.org/wiki/spectrum
Bevezetés a modern fizika fejezeteibe 4. (a) Kvantummechanika Utolsó módosítás: 2015. november 15. 1 Előzmények Az atomok színképe (1) A fehér fény komponensekre bontható: http://en.wikipedia.org/wiki/spectrum
Sugárzások kölcsönhatása az anyaggal. Dr. Vincze Árpád vincze@oah.hu
 Sugárzások kölcsönhatása az anyaggal Dr. Vincze Árpád vincze@oah.hu Mitől függ a kölcsönhatás? VÁLASZ: Az anyag felépítése A sugárzások típusai, forrásai és főbb tulajdonságai A sugárzások és az anyag
Sugárzások kölcsönhatása az anyaggal Dr. Vincze Árpád vincze@oah.hu Mitől függ a kölcsönhatás? VÁLASZ: Az anyag felépítése A sugárzások típusai, forrásai és főbb tulajdonságai A sugárzások és az anyag
Adatgyűjtés, mérési alapok, a környezetgazdálkodás fontosabb műszerei
 Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Gazdálkodási modul Gazdaságtudományi ismeretek I. Közgazdasá Adatgyűjtés, mérési alapok, a környezetgazdálkodás fontosabb műszerei KÖRNYEZETGAZDÁLKODÁSI
Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Gazdálkodási modul Gazdaságtudományi ismeretek I. Közgazdasá Adatgyűjtés, mérési alapok, a környezetgazdálkodás fontosabb műszerei KÖRNYEZETGAZDÁLKODÁSI
A radioaktív bomlás típusai
 A radioaktív bomlás típusai Párhuzamos negatív és pozitív bétabomlás/elektronbefogás 40 19 K kb.89% 0.001%, kb.11% EX 40 40 Ca Ar Felszabaduló energia Ca-40: 1311 kev Ar-40: 1505 kev Felezési idő P-40
A radioaktív bomlás típusai Párhuzamos negatív és pozitív bétabomlás/elektronbefogás 40 19 K kb.89% 0.001%, kb.11% EX 40 40 Ca Ar Felszabaduló energia Ca-40: 1311 kev Ar-40: 1505 kev Felezési idő P-40
Havancsák Károly Nagyfelbontású kétsugaras pásztázó elektronmikroszkóp az ELTÉ-n: lehetőségek, eddigi eredmények
 Havancsák Károly Nagyfelbontású kétsugaras pásztázó elektronmikroszkóp az ELTÉ-n: lehetőségek, eddigi eredmények Nanoanyagok és nanotechnológiák Albizottság ELTE TTK 2013. Havancsák Károly Nagyfelbontású
Havancsák Károly Nagyfelbontású kétsugaras pásztázó elektronmikroszkóp az ELTÉ-n: lehetőségek, eddigi eredmények Nanoanyagok és nanotechnológiák Albizottság ELTE TTK 2013. Havancsák Károly Nagyfelbontású
Általános Kémia, BMEVESAA101
 Általános Kémia, BMEVESAA101 Dr Csonka Gábor, egyetemi tanár Az anyag Készítette: Dr. Csonka Gábor egyetemi tanár, csonkagi@gmail.com 1 Jegyzet Dr. Csonka Gábor http://web.inc.bme.hu/csonka/ Óravázlatok:
Általános Kémia, BMEVESAA101 Dr Csonka Gábor, egyetemi tanár Az anyag Készítette: Dr. Csonka Gábor egyetemi tanár, csonkagi@gmail.com 1 Jegyzet Dr. Csonka Gábor http://web.inc.bme.hu/csonka/ Óravázlatok:
Modern Fizika Labor. 5. ESR (Elektronspin rezonancia) Fizika BSc. A mérés dátuma: okt. 25. A mérés száma és címe: Értékelés:
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 25. A mérés száma és címe: 5. ESR (Elektronspin rezonancia) Értékelés: A beadás dátuma: 2011. nov. 16. A mérést végezte: Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 25. A mérés száma és címe: 5. ESR (Elektronspin rezonancia) Értékelés: A beadás dátuma: 2011. nov. 16. A mérést végezte: Szőke Kálmán Benjamin
alapvető tulajdonságai
 A z a to m m a g o k alapvető tulajdonságai Mérhető mennyiségek Az atommagok mérete, tömege, töltése, spinje, mágneses momentuma, elektromos kvadrupól momentuma Az atommag töltés- és nukleon-eloszlása
A z a to m m a g o k alapvető tulajdonságai Mérhető mennyiségek Az atommagok mérete, tömege, töltése, spinje, mágneses momentuma, elektromos kvadrupól momentuma Az atommag töltés- és nukleon-eloszlása
A TÖMEGSPEKTROMETRIA ALAPJAI
 A TÖMEGSPEKTROMETRIA ALAPJAI web.inc.bme.hu/csonka/csg/oktat/tomegsp.doc alapján tömeg-töltés arány szerinti szétválasztás a legérzékenyebb módszerek közé tartozik (Nagyon kis anyagmennyiség kimutatására
A TÖMEGSPEKTROMETRIA ALAPJAI web.inc.bme.hu/csonka/csg/oktat/tomegsp.doc alapján tömeg-töltés arány szerinti szétválasztás a legérzékenyebb módszerek közé tartozik (Nagyon kis anyagmennyiség kimutatására
Modern Fizika Labor Fizika BSC
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. március 2. A mérés száma és címe: 5. Elektronspin rezonancia Értékelés: A beadás dátuma: 2009. március 5. A mérést végezte: Márton Krisztina Zsigmond
Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. március 2. A mérés száma és címe: 5. Elektronspin rezonancia Értékelés: A beadás dátuma: 2009. március 5. A mérést végezte: Márton Krisztina Zsigmond
Mágneses módszerek a mőszeres analitikában
 Mágneses módszerek a mőszeres analitikában NMR, ESR: mágneses momentummal rendelkezı anyagok minıségi és mennyiségi meghatározására alkalmas analitikai módszer Atommag spin állapotok közötti energiaátmenetek:
Mágneses módszerek a mőszeres analitikában NMR, ESR: mágneses momentummal rendelkezı anyagok minıségi és mennyiségi meghatározására alkalmas analitikai módszer Atommag spin állapotok közötti energiaátmenetek:
Neutron Aktivációs Analitika
 Neutron Aktivációs Analitika Irodalom: Alfassi, Z.B., 1994, Determination of Trace Elements,(Rehovot: Balaban Publ.) Alfassi, Z.B., 1994b, Chemical Analysis by Nuclear Methods, (Chichester: Wiley) Alfassi,
Neutron Aktivációs Analitika Irodalom: Alfassi, Z.B., 1994, Determination of Trace Elements,(Rehovot: Balaban Publ.) Alfassi, Z.B., 1994b, Chemical Analysis by Nuclear Methods, (Chichester: Wiley) Alfassi,
Magfizika tesztek. 1. Melyik részecske nem tartozik a nukleonok közé? a) elektron b) proton c) neutron d) egyik sem
 1. Melyik részecske nem tartozik a nukleonok közé? a) elektron b) proton c) neutron d) egyik sem 2. Mit nevezünk az atom tömegszámának? a) a protonok számát b) a neutronok számát c) a protonok és neutronok
1. Melyik részecske nem tartozik a nukleonok közé? a) elektron b) proton c) neutron d) egyik sem 2. Mit nevezünk az atom tömegszámának? a) a protonok számát b) a neutronok számát c) a protonok és neutronok
Fókuszált ionsugaras megmunkálás
 1 FEI Quanta 3D SEM/FIB Fókuszált ionsugaras megmunkálás Ratter Kitti 2011. január 19-21. 2 FIB = Focused Ion Beam (Fókuszált ionnyaláb) Miből áll egy SEM/FIB berendezés? elektron oszlop ion oszlop gáz
1 FEI Quanta 3D SEM/FIB Fókuszált ionsugaras megmunkálás Ratter Kitti 2011. január 19-21. 2 FIB = Focused Ion Beam (Fókuszált ionnyaláb) Miből áll egy SEM/FIB berendezés? elektron oszlop ion oszlop gáz
Adatgyőjtés, mérési alapok, a környezetgazdálkodás fontosabb mőszerei
 GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Adatgyőjtés, mérési
GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Adatgyőjtés, mérési
Modern Fizika Labor. 12. Infravörös spektroszkópia. Fizika BSc. A mérés dátuma: okt. 04. A mérés száma és címe: Értékelés:
 Modern Fizika Labor Fizika BSc A mérés dátuma: 011. okt. 04. A mérés száma és címe: 1. Infravörös spektroszkópia Értékelés: A beadás dátuma: 011. dec. 1. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 011. okt. 04. A mérés száma és címe: 1. Infravörös spektroszkópia Értékelés: A beadás dátuma: 011. dec. 1. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Modern Fizika Labor. 2. Elemi töltés meghatározása
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Atomfizika. Fizika kurzus Dr. Seres István
 Atomfizika Fizika kurzus Dr. Seres István Történeti áttekintés 440 BC Democritus, Leucippus, Epicurus 1660 Pierre Gassendi 1803 1897 1904 1911 19 193 John Dalton Joseph John (J.J.) Thomson J.J. Thomson
Atomfizika Fizika kurzus Dr. Seres István Történeti áttekintés 440 BC Democritus, Leucippus, Epicurus 1660 Pierre Gassendi 1803 1897 1904 1911 19 193 John Dalton Joseph John (J.J.) Thomson J.J. Thomson
IMFP meghatározása Co, Cu, Ge, Si és Au mintákban 56
 3.1.2. IMFP meghatározása Co, Cu, Ge, Si és Au mintákban 56 3.1.2. Elektronok rugalmatlan szórási közepes szabad úthosszának meghatározása Co, Cu, Ge, Si és Au mintákban, a 2-10 kev elektron energia tartományban
3.1.2. IMFP meghatározása Co, Cu, Ge, Si és Au mintákban 56 3.1.2. Elektronok rugalmatlan szórási közepes szabad úthosszának meghatározása Co, Cu, Ge, Si és Au mintákban, a 2-10 kev elektron energia tartományban
Radioaktivitás és mikrorészecskék felfedezése
 Radioaktivitás és mikrorészecskék felfedezése Mag és részecskefizika 1. előadás 2017. Február 17. A félév tematikája 1. Mikrorészecskék felfedezése 2. Kvark gondolat bevezetése, béta-bomlás, neutrínóhipotézis
Radioaktivitás és mikrorészecskék felfedezése Mag és részecskefizika 1. előadás 2017. Február 17. A félév tematikája 1. Mikrorészecskék felfedezése 2. Kvark gondolat bevezetése, béta-bomlás, neutrínóhipotézis
Fermi Dirac statisztika elemei
 Fermi Dirac statisztika elemei A Fermi Dirac statisztika alapjai Nagy részecskeszámú rendszerek fizikai jellemzéséhez statisztikai leírást kell alkalmazni. (Pl. gázokra érvényes klasszikus statisztika
Fermi Dirac statisztika elemei A Fermi Dirac statisztika alapjai Nagy részecskeszámú rendszerek fizikai jellemzéséhez statisztikai leírást kell alkalmazni. (Pl. gázokra érvényes klasszikus statisztika
Al-Mg-Si háromalkotós egyensúlyi fázisdiagram közelítő számítása
 l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
Modern Fizika Labor. 11. Spektroszkópia. Fizika BSc. A mérés dátuma: dec. 16. A mérés száma és címe: Értékelés: A beadás dátuma: dec. 21.
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. dec. 16. A mérés száma és címe: 11. Spektroszkópia Értékelés: A beadás dátuma: 2011. dec. 21. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. dec. 16. A mérés száma és címe: 11. Spektroszkópia Értékelés: A beadás dátuma: 2011. dec. 21. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Hadronok, atommagok, kvarkok
 Zétényi Miklós Hadronok, atommagok, kvarkok Teleki Blanka Gimnázium Székesfehérvár, 2012. február 21. www.meetthescientist.hu 1 26 Atomok Démokritosz: atom = legkisebb, oszthatatlan részecske Rutherford
Zétényi Miklós Hadronok, atommagok, kvarkok Teleki Blanka Gimnázium Székesfehérvár, 2012. február 21. www.meetthescientist.hu 1 26 Atomok Démokritosz: atom = legkisebb, oszthatatlan részecske Rutherford
3. (b) Kereszthatások. Utolsó módosítás: április 1. Dr. Márkus Ferenc BME Fizika Tanszék
 3. (b) Kereszthatások Utolsó módosítás: 2013. április 1. Vezetési együtthatók fémekben (1) 1 Az elektrongáz hővezetési együtthatója A levezetésben alkalmazott feltételek: 1. Minden elektron ugyanazzal
3. (b) Kereszthatások Utolsó módosítás: 2013. április 1. Vezetési együtthatók fémekben (1) 1 Az elektrongáz hővezetési együtthatója A levezetésben alkalmazott feltételek: 1. Minden elektron ugyanazzal
Milyen simaságú legyen a minta felülete jó minőségű EBSD mérésekhez
 1 Milyen simaságú legyen a minta felülete jó minőségű EBSD mérésekhez Havancsák Károly Dankházi Zoltán Ratter Kitti Varga Gábor Visegrád 2012. január Elektron diffrakció 2 Diffrakció - kinematikus elmélet
1 Milyen simaságú legyen a minta felülete jó minőségű EBSD mérésekhez Havancsák Károly Dankházi Zoltán Ratter Kitti Varga Gábor Visegrád 2012. január Elektron diffrakció 2 Diffrakció - kinematikus elmélet
ELEMI RÉSZECSKÉK ATOMMODELLEK
 ELEMI RÉSZECSKÉK ATOMMODELLEK Az atomok felépítése Készítette: Horváthné Vlasics Zsuzsanna Mi van az atomok belsejében? DÉMOKRITOSZ (Kr.e. 460-370) az anyag nem folytonos parányi, tovább nem bontható,
ELEMI RÉSZECSKÉK ATOMMODELLEK Az atomok felépítése Készítette: Horváthné Vlasics Zsuzsanna Mi van az atomok belsejében? DÉMOKRITOSZ (Kr.e. 460-370) az anyag nem folytonos parányi, tovább nem bontható,
Fókuszált ionsugaras megmunkálás
 FEI Quanta 3D SEM/FIB Dankházi Zoltán 2016. március 1 FIB = Focused Ion Beam (Fókuszált ionnyaláb) Miből áll egy SEM/FIB berendezés? elektron oszlop ion oszlop gáz injektorok detektor CDEM (SE, SI) 2 Dual-Beam
FEI Quanta 3D SEM/FIB Dankházi Zoltán 2016. március 1 FIB = Focused Ion Beam (Fókuszált ionnyaláb) Miből áll egy SEM/FIB berendezés? elektron oszlop ion oszlop gáz injektorok detektor CDEM (SE, SI) 2 Dual-Beam
Hőmérsékleti sugárzás
 Ideális fekete test sugárzása Hőmérsékleti sugárzás Elméleti háttér Egy ideális fekete test leírható egy egyenletes hőmérsékletű falú üreggel. A fala nemcsak kibocsát, hanem el is nyel energiát, és spektrális
Ideális fekete test sugárzása Hőmérsékleti sugárzás Elméleti háttér Egy ideális fekete test leírható egy egyenletes hőmérsékletű falú üreggel. A fala nemcsak kibocsát, hanem el is nyel energiát, és spektrális
Modern fizika laboratórium
 Modern fizika laboratórium 11. Az I 2 molekula disszociációs energiája Készítette: Hagymási Imre A mérés dátuma: 2007. október 3. A beadás dátuma: 2007. október xx. 1. Bevezetés Ebben a mérésben egy kétatomos
Modern fizika laboratórium 11. Az I 2 molekula disszociációs energiája Készítette: Hagymási Imre A mérés dátuma: 2007. október 3. A beadás dátuma: 2007. október xx. 1. Bevezetés Ebben a mérésben egy kétatomos
Periodikus struktúrák előállítása nanolitográfiával és vizsgálatuk három dimenzióban
 Periodikus struktúrák előállítása nanolitográfiával és vizsgálatuk három dimenzióban Zolnai Zsolt MTA Műszaki Fizikai és Anyagtudományi Kutatóintézet, H-1525 Budapest, P.O.B. 49, Hungary Tartalom: Kolloid
Periodikus struktúrák előállítása nanolitográfiával és vizsgálatuk három dimenzióban Zolnai Zsolt MTA Műszaki Fizikai és Anyagtudományi Kutatóintézet, H-1525 Budapest, P.O.B. 49, Hungary Tartalom: Kolloid
Szilárdtestek sávelmélete. Sávelmélet a szabadelektron-modell alapján
 Szilárdtestek sávelmélete Sávelmélet a szabadelektron-modell alapján A Fermi Dirac statisztika alapjai Nagy részecskeszámú rendszerek fizikai jellemzéséhez statisztikai leírást kell alkalmazni. (Pl. gázokra
Szilárdtestek sávelmélete Sávelmélet a szabadelektron-modell alapján A Fermi Dirac statisztika alapjai Nagy részecskeszámú rendszerek fizikai jellemzéséhez statisztikai leírást kell alkalmazni. (Pl. gázokra
Rádl Attila december 11. Rádl Attila Spalláció december / 21
 Spalláció Rádl Attila 2018. december 11. Rádl Attila Spalláció 2018. december 11. 1 / 21 Definíció Atommagok nagyenergiás részecskével történő ütközése során másodlagos részecskéket létrehozó rugalmatlan
Spalláció Rádl Attila 2018. december 11. Rádl Attila Spalláció 2018. december 11. 1 / 21 Definíció Atommagok nagyenergiás részecskével történő ütközése során másodlagos részecskéket létrehozó rugalmatlan
Hangfrekvenciás mechanikai rezgések vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
Biofizika tesztkérdések
 Biofizika tesztkérdések Egyszerű választás E kérdéstípusban A, B,...-vel jelölt lehetőségek szerepelnek, melyek közül az egyetlen megfelelőt kell kiválasztani. A választ írja a kérdés előtt lévő kockába!
Biofizika tesztkérdések Egyszerű választás E kérdéstípusban A, B,...-vel jelölt lehetőségek szerepelnek, melyek közül az egyetlen megfelelőt kell kiválasztani. A választ írja a kérdés előtt lévő kockába!
Havancsák Károly Az ELTE TTK kétsugaras pásztázó elektronmikroszkópja. Archeometriai műhely ELTE TTK 2013.
 Havancsák Károly Az ELTE TTK kétsugaras pásztázó elektronmikroszkópja Archeometriai műhely ELTE TTK 2013. Elektronmikroszkópok TEM SEM Transzmissziós elektronmikroszkóp Átvilágítós vékony minta < 100
Havancsák Károly Az ELTE TTK kétsugaras pásztázó elektronmikroszkópja Archeometriai műhely ELTE TTK 2013. Elektronmikroszkópok TEM SEM Transzmissziós elektronmikroszkóp Átvilágítós vékony minta < 100
Z bozonok az LHC nehézion programjában
 Z bozonok az LHC nehézion programjában Zsigmond Anna Julia MTA Wigner FK Max Planck Institut für Physik Fizikus Vándorgyűlés Szeged, 2016 augusztus 24-27. Nehézion-ütközések az LHC-nál A-A és p-a ütközések
Z bozonok az LHC nehézion programjában Zsigmond Anna Julia MTA Wigner FK Max Planck Institut für Physik Fizikus Vándorgyűlés Szeged, 2016 augusztus 24-27. Nehézion-ütközések az LHC-nál A-A és p-a ütközések
T I T - M T T. Hevesy György Kémiaverseny. A megyei forduló feladatlapja. 7. osztály. A versenyző jeligéje:... Megye:...
 T I T - M T T Hevesy György Kémiaverseny A megyei forduló feladatlapja 7. osztály A versenyző jeligéje:... Megye:... Elért pontszám: 1. feladat:... pont 2. feladat:... pont 3. feladat:... pont 4. feladat:...
T I T - M T T Hevesy György Kémiaverseny A megyei forduló feladatlapja 7. osztály A versenyző jeligéje:... Megye:... Elért pontszám: 1. feladat:... pont 2. feladat:... pont 3. feladat:... pont 4. feladat:...
Jelöljük meg a kérdésnek megfelelő válaszokat! 1, Hullámokról általában: alapösszefüggések a harmonikus hullámra. A Doppler-effektus
 Jelöljük meg a kérdésnek megfelelő válaszokat! 1, Hullámokról általában: alapösszefüggések a harmonikus hullámra. A Doppler-effektus Melyik egyenlet nem hullámot ír le? a) y = A sin 2π(ft x/λ) b) y = A
Jelöljük meg a kérdésnek megfelelő válaszokat! 1, Hullámokról általában: alapösszefüggések a harmonikus hullámra. A Doppler-effektus Melyik egyenlet nem hullámot ír le? a) y = A sin 2π(ft x/λ) b) y = A
Kutatási beszámoló. 2015. február. Tangens delta mérésére alkalmas mérési összeállítás elkészítése
 Kutatási beszámoló 2015. február Gyüre Balázs BME Fizika tanszék Dr. Simon Ferenc csoportja Tangens delta mérésére alkalmas mérési összeállítás elkészítése A TKI-Ferrit Fejlsztő és Gyártó Kft.-nek munkája
Kutatási beszámoló 2015. február Gyüre Balázs BME Fizika tanszék Dr. Simon Ferenc csoportja Tangens delta mérésére alkalmas mérési összeállítás elkészítése A TKI-Ferrit Fejlsztő és Gyártó Kft.-nek munkája
Mag- és neutronfizika
 Mag- és neutronfizika z elıadás célja: : megalapozni az atomenergetikai ismereteket félév során a következı témaköröket ismertetjük: Magfizikai alapfogalmak (atommagok, radioaktivitás) Sugárzás és anyag
Mag- és neutronfizika z elıadás célja: : megalapozni az atomenergetikai ismereteket félév során a következı témaköröket ismertetjük: Magfizikai alapfogalmak (atommagok, radioaktivitás) Sugárzás és anyag
