3. M AGYAR SZÁRÍTÁSI SZIM PÓZIUM
|
|
|
- Balázs Biró
- 6 évvel ezelőtt
- Látták:
Átírás
1 3. M AGYAR SZÁRÍTÁSI SZIM PÓZIUM Nyíregyháza szeptember
2 110 A szemcseméret és fajlagos felület meghatározás anyag és hőátadási folyamatokhoz Gyimes Ernő Dr. Véha Antal *- Dr. Rajkó Róbert** József Attila Tudományegyetem Szegedi Élelmiszeripari Főiskolai Kar * Élelmiszertechnológia és Környezetgazdálkodási Tanszék **Élelmiszeripari műveletek és Környezettechnika Tanszék Bevezetés, előzmények A bennünket körülvevő világban a különféle anyag- és hőátadási folyamatoknak igen nagy a szerepe. Az élet alapvető folyamatai játszódnak le a fenti transzport folyamatok szerint, kezdve az emésztéstől egészen a hőátadási szárítási feladatokig. A mezőgazdaságban, az élelmiszeriparban e területek közül kiemelten kezelt az aprítási, keverési, alakadó (formázó) és a hőátadási műveletek sokasága. A különböző anyag- illetve hőtranszport folyamatok egymással is sok esetben hasonlóságot mutatnak. Erre az elméleti és gyakorlati irodalmi forrásokban számtalan hivatkozás található, amelyek az ún. hasonlósági elveket és kritériumokat tárgyalják. A hasonlóság egyik fontos eleme a szemcseméretnek, illetve a felületnek, fajlagos felületnek a kitüntetett szerepe. A felületnek elsősorban azért, mert a hő- és anyagátadási műveletek ténylegesen a felületek mentén játszódnak le. Erre utalnak a hő- és anyagátadás fontosabb törvényei. A szemcseméretnek valamint a szemcseméret eloszlásnak hasonlóan fontos szerepe van, részben elméleti, részben gyakorlati - üzemeltetési - szempontból. Szemnagyság vagy szemcseméret alatt az adott szemcse nagyságát kifejező lineáris méretet értjük. Nem szabályos alakú szemcsék esetén - ide sorolható a mezőgazdasági anyagok tekintélyes része - a méret nagyszámú, sok esetben egymástól is eltérő adattal fejezhető ki. Ilyenek a méret szélső értékek és középérték, valamely tulajdonság hasonlóságán alapuló ún. egyenértékű szemcseméret stb. Az eltérő meghatározási módok eltérő értékeket adnak ugyanarra a szemcsenagyság értékre, ami a különféle kísérleteknél, azok reprodukálásánál gondot jelenthet. A granulometriai gyakorlatban leggyakrabban a szitaelemzés alapján meghatározott szemcseméretet használják. Ennek során adott, a szemcseméret tartományhoz
3 111 optimálisan illeszkedő szitasorozattal két, esetleg több szitálást kell végezni. A nemzetközi gyakorlatban többféle szitasorozat szabványt használnak, az USA az ún. Tyler és az ASTM sorozatot, míg Európában a Renard-féle sorozat () a jellemző. A szitálás végrehajtása után képződött szitamaradékokat visszamérve megkapható az ún. átlagos szemcseméret, amely a szitált őrlemény (vagy rostaanalízis esetén a szemestermény) méret szerinti eloszlásának leggyakoribb értéke, azaz módusza. A kiértékelést nehezíti a túlzottan széles eloszlási tartomány, amely a szemestermények őrleményeit jellemzi. A tudomány számtalan eloszlás típust ismer, amelyek közül a leggyakrabban a következőket alkalmazzák: a Gaudin-Adrejev- Schuhmann-, a Rosin-Rammler-Sperling-Bennett- és a lognormális eloszlás, vagy másképpen a Kolmogorov-Rényi eloszlás. Hasonlóan problémás a felület, illetve a fajlagos felület mérésének, meghatározásának a kérdése. A közvetlen meghatározásra többfajta módszer ismeretes, ezek közül a turbidimetriás, a gázadszorpciós-folyadékadszorpciós módszer vagy a permeabilitás alapján történő mérés. Mindegyik módszernél azonban oldódás problémájával kell számolni, amely a hibalehetőséget tovább növeli. Ezek mellett a fajlagos felület esetén is számolni kell azzal, hogy ugyanannak az anyagnak a felületértékei, az egyes módszerek között - a metodikai eltérések miatt - nagy szórást mutatnak. Az aprítási kísérletek során általában kielégítő pontosságú és viszonylag kis variáció mellett használható a Rittinger-féle (felületi) aprításelméleti összefüggésnél is alkalmazott, egyszerűsítő kritériumok szerinti képlettel megadott fajlagos felület érték: 6 Fajlagos felület = X pxx cm g 0 ) ahol p az anyag sűrűsége (kg/cm3) x a szemcse élhossza (cm) A módszer egyik előnye, hogy a szitaanalízis értékelése során, a sűrűség ismeretében a fajlagos felület meghatározása is elvégezhető. Fontos megjegyezni, hogy a sűrűség esetén a valódi, azaz a szemcsés halmazra jellemző értékkel kell számolni, ellenkező esetben az intergranuláris tér miatti értékváltozás jelentős hibát okoz. További probléma, hogy a szemestermények eredeti
4 112 formájukban kévésé hasonlítanak a kocka alakhoz, ezért abban az esetben a tényleges alak szerinti megközelítés a kívánatos. A vizsgálat célkitűzése A vizsgálatok célja hármas volt, egyrészt meghatározni több búzafajta bevonásával azok fontosabb geometriai jellemzőit, másrészt a geometriai méretek ismeretében meghatározni, a méret alakulására ható tényezőt, tényezőket. Harmadrészben arra kerestünk választ, hogy az eltérő alakú és beltartalmú fajok (búza, kukorica, szója) azonos körülmények közötti aprítása során az egyes eloszlástípusok közül melyik bizonyul a legmegbízhatóbbnak. Anyag, eszköz, módszer Kísérleteinket a JATE Szegedi Élelmiszeripari Főiskolai Karán végeztük. A szemcseméret és a felület meghatározásához étkezési búzát (Triticum Aestívum) használtunk, az egyes eloszlás típusok értékeléséhez búza (GK-öthalom), kukorica (Dekalb 524 se) és szója (Bolyi 44) került felhasználásra. Az 1. táblázat tartalmazza a búzavizsgálatok első részének adatait, a szemcseméret meghatározása a rostaelemzés módszerével történt. A táblázatból kitűnik az évben termett fajták magasabb fajlagos felület értéke, a táblázat végén találhat fajtákból nem állt rendelkezésünkre eltérő évjárat, de hipotézisünk szerint hasonló tendencia lett volna megfigyelhető. A továbbiakban a szemcseméret akkurátusabb mérését részben az 1. táblázatban közölt fajták, részben más búzafajták bevonásával is elvégeztük. A mérés ebben az esetben szemenként történt, a mintaelőkészítés után szem mindhárom geometriai méretének meghatározásával. A 2. táblázatban ennek a mérési sornak az adatai láthatók.
5 113 l.táblázat A vizsgált búzafajták fontosabb fizikai mutatói Fajta, évjárat Nedvesség - tartalom Ezerszem tömeg Sűrűség Átlag szemméret Fajlagos felület Acélosság (%) (g) (g/cm3) (mm) (cm2/g) (%) GK-Csűrös ,7 47,2 1,3133 3,38 12,11 79,1 GK-Csűrös ,63 44,2 1,3580 3,33 13,27 52,87 GK-Duna ,6 40,2 1, ,99 76,2 GK-Duna ,67 35,1 1,3107 2,95 15,54 53,89 GK-Kata ,4 44,6 1,3106 3,40 11,92 80,2 GK-Kata ,5 41,0 1,2695 3,39 12,16 60,9 GK-Kata ,98 35,8 1,3038 3,22 14,30 46,15 G K-öthalom ,4 44,6 1,3519 3,38 11,91 80,2 G K-öthalom ,3 43,9 1,2656 3,37 11,90 79,2 GK-Öthalom ,86 40,2 1,3077 3,21 14,29 65,13 Jubilejnaja-50 11,5 48,7 1,3449 3,40 11,85 81, MV ,70 37,6 1,3678 3,16 13,88 79,8 MV ,37 39,4 1,3586 3,18 13,89 82,1 MV ,91 41,8 1,3464 3,55 12,55 77,1 M V ,04 37,9 1,2978 3,25 14,23 77,7 MV ,19 32,7 1,3594 3,11 14,19 69,9 MV ,10 40,0 1,3434 3,44 12,98 53,3 M V Fatima ,94 45,0 1,3668 3,52 13,03 56,2 M V Magvas ,84 40,0 1,3339 3,30 13,61 63,0 M V Pálma ,28 38,0 1,3690 3,36 12,77 62,1 MV Summa ,28 37,0 1,4285 3,35 12,51 41,0 A három jellemző méret közül a szélességi méret alakulását az 1. ábrán mutatjuk be. Az ábrán jól nyomonkövethető az évjárati hatás szerepe. Az évben termett fajták szélességi méretei jelentősen eltérnek az egyéb évjáratoktól. Különösen szembetűnő a Kata és öthalom fajtáknál, ahol három éven tartó vizsgálat adta az értékelés alapját, és mindkét fajta esetében az 1995 és 1997-es év adatai között nem volt lényeges eltérés, szemben az 1998-as év adataival. Megállapítható a fajtánkénti eltérés a Duna és a Csűrös fajta esetén is, bár ebben az esetben két évjáratot vizsgáltunk.
6 táblázat A vizsgált búzafajták szemgeometriai méretei Fajta neve Szélesség Vastagság Hosszúság Átlag Szórás Átlag Szórás Átlag Szórás Durum ,976 0,164 2,912 0,144 6,501 0,257 GK-Bétadur ,137 0,159 2,987 0,153 8,110 0,461 GK-Csörnöc ,548 0,226 3,100 0,224 7,031 0,317 GK-Csűrös ,593 0,162 2,903 0,137 6,329 0,286 GK-Csűrös ,329 0,164 2,832 0,123 6,755 0,256 GK-Duna ,231 0,184 2,886 0,165 6,455 0,307 GK-Duna ,945 0,153 2,887 0,125 6,466 0,293 GK-Kata ,552 0,162 2,953 0,156 6,271 0,216 GK-Kata ,545 0,191 2,917 0,157 6,374 0,230 GK-Kata ,218 0,184 2,692 0,158 6,046 0,234 GK-Öthalom ,429 0,152 3,001 0,187 6,503 0,338 GK-Öthalom ,408 0,242 3,102 0,173 6,469 0,279 GK-Öthalom ,209 0,207 2,916 0,176 6,730 0,293 GK-Pinka ,525 0,220 2,923 0,184 7,010 0,389 JubiIejnaja ,360 0,154 2,932 0,115 6,954 0,320 Tambor (A) ,304 0,242 2,916 0,206 6,222 0,362 1 szélesség (mm) 1. ábra A szélességi méretek átlagértékeinek konfidencia sávjai a vizsgált búzafajták esetén
7 115 Az egyes eloszlás típusok összehasonlítása szintén figyelemre méltó eredményt hozott. A részletes adatok bemutatását mellőzve a 3. táblázatban mutatjuk be a vizsgált eloszlástípusok lineáris közelítését, azok egyenletével és a determinációs együtthatóval. A determinációs együttható a mért és számított értékek közötti kapcsolat szorosságát mutatja. Vizsgált faj RRSB GAS Kolm ogorov-rényi Egyenlet R Egyenlet R Egyenlet R Búza Y =2,7514x+l,2211 0,9304 Y=2,7322x+0,6404 0,7955 Y=l,715x+1,2635 0,9711 Kukorica Y=3,1791x+1,4446 0,8708 Y=2,3 836x+0,4846 0,8755 Y=l,906x+1,3445 0,9740 Szója Y=2,9181x+l,3841 0,8934 Y=2,5328+0,6135 0,8284 Y =l,648x+1,1682 0,9754 Megjegyzés: RRSB: Rosin-Rammler-Sperling-Bennett GAS: Gaudin-Andrejev-Schuhmann A táblázatból látható, hogy a Kolmogorov-Rényi eloszlás minden esetben jobb értéket adott, bár az RRSB egyenlet és a GAS eloszlás is szoros korrelációt feltételez. Itt kell felhívni a figyelmet arra, hogy csak a korreláció erősségét mérlegelve akár téves következtetéshez is juthatunk, hiszen transzformált koordináta rendszerben ábrázolva az adatokat jól látható törést figyelhetünk meg az RRSB és GAS eloszlás esetében. Összefoglalás Az általunk mért és közölt geometriai méret-meghatározásoknak és a fajlagos felület megállapításának nagy szerepe van a különféle anyag- és hőtranszport folyamatoknál. Az aprítástechnikai vizsgálatoknál alkalmazott fajlagos felület számítási mód - egyszerűsítő feltételezésekkel - alkalmasnak látszik egyes szárítási és egyéb hőátadási illetőleg anyagátadási feladatok megoldásánál, elsősorban őrlemények esetén. A felület kiszámításának pontossága kielégítőnek tűnik. A szemestermények eredeti formájukban eltérő számítási metódust igényelnek, amelynek lényeges eleme a valóságos alakot legjobban megközelítő geometriai alak leírása. A szemcseméret meghatározás során a táblázatokból és az ábráról is jól látható, hogy a geometriai (szélességi) méret a fajtától erősen függő, noha nem szignifikánsan változó, valamint az évjárati hatásnak nagy szerepe van a méret alakulására. Az eloszlástípusok összehasonlításának eredménye arra enged következtetni, hogy a Kolmogorov-Rényi féle lognormális eloszlás mindhárom fajnál pontosabban közelítette meg a mért értékeket.
DOKTORI (PhD) ÉRTEKEZÉS TÉZISEI
 DOKTORI (PhD) ÉRTEKEZÉS TÉZISEI NYUGAT-MAGYARORSZÁGI EGYETEM MEZŐGAZDASÁG- ÉS ÉLELMISZERTUDOMÁNYI KAR, MOSONMAGYARÓVÁR Agrárműszaki, Élelmiszeripari és Környezettechnikai Intézet Doktori Iskola vezető
DOKTORI (PhD) ÉRTEKEZÉS TÉZISEI NYUGAT-MAGYARORSZÁGI EGYETEM MEZŐGAZDASÁG- ÉS ÉLELMISZERTUDOMÁNYI KAR, MOSONMAGYARÓVÁR Agrárműszaki, Élelmiszeripari és Környezettechnikai Intézet Doktori Iskola vezető
Hangfrekvenciás mechanikai rezgések vizsgálata
 Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
Őszi búzák (Triticum aestivum) szemméreteinek és sűrűség értékeinek összefüggés-rendszere
 Őszi búzák (Triticum aestivum) szemméreteinek és sűrűség értékeinek összefüggés-rendszere Gyimes Ernő 1 Véha Antal 1 Rajkó Róbert 2 1 Szegedi Tudományegyetem Szegedi Élelmiszeripari Főiskolai Kar Élelmiszertechnológia
Őszi búzák (Triticum aestivum) szemméreteinek és sűrűség értékeinek összefüggés-rendszere Gyimes Ernő 1 Véha Antal 1 Rajkó Róbert 2 1 Szegedi Tudományegyetem Szegedi Élelmiszeripari Főiskolai Kar Élelmiszertechnológia
Biomatematika 12. Szent István Egyetem Állatorvos-tudományi Kar. Fodor János
 Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011.
 BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
SZEMKEMÉNYSÉG VIZSGÁLÓ MÓDSZEREK ÖSSZEHASONLÍTÁSA ŐSZI BÚZÁK ESETÉBEN. Véha Antal Gyimes Ernő JATE Szegedi Élelmiszeripari Főiskolai Kar, Szeged
 SZEMKEMÉNYSÉG VIZSGÁLÓ MÓDSZEREK ÖSSZEHASONLÍTÁSA ŐSZI BÚZÁK ESETÉBEN Bevezetés, célkitűzés Véha Antal Gyimes Ernő JATE Szegedi Élelmiszeripari Főiskolai Kar, Szeged A jelenlegi malomipari gyakorlatban
SZEMKEMÉNYSÉG VIZSGÁLÓ MÓDSZEREK ÖSSZEHASONLÍTÁSA ŐSZI BÚZÁK ESETÉBEN Bevezetés, célkitűzés Véha Antal Gyimes Ernő JATE Szegedi Élelmiszeripari Főiskolai Kar, Szeged A jelenlegi malomipari gyakorlatban
Nehézségi gyorsulás mérése megfordítható ingával
 Nehézségi gyorsulás mérése megfordítható ingával (Mérési jegyzőkönyv) Hagymási Imre 2007. április 21. (hétfő délelőtti csoport) 1. A mérés elmélete A nehézségi gyorsulás mérésének egy klasszikus módja
Nehézségi gyorsulás mérése megfordítható ingával (Mérési jegyzőkönyv) Hagymási Imre 2007. április 21. (hétfő délelőtti csoport) 1. A mérés elmélete A nehézségi gyorsulás mérésének egy klasszikus módja
A mérések általános és alapvető metrológiai fogalmai és definíciói. Mérések, mérési eredmények, mérési bizonytalanság. mérés. mérési elv
 Mérések, mérési eredmények, mérési bizonytalanság A mérések általános és alapvető metrológiai fogalmai és definíciói mérés Műveletek összessége, amelyek célja egy mennyiség értékének meghatározása. mérési
Mérések, mérési eredmények, mérési bizonytalanság A mérések általános és alapvető metrológiai fogalmai és definíciói mérés Műveletek összessége, amelyek célja egy mennyiség értékének meghatározása. mérési
2. Rugalmas állandók mérése
 2. Rugalmas állandók mérése Klasszikus fizika laboratórium Mérési jegyzőkönyv Mérést végezte: Vitkóczi Fanni Jegyzőkönyv leadásának időpontja: 2012. 12. 15. I. A mérés célja: Két anyag Young-modulusának
2. Rugalmas állandók mérése Klasszikus fizika laboratórium Mérési jegyzőkönyv Mérést végezte: Vitkóczi Fanni Jegyzőkönyv leadásának időpontja: 2012. 12. 15. I. A mérés célja: Két anyag Young-modulusának
y ij = µ + α i + e ij
 Elmélet STATISZTIKA 3. Előadás Variancia-analízis Lineáris modellek A magyarázat a függő változó teljes heterogenitásának két részre bontását jelenti. A teljes heterogenitás egyik része az, amelynek okai
Elmélet STATISZTIKA 3. Előadás Variancia-analízis Lineáris modellek A magyarázat a függő változó teljes heterogenitásának két részre bontását jelenti. A teljes heterogenitás egyik része az, amelynek okai
MÉRÉSI EREDMÉNYEK PONTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI
 MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
STATISZTIKA ELŐADÁS ÁTTEKINTÉSE. Matematikai statisztika. Mi a modell? Binomiális eloszlás sűrűségfüggvény. Binomiális eloszlás
 ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
Matematikai geodéziai számítások 6.
 Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Fényhullámhossz és diszperzió mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 9. MÉRÉS Fényhullámhossz és diszperzió mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 19. Szerda délelőtti csoport 1. A mérés célja
KLASSZIKUS FIZIKA LABORATÓRIUM 9. MÉRÉS Fényhullámhossz és diszperzió mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 19. Szerda délelőtti csoport 1. A mérés célja
Matematikai geodéziai számítások 6.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Tartalomjegyzék I. RÉSZ: KÍSÉRLETEK MEGTERVEZÉSE
 Tartalomjegyzék 5 Tartalomjegyzék Előszó I. RÉSZ: KÍSÉRLETEK MEGTERVEZÉSE 1. fejezet: Kontrollált kísérletek 21 1. A Salk-oltás kipróbálása 21 2. A porta-cava sönt 25 3. Történeti kontrollok 27 4. Összefoglalás
Tartalomjegyzék 5 Tartalomjegyzék Előszó I. RÉSZ: KÍSÉRLETEK MEGTERVEZÉSE 1. fejezet: Kontrollált kísérletek 21 1. A Salk-oltás kipróbálása 21 2. A porta-cava sönt 25 3. Történeti kontrollok 27 4. Összefoglalás
Statisztika I. 9. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 9. előadás Előadó: Dr. Ertsey Imre Statisztikai hipotézis vizsgálatok elsősorban a biometriában alkalmazzák, újabban reprezentatív jellegű ökonómiai vizsgálatoknál, üzemi szinten élelmiszeripari
Statisztika I. 9. előadás Előadó: Dr. Ertsey Imre Statisztikai hipotézis vizsgálatok elsősorban a biometriában alkalmazzák, újabban reprezentatív jellegű ökonómiai vizsgálatoknál, üzemi szinten élelmiszeripari
Biometria az orvosi gyakorlatban. Korrelációszámítás, regresszió
 SZDT-08 p. 1/31 Biometria az orvosi gyakorlatban Korrelációszámítás, regresszió Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Korrelációszámítás
SZDT-08 p. 1/31 Biometria az orvosi gyakorlatban Korrelációszámítás, regresszió Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Korrelációszámítás
Matematika osztályozó vizsga témakörei 9. évfolyam II. félév:
 Matematika osztályozó vizsga témakörei 9. évfolyam II. félév: 7. Függvények: - függvények fogalma, megadása, ábrázolás koordináta- rendszerben - az elsőfokú függvény, lineáris függvény - a másodfokú függvény
Matematika osztályozó vizsga témakörei 9. évfolyam II. félév: 7. Függvények: - függvények fogalma, megadása, ábrázolás koordináta- rendszerben - az elsőfokú függvény, lineáris függvény - a másodfokú függvény
Feladatok: pontdiagram és dobozdiagram. Hogyan csináltuk?
 Feladatok: pontdiagram és dobozdiagram Hogyan csináltuk? Alakmutatók: ferdeség, csúcsosság Alakmutatók a ferdeség és csúcsosság mérésére Ez eloszlás centrumát (középérték) és az adatok centrum körüli terpeszkedését
Feladatok: pontdiagram és dobozdiagram Hogyan csináltuk? Alakmutatók: ferdeség, csúcsosság Alakmutatók a ferdeség és csúcsosság mérésére Ez eloszlás centrumát (középérték) és az adatok centrum körüli terpeszkedését
1/8. Iskolai jelentés. 10.évfolyam matematika
 1/8 2009 Iskolai jelentés 10.évfolyam matematika 2/8 Matematikai kompetenciaterület A fejlesztés célja A kidolgozásra kerülő programcsomagok az alább felsorolt készségek, képességek közül a számlálás,
1/8 2009 Iskolai jelentés 10.évfolyam matematika 2/8 Matematikai kompetenciaterület A fejlesztés célja A kidolgozásra kerülő programcsomagok az alább felsorolt készségek, képességek közül a számlálás,
Szárítás során kialakuló hővezetés számítása Excel VBA makróval
 Szárítás során kalakuló hővezetés számítása Excel VBA makróval Rajkó Róbert 1 Eszes Ferenc 2 Szabó Gábor 1 1 Szeged Tudományegyetem, Szeged Élelmszerpar Főskola Kar Élelmszerpar Műveletek és Környezettechnka
Szárítás során kalakuló hővezetés számítása Excel VBA makróval Rajkó Róbert 1 Eszes Ferenc 2 Szabó Gábor 1 1 Szeged Tudományegyetem, Szeged Élelmszerpar Főskola Kar Élelmszerpar Műveletek és Környezettechnka
Géprajz - gépelemek. Előadó: Németh Szabolcs mérnöktanár. Belső használatú jegyzet 2
 Géprajz - gépelemek FELÜLETI ÉRDESSÉG Előadó: Németh Szabolcs mérnöktanár Belső használatú jegyzet http://gepesz-learning.shp.hu 1 Felületi érdesség Az alkatrészek elkészítéséhez a rajznak tartalmaznia
Géprajz - gépelemek FELÜLETI ÉRDESSÉG Előadó: Németh Szabolcs mérnöktanár Belső használatú jegyzet http://gepesz-learning.shp.hu 1 Felületi érdesség Az alkatrészek elkészítéséhez a rajznak tartalmaznia
Mérési hibák 2006.10.04. 1
 Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
Statisztika I. 11. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 11. előadás Előadó: Dr. Ertsey Imre Összefüggés vizsgálatok A társadalmi gazdasági élet jelenségei kölcsönhatásban állnak, összefüggnek egymással. Statisztika alapvető feladata: - tényszerűségek
Statisztika I. 11. előadás Előadó: Dr. Ertsey Imre Összefüggés vizsgálatok A társadalmi gazdasági élet jelenségei kölcsönhatásban állnak, összefüggnek egymással. Statisztika alapvető feladata: - tényszerűségek
Méréselmélet és mérőrendszerek 2. ELŐADÁS (1. RÉSZ)
 Méréselmélet és mérőrendszerek 2. ELŐADÁS (1. RÉSZ) KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba
Méréselmélet és mérőrendszerek 2. ELŐADÁS (1. RÉSZ) KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba
Rugalmas állandók mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 2. MÉRÉS Rugalmas állandók mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 16. Szerda délelőtti csoport 1. A mérés rövid leírása Mérésem
KLASSZIKUS FIZIKA LABORATÓRIUM 2. MÉRÉS Rugalmas állandók mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 16. Szerda délelőtti csoport 1. A mérés rövid leírása Mérésem
A vizsgálatok eredményei
 A vizsgálatok eredményei A vizsgált vetőmagvak és műtrágyák nagy száma az eredmények táblázatos bemutatását teszi szükségessé, a legfontosabb magyarázatokkal kiegészítve. A közölt adatok a felsorolt publikációkban
A vizsgálatok eredményei A vizsgált vetőmagvak és műtrágyák nagy száma az eredmények táblázatos bemutatását teszi szükségessé, a legfontosabb magyarázatokkal kiegészítve. A közölt adatok a felsorolt publikációkban
A mérési eredmény megadása
 A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
y ij = µ + α i + e ij STATISZTIKA Sir Ronald Aylmer Fisher Példa Elmélet A variancia-analízis alkalmazásának feltételei Lineáris modell
 Példa STATISZTIKA Egy gazdálkodó k kukorica hibrid termesztése között választhat. Jelöljük a fajtákat A, B, C, D-vel. Döntsük el, hogy a hibridek termesztése esetén azonos terméseredményre számíthatunk-e.
Példa STATISZTIKA Egy gazdálkodó k kukorica hibrid termesztése között választhat. Jelöljük a fajtákat A, B, C, D-vel. Döntsük el, hogy a hibridek termesztése esetén azonos terméseredményre számíthatunk-e.
Biometria gyakorló feladatok BsC hallgatók számára
 Biometria gyakorló feladatok BsC hallgatók számára 1. Egy üzem alkalmazottainak megoszlása az elért teljesítmény %-a szerint a következı: Norma teljesítmény % Dolgozók száma 60-80 30 81-90 70 91-100 90
Biometria gyakorló feladatok BsC hallgatók számára 1. Egy üzem alkalmazottainak megoszlása az elért teljesítmény %-a szerint a következı: Norma teljesítmény % Dolgozók száma 60-80 30 81-90 70 91-100 90
Statisztika I. 12. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 1. előadás Előadó: Dr. Ertsey Imre Regresszió analízis A korrelációs együttható megmutatja a kapcsolat irányát és szorosságát. A kapcsolat vizsgálata során a gyakorlatban ennél messzebb
Statisztika I. 1. előadás Előadó: Dr. Ertsey Imre Regresszió analízis A korrelációs együttható megmutatja a kapcsolat irányát és szorosságát. A kapcsolat vizsgálata során a gyakorlatban ennél messzebb
Al-Mg-Si háromalkotós egyensúlyi fázisdiagram közelítő számítása
 l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
A kálium-permanganát és az oxálsav közötti reakció vizsgálata 9a. mérés B4.9
 A kálium-permanganát és az oxálsav közötti reakció vizsgálata 9a. mérés B4.9 Név: Pitlik László Mérés dátuma: 2014.12.04. Mérőtársak neve: Menkó Orsolya Adatsorok: M24120411 Halmy Réka M14120412 Sárosi
A kálium-permanganát és az oxálsav közötti reakció vizsgálata 9a. mérés B4.9 Név: Pitlik László Mérés dátuma: 2014.12.04. Mérőtársak neve: Menkó Orsolya Adatsorok: M24120411 Halmy Réka M14120412 Sárosi
1. Adatok kiértékelése. 2. A feltételek megvizsgálása. 3. A hipotézis megfogalmazása
 HIPOTÉZIS VIZSGÁLAT A hipotézis feltételezés egy vagy több populációról. (pl. egy gyógyszer az esetek 90%-ában hatásos; egy kezelés jelentősen megnöveli a rákos betegek túlélését). A hipotézis vizsgálat
HIPOTÉZIS VIZSGÁLAT A hipotézis feltételezés egy vagy több populációról. (pl. egy gyógyszer az esetek 90%-ában hatásos; egy kezelés jelentősen megnöveli a rákos betegek túlélését). A hipotézis vizsgálat
SEGÉDANYAG az országos kompetenciamérések, érettségi és OKTV eredmények kiértékeléséhez
 SEGÉDANYAG az országos kompetenciamérések, érettségi és OKTV eredmények kiértékeléséhez 2017. március 3. Tartalomjegyzék 2 Tartalomjegyzék Általános iskolai kompetenciamérés adatainak elemzése... 3 Gimnázium
SEGÉDANYAG az országos kompetenciamérések, érettségi és OKTV eredmények kiértékeléséhez 2017. március 3. Tartalomjegyzék 2 Tartalomjegyzék Általános iskolai kompetenciamérés adatainak elemzése... 3 Gimnázium
Mérési adatok illesztése, korreláció, regresszió
 Mérési adatok illesztése, korreláció, regresszió Korreláció, regresszió Két változó mennyiség közötti kapcsolatot vizsgálunk. Kérdés: van-e kapcsolat két, ugyanabban az egyénben, állatban, kísérleti mintában,
Mérési adatok illesztése, korreláció, regresszió Korreláció, regresszió Két változó mennyiség közötti kapcsolatot vizsgálunk. Kérdés: van-e kapcsolat két, ugyanabban az egyénben, állatban, kísérleti mintában,
Korrelációs kapcsolatok elemzése
 Korrelációs kapcsolatok elemzése 1. előadás Kvantitatív statisztikai módszerek Két változó közötti kapcsolat Független: Az X ismérv szerinti hovatartozás ismerete nem ad semmilyen többletinformációt az
Korrelációs kapcsolatok elemzése 1. előadás Kvantitatív statisztikai módszerek Két változó közötti kapcsolat Független: Az X ismérv szerinti hovatartozás ismerete nem ad semmilyen többletinformációt az
A II. kategória Fizika OKTV mérési feladatainak megoldása
 Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
6. Előadás. Vereb György, DE OEC BSI, október 12.
 6. Előadás Visszatekintés: a normális eloszlás Becslés, mintavételezés Reprezentatív minta A statisztika, mint változó Paraméter és Statisztika Torzítatlan becslés A mintaközép eloszlása - centrális határeloszlás
6. Előadás Visszatekintés: a normális eloszlás Becslés, mintavételezés Reprezentatív minta A statisztika, mint változó Paraméter és Statisztika Torzítatlan becslés A mintaközép eloszlása - centrális határeloszlás
Véletlen jelenség: okok rendszere hozza létre - nem ismerhetjük mind, ezért sztochasztikus.
 Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Rugalmas állandók mérése
 Rugalmas állandók mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. április 23. (hétfő délelőtti csoport) 1. Young-modulus mérése behajlásból 1.1. A mérés menete A mérés elméleti háttere megtalálható a jegyzetben
Rugalmas állandók mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. április 23. (hétfő délelőtti csoport) 1. Young-modulus mérése behajlásból 1.1. A mérés menete A mérés elméleti háttere megtalálható a jegyzetben
2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv. Zsigmond Anna Fizika Bsc II. Mérés dátuma: Leadás dátuma:
 2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 24. Leadás dátuma: 2008. 10. 01. 1 1. Mérések ismertetése Az 1. ábrán látható összeállításban
2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 24. Leadás dátuma: 2008. 10. 01. 1 1. Mérések ismertetése Az 1. ábrán látható összeállításban
Peltier-elemek vizsgálata
 Peltier-elemek vizsgálata Mérés helyszíne: Vegyész labor Mérés időpontja: 2012.02.20. 17:00-20:00 Mérés végrehatói: Budai Csaba Sánta Botond I. Seebeck együttható közvetlen kimérése Az adott P-N átmenetre
Peltier-elemek vizsgálata Mérés helyszíne: Vegyész labor Mérés időpontja: 2012.02.20. 17:00-20:00 Mérés végrehatói: Budai Csaba Sánta Botond I. Seebeck együttható közvetlen kimérése Az adott P-N átmenetre
Iskolai jelentés. 10. évfolyam szövegértés
 2008 Iskolai jelentés 10. évfolyam szövegértés Az elmúlt évhez hasonlóan 2008-ban iskolánk is részt vett az országos kompetenciamérésben, diákjaink matematika és szövegértés teszteket, illetve egy tanulói
2008 Iskolai jelentés 10. évfolyam szövegértés Az elmúlt évhez hasonlóan 2008-ban iskolánk is részt vett az országos kompetenciamérésben, diákjaink matematika és szövegértés teszteket, illetve egy tanulói
Modern Fizika Labor. 2. Elemi töltés meghatározása
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
STATISZTIKA. A maradék független a kezelés és blokk hatástól. Maradékok leíró statisztikája. 4. A modell érvényességének ellenőrzése
 4. A modell érvényességének ellenőrzése STATISZTIKA 4. Előadás Variancia-analízis Lineáris modellek 1. Függetlenség 2. Normális eloszlás 3. Azonos varianciák A maradék független a kezelés és blokk hatástól
4. A modell érvényességének ellenőrzése STATISZTIKA 4. Előadás Variancia-analízis Lineáris modellek 1. Függetlenség 2. Normális eloszlás 3. Azonos varianciák A maradék független a kezelés és blokk hatástól
A kerék-sín között fellépő Hertz-féle érintkezési feszültség vizsgálata
 A keréksín között fellépő Hertzféle érintkezési feszültség vizsgálata közúti vasúti felépítmények esetében Dr. Kazinczy László PhD. egyetemi docens i Műszaki és Gazdaságtudományi gyetem, Út és Vasútépítési
A keréksín között fellépő Hertzféle érintkezési feszültség vizsgálata közúti vasúti felépítmények esetében Dr. Kazinczy László PhD. egyetemi docens i Műszaki és Gazdaságtudományi gyetem, Út és Vasútépítési
Populációbecslés és monitoring. Eloszlások és alapstatisztikák
 Populációbecslés és monitoring Eloszlások és alapstatisztikák Eloszlások Az eloszlás megadja, hogy milyen valószínűséggel kapunk egy adott intervallumba tartozó értéket, ha egy olyan populációból veszünk
Populációbecslés és monitoring Eloszlások és alapstatisztikák Eloszlások Az eloszlás megadja, hogy milyen valószínűséggel kapunk egy adott intervallumba tartozó értéket, ha egy olyan populációból veszünk
A hőterjedés dinamikája vékony szilikon rétegekben. Gambár Katalin, Márkus Ferenc. Tudomány Napja 2012 Gábor Dénes Főiskola
 A hőterjedés dinamikája vékony szilikon rétegekben Gambár Katalin, Márkus Ferenc Tudomány Napja 2012 Gábor Dénes Főiskola Miről szeretnék beszélni: A kutatás motivációi A fizikai egyenletek (elméleti modellek)
A hőterjedés dinamikája vékony szilikon rétegekben Gambár Katalin, Márkus Ferenc Tudomány Napja 2012 Gábor Dénes Főiskola Miről szeretnék beszélni: A kutatás motivációi A fizikai egyenletek (elméleti modellek)
Fázisátalakulások vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 6. MÉRÉS Fázisátalakulások vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. szeptember 28. Szerda délelőtti csoport 1. A mérés célja A mérés
KLASSZIKUS FIZIKA LABORATÓRIUM 6. MÉRÉS Fázisátalakulások vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. szeptember 28. Szerda délelőtti csoport 1. A mérés célja A mérés
Térfogati fajlagos felület és (tömegi) fajlagos felület
 Térfogati fajlagos felület és (tömegi) fajlagos felület A térfogati fajlagos felület az egységnyi testtérfogatú szemhalmaz szemeinek felületösszege, azaz a szemhalmaz szemei külső felülete összegének és
Térfogati fajlagos felület és (tömegi) fajlagos felület A térfogati fajlagos felület az egységnyi testtérfogatú szemhalmaz szemeinek felületösszege, azaz a szemhalmaz szemei külső felülete összegének és
Andó Mátyás Felületi érdesség matyi.misi.eu. Felületi érdesség. 1. ábra. Felületi érdességi jelek
 1. Felületi érdesség használata Felületi érdesség A műszaki rajzokon a geometria méretek tűrése mellett a felületeket is jellemzik. A felületek jellemzésére leginkább a felületi érdességet használják.
1. Felületi érdesség használata Felületi érdesség A műszaki rajzokon a geometria méretek tűrése mellett a felületeket is jellemzik. A felületek jellemzésére leginkább a felületi érdességet használják.
11. modul: LINEÁRIS FÜGGVÉNYEK
 MATEMATIK A 9. évfolyam 11. modul: LINEÁRIS FÜGGVÉNYEK KÉSZÍTETTE: CSÁKVÁRI ÁGNES Matematika A 9. évfolyam. 11. modul: LINEÁRIS FÜGGVÉNYEK Tanári útmutató 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
MATEMATIK A 9. évfolyam 11. modul: LINEÁRIS FÜGGVÉNYEK KÉSZÍTETTE: CSÁKVÁRI ÁGNES Matematika A 9. évfolyam. 11. modul: LINEÁRIS FÜGGVÉNYEK Tanári útmutató 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
Országos kompetenciamérés eredményeinek kiértékelése 6. és 8. évfolyamokon 2016
 Országos kompetenciamérés eredményeinek kiértékelése 6. és 8. évfolyamokon 2016 A hatodik osztályban 13 tanulóból 11 fő írta meg az országos kompetenciamérést. Ebből 1 fő SNI-s, 2 fő BTMN-es tanuló. Mentesítést
Országos kompetenciamérés eredményeinek kiértékelése 6. és 8. évfolyamokon 2016 A hatodik osztályban 13 tanulóból 11 fő írta meg az országos kompetenciamérést. Ebből 1 fő SNI-s, 2 fő BTMN-es tanuló. Mentesítést
Módszertani Intézeti Tanszéki Osztály. A megoldás részletes mellékszámítások hiányában nem értékelhető!
 BGF KKK Módszertani Intézeti Tanszéki Osztály Budapest, 2012.. Név:... Neptun kód:... Érdemjegy:..... STATISZTIKA II. VIZSGADOLGOZAT Feladatok 1. 2. 3. 4. 5. 6. Összesen Szerezhető pontszám 21 20 7 22
BGF KKK Módszertani Intézeti Tanszéki Osztály Budapest, 2012.. Név:... Neptun kód:... Érdemjegy:..... STATISZTIKA II. VIZSGADOLGOZAT Feladatok 1. 2. 3. 4. 5. 6. Összesen Szerezhető pontszám 21 20 7 22
Országos kompetenciamérés eredményeinek kiértékelése 6. és 8. évfolyamokon 2012
 Országos kompetenciamérés eredményeinek kiértékelése 6. és 8. évfolyamokon 2012 A hatodik osztályban 12 tanulóból 11 írta meg az országos kompetenciamérést. Ebből 1 fő SNI-s, 3 fő BTMN-es tanuló. Mentesítést
Országos kompetenciamérés eredményeinek kiértékelése 6. és 8. évfolyamokon 2012 A hatodik osztályban 12 tanulóból 11 írta meg az országos kompetenciamérést. Ebből 1 fő SNI-s, 3 fő BTMN-es tanuló. Mentesítést
Hangfrekvenciás mechanikai rezgések vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/91/106534674.jpg) [Biomatematika 2] Orvosi biometria Bódis Emőke 2016. 04. 25. J J 9 Korrelációanalízis Regresszióanalízis: hogyan változik egy vizsgált változó értéke egy másik változó változásának függvényében. Korrelációs
[Biomatematika 2] Orvosi biometria Bódis Emőke 2016. 04. 25. J J 9 Korrelációanalízis Regresszióanalízis: hogyan változik egy vizsgált változó értéke egy másik változó változásának függvényében. Korrelációs
Fázisátalakulások vizsgálata
 Klasszikus Fizika Laboratórium VI.mérés Fázisátalakulások vizsgálata Mérést végezte: Vanó Lilla VALTAAT.ELTE Mérés időpontja: 2012.10.18.. 1. Mérés leírása A mérés során egy adott minta viselkedését vizsgáljuk
Klasszikus Fizika Laboratórium VI.mérés Fázisátalakulások vizsgálata Mérést végezte: Vanó Lilla VALTAAT.ELTE Mérés időpontja: 2012.10.18.. 1. Mérés leírása A mérés során egy adott minta viselkedését vizsgáljuk
Iskolai jelentés. 10. évfolyam szövegértés
 2010 Iskolai jelentés 10. évfolyam szövegértés Szövegértési-szövegalkotási kompetenciaterület A fejlesztés célja Kommunikáció-központúság Tevékenység centrikusság Rendszeresség Differenciáltság Partnerség
2010 Iskolai jelentés 10. évfolyam szövegértés Szövegértési-szövegalkotási kompetenciaterület A fejlesztés célja Kommunikáció-központúság Tevékenység centrikusság Rendszeresség Differenciáltság Partnerség
STATISZTIKA. András hármas. Éva ötös. Nóri négyes. 5 4,5 4 3,5 3 2,5 2 1,5 ANNA BÉLA CILI 0,5 MAGY. MAT. TÖRT. KÉM.
 STATISZTIKA 5 4,5 4 3,5 3 2,5 2 1,5 1 0,5 0 MAGY. MAT. TÖRT. KÉM. ANNA BÉLA CILI András hármas. Béla Az átlag 3,5! kettes. Éva ötös. Nóri négyes. 1 mérés: dolgokhoz valamely szabály alapján szám rendelése
STATISZTIKA 5 4,5 4 3,5 3 2,5 2 1,5 1 0,5 0 MAGY. MAT. TÖRT. KÉM. ANNA BÉLA CILI András hármas. Béla Az átlag 3,5! kettes. Éva ötös. Nóri négyes. 1 mérés: dolgokhoz valamely szabály alapján szám rendelése
Szimulált vadkárok szántóföldi kultúrákban
 Szimulált vadkárok szántóföldi kultúrákban Napraforgó, kukorica és őszi búza Dr. habil. Marosán Miklós iü. szakértő Dr. Király István iü. szakértő Bevezetés A termésképzés befejeződése előtt keletkező
Szimulált vadkárok szántóföldi kultúrákban Napraforgó, kukorica és őszi búza Dr. habil. Marosán Miklós iü. szakértő Dr. Király István iü. szakértő Bevezetés A termésképzés befejeződése előtt keletkező
7. Mágneses szuszceptibilitás mérése
 7. Mágneses szuszceptibilitás mérése Klasszikus fizika laboratórium Mérési jegyzőkönyv Mérést végezte: Vitkóczi Fanni Mérés időpontja: 2012. 10. 25. I. A mérés célja: Egy mágneses térerősségmérő műszer
7. Mágneses szuszceptibilitás mérése Klasszikus fizika laboratórium Mérési jegyzőkönyv Mérést végezte: Vitkóczi Fanni Mérés időpontja: 2012. 10. 25. I. A mérés célja: Egy mágneses térerősségmérő műszer
Az ÉTI 1953. évben végzett cementvizsgálatainak kiértékelése POPOVICS SÁNDOR és UJHELYI JÁNOS
 - 1 - Építőanyag, 1954. 9. pp. 307-312 Az ÉTI 1953. évben végzett cementvizsgálatainak kiértékelése POPOVICS SÁNDOR és UJHELYI JÁNOS 1. Bevezetés Az Építéstudományi Intézet Minősítő Laboratóriumába 1953.
- 1 - Építőanyag, 1954. 9. pp. 307-312 Az ÉTI 1953. évben végzett cementvizsgálatainak kiértékelése POPOVICS SÁNDOR és UJHELYI JÁNOS 1. Bevezetés Az Építéstudományi Intézet Minősítő Laboratóriumába 1953.
Hipotézis, sejtés STATISZTIKA. Kétmintás hipotézisek. Tudományos hipotézis. Munkahipotézis (H a ) Nullhipotézis (H 0 ) 11. Előadás
 STATISZTIKA Hipotézis, sejtés 11. Előadás Hipotézisvizsgálatok, nem paraméteres próbák Tudományos hipotézis Nullhipotézis felállítása (H 0 ): Kétmintás hipotézisek Munkahipotézis (H a ) Nullhipotézis (H
STATISZTIKA Hipotézis, sejtés 11. Előadás Hipotézisvizsgálatok, nem paraméteres próbák Tudományos hipotézis Nullhipotézis felállítása (H 0 ): Kétmintás hipotézisek Munkahipotézis (H a ) Nullhipotézis (H
Mágneses szuszceptibilitás mérése
 Mágneses szuszceptibilitás mérése (Mérési jegyzőkönyv) Hagymási Imre 2006. március 12. (hétfő délelőtti csoport) 1. A mérés elmélete Az anyagok külső mágneses tér hatására polarizálódnak. Általában az
Mágneses szuszceptibilitás mérése (Mérési jegyzőkönyv) Hagymási Imre 2006. március 12. (hétfő délelőtti csoport) 1. A mérés elmélete Az anyagok külső mágneses tér hatására polarizálódnak. Általában az
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/54/33134304.jpg) [Biomatematika 2] Orvosi biometria 2016.02.29. A statisztika típusai Leíró jellegű statisztika: összegzi egy adathalmaz jellemzőit. A középértéket jelemzi (medián, módus, átlag) Az adatok változékonyságát
[Biomatematika 2] Orvosi biometria 2016.02.29. A statisztika típusai Leíró jellegű statisztika: összegzi egy adathalmaz jellemzőit. A középértéket jelemzi (medián, módus, átlag) Az adatok változékonyságát
A hőmérséklet-megoszlás és a közepes hőmérséklet számítása állandósult állapotban
 A HŐMÉRSÉKLET ÉS HŐKÖZLÉS KÉRDÉSEI BETONRÉTEGBE ÁGYAZOTT FŰTŐCSŐKÍGYÓK ESETÉBEN A LINEÁRIS HŐVEZETÉS TÖRVÉNYSZERŰSÉGEINEK FIGYELEMBEVÉTELÉVEL Általános észrevételek A sugárzó fűtőtestek konstrukciójából
A HŐMÉRSÉKLET ÉS HŐKÖZLÉS KÉRDÉSEI BETONRÉTEGBE ÁGYAZOTT FŰTŐCSŐKÍGYÓK ESETÉBEN A LINEÁRIS HŐVEZETÉS TÖRVÉNYSZERŰSÉGEINEK FIGYELEMBEVÉTELÉVEL Általános észrevételek A sugárzó fűtőtestek konstrukciójából
Anyagvizsgálati módszerek Mérési adatok feldolgozása. Anyagvizsgálati módszerek
 Anyagvizsgálati módszerek Mérési adatok feldolgozása Anyagvizsgálati módszerek Pannon Egyetem Mérnöki Kar Anyagvizsgálati módszerek Statisztika 1/ 22 Mérési eredmények felhasználása Tulajdonságok hierarchikus
Anyagvizsgálati módszerek Mérési adatok feldolgozása Anyagvizsgálati módszerek Pannon Egyetem Mérnöki Kar Anyagvizsgálati módszerek Statisztika 1/ 22 Mérési eredmények felhasználása Tulajdonságok hierarchikus
Méréselmélet és mérőrendszerek
 Méréselmélet és mérőrendszerek 6. ELŐADÁS KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba eredete o
Méréselmélet és mérőrendszerek 6. ELŐADÁS KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba eredete o
Hipotézis STATISZTIKA. Kétmintás hipotézisek. Munkahipotézis (H a ) Tematika. Tudományos hipotézis. 1. Előadás. Hipotézisvizsgálatok
 STATISZTIKA 1. Előadás Hipotézisvizsgálatok Tematika 1. Hipotézis vizsgálatok 2. t-próbák 3. Variancia-analízis 4. A variancia-analízis validálása, erőfüggvény 5. Korreláció számítás 6. Kétváltozós lineáris
STATISZTIKA 1. Előadás Hipotézisvizsgálatok Tematika 1. Hipotézis vizsgálatok 2. t-próbák 3. Variancia-analízis 4. A variancia-analízis validálása, erőfüggvény 5. Korreláció számítás 6. Kétváltozós lineáris
2. Laboratóriumi gyakorlat A TERMISZTOR. 1. A gyakorlat célja. 2. Elméleti bevezető
 . Laboratóriumi gyakorlat A EMISZO. A gyakorlat célja A termisztorok működésének bemutatása, valamint főbb paramétereik meghatározása. Az ellenállás-hőmérséklet = f és feszültség-áram U = f ( I ) jelleggörbék
. Laboratóriumi gyakorlat A EMISZO. A gyakorlat célja A termisztorok működésének bemutatása, valamint főbb paramétereik meghatározása. Az ellenállás-hőmérséklet = f és feszültség-áram U = f ( I ) jelleggörbék
Rugalmas állandók mérése (2-es számú mérés) mérési jegyzõkönyv
 (-es számú mérés) mérési jegyzõkönyv Készítette:,... Beadás ideje:.. 9. /9 A mérés leírása: A mérés során különbözõ alakú és anyagú rudak Young-moduluszát, valamint egy torziós szál torziómoduluszát akarjuk
(-es számú mérés) mérési jegyzõkönyv Készítette:,... Beadás ideje:.. 9. /9 A mérés leírása: A mérés során különbözõ alakú és anyagú rudak Young-moduluszát, valamint egy torziós szál torziómoduluszát akarjuk
KÖZPONTI STATISZTIKAI HIVATAL. Szóbeli vizsgatevékenység
 KÖZPONTI STATISZTIKAI HIVATAL A vizsgarészhez rendelt követelménymodul azonosító száma, megnevezése: 2144-06 Statisztikai szervezői és elemzési feladatok A vizsgarészhez rendelt vizsgafeladat megnevezése:
KÖZPONTI STATISZTIKAI HIVATAL A vizsgarészhez rendelt követelménymodul azonosító száma, megnevezése: 2144-06 Statisztikai szervezői és elemzési feladatok A vizsgarészhez rendelt vizsgafeladat megnevezése:
7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék)
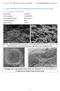 7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék) 7.1.1. SPS: 1150 C; 5 (1312 K1) Mért sűrűség: 3,795 g/cm 3 3,62 0,14 GPa Három pontos törés teszt: 105 4,2 GPa Súrlódási együttható:
7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék) 7.1.1. SPS: 1150 C; 5 (1312 K1) Mért sűrűség: 3,795 g/cm 3 3,62 0,14 GPa Három pontos törés teszt: 105 4,2 GPa Súrlódási együttható:
Aprítás 2012.09.11. Ipari gyógyszertechnológiai laboratórium gyakorlatai I. félév. Az aprítást befolyásoló tényezők GYAKORLATOK
 0.09.. Ipari gyógyszertechnológiai laboratórium gyakorlatai I. félév KÖVETELMÉNYEK. A hallgató a gyakorlatra felkészülten érkezik. A művelet típusa. Eredményt befolyásoló paraméterek (általában idő, sebesség,
0.09.. Ipari gyógyszertechnológiai laboratórium gyakorlatai I. félév KÖVETELMÉNYEK. A hallgató a gyakorlatra felkészülten érkezik. A művelet típusa. Eredményt befolyásoló paraméterek (általában idő, sebesség,
Adatok statisztikai értékelésének főbb lehetőségei
 Adatok statisztikai értékelésének főbb lehetőségei 1. a. Egy- vagy kétváltozós eset b. Többváltozós eset 2. a. Becslési problémák, hipotézis vizsgálat b. Mintázatelemzés 3. Szint: a. Egyedi b. Populáció
Adatok statisztikai értékelésének főbb lehetőségei 1. a. Egy- vagy kétváltozós eset b. Többváltozós eset 2. a. Becslési problémák, hipotézis vizsgálat b. Mintázatelemzés 3. Szint: a. Egyedi b. Populáció
Részletes összefoglaló jelentés
 Részletes összefoglaló jelentés 1. Hőátadási tényező vizsgálata egyidejű hő- és anyagátadási folyamatok esetén Az egyidejű hő- és anyagátadással járó szárítási folyamatoknál számos szerző utalt a hőátadási
Részletes összefoglaló jelentés 1. Hőátadási tényező vizsgálata egyidejű hő- és anyagátadási folyamatok esetén Az egyidejű hő- és anyagátadással járó szárítási folyamatoknál számos szerző utalt a hőátadási
A hosszúhullámú sugárzás stratocumulus felhőben történő terjedésének numerikus modellezése
 A hosszúhullámú sugárzás stratocumulus felhőben történő terjedésének numerikus modellezése Lábó Eszter 1, Geresdi István 2 1 Országos Meteorológiai Szolgálat, 2 Pécsi Tudományegyetem, Természettudományi
A hosszúhullámú sugárzás stratocumulus felhőben történő terjedésének numerikus modellezése Lábó Eszter 1, Geresdi István 2 1 Országos Meteorológiai Szolgálat, 2 Pécsi Tudományegyetem, Természettudományi
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
Kísérlettervezés alapfogalmak
 Kísérlettervezés alapfogalmak Rendszermodellezés Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Kísérlettervezés Cél: a modell paraméterezése a valóság alapján
Kísérlettervezés alapfogalmak Rendszermodellezés Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Kísérlettervezés Cél: a modell paraméterezése a valóság alapján
Kettőnél több csoport vizsgálata. Makara B. Gábor
 Kettőnél több csoport vizsgálata Makara B. Gábor Három gyógytápszer elemzéséből az alábbi energia tartalom adatok származtak (kilokalória/adag egységben) Három gyógytápszer elemzésébô A B C 30 5 00 10
Kettőnél több csoport vizsgálata Makara B. Gábor Három gyógytápszer elemzéséből az alábbi energia tartalom adatok származtak (kilokalória/adag egységben) Három gyógytápszer elemzésébô A B C 30 5 00 10
Kutatási beszámoló. 2015. február. Tangens delta mérésére alkalmas mérési összeállítás elkészítése
 Kutatási beszámoló 2015. február Gyüre Balázs BME Fizika tanszék Dr. Simon Ferenc csoportja Tangens delta mérésére alkalmas mérési összeállítás elkészítése A TKI-Ferrit Fejlsztő és Gyártó Kft.-nek munkája
Kutatási beszámoló 2015. február Gyüre Balázs BME Fizika tanszék Dr. Simon Ferenc csoportja Tangens delta mérésére alkalmas mérési összeállítás elkészítése A TKI-Ferrit Fejlsztő és Gyártó Kft.-nek munkája
BME Járműgyártás és -javítás Tanszék. Javítási ciklusrend kialakítása
 BME Járműgyártás és -javítás Tanszék Javítási ciklusrend kialakítása A javítási ciklus naptári napokban, üzemórákban vagy más teljesítmény paraméterben meghatározott időtartam, amely a jármű, gép új állapotától
BME Járműgyártás és -javítás Tanszék Javítási ciklusrend kialakítása A javítási ciklus naptári napokban, üzemórákban vagy más teljesítmény paraméterben meghatározott időtartam, amely a jármű, gép új állapotától
Mikroszkóp vizsgálata Folyadék törésmutatójának mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 8. MÉRÉS Mikroszkóp vizsgálata Folyadék törésmutatójának mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 12. Szerda délelőtti csoport
KLASSZIKUS FIZIKA LABORATÓRIUM 8. MÉRÉS Mikroszkóp vizsgálata Folyadék törésmutatójának mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 12. Szerda délelőtti csoport
NGB_IN040_1 SZIMULÁCIÓS TECHNIKÁK dr. Pozna Claudio Radu, Horváth Ernő
 SZÉCHENYI ISTVÁN EGYETEM Műszaki Tudományi Kar Informatika Tanszék BSC FOKOZATÚ MÉRNÖK INFORMATIKUS SZAK NGB_IN040_1 SZIMULÁCIÓS TECHNIKÁK dr. Pozna Claudio Radu, Horváth Ernő Fejlesztői dokumentáció GROUP#6
SZÉCHENYI ISTVÁN EGYETEM Műszaki Tudományi Kar Informatika Tanszék BSC FOKOZATÚ MÉRNÖK INFORMATIKUS SZAK NGB_IN040_1 SZIMULÁCIÓS TECHNIKÁK dr. Pozna Claudio Radu, Horváth Ernő Fejlesztői dokumentáció GROUP#6
ÉLELMISZER-IPARI ALAPISMERETEK ÉRETTSÉGI VIZSGA II. A VIZSGA LEÍRÁSA
 ÉLELMISZER-IPARI ALAPISMERETEK ÉRETTSÉGI VIZSGA A vizsga részei II. A VIZSGA LEÍRÁSA Középszint Emelt szint 180 perc 15 perc 240 perc 20 perc 100 pont 50 pont 100 pont 50 pont A vizsgán használható segédeszközök
ÉLELMISZER-IPARI ALAPISMERETEK ÉRETTSÉGI VIZSGA A vizsga részei II. A VIZSGA LEÍRÁSA Középszint Emelt szint 180 perc 15 perc 240 perc 20 perc 100 pont 50 pont 100 pont 50 pont A vizsgán használható segédeszközök
Osztályozó- és javítóvizsga témakörei MATEMATIKA tantárgyból 2016 / tanév
 9. évfolyam I. Halmazok Osztályozó- és javítóvizsga témakörei MATEMATIKA tantárgyból 2016 / 2017. tanév 1. Halmaz, részhalmaz fogalma, részhalmazok száma, jelölések 2. Intervallumok 3. Halmazműveletek
9. évfolyam I. Halmazok Osztályozó- és javítóvizsga témakörei MATEMATIKA tantárgyból 2016 / 2017. tanév 1. Halmaz, részhalmaz fogalma, részhalmazok száma, jelölések 2. Intervallumok 3. Halmazműveletek
3. Hangfrekvenciás mechanikai rezgések vizsgálata
 3. Hangfrekvenciás mechanikai rezgések vizsgálata Tóth Bence fizikus,. évfolyam 005.03.04. péntek délelőtt beadva: 005.03.. . A mérés első részében a megvastagított végű rúd (a D jelű) felharmonikusait
3. Hangfrekvenciás mechanikai rezgések vizsgálata Tóth Bence fizikus,. évfolyam 005.03.04. péntek délelőtt beadva: 005.03.. . A mérés első részében a megvastagított végű rúd (a D jelű) felharmonikusait
7. Mágneses szuszceptibilitás mérése jegyzőkönyv. Zsigmond Anna Fizika Bsc II. Mérés dátuma: Leadás dátuma:
 7. Mágneses szuszceptibilitás mérése jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 10. 22. Leadás dátuma: 2008. 11. 05. 1 1. A mérési összeállítás A mérési összeállítás sematikus ábrája
7. Mágneses szuszceptibilitás mérése jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 10. 22. Leadás dátuma: 2008. 11. 05. 1 1. A mérési összeállítás A mérési összeállítás sematikus ábrája
Statisztika 2. Dr Gősi Zsuzsanna Egyetemi adjunktus
 Statisztika 2. Dr Gősi Zsuzsanna Egyetemi adjunktus Gyakorisági sorok Mennyiségi ismérv jellemző rangsor készítünk. (pl. napi jegyeladások száma) A gyakorisági sor képzése igazából tömörítést jelent Nagyszámú
Statisztika 2. Dr Gősi Zsuzsanna Egyetemi adjunktus Gyakorisági sorok Mennyiségi ismérv jellemző rangsor készítünk. (pl. napi jegyeladások száma) A gyakorisági sor képzése igazából tömörítést jelent Nagyszámú
Fajhő mérése. (Mérési jegyzőkönyv) Hagymási Imre február 26. (hétfő délelőtti csoport)
 Fajhő mérése (Mérési jegyzőkönyv) Hagymási Imre 2006. február 26. (hétfő délelőtti csoport) 1. A mérés elméleti háttere Az anyag fajhőjének mérése legegyszerűbben a jólismert Q = cm T m (1) összefüggés
Fajhő mérése (Mérési jegyzőkönyv) Hagymási Imre 2006. február 26. (hétfő délelőtti csoport) 1. A mérés elméleti háttere Az anyag fajhőjének mérése legegyszerűbben a jólismert Q = cm T m (1) összefüggés
Országos kompetenciamérés eredményeinek kiértékelése. 6. és 8. évfolyamokon. 6. és 8. évfolyamokon 2017
 Bethlen Gábor Gimnázium, Általános Iskola, Óvoda és Alapfokú Művészeti Iskola OM azonosító: 200232 Országos kompetenciamérés Levelezési cím: H - eredményeinek 4400 Nyíregyháza, Gomba kiértékelése utca
Bethlen Gábor Gimnázium, Általános Iskola, Óvoda és Alapfokú Művészeti Iskola OM azonosító: 200232 Országos kompetenciamérés Levelezési cím: H - eredményeinek 4400 Nyíregyháza, Gomba kiértékelése utca
Vizsgáljuk elôször, hogy egy embernek mekkora esélye van, hogy a saját
 376 Statisztika, valószínûség-számítás 1500. Az elsô kérdésre egyszerû válaszolni, elég egy ellenpélda, és biztosan nem lehet akkor így kiszámolni. Pl. legyen a három szám a 3; 5;. A két kisebb szám átlaga
376 Statisztika, valószínûség-számítás 1500. Az elsô kérdésre egyszerû válaszolni, elég egy ellenpélda, és biztosan nem lehet akkor így kiszámolni. Pl. legyen a három szám a 3; 5;. A két kisebb szám átlaga
Osztályozó- és javítóvizsga. Matematika tantárgyból
 Osztályozó- és javítóvizsga Matematika tantárgyból 2018-2019 A vizsga 60 perces írásbeli vizsga (feladatlap) a megadott témakörökből. A megjelölt százalék (50%) nem teljesítése esetén szóbeli vizsga is,
Osztályozó- és javítóvizsga Matematika tantárgyból 2018-2019 A vizsga 60 perces írásbeli vizsga (feladatlap) a megadott témakörökből. A megjelölt százalék (50%) nem teljesítése esetén szóbeli vizsga is,
A VÁGÁSI KOR, A VÁGÁSI SÚLY ÉS A ROSTÉLYOS KERESZTMETSZET ALAKULÁSA FEHÉR KÉK BELGA ÉS CHAROLAIS KERESZTEZETT HÍZÓBIKÁK ESETÉBEN
 A vágási kor, a vágási súly és a rostélyos keresztmetszet alakulása fehér kék belga és charolais keresztezett hízóbikák esetében 1 () A VÁGÁSI KOR, A VÁGÁSI SÚLY ÉS A ROSTÉLYOS KERESZTMETSZET ALAKULÁSA
A vágási kor, a vágási súly és a rostélyos keresztmetszet alakulása fehér kék belga és charolais keresztezett hízóbikák esetében 1 () A VÁGÁSI KOR, A VÁGÁSI SÚLY ÉS A ROSTÉLYOS KERESZTMETSZET ALAKULÁSA
A évi országos kompetenciamérés iskolai eredményeinek elemzése
 A 2015. évi országos kompetenciamérés iskolai eredményeinek elemzése Matematika 6. osztály A szignifikánsan jobban, hasonlóan, illetve gyengébben teljesítő telephelyek száma és aránya (%) A tanulók képességeloszlása
A 2015. évi országos kompetenciamérés iskolai eredményeinek elemzése Matematika 6. osztály A szignifikánsan jobban, hasonlóan, illetve gyengébben teljesítő telephelyek száma és aránya (%) A tanulók képességeloszlása
A mágneses szuszceptibilitás vizsgálata
 Bán Marcell ETR atonosító BAMTACT.ELTE Beadási határidő: 2012.12.13 A mágneses szuszceptibilitás vizsgálata 1.1 Mérés elve Anyagokat mágneses térbe helyezve, a tér hatására az anygban mágneses dipólusmomentum
Bán Marcell ETR atonosító BAMTACT.ELTE Beadási határidő: 2012.12.13 A mágneses szuszceptibilitás vizsgálata 1.1 Mérés elve Anyagokat mágneses térbe helyezve, a tér hatására az anygban mágneses dipólusmomentum
Országos kompetenciamérés eredményeinek kiértékelése 6. és 8. évfolyamokon 2013
 Országos kompetenciamérés eredményeinek kiértékelése 6. és 8. évfolyamokon 2013 A hatodik osztályban 26 tanulóból 26 fő írta meg az országos kompetenciamérést. Ebből 0 fő SNI-s, 4 fő BTMN-es tanuló. Mentesítést
Országos kompetenciamérés eredményeinek kiértékelése 6. és 8. évfolyamokon 2013 A hatodik osztályban 26 tanulóból 26 fő írta meg az országos kompetenciamérést. Ebből 0 fő SNI-s, 4 fő BTMN-es tanuló. Mentesítést
