Őszi búzák (Triticum aestivum) szemméreteinek és sűrűség értékeinek összefüggés-rendszere
|
|
|
- Zsuzsanna Papp
- 9 évvel ezelőtt
- Látták:
Átírás
1 Őszi búzák (Triticum aestivum) szemméreteinek és sűrűség értékeinek összefüggés-rendszere Gyimes Ernő 1 Véha Antal 1 Rajkó Róbert 2 1 Szegedi Tudományegyetem Szegedi Élelmiszeripari Főiskolai Kar Élelmiszertechnológia és Környezetgazdálkodás Tanszék 2 Szegedi Tudományegyetem Szegedi Élelmiszeripari Főiskolai Kar Élelmiszeripari Műveletek és Környezettechnika Tanszék Összefoglaló A búza agrofizikai jellemzőinek ismerete alapvető fontosságú a feldolgozás során, az aratástól a malmi tisztításig. A kalászban a szemek különböző méretűek, a technológiákhoz viszont azonos méretű, kiegyenlített halmaz szükséges. A szárítás során a fizikai jellemzők szerepe alapvető, a méret mellett a méret eloszlása homogenitása -, a halmazsűrűség szerepe emelhető ki. A szerzők az étkezési, őszi búzák (Tritucum aestivum) agrofizikai jellemzői közül a szemméreteket és méreteloszlásokat, a halmaz és egyedi sűrűség értékeket és a szemtömeget vizsgálták.. Becslő egyenletet alkottak, amellyel a vastagsági méretet sikerült keménységi osztályok szerint jól becsülni. Kemény szemű mintáknál V = 2,93-0,21*H + 0,029*ESZT (R 2 =0,64) Puha szemű mintáknál V = 2,59-0,17*H + 0,031*ESZT (R 2 =0,73) Ellipszoid test alapján határozták meg a számított tömeget. A mért (ESZT) és számított ezerszem tömeg kapcsolatát az évjárattól függően r=0,75..0,91 közötti korrelációs tényezővel sikerült becsülni. Az ezerszemtömeg (ESZT) becslésére kidolgozott ellipszoid modell segítségével, a szélességi méret alapján, a mért tömeg becslése r=0,81 korrelációs tényezővel becsülhető. Megállapították, hogy a térkitöltés jellemzésére számított szemtérfogat/dm 3 jellemző az évjárattól és a termőhelytől is függ. A fajták közötti különbség lényegesen kisebb volt. Bevezetés és irodalmi áttekintés A gabonaféléknél a szemméretek ismerete döntő fontosságú. A vetőmag tisztítástól a vetésen és betakarításon át egészen a késztermék gyártásig fontos ismerni a jellemző méreteket valamint a méret kapcsolatát más fizikai jellemzőkkel. A méretek ismerete hasonlóan jelentős a betakarítás utáni (post-harvest) technológiák pontos irányításához. A szárítás előtti rostálás, betárolás előtti osztályozás eredményessége, technológiai hatásfoka nagyrészt a helyesen megválasztott rostaméretnek köszönhető, amelyhez elengedhetetlen a méretek ismerete. A szárítás során a fizikai jellemzők szerepe alapvető, a méret mellett a méret eloszlása homogenitása -, a halmazsűrűség szerepe emelhető ki (BEKE, 1997). A légáramos szállításnál és tisztításnál a megfelelő és gazdaságos légsebesség megválasztása többek között a búzahalmaz szemméreteinek ismeretét igényli. RAHEMAN és JINDAL, (2001) a függőleges pneumatikus szállítást tanulmányozva alkottak meg egy tapasztalati képletet, amelynek egyik összetevője az átlagos szemméret. 46
2 A gabonafélék szemméretének, alakjának az egyik legtermészetesebb tulajdonság, amellyel a gabona faja, esetleg fajtája azonosítható. Ugyanakkor a kalászban fejlődés során a szemek különböző méretűek. Ez utóbbi tény miatt szükséges a méret eloszlásokat is vizsgálni, hiszen technológia igény a kiegyenlített méret tulajdonság. A szemméretet jelentőségét támasztja alá MORGAN et al. (2000) valamint TROCCOLI és di FONZO (1999) kísérleti eredményei. Sűrűség alatt a szemcsék vagy a szemcsés halmaz tömegének és térfogatának hányadosát értjük. Mértékét több tényező együttes hatása alakítja, ezért is hordoz értékes információt. A gabonafélék minőségi vizsgálatakor általában 3 sűrűség értéket különböztetünk meg. Beszélhetünk halmazsűrűségről és szemsűrűségről. A halmazsűrűség mérése a malmi gyakorlatban a hektoliter tömeg meghatározását jelenti. Értékéből a halmaz várható fizikai tulajdonságaira, légellenállás, porozitás (SITKEI,1981), ürítési idő (M.CSIZMADIA-OLDAL, 2002) éppúgy lehet következtetni, mint a kiőrölhető liszt mennyiségére (KELLY et al., 1995)és minőségére SCHULER et al. (1995). Az egyedi szemeknél is értelmezhető sűrűség értékek alakulására a minta nedvesség (víztartalma) nagyobb hatást fejtett ki, mint azt CHANG (1988) valamint FANG és CAMPBELL (2000) is megállapítja. Anyag és módszer A minták a Szegedi Gabonatermesztési Kutató Kht. tenyészkertjeiből származtak. Minden tételt kisparcellás kísérletben neveltek, a vizsgált időszak között volt. A learatott búzából a nagyobb (kalászdarabok, szár) és a porszerűen kisméretű (szántóföldi por) kirostálták, a minták egyéb válogatáson nem estek keresztül. A vizsgálati minták képzése többszörös átlós mintaosztással történt. A méretek meghatározása mintánként 100 szem jellemző méreteit (szélesség, hosszúság, vastagság) digitális tolómérővel mértük. Az ezerszem mérése úgy történt, hogy a mintából kétszer 500 szemet kiszámolva a tömegét digitális mérlegen lemértük. Amennyiben az eltérés a két mérés között nagyobb volt, mint 2 %, úgy harmadik mérést is végeztünk. A halmazsűrűség érése malmi hektoliter tömeg mérlegen történt, két párhuzamos méréssel. A kapott tömegértékekből táblázat segítségével határoztuk meg a HLT értéket. Az sűrűség mérés térfogat kiszorítás elvén történt, a pontosan lemért tömegű búzát petróleummal töltött edénybe helyeztük, majd a térfogat változás mértékét lejegyeztük. A tömeg és térfogat hányadosa adta a sűrűség értéket. A valódi sűrűség mérése QUANTACHROME STEREOPYCNOMÉTERREL történt, hélium mérőgáz alkalmazásával. A pontosan lemért tömegű búza által kiszorított térfogatot a nyomásváltozás alapján lehetett kiszámítani, majd a tömeg és térfogat hányadosa szerint megkaptuk a valódi sűrűség értékét. A szemkeménység mérése Perten SKCS 4100 mérőműszerrrel történt. Az adatok kiérékelése STATISTICA (StatSoft, Inc) és STATGRAPHICS (Statistical Graphyics Corp.) programcsomaggal történt. 47
3 Eredmények A mérési eredményeket az 1. táblázatban mutatjuk be. Az egyes minták egyedi jellemzőinek közlésétől terjedelmi korlátok miatt eltekintünk. 1. táblázat A vizsgált fajták néhány jellemző értékének statisztikai adatai Szélesség Hosszúság Vastagság Ezerszem Sűrűség HLT Hi porozitás Átlag 3,19 6,40 2,75 40,16 1,35 82,03 57,43 0,39 Szórás 0,18 0,50 0,18 5,79 0,05 4,44 18,58 0,02 Min 2,67 5,32 2,26 27,72 1,19 70,36 6,10 0,34 Max 3,74 7,76 3,19 58,54 1,56 90,30 89,43 0,46 Mintaszám c.v. 5,66 7,88 6,54 14,43 3,52 5,41 32,35 5,43 Az egeys geometriai jellemzők egymástól jelentős részben függetlenek, értékük alakulására a fajta genetikai sajátosságai kisebb, a termesztés körülményei nagyobb hatással vannak. A szemszerkezet jellemzésére használt hardness index, mint szemkeménységre utaló mérőszám, alapján a minták között különbséget lehet tenni. A keményebb szemű fajtáknál a hosszúsági méret mintegy 0,2 mm-el magasabb volt, mint a puha fajtáknál. Ez a megfigyelés a szélességi méretnél nem nyert igazolást, azonban a vastagsági méret esettében igen. A puha fajtáknál a búza legkisebb mérete szignifikánsan alacsonyabb volt, mint a keményebb mintáknál. Ez utóbbi eredmény alapján sikerült egy kétváltozós egyenletet megalkotni, amely segítségével a hosszúsági méret valamint az ezerszem tömeg alapján meg lehet határozni a búza vastagsági méretét. Az egyenlet kemény fajták esetében a következőképp néz ki: V = 2,93-0,21*H + 0,029*ESZT (R 2 =0,64) Puha szemű mintáknál az egyenlet leírása: V = 2,59-0,17*H + 0,031*ESZT (R 2 =0,73) A fentiekből látható, hogy a determinációs együttható a puha fajtáknál kismértékben magasabb, amelynek lehet oka, hogy a kemény szemszerkezetű minták száma magasabb, így az adatok szórása is magasabb lehet. Az ezerszem tömeg értékeit (ESZT) viszonylag széles tartományban mértük, amely összahangban áll azzal, hogy a minták több évjáratból, köztük szélsőséges is, származtak. A nagy átlagértékű fajták között kemény és puha egyaránt előfordult. A legmagasabb átlagértéke a kemény fajták közül a Jubilejnaja-50 fajtának volt 47,45 g értékkel, a puha szemű fajták közül a Mérő (44.21 g) tömege volt a legmagasabb. A legkisebb ESZT értéket a Forrás (32,72g) adta. Az évek tekintetében a legkisebb mért értékek az 1999, a legmagasabbak a évből származtak. A sűrűség közül egyet emelnénk ki, a valódi sűrűség értékeit. Ez az érték a búza belső szrekezeti üregeit, a kapillárisok térfogatást is magába foglalja, szemben a burkot sűrűséggel, amely csak a nedvesített felületen értelmezhető térfogatból származó sűrűséget jelenti. 48
4 Vizsgálataink szerint a valódi sűrűség értékei 1,44 g/cm 3 volt. Két év adatai szerint a évi mintáknál 1,4387 g/cm 3, a évi mintáknál 1,4475 g/cm 3 értéket kaptunk. Figyelembe véve a mérés reletív hibáját, kijelenthetjük, hogy az általunk kapott átlagérték jó. Az egyes jellemzők közötti kapcsolat bemutatását a tömeg értékekkel kezdjük. A szemek számított tömegét úgy határoztuk meg, hogy a magok alakját ellipszoidnak tételeztük fel és az így kiszámított térfogatot szoroztuk meg a burkolt sűrűség értékkel. A számított és a mért (ezerszem tömeg) értékek kapcsolatát mutatja be az 1.ábra. Burkolt sűrűség adatok alapján y ( ) = 0,8553x + 5,938 R 2 = 0,765 Mért ezerszem tömeg (g) y (1999) = 0,7972x + 7,0088 R 2 = 0,5183 y (2001) = 0,8718x + 4,0787 R 2 = 0, y (2000) = 0,7769x + 10,645 R 2 = 0,6806 y( 2002) = 0,8763x + 5,0033 R 2 = 0, Számított ezerszem tömeg (g) 1. ábra A számított és mért tömegértékek a vizsgált búzafajtáknál Az egyes számításoknál gyakran alkalmazunk egyenértékű átmérőket. Egyszerűbb esetben a búza jellemző méreteként a szélességi méreteét szokás megjelölni, amely a legtöbb esetben elegendő is. Gömb, kocka és ellipszoid alakból kiindulva meghatároztuk az egyes alakokhoz tartozó térfogatot illetve tömeget. Sűrűségnek minden esetben 1,44 g/cm 3 értéket vettünk, amely vizsgálataink szerint a búza valódi sűrűségének átlagértékét jelenti. A 2.ábra az eredményeket mutatja. Látható, hogy egyszerű gömb alakot feltételezve a mért és a számított értékek között hatalmas differencia van. A számított ellipsziod értékek és a mért 49
5 értékek közötti eltérést az okozza, hogy a búza vastagsági mérete mellett nem veszi figyelembe a hasi barázda mélységét és emiatt a számított térfogat mindig nagyobb, mint a valóságos. A legjobb közelítést a kocka alakból való kiindulás jelentette, bár a valóságos búzaalakhoz ennek semmi köze, de a búza geomertiai arányai miatt mégis ez látszik a legpontosabbnak. Mért ezerszem tömeg Számított (gömb) Számított (elipszoid) Kocka Ezerszem tömeg Tömeg (g) Szélesség-ESZT y = 3,7114x 2,0457 R 2 = 0, ,5 1 1,5 2 2,5 3 3,5 4 Szélesség (mm) 2. ábra A tömeg becslése a szélességi méret alapján, különböző alakzatoknál A porozitás a szemek közötti térrész arányát mutatja. A HLT értéke fordított arányban áll a porozitással, mivel a porozitást a HLT és a sűrűség hányadosaként lehet felfogni, és a sűrűség értékének varianciája lényegesen kisebb, mint a HLT-é. Az összefüggés kapcsolati szorosságát a szemszerkezet befolyásolja. A kemény szemű minták esetében az összefüggés determinációs együtthatója 0,73 volt, míg a puha mintáknál ez 0,66 volt. A porozitás értéke elsősorban az évjárat hatására módosult. A fajták között számottevő különbséget nem lehetett felfedezni. Az évjárat mögött elsősorban a csapadék és a hőmérséklet hatása mutatható ki. Értéke az aszályos 2000 és 2002 években szignifikánsan különbözött mind egymástól, mind a többi évjárattól. A legjellemzőbb geometriai adatokra, mért és számított értékre elvégzett főkomponens elemzés szerint 3 komponens alapján lehet az összefüggés rendszert megadni. A 3. komponensben a literenkénti szemtérfogat (számított érték) súlya a legnagyobb (0,91) amely azt is jelenti, hogy ez a változó jelentősen különbözik a többitől. A főkomponens elemzésben szereplő változók elhelyezkedése a 3. ábrán látható. Megállapítható, hogy az ezerszem tömeg és a szélessségi méret gyakorlatilag nem különböztethető meg. Ez másként megfogalmazva 50
6 azt jelenti, hogy a két változó ebben az összefüggés rendszerben azonosnak tekinthető. Hasonló tendencia figyelhető meg a HLT és a gömbalakúság között. A szemek gömbszerűsége és a térkitöltési képessége között eleve feltételezhető korreláció. Az ábra továbbá azt sugallja, hogy a geometriai méretek közül mindhárom más és más tulajdonságot fed, vagy más jellemzővel áll kapcsolatban. Plot of Component Weights Component 2 0,24 0,04-0,16-0,36-0,56 porozitás Hosszúság ESZT Gömbalak Sûrûség Szemtérfogat/liter Vastagság Szélesség HLT -0,37-0,17 0,03 0,23 0,43 0,63 Component 1 3. ábra A változók súlya az első és második komponensben Következtetések és javaslatok A vastagsági méret jól becsülhető a tömeg és a hosszúság méret alapján, így közelítő számításokra alkalmas. D mesterséges látás esetén szükségtelen a legkisebb méret mérése. A mért és számított tömeg közötti kapcsolat feltehetően a hasi barázda és a szembe zárt üregre ad pontosabb információt, amelynek további vizsgálata célszerű. A modellek közül az ellipszoid és kocka alak adta alegjobb közelítést a tömeg becsléséhez. A szemszerkezet beli különbségek olyan erős minőségjegyek, amelyek még olyan jellemzőkben is megnyílvánulnak, mint a szemméret, amely pedig nem tipikusan fajta jellemző. Köszönetnyilvánítás Köszönet illeti a szegedi Gabonatermesztési Kutató Kht. Búzaigazgatóságát a kísérleti mintákért. A szerzők hálás szívvel köszönik meg Bakos Tiborné, Bodóné Lengyel Györgyi, Mészáros Gyula segítségét. Köszönet illeti mindazon hallgatóinkat, akik tevékenyen részt vettek kutatási munkánkban. 51
7 Irodalomjegyzék Sitkei, Gy. (1981): Mezőgazdasági anyagok mechanikája Akadémiai Kiadó, Budapest p Beke, J. (1997): A szemes termények szárítása (in szerk Beke:Terményszárítás Agroinform Budapest, p Chang, C. (1988): Measuring density and porosity of grain kernels using a gas pycnometer Cereal Chemistry, Vol. 65. No.(1), p Fang, C. Campbell, G. (2000): Effect of measurement method and moisture content on wheat kernel density measurement Food and Bioproducts Processing, Vol. 78, No (C4), p Fang, C. Campbell, G. (2002): Effect of roll fluting disposition and roll gap on breakage of wheat kernels during first-break roller milling Cereal Chemistry, Vol. 79, No (4), p Raheman, H. Jindal, V. (2001): Solid velocity estimation in vertical pneumatic conveying of agricultural grains Applied Engineering in Agriculture, Vol. 17. No. (2), p Morgan, B. Dexter, C. Preston, K. (2000): Relationship of kernel size to flour water absorption for Canada Western Red Spring wheat Cereal Chemistry, Vol. 77. No. 3 p Troccoli, A. di Fonzo, N. (1999): Relationship between kernel size features and test weight in triticum durum Cereal Chemistry, Vol. 76, No. 1, p Schuler, S. Bacon, R. Gbur, E. (1994): Kernel and spike character influence on test weight of soft red winter-wheat Crop Science, Vol. 34, No. 5, p Kelly, J. Bacon, R. Gbur, E. (1995): Relationship of grain-yield and test weight in soft red winter-wheat Cereal Research Communacation, Vol. 23, No. 1-2, p M. Csizmadia,B. Oldal, I. (2002): Szemcsés halmazok silóból való ürülésének problémái, Olaj-Szappan-Kozmetika, Vol. 51, No. 3, p
DOKTORI (PhD) ÉRTEKEZÉS TÉZISEI
 DOKTORI (PhD) ÉRTEKEZÉS TÉZISEI NYUGAT-MAGYARORSZÁGI EGYETEM MEZŐGAZDASÁG- ÉS ÉLELMISZERTUDOMÁNYI KAR, MOSONMAGYARÓVÁR Agrárműszaki, Élelmiszeripari és Környezettechnikai Intézet Doktori Iskola vezető
DOKTORI (PhD) ÉRTEKEZÉS TÉZISEI NYUGAT-MAGYARORSZÁGI EGYETEM MEZŐGAZDASÁG- ÉS ÉLELMISZERTUDOMÁNYI KAR, MOSONMAGYARÓVÁR Agrárműszaki, Élelmiszeripari és Környezettechnikai Intézet Doktori Iskola vezető
3. M AGYAR SZÁRÍTÁSI SZIM PÓZIUM
 3. M AGYAR SZÁRÍTÁSI SZIM PÓZIUM Nyíregyháza 1999. szeptember 22-23. 110 A szemcseméret és fajlagos felület meghatározás anyag és hőátadási folyamatokhoz Gyimes Ernő Dr. Véha Antal *- Dr. Rajkó Róbert**
3. M AGYAR SZÁRÍTÁSI SZIM PÓZIUM Nyíregyháza 1999. szeptember 22-23. 110 A szemcseméret és fajlagos felület meghatározás anyag és hőátadási folyamatokhoz Gyimes Ernő Dr. Véha Antal *- Dr. Rajkó Róbert**
SZEMKEMÉNYSÉG VIZSGÁLÓ MÓDSZEREK ÖSSZEHASONLÍTÁSA ŐSZI BÚZÁK ESETÉBEN. Véha Antal Gyimes Ernő JATE Szegedi Élelmiszeripari Főiskolai Kar, Szeged
 SZEMKEMÉNYSÉG VIZSGÁLÓ MÓDSZEREK ÖSSZEHASONLÍTÁSA ŐSZI BÚZÁK ESETÉBEN Bevezetés, célkitűzés Véha Antal Gyimes Ernő JATE Szegedi Élelmiszeripari Főiskolai Kar, Szeged A jelenlegi malomipari gyakorlatban
SZEMKEMÉNYSÉG VIZSGÁLÓ MÓDSZEREK ÖSSZEHASONLÍTÁSA ŐSZI BÚZÁK ESETÉBEN Bevezetés, célkitűzés Véha Antal Gyimes Ernő JATE Szegedi Élelmiszeripari Főiskolai Kar, Szeged A jelenlegi malomipari gyakorlatban
Matematikai geodéziai számítások 6.
 Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Matematikai geodéziai számítások 6.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
A vizsgálatok eredményei
 A vizsgálatok eredményei A vizsgált vetőmagvak és műtrágyák nagy száma az eredmények táblázatos bemutatását teszi szükségessé, a legfontosabb magyarázatokkal kiegészítve. A közölt adatok a felsorolt publikációkban
A vizsgálatok eredményei A vizsgált vetőmagvak és műtrágyák nagy száma az eredmények táblázatos bemutatását teszi szükségessé, a legfontosabb magyarázatokkal kiegészítve. A közölt adatok a felsorolt publikációkban
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011.
 BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
NYUGAT-MAGYARORSZÁGI EGYETEM MEZŐGAZDASÁG- ÉS ÉLELMISZERTUDOMÁNYI KAR, MOSONMAGYARÓVÁR Agrárműszaki, Élelmiszeripari és Környezettechnikai Intézet
 1 NYUGAT-MAGYARORSZÁGI EGYETEM MEZŐGAZDASÁG- ÉS ÉLELMISZERTUDOMÁNYI KAR, MOSONMAGYARÓVÁR Agrárműszaki, Élelmiszeripari és Környezettechnikai Intézet Doktori Iskola vezető Prof. Dr. Schmidt János MTA levelező
1 NYUGAT-MAGYARORSZÁGI EGYETEM MEZŐGAZDASÁG- ÉS ÉLELMISZERTUDOMÁNYI KAR, MOSONMAGYARÓVÁR Agrárműszaki, Élelmiszeripari és Környezettechnikai Intézet Doktori Iskola vezető Prof. Dr. Schmidt János MTA levelező
Biomatematika 12. Szent István Egyetem Állatorvos-tudományi Kar. Fodor János
 Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/91/106534674.jpg) [Biomatematika 2] Orvosi biometria Bódis Emőke 2016. 04. 25. J J 9 Korrelációanalízis Regresszióanalízis: hogyan változik egy vizsgált változó értéke egy másik változó változásának függvényében. Korrelációs
[Biomatematika 2] Orvosi biometria Bódis Emőke 2016. 04. 25. J J 9 Korrelációanalízis Regresszióanalízis: hogyan változik egy vizsgált változó értéke egy másik változó változásának függvényében. Korrelációs
DETERMINATION OF SHEAR STRENGTH OF SOLID WASTES BASED ON CPT TEST RESULTS
 Műszaki Földtudományi Közlemények, 83. kötet, 1. szám (2012), pp. 271 276. HULLADÉKOK TEHERBÍRÁSÁNAK MEGHATÁROZÁSA CPT-EREDMÉNYEK ALAPJÁN DETERMINATION OF SHEAR STRENGTH OF SOLID WASTES BASED ON CPT TEST
Műszaki Földtudományi Közlemények, 83. kötet, 1. szám (2012), pp. 271 276. HULLADÉKOK TEHERBÍRÁSÁNAK MEGHATÁROZÁSA CPT-EREDMÉNYEK ALAPJÁN DETERMINATION OF SHEAR STRENGTH OF SOLID WASTES BASED ON CPT TEST
Statisztika I. 11. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 11. előadás Előadó: Dr. Ertsey Imre Összefüggés vizsgálatok A társadalmi gazdasági élet jelenségei kölcsönhatásban állnak, összefüggnek egymással. Statisztika alapvető feladata: - tényszerűségek
Statisztika I. 11. előadás Előadó: Dr. Ertsey Imre Összefüggés vizsgálatok A társadalmi gazdasági élet jelenségei kölcsönhatásban állnak, összefüggnek egymással. Statisztika alapvető feladata: - tényszerűségek
Al-Mg-Si háromalkotós egyensúlyi fázisdiagram közelítő számítása
 l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
Andó Mátyás Felületi érdesség matyi.misi.eu. Felületi érdesség. 1. ábra. Felületi érdességi jelek
 1. Felületi érdesség használata Felületi érdesség A műszaki rajzokon a geometria méretek tűrése mellett a felületeket is jellemzik. A felületek jellemzésére leginkább a felületi érdességet használják.
1. Felületi érdesség használata Felületi érdesség A műszaki rajzokon a geometria méretek tűrése mellett a felületeket is jellemzik. A felületek jellemzésére leginkább a felületi érdességet használják.
Rugalmas állandók mérése
 Rugalmas állandók mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. április 23. (hétfő délelőtti csoport) 1. Young-modulus mérése behajlásból 1.1. A mérés menete A mérés elméleti háttere megtalálható a jegyzetben
Rugalmas állandók mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. április 23. (hétfő délelőtti csoport) 1. Young-modulus mérése behajlásból 1.1. A mérés menete A mérés elméleti háttere megtalálható a jegyzetben
Biometria az orvosi gyakorlatban. Korrelációszámítás, regresszió
 SZDT-08 p. 1/31 Biometria az orvosi gyakorlatban Korrelációszámítás, regresszió Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Korrelációszámítás
SZDT-08 p. 1/31 Biometria az orvosi gyakorlatban Korrelációszámítás, regresszió Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Korrelációszámítás
MÓDSZEREK BÚZA SZEMKEMÉNYSÉGÉNEK MEGHATÁROZÁSÁRA. Doktori értekezés tézisei. Készítette: Szabó Pál Balázs
 MÓDSZEREK BÚZA SZEMKEMÉNYSÉGÉNEK MEGHATÁROZÁSÁRA Doktori értekezés tézisei Készítette: Szabó Pál Balázs Témavezető: Dr. Fekete András egyetemi tanár Dr. habil Véha Antal egyetemi tanár Készült a Budapesti
MÓDSZEREK BÚZA SZEMKEMÉNYSÉGÉNEK MEGHATÁROZÁSÁRA Doktori értekezés tézisei Készítette: Szabó Pál Balázs Témavezető: Dr. Fekete András egyetemi tanár Dr. habil Véha Antal egyetemi tanár Készült a Budapesti
Biometria gyakorló feladatok BsC hallgatók számára
 Biometria gyakorló feladatok BsC hallgatók számára 1. Egy üzem alkalmazottainak megoszlása az elért teljesítmény %-a szerint a következı: Norma teljesítmény % Dolgozók száma 60-80 30 81-90 70 91-100 90
Biometria gyakorló feladatok BsC hallgatók számára 1. Egy üzem alkalmazottainak megoszlása az elért teljesítmény %-a szerint a következı: Norma teljesítmény % Dolgozók száma 60-80 30 81-90 70 91-100 90
Rugalmas állandók mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 2. MÉRÉS Rugalmas állandók mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 16. Szerda délelőtti csoport 1. A mérés rövid leírása Mérésem
KLASSZIKUS FIZIKA LABORATÓRIUM 2. MÉRÉS Rugalmas állandók mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 16. Szerda délelőtti csoport 1. A mérés rövid leírása Mérésem
Mérési hibák 2006.10.04. 1
 Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
A VÁGÁSI KOR, A VÁGÁSI SÚLY ÉS A ROSTÉLYOS KERESZTMETSZET ALAKULÁSA FEHÉR KÉK BELGA ÉS CHAROLAIS KERESZTEZETT HÍZÓBIKÁK ESETÉBEN
 A vágási kor, a vágási súly és a rostélyos keresztmetszet alakulása fehér kék belga és charolais keresztezett hízóbikák esetében 1 () A VÁGÁSI KOR, A VÁGÁSI SÚLY ÉS A ROSTÉLYOS KERESZTMETSZET ALAKULÁSA
A vágási kor, a vágási súly és a rostélyos keresztmetszet alakulása fehér kék belga és charolais keresztezett hízóbikák esetében 1 () A VÁGÁSI KOR, A VÁGÁSI SÚLY ÉS A ROSTÉLYOS KERESZTMETSZET ALAKULÁSA
MÉRÉSI EREDMÉNYEK PONTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI
 MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
Kettőnél több csoport vizsgálata. Makara B. Gábor
 Kettőnél több csoport vizsgálata Makara B. Gábor Három gyógytápszer elemzéséből az alábbi energia tartalom adatok származtak (kilokalória/adag egységben) Három gyógytápszer elemzésébô A B C 30 5 00 10
Kettőnél több csoport vizsgálata Makara B. Gábor Három gyógytápszer elemzéséből az alábbi energia tartalom adatok származtak (kilokalória/adag egységben) Három gyógytápszer elemzésébô A B C 30 5 00 10
Az egyszerűsítés utáni alak:
 1. gyszerűsítse a következő törtet, ahol b 6. 2 b 36 b 6 Az egyszerűsítés utáni alak: 2. A 2, 4 és 5 számjegyek mindegyikének felhasználásával elkészítjük az összes, különböző számjegyekből álló háromjegyű
1. gyszerűsítse a következő törtet, ahol b 6. 2 b 36 b 6 Az egyszerűsítés utáni alak: 2. A 2, 4 és 5 számjegyek mindegyikének felhasználásával elkészítjük az összes, különböző számjegyekből álló háromjegyű
A Kecskeméti Jubileum paradicsomfajta érésdinamikájának statisztikai vizsgálata
 Borsa Béla FVM Mezőgazdasági Gépesítési Intézet 2100 Gödöllő, Tessedik S.u.4. Tel.: (28) 511 611 E.posta: borsa@fvmmi.hu A Kecskeméti Jubileum paradicsomfajta érésdinamikájának statisztikai vizsgálata
Borsa Béla FVM Mezőgazdasági Gépesítési Intézet 2100 Gödöllő, Tessedik S.u.4. Tel.: (28) 511 611 E.posta: borsa@fvmmi.hu A Kecskeméti Jubileum paradicsomfajta érésdinamikájának statisztikai vizsgálata
y ij = µ + α i + e ij
 Elmélet STATISZTIKA 3. Előadás Variancia-analízis Lineáris modellek A magyarázat a függő változó teljes heterogenitásának két részre bontását jelenti. A teljes heterogenitás egyik része az, amelynek okai
Elmélet STATISZTIKA 3. Előadás Variancia-analízis Lineáris modellek A magyarázat a függő változó teljes heterogenitásának két részre bontását jelenti. A teljes heterogenitás egyik része az, amelynek okai
1. számú ábra. Kísérleti kályha járattal
 Kísérleti kályha tesztelése A tesztsorozat célja egy járatos, egy kitöltött harang és egy üres harang hőtároló összehasonlítása. A lehető legkisebb méretű, élére állított téglából épített héjba hagyományos,
Kísérleti kályha tesztelése A tesztsorozat célja egy járatos, egy kitöltött harang és egy üres harang hőtároló összehasonlítása. A lehető legkisebb méretű, élére állított téglából épített héjba hagyományos,
1. Adatok kiértékelése. 2. A feltételek megvizsgálása. 3. A hipotézis megfogalmazása
 HIPOTÉZIS VIZSGÁLAT A hipotézis feltételezés egy vagy több populációról. (pl. egy gyógyszer az esetek 90%-ában hatásos; egy kezelés jelentősen megnöveli a rákos betegek túlélését). A hipotézis vizsgálat
HIPOTÉZIS VIZSGÁLAT A hipotézis feltételezés egy vagy több populációról. (pl. egy gyógyszer az esetek 90%-ában hatásos; egy kezelés jelentősen megnöveli a rákos betegek túlélését). A hipotézis vizsgálat
Hangfrekvenciás mechanikai rezgések vizsgálata
 Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
A mérés problémája a pedagógiában. Dr. Nyéki Lajos 2015
 A mérés problémája a pedagógiában Dr. Nyéki Lajos 2015 A mérés fogalma Mérésen olyan tevékenységet értünk, amelynek eredményeként a vizsgált jelenség számszerűen jellemezhetővé, más hasonló jelenségekkel
A mérés problémája a pedagógiában Dr. Nyéki Lajos 2015 A mérés fogalma Mérésen olyan tevékenységet értünk, amelynek eredményeként a vizsgált jelenség számszerűen jellemezhetővé, más hasonló jelenségekkel
4/24/12. Regresszióanalízis. Legkisebb négyzetek elve. Regresszióanalízis
 1. feladat Regresszióanalízis. Legkisebb négyzetek elve 2. feladat Az iskola egy évfolyamába tartozó diákok átlagéletkora 15,8 év, standard deviációja 0,6 év. A 625 fős évfolyamból hány diák fiatalabb
1. feladat Regresszióanalízis. Legkisebb négyzetek elve 2. feladat Az iskola egy évfolyamába tartozó diákok átlagéletkora 15,8 év, standard deviációja 0,6 év. A 625 fős évfolyamból hány diák fiatalabb
Tartalomjegyzék I. RÉSZ: KÍSÉRLETEK MEGTERVEZÉSE
 Tartalomjegyzék 5 Tartalomjegyzék Előszó I. RÉSZ: KÍSÉRLETEK MEGTERVEZÉSE 1. fejezet: Kontrollált kísérletek 21 1. A Salk-oltás kipróbálása 21 2. A porta-cava sönt 25 3. Történeti kontrollok 27 4. Összefoglalás
Tartalomjegyzék 5 Tartalomjegyzék Előszó I. RÉSZ: KÍSÉRLETEK MEGTERVEZÉSE 1. fejezet: Kontrollált kísérletek 21 1. A Salk-oltás kipróbálása 21 2. A porta-cava sönt 25 3. Történeti kontrollok 27 4. Összefoglalás
Hipotézis vizsgálatok
 Hipotézis vizsgálatok Hipotézisvizsgálat Hipotézis: az alapsokaság paramétereire vagy az alapsokaság eloszlására vonatkozó feltevés. Hipotézis ellenőrzés: az a statisztikai módszer, amelynek segítségével
Hipotézis vizsgálatok Hipotézisvizsgálat Hipotézis: az alapsokaság paramétereire vagy az alapsokaság eloszlására vonatkozó feltevés. Hipotézis ellenőrzés: az a statisztikai módszer, amelynek segítségével
STATISZTIKA I. Változékonyság (szóródás) A szóródás mutatószámai. Terjedelem. Forgalom terjedelem. Excel függvények. Függvénykategória: Statisztikai
 Változékonyság (szóródás) STATISZTIKA I. 5. Előadás Szóródási mutatók A középértékek a sokaság elemeinek értéknagyságbeli különbségeit eltakarhatják. A változékonyság az azonos tulajdonságú, de eltérő
Változékonyság (szóródás) STATISZTIKA I. 5. Előadás Szóródási mutatók A középértékek a sokaság elemeinek értéknagyságbeli különbségeit eltakarhatják. A változékonyság az azonos tulajdonságú, de eltérő
Az értékelés során következtetést fogalmazhatunk meg a
 Az értékelés során következtetést fogalmazhatunk meg a a tanuló teljesítményére, a tanulási folyamatra, a célokra és követelményekre a szülők teljesítményére, a tanulási folyamatra, a célokra és követelményekre
Az értékelés során következtetést fogalmazhatunk meg a a tanuló teljesítményére, a tanulási folyamatra, a célokra és követelményekre a szülők teljesítményére, a tanulási folyamatra, a célokra és követelményekre
2013 ŐSZ. 1. Mutassa be az egymintás z-próba célját, alkalmazásának feltételeit és módszerét!
 GAZDASÁGSTATISZTIKA KIDOLGOZOTT ELMÉLETI KÉRDÉSEK A 3. ZH-HOZ 2013 ŐSZ Elméleti kérdések összegzése 1. Mutassa be az egymintás z-próba célját, alkalmazásának feltételeit és módszerét! 2. Mutassa be az
GAZDASÁGSTATISZTIKA KIDOLGOZOTT ELMÉLETI KÉRDÉSEK A 3. ZH-HOZ 2013 ŐSZ Elméleti kérdések összegzése 1. Mutassa be az egymintás z-próba célját, alkalmazásának feltételeit és módszerét! 2. Mutassa be az
Pszichometria Szemináriumi dolgozat
 Pszichometria Szemináriumi dolgozat 2007-2008. tanév szi félév Temperamentum and Personality Questionnaire pszichometriai mutatóinak vizsgálata Készítette: XXX 1 Reliabilitás és validitás A kérd ívek vizsgálatának
Pszichometria Szemináriumi dolgozat 2007-2008. tanév szi félév Temperamentum and Personality Questionnaire pszichometriai mutatóinak vizsgálata Készítette: XXX 1 Reliabilitás és validitás A kérd ívek vizsgálatának
Folyadékok és szilárd anyagok sűrűségének meghatározása különböző módszerekkel
 Folyadékok és szilárd anyagok sűrűségének meghatározása különböző módszerekkel Név: Neptun kód: _ mérőhely: _ Labor előzetes feladatok 20 C-on különböző töménységű ecetsav-oldatok sűrűségét megmérve az
Folyadékok és szilárd anyagok sűrűségének meghatározása különböző módszerekkel Név: Neptun kód: _ mérőhely: _ Labor előzetes feladatok 20 C-on különböző töménységű ecetsav-oldatok sűrűségét megmérve az
Statisztika - bevezetés Méréselmélet PE MIK MI_BSc VI_BSc 1
 Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
A termesztési tényezők hatása az őszi búza termésére és a terméselemekre 2000-ben
 A termesztési tényezők hatása az őszi búza termésére és a terméselemekre 2000-ben Lesznyák Mátyásné Debreceni Egyetem Agrártudományi Centrum, Mezőgazdaságtudományi Kar, Növénytermesztési és Tájökológiai
A termesztési tényezők hatása az őszi búza termésére és a terméselemekre 2000-ben Lesznyák Mátyásné Debreceni Egyetem Agrártudományi Centrum, Mezőgazdaságtudományi Kar, Növénytermesztési és Tájökológiai
2. Rugalmas állandók mérése jegyzőkönyv javított. Zsigmond Anna Fizika Bsc II. Mérés dátuma: Leadás dátuma:
 2. Rugalmas állandók mérése jegyzőkönyv javított Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 17. Leadás dátuma: 2008. 10. 08. 1 1. Mérések ismertetése Az első részben egy téglalap keresztmetszetű
2. Rugalmas állandók mérése jegyzőkönyv javított Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 17. Leadás dátuma: 2008. 10. 08. 1 1. Mérések ismertetése Az első részben egy téglalap keresztmetszetű
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
Hangfrekvenciás mechanikai rezgések vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
Alap-ötlet: Karl Friedrich Gauss ( ) valószínűségszámítási háttér: Andrej Markov ( )
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
A Balaton vízforgalmának a klímaváltozás hatására becsült változása
 A Balaton vízforgalmának a klímaváltozás hatására becsült változása Varga György varga.gyorgy@ovf.hu VITUKI Hungary Kft. Országos Meteorológiai Szolgálat Az előadás tartalma adatok és információk a Balaton
A Balaton vízforgalmának a klímaváltozás hatására becsült változása Varga György varga.gyorgy@ovf.hu VITUKI Hungary Kft. Országos Meteorológiai Szolgálat Az előadás tartalma adatok és információk a Balaton
Statisztika I. 9. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 9. előadás Előadó: Dr. Ertsey Imre Statisztikai hipotézis vizsgálatok elsősorban a biometriában alkalmazzák, újabban reprezentatív jellegű ökonómiai vizsgálatoknál, üzemi szinten élelmiszeripari
Statisztika I. 9. előadás Előadó: Dr. Ertsey Imre Statisztikai hipotézis vizsgálatok elsősorban a biometriában alkalmazzák, újabban reprezentatív jellegű ökonómiai vizsgálatoknál, üzemi szinten élelmiszeripari
Elemi statisztika fizikusoknak
 1. oldal Elemi statisztika fizikusoknak Pollner Péter Biológiai Fizika Tanszék pollner@elte.hu Az adatok leírása, megismerése és összehasonlítása 2-1 Áttekintés 2-2 Gyakoriság eloszlások 2-3 Az adatok
1. oldal Elemi statisztika fizikusoknak Pollner Péter Biológiai Fizika Tanszék pollner@elte.hu Az adatok leírása, megismerése és összehasonlítása 2-1 Áttekintés 2-2 Gyakoriság eloszlások 2-3 Az adatok
2. Rugalmas állandók mérése
 2. Rugalmas állandók mérése Klasszikus fizika laboratórium Mérési jegyzőkönyv Mérést végezte: Vitkóczi Fanni Jegyzőkönyv leadásának időpontja: 2012. 12. 15. I. A mérés célja: Két anyag Young-modulusának
2. Rugalmas állandók mérése Klasszikus fizika laboratórium Mérési jegyzőkönyv Mérést végezte: Vitkóczi Fanni Jegyzőkönyv leadásának időpontja: 2012. 12. 15. I. A mérés célja: Két anyag Young-modulusának
Statisztika I. 12. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 1. előadás Előadó: Dr. Ertsey Imre Regresszió analízis A korrelációs együttható megmutatja a kapcsolat irányát és szorosságát. A kapcsolat vizsgálata során a gyakorlatban ennél messzebb
Statisztika I. 1. előadás Előadó: Dr. Ertsey Imre Regresszió analízis A korrelációs együttható megmutatja a kapcsolat irányát és szorosságát. A kapcsolat vizsgálata során a gyakorlatban ennél messzebb
7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék)
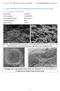 7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék) 7.1.1. SPS: 1150 C; 5 (1312 K1) Mért sűrűség: 3,795 g/cm 3 3,62 0,14 GPa Három pontos törés teszt: 105 4,2 GPa Súrlódási együttható:
7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék) 7.1.1. SPS: 1150 C; 5 (1312 K1) Mért sűrűség: 3,795 g/cm 3 3,62 0,14 GPa Három pontos törés teszt: 105 4,2 GPa Súrlódási együttható:
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/54/33134304.jpg) [Biomatematika 2] Orvosi biometria 2016.02.29. A statisztika típusai Leíró jellegű statisztika: összegzi egy adathalmaz jellemzőit. A középértéket jelemzi (medián, módus, átlag) Az adatok változékonyságát
[Biomatematika 2] Orvosi biometria 2016.02.29. A statisztika típusai Leíró jellegű statisztika: összegzi egy adathalmaz jellemzőit. A középértéket jelemzi (medián, módus, átlag) Az adatok változékonyságát
3. OSZTÁLY A TANANYAG ELRENDEZÉSE
 Jelölések: 3. OSZTÁLY A TANANYAG ELRENDEZÉSE Piros főtéma Citromsárga segítő, eszköz Narancssárga előkészítő Kék önálló melléktéma Hét Gondolkodási és megismerési módszerek Problémamegoldások, modellek
Jelölések: 3. OSZTÁLY A TANANYAG ELRENDEZÉSE Piros főtéma Citromsárga segítő, eszköz Narancssárga előkészítő Kék önálló melléktéma Hét Gondolkodási és megismerési módszerek Problémamegoldások, modellek
Heckman modell. Szelekciós modellek alkalmazásai.
 Heckman modell. Szelekciós modellek alkalmazásai. Mikroökonometria, 12. hét Bíró Anikó A tananyag a Gazdasági Versenyhivatal Versenykultúra Központja és a Tudás-Ökonómia Alapítvány támogatásával készült
Heckman modell. Szelekciós modellek alkalmazásai. Mikroökonometria, 12. hét Bíró Anikó A tananyag a Gazdasági Versenyhivatal Versenykultúra Központja és a Tudás-Ökonómia Alapítvány támogatásával készült
Víz az útpályaszerkezetben
 40. Útügyi Napok SZEGED 2015. szeptember 15-16. Víz az útpályaszerkezetben Kovácsné Igazvölgyi Zsuzsanna tanársegéd Soós Zoltán PhD hallgató dr. Tóth Csaba adjunktus Az előadás tartalma Problémafelvetés
40. Útügyi Napok SZEGED 2015. szeptember 15-16. Víz az útpályaszerkezetben Kovácsné Igazvölgyi Zsuzsanna tanársegéd Soós Zoltán PhD hallgató dr. Tóth Csaba adjunktus Az előadás tartalma Problémafelvetés
SEGÉDANYAG az országos kompetenciamérések, érettségi és OKTV eredmények kiértékeléséhez
 SEGÉDANYAG az országos kompetenciamérések, érettségi és OKTV eredmények kiértékeléséhez 2017. március 3. Tartalomjegyzék 2 Tartalomjegyzék Általános iskolai kompetenciamérés adatainak elemzése... 3 Gimnázium
SEGÉDANYAG az országos kompetenciamérések, érettségi és OKTV eredmények kiértékeléséhez 2017. március 3. Tartalomjegyzék 2 Tartalomjegyzék Általános iskolai kompetenciamérés adatainak elemzése... 3 Gimnázium
Populációbecslés és monitoring. Eloszlások és alapstatisztikák
 Populációbecslés és monitoring Eloszlások és alapstatisztikák Eloszlások Az eloszlás megadja, hogy milyen valószínűséggel kapunk egy adott intervallumba tartozó értéket, ha egy olyan populációból veszünk
Populációbecslés és monitoring Eloszlások és alapstatisztikák Eloszlások Az eloszlás megadja, hogy milyen valószínűséggel kapunk egy adott intervallumba tartozó értéket, ha egy olyan populációból veszünk
ÖDOMÉTERES VIZSGÁLAT LÉPCSŐZETES TERHELÉSSEL MSZE CEN ISO/TS 17892-5 BEÁLLÍTÁS ADAT. Zavartalan 4F/6,0 m Mintadarab mélysége (m)
 BEÁLLÍTÁS ADAT Minta leírás Barna iszap Előkészítési módszer magmintából Részecske-sűrűség (Mg/m³) 2.70 Feltételezett / Mért Feltételezett Betöltés sorrend információ Kezdeti mérések (gyűrű) Terhelési
BEÁLLÍTÁS ADAT Minta leírás Barna iszap Előkészítési módszer magmintából Részecske-sűrűség (Mg/m³) 2.70 Feltételezett / Mért Feltételezett Betöltés sorrend információ Kezdeti mérések (gyűrű) Terhelési
S Z I N T V I Z S G A F E L A D A T O K
 S Z I N T V I Z S G A F E L A D A T O K a Magyar Agrár-, Élelmiszergazdasági és Vidékfejlesztési Kamara hatáskörébe tartozó szakképesítésekhez, az 56/2016 (VIII.19.) FM rendelettel kiadott szakmai és vizsgáztatási
S Z I N T V I Z S G A F E L A D A T O K a Magyar Agrár-, Élelmiszergazdasági és Vidékfejlesztési Kamara hatáskörébe tartozó szakképesítésekhez, az 56/2016 (VIII.19.) FM rendelettel kiadott szakmai és vizsgáztatási
V átlag = (V 1 + V 2 +V 3 )/3. A szórás V = ((V átlag -V 1 ) 2 + ((V átlag -V 2 ) 2 ((V átlag -V 3 ) 2 ) 0,5 / 3
 5. gyakorlat. Tömegmérés, térfogatmérés, pipettázás gyakorlása tömegméréssel kombinálva. A mérési eredmények megadása. Sóoldat sőrőségének meghatározása, koncentrációjának megadása a mért sőrőség alapján.
5. gyakorlat. Tömegmérés, térfogatmérés, pipettázás gyakorlása tömegméréssel kombinálva. A mérési eredmények megadása. Sóoldat sőrőségének meghatározása, koncentrációjának megadása a mért sőrőség alapján.
Adatok statisztikai értékelésének főbb lehetőségei
 Adatok statisztikai értékelésének főbb lehetőségei 1. a. Egy- vagy kétváltozós eset b. Többváltozós eset 2. a. Becslési problémák, hipotézis vizsgálat b. Mintázatelemzés 3. Szint: a. Egyedi b. Populáció
Adatok statisztikai értékelésének főbb lehetőségei 1. a. Egy- vagy kétváltozós eset b. Többváltozós eset 2. a. Becslési problémák, hipotézis vizsgálat b. Mintázatelemzés 3. Szint: a. Egyedi b. Populáció
Minőségirányítási rendszerek 9. előadás
 Minőségirányítási rendszerek 9. előadás 013.05.03. MÉRŐESZKÖZÖK MÉRÉSTECHNIKAI TULAJDONSÁGAI Mérőeszköz rendszeres hibája (Systematic Error of Measurement) alatt ugyanannak az értéknek megismételhetőségi
Minőségirányítási rendszerek 9. előadás 013.05.03. MÉRŐESZKÖZÖK MÉRÉSTECHNIKAI TULAJDONSÁGAI Mérőeszköz rendszeres hibája (Systematic Error of Measurement) alatt ugyanannak az értéknek megismételhetőségi
Térfogati fajlagos felület és (tömegi) fajlagos felület
 Térfogati fajlagos felület és (tömegi) fajlagos felület A térfogati fajlagos felület az egységnyi testtérfogatú szemhalmaz szemeinek felületösszege, azaz a szemhalmaz szemei külső felülete összegének és
Térfogati fajlagos felület és (tömegi) fajlagos felület A térfogati fajlagos felület az egységnyi testtérfogatú szemhalmaz szemeinek felületösszege, azaz a szemhalmaz szemei külső felülete összegének és
MEZŐGAZDASÁGI TERMELÉS A VILÁGON. Búza Ausztráliában: előrejelzett termelést csökkentették
 MEZŐGAZDASÁGI TERMELÉS A VILÁGON Búza Ausztráliában: előrejelzett termelést csökkentették USDA a 2018/19 évre Ausztrália búza termelését 20,0 millió metrikus tonnára (mmt) becsülte, ami 2,0 mmt vagy 9%-os
MEZŐGAZDASÁGI TERMELÉS A VILÁGON Búza Ausztráliában: előrejelzett termelést csökkentették USDA a 2018/19 évre Ausztrália búza termelését 20,0 millió metrikus tonnára (mmt) becsülte, ami 2,0 mmt vagy 9%-os
Egy nyíllövéses feladat
 1 Egy nyíllövéses feladat Az [ 1 ] munkában találtuk az alábbi feladatot 1. ábra. 1. ábra forrása: [ 1 / 1 ] Igencsak tanulságos, ezért részletesen bemutatjuk a megoldását. A feladat Egy sportíjjal nyilat
1 Egy nyíllövéses feladat Az [ 1 ] munkában találtuk az alábbi feladatot 1. ábra. 1. ábra forrása: [ 1 / 1 ] Igencsak tanulságos, ezért részletesen bemutatjuk a megoldását. A feladat Egy sportíjjal nyilat
Mérési adatok illesztése, korreláció, regresszió
 Mérési adatok illesztése, korreláció, regresszió Korreláció, regresszió Két változó mennyiség közötti kapcsolatot vizsgálunk. Kérdés: van-e kapcsolat két, ugyanabban az egyénben, állatban, kísérleti mintában,
Mérési adatok illesztése, korreláció, regresszió Korreláció, regresszió Két változó mennyiség közötti kapcsolatot vizsgálunk. Kérdés: van-e kapcsolat két, ugyanabban az egyénben, állatban, kísérleti mintában,
STATISZTIKA. András hármas. Éva ötös. Nóri négyes. 5 4,5 4 3,5 3 2,5 2 1,5 ANNA BÉLA CILI 0,5 MAGY. MAT. TÖRT. KÉM.
 STATISZTIKA 5 4,5 4 3,5 3 2,5 2 1,5 1 0,5 0 MAGY. MAT. TÖRT. KÉM. ANNA BÉLA CILI András hármas. Béla Az átlag 3,5! kettes. Éva ötös. Nóri négyes. 1 mérés: dolgokhoz valamely szabály alapján szám rendelése
STATISZTIKA 5 4,5 4 3,5 3 2,5 2 1,5 1 0,5 0 MAGY. MAT. TÖRT. KÉM. ANNA BÉLA CILI András hármas. Béla Az átlag 3,5! kettes. Éva ötös. Nóri négyes. 1 mérés: dolgokhoz valamely szabály alapján szám rendelése
Az állományon belüli és kívüli hőmérséklet különbség alakulása a nappali órákban a koronatér fölötti térben május és október közötti időszak során
 Eredmények Részletes jelentésünkben a 2005-ös év adatait dolgoztuk fel. Természetesen a korábbi évek adatait is feldolgoztuk, de a terjedelmi korlátok miatt csak egy évet részletezünk. A tárgyévben az
Eredmények Részletes jelentésünkben a 2005-ös év adatait dolgoztuk fel. Természetesen a korábbi évek adatait is feldolgoztuk, de a terjedelmi korlátok miatt csak egy évet részletezünk. A tárgyévben az
Hipotézis STATISZTIKA. Kétmintás hipotézisek. Munkahipotézis (H a ) Tematika. Tudományos hipotézis. 1. Előadás. Hipotézisvizsgálatok
 STATISZTIKA 1. Előadás Hipotézisvizsgálatok Tematika 1. Hipotézis vizsgálatok 2. t-próbák 3. Variancia-analízis 4. A variancia-analízis validálása, erőfüggvény 5. Korreláció számítás 6. Kétváltozós lineáris
STATISZTIKA 1. Előadás Hipotézisvizsgálatok Tematika 1. Hipotézis vizsgálatok 2. t-próbák 3. Variancia-analízis 4. A variancia-analízis validálása, erőfüggvény 5. Korreláció számítás 6. Kétváltozós lineáris
Véletlen jelenség: okok rendszere hozza létre - nem ismerhetjük mind, ezért sztochasztikus.
 Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Korai vasbeton építmények tartószerkezeti biztonságának megítélése
 Korai vasbeton építmények tartószerkezeti biztonságának megítélése Dr. Orbán Zoltán, Dormány András, Juhász Tamás Pécsi Tudományegyetem Műszaki és Informatikai Kar Építőmérnök Tanszék A megbízhatóság értelmezése
Korai vasbeton építmények tartószerkezeti biztonságának megítélése Dr. Orbán Zoltán, Dormány András, Juhász Tamás Pécsi Tudományegyetem Műszaki és Informatikai Kar Építőmérnök Tanszék A megbízhatóság értelmezése
A magyar leányok menarche-kora az ezredforduló időszakában (Joubert Kálmán, Gyenis Gyula, Darvay Sarolta, Ágfalvi Rózsa) ...
 Tartalomjegyzék Bevezetés... 11 A vizsgálat mintavételi rendszere, az elemszám alakulása, megbízhatósági számítások... 13 A vizsgálati minta általános jellemzői és a vizsgált antropometriai adatok néhány
Tartalomjegyzék Bevezetés... 11 A vizsgálat mintavételi rendszere, az elemszám alakulása, megbízhatósági számítások... 13 A vizsgálati minta általános jellemzői és a vizsgált antropometriai adatok néhány
Statisztikai következtetések Nemlineáris regresszió Feladatok Vége
 [GVMGS11MNC] Gazdaságstatisztika 10. előadás: 9. Regressziószámítás II. Kóczy Á. László koczy.laszlo@kgk.uni-obuda.hu Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet A standard lineáris modell
[GVMGS11MNC] Gazdaságstatisztika 10. előadás: 9. Regressziószámítás II. Kóczy Á. László koczy.laszlo@kgk.uni-obuda.hu Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet A standard lineáris modell
STATISZTIKAI JELENTÉSEK
 XXII. évfolyam 4. szám 2017 STATISZTIKAI JELENTÉSEK TÁJÉKOZTATÓ JELENTÉS A NYÁRI MEZŐGAZDASÁGI MUNKÁKRÓL (2017. augusztus 14-i operatív jelentések alapján) Tájékoztató jelentés a nyári mezőgazdasági munkákról
XXII. évfolyam 4. szám 2017 STATISZTIKAI JELENTÉSEK TÁJÉKOZTATÓ JELENTÉS A NYÁRI MEZŐGAZDASÁGI MUNKÁKRÓL (2017. augusztus 14-i operatív jelentések alapján) Tájékoztató jelentés a nyári mezőgazdasági munkákról
Tavaszi Dél-Alföldi Fórum
 Tavaszi Dél-Alföldi Fórum Gazdaságos kukorica termesztés GK hibridekkel Szél Sándor és munkatársai Gabonakutató Nonprofit Kft. Szeged 2016.02.24 Mikor gazdaságos? Ha a termésért kapott bevétel meghaladja
Tavaszi Dél-Alföldi Fórum Gazdaságos kukorica termesztés GK hibridekkel Szél Sándor és munkatársai Gabonakutató Nonprofit Kft. Szeged 2016.02.24 Mikor gazdaságos? Ha a termésért kapott bevétel meghaladja
HÍDTARTÓK ELLENÁLLÁSTÉNYEZŐJE
 HÍDTARTÓK ELLENÁLLÁSTÉNYEZŐJE Csécs Ákos * - Dr. Lajos Tamás ** RÖVID KIVONAT A Budapesti Műszaki és Gazdaságtudományi Egyetem Hidak és Szerkezetek Tanszéke megbízta a BME Áramlástan Tanszékét az M8-as
HÍDTARTÓK ELLENÁLLÁSTÉNYEZŐJE Csécs Ákos * - Dr. Lajos Tamás ** RÖVID KIVONAT A Budapesti Műszaki és Gazdaságtudományi Egyetem Hidak és Szerkezetek Tanszéke megbízta a BME Áramlástan Tanszékét az M8-as
Geokémia gyakorlat. 1. Geokémiai adatok értelmezése: egyszerű statisztikai módszerek. Geológus szakirány (BSc) Dr. Lukács Réka
 Geokémia gyakorlat 1. Geokémiai adatok értelmezése: egyszerű statisztikai módszerek Geológus szakirány (BSc) Dr. Lukács Réka MTA-ELTE Vulkanológiai Kutatócsoport e-mail: reka.harangi@gmail.com ALAPFOGALMAK:
Geokémia gyakorlat 1. Geokémiai adatok értelmezése: egyszerű statisztikai módszerek Geológus szakirány (BSc) Dr. Lukács Réka MTA-ELTE Vulkanológiai Kutatócsoport e-mail: reka.harangi@gmail.com ALAPFOGALMAK:
Statisztika I. 10. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 10. előadás Előadó: Dr. Ertsey Imre Varianciaanalízis A különböző tényezők okozta szórás illetőleg szórásnégyzet összetevőire bontásán alapszik Segítségével egyszerre több mintát hasonlíthatunk
Statisztika I. 10. előadás Előadó: Dr. Ertsey Imre Varianciaanalízis A különböző tényezők okozta szórás illetőleg szórásnégyzet összetevőire bontásán alapszik Segítségével egyszerre több mintát hasonlíthatunk
Az értékelés a Móricz Zsigmond Gimnázium 3 gimnáziumi osztályának eredményei alapján készült, 102 tanuló adatai kerültek feldolgozásra.
 I. A Gimnáziumi ágazat Az értékelés a Móricz Zsigmond Gimnázium 3 gimnáziumi osztályának eredményei alapján készült, 102 tanuló adatai kerültek feldolgozásra. matematika Az eredmények szerint a 4 évfolyamos
I. A Gimnáziumi ágazat Az értékelés a Móricz Zsigmond Gimnázium 3 gimnáziumi osztályának eredményei alapján készült, 102 tanuló adatai kerültek feldolgozásra. matematika Az eredmények szerint a 4 évfolyamos
III. Kvantitatív változók kapcsolata (korreláció, regresszió)
 III. Kvantitatív változók kapcsolata (korreláció, regresszió) Tartalom Változók kapcsolata Kétdimenziós minta (pontdiagram) Regressziós előrejelzés (predikció) Korreláció Tanuló Kétdimenziós minta Tanulással
III. Kvantitatív változók kapcsolata (korreláció, regresszió) Tartalom Változók kapcsolata Kétdimenziós minta (pontdiagram) Regressziós előrejelzés (predikció) Korreláció Tanuló Kétdimenziós minta Tanulással
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
[Biomatematika 2] Orvosi biometria. Visegrády Balázs
![[Biomatematika 2] Orvosi biometria. Visegrády Balázs [Biomatematika 2] Orvosi biometria. Visegrády Balázs](/thumbs/93/112272424.jpg) [Biomatematika 2] Orvosi biometria Visegrády Balázs 2016. 03. 27. Probléma: Klinikai vizsgálatban három különböző antiaritmiás gyógyszert (ß-blokkoló) alkalmaznak, hogy kipróbálják hatásukat a szívműködés
[Biomatematika 2] Orvosi biometria Visegrády Balázs 2016. 03. 27. Probléma: Klinikai vizsgálatban három különböző antiaritmiás gyógyszert (ß-blokkoló) alkalmaznak, hogy kipróbálják hatásukat a szívműködés
Követelmény a 6. évfolyamon félévkor matematikából
 Követelmény a 6. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Halmazba rendezés adott tulajdonság alapján, részhalmaz felírása, felismerése. Két véges halmaz közös részének,
Követelmény a 6. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Halmazba rendezés adott tulajdonság alapján, részhalmaz felírása, felismerése. Két véges halmaz közös részének,
Gyakorlat 8 1xANOVA. Dr. Nyéki Lajos 2016
 Gyakorlat 8 1xANOVA Dr. Nyéki Lajos 2016 A probléma leírása Azt vizsgáljuk, hogy milyen hatása van a család jövedelmének a tanulók szövegértés teszten elért tanulmányi eredményeire. A minta 59 iskola adatait
Gyakorlat 8 1xANOVA Dr. Nyéki Lajos 2016 A probléma leírása Azt vizsgáljuk, hogy milyen hatása van a család jövedelmének a tanulók szövegértés teszten elért tanulmányi eredményeire. A minta 59 iskola adatait
FORGATTYÚS HAJTÓMŰ KISFELADAT
 Dr. Lovas László FORGATTYÚS HAJTÓMŰ KISFELADAT Segédlet a Jármű- és hajtáselemek III. tantárgyhoz Kézirat 2013 FORGATTYÚS HAJTÓMŰ KISFELADAT 1. Adatválaszték p 2 [bar] V [cm3] s/d [-] λ [-] k f [%] k a
Dr. Lovas László FORGATTYÚS HAJTÓMŰ KISFELADAT Segédlet a Jármű- és hajtáselemek III. tantárgyhoz Kézirat 2013 FORGATTYÚS HAJTÓMŰ KISFELADAT 1. Adatválaszték p 2 [bar] V [cm3] s/d [-] λ [-] k f [%] k a
Szövegértés. Xántus János Két Tanítási Nyelvű Gimnázium és Szakgimnázium OM azonosító: Telephelyi jelentés Telephely kódja: 001
 Országos kompetenciamérés 2017 22 1a Átlageredmények A telephelyek átlageredményeinek összehasonlítása Az Önök eredményei a 4 évfolyamos gimnáziumi telephelyek eredményeihez viszonyítva A szignifikánsan
Országos kompetenciamérés 2017 22 1a Átlageredmények A telephelyek átlageredményeinek összehasonlítása Az Önök eredményei a 4 évfolyamos gimnáziumi telephelyek eredményeihez viszonyítva A szignifikánsan
DIGITÁLIS TEREPMODELL A TÁJRENDEZÉSBEN
 DIGITÁLIS TEREPMODELL A TÁJRENDEZÉSBEN DR. GIMESI LÁSZLÓ Bevezetés Pécsett és környékén végzett bányászati tevékenység felszámolása kapcsán szükségessé vált az e tevékenység során keletkezett meddők, zagytározók,
DIGITÁLIS TEREPMODELL A TÁJRENDEZÉSBEN DR. GIMESI LÁSZLÓ Bevezetés Pécsett és környékén végzett bányászati tevékenység felszámolása kapcsán szükségessé vált az e tevékenység során keletkezett meddők, zagytározók,
Ax-DL100 - Lézeres Távolságmérő
 Ax-DL100 - Lézeres Távolságmérő 1. Áttekintés Köszönjük, hogy a mi termékünket választotta! A biztosnágos és megfelelő működés érdekében, kérjük alaposan olvassa át a Qick Start kézikönyvet. A globálisan
Ax-DL100 - Lézeres Távolságmérő 1. Áttekintés Köszönjük, hogy a mi termékünket választotta! A biztosnágos és megfelelő működés érdekében, kérjük alaposan olvassa át a Qick Start kézikönyvet. A globálisan
FIT-jelentés :: Telephelyi jelentés. 10. évfolyam :: Szakiskola
 FIT-jelentés :: 2012 10. évfolyam :: Szakiskola Pesti Barnabás Élelmiszeripari Szakképző Iskola és Gimnázium Almádi u. 3-5. Telephelye 1148 Budapest, Almádi u. 3-5. Létszámadatok A telephely létszámadatai
FIT-jelentés :: 2012 10. évfolyam :: Szakiskola Pesti Barnabás Élelmiszeripari Szakképző Iskola és Gimnázium Almádi u. 3-5. Telephelye 1148 Budapest, Almádi u. 3-5. Létszámadatok A telephely létszámadatai
Egyszerű számítási módszer bolygók és kisbolygók oályáj ának meghatározására
 Egyszerű számítási módszer bolygók és kisbolygók oályáj ának meghatározására A bolygók és kisbolygók pályájának analitikus meghatározása rendszerint több éves egyetemi előtanulmányokat igényel. Ennek oka
Egyszerű számítási módszer bolygók és kisbolygók oályáj ának meghatározására A bolygók és kisbolygók pályájának analitikus meghatározása rendszerint több éves egyetemi előtanulmányokat igényel. Ennek oka
2.9.34. POROK TÖMÖRÍTETLEN ÉS TÖMÖRÍTETT SŰRŰSÉGE. Tömörítetlen sűrűség
 2.9.34. Porok tömörítetlen és tömörített sűrűsége Ph.Hg.VIII. - Ph.Eur.7.6-1 2.9.34. POROK TÖMÖRÍTETLEN ÉS TÖMÖRÍTETT SŰRŰSÉGE Tömörítetlen sűrűség 01/2013:20934 Tömörítetlen sűrűségnek nevezzük a tömörítetlen
2.9.34. Porok tömörítetlen és tömörített sűrűsége Ph.Hg.VIII. - Ph.Eur.7.6-1 2.9.34. POROK TÖMÖRÍTETLEN ÉS TÖMÖRÍTETT SŰRŰSÉGE Tömörítetlen sűrűség 01/2013:20934 Tömörítetlen sűrűségnek nevezzük a tömörítetlen
Módszertani Intézeti Tanszéki Osztály. A megoldás részletes mellékszámítások hiányában nem értékelhető!
 BGF KKK Módszertani Intézeti Tanszéki Osztály Budapest, 2012.. Név:... Neptun kód:... Érdemjegy:..... STATISZTIKA II. VIZSGADOLGOZAT Feladatok 1. 2. 3. 4. 5. 6. Összesen Szerezhető pontszám 21 20 7 22
BGF KKK Módszertani Intézeti Tanszéki Osztály Budapest, 2012.. Név:... Neptun kód:... Érdemjegy:..... STATISZTIKA II. VIZSGADOLGOZAT Feladatok 1. 2. 3. 4. 5. 6. Összesen Szerezhető pontszám 21 20 7 22
Rugalmas állandók mérése
 Rugalmas állandók mérése Mérő neve: Márkus Bence Gábor Mérőpár neve: Székely Anna Krisztina Szerda délelőtti csoport Mérés ideje: 11/30/2011 Beadás ideje: 12/07/2011 1 1. A mérés rövid leírása Mérésem
Rugalmas állandók mérése Mérő neve: Márkus Bence Gábor Mérőpár neve: Székely Anna Krisztina Szerda délelőtti csoport Mérés ideje: 11/30/2011 Beadás ideje: 12/07/2011 1 1. A mérés rövid leírása Mérésem
Statisztika I. 8. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 8. előadás Előadó: Dr. Ertsey Imre Minták alapján történő értékelések A statisztika foglalkozik. a tömegjelenségek vizsgálatával Bizonyos esetekben lehetetlen illetve célszerűtlen a teljes
Statisztika I. 8. előadás Előadó: Dr. Ertsey Imre Minták alapján történő értékelések A statisztika foglalkozik. a tömegjelenségek vizsgálatával Bizonyos esetekben lehetetlen illetve célszerűtlen a teljes
Modern Fizika Labor. 2. Az elemi töltés meghatározása. Fizika BSc. A mérés dátuma: nov. 29. A mérés száma és címe: Értékelés:
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. nov. 29. A mérés száma és címe: 2. Az elemi töltés meghatározása Értékelés: A beadás dátuma: 2011. dec. 11. A mérést végezte: Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. nov. 29. A mérés száma és címe: 2. Az elemi töltés meghatározása Értékelés: A beadás dátuma: 2011. dec. 11. A mérést végezte: Szőke Kálmán Benjamin
Amit a kapacitív gabona nedvességmérésről tudni kell
 Szemestermények korszerű szárítási, tárolási, feldolgozási és mérési technológiái Gödöllő, 2018 Amit a kapacitív gabona nedvességmérésről tudni kell Dr. Gillay Zoltán, adjunktus Szent István Egyetem, Élelmiszertudományi
Szemestermények korszerű szárítási, tárolási, feldolgozási és mérési technológiái Gödöllő, 2018 Amit a kapacitív gabona nedvességmérésről tudni kell Dr. Gillay Zoltán, adjunktus Szent István Egyetem, Élelmiszertudományi
Matematika. Xántus János Két Tanítási Nyelvű Gimnázium és Szakgimnázium OM azonosító: Telephelyi jelentés Telephely kódja: 001
 Országos kompetenciamérés 2017 3 1a Átlageredmények A telephelyek átlageredményeinek összehasonlítása Az Önök eredményei a 4 évfolyamos gimnáziumi telephelyek eredményeihez viszonyítva A szignifikánsan
Országos kompetenciamérés 2017 3 1a Átlageredmények A telephelyek átlageredményeinek összehasonlítása Az Önök eredményei a 4 évfolyamos gimnáziumi telephelyek eredményeihez viszonyítva A szignifikánsan
LINEÁRIS REGRESSZIÓ (I. MODELL) ÉS KORRELÁCIÓ FELADATOK
 LINEÁRIS REGRESSZIÓ (I. MODELL) ÉS KORRELÁCIÓ FELADATOK 2004 november 29. 1.) Lisztbogarak súlyvesztése 9 lisztbogár-csapat súlyát megmérték, (mindegyik 25 bogárból állt, mert egyenként túl kis súlyúak
LINEÁRIS REGRESSZIÓ (I. MODELL) ÉS KORRELÁCIÓ FELADATOK 2004 november 29. 1.) Lisztbogarak súlyvesztése 9 lisztbogár-csapat súlyát megmérték, (mindegyik 25 bogárból állt, mert egyenként túl kis súlyúak
Matematikai geodéziai számítások 10.
 Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Miskolci Egyetem Gazdaságtudományi Kar Üzleti Információgazdálkodási és Módszertani Intézet
 Klaszteranalízis Hasonló dolgok csoportosítását jelenti, gyakorlatilag az osztályozás szinonimájaként értelmezhetjük. A klaszteranalízis célja A klaszteranalízis alapvető célja, hogy a megfigyelési egységeket
Klaszteranalízis Hasonló dolgok csoportosítását jelenti, gyakorlatilag az osztályozás szinonimájaként értelmezhetjük. A klaszteranalízis célja A klaszteranalízis alapvető célja, hogy a megfigyelési egységeket
