AZ ÓRAPARADOXONRÓL. A deszinkronizáció. Hraskó Péter PTE Elméleti Fizika Tanszék
|
|
|
- Rebeka Faragó
- 6 évvel ezelőtt
- Látták:
Átírás
1 AZ ÓRAPARADOXONRÓL Hraskó Péter PTE Elméleti Fizika Tanszék Az óraparadoxon (vagy másik nevén az ikerparadoxon) fogalmi szempontból a relativitáselmélet egyik legfontosabb következménye A jelen dolgozat a paradoxon egy tulajdonképpen tehnikai jellegû mégis zavarba ejtô aspektusával foglalkozik: A jelenség korrekt leírási módjával a gyorsuló óra (testvér) szempontjából Meg fogjuk mutatni hogy a deszinkronizáió fogalma alapján ez a tárgyalás teljesen átláthatóvá tehetô A ikk ezért két fejezetbôl áll Az elsôben a deszinkronizáióról lesz szó magát az óraparadoxont pedig a másodikban diszkutáljuk Mindezt praktikusan matematika nélkül tesszük a matematikai részleteket és kiegészítéseket a két függelékben tárgyaljuk Az óraparadoxonról nemrég jelent meg Bokor Nándor dolgozata a Szemlében Bokor azt a kérdést elemzi vajon helyes-e az az elterje vélekedés hogy az ikerparadoxon oka a gyorsulás Ha jól látom a jelen dolgozat nem kínál új szempontot e kérdés megválaszolásához A deszinkronizáió Nyugodjon egy vonat a pályatest I 0 vonatkoztatási rendszerében amelyben a Minkowski-féle (fényjelekkel szinkronizált) koordinátaidôt a sûrûn (így többek között a vonaton is) széthelyezett nyugvó virtuális (elképzelt) ideális órák mutatják Tegyük fel hogy ezek közül kettô valóságos óra amelyek a vonathoz vannak rögzítve A bal oldali óra legyen az A a jobb oldali a B Képzeljük el hogy egy nagyon rövid fényjel ikázik ide-oda az órák között A két óra helyes szinkronizáltsága következtében az a Δt idô ami alatt a jel az A -ból a B-be ér pontosan megegyezik a visszaúton eltelt Δt idôvel Ha az órák közötti távolság Δx akkor mindkét idôtartam Δx/ -vel egyenlô Az táblázat példájában Δt = Δt = 0 táblázat A nyugvó órák mutatóállása a fényjelek visszatükrözésének pillanatában Az A óra mutatóállása A B óra mutatóállása Tegyük fel most hogy a vonat elindul jobbra eléri az U sebességet és ezután ezzel a sebességgel halad tovább A konstans U sebességû vonat ineriarendszer amelyet I-vel fogunk jelölni Az A és a B óra között eközben folyamatosan ikázik ide-oda a fényjel Az oda- és a visszaút idôtartama azonban változik Az I 0 -ból (a töltésrôl) szemlélve a fényjel mozgását ezeket az idôtartamokat a Az ikerparadoxon és a gyorsulás Fizikai Szemle 6 (0) Δt 0 = Δ x 0 U Δt 0 Δt 0 = Δ x 0 U Δt 0 egyenletek határozzák meg amelyekbôl Δt 0 = Δ x 0 U Δt 0 = Δ x 0 U () () A képlet felírásánál figyelembe vettük hogy amikor a vonat mozog a nulla index segítségével meg kell különböztetnünk az I 0 -ban mért mennyiségeket az I-ben mért (index nélküli) mennyiségektôl Nekünk azonban a Δt-t és a Δt-t kifejezô képletekre van szükségünk amelyek jobb oldalán a mozgó vonaton mért Δx távolság szerepel Az () elsô egyenlete azt fejezi ki hogy az A órától elinduló fényjel és a vele egyszerre U sebességgel induló B óra Δt 0 koordinátaidôvel késôbb találkozik egymással A B órán ezalatt Δt 0 sajátidô telik el Ezt az idôtartamot jelöljük Δt -vel így Δt = Δt 0 Ez a sajátidô-intervallum egyben koordinátaidô-intervallum is hiszen a B egyike azoknak az óráknak amelyek a vonaton a t koordinátaidôt mutatják Teljesen hasonlóan látható be a Δt = Δt 0 képlet is amely az A óra sajátidejét fejezi ki égül a két óra közötti Δx vonati távolság a töltésrôl nézve kontrakiót szenved ezért Δ x 0 = Δ x Ha ()-ben a nulla indexû mennyiségeket ezen képletek segítségével index nélküli mennyiségekkel fejezzük ki a 374 FIZIKAI SZEMLE 03 /
2 képletekre jutunk (a számpéldánkban az elôbbi legyen mondjuk az utóbbi pedig 8 táblázat) táblázat A mozgó órák mutatóállása a fényjelek visszatükrözésének pillanatában Az A óra mutatóállása A B óra mutatóállása 4 6 Nyilvánvaló hogy az U sebességgel mozgó vonat nyugalmi rendszerében az I ineriarendszerben ez a két óra nins helyesen szinkronizálva Ha ugyanis megmérnénk a vonaton a fénysebességet mindkét irányban egyformán -nek találnánk Természetesen utólag szinkronizálhatnánk ôket például úgy hogy a B óra mutatóállását megfelelô mértékben (a számpéldában -vel) viszszaállítjuk (vagy az A óráét ugyanennyivel elôrevisszük) Ezt azonban most nem tesszük meg mert éppen azt akarjuk tisztázni hogy milyen következményei vannak a gyorsulásnak ha az egyszer már helyesen szinkronizált órákhoz többet már nem nyúlunk hozzá A két óra közötti deszinkronizáió mértékét a δt B = Δt Δt = U Δ x (3) formula határozza meg Az Einstein-féle szinkronizáiós eljárás szellemében ennyivel kellene visszaállítani a (gyorsulás irányába esô) B óra mutatóállását ahhoz hogy helyesen legyen szinkronizálva A -val onjuk le a következtetést: amikor egy ineriarendszert gyorsítunk a hozzá rögzített helyesen szinkronizált órák deszinkronizálódnak A deszinkronizáió nem annak a következménye hogy az órák szerkezetében a gyorsulás valamilyen változást okoz hiszen ezek az órák ideális szerkezetûek a külsô behatásoktól teljesen függetlenül a maguk monoton ritmusában járva a sajátidejüket mutatják Ha az eredetileg nyugvó vonat padlóján állt egy labda a vonat elindulásakor elkezd hátrafelé mozogni és amikor a vonat már egyenletesen halad U sebességgel a labda folyamatosan gurul hozzá képest ugyanezzel a sebességgel visszafelé (vagy legalábbis gurulna ha a vonat elég hosszú volna) Ezt a mozgást nem az okozza hogy valami hatott a labdára hanem éppen ellenkezôleg: azért gurul a labda visszafelé mert nem hatott rá semmi ami arra kényszerítené hogy átvegye a vonat sebességét A deszinkronizáió ugyanebbe a kategóriába tartozó tehetetlenségi jelenség Az órák a mozgó vonaton Lényeges pont hogy ha a fénysebesség nem lenne minden ineriarendszerben ugyanaz minden irányban akkor az ideális órák sohase deszinkronizálódnának Tegyük fel egy pillanatra hogy a relativitáselmélet téves van elektromágneses éter amely történetesen az I 0 -hoz (a töltéshez) képest nyugalomban van A két táblázat ebben az esetben lényegében érvényben maradna mégsem fejezne ki deszinkronizáiót Az I-beli fénysebesség ugyanis ilyen feltételek mellett valóban különbözne a két irányban mert kizárólag a nyugvó éterben (I 0 -ban) lenne izotróp A két táblázat adatai ezt a tényt fejeznék ki teljesen korrekt módon A deszinkronizáió ezért a fénysebesség állandóságának egyenes következménye is úgy járnak tovább ahogy a pálya I 0 ineriarendszerében szinkronizálták ôket Ez az ineriarendszer azonban kiszala alóluk de ôk nem vettek errôl tudomást agyis a deszinkronizáió végeredményben annak a következménye hogy az órákkal nem történt semmi mégis éppen olyan valóságos jelenség mint a labda megindulása hátrafelé Legnyilvánvalóbban a fénysebesség látszólagos megváltozásában jelentkezik ahogy azt a táblázat mutatja de más fontos következménye is van Mielôtt azonban erre rátérnénk foglaljuk össze a deszinkronizáió elôjelszabályát: Az órapár gyorsulás irányába esô tagja siet a gyorsulással ellentétes irányba esô tagja késik a pár másik tagjához képest A deszinkronizáió egy másik következményét a vonatos példa továbbgondolásával világítjuk meg Képzeljük el a vonat egyik mondjuk 60 méter hosszú vasúti kosiját amelyben könnyen végig lehet sétálni és méterenként faliórák találhatók rajta Az utasok között van egy fizikus aki már nagyon unja az utazást és azzal próbálja agyonütni az idôt hogy menetirányban egyenletes v sebességgel végigsétál a kosi végétôl az elejéig és közben gondosan ügyel arra hogy a faliórák alapján az útja pontosan perig tartson (Δt = 60 s) A séta idôtartamát a karóráján is leméri és azt találja hogy a séta közben pernél rövidebb idô telt el rajta Persze az idôdilatáió gondolja magában a Δτ = Δ t v képlet szerint pont ennek kellett történnie De gyakorló fizikusként ismeri a szabályt hogy egy mérés nem mérés ezért megismétli a sétáját ezúttal visszafelé úgy hogy a faliórák szerint megint per alatt érjen a kosi egyik végébôl a másikba Meglepôdve tapasztalja hogy a karóráján ezúttal hosszabb idô telt el mint az elôbb Természetesen elôször arra gyanakszik hogy valami hibát követett el de akárhányszor ismétli a kísérletet a karóráján mindig ugyanazt a két különbözô idôtartamot olvassa le: A menetirányban a sajátidô kisebb mint ellenkezô irányban ( Δτ < Δτ ) Némi töprengés után fizikusunknak eszébe jut a deszinkronizáió amirôl relativitáselmélet órán hallott Hogy is nem gondoltam rá azonnal? sap a homlokára Hiszen amikor felszálltam a vonatra láttam a szerelôket amint éppen azzal foglalkoznak hogy az álló vonaton fényjelekkel szinkronizálják a faliórákat Aztán amikor elindult a vonat bekövetkezett a deszinkronizáió Amikor elôre megyek a faliórák által meghatározott sebességgel akkor minden következô falióra a szükségesnél többet mutat A viszszaúton pont fordítva történik Ezért van az hogy a karórám az elsô esetben kevesebbet mutat mint a HRASKÓ PÉTER: AZ ÓRAPARADOXONRÓL 375
3 másodikban Mindenesetre most jól megtanultam hogy ilyen esetekben nem használhatom a A korrigált (felülhúzott) mennyiségekre érvényes az eredeti Δτ = Δ t v képletet a sajátidô meghatározására mert az mindkét irányú sétára ugyanazt a sajátidôt adja Elhatározza hogy küld egy SMS-t az egyik kollégájának és megkéri keresse már elô valahonnan a képlet Mivel dτ = v = v v Δτ = Δ t v képlet azon általánosabb alakját amelyik az ô jelenlegi helyzetében is alkalmazható Ezeket az informáiókat közli vele: Indulás elôtt a faliórákat korrekt módon fényjelekkel szinkronizálták és azóta senki sem nyúlt hozzájuk A vonat jelenleg egyenletes U sebességgel halad A faliórák meg vannak számozva 0-tól 60-ig Ezek tekinthetôk x-koordinátáknak és az egymás utáni órák közötti távolság az indulás elôtt és most az egyenletes sebesség elérése után is pontosan méter Amikor a kosin végigsétálok az órák helye és mutatóállása alapján a sebességem egy konstans v érték (történetesen v=m/ssebességet választottam de a keresett képlet szempontjából ennek nins jelentôsége) A kérés az hogy küldje el azt a képletet amely megadja a Δτ és a Δt kapsolatát ebben az esetben A kért képlet nemsokára megérkezett A figyelmes kolléga Δτ és Δt helyett az infinitezimális d τ és növekményekre írta fel mert ez akkor is alkalmazható amikor a sétálás v sebessége nem konstans (v = v (t )): Uv v d τ = (4) Ez a képlet pozitív v-nél menetirányba negatív v-nél az ellentétes irányba történô sétálásra vonatkozik Napokkal késôbb amikor utazó fizikusunk a munkahelyén találkozik a kollégájával megkéri ôt mutassa meg a képlet levezetését A magyarázat a következô: Nézzük mondjuk a pozitív irányú séta egy dx infinitezimálisan rövid A B szakaszát amely a deszinkronizált órák szerint ideig tartott Az ennek megfelelô helyesen szinkronizált idôtartam (3) szerint: = az ezzel számolt sebesség pedig v = dx Udx (5) ezt átírhatjuk a dτ = alakba amelyben (5) alapján Ezt behelyettesítve kapjuk a bizonyítandó (4) össze- függést Fogalmazzuk meg a vonatos példánk tanulságát Ha a vonat egész történetét tekintjük a veszteglését az indulás elôtt a gyorsulását és azután az egyenletes sebességû haladását akkor nyilvánvaló hogy a vonat óráit nem lehetséges úgy beállítani hogy ebben az egész idôszakban helyesen legyenek szinkronizálva A példában úgy képzeltük hogy az órákat még a nyugvó vonaton szinkronizálták fényjelekkel de akkor az indulás után a deszinkronizáió következtében már nem lesznek helyesen szinkronizálva Megtehettük volna azt is hogy az állomáson nem fényjelekkel szinkronizáljuk ôket hanem mesterséges módon olyan beállítást választunk hogy majd a deszinkronizáió következtében éppen jól legyenek szinkronizálva amikor a vonat egyenletesen halad De ekkor persze az állomáson lennének a fényjelek szempontjából rosszul szinkronizálva De választhatnánk bármilyen más szinkronizáiót ha már a legtermészetesebb einsteini szinkronizáió úgysem hajtható következetesen végre A deszinkronizáió következtében tehát Minkowski-koordinátarendszer sak ineriarendszerekhez rendelhetô Az ilyen koordinátarendszerben ugyanis a koordinátaidô definíió szerint olyan hogy a fénysebesség mindig minden irányban ugyanazzal a -vel egyenlô Gyorsuló vonatkoztatási rendszerben azonban a folyamatos deszinkronizáió az ilyen tulajdonságú koordinátaidô létezését lehetetlenné teszi Felmerül a kérdés hogy akkor a gyorsuló vonatkoztatási rendszerekben milyen eljárás (reept) alapján kell a koordinátaidôt megválasztani vagyis milyen protokoll szerint kell a vonatkoztatási rendszerben nyugvó koordinátaidôt mutató (virtuális) órákat szinkronizálni A válasz az hogy ilyen általános reept nem létezik minden eset külön döntést igényel Megjegyezzük hogy ineriarendszerben sem kötelezô a fényjelekkel szinkronizált Minkowski-koordinátaidô = v = Uv v 376 FIZIKAI SZEMLE 03 /
4 használata A koordinátarendszer választásához hasonlóan a koordinátaidô megválasztása is nagymértékben önkényes A választás fô szempontja a vizsgálandó probléma tárgyalásának az egyszerûsítése A Minkowski-koordinátaidô elônyei azonban ebbôl a nézôpontból annyira szembetûnôek hogy ineriarendszerben gyakorlatilag minden esetben ezt a koordinátaidôt használjuk Felszeg Frani Frani Ini Ini Alszeg Az óraparadoxon Az idôdilatáió mint tudjuk szimmetrikus jelenség: Ha az Inihez képest sebességgel mozgó Frani órája késik Ini órájához viszonyítva akkor Ini órája is késik Frani órájához viszonyítva Ez így elég képtelenül hangzik de nagyrészt annak következtében hogy a megfogalmazás erôsen hiányos A pontos állítás a következô: nyugodjon Ini az I I Frani pedig az I F ineriarendszerben (az egyik lehet mondjuk a vonatállomás a másik az áthaladó vonat) Mindkét ineriarendszert gondolatban telerakjuk nyugvó helyesen szinkronizált virtuális órákkal amelyek a t I illetve a t F koordinátaidôt mutatják Az állítás az hogy Ini órája késik a Frani I F ineriarendszerében nyugvó azon O F órához képest amely mellett éppen elhalad és fordítva Frani órája is késik az Ini I I ineriarendszerében nyugvó azon O I órához képest amely mellett éppen elhalad Ez így már egyáltalán nem paradoxális hanem sak figyelemre méltó Hasonlítsuk ezt össze mondjuk azzal az állítással hogy Frani határozottan magasabb mint Ini és ugyanakkor Ini is határozottan magasabb mint Frani Ez nyilván logikai képtelenség De abban a kijelentésben hogy Frani magasabb mint Ini húga és Ini is magasabb mint Frani öse már nins semmi kivetnivaló 3 Na jó de mit mondjunk a következô esetben: Ini az alszegi vasútállomáson a sín mellett áll Frani az áthaladó vonaton ül Amikor éppen egymás mellé kerülnek mindketten feljegyzik a saját órájuk mutatóállását Azután amikor a vonat jön Felszegrôl visszafelé Franival együtt megint feljegyzik mit mutat karórájuk a találkozás pillanatában Ezután egy kivonással mindketten megállapítják mennyi idô telt el a saját karórájukon a két találkozás között Mi lesz az eredmény? Az elôzôek alapján azt gondolnánk hogy Frani óráján kevesebb idô telt el mint Ini óráján de persze Ini óráján is kevesebb idô telt el mint Franién és ez már logikai ellentmondás a javából Fogalmazzuk meg megint az állítást valamivel pontosabban Azt állítjuk hogy ha az órákon eltelt sajátidôt Ini nyugalmi rendszerében számítjuk ki akkor a második találkozáskor Frani órája kevesebbet mutat mint Inié; ha azonban a számítást Frani nyugalmi rendszerében végezzük el akkor Ini órája mutat kevesebbet amikor újra találkoznak 3 A megfeleltetés nyilvánvaló: Frani órája Frani Ini órája Ini O F Frani öse O I Ini húga Frani Ini koordinátaidõt mutató órák a töltés mentén ábra Tárgyalás a töltés nyugalmi rendszerében Ha a relativitáselméletbôl valóban ez következne akkor már régen elfelejtettük volna Azonban az állításban megfogalmazott feltételek analízise arra a következtetésre vezet hogy akár az egyik akár a másik nyugalmi rendszerben végezzük is el a számítást mindig Frani órája az amelyik a második találkozáskor kevesebb idôt mutat együk alapul elôször Ini I I nyugalmi rendszerét vagyis a vasúti töltést Alszegestül és Felszegestül ( ábra) Ha a vonat oda és vissza is ugyanazzal a sebességgel halad nem tölt el semennyi idôt sem Felszegen akkor az idôdilatáió következtében Frani óráján szer kevesebb idô telik el mint Inién Mivel továbbá Ini nyugszik I I -ben ezért az óráján ugyanannyi sajátidô telik el mint koordinátaidô Ez utóbbi pedig nyilván L /-vel egyenlô ahol L Alszeg és Felszeg távolsága agyis Δτ I = L Δτ F = L (6) Hajlamosak lennénk elfogadni hogy Frani I F nyugalmi rendszerét vagyis a vonatot tekintve nyugvónak ugyanezt az eredményt kapjuk azzal a különbséggel hogy a tényezô Δτ F helyett Δτ I -ben jelenik meg Ez a relativitáselmélet halálos ítélete lenne De az ítélet kimondása elôtt gondoljuk meg jobban a dolgot Azt a helyzetet amikor a vonatot tekintjük nyugvónak (noha a valóságban persze ugyanúgy mozog mint eddig) a ábrán illusztráltuk A felsô rajzon az egész táj Alszeggel Felszeggel és Inivel együtt sebességgel úszik el a vonat mellett amelyet körülbelül ugyanolyan hosszúnak ábrázoltunk mint az Alszeg Felszeg távolság Ezt nyugoan megtehetjük hiszen a vonat valójában egy vonatkoztatási HRASKÓ PÉTER: AZ ÓRAPARADOXONRÓL 377
5 Alszeg Frani Ini Felszeg Frani Alszeg Frani Ini koordinátaidõt mutató órák a vonaton ábra Tárgyalás a vonat nyugalmi rendszerében Alszeg Ini rendszert reprezentál amely a newtoni fizikában és a speiális relativitáselmélet szerint is tetszôlegesen nagy kiterjedésû lehet Most Ini az aki mozog ezért az eddigi ismereteink alapján a két találkozás között a (6)-tal ellentétben az ô óráján kellene rövidebb idônek eltelnie De így van-e valóban? Ini pályája két részbôl áll egy odaútból és egy visszaútból Foglalkozzunk elôször az odaúttal A határozottság kedvéért tegyük fel hogy elsô találkozásukkor mindkettôjük órája éppen nulla idôt mutat és ez egyben a vonat koordinátaideje is (vagyis Frani órája szinkronban jár a vele egy helyen lévô koordinátaidôt mutató virtuális órával) Ha a vonat órái helyesen fényjelekkel vannak szinkronizálva akkor amikor a vonat végéhez ér Ini órája az idôdilatáió következtében szer kevesebb idôt fog mutatni mint az éppen ott lévô vonati óra Mekkora ez a Δ τ I idô pontosan? A Lorentz-kontrakió következtében az Alszeg Felszeg közötti L távolságnak a vonaton L távolság felel meg ezért Ini útjának ez az elsô szakasza Δ t = L ideig tart és ennek következtében Δ τ I = L = L Szabad-e ugyanígy számítani a visszaúton eltelt Δ τ I idôt is? Nem szabad mert a vonat visszafordulásakor a rajta lévô órák deszinkronizálóak és ennek következtében a sajátidô számítására már nem a dτ = hanem a (4) képletet kell használni! Mielôtt azonban idéznénk a helyes számítás végeredményét rámutatunk miért tudja a deszinkronizáió következtében Ini órája behozni a hátrányát Gondolatban helyezkedjünk el a jobbról egyenletes sebességgel érkezô vonaton Ez természetesen ineriarendszer A visszaforduláskor fellépô gyorsulás jobbra mutat ezért bármely eredetileg helyesen szinkronizált A B órapár A tagja amelyik az új menetirányhoz viszonyítva a B mögött halad kevesebbet mutat mint ha B-vel helyesen lenne szinkronizálva Ennek következtében egységnyi koordinátaidô alatt a visszaúton Ini órája többet megy elôre mint az odaúton Ez teszi lehetôvé hogy Ini órája a pályájának második szakaszában ledolgozza hátrányát és amikor újra találkozik Franival az ô órája mutasson többet A tényleges számítás (4) alapján történik Ehhez ki kell számítani a benne szereplô U -t és v-t Az U a vonat visszafordulás utáni sebessége a fordulás elôtti önmagához képest (vagyis mintha a fordulás elôtt nyugodna) A newtoni fizika szerint U nyilván -vel egyenlô de a sebességösszeadás relativisztikus szabálya ezt U = módosítja A képlet alkalmazásához ki kell még számítani azt a Δ t idôt is amely alatt a vonati deszinkronizált órák szerint Ini visszaér Franihoz A számítás egyszerû de nagyon aprólékos ezért a B Függelékben vázoljuk Az eredmény a következô: Δ τ I = Δ t Uv v Mint látjuk a Δ τ I +Δ τ I összeg ugyanannyi mint a (6)-ban felírt Δτ I Az óraparadoxonnak ez a fajta feloldása amelyet itt vázoltam 4 a deszinkronizáión alapul amely annak következménye hogy az összes különbözô egyenletes sebességgel haladó vonatkoztatási rendszerben a fénysebesség minden irányban ugyanaz a és amikor egy ilyen vonatkoztatási rendszer gyorsulni kezd a benne lévô helyesen szinkronizált ideális órák megôrzik eredeti járásukat és ezért deszinkronizálódnak Az irodalomban legelterjeebb magyarázat szerint ezzel szemben a paradoxon sak az általános relativi- re = L (7) 4 Ez a magyarázat a Basi Relativity An Introdutory Essay ímû könyvemben jelent meg elôször (Springer 0) 378 FIZIKAI SZEMLE 03 /
6 táselméletben vagyis a gravitáió figyelembe vételével oldható fel 5 alójában a speiális relativitáselmélet fogalmi struktúrája alapján elôre lehet tudni hogy a két találkozás között az egyes órákon eltelt sajátidô-intervallum értékére nem jöhet ki különbözô eredmény amikor különbözô koordinátarendszerekben számítjuk ôket Ennek az az oka hogy a sajátidô-intervallum invariáns A paradoxon feloldásán ezért igazából azt értjük hogy relativisztikus szemléletünk fejlesztése érdekében errôl az invarianiáról nem veszünk tudomást hanem különbözô konkrét szituáiókban mutatjuk be mûködését A relativitáselmélet egész matematikai formalizmusa a d τ invarianiájára van felépítve Tapasztalati szinten ez az invariania tökéletesen nyilvánvaló: egy adott órán két adott esemény (például találkozás) között eltelt idô számértékének leolvasása nem igényel koordinátarendszert A mennyiség kiszámításához azonban mindig választani kell valamilyen koordinátarendszert Az elméletnek tehát biztosítania kell hogy a számítás eredménye független legyen a választott koordinátarendszertôl A Lorentz-transzformáió képletét ebbôl az alapkövetelménybôl vezetjük le Ilyen összefüggésben rendszerint a sajátidô konstansszorosával a ds = dτ négyes intervallum négyzettel dolgozunk A dτ = v és a v = dx definíió következtében ds = dτ = v = dx amely 3D-ben ds = dx dy dz Amikor a jobb oldal pozitív ez a kifejezés a sajátidô képletével ekvivalens és invarianiája a sajátidô invarianiáját fejezi ki Amikor nullával egyenlô akkor a fénysebesség invarianiájának megfogalmazása Amikor pedig negatív akkor két közeli esemény térbeli távolságát határozza meg A Függelék Ebben a függelékben a deszinkronizáió egy másik formálisabb tárgyalását mutatjuk be Az új megközelítés lényege hogy olyan x t (röviden K) koordinátákat vezessünk be a téridôn amelyhez képest a vonat végig nyugalomban van és a koordinátaidôt folyamatosan a vonathoz rögzített órák mutatják Az eljárást úgy is nevezhetjük hogy koordinátarendszert rögzítünk a vonathoz Mint láttuk ha a vonat gyorsul egy ilyen koordinátarendszer bizonyosan nem lesz Minkowski az egész téridôn Legyenek x t Minkowski-koordináták a téridôn amelyeket összefoglalóan K-val jelölünk Az egyszerûség kedvéért tegyük fel hogy a vonat a t = 0-ban hirtelen azonnal U sebességgel indul el A még nyugvó vonaton a vonathoz rögzített x t koordinátákat azonosnak vehetjük x-szel és t -vel: t = t x = x (t <0) (A) A vonat elindulása után az x t koordináták U sebességhez tartozó Lorentz-transzformáltjai megfelelnének annak a követelménynek hogy t > 0-ban a vonat ezekhez a koordinátákhoz képest legyen nyugalomban de ahhoz hogy a vonati órák az így kapható t idôt mutassák a mozgó vonaton újra kellene szinkronizálni ôket A vonati órák akkor fogják újraszinkronizálás nélkül mutatni a koordinátaidôt ha az idôt nem a Lorentz-transzformáió hanem a t = t képletnek megfelelôen választjuk meg Ezek az órák ugyanis U sebességgel mozognak K-hoz képest ezért a járásuk K-hoz viszonyítva lelassul Így t = t x = Az inverz transzformáió t = x = x t x U t (t >0) (A) (A3) A mozgó vonathoz tartozó ívelemnégyzet a ds invarianiája következtében ds = dx = Ut (t >0) = Udx dx = = dx dx (A4) Ehhez az ívelemnégyzethez a (4) sajátidôképlet tartozik Továbbá a dx az (x x+dx) intervallum hosszával egyenlô Ha ugyanis a 5 Egy reprezentatív példa: R C Tolman: Relativity Thermodynamis and Cosmology Clarendon Press (969) 79 fejezet t = t U x x = x HRASKÓ PÉTER: AZ ÓRAPARADOXONRÓL 379
7 transzformáióval reszinkronizáljuk a mozgó vonat óráit a vesszôs koordinátákban Minkowski-ívelemnégyzetet kapunk amelyben a térkoordináta valódi térbeli távolságnak felel meg A dx/ fénysebességet a ds = 0 képletbôl kapjuk meg ha végigosztjuk -vel: U dx Az egyenlet két megoldása a jobbra és a balra haladó fényimpulzus sebességét adja meg: dx Ezt felhasználva kapjuk a már ismert =0 dx ± ± = ± ± ± U = Δ x = Δ x képleteket a terjedési idôkre B Függelék Ebben a függelékben a (7) képlet levezetését vázoljuk Ehhez jól felhasználhatók az A Függelék képletei ha az x t koordinátákon olyan Minkowski-koor- dinátarendszert értünk amelyben az érkezô (negatív irányba sebességgel mozgó) vonat nyugalomban van Ebben az esetben az (A) transzformáióval definiált x t koordináták végig rögzítve lesznek a vonathoz hasak az U sebességen a sebességgel visszafelé haladó vonat megfordulás elôtti mozgásához viszonyított sebességét értjük A sebességösszeadás relativisztikus képlete szerint U = (B) A következô feladatunk Ini pályájának meghatározása az x t koordinátákban A K-ban Ini pályája a két találkozás között x = t (t < t < t ) (B) ahol t és t a két találkozás idôpontja A vonat viszszafordulást = 0-ban történik az elsô találkozás he- lye pedig x = 0 Az Alszeg Felszeg távolság Lorentz- kontrakióját figyelembe véve t = L Az Ini óráján a pályájának elsô szakaszán eltelt sajátidô tehát Δ (B3) τ I = t = L A t = 0 pillanatban Ini már t távolságra van Franitól aki ebben a pillanatban U sebességgel indul utána és a t pillanatban éri utól Ezt az idôpontot a (t t )=U t egyenletbôl lehet meghatározni Azt találjuk hogy t = U t = L (B4) A Δ τ I számításához át kell térnünk az x t koordinátákra mert a t > 0 tartományban ezek már nem azonosak az x t koordinátákkal Ini pályájának második szakaszát úgy kapjuk meg hogy (A3)-t behelyettesítjük (B)-be A pályára az x = vt képletet kapjuk amelyben v = A t az (A3) és a (B4) alapján a következô: t = t = L (B5) (B6) Az U és a v ismeretében kiszámíthatjuk a (7)-ben szereplô négyzetgyökös kifejezést: Uv v = Ennek és (B6)-nak a szorzata adja (7) képlet jobb oldalát Számítsuk ki végül a vonat nyugalmi rendszerében a Frani óráján eltelt idôt is Frani végig nyugalomban van a vonat elején ezért sajátidejének megváltozása megegyezik koordinátaidejének megváltozásával: Δτ F = t t = a (6)-tal összhangban L 380 FIZIKAI SZEMLE 03 /
Speciális relativitás
 Fizika 1 előadás 2016. április 6. Speciális relativitás Relativisztikus kinematika Utolsó módosítás: 2016. április 4.. 1 Egy érdekesség: Fizeau-kísérlet A v sebességgel áramló n törésmutatójú folyadékban
Fizika 1 előadás 2016. április 6. Speciális relativitás Relativisztikus kinematika Utolsó módosítás: 2016. április 4.. 1 Egy érdekesség: Fizeau-kísérlet A v sebességgel áramló n törésmutatójú folyadékban
Kinematika szeptember Vonatkoztatási rendszerek, koordinátarendszerek
 Kinematika 2014. szeptember 28. 1. Vonatkoztatási rendszerek, koordinátarendszerek 1.1. Vonatkoztatási rendszerek A test mozgásának leírása kezdetén ki kell választani azt a viszonyítási rendszert, amelyből
Kinematika 2014. szeptember 28. 1. Vonatkoztatási rendszerek, koordinátarendszerek 1.1. Vonatkoztatási rendszerek A test mozgásának leírása kezdetén ki kell választani azt a viszonyítási rendszert, amelyből
Typotex Kiadó. Záró megjegyzések
 Záró megjegyzések Az olvasó esetleg hiányolhatja az éter szót, amely eddig a pillanatig egyáltalán nem fordult elő. Ez a mulasztás tudatos megfontoláson alapul: Ugyanazért nem kerítettünk szót az éterre,
Záró megjegyzések Az olvasó esetleg hiányolhatja az éter szót, amely eddig a pillanatig egyáltalán nem fordult elő. Ez a mulasztás tudatos megfontoláson alapul: Ugyanazért nem kerítettünk szót az éterre,
A modern fizika születése
 A modern fizika születése Lord Kelvin a 19. század végén azt mondta, hogy a fizika egy befejezett tudomány: Nincsen olyan probléma amit a tudomány ne tudna megoldani. A fizika egy befejezett tudomány,
A modern fizika születése Lord Kelvin a 19. század végén azt mondta, hogy a fizika egy befejezett tudomány: Nincsen olyan probléma amit a tudomány ne tudna megoldani. A fizika egy befejezett tudomány,
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
A relativitáselmélet alapjai
 A relativitáselmélet alapjai További olvasnivaló a kiadó kínálatából: Bódizs Dénes: Atommagsugárzások méréstechnikái Frei Zsolt Patkós András: Inflációs kozmológia Geszti Tamás: Kvantummechanika John D.
A relativitáselmélet alapjai További olvasnivaló a kiadó kínálatából: Bódizs Dénes: Atommagsugárzások méréstechnikái Frei Zsolt Patkós András: Inflációs kozmológia Geszti Tamás: Kvantummechanika John D.
A mechanika alapjai. A pontszerű testek dinamikája
 A mechanika alapjai A pontszerű testek dinamikája Horváth András SZE, Fizika Tsz. v 0.6 1 / 26 alapi Bevezetés Newton I. Newton II. Newton III. Newton IV. alapi 2 / 26 Bevezetés alapi Bevezetés Newton
A mechanika alapjai A pontszerű testek dinamikája Horváth András SZE, Fizika Tsz. v 0.6 1 / 26 alapi Bevezetés Newton I. Newton II. Newton III. Newton IV. alapi 2 / 26 Bevezetés alapi Bevezetés Newton
b) Ábrázolja ugyanabban a koordinátarendszerben a g függvényt! (2 pont) c) Oldja meg az ( x ) 2
 1) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) b) c) ( ) ) Határozza meg az 1. feladatban megadott, ; intervallumon
1) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) b) c) ( ) ) Határozza meg az 1. feladatban megadott, ; intervallumon
1. ábra. 24B-19 feladat
 . gyakorlat.. Feladat: (HN 4B-9) A +Q töltés egy hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld.. ábra.). Számítsuk ki az E elektromos térerősséget a vonal. ábra. 4B-9 feladat irányában lévő,
. gyakorlat.. Feladat: (HN 4B-9) A +Q töltés egy hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld.. ábra.). Számítsuk ki az E elektromos térerősséget a vonal. ábra. 4B-9 feladat irányában lévő,
Függvények Megoldások
 Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld ábra ábra
 . Gyakorlat 4B-9 A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld. 4-6 ábra.). Számítsuk ki az E elektromos térerősséget a vonal irányában lévő, annak.. ábra. 4-6 ábra végpontjától
. Gyakorlat 4B-9 A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld. 4-6 ábra.). Számítsuk ki az E elektromos térerősséget a vonal irányában lévő, annak.. ábra. 4-6 ábra végpontjától
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Speciális relativitás
 Bevezetés a modern fizika fejezeteibe 3. (a) Speciális relativitás Relativisztikus kinematika Utolsó módosítás: 2015. január 11.. 1 Egy egyszerű probléma (1) A K nyugvó vonatkoztatási rendszerben tekintsünk
Bevezetés a modern fizika fejezeteibe 3. (a) Speciális relativitás Relativisztikus kinematika Utolsó módosítás: 2015. január 11.. 1 Egy egyszerű probléma (1) A K nyugvó vonatkoztatási rendszerben tekintsünk
Q 1 D Q 2 (D x) 2 (1.1)
 . Gyakorlat 4B-9 Két pontszerű töltés az x tengelyen a következőképpen helyezkedik el: egy 3 µc töltés az origóban, és egy + µc töltés az x =, 5 m koordinátájú pontban van. Keressük meg azt a helyet, ahol
. Gyakorlat 4B-9 Két pontszerű töltés az x tengelyen a következőképpen helyezkedik el: egy 3 µc töltés az origóban, és egy + µc töltés az x =, 5 m koordinátájú pontban van. Keressük meg azt a helyet, ahol
VI. A tömeg növekedése.
 VI A tömeg nöekedése Egyszerű tárgyalás A tehetetlenség a test egy tlajdonsága, egy adata A tömeg az adott test tehetetlenségének kantitatí mértéke A tömeg meghatározásának módszere: meg kell izsgálni,
VI A tömeg nöekedése Egyszerű tárgyalás A tehetetlenség a test egy tlajdonsága, egy adata A tömeg az adott test tehetetlenségének kantitatí mértéke A tömeg meghatározásának módszere: meg kell izsgálni,
Ütközések elemzése energia-impulzus diagramokkal II. A relativisztikus rakéta
 Ütközések elemzése energia-impulzus diagramokkal II. A relativisztikus rakéta Bokor Nándor Budapesti Műszaki és Gazdaságtudományi Egyetem, Fizika Tanszék 1111 Budapest, Budafoki u. 8. Ebben a cikkben olyan
Ütközések elemzése energia-impulzus diagramokkal II. A relativisztikus rakéta Bokor Nándor Budapesti Műszaki és Gazdaságtudományi Egyetem, Fizika Tanszék 1111 Budapest, Budafoki u. 8. Ebben a cikkben olyan
Pálya : Az a vonal, amelyen a mozgó test végighalad. Út: A pályának az a része, amelyet adott idő alatt a mozgó tárgy megtesz.
 Haladó mozgások A hely és a mozgás viszonylagos. A testek helyét, mozgását valamilyen vonatkoztatási ponthoz, vonatkoztatási rendszerhez képest adjuk meg, ahhoz viszonyítjuk. pl. A vonatban utazó ember
Haladó mozgások A hely és a mozgás viszonylagos. A testek helyét, mozgását valamilyen vonatkoztatási ponthoz, vonatkoztatási rendszerhez képest adjuk meg, ahhoz viszonyítjuk. pl. A vonatban utazó ember
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I. 1 I. HALmAZOk 1. JELÖLÉSEk A halmaz fogalmát tulajdonságait gyakran használjuk a matematikában. A halmazt nem definiáljuk, ezt alapfogalomnak tekintjük. Ez nem szokatlan, hiszen
KOVÁCS BÉLA, MATEmATIkA I. 1 I. HALmAZOk 1. JELÖLÉSEk A halmaz fogalmát tulajdonságait gyakran használjuk a matematikában. A halmazt nem definiáljuk, ezt alapfogalomnak tekintjük. Ez nem szokatlan, hiszen
1. gyakorlat. Egyenletes és egyenletesen változó mozgás. 1. példa
 1. gyakorlat Egyenletes és egyenletesen változó mozgás egyenletes mozgás egyenletesen változó mozgás gyorsulás a = 0 a(t) = a = állandó sebesség v(t) = v = állandó v(t) = v(0) + a t pályakoordináta s(t)
1. gyakorlat Egyenletes és egyenletesen változó mozgás egyenletes mozgás egyenletesen változó mozgás gyorsulás a = 0 a(t) = a = állandó sebesség v(t) = v = állandó v(t) = v(0) + a t pályakoordináta s(t)
Pálya : Az a vonal, amelyen a mozgó test végighalad. Út: A pályának az a része, amelyet adott idő alatt a mozgó tárgy megtesz.
 Haladó mozgások A hely és a mozgás viszonylagos. A testek helyét, mozgását valamilyen vonatkoztatási ponthoz, vonatkoztatási rendszerhez képest adjuk meg, ahhoz viszonyítjuk. pl. A vonatban utazó ember
Haladó mozgások A hely és a mozgás viszonylagos. A testek helyét, mozgását valamilyen vonatkoztatási ponthoz, vonatkoztatási rendszerhez képest adjuk meg, ahhoz viszonyítjuk. pl. A vonatban utazó ember
Fizika példák a döntőben
 Fizika példák a döntőben F. 1. Legyen két villamosmegálló közötti távolság 500 m, a villamos gyorsulása pedig 0,5 m/s! A villamos 0 s időtartamig gyorsuljon, majd állandó sebességgel megy, végül szintén
Fizika példák a döntőben F. 1. Legyen két villamosmegálló közötti távolság 500 m, a villamos gyorsulása pedig 0,5 m/s! A villamos 0 s időtartamig gyorsuljon, majd állandó sebességgel megy, végül szintén
[ ]dx 2 # [ 1 # h( z,t)
![[ ]dx 2 # [ 1 # h( z,t) [ ]dx 2 # [ 1 # h( z,t)](/thumbs/91/105624473.jpg) A gravitációs hullámok miért mutathatók ki lézer-interferométerrel? Gravitációs hullám (GH) Newton: ha egy nagy tömegű égitest helyet változtat, annak azonnal érződik a hatása tetszőlegesen nagy távolságban
A gravitációs hullámok miért mutathatók ki lézer-interferométerrel? Gravitációs hullám (GH) Newton: ha egy nagy tömegű égitest helyet változtat, annak azonnal érződik a hatása tetszőlegesen nagy távolságban
Matematikai geodéziai számítások 10.
 Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
6. Függvények. 1. Az alábbi függvények közül melyik szigorúan monoton növekvő a 0;1 intervallumban?
 6. Függvények I. Nulladik ZH-ban láttuk: 1. Az alábbi függvények közül melyik szigorúan monoton növekvő a 0;1 intervallumban? f x g x cos x h x x ( ) sin x (A) Az f és a h. (B) Mindhárom. (C) Csak az f.
6. Függvények I. Nulladik ZH-ban láttuk: 1. Az alábbi függvények közül melyik szigorúan monoton növekvő a 0;1 intervallumban? f x g x cos x h x x ( ) sin x (A) Az f és a h. (B) Mindhárom. (C) Csak az f.
Lendület. Lendület (impulzus): A test tömegének és sebességének szorzata. vektormennyiség: iránya a sebesség vektor iránya.
 Lendület Lendület (impulzus): A test tömegének és sebességének szorzata. vektormennyiség: iránya a sebesség vektor iránya. Lendülettétel: Az lendület erő hatására változik meg. Az eredő erő határozza meg
Lendület Lendület (impulzus): A test tömegének és sebességének szorzata. vektormennyiség: iránya a sebesség vektor iránya. Lendülettétel: Az lendület erő hatására változik meg. Az eredő erő határozza meg
3. Egyenletek, egyenletrendszerek, egyenlőtlenségek
 . Egyenletek, egyenletrendszerek, egyenlőtlenségek I. Nulladik ZH-ban láttuk: 1. Mennyi a 2x 2 8x 5 = 0 egyenlet gyökeinek a szorzata? (A) 10 (B) 2 (C) 2,5 (D) 4 (E) ezek egyike sem Megoldás I.: BME 2011.
. Egyenletek, egyenletrendszerek, egyenlőtlenségek I. Nulladik ZH-ban láttuk: 1. Mennyi a 2x 2 8x 5 = 0 egyenlet gyökeinek a szorzata? (A) 10 (B) 2 (C) 2,5 (D) 4 (E) ezek egyike sem Megoldás I.: BME 2011.
Haladó mozgások A hely és a mozgás viszonylagos. A testek helyét, mozgását valamilyen vonatkoztatási ponthoz, vonatkoztatási rendszerhez képest adjuk
 Haladó mozgások A hely és a mozgás viszonylagos. A testek helyét, mozgását valamilyen vonatkoztatási ponthoz, vonatkoztatási rendszerhez képest adjuk meg, ahhoz viszonyítjuk. pl. A vonatban utazó ember
Haladó mozgások A hely és a mozgás viszonylagos. A testek helyét, mozgását valamilyen vonatkoztatási ponthoz, vonatkoztatási rendszerhez képest adjuk meg, ahhoz viszonyítjuk. pl. A vonatban utazó ember
A Hamilton-Jacobi-egyenlet
 A Hamilton-Jacobi-egyenlet Ha sikerül olyan kanonikus transzformációt találnunk, amely a Hamilton-függvényt zérusra transzformálja akkor valamennyi új koordináta és impulzus állandó lesz: H 0 Q k = H P
A Hamilton-Jacobi-egyenlet Ha sikerül olyan kanonikus transzformációt találnunk, amely a Hamilton-függvényt zérusra transzformálja akkor valamennyi új koordináta és impulzus állandó lesz: H 0 Q k = H P
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 8 VIII VEkTOROk 1 VEkTOR Vektoron irányított szakaszt értünk Jelölése: stb Vektorok hossza A vektor abszolút értéke az irányított szakasz hossza Ha a vektor hossza egységnyi akkor
KOVÁCS BÉLA MATEmATIkA I 8 VIII VEkTOROk 1 VEkTOR Vektoron irányított szakaszt értünk Jelölése: stb Vektorok hossza A vektor abszolút értéke az irányított szakasz hossza Ha a vektor hossza egységnyi akkor
Speciális relativitás
 Bevezetés a modern fizika fejezeteibe 3. (b) Speciális relativitás Relativisztikus dinamika Utolsó módosítás: 2013 október 15. 1 A relativisztikus tömeg (1) A bevezetett Lorentz-transzformáció biztosítja
Bevezetés a modern fizika fejezeteibe 3. (b) Speciális relativitás Relativisztikus dinamika Utolsó módosítás: 2013 október 15. 1 A relativisztikus tömeg (1) A bevezetett Lorentz-transzformáció biztosítja
Keresztmetszet másodrendű nyomatékainak meghatározása
 BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
Tömegpontok mozgása egyenes mentén, hajítások
 2. gyakorlat 1. Feladatok a kinematika tárgyköréből Tömegpontok mozgása egyenes mentén, hajítások 1.1. Feladat: Mekkora az átlagsebessége annak pontnak, amely mozgásának első szakaszában v 1 sebességgel
2. gyakorlat 1. Feladatok a kinematika tárgyköréből Tömegpontok mozgása egyenes mentén, hajítások 1.1. Feladat: Mekkora az átlagsebessége annak pontnak, amely mozgásának első szakaszában v 1 sebességgel
24 műhold (6 pályasíkban 4-4) & % ( )M * 26600km. T m. # 3870 m v m "1.29 #10 $5. # 460 m T a s
 A GPS-nél fellépő relativisztikus effektusok. 4 műhold 6 pályasíkban 4-4 T m = 1 óra " Mm r m = mr m % T m T r m = m % M * 66km " v m [ m s ] = r m" 87 m v m "1.9 1 5 T m s Az Egyenlítőn álló vevőkészülék:
A GPS-nél fellépő relativisztikus effektusok. 4 műhold 6 pályasíkban 4-4 T m = 1 óra " Mm r m = mr m % T m T r m = m % M * 66km " v m [ m s ] = r m" 87 m v m "1.9 1 5 T m s Az Egyenlítőn álló vevőkészülék:
A két megközelítés ellentéte ugyanakkor éppen a fizikai realitás fogalmában, értelmezésében tér el egymástól. " # $ %
 Kedves Laci és Péter! Köszönöm a vitához való hozzászólásotokat. következetesen és logikusan jeleníti meg a tárgynak - az óraparadoxonnak és ezzel egyben a relativitás elméletének mint olyannak - azt a
Kedves Laci és Péter! Köszönöm a vitához való hozzászólásotokat. következetesen és logikusan jeleníti meg a tárgynak - az óraparadoxonnak és ezzel egyben a relativitás elméletének mint olyannak - azt a
Vontatás III. A feladat
 Vontatás III Ebben a részben ázoljuk a ontatási feladat egy lehetséges numerikus megoldási módját Ezt az I részben ismertetett alapegyenletre építjük fel Itt az egy ontatott kerékpár esetét izsgáljuk feladat
Vontatás III Ebben a részben ázoljuk a ontatási feladat egy lehetséges numerikus megoldási módját Ezt az I részben ismertetett alapegyenletre építjük fel Itt az egy ontatott kerékpár esetét izsgáljuk feladat
Mozgással kapcsolatos feladatok
 Mozgással kapcsolatos feladatok Olyan feladatok, amelyekben az út, id és a sebesség szerepel. Az egyenes vonalú egyenletes mozgás esetén jelölje s= a megtett utat, v= a sebességet, t= az id t. Ekkor érvényesek
Mozgással kapcsolatos feladatok Olyan feladatok, amelyekben az út, id és a sebesség szerepel. Az egyenes vonalú egyenletes mozgás esetén jelölje s= a megtett utat, v= a sebességet, t= az id t. Ekkor érvényesek
Matematika 11 Koordináta geometria. matematika és fizika szakos középiskolai tanár. > o < szeptember 27.
 Matematika 11 Koordináta geometria Juhász László matematika és fizika szakos középiskolai tanár > o < 2015. szeptember 27. copyright: c Juhász László Ennek a könyvnek a használatát szerzői jog védi. A
Matematika 11 Koordináta geometria Juhász László matematika és fizika szakos középiskolai tanár > o < 2015. szeptember 27. copyright: c Juhász László Ennek a könyvnek a használatát szerzői jog védi. A
Fénypont a falon Feladat
 Fénypont a falon 3. Dolgozat - sorozatunk. és. részében két speiális eset vizsgálatát részleteztük. Itt az általánosabb síkbeli esettel foglalkozunk, főbb vonalaiban. Ehhez tekintsük az. ábrát is! 3. Feladat.
Fénypont a falon 3. Dolgozat - sorozatunk. és. részében két speiális eset vizsgálatát részleteztük. Itt az általánosabb síkbeli esettel foglalkozunk, főbb vonalaiban. Ehhez tekintsük az. ábrát is! 3. Feladat.
Azonos és egymással nem kölcsönható részecskékből álló kvantumos rendszer makrókanónikus sokaságban.
 Kvantum statisztika A kvantummechanika előadások során már megtanultuk, hogy az anyagot felépítő részecskék nemklasszikus, hullámtulajdonságokkal is rendelkeznek aminek következtében viselkedésük sok szempontból
Kvantum statisztika A kvantummechanika előadások során már megtanultuk, hogy az anyagot felépítő részecskék nemklasszikus, hullámtulajdonságokkal is rendelkeznek aminek következtében viselkedésük sok szempontból
First Prev Next Last Go Back Full Screen Close Quit. Matematika I
 Matematika I (Analízis) Készítette: Horváth Gábor Kötelező irodalom: Ács László, Gáspár Csaba: Analízis 1 Oktatási segédanyagok és a tantárgyi követelményrendszer megtalálható a http://rs1.szif.hu/ horvathg/horvathg.html
Matematika I (Analízis) Készítette: Horváth Gábor Kötelező irodalom: Ács László, Gáspár Csaba: Analízis 1 Oktatási segédanyagok és a tantárgyi követelményrendszer megtalálható a http://rs1.szif.hu/ horvathg/horvathg.html
A mérési eredmény megadása
 A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
Ellipszis átszelése. 1. ábra
 1 Ellipszis átszelése Adott egy a és b féltengely - adatokkal bíró ellipszis, melyet a befoglaló téglalapjának bal alsó sarkában csuklósan rögzítettnek képzelünk. Az ellipszist e C csukló körül forgatva
1 Ellipszis átszelése Adott egy a és b féltengely - adatokkal bíró ellipszis, melyet a befoglaló téglalapjának bal alsó sarkában csuklósan rögzítettnek képzelünk. Az ellipszist e C csukló körül forgatva
Optika és Relativitáselmélet II. BsC fizikus hallgatóknak
 Optika és Relativitáselmélet II. BsC fizikus hallgatóknak 11. Bevezetés a speciális relativitáselméletbe I. Tér, Idő, Téridő Cserti József, jegyzet, ELTE, 2007 (Dávid Gyula jegyzete alapján). Maxwell-egyenletek
Optika és Relativitáselmélet II. BsC fizikus hallgatóknak 11. Bevezetés a speciális relativitáselméletbe I. Tér, Idő, Téridő Cserti József, jegyzet, ELTE, 2007 (Dávid Gyula jegyzete alapján). Maxwell-egyenletek
A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a
 a Matematika mérnököknek I. című tárgyhoz Függvények. Függvények A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a szabadon eső test sebessége az idő függvénye. Konstans hőmérsékleten
a Matematika mérnököknek I. című tárgyhoz Függvények. Függvények A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a szabadon eső test sebessége az idő függvénye. Konstans hőmérsékleten
DETERMINÁNSSZÁMÍTÁS. Határozzuk meg a 1 értékét! Ez most is az egyetlen elemmel egyezik meg, tehát az értéke 1.
 DETERMINÁNSSZÁMÍTÁS A (nxn) kvadratikus (négyzetes) mátrixhoz egyértelműen hozzárendelhetünk egy D R számot, ami a mátrix determinánsa. Már most megjegyezzük, hogy a mátrix determinánsa, illetve a determináns
DETERMINÁNSSZÁMÍTÁS A (nxn) kvadratikus (négyzetes) mátrixhoz egyértelműen hozzárendelhetünk egy D R számot, ami a mátrix determinánsa. Már most megjegyezzük, hogy a mátrix determinánsa, illetve a determináns
Newton törvények és a gravitációs kölcsönhatás (Vázlat)
 Newton törvények és a gravitációs kölcsönhatás (Vázlat) 1. Az inerciarendszer fogalma. Newton I. törvénye 3. Newton II. törvénye 4. Newton III. törvénye 5. Erők szuperpozíciójának elve 6. Különböző mozgások
Newton törvények és a gravitációs kölcsönhatás (Vázlat) 1. Az inerciarendszer fogalma. Newton I. törvénye 3. Newton II. törvénye 4. Newton III. törvénye 5. Erők szuperpozíciójának elve 6. Különböző mozgások
Az időmérés pontossága fontos, mert a távolságmérést erre alapozzuk.
 A GPS-nél fellépő relativisztikus effektusok. 24 műhold (6 pályasíkban 4-4) T m = 12 óra Az Egyenlítőn álló vevőkészülék: r a = 6370km 1 Az időmérés pontossága fontos, mert a távolságmérést erre alapozzuk.
A GPS-nél fellépő relativisztikus effektusok. 24 műhold (6 pályasíkban 4-4) T m = 12 óra Az Egyenlítőn álló vevőkészülék: r a = 6370km 1 Az időmérés pontossága fontos, mert a távolságmérést erre alapozzuk.
Egyenletek, egyenlőtlenségek VII.
 Egyenletek, egyenlőtlenségek VII. Magasabbfokú egyenletek: A 3, vagy annál nagyobb fokú egyenleteket magasabb fokú egyenleteknek nevezzük. Megjegyzés: Egy n - ed fokú egyenletnek legfeljebb n darab valós
Egyenletek, egyenlőtlenségek VII. Magasabbfokú egyenletek: A 3, vagy annál nagyobb fokú egyenleteket magasabb fokú egyenleteknek nevezzük. Megjegyzés: Egy n - ed fokú egyenletnek legfeljebb n darab valós
FIZIKA ZÁRÓVIZSGA 2015
 FIZIKA ZÁRÓVIZSGA 2015 TESZT A következő feladatokban a három vagy négy megadott válasz közül pontosan egy helyes. Írd be az általad helyesnek vélt válasz betűjelét a táblázat megfelelő cellájába! Indokolni
FIZIKA ZÁRÓVIZSGA 2015 TESZT A következő feladatokban a három vagy négy megadott válasz közül pontosan egy helyes. Írd be az általad helyesnek vélt válasz betűjelét a táblázat megfelelő cellájába! Indokolni
8. Egyenletek, egyenlőtlenségek, egyenletrendszerek II.
 8 Egyenletek, egyenlőtlenségek, egyenletrendszerek II Elméleti összefoglaló Az a + b+ c, a egyenletet másodfokú egyenletnek nevezzük A D b ac kifejezést az egyenlet diszkriminánsának nevezzük Ha D >, az
8 Egyenletek, egyenlőtlenségek, egyenletrendszerek II Elméleti összefoglaló Az a + b+ c, a egyenletet másodfokú egyenletnek nevezzük A D b ac kifejezést az egyenlet diszkriminánsának nevezzük Ha D >, az
Gauss-Jordan módszer Legkisebb négyzetek módszere, egyenes LNM, polinom LNM, függvény. Lineáris algebra numerikus módszerei
 A Gauss-Jordan elimináció, mátrixinvertálás Gauss-Jordan módszer Ugyanazzal a technikával, mint ahogy a k-adik oszlopban az a kk alatti elemeket kinulláztuk, a fölötte lévő elemeket is zérussá lehet tenni.
A Gauss-Jordan elimináció, mátrixinvertálás Gauss-Jordan módszer Ugyanazzal a technikával, mint ahogy a k-adik oszlopban az a kk alatti elemeket kinulláztuk, a fölötte lévő elemeket is zérussá lehet tenni.
Pálya : Az a vonal, amelyen a mozgó tárgy, test végighalad. Út: A pályának az a része, amelyet adott idő alatt a mozgó tárgy megtesz.
 Haladó mozgások A hely és a mozgás viszonylagos. A testek helyét, mozgását valamilyen vonatkoztatási ponthoz, vonatkoztatási rendszerhez képest adjuk meg, ahhoz viszonyítjuk. pl. A vonatban utazó ember
Haladó mozgások A hely és a mozgás viszonylagos. A testek helyét, mozgását valamilyen vonatkoztatási ponthoz, vonatkoztatási rendszerhez képest adjuk meg, ahhoz viszonyítjuk. pl. A vonatban utazó ember
Meghatározás: Olyan egyenlet, amely a független változók mellett tartalmaz egy vagy több függvényt és azok deriváltjait.
 Közönséges differenciálegyenletek Meghatározás: Olyan egyenlet, amely a független változók mellett tartalmaz egy vagy több függvényt és azok deriváltjait. Célunk a függvény meghatározása Egyetlen független
Közönséges differenciálegyenletek Meghatározás: Olyan egyenlet, amely a független változók mellett tartalmaz egy vagy több függvényt és azok deriváltjait. Célunk a függvény meghatározása Egyetlen független
15. LINEÁRIS EGYENLETRENDSZEREK
 15 LINEÁRIS EGYENLETRENDSZEREK 151 Lineáris egyenletrendszer, Gauss elimináció 1 Definíció Lineáris egyenletrendszernek nevezzük az (1) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
15 LINEÁRIS EGYENLETRENDSZEREK 151 Lineáris egyenletrendszer, Gauss elimináció 1 Definíció Lineáris egyenletrendszernek nevezzük az (1) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
Alkalmazás a makrókanónikus sokaságra: A fotongáz
 Alkalmazás a makrókanónikus sokaságra: A fotongáz A fotonok az elektromágneses sugárzás hordozó részecskéi. Spinkvantumszámuk S=, tehát kvantumstatisztikai szempontból bozonok. Fotonoknak habár a spinkvantumszámuk,
Alkalmazás a makrókanónikus sokaságra: A fotongáz A fotonok az elektromágneses sugárzás hordozó részecskéi. Spinkvantumszámuk S=, tehát kvantumstatisztikai szempontból bozonok. Fotonoknak habár a spinkvantumszámuk,
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I. 4 IV. FÜGGVÉNYEk 1. LEkÉPEZÉSEk, függvények Definíció Legyen és két halmaz. Egy függvény -ből -ba egy olyan szabály, amely minden elemhez pontosan egy elemet rendel hozzá. Az
KOVÁCS BÉLA, MATEmATIkA I. 4 IV. FÜGGVÉNYEk 1. LEkÉPEZÉSEk, függvények Definíció Legyen és két halmaz. Egy függvény -ből -ba egy olyan szabály, amely minden elemhez pontosan egy elemet rendel hozzá. Az
MÉRÉSI EREDMÉNYEK PONTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI
 MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
= 163, 63V. Felírható az R 2 ellenállásra, hogy: 163,63V. blokk sorosan van kapcsolva a baloldali R 1 -gyel, és tudjuk, hogy
 Határozzuk meg és ellenállások értékét, ha =00V, = 00, az ampermérő 88mA áramot, a voltmérő,v feszültséget jelez! Az ampermérő ellenállását elhanyagolhatóan kicsinek, a voltmérőét végtelen nagynak tekinthetjük
Határozzuk meg és ellenállások értékét, ha =00V, = 00, az ampermérő 88mA áramot, a voltmérő,v feszültséget jelez! Az ampermérő ellenállását elhanyagolhatóan kicsinek, a voltmérőét végtelen nagynak tekinthetjük
Az R forgató mátrix [ 1 ] - beli képleteinek levezetése: I. rész
![Az R forgató mátrix [ 1 ] - beli képleteinek levezetése: I. rész Az R forgató mátrix [ 1 ] - beli képleteinek levezetése: I. rész](/thumbs/57/40130324.jpg) Az R forgató mátri [ ] - beli képleteinek levezetése: I rész Az [ ] forrás kötetében a ( 49 ), ( 50 ) képletek nyilván mint közismertek nem lettek levezetve Minthogy az ottani további számítások miatt
Az R forgató mátri [ ] - beli képleteinek levezetése: I rész Az [ ] forrás kötetében a ( 49 ), ( 50 ) képletek nyilván mint közismertek nem lettek levezetve Minthogy az ottani további számítások miatt
I. Vektorok. Adott A (2; 5) és B ( - 3; 4) pontok. (ld. ábra) A két pont által meghatározott vektor:
 I. Vektorok 1. Vektorok összege Általánosan: Az ábra alapján Adott: a(4; 1) és b(; 3) a + b (4 + ; 1 + 3) = (6; ) a(a 1 ; a ) és b(b 1 ; b ) a + b(a 1 + b 1 ; a + b ). Vektorok különbsége Általánosan:
I. Vektorok 1. Vektorok összege Általánosan: Az ábra alapján Adott: a(4; 1) és b(; 3) a + b (4 + ; 1 + 3) = (6; ) a(a 1 ; a ) és b(b 1 ; b ) a + b(a 1 + b 1 ; a + b ). Vektorok különbsége Általánosan:
azonos sikban fekszik. A vezetőhurok ellenállása 2 Ω. Számítsuk ki a hurok teljes 4.1. ábra ábra
 4. Gyakorlat 31B-9 A 31-15 ábrán látható, téglalap alakú vezetőhurok és a hosszúságú, egyenes vezető azonos sikban fekszik. A vezetőhurok ellenállása 2 Ω. Számítsuk ki a hurok teljes 4.1. ábra. 31-15 ábra
4. Gyakorlat 31B-9 A 31-15 ábrán látható, téglalap alakú vezetőhurok és a hosszúságú, egyenes vezető azonos sikban fekszik. A vezetőhurok ellenállása 2 Ω. Számítsuk ki a hurok teljes 4.1. ábra. 31-15 ábra
1. tétel. 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója 7 cm. Mekkora a háromszög átfogója? (4 pont)
 1. tétel 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója cm. Mekkora a háromszög átfogója? (4 pont). Adott az ábrán két vektor. Rajzolja meg a b, a b és az a b vektorokat! (6 pont)
1. tétel 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója cm. Mekkora a háromszög átfogója? (4 pont). Adott az ábrán két vektor. Rajzolja meg a b, a b és az a b vektorokat! (6 pont)
Érettségi feladatok: Trigonometria 1 /6
 Érettségi feladatok: Trigonometria 1 /6 2003. Próba 14. Egy hajó a Csendes-óceán egy szigetéről elindulva 40 perc alatt 24 km-t haladt észak felé, majd az eredeti haladási irányhoz képest 65 -ot nyugat
Érettségi feladatok: Trigonometria 1 /6 2003. Próba 14. Egy hajó a Csendes-óceán egy szigetéről elindulva 40 perc alatt 24 km-t haladt észak felé, majd az eredeti haladási irányhoz képest 65 -ot nyugat
Két naszád legkisebb távolsága. Az [ 1 ] gyűjteményben találtuk az alábbi feladatot és egy megoldását: 1. ábra.
![Két naszád legkisebb távolsága. Az [ 1 ] gyűjteményben találtuk az alábbi feladatot és egy megoldását: 1. ábra. Két naszád legkisebb távolsága. Az [ 1 ] gyűjteményben találtuk az alábbi feladatot és egy megoldását: 1. ábra.](/thumbs/91/105028162.jpg) 1 Két naszád legkisebb távolsága Az [ 1 ] gyűjteményben találtuk az alábbi feladatot és egy megoldását: 1. ábra. 1. ábra A feladat Az A és B, egymástól l távolságra lévő kikötőből egyidejűleg indul két
1 Két naszád legkisebb távolsága Az [ 1 ] gyűjteményben találtuk az alábbi feladatot és egy megoldását: 1. ábra. 1. ábra A feladat Az A és B, egymástól l távolságra lévő kikötőből egyidejűleg indul két
Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit.
 2. A VALÓS SZÁMOK 2.1 A valós számok aximómarendszere Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit. 1.Testaxiómák R-ben két művelet van értelmezve, az
2. A VALÓS SZÁMOK 2.1 A valós számok aximómarendszere Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit. 1.Testaxiómák R-ben két művelet van értelmezve, az
Gyakorlat 30B-14. a F L = e E + ( e)v B képlet, a gravitációs erőt a (2.1) G = m e g (2.2)
 2. Gyakorlat 30B-14 Az Egyenlítőnél, a földfelszín közelében a mágneses fluxussűrűség iránya északi, nagysága kb. 50µ T,az elektromos térerősség iránya lefelé mutat, nagysága; kb. 100 N/C. Számítsuk ki,
2. Gyakorlat 30B-14 Az Egyenlítőnél, a földfelszín közelében a mágneses fluxussűrűség iránya északi, nagysága kb. 50µ T,az elektromos térerősség iránya lefelé mutat, nagysága; kb. 100 N/C. Számítsuk ki,
Bevezetés a Speciális Relativitás elméletbe
 EÖTVÖS LORÁND TUDOMÁNYEGYETEM Alkalmazott matematikus szakirány Bs szakdolgozat Bevezetés a Speiális Relativitás elméletbe Szerző: Sallai Dávid Témavezető: Dr. Szeghy Dávid Péter Geometriai Tanszék Budapest,
EÖTVÖS LORÁND TUDOMÁNYEGYETEM Alkalmazott matematikus szakirány Bs szakdolgozat Bevezetés a Speiális Relativitás elméletbe Szerző: Sallai Dávid Témavezető: Dr. Szeghy Dávid Péter Geometriai Tanszék Budapest,
A brachistochron probléma megoldása
 A brachistochron probléma megoldása Adott a függőleges síkban két nem egy függőleges egyenesen fekvő P 0 és P 1 pont, amelyek közül a P 1 fekszik alacsonyabban. Azt a kérdést fogjuk vizsgálni. hogy van-e
A brachistochron probléma megoldása Adott a függőleges síkban két nem egy függőleges egyenesen fekvő P 0 és P 1 pont, amelyek közül a P 1 fekszik alacsonyabban. Azt a kérdést fogjuk vizsgálni. hogy van-e
Miért fontos számunkra az előző gyakorlaton tárgyalt lineáris algebrai ismeretek
 Az november 23-i szeminárium témája Rövid összefoglaló Miért fontos számunkra az előző gyakorlaton tárgyalt lineáris algebrai ismeretek felfrissítése? Tekintsünk ξ 1,..., ξ k valószínűségi változókat,
Az november 23-i szeminárium témája Rövid összefoglaló Miért fontos számunkra az előző gyakorlaton tárgyalt lineáris algebrai ismeretek felfrissítése? Tekintsünk ξ 1,..., ξ k valószínűségi változókat,
Modern Fizika Labor. 2. Elemi töltés meghatározása
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Másodfokú egyenletek, egyenlőtlenségek
 Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x 1x 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x 1x 16 =. 1. lépés:
Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x 1x 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x 1x 16 =. 1. lépés:
Kalkulus I. gyakorlat Fizika BSc I/1.
 . Ábrázoljuk a következő halmazokat a síkon! {, y) R 2 : + y < }, b) {, y) R 2 : 2 + y 2 < 4}, c) {, y) R 2 : 2 + y 2 < 4, + y < }, {, y) R 2 : + y < }. Kalkulus I. gyakorlat Fizika BSc I/.. gyakorlat
. Ábrázoljuk a következő halmazokat a síkon! {, y) R 2 : + y < }, b) {, y) R 2 : 2 + y 2 < 4}, c) {, y) R 2 : 2 + y 2 < 4, + y < }, {, y) R 2 : + y < }. Kalkulus I. gyakorlat Fizika BSc I/.. gyakorlat
Mérés és modellezés Méréstechnika VM, GM, MM 1
 Mérés és modellezés 2008.02.04. 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni
Mérés és modellezés 2008.02.04. 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni
Kirchhoff 2. törvénye (huroktörvény) szerint az áramkörben levő elektromotoros erők. E i = U j (3.1)
 3. Gyakorlat 29A-34 Egy C kapacitású kondenzátort R ellenálláson keresztül sütünk ki. Mennyi idő alatt csökken a kondenzátor töltése a kezdeti érték 1/e 2 ed részére? Kirchhoff 2. törvénye (huroktörvény)
3. Gyakorlat 29A-34 Egy C kapacitású kondenzátort R ellenálláson keresztül sütünk ki. Mennyi idő alatt csökken a kondenzátor töltése a kezdeti érték 1/e 2 ed részére? Kirchhoff 2. törvénye (huroktörvény)
Arany Dániel Matematikai Tanulóverseny 2015/2016-os tanév 1. forduló Haladók III. kategória
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 2015/2016-os tanév 1. forduló Haladók III. kategória Megoldások és javítási útmutató 1. Az a és b befogójú derékszögű háromszögnek
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 2015/2016-os tanév 1. forduló Haladók III. kategória Megoldások és javítási útmutató 1. Az a és b befogójú derékszögű háromszögnek
I. BESZÁLLÍTÓI TELJESÍTMÉNYEK ÉRTÉKELÉSE
 I. BESZÁLLÍTÓI TELJESÍTMÉNYEK ÉRTÉKELÉSE Komplex termékek gyártására jellemző, hogy egy-egy termékbe akár több ezer alkatrész is beépül. Ilyenkor az alkatrészek általában sok különböző beszállítótól érkeznek,
I. BESZÁLLÍTÓI TELJESÍTMÉNYEK ÉRTÉKELÉSE Komplex termékek gyártására jellemző, hogy egy-egy termékbe akár több ezer alkatrész is beépül. Ilyenkor az alkatrészek általában sok különböző beszállítótól érkeznek,
A nagyobb tömegű Peti 1,5 m-re ült a forgástengelytől. Összesen: 9p
 Jedlik 9-10. o. reg feladat és megoldás 1) Egy 5 m hosszú libikókán hintázik Évi és Peti. A gyerekek tömege 30 kg és 50 kg. Egyikük a hinta végére ült. Milyen messze ült a másik gyerek a forgástengelytől,
Jedlik 9-10. o. reg feladat és megoldás 1) Egy 5 m hosszú libikókán hintázik Évi és Peti. A gyerekek tömege 30 kg és 50 kg. Egyikük a hinta végére ült. Milyen messze ült a másik gyerek a forgástengelytől,
Tanulási cél Szorzatfüggvényekre vonatkozó integrálási technikák megismerése és különböző típusokra való alkalmazása. 5), akkor
 Integrálszámítás Integrálási szabályok Tanulási cél Szorzatfüggvényekre vonatkozó integrálási technikák megismerése és különböző típusokra való alkalmazása Motivációs feladat Valószínűség-számításnál találkozhatunk
Integrálszámítás Integrálási szabályok Tanulási cél Szorzatfüggvényekre vonatkozó integrálási technikák megismerése és különböző típusokra való alkalmazása Motivációs feladat Valószínűség-számításnál találkozhatunk
Egy érdekes statikai - geometriai feladat
 1 Egy érdekes statikai - geometriai feladat Előző dolgozatunkban melynek címe: Egy érdekes geometriai feladat egy olyan feladatot oldottunk meg, ami az itteni előtanulmányának is tekinthető. Az ottani
1 Egy érdekes statikai - geometriai feladat Előző dolgozatunkban melynek címe: Egy érdekes geometriai feladat egy olyan feladatot oldottunk meg, ami az itteni előtanulmányának is tekinthető. Az ottani
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Exponenciális és Logaritmikus kifejezések
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Eponenciális és Logaritmikus kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szoálhatnak fontos információval
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Eponenciális és Logaritmikus kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szoálhatnak fontos információval
A test tömegének és sebességének szorzatát nevezzük impulzusnak, lendületnek, mozgásmennyiségnek.
 Mozgások dinamikai leírása A dinamika azzal foglalkozik, hogy mi a testek mozgásának oka, mitől mozognak úgy, ahogy mozognak? Ennek a kérdésnek a megválaszolása Isaac NEWTON (1642 1727) nevéhez fűződik.
Mozgások dinamikai leírása A dinamika azzal foglalkozik, hogy mi a testek mozgásának oka, mitől mozognak úgy, ahogy mozognak? Ennek a kérdésnek a megválaszolása Isaac NEWTON (1642 1727) nevéhez fűződik.
2017-ben az ELTE Doktori iskoláján elhangzott előadások diái Hraskó Péter
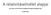 A relativitáselmélet alapjai 2017-ben az ELTE Doktori iskoláján elhangzott előadások diái Hraskó Péter 1. A speciális relativitáselmélet első posztulátuma A két posztulátum: 1. A fénysebesség minden inerciarendszerben
A relativitáselmélet alapjai 2017-ben az ELTE Doktori iskoláján elhangzott előadások diái Hraskó Péter 1. A speciális relativitáselmélet első posztulátuma A két posztulátum: 1. A fénysebesség minden inerciarendszerben
Vektorgeometria (2) First Prev Next Last Go Back Full Screen Close Quit
 Vektorgeometria (2) First Prev Next Last Go Back Full Screen Close Quit 1. Tekintsünk a térben egy P (p 1, p 2, p 3 ) pontot és egy v = (v 1, v 2, v 3 ) = 0 vektort. Ekkor pontosan egy egyenes létezik,
Vektorgeometria (2) First Prev Next Last Go Back Full Screen Close Quit 1. Tekintsünk a térben egy P (p 1, p 2, p 3 ) pontot és egy v = (v 1, v 2, v 3 ) = 0 vektort. Ekkor pontosan egy egyenes létezik,
A gravitációs hullámok miért mutathatók ki lézer-interferométerrel?
 A gravitációs hullámok miért mutathatók ki lézer-interferométerrel? Gravitációs hullám (GH) Newton: ha egy nagy tömegű égitest helyet változtat, annak azonnal érződik a hatása tetszőlegesen nagy távolságban
A gravitációs hullámok miért mutathatók ki lézer-interferométerrel? Gravitációs hullám (GH) Newton: ha egy nagy tömegű égitest helyet változtat, annak azonnal érződik a hatása tetszőlegesen nagy távolságban
Megoldások. Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma)
 Megoldások 1. Határozd meg az a és b vektor skaláris szorzatát, ha a = 5, b = 4 és a közbezárt szög φ = 55! Alkalmazzuk a megfelelő képletet: a b = a b cos φ = 5 4 cos 55 11,47. 2. Határozd meg a következő
Megoldások 1. Határozd meg az a és b vektor skaláris szorzatát, ha a = 5, b = 4 és a közbezárt szög φ = 55! Alkalmazzuk a megfelelő képletet: a b = a b cos φ = 5 4 cos 55 11,47. 2. Határozd meg a következő
BIOMATEMATIKA ELŐADÁS
 BIOMATEMATIKA ELŐADÁS 3. Hibaszámítás, lineáris regresszió Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Hibaszámítás Hibák fajtái, definíciók Abszolút, relatív, öröklött
BIOMATEMATIKA ELŐADÁS 3. Hibaszámítás, lineáris regresszió Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Hibaszámítás Hibák fajtái, definíciók Abszolút, relatív, öröklött
Kisérettségi feladatsorok matematikából
 Kisérettségi feladatsorok matematikából. feladatsor I. rész. Döntse el, hogy a következő állítások közül melyik igaz és melyik hamis! a) Ha két egész szám összege páratlan, akkor a szorzatuk páros. b)
Kisérettségi feladatsorok matematikából. feladatsor I. rész. Döntse el, hogy a következő állítások közül melyik igaz és melyik hamis! a) Ha két egész szám összege páratlan, akkor a szorzatuk páros. b)
Mérés és modellezés 1
 Mérés és modellezés 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni kell
Mérés és modellezés 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni kell
Hódmezővásárhelyi Városi Matematikaverseny április 14. A osztályosok feladatainak javítókulcsa
 Hódmezővásárhelyi Városi Matematikaverseny 2003. április 14. A 11-12. osztályosok feladatainak javítókulcsa 1. feladat Egy számtani sorozatot az első eleme és különbsége egyértelműen meghatározza, azt
Hódmezővásárhelyi Városi Matematikaverseny 2003. április 14. A 11-12. osztályosok feladatainak javítókulcsa 1. feladat Egy számtani sorozatot az első eleme és különbsége egyértelműen meghatározza, azt
Másodfokú egyenletek, egyenlőtlenségek
 Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x + 1x + 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x + 1x + 16 = 0.
Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x + 1x + 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x + 1x + 16 = 0.
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Exponenciális és Logaritmikus kifejezések
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Eponenciális és Logaritmikus kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Eponenciális és Logaritmikus kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos
A matematikai feladatok és megoldások konvenciói
 A matematikai feladatok és megoldások konvenciói Kozárné Fazekas Anna Kántor Sándor Matematika és Informatika Didaktikai Konferencia - Szatmárnémeti 2011. január 28-30. Konvenciók Mindenki által elfogadott
A matematikai feladatok és megoldások konvenciói Kozárné Fazekas Anna Kántor Sándor Matematika és Informatika Didaktikai Konferencia - Szatmárnémeti 2011. január 28-30. Konvenciók Mindenki által elfogadott
(Természetesen, nem lesz ilyen sok kérdés feladva a vizsgán!) Hogy szól a relativitási elv a lehető legjobb megfogalmazásban?
 Próba vizsgakérdések (A téridő fizikájától a tér és idő metafizikájáig) (Természetesen, nem lesz ilyen sok kérdés feladva a vizsgán!) Hogy szól a relativitási elv a lehető legjobb megfogalmazásban? Mit
Próba vizsgakérdések (A téridő fizikájától a tér és idő metafizikájáig) (Természetesen, nem lesz ilyen sok kérdés feladva a vizsgán!) Hogy szól a relativitási elv a lehető legjobb megfogalmazásban? Mit
11. Sorozatok. I. Nulladik ZH-ban láttuk:
 11. Sorozatok I. Nulladik ZH-ban láttuk: 1. Egy számtani sorozat harmadik eleme 15, a nyolcadik eleme 30. Mely n természetes számra igaz, hogy a sorozat első n elemének összege 6? A szokásos jelöléseket
11. Sorozatok I. Nulladik ZH-ban láttuk: 1. Egy számtani sorozat harmadik eleme 15, a nyolcadik eleme 30. Mely n természetes számra igaz, hogy a sorozat első n elemének összege 6? A szokásos jelöléseket
Pontműveletek. Sergyán Szabolcs Óbudai Egyetem Neumann János Informatikai Kar február 20.
 Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
