Gyakorlat 30B-14. a F L = e E + ( e)v B képlet, a gravitációs erőt a (2.1) G = m e g (2.2)
|
|
|
- Róbert Ernő Szőke
- 7 évvel ezelőtt
- Látták:
Átírás
1 2. Gyakorlat 30B-14 Az Egyenlítőnél, a földfelszín közelében a mágneses fluxussűrűség iránya északi, nagysága kb. 50µ T,az elektromos térerősség iránya lefelé mutat, nagysága; kb. 100 N/C. Számítsuk ki, hogy ebben a pontban egy 100 ev -os, kelet felé egyenes vonalban haladó elektronra mekkora gravitációs, elektromos és mágneses erők hatnak! A (-e) töltésű elektronra ható, elektromos és mágneses térből származó Lorentz erőt a F L = e E + ( e)v B képlet, a gravitációs erőt a (2.1) G = m e g (2.2) képlet adja meg. Az elektron mozgási (kinetikus) energiája E kin = 1 2 m e v 2, ahonnan v-t kifejezve és behelyettesítve az elektron sebessége: 2Ekin ev v = = 1, J/ ev = m/s (2.3) m e 9, kg Az elektronra ható egyes erők: F E = e E = 1, N felfelé mutat (2.4) F B = v B = 4, N lefele mutat (2.5) F g = 8, N lefele mutat (2.6) F g elhanyagolhatóan kicsi a többihez képest. Ennek oka az, hogy a gravitációs erő nagyon gyenge 1. (Minthogy azonban F E F B +F g az elektronra ható erők eredője nem nulla, így 1 A négy ismert természeti erő relatív nagysága: erős kölcsönhatás: 1, elektromos 1/137, gyenge: , gravitációs: ! 1
2 az elektron ellentétben a feladat megfogalmazásával a nem mozoghat egyenesvonalú pályán! 2 ) 30B-12 Egy 2keV energiájú elektron a Föld 50 µt fluxussűrűségű mágneses terében körpályán mozog. a) Számítsuk ki a pályasugarat! b) Számítsuk ki, mennyi idő alatt tesz meg az elektron egy teljes kört! c) Mutassuk meg, hogy a b) kérdésre adott válasz a részecske ciklotron-frekvenciájának megfelelő periódusidő! 2 A feladat szerint az erők eredőjének együttes hatására az elektron egyenes vonalú pályán halad, ami csak úgy lehetséges, ha ezek eredője nulla. Vegyük fel a koordináta rendszerünket úgy, hogy az x tengely kelet felé, az y észak felé, a z pedig függőlegesen felfelé mutasson! A feladat szerint v = (v, 0, 0), B = (0, B, 0) és E = (0, 0, E). Természetesen G = (0, 0, g)). Az eredő erő minden komponensének nullának kell lennie. Mivel mind E, mind v B, mind g függőleges irányúak az erőnek is csak függőleges komponense lehet: F x = F y = 0 (2.7) F z = e( E + v B) m e g = e(e v B) m e g (2.8) Tegyük fel, hogy E nagysága nem ismert. De F z = 0, ami akkor teljesül, ha E = v B + m e e g (2.9) 2Ekin E = B + m e m e e g (2.10) [ ev ] 1, 6 10 = 19 [J/ ev ] 9, [T ] + 9, kg [kg] 1, C 9, 81 m/s2 (2.11) [ = 296, 55 kg] [ m 2 ]/[ s 2 [ ] [ ] ] [V ] [ s] kg m/s + 5, V 296, 55 (2.12) [ kg] m 2 As m A második tag dimenzióját tovább alakítva látható, hogy az is rendben van: kg m/s 2 As = J/m As = V A s A s m = V m (2.13) 2
3 a) Az elektron akkor mozog körpályán, ha mozgása a B-re merőleges síkban történik és sebessége is merőleges a térre. Ekkor a Lorentz erő biztosítja számára a centripetális gyorsulást. A pályasugár ebből: mivel 1 2 m e v 2 = E kin, ahonnan 2 Ekin v = = m e F L = e v B és F L = m e v 2 e v B = m e v 2 r, tehát r (2.14) , , = 4194m/s (2.15) A pályasugár (2.14) és (2.15)-ból r = m e v e B = 9, , = 2, m (2.16) b) A kör megtételéhez szükséges idő: T = 2 r π v (= 2 π m e v e B v ) = 2 2, = s (2.17) 4194 c) Az elektron ω c ciklotron frekvenciája> ω c = eb m e ν c = ω c 2 π = e B 2 π m e (2.18) ahonnan a keringési idő valóban megegyezik a b) pontban kiszámolttal: 30B-15 T = 1 ν = 2 π m e e B = s (2.19) Egy sebességszűrőben alkalmazott elektromos és mágneses erőteret az alábbi egyenletekkel adhatjuk meg 3 : E = Eẑ, ill. B = Bŷ Ha B = 0, 015 T, számítsuk ki, mekkora E 3 A kalap (ˆ) az adott irányú egységvektort jelöli 3
4 térerősséget kell alkalmazni, hogy az x tengely pozitív irányában haladó 750eV energiájú elektron pályája egyenes maradjon! Az elektron pályája akkor egyenes, ha a rá ható eredő erő nulla. Mivel mind az elektromos, mind a mágneses Lorentz erő merőleges az elektron sebességére, mindkettő z irányú és egymással ellentétes irányúak, ezért F z = e (E v B) = 0 E = v B (2.20) Az elektron sebessége 2 Ekin v = = m e , , = m s (2.21) Vagyis 30A-16 [ m ] E = , 015 s [ ] V s = V m 2 m (2.22) Egy 12 V -os telepet mérlegre helyezünk; a telep pólusaihoz téglalap alakú dróthurkot erősítünk úgy, hogy a téglalap alsó része B = 0, 100T fluxussűrűségű mágneses téren haladjon át (2.1 ábra). A telep és a hurok együttes tömege 100 g. Mekkora legyen a huzal ellenállása, hogy a mérleg éppen zérust mutasson? Melyik a telep pozitív pólusa? 2.1. ábra. Telep a mérlegen 4
5 A huzalban folyó áramban az elektronok a telep negatív sarkától a pozitív felé mozognak v drift = áll. sebességgel. A rájuk ható Lorentz erők eredője ellensúlyozza ki a telep súlyát, ezért mutat a mérleg nullát 4. Ahhoz, hogy ez az erő felfelé mutasson a v-nek az alsó vezetőszakaszon balra kell mutatnia, ekkor ugyanis a v B lefelé, az F L = e v B pedig felfelé fog mutatni. Tehát az áramforrás bal pólusa a pozitív. Az l = 0, 2 m hosszúságú I árammal átjárt vezetőre ható erő nagysága: F L = I l B, az áramerősség I = U R, ahol U a telep kapocsfeszültsége és R a vezeték ellenállása. ahonnan m telep g = I l B = U R l B R = U m telep g l B = 12 [V ] 0, 2 m 0, 1 [T ] (2.23) 0, 1 kg 9, 81 [m/s 2 ] [ ] [ ] [ ] [ ] V m V s V s 2 V s R = 0, 245 = 0, 245 (2.24) kg m/s 2 m 2 kg m 2 Az eredmény mértékegysége valóban Ohm: 31B-16 V V s3 kg m = V 2 A A V s3 kg m 2 Ω kg m2 /s 2 s 2 kg m 2 = V A W s s2 kg m 2 = Ω J s 2 kg m 2 = A mágnesek pólusai közötti homogén mágneses erőtér a széleken inhomogén, mint ahogy azt a 2.2b ábrán vázoltuk. Az Ampere törvényt a 2.2a ábrán vázolt integrációs görbére alkalmazva mutassuk meg, hogy pólusok közötti erőtér szélén a mágneses erőtér nem ér véget hirtelen, hanem onnan kinyúlik! Az Ampere törvény szerint B zárt görbére vett integrálja egyenlő a zárt görbére fektetett tetszőleges nyílt felületen áthaladó összes árammal (azaz az áramsűrűség erre a felületre vett fluxusával, vagy felületi integráljával): B ds = I (= j da) (2.25) (g) A A = Ω 4 Feltételezzük, hogy a hurok tökéletesen merev és fel tudja emelni a telepet. 5
6 2.2. ábra. a) lehetetlen és b) valódi mágneses tér Eszerint az ábrán vázolt görbére a körintegrálnak nullát kell adnia. Viszont a körintegrál értéke az a) ábra esetében nem lesz nulla, mert a térrel párhuzamos oldalra a mágnes pólusai között egy pozítiv, a külső oldalra nulla értéket ad. A másik két szakaszra a tér merőleges az integrálási görbére, tehát ott B ds = 0. Így ellentmondásra jutottunk az Ampere törvénnyel, vagyis ilyen eset nem létezhet. Mivel az integrációs görbét tetszőlegesen felvehetjük, ezért azt kell mondani a tér kívül nem lehet nulla. A b) ábrán látható esetben a tér túlnyúlik a mágnes pólusain, ezért a körintegrál nulla lesz. Kornis 2a Határozzuk meg a mágneses indukciót egy 16 cm-es és 30 cm-es oldalhosszúságú téglalap alakú vezető keret középpontjában, ha benne 6 A-es áram folyik! Jelölések: a = c = 0, 16 m, b = d = 0, 3 m. Ha a tér csak a keret középontjában érdekel, akkor a szórt terektől eltekintve a téglalap alakú keret minden oldalát tekinthetjük egy végtelen hosszú vezető egy szakaszának. Az egyes oldalak által keltett terek a keret középpontjában az Ampere törvény alapján: I B a = B c = µ o 2 (b/2) π = µ I o π b = T (2.26) I B b = B d = µ o π a = T (2.27) Mindegyik B ugyanolyan irányú. Az eredő teret a négy oldal által keltett mágneses terek összege adja: 2 I B = B a + B b + B c + B d = µ o π b + µ 2 I o π a = T (2.28) 6
7 Kornis 2b Mekkora feszültség indukálódik a 68 A-es árammal átjárt 40 cm hosszú, 400 menetes tekercs belsejében elhelyezett 0, 6 cm 2 felületű keretben, ha a tekercs áramát kikapcsolva a mágneses tér 0,07 s alatt zérussá, válik egyenletesen? I = 68 A, l = 0, 4 m, N = 400, A = m 2 és t = 0, 07 s A tér egyenletesen változik, ezért nem kell differenciálisan kis mennyiségekkel számolnunk. Az áram által a tekercsben keltett B mágneses tér B = µ o I N l = V s 68 A 400 Am 0, 4 m = 8, T B fluxusának változási sebessége adja meg az indukált feszültséget: U i = Φ B t = B A t = 8, 545 T m 2 0, 07 s = V (2.29) Kornis 2c Állandó 400 V s mágneses indukciójú homogén mágneses térben 15 cm oldalú négyzetes m2 vezetőkeret forog 400 s 1 fordulatszámmal. A keret tengelye merőleges a térerősség vektorára és a szemközti oldalak felezőpontján megy át. Mekkora a feszültség a kivezetésben, ha a keret síkja 45 o -os szöget zár be az erővonalakkal? Az adatok: keret oldala a = 0, 15 cm, területe: A = a 2 = 0, 0225 m, B = 400 V s m 2 ν = 400 s 1, ω = 2 π ν = s 1. Az indukált feszültség: U i = dφ B dt, ahol a homogén B Φ B fluxusa a keret síkjának a B-vel bezárt szögétől függ: Φ B = B A cosω t U i = B A ω sinω t = sinω t Amikor a keret 45 o -os szöget zár be az erővonalakkal, akkor ω t = 45 o + 2 k π, ahol k = 0, 1, 2... Ekkor a feszültség = V (2.30) 7
8 Kornis 2d Egyenesvonalú hengeres, homogén, 8 mm sugarú vezetőben tengely irányú, 8 A-es áram folyik. Határozzuk meg a mágneses indukció értékét a tengelytől 6 mm és 10 mm távolságban lévő pontban! Mindkét esetben az Ampere törvényt használhatjuk. Amikor a vezető belsejében vagyunk, akkor csak azt az áramot szabad figyelembe vegyük, ami az adott távolságon belül van. Jelöljük a hengeres vezető sugarát R-rel, a tengelytől mért távolságot r-el, az áramsűrűséget j-vel! Itt j = I R 2 π. Az (2.25) Ampere törvény szerint: (g) B ds = A j da (2.31) Az r sugarú körre fektetett sík felületen áthaladó áram: I I = j r 2 π = I R 2 π r2 π = I r2 R 2 ezért B = µ I 2 r π r R µ I r 2 2 R/2 r π r < R r R r < R (2.32) A két távolságot behelyettesítve tehát µ I = r π 10 4 T r = 0, 01 m B = µ I r = R 2 π 10 4 T r = 0, 006 m Kornis 2e Négyzet alakú vezető keretben 6 A áram folyik. A vezető keret síkjában, egyik oldaltól, azzal párhuzamosan, 6,6 cm távolságban hosszú egyenes vezető helyezkedik el, melyben 8 A erősségű áram folyik. A keret oldalai 4 cm hosszúak. Mekkora erő hat a keretre az egyenes vezető részéről? 8
9 Jelölések: I k = 6 A, a = 0, 04 m, I e = 8 A, d = 0, 066 m. A keretben folyó áramok hatnak kölcsön egymással. Párhuzamos, azonos irányban folyó áramok vonzzák, ellentétes irányúak taszítják egymást, merőlegesek nem hatnak egymásra. A két árammal átjárt L hosszú vezető közötti erőhatás nagysága F = [ N A 2 ] Ik I e r L (2.33) A keret két, az egyenes vezetővel párhuzamos oldalában futó áramok ellentétes irányúak, így [ ] ( N 1 F = F közeli F távoli = I A 2 k I e d 1 ) L a + d [ ] ( ) N = [A] 8[A] A 2 0, 066 [m] 1 0, 04 [m] 0, 106 [m] = N 9
azonos sikban fekszik. A vezetőhurok ellenállása 2 Ω. Számítsuk ki a hurok teljes 4.1. ábra ábra
 4. Gyakorlat 31B-9 A 31-15 ábrán látható, téglalap alakú vezetőhurok és a hosszúságú, egyenes vezető azonos sikban fekszik. A vezetőhurok ellenállása 2 Ω. Számítsuk ki a hurok teljes 4.1. ábra. 31-15 ábra
4. Gyakorlat 31B-9 A 31-15 ábrán látható, téglalap alakú vezetőhurok és a hosszúságú, egyenes vezető azonos sikban fekszik. A vezetőhurok ellenállása 2 Ω. Számítsuk ki a hurok teljes 4.1. ábra. 31-15 ábra
3.1. ábra ábra
 3. Gyakorlat 28C-41 A 28-15 ábrán két, azonos anyagból gyártott ellenállás látható. A véglapokat vezető 3.1. ábra. 28-15 ábra réteggel vonták be. Tételezzük fel, hogy az ellenállások belsejében az áramsűrűség
3. Gyakorlat 28C-41 A 28-15 ábrán két, azonos anyagból gyártott ellenállás látható. A véglapokat vezető 3.1. ábra. 28-15 ábra réteggel vonták be. Tételezzük fel, hogy az ellenállások belsejében az áramsűrűség
Kirchhoff 2. törvénye (huroktörvény) szerint az áramkörben levő elektromotoros erők. E i = U j (3.1)
 3. Gyakorlat 29A-34 Egy C kapacitású kondenzátort R ellenálláson keresztül sütünk ki. Mennyi idő alatt csökken a kondenzátor töltése a kezdeti érték 1/e 2 ed részére? Kirchhoff 2. törvénye (huroktörvény)
3. Gyakorlat 29A-34 Egy C kapacitású kondenzátort R ellenálláson keresztül sütünk ki. Mennyi idő alatt csökken a kondenzátor töltése a kezdeti érték 1/e 2 ed részére? Kirchhoff 2. törvénye (huroktörvény)
= Φ B(t = t) Φ B (t = 0) t
 4. Gyakorlat 32B-3 Egy ellenállású, r sugarú köralakú huzalhurok a B homogén mágneses erőtér irányára merőleges felületen fekszik. A hurkot gyorsan, t idő alatt 180 o -kal átforditjuk. Számitsuk ki, hogy
4. Gyakorlat 32B-3 Egy ellenállású, r sugarú köralakú huzalhurok a B homogén mágneses erőtér irányára merőleges felületen fekszik. A hurkot gyorsan, t idő alatt 180 o -kal átforditjuk. Számitsuk ki, hogy
1. fejezet. Gyakorlat C-41
 1. fejezet Gyakorlat 3 1.1. 28C-41 A 1.1 ábrán két, azonos anyagból gyártott ellenállás látható. A véglapokat vezető réteggel vonták be. Tételezzük fel, hogy az ellenállások belsejében az áramsűrűség bármely,
1. fejezet Gyakorlat 3 1.1. 28C-41 A 1.1 ábrán két, azonos anyagból gyártott ellenállás látható. A véglapokat vezető réteggel vonták be. Tételezzük fel, hogy az ellenállások belsejében az áramsűrűség bármely,
Fizika II. feladatsor főiskolai szintű villamosmérnök szak hallgatóinak. Levelező tagozat
 Fizika. feladatsor főiskolai szintű villamosmérnök szak hallgatóinak Levelező tagozat 1. z ábra szerinti félgömb alakú, ideális vezetőnek tekinthető földelőbe = 10 k erősségű áram folyik be. föld fajlagos
Fizika. feladatsor főiskolai szintű villamosmérnök szak hallgatóinak Levelező tagozat 1. z ábra szerinti félgömb alakú, ideális vezetőnek tekinthető földelőbe = 10 k erősségű áram folyik be. föld fajlagos
Mágneses mező tesztek. d) Egy mágnesrúd északi pólusához egy másik mágnesrúd déli pólusát közelítjük.
 Mágneses mező tesztek 1. Melyik esetben nem tapasztalunk vonzóerőt? a) A mágnesrúd északi pólusához vasdarabot közelítünk. b) A mágnesrúd közepéhez vasdarabot közelítünk. c) A mágnesrúd déli pólusához
Mágneses mező tesztek 1. Melyik esetben nem tapasztalunk vonzóerőt? a) A mágnesrúd északi pólusához vasdarabot közelítünk. b) A mágnesrúd közepéhez vasdarabot közelítünk. c) A mágnesrúd déli pólusához
Gépészmérnöki alapszak, Mérnöki fizika 2. ZH, december 05. Feladatok (maximum 3x6 pont=18 pont)
 1. 2. 3. Mondat E1 E2 NÉV: Gépészmérnöki alapszak, Mérnöki fizika 2. ZH, 2017. december 05. Neptun kód: Aláírás: g=10 m/s 2 ; ε 0 = 8.85 10 12 F/m; μ 0 = 4π 10 7 Vs/Am; c = 3 10 8 m/s Előadó: Márkus /
1. 2. 3. Mondat E1 E2 NÉV: Gépészmérnöki alapszak, Mérnöki fizika 2. ZH, 2017. december 05. Neptun kód: Aláírás: g=10 m/s 2 ; ε 0 = 8.85 10 12 F/m; μ 0 = 4π 10 7 Vs/Am; c = 3 10 8 m/s Előadó: Márkus /
Mágneses erőtér. Ahol az áramtól átjárt vezetőre (vagy mágnestűre) erő hat. A villamos forgógépek mutatós műszerek működésének alapja
 Mágneses erőtér Ahol az áramtól átjárt vezetőre (vagy mágnestűre) erő hat A villamos forgógépek mutatós műszerek működésének alapja Magnetosztatikai mező: nyugvó állandó mágnesek és egyenáramok időben
Mágneses erőtér Ahol az áramtól átjárt vezetőre (vagy mágnestűre) erő hat A villamos forgógépek mutatós műszerek működésének alapja Magnetosztatikai mező: nyugvó állandó mágnesek és egyenáramok időben
MÁGNESES TÉR, INDUKCIÓ
 Egy vezetéket 2 cm átmérőjű szigetelő testre 500 menettel tekercselünk fel, 25 cm hosszúságban. Mekkora térerősség lép fel a tekercs belsejében, ha a vezetékben 5 amperes áram folyik? Mekkora a mágneses
Egy vezetéket 2 cm átmérőjű szigetelő testre 500 menettel tekercselünk fel, 25 cm hosszúságban. Mekkora térerősség lép fel a tekercs belsejében, ha a vezetékben 5 amperes áram folyik? Mekkora a mágneses
FIZIKA II. Az áram és a mágneses tér kapcsolata
 Az áram és a mágneses tér kapcsolata Mágneses tér jellemzése: Mágneses térerősség: H (A/m) Mágneses indukció: B (T = Vs/m 2 ) B = μ 0 μ r H 2Seres.Istvan@gek.szie.hu Sztatikus terek Elektrosztatikus tér:
Az áram és a mágneses tér kapcsolata Mágneses tér jellemzése: Mágneses térerősség: H (A/m) Mágneses indukció: B (T = Vs/m 2 ) B = μ 0 μ r H 2Seres.Istvan@gek.szie.hu Sztatikus terek Elektrosztatikus tér:
Mechanika. Kinematika
 Mechanika Kinematika Alapfogalmak Anyagi pont Vonatkoztatási és koordináta rendszer Pálya, út, elmozdulás, Vektormennyiségek: elmozdulásvektor Helyvektor fogalma Sebesség Mozgások csoportosítása A mozgásokat
Mechanika Kinematika Alapfogalmak Anyagi pont Vonatkoztatási és koordináta rendszer Pálya, út, elmozdulás, Vektormennyiségek: elmozdulásvektor Helyvektor fogalma Sebesség Mozgások csoportosítása A mozgásokat
FIZIKA II. Az áram és a mágneses tér kapcsolata
 Az áram és a mágneses tér kapcsolata Mágneses tér jellemzése: Mágneses térerősség: H (A/m) Mágneses indukció: B (T) B = μ 0 μ r H 2Seres.Istvan@gek.szie.hu Sztatikus terek Elektrosztatikus tér: forrásos
Az áram és a mágneses tér kapcsolata Mágneses tér jellemzése: Mágneses térerősség: H (A/m) Mágneses indukció: B (T) B = μ 0 μ r H 2Seres.Istvan@gek.szie.hu Sztatikus terek Elektrosztatikus tér: forrásos
-2σ. 1. A végtelen kiterjedésű +σ és 2σ felületi töltéssűrűségű síklapok terében az ábrának megfelelően egy dipól helyezkedik el.
 1. 2. 3. Mondat E1 E2 Össz Energetikai mérnöki alapszak Mérnöki fizika 2. ZH NÉV:.. 2018. május 15. Neptun kód:... g=10 m/s 2 ; ε 0 = 8.85 10 12 F/m; μ 0 = 4π 10 7 Vs/Am; c = 3 10 8 m/s Előadó: Márkus
1. 2. 3. Mondat E1 E2 Össz Energetikai mérnöki alapszak Mérnöki fizika 2. ZH NÉV:.. 2018. május 15. Neptun kód:... g=10 m/s 2 ; ε 0 = 8.85 10 12 F/m; μ 0 = 4π 10 7 Vs/Am; c = 3 10 8 m/s Előadó: Márkus
1 kérdés. Személyes kezdőlap Villamos Gelencsér Géza Simonyi teszt május 13. szombat Teszt feladatok 2017 Előzetes megtekintés
 Személyes kezdőlap Villamos Gelencsér Géza Simonyi teszt 2017. május 13. szombat Teszt feladatok 2017 Előzetes megtekintés Kezdés ideje 2017. május 9., kedd, 16:54 Állapot Befejezte Befejezés dátuma 2017.
Személyes kezdőlap Villamos Gelencsér Géza Simonyi teszt 2017. május 13. szombat Teszt feladatok 2017 Előzetes megtekintés Kezdés ideje 2017. május 9., kedd, 16:54 Állapot Befejezte Befejezés dátuma 2017.
a térerősség mindig az üreg falára merőleges, ezért a tér ott nem gömbszimmetrikus.
 2. Gyakorlat 25A-0 Tekintsünk egy l0 cm sugarú üreges fémgömböt, amelyen +0 µc töltés van. Legyen a gömb középpontja a koordinátarendszer origójában. A gömb belsejében az x = 5 cm pontban legyen egy 3
2. Gyakorlat 25A-0 Tekintsünk egy l0 cm sugarú üreges fémgömböt, amelyen +0 µc töltés van. Legyen a gömb középpontja a koordinátarendszer origójában. A gömb belsejében az x = 5 cm pontban legyen egy 3
1. Feladatok a dinamika tárgyköréből
 1. Feladatok a dinamika tárgyköréből Newton három törvénye 1.1. Feladat: Három azonos m tömegű gyöngyszemet fonálra fűzünk, egymástól kis távolságokban a fonálhoz rögzítünk, és az elhanyagolható tömegű
1. Feladatok a dinamika tárgyköréből Newton három törvénye 1.1. Feladat: Három azonos m tömegű gyöngyszemet fonálra fűzünk, egymástól kis távolságokban a fonálhoz rögzítünk, és az elhanyagolható tömegű
Elektrosztatika. 1.2. Mekkora két egyenlő nagyságú töltés taszítja egymást 10 m távolságból 100 N nagyságú erővel? megoldás
 Elektrosztatika 1.1. Mekkora távolságra van egymástól az a két pontszerű test, amelynek töltése 2. 10-6 C és 3. 10-8 C, és 60 N nagyságú erővel taszítják egymást? 1.2. Mekkora két egyenlő nagyságú töltés
Elektrosztatika 1.1. Mekkora távolságra van egymástól az a két pontszerű test, amelynek töltése 2. 10-6 C és 3. 10-8 C, és 60 N nagyságú erővel taszítják egymást? 1.2. Mekkora két egyenlő nagyságú töltés
Pótlap nem használható!
 1. 2. 3. Mondat E1 E2 Össz Gépészmérnöki alapszak Mérnöki fizika 2. ZH NÉV:.. 2018. november 29. Neptun kód:... Pótlap nem használható! g=10 m/s 2 ; εε 0 = 8.85 10 12 F/m; μμ 0 = 4ππ 10 7 Vs/Am; cc = 3
1. 2. 3. Mondat E1 E2 Össz Gépészmérnöki alapszak Mérnöki fizika 2. ZH NÉV:.. 2018. november 29. Neptun kód:... Pótlap nem használható! g=10 m/s 2 ; εε 0 = 8.85 10 12 F/m; μμ 0 = 4ππ 10 7 Vs/Am; cc = 3
Elektromágnesség tesztek
 Elektromágnesség tesztek 1. Melyik esetben nem tapasztalunk onzóerőt? a) A mágnesrúd északi pólusához asdarabot közelítünk. b) A mágnesrúd közepéhez asdarabot közelítünk. c) A mágnesrúd déli pólusához
Elektromágnesség tesztek 1. Melyik esetben nem tapasztalunk onzóerőt? a) A mágnesrúd északi pólusához asdarabot közelítünk. b) A mágnesrúd közepéhez asdarabot közelítünk. c) A mágnesrúd déli pólusához
Mágneses mező jellemzése
 pólusok dipólus mező mező jellemzése vonalak pólusok dipólus mező vonalak Tartalom, erőhatások pólusok dipólus mező, szemléltetése meghatározása forgatónyomaték méréssel Elektromotor nagysága különböző
pólusok dipólus mező mező jellemzése vonalak pólusok dipólus mező vonalak Tartalom, erőhatások pólusok dipólus mező, szemléltetése meghatározása forgatónyomaték méréssel Elektromotor nagysága különböző
A mágneses tulajdonságú magnetit ásvány, a görög Magnészia városról kapta nevét.
 MÁGNESES MEZŐ A mágneses tulajdonságú magnetit ásvány, a görög Magnészia városról kapta nevét. Megfigyelések (1, 2) Minden mágnesnek két pólusa van, északi és déli. A felfüggesztett mágnes - iránytű -
MÁGNESES MEZŐ A mágneses tulajdonságú magnetit ásvány, a görög Magnészia városról kapta nevét. Megfigyelések (1, 2) Minden mágnesnek két pólusa van, északi és déli. A felfüggesztett mágnes - iránytű -
Elektromágnesség tesztek
 Elektromágnesség tesztek 1. Melyik esetben nem tapasztalunk vonzóerőt? a) A mágnesrúd északi pólusához vasdarabot közelítünk. b) A mágnesrúd közepéhez vasdarabot közelítünk. c) A mágnesrúd déli pólusához
Elektromágnesség tesztek 1. Melyik esetben nem tapasztalunk vonzóerőt? a) A mágnesrúd északi pólusához vasdarabot közelítünk. b) A mágnesrúd közepéhez vasdarabot közelítünk. c) A mágnesrúd déli pólusához
Lendület. Lendület (impulzus): A test tömegének és sebességének szorzata. vektormennyiség: iránya a sebesség vektor iránya.
 Lendület Lendület (impulzus): A test tömegének és sebességének szorzata. vektormennyiség: iránya a sebesség vektor iránya. Lendülettétel: Az lendület erő hatására változik meg. Az eredő erő határozza meg
Lendület Lendület (impulzus): A test tömegének és sebességének szorzata. vektormennyiség: iránya a sebesség vektor iránya. Lendülettétel: Az lendület erő hatására változik meg. Az eredő erő határozza meg
Időben állandó mágneses mező jellemzése
 Időben állandó mágneses mező jellemzése Mágneses erőhatás Mágneses alapjelenségek A mágnesek egymásra és a vastárgyakra erőhatást fejtenek ki. vonzó és taszító erő Mágneses pólusok északi pólus: a mágnestű
Időben állandó mágneses mező jellemzése Mágneses erőhatás Mágneses alapjelenségek A mágnesek egymásra és a vastárgyakra erőhatást fejtenek ki. vonzó és taszító erő Mágneses pólusok északi pólus: a mágnestű
FIZIKA II. Dr. Rácz Ervin. egyetemi docens
 FIZIKA II. Dr. Rácz Ervin egyetemi docens Fontos tudnivalók e-mail: racz.ervin@kvk.uni-obuda.hu web: http://uni-obuda.hu/users/racz.ervin/index.htm Iroda: Bécsi út, C. épület, 124. szoba Fizika II. - ismertetés
FIZIKA II. Dr. Rácz Ervin egyetemi docens Fontos tudnivalók e-mail: racz.ervin@kvk.uni-obuda.hu web: http://uni-obuda.hu/users/racz.ervin/index.htm Iroda: Bécsi út, C. épület, 124. szoba Fizika II. - ismertetés
A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld ábra ábra
 . Gyakorlat 4B-9 A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld. 4-6 ábra.). Számítsuk ki az E elektromos térerősséget a vonal irányában lévő, annak.. ábra. 4-6 ábra végpontjától
. Gyakorlat 4B-9 A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld. 4-6 ábra.). Számítsuk ki az E elektromos térerősséget a vonal irányában lévő, annak.. ábra. 4-6 ábra végpontjától
1. ábra. 24B-19 feladat
 . gyakorlat.. Feladat: (HN 4B-9) A +Q töltés egy hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld.. ábra.). Számítsuk ki az E elektromos térerősséget a vonal. ábra. 4B-9 feladat irányában lévő,
. gyakorlat.. Feladat: (HN 4B-9) A +Q töltés egy hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld.. ábra.). Számítsuk ki az E elektromos térerősséget a vonal. ábra. 4B-9 feladat irányában lévő,
Tömegpontok mozgása egyenes mentén, hajítások
 2. gyakorlat 1. Feladatok a kinematika tárgyköréből Tömegpontok mozgása egyenes mentén, hajítások 1.1. Feladat: Mekkora az átlagsebessége annak pontnak, amely mozgásának első szakaszában v 1 sebességgel
2. gyakorlat 1. Feladatok a kinematika tárgyköréből Tömegpontok mozgása egyenes mentén, hajítások 1.1. Feladat: Mekkora az átlagsebessége annak pontnak, amely mozgásának első szakaszában v 1 sebességgel
Gyakorlat 34A-25. kapcsolunk. Mekkora a fűtőtest teljesítménye? I o = U o R = 156 V = 1, 56 A (3.1) ezekkel a pillanatnyi értékek:
 3. Gyakorlat 34-5 Egy Ω ellenállású elektromos fűtőtestre 56 V amplitúdójú váltakozó feszültséget kapcsolunk. Mekkora a fűtőtest teljesítménye? Jelölések: R = Ω, U o = 56 V fűtőtestben folyó áram amplitudója
3. Gyakorlat 34-5 Egy Ω ellenállású elektromos fűtőtestre 56 V amplitúdójú váltakozó feszültséget kapcsolunk. Mekkora a fűtőtest teljesítménye? Jelölések: R = Ω, U o = 56 V fűtőtestben folyó áram amplitudója
Fizika minta feladatsor
 Fizika minta feladatsor 10. évf. vizsgára 1. A test egyenes vonalúan egyenletesen mozog, ha A) a testre ható összes erő eredője nullával egyenlő B) a testre állandó értékű erő hat C) a testre erő hat,
Fizika minta feladatsor 10. évf. vizsgára 1. A test egyenes vonalúan egyenletesen mozog, ha A) a testre ható összes erő eredője nullával egyenlő B) a testre állandó értékű erő hat C) a testre erő hat,
Mágneses mező jellemzése
 pólusok dipólus mező mező jellemzése vonalak pólusok dipólus mező kölcsönhatás A mágnesek egymásra és a vastárgyakra erőhatást fejtenek ki. vonalak vonzó és taszító erő pólusok dipólus mező pólusok északi
pólusok dipólus mező mező jellemzése vonalak pólusok dipólus mező kölcsönhatás A mágnesek egymásra és a vastárgyakra erőhatást fejtenek ki. vonalak vonzó és taszító erő pólusok dipólus mező pólusok északi
Q 1 D Q 2 (D x) 2 (1.1)
 . Gyakorlat 4B-9 Két pontszerű töltés az x tengelyen a következőképpen helyezkedik el: egy 3 µc töltés az origóban, és egy + µc töltés az x =, 5 m koordinátájú pontban van. Keressük meg azt a helyet, ahol
. Gyakorlat 4B-9 Két pontszerű töltés az x tengelyen a következőképpen helyezkedik el: egy 3 µc töltés az origóban, és egy + µc töltés az x =, 5 m koordinátájú pontban van. Keressük meg azt a helyet, ahol
Az elektromágneses tér energiája
 Az elektromágneses tér energiája Az elektromos tér energiasűrűsége korábbról: Hasonlóképpen, a mágneses tér energiája: A tér egy adott pontjában az elektromos és mágneses terek együttes energiasűrűsége
Az elektromágneses tér energiája Az elektromos tér energiasűrűsége korábbról: Hasonlóképpen, a mágneses tér energiája: A tér egy adott pontjában az elektromos és mágneses terek együttes energiasűrűsége
Felvételi, 2018 szeptember - Alapképzés, fizika vizsga -
 Sapientia Erdélyi Magyar Tudományegyetem Marosvásárhelyi Kar Felvételi, 2018 szeptember - Alapképzés, fizika vizsga - Minden tétel kötelező Hivatalból 10 pont jár Munkaidő 3 óra I Az alábbi kérdésekre
Sapientia Erdélyi Magyar Tudományegyetem Marosvásárhelyi Kar Felvételi, 2018 szeptember - Alapképzés, fizika vizsga - Minden tétel kötelező Hivatalból 10 pont jár Munkaidő 3 óra I Az alábbi kérdésekre
KÖRMOZGÁS, REZGŐMOZGÁS, FORGÓMOZGÁS
 KÖRMOZGÁS, REZGŐMOZGÁS, FORGÓMOZGÁS 1 EGYENLETES KÖRMOZGÁS Pálya kör Út ív Definíció: Test körpályán azonos irányban haladva azonos időközönként egyenlő íveket tesz meg. Periodikus mozgás 2 PERIODICITÁS
KÖRMOZGÁS, REZGŐMOZGÁS, FORGÓMOZGÁS 1 EGYENLETES KÖRMOZGÁS Pálya kör Út ív Definíció: Test körpályán azonos irányban haladva azonos időközönként egyenlő íveket tesz meg. Periodikus mozgás 2 PERIODICITÁS
Elektrotechnika. Ballagi Áron
 Elektrotechnika Ballagi Áron Mágneses tér Elektrotechnika x/2 Mágneses indukció kísérlet Állandó mágneses térben helyezzünk el egy l hosszúságú vezetőt, és bocsássunk a vezetőbe I áramot! Tapasztalat:
Elektrotechnika Ballagi Áron Mágneses tér Elektrotechnika x/2 Mágneses indukció kísérlet Állandó mágneses térben helyezzünk el egy l hosszúságú vezetőt, és bocsássunk a vezetőbe I áramot! Tapasztalat:
7. Mágneses szuszceptibilitás mérése
 7. Mágneses szuszceptibilitás mérése Klasszikus fizika laboratórium Mérési jegyzőkönyv Mérést végezte: Vitkóczi Fanni Mérés időpontja: 2012. 10. 25. I. A mérés célja: Egy mágneses térerősségmérő műszer
7. Mágneses szuszceptibilitás mérése Klasszikus fizika laboratórium Mérési jegyzőkönyv Mérést végezte: Vitkóczi Fanni Mérés időpontja: 2012. 10. 25. I. A mérés célja: Egy mágneses térerősségmérő műszer
A nagyobb tömegű Peti 1,5 m-re ült a forgástengelytől. Összesen: 9p
 Jedlik 9-10. o. reg feladat és megoldás 1) Egy 5 m hosszú libikókán hintázik Évi és Peti. A gyerekek tömege 30 kg és 50 kg. Egyikük a hinta végére ült. Milyen messze ült a másik gyerek a forgástengelytől,
Jedlik 9-10. o. reg feladat és megoldás 1) Egy 5 m hosszú libikókán hintázik Évi és Peti. A gyerekek tömege 30 kg és 50 kg. Egyikük a hinta végére ült. Milyen messze ült a másik gyerek a forgástengelytől,
Fizika 2 - Gyakorló feladatok
 2015. június 19. ε o =8.85 10-12 AsV -1 m -1 μ o =4π10-7 VsA -1 m -1 e=1,6 10-19 C m e =9,11 10-31 kg m p =1,67 10-27 kg h=6,63 10-34 Js 1. Egy R sugarú gömbben -ρ állandó töltéssűrűség van. a. Határozza
2015. június 19. ε o =8.85 10-12 AsV -1 m -1 μ o =4π10-7 VsA -1 m -1 e=1,6 10-19 C m e =9,11 10-31 kg m p =1,67 10-27 kg h=6,63 10-34 Js 1. Egy R sugarú gömbben -ρ állandó töltéssűrűség van. a. Határozza
Gépészmérnöki alapszak, Mérnöki fizika ZH, október 10.. CHFMAX. Feladatok (maximum 3x6 pont=18 pont)
 1. 2. 3. Mondat E1 E2 Gépészmérnöki alapszak, Mérnöki fizika ZH, 2017. október 10.. CHFMAX NÉV: Neptun kód: Aláírás: g=10 m/s 2 Előadó: Márkus / Varga Feladatok (maximum 3x6 pont=18 pont) 1) Az l hosszúságú
1. 2. 3. Mondat E1 E2 Gépészmérnöki alapszak, Mérnöki fizika ZH, 2017. október 10.. CHFMAX NÉV: Neptun kód: Aláírás: g=10 m/s 2 Előadó: Márkus / Varga Feladatok (maximum 3x6 pont=18 pont) 1) Az l hosszúságú
Elektromos alapjelenségek
 Elektrosztatika Elektromos alapjelenségek Dörzselektromos jelenség: egymással szorosan érintkező, vagy egymáshoz dörzsölt testek a szétválasztásuk után vonzó, vagy taszító kölcsönhatást mutatnak. Ilyenkor
Elektrosztatika Elektromos alapjelenségek Dörzselektromos jelenség: egymással szorosan érintkező, vagy egymáshoz dörzsölt testek a szétválasztásuk után vonzó, vagy taszító kölcsönhatást mutatnak. Ilyenkor
Mechanika - Versenyfeladatok
 Mechanika - Versenyfeladatok 1. A mellékelt ábrán látható egy jobbmenetű csavar és egy villáskulcs. A kulcsra ható F erővektor nyomatékot fejt ki a csavar forgatása céljából. Az erő támadópontja és az
Mechanika - Versenyfeladatok 1. A mellékelt ábrán látható egy jobbmenetű csavar és egy villáskulcs. A kulcsra ható F erővektor nyomatékot fejt ki a csavar forgatása céljából. Az erő támadópontja és az
1. gyakorlat (pótolva: október 17.) feladatai
 1. gyakorlat (pótolva: 2012. október 17.) feladatai 30A-5 Mágneses erőtérben mozgó töltött részecskére erő hat, ami merőleges mind a részecske mozgásirányára, mind a mágneses erőteret jellemző B indukcióvektorra.
1. gyakorlat (pótolva: 2012. október 17.) feladatai 30A-5 Mágneses erőtérben mozgó töltött részecskére erő hat, ami merőleges mind a részecske mozgásirányára, mind a mágneses erőteret jellemző B indukcióvektorra.
Az Ampère-Maxwell-féle gerjesztési törvény
 Az Ampère-Maxwell-féle gerjesztési törvény Maxwell elméleti meggondolások alapján feltételezte, hogy a változó elektromos tér örvényes mágneses teret kelt (hasonlóan ahhoz ahogy a változó mágneses tér
Az Ampère-Maxwell-féle gerjesztési törvény Maxwell elméleti meggondolások alapján feltételezte, hogy a változó elektromos tér örvényes mágneses teret kelt (hasonlóan ahhoz ahogy a változó mágneses tér
Felvételi, 2017 július -Alapképzés, fizika vizsga-
 Sapientia Erdélyi Magyar Tudományegyetem Marosvásárhelyi Kar Felvételi, 2017 július -Alapképzés, fizika vizsga- Minden tétel kötelező. Hivatalból 10 pont jár. Munkaidő 3 óra. I. Az alábbi kérdésekre adott
Sapientia Erdélyi Magyar Tudományegyetem Marosvásárhelyi Kar Felvételi, 2017 július -Alapképzés, fizika vizsga- Minden tétel kötelező. Hivatalból 10 pont jár. Munkaidő 3 óra. I. Az alábbi kérdésekre adott
Bevezető fizika (VBK) zh2 tesztkérdések
 Mi a nyomás mértékegysége? NY) kg m 2 /s 2 TY) kg m 2 /s GY) kg/(m s 2 ) LY) kg/(m 2 s 2 ) Mi a fajhő mértékegysége? NY) kg m 2 /(K s 2 ) GY) J/K TY) kg m/(k s 2 ) LY) m 2 /(K s 2 ) Mi a lineáris hőtágulási
Mi a nyomás mértékegysége? NY) kg m 2 /s 2 TY) kg m 2 /s GY) kg/(m s 2 ) LY) kg/(m 2 s 2 ) Mi a fajhő mértékegysége? NY) kg m 2 /(K s 2 ) GY) J/K TY) kg m/(k s 2 ) LY) m 2 /(K s 2 ) Mi a lineáris hőtágulási
1. feladat R 1 = 2 W R 2 = 3 W R 3 = 5 W R t1 = 10 W R t2 = 20 W U 1 =200 V U 2 =150 V. Megoldás. R t1 R 3 R 1. R t2 R 2
 1. feladat = 2 W R 2 = 3 W R 3 = 5 W R t1 = 10 W R t2 = 20 W U 1 =200 V U 2 =150 V U 1 R 2 R 3 R t1 R t2 U 2 R 2 a. Számítsd ki az R t1 és R t2 ellenállásokon a feszültségeket! b. Mekkora legyen az U 2
1. feladat = 2 W R 2 = 3 W R 3 = 5 W R t1 = 10 W R t2 = 20 W U 1 =200 V U 2 =150 V U 1 R 2 R 3 R t1 R t2 U 2 R 2 a. Számítsd ki az R t1 és R t2 ellenállásokon a feszültségeket! b. Mekkora legyen az U 2
1. Feladatok munkavégzés és konzervatív erőterek tárgyköréből. Munkatétel
 1. Feladatok munkavégzés és konzervatív erőterek tárgyköréből. Munkatétel Munkavégzés, teljesítmény 1.1. Feladat: (HN 6B-8) Egy rúgót nyugalmi állapotból 4 J munka árán 10 cm-rel nyújthatunk meg. Mekkora
1. Feladatok munkavégzés és konzervatív erőterek tárgyköréből. Munkatétel Munkavégzés, teljesítmény 1.1. Feladat: (HN 6B-8) Egy rúgót nyugalmi állapotból 4 J munka árán 10 cm-rel nyújthatunk meg. Mekkora
20. Állandó mágneses mezo, mozgási indukció, váltakozó áram. Alapfeladatok
 20. Állandó mágneses mezo, mozgási indukció, váltakozó áram Mágneses mezo keltése 1. Alapfeladatok Jellemezze az áramjárta egyenes vezeto környezetében kialakult mágneses mezot! 2. Mitol függ egy tekercs
20. Állandó mágneses mezo, mozgási indukció, váltakozó áram Mágneses mezo keltése 1. Alapfeladatok Jellemezze az áramjárta egyenes vezeto környezetében kialakult mágneses mezot! 2. Mitol függ egy tekercs
Fizika 1 Elektrodinamika beugró/kis kérdések
 Fizika 1 Elektrodinamika beugró/kis kérdések 1.) Írja fel a 4 Maxwell-egyenletet lokális (differenciális) alakban! rot = j+ D rot = B div B=0 div D=ρ : elektromos térerősség : mágneses térerősség D : elektromos
Fizika 1 Elektrodinamika beugró/kis kérdések 1.) Írja fel a 4 Maxwell-egyenletet lokális (differenciális) alakban! rot = j+ D rot = B div B=0 div D=ρ : elektromos térerősség : mágneses térerősség D : elektromos
Képlet levezetése :F=m a = m Δv/Δt = ΔI/Δt
 Lendület, lendületmegmaradás Ugyanakkora sebességgel mozgó test, tárgy nagyobb erőhatást fejt ki ütközéskor, és csak nagyobb erővel fékezhető, ha nagyobb a tömege. A tömeg és a sebesség együtt jellemezheti
Lendület, lendületmegmaradás Ugyanakkora sebességgel mozgó test, tárgy nagyobb erőhatást fejt ki ütközéskor, és csak nagyobb erővel fékezhető, ha nagyobb a tömege. A tömeg és a sebesség együtt jellemezheti
A mechanikai alaptörvények ismerete
 A mechanikai alaptörvények ismerete Az oldalszám hivatkozások a Hudson-Nelson Útban a modern fizikához c. könyv megfelelő szakaszaira vonatkoznak. A Feladatgyűjtemény a Mérnöki fizika tárgy honlapjára
A mechanikai alaptörvények ismerete Az oldalszám hivatkozások a Hudson-Nelson Útban a modern fizikához c. könyv megfelelő szakaszaira vonatkoznak. A Feladatgyűjtemény a Mérnöki fizika tárgy honlapjára
Vezetők elektrosztatikus térben
 Vezetők elektrosztatikus térben Vezető: a töltések szabadon elmozdulhatnak Ha a vezető belsejében a térerősség nem lenne nulla akkor áram folyna. Ha a felületen a térerősségnek lenne tangenciális (párhuzamos)
Vezetők elektrosztatikus térben Vezető: a töltések szabadon elmozdulhatnak Ha a vezető belsejében a térerősség nem lenne nulla akkor áram folyna. Ha a felületen a térerősségnek lenne tangenciális (párhuzamos)
Fizika II minimumkérdések. A zárójelben lévő értékeket nem kötelező memorizálni, azok csak tájékoztató jellegűek.
 izika II minimumkérdések zárójelben lévő értékeket nem kötelező memorizálni, azok csak tájékoztató jellegűek. 1. Coulomb erőtörvény: = kq r 2 e r (k = 9 10 9 m2 C 2 ) 2. Coulomb állandó és vákuum permittivitás
izika II minimumkérdések zárójelben lévő értékeket nem kötelező memorizálni, azok csak tájékoztató jellegűek. 1. Coulomb erőtörvény: = kq r 2 e r (k = 9 10 9 m2 C 2 ) 2. Coulomb állandó és vákuum permittivitás
a) Valódi tekercs b) Kondenzátor c) Ohmos ellenállás d) RLC vegyes kapcsolása
 Bolyai Farkas Országos Fizika Tantárgyverseny 2016 Bolyai Farkas Elméleti Líceum, Marosvásárhely XI. Osztály 1. Adott egy alap áramköri elemen a feszültség u=220sin(314t-30 0 )V és az áramerősség i=2sin(314t-30
Bolyai Farkas Országos Fizika Tantárgyverseny 2016 Bolyai Farkas Elméleti Líceum, Marosvásárhely XI. Osztály 1. Adott egy alap áramköri elemen a feszültség u=220sin(314t-30 0 )V és az áramerősség i=2sin(314t-30
Elektrodinamika. Maxwell egyenletek: Kontinuitási egyenlet: div n v =0. div E =4 div B =0. rot E = rot B=
 Elektrodinamika Maxwell egyenletek: div E =4 div B =0 rot E = rot B= 1 B c t 1 E c t 4 c j Kontinuitási egyenlet: n t div n v =0 Vektoranalízis rot rot u=grad divu u rot grad =0 div rotu=0 udv= ud F V
Elektrodinamika Maxwell egyenletek: div E =4 div B =0 rot E = rot B= 1 B c t 1 E c t 4 c j Kontinuitási egyenlet: n t div n v =0 Vektoranalízis rot rot u=grad divu u rot grad =0 div rotu=0 udv= ud F V
A II. kategória Fizika OKTV mérési feladatainak megoldása
 Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Koordináta-geometria feladatgyűjtemény
 Koordináta-geometria feladatgyűjtemény A feladatok megoldásai a dokumentum végén találhatók Vektorok 1. Egy négyzet két szemközti csúcsának koordinátái: A( ; 7) és C(4 ; 1). Határozd meg a másik két csúcs
Koordináta-geometria feladatgyűjtemény A feladatok megoldásai a dokumentum végén találhatók Vektorok 1. Egy négyzet két szemközti csúcsának koordinátái: A( ; 7) és C(4 ; 1). Határozd meg a másik két csúcs
Az elektromágneses indukció jelensége
 Az elektromágneses indukció jelensége Korábban láttuk, hogy az elektromos áram hatására mágneses tér keletkezik (Ampère-féle gerjesztési törvény) Kérdés, hogy vajon ez megfordítható-e, és a mágneses tér
Az elektromágneses indukció jelensége Korábban láttuk, hogy az elektromos áram hatására mágneses tér keletkezik (Ampère-féle gerjesztési törvény) Kérdés, hogy vajon ez megfordítható-e, és a mágneses tér
Mágnesesség, elektromágnes, indukció Tudománytörténeti háttér Már i. e. 600 körül Thalész felfedezte, hogy Magnesia város mellett vannak olyan talált
 Mágnesesség, elektromágnes, indukció Tudománytörténeti háttér Már i. e. 600 körül Thalész felfedezte, hogy Magnesia város mellett vannak olyan talált ércek, amelyek vonzzák a vasat. Ezeket mágnesnek nevezték
Mágnesesség, elektromágnes, indukció Tudománytörténeti háttér Már i. e. 600 körül Thalész felfedezte, hogy Magnesia város mellett vannak olyan talált ércek, amelyek vonzzák a vasat. Ezeket mágnesnek nevezték
U = 24 V I = 4,8 A. Mind a két mellékágban az ellenállás külön-külön 6 Ω, ezért az áramerősség mindkét mellékágban egyenlő, azaz :...
 Jedlik Ányos Fizikaverseny regionális forduló Öveges korcsoport 08. A feladatok megoldása során végig századpontossággal kerekített értékekkel számolj! Jó munkát! :). A kapcsolási rajz adatai felhasználásával
Jedlik Ányos Fizikaverseny regionális forduló Öveges korcsoport 08. A feladatok megoldása során végig századpontossággal kerekített értékekkel számolj! Jó munkát! :). A kapcsolási rajz adatai felhasználásával
s levegő = 10 λ d sin α 10 = 10 λ (6.1.1)
 6. gyakorlat 6.. Feladat: (HN 38B-) Kettős rést 6 nm hullámhosszúságú fénnyel világitunk meg és ezzel egy ernyőn interferenciát hozunk létre. Ezután igen vékony flintüvegből (n,65) készült lemezt helyezünk
6. gyakorlat 6.. Feladat: (HN 38B-) Kettős rést 6 nm hullámhosszúságú fénnyel világitunk meg és ezzel egy ernyőn interferenciát hozunk létre. Ezután igen vékony flintüvegből (n,65) készült lemezt helyezünk
Rezgőmozgás. A mechanikai rezgések vizsgálata, jellemzői és dinamikai feltétele
 Rezgőmozgás A mechanikai rezgések vizsgálata, jellemzői és dinamikai feltétele A rezgés fogalma Minden olyan változás, amely az időben valamilyen ismétlődést mutat rezgésnek nevezünk. A rezgések fajtái:
Rezgőmozgás A mechanikai rezgések vizsgálata, jellemzői és dinamikai feltétele A rezgés fogalma Minden olyan változás, amely az időben valamilyen ismétlődést mutat rezgésnek nevezünk. A rezgések fajtái:
30A 5 Egy proton 0,5T fluxussűrűségű mágneses erőtérben 1,00 cm sugarú körpályán mozog. Mekkora a kinetikus energiája (ev egységekben kifejezve)?
 30A 5 Egy proton 0,5T fluxussűrűségű mágneses erőtérben 1,00 cm sugarú körpályán mozog. Mekkora a kinetikus energiája (ev egységekben kifejezve)? B = 0,5 T r = 0,01 m E m = ½ mv 2 v 2 2E = 2E m / m v =
30A 5 Egy proton 0,5T fluxussűrűségű mágneses erőtérben 1,00 cm sugarú körpályán mozog. Mekkora a kinetikus energiája (ev egységekben kifejezve)? B = 0,5 T r = 0,01 m E m = ½ mv 2 v 2 2E = 2E m / m v =
Fizika A2 Alapkérdések
 Fizika A2 Alapkérdések Az elektromágnesség elméletében a vektorok és skalárok (számok) megkülönböztetése nagyon fontos. A következ szövegben a vektorokat a kézírásban is jól használható nyíllal jelöljük
Fizika A2 Alapkérdések Az elektromágnesség elméletében a vektorok és skalárok (számok) megkülönböztetése nagyon fontos. A következ szövegben a vektorokat a kézírásban is jól használható nyíllal jelöljük
Fizika A2 Alapkérdések
 Fizika A2 Alapkérdések Összeállította: Dr. Pipek János, Dr. zunyogh László 20. február 5. Elektrosztatika Írja fel a légüres térben egymástól r távolságban elhelyezett Q és Q 2 pontszer pozitív töltések
Fizika A2 Alapkérdések Összeállította: Dr. Pipek János, Dr. zunyogh László 20. február 5. Elektrosztatika Írja fel a légüres térben egymástól r távolságban elhelyezett Q és Q 2 pontszer pozitív töltések
Kifejtendő kérdések június 13. Gyakorló feladatok
 Kifejtendő kérdések 2016. június 13. Gyakorló feladatok 1. Adott egy egyenletes térfogati töltéssel rendelkező, R sugarú gömb, melynek felületén a potenciál U 0. Az elektromos potenciál definíciója (1p)
Kifejtendő kérdések 2016. június 13. Gyakorló feladatok 1. Adott egy egyenletes térfogati töltéssel rendelkező, R sugarú gömb, melynek felületén a potenciál U 0. Az elektromos potenciál definíciója (1p)
Fizika feladatok - 2. gyakorlat
 Fizika feladatok - 2. gyakorlat 2014. szeptember 18. 0.1. Feladat: Órai kidolgozásra: Mekkora az átlagsebessége annak pontnak, amely mozgásának első szakaszában v 1 sebességgel s 1 utat, második szakaszában
Fizika feladatok - 2. gyakorlat 2014. szeptember 18. 0.1. Feladat: Órai kidolgozásra: Mekkora az átlagsebessége annak pontnak, amely mozgásának első szakaszában v 1 sebességgel s 1 utat, második szakaszában
Mechanikai rezgések Ismétlő kérdések és feladatok Kérdések
 Mechanikai rezgések Ismétlő kérdések és feladatok Kérdések 1. Melyek a rezgőmozgást jellemző fizikai mennyiségek?. Egy rezgés során mely helyzetekben maximális a sebesség, és mikor a gyorsulás? 3. Milyen
Mechanikai rezgések Ismétlő kérdések és feladatok Kérdések 1. Melyek a rezgőmozgást jellemző fizikai mennyiségek?. Egy rezgés során mely helyzetekben maximális a sebesség, és mikor a gyorsulás? 3. Milyen
Mit nevezünk nehézségi erőnek?
 Mit nevezünk nehézségi erőnek? Azt az erőt, amelynek hatására a szabadon eső testek g (gravitációs) gyorsulással esnek a vonzó test centruma felé, nevezzük nehézségi erőnek. F neh = m g Mi a súly? Azt
Mit nevezünk nehézségi erőnek? Azt az erőt, amelynek hatására a szabadon eső testek g (gravitációs) gyorsulással esnek a vonzó test centruma felé, nevezzük nehézségi erőnek. F neh = m g Mi a súly? Azt
A LÉGKÖRBEN HATÓ ERŐK, EGYENSÚLYI MOZGÁSOK A LÉGKÖRBEN
 A LÉGKÖRBEN HATÓ ERŐK, EGYENSÚLYI MOZGÁSOK A LÉGKÖRBEN Egy testre ható erő, a más testekkel való kölcsönhatás mértékére jellemző fizikai mennyiség. A légkörben ható erők Külső erők: A Föld tömegéből következő
A LÉGKÖRBEN HATÓ ERŐK, EGYENSÚLYI MOZGÁSOK A LÉGKÖRBEN Egy testre ható erő, a más testekkel való kölcsönhatás mértékére jellemző fizikai mennyiség. A légkörben ható erők Külső erők: A Föld tömegéből következő
Bevezető fizika (infó), 8. feladatsor Egyenáram, egyenáramú áramkörök 2.
 evezető fizika (infó), 8 feladatsor Egyenáram, egyenáramú áramkörök 04 november, 3:9 mai órához szükséges elméleti anyag: Kirchhoff törvényei: I Minden csomópontban a befolyó és kifolyó áramok előjeles
evezető fizika (infó), 8 feladatsor Egyenáram, egyenáramú áramkörök 04 november, 3:9 mai órához szükséges elméleti anyag: Kirchhoff törvényei: I Minden csomópontban a befolyó és kifolyó áramok előjeles
7. L = 100 mh és r s = 50 Ω tekercset 12 V-os egyenfeszültségű áramkörre kapcsolunk. Mennyi idő alatt éri el az áram az állandósult értékének 63 %-át?
 1. Jelöld H -val, ha hamis, I -vel ha igaz szerinted az állítás!...két elektromos töltés között fellépő erőhatás nagysága arányos a két töltés nagyságával....két elektromos töltés között fellépő erőhatás
1. Jelöld H -val, ha hamis, I -vel ha igaz szerinted az állítás!...két elektromos töltés között fellépő erőhatás nagysága arányos a két töltés nagyságával....két elektromos töltés között fellépő erőhatás
Megoldás: A feltöltött R sugarú fémgömb felületén a térerősség és a potenciál pontosan akkora, mintha a teljes töltése a középpontjában lenne:
 3. gyakorlat 3.. Feladat: (HN 27A-2) Becsüljük meg azt a legnagyo potenciált, amelyre egy 0 cm átmérőjű fémgömöt fel lehet tölteni, anélkül, hogy a térerősség értéke meghaladná a környező száraz levegő
3. gyakorlat 3.. Feladat: (HN 27A-2) Becsüljük meg azt a legnagyo potenciált, amelyre egy 0 cm átmérőjű fémgömöt fel lehet tölteni, anélkül, hogy a térerősség értéke meghaladná a környező száraz levegő
Mágneses indukcióvektor begyakorló házi feladatok
 Mágneses indukcióvektor begyakorló házi feladatok 1. Egy vezető keret (lapos tekercs) területe 10 cm 2 ; benne 8A erősségű áram folyik, a menetek száma 20. A keretre ható legnagyobb forgatónyomaték 0,005
Mágneses indukcióvektor begyakorló házi feladatok 1. Egy vezető keret (lapos tekercs) területe 10 cm 2 ; benne 8A erősségű áram folyik, a menetek száma 20. A keretre ható legnagyobb forgatónyomaték 0,005
Dinamika. A dinamika feladata a test(ek) gyorsulását okozó erők matematikai leírása.
 Dinamika A dinamika feladata a test(ek) gyorsulását okozó erők matematikai leírása. Newton törvényei: I. Newton I. axiómája: Minden nyugalomban lévő test megtartja nyugalmi állapotát, minden mozgó test
Dinamika A dinamika feladata a test(ek) gyorsulását okozó erők matematikai leírása. Newton törvényei: I. Newton I. axiómája: Minden nyugalomban lévő test megtartja nyugalmi állapotát, minden mozgó test
Magnesia. Itt találtak már az ókorban mágneses köveket. Μαγνησία. (valószínű villámok áramának a tere mágnesezi fel őket)
 Mágnesség Schay G. Magnesia Μαγνησία Itt találtak már az ókorban mágneses köveket (valószínű villámok áramának a tere mágnesezi fel őket) maghemit Köbös Fe 2 O 3 magnetit Fe 2 +Fe 3 +2O 4 mágnesvasérc
Mágnesség Schay G. Magnesia Μαγνησία Itt találtak már az ókorban mágneses köveket (valószínű villámok áramának a tere mágnesezi fel őket) maghemit Köbös Fe 2 O 3 magnetit Fe 2 +Fe 3 +2O 4 mágnesvasérc
EGYSZERŰ GÉPEK. Azok az eszközök, amelyekkel kedvezőbbé lehet tenni az erőhatás nagyságát, irányát, támadáspontjának helyét.
 EGYSZERŰ GÉPEK Azok az eszközök, amelyekkel kedvezőbbé lehet tenni az erőhatás nagyságát, irányát, támadáspontjának helyét. Az egyszerű gépekkel munkát nem takaríthatunk meg, de ugyanazt a munkát kisebb
EGYSZERŰ GÉPEK Azok az eszközök, amelyekkel kedvezőbbé lehet tenni az erőhatás nagyságát, irányát, támadáspontjának helyét. Az egyszerű gépekkel munkát nem takaríthatunk meg, de ugyanazt a munkát kisebb
28. Nagy László Fizikaverseny Szalézi Szent Ferenc Gimnázium, Kazincbarcika február 28. március osztály
 1. feladat a) A négyzet alakú vetítővászon egy oldalának hossza 1,2 m. Ahhoz, hogy a legnagyobb nagyításban is ráférjen a diafilm-kocka képe a vászonra, és teljes egészében látható legyen, ahhoz a 36 milliméteres
1. feladat a) A négyzet alakú vetítővászon egy oldalának hossza 1,2 m. Ahhoz, hogy a legnagyobb nagyításban is ráférjen a diafilm-kocka képe a vászonra, és teljes egészében látható legyen, ahhoz a 36 milliméteres
Fizika alapok. Az előadás témája
 Az előadás témája Körmozgás jellemzőinek értelmezése Általános megoldási módszer egyenletes körmozgásnál egy feladaton keresztül Testek mozgásának vizsgálata nem inerciarendszerhez képest Centripetális
Az előadás témája Körmozgás jellemzőinek értelmezése Általános megoldási módszer egyenletes körmozgásnál egy feladaton keresztül Testek mozgásának vizsgálata nem inerciarendszerhez képest Centripetális
9. ábra. A 25B-7 feladathoz
 . gyakolat.1. Feladat: (HN 5B-7) Egy d vastagságú lemezben egyenletes ρ téfogatmenti töltés van. A lemez a ±y és ±z iányokban gyakolatilag végtelen (9. ába); az x tengely zéuspontját úgy választottuk meg,
. gyakolat.1. Feladat: (HN 5B-7) Egy d vastagságú lemezben egyenletes ρ téfogatmenti töltés van. A lemez a ±y és ±z iányokban gyakolatilag végtelen (9. ába); az x tengely zéuspontját úgy választottuk meg,
ELEKTROMOSSÁG ÉS MÁGNESESSÉG
 ELEKTROMOSSÁG ÉS MÁGNESESSÉG A) változat Név:... osztály:... 1. Milyen töltésű a proton? 2. Egészítsd ki a következő mondatot! Az azonos elektromos töltések... egymást. 3. A PVC-rudat megdörzsöltük egy
ELEKTROMOSSÁG ÉS MÁGNESESSÉG A) változat Név:... osztály:... 1. Milyen töltésű a proton? 2. Egészítsd ki a következő mondatot! Az azonos elektromos töltések... egymást. 3. A PVC-rudat megdörzsöltük egy
Elektromos ellenállás, az áram hatásai, teljesítmény
 Elektromos ellenállás, az áram hatásai, teljesítmény Elektromos ellenállás Az anyag részecskéi akadályozzák a töltések mozgását. Ezt a tulajdonságot nevezzük elektromos ellenállásnak. Annak a fogyasztónak
Elektromos ellenállás, az áram hatásai, teljesítmény Elektromos ellenállás Az anyag részecskéi akadályozzák a töltések mozgását. Ezt a tulajdonságot nevezzük elektromos ellenállásnak. Annak a fogyasztónak
Koordináta-geometria feladatgyűjtemény (A feladatok megoldásai a dokumentum végén találhatók)
 Koordináta-geometria feladatgyűjtemény (A feladatok megoldásai a dokumentum végén találhatók) Vektorok 1. Egy négyzet két szemközti csúcsának koordinátái: A( ; 7) és C(4 ; 1). Határozd meg a másik két
Koordináta-geometria feladatgyűjtemény (A feladatok megoldásai a dokumentum végén találhatók) Vektorok 1. Egy négyzet két szemközti csúcsának koordinátái: A( ; 7) és C(4 ; 1). Határozd meg a másik két
Érettségi feladatok Koordinátageometria_rendszerezve / 5
 Érettségi feladatok Koordinátageometria_rendszerezve 2005-2013 1/ 5 Vektorok 2005. május 28./12. Adottak az a (4; 3) és b ( 2; 1) vektorok. a) Adja meg az a hosszát! b) Számítsa ki az a + b koordinátáit!
Érettségi feladatok Koordinátageometria_rendszerezve 2005-2013 1/ 5 Vektorok 2005. május 28./12. Adottak az a (4; 3) és b ( 2; 1) vektorok. a) Adja meg az a hosszát! b) Számítsa ki az a + b koordinátáit!
Mágneses szuszceptibilitás mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 7. MÉRÉS Mágneses szuszceptibilitás mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 5. Szerda délelőtti csoport 1. A mérés célja Az
KLASSZIKUS FIZIKA LABORATÓRIUM 7. MÉRÉS Mágneses szuszceptibilitás mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 5. Szerda délelőtti csoport 1. A mérés célja Az
1. gyakorlat. Egyenletes és egyenletesen változó mozgás. 1. példa
 1. gyakorlat Egyenletes és egyenletesen változó mozgás egyenletes mozgás egyenletesen változó mozgás gyorsulás a = 0 a(t) = a = állandó sebesség v(t) = v = állandó v(t) = v(0) + a t pályakoordináta s(t)
1. gyakorlat Egyenletes és egyenletesen változó mozgás egyenletes mozgás egyenletesen változó mozgás gyorsulás a = 0 a(t) = a = állandó sebesség v(t) = v = állandó v(t) = v(0) + a t pályakoordináta s(t)
A LÉGKÖRBEN HATÓ ERŐK, EGYENSÚLYI MOZGÁSOK A LÉGKÖRBEN
 A LÉGKÖRBEN HATÓ ERŐK, EGYENSÚLYI MOZGÁSOK A LÉGKÖRBEN Egy testre ható erő, a más testekkel való kölcsönhatás mértékére jellemző fizikai mennyiség. A légkörben ható erők Külső erők: A Föld tömegéből következő
A LÉGKÖRBEN HATÓ ERŐK, EGYENSÚLYI MOZGÁSOK A LÉGKÖRBEN Egy testre ható erő, a más testekkel való kölcsönhatás mértékére jellemző fizikai mennyiség. A légkörben ható erők Külső erők: A Föld tömegéből következő
A munkavégzés a rendszer és a környezete közötti energiacserének a D hőátadástól eltérő valamennyi más formája.
 11. Transzportfolyamatok termodinamikai vonatkozásai 1 Melyik állítás HMIS a felsoroltak közül? mechanikában minden súrlódásmentes folyamat irreverzibilis. disszipatív folyamatok irreverzibilisek. hőmennyiség
11. Transzportfolyamatok termodinamikai vonatkozásai 1 Melyik állítás HMIS a felsoroltak közül? mechanikában minden súrlódásmentes folyamat irreverzibilis. disszipatív folyamatok irreverzibilisek. hőmennyiség
EGYENÁRAM. 1. Mit mutat meg az áramerısség? 2. Mitıl függ egy vezeték ellenállása?
 EGYENÁRAM 1. Mit utat eg az áraerısség? 2. Mitıl függ egy vezeték ellenállása? Ω 2 3. Mit jelent az, hogy a vas fajlagos ellenállása 0,04? 4. Írd le Oh törvényét! 5. Milyen félvezetı eszközöket isersz?
EGYENÁRAM 1. Mit utat eg az áraerısség? 2. Mitıl függ egy vezeték ellenállása? Ω 2 3. Mit jelent az, hogy a vas fajlagos ellenállása 0,04? 4. Írd le Oh törvényét! 5. Milyen félvezetı eszközöket isersz?
LY) (1) párhuzamosan, (2) párhuzamosan
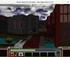 1. Egyenes vezető mágneses terében pozitív, pontszerű töltés mozog. Határozzuk meg a töltésre ható erő (Lorentz-erő) irányát az ábrán látható esetben. NY) A rajz síkjából kifelé mutat az erő. TY) A vezető
1. Egyenes vezető mágneses terében pozitív, pontszerű töltés mozog. Határozzuk meg a töltésre ható erő (Lorentz-erő) irányát az ábrán látható esetben. NY) A rajz síkjából kifelé mutat az erő. TY) A vezető
2. Ideális esetben az árammérő belső ellenállása a.) nagyobb, mint 1kΩ b.) megegyezik a mért áramkör eredő ellenállásával
 Teszt feladatok A választásos feladatoknál egy vagy több jó válasz lehet! Számításos feladatoknál csak az eredményt és a mértékegységet kell megadni. 1. Mitől függ a vezetők ellenállása? a.) a rajta esett
Teszt feladatok A választásos feladatoknál egy vagy több jó válasz lehet! Számításos feladatoknál csak az eredményt és a mértékegységet kell megadni. 1. Mitől függ a vezetők ellenállása? a.) a rajta esett
A Hamilton-Jacobi-egyenlet
 A Hamilton-Jacobi-egyenlet Ha sikerül olyan kanonikus transzformációt találnunk, amely a Hamilton-függvényt zérusra transzformálja akkor valamennyi új koordináta és impulzus állandó lesz: H 0 Q k = H P
A Hamilton-Jacobi-egyenlet Ha sikerül olyan kanonikus transzformációt találnunk, amely a Hamilton-függvényt zérusra transzformálja akkor valamennyi új koordináta és impulzus állandó lesz: H 0 Q k = H P
= 163, 63V. Felírható az R 2 ellenállásra, hogy: 163,63V. blokk sorosan van kapcsolva a baloldali R 1 -gyel, és tudjuk, hogy
 Határozzuk meg és ellenállások értékét, ha =00V, = 00, az ampermérő 88mA áramot, a voltmérő,v feszültséget jelez! Az ampermérő ellenállását elhanyagolhatóan kicsinek, a voltmérőét végtelen nagynak tekinthetjük
Határozzuk meg és ellenállások értékét, ha =00V, = 00, az ampermérő 88mA áramot, a voltmérő,v feszültséget jelez! Az ampermérő ellenállását elhanyagolhatóan kicsinek, a voltmérőét végtelen nagynak tekinthetjük
Hatvani István fizikaverseny forduló megoldások. 1. kategória. J 0,063 kg kg + m 3
 Hatvani István fizikaverseny 016-17. 1. kategória 1..1.a) Két eltérő méretű golyó - azonos magasságból - ugyanakkora végsebességgel ér a talajra. Mert a földfelszín közelében minden szabadon eső test ugyanúgy
Hatvani István fizikaverseny 016-17. 1. kategória 1..1.a) Két eltérő méretű golyó - azonos magasságból - ugyanakkora végsebességgel ér a talajra. Mert a földfelszín közelében minden szabadon eső test ugyanúgy
71. A lineáris és térfogati hőtágulási tényező közötti összefüggés:
 Összefüggések: 69. Lineáris hőtágulás: Hosszváltozás l = α l 0 T Lineáris hőtágulási Kezdeti hossz Hőmérsékletváltozás 70. Térfogati hőtágulás: Térfogatváltozás V = β V 0 T Hőmérsékletváltozás Térfogati
Összefüggések: 69. Lineáris hőtágulás: Hosszváltozás l = α l 0 T Lineáris hőtágulási Kezdeti hossz Hőmérsékletváltozás 70. Térfogati hőtágulás: Térfogatváltozás V = β V 0 T Hőmérsékletváltozás Térfogati
MÁGNESESSÉG. Türmer Kata
 MÁGESESSÉG Türmer Kata HOA? év: görög falu Magnesia, sok természetes mágnes Ezeket iodestones (iode= vonz), magnetitet tartalmaznak, Fe3O4. Kínaiak: iránytű, két olyan hely ahol maximum a vonzás Kínaiak
MÁGESESSÉG Türmer Kata HOA? év: görög falu Magnesia, sok természetes mágnes Ezeket iodestones (iode= vonz), magnetitet tartalmaznak, Fe3O4. Kínaiak: iránytű, két olyan hely ahol maximum a vonzás Kínaiak
FIZIKA FELADATLAP Megoldási útmutató
 1. C 2. A 3. X 4. B 5. C 6. D 7. D 8. C 9. D 10. B 11. D 12. C 13. A 14. C 15. C 16. D 17. C 18. C 19. C 20. B FIZIKA FELADATLAP Megoldási útmutató I. RÉSZ Összesen 1 1. téma II. RÉSZ Atommodellek: Thomson
1. C 2. A 3. X 4. B 5. C 6. D 7. D 8. C 9. D 10. B 11. D 12. C 13. A 14. C 15. C 16. D 17. C 18. C 19. C 20. B FIZIKA FELADATLAP Megoldási útmutató I. RÉSZ Összesen 1 1. téma II. RÉSZ Atommodellek: Thomson
Érettségi feladatok: Koordináta-geometria 1/5
 Érettségi feladatok: Koordináta-geometria 1/5 2003. Próba/ 13. Adott egy háromszög három csúcspontja a koordinátáival: A( 4; 4), B(4; 4) és C( 4; 8). Számítsa ki a C csúcsból induló súlyvonal és az A csúcsból
Érettségi feladatok: Koordináta-geometria 1/5 2003. Próba/ 13. Adott egy háromszög három csúcspontja a koordinátáival: A( 4; 4), B(4; 4) és C( 4; 8). Számítsa ki a C csúcsból induló súlyvonal és az A csúcsból
