Miskolci Egyetem Műszaki Anyagtudományi Kar Fémtani, Képlékenyalakítási és Nanotechnológiai Intézet
|
|
|
- Emília Szalai
- 6 évvel ezelőtt
- Látták:
Átírás
1 Miskolci Egyetem Műszaki Anyagtudományi Kar Fémtani, Képlékenyalakítási és Nanotechnológiai Intézet A szemcseszerkezet és a jellemző elemi cella orientációk változásának in situ monitorozása a Properzi technológia során DIPLOMAMUNKA Készítette: Angel Dávid Ádám Konzulensek: Dr. Benke Márton Hlavács Adrienn 2017
2 Tartalomjegyzék Bevezetés Irodalmi áttekintés A Properzi technológia bemutatása A kristálytani anizotrópia A textúra jellemzése röntgendiffrakcióval Száltextúra jellemzése Pólusábrák Az orientációs sűrűség függvény (ODF) Elvégzett vizsgálatok Hosszmetszeti próbatestek Keresztmetszeti próbatestek A szemcseszerkezet vizsgálata makromaratással A szemcseszerkezet vizsgálata színesmaratással Jellemző elemi cella orientációk meghatározása Eredmények A szemcseszerkezet jellemzése hosszmetszeten makromaratással A szemcseszerkezet jellemzése hosszmetszeten színesmaratással A szemcseszerkezet jellemzése keresztmetszeten makromaratással A szemcseszerkezet jellemzése keresztmetszeten színesmaratással Interferenciafüggvény változásának a bemutatása Jellemző elemi cella orientációk bemutatása Következtetések Összefoglalás Köszönetnyilvánítás Irodalomjegyzék sz. Melléklet - A mért {111}, {200}, {220} pólusábrák
3 Bevezetés A diplomamunkám készítése során egy Properzi technológiával készült alumínium mintasorozatot vizsgáltam. Vizsgálataimhoz a gyártó, rendelkezésemre bocsátott egy antenna nevet viselő szálat (1. ábra), mely tartalmazza minden technológiai lépésen átesett pászmaszakaszt. Ilyen teljes antennát csak a hengersor leállításával lehet kivenni a Properzi technológiai sorból. Mivel a gyártónál egy új hengerállvány került üzembe helyezésre, a próbahengerlések közbeni leállítások során lehetőség adódott egy teljes antenna kivételére, amelyet a rendelkezésemre bocsátottak. Ez azért egyedi lehetőség, mert a Properzi eljárás hengerlési lépései egy folyamatos, zárt technológiai sort alkotnak, ezért az antenna szemcseszerkezeti jellemzőinek változását a gyártás minden technológiai lépése után csak rendkívül ritka esetekben lehet elvégezni. Munkám során az antennából minden technológiai lépés utáni szakaszból mintadarabokat munkáltattam ki. A mintadarabokon szemcseszerkezet vizsgálatokat, valamint röntgendiffrakciós textúra vizsgálatokat végeztem. A vizsgálataim célja leírni a szemcseszerkezet, valamint a jellemző elemi cella orientációk változását a Properzi eljárás különleges öntési és hengerlési lépései után. 1. ábra A vizsgált Properzi eljárással készült antenna 2
4 1 Irodalmi áttekintés 1.1 A Properzi technológia bemutatása A Properzi technológia egy félfolyamatos öntvehengerlési folyamat, amely során az öntőkereket elhagyó pászmát hengersoron engedik keresztül. A hengersoron belül minden hengerlési lépés során a hengerlés 3 irányból történik, ahol a hengerek egymással 120 -ot zárnak be (2. ábra). A hengerlési lépések között a henger-hármasok 60 -kal elfordulnak. 2. ábra A hengerhármas elhelyezkedése a Properzi technológiában [1] A technológia sajátos geometriájának köszönhetően a kiinduláskor trapéz keresztmetszetű pászma az első hengerlés után közel kör keresztmetszetű lesz, ezután pedig közel háromszög, a további hengerlési lépések után a kör és háromszög keresztmetszet váltakozva követik egymást. Az utolsó lépés után kör alakú a félkész termék. A félkész termék huzalgyártás alapanyagaként szolgál. A Properzi technológiai sor sematikus ábrájának egy részletét mutatja a 3. ábra. 3
5 3. ábra Properzi technológiai sor sematikus ábrájának részlete [2] Az előállított pászma az öntőkeréken történő kristályosodással kezdődik, amely során a hőelvonás nem egyenletes a tér minden irányában, ami megfelelő kezelés hiányában orientált szemcseszerkezetet eredményez. A gyártás nem klasszikus síkhengerlési lépésekkel folytatódik, amelyek okozta képlékeny alakváltozás szintén növeli a kristálytani anizotrópiát. A Properzi gyártástechnológia jellege miatt a félkész termék kristálytanilag anizotróp. A szemcseszerkezet és a kristálytani anizotrópia jellege a teljes gyártási folyamat során drasztikus változásokon megy keresztül, melynek leírása hiányos a szakirodalomban. 1.2 A kristálytani anizotrópia Kristálytanilag izotróp az anyag, ha a kristályok orientációja (irányítottsága) véletlenszerű, és a tér minden irányában azonos tulajdonságokkal rendelkezik. Kristálytani anizotrópiának, vagy más néven textúrának nevezzük azt a jelenséget az anyagban, ha a kristályok térbeli orientációja eltér a véletlenszerűtől. Ebben az esetben, az anyagban a kristályok jelentős része egy kitüntetett kristálytani irányba állnak és a tulajdonságai (alakíthatóság, elektromos vezetőképesség) is irányfüggővé válnak. [3-7] 4
6 1.3 A textúra jellemzése röntgendiffrakcióval Száltextúra jellemzése A kristálytani textúra egyik legegyszerűbb megadási módját olyan minták esetében alkalmazhatjuk, melyekhez egy kitüntetett irány rendelhető. Ilyen minták tipikusan a huzalok, irányítottan kristályosított rudak stb.. Melyeknél a kristálytani anizotrópia kialakulását, egy meghatározott irányú folyamat befolyásolja (szálhúzásnál a húzás iránya, egykristály növesztésnél a hőelvonás iránya). Az így kialakuló textúrát, száltextúrának nevezzük. A száltextúra megadásánál a legtöbb esetben elegendő, annak a [hkl] kristálytani iránynak a megadása, amelyik párhuzamos a minta hossztengelyével (hőelvonás irányával, szálhúzás irányával). A száltextúra egyszerűen megadható a minta keresztmetszetén felvett interferencia függvénnyel, mely segítségével megadhatjuk a keresztmetszeten legnagyobb valószínűséggel előforduló (hkl) síksorozatot. A száltextúra ilyen típusú megadása, azonban nem ad teljes képet a jellemző kristálytani textúráról, ugyanis nem ad információt a keresztmetszettel párhuzamos síksorozat hossztengely körüli elfordulásáról. [3-7] Pólusábrák A textúravizsgálat során a sokkristályos anyagban lévő kristályok irányítottságát vizsgáljuk. A kvantitatív textúravizsgálat során ismernünk kell valamennyi kristály térbeli elhelyezkedését. Ennek megadásához szükségünk van a minta makroszkopikus koordinátarendszerének ismeretéhez, amely a hengerelt lemez esetén a hengerlési irány (HI), keresztirány (KI), valamint a normál irány(ni) ismeretére. Továbbá ismernünk kell valamely (hkl) sík normálisának a normál iránnyal bezárt szögét (90-α), a (hkl)-t tartalmazó sík és HI KI sík metszésvonalának a HI-val bezárt szögét (β) és a (hkl) körüli γ elforgatást. Ha ezeket valamennyi kristály esetében ismerjük, meg tudjuk adni a textúrát sűrűségfüggvénnyel (Orientation Distribution Function ODF), ami azt mutatja meg, hogy hány elemi cellára jellemző ugyanazon orientáció, lásd 4. ábra. [3-7] 5
7 4. ábra A térbeli orientáció megadásaadott kristály esetén A textúra félkvantitatív jellemzése a pólusábra alkalmazásával történhet, amely hengerelt lemezek textúrájának jellemzésére dolgoztak ki. A vizsgálathoz egy kivágott mintára van szükség, amelyen ismert a hengerlés iránya, majd úgy helyezzük fel a mintatartóba, hogy a hengerlési sík megegyezik a vizsgálati síkkal, valamint a hengerlési irány 12 óra irányába mutat (5. ábra). [3-7] 5. ábra Lemez hengerlési síkok és irányok megadása pólusábra készítéséhez [8] A mérés során a mintát körbeforgatjuk a normál irány körül, majd visszaérve a kiindulási ponthoz, kidöntjük a mintát a vizsgálati síkból adott értékkel (pl. 5 -kal)és újra körbeforgatjuk, a minta kidöntését a lehető legnagyobb (általában 0 75 ) szögtartományon belül végezzük. Az így kapott diffraktált intenzitás eloszlást, a pólusábrán a hengerlési síkhoz 6
8 és hengerlési irányhoz kötött polár koordinátarendszerben kapjuk meg. A pólusábráról egy adott irányhoz (φ, χ) tartozó intenzitás értékét úgy határozzuk meg, hogy az adott iránnyal és a hengerlési iránnyal bezárt szöget a φ tengelyről leolvasva kapjuk meg, míg a normál iránnyal bezárt szöget, pedig a χ szögértéke adja meg (lásd 6 b) ábra). [3-7] A textúra vizsgálat során χ = 0 döntési szögben a teljes vizsgált sík a fókuszsíkban van, ezért nincs intenzitás csökkenés. A minta döntésével, a fókuszsíkban lévő besugárzott terület fokozatosan csökken, kiesik a fókuszsíkból, ezért csökken a detektált intenzitás. Ezen jelenség kiküszöbölése érdekében korrigálni kell, a mért pólusábrát izotróp Al porminta értékeivel. Az 6. ábrán láthatunk egy defókuszált és egy fókuszált pólusábra közötti különbséget [3-7]. a) b) 6. ábra Az 5. minta {111} síksorozatának,defókuszált (a) és fókuszált (b) pólusábrája A pólusábra felvételekor, a mérés sajátosságaként állandó értékkel, pl. 5 -ként döntjük a mintát, valamint a vizsgálati döntési tartomány is korlátozott (pl ), ezért a hiányzó szögértékeknél nem áll rendelkezésünkre adat, lásd 7. ábra. Ennek a korrigálására bizonyos paraméterek megadásával (rácsszerkezet, alakváltozás típusa stb.) egy matematikai algoritmus segítségével újraszámítjuk, így megkapjuk az újraszámított pólusábrát. Egy újraszámított pólusábrát a 8.ábrán láthatunk. [3-7] 7
9 7. ábra A pólusábra mérések holt terei 8. ábra Az 5. minta {111} síksorozatának újraszámított pólusábrája Annak ellenére, hogy a pólusábrák röntgendiffrakciós mérési módszerét a kristálytani textúra vizsgálatával foglalkozó európai tudományos közösség általánosan elfogadott mérési paraméterekkel, illetve vizsgálati körülményekkel végzi, MSZ-EN szabványt nem találtam a pólusábrák röntgendiffrakciós mérésére vonatkozóan. Az Egyesült Államokban elfogadott szabvány azonban létezik: ASTM E81: 1977 [9] 8
10 1.3.3 Az orientációs sűrűség függvény (ODF) A pólusábra egy adott (hkl) síksorozat orientációs rendszerét adja meg, azonban ennek hátránya, hogy az adott síksorozat egy szabad tengely mentén elfordulhat, ezért az így kapott pólusábrák nem adják meg a teljes orientációját az elemi celláknak. Ezt a hiányt küszöböli ki az orientációs sűrűség függvény. Az orientációs sűrűség függvényt pólusábrákból szintetizáljuk, amelyhez legalább három síksorozat újraszámított pólusábrájára van szükség. Az orientációs sűrűség függvény számításokat a Bungenem koordiántarendszerben a φ1, Φ, φ2euler-szögek koordináta rendszerét használjuk [4]. Euler-szögek: [4] φ1 Normál irány szerinti elforgatás (Normal Direction D N Normál irány NI) lásd 9. ábra. 9. ábra Normál irány szerinti elforgatás [10] Φ A kiforgatott hengerlési irány szerinti elforgatás (Rolling Direction RD Hengerlési irány HI) lásd 10.ábra. 9
11 10. ábra A kiforgatott hengerlési irány szerinti elforgatás [10] φ2 A kiforgatott normál irány szerinti elforgatás lásd 11. ábra. 11. ábra A kiforgatott normál irány szerinti elforgatás [10] 2 Elvégzett vizsgálatok A kapott Properzi antennán szemcseszerkezeti, valamint röntgendiffrakcióstextúra vizsgálatokat végeztem. Az elvégzett vizsgálatok menetét a továbbiakban részletezem. 10
12 2.1 Hosszmetszeti próbatestek A rendelkezésemre bocsátott Properzi antennából minden két egymást követő hengerlési szúrás átmeneti szakaszából hosszmetszeti próbatesteket munkáltattam ki annak érekében, hogy a szemcseszerkezeti változását a hengerlési lépések közötti átmenetben vizsgálhassam. Erre mutat példát a 12. ábra. Ezeken a próbatesteken végeztem el a szemcseszerkezet makro és színesmaratásos vizsgálatait. 12. ábra A szemcseszerkezeti vizsgálatokhoz használt hosszmetszeti próbatest 2.2 Keresztmetszeti próbatestek A Properzi antenna mind a 12 technológiai lépésén átesett szakaszaiból három mintasorozatot munkáltattam ki. Két mintasorozatot, a keresztmetszeti makro-és színesmaratási vizsgálatokhoz készítettem elő, míg a harmadik mintasorozatból kör alakú mintákat munkáltattam ki a textúravizsgálatokhoz (13. ábra). Az ábrán a keresztmetszeti mintasorozat látható, valamint alattuk az ezekből kimunkált kör alakú textúramérésekhez használt keresztmetszeti mintasorozat. 11
13 13. ábra A szemcseszerkezeti vizsgálatokhoz, illetve a röntgendiffrakciós textúravizsgálatokhoz használt keresztmetszeti próbatestek 2.3 A szemcseszerkezet vizsgálata makromaratással A makromaratással végzett vizsgálat előkészítésének első lépése volt a kivágott minták csiszolása, 220-as, 320-as, 500-as, 800-as csiszolópapíron, majd gyémántpasztás polírozás 3µm-es és 1µm-es posztón, végül a minták lemosása, a szennyeződések eltávolítása. A maratáshoz használt marószer összetétele 2 rész 68%-os HNO3, 2 rész 37%-os HCL és 1 rész 38%-os HF. A maratási idő 3-5 másodperc volt. Maratást követően desztillált vízzel, majd alkohollal lemostam és cseppmentesre szárítottam a mintákat. A makro maratást mindkét 12
14 típusú (hosszmetszeti, keresztmetszeti) próbatesteken elvégeztem. A kész minták vizsgálatához Canon EOS 700D + EFS (60mm fókusztávolsággal) digitális tükörreflexes fényképezőgépet használtam. 2.4 A szemcseszerkezet vizsgálata színesmaratással A szemcsék jobb láthatóságának érdekében a szemcseszerkezet vizsgálatához Barker színesmaratást alkalmaztam. A minták előkészítésének folyamata a már fent említett lépésekből állt: első lépés, csiszolás 220-as, 320-as, 500-as, 800-as csiszolópapíron, majd polírozás 3µm-es és 1µm-es posztón, végül a minták lemosása, a szennyeződések eltávolítása. Ezután következett a maratás, amelyet Struers Lectro-Pol 5 típusú elektropolírozó berendezésen és Barker marószerrel végeztem. A marószer összetétele 200ml desztillált víz 5g34%-os HBF4. A maratás 20-25V és másodpercközötti beállítások mellet történt, függően a mintadarabtól. A maratás végeztével a darabokat, desztillált vízzel, majd alkohollal lemostam és cseppmentesre szárítottam. A marószer hatására Al2O3 oxidréteg keletkezik a felületen, amely a szemcsék orientációjától függően eltérő vastagságú. Polarizált fénnyel megvilágítva az eltérő orientációjú kristályok más-más színűek lesznek. A fényképeket polarizált fényben a Zeiss Axio Vert 40 típusú optikai mikroszkóppal készítettem. Barker maratást mind hosszmetszeti, mind pedig keresztmetszeti próbadarabokon is elvégeztem. 2.5 Jellemző elemi cella orientációk meghatározása A röntgendiffrakciós vizsgálatokat egy Euler bölcsővel ellátott Bruker D8 Advance röntgendiffraktométerrel végeztem el. Az általam használt röntgendiffraktométer az alábbi biztonsági szabványoknak felel meg. Elektromos biztonság: DIN EN , IEC Elektromágneses biztonság: EN , EN , EN , EN Sugárvédelem: ICRP (International Commission on Radiological Protection); IAEA (International Atomic Energy Association); EURATOM Euroaische Atomgemeinschaft); DIN Az IEC 536 szerinti biztonsági besorolás: I. osztály. Az IEC 529 szerinti biztonsági szint: IP 2 0. [11] 13
15 A textúra vizsgálatokat a pászma keresztmetszetéből kivágott kör alakú próbatesteken végeztem. Azért ilyen próbatesteket készítettem, mert a Properzi pászma fő alakváltozása a hossztengely irányú nyúlás, ami várhatóan a technológiai sor végére száltextúrát fog eredményezni. A száltextúra jellemzésére, pedig keresztmetszeti mintákat használunk [4,6,7]. A kör alakra, azért volt szükség, mert a textúravizsgálat során a mintát 0 -tól 360 -ig körbe forgatjuk, és a körbe forgatás során biztosítani kell azt, hogy a vonalfókuszú röntgen nyaláb mindig ugyanakkora területet fedjen le. A vizsgálatok során rögzítettem minden minta interferencia függvényét, valamint textúra vizsgálatokat végeztem a jellemző elemi cella orientációk meghatározásához. Annak érdekében, hogy átfogóbb képet kapjak a kialakuló elemi cella elfordulásokról, a textúra vizsgálatokat a keresztmetszeti minták mindkét oldalán elvégeztem, amelyeket a későbbiekben A és B oldallal jelöltem. A mintadarabokon feltüntettem az öntőkeréken található vályú szabad felületét (14. ábra). Erre azért volt szükség, hogy a keresztmetszeti mintasorozat minden egyes darabját azonos helyzetbe tudjam elhelyezni a röntgendiffraktométer mintatartójában a textúra vizsgálatok során. A minták felületét makromaratással készítettem elő, ezzel kiküszöbölve a mintakivágás okozta képlékeny alakváltozás hatását. A mérések során a 15. ábrán látható mintaelhelyezést alkalmaztam. 14. ábra A minták kivágásának és jelölésének folyamata 14
16 15. Ábra Az 1.minta elhelyezése a röntgendiffraktométer mintatartójában A továbbiakban az 5. mintán keresztül mutatom be a vizsgálat folyamatát. Az első lépés az interferencia függvény rögzítése, amely segítségével meghatároztam a három legerősebb intenzitású reflexiók Bragg szögét (16. ábra). A nagyszámú mintasorozatra való tekintettel a, mérési idő csökkentése érdekében az interferencia függvényeknek csak a reflexiók közelében található szakaszait rögzítettem. Az Al {111}, {200}, {220} reflexiók vizsgálatához használt 2theta szögtartomány-szakaszokat a PDF (Powder Diffraction Database) adatbázis azonosítószámú kártyája alapján határoztuk meg. A PDF adatbázist Hanawalt, Rinn és Fevel indította 1930-as években. ~100 anyag XRD spektrumát határozták meg. Ezután az ASTM ( ) és a JCPS ( )is bekapcsolódott az adatbázis bővítésébe. began to take part ban átnevezték Int. Center for Diffraction Data (ICDD) névre. Ekkor már kb. 300 studós vett részt az adatbázis bővítésében világszerte ben a (PDF) közel 62,000 spektrumot tartalmazott, évente 200 új adattal bővülve, szervetlen vegyületek, ásványok, szerves vegyületek, valamint fémes vegyületeket magába foglalva. 15
17 16. ábra Az 5. minta interferencia függvénye Az így megkapott 2Ɵ értékeknél vettem fel az {111}, {200} és {220} síksorozatokról a pólusábrákat, amelyeken elvégeztem a defókuszálási korrekciót. A mért pólusábrákat a dolgozatom érdemi részében nem mutatom be, ezeket az 1.sz Melléklet tartalmazza. A korrigált pólusábrákat újraszámítottam a röntgendiffraktométer kiértékelő szoftverével. Az öntőkerékről érkező pászma textúráját nem egy jól definiált alakítási technológia okozza, hanem az öntőkeréken történő kristályosodás, ezért az újraszámításhoz a legkisebb szimmetriával rendelkező triklin alakváltozást választottam, Az újraszámított pólusábrákból szintetizáltam az orientációs sűrűség függvényt, ennek 3D-s verziója látható a 17. ábrán. Az alkalmazott triklin alakváltozás miatt a szintetizált ODF-nek két Euler szöge (φ2, ϕ) 0 -tól 90 -ig harmadik szöge (φ1) pedig 0 - tól 360 -ig terjedt. 16
18 17. ábra 5.minta 3D-s orientációs sűrűség függvény képe A 3D-s orientációs sűrűség függvények nehéz kezelhetősége miatt, kétdimenziós metszet több sorozatot készítettem, konstans φ2 szögértékek mellet. Ezeken a metszeteken, megkerestem a lokális maximumokat (18. ábra a,b,c,d pontok) és meghatároztam ezek Eulerszögeit. Az Euler-szögek segítségével, kiszámoltam a hozzájuk tartozó térfogathányad értékeket 15 -os szögeltérés mellett. 17
19 18. ábra Az 5. minta ODF metszetei konstans φ2 értékeknél Az orientációs sűrűség függvény definiálásához használt φ1, Φ, φ2 szögek a klasszikus hengerlési technológia koordinátarendszeréhez vannak kötve (HI: hengerlési irány, KI: kereszt irány, NI: normál irány). A kiértékelő szoftver az Euler szögeket szintén ezen koordinátarendszerben értelmezi, valamint az Euler szögek elfordulási tengelyei a röntgendiffraktométer mintatartójához vannak kötve. Annak érdekében, hogy az ODF kiértékelést el tudjam végezni a Properzi eljárással készült keresztmetszeti mintákon, szükséges volt beilleszteni az Euler szögek elfordulási tengelyeit a Properzi minták koordináta-rendszerébe. Ez a kapcsolat a következő (19.ábra): 18
20 φ1 a Properzi antenna hossztengelye, vagyis a keresztmetszeti minták normálisa körüli elfordulási szög Φ az öntőkeréken található vályú szabad felülete felé mutató, φ1-elelfordított irány körüli szögelfordulás φ2 a Properzi antenna Φ-vel elfordított hossztengelye, vagyis a keresztmetszeti minták Φ-vel elfordított normálisa körüli elfordulási szög A lokális maximumokhoz tartozó elemi cella elfordulásokat SolidEdgeV20 programmal ábrázoltam. Ehhez szükséges volt az Euler-szögek elfordulási tengelyeit beilleszteni a SolidEdgeV20 program által használt koordinátarendszerbe. A SolidEdgeV20 program által használt koordinátarendszert a φ1 = 0, Φ = 0, φ2 = 0 elfordulási szögek mellett a 19. ábrán 0. lépésében látható. Ebben a pozícióban a minta hossztengelye merőleges a kép síkjára. Ehhez a helyzethez rendeltük a keresztmetszeti minták helyzetét. Ezek a következőek: φ1 az x tengely körüli elforgatásnak felel meg (lásd a 19. ábra 1. lépése) Φ az elforgatott y tengely körüli elforgatásnak felel meg (lásd a 19. ábra 2. lépése) φ2 a már kétszeresen elforgatott x tengely körüli elforgatásnak felel meg (lásd a 19. ábra 3. lépése) 19. ábra Az 5. minta egy lokális maximumához tartozó elemi cella elfordulásának ábrázolási menete SolidEdgeV20 programmal 19
21 3 Eredmények 3.1 A szemcseszerkezet jellemzése hosszmetszeten makromaratással 20. ábra A szemcseszerkezet változása hosszmetszeten makromaratással a 11 átmeneti szakaszban. A hengerlési szakaszokat számok jelzik 20
22 Ahogy azt a 20. ábrán (rácsméret 1x1 cm) is láthatjuk, a Properzi eljárással készült pászma közepén már öntött állapotban megjelenik egy sáv, amelyen belül közel ekviaksziális szemcsék találhatók. Jól látható, hogy a sáv mellet a pászma külső térfogatát jellemzően a hossztengelyre nagyjából merőleges irányú, oszlopos szemcseszerkezet fogja körbe, amely az alkalmazott beoltás ellenére is kialakul. A középső sávban található ekviaksziális szemcsék az alakítási lépések előrehaladtával fokozatosan megnyúlnak. Ezen sáv szélessége a minták keresztmetszet csökkenésével arányosan csökken. A pászma külső részében található oszlopos szemcsék fokozatosan befordulnak a hossztengely irányába és fokozatosan nyúlnak. A technológia végén a pászma teljes egészében a hossziránnyal megegyező irányú szemcsék a jellemzők. A 8. hengerlési lépéstől a központi sáv már nem különíthető el a pászma többi szemcséjétől. 3.2 A szemcseszerkezet jellemzése hosszmetszeten színesmaratással a) 21
23 b) c) d) e) 22
24 f) g) h) i) 23
25 j) k) 21. ábra A szemcseszerkezet változása hosszmetszeten színesmaratással a 11 átmeneti szakaszban. A hengerlési szakaszokat számok jelzik Az 21. ábrán láthatjuk, a 11 átmeneti szakaszból kivett hosszmetszeti próbatest szemcseszerkezetét. A különböző színek eltérő orientációjú szemcséket mutatnak. A hosszmetszeti színesmaratásos szemcseszerkezeti vizsgálatokat csak a pászma keresztmetszet csökkenésének közvetlen környezetében végeztem. Az alakítás előrehaladtával a szemcsék nyújtottságának iránya megegyezik az hossztengely irányával, illetve a megnyúlt szemcsék száma növekszik. Ahogy azt az 21. a) ábrán láthatjuk, a vizsgált látótérben található szemcsék nagy részének morfológiai orientációja a hosszmetszetre merőleges irányúak. Azonban a fokozatos alakításnak köszönhetően láthatjuk, hogy az 21. c) g) ábrákon, a felülethez közeli szemcsék nyújtottsága nagyobb mértékben változik, mint a felülettől távolabbi térfogatrészben. Az 21. e) és f) képeken már fele-fele arányban vannak az hossztengellyel, párhuzamos iránnyal megegyező és azzal közel 45 -os szöget bezáró nyújtottságú szemcsék. Az 21.h) k) ábrákon, a látótérben található összes szemcse elnyúlt a hossztengely irányában, amely az alakítás előrehaladtával arányosan egyre finomabb szerkezetű lesz. 24
26 3.3 A szemcseszerkezet jellemzése keresztmetszeten makromaratással A 22. ábrán jól látható négy zóna, amelyekben oszlopos szemcseszerkezet alakul ki. Az oszlopos szemcsék irányát a hőelvonás iránya határozta meg, ami az öntőkeréken négy irányban történt. A mintákon szabad szemmel is jól láthatóvá tett szemcsék a középpontban találkoznak össze, mind a trapéz, háromszög, illetve kör keresztmetszetű próbatesteken. a) 1. lépés b) 2. lépés c) 3.lépés d) 4.lépés e) 5.lépés f) 6.lépés 25
27 g) 7.lépés h) 8.lépés i) 9.lépés j) 10.lépés k) 11.lépés l) 12.lépés 22. A szemcseszerkezet változása keresztmetszeten makromaratással a 12 (a-l) technológiai lépés után 26
28 3.4 A szemcseszerkezet jellemzése keresztmetszeten színesmaratással 23. ábra A szemcseszerkezet az 1. technológiai lépés után a keresztmetszeten 24. ábra A szemcseszerkezet az 2. technológiai lépés után a keresztmetszeten 27
29 25. ábra A szemcseszerkezet az 3. technológiai lépés után a keresztmetszeten 26. ábra A szemcseszerkezet az 4. technológiai lépés után a keresztmetszeten 28
30 27. ábra A szemcseszerkezet az 5. technológiai lépés után a keresztmetszeten 28. ábra A szemcseszerkezet az 6. technológiai lépés után a keresztmetszeten 29
31 29. ábra A szemcseszerkezet az 7. technológiai lépés után a keresztmetszeten 30. ábra A szemcseszerkezet az 8. technológiai lépés után a keresztmetszeten 30
32 31. ábra A szemcseszerkezet az 9. technológiai lépés után a keresztmetszeten 32. ábra A szemcseszerkezet az 10. technológiai lépés után a keresztmetszeten 31
33 33. ábra A szemcseszerkezet az 11. technológiai lépés után a keresztmetszeten 34. ábra A szemcseszerkezet az 12. technológiai lépés után a keresztmetszeten 32
34 A ábrákon láthatjuk a szemcseszerkezet változását a színesmaratott keresztmetszeti mintasorozaton. Ahogy azt az ábrák is mutatják az 1. lépésnél látható az öntött dendrites szerkezet, ami az alakítás mértékének növelésével átalakul az alakításra jellemző szemcseszerkezetre. A mintasorozatokon jól látható, hogy a szemcsék hossztengelye a pászma középpontja felé mutat minden hengerlési lépés után. Mivel azonban ezek a képek a minta keresztmetszetén készültek, a pászma hossztengelye merőleges a kép síkjára, ezért a szemcsék hossztengely irányú nyújtottsága nem figyelhető meg ezeken a képeken. 3.5 Interferenciafüggvény változásának a bemutatása A mintákról kapott interferencia függvények vizsgálatával célom volt meghatározni, hogy egy mintán belül a különböző reflexiók egymáshoz viszonyított aránya milyen jelleget mutat az egyes technológiai lépések után. A teljes spektrum felvételét mind a 12 mintán elvégeztem, a minták mindkét (A és B) oldalán az alábbi síksorozatokon: {111}, {200}, {220}, {311}, {222}, {440}. A minták A oldalán mért interferencia függvényeket a 35. ábra, míg a minták B oldalán mért interferencia függvényeit a 36. ábra szemlélteti. Mivel a vizsgálat során a legfontosabb a technológia végén kialakuló textúra jellemzése a jobb láthatóság érdekében a 12-es minták spektrumait helyeztem az ábra elejére majd ehhez képest eltolva látható a többi minta spektruma. A technológia végéhez közelítve a pászma keresztmetszetének csökkenése, a kimunkált próbatestek keresztmetszetének csökkenését jelentette. Ezért a minták vizsgált térfogata és így a minták által diffraktált nyaláb intenzitása is csökkent. Ennek kiküszöbölése érdekében a mintákon kapott intenzitás értékeket a 12-es számú mintához normáltam, hiszen a végső interferencia függvény a mérvadó. A normálásnak az alapja az volt, hogy minden mintán az {111} reflexió intenzitását felszoroztam úgy, hogy az megegyezzen a 12-es minta {111} reflexiójának az intenzitásával, majd ugyanazzal a szorzóval korrigáltam az összes reflexió intenzitását. 33
35 35. ábra A keresztmetszeti minták interferencia függvénye az A oldalon 36. ábra A keresztmetszeti minták interferencia függvénye a B oldalon 34
36 Látható, hogy az öntött, valamint az első hengerlési lépéseken átesett mintákon az intenzitás arányok erős textúrát mutatnak, a relatív intenzitás nagyon változékony. Látható, hogy az öntést követően a mintákban {200} textúra a domináns. A tovább hengerlés hatására fokozatosan kialakul a 12-es mintára jellemző intenzitás arány. Megfigyelhető, hogy egy mintán belül az A és B oldalakon az intenzitás arányok eltérők is lehetnek az első technológiai lépések után. A technológiai sor végén azonban, mind az A mind a B oldalon mért intenzitás arányok közel azonosak. Az 37. ábra mutatja az utolsó hengerlési lépésen átesett minta A és B oldaláról készített diffraktogramokat, valamint a PDF adatbázisban számmal jelzett izotróp alumínium referencia minta relatív intenzitás arányait. A referencia minta intenzitás értékeit a mért spektrumok {111} reflexió intenzitásához normáltam a könnyebb összehasonlíthatóság érdekében. A referencia intenzitás értékekhez jobbra eltolva ábrázoltam az A és B oldalon mért interferencia függvényeket. Látható, hogy az A és a B oldal nagyon hasonló jelleget mutat, ami az alábbi módon tér el az izotróp referencia minta intenzitás arányától: az {111} reflexiók intenzitása megegyezik a referencia minta intenzitásával a normálásnak köszönhetően. A {200} intenzitás értéke csökken ugyan, de még egyértelműen látható, a további {220} és {311} reflexiók intenzitása drasztikus mértékben lecsökkentek, ami azt jelenti, hogy a keresztmetszeti minta A és B oldalán a vizsgált reflexiók közül az {111} a domináns, vagyis a technológia végére kialakul az <111> száltextúra, azonban még jelen van a <200> száltextúra komponens is. 35
37 37. ábra Az utolsó technológiai lépésből kivett keresztmetszeti minta A és B oldalán mért interferencia függvény és az alumínium referencia minta interferencia függvénye 3.6 Jellemző elemi cella orientációk bemutatása A ábrák mutatják a jellemző elemi cella elfordulásokat a 12 technológiai lépés után. Azokat az elemi cella orientációkat, amelyeken egyértelműen látható a <200> száltextúra, azokat zöld kerettel emeltem ki, azokat az elemi cella orientációkat, amelyeken egyértelműen látható az <111> száltextúra piros kerettel láttam el. 36
38 1. minta x=45 y =30 x =5 V/V%=17,5 x=240 y =75 x =85 V/V%=17,5 x=70 y =5 x =20 V/V%=27,6 x=215 y =20 x =0 V/V%=15,3 x=55 y =70 x =0 V/V%=8,6 x=175 y =85 x =80 V/V%=19,4 x=130 y =85 x =5 V/V%=16,6 38. ábra Az 1. minta jellemző elemi cella orientációi és térfogatszázalékai 37
39 2. minta x=315 y =15 x =40 V/V%=24,1 x=80 y =65 x =15 V/V%=19 x=160 y =10 x =15 V/V%=7,7 x=155 y =85 x =0 V/V%=11,7 x=70 y =30 x =35 V/V%=8,6 x=190 y =80 x =10 V/V%=8,5 39. ábra Az 2. minta jellemző elemi cella orientációi és térfogatszázalékai 38
40 3. minta x=110 y =5 x =65 V/V%=10,7 x=90 y =70 x =75 V/V%=18,2 x=290 y =10 x =70 V/V%=7,5 x=105 y =55 x =60 V/V%=11,56 x=140 y =45 x =35 V/V%=5,6 x=175 y =65 x =15 V/V%=5,8 40. ábra Az 3. minta jellemző elemi cella orientációi és térfogatszázalékai 39
41 4. minta x=45 y =35 x =10 V/V%=6,9 x=5 y =50 x =60 V/V%=20,8 x=20 y =0 x =0 V/V%=6,1 x=175 y =50 x =45 V/V%=4,2 x=240 y =5 x =80 V/V%=5,4 x=95 y =85 x =0 V/V%=4,9 x=35 y =75 x =15 V/V%=4,8 x=20 y =40 x =15 V/V%=4 x=120 y =60 x =35 V/V%=5,8 41. ábra Az 4. minta jellemző elemi cella orientációi és térfogatszázalékai 40
42 5. minta x=205 y =85 x =0 V/V%=29,4 x=250 y =5 x =80 V/V%=10,1 x=85 y =5 x =75 V/V%=9,7 x=120 y =45 x =40 V/V%=7,7 42. ábra Az 5. minta jellemző elemi cella orientációi és térfogatszázalékai 41
43 6. minta x=180 y =20 x =0 V/V%=13,4 x=0 y =55 x =75 V/V%=19,9 x=300 y =50 x =45 V/V%=4,4 x=220 y =60 x =50 V/V%=10,2 43. ábra Az 6. minta jellemző elemi cella orientációi és térfogatszázalékai 42
44 7. minta x=55 y =35 x =0 V/V%=6,1 x=10 y =10 x =50 V/V%=9,5 x=25 y =85 x =75 V/V%=9,8 x=170 y =80 x =85 V/V%=17 x=170 y =15 x =10 V/V%=7,7 x=0 y =50 x =35 V/V%=6,6 44. ábra Az 7. minta jellemző elemi cella orientációi és térfogatszázalékai 43
45 8. minta x=95 y =10 x =70 V/V%=6,4 x=195 y =85 x =80 V/V%=7 x=195 y =5 x =75 V/V%=8,1 x=270 y =65 x =50 V/V%=11,2 x=240 y =60 x =40 V/V%=11,5 45. ábra Az 8. minta jellemző elemi cella orientációi és térfogatszázalékai 44
46 9. minta x=155 y =55 x 40 V/V%=19,6 x=120 y =80 x =50 V/V%=7,8 x=135 y =10 x =30 V/V%=10,4 x=260 y =40 x =70 V/V%=5,6 46. ábra Az 9. minta jellemző elemi cella orientációi és térfogatszázalékai 45
47 10. minta x=90 y =10 x =35 V/V%=11,5 x=115 y =60 x =50 V/V%=12,9 x=295 y =10 x =75 V/V%=6,7 x=30 y =55 x =45 V/V%=11,8 x=85 y =65 x =45 V/V%=7,8 x=150 y =10 x =10 V/V%=5,2 x=85 y =10 x =0 V/V%=6,6 x=350 y =55 x =55 V/V%=8,3 47. ábra Az 10. minta jellemző elemi cella orientációi és térfogatszázalékai 46
48 11. minta x=115 y =10 x =0 V/V%=6,8 x=25 y =50 x =35 V/V%=8,9 x=65 y =10 x =15 V/V%=8,8 x=60 y =55 x =40 V/V%=9,8 x=220 y =50 x =60 V/V%=8,6 x=10 y =35 x =0 V/V%=4,5 48. ábra Az 11. minta jellemző elemi cella orientációi és térfogatszázalékai 47
49 12. minta x=230 y =5 x =15 V/V%=12,1 x=335 y =15 x =75 V/V%=3,2 x=30 y =0 x =0 V/V%=4,4 x=165 y =50 x =30 V/V%=7,7 x=115 y =60 x =30 V/V%=5,3 x=340 y =60 x =50 V/V%=7,8 x=210 y =10 x =65 V/V%=4,4 x=145 y =45 x =40 V/V%=8,9 49. ábra Az 12. minta jellemző elemi cella orientációi és térfogatszázalékai 48
50 Az elemi cella orientációk alátámasztják a teljes spektrumokkal kapott textúraképet. Öntés után jellemzően a <200> száltextúra alakul ki. A hengerlések hatására, pedig az <111> száltextúra alakul ki, majd erősödik. A technológia végére még megmarad a <200> textúra. A textúra térfogatszázalékaiból látható, hogy utolsó hengerlési lépés után, nem az <111> komponens, hanem a <200> komponens az erősebb. Ez némileg ellent mond az interferencia függvény mérések során kapott eredményekkel, ami azt mutatta, hogy a technológia végére az <111> komponens a domináns. A két eredmény közötti különbség abból következik, hogy a teljes spektrum vizsgálatok során vonalfókuszú röntgen nyaláb csak a minta egy részét fedte le, ellenben a textúra vizsgálat során a körbe forgatásának köszönhetően a teljes mintafelületről kaptunk információt. 49
51 4 Következtetések A vizsgálataimmal kimutattam, hogy a vizsgált Properzi technológiával gyártott pászmában az alkalmazott beoltás ellenére kristályosodáskor az oszlopos szemcseszerkezet, mely megmarad az első hengerlési lépések során. A keresztmetszeti minták két oldalának vizsgálata során azt tapasztaltam, hogy a textúrakép erősen eltérő is lehet a minta két oldalán. Ennek oka visszavezethető az oszlopos szemcseszerkezetre. Az oszlopos szemcsék hossztengelyének irányát ugyanis a kristályosodás közbeni hőelvonás iránya határozza meg, azonban a szemcsék hossztengelyük körül tetszőlegesen elfordulhatnak. Ennek köszönhetően az első technológiai lépésekben jelenlévő oszlopos szerkezetek, ugyanazon keresztmetszeti minta kétoldalán eltérő orientációjú szemcséket, tehát eltérő textúra képet eredményezhet Öntés, valamint az első hengerlési lépések után jellemzően <200> textúra van jelen a pászmában. A hengerlési lépések fokozatosan eltüntetik az oszlopos szemcseszerkezetet, valamint a hossztengellyel közel párhuzamos nyújtott szemcsék jönnek létre. Eközben fokozatosan kialakul az <111> száltextúra. A technológia végén még jelen van a <200> textúra is. Ennek oka feltehetően a kristályosodáskor kialakult oszlopos szerkezetre vezethető vissza. Tehát a kristályosodás körülményei jelentős hatással vannak a technológia végén kapott félkésztermék kristálytani textúrájára és így annak makroszkópikus tulajdonságaira. 50
52 5 Összefoglalás Diplomamunkám során Properzi technológiával gyártott pászma szemcseszerkezet és röntgendiffrakciós textúravizsgálatát végeztem. A szemcseszerkezet vizsgálatok kiterjedtek az összes technológiai lépések utáni keresztmetszeti minták, valamint az összes hengerlési lépés közti átmeneti szakaszok hosszmetszeti vizsgálataira makromaratással illetve színes maratással. Mind a 12 keresztmetszeti minta mindkét oldalán megvizsgáltam a röntgendiffrakciós interferencia függvényeket. Elvégeztem a röntgendiffrakciós textúravizsgálatokat, melyek során felvettem az {111}, {200}, {220} pólusábrákat, valamint a pólusábrákból szintetizáltam az ODF függvényeket. Kidolgoztam az eljárás, mely segítségével az ODF vizsgálata elvégezhető a Properzi technológiával előállított pászma koordinátarendszerében. Kimutattam, hogy a Properzi technológia során, öntéskor az alkalmazott beoltás mellett is kialakul az oszlopos szemcseszerkezet, ami jellemzően <200> textúrát eredményez. A hengerlési lépések során az oszlopos szemcseszerkezet fokozatosan eltűnik, és létrejön az <111> száltextúra. A technológia során gyártott félkész termékben azonban az <111> száltextúra mellett jelen van a <200> textúra is, amelynek oka a kristályosodáskor kialakuló szemcseszerkezet. 51
53 Köszönetnyilvánítás Szeretném megköszönni a munkám során nyújtott segítségét a Fémtani, Képlékenyalakítási és Nanotechnológiai Tanszék munkatársainak, Bán Róbertnek és Márkus Zoltánnak a mintadarabok ki- és megmunkálását, Márkus Zoltánnénak a szemcseszerkezeti vizsgálatok előkészítési munkálatait, valamint konzulenseimnek Dr. Benke Mártonnak és Hlavács Adriennek a szakmai útmutatást és támogatást. A kutatómunka az OTKA projekt támogatásával készült el. 52
54 Irodalomjegyzék [1] [2] [3] Dr. Bárczy Pál, Dr. Fusch Erik, Metallográfia I., Tankönyvkiadó, 1981 [4] U.F. Kocks, C.N. Tomé, H.R. Wenk, Texture and Anisotropy, Cambridge University Press, 1998 [5] Diffrac Plus TexEval: TextureAnalysis, Bruker AXS GmbH, 2000 [6] Olaf Engler, Valerie Randle,Introduction to texture analysis, SecondEdition, 2010 [7] Satyam Suwas, Ranjit Kumar Ray, Crystallographic Texture of Materials, 2014 [8] Hlavács Adrienn, A mikroszerkezet változása Properzi öntvehengerlés során, Diplomamunka, Miskolc, 2014 [9] ASTM E81: 1977 (1982) Preparing Quantitative Pole Figures of Metals [10] [11] Bruker D8 Discover X-ray Diffractometer Roplanning and Preinstallation Guide [12] 53
55 1.sz. Melléklet - A mért {111}, {200}, {220} pólusábrák Minta sorszáma {111} {200} {220} 1A 2A 3A 4A 5A 54
56 6A 7A 8A 9A 10A 11A 55
57 12A Minta sorszáma {111} {200} {220} 1B 2B 3B 4B 56
58 5B 6B 7B 8B 9B 10B 57
59 11B 12B 58
Szemcsehatárok geometriai jellemzése a TEM-ben. Lábár János
 Szemcsehatárok geometriai jellemzése a TEM-ben Lábár János Szemcsehatárok geometriai jellemzése Rácsok relatív orientációja Coincidence Site Lattice (CSL) O-lattice Határ közelítése síkkal Határsík orientációja
Szemcsehatárok geometriai jellemzése a TEM-ben Lábár János Szemcsehatárok geometriai jellemzése Rácsok relatív orientációja Coincidence Site Lattice (CSL) O-lattice Határ közelítése síkkal Határsík orientációja
Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások
 Miskolci Egyetem Műszaki Anyagtudományi Kar Anyagtudományi Intézet Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások Dr.Krállics György krallics@eik.bme.hu
Miskolci Egyetem Műszaki Anyagtudományi Kar Anyagtudományi Intézet Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások Dr.Krállics György krallics@eik.bme.hu
Modern Fizika Labor. 17. Folyadékkristályok
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 11. A mérés száma és címe: 17. Folyadékkristályok Értékelés: A beadás dátuma: 2011. okt. 23. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 11. A mérés száma és címe: 17. Folyadékkristályok Értékelés: A beadás dátuma: 2011. okt. 23. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Milyen simaságú legyen a minta felülete jó minőségű EBSD mérésekhez
 1 Milyen simaságú legyen a minta felülete jó minőségű EBSD mérésekhez Havancsák Károly Dankházi Zoltán Ratter Kitti Varga Gábor Visegrád 2012. január Elektron diffrakció 2 Diffrakció - kinematikus elmélet
1 Milyen simaságú legyen a minta felülete jó minőségű EBSD mérésekhez Havancsák Károly Dankházi Zoltán Ratter Kitti Varga Gábor Visegrád 2012. január Elektron diffrakció 2 Diffrakció - kinematikus elmélet
Fényhullámhossz és diszperzió mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 9. MÉRÉS Fényhullámhossz és diszperzió mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 19. Szerda délelőtti csoport 1. A mérés célja
KLASSZIKUS FIZIKA LABORATÓRIUM 9. MÉRÉS Fényhullámhossz és diszperzió mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 19. Szerda délelőtti csoport 1. A mérés célja
Szerkezetvizsgálat II. c. gyakorlat
 Szerkezetvizsgálat II. c. gyakorlat Miskolci Egyetem, Műszaki Anyagtudományi Kar 2011. szeptember 14. Dr. Gergely Gréta gergelygreta@freemail.hu BEVEZETÉS-SZÖVETSZERKEZET, MORFOLÓGIA Anyagtudomány: az
Szerkezetvizsgálat II. c. gyakorlat Miskolci Egyetem, Műszaki Anyagtudományi Kar 2011. szeptember 14. Dr. Gergely Gréta gergelygreta@freemail.hu BEVEZETÉS-SZÖVETSZERKEZET, MORFOLÓGIA Anyagtudomány: az
Modern Fizika Labor. A mérés száma és címe: A mérés dátuma: Értékelés: Infravörös spektroszkópia. A beadás dátuma: A mérést végezte:
 Modern Fizika Labor A mérés dátuma: 2005.10.26. A mérés száma és címe: 12. Infravörös spektroszkópia Értékelés: A beadás dátuma: 2005.11.09. A mérést végezte: Orosz Katalin Tóth Bence 1 A mérés során egy
Modern Fizika Labor A mérés dátuma: 2005.10.26. A mérés száma és címe: 12. Infravörös spektroszkópia Értékelés: A beadás dátuma: 2005.11.09. A mérést végezte: Orosz Katalin Tóth Bence 1 A mérés során egy
Alumínium ötvözetek aszimmetrikus hengerlése
 A Miskolci Egyetemen működő tudományos képzési műhelyek összehangolt minőségi fejlesztése TÁMOP-4.2.2/B-10/1-2010-0008 Tehetségeket gondozunk! Alumínium ötvözetek aszimmetrikus hengerlése 2011. November
A Miskolci Egyetemen működő tudományos képzési műhelyek összehangolt minőségi fejlesztése TÁMOP-4.2.2/B-10/1-2010-0008 Tehetségeket gondozunk! Alumínium ötvözetek aszimmetrikus hengerlése 2011. November
Kvalitatív fázisanalízis
 MISKOLCI EGYETEM ANYAG ÉS KOHÓMÉRNÖKI KAR FÉMTANI TANSZÉK GYAKORLATI ÚTMUTATÓ PHARE HU 9705000006 ÖSSZEÁLLÍTOTTA: NAGY ERZSÉBET LEKTORÁLTA: DR. MERTINGER VALÉRIA Kvalitatív fázisanalízis. A gyakorlat célja
MISKOLCI EGYETEM ANYAG ÉS KOHÓMÉRNÖKI KAR FÉMTANI TANSZÉK GYAKORLATI ÚTMUTATÓ PHARE HU 9705000006 ÖSSZEÁLLÍTOTTA: NAGY ERZSÉBET LEKTORÁLTA: DR. MERTINGER VALÉRIA Kvalitatív fázisanalízis. A gyakorlat célja
FÉMLELETEK RÖNTGENDIFFRAKCIÓS VIZSGÁLATAINAK SPECIÁLIS LEHETŐSÉGEI
 15 FÉMLELETEK RÖNTGENDIFFRAKCIÓS VIZSGÁLATAINAK SPECIÁLIS LEHETŐSÉGEI SPECIAL X-RAY DIFFRACTION METHODS FOR METALLIC ARTIFACTS MERTINGER VALÉRIA 1, BENKE MÁRTON 2 1 Miskolci Egyetem, Fémtani, képlékenyalakítási
15 FÉMLELETEK RÖNTGENDIFFRAKCIÓS VIZSGÁLATAINAK SPECIÁLIS LEHETŐSÉGEI SPECIAL X-RAY DIFFRACTION METHODS FOR METALLIC ARTIFACTS MERTINGER VALÉRIA 1, BENKE MÁRTON 2 1 Miskolci Egyetem, Fémtani, képlékenyalakítási
Robotika. Kinematika. Magyar Attila
 Robotika Kinematika Magyar Attila amagyar@almos.vein.hu Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
Robotika Kinematika Magyar Attila amagyar@almos.vein.hu Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
Laborgyakorlat. Kurzus: DFAL-MUA-003 L01. Dátum: Anyagvizsgálati jegyzőkönyv ÁLTALÁNOS ADATOK ANYAGVIZSGÁLATI JEGYZŐKÖNYV
 ÁLTALÁNOS ADATOK Megbízó adatai: Megbízott adatai: Cég/intézmény neve: Dunaújvárosi Egyetem. 1. csoport Cég/intézmény címe: 2400 Dunaújváros, Vasmű tér 1-3. H-2400 Dunaújváros, Táncsics M. u. 1/A Képviselő
ÁLTALÁNOS ADATOK Megbízó adatai: Megbízott adatai: Cég/intézmény neve: Dunaújvárosi Egyetem. 1. csoport Cég/intézmény címe: 2400 Dunaújváros, Vasmű tér 1-3. H-2400 Dunaújváros, Táncsics M. u. 1/A Képviselő
ahol m-schmid vagy geometriai tényező. A terhelőerő növekedésével a csúszó síkban fellép az un. kritikus csúsztató feszültség τ
 Egykristály és polikristály képlékeny alakváltozása A Frenkel féle modell, hibátlan anyagot feltételezve, nagyon nagy folyáshatárt eredményez. A rácshibák, különösen a diszlokációk jelenléte miatt a tényleges
Egykristály és polikristály képlékeny alakváltozása A Frenkel féle modell, hibátlan anyagot feltételezve, nagyon nagy folyáshatárt eredményez. A rácshibák, különösen a diszlokációk jelenléte miatt a tényleges
KRISTÁLYOK GEOMETRIAI LEÍRÁSA
 KRISTÁLYOK GEOMETRIAI LEÍRÁSA Kristály Bázis Pontrács Ideális Kristály: hosszútávúan rendezett hibamentes, végtelen szilárd test Kristály Bázis: a kristály legkisebb, ismétlœdœ atomcsoportja Rácspont:
KRISTÁLYOK GEOMETRIAI LEÍRÁSA Kristály Bázis Pontrács Ideális Kristály: hosszútávúan rendezett hibamentes, végtelen szilárd test Kristály Bázis: a kristály legkisebb, ismétlœdœ atomcsoportja Rácspont:
METALLOGRÁFIA. ANYAGMÉRNÖK BSC KÉPZÉS HŐKEZELÉSI ÉS KÉPLÉKENYALAKÍTÁSI SZAKIRÁNY SZAKIRÁNYOS TANTÁRGY (nappali/levelező munkarendben)
 METALLOGRÁFIA ANYAGMÉRNÖK BSC KÉPZÉS HŐKEZELÉSI ÉS KÉPLÉKENYALAKÍTÁSI SZAKIRÁNY SZAKIRÁNYOS TANTÁRGY (nappali/levelező munkarendben) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI
METALLOGRÁFIA ANYAGMÉRNÖK BSC KÉPZÉS HŐKEZELÉSI ÉS KÉPLÉKENYALAKÍTÁSI SZAKIRÁNY SZAKIRÁNYOS TANTÁRGY (nappali/levelező munkarendben) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI
 SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 6 KRISTÁLYTAN VI. A KRIsTÁLYOs ANYAG belső RENDEZETTsÉGE 1. A KRIsTÁLYOs ÁLLAPOT A szilárd ANYAG jellemzője Az ásványok néhány kivételtől eltekintve kristályos
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 6 KRISTÁLYTAN VI. A KRIsTÁLYOs ANYAG belső RENDEZETTsÉGE 1. A KRIsTÁLYOs ÁLLAPOT A szilárd ANYAG jellemzője Az ásványok néhány kivételtől eltekintve kristályos
EGYENLŐTLEN ALAKVÁLTOZÁS KIMUTATÁSA ÚJRAKRISTÁLYOSODOTT SZERKEZETBEN DETECT OF THE NON UNIFORM DEFORMATION IN RECRISATLLIZED STRUCTURE
 EGYENLŐTLEN ALAKVÁLTOZÁS KIMUTATÁSA ÚJRAKRISTÁLYOSODOTT SZERKEZETBEN DETECT OF THE NON UNIFORM DEFORMATION IN RECRISATLLIZED STRUCTURE HRABÓCZKI EDINA, BARKÓCZY PÉTER Miskolci Egyetem, Anyagtudományi Intézet
EGYENLŐTLEN ALAKVÁLTOZÁS KIMUTATÁSA ÚJRAKRISTÁLYOSODOTT SZERKEZETBEN DETECT OF THE NON UNIFORM DEFORMATION IN RECRISATLLIZED STRUCTURE HRABÓCZKI EDINA, BARKÓCZY PÉTER Miskolci Egyetem, Anyagtudományi Intézet
Mikroszkóp vizsgálata Lencse görbületi sugarának mérése Folyadék törésmutatójának mérése
 Mikroszkóp vizsgálata Lencse görbületi sugarának mérése Folyadék törésmutatójának mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. március 19. (hétfő délelőtti csoport) 1. Mikroszkóp vizsgálata 1.1. A mérés
Mikroszkóp vizsgálata Lencse görbületi sugarának mérése Folyadék törésmutatójának mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. március 19. (hétfő délelőtti csoport) 1. Mikroszkóp vizsgálata 1.1. A mérés
Descartes-féle, derékszögű koordináta-rendszer
 Descartes-féle, derékszögű koordináta-rendszer A derékszögű koordináta-rendszerben a sík minden pontjához egy rendezett valós számpár rendelhető. A számpár első tagja (abszcissza) a pont y tengelytől mért
Descartes-féle, derékszögű koordináta-rendszer A derékszögű koordináta-rendszerben a sík minden pontjához egy rendezett valós számpár rendelhető. A számpár első tagja (abszcissza) a pont y tengelytől mért
43,2 27, Alakváltozás (%)
 Záró szakmai beszámoló a Acélok karbidkiválási folyamatainak vizsgálata; a szemcsehatárok és szemcseorientáció szerepe című, T048895 számú OTKA-projekthez 1. Ausztenites acélok vizsgálata A kutatás első
Záró szakmai beszámoló a Acélok karbidkiválási folyamatainak vizsgálata; a szemcsehatárok és szemcseorientáció szerepe című, T048895 számú OTKA-projekthez 1. Ausztenites acélok vizsgálata A kutatás első
Reális kristályok, rácshibák. Anyagtudomány gyakorlat 2006/2007 I.félév Gépész BSC
 Reális kristályok, rácshibák Anyagtudomány gyakorlat 2006/2007 I.félév Gépész BSC Valódi, reális kristályok Reális rács rendezetlenségeket, rácshibákat tartalmaz Az anyagok tulajdonságainak bizonyos csoportja
Reális kristályok, rácshibák Anyagtudomány gyakorlat 2006/2007 I.félév Gépész BSC Valódi, reális kristályok Reális rács rendezetlenségeket, rácshibákat tartalmaz Az anyagok tulajdonságainak bizonyos csoportja
Lövedékálló védőmellényekben alkalmazott ballisztikai kerámia azonosítása az atomsíkok közti rácssíktávolságok alapján
 Lövedékálló védőmellényekben alkalmazott ballisztikai kerámia azonosítása az atomsíkok közti rácssíktávolságok alapján Eur.Ing. Frank György c. docens SzVMSzK mérnök szakértő (B5, B6) Személy-, Vagyonvédelmi
Lövedékálló védőmellényekben alkalmazott ballisztikai kerámia azonosítása az atomsíkok közti rácssíktávolságok alapján Eur.Ing. Frank György c. docens SzVMSzK mérnök szakértő (B5, B6) Személy-, Vagyonvédelmi
Záróvizsga szakdolgozat. Mérési bizonytalanság meghatározásának módszertana metallográfiai vizsgálatoknál. Kivonat
 Záróvizsga szakdolgozat Mérési bizonytalanság meghatározásának módszertana metallográfiai vizsgálatoknál Kivonat Csali-Kovács Krisztina Minőségirányítási szakirány 2006 1 1. Bevezetés 1.1. A dolgozat célja
Záróvizsga szakdolgozat Mérési bizonytalanság meghatározásának módszertana metallográfiai vizsgálatoknál Kivonat Csali-Kovács Krisztina Minőségirányítási szakirány 2006 1 1. Bevezetés 1.1. A dolgozat célja
Szilárd testek rugalmassága
 Fizika villamosmérnököknek Szilárd testek rugalmassága Dr. Giczi Ferenc Széchenyi István Egyetem, Fizika és Kémia Tanszék Győr, Egyetem tér 1. 1 Deformálható testek (A merev test idealizált határeset.)
Fizika villamosmérnököknek Szilárd testek rugalmassága Dr. Giczi Ferenc Széchenyi István Egyetem, Fizika és Kémia Tanszék Győr, Egyetem tér 1. 1 Deformálható testek (A merev test idealizált határeset.)
Röntgendiffrakció. Orbán József PTE, ÁOK, Biofizikai Intézet november
 Röntgendiffrakció Orbán József PTE, ÁOK, Biofizikai Intézet 2013. november Előadás vázlata Röntgen sugárzás Interferencia, diffrakció (elektromágneses hullámok) Kristályok szerkezete Röntgendiffrakció
Röntgendiffrakció Orbán József PTE, ÁOK, Biofizikai Intézet 2013. november Előadás vázlata Röntgen sugárzás Interferencia, diffrakció (elektromágneses hullámok) Kristályok szerkezete Röntgendiffrakció
Összeállította: dr. Leitold Adrien egyetemi docens
 Az R 3 tér geometriája Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. 1 Vektorok Vektor: irányított szakasz Jel.: a, a, a, AB, Jellemzői: irány, hosszúság, (abszolút érték) jel.: a Speciális
Az R 3 tér geometriája Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. 1 Vektorok Vektor: irányított szakasz Jel.: a, a, a, AB, Jellemzői: irány, hosszúság, (abszolút érték) jel.: a Speciális
Matematikai geodéziai számítások 10.
 Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
1. tétel. 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója 7 cm. Mekkora a háromszög átfogója? (4 pont)
 1. tétel 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója cm. Mekkora a háromszög átfogója? (4 pont). Adott az ábrán két vektor. Rajzolja meg a b, a b és az a b vektorokat! (6 pont)
1. tétel 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója cm. Mekkora a háromszög átfogója? (4 pont). Adott az ábrán két vektor. Rajzolja meg a b, a b és az a b vektorokat! (6 pont)
Al-Mg-Si háromalkotós egyensúlyi fázisdiagram közelítő számítása
 l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
Vázlatos tartalom. Szerkezet jellemzése és vizsgálata Szilárdtestek elektronszerkezete Rácsdinamika Transzportjelenségek Mágneses tulajdonságok
 Szilárdtestfizika Kondenzált Anyagok Fizikája Vázlatos tartalom Szerkezet jellemzése és vizsgálata Szilárdtestek elektronszerkezete Rácsdinamika Transzportjelenségek Mágneses tulajdonságok 2 Szerkezet
Szilárdtestfizika Kondenzált Anyagok Fizikája Vázlatos tartalom Szerkezet jellemzése és vizsgálata Szilárdtestek elektronszerkezete Rácsdinamika Transzportjelenségek Mágneses tulajdonságok 2 Szerkezet
Frissítve: 2015.04.29. Feszültség- és alakváltozási állapot. 1. példa: Írjuk fel az adott kockához tartozó feszültségtenzort!
 1. példa: Írjuk fel az adott kockához tartozó feszültségtenzort! 1 / 20 2. példa: Rajzoljuk fel az adott feszültségtenzorhoz tartozó kockát! 2 / 20 3. példa: Feszültségvektor számítása. Egy alkatrész egy
1. példa: Írjuk fel az adott kockához tartozó feszültségtenzort! 1 / 20 2. példa: Rajzoljuk fel az adott feszültségtenzorhoz tartozó kockát! 2 / 20 3. példa: Feszültségvektor számítása. Egy alkatrész egy
7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék)
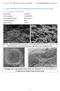 7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék) 7.1.1. SPS: 1150 C; 5 (1312 K1) Mért sűrűség: 3,795 g/cm 3 3,62 0,14 GPa Három pontos törés teszt: 105 4,2 GPa Súrlódási együttható:
7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék) 7.1.1. SPS: 1150 C; 5 (1312 K1) Mért sűrűség: 3,795 g/cm 3 3,62 0,14 GPa Három pontos törés teszt: 105 4,2 GPa Súrlódási együttható:
Mérési hibák 2006.10.04. 1
 Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
Statisztika - bevezetés Méréselmélet PE MIK MI_BSc VI_BSc 1
 Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
KÉPLÉKENYALAKÍTÁS ELMÉLETI ALAPJAI
 KÉPLÉKENYALAKÍTÁS ELMÉLETI ALAPJAI ANYAGMÉRNÖK ALAPKÉPZÉS KÉPLÉKENYALAKÍTÁSI SZAKIRÁNY TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR FÉMTANI, KÉPLÉKENYALAKÍTÁSI ÉS NANOTECHNOLÓGIA
KÉPLÉKENYALAKÍTÁS ELMÉLETI ALAPJAI ANYAGMÉRNÖK ALAPKÉPZÉS KÉPLÉKENYALAKÍTÁSI SZAKIRÁNY TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR FÉMTANI, KÉPLÉKENYALAKÍTÁSI ÉS NANOTECHNOLÓGIA
Infobionika ROBOTIKA. X. Előadás. Robot manipulátorok II. Direkt és inverz kinematika. Készült a HEFOP P /1.0 projekt keretében
 Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
METALLOGRÁFIA. ANYAGMÉRNÖK BSc KÉPZÉS. (nappali munkarendben) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR
 ANYAGMÉRNÖK BSc KÉPZÉS (nappali munkarendben) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR FÉMTANI, KÉPLÉKENYALAKÍTÁSI ÉS NANOTECHNOLÓGIAI INTÉZET Miskolc, 2018/1. II. félév
ANYAGMÉRNÖK BSc KÉPZÉS (nappali munkarendben) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR FÉMTANI, KÉPLÉKENYALAKÍTÁSI ÉS NANOTECHNOLÓGIAI INTÉZET Miskolc, 2018/1. II. félév
Példa: Normálfeszültség eloszlása síkgörbe rúd esetén
 Példa: Normálfeszültség eloszlása síkgörbe rúd esetén Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 20. Az 1. ábrán vázolt síkgörbe rúd méretei és terhelése ismert.
Példa: Normálfeszültség eloszlása síkgörbe rúd esetén Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 20. Az 1. ábrán vázolt síkgörbe rúd méretei és terhelése ismert.
9. Fényhullámhossz és diszperzió mérése jegyzőkönyv
 9. Fényhullámhossz és diszperzió mérése jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 008. 11. 1. Leadás dátuma: 008. 11. 19. 1 1. A mérési összeállítás A méréseket speciális szögmérő eszközzel
9. Fényhullámhossz és diszperzió mérése jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 008. 11. 1. Leadás dátuma: 008. 11. 19. 1 1. A mérési összeállítás A méréseket speciális szögmérő eszközzel
Az alakítással bevitt energia hatása az ausztenit átalakulási hőmérsékletére
 Az alakítással bevitt energia hatása az ausztenit átalakulási hőmérsékletére Csepeli Zsolt Bereczki Péter Kardos Ibolya Verő Balázs Workshop Miskolc, 2013.09.06. Előadás vázlata Bevezetés Vizsgálat célja,
Az alakítással bevitt energia hatása az ausztenit átalakulási hőmérsékletére Csepeli Zsolt Bereczki Péter Kardos Ibolya Verő Balázs Workshop Miskolc, 2013.09.06. Előadás vázlata Bevezetés Vizsgálat célja,
Ütőmunka meghatározása acél próbatesten, Charpy-kalapáccsal, amely ingás ütő-hajlítómű (Charpyinga) Dr. Kausay Tibor
 Ütőmunka meghatározása acél próbatesten, Charpy-kalapáccsal, amely ingás ütő-hajlítómű (Charpyinga) Dr. Kausay Tibor Dr. Kausay Tibor 1 Charpy-kalapács, 10 m kp = 100 J legnagyobb ütőenergiával A vizsgálatot
Ütőmunka meghatározása acél próbatesten, Charpy-kalapáccsal, amely ingás ütő-hajlítómű (Charpyinga) Dr. Kausay Tibor Dr. Kausay Tibor 1 Charpy-kalapács, 10 m kp = 100 J legnagyobb ütőenergiával A vizsgálatot
A végeselem módszer alapjai. 2. Alapvető elemtípusok
 A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet
 Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet 2. előadás A rugalmas lemezelmélet alapfeltevései A lemez anyaga homogén, izotróp, lineárisan rugalmas (Hooke törvény); A terheletlen állapotban
Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet 2. előadás A rugalmas lemezelmélet alapfeltevései A lemez anyaga homogén, izotróp, lineárisan rugalmas (Hooke törvény); A terheletlen állapotban
Tevékenység: Tanulmányozza a ábrát és a levezetést! Tanulja meg a fajlagos nyúlás mértékének meghatározásának módját hajlításnál!
 Tanulmányozza a.3.6. ábrát és a levezetést! Tanulja meg a fajlagos nyúlás mértékének meghatározásának módját hajlításnál! Az alakváltozás mértéke hajlításnál Hajlításnál az alakváltozást mérnöki alakváltozási
Tanulmányozza a.3.6. ábrát és a levezetést! Tanulja meg a fajlagos nyúlás mértékének meghatározásának módját hajlításnál! Az alakváltozás mértéke hajlításnál Hajlításnál az alakváltozást mérnöki alakváltozási
Optika gyakorlat 5. Gyakorló feladatok
 Optika gyakorlat 5. Gyakorló feladatok. példa: Leképezés - Fruzsika játszik Fruzsika több nagy darab ívelt üveget tart maga elé. Határozd meg, hogy milyen típusú objektívek (gyűjtő/szóró) ezek, és milyen
Optika gyakorlat 5. Gyakorló feladatok. példa: Leképezés - Fruzsika játszik Fruzsika több nagy darab ívelt üveget tart maga elé. Határozd meg, hogy milyen típusú objektívek (gyűjtő/szóró) ezek, és milyen
Mágneses szuszceptibilitás mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 7. MÉRÉS Mágneses szuszceptibilitás mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 5. Szerda délelőtti csoport 1. A mérés célja Az
KLASSZIKUS FIZIKA LABORATÓRIUM 7. MÉRÉS Mágneses szuszceptibilitás mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 5. Szerda délelőtti csoport 1. A mérés célja Az
FÉMÖTVÖZETEK HŐKEZELÉSE
 FÉMÖTVÖZETEK HŐKEZELÉSE ANYAGMÉRNÖK BSC KÉPZÉS (nappali munkarendben) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR FÉMTANI, KÉPLÉKENYALAKÍTÁSI ÉS NANOTECHNOLÓGIAI INTÉZET
FÉMÖTVÖZETEK HŐKEZELÉSE ANYAGMÉRNÖK BSC KÉPZÉS (nappali munkarendben) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR FÉMTANI, KÉPLÉKENYALAKÍTÁSI ÉS NANOTECHNOLÓGIAI INTÉZET
Modern Fizika Labor Fizika BSC
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. április 20. A mérés száma és címe: 20. Folyadékáramlások 2D-ban Értékelés: A beadás dátuma: 2009. április 28. A mérést végezte: Márton Krisztina Zsigmond
Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. április 20. A mérés száma és címe: 20. Folyadékáramlások 2D-ban Értékelés: A beadás dátuma: 2009. április 28. A mérést végezte: Márton Krisztina Zsigmond
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar. Villamos Energetika Tanszék. Világítástechnika (BME VIVEM 355)
 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Villamos Energetika Tanszék Világítástechnika (BME VIVEM 355) Beltéri mérés Világítástechnikai felülvizsgálati jegyzőkönyv
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Villamos Energetika Tanszék Világítástechnika (BME VIVEM 355) Beltéri mérés Világítástechnikai felülvizsgálati jegyzőkönyv
Transzformátor rezgés mérés. A BME Villamos Energetika Tanszéken
 Transzformátor rezgés mérés A BME Villamos Energetika Tanszéken A valóság egyszerűsítése, modellezés. A mérés tervszerűen végrehajtott tevékenység, ezért a bonyolult valóságos rendszert először egyszerűsítik.
Transzformátor rezgés mérés A BME Villamos Energetika Tanszéken A valóság egyszerűsítése, modellezés. A mérés tervszerűen végrehajtott tevékenység, ezért a bonyolult valóságos rendszert először egyszerűsítik.
CONSTEEL 8 ÚJDONSÁGOK
 CONSTEEL 8 ÚJDONSÁGOK Verzió 8.0 2013.11.20 www.consteelsoftware.com Tartalomjegyzék 1. Szerkezet modellezés... 2 1.1 Új szelvénykatalógusok... 2 1.2 Diafragma elem... 2 1.3 Merev test... 2 1.4 Rúdelemek
CONSTEEL 8 ÚJDONSÁGOK Verzió 8.0 2013.11.20 www.consteelsoftware.com Tartalomjegyzék 1. Szerkezet modellezés... 2 1.1 Új szelvénykatalógusok... 2 1.2 Diafragma elem... 2 1.3 Merev test... 2 1.4 Rúdelemek
Lengyelné Dr. Szilágyi Szilvia április 7.
 ME, Anaĺızis Tanszék 2010. április 7. , alapfogalmak 2.1. Definíció A H 1, H 2,..., H n R (ahol n 2 egész szám) nemüres valós számhalmazok H 1 H 2... H n Descartes-szorzatán a következő halmazt értjük:
ME, Anaĺızis Tanszék 2010. április 7. , alapfogalmak 2.1. Definíció A H 1, H 2,..., H n R (ahol n 2 egész szám) nemüres valós számhalmazok H 1 H 2... H n Descartes-szorzatán a következő halmazt értjük:
A technológiai paraméterek hatása az Al 2 O 3 kerámiák mikrostruktúrájára és hajlítószilárdságára
 Bevezetés A technológiai paraméterek hatása az Al 2 O 3 kerámiák mikrostruktúrájára és hajlítószilárdságára Csányi Judit 1, Dr. Gömze A. László 2 1 doktorandusz, 2 tanszékvezető egyetemi docens Miskolci
Bevezetés A technológiai paraméterek hatása az Al 2 O 3 kerámiák mikrostruktúrájára és hajlítószilárdságára Csányi Judit 1, Dr. Gömze A. László 2 1 doktorandusz, 2 tanszékvezető egyetemi docens Miskolci
Példa: Háromszög síkidom másodrendű nyomatékainak számítása
 Példa: Háromszög síkidom másodrendű nyomatékainak számítása Készítette: Dr. Kossa Attila kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék. február 6. Határozzuk meg az alábbi ábrán látható derékszögű háromszög
Példa: Háromszög síkidom másodrendű nyomatékainak számítása Készítette: Dr. Kossa Attila kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék. február 6. Határozzuk meg az alábbi ábrán látható derékszögű háromszög
Fázisátalakulások vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 6. MÉRÉS Fázisátalakulások vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. szeptember 28. Szerda délelőtti csoport 1. A mérés célja A mérés
KLASSZIKUS FIZIKA LABORATÓRIUM 6. MÉRÉS Fázisátalakulások vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. szeptember 28. Szerda délelőtti csoport 1. A mérés célja A mérés
A bifiláris felfüggesztésű rúd mozgásáról
 1 A bifiláris felfüggesztésű rúd mozgásáról A végein fonállal felfüggesztett egyenes rúd részleges erőtani vizsgálatát mutattuk be egy korábbi dolgozatunkban, melynek címe: Forgatónyomaték mérése - I.
1 A bifiláris felfüggesztésű rúd mozgásáról A végein fonállal felfüggesztett egyenes rúd részleges erőtani vizsgálatát mutattuk be egy korábbi dolgozatunkban, melynek címe: Forgatónyomaték mérése - I.
HÍDTARTÓK ELLENÁLLÁSTÉNYEZŐJE
 HÍDTARTÓK ELLENÁLLÁSTÉNYEZŐJE Csécs Ákos * - Dr. Lajos Tamás ** RÖVID KIVONAT A Budapesti Műszaki és Gazdaságtudományi Egyetem Hidak és Szerkezetek Tanszéke megbízta a BME Áramlástan Tanszékét az M8-as
HÍDTARTÓK ELLENÁLLÁSTÉNYEZŐJE Csécs Ákos * - Dr. Lajos Tamás ** RÖVID KIVONAT A Budapesti Műszaki és Gazdaságtudományi Egyetem Hidak és Szerkezetek Tanszéke megbízta a BME Áramlástan Tanszékét az M8-as
Az ipari komputer tomográfia vizsgálati lehetőségei
 Az ipari komputer tomográfia vizsgálati lehetőségei Dr. Czinege Imre, Kozma István Széchenyi István Egyetem 6. ANYAGVIZSGÁLAT A GYAKORLATBAN KONFERENCIA Cegléd, 2012. június 7-8. Tartalom A CT technika
Az ipari komputer tomográfia vizsgálati lehetőségei Dr. Czinege Imre, Kozma István Széchenyi István Egyetem 6. ANYAGVIZSGÁLAT A GYAKORLATBAN KONFERENCIA Cegléd, 2012. június 7-8. Tartalom A CT technika
Modern Fizika Labor Fizika BSC
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. február 23. A mérés száma és címe: 17. Folyadékkristályok Értékelés: A beadás dátuma: 2009. március 2. A mérést végezte: Zsigmond Anna Márton Krisztina
Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. február 23. A mérés száma és címe: 17. Folyadékkristályok Értékelés: A beadás dátuma: 2009. március 2. A mérést végezte: Zsigmond Anna Márton Krisztina
DIGITÁLIS TEREPMODELL A TÁJRENDEZÉSBEN
 DIGITÁLIS TEREPMODELL A TÁJRENDEZÉSBEN DR. GIMESI LÁSZLÓ Bevezetés Pécsett és környékén végzett bányászati tevékenység felszámolása kapcsán szükségessé vált az e tevékenység során keletkezett meddők, zagytározók,
DIGITÁLIS TEREPMODELL A TÁJRENDEZÉSBEN DR. GIMESI LÁSZLÓ Bevezetés Pécsett és környékén végzett bányászati tevékenység felszámolása kapcsán szükségessé vált az e tevékenység során keletkezett meddők, zagytározók,
Optika gyakorlat 6. Interferencia. I = u 2 = u 1 + u I 2 cos( Φ)
 Optika gyakorlat 6. Interferencia Interferencia Az interferencia az a jelenség, amikor kett vagy több hullám fázishelyes szuperpozíciója révén a térben állóhullám kép alakul ki. Ez elektromágneses hullámok
Optika gyakorlat 6. Interferencia Interferencia Az interferencia az a jelenség, amikor kett vagy több hullám fázishelyes szuperpozíciója révén a térben állóhullám kép alakul ki. Ez elektromágneses hullámok
Kondenzált anyagok fizikája 1. zárthelyi dolgozat
 Név: Neptun-kód: Kondenzált anyagok fizikája 1. zárthelyi dolgozat 2015. november 5. 16 00 18 00 Fontosabb tudnivalók Ne felejtse el beírni a nevét és a Neptun-kódját a fenti üres mezőkbe. Minden feladat
Név: Neptun-kód: Kondenzált anyagok fizikája 1. zárthelyi dolgozat 2015. november 5. 16 00 18 00 Fontosabb tudnivalók Ne felejtse el beírni a nevét és a Neptun-kódját a fenti üres mezőkbe. Minden feladat
Ipari jelölő lézergépek alkalmazása a gyógyszer- és elektronikai iparban
 Gyártás 08 konferenciára 2008. november 6-7. Ipari jelölő lézergépek alkalmazása a gyógyszer- és elektronikai iparban Szerző: Varga Bernadett, okl. gépészmérnök, III. PhD hallgató a BME VIK ET Tanszékén
Gyártás 08 konferenciára 2008. november 6-7. Ipari jelölő lézergépek alkalmazása a gyógyszer- és elektronikai iparban Szerző: Varga Bernadett, okl. gépészmérnök, III. PhD hallgató a BME VIK ET Tanszékén
A diplomaterv keretében megvalósítandó feladatok összefoglalása
 A diplomaterv keretében megvalósítandó feladatok összefoglalása Diplomaterv céljai: 1 Sclieren résoptikai módszer numerikus szimulációk validálására való felhasználhatóságának vizsgálata 2 Lamináris előkevert
A diplomaterv keretében megvalósítandó feladatok összefoglalása Diplomaterv céljai: 1 Sclieren résoptikai módszer numerikus szimulációk validálására való felhasználhatóságának vizsgálata 2 Lamináris előkevert
Rugalmas állandók mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 2. MÉRÉS Rugalmas állandók mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 16. Szerda délelőtti csoport 1. A mérés rövid leírása Mérésem
KLASSZIKUS FIZIKA LABORATÓRIUM 2. MÉRÉS Rugalmas állandók mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 16. Szerda délelőtti csoport 1. A mérés rövid leírása Mérésem
E-tananyag Matematika 9. évfolyam 2014. Függvények
 Függvények Függvények értelmezése Legyen adott az A és B két nem üres halmaz. Az A halmaz minden egyes eleméhez rendeljük hozzá a B halmaz egy-egy elemét. Ez a hozzárendelés egyértelmű, és ezt a hozzárendelést
Függvények Függvények értelmezése Legyen adott az A és B két nem üres halmaz. Az A halmaz minden egyes eleméhez rendeljük hozzá a B halmaz egy-egy elemét. Ez a hozzárendelés egyértelmű, és ezt a hozzárendelést
Szilárdságnövelés. Az előkészítő témakörei
 ANYAGTUDOMÁNY ÉS TECHNOLÓGIA TANSZÉK Alapképzés Anyagszerkezettan és anyagvizsgálat 2007/08 Szilárdságnövelés Dr. Palotás Béla palotasb@eik.bme.hu Dr. Németh Árpád arpinem@eik.bme.hu Szilárdság növelés
ANYAGTUDOMÁNY ÉS TECHNOLÓGIA TANSZÉK Alapképzés Anyagszerkezettan és anyagvizsgálat 2007/08 Szilárdságnövelés Dr. Palotás Béla palotasb@eik.bme.hu Dr. Németh Árpád arpinem@eik.bme.hu Szilárdság növelés
x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs mátrixa 3D-ben?
 . Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
. Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
2. Rugalmas állandók mérése
 2. Rugalmas állandók mérése Klasszikus fizika laboratórium Mérési jegyzőkönyv Mérést végezte: Vitkóczi Fanni Jegyzőkönyv leadásának időpontja: 2012. 12. 15. I. A mérés célja: Két anyag Young-modulusának
2. Rugalmas állandók mérése Klasszikus fizika laboratórium Mérési jegyzőkönyv Mérést végezte: Vitkóczi Fanni Jegyzőkönyv leadásának időpontja: 2012. 12. 15. I. A mérés célja: Két anyag Young-modulusának
Dankházi Z., Kalácska Sz., Baris A., Varga G., Ratter K., Radi Zs.*, Havancsák K.
 Dankházi Z., Kalácska Sz., Baris A., Varga G., Ratter K., Radi Zs.*, Havancsák K. ELTE, TTK KKMC, 1117 Budapest, Pázmány Péter sétány 1/A. * Technoorg Linda Kft., 1044 Budapest, Ipari Park utca 10. Műszer:
Dankházi Z., Kalácska Sz., Baris A., Varga G., Ratter K., Radi Zs.*, Havancsák K. ELTE, TTK KKMC, 1117 Budapest, Pázmány Péter sétány 1/A. * Technoorg Linda Kft., 1044 Budapest, Ipari Park utca 10. Műszer:
Pontműveletek. Sergyán Szabolcs Óbudai Egyetem Neumann János Informatikai Kar február 20.
 Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
Érdekes geometriai számítások Téma: A kardáncsukló kinematikai alapegyenletének levezetése gömbháromszögtani alapon
 Érdekes geometriai számítások 7. Folytatjuk a sorozatot. 7. Téma: A kardáncsukló kinematikai alapegyenletének levezetése gömbháromszögtani alapon Korábbi dolgozatainkban már többféle módon is bemutattuk
Érdekes geometriai számítások 7. Folytatjuk a sorozatot. 7. Téma: A kardáncsukló kinematikai alapegyenletének levezetése gömbháromszögtani alapon Korábbi dolgozatainkban már többféle módon is bemutattuk
Röntgen-gamma spektrometria
 Röntgen-gamma spektrométer fejlesztése radioaktív anyagok elemi összetétele és izotópszelektív radioaktivitása egyidejű meghatározására Szalóki Imre, Gerényi Anita, Radócz Gábor Nukleáris Technikai Intézet
Röntgen-gamma spektrométer fejlesztése radioaktív anyagok elemi összetétele és izotópszelektív radioaktivitása egyidejű meghatározására Szalóki Imre, Gerényi Anita, Radócz Gábor Nukleáris Technikai Intézet
Felületek differenciálgeometriai vizsgálata
 Felületek differenciálgeometriai vizsgálata Felületek differenciálgeometriai értelemben Felület: Olyan alakzat, amely előállítható az (u,v) sík egy összefüggő tartományán értelmezett r(u,v) kétparaméteres
Felületek differenciálgeometriai vizsgálata Felületek differenciálgeometriai értelemben Felület: Olyan alakzat, amely előállítható az (u,v) sík egy összefüggő tartományán értelmezett r(u,v) kétparaméteres
Elektrooptikai effektus
 Elektrooptikai effektus Alapelv: A Pockels effektus az a jelenség, amikor egy eredendően kettőstörő anyag kettőstörő tulajdonsága megváltozik az alkalmazott elektromos tér hatására, és a változás lineáris
Elektrooptikai effektus Alapelv: A Pockels effektus az a jelenség, amikor egy eredendően kettőstörő anyag kettőstörő tulajdonsága megváltozik az alkalmazott elektromos tér hatására, és a változás lineáris
A tér lineáris leképezései síkra
 A tér lineáris leképezései síkra Az ábrázoló geometria célja: A háromdimenziós térben elhelyezkedő alakzatok helyzeti és metrikus viszonyainak egyértelmű és egyértelműen rekonstruálható módon történő ábrázolása
A tér lineáris leképezései síkra Az ábrázoló geometria célja: A háromdimenziós térben elhelyezkedő alakzatok helyzeti és metrikus viszonyainak egyértelmű és egyértelműen rekonstruálható módon történő ábrázolása
Al59 VILLAMOS IPARI CÉLÚ HUZAL GYÁRTÁSÁNAK VIZSGÁLATA REVIEW OF THE PRODUCTION OF ELECTRICAL PURPOSE WIRE FROM ALLOY Al59
 Anyagmérnöki Tudományok, 37. kötet, 1. szám (01), pp. 343 349. Al59 VILLAMOS IPARI CÉLÚ HUZAL GYÁRTÁSÁNAK VIZSGÁLATA REVIEW OF THE PRODUCTION OF ELECTRICAL PURPOSE WIRE FROM ALLOY Al59 POLYÁK ATTILA, MERTINGER
Anyagmérnöki Tudományok, 37. kötet, 1. szám (01), pp. 343 349. Al59 VILLAMOS IPARI CÉLÚ HUZAL GYÁRTÁSÁNAK VIZSGÁLATA REVIEW OF THE PRODUCTION OF ELECTRICAL PURPOSE WIRE FROM ALLOY Al59 POLYÁK ATTILA, MERTINGER
Fényhullámhossz és diszperzió mérése
 Fényhullámhossz és diszperzió mérése Mérő neve: Márkus Bence Gábor Mérőpár neve: Székely Anna Krisztina Szerda délelőtti csoport Mérés ideje: 11/09/011 Beadás ideje: 11/16/011 1 1. A mérés rövid leírása
Fényhullámhossz és diszperzió mérése Mérő neve: Márkus Bence Gábor Mérőpár neve: Székely Anna Krisztina Szerda délelőtti csoport Mérés ideje: 11/09/011 Beadás ideje: 11/16/011 1 1. A mérés rövid leírása
Hangfrekvenciás mechanikai rezgések vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
Szerkezetvizsgálat ANYAGMÉRNÖK ALAPKÉPZÉS (BSc)
 Szerkezetvizsgálat ANYAGMÉRNÖK ALAPKÉPZÉS (BSc) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR ANYAGTUDOMÁNYI INTÉZET Miskolc, 2008. 1. Tantárgyleírás Szerkezetvizsgálat kommunikációs
Szerkezetvizsgálat ANYAGMÉRNÖK ALAPKÉPZÉS (BSc) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR ANYAGTUDOMÁNYI INTÉZET Miskolc, 2008. 1. Tantárgyleírás Szerkezetvizsgálat kommunikációs
Mechatronika segédlet 3. gyakorlat
 Mechatronika segédlet 3. gyakorlat 2017. február 20. Tartalom Vadai Gergely, Faragó Dénes Feladatleírás... 2 Fogaskerék... 2 Nézetváltás 3D modellezéshez... 2 Könnyítés megvalósítása... 2 A fogaskerék
Mechatronika segédlet 3. gyakorlat 2017. február 20. Tartalom Vadai Gergely, Faragó Dénes Feladatleírás... 2 Fogaskerék... 2 Nézetváltás 3D modellezéshez... 2 Könnyítés megvalósítása... 2 A fogaskerék
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI
 SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 7 KRISTÁLYTAN VII. A KRIsTÁLYOK szimmetriája 1. BEVEZETÉs Az elemi cella és ebből eredően a térrácsnak a szimmetriáját a kristályok esetében az atomok, ionok
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 7 KRISTÁLYTAN VII. A KRIsTÁLYOK szimmetriája 1. BEVEZETÉs Az elemi cella és ebből eredően a térrácsnak a szimmetriáját a kristályok esetében az atomok, ionok
Fémötvözetek hőkezelése ANYAGMÉRNÖKI ALAPKÉPZÉS (BSc) Hőkezelési szakirány
 Fémötvözetek hőkezelése ANYAGMÉRNÖKI ALAPKÉPZÉS (BSc) Hőkezelési szakirány TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR ANYAGTUDOMÁNYI INTÉZET Miskolc, 2008. 1. Tantárgyleírás
Fémötvözetek hőkezelése ANYAGMÉRNÖKI ALAPKÉPZÉS (BSc) Hőkezelési szakirány TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR ANYAGTUDOMÁNYI INTÉZET Miskolc, 2008. 1. Tantárgyleírás
Az elliptikus hengerre írt csavarvonalról
 1 Az elliptikus hengerre írt csavarvonalról Erről viszonylag ritkán olvashatunk, ezért most erről lesz szó. Az [ 1 ] munkában találtuk az alábbi részt 1. ábra. 1. ábra Itt a ( c ) feladat és annak megoldása
1 Az elliptikus hengerre írt csavarvonalról Erről viszonylag ritkán olvashatunk, ezért most erről lesz szó. Az [ 1 ] munkában találtuk az alábbi részt 1. ábra. 1. ábra Itt a ( c ) feladat és annak megoldása
5.1. ábra. Ábra a 36A-2 feladathoz
 5. Gyakorlat 36A-2 Ahogyan a 5. ábrán látható, egy fénysugár 5 o beesési szöggel esik síktükörre és a 3 m távolságban levő skálára verődik vissza. Milyen messzire mozdul el a fényfolt, ha a tükröt 2 o
5. Gyakorlat 36A-2 Ahogyan a 5. ábrán látható, egy fénysugár 5 o beesési szöggel esik síktükörre és a 3 m távolságban levő skálára verődik vissza. Milyen messzire mozdul el a fényfolt, ha a tükröt 2 o
Modern Fizika Labor. 12. Infravörös spektroszkópia. Fizika BSc. A mérés dátuma: okt. 04. A mérés száma és címe: Értékelés:
 Modern Fizika Labor Fizika BSc A mérés dátuma: 011. okt. 04. A mérés száma és címe: 1. Infravörös spektroszkópia Értékelés: A beadás dátuma: 011. dec. 1. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 011. okt. 04. A mérés száma és címe: 1. Infravörös spektroszkópia Értékelés: A beadás dátuma: 011. dec. 1. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Andó Mátyás Felületi érdesség matyi.misi.eu. Felületi érdesség. 1. ábra. Felületi érdességi jelek
 1. Felületi érdesség használata Felületi érdesség A műszaki rajzokon a geometria méretek tűrése mellett a felületeket is jellemzik. A felületek jellemzésére leginkább a felületi érdességet használják.
1. Felületi érdesség használata Felületi érdesség A műszaki rajzokon a geometria méretek tűrése mellett a felületeket is jellemzik. A felületek jellemzésére leginkább a felületi érdességet használják.
11. Előadás Gradiens törésmutatójú közeg II.
 11. Előadás Gradiens törésmutatójú közeg II. A következőkben két különleges, gradiens törésmutatójú lencsével fogunk foglalkozni, az úgynevezett Luneburg-féle lencsékkel. Annak is két típusával: a Maxwell-féle
11. Előadás Gradiens törésmutatójú közeg II. A következőkben két különleges, gradiens törésmutatójú lencsével fogunk foglalkozni, az úgynevezett Luneburg-féle lencsékkel. Annak is két típusával: a Maxwell-féle
Modern Fizika Labor Fizika BSC
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. május 4. A mérés száma és címe: 9. Röntgen-fluoreszencia analízis Értékelés: A beadás dátuma: 2009. május 13. A mérést végezte: Márton Krisztina Zsigmond
Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. május 4. A mérés száma és címe: 9. Röntgen-fluoreszencia analízis Értékelés: A beadás dátuma: 2009. május 13. A mérést végezte: Márton Krisztina Zsigmond
Aszimmetrikus nyeregtető ~ feladat 2.
 1 Aszimmetrikus nyeregtető ~ feladat 2. Ehhez tekintsük az 1. ábrát is! Itt az A és B pontok egy nyeregtető oromfali ereszpontjai, a P pont pedig a taréj pontja. Az ereszek egymástól való távolságának
1 Aszimmetrikus nyeregtető ~ feladat 2. Ehhez tekintsük az 1. ábrát is! Itt az A és B pontok egy nyeregtető oromfali ereszpontjai, a P pont pedig a taréj pontja. Az ereszek egymástól való távolságának
ESR-spektrumok különbözı kísérleti körülmények között A számítógépes értékelés alapjai anizotróp kölcsönhatási tenzorok esetén
 ESR-spektrumok különbözı kísérleti körülmények között A számítógépes értékelés alapjai anizotróp kölcsönhatási tenzorok esetén A paraméterek anizotrópiája egykristályok rögzített tengely körüli forgatásakor
ESR-spektrumok különbözı kísérleti körülmények között A számítógépes értékelés alapjai anizotróp kölcsönhatási tenzorok esetén A paraméterek anizotrópiája egykristályok rögzített tengely körüli forgatásakor
Mágneses szuszceptibilitás mérése
 Mágneses szuszceptibilitás mérése Mérő neve: Márkus Bence Gábor Mérőpár neve: Székely Anna Krisztina Szerda délelőtti csoport Mérés ideje: 10/19/2011 Beadás ideje: 10/26/2011 1 1. A mérés rövid leírása
Mágneses szuszceptibilitás mérése Mérő neve: Márkus Bence Gábor Mérőpár neve: Székely Anna Krisztina Szerda délelőtti csoport Mérés ideje: 10/19/2011 Beadás ideje: 10/26/2011 1 1. A mérés rövid leírása
A főtengelyproblémához
 1 A főtengelyproblémához Korábbi, az ellipszis perspektivikus ábrázolásával foglalkozó dolgozatainkban előkerült a másodrendű görbék kanonikus alakra hozása, majd ebben a főtengelyrendszert előállító elforgatási
1 A főtengelyproblémához Korábbi, az ellipszis perspektivikus ábrázolásával foglalkozó dolgozatainkban előkerült a másodrendű görbék kanonikus alakra hozása, majd ebben a főtengelyrendszert előállító elforgatási
Optikai méréstechnika alkalmazása járműipari mérésekben Kornis János
 Optikai méréstechnika alkalmazása járműipari mérésekben Kornis János PhD, okleveles villamosmérnök, Budapesti Műszaki és Gazdaságtudományi Egyetem Fizika Tanszék, kornis@phy.bme.hu Absztrakt: Az optikai
Optikai méréstechnika alkalmazása járműipari mérésekben Kornis János PhD, okleveles villamosmérnök, Budapesti Műszaki és Gazdaságtudományi Egyetem Fizika Tanszék, kornis@phy.bme.hu Absztrakt: Az optikai
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások
 Megoldások 1. Tekintsük az alábbi szabályos hatszögben a következő vektorokat: a = AB és b = AF. Add meg az FO, DC, AO, AC, BE, FB, CE, DF vektorok koordinátáit az (a ; b ) koordinátarendszerben! Alkalmazzuk
Megoldások 1. Tekintsük az alábbi szabályos hatszögben a következő vektorokat: a = AB és b = AF. Add meg az FO, DC, AO, AC, BE, FB, CE, DF vektorok koordinátáit az (a ; b ) koordinátarendszerben! Alkalmazzuk
MATEMATIKA HETI 5 ÓRA
 EURÓPAI ÉRETTSÉGI 2008 MATEMATIKA HETI 5 ÓRA IDŐPONT : 2008. június 5 (reggel) A VIZSGA IDŐTARTAMA: 4 óra (240 perc) MEGENGEDETT ESZKÖZÖK: Európai képletgyűjtemény Nem programozható, nem grafikus számológép
EURÓPAI ÉRETTSÉGI 2008 MATEMATIKA HETI 5 ÓRA IDŐPONT : 2008. június 5 (reggel) A VIZSGA IDŐTARTAMA: 4 óra (240 perc) MEGENGEDETT ESZKÖZÖK: Európai képletgyűjtemény Nem programozható, nem grafikus számológép
MATEMATIKA HETI 5 ÓRA. IDŐPONT: 2009. június 8.
 EURÓPAI ÉRETTSÉGI 2009 MATEMATIKA HETI 5 ÓRA IDŐPONT: 2009. június 8. A VIZSGA IDŐTARTAMA: 4 óra (240 perc) ENGEDÉLYEZETT SEGÉDESZKÖZÖK : Európai képletgyűjtemény Nem programozható, nem grafikus kalkulátor
EURÓPAI ÉRETTSÉGI 2009 MATEMATIKA HETI 5 ÓRA IDŐPONT: 2009. június 8. A VIZSGA IDŐTARTAMA: 4 óra (240 perc) ENGEDÉLYEZETT SEGÉDESZKÖZÖK : Európai képletgyűjtemény Nem programozható, nem grafikus kalkulátor
Havancsák Károly Nagyfelbontású kétsugaras pásztázó elektronmikroszkóp az ELTÉ-n: lehetőségek, eddigi eredmények
 Havancsák Károly Nagyfelbontású kétsugaras pásztázó elektronmikroszkóp az ELTÉ-n: lehetőségek, eddigi eredmények Nanoanyagok és nanotechnológiák Albizottság ELTE TTK 2013. Havancsák Károly Nagyfelbontású
Havancsák Károly Nagyfelbontású kétsugaras pásztázó elektronmikroszkóp az ELTÉ-n: lehetőségek, eddigi eredmények Nanoanyagok és nanotechnológiák Albizottság ELTE TTK 2013. Havancsák Károly Nagyfelbontású
Havancsák Károly Az ELTE TTK kétsugaras pásztázó elektronmikroszkópja. Archeometriai műhely ELTE TTK 2013.
 Havancsák Károly Az ELTE TTK kétsugaras pásztázó elektronmikroszkópja Archeometriai műhely ELTE TTK 2013. Elektronmikroszkópok TEM SEM Transzmissziós elektronmikroszkóp Átvilágítós vékony minta < 100
Havancsák Károly Az ELTE TTK kétsugaras pásztázó elektronmikroszkópja Archeometriai műhely ELTE TTK 2013. Elektronmikroszkópok TEM SEM Transzmissziós elektronmikroszkóp Átvilágítós vékony minta < 100
