Szolvatációs modellek vizsgálata pontos elméleti pka számításokhoz
|
|
|
- Áron Fekete
- 6 évvel ezelőtt
- Látták:
Átírás
1 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Vegyészmérnöki és Biomérnöki Kar Szerves Kémiai és Technológiai Tanszék Szolvatációs modellek vizsgálata pontos elméleti pka számításokhoz TDK dolgozat Készítette Kováts Benjámin Gyógyszervegyész-mérnök MSc hallgató Témavezető Dr. Nagy József Egyetemi docens Konzulens Komjáti Balázs PhD hallgató Budapest, 2015.
2 Köszönetnyilvánítás Mindenekelőtt szeretnék köszönetet mondani Dr. Nagy József egyetemi docensnek, hogy tudományos diákköri munkámat az ő témavezetésével végezhettem. Köszönettel tartozom továbbá konzulensemnek Komjáti Balázs PhD hallgatónak, aki folyamatos támogatásával hozzájárult jelen dolgozat megírásához, és felbecsülhetetlen tanácsokkal segítette szakmai fejlődésemet. Köszönet illeti a Bioorganikus kémiai kutatócsoport minden tagját, hogy tanácsaikkal, javaslataikkal segítették kutatómunkámat. 2
3 Tartalom 1. Jelölések és idegen szavak jegyzéke Bevezetés A pk a szerepe a gyógyszerfejlesztésben pk a definíciója, összefüggése a szabadentalpiával A pk a definíciója A pka összefüggése a szabadentalpiával SCRF oldószermodellek PCM C-PCM IEF-PCM IPCM és SCIPCM COSMO SMD Irodalmi előzmények Saját számítások bemutatása: Deprotonálódási szabadentalpia számítása Vizsgált vegyületek Oldószermodellek eredményeinek áttekintése Oldószermodellek vizsgálata vízre Oldószermodellek vizsgálata acetonitrilre A legjobbnak ítélt oldószermodellek ismertetése Implicit oldószermodellek vízre Explicit oldószermodellek vízre Implicit oldószermodellek acetonitrilre Explicit oldószermodellek acetonitrilre Eredmények értékelése, következtetések Felhasznált irodalom
4 1. Jelölések és idegen szavak jegyzéke SCRF: Self-Consistent Reaction Field method: ön-konzisztens reakciómező módszer PCM: Polarizable Continuum Model, polarizálható kontinuum modell C-PCM: Conductor-like PCM, vezetőszerű polarizálható kontinuum modell IEF-PCM: Integral Equation Formalism PCM, integrálegyenlet szabályozású polarizálható kontinuum modell IPCM: Isodensity Polarizable Continuum Model, homogén sűrűségű polarizálható kontinuum modell SCIPCM: Self-Consistent Isodensity Polarizable Continuum Model, önkonzisztens homogén sűrűségű polarizálható kontinuum modell COSMO: COnductor-like Screening MOdel, vezető-szerű árnyékoló modell COSMO-RS: COnductor-like Screening MOdel for Real Solvents: vezető-szerű árnyékoló modell reális oldott anyag oldószer közötti kölcsönhatások leírásához SMD: Truhlar és munkatársai által kifejlesztett oldószermodell RMSD: Root-Mean-Square Deviation, az adott mennyiség négyzetes eltérései átlagának a gyöke R 2 : reziduális szórásnégyzet Max hiba: a legnagyobb eltérés kalibrációs egyenes alapján számolt, és kísérletileg meghatározott pk a érték között, ami az adott számítási sorozatban előfordul ε: IPCM és SCIPCM oldószermodellekkel végzett számítások során az adott oldószer dielektromos állandója Isodensity érték: IPCM és SCIPCM számítások során az összelektronsűrűség által meghatározott izofelület, vagyis az azonos elektronsűrűségű pontok által határolt felület UFF, Bondi, Pauling, UAHF, UAKS: különböző atomsugár modellek G(d,p), 6-31+G(d,p): John Pople és munkatársai által kifejlesztett felhasított vegyérték (split valence) bázisok diffúz és polarizációs függvényekkel DFT: Density Functional Theory, sűrűségfunkcionál elmélet SCF: Self-Consistent Field, önkonzisztens energia számítás M06-2X: hibrid-dft funkcionál TZ: Triple Zeta, háromszoros zéta minőségű bázis 4
5 2. Bevezetés A savas disszociációs állandó (pk a) a molekulák egy fontos kémiai tulajdonsága, mely meghatározhatja kémiai és biokémiai reakciók kimenetelét, a reaktivitást, és befolyásolhatja a reakciósebességet. A vegyületek pk a értékeit különböző kísérleti módszerekkel, általában víz, DMSO, vagy acetonitril oldószerekben határozzák meg. Reakciómechanizmusok tanulmányozása, gyógyszerhatóanyagok hatásának modellezése, valamint új vegyületek szintézisének kidolgozása szempontjából elengedhetetlen, hogy a pk a elméleti úton pontosan meghatározható legyen számításos kémiai módszerek alkalmazásával. Ismert, hogy a deprotonálódás során bekövetkező szabadentalpia változás és egy vegyület pk a értéke között lineáris összefüggés van. A deprotonáláshoz szükséges szabadentalpia kvantumkémiai számítási módszerekkel számítható, de értéke erősen függ az alkalmazott oldószermodell minőségétől, és annak paramétereitől. Jelenleg az irodalomban nem található olyan módszer, amivel a deprotonálódási szabadentalpia megbízhatóan számítható lenne anélkül, hogy a vegyületeket önkényesen csoportosítanánk. Jelen tanulmányban vizsgálom, a különböző oldószermodellekkel számolt deprotonálódási szabadentalpiák és kísérletileg meghatározott pk a értékek közötti összefüggést. Összehasonlítom ezen implicit oldószermodellekkel számolt adatokat egy explicit oldószer molekulát is tartalmazó (ezáltal specifikusabb szolvatációs modellt biztosító) számításokkal. A számításokat víz és acetonitril oldószerekre végeztem el. Az eredmények függvényében értékelem, hogy szükséges-e a semleges savak és a nitrogén tartalmú szerves bázisok konjugált savainak külön kezelése. 5
6 3. A pka szerepe a gyógyszerfejlesztésben A gyógyszerhatóanyagokat farmakokinetikai szempontból az ADME betűszó szerint vizsgálják. Jelentése: abszorpció, disztribúció, metabolizáció, elimináció. Gyakran LADME-ként említik, ahol az L betű a liberációt jelöli. A pk a érték sok szempontból nagyon jelentős szerepet tölt be az ADME során [1]. A liberáció a hatóanyag gyógyszerkészítményből történő felszabadulásának kinetikájával foglalkozik, az abszorpció a hatóanyag biomembránokon (gátakon) történő átjutásával. Ahhoz, hogy egy gyógyszer hatóanyaga eljusson a kívánt receptorig, különböző gátakon kell átjutnia. Ilyenek a vízterek közötti lipoid gátak: gasztrointesztinális gát, tüdő, hajszálerek rendszere, vér-agy gát, méhlepény, vese. Az abszorpciót különböző faktorok határozzák meg, többek között a molekula mérete, és töltése. Kis, hidrofób molekulák gyorsan átjutnak a foszfolipid kettősrétegen, a hidrofilek lassabban. A nagy mérettel rendelkező, töltött molekulák egyáltalán nem képesek áthatolni a lipoid gátakon. A gyógyszerhatóanyagok molekulái csak semleges, elektromos töltéssel nem rendelkező állapotukban képesek felszívódni a tápcsatorna megfelelő szakaszából [1]. A gyomor erősen savas (ph = ), míg a vékonybél lúgos (ph = 8.3) kémhatású közeget hordoz magában. Ennek következtében a savas karakterű anyagok felszívódása a gyomorban kezdődik, bázikus karakterű anyagok pedig a vékonybélből szívódnak fel leginkább [2]. Az, hogy egy adott ph-jú közegben egy vegyület hányad része van elektromosan semleges állapotban, azt a vegyület pka értéke szabja meg. Új gyógyszerhatóanyagok kutatása, és meglévő hatóanyagok fejlesztése szempontjából fontos, hogy a pk a értéket ne csak kísérletileg tudjuk meghatározni, hanem elméleti úton is. A pk a értékének elméleti úton történő becslése különösen akkor lehet előnyös, ha az adott vegyületből nagyon kevés áll rendelkezésre, drága, vagy még csak elméletben létezik. A gyógyszerfejlesztés kezdeti szakaszaiban molekulakönyvtárakat vizsgálnak, melyek sok szerkezetileg hasonló, de nem teljesen azonos molekulát tartalmaznak. Ha a vegyületek pk a értéke pontosan számítható, akkor megbízhatóbbá tehető az in silico gyógyszertervezés. Egy vegyület savasságának nem csak a liberáció és abszorpció során van jelentősége: a disztribúció során még előfordulhat, hogy a hatóanyagnak újabb lipoid gátakat kell legyőznie, hogy eljusson a megfelelő szövetbe, amilyen a vér-agy gát vagy a méhlepény. Fontos, hogy a hatás kifejtése után a hatóanyag bomlásterméke vízoldható legyen, és így kiürülhessen a szervezetből, így a metabolizáció, és elimináció során is jelentős szerepe van a különböző metabolitok pk a értékének [3]. 6
7 4. pka definíciója, összefüggése a szabadentalpiával 4.1 A pka definíciója Arrhenius szerint sav az a vegyület, amely proton leadására képes: HA H + + A 1. egyenlet Vizes közegben a hidrogén-ion nem szabad protonként van jelen. Vízzel oxónium-iont alkot, így a reakció felírható egy sav-bázis reakcióként [4]: HA + H 2 O A + H 3 O + 2. egyenlet A Brønsted és Lowry sav-bázis elméletek ennek általánosabb megfogalmazása. Az elmélet szerint egy sav-bázis reakcióban a sav protont ad le, a bázis protont vesz fel, így a reakció során konjugált sav és konjugált bázis keletkezik [4,5]. Lewis elmélete szerint a savak olyan anyagok, melyek elektronpárakceptorként viselkednek, így datív kovalens kötést alakítanak ki [4,6]. HA + B: A + BH + 3. egyenlet A 2. egyenletben szereplő reakció egyensúlyi állandója: K = {A }{H 3 O + } {HA}{H 2 O} 4. egyenlet ahol az {A - }-ként jelölt mennyiségek aktivitásokat jelölnek. Mivel az aktivitás a koncentráció és az aktivitási koefficiens szorzata, az egyenlet felírható a következő formában: K = [A ][H 3 O + ] [HA][H 2 O] γ γ A H3 O+ = [A ][H 3 O + ] γ HA γ H2 O [HA][H 2 O] Γ 5. egyenlet Ahol az [A - ]-ként jelölt mennyiségek koncentrációkat jelölnek. A γ-val jelölt mennyiségek aktivitások, Γ pedig a megfelelő aktivitások szorzatának a hányadosa. 7
8 Az aktivitásokkal való számolás kiküszöbölésének céljából a disszociációs állandók meghatározásánál olyan körülményeket biztosítanak, hogy Γ értéke állandó legyen, így a méréseket általában nagy ionerősségű közegekben végzik. Tovább egyszerűsödik a helyzet, ha feltételezzük, hogy a víz (vagy egyéb oldószer) mennyisége a folyamtat során állandó. Az egyszerűsítések végrehajtása után az oxónium-ion koncentrációja helyére a [H + ] kifejezést bevezetve: Így a pk a definíciója: K a = [H+ ][A ] [HA] 6. egyenlet pk a = lg K a = lg ( [H+ ][A ] ) [HA] 7. egyenlet 4.2 A pka összefüggése a szabadentalpiával A hagyományos definíció szerint Brønsted-sav bármilyen vegyület, ami protont tud leadni. A folyamat gáz fázisban az alábbi módon írható fel. [7]: AH g A + g + H g 8. egyenlet ahol a folyamat egyensúlyi állandója: K a. Egy vegyület pk a értéke egyenesen arányos a gázfázisban lejátszódó deprotonálódási reakció standard szabadentalpia változásával: ΔG 0 g g g = RT ln K a = RT pka 9. egyenlet ahol a g index a gázfázist jelöli. Természetes alapú logaritmusról áttérve 10-es alapú logaritmusra, elvégezve a lg(k a g ) = pka g behelyettesítést, majd az egyenletet átrendezve a következő kifejezéshez jutunk [1,8]: pk a g = 0 ΔG g RTln(10) = ΔG 0 g RT 10. egyenlet Vizes oldatban az egyensúly a következő egyenlet szerint alakul: AH aq + H 2 O aq A aq 11. egyenlet + + H 3 O aq 8
9 Ahol a folyamat egyensúlyi állandója: K = [A aq] [H 3 O + aq ] [AH aq ] [H 2 O aq ] 12. egyenlet Ebben a modellben a H 3 O + ion a H + ion egy vízmolekulával történő szolvatációjából következik ([H 3 O + aq ] = [H + aq ]), így K és K között a kapcsolat: K = K [H 2 O aq ] 13. egyenlet A fenti összefüggések következtében a szabadentalpia változás és pk a közötti összefüggés vizes oldatban: ΔG aq 0 K = RT lg ( [H 2 O aq ] ) 14. egyenlet Ha figyelembe vesszük, hogy az egyetemes gázállandó értéke R = kcal mol K, szobahőmérsékleten (T = K) a standard deprotonálási szabadentalpia vizes oldatban [7]: ΔG 0 aq ( kcal mol ) = pk a egyenlet akkor A folyamat nem csak vízben, hanem bármilyen egyéb oldószerben is hasonlóképpen felírható. Az oldatbeli ΔG 0 deprotonálási szabadentalpia számításával így meghatározható a vegyületek pk a értéke kizárólag elméleti alapon. A tapasztalatok azt mutatják, hogy a jelenleg használt kvantumkémiai számítási módszerekkel ΔG 0 értéke nem számítható kellő pontossággal, így a pk a becslés sem lesz pontos. Erre a problémára megoldás lehet, ha megfelelő kvantumkémiai számítási módszerrel kiszámítjuk számos vegyület deprotonálási szabadentalpiáját, majd az így kapott ΔG 0 értékeket ábrázoljuk a vizsgált oldószerben mért pk a értékük függvényében, és az így nyert pontokra kalibrációs egyenest illesztünk. A pk a és ΔG 0 között fennálló lineáris összefüggés következtében a meghatározott módszerrel számolt deprotonálási szabadentalpiát a kalibrációs egyenesbe behelyettesítve kiszámítható az adott vegyület pk a értéke. A kalibrációs egyenes alapján történő pk a meghatározásnak előnye, hogy olyan hibákat is ki lehet vele küszöbölni, amelyek a tisztán elméleti számítás nem tud figyelembe venni. 9
10 5. SCRF oldószermodellek Oldatban lejátszódó kémiai folyamatok elméleti szimulációja nem könnyű feladat. Alapvetően kétfajta megközelítést használnak: implicit és explicit oldószermodelleket. Az implicit oldószermodellek az oldott molekulát egy üregbe helyezik, melyet egy kontinuum vesz körül. Az explicit oldószermodellek oldószer molekulákkal veszik körbe az oldott anyagot, és így szimulálják a szolvatációt. Általánosságban elmondható, hogy az előbbi megközelítésnek sokkal kisebb a számítási ideje, mint az utóbbi módszernek. A két módszernek több fajta ötvözetét használják, például az oldott anyag egy molekulányi explicit oldószerrel alkotott egységét helyezik bele az üregbe, amit körbevesz egy kontinuum. Ha sok explicit oldószer molekulával vesszük körbe az oldott anyagot, a rendszer szabadsági fokának nagy száma miatt jelentősen megnőhet a számítási idő, ezen felül rengeteg elrendeződésnek az átlagát kell figyelembe vennünk a számítások során [9]. Ezek a tények gátat szabnak annak, hogy tisztán kvantummechanikai szinten tanulmányozzuk az oldott rendszereket, így egyszerűsített modelleket kell használnunk [10]. Az SCRF (Self-Consistent Reaction Field) önkonzisztens reakciómező módszer szerint az oldószert egy homogén kontinuum közeg veszi körül, ami egy üregbe helyezett oldott molekula által polarizálttá válik [11][12]. 5.1 PCM A polarizálható kontinuum modell (Polarizable Continuum Model) az SCRF oldószermodellek közé tartozik. Az oldott anyag, vagy az oldott anyag és néhány oldószer molekula szupermolekula-szerű egysége egy olyan üregben helyezkedik el, amit egy végtelen, polarizálható szigetelő vesz körül. Az oldott molekula polarizálja a szigetelőt, melynek következtében fellépő dielektromos polarizáció elektrosztatikus teret létrehozva megváltoztatja az oldott anyag töltéseloszlását [13][14][15]. Az üreg, amiben az oldott molekula elhelyezkedik, az oldott anyag atomjain, vagy atom-csoportjain központosított, egymással átfedésben lévő gömbökkel van körülvéve. A gömbökhöz többféle atomsugarat használnak UFF [16], UAHF [17], UAKS [18], Bondi [19], Pauling [20]. A gömbök sugara leggyakrabban 1,10 1,20-szorosa a használt atomsugárnak [9][21]. Az üreg feloszlik kisebb egységekre, ahova a polarizációs töltések elhelyezése történik. Általános PCM számolásoknál ezeket az egységeket úgy alakítják ki, hogy minden gömbre 60 db háromszöget vetítenek, így pentakiszdodekahedronok állnak elő. Az egymással átfedésben lévő egységeket elvetik, és az alakzatokat arra alkalmas sokszögekkel helyettesítik [10][22]. 10
11 5.1.1 C-PCM A C-PCM vezetőszerű polarizálható kontinuum modellt (Conductor-like PCM) a PCM alapján fejlesztették ki. Az oldott anyag itt is az atom, vagy atom-csoport központú gömbök által határolt üregben helyezkedik el. Az üregen belül a dielektromos állandó ugyanaz, mint vákuumban, kívül pedig az oldószernek megfelelő értéket veszi fel [23]. Az üreg, meghatározása után megtörténik a kis mozaikszerű egységekre osztása, és feltérképezése. Minden kis egységet a középpontjának helye, a területe, és a felszínre normált, a közepén áthaladó elektrosztatikus vektor jellemez [18] IEF-PCM Az IEF-PCM integrál egyenlet szabályozású polarizálható kontinuum modellt (Integral Equation Formalism PCM) az elektrosztatikus szolvatációs probléma látszólagos felszíni töltésekkel (ASC Apparent Surface Charges) történő kvantummechanikai szintű megoldására fejlesztették ki [24]. A módszer lehetővé teszi az eltérő tulajdonságú szigetelő közegek, így általános izotróp folyadékok, eredendően anizotróp közegként viselkedő folyadékkristályok, szilárd mátrixok, és ionos folyadékok egyetlen megközelítésben történő kezelését [11] IPCM és SCIPCM Ha a gömbök helyett valóságosabb formájú üregekkel helyettesítjük az oldott molekula alakját, akkor numerikus integrálás lassú konvergenciája miatt megnő a számítási idő. Ennek a kiküszöbölésére megoldás, ha olyan üreget definiálunk, ami az adott módszerrel számított összelektronsűrűség által meghatározott izofelületen alapszik. Ennek a felületeknek az integrálása a gradiens vektor által definiált medencéken alapszik, vagy egyszerűen a magtöltések centrumát is használhatjuk. Csak az izofelület szintjét kell megadni (általában ), ahelyett hogy a gömbök sugarát határoznánk meg, így az üreg egyedileg az elektromos környezetből származtatható. Az IPCM oldószermodell önkonzisztens változata az SCIPCM [25]. 5.2 COSMO A COSMO vezető-szerű árnyékoló modell hasonló a PCM-hez, bár tőle függetlenül fejlesztették ki Klamt és munkatársai. A módszer alkalmazásával a szigetelőként kezelt oldószerközeg árnyékoló hatása viszonylag egyszerűen számolható, emellett lehetővé teszi üregen belüli analitikus gradiens számolását, így megbízható oldatbeli geometria optimálások is megvalósíthatóak vele [26]. A modell feltételezi, hogy az oldott molekulát körülvevő közeget jól le lehet írni vezető közegként, ami leegyszerűsíti az elektrosztatikus kölcsönhatások számítását. A korrekciókat utólag veszi figyelembe, hogy a közeg szigetelőként viselkedjen. Semleges oldószerekhez az elektrosztatikus effektusokon kívüli hatások figyelembe vételére dolgozták ki a COSMO-RS módszert, ahol termodinamikus statisztikát is használnak a teljes szolvatációs szabadentalpia számításához [9][27]. 11
12 5.3 SMD A SMD oldószermodell használata kifejezetten olyan számításoknál lehet előnyös, ahol az elektrosztatikustól eltérő kölcsönhatások is lényegesek [28]. A módszer alapja az oldott anyag és a kontinuumként kezelt oldószer között létrejövő kvantummechanikai töltéssűrűség. Kontinuum oldószermodell lévén az oldószer nem explicit jelenik meg, hanem inkább egy szigetelő közegként, ami az oldott molekula és oldószer határán létrejövő felületi feszültséget is szimulálja. A modellt univerzális alkalmazásra tervezték, azaz bármilyen töltéssel rendelkező, vagy semleges molekulára alkalmazható. Akármilyen oldószer közeget lehet alkalmazni, aminek néhány paramétere ismert, különösen a dielektromos állandója, törésmutatója, felületi feszültsége, valamint sav-bázis tulajdonságai. A modell a megfigyelhető oldódási szabadentalpiát két komponensre osztja. Az első komponens az elektrosztatikus hozzájárulás, ami az önkonzisztens reakciómezőből ered, és az elektrosztatikus kölcsönhatásokhoz használt inhomogén Poisson-egyenlet megoldását foglalja magába. A második komponenst üreg-diszperzió-oldószer-struktúra kifejezésnek hívják (cavity-dispersionsolvent-structure), és hozzájárulása az első szolvatációs burokban létrejövő, az oldott molekula és oldószer közötti rövidtávú kölcsönhatásokból ered [29]. 12
13 5.4 Irodalmi előzmények Egy 2010-es tanulmányban egy kutatócsoport 34 vegyületnek számolta ki a deprotonálási szabadentalpiáját DFT szinten B3LYP és OLYP funkcionálokkal [1]. A számítások során COSMO oldószermodellt használtak, mellyel vizes közeget modelleztek. A modellezett vegyületek között semleges savak és nitrogén tartalmú vegyületek protonált formája, azaz kationos savak is szerepeltek. Úgy találták, hogy ha csak molekulamechanikával, vagy gázfázisban optimálják a geometriát, akkor lényegesen rosszabb eredményre jutnak, mintha a geometriaoptimálást és energiaszámolást is a COSMO oldószermodell alkalmazásával végeznék. Ezen felül a szerkezetek optimálását különböző méretű bázisokkal végezték el, és azt figyelték meg, hogy egy közepes méretű bázis (6-31G*) elegendő ahhoz, hogy jó eredményt kapjanak. Nagyobb bázis alkalmazása nem javít lényegesen az eredményen, viszont sokkal hosszabb lesz a számítási ideje. Az energiák számításához a G(d,p) bázist találták a legmegfelelőbbnek. A vegyületek deprotonálási szabadentalpiájának függvényében ábrázolták a vízben kísérletileg mért pk a értéküket. A vegyületeket a következő csoportokba osztották szerkezet szerint: - alkoholok és fenolok - karbonsavak - anilinek és aminok - piridinek A különböző besorolású vegyületekhez tartozó pontokra különböző egyeneseket illesztettek a legkisebb négyzetek módszere szerint. Úgy találták, hogy egy egyenes nem illeszkedik megfelelően az ábrázolt pontokra, hanem szükséges a vegyületek szerkezet szerinti önkényes csoportosítása, és külön történő értékelése. Egy másik kutatócsoport publikációjában COSMO-RS oldószermodellt használt számításaihoz. Ez a COSMO vezetőszerű árnyékoló modellt ötvözi termodinamikus statisztikával, így valóságosabb szolvatációs szimulációt biztosít [27][30]. Tanulmányukban 93 olyan savnak számolták ki a deprotonálási szabadentalpiáját, melynek ismert az acetonitrilben mért pk a értéke. Mind az optimálásnál és energiaszámításánál is használták a COSMO oldószermodellt. Úgy találták, hogy a deprotonáláshoz szükséges szabadentalpia és a pk a közötti lineáris kapcsolat nem írható le jól anélkül, hogy a vegyületeket ne osztanánk önkényesen az anionokban fellépő delokalizáció mértéke alapján lokalizált, és delokalizált rendszerekre. 13
14 Egy tanulmány különböző paraméterek hatását vizsgálta savak elméletileg számolt pk a-ja és kísérletileg mért pk a-jának közötti összefüggésre. A savak (semleges és kationos) és konjugált bázisaik geometriáját gázfázisban optimálták, majd ebből számították ki a rezgési frekvenciákat és szolvatációs energiákat. Számításaikat a B3LYP hibrid funkcionállal és a G(d,p) bázissal végezték el. Szolvatációs energiák számítása során a C-PCM oldószermodellt alkalmazták három különböző atomsugár típussal (UFF, UAHF, Bondi) [8]. A számításokat két homológ csoportba tartozó savakra végezték el, víz, és acetonitril oldószerre egyaránt. Az egyik csoportban semleges savak, a másik csoportba konjugált savak (protonált bázisok) szerepeltek. Úgy találták, hogy acetonitrilben a semleges savak anionját minden oldószermodell jelentősen túlszolvatálja, de az anion bázicitásától való függést jobban modellezték. A konjugált savak (protonált bázisok) esetén minden oldószermodell alulszolvatálta a kationokat, de a kation savasságától való függést jól modellezték. Megvizsgálták, hogy a funkcionál változtatása milyen mértékben befolyásolja az eredményeket. Ezért a számításokat három különböző (B3LYP, B3P86, M06) hibrid sűrűségfunkcionállal is végrehajtották. Úgy találták, hogy ugyan a számított pk a értékek módosulnak a funkcionál változtatásával, de ezek a változások véletlenszerűek, így a pontokra illesztett kalibrációs egyenesek nagyon hasonlóak. A B3LYP és M06 funkcionállal számított értékekre illesztett egyenesek paraméterei szinte azonosak, míg a B3P86-tal számított értékekre illesztett egyenes meredeksége majdnem megegyezik az előzőekével, tengelymetszete némileg tér el. Egy explicit oldószer molekulát is tartalmazó rendszer vizsgálatával foglalkozó tanulmányában egy kutatócsoport 57 db egyértékű sav vizes közegű disszociációs szabadentalpiáját számította ki kísérleti és számolt, gáz-, illetve folyadékfázisú szabadentalpiák kombinálásával. Úgy találták, hogy legtöbbször, pontos implicit kontinuum modellek használata esetén, nem szükséges explicit oldószer molekulát alkalmazni a számítások során. Mindazonáltal amikor erős specifikus szolvatációs effektusok, hidrogénkötések jelenléte várható az oldott molekula és oldat között, akkor egyetlen molekula explicit víz jelentősen megnöveli a pk a számítás pontosságát [31]. 14
15 6. Saját számítások bemutatása: Deprotonálódási szabadentalpia számítása Oldószermodellek alkalmazásának nem csak a pk a elméleti számításnál van nagy jelentősége, hanem minden oldószerközegben lejátszódó kémiai és biokémiai reakció szimulációja esetén, de a pk a becslés indikátorként felhasználható annak ellenőrzésére, hogy az adott oldószermodell használatával számolt paraméterek mennyire támasztják alá a kísérleti adatokat. Különböző kvantumkémiai számítási módszerek gázfázisú kalkulációinak összehasonlítása során általánosan elfogadott, hogy az adott módszerrel számolt mennyiséget összehasonlítják az etalonként használt CCSD(T)/CBS szinten számolt értékkel. Oldószermodellek esetén jelenleg nincs olyan pontos modell, amihez a többi oldószermodellt lehetne hasonlítani. Hacsak máshol nincs egyértelműen feltűntetve, számításaim során a geometriák optimálását és frekvenciák számítását a széles körben alkalmazott M06-2X hibrid sűrűségfunkcionállal és 6-31+G(d,p) bázissal végeztem az IEF-PCM oldószermodell alkalmazásával. Az oldatbeli energiák számításához az M06-2X funkcionált és a G(d,p) bázist használtam az oldószermodellek változtatásával. A táblázatokban szereplő értékeknél az angol nyelvű programok használatából eredendően tizedes pontot használtam tizedes vessző helyett. Az M06-2X Truhlar és kutatócsoportja által fejlesztett hibrid DFT funkcionál, amit nemfémes rendszerekben előforduló nem kovalens π-π kölcsönhatások leírására paramétereztek, az intramolekuláris diszperziós effektusok pontos modellezéséhez [32 35]. A 6-31+G(d,p) és G(d,p) polarizációt és diffúz funkciót is tartalmazó felhasított vegyérték (split valence) bázisokat John Pople és munkatársai fejlesztették ki [36]. A 6-31+G(d,p) bázisban a belső pályák egyszeres zéta minőségűek és minden pálya 6 Gauss-függvényből áll, a vegyértékhéjak pedig TZ minőségűek, egy darab három primitív Gauss-függvényből, és 1 darab 1 primitív Gauss függvényből álló pályával. A G(d,p) bázisban a belső pályák egyszeres zéta minőségűek és minden pályát 6 Gauss-függvény ír le, a vegyértékhéjak pedig TZ minőségűek, egy darab 3 primitív Gauss-függvényből, és 11 db 1 primitív Gauss-függvényből álló pályával [37]. A számításokat a Budapesti Műszaki és Gazdaságtudományi Egyetem szuperszámítógépén végeztem a Gaussian 09 programmal [38]. A molekulákat, és molekulaábrákat az verziószámú Avogadro nyílt forráskódú molekulaszerkesztő és vizualizáló programmal szerkesztettem [39]. A geometria optimálások konvergenciáját a molekulák és elektronikus struktúrák folyamat előtti és folyamat utáni feldolgozásához készült Molden programmal követtem [40]. Az input és output fájlok szerkesztéséhez a Notepad++ programot, a számítások kiértékeléséhez és a dolgozat megírásához a Microsoft Office programcsomagot használtam. Az adatok feldolgozását a Microsoft Excel Visual Basic bővítményében írt makrókkal, és Unix shell scriptekkel végeztem. 15
16 6.1 Vizsgált vegyületek Munkám során semleges savak, és konjugált savak (protonált nitrogéntartalmú bázisok) deprotonálási szabadentalpiáját számítottam ki, és hoztam összefüggésbe a kísérletileg meghatározott pk a értékükkel víz, és acetonitril oldószerekben. Számításaim során implicit kontinuum oldószermodellek alkalmazásával vizsgáltam csak az oldott molekulát tartalmazó monomolekuláris rendszereket, és egy explicit oldószer molekulát is tartalmazó modelleket, amiket a továbbiakban explicit szolvatációs modellként említek. Vízben 42 db, acetonitrilben 32 db vegyületet vizsgáltam. A kationos savakon végzett számításokhoz mindkét oldószer esetén Muckerman és munkatársai publikációjában szereplő kísérleti pk a értékeket használtam fel [8]. A vizes közeg modellezésénél használt semleges savak irodalmi pk a adatait Pulay és munkatársai, az acetonitrilnél felhasznált semleges savak kísérleti pk a értékeit Eckert és munkatársai publikációja alapján használtam fel [1,27]. 6.2 Oldószermodellek eredményeinek áttekintése Kutatásom során két oldószerben (acetonitril, víz) számoltam ki a vegyületeknek a deprotonálási szabadentalpiáját, és ábrázoltam a vegyületek kísérleti pk a értékének a függvényében. Az így kapott pontokra egyenest illesztettem a legkisebb hibanégyzetek módszerével. Vizsgáltam az egyenes-illesztés jóságát, és az RMSD-t. A számításokat tisztán implicit, és egy oldószer molekulát tartalmazó implicitexplicit rendszerre is elvégeztem, ahol az oldott anyag és az egy darab oldószer molekula egysége került az implicit oldószermodell által meghatározott üregbe. A számítások kiértékelése során egyben vizsgáltam az adott sorozathoz tartozó összes vegyületet, valamint szétválasztva a kationos savakat a semleges savaktól. Kutatásom során a következő oldószermodelleket vizsgáltam: - IEF-PCM különböző atomsugarakkal (UFF, Bondi, Pauling, UAHF, UAKS) - C-PCM UFF atomsugárral (csak acetonitril esetén vizsgáltam) - SMD - IPCM különböző isodensity értékekkel (0.0003, , ) - SCIPCM különböző izodensity értékekkel ( , , , , , , , , ), illetve különböző ε értékekkel (acetonitrilre: , , ; vízre: ) A COSMO és COSMO-RS oldószermodellek nincsenek benne a Gaussian 09 programban, ezért ezeket az oldószermodelleket nem vizsgáltam. 16
17 Eredményeimet alább táblázatokban tűntetem fel. Külön értékelem az implicit, és explicit modelleket, valamint a két különböző oldószert. Az explicit oldószermodellek nem tartalmaznak IPCM és SCIPCM számításokat, mert ezek a modellek nagyon instabilnak bizonyultak, és a legtöbb esetben az molekula energiájának a számítása (SCF) nem konvergált. A legjobb 4 oldószermodellt részletesen ismertetem. A táblázatokban a Különválasztva oszlopok a kationos és semleges savak csoportjára külön-külön kapott értékeket, míg az Egyben oszlopok az összes vizsgált savra együttesen kapott értékeket mutatják be Oldószermodellek vizsgálata vízre Az implicit oldószermodellek összefoglaló táblázata: 1. táblázat: Implicit oldószermodellek vízre Különválasztva Egyben Oldószermodell R 2 RMSD R 2 RMSD Kationos Semleges Kationos Semleges UFF Bondi IEF-PCM Pauling UAHF UAKS SMD IPCM SCIPCM (ε= ) A 1. táblázatból látszik, hogy a vegyületek szétválasztása nélkül az IEF-PCM oldószermodell UAHF atomsugárral szolgáltatta a legjobb eredményt. Az egyenesek illeszkedéséből, és RMSD értékekből látszik, hogy tisztán implicit oldószermodelleknél szükséges a semleges savak elválasztása a kationos savaktól. Amennyiben végrehajtjuk a szétválasztást, az IEF-PCM oldószermodell Bondi atomsugárral való kombinálása adódik a legjobbnak a vizsgált módszerek közül. 17
18 Az explicit oldószermodellek összefoglaló táblázata: 2. táblázat: Explicit oldószermodellek vízre Különválasztva Egyben Oldószermodell R 2 RMSD R 2 RMSD Kationos Semleges Kationos Semleges UFF Bondi IEF-PCM Pauling UAHF UAKS SMD A 2. táblázatban az explicit oldószermodellek eredményeit foglaltam össze. Látható, hogy a vegyületeket egyben értékelve az IEF-PCM Pauling atomsugárral adja a legjobb eredményt, míg a vegyületeket típus szerint szétválasztva az IEF-PCM oldószermodell UAHF atomsugárral. Ez utóbbi modell nem csak explicit esetben nyújtja a legjobb eredményt. Az 1. és 2. táblázat R 2 és RMSD értékeiből leolvasható, hogy az összes vizsgált módszer közül ez bizonyul a legjobbnak, az explicit víz molekula által biztosított specifikusabb szolvatáció következtében. 1. ábra: Víz esetén használt explicit oldószermodellek szemléltetése az ecetsav példáján. Baloldalon az ecetsav semleges formája, a jobboldalon pedig konjugált bázisa látható Az 1. ábra szemlélteti az explicit oldószermodell során használt rendszert az ecetsav semleges, és deprotonált formájának példáján. A molekulák orientációján megfigyelhető, hogy a vizsgált vegyület és a víz között hidrogénkötés jön létre. 18
19 6.2.2 Oldószermodellek vizsgálata acetonitrilre Az implicit oldószermodellek összefoglaló táblázata: 3. táblázat: Implicit oldószermodellek acetonitrilre Különválasztva Egyben Oldószermodell R 2 RMSD R 2 RMSD Kationos Semleges Kationos Semleges UFF Bondi IEF-PCM Pauling UAHF UAKS C-PCM UFF SMD IPCM SCIPCM (ε=17.844) SCIPCM (ε=36.688) SCIPCM (ε=53.532) A vízhez képest két jelentős különbség van acetonitril oldószer esetén: egyrészt a 3. táblázatban feltűntetett eredményekből következik, hogy nem szükséges külön értékelni a semleges savakat a kationos savaktól, másrészt az egyenesek illeszkedése és a pk a becslés minősége is sokkal jobb, mint bármelyik modellnél víz oldószer esetén. Látszik, hogy amennyiben csak a kationos savakat vizsgáljuk, az IEF-PCM is jó eredményt ad, UAHF és Bondi atomsugár használatánál. A tisztán implicit oldószermodellnél így szétválasztás nélkül, és a vegyületek szétválasztásával is az ε=53.532, és isodensity értékű SCIPCM oldószermodell bizonyult a legjobbnak. Az SCIPCM oldószermodellel 19
20 végzett számítások során acetonitril esetén általában az ε= és isodensity értéket használják. Mivel a modellt csak ritkán alkalmazzák, nem biztos, hogy a standard paraméterek a legoptimálisabbak. Az explicit oldószermodellek összefoglaló táblázata: 4. táblázat: Explicit oldószermodell acetonitrilre Különválasztva Egyben Oldószermodell R 2 RMSD R 2 RMSD Kationos Semleges Kationos Semleges UFF Bondi IEF-PCM Pauling UAHF UAKS SMD Explicit oldószermodellt használva, a vegyületek szétválasztása nélkül a legjobb modellnek az IEF- PCM oldószermodell bizonyult UFF atomsugárral. A vegyületeket szeparálva az IEF-PCM Bondi atomsugárral adta a legjobb eredményt. 2. ábra: Acetonitilre használt explicit oldószermodellek szemléltetése a 2-klórpiridinium-kation és a 4-nitrobenzoesav példáján A 2. ábra szemlélteti a számításoknál használt explicit oldószermodellt: az ábrán a 2-klórpiridin (kationos sav) és 4-nitrobenzoesav (semleges sav) látható, amint a savas hidrogén és az acetonitril nitrogénje között hidrogénkötés jön létre. A számítások során csak a vegyületek savas formájánál használtam egy acetonitril molekulát. Ennek az az oka, hogy az acetonitril csak akceptorként működik a hidrogénkötés kialakítása során, donorként nem, így a savas vegyületeknek tud specifikus szolvatációt biztosítani, a konjugált bázisuknak nem. A legjobbnak vélt oldószermodellekkel számolt adatokra való egyenes illesztésénél az egyenes nagy tengelymetszete erre a modellre vezethető vissza. 20
21 6.3 A legjobbnak ítélt oldószermodellek ismertetése Implicit oldószermodellek vízre a) A legjobb implicit oldószermodell a vegyületek különválasztása nélkül: 5. táblázat: IEF-PCM UAHF oldószermodell vízre # Vegyület Mért pk a Számított pk a Hiba 1 2-klórpiridinium cianopiridinium anilinium piridinium ,4,6-kollidinium benzilammónium trietilammónium pirrolidinium guanidinium ,5-diklóranilinium anizidinium ,6-dimetilpiridinium hidrazinium (dimetilamino)piridinium klóranilinium cianoanilinium nitroanilinium metilammónium dimetilammónium trimetilammónium piperidinium metilpiridinium ,4-dimetilpiridinium cianopiridinium fluorpiridinium metoxipiridinium fenol metilfenol nitrofenol nitrofenol ,4-dinitrofenol ,5-dinitrofenol ,6-dinitrofenol metanol trifluoretanol hangyasav ecetsav cianoecetsav oxálsav butánsav benzoesav nitrobenzoesav RMSD 1.46 R Max hiba
22 b) A legjobb implicit oldószermodell a semleges és kationos savak különválasztásával: 6. táblázat: IEF-PCM Bondi oldószermodell vízre # Vegyület Mért pk a Számított pk a Hiba 1 2-klórpiridinium cianopiridinium anilinium piridinium ,4,6-kollidinium benzilammónium trietilammónium pirrolidinium guanidinium ,5-diklóranilinium anizidinium ,6-dimetilpiridinium hidrazinium (dimetilamino)piridinium klóranilinium cianoanilinium nitroanilinium metilammónium dimetilammónium trimetilammónium piperidinium metilpiridinium ,4-dimetilpiridinium cianopiridinium fluorpiridinium metoxipiridinium fenol metilfenol nitrofenol nitrofenol ,4-dinitrofenol ,5-dinitrofenol ,6-dinitrofenol metanol trifluoretanol hangyasav ecetsav cianoecetsav oxálsav butánsav benzoesav nitrobenzoesav RMSD 0.72 Kationos savak R Max hiba 1.29 RMSD 1.13 Semleges savak R Max hiba
23 ΔΔG [Hartree] ΔΔG [Hartree] IEF-PCM oldószermodell UAHF atomsugárral, a vegyületek különválasztása nélkül Különválasztás nélkül: y = Mért pk a 1. diagram: IEF-PCM oldószermodell vízre a vegyületek különválasztása nélkül Az 1. diagramban a fekete pontok az 5. táblázatban feltüntetett vegyületek számított deprotonálódási szabadentalpiáját jelölik, a kísérleti pk a értékük függvényében, a piros vonal pedig a pontokra illesztett egyenest. IEF-PCM oldószermodell Bondi atomsugárral, a vegyületek különválasztásával Kationos savak: x Semleges savak: x Mért pka 2. diagram: IEF-PCM Bondi oldószermodell vízre a vegyületek különválasztásával A 2. diagramban a kék pontok a 6. táblázatban lévő kationos savak deprotonálási szabadentalpiáját jelöli a kísérleti pk a értékük függvényében, a kék vonal a pontokra illesztett egyenest. A fekete pontok a 6. táblázatban lévő semleges savak deprotonálási szabadentalpiáját jelölik a kísérleti pk a értékük függvényében, a fekete vonal pedig a pontokra illesztett egyenest. 23
24 6.3.2 Explicit oldószermodellek vízre a) A legjobb explicit oldószermodell a vegyületek különválasztása nélkül: 7. táblázat: IEF-PCM Pauling oldószermodell vízre # Vegyület Mért pk a Számított pk a Hiba 1 2-klórpiridinium cianopiridinium anilinium piridinium ,4,6-kollidinium benzilammónium trietilammónium pirrolidinium guanidinium ,5-diklóranilinium anizidinium ,6-dimetilpiridinium hidrazinium (dimetilamino)piridinium klóranilinium cianoanilinium nitroanilinium metilammónium dimetilammónium trimetilammónium piperidinium metilpiridinium ,4-dimetilpiridinium cianopiridinium fluorpiridinium metoxipiridinium fenol metilfenol nitrofenol nitrofenol ,4-dinitrofenol ,5-dinitrofenol ,6-dinitrofenol metanol trifluoretanol hangyasav ecetsav cianoecetsav oxálsav butánsav benzoesav nitrobenzoesav RMSD 1.36 R Max hiba
25 b) A legjobb explicit oldószermodell a vegyületeket különválasztva: 8. táblázat: IEF-PCM UAHF oldószermodell vízre # Vegyületek Mért pk a Számított pka Hiba 1 2-klórpiridinium cianopiridinium anilinium piridinium ,4,6-kollidinium benzilammónium trietilammónium pirrolidinium guanidinium ,5-diklóranilinium anizidinium ,6-dimetilpiridinium hidrazinium (dimetilamino)piridinium klóranilinium cianoanilinium nitroanilinium metilammónium dimetilammónium trimetilammónium piperidinium metilpiridinium ,4-dimetilpiridinium cianopiridinium fluorpiridinium metoxipiridinium fenol metilfenol nitrofenol nitrofenol ,4-dinitrofenol ,5-dinitrofenol ,6-dinitrofenol metanol trifluoretanol hangyasav ecetsav cianoecetsav oxálsav butánsav benzoesav nitrobenzoesav RMSD 2.39 Kationos savak R Max hiba 4.04 RMSD 2.84 Semleges savak R Max hiba
26 ΔΔG [Hartreel] ΔΔG [Hartree] IEF-PCM oldószermodell Pauling atomsugárral, a vegyületek különválasztása nélkül Különválasztás nélkül: y = x Mért pka 3. diagram: IEF-PCM Bondi oldószermodell a vegyületek különválasztása nélkül A 3. diagramban a fekete pontok a 7. táblázatban feltüntetett vegyületek számított deprotonálódási szabadentalpiáját jelölik, a kísérleti pk a értékük függvényében, a piros vonal pedig a pontokra illesztett egyenest. IEF-PCM oldószermodell UAHF atomsugárral, a vegyületeket különválasztva Kationos savak: y = x Semleges savak: y = x Mért pk a 4. diagram: IEF-PCM UAHF oldószermodell a vegyületek különválasztásával A 4. diagramban szereplő kék pontok a kationos savak kísérleti pk a értékének a függvényében ábrázolt deprotonálási szabadentalpiák, a fekete pontok a semleges savaké. A kék vonal a kationos savak adataira illesztett egyenes, a fekete pedig a semleges savakéra. 26
27 6.3.3 Implicit oldószermodellek acetonitrilre a) A legjobb implicit oldószermodell: 9. táblázat: SCIPCM oldószermodell (ε=53.532), isodensity értékkel acetonitrilre # Vegyületek Mért pk a Számított pk a Egyben Hiba Egyben Hiba 1 2-klórpiridinium cianopiridinium anilinium piridinium ,4,6-kollidinium benzilammónium trietilammónium pirrolidinium ,5-diklóranilinium cianoanilinium anizidinium ,6-dimetilpiridinium (dimetilamino)piridinium ,6-diklóranilinium (p-tolil)-malononitril metil-(9h-fluorén-9-karboxilát) brómbenzoesav benzoesav nitrobenzoesav klórecetsav szulfanilfenol nitrofenol ,4-dinitrofenol ,4,6-triklórfenol fenol metilfenol ,3-dinitrofenoxazin nitrofenoxazin benzolszulfonamid nitrobenzolszulfonsav p-toluolszulfonsav metánszulfonsav RMSD 0.75 RMSD 1.07 Kationos R Egyben R Max hiba 1.39 Max hiba 2.14 RMSD 1.20 Semleges R Max hiba
28 ΔΔG [Hartree] SCIPCM oldószermodel (ε=53.532), isodensity értékkel Kationos savak: y = x Semleges savak: y = x Szétválasztás nélkül: y = x Mért pka 5. diagram: SCIPCM oldószermodell acetonitrilre ε=53.532, isodensity értékkel Az 5. diagramban ábrázolt kék pontok a kationos savak, a fekete pontok a semleges savak deprotonálási szabadentalpiáját jelölik a vegyületek kísérleti pk a értékük függvényében. A kék vonal a kationos savak adatpontjaira, a fekete vonal pedig a semleges savak pontjaira illesztett egyenes. A piros vonal a vegyületek szétválasztása nélkül illesztett egyenes, a 9. táblázatban szereplő összes vegyületre. Jól látható, hogy az egyenesek meredeksége és tengelymetszete hasonló, valamint a szétválasztás nélküli RMSD is kisebb, mint a szétválasztott RMSD-k átlaga, így nincs szükség a vegyületek különválasztására. 28
29 6.3.4 Explicit oldószermodellek acetonitrilre Az explicit acetonitril molekulát tartalmazó vegyületek geometriája csak sokadik számolási ciklusra konvergált. Az eddigi kiértékelésekben szereplő metil-(9h-fluorén-9-karboxilát) geometriája nem konvergált, ezért a további számításokban és kiértékelésekben nem szerepel. a) A legjobb explicit oldószermodell a vegyületek különválasztása nélkül: 10. táblázat IEF-PCM oldószermodell UFF atomsugárral acetonitrilre # Vegyület Mért pk a Számított pk a Hiba 1 2-klórpiridinium cianopiridinium anilinium piridinium ,4,6-kollidinium benzilammónium trietilammónium pirrolidinium ,5-diklóranilinium cianoanilinium anizidinium ,6-dimetilpiridinium (dimetilamino)piridinium ,6-diklóranilinium (p-tolil)-malononitril brómbenzoesav benzoesav nitrobenzoesav klórecetsav szulfanilfenol nitrofenol ,4-dinitrofenol ,4,6-triklórfenol fenol metilfenol ,3-dinitrofenoxazin nitrofenoxazin benzolszulfonamid nitrobenzolszulfonsav p-toluolszulfonsav metánszulfonsav RMSD 1.61 R Max hiba
Elektrosztatikus számítások. Elektrosztatikus számítások. Elektrosztatikus számítások. Elektrosztatikus számítások Definíciók
 Jelentősége szubsztrát kötődés szolvatáció ionizációs állapotok (pka) mechanizmus katalízis ioncsatornák szimulációk (szerkezet) all-atom dipolar fluid dipolar lattice continuum Definíciók töltéseloszlás
Jelentősége szubsztrát kötődés szolvatáció ionizációs állapotok (pka) mechanizmus katalízis ioncsatornák szimulációk (szerkezet) all-atom dipolar fluid dipolar lattice continuum Definíciók töltéseloszlás
Savak bázisok. Csonka Gábor Általános Kémia: 7. Savak és bázisok Dia 1 /43
 Savak bázisok 12-1 Az Arrhenius elmélet röviden 12-2 Brønsted-Lowry elmélet 12-3 A víz ionizációja és a p skála 12-4 Erős savak és bázisok 12-5 Gyenge savak és bázisok 12-6 Több bázisú savak 12-7 Ionok
Savak bázisok 12-1 Az Arrhenius elmélet röviden 12-2 Brønsted-Lowry elmélet 12-3 A víz ionizációja és a p skála 12-4 Erős savak és bázisok 12-5 Gyenge savak és bázisok 12-6 Több bázisú savak 12-7 Ionok
Többértékű savak és bázisok Többértékű savnak/lúgnak azokat az oldatokat nevezzük, amelyek több protont képesek leadni/felvenni.
 ELEKTROLIT EGYENSÚLYOK : ph SZÁMITÁS Általános ismeretek A savak vizes oldatban protont adnak át a vízmolekuláknak és így megnövelik az oldat H + (pontosabban oxónium - H 3 O + ) ion koncentrációját. Erős
ELEKTROLIT EGYENSÚLYOK : ph SZÁMITÁS Általános ismeretek A savak vizes oldatban protont adnak át a vízmolekuláknak és így megnövelik az oldat H + (pontosabban oxónium - H 3 O + ) ion koncentrációját. Erős
HOMOGÉN EGYENSÚLYI ELEKTROKÉMIA: ELEKTROLITOK TERMODINAMIKÁJA
 HOMOGÉN EGYENSÚLYI ELEKTROKÉMIA: ELEKTROLITOK TERMODINAMIKÁJA I. Az elektrokémia áttekintése. II. Elektrolitok termodinamikája. A. Elektrolitok jellemzése B. Ionok termodinamikai képződési függvényei C.
HOMOGÉN EGYENSÚLYI ELEKTROKÉMIA: ELEKTROLITOK TERMODINAMIKÁJA I. Az elektrokémia áttekintése. II. Elektrolitok termodinamikája. A. Elektrolitok jellemzése B. Ionok termodinamikai képződési függvényei C.
Oldódás, mint egyensúly
 Oldódás, mint egyensúly Szilárd (A) anyag oldódása: K = [A] oldott [A] szilárd állandó K [A] szilárd = [A] oldott S = telített oldat conc. Folyadék oldódása: analóg módon Gázok oldódása: [gáz] oldott =
Oldódás, mint egyensúly Szilárd (A) anyag oldódása: K = [A] oldott [A] szilárd állandó K [A] szilárd = [A] oldott S = telített oldat conc. Folyadék oldódása: analóg módon Gázok oldódása: [gáz] oldott =
Elektronegativitás. Elektronegativitás
 Általános és szervetlen kémia 3. hét Elektronaffinitás Az az energiaváltozás, ami akkor következik be, ha 1 mól gáz halmazállapotú atomból 1 mól egyszeresen negatív töltésű anion keletkezik. Mértékegysége:
Általános és szervetlen kémia 3. hét Elektronaffinitás Az az energiaváltozás, ami akkor következik be, ha 1 mól gáz halmazállapotú atomból 1 mól egyszeresen negatív töltésű anion keletkezik. Mértékegysége:
Osztályozó vizsgatételek. Kémia - 9. évfolyam - I. félév
 Kémia - 9. évfolyam - I. félév 1. Atom felépítése (elemi részecskék), alaptörvények (elektronszerkezet kiépülésének szabályai). 2. A periódusos rendszer felépítése, periódusok és csoportok jellemzése.
Kémia - 9. évfolyam - I. félév 1. Atom felépítése (elemi részecskék), alaptörvények (elektronszerkezet kiépülésének szabályai). 2. A periódusos rendszer felépítése, periódusok és csoportok jellemzése.
Oldódás, mint egyensúly
 Oldódás, mint egyensúly Szilárd (A) anyag oldódása: K = [A] oldott [A] szilárd állandó K [A] szilárd = [A] oldott S = telített oldat conc. Folyadék oldódása: analóg módon Gázok oldódása: [gáz] oldott K
Oldódás, mint egyensúly Szilárd (A) anyag oldódása: K = [A] oldott [A] szilárd állandó K [A] szilárd = [A] oldott S = telített oldat conc. Folyadék oldódása: analóg módon Gázok oldódása: [gáz] oldott K
A kovalens kötés elmélete. Kovalens kötésű molekulák geometriája. Molekula geometria. Vegyértékelektronpár taszítási elmélet (VSEPR)
 4. előadás A kovalens kötés elmélete Vegyértékelektronpár taszítási elmélet (VSEPR) az atomok kötő és nemkötő elektronpárjai úgy helyezkednek el a térben, hogy egymástól minél távolabb legyenek A központi
4. előadás A kovalens kötés elmélete Vegyértékelektronpár taszítási elmélet (VSEPR) az atomok kötő és nemkötő elektronpárjai úgy helyezkednek el a térben, hogy egymástól minél távolabb legyenek A központi
23. Indikátorok disszociációs állandójának meghatározása spektrofotometriásan
 23. Indikátorok disszociációs állandójának meghatározása spektrofotometriásan 1. Bevezetés Sav-bázis titrálások végpontjelzésére (a mőszeres indikáció mellett) ma is gyakran alkalmazunk festék indikátorokat.
23. Indikátorok disszociációs állandójának meghatározása spektrofotometriásan 1. Bevezetés Sav-bázis titrálások végpontjelzésére (a mőszeres indikáció mellett) ma is gyakran alkalmazunk festék indikátorokat.
Al-Mg-Si háromalkotós egyensúlyi fázisdiagram közelítő számítása
 l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
Savak bázisok. Csonka Gábor Általános Kémia: 7. Savak és bázisok Dia 1 /43
 Savak bázisok 121 Az Arrhenius elmélet röviden 122 BrønstedLowry elmélet 123 A víz ionizációja és a p skála 124 Erős savak és bázisok 125 Gyenge savak és bázisok 126 Több bázisú savak 127 Ionok mint savak
Savak bázisok 121 Az Arrhenius elmélet röviden 122 BrønstedLowry elmélet 123 A víz ionizációja és a p skála 124 Erős savak és bázisok 125 Gyenge savak és bázisok 126 Több bázisú savak 127 Ionok mint savak
A kovalens kötés polaritása
 Általános és szervetlen kémia 4. hét Kovalens kötés A kovalens kötés kialakulásakor szabad atomokból molekulák jönnek létre. A molekulák létrejötte mindig energia csökkenéssel jár. A kovalens kötés polaritása
Általános és szervetlen kémia 4. hét Kovalens kötés A kovalens kötés kialakulásakor szabad atomokból molekulák jönnek létre. A molekulák létrejötte mindig energia csökkenéssel jár. A kovalens kötés polaritása
A kémiai kötés magasabb szinten
 A kémiai kötés magasabb szinten 11-1 Mit kell tudnia a kötéselméletnek? 11- Vegyérték kötés elmélet 11-3 Atompályák hibridizációja 11-4 Többszörös kovalens kötések 11-5 Molekulapálya elmélet 11-6 Delokalizált
A kémiai kötés magasabb szinten 11-1 Mit kell tudnia a kötéselméletnek? 11- Vegyérték kötés elmélet 11-3 Atompályák hibridizációja 11-4 Többszörös kovalens kötések 11-5 Molekulapálya elmélet 11-6 Delokalizált
Kémiai alapismeretek 6. hét
 Kémiai alapismeretek 6. hét Horváth Attila Pécsi Tudományegyetem, Természettudományi Kar, Kémia Intézet, Szervetlen Kémiai Tanszék biner 2013. október 7-11. 1/15 2013/2014 I. félév, Horváth Attila c Egyensúly:
Kémiai alapismeretek 6. hét Horváth Attila Pécsi Tudományegyetem, Természettudományi Kar, Kémia Intézet, Szervetlen Kémiai Tanszék biner 2013. október 7-11. 1/15 2013/2014 I. félév, Horváth Attila c Egyensúly:
Víz. Az élő anyag szerkezeti egységei. A vízmolekula szerkezete. Olyan mindennapi, hogy fel sem tűnik, milyen különleges
 Az élő anyag szerkezeti egységei víz nukleinsavak fehérjék membránok Olyan mindennapi, hogy fel sem tűnik, milyen különleges A Föld felszínének 2/3-át borítja Előfordulása az emberi szövetek felépítésében
Az élő anyag szerkezeti egységei víz nukleinsavak fehérjék membránok Olyan mindennapi, hogy fel sem tűnik, milyen különleges A Föld felszínének 2/3-át borítja Előfordulása az emberi szövetek felépítésében
Kötések kialakítása - oktett elmélet
 Kémiai kötések Az elemek és vegyületek halmazai az atomok kapcsolódásával - kémiai kötések kialakításával - jönnek létre szabad atomként csak a nemesgázatomok léteznek elsődleges kémiai kötések Kötések
Kémiai kötések Az elemek és vegyületek halmazai az atomok kapcsolódásával - kémiai kötések kialakításával - jönnek létre szabad atomként csak a nemesgázatomok léteznek elsődleges kémiai kötések Kötések
[S] v' [I] [1] Kompetitív gátlás
![[S] v' [I] [1] Kompetitív gátlás [S] v' [I] [1] Kompetitív gátlás](/thumbs/93/114506146.jpg) 8. Szeminárium Enzimkinetika II. Jelen szeminárium során az enzimaktivitás szabályozásával foglalkozunk. Mivel a klinikai gyakorlatban használt gyógyszerhatóanyagok jelentős része enzimgátló hatással bír
8. Szeminárium Enzimkinetika II. Jelen szeminárium során az enzimaktivitás szabályozásával foglalkozunk. Mivel a klinikai gyakorlatban használt gyógyszerhatóanyagok jelentős része enzimgátló hatással bír
Közös elektronpár létrehozása
 Kémiai reakciók 10. hét a reagáló részecskék között közös elektronpár létrehozása valósul meg sav-bázis reakciók komplexképződés elektronátadás és átvétel történik redoxi reakciók Közös elektronpár létrehozása
Kémiai reakciók 10. hét a reagáló részecskék között közös elektronpár létrehozása valósul meg sav-bázis reakciók komplexképződés elektronátadás és átvétel történik redoxi reakciók Közös elektronpár létrehozása
Anyagvizsgálati módszerek Elektroanalitika. Anyagvizsgálati módszerek
 Anyagvizsgálati módszerek Elektroanalitika Anyagvizsgálati módszerek Pannon Egyetem Mérnöki Kar Anyagvizsgálati módszerek Optikai módszerek 1/ 18 Potenciometria Potenciometria olyan analitikai eljárások
Anyagvizsgálati módszerek Elektroanalitika Anyagvizsgálati módszerek Pannon Egyetem Mérnöki Kar Anyagvizsgálati módszerek Optikai módszerek 1/ 18 Potenciometria Potenciometria olyan analitikai eljárások
Reakciókinetika és katalízis
 Reakciókinetika és katalízis k 4. előadás: 1/14 Különbségek a gázfázisú és az oldatreakciók között: 1 Reaktáns molekulák által betöltött térfogat az oldatreakciónál jóval nagyobb. Nincs akadálytalan mozgás.
Reakciókinetika és katalízis k 4. előadás: 1/14 Különbségek a gázfázisú és az oldatreakciók között: 1 Reaktáns molekulák által betöltött térfogat az oldatreakciónál jóval nagyobb. Nincs akadálytalan mozgás.
A kémiai kötés magasabb szinten
 A kémiai kötés magasabb szinten 13-1 Mit kell tudnia a kötéselméletnek? 13- Vegyérték kötés elmélet 13-3 Atompályák hibridizációja 13-4 Többszörös kovalens kötések 13-5 Molekulapálya elmélet 13-6 Delokalizált
A kémiai kötés magasabb szinten 13-1 Mit kell tudnia a kötéselméletnek? 13- Vegyérték kötés elmélet 13-3 Atompályák hibridizációja 13-4 Többszörös kovalens kötések 13-5 Molekulapálya elmélet 13-6 Delokalizált
Mikroszkóp vizsgálata Folyadék törésmutatójának mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 8. MÉRÉS Mikroszkóp vizsgálata Folyadék törésmutatójának mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 12. Szerda délelőtti csoport
KLASSZIKUS FIZIKA LABORATÓRIUM 8. MÉRÉS Mikroszkóp vizsgálata Folyadék törésmutatójának mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 12. Szerda délelőtti csoport
Folyadékszcintillációs spektroszkópia jegyz könyv
 Folyadékszcintillációs spektroszkópia jegyz könyv Zsigmond Anna Julia Fizika MSc I. Mérés vezet je: Horváth Ákos Mérés dátuma: 2010. október 21. Leadás dátuma: 2010. november 8. 1 1. Bevezetés A mérés
Folyadékszcintillációs spektroszkópia jegyz könyv Zsigmond Anna Julia Fizika MSc I. Mérés vezet je: Horváth Ákos Mérés dátuma: 2010. október 21. Leadás dátuma: 2010. november 8. 1 1. Bevezetés A mérés
A 27/2012. (VIII. 27.) NGM rendelet (29/2016. (VIII. 26.) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján.
 A 27/2012. (VIII. 27.) NGM rendelet (29/2016. (VIII. 26.) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján. Szakképesítés azonosítószáma és megnevezése 54 524 03 Vegyész technikus Tájékoztató
A 27/2012. (VIII. 27.) NGM rendelet (29/2016. (VIII. 26.) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján. Szakképesítés azonosítószáma és megnevezése 54 524 03 Vegyész technikus Tájékoztató
Vezetők elektrosztatikus térben
 Vezetők elektrosztatikus térben Vezető: a töltések szabadon elmozdulhatnak Ha a vezető belsejében a térerősség nem lenne nulla akkor áram folyna. Ha a felületen a térerősségnek lenne tangenciális (párhuzamos)
Vezetők elektrosztatikus térben Vezető: a töltések szabadon elmozdulhatnak Ha a vezető belsejében a térerősség nem lenne nulla akkor áram folyna. Ha a felületen a térerősségnek lenne tangenciális (párhuzamos)
2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv. Zsigmond Anna Fizika Bsc II. Mérés dátuma: Leadás dátuma:
 2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 24. Leadás dátuma: 2008. 10. 01. 1 1. Mérések ismertetése Az 1. ábrán látható összeállításban
2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 24. Leadás dátuma: 2008. 10. 01. 1 1. Mérések ismertetése Az 1. ábrán látható összeállításban
KÉMIA ÍRÁSBELI ÉRETTSÉGI- FELVÉTELI FELADATOK 1995 JAVÍTÁSI ÚTMUTATÓ
 1 oldal KÉMIA ÍRÁSBELI ÉRETTSÉGI- FELVÉTELI FELADATOK 1995 JAVÍTÁSI ÚTMUTATÓ I A VÍZ - A víz molekulája V-alakú, kötésszöge 109,5 fok, poláris kovalens kötések; - a jég molekularácsos, tetraéderes elrendeződés,
1 oldal KÉMIA ÍRÁSBELI ÉRETTSÉGI- FELVÉTELI FELADATOK 1995 JAVÍTÁSI ÚTMUTATÓ I A VÍZ - A víz molekulája V-alakú, kötésszöge 109,5 fok, poláris kovalens kötések; - a jég molekularácsos, tetraéderes elrendeződés,
Kémiai kötések. Kémiai kötések kj / mol 0,8 40 kj / mol
 Kémiai kötések A természetben az anyagokat felépítő atomok nem önmagukban, hanem gyakran egymáshoz kapcsolódva léteznek. Ezeket a kötéseket összefoglaló néven kémiai kötéseknek nevezzük. Kémiai kötések
Kémiai kötések A természetben az anyagokat felépítő atomok nem önmagukban, hanem gyakran egymáshoz kapcsolódva léteznek. Ezeket a kötéseket összefoglaló néven kémiai kötéseknek nevezzük. Kémiai kötések
Kémiai reakciók. Közös elektronpár létrehozása. Általános és szervetlen kémia 10. hét. Elızı héten elsajátítottuk, hogy.
 Általános és szervetlen kémia 10. hét Elızı héten elsajátítottuk, hogy a kémiai reakciókat hogyan lehet csoportosítani milyen kinetikai összefüggések érvényesek Mai témakörök a közös elektronpár létrehozásával
Általános és szervetlen kémia 10. hét Elızı héten elsajátítottuk, hogy a kémiai reakciókat hogyan lehet csoportosítani milyen kinetikai összefüggések érvényesek Mai témakörök a közös elektronpár létrehozásával
Célkitűzés/témák Fehérje-ligandum kölcsönhatások és a kötődés termodinamikai jellemzése
 Célkitűzés/témák Fehérje-ligandum kölcsönhatások és a kötődés termodinamikai jellemzése Ferenczy György Semmelweis Egyetem Biofizikai és Sugárbiológiai Intézet Biokémiai folyamatok - Ligandum-fehérje kötődés
Célkitűzés/témák Fehérje-ligandum kölcsönhatások és a kötődés termodinamikai jellemzése Ferenczy György Semmelweis Egyetem Biofizikai és Sugárbiológiai Intézet Biokémiai folyamatok - Ligandum-fehérje kötődés
Modern Fizika Labor. 2. Elemi töltés meghatározása
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
3. A kémiai kötés. Kémiai kölcsönhatás
 3. A kémiai kötés Kémiai kölcsönhatás ELSŐDLEGES MÁSODLAGOS OVALENS IONOS FÉMES HIDROGÉN- KÖTÉS DIPÓL- DIPÓL, ION- DIPÓL, VAN DER WAALS v. DISZPERZIÓS Kémiai kötések Na Ionos kötés Kovalens kötés Fémes
3. A kémiai kötés Kémiai kölcsönhatás ELSŐDLEGES MÁSODLAGOS OVALENS IONOS FÉMES HIDROGÉN- KÖTÉS DIPÓL- DIPÓL, ION- DIPÓL, VAN DER WAALS v. DISZPERZIÓS Kémiai kötések Na Ionos kötés Kovalens kötés Fémes
Sillabusz orvosi kémia szemináriumokhoz 1. Kémiai kötések
 Sillabusz orvosi kémia szemináriumokhoz 1. Kémiai kötések Pécsi Tudományegyetem Általános Orvostudományi Kar 2010-2011. 1 A vegyületekben az atomokat kémiai kötésnek nevezett erők tartják össze. Az elektronok
Sillabusz orvosi kémia szemináriumokhoz 1. Kémiai kötések Pécsi Tudományegyetem Általános Orvostudományi Kar 2010-2011. 1 A vegyületekben az atomokat kémiai kötésnek nevezett erők tartják össze. Az elektronok
Katalízis. Tungler Antal Emeritus professzor 2017
 Katalízis Tungler Antal Emeritus professzor 2017 Fontosabb időpontok: sósav oxidáció, Deacon process 1860 kéndioxid oxidáció 1875 ammónia oxidáció 1902 ammónia szintézis 1905-1912 metanol szintézis 1923
Katalízis Tungler Antal Emeritus professzor 2017 Fontosabb időpontok: sósav oxidáció, Deacon process 1860 kéndioxid oxidáció 1875 ammónia oxidáció 1902 ammónia szintézis 1905-1912 metanol szintézis 1923
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
Összefoglaló előadás. Sav-bázis elmélet
 Összefoglaló előadás Sav-bázis elmélet SAV-BÁZIS TULAJDNSÁGKAT BEFLYÁSLÓ TÉNYEZŐK Elméletek: 1. Brönsted Lowry elmélet: sav - + donor; bázis - + akceptor; Konjugálódó (vagy korrespondáló) sav-bázis pár:
Összefoglaló előadás Sav-bázis elmélet SAV-BÁZIS TULAJDNSÁGKAT BEFLYÁSLÓ TÉNYEZŐK Elméletek: 1. Brönsted Lowry elmélet: sav - + donor; bázis - + akceptor; Konjugálódó (vagy korrespondáló) sav-bázis pár:
Általános kémia képletgyűjtemény. Atomszerkezet Tömegszám (A) A = Z + N Rendszám (Z) Neutronok száma (N) Mólok száma (n)
 Általános kémia képletgyűjtemény (Vizsgára megkövetelt egyenletek a szimbólumok értelmezésével, illetve az egyenletek megfelelő alkalmazása is követelmény) Atomszerkezet Tömegszám (A) A = Z + N Rendszám
Általános kémia képletgyűjtemény (Vizsgára megkövetelt egyenletek a szimbólumok értelmezésével, illetve az egyenletek megfelelő alkalmazása is követelmény) Atomszerkezet Tömegszám (A) A = Z + N Rendszám
Modern Fizika Labor Fizika BSC
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. május 4. A mérés száma és címe: 9. Röntgen-fluoreszencia analízis Értékelés: A beadás dátuma: 2009. május 13. A mérést végezte: Márton Krisztina Zsigmond
Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. május 4. A mérés száma és címe: 9. Röntgen-fluoreszencia analízis Értékelés: A beadás dátuma: 2009. május 13. A mérést végezte: Márton Krisztina Zsigmond
6 Ionszelektív elektródok. elektródokat kiterjedten alkalmazzák a klinikai gyakorlatban: az automata analizátorokban
 6. Szelektivitási együttható meghatározása 6.1. Bevezetés Az ionszelektív elektródok olyan potenciometriás érzékelők, melyek valamely ion aktivitásának többé-kevésbé szelektív meghatározását teszik lehetővé.
6. Szelektivitási együttható meghatározása 6.1. Bevezetés Az ionszelektív elektródok olyan potenciometriás érzékelők, melyek valamely ion aktivitásának többé-kevésbé szelektív meghatározását teszik lehetővé.
1. feladat Összesen: 8 pont. 2. feladat Összesen: 11 pont. 3. feladat Összesen: 7 pont. 4. feladat Összesen: 14 pont
 1. feladat Összesen: 8 pont 150 gramm vízmentes nátrium-karbonátból 30 dm 3 standard nyomású, és 25 C hőmérsékletű szén-dioxid gáz fejlődött 1800 cm 3 sósav hatására. A) Írja fel a lejátszódó folyamat
1. feladat Összesen: 8 pont 150 gramm vízmentes nátrium-karbonátból 30 dm 3 standard nyomású, és 25 C hőmérsékletű szén-dioxid gáz fejlődött 1800 cm 3 sósav hatására. A) Írja fel a lejátszódó folyamat
ph-számítás A víz gyenge elektrolit. Kismértékben disszociál hidrogénionokra (helyesebben hidroxónium-ionokra) és hidroxid-ionokra :
 ph-számítás A víz gyenge elektrolit. Kismértékben disszociál hidrogénionokra (helyesebben hidroxónium-ionokra) és hidroxid-ionokra : H 2 O H + + OH -, (2 H 2 O H 3 O + + 2 OH - ). Semleges oldatban a hidrogén-ion
ph-számítás A víz gyenge elektrolit. Kismértékben disszociál hidrogénionokra (helyesebben hidroxónium-ionokra) és hidroxid-ionokra : H 2 O H + + OH -, (2 H 2 O H 3 O + + 2 OH - ). Semleges oldatban a hidrogén-ion
Mikroszkóp vizsgálata és folyadék törésmutatójának mérése (8-as számú mérés) mérési jegyzõkönyv
 (-as számú mérés) mérési jegyzõkönyv Készítette:, II. éves fizikus... Beadás ideje:... / A mérés leírása: A mérés során egy mikroszkóp különbözõ nagyítású objektívjeinek nagyítását, ezek fókusztávolságát
(-as számú mérés) mérési jegyzõkönyv Készítette:, II. éves fizikus... Beadás ideje:... / A mérés leírása: A mérés során egy mikroszkóp különbözõ nagyítású objektívjeinek nagyítását, ezek fókusztávolságát
Kémiai kötés. Általános Kémia, szerkezet Slide 1 /39
 Kémiai kötés 4-1 Lewis elmélet 4-2 Kovalens kötés: bevezetés 4-3 Poláros kovalens kötés 4-4 Lewis szerkezetek 4-5 A molekulák alakja 4-6 Kötésrend, kötéstávolság 4-7 Kötésenergiák Általános Kémia, szerkezet
Kémiai kötés 4-1 Lewis elmélet 4-2 Kovalens kötés: bevezetés 4-3 Poláros kovalens kötés 4-4 Lewis szerkezetek 4-5 A molekulák alakja 4-6 Kötésrend, kötéstávolság 4-7 Kötésenergiák Általános Kémia, szerkezet
5. Az adszorpciós folyamat mennyiségi leírása a Langmuir-izoterma segítségével
 5. Az adszorpciós folyamat mennyiségi leírása a Langmuir-izoterma segítségével 5.1. Átismétlendő anyag 1. Adszorpció (előadás) 2. Langmuir-izoterma (előadás) 3. Spektrofotometria és Lambert Beer-törvény
5. Az adszorpciós folyamat mennyiségi leírása a Langmuir-izoterma segítségével 5.1. Átismétlendő anyag 1. Adszorpció (előadás) 2. Langmuir-izoterma (előadás) 3. Spektrofotometria és Lambert Beer-törvény
Az egyensúly. Általános Kémia: Az egyensúly Slide 1 of 27
 Az egyensúly 6'-1 6'-2 6'-3 6'-4 6'-5 Dinamikus egyensúly Az egyensúlyi állandó Az egyensúlyi állandókkal kapcsolatos összefüggések Az egyensúlyi állandó számértékének jelentősége A reakció hányados, Q:
Az egyensúly 6'-1 6'-2 6'-3 6'-4 6'-5 Dinamikus egyensúly Az egyensúlyi állandó Az egyensúlyi állandókkal kapcsolatos összefüggések Az egyensúlyi állandó számértékének jelentősége A reakció hányados, Q:
Reakciókinetika. Általános Kémia, kinetika Dia: 1 /53
 Reakciókinetika 9-1 A reakciók sebessége 9-2 A reakciósebesség mérése 9-3 A koncentráció hatása: a sebességtörvény 9-4 Nulladrendű reakció 9-5 Elsőrendű reakció 9-6 Másodrendű reakció 9-7 A reakciókinetika
Reakciókinetika 9-1 A reakciók sebessége 9-2 A reakciósebesség mérése 9-3 A koncentráció hatása: a sebességtörvény 9-4 Nulladrendű reakció 9-5 Elsőrendű reakció 9-6 Másodrendű reakció 9-7 A reakciókinetika
Alap-ötlet: Karl Friedrich Gauss ( ) valószínűségszámítási háttér: Andrej Markov ( )
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
5. Laboratóriumi gyakorlat
 5. Laboratóriumi gyakorlat HETEROGÉN KÉMIAI REAKCIÓ SEBESSÉGÉNEK VIZSGÁLATA A CO 2 -nak vízben történő oldódása és az azt követő egyensúlyra vezető kémiai reakció az alábbi reakcióegyenlettel írható le:
5. Laboratóriumi gyakorlat HETEROGÉN KÉMIAI REAKCIÓ SEBESSÉGÉNEK VIZSGÁLATA A CO 2 -nak vízben történő oldódása és az azt követő egyensúlyra vezető kémiai reakció az alábbi reakcióegyenlettel írható le:
Modern Fizika Labor. Fizika BSc. Értékelés: A mérés dátuma: A mérés száma és címe: 5. mérés: Elektronspin rezonancia. 2008. március 18.
 Modern Fizika Labor Fizika BSc A mérés dátuma: 28. március 18. A mérés száma és címe: 5. mérés: Elektronspin rezonancia Értékelés: A beadás dátuma: 28. március 26. A mérést végezte: 1/7 A mérés leírása:
Modern Fizika Labor Fizika BSc A mérés dátuma: 28. március 18. A mérés száma és címe: 5. mérés: Elektronspin rezonancia Értékelés: A beadás dátuma: 28. március 26. A mérést végezte: 1/7 A mérés leírása:
Sav bázis egyensúlyok vizes oldatban
 Sav bázis egyensúlyok vizes oldatban Disszociációs egyensúlyi állandó HAc H + + Ac - ecetsav disszociációja [H + ] [Ac - ] K sav = [HAc] NH 4 OH NH 4 + + OH - [NH + 4 ] [OH - ] K bázis = [ NH 4 OH] Ammóniumhidroxid
Sav bázis egyensúlyok vizes oldatban Disszociációs egyensúlyi állandó HAc H + + Ac - ecetsav disszociációja [H + ] [Ac - ] K sav = [HAc] NH 4 OH NH 4 + + OH - [NH + 4 ] [OH - ] K bázis = [ NH 4 OH] Ammóniumhidroxid
Kémiai kötés. Általános Kémia, szerkezet Dia 1 /39
 Kémiai kötés 4-1 Lewis elmélet 4-2 Kovalens kötés: bevezetés 4-3 Poláros kovalens kötés 4-4 Lewis szerkezetek 4-5 A molekulák alakja 4-6 Kötésrend, kötéstávolság 4-7 Kötésenergiák Általános Kémia, szerkezet
Kémiai kötés 4-1 Lewis elmélet 4-2 Kovalens kötés: bevezetés 4-3 Poláros kovalens kötés 4-4 Lewis szerkezetek 4-5 A molekulák alakja 4-6 Kötésrend, kötéstávolság 4-7 Kötésenergiák Általános Kémia, szerkezet
Atomfizika. A hidrogén lámpa színképei. Elektronok H atom. Fényképlemez. emisszió H 2. gáz
 Atomfizika A hidrogén lámpa színképei - Elektronok H atom emisszió Fényképlemez V + H 2 gáz Az atom és kvantumfizika fejlődésének fontos szakasza volt a hidrogén lámpa színképeinek leírása, és a vonalas
Atomfizika A hidrogén lámpa színképei - Elektronok H atom emisszió Fényképlemez V + H 2 gáz Az atom és kvantumfizika fejlődésének fontos szakasza volt a hidrogén lámpa színképeinek leírása, és a vonalas
a. 35-ös tömegszámú izotópjában 18 neutron található. b. A 3. elektronhéján két vegyértékelektront tartalmaz. c. 2 mól atomjának tömege 32 g.
 MAGYAR TANNYELVŰ KÖZÉPISKOLÁK IX. ORSZÁGOS VETÉLKEDŐJE AL IX.-LEA CONCURS PE ŢARĂ AL LICEELOR CU LIMBĂ DE PREDARE MAGHIARĂ FABINYI RUDOLF KÉMIA VERSENY - SZERVETLEN KÉMIA Marosvásárhely, Bolyai Farkas
MAGYAR TANNYELVŰ KÖZÉPISKOLÁK IX. ORSZÁGOS VETÉLKEDŐJE AL IX.-LEA CONCURS PE ŢARĂ AL LICEELOR CU LIMBĂ DE PREDARE MAGHIARĂ FABINYI RUDOLF KÉMIA VERSENY - SZERVETLEN KÉMIA Marosvásárhely, Bolyai Farkas
Elektrokémia B01. Mi a ph? Láng Győző. Kémiai Intézet, Fizikai Kémiai Tanszék Eötvös Loránd Tudományegyetem Budapest
 Elektrokémia B01 Mi a ph? Láng Győző Kémiai Intézet, Fizikai Kémiai Tanszék Eötvös Loránd Tudományegyetem Budapest Mi a ph? 1:48:51 Természetesen mindenki tudja, hogy mi az a ph, hiszen tanulta az iskolában...
Elektrokémia B01 Mi a ph? Láng Győző Kémiai Intézet, Fizikai Kémiai Tanszék Eötvös Loránd Tudományegyetem Budapest Mi a ph? 1:48:51 Természetesen mindenki tudja, hogy mi az a ph, hiszen tanulta az iskolában...
Reakció kinetika és katalízis
 Reakció kinetika és katalízis 1. előadás: Alapelvek, a kinetikai eredmények analízise Felezési idők 1/22 2/22 : A koncentráció ( ) időbeli változása, jele: mol M v, mértékegysége: dm 3. s s Legyen 5H 2
Reakció kinetika és katalízis 1. előadás: Alapelvek, a kinetikai eredmények analízise Felezési idők 1/22 2/22 : A koncentráció ( ) időbeli változása, jele: mol M v, mértékegysége: dm 3. s s Legyen 5H 2
5. gy. VIZES OLDATOK VISZKOZITÁSÁNAK MÉRÉSE OSTWALD-FENSKE-FÉLE VISZKOZIMÉTERREL
 5. gy. VIZES OLDAOK VISZKOZIÁSÁNAK MÉRÉSE OSWALD-FENSKE-FÉLE VISZKOZIMÉERREL A fluid közegek jellemző anyagi tulajdonsága a viszkozitás, mely erősen befolyásolhatja a bennük lejátszódó reakciók sebességét,
5. gy. VIZES OLDAOK VISZKOZIÁSÁNAK MÉRÉSE OSWALD-FENSKE-FÉLE VISZKOZIMÉERREL A fluid közegek jellemző anyagi tulajdonsága a viszkozitás, mely erősen befolyásolhatja a bennük lejátszódó reakciók sebességét,
Matematika A2 vizsga mgeoldása június 4.
 Matematika A vizsga mgeoldása 03. június.. (a (3 pont Definiálja az f(x, y függvény határértékét az (x 0, y 0 helyen! Megoldás: Legyen D R, f : D R. Legyen az f(x, y függvény értelmezve az (x 0, y 0 pont
Matematika A vizsga mgeoldása 03. június.. (a (3 pont Definiálja az f(x, y függvény határértékét az (x 0, y 0 helyen! Megoldás: Legyen D R, f : D R. Legyen az f(x, y függvény értelmezve az (x 0, y 0 pont
Compton-effektus. Zsigmond Anna. jegyzıkönyv. Fizika BSc III.
 Compton-effektus jegyzıkönyv Zsigmond Anna Fizika BSc III. Mérés vezetıje: Csanád Máté Mérés dátuma: 010. április. Leadás dátuma: 010. május 5. Mérés célja A kvantumelmélet egyik bizonyítékának a Compton-effektusnak
Compton-effektus jegyzıkönyv Zsigmond Anna Fizika BSc III. Mérés vezetıje: Csanád Máté Mérés dátuma: 010. április. Leadás dátuma: 010. május 5. Mérés célja A kvantumelmélet egyik bizonyítékának a Compton-effektusnak
8. Egyszerû tesztek sûrûség funkcionál módszerek minõsítésére
 8. Egyszerû tesztek sûrûség funkcionál módszerek minõsítésére XX. Csonka, G. I., Nguyen, N. A., Kolossváry, I., Simple tests for density functionals, J. Comput. Chem. 18 (1997) 1534. XXII. Csonka, G. I.,
8. Egyszerû tesztek sûrûség funkcionál módszerek minõsítésére XX. Csonka, G. I., Nguyen, N. A., Kolossváry, I., Simple tests for density functionals, J. Comput. Chem. 18 (1997) 1534. XXII. Csonka, G. I.,
Atomszerkezet. Atommag protonok, neutronok + elektronok. atompályák, alhéjak, héjak, atomtörzs ---- vegyérték elektronok
 Atomszerkezet Atommag protonok, neutronok + elektronok izotópok atompályák, alhéjak, héjak, atomtörzs ---- vegyérték elektronok periódusos rendszer csoportjai Periódusos rendszer A kémiai kötés Kémiai
Atomszerkezet Atommag protonok, neutronok + elektronok izotópok atompályák, alhéjak, héjak, atomtörzs ---- vegyérték elektronok periódusos rendszer csoportjai Periódusos rendszer A kémiai kötés Kémiai
Heterociklusos vegyületek
 Szerves kémia A gyűrű felépítésében más atom (szénatomon kívül!), ún. HETEROATOM is részt vesz. A gyűrűt alkotó heteroatomként leggyakrabban a nitrogén, oxigén, kén szerepel, (de ismerünk arzént, szilíciumot,
Szerves kémia A gyűrű felépítésében más atom (szénatomon kívül!), ún. HETEROATOM is részt vesz. A gyűrűt alkotó heteroatomként leggyakrabban a nitrogén, oxigén, kén szerepel, (de ismerünk arzént, szilíciumot,
ESR-spektrumok különbözı kísérleti körülmények között A számítógépes értékelés alapjai anizotróp kölcsönhatási tenzorok esetén
 ESR-spektrumok különbözı kísérleti körülmények között A számítógépes értékelés alapjai anizotróp kölcsönhatási tenzorok esetén A paraméterek anizotrópiája egykristályok rögzített tengely körüli forgatásakor
ESR-spektrumok különbözı kísérleti körülmények között A számítógépes értékelés alapjai anizotróp kölcsönhatási tenzorok esetén A paraméterek anizotrópiája egykristályok rögzített tengely körüli forgatásakor
Vízben oldott antibiotikumok (Fluorokinolonok) sugárzással indukált lebontása
 Vízben oldott antibiotikumok (Fluorokinolonok) sugárzással indukált lebontása Doktori beszámoló 1. félév Készítette: Tegze Anna Témavezető: Dr. Takács Erzsébet Tartalomjegyzék Bevezetés: Gyógyszerhatóanyagok
Vízben oldott antibiotikumok (Fluorokinolonok) sugárzással indukált lebontása Doktori beszámoló 1. félév Készítette: Tegze Anna Témavezető: Dr. Takács Erzsébet Tartalomjegyzék Bevezetés: Gyógyszerhatóanyagok
T I T - M T T. Hevesy György Kémiaverseny. A megyei forduló feladatlapja. 7. osztály. A versenyző jeligéje:... Megye:...
 T I T - M T T Hevesy György Kémiaverseny A megyei forduló feladatlapja 7. osztály A versenyző jeligéje:... Megye:... Elért pontszám: 1. feladat:... pont 2. feladat:... pont 3. feladat:... pont 4. feladat:...
T I T - M T T Hevesy György Kémiaverseny A megyei forduló feladatlapja 7. osztály A versenyző jeligéje:... Megye:... Elért pontszám: 1. feladat:... pont 2. feladat:... pont 3. feladat:... pont 4. feladat:...
Az élethez szükséges elemek
 Az élethez szükséges elemek 92 elemből kb. 25 szükséges az élethez Szén (C), hidrogén (H), oxigén (O) és nitrogén (N) alkotja az élő szervezetekben előforduló anyag 96%-t A fennmaradó 4% legnagyobb része
Az élethez szükséges elemek 92 elemből kb. 25 szükséges az élethez Szén (C), hidrogén (H), oxigén (O) és nitrogén (N) alkotja az élő szervezetekben előforduló anyag 96%-t A fennmaradó 4% legnagyobb része
Termoelektromos hűtőelemek vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 4. MÉRÉS Termoelektromos hűtőelemek vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 30. Szerda délelőtti csoport 1. A mérés célja
KLASSZIKUS FIZIKA LABORATÓRIUM 4. MÉRÉS Termoelektromos hűtőelemek vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 30. Szerda délelőtti csoport 1. A mérés célja
Természetes vizek, keverékek mindig tartalmaznak oldott anyagokat! Írd le milyen természetes vizeket ismersz!
 Összefoglalás Víz Természetes víz. Melyik anyagcsoportba tartozik? Sorolj fel természetes vizeket. Mitől kemény, mitől lágy a víz? Milyen okokból kell a vizet tisztítani? Kémiailag tiszta víz a... Sorold
Összefoglalás Víz Természetes víz. Melyik anyagcsoportba tartozik? Sorolj fel természetes vizeket. Mitől kemény, mitől lágy a víz? Milyen okokból kell a vizet tisztítani? Kémiailag tiszta víz a... Sorold
Az elektromos kettősréteg. Az elektromos potenciálkülönbség eredete, értéke és az azt befolyásoló tényezők. Kolloidok stabilitása.
 Az elektromos kettősréteg. Az elektromos potenciálkülönbség eredete, értéke és az azt befolyásoló tényezők. Kolloidok stabilitása. Adszorpció oldatból szilárd felületre Adszorpció oldatból Nem-elektrolitok
Az elektromos kettősréteg. Az elektromos potenciálkülönbség eredete, értéke és az azt befolyásoló tényezők. Kolloidok stabilitása. Adszorpció oldatból szilárd felületre Adszorpció oldatból Nem-elektrolitok
KONDUKTOMETRIÁS MÉRÉSEK
 A környezetvédelem analitikája KON KONDUKTOMETRIÁS MÉRÉSEK A GYAKORLAT CÉLJA: A konduktometria alapjainak megismerése. Elektrolitoldatok vezetőképességének vizsgálata. Oxálsav titrálása N-metil-glükamin
A környezetvédelem analitikája KON KONDUKTOMETRIÁS MÉRÉSEK A GYAKORLAT CÉLJA: A konduktometria alapjainak megismerése. Elektrolitoldatok vezetőképességének vizsgálata. Oxálsav titrálása N-metil-glükamin
Modern fizika laboratórium
 Modern fizika laboratórium 11. Az I 2 molekula disszociációs energiája Készítette: Hagymási Imre A mérés dátuma: 2007. október 3. A beadás dátuma: 2007. október xx. 1. Bevezetés Ebben a mérésben egy kétatomos
Modern fizika laboratórium 11. Az I 2 molekula disszociációs energiája Készítette: Hagymási Imre A mérés dátuma: 2007. október 3. A beadás dátuma: 2007. október xx. 1. Bevezetés Ebben a mérésben egy kétatomos
Az anyagi rendszer fogalma, csoportosítása
 Az anyagi rendszer fogalma, csoportosítása A bemutatót összeállította: Fogarasi József, Petrik Lajos SZKI, 2011 1 1 A rendszer fogalma A körülöttünk levő anyagi világot atomok, ionok, molekulák építik
Az anyagi rendszer fogalma, csoportosítása A bemutatót összeállította: Fogarasi József, Petrik Lajos SZKI, 2011 1 1 A rendszer fogalma A körülöttünk levő anyagi világot atomok, ionok, molekulák építik
Általános és szervetlen kémia 3. hét Kémiai kötések. Kötések kialakítása - oktett elmélet. Lewis-képlet és Lewis szerkezet
 Általános és szervetlen kémia 3. hét Kémiai kötések Az elemek és vegyületek halmazai az atomok kapcsolódásával - kémiai kötések kialakításával - jönnek létre szabad atomként csak a nemesgázatomok léteznek
Általános és szervetlen kémia 3. hét Kémiai kötések Az elemek és vegyületek halmazai az atomok kapcsolódásával - kémiai kötések kialakításával - jönnek létre szabad atomként csak a nemesgázatomok léteznek
2. Rugalmas állandók mérése jegyzőkönyv javított. Zsigmond Anna Fizika Bsc II. Mérés dátuma: Leadás dátuma:
 2. Rugalmas állandók mérése jegyzőkönyv javított Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 17. Leadás dátuma: 2008. 10. 08. 1 1. Mérések ismertetése Az első részben egy téglalap keresztmetszetű
2. Rugalmas állandók mérése jegyzőkönyv javított Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 17. Leadás dátuma: 2008. 10. 08. 1 1. Mérések ismertetése Az első részben egy téglalap keresztmetszetű
Modern Fizika Labor. 2. Az elemi töltés meghatározása. Fizika BSc. A mérés dátuma: nov. 29. A mérés száma és címe: Értékelés:
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. nov. 29. A mérés száma és címe: 2. Az elemi töltés meghatározása Értékelés: A beadás dátuma: 2011. dec. 11. A mérést végezte: Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. nov. 29. A mérés száma és címe: 2. Az elemi töltés meghatározása Értékelés: A beadás dátuma: 2011. dec. 11. A mérést végezte: Szőke Kálmán Benjamin
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KÉMIA FELVÉTELI DOLGOZAT
 KÉMIA FELVÉTELI DOLGOZAT I. Egyszerű választásos teszt Karikázza be az egyetlen helyes, vagy egyetlen helytelen választ! 1. Hány neutront tartalmaz a 127-es tömegszámú, 53-as rendszámú jód izotóp? A) 74
KÉMIA FELVÉTELI DOLGOZAT I. Egyszerű választásos teszt Karikázza be az egyetlen helyes, vagy egyetlen helytelen választ! 1. Hány neutront tartalmaz a 127-es tömegszámú, 53-as rendszámú jód izotóp? A) 74
8. osztály 2 Hevesy verseny, megyei forduló, 2008.
 8. osztály 2 Hevesy verseny, megyei forduló, 2008. Figyelem! A feladatokat ezen a feladatlapon oldd meg! Megoldásod olvasható és áttekinthető legyen! A feladatok megoldásában a gondolatmeneted követhető
8. osztály 2 Hevesy verseny, megyei forduló, 2008. Figyelem! A feladatokat ezen a feladatlapon oldd meg! Megoldásod olvasható és áttekinthető legyen! A feladatok megoldásában a gondolatmeneted követhető
Határozott integrál és alkalmazásai
 Határozott integrál és alkalmazásai 5. május 5.. Alapfeladatok. Feladat: + d = Megoldás: Egy határozott integrál kiszámolása a feladat. Ilyenkor a Newton-Leibniz-tételt használhatjuk, mely azt mondja ki,
Határozott integrál és alkalmazásai 5. május 5.. Alapfeladatok. Feladat: + d = Megoldás: Egy határozott integrál kiszámolása a feladat. Ilyenkor a Newton-Leibniz-tételt használhatjuk, mely azt mondja ki,
13 Elektrokémia. Elektrokémia Dia 1 /52
 13 Elektrokémia 13-1 Elektródpotenciálok mérése 13-2 Standard elektródpotenciálok 13-3 E cella, ΔG és K eq 13-4 E cella koncentráció függése 13-5 Elemek: áramtermelés kémiai reakciókkal 13-6 Korrózió:
13 Elektrokémia 13-1 Elektródpotenciálok mérése 13-2 Standard elektródpotenciálok 13-3 E cella, ΔG és K eq 13-4 E cella koncentráció függése 13-5 Elemek: áramtermelés kémiai reakciókkal 13-6 Korrózió:
Jegyzet. Kémia, BMEVEAAAMM1 Műszaki menedzser hallgatók számára Dr Csonka Gábor, egyetemi tanár Dr Madarász János, egyetemi docens.
 Kémia, BMEVEAAAMM Műszaki menedzser hallgatók számára Dr Csonka Gábor, egyetemi tanár Dr Madarász János, egyetemi docens Jegyzet dr. Horváth Viola, KÉMIA I. http://oktatas.ch.bme.hu/oktatas/konyvek/anal/
Kémia, BMEVEAAAMM Műszaki menedzser hallgatók számára Dr Csonka Gábor, egyetemi tanár Dr Madarász János, egyetemi docens Jegyzet dr. Horváth Viola, KÉMIA I. http://oktatas.ch.bme.hu/oktatas/konyvek/anal/
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
Biomatematika 12. Szent István Egyetem Állatorvos-tudományi Kar. Fodor János
 Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
ZÁRÓJELENTÉS. Fény hatására végbemenő folyamatok önszerveződő rendszerekben
 ZÁRÓJELENTÉS Fény hatására végbemenő folyamatok önszerveződő rendszerekben Jól megválasztott anyagok elegyítésekor, megfelelő körülmények között másodlagos kötésekkel összetartott szupramolekuláris rendszerek
ZÁRÓJELENTÉS Fény hatására végbemenő folyamatok önszerveződő rendszerekben Jól megválasztott anyagok elegyítésekor, megfelelő körülmények között másodlagos kötésekkel összetartott szupramolekuláris rendszerek
Mozgatható térlefedő szerkezetek
 Mozgatható térlefedő szerkezetek TDK Konferencia 2010 Szilárdságtani és tartószerkezeti szekció Tartalomjegyzék 1 Absztrakt 2 Bevezetés 3 Az alakzat mozgásának görbületre gyakorolt hatása 4 Teljes összenyomódás
Mozgatható térlefedő szerkezetek TDK Konferencia 2010 Szilárdságtani és tartószerkezeti szekció Tartalomjegyzék 1 Absztrakt 2 Bevezetés 3 Az alakzat mozgásának görbületre gyakorolt hatása 4 Teljes összenyomódás
TÖBBKOMPONENS RENDSZEREK FÁZISEGYENSÚLYAI II. Ismerjük fel, hogy többkomponens fázisegyensúlyokban a folyadék fázisnak kitüntetett szerepe van!
 TÖKOMPONENS RENDSZEREK FÁZISEGYENSÚLYI II Ismerjük fel hogy többkomonens fázisegyensúlyokban a folyadék fázisnak kitüntetett szeree van! Eddig: egymásban korátlanul oldódó folyadékok folyadék-gz egyensúlyai
TÖKOMPONENS RENDSZEREK FÁZISEGYENSÚLYI II Ismerjük fel hogy többkomonens fázisegyensúlyokban a folyadék fázisnak kitüntetett szeree van! Eddig: egymásban korátlanul oldódó folyadékok folyadék-gz egyensúlyai
Az atom- olvasni. 1. ábra Az atom felépítése 1. Az atomot felépítő elemi részecskék. Proton, Jele: (p+) Neutron, Jele: (n o )
 Az atom- olvasni 2.1. Az atom felépítése Az atom pozitív töltésű atommagból és negatív töltésű elektronokból áll. Az atom atommagból és elektronburokból álló semleges kémiai részecske. Az atommag pozitív
Az atom- olvasni 2.1. Az atom felépítése Az atom pozitív töltésű atommagból és negatív töltésű elektronokból áll. Az atom atommagból és elektronburokból álló semleges kémiai részecske. Az atommag pozitív
41. ábra A NaCl rács elemi cellája
 41. ábra A NaCl rács elemi cellája Mindkét rácsra jellemző, hogy egy tetszés szerint kiválasztott pozitív vagy negatív töltésű iont ellentétes töltésű ionok vesznek körül. Különbség a közvetlen szomszédok
41. ábra A NaCl rács elemi cellája Mindkét rácsra jellemző, hogy egy tetszés szerint kiválasztott pozitív vagy negatív töltésű iont ellentétes töltésű ionok vesznek körül. Különbség a közvetlen szomszédok
Modern Fizika Labor. 12. Infravörös spektroszkópia. Fizika BSc. A mérés dátuma: okt. 04. A mérés száma és címe: Értékelés:
 Modern Fizika Labor Fizika BSc A mérés dátuma: 011. okt. 04. A mérés száma és címe: 1. Infravörös spektroszkópia Értékelés: A beadás dátuma: 011. dec. 1. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 011. okt. 04. A mérés száma és címe: 1. Infravörös spektroszkópia Értékelés: A beadás dátuma: 011. dec. 1. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
ph-számítás A víz gyenge elektrolit. Kismértékben disszociál hidrogénionokra (helyesebben hidroxónium-ionokra) és hidroxid-ionokra :
 ph-számítás A víz gyenge elektrolit. Kismértékben disszociál hidrogénionokra (helyesebben hidroxónium-ionokra) és hidroxid-ionokra : H 2 O H + + OH -, (2 H 2 O H 3 O + + 2 OH - ). Semleges oldatban a hidrogén-ion
ph-számítás A víz gyenge elektrolit. Kismértékben disszociál hidrogénionokra (helyesebben hidroxónium-ionokra) és hidroxid-ionokra : H 2 O H + + OH -, (2 H 2 O H 3 O + + 2 OH - ). Semleges oldatban a hidrogén-ion
Kinetika. Általános Kémia, kinetika Dia: 1 /53
 Kinetika 15-1 A reakciók sebessége 15-2 Reakciósebesség mérése 15-3 A koncentráció hatása: a sebességtörvény 15-4 Nulladrendű reakció 15-5 Elsőrendű reakció 15-6 Másodrendű reakció 15-7 A reakció kinetika
Kinetika 15-1 A reakciók sebessége 15-2 Reakciósebesség mérése 15-3 A koncentráció hatása: a sebességtörvény 15-4 Nulladrendű reakció 15-5 Elsőrendű reakció 15-6 Másodrendű reakció 15-7 A reakció kinetika
Szerves Kémiai Problémamegoldó Verseny
 Szerves Kémiai Problémamegoldó Verseny 2015. április 24. Név: E-mail cím: Egyetem: Szak: Képzési szint: Évfolyam: Pontszám: Név: Pontszám: / 3 pont 1. feladat Egy C 4 H 10 O 3 összegképletű vegyület 0,1776
Szerves Kémiai Problémamegoldó Verseny 2015. április 24. Név: E-mail cím: Egyetem: Szak: Képzési szint: Évfolyam: Pontszám: Név: Pontszám: / 3 pont 1. feladat Egy C 4 H 10 O 3 összegképletű vegyület 0,1776
19. A fényelektromos jelenségek vizsgálata
 19. A fényelektromos jelenségek vizsgálata PÁPICS PÉTER ISTVÁN csillagász, 3. évfolyam Mérőpár: Balázs Miklós 2006.04.19. Beadva: 2006.05.15. Értékelés: A MÉRÉS LEÍRÁSA Fontos megállapítás, hogy a fénysugárzásban
19. A fényelektromos jelenségek vizsgálata PÁPICS PÉTER ISTVÁN csillagász, 3. évfolyam Mérőpár: Balázs Miklós 2006.04.19. Beadva: 2006.05.15. Értékelés: A MÉRÉS LEÍRÁSA Fontos megállapítás, hogy a fénysugárzásban
Tevékenység: Tanulmányozza a ábrát és a levezetést! Tanulja meg a fajlagos nyúlás mértékének meghatározásának módját hajlításnál!
 Tanulmányozza a.3.6. ábrát és a levezetést! Tanulja meg a fajlagos nyúlás mértékének meghatározásának módját hajlításnál! Az alakváltozás mértéke hajlításnál Hajlításnál az alakváltozást mérnöki alakváltozási
Tanulmányozza a.3.6. ábrát és a levezetést! Tanulja meg a fajlagos nyúlás mértékének meghatározásának módját hajlításnál! Az alakváltozás mértéke hajlításnál Hajlításnál az alakváltozást mérnöki alakváltozási
Gauss-Seidel iteráció
 Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Toluol (Bruckner II/1 476) µ= 0.33 Debye
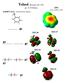 E(RHF/3-21G= -268.24021020 Hartree Toluol (Bruckner II/1 476) µ= 0.33 Debye -0.04 töltés. 0.04 φ6 MO 26 MO 27 φ4 φ5 MO 24 MO 25 φ2 MO 21 φ1 TD ρ= 0.0004 a.u. Anilin (Bruckner II/1 476) µ= 1.44 Debye E(RHF/6-311++G(d,p))=
E(RHF/3-21G= -268.24021020 Hartree Toluol (Bruckner II/1 476) µ= 0.33 Debye -0.04 töltés. 0.04 φ6 MO 26 MO 27 φ4 φ5 MO 24 MO 25 φ2 MO 21 φ1 TD ρ= 0.0004 a.u. Anilin (Bruckner II/1 476) µ= 1.44 Debye E(RHF/6-311++G(d,p))=
6. gyakorlat. Gelle Kitti. Csendes Tibor Somogyi Viktor. London András. jegyzetei alapján
 Közelítő és szimbolikus számítások 6. gyakorlat Sajátérték, Gersgorin körök Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján . Mátrixok sajátértékei
Közelítő és szimbolikus számítások 6. gyakorlat Sajátérték, Gersgorin körök Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján . Mátrixok sajátértékei
A kálium-permanganát és az oxálsav közötti reakció vizsgálata 9a. mérés B4.9
 A kálium-permanganát és az oxálsav közötti reakció vizsgálata 9a. mérés B4.9 Név: Pitlik László Mérés dátuma: 2014.12.04. Mérőtársak neve: Menkó Orsolya Adatsorok: M24120411 Halmy Réka M14120412 Sárosi
A kálium-permanganát és az oxálsav közötti reakció vizsgálata 9a. mérés B4.9 Név: Pitlik László Mérés dátuma: 2014.12.04. Mérőtársak neve: Menkó Orsolya Adatsorok: M24120411 Halmy Réka M14120412 Sárosi
Kémiai alapismeretek 3. hét
 Kémiai alapismeretek 3. hét Horváth Attila Pécsi Tudományegyetem, Természettudományi Kar, Kémia Intézet, Szervetlen Kémiai Tanszék 2013. szeptember 17.-20. 1/15 2013/2014 I. félév, Horváth Attila c : Molekulákon
Kémiai alapismeretek 3. hét Horváth Attila Pécsi Tudományegyetem, Természettudományi Kar, Kémia Intézet, Szervetlen Kémiai Tanszék 2013. szeptember 17.-20. 1/15 2013/2014 I. félév, Horváth Attila c : Molekulákon
Curie Kémia Emlékverseny 2018/2019. Országos Döntő 8. évfolyam
 A feladatokat írta: Kódszám: Harkai Jánosné, Szeged... Lektorálta: Kovács Lászlóné, Szolnok 2019. május 11. Curie Kémia Emlékverseny 2018/2019. Országos Döntő 8. évfolyam A feladatok megoldásához csak
A feladatokat írta: Kódszám: Harkai Jánosné, Szeged... Lektorálta: Kovács Lászlóné, Szolnok 2019. május 11. Curie Kémia Emlékverseny 2018/2019. Országos Döntő 8. évfolyam A feladatok megoldásához csak
