Kamera-LIDAR pár kalibrálása dobozokkal
|
|
|
- Mátyás Bakos
- 6 évvel ezelőtt
- Látták:
Átírás
1 Kamera-LIDAR pár kalibrálása dobozokkal Pusztai Zoltán 1, Hajder Levente 2 1 MTA SZTAKI, Eötvös Loránd Tudományegyetem zoltan.pusztai@mta.sztaki.hu 2 MTA SZTAKI levente.hajder@mta.sztaki.hu Kivonat Manapság egyre nagyobb az igény a minket körülvevő környezet felderítésére, szaknyelven szólva letapogatására (szkennelésére). Különösen igaz ez a robotok és önvezető autók világában, amelyeknek önmagukban kell döntéseket hozniuk a lehető legkevesebb emberi beavatkozással. Több eszköz is létezik, amelyekkel gépeinket felszerelve azok képesek lesznek a világ érzékelésére: kamerák, mikrofonok, radarok, stb. Az egyik ilyen gyakran használt eszköz a LiDAR (Light Detection And Ranging), amellyel ritka pontfelhőt készíthetünk a körülöttünk található világról. A LIDAR-os méréseket kiegészíthetik az RGB kamerák képeit feldolgozó algoritmusok, melyek például segíthetnek a kapott pontfelhő sűrítésében. Autonóm járművek és robotok esetében ezen eszközök fixálhatóak egymáshoz képest, ezért az egymáshoz képesti pozíciót és elforgatást kalibráció segítségével a működés előtt ki lehet számolni. Ebben a cikkben megmutatjuk, hogy ez a kalibráció megoldható dobozok segítségével. A javasolt eljárást részletesen bemutatjuk, a pontosságot elemezzük. 1.. Bevezetés Manapság egyre nagyobb az igény a minket körülvevő környezet felderítésére, szaknyelven szólva letapogatására (szkennelésére). Különösen igaz ez a robotok és önvezető autók világában, amelyeknek önmagukban kell döntéseket hozniuk, a lehető legkevesebb emberi beavatkozással. Több eszköz is létezik, amelyekkel gépeinket felszerelve azok képesek lesznek a világ érzékelésére: kamerák, mikrofonok, radarok, stb. Az egyik ilyen gyakran használt eszköz a LiDAR (Light Detection And Ranging), amellyel ritka pontfelhőt készíthetünk a körülöttünk található világról. A LiDAR-os méréseket kiegészíthetik az RGB kamerák képeit feldolgozó algoritmusok, melyek például segíthetnek a kapott pontfelhő sűrítésében. Autonóm járművek és robotok esetében ezen eszközök fixálhatóak egymáshoz képest, ezért az egymáshoz képesti pozíciót és elforgatást kalibráció segítségével ki lehet számolni. Ebben a cikkben megmutatjuk, hogy ez a kalibráció hatékonyan megoldható dobozok segítségével. A javasolt eljárás pontosságát részletesen bemutatjuk. Célunk, hogy egy félautomatikus eljárást hozzunk létre, amely valós helyzetekben is felhasználható. Egy GoPro Hero 4 Black kamerával és Velodyne LiDAR-ral teszteltük algoritmusunk. A kalibráció a következőek szerint ment
2 2 Pusztai Zoltán és mtsai végbe: Először egy közönséges dobozt helyeztünk a kamera elé úgy, hogy az a LiDAR szemszögéből is jól látható legyen. Felvételt készítettünk a kamerával, és lementettük a pontfelhőt a LiDAR segítségével. Kézi beavatkozással elkülönítettük a doboz pontjait a pontfelhő többi részétől, a doboz méreteit lemértük. Az algoritmus ráillesztette a dobozt a ponthalmazra, majd a felhasználónak ki kellett választania a doboz sarkaihoz tartozó pixel koordinátákat a képen. A 3D-2D megfeleltetések alapján pedig ki lehetett számolni a LiDAR és a kamera közti transzformációt. Néhány úgynevezett online módszer is elérhető a szakirodalomban, amelyekkel a kalibráció elvégezhető menet közben, azaz az eszköz használata során. Ezek közül néhány esetében nem is szükséges emberi közbelépés, viszont ezek nem olyan pontosak, mint az offline módszerek. Mi azt az esetet vizsgáljuk, amikor a kamera-lidar pár fix pozícióban helyezkedik el egymáshoz képest, ezért az egyszeri, offline kalibráció is használható. A pontosabb kalibráció elősegíti azon algoritmusok működését, amelyek felhasználják mind a két eszközt. A 3D LiDAR eszközök legnagyobb előnye a kibocsájtott fény típusa, amely különbözik a látható fénytől. Ezért bármilyen megvilágítási környezetben használható és képes a világunkról 3D pontfelhőt szkennelni nagy távolságok esetén is. Viszont ezen eszközök még mindig elég drágák és a felbontásuk limitált a Velodyne 64 LIDAR is csak 64 pontot képes horizontálisan letapogatni, lassú frissítési idővel. A kamerák olcsónak mondhatóak, így könnyen fel tudunk használni egyszerre többet is belőlük, melyekkel nagy felbontású, színes képeket nyerhetünk. Azonban használatuk nehézkes lehet különböző szélsőséges megvilágítási környezetekben, például az esti órákban. Ezen kívül árnyékok illetve takarás is nehezíti a képfeldolgozó algoritmusok dolgát. Egyértelmű, hogy a LiDAR eszközök hátrányát kompenzálhatjuk a kamerák előnyös tulajdonságaival és fordítva. Ezért a 3D LiDAR-t és a kamerákat gyakran használják egyszerre, főképp objektumok detektálásra, környezet rekonstruálásra és közlekedési feladatok megoldására. Ahhoz, hogy a két eszköz együtt tudjon dolgozni, szükséges a külső paraméterek meghatározása, ami a két eszköz relatív pozícióját és orientációját jelenti egymáshoz viszonyítva. A kalibrációs eljárás lépéseit a következőek pontokban foglaljuk össze: 1. Egy dobozt kell a kamera és a LiDAR elé helyeznünk. 2. Felvételt kell készíteni a kamerával és le kell menteni a pontfelhőt a dobozról. 3. A doboz pontjait el kell különíteni a pontfelhő többi részétől. 4. A doboz-t detektálni kell és meghatározni annak sarokpontjait. 5. Ezen sarokpontokat ki kell választani a képen. 6. Végül a 3D-2D pontmegfeleltetésekből a külső paraméterek meghatározhatóak. A cikk a következőek alapján épül fel. A 2. fejezetben egy rövid áttekintést adunk a témán belül megjelent korábbi cikkekről. A 3. fejezetben részletezzük a pontfelhő tisztítását és a doboz pontjainak elkülönítését. Az automatikus doboz illesztést a 4. szakaszban fejtjük ki, majd az 5. fejezetben lépésenként mutatjuk be az algoritmus működését egy valós példán. A 6. fejezetben összehasonlítjuk
3 Kamera-LIDAR pár kalibrálása dobozokkal 3 algoritmusunkat egy konkurens módszerrel, végül a 7. szakaszban összefoglaljuk munkánkat. 2.. Irodalmi áttekintés Több módszer is létezik a kamera-lidar pár kalibrációjára. A korábbiak még 2D LiDAR-t használtak, úgy mint [Zhang and Pless, 2004], majd az olcsóbb 3D LiDAR eszközök megjelenésének köszönhetően a kutatás átterelődött azok irányába. A módszerek több csoportra bonthatóak, sokan sakktáblákat használnak a kalibrációhoz, úgy mint [Geiger et al., 2012] és [Pandey et al., 2010], páran sík objektumokat, mint [Park et al., 2014] vagy [Veĺas et al., 2014] és páran egyáltalán nem használnak kalibrációs objektumok, mint például [Pandey et al., 2012]. A legtöbb esetben a LiDAR és a kamera már előre, külön-külön kalibrált, azaz a belső paramétereik ismertek. Léteznek olyan módszerek, melyekhez nem szükséges kalibrációs objektum vagy bármilyen előzetes tudás az eszközökről, viszont ezen módszerek pontossága bőven eltér az optimálistól. A módszer, amelyet [Park et al., 2014] tárgyal közel áll a sajátunkhoz a felhasználás módját nézve. Homogén, fehér, sík háromszög vagy négyzet alakú táblát használnak a kalibrációhoz. Bár a módszerhez egynél több képet szükséges készíteni a tábláról, vagy több táblát kell használni egy kép felvétele során a mi módszerünknél csak egy felvétel szükséges. Ezen kívül a síkbeli tábla pontjait becslésekkel közelítik, nem pedig pontos mérésekkel, ami befolyásolhatja a kalibráció pontosságát. A [Gong et al., 2013] módszer esetében több, mint 2 felvételt kell készíteni három egymásra merőleges síkról a kamerával és a LiDAR-ral egyaránt. Ez több feldolgozandó adatot jelent, a tesztjeik során 20 másodperc kellett a kalibrációhoz, melyet 9 megfigyelésből állítottak össze. Egy nagyon érdekes módszert publikált [Veĺas et al., 2014], hiszen egy nem hétköznapi kalibrációs tárgyakt választottak ki. Fehér háttér elé egy sík lapot akasztottak, melyen 4 kör alakú lyukat vágtak ki. A pontfelhőben pedig az ez által keletkeződött négy lyukat automatikusan detektálták. [Levinson and Thrun, 2013] korábbi munkáin alapul a módszer és csak egy képet szükséges készíteni a kalibrációhoz. [Geiger et al., 2012] egy új módszert mutatatott be a kamera-lidar pár kalibrálására, amelyhez elegendő egy kamera felvétel és egy LiDAR pontfelhő. A módszer teljesen automatikus, viszont több sakktáblát kell elhelyezni a kalibráció sikeréhez. Az eljárást részletesen be fogjuk mutatni a 6. fejezetben, ahol összehasonlítjuk a sajátunkkal. A LiDAR az időt méri a lézer sugár kibocsájtása és visszaérkezése között, majd kiszámolja a távolságot a fény sebessége és az előbbi időkülönbség alapján. Ám a visszaverődés különböző lehet színenként. Ezért egy sakktábla pontjai például nem fognak egy síkon maradni a LiDAR pontfelhőjében, ez a tulajdonság a [Park et al., 2014]-ban részletezve megtalálható.
4 4 Pusztai Zoltán és mtsai 3.. Pontfelhő szeparálása Általános ötlet A főbb gondolat az algoritmusunk mögött az, hogy ha a kamera belső paraméterei, a doboz sarkinak pontjai a LiDAR koordináta rendszerében és ezen sarokpontok helyzete a képen ismert, akkor a LiDAR és a kamera koordináta rendszere közti transzformáció meghatározható. A külső paramétereket a jól ismert PnP (Perspective-n-Point) probléma megoldása adja, ami egy fogatási mátrix és egy eltolás vektor. A lépések melyekkel a fenti feltételek teljesíthetőek a következő fejezetekben kerülnek részletezésre A kalibráció felépítése A sikeres kalibrációhoz legalább 4 különböző 3D-2D pontmegfeleltetésre lesz szükségünk. Ezért a kalibrációs dobozt úgy kell a kamera elé helyezni, hogy három oldalának láthatónak kell lennie a képen, illetve a pontfelhőn egyaránt. Bármilyen tetszőleges doboz használható a kalibrációhoz, de a doboz méreteit, azaz a doboz három látható oldalának a hosszát le kell mérnünk. Fontos megjegyezni, hogy a kalibráció során csak egyetlen képet és egy pontfelhőt használunk fel, viszont az eljárást ki lehet terjeszteni több kamera és több LiDAR eszköz egyidejű kalibrálásra. A részletek két LiDAR kalibrációjáról a 6.. fejezetben találhatóak. A méréseink során egy GoPro Hero 4 Black kamerát és két különböző típusú LiDAR eszközt használtunk. Az egyik egy Velodyne VLP-16, ami 16 csatornás LiDAR eszköz, ezért meglehetősen ritka pontfelhőt képes generálni. A másik pedig a Velodyne HDL-64, ami 64 csatornával felszerelt, így sűrűbb pontfelhőt észlelésére képes. A GoPro Hero 4 Black egy akciókamera, melyet főleg sportolás megörökítésére használnak. Az eszköz kalibrációja meglehetősen nehéz, mert nagy látószöggel rendelkezik, így nagyfokú torzítással kell számolni, ez a 1. ábrán is jól látható. Ipari projektek során nem használatos ez az eszköz, mi is csak a könnyű hordozhatósága miatt használtuk. A kis mérete ellenére a kamera képes 12MP fotókat és 4K videókat készíteni 30 FPS gyorsasággal. Az általunk bemutatott módszer természetesen bármilyen típusú LiDAR-kamera párosítással használható. A LiDAR-kamera pár kalibrálása előtt a kamerát be kell kalibrálnunk. Ehhez a lyukkamera modellt használtuk, jelölje P = C[R t] a projekciós transzformációt, ahol C a kamera mátrix, R a forgatási mátrix és t az eltolás vektor. Ahogy azt már említettük, a torzítást is figyelembe kell vennünk, mi radiális torzítást használtunk (k 1,k 2 ) paraméterekkel. A C és (k 1,k 2 ) adja a kamera belső paramétereit, amiket a [Zhang, 2000] által bemutatott módszerrel határoztunk meg. Az R és a t pedig a külső paraméterek, amik a LiDAR és a kamera közötti koordináta rendszer váltást jelölik. A mi kalibrációs eljárásunk célja ezen külső paraméterek meghatározása. A kalibrációs dobozt a kamera és LiDAR elé kell helyeznünk úgy, hogy annak három oldala jól látható legyen mind a két eszköz nézetéből, egy ilyen elhelyezés
5 Kamera-LIDAR pár kalibrálása dobozokkal 5 látható az 1. ábrán. Majd a kamera képét és a LiDAR pontfelhőt kell felhasználni a továbbiakban. A kalibráláshoz elegendő csak egyetlen felvételt készíteni egyetlen kalibrációs objektumról. Más módszerek esetében több felvétel szükséges egy objektumról vagy több objektumról kell egy felvételt készítenünk, ami minden esetben több adat feldolgozását jelenti. 1. ábra. Példa a kalibrációs doboz megfelelő elhelyezkedésére Pontfelhő klaszterezése Az algoritmus működéséhez szükséges a kézi beavatkozás, hogy el tudjuk különíteni a doboz pontjait a pontfelhő többi részétől. A pontok jól klaszterezhetőek a Mean-Sift algoritmus által [Fukunaga and Hostetler, 2006]. A legtöbb mérésünk során a dobozt egy székre raktuk, mert a LiDAR eszközök horizontális látószöge nagyon kicsi, ezért a Mean-Sift a széket és a rajta fekvő kalibrációs dobozt egy klaszterbe sorolta. Eljárásunk képes az ilyen klasztereket is feldolgozni, a doboz egyedi tulajdonságainak keresésével. Az kézi beavatkozás során csak a megfelelő klasztert szükséges kiválasztani, amely tartalmazza a doboz pontjait Doboz elkülönítése Az alfejezet célja, hogy pontosan el tudjuk különíteni a doboz három látható oldalát a pontfelhő többi részétől. Mivel a pontfelhő többféle tárgy pontjait is
6 6 Pusztai Zoltán és mtsai tartalmazhatja, először a dobozhoz tartozó pontokat kell felismernünk. Az előző lépésben a doboz környezete kézzel lett kiválasztva, most ebből a környezetből kell kiemelnünk azon pontokat, melyek a dobozhoz tartoznak. Habár ez a környezet már kevesebb outlier a dobozhoz nem tartozó pontot tartalmaz, erősebb szűrés szükséges a pontfelhőn. A probléma megoldása két lépésből áll. Először szekvenciális RANSAC algoritmust használtuk a pontfelhő síkokra való felbontására Euklideszi távolságot alkalmazva. Miután a pontfelhő síkjait meghatároztuk, a második lépésben kihasználjuk a doboz azon tulajdonságát, hogy a három látható oldala merőleges egymásra. Ezért azt a három síkot választjuk ki, amelyekre a következő hiba mértéke minimális: E(n 1,n 2,n 3 )= n 1 n 2 + n 1 n 3 + n 2 n 3, (1) ahol n k a k-adik sík normál vektora (k {1, 2, 3}). A pontfelhő ezen szegmense általában már nem tartalmaz sok síkot, így a síkok közötti kimerítő kereséshez nem szükséges nagy számítási idő. 4.. Doboz illesztése a pontfelhőre A doboz-illesztés két lépésből épül fel. Először megpróbáljuk a dobozhoz nem tartozó pontokat eltüntetni a pontfelhőből, majd a második lépésben egy iteratív algoritmussal ráillesztjük a dobozt a megmaradt pontokra Outlier pontok eltüntetése A méréseink során azt tapasztaltuk, hogy a kiválasztott síkokon még mindig található néhány outlier pont, ezek száma függ a doboz és LiDAR relatív orientációjától, utóbbi felbontásától és a doboz textúráltságától. A [Park et al., 2014] cikkben említettek alapján a doboz különböző színei szisztematikus visszaverődési kettősséget okozhatnak, azaz a síkon található különböző színek zajjal szennyezhetik annak pontjait. Ezért ebben a lépésben ismét egy RANSAC algoritmust használunk, de most feltételezzük a merőlegességet. Az előző lépés 3 ponthalmazt eredményezett nekünk, az egy-egy oldalhoz tartozó pontok halmazát. Jelölje L 1,L 2,L 3 rendre az első, a második és a harmadik síkhoz tartozó pontokat. A síkok sorrendje nem számít az algoritmus számára, csak a megkülönböztetés miatt jelöljük őket így. Ezután három pontot kell kiválasztanunk az L 1 halmazból, hogy meghatározzuk az első síkot. A második síknak merőlegesnek kell lennie az elsőre, így már csak 2 pont szükséges az L 2 halmazból. Végül a harmadik síknak merőlegesnek kell lennie az előző kettőre, így elegendő 1 pontot választanunk az L 3 halmazból. Majd megvizsgáljuk az inlierek számát kis hibatűréssel. Inlierek azok a pontok, amelyek közel helyezkednek el valamelyik síkhoz. Pár iteráció után azt a három síkot választjuk, amelyek a legnagyobb inlier számmal rendelkeznek és az outlier pontokat pedig eldobjuk.
7 Kamera-LIDAR pár kalibrálása dobozokkal 7 Az előző lépésben egy iteratív RANSAC algoritmust használtunk a doboz síkjainak elkülönítésére a pontfelhő többi részétől, most pedig ismét egy RAN- SAC alapú algoritmust használtunk fel. Ez a két lépés egymás után alkalmazva redundánsnak tűnhet, de nem az. A fő célunk az előző lépés során a doboz síkjainak a közelítő meghatározása volt, ezért nagyobb hibaküszöböt engedtünk meg, illetve a síkok merőlegességét sem követeltük meg. Ha kisebb hibaküszöbbel dolgoztunk volna, akkor a mérés zajossága miatt főleg a nagyobb felbontású LiDAR esetében, egyes a valóságban egy síkban lévő pontok több síkra estek volna szét, ez pedig megnehezítette volna a doboz síkjainak kiválasztását. A második RANSAC használatának célja pedig az olyan outlierek eltávolítása volt, amelyek a doboz egyik síkjához tartoznak, de túlságosan nagy zajjal terheltek, mint például az olyan esetekben, amit [Park et al., 2014] is említ. A mostanit lépés egy sokkal tisztább pontfelhőt eredményez Iteratív doboz-illesztés Az előző lépésben részletezett outlier eltávolítás után megkezdhetjük a doboz illesztést a pontfelhőre. Az algoritmusunk a legkisebb négyzetes illesztésen alapul és két lépésből épül fel, melyek egymás után ismétlődnek a konvergencia beállásáig. Először kiválasztunk két síkot a három közül, majd elforgatjuk őket a metszésvonaluk körül, majd eltoljuk a három síkot külön-külön a normál vektoruk irányába. Síkok forgatása. Az algoritmus első lépésében kiválaszt kettőt a doboz síkjai közül, és a metszési egyenesük körül elforgatja őket. A fogatás célja, hogy a négyzetes távolságot csökkentsük a síkok és a hozzájuk tartozó pontok között. Jelölje Q 1,j,j {1, 2,...m 1 } és Q 2,j,j {1, 2,...m 2 } az egyik, illetve a másik síkhoz tartozó pontokat. Legyen P 1 és P 2 egy-egy pont a síkokon (melyeknek nem feltétlenül kell benne lenniük a Q i,j,i {1, 2} halmazokban), illetve N 1 és N 2 legyenek a síkokhoz tartozó normálvektorok. A forgatást egyszerűbb úgy leírni, ha annak tengelye megegyezik a Z tengellyel. Így minden pontot és normál vektort áttranszformálunk egy új koordináta rendszerben. A Z tengely körüli φ szöggel való forgatást a következő mátrix írja le: cos(φ) sin(φ) 00 R Z (φ) = sin(φ) cos(φ) A pontok és a normál vektorok áttranszformált megfelelőit az új koordináta rendszerben jelölje rendre Q i,j, P i és N i. A következőképpen írható le a síkok és a hozzájuk tartozó pontok közötti távolságok összege, célunk ennek a minimalizálása lesz: Err = 2 m i (( Q i,j P i ) T Ni ) 2 i=1 j=1
8 8 Pusztai Zoltán és mtsai A fenti távolság felírható a forgatási paraméter φ függvényében is, ami a síkok Z tengely körüli forgatását jelöli: Err(φ) = 2 m i (( Q i,j R Z (φ) P i ) T (R Z (φ) N i )) 2 i=1 j=1 Ahhoz, hogy megkeressük a fenti függvény milyen φ értéknél veszi a fel a minimumát, a függvény deriváltját kell vennünk. A derivált függvény gyökeinek megtalálásához a [Brent, 1973]-ban bemutatott algoritmust használtuk. Ahol a Err(φ) függvény deriváltjának értéke megközelíti a nullát, ott az eredeti függvény lokális minimumot vagy lokális maximumot vesz fel. A nullához közeli φ érték a minimális forgatási szöget fogja adni, mivel a síkokhoz elég közel esnek a pontjaink. Így 0 mint kezdőérték az alkalmazott módszer esetében kielégítő. Miután megtaláltuk azt a szöget, amivel a két síkot elforgatva a legkisebb négyzetes hibát kaptuk, visszatranszformáljuk őket az eredeti koordináta rendszerükbe. Ezt a lépést megismételjük a maradék két síkpárra is. Két sík ilyen módon való elforgatása nem változtatja meg a harmadikkal való merőlegességüket. Miután mind a három síkpár elforgatásra került, az algoritmus a síkokat a normálvektoruk irányába fogja mozgatni. Síkok mozgatása. Miután a síkokat elforgattuk úgy, hogy azok a legkisebb négyzetes hibát közelítsék, a síkok mozgatásával folytatódik az algoritmus. A síkokat kizárólagosan csak a saját normálvektoruk irányába mozgatjuk, hogy megőrizzük merőlegességüket. A legjobb helyzet a síkok számára az, ahol legkisebb a négyzetes távolság a sík és pontjai között. Ahogy a forgatási lépés során, itt is bevezettünk egy hibát. Legyen m i Err(α) = ((Q i,j (α N i + P i )) T (N i )) 2 j=1 a hiba az i. síkra felírva. Keresünk az α értéket, amely az eltolás nagyságát fogja jelölni a normálvektor irányába. Az α értéket ott veszi fel a függvényünk, ahol a derivált értéke nulla. Hasonlóan forgatási lépéshez, itt is a [Brent, 1973]-ban leírt módszert használjuk 0 kezdeti értékkel. Mivel a síkjaink már közel helyezkednek el a kívánatos pozíciójukhoz, így várhatóan csak kisebb eltolásra van szükségük. Ezt a lépést megismételjük minden egyes sík esetén. A végső algoritmus A fentebb részletezett forgatás és eltolás lépések a konvergenciáig ismétlődnek. Az tapasztaltuk, hogy abból a kezdőpontból, amit az utolsó RANSAC algoritmus adott, kevesebb, mint 30 iteráció elegendő a megfelelő konvergenciához. Kipróbáltuk, hogy az origóból mint sarokpontból és a tengelyek által meghatározott síkokból indítva is képes volt konvergálni az algoritmus.
9 Kamera-LIDAR pár kalibrálása dobozokkal 9 Miután a síkokat meghatároztuk, a doboz sarkai könnyen kiszámíthatóak, ismerve a doboz méreteit. Ezután a sarkokhoz tartozó pixeleket kell kiválasztani a képen. Ezt a lépést az emberi beavatkozásra bízzuk. A kiválasztott sarokpontok a [Harris and Stephens, 1988]-ban publikált ún. Harris detektorral lettek finomítva. Ha a 3D-2D pont megfeleltetéseket ismerjük, akkor a külső paraméterek meghatározhatóak az ismert PnP probléma megoldása által. Az implementációnkban a [Lepetit et al., 2009]-ben bemutatott EPnP algoritmust alkalmaztuk. 5.. Implementációs megfontolások Amikor felvételt készítettünk a kamerával és a LiDAR-ral a kalibrációhoz, akkor a dobozt az eszközök elé kellett helyeznünk úgy, hogy annak három oldala jól látható legyen mind a két eszköz szemszögéből. A doboz pontfelhőjén látható pontjainak a száma függ a doboz és a LiDAR közötti relatív orientációtól, ezért előfordulhat, hogy az egyik oldal alig látszódik, kevesebb pontot tud a LiDAR regisztrálni rajta. Ezért a 3.4. fejezetben nem is foglalkoztunk a síkok pontjainak a számával, csak az egymásra való merőlegességükkel. Ebben a fejezetben egy példán keresztül levezetjük a kalibráció lépéseit, és példát mutatunk annak előnyeire és robusztusságára. 2. ábra. A kalibráció kiterjeszthető több doboz alkalmazására is. A 2. ábrán látható, hogy három dobozt használtunk fel a kalibrációhoz. A 3. és 4. fejezetekben bemutatott eljárás csak egy dobozt használ fel, de könnyen
10 10 Pusztai Zoltán és mtsai kiterjeszthető több doboz használatára is. A dobozok számának növelésével nagyobb pontosságot tudunk elérni. 3. ábra. Két pontfelhő ugyanarról a szobáról. A bal oldalit a Velodyne 64, a jobb oldalit a Velodyne 16-os LiDAR-ral készítettük. Ahogy a 3. ábrán látható, a pontfelhő felbontása a LiDAR eszköz típusától függ. Minél több csatornát használ a LiDAR, annál több pontot képes mintavételezni a környezetéből. A [Park et al., 2014] cikkben említett módszer megpróbálja megkeresni a LiDAR elé kihelyezett tábla szélét az oda eső pontok segítségével. Egy kisebb felbontású LiDAR esetében a pontok közötti hézag nagyobb, így a tábla széleit nehezebb megbecsülni. Ezzel szemben a mi algoritmusunk síkokat keres, majd azok metszéspontjait veszi figyelembe. Eljárásunkat nagy felbontású (64 csatornás) és kis felbontású (16 csatornás) LiDAR eszközökön is teszteltük. A következő lépés a doboz pontjainak elkülönítésre a pontfelhő többi részétől. Itt kézi beavatkozásra van szükség, a felhasználónak ki kell választania azt a klasztert, ami a dobozt tartalmazza. Ezeket a klasztereket a Mean-Sift algoritmus adja. Az 4. ábrán a dobozok megmaradt pontjai láthatóak, Velodyne 64 által felvett pontfelhőből. A következőekben ezt a pontfelhőt használjuk fel a példák során, hiszen ez jól látható nyomtatásban is. Ahhoz, hogy eltüntessük a maradék outlier pontokat, amelyek nem részei a doboznak, síkokat detektálunk a 3. fejezetben leírtak szerint. Az 5. ábrán láthatóak a detektált síkok, melyek közül azokat választjuk ki, amelyek leginkább merőlegesek egymásra. Miután a doboz három síkját megtaláltuk, a többi outlier pont kivágása következik. Ezek a pontok a nagy mérési hiba miatt befolyásolnák a legkisebb négyzetes doboz illesztő algoritmust, ezért ki kell szűrnünk őket. Példa az ilyen pontokra a 6. ábrán látható. Itt a 4. fejezetben leírtakat használjuk a doboz illesztéséhez, 10 mm-es küszöbértéket használva az inlier-ek számításához. Végül a négyzetes doboz illesztést alkalmazzuk a megmaradt pontokat. A részleteket a 4. fejezetben olvashatjuk. Az algoritmus a konvergencia beállásáig finomítja a síkokat, majd kiszámolja a doboz sarokpontjait a fizikai méretek segítségével. A végső eredményt a 7. ábrán láthatjuk.
11 Kamera-LIDAR pár kalibrálása dobozokkal ábra. A dobozok kivágott pontfelhői a Velodyne 64-es LiDAR pontfelhőjéből. A vágásnak nem kell pontosnak lennie, algoritmusunk ezeken is megtalálja a doboz pontjait. 5. ábra. A pontfelhőben megtalált síkok. Az algoritmus a piros, zöld és sárga síkot választotta a doboz síkjainak.
12 12 Pusztai Zoltán és mtsai 6. ábra. Pirossal színeztük az outlier pontokat, melyeket a merőleges sík keresése után detektáltunk. 7. ábra. A végső doboz a pontokra illesztve. A rózsaszín pontok a doboz sarkait jelölik.
13 Kamera-LIDAR pár kalibrálása dobozokkal Összehasonlítás Összehasonlítottuk algoritmusunk a [Geiger et al., 2012] -ban bemutatott eljárással. A két kalibrációs eljárás hasonló abban, hogy csak egy képet és egy LiDAR felvételt használ a kalibrációhoz. De az ő esetükben több sakktáblát kell a kamera elé helyezni, a mi esetünkben pedig dobozokat dolgozunk fel. A [Geiger et al., 2012] megemlítették, hogy több képet készítve növelhető a kalibrációjuk pontossága. Az összehasonlításunk a következőképpen ment végbe: Először a dobozokat helyeztük a kamera és a LiDAR elé, majd felvételt készítettünk a kamerával. Ezután elhelyeztünk néhány sakktáblát úgy, hogy azok jól láthatóak legyenek a pontfelhőn és a kamerán egyaránt. Majd két képet készítettünk, az egyiket pontosan az előzővel megegyező helyről, illetve egy másikat egy másik szemszögből, majd ismét lementettük a pontfelhőt. A dobozok és a sakktáblák nem lettek elmozdítva a két kép között. A Velodyne-16 LiDAR-t használtuk a teszt során, szerettük volna a nagyobb LiDAR-t is használni, de az túlságosan zajos pontfelhőt generált a sakktáblákról, így a konkurens módszer nem volt képes azokat felismerni. 8. ábra. Ezt a három pontfelhőt választottuk ki a Mean-Sift algoritmus általt adott klaszterekből a teszt során. A színes gömbök a pontfelhőkön megtalált dobozok sarkait jelölik. Az ilyen kalibrációs méréseket nehéz validálni, hiszen a valós külső paraméterek nem meghatározhatóak. Ezért úgy döntöttünk, hogy a székek pontfelhőjét fogjuk visszavetíteni a képekre, és ott vizsgáljuk a különbségeket. A visszavetítés eredménye a 9. ábrán látható.
14 14 Pusztai Zoltán és mtsai A fő különbséget a székek lábainál és a sakktáblák körül vehetjük észre. Amíg a konkurens eljárás néhány sakktábla pontot a földhöz tartozó pixelekre vetít vissza, addig a miénk a megfelelő helyen tartja azokat. Megfigyelhetjük, hogy a dobozok pontjai is különböző helyre vetítődtek vissza. 9. ábra. Ezeket a képeket készítettük a teszt során. A felsőre a konkurens módszerrel vetítettük a pontokat, az alsóra pedig a saját módszerünkkel. Az eljárásunk kiterjeszthető LiDAR-LiDAR pár kalibrálásra is. A két pontfelhő egyesítésére léteznek algoritmusok ám ezek pontossága nem megfelelő. Ebben a tesztben egy dobozt használtunk fel a kalibrációhoz, és célunk a két LiDAR koordináta rendszere közötti transzformáció meghatározása volt. A dobozt úgy helyeztük el, hogy három odala jól látható legyen mind a két pontfelhőn. Majd kivágtuk a dobozt környezetét a pontfelhőkből, ahogy azt a 3. fejezetben leírtuk. Majd az algoritmust lefuttatva mind a két pontfelhőre külön-külön megtaláltuk és párosítottuk a doboz sarokpontjait, végül a transzformációt ezekből a pontpárokból számoltuk ki SVD-alapú pontregisztrációs algoritmus segítségével. A két pontfelhő egyesítése a 10. képen látható madártávlatból.
15 Kamera-LIDAR pár kalibrálása dobozokkal ábra. Két LiDAR kalibrációja. Az egyik pontfelhő pontjait zölddel, a másik pontjait pedig kékkel rajzoltuk ki. 7.. Összegzés Cikkünkben egy LiDAR-kamera páros kalibrálására használható módszert mutattunk be, amely egy közönséges dobozt használ fel. A módszer képes a doboz pontjainak kiválasztására mind ritka, mind pedig sűrű pontfelhő esetében. Tesztjeinkhez 16 és 64 csatornás LiDAR mérőeszközt használtunk. Bemutattuk, hogy hogyan lehet a pontfelhőket megtisztítani az outlier pontoktól és részleteztük az iteratív doboz kereső algoritmust. Összehasonlítottuk módszerünk az egyetlen hasonló konkurrens módszerrel, illetve bemutattuk, hogy a módszer használható LiDAR-LiDAR pár kalibrálására is. A jövőben szeretnénk módszerünket továbbfejleszteni, az emberi beavatkozást nullára csökkenteni. A módszer pontosságát további tesztekkel tervezzük még meggyőzőbben igazolni. Hivatkozások [Brent, 1973] Brent, R. P. (1973). Algorithms for minimization without derivatives. Prentice-Hall series in automatic computation. Englewood Cliffs, N.J. Prentice-Hall. [Fukunaga and Hostetler, 2006] Fukunaga, K. and Hostetler, L. (2006). The estimation of the gradient of a density function, with applications in pattern recognition. IEEE Trans. Inf. Theor., 21(1): [Geiger et al., 2012] Geiger, A., Moosmann, F., Car, O., and Schuster, B. (2012). Automatic camera and range sensor calibration using a single shot. In IEEE International Conference on Robotics and Automation, ICRA 2012, May, 2012, St. Paul, Minnesota, USA, pages
16 16 Pusztai Zoltán és mtsai [Gong et al., 2013] Gong, X., Lin, Y., and Liu, J. (2013). 3d lidar-camera extrinsic calibration using an arbitrary trihedron. Sensors, 13(2):1902. [Harris and Stephens, 1988] Harris, C. and Stephens, M. (1988). A combined corner and edge detector. In In Proc. of Fourth Alvey Vision Conference, pages [Lepetit et al., 2009] Lepetit, V., Moreno-Noguer, F., and Fua, P. (2009). Epnp: An accurate o(n) solution to the pnp problem. Int. J. Comput. Vision, 81(2): [Levinson and Thrun, 2013] Levinson, J. and Thrun, S. (2013). Automatic online calibration of cameras and lasers. In Robotics: Science and Systems. [Pandey et al., 2010] Pandey, G., McBride, J., Savarese, S., and Eustice, R. (2010). Extrinsic calibration of a 3d laser scanner and an omnidirectional camera. In 7th IFAC Symposium on Intelligent Autonomous Vehicles, volume 7, Leece, Italy. [Pandey et al., 2012] Pandey, G., McBride, J. R., Savarese, S., and Eustice, R. M. (2012). Automatic targetless extrinsic calibration of a 3d lidar and camera by maximizing mutual information. In Proceedings of the AAAI National Conference on Artificial Intelligence, pages , Toronto, Canada. [Park et al., 2014] Park, Y., Yun, S., Won, C. S., Cho, K., Um, K., and Sim, S. (2014). Calibration between color camera and 3d lidar instruments with a polygonal planar board. Sensors, 14(3): [Veĺas et al., 2014] Veĺas, M., Španěl, M., Materna, Z., and Herout, A. (2014). Calibration of rgb camera with velodyne lidar. In WSCG 2014 Communication Papers Proceedings, volume 2014, pages Union Agency. [Zhang and Pless, 2004] Zhang, Q. and Pless, R. (2004). Extrinsic calibration of a camera and laser range finder (improves camera calibration). In 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems, Sendai, Japan, September 28 - October 2, 2004, pages [Zhang, 2000] Zhang, Z. (2000). A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell., 22(11):
3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás
 3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav54
3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav54
3D számítógépes geometria és alakzatrekonstrukció
 3D számítógépes geometria és alakzatrekonstrukció 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01
3D számítógépes geometria és alakzatrekonstrukció 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01
Infobionika ROBOTIKA. X. Előadás. Robot manipulátorok II. Direkt és inverz kinematika. Készült a HEFOP P /1.0 projekt keretében
 Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Panorámakép készítése
 Panorámakép készítése Képregisztráció, 2009. Hantos Norbert Blaskovics Viktor Összefoglalás Panoráma (image stitching, planar mosaicing): átfedő képek összeillesztése Lépések: Előfeldolgozás (pl. intenzitáskorrekciók)
Panorámakép készítése Képregisztráció, 2009. Hantos Norbert Blaskovics Viktor Összefoglalás Panoráma (image stitching, planar mosaicing): átfedő képek összeillesztése Lépések: Előfeldolgozás (pl. intenzitáskorrekciók)
Tárgy. Forgóasztal. Lézer. Kamera 3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL
 3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL. Bevezetés A lézeres letapogatás a ma elérhet legpontosabb 3D-s rekonstrukciót teszi lehet vé. Alapelve roppant egyszer : egy lézeres csíkkal megvilágítjuk a tárgyat.
3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL. Bevezetés A lézeres letapogatás a ma elérhet legpontosabb 3D-s rekonstrukciót teszi lehet vé. Alapelve roppant egyszer : egy lézeres csíkkal megvilágítjuk a tárgyat.
Robotika. Kinematika. Magyar Attila
 Robotika Kinematika Magyar Attila amagyar@almos.vein.hu Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
Robotika Kinematika Magyar Attila amagyar@almos.vein.hu Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
PONTFELHŐ REGISZTRÁCIÓ
 PONTFELHŐ REGISZTRÁCIÓ ITERATIVE CLOSEST POINT Cserteg Tamás, URLGNI, 2018.11.22. TARTALOM Röviden Alakzatrekonstrukció áttekintés ICP algoritmusok Projektfeladat Demó FORRÁSOK Cikkek Efficient Variants
PONTFELHŐ REGISZTRÁCIÓ ITERATIVE CLOSEST POINT Cserteg Tamás, URLGNI, 2018.11.22. TARTALOM Röviden Alakzatrekonstrukció áttekintés ICP algoritmusok Projektfeladat Demó FORRÁSOK Cikkek Efficient Variants
Számítógépes látás alapjai
 Számítógépes látás alapjai Csetverikov Dmitrij, Hajder Levente Eötvös Lóránd Egyetem, Informatikai Kar Csetverikov, Hajder (ELTE Informatikai Kar) Számítógépes látás 1 / 23 Rekonstrukció speciális hardverekkel
Számítógépes látás alapjai Csetverikov Dmitrij, Hajder Levente Eötvös Lóránd Egyetem, Informatikai Kar Csetverikov, Hajder (ELTE Informatikai Kar) Számítógépes látás 1 / 23 Rekonstrukció speciális hardverekkel
Mechatronika segédlet 3. gyakorlat
 Mechatronika segédlet 3. gyakorlat 2017. február 20. Tartalom Vadai Gergely, Faragó Dénes Feladatleírás... 2 Fogaskerék... 2 Nézetváltás 3D modellezéshez... 2 Könnyítés megvalósítása... 2 A fogaskerék
Mechatronika segédlet 3. gyakorlat 2017. február 20. Tartalom Vadai Gergely, Faragó Dénes Feladatleírás... 2 Fogaskerék... 2 Nézetváltás 3D modellezéshez... 2 Könnyítés megvalósítása... 2 A fogaskerék
Összeállította: dr. Leitold Adrien egyetemi docens
 Az R 3 tér geometriája Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. 1 Vektorok Vektor: irányított szakasz Jel.: a, a, a, AB, Jellemzői: irány, hosszúság, (abszolút érték) jel.: a Speciális
Az R 3 tér geometriája Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. 1 Vektorok Vektor: irányított szakasz Jel.: a, a, a, AB, Jellemzői: irány, hosszúság, (abszolút érték) jel.: a Speciális
A KLT (Kanade Lucas Tomasi) Feature Tracker Működése (jellegzetes pontok választása és követése)
 A KL (Kanade Lucas omasi) Feature racker Működése (jellegzetes pontok választása és követése) Készítette: Hajder Levente 008.11.18. 1. Feladat A rendelkezésre álló videó egy adott képkockájából minél több
A KL (Kanade Lucas omasi) Feature racker Működése (jellegzetes pontok választása és követése) Készítette: Hajder Levente 008.11.18. 1. Feladat A rendelkezésre álló videó egy adott képkockájából minél több
2014/2015. tavaszi félév
 Hajder L. és Valasek G. hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom Geometria modellezés 1 Geometria modellezés 2 Geometria modellezés
Hajder L. és Valasek G. hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom Geometria modellezés 1 Geometria modellezés 2 Geometria modellezés
x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs mátrixa 3D-ben?
 . Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
. Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
Pontfelhő létrehozás és használat Regard3D és CloudCompare nyílt forráskódú szoftverekkel. dr. Siki Zoltán
 Pontfelhő létrehozás és használat Regard3D és CloudCompare nyílt forráskódú szoftverekkel dr. Siki Zoltán siki.zoltan@epito.bme.hu Regard3D Nyílt forráskódú SfM (Structure from Motion) Fényképekből 3D
Pontfelhő létrehozás és használat Regard3D és CloudCompare nyílt forráskódú szoftverekkel dr. Siki Zoltán siki.zoltan@epito.bme.hu Regard3D Nyílt forráskódú SfM (Structure from Motion) Fényképekből 3D
Számítógépes Grafika mintafeladatok
 Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Körbelátó kamerák (oktatási segédanyag)
 Körbelátó kamerák (oktatási segédanyag) Kató Zoltán 2014 október 2 Tartalomjegyzék 1. A körbelátó kamera geometriai modellezése 7 1.1. A körbelátó optikákról......................... 7 1.2. A katadioptrikus
Körbelátó kamerák (oktatási segédanyag) Kató Zoltán 2014 október 2 Tartalomjegyzék 1. A körbelátó kamera geometriai modellezése 7 1.1. A körbelátó optikákról......................... 7 1.2. A katadioptrikus
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Geometria III.
 Geometria III. DEFINÍCIÓ: (Vektor) Az egyenlő hosszúságú és egyirányú irányított szakaszoknak a halmazát vektornak nevezzük. Jele: v. DEFINÍCIÓ: (Geometriai transzformáció) Geometriai transzformációnak
Geometria III. DEFINÍCIÓ: (Vektor) Az egyenlő hosszúságú és egyirányú irányított szakaszoknak a halmazát vektornak nevezzük. Jele: v. DEFINÍCIÓ: (Geometriai transzformáció) Geometriai transzformációnak
6. gyakorlat. Gelle Kitti. Csendes Tibor Somogyi Viktor. London András. jegyzetei alapján
 Közelítő és szimbolikus számítások 6. gyakorlat Sajátérték, Gersgorin körök Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján . Mátrixok sajátértékei
Közelítő és szimbolikus számítások 6. gyakorlat Sajátérték, Gersgorin körök Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján . Mátrixok sajátértékei
Intelligens Közlekedési Rendszerek 2
 Intelligens Közlekedési Rendszerek 2 Máté Miklós 2016 Október 11 1 / 14 Szenzor (érzékelő): mérés, detektálás Mérés elmélet emlékeztető Jó mérőműszer tulajdonságai Érzékeny a mérendő tulajdonságra Érzéketlen
Intelligens Közlekedési Rendszerek 2 Máté Miklós 2016 Október 11 1 / 14 Szenzor (érzékelő): mérés, detektálás Mérés elmélet emlékeztető Jó mérőműszer tulajdonságai Érzékeny a mérendő tulajdonságra Érzéketlen
17. előadás: Vektorok a térben
 17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
Keresztmetszet másodrendű nyomatékainak meghatározása
 BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
Alap-ötlet: Karl Friedrich Gauss ( ) valószínűségszámítási háttér: Andrej Markov ( )
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
Vektorgeometria (2) First Prev Next Last Go Back Full Screen Close Quit
 Vektorgeometria (2) First Prev Next Last Go Back Full Screen Close Quit 1. Tekintsünk a térben egy P (p 1, p 2, p 3 ) pontot és egy v = (v 1, v 2, v 3 ) = 0 vektort. Ekkor pontosan egy egyenes létezik,
Vektorgeometria (2) First Prev Next Last Go Back Full Screen Close Quit 1. Tekintsünk a térben egy P (p 1, p 2, p 3 ) pontot és egy v = (v 1, v 2, v 3 ) = 0 vektort. Ekkor pontosan egy egyenes létezik,
Láthatósági kérdések
 Láthatósági kérdések Láthatósági algoritmusok Adott térbeli objektum és adott nézőpont esetén el kell döntenünk, hogy mi látható az adott alakzatból a nézőpontból, vagy irányából nézve. Az algoritmusok
Láthatósági kérdések Láthatósági algoritmusok Adott térbeli objektum és adott nézőpont esetén el kell döntenünk, hogy mi látható az adott alakzatból a nézőpontból, vagy irányából nézve. Az algoritmusok
Sergyán Szabolcs szeptember 21.
 Éldetektálás Sergyán Szabolcs Budapesti Műszaki Főiskola Neumann János Informatikai Kar 2009. szeptember 21. Sergyán Sz. (BMF NIK) Éldetektálás 2009. szeptember 21. 1 / 28 Mit nevezünk élnek? Intuitív
Éldetektálás Sergyán Szabolcs Budapesti Műszaki Főiskola Neumann János Informatikai Kar 2009. szeptember 21. Sergyán Sz. (BMF NIK) Éldetektálás 2009. szeptember 21. 1 / 28 Mit nevezünk élnek? Intuitív
1. Olvassuk be két pont koordinátáit: (x1, y1) és (x2, y2). Határozzuk meg a két pont távolságát és nyomtassuk ki.
 Számítás:. Olvassuk be két pont koordinátáit: (, y) és (2, y2). Határozzuk meg a két pont távolságát és nyomtassuk ki. 2. Olvassuk be két darab két dimenziós vektor komponenseit: (a, ay) és (b, by). Határozzuk
Számítás:. Olvassuk be két pont koordinátáit: (, y) és (2, y2). Határozzuk meg a két pont távolságát és nyomtassuk ki. 2. Olvassuk be két darab két dimenziós vektor komponenseit: (a, ay) és (b, by). Határozzuk
Számítógépes látás alapjai
 Számítógépes látás alapjai Csetverikov Dmitrij, Hajder Levente Eötvös Lóránd Egyetem, Informatikai Kar Csetverikov, Hajder (ELTE Informatikai Kar) Számítógépes látás 1 / 44 Többkamerás 3D-s rekonstrukció
Számítógépes látás alapjai Csetverikov Dmitrij, Hajder Levente Eötvös Lóránd Egyetem, Informatikai Kar Csetverikov, Hajder (ELTE Informatikai Kar) Számítógépes látás 1 / 44 Többkamerás 3D-s rekonstrukció
International GTE Conference MANUFACTURING 2012. 14-16 November, 2012 Budapest, Hungary. Ákos György*, Bogár István**, Bánki Zsolt*, Báthor Miklós*,
 International GTE Conference MANUFACTURING 2012 14-16 November, 2012 Budapest, Hungary MÉRŐGÉP FEJLESZTÉSE HENGERES MUNKADARABOK MÉRETELLENŐRZÉSÉRE Ákos György*, Bogár István**, Bánki Zsolt*, Báthor Miklós*,
International GTE Conference MANUFACTURING 2012 14-16 November, 2012 Budapest, Hungary MÉRŐGÉP FEJLESZTÉSE HENGERES MUNKADARABOK MÉRETELLENŐRZÉSÉRE Ákos György*, Bogár István**, Bánki Zsolt*, Báthor Miklós*,
Elengedhetetlen a játékokban, mozi produkciós eszközökben Nélküle kvantum hatás lép fel. Az objektumok áthaladnak a többi objektumon
 Bevezetés Ütközés detektálás Elengedhetetlen a játékokban, mozi produkciós eszközökben Nélküle kvantum hatás lép fel Az objektumok áthaladnak a többi objektumon A valósághű megjelenítés része Nem tisztán
Bevezetés Ütközés detektálás Elengedhetetlen a játékokban, mozi produkciós eszközökben Nélküle kvantum hatás lép fel Az objektumok áthaladnak a többi objektumon A valósághű megjelenítés része Nem tisztán
Konjugált gradiens módszer
 Közelítő és szimbolikus számítások 12. gyakorlat Konjugált gradiens módszer Készítette: Gelle Kitti Csendes Tibor Vinkó Tamás Faragó István Horváth Róbert jegyzetei alapján 1 LINEÁRIS EGYENLETRENDSZEREK
Közelítő és szimbolikus számítások 12. gyakorlat Konjugált gradiens módszer Készítette: Gelle Kitti Csendes Tibor Vinkó Tamás Faragó István Horváth Róbert jegyzetei alapján 1 LINEÁRIS EGYENLETRENDSZEREK
Automatikus irányzás digitális képek. feldolgozásával TURÁK BENCE DR. ÉGETŐ CSABA
 Automatikus irányzás digitális képek feldolgozásával TURÁK BENCE DR. ÉGETŐ CSABA Koncepció Robotmérőállomásra távcsővére rögzített kamera Képek alapján a cél automatikus detektálása És az irányzás elvégzése
Automatikus irányzás digitális képek feldolgozásával TURÁK BENCE DR. ÉGETŐ CSABA Koncepció Robotmérőállomásra távcsővére rögzített kamera Képek alapján a cél automatikus detektálása És az irányzás elvégzése
OSZLOPOK DETEKTÁLÁSA 3D LIDAR PONTFELHŐKBEN
 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Irányítástechnika és Informatika Tanszék Sári András Lajos OSZLOPOK DETEKTÁLÁSA 3D LIDAR PONTFELHŐKBEN Önálló laboratórium
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Irányítástechnika és Informatika Tanszék Sári András Lajos OSZLOPOK DETEKTÁLÁSA 3D LIDAR PONTFELHŐKBEN Önálló laboratórium
Transzformációk. Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform
 Transzformációk Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform Koordinátarendszerek: modelltér Koordinátarendszerek: világtér Koordinátarendszerek: kameratér up right z eye ahead
Transzformációk Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform Koordinátarendszerek: modelltér Koordinátarendszerek: világtér Koordinátarendszerek: kameratér up right z eye ahead
EEE Kutatólaboratórium MTA-SZTAKI Magyar Tudományos Akadémia
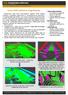 DElosztott I S T R I B U T EEsemények D EV E N T S A NElemzé A L Y S I S se R E SKutatólaboratór E A R C H L A B O R A T Oium R Y L I D A R B a s e d S u r v e i l l a n c e Városi LIDAR adathalmaz szegmentációja
DElosztott I S T R I B U T EEsemények D EV E N T S A NElemzé A L Y S I S se R E SKutatólaboratór E A R C H L A B O R A T Oium R Y L I D A R B a s e d S u r v e i l l a n c e Városi LIDAR adathalmaz szegmentációja
Élpont osztályozáson alapuló robusztus tekintetkövetés
 KÉPFELDOLGOZÁS Élpont osztályozáson alapuló robusztus tekintetkövetés HELFENBEIN TAMÁS Ipari Kommunikációs Technológiai Intézet, Bay Zoltán Alkalmazott Kutatási Közalapítvány helfenbein@ikti.hu Lektorált
KÉPFELDOLGOZÁS Élpont osztályozáson alapuló robusztus tekintetkövetés HELFENBEIN TAMÁS Ipari Kommunikációs Technológiai Intézet, Bay Zoltán Alkalmazott Kutatási Közalapítvány helfenbein@ikti.hu Lektorált
Lakóház tervezés ADT 3.3-al. Segédlet
 Lakóház tervezés ADT 3.3-al Segédlet A lakóház tervezési gyakorlathoz főleg a Tervezés és a Dokumentáció menüket fogjuk használni az AutoDesk Architectural Desktop programból. A program centiméterben dolgozik!!!
Lakóház tervezés ADT 3.3-al Segédlet A lakóház tervezési gyakorlathoz főleg a Tervezés és a Dokumentáció menüket fogjuk használni az AutoDesk Architectural Desktop programból. A program centiméterben dolgozik!!!
First Prev Next Last Go Back Full Screen Close Quit
 Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
SZENZORFÚZIÓS ELJÁRÁSOK KIDOLGOZÁSA AUTONÓM JÁRMŰVEK PÁLYAKÖVETÉSÉRE ÉS IRÁNYÍTÁSÁRA
 infokommunikációs technológiák SZENZORFÚZIÓS ELJÁRÁSOK KIDOLGOZÁSA AUTONÓM JÁRMŰVEK PÁLYAKÖVETÉSÉRE ÉS IRÁNYÍTÁSÁRA BEVEZETŐ A KUTATÁS CÉLJA Autonóm járművek és robotok esetén elsődleges feladat a robotok
infokommunikációs technológiák SZENZORFÚZIÓS ELJÁRÁSOK KIDOLGOZÁSA AUTONÓM JÁRMŰVEK PÁLYAKÖVETÉSÉRE ÉS IRÁNYÍTÁSÁRA BEVEZETŐ A KUTATÁS CÉLJA Autonóm járművek és robotok esetén elsődleges feladat a robotok
Transzformációk. Szécsi László
 Transzformációk Szécsi László A feladat Adott a 3D modell háromszögek csúcspontjai [modellezési koordináták] Háromszögkitöltő algoritmus pixeleket színez be [viewport koordináták] A feladat: számítsuk
Transzformációk Szécsi László A feladat Adott a 3D modell háromszögek csúcspontjai [modellezési koordináták] Háromszögkitöltő algoritmus pixeleket színez be [viewport koordináták] A feladat: számítsuk
9. Fényhullámhossz és diszperzió mérése jegyzőkönyv
 9. Fényhullámhossz és diszperzió mérése jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 008. 11. 1. Leadás dátuma: 008. 11. 19. 1 1. A mérési összeállítás A méréseket speciális szögmérő eszközzel
9. Fényhullámhossz és diszperzió mérése jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 008. 11. 1. Leadás dátuma: 008. 11. 19. 1 1. A mérési összeállítás A méréseket speciális szögmérő eszközzel
2. Omnidirekcionális kamera
 2. Omnidirekcionális kamera Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Omnidirekcionális kamerák típusai Omnidirekcionális, körbelátó,
2. Omnidirekcionális kamera Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Omnidirekcionális kamerák típusai Omnidirekcionális, körbelátó,
Navigáci. stervezés. Algoritmusok és alkalmazásaik. Osváth Róbert Sorbán Sámuel
 Navigáci ció és s mozgástervez stervezés Algoritmusok és alkalmazásaik Osváth Róbert Sorbán Sámuel Feladat Adottak: pálya (C), játékos, játékos ismerethalmaza, kezdőpont, célpont. Pálya szerkezete: akadályokkal
Navigáci ció és s mozgástervez stervezés Algoritmusok és alkalmazásaik Osváth Róbert Sorbán Sámuel Feladat Adottak: pálya (C), játékos, játékos ismerethalmaza, kezdőpont, célpont. Pálya szerkezete: akadályokkal
1. számú ábra. Kísérleti kályha járattal
 Kísérleti kályha tesztelése A tesztsorozat célja egy járatos, egy kitöltött harang és egy üres harang hőtároló összehasonlítása. A lehető legkisebb méretű, élére állított téglából épített héjba hagyományos,
Kísérleti kályha tesztelése A tesztsorozat célja egy járatos, egy kitöltött harang és egy üres harang hőtároló összehasonlítása. A lehető legkisebb méretű, élére állított téglából épített héjba hagyományos,
Miről lesz szó? Videó tartalom elemzés (VCA) leegyszerűsített működése Kültéri védelem Közúthálózat megfigyelés Emberszámlálás
 Videóanalitikát mindenhova! Princz Adorján Miről lesz szó? Videó tartalom elemzés (VCA) leegyszerűsített működése Kültéri védelem Közúthálózat megfigyelés Emberszámlálás VCA alapú detektorok Videótartalom
Videóanalitikát mindenhova! Princz Adorján Miről lesz szó? Videó tartalom elemzés (VCA) leegyszerűsített működése Kültéri védelem Közúthálózat megfigyelés Emberszámlálás VCA alapú detektorok Videótartalom
= Y y 0. = Z z 0. u 1. = Z z 1 z 2 z 1. = Y y 1 y 2 y 1
 Egyenes és sík a térben Elméleti áttekintés Az egyenes paraméteres egyenlete: X = u 1 λ + x 0 Y = u λ + y 0, Z = u λ + z 0 ahol a λ egy valós paraméter Az u = (u 1, u, u ) az egyenes irányvektora és P
Egyenes és sík a térben Elméleti áttekintés Az egyenes paraméteres egyenlete: X = u 1 λ + x 0 Y = u λ + y 0, Z = u λ + z 0 ahol a λ egy valós paraméter Az u = (u 1, u, u ) az egyenes irányvektora és P
Közösség detektálás gráfokban
 Közösség detektálás gráfokban Önszervező rendszerek Hegedűs István Célkitűzés: valamilyen objektumok halmaza felett minták, csoportok detektálása csakis az egyedek közötti kapcsolatok struktúrájának a
Közösség detektálás gráfokban Önszervező rendszerek Hegedűs István Célkitűzés: valamilyen objektumok halmaza felett minták, csoportok detektálása csakis az egyedek közötti kapcsolatok struktúrájának a
Számelméleti alapfogalmak
 1 Számelméleti alapfogalmak 1 Definíció Az a IN szám osztója a b IN számnak ha létezik c IN melyre a c = b Jelölése: a b 2 Példa a 0 bármely a számra teljesül, mivel c = 0 univerzálisan megfelel: a 0 =
1 Számelméleti alapfogalmak 1 Definíció Az a IN szám osztója a b IN számnak ha létezik c IN melyre a c = b Jelölése: a b 2 Példa a 0 bármely a számra teljesül, mivel c = 0 univerzálisan megfelel: a 0 =
1. tétel. 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója 7 cm. Mekkora a háromszög átfogója? (4 pont)
 1. tétel 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója cm. Mekkora a háromszög átfogója? (4 pont). Adott az ábrán két vektor. Rajzolja meg a b, a b és az a b vektorokat! (6 pont)
1. tétel 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója cm. Mekkora a háromszög átfogója? (4 pont). Adott az ábrán két vektor. Rajzolja meg a b, a b és az a b vektorokat! (6 pont)
Útjelzések, akadályok felismerése valós időben
 Útjelzések, akadályok felismerése valós időben Dr. Hidvégi Timót Széchenyi István Egyetem Győr, 9026, Egyetem tér 1. hidvegi@sze.hu 1. Bevezető Sajnos a közúton a balesetek egy része abból adódik, hogy
Útjelzések, akadályok felismerése valós időben Dr. Hidvégi Timót Széchenyi István Egyetem Győr, 9026, Egyetem tér 1. hidvegi@sze.hu 1. Bevezető Sajnos a közúton a balesetek egy része abból adódik, hogy
Kinematika szeptember Vonatkoztatási rendszerek, koordinátarendszerek
 Kinematika 2014. szeptember 28. 1. Vonatkoztatási rendszerek, koordinátarendszerek 1.1. Vonatkoztatási rendszerek A test mozgásának leírása kezdetén ki kell választani azt a viszonyítási rendszert, amelyből
Kinematika 2014. szeptember 28. 1. Vonatkoztatási rendszerek, koordinátarendszerek 1.1. Vonatkoztatási rendszerek A test mozgásának leírása kezdetén ki kell választani azt a viszonyítási rendszert, amelyből
EGY ABLAK - GEOMETRIAI PROBLÉMA
 EGY ABLAK - GEOMETRIAI PROBLÉMA Írta: Hajdu Endre A számítógépemhez tartozó két hangfal egy-egy négyzet keresztmetszetű hasáb hely - szűke miatt az ablakpárkányon van elhelyezve (. ábra).. ábra Hogy az
EGY ABLAK - GEOMETRIAI PROBLÉMA Írta: Hajdu Endre A számítógépemhez tartozó két hangfal egy-egy négyzet keresztmetszetű hasáb hely - szűke miatt az ablakpárkányon van elhelyezve (. ábra).. ábra Hogy az
Hajder Levente 2017/2018. II. félév
 Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév Tartalom 1 2 3 Geometriai modellezés feladata A világunkat modellezni kell a térben. Valamilyen koordinátarendszer
Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév Tartalom 1 2 3 Geometriai modellezés feladata A világunkat modellezni kell a térben. Valamilyen koordinátarendszer
HÁROMDIMENZIÓS SZÁMÍTÓGÉPES LÁTÁS HAJDER LEVENTE
 HÁROMDIMENZIÓS SZÁMÍTÓGÉPES LÁTÁS HAJDER LEVENTE BEMUTATKOZÁS Hajder Levente (1975-?) Tanulmányok: BME első kísérlet 1993-1995 Kandó Kálmán Műszaki Főiskola (Ma: Óbudai Egyetem) 1995-1998 BME második,
HÁROMDIMENZIÓS SZÁMÍTÓGÉPES LÁTÁS HAJDER LEVENTE BEMUTATKOZÁS Hajder Levente (1975-?) Tanulmányok: BME első kísérlet 1993-1995 Kandó Kálmán Műszaki Főiskola (Ma: Óbudai Egyetem) 1995-1998 BME második,
Keresés képi jellemzők alapján. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
Nagy András. Feladatok a koordináta-geometria, egyenesek témaköréhez 11. osztály 2010.
 Nagy András Feladatok a koordináta-geometria, egyenesek témaköréhez 11. osztály 010. Feladatok a koordináta-geometria, egyenesek témaköréhez 11. osztály 1) Döntsd el, hogy a P pont illeszkedik-e az e egyenesre
Nagy András Feladatok a koordináta-geometria, egyenesek témaköréhez 11. osztály 010. Feladatok a koordináta-geometria, egyenesek témaköréhez 11. osztály 1) Döntsd el, hogy a P pont illeszkedik-e az e egyenesre
A térképen ábrázolt vonal: - sík felület egyenese? - sík felület görbéje? - görbült felület egyenese ( geodetikus )? - görbült felület görbéje?
 Előzetes megjegyzés: 1. Az időt nyugodtan mérhetjük méterben. ct [s ] = t [m ] A film kétórás volt. = A film 2.16 milliárd kilométernyi ideig tartott. 2. A tömeget is nyugodtan mérhetjük méterben! GM [kg]
Előzetes megjegyzés: 1. Az időt nyugodtan mérhetjük méterben. ct [s ] = t [m ] A film kétórás volt. = A film 2.16 milliárd kilométernyi ideig tartott. 2. A tömeget is nyugodtan mérhetjük méterben! GM [kg]
A térképen ábrázolt vonal: - sík felület egyenese? - sík felület görbéje? - görbült felület egyenese ( geodetikus )? - görbült felület görbéje?
 Előzetes megjegyzés: 1. Az időt nyugodtan mérhetjük méterben. ct [s ] = t [m ] A film kétórás volt. = A film 2.16 milliárd kilométernyi ideig tartott. 2. A tömeget is nyugodtan mérhetjük méterben! GM [kg]
Előzetes megjegyzés: 1. Az időt nyugodtan mérhetjük méterben. ct [s ] = t [m ] A film kétórás volt. = A film 2.16 milliárd kilométernyi ideig tartott. 2. A tömeget is nyugodtan mérhetjük méterben! GM [kg]
Számítógépes képelemzés 7. előadás. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
2. Adott a valós számok halmazán értelmezett f ( x) 3. Oldja meg a [ π; π] zárt intervallumon a. A \ B = { } 2 pont. függvény.
![2. Adott a valós számok halmazán értelmezett f ( x) 3. Oldja meg a [ π; π] zárt intervallumon a. A \ B = { } 2 pont. függvény. 2. Adott a valós számok halmazán értelmezett f ( x) 3. Oldja meg a [ π; π] zárt intervallumon a. A \ B = { } 2 pont. függvény.](/thumbs/91/107500193.jpg) 1. Az A halmaz elemei a ( 5)-nél nagyobb, de 2-nél kisebb egész számok. B a pozitív egész számok halmaza. Elemeinek felsorolásával adja meg az A \ B halmazt! A \ B = { } 2. Adott a valós számok halmazán
1. Az A halmaz elemei a ( 5)-nél nagyobb, de 2-nél kisebb egész számok. B a pozitív egész számok halmaza. Elemeinek felsorolásával adja meg az A \ B halmazt! A \ B = { } 2. Adott a valós számok halmazán
ACM Snake. Orvosi képdiagnosztika 11. előadás első fele
 ACM Snake Orvosi képdiagnosztika 11. előadás első fele ACM Snake (ismétlés) A szegmentáló kontúr egy paraméteres görbe: x Zs s X s, Y s,, s A szegmentáció energia funkcionál minimalizálása: E x Eint x
ACM Snake Orvosi képdiagnosztika 11. előadás első fele ACM Snake (ismétlés) A szegmentáló kontúr egy paraméteres görbe: x Zs s X s, Y s,, s A szegmentáció energia funkcionál minimalizálása: E x Eint x
7. Koordináta méréstechnika
 7. Koordináta méréstechnika Coordinate Measuring Machine: CMM, 3D-s mérőgép Egyiptomi piramis kövek mérése i.e. 1440 Egyiptomi mérővonalzó, Amenphotep fáraó (i.e. 1550) alkarjának hossza: 524mm A koordináta
7. Koordináta méréstechnika Coordinate Measuring Machine: CMM, 3D-s mérőgép Egyiptomi piramis kövek mérése i.e. 1440 Egyiptomi mérővonalzó, Amenphotep fáraó (i.e. 1550) alkarjának hossza: 524mm A koordináta
Képrekonstrukció 3. előadás
 Képrekonstrukció 3. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Computed Tomography (CT) Elv: Röntgen-sugarak áthatolása 3D objektum 3D térfogati kép Mérések
Képrekonstrukció 3. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Computed Tomography (CT) Elv: Röntgen-sugarak áthatolása 3D objektum 3D térfogati kép Mérések
Robotika. Relatív helymeghatározás Odometria
 Robotika Relatív helymeghatározás Odometria Differenciális hajtás c m =πd n /nc e c m D n C e n = hány mm-t tesz meg a robot egy jeladó impulzusra = névleges kerék átmérő = jeladó fölbontása (impulzus/ford.)
Robotika Relatív helymeghatározás Odometria Differenciális hajtás c m =πd n /nc e c m D n C e n = hány mm-t tesz meg a robot egy jeladó impulzusra = névleges kerék átmérő = jeladó fölbontása (impulzus/ford.)
Gauss elimináció, LU felbontás
 Közelítő és szimbolikus számítások 3. gyakorlat Gauss elimináció, LU felbontás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 EGYENLETRENDSZEREK 1. Egyenletrendszerek
Közelítő és szimbolikus számítások 3. gyakorlat Gauss elimináció, LU felbontás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 EGYENLETRENDSZEREK 1. Egyenletrendszerek
9. Írjuk fel annak a síknak az egyenletét, amely átmegy az M 0(1, 2, 3) ponton és. egyenessel;
 Síkok és egyenesek FELADATLAP Írjuk fel annak az egyenesnek az egyenletét, amely átmegy az M 0(,, ) ponton és a) az M(,, 0) ponton; b) párhuzamos a d(,, 5) vektorral; c) merőleges a x y + z 0 = 0 síkra;
Síkok és egyenesek FELADATLAP Írjuk fel annak az egyenesnek az egyenletét, amely átmegy az M 0(,, ) ponton és a) az M(,, 0) ponton; b) párhuzamos a d(,, 5) vektorral; c) merőleges a x y + z 0 = 0 síkra;
5. házi feladat. AB, CD kitér élpárra történ tükrözések: Az ered transzformáció: mivel az origó xpont, így nincs szükség homogénkoordinátás
 5. házi feladat 1.feladat A csúcsok: A = (0, 1, 1) T, B = (0, 1, 1) T, C = (1, 0, 0) T, D = ( 1, 0, 0) T AB, CD kitér élpárra történ tükrözések: 1 0 0 T AB = 0 1 0, elotlási rész:(i T AB )A = (0, 0, )
5. házi feladat 1.feladat A csúcsok: A = (0, 1, 1) T, B = (0, 1, 1) T, C = (1, 0, 0) T, D = ( 1, 0, 0) T AB, CD kitér élpárra történ tükrözések: 1 0 0 T AB = 0 1 0, elotlási rész:(i T AB )A = (0, 0, )
Programozási nyelvek 2. előadás
 Programozási nyelvek 2. előadás Logo forgatás tétel Forgatás tétel Ha az ismétlendő rész T fok fordulatot végez és a kezdőhelyére visszatér, akkor az ismétlések által rajzolt ábrák egymás T fokkal elforgatottjai
Programozási nyelvek 2. előadás Logo forgatás tétel Forgatás tétel Ha az ismétlendő rész T fok fordulatot végez és a kezdőhelyére visszatér, akkor az ismétlések által rajzolt ábrák egymás T fokkal elforgatottjai
Denavit-Hartenberg konvenció alkalmazása térbeli 3DoF nyílt kinematikai láncú hengerkoordinátás és gömbi koordinátás robotra
 Budapesti M szaki És Gazdaságtudományi Egyetem Gépészmérnöki Kar M szaki Mechanikai Tanszék Denavit-Hartenberg konvenció alkalmazása térbeli 3DoF nyílt kinematikai láncú hengerkoordinátás és gömbi koordinátás
Budapesti M szaki És Gazdaságtudományi Egyetem Gépészmérnöki Kar M szaki Mechanikai Tanszék Denavit-Hartenberg konvenció alkalmazása térbeli 3DoF nyílt kinematikai láncú hengerkoordinátás és gömbi koordinátás
16. tétel Egybevágósági transzformációk. Konvex sokszögek tulajdonságai, szimmetrikus sokszögek
 16. tétel Egybevágósági transzformációk. Konvex sokszögek tulajdonságai, szimmetrikus sokszögek EGYBEVÁGÓSÁGI TRANSZFORMÁCIÓK Geometriai transzformáció Def:Olyan speciális függvény, melynek értelmezési
16. tétel Egybevágósági transzformációk. Konvex sokszögek tulajdonságai, szimmetrikus sokszögek EGYBEVÁGÓSÁGI TRANSZFORMÁCIÓK Geometriai transzformáció Def:Olyan speciális függvény, melynek értelmezési
Regresszió. Csorba János. Nagyméretű adathalmazok kezelése március 31.
 Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Általános követelmények a kép tartalmával és minőségével kapcsolatban
 Általános követelmények a kép tartalmával és minőségével kapcsolatban A következő követelmények egyrészt azért fontosak, hogy megfelelően dokumentálják az eseményeket (bizonyítékként felhasználóak legyenek),
Általános követelmények a kép tartalmával és minőségével kapcsolatban A következő követelmények egyrészt azért fontosak, hogy megfelelően dokumentálják az eseményeket (bizonyítékként felhasználóak legyenek),
Al-Mg-Si háromalkotós egyensúlyi fázisdiagram közelítő számítása
 l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
BitTorrent felhasználók értékeléseinek következtetése a viselkedésük alapján. Hegedűs István
 BitTorrent felhasználók értékeléseinek következtetése a viselkedésük alapján Hegedűs István Ajánló rendszerek Napjainkban egyre népszerűbb az ajánló rendszerek alkalmazása A cégeket is hasznos információval
BitTorrent felhasználók értékeléseinek következtetése a viselkedésük alapján Hegedűs István Ajánló rendszerek Napjainkban egyre népszerűbb az ajánló rendszerek alkalmazása A cégeket is hasznos információval
Gépi tanulás a gyakorlatban. Lineáris regresszió
 Gépi tanulás a gyakorlatban Lineáris regresszió Lineáris Regresszió Legyen adott egy tanuló adatbázis: Rendelkezésünkre áll egy olyan előfeldolgozott adathalmaz, aminek sorai az egyes ingatlanokat írják
Gépi tanulás a gyakorlatban Lineáris regresszió Lineáris Regresszió Legyen adott egy tanuló adatbázis: Rendelkezésünkre áll egy olyan előfeldolgozott adathalmaz, aminek sorai az egyes ingatlanokat írják
Grafikonok automatikus elemzése
 Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
Nem teljesen kitöltött páros összehasonlítás mátrixok sajátérték optimalizálása Newton-módszerrel p. 1/29. Ábele-Nagy Kristóf BCE, ELTE
 Nem teljesen kitöltött páros összehasonlítás mátrixok sajátérték optimalizálása Newton-módszerrel Ábele-Nagy Kristóf BCE, ELTE Bozóki Sándor BCE, MTA SZTAKI 2010. november 4. Nem teljesen kitöltött páros
Nem teljesen kitöltött páros összehasonlítás mátrixok sajátérték optimalizálása Newton-módszerrel Ábele-Nagy Kristóf BCE, ELTE Bozóki Sándor BCE, MTA SZTAKI 2010. november 4. Nem teljesen kitöltött páros
10. Koordinátageometria
 I. Nulladik ZH-ban láttuk: 0. Koordinátageometria. Melyek azok a P x; y pontok, amelyek koordinátái kielégítik az Ábrázolja a megoldáshalmazt a koordináta-síkon! x y x 0 egyenlőtlenséget? ELTE 00. szeptember
I. Nulladik ZH-ban láttuk: 0. Koordinátageometria. Melyek azok a P x; y pontok, amelyek koordinátái kielégítik az Ábrázolja a megoldáshalmazt a koordináta-síkon! x y x 0 egyenlőtlenséget? ELTE 00. szeptember
Függvények Megoldások
 Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
A lineáris programozás alapjai
 A lineáris programozás alapjai A konvex analízis alapjai: konvexitás, konvex kombináció, hipersíkok, félterek, extrém pontok, Poliéderek, a Minkowski-Weyl tétel (a poliéderek reprezentációs tétele) Lineáris
A lineáris programozás alapjai A konvex analízis alapjai: konvexitás, konvex kombináció, hipersíkok, félterek, extrém pontok, Poliéderek, a Minkowski-Weyl tétel (a poliéderek reprezentációs tétele) Lineáris
Az egyenes és a sík analitikus geometriája
 Az egyenes és a sík analitikus geometriája Az egyenes a kétdimenziós koordinátarendszerben A kétdimenziós koordinátarendszerben az egyenest egy n(a, B) normálvektorával és egy r 0 helyvektorú P(x 0,y 0
Az egyenes és a sík analitikus geometriája Az egyenes a kétdimenziós koordinátarendszerben A kétdimenziós koordinátarendszerben az egyenest egy n(a, B) normálvektorával és egy r 0 helyvektorú P(x 0,y 0
Gauss-Seidel iteráció
 Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar. Villamos Energetika Tanszék. Világítástechnika (BME VIVEM 355)
 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Villamos Energetika Tanszék Világítástechnika (BME VIVEM 355) Beltéri mérés Világítástechnikai felülvizsgálati jegyzőkönyv
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Villamos Energetika Tanszék Világítástechnika (BME VIVEM 355) Beltéri mérés Világítástechnikai felülvizsgálati jegyzőkönyv
Számítógépes geometria (mester kurzus)
 2010 sz, Debreceni Egyetem Csuklós szerkezetek animációja (Kép 1985-b l: Tony de Peltrie) Csontváz-modellek Csuklós szerkezet (robotkar) A robotkar részei: csuklók (joints) rotációs prizmatikus (transzlációs)
2010 sz, Debreceni Egyetem Csuklós szerkezetek animációja (Kép 1985-b l: Tony de Peltrie) Csontváz-modellek Csuklós szerkezet (robotkar) A robotkar részei: csuklók (joints) rotációs prizmatikus (transzlációs)
48. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY Megyei forduló HETEDIK OSZTÁLY MEGOLDÁSOK = = 2019.
 8. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY Megyei forduló HETEDIK OSZTÁLY MEGOLDÁSOK 1. Bizonyítsd be, hogy 019 db egymást követő pozitív egész szám közül mindig kiválasztható 19 db úgy, hogy az összegük
8. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY Megyei forduló HETEDIK OSZTÁLY MEGOLDÁSOK 1. Bizonyítsd be, hogy 019 db egymást követő pozitív egész szám közül mindig kiválasztható 19 db úgy, hogy az összegük
Loványi István vizsgakérdései kidolgozva (béta)
 Loványi István vizsgakérdései kidolgozva (béta) 1. Morfológiai képfeldolgozás elmélete 1. Alapvető halmazműveletek, tulajdonságaik Műveletek: egyesítés (unió) metszet negált összetett műveletek... Tulajdonságok:
Loványi István vizsgakérdései kidolgozva (béta) 1. Morfológiai képfeldolgozás elmélete 1. Alapvető halmazműveletek, tulajdonságaik Műveletek: egyesítés (unió) metszet negált összetett műveletek... Tulajdonságok:
Mérési struktúrák
 Mérési struktúrák 2007.02.19. 1 Mérési struktúrák A mérés művelete: a mérendő jellemző és a szimbólum halmaz közötti leképezés megvalósítása jel- és rendszerelméleti aspektus mérési folyamat: a leképezést
Mérési struktúrák 2007.02.19. 1 Mérési struktúrák A mérés művelete: a mérendő jellemző és a szimbólum halmaz közötti leképezés megvalósítása jel- és rendszerelméleti aspektus mérési folyamat: a leképezést
FELHASZNÁLÓI KÉZIKÖNYV
 FELHASZNÁLÓI KÉZIKÖNYV 1 BEVEZETÉS A Közlekedési Környezeti Centrum (KKC) projekt keretében létrejött ELZA (Elektronikus Levegő- és Zajvédelmi Adattár) egy online felületen elérhető alkalmazás, ahol a
FELHASZNÁLÓI KÉZIKÖNYV 1 BEVEZETÉS A Közlekedési Környezeti Centrum (KKC) projekt keretében létrejött ELZA (Elektronikus Levegő- és Zajvédelmi Adattár) egy online felületen elérhető alkalmazás, ahol a
Fényhullámhossz és diszperzió mérése
 Fényhullámhossz és diszperzió mérése Mérő neve: Márkus Bence Gábor Mérőpár neve: Székely Anna Krisztina Szerda délelőtti csoport Mérés ideje: 11/09/011 Beadás ideje: 11/16/011 1 1. A mérés rövid leírása
Fényhullámhossz és diszperzió mérése Mérő neve: Márkus Bence Gábor Mérőpár neve: Székely Anna Krisztina Szerda délelőtti csoport Mérés ideje: 11/09/011 Beadás ideje: 11/16/011 1 1. A mérés rövid leírása
DENZITOMÉTER ÁTALAKÍTÁSA HOSSZÚSÁGMÉRŐVÉ
 DENZITOMÉTER ÁTALAKÍTÁSA HOSSZÚSÁGMÉRŐVÉ Nagy Richárd MTA EK Óbudai Egyetem 2017. 01. 22. Az előadás tartalmából - Célkitűzés - Az optikai tervezés - A mérés menete - A képfeldolgozás - A pipe-line működése
DENZITOMÉTER ÁTALAKÍTÁSA HOSSZÚSÁGMÉRŐVÉ Nagy Richárd MTA EK Óbudai Egyetem 2017. 01. 22. Az előadás tartalmából - Célkitűzés - Az optikai tervezés - A mérés menete - A képfeldolgozás - A pipe-line működése
Képfeldolgozás Szegmentálás Osztályozás Képfelismerés Térbeli rekonstrukció
 Mesterséges látás Miről lesz szó? objektumok Bevezetés objektumok A mesterséges látás jelenlegi, technikai eszközökön alapuló világunkban gyakorlatilag azonos a számítógépes képfeldolgozással. Számítógépes
Mesterséges látás Miről lesz szó? objektumok Bevezetés objektumok A mesterséges látás jelenlegi, technikai eszközökön alapuló világunkban gyakorlatilag azonos a számítógépes képfeldolgozással. Számítógépes
Mérés: Millikan olajcsepp-kísérlete
 Mérés: Millikan olajcsepp-kísérlete Mérés célja: 1909-ben ezt a mérést Robert Millikan végezte el először. Mérése során meg tudta határozni az elemi részecskék töltését. Ezért a felfedezéséért Nobel-díjat
Mérés: Millikan olajcsepp-kísérlete Mérés célja: 1909-ben ezt a mérést Robert Millikan végezte el először. Mérése során meg tudta határozni az elemi részecskék töltését. Ezért a felfedezéséért Nobel-díjat
Befordulás sarkon bútorral
 Befordulás sarkon bútorral Bizonyára volt már olyan élményed, hogy bútort kellett cipelned, és nem voltál biztos benne, hogy be tudjátok - e vinni a szobába. Erről jutott eszembe az alábbi feladat. Adott
Befordulás sarkon bútorral Bizonyára volt már olyan élményed, hogy bútort kellett cipelned, és nem voltál biztos benne, hogy be tudjátok - e vinni a szobába. Erről jutott eszembe az alábbi feladat. Adott
MATEMATIKA HETI 5 ÓRA
 EURÓPAI ÉRETTSÉGI 2008 MATEMATIKA HETI 5 ÓRA IDŐPONT : 2008. június 5 (reggel) A VIZSGA IDŐTARTAMA: 4 óra (240 perc) MEGENGEDETT ESZKÖZÖK: Európai képletgyűjtemény Nem programozható, nem grafikus számológép
EURÓPAI ÉRETTSÉGI 2008 MATEMATIKA HETI 5 ÓRA IDŐPONT : 2008. június 5 (reggel) A VIZSGA IDŐTARTAMA: 4 óra (240 perc) MEGENGEDETT ESZKÖZÖK: Európai képletgyűjtemény Nem programozható, nem grafikus számológép
Érzékelők az autonóm járművekben
 Érzékelők az autonóm járművekben Gáspár Péter Szirányi Tamás 1 Érzékelők Tartalom Motivációs háttér Környezetérzékelés célja Autóipari érzékelők Széria megoldások és ipari trendek 2 Motiváció: A járműipar
Érzékelők az autonóm járművekben Gáspár Péter Szirányi Tamás 1 Érzékelők Tartalom Motivációs háttér Környezetérzékelés célja Autóipari érzékelők Széria megoldások és ipari trendek 2 Motiváció: A járműipar
5. 3D rekonstrukció. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 5. 3D rekonstrukció Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 PASSZÍV SZTEREÓ 3 Passzív sztereó 3D rekonstrukció egy sztereó kamera
5. 3D rekonstrukció Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 PASSZÍV SZTEREÓ 3 Passzív sztereó 3D rekonstrukció egy sztereó kamera
MATEMATIKA ÉRETTSÉGI május 8. EMELT SZINT
 MATEMATIKA ÉRETTSÉGI 007. május 8. EMELT SZINT 1) Oldja meg a valós számok halmazán az alábbi egyenletet! x x 4 log 9 10 sin x x 6 I. (11 pont) sin 1 lg1 0 log 9 9 x x 4 Így az 10 10 egyenletet kell megoldani,
MATEMATIKA ÉRETTSÉGI 007. május 8. EMELT SZINT 1) Oldja meg a valós számok halmazán az alábbi egyenletet! x x 4 log 9 10 sin x x 6 I. (11 pont) sin 1 lg1 0 log 9 9 x x 4 Így az 10 10 egyenletet kell megoldani,
Radioaktív anyag felezési idejének mérése
 A pályázótársam által ismertetett mérési módszer alkalmazásához Labview szoftverrel készítettem egy mérőműszert, ami lehetőséget nyújt radioaktív anyag felezési idejének meghatározására. 1. ábra: Felhasználói
A pályázótársam által ismertetett mérési módszer alkalmazásához Labview szoftverrel készítettem egy mérőműszert, ami lehetőséget nyújt radioaktív anyag felezési idejének meghatározására. 1. ábra: Felhasználói
Számítási feladatok a Számítógépi geometria órához
 Számítási feladatok a Számítógépi geometria órához Kovács Zoltán Copyright c 2012 Last Revision Date: 2012. október 15. kovacsz@nyf.hu Technikai útmutató a jegyzet használatához A jegyzet képernyőbarát
Számítási feladatok a Számítógépi geometria órához Kovács Zoltán Copyright c 2012 Last Revision Date: 2012. október 15. kovacsz@nyf.hu Technikai útmutató a jegyzet használatához A jegyzet képernyőbarát
Térbeli transzformációk, a tér leképezése síkra
 Térbeli transzformációk, a tér leképezése síkra Homogén koordináták bevezetése térben A tér minden P pontjához kölcsönösen egyértelműen egy valós (x, y, z) számhármast rendeltünk hozzá. (Descartes-féle
Térbeli transzformációk, a tér leképezése síkra Homogén koordináták bevezetése térben A tér minden P pontjához kölcsönösen egyértelműen egy valós (x, y, z) számhármast rendeltünk hozzá. (Descartes-féle
3D koordináta-rendszerek
 3D koordináta-rendszerek z z y x y x y balkezes bal-sodrású x jobbkezes jobb-sodrású z 3D transzformációk - homogén koordináták (x, y, z) megadása homogén koordinátákkal: (x, y, z, 1) (x, y, z, w) = (x,
3D koordináta-rendszerek z z y x y x y balkezes bal-sodrású x jobbkezes jobb-sodrású z 3D transzformációk - homogén koordináták (x, y, z) megadása homogén koordinátákkal: (x, y, z, 1) (x, y, z, w) = (x,
