OSZLOPOK DETEKTÁLÁSA 3D LIDAR PONTFELHŐKBEN
|
|
|
- Lídia Mezei
- 8 évvel ezelőtt
- Látták:
Átírás
1 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Irányítástechnika és Informatika Tanszék Sári András Lajos OSZLOPOK DETEKTÁLÁSA 3D LIDAR PONTFELHŐKBEN Önálló laboratórium beszámoló KONZULENS Dr. Benedek Csaba BUDAPEST, 2016
2 Tartalom Bevezetés Lidar rendszerek... 3 A feladat specifikálása... 4 Megvalósítás... 4 Talajdetekció RANSAC algoritmussal... 5 Fák lombkoronájának detektálása... 6 Klaszterezés... 7 A megfelelő objektumok kiválasztása... 8 Továbblépési lehetőségek... 9 Források
3 Bevezetés Lidar rendszerek A Lidar egy távérzékelési rendszer, használata széles körben elterjedt például a meteorológiában, térképészetben és a geológiában. A Lidar (Light Detection and Ranging) elnevezés a radar (Radio Detection And Ranging) szóból származtatott angol mozaikszó. A kettő között a különbség a távolságméréshez használt elektromágneses hullámok frekvenciájában rejlik. A radar rádióhullám tartományban sugároz, míg a Lidar az infravöröstől az ultraibolyáig terjedő frekvenciatartományban. A távolságmérés úgy történik, hogy a Lidar egység kibocsát egy energiaimpulzust, mely visszaverődik a mérni kívánt tárgyról és újra a Lidar egységbe jut. A jel által megtett út számítható az adás és a vétel időpontjából, ha az átviteli közeg törésmutatója ismert. Ahhoz, hogy több mérési pontból tudjuk végezni a térképezést, szükség van a mérési pont pozíciójára, ezért a Lidar készülékeket általában ellátják pozíció-meghatározáshoz szükséges eszközökkel (GPS, IMU) is. A Lidar rendszereknek felhasználás szempontjából különböző csoportokba sorolhatjuk. A topológiában használt Lidar rendszereket többnyire repülőgépekre szerelik és így térképezik fel a domborzatot. A hidrografikus rendszereket a tengerfenék feltérképezésére használják. Az ilyen típusú berendezések két különböző frekvenciájú nyalábbal működnek. A földi Lidar rendszereket járműre vagy talajra szerelik és általában városképek modellezésére, épületek külső vagy belső térképezésére használják, de képesek mozgó objektumok azonosítására is. Az önálló laboratórium során felhasznált adatok egy Riegl VZ 400-as Lidarral készültek. A mérés során az egységet a földre rögzítik. Másodpercenként pontot képes rögzíteni, 100 -os vertikális látószögben. A rendszer ezen kívül fel van szerelve egy kamerával is, így lehetőség nyílik a távolságon és az intenzitáson kívül RGB adatokat is hozzárendelni a pontokhoz. Az önálló laboratórium folyamán, csak a pontok pozíció (XYZ) adatait használtam fel, az RGB és intenzitásadatokat figyelmen kívül hagytam. 1 3
4 1. ábra: Velodyne Lidar által készített kép 2 2. ábra: Riegl VZ 400 által készített kép A feladat specifikálása A feladatom az önálló laboratórium során különböző, oszlopok detektálása volt, melyet később felhasználhatunk akár közúti táblák pozíciójának meghatározására. Az önálló laboratórium folyamán felhasznált mintákat a SZTAKI bocsátotta rendelkezésemre. A kapott pontfelhők több mérési pozícióból lettek felvéve, majd a BKK Közút Zrt. Közúti Adatgyűjtő REndSzer projektjének keretében, lettek egyesítve a mért adatok. Az pontfelhők, amiken dolgoztam a Fővám tér és a Gellért tér méréseiből származtak. 3. ábra: Detektálni kívánt oszlop a Fővám téren A pontfelhők feldolgozására a szabad forráskódú Point Cloud Library 3 -t használtam fel mely a pointclouds.org által van karbantartva. Így lehetőségem volt magas szinten (C++ nyelven) dolgozni. Megvalósítás Az oszlopok azonosítására a stratégiám a következő volt: Először meghatározom a talajt reprezentáló ponthalmazt és kivonom az összes pontot tartalmazó ponthalmazból. Ezzel a pontfelhő különböző objektumokra esik szét. Ezek után kivonom a fák lombkoronáját 4
5 tartalmazó felhőket, így lehetőség nyílik a fák által benőtt oszlopok detektálására is. Legvégül egy klaszterező algoritmussal azonosítom az objektumokat és különböző tulajdonságaik alapján szétválogatom őket. Talajdetekció RANSAC algoritmussal 4. ábra: talaj detektálása RANSAC algoritmussal a Szent Gelért téren A RANSAC 4 (Random Sample Consensus) algoritmus segítségével könnyedén detektálható a legtöbb pontból álló egyenes vagy sík két illetve háromdimenziós ponthalmazban. A RANSAC egy iteratív módszeren alapul, ami addig próbál javítani a talált síkon (vagy egyenesen), amíg el nem éri a paraméterben megadott maximális iterációk számát. Sík detektálásánál az első lépésként véletlenszerűen választ három pontot, amiből kiszámolja a pontokra illesztett sík paramétereit, majd megnézi, hogy a ponthalmaz többi pontja közül mennyi esik bele ebbe a síkba. Mivel a keresett pontok nem alkotnak matematikailag tökéletes síkot, ezért szükséges egy hiba paraméter megadása, mely szemléletesen a detektált sík vastagságát jelenti. Ezek után az algoritmus összeveti az így talált síkot az eddig talált legjobb síkkal, és ha ezt jobbnak ítéli, akkor ez lesz az új legjobb sík, ha nem akkor ezt a síkot eldobja. A ciklusnak akkor van vége, ha elértük az előre megadott iterációk számát. Az algoritmus működéséből adódik, hogy az iterációk számának a növelésével, nagyobb valószínűséggel kapunk az adathalmazra jól illeszkedő síkot. 5. ábra: Fővám tér talajdetekciója 6. ábra: RANSAC algoritmus hibája szintkülönbségeknél 5
6 Sajnos mivel a RANSAC a legnagyobb síkot találja meg, működése nem megfelelő olyan talajdetekciónál, melynél a talaj nem modellezhető egy síkkal (például szintkülönbségeket tartalmazó talaj). A hiba paramétert 30cm-re választottam meg, mivel azt tapasztaltam, hogyha a paraméter túl kicsi, nem lesz összefüggő a detektált talaj, viszont ha túl nagyra választom, akkor az egyéb talaj feletti részeket is a talajhoz sorolja. Mivel az oszlopok detektálása volt a cél, a szükségesnél kicsit nagyobb paraméter megengedhető, hiszen az oszlopok talpazata az oszlopfelismerésben nem kritikus. Fák lombkoronájának detektálása 7. ábra: Fák lombkoronájának detektálása A következő lépés a fák lombkoronájának detektálása volt. Ehhez azt a stratégiát választottam, hogy a felhő minden pontjára a 10 legközelebbi szomszédja alapján számolom a kovariancia mátrix sajátértékeit, amiből később a görbületet meg tudom határozni. Úgy véltem, hogy a fa lombkoronája nagy görbületet fog mutatni, mivel a lombkorona terét a pontok közel egyenletesen töltik ki. A legközelebbi pontok kereséséhez a pontfelhőt KdTree 5 struktúrába rendeztem, mely lehetővé teszi, hogy a legközelebbi k pontot megtalálása gyorsan történjen. Ezt úgy teszi, hogy a teret a koordinátatengelyekkel párhuzamosan optimálisan partícionálja. Erre azért van szükség, mert a Lidar pontfelhő nem egyenletes eloszlású a térben, ezért érdemes a felbontást csak azokon a területeken megnövelni, ahol a pontok többsége található. A sajátértékeket számítását a Point Cloud Library-be beépített PCA (Principal Component Analysis) segítségével végeztem. A PCA által szolgáltatott adatokból a görbületet a nulladik sajátérték és a sajátértékek hányadosaként számítottam. 6
7 A kapott pontokat a görbület szerint három csoportba soroltam. Pirossal jelöltem azokat a pontokat, amelyeknél a görbület nél kisebb. Ezek a síkfelületeknek felelnek meg. A től 0.03-ig terjedő intervallumban zölddel színeztem a pontokat, és a maradék pontokat kékre színeztem, melyek a lombkoronának vélt pontokat jelentik. A képek alapján jól látható, hogy ez az algoritmus is képes (kisebb módosításokkal) a talaj detektálására, esetenként jobban működik, mint a RANSAC, azonban mivel a program futása rendkívül lassú, így végül nem ezt választottam. Sajnos a fák lombkoronájának detektálása is lassúnak bizonyult, így végül ezt a módszert nem implementáltam a végső algoritmusban. Klaszterezés 8. ábra: Sík felületek és fák lombkoronájának detektálása Az objektumok szétválasztását az euklideszi klaszterező algoritmussal végeztem. Ez az eljárás tulajdonképpen a több komponensből álló gráfokra implementált BFS bejárás duálisa. Az algoritmus működése a következő: először kiválaszt egy pontot, majd megkeresi azokat a pontokat, amik a ponttól egy előre megadott távolságon belül vannak és hozzáadja őket a ponthoz tartozó listához. Ezek után kiválasztja a következő pontot a listán és ennek a környezetében lévő pontokat is hozzáadja a lista végéhez, ha azok még nem voltak rajta a listán. Ha a lista végére ért, akkor egy cluster készen van, új pontot választ és innen újraindítja 7
8 a keresést. Ha az összes pont elfogyott a klaszterezés véget ért. Mivel itt is a legközelebbi pontok kereséséről van szó (csak itt nem a legközelebbi k pontot, hanem az r sugárnál közelebb található pontokat keressük), itt is KdTree-t használtam a keresés gyorsítása végett. 9. ábra: Fővám tér a talaj eltávolítása után A megfelelő objektumok kiválasztása Ezek után, már csak az a feladat maradt, hogy eldöntsük az egyes clusterekről, hogy oszlopok-e. Ezt a következő módszerrel csináltam: megkerestem a cluster legnagyobb és legalacsonyabb z koordinátájú pontját, a z koordinátájuk különbségét egy height változóban tároltam. Ezt követően, úgy gondoltam, hogy azok az objektumok tekinthetők oszlopnak, amik magasak (height érték magasabb, mint 2,5 méter), és a magasságuk 25%-tól 75%-ig terjedő intervallumában keskenyek, azaz nem szélesebbek 3 méternél. Azért választottam viszonylag nagy értéket, mert a rajtuk lévő esetleges reklámtábláknak még bele kell férni, és ez a paraméter inkább az épülethomlokzattól való megkülönböztetésre szolgál. Ahhoz, hogy a szélességüket mérni tudjam megkerestem az ezen z tartományban 25%-75%-ig terjedő intervallumban az x és y koordináta szerinti szélsőértékeket is, és úgy határoztam, hogy se az x se az y irányú szélesség ne legyen nagyobb a megengedettnél. (Így orientációtól függően a határérték akár szerese is megengedett.) 8
9 A kívánt eredményt így nem sikerült megvalósítani, mivel az egyik oszlopról a lelógó vezetékek miatt a szélességre adott kritérium nem teljesült. A szélesség kritérium eltörlésével azonban mindkét oszlopot képesek voltunk detektálni. Továbblépési lehetőségek 10. ábra: Az algoritmus által (feltételek enyhítése után) detektált oszlopok Lehetséges továbblépési lehetőség az oszlopok különböző csoportokba sorolása, mely segítségével, akár a közúti táblák is felismerhetőek. Ehhez például felhasználhatjuk a lombkorona detektálásához használt algoritmust, mely segítségével az oszlopon lévő síkfelületeket érzékelhetnénk. Mivel a közúti tábláknak jól definiált méretei vannak, ezek szűrése viszonylag szigorú paraméterezés is alkalmazható. Másik lehetséges előrelépési lehetőség a RANSAC algoritmus lecserélése egy olyan algoritmusra, mely lehetőséget nyújt a nem sík talaj detektálására. 9
10 Források 1 Demkó Bence: Mozgó elemek által generált zaj detektálása 3D Lidar pontfelhőkben Ábra: 3 Rusu, R.B.; Cousins, S., "3D is here: Point Cloud Library (PCL)," Robotics and Automation (ICRA), 2011 IEEE International Conference on, vol., no., pp.1,4, 9-13 May Martin A. Fischler and Robert C. Bolles (June 1981). "Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography". Comm. of the ACM 24 (6): Szirmay-Kalos László, Antal György, Csonka Ferenc: Háromdimenziós grafika, animáció és játékfejlesztés ComputerBooks,
3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás
 3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav54
3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav54
3D számítógépes geometria és alakzatrekonstrukció
 3D számítógépes geometria és alakzatrekonstrukció 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01
3D számítógépes geometria és alakzatrekonstrukció 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01
3D számítógépes geometria és alakzatrekonstrukció
 3D számítógépes geometria és alakzatrekonstrukció 14. Digitális Alakzatrekonstrukció - Bevezetés http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01 Dr. Várady Tamás, Dr.
3D számítógépes geometria és alakzatrekonstrukció 14. Digitális Alakzatrekonstrukció - Bevezetés http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01 Dr. Várady Tamás, Dr.
Grafikonok automatikus elemzése
 Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
3D-s számítógépes geometria és alakzatrekonstrukció
 3D-s számítógépes geometria és alakzatrekonstrukció 14. Digitális Alakzatrekonstrukció - Bevezetés http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav08 Dr. Várady Tamás,
3D-s számítógépes geometria és alakzatrekonstrukció 14. Digitális Alakzatrekonstrukció - Bevezetés http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav08 Dr. Várady Tamás,
PONTFELHŐ REGISZTRÁCIÓ
 PONTFELHŐ REGISZTRÁCIÓ ITERATIVE CLOSEST POINT Cserteg Tamás, URLGNI, 2018.11.22. TARTALOM Röviden Alakzatrekonstrukció áttekintés ICP algoritmusok Projektfeladat Demó FORRÁSOK Cikkek Efficient Variants
PONTFELHŐ REGISZTRÁCIÓ ITERATIVE CLOSEST POINT Cserteg Tamás, URLGNI, 2018.11.22. TARTALOM Röviden Alakzatrekonstrukció áttekintés ICP algoritmusok Projektfeladat Demó FORRÁSOK Cikkek Efficient Variants
Intelligens Közlekedési Rendszerek 2
 Intelligens Közlekedési Rendszerek 2 Máté Miklós 2016 Október 11 1 / 14 Szenzor (érzékelő): mérés, detektálás Mérés elmélet emlékeztető Jó mérőműszer tulajdonságai Érzékeny a mérendő tulajdonságra Érzéketlen
Intelligens Közlekedési Rendszerek 2 Máté Miklós 2016 Október 11 1 / 14 Szenzor (érzékelő): mérés, detektálás Mérés elmélet emlékeztető Jó mérőműszer tulajdonságai Érzékeny a mérendő tulajdonságra Érzéketlen
Rendszámfelismerő rendszerek
 Problémamegoldó szeminárium Témavezető: Pataki Péter ARH Zrt. ELTE-TTK 2013 Tartalomjegyzék 1 Bevezetés 2 Út a megoldás felé 3 Felmerült problémák 4 Alkalmazott matematika 5 További lehetőségek Motiváció
Problémamegoldó szeminárium Témavezető: Pataki Péter ARH Zrt. ELTE-TTK 2013 Tartalomjegyzék 1 Bevezetés 2 Út a megoldás felé 3 Felmerült problémák 4 Alkalmazott matematika 5 További lehetőségek Motiváció
Térinformatika és Geoinformatika
 Távérzékelés 1 Térinformatika és Geoinformatika 2 A térinformatika az informatika azon része, amely térbeli adatokat, térbeli információkat dolgoz fel A geoinformatika az informatika azon része, amely
Távérzékelés 1 Térinformatika és Geoinformatika 2 A térinformatika az informatika azon része, amely térbeli adatokat, térbeli információkat dolgoz fel A geoinformatika az informatika azon része, amely
Közösség detektálás gráfokban
 Közösség detektálás gráfokban Önszervező rendszerek Hegedűs István Célkitűzés: valamilyen objektumok halmaza felett minták, csoportok detektálása csakis az egyedek közötti kapcsolatok struktúrájának a
Közösség detektálás gráfokban Önszervező rendszerek Hegedűs István Célkitűzés: valamilyen objektumok halmaza felett minták, csoportok detektálása csakis az egyedek közötti kapcsolatok struktúrájának a
Számítógépes döntéstámogatás. Genetikus algoritmusok
 BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
Pontfelhő létrehozás és használat Regard3D és CloudCompare nyílt forráskódú szoftverekkel. dr. Siki Zoltán
 Pontfelhő létrehozás és használat Regard3D és CloudCompare nyílt forráskódú szoftverekkel dr. Siki Zoltán siki.zoltan@epito.bme.hu Regard3D Nyílt forráskódú SfM (Structure from Motion) Fényképekből 3D
Pontfelhő létrehozás és használat Regard3D és CloudCompare nyílt forráskódú szoftverekkel dr. Siki Zoltán siki.zoltan@epito.bme.hu Regard3D Nyílt forráskódú SfM (Structure from Motion) Fényképekből 3D
Időjárási radarok és produktumaik
 ORSZÁGOS METEOROLÓGIAI SZOLGÁLAT Időjárási radarok és produktumaik Hadvári Marianna Országos Meteorológiai Szolgálat Távérzékelési Osztály 2018. október 6. Alapítva: 1870 Radio Detection And Ranging 1935
ORSZÁGOS METEOROLÓGIAI SZOLGÁLAT Időjárási radarok és produktumaik Hadvári Marianna Országos Meteorológiai Szolgálat Távérzékelési Osztály 2018. október 6. Alapítva: 1870 Radio Detection And Ranging 1935
Panorámakép készítése
 Panorámakép készítése Képregisztráció, 2009. Hantos Norbert Blaskovics Viktor Összefoglalás Panoráma (image stitching, planar mosaicing): átfedő képek összeillesztése Lépések: Előfeldolgozás (pl. intenzitáskorrekciók)
Panorámakép készítése Képregisztráció, 2009. Hantos Norbert Blaskovics Viktor Összefoglalás Panoráma (image stitching, planar mosaicing): átfedő képek összeillesztése Lépések: Előfeldolgozás (pl. intenzitáskorrekciók)
Városi környezet vizsgálata távérzékelési adatok osztályozásával
 Városi környezet vizsgálata távérzékelési adatok osztályozásával Verőné Dr. Wojtaszek Małgorzata Óbudai Egyetem AMK Goeinformatika Intézet 20 éves a Térinformatika Tanszék 2014. december. 15 Felvetések
Városi környezet vizsgálata távérzékelési adatok osztályozásával Verőné Dr. Wojtaszek Małgorzata Óbudai Egyetem AMK Goeinformatika Intézet 20 éves a Térinformatika Tanszék 2014. december. 15 Felvetések
Vonalas közlekedési létesítmények mobil térképezésével kapcsolatos saját fejlesztések
 www.geodezia.hu Geodézia Zrt. 31. Vándorgyűlés Szekszárd, 2017. július 6-8. Vonalas közlekedési létesítmények mobil térképezésével kapcsolatos saját fejlesztések Csörgits Péter Miről lesz szó? VONALAS
www.geodezia.hu Geodézia Zrt. 31. Vándorgyűlés Szekszárd, 2017. július 6-8. Vonalas közlekedési létesítmények mobil térképezésével kapcsolatos saját fejlesztések Csörgits Péter Miről lesz szó? VONALAS
Mikroszkóp vizsgálata Folyadék törésmutatójának mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 8. MÉRÉS Mikroszkóp vizsgálata Folyadék törésmutatójának mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 12. Szerda délelőtti csoport
KLASSZIKUS FIZIKA LABORATÓRIUM 8. MÉRÉS Mikroszkóp vizsgálata Folyadék törésmutatójának mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 12. Szerda délelőtti csoport
A 2017/2018. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. KATEGÓRIA JAVÍTÁSI ÚTMUTATÓ. Pohár rezonanciája
 Oktatási Hivatal A 017/018. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. KATEGÓRIA JAVÍTÁSI ÚTMUTATÓ Pohár rezonanciája A mérőberendezés leírása: A mérőberendezés egy változtatható
Oktatási Hivatal A 017/018. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. KATEGÓRIA JAVÍTÁSI ÚTMUTATÓ Pohár rezonanciája A mérőberendezés leírása: A mérőberendezés egy változtatható
Távérzékelés, a jöv ígéretes eszköze
 Távérzékelés, a jöv ígéretes eszköze Ritvayné Szomolányi Mária Frombach Gabriella VITUKI CONSULT Zrt. A távérzékelés segítségével: különböz6 magasságból, tetsz6leges id6ben és a kívánt hullámhossz tartományokban
Távérzékelés, a jöv ígéretes eszköze Ritvayné Szomolányi Mária Frombach Gabriella VITUKI CONSULT Zrt. A távérzékelés segítségével: különböz6 magasságból, tetsz6leges id6ben és a kívánt hullámhossz tartományokban
Milyen északi irány található a tájfutótérképen?
 Milyen északi irány található a tájfutótérképen? A felmérést a Hárshegy :000 méretarányú tájfutótérképén végeztem. Olyan pontokat választottam ki, amik a terepen és a térképen is jól azonosíthatók. ezeket
Milyen északi irány található a tájfutótérképen? A felmérést a Hárshegy :000 méretarányú tájfutótérképén végeztem. Olyan pontokat választottam ki, amik a terepen és a térképen is jól azonosíthatók. ezeket
EEE Kutatólaboratórium MTA-SZTAKI Magyar Tudományos Akadémia
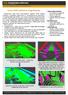 DElosztott I S T R I B U T EEsemények D EV E N T S A NElemzé A L Y S I S se R E SKutatólaboratór E A R C H L A B O R A T Oium R Y L I D A R B a s e d S u r v e i l l a n c e Városi LIDAR adathalmaz szegmentációja
DElosztott I S T R I B U T EEsemények D EV E N T S A NElemzé A L Y S I S se R E SKutatólaboratór E A R C H L A B O R A T Oium R Y L I D A R B a s e d S u r v e i l l a n c e Városi LIDAR adathalmaz szegmentációja
Navigáci. stervezés. Algoritmusok és alkalmazásaik. Osváth Róbert Sorbán Sámuel
 Navigáci ció és s mozgástervez stervezés Algoritmusok és alkalmazásaik Osváth Róbert Sorbán Sámuel Feladat Adottak: pálya (C), játékos, játékos ismerethalmaza, kezdőpont, célpont. Pálya szerkezete: akadályokkal
Navigáci ció és s mozgástervez stervezés Algoritmusok és alkalmazásaik Osváth Róbert Sorbán Sámuel Feladat Adottak: pálya (C), játékos, játékos ismerethalmaza, kezdőpont, célpont. Pálya szerkezete: akadályokkal
7. Régió alapú szegmentálás
 Digitális képek szegmentálása 7. Régió alapú szegmentálás Kató Zoltán http://www.cab.u-szeged.hu/~kato/segmentation/ Szegmentálási kritériumok Particionáljuk a képet az alábbi kritériumokat kielégítő régiókba
Digitális képek szegmentálása 7. Régió alapú szegmentálás Kató Zoltán http://www.cab.u-szeged.hu/~kato/segmentation/ Szegmentálási kritériumok Particionáljuk a képet az alábbi kritériumokat kielégítő régiókba
Digitális jelfeldolgozás
 Digitális jelfeldolgozás Kvantálás Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2010. szeptember 15. Áttekintés
Digitális jelfeldolgozás Kvantálás Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2010. szeptember 15. Áttekintés
Feladatok megoldásokkal az első gyakorlathoz (differencia- és differenciálhányados fogalma, geometriai és fizikai jelentése) (x 1)(x + 1) x 1
 Feladatok megoldásokkal az első gyakorlathoz (differencia- és differenciálhányados fogalma, geometriai és fizikai jelentése). Feladat. Határozzuk meg az f(x) x 2 függvény x 0 pontbeli differenciahányados
Feladatok megoldásokkal az első gyakorlathoz (differencia- és differenciálhányados fogalma, geometriai és fizikai jelentése). Feladat. Határozzuk meg az f(x) x 2 függvény x 0 pontbeli differenciahányados
Principal Component Analysis
 Principal Component Analysis Principal Component Analysis Principal Component Analysis Definíció Ortogonális transzformáció, amely az adatokat egy új koordinátarendszerbe transzformálja úgy, hogy a koordináták
Principal Component Analysis Principal Component Analysis Principal Component Analysis Definíció Ortogonális transzformáció, amely az adatokat egy új koordinátarendszerbe transzformálja úgy, hogy a koordináták
TÉRINFORMATIKA II. Dr. Kulcsár Balázs egyetemi docens. Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék
 TÉRINFORMATIKA II. Dr. Kulcsár Balázs egyetemi docens Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék ELSŐDLEGES ADATNYERÉSI ELJÁRÁSOK 2. Inerciális rendszerek Távérzékelés Rádiótelefonok Mobil
TÉRINFORMATIKA II. Dr. Kulcsár Balázs egyetemi docens Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék ELSŐDLEGES ADATNYERÉSI ELJÁRÁSOK 2. Inerciális rendszerek Távérzékelés Rádiótelefonok Mobil
Gauss-Seidel iteráció
 Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Mobil Térképező Rendszer hazai felhasználása
 1149 Budapest, Bosnyák tér 5. 1591 Budapest, Pf. 304. (1) 252-8222 Titkárság: (1) 363-6801 Fax: (1) 363-5808 Mobil Térképező Rendszer hazai felhasználása A lézerszkennerrel történő felmérés a legmodernebb
1149 Budapest, Bosnyák tér 5. 1591 Budapest, Pf. 304. (1) 252-8222 Titkárság: (1) 363-6801 Fax: (1) 363-5808 Mobil Térképező Rendszer hazai felhasználása A lézerszkennerrel történő felmérés a legmodernebb
MATEMATIKA HETI 5 ÓRA
 EURÓPAI ÉRETTSÉGI 2008 MATEMATIKA HETI 5 ÓRA IDŐPONT : 2008. június 5 (reggel) A VIZSGA IDŐTARTAMA: 4 óra (240 perc) MEGENGEDETT ESZKÖZÖK: Európai képletgyűjtemény Nem programozható, nem grafikus számológép
EURÓPAI ÉRETTSÉGI 2008 MATEMATIKA HETI 5 ÓRA IDŐPONT : 2008. június 5 (reggel) A VIZSGA IDŐTARTAMA: 4 óra (240 perc) MEGENGEDETT ESZKÖZÖK: Európai képletgyűjtemény Nem programozható, nem grafikus számológép
IX. Alkalmazott Informatikai Konferencia Kaposvári Egyetem február 25.
 Kaposvári Egyetem 2011. február 25. Egedy Attila, Varga Tamás, Chován Tibor Pannon Egyetem, Mérnöki Kar, Folyamatmérnöki Intézeti Tanszék Veszprém, 8200 Egyetem utca 10. Bevezetés Cellás modellezés Kvalitatív
Kaposvári Egyetem 2011. február 25. Egedy Attila, Varga Tamás, Chován Tibor Pannon Egyetem, Mérnöki Kar, Folyamatmérnöki Intézeti Tanszék Veszprém, 8200 Egyetem utca 10. Bevezetés Cellás modellezés Kvalitatív
4. Lokalizáció Magyar Attila
 4. Lokalizáció Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2011. szeptember 23. 4. Lokalizáció 2 4. Tartalom
4. Lokalizáció Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2011. szeptember 23. 4. Lokalizáció 2 4. Tartalom
Programozási módszertan. Mohó algoritmusok
 PM-08 p. 1/17 Programozási módszertan Mohó algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu PM-08 p. 2/17 Bevezetés Dinamikus programozás
PM-08 p. 1/17 Programozási módszertan Mohó algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu PM-08 p. 2/17 Bevezetés Dinamikus programozás
Modern Fizika Labor. 11. Spektroszkópia. Fizika BSc. A mérés dátuma: dec. 16. A mérés száma és címe: Értékelés: A beadás dátuma: dec. 21.
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. dec. 16. A mérés száma és címe: 11. Spektroszkópia Értékelés: A beadás dátuma: 2011. dec. 21. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. dec. 16. A mérés száma és címe: 11. Spektroszkópia Értékelés: A beadás dátuma: 2011. dec. 21. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Távérzékelés gyakorlat Fotogrammetria légifotó értelmezés
 Távérzékelés gyakorlat Fotogrammetria légifotó értelmezés I. A légifotók tájolása a térkép segítségével: a). az ábrázolt terület azonosítása a térképen b). sztereoszkópos vizsgálat II. A légifotók értelmezése:
Távérzékelés gyakorlat Fotogrammetria légifotó értelmezés I. A légifotók tájolása a térkép segítségével: a). az ábrázolt terület azonosítása a térképen b). sztereoszkópos vizsgálat II. A légifotók értelmezése:
Kontrollcsoport-generálási lehetőségek retrospektív egészségügyi vizsgálatokhoz
 Kontrollcsoport-generálási lehetőségek retrospektív egészségügyi vizsgálatokhoz Szekér Szabolcs 1, Dr. Fogarassyné dr. Vathy Ágnes 2 1 Pannon Egyetem Rendszer- és Számítástudományi Tanszék, szekersz@gmail.com
Kontrollcsoport-generálási lehetőségek retrospektív egészségügyi vizsgálatokhoz Szekér Szabolcs 1, Dr. Fogarassyné dr. Vathy Ágnes 2 1 Pannon Egyetem Rendszer- és Számítástudományi Tanszék, szekersz@gmail.com
Távérzékelés a vízgazdálkodás szolgálatában. Bíró Tibor Nemzeti Közszolgálati Egyetem Víztudományi Kar
 Távérzékelés a vízgazdálkodás szolgálatában Bíró Tibor Nemzeti Közszolgálati Egyetem Víztudományi Kar Távérzékelés Távérzékelés alkalmazásával két vagy háromdimenziós objektumok és természeti képződmények
Távérzékelés a vízgazdálkodás szolgálatában Bíró Tibor Nemzeti Közszolgálati Egyetem Víztudományi Kar Távérzékelés Távérzékelés alkalmazásával két vagy háromdimenziós objektumok és természeti képződmények
Gyakorló feladatok adatbányászati technikák tantárgyhoz
 Gyakorló feladatok adatbányászati technikák tantárgyhoz Buza Krisztián Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem Klaszterezés kiértékelése Feladat:
Gyakorló feladatok adatbányászati technikák tantárgyhoz Buza Krisztián Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem Klaszterezés kiértékelése Feladat:
Felvételi tematika INFORMATIKA
 Felvételi tematika INFORMATIKA 2016 FEJEZETEK 1. Természetes számok feldolgozása számjegyenként. 2. Számsorozatok feldolgozása elemenként. Egydimenziós tömbök. 3. Mátrixok feldolgozása elemenként/soronként/oszloponként.
Felvételi tematika INFORMATIKA 2016 FEJEZETEK 1. Természetes számok feldolgozása számjegyenként. 2. Számsorozatok feldolgozása elemenként. Egydimenziós tömbök. 3. Mátrixok feldolgozása elemenként/soronként/oszloponként.
c adatpontok és az ismeretlen pont közötti kovariancia vektora
 1. MELLÉKLET: Alkalmazott jelölések A mintaterület kiterjedése, területe c adatpontok és az ismeretlen pont közötti kovariancia vektora C(0) reziduális komponens varianciája C R (h) C R Cov{} d( u, X )
1. MELLÉKLET: Alkalmazott jelölések A mintaterület kiterjedése, területe c adatpontok és az ismeretlen pont közötti kovariancia vektora C(0) reziduális komponens varianciája C R (h) C R Cov{} d( u, X )
MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR
 KÖZÚTI ADATBÁZISOK ÉS ADAT-NYILVÁNTARTÓ RENDSZEREK Lakatos András Tartalom Bevezetés Közútra vonatkozó adatgyűjtési rendszerek története Adatbázisok, adatgyűjtési rendszerek napjainkban Adatok hasznosítása
KÖZÚTI ADATBÁZISOK ÉS ADAT-NYILVÁNTARTÓ RENDSZEREK Lakatos András Tartalom Bevezetés Közútra vonatkozó adatgyűjtési rendszerek története Adatbázisok, adatgyűjtési rendszerek napjainkban Adatok hasznosítása
Algoritmusok bonyolultsága
 Algoritmusok bonyolultsága 5. előadás http://www.ms.sapientia.ro/~kasa/komplex.htm 1 / 27 Gazdaságos faváz Kruskal-algoritmus Joseph Kruskal (1928 2010) Legyen V = {v 1, v 2,..., v n }, E = {e 1, e 2,...,
Algoritmusok bonyolultsága 5. előadás http://www.ms.sapientia.ro/~kasa/komplex.htm 1 / 27 Gazdaságos faváz Kruskal-algoritmus Joseph Kruskal (1928 2010) Legyen V = {v 1, v 2,..., v n }, E = {e 1, e 2,...,
Létesítmények felmérése 3D szkenner segítségével
 Létesítmények felmérése 3D szkenner segítségével TDK dolgozat Csizmadia Tamás Nagy András Redele Márk Konzulens: Kondor Tamás DLA, dr.habil PTE-PMMIK 2011.11.20. Pécs Létesítmények felmérése 3D szkenner
Létesítmények felmérése 3D szkenner segítségével TDK dolgozat Csizmadia Tamás Nagy András Redele Márk Konzulens: Kondor Tamás DLA, dr.habil PTE-PMMIK 2011.11.20. Pécs Létesítmények felmérése 3D szkenner
Matematikai geodéziai számítások 6.
 Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Regresszió számítás. Tartalomjegyzék: GeoEasy V2.05+ Geodéziai Kommunikációs Program
 Regresszió számítás GeoEasy V2.05+ Geodéziai Kommunikációs Program DigiKom Kft. 2006-2010 Tartalomjegyzék: Egyenes x változik Egyenes y változik Egyenes y és x változik Kör Sík z változik Sík y, x és z
Regresszió számítás GeoEasy V2.05+ Geodéziai Kommunikációs Program DigiKom Kft. 2006-2010 Tartalomjegyzék: Egyenes x változik Egyenes y változik Egyenes y és x változik Kör Sík z változik Sík y, x és z
Adatszerkezetek 2. Dr. Iványi Péter
 Adatszerkezetek 2. Dr. Iványi Péter 1 Fák Fákat akkor használunk, ha az adatok között valamilyen alá- és fölérendeltség van. Pl. könyvtárszerkezet gyökér (root) Nincsennek hurkok!!! 2 Bináris fák Azokat
Adatszerkezetek 2. Dr. Iványi Péter 1 Fák Fákat akkor használunk, ha az adatok között valamilyen alá- és fölérendeltség van. Pl. könyvtárszerkezet gyökér (root) Nincsennek hurkok!!! 2 Bináris fák Azokat
Modern Fizika Labor. 2. Az elemi töltés meghatározása. Fizika BSc. A mérés dátuma: nov. 29. A mérés száma és címe: Értékelés:
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. nov. 29. A mérés száma és címe: 2. Az elemi töltés meghatározása Értékelés: A beadás dátuma: 2011. dec. 11. A mérést végezte: Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. nov. 29. A mérés száma és címe: 2. Az elemi töltés meghatározása Értékelés: A beadás dátuma: 2011. dec. 11. A mérést végezte: Szőke Kálmán Benjamin
Tárgy. Forgóasztal. Lézer. Kamera 3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL
 3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL. Bevezetés A lézeres letapogatás a ma elérhet legpontosabb 3D-s rekonstrukciót teszi lehet vé. Alapelve roppant egyszer : egy lézeres csíkkal megvilágítjuk a tárgyat.
3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL. Bevezetés A lézeres letapogatás a ma elérhet legpontosabb 3D-s rekonstrukciót teszi lehet vé. Alapelve roppant egyszer : egy lézeres csíkkal megvilágítjuk a tárgyat.
A számítástudomány alapjai
 A számítástudomány alapjai Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem Legszélesebb utak Katona Gyula Y. (BME SZIT) A számítástudomány
A számítástudomány alapjai Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem Legszélesebb utak Katona Gyula Y. (BME SZIT) A számítástudomány
Mérés: Millikan olajcsepp-kísérlete
 Mérés: Millikan olajcsepp-kísérlete Mérés célja: 1909-ben ezt a mérést Robert Millikan végezte el először. Mérése során meg tudta határozni az elemi részecskék töltését. Ezért a felfedezéséért Nobel-díjat
Mérés: Millikan olajcsepp-kísérlete Mérés célja: 1909-ben ezt a mérést Robert Millikan végezte el először. Mérése során meg tudta határozni az elemi részecskék töltését. Ezért a felfedezéséért Nobel-díjat
Akusztikai tervezés a geometriai akusztika módszereivel
 Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Beltéri autonóm négyrotoros helikopter szabályozó rendszerének kifejlesztése és hardware-in-the-loop tesztelése
 Beltéri autonóm négyrotoros helikopter szabályozó rendszerének kifejlesztése és hardware-in-the-loop tesztelése Regula Gergely, Lantos Béla BME Villamosmérnöki és Informatikai Kar Irányítástechnika és
Beltéri autonóm négyrotoros helikopter szabályozó rendszerének kifejlesztése és hardware-in-the-loop tesztelése Regula Gergely, Lantos Béla BME Villamosmérnöki és Informatikai Kar Irányítástechnika és
Matematikai geodéziai számítások 6.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
A vasút életéhez. Örvény-áramú sínpálya vizsgáló a Shinkawa-tól. Certified by ISO9001 SHINKAWA
 SHINKAWA Certified by ISO9001 Örvény-áramú sínpálya vizsgáló a Shinkawa-tól Technikai Jelentés A vasút életéhez A Shinkawa örvény-áramú sínpálya vizsgáló rendszer, gyors állapotmeghatározásra képes, még
SHINKAWA Certified by ISO9001 Örvény-áramú sínpálya vizsgáló a Shinkawa-tól Technikai Jelentés A vasút életéhez A Shinkawa örvény-áramú sínpálya vizsgáló rendszer, gyors állapotmeghatározásra képes, még
Transzformációk. Szécsi László
 Transzformációk Szécsi László A feladat Adott a 3D modell háromszögek csúcspontjai [modellezési koordináták] Háromszögkitöltő algoritmus pixeleket színez be [viewport koordináták] A feladat: számítsuk
Transzformációk Szécsi László A feladat Adott a 3D modell háromszögek csúcspontjai [modellezési koordináták] Háromszögkitöltő algoritmus pixeleket színez be [viewport koordináták] A feladat: számítsuk
MATEMATIKA ÉRETTSÉGI május 8. KÖZÉPSZINT
 MATEMATIKA ÉRETTSÉGI 007. május 8. KÖZÉPSZINT ) Egyszerűsítse a következő törtet! (a; b valós szám, ab 0)! a b ab ab ab ( a ) a ab I. Összesen: pont ) Egy mértani sorozat második eleme 3, hatodik eleme.
MATEMATIKA ÉRETTSÉGI 007. május 8. KÖZÉPSZINT ) Egyszerűsítse a következő törtet! (a; b valós szám, ab 0)! a b ab ab ab ( a ) a ab I. Összesen: pont ) Egy mértani sorozat második eleme 3, hatodik eleme.
Szimulációs technikák
 SZÉCHENYI ISTVÁN EGYETEM Műszaki Tudományi Kar Informatikai tanszék Szimulációs technikák ( NGB_IN040_1) 2. csapat Comparator - Dokumentáció Mérnök informatikus BSc szak, nappali tagozat 2012/2013 II.
SZÉCHENYI ISTVÁN EGYETEM Műszaki Tudományi Kar Informatikai tanszék Szimulációs technikák ( NGB_IN040_1) 2. csapat Comparator - Dokumentáció Mérnök informatikus BSc szak, nappali tagozat 2012/2013 II.
Modern Fizika Labor. A mérés száma és címe: A mérés dátuma: Értékelés: Infravörös spektroszkópia. A beadás dátuma: A mérést végezte:
 Modern Fizika Labor A mérés dátuma: 2005.10.26. A mérés száma és címe: 12. Infravörös spektroszkópia Értékelés: A beadás dátuma: 2005.11.09. A mérést végezte: Orosz Katalin Tóth Bence 1 A mérés során egy
Modern Fizika Labor A mérés dátuma: 2005.10.26. A mérés száma és címe: 12. Infravörös spektroszkópia Értékelés: A beadás dátuma: 2005.11.09. A mérést végezte: Orosz Katalin Tóth Bence 1 A mérés során egy
Algoritmuselmélet. Gráfok megadása, szélességi bejárás, összefüggőség, párosítás. Katona Gyula Y.
 Algoritmuselmélet Gráfok megadása, szélességi bejárás, összefüggőség, párosítás Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem 2. előadás
Algoritmuselmélet Gráfok megadása, szélességi bejárás, összefüggőség, párosítás Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem 2. előadás
 Fotogrammetria és távérzékelés A képi tartalomban rejlő információgazdagság Dr. Jancsó Tamás Nyugat-magyarországi Egyetem, Geoinformatikai Kar MFTTT rendezvény 2012. Április 18. Székesfehérvár Tartalom
Fotogrammetria és távérzékelés A képi tartalomban rejlő információgazdagság Dr. Jancsó Tamás Nyugat-magyarországi Egyetem, Geoinformatikai Kar MFTTT rendezvény 2012. Április 18. Székesfehérvár Tartalom
Anatómiai régiók automatikus felismerése
 Anatómiai régiók automatikus felismerése Kutatási beszámoló 2015. június Készítette: Tóth Márton József Bevezetés A mai klinikai gyakorlatban a háromdimenziós orvosi képalkotó rendszerek használata igen
Anatómiai régiók automatikus felismerése Kutatási beszámoló 2015. június Készítette: Tóth Márton József Bevezetés A mai klinikai gyakorlatban a háromdimenziós orvosi képalkotó rendszerek használata igen
4. A kézfogások száma pont Összesen: 2 pont
 I. 1. A páros számokat tartalmazó részhalmazok: 6 ; 8 ; 6 ; 8. { } { } { }. 5 ( a ) 17 Összesen: t = = a a Összesen: ot kaphat a vizsgázó, ha csak két helyes részhalmazt ír fel. Szintén jár, ha a helyes
I. 1. A páros számokat tartalmazó részhalmazok: 6 ; 8 ; 6 ; 8. { } { } { }. 5 ( a ) 17 Összesen: t = = a a Összesen: ot kaphat a vizsgázó, ha csak két helyes részhalmazt ír fel. Szintén jár, ha a helyes
Heurisztikák BitTorrent hálózatok max-min méltányos sávszélesség-kiosztására
 Heurisztikák BitTorrent hálózatok max-min méltányos sávszélesség-kiosztására Dobjánné Antal Elvira és Vinkó Tamás Pallasz Athéné Egyetem, GAMF M szaki és Informatikai Kar Szegedi Tudományegyetem, Informatikai
Heurisztikák BitTorrent hálózatok max-min méltányos sávszélesség-kiosztására Dobjánné Antal Elvira és Vinkó Tamás Pallasz Athéné Egyetem, GAMF M szaki és Informatikai Kar Szegedi Tudományegyetem, Informatikai
MATEMATIKA ÉRETTSÉGI május 3. EMELT SZINT I.
 MATEMATIKA ÉRETTSÉGI 0. május. EMELT SZINT I. ) Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű számjegy
MATEMATIKA ÉRETTSÉGI 0. május. EMELT SZINT I. ) Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű számjegy
Láthatósági kérdések
 Láthatósági kérdések Láthatósági algoritmusok Adott térbeli objektum és adott nézőpont esetén el kell döntenünk, hogy mi látható az adott alakzatból a nézőpontból, vagy irányából nézve. Az algoritmusok
Láthatósági kérdések Láthatósági algoritmusok Adott térbeli objektum és adott nézőpont esetén el kell döntenünk, hogy mi látható az adott alakzatból a nézőpontból, vagy irányából nézve. Az algoritmusok
Matematikai geodéziai számítások 10.
 Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
A KLT (Kanade Lucas Tomasi) Feature Tracker Működése (jellegzetes pontok választása és követése)
 A KL (Kanade Lucas omasi) Feature racker Működése (jellegzetes pontok választása és követése) Készítette: Hajder Levente 008.11.18. 1. Feladat A rendelkezésre álló videó egy adott képkockájából minél több
A KL (Kanade Lucas omasi) Feature racker Működése (jellegzetes pontok választása és követése) Készítette: Hajder Levente 008.11.18. 1. Feladat A rendelkezésre álló videó egy adott képkockájából minél több
11. Előadás. 11. előadás Bevezetés a lineáris programozásba
 11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
GIS és Távérzékelés a közlekedési adatnyerésben
 GIS és Távérzékelés a közlekedési adatnyerésben Lovas Tamás Fotogrammetria és Térinformatika Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem Tartalom - Térinformatika Adatnyerés Távérzékelési technológiák
GIS és Távérzékelés a közlekedési adatnyerésben Lovas Tamás Fotogrammetria és Térinformatika Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem Tartalom - Térinformatika Adatnyerés Távérzékelési technológiák
GEOMETRIAI VALÓSZÍNŰSÉGEK
 GEOMETRIAI VALÓSZÍNŰSÉGEK 1. Feladat. Egy lavina területet betemetett egy síelésre gyakran használt térségben. Bence az nap síelni ment, és még nem jelentkezett, így a mentésére sietnek. Mi az esélye,
GEOMETRIAI VALÓSZÍNŰSÉGEK 1. Feladat. Egy lavina területet betemetett egy síelésre gyakran használt térségben. Bence az nap síelni ment, és még nem jelentkezett, így a mentésére sietnek. Mi az esélye,
Gépi tanulás a gyakorlatban. Kiértékelés és Klaszterezés
 Gépi tanulás a gyakorlatban Kiértékelés és Klaszterezés Hogyan alkalmazzuk sikeresen a gépi tanuló módszereket? Hogyan válasszuk az algoritmusokat? Hogyan hangoljuk a paramétereiket? Precízebben: Tegyük
Gépi tanulás a gyakorlatban Kiértékelés és Klaszterezés Hogyan alkalmazzuk sikeresen a gépi tanuló módszereket? Hogyan válasszuk az algoritmusokat? Hogyan hangoljuk a paramétereiket? Precízebben: Tegyük
Általános követelmények a kép tartalmával és minőségével kapcsolatban
 Általános követelmények a kép tartalmával és minőségével kapcsolatban A következő követelmények egyrészt azért fontosak, hogy megfelelően dokumentálják az eseményeket (bizonyítékként felhasználóak legyenek),
Általános követelmények a kép tartalmával és minőségével kapcsolatban A következő követelmények egyrészt azért fontosak, hogy megfelelően dokumentálják az eseményeket (bizonyítékként felhasználóak legyenek),
Koordinátageometria. , azaz ( ) a B halmazt pontosan azok a pontok alkotják, amelynek koordinátáira:
 005-0XX Emelt szint Koordinátageometria 1) a) Egy derékszögű háromszög egyik oldalegyenese valamelyik koordinátatengely, egy másik oldalegyenesének egyenlete x + y = 10, egyik csúcsa az origó. Hány ilyen
005-0XX Emelt szint Koordinátageometria 1) a) Egy derékszögű háromszög egyik oldalegyenese valamelyik koordinátatengely, egy másik oldalegyenesének egyenlete x + y = 10, egyik csúcsa az origó. Hány ilyen
Mikroszkóp vizsgálata és folyadék törésmutatójának mérése (8-as számú mérés) mérési jegyzõkönyv
 (-as számú mérés) mérési jegyzõkönyv Készítette:, II. éves fizikus... Beadás ideje:... / A mérés leírása: A mérés során egy mikroszkóp különbözõ nagyítású objektívjeinek nagyítását, ezek fókusztávolságát
(-as számú mérés) mérési jegyzõkönyv Készítette:, II. éves fizikus... Beadás ideje:... / A mérés leírása: A mérés során egy mikroszkóp különbözõ nagyítású objektívjeinek nagyítását, ezek fókusztávolságát
3D-s számítógépes geometria és alakzatrekonstrukció
 3D-s számítógépes geometria és alakzatrekonstrukció 2a. Háromszöghálók http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav08 Dr. Várady Tamás, Salvi Péter BME, Villamosmérnöki
3D-s számítógépes geometria és alakzatrekonstrukció 2a. Háromszöghálók http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav08 Dr. Várady Tamás, Salvi Péter BME, Villamosmérnöki
Takács Bence: Geodéziai Műszaki Ellenőrzés. Fővárosi és Pest Megyei Földmérő Nap és Továbbképzés március 22.
 Takács Bence: Geodéziai Műszaki Ellenőrzés Fővárosi és Pest Megyei Földmérő Nap és Továbbképzés 2018. március 22. VÁZLAT Mit jelent a geodéziai műszaki ellenőrzés? Példák: Ki? Mit? Miért ellenőriz? résfal
Takács Bence: Geodéziai Műszaki Ellenőrzés Fővárosi és Pest Megyei Földmérő Nap és Továbbképzés 2018. március 22. VÁZLAT Mit jelent a geodéziai műszaki ellenőrzés? Példák: Ki? Mit? Miért ellenőriz? résfal
Villamos autókból álló taxi flotta számára létesítendő töltőállomások modellezése
 Villamos autókból álló taxi flotta számára létesítendő töltőállomások modellezése 62. Vándorgyűlés, konferencia és kiállítás Siófok, 2015. 09. 16-18. Farkas Csaba egyetemi tanársegéd Dr. Dán András professor
Villamos autókból álló taxi flotta számára létesítendő töltőállomások modellezése 62. Vándorgyűlés, konferencia és kiállítás Siófok, 2015. 09. 16-18. Farkas Csaba egyetemi tanársegéd Dr. Dán András professor
Érzékelők az autonóm járművekben
 Érzékelők az autonóm járművekben Gáspár Péter Szirányi Tamás 1 Érzékelők Tartalom Motivációs háttér Környezetérzékelés célja Autóipari érzékelők Széria megoldások és ipari trendek 2 Motiváció: A járműipar
Érzékelők az autonóm járművekben Gáspár Péter Szirányi Tamás 1 Érzékelők Tartalom Motivációs háttér Környezetérzékelés célja Autóipari érzékelők Széria megoldások és ipari trendek 2 Motiváció: A járműipar
A szimplex tábla. p. 1
 A szimplex tábla Végződtetés: optimalitás és nem korlátos megoldások A szimplex algoritmus lépései A degeneráció fogalma Komplexitás (elméleti és gyakorlati) A szimplex tábla Példák megoldása a szimplex
A szimplex tábla Végződtetés: optimalitás és nem korlátos megoldások A szimplex algoritmus lépései A degeneráció fogalma Komplexitás (elméleti és gyakorlati) A szimplex tábla Példák megoldása a szimplex
MP ROTATOR Alkalmazási segédlet, telepítők számára
 MP ROTATOR Alkalmazási segédlet, telepítők számára Érjen el egyenletes csapadékkijuttatást bármilyen szórási szög és bármilyen öntözési távolság mellett. JELEN SEGÉDLET TARTALMAZZA: 1. MP Rotator alkalmazása
MP ROTATOR Alkalmazási segédlet, telepítők számára Érjen el egyenletes csapadékkijuttatást bármilyen szórási szög és bármilyen öntözési távolság mellett. JELEN SEGÉDLET TARTALMAZZA: 1. MP Rotator alkalmazása
A Megyeri híd terhelésvizsgálatának támogatása földi lézerszkenneléssel
 A Megyeri híd terhelésvizsgálatának támogatása földi lézerszkenneléssel Dr. Lovas Tamás 1 Berényi Attila 1,3 dr. Barsi Árpád 1 dr. Dunai László 2 1 Fotogrammetria és Térinformatika Tanszék, BME 2 Hidak
A Megyeri híd terhelésvizsgálatának támogatása földi lézerszkenneléssel Dr. Lovas Tamás 1 Berényi Attila 1,3 dr. Barsi Árpád 1 dr. Dunai László 2 1 Fotogrammetria és Térinformatika Tanszék, BME 2 Hidak
Hatástávolság számítás az. Ipari Park Hatvan, Robert Bosch út és M3 autópálya közötti tervezési terület (Helyrajzi szám: 0331/75.
 Hatástávolság számítás az Ipari Park Hatvan, Robert Bosch út és M3 autópálya közötti tervezési terület (Helyrajzi szám: 0331/75. ) légszennyező forrásaira (pontforrás engedélykérelemhez) Összeállítva:
Hatástávolság számítás az Ipari Park Hatvan, Robert Bosch út és M3 autópálya közötti tervezési terület (Helyrajzi szám: 0331/75. ) légszennyező forrásaira (pontforrás engedélykérelemhez) Összeállítva:
Kvalitatív elemzésen alapuló reakciómechanizmus meghatározás
 Kvalitatív elemzésen alapuló reakciómechanizmus meghatározás Varga Tamás Pannon Egyetem, Folyamatmérnöki Intézeti Tanszék IX. Alkalmazott Informatika Konferencia ~ AIK 2011 ~ Kaposvár, Február 25. Tartalom
Kvalitatív elemzésen alapuló reakciómechanizmus meghatározás Varga Tamás Pannon Egyetem, Folyamatmérnöki Intézeti Tanszék IX. Alkalmazott Informatika Konferencia ~ AIK 2011 ~ Kaposvár, Február 25. Tartalom
MOBIL TÉRKÉPEZŐ RENDSZER PROJEKT TAPASZTALATOK
 MOBIL TÉRKÉPEZŐ RENDSZER PROJEKT TAPASZTALATOK GISopen 2011 2011. március 16-18. Konasoft Project Tanácsadó Kft. Maros Olivér - projektvezető MIÉRT MOBIL TÉRKÉPEZÉS? A mobil térképezés egyetlen rendszerben
MOBIL TÉRKÉPEZŐ RENDSZER PROJEKT TAPASZTALATOK GISopen 2011 2011. március 16-18. Konasoft Project Tanácsadó Kft. Maros Olivér - projektvezető MIÉRT MOBIL TÉRKÉPEZÉS? A mobil térképezés egyetlen rendszerben
Statisztikai módszerek a skálafüggetlen hálózatok
 Statisztikai módszerek a skálafüggetlen hálózatok vizsgálatára Gyenge Ádám1 1 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Számítástudományi és Információelméleti
Statisztikai módszerek a skálafüggetlen hálózatok vizsgálatára Gyenge Ádám1 1 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Számítástudományi és Információelméleti
Problémamegoldás kereséssel. Mesterséges intelligencia március 7.
 Problémamegoldás kereséssel Mesterséges intelligencia 2014. március 7. Bevezetés Problémamegoldó ágens Kívánt állapotba vezető cselekvéseket keres Probléma megfogalmazása Megoldás megfogalmazása Keresési
Problémamegoldás kereséssel Mesterséges intelligencia 2014. március 7. Bevezetés Problémamegoldó ágens Kívánt állapotba vezető cselekvéseket keres Probléma megfogalmazása Megoldás megfogalmazása Keresési
Érzékelők csoportosítása Passzív Nem letapogató Nem képalkotó mh. radiométer, graviméter Képalkotó - Kamerák Letapogató (képalkotó) Képsíkban TV kamer
 Monitoring távérzékeléssel - aktív digitális érzékelők (E130-501) Természetvédelmi MSc szak Király Géza NyME, Erdőmérnöki Kar Geomatikai, Erdőfeltárási és Vízgazdálkodási Intézet Földmérési és Távérzékelési
Monitoring távérzékeléssel - aktív digitális érzékelők (E130-501) Természetvédelmi MSc szak Király Géza NyME, Erdőmérnöki Kar Geomatikai, Erdőfeltárási és Vízgazdálkodási Intézet Földmérési és Távérzékelési
Mozgásvizsgálatok. Mérnökgeodézia II. Ágfalvi Mihály - Tóth Zoltán
 Mérnökgeodézia II. Ágfalvi Mihály - Tóth Zoltán Célja: Várható elmozdulások előrejelzése (erőhatások alatt, Siógemenci árvízkapu) Már bekövetkezett mozgások okainak vizsgálata (Pl. kulcsi löszpart) Laboratóriumi
Mérnökgeodézia II. Ágfalvi Mihály - Tóth Zoltán Célja: Várható elmozdulások előrejelzése (erőhatások alatt, Siógemenci árvízkapu) Már bekövetkezett mozgások okainak vizsgálata (Pl. kulcsi löszpart) Laboratóriumi
Ultrahangos távolságmérő. Modell: JT-811. Használati útmutató
 Ultrahangos távolságmérő Modell: JT-811 Használati útmutató I. Funkciók 1) A mérés angolszász/metrikus mértékegységekben 2) Lehetőség van a kezdeti mérési pont kiválasztására 3) Adatrögzítés/adatok előhívása
Ultrahangos távolságmérő Modell: JT-811 Használati útmutató I. Funkciók 1) A mérés angolszász/metrikus mértékegységekben 2) Lehetőség van a kezdeti mérési pont kiválasztására 3) Adatrögzítés/adatok előhívása
MATLAB alapismeretek I.
 Alkalmazott Informatikai Intézeti Tanszék MŰSZAKI INFORMATIKA Dr.Dudás László 0. MATLAB alapismeretek I. A MATLAB bemutatása MATLAB filozófia MATLAB modulok A MATLAB felhasználói felülete MATLAB tulajdonságok
Alkalmazott Informatikai Intézeti Tanszék MŰSZAKI INFORMATIKA Dr.Dudás László 0. MATLAB alapismeretek I. A MATLAB bemutatása MATLAB filozófia MATLAB modulok A MATLAB felhasználói felülete MATLAB tulajdonságok
10. mérés. Fényelhajlási jelenségek vizsgála
 Bán Marcell ETR atonosító BAMTACT.ELTE Beadási határidő 2012.10.15 (engedélyezett késés) 10. mérés Fényelhajlási jelenségek vizsgála Bevezetés: A mérések során a fény hullámhosszából adódó jelenségeket
Bán Marcell ETR atonosító BAMTACT.ELTE Beadási határidő 2012.10.15 (engedélyezett késés) 10. mérés Fényelhajlási jelenségek vizsgála Bevezetés: A mérések során a fény hullámhosszából adódó jelenségeket
x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs mátrixa 3D-ben?
 . Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
. Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
Programozási környezetek
 KOVÁSZNAI GERGELY ÉS BIRÓ CSABA EKF TTK Információtechnológia Tanszék Programozási környezetek Alkalmazható természettudományok oktatása a tudásalapú társadalomban TÁMOP-4.1.2.A/1-11/1-2011-0038 WPF Bevezetés
KOVÁSZNAI GERGELY ÉS BIRÓ CSABA EKF TTK Információtechnológia Tanszék Programozási környezetek Alkalmazható természettudományok oktatása a tudásalapú társadalomban TÁMOP-4.1.2.A/1-11/1-2011-0038 WPF Bevezetés
Mérés és modellezés 1
 Mérés és modellezés 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni kell
Mérés és modellezés 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni kell
2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv. Zsigmond Anna Fizika Bsc II. Mérés dátuma: Leadás dátuma:
 2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 24. Leadás dátuma: 2008. 10. 01. 1 1. Mérések ismertetése Az 1. ábrán látható összeállításban
2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 24. Leadás dátuma: 2008. 10. 01. 1 1. Mérések ismertetése Az 1. ábrán látható összeállításban
3D számítógépes geometria és alakzatrekonstrukció
 3D számítógépes geometria és alakzatrekonstrukció 2a. Háromszöghálók http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01 Dr. Várady Tamás, Dr. Salvi Péter BME, Villamosmérnöki
3D számítógépes geometria és alakzatrekonstrukció 2a. Háromszöghálók http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01 Dr. Várady Tamás, Dr. Salvi Péter BME, Villamosmérnöki
Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék
 Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék 2016/17 2. félév 8. Előadás Dr. Kulcsár Gyula egyetemi docens Kereső algoritmusok alkalmazása
Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék 2016/17 2. félév 8. Előadás Dr. Kulcsár Gyula egyetemi docens Kereső algoritmusok alkalmazása
Statisztikai módszerek 7. gyakorlat
 Statisztikai módszerek 7. gyakorlat A tanult nem paraméteres próbák: PRÓBA NEVE Illeszkedés-vizsgálat Χ 2 próbával Homogenitás-vizsgálat Χ 2 próbával Normalitás-vizsgálataΧ 2 próbával MIRE SZOLGÁL? A val.-i
Statisztikai módszerek 7. gyakorlat A tanult nem paraméteres próbák: PRÓBA NEVE Illeszkedés-vizsgálat Χ 2 próbával Homogenitás-vizsgálat Χ 2 próbával Normalitás-vizsgálataΧ 2 próbával MIRE SZOLGÁL? A val.-i
2000 Szentendre, Bükköspart 74 WWW.MEVISOR.HU. MeviMR 3XC magnetorezisztív járműérzékelő szenzor
 MeviMR 3XC Magnetorezisztív járműérzékelő szenzor MeviMR3XC járműérzékelő szenzor - 3 dimenzióban érzékeli a közelében megjelenő vastömeget. - Könnyű telepíthetőség. Nincs szükség az aszfalt felvágására,
MeviMR 3XC Magnetorezisztív járműérzékelő szenzor MeviMR3XC járműérzékelő szenzor - 3 dimenzióban érzékeli a közelében megjelenő vastömeget. - Könnyű telepíthetőség. Nincs szükség az aszfalt felvágására,
Az SPC (statisztikai folyamatszabályozás) ingadozásai
 A TERMELÉSI FOLYAMAT MINÕSÉGKÉRDÉSEI, VIZSGÁLATOK 2.3 Az SPC (statisztikai folyamatszabályozás) ingadozásai Tárgyszavak: statisztikai folyamatszabályozás; Shewhart-féle szabályozókártya; többváltozós szabályozás.
A TERMELÉSI FOLYAMAT MINÕSÉGKÉRDÉSEI, VIZSGÁLATOK 2.3 Az SPC (statisztikai folyamatszabályozás) ingadozásai Tárgyszavak: statisztikai folyamatszabályozás; Shewhart-féle szabályozókártya; többváltozós szabályozás.
