Mátrixok február Feladat: Legyen ( ( B = A =
|
|
|
- Erzsébet Lukácsné
- 9 évvel ezelőtt
- Látták:
Átírás
1 Mátrixok 25. február 23.. Feladat: Legyen A ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A deníciók alapján ( A + B ( ( ( A B ( ( ( A ( 9 3 3B ( ( A 3B 2A + ( 3B A T 3 ( (B T T 3 B 4 2. Feladat: Legyen A ( B ( 2 ( 5 C 8 Határozzuk meg A + B + C, 5A + B 7C, A T 4B 6C T, mátrixokat. ( ( A + B + C ( ( A + B 7C
2 Mivel ezért A T A T 4B 6C T 3. Vizsgafeladat: Legyen A ( C T ( 5 8 ( ( 4 5 és B Határozzuk meg 3((2A B (A 3B mátrixot. ( ( ((2A B (A 3B 3(2A B A + 3B 3A + 6B ( ( ( Feladat: Határozzuk meg AB, BA, (ABA, A(BA és A 2 mátrixokat, ha ( ( A B 7 Mivel A és B 2 2-es mátrixok, a sorok és oszlopok száma azonos, a szorzások elvégezhet ek tehát AB ( tehát BA ( 3 4 Vegyük észre, hogy AB BA, azaz a mátrixok szorzása nem kommutatív tehát (ABA ( tehát A(BA (
3 Vegyük észre, hogy ABA A(BA (ABA, azaz teljesül a mátrixok szorzásra vonatkozó asszociatív tulajdonság tehát A 2 ( Feladat: Legyen A B Határozzuk meg azt az X mátrixot, amelyre 2A + X 5B teljesül. Az egyenletet átrendezve kapjuk, hogy 2 4 X 5B 2A Feladat: Legyen A ( B C ( Határozzuk meg AB + C, AB + B, CB + A és BC + A T mátrixokat. A mátrixok különböz típusúak, ezért els lépésben mindig meg kell nézni, hogy vajon a kijelölt m velet elvégezhet -e? AB + C vizsgálata: A B (2 3 (3 2 AB (2 2 Mivel A mátrix oszlopainak száma megegyezik B mátrix sorainak számával, azaz a bels indexek azonosak, a szorzás elvégezhet, a küls indexek pedig meghatározzák a szorzatmátrix típusát. Valamint AB (2 2 + C (2 2 AB + C (2 2 azaz AB és C mátrixok azonos típusúak, ezért AB + C m velet elvégezhet. Készítsük el AB szorzáshoz a táblázatot tehát AB (
4 AB + B vizsgálata: Mivel ( AB + C 8 84 ( + AB (2 2 + B (3 2 A két mátrix típusa különböz, az összeadás nem végezhet el. (BA 2 vizsgálata: B (3 2 A (2 3 BA (3 3 ( A bels indexek azonosak, BA szorzat létezik. A m velet eredménye egy négyzetes mátrix, így (BA 2 m velet is elvégezhet tehát BA CB + A vizsgálata: Mivel tehát (BA 2 C ( B (3 2 a bels indexek nem egyeznek meg, a m velet nem végezhet el. BC + A T vizsgálata: Mivel és a m velet elvégezhet. Számolás: B (3 2 BC (3 2 + AT (3 2 C (2 2 BC (3 2 4 BC + AT (3 2
5 tehát BC Az eredmény: BC + A T Feladat: Határozzuk meg AB, BA, és CA szorzatokat,ha 4 A B ( 3 ( 2 C El ször nézzük meg a szorzások elvégezhet ek-e. Mivel A B (3 ( 3 AB (3 3 a bels indexek azonosak a szorzás elvégezhet tehát AB Mivel B A ( 3 (3 BA ( a bels indexek azonosak, a szorzás elvégezhet. 4-3 tehát BA ( Mivel C A (2 3 (3 CA (2 a bels indexek azonosak, a szorzás elvégezhet tehát CA ( 5 5
6 8. Feladat: Határozzuk meg AA T és A T A mátrixokat, ha ( 3 A 5 A bels indexek megegyeznek, a m veletek elvégezhet ek. A T ( 3 5 ( ( ( AA T ( ( ( A T A Vegyük észre, hogy AA T A T A, de mindkett szimmetrikus. 9. Feladat: Határozza meg az A és T A mátrixokat, ha 3 5 A A A m velet eredménye: az A mátrix soraiban lév elemek összege. 3 5 T A (; ; 8 2 (5; 4; 8; Feladat: Végezzük el az alábbi m veleteket A e 3 és e T ( 2 3 A 5 A, ha A e 3 ( ( 3 A m velet eredménye: kiemeltük a mátrix 3. oszlopát. ( e T 2 3 A (; (2; ; 3 5 A m velet eredménye: kiemeltük a mátrix els sorát. 6
7 . Feladat: Végezzük el a következ szorzást, majd értelmezzük a m velet eredményét: 2 e T ( ( ( 3 ( 4 A m velet eredménye: kiemeltük a mátrix 2. sorát, majd a sor elemeit összeadtuk. 2. Feladat: Mutassuk meg, hogy (AB T B T A T, ha ( ( 2 5 A B 3 4 ( ( ( AB ( (AB T ( ( ( B T A T Valóban teljesül, hogy (AB T B T A T 3. Feladat: Végezze el a következ szorzást: A 2 e 2, ha ( 7 4 A 2 Végeredmény: A 2 e 2 ( Feladat: Határozza meg az A T A mátrixot, ha ( 3 A 5 2 Végeredmény: A T A (
8 5. Feladat: Határozza meg az e T 4 A szorzat eredményét, ha 3 A Végeredmény: e T 4 A 4 6. Feladat: Határozza meg az T A e 2 szorzat eredményét, ha 3 A Végeredmény: T A e Feladat: Határozza meg az A (e 3 e 4 szorzat eredményét, ha A Végeredmény: A (e 3 e 4 8. Feladat: Határozza meg az b T A d mátrixot, ha 3 5 A b 6 Végeredmény: b T A d 52. Vizsgafeladat: Legyen A Határozzuk meg (A + A 2 2 mátrixot. 2. El ször határozzuk meg A 2 mátrixot d 5 2 2
9 A + A Végül határozzuk meg (A + A 2 2 mátrixot. Az eredmény: (A + A Vizsgafeladat: Legyen A Határozzuk meg AB B 2 mátrixot. Mivel Tehát és B AB B Egyszer bb a számolás, ha észrevesszük, hogy AB B 2 (A BB. 3. Vizsgafeladat: Határozzuk meg AB és AC mátrixokat, ha A B C
10 Tehát AB AC De ebb l nem következik B C egyenl ség Vizsgafeladat: Határozzuk meg (ABC és A(BC mátrixokat, ha 2 A ( 2 B 5 3 C El ször nézzük meg, hogy a m velet elvégezhet -e. A B C (3 2 (2 4 (4 3 ABC (3 3 Az egymás mellett lév bels indexek megegyeznek, ezért a szorzások elvégezhet ek. Ebben az esetben használjuk fel, hogy a mátrixok szorzása asszociatív, azaz (ABC A(BC, így elég csak (ABC mátrixot kiszámolni. Határozzuk meg AB szorzatot
11 Határozzuk meg (ABC mátrixot Tehát (ABC A(BC Feladat: Határozzuk meg AA T és A T A mátrixokat, ha 2 A Egy négyzetes mátrix transzponáltja is vele azonos típusú négyzetes mátrix, így a szorzások elvégezhet ek Tehát AA T A T A Vegyük észre, hogy szimmetrikus mátrixokat kaptunk, de AA T A T A 6. Vizsgafeladat Egy utazási iroda 4 társasutazásra a hét els három napján különböz számú jegyet adott el. Ezeket az adatokat az alábbi A mátrix mutatja:
12 London Párizs Róma Bécs Hétf Kedd Szerda Az egyes utazások ára a táblázatban lév sorrendnek megfelel en: p T (5; ; 2, 5 pénzegység. Végezzük el az alábbi m veleteket és értelmezzük az eredményeket: Ap, e T 2 A, Ae 3, T Ap. Írja fel mátrixm velettel és számítsa ki, hogy mennyi volt a bécsi jegyek eladásából származó naponkénti bevétel! A Ap p A kapott vektor megadja a naponkénti bevételt. Azaz hénf n 72 pénzegység, kedden 64 pénzegység, szerdán 47 pénzegység e T 2 A (; ; Kedden az iroda összesen 52 repül jegyet adott el. Ae Az eredmény megmutatja, hogy naponta hány repül jegyet adtak el a Rómába. T Ap (; ; A bécsi jegyek eladásából származó naponkénti bevétel: p T e 4 Ae 4 (5; ; 2,
13 7. Vizsgafeladat Egy termel a piacon négyféle gyümölcsöt árul. Az A mátrix mutatja, hogy a hét egyes napjain mennyit adott el a különféle gyümölcsökb l. Hétf Kedd Szerda Csütörtök Péntek Szombat Szilva Körte Žszibarack Ringló A táblázat az eladott mennyiséget kg-ban mutatja. Az egyes gyümölcsfajták kilogrammonkénti árát (a táblázatbeli sorrendnek megfelel en az árvektor tartalmazza, amely a következ : p T (; 2; 3; 9. Végezzük el az alábbi m veleteket és értelmezzük az eredményeket! a p T A b e T A c Ae 3 d A(e 5 e e A f p T A g T A p T A (; 2; 3; A táblázatból leolvasható gyümölcsönként a napi bevétel e T A (; ; ; (; 5; 6; 6; 7; Megkaptuk szilvából az eladott napi mennyiséget. 6 Ae Ae 3 szerdán a gyümölcsönkénti forgalom A(e 5 e (; 4; 2; ; ; 4 A(e 5 e naponta mennyivel többet adtak el ringlóból, mint szilvából 33 A
14 A gyümölcsönként a heti forgalom p T A p T A gyümölcsönként a heti forgalom Ft-ban T A (; 3; 6; 9; 32; 36 T A naponkénti összes gyömölcs forgalom. 8. Vizsgafeladat Egy étteremben négyféle levesb l eladott adagok számát a hét els három napján az alábbi A mátrix mutatja: Rántott leves Zöldségleves Paradicsomleves Csontleves Hétf Kedd 3 2 Szerda Az egyes levesek ára: p T (5; 7; ; 2 pénzegység. (a Mennyi a leves forgalom naponként pénzegységben? (b Mennyi a leves forgalom összesen a 3 nap alatt? (c Számítsa ki és magyarázza meg a jelentését: T A. (d Számítsa ki és magyarázza meg a jelentését: Ae 2 Ae Vizsgafeladat Három étteremben négyféle ételb l egy napon eladott adagok számát mutatja az alábbi A mátrix: I. vendégl II. vendégl III. vendégl. étel étel étel étel Az egyes ételek ára: 6 Ft, 5 Ft, 8 Ft, 4 Ft. (a Mennyi az egyes vendégl k forgalma Ft-ban? (b Mennyi az egyes ételekb l eladott adagok száma a három vendégl ben együttesen? (c Mennyi az összes étel forgalom Ft-ban?. Vizsgafeladat Egy utazási iroda 4 társasutazásra a hét els három napján különböz számú jegyet adott el. Ezeket az adatokat az alábbi A mátrix mutatja: Párizs Berlin Varsó Amszterdam Hétf Kedd Szerda
15 Az egyes utazások ára: p T (9; 6; 7; 8 pénzegység. Írja fel mátrixm velettel és számítsa ki, hogy: (a mennyi volt az utazási iroda bevétele naponta; (b három nap alatt az egyes városokba hány jegyet adtak el! Számítsa ki és magyarázza meg a jelentését: (a e T 2 A (b (; ; Ap. 5
Mátrixok február Feladat: Legyen A = ( ( B =
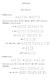Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
KOVÁCS BÉLA, MATEMATIKA I.
KOVÁCS BÉLA, MATEmATIkA I 9 IX MÁTRIxOk 1 MÁTRIx FOGALmA, TULAJDONSÁGAI A mátrix egy téglalap alakú táblázat, melyben az adatok, a mátrix elemei, sorokban és oszlopokban vannak elhelyezve Az (1) mátrixnak
Tárgyév adata 2013. december 31. Tárgyév adata 2014. december 31. A tétel megnevezése
A tétel megnevezése Tárgyév adata 2013. december 31. Tárgyév adata 2014. december 31. 1. Pénzeszközök 19 798 163 488 2. Állampapírok 411 306 73 476 a) forgatási célú 411 325 73 408 b) befektetési célú
Kereskedelmi és Hitelbank Zártkörűen Működő Részvénytársaság
Kereskedelmi és Hitelbank Zártkörűen Működő Részvénytársaság ÉVES JELENTÉS 2015. december 31. K&H BANK ZRT. ÉVES JELENTÉS 2015. DECEMBER 31. TARTALOMJEGYZÉK Kibocsátói nyilatkozat Éves Beszámoló Független
Komplex számok. 2014. szeptember 4. 1. Feladat: Legyen z 1 = 2 3i és z 2 = 4i 1. Határozza meg az alábbi kifejezés értékét!
Komplex számok 014. szeptember 4. 1. Feladat: Legyen z 1 i és z 4i 1. (z 1 z ) (z 1 z ) (( i) (4i 1)) (6 9i 8i + ) 8 17i 8 + 17i. Feladat: Legyen z 1 i és z 4i 1. Határozza meg az alábbi kifejezés értékét!
Számelméleti feladatok az általános iskolai versenyek tükrében dr. Pintér Ferenc, Nagykanizsa
Számelméleti feladatok az általános iskolai versenyek tükrében dr. Pintér Ferenc, Nagykanizsa 1. Mutasd meg, hogy a tízes számrendszerben felírt 111111111111 tizenhárom jegyű szám összetett szám, azaz
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
Matematika emelt szint 0613 ÉRETTSÉGI VIZSGA 007. május 8. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Formai előírások: Fontos tudnivalók
Mátrixaritmetika. Tartalom:
Mátrixaritmetika Tartalom: A vektor és mátrix fogalma Speciális mátrixok Relációk és műveletek mátrixokkal A mátrixok szorzása A diadikus szorzat. Hatványozás Gyakorlati alkalmazások Készítette: Dr. Ábrahám
8/2014. (X.10.) KLIK elnöki utasítás
8/2014. (X.10.) KLIK elnöki utasítás III. Fejezet A térítési díj és a tandíj 1. A térítési díj és a tandíj alapja 3. (1) Az intézményben a tanévre fizetendő térítési díj és a tandíj meghatározásának alapja
2. Az önkormányzat és költségvetési szervei 2010. évi költségvetésének teljesítése
Albertirsa Város Önkormányzata Képviselő-testületének 14/ 2011. (V.3.) önkormányzati rendelete Albertirsa Város Önkormányzata 2010. évi gazdálkodásának zárszámadásáról Albertirsa Város Önkormányzatának
ML/GL (164)
ML/GL (164) + 375 17 309-9999 + 375 29 603-9999 + 375 33 603-9999 + 375 25 603-9999 A2513203131 2321 1519 35% A164320591380 3976 2771 30% A1643206113 3554 2477 30% A1643202431 889 582 35% A2519801164 352
55 812 01 0010 55 02 Vendéglátó szakmenedzser Vendéglátó és idegenforgalmi szakmenedzser
Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján. Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
ÉVES BESZÁMOLÓ 2015.
FEGYVERNEK ÉS VIDÉKE KÖRZETI TAKARÉKSZÖVETKEZET 5231 Fegyvernek Szent Erzsébet út 138. Internet: www.fegyvernektksz.hu Cg.: 16-02-001554 ÉVES BESZÁMOLÓ 2015. Mérleg Eredmény-kimutatás Kiegészítő melléklet...
7. Feladatsor. Bérlık száma Maximális bérleti díj (Ft/hó) 100 bérlı 50000 Ft 150 bérlı 40000 Ft 250 bérlı 30000 Ft 400 bérlı 20000 Ft
7. Feladatsor 1. Hogyan és miért változik a málna egyensúlyi ára az alábbi változások hatására? (Egyszerre csak egyetlen tényezı változik.) a) Az eper ára emelkedik. b) A málnafagylalt ára emelkedik. c)
Értékelés Összesen: 100 pont 100% = 100 pont A VIZSGAFELADAT MEGOLDÁSÁRA JAVASOLT %-OS EREDMÉNY: EBBEN A VIZSGARÉSZBEN A VIZSGAFELADAT ARÁNYA 100%.
Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján. Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
43. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY MEGYEI FORDULÓ HETEDIK OSZTÁLY JAVÍTÁSI ÚTMUTATÓ
43. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY MEGYEI FORDULÓ HETEDIK OSZTÁLY JAVÍTÁSI ÚTMUTATÓ 1. Alfa tanár úr 5 tanulót vizsgáztatott matematikából. Az elért pontszámokat véletlen sorrendben írta
52 811 02 0000 00 00 Vendéglős Vendéglős 52 811 02 0100 31 01 Étkezdés Vendéglős 52 811 02 0100 31 02 Vendéglátó eladó Vendéglős
A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
a védelmi feladatokban részt vevő elektronikus hírközlési szolgáltatók kijelöléséről és felkészülési feladataik meghatározásáról
1./2009. (.) MeHVM rendelet a védelmi feladatokban részt vevő elektronikus hírközlési szolgáltatók kijelöléséről és felkészülési feladataik meghatározásáról Az elektronikus hírközlésről szóló 2003. évi
4. előadás. Vektorok
4. előadás Vektorok Vektorok bevezetése Ha adottak a térben az A és a B pontok, akkor pontosan egy olyan eltolás létezik, amely A-t B- be viszi. Ha φ egy tetszőleges eltolás, akkor ez a tér minden P pontjához
2. Halmazelmélet (megoldások)
(megoldások) 1. A pozitív háromjegy páros számok halmaza. 2. Az olyan, 3-mal osztható egész számok halmaza, amelyek ( 100)-nál nagyobbak és 100-nál kisebbek. 3. Az olyan pozitív egész számok halmaza, amelyeknek
Mezei Ildikó-Ilona. Analitikus mértan
Mezei Ildikó-Ilona Analitikus mértan feladatgyűjtemény Kolozsvár 05 Tartalomjegyzék. Vektoralgebra 3.. Műveletek vektorokkal.................................. 3.. Egyenes vektoriális egyenlete..............................
KSH:10116065-6419-122-13 Cg.:13-02-050256 Nagykáta és Vidéke Takarékszövetkezet
KSH:10116065-6419-122-13 Cg.:13-02-050256 Nagykáta és Vidéke Takarékszövetkezet MÉRLEG adatok: ezer Ft-ban S.sz. M e g n e v e z és 2014.év 2015.év a. b. c. d. E S Z K Ö Z Ö K ( A K T Í V Á K ) 01 1.Pénzeszközök
A 34/2014. (IX. 25) MNB 11/2011. (IX. 6.) MNB
A Magyar Nemzeti Bank elnökének 34/2014. (IX. 25) MNB rendelete a bankjegyek feldolgozásáról, forgalmazásáról, valamint hamisítás elleni védelmével kapcsolatos technikai feladatokról szóló 11/2011. (IX.
MATEMATIKA TANMENET SZAKKÖZÉPISKOLA 9.A-9.C-9.D OSZTÁLY HETI 4 ÓRA 37 HÉT/ ÖSSZ 148 ÓRA
MINŐSÉGIRÁNYÍTÁSI ELJÁRÁS MELLÉKLET Tanmenetborító Azonosító: ME-III.1./1 Változatszám: 2 Érvényesség 2013. 01. 01. kezdete: Oldal/összes: 1/5 Fájlnév: ME- III.1.1.Tanmenetborító SZK- DC-2013 MATEMATIKA
Pusztavám Község Önkormányzati Képviselő-testületének 1/2011.(II.17.) önkormányzati rendelete az önkormányzat 2011. évi költségvetéséről
Pusztavám Község Önkormányzati Képviselő-testületének 1/2011.(II.17.) önkormányzati rendelete az önkormányzat 2011. évi költségvetéséről Pusztavám Község Önkormányzati Képviselő-testülete az államháztartásról
43. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY MEGYEI FORDULÓ NYOLCADIK OSZTÁLY JAVÍTÁSI ÚTMUTATÓ
43. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY MEGYEI FORDULÓ NYOLCADIK OSZTÁLY JAVÍTÁSI ÚTMUTATÓ 1. Az apa, az anya és a három lányuk együtt 118 évesek. Az anya 10 évvel idősebb, mint a három lány együtt.
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten LINEÁRIS PROGRAMOZÁS Készítette: Gábor Szakmai felel s: Gábor Vázlat 1 2 3 4 A lineáris
Miskolci Egyetem GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR. Analízis I. példatár. (kidolgozott megoldásokkal) elektronikus feladatgyűjtemény
Miskolci Egyetem GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR Analízis I. példatár kidolgozott megoldásokkal) elektronikus feladatgyűjtemény Összeállította: Lengyelné Dr. Szilágyi Szilvia Miskolc, 013. Köszönetnyilvánítás
D G 0 ;8 ; 0 0 " & *!"!#$%&'" )! "#$%&' (! )* +,-. /0 )* **! / 0 1 ) " 8 9 : 7 ; 9 < = > A! B C D E +,-./0! 1#! 2 3!./0
D G 0"" @;8 < @;0 0"7@ & *!"!#$%&'" )! "#$%&'(! )*+,-./0)* **! / 0 1 ) 2 3 4 5 6 1 7 " 8 9 : 7 ; 9 < = > 9? @ A! B C D E +,-./0!1#! 2 3!./04456171#461,!FGHIJKLM 5 NO N"JPQRFGLSTUV@AW"9?@AW G X6YJK # #
KOVÁCS BÉLA, MATEMATIKA I.
KOVÁCS BÉLA, MATEmATIkA I 5 V ELEmI ALGEbRA 1 BINÁRIS műveletek Definíció Az halmazon definiált bináris művelet egy olyan függvény, amely -ből képez -be Ha akkor az elempár képét jelöljük -vel, a művelet
RENDELET - TERVEZET. A költségvetés fő összegei
RENDELET - TERVEZET Kerekegyháza Város Önkormányzat Képviselő-testületének../2012 (. ) önkormányzati rendelete Kerekegyháza Város Önkormányzatának 2012. évi költségvetéséről Kerekegyháza Város Önkormányzatának
EGER MEGYEI JOGÚ VÁROS
EGER MEGYEI JOGÚ VÁROS RENDELETEINEK ÉS HATÁROZATAINAK TÁRA 2014. február 14. 3. szám R E N D E L E T E K 3/2014. (II.15.) önk. rendelet Eger Megyei Jogú Város Önkormányzata 2014.-2017. közötti saját bevételeinek,
ÉVES BESZÁMOLÓ 2013.
Hévíz és Vidéke TAKARÉKSZÖVETKEZET 8380 Hévíz, Széchenyi u. 66. Internet: www.heviztakarek.hu Cg.: 20-02-050059 ÉVES BESZÁMOLÓ 2013. Mérleg Eredmény-kimutatás Kiegészítő melléklet Könyvvizsgálói jelentés...
Rendelet-tervezet. (2) A R. 3. -a helyébe az alábbi rendelkezés lép:
Rendelet-tervezet Kerekegyháza Város Önkormányzat Képviselő-testületének./2015.(..) önkormányzati rendelete Kerekegyháza Város Önkormányzatának 2015. évi költségvetéséről szóló 5/2015. (II. 26.) önkormányzati
Koordinátageometria. M veletek vektorokkal grakusan. Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1
Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1 Koordinátageometria M veletek vektorokkal grakusan 1. Az ABCD négyzet oldalvektorai közül a = AB és b = BC. Adja meg az AC és BD vektorokat a
2007. évi CXXVII. törvény az általános forgalmi adóról. ELSŐ RÉSZ ÁLTALÁNOS RENDELKEZÉSEK I. Fejezet ALAPVETŐ RENDELKEZÉSEK Bevezető rendelkezés
2007. évi CXXVII. törvény az általános forgalmi adóról Az Országgyűlés - figyelemmel az államháztartás feladatainak ellátásához szükséges állandó, nem konjunktúraérzékeny és értékálló bevétel biztosítására,
Hortobágy Községi Önkormányzat Képviselő-testületének
Hortobágy Községi Önkormányzat Képviselő-testületének 16/2014 (IX. 29.) Önkormányzati Rendelete a településképi véleményezési és településképi bejelentési eljárásról Hortobágy Község Önkormányzatának Képviselő-testülete
Abony Város Önkormányzat képviselő-testületének 7/2015. (II.27.) sz. önkormányzati rendelete
Abony Város Önkormányzat képviselő-testületének 7/2015. (II.27.) sz. önkormányzati rendelete A települési támogatás megállapításának, kifizetésének, folyósításának, valamint felhasználása ellenőrzésének
ÉVES BESZÁMOLÓ 2013.
Érsekvadkert és Vidéke TAKARÉKSZÖVETKEZET Érsekvadkert 2659 Érsekvadkert, Rákóczi út 122. Cg.: 12 02 000360 KSH.: 10044977 6419 122 12 ÉVES BESZÁMOLÓ 2013. Mérleg... KSH: 10044977 6419 122 12 Cg.: 12 02
5.441 eft bg) térségi fejlesztési tanácstól az államháztartás központi alrendszerén belülről kapott EU-s forrásból származó pénzeszközből,
Kozármisleny Város Önkormányzata Képviselő-testületének 5/2013. (V.15.) önkormányzati rendelete az önkormányzat és intézményei 2012. évi költségvetéséről 6/2012 (II.13.) Önkormányzati rendelet módosításáról
206/2011. (X. 7.) Korm. rendelet
206/2011. (X. 7.) Korm. rendelet a kutatási és fejlesztési megállapodások egyes csoportjainak a versenykorlátozás tilalma alóli mentesítésérıl A Kormány a tisztességtelen piaci magatartás és a versenykorlátozás
Városok Viadala JUNIOR, 1990-91. sz, második forduló ... 99
JUNIOR, 990-9. sz, els forduló. Adott két pozitív valós szám. Bizonyítsuk be, hogy ha az összegük kisebb, mint a szorzatuk, akkor az összegük nagyobb 4-nél. (N. Vasziljev, 4 pont) 2. Egy szabályos háromszög
Vektoralgebra feladatlap 2018 január 20.
1. Adott az ABCD tetraéder, határozzuk meg: a) AB + BD + DC b) AD + CB + DC c) AB + BC + DA + CD Vektoralgebra feladatlap 018 január 0.. Adott az ABCD tetraéder. Igazoljuk, hogy AD + BC = BD + AC, majd
54 582 01 0000 00 00 Épületgépész technikus Épületgépész technikus 31 582 09 0010 31 01 Energiahasznosító berendezés szerelője
A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
Láthatjuk, hogy az els szám a 19, amelyre pontosan 4 állítás teljesül, tehát ez lesz a legnagyobb. 1/5
D1. Egy pozitív egész számról az alábbi 7 állítást tették: I. A szám kisebb, mint 23. II. A szám kisebb, mint 25. III. A szám kisebb, mint 27. IV. A szám kisebb, mint 29. V. A szám páros. VI. A szám hárommal
Alulírott, mint a.., támogatást igénylő szervezet képviseletére jogosult személy a támogatást igénylő szervezet nevében az alábbiakról nyilatkozom:
A támogatást igénylő adatai: név: székhely: képviselő neve: nyilvántartási szám: nyilvántartást vezető szerv neve: adószám: Az egyedi támogatás igénylőjének (jogi személy vagy jogi személyiséggel nem rendelkező
52 811 02 0000 00 00 Vendéglős Vendéglős 52 811 02 0100 31 01 Étkezdés Vendéglős 52 811 02 0100 31 02 Vendéglátó eladó Vendéglős
A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
Az osztályozó, javító és különbözeti vizsgák (tanulmányok alatti vizsgák) témakörei matematika tantárgyból
Az osztályozó, javító és különbözeti vizsgák (tanulmányok alatti vizsgák) témakörei matematika tantárgyból A vizsga formája: Feladatlap az adott évfolyam anyagából, a megoldásra fordítható idő 60 perc.
Tanmenetjavaslat 5. osztály
Tanmenetjavaslat 5. osztály 1. A természetes számok A tanmenetjavaslatokban dőlt betűvel szedtük a tananyag legjellemzőbb részét (amelyet a naplóba írunk). Kisebb betűvel jelezzük a folyamatos ismétléssel
S a t ti a s ti z s ti z k ti a k i a i soka k s a ág Megfigyelési egység Statisztikai ismérv
Üzleti gazdaságtan Ismétlés statisztika A statisztikai alapfogalmak A statisztikaa társadalom és a gazdasági élet jelenségeinek, folyamatainak számadatok segítségével történő megismerésével, leírásával,
1. A rendelet hatálya. 2. A támogatható célok és intézkedések. 3. A támogatás igénybevételének általános feltételei
32204 M A G Y A R K Ö Z L Ö N Y 2010. évi 202. szám A vidékfejlesztési miniszter 47/2010. (XII. 31.) VM rendelete a Magyar Méhészeti Nemzeti Program alapján a 2010 2013 közötti végrehajtási idõszakokban
Feladatok a koordináta-geometria, egyenesek témaköréhez 11. osztály, középszint
TÁMOP-.1.4-08/2-2009-0011 A kompetencia alapú oktatás feltételeinek megteremtése Vas megye közoktatási intézményeiben Feladatok a koordináta-geometria, egyenesek témaköréhez 11. osztály, középszint Vasvár,
MATEMATIKA GYAKORLÓ FELADATGYŰJTEMÉNY
MATEMATIKA GYAKORLÓ FELADATGYŰJTEMÉNY (Kezdő 9. évfolyam) A feladatokat a Borbás Lászlóné MATEMATIKA a nyelvi előkészítő évfolyamok számára című könyv alapján állítottuk össze. I. Számok, műveletek számokkal.
A tervezet előterjesztője
Jelen előterjesztés csak tervezet, amelynek közigazgatási egyeztetése folyamatban van. A minisztériumok közötti egyeztetés során az előterjesztés koncepcionális kérdései is jelentősen módosulhatnak, ezért
3. Öt alma és hat narancs 20Ft-tal kerül többe, mint hat alma és öt narancs. Hány forinttal kerül többe egy narancs egy
1. forduló feladatai 1. Üres cédulákra neveket írtunk, minden cédulára egyet. Egy cédulára Annát, két cédulára Pétert, három cédulára Bencét és négy cédulára Petrát. Ezután az összes cédulát egy üres kalapba
Egy csodálatos egyenesről (A Simson-egyenes) Bíró Bálint, Eger
Egy csodálatos egyenesről (A Simson-egyenes) Bíró Bálint, Eger. feladat Állítsunk merőlegeseket egy húrnégyszög csúcsaiból a csúcsokon át nem menő átlókra. Bizonyítsuk be, hogy a merőlegesek talppontjai
343/2011. (XII. 29.) Korm. rendelet. a környezetvédelmi termékdíjról szóló 2011. évi LXXXV. törvény végrehajtásáról
a környezetvédelmi termékdíjról szóló 2011. évi LXXXV. törvény végrehajtásáról A Kormány a környezetvédelmi termékdíjról szóló 2011. évi LXXXV. törvény 38. (1) bekezdés a)-g) pontjaiban kapott felhatalmazás
Lehet vagy nem? Konstrukciók és lehetetlenségi bizonyítások Dr. Katz Sándor, Bonyhád
Dr. Katz Sándor: Lehet vagy nem? Lehet vagy nem? Konstrukciók és lehetetlenségi bizonyítások Dr. Katz Sándor, Bonyhád A kreativitás fejlesztésének legközvetlenebb módja a konstrukciós feladatok megoldása.
1.1. Gyökök és hatványozás... 1 1.1.1. Hatványozás... 1 1.1.2. Gyökök... 1 1.2. Azonosságok... 2 1.3. Egyenlőtlenségek... 3
Tartalomjegyzék 1. Műveletek valós számokkal... 1 1.1. Gyökök és hatványozás... 1 1.1.1. Hatványozás... 1 1.1.2. Gyökök... 1 1.2. Azonosságok... 2 1.3. Egyenlőtlenségek... 3 2. Függvények... 4 2.1. A függvény
Í ÍÍÍ Í Í Í Ö Ö Ö Ö Ö Ö Ö Ö Ú É Í Ö Á Á É Ö É Ö É É Á Á Ö Ú Ö Ö Í Á É É Í Á É Í Ö Ö Á Á É Í Ö Ö Ö Ö Ö Ö Á É Ö É É Ö É Ö Í Á É É Ö Ö É Ö Í Í Í Í Ö Ö Ö Í Ö É Ö É É Ö Ö Í É Ö Í É É Ö Í É Á É É Ű Ö Í É É Ö
Matematika tanmenet (A) az HHT-Arany János Tehetségfejleszt Program el készít -gazdagító évfolyama számára
Matematika tanmenet (A) az HHT-Arany János Tehetségfejleszt Program el készít -gazdagító évfolyama számára Ez a tanmenet az OM által jóváhagyott tanterv alapján készült. A tanterv az Országos Közoktatási
Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzék módosításának eljárási rendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján.
Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzék módosításának eljárási rendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján. Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
KOVÁCS BÉLA, MATEMATIKA I.
KOVÁCS BÉLA, MATEmATIkA I 11 XI LINEÁRIS EGYENLETRENDSZEREk 1 LINEÁRIS EGYENLETRENDSZER A lineáris egyenletrendszer általános alakja: (1) Ugyanez mátrix alakban: (2), ahol x az ismeretleneket tartalmazó
Konszolidált Éves Beszámoló
Budapest Bank Rt. és leányvállalatai Konszolidált Éves Beszámoló 2003. december 31. Budapest, 2004. március 16. Richard Pelly a vállalkozás vezetoje TARTALOMJEGYZÉK I. Független könyvvizsgálói jelentés
1.. NAPIREND Ügyiratszám: /2012. ELŐTERJESZTÉS a Képviselő-testület 2012. november 30.-i nyilvános ülésére
1.. NAPIREND Ügyiratszám: /2012. ELŐTERJESZTÉS a Képviselő-testület 2012. november 30.-i nyilvános ülésére Tárgy: Előterjesztő: Előkészítette: Monoszló Község Önkormányzatának 2012 évi költségvetési rendeletének
MATEMATIKA KOMPETENCIATERÜLET A
MATEMATIKA KOMPETENCIATERÜLET A Matematika 7. évfolyam TANULÓI MUNKAFÜZET 2. félév A kiadvány KHF/4002-17/2008 engedélyszámon 2008. 08. 18. időponttól tankönyvi engedélyt kapott Educatio Kht. Kompetenciafejlesztő
TISZACSEGE VÁROS ÖNKORMÁNYZATÁNAK POLGÁRMESTERE
TISZACSEGE VÁROS ÖNKORMÁNYZATÁNAK POLGÁRMESTERE 4066 Tiszacsege, Kossuth u. 5. * Tel.: 52/588-400 * Fax: 52/588-405 e-mail: pmhivatal@tiszacsege.hu * Internet: http://www.tiszacsege.hu/ MEGHÍVÓ Tiszacsege
Az OTP Bank Rt. 2001. évi auditált konszolidált jelentése
Az OTP Bank Rt. 2001. évi auditált konszolidált jelentése Jelen jelentésünket a OTP Bank Rt. auditált 2001. december 31-ére vonatkozó, Magyar Számviteli Sztandardok (HAR) szerinti konszolidált pénzügyi
Segédlet a pénzügyi számvitel oktatásához A Pénzügy számvitel szak levelező tagozatos III. évfolyamos hallgatói részére
Segédlet a pénzügyi számvitel oktatásához A Pénzügy számvitel szak levelező tagozatos III. évfolyamos hallgatói részére Térítés nélküli átvétel Összeállította: Seres Sándorné I. A tárgyi eszközök 483.
4) Az ABCD négyzet oldalvektorai körül a=ab és b=bc. Adja meg az AC és BD vektorokat a és b vektorral kifejezve!
(9/1) Vektorok, Koordináta Geometria 1) Szerkessze meg az a + b és az a b vektort, ha a és b egy szabályos háromszögnek a mellékelt ábra szerinti oldalvektorai! 2) Az ABC háromszög két oldalának vektora
Általános Szerződési Feltételek. a Pick-Up Kft.
Általános Szerződési Feltételek a Pick-Up Kft. Internet hozzáférés szolgáltatásának igénybevételéhez. Az ügyfélszolgálat elérhetősége: 2900 Komárom, Táncsics M. u. 3/b Tel./Fax.: 34/222-222, 34/342-888,
5. gyakorlat. Lineáris leképezések. Tekintsük azt a valós függvényt, amely minden számhoz hozzárendeli az ötszörösét!
5. gyakorlat Lineáris leképezések Tekintsük azt a valós függvényt, amely minden számhoz hozzárendeli az ötszörösét! f : IR IR, f(x) 5x Mit rendel hozzá ez a függvény két szám összegéhez? x, x IR, f(x +
Opticon Kft. ÁLTALÁNOS SZERZŐDÉSI FELTÉTELEI HELYHEZ KÖTÖTT TELEFON SZOLGÁLTATÁSHOZ. Hatályos: 2016. március 9. 1. oldal
Opticon Kft. ÁLTALÁNOS SZERZŐDÉSI FELTÉTELEI HELYHEZ KÖTÖTT TELEFON SZOLGÁLTATÁSHOZ Hatályos: 2016. március 9. 1. oldal Tartalomjegyzék 1. Általános adatok, elérhetőség... 6 1.1. A szolgáltató neve és
Egy emelt szintű érettségi feladat kapcsán Ábrahám Gábor, Szeged
Egy emelt szintű érettségi feladat kapcsán Ábrahám Gábor, Szeged A 01. május 8.-i emelt szintű matematika érettségin szerepelt az alábbi feladat. Egy háromszög oldalhosszai egy számtani sorozat egymást
FÖLDES NAGYKÖZSÉG POLGÁRMESTERE 4177 FÖLDES, Karácsony Sándor tér 5. /Fax: (54) 531 000 ; 531 001 E-mail: foldes.ph@gmail.com. a Képviselő-testülethez
1 FÖLDES NAGYKÖZSÉG POLGÁRMESTERE 4177 FÖLDES, Karácsony Sándor tér 5. /Fax: (54) 531 000 ; 531 001 E-mail: foldes.ph@gmail.com Iktatószám: /2015. 15. E LŐTERJESZTÉS a Képviselő-testülethez az államháztartási
2007. évi CXXVII. törvény az általános forgalmi adóról
1 / 130 2016.04.20. 11:59 2007. évi CXXVII. törvény az általános forgalmi adóról 2016.01.01 2016.04.30 44 2007. évi CXXVII. törvény az általános forgalmi adóról Az Országgyűlés figyelemmel az államháztartás
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
Matematika emelt szint 1613 ÉRETTSÉGI VIZSGA 016. május 3. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fontos tudnivalók Formai előírások:
MATEMATIKA ÉRETTSÉGI 2006. május 9. EMELT SZINT
) A PQRS négyszög csúcsai: MATEMATIKA ÉRETTSÉGI 006. május 9. EMELT SZINT P 3; I., Q ;3, R 6; és S 5; 5 Döntse el, hogy az alábbi három állítás közül melyik igaz és melyik hamis! Tegyen * jelet a táblázat
1. A rendelet hatálya. 2. A támogatható célok és intézkedések
84800 A vidékfejlesztési miniszter 118/2013. (XII. 16.) VM rendelete a Magyar Méhészeti Nemzeti Program alapján a 2013 2016 közötti végrehajtási időszakokban a központi költségvetés, valamint az Európai
evision Általános Szerződési Feltételei
evision Kereskedelmi és Szolgáltató Korlátolt Felelősségű Társaság Előfizetői hírközlési szolgáltatás (műsorterjesztés) nyújtására vonatkozó Általános Szerződési Feltételei egységes szerkezetben Hatályba
148 feladat 21 + + 20 20 ) + ( 1 21 + 2 200 > 1 2. 1022 + 1 51 + 1 52 + + 1 99 2 ) (1 1 100 2 ) =?
148 feladat a Kalmár László Matematikaversenyről 1. ( 1 19 + 2 19 + + 18 19 ) + ( 1 20 + 2 20 + + 19 20 ) + ( 1 21 + 2 21 + + 20 21 ) + ( 1 22 + 2 22 + + 21 22 ) =? Kalmár László Matematikaverseny megyei
Kadarkút Város Önkormányzat Képviselı-testületének 3/2011.(II. 11.) önkormányzati rendelete. Kadarkút Város Önkormányzata 2011. évi költségvetésérıl
Kadarkút Város Önkormányzat Képviselı-testületének 3/2011.(II. 11.) önkormányzati rendelete Kadarkút Város Önkormányzata 2011. évi költségvetésérıl Kadarkút Város Önkormányzatának Képviselı-testülete (a
LÁNG CSABÁNÉ SZÁMELMÉLET. Példák és feladatok. ELTE IK Budapest 2010-10-24 2. javított kiadás
LÁNG CSABÁNÉ SZÁMELMÉLET Példák és feladatok ELTE IK Budapest 2010-10-24 2. javított kiadás Fels oktatási tankönyv Lektorálták: Kátai Imre Bui Minh Phong Burcsi Péter Farkas Gábor Fülöp Ágnes Germán László
2014. évi előirányzat BEVÉTELEK. 2014. évi előirányzat KIADÁSOK. Költségvetési rendelet űrlapjainak összefüggései:
Költségvetési rendelet űrlapjainak összefüggései: 2014. évi előirányzat BEVÉTELEK 1. sz. melléklet Bevételek táblázat 3. oszlop 9 sora = 2.1. számú melléklet 3. oszlop 13. sor + 2.2. számú melléklet 3.
Megoldások. Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma)
Megoldások 1. Határozd meg az a és b vektor skaláris szorzatát, ha a = 5, b = 4 és a közbezárt szög φ = 55! Alkalmazzuk a megfelelő képletet: a b = a b cos φ = 5 4 cos 55 11,47. 2. Határozd meg a következő
1. Lineáris leképezések
Lineáris leképezések A lineáris leképezés fogalma Definíció (F5 Definíció) Legenek V és W vektorterek UGYANAZON T test fölött Az A : V W lineáris leképezés, ha összegtartó, azaz v,v 2 V esetén A(v +v 2
Lineáris Algebra gyakorlatok
A V 2 és V 3 vektortér áttekintése Lineáris Algebra gyakorlatok Írta: Simon Ilona Lektorálta: DrBereczky Áron Áttekintjük néhány témakör legfontosabb definícióit és a feladatokban használt tételeket kimondjuk
Mátrixok. 3. fejezet. 3.1. Bevezetés: műveletek táblázatokkal
fejezet Mátrixok Az előző fejezetben a mátrixokat csak egyszerű jelölésnek tekintettük, mely az egyenletrendszer együtthatóinak tárolására, és az egyenletrendszer megoldása közbeni számítások egyszerüsítésére
Sződ Község Önkormányzata. Képviselő-testülete. Ökt. 1/2011.(II.24.) rendelete
Sződ Község Önkormányzata Képviselő-testülete Ökt. 1/2011.(II.24.) rendelete AZ ÖNKORMÁNYZAT 2011. ÉVI KÖLTSÉGVETÉSÉRŐL 1 Sződ Község Önkormányzata képviselő-testülete 1/2011.(II.24. ) Ökt rendelete az
55 345 01 0010 55 01 Európai Uniós üzleti
A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
Matematika emelt szintû érettségi témakörök 2013. Összeállította: Kovácsné Németh Sarolta (gimnáziumi tanár)
Matematika emelt szintû érettségi témakörök 013 Összeállította: Kovácsné Németh Sarolta (gimnáziumi tanár) Tájékoztató vizsgázóknak Tisztelt Vizsgázó! A szóbeli vizsgán a tétel címében megjelölt téma kifejtését
1. sz. melléklet 1. DEFINÍCIÓK ÉS MEGHATÁROZÁSOK
1. sz. melléklet 1. DEFINÍCIÓK ÉS MEGHATÁROZÁSOK A jelen Alaptájékoztatókban szereplő egyes fogalmak definíciói, illetve rövidítések magyarázatai az alábbiakban kerülnek ismertetésre. Az egyéb, vagyis
A 2014/2015. tanévi Országos Középiskolai Tanulmányi Verseny második forduló MATEMATIKA I. KATEGÓRIA ( SZAKKÖZÉPISKOLA ) Javítási-értékelési útmutató
OktatásiHivatal A 014/01. tanévi Országos Középiskolai Tanulmányi Verseny második forduló MATEMATIKA I. KATEGÓRIA ( SZAKKÖZÉPISKOLA ) Javítási-értékelési útmutató 1. feladat: Adja meg az összes olyan (x,
3/2015. (II.16.) számú rendelet Létavértes Város önkormányzatának és intézményeinek 2015. évi költségvetéséről. 1. A rendelet hatálya
LÉTAVÉRTES VÁROSI ÖNKORMÁNYZAT KÉPVISELŐTESTÜLETÉNEK 3/2015. (II.16.) számú rendelet Létavértes Város önkormányzatának és intézményeinek 2015. évi költségvetéséről Létavértes Városi Önkormányzat Képviselő-testülete
INTERNET SZOLGÁLTATÁSÁNAK ÁLTALÁNOS SZERZŐDÉSI FELTÉTELEI
SATURNUS BT BAJA INTERNET SZOLGÁLTATÁSÁNAK ÁLTALÁNOS SZERZŐDÉSI FELTÉTELEI Készült: 2004. május 25-én Módosítva: 2012. február 22-én 1 Tartalom SATURNUS BT BAJA... 1 ÁLTALÁNOS SZERZŐDÉSI FELTÉTELEK AZ
2011. évi CIII. törvény. a népegészségügyi termékadóról
2011. évi CIII. törvény a népegészségügyi termékadóról Az Országgyűlés a népegészségügyileg nem hasznos élelmiszerek fogyasztásának visszaszorítása és az egészséges táplálkozás előmozdítása, valamint az
Budapest Főváros XIII. Kerületi Önkormányzat Képviselő-testületének /.. (.) önkormányzati rendelete
Budapest Főváros XIII. Kerületi Önkormányzat Képviselő-testületének /.. (.) önkormányzati rendelete a helyi településrendezési előírások tartalmáról szóló előzetes tájékoztatás és a tervekkel kapcsolatos
Ö Á Í Í ű ű ú ű ű ű ű ú ú ú ú ű ű ű ű ű ű ű ű ű ú ű ú ú ú ű ú Á ú ű ű Ó ú ű ű ű ú Ó ú ű ú É ú ú ú ű ű ú ű ú Ú Á ú É ú Ó ú ú ú ú ű ű ű ú É Á É É ű ű Í ú ú Ó Í ű Í ű ű ú ű ű ű É ű ú Á ű ű ú Í ű Á ű ú ú É
ö ö ö ö ö ö ö ű ű ö ö ö ö ö Ő ö Ó Ú ö Ö ö ö ö ö Ö Ő ö ö Í Ó Ó Ő ö ö ö ö ö Ő Ő Ó Ő É ö Ú ö ö Ő ö ö ö ö ö ö ö Ő ö Ő É ö Ő ö ö Ő ö ö ö Ó ű ö ö ö Ő ö ö ö Í Ő Ó Í ö ö ö ö Ő Ő Ő Ő Í Ó Ő Ő Í Ő ö ö ö ö ö Ő Ő ö
Ú ű ü ü Ü ű É É Ö Ö Á ü ü ü ű É ú Á Ö Ü ü ü ű É Á É Ű ű Ü Ü ű ü ű ü ű ü Ü ü ü Ű Á Á Á ű ú ű Á Ó Ó É Á Ó Á Ó ű ü ü ű ű ü ú ú ü ü ü ű ü ű Ü ű ü ü ú ü Ö ü ú ú ü ü ü ü ű ú ü Ó ü Ó Ó ü ü Ó ü ü Ó ű ű ú ű ű ü