BOCSKAI ZOLTÁN A SZEM BIOMECHANIKAI VISELKEDÉSÉNEK. PhD értekezés tézisei MODELLEZÉSE
|
|
|
- Ákos Illés
- 9 évvel ezelőtt
- Látták:
Átírás
1 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM TARTÓSZERKEZETEK MECHANIKÁJA TANSZÉK A SZEM BIOMECHANIKAI VISELKEDÉSÉNEK MODELLEZÉSE PhD értekezés tézisei BOCSKAI ZOLTÁN Tudományos vezető: DR. BOJTÁR IMRE Budapest, 2015
2 Tartalom 1. Bevezetés 3 2. Kutatási módszerek és eredmények A numerikus vizsgálatok céljainak bemutatása A felépített komplex végeselemes modell Az alkalmazkodóképesség vizsgálata Nem-refraktív jellegű szemműtétek numerikus elemzése Lencsefüggesztő rostok laboratóriumi vizsgálata A zonularostok geometriai vizsgálata A zonularostok mechanikai tulajdonságainak vizsgálata Az értekezés tézisei 18 Az értekezés témakörében készült publikációim 19 2
3 1. Bevezetés A különböző szemészeti beavatkozások alkalmazása napjainkban a legelőremutatóbb, és élettani szempontból az egyik legmegfelelőbb eljárás a látást akadályozó problémák elhárítására. Ezen beavatkozások többsége műtétet tesz szükségessé, mely műtét igényli a szem mélyreható élettani és biomechanikai tulajdonságainak ismeretét. Számos szemészeti műtét létezik, amellyel a különböző orvosi problémák elháríthatóak. Többek között ilyen eljárás a szaruhártya felületét érintő lézeres műtéti folyamat. Ezekben az esetekben a közelre, vagy távolra látás javítása a cél (PRK, LASIK). Olyan beavatkozások is léteznek, amelyek az ínhártya lézeres kezelését célozzák meg a szemlencse természetes alkalmazkodóképességének visszaállítása céljából (LaseACE). Másféle fontos csoportot alkotnak a szürkehályog-műtétek, melyeknél a lencse tokjának meghagyása mellett a lencsét intraokuláris (IOL) lencsére cserélik a látás megmaradása érdekében. Ezek fényében kifejezetten hasznosnak tűnt egy olyan numerikus modell létrehozása, amivel a fent említett és hasonló problémákat biomechanikai szempontból vizsgálni lehet. Az elmúlt években több tanulmány készült a szem különböző részeinek mechanikai vizsgálatára, a feladatokat általában végeselem-módszeren alapuló számítógépes programmal modellezték. Az olyan komplex modell azonban nagyon ritka, amely globális analízisre alkalmas, és megfelelően részletes a szemnél előforduló biomechanikai feladatok szinte mindegyikéhez. A legtöbb tanulmányban - a részleges, vagy kissé összetettebb modellekben - a különböző részeket homogén, izotrop és lineárisan rugalmas anyagmodellel jellemezték. Olyan publikációkban fordul elő nemlineáris anyagmodell, ahol csak bizonyos kitüntetett részek elemzését végezték el. Ez azért van így, mert a szem anyagi tulajdonságainak mérése rendkívül nehéz dolog. A lineárisan rugalmas viselkedés leírásához szükséges mechanikai jellemzőkből is hiány van a szem néhány alkotórészét tekintve, mivel a mechanikai tulajdonságok in vivo mérése szinte lehetetlen, de az in vitro mérések is igen nehézkesek a szem felépítéséből következően. A geometriai méretek meghatározása az anyagi paraméterekkel ellentétben már megoldottnak mondható, hiszen a szemészeti vizsgálatok folyamán az elülső és hátulsó szegmens geometriájának feltérképezése akár in vivo is lehetséges. PhD dolgozatom keretein belül a szem komplex háromdimenziós végeselemes modellezésével foglalkoztam, különös tekintettel az alkalmazkodóképesség vizsgálatára. A dolgozat a Semmelweis Egyetem Szemészeti Klinikájának munkatársaival szoros együttműködésben készült. Munkám egyik célja olyan numerikus szemmodell elkészítése, paraméterezése és tesztelése volt, amelynek mechanikai tulajdonságai megfelelőek az alkalmazkodóképesség vizsgálatára, de emellett egyéb numerikus vizsgálatokra (mint például különböző szemműtétek mechanikai tulajdonságainak elemzése) is alkalmas. További célom volt a szemlencse ekvátorát körbevevő lencsefüggesztő rostok (zonulák) mélyebb megismerése, és a szakirodalomban bizonytalanul közölt anyagjellemzők mérése. Ehhez szorosan kapcsolódott egy olyan egyedi kísérleti eljárás kifejlesztése, amivel reprodukálható módon elvégezhető ezen rostok rugalmassági tulajdonságainak vizsgálata. Az értekezésben rövid elméleti bevezetés után a következő részfeladatokkal foglalkoztam: - a szem komplex modelljének felépítése a biomechanikai szempontból fontos részek figyelembevételével, aminél kiemelten fontos volt - a szemlencse és a környező részek részletes modellezése, - a modell alkalmazásának bemutatása az alkalmazkodóképesség vizsgálatára, - klinikai alkalmazás a jelenleg fejlesztés alatt álló természetes alkalmazkodást visszaállító műtét geometriájának kedvezőbb kialakítására, és végül - a lencsefüggesztő rostok mechanikai tulajdonságainak vizsgálatára kifejlesztett kísérleti eljárás részletes ismertetése és a mérési eredmények kiértékelése. 3
4 Dolgozatom fejezetei a következőket tárgyalják részletesen: A szem numerikus modellezése A szemet felépítő részeket a különböző vizsgálatok céljából homogén, rugalmas kontinuummal vettem figyelembe, melynek geometriai és mechanikai tulajdonságai a valós paraméterek ismeretében szükség szerint egyszerűen módosíthatók. A felhasznált paramétereket részben saját kísérletekből, részben a szakirodalomból nyertem. A szem, mint élő szövet, élettartama során folyamatos átalakuláson megy keresztül. Az átalakulás kettős, egyrészről az életkor előrehaladtával a szemlencse geometriája változik, másrészről a szemet alkotó részek anyaga általában fokozatosan merevedik, azaz rugalmassági modulusa az öregedés során növekszik. Ezen felül a lencse optikai tulajdonságai (úgymint fénytörési mutató) is változnak. Az általam létrehozott komplex modell felépítésének algoritmusa olyan, hogy a geometriai és anyagi paraméterek tetszés szerint, a mért, vagy újonnan meghatározott adatok alapján könnyen változtathatók. Az alkalmazkodási folyamat modellezése Komplex numerikus modellem segítségével elemeztem a szemlencse alkalmazkodási folyamatának (akkomodáció) alakulását a szem időbeli változásának függvényében. Klinikai mérésekkel összehasonlítva igazoltam a modell számítási eredményeit. Megvizsgáltam, hogy a geometriai és anyagi paraméterek mellett a lencse optikai tulajdonságaiban (fénytörési mutató) történő változás milyen mértékben van hatással az alkalmazkodási folyamatra. Az ínhártyát érintő műtéti eljárás vizsgálata A természetes alkalmazkodás visszanyerését célzó, jelenleg fejlesztés alatt álló műtéti eljárás hatékonyságának növelése céljából paraméteres futtatásokat végeztem a végeselemes numerikus modell segítségével. Ez segítséget nyújthat a műtéti eljárás fejlesztésének további folyamataiban, annak érdekében, hogy a műtét eredménye a lehető legnagyobb alkalmazkodási szélességnövekedést szolgáltassa. A lencsefüggesztő rostok mechanikai tulajdonságainak laboratóriumi mérése A szemlencse működését mechanikai szempontból erősen befolyásoló rostok pontosabb mechanikai tulajdonságainak megismerése érdekében reprodukálható laboratóriumi mérési eljárást fejlesztettem ki. Ennek legfontosabb előnyei közé tartozik az in situ állapotban történő mérés. A mérési eredmények viszonylag gyors kiértékelésére analitikus és numerikus megoldásokat is adtam. A laboratóriumi mérési és kiértékelési eljárást sertésminták segítségével fejlesztettem és teszteltem, de a teljes mérési technika kiterjeszthető emberi minták vizsgálatára is. Megjegyzem, hogy a témában további kutatási lehetőséget ad például a különböző intraokuláris lencsék alkalmazása, a behelyezésük utáni helyes működés vizsgálata. 2. Kutatási módszerek és eredmények 2.1. A numerikus vizsgálatok céljainak bemutatása A numerikus modell felépítésének elsődleges célja az volt, hogy egy olyan komplex modellt építsek föl, ami akár hosszabb távon is többféle probléma vizsgálatára alkalmas. A numerikus modell végeselem-módszeren alapszik, amihez az ANSYS programrendszert használtam fel. Mivel többféle feladatra is alkalmas modellt akartam létrehozni, ezért nem kívántam korlátozni alkalmazhatóságának lehetőségeit, így a modell alapvetően háromdimenziós. A disszertációmban a komplex numerikus modellt elsősorban az alkalmazkodóképesség (a szemlencse deformációja közelre és távolra nézés során) és az 4
5 egyik ínhártyát érintő műtéti eljárás vizsgálatára használtam. Az alkalmazkodási folyamat vizsgálatával ellenőriztem a felépített modell viselkedését, és az alkalmazkodóképességet befolyásoló tényezőket, azok hatásait. Ezután a komplex modell segítségével megvizsgáltam az ínhártyát érintő látásjavító műtéti eljárás alkalmazhatóságának mechanikai kérdéseit, és ajánlást adtam a műtéti módszer hatékonyabb végrehajtására a rendelkezésre álló adatok alapján A felépített komplex végeselemes modell A szemgolyó geometriájánál kihasználtam annak tengelyszimmetriáját, de az ágyazó zsírtest geometriájánál már nem (1. és 2. ábra). Az ANSYS program paraméteres tervezési nyelvét (APDL) alkalmazva a geometria legfőbb adatai a következőkben ismertetett módon tetszőlegesen módosíthatók. A szemgolyó geometriájának felépítéséhez a következő paramétereket lehet használni (1. ábra): - a külső burok (ínhártya) külső sugara (R) gömb alakot feltételezve, - az ínhártya hátulsó (ih) és oldalsó (io) vastagsága, belső falán ellipszoid alakot feltételezve, - a szaruhártya külső sugara (s), - a szaruhártya vastagsága a szemtengelyben (szv) és a szélein (szf), - az elülső csarnokmélység, a szaruhártya és a lencse távolsága (ec), - a szemgolyó középpontja és a szaruhártya görbületi középpontjának távolsága (m), - a lencse ekvatoriális sugara (a), - a lencse vastagsága (b=b a +b p ), - a lencse görbületi viszonyaira vonatkozó paraméterek (c, d), - a lencsemag vastagsága (h), - a lencsemag sugara (r), - a lencsemag pozíciója a lencse ekvátorához viszonyítva (e), - a lencsetok vastagsága elöl (tva) és hátul (tvp), - a sugártest belső sugara (acm) ábra A geometriai paraméterek A modell felépítéséhez szükséges bemenő fájlt olyan módon hoztam létre, hogy a megadott paraméterek alapján a program automatikusan generálja a geometriai vázat és ellentmondás esetén (összemetsződés) figyelmeztetést küld. A szemgolyó a csontos szemüregben helyezkedik el az ágyazó zsírtestben. Ez utóbbit a modellemben a szemgolyót körbevevő csonka gúla alakú résszel vettem figyelembe (2. ábra). Számításaimnál a lencsemag, a kéreg, a tok, az üvegtest és a csarnok között folytatólagos kapcsolatot feltételeztem, mivel jelenleg nincsenek mérési adatok arról, hogy ezek között a részek között milyen jellegű a mechanikai kapcsolat. Modellem geometriáját az említett paramétereken 5
6 felül úgy alakítottam ki, hogy az előbb említett részek között vékony határrétegeket hoztam létre (3. ábra). Ez azért volt célszerű, mert a mechanikai kapcsolatok esetleges jövőbeli pontosabb adatainak birtokában a határrétegek merevségének módosításával a modell pontosítható. A zonulák és a lencse tokjának modellezésére héjelemeket használtam, mivel a toknak és a zonulák csoportjainak meglehetősen vékony a vastagsága (6-60 µm). A többi alkotórészt testelemekkel modelleztem. Az ellenőrzött keretek között használt automatikus hálógenerálóval a komplex modellemben többnyire háromszög és tetraéder elemeket használtam (2. ábra). Az általam létrehozott numerikus modell alkalmazásának nagy előnye, hogy az említett geometriai és anyagi paraméterek beállítása és módosítása nagyon egyszerűen végrehajtható. A számításaimnál alkalmazott anyagi és geometriai paramétereket különböző szakirodalmi adatok alapján vettem fel. (Ezek forrásainak részleteiről részletesebben lásd az értekezés megfelelő fejezetét.) 2. ábra A numerikus modell metszete, a zsírtest és a peremfeltételek Az alkalmazkodóképesség vizsgálata Az alkalmazkodási folyamat elemzéséhez a sugártestre sugárirányú erőrendszert helyeztem, ami a zonulákban húzást okozott (3. ábra). Így a szemlencsét az alkalmazkodott állapotból a távolba fókuszáló állapotba deformáltam, a deformáció után a lencsevastagság csökkent (4. ábra), vagyis a folyamatot egyfajta inverz alkalmazkodás-szimulációval modelleztem, ahogy ezt a fajta elvet több szerző is alkalmazta (a részleteket lásd az értekezésben). Ez azért volt célszerű, mert a lencse és a zonulák a Helmholtz-féle elmélet szerint az alkalmazkodott állapotban feszültségmentesek. A szemgolyót körbevevő csonka gúla alakú zsírtest külső csomópontjainak elmozdulásait megakadályoztam (2. ábra), mellyel a csontos szemüreg megtámasztó hatását szándékoztam szimulálni. Ahhoz, hogy az alkalmazkodóképesség folyamatát elemezni tudjam, szükségem volt a szemlencse tengelyében értelmezett dioptriájára (COP) a különböző vizsgált életkorokban (távolba és közelre fókuszáló állapotban). Ezt a vastag lencsék dioptriaszámítására szolgáló egyenlettel határoztam meg: 2 nl np nl np t(nl n p ) COP, ra rp rarpnl (1) ahol n l a lencse ekvivalens törésmutatója levegőre vonatkoztatva, ez általában 1,43-nak vehető érték, de nagysága függ az életkortól, n p az üvegtest és a csarnokvíz átlagos törésmutatója a levegőre vonatkoztatva, 1,336-nak vehető, r a és r p a lencse elülső és hátulsó görbületi sugara a lencse tengelyében értelmezve, illetve t a lencse vastagsága az optikai tengelyében. A COP számításához szükségem volt a lencse tengelyében értelmezett elülső és 6
7 hátulsó görbületi viszonyokra mind az alkalmazkodott (deformálatlan), mind a távolba néző (deformált) esetben. 3. ábra A sugártesten alkalmazott erőrendszer Ehhez a lencse szimmetriasíkjában és ezen belül annak külső felületén elhelyezkedő csomópontok koordinátáit használtam a deformált és a deformálatlan állapotban. Ezekre a pontokra polinomiális regressziót alkalmaztam. Az említett pontok közül azokat vizsgáltam, amelyek a lencse tengelyének 3 mm-es környezetébe estek. A deformált állapothoz tartozó csomóponti koordinátákat kapjuk meg a végeselemes számításból, ebből kifolyólag az ehhez az állapothoz tartozó lencsét leíró függvényalakot, amiből a deformált állapothoz tartozó görbületi viszonyokat számítani tudnánk, nem ismerjük. Ezt úgy küszöböltem ki, hogy az említett kezdeti (deformálatlan) felületi csomóponti koordinátákra különböző fokszámú polinomokat illesztettem a legkisebb négyzetek módszerével. A különböző fokszámú polinomokhoz meghatároztam a görbületi sugár függvényét (r pol (x)) is. A lencse kiindulási alakjából (Chien et al. [2003], (2) egyenlet, amiben a és b a befoglaló méreteket, c és d pedig a lencse alakját határozza meg) a görbületi sugár függvénye számítható (r(x)) x 1 x 1 x y( x ) b csin d sin cos sin a a a, (2) A két görbületi sugár függvény különbségnégyzetének határozott integrálját a lencse tengelyének 3 mm-es környezetében kiszámítottam ((3) egyenlet). 3mm 3mm 2 rxrpol x dxmin. (3) Ez alapján azt a polinomot fogadtam el a legjobb közelítésnek - amivel a görbületi sugár függvénye a leginkább illeszkedik az eredeti görbületi viszonyokhoz - amelyik az előző (3) egyenlet alapján a legkisebb eltérést adta (5. ábra). Az ilyen módon illesztett polinomból és az eredeti függvényből számolt görbületi sugarak függvényeit az 5. ábra szemlélteti. Miután így megkaptam az illesztett polinom legjobban illeszkedő fokszámát, amivel az eredeti függvény görbületi viszonyai a legjobban közelíthetők, ezt a fokszámú polinomot illesztettem a deformált állapothoz tartozó csomóponti koordinátákra is, és ebből számoltam a deformált (elernyedt) alakhoz tartozó görbületi sugarakat és ebből a COP értékeket. Ilyen módon az alkalmazkodási szélesség ( COP, a közelre és távolra néző lencse dioptriájának különbsége) számítható a különböző alkalmazkodóképességgel kapcsolatos vizsgálatokhoz. 7
8 4. ábra Az eltolódások ábrázolása a lencse szimmetriatengelyének irányában. 5. ábra Az illesztett polinomból és az eredeti függvényből számolt görbületi sugár közötti relatív eltérés az illesztett polinom fokszámának [n] függvényében, illetve az eredeti lencsefüggvényből számolt görbületi sugár függvénye (r(x), [mm]) és az illesztett polinomból számolt görbületi sugár függvénye (r pol (x), [mm]) Megvizsgáltam az alkalmazkodási szélességet a kor előrehaladtával (az ehhez szükséges anyagi és geometriai paramétereket részleteit lásd az értekezésben). A COP értéket négy különböző eset paraméteres vizsgálata alapján határoztam meg. Az első esetben azt feltételeztem, hogy a lencse geometriája és törésmutatója nem változik a korral, tehát csak az anyagi paramétereket, és a lencse tokjának vastagságát módosítottam a paraméteres vizsgálatban. A második esetben csak a lencse geometriája volt változatlan a paraméteres vizsgálat során. A harmadik eset a lencse geometriai és az anyagi paramétereinek változásait vette figyelembe konstans törésmutató mellett. A negyedik esetben pedig mind a lencse geometriájában, mind pedig az anyagában és törésmutatójában bekövetkező változások hatását vizsgáltam. A paraméteres vizsgálatok során kiszámítottam a lencse COP értékét az alkalmazkodott, és a távolba néző lencse esetében is. A 6. ábra mutatja ezeknek az értékeknek a tendenciáját a négy különböző paraméteres vizsgálatra a kor függvényében. Az első esetben, mivel a kiindulási geometria megegyezett (ez az alkalmazkodott lencsealak volt, és ezt a lencseállapotot húztam meg a sugárizomra hárított erővel), és a lencse törésmutatójában a korral bekövetkező változást sem vettem figyelembe, így csak a távolba néző szemlencse dioptriájában látunk változást (az alkalmazkodottnál nem), annak köszönhetően, hogy a sugárizomra tett húzóerő segítségével az alkalmazkodott lencsealakot vittem át távolba nézőnek (6. ábra). A második esetben - figyelembe véve azt, hogy a lencse törésmutatójának csökkenését is számításba vettem - a lencse dioptriájának csökkenését látjuk alkalmazkodott és távolba néző esetben is. Mivel a törésmutatót csökkenését is számításba vettem, ezért az alkalmazkodott és elernyedt állapotú lencsék dioptriája kisebb, mint az első esetben. A harmadik esetben az eredmények azt mutatták, hogy a lencse dioptriája is növekszik. 8
9 6. ábra A lencse dioptriájának változása és az alkalmazkodási szélesség változása a különböző esetekben A negyedik esetben a kezdő állapothoz tartozó értékek megegyeznek a harmadik esetben közölttel, a végállapothoz tartozó értékek pedig a kettes esetével, ahogyan azt vártam is az ottani bemenő paraméterek egyezése miatt. Az előző pont eredményei alapján az alkalmazkodási szélesség számítható, ha az alkalmazkodott állapotú lencse dioptriaértékéből kivonjuk a távolba néző lencse dioptriaértékét. Mind a négy esetben a paraméteres vizsgálat kimutatta, hogy az alkalmazkodási szélesség ( COP) csökken a kor előrehaladtával (6. ábra). Figyelembe véve az eredményeket, azok tendenciáját és azt, hogy a lencse törésmutatója csökken a korral, illetve azt, hogy a lencse vastagsága pedig növekszik, a negyedik esethez tartozó eredmények felelnek meg legjobban a valóságnak. Megállapítottam, hogy a numerikus modellel bizonyítható az alkalmazkodási szélesség csökkenése, ha a számítás során a lencse törésmutatójában történő csökkenést is figyelembe vesszük (2. és 4. eset). A numerikus számításból belátható, hogy a lencse törésmutatójában bekövetkező romlás legalább akkora hatással van az alkalmazkodási szélességre, mint a geometriai és az anyagi paraméterek változása. A 6. ábrán látható egy ötödik eset, ami a negyedik esettel megegyező bemenő értékeket tartalmazta a paraméteres vizsgálatoknál, kivéve a szaruhártya és az ínhártya rugalmassági modulusait, mivel ezeket ebben az esetben Śródka et al. [2011] által ajánlott értékekkel vettem figyelembe. Az ötödik eset tendenciája nem tér el túlzottam a korábbi négy eset paraméteres vizsgálatától. Amikor a numerikus eredményeimet összehasonlítottam Tsorbatzoglou et al. [2007] mérési eredményeivel (6. ábra), amit szubjektív alkalmazkodásmérési technikával végzett, azt tapasztaltam, hogy a tendenciák jó egyezést mutatnak. Meredekebb csökkenést látunk a mért eredmények átlagos alkalmazkodási szélességének csökkenésében, de ehhez meg kell jegyezzem, hogy a szubjektív mérési technika nagyobb értéket ad az alkalmazkodási szélességre, mint a tényleges érték Nem-refraktív jellegű szemműtétek numerikus elemzése A közvetlenül a fénytörést megváltoztató (refraktív) szemészeti beavatkozásokon kívül léteznek olyanok is, amelyeknek nem közvetlenül a szaruhártya felületének megváltoztatása a célja, hanem közvetett módon célozza meg a természetes alkalmazkodás javítását. Hipsley és McDonald [2012] alapján az egyik ilyen módszer az ínhártyával kapcsolatos, aminek köszönhetően az alkalmazkodási szélesség tartósan átlagosan 1,3 dioptriával növelhető. Ez a lézeres technika (Hipsley és McDonald [2012]) szabadalmaztatott eljárás. Az ínhártyába 36 darab 600 µm átmérőjű lyukat égetnek szemészeti lézer segítségével, bizonyos geometriai elrendezésben. A lyukak mélysége az ínhártya vastagságának 80-90%-áig ér be. A szaruhártya környezetében négy szegmensen alkalmaznak 9-9, azaz összesen 36 lyukat (7. és 8. ábra). 9
10 7. ábra A modell metszete a szemgolyó tengelye mentén, amely a lyukak pozícióját mutatja a sugártesthez és a szaruhártya pereméhez képest A 9-9 lyuk elhelyezkedése azokra a részekre lokalizálódik, ahol a legkevesebb (Hipsley és McDonald [2012]) - az elülső szegmens vérellátására szolgáló - ér helyezkedik el az ínhártyában. Ezek az erek túlnyomórészt a 8. ábrán feltüntetett négy szegmens határvonalainak sávjaiban helyezkednek el (3, 6, 9 és 12 óránál), így a lyukak ezeknek a szegmenseknek a közepére kerülnek. Az alkalmazkodóképesség tartós átlagos növekedése az operációt követően 1,3 dioptria (Hipsley és McDonald [2012]). Az alkalmazkodási szélességet minden esetben objektív módon mérték. A meglévő lézeres műtéti eljárás numerikus modellel történő alátámasztását, geometriájának elemzését és esetleges módosítását tűztem ki célul az alkalmazkodási szélesség növelése érdekében. A sugárizomra rátett konstans erő mellett elemeztem a különböző geometriai kialakításokat, és számítottam az alkalmazkodási szélességet a korábban említett inverz alkalmazkodás-vizsgálattal. Az analízissel kimutatható, hogy minél nagyobb a lyukak térfogataránya, az alkalmazkodás annál kedvezőbb lehet, de ez élettani szempontból egyéb rosszindulatú változásokhoz vezethet a szemgolyó integritása szempontjából. Ezen okokból kifolyólag jelen esetben én alapvetően a kitüntetett helyeken elhelyezett mikro-bemetszések hatását elemeztem. 8. ábra Az eljárás eredeti geometriája 9. ábra A koncentrált lyukelrendezés és a folytonos elméleti lyukelrendezés geometriája Az ilyen jellegű műtéti beavatkozások elvi hatékonysága elméletileg abban áll, hogy az ínhártyában alkalmazott gyengítések (lyukak) okozzák az alkalmazkodás valamilyen szintű javulását. A térbeli modell segítségével, melynek minden előnyét most ki tudtam használni a lyukakkal gyengített geometria már nem tengelyszimmetrikus, továbbá ha a gravitáció 10
11 hatását is figyelembe veszem a sugárirányú erők mellett, akkor a teher sem képes voltam modellezni a módosított geometria esetén az alkalmazkodási szélességnek az alakulását. A numerikus komplex modellben a bemetszések mélységét, és a szaruhártya pereméhez (limbus) képesti elhelyezkedését a 7. ábra és a 8. ábra szemlélteti. A vizsgálataim során az 50 éves korosztályhoz tartozó geometriai és anyagi paramétereket vettem figyelembe, mert Hipsley és McDonald [2012] munkájában a páciensek átlagéletkora - akiken végrehajtották a műtétet - 50,4 év volt. A 9. ábra szerinti lyukelrendezéseken is végrehajtottam a numerikus számításokat. Természetesen a 9. ábra jobb oldalán elhelyezkedő elrendezés csupán elméleti jelentőséggel bír, hiszen az ínhártyában futó artériák elhelyezkedése és a szemgolyó globális integritása miatt ez a kialakítás nem valószínű, hogy alkalmazható a gyakorlatban. 10. ábra Az eredeti geometria és a koncentrált lyukak végeselemes hálója (részlet a lyukakról és metszet) Az eredmények összehasonlíthatósága és a műtéti eljárás elméleti működésének bizonyítása céljából egy olyan eset vizsgálatát is elvégeztem, amikor az ínhártya geometriáját sértetlenül hagytam, azonban a merevségét nagyságrendekkel lecsökkentettem. A különböző geometriához tartozó számításoknál a lyukak környezetében kialakított végeselemes hálózatokat a 10. ábra és a 11. ábra szemlélteti. Az ábrákon jól látszik, hogy a lyukak környezetében sűrítettem a végeselemes hálót. Az említett eseteken végrehajtottam az alkalmazkodási folyamat elemzését az ismertetett COP számítási eljárás segítségével. 1. táblázat Az egyes esetekhez tartozó eredmények összefoglalása 50 éves korhoz tartozó anyagi és geometriai paraméterek esetén (n l =1,42; n a =1,336) Intakt Eredeti geometria Koncentrált lyukak Folytonos lyukak Elhanyagolt ínhártya (intakt) COP (alkalmazkodott) 25,800 D 25,800 D 25,800 D 25,800 D 25,800 D COP (távolra néző) 23,859 D 23,785 D 23,783 D 23,764 D 22,519 D ΔCOP 1,941 D 2,015 D 2,017 D 2,036 D 3,281 D COP változás az intakthoz képest 0,000 D 0,07382 D 0,07622 D 0,09505 D 1,3397 D a lencse vastagságváltozása 0,2866 mm 0,2878 mm 0,288 mm 0,2897 mm 0,4282 mm a lencse görbületi sugara (elülső, alkalmazkodott) 8,706 mm 8,706 mm 8,706 mm 8,706 mm 8,706 mm a lencse görbületi sugara (elülső, ernyedt) 10,821 mm 10,842 mm 10,838 mm 10,871 mm 11,861 mm a lencse görbületi sugara (hátulsó, alkalmazkodott) 5,031 mm 5,031 mm 5,031 mm 5,031 mm 5,031 mm a lencse görbületi sugara (hátulsó, ernyedt) 5,090 mm 5,109 mm 5,110 mm 5,109 mm 5,323 mm A 1. táblázat tartalmazza a számítási eredmények fontosabb adatait, végeredményeit. A táblázat tartalmazza az eredeti - Hipsley és McDonald [2012] - eljárás geometriájához a numerikus modell által számolt eredményeket. Látható, hogy a geometriában történt módosítás csupán csak 0,1 D körüli növekedést mutat az eredeti alkalmazkodási szélességen felül. Ez csupán 6%-a annak az értéknek, amit átlagosan a pácienseken a műtét után másfél évvel mértek. Az eltérés eredete sok okból lehetséges, egyrészt a geometriai és anyagi paraméterek az 50 éves átlagos korosztályhoz tartozó adatok, abból a szűk csoportból és 11
12 néhány hivatkozott szakirodalmi mérésből (a részletekről lásd az értekezést). Néhány páciens esetében az alkalmazkodási szélesség növekedése ebbe a tartományba esett (Hipsley és McDonald [2012]). A 1. táblázat tartalmazza a 8. és a 9. ábra szerinti lyukelrendezés eredményeit. A koncentrált lyukak oszlopból az látszik, hogy ez a fajta lyukséma ugyanannyi lyukat és lézerrel kiégetett ínhártya térfogatot jelent, mint az eredeti geometriája a műtétnek, azonban néhány százalékkal nagyobb dioptriaváltozást eredményez, mint az eredeti lyukelrendezés. A folytonos lyukak oszlopból látható, hogy az említett lyukelrendezéseket tekintve a dioptriaváltozás természetesen ebben az esetben a legnagyobb. Ebből levonható az a következtetés, hogy a módszer elméleti működése szempontjából a numerikus modell eredményei követik azt a tendenciát, hogy annál nagyobb a dioptriaváltozás, minél nagyobb a lézerrel eltávolított ínhártyarész térfogata. 11. ábra A folytonos lyukak végeselemes hálója (részlet a lyukakról és metszet) A technika elvi hátterét jól alátámasztja a komplex modell, ugyanis, ha a folytonos lyukelrendezéshez tartozó esetet szemléljük, akkor látható, hogy ebben az esetben a dioptriaváltozás az eredeti geometriához képest nagyobb volt, mint a megelőző esetekben (1. táblázat). Az 1. táblázat utolsó oszlopa szemlélteti annak az esetnek az eredményét is, amelynél az ínhártya merevségét lecsökkentettem. Tulajdonképpen egy olyan esetet vizsgáltam, amikor az ínhártya merevsége nem befolyásolja a lencse alkalmazkodóképességét. Ebben az esetben látható, hogy az alkalmazkodási szélesség növekedése az eredeti intakt esethez képest 1,34 D. Természetesen ez az eredmény nem reprezentatív, mivel az ínhártya szerepe a komplex modellemben ilyen módon nem elhanyagolható.. Nem volt tehát célom az élettanilag egyébként nagyon sok paramétertől függő alkalmazkodási szélességváltozás pontos követése, hanem csupán a műtéti eljárás geometriájának finomhangolása a klasszikus alkalmazkodási apparátus elemzésével. Számítási eredményeimből összegzésként kijelenthető, hogy a modellemmel a műtéti beavatkozás geometriai módosításának az alkalmazkodási szélességre gyakorolt hatása tendenciaként követhető. További módosításokkal, és a klinikai mérési eredmények pontosításával a mért és a számított érték valószínűleg közelebb hozhatók egymáshoz, de én a további kutatások fontossága és tisztasága miatt ügyeltem arra, hogy az adott keretek között a modellemből származó számítási eredményeimet semmiféle módon ne torzítsam. Ennek a pontnak a lezárásaként megjegyzem, hogy a hivatkozott műtéti eljárást fejlesztő amerikai kutatók a közelmúltban személyesen megkerestek, mivel szándékukban áll modellem használata további kísérleteik ellenőrzésére és műtéti eljárásuk javítására. 2.2 Lencsefüggesztő rostok laboratóriumi vizsgálata Az alkalmazkodási folyamat természetéből következik, hogy a zonularostok mechanikai viselkedése nagyban befolyásolja annak létrejöttét, mivel a zonulák a sugárizomból erednek, és a szemlencséhez csatlakoznak. Tulajdonképpen a zonularostokon keresztül valósulhat meg az erőátadás a szemlencse és a sugártest között. 12
13 A mechanikai vizsgálataimhoz és azok kiértékeléséhez elengedhetetlen a zonularostok geometriai méreteinek ismerete is, ezért elvégzem a zonulák hálózatának geometriai vizsgálatát elektron- és fénymikroszkópos módszerekkel. Méréseimet sertésmintákon hajtottam végre, mert a sertésszem anatómiai felépítése és geometriai méretei hasonlítanak az emberi szeméhez. A mechanikai tulajdonságok jellemzésére alkalmas vizsgálati módszert úgy fejlesztettem ki, hogy az alkalmazható legyen emberi minták esetén is A zonularostok geometriai vizsgálata A zonulákat elektronmikroszkóppal (SEM, 12. ábra), és kétfajta módon optikai mikroszkóppal (OM I. és OM II.) is megvizsgáltam. A lencsefüggesztő rostok halmazának vastagságát 15 mintán vizsgáltam, és minden mintán négy különböző helyen mértem le, ahol a szálak halmaza közel azonos vastagságú és párhuzamos volt. A három különböző eljárásból a SEM módszer adta a legkisebb átlagos vastagságot: 33,2±9,1 µm. A második eljárásból (OM1.) származó átlagos vastagság valamivel nagyobbra adódott: 43,2±9,6 µm. Az utolsó metódussal (OM2.) 73,1±12,5 µm átlagos vastagságot mértem a rostok halmazára. 12. ábra SEM képek a zonularostokról, L lencse, Z zonula, CB - sugártest A zonularostok mechanikai tulajdonságainak vizsgálata A vizsgálatokhoz 30 friss sertésszemgolyót használtam fel a kísérletek során. A mérési napon mindig aznap levágott friss sertésmintákat vizsgáltam. A mérés alapötlete három különböző méretű (összesen négy darab) előre elkészített műanyag gyűrű használata volt (13. ábra). Mindegyik gyűrűnek különböző szerepe volt a mérés során. A minta előkészítésének folyamatát az 14. ábra mutatja. 13. ábra A mérési elrendezés vázlata, preparáló gyűrű, szeparáló gyűrű, megtámasztó gyűrű Minden szövetet a lencse előtt és mögött eltávolítottam (14. F és I ábra). A megtámasztó gyűrű szerepe az, hogy kizárja a rendszerből a sugárizom rugalmasságát. A 13
14 megtámasztó gyűrűt is vékony filmréteggel a helyére ragasztottam (0,2 ml cianoakrilát) a minta hátulsó oldalán, a zonularostok sugártestből kiinduló vonalára (14. J ábra). A szeparáló gyűrűből kettőt alkalmaztam, egyiket a lencse elülső, másikat a lencse hátulsó oldalára rögzítettem (szintén 0,2 ml cianoakrilát felhasználásával), így a lencse rugalmasságát is kizártam a rendszerből (13. ábra, 14. K és L ábra). Ezen előkészítés következtében a megtámasztó és a szeparáló gyűrűk közötti sávban a zonularostok helyezkednek el in situ állapotukban (14. K ábra). Az erőmérő cella a szeparáló gyűrű tetejéhez csatlakozott, de a gyűrű tetejére egy műanyag központosító golyót helyeztem el, hogy biztosítsam az átadódó erő függőlegességét. Ennek köszönhetően a rendszer függőleges eltolódása is biztosítottá vált. Ilyen módon a szeparáló gyűrűk el tudtak mozogni a megtámasztó gyűrűben (13. ábra). A folyamat során az erő és a függőleges eltolódás értékeit rögzítettem. A mérés elmozdulásvezérelt módon történt. 14. ábra Képek egy kísérleti mintáról az előkészítés különböző fázisaiban és a kísérlet után; felülnézet A, B, H, I, L; alulnézet D, E, F, J, K; oldalnézet C, G; a minta a tönkremenetel után M; metszet N; 1 preparáló gyűrű; 2 megtámasztó gyűrű; 3 szeparáló gyűrű A mérőberendezés típusa a következő volt: Z005, Zwick Roell AG, Ulm, Németország, 10-5 N érzékenységű erőmérő cellával ellátva. Az előterhelés értéke 5 mn, az erőmérő cella sebessége 1 mm/perc volt. A mérés eredményeinek rögzítése akkor kezdődött el, amikor az erőmérő cella a központosító golyót elérte és a mért erő túllépte az előterhelés értékét. A kiindulási állapotban a lencse, a szeparáló gyűrűk és a központosító golyó tömege meghatározható. Ebből G=9 mn kezdeti erőt kapunk a rendszeren az önsúlyból az erőelmozdulás értékek mérése előtt. Ez az érték nagyon fontos, amikor a mérési eredményeket hasonlítjuk össze az analitikus és végeselemes számítás eredményeivel (15. ábra, ahol z G az eltolódás a G=9 mn nagyságú önsúly hatására). Ezért a 15. ábra alapján az összehasonlíthatóság végett a számítások eredményeit el kell tolni. A laboratóriumi mérések eredményeiből az alábbi analitikus megoldást használhatjuk a lencsefüggesztő rostok 14
15 rugalmassági modulusának meghatározására. Az analitikus megoldáshoz a következő feltételezésekkel éltem: a zonulákat lineárisan rugalmasnak és összenyomhatatlannak (ν 0,5) tekintettem. (A részletes levezetést, és a további feltételeket lásd az értekezésben.) A 15. ábra alapján az analitikus megoldás a következő: 1 z t R R z F( z ) 2Ri E 2 l z l z l 2 0 o i amiben F(z) az erő a függőleges eltolódás függvényében, R i a szeparáló gyűrű külső sugara, R o a megtámasztó gyűrű belső sugara, l 0 a zonulák kezdeti hossza, t 0 a zonulák csoportjának kezdeti vastagsága, z a függőleges eltolódás, E a zonularostok rugalmassági modulusa. Ezzel az egyenlettel a laboratóriumi kísérletek eredményei összevethetők a feladat analitikus eredményeivel különböző rugalmassági modulusok esetében., (4) 15. ábra A különbség a mért (F -z ) és a számított (F-z) erő-elmozdulás diagram között (A); jelölésrendszer egy infinitezimálisan kicsiny elemen, ss csuklósan megtámasztott perem, t a vastagság, l a zonulák hossza, l 0 a különbség a külső (R o ) és a belső (R i ) sugár között, N r a normálerő a szálakban (B); a végeselemes hálózás (C) és a terhelt rendszernek az alakja a végelemes számításból (D) 16. ábra Az analitikus megoldás összehasonlítva a végelemes számítással; E a rugalmassági modulus, ν a Poisson-tényező A numerikus vizsgálatot ANSYS Workbench programrendszerrel végeztem. A matematikai közelítéshez 8 csomópontos héj végeselemeket alkalmaztam, a kiindulási helyzethez síkbeli körgyűrűt (hártyát) feltételeztem 10,5 mm-es belső és 12,5 mm-es külső 15
16 átmérővel a kísérleti elrendezés alapján (13. ábra). A peremfeltétel a külső és a belső peremen csuklós. A terhelés a belső peremen a gyűrű síkjára merőleges irányban működő támaszeltolódás volt (15. D ábra). A számítást a nagy elmozdulások elméletének megfelelően végeztem el. A konvergenciavizsgálat eredménye alapján a paraméteres vizsgálatoknál az alkalmazott elemszám körülbelül 1000 volt. A végeselemes kiértékelési módot hasonló okok miatt végeztem el, mint az előbb bemutatott analitikus megoldást, mégpedig a zonularostok makroszkopikus szintű rugalmassági modulusának meghatározásához. A Poisson-tényező segítségével a lencsefüggesztő rostok keresztirányú hatását elemeztem, mert a SEM méréseimből arra következtettem, hogy az egymás melletti sugárirányú zonularostok között összefonódások vannak. A ν=0 Poisson-tényező jellemezte azt az esetet, amikor a rostok teljesen függetlenül, a ν=0,49 pedig a zonulák csoportjának térfogat-állandóságát modellezte, ezáltal erős keresztirányú hatást feltételezve a szomszédos szálak között (16. ábra). A végeselemes számításoknál a kezdeti feszültségek hatását is figyelembe vettem, abból az okból kifolyólag, hogy annak ellenére, hogy három órával a minták beszerzése után a sugárizom a hullamerevség állapotában volt, a preparálás után a zonularostok mégsem voltak teljesen elernyedt állapotban. 17. ábra A mért erő-elmozdulás diagramok a laboratóriumi mérésből (A); a görbék kezdeti szakaszai (B); a negyedrendű illesztett polinomok (C) és az átlagos erők a szórásokkal feltüntetve a diszkrét elmozdulásokhoz (D) A 17. ábra mutatja a mért erő-elmozdulás diagramokat a mérés kezdetétől egészen a minták tönkremeneteléig. Az alkalmazott terhelésnek a mérés kezdeti szakaszán visszaterhelés része is volt, azért hogy beálljon a rendszer (az esetleges egyenetlenségek, feltámaszkodási pontatlanságok kiszűrésére). A 14. M ábrán látható egy tipikusan tönkrement minta a mérés után. Negyedrendű polinomiális regresszió segítségével görbét illesztettem az egyes mérési eredmények erő-elmozdulás eredményeinek kezdeti szakaszaira 0 és 1 mm-es függőleges elmozdulás között (17. ábra). Az átlaggörbe nem az origóból indul, mert a rendszer az előterhelés következtében beállt. A mért erők értékeinek szórásértékeit diszkrét eltolódásoknál 0,1 mm-enként számoltam ki (17. ábra). A laboratóriumi kísérletek eredményei és az analitikus kiértékelések eredményei a (4) egyenletet felhasználva a 18. ábra alapján összevethetők, a rugalmassági modulust kpa tartomány között felvéve, 50 kpa lépésközönként. A mérési eredmények átlagából és a szórásból azt mondhatjuk, hogy a sertés zonulák rugalmassági modulusának értéke 150 és 250 kpa között van (18. ábra). A 19. ábra mutatja a végeselemes számítás parametrikus vizsgálatának eredményeit, ha a kezdeti feszültségeket a lencsefüggesztő rostokban elhanyagoltam, illetve figyelembe vettem. Ez 16
17 alapján a zonularostok rugalmassági modulusa E 200 kpa értékre adódik. Ez az érték az, ami jól jellemzi a rostok mechanikai viselkedését, mivel az adott szakaszon az ehhez tartozó eredménynek a legkisebb az eltérése a mérési eredmény átlagához képest a vizsgált esetek közül (19. ábra). Az elvégzett vizsgálatok célja kettős volt: egyrészt egy összetett laboratóriumi mérési eljárást fejlesztettem ki, hogy a zonulák mechanikai tulajdonságait in situ vizsgálni tudjam az eredeti pozíciójukban, másrészt a kísérleti eredmények többféle kiértékelését is elvégezhessem. Az analitikus és a végeselemes kiértékelő vizsgálatokból a zonularostok rugalmassági modulusa 200 kpa körüli értékre adódik. A 19. ábrán láthattuk, hogy a Poisson-tényezőnek és a kezdeti feszültségeknek csak kisebb jelentőségű hatása van az erő-elmozdulás diagramok lefutására. Mivel legjobb tudásom szerint ez az első mérés, amely sertés zonulák rugalmassági modulusának megállapításával foglalkozik, a direkt összehasonlítás más szerzők eredményeivel nem lehetséges, de nem is ez volt a fő célom, hanem az, hogy egy olyan mérési eljárást dolgozzak ki a zonulák vizsgálatára, ami az eddigi zonulák mérésére alkalmazott eljárások esetleges bizonytalanságait kiküszöböli. Ennek szellemében olyan módszert fejlesztettem ki, amely teljesen intakt pozíciójú mérésekre alapul, ami nagy különbség más szerzők zonulamérési eljárásaihoz képest. Ezenfelül az erőátadás módja is a lehető legkevesebb közvetítő elemet és bizonytalanságot tartalmazza. Ahogy bemutattam, a kifejlesztett eljárással a zonulák rugalmassági modulusa meghatározható, akár egyszerű összefüggést alkalmazva is ((4) egyenlet), továbbá a mérési módszer úgy lett kialakítva, hogy az reprodukálható és kiterjeszthető legyen emberi mintákra is. 18. ábra Az analitikus megoldás együtt ábrázolva a mérési eredmények átlagával és szórásával, E a rugalmassági modulus 19. ábra A végeselemes analízis eredményei összehasonlítva a mérési eredmények átlagával és szórásával, E a rugalmassági modulus, ν a Poisson-tényező (A); A kezdeti feszültség és a Poisson-tényező hatásainak ábrázolása a mérési eredmények átlagával és szórásával együtt, E a rugalmassági modulus, ν a Poisson-tényező, IS1=4,4 kpa és IS2=8,4 kpa a két különböző kezdeti feszültség (B) 17
18 3. Az értekezés tézisei 1. Tézis. Létrehoztam a szemgolyó olyan végeselemes modelljét, melynek a szemészeti gyakorlat szempontjából legjellemzőbb geometriai és mechanikai tulajdonságai tetszőlegesen módosíthatók. A bemenő paraméterek alapján a geometria automatikusan generálódik az igényeknek megfelelően. A komplex végeselemes modell széles körben alkalmazható, elősegítve a különböző szemészeti problémák vizsgálatát az egyes alkotórészek deformációjának és a belső erőknek a nyomon követésével. A biomechanikai szempontból minden fontosnak ítélt részt tartalmazó komplex modell használhatóságát az alkalmazkodóképesség vizsgálatával ellenőriztem, eredményeimet összehasonlítottam más szerzők numerikus eredményeivel és rámutattam a komplex modell előnyeire az eddigi modellekhez képest. Kapcsolódó publikáció: [4, 7, 10] 2. Tézis. A szakirodalomból vett geometriai, mechanikai és optikai paramétereket felhasználva a numerikus modell segítségével megvizsgáltam a szemlencse alkalmazkodási szélességének a kor előrehaladtával bekövetkező változását, beszűkülését. Ehhez - a korábbi eredményekhez képest precízebb módszerrel - meghatároztam a szemlencse dioptriáját a lencse szimmetriatengelyében. A komplex numerikus modell segítségével bizonyítottam a szemészek körében felvetett hipotézist, mely szerint a szemlencse alkalmazkodóképességének korral történő változásában a geometriai és mechanikai paraméterek hatása mellett a lencse törésmutatójában bekövetkező változás is legalább akkora szerepet játszik. Kapcsolódó publikáció: [4, 6, 9] 3. Tézis. A komplex végeselemes modell segítségével vizsgáltam egy, az alkalmazkodási szélesség növelésére kifejlesztett - ínhártyát érintő - szabadalmaztatott műtéti eljárást. Végeselemes modell segítségével először ellenőriztem a műtéti eljárás alkalmazkodásra gyakorolt hatását és működésének elvét, majd paraméteres vizsgálatsorozatot végeztem el, aminek segítségével megvizsgáltam a műtét során kialakítandó lyukak elrendezésének és mennyiségének hatását az alkalmazkodási szélességre. A numerikus modell eredményei alapján javaslatot tettem a műtéti eljárás geometriájának egy élettani szempontból lehetséges módosítására, amellyel az eredeti geometriai kialakításhoz képest nagyobb alkalmazkodási szélesség érhető el. Kapcsolódó publikáció: [4,6] 4. Tézis A zonularostok mechanikai viselkedésének és paramétereinek meghatározására kifejlesztettem egy új, és teljesen egyedi laboratóriumi kísérleti eljárást, ami egyszerű eszközökkel elvégezhető. A mérési eljárás elsődleges célja, hogy a zonularostok halmazát in-situ vizsgálni lehessen a rostok lencséhez és sugártesthez csatlakozó pontjait nem megsértve, ugyanakkor az egyéb részek merevségétől függetlenítve. Ezenfelül a mérési eljárás kifejlesztésének másik fontos célkitűzése volt a terhelési erőnek és az erőmérésnek a lehető legegyszerűbb kialakítása a minél pontosabb eredmény és kiértékelés érdekében. A mérési eljárást sertésmintákon teszteltem, ehhez a zonulák geometriáját különböző módszerekkel megmértem. Kapcsolódó publikáció: [1, 5] 5. Tézis A zonularostokkal kapcsolatos laboratóriumi mérési eredmények kiértékelésére analitikus eljárást dolgoztam ki, amivel a kísérleti eredményekből gyorsan és egyszerűen értéktartomány adható meg a zonulák csoportjának rugalmassági modulusára. Az analitikus megoldás használhatóságát a zonulák rugalmassági modulusának meghatározására végeselemes numerikus modellen a szilárdsági jellemzők és a kezdeti feltételek részletes paraméteres vizsgálatsorozatával ellenőriztem. Kapcsolódó publikáció: [1, 5] 18
19 Az értekezés témakörében készült publikációim Külföldön megjelent idegen nyelvű folyóiratcikk [1] Bocskai, Z.I., Sándor, G.L., Kiss Z., Bojtár, I., Nagy, Z.Z. (2014): Evaluation of the mechanical behaviour and estimation of the elastic properties of porcine zonular fibres. Journal of Biomechanics, 47(13), pp (IF 2,496) [2] Sándor, G.L., Kiss, Z., Bocskai, Z.I., Kolev, K., Takács, Á.I., Juhász, É., Kránitz, K., Tóth, G., Gyenes, A., Bojtár, I., Juhász, T., Nagy, Z.Z. (2014): Comperison of the mechanical properties of the anterior lens capsule following manual capsulorhexis and femtosecond laser capsulotomy, Journal of Refractive Surgery, 30, pp (IF 2,781) [3] Sándor,.L., Kiss, Z., Bocskai, Z.I., Kolev, K., Takács, Á.I., Juhász, É., Kránitz, K., Tóth, G., Gyenes, A., Bojtár, I., Juhász, T., Nagy, Z.Z. (2015): Evaluation of the mechanical properties of the anterior lens capsule following femtosecond laser capsulotomy at different pulse energy settings, Journal of Refractive Surgery, 31, pp (IF 2,781) Magyarországon megjelent idegen nyelvű folyóiratcikk [4] Bocskai, Z.I., Bojtár, I. (2013): Biomechanical modelling of the accommodation problem of human eye. Periodica Polytechnica Civil Engineering, 57(1), pp (IF 0,250) [5] Bocskai, Z.I., Kiss, Z., Sándor, G.L., Bojtár, I., Nagy, Z.Z. (2014): Scanning electron and optical microscopic studies of the system of porcine zonular fibres, Biomechanica Hungarica, 7(2), pp Magyarországon megjelent magyar nyelvű folyóiratcikk [6] Bocskai, Z.I., Bojtár, I. (2015): Az ínhártyát érintő lézeres látásjavító szemműtét végeselemes vizsgálata és elemzése, Biomechanica Hungarica, 8(2), (közlésre elfogadva) Könyvfejezet [7] Bocskai, Z.I., Bojtár, I. (2012): Emberi szem biomechanikai vizsgálata. In Kiss R.M. (szerk.), Biomechanikai modellezés, monográfia, TERC Kereskedelmi és Szolgáltató Kft., Budapest, ISBN , pp [8] Sándor, G.L., Kiss, Z., Bocskai, Z.I., Bojtár, I., Takács, Á.I., Nagy, Z.Z. (2014): Mechanical behavior of capsulotomy performed with femtosecond laser. In: Nagy, Z.Z., (szerk.), Femtosecond laser-assisted cataract surgery: facts and results, Slack Incorporated, Thorofare, ISBN , pp Helyi részvételű konferencia kiadványában megjelent idegen nyelvű konferenciacikk [9] Bocskai, Z.I. (2012): Numerical simulation of the human eye accommodation. Proceedings of the Conference of Junior Researchers in Civil Engineering, Budapest, Hungary, June, ISBN , pp Helyi részvételű konferencia kiadványában megjelent magyar nyelvű konferenciacikk [10] Bocskai, Z.I., Bojtár, I. (2011): Az emberi szem biomechanikai modellezése. Építőmérnöki Kar a Kutatóegyetemért, monográfia, kiadja az BME Építőmérnöki Kar dékánja, Budapest, ISBN , pp
20 Kivonatban megjelent előadás [11] Bocskai, Z.I., Bojtár, I. (2012): Szemészeti problémák modellezése végeselemmódszer alkalmazásával. SHIOL Societas Hungarica Ad Implantandam Oculi Lenticulam, Magyar Műlencse és Refraktív Sebészeti Társaság Kongresszusa, Budapest, Magyarország, március , pp. 34. [12] Bocskai, Z.I., Bojtár, I. (2012): The complex biomechanical analysis of the human eye, ESMC th European Solid Mechanics Conference, Graz, Austria, 9-13 July, ISBN , pp [13] Bocskai, Z. I., Bojtár, I. (2013): A szemlencse és környező részeinek mechanikai viselkedése. V. Magyar Biomechanikai Konferencia, Budapest, Magyarország, május , pp. 55. [14] Bocskai, Z.I., Kiss, Z., Sándor, G.L., Bojtár, I., Nagy, Z.Z. (2013): Measurement of porcine zonular fibres. Euromech Colloquium 533, Biomechanics of the Eye, University of Genoa, Italy, July, pp [15] Bocskai, Z.I., Bojtár, I. (2014): A LaserACE eljárás hatékonyságának biomechanikai elemzése a dinamikus akkomodáció növelése érdekében. A Magyar Szemorvostársaság évi Kongresszusa, Pécs, Magyarország, június Szemészet, 151, supplementum I., ISSN , pp. 30. Szemináriumi és konferencia előadás [16] Bocskai, Z.I., Bojtár, I. (2011): Biomechanical modelling of the human eye. 18th Inter-Institute Seminar for Young Researchers, Budapest, Magyarország, September, pp. 15. [17] Bocskai, Z.I., Bojtár, I. (2012): A presbyopia új excimer lézeres javíthatósága: akkomodáció és presbyopia a mérnök szemével modellezés végeselemmódszer segítségével. SHIOL Societas Hungarica Ad Implantandam Oculi Lenticulam, Magyar Műlencse és Refraktív Sebészeti Társaság Kongresszusa, Budapest, Magyarország, március [18] Bocskai, Z.I., Kiss, Z., Sándor, G.L., Bojtár, I., Nagy, Z.Z. (2013): Measurement of porcine eye zonular fibres. 19th Inter-Institute Seminar for Young Researchers, Institute for Mechanics of Materials and Structures, Vienna, Austria, October, ISBN , pp. 21. Hivatkozások a tézisfüzetben Chien, C.H., Huang, T., Schachar, R.A. (2003): A mathematical expression for the human crystalline lens, Comprehensive Therapy, 29, pp Hipsley, A., McDonald, M. (2012): Laser Scleral Matrix Microexcisions (LaserACE/Erbium YAG Laser), In: Pallikaris I., Plainis S., Charman W.N. (editors): Presbyopia, Origins, Effects and Treatment, SLACK Incorporated, pp Śródka, W. (2011): Evaluating the material parameters of the human cornea in a numerical model, Acta of Bioengineering and Biomechanics, 13, pp Tsorbatzoglou, A., Németh, G., Széll, N., Biró, Z., Berta, A. (2007): Anterior segment changes with age and during accommodation measured with partial coherence interferometry, Journal of Cataract and Refractive Surgery, 33, pp
Az ínhártyát érintő lézeres látásjavító szemműtét végeselemes
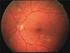 Biomechanica Hungarica VIII. évfolyam, 2. szám Az ínhártyát érintő lézeres látásjavító szemműtét végeselemes vizsgálata és elemzése Bocskai Zoltán Imre, Bojtár Imre Budapesti Műszaki és Gazdaságtudományi
Biomechanica Hungarica VIII. évfolyam, 2. szám Az ínhártyát érintő lézeres látásjavító szemműtét végeselemes vizsgálata és elemzése Bocskai Zoltán Imre, Bojtár Imre Budapesti Műszaki és Gazdaságtudományi
TERMÉKTERVEZÉS NUMERIKUS MÓDSZEREI. 1. Bevezetés
 TERMÉKTERVEZÉS NUMERIKUS MÓDSZEREI Dr. Goda Tibor egyetemi docens Gép- és Terméktervezés Tanszék 1. Bevezetés 1.1. A végeselem módszer alapjai - diszkretizáció, - szerkezet felbontása kicsi szabályos elemekre
TERMÉKTERVEZÉS NUMERIKUS MÓDSZEREI Dr. Goda Tibor egyetemi docens Gép- és Terméktervezés Tanszék 1. Bevezetés 1.1. A végeselem módszer alapjai - diszkretizáció, - szerkezet felbontása kicsi szabályos elemekre
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
FÉLMEREV KAPCSOLATOK NUMERIKUS SZIMULÁCIÓJA
 FÉLMEREV KAPCSOLATOK NUMERIKUS SZIMULÁCIÓJA Vértes Katalin * - Iványi Miklós ** RÖVID KIVONAT Acélszerkezeti kapcsolatok jellemzőinek (szilárdság, merevség, elfordulási képesség) meghatározása lehetséges
FÉLMEREV KAPCSOLATOK NUMERIKUS SZIMULÁCIÓJA Vértes Katalin * - Iványi Miklós ** RÖVID KIVONAT Acélszerkezeti kapcsolatok jellemzőinek (szilárdság, merevség, elfordulási képesség) meghatározása lehetséges
XVII. econ Konferencia és ANSYS Felhasználói Találkozó
 XVII. econ Konferencia és ANSYS Felhasználói Találkozó Hazay Máté, Bakos Bernadett, Bojtár Imre hazay.mate@epito.bme.hu PhD hallgató Budapesti Műszaki és Gazdaságtudományi Egyetem Tartószerkezetek Mechanikája
XVII. econ Konferencia és ANSYS Felhasználói Találkozó Hazay Máté, Bakos Bernadett, Bojtár Imre hazay.mate@epito.bme.hu PhD hallgató Budapesti Műszaki és Gazdaságtudományi Egyetem Tartószerkezetek Mechanikája
Mozgatható térlefedő szerkezetek
 Mozgatható térlefedő szerkezetek TDK Konferencia 2010 Szilárdságtani és tartószerkezeti szekció Tartalomjegyzék 1 Absztrakt 2 Bevezetés 3 Az alakzat mozgásának görbületre gyakorolt hatása 4 Teljes összenyomódás
Mozgatható térlefedő szerkezetek TDK Konferencia 2010 Szilárdságtani és tartószerkezeti szekció Tartalomjegyzék 1 Absztrakt 2 Bevezetés 3 Az alakzat mozgásának görbületre gyakorolt hatása 4 Teljes összenyomódás
KOMPOZITLEMEZ ORTOTRÓP
 KOMPOZITLEMEZ ORTOTRÓP ANYAGJELLEMZŐINEK MEGHATÁROZÁSA ÉS KÍSÉRLETI IGAZOLÁSA Nagy Anna anna.nagy@econengineering.com econ Engineering econ Engineering Kft. 2019 H-1116 Budapest, Kondorosi út 3. IV. emelet
KOMPOZITLEMEZ ORTOTRÓP ANYAGJELLEMZŐINEK MEGHATÁROZÁSA ÉS KÍSÉRLETI IGAZOLÁSA Nagy Anna anna.nagy@econengineering.com econ Engineering econ Engineering Kft. 2019 H-1116 Budapest, Kondorosi út 3. IV. emelet
A végeselem módszer alapjai. 2. Alapvető elemtípusok
 A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
SZIMULÁCIÓ ÉS MODELLEZÉS AZ ANSYS ALKALMAZÁSÁVAL
 SZIMULÁCIÓ ÉS MODELLEZÉS AZ ANSYS ALKALMAZÁSÁVAL MAGYAR TUDOMÁNY NAPJA KONFERENCIA 2010 GÁBOR DÉNES FŐISKOLA CSUKA ANTAL TARTALOM A KÍSÉRLET ÉS MÉRÉS JELENTŐSÉGE A MÉRNÖKI GYAKORLATBAN, MECHANIKAI FESZÜLTSÉG
SZIMULÁCIÓ ÉS MODELLEZÉS AZ ANSYS ALKALMAZÁSÁVAL MAGYAR TUDOMÁNY NAPJA KONFERENCIA 2010 GÁBOR DÉNES FŐISKOLA CSUKA ANTAL TARTALOM A KÍSÉRLET ÉS MÉRÉS JELENTŐSÉGE A MÉRNÖKI GYAKORLATBAN, MECHANIKAI FESZÜLTSÉG
Trapézlemez gerincő tartók beroppanásvizsgálata
 Trapézlemez gerincő tartók beroppanásvizsgálata Témavezetı: Dr. Dunai László Készítette: Kövesdi Balázs Bevezetés Korábbi eredmények rövid áttekintése Kísérletek bemutatása és értékelése Új kutatási irányok
Trapézlemez gerincő tartók beroppanásvizsgálata Témavezetı: Dr. Dunai László Készítette: Kövesdi Balázs Bevezetés Korábbi eredmények rövid áttekintése Kísérletek bemutatása és értékelése Új kutatási irányok
Kiválósági ösztöndíjjal támogatott kutatások az Építőmérnöki Karon c. előadóülés
 Kiválósági ösztöndíjjal támogatott kutatások az Építőmérnöki Karon c. előadóülés Hazay Máté hazay.mate@epito.bme.hu PhD hallgató Budapesti Műszaki és Gazdaságtudományi Egyetem Tartószerkezetek Mechanikája
Kiválósági ösztöndíjjal támogatott kutatások az Építőmérnöki Karon c. előadóülés Hazay Máté hazay.mate@epito.bme.hu PhD hallgató Budapesti Műszaki és Gazdaságtudományi Egyetem Tartószerkezetek Mechanikája
A SZEM BIOMECHANIKAI VISELKEDÉSÉNEK MODELLEZÉSE
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM TARTÓSZERKEZETEK MECHANIKÁJATANSZÉK BOCSKAI ZOLTÁN A SZEM BIOMECHANIKAI VISELKEDÉSÉNEK MODELLEZÉSE PHD ÉRTEKEZÉS Témavezető DR. BOJTÁR IMRE Budapest, 2015
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM TARTÓSZERKEZETEK MECHANIKÁJATANSZÉK BOCSKAI ZOLTÁN A SZEM BIOMECHANIKAI VISELKEDÉSÉNEK MODELLEZÉSE PHD ÉRTEKEZÉS Témavezető DR. BOJTÁR IMRE Budapest, 2015
GÉPI ÉS EMBERI POZICIONÁLÁSI, ÉRINTÉSI MŰVELETEK DINAMIKÁJA
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM MŰSZAKI MECHANIKAI TANSZÉK PhD Tézisfüzet GÉPI ÉS EMBERI POZICIONÁLÁSI, ÉRINTÉSI MŰVELETEK DINAMIKÁJA Szerző MAGYAR Bálint Témavezető Dr. STÉPÁN Gábor Budapest,
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM MŰSZAKI MECHANIKAI TANSZÉK PhD Tézisfüzet GÉPI ÉS EMBERI POZICIONÁLÁSI, ÉRINTÉSI MŰVELETEK DINAMIKÁJA Szerző MAGYAR Bálint Témavezető Dr. STÉPÁN Gábor Budapest,
Mikroszkóp vizsgálata Folyadék törésmutatójának mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 8. MÉRÉS Mikroszkóp vizsgálata Folyadék törésmutatójának mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 12. Szerda délelőtti csoport
KLASSZIKUS FIZIKA LABORATÓRIUM 8. MÉRÉS Mikroszkóp vizsgálata Folyadék törésmutatójának mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 12. Szerda délelőtti csoport
Mikroszkóp vizsgálata Lencse görbületi sugarának mérése Folyadék törésmutatójának mérése
 Mikroszkóp vizsgálata Lencse görbületi sugarának mérése Folyadék törésmutatójának mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. március 19. (hétfő délelőtti csoport) 1. Mikroszkóp vizsgálata 1.1. A mérés
Mikroszkóp vizsgálata Lencse görbületi sugarának mérése Folyadék törésmutatójának mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. március 19. (hétfő délelőtti csoport) 1. Mikroszkóp vizsgálata 1.1. A mérés
Rugalmas állandók mérése
 Rugalmas állandók mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. április 23. (hétfő délelőtti csoport) 1. Young-modulus mérése behajlásból 1.1. A mérés menete A mérés elméleti háttere megtalálható a jegyzetben
Rugalmas állandók mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. április 23. (hétfő délelőtti csoport) 1. Young-modulus mérése behajlásból 1.1. A mérés menete A mérés elméleti háttere megtalálható a jegyzetben
Kiöntött síncsatornás felépítmény kialakításának egyes elméleti kérdései
 Kiöntött síncsatornás felépítmény kialakításának egyes elméleti kérdései VII. Városi Villamos Vasúti Pálya Napra Budapest, 2014. április 17. Major Zoltán egyetemi tanársegéd Széchenyi István Egyetem, Győr
Kiöntött síncsatornás felépítmény kialakításának egyes elméleti kérdései VII. Városi Villamos Vasúti Pálya Napra Budapest, 2014. április 17. Major Zoltán egyetemi tanársegéd Széchenyi István Egyetem, Győr
Ejtési teszt modellezése a tervezés fázisában
 Antal Dániel, doktorandusz, Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szabó Tamás, egyetemi docens, Ph.D., Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szilágyi Attila, egyetemi adjunktus,
Antal Dániel, doktorandusz, Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szabó Tamás, egyetemi docens, Ph.D., Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szilágyi Attila, egyetemi adjunktus,
TERMÉKSZIMULÁCIÓ. Dr. Kovács Zsolt. Végeselem módszer. Elıadó: egyetemi tanár. Termékszimuláció tantárgy 6. elıadás március 22.
 TERMÉKZIMULÁCIÓ Végeselem módszer Termékszimuláció tantárgy 6. elıadás 211. március 22. Elıadó: Dr. Kovács Zsolt egyetemi tanár A végeselem módszer lényege A vizsgált, tetszıleges geometriai kialakítású
TERMÉKZIMULÁCIÓ Végeselem módszer Termékszimuláció tantárgy 6. elıadás 211. március 22. Elıadó: Dr. Kovács Zsolt egyetemi tanár A végeselem módszer lényege A vizsgált, tetszıleges geometriai kialakítású
Rugalmas állandók mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 2. MÉRÉS Rugalmas állandók mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 16. Szerda délelőtti csoport 1. A mérés rövid leírása Mérésem
KLASSZIKUS FIZIKA LABORATÓRIUM 2. MÉRÉS Rugalmas állandók mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 16. Szerda délelőtti csoport 1. A mérés rövid leírása Mérésem
A MODELLALKOTÁS ELVEI ÉS MÓDSZEREI
 SZENT ISTVÁN EGYETEM GÖDÖLLŐ MECHANIKAI ÉS GÉPTANI INTÉZET A MODELLALKOTÁS ELVEI ÉS MÓDSZEREI Dr. M. Csizmadia Béla egyetemi tanár, az MMK Gépészeti Tagozatának elnöke Budapest 2013. október. 25. BPMK
SZENT ISTVÁN EGYETEM GÖDÖLLŐ MECHANIKAI ÉS GÉPTANI INTÉZET A MODELLALKOTÁS ELVEI ÉS MÓDSZEREI Dr. M. Csizmadia Béla egyetemi tanár, az MMK Gépészeti Tagozatának elnöke Budapest 2013. október. 25. BPMK
Szemészeti optika, fénytörési hibák. Németh János
 Szemészeti optika, fénytörési hibák Németh János Témavázlat A szem, mint optikai rendszer A szem fénytörése és meghatározása Alkalmazkodóképesség Presbyopia Látóélesség Fénytörési hibák és korrigálásuk
Szemészeti optika, fénytörési hibák Németh János Témavázlat A szem, mint optikai rendszer A szem fénytörése és meghatározása Alkalmazkodóképesség Presbyopia Látóélesség Fénytörési hibák és korrigálásuk
A II. kategória Fizika OKTV mérési feladatainak megoldása
 Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Mikroelektromechanikai szerkezetek szilárdsági és megbízhatósági vizsgálata
 OTKA nyilvántartási szám: T 049848 Mikroelektromechanikai szerkezetek szilárdsági és megbízhatósági vizsgálata Témavezetı: Dr. Kovács Ádám egyetemi docens, BME Mőszaki Mechanikai Tanszék Kutatási beszámoló:
OTKA nyilvántartási szám: T 049848 Mikroelektromechanikai szerkezetek szilárdsági és megbízhatósági vizsgálata Témavezetı: Dr. Kovács Ádám egyetemi docens, BME Mőszaki Mechanikai Tanszék Kutatási beszámoló:
Acélszerkezetek korszerű tűzvédelmének néhány kérdése
 Acélszerkezetek korszerű tűzvédelmének néhány kérdése A viselkedés-alapú tervezés elemei Dr. Horváth László PhD, egyetemi docens 1 Tartalom Viselkedés-alapú tervezés fogalma Alkalmazási lehetőségei Acélszerkezetek
Acélszerkezetek korszerű tűzvédelmének néhány kérdése A viselkedés-alapú tervezés elemei Dr. Horváth László PhD, egyetemi docens 1 Tartalom Viselkedés-alapú tervezés fogalma Alkalmazási lehetőségei Acélszerkezetek
Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet
 Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet 2. előadás A rugalmas lemezelmélet alapfeltevései A lemez anyaga homogén, izotróp, lineárisan rugalmas (Hooke törvény); A terheletlen állapotban
Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet 2. előadás A rugalmas lemezelmélet alapfeltevései A lemez anyaga homogén, izotróp, lineárisan rugalmas (Hooke törvény); A terheletlen állapotban
FÉMGYURUS FAKAPCSOLATOK PALÁSTNYOMÁSI TEHERBÍRÁSÁNAK VIZSGÁLATA PONTOSÍTOTT FELÜLETI NYOMÁSELOSZLÁS ALAPJÁN
 FÉMGYURUS FAKAPCSOLATOK PALÁSTNYOMÁSI TEHERBÍRÁSÁNAK VIZSGÁLATA PONTOSÍTOTT FELÜLETI NYOMÁSELOSZLÁS ALAPJÁN Erdodi László * - Bódi István ** RÖVID KIVONAT A BME Hidak és Szerkezetek Tanszéke Szerkezetvizsgáló
FÉMGYURUS FAKAPCSOLATOK PALÁSTNYOMÁSI TEHERBÍRÁSÁNAK VIZSGÁLATA PONTOSÍTOTT FELÜLETI NYOMÁSELOSZLÁS ALAPJÁN Erdodi László * - Bódi István ** RÖVID KIVONAT A BME Hidak és Szerkezetek Tanszéke Szerkezetvizsgáló
Nanokeménység mérések
 Cirkónium Anyagtudományi Kutatások ek Nguyen Quang Chinh, Ugi Dávid ELTE Anyagfizikai Tanszék Kutatási jelentés a Nemzeti Kutatási, Fejlesztési és Innovációs Hivatal támogatásával az NKFI Alapból létrejött
Cirkónium Anyagtudományi Kutatások ek Nguyen Quang Chinh, Ugi Dávid ELTE Anyagfizikai Tanszék Kutatási jelentés a Nemzeti Kutatási, Fejlesztési és Innovációs Hivatal támogatásával az NKFI Alapból létrejött
PhD DISSZERTÁCIÓ TÉZISEI
 Budapesti Muszaki és Gazdaságtudományi Egyetem Fizikai Kémia Tanszék MTA-BME Lágy Anyagok Laboratóriuma PhD DISSZERTÁCIÓ TÉZISEI Mágneses tér hatása kompozit gélek és elasztomerek rugalmasságára Készítette:
Budapesti Muszaki és Gazdaságtudományi Egyetem Fizikai Kémia Tanszék MTA-BME Lágy Anyagok Laboratóriuma PhD DISSZERTÁCIÓ TÉZISEI Mágneses tér hatása kompozit gélek és elasztomerek rugalmasságára Készítette:
Korrodált acélszerkezetek vizsgálata
 Korrodált acélszerkezetek vizsgálata 1. Szerkezeti példák és laboratóriumi alapkutatás Oszvald Katalin Témavezető : Dr. Dunai László Budapest, 2009.12.08. 1 Általános célkitűzések Korrózió miatt károsodott
Korrodált acélszerkezetek vizsgálata 1. Szerkezeti példák és laboratóriumi alapkutatás Oszvald Katalin Témavezető : Dr. Dunai László Budapest, 2009.12.08. 1 Általános célkitűzések Korrózió miatt károsodott
Optika gyakorlat 2. Geometriai optika: planparalel lemez, prizma, hullámvezető
 Optika gyakorlat. Geometriai optika: planparalel lemez, prizma, hullámvezető. példa: Fényterjedés planparalel lemezen keresztül A plánparalel lemezen történő fényterjedés hatására a fénysugár újta távolsággal
Optika gyakorlat. Geometriai optika: planparalel lemez, prizma, hullámvezető. példa: Fényterjedés planparalel lemezen keresztül A plánparalel lemezen történő fényterjedés hatására a fénysugár újta távolsággal
Síklapokból álló üvegoszlopok laboratóriumi. vizsgálata. Jakab András, doktorandusz. BME, Építőanyagok és Magasépítés Tanszék
 Síklapokból álló üvegoszlopok laboratóriumi vizsgálata Előadó: Jakab András, doktorandusz BME, Építőanyagok és Magasépítés Tanszék Nehme Kinga, Nehme Salem Georges Szilikátipari Tudományos Egyesület Üvegipari
Síklapokból álló üvegoszlopok laboratóriumi vizsgálata Előadó: Jakab András, doktorandusz BME, Építőanyagok és Magasépítés Tanszék Nehme Kinga, Nehme Salem Georges Szilikátipari Tudományos Egyesület Üvegipari
A talajok összenyomódásának vizsgálata
 A talajok összenyomódásának vizsgálata Amit már tudni kellene Összenyomódás Konszolidáció Normálisan konszolidált talaj Túlkonszolidált talaj Túlkonszolidáltsági arányszám,ocr Konszolidáció az az időben
A talajok összenyomódásának vizsgálata Amit már tudni kellene Összenyomódás Konszolidáció Normálisan konszolidált talaj Túlkonszolidált talaj Túlkonszolidáltsági arányszám,ocr Konszolidáció az az időben
Al-Mg-Si háromalkotós egyensúlyi fázisdiagram közelítő számítása
 l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
Mikroszkóp vizsgálata és folyadék törésmutatójának mérése (8-as számú mérés) mérési jegyzõkönyv
 (-as számú mérés) mérési jegyzõkönyv Készítette:, II. éves fizikus... Beadás ideje:... / A mérés leírása: A mérés során egy mikroszkóp különbözõ nagyítású objektívjeinek nagyítását, ezek fókusztávolságát
(-as számú mérés) mérési jegyzõkönyv Készítette:, II. éves fizikus... Beadás ideje:... / A mérés leírása: A mérés során egy mikroszkóp különbözõ nagyítású objektívjeinek nagyítását, ezek fókusztávolságát
Infobionika ROBOTIKA. X. Előadás. Robot manipulátorok II. Direkt és inverz kinematika. Készült a HEFOP P /1.0 projekt keretében
 Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Szilárd testek rugalmassága
 Fizika villamosmérnököknek Szilárd testek rugalmassága Dr. Giczi Ferenc Széchenyi István Egyetem, Fizika és Kémia Tanszék Győr, Egyetem tér 1. 1 Deformálható testek (A merev test idealizált határeset.)
Fizika villamosmérnököknek Szilárd testek rugalmassága Dr. Giczi Ferenc Széchenyi István Egyetem, Fizika és Kémia Tanszék Győr, Egyetem tér 1. 1 Deformálható testek (A merev test idealizált határeset.)
Matematika 11 Koordináta geometria. matematika és fizika szakos középiskolai tanár. > o < szeptember 27.
 Matematika 11 Koordináta geometria Juhász László matematika és fizika szakos középiskolai tanár > o < 2015. szeptember 27. copyright: c Juhász László Ennek a könyvnek a használatát szerzői jog védi. A
Matematika 11 Koordináta geometria Juhász László matematika és fizika szakos középiskolai tanár > o < 2015. szeptember 27. copyright: c Juhász László Ennek a könyvnek a használatát szerzői jog védi. A
Modern Fizika Labor. 2. Az elemi töltés meghatározása. Fizika BSc. A mérés dátuma: nov. 29. A mérés száma és címe: Értékelés:
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. nov. 29. A mérés száma és címe: 2. Az elemi töltés meghatározása Értékelés: A beadás dátuma: 2011. dec. 11. A mérést végezte: Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. nov. 29. A mérés száma és címe: 2. Az elemi töltés meghatározása Értékelés: A beadás dátuma: 2011. dec. 11. A mérést végezte: Szőke Kálmán Benjamin
x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs mátrixa 3D-ben?
 . Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
. Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
Hidraulikus hálózatok robusztusságának növelése
 Dr. Dulovics Dezső Junior Szimpózium 2018. Hidraulikus hálózatok robusztusságának növelése Előadó: Huzsvár Tamás MSc. Képzés, II. évfolyam Témavezető: Wéber Richárd, Dr. Hős Csaba www.hds.bme.hu Az előadás
Dr. Dulovics Dezső Junior Szimpózium 2018. Hidraulikus hálózatok robusztusságának növelése Előadó: Huzsvár Tamás MSc. Képzés, II. évfolyam Témavezető: Wéber Richárd, Dr. Hős Csaba www.hds.bme.hu Az előadás
Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2013. szeptember 23. Javítva: 2013.10.09.
Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2013. szeptember 23. Javítva: 2013.10.09.
Mérés: Millikan olajcsepp-kísérlete
 Mérés: Millikan olajcsepp-kísérlete Mérés célja: 1909-ben ezt a mérést Robert Millikan végezte el először. Mérése során meg tudta határozni az elemi részecskék töltését. Ezért a felfedezéséért Nobel-díjat
Mérés: Millikan olajcsepp-kísérlete Mérés célja: 1909-ben ezt a mérést Robert Millikan végezte el először. Mérése során meg tudta határozni az elemi részecskék töltését. Ezért a felfedezéséért Nobel-díjat
Hangfrekvenciás mechanikai rezgések vizsgálata
 Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
2.9.1. TABLETTÁK ÉS KAPSZULÁK SZÉTESÉSE
 2.9.1 Tabletták és kapszulák szétesése Ph.Hg.VIII. Ph.Eur.6.3-1 01/2009:20901 2.9.1. TABLETTÁK ÉS KAPSZULÁK SZÉTESÉSE A szétesésvizsgálattal azt határozzuk meg, hogy az alábbiakban leírt kísérleti körülmények
2.9.1 Tabletták és kapszulák szétesése Ph.Hg.VIII. Ph.Eur.6.3-1 01/2009:20901 2.9.1. TABLETTÁK ÉS KAPSZULÁK SZÉTESÉSE A szétesésvizsgálattal azt határozzuk meg, hogy az alábbiakban leírt kísérleti körülmények
Tárgy. Forgóasztal. Lézer. Kamera 3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL
 3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL. Bevezetés A lézeres letapogatás a ma elérhet legpontosabb 3D-s rekonstrukciót teszi lehet vé. Alapelve roppant egyszer : egy lézeres csíkkal megvilágítjuk a tárgyat.
3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL. Bevezetés A lézeres letapogatás a ma elérhet legpontosabb 3D-s rekonstrukciót teszi lehet vé. Alapelve roppant egyszer : egy lézeres csíkkal megvilágítjuk a tárgyat.
DETERMINATION OF SHEAR STRENGTH OF SOLID WASTES BASED ON CPT TEST RESULTS
 Műszaki Földtudományi Közlemények, 83. kötet, 1. szám (2012), pp. 271 276. HULLADÉKOK TEHERBÍRÁSÁNAK MEGHATÁROZÁSA CPT-EREDMÉNYEK ALAPJÁN DETERMINATION OF SHEAR STRENGTH OF SOLID WASTES BASED ON CPT TEST
Műszaki Földtudományi Közlemények, 83. kötet, 1. szám (2012), pp. 271 276. HULLADÉKOK TEHERBÍRÁSÁNAK MEGHATÁROZÁSA CPT-EREDMÉNYEK ALAPJÁN DETERMINATION OF SHEAR STRENGTH OF SOLID WASTES BASED ON CPT TEST
Hangfrekvenciás mechanikai rezgések vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
HÍDTARTÓK ELLENÁLLÁSTÉNYEZŐJE
 HÍDTARTÓK ELLENÁLLÁSTÉNYEZŐJE Csécs Ákos * - Dr. Lajos Tamás ** RÖVID KIVONAT A Budapesti Műszaki és Gazdaságtudományi Egyetem Hidak és Szerkezetek Tanszéke megbízta a BME Áramlástan Tanszékét az M8-as
HÍDTARTÓK ELLENÁLLÁSTÉNYEZŐJE Csécs Ákos * - Dr. Lajos Tamás ** RÖVID KIVONAT A Budapesti Műszaki és Gazdaságtudományi Egyetem Hidak és Szerkezetek Tanszéke megbízta a BME Áramlástan Tanszékét az M8-as
3 Technology Ltd Budapest, XI. Hengermalom 14 3/24 1117. Végeselem alkalmazások a tűzvédelmi tervezésben
 1117 Végeselem alkalmazások a tűzvédelmi tervezésben 1117 NASTRAN végeselem rendszer Általános végeselemes szoftver, ami azt jelenti, hogy nem specializálták, nincsenek kimondottam valamely terület számára
1117 Végeselem alkalmazások a tűzvédelmi tervezésben 1117 NASTRAN végeselem rendszer Általános végeselemes szoftver, ami azt jelenti, hogy nem specializálták, nincsenek kimondottam valamely terület számára
Tűgörgős csapágy szöghiba érzékenységének vizsgálata I.
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Tudományos Diákköri Konferencia Tűgörgős csapágy szöghiba érzékenységének vizsgálata I. Szöghézag és a beépítésből adódó szöghiba vizsgálata
Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Tudományos Diákköri Konferencia Tűgörgős csapágy szöghiba érzékenységének vizsgálata I. Szöghézag és a beépítésből adódó szöghiba vizsgálata
CrMo4 anyagtípusok izotermikus átalakulási folyamatainak elemzése és összehasonlítása VEM alapú fázis elemeket tartalmazó TTT diagramok alkalmazásával
 CrMo4 anyagtípusok izotermikus átalakulási folyamatainak elemzése és összehasonlítása VEM alapú fázis elemeket tartalmazó TTT diagramok alkalmazásával Ginsztler J. Tanszékvezető egyetemi tanár, Anyagtudomány
CrMo4 anyagtípusok izotermikus átalakulási folyamatainak elemzése és összehasonlítása VEM alapú fázis elemeket tartalmazó TTT diagramok alkalmazásával Ginsztler J. Tanszékvezető egyetemi tanár, Anyagtudomány
A diplomaterv keretében megvalósítandó feladatok összefoglalása
 A diplomaterv keretében megvalósítandó feladatok összefoglalása Diplomaterv céljai: 1 Sclieren résoptikai módszer numerikus szimulációk validálására való felhasználhatóságának vizsgálata 2 Lamináris előkevert
A diplomaterv keretében megvalósítandó feladatok összefoglalása Diplomaterv céljai: 1 Sclieren résoptikai módszer numerikus szimulációk validálására való felhasználhatóságának vizsgálata 2 Lamináris előkevert
Akusztikai tervezés a geometriai akusztika módszereivel
 Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Modern Fizika Labor. 2. Elemi töltés meghatározása
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Szekrényes András. Delamináció nem szinguláris modellezése ortotróp kompozit lemezekben szemi-rétegmodell alkalmazásával
 Szekrényes András Delamináció nem szinguláris modellezése ortotróp kompozit lemezekben szemi-rétegmodell alkalmazásával című MTA doktori értekezésének bírálata Az értekezés általános véleményezése: Az
Szekrényes András Delamináció nem szinguláris modellezése ortotróp kompozit lemezekben szemi-rétegmodell alkalmazásával című MTA doktori értekezésének bírálata Az értekezés általános véleményezése: Az
Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 1_5. Bevezetés Végeselem-módszer Végeselem-módszer 1. A geometriai tartomány (szerkezet) felosztása (véges)elemekre.. Lokális koordináta-rendszer felvétele, kapcsolat a lokális és globális koordinátarendszerek
1_5. Bevezetés Végeselem-módszer Végeselem-módszer 1. A geometriai tartomány (szerkezet) felosztása (véges)elemekre.. Lokális koordináta-rendszer felvétele, kapcsolat a lokális és globális koordinátarendszerek
Diplomamunkám felépítése
 Üregek távolhatása gránitos kőzetkörnyezetben Tóth Szilvia Konzulensek: Dr. Török Ákos, BME Építőanyagok és Mérnökgeológia Tanszék Poromb Péter, Mott MacDonald Magyarország Kft. Diplomamunkám felépítése
Üregek távolhatása gránitos kőzetkörnyezetben Tóth Szilvia Konzulensek: Dr. Török Ákos, BME Építőanyagok és Mérnökgeológia Tanszék Poromb Péter, Mott MacDonald Magyarország Kft. Diplomamunkám felépítése
Mikroszkóp vizsgálata Lencse görbületi sugarának mérése Folyadék törésmutatójának mérése
 Mikroszkóp vizsgálata Lencse görbületi sugarának mérése Folyadék törésmutatójának mérése Mérési jegyzőkönyv Szőke Kálmán Benjamin 2010. november 16. Mérés célja: Feladat meghatározni a mikroszkópon lévő
Mikroszkóp vizsgálata Lencse görbületi sugarának mérése Folyadék törésmutatójának mérése Mérési jegyzőkönyv Szőke Kálmán Benjamin 2010. november 16. Mérés célja: Feladat meghatározni a mikroszkópon lévő
A vizsgálatok eredményei
 A vizsgálatok eredményei A vizsgált vetőmagvak és műtrágyák nagy száma az eredmények táblázatos bemutatását teszi szükségessé, a legfontosabb magyarázatokkal kiegészítve. A közölt adatok a felsorolt publikációkban
A vizsgálatok eredményei A vizsgált vetőmagvak és műtrágyák nagy száma az eredmények táblázatos bemutatását teszi szükségessé, a legfontosabb magyarázatokkal kiegészítve. A közölt adatok a felsorolt publikációkban
Lemez- és gerendaalapok méretezése
 Lemez- és gerendaalapok méretezése Az alapmerevség hatása az alap hajlékony merev a talpfeszültség egyenletes széleken nagyobb a süllyedés teknıszerő egyenletes Terhelés hatása hajlékony alapok esetén
Lemez- és gerendaalapok méretezése Az alapmerevség hatása az alap hajlékony merev a talpfeszültség egyenletes széleken nagyobb a süllyedés teknıszerő egyenletes Terhelés hatása hajlékony alapok esetén
Modern Fizika Labor. 17. Folyadékkristályok
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 11. A mérés száma és címe: 17. Folyadékkristályok Értékelés: A beadás dátuma: 2011. okt. 23. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 11. A mérés száma és címe: 17. Folyadékkristályok Értékelés: A beadás dátuma: 2011. okt. 23. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
41. ábra A NaCl rács elemi cellája
 41. ábra A NaCl rács elemi cellája Mindkét rácsra jellemző, hogy egy tetszés szerint kiválasztott pozitív vagy negatív töltésű iont ellentétes töltésű ionok vesznek körül. Különbség a közvetlen szomszédok
41. ábra A NaCl rács elemi cellája Mindkét rácsra jellemző, hogy egy tetszés szerint kiválasztott pozitív vagy negatív töltésű iont ellentétes töltésű ionok vesznek körül. Különbség a közvetlen szomszédok
Gépészeti rendszertechnika (NGB_KV002_1)
 Gépészeti rendszertechnika (NGB_KV002_1) 2. Óra Kőrös Péter Közúti és Vasúti Járművek Tanszék Tanszéki mérnök (IS201 vagy a tanszéken) E-mail: korosp@ga.sze.hu Web: http://www.sze.hu/~korosp http://www.sze.hu/~korosp/gepeszeti_rendszertechnika/
Gépészeti rendszertechnika (NGB_KV002_1) 2. Óra Kőrös Péter Közúti és Vasúti Járművek Tanszék Tanszéki mérnök (IS201 vagy a tanszéken) E-mail: korosp@ga.sze.hu Web: http://www.sze.hu/~korosp http://www.sze.hu/~korosp/gepeszeti_rendszertechnika/
Magasépítési öszvérfödémek numerikus szimuláció alapú méretezése
 BME Hidak és Szerkezetek Tanszéke Magasépítési öszvérfödémek numerikus szimuláció alapú méretezése Seres Noémi DEVSOG Témavezetı: Dr. Dunai László Bevezetés Az elıadás témája öszvérfödémek együttdolgoztató
BME Hidak és Szerkezetek Tanszéke Magasépítési öszvérfödémek numerikus szimuláció alapú méretezése Seres Noémi DEVSOG Témavezetı: Dr. Dunai László Bevezetés Az elıadás témája öszvérfödémek együttdolgoztató
Szívókönyökök veszteségeinek és sebességprofiljainak vizsgálata CFD szimuláció segítségével
 GANZ ENGINEERING ÉS ENERGETIKAI GÉPGYÁRTÓ KFT. Szívókönyökök veszteségeinek és sebességprofiljainak vizsgálata CFD szimuláció segítségével Készítette: Bogár Péter Háznagy Gergely Egyed Csaba Zombor Csaba
GANZ ENGINEERING ÉS ENERGETIKAI GÉPGYÁRTÓ KFT. Szívókönyökök veszteségeinek és sebességprofiljainak vizsgálata CFD szimuláció segítségével Készítette: Bogár Péter Háznagy Gergely Egyed Csaba Zombor Csaba
A.2. Acélszerkezetek határállapotai
 A.. Acélszerkezetek határállapotai A... A teherbírási határállapotok első osztálya: a szilárdsági határállapotok A szilárdsági határállapotok (melyek között a fáradt és rideg törést e helyütt nem tárgyaljuk)
A.. Acélszerkezetek határállapotai A... A teherbírási határállapotok első osztálya: a szilárdsági határállapotok A szilárdsági határállapotok (melyek között a fáradt és rideg törést e helyütt nem tárgyaljuk)
Fázisátalakulások vizsgálata
 Klasszikus Fizika Laboratórium VI.mérés Fázisátalakulások vizsgálata Mérést végezte: Vanó Lilla VALTAAT.ELTE Mérés időpontja: 2012.10.18.. 1. Mérés leírása A mérés során egy adott minta viselkedését vizsgáljuk
Klasszikus Fizika Laboratórium VI.mérés Fázisátalakulások vizsgálata Mérést végezte: Vanó Lilla VALTAAT.ELTE Mérés időpontja: 2012.10.18.. 1. Mérés leírása A mérés során egy adott minta viselkedését vizsgáljuk
Atomi er mikroszkópia jegyz könyv
 Atomi er mikroszkópia jegyz könyv Zsigmond Anna Julia Fizika MSc III. Mérés vezet je: Szabó Bálint Mérés dátuma: 2010. október 7. Leadás dátuma: 2010. október 20. 1. Mérés leírása A laboratóriumi mérés
Atomi er mikroszkópia jegyz könyv Zsigmond Anna Julia Fizika MSc III. Mérés vezet je: Szabó Bálint Mérés dátuma: 2010. október 7. Leadás dátuma: 2010. október 20. 1. Mérés leírása A laboratóriumi mérés
2014/2015. tavaszi félév
 Hajder L. és Valasek G. hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom Geometria modellezés 1 Geometria modellezés 2 Geometria modellezés
Hajder L. és Valasek G. hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom Geometria modellezés 1 Geometria modellezés 2 Geometria modellezés
HÁLÓZATI SZINTŰ DINAMIKUS BEHAJLÁSMÉRÉS MÚLTJA JELENE II.
 HÁLÓZATI SZINTŰ DINAMIKUS BEHAJLÁSMÉRÉS MÚLTJA JELENE II. MÉTA-Q Kft. Baksay János 2007. 06. 12. MAÚT ÚTÉPÍTÉSI AKADÉMIA 11. 1. FOGALOM: Teherbírás. Teherbíráson általában határ-igénybevételt értünk 2.
HÁLÓZATI SZINTŰ DINAMIKUS BEHAJLÁSMÉRÉS MÚLTJA JELENE II. MÉTA-Q Kft. Baksay János 2007. 06. 12. MAÚT ÚTÉPÍTÉSI AKADÉMIA 11. 1. FOGALOM: Teherbírás. Teherbíráson általában határ-igénybevételt értünk 2.
2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv. Zsigmond Anna Fizika Bsc II. Mérés dátuma: Leadás dátuma:
 2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 24. Leadás dátuma: 2008. 10. 01. 1 1. Mérések ismertetése Az 1. ábrán látható összeállításban
2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 24. Leadás dátuma: 2008. 10. 01. 1 1. Mérések ismertetése Az 1. ábrán látható összeállításban
Rugalmasan ágyazott gerenda. Szép János
 Rugalmasan ágyazott gerenda vizsgálata AXIS VM programmal Szép János 2013.10.14. LEMEZALAP TERVEZÉS 1. Bevezetés 2. Lemezalap tervezés 3. AXIS Program ismertetés 4. Példa LEMEZALAPOZÁS Alkalmazás módjai
Rugalmasan ágyazott gerenda vizsgálata AXIS VM programmal Szép János 2013.10.14. LEMEZALAP TERVEZÉS 1. Bevezetés 2. Lemezalap tervezés 3. AXIS Program ismertetés 4. Példa LEMEZALAPOZÁS Alkalmazás módjai
Kvartó elrendezésű hengerállvány végeselemes modellezése a síkkifekvési hibák kimutatása érdekében. PhD értekezés tézisei
 Kerpely Antal Anyagtudományok és Technológiák Doktori Iskola Kvartó elrendezésű hengerállvány végeselemes modellezése a síkkifekvési hibák kimutatása érdekében PhD értekezés tézisei KÉSZÍTETTE: Pálinkás
Kerpely Antal Anyagtudományok és Technológiák Doktori Iskola Kvartó elrendezésű hengerállvány végeselemes modellezése a síkkifekvési hibák kimutatása érdekében PhD értekezés tézisei KÉSZÍTETTE: Pálinkás
Statisztika I. 12. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 1. előadás Előadó: Dr. Ertsey Imre Regresszió analízis A korrelációs együttható megmutatja a kapcsolat irányát és szorosságát. A kapcsolat vizsgálata során a gyakorlatban ennél messzebb
Statisztika I. 1. előadás Előadó: Dr. Ertsey Imre Regresszió analízis A korrelációs együttható megmutatja a kapcsolat irányát és szorosságát. A kapcsolat vizsgálata során a gyakorlatban ennél messzebb
Függőleges és vízszintes vasalás hatása a téglafalazat nyírási ellenállására
 Függőleges és vízszintes vasalás hatása a téglafalazat nyírási ellenállására FÓDI ANITA Témavezető: Dr. Bódi István Budapesti Műszaki és Gazdaságtudományi Egyetem Építőmérnöki kar Hidak és Szerkezetek
Függőleges és vízszintes vasalás hatása a téglafalazat nyírási ellenállására FÓDI ANITA Témavezető: Dr. Bódi István Budapesti Műszaki és Gazdaságtudományi Egyetem Építőmérnöki kar Hidak és Szerkezetek
A szemlencse elülső tokjának biomechanikai vizsgálata manuális capsulorhexis és femtoszekundumos lézeres capsulotomia után. Dr. Sándor Gábor László
 A szemlencse elülső tokjának biomechanikai vizsgálata manuális capsulorhexis és femtoszekundumos lézeres capsulotomia után Doktori tézisek Dr. Sándor Gábor László Semmelweis Egyetem Klinikai Orvostudományok
A szemlencse elülső tokjának biomechanikai vizsgálata manuális capsulorhexis és femtoszekundumos lézeres capsulotomia után Doktori tézisek Dr. Sándor Gábor László Semmelweis Egyetem Klinikai Orvostudományok
Modern Fizika Labor Fizika BSC
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. április 20. A mérés száma és címe: 20. Folyadékáramlások 2D-ban Értékelés: A beadás dátuma: 2009. április 28. A mérést végezte: Márton Krisztina Zsigmond
Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. április 20. A mérés száma és címe: 20. Folyadékáramlások 2D-ban Értékelés: A beadás dátuma: 2009. április 28. A mérést végezte: Márton Krisztina Zsigmond
EGYIRÁNYBAN ER SÍTETT KOMPOZIT RUDAK HAJLÍTÓ KARAKTERISZTIKÁJÁNAK ÉS TÖNKREMENETELI FOLYAMATÁNAK ELEMZÉSE
 Budapest M szaki és Gazdaságtudományi Egyetem Polimertecnika Tanszék EGYIRÁNYBAN ER SÍTETT KOMPOZIT RUDAK HAJLÍTÓ KARAKTERISZTIKÁJÁNAK ÉS TÖNKREMENETELI OLYAMATÁNAK ELEMZÉSE Tézisek Rácz Zsolt Témavezet
Budapest M szaki és Gazdaságtudományi Egyetem Polimertecnika Tanszék EGYIRÁNYBAN ER SÍTETT KOMPOZIT RUDAK HAJLÍTÓ KARAKTERISZTIKÁJÁNAK ÉS TÖNKREMENETELI OLYAMATÁNAK ELEMZÉSE Tézisek Rácz Zsolt Témavezet
Műszerezett keménységmérés alkalmazhatósága a gyakorlatban
 Műszerezett keménységmérés alkalmazhatósága a gyakorlatban Rózsahegyi Péter laboratóriumvezető Tel: (46) 560-137 Mob: (30) 370-009 Műszaki Kockázatmenedzsment Osztály Mechanikai Anyagvizsgáló Laboratórium
Műszerezett keménységmérés alkalmazhatósága a gyakorlatban Rózsahegyi Péter laboratóriumvezető Tel: (46) 560-137 Mob: (30) 370-009 Műszaki Kockázatmenedzsment Osztály Mechanikai Anyagvizsgáló Laboratórium
Kutatási beszámoló. 2015. február. Tangens delta mérésére alkalmas mérési összeállítás elkészítése
 Kutatási beszámoló 2015. február Gyüre Balázs BME Fizika tanszék Dr. Simon Ferenc csoportja Tangens delta mérésére alkalmas mérési összeállítás elkészítése A TKI-Ferrit Fejlsztő és Gyártó Kft.-nek munkája
Kutatási beszámoló 2015. február Gyüre Balázs BME Fizika tanszék Dr. Simon Ferenc csoportja Tangens delta mérésére alkalmas mérési összeállítás elkészítése A TKI-Ferrit Fejlsztő és Gyártó Kft.-nek munkája
Mart gránitfelület-élek minősítése és kitöredezéseinek vizsgálata technológiai optimalizálás céljából
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki kar Gyártástudomány és technológia Tanszék DOKTORI TÉZISFÜZET Mart gránitfelület-élek minősítése és kitöredezéseinek vizsgálata technológiai
Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki kar Gyártástudomány és technológia Tanszék DOKTORI TÉZISFÜZET Mart gránitfelület-élek minősítése és kitöredezéseinek vizsgálata technológiai
Végeselem analízis. 1. el adás
 Végeselem analízis 1. el adás Pere Balázs Széchenyi István Egyetem, Alkalmazott Mechanika Tanszék 2016. szeptember 7. Mi az a VégesElem Analízis (VEA)? Parciális dierenciálegyenletek (egyenletrendszerek)
Végeselem analízis 1. el adás Pere Balázs Széchenyi István Egyetem, Alkalmazott Mechanika Tanszék 2016. szeptember 7. Mi az a VégesElem Analízis (VEA)? Parciális dierenciálegyenletek (egyenletrendszerek)
Pere Balázs október 20.
 Végeselem anaĺızis 1. előadás Széchenyi István Egyetem, Alkalmazott Mechanika Tanszék 2014. október 20. Mi az a VégesElem Anaĺızis (VEA)? Mi az a VégesElem Anaĺızis (VEA)? Mi az a VégesElem Anaĺızis (VEA)?
Végeselem anaĺızis 1. előadás Széchenyi István Egyetem, Alkalmazott Mechanika Tanszék 2014. október 20. Mi az a VégesElem Anaĺızis (VEA)? Mi az a VégesElem Anaĺızis (VEA)? Mi az a VégesElem Anaĺızis (VEA)?
Számítógépes Grafika mintafeladatok
 Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Koordináta-geometria feladatok (emelt szint)
 Koordináta-geometria feladatok (emelt szint) 1. (ESZÉV Minta (2) 2004.05/7) Egy ABC háromszögben CAB = 30, az ACB = 45. A háromszög két csúcsának koordinátái: A(2; 2) és C(4; 2). Határozza meg a harmadik
Koordináta-geometria feladatok (emelt szint) 1. (ESZÉV Minta (2) 2004.05/7) Egy ABC háromszögben CAB = 30, az ACB = 45. A háromszög két csúcsának koordinátái: A(2; 2) és C(4; 2). Határozza meg a harmadik
A kerék-sín között fellépő Hertz-féle érintkezési feszültség vizsgálata
 A keréksín között fellépő Hertzféle érintkezési feszültség vizsgálata közúti vasúti felépítmények esetében Dr. Kazinczy László PhD. egyetemi docens i Műszaki és Gazdaságtudományi gyetem, Út és Vasútépítési
A keréksín között fellépő Hertzféle érintkezési feszültség vizsgálata közúti vasúti felépítmények esetében Dr. Kazinczy László PhD. egyetemi docens i Műszaki és Gazdaságtudományi gyetem, Út és Vasútépítési
Nehézségi gyorsulás mérése megfordítható ingával
 Nehézségi gyorsulás mérése megfordítható ingával (Mérési jegyzőkönyv) Hagymási Imre 2007. április 21. (hétfő délelőtti csoport) 1. A mérés elmélete A nehézségi gyorsulás mérésének egy klasszikus módja
Nehézségi gyorsulás mérése megfordítható ingával (Mérési jegyzőkönyv) Hagymási Imre 2007. április 21. (hétfő délelőtti csoport) 1. A mérés elmélete A nehézségi gyorsulás mérésének egy klasszikus módja
Kisciklusú fárasztóvizsgálatok eredményei és energetikai értékelése
 Kisciklusú fárasztóvizsgálatok eredményei és energetikai értékelése Tóth László, Rózsahegyi Péter Bay Zoltán Alkalmazott Kutatási Közalapítvány Logisztikai és Gyártástechnikai Intézet Bevezetés A mérnöki
Kisciklusú fárasztóvizsgálatok eredményei és energetikai értékelése Tóth László, Rózsahegyi Péter Bay Zoltán Alkalmazott Kutatási Közalapítvány Logisztikai és Gyártástechnikai Intézet Bevezetés A mérnöki
2. Rugalmas állandók mérése
 2. Rugalmas állandók mérése Klasszikus fizika laboratórium Mérési jegyzőkönyv Mérést végezte: Vitkóczi Fanni Jegyzőkönyv leadásának időpontja: 2012. 12. 15. I. A mérés célja: Két anyag Young-modulusának
2. Rugalmas állandók mérése Klasszikus fizika laboratórium Mérési jegyzőkönyv Mérést végezte: Vitkóczi Fanni Jegyzőkönyv leadásának időpontja: 2012. 12. 15. I. A mérés célja: Két anyag Young-modulusának
Mágneses szuszceptibilitás mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 7. MÉRÉS Mágneses szuszceptibilitás mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 5. Szerda délelőtti csoport 1. A mérés célja Az
KLASSZIKUS FIZIKA LABORATÓRIUM 7. MÉRÉS Mágneses szuszceptibilitás mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 5. Szerda délelőtti csoport 1. A mérés célja Az
V É G E S E L E M M Ó D S Z E R M É R N Ö K I M E C H A N I K A I A L K A LM A Z Á S A I
 ALKALMAZOTT MECHANIKA TANSZÉK V É G E S E L E M M Ó D S Z E R M É R N Ö K I M E C H A N I K A I A L K A LM A Z Á S A I Előadásvázlat a Multidiszciplináris Műszaki Tudományi Doktori Iskola hallgatói számára
ALKALMAZOTT MECHANIKA TANSZÉK V É G E S E L E M M Ó D S Z E R M É R N Ö K I M E C H A N I K A I A L K A LM A Z Á S A I Előadásvázlat a Multidiszciplináris Műszaki Tudományi Doktori Iskola hallgatói számára
Fényhullámhossz és diszperzió mérése
 Fényhullámhossz és diszperzió mérése Mérő neve: Márkus Bence Gábor Mérőpár neve: Székely Anna Krisztina Szerda délelőtti csoport Mérés ideje: 11/09/011 Beadás ideje: 11/16/011 1 1. A mérés rövid leírása
Fényhullámhossz és diszperzió mérése Mérő neve: Márkus Bence Gábor Mérőpár neve: Székely Anna Krisztina Szerda délelőtti csoport Mérés ideje: 11/09/011 Beadás ideje: 11/16/011 1 1. A mérés rövid leírása
Ebben a mérnöki kézikönyvben azt mutatjuk be, hogyan számoljuk egy síkalap süllyedését és elfordulását.
 10. számú mérnöki kézikönyv Frissítve: 2016. Február Síkalap süllyedése Program: Fájl: Síkalap Demo_manual_10.gpa Ebben a mérnöki kézikönyvben azt mutatjuk be, hogyan számoljuk egy síkalap süllyedését
10. számú mérnöki kézikönyv Frissítve: 2016. Február Síkalap süllyedése Program: Fájl: Síkalap Demo_manual_10.gpa Ebben a mérnöki kézikönyvben azt mutatjuk be, hogyan számoljuk egy síkalap süllyedését
Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel
 Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel Segédlet az A végeselem módszer alapjai tárgy 4. laborgyakorlatához http://www.mm.bme.hu/~kossa/vemalap4.pdf Kossa Attila (kossa@mm.bme.hu)
Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel Segédlet az A végeselem módszer alapjai tárgy 4. laborgyakorlatához http://www.mm.bme.hu/~kossa/vemalap4.pdf Kossa Attila (kossa@mm.bme.hu)
Transzformátor rezgés mérés. A BME Villamos Energetika Tanszéken
 Transzformátor rezgés mérés A BME Villamos Energetika Tanszéken A valóság egyszerűsítése, modellezés. A mérés tervszerűen végrehajtott tevékenység, ezért a bonyolult valóságos rendszert először egyszerűsítik.
Transzformátor rezgés mérés A BME Villamos Energetika Tanszéken A valóság egyszerűsítése, modellezés. A mérés tervszerűen végrehajtott tevékenység, ezért a bonyolult valóságos rendszert először egyszerűsítik.
Acéllemezbe sajtolt nyírt kapcsolat kísérleti vizsgálata és numerikus modellezése
 Acéllemezbe sajtolt nyírt kapcsolat kísérleti vizsgálata és numerikus modellezése Seres Noémi Doktorandusz BME Tartalom Téma: öszvérfödémek együttdolgoztató kapcsolatának numerikus modellezése, nyírt együttdolgoztató
Acéllemezbe sajtolt nyírt kapcsolat kísérleti vizsgálata és numerikus modellezése Seres Noémi Doktorandusz BME Tartalom Téma: öszvérfödémek együttdolgoztató kapcsolatának numerikus modellezése, nyírt együttdolgoztató
Regresszió számítás. Tartalomjegyzék: GeoEasy V2.05+ Geodéziai Kommunikációs Program
 Regresszió számítás GeoEasy V2.05+ Geodéziai Kommunikációs Program DigiKom Kft. 2006-2010 Tartalomjegyzék: Egyenes x változik Egyenes y változik Egyenes y és x változik Kör Sík z változik Sík y, x és z
Regresszió számítás GeoEasy V2.05+ Geodéziai Kommunikációs Program DigiKom Kft. 2006-2010 Tartalomjegyzék: Egyenes x változik Egyenes y változik Egyenes y és x változik Kör Sík z változik Sík y, x és z
A mikroszkóp vizsgálata Lencse görbületi sugarának mérése Newton-gyűrűkkel Folyadék törésmutatójának mérése Abbe-féle refraktométerrel
 A mikroszkóp vizsgálata Lencse görbületi sugarának mérése Newton-gyűrűkkel Folyadék törésmutatójának mérése Abbe-féle refraktométerrel Mérő neve: Márkus Bence Gábor Mérőpár neve: Székely Anna Krisztina
A mikroszkóp vizsgálata Lencse görbületi sugarának mérése Newton-gyűrűkkel Folyadék törésmutatójának mérése Abbe-féle refraktométerrel Mérő neve: Márkus Bence Gábor Mérőpár neve: Székely Anna Krisztina
Fogorvosi anyagtan fizikai alapjai 6.
 Fogorvosi anyagtan fizikai alapjai 6. Mechanikai tulajdonságok 1. Kiemelt témák: Rugalmas alakváltozás Merevség és összefüggése a kötési energiával A geometriai tényezők szerepe egy test merevségében Tankönyv
Fogorvosi anyagtan fizikai alapjai 6. Mechanikai tulajdonságok 1. Kiemelt témák: Rugalmas alakváltozás Merevség és összefüggése a kötési energiával A geometriai tényezők szerepe egy test merevségében Tankönyv
