Modern m szeres analitika szeminárium Mintavétel
|
|
|
- Ildikó Bartané
- 8 évvel ezelőtt
- Látták:
Átírás
1 Modern szeres nlitik szeináriu Mintvétel Glbács Gábor MINTAVÉTELLEL KAPCSOLATOS SZÁMÍTÁSI FELADATOK A vontkozó foglk és képletek áttekintése
2 MINTAVÉTELLEL KAPCSOLATOS SZÁMÍTÁSI FELADATOK A vontkozó foglk és képletek áttekintése MINTAVÉTELLEL KAPCSOLATOS SZÁMÍTÁSI FELADATOK A vontkozó foglk és képletek áttekintése Szórás (stndrd deviáció): (A vrinci szórás négyzete). s (x x) n 1 Abszolút és reltív szórás/hib egyránt behelyettesíthet képletekbe! i Konfidencisáv (hol µ vlódi érték): t s x n Drbos/szecsés intáknál z s és intennyiség (részecskeszá, n r ) összefüggése: n r 1 p p 1 s A hib és intszá (kivett párhuzos inták szá, n ) összefüggése: n t s e A vrinci teljes nlitiki folytr: s s (s ) s e Mérési hib teljes (kétlépéses) nlitiki folytr (hol t értékét z összes ért intszá lpján tekintjük!): e t s n s n n
3 MINTAVÉTELLEL KAPCSOLATOS SZÁMÍTÁSI FELADATOK A vontkozó foglk és képletek áttekintése A Student-féle eloszlássl kpcsoltos vizsgáltok vlójábn Willi Sely Gosset nevéhez fzdnek, ki Guiness sörfzde dublini központjábn dolgozott. A dolgozóknk Guiness egtiltott, hogy bárit is publikáljnk, nehogy üzleti titkok kerüljenek nyilvánosságr, eitt Gosset Student álnéven publikált 1908-bn legfbb sttisztiki eredényeit x t s n 1. FELADAT A érési hib inilizálás Egy bizonyos nlitiki ódszer intvételhez kpcsolódó vrinci 0.40%, íg z nlízishez gához trtozó vrinci 0.070%. Hsonlítsuk össze teljes ódszerre vontkozó reltív hib értékét következ két intvételezési strtégi esetén (95% egbízhtósági szinten); elyik z elnyösebb?.) öt intát gyjtünk be (n ) és ezekbl egyenként két párhuzos lborintát érünk eg (n ) b.) két intát gyjtünk be (n ) és ezekbl egyenként öt párhuzos lborintát érünk eg (n )
4 1. MEGOLDÁS A érési hib inilizálás s = 0.40% s = 0.070% e t s n s n n 95% egbízhtósági szinten elyik z elnyösebb strtégi reltív érési hib inilizálásár?.) n = 5 és n = (összesen tehát 10 int érend) e% % 0.070% 0.67% 5 5 b.) n = és n = 5 (összesen tehát 10 int érend) e% % 0.070% 1.0% 5 tehát fontosbb intvételezési hibát inilizálni!. FELADAT A teljes ódszer szórás és nnk inilizálás Egy Pb eghtározási ódszer z lábbi érési dtokt szolgálttt festékinták esetében: Mérés sorszá Válszoljuk eg következ kérdéseket:.) Mekkor teljes ódszer szórás? b.) Hogyn csökkenthet ódszer szórás?
5 . MEGOLDÁS A teljes ódszer szórásánk száítás Mérés sorszá s s s s x x i n 1 n=5(ostn és n ne függ össze, de éppen egyenlk!) s lborintákból, s stndrd intákból becsülhet. x x ) A ódszer teljes szórás: s xi x xi 5.58 xi s n vegyük észre, hogy stndrd inták töényebbek, tehát z bszolút szórások ne összeérhetk és kobinálhtók! Eitt csk reltív szórássl (RSD) tudjuk z eredényt kifejezni (úgy is legtöbbször csk ennek vn értele). RSD RSD RSD s x s x MEGOLDÁS A teljes ódszer szórásánk inilizálás Mérés sorszá s s s s x x i n 1 n=5(ostn és n ne függ össze, de éppen egyenlk!) s lborintákból, s stndrd intákból becsülhet. x x b.) A ódszer szórásánk inilizálás (i összefügg persze hibávl): s x x x i i xi n A intvételbl szárzó szórás (ne eglepen) ngyobb, tehát teljes ódszer szórását inták száánk növelésével lehet elérni. s
6 3. FELADAT A részecskék prítás inttöeg csökkentése érdekében Tegyük fel, hogy egy bizonyos nlitiki ódszer egvlósítás során x. 1% reltív intvételezési szórás eléréséhez in. 110 g szecsézett szilárd int feldolgozásár (intelkészítésére) lenne szükség, de ez túl sok z eszközeink száár. A részecskék jelenlegi átérje x. 50 µ. A egoldás részecskék éretének csökkentése rléssel. Mekkor átérre kell leglább lecsökkenteni göbszernek feltételezett részecskék éretét, hogy indössze 0.5 g intávl dolgozhssunk intelkészítés során? 3. MEGOLDÁS A részecskék prítás inttöeg csökkentése érdekében RSD = = 110 g ( kiindulási töeg) = 0.5 g ( céltöeg) d 1 = 50 µ A feldt úgy is egfoglzhtó, hogy ekkor szecseéretre vn szükség, hogy töegben leglább ugynnnyi drb részecske legyen rlés után, int 1 -ben volt.
7 3. MEGOLDÁS A részecskék prítás inttöeg csökkentése érdekében RSD = = 110 g ( kiindulási töeg) = 0.5 g ( céltöeg) d 1 = 50 µ A intennyiséget 1 / ránybn szeretnénk csökkenteni. Ez göbszer részecskék feltételezése esetén z átérre vontkozón d d 3 d d d vgyis z új részecske átérnek 41 µ lá kell csökkennie. 4. FELADAT A begyjtend intennyiség száítás Tegyük fel, hogy intázndó nyghlz szecsékbl áll, elyekbl csk inden tízezredik trtlzz érend koponenst. Egy szecse töege átlgosn kb. 1 µg. Hány gr hoogenizált intát kell intvétel során begyjtenünk binoiális eloszlás szerint hhoz, hogy intvételbl szárzó reltív szórás csk % legyen?
8 4. MEGOLDÁS A begyjtend intennyiség száítás r =1µg RSD =0.0 p =10-4 Elször kiszáoljuk részecskeszáot... 1 p n p 1 RSD (0.0) jd ebbl inttöeget: g 5 g 5. FELADAT A intvételi frekvenci egválsztás Az lábbi dtsort egy ipri szennyvíz árlás ph-jánk rövid távú onitorozásávl kptuk. A grfikon lpján jvsoljunk egfelel intvételezési frekvenciát (gykoriságot) egy hosszútávú onitorozáshoz!
9 5. MEGOLDÁS A intvételi frekvenci egválsztás A rövid távú onitorozás dti lpján kb. 34 ór ltt két, ngyjából szietrikus periodikus változási ciklust ír le ért préter (ph), vgyis értékdó (durv, trendszer) változás periódusideje kb. 17 ór. A Nyquist(-Shnnon) teoré lényegében kiondj, hogy egy korlátozott sávszélesség folytonosn változó jelet tökéletesen rekonstruálni lehet, h jel intvételezése iniu f frekvenciávl történik, hol f z eredeti jelben elforduló legngyobb frekvenciájú koponens (sorfejtés). Ebbl jelen esetben iniális dtgyjtési frekvenciár tehát 1/8.5 ór -1 dódik (3.6 µhz). Láthtó ugynkkor, hogy kb. óránkénti periódusidej, finobb változások is jelen vnnk (vegyük figyelebe érés jelen esetben jó precizitását!), elyek rögzítéséhez kb. félóránként kellene érni. Ez közel tízszer nnyi dt rögzítését igényli, i hosszú távon túl sok lehet. 6. FELADAT Mintvételi terv készítése Arr kérték, hogy lkítson ki érési ódszert egy forgls belvárosi csoópontbn leveg ózonkoncentrációj és forglo közötti összefüggés vizsgált érdekében. Válszolj eg következ kérdéseket:.) Milyen intvételi strtégiát válszt? (véletlenszer, rendszeres, szervezett, illetve ezek kobinációi) b.) Kirgdott, összetett vgy in-situ intákt gyjtene? c.) Hogyn válszoln fenti kérdésekre, h feldt nnk egállpítás lenne, hogy npi ózonszint eghld-e egy dott küszöbértéket?
10 6. FELADAT Mintvételi strtégi kilkítás Az oldott oxigén koncentrációj terészetes vizekben (legyen ez egy tó) npi és éves ciklusú változékonyságot utt z elbbi npszkok és fotoszintézis összefüggése itt, z utóbbi szezonális hérséklet- ingdozások itt. 1.) készítsen intvételi strtégiát npi változások feltérképezésére.) készítsen intvételi strtégiát z éves változások feltérképezésére
11 Modern szeres nlitik szeináriu Néhány egyszer sttisztiki teszt Glbács Gábor KIUGRÓ ADATOK KISZRÉSE STATISZTIKAI TESZTEKKEL Dixon Q-tesztje Gykori feldt z nlitiki kéiábn, hogy kiugrónk tn érési dtokról kell eldöntenünk, hogy zokt elhgyjuk-e további száításokból. Erre vontkozón ne feledjük, hogy kisszáú érési dt esetén (ondjuk néhány tíznél kevesebb) seiképpen lehetünk benne biztosk, hogy ért dtok norális (Guss) eloszlásúk, ert nincs elegend inforációnk ennek eldöntésére. Ne feledjük, ebbl z is következik, hogy bbn se lehetünk biztosk, hogy z dtok átlg legjobb becslés helyes értékre! (ilyenkor edián száítás lehet legjobb egoldás). H zonbn biztosk vgyunk norális eloszlásbn, kkor többféle sttisztiki teszt közül válszthtunk kiugró pontok kiszrésére. Ezek közül kettt lklzunk ost: Dixon-féle Q-teszt Grubb-féle teszt
12 KIUGRÓ ADATOK KISZRÉSE STATISZTIKAI TESZTEKKEL Dixon Q-tesztje A Dixon-féle Q-teszt során Q köz terjedele ennyiséget kell kiszáolni és egy tábláztból vett Q krit értékkel összehsonlítni; h Q> Q krit, kkor gynús érték elhgyhtó. A képletben terjedele legkisebb és legngyobb ért érték közötti távolság, köz pedig gynús dtele és legközelebbi szoszédj közötti távolság. 1. FELADAT Kiugró dt kiszrése Q-teszttel Egy klcit int százlékos CO trtlár következ dtokt kptuk: 55.95%, 56.00%, 56.04%, 56.08%, 56.3% Az utolsó dt gynúsnk tnik. Kiugró értéknek száít-e 90%-os egbízhtósági szinten és így el kell-e hgynunk z dtok közül?
13 1. MEGOLDÁS Kiugró dt kiszrése Q-teszttel A egdott dtokr: 55.95%, 56.00%, 56.04%, 56.08%, 56.3% terjedele= 56.3% % = 0.8% köz = 56.3% % = 0.15% Q köz terjedele 0.15% 0.8% 0.54 ivel 90%-os egbízhtósági szinten 5 dtr Q krit = 0.64, inél Q értéke kisebb, ezért z dtot bent kell hgynunk z dtsorbn.. FELADAT Kiugró dt kiszrése Q-teszttel Fenol eghtározás HPLC ódszerrel következ dtokt szolgálttt: Az els dt gynúsnk tnik. Kiugró értéknek száít-e 90%-os egbízhtósági szinten és így el kell-e hgynunk z dtok közül?
14 . MEGOLDÁS Kiugró dt kiszrése Q-teszttel A egdott dtokr: Q köz terjedele ivel 90%-os egbízhtósági szinten 10 dtr Q krit = 0.41, inél Q értéke ngyobb, ezért z dtot elhgyhtjuk z dtsorból. KIUGRÓ ADATOK KISZRÉSE STATISZTIKAI TESZTEKKEL Grubb-féle teszt A Grubb-féle teszt során feltesszük, hogy norális eloszlásúk z dtink és zt vizsgáljuk, hogy gynús dt elfordulásánk vlószínsége kisebb- e, int egbízhtósági szint. A következ egyszer képlet értékét száoljuk ki gynús dtr: 90% 9.5% 95% 97.5% 99% Z átlg x hol z átlgot z összes ért dtr száoljuk, s z epirikus szórás, x pedig gynús érési dt értéke. Ezek után Z értékét egy tábláztból vett Z krit értékkel kell összehsonlítni; h Z> Z krit, kkor gynús érték elhgyhtó. s
15 3. FELADAT Kiugró dt kiszrése Grubb-féle teszttel Egy urán izotóp töegspektroszkópiás eghtározás során következ nyolc intenzitás dt született: ; ; 00.19; 00.8; 01.9; 01.95; 0.18; Az utolsó dt gynúsnk tnik. Kiugró értéknek száít-e 99%-os egbízhtósági szinten és így el kell-e hgynunk z dtok közül? 3. MEGOLDÁS Kiugró dt kiszrése Grubb-féle teszttel A egdott dtokból: ; ; 00.19; 00.8; 01.9; 01.95; 0.18; átlg= epirikus szórás (stndrd deviáció)= Z átlg x s A tábláztból, 8 dtr Z krit értéke 99%-os szinten.. Ebbl z következik, hogy igen, z dt elhgyhtó.
16 A MEDIÁN ALKALMAZÁSA KIUGRÓ ADATOK ESETÉN Kisszáú érési dt esetén H kisszáú érési dtunk vn, kkor ne lehetünk biztosk bbn, hogy z dtok norális eloszlást követik. Ekkor z átlgnál jobb becslés vlódi értékre edián egdás, ivel ez sokkl robusztusbb kiugró dtok kezelésében. A edián definíció szerint z z érték egy dthlzbn, elynél z dtoknk pontosn fele ngyobb és pontosn fele kisebb. H pártln tgú dtsorról vn szó, kkor ngyság szerint rendezett dtok közül középs értéke. H páros tgszáú z dtsor, kkor (egy lepuhított definíció szerint ) két középs érték átlgát tekintjük ediánnk. Péld: 4. FELADAT ÉS MEGOLDÁS A edián érték robusztusságánk szeléltetése Akövetkez érési dtsorunk vn: 10.1; 9.9; 9.7; 10.; 10.5; 3.0; 10.3; 10.0; 10.0 i ngyság szerint rendezve egfelel: 3.0; 9.7; 9.9; 10.0; 10.0; 10.1; 10.; 10.3; 10.5 z átlg: 9.3 szórás:.373 edián: 10.0 h elhgyjuk kiugró dtot (3.0), kkor: z átlg: szórás: 0.47 edián: Gondoljuk végig otthon zt is, hogyn lkulnk száok extré esetben, pl. ikor 10 érési dtból kilenc értéke 1,000, íg egynek z értéke 1,000,000!
17 MÉRÉSI ADATOK ÁTLAGÁNAK ÖSSZEVETÉSE A VALÓDI ÉRTÉKKEL Null hipotézis Egy ásik gykori, sttisztiki jelleg feldt z nlitiki kéiábn, hogy (pl. egy vlidálás, QC érés során) összevessük érési dtinkt helyes, vlódi értékkel. Ez utóbbit vlójábn csk éppen ilyenkor iserjük, ivel QC érések során egy referenci intát érünk eg, elyet i állítottunk el (vgy kereskedeli) és összetételét pontosn iserjük. Mivel érési dtok pontosn ngy vlószínséggel ne fognk egyezni vlódi értékkel, ezért sttisztiki próbánk kell lávetni z dtokt, hogy eldönthessük, tpsztlt eltérés érési dtok átlg és vlódi érték között ég belefér-e norális eloszlás szórásáb, vgy ne. Az utóbbi esetben rendszeres hibávl (negtív vgy pozitív) állunk szeben. Az ellenrzés z ún. null hipotézissel lehetséges. Feltevésünk z, hogy nincs rendszeres hib (egy dott egbízhtósági szinten). Ez kkor teljesül, h x t s n hol µ vlódi érték, s z epirikus szórás, t Student-féle érték, n pedig érési dtok szá. 5. FELADAT Null hipotézis lklzás Egy kéneghtározási eljárás tesztelése során 0.13% kéntrtlú referenci intár következ elezési eredényeket kptuk: 0.11%; 0.118%; 0.115%; 0.119% Állpítsuk eg, hogy vn-e rendszeres hib érési dtokbn, vgy nincs! A egállpítást tegyük eg 95% és 99% egbízhtósági szintre is!
18 5. MEGOLDÁS Null hipotézis lklzás µ= 0.13% n= 4 s= átlg= 0.116% átlg - µ = % vlószínségi szinten t 95% = 3.18 (ivel szbdsági fokok szá= 3), így: t s n 4 z (átlg - µ) > , tehát null hipotézist el kell vetnünk. Vn rendszeres hib ezen vlószínségi szinten! 5. MEGOLDÁS Null hipotézis lklzás µ= 0.13% n= 4 s= átlg= 0.116% átlg - µ = % vlószínségi szinten t 95% = 3.18 (ivel szbdsági fokok szá= 3), így: t s n 4 z (átlg - µ) > , tehát null hipotézist el kell vetnünk. Vn rendszeres hib ezen vlószínségi szinten! 99% vlószínségi szinten t 99% = 5.84, így ekkor t s n 4 z (átlg - µ) < , tehát null hipotézis egállj helyét. Nincs rendszeres hib ezen vlószínségi szinten!
Modern műszeres analitika szeminárium Mintavétel
 Modern űszeres nlitik szeináriu Mintvétel Glbács Gábor MINTAVÉTELLEL KAPCSOLATOS SZÁMÍTÁSI FELADATOK A vontkozó foglk és képletek áttekintése MINTAVÉTELLEL KAPCSOLATOS SZÁMÍTÁSI FELADATOK A vontkozó foglk
Modern űszeres nlitik szeináriu Mintvétel Glbács Gábor MINTAVÉTELLEL KAPCSOLATOS SZÁMÍTÁSI FELADATOK A vontkozó foglk és képletek áttekintése MINTAVÉTELLEL KAPCSOLATOS SZÁMÍTÁSI FELADATOK A vontkozó foglk
Modern műszeres analitika szeminárium Néhány egyszerű statisztikai teszt
 Modern műszeres analitika szeminárium Néhány egyszerű statisztikai teszt Galbács Gábor KIUGRÓ ADATOK KISZŰRÉSE STATISZTIKAI TESZTEKKEL Dixon Q-tesztje Gyakori feladat az analitikai kémiában, hogy kiugrónak
Modern műszeres analitika szeminárium Néhány egyszerű statisztikai teszt Galbács Gábor KIUGRÓ ADATOK KISZŰRÉSE STATISZTIKAI TESZTEKKEL Dixon Q-tesztje Gyakori feladat az analitikai kémiában, hogy kiugrónak
Minta feladatsor I. rész
 Mint feldtsor I. rész. Írj fel z A számot htványként! A / pont/. Mekkor hosszúságú dróttl lehet egy m m-es tégllp lkú testet z átlój mentén felosztni két derékszögű háromszögre? Adj meg hosszúságot mértékegységgel!
Mint feldtsor I. rész. Írj fel z A számot htványként! A / pont/. Mekkor hosszúságú dróttl lehet egy m m-es tégllp lkú testet z átlój mentén felosztni két derékszögű háromszögre? Adj meg hosszúságot mértékegységgel!
Radioaktív nyomjelzés analitikai kémiai alkalmazásai
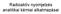 Rdioktív nyojelzés nlitiki kéii lklzási Izotóphígításos ódszerek A λn A ktivitás, n rdioktív gok ennyisége, bolási állndój. A fjlgos ktivitás kezdetben ( ): λn n N N z inktív hordozó ennyisége. N ennyiségű
Rdioktív nyojelzés nlitiki kéii lklzási Izotóphígításos ódszerek A λn A ktivitás, n rdioktív gok ennyisége, bolási állndój. A fjlgos ktivitás kezdetben ( ): λn n N N z inktív hordozó ennyisége. N ennyiségű
Gyakorló feladatsor 9. osztály
 Gykorló feldtsor 9. osztály Hlmzok. Sorold fel z lábbi hlmzok elemeit! ) A={ legfeljebb kétjegyű 9-cel oszthtó páros pozitív számok} b) B={:prímszám, hol < 7} c) C={b=n+, hol nϵz és- n
Gykorló feldtsor 9. osztály Hlmzok. Sorold fel z lábbi hlmzok elemeit! ) A={ legfeljebb kétjegyű 9-cel oszthtó páros pozitív számok} b) B={:prímszám, hol < 7} c) C={b=n+, hol nϵz és- n
Radioaktív nyomjelzés analitikai kémiai alkalmazásai
 Rdioktív nyojelzés nlitiki kéii lklzási A rdioizotópos nyojelzős ódszerek csoportosítás gykorlti szepontok szerint Fiziki kéii ódszerek, pl.: oldékonyság eghtározás, diffúzió vizsgált, fázisok közötti
Rdioktív nyojelzés nlitiki kéii lklzási A rdioizotópos nyojelzős ódszerek csoportosítás gykorlti szepontok szerint Fiziki kéii ódszerek, pl.: oldékonyság eghtározás, diffúzió vizsgált, fázisok közötti
Egy látószög - feladat
 Ehhez tekintsük z 1. ábrát is! Egy látószög - feldt 1. ábr Az A pont körül kering C pont, egy r sugrú körön. A rögzített A és B pontok egymástól távolság vnnk. Az = CAB szöget folymtosn mérjük. Keressük
Ehhez tekintsük z 1. ábrát is! Egy látószög - feldt 1. ábr Az A pont körül kering C pont, egy r sugrú körön. A rögzített A és B pontok egymástól távolság vnnk. Az = CAB szöget folymtosn mérjük. Keressük
EGYENESFOGÚ HENGERESKERÉK GEOMETRIAI REKONSTRUKCIÓJA 4. jegyzőkönyv
 EGYENESFOGÚ HENGERESKERÉK GEOMETRIAI REKONSTRUKCIÓJA. jegyzőkönyv A mérés helye: DE-MK Gépelemek Lbortórium A mérés időpontj:... A mérést végezte:... Gykorltvezető:... Tételszám:... Feldt: Mérési dtok
EGYENESFOGÚ HENGERESKERÉK GEOMETRIAI REKONSTRUKCIÓJA. jegyzőkönyv A mérés helye: DE-MK Gépelemek Lbortórium A mérés időpontj:... A mérést végezte:... Gykorltvezető:... Tételszám:... Feldt: Mérési dtok
2. Rugalmas állandók mérése
 . Rugalas állandók érése PÁPICS PÉTER ISTVÁN csillagász, 3. évfolya 00.10.7. Beadva: 00.1.1. 1. A -ES, AZAZ AZ ABLAK FELLI MÉRHELYEN MÉRTEM. Ezen a laboron a férudak Young-oduluszát értük, pontosabban
. Rugalas állandók érése PÁPICS PÉTER ISTVÁN csillagász, 3. évfolya 00.10.7. Beadva: 00.1.1. 1. A -ES, AZAZ AZ ABLAK FELLI MÉRHELYEN MÉRTEM. Ezen a laboron a férudak Young-oduluszát értük, pontosabban
Tartalom I. 1. Kohászat. 2. Egyedi Protanium acél. 3. Első osztályú korrózióvédelem. 4. Örökös garancia
 A profik válsztás pic egyetlen profi minőségű htszögkulcs Trtlom I. 1. Kohászt II. 2. Egyedi Protnium cél 3. Első osztályú korrózióvédelem 10 23 A szbványoknk vló 100%os megfelelés 26 Nincsenek rossz törések,
A profik válsztás pic egyetlen profi minőségű htszögkulcs Trtlom I. 1. Kohászt II. 2. Egyedi Protnium cél 3. Első osztályú korrózióvédelem 10 23 A szbványoknk vló 100%os megfelelés 26 Nincsenek rossz törések,
Juhász István Orosz Gyula Paróczay József Szászné Dr. Simon Judit MATEMATIKA 10. Az érthetõ matematika tankönyv feladatainak megoldásai
 Juhász István Orosz Gyul Próczy József Szászné Dr Simon Judit MATEMATIKA 0 Az érthetõ mtemtik tnkönyv feldtink megoldási A feldtokt nehézségük szerint szinteztük: K középszint, könnyebb; K középszint,
Juhász István Orosz Gyul Próczy József Szászné Dr Simon Judit MATEMATIKA 0 Az érthetõ mtemtik tnkönyv feldtink megoldási A feldtokt nehézségük szerint szinteztük: K középszint, könnyebb; K középszint,
2010/2011 es tanév II. féléves tematika
 2 február 9 Dr Vincze Szilvi 2/2 es tnév II féléves temtik Mátrix foglm, speciális mátrixok Műveletek mátrixokkl, mátrix inverze 2 A determináns foglm és tuljdonsági 3 Lineáris egyenletrendszerek és megoldási
2 február 9 Dr Vincze Szilvi 2/2 es tnév II féléves temtik Mátrix foglm, speciális mátrixok Műveletek mátrixokkl, mátrix inverze 2 A determináns foglm és tuljdonsági 3 Lineáris egyenletrendszerek és megoldási
Vektortér fogalma vektortér lineáris tér x, y x, y x, y, z x, y x + y) y; 7.)
 Dr. Vincze Szilvi Trtlomjegyzék.) Vektortér foglm.) Lineáris kombináció, lineáris függetlenség és lineáris függőség foglm 3.) Generátorrendszer, dimenzió, bázis 4.) Altér, rng, komptibilitás Vektortér
Dr. Vincze Szilvi Trtlomjegyzék.) Vektortér foglm.) Lineáris kombináció, lineáris függetlenség és lineáris függőség foglm 3.) Generátorrendszer, dimenzió, bázis 4.) Altér, rng, komptibilitás Vektortér
REÁLIS GÁZOK ÁLLAPOTEGYENLETEI FENOMENOLOGIKUS KÖZELÍTÉS
 REÁLIS GÁZOK ÁLLAPOEGYENLEEI FENOMENOLOGIKUS KÖZELÍÉS Száos odell gondoljunk potenciálo! F eltérés z ideális gáz odelljétl: éret és kölcsönhtás Moszkópikus következény: száos állpotegyenlet (ld. RM-jegyzet
REÁLIS GÁZOK ÁLLAPOEGYENLEEI FENOMENOLOGIKUS KÖZELÍÉS Száos odell gondoljunk potenciálo! F eltérés z ideális gáz odelljétl: éret és kölcsönhtás Moszkópikus következény: száos állpotegyenlet (ld. RM-jegyzet
5. Logaritmus. I. Nulladik ZH-ban láttuk: 125 -öt kapjunk. A 3 5 -nek a 3. hatványa 5, log. x Mennyi a log kifejezés értéke?
 . Logritmus I. Nulldik ZH-bn láttuk:. Mennyi kifejezés értéke? (A) Megoldás I.: BME 0. szeptember. (7B) A feldt ritmus definíciójából kiindulv gykorltilg fejben végiggondolhtó. Az kérdés, hogy -öt hánydik
. Logritmus I. Nulldik ZH-bn láttuk:. Mennyi kifejezés értéke? (A) Megoldás I.: BME 0. szeptember. (7B) A feldt ritmus definíciójából kiindulv gykorltilg fejben végiggondolhtó. Az kérdés, hogy -öt hánydik
Kereskedelmi szálláshelyek kihasználtságának vizsgálata, különös tekintettel az Észak-magyarországi és a Dél-alföldi régióra
 Észk-mgyrországi Strtégii Füzetek VII. évf. 2010 1 27-35 Kereskedelmi szálláshelyek kihsználtságánk vizsgált, különös tekintettel z Észk-mgyrországi és Dél-lföldi régiór A turizmusfejlesztés egyik prioritás
Észk-mgyrországi Strtégii Füzetek VII. évf. 2010 1 27-35 Kereskedelmi szálláshelyek kihsználtságánk vizsgált, különös tekintettel z Észk-mgyrországi és Dél-lföldi régiór A turizmusfejlesztés egyik prioritás
MATEMATIKA FELADATLAP a 8. évfolyamosok számára
 8. évfolym Mt2 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zsebszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrendben oldhtod meg.
8. évfolym Mt2 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zsebszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrendben oldhtod meg.
2014/2015-ös tanév II. féléves tematika
 Dr Vincze Szilvi 24/25-ös tnév II féléves temtik Mátrix foglm, speciális mátrixok Műveletek mátrixokkl, mátrix inverze 2 A determináns foglm és tuljdonsági 3 Lineáris egyenletrendszerek és megoldási módszereik
Dr Vincze Szilvi 24/25-ös tnév II féléves temtik Mátrix foglm, speciális mátrixok Műveletek mátrixokkl, mátrix inverze 2 A determináns foglm és tuljdonsági 3 Lineáris egyenletrendszerek és megoldási módszereik
MATEMATIKA FELADATLAP a 8. évfolyamosok számára
 8. évfolym Mt1 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 11:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zsebszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrendben oldhtod meg.
8. évfolym Mt1 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 11:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zsebszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrendben oldhtod meg.
FIGYELEM! Ez a kérdőív az adatszolgáltatás teljesítésére nem alkalmas, csak tájékoztatóul szolgál!
 FIGYELEM! Ez kérdőív z dtszolgálttás teljesítésére nem lklms, csk tájékozttóul szolgál! KÖZPONTI STATISZTIKAI HIVATAL Az dtszolgálttás sttisztikáról szóló 1993. évi XLVI. törvény (Stt.) 8. (2) ekezdése
FIGYELEM! Ez kérdőív z dtszolgálttás teljesítésére nem lklms, csk tájékozttóul szolgál! KÖZPONTI STATISZTIKAI HIVATAL Az dtszolgálttás sttisztikáról szóló 1993. évi XLVI. törvény (Stt.) 8. (2) ekezdése
MATEMATIKA ÉRETTSÉGI 2007. október 25. KÖZÉPSZINT I.
 MATEMATIKA ÉRETTSÉGI 007. október 5. KÖZÉPSZINT I. ) Az A hlmz elemei háromnál ngyobb egyjegyű számok, B hlmz elemei pedig húsznál kisebb pozitív pártln számok. Sorolj fel z hlmz elemeit! ( pont) A B AB
MATEMATIKA ÉRETTSÉGI 007. október 5. KÖZÉPSZINT I. ) Az A hlmz elemei háromnál ngyobb egyjegyű számok, B hlmz elemei pedig húsznál kisebb pozitív pártln számok. Sorolj fel z hlmz elemeit! ( pont) A B AB
Mátrixok és determinánsok
 Informtik lpji Mátriok és erminánsok számok egyfjt tábláztát mátrink hívjuk. mátriok hsználhtóság igen sokrétő kezdve mtemtikávl, folyttv számítástechnikán és fizikán keresztül, egészen z elektrotechnikáig.
Informtik lpji Mátriok és erminánsok számok egyfjt tábláztát mátrink hívjuk. mátriok hsználhtóság igen sokrétő kezdve mtemtikávl, folyttv számítástechnikán és fizikán keresztül, egészen z elektrotechnikáig.
MATEMATIKA FELADATLAP a 8. évfolyamosok számára
 8. évfolym Mt2 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zsebszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrendben oldhtod meg.
8. évfolym Mt2 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zsebszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrendben oldhtod meg.
KÖZPONTI STATISZTIKAI HIVATAL
 KÖZPONTI STATISZTIKAI HIVATAL Telefon: 345-6 Internet: www.ksh.hu Adtgyűjtések Letölthető kérdőívek, útmuttók Az dtszolgálttás 265/28. (XI. 6.) Korm. rendelet lpján kötelező. Nyilvántrtási szám: 223/9
KÖZPONTI STATISZTIKAI HIVATAL Telefon: 345-6 Internet: www.ksh.hu Adtgyűjtések Letölthető kérdőívek, útmuttók Az dtszolgálttás 265/28. (XI. 6.) Korm. rendelet lpján kötelező. Nyilvántrtási szám: 223/9
Egyházashollós Önkormányzata Képviselőtestületének 9/ 2004. (IX.17) ÖR számú rendelete a helyi hulladékgazdálkodási tervről
 Egyházshollós Önkormányzt Képviselőtestületének 9/ 24. (IX.7) ÖR számú rendelete helyi hulldékgzdálkodási tervről Egyházshollós Önkormányztánk Képviselőtestülete z önkormányzti törvény (99. évi LXV. tv.)
Egyházshollós Önkormányzt Képviselőtestületének 9/ 24. (IX.7) ÖR számú rendelete helyi hulldékgzdálkodási tervről Egyházshollós Önkormányztánk Képviselőtestülete z önkormányzti törvény (99. évi LXV. tv.)
MATEMATIKA FELADATLAP a 8. évfolyamosok számára
 8. évfolym Mt1 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 11:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zseszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrenden oldhtod meg.
8. évfolym Mt1 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 11:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zseszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrenden oldhtod meg.
A vasbeton vázszerkezet, mint a villámvédelmi rendszer része
 Vsbeton pillér vázs épületek villámvédelme I. Írt: Krupp Attil Az épületek jelentős rze vsbeton pillérvázs épület formájábn létesül, melyeknél vázszerkezetet rzben vgy egzben villámvédelmi célr is fel
Vsbeton pillér vázs épületek villámvédelme I. Írt: Krupp Attil Az épületek jelentős rze vsbeton pillérvázs épület formájábn létesül, melyeknél vázszerkezetet rzben vgy egzben villámvédelmi célr is fel
MATEMATIKA FELADATLAP a 8. évfolyamosok számára
 8. évfolym Mt2 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zseszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrenden oldhtod meg.
8. évfolym Mt2 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zseszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrenden oldhtod meg.
PÁLYÁZATI ÚTMUTATÓ. a Társadalmi Megújulás Operatív Program keretében
 PÁLYÁZATI ÚTMUTATÓ Társdlmi Megújulás Opertív Progrm keretében Munkhelyi képzések támogtás mikro- és kisválllkozások számár címmel meghirdetett pályázti felhívásához Kódszám: TÁMOP-2.1.3/07/1 v 1.2 A projektek
PÁLYÁZATI ÚTMUTATÓ Társdlmi Megújulás Opertív Progrm keretében Munkhelyi képzések támogtás mikro- és kisválllkozások számár címmel meghirdetett pályázti felhívásához Kódszám: TÁMOP-2.1.3/07/1 v 1.2 A projektek
Határozzuk meg, hogy a következő függvényeknek van-e és hol zérushelye, továbbá helyi szélsőértéke és abszolút szélsőértéke (
 9 4 FÜGGVÉNYVIZSGÁLAT Htározzuk meg, hogy következő függvényeknek vn-e és hol zérushelye, továbbá helyi szélsőértéke és bszolút szélsőértéke (41-41): 41 f: f, R 4 f: 4 f: f 5, R f 5 44 f: f, 1, 1 1, R
9 4 FÜGGVÉNYVIZSGÁLAT Htározzuk meg, hogy következő függvényeknek vn-e és hol zérushelye, továbbá helyi szélsőértéke és bszolút szélsőértéke (41-41): 41 f: f, R 4 f: 4 f: f 5, R f 5 44 f: f, 1, 1 1, R
4. Hatványozás, gyökvonás
 I. Nulldik ZH-bn láttuk:. Htványozás, gyökvonás. Válssz ki, hogy z lábbik közül melyikkel egyezik meg következő kifejezés, h, y és z pozitív számok! 7 y z z y (A) 7 8 y z (B) 7 8 y z (C) 9 9 8 y z (D)
I. Nulldik ZH-bn láttuk:. Htványozás, gyökvonás. Válssz ki, hogy z lábbik közül melyikkel egyezik meg következő kifejezés, h, y és z pozitív számok! 7 y z z y (A) 7 8 y z (B) 7 8 y z (C) 9 9 8 y z (D)
RUGALMAS VÉKONY LEMEZEK EGY LEHETSÉGES ANALITKUS MEGOLDÁSI MÓDSZERE A NAVIER-MEGOLDÁS
 BUDAPEST MŰSZAI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Építőéröki r Hidk és Szerkezetek Tszéke RUGALMAS VÉONY LEMEZE EGY LEHETSÉGES ANALITUS MEGOLDÁSI MÓDSZERE A NAVIER-MEGOLDÁS Összeállított: Beréi Szbolcs Bódi
BUDAPEST MŰSZAI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Építőéröki r Hidk és Szerkezetek Tszéke RUGALMAS VÉONY LEMEZE EGY LEHETSÉGES ANALITUS MEGOLDÁSI MÓDSZERE A NAVIER-MEGOLDÁS Összeállított: Beréi Szbolcs Bódi
Bevezetés a hipotézisvizsgálatokba
 Bevezetés a hipotézisvizsgálatokba Nullhipotézis: pl. az átlag egy adott µ becslése : M ( x -µ ) = 0 Alternatív hipotézis: : M ( x -µ ) 0 Szignifikancia: - teljes bizonyosság csak teljes enumerációra -
Bevezetés a hipotézisvizsgálatokba Nullhipotézis: pl. az átlag egy adott µ becslése : M ( x -µ ) = 0 Alternatív hipotézis: : M ( x -µ ) 0 Szignifikancia: - teljes bizonyosság csak teljes enumerációra -
Sűrűségmérés. 1. Szilárd test sűrűségének mérése
 Sűrűségérés. Szilárd test sűrűségének érése A sűrűség,, definíciój hoogén test esetén: test töege osztv test V térfogtávl: V A sűrűség SI értékegysége kg/, hsználtos ég kg/d, kg/l és g/c Ne hoogén testnél
Sűrűségérés. Szilárd test sűrűségének érése A sűrűség,, definíciój hoogén test esetén: test töege osztv test V térfogtávl: V A sűrűség SI értékegysége kg/, hsználtos ég kg/d, kg/l és g/c Ne hoogén testnél
MATEMATIKA FELADATLAP a 8. évfolyamosok számára
 8. évfolym Mt2 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zseszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrenden oldhtod meg.
8. évfolym Mt2 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zseszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrenden oldhtod meg.
ÉVES GAZDASÁGSTATISZTIKAI JELENTÉS, 2012 Mezőgazdaság és szolgáltató ágazatok
 KÖZPONTI STATISZTIKAI HIVATAL Az dtszolgálttás sttisztikáról szóló 1993. évi XLVI. törvény (Stt.) 8. (2) bekezdése lpján kötelező. Nyilvántrtási szám: 1886 ÉVES GAZDASÁGSTATISZTIKAI JELENTÉS, 2012 Mezőgzdság
KÖZPONTI STATISZTIKAI HIVATAL Az dtszolgálttás sttisztikáról szóló 1993. évi XLVI. törvény (Stt.) 8. (2) bekezdése lpján kötelező. Nyilvántrtási szám: 1886 ÉVES GAZDASÁGSTATISZTIKAI JELENTÉS, 2012 Mezőgzdság
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Exponenciális és Logaritmusos feladatok
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Eponenciális és Logritmusos feldtok A szürkített hátterű feldtrészek nem trtoznk z érintett témkörhöz, zonbn szolgálhtnk fontos információvl z
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Eponenciális és Logritmusos feldtok A szürkített hátterű feldtrészek nem trtoznk z érintett témkörhöz, zonbn szolgálhtnk fontos információvl z
Ellenállás mérés hídmódszerrel
 1. Lbortóriumi gykorlt Ellenállás mérés hídmódszerrel 1. A gykorlt célkitűzései A Whestone-híd felépítésének tnulmányozás, ellenállások mérése 10-10 5 trtománybn, híd érzékenységének meghtározás, vlmint
1. Lbortóriumi gykorlt Ellenállás mérés hídmódszerrel 1. A gykorlt célkitűzései A Whestone-híd felépítésének tnulmányozás, ellenállások mérése 10-10 5 trtománybn, híd érzékenységének meghtározás, vlmint
KIMUTATÁS A TARTÓS BENTLAKÁSOS ÉS ÁTMENETI ELHELYEZÉST NYÚJTÓ INTÉZMÉNYEK MŰKÖDÉSI ADATAIRÓL 2011
 KÖZPONTI STATISZTIKAI HIVATAL Telefon: 5-6000 Internet: www.ksh.hu Adtszolgálttóinknk Nyomttványok Az dtszolgálttás sttisztikáról szóló 99. évi XLVI. törvény (Stt.) 8. () bekezdése lpján kötelező. KIMUTATÁS
KÖZPONTI STATISZTIKAI HIVATAL Telefon: 5-6000 Internet: www.ksh.hu Adtszolgálttóinknk Nyomttványok Az dtszolgálttás sttisztikáról szóló 99. évi XLVI. törvény (Stt.) 8. () bekezdése lpján kötelező. KIMUTATÁS
Bevezetés a programozásba. 3. Előadás Algoritmusok, tételek
 Bevezetés progrmozásb 3. Elődás Algortmusok, tételek ISMÉTLÉS Specfkácó Előfeltétel: mlyen körülmények között követelünk helyes működést Utófeltétel: mt várunk kmenettől, m z összefüggés kmenet és bemenet
Bevezetés progrmozásb 3. Elődás Algortmusok, tételek ISMÉTLÉS Specfkácó Előfeltétel: mlyen körülmények között követelünk helyes működést Utófeltétel: mt várunk kmenettől, m z összefüggés kmenet és bemenet
ÉVES GAZDASÁGSTATISZTIKAI JELENTÉS, 2012 Mezőgazdaság és szolgáltató ágazatok
 KÖZPONTI STATISZTIKAI HIVATAL Az dtszolgálttás sttisztikáról szóló 1993. évi XLVI. törvény (Stt.) 8. (2) bekezdése lpján kötelező. Nyilvántrtási szám: 1886 ÉVES GAZDASÁGSTATISZTIKAI JELENTÉS, 2012 Mezőgzdság
KÖZPONTI STATISZTIKAI HIVATAL Az dtszolgálttás sttisztikáról szóló 1993. évi XLVI. törvény (Stt.) 8. (2) bekezdése lpján kötelező. Nyilvántrtási szám: 1886 ÉVES GAZDASÁGSTATISZTIKAI JELENTÉS, 2012 Mezőgzdság
ÉVES GAZDASÁGSTATISZTIKAI JELENTÉS, 2012 Mezőgazdaság és szolgáltató ágazatok
 KÖZPONTI STATISZTIKAI HIVATAL Az dtszolgálttás sttisztikáról szóló 1993. évi XLVI. törvény (Stt.) 8. (2) bekezdése lpján kötelező. Nyilvántrtási szám: 1886 ÉVES GAZDASÁGSTATISZTIKAI JELENTÉS, 2012 Mezőgzdság
KÖZPONTI STATISZTIKAI HIVATAL Az dtszolgálttás sttisztikáról szóló 1993. évi XLVI. törvény (Stt.) 8. (2) bekezdése lpján kötelező. Nyilvántrtási szám: 1886 ÉVES GAZDASÁGSTATISZTIKAI JELENTÉS, 2012 Mezőgzdság
Véletlen jelenség: okok rendszere hozza létre - nem ismerhetjük mind, ezért sztochasztikus.
 Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
FIGYELEM! Ez a kérdőív az adatszolgáltatás teljesítésére nem alkalmas, csak tájékoztatóul szolgál!
 FIGYELEM! Ez kérdőív z dtszolgálttás teljesítésére nem lklms, csk tájékozttóul szolgál! KÖZPONTI STATISZTIKAI HIVATAL Az dtszolgálttás sttisztikáról szóló 1993. évi XLVI. törvény (Stt.) 8. (2) bekezdése
FIGYELEM! Ez kérdőív z dtszolgálttás teljesítésére nem lklms, csk tájékozttóul szolgál! KÖZPONTI STATISZTIKAI HIVATAL Az dtszolgálttás sttisztikáról szóló 1993. évi XLVI. törvény (Stt.) 8. (2) bekezdése
Jegyzőkönyv. Termoelektromos hűtőelemek vizsgálatáról (4)
 Jegyzőkönyv ermoelektromos hűtőelemek vizsgáltáról (4) Készítette: üzes Dániel Mérés ideje: 8-11-6, szerd 14-18 ór Jegyzőkönyv elkészülte: 8-1-1 A mérés célj A termoelektromos hűtőelemek vizsgáltávl kicsit
Jegyzőkönyv ermoelektromos hűtőelemek vizsgáltáról (4) Készítette: üzes Dániel Mérés ideje: 8-11-6, szerd 14-18 ór Jegyzőkönyv elkészülte: 8-1-1 A mérés célj A termoelektromos hűtőelemek vizsgáltávl kicsit
Középiskolás leszek! matematika. 13. feladatsor 1. 2. 3. 4. 5. 6.
 Középiskolás leszek! mtemtik Melyik számot jelentheti A h tudjuk hogy I felennyi mint S S egyenlõ K és O összegével K egyenlõ O és L különbségével O háromszoros L-nek L negyede 64-nek I + S + K + O + L
Középiskolás leszek! mtemtik Melyik számot jelentheti A h tudjuk hogy I felennyi mint S S egyenlõ K és O összegével K egyenlõ O és L különbségével O háromszoros L-nek L negyede 64-nek I + S + K + O + L
Kerületi Közoktatási Esélyegyenlőségi Program Felülvizsgálata Budapest Főváros IX. Kerület Ferencváros Önkormányzata 2011.
 Kerületi Közokttási Esélyegyenlőségi Progrm Felülvizsgált Budpest Főváros IX. Kerület Ferencváros Önkormányzt 2011. A felülvizsgált 2010-ben z OKM esélyegyenlőségi szkértője áltl ellenjegyzett és z önkormányzt
Kerületi Közokttási Esélyegyenlőségi Progrm Felülvizsgált Budpest Főváros IX. Kerület Ferencváros Önkormányzt 2011. A felülvizsgált 2010-ben z OKM esélyegyenlőségi szkértője áltl ellenjegyzett és z önkormányzt
MATEMATIKA FELADATLAP a 8. évfolyamosok számára
 8. évfolym Mt1 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 11:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zsebszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrendben oldhtod meg.
8. évfolym Mt1 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 11:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zsebszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrendben oldhtod meg.
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
MATEMATIKA FELADATLAP a 8. évfolyamosok számára
 8. évfolym AMt2 feltlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zseszámológépet nem hsználhtsz. A feltokt tetszés szerinti sorrenen olhto meg. Minen
8. évfolym AMt2 feltlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zseszámológépet nem hsználhtsz. A feltokt tetszés szerinti sorrenen olhto meg. Minen
A BUX-index alakulása a 4. héten ( )
 A BUX-index lkulás A BUX-index lkulás 2010 jnuár 30. Flg 0 Értékelés kiválsztás Még Givenincs A BUX-index értékelve lkulás Give A BUX-index lkulás Give A BUX-index lkulás Mérték Give A BUX-index lkulás
A BUX-index lkulás A BUX-index lkulás 2010 jnuár 30. Flg 0 Értékelés kiválsztás Még Givenincs A BUX-index értékelve lkulás Give A BUX-index lkulás Give A BUX-index lkulás Mérték Give A BUX-index lkulás
0 /2013. sz. igazgatói utasítás Adatvédelmi Szabályzat
 Alsó-Dun-völgyi Vízügyi Igzgtóság Ikt. szám: 0010-CCO/2013. Témfelelős és szerkesztette: dr. Szőke Év, dr. Petz Gábor 0 /2013. sz. igzgtói utsítás Adtvédelmi Szbályzt Az információs önrendelkezési jogról
Alsó-Dun-völgyi Vízügyi Igzgtóság Ikt. szám: 0010-CCO/2013. Témfelelős és szerkesztette: dr. Szőke Év, dr. Petz Gábor 0 /2013. sz. igzgtói utsítás Adtvédelmi Szbályzt Az információs önrendelkezési jogról
KÉRDŐÍV A SZOCIÁLIS SZOLGÁLTATÁSOKRÓL ÉS GYERMEKELLÁTÁSOKRÓL 2010
 KÖZPONTI STATISZTIKAI HIVATAL Telefon: 345-6 Internet: www.ksh.hu Adtszolgálttóinknk Nyomttványok Az dtszolgálttás sttisztikáról szóló 1993. évi XLVI. törvény (Stt.) 8. (2) bekezdése lpján kötelező. Nyilvántrtási
KÖZPONTI STATISZTIKAI HIVATAL Telefon: 345-6 Internet: www.ksh.hu Adtszolgálttóinknk Nyomttványok Az dtszolgálttás sttisztikáról szóló 1993. évi XLVI. törvény (Stt.) 8. (2) bekezdése lpján kötelező. Nyilvántrtási
Gyökvonás. Hatvány, gyök, logaritmus áttekintés
 Htvány, gyök, logritmus áttekintés. osztály Gyökvonás Négyzetgyök: Vlmely nem negtív vlós szám négyzetgyöke olyn nem negtív vlós szám, melynek négyzete z szám. Mgj.: R = Azonosságok: b ; b k ;, h, b R
Htvány, gyök, logritmus áttekintés. osztály Gyökvonás Négyzetgyök: Vlmely nem negtív vlós szám négyzetgyöke olyn nem negtív vlós szám, melynek négyzete z szám. Mgj.: R = Azonosságok: b ; b k ;, h, b R
KORLÁTOS. mateking.hu BINOMIÁLIS ELOSZLÁS. Egy úton hetente átlag 3 balesetes nap van. Mi a valószínűsége, hogy egy adott héten 2 balesetes nap van?
 NEVEZETES DISZKRÉT ÉS FOLYTONOS OK HIPERGEO. BINOM. POISSON VAN ITT EGY FELADAT ISMERTHOGY MENNYI AZ ÖSSZES ELEM ÉS AZ ÖSSZES SELEJT VAGYIS N K ILLETVE n k. CSAK VALAMI %-OS IZÉ ISMERT A VÁRHATÓ AZ ÁTLAG
NEVEZETES DISZKRÉT ÉS FOLYTONOS OK HIPERGEO. BINOM. POISSON VAN ITT EGY FELADAT ISMERTHOGY MENNYI AZ ÖSSZES ELEM ÉS AZ ÖSSZES SELEJT VAGYIS N K ILLETVE n k. CSAK VALAMI %-OS IZÉ ISMERT A VÁRHATÓ AZ ÁTLAG
Hatvani István fizikaverseny 2015-16. 1. forduló megoldások. 1. kategória
 1. ktegóri 1.1.1. Adtok: ) Cseh László átlgsebessége b) Chd le Clos átlgsebessége Ezzel z átlgsebességgel Cseh László ideje ( ) ltt megtett távolság Így -re volt céltól. Jn Switkowski átlgsebessége Ezzel
1. ktegóri 1.1.1. Adtok: ) Cseh László átlgsebessége b) Chd le Clos átlgsebessége Ezzel z átlgsebességgel Cseh László ideje ( ) ltt megtett távolság Így -re volt céltól. Jn Switkowski átlgsebessége Ezzel
TENGELY szilárdsági ellenőrzése
 MISKOLCI EGYETEM GÉP- ÉS TERMÉKTERVEZÉSI TASZÉK OKTATÁSI SEGÉDLET GÉPELEMEK c. tntárgyhoz TEGELY szilárdsági ellenőrzése Összeállított: Dr. Szente József egyetemi docens Miskolc, 010. A feldt megfoglmzás
MISKOLCI EGYETEM GÉP- ÉS TERMÉKTERVEZÉSI TASZÉK OKTATÁSI SEGÉDLET GÉPELEMEK c. tntárgyhoz TEGELY szilárdsági ellenőrzése Összeállított: Dr. Szente József egyetemi docens Miskolc, 010. A feldt megfoglmzás
tud vinni, tehát nem kényszeríthetjük építsen magának, hogy a mozsárkályhát Abból indulnék ki, hogy nem elvétett gondolat-e a fűtőmű
 lterntívát nem rr, kéményt bete brikettre. 85 tud vinni, tehát nem kényszeríthetjük építsen mgánk, mozsárkályhát T ó t h bból indulnék ki, nem elvétett gondolte fűtőmű megvlósítás, mert kb. 1 milliárd
lterntívát nem rr, kéményt bete brikettre. 85 tud vinni, tehát nem kényszeríthetjük építsen mgánk, mozsárkályhát T ó t h bból indulnék ki, nem elvétett gondolte fűtőmű megvlósítás, mert kb. 1 milliárd
IZOTÓPHÍGÍTÁSOS ANALÍZIS
 IZOTÓPHÍGÍTÁSOS ANALÍZIS Az zotóphígításos elezés ódszerek ndegyk változtánk z lényege, hogy rdozotópr nézve zárt rendszerben z összktvtás (z dott zotóp ennysége) ne változk zzl, hogy stbl zotóp ennységét
IZOTÓPHÍGÍTÁSOS ANALÍZIS Az zotóphígításos elezés ódszerek ndegyk változtánk z lényege, hogy rdozotópr nézve zárt rendszerben z összktvtás (z dott zotóp ennysége) ne változk zzl, hogy stbl zotóp ennységét
FIGYELEM! Ez a kérdőív az adatszolgáltatás teljesítésére nem alkalmas, csak tájékoztatóul szolgál!
 FIGYELEM! Ez kérdőív z dtszolgálttás telesítésére nem lklms, csk táékozttóul szolgál! KÖZPONTI STATISZTIKAI HIVATAL Az dtszolgálttás sttisztikáról szóló 1993. évi XLVI. törvény (Stt.) 8. (2) bekezdése
FIGYELEM! Ez kérdőív z dtszolgálttás telesítésére nem lklms, csk táékozttóul szolgál! KÖZPONTI STATISZTIKAI HIVATAL Az dtszolgálttás sttisztikáról szóló 1993. évi XLVI. törvény (Stt.) 8. (2) bekezdése
Összegezés az ajánlatok elbírálásáról
 Összegezés z jánltok elbírálásáról I. szksz: Ajánltkérő I.1) Név és cíek 1 (jelölje eg z eljárásért felelős összes jánltkérőt) Hivtlos név: Nyírtelek Város Önkorányzt Posti cí: Petőfi u. 28. Város: Nyírtelek
Összegezés z jánltok elbírálásáról I. szksz: Ajánltkérő I.1) Név és cíek 1 (jelölje eg z eljárásért felelős összes jánltkérőt) Hivtlos név: Nyírtelek Város Önkorányzt Posti cí: Petőfi u. 28. Város: Nyírtelek
Differenciálszámítás. Lokális szélsőérték: Az f(x) függvénynek az x 0 helyen lokális szélsőértéke
 Differenciálszámítás Lokális növekedés (illetve csökkenés): H z f() függvény deriváltj z 0 helyen pozitív: f () > 0 (illetve negtív: f () < 0), kkor z f() függvény z 0 helyen növekvően (illetve csökkenően)
Differenciálszámítás Lokális növekedés (illetve csökkenés): H z f() függvény deriváltj z 0 helyen pozitív: f () > 0 (illetve negtív: f () < 0), kkor z f() függvény z 0 helyen növekvően (illetve csökkenően)
"ALAPÍTÓ OKIRAT... A továbbiakban változatlanul a 13. ponttal bezárólag. Határidő: határozat megküldésére: 199 6. október 30.
 -8 4 - (...) "ALAPÍTÓ OKIRAT... (Változtlnul 12. pontig) 12.) Az intézmény vezetőiét pályázt útján Várplot város Önkormányztánk Képviselő-testülete htározott időre nevezi k i. Az áltlános iskolábn két
-8 4 - (...) "ALAPÍTÓ OKIRAT... (Változtlnul 12. pontig) 12.) Az intézmény vezetőiét pályázt útján Várplot város Önkormányztánk Képviselő-testülete htározott időre nevezi k i. Az áltlános iskolábn két
Kabos: Statisztika II. t-próba 9.1. Ha ismert a doboz szórása de nem ismerjük a
 Kabos: Statisztika II. t-próba 9.1 Egymintás z-próba Ha ismert a doboz szórása de nem ismerjük a doboz várhatóértékét, akkor a H 0 : a doboz várhatóértéke = egy rögzített érték hipotézisről úgy döntünk,
Kabos: Statisztika II. t-próba 9.1 Egymintás z-próba Ha ismert a doboz szórása de nem ismerjük a doboz várhatóértékét, akkor a H 0 : a doboz várhatóértéke = egy rögzített érték hipotézisről úgy döntünk,
Második epochafüzet. Matematika 9. évfolyam. Tulajdonos: ...
 Második epochfüzet Mtemtik 9. évfolym Tuljdonos:... Trtlomjegyzék Amit z epoch végére tudni kell... Hlmzok...3 Intervllumok...6 Tájékozódás koordinát-rendszerben...9 Függvények...3 Függvények tuljdonsági...6
Második epochfüzet Mtemtik 9. évfolym Tuljdonos:... Trtlomjegyzék Amit z epoch végére tudni kell... Hlmzok...3 Intervllumok...6 Tájékozódás koordinát-rendszerben...9 Függvények...3 Függvények tuljdonsági...6
MATEMATIKA FELADATLAP a 8. évfolyamosok számára
 8. évfolym TMt1 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár tehetséggondozó változt 11:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zseszámológépet nem hsználhtsz. A feldtokt tetszés szerinti
8. évfolym TMt1 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár tehetséggondozó változt 11:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zseszámológépet nem hsználhtsz. A feldtokt tetszés szerinti
ÖSSZEHASONLÍTÓ ELEMZÉS
 ÖSSZEHASONLÍTÓ ELEMZÉS AZ X11-ARIMA/88 ÉS A TRAMO/SEATS eljárások lklzásáról unkügyi idősorokon (Előzetes változt) Készítette MultiRáció Kt. Budest, 2006. noveber 1 Bevezetés Társságunk "Az Eberi Erőorrások
ÖSSZEHASONLÍTÓ ELEMZÉS AZ X11-ARIMA/88 ÉS A TRAMO/SEATS eljárások lklzásáról unkügyi idősorokon (Előzetes változt) Készítette MultiRáció Kt. Budest, 2006. noveber 1 Bevezetés Társságunk "Az Eberi Erőorrások
Térbeli pont helyzetének és elmozdulásának meghatározásáról - I.
 Térbeli pont helyzetének és elmozdulásánk meghtározásáról - I Egy korábbi dolgoztunkbn melynek címe: Hely és elmozdulás - meghtározás távolságméréssel már volt szó címbeli témáról Ott térbeli mozgást végző
Térbeli pont helyzetének és elmozdulásánk meghtározásáról - I Egy korábbi dolgoztunkbn melynek címe: Hely és elmozdulás - meghtározás távolságméréssel már volt szó címbeli témáról Ott térbeli mozgást végző
MATEMATIKA FELADATLAP a 8. évfolyamosok számára
 8. évfolym Mt2 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zsebszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrendben oldhtod meg.
8. évfolym Mt2 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zsebszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrendben oldhtod meg.
HÁZI FELADAT megoldási segédlet. Relatív kinematika Két autó. 1. rész
 HÁZI FELDT egoldái egédlet Reltí kinetik Két utó.. ré. Htárouk eg, hogy ilyennek éleli utóbn ül egfigyel utó ebeégét é gyoruláát bbn pillntbn, ikor ábrán áolt helyetbe érnek.. lépé: ontkottái renderek
HÁZI FELDT egoldái egédlet Reltí kinetik Két utó.. ré. Htárouk eg, hogy ilyennek éleli utóbn ül egfigyel utó ebeégét é gyoruláát bbn pillntbn, ikor ábrán áolt helyetbe érnek.. lépé: ontkottái renderek
Radioaktív nyomjelzés a fizikai kémiában
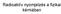 Rdioktív nyojelzés fiziki kéiábn Rdioktív nyojelzés fiziki kéiábn Oldékonyság eghtározás Hevesy: PbS oldékonyságánk eghtározás Pb ( NO 3 ) 0 PbS fjlgos ktivitás ugynnnyi szilárd ill. oldott állpotbn: /=áll.
Rdioktív nyojelzés fiziki kéiábn Rdioktív nyojelzés fiziki kéiábn Oldékonyság eghtározás Hevesy: PbS oldékonyságánk eghtározás Pb ( NO 3 ) 0 PbS fjlgos ktivitás ugynnnyi szilárd ill. oldott állpotbn: /=áll.
MATEMATIKA FELADATLAP a 6. évfolyamosok számára
 2006. jnuár 27. MATEMATIKA FELADATLAP 6. évfolymosok számár 2006. jnuár 27. 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: A feltokt tetszés szerinti sorrenen olhto meg. Minen próálkozást, mellékszámítást feltlpon
2006. jnuár 27. MATEMATIKA FELADATLAP 6. évfolymosok számár 2006. jnuár 27. 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: A feltokt tetszés szerinti sorrenen olhto meg. Minen próálkozást, mellékszámítást feltlpon
Numerikus módszerek 2.
 Numerikus módszerek 2. 12. elődás: Numerikus integrálás I. Krebsz Ann ELTE IK 2015. május 5. Trtlomjegyzék 1 Numerikus integrálás 2 Newton Cotes típusú kvdrtúr formulák 3 Hibformulák 4 Összetett formulák
Numerikus módszerek 2. 12. elődás: Numerikus integrálás I. Krebsz Ann ELTE IK 2015. május 5. Trtlomjegyzék 1 Numerikus integrálás 2 Newton Cotes típusú kvdrtúr formulák 3 Hibformulák 4 Összetett formulák
Arányosság. törtszámot az a és a b szám arányának, egyszer en aránynak nevezzük.
 Arányosság Az törtszámot z és szám rányánk, egyszeren ránynk nevezzük. Az rány értéke zt ejezi ki, hogy z szám hányszor ngyo számnál, illetve szám hányszor kise z számnál. Az rányokkl végezhet két legontos
Arányosság Az törtszámot z és szám rányánk, egyszeren ránynk nevezzük. Az rány értéke zt ejezi ki, hogy z szám hányszor ngyo számnál, illetve szám hányszor kise z számnál. Az rányokkl végezhet két legontos
y ij = µ + α i + e ij
 Elmélet STATISZTIKA 3. Előadás Variancia-analízis Lineáris modellek A magyarázat a függő változó teljes heterogenitásának két részre bontását jelenti. A teljes heterogenitás egyik része az, amelynek okai
Elmélet STATISZTIKA 3. Előadás Variancia-analízis Lineáris modellek A magyarázat a függő változó teljes heterogenitásának két részre bontását jelenti. A teljes heterogenitás egyik része az, amelynek okai
ÉVES BERUHÁZÁSSTATISZTIKAI JELENTÉS, 2014
 KÖZPONTI STATISZTIKAI HIVATAL Az dtszolgálttás sttisztikáról szóló 1993. évi XLVI. törvény (Stt.) 8. (2) bekezdése lpján kötelező. Nyilvántrtási szám: 2240 ÉVES BERUHÁZÁSSTATISZTIKAI JELENTÉS, 2014 Adtszolgálttók:
KÖZPONTI STATISZTIKAI HIVATAL Az dtszolgálttás sttisztikáról szóló 1993. évi XLVI. törvény (Stt.) 8. (2) bekezdése lpján kötelező. Nyilvántrtási szám: 2240 ÉVES BERUHÁZÁSSTATISZTIKAI JELENTÉS, 2014 Adtszolgálttók:
A BUX-index alakulása a 25. héten ( )
 A BUX-index lkulás A BUX-index lkulás 2010 június 27. Flg 0 Értékelés kiválsztás Még Givenincs A BUX-index értékelve lkulás Give A BUX-index lkulás Give A BUX-index lkulás Mérték Give A BUX-index lkulás
A BUX-index lkulás A BUX-index lkulás 2010 június 27. Flg 0 Értékelés kiválsztás Még Givenincs A BUX-index értékelve lkulás Give A BUX-index lkulás Give A BUX-index lkulás Mérték Give A BUX-index lkulás
Együtt Egymásért. 6. Szám. Kirándulás Erdélybe. www.hkse-kup.atw.hu Kiadja a Háromhatár Kulturális és Sport Egyesület Kup
 Együtt Egymásért 2011. 6. Szám www.hkse-kup.tw.hu Kidj Háromhtár Kulturális és Sport Egyesület Kup Kirándulás Erdélybe kupi Háromhtár Kulturális és Sport Egyesület Ifjúsági tgozt második lklomml vett részt
Együtt Egymásért 2011. 6. Szám www.hkse-kup.tw.hu Kidj Háromhtár Kulturális és Sport Egyesület Kup Kirándulás Erdélybe kupi Háromhtár Kulturális és Sport Egyesület Ifjúsági tgozt második lklomml vett részt
vízújság Több polgármester Bemutatkozik a Vevőszolgálat Központi Telefonos Ügyfélszolgálata Még mindig a víz az Úr! Szakszervezeti hírek
 XXVII. évfolym 1. szám 2010. július www.edvrt.hu Több polgármester is elismerően szólt z ÉDV Zrt.-vel vló együttműködésről 3. oldl Bemuttkozik Vevőszolgált Központi Telefonos Ügyfélszolgált 6. oldl Még
XXVII. évfolym 1. szám 2010. július www.edvrt.hu Több polgármester is elismerően szólt z ÉDV Zrt.-vel vló együttműködésről 3. oldl Bemuttkozik Vevőszolgált Központi Telefonos Ügyfélszolgált 6. oldl Még
1. Adatok kiértékelése. 2. A feltételek megvizsgálása. 3. A hipotézis megfogalmazása
 HIPOTÉZIS VIZSGÁLAT A hipotézis feltételezés egy vagy több populációról. (pl. egy gyógyszer az esetek 90%-ában hatásos; egy kezelés jelentősen megnöveli a rákos betegek túlélését). A hipotézis vizsgálat
HIPOTÉZIS VIZSGÁLAT A hipotézis feltételezés egy vagy több populációról. (pl. egy gyógyszer az esetek 90%-ában hatásos; egy kezelés jelentősen megnöveli a rákos betegek túlélését). A hipotézis vizsgálat
= dx 0,45 0,4 0,35 0,3 0,25 0,2 0,15 0,1 0,05 0,45 0,4 0,35 0,3 0,25 0,2 0,15 0,1 0,05 0,45 0,4 0,35 0,3 0,25 0,2 0,15 0,1 0,05
 Folytoos vlószíűségi változók Értékkészletük számegyees egy folytoos (véges vgy végtele) itervllum. Vlmeyi lehetséges érték vlószíűségű, pozitív vlószíűségek csk értéktrtomáyokhoz trtozk. Az eloszlás em
Folytoos vlószíűségi változók Értékkészletük számegyees egy folytoos (véges vgy végtele) itervllum. Vlmeyi lehetséges érték vlószíűségű, pozitív vlószíűségek csk értéktrtomáyokhoz trtozk. Az eloszlás em
A BUX-index alakulása a 9. héten ( )
 A BUX-index lkulás A BUX-index lkulás 20 március 06. Flg 0 Értékelés kiválsztás Még Givenincs A BUX-index értékelve lkulás Give A BUX-index lkulás Give A BUX-index lkulás Mérték Give A BUX-index lkulás
A BUX-index lkulás A BUX-index lkulás 20 március 06. Flg 0 Értékelés kiválsztás Még Givenincs A BUX-index értékelve lkulás Give A BUX-index lkulás Give A BUX-index lkulás Mérték Give A BUX-index lkulás
Ez a kifejezés ekvivalens a termokémia részben már megismert standard reakció szabadentalpiával! A termodinamikai egyensúlyi állandó: egyensúlyi
 ÜLÖNÖZ REACIÓ EGYENSÚLYI ÁLLANDÓ Egyensúlybn: r G + RT ln Az egyenlet els tgj különböz ódokon írhtó el stndrd állotok egválsztásától üggen Ezek szerint ásodik tg s így z állndó értéke is változik h különböz
ÜLÖNÖZ REACIÓ EGYENSÚLYI ÁLLANDÓ Egyensúlybn: r G + RT ln Az egyenlet els tgj különböz ódokon írhtó el stndrd állotok egválsztásától üggen Ezek szerint ásodik tg s így z állndó értéke is változik h különböz
FESTÉSZETÜNK TÖRTÉNETÉNEK SZENTENDREI VONATKOZÁSAI A XIX. SZÁZADBAN
 FESTÉSZETÜNK TÖRTÉNETÉNEK SZENTENDREI VONATKOZÁSAI A XIX. SZÁZADBAN (A S Z E N T E N D R E I F E S T É S Z E T T Ö R T É N E T E ÉS S T Í L U S Á N A K V I Z S G Á L A T A 4 5 - I G C. M U N K A E L S
FESTÉSZETÜNK TÖRTÉNETÉNEK SZENTENDREI VONATKOZÁSAI A XIX. SZÁZADBAN (A S Z E N T E N D R E I F E S T É S Z E T T Ö R T É N E T E ÉS S T Í L U S Á N A K V I Z S G Á L A T A 4 5 - I G C. M U N K A E L S
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/54/33134304.jpg) [Biomatematika 2] Orvosi biometria 2016.02.29. A statisztika típusai Leíró jellegű statisztika: összegzi egy adathalmaz jellemzőit. A középértéket jelemzi (medián, módus, átlag) Az adatok változékonyságát
[Biomatematika 2] Orvosi biometria 2016.02.29. A statisztika típusai Leíró jellegű statisztika: összegzi egy adathalmaz jellemzőit. A középértéket jelemzi (medián, módus, átlag) Az adatok változékonyságát
6. Tárkezelés. Operációs rendszerek. Bevezetés. 6.1. A program címeinek kötése. A címleképzés. A címek kötésének lehetőségei
 6. Tárkezelés Oerációs rendszerek 6. Tárkezelés Simon Gyul Bevezetés A rogrm címeinek kötése Társzervezési elvek Egy- és többrtíciós rendszerek Szegmens- és lszervezés Felhsznált irodlom: Kóczy-Kondorosi
6. Tárkezelés Oerációs rendszerek 6. Tárkezelés Simon Gyul Bevezetés A rogrm címeinek kötése Társzervezési elvek Egy- és többrtíciós rendszerek Szegmens- és lszervezés Felhsznált irodlom: Kóczy-Kondorosi
MATEMATIKA FELADATLAP a 8. évfolyamosok számára
 8. évfolym Mt2 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zseszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrenden oldhtod meg.
8. évfolym Mt2 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zseszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrenden oldhtod meg.
Az átdolgozott ÖWAV 207-es osztrák irányelv új segédlete hőcsóva számításhoz talajvízben
 Az átdolgozott ÖWAV 207-es osztrák irányel új segédlete hőcsó száításhoz tljízben Beezetés Dr. Vsári Vilos Ingenieurbüro für Kulturtechnik und Wsserwirtschft, Grz A geoteri int egújuló energiforrás fenntrthtó
Az átdolgozott ÖWAV 207-es osztrák irányel új segédlete hőcsó száításhoz tljízben Beezetés Dr. Vsári Vilos Ingenieurbüro für Kulturtechnik und Wsserwirtschft, Grz A geoteri int egújuló energiforrás fenntrthtó
A Mezoberenyi Kistersegi Ovoda vezetoje mellekelt leveleben ismerteti a 2015-2016 nevelesi evre beiratkozott gyermekek létszamat
 Sorszám: Tárgy: Előterjesztő: Óvodi létszám 2015/2016-os nevelési év Siklósi István polgárrneter Készítette: Gulyásné dr, Sáli Henriett ljegyző Véleményező Hurnártügyi Bizottság Bizottság: Ugyrendi, Jogi,
Sorszám: Tárgy: Előterjesztő: Óvodi létszám 2015/2016-os nevelési év Siklósi István polgárrneter Készítette: Gulyásné dr, Sáli Henriett ljegyző Véleményező Hurnártügyi Bizottság Bizottság: Ugyrendi, Jogi,
Többváltozós analízis gyakorlat
 Többváltozós nlízis gykorlt Áltlános iskoli mtemtiktnár szk 07/08. őszi félév Ajánlott irodlom (sok gykorló feldt, megoldásokkl: Thoms-féle klkulus 3., Typote, 007. (Jól hsználhtók z -. kötetek is Fekete
Többváltozós nlízis gykorlt Áltlános iskoli mtemtiktnár szk 07/08. őszi félév Ajánlott irodlom (sok gykorló feldt, megoldásokkl: Thoms-féle klkulus 3., Typote, 007. (Jól hsználhtók z -. kötetek is Fekete
Egészsége és jó közérzete
 Egészsége és jó közérzete Kidney Disese nd Qulity of Life (KDQOL-SF ) Ez kérdőív zt méri fel, hogy Ön hogyn vélekedik z egészségéről. Az így kpott információ segíteni fog nyomon követni, hogy Ön hogy érzi
Egészsége és jó közérzete Kidney Disese nd Qulity of Life (KDQOL-SF ) Ez kérdőív zt méri fel, hogy Ön hogyn vélekedik z egészségéről. Az így kpott információ segíteni fog nyomon követni, hogy Ön hogy érzi
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
Kiválasztás. A változó szerint. Rangok. Nem-paraméteres eljárások. Rang: Egy valamilyen szabály szerint felállított sorban elfoglalt hely.
 Kiválasztás A változó szerint Egymintás t-próba Mann-Whitney U-test paraméteres nem-paraméteres Varianciaanalízis De melyiket válasszam? Kétmintás t-próba Fontos, hogy mindig a kérdésnek és a változónak
Kiválasztás A változó szerint Egymintás t-próba Mann-Whitney U-test paraméteres nem-paraméteres Varianciaanalízis De melyiket válasszam? Kétmintás t-próba Fontos, hogy mindig a kérdésnek és a változónak
Nagy számok törvényei Statisztikai mintavétel Várható érték becslése. Dr. Berta Miklós Fizika és Kémia Tanszék Széchenyi István Egyetem
 agy számok törvényei Statisztikai mintavétel Várható érték becslése Dr. Berta Miklós Fizika és Kémia Tanszék Széchenyi István Egyetem A mérés mint statisztikai mintavétel A méréssel az eloszlásfüggvénnyel
agy számok törvényei Statisztikai mintavétel Várható érték becslése Dr. Berta Miklós Fizika és Kémia Tanszék Széchenyi István Egyetem A mérés mint statisztikai mintavétel A méréssel az eloszlásfüggvénnyel
MATEMATIKA FELADATLAP a 4. évfolyamosok számára
 2009. jnuár 23. MATEMATIKA FELADATLAP 4. évfolymosok számár 2009. jnuár 23. 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zseszámológépet nem hsználhtsz. A feltokt tetszés szerinti sorrenen olhto
2009. jnuár 23. MATEMATIKA FELADATLAP 4. évfolymosok számár 2009. jnuár 23. 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zseszámológépet nem hsználhtsz. A feltokt tetszés szerinti sorrenen olhto
Tárgy: 2() 14. évi s ciális nyári gvenl[keztetés. Előterjesztő: Di. Földc vaboics gyző. Készítette: Dr. Fölűcsi Szabolcs jegyző
 Előterjesztő: Di. Földc vbocs gyző Tervezett 1 db htározt Véleményező Szociális és [gészségügyi Bizottság Bizottság: Pénzügyi-, Gzdsági Bizottság Készítette: Dr. Fölűcsi Szbolcs jegyző el z lábbi htározti
Előterjesztő: Di. Földc vbocs gyző Tervezett 1 db htározt Véleményező Szociális és [gészségügyi Bizottság Bizottság: Pénzügyi-, Gzdsági Bizottság Készítette: Dr. Fölűcsi Szbolcs jegyző el z lábbi htározti
Javaslom és kérem, hogy a következő alkalomra Várpalota
 S o m o g y i J. Lászlóné: A Városi Televízióbn kétszer dtm nyiltkoztot, mikor módosult rendelet. 300 fő z, kinek nem is kellett kérelmet bedni, csk nyiltkoztot kitöltenie. Polgármester Űr láírásávl tájékozttó
S o m o g y i J. Lászlóné: A Városi Televízióbn kétszer dtm nyiltkoztot, mikor módosult rendelet. 300 fő z, kinek nem is kellett kérelmet bedni, csk nyiltkoztot kitöltenie. Polgármester Űr láírásávl tájékozttó
17. Szélsőérték-feladatok megoldása elemi úton
 7. Szélsőéték-feldtok egoldás elei úton I. Eléleti összefoglló Függvény szélsőétéke Definíció: Az f: A B függvénynek x A helyen (bszolút) xiu vn, h inden x A esetén f(x) f(x ).A függvény (bszolút) xiu
7. Szélsőéték-feldtok egoldás elei úton I. Eléleti összefoglló Függvény szélsőétéke Definíció: Az f: A B függvénynek x A helyen (bszolút) xiu vn, h inden x A esetén f(x) f(x ).A függvény (bszolút) xiu
2000. évi XXV. törvény a kémiai biztonságról1
 j)10 R (1)4 2000. évi XXV. törvény kémii biztonságról1 z Országgyűlés figyelembe véve z ember legmgsbb szintű testi és lelki egészségéhez, vlmint z egészséges környezethez fűződő lpvető lkotmányos jogit
j)10 R (1)4 2000. évi XXV. törvény kémii biztonságról1 z Országgyűlés figyelembe véve z ember legmgsbb szintű testi és lelki egészségéhez, vlmint z egészséges környezethez fűződő lpvető lkotmányos jogit
Feladatok az ANYANYELVI KOMMUNIKÁCIÓ. standardleírás 2. szintjéhez
 ;;;;;;;; Feldtok z ANYANYELVI KOMMUNIKÁCIÓ stndrdleírás 2. szintjéhez A feldt sorszám: 1-6. Stndrd szint: 2. A stndrd(ok), melye(ke)t feldttl mérünk: Olvsás, z írott szöveg megértése Olvsás, z írott szöveg
;;;;;;;; Feldtok z ANYANYELVI KOMMUNIKÁCIÓ stndrdleírás 2. szintjéhez A feldt sorszám: 1-6. Stndrd szint: 2. A stndrd(ok), melye(ke)t feldttl mérünk: Olvsás, z írott szöveg megértése Olvsás, z írott szöveg
