2.8. Képtárolási módok

Átírás

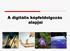
1 2.8. Képtárolási módok Ha egy A4-es lapot 6 dpi-vel akarunk beszkennelni és azt utána színes képként tárolni, akkor a mm-es lapra pixel keletkezik, s az összesen több mint 4 millió képelem tárolásához 99.6 MB-ra van szükség 24 bit/pixeles színmélységnél. A fotogrammetriai célú szkennerek használatával még jobban kidomborodik a hatékony tárolási mód szükségessége: 7 µm-es pixelmérettel a 2 2 cm-es légifénykép képmátrixa elemű! Az milliárdot is meghaladó színes képpontok.2 GB-ot foglalnának el. Mivel a fotogrammetriai feldolgozásnál általában több képpel kell dolgozni, így ekkora adatmennyiséget tekintve a mai winchestereket 4 képpel teljesen meg lehetne tölteni. Jól érzékelhető tehát, hogy effektív tárolási eszközökre és módokra van szükség. A képek tárolási módjait aszerint lehet megkülönböztetni, hogy tömörítéssel vagy anélkül dolgoznak-e. Mára a számítástechnikában igen kevés a tömörítetlen tárolás, ez még jobban érvényes a képfeldolgozásra. A viszonylag ismert DXF-formátumot lehetne ebben a témában megemlíteni. A digitális képek tárolásakor a tömörítést az teszi lehetővé, hogy a képen 8 kódolási 8 képi és 8 pszichovizuális redundancia van. A kódolási redundancia annyit tesz, hogy a képpontokat ügyes kódolással kevesebb helyen is tárolni lehet. A képi redundancia ismétlődő részleteket jelent. A pszichovizuális redundancia alatt az emberi érzékelés számára nem észrevehető különbségek, finomságok megléte. A kódolási és képi redundancia megszüntethető, így működnek a veszteségmentes (lossless) tömörítési módok. Erre a módra jó példa a Tagged Image File Format, a TIFF. A kódolási és képi redundancia megszűntetése s a pszichovizuális csökkentése veszteséges (lossy) tömörítést jelent. A két tömörített mód közötti jelentős különbség az, hogy a veszteségmentes változatban a tárolt állománynak az eredeti kép teljes információtartalmát meg kell őriznie, míg a veszteséges módok a számunkra nem érzékelhető eltéréseket, finom árnyalatkülönbségeket nem tárolják. Az orvosi, diagnosztikai gyakorlatban nem engednek meg veszteséges tárolást, a fotogrammetria és a távérzékelés bizonyos mértékű veszteséget még tolerálni képes. A számítógépes osztályozási módszerek használatánál a veszteségmentes tárolás szükséges, ellenkező esetben a pontatlan lesz a termék. A veszteséges tárolásnál mindig az a kérdés, hogy a tömörítés mértéke meddig növelhető a minőség romlása nélkül. A helytelenül paraméterezett veszteséges módot könnyen észre lehet venni a nagyobb nagyításnál jelentkező láthatóvá vált blokkok révén. A fontosabb raszteres tömörítési módokat a 29. ábra mutatja be.

2 Rasztertömörítési módok Fizikai Logikai Modell alapú módok Hullámforma alapú módok - LUT - egyéb - fraktálok - objektum alapú - egyéb Veszteségmentes eljárások Veszteséges eljárások Statisztikai módszerek - Huffman - egyéb Általános módszerek - pixel packing - RLE - aritmetikai kódolás -LZ, LZW - egyéb - Fourier - DCT - wavelet - subband - egyéb 29. ábra A tömörítési módok csoportosítása A matematikai és informatikai vívmány felhasználásával számos tárolási formátumot fejlesztettek ki. Ezen formátumokra érvényes az a dilemma, hogy a bonyolult, hatékony tárolás számításigényes, következésképp lassú, míg a gyors hozzáférésű módszerek nem jelentenek túl nagy mértékű tömörítést. Ennek a dilemmának az áthidalására néhány tárolási formátumra (pl. JPEG) működő hardvermegoldást alkalmaznak Néhány gyakori tárolási formátum A digitális képfeldolgozásban a különböző típusú (mérnöki célú, grafikus, tematikus stb.) szoftverek más-más tárolási formátumot választanak ki elsődlegesnek. Részben a rétegszerű kezelhetőség, hatékony tárkezelés, optimális hozzáférési és számítási idő miatt igen sokféle formátum alakult ki. A 6. táblázatban a fontosabb, gyakrabban előforduló formátumokat mutatom be. 4

3 Formátum Alváltozat Gyártó BMP RGB kódolt OS/2 BMP RGB kódolt Microsoft BMP RLE kódolt Microsoft CT CMYK Scitex CT CMY Scitex EPS csak kép Adobe FIF fraktáltömörítéssel Iterated Systems FPX tömörített Kodak FPX tömörítetlen Kodak GIF interlaced, 87a CompuServe GIF non-interlaced, 87a CompuServe GIF interlaced, 89a CompuServe GIF non-interlaced, 89a CompuServe JPG Huffman kódolt Joint Photogr. Expert Group JPG Progresszív kódolással Joint Photogr. Expert Group LBM tömörített Deluxe Paint LBM tömörítetlen Deluxe Paint PCX version ZSoft PCX version 2 ZSoft PCX version ZSoft PCX version 5 ZSoft PNG PSD RGB kódolt Adobe PSD indexált Adobe RAS type Sun RAW tömörítetlen RLE run length kódolt CompuServe RLE run length kódolt Microsoft TGA tömörített Truevision TGA tömörítetlen Truevision TIF Huffman kódolt Aldus TIF tömörítetlen Aldus TIF CMYK tömörítetlen Aldus TIF pack bit tömörítés Aldus TIF CMYK pack bit tömörítés Aldus TIF LZW tömörítés Aldus TIF CMYK LZW tömörítéssel Aldus TIF fax group tömörítéssel Aldus TIF fax group 4 tömörítéssel Aldus 2.. Sorfolytonos kódolás és a négyesfa 6. táblázat A gyakoribb tárolási formátumok Tételezzük fel, hogy a következő képet szeretnénk tárolni: 5

4 ábra Tárolandó képrészlet Az intezitásértékből láthatóan ez egy 8-bites radiometriai felbontású kép részlete. Az 5 5-ös részlet mentéséhez így 25 8 bitre, azaz 25 bájtra van szükség. A sorfolytonos tárolás szerint a következő sor lenne a kép reprezentációja: Természetesen tárolni kell a sorok hosszúságát is, hogy egyértelműen vissza lehessen állítani a képet. Az ismétlődő részletek azonban tömörebb leírási módot tesznek lehetővé. A következő sor az előforduló darabszámok és az intenzitásértékek megadásával teljesen egyenértékű leírás: Ha a sor elemeit megszámoljuk, azt tapasztaljuk, hogy 2 számadattal tudtuk leírni a részletet. E számok szintén beleférnek az egy bájtba, tehát így már csak 2 bájtra van szükség. A kis példában látható 5 bájtnyi (2 %) különbség lényegesen komolyabbra is adódhat nagyobb adatmennyiségnél. A bemutatott sorfolytonos kódolás angol elnevezéssel run-length encoding (RLE) megtalálható a Windows Bitmap (BMP) formátumában. Természetesen az eljárást bináris képekre is lehet alkalmazni. Eleinte a bináris képekre találták ki, majd tónusos képekre is alkalmazták a négyesfa kódolást. A négyesfa (quadtree) olyan fa, melynek egy adott szinten lévő végpontjától maximum négy ág indulhat ki. A négyesfa-felosztást használják a térképszelvények számozásában is (. ábra). A b részen látható satírozott terület a 4-as jelű. 6

5 a) szokásos fa megjelenítése b) a térképszelvényezés menete négyesfával. ábra A négyesfa és egy lehetséges felhasználása a térképszelvényezésben Az ábra a része a b rész fa reprezentációja. A felosztás algoritmusa a következő:. a képet négy egyenlő négyzetre kell osztani 2. az egyes négyzeteket meg kell vizsgálni, hogy azonos intenzitású-e minden pixel. ha igen: a négyzet változatlan marad és az intenzitásérték beíródik a fa megfelelő szintjén a megfelelő helyre ha nem: az adott négyzetet képnek tekintjük és erre vonatkoztatva ugrás az első lépésre Az algoritmust addig kell folytatni, amíg minden négyzetre el nem végeztük a vizsgálatot és tovább már nem lehet bontani a képet. Az iterációval legfeljebb a pixelméretig mehetünk el, azonban néha célszerű előre beállított négyzet-mérettel a számítást előbb megállítani. A 2. ábra tónusos kép négyesfa felosztását mutatja. A nagyobb méretű négyzetek tárolásához csupán annak a fában megadott helyzetét (szintjét) és az intenzitás értékét kell tárolni. Igen hatékony kódolási forma. 2. ábra Tónusos kép négyesfa felosztása 7

6 A műveletek végrehajtásakor a kép pixeljeihez igen sajátos sorrendben kell hozzáférni. A felfedezőjéről Peano-görbének elnevezett alakzatot a. ábra mutatja be. a) Peano-féle pixelhozzáférés b) sorfolytonos (szokásos) hozzáférés c) meanderező hozzáférés. ábra Digitális kép pixeljeihez történő hozzáférési sorrendek 2.. A TIFF-formátum és változatai A képtárolás és -feldolgozás egyik legrégebbi és legnépszerűbb formátuma a Tagged Image File Format, a TIFF. 986-ban fejlesztette ki az Aldus. A felhasználói többek között a szövegszerkesztés (DTP), az általános képfeldolgozás, a számítógépes grafika. A tárolásnál használt tag-ek a különböző adatleíró mezők. A formátum dokumentációjában részletes leírásuk megtalálható. A 7. táblázatban színes képek minimálisan szükséges tag-jeit mutatom be. A TIFF alapváltozata (Baseline TIFF) hordozható formátum, melynek öt főbb változata van: 8 bináris: 2 szín, a fekete és a fehér megkülönböztetésével 8 tónusos: 256 szürkeárnyalat kezelésével 8 indexelt: színpaletta kezelésével maximum 256 színnel 8 RGB (true color): 6.7 millió színárnyalattal az RGB alapszínekből 8 CMYK: 2 bites változat a CMYK nyomdai színekkel sávonként. A TIFF-állomány lehet tömörítetlen vagy tömörített. A tömörítésre többféle mód is kínálkozik: 8 nem tömörített 8 CCITT D 8 Group fax 8 Group 4 fax 8 LZW 8 JPEG 8 Packbits. Leggyakoribbak az LZW algoritmust használják. Ez utóbbit a három fejlesztőről nevezték el: A. Lempel, J. Ziv és T. Welch. Az LZW-tömörítés igen hatékony eljárás, melyet a hardvergyártók is alkalmaznak például modemek készítésében. Érdekes, hogy TIFF-formátum tartalmazza a JPEG-formátum tömörítési algoritmusát (Huffman-kódolás). A TIFF alkalmas telefaxon történő képtovábbításra. 8

7 Mivel a TIFF-formátum igen jó képminőséget jelent, több kiadónál a képformátumok szabványának választották. Az internet, elsősorban a World Wide Web számára közvetlenül nem, csak plug-in-okon keresztül felhasználható formátum. Tag-név Decimális Hexadec. Típus Érték érték érték ImageWidth 256 SHORT vagy LONG ImageLength 257 SHORT vagy LONG BitsPerSample SHORT 8,8,8 Compression 259 SHORT,277 PhotometricInterp SHORT 2 retation StripOffsets 27 SHORT vagy LONG SamplesPerPixel SHORT vagy több RowsPerStrip SHORT vagy LONG StripByteCounts LONG vagy SHORT XResolution 282 A RATIONAL YResolution 28 B RATIONAL ResolutionUnit SHORT,2, 7. táblázat A színes (RGB) képek tárolásához minimálisan szükséges tag-ek A jelenleg legújabb TIFF6. részletes leírása 2 oldal, mely leírja az egyes tag-ek jelentését és használatát. Újabban kidolgozták a pixelek hely-jellegű, vetületet, koordinátarendszert is tartalmazó változatát, a GeoTIFF-et. A kidolgozás irányítója és fő fejlesztője a NASA JPL Cartographic Application Group-ja volt. Napjainkra a GeoTIFF-et a képfeldolgozó és a térinformatikai cégek többsége elfogadta és támogatja. Több termékkészítő szintén használja ezt a formátumot. A SPOT műhold által készített és feldolgozott képeket lehet ilyen formátumban vásárolni. A formátumról rengeteg leírást lehet találni az interneten. A GeoTIFF-ben a raszterkoordináta rendszer mellett egy modelkoordináta rendszer is megtalálható. Ebben négyféle módon lehet helyet megadni: 8 földrajzi koordináták (geographic coordinates) 8 geocentrikus koordináták (geocentric coordinates) 8 vetületi koordináták (projected coordinates) 8 magassági koordináták (vertical coordinates). A földrajzi koordináták témakörben meg lehet adni a Földhöz illeszkedő ellipszoid paramétereit (félnagytengely, félkistengely vagy lapultság stb.), geodéziai értelemben definiált hosszúság és szélesség adatokat, geodéziai dátumokat, szabványos vagy a felhasználó által definiált földrajzi koordináta rendszereket. A geocentrikus koordinátarendszer megadásakor azonosító kódot vagy nevet lehet használni. A vonatkozási rendszerek adatai külön táblázatban áll rendelkezésre, onnan lehet az azonosítók alapján átvenni. A koordinátarendszerek közötti transzformációra szintén lehetőséget nyújt a GeoTIFF az alábbi általános összefüggés megoldásával: X a Y = e Z i m b f j n c g k o d I h J l K p () 9

8 ahol X, Y, Z a modellkoordináták, a p az együtthatómátrix elemei, I, J, K a képkoordináták. Mivel a képek 2 dimenziósak, a szabvány ezt figyelembe véve az általános esetet minimális mértékben korlátozva a következőképp írja le: X a Y = e Z b f d I h J K (2) ahol az () egyenletre figyelembe vették, hogy c = g = i = j = k = m = n = o = l = p = () A (2) kifejezésben d és h értékének nem kell feltétlen nullának lennie, így az eltolás kifejezhető. A modellméretarányokra külön kitér a formátum-leírás, a következő összefüggést mellékelik az együtthatómátrixra: S x S y S z Tx T y T z (4) ahol S a méretarányokat, T az eltolásokat (transzlációkat) jelöli. A GeoTIFF formátum a raszteradatok geokódolását is támogatja, ami a térinformatikai célú képfeldolgozásban jelent előnyt. UTM vetületi rendszerbe transzformált légifénykép számára a következő tag-eket találjuk a GeoTIFF fejlécében: ModelTiepointTag = (,,, 587.4, 568.,.) ModelPixelScaleTag = (.,.,.) GeoKeyDirectoryTag: GTModelTypeGeoKey = (ModelTypeProjected) GTRasterTypeGeoKey = (RasterPixelIsArea) ProjectedCSTypeGeoKey = 266 (PCS_WGS84_UTM_zone_6N) PCSCitationGeoKey = "UTM Zone 6 N with WGS84" 2.2. A JPEG-formátum Agyakran használt formátumok közül a JPEG-gel érdemes közelebbről is megismerkedni. A formátum nevét a Joint Photographic Expert Group-tól kapta, mely az ISO (International Organization for Standardization Nemzetközi Szabványügyi Szervezet) és a CCITT (Consultative Committee on International Telephone and 4

9 Telegraphy Nemzetközi Telefon és Távközlési Szervezet) közös munkacsoportja volt. A következőkben a fekete-fehér árnyalatos képek tömörítésének menetét írom le. Egyetlen sávra tehát a következők szerint lehet eljárni. Több sáv esetén lehetséges 8 sávonként az alábbi technikát alkalmazni 8 (luminancia-krominancia) színtranszformációt követően a levezett sávokra a transzformációt végrehajtani. A JPEG-csoport által kidolgozott formátum, melyet JPG néven is használunk, matematikai transzformáción alapuló eljárás. A betömörítési folyamatot (kódolást) a 4. ábra a része, a kitömörítést (dekódolást) az ábra b része mutatja be. bemenõ kép blokkokra bontás matematikai transzf. (DCT) kvantálás entrópia kódolás tömörített kép tábla specifikáció tábla specifikáció a) a betömörítési folyamat tömörített kép entrópia dekódolás inverz kvantálás inverz matematikai transzf. blokkok illesztése visszaállított kép tábla specifikáció tábla specifikáció b) a kitömörítési folyamat 4. ábra A JPEG be- és kitömörítési folyamatai A betömörítés első lépésében a képet blokkokra kell bontani. A blokkok mérete többnyire 2 hatványait követi (2 n 2 n ), általában 8 8 pixel. A matematikai transzformáció a diszkrét koszinusz transzformáció (DCT), melynek transzformációs egyenlete a leggyakoribb blokkméretre: F( u, v) 4 = C( u) C( v) 7 7 (2x + ) uπ (2y + ) vπ f ( x, y) cos 6 cos x= y= 6 () ahol C(u), C(v) segédfüggvények, definíciójuk pedig C ( x) = 2 ha x = egyébként (2) Megjegyzem, hogy a fenti összefüggéseken kívül más, csupán néhány apróságban eltérő definícióval is lehet találkozni a szakirodalomban. 4

10 A matematikai transzformáció abból indul ki, hogy a képblokk periodikus kétdimenziós függvénynek tekinthető. Ekkor a Fourier-transzformációhoz hasonló koszinusz bázisfüggvényeket tartalmazó transzformáció hajtható végre, melynek eredménye a növekvő frekvenciájú bázisfüggvények együtthatói. A kapott függvénysereg összegzése adja az eredeti függvényt. ( 2x + ) uπ (2y + ) vπ A cos cos tagot bázisfüggvénynek nevezzük. Igen 6 6 szemléletesen fejezi ki a transzformáció lényegét. A 5. ábra mutatja a bázisfüggvények hatását 8 8-as blokkra. A bal felső saroktól balra és lefelé növekszik a frekvencia. 5. ábra A DCT bázisfüggvényeinek hatásábrája Az ábrán látható bázisfüggvények együtthatóinak meghatározása történik meg a transzformációs lépésben. A bázisfüggvényekhez tartozó együtthatók a növekvő frekvencia szerinti tagokat jelentik. A bázisfüggvények felhasználásával a transzformáció inverz összefüggése (IDCT) is felírható: f ( x, y) = u= v= (2x + ) u C( u) C( v) F( u, v) cos 6 6 π (2y + ) vπ () cos ahol C(u)-t és C(v)-t a (2) egyenlet szerinti definíció szerint kell számítani. A betömörítés következő állomása a kvantálás, amely a transzformációs együtthatók hatékony, változtatható mértékű tömörítéséhez nélkülözhetetlen. Kiszámítását a (4) összefüggés szerint lehet megtenni: 42

11 F Q F( u, v) ( u, v) = int Q( u, v) (4) ahol Q(u,v) segédtáblázatokban tárolt kvantálási együtthatók, melyekkel F(u,v) blokk elemeit kell elemenként osztani. Lehetséges értékeit a 8. táblázat mutatja táblázat Egy lehetséges kvantálási táblázat A nagyobb értékű elemek a (4) összefüggés alapján a kisebb jelentőségű együtthatókat jelölik. A kvantálási táblázat változtatásával lehet a tömörítés mértékét s az ezzel összefüggő veszteség mértékét szabályozni. A táblázatokat emberekkel végzett pszichovizuális vizsgálatokkal határozták meg és szabványosították később. A kvantálást követően az együtthatókat a 6. ábra szerint cikkcakkban olvassa ki az algoritmus, s képez egy sort. A kapott sort entrópiakódolással veszteségmentesen kell tárolni. A JPEG által kidolgozott algoritmus a hatékony, változó hosszúságú elemekből álló kódsegédtáblázatokat használó Huffman-kódolást alkalmazza. 6. ábra A kvantált együtthatók kiolvasási sorrendje A Huffman-kódolt blokkot a háttértárolóra kell kiírni, majd a leírt műveleteket a tömörítendő kép minden blokkjára végre kell hajtani. Ezzel megtörtént a tömörített kép elkészítése. Az algoritmus a képpiramisok kialakítását is támogatja: lehetőség 4

12 van hierarchikus (piramidális) módon történő tárolásra és hozzáférésre. (Lásd 2.5. fejezet) A kitömörítés (4. ábra b része) első lépésében a blokkonként elvégzett entrópiakódolást kell "megfejteni", visszaalakítani. A dekódolás ismételten a segédtáblázatok segítségével megy végbe. A kapott együtthatósereget az (5) összefüggés alapján és a tárolt kvantálási segédtáblák révén visszaalakítjuk: Q F( u, v) = F ( u, v) Q( u, v) (5) ahol F Q (u,v) a kvantált blokk, Q(u,v) a kvantálási segédtáblázat. Az ezt követő lépés a matematikai transzformáció inverzének számítása. Az inverz diszkrét koszinusz transzformáció (IDCT) összefüggései a () egyenlet szerint számítandók. A lépés eredményeként ismételten intenzitás-jellegű mennyiségeket kapunk az eddigi frekvencia-amplitúdó mennyiségekből. Innentől a vázolt lépéseket minden tárolt, tömörített blokkra végre kell hajtani, majd azokat egymás mellé illeszteni. A végeredmény a visszaállított kép. Az eredeti és a visszaállított kép közötti különbség a tömörítési veszteség. Ennek mértéke megfelelő paraméterezéssel nem észrevehető. A JPEG-formátum felhasználásával 2:-es mértékű tömörítést is el lehet érni alig feltűnő veszteség mellett. Ez egy 7 µm-es felbontású színes légifényképre 54 MB-os, fekete-fehér képre 5 MB-os fájlméretet eredményez. A JPEG tárolási formátum igen nagy előnye, hogy az elvégzett számítások megvalósíthatók VLSI elektronikai áramkörökkel. A be- és kitömörítést ekkor a JPEG-kártya hajtja végre, amely igen gyors műveleti sebességet jelent, ugyanakkor a tömörített állománykezelés előnyeit nyújtja. A fotogrammetriai munkaállomásokban kitűnően lehet használni a formátum és a kiszolgáló hardverelem adta teljesítményt. 2.. Fraktáltömörítés A következő fejezetben az Iterated Systems Inc. által kifejlesztett fraktáltranszformáció lényegét és az ezt használó Fractal Image Format (FIF) tömörítést ismertetem. A tömörítésnél redundáns, hasonló részleteket kell keresni a képen, majd azokra vonatkozó matematikai transzformációt számítunk. A számítás menetét a 7. folyamatábra szemlélteti. bemenõ kép domainblokkokra bontás rangeblokkok kiválasztása kontraktív affin transzf. paraméterek tárolása: tömörített kép 7. ábra A fraktáltömörítés menete A tömörítendő képen elsőként ki kell jelölni az azonos méretű blokkokat, melyekkel hézag és átfedésmentesen le kell fedni a teljes képet. Ezeket a blokkokat domain-nek nevezzük (8. ábra a része). Az ezt követő lépésben a domain-nél nagyobb méretű VLSI = Very Large Scale Integration nagyon nagy integráltságú áramköri elem 44

13 blokkokat, az ún. range-et kell kiválasztani (8. ábra b része). Elméletileg a domain és a range mérete lehet azonos, azonban sok esetben szerencsésebb nagyobb méretűre választani a range-et. a) a domain-blokkok kialakítása b) lehetséges range-blokk kiválasztása 8. ábra A domain- és range-blokkok értelmezése A tömörítés legizgalmasabb része a transzformáció, amely kontraktív affin leképezés. Ez azt jelenti, hogy a range és a domain blokkok közötti kapcsolatra az affin transzformáció összefüggéseit használjuk fel: a W ( x, y) = a a2 x x + a 4 y y () ahol x,y koordinátájú pontra W(x,y) a leképezési függvény. Az leképezés akkor kontraktív (összehúzódó, zsugorodó), ha W(x,y) transzformáció az eredeti alakzatot minden méretében zsugorítja. Ez matematikailag kifejezhető a transzformáció együtthatóival: 2 4 a, a, a, a (2) A transzformációs összefüggés újabb és újabb végrehajtásával kapjuk W(W(x,y)), W(W(W(x,y))) stb. leképezéseket. A kontraktív leképezés egyetlen ponthoz, az attraktorhoz (A W ) konvergál. Például a 9. ábrán látható F betűre végrehajtott.2 W ( x, y) =.5.4x 2 +. y 5 () alakú összefüggéssel számítható kontraktív leképezés attraktora a (4.,.26) koordinátájú pont. 45

14 9. ábra Kontraktív affin leképezés Bizonyítható, hogy konkrét paraméterezésű kontraktív affin leképezés attraktora mindig ugyanaz a pont, tehát a kiindulási alakzattól, annak helyétől független. Nézzük meg, hogyan lehet ezt hasznosítani a digitális klép pixeljeire. Az affin transzformáció valamely R range-re lehetséges a következő módon (4. ábra): 8 forgatás 8 -kal 8 2 -es kicsinyítés. A range-blokk és domain-blokk összehasonlíthatósága érdekében a forgatás és kicsinyítés után átlagolással vagy újramintavételezéssel azonos felbontásra lehet hozni a két blokkot. Ezután elvégezhető annak vizsgálata, hogy milyen mértékben hasonlítanak a blokkok. Adott domain-hez több range többféle transzformációját kell elvégezni, majd ezek közül a legjobban illeszkedő transzformáció paramétereit tárolni. A hasonlóság mérésére többek között a korrelációs együttható szolgál. 4. ábra Konkrét range-blokkra elvégzett kontraktív affin transzformáció (forgatás és kicsinyítés) és egy domain-blokk összehasonlítása A digitális képrészlet esetében egyetlen kontraktív affin transzformáció paramétereit kell tárolni, melynek attraktora maga a kép. A Barnsley-féle kollázstétel szerint a blokkonként kontraktív transzformáció az egész képre végrehajtott kontraktív leképezést jelenti. Pontosan ezt használjuk ki a tömörítésnél. A formátum előnye az igen hatékony tömörítés, hátránya viszont a nagy számításigény miatti lassúság. A kitömörítés vázlatos menete a következő. Minden domain-blokk minden pixeljére kiszámítjuk annak denzitásértékét (4) alapján: 46

15 D = P( A M ) + M (4) ij ij R D ahol D ij egy domain-blokk i,j helyen lévő pixelje, P a tárolt szorzóegyütthatók, A ij a range-blokk újramintavételezett vagy átlagolt pixeljei, M R a range-blokk, M D a domain-blokk átlagdenzitása. Az összes domain minden pixeljére végrehajtott számítás után visszakapjuk a képet (visszaállított kép) Tömörítés wavelet-technikával A wavelet szó szerinti fordításban hullámocskát jelent. A szinusz-hullámmal összehasonlítva korlátozott időtartamú hullámforma, amelynek átlagértéke zérus. Elsőként 99-ben tesz róluk említést A. Haar, később intenzíven kezdtek velük foglalkozni (J. Morlet, A. Grossmann, Y. Meyer, S. Mallat, I. Daubechies, R. Coifman, V. Wickerhauser). A wavelet-elemzés a Fourier-analízishez hasonlóan a jelek felbontását végzi, csak jelen esetben nem koszinusz és szinusz, hanem a wavelet függvény alapján. A wavelet-analízis során gyakrabban használt wavelet-ek egy csoportja a 4. ábrán látható. a) Daubechies-wavelet b) Biortogonális wavelet c) Szimmetrikus wavelet (symlet) d) Mexican hat wavelet 4. ábra Néhány gyakran alkalmazott wavelet A wavelet-transzformáció lényegét legegyszerűbben a Fourier-transzformációval történő összehasonlítással lehet ismertetni. A folytonos egydimenziós f(t)-függvényre végzett Fourier-transzformáció komplex jelölési móddal az iωt = f ( t e dt F( ω ) ) () összefüggés kiszámításával ω-frekvenciához tartozó F(ω) amplitúdókat határozza meg. F(ω) értékeket Fourier-együtthatóknak is nevezik. A folytonos wavelet 47

16 transzformáció (CWT) a jelet az alapwavelet eltolt és megváltoztatott léptékű változataira bontja a következő kifejezés szerint: C ( lépték, pozíció) = f ( t) Ψ ( lépték, pozíció, t) dt (2) ahol C(lépték, pozíció) a wavelet-együtthatók, Ψ(lépték, pozíció, t) a waveletfüggvény. Az alapwavelet-függvényen végrehajtott k mértékű eltolás a Ψ(t-k) függvényt, a lépték s-szeres megváltoztatása a Ψ(st) függvényt (42. ábra) eredményezi. 42. ábra Az alapwaveletből származtatott megváltoztatott léptékű változatok A traszformáció során a jel adott pozíciójához adott léptékű wavelet-változatot illesztünk, kiszámítjuk a hasonlóságot a wavelet-együtthatókat, majd a következő pozícióhoz ugyanezeket a műveleteket hajtjuk végre és tároljuk a hasonlósági mérőszámokat. A következő lépésben megváltoztatjuk a léptéket s végigszámítjuk az előbbi műveleteket. Az összes lehetséges lépték kiszámítása után a tárolt együtthatókat meg lehet jeleníteni (4. ábra). 48

17 4. ábra Folytonos wavelet-transzformáció együtthatói Diszkrét jelek esetében a diszkrét wavelet transzformációt (DWT) alkalmazzuk. Ekkor kettő hatványaiként kifejezhető ún. diadikus léptékeket és pozíciókat választunk s hajtjuk végre a transzformációt. A gyors számítás érdekében dolgozták ki a gyors wavelet transzformációt. A diszkrét wavelet-transzformáció során a jelet (S) elsőként alul- és felüláteresztő szűrőkkel közelítés (approximation A) és részlet (detail D) részre választjuk szét. A wavelet-transzformáció és az inverz transzformáció során használatos szűrők a négyzetes tükörszűrők (quadrature mirror filter QMF). A szűrés során gyakorlatilag megduplázódna a jel, ennek megoldására alkalmazzák a downsampling-eljárást. Lényegében csupán minden második adatpontot (jelpontot) választjuk ki és tároljuk. A számítást több szinten is elvégezhetjük, melynek eredménye a wavelet felbontási (dekompozíciós) fa (44. ábra a rész). S S A D A D A2 D2 AA2 DA2 AD2 DD2 A D a) egyszerű eset AAA DAA ADA DDA AAD DAD ADD DDD b) packet-ek 44. ábra Wavelet felbontási fák 49

18 A szintekre bontásnál iteratíven járunk el, az iterációt addig folytatjuk, amíg alkalmas mérőszám, pl. entrópia alapján abba lehet hagyni. A felbontás eredményeként kapott közelítés- és részlet-együtthatókat tároljuk. Van olyan wavelet-transzformációs megoldás, amikor a szintekre bontásnál a részletrészt is felbontják. Ez a wavelet packet-analízis (44. ábra b része). Az elemzés inverz művelete a szintézis, melynek elnevezése inverz diszkrét wavelet-transzformáció. A tárolt együtthatókból visszaállítjuk az eredeti jelet úgy, hogy a downsampling megfordítását, az upsampling-műveletet hajtjuk végre: a jel pontjai közé minden második helyre nullákat szúrunk be, ezáltal meghosszabbodik a jel. Majd az inverz szűréssel az adott összetevőt visszaállítjuk. Befejezésül egyesíteni kell azokat, hogy megkapjuk a jelet. Több szintnél (több közelítéssel) tehát S = A + D = A 2 = A + D + D 2 + D + D 2 + D () illetve packet-analízisnél S = A + D = AA 2 = AAA + DA 2 + DAA + AD 2 + DD + ADA 2 + DDA + AAD + DAD + ADD + DDD (4) A packet-analízisnél a külön-külön kiszámított packet-ek szabadon kombinálhatók, például S = A + (5) + AAD + DAD DD2 Kétdimenzióban, melyre a képfeldolgozásnak is szüksége van, a wavelettranszformáció kiterjeszthető. Ekkor a képet, mint kétdimenziós jelet a következők szerint bontjuk fel (45. ábra). eredeti kép A HD VD DD A2 HD2 VD2 DD2 A HD VD DD 45. ábra Kép wavelet transzformációja 5

19 Az ábrán látható, hogy több típusú részletet kell megkülönböztetni. A felbontás a következő összetevőket adja: 8 közelítés (A) 8 horizontális részlet (HD) vízszintes komponens 8 vertikális részlet (VD) függőleges komponens 8 diagonális részlet (DD) átlós komponens. Látható, hogy kétdimenzióban is lehetséges a többszintű felbontás. A képek tömörítésénél szintén többrétegű felbontást használunk. A 46. ábrán látható egy kép többszintű felbontása. A tömörítéskor a részlet-összetevőkből hagyunk el, emiatt az eljárás a veszteséges tömörítési módok közé tartozik. 46. ábra Digitális kép wavelet-transzformációja A wavelet-transzformáción alapuló tömörítés előnyeként a megnövelt gyorsaságot és tömörítési mértéket szokás megemlíteni. A szakirodalom szerint :-es tömörítésnél sem lehet szembetűnő különbséget észrevenni az eredeti és a tömörített képek között (47. ábra). A vizsgálatok szerint a hagyományos JPEG-sebességét meghaladja a wavelet elven működő tárolás. A JPEG2 nevű, jelenleg kidolgozás alatt álló képtárolási szabvány wavelet-transzformációra fog épülni. 47. ábra Eredeti és tömörített kép 5

20 A részlet-összetevők elhagyásával a wavelet-technika szűrésre is lehetőséget nyújt. Ezt a digitális jelfeldolgozásban már használják, a képfeldolgozásban még nem terjedt el általánosan A képpiramis és használata A digitális fotogrammetria képalkotó eszközei óriási méretű képeket készítenek. Ezeknek az állományoknak a kezelésére hatékony eszközöket kell használnunk, ellenkező esetben még a mai számítógépek szintjén is hatalmas, túlzott számítási teljesítményt kellene biztosítani. Adott tulajdonságú pixelek megkeresése vagy a kép szűrése sőt csupán a megjelenítése nagyon lassú művelet lenne. Ha a 7 µm-es pixelméretű légifényképet vesszük alapul, akkor a számítógépnek több mint milliárd pixelt kell feldolgoznia! Nem szólva arról, hogy 2 2 pixeles felbontású grafikus kártya és monitor nem létezik, de értelme sem lenne, hiszen szemünk ekkora felbontóképességgel nem rendelkezik! A digitális kép jelentette hatalmas adatmennyiségek esetében nagy ötletnek bizonyult a hierarchikus tárolás, a képpiramis. A szakirodalomban hívják felbontási piramisnak is. A képpiramis működésének megértéséhez képzeljünk el egy gúlát, melynek alaplapját az eredeti felbontású digitális kép alkotja. A teljes felbontású kép 2 2 pixeljéből álló blokkok számtani középértékét kell kiszámítani (decimálás), majd az így kapott számokat egy újabb kép elemeiként elhelyezni. Ez a levezetett kép lesz a gúlában az eredeti réteg fölötti első réteg. Az új, számított képréteget piramis rétegnek, piramidális rétegnek vagy áttekintő (overview) rétegnek nevezik. A piramisréteg az eredeti sorainak és oszlopainak számát tekintve fele vagyis az összes pixel negyede lesz. Hasonló módon kell képezni a második piramisréteget az elsőből. Az átlagolások ismételt végrehajtásával kapjuk meg a gúla egyre feljebb lévő, egyre kisebb méretű, következésképp egyre kisebb felbontású rétegeit (48. ábra a és b rész). a) a piramis felépítése 52

21 b) a piramisrétegek 48. ábra A képpiramis és rétegei Hogyan lehet használni a piramisrétegeket? A belső tájékozás példáján keresztül egyszerűen belátható. A belső tájékozásnál a keretjelekre kell pontosan rámutatni. A számítógép monitorán a munka kezdetekor a képpiramis felső részén megtalálható olyan réteget használjuk, amely a rendelkezésre álló ablakot kitölti, kellő részletességgel mutatja a képet. Legyen a mérete mondjuk 5 5 pixel. Ezen a képen (áttekintőn) a mérendő keretjel helyére mutatunk rá, majd az képpiramis algoritmusa meghatározza a kurzor pozícióját ezen a rétegen és kiszámítja az ehhez a pozícióhoz tartozó kétszeres felbontású pixel raszterkoordinátáit (sor- ill. oszlopazonosítókat). A képpiramis kétszeres felbontású rétegén az új pozíció 5 5 pixeles részletét jelenítjük meg. A művelet a szemlélő ember számára ugyanolyan hatású, mintha nagyítottuk volna. Ennek az az oka, hogy a képpiramisban lefelé haladva egyre jobb felbontású rétegeket nézünk meg, míg el nem érjük a teljes felbontást. Ekkor az utolsó pozícionálás eredménye, a raszterkoordináták kerülnek felhasználásra a belső tájékozás számításában. A piramisrétegek azonban tárolókapacitás-növekedést is jelentenek, mivel a durvább felbontású rétegeket is tárolni kell. Ha az eredeti felbontású kép memóriaegységet foglal el, akkor az első piramisréteg.25 egységgel történő növekedést jelent. A további rétegek memóriaigényét a 9. táblázat mutatja. Piramisréteg Memóriaigény táblázat A piramisrétegek memóriaigénye az eredeti képhez képest Szembetűnő, hogy a piramisrétegek számának növelésével egyre kisebb mértékben változik a memóriaszükséglet. Az elméletileg szükséges memóriafogyasztás kiszámítható: 5

22 lim n n i= = lim i b b) n i= ( n b 2i () ahol n a rétegek száma, b a számítási blokk mérete. Korábbi példánk blokkmérete (2 2) alapján tehát lim n 2 = lim n 2i n i= i= n i 4 = 4 (2) A 9. táblázatban kiszámított memóriaszükségletek is ehhez a határértékhez közelítenek. A képpiramis nyújtotta gyorsabb és egyszerűbb képkezelés megéri a számított / egységnyi memórianövekedést. Természetesen lehetséges a 2 2-es blokkméret helyett 8 8 vagy más blokkméretet is alkalmazni. Ebben az esetben gyorsabban csökken a piramisrétegek memóriaszükséglete. Vannak olyan rendszerek is, ahol az egyes piramisrétegeket valamelyik hatékony tömörítési eljárással (pl. JPEG) tárolják. Ekkor még az elméleti tárolókapacitásnál is kevesebb elegendő. A képpiramis nemcsak fotogrammetriai, hanem távérzékelt vagy akár grafikai célú, nagyobb méretű kép hatékony kezelésére kiváló eszköz. Képpiramis elvű tárolást lehet találni a FotoCD-nél és a Kodak FlashPix formátumánál. Néhány rendszerben az utolsó piramisréteg megközelítőleg 5 5 pixelt tartalmaz, esetenként közbülső rétegek kimaradhatnak. Az utolsó kicsi réteg képét szokás képmorzsának (image chip) nevezni. Szerepe a fájlok között a keresett kép gyors kikeresésében van. A grafikus programok preview-nak vagy thumbnail-nek is nevezik A távérzékelés speciális formátumai A távérzékelésben használt műholdas képalkotó eszközök gyakran háromféle képtárolási formátumot használnak. E formátumok közös jellemzője, hogy támogatják a multispektrális képek tárolását. A formátumok tulajdonképpen az adatok hozzáférési rendjét adják meg. A képelemek számértékeit egyszerűen, ASCII módon találjuk meg. Ezek a tárolási módok következésképp nem tartalmaznak tömörítést, kidolgozásuk célja a minél szélesebb kör kiszolgálása volt általánosan használható formában. A képfeldolgozó szoftvercsomagok ezekből a formátumokból úgyis létrehozzák saját formátumukat, mely az adott rendszer számára optimális a hozzáférés, tömörítés stb. szempontjából. Az első a Band Sequential (BSQ) formátum. A képet sávonként tároljuk, tehát először az egész első sáv pixelről pixelre történő mentése történik, majd ezt követi a második, harmadik és sorra az összes sáv. A tárolási módok között gyakori a Band Interleaved by Line (BIL) formátum. Lényegében soronkénti a tárolás: az első sáv első sorát a második sáv első sora követi, majd a harmadik és a maradó sávok első sora. Az utolsó sáv mentése után az első sáv második sorával kell folytatni a tárolást. A Band Interleaved by Pixel (BIP) formátumban pedig pixelenként hajtjuk végre a tárolást. Az első sáv első sor első pixelje után a második sáv ugyanezen eleme következik, ezt követi a harmadik sáv képeleme, majd így haladunk végig az utolsó sávig. Ha az összes sávon az első pixelt elmentettük, a második s a többi összes képelemre hasonlóképpen járunk el. 54