Elővizsga, dec. 15. Szívhez szóló megjegyzések és megoldások Adja meg a kontrollált természetes nyelv definícióját (vendégelőadás)
|
|
|
- Marika Székelyné
- 8 évvel ezelőtt
- Látták:
Átírás
1 Elővizsga, dec. 15. Szívhez szóló megjegyzések és megoldások Tisztelt Hallgatók! Az elővizsga meglepően rossz eredménye késztet néhány megjegyzés megtételére. A félév elején hangsúlyoztam, hogy a tárgy nem nehéz, a matematikája egyszerű, nagyban a már megismert gráfelméleti, logikai és valószínűségi ismeretekre épül, de NAGYON SOK összefüggést takar. Az összefüggésekhez idő kell, a módszerek, a példák megértéséhez idő kell, az átnézett példákból, a gyorsan végig pörgetett előadás-fóliákból nem lehet ütőképes vizsgaismereteket kovácsolni. Talán segíthetett volna a kérdéses részleteket időben feltárni (jegyzet, előadás), az előadás szüneteiben, vagy más időpontban tisztázni, ha... Most a lényeges fogalmak összekeverednek és akármennyire egyszerűek is a matematikai részletek, pongyola alkalmazásukból nem születhet meg értékelhető megoldás. DT Adja meg a kontrollált természetes nyelv definícióját (vendégelőadás) "A kontrollált nyelv egy olyan mesterséges nyelv, amely a sikeres számítógépes feldolgozhatóság érdekében szűkíti egy természetes nyelv nyelvtani szabályait, szókincsét és szemantikáját megőrizve annak természetes jellegét." Magyarázza meg, hogy egy vonzat reláció fennállását, vagy hiányát két logikai állítás között hogyan lehet logikán belül eldönteni? Minél teljesebb válaszra törekedjen! Ha egy A állítás vonzata egy B állításnak, akkor ennek a tényét el tudjuk dönteni modellvizsgálattal (modellek egymásba tartozása), speciálisan szerkesztett állítások típusának vizsgálatával (B implikálja A-t egy érvényes állítás, ill. B és Nem A állítás ellentmondás), ill. egy formális bizonyítással (ha adva van egy teljes bizonyítási eljárás). Vesse össze a lokális és nem-lokális heurisztikus keresési algoritmusok tulajdonságait. Mutasson rá, ahogy egy-egy tulajdonság egyben előnyt is, hátrányt is jelenthet! Lokális nincs visszalépés: előny a kis tár, gyors működés hátrány a lokális optimum, v. akár megakadás Nem-lokális van visszalépés: előny az optimum lehetősége hátrány a nagy tár- és idő komplexitás A korlátozáskielégítés módszere nem más, mint egy keresés egy olyan keresési térben, ahol az állapotokat a rájuk érvényes korlátokkal írjuk le. Ha az alkalmazott keresés egy lokális keresés, mi a keresési tér egy-egy állapota és mi az irányító heurisztika? Lokális keresési megoldás esetén egy-egy állapot a teljes változóhalmaz egyidejű behelyettesítése valamilyen, a változók doménjeihez tartozó értékekkel. Mivel egy ilyen behelyettesítés nem biztos, hogy egy konzisztens korlátrendszerhez vezet, a sérült korlátok számát figyelni kell (ez a konfliktus heurisztika) és a változókat olyan alternatív, de legális értékekre kötni, amitől a konfliktusok száma csökkenni fog (hegymászó keresés minimum felé). Adott egy sorsjáték: [p, S1; (1-p), S2], p = 0.7, S1 = 10 Ft, S2 = 100 Ft. Mennyi a sorsjáték EMV-je? Figyelembe véve, hogy pozitív jutalmak esetén a pénz hasznossága a rizikót kerülő ember felfogásának felel meg, vegyen fel egy ezzel konzisztens sematikus ábrát és ennek alapján a megfelelő
2 U( ) hasznosság értékeket, majd elemezze az U(L) és az U(EMV(L)) viszonyát. Sematikus ábrája alapján határozza meg a sorsjáték deteminisztikus ekvivalensét DE-t! A sorsjáték monetáris ekvivalense: EMV(L) =.7 x 10 Ft +.3 x 100 Ft= 37 Ft A sorsjáték hasznossága: U(L) =.7 U(10 Ft) +.3 x U(100 Ft) --- az egyenes EMV(L) feletti pontja, a rizikót kerülő lelkület esetén kisebb, mint az EMV hasznossága, így a sorsjáték hasznosságával azonos hasznosságú determinisztikus nyerseség (determinisztikus ekvivalense) kisebb, mint az EMV(L). Fejtse ki a megerősítéses tanulás és a szekvenciális döntés kapcsolatát! A szekvenciális döntési feladat a hasznosságok meghatározása (és azok segítségével az optimális eljárásmód meghatározása) az R jutalomfüggvény és a T átmeneti valószínűségek alapján. A megerősítéses tanulás a hasznosságok tanulása (és közvetve azokból az optimális eljárásmódé) a tapasztalt állapotátmenetekből és az azokban kapott konkrét jutalmakból, nem ismervén az R és T függvények teljes, egzakt alakját. U( s) = R( s) + g max S T( s, a, s') U( s') a s' R, T ismert R, T nem ismert Milyen elemek definiálnak egy Markov döntési folyamatot, mi a leszámítolt jutalom és mi az optimális eljárásmód? Mit jelent, hogy a döntési folyamat Markov? Markov döntési folyamat elemei: kezdőállapot: állapotátmenet-modell (valószínűségek): jutalomfüggvény: S0 T(s, a, s ) R(s), v. R(s, a, s ) leszámítolt jutalom: optimális eljárásmód: maximális (leszámítolt) jutalmat biztosító cselekvésválasztás (állapotonként). döntési folyamat Markov: ha az állapot-átmeneti válószínűségek teljesítik a Markovi feltételt (az új állapot csakis a közvetlenül megelőző állapottól függ, de nem annak elődjeitől). Legyen egy történet az alábbi: (1) Minden kutya ugat éjjel.
3 (2) Akinek macskája van, annak nincs egere. (3) Aki egy könnyű-alvó, annak nincs éjjel ugató állata. (4) Jancsinak vagy macskája, vagy kutyája van. Igaz-e, hogy: (5) Ha Jancsi egy könnyű-alvó, akkor nincs egere. és legyen e történet elsőrendű logikai átírása az alábbi: (1) x Kutya(x) Ugat(x). (2) x y Van(x,y) Macska(y) ( z Van(x,z) Egér(z)). (3) x Könnyű-Alvó(x) ( y Van(x,y) Ugat(y)). (4) x Van(Jancsi, x) (Macska(x) Kutya(x)). (5) Könnyű-Alvó(Jancsi) ( z Van(Jancsi,z) Egér(z)). A kérdést rezolúciós bizonyítással kell eldönteni, amihez az (5) állítást negálni kell és mindegyik állítást (predikátum kalkulusbeli) klózzá kell átalakítani. A klózok: (1) Kutya(x1) Ugat(x1). (2) Van(x2,y1) Macska(y1) Van(x2,z1) Egér(z1). (3) Könnyű-Alvó(x3) Van(x3,y2) Ugat(y2). (4a) Van(Jancsi, S). S - Skolem konstans (4b) Macska(S) Kutya(S). (5a) Könnyű-Alvó(Jancsi). (5b) Van(Jancsi,S). (5c) Egér(S). És a rezolúciós bizonyítás egy lehetséges menete: 6: 3+5a: Van(Jancsi,y2) Ugat(y2). x2/jancsi 7: 6+5b: Ugat(S). y2/s 8: 7+1: Kutya(S). x1/s 9: 2+5c: Van(x2,y1) Macska(y1) Van(x2,S). z1/s 10: 9+5b: Van(Jancsi,y1) Macska(y1). x2/jancsi 11: 10+5b: Macska(S). y1/s 12: 11+4b: Kutya(S). 13: 12+8: üres rezolvens. Számítsa ki a háló alapján, hogy mi a P(Más Hát) valószínűség értéke? Első lépés megállapítani, hogy a teljes háló mely része releváns a lekérdezés szempontjából (bekeretezve). A 'Fáj' változóval tehát nem foglalkozunk. Áttekinthetőség kedvéért rövidítsük Széket S-re és Sport-ot P-re. Normalizálással és kiösszegzéssel:
4 P(M H) = a P(MH) = a Σ sp P(HMsp) = a Σ sp P(HMsp) P(H sp) P(M s) P(s) P(p) = = a (.9 x.9 x.8 x x.9 x.8 x x.01 x.2 x x.01 x.2 x.98) = a x.1541 P( M H) = a P( MH) = a Σ sp P(H Msp) = a Σ sp P(H Msp) P(H sp) P( M s) P(s) P(p) = = a (.9 x.1 x.8 x x.1 x.8 x x.99 x.2 x x.99 x.2 x.98) = a x.0226 a ( ) = 1, a = 5.66 azaz P(M H) = 0.87 (közelítőleg) Hasonlítsa össze a döntési háló alapján, hogy boldogabb lesz, amikor tanul, vagy amikor nem? Tipp: A 'B' Boldogság a 'Vizsgán átmegy (V)' és a 'Lottón nyer (L)' 0/1 értékeire van megadva. Azonban a 'V' és az 'L' véletlen változók a 0/1 értékkel csak bizonyos valószínűséggel fognak előfordulni, ami ráadásul a 'Tanul' cselekvés megválasztásától is függ. A 'B'-re tehát egy átlagot kell számítani. A 'T' nem véletlen változó/esemény (döntési csomópont), nincs valószínűsége. Ez a 'Tanulok', 'Nem tanulok' cselekvés-választás. A 'B' nem véletlen változó/esemény (hasznosság-csomópont), a táblázatbeli értékei nem valószínűségek, csak hasznosság-értékek egyes esetekben. Mind 'Tanulok, mind 'Nem tanulok' esetén ki kell számítani az a posteriori P(L) és P(V)-t, és ezekkel az értékekkel súlyozni a B hasznosságának egyes értékeit. Legyen a választás 'Tanulok'. P(VL T) = Σ s P(V T s) P(L s) P(s) =.9 x.25 x x.75 x.4 =.299 P(V L T) = Σ s P(V T s) P( L s) P(s) =.9 x.25 x x.75 x.6 =.67 P( VL T) = Σ s P( V T s) P(L s) P(s) =.1 x.25 x x.75 x.4 = P( V L T) = Σ s P( V T s) P( L s) P(s) =.1 x.25 x x.75 x.6 =.0295 Boldogság így:.99 x x x x.0295 =.839 Legyen a választás 'Nem tanulok'. P(VL NemT) = Σ s P(V NemT s) P(L s) P(s) =.01 x.25 x x.75 x.4 =.15 P(V L NemT) = Σ s P(V NemT s) P( L s) P(s) =.01 x.25 x x.75 x.6 =.227 P( VL NemT) = Σ s P( V NemT s) P(L s) P(s) =.99 x.25 x x.75 x.4 =.1524 P( V L NemT) = Σ s P( V NemT s) P( L s) P(s) =.99 x.25 x x.75 x.6 =.47 Boldogság így:.99 x x x x.47 =.515 (Inkább tanuljunk!) Az alábbi szekvenciális döntési feladatnál 3 eljárásmód lehetséges (S, CC, CL). 'R' az állapotonkénti pillanatnyi jutalom. A leszámoltatási tényező értéke.9. Egészítse ki az ábrát a specifikált
5 állapotátmeneteknek megfelelő valószínűség-értékekkel! Írja fel az optimális eljárásmódra vonatkozó Bellman egyenlet! Számítsa ki az állapotok hasznosságát, ha az alkalmazott eljárásmód minden állapotra a 'CL'! Az (baloldali) ábrán minden nyíl mellé 1-nyi válószínűséget kell írni, mert az állapot-átmeneti valószínűségek cselekvésenként 1-re összegződnek és itt egy-egy cselekvés esetén egyetlenegy célállapot van. Az optimális eljárásmód más-más cselekvést is diktálhat állapotonként, az ábrán látható rendszer Bellman egyenlete tehát: U(E) = g max(u(e), U(B), U(Ko)) U(B) = 20 + g max(u(e), U(Ke), U(B)) U(Ke) = g max(u(ke), U(B), U(Ko)) U(Ko) = g max(u(e), U(Ke), U(Ko)) Ha minden állapotban az alkalmazott eljárásmód a 'CL' cselekvés, akkor a feladat egyszerűsödik, az egyenletrendszer lineárissá válik: U(E) = g U(B) U(B) = 20 + g U(Ke) U(Ke) = g U(Ko) U(Ko) = g U(E) 2 U(Ke) = g U(E) 3 U(B) = g + g U(E) 2 U(E) = g g + g4 U(E) = (kb.) 67 belőle: U(B) = (kb.) 37 U(Ke) = (kb.) U(Ko) = (kb.) 60 Egy ágens példákból a Csésze logikai definícióját tanulja döntési fa módszerével. Alábbi 10 példát kap. Döntse el információelméleti mennyiségeket mérlegelve, hogy a döntési fa építését melyik attribútumteszttel kellene kezdeni (a fa építését a gyökér megválasztása után nem kell folytatni). Pl. Lapos Alja Felfelé Nyitott Drága Törékeny Fogás Tetején Csésze
6 1 V V V V - V 2 V V - V - V 3 V V V - - V 4 V V V 5 V V - V V - 6 V - - V V V V - V V - V V V - - V - - Vegye figyelembe, hogy: I(2/5,3/5) =.9710, I(1/3,2/3) =.9183, I(3/8,5/8) =.9544, I(1/5,4/5) =.7219, I(1/4,3/4) =.8113, I(4/7,3/7) = Fa információ tartalma I = I(2/5, 3/5) =.9710 Az attribútum-nyereségek: Lapos alja: I - 4/5 I(1/2,1/2) - 1/5 I(0,1) =.17 Felfelé nyitott: I - 7/10 I(4/7,3/7) - 3/10 I(0,1) =.28 Drága: I - 2/5 I(1/2,1/2) - 3/5 I(1/3,2/3) =.02 Törékeny: I - 3/5 I(1/3,2/3) - 2/5 I(1/2,1/2) =.0... Fogás tetején: I - 1/5 I(0,1) - 4/5 I(1/2,1/2) =.17 'Felfelé nyitott' attribútum a nyertes.
Bonyolult jelenség, aminek nincs jó modellje, sok empirikus adat, intelligens (ember)ágens képessége, hogy ilyen problémákkal mégis megbirkozzék.
 Vizsga, 2015. dec. 22. B cs. B1. Hogyan jellemezhetők a tanulást igénylő feladatok? (vendégelőadás) Bonyolult jelenség, aminek nincs jó modellje, sok empirikus adat, intelligens (ember)ágens képessége,
Vizsga, 2015. dec. 22. B cs. B1. Hogyan jellemezhetők a tanulást igénylő feladatok? (vendégelőadás) Bonyolult jelenség, aminek nincs jó modellje, sok empirikus adat, intelligens (ember)ágens képessége,
Mesterséges Intelligencia MI
 Mesterséges Intelligencia MI Racionalitás: a hasznosság és a döntés Dobrowiecki Tadeusz Eredics Péter, és mások BME I.E. 437, 463-28-99 dobrowiecki@mit.bme.hu, http://www.mit.bme.hu/general/staff/tade
Mesterséges Intelligencia MI Racionalitás: a hasznosság és a döntés Dobrowiecki Tadeusz Eredics Péter, és mások BME I.E. 437, 463-28-99 dobrowiecki@mit.bme.hu, http://www.mit.bme.hu/general/staff/tade
Megerősítéses tanulás 2. előadás
 Megerősítéses tanulás 2. előadás 1 Technikai dolgok Email szityu@eotvoscollegium.hu Annai levlista http://nipglab04.inf.elte.hu/cgi-bin/mailman/listinfo/annai/ Olvasnivaló: Sutton, Barto: Reinforcement
Megerősítéses tanulás 2. előadás 1 Technikai dolgok Email szityu@eotvoscollegium.hu Annai levlista http://nipglab04.inf.elte.hu/cgi-bin/mailman/listinfo/annai/ Olvasnivaló: Sutton, Barto: Reinforcement
, , A
 MI Nagy ZH, 2011. nov. 4., 14.15-16, A és B csoport - Megoldások A/1. Milyen ágenskörnyezetrıl azt mondjuk, hogy nem hozzáférhetı? Adjon példát egy konkrét ágensre, problémára és környezetre, amire igaz
MI Nagy ZH, 2011. nov. 4., 14.15-16, A és B csoport - Megoldások A/1. Milyen ágenskörnyezetrıl azt mondjuk, hogy nem hozzáférhetı? Adjon példát egy konkrét ágensre, problémára és környezetre, amire igaz
Problémamegoldás kereséssel. Mesterséges intelligencia március 7.
 Problémamegoldás kereséssel Mesterséges intelligencia 2014. március 7. Bevezetés Problémamegoldó ágens Kívánt állapotba vezető cselekvéseket keres Probléma megfogalmazása Megoldás megfogalmazása Keresési
Problémamegoldás kereséssel Mesterséges intelligencia 2014. március 7. Bevezetés Problémamegoldó ágens Kívánt állapotba vezető cselekvéseket keres Probléma megfogalmazása Megoldás megfogalmazása Keresési
Alap-ötlet: Karl Friedrich Gauss ( ) valószínűségszámítási háttér: Andrej Markov ( )
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
2. A példahalmazban n = 3 negatív és p = 3 pozitív példa van, azaz a példahalmazt képviselő döntési fa információtartalma: I = I(1/2, 1/2) = 1 bit.
 Példa 1. Döntési fa számítása/1 1. Legyen a felhasználandó példahalmaz: Példa sz. Nagy(x) Fekete(x) Ugat(x) JóKutya(x) X1 Igen Igen Igen Nem X2 Igen Igen Nem Igen X3 Nem Nem Igen Nem X4 Nem Igen Igen Igen
Példa 1. Döntési fa számítása/1 1. Legyen a felhasználandó példahalmaz: Példa sz. Nagy(x) Fekete(x) Ugat(x) JóKutya(x) X1 Igen Igen Igen Nem X2 Igen Igen Nem Igen X3 Nem Nem Igen Nem X4 Nem Igen Igen Igen
Megerősítéses tanulási módszerek és alkalmazásaik
 MISKOLCI EGYETEM GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR Megerősítéses tanulási módszerek és alkalmazásaik Tompa Tamás tanársegéd Általános Informatikai Intézeti Tanszék Miskolc, 2017. szeptember 15. Tartalom
MISKOLCI EGYETEM GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR Megerősítéses tanulási módszerek és alkalmazásaik Tompa Tamás tanársegéd Általános Informatikai Intézeti Tanszék Miskolc, 2017. szeptember 15. Tartalom
Nemlineáris programozás 2.
 Optimumszámítás Nemlineáris programozás 2. Többváltozós optimalizálás feltételek mellett. Lagrange-feladatok. Nemlineáris programozás. A Kuhn-Tucker feltételek. Konvex programozás. Sydsaeter-Hammond: 18.1-5,
Optimumszámítás Nemlineáris programozás 2. Többváltozós optimalizálás feltételek mellett. Lagrange-feladatok. Nemlineáris programozás. A Kuhn-Tucker feltételek. Konvex programozás. Sydsaeter-Hammond: 18.1-5,
Mesterséges Intelligencia MI
 Mesterséges Intelligencia MI Megerősítéses tanulás Pataki Béla BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Ágens tudása: Induláskor: vagy ismeri már a környezetet
Mesterséges Intelligencia MI Megerősítéses tanulás Pataki Béla BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Ágens tudása: Induláskor: vagy ismeri már a környezetet
Megerősítéses tanulás
 Gépi tanulás (Szekvenciális döntési probléma) Megerősítéses tanulás Pataki Béla BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Az egész világot nem tudjuk modellezni,
Gépi tanulás (Szekvenciális döntési probléma) Megerősítéses tanulás Pataki Béla BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Az egész világot nem tudjuk modellezni,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
Mesterséges Intelligencia. Csató Lehel. Csató Lehel. Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2007/2008
 Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 007/008 Az Előadások Témái Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció i stratégiák Szemantikus hálók / Keretrendszerek
Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 007/008 Az Előadások Témái Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció i stratégiák Szemantikus hálók / Keretrendszerek
Logika és informatikai alkalmazásai kiskérdések február Mikor mondjuk, hogy az F formula a G-nek részformulája?
 ,,Alap kiskérdések Logika és informatikai alkalmazásai kiskérdések 2012. február 19. 1. Hogy hívjuk a 0 aritású függvényjeleket? 2. Definiálja a termek halmazát. 3. Definiálja a formulák halmazát. 4. Definiálja,
,,Alap kiskérdések Logika és informatikai alkalmazásai kiskérdések 2012. február 19. 1. Hogy hívjuk a 0 aritású függvényjeleket? 2. Definiálja a termek halmazát. 3. Definiálja a formulák halmazát. 4. Definiálja,
Logika és informatikai alkalmazásai
 Logika és informatikai alkalmazásai 9. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2008 tavasz Egy HF múlt hétről HF1. a) Egyesíthető: s = [y/f(x,
Logika és informatikai alkalmazásai 9. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2008 tavasz Egy HF múlt hétről HF1. a) Egyesíthető: s = [y/f(x,
Logikai ágensek. Mesterséges intelligencia március 21.
 Logikai ágensek Mesterséges intelligencia 2014. március 21. Bevezetés Eddigi példák tudásra: állapotok halmaza, lehetséges operátorok, ezek költségei, heurisztikák Feltételezés: a világ (lehetséges állapotok
Logikai ágensek Mesterséges intelligencia 2014. március 21. Bevezetés Eddigi példák tudásra: állapotok halmaza, lehetséges operátorok, ezek költségei, heurisztikák Feltételezés: a világ (lehetséges állapotok
Differenciálegyenletek numerikus megoldása
 a Matematika mérnököknek II. című tárgyhoz Differenciálegyenletek numerikus megoldása Fokozatos közeĺıtés módszere (1) (2) x (t) = f (t, x(t)), x I, x(ξ) = η. Az (1)-(2) kezdeti érték probléma ekvivalens
a Matematika mérnököknek II. című tárgyhoz Differenciálegyenletek numerikus megoldása Fokozatos közeĺıtés módszere (1) (2) x (t) = f (t, x(t)), x I, x(ξ) = η. Az (1)-(2) kezdeti érték probléma ekvivalens
Példa 1. A majom és banán problémája
 Példa 1. A majom és banán problémája Egy majom ketrecében mennyezetről egy banánt lógatnak. Kézzel elérni lehetetlen, viszont egy faládát be is tesznek. Eléri-e a majom a banánt? Mit tudunk a majom képességeirõl?
Példa 1. A majom és banán problémája Egy majom ketrecében mennyezetről egy banánt lógatnak. Kézzel elérni lehetetlen, viszont egy faládát be is tesznek. Eléri-e a majom a banánt? Mit tudunk a majom képességeirõl?
Formális nyelvek - 9.
 Formális nyelvek - 9. Csuhaj Varjú Erzsébet Algoritmusok és Alkalmazásaik Tanszék Informatikai Kar Eötvös Loránd Tudományegyetem H-1117 Budapest Pázmány Péter sétány 1/c E-mail: csuhaj@inf.elte.hu 1 Véges
Formális nyelvek - 9. Csuhaj Varjú Erzsébet Algoritmusok és Alkalmazásaik Tanszék Informatikai Kar Eötvös Loránd Tudományegyetem H-1117 Budapest Pázmány Péter sétány 1/c E-mail: csuhaj@inf.elte.hu 1 Véges
Bizonytalanság. Mesterséges intelligencia április 4.
 Bizonytalanság Mesterséges intelligencia 2014. április 4. Bevezetés Eddig: logika, igaz/hamis Ha nem teljes a tudás A világ nem figyelhető meg közvetlenül Részleges tudás nem reprezentálható logikai eszközökkel
Bizonytalanság Mesterséges intelligencia 2014. április 4. Bevezetés Eddig: logika, igaz/hamis Ha nem teljes a tudás A világ nem figyelhető meg közvetlenül Részleges tudás nem reprezentálható logikai eszközökkel
ÍTÉLETKALKULUS (NULLADRENDŰ LOGIKA)
 ÍTÉLETKALKULUS SZINTAXIS ÍTÉLETKALKULUS (NULLADRENDŰ LOGIKA) jelkészlet elválasztó jelek: ( ) logikai műveleti jelek: ítéletváltozók (logikai változók): p, q, r,... ítéletkonstansok: T, F szintaxis szabályai
ÍTÉLETKALKULUS SZINTAXIS ÍTÉLETKALKULUS (NULLADRENDŰ LOGIKA) jelkészlet elválasztó jelek: ( ) logikai műveleti jelek: ítéletváltozók (logikai változók): p, q, r,... ítéletkonstansok: T, F szintaxis szabályai
Differenciaegyenletek
 Differenciaegyenletek Losonczi László Debreceni Egyetem, Közgazdaság- és Gazdaságtudományi Kar Debrecen, 2009/10 tanév, I. félév Losonczi László (DE) Differenciaegyenletek 2009/10 tanév, I. félév 1 / 11
Differenciaegyenletek Losonczi László Debreceni Egyetem, Közgazdaság- és Gazdaságtudományi Kar Debrecen, 2009/10 tanév, I. félév Losonczi László (DE) Differenciaegyenletek 2009/10 tanév, I. félév 1 / 11
Ellenőrző kérdések. 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t
 Ellenőrző kérdések 2. Kis dolgozat kérdései 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t 37. Ha t szintű indexet használunk,
Ellenőrző kérdések 2. Kis dolgozat kérdései 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t 37. Ha t szintű indexet használunk,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
Mesterséges Intelligencia MI
 Mesterséges Intelligencia MI Problémamegoldás kereséssel ha sötétben tapogatózunk Dobrowiecki Tadeusz Eredics Péter, és mások BME I.E. 437, 463-28-99 dobrowiecki@mit.bme.hu, http://www.mit.bme.hu/general/staff/tade
Mesterséges Intelligencia MI Problémamegoldás kereséssel ha sötétben tapogatózunk Dobrowiecki Tadeusz Eredics Péter, és mások BME I.E. 437, 463-28-99 dobrowiecki@mit.bme.hu, http://www.mit.bme.hu/general/staff/tade
Mesterséges Intelligencia. Csató Lehel. Csató Lehel. Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2007/2008
 Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2007/2008 Az Előadások Témái Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció Gráfkeresési stratégiák Szemantikus hálók
Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2007/2008 Az Előadások Témái Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció Gráfkeresési stratégiák Szemantikus hálók
ALGEBRAI KIFEJEZÉSEK, EGYENLETEK
 ALGEBRAI KIFEJEZÉSEK, EGYENLETEK AZ ALGEBRAI KIFEJEZÉS FOGALMÁNAK KIALAKÍTÁSA (7-9. OSZTÁLY) Racionális algebrai kifejezés (betűs kifejezés): betűket és számokat a négy alapművelet véges sokszori alkalmazásával
ALGEBRAI KIFEJEZÉSEK, EGYENLETEK AZ ALGEBRAI KIFEJEZÉS FOGALMÁNAK KIALAKÍTÁSA (7-9. OSZTÁLY) Racionális algebrai kifejezés (betűs kifejezés): betűket és számokat a négy alapművelet véges sokszori alkalmazásával
Mesterséges Intelligencia MI
 Mesterséges Intelligencia MI Valószínűségi hálók - alapok Dobrowiecki Tadeusz Eredics Péter, és mások BME I.E. 437, 463-28-99 dobrowiecki@mit.bme.hu, http://www.mit.bme.hu/general/staff/tade Valószínűségi
Mesterséges Intelligencia MI Valószínűségi hálók - alapok Dobrowiecki Tadeusz Eredics Péter, és mások BME I.E. 437, 463-28-99 dobrowiecki@mit.bme.hu, http://www.mit.bme.hu/general/staff/tade Valószínűségi
A TANTÁRGY ADATLAPJA
 A TANTÁRGY ADATLAPJA 1. A képzési program adatai 1.1 Felsőoktatási intézmény Babeş-Bolyai Tudományegyetem 1.2 Kar Matematika és Informatika 1.3 Intézet Magyar Matematika és Informatika 1.4 Szakterület
A TANTÁRGY ADATLAPJA 1. A képzési program adatai 1.1 Felsőoktatási intézmény Babeş-Bolyai Tudományegyetem 1.2 Kar Matematika és Informatika 1.3 Intézet Magyar Matematika és Informatika 1.4 Szakterület
Gyakorló feladatok: Formális modellek, temporális logikák, modellellenőrzés. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék
 Gyakorló feladatok: Formális modellek, temporális logikák, modellellenőrzés Majzik István BME Méréstechnika és Információs Rendszerek Tanszék Formális modellek használata és értelmezése Formális modellek
Gyakorló feladatok: Formális modellek, temporális logikák, modellellenőrzés Majzik István BME Méréstechnika és Információs Rendszerek Tanszék Formális modellek használata és értelmezése Formális modellek
-------------------------------------------- MIEA 18.5, --------------- Magyarázza meg, hogy milyen alapgondolat vezetett el a VKH tanuláshoz?
 2015 ZH és vizsga kérdések és feladatok tankönyv (Almanach) és előadás referenciái tankönyv (Almanach - MIEA): alfejezetszámok előadás: 2014 ősz, tárgylapján --------------------------------------------
2015 ZH és vizsga kérdések és feladatok tankönyv (Almanach) és előadás referenciái tankönyv (Almanach - MIEA): alfejezetszámok előadás: 2014 ősz, tárgylapján --------------------------------------------
1. Mire utal általában intelligens jelző sok kereskedelmi cikk esetében? 2. Milyen gépkocsi lehetne intelligens? 3. Mi ill.
 1. Mire utal általában intelligens jelző sok kereskedelmi cikk esetében? 2. Milyen gépkocsi lehetne intelligens? 3. Mi ill. milyen lehet egy intelligens város (smart city)? 4. Milyen egy intelligens informatikai
1. Mire utal általában intelligens jelző sok kereskedelmi cikk esetében? 2. Milyen gépkocsi lehetne intelligens? 3. Mi ill. milyen lehet egy intelligens város (smart city)? 4. Milyen egy intelligens informatikai
Dualitás Dualitási tételek Általános LP feladat Komplementáris lazaság 2017/ Szegedi Tudományegyetem Informatikai Intézet
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 7. Előadás Árazási interpretáció Tekintsük újra az erőforrás allokációs problémát (vonat
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 7. Előadás Árazási interpretáció Tekintsük újra az erőforrás allokációs problémát (vonat
11. Előadás. 11. előadás Bevezetés a lineáris programozásba
 11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
Előfeltétel: legalább elégséges jegy Diszkrét matematika II. (GEMAK122B) tárgyból
 ÜTEMTERV Programozás-elmélet c. tárgyhoz (GEMAK233B, GEMAK233-B) BSc gazdaságinformatikus, programtervező informatikus alapszakok számára Óraszám: heti 2+0, (aláírás+kollokvium, 3 kredit) 2019/20-es tanév
ÜTEMTERV Programozás-elmélet c. tárgyhoz (GEMAK233B, GEMAK233-B) BSc gazdaságinformatikus, programtervező informatikus alapszakok számára Óraszám: heti 2+0, (aláírás+kollokvium, 3 kredit) 2019/20-es tanév
Adaptív menetrendezés ADP algoritmus alkalmazásával
 Adaptív menetrendezés ADP algoritmus alkalmazásával Alcím III. Mechwart András Ifjúsági Találkozó Mátraháza, 2013. szeptember 10. Divényi Dániel Villamos Energetika Tanszék Villamos Művek és Környezet
Adaptív menetrendezés ADP algoritmus alkalmazásával Alcím III. Mechwart András Ifjúsági Találkozó Mátraháza, 2013. szeptember 10. Divényi Dániel Villamos Energetika Tanszék Villamos Művek és Környezet
b, Van olyan makacs ember, a senki más tanácsára nem hallgat. (Univerzum az emberek halmaza)
 Elsőrendű logika. Formalizálja az alábbi mondatokat: a, Aki másnak vermet ás, maga esik verembe. (Univerzum az emberek halmaza) ( yv ( E( ) E(: verembe esik, V(: vermet ás y-nak b, Van olyan makacs ember,
Elsőrendű logika. Formalizálja az alábbi mondatokat: a, Aki másnak vermet ás, maga esik verembe. (Univerzum az emberek halmaza) ( yv ( E( ) E(: verembe esik, V(: vermet ás y-nak b, Van olyan makacs ember,
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Abszolútértékes és gyökös kifejezések
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Abszolútértékes és gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Abszolútértékes és gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
LINEÁRIS EGYENLETRENDSZEREK október 12. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak
 LINEÁRIS EGYENLETRENDSZEREK 004. október. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László:
LINEÁRIS EGYENLETRENDSZEREK 004. október. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László:
Mesterséges Intelligencia MI
 Mesterséges Intelligencia MI Valószínűségi hálók - következtetés Dobrowiecki Tadeusz Eredics Péter, és mások BME I.E. 437, 463-28-99 dobrowiecki@mit.bme.hu, http://www.mit.bme.hu/general/staff/tade Következtetés
Mesterséges Intelligencia MI Valószínűségi hálók - következtetés Dobrowiecki Tadeusz Eredics Péter, és mások BME I.E. 437, 463-28-99 dobrowiecki@mit.bme.hu, http://www.mit.bme.hu/general/staff/tade Következtetés
Új típusú döntési fa építés és annak alkalmazása többtényezős döntés területén
 Új típusú döntési fa építés és annak alkalmazása többtényezős döntés területén Dombi József Szegedi Tudományegyetem Bevezetés - ID3 (Iterative Dichotomiser 3) Az ID algoritmusok egy elemhalmaz felhasználásával
Új típusú döntési fa építés és annak alkalmazása többtényezős döntés területén Dombi József Szegedi Tudományegyetem Bevezetés - ID3 (Iterative Dichotomiser 3) Az ID algoritmusok egy elemhalmaz felhasználásával
9. előadás. Programozás-elmélet. Programozási tételek Elemi prog. Sorozatszámítás Eldöntés Kiválasztás Lin. keresés Megszámolás Maximum.
 Programozási tételek Programozási feladatok megoldásakor a top-down (strukturált) programtervezés esetén három vezérlési szerkezetet használunk: - szekvencia - elágazás - ciklus Eddig megismertük az alábbi
Programozási tételek Programozási feladatok megoldásakor a top-down (strukturált) programtervezés esetén három vezérlési szerkezetet használunk: - szekvencia - elágazás - ciklus Eddig megismertük az alábbi
Objektumorientált Programozás III.
 Objektumorientált Programozás III. Vezérlési szerkezetek ismétlés Matematikai lehetőségek Feladatok 1 Hallgatói Tájékoztató A jelen bemutatóban található adatok, tudnivalók és információk a számonkérendő
Objektumorientált Programozás III. Vezérlési szerkezetek ismétlés Matematikai lehetőségek Feladatok 1 Hallgatói Tájékoztató A jelen bemutatóban található adatok, tudnivalók és információk a számonkérendő
Gépi tanulás a gyakorlatban. Lineáris regresszió
 Gépi tanulás a gyakorlatban Lineáris regresszió Lineáris Regresszió Legyen adott egy tanuló adatbázis: Rendelkezésünkre áll egy olyan előfeldolgozott adathalmaz, aminek sorai az egyes ingatlanokat írják
Gépi tanulás a gyakorlatban Lineáris regresszió Lineáris Regresszió Legyen adott egy tanuló adatbázis: Rendelkezésünkre áll egy olyan előfeldolgozott adathalmaz, aminek sorai az egyes ingatlanokat írják
Az informatika elméleti alapjai 2 elővizsga december 19.
 Név (aláírás): Az informatika elméleti alapjai 2 elővizsga 2017. december 19. A vizsgadolgozat 1. feladatára helyes válaszonként 1-1 pont kapható, a 2-3. feladatok megoldásáért 6-6 pont, a 4. feladatra
Név (aláírás): Az informatika elméleti alapjai 2 elővizsga 2017. december 19. A vizsgadolgozat 1. feladatára helyes válaszonként 1-1 pont kapható, a 2-3. feladatok megoldásáért 6-6 pont, a 4. feladatra
Mesterséges Intelligencia MI
 Mesterséges Intelligencia MI Problémamegoldás kereséssel - csak lokális információra alapozva Pataki Béla BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Lokálisan
Mesterséges Intelligencia MI Problémamegoldás kereséssel - csak lokális információra alapozva Pataki Béla BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Lokálisan
Intelligens Rendszerek Elmélete IRE 4/32/1
 Intelligens Rendszerek Elmélete 4 IRE 4/32/1 Problémamegoldás kereséssel http://nik.uni-obuda.hu/mobil IRE 4/32/2 Egyszerű lények intelligenciája? http://www.youtube.com/watch?v=tlo2n3ymcxw&nr=1 IRE 4/32/3
Intelligens Rendszerek Elmélete 4 IRE 4/32/1 Problémamegoldás kereséssel http://nik.uni-obuda.hu/mobil IRE 4/32/2 Egyszerű lények intelligenciája? http://www.youtube.com/watch?v=tlo2n3ymcxw&nr=1 IRE 4/32/3
Kétszemélyes játékok Gregorics Tibor Mesterséges intelligencia
 Kétszemélyes játékok Kétszemélyes, teljes információjú, véges, determinisztikus,zéró összegű játékok Két játékos lép felváltva adott szabályok szerint, amíg a játszma véget nem ér. Mindkét játékos ismeri
Kétszemélyes játékok Kétszemélyes, teljes információjú, véges, determinisztikus,zéró összegű játékok Két játékos lép felváltva adott szabályok szerint, amíg a játszma véget nem ér. Mindkét játékos ismeri
Függvények Megoldások
 Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Logikai ágens, lehetőségek és problémák 2
 Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs rendszerek Tanszék Mesterséges Intelligencia - MI Logikai ágens, lehetőségek és problémák 2 Előadó: Hullám Gábor Pataki Béla
Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs rendszerek Tanszék Mesterséges Intelligencia - MI Logikai ágens, lehetőségek és problémák 2 Előadó: Hullám Gábor Pataki Béla
NEM-DETERMINISZTIKUS PROGRAMOK HELYESSÉGE. Szekvenciális programok kategóriái. Hoare-Dijkstra-Gries módszere
 Szekvenciális programok kategóriái strukturálatlan strukturált NEM-DETERMINISZTIKUS PROGRAMOK HELYESSÉGE Hoare-Dijkstra-Gries módszere determinisztikus valódi korai nem-determinisztikus általános fejlett
Szekvenciális programok kategóriái strukturálatlan strukturált NEM-DETERMINISZTIKUS PROGRAMOK HELYESSÉGE Hoare-Dijkstra-Gries módszere determinisztikus valódi korai nem-determinisztikus általános fejlett
Megoldások MATEMATIKA II. VIZSGA (VK) NBT. NG. NMH. SZAKOS HALLGATÓK RÉSZÉRE (Kérjük, hogy a megfelelő szakot jelölje be!
 MATEMATIKA II. VIZSGA (VK) NBT. NG. NMH. SZAKOS HALLGATÓK RÉSZÉRE (Kérjük, hogy a megfelelő szakot jelölje be!) 2016. JANUÁR 21. Elérhető pontszám: 50 pont Megoldások 1. 6. 2. 7. 3. 8. 4. 9. 5. Össz.:
MATEMATIKA II. VIZSGA (VK) NBT. NG. NMH. SZAKOS HALLGATÓK RÉSZÉRE (Kérjük, hogy a megfelelő szakot jelölje be!) 2016. JANUÁR 21. Elérhető pontszám: 50 pont Megoldások 1. 6. 2. 7. 3. 8. 4. 9. 5. Össz.:
Térinformatikai algoritmusok Elemi algoritmusok
 Cserép Máté 2016. szeptember 14. Analóg programozásnak nevezzük azt, amikor egy feladat megoldásához egy már ismert és megoldott feladat megoldását használjuk fel. Általában nem pontosan ugyanazt a feladatot
Cserép Máté 2016. szeptember 14. Analóg programozásnak nevezzük azt, amikor egy feladat megoldásához egy már ismert és megoldott feladat megoldását használjuk fel. Általában nem pontosan ugyanazt a feladatot
1. Tekintsük a következő két halmazt: G = {1; 2; 3; 4; 6; 12} és H = {1; 2; 4; 8; 16}. Elemeik felsorolásával adja meg a G H és a H \ G halmazokat!
 1. Tekintsük a következő két halmazt: G = {1; 2; 3; 4; 6; 12} és H = {1; 2; 4; 8; 16}. Elemeik felsorolásával adja meg a G H és a H \ G halmazokat! G H = H \ G = 2. Ha 1 kg szalámi ára 2800 Ft, akkor hány
1. Tekintsük a következő két halmazt: G = {1; 2; 3; 4; 6; 12} és H = {1; 2; 4; 8; 16}. Elemeik felsorolásával adja meg a G H és a H \ G halmazokat! G H = H \ G = 2. Ha 1 kg szalámi ára 2800 Ft, akkor hány
Keresés képi jellemzők alapján. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Kiterjesztések sek szemantikája
 Kiterjesztések sek szemantikája Példa D Integer = {..., -1,0,1,... }; D Boolean = { true, false } D T1... T n T = D T 1... D Tn D T Az összes függvf ggvény halmaza, amelyek a D T1,..., D Tn halmazokból
Kiterjesztések sek szemantikája Példa D Integer = {..., -1,0,1,... }; D Boolean = { true, false } D T1... T n T = D T 1... D Tn D T Az összes függvf ggvény halmaza, amelyek a D T1,..., D Tn halmazokból
Gyakorló feladatok I.
 Gyakorló feladatok I. (Függvények határértéke és folytonossága) Analízis 2. (A,B, C szakirány, keresztfélév) Programtervező informatikus szak 2013-2014. tanév tavaszi félév Összeállította: Szili László
Gyakorló feladatok I. (Függvények határértéke és folytonossága) Analízis 2. (A,B, C szakirány, keresztfélév) Programtervező informatikus szak 2013-2014. tanév tavaszi félév Összeállította: Szili László
Miért fontos számunkra az előző gyakorlaton tárgyalt lineáris algebrai ismeretek
 Az november 23-i szeminárium témája Rövid összefoglaló Miért fontos számunkra az előző gyakorlaton tárgyalt lineáris algebrai ismeretek felfrissítése? Tekintsünk ξ 1,..., ξ k valószínűségi változókat,
Az november 23-i szeminárium témája Rövid összefoglaló Miért fontos számunkra az előző gyakorlaton tárgyalt lineáris algebrai ismeretek felfrissítése? Tekintsünk ξ 1,..., ξ k valószínűségi változókat,
Korszerű információs technológiák
 MISKOLCI EGYETEM GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR Korszerű információs technológiák Megerősítéses tanulási módszerek és alkalmazásaik Tompa Tamás tanársegéd Általános Informatikai Intézeti Tanszék Miskolc,
MISKOLCI EGYETEM GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR Korszerű információs technológiák Megerősítéses tanulási módszerek és alkalmazásaik Tompa Tamás tanársegéd Általános Informatikai Intézeti Tanszék Miskolc,
Számítógépes képelemzés 7. előadás. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
A dec. 19-i vizsga jellegzetes hibái:
 VIMM 3241 Gyakori hibák A dec. 19-i vizsga jellegzetes hibái: 1. A logikai indukció (általánosítás sok partikuláris esetről egy általános esetre) nem a matematikai indukció (általánosítás n-edik esetről
VIMM 3241 Gyakori hibák A dec. 19-i vizsga jellegzetes hibái: 1. A logikai indukció (általánosítás sok partikuláris esetről egy általános esetre) nem a matematikai indukció (általánosítás n-edik esetről
Logika és informatikai alkalmazásai
 Logika és informatikai alkalmazásai 9. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
Logika és informatikai alkalmazásai 9. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
 Ú Ó Ú É Ú ő ő ő ő ő ő É ő ő É ő Ú É É Ü É ő É ő Ó ő É ő ő É É É ő ő ő ő É ű ű ő ő ő Ó ű ő É ő É ő ő ő ő ő É ő Ú ű ő ő ő ő ő ű ő É Ú ő ű ű ő É ő ő É ő ő ű ő ő ő ő ő ő É Ú É É ő ő ő ű ő ő ő ő ő ő ő ő ő Ü
Ú Ó Ú É Ú ő ő ő ő ő ő É ő ő É ő Ú É É Ü É ő É ő Ó ő É ő ő É É É ő ő ő ő É ű ű ő ő ő Ó ű ő É ő É ő ő ő ő ő É ő Ú ű ő ő ő ő ő ű ő É Ú ő ű ű ő É ő ő É ő ő ű ő ő ő ő ő ő É Ú É É ő ő ő ű ő ő ő ő ő ő ő ő ő Ü
 É Á ó ö ó ö ö ő ü ö ő ö ó ö ó ü ö Í ő ö ő ő ő ő ú ö ö ú ö ó ő ő ö Ó ú ű ú Í ő ö ö ű ó ö Í ö Í Í Í Í ó ő ó ő É Ú Ű Í É Á ó É É ő ő ö ö Í ó ö ő ó ő Ő Ó Ő Á Á É Ö Á É É É É Ó Ó Á úé Á Á ö ó Ú Á Ú Ó Á Ú ő
É Á ó ö ó ö ö ő ü ö ő ö ó ö ó ü ö Í ő ö ő ő ő ő ú ö ö ú ö ó ő ő ö Ó ú ű ú Í ő ö ö ű ó ö Í ö Í Í Í Í ó ő ó ő É Ú Ű Í É Á ó É É ő ő ö ö Í ó ö ő ó ő Ő Ó Ő Á Á É Ö Á É É É É Ó Ó Á úé Á Á ö ó Ú Á Ú Ó Á Ú ő
 É Ú Ú Ü ű Ü Ú ű ű Ú Ü ű ű ű Ú ű Ú Ü ű Ú ű Ú Ü Ü Ü Ő ű ű Ú É Ú ű Ü Ü É ÜÉ É Ü É ű Ü É É ű Ú Ü ű Ú Ő ű Ö Ó Ü Ü Ó ű ű É Á ű ű Ú Ü Á ű Ü ű Ü Ú ű Ü ű ű ű Ü ű Ü Ü Ú Ü Ú Ú ű ű Ü ű Ú ű Ó Ó Ü Ü ű Ü Ü ű Ö Ü ű Ü
É Ú Ú Ü ű Ü Ú ű ű Ú Ü ű ű ű Ú ű Ú Ü ű Ú ű Ú Ü Ü Ü Ő ű ű Ú É Ú ű Ü Ü É ÜÉ É Ü É ű Ü É É ű Ú Ü ű Ú Ő ű Ö Ó Ü Ü Ó ű ű É Á ű ű Ú Ü Á ű Ü ű Ü Ú ű Ü ű ű ű Ü ű Ü Ü Ú Ü Ú Ú ű ű Ü ű Ú ű Ó Ó Ü Ü ű Ü Ü ű Ö Ü ű Ü
 Á Ö Á Ö Ö Ó ű ű Ö Ó ú Ú Ö Ú Ó ú ú ű ú ú Ö É É ú Ö ú ú ű ű Á É Á ű Ö ú Ö Ö ú ú ú Á ű Ó ű Ú ú Ö ú ú ű ú É Á Á ú ű Ú ú ú ű ú ű ú ű ú ű ű ú ú ú ű ú ű É ű Ö ú Ó ú ű ú Á ű ú É ű ú ú É ű Á ú ú ú Ó É ú ű Ú ú ú
Á Ö Á Ö Ö Ó ű ű Ö Ó ú Ú Ö Ú Ó ú ú ű ú ú Ö É É ú Ö ú ú ű ű Á É Á ű Ö ú Ö Ö ú ú ú Á ű Ó ű Ú ú Ö ú ú ű ú É Á Á ú ű Ú ú ú ű ú ű ú ű ú ű ű ú ú ú ű ú ű É ű Ö ú Ó ú ű ú Á ű ú É ű ú ú É ű Á ú ú ú Ó É ú ű Ú ú ú
 Í Ú É É Í Ö É Í É É Í É Í Ú É Í Ú ű Ú ÍÍ Ú Ú Ú ű Í Ú Ú Ú Í Ú Ú ű Ú É Ú Ú Í ű Í Ú ű Í Á Á ű Í Í Ú É Ú Ú Á Á ű Í Ú Ú Í ű Ú Ú Ú É Í ű ű ű Í ű ű Ú Ú ű Í Ú ű ű Ú Á ű ű ű Í É Í Ú Ú Í Í ű Í Ú É ű Ü Í ű Ú Ú ű
Í Ú É É Í Ö É Í É É Í É Í Ú É Í Ú ű Ú ÍÍ Ú Ú Ú ű Í Ú Ú Ú Í Ú Ú ű Ú É Ú Ú Í ű Í Ú ű Í Á Á ű Í Í Ú É Ú Ú Á Á ű Í Ú Ú Í ű Ú Ú Ú É Í ű ű ű Í ű ű Ú Ú ű Í Ú ű ű Ú Á ű ű ű Í É Í Ú Ú Í Í ű Í Ú É ű Ü Í ű Ú Ú ű
Lineáris különböz ségek
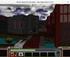 Ivanyos Gábor MTA SZTAKI 2010 december 13 A feladat Titok: u = (µ 1,..., µ n ) n dimenziós vektor Z n 3 -b l Z 3 = az egész számok modulo 3 Gombnyomásra kapunk: véletlen v i = (a i1,..., a in ) vektorokat,
Ivanyos Gábor MTA SZTAKI 2010 december 13 A feladat Titok: u = (µ 1,..., µ n ) n dimenziós vektor Z n 3 -b l Z 3 = az egész számok modulo 3 Gombnyomásra kapunk: véletlen v i = (a i1,..., a in ) vektorokat,
Kétváltozós függvények differenciálszámítása
 Kétváltozós függvények differenciálszámítása 13. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Kétváltozós függvények p. 1/1 Definíció, szemléltetés Definíció. Az f : R R R függvényt
Kétváltozós függvények differenciálszámítása 13. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Kétváltozós függvények p. 1/1 Definíció, szemléltetés Definíció. Az f : R R R függvényt
TANTÁRGYI PROGRAM Matematikai alapok 2. útmutató
 BGF PÉNZÜGYI ÉS SZÁMVITELI KAR Módszertani Intézeti Tanszéki Osztály TANTÁRGYI PROGRAM Matematikai alapok 2. útmutató 2015/2016. tanév I. félév Tantárgyi program Tantárgy megnevezése Tantárgy jellege/típusa:
BGF PÉNZÜGYI ÉS SZÁMVITELI KAR Módszertani Intézeti Tanszéki Osztály TANTÁRGYI PROGRAM Matematikai alapok 2. útmutató 2015/2016. tanév I. félév Tantárgyi program Tantárgy megnevezése Tantárgy jellege/típusa:
NGB_IN040_1 SZIMULÁCIÓS TECHNIKÁK dr. Pozna Claudio Radu, Horváth Ernő
 SZÉCHENYI ISTVÁN EGYETEM Műszaki Tudományi Kar Informatika Tanszék BSC FOKOZATÚ MÉRNÖK INFORMATIKUS SZAK NGB_IN040_1 SZIMULÁCIÓS TECHNIKÁK dr. Pozna Claudio Radu, Horváth Ernő Fejlesztői dokumentáció GROUP#6
SZÉCHENYI ISTVÁN EGYETEM Műszaki Tudományi Kar Informatika Tanszék BSC FOKOZATÚ MÉRNÖK INFORMATIKUS SZAK NGB_IN040_1 SZIMULÁCIÓS TECHNIKÁK dr. Pozna Claudio Radu, Horváth Ernő Fejlesztői dokumentáció GROUP#6
Mesterséges Intelligencia MI
 Mesterséges Intelligencia MI Egyszerű döntés Döntési fák Tanuljuk meg! Metsszük meg! Pataki Béla Bolgár Bence BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Példaprobléma:
Mesterséges Intelligencia MI Egyszerű döntés Döntési fák Tanuljuk meg! Metsszük meg! Pataki Béla Bolgár Bence BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Példaprobléma:
Rekurzió. Dr. Iványi Péter
 Rekurzió Dr. Iványi Péter 1 Függvényhívás void f3(int a3) { printf( %d,a3); } void f2(int a2) { f3(a2); a2 = (a2+1); } void f1() { int a1 = 1; int b1; b1 = f2(a1); } 2 Függvényhívás void f3(int a3) { printf(
Rekurzió Dr. Iványi Péter 1 Függvényhívás void f3(int a3) { printf( %d,a3); } void f2(int a2) { f3(a2); a2 = (a2+1); } void f1() { int a1 = 1; int b1; b1 = f2(a1); } 2 Függvényhívás void f3(int a3) { printf(
Kétfázisú szimplex algoritmus és speciális esetei
 5. gyakorlat Kétfázisú szimplex algoritmus és speciális esetei. Emlékeztető Standard alak, áttérés Standard alak Minden feltétel et tartalmaz csak. A célfüggvényünket maximalizáljuk. A b vektor (jobb oldalon
5. gyakorlat Kétfázisú szimplex algoritmus és speciális esetei. Emlékeztető Standard alak, áttérés Standard alak Minden feltétel et tartalmaz csak. A célfüggvényünket maximalizáljuk. A b vektor (jobb oldalon
Az egyenes egyenlete: 2 pont. Az összevont alak: 1 pont. Melyik ábrán látható e függvény grafikonjának egy részlete?
 1. Írja fel annak az egyenesnek az egyenletét, amely áthalad az (1; 3) ponton, és egyik normálvektora a (8; 1) vektor! Az egyenes egyenlete: 2. Végezze el a következő műveleteket, és vonja össze az egynemű
1. Írja fel annak az egyenesnek az egyenletét, amely áthalad az (1; 3) ponton, és egyik normálvektora a (8; 1) vektor! Az egyenes egyenlete: 2. Végezze el a következő műveleteket, és vonja össze az egynemű
Csuklós szerkezetek reakciói és igénybevételi ábrái. Frissítve: példa: A 12. gyakorlat 1. feladata.
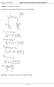 1. példa: A 12. gyakorlat 1. feladata. Számítsuk ki a reakcióerőket! Rajzoljuk meg a nyomatéki ábrát! Megjegyzés: A támaszok vízszintesen egy vonalban vannak. 1 / 20 2. példa: Számítsuk ki a reakcióerőket!
1. példa: A 12. gyakorlat 1. feladata. Számítsuk ki a reakcióerőket! Rajzoljuk meg a nyomatéki ábrát! Megjegyzés: A támaszok vízszintesen egy vonalban vannak. 1 / 20 2. példa: Számítsuk ki a reakcióerőket!
Feladatok Adja meg egy ágens rendszer meghatározását!
 Feladatok +++++++++++++++++++++++ Könnyű rövid kérdések ágensekről +++++++++++++++++++++++++++++ Adja meg egy ágens rendszer meghatározását! Környezetbe ágyazott, azt szenzoraival folyamatosan érzékelő
Feladatok +++++++++++++++++++++++ Könnyű rövid kérdések ágensekről +++++++++++++++++++++++++++++ Adja meg egy ágens rendszer meghatározását! Környezetbe ágyazott, azt szenzoraival folyamatosan érzékelő
A Számítástudomány alapjai
 Mechatronika, Optika és Gépészeti Informatika Tanszék A Számítástudomány alapjai Szemelvények az Elméleti Számítástudomány területéről Fogalmak: Számítástechnika Realizáció, technológia Elméleti számítástudomány
Mechatronika, Optika és Gépészeti Informatika Tanszék A Számítástudomány alapjai Szemelvények az Elméleti Számítástudomány területéről Fogalmak: Számítástechnika Realizáció, technológia Elméleti számítástudomány
Gépi tanulás Gregorics Tibor Mesterséges intelligencia
 Gépi tanulás Tanulás fogalma Egy algoritmus akkor tanul, ha egy feladat megoldása során olyan változások következnek be a működésében, hogy később ugyanazt a feladatot vagy ahhoz hasonló más feladatokat
Gépi tanulás Tanulás fogalma Egy algoritmus akkor tanul, ha egy feladat megoldása során olyan változások következnek be a működésében, hogy később ugyanazt a feladatot vagy ahhoz hasonló más feladatokat
7. 1. A formatív értékelés és lehetséges módjai (szóbeli, feladatlapos, számítógépes) az oktatásban. - valamilyen jelenségről, ill.
 7. 1. A formatív értékelés és lehetséges módjai (szóbeli, feladatlapos, számítógépes) az oktatásban Pedagógiai értékelés fogalma: Az értékelés során értéket állapítunk meg: közvetlenül: közvetve: - valamilyen
7. 1. A formatív értékelés és lehetséges módjai (szóbeli, feladatlapos, számítógépes) az oktatásban Pedagógiai értékelés fogalma: Az értékelés során értéket állapítunk meg: közvetlenül: közvetve: - valamilyen
Van-e kapcsolat a változók között? (példák: fizetés-távolság; felvételi pontszám - görgetett átlag)
 , rangkorreláció Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék 1111, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-16-80 Fax: 463-30-91 http://www.vizgep.bme.hu
, rangkorreláció Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék 1111, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-16-80 Fax: 463-30-91 http://www.vizgep.bme.hu
A lineáris programozás alapfeladata Standard alak Az LP feladat megoldása Az LP megoldása: a szimplex algoritmus 2018/
 Operációkutatás I. 2018/2019-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
Operációkutatás I. 2018/2019-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
Numerikus módszerek 1.
 Numerikus módszerek 1. 9. előadás: Paraméteres iterációk, relaxációs módszerek Lócsi Levente ELTE IK Tartalomjegyzék 1 A Richardson-iteráció 2 Relaxált Jacobi-iteráció 3 Relaxált Gauss Seidel-iteráció
Numerikus módszerek 1. 9. előadás: Paraméteres iterációk, relaxációs módszerek Lócsi Levente ELTE IK Tartalomjegyzék 1 A Richardson-iteráció 2 Relaxált Jacobi-iteráció 3 Relaxált Gauss Seidel-iteráció
1000 forintos adósságunkat, de csak 600 forintunk van. Egyetlen lehetőségünk, hogy a
 A merész játékok stratégiája A következő problémával foglalkozunk: Tegyük fel, hogy feltétlenül ki kell fizetnünk 000 forintos adósságunkat, de csak 600 forintunk van. Egyetlen lehetőségünk, hogy a még
A merész játékok stratégiája A következő problémával foglalkozunk: Tegyük fel, hogy feltétlenül ki kell fizetnünk 000 forintos adósságunkat, de csak 600 forintunk van. Egyetlen lehetőségünk, hogy a még
NP-teljesség röviden
 NP-teljesség röviden Bucsay Balázs earthquake[at]rycon[dot]hu http://rycon.hu 1 Turing gépek 1/3 Mi a turing gép? 1. Definíció. [Turing gép] Egy Turing-gép formálisan egy M = (K, Σ, δ, s) rendezett négyessel
NP-teljesség röviden Bucsay Balázs earthquake[at]rycon[dot]hu http://rycon.hu 1 Turing gépek 1/3 Mi a turing gép? 1. Definíció. [Turing gép] Egy Turing-gép formálisan egy M = (K, Σ, δ, s) rendezett négyessel
Logikai programozás ADMINISZTRATÍV KÉRDÉSEK KÖVETELMÉNYRENDSZER FŐBB PONTOK NÉHÁNY BIZTATÓ SZÓ
 Logikai programozás ADMINISZTRATÍV KÉRDÉSEK Bármilyen kérdéssel (akár tananyag, akár nem), örömmel, bánattal: achs.agnes@gmail.com (Ha két napon belül nem válaszolok, akkor kérek egy figyelmeztető levelet.
Logikai programozás ADMINISZTRATÍV KÉRDÉSEK Bármilyen kérdéssel (akár tananyag, akár nem), örömmel, bánattal: achs.agnes@gmail.com (Ha két napon belül nem válaszolok, akkor kérek egy figyelmeztető levelet.
Térinformatikai algoritmusok Elemi algoritmusok
 Cserép Máté Analóg programozásnak nevezzük azt, amikor egy feladat megoldásához egy már ismert és megoldott feladat megoldását használjuk fel. Általában nem pontosan ugyanazt a feladatot oldottuk meg korábban,
Cserép Máté Analóg programozásnak nevezzük azt, amikor egy feladat megoldásához egy már ismert és megoldott feladat megoldását használjuk fel. Általában nem pontosan ugyanazt a feladatot oldottuk meg korábban,
2014. szeptember 24. és 26. Dr. Vincze Szilvia
 2014. szeptember 24. és 26. Dr. Vincze Szilvia Mind a hétköznapi, mind a tudományos életben gyakran előfordul, hogy bizonyos halmazok elemei között kapcsolat figyelhető meg. A kapcsolat fogalmának matematikai
2014. szeptember 24. és 26. Dr. Vincze Szilvia Mind a hétköznapi, mind a tudományos életben gyakran előfordul, hogy bizonyos halmazok elemei között kapcsolat figyelhető meg. A kapcsolat fogalmának matematikai
ELEKTRONIKAI ALAPISMERETEK
 Elektronikai alapismeretek emelt szint 6 ÉRETTSÉGI VIZSG 06. október 7. ELEKTRONIKI LPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSG JVÍTÁSI-ÉRTÉKELÉSI ÚTMUTTÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUM Egyszerű,
Elektronikai alapismeretek emelt szint 6 ÉRETTSÉGI VIZSG 06. október 7. ELEKTRONIKI LPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSG JVÍTÁSI-ÉRTÉKELÉSI ÚTMUTTÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUM Egyszerű,
Gauss elimináció, LU felbontás
 Közelítő és szimbolikus számítások 3. gyakorlat Gauss elimináció, LU felbontás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 EGYENLETRENDSZEREK 1. Egyenletrendszerek
Közelítő és szimbolikus számítások 3. gyakorlat Gauss elimináció, LU felbontás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 EGYENLETRENDSZEREK 1. Egyenletrendszerek
egyenlőtlenségnek kell teljesülnie.
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Abszolútértékes és gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Abszolútértékes és gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
A lineáris programozás alapfeladata Standard alak Az LP feladat megoldása Az LP megoldása: a szimplex algoritmus 2017/
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
b) Ábrázolja ugyanabban a koordinátarendszerben a g függvényt! (2 pont) c) Oldja meg az ( x ) 2
 1) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) b) c) ( ) ) Határozza meg az 1. feladatban megadott, ; intervallumon
1) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) b) c) ( ) ) Határozza meg az 1. feladatban megadott, ; intervallumon
Döntéselméleti modellek
 Döntéselméleti modellek gyakorlat Berta Árpád Követelmények A félév során 40 pont szerezhető 0-19 pont : elégtelen (1) 20-24 pont : elégséges (2) 25-29 pont : közepes (3) 30-34 pont : jó (4) 35-40 pont
Döntéselméleti modellek gyakorlat Berta Árpád Követelmények A félév során 40 pont szerezhető 0-19 pont : elégtelen (1) 20-24 pont : elégséges (2) 25-29 pont : közepes (3) 30-34 pont : jó (4) 35-40 pont
2019/02/11 10:01 1/10 Logika
 2019/02/11 10:01 1/10 Logika < Számítástechnika Logika Szerző: Sallai András Copyright Sallai András, 2011, 2012, 2015 Licenc: GNU Free Documentation License 1.3 Web: http://szit.hu Boole-algebra A Boole-algebrát
2019/02/11 10:01 1/10 Logika < Számítástechnika Logika Szerző: Sallai András Copyright Sallai András, 2011, 2012, 2015 Licenc: GNU Free Documentation License 1.3 Web: http://szit.hu Boole-algebra A Boole-algebrát
Exact inference in general Bayesian networks
 Exact inference in general Bayesian networks Peter Antal antal@mit.bme.hu Overview The Probability Propagation in Trees of Cliques (a.k.a. ~in join trees) Practical inference Exercises Literature: Valószínűségi
Exact inference in general Bayesian networks Peter Antal antal@mit.bme.hu Overview The Probability Propagation in Trees of Cliques (a.k.a. ~in join trees) Practical inference Exercises Literature: Valószínűségi
Mesterséges Intelligencia MI
 Mesterséges Intelligencia MI Problémamegoldás kereséssel - lokális információval Pataki Béla Bolgár Bence BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Rugó tervezése
Mesterséges Intelligencia MI Problémamegoldás kereséssel - lokális információval Pataki Béla Bolgár Bence BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Rugó tervezése
Trigonometria Megoldások. 1) Oldja meg a következő egyenletet a valós számok halmazán! (12 pont) Megoldás:
 Trigonometria Megoldások ) Oldja meg a következő egyenletet a valós számok halmazán! cos + cos = sin ( pont) sin cos + = + = ( ) cos cos cos (+ pont) cos + cos = 0 A másodfokú egyenlet megoldóképletével
Trigonometria Megoldások ) Oldja meg a következő egyenletet a valós számok halmazán! cos + cos = sin ( pont) sin cos + = + = ( ) cos cos cos (+ pont) cos + cos = 0 A másodfokú egyenlet megoldóképletével
