FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ KÉZI CSABA
|
|
|
- Alíz Szilágyiné
- 8 évvel ezelőtt
- Látták:
Átírás
1 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ KÉZI CSABA
2 KÉZI CSABA El szó Ez a feladatgy jtemény a Debreceni Egyetem M szaki Karának Matematika I. tantárgyának tematikájához szorosan illeszkedik. Célja a m szaki képzésben részt vev hallgatók matematika tanulmányainak megkönnyítése, továbbá, hogy a hallgatók a matematika mérnöki, illetve gazdasági alkalmazásaiba is betekintést nyerjenek. A feladatgy jtemény jó néhány standard, gyakorló feladatot tartalmaz, melyeken keresztül begyakorolhatók a rutinszer en elvárt feladatok megoldásai. Ezen kívül tartalmaz nehezebb, gondolkodást igényl feladatokat, illetve szép számmal alkalmazott matematikai példákat is. Jelölésrendszerében jelöli az el adáson vagy a gyakorlati órán megoldásra szánt feladatokat, jelöli a házi feladatnak szánt példákat, és jelöli a gondolkodtatóbb, vagy a Matematika I. gyakorlat óraszámába már id hiány miatt el nem hangzott feladatokat. Ezeket a példákat a matematika iránt mélyebben érdekl d hallgatók számára ajánljuk. A példatár gondos átolvasásáért, és a felmerül hibák javításáért köszönettel tartozom Molnár Ildikó m szaki menedzser és Tóth Xénia Erzsébet mechatronika szakos hallgatóknak. Köszönettel tartozom Dr. Kocsis Imre tanszékvezet nek, Dr. Szíki Gusztáv Áron f iskolai tanárnak, akik hasznos információkkal láttak el a feladatgy jtemény megírása során. Köszönöm továbbá a M szaki Alaptárgyi Tanszék minden oktatójának, valamint jó barátomnak, Baják Szabolcsnak, akikt l a személyes beszélgetéseink során jó néhány hasznosítható ötletet meríthettem.
3 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 3 I. Mátrixm veletek, determináns kiszámítása, mátrixok invertálása (determinánsokkal), mátrixok gazdasági alkalmazásai. Tekintsük az A = meg az ( ) és a B = ( ) mátrixokat! Határozzuk a) A + B b) A 3B mátrixokat! a) Két mátrixot úgy adunk össze, hogy a megfelel helyen lév elemeket össszeadjuk, így: ( ) ( ) ( 5) A + B = = ( 9) b) El ször a skalárral való szorzásokat végezzük el (azaz az els mátrix minden elemét -vel, a második mátrix minden elemét 3-al szorozzuk), majd a kapott mátrixokat kivonjuk (az els mátrix megfelel elemeib l kivonjuk a második mátrix megfelel elemeit): ( ) ( ) ( ) A 3B = = Tekintsük az A = és a B = 5 5 mátrixokat! Határozzuk meg az a) A B b) 3A + B mátrixokat! a) Két mátrixot úgy vonunk ki, hogy a megfelel helyen lév elemeket kivonjuk, így: A B = ( ) 3 5 = b) El ször a skalárral való szorzásokat végezzük el (azaz az els mátrix minden elemét 3-mal, a második mátrix minden elemét -vel szorozzuk), majd a kapott mátrixokat összeadjuk: 3A + B = =
4 4 KÉZI CSABA 3. Határozzuk meg az x, y, z, t valós számokat úgy, hogy az ( ) ( ) ( x y x x + y 3 = + z t 6 t z + t 3 ) egyenl ség teljesüljön! Els lépésben az egyenl ség bal oldalán elvégezzük a skalárral való szorzást, jobb oldalán az összeadást, így az ( ) ( ) 3x 3y x + 5 x + y + 4 = 3z 3t z + t 6 3 t egyenl séghez jutunk. Két mátrix pontosan akkor egyenl, ha a megfelel helyen lév elemeik egyenl ek. Így az egyenl ség fennállásának szükséges és elégséges feltétele az alábbi egyenletek teljesülése 3x = x + 5 3y = x + y + 4 3z = z + t 6 3t = 3 t. Az els egyenletb l x = 5. Ezt behelyettesítve a második egyenletbe y = 4, 5 adódik. Az utolsó egyenletb l t = 0, 6. Ezt behelyettesítve a harmadik egyenletbe z =, 7 adódik. 4. Jelöljön (m n) egy m-szer n-es mátrixot. Összeszorozhatók-e az alábbi mátrixok, ha igen, határozzuk meg az eredménymátrix méretét: a) ( 4)(3 6) b) (3 5)(4 3) c) ( 5)( 5) d) (4 )( 5) e) (4 6)(6 ) f) (5 )(5 5) Két mátrix pontosan akkor szorozható össze, ha az els mátrix oszlopainak a száma megegyezik a második mátrix sorainak a számával. Ilyenkor az eredménymátrixnak annyi sora, illetve oszlopa van, amennyi sora van az els mátrixnak, illetve amennyi oszlopa van a második mátrixnak. Tehát összeszorozni csak m n és n k típusú mátrixokat lehet, s ilyenkor a szorzatmátrix m k-as lesz. Ez alapján a) nem összeszorozhatók b) nem összeszorozhatók c) nem összeszorozhatók d) összeszorozhatók, az eredménymátrix 4 5-ös lesz e) összeszorozhatók, az eredménymátrix 4 -ös lesz f) nem összeszorozhatók. 5. Tekintsük az A = az ( 3 ) és a B = ( ) mátrixokat! Határozzuk meg
5 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 5 a) AB b) BA szorzatokat! a) Az els mátrix -es, a második 3-as, így a szorzás elvégezhet, és az eredménymátrix 3-as lesz. A mátrixok szorzása úgynevezett sor-oszlop kompozíciós szorzat, azaz az i-edik sor minden elemét megszorozzuk a j-edik oszlop megfelel elemeivel, és a kapott eredményeket összeadjuk. Így kapjuk a szorzatmátrix (i, j) index elemét. Azaz ( ) ( ) ( ) ( ) AB = = = b) A BA mátrix nem létezik. 6. Tekintsük az A = és a B = ( 3 ) mátrixokat! Határozzuk meg az a) AB b) BA szorzatokat! a) b) AB = ( ) 3 4 = 3 5 BA = ( 3 ) = ( 6 ) 7. Határozzuk meg az AB és BA mátrixokat, ha ( ) A =, B = AB = ( 4 A BA mátrix nem létezik. ) 0 3. = ( ).
6 6 KÉZI CSABA 8. Határozzuk meg az alábbi mátrixok transzponáltját: A = ( ) ( 4, B = 3 ), C = Egy mátrix transzponáltját a sorainak és oszlopainak felcserélésével kapjuk meg: A T = 3 ( ) ( ) 0 4 5, B T =, C 4 3 T = Tekintsük az A = az ( ) és a B = ( ) mátrixokat! Határozzuk meg a) A T B b) B T A szorzatokat! a) b) A T B = B T A = ( ( ) = ) = Határozzuk meg az A = ( 3 ) mátrix négyzetét! Mivel A = A A, ezért A = ( 3 ) ( 3 ) = ( ).
7 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 7 ( ). Tekintsük az A = mátrixot! Határozzuk meg azokat a zéruvektortól különböz u vektorokat, melyekre Au = 5 u. Az u vektornak koordinátából álló oszlopvektornak kell lennie, ellenkez esetben a szorzás nem végezhet el. Legyenek az u koordinátái x és y. Így az Au = u egyenlet ( ) ( ) ( ) x x = 5 y y alakban írható föl. Az egyenlet bal oldalán elvégezve a szorzást ( ) ( ) x + y x = x + 5y y adódik. Két mátrix pontosan akkor egyenl, ha a megfelel helyen lév elemeik megegyeznek, így az x + y = x x + 5y = y egyenletrendszerhez jutunk. Elvégezve az összevonásokat az x + y = 0 x + 4y = 0 egyenletrendszert kapjuk. Vegyük észre, hogy a második egyenlet éppen kétszerese az els nek, így a két egyenlet ekvivalens (azaz ugyanaz a megoldásuk). Így az egyik egyenlet elhagyható. Az x + y = 0 egyenletben az egyik ismeretlent tetsz legesen választhatjuk meg. Legyen például y = t, ahol t R \ {0} tetsz leges. Ekkor x = t adódik. Tehát a feltételeknek minden ( ) t u = t alakú vektor eleget tesz, ahol t R \ {0} tetsz leges.. Határozzuk meg az A = ( 5 ) mátrix determinánsát! Kétszer kettes mátrix determinánsa a f átlóbeli és mellékátlóbeli elemek szorzatának különbsége, így det A = 5 = 0 4 = Határozzuk meg az A = ( 3 4 ) mátrix determinánsát!
8 8 KÉZI CSABA Kétszer kettes mátrix determinánsa a f átlóbeli és mellékátlóbeli elemek szorzatának különbsége, így det A = 3 4 ( ) = = Határozzuk meg az A = mátrix determinánsát Sarrus-szabállyal és kifejtési tétellel! Sarrus-szabály: Leírjuk a mátrix mellé az els két oszlopát: 3 0 0, 0 Ezután a f átlóban és vele párhuzamosan, t le jobbra lév két másik átlóban lév elemeket összeszorozzuk, e szorzatokat összeadjuk, majd a mellékátlóban és vele párhuzamosan, t le jobbra lév két másik átló elemeit összeszorozzuk, majd e szorzatot kivonjuk az el z összegb l, azaz det A = ( 0 + ( ) ) ( ( ) ) = 9. Kifejtési tétel: Eszerint egy n n-es mátrix determinánsának kiszámításához egy tetsz leges sor (vagy oszlop) minden elemét meg kell szoroznunk a hozzá tartozó el jeles aldeterminánssal, és összegeznünk kell a kapott számokat. Ha lehetséges, akkor érdemes olyan sort, vagy oszlopot választani, mely a lehet legtöbb 0-t tartalmazza. Jelen esetben válasszuk ki a mátrix második sorát. Ekkor = 0 ( ) ( ) ( )+3. Kiszámolva a -es determinánsokat det A = 0(0 3) + (0 3) ( + ) = 9. Lényeges, hogy a Sarrus-szabály CSAK 3 3-as mátrixra alkalmazható, míg a kifejtési tétel TETSZŽLEGES négyzetes mátrix determinánsának kiszámolására. 5. Határozzuk meg az A = 0 mátrix determinánsát! = ( ) = = 0.
9 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 9 6. Számoljuk ki az A = mátrix determinánsát! Az els sor szerinti kifejtést alkalmazzuk, majd a keletkez háromszor hármas determinánsokat például Sarrus szabállyal számolhatjuk ki: 3 det A = ( ) ( ) ( ) ( )( ) = ( 7) + ( ) ( ) ( 4) = Határozzuk meg az x valós számot úgy, hogy az ( ) x A = 4 mátrix invertálható legyen! Egy mátrix pontosan akkor invertálható, ha a determinánsa nem nulla. Így els lépésben kiszámoljuk a mátrix determinánsát: x 4 = ( 4) x = 8 x, ami pontosan akkor nem nulla, ha x Határozzuk meg az x valós szám értékét úgy, hogy az A = ) mátrix invertálható legyen! ( x 3 Egy mátrix pontosan akkor invertálható, ha a determinánsa nem nulla. ( ) x det A = = 3x + 3, ami pontosan akkor nem nulla, ha x Határozzuk meg az x valós számot úgy, hogy a A = x
10 0 KÉZI CSABA mátrix invertálható legyen! Egy mátrix pontosan akkor invertálható, ha a determinánsa nem nulla. Így els lépésben kiszámoljuk a mátrix determinánsát: x = 0 4x = 4x 9, 3 0 ami pontosan akkor nem nulla, ha x Határozzuk meg az (, 3) és a (, 5) vektorok által kifeszített paralelogramma területét! A keresett terület a vektorok által meghatározott determináns abszolútértéke. Mivel 3 5 = 5 ( 6) =, ezért a keresett terület.. Határozzuk meg az (,, ), (,, 0) és az (,, 3) vektorok által kifeszített paralelepipedon térfogatát! A keresett térfogat a vektorok által meghatározott determináns abszolútértéke. Mivel = = 6, 0 3 ezért a keresett terület 6. ( ) 3. Számoljuk ki az A = mátrix inverzét! 4 Az ( ) a b A = c d mátrix inverze A = det A ( d b c a ),
11 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ amennyiben a determináns nem zérus. Jelen esetben az A mátrix determinánsa det A = 4 3 ( ) =, ami nem nulla, így a mátrixnak létezik inverze. Az inverzmátrix A = ( ) Számoljuk ki az A = ( ) mátrix inverzét! Az A mátrix inverze A = det A ( d b c a ) = ( ). 4. Számoljuk ki az A = mátrix inverzét! Ellen rizzük megoldásunkat! A mátrix determinánsát kiszámolhatjuk például Sarrus-szabállyal det A = ( ( 5) ( ) 3 ) ( 0 ( 5) ( ) ) = 7, ami nem nulla, így a mátrixnak létezik inverze. Kiszámolva az algebrai adjungált aldeterminánsokat, az inverzmátrix T 0 0 A = = Ellen rzésképpen kiszámoljuk az A A szorzatot: A A = = = = Eredményül a 3 3-as egységmátrixot kaptuk, amivel ellen riztük az inverz helyességét. (Megjegyezzük, hogy az inverz helyességének ellen rzéséhez az AA szorzatot is ki kellene számolni, mivel a mátrixszorzás nem kommutatív, de ett l most eltekintünk.)
12 KÉZI CSABA 5. Számoljuk ki az A = Az A mátrix inverze A = mátrix inverzét! T = Adottak az A = 0 0, B = Határozzuk meg azt az X mátrixot, melyre A + X = B. Az X mátrixot kifejezve X = B A adóódik, így 0 X = = Adottak az A = ( 3 ) ( 0 3, B = ). Határozzuk meg azt az X mátrixot, melyre AX BX = A. Az egyenlet bal oldalán X-et jobbra kiemelve (A B)X = A adódik. Ebb l X kifejezhet, mert A B invertálható, nevezetesen X = (A B) A. Ehhez el bb kiszámoljuk az A B mátrixot, majd annak az inverzét. ( ) ( ) ( ) A B = =. Ezt felhasználva (A B) = ( 4 3 ). Ebb l az ismeretlen X mátrix X = (A B) A = ( 4 3 ) ( 3 ) = ( ).
13 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 3 8. Egy cég 3 alapanyagból 4 féle terméket állít el. Az alábbi táblázat mutatja, hogy az egyes termékek el állításához mennyi alapanyag szükséges, az egyes alapanyagok költségeit, a nyersanyagokból rendelkezésre álló mennyiségeket, valamint a kész termékek eladási árait. Az egyes termékekb l rendre 0, 0, 5, 0 darabot gyártunk. T T T3 T4 költség (Ft/db) Kapacitás A A A Egységár(Ft/db) Válaszoljunk mátrixm veletekkel az alábbi kérdésekre! a) Elegend -e a rendelkezésre álló kapacitás? b) Mennyi a megmaradt alapanyag? c) Mennyi a termékek el állítási költsége - darab el állítása esetén? d) Mekkora az összköltség? e) Mennyi a bevétel? f) Mennyi a haszon/prot? a) A megfelel eredményt egy mátrix és egy vektor szorzata adja = 45 65, így elegend a rendelkezésre álló alapanyag mennyiség. b) A megmaradt alapanyag = c) Az el állítási költség darab termék gyártása esetén: ( ) = ( ). 4 d) Az összköltség ( ) = = 3500.
14 4 KÉZI CSABA e) A bevétel ( ) = = f) A prot a bevétel és a költség különbsége: = Egy étteremben háromféle levesb l eladott adagok számát az alábbi táblázat mutatja. gulyásleves zöldségleves gyümölcsleves hétf kedd szerda csütörtök péntek Egys.ár(Ft/db) Válaszoljunk mátrixm veletekkel az alábbi kérdésekre! a) Mennyi a levesekb l származó napi bevétel? b) Mennyi a levesekb l származó összbevétel az öt nap alatt? c) Határozzuk meg az egyes levesfélékb l eladott adagok számát az öt nap alatt összesen! d) Az egyes napokon zöldséglevesb l hány adaggal többet adtak el, mint gyümölcslevesb l? a) A megfelel eredményt egy mátrix és egy vektor szorzata adja = b) A levesekb l származó összbevétel az 5 nap alatt 6500 ( ) = =
15 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 5 c) Az egyes levesekb l eladott adagok száma ( ) = ( ) d) Az egyes napokon zöldséglevesb l = adaggal adtak el többet, mint gyümölcslevesb l Egy étteremben négyféle ételb l eladott adagok számát az alábbi táblázat mutatja.. étel. étel 3. étel 4. étel hétf kedd szerda csütörtök péntek Egys.ár(Ft/db) Válaszoljunk mátrixm veletekkel az alábbi kérdésekre! a) Mennyi volt a bevétel naponta? b) Hány adag fogyott az egyes ételekb l naponta az öt nap alatt? c) A második ételb l mennyivel fogyott több, mint az els b l naponta? a) A megfelel eredményt egy mátrix és egy vektor szorzata adja =
16 6 KÉZI CSABA b) Az egyes ételekb l eladott adagok száma naponta ( ) = ( ) c) Az egyes napokon a második ételb l = adaggal fogyott több, mint az els b l. 3. Négy utazásra a hét els három napján eladott jegyek számát mutatja az alábbi táblázat. London Bécs Párizs Velence hétf kedd szerda Egys.ár(ezer Ft/db) Válaszoljunk mátrixm veletekkel az alábbi kérdésekre! a) Mennyi az utazási iroda bevétele naponta? b) Három nap alatt hány jegyet adtak el az egyes városokba? c) Mennyivel volt több a keddi bevétel, mint a hétf i? a) A megfelel eredményt egy mátrix és egy vektor szorzata adja = b) Az egyes városokba eladott jegyek száma ( ) = ( )
17 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 7 c) A hétf i bevétel ( ) = 67e forinttal volt több, mint a keddi. 3. Egy cég 3 raktárban 4 féle terméket tárol. Az alábbi táblázat mutatja a tárolt mennyiségeket, az egyes termékek egységárait, a raktározás költségét, valamint a raktár befogadó képességét. T T T3 T4 költség (Ft/db) Kapacitás R R R Egys.ár(Ft/db) Válaszoljunk mátrixm veletekkel az alábbi kérdésekre! a) Hány darabot tárolnak az egyes termékekb l? b) Mekkora az egyes raktárak szabad kapacitása? c) Mennyi az egyes termékek raktározási költsége? d) Mekkora értéket tárolnak az egyes raktárak? a) A megfelel eredményt egy mátrix és egy vektor szorzata adja = b) Az egyes raktárak szabad kapacitása = 6 c) Az egyes termékek raktározási költsége ( ) = ( )
18 8 KÉZI CSABA d) Az egyes raktárakban tárolt értékek = Négy feladóhelyr l három rendeltetési állomásra szállítunk árut. A szállítási költségeket az alábbi mátrix mutatja. R R R3 F F F F Mindegyik feladóhelyr l az els rendeltetési helyre 3, a másodikra 5, a harmadikra 4 egységnyi mennyiséget kell szállítani. Mennyi a szállítási költség feladóhelyenként? A szállítási költség feladóhelyenként = Három csoport matematika vizsgajegyeit tartalmazza az alábbi táblázat jeles (5) jó (4) közepes (3) elégséges () elégtelen () Cs Cs Cs Mátrixm veletek segítségével válaszoljunk az alábbi kérdésekre. a) Határozzuk meg a csoportonkénti létszámot! b) Határozzuk meg az összlétszámot! c) Határozzuk meg az osztályzatok megoszlását, azaz, hogy az egyes osztályzatokból összesen hány darab született! d) Számoljuk ki az egyes csoportok vizsgaátlagát!
19 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 9 a) A csoportonkénti létszám = b) Az összlétszám ( ) = = 57. c) Az osztályzatok megoszlása ( ) = ( ) d) Az egyes csoportok vizsgaátlaga ( ) ( ) ( ) = 85 = 3, 54; 4 = 40 =, 86; 4 = 67 = 3, Tegyük fel, hogy a gazdaságban három ágazat m ködik: mez gazdaság, ipar és szolgáltatás. (Nem valami realisztikus feltevés, de könnyen gondolhatunk rá úgy, hogy több szektor is van, csak azokkal mi nem foglalkozunk.) Ekkor felírható az alábbi táblázat: mez gazdaság ipar szolgáltatás mez gazdaság ipar szolgáltatás teljes ráfordítás/kibocsátás
20 0 KÉZI CSABA A táblázatot oszloponként kell olvasni, a következ módon: például a mez gazdaság összesen 85 (milliárd dollárt) költött inputokra, és ebb l 35-öt mez gazdasági termékre, 5-öt ipari termékre és 0-et szolgáltatási termékre. Nyilván 85 több, mint , de ez azért van, mert több más szektort is van, amiket itt most nem veszünk gyelembe. Írjuk fel a ráfordítási mátrixot! Ahhoz, hogy megkapjuk a ráfordítási mátrixot, az oszlopokban az elemeket le kell osztani a megfelel teljes kibocsátással, hogy egységnyire jutó adatokat kapjunk. Így az alábbi mátrixhoz jutunk 0, 4 0, 03 0, 03 0, 06 0, 38 0,. 0, 0, 6 0, Egy gazdaság ráfordítási mátrixa A = ( 0, 0, 5 0, 4 0, 3 a) Produktív-e (m köd képes-e) a gazdaság? ( ) 3 b) Mennyi legyen a teljes kibocsátás ahhoz, hogy a d = vektorral megadott nettó 4 termelést elérjük? c) Mely termékek el állítása nyereséges, ha árrendszerünk a v = (, 5) vektorral adható meg? a) Az E A mátrix inverzének az elemeit kell megvizsgálnunk, ahol E a megfelel (jelen esetben -es) egységmátrix. Az ( ) ( ) ( ) 0 0, 0, 5 0, 9 0, 5 E A = = 0 0, 4 0, 3 0, 4 0, 7 mátrix inverze (E A) = 0, 43 ( 0, 7 0, 5 0, 4 0, 9 ) = ). (, 63, 6 0, 93, 09 Mivel a Leontief inverz minden tagja nemnegatív, ezért a gazdaság m köd képes. ). b) A teljes kibocsátás (E A) d = (, 63, 6 0, 93, 09 ) ( 3 4 ) = ( 9, 53, 5 ), tehát 9,53 darabot kell az els,,5 darabot kell a második termékb l el állítani, ahhoz hogy a megadott nettó termelést elérjük.
21 c) Mivel FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ ( 0, 0, 5 va = ( 5) 0, 4 0, 3 ) = (, ;, 5), ezért az els termék el állítása, egységbe kerül, így az veszteséges (a veszteség 0, egység), a második termék el állítása, 5 egységbe kerül, így az nyereséges (a nyereség, 5 egység). 37. Igazoljuk, hogy ha A n nulla valamely n N természetes számra, akkor az E A mátrix invertálható. Mivel (E A)(E + A + A A n ) = (E + A + A A n ) (A + A + A A n ) = E A n = E, ezért az E A mátrix inverze E + A + A A n, tehát E A invertálható.
22 KÉZI CSABA II. Lineáris egyenletrendszerek megoldása (Gauss-elimináció, Cramer-szabály). Lineárisan függetlenek-e az alábbi vektorok: ( ) ( 0 a =, a = 0 )? Tekintsük az x a + x a = 0 lineáris kombinációt. Behelyettesítve az a, a értékeit ( ) ( ) ( ) 0 0 x + x =. 0 0 Elvégezve a skalárral való szorzást, majd az összeadást ( ) ( ) x 0 = x 0 adódik. Két vektor pontosan akkor egyenl, ha a megfelel helyen lév koordinátái egyenl ek, így x = 0, valamint x = 0, amib l x = 0, következésképpen a megadott vektorok lineárisan függetlenek. A lineáris függetlenséget eldönthetjük a vektorokból képzett mátrix determinánsának kiszámításával is. Ha a determináns értéke nem nulla, akkor a vektorok lineárisan függetlenek, egyébként lineárisan függ k. Jelen esetben így a vektorok lineárisan függetlenek. 0 0 = 0,. Lineárisan függetlenek-e az alábbi vektorok: ( ) ( a =, a = 4 )? Tekintsük az x a + x a = 0 lineáris kombinációt. Behelyettesítve az a, a értékeit ( ) ( ) ( ) 0 x + x = 4 0 adódik. Elvégezve a skalárral való szorzást, majd az összeadást ( ) ( ) x + x 0 =. x + 4x 0 Két vektor pontosan akkor egyenl, ha a megfelel helyen lév koordinátái egyenl ek, így x + x = 0, valamint x + 4x = 0. A két egyenlet ekvivalens egymással, így az egyik egyenlet elhagyható. Az x + x = 0 egyenletnek pedig végtelen sok megoldása van, nem csak a (0, 0) pár, következésképpen a megadott vektorok lineárisan függ k.
23 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 3 3. Lineárisan függetlenek-e az alábbi vektorok: a =, a = 0, a 3 =? 3 Tekintsük az x a + x a + x 3 a 3 = 0 lineáris kombinációt. Behelyettesítve az a, a, a 3 vektorokat x + x 0 + x 3 = adódik. Elvégzve a skalárral való szorzást és az összevonást x + x + x 3 x + x 3 = 0 0. x x + 3x 3 0 Két vektor pontosan akkor egyenl, ha a megfelel helyen lév koordinátái egyenl ek. Így az x +x +x 3 = 0, x +x 3 = 0, x x +3x 3 = 0 egyenletekb l álló egyenletrendszert kell megoldanunk. A második egyenletb l x = x 3 adódik, melyet behelyettesítve az els és a harmadik egyenletbe, az x + 3x 3 = 0 x x 3 = 0 egyenletrendszerhez jutunk. A két egyenletet összeadva x 3 = 0, amib l x 3 = 0. Ezt visszahelyettesítve x = 0, majd x = 0 adódik, így a megadott vektorok lineárisan függetlenek. 4. Lineárisan függetlenek-e az alábbi vektorok: a = 0, a =, a 3 =? 0 Tekintsük az x a + x a + x 3 a 3 = 0 lineáris kombinációt. Behelyettesítve az a, a, a 3 vektorokat x 0 + x + x 3 =
24 4 KÉZI CSABA adódik. Elvégzve a skalárral való szorzást és az összevonást x + x x 3 x x 3 = 0 0. x x 0 Két vektor pontosan akkor egyenl, ha a megfelel helyen lév koordinátái egyenl ek. Így az x + x x 3 = 0, x x 3 = 0, x x = 0 egyenletekb l álló egyenletrendszert kell megoldanunk. A második egyenletb l x = x 3 adódik, melyet behelyettesítve az els és a harmadik egyenletbe, az x + x 3 = 0 x x 3 = 0 egyenletrendszerhez jutunk. A két egyenlet ekvivalens, így az egyik elhagyható. Tehát az egyenletrendszernek végtelen sok megoládsa van, így nem csak a (0, 0, 0) számharmas megoldás, következésképpen a vektorok lineárisan függ k. 5. Tekintsük az x + y 4z = 4 x + 5y 9z = 0 3x y + 3z = egyenletrendszert! Írjuk fel az alapmátrixát, a kib vített mátrixát. Határozzuk meg az alapmátrix és a kib vített mátrix rangját. Ennek felhasználásával döntsük el, hogy megoldható-e a lineáris egyenletrendszer! Ha megoldható, osztályozzuk a megoldások száma szerint és adjuk meg a megoldást! A lineáris egyenletrendszer alapmátrixa kib vített mátrixa A = (A b) = , 4 0 Els lépésben els sor -szeresét hozzáadjuk a második sorhoz, illetve az els sor 3- szorosát hozzáadjuk a harmadik sorhoz. Második lépésben a második sor 8-szorosát hozzáadjuk a harmadik sorhoz: Gauss elimináció után kapott háromszög alakú mátrix rangja a nem csupa nulla sorok száma. Így az alapmátrix rangja 3, a kib vített mátrix rangja 3. Mivel az alapmátrix és a 4 7.
25 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 5 kib vített mátrix rangja megegyezik, ezért az egyenletrendszer megoldható. Az alapmátrix rangja megegyezik az ismeretlenek számával, így az egyenletrendszer határozott, azaz egy megoldása van. Az utolsó mátrixból felírva az egyenletrendszert x + y 4z = 4 y z = 7z = 7. adódik. Az utolsó egyenletet elosztva 7-el azt kapjuk, hogy z =. Ezt visszahelyettesítve a második egyenletbe y = adódik. Az els egyenletbe y-t és z-t behelyettesítve megkapjuk, hogy x =. 6. Tekintsük az x + y + 3z = x + 3y + 4z = 3x + 4y + 5z = 4 egyenletrendszert! Írjuk fel az alapmátrixát, a kib vített mátrixát. Határozzuk meg az alapmátrix és a kib vített mátrix rangját. Ennek felhasználásával döntsük el, hogy megoldható-e a lineáris egyenletrendszer! Ha megoldható, osztályozzuk a megoldások száma szerint és adjuk meg a megoldást! A lineáris egyenletrendszer alapmátrixa A = , kib vített mátrixa (A b) = Els lépésben az els sor -szeresét hozzáadjuk a második sorhoz, illetve az els sor 3-szorosát hozzáadjuk a harmadik sorhoz. Második lépésben a második sor -szeresét hozzáadjuk a harmadik sorhoz: Gauss elimináció után kapott háromszög alakú mátrix rangja a nem csupa nulla sorok száma. Így az alapmátrix rangja, a kib vített mátrix rangja 3. Mivel az alapmátrix és a kib vített mátrix rangja nem egyezik meg, ezért az egyenletrendszer nem megoldható, 0.
26 6 KÉZI CSABA azaz ellentmondásos. Ez a tény úgy is megállapítható, hogy az utolsó mátrixból felírjuk az egyenletrendszert x + y + 3z = y z = 0 0 =. Ekkor az utolsó egyenletb l ellentmondásra jutunk, így az egyenletrendszernek nincs megoldása. 7. Tekintsük az x + y + 3z = x + 3y + 4z = 3x + 4y + 5z = 3 egyenletrendszert! Írjuk fel az alapmátrixát, a kib vített mátrixát. Határozzuk meg az alapmátrix és a kib vített mátrix rangját. Ennek felhasználásával döntsük el, hogy megoldható-e a lineáris egyenletrendszer! Ha megoldható, osztályozzuk a megoldások száma szerint és adjuk meg a megoldást! A lineáris egyenletrendszer alapmátrixa kib vített mátrixa A = (A b) = Els lépésben az els sor -szeresét hozzáadjuk a második sorhoz, illetve az els sor 3-szorosát hozzáadjuk a harmadik sorhoz. Második lépésben a második sor -szeresét hozzáadjuk a harmadik sorhoz: , az alapmátrix rangja, a kib vített mátrix rangja. Mivel az alapmátrix és a kib vített mátrix rangja megegyezik, ezért az egyenletrendszer megoldható. Az alapmátrix rangja, míg az ismeretlenek száma 3, így az egyenletrendszer határozatlan, azaz végtelen sok megoldása van. Ezeket 3 = szabad paraméter bevezetésével kaphatjuk meg. A szabad paraméterek számát az ismeretlenek számának és az alapmátrix rangjának különbsége adja. Az utolsó mátrixból felírva az egyenletrendszert x + y + 3z = y z =
27 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 7 adódik. Legyen például z = t. Ekkor a második egyenletb l y = t. Az els egyenletbe ezeket visszahelyettesítve megkajuk az x-et: x = + t, ahol t R tetsz leges. 8. Tekintsük az x + y + 3z + 4u = x + 3y + 4z + 5u = 3x + 4y + 5z + 6u = 3 4x + 5y + 6z + 7u = 4 egyenletrendszert! Írjuk fel az alapmátrixát, a kib vített mátrixát. Határozzuk meg az alapmátrix és a kib vített mátrix rangját. Ennek felhasználásával döntsük el, hogy megoldható-e a lineáris egyenletrendszer! Ha megoldható, osztályozzuk a megoldások száma szerint és adjuk meg a megoldást! A lineáris egyenletrendszer alapmátrixa A = , kib vített mátrixa (A b) = Els lépésben az els sor -szeresét hozzáadjuk a második sorhoz, az els sor 3-szorosát hozzáadjuk a harmadik sorhoz, illetve az els sor 4-szeresét hozzáadjuk a negyedik sorhoz. Második lépésben a második sor -szeresét hozzáadjuk a harmadik sorhoz, 3-szorosát pedig a negyedikhez: az alapmátrix rangja, a kib vített mátrix rangja. Mivel az alapmátrix és a kib vített mátrix rangja megegyezik, ezért az egyenletrendszer megoldható. Az alapmátrix rangja, míg az ismeretlenek száma 4, így az egyenletrendszer határozatlan, azaz végtelen sok megoldása van. Ezeket 4 = szabad paraméter bevezetésével kaphatjuk meg. A szabad paraméterek számát az ismeretlenek számának és az alapmátrix rangjának különbsége adja. Az utolsó mátrixból felírva az egyenletrendszert x + y + 3z + 4u = y z 3u =
28 8 KÉZI CSABA adódik. Legyen például z = t, u = t. Ekkor a második egyenletb l y = z 3u = t 3t. Az els egyenletbe ezeket visszahelyettesítve megkajuk az x-et: x = y 3z 4u = + 4t + 6t 3t 4t = + t + t, t, t R 9. Tekintsük az x +x + x 3 + x 4 = 4 x x + 4x 3 x 4 = 4 3x +x x 3 + x 4 = 4. egyenletrendszert! Írjuk fel az alapmátrixát, a kib vített mátrixát. Határozzuk meg az alapmátrix és a kib vített mátrix rangját. Ennek felhasználásával döntsük el, hogy megoldható-e a lineáris egyenletrendszer! Ha megoldható, osztályozzuk a megoldások száma szerint és adjuk meg a megoldást! A lineáris egyenletrendszer alapmátrixa A = 4 3, kib vített mátrixa (A b) = Els lépésben els sor -szeresét hozzáadjuk a második sorhoz, illetve az els sor 3- szorosát hozzáadjuk a harmadik sorhoz. Második lépésben a második sor -szeresét hozzáadjuk a harmadik sorhoz: Gauss elimináció után kapott háromszög alakú mátrix rangja a nem csupa nulla sorok száma. Így az alapmátrix rangja 3, a kib vített mátrix rangja 3. Mivel az alapmátrix és a kib vített mátrix rangja megegyezik, ezért az egyenletrendszer megoldható. Az ismeretlenek száma 4, ami nem egyezik meg az alapmátrix rangjával, így az egyenletrendszer határozatlan, azaz végtelen sok megoldása van. Az utolsó mátrixból felírva az egyenletrendszert x + x + x 3 + x 4 = 4 5x + x 3 3x 4 = 4 6x 3 + x 4 =
29 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 9 adódik. Legyen x 3 = t, ahol t R. Az utolsó egyenletb l x 4 = 3t. Ezt visszahelyettesítve a második egyenletbe x = 7t adódik. Az els egyenletbe x -t, x 3 -at és x 4 -et behelyettesítve megkapjuk, hogy x =, t Oldjuk meg Cramer-szabállyal az egyenletrendszert! x y + 5z = x y + z = 3 3x + y + 6z = 5 Az egyenletrendszer alapmátrixának determinánsa 5 D = = 8 ( 37) = Az els ismeretlent úgy kapjuk meg, hogy az alapmátrix els oszlopát töröljük, majd annak helyére az egyenletrendszer jobboldalát írjuk. Ezután a kapott mátrix determinánsának és az alapmátrix determinánsának hányadosként áll el az x. Mivel D = = 45, ezért x = D D = =. A második ismeretlent úgy kapjuk meg, hogy az alapmátrix második oszlopát töröljük, majd annak helyére az egyenletrendszer jobboldalát írjuk. Ezután a kapott mátrix determinánsának és az alapmátrix determinánsának hányadosként kapjuk y-t. Mivel D = = 90, ezért y = D D = =. A harmadik ismeretlent úgy kapjuk meg, hogy az alapmátrix harmadik oszlopát töröljük, majd annak helyére az egyenletrendszer jobboldalát írjuk. Ezután a kapott mátrix determinánsának és az alapmátrix determinánsának hányadosként kapjuk z-t. Mivel D 3 = = 35, ezért z = D 3 D = = 3.
30 30 KÉZI CSABA. Tekintsük az egyenletrendszert! x + ay + z = 4 x 3y + 5z = 4 3x + 7y 3z = 7 a) Milyen a valós szám esetén alkalmazható a Cramer-szabály? b) Ha x =, akkor határozzuk meg az a értékét! a) A Cramer-szabály pontosan akkor alkalmazható, ha az alapmátrix determinánsa nem nulla. Jelen esetben az alapmátrix determinánsa a D = 3 5 = 9 + 5a + 8 ( a) = a + 0, ami pontosan akkor nem nulla, ha a 0. b) Mivel ezért azaz D = 4 a = a + 56 ( a) = 47a 6, x = D D = 47a 6 a + 0, = D D = 47a 6 a + 0. Beszorozva a nevez vel, majd rendezve az egyenletet amib l a =.. Tekintsük az egyenletrendszert! a + 0 = 47a 6 6 = 6a, x + ay + 3z = 5 x + 3y + bz = 6 3x 4y + z = a) Milyen a és b valós szám esetén alkalmazható a Cramer-szabály? b) Ha x = és y =, akkor határozzuk meg az a és b értékét!
31 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 3 a) A Cramer-szabály pontosan akkor alkalmazható, ha az alapmátrix determinánsa nem nulla. Jelen esetben az alapmátrix determinánsa a 3 D = 3 b = 6 + 3ab 4 (7 4b + 4a) = 3ab 4a + 4b 45, 3 4 ami pontosan akkor nem nulla, ha 3ab 4a + 4b b) Mivel D = 5 a b 4 = 30 + ab 7 (9 0b + a) = ab a + 0b 5, ezért azaz Továbbá D = b 3 x = D D = = ab a + 0b 5 3ab 4a + 4b 45, ab a + 0b 5 3ab 4a + 4b 45. = + 5b + 6 (54 + b + 0) = 4b 56, így azaz Tehát az y = D D = 4b 56 3ab 4a + 4b 45, = 4b 56 3ab 4a + 4b 45. ab a + 0b 5 3ab 4a + 4b 45 = 4b 56 3ab 4a + 4b 45 = egyenletrendszert kell megoldani. Beszorozva a közös nevez vel } ab a + 0b 5 = 3ab 4a + 4b 45 4b 56 = 3ab 4a + 4b 45 Elvégezve az összevonásokat az } ab + 8a 6b = 6 3ab 4a 0b =
32 3 KÉZI CSABA egyenletrendszerhez jutunk. Az els egyenlet másfélszeresét vonjuk ki a második egyenletb l. Ekkor az 6a + 4b = egyenlethez jutunk. Az egyenletet -vel osztva, majd a-t kifejezve a = + 7b. 8 Ezt visszahelyettesítve a ab+8a 6b = 6-vel ekvivalens ab+4a 8b = 3 egyenletbe: + 7b b b 8b = Beszorozva a közös nevez vel, majd elvégezve a zárójelfelbontást és az összevonást: Megoldva a másodfokú egyneletet + 7b b b 8b = ( + 7b)b + 4( + 7b) 64b = 4 b + 7b b 64b = 4 7b 35b + 8 = 0 b, = 5 ± 5 6 b 5b + 4 = 0. így b = 4, b =. Ezeket visszahelyettesítve az egyenletbe a = 9 8 és a = adódik. 3. Tekintsük az a = + 7b. 8 x y + 3z = x + y 5z = 3x y z = 0 = 5 ± 3, egyenletrendszert! Írjuk fel az alapmátrixát, a kib vített mátrixát, majd oldjuk meg Gausseliminációval! A lineáris egyenletrendszer alapmátrixa A = 3 5 3,
33 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 33 kib vített mátrixa (A b) = Els lépésben az els sor -szeresét hozzáadjuk a második sorhoz, illetve az els sor 3-szorosát hozzáadjuk a harmadik sorhoz. Második lépésben a második sor -szeresét hozzáadjuk a harmadik sorhoz: Ezen utóbbi mátrixból felírva az egyenletrendszert x y + 3z = y z = 6. Az alapmátrix rangja és a kib vített mátrix rangja is, így az egyenletrendszernek végtelen sok megoldása van. Legyen z = t, t R tetsz leges. Ekkor a második egyenletb l y = Ezt visszahelyettesítve az els egyenletbe 4. Tekintsük az x = + y 3z = t. 5 + t 5 x + y z = 3 3x + 3y + z = 4x + y + 5z = t = 0, 4 +, 4t. egyenletrendszert! Írjuk fel az alapmátrixát, a kib vített mátrixát, majd oldjuk meg Gausseliminációval! A lineáris egyenletrendszer alapmátrixa A = , kib vített mátrixa (A b) =
34 34 KÉZI CSABA Els lépésben a második sort szorozzuk -vel. Ezután az els sor 3-szorosát hozzáadjuk a második sorhoz, illetve az els sor -szeresét hozzáadjuk a harmadik sorhoz, ezt követ en cseréljük fel a második és harmadik sort: Az alapmátrix rangja 3, a kib vített mátrix rangja 3. A rang maximális, így az egyenletrendszer egyértelm en megoldható. Az utolsó mátrixból felírva az egyenletrendszert x + y z = 3 3y + 7z = 5 5z = 5. Az utolsó egyenletb l z = 3 adódik. Ezt visszahelyettesítve a második egyenletbe azt kapjuk, hogy y =. Az els egyenletbe y-t és z-t behelyettesítve x = adódik Tekintsük az 3x + y 4z = 4 3x + 3y + z = 8 4x + y + 5z = 5 egyenletrendszert! Cramer-szabállyal! Írjuk fel az alapmátrixát, a kib vített mátrixát, majd oldjuk meg Az egyenletrendszer alapmátrixának determinánsa 3 4 D = 3 3 = 37 ( 30) = Az els ismeretlent úgy kapjuk meg, hogy az alapmátrix els oszlopát töröljük, majd annak helyére az egyenletrendszer jobboldalát írjuk. Ezután a kapott mátrix determinánsának és az alapmátrix determinánsának hányadosa lesz az x. Mivel D = = 67, ezért x = D D = =. A második ismeretlent úgy kapjuk meg, hogy az alapmátrix második oszlopát töröljük, majd annak helyére az egyenletrendszer jobboldalát írjuk. Ezután a kapott mátrix determinánsának és az alapmátrix determinánsának hányadosa lesz az y. Mivel D = = 67, ezért y = D D = =.
35 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 35 A harmadik ismeretlent úgy kapjuk meg, hogy az alapmátrix harmadik oszlopát töröljük, majd annak helyére az egyenletrendszer jobboldalát írjuk. Ezután a kapott mátrix determinánsának és az alapmátrix determinánsának hányadosa lesz a z. Mivel D 3 = = 34, ezért z = D 3 D = =.
36 36 KÉZI CSABA III. Lineáris egyenletrendszerek alkalmazása, vektoralgebrai fogalmak és mérnöki alkalmazásaik.. Tekintsük az alábbi egyenáramú hálózatot! Legyen U b = 0 [V ], U b = 0 [V ], U b3 = 5 [V ], R = [Ω], R = 4 [Ω], R b = 7 [Ω], R b = 6 [Ω], R b3 = 4 [Ω]. a) Írjuk fel Kirchho els törvényét a B csomópontra! b) Írjuk fel Kirchho második törvényét az ABEF hurokra! c) Írjuk fel Kirchho második törvényét a BCDE hurokra! d) Írjuk fel a kapott egyenletrendszer alapmátrixát és kib vített mátrixát! e) Határozzuk meg az ismeretlen áramer sségeket Cramer-szabállyal! a) Kirchho els törvénye szerint egy csomópontba befolyó és onnan kifolyó áramok algebrai összege zérus, így I + I + I 3 = 0. b) Kirchho második törvénye szerint bármely hurokban körbehaladva és a feszültségeket el jelesen összegezve zérust kapunk, így I R + I 3 R b3 U b3 + I R b + U b = 0. c) Kirchho második törvényét felírva a BCDE hurokra: U b3 I 3 R b3 + I R + I R b U b = 0. d) Az adatok behelyettesítve a megoldandó egyenletrendszer I +I + I 3 = 0 8I + I 4I 3 = 5 4I 3 = 5
37 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 37 e) Az egyenletrendszer alapmátrixa , kib vített mátrixa f) Az egyenletrendszer alapmátrixának determinánsa D = = 64. Az els ismeretlent úgy kapjuk meg, hogy az alapmátrix els oszlopát töröljük, majd annak helyére az egyenletrendszer jobboldalát írjuk. Az els ismeretlen a kapott mátrix determinánsának és az alapmátrix determinánsának hányadosként. Mivel D = = 5, ezért I = D D = 5 64 [A]. A második ismeretlent úgy kapjuk meg, hogy az alapmátrix második oszlopát töröljük, majd annak helyére az egyenletrendszer jobboldalát írjuk. A második ismeretlen a kapott mátrix determinánsának és az alapmátrix determinánsának hányadosként. Mivel 0 D = = 60, ezért I = D D = [A]. A harmadik ismeretlent úgy kapjuk meg, hogy az alapmátrix harmadik oszlopát töröljük, majd annak helyére az egyenletrendszer jobboldalát írjuk. A harmadik ismeretlen a kapott mátrix determinánsának és az alapmátrix determinánsának hányadosként. Mivel 0 D 3 = = 75, ezért I 3 = D 3 D = [A].. Egy színház néz terét 8 db izzólámpa világítja meg. Egy részük 00 [W]-os, más részük 60 [W]-os, és t = 4 [h] alatt W = 5, [kwh] villamos energiát fogyasztanak. Határozzuk meg, hány 00 [W]-os, illetve 60 [W]-os izzólámpa van. A 00 [W]-os izzólámpák számát jelöljük x-el, a 60 [W]-os izzólámpák számát y-al. Ekkor a feltételek szerint x + y = 8.
38 38 KÉZI CSABA A másik egyenlet a villamosenergia-fogyasztás alapján írható föl. Az egy órára es összfogyasztás, vagyis a teljesítmény P = W t = 50 4 Ez az izzólámpák összteljesítményével egyenl = 680 [W]. 00x + 60y = 680, amit egyszer sítve 5x + 3y = 34. Tehát a megoldandó lineáris egyenletrendszer } x + y = 8 5x + 3y = 34 A lineáris egyenletrendszer alapmátrixának determinánsa D = 5 3 = 3 5 =, továbbá D = = = 68, ezért x = D D = 68 = 34. Másrészt D = = = 96, ezért y = D D = 96 = Írjuk fel a v = 0 7 a = vektort az 3 0 vektorok lineáris kombinációjaként!, a =, a 3 = 3 4 Keressük azokat az x, x, x 3 ismeretleneket, melyekre a x +a x +a 3 x 3 = v. Felhasználva a vektorok összeadására és skalárral való szorzására vonatkozó deníciókat az x + x + 3x 3 3x + x + 4x 3 = 0 7 x x 3
39 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 39 összefüggéshez jutunk. Két vektor pontosan akkor egyenl, ha a megfelel koordinátáik egyenl ek, így az el bbi egyenl ség ekvivalens az x + x + 3x 3 = 0 3x + x + 4x 3 = 7 x x 3 = egyenletrendszerrel, amit megoldhatunk például Gauss-eliminációval. A lineáris egyenletrendszer kib vített mátrixa Els lépésben az els sor 3-szorosát hozzáadjuk a második sorhoz. Második lépésben megcseréljük a második és a harmadik sort. Harmadik lépésben a második sor -szeresét hozzáadjuk a harmadik sorhoz Ezen utóbbi mátrixból felírva az egyenletrendszert x + x + 3x 3 = 0 x x 3 = 5 x 3 = 45. Az utolsó egyenletb l x 3 = 3 adódik, amit visszahelyettesítve a második egyenletbe x =. Az els egyenletb l x =. Így a keresett lineáris kombináció v = a + a + 3a 3. Visszahelyettesítéssel ellen rizhetjük megoldásunkat. 4. Írjuk fel a v = 7 vektort az 9 a =, a = 3, a 3 = 5 0 vektorok lineáris kombinációjaként! Keressük azokat az x, x, x 3 ismeretleneket, melyekre a x +a x +a 3 x 3 = v. Felhasználva a vektorok összeadására és skalárral való szorzására vonatkozó deníciókat az x + 3x + x 3 x + x + x 3 = 7 5x + x 3 9
40 40 KÉZI CSABA összefüggéshez jutunk. Két vektor pontosan akkor egyenl, ha a megfelel koordinátáik egyenl ek, így az el bbi egyenl ség ekvivalens az x + 3x + x 3 = 7 x + x + x 3 = 5x + x 3 = 9 egyenletrendszerrel, amit megoldhatunk például Gauss-eliminációval. A lineáris egyenletrendszer kib vített mátrixa Els lépésben cseréljük fel az els és második sort. Ezután az els sor -szeresét hozzáadjuk a második sorhoz, illetve az els sor 5-szörösét a harmadikhoz. Következ lépésben a második sor -szeresét hozzáadjuk a harmadik sorhoz Ezen utóbbi mátrixból felírva az egyenletrendszert x + x + x 3 = 5x + 3x 3 = 4 x 3 = 8. Az utolsó egyenletb l x 3 = adódik, amit visszahelyettesítve a második egyenletbe x =. Az els egyenletb l x =. Így a keresett lineáris kombináció v = a + a + a 3. Visszahelyettesítéssel ellen rizhetjük megoldásunkat. 5. Egy repül gép nyugodt légköri viszonyok mellett 800 [km/h] sebességgel keleti irányba repül. Egyszercsak 0 [km/h] sebesség, keleti szél támad, amelynek iránya a repülési iránnyal 60 szöget zár be. A repül a tájolót továbbra is keleti irányon tartja, de a szél miatt repülési iránya és sebessége megváltozik. Mi lesz az új irány és az új sebesség? Jelölje u a gép, v a szél sebességét! Ekkor u = 800, v = 0. Ekkor a repül gép talajhoz viszonyított sebessége az u + v ered vektorral lesz egyenl.
41 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 4 Ha az x-tengely keleti irányba mutat, az y északra, akkor u és v komponensei Így amib l Másrészt u = (800, 0), v = (0 cos 60, 0 sin 60 ) = (55, 55 3). u + v = ( , ) = (855, 55 3), u + v = (55 3) 860, 3. tgϕ = , amib l ϕ 6, 5. Tehát a repül gép talajhoz viszonyított sebessége körülbelül 860,3 [km/h], iránya pedig a keleti iránytól 6, 5 -al tér el északra. 6. Határozzuk meg az a = 3 és a = 4 vektorok skaláris szorzatát! 5 Két vektor skaláris szorzatát kiszámolhatjuk a megfelel koordináták szorzatösszegeként, így a keresett mennyiség 7. Határozzuk meg az a = a a = + 3 ( 4) + 5 = + 0 = 4. és a = 3 4 vektorok skaláris szorzatát! Két vektor skaláris szorzatát kiszámolhatjuk a megfelel koordináták szorzatösszegeként, így a keresett mennyiség a a = ( ) ( 4) = = 3.
42 4 KÉZI CSABA 8. Határozzuk meg az x valós számot úgy, hogy az a = mer legesek legyenek egymásra! 5 7 és a = x 3 vektorok Két vektor mer legességének szükséges és elégséges feltétele, hogy a két vektor skaláris szorzata 0 legyen. Az a és a vektorok skaláris szorzata a a = ( ) + 5 x = + 5x + = 5x 9. Így az 5x 9 = 0 egyenletet kell megoldanunk. Hozzáadva mindkét oldalhoz 9-et, majd mindkét oldalt 5-el elosztva 5x 9 = 0 5x = 9 x = Határozzuk meg a v = és v = vektorok által bezárt szöget! 4 Két vektor skaláris szorzatát kiszámolhatjuk a megfelel koordináták szorzatösszegeként. Másrészt a skaláris szorzatot a vektorok hosszának és a vektorok által bezárt szög koszinuszának szorzatként is kiszámolhatjuk. Ezek gyelembevételével cos ϕ = v v v v. Mivel továbbá ezért v v = + ( ) + 4 = 4, v = + ( ) + 4 =, v = + + = 6 cos ϕ = 4 = 4, 6 6 amib l ϕ 69,. 0. Határozzuk meg a v = és v = 4 4 vektorok által bezárt szöget! Két vektor skaláris szorzatát kiszámolhatjuk a megfelel koordináták szorzatösszegeként.
43 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 43 Másrészt a skaláris szorzatot a vektorok hosszának és a vektorok által bezárt szög koszinuszának szorzatként is kiszámolhatjuk. Ezek gyelembevételével cos ϕ = v v v v. Mivel v v = ( 4) 4 = 6 6 = 0, továbbá v = ( 4) = 5 = 5, v = = 36 = 6 ezért amib l ϕ 09, 47. cos ϕ = = 3,. Határozzuk meg az x valós számot úgy, hogy a v = vektorok által bezárt szög 60 legyen! Jelöljük a két vektor által bezárt szöget ϕ-vel. Ekkor cos ϕ = v v v v. 3 x és v = és Mivel v v = + 3x, v = 0 + x, v = = 5. Ezeket behelyettesítve az el bbi összefüggésbe = + 3x x. adódik. Megoldjuk a kapott egyenletet. Els lépésben az egyenlet mindkét oldalát négyzetre emeljük, majd elvégezzük a zárójel felbontását és az összevonást, nullára rendezzük az egyenletet, végül megoldjuk a kapott másodfokú egyenletet. = + 3x x ( x ) = x + 36x x = x + 36x 0 = x 88x Ebb l a megoldóképlet segítségével azt kapjuk, hogy x = , x =
44 44 KÉZI CSABA. Egy F (3, ) er hatására egy pontszer test az A(, 4) pontból a B(0, 5) pontba jut el. Mekkora a végzett munka? A végzett munka az er és az elmozdulás vekorok skaláris szorzata. Az elmozdulás vektora s = AB = B A = (, ), így a végzett munka W = F s = 3 ( ) + = 6 + = Egy F (,, 3) er hatására egy pontszer test az A(, 3, ) pontból a B(,, ) pontba jut el. Mekkora a végzett munka? A végzett munka az er és az elmozdulás vekorok skaláris szorzata. Az elmozdulás vektora s = AB = B A = (0,, 4), így a végzett munka W = F s = 0 + ( ) ( ) = Egy ifjú apa 0 [N] er vel húz egy szánkót, miközben a kötél 30 -os szöget zár be a vízszintessel. Mekkora munkát végez az apa, ha 50 métert húzza így a gyerekét? megoldás A végzett munka az er - és elmozdulsvektor skaláris szorzata, így W = F s cos ϕ = 0 50 cos 30 = , 9 [J]. 5. Mennyi munkát végzünk, ha a rakparton 0 méternyire elvonszolunk egy ládát oly módon, hogy a vízszintest l 30 -kal eltér irányban 00 [N] nagyságú er t fejtünk ki rá? A végzett munka W = F s cos ϕ = 00 0 cos 30 = [J] 3464, [J]. 6. Egy papírsárkány zsinórját [N] er vel tartjuk. A zsinór 45 szöget zár be a vízszintessel. Keressük meg az F vektor vízszintes és függ leges összetev it!
45 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 45 A vízszintes irányú összetev a függ leges itányú összeteve cos 45 = x x = = 6, sin 45 = y y = = 6. Az ábrának megfelel el jeleket is gyelembe véve F ( 6, 6 ). 7. Egy 80 [N] súlyú gyerek,5 [m] magasból csúszik le egy játszótéri csúszdán. Mekkora munkát végez a gravitációs er a gyereken? A gravitációs er, és a függ leges elmozdulás ugyanabba az irányba mutat, így a végzett munka W = 80, 5 cos 0 = 00 [J]. 8. Határozzuk meg a v = 0 és v = vektorok vektoriális szorzatát! 3 A vektoriális szorzat i j k v v = 0 3 = = 0 3 i 0 3 j + k = 6i + 3j 5k = ( 6, 3, 5). 9. Határozzuk meg a v = és v = 0 vektorok vektoriális szorzatát! A vektoriális szorzat i j k v v = 0 = = i 0 j + 0 k = i + j 4k = (,, 4). 0. Számoljuk ki az A(,, 0), B(,, ), C(,, ) pontok által meghatározott háromszög területét a vektoriális szorzat felhasználásával!
46 46 KÉZI CSABA Tekintsük az a = AB = B A = (,, ) és a b = AC = C A = (,, ) vektorokat! Ekkor a keresett terület az a és b vektorok vektoriális szorzatának a hosszának az abszolútértékének a fele. Mivel i j k a b = = i j + k = (6, 0, 6), ezért a b = = 7 = 6, így a keresett terület T = a b = 6 = 3.. Számoljuk ki az A(, 0, ), B(,, 3), C(3, 4, ) pontok által meghatározott háromszög területét a vektoriális szorzat felhasználásával! Tekintsük az a = AB = B A = (,, ) és a b = AC = C A = (, 4, 3) vektorokat! Ekkor a keresett terület az a és b vektorok vektoriális szorzatának a hosszának az abszolútértékének a fele. Mivel i j k a b = 4 3 = 4 3 i 3 j + 4 k = ( 7, 4, 0), ezért a b = ( 7) + ( 4) + ( 0) = = 65, így a keresett terület T = a b = 65.
47 FELADATGY JTEMÉNY MATEMATIKA I. GYAKORLATHOZ 47. Számoljuk ki az A(,, ), B(,, 3), C(0, 4, 5) pontok által meghatározott háromszög területét a vektoriális szorzat felhasználásával! Tekintsük az a = AB = B A = (3,, ) és a b = AC = C A = (, 6, 4) vektorokat! Ekkor a keresett terület az a és b vektorok vektoriális szorzatának a hosszának az abszolútértékének a fele. Mivel i j k a b = = 6 4 i 3 4 j k = (8, 0, 7), ezért a b = 8 + ( 0) + ( 7) = = 453, így a keresett terület T = a b = Határozzuk meg a v = szorzatát! A vegyes szorzat abc = , v = 4 3 és v 3 = = ( 6) =. 0 vektorok vegyes 4. Számoljuk ki az A(,, ), B(0,, 3), C(3, 4, 0), D(,, 0) pontok által kifeszített tetraéder térfogatát a vegyes szorzat felhasználásával! Tekintsük az a = AB = B A = (, 3, ), b = AC = C A = (, 6, ) és c = AD = D A = (0, 0, ) vektorokat! Ekkor a keresett térfogat az a, b és c vektorok vegyes szorzatának az abszolútértékének a hatoda. Mivel a vegyes szorzat 3 abc = 6 = + = 4, 0 0 ezért a keresett térfogat V = 4 6 = 4.
48 48 KÉZI CSABA 5. Számoljuk ki az A(, 0, ), B(,, ), C(3,, ), D(0,, 3) pontok által kifeszített tetraéder térfogatát a vegyes szorzat felhasználásával! Tekintsük az a = AB = B A = (,, ), b = AC = C A = (,, 0) és c = AD = D A = (,, ) vektorokat! Ekkor a keresett térfogat az a, b és c vektorok vegyes szorzatának az abszolútértékének a hatoda. Mivel a vegyes szorzat abc = 0 = 0 6 = 4, ezért a keresett térfogat V = 4 6 = A Toro f nyírógép kézikönyve azt írja el, hogy a gyertyát 0,4 [Nm] nyomatékkal kell meghúzni. Ha a gyertyakulcsra a gyertyától 5 [cm] távolságban fejtjük ki az er t, mekkora er szükséges az el írt nyomaték eléréséhez? A forgatónyomaték nagysága M = r F = r F sin ϕ, ahol M = 0, 4, r = 0, 5, ϕ = 90, így a keresett er F = M r sin ϕ = 0, 4 0, 5 sin π = 8, 6 [N]. 7. Egy sof r a sebességváltó kar P végpontjára F er vel hat. A pont és az er koordinátái adottak, P ( 5, 30, 40) [cm], F = ( 0, 30, 0) [N].
Lineáris algebra 2. Filip Ferdinánd december 7. siva.banki.hu/jegyzetek
 Lineáris algebra 2 Filip Ferdinánd filipferdinand@bgkuni-obudahu sivabankihu/jegyzetek 2015 december 7 Filip Ferdinánd 2016 februar 9 Lineáris algebra 2 1 / 37 Az el adás vázlata Determináns Determináns
Lineáris algebra 2 Filip Ferdinánd filipferdinand@bgkuni-obudahu sivabankihu/jegyzetek 2015 december 7 Filip Ferdinánd 2016 februar 9 Lineáris algebra 2 1 / 37 Az el adás vázlata Determináns Determináns
Lineáris leképezések. 2. Lineáris-e az f : R 2 R 2 f(x, y) = (x + y, x 2 )
 Lineáris leképezések 1 Lineáris-e az f : R 2 R 2 f(x, y = (3x + 2y, x y leképezés? A linearitáshoz ellen riznünk kell, hogy a leképzés additív és homogén Legyen x = (x 1, R 2, y = (y 1, y 2 R 2, c R Ekkor
Lineáris leképezések 1 Lineáris-e az f : R 2 R 2 f(x, y = (3x + 2y, x y leképezés? A linearitáshoz ellen riznünk kell, hogy a leképzés additív és homogén Legyen x = (x 1, R 2, y = (y 1, y 2 R 2, c R Ekkor
7. gyakorlat. Lineáris algebrai egyenletrendszerek megoldhatósága
 7. gyakorlat Lineáris algebrai egyenletrendszerek megoldhatósága Egy lineáris algebrai egyenletrendszerrel kapcsolatban a következ kérdések merülnek fel: 1. Létezik-e megoldása? 2. Ha igen, hány megoldása
7. gyakorlat Lineáris algebrai egyenletrendszerek megoldhatósága Egy lineáris algebrai egyenletrendszerrel kapcsolatban a következ kérdések merülnek fel: 1. Létezik-e megoldása? 2. Ha igen, hány megoldása
Lineáris egyenletrendszerek
 Lineáris egyenletrendszerek 1 Alapfogalmak 1 Deníció Egy m egyenletb l álló, n-ismeretlenes lineáris egyenletrendszer általános alakja: a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
Lineáris egyenletrendszerek 1 Alapfogalmak 1 Deníció Egy m egyenletb l álló, n-ismeretlenes lineáris egyenletrendszer általános alakja: a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
15. LINEÁRIS EGYENLETRENDSZEREK
 15 LINEÁRIS EGYENLETRENDSZEREK 151 Lineáris egyenletrendszer, Gauss elimináció 1 Definíció Lineáris egyenletrendszernek nevezzük az (1) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
15 LINEÁRIS EGYENLETRENDSZEREK 151 Lineáris egyenletrendszer, Gauss elimináció 1 Definíció Lineáris egyenletrendszernek nevezzük az (1) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 8 VIII VEkTOROk 1 VEkTOR Vektoron irányított szakaszt értünk Jelölése: stb Vektorok hossza A vektor abszolút értéke az irányított szakasz hossza Ha a vektor hossza egységnyi akkor
KOVÁCS BÉLA MATEmATIkA I 8 VIII VEkTOROk 1 VEkTOR Vektoron irányított szakaszt értünk Jelölése: stb Vektorok hossza A vektor abszolút értéke az irányított szakasz hossza Ha a vektor hossza egységnyi akkor
Vektorok. Wettl Ferenc október 20. Wettl Ferenc Vektorok október / 36
 Vektorok Wettl Ferenc 2014. október 20. Wettl Ferenc Vektorok 2014. október 20. 1 / 36 Tartalom 1 Vektorok a 2- és 3-dimenziós térben 2 Távolság, szög, orientáció 3 Vektorok koordinátás alakban 4 Összefoglalás
Vektorok Wettl Ferenc 2014. október 20. Wettl Ferenc Vektorok 2014. október 20. 1 / 36 Tartalom 1 Vektorok a 2- és 3-dimenziós térben 2 Távolság, szög, orientáció 3 Vektorok koordinátás alakban 4 Összefoglalás
7. gyakorlat. Lineáris algebrai egyenletrendszerek megoldhatósága
 7. gyakorlat Lineáris algebrai egyenletrendszerek megoldhatósága Egy lineáris algebrai egyenletrendszerrel kapcsolatban a következ kérdések merülnek fel: 1. Létezik-e megoldása? 2. Ha igen, hány megoldása
7. gyakorlat Lineáris algebrai egyenletrendszerek megoldhatósága Egy lineáris algebrai egyenletrendszerrel kapcsolatban a következ kérdések merülnek fel: 1. Létezik-e megoldása? 2. Ha igen, hány megoldása
Diszkrét matematika I., 12. előadás Dr. Takách Géza NyME FMK Informatikai Intézet takach november 30.
 1 Diszkrét matematika I, 12 előadás Dr Takách Géza NyME FMK Informatikai Intézet takach@infnymehu http://infnymehu/ takach 2005 november 30 Vektorok Definíció Egy tetszőleges n pozitív egész számra n-komponensű
1 Diszkrét matematika I, 12 előadás Dr Takách Géza NyME FMK Informatikai Intézet takach@infnymehu http://infnymehu/ takach 2005 november 30 Vektorok Definíció Egy tetszőleges n pozitív egész számra n-komponensű
Gauss-eliminációval, Cholesky felbontás, QR felbontás
 Közelítő és szimbolikus számítások 4. gyakorlat Mátrix invertálás Gauss-eliminációval, Cholesky felbontás, QR felbontás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei
Közelítő és szimbolikus számítások 4. gyakorlat Mátrix invertálás Gauss-eliminációval, Cholesky felbontás, QR felbontás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei
Feladatok megoldásokkal a harmadik gyakorlathoz (érintési paraméterek, L Hospital szabály, elaszticitás) y = 1 + 2(x 1). y = 2x 1.
 Feladatok megoldásokkal a harmadik gyakorlathoz (érintési paraméterek, L Hospital szabály, elaszticitás). Feladat. Írjuk fel az f() = függvény 0 = pontbeli érintőjének egyenletét! Az érintő egyenlete y
Feladatok megoldásokkal a harmadik gyakorlathoz (érintési paraméterek, L Hospital szabály, elaszticitás). Feladat. Írjuk fel az f() = függvény 0 = pontbeli érintőjének egyenletét! Az érintő egyenlete y
Vektorok, mátrixok, lineáris egyenletrendszerek
 a Matematika mérnököknek I. című tárgyhoz Vektorok, mátrixok, lineáris egyenletrendszerek Vektorok A rendezett valós számpárokat kétdimenziós valós vektoroknak nevezzük. Jelölésükre latin kisbetűket használunk.
a Matematika mérnököknek I. című tárgyhoz Vektorok, mátrixok, lineáris egyenletrendszerek Vektorok A rendezett valós számpárokat kétdimenziós valós vektoroknak nevezzük. Jelölésükre latin kisbetűket használunk.
9. Előadás. Megyesi László: Lineáris algebra, oldal. 9. előadás Mátrix inverze, mátrixegyenlet
 9. Előadás Megyesi László: Lineáris algebra, 75. 84. oldal. Gondolkodnivalók Mátrix rangja 1. Gondolkodnivaló Határozzuk meg a p valós paraméter értékétől függően a következő mátrix rangját: p 3 1 2 2
9. Előadás Megyesi László: Lineáris algebra, 75. 84. oldal. Gondolkodnivalók Mátrix rangja 1. Gondolkodnivaló Határozzuk meg a p valós paraméter értékétől függően a következő mátrix rangját: p 3 1 2 2
Lineáris egyenletrendszerek
 Lineáris egyenletrendszerek Lineáris egyenletrendszernek nevezzük az a 11 x 1 + a 12 x 2 +... +a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... +a 2n x n = b 2.. a k1 x 1 + a k2 x 2 +... +a kn x n = b k n ismeretlenes,
Lineáris egyenletrendszerek Lineáris egyenletrendszernek nevezzük az a 11 x 1 + a 12 x 2 +... +a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... +a 2n x n = b 2.. a k1 x 1 + a k2 x 2 +... +a kn x n = b k n ismeretlenes,
9. Előadás. Megyesi László: Lineáris algebra, oldal. 9. előadás Mátrix inverze, Leontyev-modell
 9. Előadás Megyesi László: Lineáris algebra, 75. 84. oldal. Gondolkodnivalók Mátrix rangja 1. Gondolkodnivaló Tegyük fel, hogy egy elemi bázistranszformáció kezdetekor a sor- és oszlopindexek sorban helyezkednek
9. Előadás Megyesi László: Lineáris algebra, 75. 84. oldal. Gondolkodnivalók Mátrix rangja 1. Gondolkodnivaló Tegyük fel, hogy egy elemi bázistranszformáció kezdetekor a sor- és oszlopindexek sorban helyezkednek
Bázistranszformáció és alkalmazásai 2.
 Bázistranszformáció és alkalmazásai 2. Lineáris algebra gyakorlat Összeállította: Bogya Norbert Tartalomjegyzék 1 Mátrix rangja 2 Mátrix inverze 3 Mátrixegyenlet Mátrix rangja Tartalom 1 Mátrix rangja
Bázistranszformáció és alkalmazásai 2. Lineáris algebra gyakorlat Összeállította: Bogya Norbert Tartalomjegyzék 1 Mátrix rangja 2 Mátrix inverze 3 Mátrixegyenlet Mátrix rangja Tartalom 1 Mátrix rangja
3. el adás: Determinánsok
 3. el adás: Determinánsok Wettl Ferenc 2015. február 27. Wettl Ferenc 3. el adás: Determinánsok 2015. február 27. 1 / 19 Tartalom 1 Motiváció 2 A determináns mint sorvektorainak függvénye 3 A determináns
3. el adás: Determinánsok Wettl Ferenc 2015. február 27. Wettl Ferenc 3. el adás: Determinánsok 2015. február 27. 1 / 19 Tartalom 1 Motiváció 2 A determináns mint sorvektorainak függvénye 3 A determináns
Lineáris algebra és a rang fogalma (el adásvázlat, szeptember 29.) Maróti Miklós
 Lineáris algebra és a rang fogalma (el adásvázlat, 2010. szeptember 29.) Maróti Miklós Ennek az el adásnak a megértéséhez a következ fogalmakat kell tudni: (1) A mátrixalgebrával kapcsolatban: számtest
Lineáris algebra és a rang fogalma (el adásvázlat, 2010. szeptember 29.) Maróti Miklós Ennek az el adásnak a megértéséhez a következ fogalmakat kell tudni: (1) A mátrixalgebrával kapcsolatban: számtest
Mátrixok február Feladat: Legyen A = ( ( B =
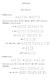 Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
A KroneckerCapelli-tételb l következik, hogy egy Bx = 0 homogén lineáris egyenletrendszernek
 10. gyakorlat Mátrixok sajátértékei és sajátvektorai Azt mondjuk, hogy az A M n mátrixnak a λ IR szám a sajátértéke, ha létezik olyan x IR n, x 0 vektor, amelyre Ax = λx. Ekkor az x vektort az A mátrix
10. gyakorlat Mátrixok sajátértékei és sajátvektorai Azt mondjuk, hogy az A M n mátrixnak a λ IR szám a sajátértéke, ha létezik olyan x IR n, x 0 vektor, amelyre Ax = λx. Ekkor az x vektort az A mátrix
Műveletek mátrixokkal. Kalkulus. 2018/2019 ősz
 2018/2019 ősz Elérhetőségek Előadó: (safaro@math.bme.hu) Fogadóóra: hétfő 9-10 (H épület 3. emelet 310-es ajtó) A pontos tárgykövetelmények a www.math.bme.hu/~safaro/kalkulus oldalon találhatóak. A mátrix
2018/2019 ősz Elérhetőségek Előadó: (safaro@math.bme.hu) Fogadóóra: hétfő 9-10 (H épület 3. emelet 310-es ajtó) A pontos tárgykövetelmények a www.math.bme.hu/~safaro/kalkulus oldalon találhatóak. A mátrix
1. Mátrixösszeadás és skalárral szorzás
 1 Mátrixösszeadás és skalárral szorzás Mátrixok tömör jelölése T test Az M = a i j T n m azt az n sorból és m oszlopból álló mátrixot jelöli, amelyben az i-edik sor j-edik eleme a i j T Példák [ ] Ha M
1 Mátrixösszeadás és skalárral szorzás Mátrixok tömör jelölése T test Az M = a i j T n m azt az n sorból és m oszlopból álló mátrixot jelöli, amelyben az i-edik sor j-edik eleme a i j T Példák [ ] Ha M
I. VEKTOROK, MÁTRIXOK
 217/18 1 félév I VEKTOROK, MÁTRIXOK I1 I2 Vektorok 1 A síkon derékszögű koordinátarendszerben minden v vektornak van vízszintes és van függőleges koordinátája, ezeket sorrendben v 1 és v 2 jelöli A v síkbeli
217/18 1 félév I VEKTOROK, MÁTRIXOK I1 I2 Vektorok 1 A síkon derékszögű koordinátarendszerben minden v vektornak van vízszintes és van függőleges koordinátája, ezeket sorrendben v 1 és v 2 jelöli A v síkbeli
Trigonometria Megoldások. 1) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( )
 Trigonometria Megoldások Trigonometria - megoldások ) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( ) akkor a háromszög egyenlő szárú vagy derékszögű!
Trigonometria Megoldások Trigonometria - megoldások ) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( ) akkor a háromszög egyenlő szárú vagy derékszögű!
1. Determinánsok. Oldjuk meg az alábbi kétismeretlenes, két egyenletet tartalmaz lineáris egyenletrendszert:
 1 Determinánsok 1 Bevezet definíció Oldjuk meg az alábbi kétismeretlenes, két egyenletet tartalmaz lineáris egyenletrendszert: a 11 x 1 +a 12 x 2 = b 1 a 21 x 1 +a 22 x 2 = b 2 Szorozzuk meg az első egyenletet
1 Determinánsok 1 Bevezet definíció Oldjuk meg az alábbi kétismeretlenes, két egyenletet tartalmaz lineáris egyenletrendszert: a 11 x 1 +a 12 x 2 = b 1 a 21 x 1 +a 22 x 2 = b 2 Szorozzuk meg az első egyenletet
DETERMINÁNSSZÁMÍTÁS. Határozzuk meg a 1 értékét! Ez most is az egyetlen elemmel egyezik meg, tehát az értéke 1.
 DETERMINÁNSSZÁMÍTÁS A (nxn) kvadratikus (négyzetes) mátrixhoz egyértelműen hozzárendelhetünk egy D R számot, ami a mátrix determinánsa. Már most megjegyezzük, hogy a mátrix determinánsa, illetve a determináns
DETERMINÁNSSZÁMÍTÁS A (nxn) kvadratikus (négyzetes) mátrixhoz egyértelműen hozzárendelhetünk egy D R számot, ami a mátrix determinánsa. Már most megjegyezzük, hogy a mátrix determinánsa, illetve a determináns
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 11 XI LINEÁRIS EGYENLETRENDSZEREk 1 LINEÁRIS EGYENLETRENDSZER A lineáris egyenletrendszer általános alakja: (1) Ugyanez mátrix alakban: (2), ahol x az ismeretleneket tartalmazó
KOVÁCS BÉLA, MATEmATIkA I 11 XI LINEÁRIS EGYENLETRENDSZEREk 1 LINEÁRIS EGYENLETRENDSZER A lineáris egyenletrendszer általános alakja: (1) Ugyanez mátrix alakban: (2), ahol x az ismeretleneket tartalmazó
11. DETERMINÁNSOK. 11.1 Mátrix fogalma, műveletek mátrixokkal
 11 DETERMINÁNSOK 111 Mátrix fogalma, műveletek mátrixokkal Bevezetés A közgazdaságtanban gyakoriak az olyan rendszerek melyek jellemzéséhez több adat szükséges Például egy k vállalatból álló csoport minden
11 DETERMINÁNSOK 111 Mátrix fogalma, műveletek mátrixokkal Bevezetés A közgazdaságtanban gyakoriak az olyan rendszerek melyek jellemzéséhez több adat szükséges Például egy k vállalatból álló csoport minden
Valasek Gábor valasek@inf.elte.hu
 Számítógépes Grafika Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2013/2014. őszi félév ( Eötvös LorándSzámítógépes TudományegyetemInformatikai Grafika Kar) 2013/2014.
Számítógépes Grafika Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2013/2014. őszi félév ( Eötvös LorándSzámítógépes TudományegyetemInformatikai Grafika Kar) 2013/2014.
2. gyakorlat. A polárkoordináta-rendszer
 . gyakorlat A polárkoordináta-rendszer Az 1. gyakorlaton megismerkedtünk a descartesi koordináta-rendszerrel. Síkvektorokat gyakran kényelmes ún. polárkoordinátákkal megadni: az r hosszúsággal és a φ irányszöggel
. gyakorlat A polárkoordináta-rendszer Az 1. gyakorlaton megismerkedtünk a descartesi koordináta-rendszerrel. Síkvektorokat gyakran kényelmes ún. polárkoordinátákkal megadni: az r hosszúsággal és a φ irányszöggel
Mátrixok 2017 Mátrixok
 2017 számtáblázatok" : számok rendezett halmaza, melyben a számok helye két paraméterrel van meghatározva. Például lineáris egyenletrendszer együtthatómátrixa 2 x 1 + 4 x 2 = 8 1 x 1 + 3 x 2 = 1 ( 2 4
2017 számtáblázatok" : számok rendezett halmaza, melyben a számok helye két paraméterrel van meghatározva. Például lineáris egyenletrendszer együtthatómátrixa 2 x 1 + 4 x 2 = 8 1 x 1 + 3 x 2 = 1 ( 2 4
12. előadás. Egyenletrendszerek, mátrixok. Dr. Szörényi Miklós, Dr. Kallós Gábor
 12. előadás Egyenletrendszerek, mátrixok Dr. Szörényi Miklós, Dr. Kallós Gábor 2015 2016 1 Tartalom Matematikai alapok Vektorok és mátrixok megadása Tömbkonstansok Lineáris műveletek Mátrixok szorzása
12. előadás Egyenletrendszerek, mátrixok Dr. Szörényi Miklós, Dr. Kallós Gábor 2015 2016 1 Tartalom Matematikai alapok Vektorok és mátrixok megadása Tömbkonstansok Lineáris műveletek Mátrixok szorzása
Matematika szigorlat június 17. Neptun kód:
 Név Matematika szigorlat 014. június 17. Neptun kód: 1.. 3. 4. 5. Elm. Fel. Össz. Oszt. Az eredményes szigorlat feltétele elméletből legalább 0 pont, feladatokból pedig legalább 30 pont elérése. A szigorlat
Név Matematika szigorlat 014. június 17. Neptun kód: 1.. 3. 4. 5. Elm. Fel. Össz. Oszt. Az eredményes szigorlat feltétele elméletből legalább 0 pont, feladatokból pedig legalább 30 pont elérése. A szigorlat
LINEÁRIS EGYENLETRENDSZEREK október 12. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak
 LINEÁRIS EGYENLETRENDSZEREK 004. október. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László:
LINEÁRIS EGYENLETRENDSZEREK 004. október. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László:
Gyakorló feladatok I.
 Gyakorló feladatok I. a Matematika Aa Vektorüggvények tárgyhoz (D D5 kurzusok) Összeállította: Szili László Ajánlott irodalmak:. G.B. Thomas, M.D. Weir, J. Hass, F.R. Giordano: Thomas-féle KALKULUS I.,
Gyakorló feladatok I. a Matematika Aa Vektorüggvények tárgyhoz (D D5 kurzusok) Összeállította: Szili László Ajánlott irodalmak:. G.B. Thomas, M.D. Weir, J. Hass, F.R. Giordano: Thomas-féle KALKULUS I.,
Komplex számok trigonometrikus alakja
 Komplex számok trigonometrikus alakja 015. február 15. 1. Alapfeladatok 1. Feladat: Határozzuk meg az alábbi algebrai alakban adott komplex számok trigonometrikus alakját! z 1 = 4 + 4i, z = 4 + i, z =
Komplex számok trigonometrikus alakja 015. február 15. 1. Alapfeladatok 1. Feladat: Határozzuk meg az alábbi algebrai alakban adott komplex számok trigonometrikus alakját! z 1 = 4 + 4i, z = 4 + i, z =
3. Egyenletek, egyenletrendszerek, egyenlőtlenségek
 . Egyenletek, egyenletrendszerek, egyenlőtlenségek I. Nulladik ZH-ban láttuk: 1. Mennyi a 2x 2 8x 5 = 0 egyenlet gyökeinek a szorzata? (A) 10 (B) 2 (C) 2,5 (D) 4 (E) ezek egyike sem Megoldás I.: BME 2011.
. Egyenletek, egyenletrendszerek, egyenlőtlenségek I. Nulladik ZH-ban láttuk: 1. Mennyi a 2x 2 8x 5 = 0 egyenlet gyökeinek a szorzata? (A) 10 (B) 2 (C) 2,5 (D) 4 (E) ezek egyike sem Megoldás I.: BME 2011.
1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás)
 Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
25 i, = i, z 1. (x y) + 2i xy 6.1
 6 Komplex számok megoldások Lásd ábra z = + i, z = + i, z = i, z = i z = 7i, z = + 5i, z = 5i, z = i, z 5 = 9, z 6 = 0 Teljes indukcióval 5 Teljes indukcióval 6 Az el z feladatból következik z = z = =
6 Komplex számok megoldások Lásd ábra z = + i, z = + i, z = i, z = i z = 7i, z = + 5i, z = 5i, z = i, z 5 = 9, z 6 = 0 Teljes indukcióval 5 Teljes indukcióval 6 Az el z feladatból következik z = z = =
9. Trigonometria. I. Nulladik ZH-ban láttuk: 1. Tegye nagyság szerint növekvő sorrendbe az alábbi értékeket! Megoldás:
 9. Trigonometria I. Nulladik ZH-ban láttuk: 1. Tegye nagyság szerint növekvő sorrendbe az alábbi értékeket! x = cos 150 ; y = sin 5 ; z = tg ( 60 ) (A) z < x < y (B) x < y < z (C) y < x < z (D) z < y
9. Trigonometria I. Nulladik ZH-ban láttuk: 1. Tegye nagyság szerint növekvő sorrendbe az alábbi értékeket! x = cos 150 ; y = sin 5 ; z = tg ( 60 ) (A) z < x < y (B) x < y < z (C) y < x < z (D) z < y
Mátrixok. 2015. február 23. 1. Feladat: Legyen ( 3 0 1 4 1 1 ( 1 0 3 2 1 0 B = A =
 Mátrixok 25. február 23.. Feladat: Legyen A ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A deníciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Mátrixok 25. február 23.. Feladat: Legyen A ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A deníciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Trigonometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
Lin.Alg.Zh.1 feladatok
 Lin.Alg.Zh. feladatok 0.. d vektorok Adott három vektor ā (0 b ( c (0 az R Euklideszi vektortérben egy ortonormált bázisban.. Mennyi az ā b skalárszorzat? ā b 0 + + 8. Mennyi az n ā b vektoriális szorzat?
Lin.Alg.Zh. feladatok 0.. d vektorok Adott három vektor ā (0 b ( c (0 az R Euklideszi vektortérben egy ortonormált bázisban.. Mennyi az ā b skalárszorzat? ā b 0 + + 8. Mennyi az n ā b vektoriális szorzat?
Matematika (mesterképzés)
 Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Jelenlegi életkor Életkor 11 év múlva Anya x x + 11 Gyermek x 29 x 29 + 11 = x 18
 Szöveges feladatok Életkori feladatok. Feladat. Egy anya 29 éves volt, amikor a a született. év múlva az életkora évvel lesz kevesebb, mint a a akkori életkorának kétszerese. Hány évesek most? Megoldás.
Szöveges feladatok Életkori feladatok. Feladat. Egy anya 29 éves volt, amikor a a született. év múlva az életkora évvel lesz kevesebb, mint a a akkori életkorának kétszerese. Hány évesek most? Megoldás.
Vektorterek. Wettl Ferenc február 17. Wettl Ferenc Vektorterek február / 27
 Vektorterek Wettl Ferenc 2015. február 17. Wettl Ferenc Vektorterek 2015. február 17. 1 / 27 Tartalom 1 Egyenletrendszerek 2 Algebrai struktúrák 3 Vektortér 4 Bázis, dimenzió 5 Valós mátrixok és egyenletrendszerek
Vektorterek Wettl Ferenc 2015. február 17. Wettl Ferenc Vektorterek 2015. február 17. 1 / 27 Tartalom 1 Egyenletrendszerek 2 Algebrai struktúrák 3 Vektortér 4 Bázis, dimenzió 5 Valós mátrixok és egyenletrendszerek
Matematika A1a Analízis
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
Lineáris algebra gyakorlat
 Lineáris algebra gyakorlat 0. gyakorlat Gyakorlatvezet : Bogya Norbert 202. április 23. Sajátérték, sajátvektor, sajátaltér Tartalom Sajátérték, sajátvektor, sajátaltér 2 Gyakorló feladatok a zh-ra (rutinfeladatok)
Lineáris algebra gyakorlat 0. gyakorlat Gyakorlatvezet : Bogya Norbert 202. április 23. Sajátérték, sajátvektor, sajátaltér Tartalom Sajátérték, sajátvektor, sajátaltér 2 Gyakorló feladatok a zh-ra (rutinfeladatok)
Matematikai statisztika 1.
 Matematikai statisztika 1 segédanyag Daróczi Gergely Szociológia Intézet 2010 Matematikai statisztika 1 01 Mátrixok A mátrix vízszintes vonalban elhelyezked elemei sorokat, függ leges vonalban elhelyezked
Matematikai statisztika 1 segédanyag Daróczi Gergely Szociológia Intézet 2010 Matematikai statisztika 1 01 Mátrixok A mátrix vízszintes vonalban elhelyezked elemei sorokat, függ leges vonalban elhelyezked
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások
 Megoldások 1. Határozd meg a szakasz hosszát, ha a végpontok koordinátái: A ( 1; ) és B (5; )! A szakasz hosszához számítsuk ki a két pont távolságát: d AB = AB = (5 ( 1)) + ( ) = 6 + 1 = 7 6,08.. Határozd
Megoldások 1. Határozd meg a szakasz hosszát, ha a végpontok koordinátái: A ( 1; ) és B (5; )! A szakasz hosszához számítsuk ki a két pont távolságát: d AB = AB = (5 ( 1)) + ( ) = 6 + 1 = 7 6,08.. Határozd
1. A kétszer kettes determináns
 1. A kétszer kettes determináns 2 2-es mátrix inverze Tétel [ ] [ ] a c 1 d c Ha ad bc 0, akkor M= inverze. b d ad bc b a Ha ad bc = 0, akkor M-nek nincs inverze. A főátló két elemét megcseréljük, a mellékátló
1. A kétszer kettes determináns 2 2-es mátrix inverze Tétel [ ] [ ] a c 1 d c Ha ad bc 0, akkor M= inverze. b d ad bc b a Ha ad bc = 0, akkor M-nek nincs inverze. A főátló két elemét megcseréljük, a mellékátló
MBNK12: Permutációk (el adásvázlat, április 11.) Maróti Miklós
 MBNK12: Permutációk el adásvázlat 2016 április 11 Maróti Miklós 1 Deníció Az A halmaz permutációin a π : A A bijektív leképezéseket értjünk Tetsz leges n pozitív egészre az {1 n} halmaz összes permutációinak
MBNK12: Permutációk el adásvázlat 2016 április 11 Maróti Miklós 1 Deníció Az A halmaz permutációin a π : A A bijektív leképezéseket értjünk Tetsz leges n pozitív egészre az {1 n} halmaz összes permutációinak
Fejezetek a lineáris algebrából PTE-PMMK, Műszaki Informatika Bsc. Dr. Kersner Róbert
 Fejezetek a lineáris algebrából PTE-PMMK, Műszaki Informatika Bsc Dr. Kersner Róbert 007 Tartalomjegyzék Előszó ii. Determináns. Mátrixok 6 3. Az inverz mátrix 9 4. Lineáris egyenletrendszerek 5. Lineáris
Fejezetek a lineáris algebrából PTE-PMMK, Műszaki Informatika Bsc Dr. Kersner Róbert 007 Tartalomjegyzék Előszó ii. Determináns. Mátrixok 6 3. Az inverz mátrix 9 4. Lineáris egyenletrendszerek 5. Lineáris
A 2014/2015. tanévi Országos Középiskolai Tanulmányi Verseny második forduló MATEMATIKA I. KATEGÓRIA ( SZAKKÖZÉPISKOLA ) Javítási-értékelési útmutató
 OktatásiHivatal A 014/01. tanévi Országos Középiskolai Tanulmányi Verseny második forduló MATEMATIKA I. KATEGÓRIA ( SZAKKÖZÉPISKOLA ) Javítási-értékelési útmutató 1. feladat: Adja meg az összes olyan (x,
OktatásiHivatal A 014/01. tanévi Országos Középiskolai Tanulmányi Verseny második forduló MATEMATIKA I. KATEGÓRIA ( SZAKKÖZÉPISKOLA ) Javítási-értékelési útmutató 1. feladat: Adja meg az összes olyan (x,
Determinánsok. A determináns fogalma olyan algebrai segédeszköz, amellyel. szolgáltat az előbbi kérdésekre, bár ez nem mindig hatékony.
 Determinánsok A determináns fogalma olyan algebrai segédeszköz, amellyel jól jellemezhető a mátrixok invertálhatósága, a mátrix rangja. Segítségével lineáris egyenletrendszerek megoldhatósága dönthető
Determinánsok A determináns fogalma olyan algebrai segédeszköz, amellyel jól jellemezhető a mátrixok invertálhatósága, a mátrix rangja. Segítségével lineáris egyenletrendszerek megoldhatósága dönthető
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Paraméter
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Paraméter A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Paraméter A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Matematika III. harmadik előadás
 Matematika III. harmadik előadás Kézi Csaba Debreceni Egyetem, Műszaki Kar Debrecen, 2013/14 tanév, I. félév Kézi Csaba (DE) Matematika III. harmadik előadás 2013/14 tanév, I. félév 1 / 13 tétel Az y (x)
Matematika III. harmadik előadás Kézi Csaba Debreceni Egyetem, Műszaki Kar Debrecen, 2013/14 tanév, I. félév Kézi Csaba (DE) Matematika III. harmadik előadás 2013/14 tanév, I. félév 1 / 13 tétel Az y (x)
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT. Koordináta-geometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT 1) Adott két pont: A 4; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. Koordináta-geometria és B 3 1; Írja fel az AB szakasz 1 3 4
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT 1) Adott két pont: A 4; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. Koordináta-geometria és B 3 1; Írja fel az AB szakasz 1 3 4
1. zárthelyi,
 1. zárthelyi, 2009.10.20. 1. Írjuk fel a tér P = (0,2,4) és Q = (6, 2,2) pontjait összekötő szakasz felezőmerőleges síkjának egyenletét. 2. Tekintsük az x + 2y + 3z = 14, a 2x + 6y + 10z = 24 és a 4x+2y
1. zárthelyi, 2009.10.20. 1. Írjuk fel a tér P = (0,2,4) és Q = (6, 2,2) pontjait összekötő szakasz felezőmerőleges síkjának egyenletét. 2. Tekintsük az x + 2y + 3z = 14, a 2x + 6y + 10z = 24 és a 4x+2y
Intergrált Intenzív Matematika Érettségi
 . Adott a mátri, determináns determináns, ahol,, d Számítsd ki:. b) Igazold, hogy a b c. Adott a az 6 0 egyenlet megoldásai. a). c) Számítsd ki a d determináns értékét. d c a b determináns, ahol abc,,.
. Adott a mátri, determináns determináns, ahol,, d Számítsd ki:. b) Igazold, hogy a b c. Adott a az 6 0 egyenlet megoldásai. a). c) Számítsd ki a d determináns értékét. d c a b determináns, ahol abc,,.
O ( 0, 0, 0 ) A ( 4, 0, 0 ) B ( 4, 3, 0 ) C ( 0, 3, 0 ) D ( 4, 0, 5 ) E ( 4, 3, 5 ) F ( 0, 3, 5 ) G ( 0, 0, 5 )
 1. feladat Írjuk föl a következő vektorokat! AC, BF, BG, DF, BD, AG, GB Írjuk föl ezen vektorok egységvektorát is! a=3 m b= 4 m c= m Írjuk föl az egyes pontok koordinátáit: O ( 0, 0, 0 ) A ( 4, 0, 0 )
1. feladat Írjuk föl a következő vektorokat! AC, BF, BG, DF, BD, AG, GB Írjuk föl ezen vektorok egységvektorát is! a=3 m b= 4 m c= m Írjuk föl az egyes pontok koordinátáit: O ( 0, 0, 0 ) A ( 4, 0, 0 )
Másodfokú egyenletek, egyenlőtlenségek
 Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x 1x 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x 1x 16 =. 1. lépés:
Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x 1x 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x 1x 16 =. 1. lépés:
LINEÁRIS ALGEBRA (A, B, C) tematika (BSc) I. éves nappali programtervező informatikus hallgatóknak évi tanév I. félév
 LINEÁRIS ALGEBRA (A, B, C) tematika (BSc) I éves nappali programtervező informatikus hallgatóknak 2010-2011 évi tanév I félév Vektoriális szorzat és tulajdonságai bizonyítás nélkül: Vegyes szorzat és tulajdonságai
LINEÁRIS ALGEBRA (A, B, C) tematika (BSc) I éves nappali programtervező informatikus hallgatóknak 2010-2011 évi tanév I félév Vektoriális szorzat és tulajdonságai bizonyítás nélkül: Vegyes szorzat és tulajdonságai
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
Permutációk véges halmazon (el adásvázlat, február 12.)
 Permutációk véges halmazon el adásvázlat 2008 február 12 Maróti Miklós Ennek az el adásnak a megértéséhez a következ fogalmakat kell tudni: ismétlés nélküli variáció leképezés indulási és érkezési halmaz
Permutációk véges halmazon el adásvázlat 2008 február 12 Maróti Miklós Ennek az el adásnak a megértéséhez a következ fogalmakat kell tudni: ismétlés nélküli variáció leképezés indulási és érkezési halmaz
: s s t 2 s t. m m m. e f e f. a a ab a b c. a c b ac. 5. Végezzük el a kijelölt m veleteket a változók lehetséges értékei mellett!
 nomosztással a megoldást visszavezethetjük egy alacsonyabb fokú egyenlet megoldására Mivel a 4 6 8 6 egyenletben az együtthatók összege 6 8 6 ezért az egyenletnek gyöke az (mert esetén a kifejezés helyettesítési
nomosztással a megoldást visszavezethetjük egy alacsonyabb fokú egyenlet megoldására Mivel a 4 6 8 6 egyenletben az együtthatók összege 6 8 6 ezért az egyenletnek gyöke az (mert esetén a kifejezés helyettesítési
rank(a) == rank([a b])
![rank(a) == rank([a b]) rank(a) == rank([a b])](/thumbs/92/110554624.jpg) Lineáris algebrai egyenletrendszerek megoldása a Matlabban Lineáris algebrai egyenletrendszerek a Matlabban igen egyszer en oldhatók meg. Legyen A az egyenletrendszer m-szer n-es együtthatómátrixa, és
Lineáris algebrai egyenletrendszerek megoldása a Matlabban Lineáris algebrai egyenletrendszerek a Matlabban igen egyszer en oldhatók meg. Legyen A az egyenletrendszer m-szer n-es együtthatómátrixa, és
Rang, sajátérték. Dr. Takách Géza NyME FMK Informatikai Intézet takach/ február 15
 Diszkrét matematika II, 2 el adás Rang, sajátérték Dr Takách Géza NyME FMK Informatikai Intézet takachinfnymehu http://infnymehu/ takach/ 25 február 5 Gyakorlati célok Ezen el adáson, és a hozzá kapcsolódó
Diszkrét matematika II, 2 el adás Rang, sajátérték Dr Takách Géza NyME FMK Informatikai Intézet takachinfnymehu http://infnymehu/ takach/ 25 február 5 Gyakorlati célok Ezen el adáson, és a hozzá kapcsolódó
Vektorok és koordinátageometria
 Vektorok és koordinátageometria Vektorral kapcsolatos alapfogalmak http://zanza.tv/matematika/geometria/vektorok-bevezetese Definíció: Ha egy szakasz két végpontját megkülönböztetjük egymástól oly módon,
Vektorok és koordinátageometria Vektorral kapcsolatos alapfogalmak http://zanza.tv/matematika/geometria/vektorok-bevezetese Definíció: Ha egy szakasz két végpontját megkülönböztetjük egymástól oly módon,
Lineáris algebra Gyakorló feladatok
 Lineáris algebra Gyakorló feladatok. október.. Feladat: Határozzuk meg a, 4b, c és a b c vektorokat, ha a = (; ; ; ; b = (; ; ; ; c = ( ; ; ; ;.. Feladat: Határozzuk meg a, 4b, a, c és a b; c + b kifejezések
Lineáris algebra Gyakorló feladatok. október.. Feladat: Határozzuk meg a, 4b, c és a b c vektorokat, ha a = (; ; ; ; b = (; ; ; ; c = ( ; ; ; ;.. Feladat: Határozzuk meg a, 4b, a, c és a b; c + b kifejezések
 XI A MÁTRIX INVERZE 1 Az inverzmátrix definíciója Determinánsok szorzástétele Az egységmátrix definíciója: 1 0 0 0 0 1 0 0 E n = 0 0 1 0 0 0 0 1 n-edrenű (azaz n n típusú) mátrix E n -nel bármely mátrixot
XI A MÁTRIX INVERZE 1 Az inverzmátrix definíciója Determinánsok szorzástétele Az egységmátrix definíciója: 1 0 0 0 0 1 0 0 E n = 0 0 1 0 0 0 0 1 n-edrenű (azaz n n típusú) mátrix E n -nel bármely mátrixot
8. Előadás. Megyesi László: Lineáris algebra, , oldal. 8. előadás Mátrix rangja, Homogén lineáris egyenletrendszer
 8. Előadás Megyesi László: Lineáris algebra, 51. 56., 70. 74. oldal. Gondolkodnivalók Elemi bázistranszformáció 1. Gondolkodnivaló Most ne vegyük figyelembe, hogy az elemi bázistranszformáció során ez
8. Előadás Megyesi László: Lineáris algebra, 51. 56., 70. 74. oldal. Gondolkodnivalók Elemi bázistranszformáció 1. Gondolkodnivaló Most ne vegyük figyelembe, hogy az elemi bázistranszformáció során ez
Budapesti Műszaki Főiskola, Neumann János Informatikai Kar. Vektorok. Fodor János
 Budapesti Műszaki Főiskola, Neumann János Informatikai Kar Lineáris algebra 1. témakör Vektorok Fodor János Copyright c Fodor@bmf.hu Last Revision Date: 2006. szeptember 11. Version 1.1 Table of Contents
Budapesti Műszaki Főiskola, Neumann János Informatikai Kar Lineáris algebra 1. témakör Vektorok Fodor János Copyright c Fodor@bmf.hu Last Revision Date: 2006. szeptember 11. Version 1.1 Table of Contents
Lineáris algebra (10A103)
 Lineáris algebra (10A103 Kátai-Urbán Kamilla Tudnivalók Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli (beugróval, feltétele a Lineáris algebra gyakorlat
Lineáris algebra (10A103 Kátai-Urbán Kamilla Tudnivalók Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli (beugróval, feltétele a Lineáris algebra gyakorlat
Vektorgeometria (1) First Prev Next Last Go Back Full Screen Close Quit
 Vektorgeometria (1) First Prev Next Last Go Back Full Screen Close Quit 1. A térbeli irányított szakaszokat vektoroknak hívjuk. Két vektort egyenlőnek tekintünk, ha párhuzamos eltolással fedésbe hozhatók.
Vektorgeometria (1) First Prev Next Last Go Back Full Screen Close Quit 1. A térbeli irányított szakaszokat vektoroknak hívjuk. Két vektort egyenlőnek tekintünk, ha párhuzamos eltolással fedésbe hozhatók.
5 = hiszen és az utóbbi mátrix determinánsa a középs½o oszlop szerint kifejtve: 3 7 ( 2) = (példa vége). 7 5 = 8. det 6.
 A pivotálás hasznáról és hatékony módjáról Adott M mátrixra pivotálás alatt a következ½ot értjük: Kijelölünk a mátrixban egy nemnulla elemet, melynek neve pivotelem, aztán az egész sort leosztjuk a pivotelemmel.
A pivotálás hasznáról és hatékony módjáról Adott M mátrixra pivotálás alatt a következ½ot értjük: Kijelölünk a mátrixban egy nemnulla elemet, melynek neve pivotelem, aztán az egész sort leosztjuk a pivotelemmel.
8. Egyenletek, egyenlőtlenségek, egyenletrendszerek II.
 8 Egyenletek, egyenlőtlenségek, egyenletrendszerek II Elméleti összefoglaló Az a + b+ c, a egyenletet másodfokú egyenletnek nevezzük A D b ac kifejezést az egyenlet diszkriminánsának nevezzük Ha D >, az
8 Egyenletek, egyenlőtlenségek, egyenletrendszerek II Elméleti összefoglaló Az a + b+ c, a egyenletet másodfokú egyenletnek nevezzük A D b ac kifejezést az egyenlet diszkriminánsának nevezzük Ha D >, az
Megoldott feladatok november 30. n+3 szigorúan monoton csökken, 5. n+3. lim a n = lim. n+3 = 2n+3 n+4 2n+1
 Megoldott feladatok 00. november 0.. Feladat: Vizsgáljuk az a n = n+ n+ sorozat monotonitását, korlátosságát és konvergenciáját. Konvergencia esetén számítsuk ki a határértéket! : a n = n+ n+ = n+ n+ =
Megoldott feladatok 00. november 0.. Feladat: Vizsgáljuk az a n = n+ n+ sorozat monotonitását, korlátosságát és konvergenciáját. Konvergencia esetén számítsuk ki a határértéket! : a n = n+ n+ = n+ n+ =
Egyenletek, egyenletrendszerek, matematikai modell. 1. Oldja meg az Ax=b egyenletrendszert Gauss módszerrel és adja meg az A mátrix LUfelbontását,
 Egyenletek egyenletrendszerek matematikai modell Oldja meg az A=b egyenletrendszert Gauss módszerrel és adja meg az A mátri LUfelbontását ahol 8 b 8 Oldja meg az A=b egyenletrendszert és határozza meg
Egyenletek egyenletrendszerek matematikai modell Oldja meg az A=b egyenletrendszert Gauss módszerrel és adja meg az A mátri LUfelbontását ahol 8 b 8 Oldja meg az A=b egyenletrendszert és határozza meg
Másodfokú egyenletek, egyenlőtlenségek
 Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x + 1x + 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x + 1x + 16 = 0.
Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x + 1x + 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x + 1x + 16 = 0.
Lin.Alg.Zh.1 feladatok
 LinAlgZh1 feladatok 01 3d vektorok Adott három vektor ā = (0 2 4) b = (1 1 4) c = (0 2 4) az R 3 Euklideszi vektortérben egy ortonormált bázisban 1 Mennyi az ā b skalárszorzat? 2 Mennyi az n = ā b vektoriális
LinAlgZh1 feladatok 01 3d vektorok Adott három vektor ā = (0 2 4) b = (1 1 4) c = (0 2 4) az R 3 Euklideszi vektortérben egy ortonormált bázisban 1 Mennyi az ā b skalárszorzat? 2 Mennyi az n = ā b vektoriális
Koordinátageometria. M veletek vektorokkal grakusan. Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1
 Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1 Koordinátageometria M veletek vektorokkal grakusan 1. Az ABCD négyzet oldalvektorai közül a = AB és b = BC. Adja meg az AC és BD vektorokat a
Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1 Koordinátageometria M veletek vektorokkal grakusan 1. Az ABCD négyzet oldalvektorai közül a = AB és b = BC. Adja meg az AC és BD vektorokat a
Az egyenlőtlenség mindkét oldalát szorozzuk meg 4 16-al:
 Bevezető matematika kémikusoknak., 04. ősz. feladatlap. Ábrázoljuk számegyenesen a következő egyenlőtlenségek megoldáshalmazát! (a) x 5 < 3 5 x < 3 x 5 < (d) 5 x
Bevezető matematika kémikusoknak., 04. ősz. feladatlap. Ábrázoljuk számegyenesen a következő egyenlőtlenségek megoldáshalmazát! (a) x 5 < 3 5 x < 3 x 5 < (d) 5 x
összeadjuk 0-t kapunk. Képletben:
 814 A ferde kifejtés tétele Ha egy determináns valamely sorának elemeit egy másik sor elemeihez tartozó adjungáltakkal szorozzuk meg és a szorzatokat összeadjuk 0-t kapunk Képletben: n a ij A kj = 0, ha
814 A ferde kifejtés tétele Ha egy determináns valamely sorának elemeit egy másik sor elemeihez tartozó adjungáltakkal szorozzuk meg és a szorzatokat összeadjuk 0-t kapunk Képletben: n a ij A kj = 0, ha
Lineáris leképezések. Wettl Ferenc március 9. Wettl Ferenc Lineáris leképezések március 9. 1 / 31
 Lineáris leképezések Wettl Ferenc 2015. március 9. Wettl Ferenc Lineáris leképezések 2015. március 9. 1 / 31 Tartalom 1 Mátrixleképezés, lineáris leképezés 2 Alkalmazás: dierenciálhatóság 3 2- és 3-dimenziós
Lineáris leképezések Wettl Ferenc 2015. március 9. Wettl Ferenc Lineáris leképezések 2015. március 9. 1 / 31 Tartalom 1 Mátrixleképezés, lineáris leképezés 2 Alkalmazás: dierenciálhatóság 3 2- és 3-dimenziós
Fizika A2E, 8. feladatsor
 Fizika AE, 8. feladatsor ida György József vidagyorgy@gmail.com. feladat: Az ábrán látható áramkörben határozzuk meg az áramer sséget! 4 5 Utolsó módosítás: 05. április 4., 0:9 El ször ki kell számolnunk
Fizika AE, 8. feladatsor ida György József vidagyorgy@gmail.com. feladat: Az ábrán látható áramkörben határozzuk meg az áramer sséget! 4 5 Utolsó módosítás: 05. április 4., 0:9 El ször ki kell számolnunk
4. Vektoralgebra (megoldások)
 (megoldások).. a) m n = (a + b) (a b) = 6b b) 4m + 4n = 8a ; c) m n = a + 5 b ; d) m + n = 9+ a + 9 b.. a) a 4b= 0 m n ; b) 5a + b= 8 m n ; c) a + b= 7 m + n ; d) a b = 4+ m + n. 0 0 5 4. A szabályos hatszög
(megoldások).. a) m n = (a + b) (a b) = 6b b) 4m + 4n = 8a ; c) m n = a + 5 b ; d) m + n = 9+ a + 9 b.. a) a 4b= 0 m n ; b) 5a + b= 8 m n ; c) a + b= 7 m + n ; d) a b = 4+ m + n. 0 0 5 4. A szabályos hatszög
10. Koordinátageometria
 I. Nulladik ZH-ban láttuk: 0. Koordinátageometria. Melyek azok a P x; y pontok, amelyek koordinátái kielégítik az Ábrázolja a megoldáshalmazt a koordináta-síkon! x y x 0 egyenlőtlenséget? ELTE 00. szeptember
I. Nulladik ZH-ban láttuk: 0. Koordinátageometria. Melyek azok a P x; y pontok, amelyek koordinátái kielégítik az Ábrázolja a megoldáshalmazt a koordináta-síkon! x y x 0 egyenlőtlenséget? ELTE 00. szeptember
λ 1 u 1 + λ 2 v 1 + λ 3 w 1 = 0 λ 1 u 2 + λ 2 v 2 + λ 3 w 2 = 0 λ 1 u 3 + λ 2 v 3 + λ 3 w 3 = 0
 Vektorok a térben Egy (v 1,v 2,v 3 ) valós számokból álló hármast vektornak nevezzünk a térben (R 3 -ban). Használni fogjuk a v = (v 1,v 2,v 3 ) jelölést. A v 1,v 2,v 3 -at a v vektor komponenseinek nevezzük.
Vektorok a térben Egy (v 1,v 2,v 3 ) valós számokból álló hármast vektornak nevezzünk a térben (R 3 -ban). Használni fogjuk a v = (v 1,v 2,v 3 ) jelölést. A v 1,v 2,v 3 -at a v vektor komponenseinek nevezzük.
Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel
 Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel Segédlet az A végeselem módszer alapjai tárgy 4. laborgyakorlatához http://www.mm.bme.hu/~kossa/vemalap4.pdf Kossa Attila (kossa@mm.bme.hu)
Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel Segédlet az A végeselem módszer alapjai tárgy 4. laborgyakorlatához http://www.mm.bme.hu/~kossa/vemalap4.pdf Kossa Attila (kossa@mm.bme.hu)
Vektoralgebra. 1.) Mekkora a pillanatnyi sebesség 3 s elteltével, ha a kezdősebesség (15;9;7) m/s, a gravitációs gyorsulás pedig (0;0;-10) m/s 2?
 Vektoralgebra Elmélet: http://digitus.itk.ppke.hu/~b_novak/dmat/vektorfolcop.pdf Mikor érdemes más, nem ortonormált bázist alkalmazni? Fizikában a ferde hajításoknál megéri úgynevezett ferdeszögű koordináta-rendszert
Vektoralgebra Elmélet: http://digitus.itk.ppke.hu/~b_novak/dmat/vektorfolcop.pdf Mikor érdemes más, nem ortonormált bázist alkalmazni? Fizikában a ferde hajításoknál megéri úgynevezett ferdeszögű koordináta-rendszert
Ortogonalizáció. Wettl Ferenc Wettl Ferenc Ortogonalizáció / 41
 Ortogonalizáció Wettl Ferenc 2016-03-22 Wettl Ferenc Ortogonalizáció 2016-03-22 1 / 41 Tartalom 1 Ortonormált bázis 2 Ortogonális mátrix 3 Ortogonalizáció 4 QR-felbontás 5 Komplex skaláris szorzás 6 Diszkrét
Ortogonalizáció Wettl Ferenc 2016-03-22 Wettl Ferenc Ortogonalizáció 2016-03-22 1 / 41 Tartalom 1 Ortonormált bázis 2 Ortogonális mátrix 3 Ortogonalizáció 4 QR-felbontás 5 Komplex skaláris szorzás 6 Diszkrét
Megoldások. Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma)
 Megoldások 1. Határozd meg az a és b vektor skaláris szorzatát, ha a = 5, b = 4 és a közbezárt szög φ = 55! Alkalmazzuk a megfelelő képletet: a b = a b cos φ = 5 4 cos 55 11,47. 2. Határozd meg a következő
Megoldások 1. Határozd meg az a és b vektor skaláris szorzatát, ha a = 5, b = 4 és a közbezárt szög φ = 55! Alkalmazzuk a megfelelő képletet: a b = a b cos φ = 5 4 cos 55 11,47. 2. Határozd meg a következő
MA1143v A. csoport Név: december 4. Gyak.vez:. Gyak. kódja: Neptun kód:.
 MAv A. csoport Név:... Tekintsük az alábbi mátriot! A 7 a Invertálható-e az A mátri? Ha igen akkor bázistranszformációval határozza meg az inverzét! Ellenőrizze számításait! b Milyen egyéb mátritulajdonságokra
MAv A. csoport Név:... Tekintsük az alábbi mátriot! A 7 a Invertálható-e az A mátri? Ha igen akkor bázistranszformációval határozza meg az inverzét! Ellenőrizze számításait! b Milyen egyéb mátritulajdonságokra
Lineáris algebra. (közgazdászoknak)
 Lineáris algebra (közgazdászoknak) 10A103 FELADATOK A GYAKORLATRA (3.) 2018/2019. tavaszi félév Lineáris egyenletrendszerek 3.1. Feladat. Oldjuk meg az alábbi lineáris egyenletrendszereket Gauss-eliminációval
Lineáris algebra (közgazdászoknak) 10A103 FELADATOK A GYAKORLATRA (3.) 2018/2019. tavaszi félév Lineáris egyenletrendszerek 3.1. Feladat. Oldjuk meg az alábbi lineáris egyenletrendszereket Gauss-eliminációval
1. Határozzuk meg, hogy mikor egyenlő egymással a következő két mátrix: ; B = 8 7 2, 5 1. Számítsuk ki az A + B, A B, 3A, B mátrixokat!
 . Mátrixok. Határozzuk meg, hogy mikor egyenlő egymással a következő két mátrix: [ ] [ ] π a A = ; B = 8 7, 5 x. 7, 5 ln y. Legyen 4 A = 4 ; B = 5 5 Számítsuk ki az A + B, A B, A, B mátrixokat!. Oldjuk
. Mátrixok. Határozzuk meg, hogy mikor egyenlő egymással a következő két mátrix: [ ] [ ] π a A = ; B = 8 7, 5 x. 7, 5 ln y. Legyen 4 A = 4 ; B = 5 5 Számítsuk ki az A + B, A B, A, B mátrixokat!. Oldjuk
Magasabbfokú egyenletek
 86 Magasabbfokú egyenletek Magasabbfokú egyenletek 5 90 a) =! ; b) =! ; c) = 5, 9 a) Legyen = y Új egyenletünk: y - 5y+ = 0 Ennek gyökei: y=, y= Tehát egyenletünk gyökei:, =!,, =! b) Új egyenletünk: y
86 Magasabbfokú egyenletek Magasabbfokú egyenletek 5 90 a) =! ; b) =! ; c) = 5, 9 a) Legyen = y Új egyenletünk: y - 5y+ = 0 Ennek gyökei: y=, y= Tehát egyenletünk gyökei:, =!,, =! b) Új egyenletünk: y
Vektorok összeadása, kivonása, szorzás számmal, koordináták
 Vektorok összeadása, kivonása, szorzás számmal, koordináták 1. Mik lesznek a P (3, 4, 8) pont C (3, 7, 2) pontra vonatkozó tükörképének a koordinátái? 2. Egy szabályos hatszög középpontja K (4, 1, 4),
Vektorok összeadása, kivonása, szorzás számmal, koordináták 1. Mik lesznek a P (3, 4, 8) pont C (3, 7, 2) pontra vonatkozó tükörképének a koordinátái? 2. Egy szabályos hatszög középpontja K (4, 1, 4),
1 p, c = p 1 és d = 4. Oldjuk meg az alábbi egyenletrendszert a c és d paraméterek minden értékére. x + 2z = 5 2x y = 8 3x + 6y + cz = d
 Bevezetés a számításelméletbe I. Zárthelyi feladatok 013. október 4. 1. Írjuk fel a háromdimenziós tér P = (1, 1, 1) és Q = (3, 1, 5) pontjait összeköt szakasz felez mer leges síkjának egyenletét. Hol
Bevezetés a számításelméletbe I. Zárthelyi feladatok 013. október 4. 1. Írjuk fel a háromdimenziós tér P = (1, 1, 1) és Q = (3, 1, 5) pontjait összeköt szakasz felez mer leges síkjának egyenletét. Hol
Mátrixok, mátrixműveletek
 Mátrixok, mátrixműveletek 1 előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Mátrixok, mátrixműveletek p 1/1 Mátrixok definíciója Definíció Helyezzünk el n m elemet egy olyan téglalap
Mátrixok, mátrixműveletek 1 előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Mátrixok, mátrixműveletek p 1/1 Mátrixok definíciója Definíció Helyezzünk el n m elemet egy olyan téglalap
