DOMBORÍTOTT FOGAZAT MATEMATIKAI MODELLEZÉSE FOGASGYŰRŰS TENGELYKAPCSOLÓKHOZ
|
|
|
- Gabi Orosz
- 9 évvel ezelőtt
- Látták:
Átírás
1 DOMBORÍTOTT FOGAZAT MATEMATIKAI MODELLEZÉSE FOGASGYŰRŰS TENGELYKAPCSOLÓKHOZ Dr. Szente József, Kelemen László PhD, Miskolci Egetem, PhD hallgató, Miskolci Egetem Miskolci Egetem, Gép- és Terméktervezési Tanszék. BEVEZETÉS A fogasgűrűs tengelkapcsoló (. ábra) fő alkotó elemei a belső fogazatú hüvel és a domborított fogazattal rendelkező ag.. ábra Fogasgűrűs tengelkapcsoló A két fogazott gépelem eg sajátos fogaskerékpárt alkot, ahol a fogszámok azonosak. A domborított fogazat révén a tengelkapcsoló képes kompenzálni az összekapcsolt tengelek szögeltérését. Ehhez egetlen ag-hüvel párosítás elegendő, azonban a gakorlatban általában két elempárt építenek be az. ábrának megfelelően. Ezzel a szöghiba mellett az összekötött tengelek egtengelűségi hibájának a kiküszöbölése is lehetővé válik. A tengelkapcsoló működése szempontjából kritikus elem a domborított fogazatú ag. A továbbiakban ennek a különleges fogaskeréknek a gártási lehetőségét vizsgáljuk meg. Ezzel összhangban előállítjuk a fogfelületek matematikai modelljét, mel alapjául szolgálhat további - a tengelkapcsoló működését célzó - vizsgálatoknak.. A DOMBORÍTOTT FOGAZATÚ FOGASKERÉK GYÁRTÁSA A tengelkapcsoló ag domborított fogazata lefejtőmarással, a munkadarab és a szerszám összehangolt mozgatásával állítható elő, a. ábrának megfelelően. 66
2 Hengeres fogaskerekek lefejtőmarása során a szerszám és a munkadarab folamatos forgómozgást végeznek, miközben a szerszám lassú előtolással mozog a munkadarab tengelével párhuzamosan. A domborított fogfelület előállításához a. ábrának megfelelően a szerszámot körpálán kell mozgatni. A lefejtőmarógép sajátos felépítése ezt általában nem teszi lehetővé, ezért a szükséges relatív mozgást a munkadarab-asztal sugáriránú és a szerszám axiális mozgásával érjük el.. ábra A domborított fogfelület gártásának elvi vázlata. Gártás közben a tengeltáv folamatosan változik. Legnagobb értéke: a = r + r () max ahol r a lefejtőmaró osztókörsugara, r a munkadarab osztókörsugara. A szerszám és a munkadarab relatív mozgásának körpáláját az A = MN sugárral jellemezhetjük, mel függ a szerszám osztókörsugarától és a fogdomborításra jellemző R mérettől (. ábra): A tengeltáv pillanatni értékét fentiek mellett a lefejtőmaró axiális helzete határozza meg, melet a. ábrán B-vel jelöltünk. Mindezek alapján a pillanatni tengeltáv: a = A B R + r () 3. A LEFEJTŐMARÁS MATEMATIKAI MODELLJE A lefejtőmarás matematikai modelljét Litvin [] két független paraméterrel képzett burkolásként mutatta be. Ez a megoldás az ideális fogfelületek leírására kiválóan alkalmas, uganakkor közelítést is tartalmaz, mivel a két paraméter nem tekinthető függetlennek. Mitome [] igen szemléletes módszert közölt a kúpos evolvens fogaskerekek lefejtőmarására. Ez a módszer módosítva alkalmas a hengeres fogaskerekek valóságos fogfelületének meghatározására [3]. 67
3 A lefejtőmarás elvi vázlata a 3. ábrán, a koordináta-rendszerek kapcsolata a 4. ábrán látható. A lefejtőmaró eg - a vágóéleire illeszkedő, állandó emelkedésű csavarfelülettel rendelkező - evolvens csigának tekinthető. Az ω szögsebességű forgás hatására a csiga fogfelülete látszólagos haladó mozgást végez az x,, z rendszerben, az tengel mentén. Az íg keletkező felület-sereg egenlete: 3. ábra A lefejtőmarás vázlata és koordinátarendszerei x z = x ( u, v), ( u, v) = + pω t, (3) = z ( u, v), ahol u és v a csavarfelület paraméterei, t az idő a munkadarab eg körülfordulásán belül, p a csiga csavarparamétere, ω a lefejtőmaró szögsebessége. 5. ábra Egenes fogú hengeres fogaskerék valóságos fogfelülete A munkadarab eg körülfordulása során a szerszám az F fogárkot hozza létre. F F k+ a munkadarab második, (k+)-edik körülfordulása során vágott fogárkot jelöli, s a szerszám eg munkadarab fordulatra vonatkoztatott előtolása. 68
4 ahol v s az előtolósebesség. A munkadarab ezalatt ω(t+kt) szöggel fordul el, ez megfelel (ωt+kπ) szögnek. Az F k+ felület vágásához a (4) egenletrendszer íg alakul: x z = x ( u, v), ( u, v) + pω ( t + kt), (6) = = z ( u, v). Állítsuk elő a (6) egenletekkel adott felület-sereget az xz rendszerben: x x = M z z (7) Az M átviteli mátrix a következő: M = cosωt -sin ωt sin Σsin ωt sin Σ cosωt cos Σ -cos Σ sin ωt -cos Σ cosωt sin Σ a cosωt -a sin ωt -v s ( ) t + kt (8) A tetszőleges F n -edik felület meghatározásához (7) megoldásával és k=n- helettesítésével jutunk, egidejűleg kapcsolatot teremtve az u, v, t paraméterek között. Ez utóbbi egik lehetséges módja, hog a D függvéndeterminánst zérussal tesszük egenlővé: x x x u v t D = = (9) u v t z z z u v t A (7) és (9) összefüggések egüttesen meghatározzák a fogfelület tetszőleges F n felületelemét. A lefejtőmarás eddig vizsgált esete hengeres fogaskerekek gártására vonatkozik. A bemutatott egenletek domborított fogazat gártására a következő feltételekkel lesznek érvénesek: - a v s axiális előtolósebesség mellett figelembe kell venni eg v r sugáriránú sebességet, - és ennek a hatásaként a tengeltáv folamatos változását. A sugáriránú és az axiális sebességek aránát az előírt szerszámpála alapján a következő összefüggés fejezi ki: 69
5 v v r s B = () A B A szerszám z= pozíciójához B=b/ tartozik, illetve érvénes a B=z+b/ kapcsolat, ahol b a fogaskerék fogszélessége. A tengeltáv változását a (3) egenlet írja le. Behelettesítve a B és z közötti összefüggést: b = A z + R () a ( z) + r adódik, mel leírja a tengeltáv változását, miközben a szerszám a fogaskerék tengele mentén, előírt pálán halad és pillanatni helzetét a z koordináta határozza meg. Mindezek alapján megállapítható, hog a hengeres fogaskerekek lefejtőmarására bemutatott matematikai modell alkalmas a domborított fogazat leírására is, ha az átviteli mátrix (8) utolsó oszlopában a tengeltáv változását figelembe vesszük. (5)-öt ()-be helettesítve a tengeltáv változása az idő függvénében: b a( t) s + r Ezt az összefüggést kell az M mátrix számításakor figelembe venni. 4. A FOGFELÜLET EGYENLETE = A v ( t + kt ) R () Az eddig leírtak alapján megállapítható, hog a kialakuló fogfelület több paraméter függvéne. Íg befolásolja a lefejtőmaró mérete (r ) és az előtolás nagsága. 6. ábra Domborított fogfelület. Tulajdonképpen hengeres fogaskerekek lefejtőmarására is igaz, hog uganaz a fogaskerék másik lefejtőmaróval, vag más előtolással előállítva, nem uganazzal a 7
6 fogfelülettel rendelkezik. A hengeres fogaskerekek evolvens fogfelületei tehát idealizált felületek. A domborított fogazatok esetében ezt az idealizált fogfelületet úg származtatjuk, hog fogak tengelmetszeteiben változó profil-eltolással rendelkező evolvens fogazatot feltételezünk. A fogfelület egenlete: x z, = r = r sinθ, cosθ, (3) ahol r tetszőleges sugár a fogprofil mentén, θ a fogszög. Számítására a θ s = + invα invα (4) r összefüggés szolgál, ahol s a fogvastagság az osztóhenger mentén, r az osztókörsugár, α az alapprofilszög, α a profilszög, mel cos α =r b /r alapján határozható meg. r b az alapkörsugár. (4)-ben inv az evolvens függvén, értelmezése: inv α = tan α α. A fogvastagság az osztóhenger mentén: s = s ( R R ) tanα (5) z ahol s a fogvastagság a z = síkban. Mindezek alapján megállapítható, hog θ az r sugártól és a z koordinátától függ, vagis (3)-ban KÖSZÖNETNYILVÁNÍTÁS x = x ( z r ) ( z r ), =, A bemutatott kutató munka a TÁMOP-4...B-//KONV-- jelű projekt részeként az Európai Unió támogatásával, az Európai Szociális Alap társfinanszírozásával valósul meg IRODALOM [] Litvin, F. L.: A fogaskerékkapcsolás elmélete. Műszaki Könvkiadó. Budapest. 97. [] Mitome, K.: Table sliding taper hobbing of clindrical gear using clindrical hob. Transactions of the ASME. Vol p [3] Szente J.: Fogazott elempárok tervezéséhez kapcsolódó vizsgálatok. A Miskolci EgetemDoktori (PhD) Tézisfüzetei. Miskolc (6) 7
7 TARTALOMJEGYZÉK Antal Dániel EJTÉSI TESZT EGYSZERSÍTETT MODELLEZÉSE A TERVEZÉS FÁZISÁBAN Bodolai Tamás MINTATESZTEL SZOFTVER FEJLESZTÉSE LINE SCAN KAMERÁS ALKALMAZÁSOKHOZ 7 Bodzás Sándor DESIGNING AND MODELLING OF WORM GEAR HOB Burmeister Dániel BUCKLING OF SHELL-STIFFENED AND AXISYMMETRICALLY LOADED ANNULAR PLATES 8 Darócz Gabriella EMOTION AND THE COMPUTATIONAL MODEL OF METAPHORS 4 Drágár Zsuzsa NEM SZABVÁNYOS SZERSZÁM-ALAPPROFIL KIALAKÍTÁSÁNAK LEHETSÉGEI FOGASKEREKEKHEZ 3 Fekete Tamás MEMBRÁNOK ALKAKMAZÁSA SZINKRON VÁLTAKOZÓ ÁRAMÚ HIDRAULIKUS HAJTÁSOKBAN 35 Ferenczi István MODELING THE BEHAVIOR OF PROFINET IRT IN GIGABIT ETHERNET NETWORK 4 Ficsor Emese AUTOMATIZÁLT AZONOSÍTÁSTECHNIKAI ÉS NYOMONKÖVETÉSI LEHETSÉGEK VIZSGÁLATA INTERMODÁLIS SZÁLLÍTÁS SORÁN 47 Gáspár Marcell Gula NAGYSZILÁRDSÁGÚ ACÉL HEGESZTÉSTECHNOLÓGIÁJÁNAK FEJLESZTÉSE A HLÉS ID ELEMZÉSÉVEL 54 Hriczó Krisztián NEMNEWTONI FOLYADÉKOK HATÁRRÉTEG ÁRAMLÁSÁNAK HASONLÓSÁGI MEGOLDÁSAI KONVEKTÍV FELÜLETI PEREMFELTÉTELEK MELLETT 6 Kelemen László Attila DOMBORÍTOTT FOGAZAT MATEMATIKAI MODELLEZÉSE FOGASGYRS TENGELYKAPCSOLÓKHOZ 66
8 Krizsán Zoltán STRUCTURAL IMPROVEMENTS OF THE OPENRTM ROBOT MIDDLEWARE 7 Mánd Zoltán A POSSIBLE NEURAL NETWORK FOR A HOLONIC MANUFACTURING SYSTEM 78 Simon Pál GRAFIKUS PROCESSZOROK ALKALMAZÁSA KÉPFELDOLGOZÁSI FELADATOKRA 84 Skapinecz Róbert OPTIMALIZÁLÁSI LEHETSÉGEK VIZSGÁLATA EGY E-PIACTÉRREL INTEGRÁLT VIRTUÁLIS SZÁLLÍTÁSI VÁLLALATNÁL 9 Somoski Gábor COLD METAL TRANSFER THE CMT PROCESS 96 Szabó Adél Anett A TELJES KÖLTSÉG KONCEPCIÓ JELENTSÉGE A VÁLLALATI BESZERZÉSI GYAKORLATBAN Szamosi Zoltán MEZGAZDASÁGI HULLADÉKOK VIZSGÁLATA 8 Sziláginé Biró Andrea BETÉTEDZÉS ACÉLOK KÜLÖNBÖZ HMÉRSÉKLET KARBONITRIDÁLÁSA 4 Tomkovics Tamás DARABÁRU OSZTÁLYOZÓ RENDSZEREK KISZOLGÁLÁSI STRATÉGIÁIT BEFOLYÁSOLÓ JELLEMZK; A RENDSZEREK MODULJAI KÖZÖTTI ÖSSZEFÜGGÉSEK FELTÁRÁSA Tóth Zsolt EL REDUKCIÓ ALKALMAZÁSA A TBL ALGORITMUS IDKÖLTSÉGÉNEK CSÖKKENTÉSÉRE 6 Varga Zoltán KONKRÉT LOGISZTIKAI MINTARENDSZER MODELLEZÉSE 3 Vincze Dávid MATLAB INTERFACE FOR THE 3D VIRTUAL COLLABORATION ARENA 37 Wagner Görg INTENZÍTÁS BÁZISÚ OPTIMALIZÁLÁS FORGÁCSOLÁSI PARAMÉTEREK MEGHATÁROZÁSÁHOZ 43
BETÉTEDZÉSŰ ACÉLOK KÜLÖNBÖZŐ HŐMÉRSÉKLETŰ KARBONITRIDÁLÁSA. Szilágyiné Biró Andrea 1, Dr. Tisza Miklós 2
 BEVEZETÉS BETÉTEDZÉSŰ ACÉLOK KÜLÖNBÖZŐ HŐMÉRSÉKLETŰ KARBONITRIDÁLÁSA Szilágyiné Biró Andrea 1, Dr. Tisza Miklós 2 1 PhD hallgató, 2 tanszékvezető, egyetemi tanár Miskolci Egyetem, Mechanikai Technológiai
BEVEZETÉS BETÉTEDZÉSŰ ACÉLOK KÜLÖNBÖZŐ HŐMÉRSÉKLETŰ KARBONITRIDÁLÁSA Szilágyiné Biró Andrea 1, Dr. Tisza Miklós 2 1 PhD hallgató, 2 tanszékvezető, egyetemi tanár Miskolci Egyetem, Mechanikai Technológiai
MEZİGAZDASÁGI HULLADÉKOK VIZSGÁLATA
 MEZİGAZDASÁGI HULLADÉKOK VIZSGÁLATA Szamosi Zoltán 1, Dr. Lakatos Károly 2, Dr. Siménfalvi Zoltán 3 doktorandusz, egyetemi docens, tanszékvezetı egyetemi docens Vegyipari Gépek Tanszéke, Áramlás- és Hıtechnikai
MEZİGAZDASÁGI HULLADÉKOK VIZSGÁLATA Szamosi Zoltán 1, Dr. Lakatos Károly 2, Dr. Siménfalvi Zoltán 3 doktorandusz, egyetemi docens, tanszékvezetı egyetemi docens Vegyipari Gépek Tanszéke, Áramlás- és Hıtechnikai
INTENZÍTÁS BÁZISÚ OPTIMALIZÁLÁS FORGÁCSOLÁSI PARAMÉTEREK MEGHATÁROZÁSÁHOZ
 INTENZÍTÁS BÁZISÚ OPTIMALIZÁLÁS FORGÁCSOLÁSI PARAMÉTEREK MEGHATÁROZÁSÁHOZ Wagner György 1, Tóth Tibor 2 egyetemi tanársegéd, ME Általános Informatikai Tanszék Prof. Dr. DSc, egyetemi tanár, ME Alkalmazott
INTENZÍTÁS BÁZISÚ OPTIMALIZÁLÁS FORGÁCSOLÁSI PARAMÉTEREK MEGHATÁROZÁSÁHOZ Wagner György 1, Tóth Tibor 2 egyetemi tanársegéd, ME Általános Informatikai Tanszék Prof. Dr. DSc, egyetemi tanár, ME Alkalmazott
KONKRÉT LOGISZTIKAI MINTARENDSZER MODELLEZÉSE
 KONKRÉT LOGISZTIKAI MINTARENDSZER MODELLEZÉSE Szerzők: Dr. Kovács László 1, Varga Zoltán 2 Egyetemi docens, PhD hallgató Miskolci Egyetem, Hatvany József Informatikai Tudományok Doktori Iskola A Miskolci
KONKRÉT LOGISZTIKAI MINTARENDSZER MODELLEZÉSE Szerzők: Dr. Kovács László 1, Varga Zoltán 2 Egyetemi docens, PhD hallgató Miskolci Egyetem, Hatvany József Informatikai Tudományok Doktori Iskola A Miskolci
ELŽ REDUKCIÓ ALKALMAZÁSA A TBL ALGORITMUS IDŽKÖLTSÉGÉNEK CSÖKKENTÉSÉRE
 ELŽ REDUKCIÓ ALKALMAZÁSA A TBL ALGORITMUS IDŽKÖLTSÉGÉNEK CSÖKKENTÉSÉRE TÓTH ZSOLT, LÁSZLÓ KOVÁCS Kivonat. A környezet független nyelvek generálása egy N P nehéz probléma, amire a TBL algoritmus[1][2] egy
ELŽ REDUKCIÓ ALKALMAZÁSA A TBL ALGORITMUS IDŽKÖLTSÉGÉNEK CSÖKKENTÉSÉRE TÓTH ZSOLT, LÁSZLÓ KOVÁCS Kivonat. A környezet független nyelvek generálása egy N P nehéz probléma, amire a TBL algoritmus[1][2] egy
A TELJES KÖLTSÉG KONCEPCIÓ JELENTŐSÉGE A VÁLLALATI BESZERZÉSI GYAKORLATBAN
 A TELJES KÖLTSÉG KONCEPCIÓ JELENTŐSÉGE A VÁLLALATI BESZERZÉSI GYAKORLATBAN Szabó Adél Anett 1, Dr. Bányainé dr. Tóth Ágota 2, Prof. Dr. Illés Béla 3 1 doktorandusz hallgató, 2 egyetemi docens témavezető,
A TELJES KÖLTSÉG KONCEPCIÓ JELENTŐSÉGE A VÁLLALATI BESZERZÉSI GYAKORLATBAN Szabó Adél Anett 1, Dr. Bányainé dr. Tóth Ágota 2, Prof. Dr. Illés Béla 3 1 doktorandusz hallgató, 2 egyetemi docens témavezető,
MEMBRÁNOK ALKAKMAZÁSA SZINKRON VÁLTAKOZÓ ÁRAMÚ HIDRAULIKUS HAJTÁSOKBAN. Fekete Tamás PhD hallgató Miskolci Egyetem, Szerszámgépek Tanszéke
 MEMBRÁNOK ALKAKMAZÁSA SZINKRON VÁLTAKOZÓ ÁRAMÚ HIDRAULIKUS HAJTÁSOKBAN Fekete Tamás PhD hallgató Miskolci Egyetem, Szerszámgépek Tanszéke 1. ASZINKRON VÁLTAKOZÓ ÁRAMÚ HIDRAULIKUS HAJTÁS A váltakozó áramú
MEMBRÁNOK ALKAKMAZÁSA SZINKRON VÁLTAKOZÓ ÁRAMÚ HIDRAULIKUS HAJTÁSOKBAN Fekete Tamás PhD hallgató Miskolci Egyetem, Szerszámgépek Tanszéke 1. ASZINKRON VÁLTAKOZÓ ÁRAMÚ HIDRAULIKUS HAJTÁS A váltakozó áramú
AUTOMATIZÁLT AZONOSÍTÁSTECHNIKAI ÉS NYOMONKÖVETÉSI LEHETŐSÉGEK VIZSGÁLATA INTERMODÁLIS SZÁLLÍTÁS SORÁN
 AUTOMATIZÁLT AZONOSÍTÁSTECHNIKAI ÉS NYOMONKÖVETÉSI LEHETŐSÉGEK VIZSGÁLATA INTERMODÁLIS SZÁLLÍTÁS SORÁN Ficsor Emese 1, Prof. Dr. Illés Béla 2 Ph.D. hallgató 1, tanszékvezető, egyetemi tanár 2 Miskolci
AUTOMATIZÁLT AZONOSÍTÁSTECHNIKAI ÉS NYOMONKÖVETÉSI LEHETŐSÉGEK VIZSGÁLATA INTERMODÁLIS SZÁLLÍTÁS SORÁN Ficsor Emese 1, Prof. Dr. Illés Béla 2 Ph.D. hallgató 1, tanszékvezető, egyetemi tanár 2 Miskolci
DARABÁRU OSZTÁLYOZÓ RENDSZEREK KISZOLGÁLÁSI STRATÉGIÁIT BEFOLYÁSOLÓ JELLEMZŐK; A RENDSZEREK MODULJAI KÖZÖTTI ÖSSZEFÜGGÉSEK FELTÁRÁSA
 DARABÁRU OSZTÁLYOZÓ RENDSZEREK KISZOLGÁLÁSI STRATÉGIÁIT BEFOLYÁSOLÓ JELLEMZŐK; A RENDSZEREK MODULJAI KÖZÖTTI ÖSSZEFÜGGÉSEK FELTÁRÁSA Tomkovics Tamás 1, Dr. Kovács László 2 Ph.D. hallgató, egyetemi docens
DARABÁRU OSZTÁLYOZÓ RENDSZEREK KISZOLGÁLÁSI STRATÉGIÁIT BEFOLYÁSOLÓ JELLEMZŐK; A RENDSZEREK MODULJAI KÖZÖTTI ÖSSZEFÜGGÉSEK FELTÁRÁSA Tomkovics Tamás 1, Dr. Kovács László 2 Ph.D. hallgató, egyetemi docens
Épületvillamosság laboratórium. Villámvédelemi felfogó-rendszer hatásosságának vizsgálata
 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék Nagyfeszültségű Technika és Berendezések Csoport Épületvillamosság laboratórium Villámvédelemi felfogó-rendszer hatásosságának
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék Nagyfeszültségű Technika és Berendezések Csoport Épületvillamosság laboratórium Villámvédelemi felfogó-rendszer hatásosságának
Kúpfogaskerék lefejtése léc-típusú szerszámmal
 Sapientia Erdélyi Magyar Tudományegyetem Műszaki és Humántudományok Kar Marosvásárhely Gépészmérnöki Tanszék Kúpfogaskerék lefejtése léc-típusú szerszámmal Sipos Bence, Sapientia EMTE, Marosvásárhely Műszaki
Sapientia Erdélyi Magyar Tudományegyetem Műszaki és Humántudományok Kar Marosvásárhely Gépészmérnöki Tanszék Kúpfogaskerék lefejtése léc-típusú szerszámmal Sipos Bence, Sapientia EMTE, Marosvásárhely Műszaki
Optimalizálási lehetőségek vizsgálata egy e-piactérrel integrált virtuális szállítási vállalatnál
 Optimalizálási lehetőségek vizsgálata egy e-piactérrel integrált virtuális szállítási vállalatnál ABSZTRAKT Skapinyecz Róbert 1, Illés Béla 2 PhD. hallgató Prof. Dr., tanszékvezető egyetemi tanár Miskolci
Optimalizálási lehetőségek vizsgálata egy e-piactérrel integrált virtuális szállítási vállalatnál ABSZTRAKT Skapinyecz Róbert 1, Illés Béla 2 PhD. hallgató Prof. Dr., tanszékvezető egyetemi tanár Miskolci
Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (13. fejezet)
 Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (3. fejezet). Egy H I = 70 m - 50000 s /m 5 Q jelleggörbéjű szivattyú a H c = 0 m + 0000 s /m 5 Q jelleggörbéjű
Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (3. fejezet). Egy H I = 70 m - 50000 s /m 5 Q jelleggörbéjű szivattyú a H c = 0 m + 0000 s /m 5 Q jelleggörbéjű
10. OPTIMÁLÁSI LEHETŐSÉGEK A MŰVELET-ELEMEK TERVEZÉSEKOR
 10. OPIMÁLÁSI LEHEŐSÉGEK A MŰVELE-ELEMEK ERVEZÉSEKOR A technológiai terezés ezen szintén a fő feladatok a köetkezők: a forgácsolási paraméterek meghatározása, a szerszám mozgásciklusok (üresárati, munkautak)
10. OPIMÁLÁSI LEHEŐSÉGEK A MŰVELE-ELEMEK ERVEZÉSEKOR A technológiai terezés ezen szintén a fő feladatok a köetkezők: a forgácsolási paraméterek meghatározása, a szerszám mozgásciklusok (üresárati, munkautak)
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 10 X DETERmINÁNSOk 1 DETERmINÁNS ÉRTELmEZÉSE, TULAJdONSÁGAI A másodrendű determináns értelmezése: A harmadrendű determináns értelmezése és annak első sor szerinti kifejtése: A
KOVÁCS BÉLA, MATEmATIkA I 10 X DETERmINÁNSOk 1 DETERmINÁNS ÉRTELmEZÉSE, TULAJdONSÁGAI A másodrendű determináns értelmezése: A harmadrendű determináns értelmezése és annak első sor szerinti kifejtése: A
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria
 005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
5. ROBOTOK IRÁNYÍTÓ RENDSZERE. 5.1. Robotok belső adatfeldolgozásának struktúrája
 TARTALOM 5. ROBOTOK IRÁNYÍTÓ RENDSZERE... 7 5.. Robotok belső adatfeldolgozásának struktúrája... 7 5.. Koordináta transzformációk... 5... Forgatás... 5... R-P-Y szögek... 5... Homogén transzformációk...
TARTALOM 5. ROBOTOK IRÁNYÍTÓ RENDSZERE... 7 5.. Robotok belső adatfeldolgozásának struktúrája... 7 5.. Koordináta transzformációk... 5... Forgatás... 5... R-P-Y szögek... 5... Homogén transzformációk...
A 27/2012 (VIII. 27.) NGM rendelet szakmai és vizsgakövetelménye alapján.
 A 27/2012 (VIII. 27.) NGM rendelet szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 54 521 03 Gépgyártástechnológiai technikus Tájékoztató A vizsgázó az első lapra írja
A 27/2012 (VIII. 27.) NGM rendelet szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 54 521 03 Gépgyártástechnológiai technikus Tájékoztató A vizsgázó az első lapra írja
MEREVSZÁRNYÚ REPÜLŐGÉPEK VEZÉRSÍK-RENDSZEREINEK KIALAKÍTÁSA 3 REPÜLŐKÉPESSÉG
 Dr. Óvári Gula 1 - Dr. Urbán István 2 MEREVSZÁRNYÚ REPÜLŐGÉPEK VEZÉRSÍK-RENDSZEREINEK KILKÍTÁS 3 cikk(soroatban)ben a merev sárnú repülőgépek veérsík rendserinek terveését és építését követheti nomon lépésről
Dr. Óvári Gula 1 - Dr. Urbán István 2 MEREVSZÁRNYÚ REPÜLŐGÉPEK VEZÉRSÍK-RENDSZEREINEK KILKÍTÁS 3 cikk(soroatban)ben a merev sárnú repülőgépek veérsík rendserinek terveését és építését követheti nomon lépésről
Mágneses szuszceptibilitás vizsgálata
 Mágneses szuszceptibilitás vizsgálata Mérést végezte: Gál Veronika I. A mérés elmélete Az anyagok külső mágnesen tér hatására polarizálódnak. Általában az anyagok mágnesezhetőségét az M mágnesezettség
Mágneses szuszceptibilitás vizsgálata Mérést végezte: Gál Veronika I. A mérés elmélete Az anyagok külső mágnesen tér hatására polarizálódnak. Általában az anyagok mágnesezhetőségét az M mágnesezettség
31 521 09 1000 00 00 Gépi forgácsoló Gépi forgácsoló
 Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján. Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján. Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
Egységes jelátalakítók
 6. Laboratóriumi gyakorlat Egységes jelátalakítók 1. A gyakorlat célja Egységes feszültség és egységes áram jelformáló áramkörök tanulmányozása, átviteli karakterisztikák felvétele, terhelésfüggőségük
6. Laboratóriumi gyakorlat Egységes jelátalakítók 1. A gyakorlat célja Egységes feszültség és egységes áram jelformáló áramkörök tanulmányozása, átviteli karakterisztikák felvétele, terhelésfüggőségük
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
FOGASKEREKEK GYÁRTÁSA ELŐADÁS
 FOGASKEREKEK GYÁRTÁSA ELŐADÁS Felhasznált irodalom: Dr. Kodácsy János: Forgácsolás szerszámai, E-tananyag, Kecskemét, 2010. Dr. Mikó Balázs: Forgácsolási folyamatok számítógépes tervezése előadásanyag,
FOGASKEREKEK GYÁRTÁSA ELŐADÁS Felhasznált irodalom: Dr. Kodácsy János: Forgácsolás szerszámai, E-tananyag, Kecskemét, 2010. Dr. Mikó Balázs: Forgácsolási folyamatok számítógépes tervezése előadásanyag,
1. Feladatok a dinamika tárgyköréből
 1. Feladatok a dinamika tárgyköréből Newton három törvénye 1.1. Feladat: Órai kidolgozásra: 1. feladat Három azonos m tömegű gyöngyszemet fonálra fűzünk, egymástól kis távolságokban a fonálhoz rögzítünk,
1. Feladatok a dinamika tárgyköréből Newton három törvénye 1.1. Feladat: Órai kidolgozásra: 1. feladat Három azonos m tömegű gyöngyszemet fonálra fűzünk, egymástól kis távolságokban a fonálhoz rögzítünk,
VASBETON LEMEZEK. Oktatási segédlet v1.0. Összeállította: Dr. Bódi István - Dr. Farkas György. Budapest, 2001. május hó
 BUDAPEST MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Építőmérnöki Kar Hidak és Szerkezetek Tanszéke VASBETON LEMEZEK Oktatási segédlet v1.0 Összeállította: Dr. Bódi István - Dr. Farkas Görg Budapest, 001. május
BUDAPEST MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Építőmérnöki Kar Hidak és Szerkezetek Tanszéke VASBETON LEMEZEK Oktatási segédlet v1.0 Összeállította: Dr. Bódi István - Dr. Farkas Görg Budapest, 001. május
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 12 XII. STATIsZTIKA ellenőrző feladatsorok 1. FELADATsOR Megoldások: láthatók nem láthatók 1. minta: 6.10, 0.01, 6.97, 6.03, 3.85, 1.11,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 12 XII. STATIsZTIKA ellenőrző feladatsorok 1. FELADATsOR Megoldások: láthatók nem láthatók 1. minta: 6.10, 0.01, 6.97, 6.03, 3.85, 1.11,
Differenciál egyenletek (rövid áttekintés) d x 2
 Differeniál egenletek (rövid áttekintés) Differeniálegenlet: olan matematikai egenlet, amel eg vag több változós ismeretlen függvén és deriváltjai közötti kasolatot írja le. Fontosabb tíusok: közönséges
Differeniál egenletek (rövid áttekintés) Differeniálegenlet: olan matematikai egenlet, amel eg vag több változós ismeretlen függvén és deriváltjai közötti kasolatot írja le. Fontosabb tíusok: közönséges
FOGASKERÉKHAJTÁSOK (Vázlat)
 FOGASKERÉKHAJTÁSOK (Vázlat) Tengelykapcsolók Hajtásrendszer (hajtáslánc): erő és munkagépek összekapcsolására szolgáló, energiát (teljesítményt, nyomatékot) továbbító, átalakító szerkezeti elemek. 1 Hajtások
FOGASKERÉKHAJTÁSOK (Vázlat) Tengelykapcsolók Hajtásrendszer (hajtáslánc): erő és munkagépek összekapcsolására szolgáló, energiát (teljesítményt, nyomatékot) továbbító, átalakító szerkezeti elemek. 1 Hajtások
DESIGNING AND MODELLING OF WORM GEAR HOB
 DESIGNING AND MODELLING OF WORM GEAR HOB Sándor Bodzás 1, Dr. Illés Dudás 2 1 PhD student, bodzassandor@nyf.hu 2 DSc professor, illes.dudas@uni-miskolc.hu 1,2 Department of Production Engineering, University
DESIGNING AND MODELLING OF WORM GEAR HOB Sándor Bodzás 1, Dr. Illés Dudás 2 1 PhD student, bodzassandor@nyf.hu 2 DSc professor, illes.dudas@uni-miskolc.hu 1,2 Department of Production Engineering, University
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
BETONACÉLOK HAJLÍTÁSÁHOZ SZÜKSÉGES l\4"yomaték MEGHATÁROZÁSÁNAK EGYSZERŰ MÓDSZERE
 BETONACÉLOK HAJLÍTÁSÁHOZ SZÜKSÉGES l\4"yomaték MEGHATÁROZÁSÁNAK EGYSZERŰ MÓDSZERE BACZY"SKI Gábor Budape?ti 1Iűszaki Egyetem, Közlekedésmérnöki Kar Epítő- és Anyagmozgató Gépek Tanszék Körkeresztmetszet{Í
BETONACÉLOK HAJLÍTÁSÁHOZ SZÜKSÉGES l\4"yomaték MEGHATÁROZÁSÁNAK EGYSZERŰ MÓDSZERE BACZY"SKI Gábor Budape?ti 1Iűszaki Egyetem, Közlekedésmérnöki Kar Epítő- és Anyagmozgató Gépek Tanszék Körkeresztmetszet{Í
Lepárlás. 8. Lepárlás
 eárlás 8. eárlás csefolós elegek szétválasztására leggakrabban használt művelet a leárlás. Míg az egszeri leárlás desztilláció néven is ismerjük az ismételt leárlás vag ismételt desztillációt rektifikálásnak
eárlás 8. eárlás csefolós elegek szétválasztására leggakrabban használt művelet a leárlás. Míg az egszeri leárlás desztilláció néven is ismerjük az ismételt leárlás vag ismételt desztillációt rektifikálásnak
Mechanika II. Szilárdságtan
 echanika II. Szilárdságtan Zalka Károl / q / B Budapest, 05 Zalka Károl, 05, e-kiadás Szabad ezt a kiadvánt sokszorosítani, terjeszteni és elektronikus vag bármel formában tárolni. Tilos viszont a kiadvánt
echanika II. Szilárdságtan Zalka Károl / q / B Budapest, 05 Zalka Károl, 05, e-kiadás Szabad ezt a kiadvánt sokszorosítani, terjeszteni és elektronikus vag bármel formában tárolni. Tilos viszont a kiadvánt
Digitális technika (VIMIAA01) Laboratórium 1
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika (VIMIAA01) Laboratórium 1 Fehér Béla Raikovich Tamás,
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika (VIMIAA01) Laboratórium 1 Fehér Béla Raikovich Tamás,
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2007. május 25. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2007. május 25. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
ÉRETTSÉGI VIZSGA 2007. május 25. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2007. május 25. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
SZILÁRDSÁGTAN A minimum teszt kérdései a gépészmérnöki szak egyetemi ágon tanuló hallgatói részére (2004/2005 tavaszi félév, szigorlat)
 SILÁRDSÁGTAN A minimum teszt kérdései a gépészmérnöki szak egetemi ágon tanuló hallgatói részére (2004/2005 tavaszi félév, szigorlat) Szilárdságtan Pontszám 1. A másodrendű tenzor értelmezése (2) 2. A
SILÁRDSÁGTAN A minimum teszt kérdései a gépészmérnöki szak egetemi ágon tanuló hallgatói részére (2004/2005 tavaszi félév, szigorlat) Szilárdságtan Pontszám 1. A másodrendű tenzor értelmezése (2) 2. A
Párhuzamos programozás
 Párhuzamos programozás Rendezések Készítette: Györkő Péter EHA: GYPMABT.ELTE Nappali tagozat Programtervező matematikus szak Budapest, 2009 május 9. Bevezetés A számítástechnikában felmerülő problémák
Párhuzamos programozás Rendezések Készítette: Györkő Péter EHA: GYPMABT.ELTE Nappali tagozat Programtervező matematikus szak Budapest, 2009 május 9. Bevezetés A számítástechnikában felmerülő problémák
NAGYSZILÁRDSÁGÚ ACÉLOK HEGESZTÉSTECHNOLÓGIÁJÁNAK FEJLESZTÉSE A HŰLÉSI IDŐ ELEMZÉSÉVEL
 NAGYSZILÁRDSÁGÚ ACÉLOK HEGESZTÉSTECHNOLÓGIÁJÁNAK FEJLESZTÉSE A HŰLÉSI IDŐ ELEMZÉSÉVEL Gáspár Marcell Gyula 1, Dr. Balogh András 2 1 PhD hallgató, 2 egyetemi docens Miskolci Egyetem Mechanikai Technológiai
NAGYSZILÁRDSÁGÚ ACÉLOK HEGESZTÉSTECHNOLÓGIÁJÁNAK FEJLESZTÉSE A HŰLÉSI IDŐ ELEMZÉSÉVEL Gáspár Marcell Gyula 1, Dr. Balogh András 2 1 PhD hallgató, 2 egyetemi docens Miskolci Egyetem Mechanikai Technológiai
2010.08.29. 05 - Hengeres fogaskerekek gyártása. Hengeres Kúp Csiga. Egyenes Ferde Ívelt. Modul: m=d/z. A modul szabványos!!!
 Óbudai Egyetem Bánki Donát Gépész és Biztonságtechnikai Mérnöki Kar Anyagtudományi és Gyártástechnológiai Intézet Forgácsolás technológia számítógépes BAGFS15NNC/NLC 05 - Hengeres fogaskerekek gyártása
Óbudai Egyetem Bánki Donát Gépész és Biztonságtechnikai Mérnöki Kar Anyagtudományi és Gyártástechnológiai Intézet Forgácsolás technológia számítógépes BAGFS15NNC/NLC 05 - Hengeres fogaskerekek gyártása
Használható segédeszköz: szabványok, táblázatok, gépkönyvek, számológép
 A 27/2012 (VIII. 27.) NGM rendelet (12/2013 (III.28) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 34 522 02 Elektromos gép és készülékszerelő
A 27/2012 (VIII. 27.) NGM rendelet (12/2013 (III.28) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 34 522 02 Elektromos gép és készülékszerelő
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 006. május 18. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 006. május 18. 1:00 Az írásbeli vizsga időtartama: 0 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI MINISZTÉRIUM
ÉRETTSÉGI VIZSGA 006. május 18. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 006. május 18. 1:00 Az írásbeli vizsga időtartama: 0 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI MINISZTÉRIUM
1. Mintapélda, amikor a fenék lekerekítési sugár (Rb) kicsi
 1 Mélyhúzott edény teríték méretének meghatározása 1. Mintapélda, amikor a fenék lekerekítési sugár (Rb) kicsi A mélyhúzott edény kiindulási teríték átmérőjének meghatározása a térfogat-állandóság alapján
1 Mélyhúzott edény teríték méretének meghatározása 1. Mintapélda, amikor a fenék lekerekítési sugár (Rb) kicsi A mélyhúzott edény kiindulási teríték átmérőjének meghatározása a térfogat-állandóság alapján
GÉPSZERKEZETTAN - TERVEZÉS. Csigahajtások
 GÉPSZERKEZETTAN - TERVEZÉS Csigahajtások Konstrukció (felsőcsigás hajtómű) Gépszerkezettan, tervezés Csigahajtások 2 Konstrukció (alsócsigás hajtómű) Gépszerkezettan, tervezés Csigahajtások 3 Műszaki jellemzők
GÉPSZERKEZETTAN - TERVEZÉS Csigahajtások Konstrukció (felsőcsigás hajtómű) Gépszerkezettan, tervezés Csigahajtások 2 Konstrukció (alsócsigás hajtómű) Gépszerkezettan, tervezés Csigahajtások 3 Műszaki jellemzők
II./2. FOGASKEREKEK ÉS FOGAZOTT HAJTÁSOK
 II./. FOGASKEREKEK ÉS FOGAZOTT HAJTÁSOK A FOGASKEREKEK FUNKCIÓJA ÉS TÍPUSAI : Az áéel (ahol az index mindig a hajó kereke jelöli): n ω i n ω A fogszámviszony (ahol az index mindig a kisebb kereke jelöli):
II./. FOGASKEREKEK ÉS FOGAZOTT HAJTÁSOK A FOGASKEREKEK FUNKCIÓJA ÉS TÍPUSAI : Az áéel (ahol az index mindig a hajó kereke jelöli): n ω i n ω A fogszámviszony (ahol az index mindig a kisebb kereke jelöli):
A mérés célja: Példák a műveleti erősítők lineáris üzemben történő felhasználására, az előadásokon elhangzottak alkalmazása a gyakorlatban.
 E II. 6. mérés Műveleti erősítők alkalmazása A mérés célja: Példák a műveleti erősítők lineáris üzemben történő felhasználására, az előadásokon elhangzottak alkalmazása a gyakorlatban. A mérésre való felkészülés
E II. 6. mérés Műveleti erősítők alkalmazása A mérés célja: Példák a műveleti erősítők lineáris üzemben történő felhasználására, az előadásokon elhangzottak alkalmazása a gyakorlatban. A mérésre való felkészülés
VASÚTI PÁLYA DINAMIKÁJA
 VASÚTI PÁLYA DINAMIKÁJA Dynamics of the railway track Liegner Nándor BME Út és Vasútépítési Tanszék A vasúti felépítmény szerkezeti elemeiben ébredő igénybevételek A Zimmermann Eisenmann elmélet alapján
VASÚTI PÁLYA DINAMIKÁJA Dynamics of the railway track Liegner Nándor BME Út és Vasútépítési Tanszék A vasúti felépítmény szerkezeti elemeiben ébredő igénybevételek A Zimmermann Eisenmann elmélet alapján
TRANZISZTOROS KAPCSOLÁSOK KÉZI SZÁMÍTÁSA
 TRNZSZTOROS KPSOLÁSOK KÉZ SZÁMÍTÁS 1. gyenáramú számítás kézi számításokhoz az ábrán látható egyszerű közelítést használjuk: = Normál aktív tartományban a tranzisztort bázis-emitter diódáját az feszültségforrással
TRNZSZTOROS KPSOLÁSOK KÉZ SZÁMÍTÁS 1. gyenáramú számítás kézi számításokhoz az ábrán látható egyszerű közelítést használjuk: = Normál aktív tartományban a tranzisztort bázis-emitter diódáját az feszültségforrással
A KÖZOP-3.5.0-09-11-2012-0018 projekt rövid bemutatása
 A KÖZOP-3.5.0-09-11-2012-0018 projekt rövid bemutatása Rétháti András Célkitűzés: az utóbbi évtizedben számos országban alkalmazott 2+1 / 1+2 sávos keresztmetszetű utak hazai bevezetési lehetőségeinek,
A KÖZOP-3.5.0-09-11-2012-0018 projekt rövid bemutatása Rétháti András Célkitűzés: az utóbbi évtizedben számos országban alkalmazott 2+1 / 1+2 sávos keresztmetszetű utak hazai bevezetési lehetőségeinek,
A Hozzárendelési feladat megoldása Magyar-módszerrel
 A Hozzárendelési feladat megoldása Magyar-módszerrel Virtuális vállalat 2013-2014/1. félév 3. gyakorlat Dr. Kulcsár Gyula A Hozzárendelési feladat Adott meghatározott számú gép és ugyanannyi független
A Hozzárendelési feladat megoldása Magyar-módszerrel Virtuális vállalat 2013-2014/1. félév 3. gyakorlat Dr. Kulcsár Gyula A Hozzárendelési feladat Adott meghatározott számú gép és ugyanannyi független
KOMPLEX TERVEZÉS TERVEZÉSI SZAKIRÁNY TARTÓSZERKEZETI FELADATRÉSZ 1. félév
 KOMPLEX TERVEZÉS TERVEZÉSI SZAKIRÁNY 1. félév engedélyezési terv szintű dokumentáció tartószerkezeti munkarészének elkészítése folyamatos konzultáció, az első konzultációnak a vázlatterv beadás előtt meg
KOMPLEX TERVEZÉS TERVEZÉSI SZAKIRÁNY 1. félév engedélyezési terv szintű dokumentáció tartószerkezeti munkarészének elkészítése folyamatos konzultáció, az első konzultációnak a vázlatterv beadás előtt meg
Szilárdságtan. Miskolci Egyetem GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR
 Miskolci Egetem GÉÉMÉRNÖKI É INORMTIKI KR ilárságtan (Oktatási segélet a Gépésmérnöki és Informatikai Kar sc leveleős hallgatói résére) Késítette: Nánori riges, irbik ánor Miskolc, 2008. Een kéirat a Gépésmérnöki
Miskolci Egetem GÉÉMÉRNÖKI É INORMTIKI KR ilárságtan (Oktatási segélet a Gépésmérnöki és Informatikai Kar sc leveleős hallgatói résére) Késítette: Nánori riges, irbik ánor Miskolc, 2008. Een kéirat a Gépésmérnöki
Jelek tanulmányozása
 Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
Dr. Kulcsár Gyula. Virtuális vállalat 2013-2014 1. félév. Projektütemezés. Virtuális vállalat 2013-2014 1. félév 5. gyakorlat Dr.
 Projektütemezés Virtuális vállalat 03-04. félév 5. gyakorlat Dr. Kulcsár Gyula Projektütemezési feladat megoldása Projekt: Projektütemezés Egy nagy, összetett, általában egyedi igény alapján előállítandó
Projektütemezés Virtuális vállalat 03-04. félév 5. gyakorlat Dr. Kulcsár Gyula Projektütemezési feladat megoldása Projekt: Projektütemezés Egy nagy, összetett, általában egyedi igény alapján előállítandó
18. előadás ÁLLANDÓ KÖLTSÉGEK ÉS A KÖLTSÉGGÖRBÉK
 18. előadás ÁLLANDÓ KÖLTSÉGEK ÉS A KÖLTSÉGGÖRBÉK Kertesi Gábor Világi Balázs Varian 21. fejezete átdolgozva 18.1 Bevezető A vállalati technológiák sajátosságainak vizsgálatát eg igen fontos elemzési eszköz,
18. előadás ÁLLANDÓ KÖLTSÉGEK ÉS A KÖLTSÉGGÖRBÉK Kertesi Gábor Világi Balázs Varian 21. fejezete átdolgozva 18.1 Bevezető A vállalati technológiák sajátosságainak vizsgálatát eg igen fontos elemzési eszköz,
Programozás I. - 9. gyakorlat
 Programozás I. - 9. gyakorlat Mutatók, dinamikus memóriakezelés Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Rendszer- és Számítástudományi Tanszék Utolsó frissítés: November 9, 2009 1 tar@dcs.vein.hu
Programozás I. - 9. gyakorlat Mutatók, dinamikus memóriakezelés Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Rendszer- és Számítástudományi Tanszék Utolsó frissítés: November 9, 2009 1 tar@dcs.vein.hu
Matematika OKTV I. kategória 2017/2018 második forduló szakgimnázium-szakközépiskola
 O k t a t á s i H i v a t a l A 017/018. tanévi Országos Középiskolai Tanulmáni Versen második forduló MATEMATIKA I. KATEGÓRIA (SZAKGIMNÁZIUM, SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató 1. Adja meg
O k t a t á s i H i v a t a l A 017/018. tanévi Országos Középiskolai Tanulmáni Versen második forduló MATEMATIKA I. KATEGÓRIA (SZAKGIMNÁZIUM, SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató 1. Adja meg
[GVMGS11MNC] Gazdaságstatisztika
![[GVMGS11MNC] Gazdaságstatisztika [GVMGS11MNC] Gazdaságstatisztika](/thumbs/40/21500887.jpg) [GVMGS11MNC] Gazdaságstatisztika 4 előadás Főátlagok összehasonlítása http://uni-obudahu/users/koczyl/gazdasagstatisztikahtm Kóczy Á László KGK-VMI Viszonyszámok (emlékeztető) Jelenség színvonalának vizsgálata
[GVMGS11MNC] Gazdaságstatisztika 4 előadás Főátlagok összehasonlítása http://uni-obudahu/users/koczyl/gazdasagstatisztikahtm Kóczy Á László KGK-VMI Viszonyszámok (emlékeztető) Jelenség színvonalának vizsgálata
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2010. május 1. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2010. május 1. 8:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
ÉRETTSÉGI VIZSGA 2010. május 1. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2010. május 1. 8:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
A forgácsolás alapjai
 NGB_AJ012_1 Forgácsoló megmunkálás (Forgácsolás és szerszámai) A forgácsolás alapjai Dr. Pintér József 2015. FONTOS! KÉREM, NE FELEDJÉK, HOGY A PowerPoint ELŐADÁS VÁZLAT NEM HELYETTESÍTI, CSAK ÖSSZEFOGLALJA,
NGB_AJ012_1 Forgácsoló megmunkálás (Forgácsolás és szerszámai) A forgácsolás alapjai Dr. Pintér József 2015. FONTOS! KÉREM, NE FELEDJÉK, HOGY A PowerPoint ELŐADÁS VÁZLAT NEM HELYETTESÍTI, CSAK ÖSSZEFOGLALJA,
Tantárgyi program. 9. A tantárgy hallgatásának előfeltétele, előképzettségi szint: 10. A tantárgy tartalma:
 Tantárgyi program 1. A tantárgy neve, kódja: AVM_VFLB111-K5 Marketing menedzsment 2. A neve, beosztása: 3. Szakcsoport (szakirány) megnevezése: Vállalkozásfejlesztés MSc szak, levelező tagozat 4. A tantárgy
Tantárgyi program 1. A tantárgy neve, kódja: AVM_VFLB111-K5 Marketing menedzsment 2. A neve, beosztása: 3. Szakcsoport (szakirány) megnevezése: Vállalkozásfejlesztés MSc szak, levelező tagozat 4. A tantárgy
Műszaki ábrázolás II. 3. Házi feladat. Hegesztett szerkezet
 Hegesztett szerkezet Feladat: Hegesztett szerkezet rajzának elkészítése. Szükséges eszközök: A3-as fehér rajzlap az összeállítási és alkatrészrajzokhoz szerkesztési táblázat az anyagminőségek és a szabványos
Hegesztett szerkezet Feladat: Hegesztett szerkezet rajzának elkészítése. Szükséges eszközök: A3-as fehér rajzlap az összeállítási és alkatrészrajzokhoz szerkesztési táblázat az anyagminőségek és a szabványos
A döntő feladatai. valós számok!
 OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
10.3. A MÁSODFOKÚ EGYENLET
 .. A MÁSODFOKÚ EGYENLET A másodfokú egenlet és függvén megoldások w9 a) ( ) + ; b) ( ) + ; c) ( + ) ; d) ( 6) ; e) ( + 8) 6; f) ( ) 9; g) (,),; h) ( +,),; i) ( ) + ; j) ( ) ; k) ( + ) + 7; l) ( ) + 9.
.. A MÁSODFOKÚ EGYENLET A másodfokú egenlet és függvén megoldások w9 a) ( ) + ; b) ( ) + ; c) ( + ) ; d) ( 6) ; e) ( + 8) 6; f) ( ) 9; g) (,),; h) ( +,),; i) ( ) + ; j) ( ) ; k) ( + ) + 7; l) ( ) + 9.
Kooperáció és intelligencia
 Kooperáció és intelligencia Tanulás többágenses szervezetekben/2 Tanulás több ágensből álló környezetben -a mozgó cél tanulás problémája (alapvetően megerősítéses tanulás) Legyen az ágens közösség formalizált
Kooperáció és intelligencia Tanulás többágenses szervezetekben/2 Tanulás több ágensből álló környezetben -a mozgó cél tanulás problémája (alapvetően megerősítéses tanulás) Legyen az ágens közösség formalizált
[MECHANIKA- HAJLÍTÁS]
![[MECHANIKA- HAJLÍTÁS] [MECHANIKA- HAJLÍTÁS]](/thumbs/39/20428431.jpg) 2010. Eötvös Loránd Szakközép és Szakiskola Molnár István [MECHANIKA- HAJLÍTÁS] 1 A hajlításra való méretezést sok helyen lehet használni, sok mechanikai probléma modelljét vissza lehet vezetni a hajlítás
2010. Eötvös Loránd Szakközép és Szakiskola Molnár István [MECHANIKA- HAJLÍTÁS] 1 A hajlításra való méretezést sok helyen lehet használni, sok mechanikai probléma modelljét vissza lehet vezetni a hajlítás
Programozható irányítóberendezések és szenzorrendszerek ZH. Távadók. Érdemjegy
 Név Neptun-kód Hallgató aláírása 0-15 pont: elégtelen (1) 16-21 pont: elégséges (2) 22-27 pont: közepes (3) 28-33 pont: jó (4) 34-40 pont: jeles (5) Érzékelők jellemzése Hőmérsékletérzékelés Erő- és nyomásmérés
Név Neptun-kód Hallgató aláírása 0-15 pont: elégtelen (1) 16-21 pont: elégséges (2) 22-27 pont: közepes (3) 28-33 pont: jó (4) 34-40 pont: jeles (5) Érzékelők jellemzése Hőmérsékletérzékelés Erő- és nyomásmérés
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2006. október 2. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2006. október 2. 1:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
ÉRETTSÉGI VIZSGA 2006. október 2. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2006. október 2. 1:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
RAISZ PÉTERNÉ PÉLDATÁR Differenciálegyenletek
 RAISZ PÉTERNÉ PÉLDATÁR Differenciálegenletek témakörből a Matematika II c tárghoz Elméleti összefoglaló 50 kidolgozott feladattal "Ez a példatár a TÁMOP-4B-0//KONV-00-000 jelű projekt részeként az Európai
RAISZ PÉTERNÉ PÉLDATÁR Differenciálegenletek témakörből a Matematika II c tárghoz Elméleti összefoglaló 50 kidolgozott feladattal "Ez a példatár a TÁMOP-4B-0//KONV-00-000 jelű projekt részeként az Európai
2011. március 9. Dr. Vincze Szilvia
 . márius 9. Dr. Vinze Szilvia Tartalomjegyzék.) Elemi bázistranszformáió.) Elemi bázistranszformáió alkalmazásai.) Lineáris függőség/függetlenség meghatározása.) Kompatibilitás vizsgálata.) Mátri/vektorrendszer
. márius 9. Dr. Vinze Szilvia Tartalomjegyzék.) Elemi bázistranszformáió.) Elemi bázistranszformáió alkalmazásai.) Lineáris függőség/függetlenség meghatározása.) Kompatibilitás vizsgálata.) Mátri/vektorrendszer
ÍRÁSBELI FELADAT MEGOLDÁSA
 54 523 04 1000 00 00-2014 MAGYAR KERESKEDELMI ÉS IPARKAMARA Országos Szakmai Tanulmányi Verseny Elődöntő ÍRÁSBELI FELADAT MEGOLDÁSA Szakképesítés: 54 523 04 1000 00 00 SZVK rendelet száma: Modulok: 6308-11
54 523 04 1000 00 00-2014 MAGYAR KERESKEDELMI ÉS IPARKAMARA Országos Szakmai Tanulmányi Verseny Elődöntő ÍRÁSBELI FELADAT MEGOLDÁSA Szakképesítés: 54 523 04 1000 00 00 SZVK rendelet száma: Modulok: 6308-11
Henger körüli áramlás. Henger körüli áramlás. Henger körüli áramlás 2015.03.02. ρ 2. R z. R z = 2 2. c A. = 4c. c p. = 2c. y/r 1.5.
 5.3.. Henger körüli áramlás y/r.5.5.5 x/r.5 3 3 R w z + z R R iϑ e r R R z ( os ϑ + i sin ϑ ) Henger körüli áramlás ( os ϑ i sin ϑ ) r R + [ ϑ + sin ϑ ] ( ) ( os ) r R r R os ϑ + os ϑ + sin ϑ 444 3 r R
5.3.. Henger körüli áramlás y/r.5.5.5 x/r.5 3 3 R w z + z R R iϑ e r R R z ( os ϑ + i sin ϑ ) Henger körüli áramlás ( os ϑ i sin ϑ ) r R + [ ϑ + sin ϑ ] ( ) ( os ) r R r R os ϑ + os ϑ + sin ϑ 444 3 r R
XII. MAGYAR MECHANIKAI KONFERENCIA MaMeK, 2015 Miskolc, 2015. augusztus 25-27.
 XII. MAGYAR MECHANIKAI KONFERENCIA MaMeK, 215 Miskolc, 215. augusztus 25-27. MARÁSI FOLYAMAT STABILITÁSA A SZERSZÁMÉLEN MEGOSZLÓ ÁLLANDÓ INTENZITÁSÚ FORGÁCSOLÓ ERŐRENDSZER ESETÉN Molnár Tamás G. 1, Insperger
XII. MAGYAR MECHANIKAI KONFERENCIA MaMeK, 215 Miskolc, 215. augusztus 25-27. MARÁSI FOLYAMAT STABILITÁSA A SZERSZÁMÉLEN MEGOSZLÓ ÁLLANDÓ INTENZITÁSÚ FORGÁCSOLÓ ERŐRENDSZER ESETÉN Molnár Tamás G. 1, Insperger
1. Írja fel prímszámok szorzataként a 420-at! 2. Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen!
 1. Írja fel prímszámok szorzataként a 40-at! 40 =. Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen! A részek: 3. Egy sejttenyészetben naponta kétszereződik meg a sejtek száma.
1. Írja fel prímszámok szorzataként a 40-at! 40 =. Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen! A részek: 3. Egy sejttenyészetben naponta kétszereződik meg a sejtek száma.
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2005. május 20. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI MINISZTÉRIM Elektronikai alapismeretek
ÉRETTSÉGI VIZSGA 2005. május 20. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI MINISZTÉRIM Elektronikai alapismeretek
TANTÁRGYI ÚTMUTATÓ. Pénzügyi-számviteli informatika 2. tanulmányokhoz
 IV. évfolyam Pénzügy és Számvitel Szak/Minden szakirány BA TANTÁRGYI ÚTMUTATÓ Pénzügyi-számviteli informatika 2. tanulmányokhoz TÁVOKTATÁS 2014/2015. I. félév A KURZUS ALAPADATAI Tárgy megnevezése: Pénzügyi-számviteli
IV. évfolyam Pénzügy és Számvitel Szak/Minden szakirány BA TANTÁRGYI ÚTMUTATÓ Pénzügyi-számviteli informatika 2. tanulmányokhoz TÁVOKTATÁS 2014/2015. I. félév A KURZUS ALAPADATAI Tárgy megnevezése: Pénzügyi-számviteli
Jelölje meg (aláhúzással vagy keretezéssel) Gyakorlatvezetőjét! Györke Gábor Kovács Viktória Barbara Könczöl Sándor. Hőközlés.
 MŰSZAKI HŐTAN II.. ZÁRTHELYI Adja meg az Ön képzési kódját! N Név: Azonosító: Terem Helyszám: K - Jelölje meg (aláhúzással vagy keretezéssel) Gyakorlatvezetőjét! Györke Gábor Kovács Viktória Barbara Könczöl
MŰSZAKI HŐTAN II.. ZÁRTHELYI Adja meg az Ön képzési kódját! N Név: Azonosító: Terem Helyszám: K - Jelölje meg (aláhúzással vagy keretezéssel) Gyakorlatvezetőjét! Györke Gábor Kovács Viktória Barbara Könczöl
MATEMATIKA HETI 3 ÓRA
 EURÓPAI ÉRETTSÉGI 010 MATEMATIKA HETI 3 ÓRA IDŐPONT : 010. június 4. A VIZSGA IDŐTARTAMA : 3 óra (180 perc) MEGENGEDETT SEGÉDESZKÖZÖK : Európai képletgyűjtemény Nem programozható, nem grafikus kalkulátor
EURÓPAI ÉRETTSÉGI 010 MATEMATIKA HETI 3 ÓRA IDŐPONT : 010. június 4. A VIZSGA IDŐTARTAMA : 3 óra (180 perc) MEGENGEDETT SEGÉDESZKÖZÖK : Európai képletgyűjtemény Nem programozható, nem grafikus kalkulátor
Vasúti pálya függőleges elmozdulásának vizsgálata
 BUDAPESTI M Ű S Z A K I É S G A Z D A S Á G T U D O M Á N Y I E G Y E T E M É p í t ő m é r n ö k i K a r Á l t a l á n o s - é s F e l s ő g e o d é z i a Ta n s z é k F o t o g r a m m e t r i a é s
BUDAPESTI M Ű S Z A K I É S G A Z D A S Á G T U D O M Á N Y I E G Y E T E M É p í t ő m é r n ö k i K a r Á l t a l á n o s - é s F e l s ő g e o d é z i a Ta n s z é k F o t o g r a m m e t r i a é s
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2010. október 18. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2010. október 18. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS
ÉRETTSÉGI VIZSGA 2010. október 18. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2010. október 18. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS
Korszerű geodéziai adatfeldolgozás Kulcsár Attila
 Korszerű geodéziai adatfeldolgozás Kulcsár Attila Nyugat-Magyarországi Egyetem Geoinformatikai Főiskolai Kar Térinformatika Tanszék 8000 Székesfehérvár, Pirosalma -3 Tel/fax: (22) 348 27 E-mail: a.kulcsar@geo.info.hu.
Korszerű geodéziai adatfeldolgozás Kulcsár Attila Nyugat-Magyarországi Egyetem Geoinformatikai Főiskolai Kar Térinformatika Tanszék 8000 Székesfehérvár, Pirosalma -3 Tel/fax: (22) 348 27 E-mail: a.kulcsar@geo.info.hu.
Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata. Az r-time és a TNS Hoffmann által végzett kutatás
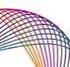 Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata Az r-time és a TNS Hoffmann által végzett kutatás 2002-2010: stabil szponzorációs részarány Televíziós reklámbevételek
Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata Az r-time és a TNS Hoffmann által végzett kutatás 2002-2010: stabil szponzorációs részarány Televíziós reklámbevételek
Vasbetonszerkezetek II. STNA252
 Szilárdságtan és Tartószerkezet Tanszéke Vasbetonszerkezetek II. STNA5 Pécs, 007. november STNA5 Szerző: Kiss Rita M. Műszaki rajzoló: Szabó Imre Gábor ISBN szám: Kézirat lezárva: 007. november 30. STNA5
Szilárdságtan és Tartószerkezet Tanszéke Vasbetonszerkezetek II. STNA5 Pécs, 007. november STNA5 Szerző: Kiss Rita M. Műszaki rajzoló: Szabó Imre Gábor ISBN szám: Kézirat lezárva: 007. november 30. STNA5
Monetáris politika. 5. el adás. Hosszú távú modell: alkalmazások. Kuncz Izabella. Makroökonómia Tanszék Budapesti Corvinus Egyetem.
 Hosszú távú modell: alkalmazások Makroökonómia Tanszék Budapesti Corvinus Egyetem Makroökonómia Mit tudunk eddig? Hogyan épül fel a hosszú távú modell? Hogyan hat a skális politika a gazdaságra? Hogyan
Hosszú távú modell: alkalmazások Makroökonómia Tanszék Budapesti Corvinus Egyetem Makroökonómia Mit tudunk eddig? Hogyan épül fel a hosszú távú modell? Hogyan hat a skális politika a gazdaságra? Hogyan
EPER E-KATA integráció
 EPER E-KATA integráció 1. Összhang a Hivatalban A hivatalban használt szoftverek összekapcsolása, integrálása révén az egyes osztályok, nyilvántartások között egyezőség jön létre. Mit is jelent az integráció?
EPER E-KATA integráció 1. Összhang a Hivatalban A hivatalban használt szoftverek összekapcsolása, integrálása révén az egyes osztályok, nyilvántartások között egyezőség jön létre. Mit is jelent az integráció?
Lineáris algebra gyakorlat
 Lineáris algebra gyakorlat 3 gyakorlat Gyakorlatvezet : Bogya Norbert 2012 február 27 Bogya Norbert Lineáris algebra gyakorlat (3 gyakorlat) Tartalom Egyenletrendszerek Cramer-szabály 1 Egyenletrendszerek
Lineáris algebra gyakorlat 3 gyakorlat Gyakorlatvezet : Bogya Norbert 2012 február 27 Bogya Norbert Lineáris algebra gyakorlat (3 gyakorlat) Tartalom Egyenletrendszerek Cramer-szabály 1 Egyenletrendszerek
Fogaskerék megmunkálás technológiája és szerszámai
 NGB_AJ012_1 Forgácsoló megmunkálás (Forgácsolás és szerszámai) Fogaskerék megmunkálás technológiája és szerszámai Dr. Pintér József 2015. Felhasznált irodalom: Pápai Gábor.ppt prezentációja 2013. Dr. Horváth
NGB_AJ012_1 Forgácsoló megmunkálás (Forgácsolás és szerszámai) Fogaskerék megmunkálás technológiája és szerszámai Dr. Pintér József 2015. Felhasznált irodalom: Pápai Gábor.ppt prezentációja 2013. Dr. Horváth
54 481 01 1000 00 00 CAD-CAM
 Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján. Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján. Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
WALTER-LIETH LIETH DIAGRAM
 TBGL0702 Meteorológia és klimatológia II. Bíróné Kircsi Andrea Egyetemi tanársegéd DE Meteorológiai Tanszék [ C] A diagram fejlécében fel kell tüntetni: - az állomás nevét, - tengerszint feletti magasságát,
TBGL0702 Meteorológia és klimatológia II. Bíróné Kircsi Andrea Egyetemi tanársegéd DE Meteorológiai Tanszék [ C] A diagram fejlécében fel kell tüntetni: - az állomás nevét, - tengerszint feletti magasságát,
A tételsor a 21/2007. (V.21.) SZMM rendeletben foglalt szakképesítés szakmai és vizsgakövetelménye alapján készült.
 A /07 (II. 27.) SzMM rendelettel módosított 1/06 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
A /07 (II. 27.) SzMM rendelettel módosított 1/06 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2012. október 15. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2012. október 15. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2012. október 15. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2012. október 15. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
GRAFIKUS PROCESSZOROK ALKALMAZÁSA KÉPFELDOLGOZÁSI FELADATOKRA
 GRAFIKUS PROCESSZOROK ALKALMAZÁSA KÉPFELDOLGOZÁSI FELADATOKRA ABSTRACT Simon Pál PhD hallgató Miskolci Egyetem Hatvany József Informatikai Tudományok Doktori Iskola The aim of this paper is the presentation
GRAFIKUS PROCESSZOROK ALKALMAZÁSA KÉPFELDOLGOZÁSI FELADATOKRA ABSTRACT Simon Pál PhD hallgató Miskolci Egyetem Hatvany József Informatikai Tudományok Doktori Iskola The aim of this paper is the presentation
Bevezetés a lágy számítás módszereibe
 BLSZM-07 p. 1/10 Bevezetés a lágy számítás módszereibe Nem fuzzy halmaz kimenetű fuzzy irányítási rendszerek Egy víztisztító berendezés szabályozását megvalósító modell Viselkedésijósló tervezési példa
BLSZM-07 p. 1/10 Bevezetés a lágy számítás módszereibe Nem fuzzy halmaz kimenetű fuzzy irányítási rendszerek Egy víztisztító berendezés szabályozását megvalósító modell Viselkedésijósló tervezési példa
Hőhidak meghatározásának bizonytalansága. Sólyomi Péter ÉMI Nonprofit Kft.
 Hőhidak meghatározásának bizonytalansága Sólyomi Péter ÉMI Nonprofit Kft. 7./2006. (V. 24.) TNM r e n d e l e t Épülethatároló szerkezet A hőátbocsátási tényező követelményértéke U W/m 2 K Külső fal 0,45
Hőhidak meghatározásának bizonytalansága Sólyomi Péter ÉMI Nonprofit Kft. 7./2006. (V. 24.) TNM r e n d e l e t Épülethatároló szerkezet A hőátbocsátási tényező követelményértéke U W/m 2 K Külső fal 0,45
1 Csoportosítsa a kötéseket a hatásmechanizmus szerint! Valamennyi csoportelemre írjon példát is!
 1 Csoportosítsa a kötéseket a hatásmechanizmus szerint! Valamennyi csoportelemre írjon példát is! Példák: Auto alváz Nyáklapok elemei Ablak műanyagkerete aknafedél Kuplung tárcsa Kólás doboz Csapágyház
1 Csoportosítsa a kötéseket a hatásmechanizmus szerint! Valamennyi csoportelemre írjon példát is! Példák: Auto alváz Nyáklapok elemei Ablak műanyagkerete aknafedél Kuplung tárcsa Kólás doboz Csapágyház
A 27/2012 (VIII. 27.) NGM rendelet szakmai és vizsgakövetelménye alapján.
 A 27/2012 (VIII. 27.) NGM rendelet szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 34 582 08 Kőműves és hidegburkoló Tájékoztató A vizsgázó az első lapra írja fel a
A 27/2012 (VIII. 27.) NGM rendelet szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 34 582 08 Kőműves és hidegburkoló Tájékoztató A vizsgázó az első lapra írja fel a
Beszámoló: a kompetenciamérés eredményének javítását célzó intézkedési tervben foglaltak megvalósításáról. Őcsény, 2015. november 20.
 Őcsényi Perczel Mór Általános Iskola székhelye: 7143 Őcsény, Perczel Mór utca 1. Tel: 74/496-782 e-mail: amk.ocseny@altisk-ocseny.sulinet.hu Ikt.sz.: /2015. OM: 036345 Ügyintéző: Ősze Józsefné Ügyintézés
Őcsényi Perczel Mór Általános Iskola székhelye: 7143 Őcsény, Perczel Mór utca 1. Tel: 74/496-782 e-mail: amk.ocseny@altisk-ocseny.sulinet.hu Ikt.sz.: /2015. OM: 036345 Ügyintéző: Ősze Józsefné Ügyintézés
Programozás alapjai Bevezetés
 Programozás alapjai Bevezetés Miskolci Egyetem Általános Informatikai Tanszék Programozás alapjai Bevezetés SWF1 / 1 Tartalom A gépi kódú programozás és hátrányai Amagasszintÿ programozási nyelv fogalma
Programozás alapjai Bevezetés Miskolci Egyetem Általános Informatikai Tanszék Programozás alapjai Bevezetés SWF1 / 1 Tartalom A gépi kódú programozás és hátrányai Amagasszintÿ programozási nyelv fogalma
Érettségi feladatok Algoritmusok egydimenziós tömbökkel (vektorokkal) 1/6. Alapműveletek
 Érettségi feladatok Algoritmusok egydimenziós tömbökkel (vektorokkal) 1/6 A tömbök deklarálásakor Pascal és C/C++ nyelvekben minden esetben meg kell adni az indexelést (Pascal) vagy az elemszámot (C/C++).
Érettségi feladatok Algoritmusok egydimenziós tömbökkel (vektorokkal) 1/6 A tömbök deklarálásakor Pascal és C/C++ nyelvekben minden esetben meg kell adni az indexelést (Pascal) vagy az elemszámot (C/C++).
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN
 GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten RACIONÁLIS TÖRTFÜGGVÉNYEK INTEGRÁLJA Készítette: Gábor Szakmai felel s: Gábor Vázlat
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten RACIONÁLIS TÖRTFÜGGVÉNYEK INTEGRÁLJA Készítette: Gábor Szakmai felel s: Gábor Vázlat
