Maga a tématerület így nagyon nagy. A fények pontos fizikai szimulációja kimondottan számításigényes
|
|
|
- Kinga Hajduné
- 9 évvel ezelőtt
- Látták:
Átírás
1 Fények a számítógépes grafikában Dr. Mileff Péter A fények és árnyékok területe különösen frekventált terület a számítógépes vizualizációban. Az utóbbi években ez tovább fokozódott Oka a hardver folyamatos fejlődése A miért egyszerű: A valóságban is a tárgyak a megvilágításoktól és árnyékoktól nyerik el igazi jellegüket. Rendkívüli vizuális élmény: egy megfelelően elkészített megvilágítási rendszerrel segítségével Ebben ma a számítógépes játékok járnak élen úttörőként. Pl: Cryengine, Unreal Engine, Source engine, stb. 2 Fények a számítógépes grafikában 3 4 1
2 Fények a számítógépes grafikában A terület sok éves fejlődésen ment keresztül. Új, további egyszerűsített megvilágítási módszerek is kialakultak Oka: a mobil eszközök megjelenése pl. Real-Time Area Lighting Maga a tématerület így nagyon nagy 5 6 A megvilágítási rendszerek alapjai A megvilágítási modellek: A valóságot modellező, különböző megközelítésű leképzések Céljuk: a valós világéval megegyező hatású képi inger előállítása Ki kell számítani: modellezni kell a fénysugarak felületekről történő visszaverődését. Meg kell határozni a képernyő pixelben látható felületi pontokat és azok szem irányú sugársűrűségét (radiancia). A sugársűrűség meghatározása: az árnyalási egyenlet (rendering equation) megoldásával a számítógépes grafika ezen egyenlet megoldásával foglalkozik Közelítő megoldások A megvilágítási rendszerek alapjai A fények pontos fizikai szimulációja kimondottan számításigényes Oka: a fényforrásból érkező fotonok útját kellene végigkövetni a felületekről való visszaverődésekkel együtt. Ezt a megvilágítási forma a globális illumináció Jellemzője: a felületeken az indirekt megvilágítás hatása is érvényesül. közvetett, más felületekről visszaverődött 7 8 2
3 A megvilágítási rendszerek alapjai A megvilágítási rendszerek alapjai A valós idejű vizualizációban jelenleg nem tudjuk ezt szimulálni a jelenlegi hardver eszközök teljesítménye nem teszi még lehetővé. Egy mai játék sok objektummal és számos fényforrással dolgozik. A megjelenítésben jelenleg alkalmazott technikák így csak a lokális illuminációt alkalmazzák. Lokális illumináció: a pont színe a fényforrásokon kívül csak a lokális anyagjellemzőktől és geometriától függ, nem vesszük figyelembe a szomszédos tárgyakról érkező szórt fényt. Ezáltal csökken a realisztikusság, de az algoritmus hatékonysága és ezáltal a sebessége nő Lokális vs Globális illumináció A megvilágítási rendszerek alapjai A fejlődés iránya: A globális illumináció közelítése. Hamis globális illumináció. Fake Global Illumination Kiegészítik a lokális illuminációs modellt új algoritmusokkal Ezek képesek: a globális illuminációhoz hasonló eredményt elérni, a lokális illuminációtól lényegesen jobban közelítő megvilágítás Ilyen technikák pl. az Ambient Occlusion, Lightmapping, Radiosity. A lokális illumináció mellett a vezető grafikus motorok kezdik bevezetni Cél a látvány minőségi növelése
4 Fényforrás típusok Absztrakt fényforrás csoportok: a valóság egy speciális foton sugárzási esetét modellező típusok Pontszerű fényforrás (point a háromdimenziós világ egy pontjában található kiterjedése nincs A háromdimenziós tér egy tetszőleges p pontjában a sugárzási iránya p pontot és a fényforrás helyét összekötő vektor Az intenzitás a távolság négyzetének arányában csökken Pl. Az elektromos izzó - jó közelítéssel Fényforrás típusok Irányfényforrás (directional végtelen távollevő sík sugárzónak felel meg. Az irány-fényforrás iránya és intenzitás a tér minden pontjában azonos. Pl. a Nap a Földről nézve jó közelítéssel irány-fényforrásnak tekinthető. Ambiens fényforrás (Ambient minden pontban és minden irányban azonos intenzitású. Spotlámpa (spot a virtuális világ egy pontjában található iránnyal és hatóterülettel rendelkezik. Pl. a zseblámpa spotlámpának tekinthető. 15 Megvilágítási modellek Feladatuk: a tárgyak árnyalásának kiszámítása A felületekre eső fények intenzitásának és jellemzőinek meghatározása Szórt háttérvilágítás (ambient az objektumok egyenletesen, minden irányból kapnak fényt Hatása a nappali fényviszonyoknak felel meg erősen felhős égbolt esetén. A számítógépes grafikában miért szükséges? a felhasználó az ábrázolt jelenet összes objektumának a megvilágítását szabályozhassa. A modellben nincs fényforrás: az objektumok saját fényüket bocsájtják ki Ez megfelel annak, hogy a jelenetet egy irányfüggetlen, szórt fény világítja meg. 16 4
5 Megvilágítási modellek Diffúz fényvisszaverődés (diffuse a matt felületek jellemzője a megvilágított felület minden irányban ugyanannyi fényt ver vissza Fényvisszaverődés fényes és csillogó felületekről (specular a sima felületekre általában az a jellemző, hogy rajtuk fényes foltokat is látunk melyek helye nézőpontunkkal együtt változik Ezek a felületek bizonyos irányokban visszatükrözik a fényforrásokat. Átmeneti eset: a matt felületekre jellemző diffúz és a tökéletesen (ideálisan) tükröző felületekre jellemző visszaverődés között Megvilágítási modellek Shininess komponens: speciális anyagtulajdonság a megvilágított anyagokon megjelenő spekuláris fényfoltok méretét és fényességét befolyásolja. Phong árnyalás ambiens, diffúz és specular összetevőkből Megvilágítási modellek Árnyalási modellek Ezek alapján az árnyalási egyenletet általános alakban a következőképpen írhatjuk fel: I a az ambiens, I d a diffúz, I = I a + I d + I s I s pedig a specular intenzitások. Ezek összege megadja a végleges színintenzitást. Árnyalási algoritmusok, amelyek az árnyalási egyenletet közelítik valamilyen szempontból. A sebesség és a minőség mérlegelendő alternatívák így többféle algoritmus alakult ki különböző optimalizálási megoldásokkal Az ideális megközelítés a pixelenkénti árnyalás ahol minden pixelre külön ki kell számolni: a fény intenzitását a normálvektorokat egyéb jellemzőket
6 Árnyalási modellek Árnyalási optimalizálásának alapelvei: érdemes az árnyalási feladatot pixeleknél nagyobb egységekben megoldani kihasználni, hogy ha a szomszédos pixelekben ugyanazon felület látszik. Ezen pixelekben látható felületi pontok optikai paraméterei igen hasonlók normálvektora, megvilágítása, akár a látható színe is. Optimalizáció: vagy változtatás nélkül használjuk a szomszédos pixelekben végzett számítások eredményeit, vagy pedig az inkrementális elv alkalmazásával egyszerű formulákkal tesszük azokat aktuálissá az új pixelben Árnyalási modellek Konstans árnyalás: Síklapok árnyalására a leggyorsabb módszer. a sokszögekre csak egyszer számítja ki az absztrakt fényforrások hatását. Színintenzitás: a legegyszerűbb esetben a beeső fénysugár és a felületi normális szögének függvényében határozzuk meg Ha valamelyik pixelben a sokszög látszik, akkor mindig ezzel a konstans színnel jelenítjük meg. Erőssége: rendkívül gyors Hátránya: Az eredmény általában nem kielégítő, A mai napig számos valósidejű alkalmazás használja gyorsasága és egyszerűsége miatt. Árnyalási modellek Gouraud árnyalás: a háromszögek csúcspontjaiban értékeli ki a fényforrásokból odajutó fény visszaverődését a csúcspontot érintő háromszögek normálvektorának átlagát felhasználva Ezen modell segítségével kiszámoljuk a csúcspontoknál a szín intenzitást: Gradiens átmeneteket számítunk a vertex pontoknál. Ezután a háromszög belső pontjainak színét a csúcspontok színéből lineárisan interpolálja Erőssége: az interpoláció, emiatt gyors raszterizáció Hátránya: a gyengébb képminőség Erősen lokalizált fény esetén az alacsony poligonszámú modellek esetén a fényvisszaverődés nem szabályos, látszanak a vertex-ek menti interpolált értékek
7 Árnyalási modellek Konstans vs Gouraud vs Phong árnyalás Phong árnyalás: A Goruaud árnyalástól abban különbözik: magát a normálvektorokat határozza meg lineáris interpolációval a csúcspont normál vektorok segítségével. A színek kiszámítása a színmodellnek megfelelően pixelenként történik. Éppen ezért a legszebb, de leglassabb árnyalási mód. A minősége nem függ a poligonok számától, a csillanás akár a poligon közepén is megjelenik Konstans vs Gouraud vs Phong árnyalás
8 Felületek normálisa A megvilágítási modellek szerves részét képezi a felületek normálisa. Célszerű tisztázni a felületi normális fogalmát Felületi normális: egy felület normálisa egy a felületre merőleges, egységnyi hosszúságú vektor. Gyakorlatban: A normálisokat vertex-ekhez és felületekhez szokás társítani. Ha egy modellen megvilágítást szeretnénk alkalmazni rendelkeznie kell kiszámított normálisokkal Mind vertex, mind pedig háromszög (face) szinten Felületek normálisa A normálisok kiszámítása egyszerű: A háromszög vertex-eiből képezni kell két darab oldalt és azok vektorait. A háromszög normálisa ilyenkor a két vektor vektoriális szorzata Normálist számító kód CVector3 Cross(CVector3 vvector1, CVector3 vvector2){ CVector3 vnormal; // The vector to hold the cross product } // The X value for the vector is: (V1.y * V2.z) - (V1.z * V2.y) vnormal.x = ((vvector1.y * vvector2.z) - (vvector1.z * vvector2.y)); // The Y value for the vector is: (V1.z * V2.x) - (V1.x * V2.z) vnormal.y = ((vvector1.z * vvector2.x) - (vvector1.x * vvector2.z)); // The Z value for the vector is: (V1.x * V2.y) - (V1.y * V2.x) vnormal.z = ((vvector1.x * vvector2.y) - (vvector1.y * vvector2.x)); return vnormal; Felületek normálisa Mikor számítsunk normálist? 1. A normálisok kiszámítását a modellek betöltésekor végezzük el 2. Már a modellező programban letárolva azt a vertex információk mellett a fájlban. Nagy modellek esetén célszerű fájlban tárolni egy-egy komplexebb modelleket alkalmazó számítógépes játék esetében a betöltési idő nagyon megnőhet
9 Mai trendek Mai trendek A fejlődés iránya jól látszik: napjainkban a fix funkciós csővezeték leváltása folyik a modern API-k már nem támogatják a fix funkciós megoldásokat. A korábban alkalmazott gllight(), glmaterial(), stb függvények már csak legacy módban használhatók. Az OpenGL 3.0 verziótól mindent árnyalók segítségével kell megoldani Előnye: az árnyalók bevezetése újabb lehetőség kínálkozik a grafikai minőség javításában, a fények és árnyékok árnyalókkal való megvalósításával. A programozók testre szabhatják a vizuális megoldásaikat. Hátránya: a programozóra több, főleg matematikai feladat megvalósítása hárul. Két fő csoport az árnyalókkal készített algoritmusoknak: vertex és pixel alapú árnyalások Attól függően, hogy egy egyszerűbb, vagy egy pontosabb számítási modellt szeretnénk alkalmazni. Az árnyalási egyenletet az árnyalókban implementált algoritmusokkal közelítjük Alapelve: Vertex árnyaló alkalmazása a számításokhoz (Minden vertex-re egyszer hajtódik végre) A fény intenzitásértékeket a vertex-ekben számítjuk ki a kiszámított intenzitásértékeket interpoláljuk a vertex-ek között elhelyezkedő pontokban Lineáris interpoláció: gyors minőségileg nem a legjobb
10 Példa (egyszerű): egy irányított fényforrás alkalmazása Csak diffúz árnyalás megvalósítása Lambert-féle fény visszaverődési modell: a visszaverődött fény intenzitása a megvilágítási szög koszinuszával arányos A modellt leíró matematikai összefüggés (OpenGL Red Book): I o jelenti a visszaverődött intenzitást, L d a fény diffúz színe, M d a material diffúz összetevője cos() pedig a két vektor által bezárt szög. Jelen példában eltekintünk az anyagjellemzőktől A két vektor által bezárt szög meghatározása: a szög éppen megegyezik a felületi normális (N) és a vizsgált felületi pontból a fényforrásba mutató vektor skaláris szorzatával Vertex árnyaló: varying float Diffuse; void main(void){ // transform the normal into eye space and normalize it vec3 Normal = normalize(gl_normalmatrix * gl_normal); // OpenGL specification, the light is stored in eye space vec3 Light = normalize(gl_lightsource[0].position.xyz); Az árnyalóban megtörténik a Lambert-féle visszaverődés kiszámítása minden vertex-re. Árnyalás megvalósítása: Elsőként a modell normál vektorait a kamera (nézeti) térbe transzformáljuk. Majd a fény irányvektorát normalizálni kell: a skaláris szorzatban azonos mértékek kerüljenek alkalmazásra. A skaláris szorzat eredménye maga a diffúz összetevő. } Diffuse = max(dot(normal, Light),0.0); gl_position = gl_modelviewprojectionmatrix * gl_vertex;
11 Fragment árnyaló: Eredmény varying float Diffuse; void main(void){ // Multiply the light Diffuse intensity by a white color gl_fragcolor = Diffuse * vec4(1,1,1,1); } A vertex árnyalóból a diffúz összetevő átadásra kerül a pixel árnyalónak. A pixel végső színét a gl_fragcolor-ban kapjuk meg, az egyszerűség kedvéért egy fehér színt alkalmazunk az árnyalás alap színeként
A bemutatott példa a Phong modell egy egyszerűsített változatát alkalmazza a Blinn-Phong-féle megközelítést
 Dr. Mileff Péter 2 Pontosabb vertex shader alapú árnyalás Phong-féle Cél: A korábbi modelltől komplexebb árnyalási modell áttekintése és megvalósítása, ahol már felhasználjuk a felület anyagtulajdonságait
Dr. Mileff Péter 2 Pontosabb vertex shader alapú árnyalás Phong-féle Cél: A korábbi modelltől komplexebb árnyalási modell áttekintése és megvalósítása, ahol már felhasználjuk a felület anyagtulajdonságait
Hajder Levente 2017/2018. II. félév
 Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév Tartalom 1 A fény elektromágneses hullám Az anyagokat olyan színűnek látjuk, amilyen színű fényt visszavernek
Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév Tartalom 1 A fény elektromágneses hullám Az anyagokat olyan színűnek látjuk, amilyen színű fényt visszavernek
Tartalom. Tartalom. Anyagok Fényforrás modellek. Hajder Levente Fényvisszaverési modellek. Színmodellek. 2017/2018. II.
 Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév 1 A fény elektromágneses hullám Az anyagokat olyan színűnek látjuk, amilyen színű fényt visszavernek
Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév 1 A fény elektromágneses hullám Az anyagokat olyan színűnek látjuk, amilyen színű fényt visszavernek
Máté: Számítógépes grafika alapjai
 Világító tárgyak Környezeti fény Szórt visszaverődés Környezeti fény és diffúz visszaverődés együtt Tükröző visszaverődés fényességének meghatározása Gouraud-féle fényesség Phong-féle fényesség a. Világító
Világító tárgyak Környezeti fény Szórt visszaverődés Környezeti fény és diffúz visszaverődés együtt Tükröző visszaverődés fényességének meghatározása Gouraud-féle fényesség Phong-féle fényesség a. Világító
Árnyalás, env mapping. Szécsi László 3D Grafikus Rendszerek 3. labor
 Árnyalás, env mapping Szécsi László 3D Grafikus Rendszerek 3. labor Egyszerű árnyaló FS legyen egy fényirány-vektor normálvektor és fényirány közötti szög koszinusza az irradiancia textúrából olvasott
Árnyalás, env mapping Szécsi László 3D Grafikus Rendszerek 3. labor Egyszerű árnyaló FS legyen egy fényirány-vektor normálvektor és fényirány közötti szög koszinusza az irradiancia textúrából olvasott
Számítógépes Grafika mintafeladatok
 Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
1. Bevezetés 1. Köszönetnyilvánítás 1. 2. A számítógépes játékfejlesztésről 3
 1. Bevezetés 1 Köszönetnyilvánítás 1 2. A számítógépes játékfejlesztésről 3 2.1. Néhány tanács játékfejlesztőknek 3 2.2. Hogyan fogjunk saját játék írásához? 4 2.3. A számítógépes játék főbb elemei 9 3.
1. Bevezetés 1 Köszönetnyilvánítás 1 2. A számítógépes játékfejlesztésről 3 2.1. Néhány tanács játékfejlesztőknek 3 2.2. Hogyan fogjunk saját játék írásához? 4 2.3. A számítógépes játék főbb elemei 9 3.
Számítógépes Graka - 4. Gyak
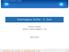 Számítógépes Graka - 4. Gyak Jámbori András andras.jambori@gmail.com 2012.03.01 Jámbori András andras.jambori@gmail.com Számítógépes Graka - 4. Gyak 1/17 Emlékeztet A múlt órákon tárgyaltuk: WinAPI programozás
Számítógépes Graka - 4. Gyak Jámbori András andras.jambori@gmail.com 2012.03.01 Jámbori András andras.jambori@gmail.com Számítógépes Graka - 4. Gyak 1/17 Emlékeztet A múlt órákon tárgyaltuk: WinAPI programozás
SZE, Doktori Iskola. Számítógépes grafikai algoritmusok. Összeállította: Dr. Gáspár Csaba. Felületmegjelenítés
 Felületmegjelenítés Megjelenítés paramétervonalakkal Drótvázas megjelenítés Megjelenítés takarással Triviális hátsólap eldobás A z-puffer algoritmus Megvilágítás és árnyalás Megjelenítés paramétervonalakkal
Felületmegjelenítés Megjelenítés paramétervonalakkal Drótvázas megjelenítés Megjelenítés takarással Triviális hátsólap eldobás A z-puffer algoritmus Megvilágítás és árnyalás Megjelenítés paramétervonalakkal
Hajder Levente 2017/2018. II. félév
 Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév Tartalom 1 Sugár és sík metszéspontja Sugár és háromszög metszéspontja Sugár és poligon metszéspontja
Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév Tartalom 1 Sugár és sík metszéspontja Sugár és háromszög metszéspontja Sugár és poligon metszéspontja
Renderelés megjelenésmódok, fények, anyagjellemzők
 Építész-informatika 2 Előadási anyag BME Építészmérnöki kar Építészeti Ábrázolás Tanszék Renderelés megjelenésmódok, fények, anyagjellemzők BMEEPAGA401 Építész-informatika 2 6. előadás Strommer László
Építész-informatika 2 Előadási anyag BME Építészmérnöki kar Építészeti Ábrázolás Tanszék Renderelés megjelenésmódok, fények, anyagjellemzők BMEEPAGA401 Építész-informatika 2 6. előadás Strommer László
OTKA Nyilvántartási szám: T ZÁRÓJELENTÉS
 OTKA Nyilvántartási szám: T042735 ZÁRÓJELENTÉS Témavezető neve: dr. Szirmay-Kalos László. A téma címe: Interaktív globális illumináció A kutatás időtartama: 4 év A kutatási tervnek megfelelően az interaktív
OTKA Nyilvántartási szám: T042735 ZÁRÓJELENTÉS Témavezető neve: dr. Szirmay-Kalos László. A téma címe: Interaktív globális illumináció A kutatás időtartama: 4 év A kutatási tervnek megfelelően az interaktív
Transzformációk. Szécsi László
 Transzformációk Szécsi László A feladat Adott a 3D modell háromszögek csúcspontjai [modellezési koordináták] Háromszögkitöltő algoritmus pixeleket színez be [viewport koordináták] A feladat: számítsuk
Transzformációk Szécsi László A feladat Adott a 3D modell háromszögek csúcspontjai [modellezési koordináták] Háromszögkitöltő algoritmus pixeleket színez be [viewport koordináták] A feladat: számítsuk
Transzformációk. Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform
 Transzformációk Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform Koordinátarendszerek: modelltér Koordinátarendszerek: világtér Koordinátarendszerek: kameratér up right z eye ahead
Transzformációk Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform Koordinátarendszerek: modelltér Koordinátarendszerek: világtér Koordinátarendszerek: kameratér up right z eye ahead
Számítógépes grafika
 Számítógépes grafika XVII. rész A grafikai modellezés A modellezés A generatív számítógépes grafikában és a képfeldolgozás során nem a valódi objektumokat (valóságbeli tárgyakat), hanem azok egy modelljét
Számítógépes grafika XVII. rész A grafikai modellezés A modellezés A generatív számítógépes grafikában és a képfeldolgozás során nem a valódi objektumokat (valóságbeli tárgyakat), hanem azok egy modelljét
Információ megjelenítés Számítógépes ábrázolás. Dr. Iványi Péter
 Információ megjelenítés Számítógépes ábrázolás Dr. Iványi Péter Raszterizáció OpenGL Mely pixelek vannak a primitíven belül fragment generálása minden ilyen pixelre Attribútumok (pl., szín) hozzárendelése
Információ megjelenítés Számítógépes ábrázolás Dr. Iványi Péter Raszterizáció OpenGL Mely pixelek vannak a primitíven belül fragment generálása minden ilyen pixelre Attribútumok (pl., szín) hozzárendelése
Sugárkövetési algoritmusok (2. rész)
 Sugárkövetési algoritmusok (2. rész) Ismét jelentkezik a sugarak szerelmeseinek szóló cikkünk, melyben tovább folytatjuk a fények birodalmában megkezdett utazásunkat. A fénysugarak rekurzív követésével
Sugárkövetési algoritmusok (2. rész) Ismét jelentkezik a sugarak szerelmeseinek szóló cikkünk, melyben tovább folytatjuk a fények birodalmában megkezdett utazásunkat. A fénysugarak rekurzív követésével
Tartalom. Tartalom. Raycasting. Hajder Levente 2017/2018. II. félév. Raycasting. Raycasting. Sugár és háromszög metszéspontja
 Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév 1 2 1 2 Albrecht Dürer, 1525 Tekintsünk minden pixelre úgy, mint egy kis ablakra a világra Milyen színértéket
Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév 1 2 1 2 Albrecht Dürer, 1525 Tekintsünk minden pixelre úgy, mint egy kis ablakra a világra Milyen színértéket
Összeállította: dr. Leitold Adrien egyetemi docens
 Az R 3 tér geometriája Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. 1 Vektorok Vektor: irányított szakasz Jel.: a, a, a, AB, Jellemzői: irány, hosszúság, (abszolút érték) jel.: a Speciális
Az R 3 tér geometriája Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. 1 Vektorok Vektor: irányított szakasz Jel.: a, a, a, AB, Jellemzői: irány, hosszúság, (abszolút érték) jel.: a Speciális
Vektorok összeadása, kivonása, szorzás számmal, koordináták
 Vektorok összeadása, kivonása, szorzás számmal, koordináták 1. Mik lesznek a P (3, 4, 8) pont C (3, 7, 2) pontra vonatkozó tükörképének a koordinátái? 2. Egy szabályos hatszög középpontja K (4, 1, 4),
Vektorok összeadása, kivonása, szorzás számmal, koordináták 1. Mik lesznek a P (3, 4, 8) pont C (3, 7, 2) pontra vonatkozó tükörképének a koordinátái? 2. Egy szabályos hatszög középpontja K (4, 1, 4),
Információ megjelenítés Számítógépes ábrázolás. Dr. Iványi Péter
 Infomáció megjelenítés Számítógépes ábázolás D. Iványi Péte Megvilágítás, ányékolás Realisztikus képhez ányékolás kell Modellezés összetett nagy számítási igenyű Megvilágítás, ányékolás OpenGL egyszeűsített
Infomáció megjelenítés Számítógépes ábázolás D. Iványi Péte Megvilágítás, ányékolás Realisztikus képhez ányékolás kell Modellezés összetett nagy számítási igenyű Megvilágítás, ányékolás OpenGL egyszeűsített
Számítógépes Grafika mintafeladatok
 Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Máté: Számítógépes grafika alapjai
 Tükröző (specular) visszaverődés Tükröző (specular) visszaverődés Fényes felületekről (tükörről) Phong-féle modell: I λ = I aλ k a + f att I pλ [ k d cos θ + W (θ) cos n α ] n: a tükrözési visszaverődés
Tükröző (specular) visszaverődés Tükröző (specular) visszaverődés Fényes felületekről (tükörről) Phong-féle modell: I λ = I aλ k a + f att I pλ [ k d cos θ + W (θ) cos n α ] n: a tükrözési visszaverődés
Modellezési transzformáció: [r lokális,1] T M = [r világ,1] Nézeti transzformáció: [r világ,1] T v = [r képernyo,1]
![Modellezési transzformáció: [r lokális,1] T M = [r világ,1] Nézeti transzformáció: [r világ,1] T v = [r képernyo,1] Modellezési transzformáció: [r lokális,1] T M = [r világ,1] Nézeti transzformáció: [r világ,1] T v = [r képernyo,1]](/thumbs/89/99513512.jpg) Inkrementális képsintéis Inkrementális 3D képsintéis Sirma-Kalos Lásló Árnalás, láthatóság nehé, különösen általános heletu objektumokra koherencia: oldjuk meg nagobb egségekre feleslegesen ne sámoljunk:
Inkrementális képsintéis Inkrementális 3D képsintéis Sirma-Kalos Lásló Árnalás, láthatóság nehé, különösen általános heletu objektumokra koherencia: oldjuk meg nagobb egségekre feleslegesen ne sámoljunk:
Láthatósági kérdések
 Láthatósági kérdések Láthatósági algoritmusok Adott térbeli objektum és adott nézőpont esetén el kell döntenünk, hogy mi látható az adott alakzatból a nézőpontból, vagy irányából nézve. Az algoritmusok
Láthatósági kérdések Láthatósági algoritmusok Adott térbeli objektum és adott nézőpont esetén el kell döntenünk, hogy mi látható az adott alakzatból a nézőpontból, vagy irányából nézve. Az algoritmusok
A számítógépes grafika alapjai kurzus, vizsgatételek és tankönyvi referenciák 2014
 Pázmány Péter Katolikus Egyetem Információs Technológiai Kar A számítógépes grafika alapjai kurzus, vizsgatételek és tankönyvi referenciák 2014 Benedek Csaba A vizsga menete: a vizsgázó egy A illetve egy
Pázmány Péter Katolikus Egyetem Információs Technológiai Kar A számítógépes grafika alapjai kurzus, vizsgatételek és tankönyvi referenciák 2014 Benedek Csaba A vizsga menete: a vizsgázó egy A illetve egy
Textúrák. Szécsi László
 Textúrák Szécsi László Textúra interpretációk kép a memóriában ugyanolyan mint a frame buffer pixel helyett texel adatok tömbje 1D, 2D, 3D tömb pl. RGB rekordok függvény diszkrét mintapontjai rácson rekonstrukció:
Textúrák Szécsi László Textúra interpretációk kép a memóriában ugyanolyan mint a frame buffer pixel helyett texel adatok tömbje 1D, 2D, 3D tömb pl. RGB rekordok függvény diszkrét mintapontjai rácson rekonstrukció:
Számítógépes grafika
 Számítógépes grafika XX. rész A GPU programozása a GLSL nyelv Az OpenGL árnyaló nyelve a GLSL (OpenGL Shading Language), amely segítségével vertex- és pixel- (fragment) shaderek által programozhatjuk a
Számítógépes grafika XX. rész A GPU programozása a GLSL nyelv Az OpenGL árnyaló nyelve a GLSL (OpenGL Shading Language), amely segítségével vertex- és pixel- (fragment) shaderek által programozhatjuk a
I. Vektorok. Adott A (2; 5) és B ( - 3; 4) pontok. (ld. ábra) A két pont által meghatározott vektor:
 I. Vektorok 1. Vektorok összege Általánosan: Az ábra alapján Adott: a(4; 1) és b(; 3) a + b (4 + ; 1 + 3) = (6; ) a(a 1 ; a ) és b(b 1 ; b ) a + b(a 1 + b 1 ; a + b ). Vektorok különbsége Általánosan:
I. Vektorok 1. Vektorok összege Általánosan: Az ábra alapján Adott: a(4; 1) és b(; 3) a + b (4 + ; 1 + 3) = (6; ) a(a 1 ; a ) és b(b 1 ; b ) a + b(a 1 + b 1 ; a + b ). Vektorok különbsége Általánosan:
x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs mátrixa 3D-ben?
 . Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
. Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
Hajder Levente 2016/2017.
 Hajder Levente hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2016/2017. Tartalom 1 Tartalom Motiváció 2 Grafikus szerelőszalag Áttekintés Modellezési transzformácó Nézeti
Hajder Levente hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2016/2017. Tartalom 1 Tartalom Motiváció 2 Grafikus szerelőszalag Áttekintés Modellezési transzformácó Nézeti
Tartalom. Tartalom. Hajder Levente 2018/2019. I. félév
 Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2018/2019. I. félév Emlékeztető Múlt órán megismerkedtünk a sugárkövetéssel Előnyei: A színtér benépesítésére minden használható,
Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2018/2019. I. félév Emlékeztető Múlt órán megismerkedtünk a sugárkövetéssel Előnyei: A színtér benépesítésére minden használható,
Tartalom. Megjegyzések. Valasek Gábor Befoglaló keretek. Felosztások. Informatikai Kar
 Tartalom Számítógépes Grafika Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2015/2016. őszi félév Rekurzív sugárkövetés Megjegyzések Sugárkövetés gyorsítása Befoglaló
Tartalom Számítógépes Grafika Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2015/2016. őszi félév Rekurzív sugárkövetés Megjegyzések Sugárkövetés gyorsítása Befoglaló
Vektorok és koordinátageometria
 Vektorok és koordinátageometria Vektorral kapcsolatos alapfogalmak http://zanza.tv/matematika/geometria/vektorok-bevezetese Definíció: Ha egy szakasz két végpontját megkülönböztetjük egymástól oly módon,
Vektorok és koordinátageometria Vektorral kapcsolatos alapfogalmak http://zanza.tv/matematika/geometria/vektorok-bevezetese Definíció: Ha egy szakasz két végpontját megkülönböztetjük egymástól oly módon,
SDL_Universe SDL, C++, 3D szoftver renderelő
 SDL_Universe SDL, C++, 3D szoftver renderelő Boros László, harmadéves mérnökinformatikus I C what you did last summer Programozói Konferencia 2014 iamsemmu@gmail.com http://progkonf.eet.bme.hu SDL_Universe
SDL_Universe SDL, C++, 3D szoftver renderelő Boros László, harmadéves mérnökinformatikus I C what you did last summer Programozói Konferencia 2014 iamsemmu@gmail.com http://progkonf.eet.bme.hu SDL_Universe
Információ megjelenítés Számítógépes ábrázolás. Dr. Iványi Péter
 Információ megjelenítés Számítógépes ábrázolás Dr. Iványi Péter (adat szerkezet) float x,y,z,w; float r,g,b,a; } vertex; glcolor3f(0, 0.5, 0); glvertex2i(11, 31); glvertex2i(37, 71); glcolor3f(0.5, 0,
Információ megjelenítés Számítógépes ábrázolás Dr. Iványi Péter (adat szerkezet) float x,y,z,w; float r,g,b,a; } vertex; glcolor3f(0, 0.5, 0); glvertex2i(11, 31); glvertex2i(37, 71); glcolor3f(0.5, 0,
1. Fénysugár követő és festő algoritmus (3p) fénysugárkövető módszer Festő algoritmus: 2. Fények, fény, fény az opengl-ben, anyagtulajdonság (12pt)
 1. Fénysugár követő és festő algoritmus (3p) A fénysugárkövető módszer azt használja ki, hogy a kép pontokból (pixelekből) épül fel. Alapötlete az, hogy meghatározza az ábrázolandó objektumnak az a pontját,
1. Fénysugár követő és festő algoritmus (3p) A fénysugárkövető módszer azt használja ki, hogy a kép pontokból (pixelekből) épül fel. Alapötlete az, hogy meghatározza az ábrázolandó objektumnak az a pontját,
O ( 0, 0, 0 ) A ( 4, 0, 0 ) B ( 4, 3, 0 ) C ( 0, 3, 0 ) D ( 4, 0, 5 ) E ( 4, 3, 5 ) F ( 0, 3, 5 ) G ( 0, 0, 5 )
 1. feladat Írjuk föl a következő vektorokat! AC, BF, BG, DF, BD, AG, GB Írjuk föl ezen vektorok egységvektorát is! a=3 m b= 4 m c= m Írjuk föl az egyes pontok koordinátáit: O ( 0, 0, 0 ) A ( 4, 0, 0 )
1. feladat Írjuk föl a következő vektorokat! AC, BF, BG, DF, BD, AG, GB Írjuk föl ezen vektorok egységvektorát is! a=3 m b= 4 m c= m Írjuk föl az egyes pontok koordinátáit: O ( 0, 0, 0 ) A ( 4, 0, 0 )
Megoldások. Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma)
 Megoldások 1. Határozd meg az a és b vektor skaláris szorzatát, ha a = 5, b = 4 és a közbezárt szög φ = 55! Alkalmazzuk a megfelelő képletet: a b = a b cos φ = 5 4 cos 55 11,47. 2. Határozd meg a következő
Megoldások 1. Határozd meg az a és b vektor skaláris szorzatát, ha a = 5, b = 4 és a közbezárt szög φ = 55! Alkalmazzuk a megfelelő képletet: a b = a b cos φ = 5 4 cos 55 11,47. 2. Határozd meg a következő
Vektoralgebra. 1.) Mekkora a pillanatnyi sebesség 3 s elteltével, ha a kezdősebesség (15;9;7) m/s, a gravitációs gyorsulás pedig (0;0;-10) m/s 2?
 Vektoralgebra Elmélet: http://digitus.itk.ppke.hu/~b_novak/dmat/vektorfolcop.pdf Mikor érdemes más, nem ortonormált bázist alkalmazni? Fizikában a ferde hajításoknál megéri úgynevezett ferdeszögű koordináta-rendszert
Vektoralgebra Elmélet: http://digitus.itk.ppke.hu/~b_novak/dmat/vektorfolcop.pdf Mikor érdemes más, nem ortonormált bázist alkalmazni? Fizikában a ferde hajításoknál megéri úgynevezett ferdeszögű koordináta-rendszert
CodeCamp Döntő feladat
 CodeCamp Döntő feladat 2014 1 CodeCamp Döntő feladat A feladatban egy játékot kell készíteni, ami az elődöntő feladatán alapul. A feladat az elődöntő során elkészített szimulációs csomagra építve egy két
CodeCamp Döntő feladat 2014 1 CodeCamp Döntő feladat A feladatban egy játékot kell készíteni, ami az elődöntő feladatán alapul. A feladat az elődöntő során elkészített szimulációs csomagra építve egy két
Tartalom. Hajder Levente 2016/2017. I. félév
 Tartalom Hajder Levente hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2016/2017. I. félév 1 Tartalom Motiváció 2 Grafikus szerelőszalag Modellezési transzformácó Nézeti transzformácó
Tartalom Hajder Levente hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2016/2017. I. félév 1 Tartalom Motiváció 2 Grafikus szerelőszalag Modellezési transzformácó Nézeti transzformácó
Koordináta-geometria feladatgyűjtemény
 Koordináta-geometria feladatgyűjtemény A feladatok megoldásai a dokumentum végén találhatók Vektorok 1. Egy négyzet két szemközti csúcsának koordinátái: A( ; 7) és C(4 ; 1). Határozd meg a másik két csúcs
Koordináta-geometria feladatgyűjtemény A feladatok megoldásai a dokumentum végén találhatók Vektorok 1. Egy négyzet két szemközti csúcsának koordinátái: A( ; 7) és C(4 ; 1). Határozd meg a másik két csúcs
Hajder Levente 2018/2019. II. félév
 Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2018/2019. II. félév Tartalom 1 2 3 4 5 Albrecht Dürer, 1525 Motiváció Tekintsünk minden pixelre úgy, mint egy kis ablakra
Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2018/2019. II. félév Tartalom 1 2 3 4 5 Albrecht Dürer, 1525 Motiváció Tekintsünk minden pixelre úgy, mint egy kis ablakra
HLSL programozás. Szécsi László
 HLSL programozás Szécsi László RESOURCES PIPELINE STAGES RENDER STATES Vertex buffer Instance buffer Constant buffers and textures Index buffer Constant buffers and textures Output buffer Constant buffers
HLSL programozás Szécsi László RESOURCES PIPELINE STAGES RENDER STATES Vertex buffer Instance buffer Constant buffers and textures Index buffer Constant buffers and textures Output buffer Constant buffers
Hajder Levente 2014/2015. tavaszi félév
 Hajder Levente hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom 1 2 3 4 5 Albrecht Dürer, 1525 Motiváció Tekintsünk minden pixelre úgy, mint
Hajder Levente hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom 1 2 3 4 5 Albrecht Dürer, 1525 Motiváció Tekintsünk minden pixelre úgy, mint
Vektorgeometria (2) First Prev Next Last Go Back Full Screen Close Quit
 Vektorgeometria (2) First Prev Next Last Go Back Full Screen Close Quit 1. Tekintsünk a térben egy P (p 1, p 2, p 3 ) pontot és egy v = (v 1, v 2, v 3 ) = 0 vektort. Ekkor pontosan egy egyenes létezik,
Vektorgeometria (2) First Prev Next Last Go Back Full Screen Close Quit 1. Tekintsünk a térben egy P (p 1, p 2, p 3 ) pontot és egy v = (v 1, v 2, v 3 ) = 0 vektort. Ekkor pontosan egy egyenes létezik,
Koordináta-geometria II.
 Koordináta-geometria II. DEFINÍCIÓ: (Alakzat egyenlete) A síkon adott egy derékszögű koordináta rendszer. A síkban levő alakzat egyenlete olyan f (x, y) = 0 egyenlet, amelyet azoknak és csak azoknak a
Koordináta-geometria II. DEFINÍCIÓ: (Alakzat egyenlete) A síkon adott egy derékszögű koordináta rendszer. A síkban levő alakzat egyenlete olyan f (x, y) = 0 egyenlet, amelyet azoknak és csak azoknak a
Skaláris szorzat: a b cos, ahol α a két vektor által bezárt szög.
 1 Összeadás: Legyen a (7; 3) és b (- 2; 4), akkor az összegük a + b (7 + (-2); 3 + 4) = (5; 7) Kivonás: Legyen a (7; 3) és b (- 2; 4), akkor a különbségük a b (7 - (-2); 3-4)=(9; - 1) Valós számmal való
1 Összeadás: Legyen a (7; 3) és b (- 2; 4), akkor az összegük a + b (7 + (-2); 3 + 4) = (5; 7) Kivonás: Legyen a (7; 3) és b (- 2; 4), akkor a különbségük a b (7 - (-2); 3-4)=(9; - 1) Valós számmal való
2. Generáció (1999-2000) 3. Generáció (2001) NVIDIA TNT2, ATI Rage, 3dfx Voodoo3. Klár Gergely tremere@elte.hu
 1. Generáció Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. őszi félév NVIDIA TNT2, ATI Rage, 3dfx Voodoo3 A standard 2d-s videokártyák kiegészítése
1. Generáció Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. őszi félév NVIDIA TNT2, ATI Rage, 3dfx Voodoo3 A standard 2d-s videokártyák kiegészítése
2D képszintézis. Szirmay-Kalos László
 2D képszintézis Szirmay-Kalos László 2D képszintézis Modell szín (200, 200) Kép Kamera ablak (window) viewport Unit=pixel Saját színnel rajzolás Világ koordinátarendszer Pixel vezérelt megközelítés: Tartalmazás
2D képszintézis Szirmay-Kalos László 2D képszintézis Modell szín (200, 200) Kép Kamera ablak (window) viewport Unit=pixel Saját színnel rajzolás Világ koordinátarendszer Pixel vezérelt megközelítés: Tartalmazás
Nem fotorealisztikus megjelenítés OpenGL segítségével
 Debreceni Egyetem Informatikai Kar Nem fotorealisztikus megjelenítés OpenGL segítségével Témavezetı: Dr. Tornai Róbert egyetemi adjunktus Készítette: Sajtos István programtervezı matematikus Debrecen 2010
Debreceni Egyetem Informatikai Kar Nem fotorealisztikus megjelenítés OpenGL segítségével Témavezetı: Dr. Tornai Róbert egyetemi adjunktus Készítette: Sajtos István programtervezı matematikus Debrecen 2010
Tartalomjegyzék. Köszönetnyilvánítás... xv. Előszó... xvii. 1. Bevezető... 1. 2. 3D-történelem... 3. 3. Matematikai alapok... 7
 Köszönetnyilvánítás... xv Előszó... xvii 1. Bevezető... 1 2. 3D-történelem... 3 3. Matematikai alapok... 7 3.1. Trigonometriai gyorstalpaló... 7 3.1.1. A szög. Fok és radián... 7 3.1.2. Szögfüggvények
Köszönetnyilvánítás... xv Előszó... xvii 1. Bevezető... 1 2. 3D-történelem... 3 3. Matematikai alapok... 7 3.1. Trigonometriai gyorstalpaló... 7 3.1.1. A szög. Fok és radián... 7 3.1.2. Szögfüggvények
8. Pontmegfeleltetések
 8. Pontmegfeleltetések Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Példa: panoráma kép készítés 1. Jellemzőpontok detektálása mindkét
8. Pontmegfeleltetések Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Példa: panoráma kép készítés 1. Jellemzőpontok detektálása mindkét
Féléves feladat. Miről lesz szó? Bemutatkozás és követelmények 2012.09.16.
 Bemutatkozás és követelmények Dr. Mileff Péter Dr. Mileff Péter Helyileg: A/1-303. szoba. Fizika Tanszék Konzultációs idő: Szerda 10-12 mileff@iit.uni-miskolc.hu Követelmények: Az órák ¾-én kötelező a
Bemutatkozás és követelmények Dr. Mileff Péter Dr. Mileff Péter Helyileg: A/1-303. szoba. Fizika Tanszék Konzultációs idő: Szerda 10-12 mileff@iit.uni-miskolc.hu Követelmények: Az órák ¾-én kötelező a
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 8 VIII VEkTOROk 1 VEkTOR Vektoron irányított szakaszt értünk Jelölése: stb Vektorok hossza A vektor abszolút értéke az irányított szakasz hossza Ha a vektor hossza egységnyi akkor
KOVÁCS BÉLA MATEmATIkA I 8 VIII VEkTOROk 1 VEkTOR Vektoron irányított szakaszt értünk Jelölése: stb Vektorok hossza A vektor abszolút értéke az irányított szakasz hossza Ha a vektor hossza egységnyi akkor
Számítógépes Grafika SZIE YMÉK
 Számítógépes Grafika SZIE YMÉK Analóg - digitális Analóg: a jel értelmezési tartománya (idő), és az értékkészletes is folytonos (pl. hang, fény) Diszkrét idejű: az értelmezési tartomány diszkrét (pl. a
Számítógépes Grafika SZIE YMÉK Analóg - digitális Analóg: a jel értelmezési tartománya (idő), és az értékkészletes is folytonos (pl. hang, fény) Diszkrét idejű: az értelmezési tartomány diszkrét (pl. a
KOVÁCS BÉLA, MATEMATIKA II.
 KOVÁCS BÉLA MATEmATIkA II 6 VI TÉRGÖRbÉk 1 Alapvető ÖSSZEFÜGGÉSEk A térgörbe (1) alakú egyenletével írható le Ez a vektoregyenlet egyenértékű az (2) skaláris egyenletrendszerrel A térgörbe három nevezetes
KOVÁCS BÉLA MATEmATIkA II 6 VI TÉRGÖRbÉk 1 Alapvető ÖSSZEFÜGGÉSEk A térgörbe (1) alakú egyenletével írható le Ez a vektoregyenlet egyenértékű az (2) skaláris egyenletrendszerrel A térgörbe három nevezetes
KOORDINÁTA-GEOMETRIA
 XIV. Témakör: feladatok 1 Huszk@ Jenő XIV.TÉMAKÖR Téma A pont koordinátageometriája A kör koordinátageometriája KOORDINÁTA-GEOMETRIA A projekt típus ú feladatok tartalmi szintézise A feladat sorszáma Oldal
XIV. Témakör: feladatok 1 Huszk@ Jenő XIV.TÉMAKÖR Téma A pont koordinátageometriája A kör koordinátageometriája KOORDINÁTA-GEOMETRIA A projekt típus ú feladatok tartalmi szintézise A feladat sorszáma Oldal
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT. Koordináta-geometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT 1) Adott két pont: A 4; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. Koordináta-geometria és B 3 1; Írja fel az AB szakasz 1 3 4
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT 1) Adott két pont: A 4; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. Koordináta-geometria és B 3 1; Írja fel az AB szakasz 1 3 4
1. Olvassuk be két pont koordinátáit: (x1, y1) és (x2, y2). Határozzuk meg a két pont távolságát és nyomtassuk ki.
 Számítás:. Olvassuk be két pont koordinátáit: (, y) és (2, y2). Határozzuk meg a két pont távolságát és nyomtassuk ki. 2. Olvassuk be két darab két dimenziós vektor komponenseit: (a, ay) és (b, by). Határozzuk
Számítás:. Olvassuk be két pont koordinátáit: (, y) és (2, y2). Határozzuk meg a két pont távolságát és nyomtassuk ki. 2. Olvassuk be két darab két dimenziós vektor komponenseit: (a, ay) és (b, by). Határozzuk
MATEMATIKA EMELT SZINTŰ SZÓBELI VIZSGA TÉMAKÖREI (TÉTELEK) 2005
 2005 1. * Halmazok, halmazműveletek, nevezetes ponthalmazok 2. Számhalmazok, halmazok számossága 3. Hatványozás, hatványfüggvény 4. Gyökvonás, gyökfüggvény 5. A logaritmus. Az exponenciális és a logaritmus
2005 1. * Halmazok, halmazműveletek, nevezetes ponthalmazok 2. Számhalmazok, halmazok számossága 3. Hatványozás, hatványfüggvény 4. Gyökvonás, gyökfüggvény 5. A logaritmus. Az exponenciális és a logaritmus
(Solid modeling, Geometric modeling) Testmodell: egy létező vagy elképzelt objektum digitális reprezentációja.
 Testmodellezés Testmodellezés (Solid modeling, Geometric modeling) Testmodell: egy létező vagy elképzelt objektum digitális reprezentációja. A tervezés (modellezés) során megadjuk a objektum geometria
Testmodellezés Testmodellezés (Solid modeling, Geometric modeling) Testmodell: egy létező vagy elképzelt objektum digitális reprezentációja. A tervezés (modellezés) során megadjuk a objektum geometria
Klár Gergely 2010/2011. tavaszi félév
 Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. tavaszi félév Tartalom Pont 1 Pont 2 3 4 5 Tartalom Pont Descartes-koordináták Homogén koordináták
Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. tavaszi félév Tartalom Pont 1 Pont 2 3 4 5 Tartalom Pont Descartes-koordináták Homogén koordináták
Plakátok, részecskerendszerek. Szécsi László
 Plakátok, részecskerendszerek Szécsi László Képalapú festés Montázs: képet képekből 2D grafika jellemző eszköze modell: kép [sprite] 3D 2D képével helyettesítsük a komplex geometriát Image-based rendering
Plakátok, részecskerendszerek Szécsi László Képalapú festés Montázs: képet képekből 2D grafika jellemző eszköze modell: kép [sprite] 3D 2D képével helyettesítsük a komplex geometriát Image-based rendering
Klár Gergely Informatikai Kar. 2010/2011. tavaszi félév
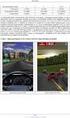 Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. tavaszi félév Tartalom I Sugárkövetés 1 Sugárkövetés 2 3 Tartalom Sugárkövetés Sugarak indítása
Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. tavaszi félév Tartalom I Sugárkövetés 1 Sugárkövetés 2 3 Tartalom Sugárkövetés Sugarak indítása
Grafikus csővezeték és az OpenGL függvénykönyvtár
 Grafikus csővezeték és az OpenGL függvénykönyvtár 1 / 32 A grafikus csővezeték 3D-s színtér objektumainak leírása primitívekkel: pontok, élek, poligonok. Primitívek szögpontjait vertexeknek nevezzük Adott
Grafikus csővezeték és az OpenGL függvénykönyvtár 1 / 32 A grafikus csővezeték 3D-s színtér objektumainak leírása primitívekkel: pontok, élek, poligonok. Primitívek szögpontjait vertexeknek nevezzük Adott
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
Koordináta-geometria feladatgyűjtemény (A feladatok megoldásai a dokumentum végén találhatók)
 Koordináta-geometria feladatgyűjtemény (A feladatok megoldásai a dokumentum végén találhatók) Vektorok 1. Egy négyzet két szemközti csúcsának koordinátái: A( ; 7) és C(4 ; 1). Határozd meg a másik két
Koordináta-geometria feladatgyűjtemény (A feladatok megoldásai a dokumentum végén találhatók) Vektorok 1. Egy négyzet két szemközti csúcsának koordinátái: A( ; 7) és C(4 ; 1). Határozd meg a másik két
Világítástechnika I. VEMIVIB544V A fény és tulajdonságai, fotometriai alapfogalmak és színmérés
 Világítástechnika I. VEMIVIB544V A fény és tulajdonságai, fotometriai alapfogalmak és színmérés tartalom Fotometriai ismétlés Fénysűrűség Színmérés Sugárzáseloszlások Lambert (reflektáló) felület egyenletesen
Világítástechnika I. VEMIVIB544V A fény és tulajdonságai, fotometriai alapfogalmak és színmérés tartalom Fotometriai ismétlés Fénysűrűség Színmérés Sugárzáseloszlások Lambert (reflektáló) felület egyenletesen
Geometriai modellezés. Szécsi László
 Geometriai modellezés Szécsi László Adatáramlás vezérlés Animáció világleírás Modellezés kamera Virtuális világ kép Képszintézis A modellezés részfeladatai Geometria megadása [1. előadás] pont, görbe,
Geometriai modellezés Szécsi László Adatáramlás vezérlés Animáció világleírás Modellezés kamera Virtuális világ kép Képszintézis A modellezés részfeladatai Geometria megadása [1. előadás] pont, görbe,
A geometriai optika. Fizika május 25. Rezgések és hullámok. Fizika 11. (Rezgések és hullámok) A geometriai optika május 25.
 A geometriai optika Fizika 11. Rezgések és hullámok 2019. május 25. Fizika 11. (Rezgések és hullámok) A geometriai optika 2019. május 25. 1 / 22 Tartalomjegyzék 1 A fénysebesség meghatározása Olaf Römer
A geometriai optika Fizika 11. Rezgések és hullámok 2019. május 25. Fizika 11. (Rezgések és hullámok) A geometriai optika 2019. május 25. 1 / 22 Tartalomjegyzék 1 A fénysebesség meghatározása Olaf Römer
OPTIKA. Fotometria. Dr. Seres István
 OPTIKA Dr. Seres István Segédmennyiségek: Síkszög: ívhossz/sugár Kör középponti szöge: 2 (radián) Térszög: terület/sugár a négyzeten sr A 2 r (szteradián = sr) i r Gömb középponti térszöge: 4 (szteradián)
OPTIKA Dr. Seres István Segédmennyiségek: Síkszög: ívhossz/sugár Kör középponti szöge: 2 (radián) Térszög: terület/sugár a négyzeten sr A 2 r (szteradián = sr) i r Gömb középponti térszöge: 4 (szteradián)
Matematika III előadás
 Matematika III. - 2. előadás Vinczéné Varga Adrienn Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Előadáskövető fóliák Vinczéné Varga Adrienn (DE-MK) Matematika III. 2016/2017/I 1 / 30 Egy
Matematika III. - 2. előadás Vinczéné Varga Adrienn Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Előadáskövető fóliák Vinczéné Varga Adrienn (DE-MK) Matematika III. 2016/2017/I 1 / 30 Egy
Diszkréten mintavételezett függvények
 Diszkréten mintavételezett függvények A függvény (jel) értéke csak rögzített pontokban ismert, de köztes pontokban is meg akarjuk becsülni időben mintavételezett jel pixelekből álló műholdkép rácson futtatott
Diszkréten mintavételezett függvények A függvény (jel) értéke csak rögzített pontokban ismert, de köztes pontokban is meg akarjuk becsülni időben mintavételezett jel pixelekből álló műholdkép rácson futtatott
10. Koordinátageometria
 I. Nulladik ZH-ban láttuk: 0. Koordinátageometria. Melyek azok a P x; y pontok, amelyek koordinátái kielégítik az Ábrázolja a megoldáshalmazt a koordináta-síkon! x y x 0 egyenlőtlenséget? ELTE 00. szeptember
I. Nulladik ZH-ban láttuk: 0. Koordinátageometria. Melyek azok a P x; y pontok, amelyek koordinátái kielégítik az Ábrázolja a megoldáshalmazt a koordináta-síkon! x y x 0 egyenlőtlenséget? ELTE 00. szeptember
Klár Gergely 2010/2011. tavaszi félév
 Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. tavaszi félév Tartalom Generációk Shader Model 3.0 (és korábban) Shader Model 4.0 Shader Model
Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. tavaszi félév Tartalom Generációk Shader Model 3.0 (és korábban) Shader Model 4.0 Shader Model
A KLT (Kanade Lucas Tomasi) Feature Tracker Működése (jellegzetes pontok választása és követése)
 A KL (Kanade Lucas omasi) Feature racker Működése (jellegzetes pontok választása és követése) Készítette: Hajder Levente 008.11.18. 1. Feladat A rendelkezésre álló videó egy adott képkockájából minél több
A KL (Kanade Lucas omasi) Feature racker Működése (jellegzetes pontok választása és követése) Készítette: Hajder Levente 008.11.18. 1. Feladat A rendelkezésre álló videó egy adott képkockájából minél több
Q 1 D Q 2 (D x) 2 (1.1)
 . Gyakorlat 4B-9 Két pontszerű töltés az x tengelyen a következőképpen helyezkedik el: egy 3 µc töltés az origóban, és egy + µc töltés az x =, 5 m koordinátájú pontban van. Keressük meg azt a helyet, ahol
. Gyakorlat 4B-9 Két pontszerű töltés az x tengelyen a következőképpen helyezkedik el: egy 3 µc töltés az origóban, és egy + µc töltés az x =, 5 m koordinátájú pontban van. Keressük meg azt a helyet, ahol
= Y y 0. = Z z 0. u 1. = Z z 1 z 2 z 1. = Y y 1 y 2 y 1
 Egyenes és sík a térben Elméleti áttekintés Az egyenes paraméteres egyenlete: X = u 1 λ + x 0 Y = u λ + y 0, Z = u λ + z 0 ahol a λ egy valós paraméter Az u = (u 1, u, u ) az egyenes irányvektora és P
Egyenes és sík a térben Elméleti áttekintés Az egyenes paraméteres egyenlete: X = u 1 λ + x 0 Y = u λ + y 0, Z = u λ + z 0 ahol a λ egy valós paraméter Az u = (u 1, u, u ) az egyenes irányvektora és P
Trigonometria Megoldások. 1) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( )
 Trigonometria Megoldások Trigonometria - megoldások ) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( ) akkor a háromszög egyenlő szárú vagy derékszögű!
Trigonometria Megoldások Trigonometria - megoldások ) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( ) akkor a háromszög egyenlő szárú vagy derékszögű!
1. ábra. 24B-19 feladat
 . gyakorlat.. Feladat: (HN 4B-9) A +Q töltés egy hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld.. ábra.). Számítsuk ki az E elektromos térerősséget a vonal. ábra. 4B-9 feladat irányában lévő,
. gyakorlat.. Feladat: (HN 4B-9) A +Q töltés egy hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld.. ábra.). Számítsuk ki az E elektromos térerősséget a vonal. ábra. 4B-9 feladat irányában lévő,
Grafikus csővezeték (Általános áttekintés) Grafikus csővezeték (Általános áttekintés)
 Dr. Mileff Péter 2 Grafikus csővezeték (Általános áttekintés) A grafikus csővezeték(graphics pipeline): feldolgozási szakaszok egy elméleti modellje ezen keresztül küldjük a grafikai adatokat, hogy megkapjuk
Dr. Mileff Péter 2 Grafikus csővezeték (Általános áttekintés) A grafikus csővezeték(graphics pipeline): feldolgozási szakaszok egy elméleti modellje ezen keresztül küldjük a grafikai adatokat, hogy megkapjuk
OPTIKA. Geometriai optika. Snellius Descartes-törvény. www.baranyi.hu 2010. szeptember 19. FIZIKA TÁVOKTATÁS
 OPTIKA Geometriai optika Snellius Descartes-törvény A fényhullám a geometriai optika szempontjából párhuzamos fénysugarakból áll. A vákuumban haladó fénysugár a geometriai egyenes fizikai megfelelője.
OPTIKA Geometriai optika Snellius Descartes-törvény A fényhullám a geometriai optika szempontjából párhuzamos fénysugarakból áll. A vákuumban haladó fénysugár a geometriai egyenes fizikai megfelelője.
14. Fotórealisztikus megjelenítés
 14. Fotórealisztikus megjelenítés 1007 14. Fotórealisztikus megjelenítés Bevezetés Napjainkban a versenyképes piac, a tervezők, az építészek olyan eszközöket igényelnek, amelyekkel megtervezett épületeket
14. Fotórealisztikus megjelenítés 1007 14. Fotórealisztikus megjelenítés Bevezetés Napjainkban a versenyképes piac, a tervezők, az építészek olyan eszközöket igényelnek, amelyekkel megtervezett épületeket
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Koordináta-geometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Koordináta-geometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Koordináta-geometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
2014/2015. tavaszi félév
 Hajder L. és Valasek G. hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom Geometria modellezés 1 Geometria modellezés 2 Geometria modellezés
Hajder L. és Valasek G. hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom Geometria modellezés 1 Geometria modellezés 2 Geometria modellezés
Orvosi Biofizika I. 12. vizsgatétel. IsmétlésI. -Fény
 Orvosi iofizika I. Fénysugárzásanyaggalvalókölcsönhatásai. Fényszóródás, fényabszorpció. Az abszorpciós spektrometria alapelvei. (Segítséga 12. tételmegértéséhezésmegtanulásához, továbbá a Fényabszorpció
Orvosi iofizika I. Fénysugárzásanyaggalvalókölcsönhatásai. Fényszóródás, fényabszorpció. Az abszorpciós spektrometria alapelvei. (Segítséga 12. tételmegértéséhezésmegtanulásához, továbbá a Fényabszorpció
Területi primitívek: Zárt görbék által határolt területek (pl. kör, ellipszis, poligon) b) Minden belső pont kirajzolásával (kitöltött)
 Grafikus primitívek kitöltése Téglalap kitöltése Poligon kitöltése Kör, ellipszis kitöltése Kitöltés mintával Grafikus primitívek kitöltése Területi primitívek: Zárt görbék által határolt területek (pl.
Grafikus primitívek kitöltése Téglalap kitöltése Poligon kitöltése Kör, ellipszis kitöltése Kitöltés mintával Grafikus primitívek kitöltése Területi primitívek: Zárt görbék által határolt területek (pl.
3D számítógépes geometria és alakzatrekonstrukció
 3D számítógépes geometria és alakzatrekonstrukció 2a. Háromszöghálók http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01 Dr. Várady Tamás, Dr. Salvi Péter BME, Villamosmérnöki
3D számítógépes geometria és alakzatrekonstrukció 2a. Háromszöghálók http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01 Dr. Várady Tamás, Dr. Salvi Péter BME, Villamosmérnöki
Geometriai és hullámoptika. Utolsó módosítás: május 10..
 Geometriai és hullámoptika Utolsó módosítás: 2016. május 10.. 1 Mi a fény? Részecske vagy hullám? Isaac Newton (1642-1727) Pierre de Fermat (1601-1665) Christiaan Huygens (1629-1695) Thomas Young (1773-1829)
Geometriai és hullámoptika Utolsó módosítás: 2016. május 10.. 1 Mi a fény? Részecske vagy hullám? Isaac Newton (1642-1727) Pierre de Fermat (1601-1665) Christiaan Huygens (1629-1695) Thomas Young (1773-1829)
Exponenciális és logaritmusos kifejezések, egyenletek
 Eponenciális és logaritmusos kifejezések, egyenletek. Hatványozási azonosságok. Számítsd ki a következő hatványok pontos értékét! a) 8 b) 4 c) d) 7 e) f) 9 0, g) 0, 9 h) 6 0, 7,, i) 8 j) 6 k) 4 l) 49,.
Eponenciális és logaritmusos kifejezések, egyenletek. Hatványozási azonosságok. Számítsd ki a következő hatványok pontos értékét! a) 8 b) 4 c) d) 7 e) f) 9 0, g) 0, 9 h) 6 0, 7,, i) 8 j) 6 k) 4 l) 49,.
A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld ábra ábra
 . Gyakorlat 4B-9 A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld. 4-6 ábra.). Számítsuk ki az E elektromos térerősséget a vonal irányában lévő, annak.. ábra. 4-6 ábra végpontjától
. Gyakorlat 4B-9 A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld. 4-6 ábra.). Számítsuk ki az E elektromos térerősséget a vonal irányában lévő, annak.. ábra. 4-6 ábra végpontjától
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Trigonometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
OPTIKA. Fotometria. Dr. Seres István
 OPTIKA Dr. Seres István Segédmennyiségek: Síkszög: ívhossz/sugár i r Kör középponti szöge: 2 (radián) Térszög: terület/sugár a négyzeten A sr (szteradián = sr) 2 r Gömb középponti térszöge: 4 (szteradián)
OPTIKA Dr. Seres István Segédmennyiségek: Síkszög: ívhossz/sugár i r Kör középponti szöge: 2 (radián) Térszög: terület/sugár a négyzeten A sr (szteradián = sr) 2 r Gömb középponti térszöge: 4 (szteradián)
Az Ampère-Maxwell-féle gerjesztési törvény
 Az Ampère-Maxwell-féle gerjesztési törvény Maxwell elméleti meggondolások alapján feltételezte, hogy a változó elektromos tér örvényes mágneses teret kelt (hasonlóan ahhoz ahogy a változó mágneses tér
Az Ampère-Maxwell-féle gerjesztési törvény Maxwell elméleti meggondolások alapján feltételezte, hogy a változó elektromos tér örvényes mágneses teret kelt (hasonlóan ahhoz ahogy a változó mágneses tér
Matematika (mesterképzés)
 Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Sergyán Szabolcs szeptember 21.
 Éldetektálás Sergyán Szabolcs Budapesti Műszaki Főiskola Neumann János Informatikai Kar 2009. szeptember 21. Sergyán Sz. (BMF NIK) Éldetektálás 2009. szeptember 21. 1 / 28 Mit nevezünk élnek? Intuitív
Éldetektálás Sergyán Szabolcs Budapesti Műszaki Főiskola Neumann János Informatikai Kar 2009. szeptember 21. Sergyán Sz. (BMF NIK) Éldetektálás 2009. szeptember 21. 1 / 28 Mit nevezünk élnek? Intuitív
Megoldás: Mindkét állítás hamis! Indoklás: a) Azonos alapú hatványokat úgy szorzunk, hogy a kitevőket összeadjuk. Tehát: a 3 * a 4 = a 3+4 = a 7
 A = {1; 3; 5; 7; 9} A B = {3; 5; 7} A/B = {1; 9} Mindkét állítás hamis! Indoklás: a) Azonos alapú hatványokat úgy szorzunk, hogy a kitevőket összeadjuk. Tehát: a 3 * a 4 = a 3+4 = a 7 Azonos alapú hatványokat
A = {1; 3; 5; 7; 9} A B = {3; 5; 7} A/B = {1; 9} Mindkét állítás hamis! Indoklás: a) Azonos alapú hatványokat úgy szorzunk, hogy a kitevőket összeadjuk. Tehát: a 3 * a 4 = a 3+4 = a 7 Azonos alapú hatványokat
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Vektorok II.
 Vektorok II. DEFINÍCIÓ: (Vektorok hajlásszöge) Két vektor hajlásszögének azt a φ (0 φ 180 ) szöget nevezzük, amelyet a vektorok egy közös pontból felmért reprezentánsai által meghatározott félegyenesek
Vektorok II. DEFINÍCIÓ: (Vektorok hajlásszöge) Két vektor hajlásszögének azt a φ (0 φ 180 ) szöget nevezzük, amelyet a vektorok egy közös pontból felmért reprezentánsai által meghatározott félegyenesek
