SZINTVONALAK AUTOMATIZÁLT, HORIZONTÁLIS GENERALIZÁLÁSA AZ ELMÉLETBEN ÉS A GYAKORLATBAN Vonalegyszerűsítő és simító eljárások
|
|
|
- Ágoston Bakos
- 6 évvel ezelőtt
- Látták:
Átírás
1 SZINTVONALAK AUTOMATIZÁLT, HORIZONTÁLIS GENERALIZÁLÁSA AZ ELMÉLETBEN ÉS A GYAKORLATBAN Vonalegyszerűsítő és simító eljárások Ungvári Zsuzsanna Eötvös Loránd Tudományegyetem, Térképtudományi és Geoinformatikai Tanszék, ungvarizs@map.elte.hu Összefoglalás A földfelszín izovonalas leképezését nagy-, közepes- és kisméretarányban egyaránt gyakran használjuk térképeken. Ahogy csökken a méretarány, egyre kevesebb segédlet vagy utasítás áll rendelkezésünkre a kartográfiai generalizálás objektív végrehajtásához, egyre jobban érvényesül a szerkesztő szubjektív szemlélete, és morfológiai ismeretei. A folyamat munkaigényessége miatt manapság egyre gyakrabban alkalmazunk számítógépes algoritmusokat, amelyekkel egy-egy izovonal szintvonal vagy batimetrikus vonal részletessége csökkenthető: azonban ismerni kell ezek tulajdonságait az optimális eredmény elérése céljából. Jelen fejezetben bemutatom és röviden jellemzem a legfontosabb vonalegyszerűsítő és simító eljárásokat, különös tekintettel azokra, amelyek szoftverekben is megtalálhatók. Az angolszász szakirodalomban két, fontosabb rendszerezés született, ezeket az általam ismert algoritmusokkal kibővítettem és rendszereztem. A vonalgeneralizálás két nagy csoportra bontható: az egyszerűsítés és a simítás. Ezeken belül az eljárás működésétől függően két illetve három kategóriát különböztetünk meg. A cikk második részében az algoritmusok gyakorlati alkalmazását mutatom be. A térinformatikai szoftverekben előforduló, valamint az ismert cikkek alapján ígéretes, jó eredményt hozó algoritmusokhoz készített programokból generált eredmények várható eredményeit és az ehhez kidolgozott értékelési folyamatot ismertetem. Abstract The representation of Earth surface by isolines such as contour and bathymetric lines is often used in multiscale maps. At topographic map scale, several directions and rules for generalization are available, but there are just a few of them for smaller scale maps. The subjective viewpoint of the cartographer is much stronger at these maps. Therefore, cartographers need thorough geographic knowledge to increase the objectivity of maps. In addition, generalizing contours needs a lot of human work, thus computer algorithms took over this task in last years. These algorithms can be classified in two main categories according to their function: line simplification routines eliminate the unnecessary vertex of polylines, and smoothing reduces the sharp peaks or broken polylines can be transformed to real curves. In this paper, these algorithms are introduced detailed into the Hungarian scientific literature for the first time. The new classification considers the previous important systems like McMaster and Li, and it is based on them. Line simplification has subgroups as scale-dependent and scaleindependent routines, and smoothing includes curve fitting, weighted averages algorithms and digital filtering methods. In the second section of this article, the author shows how these algorithms work in the practice mainly focused on routines, which can be found in geoinformatics software or in the program written by the author to test them. Finally, an evaluation sheet was created to assess the efficiency and the result of generalization algorithms. 103
2 1. Bevezetés A szintvonal- és a batimetrikus vonalrajz a földfelszín két dimenzióban leképezett mása. A szintvonalas ábrázolás technikájával több szakirodalom is foglalkozik, így RÁTÓTI 1979-ben és KLINGHAMMER PAPP-VÁRY 1983-ban is. Kevesebbet olvashatunk viszont a helyes generalizálásáról. Habár találtam néhány ábrát pl. Az automatizálások a kartográfiában II. című könyvben (STEGENA, KLINGHAMMER és FÜSI, 1977), a kartográfiai tankönyvben (KISS PAPP, 1983), valamint az EOTR T.5. szabályzatában is (T.5., 1981), de részletes útmutatók főleg kisméretarányú térképekhez nem állnak rendelkezésünkre. A generalizált rajz lényege, hogy a terep legfontosabb idomait adja vissza, Márton Mátyás szerint hiteles karikatúrája legyen (IMHOF, 1965, STEGENA, 1970 és MÁRTON, 2012). Mintául szolgálhatnak korábbi, kézzel készített térképek a területről, illetve a terület földrajzi jellemzőinek ismerete. 1. ábra Példa a helyes és helytelen szintvonal-generalizálásra a Kartográfia és térképsokszorosítás című tankönyvben (KISS PAPP, 1983) Az automatizált generalizáláshoz vonalegyszerűsítő és simító algoritmusokat használtam, ezért a következő részben röviden ismertetem a rendelkezésünkre álló eljárásokat. 2. A vonalegyszerűsítés és simítás elmélete A hagyományos térképek rajzolásánál akár manuálisan, akár térképrajzoló szoftverben a térképszerkesztő fejében zajlik a generalizálás: csökkenti a kanyarulatok számát, egyenesíti a vonalat. Ha ezt a folyamatot automatizálni szeretnénk, matematikai alapokra kell helyezni az egyes lépéseket. Alapvetően két csoportba soroljuk az e célra alkalmas algoritmusokat: egyszerűsítő és simító 104
3 algoritmusokra (SLOCUM, 2005). Egyszerűsítés során a vonal töréspontjainak száma csökken, a szerkezete egyszerűsödik. Simítás során a csúcsokat, szögleteket távolítjuk el, ezáltal kerekebbé, simábbá válik a vonallánc: új pontokat számítunk ki. Li (2007) ezzel szemben egy újabb csoportot is bevezetett, ezek a generalizáló algoritmusok. Ezekben a méretarány paraméterként megadható. Véleményem szerint ugyan mindkét csoportosítás helytálló, de a generalizáló algoritmusok besorolhatók a vonalegyszerűsítők közé, annak egy alcsoportját képezik. 2.1 Az egyszerűsítő algoritmusok áttekintése Ezeket a rutinokat többféleképpen is csoportosították, magyarul is megjelent a Térinformatikai alapismeretek c. könyvben fordításként (NCGIA CORE CURRICULUM, 1994). Li ezt használta fel és fejlesztette tovább 2007-ben. Az algoritmusok alapos ismerete alapján a következő csoportosítást javaslom: méretarány-független és méretarány-függő eljárások. A méretarány-független algoritmusoknál nem adható meg sem a kiindulási, sem a célméretarány. Ide sorolom a hagyományos vonalegyszerűsítő rutinokat, az alább felsorolt csoportokban, amely már McMaster és Shea kategorizálásán alapul. Ezeknek az algoritmusoknak a futtatásához legalább két bementi paraméter szükséges: a vonalláncok töréspontjainak koordinátái, és legalább egy tolerancia érték, ez lehet távolság, terület, szög, számosság. A teljesség igénye nélkül, a kartográfiai gyakorlatban eredményesen használható, vagy a térinformatikai szoftverekbe épített algoritmusokat tekintem át, kitérve legfontosabb jellemzőikre. Méretarány-független eljárások esetében a vonalak meglévő csomópontjainak száma csökken, általában megtartják az eredeti csomópontokat, de némely esetben előfordulhat, hogy újakat számítanak ki. Független pontok módszere. Egyszerű algoritmusok, nem veszik figyelembe a vertexek közötti kapcsolatokat. N-edik pont módszer: megtart minden n-edik pontot a vonal töréspontjai közül. N természetes szám. Túl sok töréspont esetén érdemes először ezzel ritkítani a csomópontok számát, de önmagában nem alkalmas generalizálásra. Lokális módszerű (szomszédospont-vizsgálati) eljárások. Szomszédos pontokat vizsgál, például köztük lévő távolság, általuk bezárt szög, vagy ezek kombinációja alapján. A pontok közötti távolság és az általuk bezárt szöget felhasználó algoritmust Jenk után nevezték el. A merőleges távolság esetén a vizsgált, vagy más néven a kritikus pont előtti és utáni csomópontot köti össze egy képzeletbeli egyenessel, és a kritikus pont egyenestől való távolságát vizsgálja meg. Korlátozottan kiterjesztett lokális eljárások. A pontok szélesebb szomszédságát nézik meg: például a Lang, a Deveau, és a Visvalingam Whyatt algoritmusok. A Lang-algoritmusnak két, a felhasználó által megadható paramétere van: az egy lefutásban maximálisan vizsgálandó pontok száma, és egy merőleges távolság az aktuálisan vizsgált első és utolsó pontot összekötő egyenestől (LANG, 1969). A Deveau-algoritmus a felesleges, az objektum alakját nem meghatározó pontokat törli, helyenként újakat határoz meg. Két bemeneti paramétert adhatunk meg, ezek a simasági faktor és a maximális élességi szög (DEVEAU, 1985). A Visvalingam Whyatt-rutinnál az egyetlen választható paraméter az éppen vizsgált 105
4 három pont által bezárt háromszög területe, vagyis a hatékony terület (VISVALINGAM és WHYATT, 1993). Nem korlátozott, kiterjesztett lokális eljárások. A Reumann Witkamalgoritmus esetén a vonal morfológiája szabja meg a vizsgált pontok számát: a kritikus pontot a következő ponttal összekötő egyenes irányában húzott sávon belül elhelyezkedő pontokat törli, majd áthelyezi a kritikus pontot az első, sávon kívül eső pontba. A választható toleranciaérték a sáv teljes szélességének felét jelenti. Eredményeként hosszú egyenes szakaszok jönnek létre (REUMANN és WITKAM, 1974). Ebbe a csoportba sorolom a Wang( Müller)-féle algoritmust is, amely a vonalak kanyarulatait egyszerűsíti, és amelyben egy paramétert adhatunk meg, ez a kanyar mérete (a polyline kanyart leíró része, és a kanyar alapvonala által bezárt terület). A kanyar a vonal azon szakasza, ahol az egymást követő csomópontok irányultsága vagy negatív, vagy pozitív, vagyis amíg nem következik be lokális irányváltás, azaz inflexió a vonal futásában (WANG és MÜLLER, 1998). Ide tartozik még a lineáris regresszión alapuló generalizálás is (AGÁRDI, 2014). A globális eljárások a teljes vonalláncot, vagy a vonal egy hosszabb szegmensét veszik figyelembe; iteratív módszerrel választják ki a kritikus pontokat. A legszélesebb körben alkalmazott algoritmus a (Ramer ) Douglas Peucker-féle egyszerűsítő rutin (RAMER, 1972 és DOUGLAS PEUCKER, 1973). A rekurzív eljárás merőleges távolságokkal dolgozik, ez a változtatható paramétere. Első lefutásban megvizsgálja, hogy melyik pont esik legtávolabb a kezdő- és a végpontot összekötő egyenestől. Ha ez a távolság kisebb, mint a tolerancia érték, ez lesz az új szakasz (vagy vonal); ha nagyobb; akkor rekurzívan újra hívja önmagát az eljárás, mindaddig, míg be nem fejezi a vonal vizsgálatát. A kezdő- és végpontot mindig megtartja. A méretarány-függő eljárások közé sorolom a Li által generalizálónak nevezett algoritmusokat, amelyekben meghatározható a kiindulási és célméretarány is. Perkal ötlete az automatizálási gyakorlatba nem került át. Ennek lényege, hogy a vonal mentén mindkét oldalon köröket helyezzünk el oda, ahol a vonalnak inflexiós pontja van. A kör vonalláncot érintő szakaszai lesznek a vonal új szakaszai. A belső és külső elhelyezésű körök különbségéből jön létre a generalizálási határzóna. Erre Perkal nem javasolt gyakorlati megoldást, de az örvény-algoritmus (angolul: whirlpool) működése ehhez hasonló (DOUGENIK, 1980). Méretarány szerint változó sugarú köröket helyezünk el az egyes csomópontokban. Ahol a nem szomszédos körök átfedik egymást, ott a méretarányhoz képest túl hegyes csúcs van, amit egyszerűsíteni kell. A Li Openshaw-féle eljárások figyelembe veszik az objektumok méretét. Ha az adott elem a célméretarányban kisebb, mint a minimális méret, akkor elhagyják. Bármilyen komplex felépítésű is az elem, ha nagyobb a minimális méretnél, egyszerűsíthető. A méretarány szerint definiálni kell egy raszteres rácshálót, amely az egyes celláiban elhelyezkedő objektumrészlet töréspontjaiból egy új pontot átlagol, majd ezeket köti össze (LI, 2007). Az objektumok területét megőrző kartográfiai vonalgeneralizálási algoritmus egy összetett metódus, amely két lépésben működik: először egyszerűsít, majd az ezután megmaradt, túl éles csúcsokat elsimítja. Az egyszerűsítés során csökken a vonal komplexitása: négy pontból álló csoportokból képez ponthármasokat úgy, hogy 106
5 a négyszög területe megegyezik a háromszög területével, ezáltal nem keletkeznek bezárult felületek, mint pl. a Douglas Peucker-algoritmusnál. Bemeneti paraméterként csak a célméretarány nevezőjét kell megadni (QGIS-es verzió), ehhez tartozik egy tapasztalati úton meghatározott minimális távolság (0,05 mm), amelynél a négy pontból képzett három szakasz összhosszának kisebbnek kell lennie ennél a számnál. A simítást csak ott hajtja végre, ahol túl éles szög keletkezett, az egyszerűsítésnél is alkalmazott a területmegőrző módszer ellentétjével (TUTIC, 2009). Ezáltal az algoritmus a méretarányfüggő, egyszerűsítő eljárások közé tartozik, bár simítást is végez, az csak részleges, kivitelezésében nem tartozik a simító algoritmusok közé. 2.2 A vonalsimító eljárások áttekintése A simítás megszabadítja a vonalláncokat az éles szögektől, csúcsoktól, az ún. zajoktól és részletektől. McMaster és Shea három csoportba sorolja a simító algoritmusokat (SLOCUM, 2005), míg Li már négy kategóriát állított fel (LI, 2007). A kétféle csoportosítás alapján kidolgoztam egy újabbat, amely egyesíti a kettőt. A magyar nyelvű szakirodalomban eddig még nem foglalkoztak vonalsimító eljárások csoportosításával, elnevezésével. Vannak olyan csoportok, amely mindkét szerzőnél megegyeznek. Súlyozott átlagok. A vonallánc csomópontjainak a szomszédos töréspontok átlaga alapján egy új pozíciót számít ki. Ide tartozik pl. a simítás a McMaster-féle súlyozott átlaggal, és simítás a McMaster-féle csúsztatott átlaggal. Mindkettőnél két bemeneti paraméter van, az egyik az átlagolásban részt vevő pontok száma (célszerű páratlan számú pontot átlagolni), a másik szám az új pont eredetihez való közelebb csúsztatásának mértékét fejezi ki [0,1] között, ahol 0 az eredetivel megegyező, 1 pedig az átlagolásban bevont pontokból számított új helyzetet jelenti. A csúsztatott átlag esetén az új töréspont eltolása lineáris, súlyozott átlag esetén a távolsággal fordítottan arányosan súlyozott. Boyle előretekintő algoritmusa (forward looking) esetén a megadható paraméter egy szám (x), amelytől függ az új pont helyzete. Az eredeti algoritmust kissé módosítva ültették át a gyakorlatba: a megadott szám a kritikus pont új helyzetének kiszámításához szükséges. A következő x darab pont 1/x súllyal vesz részt a kritikus pont új helyzetének számításában (BOYLE, 1970). A szerző többek között a mélységvonalak simításához ajánlja, ezért az algoritmust szintvonalakon is megvizsgáltam. Görbeillesztés során a vonalláncot görbékkel helyettesítjük. Mivel a térinformatikai szoftverek vagy fájlformátumok többségében nem támogatják a görbék leírását, ezért ezeket polyline-okkal ábrázoljuk úgy, hogy megfelelő sűrűséggel megadjuk a görbe pontjait, így a célméretarányban görbének látszanak. A görbéknek matematikai szempontból két fajtája lehet: interpolációs (a görbe átmegy a vezérlőponton) és approximációs görbék (követi a vezérlőpontot, de általában nem megy át rajta). A görbeillesztés során a gyakorlatban általában harmadfokú görbékkel helyettesítjük az eredeti törött vonalat. A szoftverekben használt görbéket harmadfokú egyenletekkel, vagy polinomokkal írhatjuk le a legegyszerűbben. A Bernstein-polinommal állítható elő a Bézier-görbe (KOVÁCS, 2011). Egy harmadfokú Bézier-görbeív futásvonala a két végpont és a két vezérlő v. más néven kontrollpont koordinátájának ismeretében írható le. Ha egy törött vonalat helyettesítek görbével, akkor az egyes görbeívek érintői a végpontokban párhuzamosak és folytonosak, így biztosítható görbe vonal sima futása. (Két görbe 107
6 folytonos illeszkedésű, ha az egyik görbe második deriváltjai a végponton megegyeznek a másik görbe második deriváltjaival a kezdőponton. Ezeket a folytonos, összetett görbéket szplájnoknak nevezzük.). Az egyes görbeívek futásvonalának számításához a két végpontra, és egy íveltségi együtthatóra van szükség: ezekből interpolálható a két kontrollpont, amivel már megadható görbe (SZIRMAY-KALOS, 2003 és AGG, 2007). A Bézier-görbéhez küllemre igen hasonló megoldást kapunk, ha Hermitegörbéket használunk fel. Ezek bár interpolációs görbék, de ugyanúgy megadhatók polinomokkal is: két pont és két érintő vektor lesz az input adat a görbeívek számításakor (KOVÁCS, 2011). A görbék ezen kívül lehetnek approximációs B-szplájnok is. Ennek két altípusa van: a NUBS (nem-uniform B-szplájn: az egymást követő görbeszegmenseknek nem egységnyi intervallum felel meg) és a NURBS (nemuniform racionális B-szplájn: az egymást követő görbeszegmenseknek nem egységnyi intervallum felel meg és a súlyfüggvények két polinom hányadosai is lehetnek). Előnyük, hogy rugalmasan alakíthatók, ezért inkább a mérnöki tervezésben használják őket, a térinformatikai szoftverekben kevésbé (SZIRMAY-KALOS, 2003). A Chaikin-algoritmussal a vonallánc szögletességét csökkentjük: veszünk három, egymást követő csomópontot (P1, P2, P3), amely a vonallánc két szakaszát (P1 P2 és P2 P3) alkotja. Mindkét szakaszra, a P2 közelében beszúrunk két új pontot, és a P2-t töröljük. Ugyanezt végrehajtjuk a teljes vonalláncra. Ha ezt a folyamatot egymás után legalább háromszor ismételjük, általában kellően sima lesz az új vonallánc, megszűnik a vonallánc sarkossága (CHAIKIN, 1974 és RIESENFELD, 1975). Az így kapott görbék másodfokú B-szplájnok. Bár a polinomiális approximáció exponenciális kernellel (PAEK) eredményeként kapott vonalak a Chaikin-algoritmushoz hasonlítanak leginkább, ezért ebbe a csoportba soroltam be, de a felhasznált matematikai módszer alapján mindhárom kategóriába illene. A görbe egyes szakaszain a csomópontok helye alapján átlagolt pontot számít ki egy, a Gauss-szűrőhöz hasonló, de azzal nem azonos kernellel (konvolúció). Ehhez másodfokú polinomokat is felhasznál (BODANSKY et al, 2002). Zajszűrés alapú simítás. A zajszűrés során a vonalláncot digitális jelnek tekintjük. A kisebb formákat reprezentáló ívek, görbületek a zajok, ezeket kiszűrjük, a nagyobb trendeket, görbületeket megtartjuk. A Fourier-transzformációt például a digitális jelfeldolgozásban is használják. A szűrés időbeli folyamatokról szól, ez a szintvonalak esetén távolságot jelent, a frekvencia pedig térfrekvenciát. Mivel a szintvonalak általában nem ábrázolhatók függvényként (többértékű függvény nem fejthető Fourier-sorba), ezért Stegena a következőképpen járt el: egy síktartományt rendel minden szintvonalhoz (egy lépcső jön létre a szintvonal két oldala között, melynél a szintvonal egyik felén lévő magasságérték 1, a másikon 0), ezen szimmetrikus, kétváltozós szűrőt futtat. A 0,5 magasságú pontokat összeköti, ez lesz a szűrt vonallánc. A szűrők közül a felülvágó szűrőt ajánlja (STEGENA, 1970). A másik lehetséges módszer a gyors Fourier-transzformáció. Többféle tudományban is gyakran használják zajszűrésre, ilyenkor a vonalakat szinusz és koszinusz függvények sorára bontják fel. Boutoura bebizonyította, hogy önmagában az 108
7 izovonalak X és Y koordinátáinak használata esetén nem működik jól, helyette inkább a vonalak meredekségét használta fel (BOUTOURA, 1989). A wavelet-transzformáció is egy spektrális felbontás, azonban nem szinusz és koszinusz összetevőkre bontjuk fel a jelet, ahogy azt a Fourier-transzformáció esetén tettük, hanem például különböző frekvenciájú négyszögjelekre (LI, 2007). A számítás folyamata a gyakorlatban igen összetett, ezért a wavelet- és a Fourier-transzformációt kevésbé használják térinformatikai szoftverekben: eredményük és hatásuk a vonalláncokon a tanulmányok szerint egymáshoz igen hasonló; a tanulmányokban bemutatott ábrák alapján nem javaslom kartográfiai alkalmazásukat. A kígyóknak (angolul: snakes) nevezett eljárás a számítás módszere miatt igen lassú, de egy kisebb, kevesebb töréspontból álló adathalmazon a gyakorlatban is használható eredményt ad. A módszer az energia-minimalizáción alapul: a vonal belső és külső energiáját kell a lehető legalacsonyabb szintre levinni. A függvénynek két, a felhasználó által választható paramétere van: a belső energia, amely a vonal alakját és karakterisztikáját írja le; és a külső energia, amely a vizsgálandó elem más térképi elemekre való hatását adja meg (BORKOWSKI, 1999). 3. A szintvonalak horizontális generalizálása a gyakorlatban A szintvonalak generalizálása összetett feladat: nemcsak horizontális, hanem vertikális generalizálás is szükséges. A horizontális generalizálást tulajdonképpen két részre bonthatjuk: a nagy- és közepes méretarányban végrehajtott generalizálásra, valamint a kisméretarányú térképek domborzatának generalizálására. Topográfiai térképeken (vagy olyan térképeken, amely alapnak a topográfiai térképek domborzatát használják, pl. tájfutó, turista térképek) a generalizálás szorosan szabályokhoz kötött, a szerkesztési utasításba foglalt: pl. mit kell ábrázolni, milyen sűrűn és hogyan kell felvenni a felezőszintvonalakat, hol szükséges kiegészítő domborzatrajz (T.5., 1981). A kis méretarányú földrajzi, autós vagy egyéb tematikájú térképen a generalizálást jobban befolyásolják térképszerkesztő földrajzi ismeretei. A horizontális generalizálás vizsgálatát ezért kétféle méretarány-tartományban végeztem, de jelen cikkben csak a kis méretarányban szerzett tapasztalataimat írom le. Itt az algoritmusokat SRTM90-es modellből generált szintvonalakon teszteltem. A következőkben az egyes algoritmusok lehetséges használatát és a várható eredmények minőségét értékelem. A horizontális generalizálás esetében többnyire az egyszerűsítő és simító eljárások kombinációját használhatjuk. Önmagában a vonalegyszerűsítés általában nem elég a megfelelő eredmény elérése érdekében, ugyanis túl szögletes, sarkos vonal keletkezik. Többféle módszerrel is kísérleteztem, de kartográfiai szempontból az egyik legjobb eredményt a Douglas Peucker-algoritmussal történő egyszerűsítés, majd utána a Chaikin-algoritmussal való simítás után kaptam. A módszer előnye, hogy végrehajtható QGIS-ben, de ArcGIS-ben is. Az utóbbi szoftverben nem érhető el a Chaikin-algoritmus (2. ábra), de helyettesíthető a polinomiális approximációval). Emellett bizonyos méretarány-tartományokban a Douglas Peucker-algoritmussal való egyszerűsítés és utána Bézier-görbékkel történő simítás is jó eredményt hozott (kivitelezhető mindkét vezető térinformatikai szoftverben, de a QGIS-ben csak Hermite-görbéket tudunk használni). A generalizálás menete az utóbbi módszerrel a következő: 109
8 2. ábra Douglas Peucker-algoritmus kifejezetten alkalmas a szögletes formák megőrzésére, pl. óceánközépi hátságoknál akár milliós méretarányban is Szükség van egy szintvonalrajzot tartalmazó állományra, ezt generálhatjuk akár SRTM domborzatmodellből is. A felhasználó választja ki a generalizálás mértékét, adja meg a Douglas Peucker-függvény paraméterét. Ha a forrásadatokat földrajzi koordinátaként tároljuk, akkor fokban; egyébként metrikus rendszerben (angolszász mértékegységekben is lehet) értelmezzük, ettől is függ a paraméter nagysága. Minél nagyobb ez a szám, annál erősebb mértékű lesz a generalizálás. Az adatsor beolvasása után vonalláncokra bontjuk az állományt. A vonallánconként megyünk végig az állományon, a Douglas Peucker-algoritmus (röv.: DP) rekurzívan hívja újra önmagát. Két függvényből áll, az egyikkel kiszámítja a merőleges távolságot az aktuális pontok között, míg a másik a toleranciaértékkel való összehasonlításért, illetve az új vonallánc töréspontjainak mentéséért felelős. Ha befejezte az egyszerűsítést a vonalláncon, a simítás következik. Egymáshoz folytonosan csatlakozó, harmadfokú Bézier-görbe íveket illeszt úgy, hogy a végpontok átmennek a vonallánc töréspontjain, a két kontrollpontot pedig interpolálja. Az eredményt olyan állományban érdemes tárolni, amely felismeri a Bézier-görbéket, pl. SVG (Scalable Vector Graphics), de lehetséges a görbe nyomvonalát megfelelő töréspontsűrűséggel pl. shapefile-ba is kiírni. Másik hatékony generalizálási módszer, amelyet Agárdi Norbert készített (AGÁRDI, 2014), a lineáris regresszió módszerén alapul. Az algoritmus az egyes görbeszakaszokat egy regressziós egyenessel helyettesíti (ahol ez a meghatározott toleranciaértéken belül található, ugyanahhoz a regressziós egyeneshez tartozik); a generalizálás mértéke a tolerancia növelésével emelhető. A regressziós egyenesek 110
9 harmadfokú Bézier-görbeívek érintői lesznek, két végpontjuk két folytonosan csatlakozó görbeív kontrollpontja. Ennek segítségével kiszámíthatók a Béziergörbeívek végpontjai. Mindkét módszernél keletkezhetnek bezárult, vagy önmagukat metsző görbeívek. Ezek többségének javítását érdemes lehet programozással megoldani. Mielőtt a vonalláncra görbét illesztene a program, megvizsgálja, hogy melyik polyline áll csupán két vertex-ből ezek a záródott görbeívek lesznek. Görbeillesztés nélkül, a kiindulási és a célméretarány ismeretében használhatjuk a Li Openshaw-módszerét raszteres-vektoros módban. A vonal mentén négyzeteket veszek fel úgy, hogy az első a vonal kezdőpontjának közepe lesz, és a többi négyzet az előző oldalát vagy sarokpontját érinti, a vonal irányának megfelelően. Minden négyzetben kiszámítottam a benne elhelyezkedő töréspontok átlagát, amely az új vonal csomópontjai lesznek. Ha egy vonal elfér egy négyzetben, akkor ez kisebb lesz a minimális méretnél, így ezt elhagyja. Az algoritmus nem hoz létre önmetszéseket, azonban kissé szögletessé válhatnak a vonalak a kevés csomópont miatt. A szögletesség pl. a Chaikin-algoritmussal eltüntethető. Az eredeti cikk alapján hoztam létre, és teszteltem ezt az algoritmust is (3. ábra). 3. ábra Az SRTM90-ből generált kiindulási szintvonalrajz, a lineáris regresszióval egyszerűsített és a Li Openshaw-féle egyszerűsítés A Wang-algoritmus, vagy másképpen a kanyarulatok egyszerűsítése (ArcGIS Bend simplify) is részben eredményes lehet. Az egyszerűsítés során a kisebb kanyarokat, íveket szünteti meg először, ehhez kisebb tolerancia érték tartozik. Ha a toleranciát növeltem, egyre inkább több utólagos, kézi helyesbítést igényelt a rajz. A Reumann Witkam-algoritmus nem használható izovonalak egyszerűsítésére, mert utána hosszú egyenes szakaszokból álló vonalszakaszok keletkeznek, amelyeket nem lehet eltüntetni simítással. 111
10 A lokális eljárású módszerek a vonal néhány csomópontból álló szakaszát vizsgálják csak az egyszerűsítésnél, ezért önmagukban általában nem adnak jó eredményt, ezért inkább a feldolgozandó adatmennyiség előszűrésére használhatók. A simító eljárásokkal is vegyesek a tapasztalataim. A görbeillesztések közül még eredményes lehet a Chaikin-algoritmus, kettő, vagy háromszori ismétléssel, ha nincsenek az állományban hosszú, egyenes vonalak. Ilyenkor előfordulhat, hogy csak a töréspontnál lesz kerek a vonal, de egyébként megőrzi szögletességét. Ehhez hasonló az ArcGIS-ben található PAEK (Polynomial Approximation with Exponential Kernel) nevű algoritmus. A Boyle előretekintő simító hatású algoritmusát önállóan, többféle paraméterrel is kipróbáltam. A kapott eredmény igen hasonló a képszűréses módszerrel simított szintvonalakhoz. Boyle szerint a mélységvonalakhoz, tapasztalataim szerint magassági vonalak generalizálásához is alkalmazható. Utólagos kézi javítások itt is szükségessé válnak: annál több javítás, minél nagyobb a toleranciaérték. Legfontosabb hibák: az önmagukba visszatérő szintvonalaknál (a térképkivágaton belül) a generalizálás kiinduló és végpontja általában csúcsosan kapcsolódik össze; hasonló méretű völgyek ismétlődnek egymás után (hullámos felszín), a generalizált vonal a morfológiai forma ellentétjét veszi fel (pl. völgyből gerincforma lesz); kissé rövidülő völgyek vagy gerincek. A súlyozott átlagokkal a szintvonalak sarkossága csökkenthető, de a töréspontok száma nem változik, ezért általában nem elegendő a szintvonalak generalizálásához. Korábban a térképszerkesztő által végzett generalizálás során, ha az alapanyag és a céltérkép között túl nagy volt méretarány-különbség, akkor a generalizálást több lépésben hajtották végre, ezen alapulnak például a topográfiai térképsorozatok. Például, ha 1: es alaptérképből szerettek volna egy 1: es térképet készíteni, szükséges volt egy köztes méretarányú térkép, pl. 1: es elkészítésére. A generalizálás automatizálásával a kiindulási és célméretarány között a különbség megnövekszik. A különbség nagysága leginkább a választott algoritmustól függ, de a szintvonalak sűrűsége (választott vertikális értékei) és a terület földrajzi jellege is befolyásoló tényező lehet. Ezentúl kipróbáltam, hogy mi történik, ha több, egymást követő lépésben alkalmazok automatizálási algoritmusokat: először ugyanazt az algoritmust hívtam meg a generalizált anyagon, második esetben egy másik algoritmus választottam. Azt vizsgáltam meg, befolyásolja-e az algoritmus választása a két esetet, illetve mennyire növelhető meg a méretarány-különbség a kiindulási és a célméretarány között. A különbségek többsége már az egyszerűsítésnél jelentkezik. Vannak olyan algoritmusok pl. DP, hogy ha két lépésben hajtom végre az egyszerűsítést, pontosan ugyanazt az eredményt kapom, mintha egy lépésben került volna sor rá. A második esetben egymás után hívtam meg két, tolerancia értékként távolságot használó algoritmust. Ha toleranciaértékként ugyanazt a távolságot használtam, alig volt különbség az eredményben (DP, majd Lang) a két lépés folyamán. Ellenkező esetben, amikor a Lang-algoritmus volt az első, és a DP a 112
11 második, a különbség jelentősebb volt. Viszont ha a két végeredményt összevetem, némi különbség ugyan itt-ott jelentkezik, de nem számottevő. Az első esetben a rövidebb vonalak pontokká alakultak. Az előbbiekből következik, hogy ha önmagában csak a DP algoritmust használtam volna, hasonló eredményt kaptam volna. Levonható a következtetés, hogy két egyszerűsítő algoritmus használata általában nem nyújtja meg annyira a kiindulási és célméretarány közti különbséget, hogy érdemes legyen ezt a módszert használni. Az óceáni területeken a mélységvonalak generalizálása már kevésbé egyértelmű, mint a szárazföldön: nemcsak az as, 70 -es, de még a 80 -as években is jelentek meg olyan szakkönyvek (KOCH, 1960 és KLINGHAMMER PAPP-VÁRY, 1983), sőt még manapság is térképek, amelyek szerint az óceáni területek kétszeresen generalizáltnak kell lenniük a szárazföldekhez képest. Ezt az óceánok kevésbé változatos domborzatával magyarázták, ami azonban nem igaz. Manapság már rendelkezésünkre állnak domborzatmodellek, amelyekből kis méretarányban a batimetrikus izovonalak (izobátok) kinyerhetők. 4. A generalizálás-vizsgálatok eredményeinek értékelése Az egyes algoritmusok kimenő adatainak értékelése szempontjából legfontosabbnak a vizuális összehasonlítást tartom, vagyis azt, hogy mennyire hasonlít az eredmény ahhoz, mintha kézzel végeztük volna el a generalizálás folyamatát. Lehetséges ugyan matematikai-statisztikai módszerekkel mérni az eredményeket a kiindulási anyag és a végeredmény között, de ez ellentmondásokhoz vezethet (pl. kedvező vizuális megjelenés, de rosszabb statisztikai eredmény, és fordítva). További nehézség az algoritmusok különbözőségéből fakad. Az sem helyes, ha hasonló tolerancia-érték megadásával hasonlítjuk össze az algoritmusokat, mert másmás lehet a toleranciaérték dimenziója pl. hosszúság vagy terület. Eldöntendő kérdés az is, hogy az eljárás értékelésénél az egyes objektumokra gyakorolt hatást vesszük figyelembe, vagy az objektumok közötti viszonyokat is. Az eredmények értékeléséhez feltétlenül szükségesek a szerkesztő geomorfológiai ismeretei. Az egyszerűsítő és a simító algoritmusok értékelését Li is külön tárgyalja (LI, 2007), ezt szintvonalak esetén nem tartom szükségesnek, mert nem az algoritmusokat, hanem az eredményüket kell elemezni, többnyire egymás után használva az egyszerűsítést és simítást. Az értékelési folyamatot és kritériumokat a következőképpen határoznám meg az automatizált generalizálásnál: 1. Vizuális értékelés: megőrizte-e az eredeti vonal karakterisztikáját? (A generalizálás minősége.) 2. A megadott paraméterekkel a célméretarányban használható eredményt kaptunk-e? Milyen mértékű utólagos korrekció szükséges? 3. Keletkeztek-e önmetszések, összezárult vonalláncok, túl kicsi objektumok? Ha igen, milyen mértékben és van-e jellegzetes előfordulásuk (LI, 2007)? (Programozással javíthatók.) 4. Keletkeznek-e metszések objektumok között? (Az algoritmus kiegészítése lehet szükséges.) 5. A vonal megváltozott futása miatt a generalizálást már korábban is megpróbálták számszerűsíteni. Stegena szerint egy szintvonal maximális helyzetváltozása a vízszintes irányú bizonytalanság minimumának kétszerese 113
12 lehet, ettől csak úgy lehet eltérni, hogy az új izovonal minél jobban megőrizze a felszín formakincsét. A vízszintes bizonytalanságot a következőképpen definiálta Koppe: m=±(k M+c ctgα), ahol az α a lejtőszög, c=0,1 m a magasságmeghatározási hiba és k=0,0002 m a helyzetkiolvasási hiba és M a méretarányszám. Vagyis pl. 1: térképen 1 os lejtőszögnél kb. 15 méter, ennek kétszerese kb. 30 m, 45 -os lejtőnél ez 10 m és 20 m (STEGENA, 1970). Egyes térképtípusoknál nagyobb eltérés is megengedhető, pl. eltolható a szintvonal a szomszédos szintvonal fele távolságáig. 6. Megnéztem, hogy keletkeztek-e új pontok, vagy csak csökkentettük az eredeti csomópontszámot? Véleményem szerint, a mérőszámok önmagukban nem adnak tájékoztatást az eredmény minőségéről, ennél sokkal fontosabb a vizuális kiértékelés.) 7. Melyik szoftverben lévő algoritmust használtuk? Az algoritmus mennyire könnyen implementálható szoftverekbe, mennyire gyors és hatékony? 8. Ha a mintaterületen létezik topográfiai térképszelvény, vagy atlasz, akkor a régi (kézi) és új (automatizálással készített) domborzatrajz összehasonlítása milyen eredményt hoz? A generalizálás-vizsgálatokat háromféle módszerrel próbáltam ki: ezek az egyszerűsítés DP-algoritmussal, majd simítás a Chaikin-féle módszerrel; lineáris regresszió módszere; és a Li Openshaw-féle raszteres-vektoros módszerű generalizálás. Ezek alapján az általánosságban levonható következések: mindegyik algoritmusnál megállapítható egy méretarány-tartomány, ahol vizuálisan szép eredményt ad, ez a tartomány a DP-algoritmus alkalmazásánál a legszűkebb. Az 5. pontban leírtak szerint a térképen helyenként kb. max. 1 mm-es eltérések észlelhetők. Ennek mértéke és gyakorisága függ a választott algoritmustól is; legtöbbször a szűk völgyeket vagy gerinceket ábrázoló kanyarulatoknál fordul elő. A 8. pontban említett összehasonlítás kivitelezése a legnehezebb: nem biztos, hogy a célméretarányban létezik megfelelő térkép (rétegszínezéses vagy szintvonalas ábrázolású, és ez megfelelő színvonalú is). Egy algoritmus tervezésénél vagy használatánál felmerül a kérdés, hogy meddig érdemes az algoritmus által produkált hibákat programozással javítani pl. önmetszés, bezáródott ívek, elemek közötti viszonyok vizsgálata, metszések javítása, szintvonalfésülés, formák felismerése (4. ábra). 4. ábra Eltérő módszerrel egyszerűsített batimetrikus vonalrajz, amely a tengerfenéki kúpokat ábrázol, a második esetben több korrekció szükséges 114
13 5. Következtetések és kitekintés Az itt bemutatott algoritmusok mindegyike felhasználható a kartográfiai generalizálás során, ugyanakkor nem mind alkalmas izovonalak egyszerűsítésére. A generalizálási folyamat szubjektivitása miatt nagyon nehéz az algoritmust mindenre felkészíteni csaknem lehetetlen. Sajnos, mint látszik teljes egészében nem automatizálható a generalizálás, szükség van utólagos korrekciókra; az egyes speciális morfológiai formák (pl. fjordok, óceánközépi hátságok ábrázolása stb.) igényelhetik a szerkesztők javításait. Addig érdemes az algoritmust fejleszteni, amíg nem válik túl bonyolulttá, és a sok feltétel nem okoz ellentmondásokat, újabb hibákat. Emellett az egyes algoritmusok, csak egy meghatározott méretarány-tartományokban használhatók jól: a tartomány felső határát az alapanyag minősége, a vertikális generalizálás mértéke, az egyszerűsítő és simító algoritmusok sorrendje, valamint a térképszerkesztő által vállalt kézi javítások mértéke és a kiegészítések (igazítás vízrajzi elemekhez és kiegészítő domborzatrajz elhelyezése) is befolyásolja. Az egyes algoritmusok felhasználhatósági méretarány-tartománya erősen függ a terület földrajzi terület jellegétől is. Vizsgálódásaim bebizonyították, hogy más-más algoritmus alkalmasabb például a magashegységek vagy fjordok valamint az óceánközépi hátságok ábrázolására. Az elmúlt évtizedben az interneten szabadon elérhető váltak különféle felbontású domborzatmodellek, ezekből nyertem a vizsgálataimhoz használt szintvonalakat is. Ugyanakkor lehetséges ezek egyszerűsítése is különféle módszerekkel pl. képszűréssel. Az eredmény vizsgálataim alapján itt sem tökéletes: ellenben, ha figyelembe vesszük a vízrajzi elemeket, akkor elkerülhetjük, hogy pl. a folyók felfelé folyjanak. Irodalomjegyzék AGÁRDI, N., Automatizálási lehetőségek a tematikus kartográfiában. Doktori értekezés, Budapest: Eötvös Loránd Tudományegyetem, pp AGG REFERENCE MANUAL, The Anti-Grain Project, nyílt forráskódú C++ függvénykönyvtár. [online] Elérhetőség: [2016. november 2.] BODANSKY, E., GRIBOV, A. és PILOUT, M., Smoothing and compression of lines obtained by raster-to-vector conversion. In: Lecture Notes in Computer Science: Graphics Recongnition Algorithms and Applications. Vol. 2390, pp BORKOWSKI, A., BURGHARDT, D. és MEIER, S., A fast snakes algorithm using the tangent angle function. International Archives of Photogrammetry and Remote Sensing, 32 (Part 3-2W5), pp BOUTOURA, C., Line generalization using spectral techniques, Cartographica, 26(3-4), pp BOYLE, A. R., The quantised line. Cartographic Journal, Vol: 7 (2) pp CHAIKIN, G., An algorithm for high speed curve generation. Computer Graphics and Image Processing, Vol. 3 (1974), pp DEVEAU, T. J., Reducing the number of points in a plane curve representation. In: Auto- Carto VII. Washington, pp DOUGENIK, J., Whirpool A geometric processor for polygon coverage data. In: Auto- Carto IV., pp
14 DOUGLAS, D. és PEUCKER, T., Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. The Canadian Cartographer 10(2), pp IMHOF, E., Kartographische Geländedarstellung. Berlin: Walter de Gruyter & Co., pp , KISS PAPP, L., Kartográfia és térképsokszorosítás. Budapest: Tankönyvkiadó Vállalat, pp KLINGHAMMER, I. és PAPP-VÁRY, Á., Földünk tükre a térkép. Budapest: Gondolat Kiadó, pp KOCH, N., A tenger. In: TASNÁDI, K. A. (szerk.): A Föld. Budapest: Gondolat Kiadó, pp KOVÁCS, E., Komputergrafika Matematikai alapok. Elektronikus jegyzet. Eger: Eszterházy Károly Főiskola, Matematikai és Informatikai Intézet, 8. fejezet: Görbék megadása, 9. fejezet: B-spline görbe és felület. LANG, T., Rules for robot draughtsmen. Geographic Magazine 42(1), pp LI, Z., Algorithmic Foundation of Multi-Scale Spatial Representation. Boca Raton USA: CRC Press, Taylor and Francis Group, pp. 1 25, 57 72, MÁRTON, M., A Világtenger kartográfus szemmel. Budapest: Eötvös Loránd Tudományegyetem, Informatikai Kar, Térképtudományi és Geoinformatikai Tanszék, pp NCGIA CORE CURRICULUM, Térinformatikai alapismeretek. GOODCHILD, M. F. és KEMP, K. K. (eredeti szerk.), MÁRTON, M., PAKSI, J. és MÁRKUS, B. (magyar szerk.): 48. fejezet Vonalgeneralizálás. Székesfehérvár: Erdészeti és Faipari Egyetem, Földmérési és Földrendezési Főiskolai Kar, Térinformatikai Tanszék, pp. (48-1) (48-10). RAMER, U., An iterative procedure for the polygonal approximation of plane curves. Computer Graphics and Image Processing. 1(3), pp RÁTÓTI, B., Gyakorlati térképszerkesztés, térképtervezés. Budapest: Kartográfiai Vállalat, pp REUMANN, K. és WITKAM, A. P. M., Optimizing curve segmentation in computer graphics. In: Proceedings of International Computing Symposium, North-Holland Publishing Company, pp RIESENFELD, R., On Chaikin's algorithm. IEEE Computer Graphics and Applications 4, 3 (1975), pp ROGERS, H. Jr., Theory of Recursive Functions and Effective Computability. Cambridge, USA: The MIT Press, p. 1. SLOCUM, T. A., McMASTER, R. B., KESSLER, F. C. és HOWARD, H. H., Thematic Cartography and Geographic Visualization. USA: Pearson Prentice Hall, 6. fejezet: Scale and generalization, pp és 15. fejezet: Symbolizing Topography, pp STEGENA, L., Térképi generalizálás és a szűrőelmélet. In: Térképi generalizálás (szerk: STEGENA, L.), kézirat. Budapest: Eötvös Loránd Tudományegyetem, Természettudományi Kar, pp és STEGENA, L., KLINGHAMMER, I. és FÜSI, L., Az automatizálás a kartográfiában II. Budapest: Tankönyvkiadó Vállalat, pp és SZIRMAY-KALOS, L., ANTAL, GY. és CSONKA, F., Háromdimenziós grafika, animáció és játékfejlesztés. Budapest: Computerbooks, 3. fejezet, pp T.5., Útmutató az egységes országos térképrendszer 1: : méretarányu levezetett topográfiai térképeinek tervezéséhez. Budapest: MÉM OFTH Földmérési Főosztály, pp TUTIC, D. és LAPAINE, M., Area Preserving Cartographic Line Generalization. Cartography and Geoinformation, Vol. 8, No. 11, pp
15 VISVALINGAM, M. és WHYATT, J. D., Line generalisation by repeated elimination of points. Cartographic Journal 30 (1), pp WANG, Z. és MÜLLER, J. C., Line generalization based on analysis of shape characteristics. Cartography and Geographic Information Systems 25 (1), pp
16 118
Domborzatmodellből nyert szintvonalak automatizált generalizálása
 Domborzatmodellből nyert szintvonalak automatizált generalizálása Agárdi Norbert 1 Ungvári Zsuzsanna 2 Zentai László 3 1 tudományos segédmunkatárs, CSFK Földrajztudományi Intézet; doktorandusz, ELTE Térképtudományi
Domborzatmodellből nyert szintvonalak automatizált generalizálása Agárdi Norbert 1 Ungvári Zsuzsanna 2 Zentai László 3 1 tudományos segédmunkatárs, CSFK Földrajztudományi Intézet; doktorandusz, ELTE Térképtudományi
Ungvári Zsuzsanna. A térképi generalizálás vizsgálata különféle méretaránytartományokban
 Eötvös Loránd Tudományegyetem Informatikai Kar Térképtudományi és Geoinformatikai Tanszék Ungvári Zsuzsanna A térképi generalizálás vizsgálata különféle méretaránytartományokban domborzatmodelleken Doktori
Eötvös Loránd Tudományegyetem Informatikai Kar Térképtudományi és Geoinformatikai Tanszék Ungvári Zsuzsanna A térképi generalizálás vizsgálata különféle méretaránytartományokban domborzatmodelleken Doktori
Hajder Levente 2018/2019. II. félév
 Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2018/2019. II. félév Tartalom 1 2 Törtvonal Felületi folytonosságok B-spline Spline variánsok Felosztott (subdivision) görbék
Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2018/2019. II. félév Tartalom 1 2 Törtvonal Felületi folytonosságok B-spline Spline variánsok Felosztott (subdivision) görbék
Görbe- és felületmodellezés. Szplájnok Felületmodellezés
 Görbe- és felületmodellezés Szplájnok Felületmodellezés Spline (szplájn) Spline: Szakaszosan, parametrikus polinomokkal leírt görbe A spline nevét arról a rugalmasan hajlítható vonalzóról kapta, melyet
Görbe- és felületmodellezés Szplájnok Felületmodellezés Spline (szplájn) Spline: Szakaszosan, parametrikus polinomokkal leírt görbe A spline nevét arról a rugalmasan hajlítható vonalzóról kapta, melyet
A Vonallánc készlet parancsai lehetővé teszik vonalláncok és sokszögek rajzolását.
 11. Geometriai elemek 883 11.3. Vonallánc A Vonallánc készlet parancsai lehetővé teszik vonalláncok és sokszögek rajzolását. A vonallánc egy olyan alapelem, amely szakaszok láncolatából áll. A sokszög
11. Geometriai elemek 883 11.3. Vonallánc A Vonallánc készlet parancsai lehetővé teszik vonalláncok és sokszögek rajzolását. A vonallánc egy olyan alapelem, amely szakaszok láncolatából áll. A sokszög
DOMBORZATMODELLEK ALKALMAZÁSA A TÉRKÉPKÉSZÍTÉSBEN. Ungvári Zsuzsanna tanársegéd
 DOMBORZATMODELLEK ALKALMAZÁSA A TÉRKÉPKÉSZÍTÉSBEN Ungvári Zsuzsanna tanársegéd TARTALOM Domborzatmodellek ismertetése Térinformatikai műveletek lehetnek szükségesek a domborzatmodellek előkészítéséhez:
DOMBORZATMODELLEK ALKALMAZÁSA A TÉRKÉPKÉSZÍTÉSBEN Ungvári Zsuzsanna tanársegéd TARTALOM Domborzatmodellek ismertetése Térinformatikai műveletek lehetnek szükségesek a domborzatmodellek előkészítéséhez:
Számítógépes Grafika SZIE YMÉK
 Számítógépes Grafika SZIE YMÉK Analóg - digitális Analóg: a jel értelmezési tartománya (idő), és az értékkészletes is folytonos (pl. hang, fény) Diszkrét idejű: az értelmezési tartomány diszkrét (pl. a
Számítógépes Grafika SZIE YMÉK Analóg - digitális Analóg: a jel értelmezési tartománya (idő), és az értékkészletes is folytonos (pl. hang, fény) Diszkrét idejű: az értelmezési tartomány diszkrét (pl. a
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 16 XVI A DIFFERENCIÁLSZÁmÍTÁS ALkALmAZÁSAI 1 Érintő ÉS NORmÁLIS EGYENES, L HOSPITAL-SZAbÁLY Az görbe abszcisszájú pontjához tartozó érintőjének egyenlete (1), normálisának egyenlete
KOVÁCS BÉLA, MATEmATIkA I 16 XVI A DIFFERENCIÁLSZÁmÍTÁS ALkALmAZÁSAI 1 Érintő ÉS NORmÁLIS EGYENES, L HOSPITAL-SZAbÁLY Az görbe abszcisszájú pontjához tartozó érintőjének egyenlete (1), normálisának egyenlete
Digitális topográfiai adatok többcélú felhasználása
 Digitális topográfiai adatok többcélú felhasználása Iván Gyula Földmérési és Távérzékelési Intézet GIS OPEN 2003. Székesfehérvár, 2003. március 10-12. Tartalom A FÖMI digitális topográfiai adatai Minőségbiztosítás
Digitális topográfiai adatok többcélú felhasználása Iván Gyula Földmérési és Távérzékelési Intézet GIS OPEN 2003. Székesfehérvár, 2003. március 10-12. Tartalom A FÖMI digitális topográfiai adatai Minőségbiztosítás
MIKOVINY SÁMUEL TÉRINFORMATIKAI EMLÉKVERSENY
 FVM VIDÉKFEJLESZTÉSI, KÉPZÉSI ÉS SZAKTANÁCSADÁSI INTÉZET NYUGAT-MAGYARORSZÁGI EGYETEM GEOINFORMATIKAI KAR MIKOVINY SÁMUEL TÉRINFORMATIKAI EMLÉKVERSENY 2009/2010. TANÉV Az I. FORDULÓ FELADATAI 1. feladat:
FVM VIDÉKFEJLESZTÉSI, KÉPZÉSI ÉS SZAKTANÁCSADÁSI INTÉZET NYUGAT-MAGYARORSZÁGI EGYETEM GEOINFORMATIKAI KAR MIKOVINY SÁMUEL TÉRINFORMATIKAI EMLÉKVERSENY 2009/2010. TANÉV Az I. FORDULÓ FELADATAI 1. feladat:
x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs mátrixa 3D-ben?
 . Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
. Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
Térképismeret 1 ELTE TTK Földtudományi és Földrajz BSc. 2007
 Térképismeret 1 ELTE TTK Földtudományi és Földrajz BSc. 2007 Török Zsolt, Draskovits Zsuzsa ELTE IK Térképtudományi és Geoinformatikai Tanszék http://lazarus.elte.hu Ismerkedés a térképekkel 1. Miért van
Térképismeret 1 ELTE TTK Földtudományi és Földrajz BSc. 2007 Török Zsolt, Draskovits Zsuzsa ELTE IK Térképtudományi és Geoinformatikai Tanszék http://lazarus.elte.hu Ismerkedés a térképekkel 1. Miért van
Tantárgycím: Térképismeret
 Eötvös Loránd Tudományegyetem Természettudományi Kar TANTÁRGYI ADATLAP és tantárgyi követelmények 2005. Tantárgycím: Térképismeret Földtudományi Szak Kötelező tantárgy 2. Tantárgy Szemeszter Követelmény
Eötvös Loránd Tudományegyetem Természettudományi Kar TANTÁRGYI ADATLAP és tantárgyi követelmények 2005. Tantárgycím: Térképismeret Földtudományi Szak Kötelező tantárgy 2. Tantárgy Szemeszter Követelmény
Diszkréten mintavételezett függvények
 Diszkréten mintavételezett függvények A függvény (jel) értéke csak rögzített pontokban ismert, de köztes pontokban is meg akarjuk becsülni időben mintavételezett jel pixelekből álló műholdkép rácson futtatott
Diszkréten mintavételezett függvények A függvény (jel) értéke csak rögzített pontokban ismert, de köztes pontokban is meg akarjuk becsülni időben mintavételezett jel pixelekből álló műholdkép rácson futtatott
ALKALMAZOTT TÉRINFORMATIKA 2.
 ALKALMAZOTT TÉRINFORMATIKA 2. FÖLDRAJZ ALAPSZAK (NAPPALI MUNKAREND) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI FÖLDTUDOMÁNYI KAR FÖLDRAJZ-GEOINFORMATIKA INTÉZET Miskolc, 2018 TARTALOMJEGYZÉK
ALKALMAZOTT TÉRINFORMATIKA 2. FÖLDRAJZ ALAPSZAK (NAPPALI MUNKAREND) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI FÖLDTUDOMÁNYI KAR FÖLDRAJZ-GEOINFORMATIKA INTÉZET Miskolc, 2018 TARTALOMJEGYZÉK
A térképi generalizálás automatizálása a vízrajz példáján
 EÖTVÖS LORÁND TUDOMÁNYEGYETEM TERMÉSZETTUDOMÁNYI KAR A térképi generalizálás automatizálása a vízrajz példáján SZAKDOLGOZAT FÖLDTUDOMÁNYI ALAPSZAK Készítette: Balogh Dániel térképész és geoinformatikus
EÖTVÖS LORÁND TUDOMÁNYEGYETEM TERMÉSZETTUDOMÁNYI KAR A térképi generalizálás automatizálása a vízrajz példáján SZAKDOLGOZAT FÖLDTUDOMÁNYI ALAPSZAK Készítette: Balogh Dániel térképész és geoinformatikus
Digitális Domborzat Modellek (DTM)
 Digitális Domborzat Modellek (DTM) Digitális Domborzat Modellek (DTM) Digitális Domborzat Modellek (DTM) DTM fogalma A földfelszín számítógéppel kezelhető topográfiai modellje Cél: tetszőleges pontban
Digitális Domborzat Modellek (DTM) Digitális Domborzat Modellek (DTM) Digitális Domborzat Modellek (DTM) DTM fogalma A földfelszín számítógéppel kezelhető topográfiai modellje Cél: tetszőleges pontban
Kartográfia, Térképészet 2. gyakorlat
 Kartográfia, Térképészet 2. gyakorlat Szintvonalas domborzatábrázolás Dr. Sümeghy Zoltán, Rajhona Gábor sumeghy@stud.u-szeged.hu szeged.hu www.sci.u-szeged.hu/eghajlattan szeged.hu/eghajlattan SZTE Éghajlattani
Kartográfia, Térképészet 2. gyakorlat Szintvonalas domborzatábrázolás Dr. Sümeghy Zoltán, Rajhona Gábor sumeghy@stud.u-szeged.hu szeged.hu www.sci.u-szeged.hu/eghajlattan szeged.hu/eghajlattan SZTE Éghajlattani
A vertikális generalizálás kérdései a kisméretarányú térképek domborzatábrázolásánál
 A vertikális generalizálás kérdései a kisméretarányú térképek domborzatábrázolásánál Dr. Márton Mátyás habilitált egyetemi docens ELTE Térképtudományi és Geoinformatikai Tanszék MTA ELTE Térképészeti és
A vertikális generalizálás kérdései a kisméretarányú térképek domborzatábrázolásánál Dr. Márton Mátyás habilitált egyetemi docens ELTE Térképtudományi és Geoinformatikai Tanszék MTA ELTE Térképészeti és
4. Felületek Forgásfelületek. Felületek 1. Legyen adott egy paramétersíkbeli T tartomány. A paramétersíkot az u és v koordinátatengelyekkel
 Felületek 1 4. Felületek Legyen adott egy paramétersíkbeli T tartomány. A paramétersíkot az u és v koordinátatengelyekkel adjuk meg. Ekkor egy F felületet az (u, v) r(u, v), (u, v) T kétváltozós vektor-vektor
Felületek 1 4. Felületek Legyen adott egy paramétersíkbeli T tartomány. A paramétersíkot az u és v koordinátatengelyekkel adjuk meg. Ekkor egy F felületet az (u, v) r(u, v), (u, v) T kétváltozós vektor-vektor
Statisztika I. 12. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 1. előadás Előadó: Dr. Ertsey Imre Regresszió analízis A korrelációs együttható megmutatja a kapcsolat irányát és szorosságát. A kapcsolat vizsgálata során a gyakorlatban ennél messzebb
Statisztika I. 1. előadás Előadó: Dr. Ertsey Imre Regresszió analízis A korrelációs együttható megmutatja a kapcsolat irányát és szorosságát. A kapcsolat vizsgálata során a gyakorlatban ennél messzebb
Űrfelvételek térinformatikai rendszerbe integrálása
 Budapest, 2005. október 18. Űrfelvételek térinformatikai rendszerbe integrálása Molnár Gábor ELTE Geofizikai Tanszék Űrkutató Csoport Témavezető: Dr. Ferencz Csaba Eötvös Loránd Tudományegyetem Geofizikai
Budapest, 2005. október 18. Űrfelvételek térinformatikai rendszerbe integrálása Molnár Gábor ELTE Geofizikai Tanszék Űrkutató Csoport Témavezető: Dr. Ferencz Csaba Eötvös Loránd Tudományegyetem Geofizikai
10. Koordinátageometria
 I. Nulladik ZH-ban láttuk: 0. Koordinátageometria. Melyek azok a P x; y pontok, amelyek koordinátái kielégítik az Ábrázolja a megoldáshalmazt a koordináta-síkon! x y x 0 egyenlőtlenséget? ELTE 00. szeptember
I. Nulladik ZH-ban láttuk: 0. Koordinátageometria. Melyek azok a P x; y pontok, amelyek koordinátái kielégítik az Ábrázolja a megoldáshalmazt a koordináta-síkon! x y x 0 egyenlőtlenséget? ELTE 00. szeptember
Súlyozott automaták alkalmazása
 Súlyozott automaták alkalmazása képek reprezentációjára Gazdag Zsolt Szegedi Tudományegyetem Számítástudomány Alapjai Tanszék Tartalom Motiváció Fraktáltömörítés Súlyozott véges automaták Képek reprezentációja
Súlyozott automaták alkalmazása képek reprezentációjára Gazdag Zsolt Szegedi Tudományegyetem Számítástudomány Alapjai Tanszék Tartalom Motiváció Fraktáltömörítés Súlyozott véges automaták Képek reprezentációja
Városi környezet vizsgálata távérzékelési adatok osztályozásával
 Városi környezet vizsgálata távérzékelési adatok osztályozásával Verőné Dr. Wojtaszek Małgorzata Óbudai Egyetem AMK Goeinformatika Intézet 20 éves a Térinformatika Tanszék 2014. december. 15 Felvetések
Városi környezet vizsgálata távérzékelési adatok osztályozásával Verőné Dr. Wojtaszek Małgorzata Óbudai Egyetem AMK Goeinformatika Intézet 20 éves a Térinformatika Tanszék 2014. december. 15 Felvetések
W = F s A munka származtatott, előjeles skalármennyiség.
 Ha az erő és az elmozdulás egymásra merőleges, akkor fizikai értelemben nem történik munkavégzés. Pl.: ha egy táskát függőlegesen tartunk, és úgy sétálunk, akkor sem a tartóerő, sem a nehézségi erő nem
Ha az erő és az elmozdulás egymásra merőleges, akkor fizikai értelemben nem történik munkavégzés. Pl.: ha egy táskát függőlegesen tartunk, és úgy sétálunk, akkor sem a tartóerő, sem a nehézségi erő nem
A szabályos sokszögek közelítő szerkesztéséhez
 1 A szabályos sokszögek közelítő szerkesztéséhez A síkmértani szerkesztések között van egy kedvencünk: a szabályos n - szög közelítő szerkesztése. Azért vívta ki nálunk ezt az előkelő helyet, mert nagyon
1 A szabályos sokszögek közelítő szerkesztéséhez A síkmértani szerkesztések között van egy kedvencünk: a szabályos n - szög közelítő szerkesztése. Azért vívta ki nálunk ezt az előkelő helyet, mert nagyon
Matematikai geodéziai számítások 6.
 Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Érettségi feladatok Koordinátageometria_rendszerezve / 5
 Érettségi feladatok Koordinátageometria_rendszerezve 2005-2013 1/ 5 Vektorok 2005. május 28./12. Adottak az a (4; 3) és b ( 2; 1) vektorok. a) Adja meg az a hosszát! b) Számítsa ki az a + b koordinátáit!
Érettségi feladatok Koordinátageometria_rendszerezve 2005-2013 1/ 5 Vektorok 2005. május 28./12. Adottak az a (4; 3) és b ( 2; 1) vektorok. a) Adja meg az a hosszát! b) Számítsa ki az a + b koordinátáit!
Klár Gergely 2010/2011. tavaszi félév
 Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. tavaszi félév Tartalom Pont 1 Pont 2 3 4 5 Tartalom Pont Descartes-koordináták Homogén koordináták
Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. tavaszi félév Tartalom Pont 1 Pont 2 3 4 5 Tartalom Pont Descartes-koordináták Homogén koordináták
Szimulációs technikák
 SZÉCHENYI ISTVÁN EGYETEM Műszaki Tudományi Kar Informatikai tanszék Szimulációs technikák ( NGB_IN040_1) 2. csapat Comparator - Dokumentáció Mérnök informatikus BSc szak, nappali tagozat 2012/2013 II.
SZÉCHENYI ISTVÁN EGYETEM Műszaki Tudományi Kar Informatikai tanszék Szimulációs technikák ( NGB_IN040_1) 2. csapat Comparator - Dokumentáció Mérnök informatikus BSc szak, nappali tagozat 2012/2013 II.
TÉRINFORMATIKA II. Dr. Kulcsár Balázs Ph.D. adjunktus. Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék
 TÉRINFORMATIKA II. Dr. Kulcsár Balázs Ph.D. adjunktus Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék MÁSODLAGOS ADATNYERÉSI ELJÁRÁSOK Meglévő (analóg) térképek manuális digitalizálása 1 A meglévő
TÉRINFORMATIKA II. Dr. Kulcsár Balázs Ph.D. adjunktus Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék MÁSODLAGOS ADATNYERÉSI ELJÁRÁSOK Meglévő (analóg) térképek manuális digitalizálása 1 A meglévő
Matematikai geodéziai számítások 1.
 Matematikai geodéziai számítások 1 Ellipszoidi számítások, ellipszoid, geoid és terep metszete Dr Bácsatyai, László Created by XMLmind XSL-FO Converter Matematikai geodéziai számítások 1: Ellipszoidi számítások,
Matematikai geodéziai számítások 1 Ellipszoidi számítások, ellipszoid, geoid és terep metszete Dr Bácsatyai, László Created by XMLmind XSL-FO Converter Matematikai geodéziai számítások 1: Ellipszoidi számítások,
6. Függvények. Legyen függvény és nem üreshalmaz. A függvényt az f K-ra való kiterjesztésének
 6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
Regresszió számítás. Tartalomjegyzék: GeoEasy V2.05+ Geodéziai Kommunikációs Program
 Regresszió számítás GeoEasy V2.05+ Geodéziai Kommunikációs Program DigiKom Kft. 2006-2010 Tartalomjegyzék: Egyenes x változik Egyenes y változik Egyenes y és x változik Kör Sík z változik Sík y, x és z
Regresszió számítás GeoEasy V2.05+ Geodéziai Kommunikációs Program DigiKom Kft. 2006-2010 Tartalomjegyzék: Egyenes x változik Egyenes y változik Egyenes y és x változik Kör Sík z változik Sík y, x és z
Információ megjelenítés Számítógépes ábrázolás. Dr. Iványi Péter
 Információ megjelenítés Számítógépes ábrázolás Dr. Iványi Péter Raszterizáció OpenGL Mely pixelek vannak a primitíven belül fragment generálása minden ilyen pixelre Attribútumok (pl., szín) hozzárendelése
Információ megjelenítés Számítógépes ábrázolás Dr. Iványi Péter Raszterizáció OpenGL Mely pixelek vannak a primitíven belül fragment generálása minden ilyen pixelre Attribútumok (pl., szín) hozzárendelése
MÉSZÁROS JÓZSEFNÉ, NUMERIKUS MÓDSZEREK
 MÉSZÁROS JÓZSEFNÉ, NUmERIKUS módszerek 9 FÜGGVÉNYKÖZELÍTÉSEK IX. SPLINE INTERPOLÁCIÓ 1. SPLINE FÜGGVÉNYEK A Lagrange interpolációnál említettük, hogy az ún. globális interpoláció helyett gyakran célszerű
MÉSZÁROS JÓZSEFNÉ, NUmERIKUS módszerek 9 FÜGGVÉNYKÖZELÍTÉSEK IX. SPLINE INTERPOLÁCIÓ 1. SPLINE FÜGGVÉNYEK A Lagrange interpolációnál említettük, hogy az ún. globális interpoláció helyett gyakran célszerű
1. tétel. 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója 7 cm. Mekkora a háromszög átfogója? (4 pont)
 1. tétel 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója cm. Mekkora a háromszög átfogója? (4 pont). Adott az ábrán két vektor. Rajzolja meg a b, a b és az a b vektorokat! (6 pont)
1. tétel 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója cm. Mekkora a háromszög átfogója? (4 pont). Adott az ábrán két vektor. Rajzolja meg a b, a b és az a b vektorokat! (6 pont)
Arany Dániel Matematikai Tanulóverseny 2010/2011-es tanév 1. forduló haladók III. kategória
 Bolyai János Matematikai Társulat Oktatásért Közalapítvány támogatásával Arany Dániel Matematikai Tanulóverseny 2010/2011-es tanév 1. forduló haladók III. kategória Megoldások és javítási útmutató 1. Határozzuk
Bolyai János Matematikai Társulat Oktatásért Közalapítvány támogatásával Arany Dániel Matematikai Tanulóverseny 2010/2011-es tanév 1. forduló haladók III. kategória Megoldások és javítási útmutató 1. Határozzuk
Egy újabb látószög - feladat
 1 Egy újabb látószög - feladat A feladat Adott az O középpontú, R sugarú körön az α szöggel jellemzett P pont. Határozzuk meg, hogy mekkora ϑ szög alatt látszik a P pontból a vízszintes átmérő - egyenes
1 Egy újabb látószög - feladat A feladat Adott az O középpontú, R sugarú körön az α szöggel jellemzett P pont. Határozzuk meg, hogy mekkora ϑ szög alatt látszik a P pontból a vízszintes átmérő - egyenes
Minõségbiztosítás és adatminõség 1
 Minõségbiztosítás és adatminõség 1 Iván Gyula, a FÖMI osztályvezetõje 1. Bevezetés A földügyi szakágban a minõségirányítás, -biztosítás, -ellenõrzés régóta ismert fogalom, hiszen az egyes szabályzatok,
Minõségbiztosítás és adatminõség 1 Iván Gyula, a FÖMI osztályvezetõje 1. Bevezetés A földügyi szakágban a minõségirányítás, -biztosítás, -ellenõrzés régóta ismert fogalom, hiszen az egyes szabályzatok,
Numerikus Matematika
 Numerikus Matematika Baran Ágnes Gyakorlat Interpoláció Baran Ágnes Numerikus Matematika 6.-7. Gyakorlat 1 / 40 Lagrange-interpoláció Példa Határozzuk meg a ( 2, 5), ( 1, 3), (0, 1), (2, 15) pontokra illeszkedő
Numerikus Matematika Baran Ágnes Gyakorlat Interpoláció Baran Ágnes Numerikus Matematika 6.-7. Gyakorlat 1 / 40 Lagrange-interpoláció Példa Határozzuk meg a ( 2, 5), ( 1, 3), (0, 1), (2, 15) pontokra illeszkedő
Adatbázisok. és s GIS műveletek pontossága
 Adatbázisok és s GIS műveletek pontossága A bizonytalansági vita résztvevői A digitális adatoktól és a létrehozott termékektől is elvárható hogy adott pontossági jellemzőkkel rendelkezzen. A pontosság
Adatbázisok és s GIS műveletek pontossága A bizonytalansági vita résztvevői A digitális adatoktól és a létrehozott termékektől is elvárható hogy adott pontossági jellemzőkkel rendelkezzen. A pontosság
3. Szűrés képtérben. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 3. Szűrés képtérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE http://www.inf.u-szeged.hu/~kato/teaching/ 2 Kép transzformációk típusai Kép értékkészletének radiometriai információ
3. Szűrés képtérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE http://www.inf.u-szeged.hu/~kato/teaching/ 2 Kép transzformációk típusai Kép értékkészletének radiometriai információ
Matematikai geodéziai számítások 9.
 Matematikai geodéziai számítások 9 Szabad álláspont kiegyenlítése Dr Bácsatyai, László Created by XMLmind XSL-FO Converter Matematikai geodéziai számítások 9: Szabad álláspont kiegyenlítése Dr Bácsatyai,
Matematikai geodéziai számítások 9 Szabad álláspont kiegyenlítése Dr Bácsatyai, László Created by XMLmind XSL-FO Converter Matematikai geodéziai számítások 9: Szabad álláspont kiegyenlítése Dr Bácsatyai,
Regresszió. Csorba János. Nagyméretű adathalmazok kezelése március 31.
 Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Diverzifikáció Markowitz-modell MAD modell CAPM modell 2017/ Szegedi Tudományegyetem Informatikai Intézet
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 11. Előadás Portfólió probléma Portfólió probléma Portfólió probléma Adott részvények (kötvények,tevékenységek,
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 11. Előadás Portfólió probléma Portfólió probléma Portfólió probléma Adott részvények (kötvények,tevékenységek,
Csoportosítás. Térinformatikai műveletek, elemzések. Csoportosítás. Csoportosítás
 Csoportosítás Térinformatikai műveletek, elemzések Leíró (attribútum) adatokra vonatkozó kérdések, műveletek, elemzések, csoportosítások,... Térbeli (geometriai) adatokra vonatkozó kérdések, műveletek
Csoportosítás Térinformatikai műveletek, elemzések Leíró (attribútum) adatokra vonatkozó kérdések, műveletek, elemzések, csoportosítások,... Térbeli (geometriai) adatokra vonatkozó kérdések, műveletek
Környezeti informatika
 Környezeti informatika Alkalmazható természettudományok oktatása a tudásalapú társadalomban TÁMOP-4.1.2.A/1-11/1-2011-0038 Eger, 2012. november 22. Utasi Zoltán Eszterházy Károly Főiskola, Földrajz Tanszék
Környezeti informatika Alkalmazható természettudományok oktatása a tudásalapú társadalomban TÁMOP-4.1.2.A/1-11/1-2011-0038 Eger, 2012. november 22. Utasi Zoltán Eszterházy Károly Főiskola, Földrajz Tanszék
Számítógépes Grafika mintafeladatok
 Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
Geofizikai kutatómódszerek I.
 Geofizikai kutatómódszerek I. A gravitációs és mágneses kutatómódszer Dr. Szabó Norbert Péter egyetemi docens Miskolci Egyetem Geofizikai Intézeti Tanszék e-mail: norbert.szabo.phd@gmail.com 1. A gravitációs
Geofizikai kutatómódszerek I. A gravitációs és mágneses kutatómódszer Dr. Szabó Norbert Péter egyetemi docens Miskolci Egyetem Geofizikai Intézeti Tanszék e-mail: norbert.szabo.phd@gmail.com 1. A gravitációs
Függvények Megoldások
 Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
 Fotogrammetria és távérzékelés A képi tartalomban rejlő információgazdagság Dr. Jancsó Tamás Nyugat-magyarországi Egyetem, Geoinformatikai Kar MFTTT rendezvény 2012. Április 18. Székesfehérvár Tartalom
Fotogrammetria és távérzékelés A képi tartalomban rejlő információgazdagság Dr. Jancsó Tamás Nyugat-magyarországi Egyetem, Geoinformatikai Kar MFTTT rendezvény 2012. Április 18. Székesfehérvár Tartalom
3. tétel Térelemek távolsága és szöge. Nevezetes ponthalmazok a síkon és a térben.
 3. tétel Térelemek távolsága és szöge. Nevezetes ponthalmazok a síkon és a térben. TÁVOLSÁG Általános definíció: két alakzat távolsága a két alakzat pontjai között húzható legrövidebb szakasz hosszaa távolság
3. tétel Térelemek távolsága és szöge. Nevezetes ponthalmazok a síkon és a térben. TÁVOLSÁG Általános definíció: két alakzat távolsága a két alakzat pontjai között húzható legrövidebb szakasz hosszaa távolság
Matematikai geodéziai számítások 6.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Kétdimenziós mesterséges festési eljárások. Hatások és alkalmazások
 Pannon Egyetem Informatikai Tudományok Doktori Iskola Tézisfüzet Kétdimenziós mesterséges festési eljárások. Hatások és alkalmazások Kovács Levente Képfeldolgozás és Neuroszámítógépek Tanszék Témavezet
Pannon Egyetem Informatikai Tudományok Doktori Iskola Tézisfüzet Kétdimenziós mesterséges festési eljárások. Hatások és alkalmazások Kovács Levente Képfeldolgozás és Neuroszámítógépek Tanszék Témavezet
GEOMETRIA 1, alapszint
 GEOMETRIA 1, alapszint Kiss György 4-723 Fogadóóra: péntek 8. 15-10. 00 email: kissgy@cs.elte.hu Előadás: 11. 15-13. 45, közben egyszer 15 perc szünet GEOMETRIA 1, alapszint Ajánlott irodalom: Hajós Gy.:
GEOMETRIA 1, alapszint Kiss György 4-723 Fogadóóra: péntek 8. 15-10. 00 email: kissgy@cs.elte.hu Előadás: 11. 15-13. 45, közben egyszer 15 perc szünet GEOMETRIA 1, alapszint Ajánlott irodalom: Hajós Gy.:
Alap-ötlet: Karl Friedrich Gauss ( ) valószínűségszámítási háttér: Andrej Markov ( )
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
Al-Mg-Si háromalkotós egyensúlyi fázisdiagram közelítő számítása
 l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Fizika középszint ÉRETTSÉGI VIZSGA 2005. november 5. FIZIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI MINISZTÉRIUM A dolgozatokat az útmutató utasításai szerint, jól követhetően
Fizika középszint ÉRETTSÉGI VIZSGA 2005. november 5. FIZIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI MINISZTÉRIUM A dolgozatokat az útmutató utasításai szerint, jól követhetően
Láthatósági kérdések
 Láthatósági kérdések Láthatósági algoritmusok Adott térbeli objektum és adott nézőpont esetén el kell döntenünk, hogy mi látható az adott alakzatból a nézőpontból, vagy irányából nézve. Az algoritmusok
Láthatósági kérdések Láthatósági algoritmusok Adott térbeli objektum és adott nézőpont esetén el kell döntenünk, hogy mi látható az adott alakzatból a nézőpontból, vagy irányából nézve. Az algoritmusok
TÉRINFORMATIKA II. Dr. Kulcsár Balázs főiskolai docens. Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék
 TÉRINFORMATIKA II. Dr. Kulcsár Balázs főiskolai docens Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék TÁJÉKOZTATÁS TANTÁRGYI TEMATIKA 1 Előadás 1. GPS műszerek és kapcsolódó szoftvereik bemutatása
TÉRINFORMATIKA II. Dr. Kulcsár Balázs főiskolai docens Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék TÁJÉKOZTATÁS TANTÁRGYI TEMATIKA 1 Előadás 1. GPS műszerek és kapcsolódó szoftvereik bemutatása
Racionális számok: Azok a számok, amelyek felírhatók két egész szám hányadosaként ( p q
 Szóbeli tételek matematikából 1. tétel 1/a Számhalmazok definíciója, jele (természetes számok, egész számok, racionális számok, valós számok) Természetes számok: A pozitív egész számok és a 0. Jele: N
Szóbeli tételek matematikából 1. tétel 1/a Számhalmazok definíciója, jele (természetes számok, egész számok, racionális számok, valós számok) Természetes számok: A pozitív egész számok és a 0. Jele: N
Döntési fák. (Klasszifikációs és regressziós fák: (Classification And Regression Trees: CART ))
 Döntési fák (Klasszifikációs és regressziós fák: (Classification And Regression Trees: CART )) Rekurzív osztályozó módszer, Klasszifikációs és regressziós fák folytonos, kategóriás, illetve túlélés adatok
Döntési fák (Klasszifikációs és regressziós fák: (Classification And Regression Trees: CART )) Rekurzív osztályozó módszer, Klasszifikációs és regressziós fák folytonos, kategóriás, illetve túlélés adatok
(Solid modeling, Geometric modeling) Testmodell: egy létező vagy elképzelt objektum digitális reprezentációja.
 Testmodellezés Testmodellezés (Solid modeling, Geometric modeling) Testmodell: egy létező vagy elképzelt objektum digitális reprezentációja. A tervezés (modellezés) során megadjuk a objektum geometria
Testmodellezés Testmodellezés (Solid modeling, Geometric modeling) Testmodell: egy létező vagy elképzelt objektum digitális reprezentációja. A tervezés (modellezés) során megadjuk a objektum geometria
TÉRINFORMATIKA I. Dr. Kulcsár Balázs egyetemi docens. Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék
 TÉRINFORMATIKA I. Dr. Kulcsár Balázs egyetemi docens Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék TÁJÉKOZTATÁS TANTÁRGYI TEMATIKA 1 Előadás 1. Bevezetés a térinformatikába. Kartográfia történet.
TÉRINFORMATIKA I. Dr. Kulcsár Balázs egyetemi docens Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék TÁJÉKOZTATÁS TANTÁRGYI TEMATIKA 1 Előadás 1. Bevezetés a térinformatikába. Kartográfia történet.
Panorámakép készítése
 Panorámakép készítése Képregisztráció, 2009. Hantos Norbert Blaskovics Viktor Összefoglalás Panoráma (image stitching, planar mosaicing): átfedő képek összeillesztése Lépések: Előfeldolgozás (pl. intenzitáskorrekciók)
Panorámakép készítése Képregisztráció, 2009. Hantos Norbert Blaskovics Viktor Összefoglalás Panoráma (image stitching, planar mosaicing): átfedő képek összeillesztése Lépések: Előfeldolgozás (pl. intenzitáskorrekciók)
Geoshop fejlesztése a FÖMI-nél
 Geoshop fejlesztése a FÖMI-nél Szolgáltató Igazgatóság Földmérési és Távérzékelési Intézet www.fomi.hu www.geoshop.hu takacs.krisztian@fomi.hu Budapest, 2014. június 12. Mi az a Geoshop? INSPIRE = térinformatikai
Geoshop fejlesztése a FÖMI-nél Szolgáltató Igazgatóság Földmérési és Távérzékelési Intézet www.fomi.hu www.geoshop.hu takacs.krisztian@fomi.hu Budapest, 2014. június 12. Mi az a Geoshop? INSPIRE = térinformatikai
Lakóház tervezés ADT 3.3-al. Segédlet
 Lakóház tervezés ADT 3.3-al Segédlet A lakóház tervezési gyakorlathoz főleg a Tervezés és a Dokumentáció menüket fogjuk használni az AutoDesk Architectural Desktop programból. A program centiméterben dolgozik!!!
Lakóház tervezés ADT 3.3-al Segédlet A lakóház tervezési gyakorlathoz főleg a Tervezés és a Dokumentáció menüket fogjuk használni az AutoDesk Architectural Desktop programból. A program centiméterben dolgozik!!!
2. előadás: A mérnöki gyakorlatban használt térkép típusok és tartalmuk
 2. előadás: A mérnöki gyakorlatban használt térkép típusok és tartalmuk Magyarországon számos olyan térkép létezik, melyek előállítását, karbantartását törvények, utasítások szabályozzák. Ezek tartalma
2. előadás: A mérnöki gyakorlatban használt térkép típusok és tartalmuk Magyarországon számos olyan térkép létezik, melyek előállítását, karbantartását törvények, utasítások szabályozzák. Ezek tartalma
Modern Fizika Labor. 5. ESR (Elektronspin rezonancia) Fizika BSc. A mérés dátuma: okt. 25. A mérés száma és címe: Értékelés:
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 25. A mérés száma és címe: 5. ESR (Elektronspin rezonancia) Értékelés: A beadás dátuma: 2011. nov. 16. A mérést végezte: Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 25. A mérés száma és címe: 5. ESR (Elektronspin rezonancia) Értékelés: A beadás dátuma: 2011. nov. 16. A mérést végezte: Szőke Kálmán Benjamin
2018/2019. Matematika 10.K
 Egész éves dolgozat szükséges felszerelés: toll, ceruza, radír, vonalzó, körző, számológép, függvénytáblázat 2 órás, 4 jegyet ér 2019. május 27-31. héten Aki hiányzik, a következő héten írja meg, e nélkül
Egész éves dolgozat szükséges felszerelés: toll, ceruza, radír, vonalzó, körző, számológép, függvénytáblázat 2 órás, 4 jegyet ér 2019. május 27-31. héten Aki hiányzik, a következő héten írja meg, e nélkül
Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea
 Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea Geometrikus deformálható modellek Görbe evolúció Level set módszer A görbe evolúció parametrizálástól független mindössze geometriai
Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea Geometrikus deformálható modellek Görbe evolúció Level set módszer A görbe evolúció parametrizálástól független mindössze geometriai
Adaptív dinamikus szegmentálás idősorok indexeléséhez
 Adaptív dinamikus szegmentálás idősorok indexeléséhez IPM-08irAREAE kurzus cikkfeldolgozás Balassi Márton 1 Englert Péter 1 Tömösy Péter 1 1 Eötvös Loránd Tudományegyetem Informatikai Kar 2013. november
Adaptív dinamikus szegmentálás idősorok indexeléséhez IPM-08irAREAE kurzus cikkfeldolgozás Balassi Márton 1 Englert Péter 1 Tömösy Péter 1 1 Eötvös Loránd Tudományegyetem Informatikai Kar 2013. november
Nagytömegű adatok (gyors) kartografálása. Rostás Sándor százados. MH GEOSZ Műszaki és információs osztály térképész főtiszt (ov. h.
 Nagytömegű adatok (gyors) kartografálása Rostás Sándor százados. MH GEOSZ Műszaki és információs osztály térképész főtiszt (ov. h.) Kialakításának feltételei - Szoftver lincence (ESRI) - Megfelelő mxd
Nagytömegű adatok (gyors) kartografálása Rostás Sándor százados. MH GEOSZ Műszaki és információs osztály térképész főtiszt (ov. h.) Kialakításának feltételei - Szoftver lincence (ESRI) - Megfelelő mxd
2. Elméleti összefoglaló
 2. Elméleti összefoglaló 2.1 A D/A konverterek [1] A D/A konverter feladata, hogy a bemenetére érkező egész számmal arányos analóg feszültséget vagy áramot állítson elő a kimenetén. A működéséhez szükséges
2. Elméleti összefoglaló 2.1 A D/A konverterek [1] A D/A konverter feladata, hogy a bemenetére érkező egész számmal arányos analóg feszültséget vagy áramot állítson elő a kimenetén. A működéséhez szükséges
Érettségi feladatok: Koordináta-geometria 1/5
 Érettségi feladatok: Koordináta-geometria 1/5 2003. Próba/ 13. Adott egy háromszög három csúcspontja a koordinátáival: A( 4; 4), B(4; 4) és C( 4; 8). Számítsa ki a C csúcsból induló súlyvonal és az A csúcsból
Érettségi feladatok: Koordináta-geometria 1/5 2003. Próba/ 13. Adott egy háromszög három csúcspontja a koordinátáival: A( 4; 4), B(4; 4) és C( 4; 8). Számítsa ki a C csúcsból induló súlyvonal és az A csúcsból
Biomatematika 12. Szent István Egyetem Állatorvos-tudományi Kar. Fodor János
 Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
Infobionika ROBOTIKA. X. Előadás. Robot manipulátorok II. Direkt és inverz kinematika. Készült a HEFOP P /1.0 projekt keretében
 Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
Grafikonok automatikus elemzése
 Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
10. Török Zsolt, Draskovits Zsuzsa ELTE IK Térképtudományi és Geoinformatikai Tanszék
 Térképszaurusz vs. Garmin GPS NASA World Wind (3D) Megint hétfő (vagy szerda)... Térképismeret 1 ELTE TTK Földtudományi és Földrajz BSc. 2007 10. Török Zsolt, Draskovits Zsuzsa ELTE IK Térképtudományi
Térképszaurusz vs. Garmin GPS NASA World Wind (3D) Megint hétfő (vagy szerda)... Térképismeret 1 ELTE TTK Földtudományi és Földrajz BSc. 2007 10. Török Zsolt, Draskovits Zsuzsa ELTE IK Térképtudományi
A tér lineáris leképezései síkra
 A tér lineáris leképezései síkra Az ábrázoló geometria célja: A háromdimenziós térben elhelyezkedő alakzatok helyzeti és metrikus viszonyainak egyértelmű és egyértelműen rekonstruálható módon történő ábrázolása
A tér lineáris leképezései síkra Az ábrázoló geometria célja: A háromdimenziós térben elhelyezkedő alakzatok helyzeti és metrikus viszonyainak egyértelmű és egyértelműen rekonstruálható módon történő ábrázolása
Matematikai geodéziai számítások 10.
 Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Biometria az orvosi gyakorlatban. Korrelációszámítás, regresszió
 SZDT-08 p. 1/31 Biometria az orvosi gyakorlatban Korrelációszámítás, regresszió Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Korrelációszámítás
SZDT-08 p. 1/31 Biometria az orvosi gyakorlatban Korrelációszámítás, regresszió Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Korrelációszámítás
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
4. gyakorlat: interpolációs és approximációs görbék implementációja
 Pázmány Péter Katolikus Egyetem Információs Technológiai Kar A számítógépes grafika alapjai kurzus, gyakorlati anyagok Benedek Csaba 4. gyakorlat: interpolációs és approximációs görbék implementációja
Pázmány Péter Katolikus Egyetem Információs Technológiai Kar A számítógépes grafika alapjai kurzus, gyakorlati anyagok Benedek Csaba 4. gyakorlat: interpolációs és approximációs görbék implementációja
Korrelációs kapcsolatok elemzése
 Korrelációs kapcsolatok elemzése 1. előadás Kvantitatív statisztikai módszerek Két változó közötti kapcsolat Független: Az X ismérv szerinti hovatartozás ismerete nem ad semmilyen többletinformációt az
Korrelációs kapcsolatok elemzése 1. előadás Kvantitatív statisztikai módszerek Két változó közötti kapcsolat Független: Az X ismérv szerinti hovatartozás ismerete nem ad semmilyen többletinformációt az
EÖTVÖS LORÁND SZAKKÖZÉP- ÉS SZAKISKOLA TANÍTÁST SEGÍTŐ OKTATÁSI ANYAGOK MÉRÉS TANTÁRGY
 EÖTVÖS LORÁND SZAKKÖZÉP- ÉS SZAKISKOLA TANÍTÁST SEGÍTŐ OKTATÁSI ANYAGOK MÉRÉS TANTÁRGY SÍKIDOMOK Síkidom 1 síkidom az a térelem, amelynek valamennyi pontja ugyan abban a síkban helyezkedik el. A síkidomokat
EÖTVÖS LORÁND SZAKKÖZÉP- ÉS SZAKISKOLA TANÍTÁST SEGÍTŐ OKTATÁSI ANYAGOK MÉRÉS TANTÁRGY SÍKIDOMOK Síkidom 1 síkidom az a térelem, amelynek valamennyi pontja ugyan abban a síkban helyezkedik el. A síkidomokat
Country Movers. Cesium alapú planetáris kartográfiai szemléltető eszköz. 5. Nyílt forráskódú térinformatikai munkaértekezlet
 Country Movers Cesium alapú planetáris kartográfiai szemléltető eszköz Mátyás Gede ELTE Térképtudományi és Geoinformatikai Tanszék 5. Nyílt forráskódú térinformatikai munkaértekezlet 2016. 11. 25. Tartalom
Country Movers Cesium alapú planetáris kartográfiai szemléltető eszköz Mátyás Gede ELTE Térképtudományi és Geoinformatikai Tanszék 5. Nyílt forráskódú térinformatikai munkaértekezlet 2016. 11. 25. Tartalom
VI. Magyar Földrajzi Konferencia 524-529
 Van Leeuwen Boudewijn Tobak Zalán Szatmári József 1 BELVÍZ OSZTÁLYOZÁS HAGYOMÁNYOS MÓDSZERREL ÉS MESTERSÉGES NEURÁLIS HÁLÓVAL BEVEZETÉS Magyarország, különösen pedig az Alföld váltakozva szenved aszályos
Van Leeuwen Boudewijn Tobak Zalán Szatmári József 1 BELVÍZ OSZTÁLYOZÁS HAGYOMÁNYOS MÓDSZERREL ÉS MESTERSÉGES NEURÁLIS HÁLÓVAL BEVEZETÉS Magyarország, különösen pedig az Alföld váltakozva szenved aszályos
Eddigi tanulmányaink alapján már egy sor, a szeizmikában általánosan használt műveletet el tudunk végezni.
 Eddigi tanulmányaink alapján már egy sor, a szeizmikában általánosan használt műveletet el tudunk végezni. Kezdjük a sort a menetidőgörbékről, illetve az NMO korrekcióról tanultakkal. A következő ábrán
Eddigi tanulmányaink alapján már egy sor, a szeizmikában általánosan használt műveletet el tudunk végezni. Kezdjük a sort a menetidőgörbékről, illetve az NMO korrekcióról tanultakkal. A következő ábrán
A loxodrómáról. Előző írásunkban melynek címe: A Gudermann - függvényről szó esett a Mercator - vetületről,illetve az ezen alapuló térképről 1. ábra.
 1 A loxodrómáról Előző írásunkban melynek címe: A Gudermann - függvényről szó esett a Mercator - vetületről,illetve az ezen alapuló térképről 1. ábra. 1. ábra forrása: [ 1 ] Ezen a térképen a szélességi
1 A loxodrómáról Előző írásunkban melynek címe: A Gudermann - függvényről szó esett a Mercator - vetületről,illetve az ezen alapuló térképről 1. ábra. 1. ábra forrása: [ 1 ] Ezen a térképen a szélességi
Térinformatika, amit tudni kell. Márkus Béla
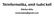 Térinformatika, amit tudni kell Márkus Béla markusbela@gmail.com GIS, a térinformatika eszköze Geographical/Geospatial/GeoInformation System Márkus, B.: Térinformatika, amit tudni kell, Corvinus GIS Meetup
Térinformatika, amit tudni kell Márkus Béla markusbela@gmail.com GIS, a térinformatika eszköze Geographical/Geospatial/GeoInformation System Márkus, B.: Térinformatika, amit tudni kell, Corvinus GIS Meetup
First Prev Next Last Go Back Full Screen Close Quit
 Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
Matematikai geodéziai számítások 5.
 Matematikai geodéziai számítások 5 Hibaterjedési feladatok Dr Bácsatyai László Matematikai geodéziai számítások 5: Hibaterjedési feladatok Dr Bácsatyai László Lektor: Dr Benedek Judit Ez a modul a TÁMOP
Matematikai geodéziai számítások 5 Hibaterjedési feladatok Dr Bácsatyai László Matematikai geodéziai számítások 5: Hibaterjedési feladatok Dr Bácsatyai László Lektor: Dr Benedek Judit Ez a modul a TÁMOP
3. Nemzetközi talajinformációs rendszerek
 Magyar Tudományos Akadémia Agrártudományi Kutatóközpont Talajtani és Agrokémiai Intézet Környezetinformatikai Osztály Pásztor László: Térbeli Talajinformációs Rendszerek/ Bevezetés a digitális talajtérképezésbe
Magyar Tudományos Akadémia Agrártudományi Kutatóközpont Talajtani és Agrokémiai Intézet Környezetinformatikai Osztály Pásztor László: Térbeli Talajinformációs Rendszerek/ Bevezetés a digitális talajtérképezésbe
Matematika III előadás
 Matematika III. - 2. előadás Vinczéné Varga Adrienn Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Előadáskövető fóliák Vinczéné Varga Adrienn (DE-MK) Matematika III. 2016/2017/I 1 / 23 paramétervonalak,
Matematika III. - 2. előadás Vinczéné Varga Adrienn Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Előadáskövető fóliák Vinczéné Varga Adrienn (DE-MK) Matematika III. 2016/2017/I 1 / 23 paramétervonalak,
Tárgyak műszaki ábrázolása. Metszeti ábrázolás
 Tárgyak műszaki ábrázolása Metszeti ábrázolás Ábrázolás metszetekkel A belső üregek, furatok, stb. szemléletes bemutatására a metszeti ábrázolás szolgál A metszeti ábrázolás elve Az üreges tárgyat egy
Tárgyak műszaki ábrázolása Metszeti ábrázolás Ábrázolás metszetekkel A belső üregek, furatok, stb. szemléletes bemutatására a metszeti ábrázolás szolgál A metszeti ábrázolás elve Az üreges tárgyat egy
