Lehetőségek és kihívások a modern bionmr spektroszkópia területén
|
|
|
- Erzsébet Fehér
- 8 évvel ezelőtt
- Látták:
Átírás
1 Lehetőségek és kihívások a modern bionmr spektroszkópia területén Perczel András és munkatársai Szerkezeti Kémia és Biológia Laboratórium és ELTE-MTA Fehérjemodellező Kutatócsoport 1
2 The Nobel Prize in Physics 1952 "for their development of new methods for nuclear magnetic precision measurements and discoveries in connection therewith Felix Bloch ( ) Edward Mills Purcell ( ) 2
3 The Nobel Prize in Chemistry 1991 "for his contributions to the development of the methodology of high resolution nuclear magnetic resonance (NMR) spectroscopy" Richard R. Ernst 3
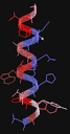
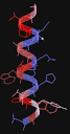
4 Fehérjék oldatban: NMR-spektroszkópia Fehérje NMR: kémiai Nobel-díj, 2002 Kurt Wüthrich A dinamikára és a belső mozgásra is reflektáló szerkezeti sokaság 4
5 NMR spektrum spinrendszerek azonosítása spinrendszerek szekvenciális rendezése kényszerfeltételek alapján szerkezetszámolás 5
6 Miért az NMR? Powerful modern structural tools for looking at complexes Crystallography ~ 45,000 structures Molecular modelling Electron microscopy ~190 Nuclear Magnetic Resonance ~7,500 - can also give 6 K d and k
7 Az NMR-spektroszkópia szükséges feltétele a nullától különböző magspin (I 0) 1) I= 0, ha mind a protonok mind a neutronok száma páros: ( 12 C, 16 O) 2) I= 1/2, ha tömegszáma páratlan ( 1 H, 3 H, 13 C, 15 N, 19 F, 57 Fe, 113 Cd) vagy a protonok, vagy a neutronok száma páratlan. 3) I= k (k=1,2,..) mind a protonok mind a neutronok száma páratlan ( 2 H, 14 N) B 0 Külső mágneses tér tér hatására hiányában rendeződött a magok és spinjei precesszáló rendezetlenül magok állnak 7
8 Feles spin esetén az impulzusmomentum (perdület) z-komponensének operátora: Î Z - két sajátfüggvénye: ψ +½ és ψ ½ - két sajátértéke van: +½ћ és ½ћ A megfelelő két sajátérték egyenlet: Î Z ψ +½ = +½ћ ψ +½ és Î Z ψ ½ = +½ћ ψ ½ vagy röviden Î Z ψ m = mћψ m ahol m ±½. A feles-spin Hamilton-operátorának sajátértékei: Az impulzusmomentum z-komponense (Î Z ) és a B 0 indukciójú mágneses tér (B 0 z) kölcsönhatását egyetlen spin esetében leíró H-operátor: Ĥ egy-spin = γb 0 Î z ( ahol γ = giromágneses együttható) a ψ +½ és ψ ½ függvények a Ĥ egy-spin nek is sajátfüggvényei (hiszen Î Z től csak a γb 0 konstansban tér el. ). Az egyik (m= +½) sajátérték egyenlet tehát : Ĥ one-spin ψ +½ = γb 0 [Î Z ψ +½ ] = γb 0 [+½ћ ψ +½ ] = ½ ћ γb 0 ψ +½ Tehát Ĥ egy-spin egyik sajátfüggvénye a ψ +½, melyhez tartozó sajátérték a ½ ћ γb 0, míg a másik sajátfüggvénye a ψ ½, melyhez tartozó sajátérték a +½ ћ γb 0. 8
9 Az egy-spin spektruma: Spin ½ esetén tehát 2 energiaszint van: E m = m ћγb 0 Tehát E +½ = ½ ћγb 0 (E α vagy spin up), illetve E ½ = +½ ћγb 0. (E β vagy spin down) ahol m ±½. A kiválasztási szabály értelmében (mivel m = +1 vagy -1) a Δm α β = ( ½) (+½) = 1, tehát az az α-ból β-ba való átmenet megengedett. υ 0 = γb 0 /2π E b E α υ 0 ΔE α β =E β E α = +½ ћγb 0 ( ½ ћγb 0 ) = ћγb 0 hυ α β = (h/2π)γb 0 υ α β = υ 0 = γb 0 /2π ami a Larmor-frekvencia E b E α B0 Pl. Ha B 0 = 9,4T és γ= 2, rad s -1 T -1 (protonra) akkor a Larmorfrekvencia = 4, Hz ~ 400MHz 9
10 Két csatolt spin spektruma: Ha az egy-spin: Ĥ egy-spin = υ 0 Î z, akkor két csatolatlan spin esetében: Ĥ két-spin, csatolatlan = υ 0,1 Î 1z + υ 0,2 Î 2z = υ I Î z + υ S Ŝ z, illetve két csatolt spin esetében: Ĥ két-spin, csatolat = υ I Î z + υ S Ŝ z + J 12 Î z Ŝ z, ahol J 12 a skaláris csatolási állandó spin1 és spin2 között. Két-spin rendszer energiadiagramja, a megengedett átmenetek és a spektrum: b b 4 Sm =-1 Sm =0 24 a b b a átmenet spin állapotok frekvencia 12 aa αβ υ S ½J βα ββ υ S +½J αα βα υ I ½J αβ ββ υ I +½J 12 Sm =+1 a a J J υ I υ S 10
11 Külső B 0 indukciójú mágneses térben a makroszkopikus mágnesezettség (M) gerjesztése, annak precessziójához vezet, amely mérhető indukált feszültséget (mv) eredményez. 11
12 A Vektor modell és a Bloch-egyenletek z-irányú mágnesezettség időbeni alakulása: dm z' /dt= (M z' M o )/T 1 M z' (t)=m o (1 exp( t/t 1 ) az x,y-síkban zajló csillapított amplitúdójú precesszió alakulása: dm x' /dt= ( o )M y' M x' /T 2 dm y' /dt= ( o )M x' M y' /T 2 Csatolt differenciál-egyenletrendszer megoldásaként a következőt kapjuk: M x' (t)=m o exp( t/t 2 )sin( o ) M y' (t)=m o exp( t/t 2 )cos( o ), ahol ( o ) a forgó referencia rendszerben a precesszió szögsebessége. A nagy felbontású NMR-spektrumok öt jellemző paramétere: csatolási állandó (J érték) félértékszélesség multiplicitás terület kémiai eltolódás =[( M - R )/ R ]
13 13
14 spinrendszerek azonosítása 1 H-spektrum I I z és S z S -I y és -S y és I x sin( I t 2 ) S x sin( S t 2 ) Ω I Ω S F1(ppm) 14 A spektrumban a J IS okozta modulációtól eltekintünk
15 spinrendszerek azonosítása Egy ~17 kda globuláris fehérje 1 H-spektruma H 2 O/D 2 O 9/1, T=300K, c 1mM amid aromás H a alifás metil ( p p m )
16 1. spinrendszerek azonosítása 2. spinrendszerek szekvenciális rendezése 3. kényszerfeltételek alapján szerkezetszámolás 16
17 spinrendszerek azonosítása Homonukleáris eljárás (homonukleáris 3 J, M<8kDa) ( 1 H- 1 H COSY, 1 H- 1 H RELAY, 1 H- 1 H TOCSY ) Heteronukleáris eljárás (heteronukleáris 1 J, 2 J, 3 J) 15 N-szerkesztés (M <15kDa) ( 1 H- 15 N TOCSY-HSQC, 1 H- 15 N NOESY-HSQC ) 15 N, 13 C-szerkesztés (M <20kDa) (HNCA, HNCOCA,.) 15 N, 13 C-szerkesztés ( 2 H) (M <30kDa) 17
18 spinrendszerek azonosítása Peptidekben és a fehérjékben az aminosavak hidrogénatomjai elkülönülő spinrendszereket alkotnak 13 J Ala Ser Glu Gly Phe Cys 18
19 A Vektor modell és a Bloch-egyenletek helyett a szorzatoperátor-elmélet Alapfogalmak: magspin-operátor vagy impulzusnyomaték-operátor: Î Î = Î x, Î y, Î z az időtől függő spinsűrűség-operátor az időtől függő Hamilton-operátor az időtől függő, normalizált állapotfüggvény (t) Ĥ(t) (t) Az alapegyenlet: d (t)/dt = i 1 [Ĥ(t), (t)] Liouville- von Neumann-egyenlet Mi kerül a Hamilton-operátorba? Az I és S spinek (AX spinrendszer) esetén, oldatfázisban: Zeeman-effektust + a skaláris csatolást + a rádiófrekvenciás gerjesztést leíró három tag. Ĥ = 1 Î x 2 Ŝ x + JÎ z Ŝ z I Î z S Ŝ z 19
20 Cél a mérhető makroszkopikus mágnesezettség-vektor (M) nagyságának és moduláltságának meghatározása: A megfigyelhető makroszkopikus mágnesezettség pl. M y összetevője a következő: M y (t) = N Tr[SI ky (t)] k ahol és mellett, N az egységnyi térfogatban vett spinek darabszáma. A feladat: A magspin operátor (I) valamint a spinsűrűség-operátor { (t)} szorzatának valamilyen bázison vett mátrixreprezentációjának a spurját (Tr) kell meghatároznunk! A nagy kérdés: mi legyen az alkalmas bázis? Mi legyen az s elemből álló báziskészletet (B s )? (t) =S b s (t)b s s A megoldás: a B s báziskészlet legyen a spin impulzusmomentum-operátor. Sorensen korábbi javaslata értelmében a Descartes-típusú I kl bázisoperátorok használata az alábbiak szerint felettébb eredményes: B s = n ( q- 2 1 ) k = 1 ( I ) kl a sk 20
21 Az I és S spinek (AX spinrendszer) 16 bázisoperátort táblázatos alakban: E S x S y S z B s elemeihez milyen fizikai kép rendelhető? mágnesezettség (populáció, NOE) E E S x S y S z I x I x 2I x S x 2I x S y 2I x S z I y I y 2I y S x 2I y S y 2I y S z I z I z 2I z S x 2I z S y 2I z S z szin-fázisú egyszeres kvantumkoherenciáik. S spinen lokalizálható ellentétesfázisú koherenciák I spinhez tartozó ellentétesfázisú koherenciák 21
22 Tipikus transzformációk a 16 bázisoperátor által kifeszített koherencia-térben: (t=0) = hb 0 ( I I y + S S z )/(8 kt) H = I I z + S S z J IS I z S z (t=0) S z [ s t] I y (t=0) (t) (t) I z [ I t] + I y cos( I t) - I x sin( I t) 2I z S z (J IS t) + I y cos( I t)cos(j IS t) - 2I x S z cos( I t) sin(j IS t) - I x sin( I t) cos(j IS t) - 2I y S z sin( I t) sin(j IS t) I y I y 22
23 + I y cos( I t)cos(j IS t): cos(a)cos(b) = 1/2[cos(A+B)+cos(A B)] következően a spektrum alakja: +1/2I y [ +cos{( I + J IS )t} + cos{( I - J IS )t} ] I y [ +a, +a] I kémiai eltolódásértéknél memo: az spektrum a Bloch-egyenlet alapján: S(t) = C*exp( t/t 2 )cos( I t). I 1 H-spektrum I z és S z S -I y és -S y és I x sin( I t 2 ) S x sin( S t 2 ) Ω I Ω S F1(ppm) A spektrumban a J IS okozta modulációtól eltekintünk 23
24 spinrendszerek azonosítása 1 H- 1 H COSY (homonukleáris korrelációs spektrum) I 2I z S y sin( I t 1 ) S S I y S x sin( I t 1 )cos( S t 2 ) I 2I y S z sin( I t 1 ) I S 24
25 spinrendszerek azonosítása 1 H- 1 H COSY NH H 2 H α H 1 H b H b H 1 H 2 H α F 1 (ppm) S NH I I S F 2 (ppm) 25 A spektrumban a J IS okozta modulációtól eltekintünk
26 spinrendszerek azonosítása Fehérje modul 1 H- 1 H COSY spektruma 26
27 spinrendszerek azonosítása 1 H- 1 H TOCSY protonok teljes korrelációját létrehozó spektrum I NH H 1 H 2 H α S 1 S 2 H b 3S H 4 1 H3S 2 3 I y K H α H b F 1 (ppm) ΣS kx b od sin( I t 1 )cos( S t 2 ) k=1 diagonális jelek diagonálison kívüli jelek NH b od = diagonálison F 2 (ppm) kívüli intenzitások 27 A spektrumban a J IS okozta modulációtól eltekintünk
28 spinrendszerek azonosítása Fehérje modul 1 H- 1 H TOCSY spektruma 28
29 Heteronukleáris egyszeres-kvantum koherencia spektrum HSQC = Heteronuclear Single-Quantum Coherence 1,1 J~90Hz H z -2H z N y +2H z N y cos( N t 1 ) H x cos( N t 1 ) N H x cos( N t 1 )cos( H t 2 ) H 29
30 A kalmodulin 1 H- 15 N HSQC spektruma A kalmodulin 1 H spektrumának amid NH és aromás tartománya J 90 Hz ( p p m )
31 spinrendszerek azonosítása 15 N-szerkesztéssel 3D-TOCSY-HSQC 2I z b od cos( K t 1 ) 2I z cos( I t 1 ) I x b od cos( K t 1 )cos(ω N t 2 ) I x b od sin(ω I t 3 ) cos(ω N t 2 ) cos( K t 1 ) -I y N K I H 2I z N y b od cos( K t 1 ) 2I z N y b od cos( K t 1 )cos(ω N t 2 ) N NH 31 b od = off diagonális intenzitás A J IK okozta modulációtól eltekintünk
32 spinrendszerek azonosítása 15 N-szerkesztett TOCSY spektrum 1 H- 1 H TOCSY amid NH (ujjlenyomat) tartománya Homonukleáris 2D TOCSY 32
33 spinrendszerek azonosítása 15 N-szerkesztett 2D TOCSY 1 H 1 H 1 H- 15 N 3D TOCSY-HSQC csíkok 1 H- 1 H TOCSYamid NH 15 N (ujjlenyomat) tartománya EVTCEPGTTFKDKCNTCRCGSDGKSAACTLKACPQ 33
34 (AMX) Ser (AX) Gly 1. spinrendszerek azonosítása (A 3 X) Ala (A 2 M 2 X) Glu 2. spinrendszerek szekvenciális rendezése 3. kényszerfeltételek alapján szerkezetszámolás 34
35 A szekvenciális hozzárendelés és a szerkezetszámolás alapja a nukláris Overhauser- effektus (NOE) 6Å (NOE) Távolság jellegű adatok 35
36 spinrendszerek azonosítása Fehérje modul 1 H- 1 H NOESY spektruma 36
37 spinrendszerek szekvenciális rendezése A spinrendszerek szekvenciális rendezését biztosító H a i-1-h NH i NOE-k Ala Ser Glu Gly Phe Cys 37
38 spinrendszerek szekvenciális rendezése Ala Glu Ser A szekvenciális hozzárendelés Phe Gly Cys Ala Ser Glu Gly Phe Cys 38
39 (AMX) Ser (AX) Gly 1. spinrendszerek azonosítása (A 3 X) Ala (A 2 M 2 X) Glu 2. spinrendszerek szekvenciális rendezése - Ala Ser Glu - Gly - 3. kényszerfeltételek alapján szerkezetszámolás 39
40 szerkezetszámolás Egy fehérje modul 1 H- 1 H NOESY spektruma 40
41 Fehérjék NMR-szerkezetvizsgálata Kurt Wüthrich (ETH, Zürich) OmpX bakteriális membránfehérje térszerkezete Mozgékony szekvenciarésszel rendelkező prion fehérje 41
42 Biomolekulák dinamikai vizsgálata GCN4 élesztő transzkripciós faktor gerinc-dinamikájának vizsgálata Arthur G. Palmer III (Columbia University) 42
43 Fehérje feltekeredés vizsgálatok (ns és ms időskálán) Alan Fersht (Cambridge University) 43
44 Our most recent targets: dutpase Beáta Vértessy Calpastatin Péter Tompa MASP-2 Péter Gál CCP Péter Gál APPase László Polgár Peptides and miniproteins Gábor Tóth Homeodomains Botond Penke P DLC László Nyitray Calmodulin Ovádi Judit 44 Inhibitors László Gráf
45 A kulcs & zár modell (Emil Fischer) Hogyan tervezzünk gyógyszert? Minél többet meg kell tudnunk a 45 fehérjék dinamikus téralkatáról!
46 A kalmodulin reorientációja célfehérje vagy antagonista hatására a molekula összecsuklik, - az N- és C-terminális közel kerül egymáshoz, - ám a D és az E α-hélixeket összekötő részről az alacsony elektronsűrűség miatt nincs krisztallográfiai információ együttműködésben Ovádi Judittal és munkatársaival (MTA SZBK Enzimológiai Intézet) 46
47 Vinca alkaloidok (biszindol) mint CaM antagonisták Catharantus (Vinca) roseus alkaloidjai (vinblasztin, vinkrisztin) VBL - sejtosztódásgátló hatás (kemoterápia) - célpontjuk a sejt mikrotubuláris hálózata - jelentős mellékhatások (neurotoxicitás) Vinblasztin KAR - In vivo kísérletekben ugyanolyan hatékonynak bizonyult, mint a természetes vinca alkaloidok - Mellékhatása jóval kisebb KAR-2 Orosz és mts. British J.Pharmacol. 1997, 121, 947 Orosz és mts. British J.Pharmacol. 1997, 121, Orosz és mts. British J.Cancer 1999, 79, 1356
48 A kalmodulin 1 H- 15 N HSQC spektruma A kalmodulin 1 H spektrumának amid NH és aromás tartománya J 90 Hz ( p p m )
49 A kalmodulin KAR2 vel való titrálása során kapott 1 H- 15 N HSQC spektrumok összevetése l5 N l H 49
50 Felület, nmr színezés alapján (két szín) ( KAR2 yes) Ligandkötés azonosítása 50
51 Az ERD-14 egy szerkezetnélküli fehérje: lombiktól az élő sejtig ΔG Tompa 51 Péter Szalainé Ágoston Bianka
52 Dehidrin = abiotikus stressz (abszcizinsav) hatására fejeződik ki a növényben: vízhiány, magas sótartalom (NaCl), hideg ERD14 = Early Response to Dehydration aminosav, 20 kda rendezetlen fehérje sok poláris, töltött aminosav kevés hidrofób aminosav 52
53 TROSY-HSQC spektrum 15 N J 90 Hz 1 H 800 MHz 10 mm MES ph K 53
54 hetnoe Az ERD14-nek nincs oldatban térszerkezete (valójában túl sok is van neki) Relaxációs mérések: merev flexibilis 5 régió, amely 5-25 % helikális hajlammal rendelkezik 54
55 Vizes oldat vagy puffer sejt Ez különösen igaz rendezetlen fehérjékre: A fehérjezsúfoltság / crowding a sejten belül sokat számíthat! Élő sejtben kell mérni! E.coli az NMR csőben 55
56 NMR élő E.coli-ban in cell NMR E.coli ERD14 kifejeztetés Sűrű sejtszuszpenzió az NMR csőben 500 MHz sejtekben 277 K Pufferben Élő sejtekben Sejtek felülúszója üres spektrumot ad 56
57 Kontroll az in cell NMR-hez Dextrán: Sejten belüli állapotot (fehérjesűrűséget és viszkozitást) utánoz Itt nem tűnnek el a jelek Puffer Puffer + 150g/L dextrán => Puffer Amit látunk, + 300g/L tényleges kötődés, dextrán kölcsönhatás! 57
58 Szerkezet sejtben = Rendezetlen Eltűnő Elmozduló Helyükön maradó csúcsok 5 régió, amely valamihez kötődik a sejtben 58
59 A molekuláris mozgás időskálái hurkok és kanyarok záródása 0.1ms 10ms másodlagos szerkezeti elemek 10ns 1ms feltekeredés 1ms 1h H/D R ex Rot. Dif. korrel. idő 1ns<t c < 10ns gerinc dinamika 1ps 10ns t lokális aggregáció 1 s 1 év Kiss Róbert t effektiv = t C +t lok. oldallánc forgás 0.1ps 1059 ps
60 A mozgás időskálái ~ 1s ~ 100 ezer 1h ~ 30 millió 1év 60
61 A fehérjék belső dinamikája NMR ps 10-9 ns 10-6 ms 10-3 ms 10 0 s 10 2 ~min sec feltekeredés kötések mozgásai domének, nagyobb szerkezeti egységek mozgásai Shifman J M et al. PNAS 2006;103:
62 A fehérjék belső dinamikája NMR ps 10-9 ns 10-6 ms 10-3 ms 10 0 s 10 2 ~min sec R 1, R 2, NOE R 1 r CPMG Line-shape analízis ZZ- csere 62
63 Fehérjék mozgása; ms-ms időskála Belső dinamikája lefedi a különböző partnerfehérjékkel alkotott komplexeiben észlelt konformációs variációkat. R 1, R 2, NOE R 1 r NMR /RDC X-ray különböző partnerfehérjékkel ms-ms időskálájú mozgások alapján számolt S 2 Ubiquitin; a halál csókja Lange és mts., Science, 2008, 320,
64 Fehérjék mozgása; ns-ps időskála R 1, R 2, NOE R 1 r NMR /NOE + S 2 MUMO szerkezeti sokaság Gáspári Zoltán X-ray a komplexről főkomponens-elemzés Az inhibitor belső dinamikájával számolt térszerkezetek lefedik az enzimmel alkotott komplexben (3 eltérő komplex) mért röntgen konformereket. 64 Gráf László
65 Fehérjék szerkezete: mit rejt a kristály? Fehérje röntgenkrisztallográfia: kémiai Nobel-díj, 1962 Max Perutz, John Kendrew kristályban az egyes atomok helye térben jól meghatározott részletgazdag szerkezet 65
66 spinrendszerek azonosítása 2H z N x C α(i-1) z cos(ω N t 1 ) és 2H z N x C α(i) 3D-NHCA z cos(ω N t 1 ) 2H z N y cos(ω N t 1 ) H z H x cos(ω N t 1 ) cos(ω Cα(i) t 2 ) cos(ω H t 3 ) és H x cos(ω N t 1 ) cos(ωc α(i-1) t 2 ) cos(ω H t 3 ) 2H z N y Cα(i) C a(i- 1) H N C a(i) 2H y N x C y α(i-1) cos(ω N t 1 ) és 2H y N x C y α(i) cos(ω N t 1 ) 2H y N x C α(i-1) y cos(ω N t 1 ) cos(ω Cα(i) t 2 ) és 2H y N x C α(i) y cos(ω N t 1 ) cos(ωc α(i-1) t 2 ) NH Cα(i-1 N 66 A skaláris csatolás okozta modulációktól eltekintünk
NMR a peptid- és fehérje-kutatásban
 NMR a peptid- és fehérje-kutatásban A PDB adatbázisban megtalálható NMR alapú fehérjeszerkezetek számának alakulása az elmúlt évek során 4000 3500 3000 2500 2000 1500 1000 500 0 1987 1988 1989 1990 1991
NMR a peptid- és fehérje-kutatásban A PDB adatbázisban megtalálható NMR alapú fehérjeszerkezetek számának alakulása az elmúlt évek során 4000 3500 3000 2500 2000 1500 1000 500 0 1987 1988 1989 1990 1991
Lehet ségek és kihívások a modern bionmr spektroszkópia területén
 Lehet ségek és kihívások a modern bionmr spektroszkópia területén Perczel András és munkatársai Szerkezeti Kémia és Biológia Laboratórium és ELTE-MTA Fehérjemodellez Kutatócsoport ELTE/TTK/FI/ Ortvay kollokvium
Lehet ségek és kihívások a modern bionmr spektroszkópia területén Perczel András és munkatársai Szerkezeti Kémia és Biológia Laboratórium és ELTE-MTA Fehérjemodellez Kutatócsoport ELTE/TTK/FI/ Ortvay kollokvium
Az NMR spektroszkópia a fehérjék szolgálatában. Bodor Andrea. ELTE Szerkezeti Kémia és Biológia Laboratórium Visegrád
 Az NMR spektroszkópia a fehérjék szolgálatában Bodor Andrea ELTE Szerkezeti Kémia és Biológia Laboratórium 2011.01.18. Visegrád Nobel díjak tükrében 1952 Fizika: Módszer és elméleti alapok Felix Bloch
Az NMR spektroszkópia a fehérjék szolgálatában Bodor Andrea ELTE Szerkezeti Kémia és Biológia Laboratórium 2011.01.18. Visegrád Nobel díjak tükrében 1952 Fizika: Módszer és elméleti alapok Felix Bloch
FEHÉRJÉK A MÁGNESEKBEN. Bodor Andrea ELTE, Szerkezeti Kémiai és Biológiai Laboratórium. Alkímia Ma, Budapest,
 FEHÉRJÉK A MÁGNESEKBEN Bodor Andrea ELTE, Szerkezeti Kémiai és Biológiai Laboratórium Alkímia Ma, Budapest, 2013.02.28. I. FEHÉRJÉK: L-α aminosavakból felépülő lineáris polimerek α H 2 N CH COOH amino
FEHÉRJÉK A MÁGNESEKBEN Bodor Andrea ELTE, Szerkezeti Kémiai és Biológiai Laboratórium Alkímia Ma, Budapest, 2013.02.28. I. FEHÉRJÉK: L-α aminosavakból felépülő lineáris polimerek α H 2 N CH COOH amino
0) I=0 I=1/2 I=k (k=1,2,..) töltéssel forog (I=1/2)
 Az NMR-spektroszkópia szükséges feltétele a nullától különbözÿ magspin (I 0) I=0 mind a protonok mind a neutronok száma páros ( 12 C, 16 O) I=1/2 ha tömegszáma páratlan ( 1, 3, 13 C, 15 N, 19 F, 57 Fe,
Az NMR-spektroszkópia szükséges feltétele a nullától különbözÿ magspin (I 0) I=0 mind a protonok mind a neutronok száma páros ( 12 C, 16 O) I=1/2 ha tömegszáma páratlan ( 1, 3, 13 C, 15 N, 19 F, 57 Fe,
Biológiailag aktív molekulák kölcsönhatásvizsgálata NMR-spektroszkópiával
 Biológiailag aktív molekulák kölcsönhatásvizsgálata MR-spektroszkópiával 1 H- 15 -HSQC Perczel András Budapest, 2004. 03. 26. Ugyanazt az MR paramétert ( 1 H, 13 C, 15, 31 P, 57 Fe) követjük. L szabad
Biológiailag aktív molekulák kölcsönhatásvizsgálata MR-spektroszkópiával 1 H- 15 -HSQC Perczel András Budapest, 2004. 03. 26. Ugyanazt az MR paramétert ( 1 H, 13 C, 15, 31 P, 57 Fe) követjük. L szabad
A BioNMR spektroszkópia alapjai
 A BioNMR spektroszkópia alapjai Az NMR-spektroszkópia szükséges feltétele a nullától különböző magspin (I 0) 1) I=0, ha mind a protonok mind a neutronok száma páros: ( 12 C, 16 O) 2) I=1/2, ha tömegszáma
A BioNMR spektroszkópia alapjai Az NMR-spektroszkópia szükséges feltétele a nullától különböző magspin (I 0) 1) I=0, ha mind a protonok mind a neutronok száma páros: ( 12 C, 16 O) 2) I=1/2, ha tömegszáma
A BioNMR spektroszkópia alapjai
 A BioNMR spektroszkópia alapjai Az NMR-spektroszkópia szükséges feltétele a nullától különböző magspin (I 0) 1) I=0, ha mind a protonok mind a neutronok száma páros: ( 12 C, 16 O) 2) I=1/2, ha tömegszáma
A BioNMR spektroszkópia alapjai Az NMR-spektroszkópia szükséges feltétele a nullától különböző magspin (I 0) 1) I=0, ha mind a protonok mind a neutronok száma páros: ( 12 C, 16 O) 2) I=1/2, ha tömegszáma
fˆ = Klasszikus mechanika Kvantummechanika Fizikai modell r: koordináta p: lendület Állapot ), komplex függvény Ψ(r 1 Fizikai mennyiség Mérés
 Klasszikus mechanika r: koordináta p: lendület f(r,p) =f(r,p) Fizikai modell Állapot Fizikai mennyiség Mérés fˆ = rˆ r Kvantummechanika Ψ(r 1, r N ), komplex függvény f (rˆ, pˆ ) fˆ Ψ * 1 Ψdr,..., r
Klasszikus mechanika r: koordináta p: lendület f(r,p) =f(r,p) Fizikai modell Állapot Fizikai mennyiség Mérés fˆ = rˆ r Kvantummechanika Ψ(r 1, r N ), komplex függvény f (rˆ, pˆ ) fˆ Ψ * 1 Ψdr,..., r
Dóczy-Bodnár Andrea október 3. Magmágneses rezonancia (NMR) és elektronspinrezonancia (ESR) alapjai
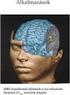 Dóczy-Bodnár Andrea 2012. október 3. Magmágneses rezonancia (NMR) és elektronspinrezonancia (ESR) alapjai Atommagok saját impulzusmomentuma (spin) protonok, neutronok (elektronhoz hasonlóan) saját impulzusmomentum
Dóczy-Bodnár Andrea 2012. október 3. Magmágneses rezonancia (NMR) és elektronspinrezonancia (ESR) alapjai Atommagok saját impulzusmomentuma (spin) protonok, neutronok (elektronhoz hasonlóan) saját impulzusmomentum
Magmágneses rezonancia (NMR) és elektronspinrezonancia (ESR) alapjai
 Magmágneses rezonancia (NMR) és elektronspinrezonancia (ESR) alapjai Dóczy-Bodnár Andrea 2011. szeptember 28. Magmágneses rezonanciához kapcsolódó Nobel-díjak * Otto Stern, USA: Nobel Prize in Physics
Magmágneses rezonancia (NMR) és elektronspinrezonancia (ESR) alapjai Dóczy-Bodnár Andrea 2011. szeptember 28. Magmágneses rezonanciához kapcsolódó Nobel-díjak * Otto Stern, USA: Nobel Prize in Physics
Alkalmazott spektroszkópia
 Alkalmazott spektroszkópia 009 Bányai István MR és a fémionok: koordinációs kémiai alkalmazások Bányai István Debreceni Egyetem TEK Kolloid- és Környezetkémiai Tanszék A mágnesség A mágneses erő: F pp
Alkalmazott spektroszkópia 009 Bányai István MR és a fémionok: koordinációs kémiai alkalmazások Bányai István Debreceni Egyetem TEK Kolloid- és Környezetkémiai Tanszék A mágnesség A mágneses erő: F pp
MÁGNESES MAGREZONANCIA A KÉMIÁBAN, GYÓGYSZERÉSZETBEN, ORVOSTUDOMÁNYBAN
 MÁGNESES MAGREZONANIA A KÉMIÁBAN, GYÓGYSZERÉSZETBEN, ORVOSTUDOMÁNYBAN 1) A jelenség 2) Nuclear Magnetic Resonance (NMR) 3) Magnetic Resonance Imaging (MRI) 4) Magnetic Resonance Spectroscopy (MRS) NMR
MÁGNESES MAGREZONANIA A KÉMIÁBAN, GYÓGYSZERÉSZETBEN, ORVOSTUDOMÁNYBAN 1) A jelenség 2) Nuclear Magnetic Resonance (NMR) 3) Magnetic Resonance Imaging (MRI) 4) Magnetic Resonance Spectroscopy (MRS) NMR
A fehérjék harmadlagos vagy térszerkezete. Még a globuláris fehérjék térszerkezete is sokféle lehet.
 A fehérjék harmadlagos vagy térszerkezete Még a globuláris fehérjék térszerkezete is sokféle lehet. A ribonukleáz redukciója és denaturálódása Chrisian B. Anfinsen A ribonukleáz renaturálódása 1972 obel-díj
A fehérjék harmadlagos vagy térszerkezete Még a globuláris fehérjék térszerkezete is sokféle lehet. A ribonukleáz redukciója és denaturálódása Chrisian B. Anfinsen A ribonukleáz renaturálódása 1972 obel-díj
Műszeres analitika II. (TKBE0532)
 Műszeres analitika II. (TKBE0532) 7. előadás NMR spektroszkópia Dr. Andrási Melinda Debreceni Egyetem Természettudományi és Technológiai Kar Szervetlen és Analitikai Kémiai Tanszék NMR, Nuclear Magnetic
Műszeres analitika II. (TKBE0532) 7. előadás NMR spektroszkópia Dr. Andrási Melinda Debreceni Egyetem Természettudományi és Technológiai Kar Szervetlen és Analitikai Kémiai Tanszék NMR, Nuclear Magnetic
Mágneses módszerek a mőszeres analitikában
 Mágneses módszerek a mőszeres analitikában NMR, ESR: mágneses momentummal rendelkezı anyagok minıségi és mennyiségi meghatározására alkalmas analitikai módszer Atommag spin állapotok közötti energiaátmenetek:
Mágneses módszerek a mőszeres analitikában NMR, ESR: mágneses momentummal rendelkezı anyagok minıségi és mennyiségi meghatározására alkalmas analitikai módszer Atommag spin állapotok közötti energiaátmenetek:
MÁGNESES MAGREZONANCIA A KÉMIÁBAN, GYÓGYSZERÉSZETBEN, ORVOSTUDOMÁNYBAN
 MÁGNESES MAGREZONANIA A KÉMIÁBAN, GYÓGYSZERÉSZETBEN, ORVOSTUDOMÁNYBAN 1) A jelenség 2) Nuclear Magnetic Resonance (NMR) 3) Magnetic Resonance Imaging (MRI) 4) Magnetic Resonance Spectroscopy (MRS) NMR
MÁGNESES MAGREZONANIA A KÉMIÁBAN, GYÓGYSZERÉSZETBEN, ORVOSTUDOMÁNYBAN 1) A jelenség 2) Nuclear Magnetic Resonance (NMR) 3) Magnetic Resonance Imaging (MRI) 4) Magnetic Resonance Spectroscopy (MRS) NMR
1D multipulzus NMR kísérletek
 D multipulzus NMR kísérletek Rohonczy János ELTE, Szervetlen Kémia Tanszék Modern szerkezetkutatási módszerek elıadás 202. . Protonlecsatolt heteronukleáris mérések Elv 3 C mag detektálása alatt a protoncsatornán
D multipulzus NMR kísérletek Rohonczy János ELTE, Szervetlen Kémia Tanszék Modern szerkezetkutatási módszerek elıadás 202. . Protonlecsatolt heteronukleáris mérések Elv 3 C mag detektálása alatt a protoncsatornán
Mágneses módszerek a műszeres analitikában
 Mágneses módszerek a műszeres analitikában NMR, ESR: mágneses momentummal rendelkező anyagok minőségi és mennyiségi meghatározására alkalmas Atommag spin állapotok közötti energiaátmenetek: NMR (magmágneses
Mágneses módszerek a műszeres analitikában NMR, ESR: mágneses momentummal rendelkező anyagok minőségi és mennyiségi meghatározására alkalmas Atommag spin állapotok közötti energiaátmenetek: NMR (magmágneses
Szerves vegyületek szerkezetfelderítése NMR spektroszkópia
 Szerves vegyületek szerkezetfelderítése NMR spektroszkópia Az anyag összeállításához Krajsovszky Gábor, Mátyus Péter és Perczel András diáit is felhasználtuk. 1 (hullámhossz) -sugárzás röntgensugárzás
Szerves vegyületek szerkezetfelderítése NMR spektroszkópia Az anyag összeállításához Krajsovszky Gábor, Mátyus Péter és Perczel András diáit is felhasználtuk. 1 (hullámhossz) -sugárzás röntgensugárzás
KÖLCSÖNHATÁS ÉS DINAMIKA. az NMR spektroszkópia, mint a modern szem. Bodor Andrea
 KÖLCSÖNHATÁS ÉS DINAMIKA az NMR spektroszkópia, mint a modern szem Bodor Andrea ELTE Szerkezeti Kémiai és Biológiai Laboratórium A Magyar Tudomány Ünnepe, 2012.11.08. Edvard Munch: A Nap (1911-1916) AZ
KÖLCSÖNHATÁS ÉS DINAMIKA az NMR spektroszkópia, mint a modern szem Bodor Andrea ELTE Szerkezeti Kémiai és Biológiai Laboratórium A Magyar Tudomány Ünnepe, 2012.11.08. Edvard Munch: A Nap (1911-1916) AZ
Alkalmazott spektroszkópia Serra Bendegúz és Bányai István
 Alkalmazott spektroszkópia 2014 Serra Bendegúz és Bányai István A mágnesség A mágneses erő: F p1 p2 r p1 p2 C ( F C ) C áll 2 2 r r r A mágneses (dipólus) momentum: m p l ( m p l ) Ahol p a póluserősség
Alkalmazott spektroszkópia 2014 Serra Bendegúz és Bányai István A mágnesség A mágneses erő: F p1 p2 r p1 p2 C ( F C ) C áll 2 2 r r r A mágneses (dipólus) momentum: m p l ( m p l ) Ahol p a póluserősség
Mi mindenről tanúskodik a Me-OH néhány NMR spektruma
 Mi mindenről tanúskodik a Me-OH néhány NMR spektruma lcélok és fogalmak: l- az NMR-rezonancia frekvencia (jel), a kémiai környezete, a kémiai eltolódás, l- az 1 H-NMR spektrum, l- az -OH és a -CH 3 csoportokban
Mi mindenről tanúskodik a Me-OH néhány NMR spektruma lcélok és fogalmak: l- az NMR-rezonancia frekvencia (jel), a kémiai környezete, a kémiai eltolódás, l- az 1 H-NMR spektrum, l- az -OH és a -CH 3 csoportokban
Spektroszkópiai módszerek 2.
 Spektroszkópiai módszerek 2. NMR spektroszkópia magspinek rendeződése külső mágneses tér hatására az eredő magspin nem nulla, ha a magot alkotó nukleonok közül legalább az egyik páratlan a szerves kémiában
Spektroszkópiai módszerek 2. NMR spektroszkópia magspinek rendeződése külső mágneses tér hatására az eredő magspin nem nulla, ha a magot alkotó nukleonok közül legalább az egyik páratlan a szerves kémiában
Mágneses rezonanciás képalkotás AZ MRI elve, fizikai alapok
 MR-ALAPTANFOLYAM 2011 SZEGED Mágneses rezonanciás képalkotás AZ MRI elve, fizikai alapok Martos János Országos Idegtudományi Intézet Az agy MR vizsgálata A gerinc MR vizsgálata Felix Bloch Edward Mills
MR-ALAPTANFOLYAM 2011 SZEGED Mágneses rezonanciás képalkotás AZ MRI elve, fizikai alapok Martos János Országos Idegtudományi Intézet Az agy MR vizsgálata A gerinc MR vizsgálata Felix Bloch Edward Mills
Hemoglobin - myoglobin. Konzultációs e-tananyag Szikla Károly
 Hemoglobin - myoglobin Konzultációs e-tananyag Szikla Károly Myoglobin A váz- és szívizom oxigén tároló fehérjéje Mt.: 17.800 153 aminosavból épül fel A lánc kb 75 % a hélix 8 db hélix, köztük nem helikális
Hemoglobin - myoglobin Konzultációs e-tananyag Szikla Károly Myoglobin A váz- és szívizom oxigén tároló fehérjéje Mt.: 17.800 153 aminosavból épül fel A lánc kb 75 % a hélix 8 db hélix, köztük nem helikális
A spin. November 28, 2006
 A spin November 28, 2006 1 A spin a kvantummechanikában Az elektronnak és sok más kvantummechanikai részecskének is van egy saját impulzusnyomatéka amely független a mozgásállapottól. (Úgy is mondhatjuk,
A spin November 28, 2006 1 A spin a kvantummechanikában Az elektronnak és sok más kvantummechanikai részecskének is van egy saját impulzusnyomatéka amely független a mozgásállapottól. (Úgy is mondhatjuk,
ERD14: egy funkcionálisan rendezetlen dehidrin fehérje szerkezeti és funkcionális jellemzése
 Doktori értekezés tézisei ERD14: egy funkcionálisan rendezetlen dehidrin fehérje szerkezeti és funkcionális jellemzése DR. SZALAINÉ ÁGOSTON Bianka Ildikó Témavezetők Dr. PERCZEL András egyetemi tanár és
Doktori értekezés tézisei ERD14: egy funkcionálisan rendezetlen dehidrin fehérje szerkezeti és funkcionális jellemzése DR. SZALAINÉ ÁGOSTON Bianka Ildikó Témavezetők Dr. PERCZEL András egyetemi tanár és
lásd: enantiotóp, diasztereotóp
 anizokrón anisochronous árnyékolási állandó shielding constant árnyékolási járulékok és empirikus értelmezésük shielding contributions diamágneses és paramágneses árnyékolás diamagnetic and paramagnetic
anizokrón anisochronous árnyékolási állandó shielding constant árnyékolási járulékok és empirikus értelmezésük shielding contributions diamágneses és paramágneses árnyékolás diamagnetic and paramagnetic
Magmágneses rezonancia. alapjai. Magmágneses rezonanciához kapcsolódó Nobel-díjak. γ N = = giromágneses hányados. v v
 Magmágneses rezonancia (MR) és elektronspinrezonancia (ESR) alapjai Dóczy-Bodnár Andrea 211. szeptember 28. Magmágneses rezonanciához kapcsolódó obel-díjak * Otto Stern, USA: obel Prize in Physics 1943,
Magmágneses rezonancia (MR) és elektronspinrezonancia (ESR) alapjai Dóczy-Bodnár Andrea 211. szeptember 28. Magmágneses rezonanciához kapcsolódó obel-díjak * Otto Stern, USA: obel Prize in Physics 1943,
Biomolekuláris szerkezeti dinamika
 Kísérletek, mérések célja Biomolekuláris szerkezeti dinamika Kellermayer Miklós Biomolekuláris szerkezet és működés pontosabb megismerése (folyamatok, állapotok, átmenetek, kölcsönhatások, mozgások, stb.)
Kísérletek, mérések célja Biomolekuláris szerkezeti dinamika Kellermayer Miklós Biomolekuláris szerkezet és működés pontosabb megismerése (folyamatok, állapotok, átmenetek, kölcsönhatások, mozgások, stb.)
Biomolekuláris szerkezeti dinamika
 Kísérletek, mérések célja Biomolekuláris szerkezeti dinamika Kellermayer Miklós Biomolekuláris szerkezet és működés pontosabb megismerése (folyamatok, állapotok, átmenetek, kölcsönhatások, stb.) Rádióspektroszkópiák
Kísérletek, mérések célja Biomolekuláris szerkezeti dinamika Kellermayer Miklós Biomolekuláris szerkezet és működés pontosabb megismerése (folyamatok, állapotok, átmenetek, kölcsönhatások, stb.) Rádióspektroszkópiák
A KAR-2, egy antimitotikus ágens egyedi farmakológiájának atomi és molekuláris alapjai
 A KAR-2, egy antimitotikus ágens egyedi farmakológiájának atomi és molekuláris alapjai A doktori értekezés tézisei Horváth István Eötvös Loránd Tudományegyetem Biológia Doktori Iskola (A Doktori Iskola
A KAR-2, egy antimitotikus ágens egyedi farmakológiájának atomi és molekuláris alapjai A doktori értekezés tézisei Horváth István Eötvös Loránd Tudományegyetem Biológia Doktori Iskola (A Doktori Iskola
M N. a. Spin = saját impulzus momentum vektor: L L nagysága:
 Az MR és MRI alapjai Magmágneses Rezonancia Spektroszkópia (MR) és Mágneses Rezonancia Képalkotás (MRI) uclear Magnetic Resonance: Alapelv felfedezéséért Fizikai obel díj, 1952 Felix Bloch és Edward M.
Az MR és MRI alapjai Magmágneses Rezonancia Spektroszkópia (MR) és Mágneses Rezonancia Képalkotás (MRI) uclear Magnetic Resonance: Alapelv felfedezéséért Fizikai obel díj, 1952 Felix Bloch és Edward M.
Hangfrekvenciás mechanikai rezgések vizsgálata
 Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
Több oxigéntartalmú funkciós csoportot tartalmazó vegyületek
 Több oxigéntartalmú funkciós csoportot tartalmazó vegyületek Hidroxikarbonsavak α-hidroxi karbonsavak -Glikolsav (kézkrémek) - Tejsav (tejtermékek, izomláz, fogszuvasodás) - Citromsav (citrusfélékben,
Több oxigéntartalmú funkciós csoportot tartalmazó vegyületek Hidroxikarbonsavak α-hidroxi karbonsavak -Glikolsav (kézkrémek) - Tejsav (tejtermékek, izomláz, fogszuvasodás) - Citromsav (citrusfélékben,
Bevezető. 1. ábra. A Trp-kalitka minifehérje szerkezetének szalagmodelje (PDB: 1L2Y).
 Bevezető A mindössze 20 aminosavból felépülő, de novo tervezett Trp-kalitka minifehérje már számos in vitro és in silico vizsgálat tárgyát képezte. Jelen doktori munka ennek a model fehérjecsaládnak a
Bevezető A mindössze 20 aminosavból felépülő, de novo tervezett Trp-kalitka minifehérje már számos in vitro és in silico vizsgálat tárgyát képezte. Jelen doktori munka ennek a model fehérjecsaládnak a
Az NMR képalkotás alapjai. Bányai István Kolloid- és Környezetkémiai Tanszék DE, TEK
 Az NMR képalkotás alapjai Bánai István Kolloid- és Körnezetkémiai Tanszék DE, TEK Az NMR alapjai alapjai Bánai István Kolloid- és Körnezetkémiai Tanszék DE, TEK A mágnesség A mágneses erı: F = pp 1 2 r
Az NMR képalkotás alapjai Bánai István Kolloid- és Körnezetkémiai Tanszék DE, TEK Az NMR alapjai alapjai Bánai István Kolloid- és Körnezetkémiai Tanszék DE, TEK A mágnesség A mágneses erı: F = pp 1 2 r
NMR spektroszkópia a fehérje biokémiában
 NMR spektroszkópia a fehérje biokémiában Závodszky Péter Beinrohr László MTA SzBK Enzimológiai Intézet NMR spektroszkópia a fehérje biokémiában Závodszky Péter Beinrohr László MTA SzBK Enzimológiai Intézet
NMR spektroszkópia a fehérje biokémiában Závodszky Péter Beinrohr László MTA SzBK Enzimológiai Intézet NMR spektroszkópia a fehérje biokémiában Závodszky Péter Beinrohr László MTA SzBK Enzimológiai Intézet
Egy antifungális diszulfid fehérje szerkezeti dinamikája és hideg/meleg kitekeredése (avagy PAF, a hűvös sárkány)
 Egy antifungális diszulfid fehérje szerkezeti dinamikája és hideg/meleg kitekeredése (avagy PAF, a hűvös sárkány) Batta Gyula Debreceni Egyetem Szerkezeti Biológiai és Molekuláris Felismerési Műhely structbiol.unideb.hu
Egy antifungális diszulfid fehérje szerkezeti dinamikája és hideg/meleg kitekeredése (avagy PAF, a hűvös sárkány) Batta Gyula Debreceni Egyetem Szerkezeti Biológiai és Molekuláris Felismerési Műhely structbiol.unideb.hu
Lin.Alg.Zh.1 feladatok
 Lin.Alg.Zh. feladatok 0.. d vektorok Adott három vektor ā (0 b ( c (0 az R Euklideszi vektortérben egy ortonormált bázisban.. Mennyi az ā b skalárszorzat? ā b 0 + + 8. Mennyi az n ā b vektoriális szorzat?
Lin.Alg.Zh. feladatok 0.. d vektorok Adott három vektor ā (0 b ( c (0 az R Euklideszi vektortérben egy ortonormált bázisban.. Mennyi az ā b skalárszorzat? ā b 0 + + 8. Mennyi az n ā b vektoriális szorzat?
NMR spektroszkópia (Nuclear Magnetic Resonance) Mágneses (atom)magrezonancia Spektroszkópia
 NMR spektroszkópia (Nuclear Magnetic Resonance) Mágneses (atom)magrezonancia Spektroszkópia Anyagszerkezeti vizsgálatok 2016. őszi félév Balogh Szabolcs sz.balogh@gmail.com Pannon Egyetem, NMR Laboratórium
NMR spektroszkópia (Nuclear Magnetic Resonance) Mágneses (atom)magrezonancia Spektroszkópia Anyagszerkezeti vizsgálatok 2016. őszi félév Balogh Szabolcs sz.balogh@gmail.com Pannon Egyetem, NMR Laboratórium
MedInProt Szinergia IV. program. Szerkezetvizsgáló módszer a rendezetlen fehérjék szerkezetének és kölcsönhatásainak jellemzésére
 MedInProt Szinergia IV. program Szerkezetvizsgáló módszer a rendezetlen fehérjék szerkezetének és kölcsönhatásainak jellemzésére Tantos Ágnes MTA TTK Enzimológiai Intézet, Rendezetlen fehérje kutatócsoport
MedInProt Szinergia IV. program Szerkezetvizsgáló módszer a rendezetlen fehérjék szerkezetének és kölcsönhatásainak jellemzésére Tantos Ágnes MTA TTK Enzimológiai Intézet, Rendezetlen fehérje kutatócsoport
BIOFIZIKA. Metodika- 4. Liliom Károly. MTA TTK Enzimológiai Intézet liliom@enzim.hu
 BIOFIZIKA 2012 11 26 Metodika- 4 Liliom Károly MTA TTK Enzimológiai Intézet liliom@enzim.hu A biofizika előadások temamkája 1. 09-03 Biofizika: fizikai szemlélet, modellalkotás, biometria 2. 09-10 SZÜNET
BIOFIZIKA 2012 11 26 Metodika- 4 Liliom Károly MTA TTK Enzimológiai Intézet liliom@enzim.hu A biofizika előadások temamkája 1. 09-03 Biofizika: fizikai szemlélet, modellalkotás, biometria 2. 09-10 SZÜNET
Atomok és molekulák elektronszerkezete
 Atomok és molekulák elektronszerkezete Szabad atomok és molekulák Schrödinger egyenlete Tekintsünk egy kvantummechanikai rendszert amely N n magból és N e elektronból áll. Koordinátáikat jelölje rendre
Atomok és molekulák elektronszerkezete Szabad atomok és molekulák Schrödinger egyenlete Tekintsünk egy kvantummechanikai rendszert amely N n magból és N e elektronból áll. Koordinátáikat jelölje rendre
I. Az NMR spektrométer
 I. Az NMR spektrométer I. Az NMR spektrométer fő részei Rádióelektronikai konzol Munkaállomás Mágnes 2 I. Ultra-árnyékolt mágnesek Kettős szupravezető tekerccsel csökkenthető a mágnes szórt tere. Kisebb
I. Az NMR spektrométer I. Az NMR spektrométer fő részei Rádióelektronikai konzol Munkaállomás Mágnes 2 I. Ultra-árnyékolt mágnesek Kettős szupravezető tekerccsel csökkenthető a mágnes szórt tere. Kisebb
Foton-visszhang alapú optikai kvantum-memóriák: koherens kontroll optikailag sűrű közegben
 Foton-visszhang alapú optikai kvantum-memóriák: koherens kontroll optikailag sűrű közegben Demeter Gábor MTA Wigner Fizikai Kutatóközpont, RMI Demeter Gábor (MTA Wigner RCP... / 4 Bevezetés / Motiváció
Foton-visszhang alapú optikai kvantum-memóriák: koherens kontroll optikailag sűrű közegben Demeter Gábor MTA Wigner Fizikai Kutatóközpont, RMI Demeter Gábor (MTA Wigner RCP... / 4 Bevezetés / Motiváció
 A polipeptidlánc szabályozott lebontása: mit mondanak a fehérjekristályok? Harmat Veronika ELTE Kémiai Intézet, Szerkezeti Kémia és Biológia Laboratórium MTA-ELTE Fehérjemodellező Kutatócsoport A magyar
A polipeptidlánc szabályozott lebontása: mit mondanak a fehérjekristályok? Harmat Veronika ELTE Kémiai Intézet, Szerkezeti Kémia és Biológia Laboratórium MTA-ELTE Fehérjemodellező Kutatócsoport A magyar
A Ca 2+ szerepe a tormaperoxidáz enzim aktív szerkezetében. Szigeti Krisztián
 A Ca 2+ szerepe a tormaperoxidáz enzim aktív szerkezetében Doktori értekezés Szigeti Krisztián Semmelweis Egyetem Gyógyszertudományok Doktori Iskola Témavezető: Hivatalos Bírálók: Szigorlati Bizottság
A Ca 2+ szerepe a tormaperoxidáz enzim aktív szerkezetében Doktori értekezés Szigeti Krisztián Semmelweis Egyetem Gyógyszertudományok Doktori Iskola Témavezető: Hivatalos Bírálók: Szigorlati Bizottság
Kvantummechanika gyakorlat Beadandó feladatsor Határid : 4. heti gyakorlatok eleje
 Kvantummechanika gyakorlat 015 1. Beadandó feladatsor Határid : 4. heti gyakorlatok eleje 1. Mutassuk meg, hogy A és B tetsz leges operátorokra igaz, hogy e B A e B = A + [B, A] + 1![ B, [B, A] ] +....
Kvantummechanika gyakorlat 015 1. Beadandó feladatsor Határid : 4. heti gyakorlatok eleje 1. Mutassuk meg, hogy A és B tetsz leges operátorokra igaz, hogy e B A e B = A + [B, A] + 1![ B, [B, A] ] +....
Mágneses magrezonancia (NMR) spektroszkópia a fehérjekutatásban. Dr. Tőke Orsolya MTA Kémiai Kutatóközpont Szerkezeti Kémiai Intézet 2007
 Mágneses magrezonancia (NMR) spektroszkópia a fehérjekutatásban Dr. Tőke Orsolya MTA Kémiai Kutatóközpont Szerkezeti Kémiai Intézet 2007 1 A fehérjék szerkezetének és működésének megértése alapvető fontosságú
Mágneses magrezonancia (NMR) spektroszkópia a fehérjekutatásban Dr. Tőke Orsolya MTA Kémiai Kutatóközpont Szerkezeti Kémiai Intézet 2007 1 A fehérjék szerkezetének és működésének megértése alapvető fontosságú
Modern Fizika Labor. 12. Infravörös spektroszkópia. Fizika BSc. A mérés dátuma: okt. 04. A mérés száma és címe: Értékelés:
 Modern Fizika Labor Fizika BSc A mérés dátuma: 011. okt. 04. A mérés száma és címe: 1. Infravörös spektroszkópia Értékelés: A beadás dátuma: 011. dec. 1. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 011. okt. 04. A mérés száma és címe: 1. Infravörös spektroszkópia Értékelés: A beadás dátuma: 011. dec. 1. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Sohár Pál Varázslat, amitől láthatóvá válnak és életre kelnek a molekulák: Az NMR spektroszkópia
 MTA -ELTE FEÉRJEMODELLEZŐ KUTATÓCSOPORT - ÁLTALÁNOS ÉS SZERVETLEN KÉMIAI TANSZÉK EÖTVÖS LORÁND TUDOMÁNYEGYETEM Sohár Pál Varázslat, amitől láthatóvá válnak és életre kelnek a molekulák: Az NMR spektroszkópia
MTA -ELTE FEÉRJEMODELLEZŐ KUTATÓCSOPORT - ÁLTALÁNOS ÉS SZERVETLEN KÉMIAI TANSZÉK EÖTVÖS LORÁND TUDOMÁNYEGYETEM Sohár Pál Varázslat, amitől láthatóvá válnak és életre kelnek a molekulák: Az NMR spektroszkópia
The magnetic pole model: two opposing poles, North (+) and South (-), separated by a distance d produce an H- field (lines).
 Preambulum: B: a mágneses indukció (mágneses fluxussűrűség), a mágneses mező (mágneses erőtér) a mozgó elektromos töltés, vagy az elektromos mező változásának következménye. SI egysége a tesla (T) - 1
Preambulum: B: a mágneses indukció (mágneses fluxussűrűség), a mágneses mező (mágneses erőtér) a mozgó elektromos töltés, vagy az elektromos mező változásának következménye. SI egysége a tesla (T) - 1
A fehérjék szerkezeti hierarchiája. Fehérje-szerkezetek! Klasszikus szerkezet-funkció paradigma. szekvencia. funkció. szerkezet! Myoglobin.
 Myoglobin Fehérje-szerkezetek! MGLSDGEWQLVLNVWGKVEADIPGGQEVLIRLFK GPETLEKFDKFKLKSEDEMKASE DLKKGATVLTALGGILKKKGEAEIKPLAQSA TKKIPVKYLEFISECIIQVLQSK PGDFGADAQGAMNKALELFRKDMASNYKELGFQG Fuxreiter Mónika! Debreceni
Myoglobin Fehérje-szerkezetek! MGLSDGEWQLVLNVWGKVEADIPGGQEVLIRLFK GPETLEKFDKFKLKSEDEMKASE DLKKGATVLTALGGILKKKGEAEIKPLAQSA TKKIPVKYLEFISECIIQVLQSK PGDFGADAQGAMNKALELFRKDMASNYKELGFQG Fuxreiter Mónika! Debreceni
MEDINPROT Gépidő Pályázat támogatásával elért eredmények
 A kisszögű röntgenszórási módszer fejlesztése fehérjék oldatfázisú mérésére Bóta Attila, Wacha András, Varga Zoltán MTA TTK Biológiai Nanokémia Kutatócsoport 1117 Bp. Magyar Tudósok krt. 2. MEDINPROT Gépidő
A kisszögű röntgenszórási módszer fejlesztése fehérjék oldatfázisú mérésére Bóta Attila, Wacha András, Varga Zoltán MTA TTK Biológiai Nanokémia Kutatócsoport 1117 Bp. Magyar Tudósok krt. 2. MEDINPROT Gépidő
Peptid- és fehérjék másodlagos-, harmadlagos- és negyedleges szerkezete
 Peptid- és fehérjék másodlagos-, harmadlagos- és negyedleges szerkezete Polipeptidek térszerkezete Tipikus (rendezett) konformerek em tipikus (rendezetlen) konformerek Periodikus vagy homokonformerek Aperiodikus
Peptid- és fehérjék másodlagos-, harmadlagos- és negyedleges szerkezete Polipeptidek térszerkezete Tipikus (rendezett) konformerek em tipikus (rendezetlen) konformerek Periodikus vagy homokonformerek Aperiodikus
Modern Fizika Labor. 5. ESR (Elektronspin rezonancia) Fizika BSc. A mérés dátuma: okt. 25. A mérés száma és címe: Értékelés:
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 25. A mérés száma és címe: 5. ESR (Elektronspin rezonancia) Értékelés: A beadás dátuma: 2011. nov. 16. A mérést végezte: Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 25. A mérés száma és címe: 5. ESR (Elektronspin rezonancia) Értékelés: A beadás dátuma: 2011. nov. 16. A mérést végezte: Szőke Kálmán Benjamin
Lin.Alg.Zh.1 feladatok
 LinAlgZh1 feladatok 01 3d vektorok Adott három vektor ā = (0 2 4) b = (1 1 4) c = (0 2 4) az R 3 Euklideszi vektortérben egy ortonormált bázisban 1 Mennyi az ā b skalárszorzat? 2 Mennyi az n = ā b vektoriális
LinAlgZh1 feladatok 01 3d vektorok Adott három vektor ā = (0 2 4) b = (1 1 4) c = (0 2 4) az R 3 Euklideszi vektortérben egy ortonormált bázisban 1 Mennyi az ā b skalárszorzat? 2 Mennyi az n = ā b vektoriális
Fluktuáló terű transzverz Ising-lánc dinamikája
 2016. szeptember 8. Phys. Rev. B 93, 134305 Modell H(t) = 1 2 L 1 σi x σi+1 x h(t) 2 i=1 h(t)-fluktuáló mágneses tér. Hogyan terjednek jelek a zajos rendszerben? L σi z, i=1 Zajok típusai 1 fehér zaj 2
2016. szeptember 8. Phys. Rev. B 93, 134305 Modell H(t) = 1 2 L 1 σi x σi+1 x h(t) 2 i=1 h(t)-fluktuáló mágneses tér. Hogyan terjednek jelek a zajos rendszerben? L σi z, i=1 Zajok típusai 1 fehér zaj 2
A fény és az anyag kölcsönhatása
 A fény és az anyag kölcsönhatása Bohr-feltétel : E = E 2 E 1 = hν abszorpció foton (hν) E 2 E 2 E 1 E 1 E 2 E 2 spontán emisszió E 1 E 1 stimulált (kényszerített) emisszió E 2 E 2 E 1 E 1 Emissziós és
A fény és az anyag kölcsönhatása Bohr-feltétel : E = E 2 E 1 = hν abszorpció foton (hν) E 2 E 2 E 1 E 1 E 2 E 2 spontán emisszió E 1 E 1 stimulált (kényszerített) emisszió E 2 E 2 E 1 E 1 Emissziós és
Sajátértékek és sajátvektorok. mf1n1a06- mf1n2a06 Csabai István
 Sajátértékek és sajátvektorok A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris transzformáció Vektorok lineáris transzformációja: általános esetben az x vektor iránya és nagysága
Sajátértékek és sajátvektorok A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris transzformáció Vektorok lineáris transzformációja: általános esetben az x vektor iránya és nagysága
Röntgen sugárzás. Wilhelm Röntgen. Röntgen feleségének keze
 Röntgendiffrakció Kardos Roland 2010.03.08. Előadás vázlata Röntgen sugárzás Interferencia Huygens teória Diffrakció Diffrakciós eljárások Alkalmazás Röntgen sugárzás 1895 röntgen sugárzás felfedezés (1901
Röntgendiffrakció Kardos Roland 2010.03.08. Előadás vázlata Röntgen sugárzás Interferencia Huygens teória Diffrakció Diffrakciós eljárások Alkalmazás Röntgen sugárzás 1895 röntgen sugárzás felfedezés (1901
2015/16/1 Kvantummechanika B 2.ZH
 2015/16/1 Kvantummechanika B 2.ZH 2015. december 10. Információk 0. A ZH ideje minimum 90 perc, maximum 180 perc. 1. Az összesen elérhet pontszám 270 pont. 2. A jeles érdemjegy eléréséhez nem szükséges
2015/16/1 Kvantummechanika B 2.ZH 2015. december 10. Információk 0. A ZH ideje minimum 90 perc, maximum 180 perc. 1. Az összesen elérhet pontszám 270 pont. 2. A jeles érdemjegy eléréséhez nem szükséges
Méréstechnika. Rezgésmérés. Készítette: Ángyán Béla. Iszak Gábor. Seidl Áron. Veszprém. [Ide írhatja a szöveget] oldal 1
![Méréstechnika. Rezgésmérés. Készítette: Ángyán Béla. Iszak Gábor. Seidl Áron. Veszprém. [Ide írhatja a szöveget] oldal 1 Méréstechnika. Rezgésmérés. Készítette: Ángyán Béla. Iszak Gábor. Seidl Áron. Veszprém. [Ide írhatja a szöveget] oldal 1](/thumbs/45/23262384.jpg) Méréstechnika Rezgésmérés Készítette: Ángyán Béla Iszak Gábor Seidl Áron Veszprém 2014 [Ide írhatja a szöveget] oldal 1 A rezgésekkel kapcsolatos alapfogalmak A rezgés a Magyar Értelmező Szótár megfogalmazása
Méréstechnika Rezgésmérés Készítette: Ángyán Béla Iszak Gábor Seidl Áron Veszprém 2014 [Ide írhatja a szöveget] oldal 1 A rezgésekkel kapcsolatos alapfogalmak A rezgés a Magyar Értelmező Szótár megfogalmazása
Az NMR és a bizonytalansági elv rejtélyes találkozása
 Az NMR és a bizonytalansági elv rejtélyes találkozása ifj. Szántay Csaba MTA Kémiai Tudományok Osztálya 2012. február 21. a magspínek pulzus-gerjesztésének értelmezési paradigmája GLOBÁLISAN ELTERJEDT
Az NMR és a bizonytalansági elv rejtélyes találkozása ifj. Szántay Csaba MTA Kémiai Tudományok Osztálya 2012. február 21. a magspínek pulzus-gerjesztésének értelmezési paradigmája GLOBÁLISAN ELTERJEDT
Kis rendszer nagy kérdés
 Tudományos Diákköri Dolgozat KOLTAI ANDRÁS Kis rendszer nagy kérdés Témavezető: Prof. Perczel András ELTE Szerkezeti Kémia és Biológia Laboratórium Eötvös Loránd Tudományegyetem Természettudományi Kar
Tudományos Diákköri Dolgozat KOLTAI ANDRÁS Kis rendszer nagy kérdés Témavezető: Prof. Perczel András ELTE Szerkezeti Kémia és Biológia Laboratórium Eötvös Loránd Tudományegyetem Természettudományi Kar
Fehérjeszerkezet, és tekeredés
 Fehérjeszerkezet, és tekeredés Futó Kinga 2013.10.08. Polimerek Polimer: hasonló alegységekből (monomer) felépülő makromolekulák Alegységek száma: tipikusan 10 2-10 4 Titin: 3,435*10 4 aminosav C 132983
Fehérjeszerkezet, és tekeredés Futó Kinga 2013.10.08. Polimerek Polimer: hasonló alegységekből (monomer) felépülő makromolekulák Alegységek száma: tipikusan 10 2-10 4 Titin: 3,435*10 4 aminosav C 132983
Bordács Sándor doktorjelölt. anyagtudományban. nyban. Dr. Kézsmárki István Prof. Yohinori Tokura Prof. Ryo Shimano
 Bordács Sándor doktorjelölt Túl l a távoli t infrán: THz spektroszkópia pia az anyagtudományban nyban Dr. Kézsmárki István Prof. Yohinori Tokura Prof. Ryo Shimano Terahertz sugárz rzás THz tartomány: frekvencia:
Bordács Sándor doktorjelölt Túl l a távoli t infrán: THz spektroszkópia pia az anyagtudományban nyban Dr. Kézsmárki István Prof. Yohinori Tokura Prof. Ryo Shimano Terahertz sugárz rzás THz tartomány: frekvencia:
Peptid- és fehérjék másodlagos-, harmadlagos- és negyedleges szerkezete
 Peptid- és fehérjék másodlagos-, harmadlagos- és negyedleges szerkezete Polipeptidek térszerkezete Tipikus (rendezett) konformerek em tipikus (rendezetlen) konformerek Periodikus vagy homokonformerek Aperiodikus
Peptid- és fehérjék másodlagos-, harmadlagos- és negyedleges szerkezete Polipeptidek térszerkezete Tipikus (rendezett) konformerek em tipikus (rendezetlen) konformerek Periodikus vagy homokonformerek Aperiodikus
palkotás alapjai Bányai István Kolloid- és Környezetkémiai Tanszék DE, TEK
 Az NMR képalkotk palkotás alapjai Bánai István Kolloid- és Körnezetkémiai Tanszék DE, TEK Az NMR alapjai alapjai Bánai István Kolloid- és Körnezetkémiai Tanszék DE, TEK Kvantummechanikai alapok Az atommag
Az NMR képalkotk palkotás alapjai Bánai István Kolloid- és Körnezetkémiai Tanszék DE, TEK Az NMR alapjai alapjai Bánai István Kolloid- és Körnezetkémiai Tanszék DE, TEK Kvantummechanikai alapok Az atommag
Egyszabadságfokú grejesztett csillapított lengõrendszer vizsgálata
 Egyszabadságfokú grejesztett csillapított lengõrendszer vizsgálata Referencia egyenlet x D Α x Α x x 0 Α sin Ω t req t,t x t D Α t x t Α x t x 0 Α Sin Ω t Α x t D Α x t x t Α Sin t Ω x 0 Homogén rész megoldása
Egyszabadságfokú grejesztett csillapított lengõrendszer vizsgálata Referencia egyenlet x D Α x Α x x 0 Α sin Ω t req t,t x t D Α t x t Α x t x 0 Α Sin Ω t Α x t D Α x t x t Α Sin t Ω x 0 Homogén rész megoldása
Röntgensugárzás az orvostudományban. Röntgen kép és Komputer tomográf (CT)
 Röntgensugárzás az orvostudományban Röntgen kép és Komputer tomográf (CT) Orbán József, Biofizikai Intézet, 2008 Hand mit Ringen: print of Wilhelm Röntgen's first "medical" x-ray, of his wife's hand, taken
Röntgensugárzás az orvostudományban Röntgen kép és Komputer tomográf (CT) Orbán József, Biofizikai Intézet, 2008 Hand mit Ringen: print of Wilhelm Röntgen's first "medical" x-ray, of his wife's hand, taken
Fourier transzformáció
 a Matematika mérnököknek II. című tárgyhoz Fourier transzformáció Fourier transzformáció, heurisztika Tekintsük egy 2L szerint periodikus függvény Fourier sorát: f (x) = a 0 2 + ( ( nπ ) ( nπ )) a n cos
a Matematika mérnököknek II. című tárgyhoz Fourier transzformáció Fourier transzformáció, heurisztika Tekintsük egy 2L szerint periodikus függvény Fourier sorát: f (x) = a 0 2 + ( ( nπ ) ( nπ )) a n cos
CD-spektroszkópia. Az ORD spektroskópia alapja
 CD-spektroszkópia Az ORD spektroskópia alapja - A XIX. század elején Biot megfigyelte, hogy bizonyos, a természetben előforduló szerves anyagok a lineárisan polarizált fény síkját elforgatják. - 1817-ben
CD-spektroszkópia Az ORD spektroskópia alapja - A XIX. század elején Biot megfigyelte, hogy bizonyos, a természetben előforduló szerves anyagok a lineárisan polarizált fény síkját elforgatják. - 1817-ben
Készítette: NÁDOR JUDIT. Témavezető: Dr. HOMONNAY ZOLTÁN. ELTE TTK, Analitikai Kémia Tanszék 2010
 Készítette: NÁDOR JUDIT Témavezető: Dr. HOMONNAY ZOLTÁN ELTE TTK, Analitikai Kémia Tanszék 2010 Bevezetés, célkitűzés Mössbauer-spektroszkópia Kísérleti előzmények Mérések és eredmények Összefoglalás EDTA
Készítette: NÁDOR JUDIT Témavezető: Dr. HOMONNAY ZOLTÁN ELTE TTK, Analitikai Kémia Tanszék 2010 Bevezetés, célkitűzés Mössbauer-spektroszkópia Kísérleti előzmények Mérések és eredmények Összefoglalás EDTA
Kémiai reakciók mechanizmusa számítógépes szimulációval
 Kémiai reakciók mechanizmusa számítógépes szimulációval Stirling András stirling@chemres.hu Elméleti Kémiai Osztály Budapest Stirling A. (MTA Kémiai Kutatóközpont) Reakciómechanizmus szimulációból 2007.
Kémiai reakciók mechanizmusa számítógépes szimulációval Stirling András stirling@chemres.hu Elméleti Kémiai Osztály Budapest Stirling A. (MTA Kémiai Kutatóközpont) Reakciómechanizmus szimulációból 2007.
Erős terek leírása a Wigner-formalizmussal
 Erős terek leírása a Wigner-formalizmussal Berényi Dániel 1, Varró Sándor 1, Vladimir Skokov 2, Lévai Péter 1 1, MTA Wigner FK, Budapest 2, RIKEN/BNL, Upton, USA Wigner 115 2017. November 15. Budapest
Erős terek leírása a Wigner-formalizmussal Berényi Dániel 1, Varró Sándor 1, Vladimir Skokov 2, Lévai Péter 1 1, MTA Wigner FK, Budapest 2, RIKEN/BNL, Upton, USA Wigner 115 2017. November 15. Budapest
Rezgőmozgás. A mechanikai rezgések vizsgálata, jellemzői és dinamikai feltétele
 Rezgőmozgás A mechanikai rezgések vizsgálata, jellemzői és dinamikai feltétele A rezgés fogalma Minden olyan változás, amely az időben valamilyen ismétlődést mutat rezgésnek nevezünk. A rezgések fajtái:
Rezgőmozgás A mechanikai rezgések vizsgálata, jellemzői és dinamikai feltétele A rezgés fogalma Minden olyan változás, amely az időben valamilyen ismétlődést mutat rezgésnek nevezünk. A rezgések fajtái:
Kvantum termodinamika
 Kvantum termodinamika Diósi Lajos MTA Wigner FK Budapest 2014. febr. 4. Diósi Lajos (MTA Wigner FKBudapest) Kvantum termodinamika 2014. febr. 4. 1 / 12 1 Miért van 1 qubitnek termodinamikája? 2 QuOszcillátor/Qubit:
Kvantum termodinamika Diósi Lajos MTA Wigner FK Budapest 2014. febr. 4. Diósi Lajos (MTA Wigner FKBudapest) Kvantum termodinamika 2014. febr. 4. 1 / 12 1 Miért van 1 qubitnek termodinamikája? 2 QuOszcillátor/Qubit:
TDK lehetőségek az MTA TTK Enzimológiai Intézetben
 TDK lehetőségek az MTA TTK Enzimológiai Intézetben Vértessy G. Beáta egyetemi tanár TDK mind 1-3 helyezettek OTDK Pro Scientia különdíj 1 második díj Diákjaink Eredményei Zsűri különdíj 2 első díj OTDK
TDK lehetőségek az MTA TTK Enzimológiai Intézetben Vértessy G. Beáta egyetemi tanár TDK mind 1-3 helyezettek OTDK Pro Scientia különdíj 1 második díj Diákjaink Eredményei Zsűri különdíj 2 első díj OTDK
MRI áttekintés. Orvosi képdiagnosztika 3. ea ősz
 MRI áttekintés Orvosi képdiagnosztika 3. ea. 2015 ősz MRI Alapelv: hogyan lehet mágneses vizsgálattal valamilyen anyag (jelen esetben az élő emberi szervezet) belső felépítéséről információt kapni? A mágneses
MRI áttekintés Orvosi képdiagnosztika 3. ea. 2015 ősz MRI Alapelv: hogyan lehet mágneses vizsgálattal valamilyen anyag (jelen esetben az élő emberi szervezet) belső felépítéséről információt kapni? A mágneses
Fizika II minimumkérdések. A zárójelben lévő értékeket nem kötelező memorizálni, azok csak tájékoztató jellegűek.
 izika II minimumkérdések zárójelben lévő értékeket nem kötelező memorizálni, azok csak tájékoztató jellegűek. 1. Coulomb erőtörvény: = kq r 2 e r (k = 9 10 9 m2 C 2 ) 2. Coulomb állandó és vákuum permittivitás
izika II minimumkérdések zárójelben lévő értékeket nem kötelező memorizálni, azok csak tájékoztató jellegűek. 1. Coulomb erőtörvény: = kq r 2 e r (k = 9 10 9 m2 C 2 ) 2. Coulomb állandó és vákuum permittivitás
Hegedüs Zsófia. Konformációsan diverz -redős szerkezetek utánzása -peptid foldamerek segítségével
 Szegedi Tudományegyetem Gyógyszertudományok Doktori Iskola Ph.D. program: Programvezető: Intézet: Témavezető: Gyógyszerkémia, gyógyszerkutatás Prof. Dr. Fülöp Ferenc Gyógyszeranalitikai Intézet Prof. Dr.
Szegedi Tudományegyetem Gyógyszertudományok Doktori Iskola Ph.D. program: Programvezető: Intézet: Témavezető: Gyógyszerkémia, gyógyszerkutatás Prof. Dr. Fülöp Ferenc Gyógyszeranalitikai Intézet Prof. Dr.
Fizikai kémia 2. ZH V. kérdések I. félévtől
 Fizikai kémia 2. ZH V. kérdések 2016-17 I. félévtől Szükséges adatok és állandók: k=1,38066 10-23 JK; c= 2,99792458 10 8 m/s; e= 1,602177 10-19 C; h=6,62608 10-34 Js; N A= 6,02214 10 23 mol -1 ; me= 9,10939
Fizikai kémia 2. ZH V. kérdések 2016-17 I. félévtől Szükséges adatok és állandók: k=1,38066 10-23 JK; c= 2,99792458 10 8 m/s; e= 1,602177 10-19 C; h=6,62608 10-34 Js; N A= 6,02214 10 23 mol -1 ; me= 9,10939
MateFIZIKA: Pörgés, forgás, csavarodás (Vektorok és axiálvektorok a fizikában)
 MateFIZIKA: Pörgés, forgás, csavarodás (Vektorok és axiálvektorok a fizikában) Tasnádi Tamás 1 2015. április 17. 1 BME, Mat. Int., Analízis Tsz. Tartalom Vektorok és axiálvektorok Forgómozgás, pörgettyűk
MateFIZIKA: Pörgés, forgás, csavarodás (Vektorok és axiálvektorok a fizikában) Tasnádi Tamás 1 2015. április 17. 1 BME, Mat. Int., Analízis Tsz. Tartalom Vektorok és axiálvektorok Forgómozgás, pörgettyűk
Az elméleti mechanika alapjai
 Az elméleti mechanika alapjai Tömegpont, a továbbiakban részecske. A jelenségeket a háromdimenziós térben és időben játszódnak le: r helyzetvektor v dr dt ṙ, a dr dt r a részecske sebessége illetve gyorsulása.
Az elméleti mechanika alapjai Tömegpont, a továbbiakban részecske. A jelenségeket a háromdimenziós térben és időben játszódnak le: r helyzetvektor v dr dt ṙ, a dr dt r a részecske sebessége illetve gyorsulása.
Gyors, multidimenzionális mérések adaptálása és tesztelése a p53 fehérje rendezetlen TAD régiójának esetében
 Tudományos Diákköri Dolgozat SEBÁK FANNI Gyors, multidimenzionális mérések adaptálása és tesztelése a p53 fehérje rendezetlen TAD régiójának esetében Témavezető: Dr. Bodor Andrea Analitikai Kémiai Tanszék
Tudományos Diákköri Dolgozat SEBÁK FANNI Gyors, multidimenzionális mérések adaptálása és tesztelése a p53 fehérje rendezetlen TAD régiójának esetében Témavezető: Dr. Bodor Andrea Analitikai Kémiai Tanszék
Vektorterek. =a gyakorlatokon megoldásra ajánlott
 Vektorterek =a gyakorlatokon megoldásra ajánlott 40. Alteret alkotnak-e a valós R 5 vektortérben a megadott részhalmazok? Ha igen, akkor hány dimenziósak? (a) L = { (x 1, x 2, x 3, x 4, x 5 ) x 1 = x 5,
Vektorterek =a gyakorlatokon megoldásra ajánlott 40. Alteret alkotnak-e a valós R 5 vektortérben a megadott részhalmazok? Ha igen, akkor hány dimenziósak? (a) L = { (x 1, x 2, x 3, x 4, x 5 ) x 1 = x 5,
Modern Fizika Labor. Fizika BSc. Értékelés: A mérés dátuma: A mérés száma és címe: 5. mérés: Elektronspin rezonancia. 2008. március 18.
 Modern Fizika Labor Fizika BSc A mérés dátuma: 28. március 18. A mérés száma és címe: 5. mérés: Elektronspin rezonancia Értékelés: A beadás dátuma: 28. március 26. A mérést végezte: 1/7 A mérés leírása:
Modern Fizika Labor Fizika BSc A mérés dátuma: 28. március 18. A mérés száma és címe: 5. mérés: Elektronspin rezonancia Értékelés: A beadás dátuma: 28. március 26. A mérést végezte: 1/7 A mérés leírása:
A fehérjék hierarchikus szerkezete
 Fehérjék felosztása A fehérjék hierarchikus szerkezete Smeller László Semmelweis Egyetem Biofizikai és Sugárbiológiai Intézet Biológiai funkció alapján Enzimek (pl.: tripszin, citokróm-c ) Transzportfehérjék
Fehérjék felosztása A fehérjék hierarchikus szerkezete Smeller László Semmelweis Egyetem Biofizikai és Sugárbiológiai Intézet Biológiai funkció alapján Enzimek (pl.: tripszin, citokróm-c ) Transzportfehérjék
Az aminosavak peptidek és fehérjék koronázatlan királyai, kémiai Nobel-díjak:
 Az aminosavak peptidek és fehérjék koronázatlan királyai, kémiai obel-díjak: Linus Pauling 1954 obel-díj fehérje szerkezet alapjai Frederick Sanger 1958 obel-díj Az inzulin szekvenálása Sir. John owdery
Az aminosavak peptidek és fehérjék koronázatlan királyai, kémiai obel-díjak: Linus Pauling 1954 obel-díj fehérje szerkezet alapjai Frederick Sanger 1958 obel-díj Az inzulin szekvenálása Sir. John owdery
 http://www.nature.com 1) Magerő-sugár: a magközéppontból mért távolság, ameddig a magerők hatótávolsága terjed. Rutherford-szórásból határozható meg. R=1,4 x 10-13 A 1/3 cm Az atommag terének potenciálja
http://www.nature.com 1) Magerő-sugár: a magközéppontból mért távolság, ameddig a magerők hatótávolsága terjed. Rutherford-szórásból határozható meg. R=1,4 x 10-13 A 1/3 cm Az atommag terének potenciálja
Gáspári Zoltán. Élő molekulák az élet molekulái
 Gáspári Zoltán Élő molekulák az élet molekulái Invokáció Kajtár Márton 1929-1991 www.eotvoskiado.hu Élő és élettelen? Élő és élettelen: a kemoton Élő kémiai rendszer, de nem élőlény (Gánti, 1975) Autokatalitikus
Gáspári Zoltán Élő molekulák az élet molekulái Invokáció Kajtár Márton 1929-1991 www.eotvoskiado.hu Élő és élettelen? Élő és élettelen: a kemoton Élő kémiai rendszer, de nem élőlény (Gánti, 1975) Autokatalitikus
Szerves spektroszkópia
 Szerves spektroszkópia ETR kód: kv1n1es5 Típus: kötelezően választható előadás (BSC, 5. félév) Heti óraszám: 2, Kreditérték: 2 Tantárgyfelelős: Vass Elemér Az előadás célkitűzése A szerves vegyületek szerkezetvizsgálatában
Szerves spektroszkópia ETR kód: kv1n1es5 Típus: kötelezően választható előadás (BSC, 5. félév) Heti óraszám: 2, Kreditérték: 2 Tantárgyfelelős: Vass Elemér Az előadás célkitűzése A szerves vegyületek szerkezetvizsgálatában
4.3. Az AcLysSerProValValGluGly heptapeptid Al(III)-kötő sajátságának jellemzése
 4.3. Az AcLysProValValGly heptapeptid Al(III)-kötő sajátságának jellemzése Az Al(III)fehérje kölcsönhatás megismerése céljából olyan neurofilamentum peptidfragmenst vizsgáltunk, mely az oldalláncban oxigén
4.3. Az AcLysProValValGly heptapeptid Al(III)-kötő sajátságának jellemzése Az Al(III)fehérje kölcsönhatás megismerése céljából olyan neurofilamentum peptidfragmenst vizsgáltunk, mely az oldalláncban oxigén
Mechanika I-II. Példatár
 Budapesti Műszaki és Gazdaságtudományi Egyetem Műszaki Mechanika Tanszék Mechanika I-II. Példatár 2012. május 24. Előszó A példatár célja, hogy támogassa a mechanika I. és mechanika II. tárgy oktatását
Budapesti Műszaki és Gazdaságtudományi Egyetem Műszaki Mechanika Tanszék Mechanika I-II. Példatár 2012. május 24. Előszó A példatár célja, hogy támogassa a mechanika I. és mechanika II. tárgy oktatását
Szilárdtestek el e ek e tr t o r n o s n zer e k r ez e et e e t
 Szilárdtestek elektronszerkezete Kvantummechanikai leírás Ismétlés: Schrödinger egyenlet, hullámfüggvény, hidrogén-atom, spin, Pauli-elv, periódusos rendszer 2 Szilárdtestek egyelektron-modellje a magok
Szilárdtestek elektronszerkezete Kvantummechanikai leírás Ismétlés: Schrödinger egyenlet, hullámfüggvény, hidrogén-atom, spin, Pauli-elv, periódusos rendszer 2 Szilárdtestek egyelektron-modellje a magok
Vektorok, mátrixok, tenzorok, T (emlékeztető)
 Vektorok, mátrixok, tenzorok, T (emlékeztető) A = T*B Tenzor: lineáris vektorfüggvény, amely két vektormennyiség közötti összefüggést ír le, egy négyzetmátrix, M reprezentálja. M M M M = M M M M M M 11
Vektorok, mátrixok, tenzorok, T (emlékeztető) A = T*B Tenzor: lineáris vektorfüggvény, amely két vektormennyiség közötti összefüggést ír le, egy négyzetmátrix, M reprezentálja. M M M M = M M M M M M 11
Hogyan bírhatjuk szóra a molekulákat, avagy mi is az a spektroszkópia?
 Hogyan bírhatjuk szóra a molekulákat, avagy mi is az a spektroszkópia? Prof. Túri László (ELTE, Kémiai Intézet) turi@chem.elte.hu 2012. november 19. Szent László Gimnázium Önképzőkör 1 Kapcsolódási pontok
Hogyan bírhatjuk szóra a molekulákat, avagy mi is az a spektroszkópia? Prof. Túri László (ELTE, Kémiai Intézet) turi@chem.elte.hu 2012. november 19. Szent László Gimnázium Önképzőkör 1 Kapcsolódási pontok
