Mechanikai alapismeretek I. (statika)
|
|
|
- Győző Nagy
- 3 évvel ezelőtt
- Látták:
Átírás
1 Mechanikai alapismeretek I. (statika) 2. előadás Síkbeli tartók egyensúlyozása, reakcióerők meghatározása, rácsos tartók számítása csomóponti módszerrel és a hármas átmetszés módszerével Szabó Imre Gábor Pécsi Tudományegyetem Műszaki és Informatikai Kar Építőmérnök Tanszék
2 1. Síkbeli tartószerkezetek, tartószerkezetek statikája 1.1 Síkbeli tartószerkezetek A teherhordásra szolgáló szerkezeteket tartóknak, a megtámasztásukra vagy helyzetük rögzítésére szolgáló berendezéseket támaszoknak (kényszereknek) nevezzük. Amennyiben az erők a tartó síkjában hatnak, akkor síkbeli tartónak, egyébként térbeli tartónak nevezzük. A tartók túlnyomó többsége olyan tömör test, amelynek a hosszirányú méreteihez viszonyítva a keresztirányú méretei kicsinyek. Az ilyen tartót rúdnak, a legkisebb síkmetszeteit keresztmetszetnek, a keresztmetszetek súlypontjait összekötő egyenest pedig rúdtengelynek nevezzük. A rúdtengely lehet egyenes, tört vagy görbevonalú.
3 1.2 A tartók megtámasztási módjait statikai szempontból osztályozhatjuk Gördülő vagy csúszó alátámasztás Ebben az esetben a támaszerő (reakcióerő) helye és iránya meghatározott. A támaszerő iránya mindig merőleges az alátámasztás síkjára. Ez a megtámasztási mód csak egyetlen ismeretlent tartalmaz. 1. kép. Gördülő alátámasztás kialakítása [Szabó I. G. 2012] 1. ábra. Gördülő alátámasztás és statikai váza [Szabó I. G. 2012]
4 2. kép. Gördülő és csúszó alátámasztás kialakítása [Szabó I. G. 2012] 2. ábra. Csúszó alátámasztás és statikai váza [Szabó I. G. 2012]
5 1.2.2 Álló csuklós alátámasztás Ebben az esetben a támaszerő helye ismert, azonban a nagysága és iránya ismeretlen. Ez a megtámasztási mód két ismeretlent tartalmaz. 3. kép. Álló csuklós alátámasztás kialakítása [Szabó I. G. 2012] 3. ábra. Álló csuklós alátámasztás és statikai váza [Szabó I. G. 2012]
6 1.2.3 Befogott (konzolos) megtámasztás Ebben az esetben a reakciók megakadályozzák a befogott tartóvég elmozdulását és elfordulását egyaránt. A tartóvég elfordulását a befogásnál keletkező nyomaték akadályozza meg. Az elmozdulást két reakcióerő gátolja. Ez a megtámasztási mód három ismeretlent tartalmaz. Fontos, hogy most először beszélhetünk a nyomaték helyhez kötéséről. Az ilyen nyomatékot koncentrált nyomatéknak nevezzük. 4. kép. Befogott (konzolos) megtámasztás kialakítása [Szabó I. G. 2012] 4. ábra. Befogott (konzolos) megtámasztás és statikai váza [Szabó I. G. 2012]
7 1.2.4 Támasztórúd (kapcsolórúd) A támasztórúd egy mindkét végén csuklóval ellátott támasztószerkezet, melynek egyik vége a megtámasztott, másik vége pedig a megtámasztó testhez kapcsolódik. A támasztórúdban értelemszerűen csak tengelyirányú rúderők keletkezhetnek. 5. kép. Kapcsolórúd csuklójának egy lehetséges kialakítása [Szabó I. G. 2012] 5. ábra. Támasztórúd és statikai váza [Szabó I. G. 2012]
8 6. kép. Támasztórúd I. 7. kép. Támasztórúd II.
9 2. Tartószerkezetek statikai osztályozása A tartószerkezeteket statikai szempontból határozott és határozatlan szerkezetekre oszthatjuk. 2.1 Statikailag határozott tartók Statikailag határozottnak nevezünk egy tartószerkezetet akkor, ha az alátámasztások (ismeretlen reakciók) száma nem több mint három. A már korábban említett három alapegyenlet segítségével az összes ismeretlen kifejezhető. M A i 0; F ix 0; F iy 0 6. ábra. Statikailag határozott szerkezetek [Szabó I. G. 2012] Ha a támaszerőt háromnál kevesebb számadat jellemzi, a támaszok nem biztosítják, hogy a tartó tetszőleges teher esetén helyben maradjon. Ekkor a tartó a helyéről képes elmozdulni, mozgatható, azaz labilis.
10 Egyensúly csak abban az esetben van, ha a tartóra ható terhek eredője függőleges. 7. ábra. Labilis tartószerkezet [Szabó I. G. 2012] 2.2 Statikailag határozatlan tartók Statikailag határozatlannak nevezünk egy tartószerkezetet akkor, ha a támaszok együttvéve háromnál több ismeretlent tartalmaznak. Ekkor már a három alapegyenlet segítségével nem oldható meg a feladat, szükséges további új, úgynevezett alakváltozási egyenletek bevezetése. 8. ábra. Statikailag határozatlan szerkezetek [Szabó I. G. 2012]
11 3. Külső erők A tartószerkezetekre ható terheket, valamint az ezek hatására az alátámasztásoknál fellépő támaszerőket (reakcióerőket) együttesen külső erőknek nevezzük. 3.1 Összpontosított (koncentrált) erő A terhelő erők a tartó valamely kisebb felület részére, mondhatni egy pontjára fejtik ki hatásukat. Jelölésük azonos az eddigi erők jelölésével. 3.2 Megoszló erők A tartószerkezetekre ható megoszló erők, vagy terhelések a gyakorlatban igen gyakoriak. Ilyen megoszló terhelés például az adott tartószerkezet önsúlya is. A megoszló terhelések mint ahogy a név is mutatja megosztják terhüket valamely nagyobb felületen vagy vonal mentén, attól függően, hogy térben vagy síkban helyezkednek el. A megoszló terhelés nagysága a tartó hosszában lehet állandó, egyenletesen megoszló vagy változó. A síkbeli megoszló erőket a rúd tengelyvonalára rajzolt diagrammal ábrázoljuk.
12 A megoszló erők nagyságát a tartó hossztengelyére általában egy egységre, például 1 méterre vonatkozó erőértékkel az úgynevezett fajlagos erőértékkel jellemezzük pl.: q = 10 kn/m. A számítások könnyítése céljából a megoszló erőket eredőjükkel helyettesíthetjük. 9. ábra. Megoszló terhelés ábrázolása és helyettesítése eredőjével [Szabó I. G. 2012] A megoszló terhelés eredőjét nagy Q val jelöljük. Az eredő nagysága a terhelési diagram területével egyenlő, hatásvonala pedig a diagram súlypontján megy át. Kiszámítása: egyenletesen megoszló teher esetén: Q q l változó nagyságú teher esetén: Q q l 2
13 4. Síkbeli rácsos tartó 4.1 Síkbeli rácsos tartó fogalma Rácsos tartóknak nevezzük azokat az összetett szerkezeteket, amelyeknek elemeit: egymáshoz csakis a két végén elhelyezett csuklók, a földhöz csuklók és/vagy görgők, támasztó rudak kapcsolják. A rácsos tartók tehát csuklókból (csomópontokból) és belső rudakból állnak. A terheket mindig a csomópontokban működtetjük. Amennyiben a rácsrúdon működik a teher, akkor azt is redukáljuk valamely csomópontra. 4.2 Statikai határozottság Amennyiben a rácsos tartóra csak a csomópontokban hat erő, akkor a rudakban csak két erő hathat, emiatt nem kell őket testnek kezelni (síkban vannak), ezért csupán a rudakat összekötő csomópontokra kell egyensúlyi feltételeket felírni. A csomópontokra közös metszéspontú erőrendszer hat, tehát csomópontonként két egymástól független egyenlet írható fel.
14 A statikai határozottság szükséges (de nem elégséges) feltétele: A független egyenletek száma: e 2c Ismeretlenek: a reakcióerők és a rúderők, melyek skaláris adattal adhatók meg: i k r független egyenletek száma = ismeretlenek száma azaz e = i 2c k r ahol: c a csuklók száma; r a rudak száma; k a külső kényszerek fokszáma. A statikai határozatlanság elégséges (de nem szükséges) feltétele: Egyenletek és ismeretlenek számának ismerete alapján: 2c k r
15 4.3 Síkbeli rácsos tartók kialakítása A rudak elhelyezkedésük alapján speciális neveket is kaphatnak: ha egy függőleges rúd több rudat is keresztez, akkor ezek közül a legfelsőt felső övrúdnak, a legalsó alsó övrúdnak nevezzük, a közbenső ferde rudak a rácsrudak, a függőleges rudak az oszlopok, vagy összekötő rudak. 10. ábra. Síkbeli rácsos tartó kialakítása [Szabó I. G. 2012] 4.4 Síkbeli rácsos tartók hálózati megoldásai Az alkalmazandó hálózat megválasztása egyrészről a megoldandó feladat, másrészről pedig a használandó anyag és technológia függvényében történhet. Lentebb a legjellemzőbb hálózati megoldások képe, vázlatos ábrája és megnevezése látható.
16 8. kép-11. ábra. Szimmetrikus rácsozás [Szabó I. G. 2012] 9. kép-12. ábra. Szimmetrikus rácsozás oszlopokkal [Szabó I. G. 2012] 10. kép-13. ábra. Oszlopos rácsozás [Szabó I. G. 2012]
17 11. kép-14. ábra. Szimmetrikus rácsozás másodlagos elemekkel [Szabó I. G. 2012] 12. kép-15. ábra. K rácsozás [Szabó I. G. 2012] 13. kép-16. ábra. X rácsozás [Szabó I. G. 2012]
18 4.5 Síkbeli rácsos tartók alakja Az alak megválasztásával kis mértékben befolyásolni lehet a belső erők, elsősorban az övrúderők nagyságát. Az alakot természetesen az alátámasztó szerkezet funkcionális követelményei és esztétikai szempontok határozzák meg. (Például csarnokszerkezetek esetében a rácsos főtartók felső övének dőlésével állítják be a tető hajlásszögét.) Alább láthatóak a leggyakrabban alkalmazott rácsos tartó alakok: 17. ábra. Párhuzamos övű rácsos tartó [Szabó I. G. 2012] 18. ábra. Kiékelt felső övű rácsos tartó [Szabó I. G. 2012] 19. ábra. Háromszög alakú rácsos tartó [Szabó I. G. 2012] 20. ábra. Szegmens alakú rácsos tartó [Szabó I. G. 2012]
19 21. ábra. Csonka (sarló) alakú rácsos tartó [Szabó I. G. 2012] 22. ábra. Lencse alakú rácsos tartó [Szabó I. G. 2012] 4.6 Statikailag határozott rácsos tartók rúderőinek meghatározása Minden esetben a rácsos tartót, mint kéttámaszú, tömör tartót kell kezelni, azaz a reakcióerők számítása az eddig megismert módon történik a nyomatéki egyenlet és a vetületi egyenletek felhasználásával. A rúderők pozitív (+) és negatív ( ) előjeleket kaphatnak. A rúderő pozitív, ha húzza a csomópontot, negatív, ha nyomja a csomópontot. Fontos, hogy a húzás és nyomás nem a rúdtengelyre van vonatkoztatva, hanem egy adott csomópontra. Azt a rudat, amelyikben nem ébred erő, vakrúdnak nevezzük.
20 Egy rúdban csak akkor keletkezik rúderő, ha a rúd mindkét végén terhelve van. A rúderő kiegyensúlyozza a rácsos tartó csomópontjait, oly módon, hogy a rúd mindkét végén ugyanolyan nagyságú, de ellenkező irányú erő működik, azaz mindkét egymás melletti csomópontot húzza, vagy nyomja a rúderő. 23. ábra. Húzó és nyomó rúderők iránya és előjele [Szabó I. G. 2012] Gyakori hiba a rúderők előjelének, illetve irányának tévesztése. A helyes előjelet a megváltozott tartóalakból viszonylag egyszerűen ki lehet következtetni. A következő ábrán egy, csak függőleges irányban lefelé ható erőkkel terhelt szimmetrikus rácsos tartó látható. Az erők hatására a görgős támasz igyekszik elmozdulni, illetve a tartó lehajlik, ezért az alsó övben húzás, a felső övben nyomás keletkezik.
21 Az alsó öv átvágott rúdja két végén lévő csomópont távolodik egymástól, tehát a rúdban húzóerő keletkezik, a rúd próbál megnyúlni, szélsőséges esetben el is szakadhat. A felső öv átvágott rúdja két végén lévő csomópont közeledik egymás felé, minek következtében a rúdban nyomóerő keletkezik, a rúd próbál összenyomódni, szélsőséges esetben kihajlás keletkezhet benne. 24. ábra. Húzó és nyomó rúderők iránya és előjele [Szabó I. G. 2012]
22 4.7 A rúderők meghatározására két módszer van 1. Csomóponti módszer A csomóponti módszer alkalmazása során minden egyes csukló (csomópont) közös metszéspontú síkbeli erőrendszernek tekintendő. Csak akkor alkalmazható, ha a csomópontban egy vagy két ismeretlen van. A két már korábban megismert vetületi egyenlet alkalmazásával az ismeretlenek meghatározhatók. A csomóponti módszer alkalmazása során a rácsos tartó minden egyes csomópontján lépésről lépésre végig kell haladni. Csak abból a csomópontból lehet kiindulni, ahol az ismeretlenek száma nem több kettőnél. E módszer alkalmazása hosszadalmas, bonyolultabb szerkezetek esetén, amennyiben nincs szükség minden rúderő nagyságának ismeretére alkalmazása nem ajánlott.
23 2. Hármas átmetszés módszer Abban az esetben célszerű alkalmazni, ha nincs szükségünk minden rúderő ismeretére. Hármas átmetszés során kettévágjuk a tartót, s a két különálló részt külön kezeljük. A továbbiakban elegendő csak az egyik résszel foglalkozni, célszerű azzal, amelyik a kisebb, illetve kevesebb külső erőt tartalmaz. Ilyenkor mindkét részre és az egészre is teljesülnie kell a Mi 0; Fix 0; Fiy 0 egyenleteknek. A három átvágott rúderőt általában egy három ismeretlenes egyenletrendszerből tudjuk meghatározni. A három átvágott rúd nem lehet közös metszéspontú (sem a közeli, sem a végtelen távolságban: azaz nem lehetnek párhuzamosak). A három ismeretlenes egyenletrendszer három darab egy egy ismeretlent tartalmazó egyenlet formájában is felírható. Mindegyik rúdhoz meg kell keresni a főpontját (a másik két rúd metszéspontját). Ha a hármas átmetszés két rúdja párhuzamos, metszéspontjuk a végtelenben van, erre a végtelenben lévő pontra felírt nyomatéki egyenlet a rudak irányára merőleges vetületi egyenletté alakul át.
24 25. ábra. Hármas átmetszés módszere [Szabó I. G. 2012]
25 Felhasznált irodalom SIPTÁR TIBOR, MARSAY ISTVÁN: Mechanika módszertani útmutató és példatár. Pollack Mihály Műszaki Főiskola Építőipari Kar, Pécs, SZABÓ IMRE GÁBOR: Mechanika I. (statika). Példatár és módszertani útmutató. Pécs, 2012.
6. MECHANIKA-STATIKA GYAKORLAT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya, Culmann-szerkesztés, Ritter-számítás
 ZÉHENYI ITVÁN EGYETE GÉPZERKEZETTN É EHNIK TNZÉK 6. EHNIK-TTIK GYKORLT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa Egy létrát egy verembe letámasztunk
ZÉHENYI ITVÁN EGYETE GÉPZERKEZETTN É EHNIK TNZÉK 6. EHNIK-TTIK GYKORLT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa Egy létrát egy verembe letámasztunk
A síkbeli Statika egyensúlyi egyenleteiről
 1 A síkbeli Statika egyensúlyi egyenleteiről Statikai tanulmányaink egyik mérföldköve az egyensúlyi egyenletek belátása és sikeres alkalmazása. Most egy erre vonatkozó lehetséges tanulási / tanítási útvonalat
1 A síkbeli Statika egyensúlyi egyenleteiről Statikai tanulmányaink egyik mérföldköve az egyensúlyi egyenletek belátása és sikeres alkalmazása. Most egy erre vonatkozó lehetséges tanulási / tanítási útvonalat
DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK. Acélszerkezetek II. IV. Előadás
 DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II IV. Előadás Rácsos tartók szerkezeti formái, kialakítása, tönkremeneteli módjai. - Rácsos tartók jellemzói - Méretezési kérdések
DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II IV. Előadás Rácsos tartók szerkezeti formái, kialakítása, tönkremeneteli módjai. - Rácsos tartók jellemzói - Méretezési kérdések
A K É T V É G É N A L Á T Á M A S Z T O T T T A R T Ó S T A T I K A I V IZS-
 A K É T V É G É N A L Á T Á M A S Z T O T T T A R T Ó S T A T I K A I V IZS- Forgatónyomaték meghatározása G Á L A T A Egy erő forgatónyomatékkal hat egy pontra, ha az az erővel össze van kötve. Például
A K É T V É G É N A L Á T Á M A S Z T O T T T A R T Ó S T A T I K A I V IZS- Forgatónyomaték meghatározása G Á L A T A Egy erő forgatónyomatékkal hat egy pontra, ha az az erővel össze van kötve. Például
6. MECHANIKA-STATIKA GYAKORLAT (kidolgozta: Triesz Péter, egy. ts.; Tarnai Gábor, mérnöktanár)
 SZÉHNYI ISTVÁN GYT LKLZOTT HNIK TNSZÉK 6. HNIK-STTIK GYKORLT (kidolgozta: Triesz Péter egy. ts.; Tarnai Gábor mérnöktanár) Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa gy létrát egy
SZÉHNYI ISTVÁN GYT LKLZOTT HNIK TNSZÉK 6. HNIK-STTIK GYKORLT (kidolgozta: Triesz Péter egy. ts.; Tarnai Gábor mérnöktanár) Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa gy létrát egy
Rácsos szerkezetek. Frissítve: Egy kis elmélet: vakrudak
 Egy kis elmélet: vakrudak Az egyik lehetőség, ha két rúd szög alatt találkozik (nem egyvonalban vannak), és nem működik a csomópontra terhelés. Ilyen az 1.ábra C csomópontja. Ekkor az ide befutó mindkét
Egy kis elmélet: vakrudak Az egyik lehetőség, ha két rúd szög alatt találkozik (nem egyvonalban vannak), és nem működik a csomópontra terhelés. Ilyen az 1.ábra C csomópontja. Ekkor az ide befutó mindkét
Mozgatható térlefedő szerkezetek
 Mozgatható térlefedő szerkezetek TDK Konferencia 2010 Szilárdságtani és tartószerkezeti szekció Tartalomjegyzék 1 Absztrakt 2 Bevezetés 3 Az alakzat mozgásának görbületre gyakorolt hatása 4 Teljes összenyomódás
Mozgatható térlefedő szerkezetek TDK Konferencia 2010 Szilárdságtani és tartószerkezeti szekció Tartalomjegyzék 1 Absztrakt 2 Bevezetés 3 Az alakzat mozgásának görbületre gyakorolt hatása 4 Teljes összenyomódás
Gyakorlati útmutató a Tartók statikája I. tárgyhoz. Fekete Ferenc. 5. gyakorlat. Széchenyi István Egyetem, 2015.
 Gyakorlati útmutató a tárgyhoz Fekete Ferenc 5. gyakorlat Széchenyi István Egyetem, 015. 1. ásodrendű hatások közelítő számítása A következőkben egy, a statikai vizsgálatoknál másodrendű hatások közelítő
Gyakorlati útmutató a tárgyhoz Fekete Ferenc 5. gyakorlat Széchenyi István Egyetem, 015. 1. ásodrendű hatások közelítő számítása A következőkben egy, a statikai vizsgálatoknál másodrendű hatások közelítő
 MECHANIKA I. /Statika/ 1. előadás SZIE-YMM 1. Bevezetés épületek, építmények fizikai hatások, köztük erőhatások részleges vagy teljes tönkremenetel használhatatlanná válás anyagi kár, emberáldozat 1 Cél:
MECHANIKA I. /Statika/ 1. előadás SZIE-YMM 1. Bevezetés épületek, építmények fizikai hatások, köztük erőhatások részleges vagy teljes tönkremenetel használhatatlanná válás anyagi kár, emberáldozat 1 Cél:
Csuklós szerkezetek reakciói és igénybevételi ábrái. Frissítve: példa: A 12. gyakorlat 1. feladata.
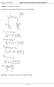 1. példa: A 12. gyakorlat 1. feladata. Számítsuk ki a reakcióerőket! Rajzoljuk meg a nyomatéki ábrát! Megjegyzés: A támaszok vízszintesen egy vonalban vannak. 1 / 20 2. példa: Számítsuk ki a reakcióerőket!
1. példa: A 12. gyakorlat 1. feladata. Számítsuk ki a reakcióerőket! Rajzoljuk meg a nyomatéki ábrát! Megjegyzés: A támaszok vízszintesen egy vonalban vannak. 1 / 20 2. példa: Számítsuk ki a reakcióerőket!
TARTÓ(SZERKEZETE)K. 05. Méretezéselméleti kérdések TERVEZÉSE II. Dr. Szép János Egyetemi docens
 TARTÓ(SZERKEZETE)K TERVEZÉSE II. 05. Méretezéselméleti kérdések Dr. Szép János Egyetemi docens 2018. 10. 15. Az előadás tartalma Az igénybevételek jellege A támaszköz szerepe Igénybevételek változása A
TARTÓ(SZERKEZETE)K TERVEZÉSE II. 05. Méretezéselméleti kérdések Dr. Szép János Egyetemi docens 2018. 10. 15. Az előadás tartalma Az igénybevételek jellege A támaszköz szerepe Igénybevételek változása A
TANTÁRGYFELELŐS INTÉZET: Építőmérnöki Intézet. OKTATÓ, ELŐADÓ címe: fogadóórája a szorgalmi időszakban:
 Mechanika 1 Mechanika I. (Statika) Mechanika I. (Statika) Neptun kódja: SGYMMET2001XA Neptun kódja: SGYMMET201XXX Tantárgy neve angolul: Mechanics 1 Építészmérnöki szak, Építőmérnöki szak Nappali tagozat
Mechanika 1 Mechanika I. (Statika) Mechanika I. (Statika) Neptun kódja: SGYMMET2001XA Neptun kódja: SGYMMET201XXX Tantárgy neve angolul: Mechanics 1 Építészmérnöki szak, Építőmérnöki szak Nappali tagozat
KERESZTMETSZETI JELLEMZŐK
 web-lap : www.hild.gor.hu DEME FERENC okl. építőmérnök, mérnöktanár e-mail : deme.ferenc1@gmail.com STATIKA 50. KERESZTMETSZETI JELLEMZŐK A TARTÓK MÉRETEZÉSE SORÁN SZÁMOS ESETBEN SZÜKSÉGÜNK VAN OLYAN ADATOKRA,
web-lap : www.hild.gor.hu DEME FERENC okl. építőmérnök, mérnöktanár e-mail : deme.ferenc1@gmail.com STATIKA 50. KERESZTMETSZETI JELLEMZŐK A TARTÓK MÉRETEZÉSE SORÁN SZÁMOS ESETBEN SZÜKSÉGÜNK VAN OLYAN ADATOKRA,
TANTÁRGYFELELŐS INTÉZET: Építőmérnöki Intézet OKTATÓK, ELŐADÓK címe: fogadóórája a szorgalmi időszakban:
 Mechanika 1 Mechanika I. (Statika) Mechanika I. (Statika) Neptun kódja: SGYMMET2001XA Neptun kódja: SGYMMET201XXX Tantárgy neve angolul: Mechanics 1 Építészmérnöki szak, Építőmérnöki szak Nappali tagozat
Mechanika 1 Mechanika I. (Statika) Mechanika I. (Statika) Neptun kódja: SGYMMET2001XA Neptun kódja: SGYMMET201XXX Tantárgy neve angolul: Mechanics 1 Építészmérnöki szak, Építőmérnöki szak Nappali tagozat
A= a keresztmetszeti felület cm 2 ɣ = biztonsági tényező
 Statika méretezés Húzás nyomás: Amennyiben a keresztmetszetre húzó-, vagy nyomóerő hat, akkor normálfeszültség (húzó-, vagy nyomó feszültség) keletkezik. Jele: σ. A feszültség: = ɣ Fajlagos alakváltozás:
Statika méretezés Húzás nyomás: Amennyiben a keresztmetszetre húzó-, vagy nyomóerő hat, akkor normálfeszültség (húzó-, vagy nyomó feszültség) keletkezik. Jele: σ. A feszültség: = ɣ Fajlagos alakváltozás:
TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ STATIKA
 TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ STATIKA GEMET001-B Miskolci Egyetem Gépészmérnöki és Informatikai Kar Műszaki Mechanikai Intézet MM/37/2018. Miskolc, 2018. február 5. HIRDETMÉNY Statika(GEMET201NB és GEMET001-B)
TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ STATIKA GEMET001-B Miskolci Egyetem Gépészmérnöki és Informatikai Kar Műszaki Mechanikai Intézet MM/37/2018. Miskolc, 2018. február 5. HIRDETMÉNY Statika(GEMET201NB és GEMET001-B)
A ferde tartó megoszló terheléseiről
 A ferde tartó megoszló terheléseiről Úgy vettem észre az idők során, hogy nem nagyon magyarázták agyon azt a kérdést, amivel itt fogunk foglalkozni. Biztos azt mondják majd megint, hogy De hisz ezt mindenki
A ferde tartó megoszló terheléseiről Úgy vettem észre az idők során, hogy nem nagyon magyarázták agyon azt a kérdést, amivel itt fogunk foglalkozni. Biztos azt mondják majd megint, hogy De hisz ezt mindenki
X i = 0 F x + B x = 0. Y i = 0 A y F y + B y = 0. M A = 0 F y 3 + B y 7 = 0. B x = 200 N. B y =
 1. feladat a = 3 m b = 4 m F = 400 N φ = 60 fok Első lépésként alkossuk meg a számítási modellt. A kényszereket helyettesítsük a bennük ébredő lehetséges erőkkel (második ábra). Az F erő felbontásával
1. feladat a = 3 m b = 4 m F = 400 N φ = 60 fok Első lépésként alkossuk meg a számítási modellt. A kényszereket helyettesítsük a bennük ébredő lehetséges erőkkel (második ábra). Az F erő felbontásával
Statika gyakorló teszt II.
 Statika gakorló teszt II. Készítette: Gönczi Dávid Témakörök: (I) Egszerű szerkezetek síkbeli statikai feladatai (II) Megoszló terhelésekkel kapcsolatos számítások (III) Összetett szerkezetek síkbeli statikai
Statika gakorló teszt II. Készítette: Gönczi Dávid Témakörök: (I) Egszerű szerkezetek síkbeli statikai feladatai (II) Megoszló terhelésekkel kapcsolatos számítások (III) Összetett szerkezetek síkbeli statikai
Gyakorlati útmutató a Tartók statikája I. tárgyhoz. Fekete Ferenc. 4. gyakorlat. Széchenyi István Egyetem,
 Gyakorlati útmutató a Tartók statikája I. tárgyhoz Fekete Ferenc 4. gyakorlat Széchenyi István Egyetem, 0..3. . Feladat Határozza meg a képen látható tartó A támaszra vonatkozó reakcióerő hatásábráját,
Gyakorlati útmutató a Tartók statikája I. tárgyhoz Fekete Ferenc 4. gyakorlat Széchenyi István Egyetem, 0..3. . Feladat Határozza meg a képen látható tartó A támaszra vonatkozó reakcióerő hatásábráját,
Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet
 Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet 2. előadás A rugalmas lemezelmélet alapfeltevései A lemez anyaga homogén, izotróp, lineárisan rugalmas (Hooke törvény); A terheletlen állapotban
Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet 2. előadás A rugalmas lemezelmélet alapfeltevései A lemez anyaga homogén, izotróp, lineárisan rugalmas (Hooke törvény); A terheletlen állapotban
Tipikus fa kapcsolatok
 Tipikus fa kapcsolatok Dr. Koris Kálmán, Dr. Bódi István BME Hidak és Szerkezetek Tanszék 1 Gerenda fal kapcsolatok Gerenda feltámaszkodás 1 Vízszintes és (lefelé vagy fölfelé irányuló) függőleges terhek
Tipikus fa kapcsolatok Dr. Koris Kálmán, Dr. Bódi István BME Hidak és Szerkezetek Tanszék 1 Gerenda fal kapcsolatok Gerenda feltámaszkodás 1 Vízszintes és (lefelé vagy fölfelé irányuló) függőleges terhek
Egymásra támaszkodó rudak
 1 Egymásra támaszkodó rudak Úgy látszik, ez is egy visszatérő téma. Egy korábbi írásunkban melynek címe: A mandala - tetőről már találkoztunk az 1. ábrán vázolthoz hasonló felülnézetű szerkezettel, foglalkoztunk
1 Egymásra támaszkodó rudak Úgy látszik, ez is egy visszatérő téma. Egy korábbi írásunkban melynek címe: A mandala - tetőről már találkoztunk az 1. ábrán vázolthoz hasonló felülnézetű szerkezettel, foglalkoztunk
UTÓFESZÍTETT SZERKEZETEK TERVEZÉSI MÓDSZEREI
 UTÓFESZÍTETT SZERKEZETEK TERVEZÉSI MÓDSZEREI DR. FARKAS GYÖRGY Professor emeritus BME Hidak és Szerkezetek Tanszék MMK Tartószerkezeti Tagozat Szakmai továbbképzés 2017 október 2. KÁBELVEZETÉS EGYENES
UTÓFESZÍTETT SZERKEZETEK TERVEZÉSI MÓDSZEREI DR. FARKAS GYÖRGY Professor emeritus BME Hidak és Szerkezetek Tanszék MMK Tartószerkezeti Tagozat Szakmai továbbképzés 2017 október 2. KÁBELVEZETÉS EGYENES
A végeselem módszer alapjai. 2. Alapvető elemtípusok
 A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
Kiegészítés a három erő egyensúlyához
 1 Kiegészítés a három erő egyensúlyához Egy régebbi dolgozatunkban melynek jele és címe : RD: Három erő egyensúlya ~ kéttámaszú tartó már sok mindent elmondtunk a címbeli témáról. Ez ugyanis egy megkerülhetetlen
1 Kiegészítés a három erő egyensúlyához Egy régebbi dolgozatunkban melynek jele és címe : RD: Három erő egyensúlya ~ kéttámaszú tartó már sok mindent elmondtunk a címbeli témáról. Ez ugyanis egy megkerülhetetlen
DEME FERENC okl. építőmérnök, mérnöktanár
 DEME FERENC okl. építőmérnök, mérnöktanár web-lap : www.sze.hu/~deme e-mail : deme.ferenc1@gmail.com HÁROMCSUKLÓS TARTÓ KÜLSŐ ÉS BELSŐ REAKCIÓ ERŐINEK SZÁMÍTÁSA, A TARTÓ IGÉNYBEVÉTELI ÁBRÁINAK RAJZOLÁSA
DEME FERENC okl. építőmérnök, mérnöktanár web-lap : www.sze.hu/~deme e-mail : deme.ferenc1@gmail.com HÁROMCSUKLÓS TARTÓ KÜLSŐ ÉS BELSŐ REAKCIÓ ERŐINEK SZÁMÍTÁSA, A TARTÓ IGÉNYBEVÉTELI ÁBRÁINAK RAJZOLÁSA
X = 0 B x = 0. M B = A y 6 = 0. B x = 0 A y = 1000 B y = 400
 1. feladat Számítsuk ki a bejelölt rúderőket! Az erők N-ban, a hosszak m-ben, a nyomatékok Nm-ben értendők Első lépésként határozzuk meg a kényszererőket. Az S 1 rúderő számítása: Egyensúlyi egyenletek:
1. feladat Számítsuk ki a bejelölt rúderőket! Az erők N-ban, a hosszak m-ben, a nyomatékok Nm-ben értendők Első lépésként határozzuk meg a kényszererőket. Az S 1 rúderő számítása: Egyensúlyi egyenletek:
DEME FERENC okl. építőmérnök, mérnöktanár TARTÓK
 web-lap : www.hild.gyor.hu DEME FERENC okl. építőmérnök, mérnöktanár e-mail : deme.ferenc1@gmail.com STATIKA 19. TARTÓK FOGALMA: TARTÓK A tartók terhek biztonságos hordására és azoknak a támaszokra történő
web-lap : www.hild.gyor.hu DEME FERENC okl. építőmérnök, mérnöktanár e-mail : deme.ferenc1@gmail.com STATIKA 19. TARTÓK FOGALMA: TARTÓK A tartók terhek biztonságos hordására és azoknak a támaszokra történő
TARTÓSZERKEZETEK II. VASBETONSZERKEZETEK
 TARTÓSZERKEZETEK II. VASBETONSZERKEZETEK 2010.04.09. VASBETON ÉPÜLETEK MEREVÍTÉSE Az épületeink vízszintes terhekkel szembeni ellenállását merevítéssel biztosítjuk. A merevítés lehetséges módjai: vasbeton
TARTÓSZERKEZETEK II. VASBETONSZERKEZETEK 2010.04.09. VASBETON ÉPÜLETEK MEREVÍTÉSE Az épületeink vízszintes terhekkel szembeni ellenállását merevítéssel biztosítjuk. A merevítés lehetséges módjai: vasbeton
Felső végükön egymásra támaszkodó szarugerendák egyensúlya
 1 Felső végükön egymásra támaszkodó szarugerendák egyensúlya Az [ 1 ] példatárban találtunk egy érdekes feladatot, melynek egy változatát vizsgáljuk meg itt. A feladat Ehhez tekintsük az 1. ábrát! 1. ábra
1 Felső végükön egymásra támaszkodó szarugerendák egyensúlya Az [ 1 ] példatárban találtunk egy érdekes feladatot, melynek egy változatát vizsgáljuk meg itt. A feladat Ehhez tekintsük az 1. ábrát! 1. ábra
Leggyakoribb fa rácsos tartó kialakítások
 Fa rácsostartók vizsgálata 1. Dr. Koris Kálmán, Dr. Bódi István BME Hidak és Szerkezetek Tanszék Leggakoribb fa rácsos tartó kialakítások Változó magasságú Állandó magasságú Kis mértékben változó magasságú
Fa rácsostartók vizsgálata 1. Dr. Koris Kálmán, Dr. Bódi István BME Hidak és Szerkezetek Tanszék Leggakoribb fa rácsos tartó kialakítások Változó magasságú Állandó magasságú Kis mértékben változó magasságú
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
Teherfelvétel. Húzott rudak számítása. 2. gyakorlat
 Teherfelvétel. Húzott rudak számítása 2. gyakorlat Az Eurocode 1. részei: (Terhek és hatások) Sűrűségek, önsúly és az épületek hasznos terhei (MSZ EN 1991-1-1) Tűznek kitett tartószerkezeteket érő hatások
Teherfelvétel. Húzott rudak számítása 2. gyakorlat Az Eurocode 1. részei: (Terhek és hatások) Sűrűségek, önsúly és az épületek hasznos terhei (MSZ EN 1991-1-1) Tűznek kitett tartószerkezeteket érő hatások
BME Gépészmérnöki Kar 3. vizsga (112A) Név: 1 Műszaki Mechanikai Tanszék január 11. Neptun: 2 Szilárdságtan Aláírás: 3
 BME Gépészmérnöki Kar 3. vizsga (2A) Név: Műszaki Mechanikai Tanszék 2. január. Neptun: 2 Szilárdságtan Aláírás: 3. feladat (2 pont) A vázolt befogott tartót a p intenzitású megoszló erőrendszer, az F
BME Gépészmérnöki Kar 3. vizsga (2A) Név: Műszaki Mechanikai Tanszék 2. január. Neptun: 2 Szilárdságtan Aláírás: 3. feladat (2 pont) A vázolt befogott tartót a p intenzitású megoszló erőrendszer, az F
Statika gyakorló teszt I.
 Statika gakorló teszt I. Készítette: Gönczi Dávid Témakörök: (I) közös ponton támadó erőrendszerek síkbeli és térbeli feladatai (1.1-1.6) (II) merev testre ható síkbeli és térbeli erőrendszerek (1.7-1.13)
Statika gakorló teszt I. Készítette: Gönczi Dávid Témakörök: (I) közös ponton támadó erőrendszerek síkbeli és térbeli feladatai (1.1-1.6) (II) merev testre ható síkbeli és térbeli erőrendszerek (1.7-1.13)
GÉPÉSZETI ALAPISMERETEK
 Gépészeti alapismeretek emelt szint 1511 ÉRETTSÉGI VIZSGA 2016. május 18. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fontos
Gépészeti alapismeretek emelt szint 1511 ÉRETTSÉGI VIZSGA 2016. május 18. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fontos
Tető - feladat. Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot és végeredményeit ld. 1. ábra.
![Tető - feladat. Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot és végeredményeit ld. 1. ábra. Tető - feladat. Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot és végeredményeit ld. 1. ábra.](/thumbs/95/123788187.jpg) 1 Tető - feladat Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot és végeredményeit ld. 1. ábra. 1. ábra forrása: [ 1 ] Most ezt oldjuk meg, részletesen. A feladat szövegének ( saját, hevenyészett
1 Tető - feladat Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot és végeredményeit ld. 1. ábra. 1. ábra forrása: [ 1 ] Most ezt oldjuk meg, részletesen. A feladat szövegének ( saját, hevenyészett
ÁGAZATI SZAKMAI ÉRETTSÉGI VIZSGA GÉPÉSZET ISMERETEK EMELT SZINTŰ SZÓBELI VIZSGA MINTAFELADATOK ÉS ÉRTÉKELÉSÜK
 GÉPÉSZET ISMERETEK EMELT SZINTŰ SZÓBELI VIZSGA MINTAFELADATOK ÉS ÉRTÉKELÉSÜK 1. tétel A. Ismertesse az anyagok tűzveszélyességi, valamint az építmények kockázati osztályba sorolását! B. Ismertesse a szerelési
GÉPÉSZET ISMERETEK EMELT SZINTŰ SZÓBELI VIZSGA MINTAFELADATOK ÉS ÉRTÉKELÉSÜK 1. tétel A. Ismertesse az anyagok tűzveszélyességi, valamint az építmények kockázati osztályba sorolását! B. Ismertesse a szerelési
GÉPÉSZETI ALAPISMERETEK TÉMAKÖRÖK
 GÉPÉSZETI ALAPISMERETEK KÖZÉPSZINTŰ ÉRETTSÉGI TÉMAKÖRÖK Preisz Csaba mérnök-tanár Műszaki mechanika Statikai alapfogalmak - Erőrendszer fogalma - Vektorokkal végezhető alapműveleteket (erők felbontása,
GÉPÉSZETI ALAPISMERETEK KÖZÉPSZINTŰ ÉRETTSÉGI TÉMAKÖRÖK Preisz Csaba mérnök-tanár Műszaki mechanika Statikai alapfogalmak - Erőrendszer fogalma - Vektorokkal végezhető alapműveleteket (erők felbontása,
11. MECHANIKA-STATIKA GYAKORLAT (kidolgozta: Triesz Péter, egy. ts.; Tarnai Gábor, mérnöktanár)
 SZÉHENYI ISTVÁN EGYETEM LKLMZOTT MEHNIK TNSZÉK.. Példa:. MEHNIK-STTIK GYKORLT (kidolgozta: Triesz Péter, eg. ts.; Tarnai Gábor, mérnöktanár) Összetett szerkezetek statikája (három csuklós ív, Gerber tartó)
SZÉHENYI ISTVÁN EGYETEM LKLMZOTT MEHNIK TNSZÉK.. Példa:. MEHNIK-STTIK GYKORLT (kidolgozta: Triesz Péter, eg. ts.; Tarnai Gábor, mérnöktanár) Összetett szerkezetek statikája (három csuklós ív, Gerber tartó)
Függőleges koncentrált erőkkel csuklóin terhelt csuklós rúdlánc számításához
 1 Függőleges koncentrált erőkkel csuklóin terhelt csuklós rúdlánc számításához Az interneten való nézelődés során találkoztunk az [ 1 ] művel, melyben egy érdekes és fontos feladat pontos(abb) megoldásához
1 Függőleges koncentrált erőkkel csuklóin terhelt csuklós rúdlánc számításához Az interneten való nézelődés során találkoztunk az [ 1 ] művel, melyben egy érdekes és fontos feladat pontos(abb) megoldásához
Egy háromlábú állvány feladata. 1. ábra forrása:
 1 Egy háromlábú állvány feladata Az interneten találtuk az alábbi versenyfeladatot 1. ábra Az egyforma hosszúságú CA, CB és CD rudak a C pontban gömbcsuklóval kapcsolódnak, az A, B, D végükön sima vízszintes
1 Egy háromlábú állvány feladata Az interneten találtuk az alábbi versenyfeladatot 1. ábra Az egyforma hosszúságú CA, CB és CD rudak a C pontban gömbcsuklóval kapcsolódnak, az A, B, D végükön sima vízszintes
Mechanika. II. előadás március 4. Mechanika II. előadás március 4. 1 / 31
 Mechanika II. előadás 219. március 4. Mechanika II. előadás 219. március 4. 1 / 31 4. Merev test megtámasztásai, statikai feladatok megtámasztás: testek érintkezése útján jön létre, az érintkezés során
Mechanika II. előadás 219. március 4. Mechanika II. előadás 219. március 4. 1 / 31 4. Merev test megtámasztásai, statikai feladatok megtámasztás: testek érintkezése útján jön létre, az érintkezés során
Navier-formula. Frissítve: Egyenes hajlítás
 Navier-formula Akkor beszélünk egyenes hajlításról, ha a nyomatékvektor egybeesik valamelyik fő-másodrendű nyomatéki tengellyel. A hajlítást mindig súlyponti koordinátarendszerben értelmezzük. Ez még a
Navier-formula Akkor beszélünk egyenes hajlításról, ha a nyomatékvektor egybeesik valamelyik fő-másodrendű nyomatéki tengellyel. A hajlítást mindig súlyponti koordinátarendszerben értelmezzük. Ez még a
MECHANIKA I. rész: Szilárd testek mechanikája
 Egészségügyi mérnökképzés MECHNIK I. rész: Szilárd testek mechanikája készítette: Németh Róbert Igénybevételek térben I. z alapelv ugyanaz, mint síkban: a keresztmetszet egyik oldalán levő szerkezetrészre
Egészségügyi mérnökképzés MECHNIK I. rész: Szilárd testek mechanikája készítette: Németh Róbert Igénybevételek térben I. z alapelv ugyanaz, mint síkban: a keresztmetszet egyik oldalán levő szerkezetrészre
TÁRGYLEÍRÁS 1. ALAPADATOK
 TÁRGYLEÍRÁS 1. ALAPADATOK 1.1. Tantárgy neve A STATIKA ÉS DINAMIKA ALAPJAI 1.2. Azonosító (tantárgykód) BMEEOTMAT41 1.3. A tantárgy jellege kontaktórás tanegység 1.4. Óraszámok gyakorlat: 5 óra/hét 1.5.
TÁRGYLEÍRÁS 1. ALAPADATOK 1.1. Tantárgy neve A STATIKA ÉS DINAMIKA ALAPJAI 1.2. Azonosító (tantárgykód) BMEEOTMAT41 1.3. A tantárgy jellege kontaktórás tanegység 1.4. Óraszámok gyakorlat: 5 óra/hét 1.5.
MUNKAANYAG. Csepcsényi Lajos Lászlóné Balogh Melinda. Egyensúlyi feltételek, reakcióerők számítása. A követelménymodul megnevezése:
 Csepcsényi Lajos Lászlóné Balogh Melinda Egyensúlyi feltételek, reakcióerők számítása A követelménymodul megnevezése: Építőipari kivitelezés tervezése A követelménymodul száma: 0688-06 A tartalomelem azonosító
Csepcsényi Lajos Lászlóné Balogh Melinda Egyensúlyi feltételek, reakcióerők számítása A követelménymodul megnevezése: Építőipari kivitelezés tervezése A követelménymodul száma: 0688-06 A tartalomelem azonosító
A magától becsukódó ajtó működéséről
 1 A magától becsukódó ajtó működéséről Az [ 1 ] műben találtunk egy érdekes feladatot, amit most mi is feldolgozunk. Az 1. ábrán látható az eredeti feladat másolata. A feladat kitűzése 1. ábra forrása:
1 A magától becsukódó ajtó működéséről Az [ 1 ] műben találtunk egy érdekes feladatot, amit most mi is feldolgozunk. Az 1. ábrán látható az eredeti feladat másolata. A feladat kitűzése 1. ábra forrása:
ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2006. február 20. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2006. február 20. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati
ÉRETTSÉGI VIZSGA 2006. február 20. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2006. február 20. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati
Egy rugalmas megtámasztású tartóról
 Egy rugalmas megtámasztású tartóról Ezzel a témával gyakran találkozunk, még ha nem is így nevezzük azt. Ne feledjük, hogy a statikailag határozatlan tartók megoldásához szinte mindig alakváltozási felté
Egy rugalmas megtámasztású tartóról Ezzel a témával gyakran találkozunk, még ha nem is így nevezzük azt. Ne feledjük, hogy a statikailag határozatlan tartók megoldásához szinte mindig alakváltozási felté
Síkbeli csuklós rúdnégyszög egyensúlya
 Síkbeli csuklós rúdnégyszög egyensúlya Két korábbi dolgozatunkban melyek címe és azonosítója: [KD ]: Egy érdekes feladat, [KD ]: Egy másik érdekes feladat azt vizsgáltuk, hogy egy csuklós rúdnégyszög milyen
Síkbeli csuklós rúdnégyszög egyensúlya Két korábbi dolgozatunkban melyek címe és azonosítója: [KD ]: Egy érdekes feladat, [KD ]: Egy másik érdekes feladat azt vizsgáltuk, hogy egy csuklós rúdnégyszög milyen
ÁGAZATI SZAKMAI ÉRETTSÉGI VIZSGA ÉPÍTŐIPAR ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA MINTAFELADATOK
 ÉPÍTŐIPAR ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA MINTAFELADATOK RÖVID FELADATOK 1. feladat 2 pont Egészítse ki az alábbi mondatokat! A statika I. alaptétele: Két erő akkor és csakis akkor van egyensúlyban,
ÉPÍTŐIPAR ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA MINTAFELADATOK RÖVID FELADATOK 1. feladat 2 pont Egészítse ki az alábbi mondatokat! A statika I. alaptétele: Két erő akkor és csakis akkor van egyensúlyban,
Használható segédeszköz: - szöveges adatok tárolására és megjelenítésére nem alkalmas számológép; - körző; - vonalzók.
 A 27/2012 (VIII. 27.) NGM rendelet a 29/2016. (VIII. 26.) NGM rendelet által módosított szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosítószáma és megnevezése 54 582 03 Magasépítő technikus
A 27/2012 (VIII. 27.) NGM rendelet a 29/2016. (VIII. 26.) NGM rendelet által módosított szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosítószáma és megnevezése 54 582 03 Magasépítő technikus
Példa: Normálfeszültség eloszlása síkgörbe rúd esetén
 Példa: Normálfeszültség eloszlása síkgörbe rúd esetén Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 20. Az 1. ábrán vázolt síkgörbe rúd méretei és terhelése ismert.
Példa: Normálfeszültség eloszlása síkgörbe rúd esetén Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 20. Az 1. ábrán vázolt síkgörbe rúd méretei és terhelése ismert.
Az igénybevételi ábrák témakörhöz az alábbi előjelszabályokat használjuk valamennyi feladat esetén.
 Alkalmazott előjelszabályok Az igénybevételi ábrák témakörhöz az alábbi előjelszabályokat használjuk valamennyi feladat esetén. A kényszererők számításánál a következő a szabály: Az erők iránya a pozitív
Alkalmazott előjelszabályok Az igénybevételi ábrák témakörhöz az alábbi előjelszabályokat használjuk valamennyi feladat esetén. A kényszererők számításánál a következő a szabály: Az erők iránya a pozitív
MUNKAANYAG. Szabó László. Szilárdságtan. A követelménymodul megnevezése:
 Szabó László Szilárdságtan A követelménymodul megnevezése: Kőolaj- és vegyipari géprendszer üzemeltetője és vegyipari technikus feladatok A követelménymodul száma: 047-06 A tartalomelem azonosító száma
Szabó László Szilárdságtan A követelménymodul megnevezése: Kőolaj- és vegyipari géprendszer üzemeltetője és vegyipari technikus feladatok A követelménymodul száma: 047-06 A tartalomelem azonosító száma
Használható segédeszköz: - szöveges adatok tárolására és megjelenítésére nem alkalmas számológép; - körző; - vonalzók.
 A 4/2015 (II. 19.) NGM rendelet és a 27/2012 (VIII. 27.) NGM rendelet a 12/2013 (III. 28.) NGM rendelet által módosított szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosítószáma és megnevezése
A 4/2015 (II. 19.) NGM rendelet és a 27/2012 (VIII. 27.) NGM rendelet a 12/2013 (III. 28.) NGM rendelet által módosított szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosítószáma és megnevezése
Egy érdekes mechanikai feladat
 1 Egy érdekes mechanikai feladat 1. ábra forrása: [ 1 ] A feladat Az 1. ábra szerinti rudazat A csomópontján átvezettek egy kötelet, melynek alsó végén egy m tömegű golyó lóg. A rudak egyező nyúlási merevsége
1 Egy érdekes mechanikai feladat 1. ábra forrása: [ 1 ] A feladat Az 1. ábra szerinti rudazat A csomópontján átvezettek egy kötelet, melynek alsó végén egy m tömegű golyó lóg. A rudak egyező nyúlási merevsége
Határfeszültségek alapanyag: σ H = 200 N/mm 2, σ ph = 350 N/mm 2 ; szegecs: τ H = 160 N/mm 2, σ ph = 350 N/mm 2. Egy szegecs teherbírása:
 ervezze meg az L10.10.1-es szögacélpár eltolt illesztését L100.100.1-es hevederekkel és Ø1 mm-es szegecsekkel. nyagminőség: 8, szegecs: SZ. atárfeszültségek alapanyag: 00 /mm, p 50 /mm szegecs: τ 160 /mm,
ervezze meg az L10.10.1-es szögacélpár eltolt illesztését L100.100.1-es hevederekkel és Ø1 mm-es szegecsekkel. nyagminőség: 8, szegecs: SZ. atárfeszültségek alapanyag: 00 /mm, p 50 /mm szegecs: τ 160 /mm,
- Elemezze a mellékelt szerkezetet, készítse el a háromcsuklós fa fedélszék igénybevételi ábráit, ismertesse a rácsostartó rúdelemeinek szilárdsági
 1. - Elemezze a mellékelt szerkezetet, készítse el a háromcsuklós fa fedélszék igénybevételi ábráit, ismertesse a rácsostartó rúdelemeinek szilárdsági vizsgálatát. - Jellemezze a vasbeton három feszültségi
1. - Elemezze a mellékelt szerkezetet, készítse el a háromcsuklós fa fedélszék igénybevételi ábráit, ismertesse a rácsostartó rúdelemeinek szilárdsági vizsgálatát. - Jellemezze a vasbeton három feszültségi
ERŐRENDSZEREK EREDŐJÉNEK MEGHATÁROZÁSA
 ALAPOGALMAK ERŐRENDSZEREK EREDŐJÉNEK MEGHATÁROZÁSA Egy testre általában nem egy erő hat, hanem több. Legalább két erőnek kell hatni a testre, ha az erő- ellenerő alaptétel alapján járunk el. A testek vizsgálatához
ALAPOGALMAK ERŐRENDSZEREK EREDŐJÉNEK MEGHATÁROZÁSA Egy testre általában nem egy erő hat, hanem több. Legalább két erőnek kell hatni a testre, ha az erő- ellenerő alaptétel alapján járunk el. A testek vizsgálatához
ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK
 Név:... osztály:... ÉRETTSÉGI VIZSGA 2007. május 25. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2007. május 25. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati
Név:... osztály:... ÉRETTSÉGI VIZSGA 2007. május 25. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2007. május 25. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati
Építészeti tartószerkezetek II.
 Építészeti tartószerkezetek II. Vasbeton szerkezetek Dr. Szép János Egyetemi docens 2019. 05. 03. Vasbeton szerkezetek I. rész o Előadás: Vasbeton lemezek o Gyakorlat: Súlyelemzés, modellfelvétel (AxisVM)
Építészeti tartószerkezetek II. Vasbeton szerkezetek Dr. Szép János Egyetemi docens 2019. 05. 03. Vasbeton szerkezetek I. rész o Előadás: Vasbeton lemezek o Gyakorlat: Súlyelemzés, modellfelvétel (AxisVM)
HELYI TANTERV. Mechanika
 HELYI TANTERV Mechanika Bevezető A mechanika tantárgy tanításának célja, hogy fejlessze a tanulók logikai készségét, alapozza meg a szakmai tantárgyak feldolgozását. A tanulók tanulási folyamata fejlessze
HELYI TANTERV Mechanika Bevezető A mechanika tantárgy tanításának célja, hogy fejlessze a tanulók logikai készségét, alapozza meg a szakmai tantárgyak feldolgozását. A tanulók tanulási folyamata fejlessze
Keresztmetszet másodrendű nyomatékainak meghatározása
 BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
Erőtani számítás Szombathely Markusovszky utcai Gyöngyös-patak hídjának ellenőrzéséhez
 Erőtani számítás Szombathely Markusovszky utcai Gyöngyös-patak hídjának ellenőrzéséhez Pécs, 2015. június . - 2 - Tartalomjegyzék 1. Felhasznált irodalom... 3 2. Feltételezések... 3 3. Anyagminőség...
Erőtani számítás Szombathely Markusovszky utcai Gyöngyös-patak hídjának ellenőrzéséhez Pécs, 2015. június . - 2 - Tartalomjegyzék 1. Felhasznált irodalom... 3 2. Feltételezések... 3 3. Anyagminőség...
Példa: Háromszög síkidom másodrendű nyomatékainak számítása
 Példa: Háromszög síkidom másodrendű nyomatékainak számítása Készítette: Dr. Kossa Attila kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék. február 6. Határozzuk meg az alábbi ábrán látható derékszögű háromszög
Példa: Háromszög síkidom másodrendű nyomatékainak számítása Készítette: Dr. Kossa Attila kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék. február 6. Határozzuk meg az alábbi ábrán látható derékszögű háromszög
KOMMUNIKÁCIÓS DOSSZIÉ MECHANIKA. Anyagmérnök BSc Szak Évfolyamszintű tárgy. Miskolci Egyetem. Gépészmérnöki és Informatikai Kar
 KOMMUNIKÁCIÓS DOSSZIÉ MECHANIKA Anyagmérnök BSc Szak Évfolyamszintű tárgy Miskolci Egyetem Gépészmérnöki és Informatikai Kar Műszaki Mechanikai Intézet 1. Tantárgyleírás Tantárgy neve: Mechanika Tantárgy
KOMMUNIKÁCIÓS DOSSZIÉ MECHANIKA Anyagmérnök BSc Szak Évfolyamszintű tárgy Miskolci Egyetem Gépészmérnöki és Informatikai Kar Műszaki Mechanikai Intézet 1. Tantárgyleírás Tantárgy neve: Mechanika Tantárgy
 A SZERKEZET SEMATIKUS ÁBRÁJA STATIKAI VÁZA ERŐI (KÜLSŐ/TÁMASZ) VALÓSÁG ÉS MODELL 01 az elemek keresztmetszeti mérete a hosszméretnél lényegesen kisebb az elemek vastagsága a másik két méretnél lényegesen
A SZERKEZET SEMATIKUS ÁBRÁJA STATIKAI VÁZA ERŐI (KÜLSŐ/TÁMASZ) VALÓSÁG ÉS MODELL 01 az elemek keresztmetszeti mérete a hosszméretnél lényegesen kisebb az elemek vastagsága a másik két méretnél lényegesen
DEBRECENI EGYETEM MŰSZAKI KAR GÉPÉSZMÉRNÖKI TANSZÉK MŰSZAKI MECHANIKA II. HÁZIFELADAT
 DEBRECENI EGYETEM MŰSZAKI KAR GÉPÉSZMÉRNÖKI TANSZÉK MŰSZAKI MECHANIKA II. HÁZIFELADAT 2013 Feladat: Adott az ábrán látható kéttámaszú tartó, amely melegen hengerelt I idomacélokból és melegen hengerelt
DEBRECENI EGYETEM MŰSZAKI KAR GÉPÉSZMÉRNÖKI TANSZÉK MŰSZAKI MECHANIKA II. HÁZIFELADAT 2013 Feladat: Adott az ábrán látható kéttámaszú tartó, amely melegen hengerelt I idomacélokból és melegen hengerelt
CAD-CAM-CAE Példatár
 CAD-CAM-CAE Példatár A példa megnevezése: A példa száma: A példa szintje: CAx rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: VEM Rúdszerkezet sajátfrekvenciája ÓE-A05 alap közepes haladó
CAD-CAM-CAE Példatár A példa megnevezése: A példa száma: A példa szintje: CAx rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: VEM Rúdszerkezet sajátfrekvenciája ÓE-A05 alap közepes haladó
TARTÓSZERKEZETEK II. VASBETONSZERKEZETEK
 TARTÓSZERKEZETEK II. VASBETONSZERKEZETEK 2010.03.26. KERETSZERKEZETEK A keretvázak kialakulása Kezdetben pillér-gerenda rendszerő tartószerkezeti váz XIX XX. Század új anyagok öntöttvas, vas, acél, vasbeton
TARTÓSZERKEZETEK II. VASBETONSZERKEZETEK 2010.03.26. KERETSZERKEZETEK A keretvázak kialakulása Kezdetben pillér-gerenda rendszerő tartószerkezeti váz XIX XX. Század új anyagok öntöttvas, vas, acél, vasbeton
Mechanika. I. előadás február 25. Mechanika I. előadás február / 31
 Mechanika I. előadás 2019. február 25. Mechanika I. előadás 2019. február 25. 1 / 31 Elérhetőségek, információk Tantárgy: Mechanika (GEMET266-ZD-B) Előadó: Dr. Lengyel Ákos József Elérhetőségek: Iroda:
Mechanika I. előadás 2019. február 25. Mechanika I. előadás 2019. február 25. 1 / 31 Elérhetőségek, információk Tantárgy: Mechanika (GEMET266-ZD-B) Előadó: Dr. Lengyel Ákos József Elérhetőségek: Iroda:
TARTALOMJEGYZÉK. 1. KIINDULÁSI ADATOK 3. 1.1 Geometria 3. 1.2 Anyagminőségek 6. 2. ALKALMAZOTT SZABVÁNYOK 6.
 statikai számítás Tsz.: 51.89/506 TARTALOMJEGYZÉK 1. KIINDULÁSI ADATOK 3. 1.1 Geometria 3. 1. Anyagminőségek 6.. ALKALMAZOTT SZABVÁNYOK 6. 3. A VASBETON LEMEZ VIZSGÁLATA 7. 3.1 Terhek 7. 3. Igénybevételek
statikai számítás Tsz.: 51.89/506 TARTALOMJEGYZÉK 1. KIINDULÁSI ADATOK 3. 1.1 Geometria 3. 1. Anyagminőségek 6.. ALKALMAZOTT SZABVÁNYOK 6. 3. A VASBETON LEMEZ VIZSGÁLATA 7. 3.1 Terhek 7. 3. Igénybevételek
Magasépítési acélszerkezetek
 Magasépítési acélszerkezetek Egyhajós acélszerkezetű csarnok tervezése Szabó Imre Gábor Pécsi Tudományegyetem Műszaki és Informatikai Kar Építőmérnök Tanszék 1. ábra. Acél csarnoképület tipikus hierarchikus
Magasépítési acélszerkezetek Egyhajós acélszerkezetű csarnok tervezése Szabó Imre Gábor Pécsi Tudományegyetem Műszaki és Informatikai Kar Építőmérnök Tanszék 1. ábra. Acél csarnoképület tipikus hierarchikus
CONSTEEL 8 ÚJDONSÁGOK
 CONSTEEL 8 ÚJDONSÁGOK Verzió 8.0 2013.11.20 www.consteelsoftware.com Tartalomjegyzék 1. Szerkezet modellezés... 2 1.1 Új szelvénykatalógusok... 2 1.2 Diafragma elem... 2 1.3 Merev test... 2 1.4 Rúdelemek
CONSTEEL 8 ÚJDONSÁGOK Verzió 8.0 2013.11.20 www.consteelsoftware.com Tartalomjegyzék 1. Szerkezet modellezés... 2 1.1 Új szelvénykatalógusok... 2 1.2 Diafragma elem... 2 1.3 Merev test... 2 1.4 Rúdelemek
Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel
 Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel Segédlet az A végeselem módszer alapjai tárgy 4. laborgyakorlatához http://www.mm.bme.hu/~kossa/vemalap4.pdf Kossa Attila (kossa@mm.bme.hu)
Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel Segédlet az A végeselem módszer alapjai tárgy 4. laborgyakorlatához http://www.mm.bme.hu/~kossa/vemalap4.pdf Kossa Attila (kossa@mm.bme.hu)
Debreceni Szakképzési Centrum Baross Gábor Középiskolája és Kollégiuma
 Debreceni Szakképzési Centrum Baross Gábor Középiskolája és Kollégiuma 4030 Debrecen, Budai Ézsaiás utca 8/A. HELYI TANTERV a IX. GÉPÉSZET ÁGAZAT kötelezően választható tantárgyaihoz a 11-on (DUÁLIS KÉPZÉSI
Debreceni Szakképzési Centrum Baross Gábor Középiskolája és Kollégiuma 4030 Debrecen, Budai Ézsaiás utca 8/A. HELYI TANTERV a IX. GÉPÉSZET ÁGAZAT kötelezően választható tantárgyaihoz a 11-on (DUÁLIS KÉPZÉSI
ACÉL TÉRRÁCSOS TETOSZERKEZET KÍSÉRLETI VIZSGÁLATA
 ACÉL TÉRRÁCSOS TETOSZERKEZET KÍSÉRLETI VIZSGÁLATA Fülöp Attila * - Iványi Miklós ** RÖVID KIVONAT Nagy terek lefedésének egyik lehetséges módja acél térrácsos tetoszerkezet alkalmazása. A térrácsos lefedéssel
ACÉL TÉRRÁCSOS TETOSZERKEZET KÍSÉRLETI VIZSGÁLATA Fülöp Attila * - Iványi Miklós ** RÖVID KIVONAT Nagy terek lefedésének egyik lehetséges módja acél térrácsos tetoszerkezet alkalmazása. A térrácsos lefedéssel
ÜVEGEZETT FELVONÓ AKNABURKOLATOK MÉRETEZÉSE
 ÜVEGEZETT FELVONÓ AKNABURKOLATOK MÉRETEZÉSE EGYSZERŰSÍTETT SZÁMÍTÁS AZ MSZ EN81-0:014 SZABVÁNY ELŐÍRÁSAINAK FIGYELEMBEVÉTELÉVEL. MAKOVSKY ZSOLT. Üvegszerkezetek .Követelmények: MSZ EN81-0:014.1 A felvonóakna
ÜVEGEZETT FELVONÓ AKNABURKOLATOK MÉRETEZÉSE EGYSZERŰSÍTETT SZÁMÍTÁS AZ MSZ EN81-0:014 SZABVÁNY ELŐÍRÁSAINAK FIGYELEMBEVÉTELÉVEL. MAKOVSKY ZSOLT. Üvegszerkezetek .Követelmények: MSZ EN81-0:014.1 A felvonóakna
Az M A vektor tehát a három vektori szorzat előjelhelyes összege:
 1. feladat Határozza meg a T i támadáspontú F i erőrendszer nyomatékát az A pontra. T 1 ( 3, 0, 5 ) T 1 ( 0, 4, 5 ) T 1 ( 3, 4, 2 ) F 1 = 0 i + 300 j + 0 k F 2 = 0 i 100 j 400 k F 3 = 100 i 100 j + 500
1. feladat Határozza meg a T i támadáspontú F i erőrendszer nyomatékát az A pontra. T 1 ( 3, 0, 5 ) T 1 ( 0, 4, 5 ) T 1 ( 3, 4, 2 ) F 1 = 0 i + 300 j + 0 k F 2 = 0 i 100 j 400 k F 3 = 100 i 100 j + 500
ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK
 Építészeti és építési alapismeretek középszint 0821 ÉRETTSÉGI VIZSGA 2008. október 20. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS
Építészeti és építési alapismeretek középszint 0821 ÉRETTSÉGI VIZSGA 2008. október 20. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS
Gyakorlat 03 Keresztmetszetek II.
 Gyakorlat 03 Keresztmetszetek II. 1. Feladat Keresztmetszetek osztályzása Végezzük el a keresztmetszet osztályzását tiszta nyomás és hajlítás esetére! Monoszimmetrikus, hegesztett I szelvény (GY02 1. példája)
Gyakorlat 03 Keresztmetszetek II. 1. Feladat Keresztmetszetek osztályzása Végezzük el a keresztmetszet osztályzását tiszta nyomás és hajlítás esetére! Monoszimmetrikus, hegesztett I szelvény (GY02 1. példája)
Egyenletek, egyenlőtlenségek VII.
 Egyenletek, egyenlőtlenségek VII. Magasabbfokú egyenletek: A 3, vagy annál nagyobb fokú egyenleteket magasabb fokú egyenleteknek nevezzük. Megjegyzés: Egy n - ed fokú egyenletnek legfeljebb n darab valós
Egyenletek, egyenlőtlenségek VII. Magasabbfokú egyenletek: A 3, vagy annál nagyobb fokú egyenleteket magasabb fokú egyenleteknek nevezzük. Megjegyzés: Egy n - ed fokú egyenletnek legfeljebb n darab valós
GÉPÉSZETI ALAPISMERETEK
 Gépészeti alapismeretek középszint 1621 ÉRETTSÉGI VIZSGA 2016. október 17. GÉPÉSZETI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐORRÁSOK MINISZTÉRIUMA ontos
Gépészeti alapismeretek középszint 1621 ÉRETTSÉGI VIZSGA 2016. október 17. GÉPÉSZETI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐORRÁSOK MINISZTÉRIUMA ontos
KERETSZERKEZETEK. Definíciók, Keretek igénybevételei, méretezése. 10. előadás
 KERETSZERKEZETEK Definíciók, Keretek igénybevételei, méretezése 10. előadás Definíciók: Oszlop definíciója: Az oszlop vonalas tartószerkezet, két keresztmetszeti mérete (h, b) lényegesen kisebb, mint a
KERETSZERKEZETEK Definíciók, Keretek igénybevételei, méretezése 10. előadás Definíciók: Oszlop definíciója: Az oszlop vonalas tartószerkezet, két keresztmetszeti mérete (h, b) lényegesen kisebb, mint a
ELŐREGYÁRTOTT VASBETON SZERKEZETEK
 ELŐREGYÁRTOTT VASBETON SZERKEZETEK Szerkezetépítés I. Széchenyi István Egyetem Győr. Előadó: Koics László TARTALOM 1. Felhasználási terület 2. Csarnokszerkezetek típusai 3. Tervezés alapjai, megrendelői
ELŐREGYÁRTOTT VASBETON SZERKEZETEK Szerkezetépítés I. Széchenyi István Egyetem Győr. Előadó: Koics László TARTALOM 1. Felhasználási terület 2. Csarnokszerkezetek típusai 3. Tervezés alapjai, megrendelői
Egy érdekes statikai feladat. Az interneten találtuk az [ 1 ] művet, benne az alábbi feladattal.
![Egy érdekes statikai feladat. Az interneten találtuk az [ 1 ] művet, benne az alábbi feladattal. Egy érdekes statikai feladat. Az interneten találtuk az [ 1 ] művet, benne az alábbi feladattal.](/thumbs/92/110379255.jpg) 1 Egy érdekes statikai feladat Az interneten találtuk az [ 1 ] művet, benne az alábbi feladattal. A feladat A szabályos n - szög alakú, A, B, C, csúcsú lap az A csúcsán egy sima függőleges fal - hoz támaszkodik,
1 Egy érdekes statikai feladat Az interneten találtuk az [ 1 ] művet, benne az alábbi feladattal. A feladat A szabályos n - szög alakú, A, B, C, csúcsú lap az A csúcsán egy sima függőleges fal - hoz támaszkodik,
Tartószerkezetek I. (Vasbeton szilárdságtan)
 Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.10.11. Vasbeton külpontos nyomása Az eső ágú σ-ε diagram miatt elvileg minden egyes esethez külön kell meghatározni a szélső szál összenyomódását.
Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.10.11. Vasbeton külpontos nyomása Az eső ágú σ-ε diagram miatt elvileg minden egyes esethez külön kell meghatározni a szélső szál összenyomódását.
Szeretném felhívni figyelmüket a feltett korábbi vizsgapéldák és az azokhoz tartozó megoldások felhasználásával kapcsolatban néhány dologra.
 Tisztelt Hallgatók! Szeretném felhívni figyelmüket a feltett korábbi vizsgapéldák és az azokhoz tartozó megoldások felhasználásával kapcsolatban néhány dologra. Az, hogy valaki egy korábbi vizsga megoldását
Tisztelt Hallgatók! Szeretném felhívni figyelmüket a feltett korábbi vizsgapéldák és az azokhoz tartozó megoldások felhasználásával kapcsolatban néhány dologra. Az, hogy valaki egy korábbi vizsga megoldását
Egy furcsa tartóról. A probléma felvetése. Adott az 1. ábra szerinti kéttámaszú tartó. 1. ábra
 Egy furcsa tartóról Az alábbi probléma ha jól emlékszem tanulói felvetés, melyet tanáruk volt kol - légánk G. A. továbbított. ( Üdv Néked, Nagy Király! ) Hogy a probléma valós - e vagy mondvacsinált, azt
Egy furcsa tartóról Az alábbi probléma ha jól emlékszem tanulói felvetés, melyet tanáruk volt kol - légánk G. A. továbbított. ( Üdv Néked, Nagy Király! ) Hogy a probléma valós - e vagy mondvacsinált, azt
TARTÓSZERKEZETEK II. VASBETONSZERKEZETEK
 TARTÓSZERKEZETEK II. VASBETONSZERKEZETEK 2012.03.11. KERETSZERKEZETEK A keretvázak kialakulása Kezdetben pillér-gerenda rendszerű tartószerkezeti váz XIX XX. Század új anyagok öntöttvas, vas, acél, vasbeton
TARTÓSZERKEZETEK II. VASBETONSZERKEZETEK 2012.03.11. KERETSZERKEZETEK A keretvázak kialakulása Kezdetben pillér-gerenda rendszerű tartószerkezeti váz XIX XX. Század új anyagok öntöttvas, vas, acél, vasbeton
Néhány feladat a ferde helyzetű kéttámaszú tartók témaköréből
 Néhány feladat a ferde helyzetű kéttámaszú tartók témaköréből Egy korábbi dolgozatunkban melynek címe: A ferde tartó megoszló terheléseiről már jeleztük, hogy a témával kapcsolatban vannak még teendők;
Néhány feladat a ferde helyzetű kéttámaszú tartók témaköréből Egy korábbi dolgozatunkban melynek címe: A ferde tartó megoszló terheléseiről már jeleztük, hogy a témával kapcsolatban vannak még teendők;
Kizárólag oktatási célra használható fel!
 DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II III. Előadás Vékonyfalú keresztmetszetek nyírófeszültségei - Nyírófolyam - Nyírási középpont - Shear lag hatás - Csavarás Összeállította:
DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II III. Előadás Vékonyfalú keresztmetszetek nyírófeszültségei - Nyírófolyam - Nyírási középpont - Shear lag hatás - Csavarás Összeállította:
Használható segédeszköz: - szöveges adatok tárolására és megjelenítésére nem alkalmas számológép; - körző; vonalzók.
 A 27/2012. (VIII. 27.) NGM rendelet, a 27/2012. (VIII. 27.) NGM rendelet a 12/2013. (III. 28.) NGM rendelet által módosított és a 27/2012. (VIII. 27.) NGM rendelet a 4/2015. (II. 19.) NGM rendelet által
A 27/2012. (VIII. 27.) NGM rendelet, a 27/2012. (VIII. 27.) NGM rendelet a 12/2013. (III. 28.) NGM rendelet által módosított és a 27/2012. (VIII. 27.) NGM rendelet a 4/2015. (II. 19.) NGM rendelet által
Segédlet: Kihajlás. Készítette: Dr. Kossa Attila BME, Műszaki Mechanikai Tanszék május 15.
 Segédlet: Kihajlás Készítette: Dr. Kossa ttila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2012. május 15. Jelen segédlet célja tömören összefoglalni a hosszú nyomott rudak kihajlásra történő ellenőrzését.
Segédlet: Kihajlás Készítette: Dr. Kossa ttila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2012. május 15. Jelen segédlet célja tömören összefoglalni a hosszú nyomott rudak kihajlásra történő ellenőrzését.
Használható segédeszköz: - szöveges adatok tárolására és megjelenítésére nem alkalmas számológép; - körző; - vonalzók.
 A 27/2012 (VIII. 27.) NGM rendelet a 29/2016. (VIII. 26.) NGM rendelet által módosított szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosítószáma és megnevezése 54 582 03 Magasépítő technikus
A 27/2012 (VIII. 27.) NGM rendelet a 29/2016. (VIII. 26.) NGM rendelet által módosított szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosítószáma és megnevezése 54 582 03 Magasépítő technikus
időpont? ütemterv számonkérés segédanyagok
 időpont? ütemterv számonkérés segédanyagok 1. Bevezetés Végeselem-módszer Számítógépek alkalmazása a szerkezettervezésben: 1. a geometria megadása, tervkészítés, 2. műszaki számítások: - analitikus számítások
időpont? ütemterv számonkérés segédanyagok 1. Bevezetés Végeselem-módszer Számítógépek alkalmazása a szerkezettervezésben: 1. a geometria megadása, tervkészítés, 2. műszaki számítások: - analitikus számítások
Csarnokszerkezet térbeli (3D-s) modellezése
 Csarnokszerkezet térbeli (3D-s) modellezése Szabályos keret főtartós kialakítású csarnokszerkezetek teljes térbeli modellezésére a gyakorlatban általában nincs szükség, mivel az elkülönítés elvén alapuló
Csarnokszerkezet térbeli (3D-s) modellezése Szabályos keret főtartós kialakítású csarnokszerkezetek teljes térbeli modellezésére a gyakorlatban általában nincs szükség, mivel az elkülönítés elvén alapuló
