6. előadás PREFERENCIÁK (2), HASZNOSSÁG
|
|
|
- Ildikó Somogyi
- 9 évvel ezelőtt
- Látták:
Átírás
1 6. előadás PREFERENCIÁK (), HASZNOSSÁG Kertesi Gábor Varian 3. fejezetének oldalai és 4. fejezete alapján
2 PREFERENCIÁK FEJEZET FOLYTATÁSA 6. A helyettesítési határarány Dolgozzunk mostantól fogva (alapértelmezésben) jól viselkedő preferenciákkal, vagyis konvex és monoton preferenciákat leíró közömbösségi görbékkel. Ha ettől a feltételezéstől eltérünk, azt mindig külön jelezzük. Tekintsük e közömbösségi görbékre a következőképpen: fogjuk föl az egyik fogyasztott jószág mennyiségét a másik jószág mennyiségének függvényeként. Legyen x = f ( x ). Ha f konvex függvény a preferenciák monotonitása miatt ennek így kell lennie, akkor nyilvánvaló, hogy az f függvény gráfjának (a közömbösségi görbének) minden egyes pontjában igaz, hogy: dx / dx < 0. Vagyis, ha x nő, akkor x csökken. Az f függvény deriváltja negatív. 6.. fólia Az analízisből tudjuk, hogy a szóban forgó differenciálhányados nem más, mint a függvény itt: a közömbösségi görbe egy adott pontban vett érintőjének meredeksége. 6.. fólia Ennek a meredekségnek igen fontos közgazdasági jelentése van: azt fejezi ki, hogy az egyik jószág ( x ) fogyasztásának egységnyi csökkenéséért ( dx ) a másik jószág ( x ) fogyasztásának hány egységnyi növelése ( + dx ) képes bennünket kárpótolni. Fordítva is megfogalmazhatjuk ugyanezt: az egyik jószág ( x ) fogyasztásának egységnyi növelése ( + dx ) érdekében a másik jószág ( x ) fogyasztásának hány egységéről ( dx ) lennénk hajlandóak lemondani. E megfogalmazásokból is világosan látszik: a szóban forgó hányados (differenciálhányados) melynek neve is van: helyettesítési határarány (marginal rate of substitution = MRS) azt fejezi ki, hogy adott jószágkosár birtokában milyen értéket tulajdonít a fogyasztó az egyik jószágnak a másik jószághoz képest. Ez az értékelés természetesen szubjektív. A fogyasztó egyéni ízlésétől függ. Kis kitérő az ízlések (preferenciák) szubjektivitásáról és különbözőségéről: 6.3 fólia Melyik az angol, és melyik a francia? Miért? Egy speciális értelmezés: a jószágteret két dimenzióban úgy is értelmezhetjük, hogy az egyik jószágot (mondjuk x -et) egy naturális mértékegységben mért, szokványos jószágnak tekintjük (alma kilóban, tej literben mérve stb.), a másik jószágot (mondjuk x - t) az általunk fogyasztott összes többi jószágra való kiadásunknak (összetett jószág). Mi is ennek a mértékegysége? Forint. Mi az ára? p =. Mit jelent ilyenkor a dx / dx helyettesítési határarány? Mennyi fogyasztásról lennénk hajlandóak lemondani x A továbbiakban, amikor röviden akarunk hivatkozni a helyettesítési határarányra, akkor MRS-nek nevezzük.
3 egységnyi növeléséért? Másképpen: Mennyi pénzt lennénk hajlandóak x egységnyi növeléséért megadni? Fizetési határhajlandóságnak nevezzük azt az összeget, amennyit hajlandóak lennénk megadni érte. 6.4 fólia Ellenőrző kérdés: a helyettesítési határarány vagy a fizetési határhajlandóság függ-e az áraktól? Nem. Itt a preferenciáinkról: a fogyasztás tárgyát képező javakkal kapcsolatos vágyainkról (szubjektív értékeléseinkről) beszélünk. Az árak (és a jövedelmek) az élet realitásait képviselik. (A döntés majd az lesz, hogy szembesítjük a vágyainkat a realitásokkal: a preferenciáinkat a költségvetési korláttal.) Amivel most küszködünk, az nem más, mint hogy megpróbáljunk technikailag jól kezelhető fogalmak segítségével leírni a vágyainkat (preferenciáinkat). Az ilyen technikailag jól kezelhető fogalmak használata különbözteti meg a tudományos gondolkodást a laikus (mindennapi) észjárástól. Hasznos segédeszközök: sokszor olyan következtetésekhez segítenek hozzá bennünket, amelyek a laikus gondolkodás számára közvetlenül nem adottak. 6. A helyettesítési határarány tulajdonságai (jól viselkedő preferenciák esetében) Mint láttuk: a preferenciák monotonitásából (ami több, az jobb is) következik, hogy a közömbösségi görbe negatív meredekségű. Így a helyettesítési határarány mindig negatív. A preferenciák monotonitásából (a több, az jobb), illetve konvexitásából (az átlagokat előnyben részesítjük a szélsőségekkel szemben) együttesen következik a helyettesítési határarány egy másik fontos tulajdonsága is: a helyettesítési határarány abszolút értékben csök-kenő. Minél többel rendelkezünk egy jószágféleségből (mondjuk x -ből), annál kevesebbet vagyunk hajlandóak feláldozni a másik jószágból (mondjuk: x -ből) annak érdekében, hogy az adott jószágból egységnyivel többet fogyaszthassunk: ha x nő, dx / dx csökken. 6.5 fólia Természetesen nem minden preferencia viselkedik jól. Mint az előző órán láttuk, vannak másmilyen preferenciák is. Például: (a) ha két jószág egymás tökéletes helyettesítője: MRS = c. 6.6 fólia (b) ha az x semleges jószág: MRS = 0. ha az x semleges jószág: MRS =. 6.7 fólia (c) ha két jószág egymás tökéletes kiegészítője: MRS = 0 vagy, és a töréspontban a közömbösségi görbe nem differenciálható. 3
4 6.8 fólia Fontos megjegyzés: a preferenciák monotonitása és konvexitása nem olyan szigorú megkötés, mint amilyennek látszik. A való életben igen ritka eset a tökéletes helyettesítés vagy a tökéletes komplementaritás. Gyakrabban találkozunk erős helyettesítéssel vagy erős komplementaritással Ezeknek az eseteknek az a sajátossága, hogy miközben nagyon hasonlítanak a tökéletes helyettesítésre, illetve a tökéletes komplementaritásra, a preferenciák konvexitását sem veszítjük el! Technikailag jól (könnyen) kezelhetők. 6.9 fólia 4
5 HASZNOSSÁG 6.3 A hasznossági függvény Továbbra is monoton és konvex preferenciákkal dolgozunk. Ha ettől eltérő esetekkel van dolgunk, azt külön jelezzük. Kanyarodjunk vissza ahhoz a gondolathoz, hogy preferenciák közömbösségi görbékkel való leírásakor a preferenciák szintjeit növekvő indexszámokkal ellátott közömbösségi görbékkel jelöljük: I3 I I. 6.0 fólia Mit is jelent ez? 6. fólia Mint a múlt órán tanultunk, ez definíció szerint azt jelenti, hogy az I közömbösségi görbe fölött elhelyezkedő H halmaz minden egyes pontja a fogyasztó számára jobb (preferált) jószágkosarat képvisel, mint az I közömbösségi görbe pontjai: H I. Vegyünk egy tetszőleges másik (mondjuk: I ) közömbösségi görbét, amely I H. Nyilvánvaló, hogy ekkor: I I. Most pedig válasszuk kályhának az I közömbösségi görbét ( H I ), és hasonló eljárással keressünk megint egy tetszőleges I H 3 közömbösségi görbét. Nyilvánvaló, hogy ekkor: I3 I. stb. Az eljárást végtelen sokszor megismételhetjük. A lényeg az, hogy amennyiben a teljesség axiómája teljesül, akkor a különböző preferenciaszinteket reprezentáló közömbösségi görbék az (x, x ) jószágtér egészét folytonosan kitöltik. Kézenfekvőnek tűnik az a gondolat, hogy a közömbösségi görbék által képviselt jószágkosarak (halmazok) közti sorbarendezést egy függvény segítségével jelenítsük meg. Ezt a függvényt nevezik a közgazdászok hasznossági függvénynek. A hasznossági függvény (u) nem más, mint a jelen kétváltozós esetben egy u : R R folytonos leképezés, amely minden lehetséges fogyasztási kosárhoz, vagyis a jószágtér minden egyes pontjához egy skaláris értéket (hasznossági értéket) rendel oly módon, hogy az egyenértékű kosarak azonos értéket, a jobban preferált kosarak a kevésbé preferált kosarakhoz képest pedig magasabb értéket kapnak. 6. fólia Mielőtt elkezdenénk a fent látható ábrát értelmezni, nyomatékosan hangsúlyozni kell: a közömbösségi görbékhez hozzárendelt értékek (hasznossági értékek) számszerű nagyságának semmi jelentősége nincsen. Nem tudjuk ugyanis azt megmondani, hogy egy jószágkosár mennyivel jobb, mint a másik. Csak annyit tudunk mondani róluk, hogy az adott fogyasztó előnyben részesíti az egyiket a másikkal szemben. Mi is az? (Bármely két kosár között tudunk választani: a preferenciarendezés a jószágtér minden egyes pontjára kiterjed.) 5
6 Most elemezzük egy kicsit a a kivetített ábrát. u : R R leképezés: a kétdimenziós térből áttérünk a háromdimenziós térbe, amelyben a hasznossági függvény gráfja egy térbeli felületet alkot. Olyan mintha egy háromdimenziós térképen ábrázolnánk egy dombot vagy hegyet (utility hill), és szintvonalakkal jeleznénk, hogy a hegy milyen magasságánál tartunk. Mivel a térképek általában kétdimenziósként készülnek, ezeket a szintvonalakat úgy szokták ábrázolni, hogy a síkra vetítik őket, és ellátják egy számmal őket, jelezve, hogy milyen magasságot képviselnek. Az analógia azonban itt véget ér. A domborzati térképnél az a jel, hogy a hegy egyik szintvonala 000, a másik meg 00 méter, valóban azt jelenti, hogy az egyik szint 00 méterrel magasabban fekszik, mint a másik. A hasznossági leképezésnél ennek az információnak nincs jelentősége. Az 00-as hasznossági indexszel ellátott közömbösségi görbe jobb (preferált) jószágkosarakat képvisel, mint a 000-es hasznossági értékkel ellátott görbe. Azt azonban nem mondhatjuk, hogy 00 hasznosságegységgel több értéket képviselne, ennek ugyanis semmi értelme nincsen. A hasznossági függvényen értelmezett távolságfogalom önkényes. A jószágkosarakhoz hozzárendelt hasznossági értékek merőben technikai szerepet játszanak: arra szolgálnak, hogy rangsoroljuk (sorba rendezzük) az egyenértékű jószágkombinációkat: ordinális hasznosság. (A hasznosság kardinális mérőszámáról lásd Varian tankönyvét! elmélettörténeti kitérő). De ha egyszer a távolságfogalomnak nincs értelme, miért használunk mégis egy folytonos indexfüggvényt, melynek használata azt a látszatot kelti, mintha a távolságfogalomnak mégis lenne valami értelme? ( 00-zal nagyobb hasznosságú ). Valóban önkényes a hasznossági függvényen értelmezett távolságfogalom? A válasz két elemből áll: (a) a távolságfogalom valóban önkényes; egy preferenciarendezést jól leírhatunk végtelen sok hasznossági függvénnyel; (b) a közgazdaságtanra sajátosan jellemző döntési problémák elemzésének az ily módon definiált hasznossági függvény egy technikailag igen jól kezelhető eszköze: kényelmes mankó, amire rátámaszkodhatunk. Ezért használjuk. Lássuk az érveket! (a) (b) A hasznossági függvényen értelmezett távolságfogalom önkényessége azonnal nyilvánvalóvá válik, ha számításba vesszük, hogy egy preferenciarendezéshez végtelen sok lehetséges hasznossági függvény tartozhat. Ha már van egy hasznossági függvényünk, akkor minden olyan további hasznossági függvényről elmondhatjuk, hogy megfelelően reprezentálja az alapjául szolgáló preferenciarendezést, amely a jószágkosarak eredeti preferenciasorrendjét nem változtatja meg. (Pl. ha egy hasznossági függvényhez hozzáadunk egy pozitív számot, vagy megszorozzuk egy pozitív számmal, akkor a transzformált hasznossági függvény szerint pontosan ugyanolyan módon rendezzük sorba az alternatívákat, mint az eredetileg választott hasznossági függvény szerint: a preferenciaszintek közti távolságok teljesen önkényesen változhatnak.) Itt még sok mindent tisztáznunk kellene. Erre hamarosan sort is kerítünk. Lássuk előbb azonban a válasz másik elemét. Miért van szükségünk nekünk, közgazdászoknak erre a konstrukcióra? Emlékezzünk csak vissza arra, ahonnan a múlt óra elején elindultunk. Hogyan is fest a fogyasztói döntés elméletének a szerkezete? A fogyasztó a számára megfizethető legjobb jószágkosarat választja. Általánosabban fogalmazva: a 6
7 számára megvalósítható lehetőségek közül a legjobb lehetőséget választja. A közgazdasági problémák jó része pontosan ilyen szerkezetű. Matematikai természetét tekintve nem más, mint egy feltételes optimalizálási feladat (erről már tanultak az első félévi matekban, illetve a mikro előadások során Simonovits tanár úr előadásán). Pl. A téglalap kerületét rögzítjük (mondjuk 0 cm-ben), és keressük azt a téglalapot, amelynek területe (T) a rögzített 0 cm-es kerület mint korlát mellett a legnagyobb. 6.3 fólia A folytonos (és differenciálható) hasznossági függvények technikailag igen jól kezelhető célfüggvényei az ilyen jellegű feltételes optimalizálási problémáknak. Most pontosítani fogjuk azt a megjegyzést, hogy egy preferenciarendezéshez végtelen sok lehetséges hasznossági függvény tartozhat. Mivel a közömbösségi görbék által reprezentált jószágkosaraknak csak a preferenciasorrendje számít, így egy tetszőleges u ( x, x ) hasznossági függvény helyett bármely f [ u ( x, x )] is megteszi, amely a szóban forgó halmazok rangsorát nem változtatja meg. Az ilyen f : R R transzformációkat pozitív monoton transzformációknak nevezzük. 6.4 fólia A monoton transzformációk révén a közömbösségi görbék újraszámozzuk. 6.4 A határhaszon A hasznossági függvény lesz mostantól fogva az az elemzési eszköz, melynek segítségével a preferenciákat megjelenítjük. Induljunk ki egy fogyasztóból, aki egy tetszőleges ( x, x ) jószágkosarat fogyaszt. Hasznossági mértékegységben kifejezve, milyen értéket képvisel a számára az, ha az egyik termék mondjuk az x mennyiségét egy kis mértékben (mondjuk: dx > 0 mennyiséggel) növeli, miközben a másik (x ) jószág fogyasztott mennyiségét változatlanul hagyja? Mivel a jól viselkedő preferenciák monotonok (ami több, az jobb is) => átkerülünk egy magasabb szintet képviselő közömbösségi görbére => magasabb hasznossági szintre: du > fólia A határhaszon nagysága függ a választott hasznossági mértéktől (függ az alkalmazott speciális hasznossági függvénytől). 6.6 fólia Ez nem túl előnyös tulajdonság, hiszen mint korábban erősen hangsúlyoztuk a jószágkosarak sorrendje a lényeg, nem pedig az a konkrét indexelési eljárás, ahogyan a 7
8 közömbösségi görbéket beszámozzuk. A határhaszonnak önmagában nincs magatartási tartalma. Hamarosan azonban látni fogjuk, hogy a határhaszon fogalmát fölhasználhatjuk egy olyan (már ismerős) fogalom meghatározására, amelynek már van magatartási tartalma => helyettesítési határarány. 6.5 A határhaszon és a helyettesítési határarány Változzon most úgy a fogyasztás mindkét jószágból olyan mértékben ( dx, dx ), hogy az összhaszon változatlan maradjon. A közömbösségi görbe mentén (pontosabban: egy kontúrvonal mentén) mozgunk. 6.7 fólia Konvex preferenciák esetén (jól viselkedő preferenciák!) az egyik jószágból (mondjuk x - ből) való fogyasztásunkat növeljük, a másikból (mondjuk x -ből) csökkentjük. Mekkora értéket képvisel számunkra hasznosságegységben kifejezve x mennyiségének növekedése, illetve hasznosságegységben kifejezve x mennyiségének csökkenése? A növekményt, illetve csökkenést (melyet naturális mértékegységben kg, liter, méter mérünk) beárazzuk a szóban forgó termék határhasznával (azzal, amilyen értéket számunkra annak egy egysége képvisel). S minthogy egy közömbösségi görbén mozgunk, a változások (hasznossági egységben mérve) kioltják egymást: du = 0. Matematikai nyelven kifejezve: a hasznossági szint változatlanul hagyása mellett teljesen differenciáljuk a hasznossági függvényt: 6.8 fólia A helyettesítési határarány nem más, mint a határhasznok aránya. Jól viselkedő preferenciák esetén ez mindig negatív szám. Konvenció szerint azonban, amikor helyettesítési határarányról beszélünk, a helyettesítési határráta abszolút értékét szoktuk használni! MRS előnyös tulajdonsága, hogy invariáns a hasznossági függvény pozitív monoton transzformációira. 6.9 fólia Vagyis: bármely hasznossági függvényből ugyanaz az MRS nyerhető. => magatartási tartalma: adott jószágkosár birtokában milyen értéket tulajdonít a fogyasztó az egyik jószágnak a másik jószághoz képest. => A jövő heti szemináriumon majd látnak erre egy gyakorlati szempontból is fontos példát (Varian ingázási példája, old.) 8
9 6.6 Technikai trükkök Hasznossági függvény szerkesztése (jól viselkedő preferenciák esetén) közömbösségi görbék segítségével. (lásd könyv, old.) Közömbösségi görbék, illetve a nekik megfelelő hasznossági függvények: (a) u ( x, x) = xx => x = k / x, k =,,3... Hiperbola. 6.0 fólia a (b) Cobb-Douglas hasznossági függvény ( x a v( x, x) = x, ahol: 0 < a <, még nagy hasznát fogjuk venni). Hiperbola, akárcsak 6.0-as fólián. 6. fólia (c) k a tökéletes helyettesítés: u ( x, x) = ax + bx => x = x, b b k =,, fólia (d) tökéletes kiegészítés: u ( x, x) = min{ ax, bx} 6.3 fólia (e) kvázilineáris hasznossági függvény: u ( x, x) = v( x ) + x => x = k v( x ), k =,,3... Nem mások, mint x -ben lineáris közömbösségi görbék párhuzamos eltolásai: 6.4 fólia 9
10 A hasznossági elmélet első megfogalmazása Jeremy Bentham (748-83) brit morálfilozófus nevéhez fűződik: A természet az emberi nemet két szuverén úr a fájdalom és az élvezet kormányzata alá helyezte. Egyedül az ő dolguk kijelölni, mit kell tennünk, csakúgy, mint meghatározni, hogy mit fogunk tenni. Az ember szavakban tagadhatja uralmukat: de a valóságban mindvégig annak alávetve marad. A hasznosság elve elismeri ezen alávetettséget.. A hasznosság elvén azt az elvet értjük, mely szerint bármely cselekedetet azon irányultság szerint helyeslünk vagy helytelenítünk, hogy az az érintett fél boldogságát növelni, vagy csökkenteni látszik, vagy ami ugyanaz más szavakkal: e boldogságot előmozdítani vagy akadályozni látszik. Jeremy Bentham: Bevezetés az erkölcsök és a törvényhozás alapelveibe, fejezet Jeremy Bentham (748 83) 0
11 6. előadás PREFERENCIÁK (), HASZNOSSÁG MELLÉKLET Kertesi Gábor
12 6. A közömbösségi görbe lejtése negatív dx < 0 f < 0 dx
13 6. Helyettesítési határarány dx dx x < 0 : x x x 3
14 6.3 Melyik az angol és melyik a francia? 4
15 6.4 Fizetési határhajlandóság 5
16 6.5 Csökkenő helyettesítési határarány dx dx A > dx dx B 6
17 6.6 Tökéletes helyettesítés 7
18 6.7 Semleges jószág 8
19 6.8 Tökéletes kiegészítés (komplementaritás) 9
20 6.9 Erős helyettesítés és erős komplementaritás 0
21 6.0 A közömbösségi görbéket indexekkel látjuk el
22 6. A közömbösségi görbék a jószágtér egészét folytonosan kitöltik ( H I és I H ) I I ( H I és I H ) I 3 I 3
23 6. Közömbösségi görbék és hasznossági függvény 3
24 6.3 Feltételes optimalizálási probléma Keressük azt az a* és b* értéket, amelynél a T (a,b) = ab függvény felveszi a maximumát, a a + b = 0 korlátozó feltétel mellett T (a,b) = ab célfüggvény a + b = 0 korlátozó feltétel Rövidített jelölésmóddal: k.f. : a ( ) max T a,b a,b = ab + b = 0 Optimális megoldás (optimum): a * = b* = 5 4
25 6.4 Pozitív monoton transzformáció Ha ( b,b ) ( a, ) u ( b,b ) > u( a, ) a Példák: v = f ( u) f [ u ( b, )] > f[ u( a, )] b a a f f = αu + β α, β > 0 = u stb 5
26 6.5 Határhaszon ( x + x,x ) ( x,x ) u( x + x, ) > u ( x, ) () x x u ( x + x,x ) u( x,x ) x ( ) lim u ( x + x,x ) u( x,x ) u = ( 3) x x 0 x MU = u x ; () 4 du u = dx x x mennyisége rögzítve MU = u x ; ( 5) du u = dx x x mennyisége rögzítve 6
27 7
28 6.6 A határhaszon nagysága a hasznossági függvénytől függ ( x, x ) = x c x c,d >0 ( ) u d v = lnu ( ) v c ln x + d ln x = ( 3) u / x = (c ) c x x d ( 4) v / x c / x = ( 5) u / x v / x ( 6) 8
29 6.7 A hasznossági domb kontúrvonalai és szintvonalai 9
30 6.8 Helyettesítési határarány kiszámítása a hasznossági függvényből ( x, ) u = u () x u u du = dx + dx = 0 () x x MRS dx u / x = = (3) dx u / x 30
31 6.9 A MRS invariáns a hasznossági függvény pozitív monoton transzformációira = u(x, x ) () u f : R R u pozitív monoton transzformációja ( ) = f[ u(x,x )] v(x,x ) ( 3) v = Helyettesítési határráta: dx dx v / x = ( 4) v / x A láncszabályt alkalmazva: v / x v / x = f u u x f u u x = u / x ( 5) u / x 3
32 6.0 Hasznossági függvény közömbösségi görbék ( x, x ) xx u = k x x = ( k =,,3...) ( x, x ) = u [ u( x, )] v = x k k =,4,9... x x = ( ) 3
33 6. Cobb-Douglas hasznossági függvény u c d ( x, x ) x x = c,d > 0 () v egy monoton transzformációja: ( x, x ) = lnu = c ln x + d ln x ( ) egy másik transzformációja: ( x, ) v u ( x, )[ /(c + = d) ] x x = [ c /( c+ d) ] [ d /( c+ d) x ] x a = x x ( a) ( 3) c ahol: a =, c + d a = d c + d Cobb Douglas hasznossági függvény nevezetes változata: u a ( a) ( x,x ) = x x ( 4) 0 < a < 33
34 6. Tökéletes helyettesítés ( x,x ) = ax bx u + x k a = b b x 34
35 6.3 Tökéletes kiegészítés ( x,x ) min { ax, } u = bx 35
36 6.4 Kvázilineáris hasznossági függvény ( x,x ) = v( x ) x u + x ( ) = k v, k =,,3... x 36
MIKROÖKONÓMIA I. Készítette: K hegyi Gergely és Horn Dániel. Szakmai felel s: K hegyi Gergely. 2010. június
 MIKROÖKONÓMIA I. Készült a TÁMOP-4.1.2-08/2/a/KMR-2009-0041 pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék az MTA Közgazdaságtudományi
MIKROÖKONÓMIA I. Készült a TÁMOP-4.1.2-08/2/a/KMR-2009-0041 pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék az MTA Közgazdaságtudományi
8. előadás EGYÉNI KERESLET
 8. előadás EGYÉNI KERESLET Kertesi Gábor Varian 6. fejezete, enyhe változtatásokkal 8. Bevezető megjegyzések Az elmúlt héten az optimális egyéni döntést elemeztük grafikus és algebrai eszközökkel: a preferenciatérkép
8. előadás EGYÉNI KERESLET Kertesi Gábor Varian 6. fejezete, enyhe változtatásokkal 8. Bevezető megjegyzések Az elmúlt héten az optimális egyéni döntést elemeztük grafikus és algebrai eszközökkel: a preferenciatérkép
Mikroökonómia I. ELTE TáTK Közgazdaságtudományi Tanszék. 6. hét PREFERENCIÁK, HASZNOSSÁG 2. RÉSZ
 MIKROÖKONÓMI I. ELTE TáTK Közgazdaságtudományi Tanszék Mikroökonómia I. PREFERENCIÁK, HSZNOSSÁG 2. RÉSZ Készítette: K hegyi Gergely, Horn Dániel Szakmai felel s: K hegyi Gergely 2010. június tananyagot
MIKROÖKONÓMI I. ELTE TáTK Közgazdaságtudományi Tanszék Mikroökonómia I. PREFERENCIÁK, HSZNOSSÁG 2. RÉSZ Készítette: K hegyi Gergely, Horn Dániel Szakmai felel s: K hegyi Gergely 2010. június tananyagot
Mikroökonómia II. B. ELTE TáTK Közgazdaságtudományi Tanszék. 2. hét TÉNYEZŽPIACOK ÉS JÖVEDELEMELOSZTÁS 2. RÉSZ
 MIKROÖKONÓMIA II. B ELTE TáTK Közgazdaságtudományi Tanszék Mikroökonómia II. B TÉNYEZŽPIACOK ÉS JÖVEDELEMELOSZTÁS 2. RÉSZ Készítette: Szakmai felel s: 2011. február A tananyagot készítette: Jack Hirshleifer,
MIKROÖKONÓMIA II. B ELTE TáTK Közgazdaságtudományi Tanszék Mikroökonómia II. B TÉNYEZŽPIACOK ÉS JÖVEDELEMELOSZTÁS 2. RÉSZ Készítette: Szakmai felel s: 2011. február A tananyagot készítette: Jack Hirshleifer,
MIKROÖKONÓMIA I. B. Készítette: K hegyi Gergely, Horn Dániel és Major Klára. Szakmai felel s: K hegyi Gergely. 2010. június
 MIKROÖKONÓMIA I. B Készült a TÁMOP-4.1.2-08/2/a/KMR-2009-0041 pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék az MTA Közgazdaságtudományi
MIKROÖKONÓMIA I. B Készült a TÁMOP-4.1.2-08/2/a/KMR-2009-0041 pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék az MTA Közgazdaságtudományi
Mikroökonómia I. feladatok
 Mikroökonómia I. feladatok 2014 december Írta: Rózemberczki Benedek András Alkalmazott közgazdaságtan szak Got It! konzultáció 2014 TARTALOMJEGYZÉK TARTALOMJEGYZÉK Tartalomjegyzék 1. Preferenciák 3 2.
Mikroökonómia I. feladatok 2014 december Írta: Rózemberczki Benedek András Alkalmazott közgazdaságtan szak Got It! konzultáció 2014 TARTALOMJEGYZÉK TARTALOMJEGYZÉK Tartalomjegyzék 1. Preferenciák 3 2.
Nevezetes függvények
 Nevezetes függvények Függvények értelmezése Legyen adott az A és B két nem üres halmaz. Az A halmaz minden egyes eleméhez rendeljük hozzá a B halmaz egy-egy elemét. Ez a hozzárendelés egyértelmű, és ezt
Nevezetes függvények Függvények értelmezése Legyen adott az A és B két nem üres halmaz. Az A halmaz minden egyes eleméhez rendeljük hozzá a B halmaz egy-egy elemét. Ez a hozzárendelés egyértelmű, és ezt
MIKROÖKONÓMIA - konzultáció - Piac és fogyasztás
 MIKROÖKONÓMIA - konzultáció - Piac és fogyasztás Révész Sándor szuperkonzultacio.hu 2012. január 7. Dierenciálszámítási alapok A mikroökonómiai problémák megoldása két formában fog történni: 1. egyensúly
MIKROÖKONÓMIA - konzultáció - Piac és fogyasztás Révész Sándor szuperkonzultacio.hu 2012. január 7. Dierenciálszámítási alapok A mikroökonómiai problémák megoldása két formában fog történni: 1. egyensúly
Szeminárium-Rekurziók
 1 Szeminárium-Rekurziók 1.1. A sorozat fogalma Számsorozatot kapunk, ha pozitív egész számok mindegyikéhez egyértelműen hozzárendelünk egy valós számot. Tehát a számsorozat olyan függvény, amelynek az
1 Szeminárium-Rekurziók 1.1. A sorozat fogalma Számsorozatot kapunk, ha pozitív egész számok mindegyikéhez egyértelműen hozzárendelünk egy valós számot. Tehát a számsorozat olyan függvény, amelynek az
FOGYASZTÓI MAGATARTÁS 1.
 KÖZGAZDASÁGTAN I. BMEGT30A003 HÉTFŐ: 8:15 10:00 (Q-II) HÉTFŐ: 10.15 12:00 (QAF15) FOGYASZTÓI MAGATARTÁS 1. 2 5. FEJEZETEK Dr. Ligeti Zsombor ligetizs@kgt.bme.hu Fogadóóra: Kedd 12 14, QA215 2018.09.17.
KÖZGAZDASÁGTAN I. BMEGT30A003 HÉTFŐ: 8:15 10:00 (Q-II) HÉTFŐ: 10.15 12:00 (QAF15) FOGYASZTÓI MAGATARTÁS 1. 2 5. FEJEZETEK Dr. Ligeti Zsombor ligetizs@kgt.bme.hu Fogadóóra: Kedd 12 14, QA215 2018.09.17.
FOGYASZTÓI MAGATARTÁS 1.
 KÖZGAZDASÁGTAN I. BMEGT30A003 HÉTFŐ: 8:15 10:00 (Q-II) KEDD: 10.15 12:00 (E1A) FOGYASZTÓI MAGATARTÁS 1. 2 5. FEJEZETEK Dr. Ligeti Zsombor ligetizs@kgt.bme.hu Ligeti Zsombor 1 TARTALOM 1. NEMLINEÁRIS VILÁG
KÖZGAZDASÁGTAN I. BMEGT30A003 HÉTFŐ: 8:15 10:00 (Q-II) KEDD: 10.15 12:00 (E1A) FOGYASZTÓI MAGATARTÁS 1. 2 5. FEJEZETEK Dr. Ligeti Zsombor ligetizs@kgt.bme.hu Ligeti Zsombor 1 TARTALOM 1. NEMLINEÁRIS VILÁG
Analízisfeladat-gyűjtemény IV.
 Oktatási segédanyag a Programtervező matematikus szak Analízis. című tantárgyához (003 004. tanév tavaszi félév) Analízisfeladat-gyűjtemény IV. (Függvények határértéke és folytonossága) Összeállította
Oktatási segédanyag a Programtervező matematikus szak Analízis. című tantárgyához (003 004. tanév tavaszi félév) Analízisfeladat-gyűjtemény IV. (Függvények határértéke és folytonossága) Összeállította
Beadható feladatok. 2006. december 4. 1. Add meg az alábbi probléma állapottér-reprezentációját!
 Beadható feladatok 2006. december 4. 1. Feladatok 2006. szeptember 13-án kitűzött feladat: 1. Add meg az alábbi probléma állapottér-reprezentációját! Adott I 1,..., I n [0, 1] intervallumokból szeretnénk
Beadható feladatok 2006. december 4. 1. Feladatok 2006. szeptember 13-án kitűzött feladat: 1. Add meg az alábbi probléma állapottér-reprezentációját! Adott I 1,..., I n [0, 1] intervallumokból szeretnénk
Analízis lépésről - lépésre
 Analízis lépésről - lépésre interaktív tananyag Dr. Stettner Eleonóra Klingné Takács Anna Analízis lépésről - lépésre: interaktív tananyag írta Dr. Stettner Eleonóra és Klingné Takács Anna Tartalom Előszó...
Analízis lépésről - lépésre interaktív tananyag Dr. Stettner Eleonóra Klingné Takács Anna Analízis lépésről - lépésre: interaktív tananyag írta Dr. Stettner Eleonóra és Klingné Takács Anna Tartalom Előszó...
2. Hatványozás, gyökvonás
 2. Hatványozás, gyökvonás I. Elméleti összefoglaló Egész kitevőjű hatvány értelmezése: a 1, ha a R; a 0; a a, ha a R. Ha a R és n N; n > 1, akkor a olyan n tényezős szorzatot jelöl, aminek minden tényezője
2. Hatványozás, gyökvonás I. Elméleti összefoglaló Egész kitevőjű hatvány értelmezése: a 1, ha a R; a 0; a a, ha a R. Ha a R és n N; n > 1, akkor a olyan n tényezős szorzatot jelöl, aminek minden tényezője
MIKROÖKONÓMIA I. Készítette: K hegyi Gergely és Horn Dániel. Szakmai felel s: K hegyi Gergely. 2010. június
 MIKROÖKONÓMIA I. Készült a TÁMOP-4.1.2-08/2/a/KMR-2009-0041 pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék az MTA Közgazdaságtudományi
MIKROÖKONÓMIA I. Készült a TÁMOP-4.1.2-08/2/a/KMR-2009-0041 pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék az MTA Közgazdaságtudományi
Miskolci Egyetem GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR. Analízis I. példatár. (kidolgozott megoldásokkal) elektronikus feladatgyűjtemény
 Miskolci Egyetem GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR Analízis I. példatár kidolgozott megoldásokkal) elektronikus feladatgyűjtemény Összeállította: Lengyelné Dr. Szilágyi Szilvia Miskolc, 013. Köszönetnyilvánítás
Miskolci Egyetem GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR Analízis I. példatár kidolgozott megoldásokkal) elektronikus feladatgyűjtemény Összeállította: Lengyelné Dr. Szilágyi Szilvia Miskolc, 013. Köszönetnyilvánítás
Komputer statisztika gyakorlatok
 Eszterházy Károly Főiskola Matematikai és Informatikai Intézet Tómács Tibor Komputer statisztika gyakorlatok Eger, 2010. október 26. Tartalomjegyzék Előszó 4 Jelölések 5 1. Mintagenerálás 7 1.1. Egyenletes
Eszterházy Károly Főiskola Matematikai és Informatikai Intézet Tómács Tibor Komputer statisztika gyakorlatok Eger, 2010. október 26. Tartalomjegyzék Előszó 4 Jelölések 5 1. Mintagenerálás 7 1.1. Egyenletes
MIKROÖKONÓMIA I. Készítette: K hegyi Gergely és Horn Dániel. Szakmai felel s: K hegyi Gergely. 2010. június
 MIKROÖKONÓMIA I Készült a TÁMOP-412-08/2/a/KMR-2009-0041 pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék az MTA Közgazdaságtudományi
MIKROÖKONÓMIA I Készült a TÁMOP-412-08/2/a/KMR-2009-0041 pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék az MTA Közgazdaságtudományi
ÉS TESZTEK A DEFINITSÉG
 MÁTRIX DEFINITSÉGÉNEK FOGALMA ÉS TESZTEK A DEFINITSÉG ELDÖNTÉSÉRE DR. NAGY TAMÁS egyetemi docens Miskolci Egyetem Alkalmazott Matematikai Tanszék A bemutatott kutató munka a TÁMOP-..1.B-10//KONV-010-0001
MÁTRIX DEFINITSÉGÉNEK FOGALMA ÉS TESZTEK A DEFINITSÉG ELDÖNTÉSÉRE DR. NAGY TAMÁS egyetemi docens Miskolci Egyetem Alkalmazott Matematikai Tanszék A bemutatott kutató munka a TÁMOP-..1.B-10//KONV-010-0001
választással azaz ha c 0 -t választjuk sebesség-egységnek: c 0 :=1, akkor a Topa-féle sebességkör teljes hossza 4 (sebesség-)egységnyi.
 Egy kis számmisztika Az elmúlt másfél-két évben elért kutatási eredményeim szerint a fizikai téridő geometriai jellege szerint háromosztatú egységet alkot: egymáshoz (a lokális éterhez mért v sebesség
Egy kis számmisztika Az elmúlt másfél-két évben elért kutatási eredményeim szerint a fizikai téridő geometriai jellege szerint háromosztatú egységet alkot: egymáshoz (a lokális éterhez mért v sebesség
10. Valószínűségszámítás
 . Valószínűségszámítás.. Események A valószínűségszámítás nagyon leegyszerűsítve események bekövetkezésének valószínűségével foglalkozik. Példák: Ha egy játékban egy dobókockával dobunk, akkor a kockadobás
. Valószínűségszámítás.. Események A valószínűségszámítás nagyon leegyszerűsítve események bekövetkezésének valószínűségével foglalkozik. Példák: Ha egy játékban egy dobókockával dobunk, akkor a kockadobás
matematikai statisztika 2006. október 24.
 Valószínűségszámítás és matematikai statisztika 2006. október 24. ii Tartalomjegyzék I. Valószínűségszámítás 1 1. Véletlen jelenségek matematikai modellje 3 1.1. Valószínűségi mező..............................
Valószínűségszámítás és matematikai statisztika 2006. október 24. ii Tartalomjegyzék I. Valószínűségszámítás 1 1. Véletlen jelenségek matematikai modellje 3 1.1. Valószínűségi mező..............................
Lineáris programozás. Modellalkotás Grafikus megoldás Feladattípusok Szimplex módszer
 Lineáris programozás Modellalkotás Grafikus megoldás Feladattípusok Szimplex módszer Feladat: Egy gyár kétféle terméket gyárt (A, B): /db Eladási ár 1000 800 Technológiai önköltség 400 300 Normaóraigény
Lineáris programozás Modellalkotás Grafikus megoldás Feladattípusok Szimplex módszer Feladat: Egy gyár kétféle terméket gyárt (A, B): /db Eladási ár 1000 800 Technológiai önköltség 400 300 Normaóraigény
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN
 GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten ANALÍZIS Készítette: Gábor Szakmai felel s: Gábor Vázlat 1 2 3 Nevezetes halmazok
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten ANALÍZIS Készítette: Gábor Szakmai felel s: Gábor Vázlat 1 2 3 Nevezetes halmazok
Idő és tér. Idő és tér. Tartalom. Megjegyzés
 Tartalom Az idő és tér fogalma és legfontosabb sajátosságaik. Megjegyzés Ez egy rövid, de meglehetősen elvont téma. Annyiból érdekes, hogy tér és idő a világunk legalapvetőbb jellemzői, és mindannyian
Tartalom Az idő és tér fogalma és legfontosabb sajátosságaik. Megjegyzés Ez egy rövid, de meglehetősen elvont téma. Annyiból érdekes, hogy tér és idő a világunk legalapvetőbb jellemzői, és mindannyian
JANUS PANNONIUS TUDOMÁNYEGYETEM. Schipp Ferenc ANALÍZIS I. Sorozatok és sorok
 JANUS PANNONIUS TUDOMÁNYEGYETEM Schipp Ferenc ANALÍZIS I. Sorozatok és sorok Pécs, 1994 Lektorok: Dr. FEHÉR JÁNOS egyetemi docens, kandidtus. Dr. SIMON PÉTER egyetemi docens, kandidtus 1 Előszó Ez a jegyzet
JANUS PANNONIUS TUDOMÁNYEGYETEM Schipp Ferenc ANALÍZIS I. Sorozatok és sorok Pécs, 1994 Lektorok: Dr. FEHÉR JÁNOS egyetemi docens, kandidtus. Dr. SIMON PÉTER egyetemi docens, kandidtus 1 Előszó Ez a jegyzet
Elméleti közgazdaságtan I.
 Elméleti közgazdaságtan I. lapfogalmak és Mikroökonómia FOGYSZTÓI MGTRTÁS (I. rész) fogasztói preferenciák Eg játék fogasztónak felkínálunk két kosarat azzal, hog bármelik az övé lehet minden egéb feltétel
Elméleti közgazdaságtan I. lapfogalmak és Mikroökonómia FOGYSZTÓI MGTRTÁS (I. rész) fogasztói preferenciák Eg játék fogasztónak felkínálunk két kosarat azzal, hog bármelik az övé lehet minden egéb feltétel
Válasz Páles Zsolt opponensi véleményére
 Válasz az opponenseknek Köszönöm az opponensek elismerő szavait és a játékelmélet szerepének az értekezésen túlmutató pozitív értékelését. A bírálatra válaszaimat a bírálóknak külön-külön tételesen, az
Válasz az opponenseknek Köszönöm az opponensek elismerő szavait és a játékelmélet szerepének az értekezésen túlmutató pozitív értékelését. A bírálatra válaszaimat a bírálóknak külön-külön tételesen, az
Adó: kényszer útján beszedett pénzösszeg, amellyel szemben közvetlen ellenszolgáltatás nem követelhető Adósságcsapda: kezelése hitelfelvétellel
 Adó: kényszer útján beszedett pénzösszeg, amellyel szemben közvetlen ellenszolgáltatás nem követelhető Adósságcsapda: kezelése hitelfelvétellel történik Alacsony (inferior) javak: azok melynek jöv.rugja.
Adó: kényszer útján beszedett pénzösszeg, amellyel szemben közvetlen ellenszolgáltatás nem követelhető Adósságcsapda: kezelése hitelfelvétellel történik Alacsony (inferior) javak: azok melynek jöv.rugja.
Analízis előadás és gyakorlat vázlat
 Analízis előadás és gyakorlat vázlat Készült a PTE TTK GI szakos hallgatóinak Király Balázs 00-. I. Félév . fejezet Számhalmazok és tulajdonságaik.. Nevezetes számhalmazok ➀ a) jelölése: N b) elemei:
Analízis előadás és gyakorlat vázlat Készült a PTE TTK GI szakos hallgatóinak Király Balázs 00-. I. Félév . fejezet Számhalmazok és tulajdonságaik.. Nevezetes számhalmazok ➀ a) jelölése: N b) elemei:
Csődvalószínűségek becslése a biztosításban
 Csődvalószínűségek becslése a biztosításban Diplomamunka Írta: Deák Barbara Matematikus szak Témavezető: Arató Miklós, egyetemi docens Valószínűségelméleti és Statisztika Tanszék Eötvös Loránd Tudományegyetem,
Csődvalószínűségek becslése a biztosításban Diplomamunka Írta: Deák Barbara Matematikus szak Témavezető: Arató Miklós, egyetemi docens Valószínűségelméleti és Statisztika Tanszék Eötvös Loránd Tudományegyetem,
Matematikai programozás gyakorlatok
 VÁRTERÉSZ MAGDA Matematikai programozás gyakorlatok 2003/04-es tanév 1. félév Tartalomjegyzék 1. Számrendszerek 3 1.1. Javasolt órai feladat.............................. 3 1.2. Javasolt házi feladatok.............................
VÁRTERÉSZ MAGDA Matematikai programozás gyakorlatok 2003/04-es tanév 1. félév Tartalomjegyzék 1. Számrendszerek 3 1.1. Javasolt órai feladat.............................. 3 1.2. Javasolt házi feladatok.............................
Kőszegi Irén MATEMATIKA. 9. évfolyam
 -- Kőszegi Irén MATEMATIKA 9. évfolyam (a b) 2 = a 2 2ab + b 2 2015 1 2 Tartalom 1. HALMAZOK... 5 2. SZÁMHALMAZOK... 8 3. HATVÁNYOK... 12 4. OSZTHATÓSÁG... 14 5. ALGEBRAI KIFEJEZÉSEK... 17 6. FÜGGVÉNYEK...
-- Kőszegi Irén MATEMATIKA 9. évfolyam (a b) 2 = a 2 2ab + b 2 2015 1 2 Tartalom 1. HALMAZOK... 5 2. SZÁMHALMAZOK... 8 3. HATVÁNYOK... 12 4. OSZTHATÓSÁG... 14 5. ALGEBRAI KIFEJEZÉSEK... 17 6. FÜGGVÉNYEK...
Mesterséges intelligencia, 7. előadás 2008. október 13. Készítette: Masa Tibor (KPM V.)
 Mesterséges intelligencia, 7. előadás 2008. október 13. Készítette: Masa Tibor (KPM V.) Bizonytalanságkezelés: Az eddig vizsgáltakhoz képest teljesen más világ. A korábbi problémák nagy része logikai,
Mesterséges intelligencia, 7. előadás 2008. október 13. Készítette: Masa Tibor (KPM V.) Bizonytalanságkezelés: Az eddig vizsgáltakhoz képest teljesen más világ. A korábbi problémák nagy része logikai,
4. sz. Füzet. A hibafa számszerű kiértékelése 2002.
 M Ű S Z A K I B I Z O N S Á G I F Ő F E L Ü G Y E L E 4. sz. Füzet A hibafa számszerű kiértékelése 00. Sem a Műszaki Biztonsági Főfelügyelet, sem annak nevében, képviseletében vagy részéről eljáró személy
M Ű S Z A K I B I Z O N S Á G I F Ő F E L Ü G Y E L E 4. sz. Füzet A hibafa számszerű kiértékelése 00. Sem a Műszaki Biztonsági Főfelügyelet, sem annak nevében, képviseletében vagy részéről eljáró személy
Mikroökonómia szeminárium 2. Konzultáció
 Mikroökonómia szeminárium 2. Konzultáció Révész Sándor Budapesti Corvinus Egyetem Makroökonómia Tanszék 2011. október 12. Tesztek - Preferenciák, közömbösségi görbék Egy közömbösségi görbe mentén biztosan
Mikroökonómia szeminárium 2. Konzultáció Révész Sándor Budapesti Corvinus Egyetem Makroökonómia Tanszék 2011. október 12. Tesztek - Preferenciák, közömbösségi görbék Egy közömbösségi görbe mentén biztosan
BEVEZETÉS AZ ÁBRÁZOLÓ GEOMETRIÁBA
 Pék Johanna BEVEZETÉS AZ ÁBRÁZOLÓ GEOMETRIÁBA (Matematika tanárszakos hallgatók számára) Tartalomjegyzék Előszó ii 0. Alapismeretek 1 0.1. Térgeometriai alapok............................. 1 0.2. Az ábrázoló
Pék Johanna BEVEZETÉS AZ ÁBRÁZOLÓ GEOMETRIÁBA (Matematika tanárszakos hallgatók számára) Tartalomjegyzék Előszó ii 0. Alapismeretek 1 0.1. Térgeometriai alapok............................. 1 0.2. Az ábrázoló
Geometriai axiómarendszerek és modellek
 Verhóczki László Geometriai axiómarendszerek és modellek ELTE TTK Matematikai Intézet Geometriai Tanszék Budapest, 2011 1) Az axiómákra vonatkozó alapvető ismeretek Egy matematikai elmélet felépítésének
Verhóczki László Geometriai axiómarendszerek és modellek ELTE TTK Matematikai Intézet Geometriai Tanszék Budapest, 2011 1) Az axiómákra vonatkozó alapvető ismeretek Egy matematikai elmélet felépítésének
Közbeszerzési referens képzés Gazdasági és pénzügyi ismeretek modul 1. alkalom. A közgazdaságtan alapfogalmai Makro- és mikroökonómiai alapfogalmak
 Közbeszerzési referens képzés Gazdasági és pénzügyi ismeretek modul 1. alkalom A közgazdaságtan alapfogalmai Makro- és mikroökonómiai alapfogalmak ALAPKÉRDÉSEK TISZTÁZÁSA I. A gazdasági törvények lényege:
Közbeszerzési referens képzés Gazdasági és pénzügyi ismeretek modul 1. alkalom A közgazdaságtan alapfogalmai Makro- és mikroökonómiai alapfogalmak ALAPKÉRDÉSEK TISZTÁZÁSA I. A gazdasági törvények lényege:
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN
 GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten LINEÁRIS PROGRAMOZÁS Készítette: Gábor Szakmai felel s: Gábor Vázlat 1 2 3 4 A lineáris
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten LINEÁRIS PROGRAMOZÁS Készítette: Gábor Szakmai felel s: Gábor Vázlat 1 2 3 4 A lineáris
* Modern piacelmélet. ELTE TáTK Közgazdaságtudományi Tanszék. Tárgyfelelős neve * Modern piacelmélet Összejátszás, kartell
 * Modern piacelmélet ELTE TáTK Közgazdaságtudományi Tanszék Tárgyfelelős neve * Modern piacelmélet Összejátszás, kartell ELTE TáTK Közgazdaságtudományi Tanszék Készítette: Hidi János * Verseny és versenyellenesség
* Modern piacelmélet ELTE TáTK Közgazdaságtudományi Tanszék Tárgyfelelős neve * Modern piacelmélet Összejátszás, kartell ELTE TáTK Közgazdaságtudományi Tanszék Készítette: Hidi János * Verseny és versenyellenesség
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 5 V ELEmI ALGEbRA 1 BINÁRIS műveletek Definíció Az halmazon definiált bináris művelet egy olyan függvény, amely -ből képez -be Ha akkor az elempár képét jelöljük -vel, a művelet
KOVÁCS BÉLA, MATEmATIkA I 5 V ELEmI ALGEbRA 1 BINÁRIS műveletek Definíció Az halmazon definiált bináris művelet egy olyan függvény, amely -ből képez -be Ha akkor az elempár képét jelöljük -vel, a művelet
Tető nem állandó hajlású szarufákkal
 1 Tető nem állandó hajlású szarufákkal Már korábbi dolgozatainkban is szó volt a címbeli témáról. Most azért vettük újra elő, mert szép és érdekes ábrákat találtunk az interneten, ezzel kapcsolatban, és
1 Tető nem állandó hajlású szarufákkal Már korábbi dolgozatainkban is szó volt a címbeli témáról. Most azért vettük újra elő, mert szép és érdekes ábrákat találtunk az interneten, ezzel kapcsolatban, és
ÉLETPÁLYA- ÉPÍTÉS MATEMATIKA TANÁRI ÚTMUTATÓ KOMPETENCIATERÜLET B. 6. évfolyam
 ÉLETPÁLYA- ÉPÍTÉS KOMPETENCIATERÜLET B MATEMATIKA TANÁRI ÚTMUTATÓ 6. évfolyam A kiadvány az Educatio Kht. kompetenciafejlesztő oktatási program kerettanterve alapján készült. A kiadvány a Nemzeti Fejlesztési
ÉLETPÁLYA- ÉPÍTÉS KOMPETENCIATERÜLET B MATEMATIKA TANÁRI ÚTMUTATÓ 6. évfolyam A kiadvány az Educatio Kht. kompetenciafejlesztő oktatási program kerettanterve alapján készült. A kiadvány a Nemzeti Fejlesztési
Valószínűségszámítás
 Eszterházy Károly Főiskola Matematikai és Informatikai Intézet Tómács Tibor Valószínűségszámítás programtervező informatikusok részére Eger, 010. szeptember 0. Tartalomjegyzék 1. Véletlen események...............................
Eszterházy Károly Főiskola Matematikai és Informatikai Intézet Tómács Tibor Valószínűségszámítás programtervező informatikusok részére Eger, 010. szeptember 0. Tartalomjegyzék 1. Véletlen események...............................
MATEMATIKA 1-12. ÉVFOLYAM
 MATEMATIKA 1-12. ÉVFOLYAM SZERZŐK: Veppert Károlyné, Ádám Imréné, Heibl Sándorné, Rimainé Sz. Julianna, Kelemen Ildikó, Antalfiné Kutyifa Zsuzsanna, Grószné Havasi Rózsa 1 1-2. ÉVFOLYAM Gondolkodási, megismerési
MATEMATIKA 1-12. ÉVFOLYAM SZERZŐK: Veppert Károlyné, Ádám Imréné, Heibl Sándorné, Rimainé Sz. Julianna, Kelemen Ildikó, Antalfiné Kutyifa Zsuzsanna, Grószné Havasi Rózsa 1 1-2. ÉVFOLYAM Gondolkodási, megismerési
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Geometria I.
 Geometria I. Alapfogalmak: Az olyan fogalmakat, amelyeket nem tudunk egyszerűbb fogalmakra visszavezetni, alapfogalmaknak nevezzük, s ezeket nem definiáljuk. Pl.: pont, egyenes, sík, tér, illeszkedés.
Geometria I. Alapfogalmak: Az olyan fogalmakat, amelyeket nem tudunk egyszerűbb fogalmakra visszavezetni, alapfogalmaknak nevezzük, s ezeket nem definiáljuk. Pl.: pont, egyenes, sík, tér, illeszkedés.
Természetes számok: a legegyszerűbb halmazok elemeinek. halmazokat alkothatunk, ezek elemszámai természetes 3+2=5
 1. Valós számok (ismétlés) Természetes számok: a legegyszerűbb halmazok elemeinek megszámlálására használjuk őket: N := {1, 2, 3,...,n,...} Például, egy zsák bab felhasználásával babszemekből halmazokat
1. Valós számok (ismétlés) Természetes számok: a legegyszerűbb halmazok elemeinek megszámlálására használjuk őket: N := {1, 2, 3,...,n,...} Például, egy zsák bab felhasználásával babszemekből halmazokat
Hosszú élettartamú fényforrások megbízhatóságának vizsgálata Tóth Zoltán. 1. Bevezetés
 Tóth Zoltán A cikk bemutatja, hogy tipikusan milyen formában adják meg a gyártók az élettartamgörbéket, ezek különböző fajtáit, hogyan kell értelmezni őket. Kitér néhány felhasználási területetre, például
Tóth Zoltán A cikk bemutatja, hogy tipikusan milyen formában adják meg a gyártók az élettartamgörbéket, ezek különböző fajtáit, hogyan kell értelmezni őket. Kitér néhány felhasználási területetre, például
Matematikai modellalkotás
 Konferencia A Korszerű Oktatásért Almássy Téri Szabadidőközpont, 2004. november 22. Matematikai modellalkotás (ötletek, javaslatok) Kosztolányi József I. Elméleti kitekintés oktatási koncepciók 1. Realisztikus
Konferencia A Korszerű Oktatásért Almássy Téri Szabadidőközpont, 2004. november 22. Matematikai modellalkotás (ötletek, javaslatok) Kosztolányi József I. Elméleti kitekintés oktatási koncepciók 1. Realisztikus
Dualitás Dualitási tételek Általános LP feladat Komplementáris lazaság 2015/2016-2. Szegedi Tudományegyetem Informatikai Tanszékcsoport
 Operációkutatás I. 2015/2016-2. Szegedi Tudományegyetem Informatikai Tanszékcsoport Számítógépes Optimalizálás Tanszék 6. Előadás Árazási interpretáció Tekintsük újra az erőforrás allokációs problémát
Operációkutatás I. 2015/2016-2. Szegedi Tudományegyetem Informatikai Tanszékcsoport Számítógépes Optimalizálás Tanszék 6. Előadás Árazási interpretáció Tekintsük újra az erőforrás allokációs problémát
4. modul Poliéderek felszíne, térfogata
 Matematika A 1. évfolyam 4. modul Poliéderek felszíne, térfogata Készítette: Vidra Gábor Matematika A 1. évfolyam 4. modul: POLIÉDEREK FELSZÍNE, TÉRFOGATA Tanári útmutató A modul célja Időkeret Ajánlott
Matematika A 1. évfolyam 4. modul Poliéderek felszíne, térfogata Készítette: Vidra Gábor Matematika A 1. évfolyam 4. modul: POLIÉDEREK FELSZÍNE, TÉRFOGATA Tanári útmutató A modul célja Időkeret Ajánlott
III. rész: A VÁLLALATI MAGATARTÁS
 III. rész: A VÁAATI MAGATARTÁS Az árupiacon a kínálati oldalon a termelőegységek, a vállalatok állnak. A vállalatok különböznek tevékenységük, méretük, tulajdonformájuk szerint. Különböző vállalatok közös
III. rész: A VÁAATI MAGATARTÁS Az árupiacon a kínálati oldalon a termelőegységek, a vállalatok állnak. A vállalatok különböznek tevékenységük, méretük, tulajdonformájuk szerint. Különböző vállalatok közös
ERWIN PANOFSKY: GÓTIKUS ÉPÍTÉSZET ÉS SKOLASZTIKUS GONDOLKODÁS
 Mindezt figyelembe véve elmondhatjuk, hogy ez a könyv szellemi életünk kiterebélyesedéséről tanúskodik. Arról, hogy már van olyan értelmiségi erőnk, amely képessé tesz bennünket arra, hogy vállalkozzunk
Mindezt figyelembe véve elmondhatjuk, hogy ez a könyv szellemi életünk kiterebélyesedéséről tanúskodik. Arról, hogy már van olyan értelmiségi erőnk, amely képessé tesz bennünket arra, hogy vállalkozzunk
MATEMATIKA C 8. évfolyam 6. modul ATTÓL FÜGG?
 MATEMATIKA C 8. évfolyam 6. modul ATTÓL FÜGG? Készítette: Surányi Szabolcs MATEMATIKA C 8. ÉVFOLYAM 6. MODUL: ATTÓL FÜGG? TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
MATEMATIKA C 8. évfolyam 6. modul ATTÓL FÜGG? Készítette: Surányi Szabolcs MATEMATIKA C 8. ÉVFOLYAM 6. MODUL: ATTÓL FÜGG? TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
5. Trigonometria. 2 cos 40 cos 20 sin 20. BC kifejezés pontos értéke?
 5. Trigonometria I. Feladatok 1. Mutassuk meg, hogy cos 0 cos 0 sin 0 3. KöMaL 010/október; C. 108.. Az ABC háromszög belsejében lévő P pontra PAB PBC PCA φ. Mutassuk meg, hogy ha a háromszög szögei α,
5. Trigonometria I. Feladatok 1. Mutassuk meg, hogy cos 0 cos 0 sin 0 3. KöMaL 010/október; C. 108.. Az ABC háromszög belsejében lévő P pontra PAB PBC PCA φ. Mutassuk meg, hogy ha a háromszög szögei α,
EGÉSZSÉGÜGYI DÖNTÉS ELŐKÉSZÍTŐ
 EGÉSZSÉGÜGYI DÖNTÉS ELŐKÉSZÍTŐ MODELLEZÉS Brodszky Valentin, Jelics-Popa Nóra, Péntek Márta BCE Közszolgálati Tanszék A tananyag a TÁMOP-4.1.2/A/2-10/1-2010-0003 "Képzés- és tartalomfejlesztés a Budapesti
EGÉSZSÉGÜGYI DÖNTÉS ELŐKÉSZÍTŐ MODELLEZÉS Brodszky Valentin, Jelics-Popa Nóra, Péntek Márta BCE Közszolgálati Tanszék A tananyag a TÁMOP-4.1.2/A/2-10/1-2010-0003 "Képzés- és tartalomfejlesztés a Budapesti
MATEMATIKA 9. osztály Segédanyag 4 óra/hét
 MATEMATIKA 9. osztály Segédanyag 4 óra/hét - 1 - Az óraszámok az AROMOBAN követhetőek nyomon! A tananyag feldolgozása a SOKSZÍNŰ MATEMATIKA (Mozaik, 013) tankönyv és a SOKSZÍNŰ MATEMATIKA FELADATGYŰJTEMÉNY
MATEMATIKA 9. osztály Segédanyag 4 óra/hét - 1 - Az óraszámok az AROMOBAN követhetőek nyomon! A tananyag feldolgozása a SOKSZÍNŰ MATEMATIKA (Mozaik, 013) tankönyv és a SOKSZÍNŰ MATEMATIKA FELADATGYŰJTEMÉNY
A kvantummechanika általános formalizmusa
 A kvantummechanika általános formalizmusa October 4, 2006 Jelen fejezetünk célja bevezetni egy általános matematikai formalizmust amelynek segítségével a végtelen dimenziós vektorterek elegánsan tárgyalhatók.
A kvantummechanika általános formalizmusa October 4, 2006 Jelen fejezetünk célja bevezetni egy általános matematikai formalizmust amelynek segítségével a végtelen dimenziós vektorterek elegánsan tárgyalhatók.
Hraskó András, Surányi László: 11-12. spec.mat szakkör Tartotta: Surányi László. Feladatok
 Feladatok 1. Színezzük meg a koordinátarendszer rácspontjait két színnel, kékkel és pirossal úgy, hogy minden vízszintes egyenesen csak véges sok kék rácspont legyen és minden függőleges egyenesen csak
Feladatok 1. Színezzük meg a koordinátarendszer rácspontjait két színnel, kékkel és pirossal úgy, hogy minden vízszintes egyenesen csak véges sok kék rácspont legyen és minden függőleges egyenesen csak
építészeti mű leírás_2007. június 26.
 építészeti mű leírás_2007. június 26. BEVEZETÉS, HELYSZÍN A keszthelyi Georgikon Egyetem Mezőgazdaságtudományi kar Állatélettani és Takarmányozási Tanszékének professzorai az elmúlt években több tanulmányt
építészeti mű leírás_2007. június 26. BEVEZETÉS, HELYSZÍN A keszthelyi Georgikon Egyetem Mezőgazdaságtudományi kar Állatélettani és Takarmányozási Tanszékének professzorai az elmúlt években több tanulmányt
MATEMATIKA GYAKORLÓ FELADATGYŰJTEMÉNY
 MATEMATIKA GYAKORLÓ FELADATGYŰJTEMÉNY (Kezdő 9. évfolyam) A feladatokat a Borbás Lászlóné MATEMATIKA a nyelvi előkészítő évfolyamok számára című könyv alapján állítottuk össze. I. Számok, műveletek számokkal.
MATEMATIKA GYAKORLÓ FELADATGYŰJTEMÉNY (Kezdő 9. évfolyam) A feladatokat a Borbás Lászlóné MATEMATIKA a nyelvi előkészítő évfolyamok számára című könyv alapján állítottuk össze. I. Számok, műveletek számokkal.
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Matematika emelt szint 0613 ÉRETTSÉGI VIZSGA 007. május 8. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Formai előírások: Fontos tudnivalók
Matematika emelt szint 0613 ÉRETTSÉGI VIZSGA 007. május 8. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Formai előírások: Fontos tudnivalók
(11) Lajstromszám: E 004 142 (13) T2 EURÓPAI SZABADALOM SZÖVEGÉNEK FORDÍTÁSA
 !HU000004142T2! (19) HU (11) Lajstromszám: E 004 142 (13) T2 MAGYAR KÖZTÁRSASÁG Magyar Szabadalmi Hivatal EURÓPAI SZABADALOM SZÖVEGÉNEK FORDÍTÁSA (21) Magyar ügyszám: E 04 72816 (22) A bejelentés napja:
!HU000004142T2! (19) HU (11) Lajstromszám: E 004 142 (13) T2 MAGYAR KÖZTÁRSASÁG Magyar Szabadalmi Hivatal EURÓPAI SZABADALOM SZÖVEGÉNEK FORDÍTÁSA (21) Magyar ügyszám: E 04 72816 (22) A bejelentés napja:
2) = 0 ahol x 1 és x 2 az ax 2 + bx + c = 0 ( a,b, c R és a 0 )
 Fogalom gyűjtemény Abszcissza: az x tengely Abszolút értékes egyenletek: azok az egyenletek, amelyekben abszolút érték jel szerepel. Abszolútérték-függvény: egy elemi egyváltozós valós függvény, mely minden
Fogalom gyűjtemény Abszcissza: az x tengely Abszolút értékes egyenletek: azok az egyenletek, amelyekben abszolút érték jel szerepel. Abszolútérték-függvény: egy elemi egyváltozós valós függvény, mely minden
SZÁMOLÁSTECHNIKAI ISMERETEK
 SZÁMOLÁSTECHNIKAI ISMERETEK Műveletek szögekkel Geodéziai számításaink során gyakran fogunk szögekkel dolgozni. Az egyszerűbb írásmód kedvéért ilyenkor a fok ( o ), perc (, ), másodperc (,, ) jelét el
SZÁMOLÁSTECHNIKAI ISMERETEK Műveletek szögekkel Geodéziai számításaink során gyakran fogunk szögekkel dolgozni. Az egyszerűbb írásmód kedvéért ilyenkor a fok ( o ), perc (, ), másodperc (,, ) jelét el
Környezetszabályozás elméleti alapjai
 Környezetszabályozás elméleti alapjai PTE PMMIK Környezetmérnök BSc Dr. Kiss Tibor Tudományos főmunkatárs PTE PMMIK Környezetmérnöki Tanszék Terepbejárás 2015.04.30 Összevont Településgazgálkodás- és üzemeltetés
Környezetszabályozás elméleti alapjai PTE PMMIK Környezetmérnök BSc Dr. Kiss Tibor Tudományos főmunkatárs PTE PMMIK Környezetmérnöki Tanszék Terepbejárás 2015.04.30 Összevont Településgazgálkodás- és üzemeltetés
Vargha András PSZICHOLÓGIAI STATISZTIKA DIÓHÉJBAN 1. X.1. táblázat: Egy iskolai bizonyítvány. Magyar irodalom. Biológia Földrajz
 Megjelent: Vargha A. (7). Pszichológiai statisztika dióhéjban. In: Czigler I. és Oláh A. (szerk.), Találkozás a pszichológiával. Osiris Kiadó, Budapest, 7-46. Mi az, hogy statisztika? Vargha András PSZICHOLÓGIAI
Megjelent: Vargha A. (7). Pszichológiai statisztika dióhéjban. In: Czigler I. és Oláh A. (szerk.), Találkozás a pszichológiával. Osiris Kiadó, Budapest, 7-46. Mi az, hogy statisztika? Vargha András PSZICHOLÓGIAI
14. előadás JÓLÉTI TÉTELEK
 4. előadás JÓLÉTI TÉTELEK Kertesi Gábor Varian 9. fejezetének 9-3. alfejezetei átdolgozva 4. evezető Ennek az előadásnak a során az előző órán vett kéttermékes, kétszereplős, termelés nélküli általános
4. előadás JÓLÉTI TÉTELEK Kertesi Gábor Varian 9. fejezetének 9-3. alfejezetei átdolgozva 4. evezető Ennek az előadásnak a során az előző órán vett kéttermékes, kétszereplős, termelés nélküli általános
AZ ORSZÁGOS RÁDIÓ ÉS TELEVÍZIÓ TESTÜLET 222/2010. (II.3.) VÉGZÉSE
 AZ ORSZÁGOS RÁDIÓ ÉS TELEVÍZIÓ TESTÜLET 222/2010. (II.3.) VÉGZÉSE Az Országos Rádió és Televízió Testület (a továbbiakban: Testület) a rádiózásról és televíziózásról szóló 1996. évi I. törvény (a továbbiakban:
AZ ORSZÁGOS RÁDIÓ ÉS TELEVÍZIÓ TESTÜLET 222/2010. (II.3.) VÉGZÉSE Az Országos Rádió és Televízió Testület (a továbbiakban: Testület) a rádiózásról és televíziózásról szóló 1996. évi I. törvény (a továbbiakban:
A racionalitás értelmezése és korlátai a közgazdaságtanban
 A racionalitás értelmezése és korlátai a közgazdaságtanban Kovács Máté 2010. szeptember 30. Kivonat A munkában a közgazdasági racionalitás értelmezési lehetőségeit vizsgáljuk. Miután számba vettük a lehetőségeket,
A racionalitás értelmezése és korlátai a közgazdaságtanban Kovács Máté 2010. szeptember 30. Kivonat A munkában a közgazdasági racionalitás értelmezési lehetőségeit vizsgáljuk. Miután számba vettük a lehetőségeket,
II. A következtetési statisztika alapfogalmai
 II. A következtetési statisztika alapfogalmai Tartalom Statisztikai következtetések A véletlen minta fogalma Pontbecslés és hibája Intervallumbecslés A hipotézisvizsgálat alapfogalmai A legegyszerűbb statisztikai
II. A következtetési statisztika alapfogalmai Tartalom Statisztikai következtetések A véletlen minta fogalma Pontbecslés és hibája Intervallumbecslés A hipotézisvizsgálat alapfogalmai A legegyszerűbb statisztikai
KB: Jövőre lesz 60 éve, hogy üzembe állították a világ első atomerőművét, amely 1954-ben Obnyinszkban kezdte meg működését.
 Kossuth Rádió, Krónika, 2013.10.18. Közelről MV: Jó napot kívánok mindenkinek, azoknak is akik most kapcsolódnak be. Kedvükért is mondom, hogy mivel fogunk foglalkozunk ebben az órában itt a Kossuth Rádióban.
Kossuth Rádió, Krónika, 2013.10.18. Közelről MV: Jó napot kívánok mindenkinek, azoknak is akik most kapcsolódnak be. Kedvükért is mondom, hogy mivel fogunk foglalkozunk ebben az órában itt a Kossuth Rádióban.
9. modul Szinusz- és koszinusztétel. Készítette: Csákvári Ágnes
 9. modul Szinusz- és koszinusztétel Készítette: Csákvári Ágnes Matematika A 11. évfolyam 9. modul: Szinusz- és koszinusztétel Tanári útmutató A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
9. modul Szinusz- és koszinusztétel Készítette: Csákvári Ágnes Matematika A 11. évfolyam 9. modul: Szinusz- és koszinusztétel Tanári útmutató A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
Matematikai és matematikai statisztikai alapismeretek
 Kézirat a Matematikai és matematikai statisztikai alapismeretek című előadáshoz Dr. Győri István NEVELÉSTUDOMÁNYI PH.D. PROGRM 1999/2000 1 1. MTEMTIKI LPOGLMK 1.1. Halmazok Halmazon mindig bizonyos dolgok
Kézirat a Matematikai és matematikai statisztikai alapismeretek című előadáshoz Dr. Győri István NEVELÉSTUDOMÁNYI PH.D. PROGRM 1999/2000 1 1. MTEMTIKI LPOGLMK 1.1. Halmazok Halmazon mindig bizonyos dolgok
Lineáris Algebra gyakorlatok
 A V 2 és V 3 vektortér áttekintése Lineáris Algebra gyakorlatok Írta: Simon Ilona Lektorálta: DrBereczky Áron Áttekintjük néhány témakör legfontosabb definícióit és a feladatokban használt tételeket kimondjuk
A V 2 és V 3 vektortér áttekintése Lineáris Algebra gyakorlatok Írta: Simon Ilona Lektorálta: DrBereczky Áron Áttekintjük néhány témakör legfontosabb definícióit és a feladatokban használt tételeket kimondjuk
Tómács Tibor. Matematikai statisztika
 Tómács Tibor Matematikai statisztika Eszterházy Károly Főiskola Matematikai és Informatikai Intézet Tómács Tibor Matematikai statisztika Eger, 01 Szerző: Dr. Tómács Tibor főiskolai docens Eszterházy Károly
Tómács Tibor Matematikai statisztika Eszterházy Károly Főiskola Matematikai és Informatikai Intézet Tómács Tibor Matematikai statisztika Eger, 01 Szerző: Dr. Tómács Tibor főiskolai docens Eszterházy Károly
Gondolkodjunk a fizika segı tse ge vel!
 SZAKDOLGOZAT Gondolkodjunk a fizika segı tse ge vel! Simon Ju lia Matematika BSc., tana ri szakira ny Te mavezeto : Besenyei A da m adjunktus Alkalmazott Analı zis e s Sza mı ta smatematikai Tansze k Eo
SZAKDOLGOZAT Gondolkodjunk a fizika segı tse ge vel! Simon Ju lia Matematika BSc., tana ri szakira ny Te mavezeto : Besenyei A da m adjunktus Alkalmazott Analı zis e s Sza mı ta smatematikai Tansze k Eo
A felmérési egység kódja:
 A felmérési egység lajstromszáma: 0056 ÚMFT Programiroda A felmérési egység adatai A felmérési egység kódja: A kódrészletek jelentése: Iterköz//30/Rea//Ált Informatika közös szakképesítés-csoportban, a
A felmérési egység lajstromszáma: 0056 ÚMFT Programiroda A felmérési egység adatai A felmérési egység kódja: A kódrészletek jelentése: Iterköz//30/Rea//Ált Informatika közös szakképesítés-csoportban, a
Valószín ségelmélet házi feladatok
 Valószín ségelmélet házi feladatok Minden héten 3-4 házi feladatot adok ki. A megoldásokat a következ órán kell beadni, és kés bb már nem lehet pótolni. Csak az mehet vizsgázni, aki a 13 hét során kiadott
Valószín ségelmélet házi feladatok Minden héten 3-4 házi feladatot adok ki. A megoldásokat a következ órán kell beadni, és kés bb már nem lehet pótolni. Csak az mehet vizsgázni, aki a 13 hét során kiadott
MATEMATIKA A 10. évfolyam
 MATEMATIKA A 10. évfolyam 8. modul Hasonlóság és alkalmazásai Készítették: Vidra Gábor, Lénárt István Matematika A 10. évfolyam 8. modul: Hasonlóság és alkalmazásai A modul célja Időkeret Ajánlott korosztály
MATEMATIKA A 10. évfolyam 8. modul Hasonlóság és alkalmazásai Készítették: Vidra Gábor, Lénárt István Matematika A 10. évfolyam 8. modul: Hasonlóság és alkalmazásai A modul célja Időkeret Ajánlott korosztály
Vektorszámítás Fizika tanárszak I. évfolyam
 Vektorszámítás Fizika tanárszak I. évfolyam Lengyel Krisztián TARTALOMJEGYZÉK Tartalomjegyzék. Deriválás.. Elmélet........................................... Deriválási szabályok..................................
Vektorszámítás Fizika tanárszak I. évfolyam Lengyel Krisztián TARTALOMJEGYZÉK Tartalomjegyzék. Deriválás.. Elmélet........................................... Deriválási szabályok..................................
Működési kockázati önértékelések veszteségeloszlás-alapú modellezése
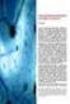 506 HITELINTÉZETI SZEMLE HAJNAL BÉLA KÁLLAI ZOLTÁN NAGY GÁBOR Működési kockázati önértékelések veszteségeloszlás-alapú modellezése Tanulmányunkban a működési kockázatok önértékelésen alapuló modellezését
506 HITELINTÉZETI SZEMLE HAJNAL BÉLA KÁLLAI ZOLTÁN NAGY GÁBOR Működési kockázati önértékelések veszteségeloszlás-alapú modellezése Tanulmányunkban a működési kockázatok önértékelésen alapuló modellezését
MUNKAANYAG. Szabó László. Szilárdságtan. A követelménymodul megnevezése:
 Szabó László Szilárdságtan A követelménymodul megnevezése: Kőolaj- és vegyipari géprendszer üzemeltetője és vegyipari technikus feladatok A követelménymodul száma: 047-06 A tartalomelem azonosító száma
Szabó László Szilárdságtan A követelménymodul megnevezése: Kőolaj- és vegyipari géprendszer üzemeltetője és vegyipari technikus feladatok A követelménymodul száma: 047-06 A tartalomelem azonosító száma
Load-flow jellegű feladat a villamos rendszerirányításban
 NASZVADI PÉTER Load-flow jellegű feladat a villamos rendszerirányításban TDK dolgozat 2006 Előszó: Adott egy (villamosenergiaellátást biztosító) villamoshálózat, és ezen hálózathoz csatlakozó energiatermelők
NASZVADI PÉTER Load-flow jellegű feladat a villamos rendszerirányításban TDK dolgozat 2006 Előszó: Adott egy (villamosenergiaellátást biztosító) villamoshálózat, és ezen hálózathoz csatlakozó energiatermelők
2. OPTIKA 2.1. Elmélet 2.1.1. Geometriai optika
 2. OPTIKA 2.1. Elmélet Az optika tudománya a látás élményéből fejlődött ki. A tárgyakat azért látjuk, mert fényt bocsátanak ki, vagy a rájuk eső fényt visszaverik, és ezt a fényt a szemünk érzékeli. A
2. OPTIKA 2.1. Elmélet Az optika tudománya a látás élményéből fejlődött ki. A tárgyakat azért látjuk, mert fényt bocsátanak ki, vagy a rájuk eső fényt visszaverik, és ezt a fényt a szemünk érzékeli. A
Hipotézisvizsgálat. A sokaság valamely paraméteréről állítunk valamit,
 II. Hipotézisvizsgálat Lényege: A sokaság valamely paraméteréről állítunk valamit, majd az állításunk helyességét vizsgáljuk. A hipotézisvizsgálat eszköze: a statisztikai próba Menete: 1.Hipotézisek matematikai
II. Hipotézisvizsgálat Lényege: A sokaság valamely paraméteréről állítunk valamit, majd az állításunk helyességét vizsgáljuk. A hipotézisvizsgálat eszköze: a statisztikai próba Menete: 1.Hipotézisek matematikai
Áttekintés a felhasznált lineáris algebrai ismeretekről.
 Kiegészítés az előadássorozathoz. Áttekintés a felhasznált lineáris algebrai ismeretekről. A valószínűségszámítás (és a matematika) bizonyos kérdéseiben fontos szerepet játszik a lineáris algebra néhány
Kiegészítés az előadássorozathoz. Áttekintés a felhasznált lineáris algebrai ismeretekről. A valószínűségszámítás (és a matematika) bizonyos kérdéseiben fontos szerepet játszik a lineáris algebra néhány
Breitner Péter. országjelentžshez
 Breitner Péter Zárszó a 2009. Žvi hajlžktalanügyi országjelentžshez A hajléktalanügyben kifejtett, lassan húszéves munkánknak egyesek szerint nincs látszatja, mások azt állítják, hogy a segítők életfontosságú
Breitner Péter Zárszó a 2009. Žvi hajlžktalanügyi országjelentžshez A hajléktalanügyben kifejtett, lassan húszéves munkánknak egyesek szerint nincs látszatja, mások azt állítják, hogy a segítők életfontosságú
2.3.2.2.1.2.1 Visszatérítő nyomaték és visszatérítő kar
 2.3.2.2.1.2 Keresztirányú stabilitás nagy dőlésszögeknél A keresztirányú stabilitás számszerűsítésénél, amint korábban láttuk, korlátozott a metacentrikus magasságra való támaszkodás lehetősége. Csak olyankor
2.3.2.2.1.2 Keresztirányú stabilitás nagy dőlésszögeknél A keresztirányú stabilitás számszerűsítésénél, amint korábban láttuk, korlátozott a metacentrikus magasságra való támaszkodás lehetősége. Csak olyankor
Gyakorló feladatok a Közönséges dierenciálegyenletek kurzushoz
 Gyakorló feladatok a Közönséges dierenciálegyenletek kurzushoz Vas Gabriella 204. február A feladatgy jtemény a TÁMOP-4.2.4.A/2-/-202-000 azonosító számú Nemzeti Kiválóság Program Hazai hallgatói, illetve
Gyakorló feladatok a Közönséges dierenciálegyenletek kurzushoz Vas Gabriella 204. február A feladatgy jtemény a TÁMOP-4.2.4.A/2-/-202-000 azonosító számú Nemzeti Kiválóság Program Hazai hallgatói, illetve
Kutatási beszámoló. a KDOP-3.1.1/D2/13-k2-2013-0004 jelű, Szociális város-rehabilitáció Szárazréten elnevezésű projekt hatásának mérése
 Kutatási beszámoló a KDOP-3.1.1/D2/13-k2-2013-0004 jelű, Szociális város-rehabilitáció Szárazréten elnevezésű projekt hatásának mérése 2015. május Tartalomjegyzék I. A kutatás háttere... 3 II. Az empirikus
Kutatási beszámoló a KDOP-3.1.1/D2/13-k2-2013-0004 jelű, Szociális város-rehabilitáció Szárazréten elnevezésű projekt hatásának mérése 2015. május Tartalomjegyzék I. A kutatás háttere... 3 II. Az empirikus
Komáromi Éva LINEÁRIS PROGRAMOZÁS
 OPERÁCIÓKUTATÁS No.2. Komáromi Éva LINEÁRIS PROGRAMOZÁS Budapest 2005 Komáromi Éva LINEÁRIS PROGRAMOZÁS Javított kiadás OPERÁCIÓKUTATÁS No.2 Megjelenik az FKFP 0231 Program támogatásával a Budapesti Közgazdaságtudományi
OPERÁCIÓKUTATÁS No.2. Komáromi Éva LINEÁRIS PROGRAMOZÁS Budapest 2005 Komáromi Éva LINEÁRIS PROGRAMOZÁS Javított kiadás OPERÁCIÓKUTATÁS No.2 Megjelenik az FKFP 0231 Program támogatásával a Budapesti Közgazdaságtudományi
MIKROÖKONÓMIA II. B. Készítette: K hegyi Gergely. Szakmai felel s: K hegyi Gergely. 2011. február
 MIKROÖKONÓMIA II. B Készült a TÁMOP-4.1.2-08/2/a/KMR-2009-0041 pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék az MTA Közgazdaságtudományi
MIKROÖKONÓMIA II. B Készült a TÁMOP-4.1.2-08/2/a/KMR-2009-0041 pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék az MTA Közgazdaságtudományi
Lehet vagy nem? Konstrukciók és lehetetlenségi bizonyítások Dr. Katz Sándor, Bonyhád
 Dr. Katz Sándor: Lehet vagy nem? Lehet vagy nem? Konstrukciók és lehetetlenségi bizonyítások Dr. Katz Sándor, Bonyhád A kreativitás fejlesztésének legközvetlenebb módja a konstrukciós feladatok megoldása.
Dr. Katz Sándor: Lehet vagy nem? Lehet vagy nem? Konstrukciók és lehetetlenségi bizonyítások Dr. Katz Sándor, Bonyhád A kreativitás fejlesztésének legközvetlenebb módja a konstrukciós feladatok megoldása.
A rádió* I. Elektromos rezgések és hullámok.
 A rádió* I. Elektromos rezgések és hullámok. A legtöbb test dörzsölés, nyomás következtében elektromos töltést nyer. E töltéstől függ a test elektromos feszültsége, akárcsak a hőtartalomtól a hőmérséklete;
A rádió* I. Elektromos rezgések és hullámok. A legtöbb test dörzsölés, nyomás következtében elektromos töltést nyer. E töltéstől függ a test elektromos feszültsége, akárcsak a hőtartalomtól a hőmérséklete;
Országos kompetenciamérés. Országos jelentés
 Országos kompetenciamérés 2009 Országos jelentés Országos jelentés TARTALOMJEGYZÉK JOGSZABÁLYI HÁTTÉR... 7 A 2009. ÉVI ORSZÁGOS KOMPETENCIAMÉRÉS SZÁMOKBAN... 8 A FELMÉRÉSRŐL... 9 EREDMÉNYEK... 11 AJÁNLÁS...
Országos kompetenciamérés 2009 Országos jelentés Országos jelentés TARTALOMJEGYZÉK JOGSZABÁLYI HÁTTÉR... 7 A 2009. ÉVI ORSZÁGOS KOMPETENCIAMÉRÉS SZÁMOKBAN... 8 A FELMÉRÉSRŐL... 9 EREDMÉNYEK... 11 AJÁNLÁS...
IFJÚSÁG-NEVELÉS. Nevelés, gondolkodás, matematika
 IFJÚSÁG-NEVELÉS Nevelés, gondolkodás, matematika Érdeklődéssel olvastam a Korunk 1970. novemberi számában Édouard Labin cikkét: Miért érthetetlen a matematika? Egyetértek a cikk megállapításaival, a vázolt
IFJÚSÁG-NEVELÉS Nevelés, gondolkodás, matematika Érdeklődéssel olvastam a Korunk 1970. novemberi számában Édouard Labin cikkét: Miért érthetetlen a matematika? Egyetértek a cikk megállapításaival, a vázolt
AZ ÁLTALÁNOS ISKOLÁSOK IDEGENNYELV-TANULÁSI ATTITŰDJEI ÉS MOTIVÁCIÓJA
 MAGYAR PEDAGÓGIA 0. évf.. szám 5. (00) AZ ÁLTALÁNOS ISKOLÁSOK IDEGENNYELV-TANULÁSI ATTITŰDJEI ÉS MOTIVÁCIÓJA Csizér Kata és Dörnyei Zoltán Eötvös Loránd Tudományegyetem és Nottigham University Az általános
MAGYAR PEDAGÓGIA 0. évf.. szám 5. (00) AZ ÁLTALÁNOS ISKOLÁSOK IDEGENNYELV-TANULÁSI ATTITŰDJEI ÉS MOTIVÁCIÓJA Csizér Kata és Dörnyei Zoltán Eötvös Loránd Tudományegyetem és Nottigham University Az általános
