DIPLOMAMUNKA. Székely Péter 2004.
|
|
|
- József Vincze
- 6 évvel ezelőtt
- Látták:
Átírás
1 DIPLOMAMUNKA Székely Péter 2004.
2 SZEGEDI TUDOMÁNYEGYETEM Természettudományi Kar Kísérleti Fizikai Tanszék Csillagász szak DIPLOMAMUNKA Alulészlelt kisbolygók CCD-fotometriája Székely Péter Témavezető: Dr. Kiss L. László Konzulens: Dr. Kiss L. László 2004.
3 Összefoglaló Diplomamunkám célja, hogy bemutassa a tudományos célból végzett észlelés szempontjából elhanyagolt, vagy nem vizsgált kisbolygókon az elmúlt években végzett fotometriai méréseimet és azok eredményeit. Megfigyeléseim során számos aszteroidáról vettem fel fotometriai adatsort, melyek felhasználásával több esetben sikerült meghatározni a forgási periódusukat és a későbbiekben, reményeim szerint elvégzendő méréseimmel kiegészítve, lehetővé válik majd a hozzávetőleges alakmodellek elkészítése. A méréseket 2000 októbere és 2002 augusztusa között végeztem, összesen 37 éjszakán. Ezen vizsgálatok során mérési pontot vettem fel, de az elkészített CCD-felvételek száma ennél több, ugyanis ez a szám nem tartalmazza a flatképeket és a különböző okokból használhatatlannak bizonyult képeket. 138 kbyte-os képméretet véve a feldolgozott adatok terjedelme meghaladja az 1,3 Gbyte-ot. A munkám során elsődlegesen használt műszer a Szegedi Csillagvizsgáló 40 cm-es, nemrégiben felújított Cassegrain távcsöve volt, és az arra szerelt Santa Barbara Instruments Group Inc. ST 9E típusú CCD-kamera. Ezenkívül a Magyar Tudományos Akadémia Konkoly Thege Miklós Csillagászati Kutatóintézetének piszkéstetői 0,6/0,9/1,8 m-es Schmidt távcsövével és Photometrics AT-200 kamerájával dolgoztam. Diplomamunkám első részében ismertetem a kisbolygók fotometriai mérésének fontosságát, ezután kitérek a mérések tervezésére, az azoknál adódó buktatókra, valamint az adatfeldolgozás mikéntjére. A következő fejezetben részletesen beszámolok vizsgálataim eredményeiről, legvégül összefoglalást készítek az elvégzett munkáról. A diplomamunka mellékletében megtalálhatóak az adatok feldolgozása során használt programok forráskódjai, valamint az összes mérésemből származó fénygörbe is. 3
4 Tartalomjegyzék 1. Célkitűzések 5 2. A mérések tervezése Mit és hogyan észleljek? Az adatok feldolgozása Elért eredmények Kisbolygók Egyéb eredmények A 360 Carlova - HIP 9975 okkultációja A GSC fényváltozása Mérési adatok Összefoglalás Köszönetnyilvánítás 28 A. Mellékletek 29 A.1. Az adatok feldolgozása A.2. A medián képzése A.3. Fluxus azonos szintre hozása A.4. Összes mérésem fénygörbéje
5 1. Célkitűzések Több, mint 200 éve, hogy a palermói Giuseppe Piazzi csillagkatalógus készítése közben rábukkant egy elmozduló objektumra, amelyet ma az 1 es sorszámú Ceres nevű kisbolygóként ismerünk. Akkoriban a Naprendszer elképzelt szerkezete sokkal egyszerűbb volt az addig ismert 7 bolygóval. Az azóta eltelt két század számos új és az addigi ismereteket alaposan módosító felfedezéssel gazdagította a szűkebb kozmikus otthonunknak nevezhető Naprendszerről alkotott világképünket. Elég csak megemlítenünk a Kuiper-övet, a több száz csillagászati egységnyi afélium ponttal rendelkező tagjaival, vagy akár az Oort-felhőt a milliárdnyi fagyott üstökösmaggal. Tény, hogy az Univerzum tőlünk távol eső részei titkainak kifürkészésén túl továbbra sem szabad elhanyagolni a Naprendszer kutatását, már csak azért sem, mert a média által oly felkapott téma a Föld és egy kisbolygó esetleges ütközése szakavatott, biztos kezeléséhez pontos pályaszámításokra és a potenciális veszélyt jelentő objektumok felfedezésére, nyomon követésére feltétlen szükség van. Bolygórendszerünkről alkotott árnyalt és kifinomult képünk tudományos megértéséhez ezért is elengedhetetlen a kisbolygók kutatása. Naprendszerünk ezen kis égitestjeinek döntő többsége a Mars és a Jupiter pályája között kering, átlagosan 2-5 csillagászati egységre központi csillagunktól. Ezek a főövbeli kisbolygók. Az 1. ábrán, amely a Minor Planet Center honlapjáról származik, a sorszámozott kisbolygók láthatóak. Minden apró pötty egy-egy aszteroidát reprezentál. Látható, hogy a két említett bolygó közötti térség csillagászati mértékben zsúfoltnak tekinthető. Jelen dolgozatomban szereplő vizsgálataim az úgynevezett főövbeli kisbolygókra vonatkoznak. Ezek az égitestek több nagyobb méretű, a Jupiter erős gravitációs perturbációi miatt nagybolygóvá soha össze nem állt bolygócsíra építőanyagaiból keletkeztek. Az aszteroidák különböző családokba sorolhatóak. Ezen osztályozás alapja a családhoz tartozó égitestek bizonyos paramétereinek például a pálya fél nagytengelyének nagysága, az inklináció mértéke stb. hasonlósága. A család névadója legtöbbször az elsőként felfedezett ilyen tulajdonságú égitest. Az utóbbi években nagyarányú kutatás indult meg a Naprendszer külső tartományait benépesítő objektumok területén. A jövőben, amennyiben lehetőségem nyílik nagyobb távcsöveket használni, vizsgálataimat én is szeretném kiterjeszteni ezen égitestekre. /KBO, azaz Kuiper Belt Object/ Az úgynevezett TNO-k, azaz Trans Neptunian Object-ek száma ma (2002. november 13.) már 617, plusz a Plútó és Charon, valamint 7 darab kettős TNO. A Kentaurok, illetve SDO-k (Scattered Disk Object) száma Újabb megfigyelési és statisztikai vizsgálatok szerint a Naprendszerben hozzávetőleg tízmillió olyan kisbolygó található, melynek mérete eléri a 30 métert és keresztezheti a Föld 1 5
6 1. ábra. A Naprendszer belső vidéke pályáját. 2 Ez a méret a jelentős, szerencsére csak természeti és nem emberi katasztrófát okozó 1908-as híres Tunguz-meteorit karakterisztikus méretével vethető össze. Jelen dolgozatomban azonban hétköznapibb területen végzett munkámat mutatom be. A nagy égboltfelmérő és automatikus kisbolygó kereső programoknak köszönhetően elképesztő ütemben gyarapodik az ismert aszteroidák száma. Havonta néhány ezer új objektummal gyarapszik a felfedezett kisbolygók listája, azonban a pályaelemek és a fizikai paraméterek pontosítása erősen lemaradva követi csak a felfedezéseket és ez a tendencia egyre erősödni látszik. Az ideiglenes elnevezést kapott égitest optimális körülmények közt pontos pályaelemeket, így sorszámot, kivételesen gyors esetben nevet kap, majd leggyakrabban eltűnik az elektronikus katalógusok mélyén anélkül, hogy valódi fizikai tulajdonságairól 2 6
7 egzakt képet kaphatnánk. Már egy a nyugati körülményekhez viszonyított szerény távcsővel és CCD-kamerával több száz kisbolygóról végezhetünk komoly tudományos eredményekkel kecsegtető vizsgálatokat. Jelen munkám célja ezen tudományos tevékenység során nyert eredmények bemutatása. Jelenleg több, mint sorszámozott aszteroidát ismerünk, de legtöbbjükről a pontos pályaelemeken kívül nem áll rendelkezésre bővebb információ. A változócsillagok területén alkalmazott egyszerű apertúra fotometria a kisbolygók kutatásának területén is számos tudományos szempontból értékes eredményt nyújthat. A kapott fénygörbe alakja árulkodik a forgási periódusról, a kisbolygó alakjáról, a forgástengely térbeli helyzetéről, annak esetleges precessziójáról, valamint elkészíthető az aszteroida alakmodellje is. Természetesen ez utóbbiak precíz meghatározásához számos, különböző ekliptikai hosszúságnál elvégzett mérésre van szükség (L.L. Kiss et al., 1999 és C.A. Angeli et al., 2001). Az alakmodellek elkészítése legegyszerűbb esetben egy háromtengelyű ellipszoid illesztéséből áll. A forgó ellipszoid különböző látóirányú vetületei okozzák a fényváltozást amennyiben ezen változás okaként a napfényt reflektáló felület méretváltozását értjük. A kis égitestek forgási periódusaira vonatkozó vizsgálatok fontos információkat nyújthatnak a kisbolygók populációján belüli ütközésekről és ezen keresztül magának a Naprendszernek az időbeli fejlődéséről (Fulchignoni et al., 1995) A kisbolygók feltételezett fényviszszaverő képessége (albedó) 0,02 és 0,6 közötti tartományban mozog (D illetve E osztály). Ez az érték a Földre vonatkoztatva 0,39. Az égitestek hipotetikus méretét alapvetően ez a paraméter határozza meg. A legutóbbi idők vizsgálatai szerint még mindig rendkívül bizonytalanok ezen elméleteink. A Stardust szonda által megvizsgált 5535 Annefrank kisbolygó reflexiós képessége a feltételezett érték fele, aminek következtében az objektum valódi mérete az elméletileg jósoltnak a kétszerese. Ezek az eredmények alaposan módosíthatják a kisbolygók világáról alkotott szemléletünket. Elég csak arra gondolnunk, hogy ez mennyiben érinti a kisbolygók tömegét, sűrűségét, anyagi összetételét mind egyedileg tekintve, mind a Naprendszer egészére vetítve. 7
8 2. A mérések tervezése Az Egyesült Államokban, Cambridge-ben működő, interneten keresztül elérhető Minor Planet Center 3 rendkívül sok hasznos információt biztosít a magát kisbolygók kutatására elszánó csillagász számára. Számomra a két legfontosabb szolgáltatás az efemeris generátor és a korábban már mások által vizsgált kisbolygók, valamint a fénygörbékből nyert rotációs periódus és amplitúdó adatok listája volt. A fénygörbe adatok listáját tanulmányozva azonnal feltűnik a figyelmes szemlélőnek, hogy a vizsgált apró égitestek eloszlása rendkívül egyenetlen. Az első ezer sorszámozott, korán felfedezett, tehát viszonylag fényes kisbolygó közel 90 százalékának fényváltozását alaposan tanulmányozták, a rotációt jellemző paraméterek nagy bizonyossággal ismertek (amplitúdó, forgási periódus). A nagyobb sorszámú, később, fotografikus úton felfedezett égitestek közül egyre kevesebb szerepel a listán, illetve ahogy a magasabb sorszámok felé haladunk a forgási paramétereket egyre nagyobb bizonytalanság terheli. Ezek a pontatlanságokat négyfokozatú skálán osztályozzák: 1. Az eredmények töredékes fénygörbén alapulnak s így teljesen rosszak is lehetnek. 2. A paramétereket nem a teljesen lefedett fénygörbe alapján határozták meg, ezért a periódust akár 30 % hiba is terhelheti. 3. Bizonytalanságok nélküli stabil eredmény a fénygörbe teljes lefedettségével. 4. Az előbbieken kívül a forgástengely helyzete is adott. A periódusokat órákban mérve három tizedesjegy erejéig szokás megadni. Már két évvel ezelőtt amikor elhatároztam, hogy a Naprendszer apró égitestjeinek kitüntetett figyelmet szentelek világos volt számomra, hogy a fotometrialig alig, vagy egyáltalán nem vizsgált kisbolygók fontos és aránylag nagy részt kapnak kutatási profilomból. Ennek megfelelően állítottam össze észlési terveimet Mit és hogyan észleljek? A rendelkezésemre álló műszeregyüttes távcső + CCD kamera egyértelmű választ adott erre a kérdésre. Az egyetemi csillagvizsgáló 40 centiméteres Cassegrain távcsöve, az SBIG ST 9E kamera 6 6 ívperces látómezejével és a felújított Fornax gyártmányú, német ekvatoriális szerelésű mechanika korlátozott megbízhatóságú vezetésével megszabta a határokat
9 Az izgalmasnak ígérkező 14+ magnitúdós tartomány küszöbénél kellett megállni: az adott feltételek mellett 60, esetleg 90 másodperces expozíciós időkkel az említett fényességű aszteroidákról készített képeken a jel/zaj viszony 2-3 körüli érték volt. A piszkéstetői Schmidt távcső a ívperces látómezőnek, a 40 C-ra hűtött kamerának és a kitűnő vezetésnek köszönhetően minden kisbolygókat követő csillagász igényének megfelel: és még halványabb magnitúdó tartományban rendkívül sok fotometriailag egyáltalán nem vizsgált aszteroida létezik. A méréseim előzetes tervezésekor egész éjszaka során elegendően magasan látszó, megfelelően fényes objektumokat kerestem. ( Piirone, 1990.; Pravec et al., 2001.) A keresésben az MPC adatain kívül a ProjectPluto Guide 6.0 és 7.0 csillagászati programra támaszkodtam, amely a Hubble Űrtávcső számára készült Guide Star Catalog nevű csillagkatalógust jeleníti meg grafikus formában. A mérés tervezésekor ügyelni kell, hogy a fenti kívánalmakon túl a kisbolygó látszó mozgása ne legyen túlságosan nagy, illetve e mozgás során lehetőleg minél kevesebb állócsillag képén haladjon keresztül. A túl nagy elmozdulás elkent profilokat okoz és az éjszaka közben fellépő több látómezőnyi elmozdulás miatt nehéz minden felvételen látható összehasonlító, ellenőrző csillagot találni (K. Sárneczky et al., 1999). Ez utóbbi jelenség főként a szegedi távcsőnél okozhat kellemetlenségeket. Többek között ezért is hiányzanak méréseimből a nagy látszó elmozdulással bíró földsúroló kisbolygók. A kisbolygók jelentős hányada alacsony inklinációjú pályákon kering a Nap körül, ezért főként az ekliptika környékén összpontosulnak. A nyári hónapok éjszakáin végzett mérések alatt a Nap látszó pályája belemetsz a Tejút csillagokkal zsúfolt mezőibe, megnehezítve ezzel a CCD képek feldolgozását a sok látszólagos okkultáció miatt. E jelenség kiküszöbölésére külön eljárás kidolgozása vált szükségessé, melynek ötlete Szabó Gyula okleveles csillagász, PhD ösztöndíjas hallgatótól származik. Részletes leírása a későbbiekben következik Az adatok feldolgozása Egy éjszaka során tipikusan 400 felvételt készítettem el, amelyek feldolgozása manuálisan történt. Ennek oka részben a vizsgált objektum elmozdulása, másrészt a gyorsabb eredmény elérése volt. A CCD felvételeken található hullámoptikai megfontolásokból soha nem pontszerű égi objektum fényességének meghatározására több módszer is szolgálhat. A kisbolygók elmozdulása miatt az illesztéses (PSF point spread function) fotometria nem használható, ugyanis az intenzitás profilra illesztett haranggörbe erősen torzulhat. Ennek térbeli megforgatása és a bezárt térfogat integrálása után nem kapunk pontos eredményt. Célravezetőbb ilyenkor az egyszerűbb megoldások választása. Az apertúra fotometria során a mérendő kisbolygó képére néhány pixel sugarú, kör alakú nyílást illesztünk, majd összegezzük az ezen belüli pixelek intenzitását. Ezt a folyam- 9
10 atot elvégezzük az összehasonlító és az ellenőrző csillagokra is. Ezt a munkaszakaszt a UNIX/Linux alatt futó, népszerű Image Reduction and Analysis Facility (IRAF) programcsomag quickphot taszkjával végeztem. Az illesztett apertúra méretét illetően figyelembe kellett venni, hogy túl kicsi nyílás esetén a vezetés pontatlansága miatt szétkent kisbolygó profil egy része lemaradhat, másrészt a kelleténél nagyobb apertúra esetén a szomszédos csillagok pixelei is bekerülhettek az apertúrába. Tipikusan alkalmazott érték volt a 6 pixel sugarú környílás. A kezdeti nehézségek után a kiértékelés sebessége elérte a kép/órát. A kinyert instrumentális relatív magnitúdók egy fájlba kerültek, hasonlóan a felvételek készítésének Julián dátuma. Egy általam írt, körülbelül 60 soros, rövid C nyelvű program végezte el a magnitúdó különbségek képzését, valamint ezek összepárosítását a megfelelő időponttal, majd az eredmény szintén egy fájlba került. A kétoszlopos egyszerű adatfájl ábrázolására a Linux alatt használható Grace nevű alkalmazást használtam. A kompozit fénygörbék elkészítésére az apc11 nevű /Asteroid Photometric Catalogue Software 1.0/, DOS-os használatra írt programot szintén Linux alatt futtattam. A periódus meghatározát ezen alkalmazás segítségével úgynevezett fázisdiszperzió minimalizációs módszerrel (PDM) végeztem. Az eljárás lényege, hogy a helyes periódussal elkészített fázisdiagramon az adatok szórásának minimuma van. A heliocentrikus ekliptikai koordináták kiszámítására írtam egy kis C nyelvű szkriptet, ami a szükséges adatokat a Guide szöveges állományba elmentett információból veszi. Gyakran szükségessé vált a sok mérési pont átlagolása, a csillagászatban gyakran használt medián képzésére szintén egy C ben írt program szolgált. Méréseim becsült fotometriai pontossága az alkalmazott műszeregyüttes és a légkör állapotának függvénye. A szegedi körülményekre a 0,05 0,2, a piszkéstetői felvételekre 0,02 0,05 magnitúdó volt a jellemző érték. A fényváltozás amplitúdójából egyszerű modell segítségével lehet következtetni a kisbolygó hozzávetőleges alakjára. A számítások során feltételezzük, hogy az aszteroida alakja kéttengelyű ellipszoiddal közelíthető, forgástengelye a látóirányunkra merőleges és a detektált fluxus a megvilágított felülettel arányos. m 1 m 2 = 2,5 log F 1 F 2 F 1 F 2 = t 1 t2 = abπ b 2 π = a b a b = A 10 2,5 A = m 1 m 2 A a fényváltozás amplitúdója, F a fluxus, ami az ellipszoidok t területével arányos, a illetve b az ellipszoid tengelyei. Pontos alakmodell elkészítéséhez természetesen több, külön- 10
11 böző ekliptikai hosszúságnál és oppozíciónál elvégzett mérésre és lényegesen bonyolultabb számításokra van szükség. 3. Elért eredmények 3.1. Kisbolygók Az ismertetett kisbolygók ebben a fejezetben bemutatott fénygörbéi mellett a mellékletben további fénygörbék találhatók meg, növekvő sorszám szerint rendezve. A feldolgozás során elért eredmények a harmadik táblázatban olvashatóak. A négy szegedi éjszakán át mért 1400 Tirela halványsága ellenére meglepő eredményt nyújtott a 40 centiméteres távcsővel. Sajnos a Tejút sűrű csillagmezőin való áthaladása miatt számos hézag tarkítja a fénygörbét, de ez nem csökkenti a kisbolygó annak kompozit diagramjáról leolvasható nagy mértékű fényváltozásának jelentőségét. Az aszteroida fénygörbéje nagy amplitúdójú fényességingadozást mutat, amire kisebb nagyobb hullámok ülnek (2. ábra). A változás nagysága meghaladja az egy magnitúdót, ami kevés kisbolygónál mutatható ki. Az égitest 1:3 tengelyarányú ellipszoiddal modellezhető. A rövid nyári éjszakákon végzett mérések miatt azonban szükségesnek tartom a télen végzett fotometriai vizsgálatokat a teljes periódus lefedésének érdekében Tirela composite lightcurve -1, ,5 0 0,2 0,4 0,6 0,8 1 phase 2. ábra. Az 1400 Tirela kompozit fénygörbéje A soron lévő mérésem megközelíti az ideális obszerváció kritériumait. A kifogástalan égbolt és a kiváló műszer mellé nagy fényváltozást mutató aszteroida párosult, amely kedvező találkozás eredménye a 42. ábrán látható. A 3. ábrán egy kompozit diagram látható. Az 1503 Kuopio nevű kisbolygó jó választásnak bizonyult. A 2001 őszén, Piszkéstetőn 11
12 elvégzett mérések tekintélyes amplitúdójú, aszimmetrikus fényváltozást mutatnak. A fényváltozás 1:2 arányban elnyúlt égitest forgásával írható le. A 0,7 magnitúdónyi tartományt átívelő görbe szórása elhanyagolható Kuopio composite lightcurve -3,3-3,2-3,1-3 -2,9-2,8-2,7-2, ,2 0,4 0,6 0,8 1 phase 3. ábra. Az 1503 Kuopio kompozit fénygörbéje Bár a 7505=1997 AM2 jelzésű aszteroidát előttünk már mérték és periódusa, valamint nagy amplitúdójú fényváltozása már ismert volt, Piszkéstetőn mégis készítettünk róla felvételeket. A Minor Planet Center fénygörbe listáján 4,14 órás periódus szerepelt meglehetősen tekintélyes, 0,75 magnitúdós intenzitásváltozással. Méréseink is alátámasztották ezeket az adatokat, amint az a kompozit diagramon jól látszik (4. ábra). Azonban feltételezhető, hogy az illesztett periódus nem jó, mivel könnyen lehetséges, hogy a görbe valójában nem kettő, hanem három púppal rendelkezik. A periódus pontosítására további vizsgálatok szükségesek. A megfigyelt amplitúdóra 1:2 tengelyarányú ellipszoid rotációja adhat magyarázatot. A 756 Lilliana az első mért kisbolygók közé tartozik. A görbe vastagsága a szűrő alkalmazása miatti alacsony jel/zaj viszonynak tudható be (5. ábra). Mindenesetre jól nyomon követhető a több, mint fél magnitúdónyi változás és a nem szimmetrikus fénymenet. Az alakmodell elkészítéséhez későbbi vizsgálatok szeretnék végezni erről az objektumról. Első közelítésben 3:5 arányban elnyúlt alakkal rendelkezhet az objektum. Az észlelések elkészítésében nyújtott segítségéért köszönet illeti Mészáros Szabolcs évfolyamtársamat, aki két éjszakán végzett megfigyeléseket. A következő kisbolygót, a 7505=1997 AM2 és 5690=1992 EU aszteroidákkal egyetemben 2000 őszén mértük Kiss Lászlóval és Sárneczky Krisztiánnal. Bár az 1270 Datura és a másik két aszteroida vizsgálatára már előttünk történtek kisérletek, a mi méréseink is szolgáltak érdekességgel. Az MPC által közölt 0,41 magnitúdós amplitúdóval szemben a piszkéstetői észlelések 0,6 magnitúdós fényességváltozást sugallnak (6. ábra). A forgási 12
13 0 7505=1997 AM2 P=4.14h 0,2 0,4 0,6 0, ,2 0,4 0,6 0,8 1 phase 4. ábra. A 7505=1997 AM2 kompozit fénygörbéje 756 Lilliana ,8 2,1 2,4 2,7 2102,3 2102, ,4 2102, ,5 2102, ,6 5. ábra. A 756 Lilliana fénygörbéje periódus 3,36 órára tehető, míg a Minor Planet Center szerint ez 3,2 óra. Az intenzitás változására 5:9 tengelyarányú alak adhat magyarázatot. A 3682 Welther kisbolygó fénygörbéjét tavaly augusztusban, illetve októberben vettem fel. Két éjszakán Szegeden, míg három éjszaka során Piszkéstetőn végeztem fotometriai vizsgálatokat az aszteroidáról. Az érdekes alakú, mély és hegyes főminimumokat mutató fénygörbét a 7. és 8. ábrán mutatom be. Az ondrejovoi obszervatórium honlapján szintén található fénygörbe az aszteroidáról, feltételezésük szerint az objektum kettős 4. A piszkéstetői méréseimet a ködös, párás időjárás tette ilyen szaggatottá. Az égitest alakja hozzávatőlegesen 3:4 arányban elnyúlt ellipszoid. Az 5690=1992 EU sorszámú aszteroidát 2000 őszén mértük Piszkéstetőn. A két éjszaka eredménye a jól detektálható, több tizedmagnitúdós fényváltozás, azonban a periodicitás 4 ppravec/welther.htm 13
14 -0, Datura clear filter 60/90/180 Schmidt 0 0,1 0,2 0,3 0,4 0,5 0,6 1831, , ,5 1831, , , ,62 6. ábra. Az 1270 Datura fénygörbéje 3682 Welther ábra. Az 3682 Welther fénygörbéje létének, illetve pontos mértékének megállapításához kevésnek bizonyult a rendelkezésre álló idő (9. ábra). A fényességváltozás további vizsgálata szükséges ezen kis égitest esetében is. A következő fénygörbe (10. ábra) első pillantásra is eredményes mérést mutat. A 6510 Tarry kisbolygó kis mérete miatt valószínűleg kevésbe szabályos alakú és tapasztalataim szerint minél kisebb méretű az objektum, annál nagyobb valószínűséggel találunk nagy amplitúdójú, esetleg aszimmetrikus fényváltozást. Természetesen ezen megállapításom érvényesítéséhez hosszú távú, statisztikai jellegű adathalmazra is szükség van. Nincs kizárva, hogy az 1000 alatti sorszámú, tehát viszonylag fényes, de az MPC listájában nem szereplő kisbolygók többségét már mérték fotometriai úton, de az eredményül kapott lapos 14
15 3682 Welther /0.9/1.8 m Schmidt 1,1 1,2 1,3 1,4 1,5 2191,2 2191, ,3 2191, ,4 8. ábra. Az 3682 Welther fénygörbéje 5690=1992 EU clear filter 60/90/180 Schmidt 2,6 2,7 2,8 1831, ,3 1831, ,4 1831,45 9. ábra. Az 5690=1992 EU fénygörbéje fénygörbék, vagy a nagy, csak sejthető periódusok nem győzik meg a szerzőket az eredmények publikálásáról. Mindenesetre ez a kisbolygó szép fényváltozást produkált ezen az egy végigmért éjszakán. A görbén látható űr csillaggal való összeolvadásnak tudható be. Az ábrán feltűnő az aszimmetrikus fényváltozás, amelynek másik ága nem látható teljes mértékben, mivel a hajnal erőteljes közeledtével be kellett fejeznünk a mérést, bármennyire is szerettük volna folytatni a felszálló ág követését. Mindenesetre az biztos, hogy a fényváltozás amplitúdója eléri a fél magnitúdót, így feltétlenül szeretnék további vizsgálatokat elvégezni erről a kisbolygóról, már csak a kompozit diagram elkészítése miatt is. Az amplitúdóra 3:5 tengelyarányú test forgása illeszthető januárja nem biztosított túl sok derült éjszakát. A 469 Argentina nevű aszteroida 15
16 1, Tarry /90/180 Schmidt, R filter 1,8 1,9 2 2,1 2,2 2,3 2438, ,4 2438, ,5 2438, ,6 10. ábra. Az 6510 Tarry fénygörbéje 1,7 469 Argentina ,8 1,9 2 2,1 2305,2 2305,3 2305,4 2305,5 2305,6 11. ábra. A 469 Argentina fénygörbéje fénygörbéjének nagy szórása (11. ábra) tanúsítja a párás égboltot, ennek ellenére szépen kirajzolódik a mindössze másfél tized magnitúdónyi fényességváltozás. Az éjszaka második felében a rossz átlátszóság használhatatlan szélességűvé keni el a görbét. Érdemes felfigyelni a közel lineáris ágakra. A kis amplitúdóval jellemezhető fényváltozás további vizsgálatához nagyobb teljesítőképességű műszer és jobb légköri állapotok szükségesek. Első közelítésban a kisbolygó alakja 8:9 tengelyarányú ellipszoid. Az 531 Zerlina nevű aszteroida lassan, kis amplitúdóval változtatja fényességét (12. ábra). A bal szélen látható púp hamis, csupán csillaggal történő összeolvadás eredménye. Az ábra jobb oldalán a görbe erős kiszélesedése az égbolt állapotának és vele együtt a jel/zaj viszony gyors leromlásának tudható be. A rövid nyári éjszaka miatt valójában nem is sötétedett be teljes mértékig, a horizont alatt végig sejthető volt a Nap fénye a periódus megállapítása lehetetlen volt, talán egy hosszú, téli éjszakai mérés többet felfedne a kisbolygó fényváltozásáról. 16
17 531 Zerlina /90/180 Schmidt, R-filter 1 rel.magnitude 1,2 1,4 2434, ,5 2434, ,6 2434, ábra. Az 531 Zerlina kompozit fénygörbéje 546 Herodias ,4 rel.magnitude -0,3-0,2-0, ,4 2298,5 2298,6 2298,7 13. ábra. Az 546 Herodias fénygörbéje A két januári éjszakán mért 546 Herodias kisbolygó fénygörbéire ráillenek az 469 Argentina-nál említettek. A csupán egytized magnitudóval jellemezhető, de jól definiált fényváltozás elmosódik a hajnali ködösség és a város reflexió miatti fénybúrája következtében (13. ábra). Jobb észlelési feltételek mellett minden bizonnyal meghatározható lenne az esetleges rotáció indukálta fényváltozási periódus. A következő két görbe nem jelez jelentős fényváltozást. Az 549 Jessonda csupán kismértékű elhalványodást mutatott a mérés 3 órája során, ami sajnos a kedvezőtlen időjárás miatti vastag szórással párosult (14. ábra). Az 551 Ortrud néhány mérési pontja Piszkéstetőn született egy rövid ködszünetet próbálván hasznosítani. Sajnos az időjárás nem tette lehetővé a kis égitest további tanulmányozását a fenn töltött egy hét alatt. Így ez a néhány mérési pont csupán a Schmidt-távcső hazai viszonylatban kimagaslóan jó paramétereit mutatja, amit a párás őszi ég ellenére elért néhány század magnitúdónyi szórás jelez (15. ábra). A következő fénygörbén (16. ábra) látható meredek intenzitásesést a későbbi mérések során nem sikerült újra megfigyelni. A jelenségért talán a 894 Erda jellemzője a kisbolygó 17
18 549 Jessonda ,4 1,2 1 0,8 0,6 2321, ,4 2321, , , , ábra. Az 549 Jessonda fénygörbéje 551 Ortrud /0.9/1.8 m Schmidt 1,77 1,8 1, , , , , ábra. Az 551 Ortrud fénygörbéje 2,1 894 Erda ,2 2,3 2,4 2,5 2109, , , , , ,6 16. ábra. A 894 Erda fénygörbéje esetleges kettőssége felelhet, vagyis épp egy sötétebb kísérő általi fedést sikerült megfigyelnünk. Bár a későbbi vizsgálatok ezt nem erősítették meg, a lehetőséget nem zárhatjuk ki végérvényesen. Az 1108 Demeter fényváltozása a 17. ábrán jól követhető. A néhány tized magnitúdós amplitúdó sajnos nem párosul detektálható periodicitással, bár a mért intenzitás hullámzása minden éjszakán megfigyelhető. A 14 magnitúdónál is halványabb kisbolygó mérése sajnos 18
19 nagyon alacsony jel/zaj viszonnyal terhelt, ráadásul a mezőcsillagokkal való összeolvadásnak betudható hézagok tovább csökkentik a görbe értékelhetőségét. Érdekességképpen megemlíthető, hogy az összehasonlítónak választott csillag változtatja a fényességét, mint az a későbbiekben kiderült. A mellékelt részfénygörbe alakjából pulzációra vagy kontakt kettőscsillag jellegre következtethetünk a változás okaként. Ez az eset is alátámasztja azt az követelményt, hogy minden kimérési munkaszakasznál minimum kettő, de inkább több csillagra végezzük el az apertúra fotometriát. A csillag azonosítója: GSC , Demeter ast-chk 2,3 2,4 2,5 2,6 2123,3 2123,4 2123,5 2123,6 17. ábra. Az 1108 Demeter fénygörbéje 1170 Siva /0.9/1.8 m Schmidt 0,25 0,3 0, , , , , , ,74 Julian Date ábra. Az 1170 Siva fénygörbéje Az 1170 Siva grafikonja (18. ábra) ismét demonstrálja a piszkéstetői Schmidt távcső kvalitását. Érdemes megemlíteni, hogy a mellékelt ábra teljes magassága mindössze 0,1 magnitúdó - mégis a kisbolygó fényváltozása egyértelműen azonosítható. A mérés szórása 0,02, azaz kétszázad magnitúdó! Sajnos az adott megfigyelési időszakban nem állt módunkban több mérést végezni erről a kis égitestről, csupán ez a néhány órás idősor mutatja a precessziót is sejtető fényváltozást. Az 1286 Banachiewicza-ról készült, mindössze egy órás adatsor nem fed fel sokat a kisbolygó fényváltozásából (19. ábra). A görbe emelkedésén a tekintélyes szórás el- 19
20 lenére látszik az emelkedő ág, ami az égitest esetleges periódikus fényesség változására utalhat. Sajnos a későbbiekben nem volt lehetőségem az aszteroida további fotometriai vizsgálatára, így ez az égitest is felkerült az alaposabb méréseket igénylő kisbolygókat tartalmazó listámra. 0, Banachiewicza ,8 1 1,2 1,4 2136, , , , ,6 2136, ábra. Az 1286 Banachiewicza fénygörbéje 1506 Xosa ,7 0,8 0, , ,4 2121, ,5 2121, ,6 20. ábra. Az 1506 Xosa fénygörbéje Az 1506 Xosa mérése nem nyújtott a fényváltozás szempontjából pozitívan értékelhető eredményt. Három értékes éjszakát töltöttem ezen kisbolygó fotometriai vizsgálatával. Amint az a 20. ábrán is látható, a kisméretű égitest fényváltozása nem túl jelentős: a kéttizedes szórásból nehezen vehető ki értelmezhető periódus. Mindazonáltal sejthető némi szabályosság, így teljes bizonyossággal nem zárható ki a mérhető periodicitás megléte, amit egy esetleges - jobb feltételek mellett végzett - mérési sorozat alátámaszthat. Az 1695 Walbeck esetére az előzőekben említettek szinte szó szerint átvihetők. A 21. ábrán mintha három csúccsal rendelkező fényváltozás lenne felismerhető. Mindenesetre ezen kisbolygó megérdemelne egy nagyobb műszerrel történő alaposabb vizsgálatot. A fenti eredményeket 2002 májusában, a horvátországi Višnjan ban megrendezett Meeting on Asteroids and Comets in Europe, 2002 konferencián poszter formájában mutattam be. 20
21 1, Walbeck ,3 1,4 1,5 1,6 2151,3 2151,4 2151,5 21. ábra. Az 1695 Walbeck fénygörbéje Az említett és más kisbolygók fénygörbéi - változócsillagok méréseivel egyetemben - megtalálhatók elektronikus formátumban a honlapomon Egyéb eredmények A 360 Carlova - HIP 9975 okkultációja 2000 októberében kedvező alkalom kínálkozott egy kisbolygó csillag okkultáció magyarországi pozitív megfigyelésére. Ekkor nem csak a CCD képen látszanak összeolvadni a két égi objektum pixelei, hanem a valóságban is a megfigyelő és a távoli csillag közé kerül a kisbolygó, azaz csillagfogyatkozásra kerül sor. Esetünkben a 360 Carlova nevű kisbolygó fedte el a HIP 9975 katalógusszámú, 8,3 magnitúdós csillagot. Ebben az időszakban Kiss L. Lászlóval és Sárneczky Krisztiánnal Piszkéstetőn tartózkodtunk, kisbolygók mérési programján dolgozva. A fedés előre kiszámított időpontja körül készítettünk egy 90 másodperc expozíciós idejű CCD-felvételt kikapcsolt óragéppel, ezért a csillagok hosszú nyomot hagytak a képen (22. ábra). A legfényesebb sávon látszik egy sötét szakasz, ami a sikeres megfigyelés ékes bizonyítéka! Az 1283 pixelnyi csillagnyom 3. harmadában egy 130 pixelnyi fedés látszik. A felvétel készítésének időpontjából kiszámítható volt az okkultáció bekövetkeztének pontos időpontja és a fedés hosszúsága is. Ezek szerint az esemény 1:12:50,3 UT-kor történt és 9,1 másodpercig tartott. 22. ábra. A 360 Carlova csillagfedése 5 pierre/meas.htm 21
22 Sikerünkhöz az alapos tervezésen kívül számos külső körülmény szerencsés összjátékára is szükség volt, hiszen az ilyen előrejelzések elég nagy bizonytalansággal terheltek és az őszi időjárás is könnyen meghiúsíthatta volna terveinket. Mindenesetre nem ez történt, így másokéi mellett a mi megfigyelésünket is felhasználhatták a kisbolygó alakjának modellezésére. Ezek alapján az aszteroida meglehetősen elnyúlt alakú, mintegy 1:6 arányban (23. ábra). A rajz az eltérő földrajzi helyen lévő megfigyelők pozitív észleléseinek időtartamaiból származó alakot mutatja (piros körök). A különálló zöld körök sikertelen megfigyelést reprezentálnak. Természetesen az alak így nem határozható meg túl nagy pontossággal, ehhez nagyon sok, különböző helyeken történő észlelésre, majd a földrajzi koordináták és az esemény időpontjainak összevetésére lenne szükség. 23. ábra. A 360 Carlova alakmodellje A GSC fényváltozása Kisbolygók fotometria megfigyelésénél számos más égi objektumot is rögzítünk a CCDkamerával. A sikeres mérés feltétele, hogy legyen a képen néhány, a kisbolygó intenzitásával egy nagyságrendbe eső intenzitású csillag is, amihez képest a differenciális fotometrálást elvégezhetjük. Halvány aszteroidák vizsgálatánál a megfelelő jel/zaj viszony eléréséhez viszonylag nagy tipikusan másodperc expozíciós idejű felvételeket készítünk, ennek következtében az objektumunk fényességéhez hasonló csillagokat is kimérésre alkalmas állapotban rögzítünk. A magnitúdós tartományban, minden bizonnyal állítható, ezerszámra találhatók még felfedezetlen változócsillagok. Ilyen határfényességű képek feldolgozásakor nagy valószínűséggel akadunk ilyen érdekes objektumra. Tavaly augusztus elsején az 1108 Demeter kisbolygóról készült képeken a GSC
23 56 katalógusszámú 12,3 magnitúdós csillag fényességét változó mértékűnek találtam, amit a 24. ábra is szemléltet. A következő éjszakákon a vizsgált égitestem már egy látómezőnél messzebb járt ettől a csillagtól, így sajnos ezen időszakban nem készült több mérés a változóról. Az említett mérés kiértékelése is későbbi időben történt, amikor a csillag már csak az éjszaka első felében, rövid ideig és alacsony magasságban volt megfigyelhető. A fénygörbe alapján a változás lehetséges oka csillagpulzáció, esetleg egy fedési kettős minimumát rögzítettem. Az utóbbi feltevés a valószínűbb, ez esetben a csillag W UMa vagy β Lyr típusú. Amennyit a rész fénygörbéből elmondhatunk, az annyi, hogy a periódus bizonyosan nagyobb 0,4 napnál, az amplitúdó pedig 0,2 magnitúdónál. A fényváltozás okának kiderítése és a paraméterek pontosítása érdekében további vizsgálatokat szeretnék a jövőben végezni erről a csillagról Demeter comp-chk 0,55 0,6 0,65 0,7 0, ,3 2123,4 2123,5 2123,6 24. ábra. Az 1108 Demeter mérésénél talált változócsillag (GSC ) fénygörbéje Az egyetemen eddig elvégzett kisbolygós vizsgálatokból származó CCD-felvételeken talált változócsillagokat IBVS cikkek is bemutatják októberében az 5690=1992 EU jelzésű kis égitestről készített képeken két W UMa típusú fedési kettőst találtunk (Csák et al., 2001). 23
24 4. Mérési adatok Az alábbi táblázatokban részletesen megtalálhatóak a vizsgált kisbolygókra felfedező, felfedezés ideje, méretek valamint az észlelés körülményeire aspektus adatok, mérés helye, ideje, alkalmazott távcső, szűrő és expozíciós idő vonatkozó adatok. Itt tüntettem fel a fénygörbék analízise után nyert periódus és amplitúdó értékeket is. Végül statisztikai összegzést készítettem méréseimről. 1. táblázat. Vizsgált kisbolygók Név Felfedező Felfedezés ideje Átmérő km-ben 469 Argentina L. Carnera ±3 531 Zerlina M. Wolf ,8±3,7 546 Herodias P. Gotz ,7±1,5 549 Jessonda M. Wolf ,5±2,1 756 Lilliana J.H. Metcalf ,3±1,5 894 Erda M. Wolf ,8±1, Demeter K. Reinmuth , Siva E. Delporte ,3±0, Datura G. Van Biesbroeck ,5±0, Banachiewicza S.J. Arend ,8±4, Tirela L. Boyer , Kuopio Y. Vaisala ,0±1, Xosa C. Jackson , Walbeck L. Oterma ,0±0, Welther K. Reinmuth , EU S. Ueda, H. Kaneda , Tarry C. S. Shoemaker , AM2 T. Kobayashi ,5 24
25 2. táblázat. Geocentrikus és heliocentrikus geometriai adatok Név Mag. R Fázis λ β 469 Argentina 12, m 9 2,85 1,92 7,69 110,88 10, Zerlina 15, m 4 2,232 1,444 20, ,07 50, Herodias 13, m 2 2,32 1,45 14,9 95,3 24,0 549 Jessonda 13, m 6 2,114 1,168 10, ,65-2, Lilliana 14, m 2 2,949 2,040 10,471 86,169 28, Erda 13, m 4 2,741 1,768 7,536 52,181 18, Demeter 14, m 3 1,80 0,97 25,01 66,02 47, Siva 13, m 5 1,744 0,754 7,044 14,765 12, Datura 15, m 8 1,955 1,341 28,176 88,237-5, Banachiewicza 14, m 7 2,755 1,759 4,715 36,959 14, Tirela 15, m 0 2,374 1,479 14,345 65,318 25, Kuopio 14, m 5 2,739 1,768 6,113 11,303 16, Xosa 13, m 8 1,935 0,97 13,041 61,439 23, Walbeck 15, m 3 2,07 1,19 18,2 52,75 28, Welther 13, m 7 1,928 0,984 14,769 10,934 27, Welther 13, m 9 1,887 1,002 19,477 16,902 25, Welther 13, m 9 1,886 1,01 20,056 17,01 25, EU 15, m 6 1,775 1,218 32,774 89,852 36, Tarry 15, m 3 1,853 1,01 23,485 73,609 42, AM2 14, m 3 1,719 0,967 29,489 79,587-6,771 LEÍRÁS: R = HELIOCENTRIKUS TÁVOLSÁG (AU) = GEOCENTRIKUS TÁVOLSÁG (AU) λ = GEOCENTRIKUS HOSSZÚSÁG (FOK) β = GEOCENTRIKUS SZÉLESSÉG (FOK) 25
26 3. táblázat. Elért eredmények Név Mérés ideje Távcső&Szűrő Exp. idő Periódus Ampl. 469 Argentina ,4m Cass., X 40 sec. 8,2h? 0, m Zerlina ,6m Sch., R 90 sec. >0,4d >0, m Herodias ,4m Cass., X 45 sec. 8,450h 0, m Jessonda ,4m Cass., X 30 sec. - <0, m Lilliana ,4m Cass., R 45 sec. 4,683h 0, m Erda ,4m Cass., R 45 sec. - <0, m Demeter ,4m Cass., R 45 sec. - <0, m Siva ,6m Sch., R 60 sec. - <0, m Datura ,6m Sch., X 180 sec. 3,36h 0, m Banachiewicza ,4m Cass., X 40 sec. - <0, m Tirela ,4m Cass., X 45 sec. 15,0h? 0, m Kuopio ,6m Sch., R 60 sec. 9,96h 0, m Xosa ,4m Cass., R 45 sec. 6,7h? <0, m Walbeck ,4m Cass., X 60 sec. 8,93h? 0, m Welther ,6m Sch., R 60 sec. 3,43h? 0, m EU ,6m Sch., X 120 sec.? >0, m Tarry ,6m Sch., R 120 sec. >6,h24 >0, m AM ,6m Sch., V 180 sec. 4,h14 0, m táblázat. Statisztika Név Idő Pontok Név Idő Pontok 469 Argentina Xosa Zerlina Herodias Tirela Jessonda Ortrud Lilliana Walbeck Welther Erda Demeter EU Siva Tarry Datura AM Banachiewicza Kuopio Összesen: darab felhasznált CCD frame 37 éjszaka során. 26
27 5. Összefoglalás Az objektumok döntő hányada mutatott érdemleges fényváltozást, így számos kisbolygó további alapos méréseket igényel, talán akár többszín fotometria keretében is. Ezenkívül szeretném lefedni az első ezer sorszámozott kisbolygó fotometriai adatsorát, azaz minden hiányzó objektumról végezni legalább egy éjszaka során mérést CCD kamera segítségével. Az adatfeldolgozás automatizálásának területén is számos feladat vár még rám. A kimérés folyamatának felgyorsítására szolgálhat a kisbolygó CCD képen lévő pozíciójának lineáris interpolációval történő meghatározása. Ekkor a kezdő és a legutolsó felvétel x, illetve y koordinátája alapján válik lehetségessé az égitest pozíciójának meghatározása a közbenső felvételekre. Majd ezen képterület apertúra fotometriájával nyerhető a kisbolygó intenzitása. Az összehasonlító és ellenőrző csillagok fényessége egymásra csúsztatott képek automatikus kimérésével kapható. Új változócsillagok keresésének egyik járható útja az elkészített CCD felvételek utólagos ellenőrzése és kimérése, amikor is a képen található összes csillag fényességét meghatározzuk. Egyszerű különbségi fotometria alkalmazásával a változócsillagok könnyedén kiszűrhetőek. Ezeket a feladatokat tervezem elvégezni a kisbolygós képeimre vonatkozóan. A dolgozatban említett eredmények publikálás alatt vannak a Planetary and Space Science című szakfolyóiratban. 27
28 6. Köszönetnyilvánítás Az alábbi személyeknek tartozom hálával: Dr. Kiss L. Lászlónak a témavezetésért, Sárneczky Krisztiánnak, Szabó M. Gyulának és Csák Balázsnak az értékes ötletekért és a mérések kivitelezése során nyújtott segítségükért. A berendezések rendelkezésre bocsájtásáért köszönet illeti a Szegedi Tudományegyetem Fizikus Tanszékcsoportját, valamint az MTA KTM CSKI piszkéstetői obszervatóriumát. Munkámat az FKFP 0010/2001 pályázat és a Pro Renovanda Cultura Hungariae Diákok a tudományért szakalapítvány támogatta. 28
29 A. Mellékletek A.1. Az adatok feldolgozása A következő sorokban található az adatok kiértékelését segítő rövid C nyelvű program, melynek feladata az idő és magnitúdó listák összehangolása, illetve a különbségi fotometria elvégzése egyszerű kivonás segítségével. /* Kisbolygó adatok redukálása, Pierre 2001 */ #include <stdio.h> #include <stdlib.h> main () { int i=0, n=0, a=0; int jdfix= ; /* Julian-dátum */ double ast,comp,chk; double jd[1000]; char imgs[1000] [20]; char image[20]; char im; FILE * file; FILE * reduc; if ((reduc = fopen( "red.dat", "wt"))== NULL) { fprintf (stderr, "Unsuccesfull file creating! \n"); exit (-1); } else; if ((file = fopen( "times", "rt"))== NULL) { fprintf (stderr, "Unsuccesfull file opening! \n"); exit (-1); } else; do { fscanf (file, "%s %lf ", &imgs[i], &jd[i]); i++; } while (!feof(file)); fclose (file); if ((file = fopen( "mags", "rt"))== NULL) { 29
30 fprintf (stderr, "Unsuccesfull file opening! \n"); exit(-1); } else; n=i-1; do { fscanf (file, "%s %lf ", &image, &ast); fscanf (file, "%s %lf ", &image, &comp); fscanf (file, "%s %lf ", &image, &chk); for ( a=0; a<=n; a++) if ( strcmp(image,imgs[a])); else { printf (" %lf %lf %lf \n", jd[a]-jdfix, ast-comp, chk-comp); fprintf (reduc, " %lf %lf %lf \n", jd[a]-jdfix, ast-comp, chk-comp); } } while (!feof(file)); fclose(file); fclose(reduc); printf (" \n \n red.dat file writing done. \n \n "); } A.2. A medián képzése Az adatfeldolgozás során szükségessé vált valamilyen módszer kidolgozása a különböző okok miatt a kelleténél vastagabb fénygörbék keskenyítésére, a fényváltozás grafikus ábrázolásának szépítésére információvesztés vagy ami még rosszabb, az adatok meghamisítása nélkül. A csillagászatban széles körben elterjedt fogalom az úgynevezett medián eljárás, amely egyfajta átlag képzésére szolgál. A metódus lényege rendkívül egyszerű: a mértani, a geometriai vagy más középértékektől eltérően itt nem szükséges a rendelkezésre álló minden adatokból egy új, a céljainknak megfelelő érték kiszámítása, szimplán a mért értékek közül választunk ki egyet. A median eljárás egyszerűsége a következőben rejlik: páratlan számú adat esetén azt számot választjuk ki középértéknek, amely a nagyság szerint felsorolt elemek sorában középen található, azaz ugyanannyi értéktől nagyobb, mint amennyitől kisebb. Páros számú adat estén az így sorrendbe állított elemek közül a két középső aritmetikai átlagát vesszük. A medián-képzés gyakorlati jelentőségét a mérés során szinte elkerülhetetlenül bekövetkező tekintélyes mérési hibák növelik. CCD felvételeken gyakran láthatunk kozmikus sug- 30
31 araktól eredő hamis beütésnyomokat. Az apertúránkba kerülő ilyen hamis felfényesedés jelentősen megváltoztathatja az objektum valódi fényességértékét. Tekintsük példának okáért a következő számsorozatot, amelyek akár mérési sorozatot is reprezentálhatnak: 51, 49, 50, 52, 48, 51, 250, 49, 52, ahol a hetedik érték szemmel láthatólag erősen kilóg a többi pont közül, amelyet nyugodtan tekinthetünk mérési hibának is. A különböző módon képzett középértékek a következő eredményeket adják: aritmetikai: A = 1 n Σn i=1 a i = geometriai: G = n Π n i=1 a i = harmonikus: H = n Σ n i=1 1 a i = négyzetes: Q = Σ n i=1 a2 i n = A median eljárás a valódi értékhez közelebb eső 51-et fogja szolgáltatni. A következő, általam írt kis C-nyelvű program segítségével végeztem el a fénygörbék simítását. /* Median átlagot képző program, (c) Pierre */ #include <stdio.h> #include <stdlib.h> main () { int i=1; /* első tömbindex */ int z,j,l,n,d; /* csereparaméter és median típus: n */ int a=1,e=1; /* ciklusváltozók */ 31
32 double value[1000]; /* kezdeti tömb */ double time[1000]; double newvalue; /* új adatok*/ double newtime; double q[10]; /* csereparaméter */ double x; /* csereparaméter */ FILE * file; FILE * newf; if ((file = fopen( "red.dat", "rt"))== NULL) { fprintf (stderr, "Unsuccesfull file opening! \n"); exit(-1); else; } do { fscanf (file, "%lf %lf ", &time[i], &value[i]); printf (" %lf %lf \n", time[i], value[i]); i++; } while (!feof(file)); fclose(file); printf ("\n Median type (3,5,7)? "); scanf ("%d",&n); if ((newf = fopen ( "median.dat", "wt" ))== NULL) { fprintf (stderr, "Unsuccesfull file creating! \n"); exit(-1); else; } for (e=1; e<i; e=e+n) { l=0; for (a=e; a<=e+n-1; a++) { l++; q[l]=value[a]; } for(z=1; z<=l-1; z++) { for(j=z; j<=l; j++) if(q[z] > q[j]) 32
33 { x=q[j]; q[j]=q[z]; q[z]=x; } } d=(l/2)+1; newvalue=q[d]; newtime=time[d+e-1]; fprintf (newf, "%lf %lf \n", newtime, newvalue); d=0; } fflush (newf); fclose (newf); printf ("\n\nwith parameter %d median.dat file writing done. } \n \n ", n); Egy éjszaka során átlagosan felvételt készítettem 8 órára vetítve és egy perces expozíciós idővel számolva. Egy, hasonló tengely körüli forgási periódusidővel rendelkező kisbolygó teljes rotációs periódusára tehát ennyi kép esik, ami bőven elégséges felbontást biztosít. A különböző mértékű medián-képzés eredményeit a következő ábrák szemléltetik. A 3682 sorszámú, Welther nevű kisbolygó fénygörbéjét felhasználva 3,5 illetve 7 mérésre végeztem az eljárást, azaz ennyi kép közül választottam ki a középső mérési értékeket. Az ábrák jól mutatják a megoldás hatékonyságát: az ábrázolt görbe minden esetben relevánsan keskenyebb lett, míg az alakjából egyáltalán nem vesztett, sőt kifejezetten előnyösebb lett az eredmény a fényváltozás szemléltetése szempontjából. 33
34 rel. mag Welther eredeti JD rel. mag Welther 3-as medián JD Welther 5-ös medián Welther 7-es medián rel. mag rel. mag JD JD ábra Welther fénygörbéi 34
35 A.3. Fluxus azonos szintre hozása Az eljárás alapját Szabó Gyula ötlete képezi. A mérési adatok ilyen úton történő feldolgozását az teszi szükségessé, hogy a CCD-felvételen a kisbolygó nagyon gyakran zsúfolt csillagkörnyezetben található. Az éjszaka kezdetén sokszor az égitest azonosítása is nehézségekbe ütközik. A Guide ugyanis nem ábrázol minden csillagot a beállított határmagnitúdóig az adott égterületen, a katalógus célja előre megadott csillagszám biztosítása fix égterületre a referenciacsillagok számának szinten tartása érdekében. Így a Tejút környezetében a program határmagnitúdója lecsökken, csupán a fényesebb csillagok szerepelnek a térképen. Ehhez járul még hozzá a szegedi berendezés kicsi látómezeje, a 6 6 ívperces égterület megnehezíti a tájékozódást. Célszerű a mérés megkezdése előtt az internetről letölteni az adott területről a Digitized Sky Survey (DSS) 6 egy ide vonatkozó, beállítható méretű felvételét. A nagy határfényességű kép jobban visszaadja a valóság látványát, mint a Guide által kinyomtatott térkép. 26. ábra. A 6510 Tarry egyik felvétele Az azonosítási nehézségeknél azonban sokkal nagyobb probléma, hogy a csillagokkal történő számos látszólagos ütközésnél rengeteg fotometriai információ elveszik. A PSF fotometriával ellentétben az apertúra fotometria nem teszi lehetővé egymásba lógó csillagprofilok kiértékelését. Ha a kisbolygó látszólagos elmozdulása kicsi, nagyon sok időt tölt a csillag környezetében, ha gyorsan mozog, számos csillagot talál el. A 26. ábra, ami idén júniusban készült a piszkéstetői Schmidt-távcsővel, jól szemlélteti a fentebb említett gondokat
36 Ezen problémák kiküszöbölésére alkalmas a fluxus azonos szintre hozásának módszere. Az eljárás lépései a következőek: 1. A felvételeket koordináta szerint rendezzük. A képek összetolására alkalmas taszk az IRAF-on belül az imalign. 2. Az így kapott képek mindegyikét leosztjuk az adott képen található előre rögzített csillag fluxusával. 3. Vesszük ezen képek mediánját. 4. Minden leosztott képből kivonjuk ezt az eredményt. 5. Így a felvételeken csak egy csillag marad, maga a kisbolygó, ami így kifotometrálható. Az eljárás gyors alkalmazására egy C nyelvű program szolgálhat, amit a közeljövőben szeretnék elkészíteni. 36
37 A.4. Összes mérésem fénygörbéje A következő oldalakon a 4.1. alfejezetben bemutatott adatsorok kivételével megtalálható minden egyes mérésemből származó fénygörbe. Az ábrák vízszintes tengelyén a mérés időpontja található Julián-dátum formájában kifejezve, míg a függőleges tengelyen relatív magnitúdó különbség látható. A méréseim ábrázolásának döntő többségénél kiszedtem a csillaggal való látszólagos összeolvadások miatti hamis csúcsokat adó pontokat. Ezért több görbén az emiatti űrök sajnos fellelhetőek. 1,6 469 Argentina ,7 1,8 1,9 2 2,1 2,2 2303,2 2303, ,3 2303, ,4 2303, ,5 27. ábra. A 469 Argentina fénygörbéje 469 Argentina ,2 1 0,8 0,6 0,4 2307,3 2307,4 2307,5 2307,6 28. ábra. A 469 Argentina fénygörbéje 37
A csillagképek története és látnivalói február 14. Bevezetés: Az alapvető égi mozgások
 A csillagképek története és látnivalói 2018. február 14. Bevezetés: Az alapvető égi mozgások A csillagok látszólagos mozgása A Föld kb. 24 óra alatt megfordul a tengelye körül a földi megfigyelő számára
A csillagképek története és látnivalói 2018. február 14. Bevezetés: Az alapvető égi mozgások A csillagok látszólagos mozgása A Föld kb. 24 óra alatt megfordul a tengelye körül a földi megfigyelő számára
Véletlen jelenség: okok rendszere hozza létre - nem ismerhetjük mind, ezért sztochasztikus.
 Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Pulzáló változócsillagok és megfigyelésük I.
 Pulzáló változócsillagok és megfigyelésük I. 7. Cephei és SPB csillagok, megfigyelés Sódor Ádám ELTE MTA CSFK CSI 2015.11.10. 2 Sódor Ádám Pulzáló váltcsill. és megfigy. I. 6. Cep, SPB, megfigyelés 2 /
Pulzáló változócsillagok és megfigyelésük I. 7. Cephei és SPB csillagok, megfigyelés Sódor Ádám ELTE MTA CSFK CSI 2015.11.10. 2 Sódor Ádám Pulzáló váltcsill. és megfigy. I. 6. Cep, SPB, megfigyelés 2 /
Egyszerű számítási módszer bolygók és kisbolygók oályáj ának meghatározására
 Egyszerű számítási módszer bolygók és kisbolygók oályáj ának meghatározására A bolygók és kisbolygók pályájának analitikus meghatározása rendszerint több éves egyetemi előtanulmányokat igényel. Ennek oka
Egyszerű számítási módszer bolygók és kisbolygók oályáj ának meghatározására A bolygók és kisbolygók pályájának analitikus meghatározása rendszerint több éves egyetemi előtanulmányokat igényel. Ennek oka
Asztrometria egy klasszikus tudományág újjászületése. ELFT Fizikus Vándorgyűlés, Szeged, augusztus 25.
 Asztrometria egy klasszikus tudományág újjászületése ELFT Fizikus Vándorgyűlés, Szeged, 2016. augusztus 25. Történeti visszapillantás Asztrometria: az égitestek helyzetének és mozgásának meghatározásával
Asztrometria egy klasszikus tudományág újjászületése ELFT Fizikus Vándorgyűlés, Szeged, 2016. augusztus 25. Történeti visszapillantás Asztrometria: az égitestek helyzetének és mozgásának meghatározásával
Kettőscsillagok vizuális észlelése. Hannák Judit
 Kettőscsillagok vizuális észlelése Hannák Judit Miért észleljünk kettősöket? A kettőscsillagok szépek: Rengeteg féle szín, fényesség, szinte nincs is két egyforma. Többes rendszerek különösen érdekesek.
Kettőscsillagok vizuális észlelése Hannák Judit Miért észleljünk kettősöket? A kettőscsillagok szépek: Rengeteg féle szín, fényesség, szinte nincs is két egyforma. Többes rendszerek különösen érdekesek.
Hogyan lehet meghatározni az égitestek távolságát?
 Hogyan lehet meghatározni az égitestek távolságát? Először egy régóta használt, praktikus módszerről lesz szó, amelyet a térképészetben is alkalmaznak. Ez a geometriai háromszögelésen alapul, trigonometriai
Hogyan lehet meghatározni az égitestek távolságát? Először egy régóta használt, praktikus módszerről lesz szó, amelyet a térképészetben is alkalmaznak. Ez a geometriai háromszögelésen alapul, trigonometriai
Összeállította: Juhász Tibor 1
 A távcsövek típusai Refraktorok és reflektorok Lencsés távcső (refraktor) Galilei, 1609 A TÁVCSŐ objektív Kepler, 1611 Tükrös távcső (reflektor) objektív Newton, 1668 refraktor reflektor (i) Legnagyobb
A távcsövek típusai Refraktorok és reflektorok Lencsés távcső (refraktor) Galilei, 1609 A TÁVCSŐ objektív Kepler, 1611 Tükrös távcső (reflektor) objektív Newton, 1668 refraktor reflektor (i) Legnagyobb
Méréselmélet és mérőrendszerek 2. ELŐADÁS (1. RÉSZ)
 Méréselmélet és mérőrendszerek 2. ELŐADÁS (1. RÉSZ) KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba
Méréselmélet és mérőrendszerek 2. ELŐADÁS (1. RÉSZ) KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba
Matematikai alapok és valószínőségszámítás. Középértékek és szóródási mutatók
 Matematikai alapok és valószínőségszámítás Középértékek és szóródási mutatók Középértékek A leíró statisztikák talán leggyakrabban használt csoportját a középértékek jelentik. Legkönnyebben mint az adathalmaz
Matematikai alapok és valószínőségszámítás Középértékek és szóródási mutatók Középértékek A leíró statisztikák talán leggyakrabban használt csoportját a középértékek jelentik. Legkönnyebben mint az adathalmaz
Nehézségi gyorsulás mérése megfordítható ingával
 Nehézségi gyorsulás mérése megfordítható ingával (Mérési jegyzőkönyv) Hagymási Imre 2007. április 21. (hétfő délelőtti csoport) 1. A mérés elmélete A nehézségi gyorsulás mérésének egy klasszikus módja
Nehézségi gyorsulás mérése megfordítható ingával (Mérési jegyzőkönyv) Hagymási Imre 2007. április 21. (hétfő délelőtti csoport) 1. A mérés elmélete A nehézségi gyorsulás mérésének egy klasszikus módja
0.1. A CCD és infravörös felvételek feldolgozása
 Részletek Balog Zoltán PhD értekezéséből 0.1. A CCD és infravörös felvételek feldolgozása A dolgozatban közölt eredmények különböző CCD és infravörös kamerákkal elvégzett méréseken alapulnak. A képek különböző
Részletek Balog Zoltán PhD értekezéséből 0.1. A CCD és infravörös felvételek feldolgozása A dolgozatban közölt eredmények különböző CCD és infravörös kamerákkal elvégzett méréseken alapulnak. A képek különböző
Nemzetközi Csillagászati és Asztrofizikai Diákolimpia Szakkör Asztrofizika II. és Műszerismeret Megoldások
 Nemzetközi Csillagászati és Asztrofizikai Diákolimpia Szakkör 2015-16 4. Asztrofizika II. és Műszerismeret Megoldások Dálya Gergely, Bécsy Bence 1. Bemelegítő feladatok B.1. feladat Írjuk fel a Pogson-képletet:
Nemzetközi Csillagászati és Asztrofizikai Diákolimpia Szakkör 2015-16 4. Asztrofizika II. és Műszerismeret Megoldások Dálya Gergely, Bécsy Bence 1. Bemelegítő feladatok B.1. feladat Írjuk fel a Pogson-képletet:
Elfedett pulzációk vizsgálata a KIC fedési kettősrendszerben
 Elfedett pulzációk vizsgálata a KIC 3858884 fedési kettősrendszerben Bókon András II. éves Fizikus MSc szakos hallgató Témavezető: Dr. Bíró Imre Barna tudományos munkatárs, 216. 11. 25. Csillagok pulzációja
Elfedett pulzációk vizsgálata a KIC 3858884 fedési kettősrendszerben Bókon András II. éves Fizikus MSc szakos hallgató Témavezető: Dr. Bíró Imre Barna tudományos munkatárs, 216. 11. 25. Csillagok pulzációja
Fedési kett scsillagok fénygörbéinek el állítása
 Szegedi Tudományegyetem TTIK Kísérleti Fizikai Tanszék Fedési kett scsillagok fénygörbéinek el állítása BSc Szakmai gyakorlat Készítette: Mitnyan Tibor Fizika BSc hallgató Témavezet : Dr. Székely Péter
Szegedi Tudományegyetem TTIK Kísérleti Fizikai Tanszék Fedési kett scsillagok fénygörbéinek el állítása BSc Szakmai gyakorlat Készítette: Mitnyan Tibor Fizika BSc hallgató Témavezet : Dr. Székely Péter
Az éggömb. Csillagászat
 Az éggömb A csillagászati koordináta-rendszerek típusai topocentrikus geocentrikus heliocentrikus baricentrikus galaktocentrikus alapsík, kiindulási pont, körüljárási irány (ábra forrása: Marik Miklós:
Az éggömb A csillagászati koordináta-rendszerek típusai topocentrikus geocentrikus heliocentrikus baricentrikus galaktocentrikus alapsík, kiindulási pont, körüljárási irány (ábra forrása: Marik Miklós:
Naprendszer mozgásai
 Bevezetés a csillagászatba 2. Muraközy Judit Debreceni Egyetem, TTK 2017. 09. 28. Bevezetés a csillagászatba- Naprendszer mozgásai 2017. szeptember 28. 1 / 33 Kitekintés Miről lesz szó a mai órán? Naprendszer
Bevezetés a csillagászatba 2. Muraközy Judit Debreceni Egyetem, TTK 2017. 09. 28. Bevezetés a csillagászatba- Naprendszer mozgásai 2017. szeptember 28. 1 / 33 Kitekintés Miről lesz szó a mai órán? Naprendszer
Modern Fizika Labor. 2. Elemi töltés meghatározása
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Méréselmélet és mérőrendszerek
 Méréselmélet és mérőrendszerek 6. ELŐADÁS KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba eredete o
Méréselmélet és mérőrendszerek 6. ELŐADÁS KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba eredete o
Az Univerzum szerkezete
 Az Univerzum szerkezete Készítette: Szalai Tamás (csillagász, PhD-hallgató, SZTE) Lektorálta: Dr. Szatmáry Károly (egy. docens, SZTE Kísérleti Fizikai Tsz.) 2011. március Kifelé a Naprendszerből: A Kuiper(-Edgeworth)-öv
Az Univerzum szerkezete Készítette: Szalai Tamás (csillagász, PhD-hallgató, SZTE) Lektorálta: Dr. Szatmáry Károly (egy. docens, SZTE Kísérleti Fizikai Tsz.) 2011. március Kifelé a Naprendszerből: A Kuiper(-Edgeworth)-öv
Földünk a világegyetemben
 Földünk a világegyetemben A Tejútrendszer a Lokális Galaxiscsoport egyik küllős spirálgalaxisa, melyben a Naprendszer és ezen belül Földünk található. 200-400 milliárd csillag található benne, átmérője
Földünk a világegyetemben A Tejútrendszer a Lokális Galaxiscsoport egyik küllős spirálgalaxisa, melyben a Naprendszer és ezen belül Földünk található. 200-400 milliárd csillag található benne, átmérője
7. gyakorlat Sorozatok, Fájlkezelés
 7. gyakorlat Sorozatok, Fájlkezelés Házi ellenőrzés - f0124 Írj programot, amelyben a felhasználónak egy, a program által meghatározott számot kell kitalálnia! A felhasználó tippjét a program vagy elfogadja,
7. gyakorlat Sorozatok, Fájlkezelés Házi ellenőrzés - f0124 Írj programot, amelyben a felhasználónak egy, a program által meghatározott számot kell kitalálnia! A felhasználó tippjét a program vagy elfogadja,
Grafikonok automatikus elemzése
 Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
CSAPADÉK ÉS TALAJVÍZSZINT ÉRTÉKEK SPEKTRÁLIS ELEMZÉSE A MEZŐKERESZTES-I ADATOK ALAPJÁN*
 A Miskolci Egyetem Közleménye A sorozat, Bányászat, 66. kötet, (2004) p. 103-108 CSAPADÉK ÉS TALAJVÍZSZINT ÉRTÉKEK SPEKTRÁLIS ELEMZÉSE A MEZŐKERESZTES-I ADATOK ALAPJÁN* Dr.h.c.mult. Dr. Kovács Ferenc az
A Miskolci Egyetem Közleménye A sorozat, Bányászat, 66. kötet, (2004) p. 103-108 CSAPADÉK ÉS TALAJVÍZSZINT ÉRTÉKEK SPEKTRÁLIS ELEMZÉSE A MEZŐKERESZTES-I ADATOK ALAPJÁN* Dr.h.c.mult. Dr. Kovács Ferenc az
Múltunk és jövőnk a Naprendszerben
 Múltunk és jövőnk a Naprendszerben Holl András MTA Konkoly Thege Miklós Csillagászati Kutatóintézete Szöveges változat: http://www.konkoly.hu/staff/holl/petofi/nemesis_text.pdf 1 2 Az emberiség a Naprendszerben
Múltunk és jövőnk a Naprendszerben Holl András MTA Konkoly Thege Miklós Csillagászati Kutatóintézete Szöveges változat: http://www.konkoly.hu/staff/holl/petofi/nemesis_text.pdf 1 2 Az emberiség a Naprendszerben
A magyar teljesítménytúra-naptár fejlődése,
 A magyar teljesítménytúra-naptár fejlődése, 28-216 Tartalomjegyzék Ferenci Tamás, tamas.ferenci@medstat.hu 217. február 2. Cél 1 Számítástechnikai megjegyzések 1 Eredmények 2 Túrák és túrázok száma..........................................
A magyar teljesítménytúra-naptár fejlődése, 28-216 Tartalomjegyzék Ferenci Tamás, tamas.ferenci@medstat.hu 217. február 2. Cél 1 Számítástechnikai megjegyzések 1 Eredmények 2 Túrák és túrázok száma..........................................
matematikai statisztika
 Az újságokban, plakátokon, reklámkiadványokban sokszor találkozunk ilyen grafikonokkal, ezért szükséges, hogy megértsük, és jól tudjuk értelmezni őket. A második grafikon ismerős lehet, hiszen a függvények
Az újságokban, plakátokon, reklámkiadványokban sokszor találkozunk ilyen grafikonokkal, ezért szükséges, hogy megértsük, és jól tudjuk értelmezni őket. A második grafikon ismerős lehet, hiszen a függvények
3. jegyz könyv: Bolygómozgás
 3. jegyz könyv: Bolygómozgás Harangozó Szilveszter Miklós, HASPABT.ELTE 21. április 6. 1. Bevezetés Mostani feladatunk a bolygók mozgásának modellezése. Mint mindig a program forráskódját a honlapon [1]
3. jegyz könyv: Bolygómozgás Harangozó Szilveszter Miklós, HASPABT.ELTE 21. április 6. 1. Bevezetés Mostani feladatunk a bolygók mozgásának modellezése. Mint mindig a program forráskódját a honlapon [1]
A napenergia magyarországi hasznosítását támogató új fejlesztések az Országos Meteorológiai Szolgálatnál
 A napenergia magyarországi hasznosítását támogató új fejlesztések az Országos Meteorológiai Szolgálatnál Nagy Zoltán, Tóth Zoltán, Morvai Krisztián, Szintai Balázs Országos Meteorológiai Szolgálat A globálsugárzás
A napenergia magyarországi hasznosítását támogató új fejlesztések az Országos Meteorológiai Szolgálatnál Nagy Zoltán, Tóth Zoltán, Morvai Krisztián, Szintai Balázs Országos Meteorológiai Szolgálat A globálsugárzás
A II. kategória Fizika OKTV mérési feladatainak megoldása
 Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Elveszett m²-ek? (Az akaratlanul elveszett információ)
 Elveszett m²-ek? (Az akaratlanul elveszett információ) A mérés és a térkép I. A földrészletek elméleti határvonalait definiáló geodéziai/geometriai pontok (mint térképi objektumok) 0[null] dimenziósak,
Elveszett m²-ek? (Az akaratlanul elveszett információ) A mérés és a térkép I. A földrészletek elméleti határvonalait definiáló geodéziai/geometriai pontok (mint térképi objektumok) 0[null] dimenziósak,
Mérési hibák 2006.10.04. 1
 Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
PÁPICS PÉTER ISTVÁN CSILLAGÁSZATI SPEKTROSZKÓPIA HF FELADAT: egy tetszőleges nyers csillagspektrum választása, ábrakészítés IDL-ben (leírása az
 PÁPICS PÉTER ISTVÁN CSILLAGÁSZATI SPEKTROSZKÓPIA 1. 3. HF FELADAT: egy tetszőleges nyers csillagspektrum választása, ábrakészítés IDL-ben (leírása az objektum, a műszer, és az időpont megjelölésével).
PÁPICS PÉTER ISTVÁN CSILLAGÁSZATI SPEKTROSZKÓPIA 1. 3. HF FELADAT: egy tetszőleges nyers csillagspektrum választása, ábrakészítés IDL-ben (leírása az objektum, a műszer, és az időpont megjelölésével).
A változócsillagok. A pulzáló változók.
 A változócsillagok. Tulajdonképpen minden csillag változik az élete során. Például a kémiai összetétele, a luminozitása, a sugara, az átlagsűrűsége, stb. Ezek a változások a mi emberi élethosszunkhoz képest
A változócsillagok. Tulajdonképpen minden csillag változik az élete során. Például a kémiai összetétele, a luminozitása, a sugara, az átlagsűrűsége, stb. Ezek a változások a mi emberi élethosszunkhoz képest
Hogyan mozognak a legjobb égi referenciapontok?
 Hogyan mozognak a legjobb égi referenciapontok? Moór Attila, Frey Sándor, Sebastien Lambert, Oleg Titov, Bakos Judit FÖMI Kozmikus Geodéziai Obszervatóriuma, Penc MTA Fizikai Geodézia és Geodinamikai Kutatócsoport,
Hogyan mozognak a legjobb égi referenciapontok? Moór Attila, Frey Sándor, Sebastien Lambert, Oleg Titov, Bakos Judit FÖMI Kozmikus Geodéziai Obszervatóriuma, Penc MTA Fizikai Geodézia és Geodinamikai Kutatócsoport,
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011.
 BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
A mérések általános és alapvető metrológiai fogalmai és definíciói. Mérések, mérési eredmények, mérési bizonytalanság. mérés. mérési elv
 Mérések, mérési eredmények, mérési bizonytalanság A mérések általános és alapvető metrológiai fogalmai és definíciói mérés Műveletek összessége, amelyek célja egy mennyiség értékének meghatározása. mérési
Mérések, mérési eredmények, mérési bizonytalanság A mérések általános és alapvető metrológiai fogalmai és definíciói mérés Műveletek összessége, amelyek célja egy mennyiség értékének meghatározása. mérési
A mérés problémája a pedagógiában. Dr. Nyéki Lajos 2015
 A mérés problémája a pedagógiában Dr. Nyéki Lajos 2015 A mérés fogalma Mérésen olyan tevékenységet értünk, amelynek eredményeként a vizsgált jelenség számszerűen jellemezhetővé, más hasonló jelenségekkel
A mérés problémája a pedagógiában Dr. Nyéki Lajos 2015 A mérés fogalma Mérésen olyan tevékenységet értünk, amelynek eredményeként a vizsgált jelenség számszerűen jellemezhetővé, más hasonló jelenségekkel
Pósfay Péter. ELTE, Wigner FK Témavezetők: Jakovác Antal, Barnaföldi Gergely G.
 Pósfay Péter ELTE, Wigner FK Témavezetők: Jakovác Antal, Barnaföldi Gergely G. A Naphoz hasonló tömegű csillagok A Napnál 4-8-szor nagyobb tömegű csillagok 8 naptömegnél nagyobb csillagok Vörös óriás Szupernóva
Pósfay Péter ELTE, Wigner FK Témavezetők: Jakovác Antal, Barnaföldi Gergely G. A Naphoz hasonló tömegű csillagok A Napnál 4-8-szor nagyobb tömegű csillagok 8 naptömegnél nagyobb csillagok Vörös óriás Szupernóva
Osztályozó, javító vizsga 9. évfolyam gimnázium. Írásbeli vizsgarész ELSŐ RÉSZ
 Írásbeli vizsgarész ELSŐ RÉSZ 1. Egy téglalap alakú háztömb egyik sarkából elindulva 80 m, 150 m, 80 m utat tettünk meg az egyes házoldalak mentén, míg a szomszédos sarokig értünk. Mekkora az elmozdulásunk?
Írásbeli vizsgarész ELSŐ RÉSZ 1. Egy téglalap alakú háztömb egyik sarkából elindulva 80 m, 150 m, 80 m utat tettünk meg az egyes házoldalak mentén, míg a szomszédos sarokig értünk. Mekkora az elmozdulásunk?
A Hisztogram használata a digitális képszerkesztésben
 Mechatronika, Optika és Mûszertechnika Tanszék A Hisztogram használata a digitális képszerkesztésben Tárgy: Fotó és Készítette: Curávy Tamás képszerkesztési technikák B1Y6IV Elõadó: Antal Á kos Budapest,
Mechatronika, Optika és Mûszertechnika Tanszék A Hisztogram használata a digitális képszerkesztésben Tárgy: Fotó és Készítette: Curávy Tamás képszerkesztési technikák B1Y6IV Elõadó: Antal Á kos Budapest,
A mérési eredmény megadása
 A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
A 2017/2018. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. KATEGÓRIA JAVÍTÁSI ÚTMUTATÓ. Pohár rezonanciája
 Oktatási Hivatal A 017/018. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. KATEGÓRIA JAVÍTÁSI ÚTMUTATÓ Pohár rezonanciája A mérőberendezés leírása: A mérőberendezés egy változtatható
Oktatási Hivatal A 017/018. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. KATEGÓRIA JAVÍTÁSI ÚTMUTATÓ Pohár rezonanciája A mérőberendezés leírása: A mérőberendezés egy változtatható
1/8. Iskolai jelentés. 10.évfolyam matematika
 1/8 2009 Iskolai jelentés 10.évfolyam matematika 2/8 Matematikai kompetenciaterület A fejlesztés célja A kidolgozásra kerülő programcsomagok az alább felsorolt készségek, képességek közül a számlálás,
1/8 2009 Iskolai jelentés 10.évfolyam matematika 2/8 Matematikai kompetenciaterület A fejlesztés célja A kidolgozásra kerülő programcsomagok az alább felsorolt készségek, képességek közül a számlálás,
Eddigi tanulmányaink alapján már egy sor, a szeizmikában általánosan használt műveletet el tudunk végezni.
 Eddigi tanulmányaink alapján már egy sor, a szeizmikában általánosan használt műveletet el tudunk végezni. Kezdjük a sort a menetidőgörbékről, illetve az NMO korrekcióról tanultakkal. A következő ábrán
Eddigi tanulmányaink alapján már egy sor, a szeizmikában általánosan használt műveletet el tudunk végezni. Kezdjük a sort a menetidőgörbékről, illetve az NMO korrekcióról tanultakkal. A következő ábrán
A mérés célkitűzései: A matematikai inga lengésidejének kísérleti vizsgálata, a nehézségi gyorsulás meghatározása.
 A mérés célkitűzései: A matematikai inga lengésidejének kísérleti vizsgálata, a nehézségi gyorsulás meghatározása. Eszközszükséglet: Bunsen állvány lombik fogóval 50 g-os vasból készült súlyok fonál mérőszalag,
A mérés célkitűzései: A matematikai inga lengésidejének kísérleti vizsgálata, a nehézségi gyorsulás meghatározása. Eszközszükséglet: Bunsen állvány lombik fogóval 50 g-os vasból készült súlyok fonál mérőszalag,
10. mérés. Fényelhajlási jelenségek vizsgála
 Bán Marcell ETR atonosító BAMTACT.ELTE Beadási határidő 2012.10.15 (engedélyezett késés) 10. mérés Fényelhajlási jelenségek vizsgála Bevezetés: A mérések során a fény hullámhosszából adódó jelenségeket
Bán Marcell ETR atonosító BAMTACT.ELTE Beadási határidő 2012.10.15 (engedélyezett késés) 10. mérés Fényelhajlási jelenségek vizsgála Bevezetés: A mérések során a fény hullámhosszából adódó jelenségeket
Kisérettségi feladatsorok matematikából
 Kisérettségi feladatsorok matematikából. feladatsor I. rész. Döntse el, hogy a következő állítások közül melyik igaz és melyik hamis! a) Ha két egész szám összege páratlan, akkor a szorzatuk páros. b)
Kisérettségi feladatsorok matematikából. feladatsor I. rész. Döntse el, hogy a következő állítások közül melyik igaz és melyik hamis! a) Ha két egész szám összege páratlan, akkor a szorzatuk páros. b)
JUICE: navigáció a Jupiternél, rádiótávcsövekkel
 JUICE: navigáció a Jupiternél, rádiótávcsövekkel Frey Sándor MTA Csillagászati és Földtudományi Kutatóközpont Konkoly Thege Miklós Csillagászati Intézet Budapest frey.sandor@csfk.mta.hu ESA GISOpen 2019
JUICE: navigáció a Jupiternél, rádiótávcsövekkel Frey Sándor MTA Csillagászati és Földtudományi Kutatóközpont Konkoly Thege Miklós Csillagászati Intézet Budapest frey.sandor@csfk.mta.hu ESA GISOpen 2019
Statisztikai módszerek a skálafüggetlen hálózatok
 Statisztikai módszerek a skálafüggetlen hálózatok vizsgálatára Gyenge Ádám1 1 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Számítástudományi és Információelméleti
Statisztikai módszerek a skálafüggetlen hálózatok vizsgálatára Gyenge Ádám1 1 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Számítástudományi és Információelméleti
NYOMÁS ÉS NYOMÁSKÜLÖNBSÉG MÉRÉS. Mérési feladatok
 Hidrodinamikai Rendszerek Tanszék Készítette:... kurzus Elfogadva: Dátum:...év...hó...nap NYOMÁS ÉS NYOMÁSKÜLÖNBSÉG MÉRÉS Mérési feladatok 1. Csővezetékben áramló levegő nyomásveszteségének mérése U-csöves
Hidrodinamikai Rendszerek Tanszék Készítette:... kurzus Elfogadva: Dátum:...év...hó...nap NYOMÁS ÉS NYOMÁSKÜLÖNBSÉG MÉRÉS Mérési feladatok 1. Csővezetékben áramló levegő nyomásveszteségének mérése U-csöves
Galaxisfelmérések: az Univerzum térképei. Bevezetés a csillagászatba május 12.
 Galaxisfelmérések: az Univerzum térképei Bevezetés a csillagászatba 4. 2015. május 12. Miről lesz szó? Hubble vagy nem Hubble? Galaxisok, galaxishalmazok és az Univerzum szerkezete A műszerfejlődés útjai
Galaxisfelmérések: az Univerzum térképei Bevezetés a csillagászatba 4. 2015. május 12. Miről lesz szó? Hubble vagy nem Hubble? Galaxisok, galaxishalmazok és az Univerzum szerkezete A műszerfejlődés útjai
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar. Villamos Energetika Tanszék. Világítástechnika (BME VIVEM 355)
 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Villamos Energetika Tanszék Világítástechnika (BME VIVEM 355) Beltéri mérés Világítástechnikai felülvizsgálati jegyzőkönyv
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Villamos Energetika Tanszék Világítástechnika (BME VIVEM 355) Beltéri mérés Világítástechnikai felülvizsgálati jegyzőkönyv
Mechanika. Kinematika
 Mechanika Kinematika Alapfogalmak Anyagi pont Vonatkoztatási és koordináta rendszer Pálya, út, elmozdulás, Vektormennyiségek: elmozdulásvektor Helyvektor fogalma Sebesség Mozgások csoportosítása A mozgásokat
Mechanika Kinematika Alapfogalmak Anyagi pont Vonatkoztatási és koordináta rendszer Pálya, út, elmozdulás, Vektormennyiségek: elmozdulásvektor Helyvektor fogalma Sebesség Mozgások csoportosítása A mozgásokat
A kálium-permanganát és az oxálsav közötti reakció vizsgálata 9a. mérés B4.9
 A kálium-permanganát és az oxálsav közötti reakció vizsgálata 9a. mérés B4.9 Név: Pitlik László Mérés dátuma: 2014.12.04. Mérőtársak neve: Menkó Orsolya Adatsorok: M24120411 Halmy Réka M14120412 Sárosi
A kálium-permanganát és az oxálsav közötti reakció vizsgálata 9a. mérés B4.9 Név: Pitlik László Mérés dátuma: 2014.12.04. Mérőtársak neve: Menkó Orsolya Adatsorok: M24120411 Halmy Réka M14120412 Sárosi
Matematikai geodéziai számítások 6.
 Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Fizika példák a döntőben
 Fizika példák a döntőben F. 1. Legyen két villamosmegálló közötti távolság 500 m, a villamos gyorsulása pedig 0,5 m/s! A villamos 0 s időtartamig gyorsuljon, majd állandó sebességgel megy, végül szintén
Fizika példák a döntőben F. 1. Legyen két villamosmegálló közötti távolság 500 m, a villamos gyorsulása pedig 0,5 m/s! A villamos 0 s időtartamig gyorsuljon, majd állandó sebességgel megy, végül szintén
HÁZI DOLGOZAT. Érmefeldobások eredményei és statisztikája. ELTE-TTK Kémia BSc Tantárgy: Kémia felzárkóztató (A kémia alapjai)
 ELTE-TTK Kémia BSc Tantárgy: Kémia felzárkóztató (A kémia alapjai) HÁZI DOLGOZAT Érmefeldobások eredményei és statisztikája Készítette: Babinszki Bence EHA-kód: BABSAET.ELTE E-mail cím: Törölve A jelentés
ELTE-TTK Kémia BSc Tantárgy: Kémia felzárkóztató (A kémia alapjai) HÁZI DOLGOZAT Érmefeldobások eredményei és statisztikája Készítette: Babinszki Bence EHA-kód: BABSAET.ELTE E-mail cím: Törölve A jelentés
Biomatematika 12. Szent István Egyetem Állatorvos-tudományi Kar. Fodor János
 Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
MATEMATIKA HETI 5 ÓRA
 EURÓPAI ÉRETTSÉGI 2008 MATEMATIKA HETI 5 ÓRA IDŐPONT : 2008. június 5 (reggel) A VIZSGA IDŐTARTAMA: 4 óra (240 perc) MEGENGEDETT ESZKÖZÖK: Európai képletgyűjtemény Nem programozható, nem grafikus számológép
EURÓPAI ÉRETTSÉGI 2008 MATEMATIKA HETI 5 ÓRA IDŐPONT : 2008. június 5 (reggel) A VIZSGA IDŐTARTAMA: 4 óra (240 perc) MEGENGEDETT ESZKÖZÖK: Európai képletgyűjtemény Nem programozható, nem grafikus számológép
STATISZTIKA ELŐADÁS ÁTTEKINTÉSE. Matematikai statisztika. Mi a modell? Binomiális eloszlás sűrűségfüggvény. Binomiális eloszlás
 ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
Csillagászati földrajz I-II.
 Tantárgy neve Csillagászati földrajz I-II. Tantárgy kódja FDB1305; FDB1306 Meghirdetés féléve 2 Kreditpont 2+1 Összóraszám (elm.+gyak.) 1+0, 0+1 Számonkérés módja kollokvium + gyakorlati jegy Előfeltétel
Tantárgy neve Csillagászati földrajz I-II. Tantárgy kódja FDB1305; FDB1306 Meghirdetés féléve 2 Kreditpont 2+1 Összóraszám (elm.+gyak.) 1+0, 0+1 Számonkérés módja kollokvium + gyakorlati jegy Előfeltétel
Csillagászati észlelési gyakorlatok I. 4. óra Az éggömb látszólagos mozgása, csillagászati koordináta-rendszerek, a téli égbolt csillagképei
 Csillagászati észlelési gyakorlatok I. 4. óra Az éggömb látszólagos mozgása, csillagászati koordináta-rendszerek, a téli égbolt csillagképei Hajdu Tamás & Perger Krisztina & B gner Rebeka & Császár Anna
Csillagászati észlelési gyakorlatok I. 4. óra Az éggömb látszólagos mozgása, csillagászati koordináta-rendszerek, a téli égbolt csillagképei Hajdu Tamás & Perger Krisztina & B gner Rebeka & Császár Anna
DIGITÁLIS TEREPMODELL A TÁJRENDEZÉSBEN
 DIGITÁLIS TEREPMODELL A TÁJRENDEZÉSBEN DR. GIMESI LÁSZLÓ Bevezetés Pécsett és környékén végzett bányászati tevékenység felszámolása kapcsán szükségessé vált az e tevékenység során keletkezett meddők, zagytározók,
DIGITÁLIS TEREPMODELL A TÁJRENDEZÉSBEN DR. GIMESI LÁSZLÓ Bevezetés Pécsett és környékén végzett bányászati tevékenység felszámolása kapcsán szükségessé vált az e tevékenység során keletkezett meddők, zagytározók,
Matematikai geodéziai számítások 10.
 Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Távérzékelés gyakorlat Fotogrammetria légifotó értelmezés
 Távérzékelés gyakorlat Fotogrammetria légifotó értelmezés I. A légifotók tájolása a térkép segítségével: a). az ábrázolt terület azonosítása a térképen b). sztereoszkópos vizsgálat II. A légifotók értelmezése:
Távérzékelés gyakorlat Fotogrammetria légifotó értelmezés I. A légifotók tájolása a térkép segítségével: a). az ábrázolt terület azonosítása a térképen b). sztereoszkópos vizsgálat II. A légifotók értelmezése:
Modern műszeres analitika szeminárium Néhány egyszerű statisztikai teszt
 Modern műszeres analitika szeminárium Néhány egyszerű statisztikai teszt Galbács Gábor KIUGRÓ ADATOK KISZŰRÉSE STATISZTIKAI TESZTEKKEL Dixon Q-tesztje Gyakori feladat az analitikai kémiában, hogy kiugrónak
Modern műszeres analitika szeminárium Néhány egyszerű statisztikai teszt Galbács Gábor KIUGRÓ ADATOK KISZŰRÉSE STATISZTIKAI TESZTEKKEL Dixon Q-tesztje Gyakori feladat az analitikai kémiában, hogy kiugrónak
Akusztikai tervezés a geometriai akusztika módszereivel
 Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Modern fizika laboratórium
 Modern fizika laboratórium 11. Az I 2 molekula disszociációs energiája Készítette: Hagymási Imre A mérés dátuma: 2007. október 3. A beadás dátuma: 2007. október xx. 1. Bevezetés Ebben a mérésben egy kétatomos
Modern fizika laboratórium 11. Az I 2 molekula disszociációs energiája Készítette: Hagymási Imre A mérés dátuma: 2007. október 3. A beadás dátuma: 2007. október xx. 1. Bevezetés Ebben a mérésben egy kétatomos
2. A 2016.évi Országos kompetencia mérés eredményeinek feldolgozása
 2. A 2016.évi Országos kompetencia mérés eredményeinek feldolgozása A 2016.évi Országos kompetenciamérésen résztvevő 10 évfolyamos osztályok osztályfőnökei; a könnyebb beazonosíthatóság végett: 10.A: Ányosné
2. A 2016.évi Országos kompetencia mérés eredményeinek feldolgozása A 2016.évi Országos kompetenciamérésen résztvevő 10 évfolyamos osztályok osztályfőnökei; a könnyebb beazonosíthatóság végett: 10.A: Ányosné
1. Adatok kiértékelése. 2. A feltételek megvizsgálása. 3. A hipotézis megfogalmazása
 HIPOTÉZIS VIZSGÁLAT A hipotézis feltételezés egy vagy több populációról. (pl. egy gyógyszer az esetek 90%-ában hatásos; egy kezelés jelentősen megnöveli a rákos betegek túlélését). A hipotézis vizsgálat
HIPOTÉZIS VIZSGÁLAT A hipotézis feltételezés egy vagy több populációról. (pl. egy gyógyszer az esetek 90%-ában hatásos; egy kezelés jelentősen megnöveli a rákos betegek túlélését). A hipotézis vizsgálat
BSc hallgatók szakdolgozatával szemben támasztott követelmények SZTE TTIK Földrajzi és Földtani Tanszékcsoport
 BSc hallgatók szakdolgozatával szemben támasztott követelmények SZTE TTIK Földrajzi és Földtani Tanszékcsoport Az alapszakon a záróvizsgára bocsátás feltétele szakdolgozat készítése. A szakdolgozat kreditértéke:
BSc hallgatók szakdolgozatával szemben támasztott követelmények SZTE TTIK Földrajzi és Földtani Tanszékcsoport Az alapszakon a záróvizsgára bocsátás feltétele szakdolgozat készítése. A szakdolgozat kreditértéke:
Diplomamunka, Szakdolgozat, Projekt munka, Komplex tervezés felépítésének tartalmi és formai követelményei
 Diplomamunka, Szakdolgozat, Projekt munka, Komplex tervezés felépítésének tartalmi és formai követelményei 1. Kötelezően leadandó Az Automatizálási és Infokommunikációs Intézet honlapján található tervezési
Diplomamunka, Szakdolgozat, Projekt munka, Komplex tervezés felépítésének tartalmi és formai követelményei 1. Kötelezően leadandó Az Automatizálási és Infokommunikációs Intézet honlapján található tervezési
SZEGEDI TUDOMÁNYEGYETEM Természettudományi és Informatikai Kar Kísérleti Fizikai Tanszék. Doktori/Ph.D. értekezés tézisfüzet
 SZEGEDI TUDOMÁNYEGYETEM Természettudományi és Informatikai Kar Kísérleti Fizikai Tanszék Doktori/Ph.D. értekezés tézisfüzet Csillagok, csillaghalmazok és kisbolygók fizikai paramétereinek meghatározása
SZEGEDI TUDOMÁNYEGYETEM Természettudományi és Informatikai Kar Kísérleti Fizikai Tanszék Doktori/Ph.D. értekezés tézisfüzet Csillagok, csillaghalmazok és kisbolygók fizikai paramétereinek meghatározása
STATISZTIKA I. Centrális mutatók. Helyzeti középértékek. Középértékek. Bimodális eloszlás, U. Módusz, Mo. 4. Előadás.
 Centrális mutatók STATISZTIKA I. 4. Előadás Centrális mutatók 1/51 2/51 Középértékek Helyzeti középértékek A meghatározása gyakoriság vagy sorszám alapján Számítás nélkül Az elemek nagyság szerint rendezett
Centrális mutatók STATISZTIKA I. 4. Előadás Centrális mutatók 1/51 2/51 Középértékek Helyzeti középértékek A meghatározása gyakoriság vagy sorszám alapján Számítás nélkül Az elemek nagyság szerint rendezett
2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv. Zsigmond Anna Fizika Bsc II. Mérés dátuma: Leadás dátuma:
 2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 24. Leadás dátuma: 2008. 10. 01. 1 1. Mérések ismertetése Az 1. ábrán látható összeállításban
2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 24. Leadás dátuma: 2008. 10. 01. 1 1. Mérések ismertetése Az 1. ábrán látható összeállításban
Mit nevezünk nehézségi erőnek?
 Mit nevezünk nehézségi erőnek? Azt az erőt, amelynek hatására a szabadon eső testek g (gravitációs) gyorsulással esnek a vonzó test centruma felé, nevezzük nehézségi erőnek. F neh = m g Mi a súly? Azt
Mit nevezünk nehézségi erőnek? Azt az erőt, amelynek hatására a szabadon eső testek g (gravitációs) gyorsulással esnek a vonzó test centruma felé, nevezzük nehézségi erőnek. F neh = m g Mi a súly? Azt
A SZÉL ENERGIÁJÁNAK HASZNOSÍTÁSA Háztartási Méretű Kiserőművek (HMKE)
 A SZÉL ENERGIÁJÁNAK HASZNOSÍTÁSA Háztartási Méretű Kiserőművek (HMKE) A szél mechanikai energiáját szélgenerátorok segítségével tudjuk elektromos energiává alakítani. Természetesen a szél energiáját mechanikus
A SZÉL ENERGIÁJÁNAK HASZNOSÍTÁSA Háztartási Méretű Kiserőművek (HMKE) A szél mechanikai energiáját szélgenerátorok segítségével tudjuk elektromos energiává alakítani. Természetesen a szél energiáját mechanikus
A Föld helye a Világegyetemben. A Naprendszer
 A Föld helye a Világegyetemben A Naprendszer Mértékegységek: Fényév: az a távolság, amelyet a fény egy év alatt tesz meg. (A fény terjedési sebessége: 300.000 km.s -1.) Egy év alatt: 60.60.24.365.300 000
A Föld helye a Világegyetemben A Naprendszer Mértékegységek: Fényév: az a távolság, amelyet a fény egy év alatt tesz meg. (A fény terjedési sebessége: 300.000 km.s -1.) Egy év alatt: 60.60.24.365.300 000
Méréstechnika. Rezgésmérés. Készítette: Ángyán Béla. Iszak Gábor. Seidl Áron. Veszprém. [Ide írhatja a szöveget] oldal 1
![Méréstechnika. Rezgésmérés. Készítette: Ángyán Béla. Iszak Gábor. Seidl Áron. Veszprém. [Ide írhatja a szöveget] oldal 1 Méréstechnika. Rezgésmérés. Készítette: Ángyán Béla. Iszak Gábor. Seidl Áron. Veszprém. [Ide írhatja a szöveget] oldal 1](/thumbs/45/23262384.jpg) Méréstechnika Rezgésmérés Készítette: Ángyán Béla Iszak Gábor Seidl Áron Veszprém 2014 [Ide írhatja a szöveget] oldal 1 A rezgésekkel kapcsolatos alapfogalmak A rezgés a Magyar Értelmező Szótár megfogalmazása
Méréstechnika Rezgésmérés Készítette: Ángyán Béla Iszak Gábor Seidl Áron Veszprém 2014 [Ide írhatja a szöveget] oldal 1 A rezgésekkel kapcsolatos alapfogalmak A rezgés a Magyar Értelmező Szótár megfogalmazása
2. Rugalmas állandók mérése
 2. Rugalmas állandók mérése Klasszikus fizika laboratórium Mérési jegyzőkönyv Mérést végezte: Vitkóczi Fanni Jegyzőkönyv leadásának időpontja: 2012. 12. 15. I. A mérés célja: Két anyag Young-modulusának
2. Rugalmas állandók mérése Klasszikus fizika laboratórium Mérési jegyzőkönyv Mérést végezte: Vitkóczi Fanni Jegyzőkönyv leadásának időpontja: 2012. 12. 15. I. A mérés célja: Két anyag Young-modulusának
Mechatronika segédlet 3. gyakorlat
 Mechatronika segédlet 3. gyakorlat 2017. február 20. Tartalom Vadai Gergely, Faragó Dénes Feladatleírás... 2 Fogaskerék... 2 Nézetváltás 3D modellezéshez... 2 Könnyítés megvalósítása... 2 A fogaskerék
Mechatronika segédlet 3. gyakorlat 2017. február 20. Tartalom Vadai Gergely, Faragó Dénes Feladatleírás... 2 Fogaskerék... 2 Nézetváltás 3D modellezéshez... 2 Könnyítés megvalósítása... 2 A fogaskerék
Feladatok: pontdiagram és dobozdiagram. Hogyan csináltuk?
 Feladatok: pontdiagram és dobozdiagram Hogyan csináltuk? Alakmutatók: ferdeség, csúcsosság Alakmutatók a ferdeség és csúcsosság mérésére Ez eloszlás centrumát (középérték) és az adatok centrum körüli terpeszkedését
Feladatok: pontdiagram és dobozdiagram Hogyan csináltuk? Alakmutatók: ferdeség, csúcsosság Alakmutatók a ferdeség és csúcsosság mérésére Ez eloszlás centrumát (középérték) és az adatok centrum körüli terpeszkedését
CSILLAGÁSZATI FÖLDRAJZ
 CSILLAGÁSZATI FÖLDRAJZ FÖLDRAJZ ALAPSZAK (NAPPALI MUNKAREND) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI FÖLDTUDOMÁNYI KAR FÖLDRAJZ-GEOINFORMATIKA INTÉZET Miskolc, 2019 TARTALOMJEGYZÉK 1.
CSILLAGÁSZATI FÖLDRAJZ FÖLDRAJZ ALAPSZAK (NAPPALI MUNKAREND) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI FÖLDTUDOMÁNYI KAR FÖLDRAJZ-GEOINFORMATIKA INTÉZET Miskolc, 2019 TARTALOMJEGYZÉK 1.
A mechanika alapjai. A pontszerű testek dinamikája
 A mechanika alapjai A pontszerű testek dinamikája Horváth András SZE, Fizika Tsz. v 0.6 1 / 26 alapi Bevezetés Newton I. Newton II. Newton III. Newton IV. alapi 2 / 26 Bevezetés alapi Bevezetés Newton
A mechanika alapjai A pontszerű testek dinamikája Horváth András SZE, Fizika Tsz. v 0.6 1 / 26 alapi Bevezetés Newton I. Newton II. Newton III. Newton IV. alapi 2 / 26 Bevezetés alapi Bevezetés Newton
kompetenciakompetenciakompetenci akompetenciakompetenciakompeten ciakompetenciakompetenciakompete nciakompetenciakompetenciakompet
 kompetenciakompetenciakompetenci akompetenciakompetenciakompeten ciakompetenciakompetenciakompete nciakompetenciakompetenciakompet A 2017. évi kompetenciamérés eredményei enciakompetenciakompetenciakomp
kompetenciakompetenciakompetenci akompetenciakompetenciakompeten ciakompetenciakompetenciakompete nciakompetenciakompetenciakompet A 2017. évi kompetenciamérés eredményei enciakompetenciakompetenciakomp
6. Előadás. Vereb György, DE OEC BSI, október 12.
 6. Előadás Visszatekintés: a normális eloszlás Becslés, mintavételezés Reprezentatív minta A statisztika, mint változó Paraméter és Statisztika Torzítatlan becslés A mintaközép eloszlása - centrális határeloszlás
6. Előadás Visszatekintés: a normális eloszlás Becslés, mintavételezés Reprezentatív minta A statisztika, mint változó Paraméter és Statisztika Torzítatlan becslés A mintaközép eloszlása - centrális határeloszlás
Akusztikus aktivitás AE vizsgálatoknál
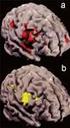 Akusztikus aktivitás AE vizsgálatoknál Kindlein Melinda, Fodor Olivér ÁEF Anyagvizsgáló Laboratórium Kft. 1112. Bp. Budaörsi út 45. Az akusztikus emissziós vizsgálat a roncsolásmentes vizsgálati módszerek
Akusztikus aktivitás AE vizsgálatoknál Kindlein Melinda, Fodor Olivér ÁEF Anyagvizsgáló Laboratórium Kft. 1112. Bp. Budaörsi út 45. Az akusztikus emissziós vizsgálat a roncsolásmentes vizsgálati módszerek
Térinformatikai DGPS NTRIP vétel és feldolgozás
 Térinformatikai DGPS NTRIP vétel és feldolgozás Méréseinkhez a Thales Mobile Mapper CE térinformatikai GPS vevıt használtunk. A mérést a Szegedi Tudományegyetem Egyetem utcai épületének tetején található
Térinformatikai DGPS NTRIP vétel és feldolgozás Méréseinkhez a Thales Mobile Mapper CE térinformatikai GPS vevıt használtunk. A mérést a Szegedi Tudományegyetem Egyetem utcai épületének tetején található
Információk. Ismétlés II. Ismétlés. Ismétlés III. A PROGRAMOZÁS ALAPJAI 2. Készítette: Vénné Meskó Katalin. Algoritmus. Algoritmus ábrázolása
 1 Információk 2 A PROGRAMOZÁS ALAPJAI 2. Készítette: Vénné Meskó Katalin Elérhetőség mesko.katalin@tfk.kefo.hu Fogadóóra: szerda 9:50-10:35 Számonkérés időpontok Április 25. 9 00 Május 17. 9 00 Június
1 Információk 2 A PROGRAMOZÁS ALAPJAI 2. Készítette: Vénné Meskó Katalin Elérhetőség mesko.katalin@tfk.kefo.hu Fogadóóra: szerda 9:50-10:35 Számonkérés időpontok Április 25. 9 00 Május 17. 9 00 Június
Programozási segédlet
 Programozási segédlet Programozási tételek Az alábbiakban leírtam néhány alap algoritmust, amit ismernie kell annak, aki programozásra adja a fejét. A lista korántsem teljes, ám ennyi elég kell legyen
Programozási segédlet Programozási tételek Az alábbiakban leírtam néhány alap algoritmust, amit ismernie kell annak, aki programozásra adja a fejét. A lista korántsem teljes, ám ennyi elég kell legyen
WLAN lefedettségi terv készítés - Site Survey
 WLAN lefedettségi terv készítés - Site Survey 1. Mérés célja Az ISM és U-NII sávok közkedvelt használata, az egyre dizájnosabb és olcsóbb Wi- Wi képes eszközök megjelenése, dinamikus elterjedésnek indította
WLAN lefedettségi terv készítés - Site Survey 1. Mérés célja Az ISM és U-NII sávok közkedvelt használata, az egyre dizájnosabb és olcsóbb Wi- Wi képes eszközök megjelenése, dinamikus elterjedésnek indította
1. Gauss-eloszlás, természetes szórás
 1. Gauss-eloszlás, természetes szórás A Gauss-eloszlásnak megfelelő függvény: amely egy σ szélességű, µ középpontú, 1-re normált (azaz a teljes görbe alatti terület 1) görbét ír le. A természetben a centrális
1. Gauss-eloszlás, természetes szórás A Gauss-eloszlásnak megfelelő függvény: amely egy σ szélességű, µ középpontú, 1-re normált (azaz a teljes görbe alatti terület 1) görbét ír le. A természetben a centrális
A DIPLOMAMUNKA FORMAI KÖVETELMÉNYEI JAVASLAT
 A DIPLOMAMUNKA FORMAI KÖVETELMÉNYEI JAVASLAT A diplomamunka kötelező részei (bekötési sorrendben) 1. Fedőlap - Bal felső sarokban a kiíró tanszék megnevezése (ha két tanszékkel együttműködve dolgozzuk
A DIPLOMAMUNKA FORMAI KÖVETELMÉNYEI JAVASLAT A diplomamunka kötelező részei (bekötési sorrendben) 1. Fedőlap - Bal felső sarokban a kiíró tanszék megnevezése (ha két tanszékkel együttműködve dolgozzuk
MÉRÉSI EREDMÉNYEK PONTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI
 MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
Abszorpciós spektroszkópia
 Tartalomjegyzék Abszorpciós spektroszkópia (Nyitrai Miklós; 2011 február 1.) Dolgozat: május 3. 18:00-20:00. Egész éves anyag. Korábbi dolgozatok nem számítanak bele. Felmentés 80% felett. A fény; Elektromágneses
Tartalomjegyzék Abszorpciós spektroszkópia (Nyitrai Miklós; 2011 február 1.) Dolgozat: május 3. 18:00-20:00. Egész éves anyag. Korábbi dolgozatok nem számítanak bele. Felmentés 80% felett. A fény; Elektromágneses
A fejlesztés várt eredményei a 1. évfolyam végén
 A tanuló legyen képes: A fejlesztés várt eredményei a 1. évfolyam végén - Halmazalkotásra, összehasonlításra az elemek száma szerint; - Állítások igazságtartalmának eldöntésére, állítások megfogalmazására;
A tanuló legyen képes: A fejlesztés várt eredményei a 1. évfolyam végén - Halmazalkotásra, összehasonlításra az elemek száma szerint; - Állítások igazságtartalmának eldöntésére, állítások megfogalmazására;
Populációbecslések és monitoring
 Populációbecslések és monitoring A becslés szerepe az ökológiában és a vadgazdálkodásban. A becslési módszerek csoportosítása. Teljes számlálás. Statisztikai alapfogalmak. Fontos lehet tudnunk, hogy hány
Populációbecslések és monitoring A becslés szerepe az ökológiában és a vadgazdálkodásban. A becslési módszerek csoportosítása. Teljes számlálás. Statisztikai alapfogalmak. Fontos lehet tudnunk, hogy hány
A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a
 a Matematika mérnököknek I. című tárgyhoz Függvények. Függvények A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a szabadon eső test sebessége az idő függvénye. Konstans hőmérsékleten
a Matematika mérnököknek I. című tárgyhoz Függvények. Függvények A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a szabadon eső test sebessége az idő függvénye. Konstans hőmérsékleten
Készítette: Bruder Júlia
 Készítette: Bruder Júlia nkp.hu Megfigyelés Kísérlet Mérés Feladat: Lakóhely időjárásának megfigyelése 2 hétig: max. hőmérséklet, min. hőmérséklet, szél (nincs, gyenge, erős), csapadék. Az adatokat táblázatba
Készítette: Bruder Júlia nkp.hu Megfigyelés Kísérlet Mérés Feladat: Lakóhely időjárásának megfigyelése 2 hétig: max. hőmérséklet, min. hőmérséklet, szél (nincs, gyenge, erős), csapadék. Az adatokat táblázatba
