Formális szemantika. Kifejezések szemantikája. Horpácsi Dániel ELTE Informatikai Kar
|
|
|
- Lili Balog
- 7 évvel ezelőtt
- Látták:
Átírás
1 Formális szemantika Kifejezések szemantikája Horpácsi Dániel ELTE Informatikai Kar
2 Az előadás témája Egyszerű kifejezések formális szemantikája Az első lépés a programozási nyelvek szemantikájának megadása felé
3 Konkrét szintaxis kontra absztrakt szintaxis A konkrét szintaxis definiálja, hogyan lehet a tárgyalt programozási nyelven jól formázott mondatokat leírni Megadja a nyelvi elemek precíz, konkrét leírását; milyen más elemekből, hogyan konstruálhatunk összetett szerkezeteket Szintaktikus elemzőt tudunk ezen definíció alapján készíteni a nyelvhez, automatikusan <assignment> ::= LET <variable> := <expression> ; Az absztrakt szintaxis csak azt írja le, milyen alapvető szintaktikus kategóriák vannak a nyelvben és azok milyen minták mentén épülnek fel Megadja, hogyan épülnek majd fel az absztrakt szintaktikus termek, szintaxisfák A ::= assignment(v, E) Kifejezések szemantikája (2/28)
4 Konkrét szintaxis kontra absztrakt szintaxis Az absztrakt szitaxisból kimaradnak például Konkrét kulcsszavak Precedenciák, asszociativitási szabályok Zárójelek A szintaktikus elemzést segítő elválasztó és termináló szimbólumok Az olvasást (megértést) segítő szimbólumok, jelek Vajon hogyan reprezentálhatjuk az absztrakt szintaxist? Visszaalakítható az absztrakt konkréttá? Kifejezések szemantikája (3/28)
5 Emlékeztető: formális szemantikadefiníciók A programozási nyelvek szemantikája általában informálisan kerül leírásra, továbbá praktikusan a nyelv fordítóprogramja definiálja Ezek közül egyiket sem tekintjük formális definíciónak, nem használhatóak bizonyításhoz Megoldás: használjuk a jó öreg matematikát és logikát! Két alapvető megközelítés: Operációs (műveleti) deduktív levezetésekkel Megadja, hogyan kell végrehajtani a programot Denotációs (leíró) matematikai objektumokkal A jelentést denotációk hozzárendelésével adja meg Kifejezések szemantikája (4/28)
6 Kifejezések mint egyszerűbb nyelvi elemek A formális szemantikadefiníciók alapvető fogalmainak tisztázására először olyan egyszerű aritmetikai és logikai kifejezések jelentését adjuk meg, amelyek a legtöbb programozási nyelvben megtalálhatóak. Operációs és denotációs szematikát is definiálunk, hogy felfedjük a két megközelítés közötti alapvető különbségeket A formális szemantika definiálásakor feltesszük, hogy a kifejezések szintaktikusan és statikus szemantikusan is helyesek, tehát biztosan van jelentésük Kifejezések szemantikája (5/28)
7 Kifejezések: absztrakt szintaxis A szintaktikus kategóriák és metaváltozóik n Num (számliterálok) (token) x Var (változó szimbólumok) (token) a Aexp (aritmetikai kifejezések) b Bexp (logikai kifejezések) Absztrakt produkciós szabályok a ::= n x a 1 + a 2 a 1 a 2 -a b ::= true false a 1 = a 2 a 1 < a 2 b b 1 b 2 Feltesszük, hogy n és x már definiáltak Vegyük észre a bázis- és rekurzív esetek közötti különbséget a 1 + a 2 termként pl. addition(a 1, a 2 ) formában lenne írható Kifejezések szemantikája (6/28)
8 Állapotok A kifejezésekben szerepelhetnek változószimbólumok, tehát függhetnek a környezetüktől, az állapottól, amelyben kiértékeljük őket Az egyszerűsítés végett csak egész változókat engedünk meg, de a módszer általánosítható A lehetséges állapotokat függvényekkel reprezentáljuk s State = Var Z Minden ilyen függvény egy lehetséges állapotot ad meg: a változókhoz rendelt értékeket Jelölni listaként szoktuk: [x 1, y 2, z 3] Kifejezések szemantikája (7/28)
9 Állapotok: lekérdezés és módosítás Vegyük a következő állapotot: s State = Var Z Ha hivatkozunk egy változó értékére, ki kell olvasnunk a memóriából s[x] megadja az x változó értékét az s állapotban Amikor értéket adunk egy változónak, frissíteni kell az állapotot s[y v] megad egy olyan állapotot, amely megegyezik az s állapottal, de y helyen az értéke v Következésképp teljesül, hogy (s[y v])[x] = { v s[x] if x = y if x = y Kifejezések szemantikája (8/28)
10 Operációs szemantika Hogyan értékelnénk ki egy ideális, absztrakt gépen? Valójában átmeneteket definiál megfelelő konfigurációk között Az átmeneteket általános következtetési szabályokkal adjuk meg Ezek tulajdonképp sémák, amelyeket tetszőleges szintaktikus elemmel példányosíthatunk A levezetések szintaxis-vezéreltek A dedukcióval definiált átmenetrendszert használjuk a kifejezések eredményének (vagy normálformájának) meghatározására A következő pár dián strukturális operációs szematikát definiálunk kifejezéseknek, amellyel megadjuk a részletes kiértékelési lépéseket. Kifejezések szemantikája (9/28)
11 Konfigurációk, átmenetek Ahogy már említettük, a kiértékelés függ a környezettől az állapotot egy függvénnyel adjuk meg A konfigurációknak két megengedett formája lesz: egy kifejezés és egy állapot párja, vagy pedig a kifejezés eredménye (szemantikája) A konfigurációk közötti átmeneteket a következőképp jelöljük: Egy köztes lépés a számításban: a, s a, s Egy (rész)kifejezés kiértékelése végén a végkonfiguráció az érték: a, s v ahol v Z {tt, ff} (Vegyük észre, hogy ezekben a számításokban az állapotokat még nem változtatjuk, tehát csak lemásolódnak az egyes átmenetekkel.) Kifejezések szemantikája (10/28)
12 Következtetési szabályok Definiáltuk, mit értünk konfiguráció alatt, most azt kellene megadnunk, hogyan viselkedik az átmenet-reláció: mely konfigurációkból mely más konfigurációkba léphet az absztrakt gép. Következtetési szabályokkal ( azok sémáival) adjuk meg A szabályok három részből állnak: premissza (előfeltétel), konklúzió és további feltételek Premises Conditions Conclusion A szabály szerint a konklúzió akkor érvényes, ha a premissza kikövetkeztethető és a feltételek teljesülnek. A feltételek nélküli szabályok az axiómák Axiom Conditions Az axiómák példányai lesznek a levezetések gyökerében. Kifejezések szemantikája (11/28)
13 Kifejezések operációs szemantikája (1) Számliterálok n, s N [[n]] Változók x, s s[x] Bináris műveletek (LHS) a 1, s a 1, s a 1 a 2, s a 1 a 2, s a 1, s i a 1 a 2, s n a 2, s {+,, <, =} {+,, <, =}, i Z, N [[n]] = i Kifejezések szemantikája (12/28)
14 Kifejezések operációs szemantikája (2) Bináris műveletek (RHS) a 2, s a 2, s n a 2, s n a 2, s {+,, <, =} Bináris műveletek (utolsó lépés) a 2, s i {+,, <, =}, i Z n a 2, s N [[n]] i Az utolsó szabályban az N [[n]] i a művelet tényleges végrehajtása az egész számok körében (< és = a tt vagy ff logikai értékek valamelyikét eredményezik) Aritmetikai negáció a, s a, s -a, s -a, s a, s i -a, s 0 i i Z Kifejezések szemantikája (13/28)
15 Kifejezések operációs szemantikája (3) Logikai literálok true, s tt false, s ff Negáció b, s b, s b, s b, s b, s l b, s l l {tt, ff} Megjegyzés: vegyük észre, hogy az utolsó szabály konklúziójában szereplő szimbólum különböző jelentéssel bír az átmenet jobb és bal oldalán: a bal oldalon az absztrakt szintaxis egy szimbóluma, a jobb oldalon a logikai tagadás művelete. Hasonló megjegyzés igaz a legtöbb művelet leírására. Az utolsó szabályt helyettesíthetnénk ezzel a kettővel: b, s tt b, s ff b, s ff b, s tt Kifejezések szemantikája (14/28)
16 Kifejezések operációs szemantikája (4) Konjunkció (LHS) b 1, s b 1, s b 1 b 2, s b 1 b 2, s b 1, s tt b 1 b 2, s true b 2, s b 1, s ff b 1 b 2, s false b 2, s Konjunkció (RHS) b 2, s b 2, s b b 2, s b b 2, s b {true, false} Konjunkció (utolsó átmenet) b 2, s l b 2, s l true b 2, s l false b 2, s ff l {tt, ff} Kifejezések szemantikája (15/28)
17 A számliterálokról A formális szemantikában éles különbséget teszünk a számliterálok és azok jelentése között. A számokat sokféle formában le lehet írni (pl. különböző számrendszerekben), de a jelentésük minden esetben egy egész szám. Ezt a jelentést az N függvény adja meg, amelyről feltesszük, hogy definiált. Például, ha a számliterálokat decimális számrendszerben írjuk, akkor a leképezés triviális: N [[n]] = n minden n Z esetén. A szemantikus számokat félkövéren szedjük, a nem félkövér számok szintaktikus elemek. Az N [[n]] formulában használt speciális zárójeleket gyakran használják szemantika definíciókban; ami a zárójelek között van, azt szintaktikus egységként (vagy annak mintájaként) kell kezelni. Bizonyos irodalmakban és a gyakorlatban kiterjesztik a szintaxist a szemantikus értékekkel, ezzel egyszerűsítve a leírást. Kifejezések szemantikája (16/28)
18 Levezetés példa Számoljuk ki az (y + 5) + z kifejezés értékét abban az állapotban, ahol y értéke 12 és z értéke 34! A lineáris levezetés (konfigurációsorozat) a következőképp néz ki: (y + 5) + z, [y 12, z 34] (12 + 5) + z, [y 12, z 34] 17 + z, [y 12, z 34] 51 Változó (axióma) y, s 12 Bináris kifejezés LHS (utolsó átmenet) y + 5, s , s Bináris kifejezés LHS (y + 5) + z, s (12 + 5) + z, s Kifejezések szemantikája (17/28)
19 Érdekesség Ha tranzitívvá tesszük az átmenetrelációt, c 1 c 2 c 2 c 3 c 1 c 3 a levezetést faként tudjuk ábrázolni: y, s 12 y + 5, s , s 5, s , s 12+5 y + 5, s 17 (y + 5) + z, s 17 + z, s z, s z, s (y + 5) + z, s 51 Kifejezések szemantikája (18/28)
20 Denotációs szemantika Csakúgy, mint eddig, az absztrakt szintaxison definiáljuk Matematikai objektumokat (pl. számokat, n-eseket, függvényeket) rendelünk a nyelvi szerkezetekhez Szemantikus függvények klózait (különböző mintákra vett eseteit) fogjuk megadni Általában totálisak és kompozicionálisak a definíciók Kifejezések szemantikája (19/28)
21 Szemantikus tartományok (semantic domains) Az absztrakt szintaktikus szerkezeteket szemantikus objektumokra képezzük le, amelyeket a szemantikus tartományok definiálnak. Semantic domains Integer = {..., -2, -1, 0, 1, 2,... } = Z Boolean = {tt, ff} (igazságértékek halmaza) A jelentést úgy adjuk meg, hogy definiáljuk a kifejezések értékét az állapot függvényében Az aritmetikai kifejezések értéke egy egész szám, a logikai kifejezések értéke egy igazságérték Vegyük észre, hogy a szemantikus értékek (tt, ff ) itt is megkülönböztetésre kerültek a szintaktikus elemektől (true és false) Kifejezések szemantikája (20/28)
22 Szemantikus függvények Szemantikus függvények A : Aexp (State Integer) B : Bexp (State Boolean) Minden szintaktikus kategóriához (nemterminálishoz) készítünk egy szemantikus függvényt A szintaktikus kategória szabályaihoz függvényklózokat írunk fel A függvényeket Curry-formában adjuk meg, tehát a szemantikus függvény egy szintaktikus elemre egy újabb függvényt határoz meg, amely az állapotokhoz szemantikus értékeket rendel Kifejezések szemantikája (21/28)
23 Kifejezések denotációs szemantikája (1) A szemantikus függvényt definiáljuk az adott szintaktikus kategória minden bázis elemére és összetett elemére (ügyelve arra, hogy a definíciók kompozicionálisak legyenek). Szemantikus megfeleltetések (aritmetikai kifejezések) A[[n]]s = N [[n]] A[[x]]s = s[x] A[[a 1 + a 2 ]]s = A[[a 1 ]]s + A[[a 2 ]]s A[[a 1 a 2 ]]s = A[[a 1 ]]s A[[a 2 ]]s A[[-a]]s = 0 A[[a]]s Az a 1 + a 2 jelentése csak a részkifejezéseitől (a 1 és a 2 ) függ, ahogy a többi klóz esetében is, tehát a definíció kompozicionális. Kifejezések szemantikája (22/28)
24 Kifejezések denotációs szemantikája (2) Szemantikus megfeleltetések (logikai kifejezések) B[[true]]s = tt B[[false]]s = ff { tt B[[a 1 = a 2 ]]s = B[[a 1 < a 2 ]]s = ff { tt ff { tt ha A[[a 1 ]]s = A[[a 2 ]]s ha A[[a 1 ]]s = A[[a 2 ]]s ha A[[a 1 ]]s < A[[a 2 ]]s ha A[[a 1 ]]s A[[a 2 ]]s ha B[[b]]s = ff B[[ b]]s = ff ha B[[b]]s = tt { tt ha B[[b 1 ]]s = tt és B[[b 2 ]]s = tt B[[b 1 b 2 ]]s = ff ha B[[b 1 ]]s = ff vagy B[[b 2 ]]s = ff Kifejezések szemantikája (23/28)
25 Denotációs szemantika Számítsuk ki a denotációs szemantikában ugyanannak a kifejezésnek az értékét, amelynek az operációsban már kiszámoltuk! Legyen az s állapot [y 12, z 34], ekkor A[[(y + 5) + z]]s = A[[y + 5]]s + A[[z]]s = A[[y + 5]]s + 34 = (A[[y]]s + A[[5]]s) + 34 = (12 + N [[5]]) + 34 = (12 + 5) + 34 = 51 Kifejezések szemantikája (24/28)
26 Kompozicionalitás A megadott denotációs szemantika kompozicionálisan definiált: Minden szintaktikai elemhez megadtunk egy függvényklózt Az összetett kifejezések jelentése a részkifejezések jelentésének függvényében került megadásra Érdemes megfigyelni az aritmetikai negációt, amelyet tipikusan rosszul szoktak definiálni (pl. A[[-a]]s = A[[0 a]]s) A kompozicionalitásnak nagy jelentősége lesz a későbbiekben, hiszen szükséges ahhoz, hogy strukturális indukciós bizonyításokat végezhessünk a szemantikára vonatkozóan Kifejezések szemantikája (25/28)
27 Megjegyzések Indukcióval bizonyítható, hogy A megadott szemantikadefiníció teljes: minden lehetséges kifejezésnek megadtuk a jelentését A szemantikadefiníció konzisztens: ha két különböző jelentés is levezethető egy kifejezéshez, akkor azok ekvivalensek (ebben az esetben megegyeznek) A kifejezésekre definiált operációs és a denotációs szemantika ekvivalens Kifejezések szemantikája (26/28)
28 Összegzés Konkrét szintaxis kontra absztrakt szintaxis Kifejezések absztrakt szintaxisa, metaváltozók Strukturális operációs szemantika Denotációs szemantika A szemantikadefiníciók tulajdonságai Kifejezések szemantikája (27/28)
29 Show me the code! K Egy egyszerű kifejezéseket leíró nyelv szemantikája elérhető a kurzus anyagai között, amely segít megérteni a konfiguráció és az állapot fogalmát. (A példában a szintaktikus és a szemantikus számok nincsenek különválasztva.) A small-step stílusú operációs szemantikát a K keretrendszerben definiáltuk, kipróbálható a 3.5 és a 3.6 verziókkal. Kifejezések szemantikája (28/28)
Programok értelmezése
 Programok értelmezése Kód visszafejtés. Izsó Tamás 2016. szeptember 22. Izsó Tamás Programok értelmezése/ 1 Section 1 Programok értelmezése Izsó Tamás Programok értelmezése/ 2 programok szemantika értelmezése
Programok értelmezése Kód visszafejtés. Izsó Tamás 2016. szeptember 22. Izsó Tamás Programok értelmezése/ 1 Section 1 Programok értelmezése Izsó Tamás Programok értelmezése/ 2 programok szemantika értelmezése
Formális szemantika. Bevezetés. Horpácsi Dániel
 Formális szemantika Bevezetés Horpácsi Dániel daniel-h@elte.hu Az előadás témája Programozási nyelvek formális definíciói: Motiváció, alapfogalmak, módszerek Nyelvek A gondolatainkat szavakban, mondatokban
Formális szemantika Bevezetés Horpácsi Dániel daniel-h@elte.hu Az előadás témája Programozási nyelvek formális definíciói: Motiváció, alapfogalmak, módszerek Nyelvek A gondolatainkat szavakban, mondatokban
Kiterjesztések sek szemantikája
 Kiterjesztések sek szemantikája Példa D Integer = {..., -1,0,1,... }; D Boolean = { true, false } D T1... T n T = D T 1... D Tn D T Az összes függvf ggvény halmaza, amelyek a D T1,..., D Tn halmazokból
Kiterjesztések sek szemantikája Példa D Integer = {..., -1,0,1,... }; D Boolean = { true, false } D T1... T n T = D T 1... D Tn D T Az összes függvf ggvény halmaza, amelyek a D T1,..., D Tn halmazokból
Logika es sz am ıt aselm elet I. r esz Logika 1/36
 1/36 Logika és számításelmélet I. rész Logika 2/36 Elérhetőségek Tejfel Máté Déli épület, 2.606 matej@inf.elte.hu http://matej.web.elte.hu Tankönyv 3/36 Tartalom 4/36 Bevezető fogalmak Ítéletlogika Ítéletlogika
1/36 Logika és számításelmélet I. rész Logika 2/36 Elérhetőségek Tejfel Máté Déli épület, 2.606 matej@inf.elte.hu http://matej.web.elte.hu Tankönyv 3/36 Tartalom 4/36 Bevezető fogalmak Ítéletlogika Ítéletlogika
Elsőrendű logika. Mesterséges intelligencia március 28.
 Elsőrendű logika Mesterséges intelligencia 2014. március 28. Bevezetés Ítéletkalkulus: deklaratív nyelv (mondatok és lehetséges világok közti igazságrelációk) Részinformációkat is kezel (diszjunkció, negáció)
Elsőrendű logika Mesterséges intelligencia 2014. március 28. Bevezetés Ítéletkalkulus: deklaratív nyelv (mondatok és lehetséges világok közti igazságrelációk) Részinformációkat is kezel (diszjunkció, negáció)
Logika és informatikai alkalmazásai kiskérdések február Mikor mondjuk, hogy az F formula a G-nek részformulája?
 ,,Alap kiskérdések Logika és informatikai alkalmazásai kiskérdések 2012. február 19. 1. Hogy hívjuk a 0 aritású függvényjeleket? 2. Definiálja a termek halmazát. 3. Definiálja a formulák halmazát. 4. Definiálja,
,,Alap kiskérdések Logika és informatikai alkalmazásai kiskérdések 2012. február 19. 1. Hogy hívjuk a 0 aritású függvényjeleket? 2. Definiálja a termek halmazát. 3. Definiálja a formulák halmazát. 4. Definiálja,
ÍTÉLETKALKULUS (NULLADRENDŰ LOGIKA)
 ÍTÉLETKALKULUS SZINTAXIS ÍTÉLETKALKULUS (NULLADRENDŰ LOGIKA) jelkészlet elválasztó jelek: ( ) logikai műveleti jelek: ítéletváltozók (logikai változók): p, q, r,... ítéletkonstansok: T, F szintaxis szabályai
ÍTÉLETKALKULUS SZINTAXIS ÍTÉLETKALKULUS (NULLADRENDŰ LOGIKA) jelkészlet elválasztó jelek: ( ) logikai műveleti jelek: ítéletváltozók (logikai változók): p, q, r,... ítéletkonstansok: T, F szintaxis szabályai
Ítéletkalkulus. 1. Bevezet. 2. Ítéletkalkulus
 Ítéletkalkulus Logikai alapfogalmak, m veletek, formalizálás, logikai ekvivalencia, teljes diszjunktív normálforma, tautológia. 1. Bevezet A matematikai logikában az állításoknak nem a tényleges jelentésével,
Ítéletkalkulus Logikai alapfogalmak, m veletek, formalizálás, logikai ekvivalencia, teljes diszjunktív normálforma, tautológia. 1. Bevezet A matematikai logikában az állításoknak nem a tényleges jelentésével,
Logika es sz am ıt aselm elet I. r esz Logika Negyedik el oad as 1/26
 1/26 Logika és számításelmélet I. rész Logika Negyedik előadás Tartalom 2/26 Az elsőrendű logika szemantikája Formulák és formulahalmazok szemantikus tulajdonságai Elsőrendű logikai nyelv interpretációja
1/26 Logika és számításelmélet I. rész Logika Negyedik előadás Tartalom 2/26 Az elsőrendű logika szemantikája Formulák és formulahalmazok szemantikus tulajdonságai Elsőrendű logikai nyelv interpretációja
Logikai ágensek. Mesterséges intelligencia március 21.
 Logikai ágensek Mesterséges intelligencia 2014. március 21. Bevezetés Eddigi példák tudásra: állapotok halmaza, lehetséges operátorok, ezek költségei, heurisztikák Feltételezés: a világ (lehetséges állapotok
Logikai ágensek Mesterséges intelligencia 2014. március 21. Bevezetés Eddigi példák tudásra: állapotok halmaza, lehetséges operátorok, ezek költségei, heurisztikák Feltételezés: a világ (lehetséges állapotok
Logika es sz am ıt aselm elet I. r esz Logika Harmadik el oad as 1/33
 1/33 Logika és számításelmélet I. rész Logika Harmadik előadás Tartalom 2/33 Elsőrendű logika bevezetés Az elsőrendű logika szintaxisa 3/33 Nulladrendű állítás Az ítéletlogikában nem foglalkoztunk az álĺıtások
1/33 Logika és számításelmélet I. rész Logika Harmadik előadás Tartalom 2/33 Elsőrendű logika bevezetés Az elsőrendű logika szintaxisa 3/33 Nulladrendű állítás Az ítéletlogikában nem foglalkoztunk az álĺıtások
Logika es sz am ıt aselm elet I. r esz Logika M asodik el oad as 1/26
 1/26 Logika és számításelmélet I. rész Logika Második előadás Tartalom 2/26 Ítéletlogika - Szemantika (folytatás) Formulák és formulahalmazok szemantikus tulajdonságai Szemantikus következményfogalom Formalizálás
1/26 Logika és számításelmélet I. rész Logika Második előadás Tartalom 2/26 Ítéletlogika - Szemantika (folytatás) Formulák és formulahalmazok szemantikus tulajdonságai Szemantikus következményfogalom Formalizálás
Elsőrendű logika szintaktikája és szemantikája. Logika (3. gyakorlat) 0-adrendű szemantika 2009/10 II. félév 1 / 1
 Elsőrendű logika szintaktikája és szemantikája Logika és számításelmélet, 3. gyakorlat 2009/10 II. félév Logika (3. gyakorlat) 0-adrendű szemantika 2009/10 II. félév 1 / 1 Az elsőrendű logika Elemek egy
Elsőrendű logika szintaktikája és szemantikája Logika és számításelmélet, 3. gyakorlat 2009/10 II. félév Logika (3. gyakorlat) 0-adrendű szemantika 2009/10 II. félév 1 / 1 Az elsőrendű logika Elemek egy
... S n. A párhuzamos programszerkezet két vagy több folyamatot tartalmaz, melyek egymással közös változó segítségével kommunikálnak.
 Párhuzamos programok Legyen S parbegin S 1... S n parend; program. A párhuzamos programszerkezet két vagy több folyamatot tartalmaz, melyek egymással közös változó segítségével kommunikálnak. Folyamat
Párhuzamos programok Legyen S parbegin S 1... S n parend; program. A párhuzamos programszerkezet két vagy több folyamatot tartalmaz, melyek egymással közös változó segítségével kommunikálnak. Folyamat
Kifejezések. Kozsik Tamás. December 11, 2016
 Kifejezések Kozsik Tamás December 11, 2016 Kifejezések Lexika Szintaktika Szemantika Lexika azonosítók (változó-, metódus-, típus- és csomagnevek) literálok operátorok, pl. + zárójelek: (), [], {},
Kifejezések Kozsik Tamás December 11, 2016 Kifejezések Lexika Szintaktika Szemantika Lexika azonosítók (változó-, metódus-, típus- és csomagnevek) literálok operátorok, pl. + zárójelek: (), [], {},
A szemantikus elemzés helye. A szemantikus elemzés feladatai. A szemantikus elemzés feladatai. Deklarációk és láthatósági szabályok
 A szemantikus elemzés helye Forrásprogram Forrás-kezelő (source handler) Lexikális elemző (scanner) A szemantikus elemzés feladatai Fordítóprogramok előadás (A, C, T szakirány) Szintaktikus elemző (parser)
A szemantikus elemzés helye Forrásprogram Forrás-kezelő (source handler) Lexikális elemző (scanner) A szemantikus elemzés feladatai Fordítóprogramok előadás (A, C, T szakirány) Szintaktikus elemző (parser)
A Formális nyelvek vizsga teljesítése. a) Normál A vizsgán 60 pont szerezhet, amely két 30 pontos részb l áll össze az alábbi módon:
 A Formális nyelvek vizsga teljesítése a) Normál A vizsgán 60 pont szerezhet, amely két 30 pontos részb l áll össze az alábbi módon: 1. Öt rövid kérdés megválaszolása egyenként 6 pontért, melyet minimum
A Formális nyelvek vizsga teljesítése a) Normál A vizsgán 60 pont szerezhet, amely két 30 pontos részb l áll össze az alábbi módon: 1. Öt rövid kérdés megválaszolása egyenként 6 pontért, melyet minimum
Kifejezések. Kozsik Tamás. December 11, 2016
 Kifejezések Kozsik Tamás December 11, 2016 Kifejezés versus utasítás C/C++: kifejezés plusz pontosvessző: utasítás kiértékeli a kifejezést jellemzően: mellékhatása is van például: értékadás Ada: n = 5;
Kifejezések Kozsik Tamás December 11, 2016 Kifejezés versus utasítás C/C++: kifejezés plusz pontosvessző: utasítás kiértékeli a kifejezést jellemzően: mellékhatása is van például: értékadás Ada: n = 5;
Magyarok: Bereczki Ilona, Kalmár László, Neumann, Péter Rózsa, Pásztorné Varga Katalin, Urbán János, Lovász László
 MATEMATIKAI LOGIKA A gondolkodás tudománya Diszkrét matematika Arisztotelész(i.e. 384-311) Boole, De Morgan, Gödel, Cantor, Church, Herbrand, Hilbert, Kleene, Lukesiewicz, Löwenheim, Ackermann, McKinsey,
MATEMATIKAI LOGIKA A gondolkodás tudománya Diszkrét matematika Arisztotelész(i.e. 384-311) Boole, De Morgan, Gödel, Cantor, Church, Herbrand, Hilbert, Kleene, Lukesiewicz, Löwenheim, Ackermann, McKinsey,
LOGIKA. Magyarok: Bereczki Ilona, Kalmár László, Neumann, Péter Rózsa, Pásztorné Varga Katalin, Urbán János, Lovász László.
 MATEMATIKAI A gondolkodás tudománya Arisztotelész(i.e. 384-311) Boole, De Morgan, Gödel, Cantor, Church, Herbrand, Hilbert, Kleene, Lukesiewicz, Löwenheim, Ackermann, McKinsey, Tarski, Ramsey, Russel,
MATEMATIKAI A gondolkodás tudománya Arisztotelész(i.e. 384-311) Boole, De Morgan, Gödel, Cantor, Church, Herbrand, Hilbert, Kleene, Lukesiewicz, Löwenheim, Ackermann, McKinsey, Tarski, Ramsey, Russel,
A szemantikus elemzés elmélete. Szemantikus elemzés (attribútum fordítási grammatikák) A szemantikus elemzés elmélete. A szemantikus elemzés elmélete
 A szemantikus elemzés elmélete Szemantikus elemzés (attribútum fordítási grammatikák) a nyelvtan szabályait kiegészítjük a szemantikus elemzés tevékenységeivel fordítási grammatikák Fordítóprogramok előadás
A szemantikus elemzés elmélete Szemantikus elemzés (attribútum fordítási grammatikák) a nyelvtan szabályait kiegészítjük a szemantikus elemzés tevékenységeivel fordítási grammatikák Fordítóprogramok előadás
I. A DIGITÁLIS ÁRAMKÖRÖK ELMÉLETI ALAPJAI
 I. A DIGITÁLIS ÁRAMKÖRÖK ELMÉLETI ALAPJAI 1 A digitális áramkörökre is érvényesek a villamosságtanból ismert Ohm törvény és a Kirchhoff törvények, de az elemzés és a tervezés rendszerint nem ezekre épül.
I. A DIGITÁLIS ÁRAMKÖRÖK ELMÉLETI ALAPJAI 1 A digitális áramkörökre is érvényesek a villamosságtanból ismert Ohm törvény és a Kirchhoff törvények, de az elemzés és a tervezés rendszerint nem ezekre épül.
Komputeralgebra rendszerek
 Komputeralgebra rendszerek III. Változók Czirbusz Sándor czirbusz@gmail.com Komputeralgebra Tanszék ELTE Informatika Kar 2009-2010 ősz Index I 1 Szimbolikus konstansok kezelés A konstansok Nevek levédése
Komputeralgebra rendszerek III. Változók Czirbusz Sándor czirbusz@gmail.com Komputeralgebra Tanszék ELTE Informatika Kar 2009-2010 ősz Index I 1 Szimbolikus konstansok kezelés A konstansok Nevek levédése
A logikai következmény
 Logika 3 A logikai következmény A logika egyik feladata: helyes következtetési sémák kialakítása. Példa következtetésekre : Minden veréb madár. Minden madár gerinces. Minden veréb gerinces 1.Feltétel 2.Feltétel
Logika 3 A logikai következmény A logika egyik feladata: helyes következtetési sémák kialakítása. Példa következtetésekre : Minden veréb madár. Minden madár gerinces. Minden veréb gerinces 1.Feltétel 2.Feltétel
A Formális nyelvek vizsga teljesítése. a) Normál A vizsgán 60 pont szerezhet, amely két 30 pontos részb l áll össze az alábbi módon:
 A Formális nyelvek vizsga teljesítése a) Normál A vizsgán 60 pont szerezhet, amely két 30 pontos részb l áll össze az alábbi módon: 1. Öt kis kérdés megválaszolása egyenként 6 pontért, melyet minimum 12
A Formális nyelvek vizsga teljesítése a) Normál A vizsgán 60 pont szerezhet, amely két 30 pontos részb l áll össze az alábbi módon: 1. Öt kis kérdés megválaszolása egyenként 6 pontért, melyet minimum 12
Predikátumkalkulus. 1. Bevezet. 2. Predikátumkalkulus, formalizálás. Predikátumkalkulus alapfogalmai, formalizálás, tagadás, logikailag igaz formulák.
 Predikátumkalkulus Predikátumkalkulus alapfogalmai, formalizálás, tagadás, logikailag igaz formulák. 1. Bevezet Nézzük meg a következ két kijelentést: Minden almához tartozik egy fa, amir l leesett. Bármely
Predikátumkalkulus Predikátumkalkulus alapfogalmai, formalizálás, tagadás, logikailag igaz formulák. 1. Bevezet Nézzük meg a következ két kijelentést: Minden almához tartozik egy fa, amir l leesett. Bármely
Hardver és szoftver rendszerek verifikációja Röviden megválaszolható kérdések
 Hardver és szoftver rendszerek verifikációja Röviden megválaszolható kérdések 1. Az informatikai rendszereknél mit ellenőriznek validációnál és mit verifikációnál? 2. A szoftver verifikációs technikák
Hardver és szoftver rendszerek verifikációja Röviden megválaszolható kérdések 1. Az informatikai rendszereknél mit ellenőriznek validációnál és mit verifikációnál? 2. A szoftver verifikációs technikák
Komputeralgebra rendszerek
 Komputeralgebra rendszerek III. Változók Czirbusz Sándor czirbusz@gmail.com Komputeralgebra Tanszék ELTE Informatika Kar 2009-2010 ősz Index I 1 Szimbolikus konstansok kezelés A konstansok Nevek levédése
Komputeralgebra rendszerek III. Változók Czirbusz Sándor czirbusz@gmail.com Komputeralgebra Tanszék ELTE Informatika Kar 2009-2010 ősz Index I 1 Szimbolikus konstansok kezelés A konstansok Nevek levédése
Logika és informatikai alkalmazásai
 Logika és informatikai alkalmazásai 4. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
Logika és informatikai alkalmazásai 4. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
Ítéletkalkulus. 1. Bevezet. 2. Ítéletkalkulus
 Ítéletkalkulus Logikai alapfogalmak, m veletek, formalizálás, logikai ekvivalencia, teljes diszjunktív normálforma, tautológia. 1. Bevezet A matematikai logikában az állításoknak nem a tényleges jelentésével,
Ítéletkalkulus Logikai alapfogalmak, m veletek, formalizálás, logikai ekvivalencia, teljes diszjunktív normálforma, tautológia. 1. Bevezet A matematikai logikában az állításoknak nem a tényleges jelentésével,
A fröccs szintaxisa és operációs szemantikája
 A fröccs szintaxisa és operációs szemantikája Kaposi Ambrus Eötvös Loránd Tudományegyetem akaposi@inf.elte.hu 2017. október 2. 1. Bevezetés Ipari partnerünk megkereste az Informatikai Kar Programozási
A fröccs szintaxisa és operációs szemantikája Kaposi Ambrus Eötvös Loránd Tudományegyetem akaposi@inf.elte.hu 2017. október 2. 1. Bevezetés Ipari partnerünk megkereste az Informatikai Kar Programozási
Matematikai logika és halmazelmélet
 Matematikai logika és halmazelmélet Wettl Ferenc előadása alapján 2015-09-07 Wettl Ferenc előadása alapján Matematikai logika és halmazelmélet 2015-09-07 1 / 21 Tartalom 1 Matematikai kijelentések szerkezete
Matematikai logika és halmazelmélet Wettl Ferenc előadása alapján 2015-09-07 Wettl Ferenc előadása alapján Matematikai logika és halmazelmélet 2015-09-07 1 / 21 Tartalom 1 Matematikai kijelentések szerkezete
Logika és informatikai alkalmazásai
 Logika és informatikai alkalmazásai 4. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
Logika és informatikai alkalmazásai 4. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I. 4 IV. FÜGGVÉNYEk 1. LEkÉPEZÉSEk, függvények Definíció Legyen és két halmaz. Egy függvény -ből -ba egy olyan szabály, amely minden elemhez pontosan egy elemet rendel hozzá. Az
KOVÁCS BÉLA, MATEmATIkA I. 4 IV. FÜGGVÉNYEk 1. LEkÉPEZÉSEk, függvények Definíció Legyen és két halmaz. Egy függvény -ből -ba egy olyan szabály, amely minden elemhez pontosan egy elemet rendel hozzá. Az
Időzített átmeneti rendszerek
 Időzített átmeneti rendszerek Legyen A egy ábécé, A = A { (d) d R 0 }. A feletti (valós idejű) időzített átmeneti rendszer olyan A = (S, T,,, ) címkézett átmeneti rendszert ( : T A ), melyre teljesülnek
Időzített átmeneti rendszerek Legyen A egy ábécé, A = A { (d) d R 0 }. A feletti (valós idejű) időzített átmeneti rendszer olyan A = (S, T,,, ) címkézett átmeneti rendszert ( : T A ), melyre teljesülnek
Segédanyagok. Formális nyelvek a gyakorlatban. Szintaktikai helyesség. Fordítóprogramok. Formális nyelvek, 1. gyakorlat
 Formális nyelvek a gyakorlatban Formális nyelvek, 1 gyakorlat Segédanyagok Célja: A programozási nyelvek szintaxisának leírására használatos eszközök, módszerek bemutatása Fogalmak: BNF, szabály, levezethető,
Formális nyelvek a gyakorlatban Formális nyelvek, 1 gyakorlat Segédanyagok Célja: A programozási nyelvek szintaxisának leírására használatos eszközök, módszerek bemutatása Fogalmak: BNF, szabály, levezethető,
S0-02 Típusmodellek (Programozás elmélet)
 S0-02 Típusmodellek (Programozás elmélet) Tartalom 1. Absztrakt adattípus 2. Adattípus specifikációja 3. Adattípus osztály 4. Paraméterátadás 5. Reprezentációs függvény 6. Öröklődés és polimorfizmus 7.
S0-02 Típusmodellek (Programozás elmélet) Tartalom 1. Absztrakt adattípus 2. Adattípus specifikációja 3. Adattípus osztály 4. Paraméterátadás 5. Reprezentációs függvény 6. Öröklődés és polimorfizmus 7.
Logikai következmény, tautológia, inkonzisztens, logikai ekvivalencia, normálformák
 08EMVI3b.nb 1 In[2]:= Theorema Ítéletlogika 1 Ismétlés Szintaxis Szemantika Logikai következmény, tautológia, inkonzisztens, logikai ekvivalencia, normálformák 2 Kalkulusok Kalkulus Levezethetõség Dedukciós
08EMVI3b.nb 1 In[2]:= Theorema Ítéletlogika 1 Ismétlés Szintaxis Szemantika Logikai következmény, tautológia, inkonzisztens, logikai ekvivalencia, normálformák 2 Kalkulusok Kalkulus Levezethetõség Dedukciós
Az informatika logikai alapjai
 Az informatika logikai alapjai Várterész Magda DE, Informatikai Kar PTI BSc és informatikatanár hallgatók számára 2017. Az elsőrendű logikai nyelv interpretációja L interpretációja egy I-vel jelölt függvénynégyes,
Az informatika logikai alapjai Várterész Magda DE, Informatikai Kar PTI BSc és informatikatanár hallgatók számára 2017. Az elsőrendű logikai nyelv interpretációja L interpretációja egy I-vel jelölt függvénynégyes,
5. előadás Reguláris kifejezések, a reguláris nyelvek jellemzése 1.
 5. előadás Reguláris kifejezések, a reguláris nyelvek jellemzése 1. Dr. Kallós Gábor 2014 2015 1 Tartalom Reguláris kifejezések Meghatározás, tulajdonságok Kapcsolat a reguláris nyelvekkel A reguláris
5. előadás Reguláris kifejezések, a reguláris nyelvek jellemzése 1. Dr. Kallós Gábor 2014 2015 1 Tartalom Reguláris kifejezések Meghatározás, tulajdonságok Kapcsolat a reguláris nyelvekkel A reguláris
Felmentések. Logika (1. gyakorlat) 0-adrendű szintaktika 2009/10 II. félév 1 / 21
 Felmentések Logika (1. gyakorlat) 0-adrendű szintaktika 2009/10 II. félév 1 / 21 Felmentések Ha valaki tanár szakos, akkor mivel neki elvileg a hálóban nincs logika rész, felmentést kaphat a logika gyakorlat
Felmentések Logika (1. gyakorlat) 0-adrendű szintaktika 2009/10 II. félév 1 / 21 Felmentések Ha valaki tanár szakos, akkor mivel neki elvileg a hálóban nincs logika rész, felmentést kaphat a logika gyakorlat
Komputeralgebra Rendszerek
 Komputeralgebra Rendszerek Konstansok, változók, típusok Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2015. február 24. TARTALOMJEGYZÉK 1 of 110 TARTALOMJEGYZÉK I 1 TARTALOMJEGYZÉK 2 Nevek kezelése
Komputeralgebra Rendszerek Konstansok, változók, típusok Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2015. február 24. TARTALOMJEGYZÉK 1 of 110 TARTALOMJEGYZÉK I 1 TARTALOMJEGYZÉK 2 Nevek kezelése
BOOLE ALGEBRA Logika: A konjunkció és diszjunkció tulajdonságai
 BOOLE ALGEBRA Logika: A konjunkció és diszjunkció tulajdonságai 1.a. A B B A 2.a. (A B) C A (B C) 3.a. A (A B) A 4.a. I A I 5.a. A (B C) (A B) (A C) 6.a. A A I 1.b. A B B A 2.b. (A B) C A (B C) 3.b. A
BOOLE ALGEBRA Logika: A konjunkció és diszjunkció tulajdonságai 1.a. A B B A 2.a. (A B) C A (B C) 3.a. A (A B) A 4.a. I A I 5.a. A (B C) (A B) (A C) 6.a. A A I 1.b. A B B A 2.b. (A B) C A (B C) 3.b. A
9. előadás. Programozás-elmélet. Programozási tételek Elemi prog. Sorozatszámítás Eldöntés Kiválasztás Lin. keresés Megszámolás Maximum.
 Programozási tételek Programozási feladatok megoldásakor a top-down (strukturált) programtervezés esetén három vezérlési szerkezetet használunk: - szekvencia - elágazás - ciklus Eddig megismertük az alábbi
Programozási tételek Programozási feladatok megoldásakor a top-down (strukturált) programtervezés esetén három vezérlési szerkezetet használunk: - szekvencia - elágazás - ciklus Eddig megismertük az alábbi
Bisonc++ tutorial. Dévai Gergely. A szabály bal- és jobboldalát : választja el egymástól. A szabályalternatívák sorozatát ; zárja le.
 Bisonc++ tutorial Dévai Gergely A Bisonc++ egy szintaktikuselemz -generátor: egy környezetfüggetlen nyelvtanból egy C++ programot generál, ami egy tokensorozat szintaktikai helyességét képes ellen rizni.
Bisonc++ tutorial Dévai Gergely A Bisonc++ egy szintaktikuselemz -generátor: egy környezetfüggetlen nyelvtanból egy C++ programot generál, ami egy tokensorozat szintaktikai helyességét képes ellen rizni.
Kaposi Ambrus. University of Nottingham Functional Programming Lab. Hackerspace Budapest 2015. január 6.
 Bizonyítás és programozás Kaposi Ambrus University of Nottingham Functional Programming Lab Hackerspace Budapest 2015. január 6. Bizonyítás, érvelés Példa: sáros a csizmám ha vizes a föld, esett az eső
Bizonyítás és programozás Kaposi Ambrus University of Nottingham Functional Programming Lab Hackerspace Budapest 2015. január 6. Bizonyítás, érvelés Példa: sáros a csizmám ha vizes a föld, esett az eső
MATEMATIK A 9. évfolyam. 2. modul: LOGIKA KÉSZÍTETTE: VIDRA GÁBOR
 MATEMATIK A 9. évfolyam 2. modul: LOGIKA KÉSZÍTETTE: VIDRA GÁBOR Matematika A 9. évfolyam. 2. modul: LOGIKA Tanári útmutató 2 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok
MATEMATIK A 9. évfolyam 2. modul: LOGIKA KÉSZÍTETTE: VIDRA GÁBOR Matematika A 9. évfolyam. 2. modul: LOGIKA Tanári útmutató 2 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok
Térinformatikai algoritmusok Elemi algoritmusok
 Cserép Máté 2016. szeptember 14. Analóg programozásnak nevezzük azt, amikor egy feladat megoldásához egy már ismert és megoldott feladat megoldását használjuk fel. Általában nem pontosan ugyanazt a feladatot
Cserép Máté 2016. szeptember 14. Analóg programozásnak nevezzük azt, amikor egy feladat megoldásához egy már ismert és megoldott feladat megoldását használjuk fel. Általában nem pontosan ugyanazt a feladatot
Felmentések. Ha valaki tanár szakos, akkor mivel neki elvileg a hálóban nincs logika rész, felmentést kaphat a logika gyakorlat és vizsga alól.
 Felmentések Ha valaki tanár szakos, akkor mivel neki elvileg a hálóban nincs logika rész, felmentést kaphat a logika gyakorlat és vizsga alól. Az eredménye, ezek után a számításelélet részből elért eredmény
Felmentések Ha valaki tanár szakos, akkor mivel neki elvileg a hálóban nincs logika rész, felmentést kaphat a logika gyakorlat és vizsga alól. Az eredménye, ezek után a számításelélet részből elért eredmény
3. Magyarország legmagasabb hegycsúcsa az Istállós-kő.
 1. Bevezetés A logika a görög,,logosz szóból származik, melynek jelentése gondolkodás, beszéd, szó. A logika az emberi gondolkodás vizsgálatával foglalkozik, célja pedig a gondolkodás során használt helyes
1. Bevezetés A logika a görög,,logosz szóból származik, melynek jelentése gondolkodás, beszéd, szó. A logika az emberi gondolkodás vizsgálatával foglalkozik, célja pedig a gondolkodás során használt helyes
Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé.
 HA 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) HA 2 Halmazok HA 3 Megjegyzések A halmaz, az elem és az eleme fogalmakat nem definiáljuk, hanem alapfogalmaknak
HA 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) HA 2 Halmazok HA 3 Megjegyzések A halmaz, az elem és az eleme fogalmakat nem definiáljuk, hanem alapfogalmaknak
Diszkrét matematika MATEMATIKAI LOGIKA
 NULLADRENDŰ LOGIKA (ÍTÉLETKALKULUS) A logikát, mint a filozófia egy részét, már az ókori a görög tudósok is igen magas szinten művelték, pl. Platón (Kr. e. 427- Kr. e. 347), Arisztotelész (Kr.e. 384- Kr.
NULLADRENDŰ LOGIKA (ÍTÉLETKALKULUS) A logikát, mint a filozófia egy részét, már az ókori a görög tudósok is igen magas szinten művelték, pl. Platón (Kr. e. 427- Kr. e. 347), Arisztotelész (Kr.e. 384- Kr.
6. Közös változóval rendelkező párhuzamos program, Közös változó,
 6. Közös változóval rendelkező párhuzamos program, Közös változó, Reynold kritérium. Atomi művelet, atomi utasítás. szintaxis, szemantika, tulajdonságok. Szinkronizációs párhuzamos program, szintaxis,
6. Közös változóval rendelkező párhuzamos program, Közös változó, Reynold kritérium. Atomi művelet, atomi utasítás. szintaxis, szemantika, tulajdonságok. Szinkronizációs párhuzamos program, szintaxis,
Automaták mint elfogadók (akceptorok)
 Automaták mint elfogadók (akceptorok) Ha egy iniciális Moore-automatában a kimenőjelek halmaza csupán kételemű: {elfogadom, nem fogadom el}, és az utolsó kimenőjel dönti el azt a kérdést, hogy elfogadható-e
Automaták mint elfogadók (akceptorok) Ha egy iniciális Moore-automatában a kimenőjelek halmaza csupán kételemű: {elfogadom, nem fogadom el}, és az utolsó kimenőjel dönti el azt a kérdést, hogy elfogadható-e
1. Alapfogalmak Algoritmus Számítási probléma Specifikáció Algoritmusok futási ideje
 1. Alapfogalmak 1.1. Algoritmus Az algoritmus olyan elemi műveletekből kompozíciós szabályok szerint felépített összetett művelet, amelyet megadott feltételt teljesítő bemeneti adatra végrehajtva, a megkívánt
1. Alapfogalmak 1.1. Algoritmus Az algoritmus olyan elemi műveletekből kompozíciós szabályok szerint felépített összetett művelet, amelyet megadott feltételt teljesítő bemeneti adatra végrehajtva, a megkívánt
Matematikai logika. Nagy Károly 2009
 Matematikai logika előadások összefoglalója (Levelezős hallgatók számára) Nagy Károly 2009 1 1. Elsőrendű nyelvek 1.1. Definíció. Az Ω =< Srt, Cnst, F n, P r > komponensekből álló rendezett négyest elsőrendű
Matematikai logika előadások összefoglalója (Levelezős hallgatók számára) Nagy Károly 2009 1 1. Elsőrendű nyelvek 1.1. Definíció. Az Ω =< Srt, Cnst, F n, P r > komponensekből álló rendezett négyest elsőrendű
A TANTÁRGY ADATLAPJA
 A TANTÁRGY ADATLAPJA 1. A képzési program adatai 1.1 Felsőoktatási intézmény Babeş-Bolyai Tudományegyetem 1.2 Kar Matematika és Informatika 1.3 Intézet Magyar Matematika és Informatika 1.4 Szakterület
A TANTÁRGY ADATLAPJA 1. A képzési program adatai 1.1 Felsőoktatási intézmény Babeş-Bolyai Tudományegyetem 1.2 Kar Matematika és Informatika 1.3 Intézet Magyar Matematika és Informatika 1.4 Szakterület
Matematikai logika NULLADRENDŰ LOGIKA
 Matematikai logika NULLADRENDŰ LOGIKA Kijelentő mondatokhoz, melyeket nagy betűkkel jelölünk, interpretáció (egy függvény) segítségével igazságértéket rendelünk (I,H). Szintaxisból (nyelvtani szabályok,
Matematikai logika NULLADRENDŰ LOGIKA Kijelentő mondatokhoz, melyeket nagy betűkkel jelölünk, interpretáció (egy függvény) segítségével igazságértéket rendelünk (I,H). Szintaxisból (nyelvtani szabályok,
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2013 ősz 1. Diszkrét matematika I. középszint 8. előadás Mérai László merai@compalg.inf.elte.hu compalg.inf.elte.hu/ merai Komputeralgebra Tanszék 2013 ősz Kombinatorika
Diszkrét matematika I. középszint 2013 ősz 1. Diszkrét matematika I. középszint 8. előadás Mérai László merai@compalg.inf.elte.hu compalg.inf.elte.hu/ merai Komputeralgebra Tanszék 2013 ősz Kombinatorika
ALGORITMUSOK ÉS BONYOLULTSÁGELMÉLET Matematika MSc hallgatók számára
 ALGORITMUSOK ÉS BONYOLULTSÁGELMÉLET Matematika MSc hallgatók számára 7. Előadás: Hálózatok, P- és N P-teljes problémák Előadó: Hajnal Péter 2015. tavasz 1. Hálózatok és egy P-teljes probléma Emlékeztető.
ALGORITMUSOK ÉS BONYOLULTSÁGELMÉLET Matematika MSc hallgatók számára 7. Előadás: Hálózatok, P- és N P-teljes problémák Előadó: Hajnal Péter 2015. tavasz 1. Hálózatok és egy P-teljes probléma Emlékeztető.
AZ INFORMATIKA LOGIKAI ALAPJAI
 AZ INFORMATIKA LOGIKAI ALAPJAI Előadó: Dr. Mihálydeák Tamás Sándor Gyakorlatvezető: Kovács Zita 2017/2018. I. félév 4. gyakorlat Interpretáció A ϱ függvényt az L (0) = LC, Con, Form nulladrendű nyelv egy
AZ INFORMATIKA LOGIKAI ALAPJAI Előadó: Dr. Mihálydeák Tamás Sándor Gyakorlatvezető: Kovács Zita 2017/2018. I. félév 4. gyakorlat Interpretáció A ϱ függvényt az L (0) = LC, Con, Form nulladrendű nyelv egy
2019/02/11 10:01 1/10 Logika
 2019/02/11 10:01 1/10 Logika < Számítástechnika Logika Szerző: Sallai András Copyright Sallai András, 2011, 2012, 2015 Licenc: GNU Free Documentation License 1.3 Web: http://szit.hu Boole-algebra A Boole-algebrát
2019/02/11 10:01 1/10 Logika < Számítástechnika Logika Szerző: Sallai András Copyright Sallai András, 2011, 2012, 2015 Licenc: GNU Free Documentation License 1.3 Web: http://szit.hu Boole-algebra A Boole-algebrát
NEM-DETERMINISZTIKUS PROGRAMOK HELYESSÉGE. Szekvenciális programok kategóriái. Hoare-Dijkstra-Gries módszere
 Szekvenciális programok kategóriái strukturálatlan strukturált NEM-DETERMINISZTIKUS PROGRAMOK HELYESSÉGE Hoare-Dijkstra-Gries módszere determinisztikus valódi korai nem-determinisztikus általános fejlett
Szekvenciális programok kategóriái strukturálatlan strukturált NEM-DETERMINISZTIKUS PROGRAMOK HELYESSÉGE Hoare-Dijkstra-Gries módszere determinisztikus valódi korai nem-determinisztikus általános fejlett
Lekérdezések az SQL-ben 1.rész
 Lekérdezések az SQL-ben 1.rész Tankönyv: Ullman-Widom: Adatbázisrendszerek Alapvetés Második, átdolgozott kiadás, Panem, 2009 6.1. Egyszerű (egy-relációs) lekérdezések az SQL-ben - Select-From-Where utasítás
Lekérdezések az SQL-ben 1.rész Tankönyv: Ullman-Widom: Adatbázisrendszerek Alapvetés Második, átdolgozott kiadás, Panem, 2009 6.1. Egyszerű (egy-relációs) lekérdezések az SQL-ben - Select-From-Where utasítás
5.3. Logika a relációkhoz
 236 5. Algebrai és logikai lekérdező nyelvek! 5.2.3. feladat. Az egyik dolog, amit az eredeti 2.4.5. alfejezetben definiált vetítési művelettel szemben elérhetünk a kiterjesztett vetítési művelet segítségével,
236 5. Algebrai és logikai lekérdező nyelvek! 5.2.3. feladat. Az egyik dolog, amit az eredeti 2.4.5. alfejezetben definiált vetítési művelettel szemben elérhetünk a kiterjesztett vetítési művelet segítségével,
Java II. I A Java programozási nyelv alapelemei
 Java II. I A Java programozási nyelv alapelemei Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2008. 02. 19. Java II.: Alapelemek JAVA2 / 1 A Java formalizmusa A C, illetve az annak
Java II. I A Java programozási nyelv alapelemei Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2008. 02. 19. Java II.: Alapelemek JAVA2 / 1 A Java formalizmusa A C, illetve az annak
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 2. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Matematikai logika Diszkrét matematika I. középszint
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 2. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Matematikai logika Diszkrét matematika I. középszint
Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) Halmazok 1
 Halmazok 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) Halmazok 2 A fejezet legfontosabb elemei Halmaz megadási módjai Halmazok közti műveletek (metszet,
Halmazok 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) Halmazok 2 A fejezet legfontosabb elemei Halmaz megadási módjai Halmazok közti műveletek (metszet,
Lekérdezések az SQL-ben 1.rész
 Lekérdezések az SQL-ben 1.rész Tankönyv: Ullman-Widom: Adatbázisrendszerek Alapvetés Második, átdolgozott kiadás, Panem, 2009 6.1. Egyszerű (egy-relációs) lekérdezések az SQL-ben - Select-From-Where utasítás
Lekérdezések az SQL-ben 1.rész Tankönyv: Ullman-Widom: Adatbázisrendszerek Alapvetés Második, átdolgozott kiadás, Panem, 2009 6.1. Egyszerű (egy-relációs) lekérdezések az SQL-ben - Select-From-Where utasítás
Fordítóprogramok (A,C,T szakirány) Feladatgy jtemény
 Fordítóprogramok (A,C,T szakirány) Feladatgy jtemény ELTE IK 1 Lexikális elemzés 1. Add meg reguláris nyelvtannal, reguláris kifejezéssel és véges determinisztikus automatával a következ lexikális elemeket!
Fordítóprogramok (A,C,T szakirány) Feladatgy jtemény ELTE IK 1 Lexikális elemzés 1. Add meg reguláris nyelvtannal, reguláris kifejezéssel és véges determinisztikus automatával a következ lexikális elemeket!
Knoch László: Információelmélet LOGIKA
 Mi az ítélet? Az ítélet olyan mondat, amely vagy igaz, vagy hamis. Azt, hogy az adott ítélet igaz vagy hamis, az ítélet logikai értékének nevezzük. Jelölése: i igaz h hamis A 2 páros és prím. Logikai értéke
Mi az ítélet? Az ítélet olyan mondat, amely vagy igaz, vagy hamis. Azt, hogy az adott ítélet igaz vagy hamis, az ítélet logikai értékének nevezzük. Jelölése: i igaz h hamis A 2 páros és prím. Logikai értéke
definiálunk. Legyen egy konfiguráció, ahol és. A következő három esetet különböztetjük meg. 1. Ha, akkor 2. Ha, akkor, ahol, ha, és egyébként.
 Számításelmélet Kiszámítási problémának nevezünk egy olyan, a matematika nyelvén megfogalmazott kérdést, amire számítógéppel szeretnénk megadni a választ. (A matematika nyelvén precízen megfogalmazott
Számításelmélet Kiszámítási problémának nevezünk egy olyan, a matematika nyelvén megfogalmazott kérdést, amire számítógéppel szeretnénk megadni a választ. (A matematika nyelvén precízen megfogalmazott
Térinformatikai algoritmusok Elemi algoritmusok
 Cserép Máté Analóg programozásnak nevezzük azt, amikor egy feladat megoldásához egy már ismert és megoldott feladat megoldását használjuk fel. Általában nem pontosan ugyanazt a feladatot oldottuk meg korábban,
Cserép Máté Analóg programozásnak nevezzük azt, amikor egy feladat megoldásához egy már ismert és megoldott feladat megoldását használjuk fel. Általában nem pontosan ugyanazt a feladatot oldottuk meg korábban,
Általános algoritmustervezési módszerek
 Általános algoritmustervezési módszerek Ebben a részben arra mutatunk példát, hogy miként használhatóak olyan általános algoritmustervezési módszerek mint a dinamikus programozás és a korlátozás és szétválasztás
Általános algoritmustervezési módszerek Ebben a részben arra mutatunk példát, hogy miként használhatóak olyan általános algoritmustervezési módszerek mint a dinamikus programozás és a korlátozás és szétválasztás
ködös határ (félreértés, hiba)
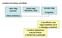 probléma formálisan specifikált: valós világ (domain) (hibás eredmény) ködös határ (félreértés, hiba) formális világ (megoldás) A szoftver fejlesztőnek meg kell értenie a felhasználó problémáját. A specifikáció
probléma formálisan specifikált: valós világ (domain) (hibás eredmény) ködös határ (félreértés, hiba) formális világ (megoldás) A szoftver fejlesztőnek meg kell értenie a felhasználó problémáját. A specifikáció
Nyelvek típusrendszere (jegyzet)
 Nyelvek típusrendszere (jegyzet) Kaposi Ambrus Eötvös Loránd Tudományegyetem akaposi@inf.elte.hu 2017. november 6. Lektorálta: Csörnyei Zoltán Az ELTE tankönyv- és jegyzettámogatási pályázatán elnyert
Nyelvek típusrendszere (jegyzet) Kaposi Ambrus Eötvös Loránd Tudományegyetem akaposi@inf.elte.hu 2017. november 6. Lektorálta: Csörnyei Zoltán Az ELTE tankönyv- és jegyzettámogatási pályázatán elnyert
3. előadás. Programozás-elmélet. A változó fogalma Kiterjesztések A feladat kiterjesztése A program kiterjesztése Kiterjesztési tételek Példa
 A változó fogalma Definíció Legyen A = A 1 A 2... A n állapottér. A pr Ai projekciós függvényeket változóknak nevezzük: : A A i pr Ai (a) = a i ( a = (a 1, a 2,..., a n ) A). A változók jelölése: v i =
A változó fogalma Definíció Legyen A = A 1 A 2... A n állapottér. A pr Ai projekciós függvényeket változóknak nevezzük: : A A i pr Ai (a) = a i ( a = (a 1, a 2,..., a n ) A). A változók jelölése: v i =
1. Tétel - Az ítéletkalkulus alapfogalmai
 A tételhez hozzátartozik az elsőrendű nyelv szemantikája! 1. Tétel - Az ítéletkalkulus alapfogalmai Ítéletkalkulus - Az elsőrendű logika azon speciális este, amikor csak 0 ad rendű predikátumszimbólumok
A tételhez hozzátartozik az elsőrendű nyelv szemantikája! 1. Tétel - Az ítéletkalkulus alapfogalmai Ítéletkalkulus - Az elsőrendű logika azon speciális este, amikor csak 0 ad rendű predikátumszimbólumok
Memo: Az alábbi, "természetes", Gentzen típusú dedukciós rendszer szerint készítjük el a levezetéseket.
 Untitled 2 1 Theorema Predikátumlogika 1 3 Natural Deduction (Gentzen mag/alap kalkulus) Cél: a logikai (szematikai) következményfogalom helyett a (szintaktikai) levethetõség vizsgálata. A bizonyítási
Untitled 2 1 Theorema Predikátumlogika 1 3 Natural Deduction (Gentzen mag/alap kalkulus) Cél: a logikai (szematikai) következményfogalom helyett a (szintaktikai) levethetõség vizsgálata. A bizonyítási
Automaták és formális nyelvek
 Automaták és formális nyelvek Bevezetés a számítástudomány alapjaiba 1. Formális nyelvek 2006.11.13. 1 Automaták és formális nyelvek - bevezetés Automaták elmélete: információs gépek általános absztrakt
Automaták és formális nyelvek Bevezetés a számítástudomány alapjaiba 1. Formális nyelvek 2006.11.13. 1 Automaták és formális nyelvek - bevezetés Automaták elmélete: információs gépek általános absztrakt
Házi feladatok megoldása. Nyelvtani transzformációk. Házi feladatok megoldása. Házi feladatok megoldása. Formális nyelvek, 6. gyakorlat.
 Nyelvtani transzformációk Formális nyelvek, 6. gyakorlat a. S (S) SS ε b. S XS ε és X (S) c. S (SS ) Megoldás: Célja: A nyelvtani transzformációk bemutatása Fogalmak: Megszorított típusok, normálformák,
Nyelvtani transzformációk Formális nyelvek, 6. gyakorlat a. S (S) SS ε b. S XS ε és X (S) c. S (SS ) Megoldás: Célja: A nyelvtani transzformációk bemutatása Fogalmak: Megszorított típusok, normálformák,
Formális módszerek GM_IN003_1 Program verifikálás, formalizmusok
 Formális módszerek GM_IN003_1 Program verifikálás, formalizmusok Program verifikálás Konkurens programozási megoldások terjedése -> verifikálás szükséges, (nehéz) logika Legszélesebb körben alkalmazott
Formális módszerek GM_IN003_1 Program verifikálás, formalizmusok Program verifikálás Konkurens programozási megoldások terjedése -> verifikálás szükséges, (nehéz) logika Legszélesebb körben alkalmazott
Bevezetés az informatikába
 Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Ellenőrző kérdések. 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t
 Ellenőrző kérdések 2. Kis dolgozat kérdései 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t 37. Ha t szintű indexet használunk,
Ellenőrző kérdések 2. Kis dolgozat kérdései 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t 37. Ha t szintű indexet használunk,
ALAPFOGALMAK 1. A reláció az program programfüggvénye, ha. Azt mondjuk, hogy az feladat szigorúbb, mint az feladat, ha
 ALAPFOGALMAK 1 Á l l a p o t t é r Legyen I egy véges halmaz és legyenek A i, i I tetszőleges véges vagy megszámlálható, nem üres halmazok Ekkor az A= A i halmazt állapottérnek, az A i halmazokat pedig
ALAPFOGALMAK 1 Á l l a p o t t é r Legyen I egy véges halmaz és legyenek A i, i I tetszőleges véges vagy megszámlálható, nem üres halmazok Ekkor az A= A i halmazt állapottérnek, az A i halmazokat pedig
SZÁMÍTÓGÉPES PROBLÉMAMEGOLDÁS
 SZÁMÍTÓGÉPES PROBLÉMAMEGOLDÁS 2.ELŐADÁS A VB programozási nyelv Az Excel programozása 2 A VB programozási nyelv Adattípusok Adatok kezelése Vezérlőszerkezetek Adattípusok és műveletek Egész adattípusok
SZÁMÍTÓGÉPES PROBLÉMAMEGOLDÁS 2.ELŐADÁS A VB programozási nyelv Az Excel programozása 2 A VB programozási nyelv Adattípusok Adatok kezelése Vezérlőszerkezetek Adattípusok és műveletek Egész adattípusok
Absztrakt adattípus - algebrai specifikáció - Lists (paraméteres) module imports end exports parameters variables sorts operations equations
 Absztrakt adattípus -algebrai specifikáció -Lists (paraméteres) module Lists imports Booleans, Naturals parameters Items sorts Item operations erroritem : Item eq? : Item, Item Boolean variables a, b,
Absztrakt adattípus -algebrai specifikáció -Lists (paraméteres) module Lists imports Booleans, Naturals parameters Items sorts Item operations erroritem : Item eq? : Item, Item Boolean variables a, b,
ADATBÁZIS-KEZELÉS. Relációalgebra, 5NF
 ADATBÁZIS-KEZELÉS Relációalgebra, 5NF ABSZTRAKT LEKÉRDEZŐ NYELVEK relációalgebra relációkalkulus rekord alapú tartomány alapú Relációalgebra a matematikai halmazelméleten alapuló lekérdező nyelv a lekérdezés
ADATBÁZIS-KEZELÉS Relációalgebra, 5NF ABSZTRAKT LEKÉRDEZŐ NYELVEK relációalgebra relációkalkulus rekord alapú tartomány alapú Relációalgebra a matematikai halmazelméleten alapuló lekérdező nyelv a lekérdezés
Formális nyelvek és automaták
 Formális nyelvek és automaták Nagy Sára gyakorlatai alapján Készítette: Nagy Krisztián 2. gyakorlat Ismétlés: Megjegyzés: Az ismétlés egy része nem szerepel a dokumentumban, mivel lényegében a teljes 1.
Formális nyelvek és automaták Nagy Sára gyakorlatai alapján Készítette: Nagy Krisztián 2. gyakorlat Ismétlés: Megjegyzés: Az ismétlés egy része nem szerepel a dokumentumban, mivel lényegében a teljes 1.
2. Ítéletkalkulus szintaxisa
 2. Ítéletkalkulus szintaxisa (4.1) 2.1 Az ítéletlogika abc-je: V 0 V 0 A következő szimbólumokat tartalmazza: ítélet- vagy állításváltozók (az állítások szimbolizálására). Esetenként logikai változónak
2. Ítéletkalkulus szintaxisa (4.1) 2.1 Az ítéletlogika abc-je: V 0 V 0 A következő szimbólumokat tartalmazza: ítélet- vagy állításváltozók (az állítások szimbolizálására). Esetenként logikai változónak
BASH script programozás II. Vezérlési szerkezetek
 06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
Modell alapú tesztelés mobil környezetben
 Modell alapú tesztelés mobil környezetben Micskei Zoltán Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék A terület behatárolása Testing is an activity performed
Modell alapú tesztelés mobil környezetben Micskei Zoltán Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék A terület behatárolása Testing is an activity performed
Adattípusok, vezérlési szerkezetek. Informatika Szabó Adrienn szeptember 14.
 Informatika 1 2011 Második előadás, vezérlési szerkezetek Szabó Adrienn 2011. szeptember 14. Tartalom Algoritmusok, vezérlési szerkezetek If - else: elágazás While ciklus For ciklus Egyszerű típusok Összetett
Informatika 1 2011 Második előadás, vezérlési szerkezetek Szabó Adrienn 2011. szeptember 14. Tartalom Algoritmusok, vezérlési szerkezetek If - else: elágazás While ciklus For ciklus Egyszerű típusok Összetett
LOGIKA ÉS ÉRVELÉSTECHNIKA
 LOGIKA ÉS ÉRVELÉSTECHNIKA ELTE TáTK Közgazdaságtudományi Tanszék Logika és érveléstechnika NULLADREND LOGIKA 1. Készítette: Szakmai felel s: 2011. február Készült a következ m felhasználásával: Ruzsa
LOGIKA ÉS ÉRVELÉSTECHNIKA ELTE TáTK Közgazdaságtudományi Tanszék Logika és érveléstechnika NULLADREND LOGIKA 1. Készítette: Szakmai felel s: 2011. február Készült a következ m felhasználásával: Ruzsa
A digitális számítás elmélete
 A digitális számítás elmélete 8. előadás ápr. 16. Turing gépek és nyelvtanok A nyelvosztályok áttekintése Turing gépek és a természetes számokon értelmezett függvények Áttekintés Dominó Bizonyítások: L
A digitális számítás elmélete 8. előadás ápr. 16. Turing gépek és nyelvtanok A nyelvosztályok áttekintése Turing gépek és a természetes számokon értelmezett függvények Áttekintés Dominó Bizonyítások: L
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Logika
 Logika Indukció: A fogalomalkotásnak azt a módját, amikor a konkrét tapasztalatokra támaszkodva jutunk el az általános fogalomhoz, indukciónak nevezzük. Dedukció: A fogalomalkotásnak azt a módját, amikor
Logika Indukció: A fogalomalkotásnak azt a módját, amikor a konkrét tapasztalatokra támaszkodva jutunk el az általános fogalomhoz, indukciónak nevezzük. Dedukció: A fogalomalkotásnak azt a módját, amikor
Házi feladatok megoldása. Nyelvek használata adatszerkezetek, képek leírására
 Nyelvek használata adatszerkezetek, képek leírására Formális nyelvek, 2. gyakorlat 1. feladat Módosított : belsejében lehet _ jel is. Kezdődhet, de nem végződhet vele, két aláhúzás nem lehet egymás mellett.
Nyelvek használata adatszerkezetek, képek leírására Formális nyelvek, 2. gyakorlat 1. feladat Módosított : belsejében lehet _ jel is. Kezdődhet, de nem végződhet vele, két aláhúzás nem lehet egymás mellett.
Miért fontos számunkra az előző gyakorlaton tárgyalt lineáris algebrai ismeretek
 Az november 23-i szeminárium témája Rövid összefoglaló Miért fontos számunkra az előző gyakorlaton tárgyalt lineáris algebrai ismeretek felfrissítése? Tekintsünk ξ 1,..., ξ k valószínűségi változókat,
Az november 23-i szeminárium témája Rövid összefoglaló Miért fontos számunkra az előző gyakorlaton tárgyalt lineáris algebrai ismeretek felfrissítése? Tekintsünk ξ 1,..., ξ k valószínűségi változókat,
1. A matematikai logika alapfogalmai. 2. A matematikai logika műveletei
 1. A matematikai logika alapfogalmai Megjegyzések: a) A logikában az állítás (kijelentés), valamint annak igaz vagy hamis voltát alapfogalomnak tekintjük, nem definiáljuk. b) Minden állítással kapcsolatban
1. A matematikai logika alapfogalmai Megjegyzések: a) A logikában az állítás (kijelentés), valamint annak igaz vagy hamis voltát alapfogalomnak tekintjük, nem definiáljuk. b) Minden állítással kapcsolatban
