Formális módszerek GM_IN003_1 Program verifikálás, formalizmusok
|
|
|
- Erzsébet Csenge Magyarné
- 5 évvel ezelőtt
- Látták:
Átírás
1 Formális módszerek GM_IN003_1 Program verifikálás, formalizmusok Program verifikálás Konkurens programozási megoldások terjedése -> verifikálás szükséges, (nehéz) logika Legszélesebb körben alkalmazott gyakorlat program formális specifikálása: temporális bizonyítás: a helyes m!ködés tétel (adott deduktív rendszer mellett) bizonyítás géppel ellen"rizhet"
2 Véges állapotú programok Program változóinak értékkészlete véges domén Az állapotot véges információmennyiség írja le leírható elemi propozíciókkal véges propozícionális Kripke struktúra Számítások A számítások alapvet"en végtelen állapot szekvenciák az elemi propozíciók igazságértékeinek A temporális logikák tekinthet"k véges állapotú elfogadóknak (gépeknek) megfelel" végtelen szavak egy ABC felett azaz konstruálható olyan véges állapotú automata, mely pontosan az adott propozícionális temporális logikai kifejezéseket fogadja el
3 Modell ellen"rzés Véges állapotú program (P), mint végtelen kifejezések véges generátora Program specifikáció (#), mint véges állapotú elfogadó P " # üres, azaz nem fogad el kifejezést Temporális logikák Propozíciós ill. els"rend! logikák Pont ill. intervallum logikák Diszkrét ill. folytonos idej! logikák Lineáris és elágazó idej! logikák Múlt és jöv" kezelése
4 Propozíciós temporális logika Wff-ok elemi propozíciókból (boole operátorokra zártak) Jöv" kezelés Unáris temporális kapcsolat X (next) Bináris temporális kapcsolat U (until) " :# $ 2 Prop i % # Propozíciós temporális logika Múlt kezelés Unáris temporális kapcsolat Y (previous) Bináris temporális kapcsolat S (since) p Xp p p q puq p Yp q p p psq
5 Kripke struktúrák KS=(S,R,L) S: állapotok véges halmaza R: állapot átmeneti relációk L: S$2 Prop állapotok címkézése elemi propozíciókkal KS teljes, ha "s # S : $t # S (s,t) # R Címkézett állapotátmeneti rendszerek LTS=(S,Act,$) S: állapotok halmaza (véges, vagy megszámlálhatóan végtelen) Act: akciók halmaza $!S x Act x S: címkézett állapotátmeneti reláció ( s,",s' ) #$ helyett s " % $ s' jelölés
6 Kripke állapotátmenet rendszerek KTS=(S,$,L) adott Prop és Act mellett Jól használható programok m!ködésének leírására utasítások (akciók) és változók (állapot) megadása Automaták (%,Q,&,q0,F) %: véges ABC (szimbólum halmaz) Q: állapotok véges halmaza &: tranzíció függvény Qx%$Q q 0"Q: kezd" állapot F!Q: elfogadási állapotok halmaza
7 Automaták (folyt.) Automata futása a 1a2..an"%* inputra: q0,q1,..qn szekvencia úgy, hogy qi=&(qi-1,ai) Szó elfogadása q n"f Felismert nyelv L!%* az összes felismert szó halmaza Input véges végtelen Temporális logika és automaták Elfogadó automata PTL-hoz Büchi automata A=(%,S,',S0,F)
8 Büchi automata Egy futás akkor elfogadó egy végtelen szóra, ha vannak olyan F-beli állapotok, melyek végtelenszer ismétl"dnek (-automaták w"%( végtelen szekvenciák! (!% ( (-nyelv Büchi automata (pl.) %={a,b},s={q0,q1,q2},s0={q0},f={q2} a,b b start a q 0 q 1 q 2 a (a+b) * (ab) (
9 PTL és Büchi automata Tétel: Adott # PTL kifejezéshez konstruálható A# Büchi automata, ahol %=2 Prop és S )2 O( # ), hogy L(A#) pontosan a #-t kielégít" számítások halmaza. PTL és Büchi automata (pl.) Prop={r,s} %:=2Prop ={#,{r},{s},{r,s}} Automata, ami r-t kielégit" futásokat fogad el: {r},{r,s} start!
10 Ürességi probléma Az adott automata egyáltalán elfogad-e valamilyen szavakat az ürességi probléma lineáris id"ben és nem determinisztikus logaritmikus térben megoldható Modell ellen"rzés Véges állapotú program P=(W,s0,R,V) W: véges állapot halmaz s 0"W :kezd" állapot R!W2 :elérhet"ségi reláció V:W$2 Prop propozíciók igazság értékei az egyes állapotokban
11 Modell ellen"rzés (folyt.) u: végtelen szekvencia u0,u1... u0=s0 és uirui+1 i*0 V(u0),V(u1)... P egy számítása P kielégít egy # PTL kifejezést, ha P minden számítása kielégíti #-t Modell ellen"rzés (folyt.) Véges állapotú program, mint Büchi automata Ap=(%,W,s0, ',W) %=2 Prop s "'(s,a) iff (s,s )"R és a=v(s) a teljes állapottér elfogadási állapot
12 Modell ellen"rzés (folyt.) Véges állapotú program P PTL kifejezés! Büchi automata A P Büchi automata A! Szorzat automata A P xa! Igen Üresség vizsgálat Nem Komplementer automata Teljesen definiált, determinisztikus esetben elfogadó és nem elfogadó állapotok felcserélése pl.: {Q} {Q},{P,Q} {Q} {Q},{P,Q} A! A {P,Q}! {P,Q} > 1 2 > 1 2 {},{P} 3 {},{P} {},{P} 3 {},{P} {},{P},{Q},{P,Q} {},{P},{Q},{P,Q}
13 Szorzat automata konstruálása B1= (%,S1,'1,S01,F1) B2= (%,S2,'2,S02,F2) B 1+2=(%,S1,S2,{1,2},',S01,S02,{1},{(s1,s2,1) s1"f1}) ': {((s 1,s2,1),a,(s 1,s 2,i)) if s1"f1 then i=2 else 1}$ {((s 1,s2,2),a,(s 1,s 2,i)) if s2"f2 then i=1 else 2} (s 1,a,s 1)"'1 and (s2,a,s 2)"'2 Szorzat automata (pl.)
Modellellenőrzés. dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék
 Modellellenőrzés dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mit szeretnénk elérni? Informális vagy félformális tervek Informális követelmények Formális modell: KS, LTS, TA
Modellellenőrzés dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mit szeretnénk elérni? Informális vagy félformális tervek Informális követelmények Formális modell: KS, LTS, TA
Temporális logikák és modell ellenırzés
 Temporális logikák és modell ellenırzés Temporális logikák Modális logika: kijelentések különböző módjainak tanulmányozására vezették be (eredetileg filozófusok). Ilyen módok: esetleg, mindig, szükségszerűen,
Temporális logikák és modell ellenırzés Temporális logikák Modális logika: kijelentések különböző módjainak tanulmányozására vezették be (eredetileg filozófusok). Ilyen módok: esetleg, mindig, szükségszerűen,
Alapszintű formalizmusok
 Alapszintű formalizmusok dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mit szeretnénk elérni? Informális tervek Informális követelmények Formális modell Formalizált követelmények
Alapszintű formalizmusok dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mit szeretnénk elérni? Informális tervek Informális követelmények Formális modell Formalizált követelmények
Részletes szoftver tervek ellenőrzése
 Részletes szoftver tervek ellenőrzése Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/~majzik/ Tartalomjegyzék A részletes
Részletes szoftver tervek ellenőrzése Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/~majzik/ Tartalomjegyzék A részletes
A Formális nyelvek vizsga teljesítése. a) Normál A vizsgán 60 pont szerezhet, amely két 30 pontos részb l áll össze az alábbi módon:
 A Formális nyelvek vizsga teljesítése a) Normál A vizsgán 60 pont szerezhet, amely két 30 pontos részb l áll össze az alábbi módon: 1. Öt kis kérdés megválaszolása egyenként 6 pontért, melyet minimum 12
A Formális nyelvek vizsga teljesítése a) Normál A vizsgán 60 pont szerezhet, amely két 30 pontos részb l áll össze az alábbi módon: 1. Öt kis kérdés megválaszolása egyenként 6 pontért, melyet minimum 12
A Formális nyelvek vizsga teljesítése. a) Normál A vizsgán 60 pont szerezhet, amely két 30 pontos részb l áll össze az alábbi módon:
 A Formális nyelvek vizsga teljesítése a) Normál A vizsgán 60 pont szerezhet, amely két 30 pontos részb l áll össze az alábbi módon: 1. Öt rövid kérdés megválaszolása egyenként 6 pontért, melyet minimum
A Formális nyelvek vizsga teljesítése a) Normál A vizsgán 60 pont szerezhet, amely két 30 pontos részb l áll össze az alábbi módon: 1. Öt rövid kérdés megválaszolása egyenként 6 pontért, melyet minimum
Modellellenőrzés. dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék
 Modellellenőrzés dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mit szeretnénk elérni? Informális vagy félformális tervek Informális követelmények Formális modell: KS, LTS, TA
Modellellenőrzés dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mit szeretnénk elérni? Informális vagy félformális tervek Informális követelmények Formális modell: KS, LTS, TA
Térinformatikai algoritmusok Elemi algoritmusok
 Cserép Máté Analóg programozásnak nevezzük azt, amikor egy feladat megoldásához egy már ismert és megoldott feladat megoldását használjuk fel. Általában nem pontosan ugyanazt a feladatot oldottuk meg korábban,
Cserép Máté Analóg programozásnak nevezzük azt, amikor egy feladat megoldásához egy már ismert és megoldott feladat megoldását használjuk fel. Általában nem pontosan ugyanazt a feladatot oldottuk meg korábban,
Hardver és szoftver rendszerek verifikációja Röviden megválaszolható kérdések
 Hardver és szoftver rendszerek verifikációja Röviden megválaszolható kérdések 1. Az informatikai rendszereknél mit ellenőriznek validációnál és mit verifikációnál? 2. A szoftver verifikációs technikák
Hardver és szoftver rendszerek verifikációja Röviden megválaszolható kérdések 1. Az informatikai rendszereknél mit ellenőriznek validációnál és mit verifikációnál? 2. A szoftver verifikációs technikák
Térinformatikai algoritmusok Elemi algoritmusok
 Cserép Máté 2016. szeptember 14. Analóg programozásnak nevezzük azt, amikor egy feladat megoldásához egy már ismert és megoldott feladat megoldását használjuk fel. Általában nem pontosan ugyanazt a feladatot
Cserép Máté 2016. szeptember 14. Analóg programozásnak nevezzük azt, amikor egy feladat megoldásához egy már ismert és megoldott feladat megoldását használjuk fel. Általában nem pontosan ugyanazt a feladatot
Hatékony technikák modellellenőrzéshez: Szimbolikus technikák (ROBDD)
 Hatékony technikák modellellenőrzéshez: Szimbolikus technikák (ROBDD) dr. Majzik István dr. Pataricza András dr. Bartha Tamás BME Méréstechnika és Információs Rendszerek Tanszék 1 Hol tartunk? Alacsony
Hatékony technikák modellellenőrzéshez: Szimbolikus technikák (ROBDD) dr. Majzik István dr. Pataricza András dr. Bartha Tamás BME Méréstechnika és Információs Rendszerek Tanszék 1 Hol tartunk? Alacsony
Gyakorló feladatok: Formális modellek, temporális logikák, modellellenőrzés. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék
 Gyakorló feladatok: Formális modellek, temporális logikák, modellellenőrzés Majzik István BME Méréstechnika és Információs Rendszerek Tanszék Formális modellek használata és értelmezése Formális modellek
Gyakorló feladatok: Formális modellek, temporális logikák, modellellenőrzés Majzik István BME Méréstechnika és Információs Rendszerek Tanszék Formális modellek használata és értelmezése Formális modellek
Logika es sz am ıt aselm elet I. r esz Logika Negyedik el oad as 1/26
 1/26 Logika és számításelmélet I. rész Logika Negyedik előadás Tartalom 2/26 Az elsőrendű logika szemantikája Formulák és formulahalmazok szemantikus tulajdonságai Elsőrendű logikai nyelv interpretációja
1/26 Logika és számításelmélet I. rész Logika Negyedik előadás Tartalom 2/26 Az elsőrendű logika szemantikája Formulák és formulahalmazok szemantikus tulajdonságai Elsőrendű logikai nyelv interpretációja
5. előadás. Programozás-elmélet. Programozás-elmélet 5. előadás
 Elemi programok Definíció Az S A A program elemi, ha a A : S(a) { a, a, a, a,..., a, b b a}. A definíció alapján könnyen látható, hogy egy elemi program tényleg program. Speciális elemi programok a kövekezők:
Elemi programok Definíció Az S A A program elemi, ha a A : S(a) { a, a, a, a,..., a, b b a}. A definíció alapján könnyen látható, hogy egy elemi program tényleg program. Speciális elemi programok a kövekezők:
Követelmények formalizálása: Temporális logikák. dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék
 Követelmények formalizálása: Temporális logikák dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mire kellenek a temporális logikák? 2 Motivációs mintapélda: Kölcsönös kizárás 2
Követelmények formalizálása: Temporális logikák dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mire kellenek a temporális logikák? 2 Motivációs mintapélda: Kölcsönös kizárás 2
Kiterjesztések sek szemantikája
 Kiterjesztések sek szemantikája Példa D Integer = {..., -1,0,1,... }; D Boolean = { true, false } D T1... T n T = D T 1... D Tn D T Az összes függvf ggvény halmaza, amelyek a D T1,..., D Tn halmazokból
Kiterjesztések sek szemantikája Példa D Integer = {..., -1,0,1,... }; D Boolean = { true, false } D T1... T n T = D T 1... D Tn D T Az összes függvf ggvény halmaza, amelyek a D T1,..., D Tn halmazokból
Formális nyelvek - 9.
 Formális nyelvek - 9. Csuhaj Varjú Erzsébet Algoritmusok és Alkalmazásaik Tanszék Informatikai Kar Eötvös Loránd Tudományegyetem H-1117 Budapest Pázmány Péter sétány 1/c E-mail: csuhaj@inf.elte.hu 1 Véges
Formális nyelvek - 9. Csuhaj Varjú Erzsébet Algoritmusok és Alkalmazásaik Tanszék Informatikai Kar Eötvös Loránd Tudományegyetem H-1117 Budapest Pázmány Péter sétány 1/c E-mail: csuhaj@inf.elte.hu 1 Véges
Hatékony technikák modellellenőrzéshez: Szimbolikus technikák (ROBDD)
 Hatékony technikák modellellenőrzéshez: Szimbolikus technikák (ROBDD) dr. Majzik István dr. Pataricza András dr. Bartha Tamás BME Méréstechnika és Információs Rendszerek Tanszék 1 Hol tartunk? Alacsony
Hatékony technikák modellellenőrzéshez: Szimbolikus technikák (ROBDD) dr. Majzik István dr. Pataricza András dr. Bartha Tamás BME Méréstechnika és Információs Rendszerek Tanszék 1 Hol tartunk? Alacsony
Előfeltétel: legalább elégséges jegy Diszkrét matematika II. (GEMAK122B) tárgyból
 ÜTEMTERV Programozás-elmélet c. tárgyhoz (GEMAK233B, GEMAK233-B) BSc gazdaságinformatikus, programtervező informatikus alapszakok számára Óraszám: heti 2+0, (aláírás+kollokvium, 3 kredit) 2019/20-es tanév
ÜTEMTERV Programozás-elmélet c. tárgyhoz (GEMAK233B, GEMAK233-B) BSc gazdaságinformatikus, programtervező informatikus alapszakok számára Óraszám: heti 2+0, (aláírás+kollokvium, 3 kredit) 2019/20-es tanév
Szoftverminőségbiztosítás
 NGB_IN003_1 SZE 2014-15/2 (13) Szoftverminőségbiztosítás Szoftverminőség és formális módszerek Formális módszerek Formális módszer formalizált módszer(tan) Formális eljárások alkalmazása a fejlesztésben
NGB_IN003_1 SZE 2014-15/2 (13) Szoftverminőségbiztosítás Szoftverminőség és formális módszerek Formális módszerek Formális módszer formalizált módszer(tan) Formális eljárások alkalmazása a fejlesztésben
Programozási Módszertan definíciók, stb.
 Programozási Módszertan definíciók, stb. 1. Bevezetés Egy adat típusát az adat által felvehető lehetséges értékek halmaza (típusérték halmaz, TÉH), és az ezen értelmezett műveletek (típusműveletek) együttesen
Programozási Módszertan definíciók, stb. 1. Bevezetés Egy adat típusát az adat által felvehető lehetséges értékek halmaza (típusérték halmaz, TÉH), és az ezen értelmezett műveletek (típusműveletek) együttesen
A modellellenőrzés érdekes alkalmazása: Tesztgenerálás modellellenőrzővel
 A modellellenőrzés érdekes alkalmazása: Tesztgenerálás modellellenőrzővel Majzik István Micskei Zoltán BME Méréstechnika és Információs Rendszerek Tanszék 1 Modell alapú fejlesztési folyamat (részlet)
A modellellenőrzés érdekes alkalmazása: Tesztgenerálás modellellenőrzővel Majzik István Micskei Zoltán BME Méréstechnika és Információs Rendszerek Tanszék 1 Modell alapú fejlesztési folyamat (részlet)
Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) Halmazok 1
 Halmazok 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) Halmazok 2 A fejezet legfontosabb elemei Halmaz megadási módjai Halmazok közti műveletek (metszet,
Halmazok 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) Halmazok 2 A fejezet legfontosabb elemei Halmaz megadási módjai Halmazok közti műveletek (metszet,
Szoftverminőségbiztosítás
 NGB_IN003_1 SZE 2017-18/2 (9) Szoftverminőségbiztosítás Specifikáció alapú (black-box) technikák A szoftver mint leképezés Szoftverhiba Hibát okozó bement Hibás kimenet Input Szoftver Output Funkcionális
NGB_IN003_1 SZE 2017-18/2 (9) Szoftverminőségbiztosítás Specifikáció alapú (black-box) technikák A szoftver mint leképezés Szoftverhiba Hibát okozó bement Hibás kimenet Input Szoftver Output Funkcionális
Rendszermodellezés. Modellellenőrzés. Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék
 Rendszermodellezés Modellellenőrzés Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Ismétlés: Mire használunk modelleket? Kommunikáció, dokumentáció Gondolkodás,
Rendszermodellezés Modellellenőrzés Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Ismétlés: Mire használunk modelleket? Kommunikáció, dokumentáció Gondolkodás,
Korlátos modellellenőrzés. dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék
 Korlátos modellellenőrzés dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Hol tartunk most? Alacsony szintű formalizmusok (KS, LTS, KTS) Magasabb szintű formalizmusok Temporális
Korlátos modellellenőrzés dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Hol tartunk most? Alacsony szintű formalizmusok (KS, LTS, KTS) Magasabb szintű formalizmusok Temporális
Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé.
 HA 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) HA 2 Halmazok HA 3 Megjegyzések A halmaz, az elem és az eleme fogalmakat nem definiáljuk, hanem alapfogalmaknak
HA 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) HA 2 Halmazok HA 3 Megjegyzések A halmaz, az elem és az eleme fogalmakat nem definiáljuk, hanem alapfogalmaknak
Turing-gépek. Számításelmélet (7. gyakorlat) Turing-gépek 2009/10 II. félév 1 / 1
 Turing-gépek Logika és számításelmélet, 7. gyakorlat 2009/10 II. félév Számításelmélet (7. gyakorlat) Turing-gépek 2009/10 II. félév 1 / 1 A Turing-gép Az algoritmus fogalmának egy intuitív definíciója:
Turing-gépek Logika és számításelmélet, 7. gyakorlat 2009/10 II. félév Számításelmélet (7. gyakorlat) Turing-gépek 2009/10 II. félév 1 / 1 A Turing-gép Az algoritmus fogalmának egy intuitív definíciója:
A digitális számítás elmélete
 A digitális számítás elmélete 8. előadás ápr. 16. Turing gépek és nyelvtanok A nyelvosztályok áttekintése Turing gépek és a természetes számokon értelmezett függvények Áttekintés Dominó Bizonyítások: L
A digitális számítás elmélete 8. előadás ápr. 16. Turing gépek és nyelvtanok A nyelvosztályok áttekintése Turing gépek és a természetes számokon értelmezett függvények Áttekintés Dominó Bizonyítások: L
A számítógépes nyelvészet elmélete és gyakorlata. Automaták
 A számítógépes nyelvészet elmélete és gyakorlata Automaták Nyelvek és automaták A nyelvek automatákkal is jellemezhetőek Automaták hierarchiája Chomsky-féle hierarchia Automata: új eszköz a nyelvek komplexitásának
A számítógépes nyelvészet elmélete és gyakorlata Automaták Nyelvek és automaták A nyelvek automatákkal is jellemezhetőek Automaták hierarchiája Chomsky-féle hierarchia Automata: új eszköz a nyelvek komplexitásának
Véges automaták, reguláris nyelvek
 Véges automaták, reguláris nyelvek Kiegészítő anyag az lgoritmuselmélet tárgyhoz (a Rónyai Ivanyos Szabó: lgoritmusok könyv mellé) Friedl Katalin BME SZIT friedl@cs.bme.hu 27. augusztus 3. véges automata
Véges automaták, reguláris nyelvek Kiegészítő anyag az lgoritmuselmélet tárgyhoz (a Rónyai Ivanyos Szabó: lgoritmusok könyv mellé) Friedl Katalin BME SZIT friedl@cs.bme.hu 27. augusztus 3. véges automata
Automaták mint elfogadók (akceptorok)
 Automaták mint elfogadók (akceptorok) Ha egy iniciális Moore-automatában a kimenőjelek halmaza csupán kételemű: {elfogadom, nem fogadom el}, és az utolsó kimenőjel dönti el azt a kérdést, hogy elfogadható-e
Automaták mint elfogadók (akceptorok) Ha egy iniciális Moore-automatában a kimenőjelek halmaza csupán kételemű: {elfogadom, nem fogadom el}, és az utolsó kimenőjel dönti el azt a kérdést, hogy elfogadható-e
A modellellenőrzés érdekes alkalmazása: Tesztgenerálás modellellenőrzővel
 A modellellenőrzés érdekes alkalmazása: Tesztgenerálás modellellenőrzővel Majzik István Micskei Zoltán BME Méréstechnika és Információs Rendszerek Tanszék 1 Modell alapú fejlesztési folyamat (részlet)
A modellellenőrzés érdekes alkalmazása: Tesztgenerálás modellellenőrzővel Majzik István Micskei Zoltán BME Méréstechnika és Információs Rendszerek Tanszék 1 Modell alapú fejlesztési folyamat (részlet)
ALAPFOGALMAK 1. A reláció az program programfüggvénye, ha. Azt mondjuk, hogy az feladat szigorúbb, mint az feladat, ha
 ALAPFOGALMAK 1 Á l l a p o t t é r Legyen I egy véges halmaz és legyenek A i, i I tetszőleges véges vagy megszámlálható, nem üres halmazok Ekkor az A= A i halmazt állapottérnek, az A i halmazokat pedig
ALAPFOGALMAK 1 Á l l a p o t t é r Legyen I egy véges halmaz és legyenek A i, i I tetszőleges véges vagy megszámlálható, nem üres halmazok Ekkor az A= A i halmazt állapottérnek, az A i halmazokat pedig
Hatékony technikák modellellenőrzéshez: Korlátos modellellenőrzés. dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék
 Hatékony technikák modellellenőrzéshez: Korlátos modellellenőrzés dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Hol tartunk most? Alacsony szintű formalizmusok (KS, LTS, KTS)
Hatékony technikák modellellenőrzéshez: Korlátos modellellenőrzés dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Hol tartunk most? Alacsony szintű formalizmusok (KS, LTS, KTS)
Informatika 1 2. el adás: Absztrakt számítógépek
 Informatika 1 2. el adás: Budapesti M szaki és Gazdaságtudományi Egyetem 2015-09-08 1 2 3 A egy M = Q, Γ, b, Σ, δ, q 0, F hetes, ahol Q az 'állapotok' nem üres halmaza, Γ a 'szalag ábécé' véges, nem üres
Informatika 1 2. el adás: Budapesti M szaki és Gazdaságtudományi Egyetem 2015-09-08 1 2 3 A egy M = Q, Γ, b, Σ, δ, q 0, F hetes, ahol Q az 'állapotok' nem üres halmaza, Γ a 'szalag ábécé' véges, nem üres
Programozási módszertan
 1 Programozási módszertan 1. Alapfogalmak Feldhoffer Gergely 2012 Féléves tananyag terve 2 Program helyességének bizonyítása Reprezentáció Logikai-matematikai eszköztár Programozási tételek bizonyítása
1 Programozási módszertan 1. Alapfogalmak Feldhoffer Gergely 2012 Féléves tananyag terve 2 Program helyességének bizonyítása Reprezentáció Logikai-matematikai eszköztár Programozási tételek bizonyítása
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 1. estis képzés 2017. ősz 1. Diszkrét matematika 1. estis képzés 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
Diszkrét matematika 1. estis képzés 2017. ősz 1. Diszkrét matematika 1. estis képzés 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
9. előadás. Programozás-elmélet. Programozási tételek Elemi prog. Sorozatszámítás Eldöntés Kiválasztás Lin. keresés Megszámolás Maximum.
 Programozási tételek Programozási feladatok megoldásakor a top-down (strukturált) programtervezés esetén három vezérlési szerkezetet használunk: - szekvencia - elágazás - ciklus Eddig megismertük az alábbi
Programozási tételek Programozási feladatok megoldásakor a top-down (strukturált) programtervezés esetén három vezérlési szerkezetet használunk: - szekvencia - elágazás - ciklus Eddig megismertük az alábbi
Valószínűségi modellellenőrzés Markov döntési folyamatokkal
 Valószínűségi modellellenőrzés Markov döntési folyamatokkal Hajdu Ákos Szoftver verifikáció és validáció 2015.12.09. Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek
Valószínűségi modellellenőrzés Markov döntési folyamatokkal Hajdu Ákos Szoftver verifikáció és validáció 2015.12.09. Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek
Múlt és jövő: Új algoritmusok lineáris temporális tulajdonságok szaturáció-alapú modellellenőrzésére
 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Méréstechnika és Információs Rendszerek Tanszék Múlt és jövő: Új algoritmusok lineáris temporális tulajdonságok szaturáció-alapú
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Méréstechnika és Információs Rendszerek Tanszék Múlt és jövő: Új algoritmusok lineáris temporális tulajdonságok szaturáció-alapú
... S n. A párhuzamos programszerkezet két vagy több folyamatot tartalmaz, melyek egymással közös változó segítségével kommunikálnak.
 Párhuzamos programok Legyen S parbegin S 1... S n parend; program. A párhuzamos programszerkezet két vagy több folyamatot tartalmaz, melyek egymással közös változó segítségével kommunikálnak. Folyamat
Párhuzamos programok Legyen S parbegin S 1... S n parend; program. A párhuzamos programszerkezet két vagy több folyamatot tartalmaz, melyek egymással közös változó segítségével kommunikálnak. Folyamat
Algoritmuselmélet 12. előadás
 Algoritmuselmélet 12. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu 2002 Április 9. ALGORITMUSELMÉLET 12. ELŐADÁS 1 Turing-gépek
Algoritmuselmélet 12. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu 2002 Április 9. ALGORITMUSELMÉLET 12. ELŐADÁS 1 Turing-gépek
Modellek ellenőrzése és tesztelése
 Modellek ellenőrzése és tesztelése Rendszermodellezés imsc gyakorlat Budapesti Műszaki és Gazdaságtudományi Egyetem Hibatűrő Rendszerek Kutatócsoport Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika
Modellek ellenőrzése és tesztelése Rendszermodellezés imsc gyakorlat Budapesti Műszaki és Gazdaságtudományi Egyetem Hibatűrő Rendszerek Kutatócsoport Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika
Hardver és szoftver rendszerek verifikációja Röviden megválaszolható kérdések
 Hardver és szoftver rendszerek verifikációja Röviden megválaszolható kérdések 1. Az informatikai rendszereknél mit ellenőriznek validációnál és mit verifikációnál? 2. A szoftver verifikációs technikák
Hardver és szoftver rendszerek verifikációja Röviden megválaszolható kérdések 1. Az informatikai rendszereknél mit ellenőriznek validációnál és mit verifikációnál? 2. A szoftver verifikációs technikák
Logika és informatikai alkalmazásai kiskérdések február Mikor mondjuk, hogy az F formula a G-nek részformulája?
 ,,Alap kiskérdések Logika és informatikai alkalmazásai kiskérdések 2012. február 19. 1. Hogy hívjuk a 0 aritású függvényjeleket? 2. Definiálja a termek halmazát. 3. Definiálja a formulák halmazát. 4. Definiálja,
,,Alap kiskérdések Logika és informatikai alkalmazásai kiskérdések 2012. február 19. 1. Hogy hívjuk a 0 aritású függvényjeleket? 2. Definiálja a termek halmazát. 3. Definiálja a formulák halmazát. 4. Definiálja,
Zárthelyi mintapéldák. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék
 Zárthelyi mintapéldák Majzik István BME Méréstechnika és Információs Rendszerek Tanszék Elméleti kérdések Indokolja meg, hogy az A (X Stop F Start) kifejezés szintaktikailag helyes kifejezés-e CTL illetve
Zárthelyi mintapéldák Majzik István BME Méréstechnika és Információs Rendszerek Tanszék Elméleti kérdések Indokolja meg, hogy az A (X Stop F Start) kifejezés szintaktikailag helyes kifejezés-e CTL illetve
Formális módszerek GM_IN003_1 Bevezetés
 Formális módszerek GM_IN003_1 Formális módszerek Formális módszer! formalizált módszer(tan) Formális eljárások alkalmazása a fejlesztésben nincs olyan formális eljárás, ami egy komplex rendszer minden
Formális módszerek GM_IN003_1 Formális módszerek Formális módszer! formalizált módszer(tan) Formális eljárások alkalmazása a fejlesztésben nincs olyan formális eljárás, ami egy komplex rendszer minden
Kriptográfia 0. A biztonság alapja. Számítás-komplexitási kérdések
 Kriptográfia 0 Számítás-komplexitási kérdések A biztonság alapja Komplexitás elméleti modellek független, egyenletes eloszlású véletlen változó értéke számítással nem hozható kapcsolatba más információval
Kriptográfia 0 Számítás-komplexitási kérdések A biztonság alapja Komplexitás elméleti modellek független, egyenletes eloszlású véletlen változó értéke számítással nem hozható kapcsolatba más információval
folyamatrendszerek modellezése
 Diszkrét eseményű folyamatrendszerek modellezése Hangos Katalin Számítástudomány Alkalmazása Tanszék Veszprémi Egyetem Haladó Folyamatmodellezés és modell analízis PhD kurzus p. 1/36 Tartalom Diszkrét
Diszkrét eseményű folyamatrendszerek modellezése Hangos Katalin Számítástudomány Alkalmazása Tanszék Veszprémi Egyetem Haladó Folyamatmodellezés és modell analízis PhD kurzus p. 1/36 Tartalom Diszkrét
Algoritmusok helyességének bizonyítása. A Floyd-módszer
 Algoritmusok helyességének bizonyítása A Floyd-módszer Algoritmusok végrehajtása Egy A algoritmus esetében a változókat három változótípusról beszélhetünk, melyeket az X, Y és Z vektorokba csoportosítjuk
Algoritmusok helyességének bizonyítása A Floyd-módszer Algoritmusok végrehajtása Egy A algoritmus esetében a változókat három változótípusról beszélhetünk, melyeket az X, Y és Z vektorokba csoportosítjuk
Formális nyelvek és automaták vizsgához statisztikailag igazolt várható vizsgakérdések
 1. Feladat Az első feladatban szereplő - kérdések 1 Minden környezet független nyelv felismerhető veremautomatával. Minden környezet független nyelv felismerhető 1 veremmel. Minden 3. típusú nyelv felismerhető
1. Feladat Az első feladatban szereplő - kérdések 1 Minden környezet független nyelv felismerhető veremautomatával. Minden környezet független nyelv felismerhető 1 veremmel. Minden 3. típusú nyelv felismerhető
Időzített átmeneti rendszerek
 Időzített átmeneti rendszerek Legyen A egy ábécé, A = A { (d) d R 0 }. A feletti (valós idejű) időzített átmeneti rendszer olyan A = (S, T,,, ) címkézett átmeneti rendszert ( : T A ), melyre teljesülnek
Időzített átmeneti rendszerek Legyen A egy ábécé, A = A { (d) d R 0 }. A feletti (valós idejű) időzített átmeneti rendszer olyan A = (S, T,,, ) címkézett átmeneti rendszert ( : T A ), melyre teljesülnek
Temporális logikai specifikációk vizsgálata
 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Méréstechnika és Információs Rendszerek Tanszék Temporális logikai specifikációk vizsgálata Diplomaterv Készítette Segesdi
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Méréstechnika és Információs Rendszerek Tanszék Temporális logikai specifikációk vizsgálata Diplomaterv Készítette Segesdi
Programkonstrukciók A programkonstrukciók programfüggvényei Levezetési szabályok. 6. előadás. Programozás-elmélet. Programozás-elmélet 6.
 Programkonstrukciók Definíció Legyen π feltétel és S program A-n. A DO A A relációt az S-ből a π feltétellel képezett ciklusnak nevezzük, és (π, S)-sel jelöljük, ha 1. a / [π] : DO (a) = { a }, 2. a [π]
Programkonstrukciók Definíció Legyen π feltétel és S program A-n. A DO A A relációt az S-ből a π feltétellel képezett ciklusnak nevezzük, és (π, S)-sel jelöljük, ha 1. a / [π] : DO (a) = { a }, 2. a [π]
Számításelmélet. Második előadás
 Számításelmélet Második előadás Többszalagos Turing-gép Turing-gép k (konstans) számú szalaggal A szalagok mindegyike rendelkezik egy független író / olvasó fejjel A bemenet az első szalagra kerül, a többi
Számításelmélet Második előadás Többszalagos Turing-gép Turing-gép k (konstans) számú szalaggal A szalagok mindegyike rendelkezik egy független író / olvasó fejjel A bemenet az első szalagra kerül, a többi
Dinamikus modellek szerkezete, SDG modellek
 Diagnosztika - 3. p. 1/2 Modell Alapú Diagnosztika Diszkrét Módszerekkel Dinamikus modellek szerkezete, SDG modellek Hangos Katalin PE Villamosmérnöki és Információs Rendszerek Tanszék Diagnosztika - 3.
Diagnosztika - 3. p. 1/2 Modell Alapú Diagnosztika Diszkrét Módszerekkel Dinamikus modellek szerkezete, SDG modellek Hangos Katalin PE Villamosmérnöki és Információs Rendszerek Tanszék Diagnosztika - 3.
ZH feladatok megoldásai
 ZH feladatok megoldásai A CSOPORT 5. Írja le, hogy milyen szabályokat tartalmazhatnak az egyes Chomskynyelvosztályok (03 típusú nyelvek)! (4 pont) 3. típusú, vagy reguláris nyelvek szabályai A ab, A a
ZH feladatok megoldásai A CSOPORT 5. Írja le, hogy milyen szabályokat tartalmazhatnak az egyes Chomskynyelvosztályok (03 típusú nyelvek)! (4 pont) 3. típusú, vagy reguláris nyelvek szabályai A ab, A a
Programok értelmezése
 Programok értelmezése Kód visszafejtés. Izsó Tamás 2016. szeptember 22. Izsó Tamás Programok értelmezése/ 1 Section 1 Programok értelmezése Izsó Tamás Programok értelmezése/ 2 programok szemantika értelmezése
Programok értelmezése Kód visszafejtés. Izsó Tamás 2016. szeptember 22. Izsó Tamás Programok értelmezése/ 1 Section 1 Programok értelmezése Izsó Tamás Programok értelmezése/ 2 programok szemantika értelmezése
ködös határ (félreértés, hiba)
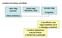 probléma formálisan specifikált: valós világ (domain) (hibás eredmény) ködös határ (félreértés, hiba) formális világ (megoldás) A szoftver fejlesztőnek meg kell értenie a felhasználó problémáját. A specifikáció
probléma formálisan specifikált: valós világ (domain) (hibás eredmény) ködös határ (félreértés, hiba) formális világ (megoldás) A szoftver fejlesztőnek meg kell értenie a felhasználó problémáját. A specifikáció
1. Alapfogalmak Algoritmus Számítási probléma Specifikáció Algoritmusok futási ideje
 1. Alapfogalmak 1.1. Algoritmus Az algoritmus olyan elemi műveletekből kompozíciós szabályok szerint felépített összetett művelet, amelyet megadott feltételt teljesítő bemeneti adatra végrehajtva, a megkívánt
1. Alapfogalmak 1.1. Algoritmus Az algoritmus olyan elemi műveletekből kompozíciós szabályok szerint felépített összetett művelet, amelyet megadott feltételt teljesítő bemeneti adatra végrehajtva, a megkívánt
Feladatok. 6. A CYK algoritmus segítségével döntsük el, hogy aabbcc eleme-e a G = {a, b, c}, {S, A, B, C}, P, S nyelvtan által generált nyelvnek!
 Feladatok 1. A CYK algoritmus segítségével döntsük el, hogy cabcab eleme-e a G = {a, b, c}, {S, A, B, C, D, E}, P, S nyelvtan által generált nyelvnek! P: S AD EB SS A AB a B DD b C CB c D EC a E AD b 2.
Feladatok 1. A CYK algoritmus segítségével döntsük el, hogy cabcab eleme-e a G = {a, b, c}, {S, A, B, C, D, E}, P, S nyelvtan által generált nyelvnek! P: S AD EB SS A AB a B DD b C CB c D EC a E AD b 2.
Deníciók és tételek a beugró vizsgára
 Deníciók és tételek a beugró vizsgára (a szóbeli viszgázás jogáért) Utolsó módosítás: 2008. december 2. 2 Bevezetés Számítási problémának nevezünk egy olyan, a matematika nyelvén megfogalmazott kérdést,
Deníciók és tételek a beugró vizsgára (a szóbeli viszgázás jogáért) Utolsó módosítás: 2008. december 2. 2 Bevezetés Számítási problémának nevezünk egy olyan, a matematika nyelvén megfogalmazott kérdést,
Emlékeztető: LR(0) elemzés. LR elemzések (SLR(1) és LR(1) elemzések)
 Emlékeztető Emlékeztető: LR(0) elemzés A lexikális által előállított szimbólumsorozatot balról jobbra olvassuk, a szimbólumokat az vermébe tesszük. LR elemzések (SLR() és LR() elemzések) Fordítóprogramok
Emlékeztető Emlékeztető: LR(0) elemzés A lexikális által előállított szimbólumsorozatot balról jobbra olvassuk, a szimbólumokat az vermébe tesszük. LR elemzések (SLR() és LR() elemzések) Fordítóprogramok
I. A DIGITÁLIS ÁRAMKÖRÖK ELMÉLETI ALAPJAI
 I. A DIGITÁLIS ÁRAMKÖRÖK ELMÉLETI ALAPJAI 1 A digitális áramkörökre is érvényesek a villamosságtanból ismert Ohm törvény és a Kirchhoff törvények, de az elemzés és a tervezés rendszerint nem ezekre épül.
I. A DIGITÁLIS ÁRAMKÖRÖK ELMÉLETI ALAPJAI 1 A digitális áramkörökre is érvényesek a villamosságtanból ismert Ohm törvény és a Kirchhoff törvények, de az elemzés és a tervezés rendszerint nem ezekre épül.
Bevezetés az informatikába
 Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Matematika alapjai; Feladatok
 Matematika alapjai; Feladatok 1. Hét 1. Tekintsük a,, \ műveleteket. Melyek lesznek a.) kommutativok b.) asszociativak c.) disztributívak-e a, műveletek? Melyik melyikre? 2. Fejezzük ki a műveletet a \
Matematika alapjai; Feladatok 1. Hét 1. Tekintsük a,, \ műveleteket. Melyek lesznek a.) kommutativok b.) asszociativak c.) disztributívak-e a, műveletek? Melyik melyikre? 2. Fejezzük ki a műveletet a \
NEM-DETERMINISZTIKUS PROGRAMOK HELYESSÉGE. Szekvenciális programok kategóriái. Hoare-Dijkstra-Gries módszere
 Szekvenciális programok kategóriái strukturálatlan strukturált NEM-DETERMINISZTIKUS PROGRAMOK HELYESSÉGE Hoare-Dijkstra-Gries módszere determinisztikus valódi korai nem-determinisztikus általános fejlett
Szekvenciális programok kategóriái strukturálatlan strukturált NEM-DETERMINISZTIKUS PROGRAMOK HELYESSÉGE Hoare-Dijkstra-Gries módszere determinisztikus valódi korai nem-determinisztikus általános fejlett
Alapszintű formalizmusok
 Alapszintű formalizmusok dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mit szeretnénk elérni? Informális tervek Informális követelmények Formális modell Formalizált követelmények
Alapszintű formalizmusok dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mit szeretnénk elérni? Informális tervek Informális követelmények Formális modell Formalizált követelmények
Algoritmizálás és adatmodellezés tanítása 1. előadás
 Algoritmizálás és adatmodellezés tanítása 1. előadás Algoritmus-leíró eszközök Folyamatábra Irányított gráf, amely csomópontokból és őket összekötő élekből áll, egyetlen induló és befejező éle van, az
Algoritmizálás és adatmodellezés tanítása 1. előadás Algoritmus-leíró eszközök Folyamatábra Irányított gráf, amely csomópontokból és őket összekötő élekből áll, egyetlen induló és befejező éle van, az
Alapszintű formalizmusok
 Alapszintű formalizmusok dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Modellek a formális ellenőrzéshez Leképzések Mérnöki modellek Magasabb szintű formalizmusok PN, CPN, DFN,
Alapszintű formalizmusok dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Modellek a formális ellenőrzéshez Leképzések Mérnöki modellek Magasabb szintű formalizmusok PN, CPN, DFN,
2. Alapfogalmak, műveletek
 2. Alapfogalmak, műveletek Gépi intelligencia I. Fodor János BMF NIK IMRI NIMGIMIEM Tartalomjegyzék I Mit tudunk eddig? 2 Fuzzy halmazokkal kapcsolatos alapvető fogalmak Fuzzy halmaz tartója Fuzzy halmaz
2. Alapfogalmak, műveletek Gépi intelligencia I. Fodor János BMF NIK IMRI NIMGIMIEM Tartalomjegyzék I Mit tudunk eddig? 2 Fuzzy halmazokkal kapcsolatos alapvető fogalmak Fuzzy halmaz tartója Fuzzy halmaz
Komputeralgebra Rendszerek
 Komputeralgebra Rendszerek Programozás Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2014. február 23. TARTALOMJEGYZÉK 1 of 28 TARTALOMJEGYZÉK I 1 TARTALOMJEGYZÉK 2 Értékadás MAPLE -ben SAGE -ben 3
Komputeralgebra Rendszerek Programozás Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2014. február 23. TARTALOMJEGYZÉK 1 of 28 TARTALOMJEGYZÉK I 1 TARTALOMJEGYZÉK 2 Értékadás MAPLE -ben SAGE -ben 3
2014. szeptember 24. és 26. Dr. Vincze Szilvia
 2014. szeptember 24. és 26. Dr. Vincze Szilvia Mind a hétköznapi, mind a tudományos életben gyakran előfordul, hogy bizonyos halmazok elemei között kapcsolat figyelhető meg. A kapcsolat fogalmának matematikai
2014. szeptember 24. és 26. Dr. Vincze Szilvia Mind a hétköznapi, mind a tudományos életben gyakran előfordul, hogy bizonyos halmazok elemei között kapcsolat figyelhető meg. A kapcsolat fogalmának matematikai
Algoritmusok Tervezése. Fuzzy rendszerek Dr. Bécsi Tamás
 Algoritmusok Tervezése Fuzzy rendszerek Dr. Bécsi Tamás Bevezetés Mese a homokkupacról és a hidegről és a hegyekről Bevezetés, Fuzzy történet Két értékű logika, Boole algebra Háromértékű logika n értékű
Algoritmusok Tervezése Fuzzy rendszerek Dr. Bécsi Tamás Bevezetés Mese a homokkupacról és a hidegről és a hegyekről Bevezetés, Fuzzy történet Két értékű logika, Boole algebra Háromértékű logika n értékű
Programozási nyelvek 6. előadás
 Programozási nyelvek 6. előadás Szempontok Programozási nyelvek osztályozása Felhasználói kör (amatőr, professzionális) Emberközelség (gépi nyelvektől a természetes nyelvekig) Számítási modell (hogyan
Programozási nyelvek 6. előadás Szempontok Programozási nyelvek osztályozása Felhasználói kör (amatőr, professzionális) Emberközelség (gépi nyelvektől a természetes nyelvekig) Számítási modell (hogyan
Logika es sz am ıt aselm elet I. r esz Logika Harmadik el oad as 1/33
 1/33 Logika és számításelmélet I. rész Logika Harmadik előadás Tartalom 2/33 Elsőrendű logika bevezetés Az elsőrendű logika szintaxisa 3/33 Nulladrendű állítás Az ítéletlogikában nem foglalkoztunk az álĺıtások
1/33 Logika és számításelmélet I. rész Logika Harmadik előadás Tartalom 2/33 Elsőrendű logika bevezetés Az elsőrendű logika szintaxisa 3/33 Nulladrendű állítás Az ítéletlogikában nem foglalkoztunk az álĺıtások
Programozási nyelvek (ADA)
 Programozási nyelvek (ADA) Kozsik Tamás előadása alapján Készítette: Nagy Krisztián 3. előadás Programozási nyelv felépítése szabályok megadása Lexika Milyen egységek építik fel? Szintaktikus szabályok
Programozási nyelvek (ADA) Kozsik Tamás előadása alapján Készítette: Nagy Krisztián 3. előadás Programozási nyelv felépítése szabályok megadása Lexika Milyen egységek építik fel? Szintaktikus szabályok
Összetett programozási tételek Rendezések Keresések PT egymásra építése. 10. előadás. Programozás-elmélet. Programozás-elmélet 10.
 Összetett programozási tételek Sorozathoz sorozatot relő feladatokkal foglalkozunk. A bemenő sorozatot le kell másolni, s közben az elemekre vonatkozó átalakításokat lehet végezni rajta: Input : n N 0,
Összetett programozási tételek Sorozathoz sorozatot relő feladatokkal foglalkozunk. A bemenő sorozatot le kell másolni, s közben az elemekre vonatkozó átalakításokat lehet végezni rajta: Input : n N 0,
Részletes tervek ellenőrzése
 Szoftverellenőrzési technikák Részletes tervek ellenőrzése Majzik István http://www.inf.mit.bme.hu/ 1 Tartalomjegyzék Áttekintés Milyen szerepe van a részletes terveknek? Milyen ellenőrzési módszerek vannak?
Szoftverellenőrzési technikák Részletes tervek ellenőrzése Majzik István http://www.inf.mit.bme.hu/ 1 Tartalomjegyzék Áttekintés Milyen szerepe van a részletes terveknek? Milyen ellenőrzési módszerek vannak?
Programozási nyelvek (ADA)
 Programozási nyelvek (ADA) Kozsik Tamás előadása alapján Készítette: Nagy Krisztián 1. előadás Hasznos weboldal http://kto.web.elte.hu Program felépítése Programegységek (program unit) eljárások (procedure)
Programozási nyelvek (ADA) Kozsik Tamás előadása alapján Készítette: Nagy Krisztián 1. előadás Hasznos weboldal http://kto.web.elte.hu Program felépítése Programegységek (program unit) eljárások (procedure)
Dicsőségtabló Beadós programozási feladatok
 Dicsőségtabló Beadós programozási feladatok Hallgatói munkák 2017 2018 Szavak kiírása ábécé felett Készítő: Maurer Márton (GI, nappali, 2017) Elméleti háttér Adott véges Ʃ ábécé felett megszámlálhatóan
Dicsőségtabló Beadós programozási feladatok Hallgatói munkák 2017 2018 Szavak kiírása ábécé felett Készítő: Maurer Márton (GI, nappali, 2017) Elméleti háttér Adott véges Ʃ ábécé felett megszámlálhatóan
Elsőrendű logika szintaktikája és szemantikája. Logika (3. gyakorlat) 0-adrendű szemantika 2009/10 II. félév 1 / 1
 Elsőrendű logika szintaktikája és szemantikája Logika és számításelmélet, 3. gyakorlat 2009/10 II. félév Logika (3. gyakorlat) 0-adrendű szemantika 2009/10 II. félév 1 / 1 Az elsőrendű logika Elemek egy
Elsőrendű logika szintaktikája és szemantikája Logika és számításelmélet, 3. gyakorlat 2009/10 II. félév Logika (3. gyakorlat) 0-adrendű szemantika 2009/10 II. félév 1 / 1 Az elsőrendű logika Elemek egy
BASH script programozás II. Vezérlési szerkezetek
 06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
5. A kiterjesztési elv, nyelvi változók
 5. A kiterjesztési elv, nyelvi változók Gépi intelligencia I. Fodor János BMF NIK IMRI NIMGI1MIEM Tartalomjegyzék I 1 A kiterjesztési elv 2 Nyelvi változók A kiterjesztési elv 237 A KITERJESZTÉSI ELV A
5. A kiterjesztési elv, nyelvi változók Gépi intelligencia I. Fodor János BMF NIK IMRI NIMGI1MIEM Tartalomjegyzék I 1 A kiterjesztési elv 2 Nyelvi változók A kiterjesztési elv 237 A KITERJESZTÉSI ELV A
A modell-ellenőrzés gyakorlata UPPAAL
 A modell-ellenőrzés gyakorlata UPPAAL Uppsalai Egyetem + Aalborgi Egyetem közös fejlesztése; 1995. első verzió megjelenése; részei: - grafikus modellt leíró eszköz (System editor) - szimulátor (Simulator)
A modell-ellenőrzés gyakorlata UPPAAL Uppsalai Egyetem + Aalborgi Egyetem közös fejlesztése; 1995. első verzió megjelenése; részei: - grafikus modellt leíró eszköz (System editor) - szimulátor (Simulator)
 Á É Á É Ü É í ö ö ö í ö ö í í ö í ö Ö ö í í í í Ö ö Ö É ö ö Ö ö É ö Í Í ö ö ö í ö ö ö í ö ö ú ö Í ö Ö ö Ö ö í ö í ú ö Ö ö Ö ö í ö í É ö É í í ö í í ö í É ö ö É É É ö ö í ú í ű ö ö Í ö ö í ö Ü ö ö É ö ú
Á É Á É Ü É í ö ö ö í ö ö í í ö í ö Ö ö í í í í Ö ö Ö É ö ö Ö ö É ö Í Í ö ö ö í ö ö ö í ö ö ú ö Í ö Ö ö Ö ö í ö í ú ö Ö ö Ö ö í ö í É ö É í í ö í í ö í É ö ö É É É ö ö í ú í ű ö ö Í ö ö í ö Ü ö ö É ö ú
Bonyolultságelmélet. Thursday 1 st December, 2016, 22:21
 Bonyolultságelmélet Thursday 1 st December, 2016, 22:21 Tárbonyolultság A futásidő mellett a felhasznált tárterület a másik fontos erőforrás. Ismét igaz, hogy egy Ram-program esetében ha csak a használt
Bonyolultságelmélet Thursday 1 st December, 2016, 22:21 Tárbonyolultság A futásidő mellett a felhasznált tárterület a másik fontos erőforrás. Ismét igaz, hogy egy Ram-program esetében ha csak a használt
Valószínűségi változók. Várható érték és szórás
 Matematikai statisztika gyakorlat Valószínűségi változók. Várható érték és szórás Valószínűségi változók 2016. március 7-11. 1 / 13 Valószínűségi változók Legyen a (Ω, A, P) valószínűségi mező. Egy X :
Matematikai statisztika gyakorlat Valószínűségi változók. Várható érték és szórás Valószínűségi változók 2016. március 7-11. 1 / 13 Valószínűségi változók Legyen a (Ω, A, P) valószínűségi mező. Egy X :
Hardver leíró nyelvek (HDL)
 Hardver leíró nyelvek (HDL) Benesóczky Zoltán 2004 A jegyzetet a szerzıi jog védi. Azt a BME hallgatói használhatják, nyomtathatják tanulás céljából. Minden egyéb felhasználáshoz a szerzı belegyezése szükséges.
Hardver leíró nyelvek (HDL) Benesóczky Zoltán 2004 A jegyzetet a szerzıi jog védi. Azt a BME hallgatói használhatják, nyomtathatják tanulás céljából. Minden egyéb felhasználáshoz a szerzı belegyezése szükséges.
Sorozatok határértéke SOROZAT FOGALMA, MEGADÁSA, ÁBRÁZOLÁSA; KORLÁTOS ÉS MONOTON SOROZATOK
 Sorozatok határértéke SOROZAT FOGALMA, MEGADÁSA, ÁBRÁZOLÁSA; KORLÁTOS ÉS MONOTON SOROZATOK Sorozat fogalma Definíció: Számsorozaton olyan függvényt értünk, amelynek értelmezési tartománya a pozitív egész
Sorozatok határértéke SOROZAT FOGALMA, MEGADÁSA, ÁBRÁZOLÁSA; KORLÁTOS ÉS MONOTON SOROZATOK Sorozat fogalma Definíció: Számsorozaton olyan függvényt értünk, amelynek értelmezési tartománya a pozitív egész
PROGRAMOZÁS tantárgy. Gregorics Tibor egyetemi docens ELTE Informatikai Kar
 PROGRAMOZÁS tantárgy Gregorics Tibor egyetemi docens ELTE Informatikai Kar Követelmények A,C,E szakirány B szakirány Előfeltétel Prog. alapismeret Prog. alapismeret Diszkrét matematika I. Óraszám 2 ea
PROGRAMOZÁS tantárgy Gregorics Tibor egyetemi docens ELTE Informatikai Kar Követelmények A,C,E szakirány B szakirány Előfeltétel Prog. alapismeret Prog. alapismeret Diszkrét matematika I. Óraszám 2 ea
Államvizsga kérdések a matematikus szakon, 2001.
 Államvizsga '01, 12. tétel: Algoritmusok bonyolultsága... 1 Államvizsga kérdések a matematikus szakon, 2001. 10. tétel : Algoritmusok bonyolultsága (Számítási modellek, véges automaták, Turinggépek, eldönthet
Államvizsga '01, 12. tétel: Algoritmusok bonyolultsága... 1 Államvizsga kérdések a matematikus szakon, 2001. 10. tétel : Algoritmusok bonyolultsága (Számítási modellek, véges automaták, Turinggépek, eldönthet
Algoritmusok Tervezése. 6. Előadás Algoritmusok 101 Dr. Bécsi Tamás
 Algoritmusok Tervezése 6. Előadás Algoritmusok 101 Dr. Bécsi Tamás Mi az algoritmus? Lépések sorozata egy feladat elvégzéséhez (legáltalánosabban) Informálisan algoritmusnak nevezünk bármilyen jól definiált
Algoritmusok Tervezése 6. Előadás Algoritmusok 101 Dr. Bécsi Tamás Mi az algoritmus? Lépések sorozata egy feladat elvégzéséhez (legáltalánosabban) Informálisan algoritmusnak nevezünk bármilyen jól definiált
Elérhetőségi analízis Petri hálók dinamikus tulajdonságai
 Elérhetőségi analízis Petri hálók dinamikus tulajdonságai dr. Bartha Tamás Dr. Pataricza András BME Méréstechnika és Információs Rendszerek Tanszék Petri hálók vizsgálata Az elemzés mélysége szerint: Vizsgálati
Elérhetőségi analízis Petri hálók dinamikus tulajdonságai dr. Bartha Tamás Dr. Pataricza András BME Méréstechnika és Információs Rendszerek Tanszék Petri hálók vizsgálata Az elemzés mélysége szerint: Vizsgálati
A félév során előkerülő témakörök
 A félév során előkerülő témakörök rekurzív algoritmusok rendező algoritmusok alapvető adattípusok, adatszerkezetek, és kapcsolódó algoritmusok dinamikus programozás mohó algoritmusok gráf algoritmusok
A félév során előkerülő témakörök rekurzív algoritmusok rendező algoritmusok alapvető adattípusok, adatszerkezetek, és kapcsolódó algoritmusok dinamikus programozás mohó algoritmusok gráf algoritmusok
9. előadás Veremautomaták 1.
 9. előadás 1. Dr. Kallós Gábor 2014 2015 1 Tartalom Motiváció Verem és végtelen automata Felépítés, konfigurációk és átmenetek Szavak felismerése, felismert nyelv Az elfogadó állapottal és az üres veremmel
9. előadás 1. Dr. Kallós Gábor 2014 2015 1 Tartalom Motiváció Verem és végtelen automata Felépítés, konfigurációk és átmenetek Szavak felismerése, felismert nyelv Az elfogadó állapottal és az üres veremmel
Szaturáció alapú modellellenőrzés lineáris idejű tulajdonságokhoz
 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Méréstechnika és Információs Rendszerek Tanszék Szaturáció alapú modellellenőrzés lineáris idejű tulajdonságokhoz TDK-dolgozat
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Méréstechnika és Információs Rendszerek Tanszék Szaturáció alapú modellellenőrzés lineáris idejű tulajdonságokhoz TDK-dolgozat
Logikai hálózatok. Dr. Bede Zsuzsanna St. I. em. 104.
 Logikai hálózatok Dr. Bede Zsuzsanna bede.zsuzsanna@mail.bme.hu St. I. em. 04. Tanszéki honlap: www.kjit.bme.hu/hallgatoknak/bsc-targyak-3/logikai-halozatok Gyakorlatok: hétfő + 08:5-0:00 J 208 HF: 4.
Logikai hálózatok Dr. Bede Zsuzsanna bede.zsuzsanna@mail.bme.hu St. I. em. 04. Tanszéki honlap: www.kjit.bme.hu/hallgatoknak/bsc-targyak-3/logikai-halozatok Gyakorlatok: hétfő + 08:5-0:00 J 208 HF: 4.
HALMAZELMÉLET feladatsor 1.
 HALMAZELMÉLET feladatsor 1. Egy (H,, ) algebrai struktúra háló, ha (H, ) és (H, ) kommutatív félcsoport, és teljesül az ún. elnyelési tulajdonság: A, B H: A (A B) = A, A (A B) = A. A (H,, ) háló korlátos,
HALMAZELMÉLET feladatsor 1. Egy (H,, ) algebrai struktúra háló, ha (H, ) és (H, ) kommutatív félcsoport, és teljesül az ún. elnyelési tulajdonság: A, B H: A (A B) = A, A (A B) = A. A (H,, ) háló korlátos,
