Duopólium részben állami tulajdonú vállalattal
|
|
|
- Zoltán Budai
- 9 évvel ezelőtt
- Látták:
Átírás
1 Duopólium részben állami tulajdonú vállalattal Tasnádi Attila Budapesti Corvinus Egyetem, Matematika Tanszék, MTA-BCE Lendület Stratégiai Interakciók Kutatócsoport január 6. Kivonat A piaci szabályozás egyik lehetséges eszköze, hogy az állam egy oligopol piacon egyik versenyző vállalatban megszerzett részesedésén keresztül terelje a piacot a kívánt irányba, a társadalmi jólét növelése érdekében. Ebben a tanulmányban egy Bertrand-Edgeworth típusú versenykörnyezetben vizsgáljuk meg a részben állami tulajdonú vállalat lehetséges jólétnövelő hatását. Választ keresünk arra a kérdésre is, hogy mekkora legyen az állam optimális részesedése az általa részben irányított vállalatban. Kulcsszavak: Bertrand Edgeworth-duopólium, állami vállalat, privatizáció. JEL Classification Number: D43, L Bevezetés Az állami érdekeltségű vállalatok hosszú múltra tekintenek vissza. Jelenleg is nagyon sok országban találhatók állami, illetve részben állami vállalatok Megjelent in: Matematikai közgazdaságtan: elmélet, modellezés, oktatás - Tanulmányok Zalai Ernőnek szerk. Matematikai Közgazdaságtan és Gazdaságelemzés Tanszékének munkatársai, Műszaki Könvykiadó, Budapest, , (2013). A szerző kutatásait az OTKA K pályázat támogatta Budapest, Fővám tér , attila.tasnadi@uni-corvinus.hu, URL: tasnadi. 1
2 piaci versenykörnyezetben. Hazai példaként felhozható a MOL, a tervezett negyedik állami tulajdonú mobilszolgáltató vagy a tervezett részben állami tulajdonú Webbank. Külföldi példaként felhozható az állami tulajdonú Új- Zélandi Kiwibank, amely egy teljes jogú kereskedelmi bank, vagy a több mint 60 százalékos állami tulajdonban lévő norvég Statoil, amely egy elsődlegesen az olaj- és gázkitermelésre koncentrált nemzetközi energiaipari társaság. 1 Az állami tulajdon révén az állam stratégai célokat valósíthat meg, alapvető szolgáltatásokat biztosíthat vagy indirekte szabályozhatja a piacot, a társadalmi jólét növelése érdekében. A részben állami tulajdonú vállalatok esetén az optimális állami tulajdonhányad meghatározása egy elméletileg is érdekes kérdés. Állami vállalatos oligopóliumokat, úgynevezett vegyes oligopóliumokat először Merrill és Schneider (1966) vizsgált. Ők és az őket követő irodalom elsősorban az állami vállalat optimális stratégiáját és annak jelenlétének jóléti hatásait határozták meg. Részben állami tulajdonú, úgynevezett félig-vegyes duopóliumok elemzését Matsumura (1998) kezdeményezte, amelyben a részben állami tulajdonú vállalat célfüggvénye a vállalat profitfüggvényének és a társadalmi jólétnek egy súlyozott összege. Matsumura (1998) egy homogén termékű mennyiségi duopol modellben meghatározta az optimális állami tulajdonhányadot, amelynek eredményeként rámutatott arra is, hogy a részben állami vállalat magasabb társadalmi jólétet eredményez, mint a tiszta állami vállalat. Hasonló vizsgálatokat végzett Barcéna-Ruiz és Sedano (2011) differenciát termékű árduopóliumok esetére. Az, hogy milyen típusú duopol modellből célszerű kiindulni a modellezendő piac és a termék jellegének függvénye. Jelen tanulmányban a homogén termékű kapacitáskorlátos Bertrand Edgeworth-duopóliumból indulunk ki, amelyet például energiaszektorbeli piacok modellezésének építőköveiként is szoktak használni (lásd Crampes és Creti, 2005 vagy Taylor és mások, 2012). A tiszta állami vállalat esetét Balogh és Tasnádi (2012) elemezte. Most a modell félig vegyes változatát elemezzük: meghatározzuk a modell tiszta Nashegyensúlyát, létezésének szükséges és elégséges feltételét, igazoljuk a kevert Nash-egyensúly létezését és a végén megállapítjuk, hogy a tiszta állami vállalat magasabb társadalmi jólétet eredményez a részben állami vállalatnál. 2. Modellkeret Megköveteljük, hogy a D keresleti görbe elégítse ki a következő feltevéseket: fel. 1 A közlekedés és a kommunikáció területén számos nyugat-európai példát hozhatnánk 2
3 2.1. feltevés. A D keresleti görbe a vízszintes tengelyt a outputnál, míg a függőleges tengelyt b árnál metszi. Legyen D szigorúan monoton csökkenő, konkáv és kétszer folytonosan differenciálható a (0, a) intervallumon; továbbá legyen D jobbról folytonos 0-ban, balról folytonos b-ben és D(p) = 0 minden p b-re. A feltevéseink mellett a vállalatok nyilván nem állapítanak meg b-nél nagyobb árat. Jelölje P az inverz keresleti görbét. Ekkor P (q) = D 1 (q) minden 0 < q a-ra, P (0) = b, és P (q) = 0 minden q > a-ra. A termelői oldalon egy részben állami tulajdonú vállalat és egy teljesen magán tulajdonban lévő vállalat található. A vállalatok halmaza {1, 2}, ahol 1 a részben állami tulajdonú és 2 a magántulajdonú vállalat. Az ilyen típusú duopóliumokat félig-vegyes 2 duopóliumoknak nevezzük. A duopolisták költségfüggvényei a következő alakúak feltevés. A két vállalat egységköltsége, a vállalatspecifikus pozitív k 1 és k 2 kapacitáskorlátokig, zerus. 3 Az egyszerűség kedvéért feltesszük még, hogy az állami vállalat egyedül nem képes a maximális piaci igény kielégítésére, azaz k 1 < a. 4 Jelölje p c a piactisztító árat és p M a kapacitáskorlát-mentes monopolista profitmaximalizáló árát, azaz p c = P (k 1 + k 2 ) és p M = arg max p [0,b] pd (p). A továbbiakban p 1, p 2 [0, b] a vállalatok árait jelölik. Jelölje p m i az i {1, 2} vállalat egyértelmű bevétel-maximalizáló árát a Di r (p) = (D(p) k j ) + reziduális keresleti görbéjén, ahol j {1, 2} és j i. Formálisan p m i = arg max p [0,b] pdi r (p). Jelöljék R 1 és R 2 rendre a vállalatok inverz reziduális keresleti görbéit. A 2.1. és a 2.2. feltevések mellett p c és p m i jól definiáltak, sőt k 1 < a miatt p m 2 > 0. Könnyen igazolható, hogy k i > k j esetén p m i > p m j. A p m i ár mellett fontos szerepet játszik a p d i ár, amely a reziduális keresleti görbén elérhető maximális profittal azonos profitot eredményez a teljes piaci kereslettel és a ( kapacitáskorláttal ) szembesülve. Másképpen mondva a p d i ár a p d i min{k i, D i p d i } = p m i Di r (p m i ) egyenlőséget kielégítő legkisebb ár, amennyiben létezik a kérdéses egyenlőséget kielégítő ár. 5 Tehát egy elégséges kapacitással (azaz p c < p m 2 ) rendelkező magánvállalatnak mindegy, hogy 2 Angolul a semi-mixed duopoly elnevezés használatos. 3 Ha már feltesszük az egységköltségek azonosságát, akkor azok nullára normálása nem jelenti az általánosság megszorítását, amennyiben a vállalatok rendelésre termelnek, azaz áraik meghatározása és a kereslet megismerése után a felmerülő igényeket kielégítve termelnek. 4 A k 1 a esetben a tiszta egyensúly nem feltétlenül egyértelmű, azonban értékesítés csak 0 áron történhet. 5 Az egyenlőségnek létezik megoldása, ha p m i p c. A p d i árat csak akkor fogjuk használni, ha létezik. 3
4 ( ) a reziduális keresletet elégíti ki p m i áron vagy min{k i, D i p d i } mennyiséget értékesít p d i áron. Megjegyzendő, hogy Deneckere és Kovenock (1992) 1. lemmája alapján p d i > p d j, ha k i > k j. Mivel az alacsonyabb árat megállapító vállalat a kapacitáskorlátja miatt általában nem képes a keresletének maradéktalan kielégítésére, a magasabb árat meghatározó vállalat kereslete függ az alacsonyabb áron kiszolgált fogyasztói körtől. Az egyik leggyakrabban alkalmazott eljárás, az úgynevezett hatékony vagy más néven párhuzamos adagolási szabály szerint az alacsonyabb áron kínáló vállalat előbb a magasabb rezervációs árú fogyasztókat elégíti ki, amely eljárás elsősorban akkor realisztikus, ha a terméknek van másodlagos piaca. Ekkor ugyanis egy alacsonyabb rezervációs árú fogyasztó haszonnal továbbadhatja az alacsonyabb áron megvásárolt terméket egy nála magasabb rezervációs árú fogyasztónak, amennyiben annak igényét nem sikerült az alacsonyabb áron kielégíteni. A hatékony adagolási szabály szerint a reziduális keresleti görbe a keresleti görbének az alacsonyabb áron értékesített mennyiséggel történő balra eltolásával kapható meg feltevés. A piacon a hatékony adagolási szabály valósul meg. A hatékony adagolási szabály mellett az i {1, 2} vállalat kereslete D (p i ), ha p i < p j ; k i (D, p 1, k 1, p 2, k 2 ) = i k 1 +k 2 D (p i ), ha p = p i = p j ; (D (p i ) k j ) +, ha p i > p j. Mint látható, azonos árak esetén a két vállalat kapacitás arányosan osztozik a keresleten. Valójában sok más törési szabályt is megengedhetünk a következő fejezetekben ismertetett eredmények szempontjából. Csak az olyan törési szabályok kerülendők, amelyek teljes mértékben valamelyik vállalatot részesítenék előnyben a másik vállalattal szemben. A vállalatok keresleteinek ismeretében megadjuk a profitfüggvényeiket. Ehhez feltesszük, hogy α (0, 1) adja meg az állami tulajdon hányadot az 1 vállalatban. Az α = 0 és az α = 1 esetek elemzésétől eltekintünk, mivel az előbbi a jól ismert sztenderd magánvállalatos Bertrand Edgeworthduopóliumot adja, míg az utóbbi esetet tiszta állami vállalattal Balogh és Tasnádi (2012) vizsgálta. Természetesen a következő fejezetekben levezetett eredményeinket viszonyítani fogjuk a két szélsőséges eset egyensúlyi kimeneteleihez. A részben állami vállalat célfüggvénye tekintetében feltesszük, hogy az állam α súlyú tulajdoni hányada miatt az 1 vállalat α súllyal társadalmi jólét maximalizáló és 1 α súllyal profitmaximalizáló. Ezek alapján a részben 4
5 állami tulajdonú vállalat célfüggvénye π 1 (p 1, p 2 ) = (1 α)p 1 min {k 1, 1 (D, p 1, k 1, p 2, k 2 )} + min{(d(pj ) k i ) +,k j} α R j (q)dq + α 0 min{a,ki } 0 P (q)dq, (1) ahol 0 p i p j b. Vegyük észre, hogy a hatékony adagolási szabály miatt, a két ár közül, a legmagasabb pozitív értékesítésű eladási ár határozza meg a társadalmi jólétet. A magánvállalat profitmaximalizáló, így célfüggvénye π 2 (p 1, p 2 ) = p 2 min {k 2, 2 (D, p 1, k 1, p 2, k 2 )}. (2) Végül definiáljuk még a magánvállalat reziduális keresleti görbéjén profitmaximalizáló p m 2 árhoz hasonlóan a részben állami vállalat reziduális keresleti görbéjén profitmaximalizáló p s 1 árat a következőképpen: { } p s 1 = arg max p 1 [0,b] (1 α)p 1 D r 1 (p 1 ) + α D(p1 ) 0 P (q)dq Ellenőrizhető, hogy a fenti feladat célfüggvénye szigorúan konkáv, a p s 1 ár egyértelműen létezik és p s 1 < p m 1 a feltevések mellett.. 3. Tiszta Nash-egyensúly Ebben a szakaszban meghatározzuk, hogy mikor létezik a félig-vegyes Bertrand Edgeworth-duopóliumnak tiszta Nash-egyensúlya. Továbbá ha létezik, akkor megadjuk a tiszta egyensúlyt állítás. A feltevések teljesülése esetén a félig-vegyes Bertrand Edgeworth duopol játéknak pontosan akkor létezik tiszta egyensúlya, ha max{p s 1, p m 2 } p c, és ekkor a tiszta egyensúly p 1 = p 2 = p c = P (k 1 + k 2 ). (3) Bizonyítás. Először megmutatjuk, hogy Nash egyensúlyként csak (3) jöhet szóba. Tegyük fel, hogy p 1 < p 2. Tekintsük előbb a D(p 1) > k 1 esetet. Ha D r 2(p 2) > 0, akkor a részben állami vállalat árának emelésével növelheti a profitját anélkül, hogy változna a társadalmi jólét. Ha pedig D r 2(p 2) 0, akkor a magánvállalat árának csökkentésével profitra tehet szert. Térjünk rá a D(p 1) k 1 esetre. Ekkor pedig a magánvállalat p 1 árra való áttéréssel 5
6 piacra tehet szert, és ezzel D(0) > k 1 miatt profitot realizálhat. Tehát nem létezik a p 1 < p 2 egyenlőtlenséget kielégítő egyensúly. Valamivel egyszerűbb annak igazolása, hogy nem létezik a p 1 > p 2 egyenlőtlenséget kielégítő egyensúly. A p 1 > p 2 esetben ugyanis ha D(p 2) > k 2, akkor a magánvállalat p 2-nál magasabb árakon is értékesítheti teljes kapacitását, és ha D(p 2) k 2, akkor pedig a részben állami vállalatnak érdemes árát p 2 alá csökkentenie, mivel ezzel ugyan nem változna a társadalmi jólét, de növekedne a profitja. 6 Közvetlenül látható, hogy a p 1 = p 2 > p c eset sem egyensúlyi, ugyanis ekkor mindkét cég egyoldalúan érdekelt árának kis mértékű csökkentésében. A p c alatti árak választása nyilván irracionális. Tehát az egyetlen lehetséges tiszta Nash-egyensúly a (3). Végül annak szükséges és elégséges feltétele, hogy egyik duopolistának se álljon érdekében egyoldalúan árát p c fölé emelnie, a p s 1, p m 2 árak definícióiból és a megfelelő reziduális profitfüggvények szigorú konkavitásából adódik. A kapott eredményt célszerű a két szélsőséges esethez viszonyítani. A félig-vegyes duopólium abban a tekintetben a tiszta magánvállalatos duopóliumhoz (α = 0) hasonlít, hogy nem mindig létezik tiszta Nash-egyensúlya. Ezzel szemben a tiszta állami vállalatos duopóliumnak (α = 1) mindig van tiszta Nash-egyensúlya (lásd Balogh és Tasnádi, 2012). A két szélsőséges eset közötti átmenet azonban bizonyos szempontból α-ban folytonos : nevezetesen p s 1 értéke kisebb α-ákra közelebb lesz p m 1 -hez, amiből adódóan a kapacitások azon tartománya, amelyekre létezik a félig-vegyes duopóliumnak tiszta Nash-egyensúlya α-ban szűkülő. Ilyen értelemben a nagyobb állami részesedés a determinisztikusság irányába mutat (a tiszta Nash-egyensúlyt előnyben szoktuk részesíteni a nem-degenerált kevert Nash-egyensúllyal szemben). A pontosabb helyzetkép kialakításához szükséges azzal az érdekesebb esettel foglakoznunk, amikor a félig-vegyes duopóliumnak nincsen tiszta Nash-egyensúlya. 4. Kevert Nash-egyensúly létezése Mivel a félig-vegyes Bertrand Edgeworth-duopólium kifizetőfüggvényei nem folytonosak, a kevert Nash-egyensúly létezését speciális tételek segítségével láthatjuk be. Az első ilyen, a közgazdaságtanban gyakran előforduló játékokra alkalmazható tételeket Dasgupta és Maskin (1986a) igazolta. Egyik tételük segítségével Dasgupta és Maskin (1986b) belátta, hogy a sztenderd 6 A részben állami vállalat árával azért mehet a magánvállalat ára alá, mert p 1 > p 2 esetén p 2 = 0 nem lehet egyensúlyi. 6
7 Bertrand Edgeworth-duopóliumnak létezik kevert egyensúlya. Sajnos a féligvegyes Bertrand Edgeworth-duopóliumokra az 5. tételük nem alkalmazható, mivel sérül a π 1 + π 2 függvény felülről-félig folytonossága. 7 Szóba jöhetne még Dasgupta és Maskin (1986a) 5b. tétele, azonban ennek hiányosságaira Bagh (2010) mutatott rá. Bagh (2010) 5.1. tétele helyett amely segítségével a Bertrand Edgeworth-duopóliumok széles körére igazolta a kevert Nash-egyensúly létezését inkább Prokopovych és Yannelis (2012) valamivel rövidebben kimondható 3. tételét alkalmazzuk. Prokopovych és Yannelis (2012) egzisztencia tételének kimondásához be kell vezetnünk néhány új jelölést. Legyen S 1 = {(x 1, x 2 ) [0, b] 2 x 2 > x 1 } S 2 = {(x 1, x 2 ) [0, b] 2 x 1 > x 2 } S = {(x 1, x 2 ) [0, b] 2 x 1 = x 2 } S D = { (x 1, x 2 ) [0, b] 2 lim sup y x u 1 (y) + u 2 (y) > u 1 (x) + u 2 (x) }. Most már kimondhatjuk Prokopovych és Yannelis (2012) egzisztencia tételét tétel (Prokopovych és Yannelis (2012)). Az ({1, 2}, [0, b] 2, (u 1, u 2 )) játéknak létezik kevert Nash-egyensúlya, ha (i) u 1 + u 2 függvény megszorítása S-re folytonos; (ii) léteznek olyan l j i : S j R folytonos függvények (i, j {1, 2}), hogy u i (x) = l j i (x) minden x Sj -re és minden i, j {1, 2}-re; (iii) minden i {1, 2}-höz és minden x S-hez létezik olyan j {1, 2}, hogy l j i (x) u i(x) l j i (x), ahol j az j-től különböző másik indexet jelöli; (iv) minden x = (z, z) S D -hez léteznek olyan i, j {1, 2} indexek és olyan S j -beli elemekből álló x-hez tartó {(x k i, z)} k=1 sorozat, amelyre lim k l j i (xk i, z) > u i (x); (v) ha léteznek olyan i, j {1, 2} indexek és olyan x = (z, z) S D -hez tartó S j -beli elemekből álló {(x k i, z)} k=1 sorozat, hogy lim k l j i (xk i, z) > u i (x), akkor lim k l j i (z, xk i ) < u i (x). 7 Az azonos árak megállapítása esetén alkalmazandó törési szabályunk módosításával helyreállítható volna a π 1 +π 2 függvény felülről-félig folytonossága. Ehhez azonban a törési szabályunknak teljes mértékben a magánvállalatot kellene előnyben részesítenie. Mivel ez egy meglehetősen szélsőséges eset, ezért nem ezt az utat választjuk. 7
8 Ellenőrizzük le a fenti tételben szereplő öt pontot a félig-vegyes Bertrand Edgeworth-duopóliumunkra. Mivel π 1 (p, p) + π 2 (p, p)-ben a társadalmi jólét egyébként is folytonos [0, b] 2 -ön és mindkét vállalat profitfüggvénye azonos árak mentén az alacsonyabb ártartományban (p [0, p c ]) lineáris p-ben, míg a magasabb ártartományban (p (p c, b)) a törési szabály szerint a keresleti görbe konstansszorosa, teljesül (i). A (ii) pontban szereplő függvények legyenek l 1 1(p 1, p 2 ) = π 1 (p 1, p 2 ) az S 1 -en, l 2 1(p 1, p 2 ) = π 1 (p 1, p 2 ) az S 2 -ön, l 1 2(p 1, p 2 ) = π 2 (p 1, p 2 ) az S 1 -en és l 2 2(p 1, p 2 ) = π 2 (p 1, p 2 ) az S 2 -ön. Ekkor l 1 1 a részben állami vállalat profitja, ha a teljes kereslettel szembesül, l 2 1 a részben állami vállalat profitja, ha a reziduális kereslet jelentkezik nála, l 1 2 a magánvállalat profitja, ha a reziduális kereslet jelentkezik nála, és l 2 2 a magánvállalat profitja, ha a teljes kereslettel szembesül. Ezek után (iii) abból adódik, hogy az l j i folytonos kiterjesztéseit véve l 1 1(p, p) π 1 (p, p) l 2 1(p, p) és l 1 2(p, p) π 2 (p, p) l 2 2(p, p) minden p S-re. A (iv) és (v) pontok teljesüléséhez vegyük figyelembe, hogy S D = {(p, p) [0, b] 2 p c < p < b}. A (iv) ponthoz legyen j = i = 1 (a j = i = 2 választása is alkalmas volna). Ekkor bármely (p, p) S D -hez bármely alulról monoton p- hez tartó {p k 1} k=1 sorozatra lim k l 1 1(p k 1, p) > π 1 (p, p) abból adódóan, hogy p-nél kisebb árakon az állami vállalat min{k 1, D(p)} mennyiséget értékesít, míg p áron osztoznia kell a D(p) piacon, ami p > p c miatt min{k 1, D(p)}-nél jóval kisebb értékesítést eredményez. Ehhez az (v) pont belátásához még azt kell figyelembe venni, hogy lim k l 1 2(p, p k 1) < π 2 (p, p), mivel a magánvállalat (p, p k 1) árak mellett a reziduális keresleti görbén kevesebbet értékesít, mint (p, p) áron a piacon való osztozkodással p > p c miatt. Az eddigieket összegezve kimondhatjuk a következő tételt tétel. A feltevések teljesülése esetén a félig-vegyes Bertrand Edgeworth-duopóliumnak létezik kevert Nash-egyensúlya. Megjegyzendő, hogy a kevert Nash-egyensúly létezése nem igényli a keresleti görbe konkavitását. 5. Összegzés A Bertrand Edgeworth típusú modellkeretet alapul véve megvizsgáltuk annak félig-vegyes változatát, meghatároztuk a tiszta Nash-egyensúlyát annak létezése esetén és igazoltuk a kevert Nash-egyensúly létezését. Ha a félig-vegyes Bertrand Edgeworth-duopóliumnak létezik tiszta Nashegyensúlya, akkor jóléti szempontból ekvivalens a sztenderd és a tiszta vegyes Bertrand Edgeworth-duopóliumokkal. A kevert egyensúly létezésének 8
9 tudtában a jóléti összehasonlítást elvégezhetjük abban az esetben is, amikor a félig-vegyes játéknak nincsen tiszta Nash-egyensúlya. Könnyen meggyőződhetünk arról, hogy ha p m 2 > p c, akkor a magánvállalat kevert egyensúlyban nem fog p d 2 alatti árat megállapítani, és emiatt a részben állami vállalat sem. Ekkor a (p d 2, p d 2) stratégiaegyüttessel szemben, amely Balogh és Tasnádi (2012) szerint a tiszta vegyes Bertrand Edgeworth-duopólium kitűntetett tiszta Nash-egyensúlya, a vállalatok a játék félig-vegyes változatában pozitív valószínűséggel állapítanak meg p d 2-nél magasabb árakat. Tehát arra a következtetésre jutunk, hogy tiszta állami vállalat esetén magasabb a társadalmi jólét, mint részben állami vállalat esetén. A másik nem elfajult kevert egyensúlyt eredményező p s 1 > p c p m 2 esetben Balogh és Tasnádi (2012) szerint a tiszta állami vállalatos duopólium tiszta Nash-egyensúlya (p c, p c ). 8 Mivel ekkor a félig-vegyes duopóliumnak (p c, p c ) nem lehet tiszta Nash-egyensúlya, a vállalatok nem választanak p c -nél kisebb árakat és a kevert egyensúlyban pozitív valószínűséggel játsszanak p c -nél magasabb árakat, ezért ebben az esetben is alacsonyabb a társadalmi jólét félig-vegyes duopóliumban. A kevert Nash-egyensúly karakterizációja mellett a jövőben érdemes megvizsgálni, hogy az állami tulajdonhányad növelésével csökken-e az egyensúlyi stratégiák tartója, azaz rászűkülünk-e a tiszta állami vállalatos (p d 2, p d 2) egyensúlyra. Hivatkozások [1] Bagh, A. (2010): Variational Convergence: Approximation and Existence of Equilibria in Discontinuous Games. Journal of Economic Theory, 145: o. [2] Balogh, T. Tasnádi, A. (2012): Does timing of decisions in a mixed duopoly matter? Journal of Economics (Zeitschrift für Nationalökonomie), 106: o. [3] Bárcena-Ruiz, J. C. Sedano, M. (2011): Endogenous timing in mixed duopolies: Weighted welfare and price competition. Japanese Economic Review, 62: o. [4] Crampes, C. Creti, A. (2005): Capacity Competition in Electricity Markets. Economia delle fonti di energia e dell ambiente 2: o. [5] Dasgupta, P. Maskin, E. (1986a): The Existence of Equilibria in Discontinuous Games I: Theory. Review of Economic Studies, 53: o. 8 Léteznek a társadalmi jólét szempontjából (p c, p c )-vel ekvivalens tiszta egyensúlyok, amelyekben az állami vállalat p c -nél kisebb árakat állapít meg. 9
10 [6] Dasgupta, P. Maskin, E. (1986b): The Existence of Equilibria in Discontinuous Games II: Applications. Review of Economic Studies, 53: o. [7] Deneckere, R. Kovenock, D. (1992): Price Leadership. Review of Economic Studies, 59: [8] Matsumura, T. (1998): Partial privatization in mixed duopoly. Journal of Public Economics, 70: o. [9] Merrill, W. Schneider, N. (1966): Government Firms in Oligopoly Industries: A Short-run Analysis. Quarterly Journal of Economics, 80: o. [10] Prokopovych, P. Yannelis, N.C. (2012): On Uniform Conditions for the Existence of Mixed Strategy Equilibria. Kyiv School of Economics & Kyiv Economics Institute, Discussion Paper Series, 48. [11] Taylor, J.A. Mathieu, J.L. Callaway, D.S. Poolla, K. (2012): Price and capacity competition in storage and zero-mean energy markets. 50th Annual Allerton Conference on Communication, Control, and Computing, megjelenés alatt. 10
Példák. Duopólium részben állami tulajdonú vállalattal. Gyakran feltett kérdések. Alapvető források
 Példák Duopólum részben állam tulajdonú vállalattal Tasnád Attla Budapest Corvnus Egyetem Matematka Tanszék MTA-BCE Lendület Stratéga Interakcók Kutatócsoport 2013. áprls 25. A részben állam tulajdonú
Példák Duopólum részben állam tulajdonú vállalattal Tasnád Attla Budapest Corvnus Egyetem Matematka Tanszék MTA-BCE Lendület Stratéga Interakcók Kutatócsoport 2013. áprls 25. A részben állam tulajdonú
A kompetitív piac közelítése sokszereplős Cournot-oligopóliumokkal
 A kompetitív piac közelítése sokszereplős Cournot-oligopóliumokkal Tasnádi Attila Kivonat Mikroökonómia tankönyvekből és példatárakból ismert, hogy egy homogén termékű Cournot-oligopol piacon a termelők
A kompetitív piac közelítése sokszereplős Cournot-oligopóliumokkal Tasnádi Attila Kivonat Mikroökonómia tankönyvekből és példatárakból ismert, hogy egy homogén termékű Cournot-oligopol piacon a termelők
Játékok (domináns stratégia, alkalmazása. 2016.03.30.
 Játékok (domináns stratégia, Nash-egyensúly). A Nashegyensúly koncepciójának alkalmazása. 2016.03.30. Játékelmélet és közgazdaságtan 1914: Zermelo (sakk) 1944. Neumann-Morgenstern: Game Theory and Economic
Játékok (domináns stratégia, Nash-egyensúly). A Nashegyensúly koncepciójának alkalmazása. 2016.03.30. Játékelmélet és közgazdaságtan 1914: Zermelo (sakk) 1944. Neumann-Morgenstern: Game Theory and Economic
Analízis elo adások. Vajda István. 2012. október 3. Neumann János Informatika Kar Óbudai Egyetem. Vajda István (Óbudai Egyetem)
 Vajda István Neumann János Informatika Kar Óbudai Egyetem / 40 Fogalmak A függvények értelmezése Definíció: Az (A, B ; R ) bináris relációt függvénynek nevezzük, ha bármely a A -hoz pontosan egy olyan
Vajda István Neumann János Informatika Kar Óbudai Egyetem / 40 Fogalmak A függvények értelmezése Definíció: Az (A, B ; R ) bináris relációt függvénynek nevezzük, ha bármely a A -hoz pontosan egy olyan
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria
 005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
Párhuzamos programozás
 Párhuzamos programozás Rendezések Készítette: Györkő Péter EHA: GYPMABT.ELTE Nappali tagozat Programtervező matematikus szak Budapest, 2009 május 9. Bevezetés A számítástechnikában felmerülő problémák
Párhuzamos programozás Rendezések Készítette: Györkő Péter EHA: GYPMABT.ELTE Nappali tagozat Programtervező matematikus szak Budapest, 2009 május 9. Bevezetés A számítástechnikában felmerülő problémák
Algebra es sz amelm elet 3 el oad as Rel aci ok Waldhauser Tam as 2014 oszi f el ev
 Algebra és számelmélet 3 előadás Relációk Waldhauser Tamás 2014 őszi félév Relációk reláció lat. 1. kapcsolat, viszony; összefüggés vmivel 2. viszonylat, vonatkozás reláció lat. 3. mat halmazok elemei
Algebra és számelmélet 3 előadás Relációk Waldhauser Tamás 2014 őszi félév Relációk reláció lat. 1. kapcsolat, viszony; összefüggés vmivel 2. viszonylat, vonatkozás reláció lat. 3. mat halmazok elemei
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
Arany Dániel Matematikai Tanulóverseny 2011/2012-es tanév első (iskolai) forduló haladók I. kategória
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 011/01-es tanév első (iskolai) forduló haladók I. kategória Megoldások és javítási útmutató 1. Az ábrán látható ABC derékszögű háromszög
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 011/01-es tanév első (iskolai) forduló haladók I. kategória Megoldások és javítási útmutató 1. Az ábrán látható ABC derékszögű háromszög
Az aktiválódásoknak azonban itt még nincs vége, ugyanis az aktiválódások 30 évenként ismétlődnek!
 1 Mindannyiunk életében előfordulnak jelentős évek, amikor is egy-egy esemény hatására a sorsunk új irányt vesz. Bár ezen események többségének ott és akkor kevésbé tulajdonítunk jelentőséget, csak idővel,
1 Mindannyiunk életében előfordulnak jelentős évek, amikor is egy-egy esemény hatására a sorsunk új irányt vesz. Bár ezen események többségének ott és akkor kevésbé tulajdonítunk jelentőséget, csak idővel,
A döntő feladatai. valós számok!
 OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
FENNTARTHATÓ FEJLŐDÉS
 FENNTARTHATÓ FEJLŐDÉS Kump Edina ÖKO-Pack Nonprofit Kft. E-mail: edina@okopack.hu Web: www.okopack.hu Dunaújváros, 2014. november 07. A FENNTARTHATÓ FEJLŐDÉS FOGALMA A fenntartható fejlődés a fejlődés
FENNTARTHATÓ FEJLŐDÉS Kump Edina ÖKO-Pack Nonprofit Kft. E-mail: edina@okopack.hu Web: www.okopack.hu Dunaújváros, 2014. november 07. A FENNTARTHATÓ FEJLŐDÉS FOGALMA A fenntartható fejlődés a fejlődés
Tasnádi Attila Tiszta és vegyes oligopóliumok című MTA doktori értekezéséről
 Opponensi vélemény Tasnádi Attila Tiszta és vegyes oligopóliumok című MTA doktori értekezéséről Bevezetés Tasnádi Attila doktori értekezése a matematikai közgazdaságtan, a piacelmélet területén belül az
Opponensi vélemény Tasnádi Attila Tiszta és vegyes oligopóliumok című MTA doktori értekezéséről Bevezetés Tasnádi Attila doktori értekezése a matematikai közgazdaságtan, a piacelmélet területén belül az
Mágneses szuszceptibilitás vizsgálata
 Mágneses szuszceptibilitás vizsgálata Mérést végezte: Gál Veronika I. A mérés elmélete Az anyagok külső mágnesen tér hatására polarizálódnak. Általában az anyagok mágnesezhetőségét az M mágnesezettség
Mágneses szuszceptibilitás vizsgálata Mérést végezte: Gál Veronika I. A mérés elmélete Az anyagok külső mágnesen tér hatására polarizálódnak. Általában az anyagok mágnesezhetőségét az M mágnesezettség
Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata. Az r-time és a TNS Hoffmann által végzett kutatás
 Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata Az r-time és a TNS Hoffmann által végzett kutatás 2002-2010: stabil szponzorációs részarány Televíziós reklámbevételek
Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata Az r-time és a TNS Hoffmann által végzett kutatás 2002-2010: stabil szponzorációs részarány Televíziós reklámbevételek
Analízis elo adások. Vajda István. 2012. szeptember 24. Neumann János Informatika Kar Óbudai Egyetem. Vajda István (Óbudai Egyetem)
 Vajda István Neumann János Informatika Kar Óbudai Egyetem 1/8 A halmaz alapfogalom, tehát nem definiáljuk. Jelölés: A halmazokat általában nyomtatott nagybetu vel jelöljük Egy H halmazt akkor tekintünk
Vajda István Neumann János Informatika Kar Óbudai Egyetem 1/8 A halmaz alapfogalom, tehát nem definiáljuk. Jelölés: A halmazokat általában nyomtatott nagybetu vel jelöljük Egy H halmazt akkor tekintünk
Operációkutatás. 2. konzultáció: Lineáris programozás (2. rész) Feladattípusok
 Operációkutatás NYME KTK, gazdálkodás szak, levelező alapképzés 00/003 tanév, II évf félév Előadó: Dr Takách Géza NyME FMK Információ Technológia Tanszék 9400 Sopron, Bajcsy Zs u 9 GT fszt 3 (99) 58 640
Operációkutatás NYME KTK, gazdálkodás szak, levelező alapképzés 00/003 tanév, II évf félév Előadó: Dr Takách Géza NyME FMK Információ Technológia Tanszék 9400 Sopron, Bajcsy Zs u 9 GT fszt 3 (99) 58 640
[GVMGS11MNC] Gazdaságstatisztika
![[GVMGS11MNC] Gazdaságstatisztika [GVMGS11MNC] Gazdaságstatisztika](/thumbs/40/21500887.jpg) [GVMGS11MNC] Gazdaságstatisztika 4 előadás Főátlagok összehasonlítása http://uni-obudahu/users/koczyl/gazdasagstatisztikahtm Kóczy Á László KGK-VMI Viszonyszámok (emlékeztető) Jelenség színvonalának vizsgálata
[GVMGS11MNC] Gazdaságstatisztika 4 előadás Főátlagok összehasonlítása http://uni-obudahu/users/koczyl/gazdasagstatisztikahtm Kóczy Á László KGK-VMI Viszonyszámok (emlékeztető) Jelenség színvonalának vizsgálata
GAZDASÁGI MATEMATIKA 1. 1. Gyakorlat
 GAZDASÁGI MATEMATIKA 1. 1. Gyakorlat Bemutatkozás Chmelik Gábor óraadó BGF-KKK Módszertani Intézeti Tanszéki Osztály chmelik.gabor@kkk.bgf.hu http://www.cs.elte.hu/ chmelik Fogadóóra: e-mailben egyeztetett
GAZDASÁGI MATEMATIKA 1. 1. Gyakorlat Bemutatkozás Chmelik Gábor óraadó BGF-KKK Módszertani Intézeti Tanszéki Osztály chmelik.gabor@kkk.bgf.hu http://www.cs.elte.hu/ chmelik Fogadóóra: e-mailben egyeztetett
2011. március 9. Dr. Vincze Szilvia
 . márius 9. Dr. Vinze Szilvia Tartalomjegyzék.) Elemi bázistranszformáió.) Elemi bázistranszformáió alkalmazásai.) Lineáris függőség/függetlenség meghatározása.) Kompatibilitás vizsgálata.) Mátri/vektorrendszer
. márius 9. Dr. Vinze Szilvia Tartalomjegyzék.) Elemi bázistranszformáió.) Elemi bázistranszformáió alkalmazásai.) Lineáris függőség/függetlenség meghatározása.) Kompatibilitás vizsgálata.) Mátri/vektorrendszer
ELLENÁLLÁSOK PÁRHUZAMOS KAPCSOLÁSA, KIRCHHOFF I. TÖRVÉNYE, A CSOMÓPONTI TÖRVÉNY ELLENÁLLÁSOK PÁRHUZAMOS KAPCSOLÁSA. 1. ábra
 ELLENÁLLÁSOK PÁRHUZAMOS KAPCSOLÁSA Három háztartási fogyasztót kapcsoltunk egy feszültségforrásra (hálózati feszültségre: 230V), vagyis közös kapocspárra, tehát párhuzamosan. A PÁRHUZAMOS KAPCSOLÁS ISMÉRVE:
ELLENÁLLÁSOK PÁRHUZAMOS KAPCSOLÁSA Három háztartási fogyasztót kapcsoltunk egy feszültségforrásra (hálózati feszültségre: 230V), vagyis közös kapocspárra, tehát párhuzamosan. A PÁRHUZAMOS KAPCSOLÁS ISMÉRVE:
Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (13. fejezet)
 Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (3. fejezet). Egy H I = 70 m - 50000 s /m 5 Q jelleggörbéjű szivattyú a H c = 0 m + 0000 s /m 5 Q jelleggörbéjű
Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (3. fejezet). Egy H I = 70 m - 50000 s /m 5 Q jelleggörbéjű szivattyú a H c = 0 m + 0000 s /m 5 Q jelleggörbéjű
http://www.olcsoweboldal.hu ingyenes tanulmány GOOGLE INSIGHTS FOR SEARCH
 2008. augusztus 5-én elindult a Google Insights for Search, ami betekintést nyújt a keresőt használók tömegeinek lelkivilágába, és időben-térben szemlélteti is, amit tud róluk. Az alapja a Google Trends,
2008. augusztus 5-én elindult a Google Insights for Search, ami betekintést nyújt a keresőt használók tömegeinek lelkivilágába, és időben-térben szemlélteti is, amit tud róluk. Az alapja a Google Trends,
Növelhető-e a hazai szélerőmű kapacitás energiatárolás alkalmazása esetén?
 Növelhető-e a hazai szélerőmű kapacitás energiatárolás alkalmazása esetén? Okos hálózatok, okos mérés konferencia Magyar Regula 2012 2012. március 21. Hartmann Bálint, Dr. Dán András Villamos Energetika
Növelhető-e a hazai szélerőmű kapacitás energiatárolás alkalmazása esetén? Okos hálózatok, okos mérés konferencia Magyar Regula 2012 2012. március 21. Hartmann Bálint, Dr. Dán András Villamos Energetika
Kerékpárlabda kvalifikációs szabályzat
 Kerékpárlabda kvalifikációs szabályzat Érvényesség kezdete: Junior kategória 2016 június 1 Felnőtt kategória 2016 január 1 Tartalom I. Célja... 3 II. Szabályozás... 3 1) A versenyek meghatározása... 3
Kerékpárlabda kvalifikációs szabályzat Érvényesség kezdete: Junior kategória 2016 június 1 Felnőtt kategória 2016 január 1 Tartalom I. Célja... 3 II. Szabályozás... 3 1) A versenyek meghatározása... 3
Halmazok és függvények
 Halmazok és függvények Óraszám: 2+2 Kreditszám: 6 Meghirdető tanszék: Analízis Debrecen, 2005. A tárgy neve: Halmazok és függvények (előadás) A tárgy oktatója: Dr. Gilányi Attila Óraszám/hét: 2 Kreditszám:
Halmazok és függvények Óraszám: 2+2 Kreditszám: 6 Meghirdető tanszék: Analízis Debrecen, 2005. A tárgy neve: Halmazok és függvények (előadás) A tárgy oktatója: Dr. Gilányi Attila Óraszám/hét: 2 Kreditszám:
Conjoint-analízis példa (egyszerűsített)
 Conjoint-analízis példa (egyszerűsített) Az eljárás meghatározza, hogy a fogyasztók a vásárlás szempontjából lényeges terméktulajdonságoknak mekkora relatív fontosságot tulajdonítanak és megadja a tulajdonságok
Conjoint-analízis példa (egyszerűsített) Az eljárás meghatározza, hogy a fogyasztók a vásárlás szempontjából lényeges terméktulajdonságoknak mekkora relatív fontosságot tulajdonítanak és megadja a tulajdonságok
MBLK12: Relációk és műveletek (levelező) (előadásvázlat) Maróti Miklós, Kátai-Urbán Kamilla
 MBLK12: Relációk és műveletek (levelező) (előadásvázlat) Maróti Miklós, Kátai-Urbán Kamilla Jelölje Z az egész számok halmazát, N a pozitív egészek halmazát, N 0 a nem negatív egészek halmazát, Q a racionális
MBLK12: Relációk és műveletek (levelező) (előadásvázlat) Maróti Miklós, Kátai-Urbán Kamilla Jelölje Z az egész számok halmazát, N a pozitív egészek halmazát, N 0 a nem negatív egészek halmazát, Q a racionális
[MECHANIKA- HAJLÍTÁS]
![[MECHANIKA- HAJLÍTÁS] [MECHANIKA- HAJLÍTÁS]](/thumbs/39/20428431.jpg) 2010. Eötvös Loránd Szakközép és Szakiskola Molnár István [MECHANIKA- HAJLÍTÁS] 1 A hajlításra való méretezést sok helyen lehet használni, sok mechanikai probléma modelljét vissza lehet vezetni a hajlítás
2010. Eötvös Loránd Szakközép és Szakiskola Molnár István [MECHANIKA- HAJLÍTÁS] 1 A hajlításra való méretezést sok helyen lehet használni, sok mechanikai probléma modelljét vissza lehet vezetni a hajlítás
Jelek tanulmányozása
 Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
Kombinatorika. 9. előadás. Farkas István. DE ATC Gazdaságelemzési és Statisztikai Tanszék. Kombinatorika p. 1/
 Kombinatorika 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Kombinatorika p. 1/ Permutáció Definíció. Adott n különböző elem. Az elemek egy meghatározott sorrendjét az adott
Kombinatorika 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Kombinatorika p. 1/ Permutáció Definíció. Adott n különböző elem. Az elemek egy meghatározott sorrendjét az adott
Sikeres E-DETAILING KAMPÁNY receptje. GYÓGYKOMM 2016. KONFERENCIA Budapest, 2016. február 25. BALOGH JUDIT, PharmaPromo Kft.
 Sikeres E-DETAILING KAMPÁNY receptje GYÓGYKOMM 2016. KONFERENCIA Budapest, 2016. február 25. BALOGH JUDIT, PharmaPromo Kft. AZ ORVOSOK SZÍVESEN FOGADJÁK Szinapszis, 2016. 01., Online (CAWI) kérdőíves kutatás,
Sikeres E-DETAILING KAMPÁNY receptje GYÓGYKOMM 2016. KONFERENCIA Budapest, 2016. február 25. BALOGH JUDIT, PharmaPromo Kft. AZ ORVOSOK SZÍVESEN FOGADJÁK Szinapszis, 2016. 01., Online (CAWI) kérdőíves kutatás,
Országos Középiskolai Tanulmányi Verseny 2011/2012 Matematika I. kategória (SZAKKÖZÉPISKOLA) Döntő. x 3x 2 <
 Oktatási Hivatal Országos Középiskolai Tanulmányi Verseny 011/01 Matematika I. kategória (SZKKÖZÉPISKOL) Döntő 1. Határozza meg az összes olyan egész számot, amely eleget tesz az egyenlőtlenségnek! log
Oktatási Hivatal Országos Középiskolai Tanulmányi Verseny 011/01 Matematika I. kategória (SZKKÖZÉPISKOL) Döntő 1. Határozza meg az összes olyan egész számot, amely eleget tesz az egyenlőtlenségnek! log
Dr. Kulcsár Gyula. Virtuális vállalat 2013-2014 1. félév. Projektütemezés. Virtuális vállalat 2013-2014 1. félév 5. gyakorlat Dr.
 Projektütemezés Virtuális vállalat 03-04. félév 5. gyakorlat Dr. Kulcsár Gyula Projektütemezési feladat megoldása Projekt: Projektütemezés Egy nagy, összetett, általában egyedi igény alapján előállítandó
Projektütemezés Virtuális vállalat 03-04. félév 5. gyakorlat Dr. Kulcsár Gyula Projektütemezési feladat megoldása Projekt: Projektütemezés Egy nagy, összetett, általában egyedi igény alapján előállítandó
Az Európai Szabadalmi Egyezmény végrehajtási szabályainak 2010. április 1-étől hatályba lépő lényeges változásai
 DANUBIA Szabadalmi és Védjegy Iroda Kft. Az Európai Szabadalmi Egyezmény végrehajtási szabályainak 2010. április 1-étől hatályba lépő lényeges változásai A Magyar Iparjogvédelmi és Szerzői Jogi Egyesület
DANUBIA Szabadalmi és Védjegy Iroda Kft. Az Európai Szabadalmi Egyezmény végrehajtási szabályainak 2010. április 1-étől hatályba lépő lényeges változásai A Magyar Iparjogvédelmi és Szerzői Jogi Egyesület
1. Írja fel prímszámok szorzataként a 420-at! 2. Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen!
 1. Írja fel prímszámok szorzataként a 40-at! 40 =. Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen! A részek: 3. Egy sejttenyészetben naponta kétszereződik meg a sejtek száma.
1. Írja fel prímszámok szorzataként a 40-at! 40 =. Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen! A részek: 3. Egy sejttenyészetben naponta kétszereződik meg a sejtek száma.
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN
 GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten RACIONÁLIS TÖRTFÜGGVÉNYEK INTEGRÁLJA Készítette: Gábor Szakmai felel s: Gábor Vázlat
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten RACIONÁLIS TÖRTFÜGGVÉNYEK INTEGRÁLJA Készítette: Gábor Szakmai felel s: Gábor Vázlat
Épületvillamosság laboratórium. Villámvédelemi felfogó-rendszer hatásosságának vizsgálata
 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék Nagyfeszültségű Technika és Berendezések Csoport Épületvillamosság laboratórium Villámvédelemi felfogó-rendszer hatásosságának
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék Nagyfeszültségű Technika és Berendezések Csoport Épületvillamosság laboratórium Villámvédelemi felfogó-rendszer hatásosságának
Pénzmosás és fellépés a terrorizmus ellen (változó szabályok) Dr. Király Júlia MNB Budapest, 2007. november 12.
 Pénzmosás és fellépés a terrorizmus ellen (változó szabályok) Dr. Király Júlia MNB Budapest, 2007. november 12. MNB szerepe pénzügyi rendszer stabilitása a pénzforgalom szabályozása, zökkenőmentes lebonyolítása
Pénzmosás és fellépés a terrorizmus ellen (változó szabályok) Dr. Király Júlia MNB Budapest, 2007. november 12. MNB szerepe pénzügyi rendszer stabilitása a pénzforgalom szabályozása, zökkenőmentes lebonyolítása
Gyakorló feladatok Nemzetközi gazdaságtanból. BA II. év GTGKG113BNV
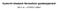 BA II. év GTGKG113BNV 1) Legyen az alábbi egy ricardói modell, amely a termelékenység előállításához szükséges ráfordításokat tartalmazza munkaórában: Bor Posztó Anglia 2 mó/egység 4 mó/egység Portugália
BA II. év GTGKG113BNV 1) Legyen az alábbi egy ricardói modell, amely a termelékenység előállításához szükséges ráfordításokat tartalmazza munkaórában: Bor Posztó Anglia 2 mó/egység 4 mó/egység Portugália
1. forduló. MEGOLDÁSOK Pontszerző Matematikaverseny 2015/2016-os tanév
 MEGOLDÁSOK Pontszerző Matematikaverseny 2015/2016-os tanév 1. forduló 1. feladat: Jancsi és Juliska Matematikai Memory-t játszik. A játék lényege, hogy négyzet alakú kártyákra vagy műveletsorokat írnak
MEGOLDÁSOK Pontszerző Matematikaverseny 2015/2016-os tanév 1. forduló 1. feladat: Jancsi és Juliska Matematikai Memory-t játszik. A játék lényege, hogy négyzet alakú kártyákra vagy műveletsorokat írnak
Kooperáció és intelligencia
 Kooperáció és intelligencia Tanulás többágenses szervezetekben/2 Tanulás több ágensből álló környezetben -a mozgó cél tanulás problémája (alapvetően megerősítéses tanulás) Legyen az ágens közösség formalizált
Kooperáció és intelligencia Tanulás többágenses szervezetekben/2 Tanulás több ágensből álló környezetben -a mozgó cél tanulás problémája (alapvetően megerősítéses tanulás) Legyen az ágens közösség formalizált
Egyre nagyobb profitot generálnak a mobiltelefonnal végzett vásárlások, és egyre többet hezitálunk vásárlás előtt
 Egyre nagyobb profitot generálnak a mobiltelefonnal végzett vásárlások, és egyre többet hezitálunk vásárlás előtt 2016 ban még nagyobb hangsúlyt kapnak az e kereskedelmeben az okostelefonok. 2015 ben még
Egyre nagyobb profitot generálnak a mobiltelefonnal végzett vásárlások, és egyre többet hezitálunk vásárlás előtt 2016 ban még nagyobb hangsúlyt kapnak az e kereskedelmeben az okostelefonok. 2015 ben még
BOLYAI MATEMATIKA CSAPATVERSENY FŐVÁROSI DÖNTŐ SZÓBELI (2005. NOVEMBER 26.) 5. osztály
 5. osztály Írd be az ábrán látható hat üres körbe a 10, 30, 40, 60, 70 és 90 számokat úgy, hogy a háromszög mindhárom oldala mentén a számok összege 200 legyen! 50 20 80 Egy dobozban háromféle színű: piros,
5. osztály Írd be az ábrán látható hat üres körbe a 10, 30, 40, 60, 70 és 90 számokat úgy, hogy a háromszög mindhárom oldala mentén a számok összege 200 legyen! 50 20 80 Egy dobozban háromféle színű: piros,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 5 V. BECsLÉsELMÉLET 1. STATIsZTIKAI becslés A becsléselméletben gyakran feltesszük, hogy a megfigyelt mennyiségek független valószínűségi
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 5 V. BECsLÉsELMÉLET 1. STATIsZTIKAI becslés A becsléselméletben gyakran feltesszük, hogy a megfigyelt mennyiségek független valószínűségi
KÖZGAZDASÁGTAN I. Készítette: Bíró Anikó, K hegyi Gergely, Major Klára. Szakmai felel s: K hegyi Gergely. 2010. június
 KÖZGAZDASÁGTAN I. Készült a TÁMOP-4.1.2-08/2/a/KMR-2009-0041 pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék az MTA Közgazdaságtudományi
KÖZGAZDASÁGTAN I. Készült a TÁMOP-4.1.2-08/2/a/KMR-2009-0041 pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék az MTA Közgazdaságtudományi
EURÓPAI UNIÓ AZ EURÓPAI PARLAMENT 2006/0287 (COD) PE-CONS 3648/2/07 REV 2
 EURÓPAI UNIÓ AZ EURÓPAI PARLAMENT A TANÁCS Brüsszel, 2008. február 26. (OR. en) 2006/0287 (COD) PE-CONS 3648/2/07 REV 2 ENV 447 ENT 104 CODEC 899 JOGI AKTUSOK ÉS EGYÉB ESZKÖZÖK Tárgy: AZ EURÓPAI PARLAMENT
EURÓPAI UNIÓ AZ EURÓPAI PARLAMENT A TANÁCS Brüsszel, 2008. február 26. (OR. en) 2006/0287 (COD) PE-CONS 3648/2/07 REV 2 ENV 447 ENT 104 CODEC 899 JOGI AKTUSOK ÉS EGYÉB ESZKÖZÖK Tárgy: AZ EURÓPAI PARLAMENT
Fábián Zoltán Hálózatok elmélet
 Fábián Zoltán Hálózatok elmélet Minden olyan dologi és személyi eszköz, ami egy cél eléréséhez szükséges Dologi erőforrás Olyan eszközök, amelyek kellenek a cél eléréséhez Emberi erőforrás Emberi munkaidő.
Fábián Zoltán Hálózatok elmélet Minden olyan dologi és személyi eszköz, ami egy cél eléréséhez szükséges Dologi erőforrás Olyan eszközök, amelyek kellenek a cél eléréséhez Emberi erőforrás Emberi munkaidő.
 Felépítettünk egy modellt, amely dinamikus, megfelel a Lucas kritikának képes reprodukálni bizonyos makro aggregátumok alakulásában megfigyelhető szabályszerűségeket (üzleti ciklus, a fogyasztás simítottab
Felépítettünk egy modellt, amely dinamikus, megfelel a Lucas kritikának képes reprodukálni bizonyos makro aggregátumok alakulásában megfigyelhető szabályszerűségeket (üzleti ciklus, a fogyasztás simítottab
Azonosító jel: Matematika emelt szint
 I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
Korszerű geodéziai adatfeldolgozás Kulcsár Attila
 Korszerű geodéziai adatfeldolgozás Kulcsár Attila Nyugat-Magyarországi Egyetem Geoinformatikai Főiskolai Kar Térinformatika Tanszék 8000 Székesfehérvár, Pirosalma -3 Tel/fax: (22) 348 27 E-mail: a.kulcsar@geo.info.hu.
Korszerű geodéziai adatfeldolgozás Kulcsár Attila Nyugat-Magyarországi Egyetem Geoinformatikai Főiskolai Kar Térinformatika Tanszék 8000 Székesfehérvár, Pirosalma -3 Tel/fax: (22) 348 27 E-mail: a.kulcsar@geo.info.hu.
Bár a digitális technológia nagyon sokat fejlődött, van még olyan dolog, amit a digitális fényképezőgépek nem tudnak: minden körülmények között
 Dr. Nyári Tibor Bár a digitális technológia nagyon sokat fejlődött, van még olyan dolog, amit a digitális fényképezőgépek nem tudnak: minden körülmények között tökéletes színeket visszaadni. A digitális
Dr. Nyári Tibor Bár a digitális technológia nagyon sokat fejlődött, van még olyan dolog, amit a digitális fényképezőgépek nem tudnak: minden körülmények között tökéletes színeket visszaadni. A digitális
Földrajzi helymeghatározás
 A mérés megnevezése, célkitűzései: Földrajzi fokhálózat jelentősége és használata a gyakorlatban Eszközszükséglet: Szükséges anyagok: narancs Szükséges eszközök: GPS készülék, földgömb, földrajz atlasz,
A mérés megnevezése, célkitűzései: Földrajzi fokhálózat jelentősége és használata a gyakorlatban Eszközszükséglet: Szükséges anyagok: narancs Szükséges eszközök: GPS készülék, földgömb, földrajz atlasz,
A gazdaság rövid távon. Gazdasági ingadozások. A makroökonómia időhorizontjának jelentősége
 gazdaság rövid távon Gazdasági ingadozások EVEZETÉS GZDSÁGI INGDOZÁSOK ELMÉLETÉE gazdasági ingadozások visszatérő problémát jelentenek a közgazdászoknak és a gazdaságpolitikusoknak. közgazdászok k ülti
gazdaság rövid távon Gazdasági ingadozások EVEZETÉS GZDSÁGI INGDOZÁSOK ELMÉLETÉE gazdasági ingadozások visszatérő problémát jelentenek a közgazdászoknak és a gazdaságpolitikusoknak. közgazdászok k ülti
SOLARCAPITAL MARKETS ZRT. WWW.SOLARCAPITAL.HU SOLAR@SOLARCAPITAL.HU. Összefoglaló
 WWW.CAPITAL.HU @CAPITAL.HU Napi Elemzés 2010. november 9. INDEXEK Záróérték Napi változás (%) Dow Jones IA 11406.46-0.33% S&P 500 1223.23-0.22% Nasdaq 100 2188.94 +0.10% DAX 6750.50-0.05% BUX 23127.36-0.34%
WWW.CAPITAL.HU @CAPITAL.HU Napi Elemzés 2010. november 9. INDEXEK Záróérték Napi változás (%) Dow Jones IA 11406.46-0.33% S&P 500 1223.23-0.22% Nasdaq 100 2188.94 +0.10% DAX 6750.50-0.05% BUX 23127.36-0.34%
Kiterjesztett csomagolás Hiteles fogyasztói tájékoztatás
 Kiterjesztett csomagolás Hiteles fogyasztói tájékoztatás By David Twice Global Comics 2013 All rights reserved Egy reggelem a SafeBrand-del reggel 8.00 Jaj! Feleségecském nincs szabin reggeli reggeli??
Kiterjesztett csomagolás Hiteles fogyasztói tájékoztatás By David Twice Global Comics 2013 All rights reserved Egy reggelem a SafeBrand-del reggel 8.00 Jaj! Feleségecském nincs szabin reggeli reggeli??
6. SZÁMÚ FÜGGELÉK: AZ E.ON ENERGIASZOLGÁLTATÓ KFT. ÁLTAL E.ON KLUB KATEGÓRIÁBA SOROLT ÜGYFELEKNEK NYÚJTOTT ÁRAK, SZOLGÁLTATÁSOK
 6. SZÁMÚ FÜGGELÉK: AZ E.ON ENERGIASZOLGÁLTATÓ KFT. ÁLTAL E.ON KLUB KATEGÓRIÁBA SOROLT ÜGYFELEKNEK NYÚJTOTT ÁRAK, SZOLGÁLTATÁSOK 1. A függelék hatálya A jelen függelékben foglaltak azon Felhasználókra terjednek
6. SZÁMÚ FÜGGELÉK: AZ E.ON ENERGIASZOLGÁLTATÓ KFT. ÁLTAL E.ON KLUB KATEGÓRIÁBA SOROLT ÜGYFELEKNEK NYÚJTOTT ÁRAK, SZOLGÁLTATÁSOK 1. A függelék hatálya A jelen függelékben foglaltak azon Felhasználókra terjednek
DPR Szakmai nap. 2011. október 17. PTE Felnőttképzési és Emberi Erőforrás Fejlesztési Kar
 PTE Felnőttképzési és Emberi Erőforrás Fejlesztési Kar A diplomás pályakövetés eredményei és a lehetséges fejlesztési irányok DPR Szakmai nap 2011. október 17. Horváth Judit A vizsgálat reprezentativitása
PTE Felnőttképzési és Emberi Erőforrás Fejlesztési Kar A diplomás pályakövetés eredményei és a lehetséges fejlesztési irányok DPR Szakmai nap 2011. október 17. Horváth Judit A vizsgálat reprezentativitása
Koordináta - geometria I.
 Koordináta - geometria I. DEFINÍCIÓ: (Helyvektor) A derékszögű koordináta - rendszerben a pont helyvektora az origóból a pontba mutató vektor. TÉTEL: Ha i az (1; 0) és j a (0; 1) pont helyvektora, akkor
Koordináta - geometria I. DEFINÍCIÓ: (Helyvektor) A derékszögű koordináta - rendszerben a pont helyvektora az origóból a pontba mutató vektor. TÉTEL: Ha i az (1; 0) és j a (0; 1) pont helyvektora, akkor
A fiatalok pénzügyi kultúrája Számít-e a gazdasági oktatás?
 A fiatalok pénzügyi kultúrája Számít-e a gazdasági oktatás? XXXII. OTDK Konferencia 2015. április 9-11. Készítette: Pintye Alexandra Konzulens: Dr. Kiss Marietta A kultúrától a pénzügyi kultúráig vezető
A fiatalok pénzügyi kultúrája Számít-e a gazdasági oktatás? XXXII. OTDK Konferencia 2015. április 9-11. Készítette: Pintye Alexandra Konzulens: Dr. Kiss Marietta A kultúrától a pénzügyi kultúráig vezető
3. Térvezérlésű tranzisztorok
 1 3. Térvezérlésű tranzisztorok A térvezérlésű tranzisztorok (Field Effect Transistor = FET) működési elve alapjaiban eltér a bipoláris tranzisztoroktól. Az áramvezetés mértéke statikus feszültséggel befolyásolható.
1 3. Térvezérlésű tranzisztorok A térvezérlésű tranzisztorok (Field Effect Transistor = FET) működési elve alapjaiban eltér a bipoláris tranzisztoroktól. Az áramvezetés mértéke statikus feszültséggel befolyásolható.
Nyomott - hajlított fagerenda szilárdsági méretezése ~ egy régi - új megoldás
 Nyomott - ajlított fagerenda szilárdsági méretezése ~ egy régi - új oldás Már régóta foglalkozom erőtani problémákkal, ám nagy lepetésemre a minap egy olyan érdekes feladat - oldást találtam, amilyet még
Nyomott - ajlított fagerenda szilárdsági méretezése ~ egy régi - új oldás Már régóta foglalkozom erőtani problémákkal, ám nagy lepetésemre a minap egy olyan érdekes feladat - oldást találtam, amilyet még
KÖZGAZDASÁGI- MARKETING ALAPISMERETEK
 Közgazdasági-marketing alapismeretek emelt szint 0631 ÉRETTSÉGI VIZSGA 2006. október 24. KÖZGAZDASÁGI- MARKETING ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI
Közgazdasági-marketing alapismeretek emelt szint 0631 ÉRETTSÉGI VIZSGA 2006. október 24. KÖZGAZDASÁGI- MARKETING ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI
MŰTRÁGYA ÉRTÉKESÍTÉS 2009. I-III. negyedév
 Agrárgazdasági Kutató Intézet Statisztikai Osztály MŰTRÁGYA ÉRTÉKESÍTÉS 2009. I-III. negyedév A K I BUDAPEST 2009. december Készült: Agrárgazdasági Kutató Intézet Gazdaságelemzési Igazgatóság Statisztikai
Agrárgazdasági Kutató Intézet Statisztikai Osztály MŰTRÁGYA ÉRTÉKESÍTÉS 2009. I-III. negyedév A K I BUDAPEST 2009. december Készült: Agrárgazdasági Kutató Intézet Gazdaságelemzési Igazgatóság Statisztikai
5. sz. melléklet: Nyereség- és költségelszámolásra vonatkozó eljárásrend
 5. sz. melléklet: Nyereség- és költségelszámolásra vonatkozó eljárásrend 1. Fogalmak: 1.1. nyitó készletérték (HUF): szerződés indulását követő 15 napban betárolt gáz energia (kwh) * a Day ahead Close
5. sz. melléklet: Nyereség- és költségelszámolásra vonatkozó eljárásrend 1. Fogalmak: 1.1. nyitó készletérték (HUF): szerződés indulását követő 15 napban betárolt gáz energia (kwh) * a Day ahead Close
The Kreps and Scheinkman result remains valid for mixed duopolies with linear demand
 MPRA Munich Personal RePEc Archive The Kreps and Scheinkman result remains valid for mixed duopolies with linear demand Barna Bakó and Attila Tasnádi Corvinus University of Budapest 6. January 014 Online
MPRA Munich Personal RePEc Archive The Kreps and Scheinkman result remains valid for mixed duopolies with linear demand Barna Bakó and Attila Tasnádi Corvinus University of Budapest 6. January 014 Online
MIT VÁR EL A PSZICHOLÓGUS A JÓ KRESZTŐL? ARANYOS JUDIT közlekedés szakpszichológus
 MIT VÁR EL A PSZICHOLÓGUS A JÓ KRESZTŐL? ARANYOS JUDIT közlekedés szakpszichológus KRESZ: Közúti Rendelkezések Egységes Szabályozása, 1975 óta: rendeletekbe foglalt szabálygyűjtemény, mely a közlekedést
MIT VÁR EL A PSZICHOLÓGUS A JÓ KRESZTŐL? ARANYOS JUDIT közlekedés szakpszichológus KRESZ: Közúti Rendelkezések Egységes Szabályozása, 1975 óta: rendeletekbe foglalt szabálygyűjtemény, mely a közlekedést
Jelentéskészítő TEK-IK () Válaszadók száma = 610
 Jelentéskészítő TEK-IK () Válaszadók száma = 0 Általános mutatók Szak értékelése - + átl.=. Felmérés eredmények Jelmagyarázat Kérdésszöveg Válaszok relatív gyakorisága Bal pólus Skála Átl. elt. Átlag Medián
Jelentéskészítő TEK-IK () Válaszadók száma = 0 Általános mutatók Szak értékelése - + átl.=. Felmérés eredmények Jelmagyarázat Kérdésszöveg Válaszok relatív gyakorisága Bal pólus Skála Átl. elt. Átlag Medián
ORSZÁGOS KÖRNYEZETEGÉSZSÉGÜGYI INTÉZET
 ORSZÁGOS KÖRNYEZETEGÉSZSÉGÜGYI INTÉZET 197 Budapest, Gyáli út 2-6. Levélcím: 1437 Budapest Pf.: 839 Telefon: (6-1) 476-11 Fax: (6-1) 21-148 http://efrirk.antsz.hu/oki/ A PARLAGFŰ POLLENSZÓRÁSÁNAK ALAKULÁSA
ORSZÁGOS KÖRNYEZETEGÉSZSÉGÜGYI INTÉZET 197 Budapest, Gyáli út 2-6. Levélcím: 1437 Budapest Pf.: 839 Telefon: (6-1) 476-11 Fax: (6-1) 21-148 http://efrirk.antsz.hu/oki/ A PARLAGFŰ POLLENSZÓRÁSÁNAK ALAKULÁSA
Lineáris algebra gyakorlat
 Lineáris algebra gyakorlat 3 gyakorlat Gyakorlatvezet : Bogya Norbert 2012 február 27 Bogya Norbert Lineáris algebra gyakorlat (3 gyakorlat) Tartalom Egyenletrendszerek Cramer-szabály 1 Egyenletrendszerek
Lineáris algebra gyakorlat 3 gyakorlat Gyakorlatvezet : Bogya Norbert 2012 február 27 Bogya Norbert Lineáris algebra gyakorlat (3 gyakorlat) Tartalom Egyenletrendszerek Cramer-szabály 1 Egyenletrendszerek
HWDEV-02A GSM TERMOSZTÁT
 HWDEV-02A GSM TERMOSZTÁT 2010 HASZNÁLATI ÚTMUTATÓ A termosztát egy beépített mobiltelefonnal rendelkezik. Ez fogadja az Ön hívását ha felhívja a termosztát telefonszámát. Érdemes ezt a telefonszámot felírni
HWDEV-02A GSM TERMOSZTÁT 2010 HASZNÁLATI ÚTMUTATÓ A termosztát egy beépített mobiltelefonnal rendelkezik. Ez fogadja az Ön hívását ha felhívja a termosztát telefonszámát. Érdemes ezt a telefonszámot felírni
Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Szászné Simon Judit; dátum: 2005. november. I. rész
 Szászné Simon Judit, 005. november Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Szászné Simon Judit; dátum: 005. november. feladat I. rész Oldjuk meg a valós számok halmazán a x 5x
Szászné Simon Judit, 005. november Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Szászné Simon Judit; dátum: 005. november. feladat I. rész Oldjuk meg a valós számok halmazán a x 5x
Diszkrét matematika I. gyakorlat
 Diszkrét matematika I. gyakorlat 1. Gyakorlat Bogya Norbert Bolyai Intézet 2012. szeptember 4-5. Bogya Norbert (Bolyai Intézet) Diszkrét matematika I. gyakorlat 2012. szeptember 4-5. 1 / 21 Információk
Diszkrét matematika I. gyakorlat 1. Gyakorlat Bogya Norbert Bolyai Intézet 2012. szeptember 4-5. Bogya Norbert (Bolyai Intézet) Diszkrét matematika I. gyakorlat 2012. szeptember 4-5. 1 / 21 Információk
III. rész: A VÁLLALATI MAGATARTÁS
 III. rész: A VÁAATI MAGATARTÁS Az árupiacon a kínálati oldalon a termelőegységek, a vállalatok állnak. A vállalatok különböznek tevékenységük, méretük, tulajdonformájuk szerint. Különböző vállalatok közös
III. rész: A VÁAATI MAGATARTÁS Az árupiacon a kínálati oldalon a termelőegységek, a vállalatok állnak. A vállalatok különböznek tevékenységük, méretük, tulajdonformájuk szerint. Különböző vállalatok közös
2010.05.12. 1300 Infó Rádió. Hírek
 2010.05.12. 1300 Infó Rádió Hírek 100512 1303 [1127h GAZ MKIK - pozitív index MTI km 100512] Jelentősen javultak a magyar vállalatok várakozásai a következő félévre a Magyar Kereskedelmi és Iparkamara
2010.05.12. 1300 Infó Rádió Hírek 100512 1303 [1127h GAZ MKIK - pozitív index MTI km 100512] Jelentősen javultak a magyar vállalatok várakozásai a következő félévre a Magyar Kereskedelmi és Iparkamara
3. KÖRGEOMETRIA. 3.1. Körrel kapcsolatos alapismeretek
 3. KÖRGEOMETRIA Hajós György: Bevezetés a geometriába, Tankönyvkiadó, Budapest, 89 109. és 121. oldal. Pelle Béla: Geometria, Tankönyvkiadó, Budapest, 86 97. és 117 121. oldal. Kovács Zoltán: Geometria,
3. KÖRGEOMETRIA Hajós György: Bevezetés a geometriába, Tankönyvkiadó, Budapest, 89 109. és 121. oldal. Pelle Béla: Geometria, Tankönyvkiadó, Budapest, 86 97. és 117 121. oldal. Kovács Zoltán: Geometria,
118. Szerencsi Többcélú Kistérségi Társulás
 BAZ MTrT TERVEZŐI VÁLASZ 118. Szerencsi Többcélú Kistérségi Társulás 1. Szakmai szempontból elhibázott döntésnek tartjuk a Tokaji Borvidék Világörökségi terület közvetlen környezetében erőmű létesítését.
BAZ MTrT TERVEZŐI VÁLASZ 118. Szerencsi Többcélú Kistérségi Társulás 1. Szakmai szempontból elhibázott döntésnek tartjuk a Tokaji Borvidék Világörökségi terület közvetlen környezetében erőmű létesítését.
Kedves 9. évfolyamos tanulónk!
 Kedves 9. évfolyamos tanulónk! A 9. osztály befejezését követően a nyári szünetben kéthetes szakmai gyakorlaton kell részt venned. A beosztás az előzetesen megkaptátok, az áruházak felhívtak titeket. Ne
Kedves 9. évfolyamos tanulónk! A 9. osztály befejezését követően a nyári szünetben kéthetes szakmai gyakorlaton kell részt venned. A beosztás az előzetesen megkaptátok, az áruházak felhívtak titeket. Ne
8. Feladat Egy bútorgyár asztalosműhelyében évek óta gyártják a Badacsony elnevezésű konyhaasztalt. Az asztal gyártási anyagjegyzéke a következő:
 MRP számítások 1 8. Feladat Egy bútorgyár asztalosműhelyében évek óta gyártják a Badacsony elnevezésű konyhaasztalt. Az asztal gyártási anyagjegyzéke a következő: asztal lábszerkezet asztallap Csavar (
MRP számítások 1 8. Feladat Egy bútorgyár asztalosműhelyében évek óta gyártják a Badacsony elnevezésű konyhaasztalt. Az asztal gyártási anyagjegyzéke a következő: asztal lábszerkezet asztallap Csavar (
Feladatok megoldásokkal a negyedik gyakorlathoz (Függvényvizsgálat) f(x) = 2x 2 x 4. 2x 2 x 4 = 0, x 2 (2 x 2 ) = 0.
 Feladatok megoldásokkal a negyedik gyakorlathoz (Függvényvizsgálat). Feladat. Végezzük el az f(x) = x x 4 ) Értelmezési tartomány: x R. ) A zérushelyet az f(x) = 0 egyenlet megoldásával kapjuk: amiből
Feladatok megoldásokkal a negyedik gyakorlathoz (Függvényvizsgálat). Feladat. Végezzük el az f(x) = x x 4 ) Értelmezési tartomány: x R. ) A zérushelyet az f(x) = 0 egyenlet megoldásával kapjuk: amiből
MIÉRT SIKERESEK A CSALÁDI VÁLLALKOZÁSOK?
 o Családi vállalkozások mérettől függetlenül azok a vállalkozások, amelyek irányításában a tulajdonos (alapító) mellett o Legalább 1 családtag részt vesz, o Valamint a család tulajdoni hányada meghatározó,
o Családi vállalkozások mérettől függetlenül azok a vállalkozások, amelyek irányításában a tulajdonos (alapító) mellett o Legalább 1 családtag részt vesz, o Valamint a család tulajdoni hányada meghatározó,
Borpiaci információk. V. évfolyam / 11. szám 2007. június 20. 22-23. hét. Borpiaci jelentés. Hazai borpiaci tendenciák
 A K I Borpiaci információk V. évfolyam / 11. szám 2007. június 20. 22-23. hét Borpiaci jelentés Hazai borpiaci tendenciák 2. old. 1-2. táblázat, 1-8. ábra: Belföldön termelt fehérborok értékesített mennyisége
A K I Borpiaci információk V. évfolyam / 11. szám 2007. június 20. 22-23. hét Borpiaci jelentés Hazai borpiaci tendenciák 2. old. 1-2. táblázat, 1-8. ábra: Belföldön termelt fehérborok értékesített mennyisége
Egyetemi doktori (PhD) értekezés tézisei
 Egyetemi doktori (PhD) értekezés tézisei Vegyes Bertrand-Edgeworth duopóliumok játékelméleti modellezése Szerző: Balogh Tamás László Témavezető: Dr. Kormos János Debreceni Egyetem Közgazdaságtudományi
Egyetemi doktori (PhD) értekezés tézisei Vegyes Bertrand-Edgeworth duopóliumok játékelméleti modellezése Szerző: Balogh Tamás László Témavezető: Dr. Kormos János Debreceni Egyetem Közgazdaságtudományi
Analízis előadások. Vajda István. 2013. február 10. Neumann János Informatika Kar Óbudai Egyetem
 Analízis előadások Vajda István Neumann János Informatika Kar Óbudai Egyetem 013. február 10. Vajda István (Óbudai Egyetem) Analízis előadások 013. február 10. 1 / 3 Az elemi függvények csoportosítása
Analízis előadások Vajda István Neumann János Informatika Kar Óbudai Egyetem 013. február 10. Vajda István (Óbudai Egyetem) Analízis előadások 013. február 10. 1 / 3 Az elemi függvények csoportosítása
Fordítóprogramok Készítette: Nagy Krisztián
 Fordítóprogramok Készítette: Nagy Krisztián Reguláris kifejezések (FLEX) Alapelemek kiválasztása az x karakter. tetszőleges karakter (kivéve újsor) [xyz] karakterhalmaz; vagy egy x, vagy egy y vagy egy
Fordítóprogramok Készítette: Nagy Krisztián Reguláris kifejezések (FLEX) Alapelemek kiválasztása az x karakter. tetszőleges karakter (kivéve újsor) [xyz] karakterhalmaz; vagy egy x, vagy egy y vagy egy
ADATLAP Sorszám: SZAKÉRTŐI INTERJÚ-VÁZLAT
 Moderátor neve: Megkérdezés ideje: Cég neve: Válaszadó neve: ADATLAP Sorszám: Megkérdezés helye: Cég tevékenysége: Válaszadó beosztása: SZAKÉRTŐI INTERJÚ-VÁZLAT 1. BEVEZETÉS [5 PERC] MODERÁTOR Bemutatkozás
Moderátor neve: Megkérdezés ideje: Cég neve: Válaszadó neve: ADATLAP Sorszám: Megkérdezés helye: Cég tevékenysége: Válaszadó beosztása: SZAKÉRTŐI INTERJÚ-VÁZLAT 1. BEVEZETÉS [5 PERC] MODERÁTOR Bemutatkozás
Útmutató a vízumkérő lap kitöltéséhez
 Útmutató a vízumkérő lap kitöltéséhez A vízumkérő lap ( Visa application form of the People s Republic of China, Form V. 2013 ) az egyik legfontosabb dokumentum, amit a kínai vízumra való jelentkezésnél
Útmutató a vízumkérő lap kitöltéséhez A vízumkérő lap ( Visa application form of the People s Republic of China, Form V. 2013 ) az egyik legfontosabb dokumentum, amit a kínai vízumra való jelentkezésnél
Tájékoztató a szerződés módosításáról_munkaruházati termékek szállítása (5. rész)
 Tájékoztató a szerződés módosításáról_munkaruházati termékek szállítása (5. rész) Közbeszerzési Értesítő száma: 2016/61 Beszerzés tárgya: Árubeszerzés Hirdetmény típusa: Tájékoztató a szerződés módosításáról/2015
Tájékoztató a szerződés módosításáról_munkaruházati termékek szállítása (5. rész) Közbeszerzési Értesítő száma: 2016/61 Beszerzés tárgya: Árubeszerzés Hirdetmény típusa: Tájékoztató a szerződés módosításáról/2015
Agrárgazdasági Kutató Intézet Piac-árinformációs Szolgálat. Borpiaci információk. III. évfolyam / 7. szám 2005. április 28. 14-15.
 A K I Borpiaci információk III. évfolyam / 7. szám 25. április 28. 14- Bor piaci jelentés Borpiaci információk 1-4. táblázat, 1-8. ábra: Belföldi értékesítési-árak és mennyiségi adatok 2. oldal 3-7. oldal
A K I Borpiaci információk III. évfolyam / 7. szám 25. április 28. 14- Bor piaci jelentés Borpiaci információk 1-4. táblázat, 1-8. ábra: Belföldi értékesítési-árak és mennyiségi adatok 2. oldal 3-7. oldal
54 345 03 0000 00 00 Munkaerőpiaci szervező, elemző Munkaerőpiaci szervező, elemző 54 345 06 0000 00 00 Személyügyi gazdálkodó és fejlesztő
 A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
Lécgerenda. 1. ábra. 2. ábra
 Lécgerenda Egy korábbi dolgozatunkban melynek címe: Karimás csőillesztés már szóltunk arról, hogy a szeezetek számításaiban néha célszerű lehet a diszkrét mennyiségeket folyto - nosan megoszló mennyiségekkel
Lécgerenda Egy korábbi dolgozatunkban melynek címe: Karimás csőillesztés már szóltunk arról, hogy a szeezetek számításaiban néha célszerű lehet a diszkrét mennyiségeket folyto - nosan megoszló mennyiségekkel
A táblázatkezelő felépítése
 A táblázatkezelés A táblázatkezelő felépítése A táblázatkezelő felépítése Címsor: A munkafüzet címét mutatja, és a program nevét, amivel megnyitottam. Menüszalag: A menüsor segítségével használhatjuk az
A táblázatkezelés A táblázatkezelő felépítése A táblázatkezelő felépítése Címsor: A munkafüzet címét mutatja, és a program nevét, amivel megnyitottam. Menüszalag: A menüsor segítségével használhatjuk az
Tartószerkezetek I. (Vasbeton szilárdságtan)
 Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.09.27. Hajlított vasbeton keresztmetszetek vizsgálata 2 3 Jelölések, elnevezések b : a keresztmetszet szélessége h : a keresztmetszet magassága
Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.09.27. Hajlított vasbeton keresztmetszetek vizsgálata 2 3 Jelölések, elnevezések b : a keresztmetszet szélessége h : a keresztmetszet magassága
A Hozzárendelési feladat megoldása Magyar-módszerrel
 A Hozzárendelési feladat megoldása Magyar-módszerrel Virtuális vállalat 2013-2014/1. félév 3. gyakorlat Dr. Kulcsár Gyula A Hozzárendelési feladat Adott meghatározott számú gép és ugyanannyi független
A Hozzárendelési feladat megoldása Magyar-módszerrel Virtuális vállalat 2013-2014/1. félév 3. gyakorlat Dr. Kulcsár Gyula A Hozzárendelési feladat Adott meghatározott számú gép és ugyanannyi független
Bevezetés a lágy számítás módszereibe
 BLSZM-07 p. 1/10 Bevezetés a lágy számítás módszereibe Nem fuzzy halmaz kimenetű fuzzy irányítási rendszerek Egy víztisztító berendezés szabályozását megvalósító modell Viselkedésijósló tervezési példa
BLSZM-07 p. 1/10 Bevezetés a lágy számítás módszereibe Nem fuzzy halmaz kimenetű fuzzy irányítási rendszerek Egy víztisztító berendezés szabályozását megvalósító modell Viselkedésijósló tervezési példa
HUPX anomáliák, azaz mi történik itt 2011. július óta? dr. Uzonyi Zoltán és Turai József MVKE közgyűlés 2012. május 8.
 HUPX anomáliák, azaz mi történik itt 2011. július óta? dr. Uzonyi Zoltán és Turai József MVKE közgyűlés 2012. május 8. Tartalom 1. Hisztorikus forward zsinór árak alakulása, DE vs HU 2. Hisztorikus spot
HUPX anomáliák, azaz mi történik itt 2011. július óta? dr. Uzonyi Zoltán és Turai József MVKE közgyűlés 2012. május 8. Tartalom 1. Hisztorikus forward zsinór árak alakulása, DE vs HU 2. Hisztorikus spot
MATEMATIKA ÍRÁSBELI VIZSGA 2011. május 3.
 MATEMATIKA ÍRÁSBELI VIZSGA I. rész Fontos tudnivalók A megoldások sorrendje tetszőleges. A feladatok megoldásához szöveges adatok tárolására és megjelenítésére nem alkalmas zsebszámológépet és bármelyik
MATEMATIKA ÍRÁSBELI VIZSGA I. rész Fontos tudnivalók A megoldások sorrendje tetszőleges. A feladatok megoldásához szöveges adatok tárolására és megjelenítésére nem alkalmas zsebszámológépet és bármelyik
A SZÁMFOGALOM KIALAKÍTÁSA
 A SZÁMFOGALOM KIALAKÍTÁSA TERMÉSZETES SZÁMOK ÉRTELMEZÉSE 1-5. OSZTÁLY Számok értelmezése 0-tól 10-ig: Véges halmazok számosságaként Mérőszámként Sorszámként Jelzőszámként A számok fogalmának kiterjesztése
A SZÁMFOGALOM KIALAKÍTÁSA TERMÉSZETES SZÁMOK ÉRTELMEZÉSE 1-5. OSZTÁLY Számok értelmezése 0-tól 10-ig: Véges halmazok számosságaként Mérőszámként Sorszámként Jelzőszámként A számok fogalmának kiterjesztése
Tantárgyi program. 9. A tantárgy hallgatásának előfeltétele, előképzettségi szint: 10. A tantárgy tartalma:
 Tantárgyi program 1. A tantárgy neve, kódja: AVM_VFLB111-K5 Marketing menedzsment 2. A neve, beosztása: 3. Szakcsoport (szakirány) megnevezése: Vállalkozásfejlesztés MSc szak, levelező tagozat 4. A tantárgy
Tantárgyi program 1. A tantárgy neve, kódja: AVM_VFLB111-K5 Marketing menedzsment 2. A neve, beosztása: 3. Szakcsoport (szakirány) megnevezése: Vállalkozásfejlesztés MSc szak, levelező tagozat 4. A tantárgy
