Számítógépes Hálózatok. 7. gyakorlat
|
|
|
- Judit Bodnár
- 6 évvel ezelőtt
- Látták:
Átírás
1 Számítógépes Hálózatok 7. gyakorlat
2 Gyakorlat tematika Hibajelző kód: CRC számítás Órai / házi feladat Számítógépes Hálózatok Gyakorlat 7. 2
3 CRC hibajelző kód emlékeztető Forrás: Dr. Lukovszki Tamás fóliái alapján Számítógépes Hálózatok Gyakorlat 7. 3
4 Példa CRC számításra emlékeztető Keret (M(x)): Generátor (G(x)): Végezzük el a következő maradékos osztást: (A maradék lesz a CRC ellenőrzőösszeg) Ellenőrzés: _ Számítógépes Hálózatok Gyakorlat 7. 4
5 Példa CRC számításra kiegészítés Az előbbi osztásnál: megfelel a 1 x x x x x x x 4, megfelel a 1 x x + 1 polinomnak Ha a polinom alakjukban végeznénk az osztást, akkor először az osztó legnagyobb fokú tagjával (x 4 ) leosztanánk az osztandó legnagyobb fokú tagját (x 13 ) Ez x 9 -et eredményezi. Lekönyveljük, és összeszorozzuk az osztóval: x 9 1 x x + 1 = x 13 + x 10 + x 9 (Vegyük észre, hogy ez az osztó eltoltját fogja mindig eredményezni bináris reprezentációval nézve.) Ezt kivonjuk az eredeti osztandóból, amely az 1 x 12 + ( 1) x x x (mod 2) x x 4 polinomot eredményezi. Bináris alakban ez a polinom: Számítógépes Hálózatok Gyakorlat 7. 5
6 Példa CRC számításra kiegészítés Ennek a polinomnak a legnagyobb fokú tagját osztjuk majd tovább az osztó legnagyobb fokú tagjával az előző lépésekhez hasonlóan, amely x 8 -at eredményezi. Lekönyveljük, és összeszorozzuk az osztóval: x 8 1 x x + 1 = x 12 + x 9 + x 8 Ezt kivonjuk az eredeti osztandóból, amely az 1 x x x 4 polinomot eredményezi. Bináris alakban ez a polinom: Ezt folytatjuk. A végén a lekönyvelt tagokat összeadjuk, amely az eredményt adja, továbbá a megmaradt, az osztónál kisebb fokú polinom a maradékot. Számítógépes Hálózatok Gyakorlat 7. 6
7 Példa CRC számításra kiegészítés Az előbbi szorzásnál: megfelel a 1 x x x x, megfelel a 1 x x + 1 polinomnak Ha a polinom alakjukban összeszoroznánk: 1 x x x x 1 x x + 1 = 1 x x x x x x x x x x x x = 1 x x x 10 + (1 + 1) x x x x x x x x 0 (mod 2) Ez bináris alakban éppen a lesz Számítógépes Hálózatok Gyakorlat 7. 7
8 Feladat 1 Adva a G(x) = x 4 + x generátor polinom. Számoljuk ki bemenethez a 4-bit CRC ellenőrzőösszeget! Adjuk meg az átviteli üzenetet (a csatornára kerülő bitsorozatot)! Számítógépes Hálózatok Gyakorlat 7. 8
9 Feladat 1 megoldása Mivel a generátor polinom foka 4, ezért négy 0-t írunk a bemenet végéhez. A G(x) bináris alakban: lesz, tehát a maradékos osztást kell elvégeznünk: Számítógépes Hálózatok Gyakorlat 7. 9
10 / _ a CRC ellenőrzőösszeg Számítógépes Hálózatok Gyakorlat 7. 10
11 Feladat 1 megoldása Az átviteli üzenet: Számítógépes Hálózatok Gyakorlat 7. 11
12 Feladat 2 Adva a G(x) = x 4 + x + 1 generátor polinom. Történt-e hiba az átvitel során, ha a vevő a következő üzenetet kapja: Számítógépes Hálózatok Gyakorlat 7. 12
13 Feladat 2 megoldása A G(x) bináris alakban: lesz, tehát a maradékos osztást kell elvégeznünk, és ha nem nulla jön ki maradéknak, akkor hiba történt: Számítógépes Hálózatok Gyakorlat 7. 13
14 / Nem nulla a maradék hiba történt Számítógépes Hálózatok Gyakorlat 7. 14
15 Feladat 3 Adva a G x = x 4 + x 3 + x + 1 generátor polinom. Számoljuk ki a bemenethez a 4-bit CRC ellenőrzőösszeget! A fenti üzenet az átvitel során sérül, a vevő adatkapcsolati rétege az bitsorozatot kapja. Történt-e olyan hiba az átvitel során, amit a generátor polinommal fel lehet ismerni? Ha nem, akkor ennek mi lehet az oka? Számítógépes Hálózatok Gyakorlat 7. 15
16 Feladat 3 megoldása Mivel a generátor polinom foka 4, ezért négy 0-t írunk a bemenet végéhez. A G(x) bináris alakban: lesz, tehát a maradékos osztást kell elvégeznünk: Számítógépes Hálózatok Gyakorlat 7. 16
17 / a CRC ellenőrzőösszeg Számítógépes Hálózatok Gyakorlat 7. 17
18 Feladat 3 megoldása Az előbbi számításnál az jött ki, hogy lenne az a bitsorozat, amelyet a vevő kapna. Ha ebből kivonjuk az alfeladatban megadott sorozatot, az alábbi eredmény jön ki: Tehát a két bitsorozat pontosan a generátor polinom többszörösével tér egymástól, amely tehát a hiba polinom. Ezt pedig nem lehet felismerni. Számítógépes Hálózatok Gyakorlat 7. 18
19 Feladat 4 Készítsünk egy kliens-proxy-szerver alkalmazást, ahol: a szerver egy UDP szerver, a proxy a szerver irányába egy UDP kliens, a kliens irányába egy TCP szerver, a kliens egy TCP kliens a proxy irányába Folyamat: a kliens küldje a Hello Server üzenetet a proxynak, amely küldje tovább azt a szervernek, amely válaszolja vissza a Hello Kliens üzenetet a proxynak, amely küldje tovább azt a kliensnek Számítógépes Hálózatok Gyakorlat 7. 19
20 CRC Órai / házi feladat Legyen tetszőleges számú küldő, egy csatorna szerver és egy fogadó Adott a generátor polinom: G x = x 4 + x 3 + x + 1, amelyet mindenki ismer Egy küldő indításkor csatlakozik a csatorna szerverhez A csatorna szerver egy időben figyel több socketet A bejövő kapcsolódásokra és a meglevő kapcsolatokból való olvasásra is használjunk select függvényt! Számítógépes Hálózatok Gyakorlat 7. 20
21 CRC Órai / házi feladat A küldő oldalon folyamatosan megadhatunk egyszerű 0-1 bitekből álló üzeneteket, amelyre az alkalmazás a 4-bit CRC ellenőrzőösszeggel ellátott átviteli üzenetet számolja ki, és küldi tovább a csatorna szervernek Számítógépes Hálózatok Gyakorlat 7. 21
22 Órai / házi feladat CRC A csatorna szerver ciklikus módon váltakozva az alábbi hiba polinomokat adja az átviteli üzenetekhez: 1. Nincs hiba polinom 2. Van hiba polinom, és nem többszöröse a generátor polinomnak 3. Van hiba polinom, de többszöröse a generátor polinomnak (Megjegyzés: ezek a hiba polinomok lehetnek előre adottak) Azután továbbítja UDP protokoll használatával a fogadónak a hibával terhelt üzenetet Figyelem! Ehhez még egy socketet definiálni kell egy új porttal a csatorna szervernél (és datagram típusú legyen ez a socket) Itt a csatorna szerver legyen az UDP kliens, és a fogadó legyen az UDP szerver (azaz a fogadónál történjen meg a bind függvény hívása) Számítógépes Hálózatok Gyakorlat 7. 22
23 Órai / házi feladat CRC A fogadó egy végtelen ciklusban folyamatosan várja a beérkező üzeneteket A socketjén definiáljunk timeoutot (pl. 1 másodperccel), hogy le lehessen állítani, akkor is ha nem jön üzenet a csatorna szervertől Így socket.timeout kivétel fog jönni, de azt kezeljük le úgy, hogy continue (vagy egy üres pass utasítás) szerepeljen a kivételkezelésnél A fogadó megpróbálja leellenőrzi a generátor polinom segítségével bejövő üzenetre, hogy történt-e hiba, és kiírja a kimenetre az eredményt (Nyilván minden harmadik üzenetre tévesen azt a következtetést fogja levonni, hogy nincs hiba, hiszen abban az esetben a hiba rejtve marad) Számítógépes Hálózatok Gyakorlat 7. 23
24 Órai / házi feladat CRC Természetesen ne használjunk a CRC számításhoz mások által megírt CRC számító modult! Ennek implementálása is a feladat része! Mivel CRC számítást a küldő és fogadó is végez, ezért érdemes ezt a funkcionalitást kiszervezni egy külön modulba Ehhez segítség: ha a hazicrccalculator.py tartalmazza a szükséges funkcionalitást pl. calculateremainder(...) néven, akkor a többi forrásfájlba egyszerűen az alábbi módon tudunk erre ráhívni (ha ugyanabban a könyvtárban vannak): import hazicrccalculator... hazicrccalculator.calculateremainder(...) Számítógépes Hálózatok Gyakorlat 7. 24
25 Órai / házi feladat CRC Segítség a CRC számításhoz (de nem kötelező ezt használni): Pythonnál az int(str1,base2) konverzió a bemeneti str1 sztringből a megadott base2 alapján, - amely a számrendszert jelöli, - egész számot készít: >>> i1 = int(' ',2) >>> i >>> i2 = int(' ',2) >>> i Bitenkénti műveletek: <<, >>, &,, ~, ^, pl. a bitenkénti XOR: >>> i1^i Az előbbi sztring reprezentációja: >>> "{0:b}".format(i1^i2) ' ' Számítógépes Hálózatok Gyakorlat 7. 25
26 TCP Órai / házi feladat Küldő 1 Küldő 2 Csatorna szerver UDP Fogadó Küldő 3 Számítógépes Hálózatok Gyakorlat 7. 26
27 Számítógépes Hálózatok Gyakorlat 7. 27
28 VÉGE Számítógépes Hálózatok Gyakorlat 7. 28
Számítógépes Hálózatok 2012
 Számítógépes Hálózatok 22 4. Adatkapcsolati réteg CRC, utólagos hibajavítás Hálózatok, 22 Hibafelismerés: CRC Hatékony hibafelismerés: Cyclic Redundancy Check (CRC) A gyakorlatban gyakran használt kód
Számítógépes Hálózatok 22 4. Adatkapcsolati réteg CRC, utólagos hibajavítás Hálózatok, 22 Hibafelismerés: CRC Hatékony hibafelismerés: Cyclic Redundancy Check (CRC) A gyakorlatban gyakran használt kód
Számítógépes Hálózatok. 5. gyakorlat
 Számítógépes Hálózatok 5. gyakorlat PYTHON ALAPOK V. Socket programozás, UDP 2 Óra eleji kiszh Elérés: https://canvas.elte.hu Számítógépes Hálózatok Gyakorlat 1 3 A kommunikációs csatorna kétféle típusa
Számítógépes Hálózatok 5. gyakorlat PYTHON ALAPOK V. Socket programozás, UDP 2 Óra eleji kiszh Elérés: https://canvas.elte.hu Számítógépes Hálózatok Gyakorlat 1 3 A kommunikációs csatorna kétféle típusa
Számítógépes Hálózatok. 5. gyakorlat
 Számítógépes Hálózatok 5. gyakorlat Óra eleji kiszh Elérés: https://oktnb6.inf.elte.hu Számítógépes Hálózatok Gyakorlat 2 Gyakorlat tematika Szinkron CDMA Órai / házi feladat Számítógépes Hálózatok Gyakorlat
Számítógépes Hálózatok 5. gyakorlat Óra eleji kiszh Elérés: https://oktnb6.inf.elte.hu Számítógépes Hálózatok Gyakorlat 2 Gyakorlat tematika Szinkron CDMA Órai / házi feladat Számítógépes Hálózatok Gyakorlat
Számítógépes Hálózatok GY 6.hét
 Számítógépes Hálózatok GY 6.hét Laki Sándor ELTE-Ericsson Kommunikációs Hálózatok Laboratórium ELTE IK - Információs Rendszerek Tanszék lakis@elte.hu http://lakis.web.elte.hu Teszt 10 kérdés 10 perc canvas.elte.hu
Számítógépes Hálózatok GY 6.hét Laki Sándor ELTE-Ericsson Kommunikációs Hálózatok Laboratórium ELTE IK - Információs Rendszerek Tanszék lakis@elte.hu http://lakis.web.elte.hu Teszt 10 kérdés 10 perc canvas.elte.hu
Számítógépes Hálózatok GY 7.hét
 Számítógépes Hálózatok GY 7.hét Laki Sándor ELTE-Ericsson Kommunikációs Hálózatok Laboratórium ELTE IK - Információs Rendszerek Tanszék lakis@elte.hu http://lakis.web.elte.hu Teszt 10 kérdés 10 perc canvas.elte.hu
Számítógépes Hálózatok GY 7.hét Laki Sándor ELTE-Ericsson Kommunikációs Hálózatok Laboratórium ELTE IK - Információs Rendszerek Tanszék lakis@elte.hu http://lakis.web.elte.hu Teszt 10 kérdés 10 perc canvas.elte.hu
Hibafelismerés: CRC. Számítógépes Hálózatok Polinóm aritmetika modulo 2. Számolás Z 2 -ben
 Hibafelismerés: CRC Számítógépes Hálózatok 27 6. Adatkapcsolati réteg CRC, utólagos hibajavítás, csúszó ablakok Hatékony hibafelismerés: Cyclic Redundancy Check (CRC) A gyakorlatban gyakran használt kód
Hibafelismerés: CRC Számítógépes Hálózatok 27 6. Adatkapcsolati réteg CRC, utólagos hibajavítás, csúszó ablakok Hatékony hibafelismerés: Cyclic Redundancy Check (CRC) A gyakorlatban gyakran használt kód
Számítógépes Hálózatok 2008
 Számítógépes Hálózatok 28 5. Adatkapcsolati réteg CRC, utólagos hibajavítás, csúszó ablakok Hibafelismerés: CRC Hatékony hibafelismerés: Cyclic Redundancy Check (CRC) A gyakorlatban gyakran használt kód
Számítógépes Hálózatok 28 5. Adatkapcsolati réteg CRC, utólagos hibajavítás, csúszó ablakok Hibafelismerés: CRC Hatékony hibafelismerés: Cyclic Redundancy Check (CRC) A gyakorlatban gyakran használt kód
Számítógépes Hálózatok. 4. gyakorlat
 Számítógépes Hálózatok 4. gyakorlat Feladat 0 Számolja ki a CRC kontrollösszeget az 11011011001101000111 üzenetre, ha a generátor polinom x 4 +x 3 +x+1! Mi lesz a 4 bites kontrollösszeg? A fenti üzenet
Számítógépes Hálózatok 4. gyakorlat Feladat 0 Számolja ki a CRC kontrollösszeget az 11011011001101000111 üzenetre, ha a generátor polinom x 4 +x 3 +x+1! Mi lesz a 4 bites kontrollösszeg? A fenti üzenet
Számítógépes Hálózatok. 5. gyakorlat
 Számítógépes Hálózatok 5. gyakorlat Feladat 0 Számolja ki a CRC kontrollösszeget az 11011011001101000111 üzenetre, ha a generátor polinom x 4 +x 3 +x+1! Mi lesz a 4 bites kontrollösszeg? A fenti üzenet
Számítógépes Hálózatok 5. gyakorlat Feladat 0 Számolja ki a CRC kontrollösszeget az 11011011001101000111 üzenetre, ha a generátor polinom x 4 +x 3 +x+1! Mi lesz a 4 bites kontrollösszeg? A fenti üzenet
Diszkrét matematika II. feladatok
 Diszkrét matematika II. feladatok 1. Gráfelmélet 1.1. Könnyebb 1. Rajzold le az összes, páronként nem izomorf 3, 4, illetve 5 csúcsú egyszerű gráfot! 2. Van-e olyan (legalább kétpontú) gráf, melyben minden
Diszkrét matematika II. feladatok 1. Gráfelmélet 1.1. Könnyebb 1. Rajzold le az összes, páronként nem izomorf 3, 4, illetve 5 csúcsú egyszerű gráfot! 2. Van-e olyan (legalább kétpontú) gráf, melyben minden
Számítógépes Hálózatok. 4. gyakorlat
 Számítógépes Hálózatok 4. gyakorlat Teszt canvas.elte.hu Számítógépes Hálózatok Gyakorlat 2 TCP Számítógépes Hálózatok Gyakorlat 3 TCP socket() bind() listen() accept() sock = socket.socket(socket.af_inet,
Számítógépes Hálózatok 4. gyakorlat Teszt canvas.elte.hu Számítógépes Hálózatok Gyakorlat 2 TCP Számítógépes Hálózatok Gyakorlat 3 TCP socket() bind() listen() accept() sock = socket.socket(socket.af_inet,
Hibafelismerés: CRC. Számítógépes Hálózatok Polinóm aritmetika modulo 2. Számolás Z 2 -ben
 Hibafelismerés: CRC Számítógépes Hálózatok 2 4. Adatkapcsolati réteg CRC, utólagos hibajavítás, csúszó ablakok Hatékony hibafelismerés: Cyclic Redundancy Check (CRC) A gyakorlatban gyakran használt kód
Hibafelismerés: CRC Számítógépes Hálózatok 2 4. Adatkapcsolati réteg CRC, utólagos hibajavítás, csúszó ablakok Hatékony hibafelismerés: Cyclic Redundancy Check (CRC) A gyakorlatban gyakran használt kód
Számítógépes Hálózatok GY 4.hét
 Számítógépes Hálózatok GY 4.hét Laki Sándor ELTE-Ericsson Kommunikációs Hálózatok Laboratórium ELTE IK - Információs Rendszerek Tanszék lakis@elte.hu http://lakis.web.elte.hu Teszt 10 kérdés 10 perc canvas.elte.hu
Számítógépes Hálózatok GY 4.hét Laki Sándor ELTE-Ericsson Kommunikációs Hálózatok Laboratórium ELTE IK - Információs Rendszerek Tanszék lakis@elte.hu http://lakis.web.elte.hu Teszt 10 kérdés 10 perc canvas.elte.hu
Az adatkapcsolati réteg
 Az adatkapcsolati réteg Programtervező informatikus BSc Számítógép hálózatok és architektúrák előadás Az adatkapcsolati réteg A fizikai átviteli hibáinak elfedése a hálózati réteg elől Keretezés Adatfolyam
Az adatkapcsolati réteg Programtervező informatikus BSc Számítógép hálózatok és architektúrák előadás Az adatkapcsolati réteg A fizikai átviteli hibáinak elfedése a hálózati réteg elől Keretezés Adatfolyam
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 2017. tavasz 1. Diszkrét matematika 2.C szakirány 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 2.C szakirány 2017. tavasz 1. Diszkrét matematika 2.C szakirány 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 4. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 4. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Számítógépes Hálózatok GY 3-4.hét
 Számítógépes Hálózatok GY 3-4.hét Laki Sándor ELTE-Ericsson Kommunikációs Hálózatok Laboratórium ELTE IK - Információs Rendszerek Tanszék lakis@elte.hu http://lakis.web.elte.hu 1 Teszt canvas.elte.hu Kód:
Számítógépes Hálózatok GY 3-4.hét Laki Sándor ELTE-Ericsson Kommunikációs Hálózatok Laboratórium ELTE IK - Információs Rendszerek Tanszék lakis@elte.hu http://lakis.web.elte.hu 1 Teszt canvas.elte.hu Kód:
1. fogalom. Add meg az összeadásban szereplő számok elnevezéseit! Milyen tulajdonságai vannak az összeadásnak? Hogyan ellenőrizzük az összeadást?
 1. fogalom Add meg az összeadásban szereplő számok 73 + 19 = 92 összeadandók (tagok) összeg Összeadandók (tagok): amiket összeadunk. Összeg: az összeadás eredménye. Milyen tulajdonságai vannak az összeadásnak?
1. fogalom Add meg az összeadásban szereplő számok 73 + 19 = 92 összeadandók (tagok) összeg Összeadandók (tagok): amiket összeadunk. Összeg: az összeadás eredménye. Milyen tulajdonságai vannak az összeadásnak?
Számítógépes Hálózatok
 Számítógépes Hálózatok 4. Előadás: Adatkapcsolati réteg Based on slides from Zoltán Ács ELTE and D. Choffnes Northeastern U., Philippa Gill from StonyBrook University, Revised Spring 2016 by S. Laki Adatkapcsolati
Számítógépes Hálózatok 4. Előadás: Adatkapcsolati réteg Based on slides from Zoltán Ács ELTE and D. Choffnes Northeastern U., Philippa Gill from StonyBrook University, Revised Spring 2016 by S. Laki Adatkapcsolati
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Számítógépes Hálózatok. 3. gyakorlat
 Számítógépes Hálózatok 3. gyakorlat Teszt canvas.elte.hu Számítógépes Hálózatok Gyakorlat 2 NC-NetCat (SoCat), avagy hálózati svájcibicska # szerver imitálása nc -l -p 1234 # kliens imitálása nc destination_host
Számítógépes Hálózatok 3. gyakorlat Teszt canvas.elte.hu Számítógépes Hálózatok Gyakorlat 2 NC-NetCat (SoCat), avagy hálózati svájcibicska # szerver imitálása nc -l -p 1234 # kliens imitálása nc destination_host
III. Felzárkóztató mérés SZÉCHENYI ISTVÁN EGYETEM GYŐR TÁVKÖZLÉSI TANSZÉK
 Mérési utasítás ARP, ICMP és DHCP protokollok vizsgálata Ezen a mérésen a hallgatók az ARP, az ICMP és a DHCP protokollok működését tanulmányozzák az előző mérésen megismert Wireshark segítségével. A mérés
Mérési utasítás ARP, ICMP és DHCP protokollok vizsgálata Ezen a mérésen a hallgatók az ARP, az ICMP és a DHCP protokollok működését tanulmányozzák az előző mérésen megismert Wireshark segítségével. A mérés
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 2. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 2. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Bevezetés az informatikába gyakorló feladatok Utoljára módosítva:
 Tartalom 1. Számrendszerek közti átváltás... 2 1.1. Megoldások... 4 2. Műveletek (+, -, bitműveletek)... 7 2.1. Megoldások... 8 3. Számítógépes adatábrázolás... 10 3.1. Megoldások... 12 A gyakorlósor lektorálatlan,
Tartalom 1. Számrendszerek közti átváltás... 2 1.1. Megoldások... 4 2. Műveletek (+, -, bitműveletek)... 7 2.1. Megoldások... 8 3. Számítógépes adatábrázolás... 10 3.1. Megoldások... 12 A gyakorlósor lektorálatlan,
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 3. estis képzés 2016. ősz 1. Diszkrét matematika 3. estis képzés 3. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2016. ősz 1. Diszkrét matematika 3. estis képzés 3. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
2018, Diszkrét matematika
 Diszkrét matematika 3. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia 2018, őszi félév Miről volt szó az elmúlt előadáson? számtartományok: természetes
Diszkrét matematika 3. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia 2018, őszi félév Miről volt szó az elmúlt előadáson? számtartományok: természetes
1. A maradékos osztás
 1. A maradékos osztás Egész számok osztása Példa 223 = 7 31+6. Visszaszorzunk Kivonunk 223 : 7 = 31 21 13 7 6 Állítás (számelméletből) Minden a,b Z esetén, ahol b 0, létezik olyan q,r Z, hogy a = bq +
1. A maradékos osztás Egész számok osztása Példa 223 = 7 31+6. Visszaszorzunk Kivonunk 223 : 7 = 31 21 13 7 6 Állítás (számelméletből) Minden a,b Z esetén, ahol b 0, létezik olyan q,r Z, hogy a = bq +
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 11. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Kongruenciák Diszkrét matematika I. középszint 2014.
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 11. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Kongruenciák Diszkrét matematika I. középszint 2014.
2. Fejezet : Számrendszerek
 2. Fejezet : Számrendszerek The Architecture of Computer Hardware and Systems Software: An Information Technology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson Wong, Bentley College
2. Fejezet : Számrendszerek The Architecture of Computer Hardware and Systems Software: An Information Technology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson Wong, Bentley College
Komputeralgebra Rendszerek
 Komputeralgebra Rendszerek Számkezelés Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2015. február 24. TARTALOMJEGYZÉK 1 of 53 TARTALOMJEGYZÉK 1 TARTALOMJEGYZÉK 2 Az egzakt aritmetika Bignum aritmetika
Komputeralgebra Rendszerek Számkezelés Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2015. február 24. TARTALOMJEGYZÉK 1 of 53 TARTALOMJEGYZÉK 1 TARTALOMJEGYZÉK 2 Az egzakt aritmetika Bignum aritmetika
Számítógépes hálózatok
 Számítógépes hálózatok 7. gyakorlat: SOCKET programozás (C) Gyakorlatvezető: Ács Zoltán Hatodik házi-feladat 1/2 ADAPTÍV FA Tekintsünk 16 állomást, melyek adaptív fabejárás protokollal visznek át csomagokat.
Számítógépes hálózatok 7. gyakorlat: SOCKET programozás (C) Gyakorlatvezető: Ács Zoltán Hatodik házi-feladat 1/2 ADAPTÍV FA Tekintsünk 16 állomást, melyek adaptív fabejárás protokollal visznek át csomagokat.
Kommunikáció. 3. előadás
 Kommunikáció 3. előadás Kommunikáció A és B folyamatnak meg kell egyeznie a bitek jelentésében Szabályok protokollok ISO OSI Többrétegű protokollok előnyei Kapcsolat-orientált / kapcsolat nélküli Protokollrétegek
Kommunikáció 3. előadás Kommunikáció A és B folyamatnak meg kell egyeznie a bitek jelentésében Szabályok protokollok ISO OSI Többrétegű protokollok előnyei Kapcsolat-orientált / kapcsolat nélküli Protokollrétegek
The Architecture of Computer Hardware and Systems Software: An InformationTechnology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003
 . Fejezet : Számrendszerek The Architecture of Computer Hardware and Systems Software: An InformationTechnology Approach. kiadás, Irv Englander John Wiley and Sons Wilson Wong, Bentley College Linda Senne,
. Fejezet : Számrendszerek The Architecture of Computer Hardware and Systems Software: An InformationTechnology Approach. kiadás, Irv Englander John Wiley and Sons Wilson Wong, Bentley College Linda Senne,
Diszkrét matematika 2.
 Diszkrét matematika 2. 2018. november 23. 1. Diszkrét matematika 2. 9. előadás Fancsali Szabolcs Levente nudniq@cs.elte.hu www.cs.elte.hu/ nudniq Komputeralgebra Tanszék 2018. november 23. Diszkrét matematika
Diszkrét matematika 2. 2018. november 23. 1. Diszkrét matematika 2. 9. előadás Fancsali Szabolcs Levente nudniq@cs.elte.hu www.cs.elte.hu/ nudniq Komputeralgebra Tanszék 2018. november 23. Diszkrét matematika
Bevezetés az informatikába gyakorló feladatok Utoljára módosítva:
 Tartalom 1. Számrendszerek közti átváltás... 2 1.1. Megoldások... 4 2. Műveletek (+, -, bitműveletek)... 7 2.1. Megoldások... 8 3. Számítógépes adatábrázolás... 12 3.1. Megoldások... 14 A gyakorlósor lektorálatlan,
Tartalom 1. Számrendszerek közti átváltás... 2 1.1. Megoldások... 4 2. Műveletek (+, -, bitműveletek)... 7 2.1. Megoldások... 8 3. Számítógépes adatábrázolás... 12 3.1. Megoldások... 14 A gyakorlósor lektorálatlan,
Imperatív programozás
 Imperatív programozás 7. Előadás Függvények, láthatóság (folytatás) Modulok Kivételkezelés Beágyazott függvény def lnko(x, y): def kivon(m, n): return m - n while not (x == y) : if x > y : x = kivon(x,y)
Imperatív programozás 7. Előadás Függvények, láthatóság (folytatás) Modulok Kivételkezelés Beágyazott függvény def lnko(x, y): def kivon(m, n): return m - n while not (x == y) : if x > y : x = kivon(x,y)
Számítógépes Hálózatok
 Számítógépes Hálózatok 4. Előadás: Adatkapcsolati réteg II. Based on slides from Zoltán Ács ELTE and D. Choffnes Northeastern U., Philippa Gill from StonyBrook University, Revised Spring 2016 by S. Laki
Számítógépes Hálózatok 4. Előadás: Adatkapcsolati réteg II. Based on slides from Zoltán Ács ELTE and D. Choffnes Northeastern U., Philippa Gill from StonyBrook University, Revised Spring 2016 by S. Laki
1. A maradékos osztás
 1. A maradékos osztás Egész számok osztása. 223 = 7 31 + 6. Visszaszorzunk 223 : 7 = 31 21 13 7 6 Állítás (számelméletből) Minden a, b Z esetén, ahol b 0, létezik olyan q, r Z, hogy a = bq + r és r < b.
1. A maradékos osztás Egész számok osztása. 223 = 7 31 + 6. Visszaszorzunk 223 : 7 = 31 21 13 7 6 Állítás (számelméletből) Minden a, b Z esetén, ahol b 0, létezik olyan q, r Z, hogy a = bq + r és r < b.
* Rendelje a PPP protokollt az TCP/IP rétegmodell megfelelő rétegéhez. Kapcsolati réteg
 ét * Rendelje a PPP protokollt az TCP/IP rétegmodell megfelelő Kapcsolati réteg A Pont-pont protokoll (általánosan használt rövidítéssel: PPP az angol Point-to-Point Protocol kifejezésből) egy magas szintű
ét * Rendelje a PPP protokollt az TCP/IP rétegmodell megfelelő Kapcsolati réteg A Pont-pont protokoll (általánosan használt rövidítéssel: PPP az angol Point-to-Point Protocol kifejezésből) egy magas szintű
Törtek. Rendelhetőek nagyon jó szemléltethető eszközök könyvesboltokban és internetek is, pl:
 Törtek A törteknek kétféle értelmezése van: - Egy egészet valamennyi részre (nevező) osztunk, és abból kiválasztunk valahány darabot (számláló) - Valamennyi egészet (számláló), valahány részre osztunk
Törtek A törteknek kétféle értelmezése van: - Egy egészet valamennyi részre (nevező) osztunk, és abból kiválasztunk valahány darabot (számláló) - Valamennyi egészet (számláló), valahány részre osztunk
Programozás alapjai gyakorlat. 2. gyakorlat C alapok
 Programozás alapjai gyakorlat 2. gyakorlat C alapok 2016-2017 Bordé Sándor 2 Forráskód, fordító, futtatható állomány Először megírjuk a programunk kódját (forráskód) Egyszerű szövegszerkesztőben vagy fejlesztőkörnyezettel
Programozás alapjai gyakorlat 2. gyakorlat C alapok 2016-2017 Bordé Sándor 2 Forráskód, fordító, futtatható állomány Először megírjuk a programunk kódját (forráskód) Egyszerű szövegszerkesztőben vagy fejlesztőkörnyezettel
Hibadetektáló és javító kódolások
 Hibadetektáló és javító kódolások Számítógépes adatbiztonság Hibadetektálás és javítás Zajos csatornák ARQ adatblokk meghibásodási valószínségének csökkentése blokk bvítése redundáns információval Hálózati
Hibadetektáló és javító kódolások Számítógépes adatbiztonság Hibadetektálás és javítás Zajos csatornák ARQ adatblokk meghibásodási valószínségének csökkentése blokk bvítése redundáns információval Hálózati
Számítógépes hálózatok
 Számítógépes hálózatok 3.gyakorlat Fizikai réteg Kódolások, moduláció, CDMA Laki Sándor lakis@inf.elte.hu http://lakis.web.elte.hu 1 Második házi feladat 2 AM és FM analóg jel modulációja esetén Forrás:
Számítógépes hálózatok 3.gyakorlat Fizikai réteg Kódolások, moduláció, CDMA Laki Sándor lakis@inf.elte.hu http://lakis.web.elte.hu 1 Második házi feladat 2 AM és FM analóg jel modulációja esetén Forrás:
Szoftvertervezés és -fejlesztés I.
 Szoftvertervezés és -fejlesztés I. Operátorok Vezérlési szerkezetek Gyakorlás 1 Hallgatói Tájékoztató A jelen bemutatóban található adatok, tudnivalók és információk a számonkérendő anyag vázlatát képezik.
Szoftvertervezés és -fejlesztés I. Operátorok Vezérlési szerkezetek Gyakorlás 1 Hallgatói Tájékoztató A jelen bemutatóban található adatok, tudnivalók és információk a számonkérendő anyag vázlatát képezik.
2018, Diszkre t matematika. 8. elo ada s
 Diszkre t matematika 8. elo ada s MA RTON Gyo ngyve r mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tansze k Marosva sa rhely, Roma nia 2018, o szi fe le v MA RTON Gyo ngyve r 2018,
Diszkre t matematika 8. elo ada s MA RTON Gyo ngyve r mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tansze k Marosva sa rhely, Roma nia 2018, o szi fe le v MA RTON Gyo ngyve r 2018,
Számítógépes Hálózatok. 3. gyakorlat
 Számítógépes Hálózatok 3. gyakorlat Áramkörkapcsolt hálózatok ÓRAI FELADAT (1 PONT) Számítógépes Hálózatok Gyakorlat 2 Topológia cs1.json D A S1 S4 C B S2 S3 Irányítatlan legyen a gráf!!! Számítógépes
Számítógépes Hálózatok 3. gyakorlat Áramkörkapcsolt hálózatok ÓRAI FELADAT (1 PONT) Számítógépes Hálózatok Gyakorlat 2 Topológia cs1.json D A S1 S4 C B S2 S3 Irányítatlan legyen a gráf!!! Számítógépes
2018, Diszkre t matematika. 10. elo ada s
 Diszkre t matematika 10. elo ada s MA RTON Gyo ngyve r mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tansze k Marosva sa rhely, Roma nia 2018, o szi fe le v MA RTON Gyo ngyve r 2018,
Diszkre t matematika 10. elo ada s MA RTON Gyo ngyve r mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tansze k Marosva sa rhely, Roma nia 2018, o szi fe le v MA RTON Gyo ngyve r 2018,
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 3. estis képzés 2016. ősz 1. Diszkrét matematika 3. estis képzés 4. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2016. ősz 1. Diszkrét matematika 3. estis képzés 4. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Algoritmuselmélet gyakorlat (MMN111G)
 Algoritmuselmélet gyakorlat (MMN111G) 2014. január 14. 1. Gyakorlat 1.1. Feladat. Adott K testre rendre K[x] és K(x) jelöli a K feletti polinomok és racionális törtfüggvények halmazát. Mutassuk meg, hogy
Algoritmuselmélet gyakorlat (MMN111G) 2014. január 14. 1. Gyakorlat 1.1. Feladat. Adott K testre rendre K[x] és K(x) jelöli a K feletti polinomok és racionális törtfüggvények halmazát. Mutassuk meg, hogy
Véges állapotú gépek (FSM) tervezése
 Véges állapotú gépek (FSM) tervezése F1. A 2. gyakorlaton foglalkoztunk a 3-mal vagy 5-tel osztható 4 bites számok felismerésével. Abban a feladatban a bemenet bitpárhuzamosan, azaz egy időben minden adatbit
Véges állapotú gépek (FSM) tervezése F1. A 2. gyakorlaton foglalkoztunk a 3-mal vagy 5-tel osztható 4 bites számok felismerésével. Abban a feladatban a bemenet bitpárhuzamosan, azaz egy időben minden adatbit
Tűzfalak működése és összehasonlításuk
 Tűzfalak működése és összehasonlításuk Készítette Sári Zoltán YF5D3E Óbudai Egyetem Neumann János Informatikai Kar 1 1. Bevezetés A tűzfalak fejlődése a számítógépes hálózatok evolúciójával párhuzamosan,
Tűzfalak működése és összehasonlításuk Készítette Sári Zoltán YF5D3E Óbudai Egyetem Neumann János Informatikai Kar 1 1. Bevezetés A tűzfalak fejlődése a számítógépes hálózatok evolúciójával párhuzamosan,
SZÁMÉRTÉKEK (ÁT)KÓDOLÁSA
 1 ELSŐ GYAKORLAT SZÁMÉRTÉKEK (ÁT)KÓDOLÁSA A feladat elvégzése során a következőket fogjuk gyakorolni: Számrendszerek közti átváltás előjelesen és előjel nélkül. Bináris, decimális, hexadexcimális számrendszer.
1 ELSŐ GYAKORLAT SZÁMÉRTÉKEK (ÁT)KÓDOLÁSA A feladat elvégzése során a következőket fogjuk gyakorolni: Számrendszerek közti átváltás előjelesen és előjel nélkül. Bináris, decimális, hexadexcimális számrendszer.
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 8. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Elemi számelmélet Diszkrét matematika I. középszint
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 8. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Elemi számelmélet Diszkrét matematika I. középszint
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 8. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 8. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Minden egész szám osztója önmagának, azaz a a minden egész a-ra.
 1. Számelmélet Definíció: Az a egész szám osztója a egész számnak, ha létezik olyan c egész szám, melyre = ac. Ezt a következőképpen jelöljük: a Tulajdonságok: Minden egész szám osztója önmagának, azaz
1. Számelmélet Definíció: Az a egész szám osztója a egész számnak, ha létezik olyan c egész szám, melyre = ac. Ezt a következőképpen jelöljük: a Tulajdonságok: Minden egész szám osztója önmagának, azaz
7. Adatkapcsolati réteg
 7. Adatkapcsolati réteg A fejezet tárgya a megbízható, hatékony kommunikáció megvalósítása két szomszédos gép között. Az alapvető követelmény az, hogy a továbbított bitek helyesen, s a küldés sorrendjében
7. Adatkapcsolati réteg A fejezet tárgya a megbízható, hatékony kommunikáció megvalósítása két szomszédos gép között. Az alapvető követelmény az, hogy a továbbított bitek helyesen, s a küldés sorrendjében
URL-LEL ADOTT OBJEKTUM LETÖLTÉSE (1) URL-LEL ADOTT OBJEKTUM LETÖLTÉSE
 Programozás III HÁLÓZATKEZELÉS A hálózatkezeléshez használatos java csomag: java. net Hol találkoztunk már vele? Pl.: URL cim = this.getclass().getresource("/zene/valami_zene.wav"); De pl. adott URL-ről
Programozás III HÁLÓZATKEZELÉS A hálózatkezeléshez használatos java csomag: java. net Hol találkoztunk már vele? Pl.: URL cim = this.getclass().getresource("/zene/valami_zene.wav"); De pl. adott URL-ről
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. estis képzés 017. ősz 1. Diszkrét matematika 1. estis képzés 4. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
Diszkrét matematika 1. estis képzés 017. ősz 1. Diszkrét matematika 1. estis képzés 4. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Számelmélet I.
 Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
2018, Diszkrét matematika
 Diszkrét matematika 7. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia 2018, őszi félév Miről volt szó az elmúlt előadáson? számrendszerek számrendszerek
Diszkrét matematika 7. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia 2018, őszi félév Miről volt szó az elmúlt előadáson? számrendszerek számrendszerek
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 3. estis képzés 2016. ősz 1. Diszkrét matematika 3. estis képzés 4. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2016. ősz 1. Diszkrét matematika 3. estis képzés 4. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Segédlet az Informatika alapjai I. című tárgy számrendszerek fejezetéhez
 Segédlet az Informatika alapjai I. című tárgy számrendszerek fejezetéhez Sándor Tamás, sandor.tamas@kvk.bmf.hu Takács Gergely, takacs.gergo@kvk.bmf.hu Lektorálta: dr. Schuster György PhD, hal@k2.jozsef.kando.hu
Segédlet az Informatika alapjai I. című tárgy számrendszerek fejezetéhez Sándor Tamás, sandor.tamas@kvk.bmf.hu Takács Gergely, takacs.gergo@kvk.bmf.hu Lektorálta: dr. Schuster György PhD, hal@k2.jozsef.kando.hu
1. A polinom fogalma. Számolás formális kifejezésekkel. Feladat Oldjuk meg az x2 + x + 1 x + 1. = x egyenletet.
 1. A polinom fogalma Számolás formális kifejezésekkel. Feladat Oldjuk meg az x2 + x + 1 x + 1 = x egyenletet. Megoldás x + 1-gyel átszorozva x 2 + x + 1 = x 2 + x. Innen 1 = 0. Ez ellentmondás, így az
1. A polinom fogalma Számolás formális kifejezésekkel. Feladat Oldjuk meg az x2 + x + 1 x + 1 = x egyenletet. Megoldás x + 1-gyel átszorozva x 2 + x + 1 = x 2 + x. Innen 1 = 0. Ez ellentmondás, így az
Laborgyakorlat Logikai áramkörök számítógéppel segített tervezése (CAD)
 Laborgyakorlat Logikai áramkörök számítógéppel segített tervezése (CAD) Bevezetés A laborgyakorlatok alapvető célja a tárgy későbbi laborgyakorlataihoz szükséges ismeretek átadása, az azokban szereplő
Laborgyakorlat Logikai áramkörök számítógéppel segített tervezése (CAD) Bevezetés A laborgyakorlatok alapvető célja a tárgy későbbi laborgyakorlataihoz szükséges ismeretek átadása, az azokban szereplő
Számítógépes hálózatok
 Számítógépes hálózatok HETEDIK ELŐADÁS SOCKET programozás C/C++ nyelven AZ ELŐADÁS DIÁKAT KÉSZÍTETTE: ÁCS ZOLTÁN Hálózati programozás bevezetés Általában egy klasszikus hálózati alkalmazás két fő részre
Számítógépes hálózatok HETEDIK ELŐADÁS SOCKET programozás C/C++ nyelven AZ ELŐADÁS DIÁKAT KÉSZÍTETTE: ÁCS ZOLTÁN Hálózati programozás bevezetés Általában egy klasszikus hálózati alkalmazás két fő részre
Hibajavítás, -jelzés. Informatikai rendszerek alapjai. Horváth Árpád november 24.
 Hibajavítás és hibajelzés Informatikai rendszerek alapjai Óbudai Egyetem Alba Regia M szaki Kar (AMK) Székesfehérvár 2016. november 24. Vázlat 1 Hibákról 2 Információátvitel diagrammja forrás csatorna
Hibajavítás és hibajelzés Informatikai rendszerek alapjai Óbudai Egyetem Alba Regia M szaki Kar (AMK) Székesfehérvár 2016. november 24. Vázlat 1 Hibákról 2 Információátvitel diagrammja forrás csatorna
Intergrált Intenzív Matematika Érettségi
 . Adott a mátri, determináns determináns, ahol,, d Számítsd ki:. b) Igazold, hogy a b c. Adott a az 6 0 egyenlet megoldásai. a). c) Számítsd ki a d determináns értékét. d c a b determináns, ahol abc,,.
. Adott a mátri, determináns determináns, ahol,, d Számítsd ki:. b) Igazold, hogy a b c. Adott a az 6 0 egyenlet megoldásai. a). c) Számítsd ki a d determináns értékét. d c a b determináns, ahol abc,,.
Gyakorló feladatok. /2 Maradék /16 Maradék /8 Maradék
 Gyakorló feladatok Számrendszerek: Feladat: Ábrázold kettes számrendszerbe a 639 10, 16-os számrendszerbe a 311 10, 8-as számrendszerbe a 483 10 számot! /2 Maradék /16 Maradék /8 Maradék 639 1 311 7 483
Gyakorló feladatok Számrendszerek: Feladat: Ábrázold kettes számrendszerbe a 639 10, 16-os számrendszerbe a 311 10, 8-as számrendszerbe a 483 10 számot! /2 Maradék /16 Maradék /8 Maradék 639 1 311 7 483
1. Kombinációs hálózatok mérési gyakorlatai
 1. Kombinációs hálózatok mérési gyakorlatai 1.1 Logikai alapkapuk vizsgálata A XILINX ISE DESIGN SUITE 14.7 WebPack fejlesztőrendszer segítségével és töltse be a rendelkezésére álló SPARTAN 3E FPGA ba:
1. Kombinációs hálózatok mérési gyakorlatai 1.1 Logikai alapkapuk vizsgálata A XILINX ISE DESIGN SUITE 14.7 WebPack fejlesztőrendszer segítségével és töltse be a rendelkezésére álló SPARTAN 3E FPGA ba:
Hatványozás. A hatványozás azonosságai
 Hatványozás Definíció: a 0 = 1, ahol a R, azaz bármely szám nulladik hatványa mindig 1. a 1 = a, ahol a R, azaz bármely szám első hatványa önmaga a n = a a a, ahol a R, n N + n darab 3 4 = 3 3 3 3 = 84
Hatványozás Definíció: a 0 = 1, ahol a R, azaz bármely szám nulladik hatványa mindig 1. a 1 = a, ahol a R, azaz bármely szám első hatványa önmaga a n = a a a, ahol a R, n N + n darab 3 4 = 3 3 3 3 = 84
Számítógépes hálózatok
 Számítógépes hálózatok Harmadik gyakorlat forgalomszűrés, DNS, HTTP forgalom elemzés Előadó: Ács Zoltán Hálózati forgalom elemzése 1/3 Különböző célok miatt szükség lehet a hálózati forgalom megfigyelésére
Számítógépes hálózatok Harmadik gyakorlat forgalomszűrés, DNS, HTTP forgalom elemzés Előadó: Ács Zoltán Hálózati forgalom elemzése 1/3 Különböző célok miatt szükség lehet a hálózati forgalom megfigyelésére
Adatbiztonság PPZH 2011. május 20.
 Adatbiztonság PPZH 2011. május 20. 1. Mutassa meg, hogy a CBC-MAC kulcsolt hashing nem teljesíti az egyirányúság követelményét egy a k kulcsot ismerő fél számára, azaz tetszőleges MAC ellenőrzőösszeghez
Adatbiztonság PPZH 2011. május 20. 1. Mutassa meg, hogy a CBC-MAC kulcsolt hashing nem teljesíti az egyirányúság követelményét egy a k kulcsot ismerő fél számára, azaz tetszőleges MAC ellenőrzőösszeghez
Programozás alapjai gyakorlat. 4. gyakorlat Konstansok, tömbök, stringek
 Programozás alapjai gyakorlat 4. gyakorlat Konstansok, tömbök, stringek Házi ellenőrzés (f0069) Valósítsd meg a linuxos seq parancs egy egyszerűbb változatát, ami beolvas két egész számot, majd a kettő
Programozás alapjai gyakorlat 4. gyakorlat Konstansok, tömbök, stringek Házi ellenőrzés (f0069) Valósítsd meg a linuxos seq parancs egy egyszerűbb változatát, ami beolvas két egész számot, majd a kettő
Számrendszerek. A római számok írására csak hét jelt használtak. Ezek segítségével, jól meghatározott szabályok szerint képezték a különböz számokat.
 Számrendszerek A római számok írására csak hét jelt használtak Ezek segítségével, jól meghatározott szabályok szerint képezték a különböz számokat Római számjegyek I V X L C D M E számok értéke 1 5 10
Számrendszerek A római számok írására csak hét jelt használtak Ezek segítségével, jól meghatározott szabályok szerint képezték a különböz számokat Római számjegyek I V X L C D M E számok értéke 1 5 10
Bérprogram vásárlásakor az Ügyfélnek e-mailben és levélben is megküldjük a termék letöltéséhez és aktiválásához szükséges termékszámot.
 Telepítés Bérprogram vásárlásakor az Ügyfélnek e-mailben és levélben is megküldjük a termék letöltéséhez és aktiválásához szükséges termékszámot. A programot honlapunkról, az alábbi linkről tudják letölteni:
Telepítés Bérprogram vásárlásakor az Ügyfélnek e-mailben és levélben is megküldjük a termék letöltéséhez és aktiválásához szükséges termékszámot. A programot honlapunkról, az alábbi linkről tudják letölteni:
A függvény kód szekvenciáját kapcsos zárójelek közt definiáljuk, a { } -ek közti részt a Bash héj kód blokknak (code block) nevezi.
 Függvények 1.Függvények...1 1.1.A függvény deníció szintaxisa... 1..Függvények érték visszatérítése...3 1.3.Környezettel kapcsolatos kérdések...4 1.4.Lokális változók használata...4 1.5.Rekurzív hívások...5.kód
Függvények 1.Függvények...1 1.1.A függvény deníció szintaxisa... 1..Függvények érték visszatérítése...3 1.3.Környezettel kapcsolatos kérdések...4 1.4.Lokális változók használata...4 1.5.Rekurzív hívások...5.kód
Információk. Ismétlés II. Ismétlés. Ismétlés III. A PROGRAMOZÁS ALAPJAI 2. Készítette: Vénné Meskó Katalin. Algoritmus. Algoritmus ábrázolása
 1 Információk 2 A PROGRAMOZÁS ALAPJAI 2. Készítette: Vénné Meskó Katalin Elérhetőség mesko.katalin@tfk.kefo.hu Fogadóóra: szerda 9:50-10:35 Számonkérés időpontok Április 25. 9 00 Május 17. 9 00 Június
1 Információk 2 A PROGRAMOZÁS ALAPJAI 2. Készítette: Vénné Meskó Katalin Elérhetőség mesko.katalin@tfk.kefo.hu Fogadóóra: szerda 9:50-10:35 Számonkérés időpontok Április 25. 9 00 Május 17. 9 00 Június
Bevezető. PoC kit felépítése. NX appliance. SPAN-Proxy
 Bevezető A dokumentum célja összefoglalni a szükséges technikai előkészületeket a FireEye PoC előtt, hogy az sikeresen végig mehessen. PoC kit felépítése A FireEye PoC kit 3 appliance-t tartalmaz: NX series:
Bevezető A dokumentum célja összefoglalni a szükséges technikai előkészületeket a FireEye PoC előtt, hogy az sikeresen végig mehessen. PoC kit felépítése A FireEye PoC kit 3 appliance-t tartalmaz: NX series:
Hálózati architektúrák laborgyakorlat
 Hálózati architektúrák laborgyakorlat 10. hét Dr. Orosz Péter, Skopkó Tamás 2012. szeptember A Unix (C) socket A kommunikációt lehetővé tevő programozási eszköz UNIX fájlleíró (ld. minden egy fájl filozófia)
Hálózati architektúrák laborgyakorlat 10. hét Dr. Orosz Péter, Skopkó Tamás 2012. szeptember A Unix (C) socket A kommunikációt lehetővé tevő programozási eszköz UNIX fájlleíró (ld. minden egy fájl filozófia)
Socket programozás Példák
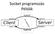 Socket programozás Példák Áttekintés Client Server socket socket bind connect Connection request listen accept Client / Server Session write read read write close EOF read close 3 Select demo Beej s guide
Socket programozás Példák Áttekintés Client Server socket socket bind connect Connection request listen accept Client / Server Session write read read write close EOF read close 3 Select demo Beej s guide
Sapientia Egyetem, Műszaki és Humántudományok Tanszék. mgyongyi@ms.sapientia.ro
 Kriptográfia és Információbiztonság 4. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2015 Miről volt szó az elmúlt előadáson? blokk-titkosító
Kriptográfia és Információbiztonság 4. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2015 Miről volt szó az elmúlt előadáson? blokk-titkosító
Véges állapotú gépek (FSM) tervezése
 Véges állapotú gépek (FSM) tervezése F1. Tervezzünk egy soros mintafelismerőt, ami a bemenetére ciklikusan, sorosan érkező 4 bites számok közül felismeri azokat, amelyek 3-mal vagy 5-tel oszthatók. A fenti
Véges állapotú gépek (FSM) tervezése F1. Tervezzünk egy soros mintafelismerőt, ami a bemenetére ciklikusan, sorosan érkező 4 bites számok közül felismeri azokat, amelyek 3-mal vagy 5-tel oszthatók. A fenti
Easton420. Automata Telefon hangrögzítő. V 6.0 Telepítése Windows XP rendszerre
 Easton420 Automata Telefon hangrögzítő V 6.0 Telepítése Windows XP rendszerre A mellékelt telepítő CD-t helyezze a számítógép lemez olvasó egységbe, várja meg az automatikus indítási képernyőt. Majd válassza
Easton420 Automata Telefon hangrögzítő V 6.0 Telepítése Windows XP rendszerre A mellékelt telepítő CD-t helyezze a számítógép lemez olvasó egységbe, várja meg az automatikus indítási képernyőt. Majd válassza
Diszkrét matematika 2.
 Diszkrét matematika 2. A szakirány 11. előadás Ligeti Péter turul@cs.elte.hu www.cs.elte.hu/ turul Nagy hálózatok Nagy hálózatok jellemzése Internet, kapcsolati hálók, biológiai hálózatok,... globális
Diszkrét matematika 2. A szakirány 11. előadás Ligeti Péter turul@cs.elte.hu www.cs.elte.hu/ turul Nagy hálózatok Nagy hálózatok jellemzése Internet, kapcsolati hálók, biológiai hálózatok,... globális
Raszteres elemzés végrehajtása QGIS GRASS moduljával 1.7 dr. Siki Zoltán
 Raszteres elemzés végrehajtása QGIS GRASS moduljával 1.7 dr. Siki Zoltán Egy mintapéldán keresztül mutatjuk be a GRASS raszteres elemzési műveleteit. Az elemzési mintafeladat során gumipitypang termesztésére
Raszteres elemzés végrehajtása QGIS GRASS moduljával 1.7 dr. Siki Zoltán Egy mintapéldán keresztül mutatjuk be a GRASS raszteres elemzési műveleteit. Az elemzési mintafeladat során gumipitypang termesztésére
Bevezetés a Python programozási nyelvbe
 Bevezetés a Python programozási nyelvbe 8. Gyakorlat modulok random számok (utolsó módosítás: 2017. aug. 3.) Szathmáry László Debreceni Egyetem Informatikai Kar 2017-2018, 1. félév Modulok Amint a programunk
Bevezetés a Python programozási nyelvbe 8. Gyakorlat modulok random számok (utolsó módosítás: 2017. aug. 3.) Szathmáry László Debreceni Egyetem Informatikai Kar 2017-2018, 1. félév Modulok Amint a programunk
Titkosítás NetWare környezetben
 1 Nyílt kulcsú titkosítás titkos nyilvános nyilvános titkos kulcs kulcs kulcs kulcs Nyilvános, bárki által hozzáférhető csatorna Nyílt szöveg C k (m) Titkosított szöveg Titkosított szöveg D k (M) Nyílt
1 Nyílt kulcsú titkosítás titkos nyilvános nyilvános titkos kulcs kulcs kulcs kulcs Nyilvános, bárki által hozzáférhető csatorna Nyílt szöveg C k (m) Titkosított szöveg Titkosított szöveg D k (M) Nyílt
Általános e-mail fiók beállítási útmutató
 Általános e-mail fiók beállítási útmutató Ennek az összeállításnak az a célja, hogy segítséget nyújtsunk azon Ügyfeleink számára, akik az IntroWeb Kft. által nyújtott e-mail szolgáltatáshoz be szeretnék
Általános e-mail fiók beállítási útmutató Ennek az összeállításnak az a célja, hogy segítséget nyújtsunk azon Ügyfeleink számára, akik az IntroWeb Kft. által nyújtott e-mail szolgáltatáshoz be szeretnék
DIGITÁLIS TECHNIKA feladatgyűjtemény
 IGITÁLIS TEHNIK feladatgyűjtemény Írta: r. Sárosi József álint Ádám János Szegedi Tudományegyetem Mérnöki Kar Műszaki Intézet Szerkesztette: r. Sárosi József Lektorálta: r. Gogolák László Szabadkai Műszaki
IGITÁLIS TEHNIK feladatgyűjtemény Írta: r. Sárosi József álint Ádám János Szegedi Tudományegyetem Mérnöki Kar Műszaki Intézet Szerkesztette: r. Sárosi József Lektorálta: r. Gogolák László Szabadkai Műszaki
FFT. Második nekifutás. Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék október 2.
 TARTALOMJEGYZÉK Polinomok konvolúviója A DFT és a maradékos osztás Gyűrűk támogatás nélkül Második nekifutás Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2015. október 2. TARTALOMJEGYZÉK Polinomok
TARTALOMJEGYZÉK Polinomok konvolúviója A DFT és a maradékos osztás Gyűrűk támogatás nélkül Második nekifutás Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2015. október 2. TARTALOMJEGYZÉK Polinomok
Waldhauser Tamás december 1.
 Algebra és számelmélet előadás Waldhauser Tamás 2016. december 1. Tizedik házi feladat az előadásra Hányféleképpen lehet kiszínezni az X-pentominót n színnel, ha a forgatással vagy tükrözéssel egymásba
Algebra és számelmélet előadás Waldhauser Tamás 2016. december 1. Tizedik házi feladat az előadásra Hányféleképpen lehet kiszínezni az X-pentominót n színnel, ha a forgatással vagy tükrözéssel egymásba
4. Hivatkozási modellek
 4. Hivatkozási modellek Az előző fejezetben megismerkedtünk a rétegekbe szervezett számítógépes hálózatokkal, s itt az ideje, hogy megemlítsünk néhány példát is. A következő részben két fontos hálózati
4. Hivatkozási modellek Az előző fejezetben megismerkedtünk a rétegekbe szervezett számítógépes hálózatokkal, s itt az ideje, hogy megemlítsünk néhány példát is. A következő részben két fontos hálózati
OSZTHATÓSÁG. Osztók és többszörösök : a 3 többszörösei : a 4 többszörösei Ahol mindkét jel megtalálható a 12 többszöröseit találjuk.
 Osztók és többszörösök 1783. A megadott számok elsõ tíz többszöröse: 3: 3 6 9 12 15 18 21 24 27 30 4: 4 8 12 16 20 24 28 32 36 40 5: 5 10 15 20 25 30 35 40 45 50 6: 6 12 18 24 30 36 42 48 54 60 1784. :
Osztók és többszörösök 1783. A megadott számok elsõ tíz többszöröse: 3: 3 6 9 12 15 18 21 24 27 30 4: 4 8 12 16 20 24 28 32 36 40 5: 5 10 15 20 25 30 35 40 45 50 6: 6 12 18 24 30 36 42 48 54 60 1784. :
RSA algoritmus. Smidla József. Rendszer- és Számítástudományi Tanszék Pannon Egyetem
 RSA algoritmus Smidla József Rendszer- és Számítástudományi Tanszék Pannon Egyetem 2012. 3. 27. Smidla József (RSZT) RSA algoritmus 2012. 3. 27. 1 / 29 Tartalom 1 Aszimmetrikus kódolók 2 Matematikai alapok
RSA algoritmus Smidla József Rendszer- és Számítástudományi Tanszék Pannon Egyetem 2012. 3. 27. Smidla József (RSZT) RSA algoritmus 2012. 3. 27. 1 / 29 Tartalom 1 Aszimmetrikus kódolók 2 Matematikai alapok
Programozás alapjai. 6. gyakorlat Futásidő, rekurzió, feladatmegoldás
 Programozás alapjai 6. gyakorlat Futásidő, rekurzió, feladatmegoldás Háziellenőrzés Egészítsd ki úgy a simplemaths.c programot, hogy megfelelően működjön. A program feladata az inputon soronként megadott
Programozás alapjai 6. gyakorlat Futásidő, rekurzió, feladatmegoldás Háziellenőrzés Egészítsd ki úgy a simplemaths.c programot, hogy megfelelően működjön. A program feladata az inputon soronként megadott
Számelmélet (2017. február 8.) Bogya Norbert, Kátai-Urbán Kamilla
 Számelmélet (2017 február 8) Bogya Norbert, Kátai-Urbán Kamilla 1 Oszthatóság 1 Definíció Legyen a, b Z Az a osztója b-nek, ha létezik olyan c Z egész szám, melyre ac = b Jelölése: a b 2 Példa 3 12, 2
Számelmélet (2017 február 8) Bogya Norbert, Kátai-Urbán Kamilla 1 Oszthatóság 1 Definíció Legyen a, b Z Az a osztója b-nek, ha létezik olyan c Z egész szám, melyre ac = b Jelölése: a b 2 Példa 3 12, 2
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. estis képzés 2017. ősz 1. Diszkrét matematika 1. estis képzés 9. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
Diszkrét matematika 1. estis képzés 2017. ősz 1. Diszkrét matematika 1. estis képzés 9. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
Sapientia Egyetem, Matematika-Informatika Tanszék.
 Kriptográfia és Információbiztonság 7. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018 Miről volt szó az elmúlt előadáson? Kriptográfiai
Kriptográfia és Információbiztonság 7. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018 Miről volt szó az elmúlt előadáson? Kriptográfiai
Komputeralgebrai Algoritmusok
 Komputeralgebrai Algoritmusok Adatábrázolás Czirbusz Sándor, Komputeralgebra Tanszék 2015-2016 Ősz Többszörös pontosságú egészek Helyiértékes tárolás: l 1 s d i B i i=0 ahol B a számrendszer alapszáma,
Komputeralgebrai Algoritmusok Adatábrázolás Czirbusz Sándor, Komputeralgebra Tanszék 2015-2016 Ősz Többszörös pontosságú egészek Helyiértékes tárolás: l 1 s d i B i i=0 ahol B a számrendszer alapszáma,
Digitális technika VIMIAA hét
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK VIMIAA02 14. hét Fehér Béla BME MIT Rövid visszatekintés, összefoglaló
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK VIMIAA02 14. hét Fehér Béla BME MIT Rövid visszatekintés, összefoglaló
