BALOG DÓRA TŐKEALLOKÁCIÓ A BIZTOSÍTÁSI SZEKTORBAN, ELMÉLETI ÉS GYAKORLATI MEGKÖZELÍTÉSBEN
|
|
|
- Csongor Fülöp
- 6 évvel ezelőtt
- Látták:
Átírás
1 BALOG DÓRA TŐKEALLOKÁCIÓ A BIZTOSÍTÁSI SZEKTORBAN, ELMÉLETI ÉS GYAKORLATI MEGKÖZELÍTÉSBEN
2 Befektetések és Vállalati Pénzügy Tanszék Témavezető: Csóka Péter, PhD Copyright Balog Dóra
3 BUDAPESTI CORVINUS EGYETEM ÁLTALÁNOS ÉS KVANTITATÍV KÖZGAZDASÁGTAN DOKTORI ISKOLA TŐKEALLOKÁCIÓ A BIZTOSÍTÁSI SZEKTORBAN, ELMÉLETI ÉS GYAKORLATI MEGKÖZELÍTÉSBEN DOKTORI ÉRTEKEZÉS BALOG DÓRA BARBARA Budapest, 2018
4 TARTALOMJEGYZÉK Tartalomjegyzék... 4 Táblázatok jegyzéke... 7 Ábrajegyzék... 9 Bevezetés rész: Tőke, kockázatmérés A kockázat mérése Az alkalmazott jelölések Koherens kockázatmérés A leggyakrabban alkalmazott kockázatmértékek Tőkekövetelmény és tőkefogalmak a biztosítási szektorban Szabályozói tőkekövetelmény Szolvencia II Gazdasági tőkeszükséglet Költségjátékok kooperatív játékelméleti kitérő rész: A tőkeallokáció elméleti modellje: az alkalmazható módszerek összehasonlítása A tőkeallokációs probléma, jelölések A hét módszer analitikus elemzésének eredményei Egyéni kockázattal arányos módszer
5 2.2.2 Béta módszer Növekményi módszer Költségrés módszer Marginális kockázati hozzájárulás Shapley-módszer Nukleolusz módszer Az analitikus eredmények összegzése Szimulációs eredmények a magkompatibilitás ellenőrzésére Következtetések rész: A tőkeallokáció gyakorlati alkalmazása Miért a tőkeallokáció különböző alkalmazásai Teljesítményértékelés Stratégiai döntések Árazás Milyen típusú tőkét allokálunk? Tőkefogalmak ismétlés Tőkefogalmak megfeleltetése Mi kerüljön szétosztásra? Milyen egységekre irányul a tőke szétosztása? Az allokációs módszer kiválasztása Az alkalmazható módszerek csoportosítása Módszerválasztás az alkalmazás függvényében
6 3.5 Következtetések rész: Esettanulmány Teljesítményértékelés az ABC Biztosító Zrt-nél A modell felépítése Gépjármű felelősségbiztosítás Lakásbiztosítás Szakmai felelősségbiztosítás Befektetések Kockázat- és tőkekövetelmény számítás Tőkeallokáció és teljesítményértékelés Nettó eredmények Tőkeallokáció A teljesítményértékelés Összegzés Mellékletek Felhasznált irodalom Publikációs jegyzék
7 TÁBLÁZATOK JEGYZÉKE 1. TÁBLÁZAT: A SZÓRÁS NEM KOHERENS TÁBLÁZAT: A VAR NEM KOHERENS TÁBLÁZAT: AZ EXPECTED SHORTFALL ÉS A FELTÉTELES VAR ELTÉRÉSE DISZKRÉT ESET TÁBLÁZAT: AZ XNΡ TŐKEALLOKÁCIÓS SZITUÁCIÓ TÁBLÁZAT: A PÉLDABELI KOCKÁZATI TŐKE ALLOKÁCIÓJA TÁBLÁZAT: AZ EGYÉNI KOCKÁZATTAL ARÁNYOS MÓDSZER NEM TELJESÍTI A DIVERZIFIKÁLÓ, MAGBELI, ÖSZTÖNZŐ, ERŐSEN MONOTON, KOCKÁZATMENTES ÉS KOVARIÁNS TULAJDONSÁGOKAT TÁBLÁZAT: AZ EGYÉNI KOCKÁZATTAL ARÁNYOS MÓDSZER NEM TELJESÍTI A DEKOMPOZÍCIÓ INVARIANCIA TULAJDONSÁGOT TÁBLÁZAT: A BÉTA MÓDSZER NEM TELJESÍTI A DIVERZIFIKÁLÓ, MAGBELI, ÖSZTÖNZŐ, ERŐSEN MONOTON, KOCKÁZATMENTES ÉS KOVARIÁNS TULAJDONSÁGOKAT TÁBLÁZAT: A NÖVEKMÉNYI MÓDSZER NEM TELJESÍTI AZ ÖSZTÖNZÉS ÉS ERŐS MONOTONITÁS TULAJDONSÁGOKAT TÁBLÁZAT: A NÖVEKMÉNYI MÓDSZER NEM TELJESÍTI A KOCKÁZATMENTES TULAJDONSÁGOT TÁBLÁZAT: A NÖVEKMÉNYI MÓDSZER NEM DEKOMPOZÍCIÓ INVARIÁNS TÁBLÁZAT: EGY XNΡ TŐKEALLOKÁCIÓS SZITUÁCIÓ, AHOL A KÖLTSÉGRÉS MÓDSZER NEM MAGBELI ALLOKÁCIÓT EREDMÉNYEZ TÁBLÁZAT: XNΡ ÉS YNΡ (ZÁRÓJELBEN) TŐKEALLOKÁCIÓS SZITUÁCIÓK, AHOL A KÖLTSÉGRÉS MÓDSZER NEM ÖSZTÖNZŐ TÁBLÁZAT: A KÖLTSÉGRÉS MÓDSZER NEM DEKOMPOZÍCIÓ INVARIÁNS TÁBLÁZAT. A MARGINÁLIS KOCKÁZATI HOZZÁJÁRULÁS IRÁNYMENTI DERIVÁLTKÉNT ÉRTELMEZVE NEM TELJESÍTI A HATÉKONY, DIVERZIFIKÁLÓ ÉS MAGBELI TULAJDONSÁGOKAT TÁBLÁZAT: XNΡ ÉS YNΡ TŐKEALLOKÁCIÓS SZITUÁCIÓK, MELYEKBEN A MARGINÁLIS KOCKÁZATI HOZZÁJÁRULÁS NEM ÖSZTÖNZŐ ÉS NEM ERŐSEN MONOTON TÁBLÁZAT: A SHAPLEY-MÓDSZER NEM MAGBELI ÉS NEM DEKOMPOZÍCIÓ INVARIÁNS TÁBLÁZAT: A NUKLEOLUSZ MÓDSZER NEM DEKOMPOZÍCIÓ INVARIÁNS TÁBLÁZAT: A VIZSGÁLT TŐKEALLOKÁCIÓS MÓDSZEREK TULAJDONSÁGAI TÁBLÁZAT: M-ARÁNYOK ÉS STANDARD HIBÁK AZONOS PORTFÓLIÓ MÉRET, NAGY SZÓRÁS, NORMÁLIS ELOSZLÁS ÉS 95%- EXPECTED SHORTFALL MELLETT TÁBLÁZAT: M-ARÁNYOK ÉS STANDARD HIBÁK AZONOS PORTFÓLIÓ MÉRET, NAGY SZÓRÁS, T-ELOSZLÁS ÉS 95%-EXPECTED SHORTFALL MELLETT 85 7
8 22. TÁBLÁZAT: M-ARÁNYOK ÉS STANDARD HIBÁK KÜLÖNBÖZŐ PORTFÓLIÓ MÉRET, NAGY SZÓRÁS, T-ELOSZLÁS ÉS 95%-EXPECTED SHORTFALL MELLETT TÁBLÁZAT: AZ EGYES ALKALMAZÁSOKHOZ JAVASOLT MÓDSZEREK ELŐNYEI ÉS HÁTRÁNYAI TÁBLÁZAT: AZ ABC ZRT. ÜZLETÁGAI ÁLTAL ELÉRT NETTÓ EREDMÉNY TÁBLÁZAT: AZ EGYES ÜZLETÁGAK ÉS A TELJES ABC ZRT. KOCKÁZATA (99% EXPECTED SHORTFALL) TÁBLÁZAT: A GAZDASÁGI TŐKE ALLOKÁCIÓJA 4 KÜLÖNBÖZŐ MÓDSZER SEGÍTSÉGÉVEL TÁBLÁZAT: A RORAC MUTATÓ ALAKULÁSA ÜZLETÁGANKÉNT TÁBLÁZAT: M-ARÁNYOK ÉS STANDARD HIBÁK AZONOS PORTFÓLIÓ MÉRET, KIS SZÓRÁS, NORMÁLIS ELOSZLÁS ÉS 95%-EXPECTED SHORTFALL MELLETT TÁBLÁZAT: M-ARÁNYOK ÉS STANDARD HIBÁK AZONOS PORTFÓLIÓ MÉRET, KIS SZÓRÁS, T-ELOSZLÁS ÉS MAXIMÁLIS VESZTESÉG MELLETT TÁBLÁZAT: M-ARÁNYOK ÉS STANDARD HIBÁK KÜLÖNBÖZŐ PORTFÓLIÓ MÉRET, KIS SZÓRÁS, T-ELOSZLÁS ÉS MAXIMÁLIS VESZTESÉG MELLETT TÁBLÁZAT: M-ARÁNYOK ÉS STANDARD HIBÁK AZONOS PORTFÓLIÓ MÉRET, NAGY SZÓRÁS, NORMÁLIS ELOSZLÁS ÉS 84,14% VAR MELLETT 134 8
9 ÁBRAJEGYZÉK 1. ÁBRA: AZ EXPECTED SHORTFALL ÉS A FELTÉTELES VAR SZÁMÍTÁSÁNAK KÜLÖNBSÉGE ÁBRA: A SZABÁLYOZÓI TŐKEKÖVETELMÉNY A SZOLVENCIA I ÉS II IRÁNYELVEK SZERINT ÁBRA: A VIZSGÁLT TULAJDONSÁGOK KÖZÖTTI ÖSSZEFÜGGÉS ÁBRA: A BIZTOSÍTÓ SEMATIKUS MÉRLEGE ÁBRA: AZ ABC ZRT. EGYES ÜZLETÁGAI ÁLTAL ELÉRT MŰKÖDÉSI EREDMÉNY ÁBRA: AZ ABC ZRT. ÉVES NETTÓ EREDMÉNYÉNEK ELOSZLÁSA ÉS KOCKÁZATA
10 BEVEZETÉS Disszertációm témája a pénzügyi szektorban alkalmazott belső tőkeallokáció. A tőkeallokáció a nem várt kockázatok fedezésére szükséges tőkének az egyes üzletágakra, portfólióelemekre, vagy más módon meghatározott egységekre való felosztásának folyamata. A tőkeallokáció gyakorlati oldalról való megközelítése során a pénzügyi vállalatokon belül a biztosítási szektorra koncentrálok, mivel leginkább ebben a szektorban alkalmaznak szofisztikált tőkeallokációs módszereket. A különböző biztosítási események bekövetkezése sztochasztikus, így a legfejlettebb statisztikai módszerek alkalmazása esetén is előfordulhat, hogy a beszedett díjak és a tartalékok nem fedezik a biztosítóval szembeni követeléseket. Ilyen esetekben a szavatoló tőke biztosítja, hogy a biztosító továbbra is eleget tudjon tenni kötelezettségeinek. Máshogy fogalmazva a szavatoló tőke az események nem várt, kedvezőtlen alakulása esetén felmerülő veszteségek fedezésére szolgál. Bár e szavatoló tőke egyaránt védelmet nyújt bármely üzletág által elszenvedett veszteséggel szemben, számos okból fontos mégis tudni, hogy az egyes üzletágak milyen mértékben járulnak hozzá a biztosító tőkeigényéhez. Tőkét tartani költséges, e költségnek az allokálása pedig igen fontos tényező az üzletágak és egyes termékportfóliók teljesítményének értékelése, termékárazási és bizonyos stratégiai döntések (felvásárlások, összeolvadások, új üzletág indítása, vagy meglévő megszüntetése) során. A biztosítótársaságok jellemzően üzletágakra, leányvállalatokra, termékekre vagy termékcsoportokra allokálják a tőkéjüket, de találkozhatunk különböző földrajzi régiókra, vagy akár értékesítési csatornákra történő felosztással is. 10
11 A probléma nem új keletű, különösen aktuálissá teszi azonban a biztosítótársaságok esetében nemrég, január 1-gyel életbe lépett Szolvencia II 1 direktíva. Az irányelv első pillére a tőke és tőkeszükséglet számítására hoz új szabályokat (így megváltozhat maga az allokálandó tőke mennyisége). A második pillérben előírt saját kockázat és szavatolótőke értékelés (a továbbiakban ORSA, Own Risk and Solvency Assessment) folyamat keretében pedig maga a tőkeallokációs folyamat is a szabályozó ellenőrzése alá kerül (az integrált vállalati kockázatkezelési rendszerre vonatkozó elvárásokon keresztül). Maume-Deschamps et al. (2016) tanulmányát idézve: A második pillér ORSA gyakorlata a tőkeallokációt fontos kérdéssé teszi minden biztosító számára [ ]. Az integrált vállalati kockázatkezelési rendszerek 2 (Enterprise Risk Management, ERM) fejlesztése a biztosítók számára nem csak a Szolvencia II előírásai miatt kiemelten fontos feladat. Ahogyan arra a McKinsey felhívja a figyelmet (Bongiovanni et al., 2016), a fejlettebb vállalati kockázatkezelési rendszerrel rendelkező biztosítók szignifikánsan jobban teljesítettek társaiknál a válság (2008 és 2009) során. Ezt felismerve maguk a biztosítók is jelentős erőforrásokat kezdtek áldozni ERM rendszereik fejlesztésére, melyeknek pedig fontos alkotóeleme a tőkeallokáció, hiszen a teljesítményértékelésen keresztül a biztosító egy-egy üzletága (leányvállalata, portfóliója) által elért hozamot (ami az üzlet jövedelmezőségét jellemzi) veti össze az adott egységre allokált tőkekövetelménnyel (ami pedig egy fontos kockázati mutató). A biztosítási szektorban tehát a Szolvencia II szabályozás bevezetésével párhuzamosan a tőkeallokáció egyre nagyobb szerephez jut napjainkban Európában, miközben az USA-ban a szabályozó hatóság már korábban is kötelezővé tette a biztosítók számára a tőkeallokációt. A tőkeallokáció kérdése régóta foglalkoztatja az akadémiai világot is. Ez kevéssé meglepő, hiszen egy matematikailag is jól megfogalmazható, távolról sem triviális probléma, amely 1 Az Európai Parlament és a Tanács 2009/138/Ek Irányelve 2 Ld. pl. McKinsey&Company (2014) 11
12 számos különböző megközelítésben vizsgálható: a játékelmélet eszközeivel (pl. Denault, 2001; Csóka et al., 2009, Csóka és Pintér, 2016), opcióárazási (pl. Myers és Read, 2001; Sherris, 2006; Kim és Hardy, 2007) vagy egyéb statisztikai megközelítésben (pl. Kalkberener, 2005; Homburg és Scherpereel, 2008; Buch és Dorfleitner, 2008). A tőkeallokációs probléma megoldására számtalan különböző módszer áll az alkalmazók rendelkezésére, azonban részben pont emiatt az elméleti kutatások és a gyakorlati alkalmazás között egyelőre elég nagy a távolság. Ahogy Kim és Hardy (2007, p23) írja, a tőkeallokációs módszerek nagyobb részt axiómák alapján kerültek kialakításra, nem pedig [a felhasználás 3 ] céljai szerint, és kevés kutatási eredmény áll rendelkezésre a célok fényében történő alkalmazásra vonatkozóan. Hasonló véleményt fogalmaz meg Meyers (2005, p26) is: Sajnos kiderült, hogy a gazdasági allokáció nem ekvivalens az axiomatikus allokációval. A disszertációban emiatt olyan, az irodalomban igen ritka megközelítést alkalmazok (Vrieze és Brehm, 2003; Zec, 2014, illetve Balogh, 2006 a bankokra koncentrálva), amely a tőkeallokáció elméleti és gyakorlati oldalával egyaránt foglalkozik; a módszertani kérdések vizsgálata mellett a módszerek gyakorlati használatával kapcsolatban is támpontokat adok. A disszertáció legfontosabb fejezetei a 2., 3. és 4. részekben találhatóak, az 1. rész felvezetésként szolgál a később tárgyaltakhoz: bevezetem a kockázat mérésével kapcsolatos szükséges fogalmakat, bemutatom a később alkalmazott kockázatmértékeket, illetve a szükséges tőkefogalmakat is ebben a részben tisztázom. A 2. rész (mely Bátyi Tamással, Csóka Péterrel és Pintér Miklóssal való közös munkánk eredménye) tekinthető a disszertáció elméleti részének, itt a tőkeallokáció módszertani kérdésével foglalkozunk, azonban már az itt közölt eredmények is bizonyos mértékben 3 A fordító kiegészítése 12
13 gyakorlat-orientáltak. Tíz fontos követelménynek való megfelelés szempontjából vizsgálunk hét, az irodalomban gyakran előforduló, illetve a gyakorlatban alkalmazott módszert, melyek a következők: egyéni kockázattal arányos módszer (Hamlen et al., 1977); béta módszer (ld. pl. Homburg és Scherpereel, 2008); növekményi módszer (ld. pl. Jorion, 2007); költségrés módszer (Tijs és Driessen, 1986); marginális kockázati hozzájárulás mint iránymenti derivált (Cherny és Orlov, 2011), és mint parciális derivált, más néven Euler módszer (ld. pl. Denault, 2001, vagy Buch és Dorfleitner, 2008); a Shapley-módszer (Shapley, 1953) és a nukleolusz módszer (Schmeidler, 1969). A módszerek vizsgálata során az egyes követelmények teljesítését csak az adott módszer értelmezési tartományán várjuk el: vannak módszerek, melyek nem mindig definiáltak, azaz nem teljesítik az első vizsgált tulajdonságot, a teljes értelmezési tartományon való definiáltságot (mindig értelmezettség). A további kilenc vizsgált tulajdonságot két csoportba sorolhatjuk. Az első csoport tulajdonságai az egyes alegységekből álló halmazok (koalíciók) kockázataival foglalkozó kooperatív játékelmélethez kapcsolódnak: magbeliség; diverzifikáció; erős monotonitás; hatékonyság; egyenlően kezelés. A második csoport tulajdonságai közvetlenül a portfólión definiáltak, a kockázatmérték használata nélkül: az ösztönzés, a kockázatmentes allokáció, a kovariancia és a dekompozíció invariancia. Minden módszer és tulajdonság esetében bizonyítással vagy ellenpéldával mutatjuk meg, hogy az adott módszer teljesíti-e a szóban forgó tulajdonságot. Az analitikus eredményeinket összegző táblázat hasznos támpontként szolgálhat a gyakorlati alkalmazóknak a módszerek közötti választásban, továbbá segítséget nyújthat abban is, hogy egy adott módszer alkalmazása esetén milyen esetleges problémára kell felkészülni az alkalmazás során. Ha egy módszer egy adott tulajdonságot nem teljesít, az még nem biztos, hogy problémát jelent az alkalmazás során, ha a tulajdonság megsértése csak bizonyos elméletileg lehetséges, ám a gyakorlatban nem releváns esetekben fordul elő. Emiatt a magallokáció 13
14 követelményének teljesítését szimuláció segítségével is vizsgáljuk: legfeljebb kilenc alegységet tartalmazó portfóliók esetén, véletlenszerűen generált tőkeallokációs szituációkban 4 milyen arányban eredményez magbeli elosztást az egyéni kockázattal arányos, a béta, a növekményi, a költségrés és a Shapley-módszer. Mivel a nukleolusz módszer, illetve a szimulált környezetben a marginális kockázati hozzájárulás mindkét típusa mindig eleget tesz a magbeliség követelményének, ezek nem képzik tárgyát a szimulációs vizsgálatnak. Megmutatjuk, hogy legjobban a költségrés módszer teljesít: jellemzően 90% feletti arányban ad magbeli elosztást, bár ez egyes esetekben akár 30%-ig is lemehet. Általában a magbeli elosztások aránya nagyban függ a szimuláció paramétereitől, de minden esetben csökken az alegységek számának csökkenésével. A 3. rész már teljes mértékben a gyakorlati felhasználásra koncentrál, ugyanakkor épít a 2. rész előbb említett eredményére is, mely szerint az egyes módszerek által eredményezett elosztás tulajdonságai igen nagymértékben függenek az alap probléma paramétereitől. Ebben a részben egyfajta útmutatóként szolgálva a tőkeallokációs problémának a szakirodalomban megszokott, igen absztrakt megfogalmazását a biztosítóknál az implementáció során felmerülő gyakorlati kérdésekre fordítom le, ezzel segítséget nyújtva az elméletileg lehetséges módszerek közötti eligazodásban. Bemutatom a lehetséges alkalmazásokat, vagyis azt, hogy miért fontos, mire használják a biztosítótársaságok a tőkeallokációt. Ez meghatározó, hiszen mint látni fogjuk, végső soron mindig a felhasználás célja szerint kell az alkalmazott módszert kiválasztani, mivel a tőkeallokációs problémának nincs univerzális, minden helyzetben alkalmazható legjobb megoldása. Ehhez a választáshoz igyekszem praktikus támpontokat adni a lehetséges módszerek 4 Egy-egy tőkeallokációs szituáció összetevői az alábbiak: az alegységek, a portfólióik, és egy koherens kockázatmérték. 14
15 csoportosításával, illetve annak meghatározásával, hogy a felhasználás céljai szerint mely módszertípust érdemes alkalmazni. A 4. részben végül egy esettanulmány segítségével szeretném még kézzelfoghatóbban bemutatni a tőkeallokációt, illetve annak egy lehetséges felhasználását. Az esettanulmányban az ABC Zrt., egy fiktív biztosítótársaság példáján keresztül természetesen sok szempontból egyszerűsítéseket alkalmazva mutatom be, hogyan alkalmazhat egy biztosító tőkeallokációs módszereket az egyes üzletágainak teljesítményének értékelésére. 15
16 1. RÉSZ: TŐKE, KOCKÁZATMÉRÉS A pénzügyi intézményekben a kockázat mai értelemben vett mérésével csak az elmúlt néhány évtizedben kezdtek komolyabban foglalkozni, a modern kockázatkezelés születését az irodalomban körülre datálják (Dionne, 2013). Ugyanakkor az első biztosítás jellegű ügyletek már jóval időszámításunk előtt köttettek: a legkorábbi utalást Hamurappi törvénykönyve tartalmazza. A törvénykönyv olyan kölcsönökről számol be, amelyek mellé többlet díj ellenében biztosítást is köthettek a tengeri kereskedők, azaz amennyiben hajójuk elsüllyedt, a felvett kölcsönt nem kellett visszafizetniük. Később, a középkorban az egyház megtiltotta a kamat ellenében történő hitel nyújtását, IX. Gergely Pápa azonban a különféle kockázatok átvállalását (s ezért díj felszámítását) kimondottan külön engedélyezte: a történelem során ekkor vált el először a biztosítás, mint termék a hitelügylettől. Néhány száz év elteltével, a 18. században jelentek meg Európában az első biztosító részvénytársaságok, amelyek az egymás közötti kölcsönös kármegosztást alkalmazták kockázataik csökkentésére. Alig száz évvel később, az 1800-as évek közepén ez a típusú kockázatmegosztás elégtelennek bizonyult, mikor Németországban az 1842-es hamburgi nagy tűz, illetve Svájcban az 1861-es glarusi nagy tűz számos biztosítótársaság csődjét okozta, s rövid időn belül létrejöttek az első viszontbiztosítók: a Cologne Re, illetve a Swiss Re. A biztosítási szektoron kívül a Második Világháborút követően erősödött meg az igény a pénzügyi kockázatkezelés iránt. Az értékes eszközöket, készleteket birtokló nagyvállalatok ekkoriban kezdtek saját biztosítás jellegű termékeket fejleszteni. Az 1900-as években 5 eközben elkezdődött a pénzügy, mint önálló tudományterület fejlődése is. Az első nagy mérföldkőnek Louis Bachelier 1900-as műve (Davis és Etheridge, 2006) 5 Az összefoglaló további részében Dionne (2013) munkájára támaszkodunk, míg az előző bekezdésben az elsődleges forrás a oldal volt. 16
17 tekinthető. A pénzügyi termékek árfolyam-mozgásaira irányulóan az 1930-as éveket követően kezdődtek komolyabb kutatások. Az USA-ban létrejöttek az első kockázatkezeléssel foglalkozó társaságok (American Finance Association, American Risk and Insurance Association), s elindult a Journal of Insurance folyóirat (melyet 1964-ben neveztek át Journal of Risk and Insurance-ra). Az 50-es, 60-as évek ismét igen nagy fejlődést jelentettek, többek között Markowitz, Lintner és Sharpe munkásságának eredményeként a modern portfólióelmélet és a CAPM (Capital Asset Pricing Model, magyarul: tőkepiaci árfolyamok modellje) születésével. Az 1970-es években indult meg a derivatív jellegű pénzügyi termékek robbanásszerű fejlődése. E termékek célja kezdetben a biztosításokéhoz nagyon hasonló volt: vagyis a nagymértékű veszteségek elkerülése érdekében hozták létre és vásárolták ezeket, azonban a biztosításoktól egy nagyon fontos tulajdonság megkülönböztette őket: ezek az ügyletek egy kereskedett alaptermékhez kötöttek (pl. egy részvény, egy tőzsdén kereskedett áru), szemben a biztosításokkal, melyek esetében maga a biztosítási esemény teljesen más jellegű (nem kereskedett), pl. haláleset, betegség, tűzeset, vagy egyéb baleset ban jelent meg Black és Scholes forradalmi jelentőségű opcióárazási modellje (Black és Scholes, 1973). A tanulmány publikálását előbb több lap is elutasította, olyannyira újdonságnak számítottak a benne leírtak, végül a Journal of Political Economy folyóirat jelentette meg. Még ugyanebben az évben publikálta Merton az árazási modell általánosított, európai opciókra 6 is alkalmazható változatát a Bell Journal of Economics and Management Science című folyóiratban (Merton, 1973). Szintén 1973-ban létrejött a Chicago Board of Options Exchange, a világ első, s a mai napig legnagyobb forgalmat lebonyolító tőzsdéje, ahol opciókkal kereskednek. A következő évtizedekben a derivatív termékek iránti kereslet 6 Olyan opció, amely kizárólag a lejárat időpontjában lehívható szemben az amerikai opcióval, melynek esetében az opciós jog a lejárat időpontjáig bármikor gyakorolható. 17
18 folyamatosan növekedett, ahogyan a piaci szereplők számára is egyre inkább központi kérdéssé vált a tevékenységükkel kapcsolatos kockázat fedezése. A kockázatkezelés, mint kutatási terület fejlődésének szintén nagy lökést adott néhány, a 20. század utolsó évtizedeiben bekövetkezett esemény is. A legfontosabbak közé sorolható a Bretton Woods-i árfolyamrendszer 7 összeomlása 1971-ben, illetve az olajár-robbanás az 1970-es években. Jelentős mérföldkőnek tekinthető a hírhedt Fekete Hétfő is (1987. október 19-én az egyik legnagyobb amerikai részvényindex, a Dow Jones 23%-ot zuhant egyetlen nap alatt), illetve az 1998-as orosz válság is, melyek mind piaci kockázati eseménynek tekinthetők. Ugyanakkor fontos megemlíteni néhány igen nagy jelentőségű működési kockázati eseményt is: az amerikai Orange megye csődje 1994-ben (egy megyei tisztségviselő, hatalmas tőkeáttétellel járó befektetési stratégiájának köszönhetően közel 2 milliárd dollárt veszített; a tisztségviselőt csalásért 14 évre elítélték, ld. pl. Jorion 2007); a brit Barings Bank csődje 1995-ben (amelyet a pénzintézet szingapúri leányának vezetőjeként az akkor 28 éves Nick Leeson idézett elő, aki tőzsdei spekulatív ügyleteivel melyek veszteségét egy titkos számla segítségével próbálta eltitkolni végül körülbelül 850 millió fontos veszteséget okozott, ld. Greener, 2006); vagy a 2001-es Enron botrány (az energiaipar egyik fontos szereplőjének számító Enron Corporation pénzügyi igazgatójának vezetésével a cégben hosszú időn keresztül meghamisították a pénzügyi jelentéseket, hogy a bedőlt projektek veszteségeit láthatatlanná tegyék, amely végül mind a vállalat csődjéhez, mint a céget auditáló Arthur Andersen könyvvizsgálati üzletágának bezárásához vezetett, ld. pl. Gordon, 2002). A kockázatkezelés tehát egyre inkább a pénzügyi világ figyelmének fókuszába került, s az alkalmazott matematikai eszköztár is jelentős fejlődésnek indult. A nagy befektetési bankok 7 Az amerikai dollár (s a rendszerhez csatlakozott többi állam valutáinak) kötött árfolyamon történő aranyra váltása, melyet az Egyesült Államok 1971-ben felfüggesztett. 18
19 jelentős erőforrást fektettek kockázatkezelési rendszereik fejlesztésébe, és néhányuk azt külső szereplők számára is elérhetővé tette: a JP Morgan 1994-ben dobta piacra a piaci kockázatok kezelésére szolgáló RiskMetrics, majd 1997-ben a hitelezési kockázatok kezelésére született CreditMetrics modellt. Nagyban köthető a RiskMetrics modell alkalmazásához a VaR (Value at Risk, magyarul kockáztatott érték, ld. az fejezetben) módszer elterjedése, amely széles körben ismertté és elfogadottá vált a pénzügyi szektorban. Számtalan további kockázatmérték, rengeteg módszertan és szoftver született a kockázat mérésére, és a szabályozók is egyre nagyobb hangsúlyt fektettek a pénzügyi vállalatok által vállalt kockázat korlátozására és szofisztikált mérésére. Többek közt a fent említett működési és piaci kockázati eseményeket s több nagy bank és egyéb vállalat csődjét követően a tőkekövetelmény számítás is egyre hangsúlyosabb szabályozói kérdéssé vált. A bankszektorban az 1988-as Bázel I szabályozást jelentősen továbbfejlesztette és (a működési és piaci kockázatok figyelembe vételével) kiegészítette a 2004-es Bázel II, majd a Bázel III egyezmény. A biztosítási szektor bizonyos szempontból előrébb járt a szabályozásban: a Szolvencia I irányelv már 1973 óta hatályban volt, de a kockázatérzékenyebb értékelést előíró (és a Bázel II/III szabályozással analóg módon már három pillérre épülő) Szolvencia II irányelv életbelépése 2016-ig váratott magára (ld. majd az fejezetben). A tanulmány 1. részének felépítése a továbbiakban a következő. Az 1.1. fejezetben a kockázat mérésére rendelkezésre álló lehetséges kockázatmértékeket tekintem át röviden. Az áttekintés távolról sem teljes körű, célom elsősorban az, hogy a tanulmány további részeiben alkalmazott kockázatmértékeket bemutassam. Az 1.2. fejezetben a különböző lehetséges tőkefogalmakkal, és a biztosítókra vonatkozó tőkekövetelményekkel foglalkozom. 19
20 1.1 A KOCKÁZAT MÉRÉSE A biztosítók alaptevékenysége a kockázatok (át)vállalásán alapul, de a kockázatvállalás hasonlóan központi szerepet játszik az egyéb pénzügyi intézmények esetében is (pl. bankok esetében legmeghatározóbb a hitelezési kockázat, alapkezelőknél a piaci kockázat). A kockázatok kezelésére ma már igen széles eszköztár áll a pénzügyi vállalatok rendelkezésére. A kockázatkezeléssel erre specializálódott szakemberek foglalkoznak, jellemzően a cég struktúrájában elkülönült szervezeti egységben. A terület általában erős IT támogatottsággal is rendelkezik: a cégek szofisztikált kockázatkezelési szoftvereket, vagy belső fejlesztésű modelleket alkalmaznak. Számtalan különböző tartalmú és különböző célközönségnek készülő kockázatkezelési riport születik nap mint nap, melyek segítségével ideális esetben a vezetőség is naprakész információval rendelkezik a vállalt kockázatokról. A bankok és biztosítók által alkalmazott kockázatkezelési módszerek között egyaránt jelen vannak a kvantitatív és kvalitatív eljárások. A kvantitatív módszerek (melyek egy, vagy néhány mutatószám segítségével jellemzik a vállalt kockázatot) természetesen nagyon fontos információt hordoznak, de kizárólag ezekre támaszkodni veszélyes, ahogyan erre a as válság is felhívta a figyelmet. A válság során a pénzügyi intézmények által elszenvedett hatalmas veszteségekhez ugyanis sokak véleménye szerint részben a VaR (kockáztatott érték, Value at Risk) kockázatmérték nem megfelelő alkalmazása vezetett. A válság során a VaR alkalmazása sokaknak hamis biztonságérzetet adott, ami egy fontos tényező volt abban, hogy az elszenvedett veszteségek ilyen hatalmas mértékűek legyenek. Ahogyan a későbbiekben látni fogjuk, a VaR kockázatmértékkel szemben több kritikát is meg lehet fogalmazni, azonban a konkrét mérték tulajdonságaitól függetlenül is elmondható, hogy egyetlen mérőszámra támaszkodni a kockázatok értékelése során nem célszerű. Fontos tehát, hogy a kvalitatív kockázatértékelési módszerek jelentőségéről se felejtkezzünk meg 20
21 legyen az akár egy kockázati térkép, a kockázatvállalási étvágy ( risk appetite ) meghatározása, egy különböző kockázati szintekhez kötött korai figyelmeztető mechanizmus, vagy akár csak a kockázatkezelők szubjektív, szakértői kockázatértékelése. Ugyanakkor tény, hogy a kockázatok számszerűsítésére alkalmazott kockázatmértékek elengedhetetlen, alapvető építőkövei a kockázatkezelésnek. Kockázatmérték alatt azt a leképezést értjük, amely egy valós számot rendel a portfólió nyereségét/veszteségét leíró valószínűségi változóhoz. Ez a számot úgy is értelmezhető, mint azt a készpénz mennyiség, melyet a portfólióhoz adva a portfólió kockázatossága elfogadható lesz a szóban forgó kockázatmérték mellett. A következő alfejezetekben előbb néhány szükséges jelölést vezetek be, hogy formálisan is definiálni tudjam a kockázatmérték fogalmát, majd a koherens kockázatmérés axiómáit veszem sorra, ezt követően pedig a leggyakrabban alkalmazott kockázatmértékeket, s ezek fontosabb tulajdonságait mutatom be AZ ALKALMAZOTT JELÖLÉSEK Mivel a 2. részben Balog et al. (2017) cikkének eredményeit közlöm, a konzisztencia jegyében az egész disszertációban az ott alkalmazott jelöléseket használom. Feltesszük, hogy egy-egy pénzügyi egység (portfólió) által elért hozamot (veszteséget) véletlen valószínűségi változók írják le a (Ω, M, P) diszkrét valószínűségi mezőn, ahol Ω a lehetséges kimenetelek halmaza, M jelöli Ω összes lehetséges részhalmazát, P pedig egy valószínűség eloszlás (Ω, M)-n. A (Ω, M, P)-n értelmezett valószínűségi változók halmaza Χ. Mivel véges számú lehetséges kimenetel van, X: Ω R valószínűségi változó tekinthető egy s elemű realizációs vektornak is, ahol s a lehetséges világállapotok számát jelöli. Jelölje tehát X i Χ az i egység realizációs vektorát, amely tehát az egyes világállapotokban 21
22 megadja az egység által adott idő alatt elért profitot (a negatív értékek veszteséget jelentenek), azaz X i ω j az i egység kifizetését jelenti az ωj Ω világállapotban. A továbbiakban két tetszőleges realizációs vektor, Y és X vonatkozásában Y X azt jelenti, hogy minden lehetséges ω j Ω világállapotban Y ω j X ω j. A ρ: Χ R függvényt kockázatmértéknek nevezzük. A kockázatmérték minden valószínűségi változóhoz egy valós számot rendel, megadja az egyes portfóliók kockázatát. Az így értelmezett kockázatot tekinthetjük annak az összegnek tőke, amelyet a portfólióhoz adva annak kockázata elfogadhatóvá válik. A kockázatmértékek között kiemelt szerepet töltenek be a koherens kockázatmértékek, melyeket a következő alfejezetben definiálok KOHERENS KOCKÁZATMÉRÉS Mind az irodalomban, mind pedig a gyakorlatban számos különböző kockázatmértékkel találkozhatunk. Ezek összevetése, értékelése kapcsán talán a legfontosabb, az akadémiai és a pénzügyi világban egyaránt elfogadott referencia pontnak a koherencia Artzner és szerzőtársai (1999) által definiált négy követelménye tekinthető. A konkrét kockázatmértékek sorra vétele előtt tekintsük át tehát a koherens kockázatmérés követelményeit. A fogalom elméleti alapjairól bővebben Csóka et al. (2007), illetve Acerbi és Scandolo (2008) cikkében, a gyakorlati alkalmazásairól a Bázeli Bankfelügyelet tanulmányában (BCoBS, 2014) olvashat az érdeklődő definíció (Artzner et al., 1999). A ρ: Χ R függvényt koherens kockázatmértéknek nevezzük, amennyiben teljesíti a következő axiómákat: Monotonitás: minden X 1, X 2 Χ-re, amennyiben X 1 X 2, ρ(x 1 ) ρ(x 2 ). Szubadditivitás: minden X 1, X 2 Χ-re ρ(x 1 + X 2 ) ρ(x 1 ) + ρ(x 2 ). 22
23 Pozitív homogenitás: minden X 1 Χ és h R + -ra ρ(hx 1 ) = hρ(x 1 ). Transzláció invariancia: minden X 1 Χ és a R-re, ρ(x 1 + aχ Ω ) = ρ(x 1 ) a, ahol χ Ω egy olyan vektor R Ω -n, melynek minden koordinátája 1. A fenti axiómák magyarázata sorra a következő. A monotonitás azt a meglehetősen kézenfekvő elvárást fejezi ki, hogy ha egy adott X 2 portfólió hozama soha nem rosszabb, mint X 1 -é, akkor a kockázata se legyen nagyobb. Vagyis, ha egy portfólió minden lehetséges kimenetel esetén legalább akkora profitot termel, mint egy másik portfólió, akkor a kockázata ne legyen magasabb a másik portfólióénál. A szubadditivitás azt jelenti, hogy két portfólió (üzletág, stb.) egyesítése esetén a kockázat nem növekszik. Ha a szubadditivitás nem teljesülne, akkor egy olyan befektető, aki az X 1 és X 2 portfóliókat is tartani szeretné, jobban járhatna, ha két külön számlán tartaná a két befektetést, mint egy közös számla esetén. A szubbaditivitás által válik lehetővé a diverzifikáció: X 1 és X 2 egyesítése esetén az új kockázat, ρ(x 1 + X 2 ) alacsonyabb lehet, de magasabb nem a két egység külön-külön számított kockázatának összegénél, ρ(x 1 ) + ρ(x 2 )-nél. A pozitív homogenitás követelménye is világos: konstansszorosára növelve az adott kockázatos portfóliót a kockázat is konstansszorosára nő. A pozitív homogenitás elvárása azt is jelenti tehát, hogy a portfólió kockázata egyenes arányban változik annak méretével. Az alábbiakban röviden kitérünk rá, hogy bár elméletben ez igen logikusan hangzik, de a gyakorlatban nem feltétlenül igaz, amennyiben az adott piacon a likviditási kockázattal is számolnunk kell. Végül a transzláció invariancia elvárása azt fejezi ki, hogy egy kockázatmentes eszközt (amelynek hozamát tehát előre biztosan ismerjük, legyen a) adva bármely más portfólióhoz, annak a kockázata a kockázatmentes eszköz hozamával, a-val csökkenjen. Vagyis például 23
24 ha egy adott befektetett portfólióhoz készpénzt adunk, akkor a befektetésünk kockázata pontosan a készpénz mennyiségével kell, hogy csökkenjen. Bár a koherens kockázatmértékek széles körben elfogadottak, azonban fontos tisztában lennünk azzal is, hogy ezek a kockázatmértékek sem hibátlanok. A leggyakrabban felmerülő kritika a koherens kockázatmértékekkel szemben, hogy egy fontos jelenséget: a likviditási kockázatot nem kezelik megfelelően. Többek között Acerbi és Scandolo (2008) hívta fel arra a figyelmet, hogy a gyakorlatban a portfólió mérete nagyban befolyásolja annak kockázatát, hiszen a portfólió méretének többszörösére növelése sok esetben a méret növekedésénél nagyobb mértékben növeli annak a kockázatát (jellemzően, ha az adott portfólió mérete már nem elhanyagolható a teljes piac méretéhez képest) a likviditási kockázat jelenléte miatt. Amennyiben pedig elfogadjuk, hogy a valóságban egy kétszer nagyobb portfólió kockázata az eredeti portfólió kockázatának több, mint kétszerese is lehet (mert pl. nehezebb, több idő értékesíteni, készpénzzé tenni azt), akkor a koherens kockázatmérés axiómái közül kettő, a pozitív homogenitás és a szubadditivitás is sérül. Acerbi és Scandolo (2008) viszont egyszerű megoldást is kínál a probléma feloldására azzal, hogy a portfólió értékét módosítják (attól függően, hogy mi a cél az adott portfólióval), melyet a likviditási politika segítségével számszerűsítenek, ami tehát annak függvényében határozza meg a portfólió értékét, hogy pl. csak tartani akarjuk, vagy szükséges lehet egy részét likvidálni, készpénzzé tenni. Erre a módosított portfólióértékre pedig továbbra is logikusan elvárható a koherens kockázatmérés négy axiómájának teljesítése A LEGGYAKRABBAN ALKALMAZOTT KOCKÁZATMÉRTÉKEK Az alábbiakban természetesen a teljesség igénye nélkül lehetséges alternatívákat mutatok be a kockázat számszerűsítésére használható kockázatmértékekre. Csak néhány, a gyakorlatban gyakran alkalmazott kockázatmértékkel foglalkozom, melyek közül a 24
25 következő részekben elsősorban a VaR és az Expected Shortfall kockázatmértékeket fogom alkalmazni. Kimondottan a biztosítási szektorban alkalmazott kockázatmértékekkel kapcsolatban részletesebb összefoglalót ad Kaye (2005), Hardy (2006), Goldfarb (2010), vagy Zec (2014) Szórás Az egyik legrégebben alkalmazott kockázatmérték a valószínűségszámításból átvett, ugyanakkor a nem-akadémiai közönség számára is ismerős szórás (jelöljük D-vel), melynek formális definíciója a következő: D(X) = E(X 2 ) E 2 (X), ahol E(X) szokás szerint az X változó várható értékét jelöli. A szórást viszonylag gyakran alkalmazzák a kockázat mérésére, ugyanakkor fontos tisztában lenni azzal, mennyire limitált az információtartalma. A szórás az eloszlást egyetlen számban jellemzi, s könnyen konstruálható két meglehetősen különböző eloszlású valószínűségi változó, melyek szórása megegyezik. A biztosításokhoz kapcsolódó eloszlások az esetek túlnyomó többségében távolról sem normálisak, nem is szimmetrikusak, így a szórás önmagában nem jellemzi jól az eloszlást, mellette fontos a harmadik, negyedik momentumok ismerete is (ld. pl. Kaye, 2005). A szórás a koherencia axiómáinak való megfelelés szempontjából sem teljesít jól, kettőt is megsért közülük: nem monoton, és nem is transzláció invariáns. Ennek bizonyítására tekintsük a következő példát példa. Tekintsük a lenti X 1, X 2, Y 1, Y 2 X portfóliókat, és legyen a lehetséges kimenetelek halmaza Ω = {ω 1, ω 2, ω 3, ω 4 }, P pedig olyan, hogy P = P({ω 1 }) = P({ω 2 }) = P({ω 3 }) = P({ω 4 }) = 1/4. A kockázatot a szórással mérjük. A különböző 25
26 világállapotokban az egyes portfóliók értékeit, illetve az ezekből számított kockázatot a lenti 1. táblázat tartalmazza. 1. táblázat: A szórás nem koherens Ω / X S X 1 X 2 Ω / Y S Y 1 Y 2 ω ω ω ω ω ω ω ω D{X S } 0,5 1 D{Y S } 0,5 0,5 A monotonitást vizsgálva látjuk, hogy bár X2 kifizetése mindig meghaladja X1-ét, a két portfólió szórása: D(X 1 ) = 0,5, viszont D(X 2 ) = 1, azaz X2 kockázata meghaladja X1-ét, tehát ez a követelmény nem teljesül. Szintén látható, hogy Y 2 = Y 1 + 1, ugyanakkor a transzláció invariancia teljesülése esetén D(Y 2 ) = D(Y 1 + 1) = D(Y 1 ) 1 = 0,5 állna fenn, ami láthatóan nem igaz Kockáztatott érték (Value at Risk, VaR) Napjainkban továbbra is talán a legelterjedtebb módszer a kockázatott érték, ismertebb nevén VaR (Value at Risk). Az adott α [0,1) szignifikancia szint mellett számított VaR egyszerűen X eloszlásának az adott α mellett számított kvantilisének ellentettje: VaR α (X) = inf{x R: P(X x) 1 α}. Tehát például α = esetén azt értéket kapjuk, amelyet meghatározott időtávon (jellemzően 1 nap, 10 nap, 1 év) 99,5%-os valószínűséggel (ami gyakran alkalmazott szignifikancia szint a gyakorlatban) nem fog meghaladni a veszteségünk. 26
27 A VaR kockázatmérték alkalmazása az 1990-es években terjedt robbanásszerűen a pénzügyi szektorban, különösen a befektetési bankok, alapkezelők körében. (Fontos megjegyezni, hogy a VaR-t alapvetően kereskedett termékek kockázatának mérésére vezették be, szemben például az előzőekben tárgyalt szórással.) A legnagyobb szerepe a VaR népszerűsítésében a JP Morgan RiskMetrics modelljének volt, amely egy VaR-ra épülő piaci kockázatkezelési szisztéma. Nagyon hasonló kockázatmértéket, a maximális várható éves veszteséget (MPY, Maximum Probable Yearly Aggregate Loss) a biztosítási szektorban már jóval korábban használták (ld. pl. Cummins és Freifelder, 1978). Zec (2014) ugyanakkor azt is megemlíti, hogy a VaR elvének megfelelő kockázatméréssel már a 18. és 19. században is foglalkoztak (pénzügyi) kockázatok elemzése során (pl. Condorcet, Edgeworth vagy Hicks). Bármi volt is a forrás, kétségtelen azonban, hogy a RiskMetrics modell terjedésével a VaR rendkívül széles körben elfogadott és alkalmazott kockázatmértékké vált a pénzügyi világban. A VaR kockázatmérték interpretációja meglehetősen kézenfekvő: mennyi az a veszteség, amelynél többet adott időtávon nem szenved el a portfólió valamely kellően magas szignifikancia szint mellett. A VaR terjedésében nagy szerepet játszott az is, hogy mind a bankok, mind Európában a biztosítók felügyeletéért felelős szervezetek is validálták azt, hiszen mind a Bázeli szabályozásban, mind a Szolvencia II-ben a tőkekövetelmény számítása a VaR elve alapján történik. Ugyanakkor azt is fontos megjegyezni, hogy bár az európai biztosítókat szabályozó Szolvencia II tőkekövetelmény meghatározása is a VaR elvén alapszik, az aktuáriusok körében a VaR mindig sokkal kevésbé volt népszerű, mint a bankok és alapkezelők kockázatkezelői körében (Ingram, 2004). Egyfelől talán az aktuáriusok tisztábban látták már a pénzügyi válság előtt is, hogy a VaR egy igencsak kétélű fegyver, másfelől nem szabad elfejtenünk azt sem, hogy a VaR-t eredetileg kereskedett termékek kockázatának mérésére vezették be (implicit módon azt feltételezi, hogy a pozíció 27
28 adott időn belül lezárható), s ez már önmagában is megmagyarázza, miért volt kevésbé jellemző a használata biztosítók esetében. Részben a felelősséget hárítva, de sokan okolják a VaR-t amiatt, hogy a as válság során ekkora veszteségeket szenvedtek el pénzintézetek 8. A VaR ugyanis hamis biztonságérzetet is adhat, hiszen arról, hogy a kimenetelek legrosszabb α százalékában mi történik, nem ad semmilyen információt. Ahogyan David Einhorn, egy neves alapkezelő alapítója fogalmazott, a VaR olyan, mint egy légzsák, ami mindig működik, kivéve baleset esetén (Nocera, 2009). Valójában a VaR hibája inkább annak manipulálhatósága, azaz arra való alkalmassága, hogy az eloszlás szélébe rejtsék el vele a veszteséget azonban pont ez mutatja, hogy a válság értelemszerűen nem egy kockázatmérték hibája volt, a VaR mindössze egy jó eszköznek bizonyult a kimutatott kockázatok manipulálására. A VaR mellett, illetve ellene szóló érvekről részletes összefoglalót közölt 2009-ben a New York Times (Nocera, 2009), amely egyben azt is jól mutatja, hogy a kockázatmértékek között a VaR milyen kiemelt figyelmet kapott. Matematikai szempontból vizsgálva a VaR alkalmazásával kapcsolatos problémák nagyon hasonlóak a szórás kapcsán felmerültekhez. Normális eloszlású változó esetén ugyanis bár a VaR jól használható, de semmilyen plusz információtartalma nincs a nála egyszerűbben számítható szóráshoz képest, ekkor ugyanis a VaR a szórás konstansszorosa a választott szignifikancia szint függvényében: VaR α (X) = Φ 1 (α) D(X) E(X), 8 A válság okairól szóló egyéb, legfrissebb hipotézisekről ld. pl. Bolton et al. (2017), Shin (2012), Borio és Disyatat (2011). 28
29 ahol E(X) a várható értéket jelöli, Φ 1 pedig a standard normális eloszlásfüggvény inverze. Egyéb esetben pedig az a nagy probléma a VaR-ral, hogy pont az eloszlás széléről (azaz a lehetséges legrosszabb kimenetelekről) nem mond semmit. Hasonlóan a szóráshoz, konstruálható két teljesen azonos VaR-ral jellemezhető eloszlás, melyek kockázatosság szempontjából teljesen eltérnek egymástól (pl. a maximális veszteség egyik esetben mondjuk 100-szoros a másikhoz képest). Ha a VaR-t a koherencia szempontjából vizsgáljuk, akkor azt találjuk, hogy ez a kockázatmérték sem koherens, mivel nem tesz eleget a szubadditivitás követelményének. Így például előfordulhat, hogy két portfólió (üzletág) egyesítése után a kockázat nagyobb lesz, mint előzőleg a külön-külön számított két kockázat összege. Ez természetesen nem kívánatos. A VaR nem koherens voltát a következő egyszerű példa szemlélteti példa. Tekintsük a lenti X 1, X 2, X portfóliókat, és legyen a lehetséges kimenetelek halmaza Ω = {ω 1, ω 2, ω 3, ω 4 }, Mjelöli Ω lehetséges részhalmazait, P pedig olyan, hogy P = P({ω 1 }) = P({ω 2 }) = P({ω 3 }) = P({ω 4 }) = 1/4. A kockázatot a VaR kockázatmértékkel mérjük, α = 0,7 mellett, azaz 70%-os szignifikancia szinten. A különböző világállapotokban az egyes portfóliók értékeit, illetve az ezekből számított kockázatot a lenti 2. táblázat tartalmazza. 2. táblázat: A VaR nem koherens Ω / X i X1 X2 X1+ X2 ω ω ω ω Var 0,7 (X i )
30 A fenti esetben, Var 0,7 (X 1 ) + Var 0,7 (X 2 ) = 0, viszont Var 0,7 (X 1 + X 2 ) = 1, tehát Var 0,7 (X 1 + X 2 ) > Var 0,7 (X 1 ) + Var 0,7 (X 2 ), azaz nem teljesül a szubadditivitás Az Expected Shortfall A koherens kockázatmértékek közül talán a legszélesebb körben alkalmazott az Expected Shortfall (Acerbi és Tasche, 2002). Az Expected Shortfall az irodalomban több különböző néven is megtalálható, a biztosítási szakma leggyakrabban a Conditional Tail Expectation néven hivatkozik rá (ld. pl. Ingram, 2004), de nevezik Tail Value at Risk-nek is (Zec, 2014). Az α (α [0,1)) szignifikancia szint mellett számított Expected Shortfall a veszteségek közül a legrosszabb ( 1 α) 100 százalék átlagát jelenti. Formálisan, legyen X Χ valószínűségi változó és α (0,1]. Ekkor az Expected Shortfall a következőképp definiálható: 1 α ES α (X) = 1 1 α VaR β(x)dβ. Vegyük észre, hogy amennyiben 1 α kisebb-egyenlő, mint a legrosszabb kimenetel valószínűsége, akkor a maximális veszteséget kapjuk koherens kockázatmértékként. Az Expected Shortfall koherenciájára bizonyítást ad pl. Acerbi és Tasche (2002), vagy Kalkbrener (2005). 0 Míg tehát a VaR arra a kérdésre ad választ, hogy melyik az a veszteségszint, amelynél adott valószínűséggel nem szenvedünk el többet de semmit nem mond arról, hogy pont ezen legrosszabb kimenetelek esetén mire kell számítanunk, az Expected Shortfall azt mutatja meg, hogy a legrosszabb kimenetelek bekövetkezése esetén várhatóan mennyit veszítünk. Az Expected Shortfall számos kedvező gyakorlati tulajdonsággal rendelkezik (nem manipulálható, könnyen interpretálható), ugyanakkor a matematikai tulajdonságok terén is 30
31 jól teljesít, hiszen a VaR-ral ellentétben koherens (bővebben ld. Acerbi és Tasche, 2002, illetve Tasche, 2002). Nem véletlen, hogy az USA-ban és Kanadában a biztosítók a tőkekövetelményüket az Expected Shortfall mértékkel kell, hogy számszerűsítsék (Ingram, 2004). Az Expected Shortfall bevezetése körüli vitában komoly vihart kavart, hogy az nem felel meg az elicitabilitás követelményének, ami miatt sokan azt hitték, hogy teljesítménye egyáltalán nem is visszamérhető (ld. pl. Acerbi és Székely, 2017). Az Expected Shortfall csak e kérdésnek a tisztázását követően kerülhetett be a szabályozásba Feltételes VaR ( Conditional Value at Risk ) Az Expected Shortfall mellett röviden kitérek még egy koncepciójában igen hasonló kockázatmértékre, a feltételes VaR-ra is. A teljesség kedvéért megjegyzendő, hogy még a szakirodalomban sem egységes a névhasználat: az Expected Shortfall, a feltételes VaR, a Conditional Tail Expectation és a Tail VaR fogalmak használata nem egységes. A feltételes VaR azt mutatja meg, hogy mekkora a várható veszteség azokban az esetekben, amikor a veszteségünk meghaladja a VaR értékét, formálisan: CVaR α (X) = E(X X VaR α (X)) A feltételes VaR folytonos esetben megegyezik az Expected Shortfallal (részben ez magyarázza a nem konzisztens névhasználatot), diszkrét esetben azonban nem feltétlenül. A két kockázatmérték közül csak az Expected Shortfall koherens, a feltételes VaR nem az, így a továbbiakban a CVaR-t nem, csak az ES-t fogom használni. A két kockázatmérték közötti eltérést az alábbi példán mutatom be példa. Tekintsük a lenti X X portfóliót, és legyen a lehetséges kimenetelek halmaza Ω = {ω 1, ω 2, ω 3, ω 4 }, P pedig olyan, hogy P = P({ω 1 }) = P({ω 2 }) = P({ω 3 }) = P({ω 4 }) = 1/4. Számítsuk ki a portfólió kockázatát az Expected Shortfall, illetve a 31
32 feltételes VaR kockázatmértékkel is, α = 0,7 esetén. A különböző világállapotokban az egyes portfóliók értékeit, illetve az ezekből számított kockázatot a lenti tartalmazza. 3. táblázat: Az Expected Shortfall és a feltételes VaR eltérése diszkrét eset Ω / X X ω 1-4 ω 2-3 ω 3-2 ω 4-1 ES 0,7 (X) 3,8333 CVaR 0,7 (X) 3,5 Egyszerű számítással ellenőrizhető, hogy a fenti esetben ES 0,7 (X) = 0,25 ( 4)+0,05 ( 3) 0,3 3,8333, ugyanakkor CVaR 0,7 = 0,25 ( 4)+0,25 ( 3) 0,5 jobban szemléltethető, melyet a következő ábra mutat. = 3,5. Grafikusan az eltérés talán még = 32
33 1. ábra: Az Expected Shortfall és a feltételes VaR számításának különbsége 1.2 TŐKEKÖVETELMÉNY ÉS TŐKEFOGALMAK A BIZTOSÍTÁSI SZEKTORBAN Az előző fejezetben a pénzügyi vállalatok által vállalt kockázatok mérésével foglalkoztam. A kockázatok mérésének egyik legfontosabb célja, hogy e vállalatok tőkekövetelményét számszerűsíteni lehessen vagyis meghatározzuk, mennyi forrást kell a vállalat tulajdonosainak rendelkezésre bocsátania annak érdekében, hogy az nagy biztonsággal ne váljon fizetésképtelenné. Tőke alatt a továbbiakban a nem várt veszteségek fedezésére szolgáló, elsősorban az ügyfelek követeléseit biztosító tartalékot tekintem. Bár a kérdés, hogy mit is tekintünk egy vállalat tőkéjének, triviálisnak tűnhet, valójában rengeteg tőkefogalommal találkozunk akár az irodalomban, akár egy-egy bank vagy biztosító mérlegét tanulmányozva (szabályozói tőke, gazdasági tőke, különböző számviteli kategóriák). A lehetséges tőkefogalmakat vizsgálva első lépésben (ahogyan Farr et al., 2008 is javasolja), meg kell különböztetnünk az elvárt (valamilyen kockázatmérési módszerrel számszerűsített, elméleti) tőkeigény és a 33
34 rendelkezésre álló tőke fogalmát. A rendelkezésre álló tőke egy számviteli kategória, amely egyszerűen a biztosító mérlegéből kiolvasható, némi egyszerűsítéssel élve az eszközök és kötelezettségek különbségeként. Albrecht (2006) a szintén beszédes fizikai tőke elnevezést használja. Az elvárt tőkét is célszerű még legalább két osztályra bontani, ahogyan azt az Aktuáriusok Szövetsége által jegyzett Specialty Guide on Economic Capital c. kiadvány is javasolja (Mueller et al., 2004): szabályozói tőkekövetelményre és gazdasági tőkeszükségletre. Szolvens pénzügyi vállalkozások esetében a rendelkezésre álló tőke szintje meghaladja mind a szabályozói tőkekövetelmény, mind a gazdasági tőkeszükséglet értékét, míg az utóbbi kettő szintje között nincs általánosan érvényes reláció SZABÁLYOZÓI TŐKEKÖVETELMÉNY SZOLVENCIA II Szabályozói tőkeszükséglet alatt a szabályozó által előírt kötelező minimum tőkekövetelményt értjük az Európai Gazdasági Térségben ez a Szolvencia II irányelv (a továbbiakban Szolvencia II, vagy az Irányelv) szerinti tőkekövetelményt jelenti. Az alábbiakban röviden bemutatom a 2016 januárjában bevezetett, így az európai biztosítási szektor szereplői számára meglehetősen fontos aktualitást jelentő irányelv követelményeit. A Szolvencia II a bankokra vonatkozó Bázel II-vel (illetve Bázel III-mal) teljesen analóg módon három pillérre épül. Az első pillér tartalmazza a kvantitatív előírásokat: a kötelező tőkeszámítás módszertanát valamint az egyes mérlegtételek értékelésének szabályait. A tőkekövetelmény számítása során a biztosítók a standard módszer, részleges vagy teljes belső modell alkalmazása mellett dönthetnek, utóbbi kettő előzetes felügyeleti engedélyhez kötött. Maga a Szolvencia II tőkekövetelmény (SCR) akár belső modellel, akár a standard módszerrel kerül kiszámításra, 99,5%-os szignifikancia szint és egy éves időhorizont mellett számított kockázatott értéknek (VaR) felel meg (azaz az a veszteségszint, amelynél nagyobb várhatóan csak 200 évente egyszer következik be). Az SCR mellett az irányelv még egy 34
35 mutató: a minimális tőkeszükséglet (MCR) számítását is előírja. Az MCR 85%-os szignifikancia szint mellett számított kockázatott értéknek felel meg, és azonnali felügyeleti intézkedést von maga után, ha az intézmény tőkéje ez alá a szint alá csökken (természetesen a felügyelet már az SCR szint átlépésekor beavatkozik, de fokozatosan, eleinte kevésbé kemény intézkedésekkel). A VaR koncepciójának megfeleltethető tőkekövetelmény számítás jelentős előrelépés a Szolvencia I jóval kevésbé kockázatérzékeny, arányszám alapú tőkeszámítási gyakorlatához képest. Szintén fontos különbség, hogy az új irányelv piaci árakon alapuló értékelést ír elő a korábbi, könyv szerinti (az adott országban alkalmazott értékelési standardok szerinti) értékelés helyett. A régi és az új direktíva megközelítése közötti különbséget az alábbi ábra szemlélteti. 2. ábra: A szabályozói tőkekövetelmény a Szolvencia I és II irányelvek szerint A második pillér az első pillér kvantitatív követelményeit kvalitatív jellegű előírásokkal egészíti ki. A biztosítók felügyeletének eljárásrendje mellett a második pillér tartalmazza a 35
Tőkeallokáció a biztosítási szektorban*
 Hitelintézeti Szemle, 16. évf. 3. szám, 2017. szeptember, 74 97. o. Tőkeallokáció a biztosítási szektorban* Balog Dóra A tőkeallokáció fontos szerepet tölt be a biztosítók vállalati kockázatkezelési rendszerében:
Hitelintézeti Szemle, 16. évf. 3. szám, 2017. szeptember, 74 97. o. Tőkeallokáció a biztosítási szektorban* Balog Dóra A tőkeallokáció fontos szerepet tölt be a biztosítók vállalati kockázatkezelési rendszerében:
Tőkeallokáció nem likvid portfóliók esetén 1
 604 BALOG DÓRA CSÓKA PÉTER PINTÉR MIKLÓS Tőkeallokáció nem likvid portfóliók esetén 1 A kockázat jó mérése és elosztása elengedhetetlen a bankok, biztosítók, befektetési alapok és egyéb pénzügyi vállalkozások
604 BALOG DÓRA CSÓKA PÉTER PINTÉR MIKLÓS Tőkeallokáció nem likvid portfóliók esetén 1 A kockázat jó mérése és elosztása elengedhetetlen a bankok, biztosítók, befektetési alapok és egyéb pénzügyi vállalkozások
Diverzifikáció Markowitz-modell MAD modell CAPM modell 2017/ Szegedi Tudományegyetem Informatikai Intézet
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 11. Előadás Portfólió probléma Portfólió probléma Portfólió probléma Adott részvények (kötvények,tevékenységek,
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 11. Előadás Portfólió probléma Portfólió probléma Portfólió probléma Adott részvények (kötvények,tevékenységek,
Volatilitási tőkepuffer a szolvencia IIes tőkekövetelmények megsértésének kivédésére
 Volatilitási tőkepuffer a szolvencia IIes tőkekövetelmények megsértésének kivédésére Zubor Zoltán MNB - Biztosításfelügyeleti főosztály MAT Tavaszi Szimpózium 2016. május 7. 1 Háttér Bit. 99. : folyamatos
Volatilitási tőkepuffer a szolvencia IIes tőkekövetelmények megsértésének kivédésére Zubor Zoltán MNB - Biztosításfelügyeleti főosztály MAT Tavaszi Szimpózium 2016. május 7. 1 Háttér Bit. 99. : folyamatos
Valószínűségi változók. Várható érték és szórás
 Matematikai statisztika gyakorlat Valószínűségi változók. Várható érték és szórás Valószínűségi változók 2016. március 7-11. 1 / 13 Valószínűségi változók Legyen a (Ω, A, P) valószínűségi mező. Egy X :
Matematikai statisztika gyakorlat Valószínűségi változók. Várható érték és szórás Valószínűségi változók 2016. március 7-11. 1 / 13 Valószínűségi változók Legyen a (Ω, A, P) valószínűségi mező. Egy X :
Tőkeallokációs módszerek és tulajdonságaik a gyakorlatban
 Közgazdasági Szemle, LVIII. évf., 2011. július augusztus (619 632. o.) Balog Dóra Bátyi Tamás László Csóka Péter Pintér Miklós Tőkeallokációs módszerek és tulajdonságaik a gyakorlatban A pénzügyekben mind
Közgazdasági Szemle, LVIII. évf., 2011. július augusztus (619 632. o.) Balog Dóra Bátyi Tamás László Csóka Péter Pintér Miklós Tőkeallokációs módszerek és tulajdonságaik a gyakorlatban A pénzügyekben mind
A portfólió elmélet általánosításai és következményei
 A portfólió elmélet általánosításai és következményei Általánosan: n kockázatos eszköz allokációja HOZAM: KOCKÁZAT: variancia-kovariancia mátrix segítségével! ) ( ) ( ) / ( ) ( 1 1 1 n s s s p t t t s
A portfólió elmélet általánosításai és következményei Általánosan: n kockázatos eszköz allokációja HOZAM: KOCKÁZAT: variancia-kovariancia mátrix segítségével! ) ( ) ( ) / ( ) ( 1 1 1 n s s s p t t t s
QIS4 Az ING tapasztalatai
 QIS4 Az ING tapasztalatai Diószeghy Zoltán Aktárius, ING PSZÁF konzultáció 2008.12.10 Kockázatok szabályozása a csoporton belül Végrehajtás Szabályozás Kockázati stratégia Kockázati étvágy 3 védelmi vonal
QIS4 Az ING tapasztalatai Diószeghy Zoltán Aktárius, ING PSZÁF konzultáció 2008.12.10 Kockázatok szabályozása a csoporton belül Végrehajtás Szabályozás Kockázati stratégia Kockázati étvágy 3 védelmi vonal
Basel II, avagy a tőkekövetelmények és azok számítása a pénz- és tőkepiaci szervezeteknél - számítás gyakorlati
 Basel II, avagy a tőkekövetelmények és azok számítása a pénz- és tőkepiaci szervezeteknél - számítás gyakorlati példákon Dr. Pálosi-Németh Balázs, Tamás Sándor Budapest, 18 November 2010 A Bank tőkemegfelelésének
Basel II, avagy a tőkekövetelmények és azok számítása a pénz- és tőkepiaci szervezeteknél - számítás gyakorlati példákon Dr. Pálosi-Németh Balázs, Tamás Sándor Budapest, 18 November 2010 A Bank tőkemegfelelésének
Mérleg. Szolvencia II. szerinti érték Eszközök
 Mérleg Szolvencia II. szerinti érték Eszközök C0010 Immateriális javak R0030 - Halasztott adókövetelések R0040 - Nyugdíjszolgáltatások többlete R0050 - Saját használatú ingatlanok, gépek és berendezések
Mérleg Szolvencia II. szerinti érték Eszközök C0010 Immateriális javak R0030 - Halasztott adókövetelések R0040 - Nyugdíjszolgáltatások többlete R0050 - Saját használatú ingatlanok, gépek és berendezések
A KBC Equitas Zrt kockázatvállalására és kockázatkezelésére vonatkozó tájékoztatása.
 A KBC Equitas Zrt kockázatvállalására és kockázatkezelésére vonatkozó tájékoztatása. A KBC Equitas Zrt (székhely: 1051 Budapest, Roosevelt tér 7-8.; cégjegyzékszám: 01-10- 042685, a továbbiakban: Társaság)
A KBC Equitas Zrt kockázatvállalására és kockázatkezelésére vonatkozó tájékoztatása. A KBC Equitas Zrt (székhely: 1051 Budapest, Roosevelt tér 7-8.; cégjegyzékszám: 01-10- 042685, a továbbiakban: Társaság)
Hitelintézetek és befektetési vállalkozások tőkekövetelményeinek változásai
 Hitelintézetek és befektetési vállalkozások tőkekövetelményeinek változásai Seregdi László 2006. december 11. 2006. november 16. Előadás témái I. Bevezetés a hitelintézetek tőkekövetelmény számításába
Hitelintézetek és befektetési vállalkozások tőkekövetelményeinek változásai Seregdi László 2006. december 11. 2006. november 16. Előadás témái I. Bevezetés a hitelintézetek tőkekövetelmény számításába
MÜBSE. Szolvencia és pénzügyi állapotjelentés. Közzétételek. december 31. (Monetáris összegek ezer Ft-ban)
 MÜBSE Szolvencia és pénzügyi állapotjelentés Közzétételek 217 december 31. (Monetáris összegek ezer Ft-ban) Vállalkozás neve MÜBSE A vállalkozás azonosító kódja 529973SWRVST25IQ23 A vállalkozás azonosító
MÜBSE Szolvencia és pénzügyi állapotjelentés Közzétételek 217 december 31. (Monetáris összegek ezer Ft-ban) Vállalkozás neve MÜBSE A vállalkozás azonosító kódja 529973SWRVST25IQ23 A vállalkozás azonosító
Kockázat alapú felügyelés
 Kockázat alapú felügyelés A felügyelet intézkedései a Solvency II. követelményei tükrében dr. Hajdu Gabriella főosztályvezető helyettes 2005. április 27. dátum Solvency I. - Finomítások, szigorítások,
Kockázat alapú felügyelés A felügyelet intézkedései a Solvency II. követelményei tükrében dr. Hajdu Gabriella főosztályvezető helyettes 2005. április 27. dátum Solvency I. - Finomítások, szigorítások,
A kockázat fogalma. A kockázat fogalma. Fejezetek a környezeti kockázatok menedzsmentjéből 2 Bezegh András
 Fejezetek a környezeti kockázatok menedzsmentjéből 2 Bezegh András A kockázat fogalma A kockázat (def:) annak kifejezése, hogy valami nem kívánt hatással lesz a valaki/k értékeire, célkitűzésekre. A kockázat
Fejezetek a környezeti kockázatok menedzsmentjéből 2 Bezegh András A kockázat fogalma A kockázat (def:) annak kifejezése, hogy valami nem kívánt hatással lesz a valaki/k értékeire, célkitűzésekre. A kockázat
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
I. sz. melléklet S Mérleg
 S.02.01.02 Mérleg Szolvencia II. szerinti érték Eszközök C0010 Immateriális javak R0030 0 Halasztott adókövetelések R0040 0 Nyugdíjszolgáltatások többlete R0050 0 Saját használatú ingatlanok, gépek és
S.02.01.02 Mérleg Szolvencia II. szerinti érték Eszközök C0010 Immateriális javak R0030 0 Halasztott adókövetelések R0040 0 Nyugdíjszolgáltatások többlete R0050 0 Saját használatú ingatlanok, gépek és
Módszertani megjegyzések a biztosítók felügyeleti célú adatszolgáltatásán alapuló idősorhoz és a tájékoztatóhoz
 Módszertani megjegyzések a biztosítók felügyeleti célú adatszolgáltatásán alapuló idősorhoz és a tájékoztatóhoz Általános megállapítások 1. Az idősorok a biztosítók rendszeres felügyeleti célú adatszolgáltatási
Módszertani megjegyzések a biztosítók felügyeleti célú adatszolgáltatásán alapuló idősorhoz és a tájékoztatóhoz Általános megállapítások 1. Az idősorok a biztosítók rendszeres felügyeleti célú adatszolgáltatási
C0010 Eszközök Üzleti vagy cégérték
 S.02.01.02 Mérleg Szolvencia II. szerinti érték C0010 Eszközök Üzleti vagy cégérték R0010 Halasztott szerzési költség R0020 Immateriális javak R0030 0 Halasztott adókövetelések R0040 66.672 Nyugdíjszolgáltatások
S.02.01.02 Mérleg Szolvencia II. szerinti érték C0010 Eszközök Üzleti vagy cégérték R0010 Halasztott szerzési költség R0020 Immateriális javak R0030 0 Halasztott adókövetelések R0040 66.672 Nyugdíjszolgáltatások
Az ICAAP felülvizsgálati folyamat bemutatása
 Az ICAAP felülvizsgálati folyamat bemutatása Kutasi Dávid főosztályvezető Validáció és SREP Főosztály Budapesti Corvinus Egyetem 2017.05.04. 1 Komplex SREP a magyar bankrendszer ~80%-át fedi le Eltérő
Az ICAAP felülvizsgálati folyamat bemutatása Kutasi Dávid főosztályvezető Validáció és SREP Főosztály Budapesti Corvinus Egyetem 2017.05.04. 1 Komplex SREP a magyar bankrendszer ~80%-át fedi le Eltérő
ORSA, Own Risk and Solvency Assessment saját kockázat és szolvencia értékelés / egyedi intézményi kör
 dr. Hajdu Gabriella 2011. november 18. SZOLVENCIA II PSZÁF külső oktatás 2011 ORSA, Own Risk and Solvency Assessment saját kockázat és szolvencia értékelés / egyedi intézményi kör Tartalom 1. Mi is az
dr. Hajdu Gabriella 2011. november 18. SZOLVENCIA II PSZÁF külső oktatás 2011 ORSA, Own Risk and Solvency Assessment saját kockázat és szolvencia értékelés / egyedi intézményi kör Tartalom 1. Mi is az
OTP Bank Nyrt. csoportszintű adatai
 OTP Bank Nyrt. csoportszintű adatai (A Hitelintézetekről és a pénzügyi vállalkozásokról szóló 2013. évi CCXXXVII. törvény, valamint a hitelintézetekre és befektetési vállalkozásokra vonatkozó prudenciális
OTP Bank Nyrt. csoportszintű adatai (A Hitelintézetekről és a pénzügyi vállalkozásokról szóló 2013. évi CCXXXVII. törvény, valamint a hitelintézetekre és befektetési vállalkozásokra vonatkozó prudenciális
ORSA / SAKSZÉ Folyamatok Eljárások
 ORSA / SAKSZÉ avagy a CRO / VKK dicsérete 21. Altenburger Gyula Szimpózium 2011. május 21. Hanák Gábor Egy interdiszciplináris otthon ORSA / SAKSZÉ Folyamatok Eljárások 1. Pillér: Kvantitatív követelmények
ORSA / SAKSZÉ avagy a CRO / VKK dicsérete 21. Altenburger Gyula Szimpózium 2011. május 21. Hanák Gábor Egy interdiszciplináris otthon ORSA / SAKSZÉ Folyamatok Eljárások 1. Pillér: Kvantitatív követelmények
KÖZZÉTÉTEL. - éves kockázatkezelési jelentés -
 KÖZZÉTÉTEL - éves kockázatkezelési jelentés - A GlobalFX Investment Zártkörűen Működő Részvénytársaság (székhely: 1113 Budapest, Nagyszőlős utca 11-15., cégjegyzékszám: 01-10-046511; továbbiakban: Társaság)
KÖZZÉTÉTEL - éves kockázatkezelési jelentés - A GlobalFX Investment Zártkörűen Működő Részvénytársaság (székhely: 1113 Budapest, Nagyszőlős utca 11-15., cégjegyzékszám: 01-10-046511; továbbiakban: Társaság)
Az ALTERA VAGYONKEZELŐ Nyrt. kockázatkezelési irányelvei
 Az ALTERA VAGYONKEZELŐ Nyrt. kockázatkezelési irányelvei I. A dokumentum célja és alkalmazási területe A Kockázatkezelési Irányelvek az ALTERA Vagyonkezelő Nyilvánosan Működő Részvénytársaság (1068 Budapest,
Az ALTERA VAGYONKEZELŐ Nyrt. kockázatkezelési irányelvei I. A dokumentum célja és alkalmazási területe A Kockázatkezelési Irányelvek az ALTERA Vagyonkezelő Nyilvánosan Működő Részvénytársaság (1068 Budapest,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
ALKALMASSÁGI TESZT (TERMÉSZETES SZEMÉLY ÜGYFELEKNEK)
 8.a. sz. melléklet ALKALMASSÁGI TESZT (TERMÉSZETES SZEMÉLY ÜGYFELEKNEK) Tisztelt Ügyfelünk! A befektetési vállalkozásokról és az árutőzsdei szolgáltatókról, valamint az általuk végezhető tevékenységek
8.a. sz. melléklet ALKALMASSÁGI TESZT (TERMÉSZETES SZEMÉLY ÜGYFELEKNEK) Tisztelt Ügyfelünk! A befektetési vállalkozásokról és az árutőzsdei szolgáltatókról, valamint az általuk végezhető tevékenységek
OTP Bank Nyrt. csoportszintű adatai
 OTP Bank Nyrt. csoportszintű adatai (A Hitelintézetekről és a pénzügyi vállalkozásokról szóló 2013. évi CCXXXVII. törvény, valamint a hitelintézetekre és befektetési vállalkozásokra vonatkozó prudenciális
OTP Bank Nyrt. csoportszintű adatai (A Hitelintézetekről és a pénzügyi vállalkozásokról szóló 2013. évi CCXXXVII. törvény, valamint a hitelintézetekre és befektetési vállalkozásokra vonatkozó prudenciális
Szolvencia II: Tőkekövetelmény
 Szolvencia II: Tőkekövetelmény Szabó Péter 2005. április 27. 2005. 04. 27. 1/30 Áttekintés Szervezeti keretek A tőkeszükséglet szintjei Minimális Tőkeszükséglet Szavatoló Tőkeszükséglet: Átfogó kérdések
Szolvencia II: Tőkekövetelmény Szabó Péter 2005. április 27. 2005. 04. 27. 1/30 Áttekintés Szervezeti keretek A tőkeszükséglet szintjei Minimális Tőkeszükséglet Szavatoló Tőkeszükséglet: Átfogó kérdések
A pénzügyi kockázat mérése és kezelése
 A pénzügyi kockázat mérése és kezelése Varga-Haszonits István Gazdasági Fizika Téli Iskola, 2009. január 31. Áttekintés 1 Bevezetés 2 A portfólióválasztási probléma 3 Kockázati mértékek 4 A hatékony portfóliók
A pénzügyi kockázat mérése és kezelése Varga-Haszonits István Gazdasági Fizika Téli Iskola, 2009. január 31. Áttekintés 1 Bevezetés 2 A portfólióválasztási probléma 3 Kockázati mértékek 4 A hatékony portfóliók
ESZKÖZÖK TERVEZÉSE millió Ft-ban 2014-12-31 2015-12-31 1. Pénzeszközök 410 420 MTB-nél lévő elszámolási számla
 ESZKÖZÖK TERVEZÉSE millió Ft-ban 214-12-31 215-12-31 1. Pénzeszközök 41 42 MTB-nél lévő elszámolási számla 22 23 pénztár és egyéb elszámolási számlák 19 19 2. Értékpapírok Hitelviszonyt megtestesítő értékpapírok
ESZKÖZÖK TERVEZÉSE millió Ft-ban 214-12-31 215-12-31 1. Pénzeszközök 41 42 MTB-nél lévő elszámolási számla 22 23 pénztár és egyéb elszámolási számlák 19 19 2. Értékpapírok Hitelviszonyt megtestesítő értékpapírok
ALKALMASSÁGI ÉS MEGFELELÉSI TESZT
 Ügyfélnév: MIFID KÉRDŐÍV Ügyfélkód: ALKALMASSÁGI ÉS MEGFELELÉSI TESZT MAGÁNSZEMÉLYEK ÉS JOGI SZEMÉLYEK, VALAMINT JOGI SZEMÉLYISÉGGEL NEM RENDELKEZŐ GAZDASÁGI TÁRSASÁGOK RÉSZÉRE Felhívjuk Tisztelt Ügyfelünk
Ügyfélnév: MIFID KÉRDŐÍV Ügyfélkód: ALKALMASSÁGI ÉS MEGFELELÉSI TESZT MAGÁNSZEMÉLYEK ÉS JOGI SZEMÉLYEK, VALAMINT JOGI SZEMÉLYISÉGGEL NEM RENDELKEZŐ GAZDASÁGI TÁRSASÁGOK RÉSZÉRE Felhívjuk Tisztelt Ügyfelünk
KOCKÁZATKEZELÉSI JELENTÉS A belső tőkemegfelelés értékelési folyamatára vonatkozó elvekről és stratégiákról
 KOCKÁZATKEZELÉSI JELENTÉS A belső tőkemegfelelés értékelési folyamatára vonatkozó elvekről és stratégiákról A Random Capital Broker Zrt. (cj: 01-10-046204 székhely: 1053 Budapest, Szép u. 2.) (Továbbiakban:
KOCKÁZATKEZELÉSI JELENTÉS A belső tőkemegfelelés értékelési folyamatára vonatkozó elvekről és stratégiákról A Random Capital Broker Zrt. (cj: 01-10-046204 székhely: 1053 Budapest, Szép u. 2.) (Továbbiakban:
Módszertani megjegyzések a biztosítók felügyeleti célú adatszolgáltatásán alapuló idősorhoz és a tájékoztatóhoz
 Módszertani megjegyzések a biztosítók felügyeleti célú adatszolgáltatásán alapuló idősorhoz és a tájékoztatóhoz Általános megállapítások 1. A biztosítók idősorai az MNB adatszolgáltatási táblái alapján
Módszertani megjegyzések a biztosítók felügyeleti célú adatszolgáltatásán alapuló idősorhoz és a tájékoztatóhoz Általános megállapítások 1. A biztosítók idősorai az MNB adatszolgáltatási táblái alapján
Széchenyi Kereskedelmi Bank Zrt. 1
 Széchenyi Kereskedelmi Bank Zrt. 1 Bemutatkozás Burány Gábor 2014-től SZÉCHENYI Kereskedelmi Bank Zrt. Befektetési Szolgáltatások, vezető üzletkötő 2008-2013 Strategon Értékpapír Zrt. üzletkötő, határidős
Széchenyi Kereskedelmi Bank Zrt. 1 Bemutatkozás Burány Gábor 2014-től SZÉCHENYI Kereskedelmi Bank Zrt. Befektetési Szolgáltatások, vezető üzletkötő 2008-2013 Strategon Értékpapír Zrt. üzletkötő, határidős
Gépjárműfelelősségbiztosítás. Üzemi balesetbiztosítás
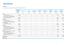 Melléklet S.05.01.02 Biztosítási díjak, kárigények és ráfordítások üzletáganként (1/3) Gyógyászati költségek térítésére vonatkozó biztosítás Jövedelembiztosítás Üzemi balesetbiztosítás Gépjárműfelelősségbiztosítás
Melléklet S.05.01.02 Biztosítási díjak, kárigények és ráfordítások üzletáganként (1/3) Gyógyászati költségek térítésére vonatkozó biztosítás Jövedelembiztosítás Üzemi balesetbiztosítás Gépjárműfelelősségbiztosítás
A Pénzügyi Szervezetek Állami Felügyelete Elnökének 1/2010. számú ajánlása a javadalmazási politika alkalmazásáról. I. Az ajánlás célja és hatálya
 A Pénzügyi Szervezetek Állami Felügyelete Elnökének 1/2010. számú ajánlása a javadalmazási politika alkalmazásáról I. Az ajánlás célja és hatálya 1. Az ajánlásban foglalt elvárások követése a Pénzügyi
A Pénzügyi Szervezetek Állami Felügyelete Elnökének 1/2010. számú ajánlása a javadalmazási politika alkalmazásáról I. Az ajánlás célja és hatálya 1. Az ajánlásban foglalt elvárások követése a Pénzügyi
Az ERGO Életbiztosító Zrt. üzleti jelentése április december 31.
 Az ERGO Életbiztosító Zrt. üzleti jelentése 2008. április 16. 2008. december 31. Tartalom AZ ERGO BIZTOSÍTÓ PIACRA LÉPÉSE... 3 AZ ERGO BIZTOSÍTÓ FEJLŐDÉSE... 3 DÍJBEVÉTEL, BIZTOSÍTÁSI SZOLGÁLTATÁSOK, MŰKÖDÉSI
Az ERGO Életbiztosító Zrt. üzleti jelentése 2008. április 16. 2008. december 31. Tartalom AZ ERGO BIZTOSÍTÓ PIACRA LÉPÉSE... 3 AZ ERGO BIZTOSÍTÓ FEJLŐDÉSE... 3 DÍJBEVÉTEL, BIZTOSÍTÁSI SZOLGÁLTATÁSOK, MŰKÖDÉSI
CONCORDE USD PÉNZPIACI BEFEKTETÉSI ALAP
 CONCORDE USD PÉNZPIACI BEFEKTETÉSI ALAP Féléves jelentés 2017. FÉLÉVES JELENTÉS A Concorde USD Pénzpiaci Befektetési Alap Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült.
CONCORDE USD PÉNZPIACI BEFEKTETÉSI ALAP Féléves jelentés 2017. FÉLÉVES JELENTÉS A Concorde USD Pénzpiaci Befektetési Alap Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült.
Megfelelési teszt. Név: Cím: Ügyfélszám: Számlatulajdonos: Meghatalmazott/képviselő:
 Megfelelési teszt Felhívjuk Tisztelt Ügyfelünk figyelmét, hogy a Random Capital Zrt. a befektetési szolgáltatási tevékenysége és kiegészítő tevékenysége és kiegészítő szolgáltatása keretében történő szerződéskötést,
Megfelelési teszt Felhívjuk Tisztelt Ügyfelünk figyelmét, hogy a Random Capital Zrt. a befektetési szolgáltatási tevékenysége és kiegészítő tevékenysége és kiegészítő szolgáltatása keretében történő szerződéskötést,
OP, KOP A HITELINTÉZETEK MŰKÖDÉSI KOCKÁZATA TŐKEKÖVETELMÉNYÉNEK SZÁMÍTÁSA
 OP, KOP A HITELINTÉZETEK MŰKÖDÉSI KOCKÁZATA TŐKEKÖVETELMÉNYÉNEK SZÁMÍTÁSA Azonosító Megnevezés HIVATKOZÁSOK MAGYAR JOGSZABÁLYOKRA ÉS MEGJEGYZÉSEK OSZLOPOK 1,2,3 Bruttó jövedelem A bruttó jövedelem meghatározását
OP, KOP A HITELINTÉZETEK MŰKÖDÉSI KOCKÁZATA TŐKEKÖVETELMÉNYÉNEK SZÁMÍTÁSA Azonosító Megnevezés HIVATKOZÁSOK MAGYAR JOGSZABÁLYOKRA ÉS MEGJEGYZÉSEK OSZLOPOK 1,2,3 Bruttó jövedelem A bruttó jövedelem meghatározását
CONCORDE RÖVID KÖTVÉNY BEFEKTETÉSI ALAP
 CONCORDE RÖVID KÖTVÉNY BEFEKTETÉSI ALAP Féléves jelentés 2017. FÉLÉVES JELENTÉS A Concorde Rövid Kötvény Befektetési Alap Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült.
CONCORDE RÖVID KÖTVÉNY BEFEKTETÉSI ALAP Féléves jelentés 2017. FÉLÉVES JELENTÉS A Concorde Rövid Kötvény Befektetési Alap Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült.
Immateriális javak Halasztott adókövetelések 0 Nyugdíjszolgáltatások többlete Saját használatú ingatlanok, gépek és berendezések
 MELLÉKLET S.02.01.02 Mérleg Eszközök Eszközök Szolvencia II. szerinti érték C0010 Immateriális javak Halasztott adókövetelések 0 Nyugdíjszolgáltatások többlete Saját használatú ingatlanok, gépek és berendezések
MELLÉKLET S.02.01.02 Mérleg Eszközök Eszközök Szolvencia II. szerinti érték C0010 Immateriális javak Halasztott adókövetelések 0 Nyugdíjszolgáltatások többlete Saját használatú ingatlanok, gépek és berendezések
(Independence, dependence, random variables)
 Két valószínűségi változó együttes vizsgálata Feltételes eloszlások Két diszkrét változó együttes eloszlása a lehetséges értékpárok és a hozzájuk tartozó valószínűségek (táblázat) Példa: Egy urna 3 fehér,
Két valószínűségi változó együttes vizsgálata Feltételes eloszlások Két diszkrét változó együttes eloszlása a lehetséges értékpárok és a hozzájuk tartozó valószínűségek (táblázat) Példa: Egy urna 3 fehér,
Kockázatkezelés és biztosítás 1. konzultáció 2. rész
 Kockázatkezelés és biztosítás 1. konzultáció 2. rész Témák 1) A kockázatkezelés eszközei 2) A kockázatkezelés szakmai területei 3) A kockázatelemzés nem holisztikus technikái 4) Kockázatfinanszírozás 5)
Kockázatkezelés és biztosítás 1. konzultáció 2. rész Témák 1) A kockázatkezelés eszközei 2) A kockázatkezelés szakmai területei 3) A kockázatelemzés nem holisztikus technikái 4) Kockázatfinanszírozás 5)
Bankkonferencia Visegrád, november panel: Validációs és prevalidációs tapasztalatok
 Bankkonferencia Visegrád, 2006. november 13-14. 2. panel: Validációs és prevalidációs tapasztalatok 1. Magyarországi bankoknál bevezetésre kerülő módszerek 2. Szabályozás és a kapcsolódó CEBS anyagok 3.
Bankkonferencia Visegrád, 2006. november 13-14. 2. panel: Validációs és prevalidációs tapasztalatok 1. Magyarországi bankoknál bevezetésre kerülő módszerek 2. Szabályozás és a kapcsolódó CEBS anyagok 3.
A kockázat alapú felügyelés módszertana Mérő Katalin ügyvezető igazgató PSZÁF november 13
 A kockázat alapú felügyelés módszertana Mérő Katalin ügyvezető igazgató PSZÁF 2006. november 13 A felügyelés közeljövője a kockázat alapú felügyelés Miért? Mert a Felügyelet sok,különböző típusú és nagyságú
A kockázat alapú felügyelés módszertana Mérő Katalin ügyvezető igazgató PSZÁF 2006. november 13 A felügyelés közeljövője a kockázat alapú felügyelés Miért? Mert a Felügyelet sok,különböző típusú és nagyságú
A kockázatkezelő feladatai az AEGON gyakorlatában Zombor Zsolt 2013. május 30.
 A kockázatkezelő feladatai az AEGON gyakorlatában Zombor Zsolt 2013. május 30. aegon.com Védelmi vonalak Kockázat 1. védelmi vonal Mindenki (Aktuáriusok) 2. védelmi vonal Kockázatkezelés, Compliance 3.
A kockázatkezelő feladatai az AEGON gyakorlatában Zombor Zsolt 2013. május 30. aegon.com Védelmi vonalak Kockázat 1. védelmi vonal Mindenki (Aktuáriusok) 2. védelmi vonal Kockázatkezelés, Compliance 3.
ORSA ORSA ORSA. ORSA konzultáció I. pilléres aspektusok. Tatai Ágnes 2011 november 18
 ORSA konzultáció I. pilléres aspektusok Tatai Ágnes 2011 november 18 1 Vázlat Mi az ORSA, miért jó ez nekünk? Az ORSA mennyiségi aspektusai tartalékok szavatoló tőkeszükséglet szavatoló tőke Összegzés
ORSA konzultáció I. pilléres aspektusok Tatai Ágnes 2011 november 18 1 Vázlat Mi az ORSA, miért jó ez nekünk? Az ORSA mennyiségi aspektusai tartalékok szavatoló tőkeszükséglet szavatoló tőke Összegzés
A Szolvencia II harmadik mennyiségi hatástanulmányának (QIS3) eredményei. Gaálné Kodila Diána március 20.
 A Szolvencia II harmadik mennyiségi hatástanulmányának (QIS3) eredményei Gaálné Kodila Diána 2008. március 20. 1 Korábbi hatástanulmányok Előkészítő helyszíni tanulmány (Preparatory Field Study, PFS) 2005.
A Szolvencia II harmadik mennyiségi hatástanulmányának (QIS3) eredményei Gaálné Kodila Diána 2008. március 20. 1 Korábbi hatástanulmányok Előkészítő helyszíni tanulmány (Preparatory Field Study, PFS) 2005.
Iránymutatások az illetékes hatóságok és az ÁÉKBV alapkezelő társaságok számára
 Iránymutatások az illetékes hatóságok és az ÁÉKBV alapkezelő társaságok számára Az egyes strukturált ÁÉKBV-k kockázatának mérésére és teljes kitettségének számítására vonatkozó iránymutatások ESMA/2012/197
Iránymutatások az illetékes hatóságok és az ÁÉKBV alapkezelő társaságok számára Az egyes strukturált ÁÉKBV-k kockázatának mérésére és teljes kitettségének számítására vonatkozó iránymutatások ESMA/2012/197
Szolvencia II: A QIS4 hatástanulmány magyarországi eredményei. Szabó Péter december 10.
 Szolvencia II: A QIS4 hatástanulmány magyarországi eredményei Szabó Péter 2008. december 10. Miről lesz szó? Részvétel Pénzügyi helyzet alakulása Értékelés: Eszközök és nem biztosítási kötelezettségek
Szolvencia II: A QIS4 hatástanulmány magyarországi eredményei Szabó Péter 2008. december 10. Miről lesz szó? Részvétel Pénzügyi helyzet alakulása Értékelés: Eszközök és nem biztosítási kötelezettségek
Szakdolgozat. Írta: Herczeg Bonifác
 Tőkeallokáció illikvid portfólió esetén Szakdolgozat Írta: Herczeg Bonifác Biztosítási és Pénzügyi Matematika MSc Kvantitatív pénzügyek szakirány 2015 Témavezető: Dr. Csóka Péter Befektetések és Vállalati
Tőkeallokáció illikvid portfólió esetén Szakdolgozat Írta: Herczeg Bonifác Biztosítási és Pénzügyi Matematika MSc Kvantitatív pénzügyek szakirány 2015 Témavezető: Dr. Csóka Péter Befektetések és Vállalati
Gazdasági matematika II. vizsgadolgozat, megoldással,
 Gazdasági matematika II. vizsgadolgozat, megoldással, levelező képzés Definiálja az alábbi fogalmakat! 1. Kvadratikus mátrix invertálhatósága és inverze. (4 pont) Egy A kvadratikus mátrixot invertálhatónak
Gazdasági matematika II. vizsgadolgozat, megoldással, levelező képzés Definiálja az alábbi fogalmakat! 1. Kvadratikus mátrix invertálhatósága és inverze. (4 pont) Egy A kvadratikus mátrixot invertálhatónak
Jó befektetési lehetőség kell? - Ebben van minden, amit keresel
 Jó befektetési lehetőség kell? - Ebben van minden, amit keresel 2014.11.18 14:17 Árgyelán Ágnes A jelenlegi hozamsivatagban különösen felértékelődik egy-egy jó befektetési lehetőség. A pénzpiaci- és kötvényalapok
Jó befektetési lehetőség kell? - Ebben van minden, amit keresel 2014.11.18 14:17 Árgyelán Ágnes A jelenlegi hozamsivatagban különösen felértékelődik egy-egy jó befektetési lehetőség. A pénzpiaci- és kötvényalapok
CONCORDE HOLD ALAPOK ALAPJA
 CONCORDE HOLD ALAPOK ALAPJA Féléves jelentés 2017. FÉLÉVES JELENTÉS A Concorde Hold Alapok Alapja Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült. I. Vagyonkimutatás 2016.12.31
CONCORDE HOLD ALAPOK ALAPJA Féléves jelentés 2017. FÉLÉVES JELENTÉS A Concorde Hold Alapok Alapja Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült. I. Vagyonkimutatás 2016.12.31
Budapesti Értéktőzsde
 Budapesti Értéktőzsde Részvénytársaság Pénztárak, mint a tőzsdei társaságok tulajdonosai Horváth Zsolt a BÉT vezérigazgatója Gondolkozzunk hosszú távon! A pénztárak természetükből adódóan hosszú távú befektetésekben
Budapesti Értéktőzsde Részvénytársaság Pénztárak, mint a tőzsdei társaságok tulajdonosai Horváth Zsolt a BÉT vezérigazgatója Gondolkozzunk hosszú távon! A pénztárak természetükből adódóan hosszú távú befektetésekben
Bankismeretek 4. Lamanda Gabriella
 Bankismeretek 4. Lamanda Gabriella lamanda@finance.bme.hu Miről volt szó? Monetáris alrendszer: Kétszintű bankrendszer Jegybankok: Cél: inflációs célkövetés rendszere, árstabilitás Eszköz: irányadó ráta
Bankismeretek 4. Lamanda Gabriella lamanda@finance.bme.hu Miről volt szó? Monetáris alrendszer: Kétszintű bankrendszer Jegybankok: Cél: inflációs célkövetés rendszere, árstabilitás Eszköz: irányadó ráta
CONCORDE PB3 ALAPOK ALAPJA
 CONCORDE PB3 ALAPOK ALAPJA Féléves jelentés 2017. FÉLÉVES JELENTÉS A Concorde PB3 Alapok Alapja Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült. I. Vagyonkimutatás 2016.12.31
CONCORDE PB3 ALAPOK ALAPJA Féléves jelentés 2017. FÉLÉVES JELENTÉS A Concorde PB3 Alapok Alapja Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült. I. Vagyonkimutatás 2016.12.31
Vagyonkezelési témavizsgálat
 Vagyonkezelési témavizsgálat Erdős Mihály 2005. 11. 10. Előadás felépítése témavizsgálat előkészítése, koordinálása lebonyolítása fontosabb megállapítások javaslatok 2005. 11. 10. 2 Témavizsgálat Előkészítése,
Vagyonkezelési témavizsgálat Erdős Mihály 2005. 11. 10. Előadás felépítése témavizsgálat előkészítése, koordinálása lebonyolítása fontosabb megállapítások javaslatok 2005. 11. 10. 2 Témavizsgálat Előkészítése,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
MÉRÉSI EREDMÉNYEK PONTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI
 MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
CONCORDE FORTE HUF ALAPOKBA FEKTETŐ RÉSZALAP PRÉM SOROZAT
 CONCORDE FORTE HUF ALAPOKBA FEKTETŐ RÉSZALAP PRÉM SOROZAT Féléves jelentés 2017. FÉLÉVES JELENTÉS A ának Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült. I. Vagyonkimutatás
CONCORDE FORTE HUF ALAPOKBA FEKTETŐ RÉSZALAP PRÉM SOROZAT Féléves jelentés 2017. FÉLÉVES JELENTÉS A ának Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült. I. Vagyonkimutatás
CONCORDE HOLD EURO ALAPOK ALAPJA
 CONCORDE HOLD EURO ALAPOK ALAPJA Féléves jelentés 2017. FÉLÉVES JELENTÉS A Concorde Hold Euro Alapok Alapja Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült. I. Vagyonkimutatás
CONCORDE HOLD EURO ALAPOK ALAPJA Féléves jelentés 2017. FÉLÉVES JELENTÉS A Concorde Hold Euro Alapok Alapja Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült. I. Vagyonkimutatás
Kockázatos pénzügyi eszközök
 Kockázatos pénzügyi eszközök Tulassay Zsolt zsolt.tulassay@uni-corvinus.hu Tőkepiaci és vállalati pénzügyek 2006. tavasz Budapesti Corvinus Egyetem 2006. március 1. Motiváció Mi a fő különbség (pénzügyi
Kockázatos pénzügyi eszközök Tulassay Zsolt zsolt.tulassay@uni-corvinus.hu Tőkepiaci és vállalati pénzügyek 2006. tavasz Budapesti Corvinus Egyetem 2006. március 1. Motiváció Mi a fő különbség (pénzügyi
TÁJÉKOZTATÓ. K&H hozamlépcső 2 származtatott zártvégű alap
 TÁJÉKOZTATÓ a K&H hozamlépcső 2 származtatott zártvégű alap befektetési jegyeinek forgalomba hozatalához a Magyar Nemzeti Bank által kiadott engedély száma: H-KE-III-236/2014. Alapkezelő: K&H Befektetési
TÁJÉKOZTATÓ a K&H hozamlépcső 2 származtatott zártvégű alap befektetési jegyeinek forgalomba hozatalához a Magyar Nemzeti Bank által kiadott engedély száma: H-KE-III-236/2014. Alapkezelő: K&H Befektetési
Az önkéntes nyugdíjpénztárak működése és sajátosságai
 MOTTÓ: MAGUNK FORMÁLJUK SZERENCSÉNKET, S ÚGY HÍVJUK SORS... Az önkéntes nyugdíjpénztárak működése és sajátosságai Előadók: Hanák Márta ügyvezető Jakab Ilona befektetési kontroller 2015. augusztus 31. TARTALOM
MOTTÓ: MAGUNK FORMÁLJUK SZERENCSÉNKET, S ÚGY HÍVJUK SORS... Az önkéntes nyugdíjpénztárak működése és sajátosságai Előadók: Hanák Márta ügyvezető Jakab Ilona befektetési kontroller 2015. augusztus 31. TARTALOM
Készítette: Fegyverneki Sándor
 VALÓSZÍNŰSÉGSZÁMÍTÁS Összefoglaló segédlet Készítette: Fegyverneki Sándor Miskolci Egyetem, 2001. i JELÖLÉSEK: N a természetes számok halmaza (pozitív egészek) R a valós számok halmaza R 2 {(x, y) x, y
VALÓSZÍNŰSÉGSZÁMÍTÁS Összefoglaló segédlet Készítette: Fegyverneki Sándor Miskolci Egyetem, 2001. i JELÖLÉSEK: N a természetes számok halmaza (pozitív egészek) R a valós számok halmaza R 2 {(x, y) x, y
Kutatásmódszertan és prezentációkészítés
 Kutatásmódszertan és prezentációkészítés 10. rész: Az adatelemzés alapjai Szerző: Kmetty Zoltán Lektor: Fokasz Nikosz Tizedik rész Az adatelemzés alapjai Tartalomjegyzék Bevezetés Leíró statisztikák I
Kutatásmódszertan és prezentációkészítés 10. rész: Az adatelemzés alapjai Szerző: Kmetty Zoltán Lektor: Fokasz Nikosz Tizedik rész Az adatelemzés alapjai Tartalomjegyzék Bevezetés Leíró statisztikák I
A csoport ORSA és a hazai leánybiztosítók
 SZOLVENCIA II PSZÁF konzultáció 2011 A csoport ORSA és a hazai leánybiztosítók Ph.D. Bethlendi András 2011. November 18. ORSA ajánlás group specificities of the ORSA - 1 Egyedi szabályok mutatis mutandis,
SZOLVENCIA II PSZÁF konzultáció 2011 A csoport ORSA és a hazai leánybiztosítók Ph.D. Bethlendi András 2011. November 18. ORSA ajánlás group specificities of the ORSA - 1 Egyedi szabályok mutatis mutandis,
CONCORDE KÖTVÉNY BEFEKTETÉSI ALAP
 CONCORDE KÖTVÉNY BEFEKTETÉSI ALAP Féléves jelentés 2017. FÉLÉVES JELENTÉS A Concorde Kötvény Befektetési Alap Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült. I. Vagyonkimutatás
CONCORDE KÖTVÉNY BEFEKTETÉSI ALAP Féléves jelentés 2017. FÉLÉVES JELENTÉS A Concorde Kötvény Befektetési Alap Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült. I. Vagyonkimutatás
Loss Distribution Approach
 Modeling operational risk using the Loss Distribution Approach Tartalom»Szabályozói környezet»modellezési struktúra»eseményszám eloszlás»káreloszlás»aggregált veszteségek»további problémák 2 Szabályozói
Modeling operational risk using the Loss Distribution Approach Tartalom»Szabályozói környezet»modellezési struktúra»eseményszám eloszlás»káreloszlás»aggregált veszteségek»további problémák 2 Szabályozói
Társaságok pénzügyei kollokvium
 udapesti Gazdasági Főiskola Pénzügyi és Számviteli Főiskolai Kar udapesti Intézet Továbbképzési Osztály Társaságok pénzügyei kollokvium F Név: soport: Tagozat: Elért pont: Érdemjegy: Javította: 55 60 pont
udapesti Gazdasági Főiskola Pénzügyi és Számviteli Főiskolai Kar udapesti Intézet Továbbképzési Osztály Társaságok pénzügyei kollokvium F Név: soport: Tagozat: Elért pont: Érdemjegy: Javította: 55 60 pont
1. tétel. Valószínűségszámítás vizsga Frissült: 2013. január 19. Valószínűségi mező, véletlen tömegjelenség.
 1. tétel Valószínűségszámítás vizsga Frissült: 2013. január 19. Valószínűségi mező, véletlen tömegjelenség. A valószínűségszámítás tárgya: véletlen tömegjelenségek vizsgálata. véletlen: a kísérlet kimenetelét
1. tétel Valószínűségszámítás vizsga Frissült: 2013. január 19. Valószínűségi mező, véletlen tömegjelenség. A valószínűségszámítás tárgya: véletlen tömegjelenségek vizsgálata. véletlen: a kísérlet kimenetelét
A L Hospital-szabály, elaszticitás, monotonitás, konvexitás
 A L Hospital-szabály, elaszticitás, monotonitás, konvexitás 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék A L Hospital-szabály, elaszticitás, monotonitás, konvexitás p. / A L
A L Hospital-szabály, elaszticitás, monotonitás, konvexitás 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék A L Hospital-szabály, elaszticitás, monotonitás, konvexitás p. / A L
Javadalmazási politika
 Javadalmazási politika Tartalom I. A javadalmazási politika szabályozása II. A javadalmazási politikával szembeni elvárások 2 I. A javadalmazási politika szabályozása II. A javadalmazási politikával szembeni
Javadalmazási politika Tartalom I. A javadalmazási politika szabályozása II. A javadalmazási politikával szembeni elvárások 2 I. A javadalmazási politika szabályozása II. A javadalmazási politikával szembeni
A Random Capital Zrt március 25. napjára összehívott éves rendes közgyűlésén az alábbi döntések születtek:
 A Random Capital Zrt. 2010. március 25. napjára összehívott éves rendes közgyűlésén az alábbi döntések születtek: 1. A Közgyűlés a Társaság 2009. évi éves beszámolóját az igazgatóság által előterjesztett
A Random Capital Zrt. 2010. március 25. napjára összehívott éves rendes közgyűlésén az alábbi döntések születtek: 1. A Közgyűlés a Társaság 2009. évi éves beszámolóját az igazgatóság által előterjesztett
QIS 3 tapasztalatai a nem-élet területen. Malicskó László Gábor
 QIS 3 tapasztalatai a nem-élet területen Malicskó László Gábor (malicsko@allianz.hu) Vázlat Standard modell vázlatos felépítése U/W kockázat: Díj, tartalék és katasztrófa Cégspecifikus adatok figyelembe
QIS 3 tapasztalatai a nem-élet területen Malicskó László Gábor (malicsko@allianz.hu) Vázlat Standard modell vázlatos felépítése U/W kockázat: Díj, tartalék és katasztrófa Cégspecifikus adatok figyelembe
Elméleti összefoglaló a Valószín ségszámítás kurzushoz
 Elméleti összefoglaló a Valószín ségszámítás kurzushoz Véletlen kísérletek, események valószín sége Deníció. Egy véletlen kísérlet lehetséges eredményeit kimeneteleknek nevezzük. A kísérlet kimeneteleinek
Elméleti összefoglaló a Valószín ségszámítás kurzushoz Véletlen kísérletek, események valószín sége Deníció. Egy véletlen kísérlet lehetséges eredményeit kimeneteleknek nevezzük. A kísérlet kimeneteleinek
SAJTÓKÖZLEMÉNY. A hitelintézeti idősorok és sajtóközlemény az MNB-nek ig jelentett összesített adatokat tartalmazzák. 3
 SAJTÓKÖZLEMÉNY a hitelintézetekről 1 a IV. negyedév végi 2 prudenciális adataik alapján Budapest, 2018. február 28. A hitelintézetek mérlegfőösszege IV. negyedévben további 1,5%-kal nőtt, év egészében
SAJTÓKÖZLEMÉNY a hitelintézetekről 1 a IV. negyedév végi 2 prudenciális adataik alapján Budapest, 2018. február 28. A hitelintézetek mérlegfőösszege IV. negyedévben további 1,5%-kal nőtt, év egészében
Magyar Könyvvizsgálói Kamara. XX. Országos Könyvvizsgálói Konferencia. Kihívások az elkövetkező 5 évben
 Kihívások az elkövetkező 5 évben (hogyan kell módosítani a könyvvizsgálati módszertant a várható új IFRS-ek követelményeinek figyelembevételével) Új IFRS standardok - Összefoglaló Standard Mikortól hatályos?
Kihívások az elkövetkező 5 évben (hogyan kell módosítani a könyvvizsgálati módszertant a várható új IFRS-ek követelményeinek figyelembevételével) Új IFRS standardok - Összefoglaló Standard Mikortól hatályos?
ERSTE DAX NÖVEKEDÉSI KÖTVÉNY
 ERSTE DAX NÖVEKEDÉSI KÖTVÉNY 100%-os tőkevédelem és részesedés a legmeghatározóbb német részvényeket tartalmazó DAX index teljesítményéből! 1. Kinek ajánljuk a figyelmébe az Erste DAX Növekedési Kötvény-t?
ERSTE DAX NÖVEKEDÉSI KÖTVÉNY 100%-os tőkevédelem és részesedés a legmeghatározóbb német részvényeket tartalmazó DAX index teljesítményéből! 1. Kinek ajánljuk a figyelmébe az Erste DAX Növekedési Kötvény-t?
CONCORDE 2016 DEVIZÁS VÁLLALATI KÖTVÉNY SZÁRMAZTATOTT BEFEKTETÉSI ALAP
 CONCORDE 2016 DEVIZÁS VÁLLALATI KÖTVÉNY SZÁRMAZTATOTT BEFEKTETÉSI ALAP Féléves jelentés 2016. FÉLÉVES JELENTÉS A Féléves jelentése a Tpt. V. fejezetében foglaltak alapján készült. I. Vagyonkimutatás Piaci
CONCORDE 2016 DEVIZÁS VÁLLALATI KÖTVÉNY SZÁRMAZTATOTT BEFEKTETÉSI ALAP Féléves jelentés 2016. FÉLÉVES JELENTÉS A Féléves jelentése a Tpt. V. fejezetében foglaltak alapján készült. I. Vagyonkimutatás Piaci
Statisztika - bevezetés Méréselmélet PE MIK MI_BSc VI_BSc 1
 Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
I. BESZÁLLÍTÓI TELJESÍTMÉNYEK ÉRTÉKELÉSE
 I. BESZÁLLÍTÓI TELJESÍTMÉNYEK ÉRTÉKELÉSE Komplex termékek gyártására jellemző, hogy egy-egy termékbe akár több ezer alkatrész is beépül. Ilyenkor az alkatrészek általában sok különböző beszállítótól érkeznek,
I. BESZÁLLÍTÓI TELJESÍTMÉNYEK ÉRTÉKELÉSE Komplex termékek gyártására jellemző, hogy egy-egy termékbe akár több ezer alkatrész is beépül. Ilyenkor az alkatrészek általában sok különböző beszállítótól érkeznek,
STATISZTIKA ELŐADÁS ÁTTEKINTÉSE. Matematikai statisztika. Mi a modell? Binomiális eloszlás sűrűségfüggvény. Binomiális eloszlás
 ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
CONCORDE USD PB3 ALAPOK ALAPJA
 CONCORDE USD PB3 ALAPOK ALAPJA Féléves jelentés 2016. FÉLÉVES JELENTÉS A Concorde USD PB3 Alapok Alapja Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült. I. Vagyonkimutatás
CONCORDE USD PB3 ALAPOK ALAPJA Féléves jelentés 2016. FÉLÉVES JELENTÉS A Concorde USD PB3 Alapok Alapja Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült. I. Vagyonkimutatás
1. árfolyam alapú értékeltségi mutatók
 Egyre nagyobbra fújódik a tőzsdei lufi 2016.07.22 10:48 Eddig sem volt olcsó az amerikai részvénypiac, az árfolyamok legutóbb látott meredek emelkedése pedig még inkább feszítetté tette az értékeltséget.
Egyre nagyobbra fújódik a tőzsdei lufi 2016.07.22 10:48 Eddig sem volt olcsó az amerikai részvénypiac, az árfolyamok legutóbb látott meredek emelkedése pedig még inkább feszítetté tette az értékeltséget.
Szolvencia II - áttekintés. Tatai Ágnes 2011. Január 17. 24. Piaci konzultáció
 Szolvencia II - áttekintés Tatai Ágnes 2011. Január 17. 24. Piaci konzultáció 1 A Szolvencia II projekt állása, a felügyelés alapjai 2 Hol tart a folyamat? 1. szintű szabályozás elfogadva: 2009 év végén
Szolvencia II - áttekintés Tatai Ágnes 2011. Január 17. 24. Piaci konzultáció 1 A Szolvencia II projekt állása, a felügyelés alapjai 2 Hol tart a folyamat? 1. szintű szabályozás elfogadva: 2009 év végén
A Magyar Nemzeti Bank 21/2018. (IV.18.) számú ajánlása
 A Magyar Nemzeti Bank 21/2018. (IV.18.) számú ajánlása az IFRS 9 standard bevezetése által a szavatolótőkére gyakorolt hatás enyhítésére szolgáló átmeneti szabályokhoz kapcsolódó egységes nyilvánosságra
A Magyar Nemzeti Bank 21/2018. (IV.18.) számú ajánlása az IFRS 9 standard bevezetése által a szavatolótőkére gyakorolt hatás enyhítésére szolgáló átmeneti szabályokhoz kapcsolódó egységes nyilvánosságra
2013.06.05. A TakarékBank. és a Magyar Takarékszövetkezeti Szektor. MKVK Pénz és Tőkepiaci Tagozat rendezvénye. Budapest, 2013. június 5.
 A TakarékBank és a Magyar Takarékszövetkezeti Szektor A TakarékBank tulajdonosi struktúrája megváltozott 2012. december 31. 2013. május 15. 5.07% 0.01% 3.22% 36.05% 55.65% 39.28% Takarékszövetkezetek MFB
A TakarékBank és a Magyar Takarékszövetkezeti Szektor A TakarékBank tulajdonosi struktúrája megváltozott 2012. december 31. 2013. május 15. 5.07% 0.01% 3.22% 36.05% 55.65% 39.28% Takarékszövetkezetek MFB
CONCORDE EURO PB3 ALAPOK ALAPJA
 CONCORDE EURO PB3 ALAPOK ALAPJA Féléves jelentés 2017. FÉLÉVES JELENTÉS A Concorde Euro PB3 Alapok Alapja Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült. I. Vagyonkimutatás
CONCORDE EURO PB3 ALAPOK ALAPJA Féléves jelentés 2017. FÉLÉVES JELENTÉS A Concorde Euro PB3 Alapok Alapja Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült. I. Vagyonkimutatás
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT.
 CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2014. MÁSODIK NEGYEDÉV 2014. augusztus 12. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2014. MÁSODIK NEGYEDÉV 2014. augusztus 12. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
CRD IV/CRR hitelintézetek és befektetési vállalkozások prudenciális szabályozásának várható változásai
 CRD IV/CRR hitelintézetek és befektetési vállalkozások prudenciális szabályozásának várható változásai dr. Kardosné Vadászi Zsuzsanna 2012. április CRR/CRD IV javaslat áttekintése A 2006/48/EK és 2006/49/EK
CRD IV/CRR hitelintézetek és befektetési vállalkozások prudenciális szabályozásának várható változásai dr. Kardosné Vadászi Zsuzsanna 2012. április CRR/CRD IV javaslat áttekintése A 2006/48/EK és 2006/49/EK
Banki kockázatok. Kockázat. Befektetési kockázat: Likviditási kockázat
 Bankrendszer II. Banki kockázatok Kockázat A hitelintézet tevékenysége, a tevékenység tárgya alapján eredendően kockázatos Igen nagy, szerteágazó a pénzügyi szolgáltatások eredményét befolyásoló veszélyforrások
Bankrendszer II. Banki kockázatok Kockázat A hitelintézet tevékenysége, a tevékenység tárgya alapján eredendően kockázatos Igen nagy, szerteágazó a pénzügyi szolgáltatások eredményét befolyásoló veszélyforrások
CONCORDE USD PÉNZPIACI BEFEKTETÉSI ALAP
 CONCORDE USD PÉNZPIACI BEFEKTETÉSI ALAP Féléves jelentés 2015. A Concorde USD Pénzpiaci Befektetési Alap Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült. I. Vagyonkimutatás
CONCORDE USD PÉNZPIACI BEFEKTETÉSI ALAP Féléves jelentés 2015. A Concorde USD Pénzpiaci Befektetési Alap Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült. I. Vagyonkimutatás
Balogh Csaba. Tőkeszükséglet és tőkeallokáció a pénzügyi intézményekben
 Tőkeszükséglet és tőkeallokáció a pénzügyi intézményekben BEFEKTETÉSEK ÉS VÁLLALATI PÉNZÜGY TANSZÉK TÉMAVEZETŐ: KIRÁLY JÚLIA, EGYETEMI DOCENS Copyright Balogh Csaba, 2005 BUDAPESTI CORVINUS EGYETEM GAZDÁLKODÁSTANI
Tőkeszükséglet és tőkeallokáció a pénzügyi intézményekben BEFEKTETÉSEK ÉS VÁLLALATI PÉNZÜGY TANSZÉK TÉMAVEZETŐ: KIRÁLY JÚLIA, EGYETEMI DOCENS Copyright Balogh Csaba, 2005 BUDAPESTI CORVINUS EGYETEM GAZDÁLKODÁSTANI
CONCORDE KÖTVÉNY BEFEKTETÉSI ALAP
 CONCORDE KÖTVÉNY BEFEKTETÉSI ALAP Féléves jelentés 2016. FÉLÉVES JELENTÉS A Concorde Kötvény Befektetési Alap Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült. I. Vagyonkimutatás
CONCORDE KÖTVÉNY BEFEKTETÉSI ALAP Féléves jelentés 2016. FÉLÉVES JELENTÉS A Concorde Kötvény Befektetési Alap Féléves jelentése a 2014. évi XVI. törvény 6. számú melléklete alapján készült. I. Vagyonkimutatás
Piackutatás versenytárs elemzés
 Piackutatás versenytárs elemzés 2015 TÁJÉKOZTATÓ Jelen szigorúan bizalmas piackutatást / versenytárs elemzést (a továbbiakban mellékleteivel és kiegészítéseivel együtt Elemzés ) az Elemző (a továbbiakban
Piackutatás versenytárs elemzés 2015 TÁJÉKOZTATÓ Jelen szigorúan bizalmas piackutatást / versenytárs elemzést (a továbbiakban mellékleteivel és kiegészítéseivel együtt Elemzés ) az Elemző (a továbbiakban
CEBS Consultative Paper 10 (folytatás) Krekó Béla PSZÁF, 2005. szeptember 15.
 CEBS Consultative Paper 10 (folytatás) Krekó Béla PSZÁF, 2005. szeptember 15. 1 3.3.3 Minősítési rendszerek és a kockázatok számszerűsítése Minősítések hozzárendelése PD, LGD, CF meghatározása Közös vizsgálati
CEBS Consultative Paper 10 (folytatás) Krekó Béla PSZÁF, 2005. szeptember 15. 1 3.3.3 Minősítési rendszerek és a kockázatok számszerűsítése Minősítések hozzárendelése PD, LGD, CF meghatározása Közös vizsgálati
