Az ötszög keresztmetszetű élszarufa keresztmetszeti jellemzőiről
|
|
|
- Jenő Székely
- 6 évvel ezelőtt
- Látták:
Átírás
1 1 Az ötszög keresztmetszetű élszarufa keresztmetszeti jellemzőiről Bevezetés A kontytetők és az összetett alaprajzú tetők akár nyeregtetők szerkezeti elemei között megtaláljuk az él - és a vápaszarufákat is 1. ábra. 1. ábra forrása: Ezek keresztmetszete ötszögletű, ha azt akarjuk, hogy az él - vagy a vápaszarufa pontosan illeszkedjen a tetősíkokhoz. A mai számítógépes világban gyakran találkozhatunk ilyen módon megjelenített tető - szerkezeti részletekkel; hasonlók láthatók az 1. ábrán is. ( Ez egy makettet szemléltet. ) Annál kevésbé találunk olyan elemzéseket, melyek érdemben vizsgálnák az él - és vápa - szarufák erőtani viselkedését. Ennek okai sokfélék lehetnek; ilyenek pl.: ~ a szükséges erőtani számítások hosszúak, bonyolultak, leginkább közelítőek; ~ az erőtani modell felvétele / a tetőszerkezet feltételezett viselkedése bizonytalan; ~ az alkalmazott faanyagok anyagjellemzői kevéssé megbízhatóak, illetve a szabvány által előírt értékek nehezen biztosíthatók, stb. Ennek ellenére látunk néha olyan internetes oldalakat, ahol összetettebb tetőszerkezet erő - tani vizsgálatának eredményeit közlik. Sajnos, ezzel kevéssé vagyunk kisegítve, hiszen erről csak annyit tudhatunk / sejthetünk, hogy a vonatkozó szabványok, valamint az épí - tészeti program tervezői által adott / felvett erőtani modellhez tartozó számítások eredmé - nyeként álltak elő.
2 2 A következőkben ez egy hosszabb időszak is lehet megkísérelünk használható érveket, gondolatokat, számításokat közreadni ebben a mostohagyerek témakörben. Máris kezdjük, a keresztmetszeti jellemzők számításával. Az ötszög alakú élszarufa - keresztmetszet néhány jellemzőjének meghatározása Itt a húzás - nyomás - hajlítással kapcsolatos geometriai adatok előállításáról lesz szó. Ezek: ~ a keresztmetszeti síkidom területe; ~ a keresztmetszeti síkidom elsőrendű vagy statikai nyomatékai; ~ a keresztmetszeti síkidom másodrendű nyomatékai. Most tekintsük a 2. ábrát! 2. ábra Ezt egy korábbi dolgozatunkból vettük át, melynek címe: Az ötszög keresztmetszetű élszarufa keresztmetszetének kialakításáról. Itt azt láthatjuk, hogy az élszarufák keresztmetszetének két különböző kialakítása is lehet - séges. Mi itt az 1. típusúval foglalkozunk, vagyis azzal, amelyiknél az élszarufa felső éle éppen középen helyezkedik el. Lényeges, hogy a kiindulási alap mindig a szabványos fűrészáru, melynek keresztmetszete egy b x h befoglaló méretű téglalap. Az itt elvégzendő számításokkal máshol még nem találkoztunk, pont ezen a módon. Természetesen a szilárdságtani szakirodalomban, mérnöki kézikönyvekben találhatók olyan képletek, melyek a mi keresztmetszeteinket alkotó téglalapra, háromszögre, illetve trapézra vonatkoznak, amelyekből összerakhattuk volna eredményeinket. Úgy döntöttünk, hogy nem ezt az utat járjuk, hanem közvetlenül a definíciós képletekből kiindulva végez - zük a számításokat. Ez valószínűleg könnyebben áttekinthető, kevesebb tévesztési lehető - séggel. Az előkészületekhez, ismétléshez ajánlott irodalom:[ 1 ]. Először tekintsük a számításainkhoz alkalmazott koordináta - rendszert 3. ábra!
3 3 Ebben feltüntettük a számításaink alapadatait is; ezek: b, h, γ 1, γ 2, melyek előre ismertek. 3. ábra 1. A keresztmetszeti síkidom területének számítása A 3. ábra alapján: ( 1 ) ( 2 ) így ( 1 ) és ( 2 ) - vel: ( 3 ) 2. Az X tengelyre vett statikai nyomaték számítása Ehhez tekintsük a 4. ábrát! Ez alapján és a definíció szerint: ( 4 ) Az első összeadandó számítását részletezzük. ( A másodikat nem, mert az teljesen hasonlóan megy. )
4 4 4. ábra ( 5 ) mivel a felső határoló egyenes egyenlete: ( 6 ) így ( 5 ) és ( 6 ) - tal: ( 7 ) Részletezve: ( 8 ) majd ( 7 ) és ( 8 ) - cal:
5 5 ( 9 ) Hasonló számítással, illetve indexcserével: ( 10 ) Most ( 4 ), ( 9 ) és ( 10 ) - zel: ( 11 ) Ismét definíció szerint a keresztmetszeti síkidom S súlypontjának Y S koordinátájára: ( 12 ) Most ( 3 ), ( 11 ) és ( 12 ) - vel: ( 13 ) 1. Speciális eset 5 / a ábra : ( 14 ) ekkor ( 13 ) és ( 14 ) szerint:
6 6 ( 15 ) 5. ábra 2. Speciális eset 5 / b ábra: ekkor ( 15 ) és ( 16 ) szerint: ( 16 ) ( 17 ) ahogyan azt a szemlélet alapján vártuk is. 3. Az Y tengelyre vett statikai nyomaték számítása Definíció szerint: ( 18 ) ( 18 ) első összeadandója részletezve, a 4. ábrával is:
7 7 ( 19 ) ( 18 ) második összeadandója részletezve, a 6. ábrával is: 6. ábra ( 20 )
8 8 Majd ( 18 ), ( 19 ) és ( 20 ) - szal: ( 21 ) Ismét definíció szerint a keresztmetszeti síkidom S súlypontjának X S koordinátájára: ( 22 ) Most ( 3 ), ( 21 ) és ( 22 ) szerint: ( 23 ) 1. Speciális eset 5 / a ábra : ( 14 ) ekkor ( 23 ) és ( 14 ) szerint: ( 24 ) 2. Speciális eset 5 / b ábra: minthogy ( 24 ) független γ - tól, így ( 16 ) és ( 24 ) - ből: ( 16 ) ( 25 ) A ( 24 ) és ( 25 ) képleteket a szemlélet alapján is vártuk, a szimmetria miatt.
9 9 4. Az X tengelyre vett másodrendű nyomaték számítása Definíció szerint: ( 26 ) Az első összeadandó számítását részletezzük. ( A másodikat nem, mert az teljesen hasonlóan megy. ) A 4. ábrával is: ( 27 ) helyettesítéssel: ( 28 ) most ( 27 ) és ( 28 ) - cal: ( 29 ) Felhasználjuk az alábbi azonosságot: ( 30 ) most ( 29 ) és ( 30 ) - cal: ( 31 ) a szorzatokat részletezve: ( 32 ) hasonlóan:
10 10 ( 33 ) most ( 31 ), ( 32 ), ( 33 ) szerint: ( 34 ) Hasonló számítással, illetve indexcserével: ( 35 ) Majd ( 26 ), ( 34 ) és ( 35 ) - tel: ( 36 ) 1. Speciális eset 5 / a ábra : ekkor ( 36 ) és ( 14 ) - gyel: ( 14 ) ( 37 ) 2. Speciális eset 5 / b ábra: ekkor ( 37 ) és ( 16 ) szerint: ( 16 ) ( 38 ) Ez megint egy ismert eredmény [ 1 ].
11 11 5. Az Y tengelyre vett másodrendű nyomaték számítása Definíció szerint: ( 39 ) ( 39 ) első tagjának részletezése: ( 40 ) ( 39 ) második tagjának részletezése:
12 12 ( 41 ) Most ( 39 ), ( 40 ) és ( 41 ) - gyel: ( 42 ) 1. Speciális eset 5 / a ábra : ( 14 ) ekkor ( 42 ) és ( 14 ) - gyel: ( 43 ) 2. Speciális eset 5 / b ábra: ekkor ( 43 ) és ( 16 ) szerint: ( 16 ) ( 44 ) 6. Az XY tengelypárra vett deviációs másodrendű nyomaték számítása Definíció szerint: ( 45 ) ( 45 ) első tagjának részletezése:
13 13 ( 46 ) Átalakításokkal: tehát ( 46 ) - ból: ( 47 )
14 14 ( 45 ) második tagjának részletezése: Átalakításokkal: ( 48 ) Most ( 45 ), ( 47 ) és ( 48 ) - cal:
15 15 ( 49 ) 1. Speciális eset 5 / a ábra : ekkor ( 49 ) és ( 14 ) - gyel: ( 14 ) ( 50 ) 2. Speciális eset 5 / b ábra: ekkor ( 50 ) és ( 16 ) - tal: ( 16 ) ( 51 ) Ez megint egy ismert eredmény [ 1 ]. Megjegyzések: M1. Képleteinket bár egyszerűbb esetekre jó eredményt adtak még további ellenőr - zésnek kell alávetni. Ugyanis ha pl. a ( 43 ) képlet zárójelében + előjel állna, a ( 16 ) és ( 43 ) képletek akkor is a helyes ( 44 ) eredményt adnák. Vagyis egy speciális esetre kapott helyes eredmény még nem garantálja az általánosabb esetre vonatkozó képlet jóságát. Ez az ellenőrzés történhet számszerű adatokkal bíró esetekben, pl. numerikus integrálás segítségével. Az analitikusan és a numerikusan meghatározott integrállal kapott eredmé - nyek egyezése már eléggé meggyőző lehet, a levezetett képlet jóságára nézve. A mondottakat két konkrét számpéldával szemléltetjük. 1. SZÁMPÉLDA
16 16 Ellenőrizendő az ( 43 ) képlet! Adatok: b = 10 cm; h = 14 cm; γ = 45. ( A ) Most ( 43 ) és ( A ) - val: ( a ) Majd a numerikus integráláshoz előkészületként: ( b ) Ezután a Graph ingyenes szoftvert alkalmazva, numerikus integrálással kapjuk, hogy: tehát megállapíthatjuk, hogy ( c ) vagyis a ( 43 ) képlet valószínűleg helyes. 2. SZÁMPÉLDA Ellenőrizendő az ( 50 ) képlet! Adatok: b = 10 cm; h = 14 cm; γ = 45. ( A ) Most ( 50 ) és ( A ) - val: Majd a numerikus integráláshoz előkészületként: ( d ) ( e )
17 Ezután a Graph ingyenes szoftvert alkalmazva, numerikus integrálással kapjuk, hogy: 17 tehát megállapíthatjuk, hogy vagyis az ( 50 ) képlet valószínűleg helyes. M2. Gyakori, hogy a keresztmetszeti jellemzők számítását eleve numerikus integrálással végzik, nem foglalkoznak zárt alakú pontos képletek előállításával. Ilyen közelítő kép - leteket találunk pl. [ 1 ] - ben is, melyeket a trapézszabály alkalmazásával nyertek. M3. A zárt alakú pontos képletek felírását azért is szorgalmazzuk, mert nem mindenki tud saját számítógépi programot készíteni és működtetni. Bár a nagyobb tervező irodák, egye - temi tanszékek, kutató intézmények bizonyára rendelkeznek a szükséges tárgyi és szemé - lyi erőforrásokkal, azonban a mezei felhasználó dolgozóknak pl: ilyenek lehetnek a mérnökök és a tanárok szükségük lehet számításaikhoz a szakirodalomban nem fellelt fenti képletekre is. M4. A 2. ábra jobb oldalán látható 2. típusú élszarufa - keresztmetszet jellemzőinek szá - mítása a fentiekhez hasonlóan végezhető el, a megfelelő újabb képletek előállításával. Megeshet, hogy ezt nem végezzük el, hanem az alábbi kézenfekvő egyszerűsítéssel élünk: a b x h 0 méretű dolgozó keresztmetszet - részre, azaz téglalapra alkalmazzuk az ismert szilárdságtani képleteket. Ezt azzal is indokolhatjuk, hogy ennél a keresztmetszet - alaknál kisebb a b x h befoglaló méretű téglalap gyengítése, így a felső ferde részeket úgy tekint - jük, mint egy rászerelt támasztó felület részeit. A hazai építési gyakorlatban ténylegesen előfordul ez a ráépítés, csak nem igazán megmunkáltan, hanem pl. léceknek a szarugeren - dára való rászegezésével. M5. A nagy kérdés, amit eddig még nem tettünk fel, hogy mire használjuk a nem annyira egyszerű képleteinket. Erre a választ talán későbbi dolgozatainkban adjuk meg. Ne feled - jük, hogy képleteink bemenő adatait ismernünk kell, amelyek szintén valamely ( elő )ter - vezési munka eredményeként állnak elő. Ezek főként geometriai, mechanikai, gazdasági és építés - technológiai természetűek lehetnek. Terveink szerint ezekhez hasonló kérdésekre a későbbiekben még visszatérünk.
18 18 Ajánlott irodalom: [ 1 ] Muttnyánszky Ádám: Szilárdságtan Műszaki Könyvkiadó, Budapest, 1981., 136. o, 148. o. Sződliget, Összeállította: Galgóczi Gyula mérnöktanár
Ellipszis átszelése. 1. ábra
 1 Ellipszis átszelése Adott egy a és b féltengely - adatokkal bíró ellipszis, melyet a befoglaló téglalapjának bal alsó sarkában csuklósan rögzítettnek képzelünk. Az ellipszist e C csukló körül forgatva
1 Ellipszis átszelése Adott egy a és b féltengely - adatokkal bíró ellipszis, melyet a befoglaló téglalapjának bal alsó sarkában csuklósan rögzítettnek képzelünk. Az ellipszist e C csukló körül forgatva
Az ötszög keresztmetszetű élszarufa kis elmozdulásainak számításáról
 1 Az ötszög keresztmetszetű élszarufa kis elmozdulásainak számításáról Előző dolgozatunkban melynek címe: ED: Az ötszög keresztmetszetű élszarufa σ - feszültségeinek számításáról elkezdtük / folytattuk
1 Az ötszög keresztmetszetű élszarufa kis elmozdulásainak számításáról Előző dolgozatunkban melynek címe: ED: Az ötszög keresztmetszetű élszarufa σ - feszültségeinek számításáról elkezdtük / folytattuk
Ellipszis vezérgörbéjű ferde kúp felszínének meghatározásához
 1 Ellipszis vezérgörbéjű ferde kúp felszínének meghatározásához Előző dolgozatunkkal melynek címe: A ferde körkúp palástfelszínének meghatározásához már mintegy megágyaztunk a jelen írásnak. Több mindent
1 Ellipszis vezérgörbéjű ferde kúp felszínének meghatározásához Előző dolgozatunkkal melynek címe: A ferde körkúp palástfelszínének meghatározásához már mintegy megágyaztunk a jelen írásnak. Több mindent
Érdekes geometriai számítások 10.
 1 Érdekes geometriai számítások 10. Találtunk az interneten egy könyvrészletet [ 1 ], ahol egy a triéder - geometriában fontos összefüggést egyszerű módon vezetnek le. Ennek eredményét összevetjük más
1 Érdekes geometriai számítások 10. Találtunk az interneten egy könyvrészletet [ 1 ], ahol egy a triéder - geometriában fontos összefüggést egyszerű módon vezetnek le. Ennek eredményét összevetjük más
A főtengelyproblémához
 1 A főtengelyproblémához Korábbi, az ellipszis perspektivikus ábrázolásával foglalkozó dolgozatainkban előkerült a másodrendű görbék kanonikus alakra hozása, majd ebben a főtengelyrendszert előállító elforgatási
1 A főtengelyproblémához Korábbi, az ellipszis perspektivikus ábrázolásával foglalkozó dolgozatainkban előkerült a másodrendű görbék kanonikus alakra hozása, majd ebben a főtengelyrendszert előállító elforgatási
Szabályos fahengeres keresztmetszet geometriai jellemzőinek meghatározása számítással
 Szabályos fahengeres keresztmetszet geometriai jellemzőinek meghatározása számítással Előző dolgozatunkban jele: ( E ), címe: Szimmetrikusan szélezett körkeresztmetszet geometriai jellemzőinek meghatározása
Szabályos fahengeres keresztmetszet geometriai jellemzőinek meghatározása számítással Előző dolgozatunkban jele: ( E ), címe: Szimmetrikusan szélezett körkeresztmetszet geometriai jellemzőinek meghatározása
Egy gyakorlati szélsőérték - feladat. 1. ábra forrása: [ 1 ]
![Egy gyakorlati szélsőérték - feladat. 1. ábra forrása: [ 1 ] Egy gyakorlati szélsőérték - feladat. 1. ábra forrása: [ 1 ]](/thumbs/101/151445602.jpg) 1 Egy gyakorlati szélsőérték - feladat Az [ 1 ] munkában találtuk az alábbi feladatot. 1. ábra forrása: [ 1 ] Magyarul: Három egyforma széles deszkából egy (eresz - )csatornát szegezünk össze. Az oldalfal
1 Egy gyakorlati szélsőérték - feladat Az [ 1 ] munkában találtuk az alábbi feladatot. 1. ábra forrása: [ 1 ] Magyarul: Három egyforma széles deszkából egy (eresz - )csatornát szegezünk össze. Az oldalfal
Fiók ferde betolása. A hűtőszekrényünk ajtajának és kihúzott fiókjának érintkezése ihlette az alábbi feladatot. Ehhez tekintsük az 1. ábrát!
 1 Fiók ferde betolása A hűtőszekrényünk ajtajának és kihúzott fiókjának érintkezése ihlette az alábbi feladatot. Ehhez tekintsük az 1. ábrát! 1. ábra Itt azt látjuk, hogy egy a x b méretű kis kék téglalapot
1 Fiók ferde betolása A hűtőszekrényünk ajtajának és kihúzott fiókjának érintkezése ihlette az alábbi feladatot. Ehhez tekintsük az 1. ábrát! 1. ábra Itt azt látjuk, hogy egy a x b méretű kis kék téglalapot
Példa: Háromszög síkidom másodrendű nyomatékainak számítása
 Példa: Háromszög síkidom másodrendű nyomatékainak számítása Készítette: Dr. Kossa Attila kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék. február 6. Határozzuk meg az alábbi ábrán látható derékszögű háromszög
Példa: Háromszög síkidom másodrendű nyomatékainak számítása Készítette: Dr. Kossa Attila kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék. február 6. Határozzuk meg az alábbi ábrán látható derékszögű háromszög
Az R forgató mátrix [ 1 ] - beli képleteinek levezetése: I. rész
![Az R forgató mátrix [ 1 ] - beli képleteinek levezetése: I. rész Az R forgató mátrix [ 1 ] - beli képleteinek levezetése: I. rész](/thumbs/57/40130324.jpg) Az R forgató mátri [ ] - beli képleteinek levezetése: I rész Az [ ] forrás kötetében a ( 49 ), ( 50 ) képletek nyilván mint közismertek nem lettek levezetve Minthogy az ottani további számítások miatt
Az R forgató mátri [ ] - beli képleteinek levezetése: I rész Az [ ] forrás kötetében a ( 49 ), ( 50 ) képletek nyilván mint közismertek nem lettek levezetve Minthogy az ottani további számítások miatt
Az eltérő hajlású szarufák és a taréjszelemen kapcsolatáról 1. rész. Eltérő keresztmetszet - magasságú szarufák esete
 1 Az eltérő hajlású szarufák és a taréjszelemen kapcsolatáról 1. rész Eltérő keresztmetszet - magasságú szarufák esete Az alábbi ábrát találtuk az interneten 1. ábra 1. ábra forrás( ok ): http://www.sema-soft.com/de/forum/files/firstpfettenverschiebung_432.jpg
1 Az eltérő hajlású szarufák és a taréjszelemen kapcsolatáról 1. rész Eltérő keresztmetszet - magasságú szarufák esete Az alábbi ábrát találtuk az interneten 1. ábra 1. ábra forrás( ok ): http://www.sema-soft.com/de/forum/files/firstpfettenverschiebung_432.jpg
Egy geometriai szélsőérték - feladat
 1 Egy geometriai szélsőérték - feladat A feladat: Szerkesztendő egy olyan legnagyobb területű háromszög, melynek egyik csúcsa az a és b féltengelyeivel adott ellipszis tetszőlegesen felvett pontja. Keresendő
1 Egy geometriai szélsőérték - feladat A feladat: Szerkesztendő egy olyan legnagyobb területű háromszög, melynek egyik csúcsa az a és b féltengelyeivel adott ellipszis tetszőlegesen felvett pontja. Keresendő
Ellipszis perspektivikus képe 2. rész
 1 Ellipszis perspektivikus képe 2. rész Dolgozatunk 1. részében nem mentünk tovább a matematikai kifejtésben. Ezzel mintegy felhagytunk a belső összefüggések feltárásával. A jelen 2. részben megkíséreljük
1 Ellipszis perspektivikus képe 2. rész Dolgozatunk 1. részében nem mentünk tovább a matematikai kifejtésben. Ezzel mintegy felhagytunk a belső összefüggések feltárásával. A jelen 2. részben megkíséreljük
Egy felszínszámítási feladat a tompaélű fagerendák témaköréből
 1 Egy felszínszámítási feladat a tompaélű fagerendák témaköréből Előző dolgozatunkban melynek címe: Ismét a fahengeres keresztmetszetű gerenda témájáról már sok min - dent előkészítettünk az itteni címbeli
1 Egy felszínszámítási feladat a tompaélű fagerendák témaköréből Előző dolgozatunkban melynek címe: Ismét a fahengeres keresztmetszetű gerenda témájáról már sok min - dent előkészítettünk az itteni címbeli
Fa rudak forgatása II.
 Fa rudak forgatása II. Dolgozatunk I. részében egy speciális esetre oldottuk meg a kitűzött feladatokat. Most egy általánosabb elrendezés vizsgálatát végezzük el. A számítás a korábbi úton halad, ügyelve
Fa rudak forgatása II. Dolgozatunk I. részében egy speciális esetre oldottuk meg a kitűzött feladatokat. Most egy általánosabb elrendezés vizsgálatát végezzük el. A számítás a korábbi úton halad, ügyelve
Ismét a fahengeres keresztmetszetű gerenda témájáról. 1. ábra forrása: [ 1 ]
![Ismét a fahengeres keresztmetszetű gerenda témájáról. 1. ábra forrása: [ 1 ] Ismét a fahengeres keresztmetszetű gerenda témájáról. 1. ábra forrása: [ 1 ]](/thumbs/50/26108823.jpg) 1 Ismét a fahengeres keresztmetszetű gerenda témájáról Az 1. ábrával már korábban is találkozhatott az Olvasó. 1. ábra forrása: [ 1 ] Ezen azt láthatjuk, hogy bizonyos esetekben a fűrészelt fagerenda a
1 Ismét a fahengeres keresztmetszetű gerenda témájáról Az 1. ábrával már korábban is találkozhatott az Olvasó. 1. ábra forrása: [ 1 ] Ezen azt láthatjuk, hogy bizonyos esetekben a fűrészelt fagerenda a
Aszimmetrikus nyeregtető ~ feladat 2.
 1 Aszimmetrikus nyeregtető ~ feladat 2. Ehhez tekintsük az 1. ábrát is! Itt az A és B pontok egy nyeregtető oromfali ereszpontjai, a P pont pedig a taréj pontja. Az ereszek egymástól való távolságának
1 Aszimmetrikus nyeregtető ~ feladat 2. Ehhez tekintsük az 1. ábrát is! Itt az A és B pontok egy nyeregtető oromfali ereszpontjai, a P pont pedig a taréj pontja. Az ereszek egymástól való távolságának
Egy általános helyzetű lekerekített sarkú téglalap paraméteres egyenletrendszere. Az egyenletek felírása
 1 Egy általános helyzetű lekerekített sarkú téglalap paraméteres egyenletrendszere Az egyenletek felírása Korábbi dolgozataink már mintegy előkészítették a mostanit; ezek: ~ KD - 1: Általános helyzetű
1 Egy általános helyzetű lekerekített sarkú téglalap paraméteres egyenletrendszere Az egyenletek felírása Korábbi dolgozataink már mintegy előkészítették a mostanit; ezek: ~ KD - 1: Általános helyzetű
Csúcsívek rajzolása. Kezdjük egy általános csúcsív rajzolásával! Ehhez tekintsük az 1. ábrát!
 1 Csúcsívek rajzolása Előző dolgozatunk kapcsán melynek címe: Íves nyeregtető főbb számítási képleteiről találkoztunk a csúcsívvel, mint az építészetben igen gyakran előforduló vonalidommal. Most egy másik
1 Csúcsívek rajzolása Előző dolgozatunk kapcsán melynek címe: Íves nyeregtető főbb számítási képleteiről találkoztunk a csúcsívvel, mint az építészetben igen gyakran előforduló vonalidommal. Most egy másik
Az elforgatott ellipszisbe írható legnagyobb területű téglalapról
 1 Az elforgatott ellipszisbe írható legnagyobb területű téglalapról Előző dolgozatunkban melynek címe: Az ellipszisbe írható legnagyobb területű négyszögről már beharangoztuk, hogy találtunk valami érdekeset
1 Az elforgatott ellipszisbe írható legnagyobb területű téglalapról Előző dolgozatunkban melynek címe: Az ellipszisbe írható legnagyobb területű négyszögről már beharangoztuk, hogy találtunk valami érdekeset
Egy forgáskúp metszéséről. Egy forgáskúpot az 1. ábra szerint helyeztünk el egy ( OXYZ ) derékszögű koordináta - rendszerben.
 Egy forgáskúp metszéséről Egy forgáskúpot az 1. ábra szerint helyeztünk el egy ( OXYZ ) derékszögű koordináta - rendszerben. Az O csúcsú, O tengelyű, γ félnyílásszögű kúpot az ( XY ) sík itt két alkotóban
Egy forgáskúp metszéséről Egy forgáskúpot az 1. ábra szerint helyeztünk el egy ( OXYZ ) derékszögű koordináta - rendszerben. Az O csúcsú, O tengelyű, γ félnyílásszögű kúpot az ( XY ) sík itt két alkotóban
Függőleges koncentrált erőkkel csuklóin terhelt csuklós rúdlánc számításához
 1 Függőleges koncentrált erőkkel csuklóin terhelt csuklós rúdlánc számításához Az interneten való nézelődés során találkoztunk az [ 1 ] művel, melyben egy érdekes és fontos feladat pontos(abb) megoldásához
1 Függőleges koncentrált erőkkel csuklóin terhelt csuklós rúdlánc számításához Az interneten való nézelődés során találkoztunk az [ 1 ] művel, melyben egy érdekes és fontos feladat pontos(abb) megoldásához
Egy érdekes statikai - geometriai feladat
 1 Egy érdekes statikai - geometriai feladat Előző dolgozatunkban melynek címe: Egy érdekes geometriai feladat egy olyan feladatot oldottunk meg, ami az itteni előtanulmányának is tekinthető. Az ottani
1 Egy érdekes statikai - geometriai feladat Előző dolgozatunkban melynek címe: Egy érdekes geometriai feladat egy olyan feladatot oldottunk meg, ami az itteni előtanulmányának is tekinthető. Az ottani
A ferde tartó megoszló terheléseiről
 A ferde tartó megoszló terheléseiről Úgy vettem észre az idők során, hogy nem nagyon magyarázták agyon azt a kérdést, amivel itt fogunk foglalkozni. Biztos azt mondják majd megint, hogy De hisz ezt mindenki
A ferde tartó megoszló terheléseiről Úgy vettem észre az idők során, hogy nem nagyon magyarázták agyon azt a kérdést, amivel itt fogunk foglalkozni. Biztos azt mondják majd megint, hogy De hisz ezt mindenki
Az elliptikus hengerre írt csavarvonalról
 1 Az elliptikus hengerre írt csavarvonalról Erről viszonylag ritkán olvashatunk, ezért most erről lesz szó. Az [ 1 ] munkában találtuk az alábbi részt 1. ábra. 1. ábra Itt a ( c ) feladat és annak megoldása
1 Az elliptikus hengerre írt csavarvonalról Erről viszonylag ritkán olvashatunk, ezért most erről lesz szó. Az [ 1 ] munkában találtuk az alábbi részt 1. ábra. 1. ábra Itt a ( c ) feladat és annak megoldása
A tűzfalakkal lezárt nyeregtető feladatához
 1 A tűzfalakkal lezárt nyeregtető feladatához Bevezetés Ehhez először tekintsük az 1. ábrát! 1 Itt azt szemlélhetjük, hogy hogyan lehet el - kerülni egy épület tűzfalának eláztatását. A felső ábrarészen
1 A tűzfalakkal lezárt nyeregtető feladatához Bevezetés Ehhez először tekintsük az 1. ábrát! 1 Itt azt szemlélhetjük, hogy hogyan lehet el - kerülni egy épület tűzfalának eláztatását. A felső ábrarészen
Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1.
![Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1. Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1.](/thumbs/27/12197964.jpg) 1 Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1. Feladat Egy G gépkocsi állandó v 0 nagyságú sebességgel egyenes úton
1 Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1. Feladat Egy G gépkocsi állandó v 0 nagyságú sebességgel egyenes úton
A gúla ~ projekthez 1. rész
 1 A gúla ~ projekthez 1. rész Megint találtunk az interneten valami érdekeset: az [ 1 ], [ 2 ], [ 3 ] anyagokat. Úgy véljük, hogy az alábbi téma / témakör kiválóan alkalmas lehet projekt - módszerrel történő
1 A gúla ~ projekthez 1. rész Megint találtunk az interneten valami érdekeset: az [ 1 ], [ 2 ], [ 3 ] anyagokat. Úgy véljük, hogy az alábbi téma / témakör kiválóan alkalmas lehet projekt - módszerrel történő
Egy érdekes nyeregtetőről
 Egy érdekes nyeregtetőről Adott egy nyeregtető, az 1 ábra szerinti adatokkal 1 ábra Végezzük el vetületi ábrázolását, az alábbi számszerű adatokkal: a = 10,00 m; b = 6,00 m; c = 3,00 m; α = 45 ; M 1:100!
Egy érdekes nyeregtetőről Adott egy nyeregtető, az 1 ábra szerinti adatokkal 1 ábra Végezzük el vetületi ábrázolását, az alábbi számszerű adatokkal: a = 10,00 m; b = 6,00 m; c = 3,00 m; α = 45 ; M 1:100!
A hordófelület síkmetszeteiről
 1 A hordófelület síkmetszeteiről Előző dolgozatunkban melynek címe: Ismét egy érdekes mechanizmusról azon hiányérzetünknek adtunk hangot, hogy a hordószerű test görbe felülete nem kapott nevet. Itt elneveztük
1 A hordófelület síkmetszeteiről Előző dolgozatunkban melynek címe: Ismét egy érdekes mechanizmusról azon hiányérzetünknek adtunk hangot, hogy a hordószerű test görbe felülete nem kapott nevet. Itt elneveztük
Két körhenger általánosabban ( Alkalmazzuk a vektoralgebrát! ) 1. ábra
 Két körhenger általánosabban ( Alkalmazzuk a vektoralgebrát! ) Egy korábbi dolgozatunkban címe: Két egyenes körhenger a merőlegesen metsződő tengelyű körhengerek áthatási feladatával foglalkoztunk. Most
Két körhenger általánosabban ( Alkalmazzuk a vektoralgebrát! ) Egy korábbi dolgozatunkban címe: Két egyenes körhenger a merőlegesen metsződő tengelyű körhengerek áthatási feladatával foglalkoztunk. Most
Egy újabb térmértani feladat. Az [ 1 ] könyvben az interneten találtuk az alábbi érdekes feladatot is 1. ábra.
![Egy újabb térmértani feladat. Az [ 1 ] könyvben az interneten találtuk az alábbi érdekes feladatot is 1. ábra. Egy újabb térmértani feladat. Az [ 1 ] könyvben az interneten találtuk az alábbi érdekes feladatot is 1. ábra.](/thumbs/98/136939744.jpg) 1 Egy újabb térmértani feladat Az [ 1 ] könyvben az interneten találtuk az alábbi érdekes feladatot is 1. ábra. Úgy látjuk, érdekes és tanulságos lesz végigvenni. 2 A feladat Egy szabályos n - szög alapú
1 Egy újabb térmértani feladat Az [ 1 ] könyvben az interneten találtuk az alábbi érdekes feladatot is 1. ábra. Úgy látjuk, érdekes és tanulságos lesz végigvenni. 2 A feladat Egy szabályos n - szög alapú
Egy kötélstatikai alapfeladat megoldása másként
 1 Egy kötélstatikai alapfeladat megoldása másként Most megint egyik kedvenc témánkat vesszük elő. Bízunk benne, hogy az itt előforduló ismétlések szükségesek, ámde nem feleslegesek. A más módon való megoldás
1 Egy kötélstatikai alapfeladat megoldása másként Most megint egyik kedvenc témánkat vesszük elő. Bízunk benne, hogy az itt előforduló ismétlések szükségesek, ámde nem feleslegesek. A más módon való megoldás
Érdekes geometriai számítások Téma: Szimmetrikus kontytető tetősíkjai lapszögének meghatározásáról
 1 Folytatjuk a sorozatot. Érdekes geometriai számítások 9. 9. Téma: Szimmetrikus kontytető tetősíkjai lapszögének meghatározásáról Már több dolgozatunk témája volt két metsződő tetősík közbezárt szögének
1 Folytatjuk a sorozatot. Érdekes geometriai számítások 9. 9. Téma: Szimmetrikus kontytető tetősíkjai lapszögének meghatározásáról Már több dolgozatunk témája volt két metsződő tetősík közbezárt szögének
Néhány véges trigonometriai összegről. Határozzuk meg az alábbi véges összegek értékét!, ( 1 ) ( 2 )
 1 Néhány véges trigonometriai összegről A Fizika számos területén találkozhatunk véges számú tagból álló trigonometriai össze - gekkel, melyek a számítások során állnak elő. Ezek értékét kinézhetjük matematikai
1 Néhány véges trigonometriai összegről A Fizika számos területén találkozhatunk véges számú tagból álló trigonometriai össze - gekkel, melyek a számítások során állnak elő. Ezek értékét kinézhetjük matematikai
Egy kinematikai feladathoz
 1 Egy kinematikai feladathoz Az [ 1 ] példatárból való az alábbi feladat. Egy bütyök v 0 állandó nagyságú sebességgel halad jobbról balra. Kontúrjának egyenlete a hozzá kötött, vele együtt haladó O 1 xy
1 Egy kinematikai feladathoz Az [ 1 ] példatárból való az alábbi feladat. Egy bütyök v 0 állandó nagyságú sebességgel halad jobbról balra. Kontúrjának egyenlete a hozzá kötött, vele együtt haladó O 1 xy
További adalékok a merőleges axonometriához
 1 További adalékok a merőleges axonometriához Egy szép összefoglaló munkát [ 1 ] találtunk az interneten, melynek előző dolgoza - tunkhoz csatlakozó részeit itt dolgozzuk fel. Előző dolgozatunk címe: Kiegészítés
1 További adalékok a merőleges axonometriához Egy szép összefoglaló munkát [ 1 ] találtunk az interneten, melynek előző dolgoza - tunkhoz csatlakozó részeit itt dolgozzuk fel. Előző dolgozatunk címe: Kiegészítés
Síkbeli csuklós rúdnégyszög egyensúlya
 Síkbeli csuklós rúdnégyszög egyensúlya Két korábbi dolgozatunkban melyek címe és azonosítója: [KD ]: Egy érdekes feladat, [KD ]: Egy másik érdekes feladat azt vizsgáltuk, hogy egy csuklós rúdnégyszög milyen
Síkbeli csuklós rúdnégyszög egyensúlya Két korábbi dolgozatunkban melyek címe és azonosítója: [KD ]: Egy érdekes feladat, [KD ]: Egy másik érdekes feladat azt vizsgáltuk, hogy egy csuklós rúdnégyszög milyen
Felső végükön egymásra támaszkodó szarugerendák egyensúlya
 1 Felső végükön egymásra támaszkodó szarugerendák egyensúlya Az [ 1 ] példatárban találtunk egy érdekes feladatot, melynek egy változatát vizsgáljuk meg itt. A feladat Ehhez tekintsük az 1. ábrát! 1. ábra
1 Felső végükön egymásra támaszkodó szarugerendák egyensúlya Az [ 1 ] példatárban találtunk egy érdekes feladatot, melynek egy változatát vizsgáljuk meg itt. A feladat Ehhez tekintsük az 1. ábrát! 1. ábra
Példa: Normálfeszültség eloszlása síkgörbe rúd esetén
 Példa: Normálfeszültség eloszlása síkgörbe rúd esetén Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 20. Az 1. ábrán vázolt síkgörbe rúd méretei és terhelése ismert.
Példa: Normálfeszültség eloszlása síkgörbe rúd esetén Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 20. Az 1. ábrán vázolt síkgörbe rúd méretei és terhelése ismert.
Egy sajátos ábrázolási feladatról
 1 Egy sajátos ábrázolási feladatról Régen volt, ha volt egyáltalán. Én bizony nem emlékszem a ferde gerincvonalú túleme - lés ~ átmeneti megoldásra 1. ábra az ( erdészeti ) útépítésben. 1. ábra forrása:
1 Egy sajátos ábrázolási feladatról Régen volt, ha volt egyáltalán. Én bizony nem emlékszem a ferde gerincvonalú túleme - lés ~ átmeneti megoldásra 1. ábra az ( erdészeti ) útépítésben. 1. ábra forrása:
A síkbeli Statika egyensúlyi egyenleteiről
 1 A síkbeli Statika egyensúlyi egyenleteiről Statikai tanulmányaink egyik mérföldköve az egyensúlyi egyenletek belátása és sikeres alkalmazása. Most egy erre vonatkozó lehetséges tanulási / tanítási útvonalat
1 A síkbeli Statika egyensúlyi egyenleteiről Statikai tanulmányaink egyik mérföldköve az egyensúlyi egyenletek belátása és sikeres alkalmazása. Most egy erre vonatkozó lehetséges tanulási / tanítási útvonalat
A szabályos sokszögek közelítő szerkesztéséhez
 1 A szabályos sokszögek közelítő szerkesztéséhez A síkmértani szerkesztések között van egy kedvencünk: a szabályos n - szög közelítő szerkesztése. Azért vívta ki nálunk ezt az előkelő helyet, mert nagyon
1 A szabályos sokszögek közelítő szerkesztéséhez A síkmértani szerkesztések között van egy kedvencünk: a szabályos n - szög közelítő szerkesztése. Azért vívta ki nálunk ezt az előkelő helyet, mert nagyon
Egy háromlábú állvány feladata. 1. ábra forrása:
 1 Egy háromlábú állvány feladata Az interneten találtuk az alábbi versenyfeladatot 1. ábra Az egyforma hosszúságú CA, CB és CD rudak a C pontban gömbcsuklóval kapcsolódnak, az A, B, D végükön sima vízszintes
1 Egy háromlábú állvány feladata Az interneten találtuk az alábbi versenyfeladatot 1. ábra Az egyforma hosszúságú CA, CB és CD rudak a C pontban gömbcsuklóval kapcsolódnak, az A, B, D végükön sima vízszintes
Henger és kúp metsződő tengelyekkel
 Henger és kúp metsződő tengelyekkel Ebben a dolgozatban egy forgáshenger és egy forgáskúp áthatását tanulmányozzuk abban az egyszerűbb esetben, amikor a két test tengelye egyazon síkban fekszik, vagyis
Henger és kúp metsződő tengelyekkel Ebben a dolgozatban egy forgáshenger és egy forgáskúp áthatását tanulmányozzuk abban az egyszerűbb esetben, amikor a két test tengelye egyazon síkban fekszik, vagyis
Érdekes geometriai számítások Téma: A kardáncsukló kinematikai alapegyenletének levezetése gömbháromszögtani alapon
 Érdekes geometriai számítások 7. Folytatjuk a sorozatot. 7. Téma: A kardáncsukló kinematikai alapegyenletének levezetése gömbháromszögtani alapon Korábbi dolgozatainkban már többféle módon is bemutattuk
Érdekes geometriai számítások 7. Folytatjuk a sorozatot. 7. Téma: A kardáncsukló kinematikai alapegyenletének levezetése gömbháromszögtani alapon Korábbi dolgozatainkban már többféle módon is bemutattuk
Kiegészítés a három erő egyensúlyához
 1 Kiegészítés a három erő egyensúlyához Egy régebbi dolgozatunkban melynek jele és címe : RD: Három erő egyensúlya ~ kéttámaszú tartó már sok mindent elmondtunk a címbeli témáról. Ez ugyanis egy megkerülhetetlen
1 Kiegészítés a három erő egyensúlyához Egy régebbi dolgozatunkban melynek jele és címe : RD: Három erő egyensúlya ~ kéttámaszú tartó már sok mindent elmondtunk a címbeli témáról. Ez ugyanis egy megkerülhetetlen
Egy furcsa tartóról. A probléma felvetése. Adott az 1. ábra szerinti kéttámaszú tartó. 1. ábra
 Egy furcsa tartóról Az alábbi probléma ha jól emlékszem tanulói felvetés, melyet tanáruk volt kol - légánk G. A. továbbított. ( Üdv Néked, Nagy Király! ) Hogy a probléma valós - e vagy mondvacsinált, azt
Egy furcsa tartóról Az alábbi probléma ha jól emlékszem tanulói felvetés, melyet tanáruk volt kol - légánk G. A. továbbított. ( Üdv Néked, Nagy Király! ) Hogy a probléma valós - e vagy mondvacsinált, azt
Egymásra támaszkodó rudak
 1 Egymásra támaszkodó rudak Úgy látszik, ez is egy visszatérő téma. Egy korábbi írásunkban melynek címe: A mandala - tetőről már találkoztunk az 1. ábrán vázolthoz hasonló felülnézetű szerkezettel, foglalkoztunk
1 Egymásra támaszkodó rudak Úgy látszik, ez is egy visszatérő téma. Egy korábbi írásunkban melynek címe: A mandala - tetőről már találkoztunk az 1. ábrán vázolthoz hasonló felülnézetű szerkezettel, foglalkoztunk
A magától becsukódó ajtó működéséről
 1 A magától becsukódó ajtó működéséről Az [ 1 ] műben találtunk egy érdekes feladatot, amit most mi is feldolgozunk. Az 1. ábrán látható az eredeti feladat másolata. A feladat kitűzése 1. ábra forrása:
1 A magától becsukódó ajtó működéséről Az [ 1 ] műben találtunk egy érdekes feladatot, amit most mi is feldolgozunk. Az 1. ábrán látható az eredeti feladat másolata. A feladat kitűzése 1. ábra forrása:
A merőleges axonometria néhány régi - új összefüggéséről
 1 A merőleges axonometria néhány régi - új összefüggéséről Most néhány régebben már megbeszélt összefüggés újabb igazolását adjuk meg, illetve más, eddig még nem látott képlet - alakokat állítunk elő.
1 A merőleges axonometria néhány régi - új összefüggéséről Most néhány régebben már megbeszélt összefüggés újabb igazolását adjuk meg, illetve más, eddig még nem látott képlet - alakokat állítunk elő.
Az élszarufa és a szelemenek kapcsolódásáról
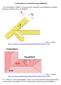 Az élszarufa és a szelemenek kapcsolódásáról A következőkben a címbeli viszonylag nehéz anyagrész megvilágítását szeretnénk elősegíteni főként szép és jó ábrákkal.. ábra forrása: http://www.dikraus.at/ingenieurbau/baustatik/baustatikflyer/s6_0.pdf.
Az élszarufa és a szelemenek kapcsolódásáról A következőkben a címbeli viszonylag nehéz anyagrész megvilágítását szeretnénk elősegíteni főként szép és jó ábrákkal.. ábra forrása: http://www.dikraus.at/ingenieurbau/baustatik/baustatikflyer/s6_0.pdf.
Végein függesztett rúd egyensúlyi helyzete. Az interneten találtuk az [ 1 ] munkát, benne az alábbi érdekes feladatot 1. ábra. Most erről lesz szó.
![Végein függesztett rúd egyensúlyi helyzete. Az interneten találtuk az [ 1 ] munkát, benne az alábbi érdekes feladatot 1. ábra. Most erről lesz szó. Végein függesztett rúd egyensúlyi helyzete. Az interneten találtuk az [ 1 ] munkát, benne az alábbi érdekes feladatot 1. ábra. Most erről lesz szó.](/thumbs/92/108783591.jpg) 1 Végein függesztett rúd egyensúlyi helyzete Az interneten találtuk az [ 1 ] munkát, benne az alábbi érdekes feladatot 1. ábra. Most erről lesz szó. A feladat Ehhez tekintsük a 2. ábrát is! 1. ábra forrása:
1 Végein függesztett rúd egyensúlyi helyzete Az interneten találtuk az [ 1 ] munkát, benne az alábbi érdekes feladatot 1. ábra. Most erről lesz szó. A feladat Ehhez tekintsük a 2. ábrát is! 1. ábra forrása:
A visszacsapó kilincs működéséről
 1 A visszacsapó kilincs működéséről A faipari forgácsoló gépek egy részén a munkadarab visszasodródása ellen visszacsapó kilincset / kilincssort alkalmaznak. Ilyen gépek például a felülről vágó körfűrészek
1 A visszacsapó kilincs működéséről A faipari forgácsoló gépek egy részén a munkadarab visszasodródása ellen visszacsapó kilincset / kilincssort alkalmaznak. Ilyen gépek például a felülről vágó körfűrészek
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 19 XIX A HATÁROZOTT INTEGRÁL ALkALmAZÁSAI 1 TERÜLET ÉS ÍVHOSSZ SZÁmÍTÁSA Területszámítás Ha f az [a,b] intervallumon nemnegatív, folytonos függvény, akkor az görbe, az x tengely,
KOVÁCS BÉLA, MATEmATIkA I 19 XIX A HATÁROZOTT INTEGRÁL ALkALmAZÁSAI 1 TERÜLET ÉS ÍVHOSSZ SZÁmÍTÁSA Területszámítás Ha f az [a,b] intervallumon nemnegatív, folytonos függvény, akkor az görbe, az x tengely,
Az egyenes ellipszishenger ferde síkmetszeteiről
 1 Az egyenes ellipszishenger ferde síkmetszeteiről Vegyünk egy a és b féltengelyekkel bíró ellipszist a vezérgörbét, majd az ellipszis O centrumában állítsunk merőlegest az ellipszis síkjára. Ez a merőleges
1 Az egyenes ellipszishenger ferde síkmetszeteiről Vegyünk egy a és b féltengelyekkel bíró ellipszist a vezérgörbét, majd az ellipszis O centrumában állítsunk merőlegest az ellipszis síkjára. Ez a merőleges
KERESZTMETSZETI JELLEMZŐK
 web-lap : www.hild.gor.hu DEME FERENC okl. építőmérnök, mérnöktanár e-mail : deme.ferenc1@gmail.com STATIKA 50. KERESZTMETSZETI JELLEMZŐK A TARTÓK MÉRETEZÉSE SORÁN SZÁMOS ESETBEN SZÜKSÉGÜNK VAN OLYAN ADATOKRA,
web-lap : www.hild.gor.hu DEME FERENC okl. építőmérnök, mérnöktanár e-mail : deme.ferenc1@gmail.com STATIKA 50. KERESZTMETSZETI JELLEMZŐK A TARTÓK MÉRETEZÉSE SORÁN SZÁMOS ESETBEN SZÜKSÉGÜNK VAN OLYAN ADATOKRA,
Szökőkút - feladat. 1. ábra. A fotók forrása:
 Szökőkút - feladat Nemrégen Gyulán jártunk, ahol sok szép szökőkutat láttunk. Az egyik különösen megtetszett, ezért elhatároztam, hogy megpróbálom elemi módon leírni a ízsugarak, illete az általuk leírt
Szökőkút - feladat Nemrégen Gyulán jártunk, ahol sok szép szökőkutat láttunk. Az egyik különösen megtetszett, ezért elhatároztam, hogy megpróbálom elemi módon leírni a ízsugarak, illete az általuk leírt
Egy újabb látószög - feladat
 1 Egy újabb látószög - feladat A feladat Adott az O középpontú, R sugarú körön az α szöggel jellemzett P pont. Határozzuk meg, hogy mekkora ϑ szög alatt látszik a P pontból a vízszintes átmérő - egyenes
1 Egy újabb látószög - feladat A feladat Adott az O középpontú, R sugarú körön az α szöggel jellemzett P pont. Határozzuk meg, hogy mekkora ϑ szög alatt látszik a P pontból a vízszintes átmérő - egyenes
Egy általánosabb súrlódásos alapfeladat
 Egy általánosabb súrlódásos alapfeladat Az előző dolgozatunkban címe: Egy súrlódásos alapfeladat, jele: ( E D ) tárgyalt probléma általánosítása az alábbi, melynek forrása [ 1 ]. Tekintsük az 1. ábrát!
Egy általánosabb súrlódásos alapfeladat Az előző dolgozatunkban címe: Egy súrlódásos alapfeladat, jele: ( E D ) tárgyalt probléma általánosítása az alábbi, melynek forrása [ 1 ]. Tekintsük az 1. ábrát!
A csavarvonal axonometrikus képéről
 A avarvonal axonometrikus képéről Miután egyre jobban megy a Graph ingyenes függvény - ábrázoló szoftver használata, kipróbáltuk, hogy tudunk - e vele avarvonalat ábrázolni, axonometrikusan. A válasz:
A avarvonal axonometrikus képéről Miután egyre jobban megy a Graph ingyenes függvény - ábrázoló szoftver használata, kipróbáltuk, hogy tudunk - e vele avarvonalat ábrázolni, axonometrikusan. A válasz:
Egy másik érdekes feladat. A feladat
 Egy másik érdekes feladat Az előző dolgozatban melynek címe: Egy érdekes feladat az itteninek egy speciális esetét vizsgáltuk. Az általánosabb feladat az alábbi [ 1 ]. A feladat Adott: az ABCD zárt négyszög
Egy másik érdekes feladat Az előző dolgozatban melynek címe: Egy érdekes feladat az itteninek egy speciális esetét vizsgáltuk. Az általánosabb feladat az alábbi [ 1 ]. A feladat Adott: az ABCD zárt négyszög
Ellipszissel kapcsolatos képletekről
 1 Ellipszissel kapcsolatos képletekről Előző dolgozatunkban melynek címe: A Lenz - vektorról viszonylag sokat kellett ellipszissel kapcsolatos képletekkel dolgozni. Ennek során is adódott pár észrevételünk,
1 Ellipszissel kapcsolatos képletekről Előző dolgozatunkban melynek címe: A Lenz - vektorról viszonylag sokat kellett ellipszissel kapcsolatos képletekkel dolgozni. Ennek során is adódott pár észrevételünk,
Két naszád legkisebb távolsága. Az [ 1 ] gyűjteményben találtuk az alábbi feladatot és egy megoldását: 1. ábra.
![Két naszád legkisebb távolsága. Az [ 1 ] gyűjteményben találtuk az alábbi feladatot és egy megoldását: 1. ábra. Két naszád legkisebb távolsága. Az [ 1 ] gyűjteményben találtuk az alábbi feladatot és egy megoldását: 1. ábra.](/thumbs/91/105028162.jpg) 1 Két naszád legkisebb távolsága Az [ 1 ] gyűjteményben találtuk az alábbi feladatot és egy megoldását: 1. ábra. 1. ábra A feladat Az A és B, egymástól l távolságra lévő kikötőből egyidejűleg indul két
1 Két naszád legkisebb távolsága Az [ 1 ] gyűjteményben találtuk az alábbi feladatot és egy megoldását: 1. ábra. 1. ábra A feladat Az A és B, egymástól l távolságra lévő kikötőből egyidejűleg indul két
A manzárdtetőről. 1. ábra Forrás: http://upload.wikimedia.org/wikipedia/commons/0/0a/drawing_in_perspective_ of_gambrel-roofed_building.
 A manzárdtetőről Az építőipari tanulók ácsok, magasépítő technikusok részére kötelező gyakorlat a manzárdtetőkkel való foglalkozás. Egy manzárd nyeregtetőt mutat az. ábra.. ábra Forrás: http://upload.wikimedia.org/wikipedia/commons/0/0a/drawing_in_perspective_
A manzárdtetőről Az építőipari tanulók ácsok, magasépítő technikusok részére kötelező gyakorlat a manzárdtetőkkel való foglalkozás. Egy manzárd nyeregtetőt mutat az. ábra.. ábra Forrás: http://upload.wikimedia.org/wikipedia/commons/0/0a/drawing_in_perspective_
Egy érdekes mechanikai feladat
 1 Egy érdekes mechanikai feladat 1. ábra forrása: [ 1 ] A feladat Az 1. ábra szerinti rudazat A csomópontján átvezettek egy kötelet, melynek alsó végén egy m tömegű golyó lóg. A rudak egyező nyúlási merevsége
1 Egy érdekes mechanikai feladat 1. ábra forrása: [ 1 ] A feladat Az 1. ábra szerinti rudazat A csomópontján átvezettek egy kötelet, melynek alsó végén egy m tömegű golyó lóg. A rudak egyező nyúlási merevsége
Fénypont a falon Feladat
 Fénypont a falon 3. Dolgozat - sorozatunk. és. részében két speiális eset vizsgálatát részleteztük. Itt az általánosabb síkbeli esettel foglalkozunk, főbb vonalaiban. Ehhez tekintsük az. ábrát is! 3. Feladat.
Fénypont a falon 3. Dolgozat - sorozatunk. és. részében két speiális eset vizsgálatát részleteztük. Itt az általánosabb síkbeli esettel foglalkozunk, főbb vonalaiban. Ehhez tekintsük az. ábrát is! 3. Feladat.
Egy kérdés: merre folyik le az esővíz az úttestről? Ezt a kérdést az után tettük fel magunknak, hogy megláttuk az 1. ábrát.
 1 Egy kérdés: merre folyik le az esővíz az úttestről? Ezt a kérdést az után tettük fel magunknak, hogy megláttuk az 1. ábrát. 1. ábra forrása: [ 1 ] Ezen egy út tengelyvonalának egy pontjában tüntették
1 Egy kérdés: merre folyik le az esővíz az úttestről? Ezt a kérdést az után tettük fel magunknak, hogy megláttuk az 1. ábrát. 1. ábra forrása: [ 1 ] Ezen egy út tengelyvonalának egy pontjában tüntették
Példa keresztmetszet másodrendű nyomatékainak számítására
 Példa keresztmetszet másodrendű nyomatékainak számítására Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. február 22. Tekintsük az alábbi keresztmetszetet. 1. ábra. A vizsgált
Példa keresztmetszet másodrendű nyomatékainak számítására Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. február 22. Tekintsük az alábbi keresztmetszetet. 1. ábra. A vizsgált
Egy sík és a koordinátasíkok metszésvonalainak meghatározása
 1 Egy sík és a koordinátasíkok metszésvonalainak meghatározása Ehhez tekintsük az 1. ábrát! 1. ábra Itt az ( u, v, w ) tengelymetszeteivel adott S síkot látjuk, az Oxyz térbeli derékszögű koordináta -
1 Egy sík és a koordinátasíkok metszésvonalainak meghatározása Ehhez tekintsük az 1. ábrát! 1. ábra Itt az ( u, v, w ) tengelymetszeteivel adott S síkot látjuk, az Oxyz térbeli derékszögű koordináta -
Kocka perspektivikus ábrázolása. Bevezetés
 1 Kocka perspektivikus ábrázolása Bevezetés Előző három dolgozatunkban ~ melyek címe: 1. Sínpár perspektivikus ábrázolása, 2. Sínpár perspektivikus ábrázolása másként, 3. Sínpár perspektivikus ábrázolása
1 Kocka perspektivikus ábrázolása Bevezetés Előző három dolgozatunkban ~ melyek címe: 1. Sínpár perspektivikus ábrázolása, 2. Sínpár perspektivikus ábrázolása másként, 3. Sínpár perspektivikus ábrázolása
A szabályos sokszög keresztmetszetű rúd keresztmetszeti jellemzőiről
 1 A szabályos sokszög keresztmetszetű rúd keresztmetszeti jellemzőiről Már megint az történt, hogy egy képletgyűjteményt nézegetve furcsának találtunk pár képletet: hibára gyanakodtunk. Most erről lesz
1 A szabályos sokszög keresztmetszetű rúd keresztmetszeti jellemzőiről Már megint az történt, hogy egy képletgyűjteményt nézegetve furcsának találtunk pár képletet: hibára gyanakodtunk. Most erről lesz
A gúla ~ projekthez 2. rész
 1 A gúla ~ projekthez 2. rész Dolgozatunk 1. részében egy speciális esetre a négyzet alapú egyenes gúla esetére írtuk fel és alkalmaztuk képleteinket. Most a tetszőleges oldalszámú szabályos sokszög alakú
1 A gúla ~ projekthez 2. rész Dolgozatunk 1. részében egy speciális esetre a négyzet alapú egyenes gúla esetére írtuk fel és alkalmaztuk képleteinket. Most a tetszőleges oldalszámú szabályos sokszög alakú
Keresztezett pálcák II.
 Keresztezett pálcák II Dolgozatunk I részéen a merőleges tengelyű pálcák esetét vizsgáltuk Most nézzük meg azt az esetet amikor a pálcák tengelyei nem merőlegesen keresztezik egymást Ehhez tekintsük az
Keresztezett pálcák II Dolgozatunk I részéen a merőleges tengelyű pálcák esetét vizsgáltuk Most nézzük meg azt az esetet amikor a pálcák tengelyei nem merőlegesen keresztezik egymást Ehhez tekintsük az
A konfokális és a nem - konfokális ellipszis - seregekről és ortogonális trajektóriáikról
 1 A konfokális és a nem - konfokális ellipszis - seregekről és ortogonális trajektóriáikról Előző dolgozatunk melynek címe: Ha az évgyűrűk ellipszis alakúak lennének készítése során böngész - gettük az
1 A konfokális és a nem - konfokális ellipszis - seregekről és ortogonális trajektóriáikról Előző dolgozatunk melynek címe: Ha az évgyűrűk ellipszis alakúak lennének készítése során böngész - gettük az
Lövés csúzlival. Egy csúzli k merevségű gumival készült. Adjuk meg az ebből kilőtt m tömegű lövedék sebességét, ha a csúzlit L - re húztuk ki!
 1 Lövés csúzlival Az [ 1 ] munkában találtuk az alábbi feladatot 1. ábra. A feladat Egy csúzli k merevségű gumival készült. Adjuk meg az ebből kilőtt m tömegű lövedék sebességét, ha a csúzlit L - re húztuk
1 Lövés csúzlival Az [ 1 ] munkában találtuk az alábbi feladatot 1. ábra. A feladat Egy csúzli k merevségű gumival készült. Adjuk meg az ebből kilőtt m tömegű lövedék sebességét, ha a csúzlit L - re húztuk
Rugalmas láncgörbe alapvető összefüggések és tudnivalók I. rész
 Rugalmas láncgörbe alapvető összefüggések és tudnivalók I rész evezetés rugalmas láncgörbe magyar nyelvű szakirodalma nem túl gazdag Egy viszonylag rövid ismertetés található [ 1 ] - ben közönséges ( azaz
Rugalmas láncgörbe alapvető összefüggések és tudnivalók I rész evezetés rugalmas láncgörbe magyar nyelvű szakirodalma nem túl gazdag Egy viszonylag rövid ismertetés található [ 1 ] - ben közönséges ( azaz
Keresztmetszet másodrendű nyomatékainak meghatározása
 BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
A felcsapódó kavicsról. Az interneten találtuk az alábbi, a hajítás témakörébe tartozó érdekes feladatot 1. ábra.
 1 A felcsapódó kavicsról Az interneten találtuk az alábbi, a hajítás témakörébe tartozó érdekes feladatot 1. ábra. 1. ábra forrása: [ 1 ] Ez azért is érdekes, mert autóvezetés közben már többször is eszünkbe
1 A felcsapódó kavicsról Az interneten találtuk az alábbi, a hajítás témakörébe tartozó érdekes feladatot 1. ábra. 1. ábra forrása: [ 1 ] Ez azért is érdekes, mert autóvezetés közben már többször is eszünkbe
Egy kinematikai feladat
 1 Egy kinematikai feladat Valami geometriai dologról ötlött eszembe az alábbi feladat 1. ábra. 1. ábra Adott az a és b egyenes, melyek α szöget zárnak be egymással. A b egyenesre ráfektetünk egy d hosszúságú
1 Egy kinematikai feladat Valami geometriai dologról ötlött eszembe az alábbi feladat 1. ábra. 1. ábra Adott az a és b egyenes, melyek α szöget zárnak be egymással. A b egyenesre ráfektetünk egy d hosszúságú
MECHANIKA I. rész: Szilárd testek mechanikája
 Egészségügyi mérnökképzés MECHNIK I. rész: Szilárd testek mechanikája készítette: Németh Róbert Igénybevételek térben I. z alapelv ugyanaz, mint síkban: a keresztmetszet egyik oldalán levő szerkezetrészre
Egészségügyi mérnökképzés MECHNIK I. rész: Szilárd testek mechanikája készítette: Németh Róbert Igénybevételek térben I. z alapelv ugyanaz, mint síkban: a keresztmetszet egyik oldalán levő szerkezetrészre
Egy kétszeresen aszimmetrikus kontytető főbb geometriai adatainak meghatározásáról
 1 Egy kétszeresen aszimmetrikus kontytető főbb geometriai adatainak meghatározásáról Korábban már több egyszerűbb tető - alak geometriáját leírtuk. Most egy kicsit nehezebb feladat megoldását tűzzük ki
1 Egy kétszeresen aszimmetrikus kontytető főbb geometriai adatainak meghatározásáról Korábban már több egyszerűbb tető - alak geometriáját leírtuk. Most egy kicsit nehezebb feladat megoldását tűzzük ki
Példa: Csúsztatófeszültség-eloszlás számítása I-szelvényben
 Példa: Csúsztatófeszültség-eloszlás számítása I-szelvényben Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 14. Határozzuk meg a nyírásból adódó csúsztatófeszültség
Példa: Csúsztatófeszültség-eloszlás számítása I-szelvényben Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 14. Határozzuk meg a nyírásból adódó csúsztatófeszültség
A kötélsúrlódás képletének egy általánosításáról
 1 A kötélsúrlódás képletének egy általánosításáról Sok korábbi dolgozatunkban foglalkoztunk kötélstatikai feladatokkal. Ez a mostani azon - ban még nem került szóba. A feladat: az egyenes körhengerre feltekert,
1 A kötélsúrlódás képletének egy általánosításáról Sok korábbi dolgozatunkban foglalkoztunk kötélstatikai feladatokkal. Ez a mostani azon - ban még nem került szóba. A feladat: az egyenes körhengerre feltekert,
A lengőfűrészelésről
 A lengőfűrészelésről Az [ 1 ] tankönyvben ezt írják a lengőfűrészről, működéséről, használatáról: A lengőfűrész árkolásra, csaprések készítésére alkalmazott, 150 00 mm átmérőjű, 3 4 mm vastag, sűrű fogazású
A lengőfűrészelésről Az [ 1 ] tankönyvben ezt írják a lengőfűrészről, működéséről, használatáról: A lengőfűrész árkolásra, csaprések készítésére alkalmazott, 150 00 mm átmérőjű, 3 4 mm vastag, sűrű fogazású
A bifiláris felfüggesztésű rúd mozgásáról
 1 A bifiláris felfüggesztésű rúd mozgásáról A végein fonállal felfüggesztett egyenes rúd részleges erőtani vizsgálatát mutattuk be egy korábbi dolgozatunkban, melynek címe: Forgatónyomaték mérése - I.
1 A bifiláris felfüggesztésű rúd mozgásáról A végein fonállal felfüggesztett egyenes rúd részleges erőtani vizsgálatát mutattuk be egy korábbi dolgozatunkban, melynek címe: Forgatónyomaték mérése - I.
A Lenz - vektorról. Ha jól emlékszem, először [ 1 ] - ben találkoztam a címbeli fogalommal 1. ábra.
![A Lenz - vektorról. Ha jól emlékszem, először [ 1 ] - ben találkoztam a címbeli fogalommal 1. ábra. A Lenz - vektorról. Ha jól emlékszem, először [ 1 ] - ben találkoztam a címbeli fogalommal 1. ábra.](/thumbs/93/112395793.jpg) 1 A Lenz - vektorról Ha jól emlékszem, először [ 1 ] - ben találkoztam a címbeli fogalommal 1. ábra. 1. ábra forrása: [ 1 ] Ez nem régen történt. Meglepett, hogy eddig ez kimaradt. Annál is inkább, mert
1 A Lenz - vektorról Ha jól emlékszem, először [ 1 ] - ben találkoztam a címbeli fogalommal 1. ábra. 1. ábra forrása: [ 1 ] Ez nem régen történt. Meglepett, hogy eddig ez kimaradt. Annál is inkább, mert
Rönk kiemelése a vízből
 1 Rönk kiemelése a vízből Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot 1. ábra. A feladat 1. ábra forrása: [ 1 ] Egy daru kötél segítségével lassan emeli ki a vízből a benne úszó gerendát
1 Rönk kiemelése a vízből Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot 1. ábra. A feladat 1. ábra forrása: [ 1 ] Egy daru kötél segítségével lassan emeli ki a vízből a benne úszó gerendát
Már megint az esővíz lefolyásáról
 1 Már megint az esővíz lefolyásáról Már korábban is elmélkedtünk e témáról; ennek honlapunkon bemutatott eredményei: ~ KD 1: Két kereszttetőről; ~ KD 2: Egy modellről; ~ KD 3: Egy kérdés: merre folyik
1 Már megint az esővíz lefolyásáról Már korábban is elmélkedtünk e témáról; ennek honlapunkon bemutatott eredményei: ~ KD 1: Két kereszttetőről; ~ KD 2: Egy modellről; ~ KD 3: Egy kérdés: merre folyik
Egy rugalmas megtámasztású tartóról
 Egy rugalmas megtámasztású tartóról Ezzel a témával gyakran találkozunk, még ha nem is így nevezzük azt. Ne feledjük, hogy a statikailag határozatlan tartók megoldásához szinte mindig alakváltozási felté
Egy rugalmas megtámasztású tartóról Ezzel a témával gyakran találkozunk, még ha nem is így nevezzük azt. Ne feledjük, hogy a statikailag határozatlan tartók megoldásához szinte mindig alakváltozási felté
w u R. x 2 x w w u 2 u y y l ; x d y r ; x 2 x d d y r ; l 2 r 2 2 x w 2 x d w 2 u 2 d 2 2 u y ; x w u y l ; l r 2 x w 2 x d R d 2 u y ;
 A négysuklós mehanizmus alapfeladata másképpen Előző dolgozatunkban melynek íme: A négysuklós mehanizmus alapfeladatáról egy általunk legegyszerűbbnek gondolt megoldási módot ismertettünk. Ott megemlítet
A négysuklós mehanizmus alapfeladata másképpen Előző dolgozatunkban melynek íme: A négysuklós mehanizmus alapfeladatáról egy általunk legegyszerűbbnek gondolt megoldási módot ismertettünk. Ott megemlítet
Kosárra dobás I. Egy érdekes feladattal találkoztunk [ 1 ] - ben, ahol ezt szerkesztéssel oldották meg. Most itt számítással oldjuk meg ugyanezt.
![Kosárra dobás I. Egy érdekes feladattal találkoztunk [ 1 ] - ben, ahol ezt szerkesztéssel oldották meg. Most itt számítással oldjuk meg ugyanezt. Kosárra dobás I. Egy érdekes feladattal találkoztunk [ 1 ] - ben, ahol ezt szerkesztéssel oldották meg. Most itt számítással oldjuk meg ugyanezt.](/thumbs/27/11117124.jpg) osárra dobás I. Egy érdekes feladattal találkoztunk [ 1 ] - ben, ahol ezt szerkesztéssel oldották meg. Most itt számítással oldjuk meg ugyanezt. A feladat Az 1. ábrán [ 1 ] egy tornaterem hosszmetszetét
osárra dobás I. Egy érdekes feladattal találkoztunk [ 1 ] - ben, ahol ezt szerkesztéssel oldották meg. Most itt számítással oldjuk meg ugyanezt. A feladat Az 1. ábrán [ 1 ] egy tornaterem hosszmetszetét
Poncelet egy tételéről
 1 Poncelet egy tételéről Már régebben találkoztunk az [ 1 ] műben egy problémával, mostanában pedig a [ 2 ] műben a megoldásával. A probléma lényege: határozzuk meg a egyenletben szereplő α, β együtthatókat,
1 Poncelet egy tételéről Már régebben találkoztunk az [ 1 ] műben egy problémával, mostanában pedig a [ 2 ] műben a megoldásával. A probléma lényege: határozzuk meg a egyenletben szereplő α, β együtthatókat,
Egy mozgástani feladat
 1 Egy mozgástani feladat Előző dolgozatunk melynek jele és címe: ED ~ Ismét az ellipszis egyenleteiről folytatásának tekinthető ez az írás. Leválasztottuk róla, mert bár szorosan kapcsolódnak, más a céljuk.
1 Egy mozgástani feladat Előző dolgozatunk melynek jele és címe: ED ~ Ismét az ellipszis egyenleteiről folytatásának tekinthető ez az írás. Leválasztottuk róla, mert bár szorosan kapcsolódnak, más a céljuk.
A tetők ferde összekötési feladatainak megoldása
 1 A tetők ferde összekötési feladatainak megoldása Előző dolgozatunkban melynek címe: Két tető összekötése ferdén három önállóan megoldandó feladattal zártunk. Most részletezzük a megoldásokat, azok hasznossága
1 A tetők ferde összekötési feladatainak megoldása Előző dolgozatunkban melynek címe: Két tető összekötése ferdén három önállóan megoldandó feladattal zártunk. Most részletezzük a megoldásokat, azok hasznossága
t, u v. u v t A kúpra írt csavarvonalról I. rész
 A kúpra írt csavarvonalról I. rész Sokféle kúpra írt csavarvonal létezik. Ezek közül először a legegyszerűbbel foglalko - zunk. Ezt azért tesszük mert meglepő az a tény hogy eddig még szinte sehol nem
A kúpra írt csavarvonalról I. rész Sokféle kúpra írt csavarvonal létezik. Ezek közül először a legegyszerűbbel foglalko - zunk. Ezt azért tesszük mert meglepő az a tény hogy eddig még szinte sehol nem
Vontatás III. A feladat
 Vontatás III Ebben a részben ázoljuk a ontatási feladat egy lehetséges numerikus megoldási módját Ezt az I részben ismertetett alapegyenletre építjük fel Itt az egy ontatott kerékpár esetét izsgáljuk feladat
Vontatás III Ebben a részben ázoljuk a ontatási feladat egy lehetséges numerikus megoldási módját Ezt az I részben ismertetett alapegyenletre építjük fel Itt az egy ontatott kerékpár esetét izsgáljuk feladat
Érdekes geometriai számítások 9.
 1 Érdekes geometriai számítások 9. Folytatjuk a sorozatot. 9. Téma: Szimmetrikus kontytető tetősíkjai lapszögének maghatározásáról Már több dolgozatunk témája volt két metsződő tetősík közbezárt szögének
1 Érdekes geometriai számítások 9. Folytatjuk a sorozatot. 9. Téma: Szimmetrikus kontytető tetősíkjai lapszögének maghatározásáról Már több dolgozatunk témája volt két metsződő tetősík közbezárt szögének
Egy ismerős fizika - feladatról. Az interneten találtuk az [ 1 ] könyvet, benne egy ismerős fizika - feladattal 1. ábra.
![Egy ismerős fizika - feladatról. Az interneten találtuk az [ 1 ] könyvet, benne egy ismerős fizika - feladattal 1. ábra. Egy ismerős fizika - feladatról. Az interneten találtuk az [ 1 ] könyvet, benne egy ismerős fizika - feladattal 1. ábra.](/thumbs/54/33921873.jpg) 1 Egy ismerős fizika - feladatról Az interneten találtuk az [ 1 ] könyvet, benne egy ismerős fizika - feladattal 1. ábra. 1. ábra forrása: [ 1 ] A feladat szerint beleejtünk egy kútba / aknába egy követ,
1 Egy ismerős fizika - feladatról Az interneten találtuk az [ 1 ] könyvet, benne egy ismerős fizika - feladattal 1. ábra. 1. ábra forrása: [ 1 ] A feladat szerint beleejtünk egy kútba / aknába egy követ,
A fűrészáru száradása miatt fellépő méret - és alakváltozása meghatározásának egy újabb módszeréről
 1 A fűrészáru száradása miatt fellépő méret - és alakváltozása meghatározásának egy újabb módszeréről Előző dolgozatunkban melynek címe: A zsugorodási viszonyszám, illetve százalék Keylwerth - féle képletének
1 A fűrészáru száradása miatt fellépő méret - és alakváltozása meghatározásának egy újabb módszeréről Előző dolgozatunkban melynek címe: A zsugorodási viszonyszám, illetve százalék Keylwerth - féle képletének
