Marsall László két versének értelmezése
|
|
|
- Boglárka Takács
- 8 évvel ezelőtt
- Látták:
Átírás
1 Vajna Gyöngyi Marsall László két versének értelmezése Bevezető Dolgozatomban olyan versek vizsgálatára vállalkozom, melyek szoros kapcsolatban állnak a matematikával. Az elemzés nehézségét az adja, hogy sok esetben a versekben megjelenő tételek, műveletek, elméletek megértése alapos számtani ismereteket igényel. Ezért célom egy olyan beszédmód kialakítása, mely hidat alkot irodalom és matematika között. Segítségével érthetőbbé válnak a literatúra határán kívül rekedt elemek, s közelebb juthatunk a művek értelmezéséhez. Így az elemzést fogalommagyarázatok segítik, melyek a szöveg végén, Jegyzet címszó alatt találhatók. Megírásakor a pontos matematikai definíciók helyett a közérthető megfogalmazásra törekedtem. Mivel a matematika és az irodalom által használt terminusok jelentősen eltérnek, illetve kevés átfedést tartalmaznak, így sem az irodalomértelmezés megszokott konvencióihoz, sem a matematika precíz és aprólékos szóhasználatához nem tudok maradéktalanul igazodni. De ezekről a járt utakról való letérés teszi lehetővé a művek újszerű, pontos és alapos megközelítését. Kezdjük a halmaz fogalmával! Ez a kifejezés a matematikában másképp értendő, mint az irodalomban. Ugyanis nem helyes az a megfogalmazás, hogy a halmaz azonos tulajdonságú dolgok összessége, mert a közös tulajdonság nem szükséges feltétele a halmaz létezésének. (Példa erre az üres halmaz vagy az egyelemű halmazok.) Köznapi értelemben azonban hasonló sajátosságokkal bíró elemek összességét, sokaságát értjük alatta. E példa jól reprezentálja annak a párhuzamos fogalomrendszernek a működését, mely a verseket mozgatja, s mely az értelmezés kettős aspektusát megadja. Az irodalom egy részhalmaza Marsall számos verse olyan részhalmazát alkotja az irodalomnak, ahol a költészet találkozik a matematikával. Hol képletek, fogalmak, műveletek, elméletek bújnak irodalmi köntösbe, hol pedig az alkotás eszközévé válnak a matematikai elemek. Ezzel a gesztussal a költő nemcsak művészi technikáinak tárházát bővíti, hanem az értelmezési lehetőségek új dimenzióját is megnyitja. Marsall egész kötetet szentelt matematikaverseinek. 1 A Pókhálófüggvények költeményei megmerítkeznek a matematikában. Hol harsány és merész a kapcsolat, hol szinte láthatatlan. E kötet Anthropos tézisei ciklusának egyik darabja Az ún. Heine Borel lefedési tétel bizonyítása félálomban. A vers fő motívuma a keresés. Ennek a cselekvésnek a leírására 1 Az elnevezés Kemsei Istvántól származik (Kemsei I.: A szavak fikciós fortyogása. ISz, 2000/ ) 88
2 használ fel Marsall matematikai eszközt. A szöveg egy bizonyítási módszerre épül, mely a címben szereplő tézis igazolásának kulcslépése. A tétel így hangzik: Heine Borel tétel: Ha a H ponthalmaz korlátos és zárt, akkor akármilyen módon fedjük is be[1] H-t végtelen sok nyitott[2] intervallummal[3], vagy általánosabban végtelen sok nyitott halmazzal, ezek közül mindig kiválasztható véges sok, amelyek a H halmazt szintén befedik. 2 Másképpen megfogalmazva: minden korlátos[4] és zárt[5] halmaz kompakt[6]. Az állítás többféleképpen is igazolható, ám ezek ismertetése a vers értelmezése szempontjából irreleváns. A mű egy olyan általános matematikai módszeren alapszik, mely több bizonyításnak is részlépése. Lényege, hogy úgy közelítünk meg egy pontot vagy pontokat egy adott intervallumon belül, hogy az intervallumot a keresett objektum irányába szűkítjük. Ez a módszer oroszlánfogás néven is ismert. Játékos formában megfogalmazva így hangzik: oroszlánt akarunk fogni a sivatagban. Ezt úgy tehetjük, hogy a sivatagot kettéosztjuk egy vonallal. Az oroszlán vagy a jobb oldalon, vagy a felezővonalon, vagy a bal oldalon van. Ha a felezővonalon találjuk, akkor készen vagyunk, elkaptuk. Ha nincs ott, akkor csak a sivatag egyik felében lehet. Most osszuk ketté azt az oldalt, amelyikben az oroszlán van! Amennyiben a kettéosztó vonalon van, akkor elkaptuk. Ha nem, akkor megint csak egyik felében lehet a fél sivatagnak. Ismételjük az eljárást addig, míg így el nem fogjuk az oroszlánt[7]. (Mivel az oroszlán véges, nem zéró kiterjedésű [kit érdekel egy pont-oroszlán?], feltételezzük, hogy az eljárás egyszer véget ér, és a sivatag felezgetésével előbb-utóbb kisebb darabot hozunk létre, mint maga az állat.) Marsall ezt az eljárást futtatja végig egy százszor-százszor-százas borzalmatos faládában. Ám oroszlán helyett egy aprócska létezőt (neutrino, izink, monád stb.) kerget. E jelentéktelennek tűnő dolognak a keresés alapossága, pontossága és leírásának részletessége ad jelentőséget. A matematikai alap adja azt a bizonyosságot, hogy bármely dolog legyen az akármilyen kicsi elérhető. Így rögzíti Marsall a megragadhatatlan képzelet szálait a valósághoz. Az álomszerű képzelgés szürreális közegének és a szilárd rendszerben létező tényeknek az együttese adja a vers dinamizmusát. Míg a tétel bizonyításakor az eredmény kapja a nagyobb nyomatékot, addig a versben a keresés mechanizmusa válik hangsúlyossá. Ez a folyamat hosszadalmas és fárasztó, mégis ez az út elvezet a végcélhoz. Marsall másik jelentős matematikaverse a Portáncfigurák kötet amíg a föld forog ciklusának darabja, a 2 2-es mátrixszorzatok. A szöveg egyediségét az adja, hogy struktúráját a mátrix fogalma, illetve két művelet, a mátrixszorzás és a mátrix transzponálása határozzák meg. A versszerkezet felépítésének megértéséhez szükség van ezek definícióira. A mátrix pontos matematikai meghatározása így hangzik: Definíció: Legyen T test[8], k és n pozitív egész számok. A T test feletti k n-típusú vagy k n-es mátrixon olyan téglalap alakú táblázatot értünk, amely T-nek k n elemét tartalmazza k sorba és n oszlopba rendezve. 3 Eszerint egy olyan sorokba és oszlopokba rendezett adathalmazról van szó, mely k sorból és n oszlopból áll, tehát k n elemet tartalmaz. Ezeket a téglalap alakú táblázatba rendezett adatokat kerek zárójel határolja. Egy k n típusú mátrix a következő alakban írható fel: 2 Szőkefalvi-Nagy Béla: Valós függvények és függvénysorok. Szeged, Polygon, 2002, Megyesi László: Lineáris algebra. Szeged, Polygon, Szeged, 2007,
3 Ezek alapján egy 2 2-es mátrix általános alakja: Így egy 2 2-es mátrixnak 2 sora, két oszlopa és összesen 2 2, azaz 4 eleme van. Így a vers mindkét szakaszának első fele 2 2-es mátrixnak tekinthető. A könnyebb érthetőség és kezelhetőség kedvéért vezessünk be új mátrix-jelöléseket! Rendeljünk hozzá indexelt betűt mindkét szakasz két első sorának minden szavához a következő sorrendben: Ennek a négy mátrixnak a szorzata adja mindkét szakasz befejező sorait. A mátrixszorzás matematikai definíciója a következő: Definíció: Legyen az A mátrix k n típusú, a B mátrix n m típusú T feletti mátrix. Az AB mátrix k m típusú és az AB = C mátrix i-edik sorának j-edik elemét az A mátrix i-edik sorának és a B mátrix j-edik oszlopának belső szorzata[9] adja (bármely i = 1, 2,..., k-ra és j = 1, 2,..., m-re). 4 A mátrixok szorzásával kapcsolatban alapvető fontosságú, hogy ez a művelet nem kommutatív[10]. Sok esetben a fordított sorrendben való szorzás nem is végezhető el, de ha elvégezhető is, általában más eredményt ad, mint az eredeti. Két mátrix csak akkor szorozható össze, ha legalább az egyik sorainak száma megegyezik a másik oszlopainak számával. Tehát egy k n és egy n m típusú mátrix (ha k m) összeszorozható, de csak ebben a sorrendben. 2 2-es mátrixok esetén, mivel sorainak és oszlopainak száma megegyezik, így mindkét oldalról vett szorzat létezik, azaz AB és BA szorzat is lehetséges. A művelet eredménye szintén egy 2 2-es mátrix lesz. Nézzük, hogyan számolható ki ennek egy eleme! Foglaljuk táblázatba a két mátrix elemeit a következőképpen: b 11 b 12 b 21 b 22 a 11 a 12 a 21 a 22 4 Megyesi László: Lineáris algebra. Szeged, Polygon, Szeged, 2007,
4 A szürke mezőben lévő elemet mely a szorzatmátrix első eleme lesz úgy kapjuk, hogy vesszük a vele egy sorban lévő elemeit az A mátrixnak, valamint a vele egy oszlopban lévő elemeit a B mátrixnak, s ezeknek képezzük a belső szorzatát. A belső szorzatot úgy számoljuk ki, hogy a 11 és b 11 elemet, valamint a 12 és b 21 elemeket összeszorozzuk, majd az így kapott két szorzatot összeadjuk: a 11 b 11 +a 12 b 21. Hasonlóan képezzük a többi elemet is, mindig a megfelelő sorból és oszlopból. Így tehát két darab 2 2-es mátrix szorzata a következőképpen írható le általános alakban: Ez alapján a keletkezett A B szorzat a vers első szakaszának elemeivel: Ha megvizsgáljuk a matematikai úton kapott eredményt és az eredeti verset, különbséget tapasztalunk. Ez az eltérés azonban egy matematikai művelettel megszüntethető. Ez az eljárás a mátrix transzponálása. Mátrixok transzponáltja definíció szerint a következő: Definíció: A T számtest feletti A=(a ij ) k n mátrix transzponáltján azt az A T -vel jelölt (b ij ) n k mátrixot értjük, melyre (b ij ) = a ji, 1 i n, l j k. Tehát Tehát vegyük észre, hogy A T megkapható A-ból, ha tükrözzük az a 11, a 22, elemeken áthaladó egyenesre. 5 Így az előbb kapott AB mátrix transzponálása megadja a vers eredeti szövegét: 5 Szabó László: Bevezetés a lineáris algebrába. Szeged, Polygon, Szeged, 2003, 7. 91
5 A szorzás és transzponálás műveleteit hasonlóképpen elvégezve a C és D mátrixokon, megkapjuk a második szakasz második felének szómátrixát. A vers keletkezése tehát pontos matematikai műveletekhez kötött. Úgy tűnik, a szavak egymás mellé kerülése determinált. Ám éppen ilyen logikus úton képződhetett volna meg egy teljesen más vers az adott szómátrixokból, a szorzótényezők felcserélésével. A vers első szakaszának mátrixaiból képzett BA szorzat transzponáltja a következő konstrukciót adja: További variációs lehetőségeket ad a mátrixszorzaton belül elvégzett műveletek tagjainak és tényezőinek sorrendje. Ha a vers első szakaszának szómátrixából az első elemet vizsgáljuk, a következő variációkat kaphatjuk: Az eredeti elem: Variációk: füst száll szó forr szó forr füst száll száll füst szó forr szó forr száll füst füst száll forr szó forr szó füst száll száll füst forr szó forr szó száll füst Jól mutatja ez a példa, hogyan jön létre számtalan variáció egy determinált közegben, és hogyan dolgozik az alkotói szabadság egy zárt és szabályozott rendszerben. A szavak többféle összevegyítése mellett fontos az elemek közti kapcsolatok vizsgálata. Az első szakasz kezdő szómátrixainak elemei egyszótagú szavak. 1. füst száll szó forr 2. szó száll ár forr 3. füst mész szó szék 4. szómész árszék Ezeknek az egységeknek az összetartozását matematikai alapokra is helyezhetjük. Ha figyelembe vesszük a szavak közötti jelöletlen műveleteket, akkor azt kapjuk, hogy mindegyik elemben az első és második szó, illetve a harmadik és negyedik szó szorosan összetartozik. (A köztük lévő művelet szorzás, ami erősebb a második és harmadik szó közti összeadásnál, pl. füst száll+szó forr.) Ám ezek a viszonyok csak a matematika nyelvén bírnak jelentéssel, hisz a versben jelöletlenek maradnak. Ha a szavakat és szószorzatokat megvizsgáljuk, akkor szinte végtelen azoknak a kapcsolatoknak a száma, mely hangalak vagy jelentés alapján, illetve a keltett asszociációk révén egybefűzik ezeket az elemeket. Csak néhány példa: madár sirály fehér, közepe magja, szó láthatatlan, mész fehér, szó szék száll, füst forr fehér stb. S bár a vers szinte végtelen számú interpretációt tesz lehetővé, a szövegben ott van a Marsall által elgondolt 92
6 értelmezés kulcsa. A verset Constantin Brâncuşi román szobrász emlékének ajánlja. S a látszólag találomra választott szavak megelevenednek a szobrokban. A márványcsíra, a mész szó szék vagy a madár láthatatlan fehér sirály mind hozzákapcsolható Brâncuşi egy-egy alkotásához. Ahogy a szavak matematikai fogalmak és műveletek nyomán válnak összetett jelentéshálót alkotó szöveggé a fent vizsgált versekben, úgy kelnek életre a tömör, egyszerű formák a szobrász címadása nyomán. Így, mint egy műveletsorozat által, ahogy Brâncuşi eljut a faragvány és a cím összepárosításával a szoborig, úgy jut el Marsall László a szavak és a matematika összeművelésével a szövegig. Az újszülött (1920, bronz) Az újszülött (1915, márvány) Madár a térben (1928) Fiatal madár (1928) Maiastra (1911) Mészkő szék 93
7 Jegyzetek: [1] befedés: az, hogy egy H ponthalmazt bizonyos szabály szerint adódott intervallumok befednek, azt jelenti, hogy H minden pontja legalább az egyik ilyen intervallumba beletartozik. [2] nyitott: egy halmaz (pl. intervallum) nyitott, ha nem tartalmazza határpontjait. [3] intervallum: azoknak a számoknak a halmaza, amik két adott szám közé esnek. Megkülönböztetünk zárt és nyílt intervallumokat aszerint, hogy a határoló számok beletartoznak (zárt) vagy sem (nyílt). [4] korlátos: egy halmaz korlátos, ha annak kiterjedése valamilyen értelemben véges. [5] zárt: egy halmaz zárt, ha minden határpontját tartalmazza. [6] kompakt: egy halmaz (K) kompakt, ha minden nyílt halmazrendszerből, melynek uniója lefedi K-t, kiválasztható véges sok nyílt halmaz is, melyek véges uniója még mindig lefedi K-t. [7] oroszlánfogás: ¼ ½ ¹ ₁₆ ¹ ₃₂ ⅛ [8] test: számok (vagy más matematikai objektumok) olyan halmaza, melyen a négy alapművelet elvégezhető (kivéve a 0-val való osztás). [9] belső szorzat: az adott sor és adott oszlop megfelelő elemeinek szorzatából képzett összeg. [10] kommutatív: egy matematikai művelet kommutatív volta azt jelenti, a művelet elvégzésekor az összetevők sorrendjének felcserélése nem változtatja meg a művelet eredményét. Például a pozitív egész számok között az összeadás vagy a szorzás. (Pl.: 2+3=3+2; vagy 5 6=6 5). Bibliográfia: Ágh István: Egy világ mintája : Marsall László új könyvéről. Je, 1987/10. Alföldy Jenő: Két sarkpont között: Marsall László: Holdraforgó. Ttáj, 1991/12. Balogh Piroska: f (poesis): Marsall László: Pókhálófüggvények. Ttáj, 1999/11. Dérczy Péter: Árva Sziszifusz: Vázlat Marsall Lászlóról. Mozgó Világ, 1981/7. Gál Ferenc: Egy világ mintája: Marsall László költészete. Életünk, 1988/9. Kemsei István: Szavak fickós fortyogása : Marsall Lászlóról. Hitel, 2000/8. Keresztury Tibor: Minták és vízjelek: Marsall László költészetéről. Alf, 1992/4. Kovács Béla Lóránt: A lírikus matematikája: Marsall László: Pókhálófüggvények. Alf, 1999/7. Lator László, Varga Lajos Márton: Életen túli érvényesség: Marsall László: Holdraforgó. Je, 1991/12. Megyesi László: Lineáris algebra. Szeged, Polygon, Szeged, 2007 Pécsi Györgyi: Pókhálófüggvények: Marsall László verseiről. Hitel, 1998/12. Rába György: Valóság és költészet összhangja felé: Marsall László: Holdraforgó. Holmi, 1992/5. Szabó László: Bevezetés a lineáris algebrába. Polygon, Szeged, 2003 Szincsok György: Egy lehetőség dimenziói: Marsall László: Város papírmadárból. Je, 1994/3. 94
8 Szőkefalvi-Nagy Béla: Valós függvények és függvénysorok. Polygon, Szeged, 2002 Tandori Dezső: Időkben és mezekben mindenki helyett élni : Marsall László: Egy világ mintája. ÚÍ, 1988/7. Vasy Géza: A változó és a változatlan: Marsall László új verseskönyve. Ttáj, 1994/10. Képek: Madár a térben: Az újszülött (márvány): Az újszülött (bronz): Maiastra: Fiatal madár: Mészkő szék: Az elemzett versek: Marsall László Szélketrec pókhálófüggvények Anthropos tézisei Az ún. Heine Borel lefedési tétel bizonyítása félálomban Egy százszor-százszor-százas (méterről van szó tudjuk) borzalmatos faládát vágtam félbe középütt, tudván, valamely félben rejlik, mint neutrino (?) (ősanya olló-vágta szemölcse, a padlásnak eldugott zugolyában). Ládám egyik felében mezítláb osonkodtam zseblámpámmal, talpamba szálka ment, kivájtam, nem volt ott, kit kerestem, (bár tüzetesen néztem érzékeny műszeremmel, s ijedtemben csuklottam, hogy visszhangzott a bódé), tüsszentettem, hogy mentem elfelé ki a külső térbe és bammegeltem. 95
9 Már tudom, te paránykám vagy: másik láda-térben, s most véled én elmésen vágom félbe az első fél-ládát, fűrészemmel. Ódon-mód átkozódom, izzadtságom törölve, támad okádhatnékom. Ám torna lábtyűt húzok, s fél-láda fél-felébe bújok a műszeremmel már csak avval kerestem a rejtőző monádot. Nem volt szemszegletemben semmi jelzés, a műszer K.O.-t mond önmagának. Itt nincs szálka, de vikszos padló, hogy esem seggre (vén tanár-hang: va bene ). Mentemben káromkodtam, mint züllött alkimista, elfelé külső térbe. Az egész negyed részét fűrészeltem épp félbe, jócskán kisebb kazettát, hátha e partiumban a virtuális izink Mol-tojás nincs se párja. Nyolcadolok fűrésszel, trancsírozok továbbá, már unom részletezni: százszor-százszor százas kóbli szőrhagyma-féle szektorában találtam a láthatatlan pöttyöt. Áldomást ittunk rája Heine és Borel úrral, kik elméjük zsákjával röptében is elkaptak zárt tartományban egykor rejtőzködő kis légyfit. 96
10 Szélketrec portáncfigurák amíg a föld forog 2 2-es mátrixszorzatok Brâncuşi emlékére 1. füst szó száll mész szó ár forr szék füst száll szó forr füst mész szó szék szó száll ár forr szómészárszék 2. közepe önmaga márványcsíra láthatatlan madár fehér magja sirály közepe márványcsíra önmaga magja madár márványcsíra fehér magja közepe láthatatlan önmaga sirály madár láthatatlan fehér sirály 97
Lineáris algebra (10A103)
 Lineáris algebra (10A103 Kátai-Urbán Kamilla Tudnivalók Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli (beugróval, feltétele a Lineáris algebra gyakorlat
Lineáris algebra (10A103 Kátai-Urbán Kamilla Tudnivalók Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli (beugróval, feltétele a Lineáris algebra gyakorlat
Diszkrét matematika I., 12. előadás Dr. Takách Géza NyME FMK Informatikai Intézet takach november 30.
 1 Diszkrét matematika I, 12 előadás Dr Takách Géza NyME FMK Informatikai Intézet takach@infnymehu http://infnymehu/ takach 2005 november 30 Vektorok Definíció Egy tetszőleges n pozitív egész számra n-komponensű
1 Diszkrét matematika I, 12 előadás Dr Takách Géza NyME FMK Informatikai Intézet takach@infnymehu http://infnymehu/ takach 2005 november 30 Vektorok Definíció Egy tetszőleges n pozitív egész számra n-komponensű
Irodalom. (a) A T, B T, (b) A + B, C + D, D C, (c) 3A, (d) AD, DA, B T A, 1 2 B = 1 C = A = 1 0 D = (a) 1 1 3, B T = = ( ) ; A T = 1 0
 Irodalom ezek egyrészt el- A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: hangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László: Bevezetés a lineáris algebrába, Polygon
Irodalom ezek egyrészt el- A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: hangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László: Bevezetés a lineáris algebrába, Polygon
Lineáris algebra (10A103)
 Lineáris algebra (10A103) Dr. Hartmann Miklós Tudnivalók Honlap: http://www.math.u-szeged.hu/~hartm Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli, feltétele a Lineáris algebra gyakorlat teljesítése.
Lineáris algebra (10A103) Dr. Hartmann Miklós Tudnivalók Honlap: http://www.math.u-szeged.hu/~hartm Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli, feltétele a Lineáris algebra gyakorlat teljesítése.
Lineáris algebra (10A103)
 Lineáris algebra (10A103) Kátai-Urbán Kamilla (1. előadás) Mátrixok 2019. február 6. 1 / 35 Bevezetés Előadás Tudnivalók (I.) Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Az előadáson készített
Lineáris algebra (10A103) Kátai-Urbán Kamilla (1. előadás) Mátrixok 2019. február 6. 1 / 35 Bevezetés Előadás Tudnivalók (I.) Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Az előadáson készített
I. VEKTOROK, MÁTRIXOK
 217/18 1 félév I VEKTOROK, MÁTRIXOK I1 I2 Vektorok 1 A síkon derékszögű koordinátarendszerben minden v vektornak van vízszintes és van függőleges koordinátája, ezeket sorrendben v 1 és v 2 jelöli A v síkbeli
217/18 1 félév I VEKTOROK, MÁTRIXOK I1 I2 Vektorok 1 A síkon derékszögű koordinátarendszerben minden v vektornak van vízszintes és van függőleges koordinátája, ezeket sorrendben v 1 és v 2 jelöli A v síkbeli
Műveletek mátrixokkal. Kalkulus. 2018/2019 ősz
 2018/2019 ősz Elérhetőségek Előadó: (safaro@math.bme.hu) Fogadóóra: hétfő 9-10 (H épület 3. emelet 310-es ajtó) A pontos tárgykövetelmények a www.math.bme.hu/~safaro/kalkulus oldalon találhatóak. A mátrix
2018/2019 ősz Elérhetőségek Előadó: (safaro@math.bme.hu) Fogadóóra: hétfő 9-10 (H épület 3. emelet 310-es ajtó) A pontos tárgykövetelmények a www.math.bme.hu/~safaro/kalkulus oldalon találhatóak. A mátrix
Valasek Gábor valasek@inf.elte.hu
 Számítógépes Grafika Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2013/2014. őszi félév ( Eötvös LorándSzámítógépes TudományegyetemInformatikai Grafika Kar) 2013/2014.
Számítógépes Grafika Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2013/2014. őszi félév ( Eötvös LorándSzámítógépes TudományegyetemInformatikai Grafika Kar) 2013/2014.
Algebrai egész kifejezések (polinomok)
 Algebrai egész kifejezések (polinomok) Betűk használata a matematikában Feladat Mekkora a 107m 68m oldalhosszúságú téglalap alakú focipála kerülete, területe? a = 107 m b = 68 m Terület T = a b = 107m
Algebrai egész kifejezések (polinomok) Betűk használata a matematikában Feladat Mekkora a 107m 68m oldalhosszúságú téglalap alakú focipála kerülete, területe? a = 107 m b = 68 m Terület T = a b = 107m
1. előadás: Halmazelmélet, számfogalom, teljes
 1. előadás: Halmazelmélet, számfogalom, teljes indukció Szabó Szilárd Halmazok Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) összessége. Egy halmaz akkor adott, ha minden objektumról eldönthető,
1. előadás: Halmazelmélet, számfogalom, teljes indukció Szabó Szilárd Halmazok Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) összessége. Egy halmaz akkor adott, ha minden objektumról eldönthető,
12. előadás. Egyenletrendszerek, mátrixok. Dr. Szörényi Miklós, Dr. Kallós Gábor
 12. előadás Egyenletrendszerek, mátrixok Dr. Szörényi Miklós, Dr. Kallós Gábor 2015 2016 1 Tartalom Matematikai alapok Vektorok és mátrixok megadása Tömbkonstansok Lineáris műveletek Mátrixok szorzása
12. előadás Egyenletrendszerek, mátrixok Dr. Szörényi Miklós, Dr. Kallós Gábor 2015 2016 1 Tartalom Matematikai alapok Vektorok és mátrixok megadása Tömbkonstansok Lineáris műveletek Mátrixok szorzása
Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) Halmazok 1
 Halmazok 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) Halmazok 2 A fejezet legfontosabb elemei Halmaz megadási módjai Halmazok közti műveletek (metszet,
Halmazok 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) Halmazok 2 A fejezet legfontosabb elemei Halmaz megadási módjai Halmazok közti műveletek (metszet,
Matematika. 1. évfolyam. I. félév
 Matematika 1. évfolyam - Biztos számfogalom a 10-es számkörben - Egyjegyű szám fogalmának ismerete - Páros, páratlan fogalma - Sorszám helyes használata szóban - Növekvő, csökkenő számsorozatok felismerése
Matematika 1. évfolyam - Biztos számfogalom a 10-es számkörben - Egyjegyű szám fogalmának ismerete - Páros, páratlan fogalma - Sorszám helyes használata szóban - Növekvő, csökkenő számsorozatok felismerése
Egész számok. pozitív egész számok: 1; 2; 3; 4;... negatív egész számok: 1; 2; 3; 4;...
 Egész számok természetes számok ( ) pozitív egész számok: 1; 2; 3; 4;... 0 negatív egész számok: 1; 2; 3; 4;... egész számok ( ) 1. Írd a következõ számokat a halmazábra megfelelõ helyére! 3; 7; +6 ; (
Egész számok természetes számok ( ) pozitív egész számok: 1; 2; 3; 4;... 0 negatív egész számok: 1; 2; 3; 4;... egész számok ( ) 1. Írd a következõ számokat a halmazábra megfelelõ helyére! 3; 7; +6 ; (
Követelmény az 5. évfolyamon félévkor matematikából
 Követelmény az 5. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Néhány elem kiválasztása adott szempont szerint. Néhány elem sorba rendezése, az összes lehetséges sorrend felsorolása.
Követelmény az 5. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Néhány elem kiválasztása adott szempont szerint. Néhány elem sorba rendezése, az összes lehetséges sorrend felsorolása.
Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé.
 HA 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) HA 2 Halmazok HA 3 Megjegyzések A halmaz, az elem és az eleme fogalmakat nem definiáljuk, hanem alapfogalmaknak
HA 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) HA 2 Halmazok HA 3 Megjegyzések A halmaz, az elem és az eleme fogalmakat nem definiáljuk, hanem alapfogalmaknak
Mátrixok, mátrixműveletek
 Mátrixok, mátrixműveletek 1 előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Mátrixok, mátrixműveletek p 1/1 Mátrixok definíciója Definíció Helyezzünk el n m elemet egy olyan téglalap
Mátrixok, mátrixműveletek 1 előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Mátrixok, mátrixműveletek p 1/1 Mátrixok definíciója Definíció Helyezzünk el n m elemet egy olyan téglalap
Halmazelmélet. 1. előadás. Farkas István. DE ATC Gazdaságelemzési és Statisztikai Tanszék. Halmazelmélet p. 1/1
 Halmazelmélet 1. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Halmazelmélet p. 1/1 A halmaz fogalma, jelölések A halmaz fogalmát a matematikában nem definiáljuk, tulajdonságaival
Halmazelmélet 1. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Halmazelmélet p. 1/1 A halmaz fogalma, jelölések A halmaz fogalmát a matematikában nem definiáljuk, tulajdonságaival
Permutációk véges halmazon (el adásvázlat, február 12.)
 Permutációk véges halmazon el adásvázlat 2008 február 12 Maróti Miklós Ennek az el adásnak a megértéséhez a következ fogalmakat kell tudni: ismétlés nélküli variáció leképezés indulási és érkezési halmaz
Permutációk véges halmazon el adásvázlat 2008 február 12 Maróti Miklós Ennek az el adásnak a megértéséhez a következ fogalmakat kell tudni: ismétlés nélküli variáció leképezés indulási és érkezési halmaz
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Számelmélet I.
 Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
Követelmény a 6. évfolyamon félévkor matematikából
 Követelmény a 6. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Halmazba rendezés adott tulajdonság alapján, részhalmaz felírása, felismerése. Két véges halmaz közös részének,
Követelmény a 6. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Halmazba rendezés adott tulajdonság alapján, részhalmaz felírása, felismerése. Két véges halmaz közös részének,
A valós számok halmaza
 VA 1 A valós számok halmaza VA 2 A valós számok halmazának axiómarendszere és alapvető tulajdonságai Definíció Az R halmazt a valós számok halmazának nevezzük, ha teljesíti a következő axiómarendszerben
VA 1 A valós számok halmaza VA 2 A valós számok halmazának axiómarendszere és alapvető tulajdonságai Definíció Az R halmazt a valós számok halmazának nevezzük, ha teljesíti a következő axiómarendszerben
17. előadás: Vektorok a térben
 17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
1. Mátrixösszeadás és skalárral szorzás
 1 Mátrixösszeadás és skalárral szorzás Mátrixok tömör jelölése T test Az M = a i j T n m azt az n sorból és m oszlopból álló mátrixot jelöli, amelyben az i-edik sor j-edik eleme a i j T Példák [ ] Ha M
1 Mátrixösszeadás és skalárral szorzás Mátrixok tömör jelölése T test Az M = a i j T n m azt az n sorból és m oszlopból álló mátrixot jelöli, amelyben az i-edik sor j-edik eleme a i j T Példák [ ] Ha M
Mátrixok 2017 Mátrixok
 2017 számtáblázatok" : számok rendezett halmaza, melyben a számok helye két paraméterrel van meghatározva. Például lineáris egyenletrendszer együtthatómátrixa 2 x 1 + 4 x 2 = 8 1 x 1 + 3 x 2 = 1 ( 2 4
2017 számtáblázatok" : számok rendezett halmaza, melyben a számok helye két paraméterrel van meghatározva. Például lineáris egyenletrendszer együtthatómátrixa 2 x 1 + 4 x 2 = 8 1 x 1 + 3 x 2 = 1 ( 2 4
Analízis. 11 12. évfolyam. Szerkesztette: Surányi László. 2015. július 5.
 Analízis 11 12. évfolyam Szerkesztette: Surányi László 2015. július 5. Technikai munkák (MatKönyv project, TEX programozás, PHP programozás, tördelés...) Dénes Balázs, Grósz Dániel, Hraskó András, Kalló
Analízis 11 12. évfolyam Szerkesztette: Surányi László 2015. július 5. Technikai munkák (MatKönyv project, TEX programozás, PHP programozás, tördelés...) Dénes Balázs, Grósz Dániel, Hraskó András, Kalló
Matematika A1a Analízis
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
Tanmenetjavaslat. Téma Óraszám Tananyag Fogalmak Összefüggések Eszközök Kitekintés. Helyi érték, alaki érték. Számegyenes.
 Heti 4 óra esetén, 37 tanítási hétre összesen 148 óra áll rendelkezésre. A tanmenet 132 óra beosztását tartalmazza. Heti 5 óra esetén összesen 37-tel több órában dolgozhatunk. Ez összesen 185 óra. Itt
Heti 4 óra esetén, 37 tanítási hétre összesen 148 óra áll rendelkezésre. A tanmenet 132 óra beosztását tartalmazza. Heti 5 óra esetén összesen 37-tel több órában dolgozhatunk. Ez összesen 185 óra. Itt
2014. november 5-7. Dr. Vincze Szilvia
 24. november 5-7. Dr. Vincze Szilvia A differenciálszámítás az emberiség egyik legnagyobb találmánya és ez az állítás nem egy matek-szakbarbár fellengzős kijelentése. A differenciálszámítás segítségével
24. november 5-7. Dr. Vincze Szilvia A differenciálszámítás az emberiség egyik legnagyobb találmánya és ez az állítás nem egy matek-szakbarbár fellengzős kijelentése. A differenciálszámítás segítségével
A Matematika I. előadás részletes tematikája
 A Matematika I. előadás részletes tematikája 2005/6, I. félév 1. Halmazok és relációk 1.1 Műveletek halmazokkal Definíciók, fogalmak: halmaz, elem, üres halmaz, halmazok egyenlősége, részhalmaz, halmazok
A Matematika I. előadás részletes tematikája 2005/6, I. félév 1. Halmazok és relációk 1.1 Műveletek halmazokkal Definíciók, fogalmak: halmaz, elem, üres halmaz, halmazok egyenlősége, részhalmaz, halmazok
1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás)
 Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
 1. Bevezetés A félév anyaga. Lineáris algebra Vektorterek, alterek Függés, függetlenség, bázis, dimenzió Skaláris szorzat R n -ben, vektorok hossza és szöge Lineáris leképezések, mátrixuk, bázistranszformáció
1. Bevezetés A félév anyaga. Lineáris algebra Vektorterek, alterek Függés, függetlenség, bázis, dimenzió Skaláris szorzat R n -ben, vektorok hossza és szöge Lineáris leképezések, mátrixuk, bázistranszformáció
Matematika szigorlat június 17. Neptun kód:
 Név Matematika szigorlat 014. június 17. Neptun kód: 1.. 3. 4. 5. Elm. Fel. Össz. Oszt. Az eredményes szigorlat feltétele elméletből legalább 0 pont, feladatokból pedig legalább 30 pont elérése. A szigorlat
Név Matematika szigorlat 014. június 17. Neptun kód: 1.. 3. 4. 5. Elm. Fel. Össz. Oszt. Az eredményes szigorlat feltétele elméletből legalább 0 pont, feladatokból pedig legalább 30 pont elérése. A szigorlat
FRAKTÁLGEOMETRIA. Metrikus terek, szeparábilitás, kompaktság. Czirbusz Sándor czirbusz@gmail.com. Komputeralgebra Tanszék ELTE Informatika Kar
 Metrikus terek, szeparábilitás, kompaktság Czirbusz Sándor czirbusz@gmail.com Komputeralgebra Tanszék ELTE Informatika Kar 2010. március 7. Vázlat 1 Szeparábilitás Definíciók A szeparábilitás ekvivalens
Metrikus terek, szeparábilitás, kompaktság Czirbusz Sándor czirbusz@gmail.com Komputeralgebra Tanszék ELTE Informatika Kar 2010. március 7. Vázlat 1 Szeparábilitás Definíciók A szeparábilitás ekvivalens
BUDAPESTI KÖZGAZDASÁGTUDOMÁNYI EGYETEM. Puskás Csaba, Szabó Imre, Tallos Péter LINEÁRIS ALGEBRA JEGYZET
 BUDAPESTI KÖZGAZDASÁGTUDOMÁNYI EGYETEM Puskás Csaba, Szabó Imre, Tallos Péter LINEÁRIS ALGEBRA JEGYZET BUDAPEST, 1997 A szerzők Lineáris Algebra, illetve Lineáris Algebra II c jegyzeteinek átdolgozott
BUDAPESTI KÖZGAZDASÁGTUDOMÁNYI EGYETEM Puskás Csaba, Szabó Imre, Tallos Péter LINEÁRIS ALGEBRA JEGYZET BUDAPEST, 1997 A szerzők Lineáris Algebra, illetve Lineáris Algebra II c jegyzeteinek átdolgozott
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 6. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 6. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika II., 8. előadás. Vektorterek
 1 Diszkrét matematika II., 8. előadás Vektorterek Dr. Takách Géza NyME FMK Informatikai Intézet takach@inf.nyme.hu http://inf.nyme.hu/ takach/ 2007.??? Vektorterek Legyen T egy test (pl. R, Q, F p ). Definíció.
1 Diszkrét matematika II., 8. előadás Vektorterek Dr. Takách Géza NyME FMK Informatikai Intézet takach@inf.nyme.hu http://inf.nyme.hu/ takach/ 2007.??? Vektorterek Legyen T egy test (pl. R, Q, F p ). Definíció.
Matematika III. 2. Eseményalgebra Prof. Dr. Závoti, József
 Matematika III. 2. Eseményalgebra Prof. Dr. Závoti, József Matematika III. 2. : Eseményalgebra Prof. Dr. Závoti, József Lektor : Bischof, Annamária Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027 Tananyagfejlesztéssel
Matematika III. 2. Eseményalgebra Prof. Dr. Závoti, József Matematika III. 2. : Eseményalgebra Prof. Dr. Závoti, József Lektor : Bischof, Annamária Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027 Tananyagfejlesztéssel
1. Halmazok, számhalmazok, alapműveletek
 1. Halmazok, számhalmazok, alapműveletek I. Nulladik ZH-ban láttuk: 1. Határozza meg az (A B)\C halmaz elemszámát, ha A tartalmazza az összes 19-nél kisebb természetes számot, továbbá B a prímszámok halmaza
1. Halmazok, számhalmazok, alapműveletek I. Nulladik ZH-ban láttuk: 1. Határozza meg az (A B)\C halmaz elemszámát, ha A tartalmazza az összes 19-nél kisebb természetes számot, továbbá B a prímszámok halmaza
Analízis előadás és gyakorlat vázlat
 Analízis előadás és gyakorlat vázlat Készült a PTE TTK GI szakos hallgatóinak Király Balázs 2010-11. I. Félév 2 1. fejezet Számhalmazok és tulajdonságaik 1.1. Nevezetes számhalmazok ➀ a) jelölése: N b)
Analízis előadás és gyakorlat vázlat Készült a PTE TTK GI szakos hallgatóinak Király Balázs 2010-11. I. Félév 2 1. fejezet Számhalmazok és tulajdonságaik 1.1. Nevezetes számhalmazok ➀ a) jelölése: N b)
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 6. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 6. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
DISZKRÉT MATEMATIKA: STRUKTÚRÁK Előadáson mutatott példa: Bércesné Novák Ágnes
 1. Algebrai alapok: DISZKRÉT MATEMATIKA: STRUKTÚRÁK Művelet: Egy H nemüres halmazon értelmezett (kétváltozós) műveleten egy H H H függvényt értünk, azaz egy olyan leképezést, amely bármely a,b H elempárhoz
1. Algebrai alapok: DISZKRÉT MATEMATIKA: STRUKTÚRÁK Művelet: Egy H nemüres halmazon értelmezett (kétváltozós) műveleten egy H H H függvényt értünk, azaz egy olyan leképezést, amely bármely a,b H elempárhoz
A matematikai feladatok és megoldások konvenciói
 A matematikai feladatok és megoldások konvenciói Kozárné Fazekas Anna Kántor Sándor Matematika és Informatika Didaktikai Konferencia - Szatmárnémeti 2011. január 28-30. Konvenciók Mindenki által elfogadott
A matematikai feladatok és megoldások konvenciói Kozárné Fazekas Anna Kántor Sándor Matematika és Informatika Didaktikai Konferencia - Szatmárnémeti 2011. január 28-30. Konvenciók Mindenki által elfogadott
1. Részcsoportok (1) C + R + Q + Z +. (2) C R Q. (3) Q nem részcsoportja C + -nak, mert más a művelet!
 1. Részcsoportok A részcsoport fogalma. 2.2.15. Definíció Legyen G csoport. A H G részhalmaz részcsoport, ha maga is csoport G műveleteire nézve. Jele: H G. Az altér fogalmához hasonlít. Példák (1) C +
1. Részcsoportok A részcsoport fogalma. 2.2.15. Definíció Legyen G csoport. A H G részhalmaz részcsoport, ha maga is csoport G műveleteire nézve. Jele: H G. Az altér fogalmához hasonlít. Példák (1) C +
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I. 1 I. HALmAZOk 1. JELÖLÉSEk A halmaz fogalmát tulajdonságait gyakran használjuk a matematikában. A halmazt nem definiáljuk, ezt alapfogalomnak tekintjük. Ez nem szokatlan, hiszen
KOVÁCS BÉLA, MATEmATIkA I. 1 I. HALmAZOk 1. JELÖLÉSEk A halmaz fogalmát tulajdonságait gyakran használjuk a matematikában. A halmazt nem definiáljuk, ezt alapfogalomnak tekintjük. Ez nem szokatlan, hiszen
Mátrixok február Feladat: Legyen A = ( ( B =
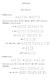 Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Numerikus módszerek 1.
 Numerikus módszerek 1. 3. előadás: Mátrixok LU-felbontása Lócsi Levente ELTE IK 2013. szeptember 23. Tartalomjegyzék 1 Alsó háromszögmátrixok és Gauss-elimináció 2 Háromszögmátrixokról 3 LU-felbontás Gauss-eliminációval
Numerikus módszerek 1. 3. előadás: Mátrixok LU-felbontása Lócsi Levente ELTE IK 2013. szeptember 23. Tartalomjegyzék 1 Alsó háromszögmátrixok és Gauss-elimináció 2 Háromszögmátrixokról 3 LU-felbontás Gauss-eliminációval
Műveletek egész számokkal
 Mit tudunk az egész számokról? 1. Döntsd el, hogy igazak-e a következő állítások az A halmaz elemeire! a) Az A halmaz elemei között 3 pozitív szám van. b) A legkisebb szám abszolút értéke a legnagyobb.
Mit tudunk az egész számokról? 1. Döntsd el, hogy igazak-e a következő állítások az A halmaz elemeire! a) Az A halmaz elemei között 3 pozitív szám van. b) A legkisebb szám abszolút értéke a legnagyobb.
SULINOVA PROGRAMTANTERVÉHEZ ILLESZKEDŐ TANMENET 9. ÉVFOLYAM SZÁMÁRA
 1 SULINOVA PROGRAMTANTERVÉHEZ ILLESZKEDŐ TANMENET 9. ÉVFOLYAM SZÁMÁRA Heti óraszám: 3 Éves óraszám: 37 x 3 = 111 A tanmenet 101 óra beosztását tartalmazza. A dolgozatok írása és javítása 10 órát foglal
1 SULINOVA PROGRAMTANTERVÉHEZ ILLESZKEDŐ TANMENET 9. ÉVFOLYAM SZÁMÁRA Heti óraszám: 3 Éves óraszám: 37 x 3 = 111 A tanmenet 101 óra beosztását tartalmazza. A dolgozatok írása és javítása 10 órát foglal
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 5. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Számfogalom bővítése Diszkrét matematika I. középszint
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 5. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Számfogalom bővítése Diszkrét matematika I. középszint
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
Funkcionálanalízis. n=1. n=1. x n y n. n=1
 Funkcionálanalízis 2011/12 tavaszi félév - 2. előadás 1.4. Lényeges alap-terek, példák Sorozat terek (Folytatás.) C: konvergens sorozatok tere. A tér pontjai sorozatok: x = (x n ). Ezen belül C 0 a nullsorozatok
Funkcionálanalízis 2011/12 tavaszi félév - 2. előadás 1.4. Lényeges alap-terek, példák Sorozat terek (Folytatás.) C: konvergens sorozatok tere. A tér pontjai sorozatok: x = (x n ). Ezen belül C 0 a nullsorozatok
1. Interpoláció. Egyértelműség Ha f és g ilyen polinomok, akkor n helyen megegyeznek, így a polinomok azonossági tétele miatt egyenlők.
 1. Interpoláció Az interpoláció alapproblémája. Feladat Olyan polinomot keresünk, amely előre megadott helyeken előre megadott értékeket vesz fel. A helyek: páronként különböző a 1, a,...,a n számok. Az
1. Interpoláció Az interpoláció alapproblémája. Feladat Olyan polinomot keresünk, amely előre megadott helyeken előre megadott értékeket vesz fel. A helyek: páronként különböző a 1, a,...,a n számok. Az
Vektorterek. Wettl Ferenc február 17. Wettl Ferenc Vektorterek február / 27
 Vektorterek Wettl Ferenc 2015. február 17. Wettl Ferenc Vektorterek 2015. február 17. 1 / 27 Tartalom 1 Egyenletrendszerek 2 Algebrai struktúrák 3 Vektortér 4 Bázis, dimenzió 5 Valós mátrixok és egyenletrendszerek
Vektorterek Wettl Ferenc 2015. február 17. Wettl Ferenc Vektorterek 2015. február 17. 1 / 27 Tartalom 1 Egyenletrendszerek 2 Algebrai struktúrák 3 Vektortér 4 Bázis, dimenzió 5 Valós mátrixok és egyenletrendszerek
Lineáris leképezések (előadásvázlat, szeptember 28.) Maróti Miklós, Kátai-Urbán Kamilla
 Lineáris leképezések (előadásvázlat, 2012. szeptember 28.) Maróti Miklós, Kátai-Urbán Kamilla Ennek az előadásnak a megértéséhez a következő fogalmakat kell tudni: homogén lineáris egyenletrendszer és
Lineáris leképezések (előadásvázlat, 2012. szeptember 28.) Maróti Miklós, Kátai-Urbán Kamilla Ennek az előadásnak a megértéséhez a következő fogalmakat kell tudni: homogén lineáris egyenletrendszer és
Egyenletek, egyenlőtlenségek, egyenletrendszerek I.
 Egyenletek, egyenlőtlenségek, egyenletrendszerek I. DEFINÍCIÓ: (Nyitott mondat) Az olyan állítást, amelyben az alany helyén változó szerepel, nyitott mondatnak nevezzük. A nyitott mondatba írt változót
Egyenletek, egyenlőtlenségek, egyenletrendszerek I. DEFINÍCIÓ: (Nyitott mondat) Az olyan állítást, amelyben az alany helyén változó szerepel, nyitott mondatnak nevezzük. A nyitott mondatba írt változót
15. LINEÁRIS EGYENLETRENDSZEREK
 15 LINEÁRIS EGYENLETRENDSZEREK 151 Lineáris egyenletrendszer, Gauss elimináció 1 Definíció Lineáris egyenletrendszernek nevezzük az (1) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
15 LINEÁRIS EGYENLETRENDSZEREK 151 Lineáris egyenletrendszer, Gauss elimináció 1 Definíció Lineáris egyenletrendszernek nevezzük az (1) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
Fuzzy halmazok jellemzői
 A Fuzzy rendszerek, számítási intelligencia gyakorló feladatok megoldása Fuzzy halmazok jellemzői A fuzzy halmaz tartója az alaphalmaz azon elemeket tartalmazó részhalmaza, melyek tagsági értéke 0-nál
A Fuzzy rendszerek, számítási intelligencia gyakorló feladatok megoldása Fuzzy halmazok jellemzői A fuzzy halmaz tartója az alaphalmaz azon elemeket tartalmazó részhalmaza, melyek tagsági értéke 0-nál
Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) Egy halmaz akkor adott, ha minden objektumról eldönthető, hogy
 1. előadás: Halmazelmélet Szabó Szilárd Halmazok Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) összessége. Egy halmaz akkor adott, ha minden objektumról eldönthető, hogy hozzátartozik-e,
1. előadás: Halmazelmélet Szabó Szilárd Halmazok Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) összessége. Egy halmaz akkor adott, ha minden objektumról eldönthető, hogy hozzátartozik-e,
HALMAZELMÉLET feladatsor 1.
 HALMAZELMÉLET feladatsor 1. Egy (H,, ) algebrai struktúra háló, ha (H, ) és (H, ) kommutatív félcsoport, és teljesül az ún. elnyelési tulajdonság: A, B H: A (A B) = A, A (A B) = A. A (H,, ) háló korlátos,
HALMAZELMÉLET feladatsor 1. Egy (H,, ) algebrai struktúra háló, ha (H, ) és (H, ) kommutatív félcsoport, és teljesül az ún. elnyelési tulajdonság: A, B H: A (A B) = A, A (A B) = A. A (H,, ) háló korlátos,
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I. 4 IV. FÜGGVÉNYEk 1. LEkÉPEZÉSEk, függvények Definíció Legyen és két halmaz. Egy függvény -ből -ba egy olyan szabály, amely minden elemhez pontosan egy elemet rendel hozzá. Az
KOVÁCS BÉLA, MATEmATIkA I. 4 IV. FÜGGVÉNYEk 1. LEkÉPEZÉSEk, függvények Definíció Legyen és két halmaz. Egy függvény -ből -ba egy olyan szabály, amely minden elemhez pontosan egy elemet rendel hozzá. Az
HALMAZOK. A racionális számok halmazát olyan számok alkotják, amelyek felírhatók b. jele:. A racionális számok halmazának végtelen sok eleme van.
 HALMAZOK Tanulási cél Halmazok megadása, halmazműveletek megismerése és alkalmazása, halmazok ábrázolása Venn diagramon. Motivációs példa Egy fogyasztó 80 000 pénzegység jövedelmet fordít két termék, x
HALMAZOK Tanulási cél Halmazok megadása, halmazműveletek megismerése és alkalmazása, halmazok ábrázolása Venn diagramon. Motivációs példa Egy fogyasztó 80 000 pénzegység jövedelmet fordít két termék, x
2. előadás. Lineáris algebra numerikus módszerei. Mátrixok Mátrixműveletek Speciális mátrixok, vektorok Norma
 Mátrixok Definíció Az m n típusú (méretű) valós A mátrixon valós a ij számok alábbi táblázatát értjük: a 11 a 12... a 1j... a 1n.......... A = a i1 a i2... a ij... a in........... a m1 a m2... a mj...
Mátrixok Definíció Az m n típusú (méretű) valós A mátrixon valós a ij számok alábbi táblázatát értjük: a 11 a 12... a 1j... a 1n.......... A = a i1 a i2... a ij... a in........... a m1 a m2... a mj...
1. ábra ábra
 A kifejtési tétel A kifejtési tétel kimondásához először meg kell ismerkedni az előjeles aldetermináns fogalmával. Ha az n n-es A mátrix i-edik sorának és j-edik oszlopának kereszteződésében az elem áll,
A kifejtési tétel A kifejtési tétel kimondásához először meg kell ismerkedni az előjeles aldetermináns fogalmával. Ha az n n-es A mátrix i-edik sorának és j-edik oszlopának kereszteződésében az elem áll,
Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit.
 2. A VALÓS SZÁMOK 2.1 A valós számok aximómarendszere Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit. 1.Testaxiómák R-ben két művelet van értelmezve, az
2. A VALÓS SZÁMOK 2.1 A valós számok aximómarendszere Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit. 1.Testaxiómák R-ben két művelet van értelmezve, az
Determinánsok. A determináns fogalma olyan algebrai segédeszköz, amellyel. szolgáltat az előbbi kérdésekre, bár ez nem mindig hatékony.
 Determinánsok A determináns fogalma olyan algebrai segédeszköz, amellyel jól jellemezhető a mátrixok invertálhatósága, a mátrix rangja. Segítségével lineáris egyenletrendszerek megoldhatósága dönthető
Determinánsok A determináns fogalma olyan algebrai segédeszköz, amellyel jól jellemezhető a mátrixok invertálhatósága, a mátrix rangja. Segítségével lineáris egyenletrendszerek megoldhatósága dönthető
Matematika alapjai; Feladatok
 Matematika alapjai; Feladatok 1. Hét 1. Tekintsük a,, \ műveleteket. Melyek lesznek a.) kommutativok b.) asszociativak c.) disztributívak-e a, műveletek? Melyik melyikre? 2. Fejezzük ki a műveletet a \
Matematika alapjai; Feladatok 1. Hét 1. Tekintsük a,, \ műveleteket. Melyek lesznek a.) kommutativok b.) asszociativak c.) disztributívak-e a, műveletek? Melyik melyikre? 2. Fejezzük ki a műveletet a \
f(x) vagy f(x) a (x x 0 )-t használjuk. lim melyekre Mivel itt ɛ > 0 tetszőlegesen kicsi, így a a = 0, a = a, ami ellentmondás, bizonyítva
 6. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 6.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
6. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 6.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
Szöveges feladatok a mátrixaritmetika alkalmazására
 Szöveges feladatok a mátrixaritmetika alkalmazására Bevezetés: Tekintsük az alábbi -es mátrixot: A. Szorozzuk meg ezt jobbról egy alkalmas méretű (azaz -es) oszlopvektorral, amely az R tér kanonikus bázisának
Szöveges feladatok a mátrixaritmetika alkalmazására Bevezetés: Tekintsük az alábbi -es mátrixot: A. Szorozzuk meg ezt jobbról egy alkalmas méretű (azaz -es) oszlopvektorral, amely az R tér kanonikus bázisának
A valós számok halmaza 5. I. rész MATEMATIKAI ANALÍZIS
 A valós számok halmaza 5 I rész MATEMATIKAI ANALÍZIS 6 A valós számok halmaza A valós számok halmaza 7 I A valós számok halmaza A valós számokra vonatkozó axiómák A matematika lépten-nyomon felhasználja
A valós számok halmaza 5 I rész MATEMATIKAI ANALÍZIS 6 A valós számok halmaza A valós számok halmaza 7 I A valós számok halmaza A valós számokra vonatkozó axiómák A matematika lépten-nyomon felhasználja
Klasszikus algebra előadás. Waldhauser Tamás április 14.
 Klasszikus algebra előadás Waldhauser Tamás 2014. április 14. Többhatározatlanú polinomok 4.3. Definíció. Adott T test feletti n-határozatlanú monomnak nevezzük az ax k 1 1 xk n n alakú formális kifejezéseket,
Klasszikus algebra előadás Waldhauser Tamás 2014. április 14. Többhatározatlanú polinomok 4.3. Definíció. Adott T test feletti n-határozatlanú monomnak nevezzük az ax k 1 1 xk n n alakú formális kifejezéseket,
Elemi matematika szakkör
 Elemi matematika szakkör Kolozsvár, 2015. október 5. 1.1. Feladat. Egy pozitív egész számot K tulajdonságúnak nevezünk, ha számjegyei nullától különböznek és nincs két azonos számjegye. Határozd meg az
Elemi matematika szakkör Kolozsvár, 2015. október 5. 1.1. Feladat. Egy pozitív egész számot K tulajdonságúnak nevezünk, ha számjegyei nullától különböznek és nincs két azonos számjegye. Határozd meg az
2014. szeptember 24. és 26. Dr. Vincze Szilvia
 2014. szeptember 24. és 26. Dr. Vincze Szilvia Mind a hétköznapi, mind a tudományos életben gyakran előfordul, hogy bizonyos halmazok elemei között kapcsolat figyelhető meg. A kapcsolat fogalmának matematikai
2014. szeptember 24. és 26. Dr. Vincze Szilvia Mind a hétköznapi, mind a tudományos életben gyakran előfordul, hogy bizonyos halmazok elemei között kapcsolat figyelhető meg. A kapcsolat fogalmának matematikai
6. OSZTÁLY. Az évi munka szervezése, az érdeklõdés felkeltése Feladatok a 6. osztály anyagából. Halmazok Ismétlés (halmaz megadása, részhalmaz)
 6. OSZTÁLY Óraszám 1. 1. Az évi munka szervezése, az érdeklõdés felkeltése a 6. osztály anyagából Tk. 13/elsõ mintapélda 42/69 70. 96/elsõ mintapélda 202/16. 218/69. 2 3. 2 3. Halmazok Ismétlés (halmaz
6. OSZTÁLY Óraszám 1. 1. Az évi munka szervezése, az érdeklõdés felkeltése a 6. osztály anyagából Tk. 13/elsõ mintapélda 42/69 70. 96/elsõ mintapélda 202/16. 218/69. 2 3. 2 3. Halmazok Ismétlés (halmaz
1. Generátorrendszer. Házi feladat (fizikából tudjuk) Ha v és w nem párhuzamos síkvektorok, akkor generátorrendszert alkotnak a sík vektorainak
 1. Generátorrendszer Generátorrendszer. Tétel (Freud, 4.3.4. Tétel) Legyen V vektortér a T test fölött és v 1,v 2,...,v m V. Ekkor a λ 1 v 1 + λ 2 v 2 +... + λ m v m alakú vektorok, ahol λ 1,λ 2,...,λ
1. Generátorrendszer Generátorrendszer. Tétel (Freud, 4.3.4. Tétel) Legyen V vektortér a T test fölött és v 1,v 2,...,v m V. Ekkor a λ 1 v 1 + λ 2 v 2 +... + λ m v m alakú vektorok, ahol λ 1,λ 2,...,λ
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 2017. tavasz 1. Diszkrét matematika 2.C szakirány 4. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2017.
Diszkrét matematika 2.C szakirány 2017. tavasz 1. Diszkrét matematika 2.C szakirány 4. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2017.
összeadjuk 0-t kapunk. Képletben:
 814 A ferde kifejtés tétele Ha egy determináns valamely sorának elemeit egy másik sor elemeihez tartozó adjungáltakkal szorozzuk meg és a szorzatokat összeadjuk 0-t kapunk Képletben: n a ij A kj = 0, ha
814 A ferde kifejtés tétele Ha egy determináns valamely sorának elemeit egy másik sor elemeihez tartozó adjungáltakkal szorozzuk meg és a szorzatokat összeadjuk 0-t kapunk Képletben: n a ij A kj = 0, ha
Követelmény a 7. évfolyamon félévkor matematikából
 Követelmény a 7. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Elemek halmazba rendezése több szempont alapján. Halmazok ábrázolása. A nyelv logikai elemeinek helyes használata.
Követelmény a 7. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Elemek halmazba rendezése több szempont alapján. Halmazok ábrázolása. A nyelv logikai elemeinek helyes használata.
ÍRÁSBELI BELSŐ VIZSGA MATEMATIKA 8. évfolyam reál tagozat Az írásbeli vizsga gyakorlati és elméleti feladatai a következő témakörökből származnak.
 ÍRÁSBELI BELSŐ VIZSGA MATEMATIKA 8. évfolyam reál tagozat Az írásbeli vizsga gyakorlati és elméleti feladatai a következő témakörökből származnak. Időtartam: 60 perc 1. Halmazműveletek konkrét halmazokkal.
ÍRÁSBELI BELSŐ VIZSGA MATEMATIKA 8. évfolyam reál tagozat Az írásbeli vizsga gyakorlati és elméleti feladatai a következő témakörökből származnak. Időtartam: 60 perc 1. Halmazműveletek konkrét halmazokkal.
Gráfelmélet. I. Előadás jegyzet (2010.szeptember 9.) 1.A gráf fogalma
 Készítette: Laczik Sándor János Gráfelmélet I. Előadás jegyzet (2010.szeptember 9.) 1.A gráf fogalma Definíció: a G=(V,E) párt egyszerű gráfnak nevezzük, (V elemeit a gráf csúcsainak/pontjainak,e elemeit
Készítette: Laczik Sándor János Gráfelmélet I. Előadás jegyzet (2010.szeptember 9.) 1.A gráf fogalma Definíció: a G=(V,E) párt egyszerű gráfnak nevezzük, (V elemeit a gráf csúcsainak/pontjainak,e elemeit
RE 1. Relációk Függvények. A diákon megjelenő szövegek és képek csak a szerző (Kocsis Imre, DE MFK) engedélyével használhatók fel!
 RE 1 Relációk Függvények RE 2 Definíció: Ha A, B és ρ A B, akkor azt mondjuk, hogy ρ reláció A és B között, vagy azt, hogy ρ leképezés A-ból B-be. Ha speciálisan A=B, azaz ρ A A, akkor azt mondjuk, hogy
RE 1 Relációk Függvények RE 2 Definíció: Ha A, B és ρ A B, akkor azt mondjuk, hogy ρ reláció A és B között, vagy azt, hogy ρ leképezés A-ból B-be. Ha speciálisan A=B, azaz ρ A A, akkor azt mondjuk, hogy
3. Előadás. Megyesi László: Lineáris algebra, oldal. 3. előadás Lineáris egyenletrendszerek
 3. Előadás Megyesi László: Lineáris algebra, 47. 50. oldal. Gondolkodnivalók Determinánsok 1. Gondolkodnivaló Determinánselméleti tételek segítségével határozzuk meg a következő n n-es determinánst: 1
3. Előadás Megyesi László: Lineáris algebra, 47. 50. oldal. Gondolkodnivalók Determinánsok 1. Gondolkodnivaló Determinánselméleti tételek segítségével határozzuk meg a következő n n-es determinánst: 1
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 2017. tavasz 1. Diszkrét matematika 2.C szakirány 10. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 2.C szakirány 2017. tavasz 1. Diszkrét matematika 2.C szakirány 10. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
TANMENETJAVASLAT. Dr. Korányi Erzsébet MATEMATIKA. tankönyv ötödikeseknek. címû tankönyvéhez
 TANMENETJAVASLAT Dr. Korányi Erzsébet MATEMATIKA tankönyv ötödikeseknek címû tankönyvéhez A heti 3 óra, évi 111 óra B heti 4 óra, évi 148 óra Javaslat témazáró dolgozatra: Dr. Korányi Erzsébet: Matematika
TANMENETJAVASLAT Dr. Korányi Erzsébet MATEMATIKA tankönyv ötödikeseknek címû tankönyvéhez A heti 3 óra, évi 111 óra B heti 4 óra, évi 148 óra Javaslat témazáró dolgozatra: Dr. Korányi Erzsébet: Matematika
1.1. Definíció. Azt mondjuk, hogy a oszója b-nek, vagy más szóval, b osztható a-val, ha létezik olyan x Z, hogy b = ax. Ennek jelölése a b.
 1. Oszthatóság, legnagyobb közös osztó Ebben a jegyzetben minden változó egész számot jelöl. 1.1. Definíció. Azt mondjuk, hogy a oszója b-nek, vagy más szóval, b osztható a-val, ha létezik olyan x Z, hogy
1. Oszthatóság, legnagyobb közös osztó Ebben a jegyzetben minden változó egész számot jelöl. 1.1. Definíció. Azt mondjuk, hogy a oszója b-nek, vagy más szóval, b osztható a-val, ha létezik olyan x Z, hogy
1. Determinánsok. Oldjuk meg az alábbi kétismeretlenes, két egyenletet tartalmaz lineáris egyenletrendszert:
 1 Determinánsok 1 Bevezet definíció Oldjuk meg az alábbi kétismeretlenes, két egyenletet tartalmaz lineáris egyenletrendszert: a 11 x 1 +a 12 x 2 = b 1 a 21 x 1 +a 22 x 2 = b 2 Szorozzuk meg az első egyenletet
1 Determinánsok 1 Bevezet definíció Oldjuk meg az alábbi kétismeretlenes, két egyenletet tartalmaz lineáris egyenletrendszert: a 11 x 1 +a 12 x 2 = b 1 a 21 x 1 +a 22 x 2 = b 2 Szorozzuk meg az első egyenletet
1. A polinom fogalma. Számolás formális kifejezésekkel. Feladat Oldjuk meg az x2 + x + 1 x + 1. = x egyenletet.
 1. A polinom fogalma Számolás formális kifejezésekkel. Feladat Oldjuk meg az x2 + x + 1 x + 1 = x egyenletet. Megoldás x + 1-gyel átszorozva x 2 + x + 1 = x 2 + x. Innen 1 = 0. Ez ellentmondás, így az
1. A polinom fogalma Számolás formális kifejezésekkel. Feladat Oldjuk meg az x2 + x + 1 x + 1 = x egyenletet. Megoldás x + 1-gyel átszorozva x 2 + x + 1 = x 2 + x. Innen 1 = 0. Ez ellentmondás, így az
Többváltozós, valós értékű függvények
 TÖ Többváltozós, valós értékű függvények TÖ Definíció: többváltozós függvények Azokat a függvényeket, melyeknek az értelmezési tartománya R n egy részhalmaza, n változós függvényeknek nevezzük. TÖ Példák:.
TÖ Többváltozós, valós értékű függvények TÖ Definíció: többváltozós függvények Azokat a függvényeket, melyeknek az értelmezési tartománya R n egy részhalmaza, n változós függvényeknek nevezzük. TÖ Példák:.
Vektorok, mátrixok, lineáris egyenletrendszerek
 a Matematika mérnököknek I. című tárgyhoz Vektorok, mátrixok, lineáris egyenletrendszerek Vektorok A rendezett valós számpárokat kétdimenziós valós vektoroknak nevezzük. Jelölésükre latin kisbetűket használunk.
a Matematika mérnököknek I. című tárgyhoz Vektorok, mátrixok, lineáris egyenletrendszerek Vektorok A rendezett valós számpárokat kétdimenziós valós vektoroknak nevezzük. Jelölésükre latin kisbetűket használunk.
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 3. estis képzés 2016. ősz 1. Diszkrét matematika 3. estis képzés 3. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2016. ősz 1. Diszkrét matematika 3. estis képzés 3. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Miskolci Egyetem. Diszkrét matek I. Vizsga-jegyzet. Hegedűs Ádám Imre 2010.12.28.
 Miskolci Egyetem Diszkrét matek I. Vizsga-jegyzet Hegedűs Ádám Imre 2010.12.28. KOMBINATORIKA Permutáció Ismétlés nélküli permutáció alatt néhány különböző dolognak a sorba rendezését értjük. Az "ismétlés
Miskolci Egyetem Diszkrét matek I. Vizsga-jegyzet Hegedűs Ádám Imre 2010.12.28. KOMBINATORIKA Permutáció Ismétlés nélküli permutáció alatt néhány különböző dolognak a sorba rendezését értjük. Az "ismétlés
2016/2017. Matematika 9.Kny
 2016/2017. Matematika 9.Kny Gondolkodási módszerek 1. Számhalmazok: N, Z, Q, Q*, R a számhalmazok kapcsolata, halmazábra 2. Ponthalmazok: o 4. oldal K I. fejezet: 172-178., 180-185., 191. feladat távolsággal
2016/2017. Matematika 9.Kny Gondolkodási módszerek 1. Számhalmazok: N, Z, Q, Q*, R a számhalmazok kapcsolata, halmazábra 2. Ponthalmazok: o 4. oldal K I. fejezet: 172-178., 180-185., 191. feladat távolsággal
Halmazelméleti alapfogalmak
 Halmazelméleti alapfogalmak halmaz (sokaság) jól meghatározott, megkülönböztetett dolgok (tárgyak, fogalmak, stb.) összessége. - halmaz alapfogalom. z azt jelenti, hogy csak példákon keresztül magyarázzuk,
Halmazelméleti alapfogalmak halmaz (sokaság) jól meghatározott, megkülönböztetett dolgok (tárgyak, fogalmak, stb.) összessége. - halmaz alapfogalom. z azt jelenti, hogy csak példákon keresztül magyarázzuk,
VEKTORTEREK I. VEKTORTÉR, ALTÉR, GENERÁTORRENDSZER október 15. Irodalom. További ajánlott feladatok
 VEKTORTEREK I. VEKTORTÉR, ALTÉR, GENERÁTORRENDSZER 2004. október 15. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak az előadáson, másrészt megtalálják
VEKTORTEREK I. VEKTORTÉR, ALTÉR, GENERÁTORRENDSZER 2004. október 15. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak az előadáson, másrészt megtalálják
2016/2017. Matematika 9.Kny
 2016/2017. Matematika 9.Kny Gondolkodási módszerek 1. Számhalmazok: N, Z, Q, Q*, R a számhalmazok kapcsolata, halmazábra 2. Ponthalmazok: o 5. oldal K I. fejezet: 172-178., 180-185., 191. feladat távolsággal
2016/2017. Matematika 9.Kny Gondolkodási módszerek 1. Számhalmazok: N, Z, Q, Q*, R a számhalmazok kapcsolata, halmazábra 2. Ponthalmazok: o 5. oldal K I. fejezet: 172-178., 180-185., 191. feladat távolsággal
Mátrixjátékok tiszta nyeregponttal
 1 Mátrixjátékok tiszta nyeregponttal 1. Példa. Két játékos Aladár és Bendegúz rendelkeznek egy-egy tetraéderrel, melyek lapjaira rendre az 1, 2, 3, 4 számokat írták. Egy megadott jelre egyszerre felmutatják
1 Mátrixjátékok tiszta nyeregponttal 1. Példa. Két játékos Aladár és Bendegúz rendelkeznek egy-egy tetraéderrel, melyek lapjaira rendre az 1, 2, 3, 4 számokat írták. Egy megadott jelre egyszerre felmutatják
First Prev Next Last Go Back Full Screen Close Quit. Matematika I
 Matematika I (Analízis) Készítette: Horváth Gábor Kötelező irodalom: Ács László, Gáspár Csaba: Analízis 1 Oktatási segédanyagok és a tantárgyi követelményrendszer megtalálható a http://rs1.szif.hu/ horvathg/horvathg.html
Matematika I (Analízis) Készítette: Horváth Gábor Kötelező irodalom: Ács László, Gáspár Csaba: Analízis 1 Oktatási segédanyagok és a tantárgyi követelményrendszer megtalálható a http://rs1.szif.hu/ horvathg/horvathg.html
MATEMATIKA TANMENET SZAKKÖZÉPISKOLA. 9. Nyelvi előkészítő osztály
 MINŐSÉGIRÁNYÍTÁSI ELJÁRÁS MELLÉKLET Tanmenetborító Azonosító: ME-III.1./1 Változatszám: 2 Érvényesség 2013. 01. 01. kezdete: Oldal/összes: 1/6 Fájlnév: ME- III.1.1.Tanmenetborító SZK- DC-2013 MATEMATIKA
MINŐSÉGIRÁNYÍTÁSI ELJÁRÁS MELLÉKLET Tanmenetborító Azonosító: ME-III.1./1 Változatszám: 2 Érvényesség 2013. 01. 01. kezdete: Oldal/összes: 1/6 Fájlnév: ME- III.1.1.Tanmenetborító SZK- DC-2013 MATEMATIKA
Meghirdetés féléve 2 Kreditpont Összóraszám (elm+gyak) 2+0
 Tantárgy neve Lineáris algebra I Tantárgy kódja MTB1004 Meghirdetés féléve 2 Kreditpont 3k Összóraszám elm+gyak 2+0 Számonkérés módja kollokvium Előfeltétel tantárgyi kód MTB1003 Tantárgyfelelős neve Kurdics
Tantárgy neve Lineáris algebra I Tantárgy kódja MTB1004 Meghirdetés féléve 2 Kreditpont 3k Összóraszám elm+gyak 2+0 Számonkérés módja kollokvium Előfeltétel tantárgyi kód MTB1003 Tantárgyfelelős neve Kurdics
MATE-INFO UBB verseny, március 25. MATEMATIKA írásbeli vizsga
 BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR MATE-INFO UBB verseny, 218. március 25. MATEMATIKA írásbeli vizsga FONTOS TUDNIVALÓK: 1 A feleletválasztós feladatok,,a rész esetén
BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR MATE-INFO UBB verseny, 218. március 25. MATEMATIKA írásbeli vizsga FONTOS TUDNIVALÓK: 1 A feleletválasztós feladatok,,a rész esetén
