MEO. Magyar Egységes Ontológia Hungarian Unified Ontology. Extenzionális relációelmélet Extensional Relation Theory
|
|
|
- Gusztáv Bakos
- 8 évvel ezelőtt
- Látták:
Átírás
1 MEO Magyar Egységes Ontológia Hungarian Unified Ontology Extenzionális relációelmélet Extensional Relation Theory Szakadát István,Szőts Miklós,Gyepesi György web: NKFP-2/042/ december 28. v
2 Extenzionális relációelmélet Extensional Relation Theory MEO ERT 1.1. Szintaxis / Syntax: A RELÁCIÓFOGALOM METANYELVI MEGNEVEZÉSE / METALANGUAGE BINDING OF THE RELATIONAL CONCEPT (1) a metafogalom formulája / formula of the concept a nyelvi rétegbe tartozó megnevezések listája, zárójelben a nyelvi kapcsolattal / natural language expressions of the concept in the language layer 1. Reláció Relation ORDERED-PAIR def (2) a, b = c, d a = b c = d rendezett pár (HUN) ordered pair (ENG) R def (3) a, b {{a}, {a, b}} reláció (HUN) relation (ENG) ARITY (4) a relátumok, a reláció argumentumainak száma / number of relata aritás (HUN) arity (ENG) valence (ENG) adicity (ENG) UNARY (5) arity = 1 unáris (HUN) unary (ENG) 2
3 BINARY (6) arity = 2 bináris (HUN) binary (ENG) N-ARY (7) arity = n n-áris (HUN) n-ary (ENG) DOM (8) R A B Dom(R) = A értelmezési tartomány (HUN) domain (ENG) Dom (MAT) RNG (9) R A B Rng(R) = B értékkészlet (HUN) range (ENG) Rng (MAT) HETEROGENEOUS (10) Dom(R) Rng(R) heterogén reláció (HUN) heterogeneous relation (ENG) HOMOGENEOUS (11) Dom(R) = Rng(R) homogén reláció (HUN) homogeneous relation (ENG) 2. Logikai relációk Logical relations U (12) x y(r(x, y)) teljes reláció (HUN) univerzális reláció (HUN) universal relation (ENG) (13) x y( R(x, y)) üres reláció (HUN) null reláció (HUN) empty relation (ENG) 3
4 I (14) x y(r(x, y) x = y) azonossági reláció (HUN) azonosság (HUN) egység reláció (HUN) diagonális reláció (HUN) egyenlőségi reláció (HUN) egyenlőség (HUN) identitás reláció (HUN) identity (ENG) diagonal (ENG) D (15) x y(r(x, y) x y) különbözőségi reláció (HUN) különbözőség (HUN) egyenlőtlenségi reláció (HUN) egyenlőtlenség (HUN) antidiagonális reláció (HUN) differencia reláció (HUN) inkompatibilitási reláció (HUN) diverzitási reláció (HUN) difference (ENG) incompatibility relation (ENG) antidiagonal relation (ENG) diversity relation (ENG) 3. Relációtípusok, relációtulajdonságok Relation types, relation properties REFLEXIVE (16) x(r(x, x)) reflexív reláció (HUN) reflexive relation (ENG) NON-REFLEXIVE (17) x( R(x, x)) nem-reflexív reláció (HUN) non-reflexive relation (ENG) IRREFLEXIVE (18) x( R(x, x)) irreflexív reláció (HUN) antireflexív reláció (HUN) irreflexive relation (ENG) antireflexive relation (ENG) LEFT-TOTAL (19) x y(r(x, y)) balról totális reláció (HUN) totális reláció (HUN) sorozatos reláció (HUN) szeriális reláció (HUN) serial relation (ENG) sorozat (HUN) left-total relation (ENG) extendable relation (ENG) RIGHT-TOTAL (20) y x(r(x, y)) jobbról totális reláció (HUN) right-total relation (ENG) 4
5 SECONDARILY_REFLEXIVE (21) x y(r(x, y) R(y, y)) másodlagosan reflexív reláció (HUN) szekunder reflexív reláció (HUN) secondarily reflexive relation (ENG) shift reflexive relation (ENG) INVERSE_SECONDARILY_REFLEXIVE (22) x y(r(x, y) R(x, x)) fordítottan másodlagos reflexív reláció (HUN) feltételesen reflexív reláció (HUN) conditional reflexive relation (ENG) inverse secondarily reflexive relation (ENG) COREFLEXIVE (23) x y(r(x, y) x = y) koreflexív reláció (HUN) vákumos reláció (HUN) vacuous relation (ENG) coreflexive relation (ENG) SYMMETRIC (24) x y(r(x, y) R(y, x)) szimmetrikus reláció (HUN) symmetric relation (ENG) SymmetricProperty (OWL) NON-SYMMETRIC (25) x y(r(x, y) R(y, x)) nem-szimmetrikus reláció (HUN) non-symmetric relation (ENG) ASYMMETRIC (26) x y(r(x, y) R(y, x)) aszimmetrikus reláció (HUN) antiszimmetrikus reláció (HUN) szigorúan antiszimmetrikus reláció (HUN) asymmetric relation (ENG) antisymmetric relation (ENG) ANTISYMMETRIC (27) x y((r(x, y) R(y, x)) x = y) antiszimmetrikus reláció (HUN) identitív reláció (HUN) antisymmetric relation (ENG) identitive relation (ENG) CONNEX (28) x y(x y (R(x, y) R(y, x))) 5
6 összefüggő reláció (HUN) konnex reláció (HUN) connex relation (ENG) connected relation (ENG) lineáris reláció (HUN) összehasonlítható reláció (HUN) comparable relation (ENG) teljes reláció (HUN) complete relation (ENG) totális reláció (HUN) STRONGLY-CONNEX (29) x y(r(x, y) R(y, x)) erősen összefüggő reláció (HUN) strongly connex (ENG) strongly connected (ENG) teljes reláció (HUN) WEAKLY-CONNEX (30) x y z(r(x, y) R(x, z) (y = z R(y, z) R(z, y))). gyengén összefüggő (HUN) weakly connected relation (ENG) weakly connex relation (ENG) DICHOTOMOUS (31) x y(x y ((R(x, y) R(y, x)) ( R(x, y) R(y, x)))) dichotóm reláció (HUN) összehasonlítható reláció (HUN) comparable relation (ENG) totális reláció (HUN) teljes reláció (HUN) total relation (ENG) dichotomous (ENG) complete (ENG) TRICHOTOMOUS (32) x y((r(x, y) R(y, x) x y) ( R(x, y) R(y, x) x y) x = y) trichotóm reláció (HUN) lineáris reláció (HUN) trichotomous relation (ENG) RIGHT-UNIQUE (33) x y z((r(x, y) R(x, z)) y = z) jobbról egyértelmű reláció (HUN) funkcionális reláció (HUN) parciális függvény (HUN) partial function (ENG) functional relation (ENG) right-unique (ENG) FunctionalProperty (OWL) LEFT-UNIQUE (34) x y z((r(x, z) R(y, z)) x = y) balról egyértelmű reláció (HUN) inverz-funkcionális reláció (HUN) inverse functional relation (ENG) InverseFunctionalProperty (OWL) NON-RIGHT-UNIQUE (35) x y z((r(x, y) R(x, z)) y z) jobbról nem egyértelmű reláció (HUN) jobbról többértelmű reláció (HUN) non-right-unique relation (ENG) 6
7 NON-LEFT-UNIQUE (36) x y z((r(x, z) R(y, z)) x y) balról nem egyértelmű reláció (HUN) balról többértelmű reláció (HUN) non-left-unique relation (ENG) TRANSITIVE (37) x y z((r(x, y) R(y, z)) R(x, z)) tranzitív reláció (HUN) transitive relation (ENG) INTRANSITIVE (38) x y z((r(x, y) R(y, z)) R(x, z)) intranzitív reláció (HUN) atranzitív reláció (HUN) antitranzitív reláció (HUN) intransitive relation (ENG) atransitive relation (ENG) antitransitive relation (ENG) TransitiveProperty (OWL) QUASI-TRANSITIVE (39) x y z((r(x, y) R(y, z) x z) R(x, z)) kvázitranzitív reláció (HUN) quasi-transitive relation (ENG) ALIOTRANSITIVE (40) x y z((r(x, y) R(y, z)) (R(x, z) x = z)) aliotranzitív reláció (HUN) aliotransitive relation (ENG) NON-TRANSITIVE (41) x y z((r(x, y) R(y, z)) R(x, z)) nem-tranzitív reláció (HUN) atranzitív reláció (HUN) intranzitív reláció (HUN) non-transitive (ENG) intransitive relation (ENG) atransitive relation (ENG) EUCLIDEAN (42) x y z((r(x, y) R(x, z)) R(y, z)) euklideszi reláció (HUN) euclidean relation (ENG) ANEUCLIDEAN (43) x y z((r(x, y) R(x, z)) ( R(y, z) R(z, y))) aneuklideszi reláció (HUN) antieuclidean relation (ENG) aneuclidean relation (ENG) ineuclidean relation (ENG) antitransitive relation (ENG) 7
8 CATENARY (44) x y z(r(x, y) ((R(y, z) R(z, x))) katenáris reláció (HUN) láncolt reláció (HUN) nem bipoláris reláció (HUN) catenary relation (ENG) non-bipolar relation (ENG) ACATENARY (45) x y z(r(x, y) ( R(y, z) R(z, x))) akatenáris reláció (HUN) nem-láncolt reláció (HUN) bipoláris reláció (HUN) non-catenary relation (ENG) acatenary relation (ENG) bipolar relation (ENG) CIRCULAR (46) x y z((r(x, y) R(y, z)) R(z, x)) cirkuláris (HUN) körkörös reláció (HUN) circular relation (ENG) ACIRCULAR (47) x y z((r(x, y) R(y, z)) R(z, x)) acirkuláris (HUN) nem-körkörös reláció (HUN) acircular relation (ENG) CONFLUENT (48) x y w z((r(x, y) R(x, w)) (R(y, z) R(w, z))) konfluens reláció (HUN) incesztuális reláció (HUN) incestual relation (ENG) confluent relation (ENG) ACONFLUENT (49) x y w z((r(x, y) R(x, w)) (R(y, z) R(w, z))) akonfluens reláció (HUN) anincesztuális reláció (HUN) anincestual relation (ENG) aconfluent relation (ENG) 8
9 4. Relációtulajdonságok összefoglaló táblázata Summary of relation properties reflexív irreflexív nem-reflexív balról totális jobbról totális x(r(x, x)) x( R(x, x)) x( R(x, x)) x y(r(x, y)) y x(r(x, y)) másodlagosan reflexív x y(r(x, y) R(y, y)) ford.másodlagosan reflexív x y(r(x, y) R(x, x)) koreflexív x y(r(x, y) x = y) szimmetrikus x y(r(x, y) R(y, x)) aszimmetrikus x y(r(x, y) R(y, x)) antiszimmetrikus x y((r(x, y) R(y, x)) x = y) nem-szimmetrikus x y(r(x, y) R(y, x)) összefüggő x y(x y (R(x, y) R(y, x))) erősen összefüggő x y(r(x, y) R(y, x)) gyengén összefüggő x y z(r(x, y) R(x, z) (y = z R(y, z) R(z, y))) dichotóm x y(x y (R(x, y) R(y, x)) ( R(x, y) R(y, x))) trichotóm x y(r(x, y) R(y, x) x y) ( R(x, y) R(y, x) x y) x = y balról egyértelmű x y z((r(x, z) R(y, z)) x = y) jobbról egyértelmű x y z((r(x, y) R(x, z)) y = z) tranzitív intranzitív kvázitranzitív aliotranzitív nem-tranzitív cirkuláris acirkuláris euklideszi aneuklideszi katenáris akatenáris konfluens akonfluens x y z((r(x, y) R(y, z)) R(x, z)) x y z((r(x, y) R(y, z)) R(x, z)) x y z((r(x, y) R(y, z) x z) R(x, z)) x y z((r(x, y) R(y, z)) (R(x, z) x = z)) x y z((r(x, y) R(y, z)) R(x, z)) x y z((r(x, y) R(y, z)) R(z, x)) x y z((r(x, y) R(y, z)) R(z, x)) x y z((r(x, y) R(x, z)) R(y, z)) x y z((r(x, y) R(x, z)) ( R(y, z) R(z, y))) x y z(r(x, y) ((R(y, z) R(z, x))) x y z(r(x, y) ( R(y, z) R(z, x))) x y w z((r(x, y) R(x, w)) (R(y, z) R(w, z))) x y w z((r(x, y) R(x, w)) (R(y, z) R(w, z))) 9
10 5. Összefüggések egyszerű relációk közt Lemmas between simple relations (50) asymmetric irre f lexive (51) asymmetric antisymmetric (52) intransitive irre f lexive (53) symmetric transitive dichotomous re f lexive (54) irre f lexive transitive asymmetric (55) identity (re f lexive symmetric antisymmetric transitive) (56) acatenary (asymmetric transitive intransitive) (57) le f t-unique intransitive (58) re f lexive le ft-total (59) re f lexive secondarily-re f lexive (60) re f lexive inverse-secondarily-re f lexive (61) euclidean secondarily-re f lexive (62) euclidean con f luent 10
11 (63) secondarily-re f lexive dense (64) symmetric con f luent (65) (symmetric transitive) euclidean (66) (le ft-total (core f lexive secondarily-re f lexive)) re f lexive (67) core f lexive symmetric (68) core f lexive transitive (69) core f lexive euklidean (70) core f lexive right-unique (71) re f lexive right-unique core f lexive (72) empty core f lexive (73) intransitive re f lexive 6. Összetett relációk Compound relations TOLERANCE 11
12 (74) re f lexive symmetric tolerancia reláció (HUN) kompatibilitási reláció (HUN) hasonlósági reláció (HUN) compatibility relation (ENG) similarity relation (ENG) tolerance relation (ENG) PARTIAL_EQUIVALENCE (75) transitive symmetric részleges ekvivalencia reláció (HUN) partial equivalence relation (ENG) per (ENG) EQUIVALENCE (76) re f lexive symmetric transitive ekvivalenciareláció (HUN) ekvivalencia (HUN) equivalence (ENG) COVER (77) asymmetric intransitive rákövetkezés reláció (HUN) követés (HUN) közvetlen követés (HUN) közvetlen rákövetkezés (HUN) immediate successor (ENG) direct successor (ENG) fedés (HUN) cover (ENG) PARTIAL_ORDER (78) re f lexive antisymmetric transitive részben rendezés (HUN) parciális rendezés (HUN) részleges rendezés (HUN) gyenge rendezés (HUN) gyenge részben rendezés (HUN) nem szigorú rendezés (HUN) weak order (ENG) weak partial order (ENG) partial order (ENG) STRICT_ORDER (79) irre f lexive transitive szigorú rendezés (HUN) szigorú rendezési reláció (HUN) erős részben rendezés (HUN) irreflexív rendezés (HUN) strict order (ENG) strict weak order (ENG) strong order (ENG) strong weak order (ENG) LINEAR_PARTIAL_ORDER (80) re f lexive antisymmetric transitive dichotomous nem szigorú elrendezés reláció (HUN) teljes parciális rendezés (HUN) lineáris parciális rendezés (HUN) totális parciális rendezés (HUN) total partial order (ENG) linear partial order (ENG) LINEAR_STRICT_ORDER 12
13 (81) irre f lexive transitive dichotomous szigorú elrendezés (HUN) teljes szigorú rendezés (HUN) lineáris szigorú rendezés (HUN) totális szigorú rendezés (HUN) total strict order (ENG) linear strict order (ENG) total strong order (ENG) linear strong order (ENG) PREORDER (82) re f lexive transitive előrendezés (HUN) kvázirendezés (HUN) preorder (ENG) quasi order (ENG) WEAK_ORDER (83) re f lexive transitive dichotomous gyenge rendezés (HUN) lineáris előrendezés (HUN) weak order (ENG) linear preorder (ENG) WEAK_PARTIAL_ORDER (84) antisymmetric transitive gyenge részben rendezés (HUN) partial order (ENG) weak partial order (ENG) LINEAR_WEAK_PARTIAL_ORDER (85) antisymmetric transitive dichotomous részben elrendezés (HUN) teljes gyenge részben rendezés (HUN) total weak partial order (ENG) linear weak partial order (ENG) 1 :1-RELATION (86) le f t-total right-total 1:1-es reláció (HUN) bitotális reláció (HUN) bitotal relation (ENG) 1:1 relation (ENG) 1 :N-RELATION (87) le f t-total non-right-total 1:N-es reláció (HUN) 1:N-relation (ENG) N :1-RELATION (88) non-le f t-total right-total N:1-es reláció (HUN) N:1-relation (ENG) N :M-RELATION (89) non-le f t-total non-right-total N:M-es reláció (HUN) N:M-relation (ENG) 13
14 7. Az összetett relációk összefoglaló táblázata Summary of compound relations tolerance partial_equivalence equivalence cover partial_order strict_order linear_partial_order linear_strict_order preorder weak_partial_order linear_weak_partial_order 1:1 le f t-total right-total 1:N le f t-total right-total N:1 le f t-total right-total N:M le f t-total right-total re f lexive symmetric transitive symmetric re f lexive symmetric transitive asymmetric intransitive re f lexive antisymmetric transitive irre f lexive transitive( asymmetric antisymmetric) re f lexive antisymmetric transitive dichotomous irre f lexive transitive dichotomous re f lexive transitive antisymmetric transitive antisymmetric transitive dichotomous reflexive irreflexive asymmetric antisymmetric transitive dichotomous preorder weak_partial_order partial_order strict_order ( ) ( ) weak order linear_weak_partial_order linear_partial_order linear_strict_order ( ) ( ) reflexive ireflexive symmetric asymmetric transitive intransitive tolerance partial_equivalence equivalence cover bipolar (acatenary) 8. Összefüggések összetett relációk között Lemmas between compound relations (90) identity (equivalence partial order) (91) (re f lexive symmetric transitive) equivalence (92) (le f t-total symmetric transitive) equivalence 14
15 (93) (le f t-total symmetric euclidean) equivalence (94) di f f erence (irre f lexive symmetric transitive) (95) equivalence (re f lexive circular) 9. A rendezés tulajdonságai Order properties ORDER (96) preorder weak partial order partial order strict order rendezés (HUN) rendezési reláció (HUN) order relation (ENG) ordering (ENG) (MATH) ATOM-FREE (97) x y(order(y, x) order(x, y)) atommentes reláció (HUN) atom free relation (ENG) atomless relation (ENG) ATOMIC (98) x y(order(y, x) z(order(z, y) order(y, z))) atomos reláció (HUN) atomic relation (ENG) atomistic relation (ENG) DENSE (99) x y z(order(x, y) (order(x, z) order(z, y))) sűrű reláció (HUN) gyengén sűrű reláció (HUN) density relation (ENG) dense relation (ENG) HAS_LEAST_ELEMENT (100) order right-total legkisebb elemmel rendelkező reláció (HUN) van legkisebb eleme reláció (HUN) bottom (ENG) zero (ENG) 15
16 HAS_GREATEST_ELEMENT (101) order le f t-total legnagyobb elemmel rendelkező reláció (HUN) van legnagyobb eleme reláció (HUN) top (ENG) unit (ENG) HAS_MINIMAL_ELEMENT (102) x y(order(y, x) x = y) kezdőpontos reláció (HUN) minimális elemű reláció (HUN) van minimális eleme reláció (HUN) has minimal element relation (ENG) HAS_NO_MINIMAL_ELEMENT (103) x y(order(y, x) x y) kezdőpontmentes reláció (HUN) nem-kezdőpontos reláció (HUN) nincs minimális eleme reláció (HUN) has no minimal element relation (ENG) HAS_MAXIMAL_ELEMENT (104) x y(order(y, x) x = y) végpontos reláció (HUN) maximális elemű reláció (HUN) van maximális eleme reláció (HUN) has maximal element relation (ENG) HAS_NO_MAXIMAL_ELEMENT (105) x y(order(x, y) x y) végpontmentes reláció (HUN) nincs maximális eleme reláció (HUN) has no maximal element relation (ENG) HAS_IMMEDIATE_PREDECESSOR (106) x( y(order(y, x) x y) y(order(y, x) x y z(order(z, x) z = x order(z, y)))) van közvetlen megelőző eleme reláció (HUN) has immediate predecessor relation (ENG) HAS_IMMEDIATE_SUCCESSOR (107) x( y(order(x, y) x y) y(order(x, y) x y z(order(x, z) z = x order(y, z)))) van közvetlen rákövetkező eleme reláció (HUN) has immediate successor relation (ENG) CONVERGENT 16
17 (108) x y z(x y (order(x, z) order(y, z))) konvergens reláció (HUN) convergent relation (ENG) STRONGLY_CONVERGENT (109) x y z(order(x, z) order(y, z)) erősen konvergens reláció (HUN) strongly convergent relation (ENG) NON-CONVERGENT (110) x y z((order(x, z) order(y, z) y z) (order(x, y) order(y, x))) nem-konvergens reláció (HUN) non-convergent relation (ENG) NON-DIVERGENT (111) x y z((order(x, y) order(x, z) y z) (order(y, z) order(z, y))) nem divergens reláció (HUN) non-divergent relation (ENG) 10. A rendezés tulajdonságainak összefoglaló táblázata Summary of order properties atom-free x y(r(y, x) R(x, y)) kezdőpontmentes x y(r(y, x) x y) kezdőpontos x y(r(y, x) x = y) végpontmentes x y(r(x, y) x y) végpontos x y(r(y, x) x = y) atomic x y(r(y, x) z(r(z, y) R(y, z))) dense x y z(r(x, y) (R(x, z) R(z, y))) convergent x y z(x y (R(x, z) R(y, z))) strongly_convergent x y z(r(x, z) R(y, z)) non-convergent x y z((r(x, z) R(y, z) y z) (R(x, y) R(y, x))) non-divergent x y z((r(x, y) R(x, z) y z) (R(y, z) R(z, y))) van közv. előzője x( y(r(y, x) x y) y(r(y, x) x y z(r(z, x) z = x R(z, y)))) van közv. ráköv. x( y(r(x, y) x y) y(r(x, y) x y z(r(x, z) z = x R(y, z)))) 11. Sorozat, függvény, művelet Series, function, operation FUNCTION (112) le f t-total right-unique függvény (HUN) leképezés (HUN) function (ENG) 17
18 INVERSE_FUNCTION (113) right-total le f t-unique inverz függvény (HUN) inverz leképezés (HUN) inverse function (ENG) BIUNIQUE (114) le f t-unique right-unique egy-egyértelmű függvény (HUN) egy-egyértelmű reláció (HUN) biunique relation (ENG) unique relation (ENG) BITOTAL (115) le f t-total right-total bitotális függvény (HUN) 1:1-es reláció (HUN) bitotal function (ENG) bitotal relation (ENG) 1-1 relation (ENG) INJECTIVE (116) f unction le ft-unique injektív függvény (HUN) egyrétű függvény (HUN) injective function (ENG) SURJECTIVE (117) f unction right-total szürjektív függvény (HUN) ráképzés (HUN) szuperjektív fügvény (HUN) lefedő függvény (HUN) surjective function (ENG) BIJECTIVE (118) in jective sur jective bijektív függvény (HUN) egyrétűen lefedő függvény (HUN) bijective function (ENG) SERIES (119) f unction (Dom = IN) sorozat (HUN) series (ENG) OPERATION (120) f unction (Dom = Rng) művelet (HUN) operáció (HUN) belső összekapcsolás (HUN) operation (ENG) 18
19 left-unique right-unique left-total right-total biunique bitotal inverse_function function 1? 2? 3? 4? surjective injective bijective 12. Művelettulajdonságok Operation properties ASSOCIATIVE (121) x y z(x (y z) = (x y) z) asszociatív művelet (HUN) társítható művelet (HUN) associative operation (ENG) COMMUTATIVE (122) x y(x y = y x) kommutatív művelet (HUN) felcserélhető művelet (HUN) commutative operation (ENG) DISTRIBUTIVE (123a) x y z((x (y z) = (x y) (x z)) (123b) x y z((y z) x = (y x) (z x)) disztributív művelet (HUN) szétosztható művelet (HUN) széttagolható művelet (HUN) distributive operation (ENG) IDEMPOTENT (124) x(x x = x) idempotens művelet (HUN) önhatványozó (HUN) azonos hatványú (HUN) idempotent operation (ENG) ABSORPTIVE (125a) x y(x (x y) = x) (125b) x y(x (x y) = x) abszorbtív művelet (HUN) elnyelő művelet (HUN) adjunktív művelet (HUN) absorptive operation (ENG) 19
20 13. Művelettulajdonságok összefoglaló táblázata Summary of properties of operation kommutatív x y = y x asszociatív (x y) z = y (x z) idempotens x x = x komplementer eleme x x c = /0 egységeleme x E = x neutrális eleme x /0 = /0 disztributív -ra nézve (x y) z = (x z) (y z) kommutatív x y = y x asszociatív (x y) z = y (x z) idempotens x x = x komplementer eleme x x c = /0 egységeleme x E = x neutrális eleme x /0 = /0 disztributív -ra nézve (x y) z = (x z) (y z) 14. Relációműveletek Relational operations 1 (126) x y(r 1 (x, y) R(y, x)) relációinvertálás művelet (HUN) inverzképzés (HUN) relation conversion operation (ENG) relation converse operation (ENG) relation inverse operation (ENG) inverseof (OWL) c (127) x y(r c (x, y) R(x, y) relációkomplementálás (HUN) relation complementation (ENG) complementof (OWL) (128) x y(r Q(x, y) (R(x, y) Q(x, y)) relációmetszés (HUN) relation intersection (ENG) + (129) x y(r+q(x, y) (R(x, y) Q(x, y)) relációegyesítés (HUN) relációúnió (HUN) relációegyesítés (HUN) relation union (ENG) 20
21 (130) x y(r Q(x, y)) (R(x, z) Q(z, y)) relációszorzás (HUN) relatív szorzat (HUN) kompozíció (HUN) multiplikáció (HUN) relációkompozíció (HUN) relation product (ENG) relative multiplication (ENG) relative product (ENG) composition (ENG) (131) x y(r Q(x, y)) (R(x, z) Q(z, y)) relációösszeadás (HUN) összeadás (HUN) relatív összeadás (HUN) relative addition (ENG) relative sum (ENG) 15. A relációműveletek összefoglaló táblázata Summary of relational operations alaprelációk: U I D unáris műveletek: c 1 teljes reláció üres reláció azonosság reláció differencia reláció relációkomplementálás relációinvertálás bináris műveletek: relációszorzás relációösszeadás relációmetszés + relációegyesítés unáris művelettel kapott relációk: R c R 1 bináris művelettel kapott relációk: R Q R Q R Q R+Q relációkomplementum relációinverz relációszorzat relációösszeg relációmetszet relációegyesület 16. Lemmák: műveletek közti összefüggések Lemmas between operations (132) x y(r Q = (R c +Q c ) c ) (133) x y(r+q = (R c Q c ) c ) 21
22 (134) x y(r Q = (R c Q c ) c ) (135) x y(r Q = (R c Q c ) c ) 17. Relációalgebra, relációkalkulus Relation algebra, relation calculus (136) (R = P R = Q) P = Q (137) R = P (R+Q = P+Q R Q = P Q) (138) R+Q = Q+R R Q = Q R (139) (R+P) Q = R Q+P Q (R P)+Q = (R+Q) (P+Q) (140) (R+ = R) (R U = R) (141) (R+R c = U) (R R c = ) (142a) (142b) (U = ) U = (143) (R 1 ) 1 = R (144) (R Q) 1 = R 1 Q 1 (145) R (P Q) = (R P) Q 22
23 (146) R I = R (147a) (147b) R U = U U R c = U (148) ((R P) Q 1 = ) ((P Q) R 1 = ) (149) D = I c (150) R Q = (R c Q c ) c 18. Relációkalkulus összefoglaló táblázata Summary of relation calculus (1) (R = P R = Q) P = Q (2) R = P (R+Q = P+Q R Q = P Q) (3) R+Q = Q+R R Q = Q R (4) (R+P) Q = R Q+P Q (R P)+Q = (R+Q) (P+Q) (5) R+ = R R U = R (6) (R+R c = U) (R R c = ) (7a) (U = ) (7b) U = (8) (R 1 ) 1 = R (9) (R Q) 1 = R 1 Q 1 (10) R (P Q) = (R P) Q (11) R I = R (12a) R U = U (12b) U R c = U (13) ((R P) Q 1 = ) ((P Q) R 1 = ) (14) D = I c (15) R Q = (R c Q c ) c 23
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 3. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Relációk Diszkrét matematika I. középszint 2014.
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 3. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Relációk Diszkrét matematika I. középszint 2014.
Relációk Függvények. A diákon megjelenő szövegek és képek csak a szerző (Kocsis Imre, DE MFK) engedélyével használhatók fel!
 függvények RE 1 Relációk Függvények függvények RE 2 Definíció Ha A, B és ρ A B, akkor azt mondjuk, hogy ρ reláció A és B között, vagy azt, hogy ρ leképezés A-ból B-be. Ha speciálisan A=B, azaz ρ A A, akkor
függvények RE 1 Relációk Függvények függvények RE 2 Definíció Ha A, B és ρ A B, akkor azt mondjuk, hogy ρ reláció A és B között, vagy azt, hogy ρ leképezés A-ból B-be. Ha speciálisan A=B, azaz ρ A A, akkor
RE 1. Relációk Függvények. A diákon megjelenő szövegek és képek csak a szerző (Kocsis Imre, DE MFK) engedélyével használhatók fel!
 RE 1 Relációk Függvények RE 2 Definíció: Ha A, B és ρ A B, akkor azt mondjuk, hogy ρ reláció A és B között, vagy azt, hogy ρ leképezés A-ból B-be. Ha speciálisan A=B, azaz ρ A A, akkor azt mondjuk, hogy
RE 1 Relációk Függvények RE 2 Definíció: Ha A, B és ρ A B, akkor azt mondjuk, hogy ρ reláció A és B között, vagy azt, hogy ρ leképezés A-ból B-be. Ha speciálisan A=B, azaz ρ A A, akkor azt mondjuk, hogy
1. Mondjon legalább három példát predikátumra. 4. Mikor van egy változó egy kvantor hatáskörében?
 Definíciók, tételkimondások 1. Mondjon legalább három példát predikátumra. 2. Sorolja fel a logikai jeleket. 3. Milyen kvantorokat ismer? Mi a jelük? 4. Mikor van egy változó egy kvantor hatáskörében?
Definíciók, tételkimondások 1. Mondjon legalább három példát predikátumra. 2. Sorolja fel a logikai jeleket. 3. Milyen kvantorokat ismer? Mi a jelük? 4. Mikor van egy változó egy kvantor hatáskörében?
4. Fuzzy relációk. Gépi intelligencia I. Fodor János NIMGI1MIEM BMF NIK IMRI
 4. Fuzzy relációk Gépi intelligencia I. Fodor János BMF NIK IMRI NIMGI1MIEM Tartalomjegyzék I 1 Klasszikus relációk Halmazok Descartes-szorzata Relációk 2 Fuzzy relációk Fuzzy relációk véges alaphalmazok
4. Fuzzy relációk Gépi intelligencia I. Fodor János BMF NIK IMRI NIMGI1MIEM Tartalomjegyzék I 1 Klasszikus relációk Halmazok Descartes-szorzata Relációk 2 Fuzzy relációk Fuzzy relációk véges alaphalmazok
A relációelmélet alapjai
 A relációelmélet alapjai A reláció latin eredet szó, jelentése kapcsolat. A reláció, két vagy több nem feltétlenül különböz halmaz elemei közötti viszonyt, kapcsolatot fejez ki. A reláció értelmezése gráffal
A relációelmélet alapjai A reláció latin eredet szó, jelentése kapcsolat. A reláció, két vagy több nem feltétlenül különböz halmaz elemei közötti viszonyt, kapcsolatot fejez ki. A reláció értelmezése gráffal
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 5. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 5. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Itt és a továbbiakban a számhalmazokra az alábbi jelöléseket használjuk:
 1. Halmazok, relációk, függvények 1.A. Halmazok A halmaz bizonyos jól meghatározott dolgok (tárgyak, fogalmak), a halmaz elemeinek az összessége. Azt, hogy az a elem hozzátartozik az A halmazhoz így jelöljük:
1. Halmazok, relációk, függvények 1.A. Halmazok A halmaz bizonyos jól meghatározott dolgok (tárgyak, fogalmak), a halmaz elemeinek az összessége. Azt, hogy az a elem hozzátartozik az A halmazhoz így jelöljük:
1.1 Halmazelméleti fogalmak, jelölések
 1.1 Halmazelméleti fogalmak, jelölések Alapfogalmak (nem definiáljuk) Halmaz x eleme az A halmaznak x nem eleme A halmaznak Jelölések A,B,C, x A x A SiUDWODQ V]iRN Halmaz megadása: Elemeinek felsorolásával:
1.1 Halmazelméleti fogalmak, jelölések Alapfogalmak (nem definiáljuk) Halmaz x eleme az A halmaznak x nem eleme A halmaznak Jelölések A,B,C, x A x A SiUDWODQ V]iRN Halmaz megadása: Elemeinek felsorolásával:
Mikor van egy változó egy kvantor hatáskörében? Milyen tulajdonságokkal rendelkezik a,,részhalmaz fogalom?
 Definíciók, tételkimondások Mondjon legalább három példát predikátumra. Sorolja fel a logikai jeleket. Milyen kvantorokat ismer? Mi a jelük? Hogyan kapjuk a logikai formulákat? Mikor van egy változó egy
Definíciók, tételkimondások Mondjon legalább három példát predikátumra. Sorolja fel a logikai jeleket. Milyen kvantorokat ismer? Mi a jelük? Hogyan kapjuk a logikai formulákat? Mikor van egy változó egy
Logika és informatikai alkalmazásai
 Logika és informatikai alkalmazásai 2. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2008 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
Logika és informatikai alkalmazásai 2. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2008 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
A fontosabb definíciók
 A legfontosabb definíciókat jelöli. A fontosabb definíciók [Descartes szorzat] Az A és B halmazok Descartes szorzatán az A és B elemeiből képezett összes (a, b) a A, b B rendezett párok halmazát értjük,
A legfontosabb definíciókat jelöli. A fontosabb definíciók [Descartes szorzat] Az A és B halmazok Descartes szorzatán az A és B elemeiből képezett összes (a, b) a A, b B rendezett párok halmazát értjük,
HALMAZELMÉLET feladatsor 1.
 HALMAZELMÉLET feladatsor 1. Egy (H,, ) algebrai struktúra háló, ha (H, ) és (H, ) kommutatív félcsoport, és teljesül az ún. elnyelési tulajdonság: A, B H: A (A B) = A, A (A B) = A. A (H,, ) háló korlátos,
HALMAZELMÉLET feladatsor 1. Egy (H,, ) algebrai struktúra háló, ha (H, ) és (H, ) kommutatív félcsoport, és teljesül az ún. elnyelési tulajdonság: A, B H: A (A B) = A, A (A B) = A. A (H,, ) háló korlátos,
Térinformatikai algoritmusok Elemi algoritmusok
 Cserép Máté 2016. szeptember 14. Analóg programozásnak nevezzük azt, amikor egy feladat megoldásához egy már ismert és megoldott feladat megoldását használjuk fel. Általában nem pontosan ugyanazt a feladatot
Cserép Máté 2016. szeptember 14. Analóg programozásnak nevezzük azt, amikor egy feladat megoldásához egy már ismert és megoldott feladat megoldását használjuk fel. Általában nem pontosan ugyanazt a feladatot
1. tétel Halmazok és halmazok számossága. Halmazműveletek és logikai műveletek kapcsolata.
 1. tétel Halmazok és halmazok számossága. Halmazműveletek és logikai műveletek kapcsolata. HLMZOK halmaz axiomatikus fogalom, nincs definíciója. benne van valami a halmazban szintén axiomatikus fogalom,
1. tétel Halmazok és halmazok számossága. Halmazműveletek és logikai műveletek kapcsolata. HLMZOK halmaz axiomatikus fogalom, nincs definíciója. benne van valami a halmazban szintén axiomatikus fogalom,
Térinformatikai algoritmusok Elemi algoritmusok
 Cserép Máté Analóg programozásnak nevezzük azt, amikor egy feladat megoldásához egy már ismert és megoldott feladat megoldását használjuk fel. Általában nem pontosan ugyanazt a feladatot oldottuk meg korábban,
Cserép Máté Analóg programozásnak nevezzük azt, amikor egy feladat megoldásához egy már ismert és megoldott feladat megoldását használjuk fel. Általában nem pontosan ugyanazt a feladatot oldottuk meg korábban,
Logika és informatikai alkalmazásai
 Logika és informatikai alkalmazásai 2. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
Logika és informatikai alkalmazásai 2. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
Diszkrét matematika I.
 EÖTVÖS LORÁND TUDOMÁNYEGYETEM - INFORMATIKAI KAR Diszkrét matematika I. Vizsgaanyag Cserép Máté 2009.01.20. A dokumentum a programtervező informatikus szak Diszkrét matematika I. kurzusának vizsgaanyagát
EÖTVÖS LORÁND TUDOMÁNYEGYETEM - INFORMATIKAI KAR Diszkrét matematika I. Vizsgaanyag Cserép Máté 2009.01.20. A dokumentum a programtervező informatikus szak Diszkrét matematika I. kurzusának vizsgaanyagát
1. előadás: Halmazelmélet, számfogalom, teljes
 1. előadás: Halmazelmélet, számfogalom, teljes indukció Szabó Szilárd Halmazok Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) összessége. Egy halmaz akkor adott, ha minden objektumról eldönthető,
1. előadás: Halmazelmélet, számfogalom, teljes indukció Szabó Szilárd Halmazok Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) összessége. Egy halmaz akkor adott, ha minden objektumról eldönthető,
Matematika szigorlat, Mérnök informatikus szak I máj. 12. Név: Nept. kód: Idő: 1. f. 2. f. 3. f. 4. f. 5. f. 6. f. Össz.: Oszt.
 Matematika szigorlat, Mérnök informatikus szak I. 2009. máj. 12. Név: Nept. kód: Idő: 1. f. 2. f. 3. f. 4. f. 5. f. 6. f. Össz.: Oszt.: 180 perc 0-49 pont: elégtelen, 50-61 pont: elégséges, 62-73 pont:
Matematika szigorlat, Mérnök informatikus szak I. 2009. máj. 12. Név: Nept. kód: Idő: 1. f. 2. f. 3. f. 4. f. 5. f. 6. f. Össz.: Oszt.: 180 perc 0-49 pont: elégtelen, 50-61 pont: elégséges, 62-73 pont:
Diszkrét matematika I. gyakorlat
 Vizsgafeladatok megoldása 2012. december 5. Tartalom Teljes feladatsor #1 1 Teljes feladatsor #1 2 Teljes feladatsor #2 3 Teljes feladatsor #3 4 Teljes feladatsor #4 5 Válogatott feladatok 6 Végső bölcsesség
Vizsgafeladatok megoldása 2012. december 5. Tartalom Teljes feladatsor #1 1 Teljes feladatsor #1 2 Teljes feladatsor #2 3 Teljes feladatsor #3 4 Teljes feladatsor #4 5 Válogatott feladatok 6 Végső bölcsesség
Bevezetés a számításelméletbe (MS1 BS)
 Matematika szigorlat - konzultációs szeminárium Azoknak, akik másodszorra vagy többedszerre veszik fel a Matematika szigorlat (NAMMS1SAND) tárgyat. Bevezetés a számításelméletbe (MS1 BS) FŐBB TÉMAKÖRÖK
Matematika szigorlat - konzultációs szeminárium Azoknak, akik másodszorra vagy többedszerre veszik fel a Matematika szigorlat (NAMMS1SAND) tárgyat. Bevezetés a számításelméletbe (MS1 BS) FŐBB TÉMAKÖRÖK
2014. szeptember 24. és 26. Dr. Vincze Szilvia
 2014. szeptember 24. és 26. Dr. Vincze Szilvia Mind a hétköznapi, mind a tudományos életben gyakran előfordul, hogy bizonyos halmazok elemei között kapcsolat figyelhető meg. A kapcsolat fogalmának matematikai
2014. szeptember 24. és 26. Dr. Vincze Szilvia Mind a hétköznapi, mind a tudományos életben gyakran előfordul, hogy bizonyos halmazok elemei között kapcsolat figyelhető meg. A kapcsolat fogalmának matematikai
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 1. estis képzés 2017. ősz 1. Diszkrét matematika 1. estis képzés 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
Diszkrét matematika 1. estis képzés 2017. ősz 1. Diszkrét matematika 1. estis képzés 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
A Matematika I. előadás részletes tematikája
 A Matematika I. előadás részletes tematikája 2005/6, I. félév 1. Halmazok és relációk 1.1 Műveletek halmazokkal Definíciók, fogalmak: halmaz, elem, üres halmaz, halmazok egyenlősége, részhalmaz, halmazok
A Matematika I. előadás részletes tematikája 2005/6, I. félév 1. Halmazok és relációk 1.1 Műveletek halmazokkal Definíciók, fogalmak: halmaz, elem, üres halmaz, halmazok egyenlősége, részhalmaz, halmazok
Diszkrét matematika gyakorlat 1. ZH október 10. α csoport
 Diszkrét matematika gyakorlat 1. ZH 2016. október 10. α csoport 1. Feladat. (5 pont) Adja meg az α 1 β szorzatrelációt, amennyiben ahol A {1, 2, 3, 4}. α {(1, 2), (1, 3), (2, 1), (3, 1), (3, 4), (4, 4)}
Diszkrét matematika gyakorlat 1. ZH 2016. október 10. α csoport 1. Feladat. (5 pont) Adja meg az α 1 β szorzatrelációt, amennyiben ahol A {1, 2, 3, 4}. α {(1, 2), (1, 3), (2, 1), (3, 1), (3, 4), (4, 4)}
Logika és informatikai alkalmazásai
 Logika és informatikai alkalmazásai 2. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2009 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
Logika és informatikai alkalmazásai 2. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2009 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
Diszkrét Matematika I.
 Orosz Ágota Kaiser Zoltán Diszkrét Matematika I példatár mobidiák könyvtár Orosz Ágota Kaiser Zoltán Diszkrét Matematika I példatár mobidiák könyvtár SOROZATSZERKESZTŐ Fazekas István Orosz Ágota Kaiser
Orosz Ágota Kaiser Zoltán Diszkrét Matematika I példatár mobidiák könyvtár Orosz Ágota Kaiser Zoltán Diszkrét Matematika I példatár mobidiák könyvtár SOROZATSZERKESZTŐ Fazekas István Orosz Ágota Kaiser
? szimmetrikus antiszimmetrikus reflexív tranzitív egyik sem?
 Czédli Gábor: Diszkr.mat. I. (új) Feladatsor azonosítója: Olvaható név= EHAkód= Tisztelt Vizsgázó! Minden egyes feladatnál a választ, illetve a végeredményt a feladathoz tartozó, előre nyomtatott téglalap(ok)ban
Czédli Gábor: Diszkr.mat. I. (új) Feladatsor azonosítója: Olvaható név= EHAkód= Tisztelt Vizsgázó! Minden egyes feladatnál a választ, illetve a végeredményt a feladathoz tartozó, előre nyomtatott téglalap(ok)ban
BOOLE ALGEBRA Logika: A konjunkció és diszjunkció tulajdonságai
 BOOLE ALGEBRA Logika: A konjunkció és diszjunkció tulajdonságai 1.a. A B B A 2.a. (A B) C A (B C) 3.a. A (A B) A 4.a. I A I 5.a. A (B C) (A B) (A C) 6.a. A A I 1.b. A B B A 2.b. (A B) C A (B C) 3.b. A
BOOLE ALGEBRA Logika: A konjunkció és diszjunkció tulajdonságai 1.a. A B B A 2.a. (A B) C A (B C) 3.a. A (A B) A 4.a. I A I 5.a. A (B C) (A B) (A C) 6.a. A A I 1.b. A B B A 2.b. (A B) C A (B C) 3.b. A
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 5. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Számfogalom bővítése Diszkrét matematika I. középszint
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 5. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Számfogalom bővítése Diszkrét matematika I. középszint
Relációs struktúrák Relációs elméletek Modális elméletek Gyakorlás Modellezés Házifeladatok MODÁLIS LOGIKAI ALAPOK
 DEONTIKUS LOGIKA MODÁLIS LOGIKAI ALAPOK Molnár Attila, Markovich Réka Eötvös Loránd University March 14, 2015 Relációs struktúrák DEONTIKUS RENDSZER MINT RELÁCIÓS STRUKTÚRA Modellezni szeretnénk a cselekvéseket
DEONTIKUS LOGIKA MODÁLIS LOGIKAI ALAPOK Molnár Attila, Markovich Réka Eötvös Loránd University March 14, 2015 Relációs struktúrák DEONTIKUS RENDSZER MINT RELÁCIÓS STRUKTÚRA Modellezni szeretnénk a cselekvéseket
Analízis I. beugró vizsgakérdések
 Analízis I. beugró vizsgakérdések Programtervező Informatikus szak 2008-2009. 2. félév Készítette: Szabó Zoltán SZZNACI.ELTE zotyo@bolyaimk.hu v1.7 Forrás: Dr. Weisz Ferenc: Prog. Mat. 2006-2007 definíciók
Analízis I. beugró vizsgakérdések Programtervező Informatikus szak 2008-2009. 2. félév Készítette: Szabó Zoltán SZZNACI.ELTE zotyo@bolyaimk.hu v1.7 Forrás: Dr. Weisz Ferenc: Prog. Mat. 2006-2007 definíciók
4. Fogyasztói preferenciák elmélete
 4. Fogyasztói preferenciák elmélete (ld. Temesi J.: A döntéselmélet alapjai, 47-63) 4.1 Preferencia relációk Mit jelent a fogyasztó választása? Legyen X egy olyan halmaz amelynek az elemei azok a lehetőségek
4. Fogyasztói preferenciák elmélete (ld. Temesi J.: A döntéselmélet alapjai, 47-63) 4.1 Preferencia relációk Mit jelent a fogyasztó választása? Legyen X egy olyan halmaz amelynek az elemei azok a lehetőségek
SZÁMÍTÁSTUDOMÁNY ALAPJAI
 SZÁMÍTÁSTUDOMÁNY ALAPJAI INBGM0101-17 Előadó: Dr. Mihálydeák Tamás Sándor Gyakorlatvezető: Kovács Zita 2017/2018. I. félév 2. gyakorlat Az alábbi összefüggések közül melyek érvényesek minden A, B halmaz
SZÁMÍTÁSTUDOMÁNY ALAPJAI INBGM0101-17 Előadó: Dr. Mihálydeák Tamás Sándor Gyakorlatvezető: Kovács Zita 2017/2018. I. félév 2. gyakorlat Az alábbi összefüggések közül melyek érvényesek minden A, B halmaz
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2013 ősz 1. Diszkrét matematika I. középszint 9. előadás Mérai László merai@compalg.inf.elte.hu compalg.inf.elte.hu/ merai Komputeralgebra Tanszék 2013 ősz Halmazok Diszkrét
Diszkrét matematika I. középszint 2013 ősz 1. Diszkrét matematika I. középszint 9. előadás Mérai László merai@compalg.inf.elte.hu compalg.inf.elte.hu/ merai Komputeralgebra Tanszék 2013 ősz Halmazok Diszkrét
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 6. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 6. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
A rokonsági fogalmak ontológiája
 A rokonsági fogalmak ontológiája Szakadát István BME SZKT MOKK http://si.hu Magarországi Web Konferencia 2007 - W3C-szekció célok, tartalom szemantika, ontológia szemantikus web Tim Berners-Lee: a szöveget
A rokonsági fogalmak ontológiája Szakadát István BME SZKT MOKK http://si.hu Magarországi Web Konferencia 2007 - W3C-szekció célok, tartalom szemantika, ontológia szemantikus web Tim Berners-Lee: a szöveget
Diszkrét matematika 2. estis képzés
 Diszkrét matematika 2. estis képzés 2018. tavasz 1. Diszkrét matematika 2. estis képzés 1. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
Diszkrét matematika 2. estis képzés 2018. tavasz 1. Diszkrét matematika 2. estis képzés 1. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
DISZKRÉT MATEMATIKA RENDEZETT HALMAZOKKAL KAPCSOLATOS PÉLDÁK. Rendezett halmaz. (a, b) R a R b 1. Reflexív 2. Antiszimmetrikus 3.
 Rendezett halmaz R A x A rendezési reláció A-n, ha R Másképpen: (a, b) R a R b 1. Reflexív 2. Antiszimmetrikus 3. Tranzitív arb for (a, b) R. 1. a A ara 2. a,b A (arb bra a = b 3. a,b,c A (arb brc arc
Rendezett halmaz R A x A rendezési reláció A-n, ha R Másképpen: (a, b) R a R b 1. Reflexív 2. Antiszimmetrikus 3. Tranzitív arb for (a, b) R. 1. a A ara 2. a,b A (arb bra a = b 3. a,b,c A (arb brc arc
Miskolci Egyetem. Diszkrét matek I. Vizsga-jegyzet. Hegedűs Ádám Imre 2010.12.28.
 Miskolci Egyetem Diszkrét matek I. Vizsga-jegyzet Hegedűs Ádám Imre 2010.12.28. KOMBINATORIKA Permutáció Ismétlés nélküli permutáció alatt néhány különböző dolognak a sorba rendezését értjük. Az "ismétlés
Miskolci Egyetem Diszkrét matek I. Vizsga-jegyzet Hegedűs Ádám Imre 2010.12.28. KOMBINATORIKA Permutáció Ismétlés nélküli permutáció alatt néhány különböző dolognak a sorba rendezését értjük. Az "ismétlés
D(x, y) - x osztója y-nak
 1. Mondjon legalább három példát predikátumra! P (x) - x prím M(x, y) - x merőleges y-ra E(x) - x egyenes D(x, y) - x osztója y-nak 2. Sorolja fel a logikai jeleket! - és (konjunkció) - vagy (diszjunkció)
1. Mondjon legalább három példát predikátumra! P (x) - x prím M(x, y) - x merőleges y-ra E(x) - x egyenes D(x, y) - x osztója y-nak 2. Sorolja fel a logikai jeleket! - és (konjunkció) - vagy (diszjunkció)
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I. 3 III. MEGFELELTETÉSEk, RELÁCIÓk 1. BEVEZETÉS Emlékeztetünk arra, hogy az rendezett párok halmazát az és halmazok Descartes-féle szorzatának nevezzük. Más szóval az és halmazok
KOVÁCS BÉLA, MATEmATIkA I. 3 III. MEGFELELTETÉSEk, RELÁCIÓk 1. BEVEZETÉS Emlékeztetünk arra, hogy az rendezett párok halmazát az és halmazok Descartes-féle szorzatának nevezzük. Más szóval az és halmazok
Diszkrét matematika I. feladatok
 Diszkrét matematika I. feladatok 1. Komplex számok Fogalmak Új jel: i, amire igaz: i 2 = 1. Minden z komplex szám a következő alakba írható: z = a + i b, ezt nevezzük z algebrai alakjának. a-t a komplex
Diszkrét matematika I. feladatok 1. Komplex számok Fogalmak Új jel: i, amire igaz: i 2 = 1. Minden z komplex szám a következő alakba írható: z = a + i b, ezt nevezzük z algebrai alakjának. a-t a komplex
Logika és informatikai alkalmazásai
 Logika és informatikai alkalmazásai 2. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2009 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
Logika és informatikai alkalmazásai 2. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2009 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
ADATBÁZIS-KEZELÉS. Relációalgebra, 5NF
 ADATBÁZIS-KEZELÉS Relációalgebra, 5NF ABSZTRAKT LEKÉRDEZŐ NYELVEK relációalgebra relációkalkulus rekord alapú tartomány alapú Relációalgebra a matematikai halmazelméleten alapuló lekérdező nyelv a lekérdezés
ADATBÁZIS-KEZELÉS Relációalgebra, 5NF ABSZTRAKT LEKÉRDEZŐ NYELVEK relációalgebra relációkalkulus rekord alapú tartomány alapú Relációalgebra a matematikai halmazelméleten alapuló lekérdező nyelv a lekérdezés
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I. 4 IV. FÜGGVÉNYEk 1. LEkÉPEZÉSEk, függvények Definíció Legyen és két halmaz. Egy függvény -ből -ba egy olyan szabály, amely minden elemhez pontosan egy elemet rendel hozzá. Az
KOVÁCS BÉLA, MATEmATIkA I. 4 IV. FÜGGVÉNYEk 1. LEkÉPEZÉSEk, függvények Definíció Legyen és két halmaz. Egy függvény -ből -ba egy olyan szabály, amely minden elemhez pontosan egy elemet rendel hozzá. Az
Diszkrét matematika HALMAZALGEBRA. Halmazalgebra
 Halmazalgebra Ebben a fejezetben összefoglaljuk a halmazokról tanult középiskolai ismeretanyagot, és néhány érdekességgel, módszerrel ki is egészítjük. A halmaz alapfogalom. Mondhatjuk, hogy tárgyak, fogalmak,
Halmazalgebra Ebben a fejezetben összefoglaljuk a halmazokról tanult középiskolai ismeretanyagot, és néhány érdekességgel, módszerrel ki is egészítjük. A halmaz alapfogalom. Mondhatjuk, hogy tárgyak, fogalmak,
Diszkrét matematika I. feladatok
 Diszkrét matematika I. feladatok 1. Komplex számok 1.1. Fogalmak Új jel: i, amire igaz: i 2 = 1. Minden z komplex szám a következő alakba írható: z = a + i b, ezt nevezzük z algebrai alakjának. a-t a komplex
Diszkrét matematika I. feladatok 1. Komplex számok 1.1. Fogalmak Új jel: i, amire igaz: i 2 = 1. Minden z komplex szám a következő alakba írható: z = a + i b, ezt nevezzük z algebrai alakjának. a-t a komplex
Bevezetés a matematikába 1. Definíciók, vizsgakérdések
 Bevezet a matematikába 1 Definíciók, vizsgakérdek Tételek15 Mi lehet predikátumok értéke? Hogyan jelöljük?15 Mondjon legalább három példát predikátumra15 Sorolja fel a logikai jeleket15 Milyen kvantortokat
Bevezet a matematikába 1 Definíciók, vizsgakérdek Tételek15 Mi lehet predikátumok értéke? Hogyan jelöljük?15 Mondjon legalább három példát predikátumra15 Sorolja fel a logikai jeleket15 Milyen kvantortokat
Diszkrét Matematika. zöld könyv ): XIII. fejezet: 1583, 1587, 1588, 1590, Matematikai feladatgyűjtemény II. (
 FELADATOK A LEKÉPEZÉSEK, PERMUTÁCIÓK TÉMAKÖRHÖZ Diszkrét Matematika 4. LEKÉPEZÉSEK Értelmezési tartomány és értékkészlet meghatározása : Összefoglaló feladatgyűjtemény matematikából ( zöld könyv ): XIII.
FELADATOK A LEKÉPEZÉSEK, PERMUTÁCIÓK TÉMAKÖRHÖZ Diszkrét Matematika 4. LEKÉPEZÉSEK Értelmezési tartomány és értékkészlet meghatározása : Összefoglaló feladatgyűjtemény matematikából ( zöld könyv ): XIII.
0-49 pont: elégtelen, pont: elégséges, pont: közepes, pont: jó, pont: jeles
 Matematika szigorlat, Mérnök informatikus szak I. 2013. jan. 10. Név: Neptun kód: Idő: 180 perc Elm.: 1. f. 2. f. 3. f. 4. f. 5. f. Fel. össz.: Össz.: Oszt.: Az elérhető pontszám 40 (elmélet) + 60 (feladatok)
Matematika szigorlat, Mérnök informatikus szak I. 2013. jan. 10. Név: Neptun kód: Idő: 180 perc Elm.: 1. f. 2. f. 3. f. 4. f. 5. f. Fel. össz.: Össz.: Oszt.: Az elérhető pontszám 40 (elmélet) + 60 (feladatok)
Gy ur uk aprilis 11.
 Gyűrűk 2014. április 11. 1. Hányadostest 2. Karakterisztika, prímtest 3. Egyszerű gyűrűk [F] III/8 Tétel Minden integritástartomány beágyazható testbe. Legyen R integritástartomány, és értelmezzünk az
Gyűrűk 2014. április 11. 1. Hányadostest 2. Karakterisztika, prímtest 3. Egyszerű gyűrűk [F] III/8 Tétel Minden integritástartomány beágyazható testbe. Legyen R integritástartomány, és értelmezzünk az
I. NÉHÁNY FONTOS FOGALOM
 I. NÉHÁNY FONTOS FOGALOM 1. Halmazok, relációk, függvények A matematika alapfogalma a halmaz, amely szemléletesen dolgok összességét jelenti. Az alábbiakban az úgynevezett naív halmazelméletet ismertetjük,
I. NÉHÁNY FONTOS FOGALOM 1. Halmazok, relációk, függvények A matematika alapfogalma a halmaz, amely szemléletesen dolgok összességét jelenti. Az alábbiakban az úgynevezett naív halmazelméletet ismertetjük,
Logika és informatikai alkalmazásai
 Logika és informatikai alkalmazásai 1. levelezős gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2009 tavasz Követelmények A tárgy (ea+gyak) teljesítésének
Logika és informatikai alkalmazásai 1. levelezős gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2009 tavasz Követelmények A tárgy (ea+gyak) teljesítésének
1 2. gyakorlat Matematikai és nyelvi alapfogalmak. dr. Kallós Gábor
 1 2. gyakorlat Matematikai és nyelvi alapfogalmak dr. Kallós Gábor 2017 2018 Köszönetnyilvánítás Köszönetnyilvánítás (Acknowledgement) Ez a gyakorlati feladatsor nagyban épít a következő könyvre Elements
1 2. gyakorlat Matematikai és nyelvi alapfogalmak dr. Kallós Gábor 2017 2018 Köszönetnyilvánítás Köszönetnyilvánítás (Acknowledgement) Ez a gyakorlati feladatsor nagyban épít a következő könyvre Elements
Vektorterek. Wettl Ferenc február 17. Wettl Ferenc Vektorterek február / 27
 Vektorterek Wettl Ferenc 2015. február 17. Wettl Ferenc Vektorterek 2015. február 17. 1 / 27 Tartalom 1 Egyenletrendszerek 2 Algebrai struktúrák 3 Vektortér 4 Bázis, dimenzió 5 Valós mátrixok és egyenletrendszerek
Vektorterek Wettl Ferenc 2015. február 17. Wettl Ferenc Vektorterek 2015. február 17. 1 / 27 Tartalom 1 Egyenletrendszerek 2 Algebrai struktúrák 3 Vektortér 4 Bázis, dimenzió 5 Valós mátrixok és egyenletrendszerek
Dr. Vincze Szilvia;
 2014. szeptember 17. és 19. Dr. Vincze Szilvia; vincze@agr.unideb.hu https://portal.agr.unideb.hu/oktatok/drvinczeszilvia/oktatas/oktatott_targyak/index/index.html 2010/2011-es tanév I. féléves tematika
2014. szeptember 17. és 19. Dr. Vincze Szilvia; vincze@agr.unideb.hu https://portal.agr.unideb.hu/oktatok/drvinczeszilvia/oktatas/oktatott_targyak/index/index.html 2010/2011-es tanév I. féléves tematika
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 3. estis képzés 2016. ősz 1. Diszkrét matematika 3. estis képzés 3. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2016. ősz 1. Diszkrét matematika 3. estis képzés 3. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 2.
 Diszkrét matematika 2. 2018. november 23. 1. Diszkrét matematika 2. 9. előadás Fancsali Szabolcs Levente nudniq@cs.elte.hu www.cs.elte.hu/ nudniq Komputeralgebra Tanszék 2018. november 23. Diszkrét matematika
Diszkrét matematika 2. 2018. november 23. 1. Diszkrét matematika 2. 9. előadás Fancsali Szabolcs Levente nudniq@cs.elte.hu www.cs.elte.hu/ nudniq Komputeralgebra Tanszék 2018. november 23. Diszkrét matematika
DISZKRÉT MATEMATIKA: STRUKTÚRÁK Előadáson mutatott példa: Bércesné Novák Ágnes
 1. Algebrai alapok: DISZKRÉT MATEMATIKA: STRUKTÚRÁK Művelet: Egy H nemüres halmazon értelmezett (kétváltozós) műveleten egy H H H függvényt értünk, azaz egy olyan leképezést, amely bármely a,b H elempárhoz
1. Algebrai alapok: DISZKRÉT MATEMATIKA: STRUKTÚRÁK Művelet: Egy H nemüres halmazon értelmezett (kétváltozós) műveleten egy H H H függvényt értünk, azaz egy olyan leképezést, amely bármely a,b H elempárhoz
DISZKRÉT MATEMATIKA I. TÉTELEK
 DISZKRÉT MATEMATIKA I. TÉTELEK Szerkesztette: Bókay Csongor 2011 őszi félév Az esetleges hibákat kérlek a csongor@csongorbokay.com címen jelezd! Utolsó módosítás: 2012. január 16. Ez a Mű a Creative Commons
DISZKRÉT MATEMATIKA I. TÉTELEK Szerkesztette: Bókay Csongor 2011 őszi félév Az esetleges hibákat kérlek a csongor@csongorbokay.com címen jelezd! Utolsó módosítás: 2012. január 16. Ez a Mű a Creative Commons
Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) Egy halmaz akkor adott, ha minden objektumról eldönthető, hogy
 1. előadás: Halmazelmélet Szabó Szilárd Halmazok Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) összessége. Egy halmaz akkor adott, ha minden objektumról eldönthető, hogy hozzátartozik-e,
1. előadás: Halmazelmélet Szabó Szilárd Halmazok Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) összessége. Egy halmaz akkor adott, ha minden objektumról eldönthető, hogy hozzátartozik-e,
Klasszikus algebra előadás. Waldhauser Tamás április 28.
 Klasszikus algebra előadás Waldhauser Tamás 2014. április 28. 5. Számelmélet integritástartományokban Oszthatóság Mostantól R mindig tetszőleges integritástartományt jelöl. 5.1. Definíció. Azt mondjuk,
Klasszikus algebra előadás Waldhauser Tamás 2014. április 28. 5. Számelmélet integritástartományokban Oszthatóság Mostantól R mindig tetszőleges integritástartományt jelöl. 5.1. Definíció. Azt mondjuk,
Ontológia nyelvek (Szemantikus Világhálótól...)
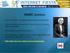 Ontológia nyelvek (Szemantikus Világhálótól...) XML XML, DTD RDF Tudásreprezentáció Univerzális kifejező erő Szintaktikai interoperabilitás Szemantikai interoperabilitás RDFS DAML+OIL OWL OWL-Lite OWL-DL
Ontológia nyelvek (Szemantikus Világhálótól...) XML XML, DTD RDF Tudásreprezentáció Univerzális kifejező erő Szintaktikai interoperabilitás Szemantikai interoperabilitás RDFS DAML+OIL OWL OWL-Lite OWL-DL
Debreceni Egyetem. Kalkulus I. Gselmann Eszter
 Debreceni Egyetem Természettudományi és Technológiai Kar Kalkulus I. Gselmann Eszter Debrecen, 2011 A matematikában a gondolat, ami számít. (Szofja Vasziljevna Kovalevszkaja) Tartalomjegyzék 1. Halmazok,
Debreceni Egyetem Természettudományi és Technológiai Kar Kalkulus I. Gselmann Eszter Debrecen, 2011 A matematikában a gondolat, ami számít. (Szofja Vasziljevna Kovalevszkaja) Tartalomjegyzék 1. Halmazok,
Lineáris algebra (10A103)
 Lineáris algebra (10A103 Kátai-Urbán Kamilla Tudnivalók Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli (beugróval, feltétele a Lineáris algebra gyakorlat
Lineáris algebra (10A103 Kátai-Urbán Kamilla Tudnivalók Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli (beugróval, feltétele a Lineáris algebra gyakorlat
DEFINICIÓK. Például a síkgeometriában predikátumok: ( egyenes ), ( pont ), ( illeszkedik - ra ).
 DEFINICIÓK 1. Mondjon legalább három példát predikátumra. Például a síkgeometriában predikátumok: ( egyenes ), ( pont ), ( illeszkedik - ra ). 2. Sorolja fel a logikai jeleket. A logikai formulák alkotóelemei:
DEFINICIÓK 1. Mondjon legalább három példát predikátumra. Például a síkgeometriában predikátumok: ( egyenes ), ( pont ), ( illeszkedik - ra ). 2. Sorolja fel a logikai jeleket. A logikai formulák alkotóelemei:
Halmazelméleti alapfogalmak
 Halmazelméleti alapfogalmak halmaz (sokaság) jól meghatározott, megkülönböztetett dolgok (tárgyak, fogalmak, stb.) összessége. - halmaz alapfogalom. z azt jelenti, hogy csak példákon keresztül magyarázzuk,
Halmazelméleti alapfogalmak halmaz (sokaság) jól meghatározott, megkülönböztetett dolgok (tárgyak, fogalmak, stb.) összessége. - halmaz alapfogalom. z azt jelenti, hogy csak példákon keresztül magyarázzuk,
Matematika szigorlat javítókulcs, Informatika I máj. 30.
 Matematika szigorlat javítókulcs, Informatika I. 006. máj. 0.. Legyen f : [0, [ R, f (x)= x x +. a) Vizsgálja meg a függvényt monotonitás szempontjából! f (x)= x (x + ). x=0 0
Matematika szigorlat javítókulcs, Informatika I. 006. máj. 0.. Legyen f : [0, [ R, f (x)= x x +. a) Vizsgálja meg a függvényt monotonitás szempontjából! f (x)= x (x + ). x=0 0
Diszkrét matematika I. feladatok
 Diszkrét matematika I feladatok 1 Teljes indukció 11 Könnyebb Teljes indukcióval bizonyítsd be az alábbi összefüggéseket: 1 1 + + 3 + + n = 1 + + 3 + + n = n(n + 1) 3 1 + 3 + + n(n + 1) = n(n + 1)(n +
Diszkrét matematika I feladatok 1 Teljes indukció 11 Könnyebb Teljes indukcióval bizonyítsd be az alábbi összefüggéseket: 1 1 + + 3 + + n = 1 + + 3 + + n = n(n + 1) 3 1 + 3 + + n(n + 1) = n(n + 1)(n +
Általános algebra. 1. Algebrai struktúra, izomorfizmus. 3. Kongruencia, faktoralgebra március Homomorfizmus, homomorfiatétel
 1. Algebrai struktúra, izomorfizmus Általános algebra 2. Részalgebra, generálás 3. Kongruencia, faktoralgebra 2013 március 8. 4. Homomorfizmus, homomorfiatétel 1. Algebrai struktúra, izomorfizmus 2. Részalgebra,
1. Algebrai struktúra, izomorfizmus Általános algebra 2. Részalgebra, generálás 3. Kongruencia, faktoralgebra 2013 március 8. 4. Homomorfizmus, homomorfiatétel 1. Algebrai struktúra, izomorfizmus 2. Részalgebra,
Logika es sz am ıt aselm elet I. r esz Logika Harmadik el oad as 1/33
 1/33 Logika és számításelmélet I. rész Logika Harmadik előadás Tartalom 2/33 Elsőrendű logika bevezetés Az elsőrendű logika szintaxisa 3/33 Nulladrendű állítás Az ítéletlogikában nem foglalkoztunk az álĺıtások
1/33 Logika és számításelmélet I. rész Logika Harmadik előadás Tartalom 2/33 Elsőrendű logika bevezetés Az elsőrendű logika szintaxisa 3/33 Nulladrendű állítás Az ítéletlogikában nem foglalkoztunk az álĺıtások
Követelmény- és funkcionális specifikáció
 Szakadát István Ontológiai konzisztenciavizsgálat Követelmény- és funkcionális specifikáció Az ontológiák értékelését sokféle szempont szerint végezhetjük a technikai, logikai követelményektől kezdve a
Szakadát István Ontológiai konzisztenciavizsgálat Követelmény- és funkcionális specifikáció Az ontológiák értékelését sokféle szempont szerint végezhetjük a technikai, logikai követelményektől kezdve a
Matematika szigorlat június 17. Neptun kód:
 Név Matematika szigorlat 014. június 17. Neptun kód: 1.. 3. 4. 5. Elm. Fel. Össz. Oszt. Az eredményes szigorlat feltétele elméletből legalább 0 pont, feladatokból pedig legalább 30 pont elérése. A szigorlat
Név Matematika szigorlat 014. június 17. Neptun kód: 1.. 3. 4. 5. Elm. Fel. Össz. Oszt. Az eredményes szigorlat feltétele elméletből legalább 0 pont, feladatokból pedig legalább 30 pont elérése. A szigorlat
A valós számok halmaza
 VA 1 A valós számok halmaza VA 2 A valós számok halmazának axiómarendszere és alapvető tulajdonságai Definíció Az R halmazt a valós számok halmazának nevezzük, ha teljesíti a következő axiómarendszerben
VA 1 A valós számok halmaza VA 2 A valós számok halmazának axiómarendszere és alapvető tulajdonságai Definíció Az R halmazt a valós számok halmazának nevezzük, ha teljesíti a következő axiómarendszerben
Permutációk véges halmazon (el adásvázlat, február 12.)
 Permutációk véges halmazon el adásvázlat 2008 február 12 Maróti Miklós Ennek az el adásnak a megértéséhez a következ fogalmakat kell tudni: ismétlés nélküli variáció leképezés indulási és érkezési halmaz
Permutációk véges halmazon el adásvázlat 2008 február 12 Maróti Miklós Ennek az el adásnak a megértéséhez a következ fogalmakat kell tudni: ismétlés nélküli variáció leképezés indulási és érkezési halmaz
5. A kiterjesztési elv, nyelvi változók
 5. A kiterjesztési elv, nyelvi változók Gépi intelligencia I. Fodor János BMF NIK IMRI NIMGI1MIEM Tartalomjegyzék I 1 A kiterjesztési elv 2 Nyelvi változók A kiterjesztési elv 237 A KITERJESZTÉSI ELV A
5. A kiterjesztési elv, nyelvi változók Gépi intelligencia I. Fodor János BMF NIK IMRI NIMGI1MIEM Tartalomjegyzék I 1 A kiterjesztési elv 2 Nyelvi változók A kiterjesztési elv 237 A KITERJESZTÉSI ELV A
Diszkrét matematika 1. középszint
 Diszkrét matematika 1. középszint 2017. sz 1. Diszkrét matematika 1. középszint 3. el adás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2017. sz 1. Diszkrét matematika 1. középszint 3. el adás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
A félév során előkerülő témakörök
 A félév során előkerülő témakörök rekurzív algoritmusok rendező algoritmusok alapvető adattípusok, adatszerkezetek, és kapcsolódó algoritmusok dinamikus programozás mohó algoritmusok gráf algoritmusok
A félév során előkerülő témakörök rekurzív algoritmusok rendező algoritmusok alapvető adattípusok, adatszerkezetek, és kapcsolódó algoritmusok dinamikus programozás mohó algoritmusok gráf algoritmusok
Matematika szigorlat, Mérnök informatikus szak I máj. 29.
 Matematika szigorlat, Mérnök informatikus szak I. 2007. máj. 29. Megoldókulcs 1. Adott az S : 3x 6y + 2z = 6 sík a három dimenziós térben. (a) Írja fel egy tetszőleges, az S-re merőleges S síknak az egyenletét!
Matematika szigorlat, Mérnök informatikus szak I. 2007. máj. 29. Megoldókulcs 1. Adott az S : 3x 6y + 2z = 6 sík a három dimenziós térben. (a) Írja fel egy tetszőleges, az S-re merőleges S síknak az egyenletét!
Diszkrét matematika 2. estis képzés
 Diszkrét matematika 2. estis képzés 2018. tavasz 1. Diszkrét matematika 2. estis képzés 4-6. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 2. estis képzés 2018. tavasz 1. Diszkrét matematika 2. estis képzés 4-6. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Algoritmuselmélet gyakorlat (MMN111G)
 Algoritmuselmélet gyakorlat (MMN111G) 2014. január 14. 1. Gyakorlat 1.1. Feladat. Adott K testre rendre K[x] és K(x) jelöli a K feletti polinomok és racionális törtfüggvények halmazát. Mutassuk meg, hogy
Algoritmuselmélet gyakorlat (MMN111G) 2014. január 14. 1. Gyakorlat 1.1. Feladat. Adott K testre rendre K[x] és K(x) jelöli a K feletti polinomok és racionális törtfüggvények halmazát. Mutassuk meg, hogy
Intergrált Intenzív Matematika Érettségi
 . Adott a mátri, determináns determináns, ahol,, d Számítsd ki:. b) Igazold, hogy a b c. Adott a az 6 0 egyenlet megoldásai. a). c) Számítsd ki a d determináns értékét. d c a b determináns, ahol abc,,.
. Adott a mátri, determináns determináns, ahol,, d Számítsd ki:. b) Igazold, hogy a b c. Adott a az 6 0 egyenlet megoldásai. a). c) Számítsd ki a d determináns értékét. d c a b determináns, ahol abc,,.
Logika feladatgyűjtemény
 Debreceni Egyetem Informatikai Kar Logika feladatgyűjtemény 2005. május 19. Készítette: Lengyel Zoltán lengyelz@inf.unideb.hu Tartalomjegyzék 1. Ítéletlogika 2 2. Elsőrendű logika 17 2.1. Prenex alak......................................
Debreceni Egyetem Informatikai Kar Logika feladatgyűjtemény 2005. május 19. Készítette: Lengyel Zoltán lengyelz@inf.unideb.hu Tartalomjegyzék 1. Ítéletlogika 2 2. Elsőrendű logika 17 2.1. Prenex alak......................................
Matematika B/1. Tartalomjegyzék. 1. Célkit zések. 2. Általános követelmények. 3. Rövid leírás. 4. Oktatási módszer. Biró Zsolt. 1.
 Matematika B/1 Biró Zsolt Tartalomjegyzék 1. Célkit zések 1 2. Általános követelmények 1 3. Rövid leírás 1 4. Oktatási módszer 1 5. Követelmények, pótlások 2 6. Program (el adás) 2 7. Program (gyakorlat)
Matematika B/1 Biró Zsolt Tartalomjegyzék 1. Célkit zések 1 2. Általános követelmények 1 3. Rövid leírás 1 4. Oktatási módszer 1 5. Követelmények, pótlások 2 6. Program (el adás) 2 7. Program (gyakorlat)
azonosságot minden 1 i, l n, 1 j k, indexre teljesítő együtthatókkal, amelyekre érvényes a = c (j) i,l l,i
 A Cochran Fisher tételről A matematikai statisztika egyik fontos eredménye a Cochran Fisher tétel, amely a variancia analízisben játszik fontos szerepet. Ugyanakkor ez a tétel lényegét tekintve valójában
A Cochran Fisher tételről A matematikai statisztika egyik fontos eredménye a Cochran Fisher tétel, amely a variancia analízisben játszik fontos szerepet. Ugyanakkor ez a tétel lényegét tekintve valójában
Megoldások. 2001. augusztus 8.
 Megoldások 2001. augusztus 8. 1 1. El zetes tudnivalók a különböz matematikai logikai nyelvekr l 1.1. (a) Igen (b) Igen (c) Nem, mert nem kijelent mondat. (d) Nem fejez ki önmagában állítást. "Ádám azt
Megoldások 2001. augusztus 8. 1 1. El zetes tudnivalók a különböz matematikai logikai nyelvekr l 1.1. (a) Igen (b) Igen (c) Nem, mert nem kijelent mondat. (d) Nem fejez ki önmagában állítást. "Ádám azt
Diszkrét Matematika - Beadandó Feladatok
 Diszkrét Matematika - Beadandó Feladatok Demjan Adalbert - SFDAGZ 2014. december 6. Tartalomjegyzék 1. 2.1-2/c 2 2. 2.2-1/c 3 3. 2.3-13/a 4 4. 2.3-13/b 5 5. 4.1-5/a 6 6. 4.1-5/b 7 7. 4.1-5/c 8 8. 4.4-16
Diszkrét Matematika - Beadandó Feladatok Demjan Adalbert - SFDAGZ 2014. december 6. Tartalomjegyzék 1. 2.1-2/c 2 2. 2.2-1/c 3 3. 2.3-13/a 4 4. 2.3-13/b 5 5. 4.1-5/a 6 6. 4.1-5/b 7 7. 4.1-5/c 8 8. 4.4-16
 Adatbázis rendszerek I Relációs adatmodell műveleti rész (relációs algebra) ME- GEIAL Dr. Kovács László Relációs adatmodell strukturális rész tárolási struktúra séma R(m1,m2, ) adatmodell integritási rész
Adatbázis rendszerek I Relációs adatmodell műveleti rész (relációs algebra) ME- GEIAL Dr. Kovács László Relációs adatmodell strukturális rész tárolási struktúra séma R(m1,m2, ) adatmodell integritási rész
FUNKCIONÁLIS PROGRAMOZÁS
 FUNKCIONÁLIS PROGRAMOZÁS A funkcionális programozás néhány jellemzője Funkcionális programozás 1-2 Funkcionális, más néven applikatív programozás Funkcionális = függvényalapú, függvényközpontú Applikatív
FUNKCIONÁLIS PROGRAMOZÁS A funkcionális programozás néhány jellemzője Funkcionális programozás 1-2 Funkcionális, más néven applikatív programozás Funkcionális = függvényalapú, függvényközpontú Applikatív
Analízis ZH konzultáció
 Analízis ZH konzultáció 1. Teljes indukció Elméleti segítség: n=1-re bebizonyítani (vagy arra az n-re, ahonnan az állítást igazolni szeretnénk) feltesszük, hogy n-re igaz az állítás -> n+1-re is igaz lesz?
Analízis ZH konzultáció 1. Teljes indukció Elméleti segítség: n=1-re bebizonyítani (vagy arra az n-re, ahonnan az állítást igazolni szeretnénk) feltesszük, hogy n-re igaz az állítás -> n+1-re is igaz lesz?
n =
 15. PÉLDÁK FÉLCSOPORTOKRA ÉS CSOPORTOKRA 1. Az R 3 tér vektorai a derékszög½u koordinátarendszerben az a = (a 1 ; a 2 ; a 3 ) alakban adottak az a 1 ; a 2 ; a 3 2 R valós számokkal. A vektoriális szorzás
15. PÉLDÁK FÉLCSOPORTOKRA ÉS CSOPORTOKRA 1. Az R 3 tér vektorai a derékszög½u koordinátarendszerben az a = (a 1 ; a 2 ; a 3 ) alakban adottak az a 1 ; a 2 ; a 3 2 R valós számokkal. A vektoriális szorzás
HALMAZOK. A racionális számok halmazát olyan számok alkotják, amelyek felírhatók b. jele:. A racionális számok halmazának végtelen sok eleme van.
 HALMAZOK Tanulási cél Halmazok megadása, halmazműveletek megismerése és alkalmazása, halmazok ábrázolása Venn diagramon. Motivációs példa Egy fogyasztó 80 000 pénzegység jövedelmet fordít két termék, x
HALMAZOK Tanulási cél Halmazok megadása, halmazműveletek megismerése és alkalmazása, halmazok ábrázolása Venn diagramon. Motivációs példa Egy fogyasztó 80 000 pénzegység jövedelmet fordít két termék, x
Elsőrendű logika szintaktikája és szemantikája. Logika (3. gyakorlat) 0-adrendű szemantika 2009/10 II. félév 1 / 1
 Elsőrendű logika szintaktikája és szemantikája Logika és számításelmélet, 3. gyakorlat 2009/10 II. félév Logika (3. gyakorlat) 0-adrendű szemantika 2009/10 II. félév 1 / 1 Az elsőrendű logika Elemek egy
Elsőrendű logika szintaktikája és szemantikája Logika és számításelmélet, 3. gyakorlat 2009/10 II. félév Logika (3. gyakorlat) 0-adrendű szemantika 2009/10 II. félév 1 / 1 Az elsőrendű logika Elemek egy
Relációk. 1. Descartes-szorzat. 2. Relációk
 Relációk Descartes-szorzat. Relációk szorzata, inverze. Relációk tulajdonságai. Ekvivalenciareláció, osztályozás. Részbenrendezés, Hasse-diagram. 1. Descartes-szorzat 1. Deníció. Tetsz leges két a, b objektum
Relációk Descartes-szorzat. Relációk szorzata, inverze. Relációk tulajdonságai. Ekvivalenciareláció, osztályozás. Részbenrendezés, Hasse-diagram. 1. Descartes-szorzat 1. Deníció. Tetsz leges két a, b objektum
2011. szeptember 14. Dr. Vincze Szilvia;
 2011. szeptember 14. Dr. Vincze Szilvia; vincze@fin.unideb.hu https://portal.agr.unideb.hu/oktatok/drvinczeszilvia Első pillantásra hihetetlennek tűnik, hogy egy olyan tiszta és érzelmektől mentes tudomány,
2011. szeptember 14. Dr. Vincze Szilvia; vincze@fin.unideb.hu https://portal.agr.unideb.hu/oktatok/drvinczeszilvia Első pillantásra hihetetlennek tűnik, hogy egy olyan tiszta és érzelmektől mentes tudomány,
Logika és informatikai alkalmazásai
 Logika és informatikai alkalmazásai 1. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Követelmények A tárgy (ea+gyak) teljesítésének követlményeit
Logika és informatikai alkalmazásai 1. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Követelmények A tárgy (ea+gyak) teljesítésének követlményeit
2016/11/29 11:13 1/6 Digitális átvitel
 2016/11/29 11:13 1/6 Digitális átvitel < Hálózat Digitális átvitel Szerző: Sallai András Copyright Sallai András, 2013, 2014 Licenc: GNU Free Documentation License 1.3 Web: http://szit.hu Szinkron átvitel
2016/11/29 11:13 1/6 Digitális átvitel < Hálózat Digitális átvitel Szerző: Sallai András Copyright Sallai András, 2013, 2014 Licenc: GNU Free Documentation License 1.3 Web: http://szit.hu Szinkron átvitel
AZ INFORMATIKA LOGIKAI ALAPJAI
 AZ INFORMATIKA LOGIKAI ALAPJAI Előadó: Dr. Mihálydeák Tamás Sándor Gyakorlatvezető: Kovács Zita 2017/2018. I. félév 4. gyakorlat Interpretáció A ϱ függvényt az L (0) = LC, Con, Form nulladrendű nyelv egy
AZ INFORMATIKA LOGIKAI ALAPJAI Előadó: Dr. Mihálydeák Tamás Sándor Gyakorlatvezető: Kovács Zita 2017/2018. I. félév 4. gyakorlat Interpretáció A ϱ függvényt az L (0) = LC, Con, Form nulladrendű nyelv egy
