FEJLESZTŐPROGRAMOK HATÁSVIZSGÁLATÁNAK MATEMATIKAI STATISZTIKAI ALAPFOGALMAI
|
|
|
- Lőrinc Bognár
- 9 évvel ezelőtt
- Látták:
Átírás
1 FEJLESZTŐPROGRAMOK HATÁSVIZSGÁLATÁNAK MATEMATIKAI STATISZTIKAI ALAPFOGALMAI Szerzők: Máth János Debreceni Egyetem Mező Ferenc Debreceni Egyetem Abari Kálmán Debreceni Egyetem Mező Katalin Debreceni Egyetem Lektorok: Demetrovics János Eötvös Lóránd Tudományegyetem Nagy Dénes Nemzetközi Szimmetria Társaság Varga Imre Szegedi Tudományegyetem Koncz István Professzorok az Európai Magyarországért Első szerző címe: Máth János, Mező Ferenc, Abari Kálmán és Mező Katalin (2015): Fejlesztőprogramok hatásvizsgálatának matematikai statisztikai alapfogalmai. Különleges Bánásmód, I. évf. 2015/1. szám, DOI /KB Absztrakt Pedagógusok, óvodapedagógusok, gyógypedagógusok, fejlesztőpedagógusok, pszichológusok egy csokorra való azon szakemberek köréből, akik képesség- és/vagy személyiségfejlesztő programokat hozhatnak létre, valósíthatnak meg. E programokkal szemben elvárható azonban, hogy az általuk ígért fejlesztőhatást akár matematikai statisztikai elemzéssel is alá lehessen támasztani. Ez azonban nem mindig történik meg ennek hátterében pedig részben a matematikai statisztikai fogalmi és módszertani hiányosságok, valamint a drága statisztikai szoftverek állnak. E tanulmány a különleges bánásmódot igénylők számára készült fejlesztőprogramok hatásvizsgálatának matematikai statisztikai elemzéséhez nyújt elméleti összefoglalót. Kulcsszavak: fejlesztőprogram, hatásvizsgálat, statisztika Diszciplinák: matematika, pszichológia, gyógypedagógia, pedagógia Abstract BASIC TERMS IN MATHEMATICAL STATISTICS OF IMPACT STUDIES FOR DEVELOPMENTAL PROGRAMS Pedagogues, kindergarten pedagogues, special needs teacher (also known as remedial teachers) and psychologists just a few of those people who can create and use development 69
2 programmes. These programmes are expected to be proven in their effects by using mathematical analysis. However, it doesn t happen in every case partly due to shortage of definitions of mathematical statistics, methodology problems and expensive softwares. This paper is a theoretical summary about mathematical statistical analysis of effectiveness studies of remedial courses designed for those who live with special needs. Key words: development programmes, effectiveness studies, statitics Disciplines: mathematics, psychology, special education, pedagogy A sajátos nevelési igényű és/vagy beilleszkedési, tanulási és magatartászavaros és/vagy tehetséges tanulók felé irányuló különleges bánásmód többek között egyéni vagy csoportos fejlesztő-programokban nyilvánulhat meg. E fejlesztések központi kérdése, hogy vajon hatékonyak-e, elérik-e a fejlesztési tervben kitűzött céljukat; illetve, hogy valóban bizonyítható-e, hogy fejlesztés történt (vö.: Berényi és Katona, 2013, de lényegében ugyanezt a kérdést járja körbe medicinálisabb aspektusból: Guyatt, Cook és Haynes, 2004). Egyéni fejlesztés hatékonyságának vizsgálata fejlesztő program hatásvizsgálata Ha egy adott gyermek fejlesztésének hatékonyságáról kívánunk képet kapni, akkor a fejlesztő folyamat adott pontján tapasztalható eredményeit vethetjük egybe a saját korábbi (pl. fejlesztés előtti) eredményeivel és/vagy a fejlesztési tervben kitűzött célértékkel és/vagy a kortársak eredményeivel. Ez a helyzet nem igényel különösebb statisztikai felkészültséget. Ha egyáltalán számszerűsítenünk kell az eredményeket, akkor a vizsgáló eljárás leírásában szereplő útmutató révén összesítenünk kell a vizsgálati eredményeket (szükséges matematikai műveletek általában: összeadás, kivonás, szorzás, osztás, átlag- és százalékszámítás), majd össze kell hasonlítanunk a kapott végeredményeket a fejlesztési tervben meghatározott célértékkel, korábbi eredménnyel, mások eredményével (elvégzendő művelet: két érték között a kisebb, nagyobb, egyenlő reláció megállapítása). De: néhány egyéni, eseti jó/rossz eredmény alapján még nem biztos, hogy valóban általánosítható, ténylegesen a programról szóló információkat kapunk. Az előzőnél bonyolultabb matematikai statisztikai feladat előtt állunk akkor, ha nem egy adott gyermek fejlesztésének a hatékonyságáról, hanem magának a fejlesztő programnak a hatásáról kívánunk képet alkotni. Egyrészt ez olyan esetben történhet meg, amikor ugyanolyan fejlesztési terv alapján megvalósult sok egyéni/csoportos fejlesztés eredményének összesítése után szeretnénk a program eredményességére következtetni. Másrészt, ha egy adott tulajdonságokkal rendelkező csoport (nevezzük ezt a csoportot: vizsgálati csoportnak vagy mintának!) vizsgálati eredményei alapján szeretnénk következtetni arra, hogy a hasonló adottságokkal rendelkező többi személyre (egy szóval: a populáció -ra) is általánosíthatók lehetnek-e a fejlesztő program hatásáról szóló megállapításaink. Ilyen esetekben tehát statisztikai következtetéseket kell tennünk (Bolla és Krámli, 2012; Obádovics, 2003). A fejlesztőprogramok hatásvizsgálata alkalmával arra vagyunk kíváncsiak, hogy a program következtében jelentős különbség adódik-e két vizsgálat eredményei között - pl. az elő- és utóvizsgálat(ok) és/vagy a fejlesztésbe különböző módon bevont csoportok eredményei, vagy ezen eredmények változásai között -, illetve egy vizsgálat és egy általunk meghatározott kritériumszint (pl. tehetségküszöb vagy a fejlesztési célban meghatározott érték) között. Az ilyen összehasonlításokat összefoglaló néven különbségvizsgálatoknak nevezzük. 70
3 Ha a kapott különbség, eltérés jelentős (tudományosan fogalmazva szignifikáns), akkor nagy valószínűséggel valós hatást jeleznek. Ellenkező esetben a kapott eltérések véletlenszerű, eseti jelenségnek tekinthetők, melyek semmit sem bizonyítanak. A továbbiakban vegyük szemügyre közelebbről a minta, a populáció, a változó, a skála, a statisztikai próba, a leíró statisztika és a matematikai statisztika, a hipotézisvizsgálat és a szignifikancia, a különbségvizsgálat és a kapcsolatvizsgálat fogalmát! Minta és populáció Egy konkrét fejlesztőprogram hatásvizsgálata kapcsán elsősorban az érdekli a szervezőket és a résztvevőket, hogy a programban résztvevő személyek milyen eredményt értek el. Más esetben például a fejlesztőprogram tágabb értelemben vett tudományos jellegű hatásvizsgálata során arra a kérdésre is szeretnénk választ kapni, hogy amennyiben a programban résztvevőket egy nagyobb közösség (populáció) tipikus képviselőinek tekintjük, akkor általánosítható-e a populációra (vagyis a nagy többségre) a résztvevők eredményei alapján kirajzolódó kép. A kérdésfeltevéseink utóbbi típusa tehát az emberek tágabb körére vonatkozik, mint azokra, akikről adatokat tudunk gyűjteni. Ha egy fejlesztőmódszer hatékonyságát vizsgáljuk egy csoportban, valójában azt kérdezzük, a csoporttagokra általában, vagy bizonyos csoporttagokra általában miként hat ez a módszer? Ebben az esetben tehát nem a konkrét csoport érdekel minket, hanem a módszernek egy bizonyos népességre gyakorolt hatása. Ezt a szélesebb népességet szokás populációnak nevezni, a konkrétan megvizsgált személyeket pedig mintának. Fontos megérteni, hogy a statisztikai eljárások mindig a mintát vizsgálják, de a populációról kívánnak állításokat megfogalmazni. Ez az általánosítás statisztikailag akkor megalapozott, ha a minta a releváns változók tekintetében hasonló a populációhoz (vö.: 1. ábra). 1. ábra: a populáció és a minta két lehetséges viszonya (Forrás: Mező, Máth és Abari, 2008) Változók, skálák és statisztikai próbák Ha emberek tulajdonságaival kapcsolatban mint pl. nem, életkor, kreativitás, IQ, agresszió, feladatmegoldás pontszáma, irodalom jegy méréseket végzünk, akkor a mért tulajdonságokat változóknak szokás nevezni. E változók megítélhetők abból a szempontból is, 71
4 hogy a lehetséges értékeik mennyire rendelkeznek a számok tulajdonságaival. Ez alapján mondhatjuk egy változóról, hogy nominális, ordinális vagy kvantitatív skálát képvisel: Nominális skála esetén a lehetséges értékek között nem értelmezhető a kisebb/nagyobb fogalma sem, így sorrend sem kínálkozik közöttük. Példa lehet nominális változóra diákok esetén a kedvenc tantárgyuk. Ordinális skála esetén a lehetséges értékek között van sorrend, de ezen értékek különbsége nem értelmezhető. Példaként tekintsük az iskolai végzettséget a következő 4 értékkel: legfeljebb 8 általános, szakmunkásképző, érettségi, felsőfokú végzettség. Bár a végzettség fokozatai egyértelműen sorba rakhatók, az nem jelenthető ki, hogy a főiskola éppen annyival jelent magasabb végzettséget az érettséginél, mint a szakmunkásképző a 8 általánosnál. Valójában a kérdés ennyiből nem is értelmezhető. További példák ordinális változóra: a diákoknak rangsorolni kell, hogy adott dolog hol helyezkedik el számukra egy fontossági sorban, vagy hogy mekkora erőfeszítést tesznek egy ügy érdekében és a lehetséges választások pl. a következők: semmilyet, épphogy csak, amennyit szükséges, mindent beleadok. Egy másik példa, hogy a diákok órai teljesítményét a következő fokozatokkal ítélik meg: gyenge, megfelelő, kiváló. Kvantitatív (vagy: Intervallum) skáláról akkor beszélünk, ha a változó értékei között nem csak a sorrend értelmes, de ezen értékek különbsége is értelmezhető. Az ilyen változókat kvantitatívnak is szokás nevezni. Ilyennek tekinthető pl. a legtöbb teljesítményteszt, képességteszt (pl. IQ teszt), ami tehát azzal a plusz tulajdonsággal jár, hogy kijelenthetjük: a 120 pont éppen annyival jobb eredmény a 100-nál, mint a 140 a 120-nál. A változók egy másik szempont szerint lehetnek diszkrétek és folytonosak. A diszkrét változó lehetséges értékei jól elkülönülnek egymástól, mint például a kedvenc tantárgy vagy az iskolai végzettség. Az olyan változót, amely eredendően folytonos jelenséget mér és a lehetséges értékei között kellően kicsi különbség van (vagyis a mérés kellő pontossággal rendelkezik), folytonosnak nevezzük. Például a legtöbb IQ teszt folytonosnak tekinthető, mert az intelligencia (vélhetően) folytonos és a mérés kellően árnyalt. Ugyanakkor nem folytonos az intelligenciának az a mérése, ahol csak átlag alatti, átlagos és átlag feletti kategóriákat használjuk. A folytonosság kérdése azért fontos, mert ha egy változó legalább ordinális, általában egyszerűbb és hatékonyabb az elemzés, ha a változót folytonosnak tekinthetjük. Minél finomabb a skála, annál inkább megtehetjük ezt. A statisztikai gyakorlatban az ötfokú skálákra már szokták alkalmazni a folytonos változókra vonatkozó eljárásokat. Leíró és matematikai statisztikák A leíró statisztikák a minták számszerű jellemzésére valók. A minta közepét (kvantitatív változó esetén) általában az átlaggal vagy (legalább ordinális változó esetén) a mediánnal szokás megragadni. A minta átlaga az, amit mindenki ért ezen: a minta értékeinek átlagát. A medián talán rövid magyarázatra szorul. Némi leegyszerűsítéssel azt az értéket jelenti, amely megfelezi a mintát abban az értelemben, hogy annyi érték van felette, mint alatta. Ha pl. 5 diák IQ értékei: 80, 86, 101, 140, 90, akkor ennek az 5 elemű mintának a mediánja 90 (két érték a 80 és a 86 kisebb, mint 90; két érték a 101 és a 140 pedig nagyobb, mint 90). Ha a mintát 6 eleműre bővítjük: 80, 85, 101, 140, 90, 70, akkor a medián (a növekvő sorrendbe állított 70, 80, 85, 86, 90, 101, 140 számsor) a két középső értékének, vagyis a 86- nak és a 90-nek az átlaga, tehát: 88. Az átlag intervallum skálák esetén használatos, míg a medián csupán ordinális skálát igényel (Falus és Ollé, 2000; Szűcs, 2002). Gyakran felmerül a közép körüli ingadozás nagysága. Ennek leggyakoribb mérőszáma a szórás. Némi leegyszerűsítéssel azt mondhatjuk, a szórás az átlagtól való eltérésnek egy olyan középértéke, ami közel áll az átlaghoz: az átlagtól való átlagos eltérés. 72
5 A matematikai statisztikai eljárások a leíró statisztikák adatait felhasználó, illetve azok alapján megválasztható számítások (Vargha, 2000). A vizsgálatok egy része olyan eszközökkel (tesztek, feladatsorok, osztályzatok) történik, melyek lehetséges értékei kvantitatívskálát képviselnek és lényegében folytonosak is (vagyis elég finom beosztásúak). Itt a további elemzés azon múlik, hogy a minta eloszlása normálisnak tekinthető-e? Ha igen, akkor az átlagok eltérését vizsgáló eljárások (t-próbák, varianciaanalízis) alkalmazhatók, melyek a legerősebb eszközök a különböző (csoportok közötti, időpontok közötti) eltérések kimutatására. A normalitás vizsgálata (többek között) a Shapiro-Wilk-próba segítségével történhet. Ha a Shapiro-Wilk-próba eredményeként kapott szignifikancia érték (p-value) 0,05 alatt van, akkor a normalitást el szokás vetni. A 2. ábrán néhány példát láthatunk, ahol az első minta még normálisnak tekinthető, a második kettő már nem. (Megjegyezzük, hogy a varianciaanalízis nem túlságosan érzékeny a normalitás hiányára, ezért ha az említett p-value néhány századdal 0,05 alatt marad, a varianciaanalízis által adott eredmények még jól használhatók) Ha azt kaptuk, hogy a normalitás nem áll fenn, vagy a skála ordinális, akkor az ún. rangokon alapuló eljárásokat alkalmazhatjuk pl. (Wilcoxon-próba), melyek az adatok tényleges értéke helyett a nagysági sorrendben elfoglalt helyükkel számol. Némi leegyszerűsítéssel azt mondhatjuk, itt az átlagok helyett a mediánok eltérését vizsgálják. Ha a minta (csoportonkénti) eloszlása a 2. ábra nem normális eloszlást mutató eseteiben látható eloszlásnál is csúnyább képet mutat (pl. több púpja van), érdemes statisztikussal konzultálni (kapcsolat: mert sok minden lehet a dolog hátterében. 2. ábra: példák normális és nem normális eloszlásra (Forrás: Mező, Máth és Abari, 2008) F re q u e n c y F re q u e n c y F re q u e n c y Shapiro-Wilk normality test data: y1 W = p-value = y Shapiro-Wilk normality test data: y2 W = p-value = y Shapiro-Wilk normality test data: y3 W = , p-value = y2 Eloszlás: normális Eloszlás: nem normális Eloszlás: nem normális Az is lehetséges, hogy a mérés nominális skálán történik. Hatásvizsgálatokban talán a kétértékű nominális változó fordul elő leggyakrabban, melynek tipikus példája az igen/nem, a siker/kudarc, fiú/lány. Kétértékű változók esetén több eljárás kínálkozik a fejlődés detektálására, de többértékű esetben is vizsgálható a változás. Ha több csoportot egyszerre vizsgálunk, a változások értelmezése bonyolulttá válik, melynek elméleti hátterét a loglineáris elemzés adja. Ennek ismertetése túlmutat e mű keretein (Máth, 2004). A matematikai statisztikai vizsgálatok két átfogóbb csoportját képezik a különbségvizsgálatok, illetve a kapcsolatvizsgálatok. Amíg az előzőek összehasonlítanak egy vagy több adatsort, addig az utóbbiak az adatsorok közötti bejósolhatóságot, együtt járást vizsgálják. 73
6 Hipotézisvizsgálat A hipotézisvizsgálat lényege, hogy legalább két versengő hipotézis között (H 0 és H 1 hipotézis) kell döntenünk (Borovkov, 2012). H 0 (más szóval: nullhipotézis) jelentése: az eltérés (a csoportok, időpontok között) nem jelentős, véletlenszerű, csak a vizsgált mintában van jelen, az egész populáció esetében már nem áll fenn. H 1 jelentése: az eltérés a véletlent meghaladó, lényeges különbség, az egész populációra vonatkozó, azaz szignifikáns. A szignifikancia annak a valószínűségét jelenti, hogy a kapott (vagy annál is nagyobb) eltérés H 0 esetén is bekövetkezhet. Minél kisebb a szignifikancia, annál nagyobb meglepetést jelent az adott eltérés H 0 -t feltételezve. A pedagógiai kutatásokban a 0,05-nél kisebb szignifikanciaérték (a továbbiakban: p-érték vagy p-value) esetén szokás úgy dönteni, hogy H 1 -et választjuk, vagyis hogy a kapott eltérés lényeges, nem a véletlen műve, azaz szignifikáns (2. ábra). 2. ábra: a szignifikancia értékének (a p-értéknek az) értelmezési lehetőségei HA a szignifikanciát számszerűsítő p-érték (p-value) = 0 0,05 1 AKKOR: Mekkora a valószínűsége, hogy véletlen folytán legalább ekkora különbség keletkezzen két vizsgálati eredmény között (feltéve, hogy a módszer teljesen hatástalan)? 0% - 5% 100% Mekkora a valószínűsége (=1-p), hogy véletlen esetén legfeljebb ekkora különbség mutatkozik (feltéve, hogy a módszer teljesen hatástalan)? 100% 95 % 0% Az eredmény szignifikáns? IGEN NEM H 0 (=a különbség nem jelentős, véletlenszerű, csak a vizsgált mintában van jelen, a populációra nem érvényes) igaz? NEM IGEN H 1 (=a különbség jelentős, a populáció egészére is érvényes, nemcsak a mintára) igaz? IGEN NEM Példaként tegyük fel, arra vagyunk kíváncsiak, hogy egy csoport év végi átlagteljesítménye (55,6) fejlődést mutat-e az év elejivel (52,7) összevetve egy képzeletbeli tesztben? A szignifikanciavizsgálat eredménye lehet: a szignifikancia értéke (a p-érték) 1: ez arra utal, hogy a két átlag hajszálra megegyezik és semmi okunk bármilyen fejlődésre gyanakodni. a kapott szignifikancia érték (p-érték) nagyobb, mint 0,05. Ha például: p=0,16, ez azt jelenti, hogy ekkora (vagyis 55,6-52,7=2,9 pontos) vagy ennél is nagyobb eltérés 0,16 (azaz 16%-os) valószínűséggel akkor is előfordulhat, ha valójában semmilyen érdemi változás nem történt a csoportban, ezért ebben az esetben nem tudtuk igazolni, hogy fejlődés történt volna: tehát az eltérés nem szignifikáns. a kapott szignifikancia érték (p-érték) kisebb 0,05 vagy pontosan 0,05. Például: ha p=0,02, akkor kijelenthetjük, érdemi fejlődés áll fenn, az év eleji és az év végi vizsgálat eredményei között az eltérés szignifikáns. Meg kell jegyezni, hogy a hipotézisvizsgálat logikája sem zárja ki a tévedés lehetőségét. Példánknál maradva előfordulhat, hogy a csoport noha semmit sem fejlődött mégis szignifikánsan jobban teljesít, mert az első mérés eredménye volt túl rossz (pl. a vizsgálati személyek mással voltak elfoglalva a méréskor) vagy a második túl jó (pl. könnyűek voltak a 74
7 feladatok, jó napot fogtak ki, stb ). Ilyenkor tévesen H 1 et választjuk. E hiba elkövetésének valószínűségét maximalizálja a 0,05-ös szint. Ennek az ellenkezője is megeshet, amikor tényleges fejlődés van az osztályban, de az első mérés sikerült túl jól vagy a második túl rosszul és az átlagok nem térnek el eléggé. Ebben az esetben tévesen azt mondjuk, nem tudtunk érdemi, azaz szignifikáns fejlődést kimutatni. Különösen nagy e hiba esélye akkor, ha túl kicsi a vizsgált minta és/vagy túl kicsi a kapott eltérés és/vagy túl nagy a mérés hibája. Különbségvizsgálatok A különbségvizsgálatokon alapuló hatásvizsgálatok kilenc jellegzetes esetét különböztethetjük meg aszerint, hogy hány csoportról hány alkalommal nyert eredményeket vetjük össze egymással (1. táblázat). 1. táblázat: A legalapvetőbb különbségvizsgálatokra vonatkozó példák Vizsgált csoportok száma Egy vizsgálat: Két vizsgálat: elő- és utóvizsgálat Több vizsgálat: nyomon követéses vizsgálat 1 Pl.: egy fejlesztőprogramba bevont csoport 2015-ben nyújtott teljesítménye különbözik-e egy meghatározott (pl. fejlesztési tervben kitűzött) célértéktől? Pl.: a fejlesztőprogramba bevont csoport program előtti (pl ös) és utáni (pl ös) teljesítménye különbözik-e egymástól? Pl.: a fejlesztett csoport ben, 2010-ben, 2015-ben stb. nyújtott teljesítménye különbözik-e egymástól? 2 Pl.: a fejlesztett (vizsgálati) csoport 2015-ös teljesítménye különbözik egy fejlesztésbe be nem vont (kontroll-)csoport teljesítményétől? Pl.: a fejlesztőprogramba bevont csoport és a kontrollcsoport teljesítménye különbözik-e önmagától, illetve egymástól program előtt (pl ben) és után (pl ben) ill. az esetleges változás mértéke eltér-e a két csoportban? Pl.: a fejlesztőprogramba bevont csoport és a kontrollcsoport teljesítménye különbözik-e önmagától, illetve egymástól a program előtt (pl ben) és után (pl ben), s a további években (2015-ben stb.) ill. az esetleges változás görbéje eltér-e a két csoportban? 3 vagy több Pl.: a különböző fejlesztésben részesülő csoportok teljesítménye különböző 2015-ben? Pl.: a csoportok teljesítménye különbözik-e a saját, illetve a többi csoport teljesítményétől a program előtt (pl ben) és után (pl ben) ill. az esetleges változás mértéke eltére az egyes csoportokban? Pl.: a csoportok teljesítménye különbözik-e a saját, illetve a többi csoport teljesítményétől a program előtt (pl ben) és után (pl ben), s a további években (2015-ben stb.) ill. az esetleges változás görbéje eltér-e a az egyes csoportokban? A különbségvizsgálatokban résztvevő minták jellegzetességei alapján egymintás, összetartozó mintás, illetve független mintás eseteket különböztethetünk meg. Egymintás különbségvizsgálatról van szó abban az esetben, ha egy csoport eredményét egy (pl. fejlesztési tervben) kitűzött célértékhez (kritériumszinthez) hasonlítjuk. Összetartozó mintás vizsgálatoknak tekinthetjük azokat a helyzeteket, amelyek alkalmával ugyanannak a mintának két (e speciális esetben: páros vagy paired vizsgálat megnevezéssel is találkozhatunk) vagy több 75
8 adatgyűjtés során nyert eredményeit vetjük össze egymással. A független minták összehasonlításakor két vagy több csoport teljesítményét hasonlítjuk össze azonos változó(k) mentén ilyen változók lehetnek például: IQ, szófluencia stb.. Kapcsolatvizsgálatok Fejlesztőprogramok hatásvizsgálata során felmerülhet annak igénye is, hogy a vizsgálatok során gyűjtött adatok közötti összefüggéseket (például két változó közötti egyenes/fordított arányosságot, együtt járást stb.) is feltárjuk. Ez történik olyan esetekben, amikor arra keressük a választ, hogy az egyik változó (például: általános intelligencia, motoros fejlettség, kreativitás stb.) értékének növekedése esetén a másik változó (például önértékelés önismeret, tanulmányi átlag stb.) értéke vajon szisztematikusan nő, csökken, vagy teljesen bejósolhatatlanul változik-e. A kapcsolatvizsgálatok alkalmazásakor tehát arra vagyunk kíváncsiak, hogy egy(néhány) változó aktuális értékének ismeretében érvényes és megbízható következtetéseket tehetünk-e más változó(k) értékére. Ha csak két változó kapcsolatát vizsgáljuk, akkor a leggyakrabban használt mutatók folytonos változók esetén (tehát ha a teljesítményt egy árnyalt pontszámmal mérjük) a Pearson-féle és a Spearman-féle korreláció, illetve az egyváltozós regressziószámítás. Ha a mérésünk csak néhány fokozatot jelent, esetleg csak nominális skálán mérünk (tehát a lehetséges értékek még sorban sem rendezhetők), akkor használhatjuk a Kendall tau-b mutatót, vagy a Khi-négyzet próbával együtt a lambda együtthatót. Ha egyszerre több változónk is van, melyekből következtetni kívánunk a megfelelő, teljesítmény változóra (például önértékelés önismeret, tanulmányi átlag), akkor a következő többváltozós eljárásokat alkalmazhatjuk (vö.: Vargha, 2000): Parciális korrelációszámítás; Többváltozós lineáris regressziószámítás; Diszkriminancia analízis; Logisztikus regressziószámítás. A kapcsolatvizsgálatok sajátos esete a faktoranalízis, amikor nagy számú vizsgálati változónk mögött meghúzódó (rejtett, latens módon megnyilvánuló) háttérváltozókat keresünk. Zárógondolatok A fentiekben áttekintettük néhány jellegzetes esetét és alapfogalmát a bizonyítékokon alapuló hatásvizsgálatok matematikai statisztikai világának. A matematikai statisztikai számítások végrehajtására napjainkban már szoftverek is rendelkezésre állnak - ezek többsége azonban olyan összegbe kerül, hogy megvásárlásuk sokszor intézményi szinten is kihívást jelenthet. Utolérhetők azonban az internetről ingyenesen letölthető, matematikai statisztikai számítások végzésére alkalmas programcsomagok is. Az egyik ilyen ingyenesen elérhető, sokoldalú és magyar nyelven is utolérhető szakirodalmi segédletekkel (Abari, 2008; Mező, Máth és Abari, 2008; Solymosi, 2005) rendelkező szoftver az úgynevezett R-nyelv. E lap következő számaiban igyekszünk közzé tenni a jövőben az R-nyelvvel és a hatásvizsgálatokkal kapcsolatos további módszertani tanulmányokat, amelyeket ezúton is ajánlunk az érdeklődők figyelmébe! Irodalom Abari K. (2008): A tehetségdiagnosztika adatkezelésbeli alapjai R környezetben. In Mező F. (szerk.): Tehetségdiagnosztika. Kocka Kör & Faculty of Central European Studies, Constantine the Philosopher University in Nitra, Debrecen. pp
9 Berényi Marianne - Katona Ferenc (2013): Fejlesztések és terápiák. Fogalomzavar, vagy vetélkedés a mindennapokért? Gyógypedagógiai Szemle, 2013, XLI. évf. 3., Bolla M. és Krámli A. (2012): Statisztikai következtetések elmélete. Typotex Kiadó, Budapest. Borovkov, A. A. (2012): Matematikai statisztika. Paraméterek becslése, hipotézisvizsgálat. Typotex, Budapest. Falus I. és Ollé J. (2000): Statisztikai módszerek pedagógusok számára. Okker Kiadói Kft., Budapest. Guyatt, G., Cook, D. és Haynes, B. (2004): Evidence based medicine has come a long way. BMJ, Oct (7473), Mező F., Máth J. és Abari K. (2008): A különbségvizsgálatokon alapuló tehetségdiagnosztika matematikai statisztikai alapjai (adatelemzési útmutató). In Mező F. (Szerk.): Tehetségdiagnosztika. Kocka Kör & Faculty of Central European Studies, Constantine the Philosopher University in Nitra, Debrecen. pp Obádovics J. Gy. (2003): Valószínűségszámítás és matematikai statisztika. Scolar Kiadó, Budapest. Solymosi N. (2005): R<- erre, erre! Internetes R-jegyzet. Letöltés: Web: Szűcs István (2002): Alkalmazott statisztika. Agroinform Kiadó, Budapest. Vargha A. (2000): Matematikai statisztika pszichológiai, nyelvészeti és biológiai alkalmazásokkal. Pólya Kiadó, Budapest. 77
FEJLESZTŐPROGRAMOK EGYMINTÁS, KRITÉRIUMORIENTÁLT HATÁSVIZSGÁLATÁNAK MATEMATIKAI STATISZTIKAI HÁTTERE
 FEJLESZTŐPROGRAMOK EGYMINTÁS, KRITÉRIUMORIENTÁLT HATÁSVIZSGÁLATÁNAK MATEMATIKAI STATISZTIKAI HÁTTERE Szerzők: Mező Ferenc Debreceni Egyetem Máth János Debreceni Egyetem Abari Kálmán Debreceni Egyetem Mező
FEJLESZTŐPROGRAMOK EGYMINTÁS, KRITÉRIUMORIENTÁLT HATÁSVIZSGÁLATÁNAK MATEMATIKAI STATISZTIKAI HÁTTERE Szerzők: Mező Ferenc Debreceni Egyetem Máth János Debreceni Egyetem Abari Kálmán Debreceni Egyetem Mező
Matematikai statisztikai elemzések 2.
 Matematikai statisztikai elemzések 2. Helyzetmutatók, átlagok, kvantilisek. A szórás és szóródás Prof. Dr. Závoti, József Matematikai statisztikai elemzések 2.: Helyzetmutatók, átlagok, Prof. Dr. Závoti,
Matematikai statisztikai elemzések 2. Helyzetmutatók, átlagok, kvantilisek. A szórás és szóródás Prof. Dr. Závoti, József Matematikai statisztikai elemzések 2.: Helyzetmutatók, átlagok, Prof. Dr. Závoti,
Turmezeyné Dr. Heller Erika (2012): A zenei tehetség azonosításának rendszere, módszerei. Parlando, 54(2),
 Turmezeyné Dr. Heller Erika (2012): A zenei tehetség azonosításának rendszere, módszerei. Parlando, 54(2), A ZENEI TEHETSÉG AZONOSÍTÁSÁNAK RENDSZERE, MÓDSZEREI A tehetséggondozó, -fejlesztő programokra
Turmezeyné Dr. Heller Erika (2012): A zenei tehetség azonosításának rendszere, módszerei. Parlando, 54(2), A ZENEI TEHETSÉG AZONOSÍTÁSÁNAK RENDSZERE, MÓDSZEREI A tehetséggondozó, -fejlesztő programokra
Általános statisztika II. Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László
 Általános statisztika II Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László Általános statisztika II Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László Publication
Általános statisztika II Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László Általános statisztika II Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László Publication
Elméleti összefoglalók dr. Kovács Péter
 Elméleti összefoglalók dr. Kovács Péter 1. Adatállományok létrehozása, kezelése... 2 2. Leíró statisztikai eljárások... 3 3. Várható értékek (átlagok) vizsgálatára irányuló próbák... 5 4. Eloszlások vizsgálata...
Elméleti összefoglalók dr. Kovács Péter 1. Adatállományok létrehozása, kezelése... 2 2. Leíró statisztikai eljárások... 3 3. Várható értékek (átlagok) vizsgálatára irányuló próbák... 5 4. Eloszlások vizsgálata...
KIFEJEZÉSE: A GAMMA KOEFFICIENS. Csapó Benő Szegedi Tudományegyetem, Neveléstudományi Tanszék MTA-SZTE Képességkutató Csoport
 MAGYAR PEDAGÓGIA 102. évf. 3. szám 391 410. (2002) A KÉPESSÉGEK FEJLŐDÉSI ÜTEMÉNEK EGYSÉGES KIFEJEZÉSE: A GAMMA KOEFFICIENS Csapó Benő Szegedi Tudományegyetem, Neveléstudományi Tanszék MTA-SZTE Képességkutató
MAGYAR PEDAGÓGIA 102. évf. 3. szám 391 410. (2002) A KÉPESSÉGEK FEJLŐDÉSI ÜTEMÉNEK EGYSÉGES KIFEJEZÉSE: A GAMMA KOEFFICIENS Csapó Benő Szegedi Tudományegyetem, Neveléstudományi Tanszék MTA-SZTE Képességkutató
A KÜLÖNLEGES BÁNÁSMÓD DIAGNOSZTIKAI ÉS FEJLESZTÉSI CENTRUM KUTATÓMŰHELY BEMUTATÁSA
 A KÜLÖNLEGES BÁNÁSMÓD DIAGNOSZTIKAI ÉS FEJLESZTÉSI CENTRUM KUTATÓMŰHELY BEMUTATÁSA Szerzők: Mező Ferenc Mező Katalin Lektorok: Szabó Edina Szilágyi Barnabás Schréder Veronika Első szerző e-mail címe: mezo.ferenc@ped.unideb.hu
A KÜLÖNLEGES BÁNÁSMÓD DIAGNOSZTIKAI ÉS FEJLESZTÉSI CENTRUM KUTATÓMŰHELY BEMUTATÁSA Szerzők: Mező Ferenc Mező Katalin Lektorok: Szabó Edina Szilágyi Barnabás Schréder Veronika Első szerző e-mail címe: mezo.ferenc@ped.unideb.hu
Ittfoglalomösszea legfontosabbtudnivalókat, részleteka honlapon, illetvea gyakorlatvezetőtől is kaptok információkat.
 1 Ittfoglalomösszea legfontosabbtudnivalókat, részleteka honlapon, illetvea gyakorlatvezetőtől is kaptok információkat. A statisztika tanulásához a legtöbb infomrációkat az előadásokon és számítógépes
1 Ittfoglalomösszea legfontosabbtudnivalókat, részleteka honlapon, illetvea gyakorlatvezetőtől is kaptok információkat. A statisztika tanulásához a legtöbb infomrációkat az előadásokon és számítógépes
Nyugat-magyarországi Egyetem Geoinformatikai Kara. Prof. Dr. Závoti József. Matematika III. 6. MA3-6 modul. A statisztika alapfogalmai
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Prof. Dr. Závoti József Matematika III. 6. MA3-6 modul A statisztika alapfogalmai SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról szóló 1999.
Nyugat-magyarországi Egyetem Geoinformatikai Kara Prof. Dr. Závoti József Matematika III. 6. MA3-6 modul A statisztika alapfogalmai SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról szóló 1999.
1/8. Iskolai jelentés. 10.évfolyam matematika
 1/8 2008 Iskolai jelentés 10.évfolyam matematika 2/8 Matematikai kompetenciaterület A fejlesztés célja A kidolgozásra kerülő programcsomagok az alább felsorolt készségek, képességek közül a számlálás,
1/8 2008 Iskolai jelentés 10.évfolyam matematika 2/8 Matematikai kompetenciaterület A fejlesztés célja A kidolgozásra kerülő programcsomagok az alább felsorolt készségek, képességek közül a számlálás,
FELADATMEGOLDÁSI SZOKÁSAINAK VIZSGÁLATA. Baranyai Tünde
 Volume 3, Number 1, 2013 3. kötet, 1. szám, 2013 A SZATMÁRNÉMETI TANÍTÓ- ÉS ÓVÓKÉPZŐS HALLGATÓK FELADATMEGOLDÁSI SZOKÁSAINAK VIZSGÁLATA THE EXAMINATION OF TEACHER TRAINING COLLEGE STUDENTS PROBLEM-SOLVING
Volume 3, Number 1, 2013 3. kötet, 1. szám, 2013 A SZATMÁRNÉMETI TANÍTÓ- ÉS ÓVÓKÉPZŐS HALLGATÓK FELADATMEGOLDÁSI SZOKÁSAINAK VIZSGÁLATA THE EXAMINATION OF TEACHER TRAINING COLLEGE STUDENTS PROBLEM-SOLVING
TAGOZATÁN SATU MARE EXTENSION. Baranyai Tünde, Stark Gabriella
 Volume 3, Number 2, 2013 3. kötet, 2. szám, 2013 PEDAGÓGIAI GYAKORLAT A BBTE SZATMÁRNÉMETI TAGOZATÁN THE EXAMINATION OF PEDAGOGICAL PRACTICE AT THE SATU MARE EXTENSION Baranyai Tünde, Stark Gabriella Abstract:
Volume 3, Number 2, 2013 3. kötet, 2. szám, 2013 PEDAGÓGIAI GYAKORLAT A BBTE SZATMÁRNÉMETI TAGOZATÁN THE EXAMINATION OF PEDAGOGICAL PRACTICE AT THE SATU MARE EXTENSION Baranyai Tünde, Stark Gabriella Abstract:
ÉRTÉKREND VIZSGÁLATA A VONULÓS TŰZOLTÓK KÖRÉBEN
 IV. Évfolyam 1. szám - 2009. március Kozák Mónika Jász-Nagykun-Szolnok Megyei Katasztrófavédelmi Igazgatóság monika.kozak@katved.hu ÉRTÉKREND VIZSGÁLATA A VONULÓS TŰZOLTÓK KÖRÉBEN Absztrakt Tanulmányom
IV. Évfolyam 1. szám - 2009. március Kozák Mónika Jász-Nagykun-Szolnok Megyei Katasztrófavédelmi Igazgatóság monika.kozak@katved.hu ÉRTÉKREND VIZSGÁLATA A VONULÓS TŰZOLTÓK KÖRÉBEN Absztrakt Tanulmányom
Matematika III. 8. A szórás és a szóródás egyéb mérőszámai Prof. Dr. Závoti, József
 Matematika III. 8. A szórás és a szóródás egyéb Prof. Dr. Závoti, József Matematika III. 8. : A szórás és a szóródás egyéb Prof. Dr. Závoti, József Lektor : Bischof, Annamária Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027
Matematika III. 8. A szórás és a szóródás egyéb Prof. Dr. Závoti, József Matematika III. 8. : A szórás és a szóródás egyéb Prof. Dr. Závoti, József Lektor : Bischof, Annamária Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027
Matematikai statisztikai elemzések 1.
 Matematikai statisztikai elemzések 1. A statisztika alapfogalmai, feladatai, Prof. Dr. Závoti, József Matematikai statisztikai elemzések 1.: A statisztika alapfogalmai, feladatai, statisztika, osztályozás,
Matematikai statisztikai elemzések 1. A statisztika alapfogalmai, feladatai, Prof. Dr. Závoti, József Matematikai statisztikai elemzések 1.: A statisztika alapfogalmai, feladatai, statisztika, osztályozás,
Megjelent: Magyar Földrajzi Konferencia tudományos közleményei (CD), Szeged, 2001
 Megjelent: Magyar Földrajzi Konferencia tudományos közleményei (CD), Szeged, 2001 A területi lehatárolások statisztikai következményei A területi lehatárolások statisztikai következményeinek megközelítése
Megjelent: Magyar Földrajzi Konferencia tudományos közleményei (CD), Szeged, 2001 A területi lehatárolások statisztikai következményei A területi lehatárolások statisztikai következményeinek megközelítése
Vargha András PSZICHOLÓGIAI STATISZTIKA DIÓHÉJBAN 1. X.1. táblázat: Egy iskolai bizonyítvány. Magyar irodalom. Biológia Földrajz
 Megjelent: Vargha A. (7). Pszichológiai statisztika dióhéjban. In: Czigler I. és Oláh A. (szerk.), Találkozás a pszichológiával. Osiris Kiadó, Budapest, 7-46. Mi az, hogy statisztika? Vargha András PSZICHOLÓGIAI
Megjelent: Vargha A. (7). Pszichológiai statisztika dióhéjban. In: Czigler I. és Oláh A. (szerk.), Találkozás a pszichológiával. Osiris Kiadó, Budapest, 7-46. Mi az, hogy statisztika? Vargha András PSZICHOLÓGIAI
Reiczigel Jenő, 2006 1
 Reiczigel Jenő, 2006 1 Egytényezős (egyszempontos) varianciaelemzés k független minta (k kezelés vagy k csoport), a célváltozó minden csoportban normális eloszlású, a szórások azonosak, az átlagok vagy
Reiczigel Jenő, 2006 1 Egytényezős (egyszempontos) varianciaelemzés k független minta (k kezelés vagy k csoport), a célváltozó minden csoportban normális eloszlású, a szórások azonosak, az átlagok vagy
Nyugat-magyarországi Egyetem Geoinformatikai Kara. Prof. Dr. Závoti József. Matematika III. 7. MA3-7 modul. Helyzetmutatók, átlagok, kvantilisek
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Prof. Dr. Závoti József Matematika III. 7. MA3-7 modul Helyzetmutatók, átlagok, kvantilisek SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról
Nyugat-magyarországi Egyetem Geoinformatikai Kara Prof. Dr. Závoti József Matematika III. 7. MA3-7 modul Helyzetmutatók, átlagok, kvantilisek SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról
statisztikai menürendszere Dr. Vargha András 2007
 A statisztikai menürendszere Dr. Vargha András 2007 2 tartalomjegyzék 1. Alapok (egymintás elemzések Alapstatisztikák Részletesebb statisztikák számítása Gyakorisági eloszlás, hisztogram készítése Középértékekre
A statisztikai menürendszere Dr. Vargha András 2007 2 tartalomjegyzék 1. Alapok (egymintás elemzések Alapstatisztikák Részletesebb statisztikák számítása Gyakorisági eloszlás, hisztogram készítése Középértékekre
SZOFTVEREK A SORBANÁLLÁSI ELMÉLET OKTATÁSÁBAN
 SZOFTVEREK A SORBANÁLLÁSI ELMÉLET OKTATÁSÁBAN Almási Béla, almasi@math.klte.hu Sztrik János, jsztrik@math.klte.hu KLTE Matematikai és Informatikai Intézet Abstract This paper gives a short review on software
SZOFTVEREK A SORBANÁLLÁSI ELMÉLET OKTATÁSÁBAN Almási Béla, almasi@math.klte.hu Sztrik János, jsztrik@math.klte.hu KLTE Matematikai és Informatikai Intézet Abstract This paper gives a short review on software
A KÖRNYEZETI INNOVÁCIÓK MOZGATÓRUGÓI A HAZAI FELDOLGOZÓIPARBAN EGY VÁLLALATI FELMÉRÉS TANULSÁGAI
 A KÖRNYEZETI INNOVÁCIÓK MOZGATÓRUGÓI A HAZAI FELDOLGOZÓIPARBAN EGY VÁLLALATI FELMÉRÉS TANULSÁGAI Széchy Anna Zilahy Gyula Bevezetés Az innováció, mint versenyképességi tényező a közelmúltban mindinkább
A KÖRNYEZETI INNOVÁCIÓK MOZGATÓRUGÓI A HAZAI FELDOLGOZÓIPARBAN EGY VÁLLALATI FELMÉRÉS TANULSÁGAI Széchy Anna Zilahy Gyula Bevezetés Az innováció, mint versenyképességi tényező a közelmúltban mindinkább
MŰSZAKI TUDOMÁNY AZ ÉSZAK-ALFÖLDI RÉGIÓBAN 2010
 MŰSZAKI TUDOMÁNY AZ ÉSZAK-ALFÖLDI RÉGIÓBAN 2010 KONFERENCIA ELŐADÁSAI Nyíregyháza, 2010. május 19. Szerkesztette: Edited by Pokorádi László Kiadja: Debreceni Akadémiai Bizottság Műszaki Szakbizottsága
MŰSZAKI TUDOMÁNY AZ ÉSZAK-ALFÖLDI RÉGIÓBAN 2010 KONFERENCIA ELŐADÁSAI Nyíregyháza, 2010. május 19. Szerkesztette: Edited by Pokorádi László Kiadja: Debreceni Akadémiai Bizottság Műszaki Szakbizottsága
6. AZ EREDMÉNYEK ÉRTELMEZÉSE
 6. AZ EREDMÉNYEK ÉRTELMEZÉSE A kurzus anyagát felhasználva összeállíthatunk egy kitűnő feladatlapot, de még nem dőlhetünk nyugodtan hátra. Diákjaink teljesítményét még osztályzatokra kell átváltanunk,
6. AZ EREDMÉNYEK ÉRTELMEZÉSE A kurzus anyagát felhasználva összeállíthatunk egy kitűnő feladatlapot, de még nem dőlhetünk nyugodtan hátra. Diákjaink teljesítményét még osztályzatokra kell átváltanunk,
A STRATÉGIAALKOTÁS FOLYAMATA
 BUDAPESTI CORVINUS EGYETEM VÁLLALATGAZDASÁGTAN INTÉZET VERSENYKÉPESSÉG KUTATÓ KÖZPONT Szabó Zsolt Roland: A STRATÉGIAALKOTÁS FOLYAMATA VERSENYBEN A VILÁGGAL 2004 2006 GAZDASÁGI VERSENYKÉPESSÉGÜNK VÁLLALATI
BUDAPESTI CORVINUS EGYETEM VÁLLALATGAZDASÁGTAN INTÉZET VERSENYKÉPESSÉG KUTATÓ KÖZPONT Szabó Zsolt Roland: A STRATÉGIAALKOTÁS FOLYAMATA VERSENYBEN A VILÁGGAL 2004 2006 GAZDASÁGI VERSENYKÉPESSÉGÜNK VÁLLALATI
Dr. Szőke Szilvia Dr. Balogh Péter: Nemparaméteres eljárások
 Dr. Szőke Szilvia Dr. Balogh Péter: Nemparaméteres eljárások Bevezetés A magas mérési szintű változók adataiból számolhatunk átlagot, szórást. Fontos módszerek alapulnak ezeknek a származtatott paramétereknek
Dr. Szőke Szilvia Dr. Balogh Péter: Nemparaméteres eljárások Bevezetés A magas mérési szintű változók adataiból számolhatunk átlagot, szórást. Fontos módszerek alapulnak ezeknek a származtatott paramétereknek
Útmutató szakdolgozatok készítéséhez Ez az útmutató a Szent István Egyetem Alkalmazott Bölcsészeti és Pedagógiai Karán készülő szakdolgozatokkal
 Útmutató szakdolgozatok készítéséhez Ez az útmutató a Szent István Egyetem Alkalmazott Bölcsészeti és Pedagógiai Karán készülő szakdolgozatokkal kapcsolatos formai követelményeket tartalmazza. A dolgozat
Útmutató szakdolgozatok készítéséhez Ez az útmutató a Szent István Egyetem Alkalmazott Bölcsészeti és Pedagógiai Karán készülő szakdolgozatokkal kapcsolatos formai követelményeket tartalmazza. A dolgozat
A nyomási fekély ellátásának vizsgálata a minőségi betegellátás kritériumai szerint
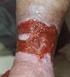 A nyomási fekély ellátásának vizsgálata a minőségi betegellátás kritériumai szerint Doktori értekezés Raskovicsné Csernus Mariann Semmelweis Egyetem Patológiai Tudományok Doktori Iskola Témavezető: Hivatalos
A nyomási fekély ellátásának vizsgálata a minőségi betegellátás kritériumai szerint Doktori értekezés Raskovicsné Csernus Mariann Semmelweis Egyetem Patológiai Tudományok Doktori Iskola Témavezető: Hivatalos
Esetelemzés az SPSS használatával
 Esetelemzés az SPSS használatával A gepj.sav fileban négy különböző típusú, összesen 80 db gépkocsi üzemanyag fogyasztási adatai találhatók. Vizsgálja meg, hogy befolyásolja-e az üzemanyag fogyasztás mértékét
Esetelemzés az SPSS használatával A gepj.sav fileban négy különböző típusú, összesen 80 db gépkocsi üzemanyag fogyasztási adatai találhatók. Vizsgálja meg, hogy befolyásolja-e az üzemanyag fogyasztás mértékét
INTELLIGENS ADATELEMZÉS
 Írta: FOGARASSYNÉ VATHY ÁGNES STARKNÉ WERNER ÁGNES INTELLIGENS ADATELEMZÉS Egyetemi tananyag 2011 COPYRIGHT: 2011 2016, Dr. Fogarassyné Dr. Vathy Ágnes, Pannon Egyetem Műszaki Informatikai Kar Matematika
Írta: FOGARASSYNÉ VATHY ÁGNES STARKNÉ WERNER ÁGNES INTELLIGENS ADATELEMZÉS Egyetemi tananyag 2011 COPYRIGHT: 2011 2016, Dr. Fogarassyné Dr. Vathy Ágnes, Pannon Egyetem Műszaki Informatikai Kar Matematika
MÛHELY. A nemek és generációk jellegzetességei az információs technológiák használatában és megítélésében*
 MÛHELY Nagy Beáta KIREKESZTÉS VAGY BEFOGADÁS? A nemek és generációk jellegzetességei az információs technológiák használatában és megítélésében* Az információs technológiák folyamatos és egyre felgyorsuló
MÛHELY Nagy Beáta KIREKESZTÉS VAGY BEFOGADÁS? A nemek és generációk jellegzetességei az információs technológiák használatában és megítélésében* Az információs technológiák folyamatos és egyre felgyorsuló
TANMENETJAVASLAT AZ ÚJ KERETTANTERVHEZ MATEMATIKA 1. ÉVFOLYAM KÉSZÍTETTÉK: KURUCZNÉ BORBÉLY MÁRTA ÉS VARGA LÍVIA TANKÖNYVSZERZŐK 2013
 TANMENETJAVASLAT AZ ÚJ KERETTANTERVHEZ MATEMATIKA 1. ÉVFOLYAM KÉSZÍTETTÉK: KURUCZNÉ BORBÉLY MÁRTA ÉS VARGA LÍVIA TANKÖNYVSZERZŐK 2013 1 Kedves Kollégák! Tanmenet javaslatunkkal segítséget kívánunk nyújtani
TANMENETJAVASLAT AZ ÚJ KERETTANTERVHEZ MATEMATIKA 1. ÉVFOLYAM KÉSZÍTETTÉK: KURUCZNÉ BORBÉLY MÁRTA ÉS VARGA LÍVIA TANKÖNYVSZERZŐK 2013 1 Kedves Kollégák! Tanmenet javaslatunkkal segítséget kívánunk nyújtani
Országos kompetenciamérés. Országos jelentés
 Országos kompetenciamérés 2009 Országos jelentés Országos jelentés TARTALOMJEGYZÉK JOGSZABÁLYI HÁTTÉR... 7 A 2009. ÉVI ORSZÁGOS KOMPETENCIAMÉRÉS SZÁMOKBAN... 8 A FELMÉRÉSRŐL... 9 EREDMÉNYEK... 11 AJÁNLÁS...
Országos kompetenciamérés 2009 Országos jelentés Országos jelentés TARTALOMJEGYZÉK JOGSZABÁLYI HÁTTÉR... 7 A 2009. ÉVI ORSZÁGOS KOMPETENCIAMÉRÉS SZÁMOKBAN... 8 A FELMÉRÉSRŐL... 9 EREDMÉNYEK... 11 AJÁNLÁS...
Educatio 2013/4 Fehérvári Anikó: Szakiskolások rekrutációja. pp. 516 528.
 Szakiskolások rekrutációja Atársadalmat vizsgáló kutatók egyik célja annak meghatározása, hogy mely társadalmak nyitottabbak, illetve mekkora szerepet játszanak egy-egy társadalomban az öröklött (pl. család)
Szakiskolások rekrutációja Atársadalmat vizsgáló kutatók egyik célja annak meghatározása, hogy mely társadalmak nyitottabbak, illetve mekkora szerepet játszanak egy-egy társadalomban az öröklött (pl. család)
2. MÉRÉSELMÉLETI ISMERETEK
 2. MÉRÉSELMÉLETI ISMERETEK A fejezet célja azoknak a módszereknek a bemutatása, amelyekkel adatokat gyűjthetünk annak érdekében, hogy kérdéseinkre választ kapjunk. Megvizsgáljuk azokat a feltételeket is,
2. MÉRÉSELMÉLETI ISMERETEK A fejezet célja azoknak a módszereknek a bemutatása, amelyekkel adatokat gyűjthetünk annak érdekében, hogy kérdéseinkre választ kapjunk. Megvizsgáljuk azokat a feltételeket is,
II. A következtetési statisztika alapfogalmai
 II. A következtetési statisztika alapfogalmai Tartalom Statisztikai következtetések A véletlen minta fogalma Pontbecslés és hibája Intervallumbecslés A hipotézisvizsgálat alapfogalmai A legegyszerűbb statisztikai
II. A következtetési statisztika alapfogalmai Tartalom Statisztikai következtetések A véletlen minta fogalma Pontbecslés és hibája Intervallumbecslés A hipotézisvizsgálat alapfogalmai A legegyszerűbb statisztikai
11. Matematikai statisztika
 11. Matematikai statisztika 11.1. Alapfogalmak A statisztikai minta valamely valószínűségi változóra vonatkozó véges számú független kisérlet eredménye. Ez véges sok, azonos eloszlású valószínűségi változó
11. Matematikai statisztika 11.1. Alapfogalmak A statisztikai minta valamely valószínűségi változóra vonatkozó véges számú független kisérlet eredménye. Ez véges sok, azonos eloszlású valószínűségi változó
A korai kéttannyelvű oktatás hatása a kisiskolások anyanyelvi szövegértési és helyesírási kompetenciájára
 Gyermeknevelés 4. évf. 1. szám 55 64. (2016) A korai kéttannyelvű oktatás hatása a kisiskolások anyanyelvi szövegértési és helyesírási kompetenciájára Szaszkó Rita Jezsik Kata Szent István Egyetem Alkalmazott
Gyermeknevelés 4. évf. 1. szám 55 64. (2016) A korai kéttannyelvű oktatás hatása a kisiskolások anyanyelvi szövegértési és helyesírási kompetenciájára Szaszkó Rita Jezsik Kata Szent István Egyetem Alkalmazott
Mobilizált kémia. Azaz: lehet-e az okostelefon a kémiatanítás hatékony eszköze?
 Mobilizált kémia. Azaz: lehet-e az okostelefon a kémiatanítás hatékony eszköze? Murányi Zoltán Eszterházy Károly Főiskola Kémiai és Élelmiszerkémiai Tanszék, Eger mzperx@ektf.hu Farkasné Ökrös Marianna
Mobilizált kémia. Azaz: lehet-e az okostelefon a kémiatanítás hatékony eszköze? Murányi Zoltán Eszterházy Károly Főiskola Kémiai és Élelmiszerkémiai Tanszék, Eger mzperx@ektf.hu Farkasné Ökrös Marianna
Kulcsszavak: különleges bánásmód, játék Diszciplinák: pszichológia, pedagógia, gyógypedagógia
 JÁTÉKKAL A KÜLÖNLEGES BÁNÁSMÓDOT IGÉNYLŐ GYERMEKEKÉRT (RECENZIÓ) A recenzió szerzője: Varga Gréta Debreceni Egyetem Lektorok: Mező Katalin Debreceni Egyetem Schéder Veronika Debreceni Egyetem Szilágyi
JÁTÉKKAL A KÜLÖNLEGES BÁNÁSMÓDOT IGÉNYLŐ GYERMEKEKÉRT (RECENZIÓ) A recenzió szerzője: Varga Gréta Debreceni Egyetem Lektorok: Mező Katalin Debreceni Egyetem Schéder Veronika Debreceni Egyetem Szilágyi
A rosszindulatú daganatos halálozás változása 1975 és 2001 között Magyarországon
 A rosszindulatú daganatos halálozás változása és között Eredeti közlemény Gaudi István 1,2, Kásler Miklós 2 1 MTA Számítástechnikai és Automatizálási Kutató Intézete, Budapest 2 Országos Onkológiai Intézet,
A rosszindulatú daganatos halálozás változása és között Eredeti közlemény Gaudi István 1,2, Kásler Miklós 2 1 MTA Számítástechnikai és Automatizálási Kutató Intézete, Budapest 2 Országos Onkológiai Intézet,
Matematikai statisztikai elemzések 6.
 Matematikai statisztikai elemzések 6. Regressziószámítás: kétváltozós lineáris és nemlineáris regresszió, többváltozós regresszió Prof. Dr. Závoti, József Matematikai statisztikai elemzések 6.: Regressziószámítás:
Matematikai statisztikai elemzések 6. Regressziószámítás: kétváltozós lineáris és nemlineáris regresszió, többváltozós regresszió Prof. Dr. Závoti, József Matematikai statisztikai elemzések 6.: Regressziószámítás:
Az agrár-környezetgazdálkodási támogatási rendszer fejlesztési lehetőségei (Hogyan tovább agrárkörnyezetgazdálkodás?)
 Természetvédelmi Közlemények 21, pp. 232 242, 2015 Az agrár-környezetgazdálkodási támogatási rendszer fejlesztési lehetőségei (Hogyan tovább agrárkörnyezetgazdálkodás?) Marticsek József 1, Molnár Dániel
Természetvédelmi Közlemények 21, pp. 232 242, 2015 Az agrár-környezetgazdálkodási támogatási rendszer fejlesztési lehetőségei (Hogyan tovább agrárkörnyezetgazdálkodás?) Marticsek József 1, Molnár Dániel
Alapfogalmak áttekintése. Pszichológiai statisztika, 1. alkalom
 Alapfogalmak áttekintése Pszichológiai statisztika, 1. alkalom Hipotézisek Milyen a jó null hipotézis?? H0: Léteznek kitőnı tanuló diszlexiások.? H1: Nem léteznek. Sokkal inkább: H0: Nincs diszlexiás kitőnı
Alapfogalmak áttekintése Pszichológiai statisztika, 1. alkalom Hipotézisek Milyen a jó null hipotézis?? H0: Léteznek kitőnı tanuló diszlexiások.? H1: Nem léteznek. Sokkal inkább: H0: Nincs diszlexiás kitőnı
Gyarmati Dezső Sport Általános Iskola MATEMATIKA HELYI TANTERV 1-4. OSZTÁLY
 Gyarmati Dezső Sport Általános Iskola MATEMATIKA HELYI TANTERV 1-4. OSZTÁLY KÉSZÍTETTE: Bartháné Jáger Ottília, Holndonnerné Zátonyi Katalin, Krivánné Czirba Zsuzsanna, Migléczi Lászlóné MISKOLC 2015 Összesített
Gyarmati Dezső Sport Általános Iskola MATEMATIKA HELYI TANTERV 1-4. OSZTÁLY KÉSZÍTETTE: Bartháné Jáger Ottília, Holndonnerné Zátonyi Katalin, Krivánné Czirba Zsuzsanna, Migléczi Lászlóné MISKOLC 2015 Összesített
VI.9. KÖRÖK. A feladatsor jellemzői
 VI.9. KÖRÖK Tárgy, téma A feladatsor jellemzői A kör területe, arányok változatlansága sokszorozás esetén. Előzmények Cél A kör részeinek területe egyszerű esetben, szimmetriák, a négyzet és átlójának
VI.9. KÖRÖK Tárgy, téma A feladatsor jellemzői A kör területe, arányok változatlansága sokszorozás esetén. Előzmények Cél A kör részeinek területe egyszerű esetben, szimmetriák, a négyzet és átlójának
Könyvszemle. Szakirodalom
 Könyvszemle Pontossági követelmények és varianciabecslés az Európai Statisztikai Rendszer háztartás-statisztikai felvételeihez. Kézikönyv. Handbook on Precision Requirements and Variance Estimation for
Könyvszemle Pontossági követelmények és varianciabecslés az Európai Statisztikai Rendszer háztartás-statisztikai felvételeihez. Kézikönyv. Handbook on Precision Requirements and Variance Estimation for
A hátrányos helyzetű gyermekek tehetséggondozásának rendszerszemléletű megközelítése
 A hátrányos helyzetű gyermekek tehetséggondozásának rendszerszemléletű megközelítése DUDÁS Marianna Nyíregyházi Főiskola Pedagógus Képző Kar, Nyíregyháza dudasm@nyf.hu A hétköznapi életben, a tehetség
A hátrányos helyzetű gyermekek tehetséggondozásának rendszerszemléletű megközelítése DUDÁS Marianna Nyíregyházi Főiskola Pedagógus Képző Kar, Nyíregyháza dudasm@nyf.hu A hétköznapi életben, a tehetség
A nyomon követhetőség fogyasztói megítélése az élelmiszeriparban
 A nyomon követhetőség fogyasztói megítélése az élelmiszeriparban Rózsa Norbert V. évfolyam, gazdasági agrármérnök szak Konzulensek: Dr. Biacs Péter, egyetemi tanár Solymosi Viktor, PhD hallgató Kaposvári
A nyomon követhetőség fogyasztói megítélése az élelmiszeriparban Rózsa Norbert V. évfolyam, gazdasági agrármérnök szak Konzulensek: Dr. Biacs Péter, egyetemi tanár Solymosi Viktor, PhD hallgató Kaposvári
A 49/2011. (IX. 20.) HSZB. határozat 8. számú melléklete
 A 49/2011. (IX. 20.) HSZB. határozat 8. számú melléklete SZONDI GYÖRGY SZAKKÖZÉPISKOLA, SZAKISKOLA ÉS SPECIÁLIS SZAKISKOLA Beszámoló az intézményi minőségirányítási program teljesítéséről a 2010/2011-es
A 49/2011. (IX. 20.) HSZB. határozat 8. számú melléklete SZONDI GYÖRGY SZAKKÖZÉPISKOLA, SZAKISKOLA ÉS SPECIÁLIS SZAKISKOLA Beszámoló az intézményi minőségirányítási program teljesítéséről a 2010/2011-es
MILYEN A JÓ EGÉSZSÉGÜGY?
 FERNEZELYI BORI 1 MILYEN A JÓ EGÉSZSÉGÜGY? Gulácsi László (szerk.) (2012) Egészség-gazdaságtan és technológiaelemzés. Az egészség -gazdaságtani döntéstől a klinikai és finanszírozási döntéshozatalig. Budapest:
FERNEZELYI BORI 1 MILYEN A JÓ EGÉSZSÉGÜGY? Gulácsi László (szerk.) (2012) Egészség-gazdaságtan és technológiaelemzés. Az egészség -gazdaságtani döntéstől a klinikai és finanszírozási döntéshozatalig. Budapest:
STATISZTIKUS TÖRVÉNYSZERŰSÉGEK EGYSZERŰ DEMONSTRÁLÁSA GALTON-DESZKÁVAL SIMPLE DEMONSTRATION OF STATISTICAL LAWS WITH GALTON-BOARD
 STATISZTIKUS TÖRVÉNYSZERŰSÉGEK EGYSZERŰ DEMONSTRÁLÁSA GALTON-DESZKÁVAL SIMPLE DEMONSTRATION OF STATISTICAL LAWS WITH GALTON-BOARD Gyertyán Attila 1, Dr. Juhász András 2 1 ELTE Apáczai Csere János Gyakorlóiskola,
STATISZTIKUS TÖRVÉNYSZERŰSÉGEK EGYSZERŰ DEMONSTRÁLÁSA GALTON-DESZKÁVAL SIMPLE DEMONSTRATION OF STATISTICAL LAWS WITH GALTON-BOARD Gyertyán Attila 1, Dr. Juhász András 2 1 ELTE Apáczai Csere János Gyakorlóiskola,
Kapacitív áramokkal működtetett relés áramkörök 621.316.92S:621.318.B7:S21.3S2.$
 DR. GÁL JÓZSEF Budapesti Műszaki Egyetem Kapacitív áramokkal működtetett relés áramkörök BTO 621.316.92S:621.318.B7:S21.3S2.$ A cikk cím szerinti témáját két, egymástól időben nagyon távoleső kapcsolási
DR. GÁL JÓZSEF Budapesti Műszaki Egyetem Kapacitív áramokkal működtetett relés áramkörök BTO 621.316.92S:621.318.B7:S21.3S2.$ A cikk cím szerinti témáját két, egymástól időben nagyon távoleső kapcsolási
1. A kutatás célja, a munkatervben vállalt kutatási program ismertetése
 1 1. A kutatás célja, a munkatervben vállalt kutatási program ismertetése A kutatás célja a természetgyógyászat néven összefoglalható, alternatív és komplementer gyógyító módszerek (röviden: alternatív
1 1. A kutatás célja, a munkatervben vállalt kutatási program ismertetése A kutatás célja a természetgyógyászat néven összefoglalható, alternatív és komplementer gyógyító módszerek (röviden: alternatív
MARKETING MESTERSZAK Marketingkutatás 5. előadás KÉRDŐÍVSZERKESZTÉS. 2015. 03. 14. Magyar Mária - BME MVT
 MARKETING MESTERSZAK Marketingkutatás 5. előadás KÉRDŐÍVSZERKESZTÉS 2015. 03. 14. Magyar Mária - BME MVT 2 A mai anyag Kérdőívszerkesztés folyamata Kérdőív logikai/szerkezeti felépítése Kérdéstípusok Kérdések
MARKETING MESTERSZAK Marketingkutatás 5. előadás KÉRDŐÍVSZERKESZTÉS 2015. 03. 14. Magyar Mária - BME MVT 2 A mai anyag Kérdőívszerkesztés folyamata Kérdőív logikai/szerkezeti felépítése Kérdéstípusok Kérdések
Mit tapasztaltak a bizottságok a tanári alkalmassági vizsgán?
 Sági Matild Nikitscher Péter Oktatáskutató és Fejlesztő Intézet, tudományos főmunkatárs, PhD Oktatáskutató és Fejlesztő Intézet, kutató-elemző Mit tapasztaltak a bizottságok a tanári alkalmassági vizsgán?
Sági Matild Nikitscher Péter Oktatáskutató és Fejlesztő Intézet, tudományos főmunkatárs, PhD Oktatáskutató és Fejlesztő Intézet, kutató-elemző Mit tapasztaltak a bizottságok a tanári alkalmassági vizsgán?
Vállalkozás alapítás és vállalkozóvá válás kutatás zárójelentés
 TÁMOP-4.2.1-08/1-2008-0002 projekt Vállalkozás alapítás és vállalkozóvá válás kutatás zárójelentés Készítette: Dr. Imreh Szabolcs Dr. Lukovics Miklós A kutatásban részt vett: Dr. Kovács Péter, Prónay Szabolcs,
TÁMOP-4.2.1-08/1-2008-0002 projekt Vállalkozás alapítás és vállalkozóvá válás kutatás zárójelentés Készítette: Dr. Imreh Szabolcs Dr. Lukovics Miklós A kutatásban részt vett: Dr. Kovács Péter, Prónay Szabolcs,
Doktori munka. Solymosi József: NUKLEÁRIS KÖRNYEZETELLENŐRZŐ MÉRŐRENDSZEREK. Alkotás leírása
 Doktori munka Solymosi József: NUKLEÁRIS KÖRNYEZETELLENŐRZŐ MÉRŐRENDSZEREK Alkotás leírása Budapest, 1990. 2 KÖSZÖNETNYILVÁNÍTÁS A doktori munka célja az egyéni eredmény bemutatása. Feltétlenül hangsúlyoznom
Doktori munka Solymosi József: NUKLEÁRIS KÖRNYEZETELLENŐRZŐ MÉRŐRENDSZEREK Alkotás leírása Budapest, 1990. 2 KÖSZÖNETNYILVÁNÍTÁS A doktori munka célja az egyéni eredmény bemutatása. Feltétlenül hangsúlyoznom
TBL05A01 Bevezetés a matematikába. 2 7 m K I.
 TBL05A01 Bevezetés a matematikába 2 7 m K I. CÉL: A matematikatanítás feladatainak, lehetőségeinek megismertetése. A legfontosabb matematikai alapok felfrissítése, a hallgatók matematikai kompetenciájának
TBL05A01 Bevezetés a matematikába 2 7 m K I. CÉL: A matematikatanítás feladatainak, lehetőségeinek megismertetése. A legfontosabb matematikai alapok felfrissítése, a hallgatók matematikai kompetenciájának
GAZDASÁGI STATISZTIKA
 GAZDASÁGI STATISZTIKA Dr. Kun István GÁBOR DÉNES FŐISKOLA Tantárgy: Gazdasági statisztika Kódszám: 224 Lapszám: 1 TÉMAKÖRÖK A STATISZTIKA ALAPFOGALMAI STATISZTIKAI SOROK STATISZTIKAI TÁBLÁK ÖSSZETETT VISZONYSZÁMOK
GAZDASÁGI STATISZTIKA Dr. Kun István GÁBOR DÉNES FŐISKOLA Tantárgy: Gazdasági statisztika Kódszám: 224 Lapszám: 1 TÉMAKÖRÖK A STATISZTIKA ALAPFOGALMAI STATISZTIKAI SOROK STATISZTIKAI TÁBLÁK ÖSSZETETT VISZONYSZÁMOK
1. Katona János publikációs jegyzéke
 1. Katona János publikációs jegyzéke 1.1. Referált, angol nyelvű, nyomtatott publikációk [1] J.KATONA-E.MOLNÁR: Visibility of the higher-dimensional central projection into the projective sphere Típus:
1. Katona János publikációs jegyzéke 1.1. Referált, angol nyelvű, nyomtatott publikációk [1] J.KATONA-E.MOLNÁR: Visibility of the higher-dimensional central projection into the projective sphere Típus:
IT KOCKÁZATOK, ELEMZÉSÜK, KEZELÉSÜK
 Póserné Oláh Valéria Budapesti Műszaki Főiskola NIK, poserne.valeria@nik.bmf.hu IT KOCKÁZATOK, ELEMZÉSÜK, KEZELÉSÜK Absztrakt Napjainkban már a legtöbb szervezet működése elképzelhetetlen informatikai
Póserné Oláh Valéria Budapesti Műszaki Főiskola NIK, poserne.valeria@nik.bmf.hu IT KOCKÁZATOK, ELEMZÉSÜK, KEZELÉSÜK Absztrakt Napjainkban már a legtöbb szervezet működése elképzelhetetlen informatikai
Gyorsjelentés. az informatikai eszközök iskolafejlesztő célú alkalmazásának országos helyzetéről 2011. február 28-án, elemér napján KÉSZÍTETTÉK:
 Gyorsjelentés az informatikai eszközök iskolafejlesztő célú alkalmazásának országos helyzetéről 2011. február 28-án, elemér napján KÉSZÍTETTÉK: Hunya Márta PhD Kőrösné dr. Mikis Márta Tartsayné Németh
Gyorsjelentés az informatikai eszközök iskolafejlesztő célú alkalmazásának országos helyzetéről 2011. február 28-án, elemér napján KÉSZÍTETTÉK: Hunya Márta PhD Kőrösné dr. Mikis Márta Tartsayné Németh
A SZÁMÍTÓGÉPPEL SEGÍTETT VIZSGÁZTATÁS EGY SAJÁT FEJLESZTÉSŰ ALKALMAZÁSA
 A SZÁMÍTÓGÉPPEL SEGÍTETT VIZSGÁZTATÁS EGY SAJÁT FEJLESZTÉSŰ ALKALMAZÁSA Dr. Kadocsa László kadocsa@mail.duf.hu Dunaújvárosi Főiskola Ludik Péter luidikp@mail.duf.hu Dunaújvárosi Főiskola Willinger László
A SZÁMÍTÓGÉPPEL SEGÍTETT VIZSGÁZTATÁS EGY SAJÁT FEJLESZTÉSŰ ALKALMAZÁSA Dr. Kadocsa László kadocsa@mail.duf.hu Dunaújvárosi Főiskola Ludik Péter luidikp@mail.duf.hu Dunaújvárosi Főiskola Willinger László
MARKOLT NORBERT. Alegységszintű vezetők megítélésének pszichológiai dimenziói. Psychological dimension in subunit military leader s assessment
 MARKOLT NORBERT Alegységszintű vezetők megítélésének pszichológiai dimenziói Absztrakt Psychological dimension in subunit military leader s assessment A kutatás célja, az alegységszintű vezetők megítélésében
MARKOLT NORBERT Alegységszintű vezetők megítélésének pszichológiai dimenziói Absztrakt Psychological dimension in subunit military leader s assessment A kutatás célja, az alegységszintű vezetők megítélésében
A csõdelõrejelzés és a nem fizetési valószínûség számításának módszertani kérdéseirõl
 MÛHELY Közgazdasági Szemle, LV. évf., 2008. május (441 461. o.) KRISTÓF TAMÁS A csõdelõrejelzés és a nem fizetési valószínûség számításának módszertani kérdéseirõl A Bázel 2 tõkeegyezmény magyarországi
MÛHELY Közgazdasági Szemle, LV. évf., 2008. május (441 461. o.) KRISTÓF TAMÁS A csõdelõrejelzés és a nem fizetési valószínûség számításának módszertani kérdéseirõl A Bázel 2 tõkeegyezmény magyarországi
A fogyatékossághoz vezetõ út
 07Kende-Nemenyi(1).qxd 2005.02.23. 9:37 Page 199 KENDE ANNA NEMÉNYI MÁRIA A fogyatékossághoz vezetõ út A 2003-as év elsõ felében, az iskolaérettségi vizsgálatok idõszakában kutatást végeztünk beiskolázás
07Kende-Nemenyi(1).qxd 2005.02.23. 9:37 Page 199 KENDE ANNA NEMÉNYI MÁRIA A fogyatékossághoz vezetõ út A 2003-as év elsõ felében, az iskolaérettségi vizsgálatok idõszakában kutatást végeztünk beiskolázás
gyógypedagógus, SZT Bárczi Gusztáv Egységes Gyógypedagógiai Módszertani Intézmény 2
 Iskolakultúra, 25. évfolyam, 2015/4. szám DOI: 10.17543/ISKKULT.2015.4.3 Köböl Erika 1 Vidákovich Tibor 2 1 gyógypedagógus, SZT Bárczi Gusztáv Egységes Gyógypedagógiai Módszertani Intézmény 2 egyetemi
Iskolakultúra, 25. évfolyam, 2015/4. szám DOI: 10.17543/ISKKULT.2015.4.3 Köböl Erika 1 Vidákovich Tibor 2 1 gyógypedagógus, SZT Bárczi Gusztáv Egységes Gyógypedagógiai Módszertani Intézmény 2 egyetemi
Az alábbi áttekintés Délkelet-Európa (a volt Jugoszlávia országai
 OKTATÁSIRÁNYÍTÁS ÉS OKTATÁSPOLITIKA A BALKÁNON Az alábbi áttekintés Délkelet-Európa (a volt Jugoszlávia országai Szlovénia kivételével, Bulgária, Románia és Albánia) oktatási rendszerei előtt álló kihívásokat
OKTATÁSIRÁNYÍTÁS ÉS OKTATÁSPOLITIKA A BALKÁNON Az alábbi áttekintés Délkelet-Európa (a volt Jugoszlávia országai Szlovénia kivételével, Bulgária, Románia és Albánia) oktatási rendszerei előtt álló kihívásokat
Működési kockázati önértékelések veszteségeloszlás-alapú modellezése
 506 HITELINTÉZETI SZEMLE HAJNAL BÉLA KÁLLAI ZOLTÁN NAGY GÁBOR Működési kockázati önértékelések veszteségeloszlás-alapú modellezése Tanulmányunkban a működési kockázatok önértékelésen alapuló modellezését
506 HITELINTÉZETI SZEMLE HAJNAL BÉLA KÁLLAI ZOLTÁN NAGY GÁBOR Működési kockázati önértékelések veszteségeloszlás-alapú modellezése Tanulmányunkban a működési kockázatok önértékelésen alapuló modellezését
Matematikai statisztikai elemzések 5.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Prof. Dr. Závoti József Matematikai statisztikai elemzések. MSTE modul Kapcsolatvizsgálat: asszociáció vegyes kapcsolat korrelációszámítás. Varianciaanalízis
Nyugat-magyarországi Egyetem Geoinformatikai Kara Prof. Dr. Závoti József Matematikai statisztikai elemzések. MSTE modul Kapcsolatvizsgálat: asszociáció vegyes kapcsolat korrelációszámítás. Varianciaanalízis
A foglalkoztatottság és a munkanélküliség szerkezetét befolyásoló társadalmi-területi tényezők
 Forray R. Katalin Híves Tamás A foglalkoztatottság és a munkanélküliség szerkezetét befolyásoló társadalmi-területi tényezők Az OFA/6341/26 sz. kutatási összefoglaló Budapest, 2008. március 31. Oktatáskutató
Forray R. Katalin Híves Tamás A foglalkoztatottság és a munkanélküliség szerkezetét befolyásoló társadalmi-területi tényezők Az OFA/6341/26 sz. kutatási összefoglaló Budapest, 2008. március 31. Oktatáskutató
A közvetett hatások értékelésének lehetőségei
 A közvetett hatások értékelésének lehetőségei Összefoglaló jelentés Készült A VKI végrehajtásának elősegítése II. fázis című projekt keretében Készítették: Marjainé Dr. Szerényi Zsuzsanna Harangozó Gábor
A közvetett hatások értékelésének lehetőségei Összefoglaló jelentés Készült A VKI végrehajtásának elősegítése II. fázis című projekt keretében Készítették: Marjainé Dr. Szerényi Zsuzsanna Harangozó Gábor
KÉPI INFORMÁCIÓK KEZELHETŐSÉGE. Forczek Erzsébet SZTE ÁOK Orvosi Informatikai Intézet. Összefoglaló
 KÉPI INFORMÁCIÓK KEZELHETŐSÉGE Forczek Erzsébet SZTE ÁOK Orvosi Informatikai Intézet Összefoglaló Tanórákon és az önálló tanulás részeként is, az informatika világában a rendelkezésünkre álló óriási mennyiségű
KÉPI INFORMÁCIÓK KEZELHETŐSÉGE Forczek Erzsébet SZTE ÁOK Orvosi Informatikai Intézet Összefoglaló Tanórákon és az önálló tanulás részeként is, az informatika világában a rendelkezésünkre álló óriási mennyiségű
AZ I990 - ES ÉVEK ELEJÉN AZ ÁLLAMI tankönyvkiadás monopóliumát gyors ütemben
 TANKÖNYVRENDELÉS AZ I990 - ES ÉVEK ELEJÉN AZ ÁLLAMI tankönyvkiadás monopóliumát gyors ütemben váltotta fel a "kvázi" piaci alapú kiadás és értékesítés (kvázi piac, hiszen nem pusztán az eladó és a fogyasztó,
TANKÖNYVRENDELÉS AZ I990 - ES ÉVEK ELEJÉN AZ ÁLLAMI tankönyvkiadás monopóliumát gyors ütemben váltotta fel a "kvázi" piaci alapú kiadás és értékesítés (kvázi piac, hiszen nem pusztán az eladó és a fogyasztó,
Vezetői információs rendszerek
 Vezetői információs rendszerek 7. előadás: Stratégiai menedzsment és informatikai támogatás 2. Elekes Edit, 2015. E-mail: elekes.edit@eng.unideb.hu Anyagok: eng.unideb.hu/userdir/elekes Edit/Vezetoi_inf_rd
Vezetői információs rendszerek 7. előadás: Stratégiai menedzsment és informatikai támogatás 2. Elekes Edit, 2015. E-mail: elekes.edit@eng.unideb.hu Anyagok: eng.unideb.hu/userdir/elekes Edit/Vezetoi_inf_rd
Educatio 2013/4 Forray R. Katalin & Híves Tamás: Az iskolázottság térszerkezete, 2011. pp. 493 504.
 Az iskolázottság térszerkezete, 2011 Az iskolázottság alakulása egyike azoknak a nagy népesedési folyamatoknak, amelyekre különös figyelem irányul. Természetesen nemcsak az e területtel hivatásszerűen
Az iskolázottság térszerkezete, 2011 Az iskolázottság alakulása egyike azoknak a nagy népesedési folyamatoknak, amelyekre különös figyelem irányul. Természetesen nemcsak az e területtel hivatásszerűen
EMMI kerettanterv 51/2012. (XII. 21.) EMMI rendelet 1. sz. melléklet 1.2.3. Matematika az általános iskolák 1 4. évfolyama számára
 EMMI kerettanterv 51/2012. (XII. 21.) EMMI rendelet 1. sz. melléklet 1.2.3 Matematika az általános iskolák 1 4. évfolyama számára Célok és feladatok Az iskolai matematikatanítás célja, hogy hiteles képet
EMMI kerettanterv 51/2012. (XII. 21.) EMMI rendelet 1. sz. melléklet 1.2.3 Matematika az általános iskolák 1 4. évfolyama számára Célok és feladatok Az iskolai matematikatanítás célja, hogy hiteles képet
Beton-nyomószilárdság értékelésének alulmaradási tényezője
 Beton-nyomószilárdság értékelésének alulmaradási tényezője Acceptance constant of concrete compressive strength evaluation Dr. KAUSAY Tibor okl. vasbetonépítési szakmérnök, címzetes egyetemi tanár Budapesti
Beton-nyomószilárdság értékelésének alulmaradási tényezője Acceptance constant of concrete compressive strength evaluation Dr. KAUSAY Tibor okl. vasbetonépítési szakmérnök, címzetes egyetemi tanár Budapesti
INTERAKTÍV MATEMATIKA MINDENKINEK GEOGEBRA MÓDRA. Papp-Varga Zsuzsanna ELTE IK, Média- és Oktatásinformatika Tanszék vzsuzsa@elte.
 INTERAKTÍV MATEMATIKA MINDENKINEK GEOGEBRA MÓDRA Papp-Varga Zsuzsanna ELTE IK, Média- és Oktatásinformatika Tanszék vzsuzsa@elte.hu Abstract/Absztrakt A GeoGebra egy olyan világszerte 190 országban ismert,
INTERAKTÍV MATEMATIKA MINDENKINEK GEOGEBRA MÓDRA Papp-Varga Zsuzsanna ELTE IK, Média- és Oktatásinformatika Tanszék vzsuzsa@elte.hu Abstract/Absztrakt A GeoGebra egy olyan világszerte 190 országban ismert,
Mérés és értékelés a tanodában egy lehetséges megközelítés
 Mérés és értékelés a tanodában egy lehetséges megközelítés Baráth Szabolcs Fejes József Balázs Kasik László Lencse Máté 2016 Javaslat tanodák számára a mérési és értékelési kultúrájuk megújításához Tartalom
Mérés és értékelés a tanodában egy lehetséges megközelítés Baráth Szabolcs Fejes József Balázs Kasik László Lencse Máté 2016 Javaslat tanodák számára a mérési és értékelési kultúrájuk megújításához Tartalom
Matematika. 1 4. évfolyam. Vass Lajos Általános Iskola Helyi tanterv Matematika 1 4. osztály
 Matematika 1 4. évfolyam Célok és feladatok Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról, mint tudásrendszerről, és mint sajátos emberi megismerési, gondolkodási, szellemi
Matematika 1 4. évfolyam Célok és feladatok Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról, mint tudásrendszerről, és mint sajátos emberi megismerési, gondolkodási, szellemi
SZAKIRÁNYOK A MISKOLCI EGYETEM MÛSZAKI INFORMATIKAI SZAKÁN
 SZAKIRÁNYOK A MISKOLCI EGYETEM MÛSZAKI INFORMATIKAI SZAKÁN Dr. Vadász Dénes, vadasz@iit.uni-miskolc.hu Miskolci Egyetem, Informatikai Intézet, Általános Informatikai Tanszék Abstract Our recently established
SZAKIRÁNYOK A MISKOLCI EGYETEM MÛSZAKI INFORMATIKAI SZAKÁN Dr. Vadász Dénes, vadasz@iit.uni-miskolc.hu Miskolci Egyetem, Informatikai Intézet, Általános Informatikai Tanszék Abstract Our recently established
különösen a média közleményeiben való reális tájékozódást. Mindehhez elengedhetetlen egyszerű matematikai szövegek értelmezése, elemzése.
 MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
HALLGATÓI KÉRDŐÍV ÉS TESZT ÉRTÉKELÉSE
 HALLGATÓI KÉRDŐÍV ÉS TESZT ÉRTÉKELÉSE EVALUATION OF STUDENT QUESTIONNAIRE AND TEST Daragó László, Dinyáné Szabó Marianna, Sára Zoltán, Jávor András Semmelweis Egyetem, Egészségügyi Informatikai Fejlesztő
HALLGATÓI KÉRDŐÍV ÉS TESZT ÉRTÉKELÉSE EVALUATION OF STUDENT QUESTIONNAIRE AND TEST Daragó László, Dinyáné Szabó Marianna, Sára Zoltán, Jávor András Semmelweis Egyetem, Egészségügyi Informatikai Fejlesztő
OPERÁCIÓKUTATÁS, AZ ELFELEDETT TUDOMÁNY A LOGISZTIKÁBAN (A LOGISZTIKAI CÉL ELÉRÉSÉNEK ÉRDEKÉBEN)
 OPERÁCIÓKUTATÁS, AZ ELFELEDETT TUDOMÁNY A LOGISZTIKÁBAN (A LOGISZTIKAI CÉL ELÉRÉSÉNEK ÉRDEKÉBEN) Fábos Róbert 1 Alapvető elvárás a logisztika területeinek szereplői (termelő, szolgáltató, megrendelő, stb.)
OPERÁCIÓKUTATÁS, AZ ELFELEDETT TUDOMÁNY A LOGISZTIKÁBAN (A LOGISZTIKAI CÉL ELÉRÉSÉNEK ÉRDEKÉBEN) Fábos Róbert 1 Alapvető elvárás a logisztika területeinek szereplői (termelő, szolgáltató, megrendelő, stb.)
különösen a média közleményeiben való reális tájékozódást. Mindehhez elengedhetetlen egyszerű matematikai szövegek értelmezése, elemzése.
 MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson amatematikáról, mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson amatematikáról, mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
Összeállította: Magyar Turizmus Zrt., Kutatási Csoport 1
 a a a Kedves Olvasók! Ismét tematikus számmal szeretnénk az Önök ismereteit gyarapítani. A Magyar Turizmus Zrt. 2009-re a Kulturális Turizmus Évét hirdette meg, elsôsorban belföldi marketingtevékenységében.
a a a Kedves Olvasók! Ismét tematikus számmal szeretnénk az Önök ismereteit gyarapítani. A Magyar Turizmus Zrt. 2009-re a Kulturális Turizmus Évét hirdette meg, elsôsorban belföldi marketingtevékenységében.
SZEGEDI ZOLTÁN. Konfliktuskezelési stratégiák. Conflict management
 SZEGEDI ZOLTÁN Konfliktuskezelési stratégiák Conflict management Absztrakt A konfliktus kialakulásának folyamata. Konfliktuskezelési stratégiák alkalmazása munkahelyi környezetben. Az empirikus kutatás
SZEGEDI ZOLTÁN Konfliktuskezelési stratégiák Conflict management Absztrakt A konfliktus kialakulásának folyamata. Konfliktuskezelési stratégiák alkalmazása munkahelyi környezetben. Az empirikus kutatás
Táblagépes alkalmazások a gyógypedagógiai gyakorlatban, súlyosan-halmozottan sérült gyermekek körében
 Táblagépes alkalmazások a gyógypedagógiai gyakorlatban, súlyosan-halmozottan sérült gyermekek körében Aknai Dóra Orsolya IKT MasterMinds Kutatócsoport, Veszprém doraorsolya@gmail.com Nyolcadik éve foglalkozom
Táblagépes alkalmazások a gyógypedagógiai gyakorlatban, súlyosan-halmozottan sérült gyermekek körében Aknai Dóra Orsolya IKT MasterMinds Kutatócsoport, Veszprém doraorsolya@gmail.com Nyolcadik éve foglalkozom
A diplomás nők munkaerőpiaci sikerességét befolyásoló tényezők és a gyerekvállalás hatásai
 FÓKUSZ A diplomás nők munkaerőpiaci sikerességét befolyásoló tényezők és a gyerekvállalás hatásai Engler Ágnes, Fényes Hajnalka Kutatásunkban a 2008-ban és 2010-ben végzett, volt levelezős felsőoktatási
FÓKUSZ A diplomás nők munkaerőpiaci sikerességét befolyásoló tényezők és a gyerekvállalás hatásai Engler Ágnes, Fényes Hajnalka Kutatásunkban a 2008-ban és 2010-ben végzett, volt levelezős felsőoktatási
Havasi Éva Rakovics Márton
 Havasi Éva Rakovics Márton Súlyos gender kérdés, avagy a túlsúlyban, az elhízottságban megnyilvánuló nemi különbségek 1 Ebben a rövid terjedelmű írásban a férfiak és a nők testsúlyában meglevő különbségekről
Havasi Éva Rakovics Márton Súlyos gender kérdés, avagy a túlsúlyban, az elhízottságban megnyilvánuló nemi különbségek 1 Ebben a rövid terjedelmű írásban a férfiak és a nők testsúlyában meglevő különbségekről
T Ö. Irodalom http://www V Á
 T Ö BB V Á T O Z Ó TAT I Z T I K A Irodalom http://www www.szit.bme.hu/~kela/ind2 - Bolla-Krámli: tatisztikai következések elmélete, Typotex, 2005 - Vargha A.: Matematikai statisztika, Pólya, 2000 - Bryman,
T Ö BB V Á T O Z Ó TAT I Z T I K A Irodalom http://www www.szit.bme.hu/~kela/ind2 - Bolla-Krámli: tatisztikai következések elmélete, Typotex, 2005 - Vargha A.: Matematikai statisztika, Pólya, 2000 - Bryman,
Csicsman József-Sipos Szabó Eszter csicsman@calculus.hu, siposeszti@gmail.com. Matematikai alapok az adatbányászati szoftverek első megismeréséhez
 Csicsman József-Sipos Szabó Eszter csicsman@calculus.hu, siposeszti@gmail.com Matematikai alapok az adatbányászati szoftverek első megismeréséhez 1.1 A statisztikai sokaság A statisztika a valóság számszerű
Csicsman József-Sipos Szabó Eszter csicsman@calculus.hu, siposeszti@gmail.com Matematikai alapok az adatbányászati szoftverek első megismeréséhez 1.1 A statisztikai sokaság A statisztika a valóság számszerű
képességgel és készséggel, hogy alkalmazni tudják matematikai tudásukat, és felismerjék, hogy a megismert fogalmakat és tételeket változatos
 MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
A BÜKKI KARSZTVÍZSZINT ÉSZLELŐ RENDSZER KERETÉBEN GYŰJTÖTT HIDROMETEOROLÓGIAI ADATOK ELEMZÉSE
 KARSZTFEJLŐDÉS XIX. Szombathely, 2014. pp. 137-146. A BÜKKI KARSZTVÍZSZINT ÉSZLELŐ RENDSZER KERETÉBEN GYŰJTÖTT HIDROMETEOROLÓGIAI ADATOK ELEMZÉSE ANALYSIS OF HYDROMETEOROLIGYCAL DATA OF BÜKK WATER LEVEL
KARSZTFEJLŐDÉS XIX. Szombathely, 2014. pp. 137-146. A BÜKKI KARSZTVÍZSZINT ÉSZLELŐ RENDSZER KERETÉBEN GYŰJTÖTT HIDROMETEOROLÓGIAI ADATOK ELEMZÉSE ANALYSIS OF HYDROMETEOROLIGYCAL DATA OF BÜKK WATER LEVEL
MUNKAERŐ-PIACI ESÉLYEK, MUNKAERŐ-PIACI STRATÉGIÁK 1
 GYÖRGYI ZOLTÁN MUNKAERŐ-PIACI ESÉLYEK, MUNKAERŐ-PIACI STRATÉGIÁK 1 Bevezetés Átfogó statisztikai adatok nem csak azt jelzik, hogy a diplomával rendelkezők viszonylag könynyen el tudnak helyezkedni, s jövedelmük
GYÖRGYI ZOLTÁN MUNKAERŐ-PIACI ESÉLYEK, MUNKAERŐ-PIACI STRATÉGIÁK 1 Bevezetés Átfogó statisztikai adatok nem csak azt jelzik, hogy a diplomával rendelkezők viszonylag könynyen el tudnak helyezkedni, s jövedelmük
IFJÚSÁG-NEVELÉS. Nevelés, gondolkodás, matematika
 IFJÚSÁG-NEVELÉS Nevelés, gondolkodás, matematika Érdeklődéssel olvastam a Korunk 1970. novemberi számában Édouard Labin cikkét: Miért érthetetlen a matematika? Egyetértek a cikk megállapításaival, a vázolt
IFJÚSÁG-NEVELÉS Nevelés, gondolkodás, matematika Érdeklődéssel olvastam a Korunk 1970. novemberi számában Édouard Labin cikkét: Miért érthetetlen a matematika? Egyetértek a cikk megállapításaival, a vázolt
KVANTITATÍV MÓDSZEREK
 KVANTITATÍV MÓDSZEREK Dr. Kövesi János Tóth Zsuzsanna Eszter 6 Tartalomjegyzék Kvantitatív módszerek. Valószínűségszámítási tételek. eltételes valószínűség. Események függetlensége.... 3.. eltételes valószínűség...
KVANTITATÍV MÓDSZEREK Dr. Kövesi János Tóth Zsuzsanna Eszter 6 Tartalomjegyzék Kvantitatív módszerek. Valószínűségszámítási tételek. eltételes valószínűség. Események függetlensége.... 3.. eltételes valószínűség...
Növelhető-e a csőd-előrejelző modellek előre jelző képessége az új klasszifikációs módszerek nélkül?
 Közgazdasági Szemle, LXI. évf., 2014. május (566 585. o.) Nyitrai Tamás Növelhető-e a csőd-előrejelző modellek előre jelző képessége az új klasszifikációs módszerek nélkül? A Bázel 2. tőkeegyezmény bevezetését
Közgazdasági Szemle, LXI. évf., 2014. május (566 585. o.) Nyitrai Tamás Növelhető-e a csőd-előrejelző modellek előre jelző képessége az új klasszifikációs módszerek nélkül? A Bázel 2. tőkeegyezmény bevezetését
