Diszkrét tomográfiai és PACS képfeldolgozó rendszerek
|
|
|
- Artúr Papp
- 9 évvel ezelőtt
- Látták:
Átírás
1 Szegedi Tudományegyetem Képfeldolgozás és Számítógépes Grafika Tanszék Diszkrét tomográfiai és PACS képfeldolgozó rendszerek Doktori értekezés Nagy Antal Témavezető Dr. Kuba Attila Szeged 26
2
3 Édesanyám emlékére...
4
5 Köszönetnyilvánítás Köszönetet szeretnék mondani az Informatikai Tanszékcsoport vezetőségének, hogy használhattam a tanszék infrastruktúráját kutatásaim során, valamint, hogy lehetőséget biztosítottak számomra a dolgozat elkészítéséhez. Hálás vagyok témavezetőmnek, Kuba Attilának, aki mind szakmailag, mind pedig emberileg munkám során végig támogatott. Köszönettel tartozom neki, hogy időt és fáradtságot nem kímélve irányította munkámat, megjegyzéseivel és javaslataival segítette dolgozatom elkészülését. Köszönetet szeretnék mondani Kiss Zoltánnak, Sven Krimmelnek, Dr. Martin Samalnak, Dr. Balaskó Mártonnak, Rodek Lajosnak és Ruskó Lászlónak, hogy közreműködésükkel a diszkrét tomográfia témakörben együtt dolgozhattunk. Szeretnék köszönetet mondani Dr. Werner Backfriedernek és a müncheni Corporate Technology PS 9, Siemens AG -nek, hogy kutatásaimhoz adatokat bocsátottak rendelkezésre. A képarchiváló- és továbbító rendszer (PACS) fejlesztése és az ahhoz kapcsolódó kutatások során Dr. Csernay László professzor, Dr. Almási László megjegyzései és javaslatai nagyban hozzájárultak ahhoz, hogy egy klinikai környezetben használható rendszer jöjjön létre. Ezúton szeretnék köszönetet mondani nekik és munkatársaiknak a kutatás és fejlesztés során nyújtott segítségükért. Köszönettel tartozom kollégáimnak Máté Eörsnek, Dudásné Nagy Mariannának, Palágyi Kálmánnak, Nyúl Lászlónak, Tanács Attilának és Kató Zoltánnak, akik munkám során gondolataikkal, javaslataikkal és biztatásukkal segítették a munkámat. Külön szeretnék köszönetet mondani Nyúl László kollégámnak, barátomnak, aki rendelkezésemre bocsátotta a dolgozat stílusát, valamint a dolgozat írása közben nyújtott technikai segítségéért. Köszönettel tartozom szüleimnek is, hogy szeretetükkel és bizalmukkal támogattak, annak ellenére, hogy ilyen messze kerültem a szülői háztól. Szavakkal nem írható le az a hála, amivel feleségemnek tartozom azért, hogy mindig mellettem állt a nehéz pillanatokban. Köszönöm neki, hogy a világ legjobb édesanyjaként Kristóf fiamnak megadta azt, amit sűrű teendőim miatt néha elmulasztottam és biztosította számunkra a biztos családi hátteret. A munkámat a következő pályázatok segítették: Felzárkózás az Európai Felsőoktatáshoz Alap (FEFA) III, FEFA IV, Felsőoktatási Kutatási és Fejlesztési Pályázatok (FKFP) 98/1997, Országos Tudományos Kutatási Alapprogram (OTKA) T32241, OTKA T48476 és National Science Foundation (NSF) DMS iii
6
7 Rövidítések ACR American College of Radiology DT discrete tomography Amerikai Radiológus Társaság diszkrét tomográfia ART Algebraic Reconstruction Techniques EDT emission discrete tomography emissziós diszkrét tomográfia CD Algebrai Rekonstrukciós Módszerek Compact Disc FEFA Felzárkózás az Európai Felsőoktatáshoz Alap (pályázati szervezet) CR computed radiography digitális radiográfia FKFP Felsőoktatási Kutatási és Fejlesztési Pályázatok (pályázati szervezet) CS code string kód FTP HTML File Transfer Protocol HyperText Markup Language CMYK cyan, magenta, yellow, black (színmodell) HSV hue, saturation, value (színmodell) CT computerized tomography, computer tomograph számítógépes tomográfia, számítógépes tomográf IAEA International Atomic Energy Agency Nemzetközi Atomenergetikai Ügynökség DAT Digital Audio Tape JATE József Attila Tudományegyetem DICOM DSA digitális audió szalag Digital Imaging and Communications in Medicine digitális képalkotás- és kommunikáció az orvostudományban (szabvány) digital subtraction angiography digitális szubtrakciós angiográfia JPEG NEMA NFS NM NSF MS Joint Photographic Experts Group National Electrical Manufacturers Association Nemzeti Elektromos Készülékgyártók Szervezete Network File System nuclear medicine nukleáris medicina National Science Foundation Microsoft v
8 MR magnetic resonance RIS Radiology Information System MRI mágneses rezonancia magnetic resonance imaging mágneses rezonanciás képalkotás SQL radiológiai információs rendszer Standard Query Language szabványos lekérdező nyelv OTKA PACS PC PNG RGB RGBA Országos Tudományos Kutatási Alapprogram (pályázati szervezet) Picture Archiving and Communication System képarchiváló- és továbbító rendszer personal computer személyi számítógép Portable Network Graphics (képformátum) red, green, blue (színmodell) red, green, blue, alpha (színmodell) TIFF US UID SA Tagged Image File Format (képformátum) ultra sound ultrahang Unique Identifier egyedi azonosító simulated annealing szimulált hűtés SPECT Single Photon Emission Computed Tomography SZOTE Szent-Györgyi Albert Orvostudományi Egyetem VR value representation érték reprezentáció vi
9 Tartalomjegyzék Köszönetnyilvánítás Rövidítések iii v 1. Bevezetés 1 2. Diszkrét tomográfiai rendszer Rekonstrukciós probléma legyező-nyalábvetületekre A legyező-nyalábmodell A rekonstrukció, mint optimalizálási feladat Szimulált hűtés Szimulációskísérletek Vetületek számítása vonalmenti integrállal Vetületek számítása területi integrállal Eredmények Diszkusszió Alkalmazások Nemroncsoló anyagvizsgálat röntgensugárzás esetén Csővezetékek vizsgálata neutron tomográfiai módszerrel Diszkusszió Összefoglalás Emissziós diszkrét tomográfiai rendszer EDTspeciálisabszorpciósértékre β-alapúszámrendszerbenvalószámábrázolás A hv-konvex bináris mátrixok variáns és invariáns pozíciói Egy algoritmus variáns és invariáns pozíciók meghatározására Diszkusszió Emissziós diszkrét tomográfiai alkalmazás faktorstruktúrákra Afantom Faktoranalízis Eredmények Diszkusszió Összefoglalás vii
10 4. Képarchiváló- és továbbító rendszer Bevezetés SZOTE-PACS felépítése Vizsgálatok begyűjtése Archiválás Megjelenítés és feldolgozás Szalagos mentés Aképarchiválórendszermegvalósítása Biztonság RISkapcsolat Automatikusfolyamatok IDICON programcsomag Képtömörítés Tapasztalatok a SZOTE-PACS üzemeltetésével kapcsolatban DICOM problémák Megjegyzések a DICOM szabvánnyal kapcsolatban Megjegyzések az IDICON programcsomaggal kapcsolatban Összefoglalás Irodalomjegyzék 87 Összefoglaló 93 Summary 97 Publikációk 11 viii
11 1. fejezet Bevezetés A képfeldolgozás az informatika egyik legdinamikusabban fejlődő ága.ahardverfejlődé- sével újabb és újabb területen használnak digitális képeket, amelyeket bonyolult rendszerekben archiválnak, kódolnak, továbbítanak, dolgoznak fel és jelenítenek meg. A képfeldolgozó rendszerek egyre fontosabb szerepet játszanak az orvostudományban, az űrkutatásban, a meteorológiában, sőt azt lehet mondani, hogy szinte minden tudományterületen. Az általános célú képfeldolgozó rendszerek mellett kifejlődtek speciális, egy-egy adott feladat megoldására alkalmas rendszerek is. Ma már a fontosabb alkalmazásokban inkább ezek a képfeldolgozó rendszerek használatosak. Így van ez akkor is, amikor 3-dimenziós (3D) tárgyak keresztmetszeti képeit állítják elő azok vetületi képeiből vagy amikor orvosi vizsgálatok képeit gyűjtik be és továbbítják egy képarchiváló központba. Mindkét speciális rendszer az újabb fejlesztések közé tartozik és a dolgozatnak is ezek a rendszerek a témái. A tomográfia mára általánosan elfogadott eszköz a 3D-s tárgyak szerkezetének vizsgálatában, amikor a tárgyat nem lehet vagy nem szabad szétdarabolni (pl. betegvizsgálatok vagy az ún. nemroncsoló anyagvizsgálatnál). Ezek nélkül ma már nem lehetne például hatékony orvosi diagnózisokat készíteni. A tomográfiának egy speciális ága az, amikor a rekonstruálandó tárgy anyagait ismerjük és csak ezeknek az anyagoknak a térbeli eloszlását kell meghatározni. Ilyen például a tomográfia ipari alkalmazásainak nagy része. Ebben az esetben lehet alkalmazni az ún. diszkrét tomográfiát, ahol tehát a rekonstruálandó objektumot reprezentáló függvény értékkészlete ismert, véges (lehetőleg kis elemszámú) diszkrét halmazzal reprezentálható. Például, ha a tárgy vasból készült, akkor a rekonstruált térben csak vas és levegő van jelen. A diszkrét tomográfia módszereit ekkor azért érdemes használni, mert a diszkrét értékkészlet ismerete, mint járulékos információ használható a rekonstrukciós eljárásban, ami lehetővé teszi, hogy kis számú (2 2) vetületből végezzünk rekonstrukciót a hagyományos rekonstrukciós eljárásokhoz szükséges párszáz vetület helyett. Természetesen a diszkrét tomográfia speciális, diszkrét tomográfiai rekonstrukciós eljárásokat igényel. Ilyen eljárások kifejlesztése jelenleg több helyen is folyik a világon [11, 13, 16, 21, 25, 62]. Az algoritmusok tesztelése és összehasonlítása egy természetes feladat, amihez egy diszkrét tomográfiai (DT) rendszert fejlesztettünk ki 21-től kezdve. Ebben a DT rendszerben lehetőség van az ún. legyező-nyaláb geometriával begyűjtött vetületekből végezni rekonstrukciót. A mi rendszerünk egy virtuális DT rendszer, amelyben a különféle geometriai és rekonstrukciós paramétereket lehet változtatni, ezáltal egy később megvalósítandó fizikai DT rendszer várható teljesítményéről lehet információkat gyűjteni. Ennek a rendszernek a leírását és a rendszerrel elvégzett kísérletek eredményeit foglaljuk össze a 2. fejezetben. Megmutatjuk, hogyan változik a rekonstruált kép minősége például a vetületek számától vagy a mérési adatok számától függően. A diszkrét tomográ- 1
12 2 Bevezetés fiai rendszer felhasználhatóságának szemléltetésére a 2.5. fejezetben két, nemroncsoló ipari alkalmazást mutatunk be. A tomográfiai eljárások egy fontos részét képezik azok, amikor a vetületeket valamilyen sugárzást kibocsátó tárgyakról gyűjtik be (emissziós tomográfia) szemben az általánosan ismert ún. transzmissziós tomográfiával, amikor a vetületek a külső sugárforrásból kiinduló és a tárgyon áthaladó sugárzás mérésével állnak elő. Az emissziós tomográfia akkor igényel speciális, a transzmisszióstól eltérő rekonstrukciós módszert, amikor a rekonstruálandó függvény vetületeit nemcsak a tárgyban levő (radioaktív) anyag aktivitás eloszlása, hanem a tárgyat körülvevő abszorbens anyag is befolyásolja. Az emissziós tomográfia speciális esete az emissziós diszkrét tomográfia (EDT), amikor az aktivitás eloszlás ismert diszkrét értékekkel jellemezhető (pl. 1: egységnyi aktivitás, : nincs aktivitás). A 3.1. fejezetben egy speciális abszorpciós problémát és annak megoldását ismertetjük. Ezt követően, a 3.2. fejezetben, az emissziós diszkrét tomográfia egy lehetséges alkalmazását mutatjuk be, amikor 4 abszorpciós vetületből rekonstruáltunk 3D-s struktúrákat. A képfeldolgozó rendszerek egy másik fontos feladata a különböző módszerekkel előállított képek tárolása. A feladat nehézségét fokozza az, ha a képekhez egyéb információk, például betegek adatai kapcsolódnak az orvosi vizsgálatok során. Ráadásul az orvosi képek mérete sem elhanyagolható az archiválási folyamat során. Az orvosi képeket képalkotó berendezések széles tárháza állítja elő, mint például számítógépes tomográfia (CT), mágneses rezonanciás képalkotás (MRI), ultrahang (US), digitális radiográfia (CR), nukleáris medicina (NM) stb. Az orvosi képek archiválása hozzáférést biztosít a betegek digitális képeinek visszakereséséhez. Ezeket a képeket klinikai diagnózisra lehet használni a betegek aktuális vizsgálatainak az összevetésével. Az archívum továbbá felhasználható a kapcsolódó kutatásokhoz és az oktatásban is. Egy képarchiváló- és továbbító rendszer (PACS) megvalósításához szükség van az archiváló rendszer, az egyedi képalkotó berendezések és PACS összetevők (felvevő, archiváló és megjelenítő állomások) közötti kapcsolatra és együttműködésre. Ennek az együttműködésnek a megvalósítása különösen nehéz akkor, amikor több platformon és a gyártó cégek különböző protokolljain kommunikálnak az adott képalkotó berendezések. Hasonló helyzettel néztünk szembe 1995-ben, amikor elkezdtük fejleszteni a SZOTE-PACS rendszert. Az volt a cél, hogy egy olyan archiváló rendszert fejlesszünk ki, amely egyaránt használható oktatási, kutatási és klinikai környezetben. Az orvosi egyetem különböző klinikáin található képalkotó berendezéseket kellett integrálni egy PACS rendszerbe. Ezek az eszközök nagyon eltérőek voltak (különböző formátumokban tárolták/szolgáltatták az orvosi vizsgálatokat). Annak érdekében, hogy ezeket a vizsgálatokat egységes formátumban tárolhassuk, a Digital Imaging and Communications in Medicine (DICOM) szabványt választottuk. Ez a szabvány lehetővé tette az összes eddig alkalmazott orvosi vizsgálati mód adatainak tárolását egy központi archívumban, illetve a hozzá tartozó adatbázisban. A SZOTE-PACS felépítését a 4. fejezetben adjuk meg. Ismertetjük továbbá a rendszer fejlesztéséhez kapcsolódó tapasztalatokat és eredményeket is.
13 2. fejezet Diszkrét tomográfiai rendszer A tomográfia egy olyan képalkotó eljárás, ahol a leképezendő tárgy szerkezetét annak vetületeiből határozzuk meg. A vetületi képeket elő lehet állítani valamilyen sugarak segítségével, amelyek egy adott forrásból (pl. Röntgen-cső) lépnek ki, majd áthaladnak az adott tárgyon, amiben részlegesen elnyelődnek, végül az áthatolt sugarak pontról pontra történő detektálásával alakul ki a detektált kép. Röntgensugár esetén a kép pontjaiban a következő értékeket mérhetjük (Beer törvénye): I = I e dr µ(x)dx, (2.1) ahol I a forrásból kilépő röntgensugár intenzitása, I a detektált intenzitás, µ atárgy anyagának elnyelődési együtthatója és d a forrás és az áthatolt sugár intenzitását érzékelő detektor távolsága. A detektált kép egy pontja annak a sugárnak az intenzitását adja meg, amely a forrást és az adott detektort összekötő egyenes mentén halad. A detektált képből az abszorpciós együtthatót reprezentáló µ függvény vonalmenti integráljait tartalmazó ún. vetületi képet (2.1. ábra) a (2.1) egyenlet logaritmus transzformáltjával kapjuk meg, azaz d µ(x)dx = log(i /I). (2.2) Az adott tárgyról általában több vetületi képet állítanak elő különböző irányokból. Ezt követően az a feladat, hogy kiszámítsuk a tárgy keresztmetszetein az elnyelődési együtthatót valamilyen matematikai eljárás segítségével, amit vetületekből való rekonstruálásnak [18] nevezünk. Ezt a módszert rutinszerűen használják például a számítógépes tomográfiában (Computerized Tomography, CT), ahol az elnyelődési együtthatót az emberi test metszetein az áthatolt röntgensugarak intenzitásának detektálásán alapuló vetületekből számítják ki. 3D-s tárgyak rekonstruálásának a problémáját általában leegyszerűsítik a tárgy 2D-s keresztmetszeteinek a rekonstruálására. Ily módon a 3D-s rekonstrukciós probléma 2D-s rekonstrukciós problémák sorozatára redukálódik. A diszkrét tomográfia (DT) egy speciális rekonstrukciós módszer, amit olyan egyszerű tárgyak rekonstrukciójára lehet használni, amelyek néhány homogén anyagú régióra bonthatók (pl. fém és fa). Azt az információt, hogy a tárgy néhány ismert abszorpciójú anyagból áll, bele lehet foglalni a rekonstrukciós eljárásba, ezáltal sokkal kevesebb vetületből rekonstruálhatunk, mint összetettebb tárgyak esetében. Így a diszkrét tomográfia fontos olyan alkalmazások esetében, ahol az adott tárgyak egyszerűek és nincs lehetőség a nagy 3
14 4 Diszkrét tomográfiai rendszer vetület vetület 2.1. ábra. Egy homogén tárgy és annak vetületei két irányból. számú vetületi kép előállítására vagy azok elkészítése túl drága, mint például a nemroncsoló anyagvizsgálat, elektron mikroszkópia vagy az orvosi diagnosztika bizonyos vizsgáló eljárásai [19]. Általában kétféle módon szokás begyűjteni a szükséges vetületi képeket (2.2. ábra). Párhuzamos vetületek esetében az egyes vetületi képek adott irányú, egymással párhuzamos sugarak segítségével állnak elő. Legyező-nyaláb vetületek esetében a sugarak egy pontszerű forrásból indulnak ki és legyezőszerűen terülnek szét a térben. Mindkét esetben a tárgy vagy pedig a forrás és a detektorok együttes elforgatásával újabb vetület képezhető. Nagy számú vetület esetén a kétféle vetület a rekonstrukcióhoz szükséges információ szempontjából egyenértékű (a sugarak megfelelő átrendezésével egymásba átalakítható), de algoritmikusan különböző rekonstrukciós módszerek léteznek párhuzamos és legyező-nyaláb vetületekre. Ebben a fejezetben egy speciális diszkrét tomográfiai problémát tárgyalunk, nevezetesen bináris mátrixok rekonstruálását legyező-nyaláb vetületekből. Bináris mátrixok párhuzamos vetületekből való rekonstruálása egy klasszikus probléma, amelyhez ma már alaposan kidolgozott matematikai elmélet tartozik [12, 19]. A rekonstrukció legyező-nyaláb vetületekből is jól ismert probléma a klasszikus (nem diszkrét) tomográfiában [17, 22], ugyanakkor csak nagyon kevés algoritmust lehet találni, amely legyező-nyaláb vetületekből végzi a rekonstrukciót diszkrét tomográfiai módszer segítségével. Tudomásunk szerint ezidáig csak Peyrin és m.társai [61] által publikált cikk foglalkozik ezzel a problémával. Ebben a cikkben valódi 3D-s tárgy rekonstruálását tárgyalják kúp-nyaláb vetületekből (a teljes 3D-s tárgyon áthaladó 3 dimenziós sugárnyalábok). Habár bizonyos rekonstrukciós eljárások viszonylag könnyen átvihetők a párhuzamos vetületekről a legyező-nyaláb vetületekre, sok elméleti kérdés nyitott még az utóbbi esetben (pl. unicitás és egzisztencia problémák). Ugyanakkor számos diszkrét tomográfiai alkalmazásban legyező-nyaláb vetületeket használnak, mint például nemroncsoló anyagvizsgálatban röntgensugarak [14] vagy neutron sugarak [43] felhasználásakor. Ennek a fejezetnek az elején bemutatjuk, hogy a legyező-nyaláb vetületi paraméterek-
15 Forrás 5 Detektorok Detektorok (a) Párhuzamos vetület Forrás (b) Legyező-nyaláb vetület 2.2. ábra. Párhuzamos és legyező-nyaláb vetületek. től illetve az alkalmazott rekonstrukciós eljárás paramétereitől hogyan függ a rekonstrukció minősége. Ehhez azt a módszert választottuk, hogy szimuláljuk a felvételi technikát, majd a szimulált adatokból végezzük el a rekonstrukciót. Az alkalmazott szimulációs módszer szerint végigkísérjük a teljes eljárást a vetületek létrehozásától egészen a rekonstruált képeknek az eredeti fantommal való összehasonlításáig. A szimulációs folyamat során az első lépés azoknak a 2D-s bináris mátrixoknak az előállítása, amelyek a rekonstruálandó tárgyakat reprezentálják a szimulációban. Ezek után a legyező-nyaláb vetületek előállítása következik. A legyező-nyaláb modellben különböző paraméterek találhatók, mint például a források, illetve a detektor elemek száma. A megfelelő paraméterek segítségével különböző legyező-nyaláb vetületeket előállító rendszert szimulálunk. A vetületeket analitikus módon számítjuk ki a legyező-nyaláb paraméterek értékeinek megfelelően. A mérési hibát és egyéb lehetséges zavaró tényezőket a rendszerben véletlenszerű additív zajjal szimuláljuk. A bináris mátrixok rekonstruálására egy véletlen-keresésen alapuló optimalizálási eljárást valósítottunk meg. A rekonstruált és az eredeti képek eltérésének mérésére több módszert próbáltunk ki. Ezek közül a relatív átlagos hiba bizonyult a legjobbnak (legkifejezőbbnek). A paramétereknek a hatását úgy mutatjuk be, hogy rekonstrukciók sorozatát hajtjuk végre a kiválasztott paramétert változtatva, míg a többi paraméter értéke rögzítve marad. Ily módon előállíthatunk egy görbét, ami az éppen változó paraméter hatását mutatja be a relatív átlagos hiba függvényében. A 2.1. fejezetben ismertetjük a rekonstrukciós problémát a szükséges definíciókkal és jelölésekkel. Ezek után a 2.2. fejezetben részletesen bemutatjuk a rekonstrukciók során használt legyező-nyaláb modellt. A 2.3. fejezetben a diszkrét tomográfiai feladatot optimalizálási problémaként fogalmazzuk át. A 2.4. fejezetben ismertetett szimulációs kísérletek
16 6 Diszkrét tomográfiai rendszer tárgyalása után a 2.5.fejezetben bemutatjuk az adott diszkrét tomográfiai rekonstrukciós módszer két lehetséges alkalmazását. Az eredményeket a 2.6. fejezetben foglaljuk össze. A fejezet eredményei a [8, 26, 51] cikkekben jelentek meg. A legfrissebb eredményeket tartalmazó kézirat [24] cikk könyv fejezetben fog megjelenni (publikálásra elfogadva), a [5]-t pedig publikálásra küldtük be Rekonstrukciós probléma legyező-nyaláb vetületekre Legyen f egy integrálható valós függvény az R 2 síkon. Legyen S R 2 egy pont, melyet nevezzünk forrásnak. Vegyük f integrálját az S-ből induló v θ irányú félegyenes mentén [Rf](S, θ) = f(s + u v θ )du, (2.3) ahol θ szög értéke és 2π között változik és v θ egy θ-irányú egységvektor. A (2.3) egyenlet által definiált transzformációt, amely f függvény S pontból θ irányában képzett vetületi értékeit adja meg, az f-nek S pontból vett legyező-nyaláb vetületének hívjuk. Ilyen vetületi modellt használnak ma már a számítógépes tomográfia esetében (például [18]), ahol a vetületeket az adott tárgy körül forgatott forrás segítségével képezik le néhány száz legyezőnyaláb vetületnek megfelelő adatmennyiséget begyűjtve, majd ezekből rekonstruálják a tárgyat. Adott forrásoknak egy halmaza, jelöljük ezt S-sel. A legyező-nyaláb vetületekből való rekonstrukciós probléma a következőképpen adható meg: FB(S) REKONSTRUKCIÓS PROBLÉMA Adott: egy g függvény: S [, 2π) R. Feladat: állítsunk elő egy f függvényt, amelyre teljesül, hogy minden S Sés θ [, 2π)-re. [Rf](S, θ) = g(s, θ) Ennek a problémának az alkalmazásokban általában nincs pontos megoldása a kiindulási (mérési) adatok pontatlansága, ellentmondásossága miatt, ezért a probléma megoldásán általában közelítő megoldást értünk. Több módszer is létezik az FB rekonstrukciós probléma megoldására [18]. Először speciális függvények legyező-nyaláb vetületekből való rekonstruálását tárgyaljuk. Tegyük fel, hogy f értelmezési tartománya egy n n-es, szabályos W ráccsal lefedhető, f mindegyik 1 1-es rácsnégyzetben konstans, és a D = {, 1} értékek valamelyikét veszi fel. Ily módon, f megadható egy mátrixszal, másképpen, egy x {, 1} J vektorral, ahol x j amátrixj-edik elemét jelöli sorfolytonos bejárás esetén (j =1,...,J és J = n 2 ). Az alkalmazásokban a vetületeket véges számú S k (k =1, 2,...,K) forrásból nyerik, véges számú (L) félegyenes mentén képezve azokat. Az S k forrásból kiinduló v l irányú egyenes mentén számítható ki a b i érték, ahol i =(k 1) K + l (l =1, 2,...,L): J a ij x j = b i, i =1, 2,...,I, (2.4) j=
17 2.2 A legyező-nyaláb modell 7 Detektorok S k Detektorok S k S S C r C r Detektorok Detektorok (a) Vonal-menti integrálok alkalmazása (b) Terület integrálok alkalmazása 2.3. ábra. A legyező-nyaláb modell geometriai paraméterei. ahol I = K L és a ij az i-edik vetületi értéket meghatározó félegyenesnek a W rács j-edik egységnégyzetén belüli szakaszának a hossza más szóval a W rács j-edik egységnégyzetének a súlya. Az A =(a ij ) I J mátrix elemei meghatározhatóak a W -ben lévő négyzetek pozícióinak és a forrásból kiinduló félegyenesek ismeretében. A (2.4) speciális tulajdonsága az, hogy ebben az esetben az ismeretlen x vektor bináris, azaz x j {, 1} minden j = 1, 2,..., J-re A legyező-nyaláb modell A diszkrét tomográfiai alkalmazások többségében, ahogy a mi legyező-nyaláb modellünkben is (2.3. ábra), az S k (k =1, 2,...,K) források az O origó körül lévő C r = {(x, y) x 2 + y 2 = r 2 } körön helyezkednek el, ahol r> elég nagy ahhoz, hogy a W rács teljes egészében benne legyen az egyes forrásokból kiinduló, szélső sugarak által lefedett szögtartományban. Továbbá az is szokásos, hogy a források egyenletesen vannak elhelyezve a C r körön, vagyis S k =(r cos θ k,r sin θ k ),aholθ k = θ +(k 1) 2π/K, mindenk =1, 2,...,K-ra. Rögzített K esetén θ [, 2π) kezdő szög nemcsak az első forrás helyét határozza meg, hanem az összes többiét is. A modellünkben azért volt szükség a θ kezdő szögre, mert általában kevés (2 4) vetület áll rendelkezésre és a vetületek száma, valamint a források helyzete erősen befolyásolhatja a rekonstrukció minőségét, ahogy később ezt szemléltetni fogjuk. Például, kezdő szög azt jelenti, hogy az első forrás az x tengely pozitív része és a C r kör metszés pontjában található. Az egyszerűség kedvéért tételezzük fel, hogy a W rács középpontja a koordinátarendszer origójában található (2.3. ábra). Modellünkben L darab detektor méri az S k forrásból (k =1, 2,...,K) kiinduló sugarak intenzitását, amelyek az objektumon áthaladva részlegesen elnyelődnek. A detektált sugár intenzitása összefügg az elnyelődéssel, amiből a (2.1) egyenlet szerint számítható a forrásokból kiinduló félegyenesek mentén vett integrál. A detektorok egyenletesen vannak elhelyezve a detektor íven. A detektor ív a tárgynak a forrással ellentétes oldalán van elhelyezve és a detektorok ívének a középpontja S k -ban található (2.3. ábra). A detektor ív szélső sugarai érintik a W rácsot tartalmazó kört. A két érintő által bezárt szöget ϕ-vel jelöljük (2.3. ábra). A detektor ív mindegyik detektora egy b i vetületi értéket detektál, ezért
18 8 Diszkrét tomográfiai rendszer egy-egy pixel hatását vonalmenti és területi integrál segítségével is meghatározhatjuk. Attól függően, hogy vonalmenti vagy területi integrál segítségével határozzuk meg a vetületi értékeket, más és más módon kell kiszámítanunk az a ij súlyokat a (2.4) egyenlet esetében: vonalmenti integrál esetén, a súlyokat a W rács, j-edik egységnégyzete és az i-edik vetületi értéket meghatározó félegyenes által kimetszett szakasz hossza adja meg (2.3(a) ábra), területi integrál esetén a detektorok közötti lehetséges hézagok miatt az i-edik vetületi értéket meghatározó 2i és 2i +1félegyenesek által közbezárt területek és a W rács j-edik egységnégyzet közös részét értjük a ij súlyon. A területhez tartozó félegyenesek által bezárt szöget α-val jelöljük (2.3(b) ábra). Ily módon, az r, L és (területi integrál esetén) α paraméterek egyértelműen jellemzik a legyező-nyalábot. Valódi mérés esetén a vetületeket általában csak bizonyos hibával (zaj) tudjuk megkapni. Ezért a zajos vetületek szimulálására Gauss eloszlású zajt adunk a pontos (analitikus úton kiszámított) vetületi értékekhez. A mi legyező-nyaláb modellünket a következő paraméterek határozzák meg: n: a rekonstruálandó bináris mátrix mérete (n n); h: egy mátrix elemhez tartozó négyzet oldalélének hossza (lehet egységnyi); r: a C r kör sugara, azaz a forrás és az origó távolsága; θ : akezdő szög, amely meghatározza az első forrás helyét; K: a források száma; L: a detektorok száma, vagyis az egy forrásból mért adatok száma; α: területi integrál esetén a sugárnyaláb nyílásszöge; η: a vetületi értékekhez adott Gauss eloszlású zaj százalékos aránya A rekonstrukció, mint optimalizálási feladat Ahogyan korábban láttuk, az FB(S) rekonstrukciós probléma (2.1. fejezet) megoldása a legyező-nyaláb modell esetén ekvivalens a következő lineáris egyenletrendszer megoldásával: Ax = b, ahol x egy D-beli vektor. (2.5) A hagyományos rekonstrukciós módszerek, mint például az Algebraic Reconstruction Techniques (ART) [18] nem feltétlenül adnak D-beli x vektort a (2.4) egyenletrendszer megoldásaként. Mivel modellünkben a sugarak/sugárnyalábok a W rácson legfeljebb O(n) négyzetet metszenek, az A =(a ij ) I J mátrix ritka lesz (csak néhány nem nulla értéket fog tartalmazni). A diszkrét tomográfiai alkalmazásokban egy másik fontos tulajdonsága ennek a mátrix egyenletnek az, hogy az egyenletek száma (azaz a mérési (vetületi) adatok száma) jóval kisebb, mint az ismeretlenek száma, ennélfogva I J. Ez azt jelenti, hogy ennek az egyenletrendszernek sok megoldása lehet, közöttük akár bináris-értékűek is.
19 2.3 A rekonstrukció, mint optimalizálási feladat 9 A mérési hibák miatt az is lehetséges, hogy a (2.5) egyenletrendszernek nincs megoldása, ezért a (2.5) egyenletrendszer megoldása helyett megelégszünk egy közelítő eredmény megkeresésével úgy, hogy a problémát optimalizálási feladatként oldjuk meg. Formálisan, keressük meg a következő célfüggvénynek a minimumhelyét C(x) = Ax b +Ψ(x), (2.6) ahol x egy D-beli vektor és Ψ(x) =γ Φ(x) alakban írható fel. A fenti kifejezés első tagja azt biztosítja, hogy egy olyan x vektort kapjunk, amely a (2.5) egyenletrendszert legalább megközelítőleg kielégíti. A célfüggvény második tagjának a segítségével további tulajdonságokat követelhetünk meg az x vektortól. A második tag (2.6)-ben azt biztosítja, hogy az első tagra kis értéket adó x-ek közül olyat kapjunk, amelyikre Ψ(x) is kicsi lesz, azaz a kívánt tulajdonságot is teljesíti. Például Φ(x) = x x (proto) lehet, ahol x (proto) egy D-beli prototípus vektor, amely az x vektorral azonos dimenziójú. Ilyen Φ(x) esetén olyan x vektort kaphatunk megoldásul, amely az x (proto) prototípus vektorhoz közeli. A γ regularizációs együttható a C(x)-ben lévő Φ(x) tag súlyozására szolgál. Például, ha a mért értékek nagyon zajosak, akkor egy nagyobb γ-t választva nagyobb hangsúlyt adhatunk a (2.6) egyenletben lévő második tagnak, így az fontosabb szerepet fog játszani az optimalizálási folyamatban. A (2.6) kifejezés optimalizálása során D-beli megoldást keresünk, ezért a szokásos numerikus optimalizálási módszerek használata nem látszik alkalmasnak. A kombinatorikus optimalizálási módszerek sokkal ígéretesebbnek tűntek és hasznosabbaknak is bizonyultak. Ezek közül mi a szimulált hűtés (simulated annealing, SA) optimalizálási eljárást választottuk [49]. A választás oka az volt, hogy az SA-t könnyen lehetett megvalósítani és a célfüggvényhez igazítani (azaz kis módosításokkal a program egy másik célfüggvény optimalizálására is alkalmas volt) Szimulált hűtés Az SA egy véletlenszerű keresési technika [49], amely a fémek hűtésének a fizikai jelenségén alapszik. A folyékony fém részecskéi hűtés közben fokozatosan érik el a minimális energiaszintet, a fém kristályos szerkezetet vesz fel és megfagy. Az SA algoritmust többféle módon lehet megvalósítani az adott feladatnak megfelelően. Ezek a megvalósítások eltérhetnek a minimalizálandó célfüggvény értékkészletéből való pontok kiválasztásában, a hűtés módjában és a megállási feltétel megfogalmazásában. A dolgozatban bináris képek rekonstrukciójával foglalkozunk, ezért D = {, 1}. Az x komponensei D-ből valók. Többértékű képek esetén a szimulált hűtés során alkalmazott módosításokat a bináristól eltérő stratégiával kell végrehajtani. A bináris képek rekonstrukciójához megvalósított szimulált hűtés algoritmusokat a pozíciók kiválasztása szerint két csoportba osztottuk [68]. Inhomogén SA Az algoritmus egy tetszőleges x () iniciális bináris képből és egy T = T () hőmérsékletről indul ki (2.4. ábra). Kiszámítja a C(x) célfüggvény kezdő értékét. Ezután véletlenszerűen kiválaszt egy j pozíciót az x vektorban. Legyen x az a kép, amely csak a j-edik pozícióban tér el az x képtől, azaz x j =1 x j. Ezt a változtatást az algoritmus elfogadja, azaz x lesz az új x vektor, ha C(x ) <C(x). Ellenkező esetben a változtatást csak a C = C(x ) C(x) értékétől függő valószínűséggel fogadja el. Pontosan csak akkor, ha exp( C/κT) >z, (2.7)
20 1 Diszkrét tomográfiai rendszer ahol κ a Boltzmann állandó ( m 2 kgs 2 K 1 ), T az aktuális hőmérséklet, z pedig a [, 1] intervallumon egyenletes eloszlású pszeudó véletlenszám-generátorral előállított szám. () () x:= x, T:=T C( x) kiszámítása j véletlen kiválasztása x j:=1-xj T:=hT Igen C ( x ) kiszámítása Nem T>T min? Elfogadja a változást? Igen Aktualizál Nem Igen Eldobja Nem Egyensúlyi állapot? Nem Alacsony hatékonyság? Igen Kilépés 2.4. ábra. A megvalósított inhomogén SA algoritmus folyamatábrája. Ha a változtatást nem fogadtuk el, akkor ellenőrizzük a képben a változtatások hatékonysági szintjét a megadott számú utolsó iterációs lépésekben. Ez azt jelenti, hogy számoljuk az elvetett iterációs lépéseket az utolsó N iter iterációban. Ha ez az érték nagyobb egy előre megadott R thr küszöb értéknél, akkor a hatékonyság alacsony és az algoritmus futása befejeződik. Ellenkező esetben megvizsgáljuk, hogy az algoritmus egyensúlyi ál-
21 2.4 Szimulációs kísérletek 11 lapotba került-e. Ennek eldöntéséhez kiszámoljuk a C szórását az utolsó N var iterációs lépésben. Amennyiben a C szórásának a becslése nagyobb, mint az előző N var becsléséé, akkor egyensúlyi állapotban vagyunk. Egyensúlyi állapotban csökkentjük a hőmérsékletet, az aktuális T hőmérséklet értékét h T -re módosítjuk, ahol h az úgynevezett hűtési együttható. A mi esetünkben ugyanazt az értéket választottuk, mint a [61] cikkben, nevezetesen h =.9. Az alacsonyabb hőmérséklet azt jelenti, hogy kisebb valószínűséggel engedjük meg a változtatás elfogadását abban az esetben, ha a célfüggvény értéke nő. Új iterációt kezdünk alacsonyabb hőmérséklettel. A homogén SA algoritmusunk a következő paraméterekkel rendelkezik: x () : kezdő kép; T () : kezdő hőmérséklet; N iter : a hatékonyság meghatározásához használt iterációs lépések száma; R thr : az elutasított változtatások számának a küszöbértéke az utolsó N iter iterációban; N var : a célfüggvény szórásának kiszámításához használt elfogadott változtatások száma. Homogén SA A homogén SA abban tér el az inhomogén SA algoritmustól (2.5. ábra), hogy egy iterációs lépésben az x vektor összes elemén végighaladva hajtjuk végre a változtatásokat (az adott elemet -ról 1-re illetve 1-ről -ra változtatjuk). A változtatásokat a homogén megvalósításhoz hasonlóan vagy elfogadjuk vagy elutasítjuk. Az egyes iterációs lépések végén csökkentjük az aktuális hőmérsékletet és egy új iterációs lépést kezdünk. Az algoritmus akkor fejeződik be, ha az aktuális célfüggvény értékének és a célfüggvény kezdőértékének aránya egy előre megadott küszöbérték alá esik (C(x )/C(x () ) <C thr ) vagy az aktuális hőmérséklet egy adott hőmérsékleti pont alá kerül (T <T thr ). A homogén SA algoritmusunk a következő paraméterekkel rendelkezik: x () : kezdő kép; T () : kezdő hőmérséklet; C thr : az aktuális célfüggvény érték és a kezdő érték arányához tartozó küszöbérték; T thr : ahőmérsékleti küszöbérték Szimulációs kísérletek Munkánk során szimulációs kísérleteket végeztünk a legyező-nyaláb vetületek illetve az inhomogén SA paramétereinek változtatásával abból a célból, hogy bemutassuk azoknak a hatását a rekonstrukció minőségére. Ezeknek a kísérleteknek az volt a célja, hogy előzetesen információkat adjunk egy diszkrét tomográfiai rendszer várható teljesítményéről a különféle paraméterek függvényében. A tapasztalatokat az alkalmazások és a leképezést megvalósító hardver kialakítása során fel is használtuk [8, 26]. A szimulációs kísérleteket 2 2-as (azaz n = 2) méretű fantom képeken hajtottuk végre. A fantom képek vetületeit a (2.4) egyenlet alapján számítottuk ki. A képeket ezekből a vetületekből rekonstruáltuk az inhomogén szimulált hűtést felhasználva. Ahhoz, hogy a
22 12 Diszkrét tomográfiai rendszer () () x:= x, T:=T, j=, C( x) kiszámítása x :=1-x j j T:=hT C( x ) kiszámítása j:=j+1 Nem Igen T>T min? Elfogadja a változást? Nem Igen Aktualizál Nem Eldobja C( x )/ C( x () )<C vagy T<T thr thr Nem j<n 2 Igen Igen Kilépés 2.5. ábra. A megvalósított homogén SA algoritmus folyamatábrája. rekonstrukció minőségét mérni tudjuk, az eredeti fantom képeket pixelenként hasonlítottuk össze a kapott eredmény képpel a relatív átlagos hiba definíciója szerint (2.8), azaz M e = J x j ˆx j j=1, (2.8) J ˆx j j=1 ahol az ˆx = { ˆx j } J j=1 jelöli az eredeti képet. Tehát M e és az alacsonyabb érték a jobb eredményt jelzi. Továbbá, M e =, akkor és csak akkor igaz, ha x = ˆx. A relatív átlagos hiba lényegében az eredmény és az eredeti képen lévő pixelek eltérésének és az eredeti képen lévő 1-esekaránya. Mivel az optimalizálási feladatot egy véletlen-keresésen alapuló módszer segítségével oldottuk meg, ezért minden egyes paraméter-beállítás esetén 1-szor ismételtük meg a rekonstrukciós eljárást. A 1 darab M e érték átlagát számítottuk ki és ábrázoltuk az adott
23 2.4 Szimulációs kísérletek 13 paraméter-beállításra. A rekonstrukció eredményét ugyanúgy, 1 rekonstruált bináris kép átlagaként adtuk meg egy adott paraméter-beállításra. Az így kapott átlag képen a sötétebb pixelek mutatják azokat a helyeket, amelyekhez a 1 rekonstrukció során kevesebb 1-es pixelt kaptunk. Természetesen több paraméter-beállítást teszteltünk. Mindegyik kísérleti paraméterhez hozzárendeltünk egy intervallumot. Egy adott paraméter intervallum azon értékét választottuk alap paraméter-beállításként, amely az előzetes tapasztalatok alapján optimális eredményt adott. A kísérletek során az egyes paraméterek hatását úgy vizsgáltuk, hogy csak a megfelelő paramétert változtattuk az intervallumon belül, a többi paraméter értékét az alap paraméter-beállításnak megfelelően állítottuk be. Például ahhoz, hogy lássuk a források számának a hatását, a modellünkben a K értékét változtattuk (2 32 intervallumban). Kiszámoltuk a vetületeit az adott fantomnak, 1-szor futtattuk a rekonstrukciós algoritmust, vettük a 1 rekonstruált képet, majd kiszámoltuk a 1 M e értéket a rekonstruált és az eredeti képre nézve, illetve kiszámoltuk az átlag képeket is. Végezetül megrajzoltuk az M e változásának görbéjét a várható értékek alapján a források számának függvényében. Ezt a görbét mutatjuk be, mint az adott paraméter változtatásával kapott végső megfigyelés eredményét Vetületek számítása vonalmenti integrállal Vonalmenti integrál esetén a 2.1. táblázat tartalmazza az elvégzett kísérletek alap paraméterbeállításait, valamint a paraméterek lehetséges értékeit táblázat. Alap paraméter-beállítások és az egyes paraméter-értékeknek az intervalluma vonalmenti integrál esetén. Paraméter Alap érték Intervallum A forrás távolsága az origótól (r) 25 [25, 175] Akezdőszög(θ ) [, 36 /K] A források száma (K) K {22, 32} [2, 32] A detektorok száma (L) 41 [11, 41] Hozzáadott zaj aránya (η) η {%, 5%} [%, 45%] Kezdő hőmérséklet (T () ) 4 [4, 14 ] Megfigyelendő iterációk száma (N iter ) 1 [1, 1] El nem fogadott változtatások küszöbértéke (R thr ) 999 [99, 999] A szórás számításához felhasznált iterációk száma (N var ) 5 [5, 5] Elsődleges regularizációs paraméter (γ poz ) 145 [, 145] Másodlagos regularizációs paraméter (γ sm ) [, 49] A kísérletek a Ψ(x) =Ψ poz (x) =γ poz Φ poz (x) regularizációs kifejezéssel és a γ poz = 145 regularizációs paraméterrel hajtottuk végre a (2.9) és (2.1) egyenletek alapján. Annak érdekében, hogy a zaj hatását is bemutassuk az adott rekonstrukciós módszer alkalmazása során, a kísérleteket %-os és 5%-os zaj hozzáadásával is elvégeztük. Ezzel két görbét kaptunk a teszt eredményekre nézve: egyet a zajmentes, egyet pedig az 5%-os zajos esetre. A legtöbb kísérletet elvégeztük K =32és K =22paraméter beállításokra is. Ezzel két további görbét kaptunk. A paramétereket és a hozzájuk tartozó eredményeket négy csoportra oszthatjuk. A következő alfejezetekben ezeket elkülönítve tárgyaljuk. Ezek bemutatják a legyező-nyaláb il-
24 14 Diszkrét tomográfiai rendszer 2.6. ábra. A kísérletek során használt alap szoftver fantom. letve a szimulált hűtés paramétereinek, a fantom kép összetettségének, a regularizációs paraméter változtatásának és a hozzáadott zajnak a hatását. A legyező-nyaláb modell paraméterei Ebben a csoportban a legyező-nyaláb geometriához kapcsolódó paraméterek (2.2. fejezet) változtatásának a hatását vizsgáljuk. A forrás távolsága az origótól Ezt a paramétert 25 és 175 között változtattuk, amíg a félkör detektor sor nyílásszöge a rekonstruálandó W rácsot befoglaló kör egészét lefedte és a detektorok L száma nem változott (2.7. ábra). Ahogyan a forrás távolodik az origótól, a legyező-nyaláb modell közelít a hasonló detektor paraméterekkel rendelkező párhuzamos-nyaláb modellhez. D D S S 2.7. ábra. A forrás és az origó közötti távolság változtatása. A D detektor ív az S forráshoz, a D detektor ív az S forráshoz tartozik. A 2.8. ábrán lévő görbék azt mutatják, hogy a forrás origótól való távolsága nem befolyásolja lényegesen a rekonstrukció minőségét. Vagyis ezt az eredményt úgy is átfogalmazhatjuk, hogy nincs igazi különbség a legyező-nyaláb és a párhuzamos-nyaláb vetületi modellek között, mivel a forrás távolságának a növelésével a legyező-nyaláb sugarak párhuzamossá válnak, ami viszont már megfelel a párhuzamos-nyaláb vetületi modellnek.
25 2.4 Szimulációs kísérletek 15,18,18,15,15 Relatív átlagos hiba,12,9,6 K=32 K=22 Relatív átlagos hiba,12,9,6 K=32 K=22,3, A forrás távolsága az origótól A forrás távolsága az origótól (a) Zajmentes (b) 5% Gauss eloszlású zaj 2.8. ábra. A relatív átlagos hiba a forrás és az origó közötti távolság (r) függvényében vonalmenti integrál esetén. Kezdő szög Akezdő szög paramétert és 36 /K szögek között változtattuk. Nyilvánvaló, hogy az első forrás pozíciójának a meghatározásával a C r körön lévő összes forrás helyét is megadjuk (ha a források száma nem változik). A 2.9(a). ábra mutatja a kezdő szög választásának a hatását, ha elég sok forrással rendelkezünk (a források száma 32). A görbék azt jelzik, hogy nincs lényeges eltérés, ha elég sok forrással rendelkezünk. Egészen más görbéket kapunk abban az esetben, ha a vetületek száma kicsi. Például, ha a források száma 4, akkor olyan görbéket kapunk, amelyek azt mutatják, hogy a rekonstrukció minősége függ a források pozíciójától (2.9(b). ábra).,9,9,8,8,7,7 Relatív átlagos hiba,6,5,4,3 Zajmentes Zajos Relatív átlagos hiba,6,5,4,3 Zajmentes Zajos,2,2,1, Kezdoõ szög Kezdo õ szög (a) 32 vetület (b) 4 vetület 2.9. ábra. A relatív átlagos hiba a kezdőszög(θ ) függvényében vonalmenti integrál esetén. A 2.9(b) görbe alakjára az lehet a magyarázat, hogy létezik egy bizonyos vetületi irány, ami több információt ad (pl. sok vonalmenti integrál ) a rekonstrukciós módszernek, mint a többi. Például a vetületi érték azt jelenti, hogy a megfelelő félegyenes mentén az összes pixel értékű (amit üres pixel sornak is nevezhetünk). Egy másik esetben, amikor a vetületi érték megegyezik a W négyzet és az adott félegyenes metszetével; ekkor a félegyenes mentén csupa 1-es értékű pixel található (nevezzük ezt teljes pixel sornak).ha a források olyan pozícióban vannak, ahol sok pixel található üres vagy teljes sorban, akkor a kép nagy része rekonstruálható kevés számú vetületből. A 2.6. ábrára nézve észrevehetjük, hogy ez az eset
26 16 Diszkrét tomográfiai rendszer kb. 4 -os forrás pozícióban található. A 4 vetületből rekonstruált képek a 2.1. ábrán láthatók. Ezek az ábrák megerősítik azt az előzetes feltevést, amikor is a rekonstrukció minősége jobb lesz abban az esetben, ha legalább egy forrás pozíciója majdnem ugyanabban a vonalban található, mint amin a fantomkép 3 körlapjának középpontja is fekszik. (a) kezdő szög, zajmentes (b) kezdő szög, 5%-os Gauss zaj (c) 4 kezdő szög, zajmentes (d) 4 kezdő szög,5%-osgauss zaj 2.1. ábra. 4 vetületből rekonstruált átlag képek különböző kezdő szögek és vonalmenti integrál esetében. Források száma A források száma a szimulációs tesztek során 2 és 32 között változott. Nem okozott meglepetést az, hogy a források számának növelésével, a rekonstrukció minősége javult. A tényleges kérdés az, hogy mi az a minimális szám, ami elegendő ahhoz, hogy jó minőségben állítsuk helyre az adott képet. A ábra alapján kapunk választ erre a kérdésre. Zajos esetben 12-nél több forrás esetén már alig csökken a hiba. Zajmentes esetben 22 forrás elegendő a jó minőségű rekonstrukció elvégzésére. A 2.11(a). ábra alapján azt a következtetést lehet levonni, hogy 22 vagy annál több forrás alig van hatással a rekonstrukció minőségére. Ugyanakkor zajmentes esetben, a fantom 22 vetületből való rekonstruálása több időt vesz igénybe, mint 32 vetület esetén (2.11(b) ábra). A ábrán láthatók a 12 illetve 22 forrásra kapott zajmentes, illetve 5%-os zajos vetületekből rekonstruált átlag képek.
27 2.4 Szimulációs kísérletek ,9 4,8 35 Relatív átlagos hiba,7,6,5,4,3 Zajmentes Zajos Ido (sec) õ Zaj mentes Zajos,2 1, Források száma Források száma (a) Relatív átlagos hiba (b) Idő (sec) ábra. A források számának (K) változtatásával elért hatás vonalmenti integrál esetén. (a) 12 forrás, zajmentes (b) 12 forrás, 5%-os Gauss zaj (c) 22 forrás, zajmentes (d) 22 forrás, 5%-os Gauss zaj ábra. Különböző számú forrás felhasználásával rekonstruált átlag képek vonalmenti integrál esetén.
28 18 Diszkrét tomográfiai rendszer Detektorok száma A detektorok száma megadja az egy forrásból mért vetületi értékek számát. Ha több detektorral rendelkezünk, akkor több egyenlet áll rendelkezésünkre a (2.4) egyenletrendszerben.,6,6,5,5 Relatív átlagos hiba,4,3,2 K=32 K=22 Relatív átlagos hiba,4,3,2 K=32 K=22,1, Detektorok száma Detektorok száma (a) Zajmentes (b) 5%-os Gauss eloszlású zaj ábra. A detektorok számának (L) változtatásával kapott relatív átlagos hiba vonalmenti integrál esetén. A detektorok számának a növelése egy adott határig javítja a rekonstrukció minőségét (2.13. ábra). Ez az érték 32 forrás esetén ebben az esetben L = 281 (2.13. és ábra). A rekonstruált bináris képből az tűnik ki, hogy ilyen paraméterek esetén csaknem tökéletes a rekonstrukció. Ezt a kísérletet megismételtük 22 vetületre is. Körülbelül ugyanazt a relatív átlagos hiba szintet L = 41 értékre kaptuk zajmentes esetben (2.13(a). ábra). A (2.6)-ban szereplő egyenletek száma csaknem megegyezik a két esetben (azaz = = 8822), ez megmagyarázza a két eredmény hasonlóságát. Az SA optimalizálási algoritmus paraméterei A megvalósított inhomogén SA algoritmus különböző paraméterekkel rendelkezik. Ebben a részben azt vizsgáljuk, hogy mi történik, ha a kezdő hőmérsékletet és a megállási feltételt változtatjuk. Kezdő hőmérséklet A szimulált hűtés algoritmusban az alacsony hőmérséklet azt jelenti, hogy kis valószínűséggel fogad el az algoritmus olyan változtatásokat, amelyek a célfüggvény értékének növelését vonják maguk után, azaz az algoritmus nehezen hagyja el egy lokális minimum vonzáskörzetét. Magasabb hőmérséklet esetén a rossz irányú lépés valószínűsége nagyobb, ennek megfelelően nagyobb valószínűséggel hagyja el a vonzáskörzetet, ennek következtében nagyobb valószínűséggel talál rá a globális minimumra. Mindamellett, egy túlzottan magas kezdő hőmérséklet esetén felesleges iterációs lépéseket hajt végre az algoritmus. Így a kezdő hőmérséklet paraméter beállítását gondosan kell elvégezni. Ebben a kísérletben a kezdő hőmérséklet 4 és 14 között változott. A görbék alapján láthatjuk (2.15. ábra), hogy a kezdő hőmérsékletnek az alap beállítások mellett nagyon korlátozott hatása van a relatív átlagos hibára. Ez azért lehetséges, mert az adott kezdő hőmérsékletek elég szabadságot adnak az SA algoritmusnak a globális minimum megtalálására. A végrehajtási idő görbéi (2.16. ábra) nem mutatnak nagy különbséget a maga-
29 2.4 Szimulációs kísérletek 19 (a) 11 detektor, zajmentes (b) 11 detektor, 5%-os Gauss zaj (c) 281 detektor, zajmentes (d) 281 detektor, 5%-os Gauss zaj ábra. 32 vetületből rekonstruált átlag képek különböző számú detektor felhasználásával vonalmenti integrál esetén.,18,18,15,15 Relatív átlagos hiba,12,9,6 K=32 K=22 Relatív átlagos hiba,12,9,6 K=32 K=22,3, Kezdoõ homérséklet õ Kezdo õ homérséklet õ (a) Zajmentes (b) 5%-os Gauss eloszlású zaj ábra. Relatív átlagos hiba a kezdőhőmérséklet (T () ) függvényében vonalmenti integrál esetén.
30 2 Diszkrét tomográfiai rendszer Ido (sec) õ K=32 K=22 Ido (sec) õ K=32 K= Kezdo õ homérséklet õ Kezdoõ homérséklet õ (a) Zajmentes (b) 5%-os Gauss eloszlású zaj ábra. A végrehajtási időakezdőhőmérséklet (T () ) függvényében vonalmenti integrál esetén. sabb kezdő hőmérsékletet tekintve. Megfigyelhető azonban, hogy 22 vetületből való rekonstrukció több időt vett igénybe, amikor nem adtunk zajt a vetületekhez. Ekkor a kevesebb egyenlet azt jelenti, hogy az egyenletrendszer alulhatározott és valószínűleg a célfüggvénynek ebben az esetben több lokális minimuma van. Fordított eredményt kapunk, amikor a vetületekhez 5%-os Gauss eloszlású zajt adtunk. Az lehet erre a magyarázat, hogy zaj és 32 vetület esetén több egyenletünk van és több lokális minimuma van a célfüggvénynek, mint K =22esetben. Megállási feltétel A megállási feltételt az inhomogén SA algoritmusban a nem elfogadott változtatások R thr számával határozzuk meg az utolsó N iter számú iterációs lépésben. Ha ez a szám nagyobb, mint egy előre megadott R thr küszöbérték, akkor azt mondjuk, hogy a hatékonyság alacsony, mert túl kevés változtatást fogadott el az algoritmus. A két paraméter hatását elkülönítve vizsgáltuk. Először az N iter értékét változtattuk és az R thr értékét ehhez képest magasan tartottuk (2.17 és ábra). A C célfüggvény eltérés szórásának a becslését az utolsó N var = N iter /2 elfogadott változtatás értékéből számítottuk ki. Másodszor rögzítettük az N iter értékét és hatékonyság küszöbértékét (azaz R thr -t) növeltük. Az eredményt a és a 2.2. ábrákon láthatjuk. A relatív átlagos hiba csökkenő, a végrehajtási idő emelkedő tendenciát mutatott mind a két kísérletben. Ezekből a megfigyelésekből azt a következtetést vonhatjuk le, hogy a nagyobb hatékonyság megkövetelése jobb eredményt produkál, de a rekonstrukció több időt vesz igénybe. A fantomkép bonyolultsága 1 különböző szoftver fantomot állítottunk elő. Ezek a fantomok 1, 2,..., 1 kört tartalmaznak egy adott méretű körgyűrűn belül (2.21. ábra). A kísérletet mindegyik szoftver fantom esetében 1-szor ismételtük meg. Ezeknek a kísérleteknek az eredményét a ábrán láthatjuk. A görbék alapján egyértelműen megállapíthatjuk, hogy a zajmentes és a zajos esetben eltérő eredményt kapunk. 22 zajmentes vetület esetén bonyolultabb képek csak nagyobb hibával rekonstruálhatóak. 32 vetület esetén elegendő információ áll rendelkezésre az összetett képek rekonstruálásához. 5%-os Gauss eloszlású zajt adva a vetületi értékekhez a rekonstrukció minősége nem változik lényegesen a fantomban lévő körök számával.
Diszkrét tomográfiai és PACS képfeldolgozó rendszerek
 Szegedi Tudományegyetem Képfeldolgozás és Számítógépes Grafika Tanszék Diszkrét tomográfiai és PACS képfeldolgozó rendszerek Doktori értekezés tézisei Nagy Antal Témavezető: Dr. Kuba Attila Szeged 2006
Szegedi Tudományegyetem Képfeldolgozás és Számítógépes Grafika Tanszék Diszkrét tomográfiai és PACS képfeldolgozó rendszerek Doktori értekezés tézisei Nagy Antal Témavezető: Dr. Kuba Attila Szeged 2006
Nem roncsoló tesztelés diszkrét tomográfiával
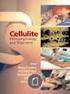 Nem roncsoló tesztelés diszkrét tomográfiával Dr. Balázs Péter, adjunktus Képfeldolgozás és Számítógépes Grafika Tanszék SZTE TTIK, Informatikai Tanszékcsoport A teszteléshez használt CT berendezés lapdetektor
Nem roncsoló tesztelés diszkrét tomográfiával Dr. Balázs Péter, adjunktus Képfeldolgozás és Számítógépes Grafika Tanszék SZTE TTIK, Informatikai Tanszékcsoport A teszteléshez használt CT berendezés lapdetektor
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
Képrekonstrukció 3. előadás
 Képrekonstrukció 3. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Computed Tomography (CT) Elv: Röntgen-sugarak áthatolása 3D objektum 3D térfogati kép Mérések
Képrekonstrukció 3. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Computed Tomography (CT) Elv: Röntgen-sugarak áthatolása 3D objektum 3D térfogati kép Mérések
Képrekonstrukció 6. előadás
 Képrekonstrukció 6. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Diszkrét tomográfia (DT) A CT-hez több száz vetület szükséges időigényes költséges károsíthatja
Képrekonstrukció 6. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Diszkrét tomográfia (DT) A CT-hez több száz vetület szükséges időigényes költséges károsíthatja
Konjugált gradiens módszer
 Közelítő és szimbolikus számítások 12. gyakorlat Konjugált gradiens módszer Készítette: Gelle Kitti Csendes Tibor Vinkó Tamás Faragó István Horváth Róbert jegyzetei alapján 1 LINEÁRIS EGYENLETRENDSZEREK
Közelítő és szimbolikus számítások 12. gyakorlat Konjugált gradiens módszer Készítette: Gelle Kitti Csendes Tibor Vinkó Tamás Faragó István Horváth Róbert jegyzetei alapján 1 LINEÁRIS EGYENLETRENDSZEREK
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Képrekonstrukció 9. előadás
 Képrekonstrukció 9. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem hv-konvex összefüggő halmazok Mag-burok-szerű rekonstrukció: S. Brunetti, A. Del Lungo, F.
Képrekonstrukció 9. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem hv-konvex összefüggő halmazok Mag-burok-szerű rekonstrukció: S. Brunetti, A. Del Lungo, F.
Infobionika ROBOTIKA. X. Előadás. Robot manipulátorok II. Direkt és inverz kinematika. Készült a HEFOP P /1.0 projekt keretében
 Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Alap-ötlet: Karl Friedrich Gauss ( ) valószínűségszámítási háttér: Andrej Markov ( )
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
b) Ábrázolja ugyanabban a koordinátarendszerben a g függvényt! (2 pont) c) Oldja meg az ( x ) 2
 1) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) b) c) ( ) ) Határozza meg az 1. feladatban megadott, ; intervallumon
1) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) b) c) ( ) ) Határozza meg az 1. feladatban megadott, ; intervallumon
6. Függvények. Legyen függvény és nem üreshalmaz. A függvényt az f K-ra való kiterjesztésének
 6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Grafikonok automatikus elemzése
 Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
Biomatematika 12. Szent István Egyetem Állatorvos-tudományi Kar. Fodor János
 Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
Orvosi tomográkus képalkotás/ct technika alapja
 Orvosi tomográkus képalkotás/ct technika alapja Kis Sándor Attila DEOEC, Nukléáris Medicina Intézet Outline 1 Bevezetés 2 A planáris transzmissziós leképzési technikák esetén a vizsgált objektumról összegképet
Orvosi tomográkus képalkotás/ct technika alapja Kis Sándor Attila DEOEC, Nukléáris Medicina Intézet Outline 1 Bevezetés 2 A planáris transzmissziós leképzési technikák esetén a vizsgált objektumról összegképet
Függvények Megoldások
 Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
A mérési eredmény megadása
 A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
Számítási feladatok a Számítógépi geometria órához
 Számítási feladatok a Számítógépi geometria órához Kovács Zoltán Copyright c 2012 Last Revision Date: 2012. október 15. kovacsz@nyf.hu Technikai útmutató a jegyzet használatához A jegyzet képernyőbarát
Számítási feladatok a Számítógépi geometria órához Kovács Zoltán Copyright c 2012 Last Revision Date: 2012. október 15. kovacsz@nyf.hu Technikai útmutató a jegyzet használatához A jegyzet képernyőbarát
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
15. LINEÁRIS EGYENLETRENDSZEREK
 15 LINEÁRIS EGYENLETRENDSZEREK 151 Lineáris egyenletrendszer, Gauss elimináció 1 Definíció Lineáris egyenletrendszernek nevezzük az (1) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
15 LINEÁRIS EGYENLETRENDSZEREK 151 Lineáris egyenletrendszer, Gauss elimináció 1 Definíció Lineáris egyenletrendszernek nevezzük az (1) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
Mátrixjátékok tiszta nyeregponttal
 1 Mátrixjátékok tiszta nyeregponttal 1. Példa. Két játékos Aladár és Bendegúz rendelkeznek egy-egy tetraéderrel, melyek lapjaira rendre az 1, 2, 3, 4 számokat írták. Egy megadott jelre egyszerre felmutatják
1 Mátrixjátékok tiszta nyeregponttal 1. Példa. Két játékos Aladár és Bendegúz rendelkeznek egy-egy tetraéderrel, melyek lapjaira rendre az 1, 2, 3, 4 számokat írták. Egy megadott jelre egyszerre felmutatják
Matematikai geodéziai számítások 10.
 Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Hódmezővásárhelyi Városi Matematikaverseny április 14. A osztályosok feladatainak javítókulcsa
 Hódmezővásárhelyi Városi Matematikaverseny 2003. április 14. A 11-12. osztályosok feladatainak javítókulcsa 1. feladat Egy számtani sorozatot az első eleme és különbsége egyértelműen meghatározza, azt
Hódmezővásárhelyi Városi Matematikaverseny 2003. április 14. A 11-12. osztályosok feladatainak javítókulcsa 1. feladat Egy számtani sorozatot az első eleme és különbsége egyértelműen meghatározza, azt
Számítógépes döntéstámogatás. Genetikus algoritmusok
 BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
MÉRÉSI EREDMÉNYEK PONTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI
 MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
Mérési hibák 2006.10.04. 1
 Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x
Szakmai zárójelentés a Diszkrét tomográfia új irányzatai és alkalmazása a neutron radiográfiában című OTKA 48476 pályázathoz
 Szakmai zárójelentés a Diszkrét tomográfia új irányzatai és alkalmazása a neutron radiográfiában című OTKA 48476 pályázathoz A számítógépes tomográfia alapfeladata egy adott objektum belsejének vizsgálata
Szakmai zárójelentés a Diszkrét tomográfia új irányzatai és alkalmazása a neutron radiográfiában című OTKA 48476 pályázathoz A számítógépes tomográfia alapfeladata egy adott objektum belsejének vizsgálata
A maximum likelihood becslésről
 A maximum likelihood becslésről Definíció Parametrikus becsléssel foglalkozunk. Adott egy modell, mellyel elképzeléseink szerint jól leírható a meghatározni kívánt rendszer. (A modell típusának és rendszámának
A maximum likelihood becslésről Definíció Parametrikus becsléssel foglalkozunk. Adott egy modell, mellyel elképzeléseink szerint jól leírható a meghatározni kívánt rendszer. (A modell típusának és rendszámának
Al-Mg-Si háromalkotós egyensúlyi fázisdiagram közelítő számítása
 l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
3D számítógépes geometria és alakzatrekonstrukció
 3D számítógépes geometria és alakzatrekonstrukció 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01
3D számítógépes geometria és alakzatrekonstrukció 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01
6. gyakorlat. Gelle Kitti. Csendes Tibor Somogyi Viktor. London András. jegyzetei alapján
 Közelítő és szimbolikus számítások 6. gyakorlat Sajátérték, Gersgorin körök Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján . Mátrixok sajátértékei
Közelítő és szimbolikus számítások 6. gyakorlat Sajátérték, Gersgorin körök Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján . Mátrixok sajátértékei
STATISZTIKAI PROBLÉMÁK A
 STATISZTIKAI PROBLÉMÁK A HULLÁMTÉR REPRODUKCIÓ TERÜLETÉN 2012. május 3., Budapest Firtha Gergely PhD hallgató, Akusztikai Laboratórium BME Híradástechnikai Tanszék firtha@hit.bme.hu Tartalom A hangtér
STATISZTIKAI PROBLÉMÁK A HULLÁMTÉR REPRODUKCIÓ TERÜLETÉN 2012. május 3., Budapest Firtha Gergely PhD hallgató, Akusztikai Laboratórium BME Híradástechnikai Tanszék firtha@hit.bme.hu Tartalom A hangtér
Az ipari komputer tomográfia vizsgálati lehetőségei
 Az ipari komputer tomográfia vizsgálati lehetőségei Dr. Czinege Imre, Kozma István Széchenyi István Egyetem 6. ANYAGVIZSGÁLAT A GYAKORLATBAN KONFERENCIA Cegléd, 2012. június 7-8. Tartalom A CT technika
Az ipari komputer tomográfia vizsgálati lehetőségei Dr. Czinege Imre, Kozma István Széchenyi István Egyetem 6. ANYAGVIZSGÁLAT A GYAKORLATBAN KONFERENCIA Cegléd, 2012. június 7-8. Tartalom A CT technika
6. Függvények. 1. Az alábbi függvények közül melyik szigorúan monoton növekvő a 0;1 intervallumban?
 6. Függvények I. Nulladik ZH-ban láttuk: 1. Az alábbi függvények közül melyik szigorúan monoton növekvő a 0;1 intervallumban? f x g x cos x h x x ( ) sin x (A) Az f és a h. (B) Mindhárom. (C) Csak az f.
6. Függvények I. Nulladik ZH-ban láttuk: 1. Az alábbi függvények közül melyik szigorúan monoton növekvő a 0;1 intervallumban? f x g x cos x h x x ( ) sin x (A) Az f és a h. (B) Mindhárom. (C) Csak az f.
Geometria 1 normál szint
 Geometria 1 normál szint Naszódi Márton nmarci@math.elte.hu www.math.elte.hu/ nmarci ELTE TTK Geometriai Tsz. Budapest Geometria 1 p.1/4 Vizsga 1. Írásban, 90 perc. 2. Index nélkül nem lehet vizsgázni!
Geometria 1 normál szint Naszódi Márton nmarci@math.elte.hu www.math.elte.hu/ nmarci ELTE TTK Geometriai Tsz. Budapest Geometria 1 p.1/4 Vizsga 1. Írásban, 90 perc. 2. Index nélkül nem lehet vizsgázni!
Az egyenes egyenlete: 2 pont. Az összevont alak: 1 pont. Melyik ábrán látható e függvény grafikonjának egy részlete?
 1. Írja fel annak az egyenesnek az egyenletét, amely áthalad az (1; 3) ponton, és egyik normálvektora a (8; 1) vektor! Az egyenes egyenlete: 2. Végezze el a következő műveleteket, és vonja össze az egynemű
1. Írja fel annak az egyenesnek az egyenletét, amely áthalad az (1; 3) ponton, és egyik normálvektora a (8; 1) vektor! Az egyenes egyenlete: 2. Végezze el a következő műveleteket, és vonja össze az egynemű
Lineáris egyenletrendszerek
 Lineáris egyenletrendszerek Lineáris egyenletrendszernek nevezzük az a 11 x 1 + a 12 x 2 +... +a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... +a 2n x n = b 2.. a k1 x 1 + a k2 x 2 +... +a kn x n = b k n ismeretlenes,
Lineáris egyenletrendszerek Lineáris egyenletrendszernek nevezzük az a 11 x 1 + a 12 x 2 +... +a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... +a 2n x n = b 2.. a k1 x 1 + a k2 x 2 +... +a kn x n = b k n ismeretlenes,
3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás
 3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav54
3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav54
1. tétel. 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója 7 cm. Mekkora a háromszög átfogója? (4 pont)
 1. tétel 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója cm. Mekkora a háromszög átfogója? (4 pont). Adott az ábrán két vektor. Rajzolja meg a b, a b és az a b vektorokat! (6 pont)
1. tétel 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója cm. Mekkora a háromszög átfogója? (4 pont). Adott az ábrán két vektor. Rajzolja meg a b, a b és az a b vektorokat! (6 pont)
almasi@dmi.u-szeged.hu, palko@radio.szote.u-szeged.hu, csernay@ss10.numed.szote.u-szeged.hu
 Radiológiai gyakorlatok a Szegedi Egyetemen PACS és multimédia támogatással Almási László 1, Palkó András 2, Csernay László 3 1 SZTE ÁOK Orvosi Informatikai Intézet, 2 SZTE ÁOK Radiológiai Klinika, 3 Nemzetközi
Radiológiai gyakorlatok a Szegedi Egyetemen PACS és multimédia támogatással Almási László 1, Palkó András 2, Csernay László 3 1 SZTE ÁOK Orvosi Informatikai Intézet, 2 SZTE ÁOK Radiológiai Klinika, 3 Nemzetközi
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Matematikai geodéziai számítások 6.
 Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Tárgy. Forgóasztal. Lézer. Kamera 3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL
 3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL. Bevezetés A lézeres letapogatás a ma elérhet legpontosabb 3D-s rekonstrukciót teszi lehet vé. Alapelve roppant egyszer : egy lézeres csíkkal megvilágítjuk a tárgyat.
3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL. Bevezetés A lézeres letapogatás a ma elérhet legpontosabb 3D-s rekonstrukciót teszi lehet vé. Alapelve roppant egyszer : egy lézeres csíkkal megvilágítjuk a tárgyat.
First Prev Next Last Go Back Full Screen Close Quit
 Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
Molekuláris dinamika I. 10. előadás
 Molekuláris dinamika I. 10. előadás Miről is szól a MD? nagy részecskeszámú rendszerek ismerjük a törvényeket mikroszkópikus szinten minden részecske mozgását szimuláljuk? Hogyan tudjuk megérteni a folyadékok,
Molekuláris dinamika I. 10. előadás Miről is szól a MD? nagy részecskeszámú rendszerek ismerjük a törvényeket mikroszkópikus szinten minden részecske mozgását szimuláljuk? Hogyan tudjuk megérteni a folyadékok,
2014/2015. tavaszi félév
 Hajder L. és Valasek G. hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom Geometria modellezés 1 Geometria modellezés 2 Geometria modellezés
Hajder L. és Valasek G. hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom Geometria modellezés 1 Geometria modellezés 2 Geometria modellezés
3. Előadás. Megyesi László: Lineáris algebra, oldal. 3. előadás Lineáris egyenletrendszerek
 3. Előadás Megyesi László: Lineáris algebra, 47. 50. oldal. Gondolkodnivalók Determinánsok 1. Gondolkodnivaló Determinánselméleti tételek segítségével határozzuk meg a következő n n-es determinánst: 1
3. Előadás Megyesi László: Lineáris algebra, 47. 50. oldal. Gondolkodnivalók Determinánsok 1. Gondolkodnivaló Determinánselméleti tételek segítségével határozzuk meg a következő n n-es determinánst: 1
A röntgendiagnosztika alapjai
 A röngtgendiagnosztika alapja: a sugárzás elnyelődése A röntgendiagnosztika alapjai A foton kölcsönhatásának lehetőségei: Compton-szórás Comptonszórás elnyelődés fotoeffektusban fotoeffektus nincs kölcsönhatás
A röngtgendiagnosztika alapja: a sugárzás elnyelődése A röntgendiagnosztika alapjai A foton kölcsönhatásának lehetőségei: Compton-szórás Comptonszórás elnyelődés fotoeffektusban fotoeffektus nincs kölcsönhatás
Lineáris leképezések. Wettl Ferenc március 9. Wettl Ferenc Lineáris leképezések március 9. 1 / 31
 Lineáris leképezések Wettl Ferenc 2015. március 9. Wettl Ferenc Lineáris leképezések 2015. március 9. 1 / 31 Tartalom 1 Mátrixleképezés, lineáris leképezés 2 Alkalmazás: dierenciálhatóság 3 2- és 3-dimenziós
Lineáris leképezések Wettl Ferenc 2015. március 9. Wettl Ferenc Lineáris leképezések 2015. március 9. 1 / 31 Tartalom 1 Mátrixleképezés, lineáris leképezés 2 Alkalmazás: dierenciálhatóság 3 2- és 3-dimenziós
DIGITÁLIS KÉPANALÍZIS KÉSZÍTETTE: KISS ALEXANDRA ELÉRHETŐSÉG:
 DIGITÁLIS KÉPANALÍZIS KÉSZÍTETTE: KISS ALEXANDRA ELÉRHETŐSÉG: kisszandi@mailbox.unideb.hu ImageJ (Fiji) Nyílt forrás kódú, java alapú képelemző szoftver https://fiji.sc/ Számos képformátumhoz megfelelő
DIGITÁLIS KÉPANALÍZIS KÉSZÍTETTE: KISS ALEXANDRA ELÉRHETŐSÉG: kisszandi@mailbox.unideb.hu ImageJ (Fiji) Nyílt forrás kódú, java alapú képelemző szoftver https://fiji.sc/ Számos képformátumhoz megfelelő
Bevezetés az elméleti zikába
 Bevezetés az elméleti zikába egyetemi jegyzet Kúpszeletek Lázár Zsolt, Lázár József Babe³Bolyai Tudományegyetem Fizika Kar 2011 TARTALOMJEGYZÉK 6 TARTALOMJEGYZÉK Azokat a görbéket, amelyeknek egyenlete
Bevezetés az elméleti zikába egyetemi jegyzet Kúpszeletek Lázár Zsolt, Lázár József Babe³Bolyai Tudományegyetem Fizika Kar 2011 TARTALOMJEGYZÉK 6 TARTALOMJEGYZÉK Azokat a görbéket, amelyeknek egyenlete
Koordináta-geometria feladatok (középszint)
 Koordináta-geometria feladatok (középszint) 1. (KSZÉV Minta (1) 2004.05/I/4) Adott az A(2; 5) és B(1; 3) pont. Adja meg az AB szakasz felezőpontjának koordinátáit! 2. (KSZÉV Minta (2) 2004.05/I/7) Egy
Koordináta-geometria feladatok (középszint) 1. (KSZÉV Minta (1) 2004.05/I/4) Adott az A(2; 5) és B(1; 3) pont. Adja meg az AB szakasz felezőpontjának koordinátáit! 2. (KSZÉV Minta (2) 2004.05/I/7) Egy
Fázisátalakulások vizsgálata
 Klasszikus Fizika Laboratórium VI.mérés Fázisátalakulások vizsgálata Mérést végezte: Vanó Lilla VALTAAT.ELTE Mérés időpontja: 2012.10.18.. 1. Mérés leírása A mérés során egy adott minta viselkedését vizsgáljuk
Klasszikus Fizika Laboratórium VI.mérés Fázisátalakulások vizsgálata Mérést végezte: Vanó Lilla VALTAAT.ELTE Mérés időpontja: 2012.10.18.. 1. Mérés leírása A mérés során egy adott minta viselkedését vizsgáljuk
Matematika A1a Analízis
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Matematika középszint 063 ÉRETTSÉGI VIZSGA 006. február. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI MINISZTÉRIUM Fontos tudnivalók Formai előírások: A dolgozatot
Matematika középszint 063 ÉRETTSÉGI VIZSGA 006. február. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI MINISZTÉRIUM Fontos tudnivalók Formai előírások: A dolgozatot
1. A Hilbert féle axiómarendszer
 {Euklideszi geometria} 1. A Hilbert féle axiómarendszer Az axiómarendszer alapfogalmai: pont, egyenes, sík, illeszkedés (pont egyenesre, pont síkra, egyenes síkra), közte van reláció, egybevágóság (szögeké,
{Euklideszi geometria} 1. A Hilbert féle axiómarendszer Az axiómarendszer alapfogalmai: pont, egyenes, sík, illeszkedés (pont egyenesre, pont síkra, egyenes síkra), közte van reláció, egybevágóság (szögeké,
Matematika (mesterképzés)
 Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Véletlenszám generátorok és tesztelésük. Tossenberger Tamás
 Véletlenszám generátorok és tesztelésük Tossenberger Tamás Érdekességek Pénzérme feldobó gép: $0,25-os érme 1/6000 valószínűséggel esik az élére 51% eséllyel érkezik a felfelé mutató oldalára Pörgetésnél
Véletlenszám generátorok és tesztelésük Tossenberger Tamás Érdekességek Pénzérme feldobó gép: $0,25-os érme 1/6000 valószínűséggel esik az élére 51% eséllyel érkezik a felfelé mutató oldalára Pörgetésnél
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
Pontműveletek. Sergyán Szabolcs Óbudai Egyetem Neumann János Informatikai Kar február 20.
 Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
3. Lineáris differenciálegyenletek
 3. Lineáris differenciálegyenletek A közönséges differenciálegyenletek két nagy csoportba oszthatók lineáris és nemlineáris egyenletek csoportjába. Ez a felbontás kicsit önkényesnek tűnhet, a megoldásra
3. Lineáris differenciálegyenletek A közönséges differenciálegyenletek két nagy csoportba oszthatók lineáris és nemlineáris egyenletek csoportjába. Ez a felbontás kicsit önkényesnek tűnhet, a megoldásra
KÉPARCHIVÁLÓ ÉS -TOVÁBBÍTÓ RENDSZER SZOFTVERÉNEK FEJLESZTÉSE (SZOTE-PACS)
 KÉPARCHIVÁLÓ ÉS -TOVÁBBÍTÓ RENDSZER SZOFTVERÉNEK FEJLESZTÉSE (SZOTE-PACS) Kuba Attila, kuba@inf.u-szeged.hu Alexin Zoltán, alexin@inf.u-szeged.hu Nagy Antal, nagya@inf.u-szeged.hu Nyúl László, nyul@inf.u-szeged.hu
KÉPARCHIVÁLÓ ÉS -TOVÁBBÍTÓ RENDSZER SZOFTVERÉNEK FEJLESZTÉSE (SZOTE-PACS) Kuba Attila, kuba@inf.u-szeged.hu Alexin Zoltán, alexin@inf.u-szeged.hu Nagy Antal, nagya@inf.u-szeged.hu Nyúl László, nyul@inf.u-szeged.hu
A II. kategória Fizika OKTV mérési feladatainak megoldása
 Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Skalárszorzat, norma, szög, távolság. Dr. Takách Géza NyME FMK Informatikai Intézet takach@inf.nyme.hu http://inf.nyme.hu/ takach/ 2005.
 1 Diszkrét matematika II., 4. el adás Skalárszorzat, norma, szög, távolság Dr. Takách Géza NyME FMK Informatikai Intézet takach@inf.nyme.hu http://inf.nyme.hu/ takach/ 2005. március 1 A téma jelent sége
1 Diszkrét matematika II., 4. el adás Skalárszorzat, norma, szög, távolság Dr. Takách Géza NyME FMK Informatikai Intézet takach@inf.nyme.hu http://inf.nyme.hu/ takach/ 2005. március 1 A téma jelent sége
Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Pataki János; dátum: november. I. rész
 Pataki János, november Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Pataki János; dátum: november I rész feladat Oldja meg az alábbi egyenleteket: a) log 7 log log log 7 ; b) ( )
Pataki János, november Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Pataki János; dátum: november I rész feladat Oldja meg az alábbi egyenleteket: a) log 7 log log log 7 ; b) ( )
egyenlőtlenségnek kell teljesülnie.
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Abszolútértékes és gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Abszolútértékes és gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
Hipotézis STATISZTIKA. Kétmintás hipotézisek. Munkahipotézis (H a ) Tematika. Tudományos hipotézis. 1. Előadás. Hipotézisvizsgálatok
 STATISZTIKA 1. Előadás Hipotézisvizsgálatok Tematika 1. Hipotézis vizsgálatok 2. t-próbák 3. Variancia-analízis 4. A variancia-analízis validálása, erőfüggvény 5. Korreláció számítás 6. Kétváltozós lineáris
STATISZTIKA 1. Előadás Hipotézisvizsgálatok Tematika 1. Hipotézis vizsgálatok 2. t-próbák 3. Variancia-analízis 4. A variancia-analízis validálása, erőfüggvény 5. Korreláció számítás 6. Kétváltozós lineáris
Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) Halmazok 1
 Halmazok 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) Halmazok 2 A fejezet legfontosabb elemei Halmaz megadási módjai Halmazok közti műveletek (metszet,
Halmazok 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) Halmazok 2 A fejezet legfontosabb elemei Halmaz megadási módjai Halmazok közti műveletek (metszet,
10. Koordinátageometria
 I. Nulladik ZH-ban láttuk: 0. Koordinátageometria. Melyek azok a P x; y pontok, amelyek koordinátái kielégítik az Ábrázolja a megoldáshalmazt a koordináta-síkon! x y x 0 egyenlőtlenséget? ELTE 00. szeptember
I. Nulladik ZH-ban láttuk: 0. Koordinátageometria. Melyek azok a P x; y pontok, amelyek koordinátái kielégítik az Ábrázolja a megoldáshalmazt a koordináta-síkon! x y x 0 egyenlőtlenséget? ELTE 00. szeptember
A brachistochron probléma megoldása
 A brachistochron probléma megoldása Adott a függőleges síkban két nem egy függőleges egyenesen fekvő P 0 és P 1 pont, amelyek közül a P 1 fekszik alacsonyabban. Azt a kérdést fogjuk vizsgálni. hogy van-e
A brachistochron probléma megoldása Adott a függőleges síkban két nem egy függőleges egyenesen fekvő P 0 és P 1 pont, amelyek közül a P 1 fekszik alacsonyabban. Azt a kérdést fogjuk vizsgálni. hogy van-e
Összeállította Horváth László egyetemi tanár
 Óbudai Egyetem Neumann János Informatikai Kar Intelligens Mérnöki Rendszerek Intézet Intelligens Mérnöki Rendszerek Szakirány a Mérnök informatikus alapszakon Összeállította Horváth László Budapest, 2011
Óbudai Egyetem Neumann János Informatikai Kar Intelligens Mérnöki Rendszerek Intézet Intelligens Mérnöki Rendszerek Szakirány a Mérnök informatikus alapszakon Összeállította Horváth László Budapest, 2011
3. előadás Stabilitás
 Stabilitás 3. előadás 2011. 09. 19. Alapfogalmak Tekintsük dx dt = f (t, x), x(t 0) = x 0 t (, ), (1) Jelölje t x(t; t 0, x 0 ) vagy x(.; t 0, x 0 ) a KÉF megoldását. Kívánalom: kezdeti állapot kis megváltozása
Stabilitás 3. előadás 2011. 09. 19. Alapfogalmak Tekintsük dx dt = f (t, x), x(t 0) = x 0 t (, ), (1) Jelölje t x(t; t 0, x 0 ) vagy x(.; t 0, x 0 ) a KÉF megoldását. Kívánalom: kezdeti állapot kis megváltozása
Diverzifikáció Markowitz-modell MAD modell CAPM modell 2017/ Szegedi Tudományegyetem Informatikai Intézet
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 11. Előadás Portfólió probléma Portfólió probléma Portfólió probléma Adott részvények (kötvények,tevékenységek,
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 11. Előadás Portfólió probléma Portfólió probléma Portfólió probléma Adott részvények (kötvények,tevékenységek,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 3 III. VÉLETLEN VEKTOROK 1. A KÉTDIMENZIÓs VÉLETLEN VEKTOR Definíció: Az leképezést (kétdimenziós) véletlen vektornak nevezzük, ha Definíció:
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 3 III. VÉLETLEN VEKTOROK 1. A KÉTDIMENZIÓs VÉLETLEN VEKTOR Definíció: Az leképezést (kétdimenziós) véletlen vektornak nevezzük, ha Definíció:
Gauss-Jordan módszer Legkisebb négyzetek módszere, egyenes LNM, polinom LNM, függvény. Lineáris algebra numerikus módszerei
 A Gauss-Jordan elimináció, mátrixinvertálás Gauss-Jordan módszer Ugyanazzal a technikával, mint ahogy a k-adik oszlopban az a kk alatti elemeket kinulláztuk, a fölötte lévő elemeket is zérussá lehet tenni.
A Gauss-Jordan elimináció, mátrixinvertálás Gauss-Jordan módszer Ugyanazzal a technikával, mint ahogy a k-adik oszlopban az a kk alatti elemeket kinulláztuk, a fölötte lévő elemeket is zérussá lehet tenni.
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011.
 BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
Kísérlettervezés alapfogalmak
 Kísérlettervezés alapfogalmak Rendszermodellezés Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Kísérlettervezés Cél: a modell paraméterezése a valóság alapján
Kísérlettervezés alapfogalmak Rendszermodellezés Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Kísérlettervezés Cél: a modell paraméterezése a valóság alapján
Matematika 11 Koordináta geometria. matematika és fizika szakos középiskolai tanár. > o < szeptember 27.
 Matematika 11 Koordináta geometria Juhász László matematika és fizika szakos középiskolai tanár > o < 2015. szeptember 27. copyright: c Juhász László Ennek a könyvnek a használatát szerzői jog védi. A
Matematika 11 Koordináta geometria Juhász László matematika és fizika szakos középiskolai tanár > o < 2015. szeptember 27. copyright: c Juhász László Ennek a könyvnek a használatát szerzői jog védi. A
Akusztikai tervezés a geometriai akusztika módszereivel
 Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Matematikai geodéziai számítások 6.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Modern Fizika Labor. 2. Elemi töltés meghatározása
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Függvények növekedési korlátainak jellemzése
 17 Függvények növekedési korlátainak jellemzése A jellemzés jól bevált eszközei az Ω, O, Θ, o és ω jelölések. Mivel az igények általában nemnegatívak, ezért az alábbi meghatározásokban mindenütt feltesszük,
17 Függvények növekedési korlátainak jellemzése A jellemzés jól bevált eszközei az Ω, O, Θ, o és ω jelölések. Mivel az igények általában nemnegatívak, ezért az alábbi meghatározásokban mindenütt feltesszük,
Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé.
 HA 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) HA 2 Halmazok HA 3 Megjegyzések A halmaz, az elem és az eleme fogalmakat nem definiáljuk, hanem alapfogalmaknak
HA 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) HA 2 Halmazok HA 3 Megjegyzések A halmaz, az elem és az eleme fogalmakat nem definiáljuk, hanem alapfogalmaknak
Határozatlan integrál (2) First Prev Next Last Go Back Full Screen Close Quit
 Határozatlan integrál () First Prev Next Last Go Back Full Screen Close Quit 1. Az összetett függvények integrálására szolgáló egyik módszer a helyettesítéssel való integrálás. Az idevonatkozó tétel pontos
Határozatlan integrál () First Prev Next Last Go Back Full Screen Close Quit 1. Az összetett függvények integrálására szolgáló egyik módszer a helyettesítéssel való integrálás. Az idevonatkozó tétel pontos
Least Squares becslés
 Least Squares becslés A négyzetes hibafüggvény: i d i ( ) φx i A négyzetes hibafüggvény mellett a minimumot biztosító megoldás W=( d LS becslés A gradiens számítása és nullává tétele eredményeképp A megoldás
Least Squares becslés A négyzetes hibafüggvény: i d i ( ) φx i A négyzetes hibafüggvény mellett a minimumot biztosító megoldás W=( d LS becslés A gradiens számítása és nullává tétele eredményeképp A megoldás
Véletlen jelenség: okok rendszere hozza létre - nem ismerhetjük mind, ezért sztochasztikus.
 Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Biometria az orvosi gyakorlatban. Regresszió Túlélésanalízis
 SZDT-09 p. 1/36 Biometria az orvosi gyakorlatban Regresszió Túlélésanalízis Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Logisztikus regresszió
SZDT-09 p. 1/36 Biometria az orvosi gyakorlatban Regresszió Túlélésanalízis Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Logisztikus regresszió
SZÍNES KÉPEK FELDOLGOZÁSA
 SZÍNES KÉPEK FELDOLGOZÁSA Színes képek feldolgozása Az emberi szem többezer színt képes megkülönböztetni, de csupán 20-30 különböző szürkeárnyalatot A színes kép feldolgozása két csoportba sorolható -
SZÍNES KÉPEK FELDOLGOZÁSA Színes képek feldolgozása Az emberi szem többezer színt képes megkülönböztetni, de csupán 20-30 különböző szürkeárnyalatot A színes kép feldolgozása két csoportba sorolható -
NGB_IN040_1 SZIMULÁCIÓS TECHNIKÁK dr. Pozna Claudio Radu, Horváth Ernő
 SZÉCHENYI ISTVÁN EGYETEM Műszaki Tudományi Kar Informatika Tanszék BSC FOKOZATÚ MÉRNÖK INFORMATIKUS SZAK NGB_IN040_1 SZIMULÁCIÓS TECHNIKÁK dr. Pozna Claudio Radu, Horváth Ernő Fejlesztői dokumentáció GROUP#6
SZÉCHENYI ISTVÁN EGYETEM Műszaki Tudományi Kar Informatika Tanszék BSC FOKOZATÚ MÉRNÖK INFORMATIKUS SZAK NGB_IN040_1 SZIMULÁCIÓS TECHNIKÁK dr. Pozna Claudio Radu, Horváth Ernő Fejlesztői dokumentáció GROUP#6
Készítette: Fegyverneki Sándor
 VALÓSZÍNŰSÉGSZÁMÍTÁS Összefoglaló segédlet Készítette: Fegyverneki Sándor Miskolci Egyetem, 2001. i JELÖLÉSEK: N a természetes számok halmaza (pozitív egészek) R a valós számok halmaza R 2 {(x, y) x, y
VALÓSZÍNŰSÉGSZÁMÍTÁS Összefoglaló segédlet Készítette: Fegyverneki Sándor Miskolci Egyetem, 2001. i JELÖLÉSEK: N a természetes számok halmaza (pozitív egészek) R a valós számok halmaza R 2 {(x, y) x, y
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I. 4 IV. FÜGGVÉNYEk 1. LEkÉPEZÉSEk, függvények Definíció Legyen és két halmaz. Egy függvény -ből -ba egy olyan szabály, amely minden elemhez pontosan egy elemet rendel hozzá. Az
KOVÁCS BÉLA, MATEmATIkA I. 4 IV. FÜGGVÉNYEk 1. LEkÉPEZÉSEk, függvények Definíció Legyen és két halmaz. Egy függvény -ből -ba egy olyan szabály, amely minden elemhez pontosan egy elemet rendel hozzá. Az
Compton-effektus. Zsigmond Anna. jegyzıkönyv. Fizika BSc III.
 Compton-effektus jegyzıkönyv Zsigmond Anna Fizika BSc III. Mérés vezetıje: Csanád Máté Mérés dátuma: 010. április. Leadás dátuma: 010. május 5. Mérés célja A kvantumelmélet egyik bizonyítékának a Compton-effektusnak
Compton-effektus jegyzıkönyv Zsigmond Anna Fizika BSc III. Mérés vezetıje: Csanád Máté Mérés dátuma: 010. április. Leadás dátuma: 010. május 5. Mérés célja A kvantumelmélet egyik bizonyítékának a Compton-effektusnak
Oktatási Hivatal. 1 pont. A feltételek alapján felírhatók az. összevonás után az. 1 pont
 Oktatási Hivatal Öt pozitív egész szám egy számtani sorozat első öt eleme A sorozatnak a különbsége prímszám Tudjuk hogy az első négy szám köbének összege megegyezik az ezen öt tag közül vett páros sorszámú
Oktatási Hivatal Öt pozitív egész szám egy számtani sorozat első öt eleme A sorozatnak a különbsége prímszám Tudjuk hogy az első négy szám köbének összege megegyezik az ezen öt tag közül vett páros sorszámú
Adaptív dinamikus szegmentálás idősorok indexeléséhez
 Adaptív dinamikus szegmentálás idősorok indexeléséhez IPM-08irAREAE kurzus cikkfeldolgozás Balassi Márton 1 Englert Péter 1 Tömösy Péter 1 1 Eötvös Loránd Tudományegyetem Informatikai Kar 2013. november
Adaptív dinamikus szegmentálás idősorok indexeléséhez IPM-08irAREAE kurzus cikkfeldolgozás Balassi Márton 1 Englert Péter 1 Tömösy Péter 1 1 Eötvös Loránd Tudományegyetem Informatikai Kar 2013. november
11. Előadás. 11. előadás Bevezetés a lineáris programozásba
 11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
Alkalmazás a makrókanónikus sokaságra: A fotongáz
 Alkalmazás a makrókanónikus sokaságra: A fotongáz A fotonok az elektromágneses sugárzás hordozó részecskéi. Spinkvantumszámuk S=, tehát kvantumstatisztikai szempontból bozonok. Fotonoknak habár a spinkvantumszámuk,
Alkalmazás a makrókanónikus sokaságra: A fotongáz A fotonok az elektromágneses sugárzás hordozó részecskéi. Spinkvantumszámuk S=, tehát kvantumstatisztikai szempontból bozonok. Fotonoknak habár a spinkvantumszámuk,
