GYIMESI LÁSZLÓ Gyôri Széchenyi István Egyetem, Digitális Elektronikai Laboratórium,
|
|
|
- Valéria Hegedűs
- 9 évvel ezelőtt
- Látták:
Átírás
1 Hallásmodellre alapozott optimális jeltisztítási eljárás alkalmazásával szerzett tapasztalatok FÖLDVÁRI RUDOLF Budapesti Mûszaki és Gazdaságtudományi Egyetem, Távközlési Tanszék GYIMESI LÁSZLÓ Gyôri Széchenyi István Egyetem, Digitális Elektronikai Laboratórium, Kulcsszavak: akusztika, hangosság érzet, kritikus sávszélesség, szûrôk, transzformációk A Földvári-féle hallásmodellben használt általánosított amplitúdó- és frekvencia-transzformáció (GAFT Generalized Amplitude and Frequency Transformation) ismertetése után bizonyítások nélkül felsoroljuk annak tulajdonságait. Bemutatjuk az optimális jeltisztítási eljárás blokkvázlatát, és a háttérzaj becslésének módszerét. Számos DEMO-t adunk, melyekhez rövid értékeléseket mellékelünk, továbbá közöljük az eredeti és a tisztított wav fájlok, valamint a PC-n futtatható exe fálj elérhetôségét. 1. Hallásmodellezés A hallás és a hallásmechanizmussal kapcsolatos kérdések évezredek óta foglalkoztatják az emberiséget [6]. Egészen a 20-ik század végéig rendkívül ellentmondásos elméletek kerültek napvilágra [1, 2, 3, 4 és 9]. A 60-as évek közepétôl azonban már nyilvánvalóvá vált, hogy lineáris transzformációk segítségével nem magyarázható, ennek egyik legalapvetôbb tulajdonsága, az idô- és frekvenciatartományban való igen jó felbontóképessége [7]. Fizikai-érzeti leképzés A hangforrás fizikailag mérhetô mennyiségei, az intenzitás, frekvencia, idôtartam, hangszín és irány, pszichológiai érzeteket váltanak ki a megfigyelôben. A fizikai inger az érzékszerven, idegi vezetésen és agymûködésen keresztül alakítja ki az érzetet. Az egyes ingerek, azaz a fizikai összetevôk és az érzet, azaz pszichológiai összetevôk között nincs kölcsönösen egyértelmû kapcsolat, összefüggéseik rendkívül bonyolultak [9]. Az érzeti oldal egyes mennyiségeit módunkban áll számszerûleg megismerni, ha a méréshez elôzetesen sikerül skálát felállítani. Ez minden pszichológiai kísérlet alapja, és egyben a legnehezebb lépése is. Az érzékelt hangosság és hangmagasság elsôsorban a hang intenzitásától és frekvenciájától függ, de a színkép, idôtartam és irány is befolyásolja hangosság és hangmagasság érzetünket. Hangosság Barkhausen (1927) vezette be a phon fogalmát, amely definíciószerûen a db értékekkel egyezik meg 1000 Hz-en, más frekvenciákon pedig a Fletcher-Munson görbékrôl olvasható le [5]. Hangmagasság A hangmagasság érzete a frekvenciával logaritmikusan növekszik és a legjellegzetesebb intervallum az oktáv. A hangmagasság érzet rendkívül erôsen függ attól, hogy a hangokat egyszerre, vagy egymásután szólaltatjuk meg. Kétféle hangmagasság érzetünk mûködik, egy melodikus és egy harmonikus. Hangmagasságnak a melodikus skálát fogadjuk el, ugyanis az egyszerre megszólaltatott hangok harmónia érzetet váltanak ki, melynek nincs közvetlen köze a hangmagasság érzethez [9]. A melodikus hangmagasság skála kísérletileg meghatározott összefüggés a frekvencia és a hangmagasság érzet között. Az érzeti skála sem lineárisan, sem logaritmikusan nem függ a frekvenciától. Az alaphang felismerése A természetben tisztán szinuszos hang alig fordul elô. A tiszta szinuszhoz a furulya, fuvola és az orgona hangja áll a legközelebb. Az alaphangon kívül annak az egészszámú többszörösei is jelen vannak. Az alaphang érzékelésével áttekinthetetlenül sok irodalom foglalkozik, melyek részben ellentmondóak. Az akusztikai Ohm törvény (1843) szerint a hang magassága a legalacsonyabb Fourier összetevô értékével azonos. Késôbb Helmholtz is csatlakozott Ohm elképzeléséhez [1, 2]. Az alaphang azonban akkor is tisztán hallható, ha a megszólaltatott hang a legmélyebb összetevôt nem tartalmazza. Ajelenség legegyszerûbb, de a valóságnak egyáltalán nem megfelelô magyarázata, a közép- és belsôfül nonlinearitására való hivatkozás, mely szerint a hiányzó alaphang torzítás eredményeképpen keletkezô különbségi hang. A legmeggyôzôbb kísérlet, mely bizonyítja, hogy nem különbségi hang jön létre, rendkívül egyszerû. Egy 2f o frekvenciájú hangot az egyik, 3f o frekvenciájút pedig a másik fülben megszólaltatva, az f o frekvenciájú virtuális hang változatlanul hallható, pedig ez esetben az egyik alaphártyát csak az egyik, a másik alaphártyát pedig csak a másik hanggal ingereltük. Ezzel bizonyítható, hogy a virtuális hang agyi eredetû, és semmi köze sincs a különbségi hanghoz, mely nem jöhet létre kétfülû (dichotikus) gerjesztés esetén. LIX. ÉVFOLYAM 2004/1 25
2 HÍRADÁSTECHNIKA 2. Kritikus sávok, fázishatár-frekvencia és két frekvencia-határ fogalma Kritikus sávok értelmezése A hangosságérzetünk függ az ingerlô jel sávszélességétôl. Akár sok szinuszos hanggal, akár zajjal gerjesztjük a fület, a sáv szélesedésével csak a fizikai hangintenzitás változásával halljuk a jelet hangosabbnak. Ha azonban ez a sávszélesség egy határértéket túllép, akkor megváltozik a helyzet, erôteljesebben növekszik a hangosság érzete, mint ahogy azt az ingerlô hatás növekedése indokolná. Gondos vizsgálatokkal sikerült tisztázni ezeknek az összefoglaló képességgel rendelkezô frekvenciasávoknak az értékét, melyeket kritikus sávoknak nevezünk [6]. ahol A(t)-t (mely negatív is lehet) általánosított pillanatnyi amplitúdónak, Ω(t)-t pillanatnyi frekvenciának nevezzük. Ezt a függvénytranszformációt Z(ω,t)-vel jelöljük, és GAFT-nak (Generalized Amplitude Frequency Transformation) hívjuk [10]. Az (1) egyenlettel adott pillanatnyi paraméterek úgy tekinthetôk, mint kölcsönösen független és ideális AM és FM demodulátorokat megvalósító transzformáltak. Az elmondottakat az 1. ábra szemlélteti., (1) Fázishatár-frekvencia értelmezése Az emberi hallás nemcsak a hangosság érzékelése során mutat egy kritikus sávon belül más tulajdonságot, mint szélessávban, hanem egy adott frekvencia környezetében a fázisra is érzékeny. Ha a frekvenciasávot szélesítjük, akkor egy határ után ez az érzékenység megszûnik, és már nem tudunk az amplitúdó- modulált és a frekvenciamodulált jel között különbséget tenni [6]. Feltûnô megegyezés, hogy ezen a területen belül a különbözô frekvenciák hangingere az energiával arányosan okoz hangosságérzetet, azaz megegyezik a kritikus sávokkal. Érdekes, hogy míg a hallásküszöb görbe alakulásában az egyes egyedek között nagy szórás mutatkozik, ezeknek az összefoglaló tulajdonságú sávoknak az értéke egyénektôl függetlenül egyetemlegesen érvényes adatnak tûnik. Két tiszta hang érzékelése Ha két tiszta hang egyszerre szólal meg, és frekvenciájuk azonos, akkor a hangmagasság nem változik, de ha kissé eltérnek egymástól, akkor elôbb lebegést, majd ha még jobban különböznek, érdességet észlelünk. Nem két különbözô frekvenciájú hangot, hanem a két frekvencia számtani átlagának megfelelô egyetlen hangmagasságú hangot hallunk. További távolodáskor az érdes, kellemetlen hang egyszer csak két külön hangra hasad szét. Ezt az értéket megkülönböztetési frekvenciatávolságnak, vagy két hang érzeti határnak nevezzük. Nagyjából a kritikus sáv távolságában megszûnik az érdességi megítélés, és ekkor hallunk egymás mellett két sima, zavartalan hangot [6]. 3. Általánosított amplitúdó és frekvencia transzformáció Ha egy x(t) idôfüggvény Fourier-transzformálható, továbbá nem tartalmaz egyen komponenst, akkor létezik a Hilbert párja, és ezt jelöljük y(t)-vel. Felhasználva x(t) és y(t) idôfüggvényeket bevezethetjük a következô transzformációt: 1. ábra a) modulálatlan vivô b) amplitúdó moduláció c) frekvencia moduláció d) együttes amplitúdó és frekvencia moduláció A pillanatnyi paraméterek (GAFT) tulajdonságai Apillanatnyi paraméterek az idô-frekvencia sík felett egy görbét határoznak meg (1. ábra). Az (1) egyenletbôl látható, hogy a kapcsolat nemlineáris, a pillanatnyi paraméterekre a szuperpozíció elve nem érvényes. A GAFT a geometriai értelemben hasonló jeleket hasonló függvényekbe képezi le. A GAFT invariáns az idôeltolással szemben. A jel pillanatnyi teljesítménye A 2 (t). Az általánosított amplitúdó és pillanatnyi frekvencia tartója azonos a jel idôtartománybeli tartójával. A GAFT tetszôlegesen sokszor ismételhetô, ha az A(t) és Ω(t) jelek DC komponenseit leválasztjuk. Ilyenkor hasonló tulajdonságú függvényeket kapunk, mint az x(t). Ha egy jel periodikus, akkor A(t) és Ω(t) szintén periodikus. 26 LIX. ÉVFOLYAM 2004/1
3 Hallásmodellre alapozott optimális jeltisztítási eljárás... Az úgynevezett bizonytalansági reláció közvetlenül nem értelmezhetô a GAFT esetében. A pillanatnyi paraméterek által meghatározott A(t), Ω(t), mint az a (1) egyenletbôl látható, csak az idôtôl függ, zérus szórású. Az illesztett mintavételezés hasonló tulajdonságokkal rendelkezik. 4. Illesztett mintavételezés Egy sávkorlátos periodikus jel mindig felírható a következô alakban (2): Legyen x(t) a (2)-nek megfelelô alakú, és a (0,T) intervallumban vegyünk mintát a jel helyi szélsôértékeinél a 2. ábrának megfelelôen. Bizonyítható, hogy a {x 1,t 1, x 2, t 2,..., x i, t i,} halmaz egyértelmûen meghatározza x(t)-t, ha ω H <2ω L, azaz ha x(t) komponensei egy oktávnál szûkebb sávba esnek [8]. Ez a feltétel esetünkben teljesül, ugyanis a Zwicker-szûrôk kb. terc szélességûek. 2. ábra Periodikus, véges sávszélességû jel helyi szélsôértékei 5. A hallásmodell felépítése és tulajdonságai Az emberi hallás alapvetô tulajdonságaira pontos magyarázat adható a Zwicker-féle szûrôsor kimenetein alkalmazott GAFT (vagy illesztett mintavételezés) felhasználásával (3. ábra). 3. ábra Zwicker-féle szûrôk (0-24) karakterisztikái és eredôjük 4. ábra A hallásmodell tömbvázlata Az általunk javasolt legegyszerûbb hallásmodell blokkvázlata a 4. ábrán látható. A váltószûrôk feladata a lassan változó komponens és a kváziperiodikusan változó komponensek szétválasztása. További kiegészítésekre attól függôen van szükség, hogy a modell felhasználásával milyen feladatot kívánunk megoldani. Ahallásmodell alapvetô tulajdonságai: A 3. ábrán jól látható, hogy a szûrôbank eredô karakterisztikája tökéletesen meghatározza a bemeneti x(t) jelet. Az ingadozás kisebb, mint 0.5 db, a késleltetés kb. 10 ms. Az összegezett jel, még zene esetén sem különböztethetô meg az eredetitôl. Tekintettel arra, hogy mind a GAFT, mind az illesztett mintavétel egzakt transzformáció, a A k (t) és Ω k (t) jelek, illetve a váltószûrôk kimeneti jelei, egyértelmûen meghatározzák az x(t) jelet. A kapcsolat egyértelmû, de a nemlineáris transzformáció miatt rendkívül bonyolult. Minden x(t)-hez különbözô válaszfüggvények tartoznak, és természetesen a lineáris szuperpozíció nem érvényes. Az A k (t) jelek felhasználásával meghatározható az x(t) jel által okozott hangosság érzet. A szûrôbankot az igazi hangosság méréséhez használják, hiszen hangosság érzetünk döntôen függ attól, hogy az inger komponensei melyik frekvenciatartományba esnek. Hosszan megszólaltatott tiszta hang esetén a modell szinte tetszôleges felbontást valósít meg a frekvenciatartományban. Triviális, hogy végtelen hosszú szinuszos jel esetén a Zwicker-féle szûrôsor a jelre nincs hatással, kimenetein a pillanatnyi paraméterek elvileg bármilyen pontossággal meghatározhatók. Két szinuszos jellel vizsgálva a modellt, a fent elmondottak továbbra is érvényesek, ha a frekvenciák között több kritikus sáv távolság van. Ha a két jel ugyanabba a részsávba esik, akkor Ω k (t) átlaga a két frekvencia számtani átlaga. A modell felhasználásával meghatározható a virtuális hang, ugyanis a hiányzó alaphang feletti részsávok jelébôl Ω i (t) és Ω k (t) meghatározható a váltóáramú komponensek periódusideje, melyek a hiányzó alaphang pe- LIX. ÉVFOLYAM 2004/1 27
4 HÍRADÁSTECHNIKA riódusidejével egyeznek meg. Az így meghatározott periódusidôt nem lehet befolyásolni a hiányzó alaphang helyére beadott keskenysávú zajjal, és nem lehetséges a hiányzó alaphang környezetében lebegést elérni. Ha azonban a jel az alapot tartalmazza, akkor lebegés jön létre, hiszen a szóban forgó részsáv pillanatnyi paraméterei pontosan követik a lebegést. A modellen a bizonytalansági reláció csak meglehetôsen bonyolultan értelmezhetô. Azonban megmutatható, hogy a modell felhasználásával kisebb felbontás is elérhetô, mint a hallásra publikált érték [7]. 6. Beszéd kiemelése háttérzajból A zajos háttérbôl történô beszédkiemelésre a hallásmodell egyszerûsített változatát célszerû használni. Az eljárás blokkvázlatát az 5. ábra mutatja. Ebben az egyenletben a teljesítmény sûrûségspektrumok nem ismertek, de igen jó becslések adhatók értékükre. Abból a felismerésbôl kiindulva, hogy a beszéd mindig tartalmaz szüneteket, következik, hogy A k L (t) minimumának négyzete arányos a háttérzaj teljesítményével, azaz továbbá A L k (t) pillanatnyi értékének négyzete arányos a jel és a zaj teljesítményének az összegével, hiszen a jel és a zaj kölcsönösen független folyamatok. Mindezek alapján írhatjuk, hogy (7) (5) (6) Normalizáljuk A k L (t) értékét a minimumával, és vezessük be a következô egyszerûsítô jelölést: (8) Fentieket felhasználva néhány egyszerû átalakítás után azt kapjuk, hogy a súlytényezô értéke: (9) 5. ábra Zajos háttérbôl történô beszédkiemelés egyszerûsített blokkvázlata A megoldás elméleti alapját az úgynevezett optimumszûrô szolgáltatja [11]. Ha egy rendszer bemenetére zajos jel kerül, azaz x(t) = s(t) + n(t), (3) akkor a rendszer jellemzôit úgy célszerû megválasztani, hogy a kimeneti y(t) jel minél többet tartalmazzon a hasznos jelbôl, és minél kevesebbet a zavaró jelbôl. A feladat általános esetben nem oldható meg, ezért a feladatot célszerû lineáris rendszerre korlátozni. Az így nyert lineáris rendszer az optimumszûrô. A Wiener-Hopf integrálegyenlet megoldása adja a keresett rendszer K(ω) átviteli karakterisztikáját, amely a jel és a zaj teljesítmény sûrûség spektrumával kifejezve a következô: Ennek alapján a k-adik csatornában az A k *(t) súlytényezôt a következô értékre kell beállítani: (4) Ez a lassan változó jel (az 5. ábra közepén A ~ (t) -vel jelölve) kerül a (9) által meghatározott nemlineáris karakterisztikára, melynek kimeneti jele állítja be minden egyes részsáv erôsítését. Természetesen, ha a beszéd nem tartalmaz háttérzajt, akkor a csatorna jele változatlanul kerül az öszszegzôre, hiszen ebben az esetben minden súlytényezô értéke A k (t) = Záró megjegyzések A) A 6. pontban ismertetett eljárás igen jól használható régi zajos felvételek, hanglemezek tûzörejének, valamint régi filmek hanganyagának tisztítására. Ezekben az esetekben az optimálisan megtisztított jel hangzása nem a legkellemesebb, ezért a normalizálást nem a minimummal, hanem egy kisebb értékkel célszerû elvégezni. Természetesen így kevesebb háttérzaj kerül eltávolításra, de kellemesebbnek halljuk a megtisztított anyagot. A legjobb megoldásnak azt tartjuk, ha a helyes arány beállítását hangmérnök végzi. 28 LIX. ÉVFOLYAM 2004/1
5 Hallásmodellre alapozott optimális jeltisztítási eljárás... B) Ha a háttérzaj egészen speciális (pl. egy üzemcsarnokban a beszédnél is hangosabb csattanások), az eljárás természetesen csak a beszédszünetekben hallható zajt csökkenti, a csattanásokat nem, hiszen a háttérzajból éppen úgy kiemelkedik, mint a beszéd. Ilyen speciális zavarok csökkentéséhez további kiegészítésekre van szükség. Például pitch detektor felhasználásával a beszéd maximumai meghatározhatók. A csattanások szintje egy, a zajforráshoz közel elhelyezett mikrofon segítségével csökkenthetô (ismert jel elnyomás). Ez a megoldás bármilyen típusú zaj esetén használható, ha háttérzaj jól definiálható forrásból származik. Ha ez nem áll fenn, akkor ez a megoldás igen kevés eredménnyel kecsegtet. Például egy autóban a szélvédô bal és jobb oldalánál elhelyezett mikrofonok jelei gyakorlatilag függetlenek, ezért egyik jel sem csökkenthetô a másik felhasználásával. C) Ha a háttérzaj összemérhetô a beszéd hangosságával, azaz a jel-zaj viszony kisebb 10 db-nél, akkor elôfordulhat, hogy a tisztított beszéd rosszabbul érthetô, mint az eredeti. Ilyen esetben a tisztítás hatásfokát csökkenteni kell. Ez a feladat megoldható, ha a minimumokon kívül a maximumokat is figyeljük, és megpróbálunk a jel-zaj viszonyra becslést adni. Sajnos minden típusra más-más algoritmust kellene kidolgozni (pl. a jelbôl kiemelkedô csattanás ad egy maximumot, de ennek semmi köze sincs a jel-zaj viszonyhoz). D) A nemlineáris hallásmodell [10] felhasználásával és további kiegészítésével majdnem minden feladat megoldását sikerült szimulálni. Rendkívül jól használható ismert jel elnyomásra, források szétválasztására, visszhang csökkentésére, zöngés-zöngétlen döntô, valamint pitch detektor készítésére, továbbá beszéd tömörítésére [12, 13]. A minôség még tökéletes (az eredetitôl megkülönböztethetetlen) maradt 1000 bit/s átviteli sebesség esetén is (késleltetési idô kb. 100 ms). Kisebb sebességû átvitel is megvalósítható, de természetesen csak minôségromlás és a késleltetési idô további növekedése árán. Köszönetnyilvánítás A hallásmodell elméleti hátterének kidolgozásában nyújtott segítségért ezúton is szeretnénk köszönetet mondani dr. Papp Lászlónak és dr. Osváth Lászlónak. Irodalom [1] G. S. Ohm: Über die Definition des Tones, nebst daran geknüpfter Theorie der Sirene und ähnlicher tonbildender Vorrichtungen. Ann. der Phisik, Vol. 59, No. 8, , [2] H.v. Helmholtz: Die Lehre von den Tonempfindungen. Braunschweig, 1863, [3] D. Gabor: Acoustical Quanta and the Theory of Hearing. Nature, Vol. 159, , [4] Békésy, Gy., Rosenblith, W. A.: The early history of hearing observations and theories. J. Acoust. Soc. Am. Vol. 20, [5] H. Fletcher: Speech and Hearing. Nostrand C., New York, [6] E. Zwicker, R. Feldtkeller: Das Ohr als Nachrichtenempfnger. Hirzel V., Stuttgart, [7] L. M. Grobben: Appreciation of Short Tones. Seventh International Congress on Acoustics, Budapest, Vol. 3, , [8] R. Földvári: Adaptive Sampling. Periodica Politechnica Electrical Engineering, Vol. 33, No. 3, Budapest, [9] Tarnóczy T.: Einführung in die musikalische Akustik. Akadémiai Kiadó, Budapest, [10] R. Földvári: Generalized instantaneous amplitude and frequency functions and their application for pitch frequency determination. Journal of Circuits, Systems, and Computers, Vol. 5, No. 2, [11] R. Földvári, Gy. Ács: Speech Enhancement Based on a New Hearing Model. 19th Czech-Hungarian-Polish Workshop on Circuit Theory and Applications, Prague, [12] R. Földvári, Gy. Ács: Speech and Music Coder Based on a New Hearing Model. 7th Conference and Exhibition on Television and Sound Technique, Budapest, [13] R. Földvári, L. Gyimesi: Very Low Bit Rate Voice Coder Based on a Nonlinear Hearing Model. Eurospeech 99 6th European Conference of Speech Communication and Technology, Budapest, LIX. ÉVFOLYAM 2004/1 29
Hallás időállandói. Következmények: 20Hz alatti hang nem hallható 12Hz kattanás felismerhető
 Hallás időállandói Fizikai terjedési idők Dobhártya: végtelenül gyors Hallócsontok: 0.08ms késés Csiga: 20Hz: 3ms késés 100Hz: 1.5 ms késés 1000Hz: 0.3ms késés >3000Hz: késés nélkül Ideg-impulzus időtartam:
Hallás időállandói Fizikai terjedési idők Dobhártya: végtelenül gyors Hallócsontok: 0.08ms késés Csiga: 20Hz: 3ms késés 100Hz: 1.5 ms késés 1000Hz: 0.3ms késés >3000Hz: késés nélkül Ideg-impulzus időtartam:
2. Az emberi hallásról
 2. Az emberi hallásról Élettani folyamat. Valamilyen vivőközegben terjedő hanghullámok hatására, az élőlényben szubjektív hangérzet jön létre. A hangérzékelés részben fizikai, részben fiziológiai folyamat.
2. Az emberi hallásról Élettani folyamat. Valamilyen vivőközegben terjedő hanghullámok hatására, az élőlényben szubjektív hangérzet jön létre. A hangérzékelés részben fizikai, részben fiziológiai folyamat.
A hang mint mechanikai hullám
 A hang mint mechanikai hullám I. Célkitűzés Hullámok alapvető jellemzőinek megismerése. A hanghullám fizikai tulajdonságai és a hangérzet közötti összefüggések bemutatása. Fourier-transzformáció alapjainak
A hang mint mechanikai hullám I. Célkitűzés Hullámok alapvető jellemzőinek megismerése. A hanghullám fizikai tulajdonságai és a hangérzet közötti összefüggések bemutatása. Fourier-transzformáció alapjainak
1. A hang, mint akusztikus jel
 1. A hang, mint akusztikus jel Mechanikai rezgés - csak anyagi közegben terjed. A levegő molekuláinak a hangforrástól kiinduló, egyre csillapodva tovaterjedő mechanikai rezgése. Nemcsak levegőben, hanem
1. A hang, mint akusztikus jel Mechanikai rezgés - csak anyagi közegben terjed. A levegő molekuláinak a hangforrástól kiinduló, egyre csillapodva tovaterjedő mechanikai rezgése. Nemcsak levegőben, hanem
Teremakusztikai méréstechnika
 Teremakusztikai méréstechnika Tantermek akusztikája Fürjes Andor Tamás 1 Tartalomjegyzék 1. A teremakusztikai mérések célja 2. Teremakusztikai paraméterek 3. Mérési módszerek 4. ISO 3382 szabvány 5. Méréstechnika
Teremakusztikai méréstechnika Tantermek akusztikája Fürjes Andor Tamás 1 Tartalomjegyzék 1. A teremakusztikai mérések célja 2. Teremakusztikai paraméterek 3. Mérési módszerek 4. ISO 3382 szabvány 5. Méréstechnika
π π A vivőhullám jelalakja (2. ábra) A vivőhullám periódusideje T amplitudója A az impulzus szélessége szögfokban 2p. 2p [ ]
![π π A vivőhullám jelalakja (2. ábra) A vivőhullám periódusideje T amplitudója A az impulzus szélessége szögfokban 2p. 2p [ ] π π A vivőhullám jelalakja (2. ábra) A vivőhullám periódusideje T amplitudója A az impulzus szélessége szögfokban 2p. 2p [ ]](/thumbs/92/108201304.jpg) Pulzus Amplitúdó Moduláció (PAM) A Pulzus Amplitúdó Modulációról abban az esetben beszélünk, amikor egy impulzus sorozatot használunk vivőhullámnak és ezen a vivőhullámon valósítjuk meg az amplitúdómodulációt
Pulzus Amplitúdó Moduláció (PAM) A Pulzus Amplitúdó Modulációról abban az esetben beszélünk, amikor egy impulzus sorozatot használunk vivőhullámnak és ezen a vivőhullámon valósítjuk meg az amplitúdómodulációt
Digitális mérőműszerek. Kaltenecker Zsolt Hiradástechnikai Villamosmérnök Szinusz Hullám Bt.
 Digitális mérőműszerek Digitális jelek mérése Kaltenecker Zsolt Hiradástechnikai Villamosmérnök Szinusz Hullám Bt. MIRŐL LESZ SZÓ? Mit mérjünk? Hogyan jelentkezik a minőségromlás digitális jel esetében?
Digitális mérőműszerek Digitális jelek mérése Kaltenecker Zsolt Hiradástechnikai Villamosmérnök Szinusz Hullám Bt. MIRŐL LESZ SZÓ? Mit mérjünk? Hogyan jelentkezik a minőségromlás digitális jel esetében?
Gyakorló többnyire régebbi zh feladatok. Intelligens orvosi műszerek október 2.
 Gyakorló többnyire régebbi zh feladatok Intelligens orvosi műszerek 2018. október 2. Régebbi zh feladat - #1 Az ábrán látható két jelet, illetve összegüket mozgóablak mediánszűréssel szűrjük egy 11 pontos
Gyakorló többnyire régebbi zh feladatok Intelligens orvosi műszerek 2018. október 2. Régebbi zh feladat - #1 Az ábrán látható két jelet, illetve összegüket mozgóablak mediánszűréssel szűrjük egy 11 pontos
Rezgés, Hullámok. Rezgés, oszcilláció. Harmonikus rezgő mozgás jellemzői
 Rezgés, oszcilláció Rezgés, Hullámok Fogorvos képzés 2016/17 Szatmári Dávid (david.szatmari@aok.pte.hu) 2016.09.26. Bármilyen azonos időközönként ismétlődő mozgást, periodikus mozgásnak nevezünk. A rezgési
Rezgés, oszcilláció Rezgés, Hullámok Fogorvos képzés 2016/17 Szatmári Dávid (david.szatmari@aok.pte.hu) 2016.09.26. Bármilyen azonos időközönként ismétlődő mozgást, periodikus mozgásnak nevezünk. A rezgési
Jelek és rendszerek 1. 10/9/2011 Dr. Buchman Attila Informatikai Rendszerek és Hálózatok Tanszék
 Jelek és rendszerek 1 10/9/2011 Dr. Buchman Attila Informatikai Rendszerek és Hálózatok Tanszék 1 Ajánlott irodalom: FODOR GYÖRGY : JELEK ÉS RENDSZEREK EGYETEMI TANKÖNYV Műegyetemi Kiadó, Budapest, 2006
Jelek és rendszerek 1 10/9/2011 Dr. Buchman Attila Informatikai Rendszerek és Hálózatok Tanszék 1 Ajánlott irodalom: FODOR GYÖRGY : JELEK ÉS RENDSZEREK EGYETEMI TANKÖNYV Műegyetemi Kiadó, Budapest, 2006
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 3. MÉRÉSFELDOLGOZÁS
 ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 3. MÉRÉSFELDOLGOZÁS Dr. Soumelidis Alexandros 2018.10.04. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG Mérés-feldolgozás
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 3. MÉRÉSFELDOLGOZÁS Dr. Soumelidis Alexandros 2018.10.04. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG Mérés-feldolgozás
Digitális mérőműszerek
 KTE Szakmai nap, Tihany Digitális mérőműszerek Digitális jelek mérése Kaltenecker Zsolt KT-Electronic MIRŐL LESZ SZÓ? Mit mérjünk? Hogyan jelentkezik a minőségromlás digitális TV jel esetében? Milyen paraméterekkel
KTE Szakmai nap, Tihany Digitális mérőműszerek Digitális jelek mérése Kaltenecker Zsolt KT-Electronic MIRŐL LESZ SZÓ? Mit mérjünk? Hogyan jelentkezik a minőségromlás digitális TV jel esetében? Milyen paraméterekkel
A mintavételezéses mérések alapjai
 A mintavételezéses mérések alapjai Sok mérési feladat során egy fizikai mennyiség időbeli változását kell meghatároznunk. Ha a folyamat lassan változik, akkor adott időpillanatokban elvégzett méréssel
A mintavételezéses mérések alapjai Sok mérési feladat során egy fizikai mennyiség időbeli változását kell meghatároznunk. Ha a folyamat lassan változik, akkor adott időpillanatokban elvégzett méréssel
5. témakör. Szögmodulációk: Fázis és frekvenciamoduláció FM modulátorok, demodulátorok
 5. témakör Szögmodulációk: Fázis és frekvenciamoduláció FM modulátorok, demodulátorok Szögmoduláció Általánosan felírva a vivőfrekvenciás jelet (AM-nél megismert módon): Amennyiben a vivő pillanatnyi amplitúdója
5. témakör Szögmodulációk: Fázis és frekvenciamoduláció FM modulátorok, demodulátorok Szögmoduláció Általánosan felírva a vivőfrekvenciás jelet (AM-nél megismert módon): Amennyiben a vivő pillanatnyi amplitúdója
Informatikai eszközök fizikai alapjai Lovász Béla
 Informatikai eszközök fizikai alapjai Lovász Béla Kódolás Moduláció Morzekód Mágneses tárolás merevlemezeken Modulációs eljárások típusai Kódolás A kód megállapodás szerinti jelek vagy szimbólumok rendszere,
Informatikai eszközök fizikai alapjai Lovász Béla Kódolás Moduláció Morzekód Mágneses tárolás merevlemezeken Modulációs eljárások típusai Kódolás A kód megállapodás szerinti jelek vagy szimbólumok rendszere,
Akusztikus MEMS szenzor vizsgálata. Sós Bence JB2BP7
 Akusztikus MEMS szenzor vizsgálata Sós Bence JB2BP7 Tartalom MEMS mikrofon felépítése és típusai A PDM jel Kinyerhető információ CIC szűrő Mérési tapasztalatok. Konklúzió MEMS (MicroElectrical-Mechanical
Akusztikus MEMS szenzor vizsgálata Sós Bence JB2BP7 Tartalom MEMS mikrofon felépítése és típusai A PDM jel Kinyerhető információ CIC szűrő Mérési tapasztalatok. Konklúzió MEMS (MicroElectrical-Mechanical
Értékelés Összesen: 100 pont 100% = 100 pont A VIZSGAFELADAT MEGOLDÁSÁRA JAVASOLT %-OS EREDMÉNY: EBBEN A VIZSGARÉSZBEN A VIZSGAFELADAT ARÁNYA 35%.
 Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzék módosításának eljárásrendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján: Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzék módosításának eljárásrendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján: Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
Modern Fizika Labor. 5. ESR (Elektronspin rezonancia) Fizika BSc. A mérés dátuma: okt. 25. A mérés száma és címe: Értékelés:
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 25. A mérés száma és címe: 5. ESR (Elektronspin rezonancia) Értékelés: A beadás dátuma: 2011. nov. 16. A mérést végezte: Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 25. A mérés száma és címe: 5. ESR (Elektronspin rezonancia) Értékelés: A beadás dátuma: 2011. nov. 16. A mérést végezte: Szőke Kálmán Benjamin
A MEGTÖRT CSEND. Muntag András december 9. L DEN + L NIGHT. A megtört csend
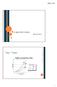 A MEGTÖRT CSEND Muntag András L DEN + L NIGHT 2 1 UNBIASED ANNOYANCE (ELŐÍTÉLETMENTES ZAVARÁS) UBA d 1 N 0.3 N 1.3 10 N 1 0.25S 1 lgn 10 0.3F au 10 N10 d 1 5 0,5 S 0.11 10 24bark 0 ' N z g N z dz 10 acum
A MEGTÖRT CSEND Muntag András L DEN + L NIGHT 2 1 UNBIASED ANNOYANCE (ELŐÍTÉLETMENTES ZAVARÁS) UBA d 1 N 0.3 N 1.3 10 N 1 0.25S 1 lgn 10 0.3F au 10 N10 d 1 5 0,5 S 0.11 10 24bark 0 ' N z g N z dz 10 acum
Az emberi hallás. A fül felépítése
 Az emberi hallás A fül felépítése Külső fül: Hangösszegyűjtés, ami a dobhártyán rezgéssé alakul át. Középfül: mechanikai csatolás a dobhártya és a belső fül folyadékkal töltött részei között. Kb. 2 cm
Az emberi hallás A fül felépítése Külső fül: Hangösszegyűjtés, ami a dobhártyán rezgéssé alakul át. Középfül: mechanikai csatolás a dobhártya és a belső fül folyadékkal töltött részei között. Kb. 2 cm
X. ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ
 X. ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ Ma az analóg jelek feldolgozása (is) mindinkább digitális eszközökkel és módszerekkel történik. A feldolgozás előtt az analóg jeleket digitalizálni kell.
X. ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ Ma az analóg jelek feldolgozása (is) mindinkább digitális eszközökkel és módszerekkel történik. A feldolgozás előtt az analóg jeleket digitalizálni kell.
Szent István Egyetem Fizika és folyamatirányítási Tanszék FIZIKA. rezgések egydimenziós hullám hangok fizikája. Dr. Seres István
 Szent István Egyetem Fizika és folyamatirányítási Tanszék rezgések egydimenziós hullám hangok fizikája Dr. Seres István Harmonikus rezgőmozgás ( sin(ct) ) ( c cos(ct) ) c sin(ct) ( cos(ct) ) ( c sin(ct)
Szent István Egyetem Fizika és folyamatirányítási Tanszék rezgések egydimenziós hullám hangok fizikája Dr. Seres István Harmonikus rezgőmozgás ( sin(ct) ) ( c cos(ct) ) c sin(ct) ( cos(ct) ) ( c sin(ct)
Villamosságtan szigorlati tételek
 Villamosságtan szigorlati tételek 1.1. Egyenáramú hálózatok alaptörvényei 1.2. Lineáris egyenáramú hálózatok elemi számítása 1.3. Nemlineáris egyenáramú hálózatok elemi számítása 1.4. Egyenáramú hálózatok
Villamosságtan szigorlati tételek 1.1. Egyenáramú hálózatok alaptörvényei 1.2. Lineáris egyenáramú hálózatok elemi számítása 1.3. Nemlineáris egyenáramú hálózatok elemi számítása 1.4. Egyenáramú hálózatok
Ellenőrző kérdések a Jelanalízis és Jelfeldolgozás témakörökhöz
 Ellenőrző kérdések a Jelanalízis és Jelfeldolgozás témakörökhöz 1. Hogyan lehet osztályozni a jeleket időfüggvényük időtartama szerint? 2. Mi a periodikus jelek definiciója? (szöveg, képlet, 3. Milyen
Ellenőrző kérdések a Jelanalízis és Jelfeldolgozás témakörökhöz 1. Hogyan lehet osztályozni a jeleket időfüggvényük időtartama szerint? 2. Mi a periodikus jelek definiciója? (szöveg, képlet, 3. Milyen
Zaj- és rezgés. Törvényszerűségek
 Zaj- és rezgés Törvényszerűségek A hang valamilyen közegben létrejövő rezgés. A vivőközeg szerint megkülönböztetünk: léghangot (a vivőközeg gáz, leggyakrabban levegő); folyadékhangot (a vivőközeg folyadék,
Zaj- és rezgés Törvényszerűségek A hang valamilyen közegben létrejövő rezgés. A vivőközeg szerint megkülönböztetünk: léghangot (a vivőközeg gáz, leggyakrabban levegő); folyadékhangot (a vivőközeg folyadék,
Fourier-sorfejtés vizsgálata Négyszögjel sorfejtése, átviteli vizsgálata
 Fourier-sorfejtés vizsgálata Négyszögjel sorfejtése, átviteli vizsgálata Reichardt, András 27. szeptember 2. 2 / 5 NDSM Komplex alak U C k = T (T ) ahol ω = 2π T, k módusindex. Időfüggvény előállítása
Fourier-sorfejtés vizsgálata Négyszögjel sorfejtése, átviteli vizsgálata Reichardt, András 27. szeptember 2. 2 / 5 NDSM Komplex alak U C k = T (T ) ahol ω = 2π T, k módusindex. Időfüggvény előállítása
Digitális jelfeldolgozás
 Digitális jelfeldolgozás Mintavételezés és jel-rekonstrukció Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2010.
Digitális jelfeldolgozás Mintavételezés és jel-rekonstrukció Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2010.
11. Egy Y alakú gumikötél egyik ága 20 cm, másik ága 50 cm. A két ág végeit azonos, f = 4 Hz
 Hullámok tesztek 1. Melyik állítás nem igaz a mechanikai hullámok körében? a) Transzverzális hullám esetén a részecskék rezgésének iránya merőleges a hullámterjedés irányára. b) Csak a transzverzális hullám
Hullámok tesztek 1. Melyik állítás nem igaz a mechanikai hullámok körében? a) Transzverzális hullám esetén a részecskék rezgésének iránya merőleges a hullámterjedés irányára. b) Csak a transzverzális hullám
ZAJ ÉS REZGÉSVÉDELEM Hallás
 Budapesti Műszaki és Gazdaságtudományi Egyetem Közlekedésmérnöki és Járműmérnöki Kar Felsőfokú munkavédelmi szakirányú továbbképzés ZAJ ÉS REZGÉSVÉDELEM Hallás MÁRKUS MIKLÓS ZAJ ÉS REZGÉSVÉDELMI SZAKÉRTŐ
Budapesti Műszaki és Gazdaságtudományi Egyetem Közlekedésmérnöki és Járműmérnöki Kar Felsőfokú munkavédelmi szakirányú továbbképzés ZAJ ÉS REZGÉSVÉDELEM Hallás MÁRKUS MIKLÓS ZAJ ÉS REZGÉSVÉDELMI SZAKÉRTŐ
Hangtechnika. Médiatechnológus asszisztens
 Vázlat 3. Előadás - alapjai Pécsi Tudományegyetem, Pollack Mihály Műszaki Kar Műszaki Informatika és Villamos Intézet Műszaki Informatika Tanszék Ismétlés Vázlat I.rész: Ismétlés II.rész: A digitális Jelfeldolgozás
Vázlat 3. Előadás - alapjai Pécsi Tudományegyetem, Pollack Mihály Műszaki Kar Műszaki Informatika és Villamos Intézet Műszaki Informatika Tanszék Ismétlés Vázlat I.rész: Ismétlés II.rész: A digitális Jelfeldolgozás
A Brüel & Kjaer zajdiagnosztikai módszereinek elméleti alapjai és ipari alkalmazása
 A Brüel & Kjaer zajdiagnosztikai módszereinek elméleti alapjai és ipari alkalmazása Összeállította: dr. Szuhay Péter Budapest, 2013 Filename, 1 Hang és zaj 1. rész Dr. Szuhay Péter B & K Components Kft
A Brüel & Kjaer zajdiagnosztikai módszereinek elméleti alapjai és ipari alkalmazása Összeállította: dr. Szuhay Péter Budapest, 2013 Filename, 1 Hang és zaj 1. rész Dr. Szuhay Péter B & K Components Kft
6. Függvények. Legyen függvény és nem üreshalmaz. A függvényt az f K-ra való kiterjesztésének
 6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
STATISZTIKAI PROBLÉMÁK A
 STATISZTIKAI PROBLÉMÁK A HULLÁMTÉR REPRODUKCIÓ TERÜLETÉN 2012. május 3., Budapest Firtha Gergely PhD hallgató, Akusztikai Laboratórium BME Híradástechnikai Tanszék firtha@hit.bme.hu Tartalom A hangtér
STATISZTIKAI PROBLÉMÁK A HULLÁMTÉR REPRODUKCIÓ TERÜLETÉN 2012. május 3., Budapest Firtha Gergely PhD hallgató, Akusztikai Laboratórium BME Híradástechnikai Tanszék firtha@hit.bme.hu Tartalom A hangtér
Fizikai hangtan, fiziológiai hangtan és építészeti hangtan
 Fizikai hangtan, fiziológiai hangtan és építészeti hangtan Témakörök: A hang terjedési sebessége levegőben Weber Fechner féle pszicho-fizikai törvény Hangintenzitás szint Hangosságszint Álló hullámok és
Fizikai hangtan, fiziológiai hangtan és építészeti hangtan Témakörök: A hang terjedési sebessége levegőben Weber Fechner féle pszicho-fizikai törvény Hangintenzitás szint Hangosságszint Álló hullámok és
Hangfrekvenciás mechanikai rezgések vizsgálata
 Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
Mechanikai hullámok. Hullámhegyek és hullámvölgyek alakulnak ki.
 Mechanikai hullámok Mechanikai hullámnak nevezzük, ha egy anyagban az anyag részecskéinek rezgésállapota továbbterjed. A mechanikai hullám terjedéséhez tehát szükség van valamilyen anyagra (légüres térben
Mechanikai hullámok Mechanikai hullámnak nevezzük, ha egy anyagban az anyag részecskéinek rezgésállapota továbbterjed. A mechanikai hullám terjedéséhez tehát szükség van valamilyen anyagra (légüres térben
2. gyakorlat Mintavételezés, kvantálás
 2. gyakorlat Mintavételezés, kvantálás x(t) x[k]= =x(k T) Q x[k] ^ D/A x(t) ~ ampl. FOLYTONOS idı FOLYTONOS ANALÓG DISZKRÉT MINTAVÉTELEZETT DISZKRÉT KVANTÁLT DIGITÁLIS Jelek visszaállítása egyenköző mintáinak
2. gyakorlat Mintavételezés, kvantálás x(t) x[k]= =x(k T) Q x[k] ^ D/A x(t) ~ ampl. FOLYTONOS idı FOLYTONOS ANALÓG DISZKRÉT MINTAVÉTELEZETT DISZKRÉT KVANTÁLT DIGITÁLIS Jelek visszaállítása egyenköző mintáinak
Elektronika Előadás. Modulátorok, demodulátorok, lock-in erősítők
 Elektronika 2 10. Előadás Modulátorok, demodulátorok, lock-in erősítők Irodalom - Megyeri János: Analóg elektronika, Tankönyvkiadó, 1990 - U. Tiecze, Ch. Schenk: Analóg és digitális áramkörök, Műszaki
Elektronika 2 10. Előadás Modulátorok, demodulátorok, lock-in erősítők Irodalom - Megyeri János: Analóg elektronika, Tankönyvkiadó, 1990 - U. Tiecze, Ch. Schenk: Analóg és digitális áramkörök, Műszaki
2. Elméleti összefoglaló
 2. Elméleti összefoglaló 2.1 A D/A konverterek [1] A D/A konverter feladata, hogy a bemenetére érkező egész számmal arányos analóg feszültséget vagy áramot állítson elő a kimenetén. A működéséhez szükséges
2. Elméleti összefoglaló 2.1 A D/A konverterek [1] A D/A konverter feladata, hogy a bemenetére érkező egész számmal arányos analóg feszültséget vagy áramot állítson elő a kimenetén. A működéséhez szükséges
Függvények Megoldások
 Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Objektív beszédminősítés
 Objektív beszédminősítés Fegyó Tibor fegyo@tmit.bme.hu Beszédinformációs rendszerek -- Objektív beszédminõsítés 1 Beszédinformációs rendszerek -- Objektív beszédminõsítés 2 Bevezető kérdések Mi a [beszéd]
Objektív beszédminősítés Fegyó Tibor fegyo@tmit.bme.hu Beszédinformációs rendszerek -- Objektív beszédminõsítés 1 Beszédinformációs rendszerek -- Objektív beszédminõsítés 2 Bevezető kérdések Mi a [beszéd]
Hangfrekvenciás mechanikai rezgések vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
Analóg digitális átalakítók ELEKTRONIKA_2
 Analóg digitális átalakítók ELEKTRONIKA_2 TEMATIKA Analóg vs. Digital Analóg/Digital átalakítás Mintavételezés Kvantálás Kódolás A/D átalakítók csoportosítása A közvetlen átalakítás A szukcesszív approximációs
Analóg digitális átalakítók ELEKTRONIKA_2 TEMATIKA Analóg vs. Digital Analóg/Digital átalakítás Mintavételezés Kvantálás Kódolás A/D átalakítók csoportosítása A közvetlen átalakítás A szukcesszív approximációs
Hullámok, hanghullámok
 Hullámok, hanghullámok Hullámokra jellemző mennyiségek: Amplitúdó: a legnagyobb, maximális kitérés nagysága jele: A, mértékegysége: m (egyéb mértékegységek: dm, cm, mm, ) Hullámhossz: két azonos rezgési
Hullámok, hanghullámok Hullámokra jellemző mennyiségek: Amplitúdó: a legnagyobb, maximális kitérés nagysága jele: A, mértékegysége: m (egyéb mértékegységek: dm, cm, mm, ) Hullámhossz: két azonos rezgési
Számítógépes gyakorlat MATLAB, Control System Toolbox
 Számítógépes gyakorlat MATLAB, Control System Toolbox Bevezetés A gyakorlatok célja az irányítási rendszerek korszerű számítógépes vizsgálati és tervezési módszereinek bemutatása, az alkalmazáshoz szükséges
Számítógépes gyakorlat MATLAB, Control System Toolbox Bevezetés A gyakorlatok célja az irányítási rendszerek korszerű számítógépes vizsgálati és tervezési módszereinek bemutatása, az alkalmazáshoz szükséges
Négyszög - Háromszög Oszcillátor Mérése Mérési Útmutató
 ÓBUDAI EGYETEM Kandó Kálmán Villamosmérnöki Kar Híradástechnika Intézet Négyszög - Háromszög Oszcillátor Mérése Mérési Útmutató A mérést végezte: Neptun kód: A mérés időpontja: A méréshez szükséges eszközök:
ÓBUDAI EGYETEM Kandó Kálmán Villamosmérnöki Kar Híradástechnika Intézet Négyszög - Háromszög Oszcillátor Mérése Mérési Útmutató A mérést végezte: Neptun kód: A mérés időpontja: A méréshez szükséges eszközök:
Milyen elvi mérési és számítási módszerrel lehet a Thevenin helyettesítő kép elemeit meghatározni?
 1. mérés Definiálja a korrekciót! Definiálja a mérés eredményét metrológiailag helyes formában! Definiálja a relatív formában megadott mérési hibát! Definiálja a rendszeres hibát! Definiálja a véletlen
1. mérés Definiálja a korrekciót! Definiálja a mérés eredményét metrológiailag helyes formában! Definiálja a relatív formában megadott mérési hibát! Definiálja a rendszeres hibát! Definiálja a véletlen
Analóg elektronika - laboratóriumi gyakorlatok
 Analóg elektronika - laboratóriumi gyakorlatok. Mûveleti erõsítõk váltakozó-áramú alkalmazásai. Elmélet Az integrált mûveleti erõsítõk váltakozó áramú viselkedését a. fejezetben (jegyzet és prezentáció)
Analóg elektronika - laboratóriumi gyakorlatok. Mûveleti erõsítõk váltakozó-áramú alkalmazásai. Elmélet Az integrált mûveleti erõsítõk váltakozó áramú viselkedését a. fejezetben (jegyzet és prezentáció)
Mintavételezés és AD átalakítók
 HORVÁTH ESZTER BUDAPEST MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM JÁRMŰELEMEK ÉS JÁRMŰ-SZERKEZETANALÍZIS TANSZÉK ÉRZÉKELÉS FOLYAMATA Az érzékelés, jelfeldolgozás általános folyamata Mérés Adatfeldolgozás 2/31
HORVÁTH ESZTER BUDAPEST MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM JÁRMŰELEMEK ÉS JÁRMŰ-SZERKEZETANALÍZIS TANSZÉK ÉRZÉKELÉS FOLYAMATA Az érzékelés, jelfeldolgozás általános folyamata Mérés Adatfeldolgozás 2/31
1. témakör. A hírközlés célja, általános modellje A jelek osztályozása Periodikus jelek leírása időtartományban
 1. témakör A hírközlés célja, általános modellje A jelek osztályozása Periodikus jelek leírása időtartományban A hírközlés célja, általános modellje Üzenet: Hír: Jel: Zaj: Továbbításra szánt adathalmaz
1. témakör A hírközlés célja, általános modellje A jelek osztályozása Periodikus jelek leírása időtartományban A hírközlés célja, általános modellje Üzenet: Hír: Jel: Zaj: Továbbításra szánt adathalmaz
10.1. ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ
 101 ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ Ma az analóg jelek feldolgozása (is) mindinkább digitális eszközökkel történik A feldolgozás előtt az analóg jeleket digitalizálni kell Rendszerint az
101 ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ Ma az analóg jelek feldolgozása (is) mindinkább digitális eszközökkel történik A feldolgozás előtt az analóg jeleket digitalizálni kell Rendszerint az
Véletlen jelenség: okok rendszere hozza létre - nem ismerhetjük mind, ezért sztochasztikus.
 Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Transzformátor rezgés mérés. A BME Villamos Energetika Tanszéken
 Transzformátor rezgés mérés A BME Villamos Energetika Tanszéken A valóság egyszerűsítése, modellezés. A mérés tervszerűen végrehajtott tevékenység, ezért a bonyolult valóságos rendszert először egyszerűsítik.
Transzformátor rezgés mérés A BME Villamos Energetika Tanszéken A valóság egyszerűsítése, modellezés. A mérés tervszerűen végrehajtott tevékenység, ezért a bonyolult valóságos rendszert először egyszerűsítik.
Orvosi Fizika és Statisztika
 Orvosi Fizika és Statisztika Szegedi Tudományegyetem Általános Orvostudományi Kar Természettudományi és Informatikai Kar Orvosi Fizikai és Orvosi Informatikai Intézet www.szote.u-szeged.hu/dmi Orvosi fizika
Orvosi Fizika és Statisztika Szegedi Tudományegyetem Általános Orvostudományi Kar Természettudományi és Informatikai Kar Orvosi Fizikai és Orvosi Informatikai Intézet www.szote.u-szeged.hu/dmi Orvosi fizika
Következõ: Lineáris rendszerek jellemzõi és vizsgálatuk. Jelfeldolgozás. Lineáris rendszerek jellemzõi és vizsgálatuk
 1 1 Következõ: Lineáris rendszerek jellemzõi és vizsgálatuk Jelfeldolgozás 1 Lineáris rendszerek jellemzõi és vizsgálatuk 2 Bevezetés 5 Kérdések, feladatok 6 Fourier sorok, Fourier transzformáció 7 Jelek
1 1 Következõ: Lineáris rendszerek jellemzõi és vizsgálatuk Jelfeldolgozás 1 Lineáris rendszerek jellemzõi és vizsgálatuk 2 Bevezetés 5 Kérdések, feladatok 6 Fourier sorok, Fourier transzformáció 7 Jelek
Mérési hibák 2006.10.04. 1
 Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
Feszültségérzékelők a méréstechnikában
 5. Laboratóriumi gyakorlat Feszültségérzékelők a méréstechnikában 1. A gyakorlat célja Az elektronikus mérőműszerekben használatos különböző feszültségdetektoroknak tanulmányozása, átviteli karakterisztika
5. Laboratóriumi gyakorlat Feszültségérzékelők a méréstechnikában 1. A gyakorlat célja Az elektronikus mérőműszerekben használatos különböző feszültségdetektoroknak tanulmányozása, átviteli karakterisztika
Bevezetés az állapottér-elméletbe Dinamikus rendszerek állapottér reprezentációi
 Tartalom Bevezetés az állapottér-elméletbe Irányítható alak Megfigyelhetőségi alak Diagonális alak Állapottér transzformáció 2018 1 A szabályozáselmélet klasszikus, BODE, NICHOLS, NYQUIST nevéhez kötődő,
Tartalom Bevezetés az állapottér-elméletbe Irányítható alak Megfigyelhetőségi alak Diagonális alak Állapottér transzformáció 2018 1 A szabályozáselmélet klasszikus, BODE, NICHOLS, NYQUIST nevéhez kötődő,
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Villamos jelek mintavételezése, feldolgozása. LabVIEW előadás
 Villamos jelek mintavételezése, feldolgozása (ellenállás mérés LabVIEW támogatással) LabVIEW 7.1 2. előadás Dr. Iványi Miklósné, egyetemi tanár LabVIEW-7.1 EA-2/1 Ellenállás mérés és adatbeolvasás Rn ismert
Villamos jelek mintavételezése, feldolgozása (ellenállás mérés LabVIEW támogatással) LabVIEW 7.1 2. előadás Dr. Iványi Miklósné, egyetemi tanár LabVIEW-7.1 EA-2/1 Ellenállás mérés és adatbeolvasás Rn ismert
GYAKORLATI ÉPÜLETFIZIKA
 GYAKORLATI ÉPÜLETFIZIKA Akusztika: A hang, és általában a rezgések tudománya. Görögből: akuein hallani. Igen széles tudományterületet ölel fel, néhány szokásos szakterületi elnevezés: épületakusztika,
GYAKORLATI ÉPÜLETFIZIKA Akusztika: A hang, és általában a rezgések tudománya. Görögből: akuein hallani. Igen széles tudományterületet ölel fel, néhány szokásos szakterületi elnevezés: épületakusztika,
Wavelet transzformáció
 1 Wavelet transzformáció Más felbontás: Walsh, Haar, wavelet alapok! Eddig: amplitúdó vagy frekvencia leírás: Pl. egy rövid, Dirac-delta jellegű impulzus Fourier-transzformált: nagyon sok, kb. ugyanolyan
1 Wavelet transzformáció Más felbontás: Walsh, Haar, wavelet alapok! Eddig: amplitúdó vagy frekvencia leírás: Pl. egy rövid, Dirac-delta jellegű impulzus Fourier-transzformált: nagyon sok, kb. ugyanolyan
Irányítástechnika 2. előadás
 Irányítástechnika 2. előadás Dr. Kovács Levente 2013. 03. 19. 2013.03.19. Tartalom Tipikus vizsgálójelek és azok információtartalma Laplace transzformáció, állapotegyenlet, átviteli függvény Alaptagok
Irányítástechnika 2. előadás Dr. Kovács Levente 2013. 03. 19. 2013.03.19. Tartalom Tipikus vizsgálójelek és azok információtartalma Laplace transzformáció, állapotegyenlet, átviteli függvény Alaptagok
Villamos jelek mintavételezése, feldolgozása. LabVIEW 7.1
 Villamos jelek mintavételezése, feldolgozása (ellenállás mérés LabVIEW támogatással) LabVIEW 7.1 előadás Dr. Iványi Miklósné, egyetemi tanár LabVIEW-7.1 KONF-5_2/1 Ellenállás mérés és adatbeolvasás Rn
Villamos jelek mintavételezése, feldolgozása (ellenállás mérés LabVIEW támogatással) LabVIEW 7.1 előadás Dr. Iványi Miklósné, egyetemi tanár LabVIEW-7.1 KONF-5_2/1 Ellenállás mérés és adatbeolvasás Rn
Méréstechnika. Rezgésmérés. Készítette: Ángyán Béla. Iszak Gábor. Seidl Áron. Veszprém. [Ide írhatja a szöveget] oldal 1
![Méréstechnika. Rezgésmérés. Készítette: Ángyán Béla. Iszak Gábor. Seidl Áron. Veszprém. [Ide írhatja a szöveget] oldal 1 Méréstechnika. Rezgésmérés. Készítette: Ángyán Béla. Iszak Gábor. Seidl Áron. Veszprém. [Ide írhatja a szöveget] oldal 1](/thumbs/45/23262384.jpg) Méréstechnika Rezgésmérés Készítette: Ángyán Béla Iszak Gábor Seidl Áron Veszprém 2014 [Ide írhatja a szöveget] oldal 1 A rezgésekkel kapcsolatos alapfogalmak A rezgés a Magyar Értelmező Szótár megfogalmazása
Méréstechnika Rezgésmérés Készítette: Ángyán Béla Iszak Gábor Seidl Áron Veszprém 2014 [Ide írhatja a szöveget] oldal 1 A rezgésekkel kapcsolatos alapfogalmak A rezgés a Magyar Értelmező Szótár megfogalmazása
Hullámok tesztek. 3. Melyik állítás nem igaz a mechanikai hullámok körében?
 Hullámok tesztek 1. Melyik állítás nem igaz a mechanikai hullámok körében? a) Transzverzális hullám esetén a részecskék rezgésének iránya merıleges a hullámterjedés irányára. b) Csak a transzverzális hullám
Hullámok tesztek 1. Melyik állítás nem igaz a mechanikai hullámok körében? a) Transzverzális hullám esetén a részecskék rezgésének iránya merıleges a hullámterjedés irányára. b) Csak a transzverzális hullám
Függvények határértéke, folytonossága
 Függvények határértéke, folytonossága 25. február 22.. Alapfeladatok. Feladat: Határozzuk meg az f() = 23 4 5 3 + 9 a végtelenben és a mínusz végtelenben! függvény határértékét Megoldás: Vizsgáljuk el
Függvények határértéke, folytonossága 25. február 22.. Alapfeladatok. Feladat: Határozzuk meg az f() = 23 4 5 3 + 9 a végtelenben és a mínusz végtelenben! függvény határértékét Megoldás: Vizsgáljuk el
ÁRAMKÖRÖK SZIMULÁCIÓJA
 ÁRAMKÖRÖK SZIMULÁCIÓJA Az áramkörök szimulációja révén betekintést nyerünk azok működésébe. Meg tudjuk határozni az áramkörök válaszát különböző gerjesztésekre, különböző üzemmódokra. Végezhetők analóg
ÁRAMKÖRÖK SZIMULÁCIÓJA Az áramkörök szimulációja révén betekintést nyerünk azok működésébe. Meg tudjuk határozni az áramkörök válaszát különböző gerjesztésekre, különböző üzemmódokra. Végezhetők analóg
Mérés és adatgyűjtés
 Mérés és adatgyűjtés 4. óra Mingesz Róbert Szegedi Tudományegyetem 2012. február 27. MA - 4. óra Verzió: 2.1 Utolsó frissítés: 2012. március 12. 1/41 Tartalom I 1 Jelek 2 Mintavételezés 3 A/D konverterek
Mérés és adatgyűjtés 4. óra Mingesz Róbert Szegedi Tudományegyetem 2012. február 27. MA - 4. óra Verzió: 2.1 Utolsó frissítés: 2012. március 12. 1/41 Tartalom I 1 Jelek 2 Mintavételezés 3 A/D konverterek
A beszéd. Segédlet a Kommunikáció-akusztika tanulásához
 A beszéd Segédlet a Kommunikáció-akusztika tanulásához Bevezetés Nyelv: az emberi társadalom egyedei közötti kommunikáció az egyed gondolkodásának legfőbb eszköze Beszéd: a nyelv elsődleges megnyilvánulása
A beszéd Segédlet a Kommunikáció-akusztika tanulásához Bevezetés Nyelv: az emberi társadalom egyedei közötti kommunikáció az egyed gondolkodásának legfőbb eszköze Beszéd: a nyelv elsődleges megnyilvánulása
A 2017/2018. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. KATEGÓRIA JAVÍTÁSI ÚTMUTATÓ. Pohár rezonanciája
 Oktatási Hivatal A 017/018. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. KATEGÓRIA JAVÍTÁSI ÚTMUTATÓ Pohár rezonanciája A mérőberendezés leírása: A mérőberendezés egy változtatható
Oktatási Hivatal A 017/018. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. KATEGÓRIA JAVÍTÁSI ÚTMUTATÓ Pohár rezonanciája A mérőberendezés leírása: A mérőberendezés egy változtatható
Nehézségi gyorsulás mérése megfordítható ingával
 Nehézségi gyorsulás mérése megfordítható ingával (Mérési jegyzőkönyv) Hagymási Imre 2007. április 21. (hétfő délelőtti csoport) 1. A mérés elmélete A nehézségi gyorsulás mérésének egy klasszikus módja
Nehézségi gyorsulás mérése megfordítható ingával (Mérési jegyzőkönyv) Hagymási Imre 2007. április 21. (hétfő délelőtti csoport) 1. A mérés elmélete A nehézségi gyorsulás mérésének egy klasszikus módja
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
Analóg-digitális átalakítás. Rencz Márta/ Ress S. Elektronikus Eszközök Tanszék
 Analóg-digitális átalakítás Rencz Márta/ Ress S. Elektronikus Eszközök Tanszék Mai témák Mintavételezés A/D átalakítók típusok D/A átalakítás 12/10/2007 2/17 A/D ill. D/A átalakítók A világ analóg, a jelfeldolgozás
Analóg-digitális átalakítás Rencz Márta/ Ress S. Elektronikus Eszközök Tanszék Mai témák Mintavételezés A/D átalakítók típusok D/A átalakítás 12/10/2007 2/17 A/D ill. D/A átalakítók A világ analóg, a jelfeldolgozás
2. témakör. Sztochasztikus, stacionárius és ergodikus jelek leírása idő és frekvenciatartományban
 2. témakör Sztochasztikus, stacionárius és ergodikus jelek leírása idő és frekvenciatartományban Bevezetés Egy összetett jel, amely nem feltétlen periodikus, de stabil amplitúdójó és frekvenciájú diszkrét
2. témakör Sztochasztikus, stacionárius és ergodikus jelek leírása idő és frekvenciatartományban Bevezetés Egy összetett jel, amely nem feltétlen periodikus, de stabil amplitúdójó és frekvenciájú diszkrét
NEPTUN-kód: KHTIA21TNC
 Kredit: 5 Informatika II. KHTIA21TNC Programozás II. oratórium nappali: 2 ea+ 0 gy+ 0 KMAPR22TNC Dr. Beinschróth József Az aláírás megszerzésnek feltétele: a félév folyamán 2db. ZH mindegyikének legalább
Kredit: 5 Informatika II. KHTIA21TNC Programozás II. oratórium nappali: 2 ea+ 0 gy+ 0 KMAPR22TNC Dr. Beinschróth József Az aláírás megszerzésnek feltétele: a félév folyamán 2db. ZH mindegyikének legalább
Értékelés Összesen: 100 pont 100% = 100 pont A VIZSGAFELADAT MEGOLDÁSÁRA JAVASOLT %-OS EREDMÉNY: EBBEN A VIZSGARÉSZBEN A VIZSGAFELADAT ARÁNYA 15%.
 Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzék módosításának eljárásrendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján: Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzék módosításának eljárásrendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján: Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
Képrestauráció Képhelyreállítás
 Képrestauráció Képhelyreállítás Képrestauráció - A képrestauráció az a folyamat mellyel a sérült képből eltávolítjuk a degradációt, eredményképpen pedig az eredetihez minél közelebbi képet szeretnénk kapni
Képrestauráció Képhelyreállítás Képrestauráció - A képrestauráció az a folyamat mellyel a sérült képből eltávolítjuk a degradációt, eredményképpen pedig az eredetihez minél közelebbi képet szeretnénk kapni
Modern Fizika Labor. Fizika BSc. Értékelés: A mérés dátuma: A mérés száma és címe: 5. mérés: Elektronspin rezonancia. 2008. március 18.
 Modern Fizika Labor Fizika BSc A mérés dátuma: 28. március 18. A mérés száma és címe: 5. mérés: Elektronspin rezonancia Értékelés: A beadás dátuma: 28. március 26. A mérést végezte: 1/7 A mérés leírása:
Modern Fizika Labor Fizika BSc A mérés dátuma: 28. március 18. A mérés száma és címe: 5. mérés: Elektronspin rezonancia Értékelés: A beadás dátuma: 28. március 26. A mérést végezte: 1/7 A mérés leírása:
Mérési útmutató. Széchenyi István Egyetem Távközlési Tanszék. Rádiófrekvenciás sáverősítők. intermodulációs torzításának vizsgálata
 Széchenyi István Egyetem Távközlési Tanszék Mérési útmutató Rádiórendszerek tárgy laboratóriumi gyakorlatához Rádiófrekvenciás sáverősítők intermodulációs torzításának vizsgálata Készítette: Mórocz Tamás
Széchenyi István Egyetem Távközlési Tanszék Mérési útmutató Rádiórendszerek tárgy laboratóriumi gyakorlatához Rádiófrekvenciás sáverősítők intermodulációs torzításának vizsgálata Készítette: Mórocz Tamás
Mechanika I-II. Példatár
 Budapesti Műszaki és Gazdaságtudományi Egyetem Műszaki Mechanika Tanszék Mechanika I-II. Példatár 2012. május 24. Előszó A példatár célja, hogy támogassa a mechanika I. és mechanika II. tárgy oktatását
Budapesti Műszaki és Gazdaságtudományi Egyetem Műszaki Mechanika Tanszék Mechanika I-II. Példatár 2012. május 24. Előszó A példatár célja, hogy támogassa a mechanika I. és mechanika II. tárgy oktatását
Zaj (bevezetés) A zaj hatása Zaj Környezeti zaj Zajimisszió Zajemisszió Zaj szabályozás Zaj környezeti és gazdasági szerepe:
 Zaj (bevezetés) A zaj hatása: elhanyagolhatótól az elviselhetetlenig. Zaj: nem akart hang. Környezeti zaj: állandó zaj (l. ha nincs közlekedés). Zajimisszió: Zajterhelés az érzékelés helyén. Zajemisszió:
Zaj (bevezetés) A zaj hatása: elhanyagolhatótól az elviselhetetlenig. Zaj: nem akart hang. Környezeti zaj: állandó zaj (l. ha nincs közlekedés). Zajimisszió: Zajterhelés az érzékelés helyén. Zajemisszió:
Házi Feladat. Méréstechnika 1-3.
 Házi Feladat Méréstechnika 1-3. Tantárgy: Méréstechnika Tanár neve: Tényi V. Gusztáv Készítette: Fazekas István AKYBRR 45. csoport 2010-09-18 1/1. Ismertesse a villamos jelek felosztását, és az egyes csoportokban
Házi Feladat Méréstechnika 1-3. Tantárgy: Méréstechnika Tanár neve: Tényi V. Gusztáv Készítette: Fazekas István AKYBRR 45. csoport 2010-09-18 1/1. Ismertesse a villamos jelek felosztását, és az egyes csoportokban
A maximum likelihood becslésről
 A maximum likelihood becslésről Definíció Parametrikus becsléssel foglalkozunk. Adott egy modell, mellyel elképzeléseink szerint jól leírható a meghatározni kívánt rendszer. (A modell típusának és rendszámának
A maximum likelihood becslésről Definíció Parametrikus becsléssel foglalkozunk. Adott egy modell, mellyel elképzeléseink szerint jól leírható a meghatározni kívánt rendszer. (A modell típusának és rendszámának
Szinkronizmusból való kiesés elleni védelmi funkció
 Budapest, 2011. december Szinkronizmusból való kiesés elleni védelmi funkció Szinkronizmusból való kiesés elleni védelmi funkciót főleg szinkron generátorokhoz alkalmaznak. Ha a generátor kiesik a szinkronizmusból,
Budapest, 2011. december Szinkronizmusból való kiesés elleni védelmi funkció Szinkronizmusból való kiesés elleni védelmi funkciót főleg szinkron generátorokhoz alkalmaznak. Ha a generátor kiesik a szinkronizmusból,
Hullámmozgás. Mechanikai hullámok A hang és jellemzői A fény hullámtermészete
 Hullámmozgás Mechanikai hullámok A hang és jellemzői A fény hullámtermészete A hullámmozgás fogalma A rezgési energia térbeli továbbterjedését hullámmozgásnak nevezzük. Hullámmozgáskor a közeg, vagy mező
Hullámmozgás Mechanikai hullámok A hang és jellemzői A fény hullámtermészete A hullámmozgás fogalma A rezgési energia térbeli továbbterjedését hullámmozgásnak nevezzük. Hullámmozgáskor a közeg, vagy mező
Folytonos rendszeregyenletek megoldása. 1. Folytonos idejű (FI) rendszeregyenlet általános alakja
 Folytonos rendszeregyenletek megoldása 1. Folytonos idejű (FI) rendszeregyenlet általános alakja A folytonos rendszeregyenletek megoldásakor olyan rendszerekkel foglalkozunk, amelyeknek egyetlen u = u(t)
Folytonos rendszeregyenletek megoldása 1. Folytonos idejű (FI) rendszeregyenlet általános alakja A folytonos rendszeregyenletek megoldásakor olyan rendszerekkel foglalkozunk, amelyeknek egyetlen u = u(t)
RÖVID ÚTMUTATÓ A FELÜLETI ÉRDESSÉG MÉRÉSÉHEZ
 RÖVID ÚTMUTATÓ A FELÜLETI ÉRDESSÉG MÉRÉSÉHEZ Referencia útmutató laboratórium és műhely részére Magyar KIADÁS lr i = kiértékelési hossz Profilok és szűrők (EN ISO 4287 és EN ISO 16610-21) 01 A tényleges
RÖVID ÚTMUTATÓ A FELÜLETI ÉRDESSÉG MÉRÉSÉHEZ Referencia útmutató laboratórium és műhely részére Magyar KIADÁS lr i = kiértékelési hossz Profilok és szűrők (EN ISO 4287 és EN ISO 16610-21) 01 A tényleges
A fázismoduláció és frekvenciamoduláció közötti különbség
 Fázismoduláció (PM) A fázismoduláció és frekvenciamoduláció közötti különbség A fázismoduláció, akárcsak a frekvenciamoduláció, a szögmoduláció kategóriájába sorolható. Mivel a modulációs index és a fázislöket
Fázismoduláció (PM) A fázismoduláció és frekvenciamoduláció közötti különbség A fázismoduláció, akárcsak a frekvenciamoduláció, a szögmoduláció kategóriájába sorolható. Mivel a modulációs index és a fázislöket
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 6. A MINTAVÉTELI TÖRVÉNY
 ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 6. A MINTAVÉTELI TÖRVÉNY Dr. Soumelidis Alexandros 2018.10.25. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG Mintavételezés
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 6. A MINTAVÉTELI TÖRVÉNY Dr. Soumelidis Alexandros 2018.10.25. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG Mintavételezés
Akusztikus mérőműszerek
 Akusztikus mérőműszerek Hangszintmérő: méri a frekvencia súlyozott, és nyomásátlagolt hangnyomás szintet (hangszintet). Felépítése Mikrofon + Erősítő Frekvencia Szint tartomány Időátlagolás Kijelzés Előerősítő
Akusztikus mérőműszerek Hangszintmérő: méri a frekvencia súlyozott, és nyomásátlagolt hangnyomás szintet (hangszintet). Felépítése Mikrofon + Erősítő Frekvencia Szint tartomány Időátlagolás Kijelzés Előerősítő
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
A 2014/2015. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. KATEGÓRIA MEGOLDÁSI ÚTMUTATÓ
 Oktatási Hivatal A 2014/2015. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. KATEGÓRIA MEGOLDÁSI ÚTMUTATÓ 1./ Bevezetés Ha egy rezgésre képes rugalmas testet például ütéssel rezgésbe
Oktatási Hivatal A 2014/2015. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. KATEGÓRIA MEGOLDÁSI ÚTMUTATÓ 1./ Bevezetés Ha egy rezgésre képes rugalmas testet például ütéssel rezgésbe
Aktív zajcsökkentő rendszerek megvalósítása szenzorhálózattal
 Aktív zajcsökkentő rendszerek megvalósítása szenzorhálózattal Lajkó László, Orosz György Konzulens: Dr. Sujbert László Méréstechnika és Információs Rendszerek Tanszék Önálló laboratórium beszámoló 2005.
Aktív zajcsökkentő rendszerek megvalósítása szenzorhálózattal Lajkó László, Orosz György Konzulens: Dr. Sujbert László Méréstechnika és Információs Rendszerek Tanszék Önálló laboratórium beszámoló 2005.
A gyakorlat célja a fehér és a színes zaj bemutatása.
 A gyakorlat célja a fehér és a színes zaj bemutatása. 1.@. FFT begyakorlása n = [:9]; % Harminc minta x = cos(*pi*n/1); % 1 mintát veszünk periodusonként N1 = 64; % Három módon számoljuk az FFT-t N = 18;
A gyakorlat célja a fehér és a színes zaj bemutatása. 1.@. FFT begyakorlása n = [:9]; % Harminc minta x = cos(*pi*n/1); % 1 mintát veszünk periodusonként N1 = 64; % Három módon számoljuk az FFT-t N = 18;
Az Ampère-Maxwell-féle gerjesztési törvény
 Az Ampère-Maxwell-féle gerjesztési törvény Maxwell elméleti meggondolások alapján feltételezte, hogy a változó elektromos tér örvényes mágneses teret kelt (hasonlóan ahhoz ahogy a változó mágneses tér
Az Ampère-Maxwell-féle gerjesztési törvény Maxwell elméleti meggondolások alapján feltételezte, hogy a változó elektromos tér örvényes mágneses teret kelt (hasonlóan ahhoz ahogy a változó mágneses tér
Optika és Relativitáselmélet II. BsC fizikus hallgatóknak
 Optika és Relativitáselmélet II. BsC fizikus hallgatóknak 2. Fényhullámok tulajdonságai Cserti József, jegyzet, ELTE, 2007. Az elektromágneses spektrum Látható spektrum (erre állt be a szemünk) UV: ultraibolya
Optika és Relativitáselmélet II. BsC fizikus hallgatóknak 2. Fényhullámok tulajdonságai Cserti József, jegyzet, ELTE, 2007. Az elektromágneses spektrum Látható spektrum (erre állt be a szemünk) UV: ultraibolya
Objektív beszédminısítés
 Objektív beszédminısítés Fegyó Tibor fegyo@tmit.bme.hu Beszédinformációs rendszerek -- Objektív beszédminõsítés 1 Bevezetı kérdések Mi a [beszéd] minıség [a beszédkommunikációban]? Mi befolyásolja a minıséget?
Objektív beszédminısítés Fegyó Tibor fegyo@tmit.bme.hu Beszédinformációs rendszerek -- Objektív beszédminõsítés 1 Bevezetı kérdések Mi a [beszéd] minıség [a beszédkommunikációban]? Mi befolyásolja a minıséget?
Zh1 - tételsor ELEKTRONIKA_2
 Zh1 - tételsor ELEKTRONIKA_2 1.a. I1 I2 jelforrás U1 erősítő U2 terhelés 1. ábra Az 1-es ábrán látható erősítő bemeneti jele egy U1= 1V amplitúdójú f=1khz frekvenciájú szinuszos jel. Ennek megfelelően
Zh1 - tételsor ELEKTRONIKA_2 1.a. I1 I2 jelforrás U1 erősítő U2 terhelés 1. ábra Az 1-es ábrán látható erősítő bemeneti jele egy U1= 1V amplitúdójú f=1khz frekvenciájú szinuszos jel. Ennek megfelelően
