Klár Gergely 2010/2011. tavaszi félév
|
|
|
- Amanda Anna Pásztor
- 8 évvel ezelőtt
- Látták:
Átírás
1 Számítógépes Grafika Klár Gergely Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. tavaszi félév
2 Tartalom Virtuális világ tárolása 1 Virtuális világ tárolása 2 3 4
3 Virtuális világ tárolása - kérdések Hol táruljuk az adatokat? Mem. vagy HDD? Mire optimalizálunk? Rajzolás vagy szerkesztés? Milyen koordináta-rendszerben tároljuk őket? Világ vagy modell kr?
4 Virtuális világ tárolása - kérdések Hol táruljuk az adatokat? Mem. vagy HDD? Mire optimalizálunk? Rajzolás vagy szerkesztés? Milyen koordináta-rendszerben tároljuk őket? Világ vagy modell kr?
5 Virtuális világ tárolása - kérdések Hol táruljuk az adatokat? Mem. vagy HDD? Mire optimalizálunk? Rajzolás vagy szerkesztés? Milyen koordináta-rendszerben tároljuk őket? Világ vagy modell kr?
6 Tartalom Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet 1 Virtuális világ tárolása 2 Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet 3 4
7 Geometria brute force tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Legyenek a primitíveink poligonok. Legyünk lusták, és minden poligont tartsuk nyílván az összes csúcsával. Poligonokkal kapcsolatos feladatok: tárolás transzformálás szomszédsági lekérdezések
8 Geometria brute force tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Legyenek a primitíveink poligonok. Legyünk lusták, és minden poligont tartsuk nyílván az összes csúcsával. Poligonokkal kapcsolatos feladatok: tárolás transzformálás szomszédsági lekérdezések
9 Geometria brute force tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Legyenek a primitíveink poligonok. Legyünk lusták, és minden poligont tartsuk nyílván az összes csúcsával. Poligonokkal kapcsolatos feladatok: tárolás transzformálás szomszédsági lekérdezések
10 Geometria brute force tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet s t r u c t t r i a n g l e { f l o a t x1, y1, z1 ; f l o a t x2, y2, z2 ; f l o a t x3, y3, z3 ; } ;
11 A brute force tárolás elemzése Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Tárolás: ha vannak poligonoknak közös csúcsai, akkor ezeket többször tároljuk feleslegesen Ñ nem túl jó. Transzformálás: a közös csúcsokra annyiszor fogjuk el végezni a transzformációkat, ahányszor szerepelnek Ñ nem hatékony. Lekérdezések: fogalmunk sincs, ki kinek a szomszédja, csak az összes csúcs bejárásával tudunk eredményre jutni Ñ katasztrófa. Egyetlen előnye, hogy ennél egyszerűbben már nem is lehetne tárolni.
12 A brute force tárolás elemzése Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Tárolás: ha vannak poligonoknak közös csúcsai, akkor ezeket többször tároljuk feleslegesen Ñ nem túl jó. Transzformálás: a közös csúcsokra annyiszor fogjuk el végezni a transzformációkat, ahányszor szerepelnek Ñ nem hatékony. Lekérdezések: fogalmunk sincs, ki kinek a szomszédja, csak az összes csúcs bejárásával tudunk eredményre jutni Ñ katasztrófa. Egyetlen előnye, hogy ennél egyszerűbben már nem is lehetne tárolni.
13 A brute force tárolás elemzése Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Tárolás: ha vannak poligonoknak közös csúcsai, akkor ezeket többször tároljuk feleslegesen Ñ nem túl jó. Transzformálás: a közös csúcsokra annyiszor fogjuk el végezni a transzformációkat, ahányszor szerepelnek Ñ nem hatékony. Lekérdezések: fogalmunk sincs, ki kinek a szomszédja, csak az összes csúcs bejárásával tudunk eredményre jutni Ñ katasztrófa. Egyetlen előnye, hogy ennél egyszerűbben már nem is lehetne tárolni.
14 A brute force tárolás elemzése Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Tárolás: ha vannak poligonoknak közös csúcsai, akkor ezeket többször tároljuk feleslegesen Ñ nem túl jó. Transzformálás: a közös csúcsokra annyiszor fogjuk el végezni a transzformációkat, ahányszor szerepelnek Ñ nem hatékony. Lekérdezések: fogalmunk sincs, ki kinek a szomszédja, csak az összes csúcs bejárásával tudunk eredményre jutni Ñ katasztrófa. Egyetlen előnye, hogy ennél egyszerűbben már nem is lehetne tárolni.
15 Index buffer-ek Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Alapötlet: tároljunk minden csúcsot egyszer, egy nagy közös tömbben! A poligonok csak hivatkozzanak a csúcsok tömbjének elemeire. Ez az index buffer. Minden GPU támogatja.
16 Index buffer-ek Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Alapötlet: tároljunk minden csúcsot egyszer, egy nagy közös tömbben! A poligonok csak hivatkozzanak a csúcsok tömbjének elemeire. Ez az index buffer. Minden GPU támogatja.
17 Index buffer-ek Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Alapötlet: tároljunk minden csúcsot egyszer, egy nagy közös tömbben! A poligonok csak hivatkozzanak a csúcsok tömbjének elemeire. Ez az index buffer. Minden GPU támogatja.
18 Index buffer-ek Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Alapötlet: tároljunk minden csúcsot egyszer, egy nagy közös tömbben! A poligonok csak hivatkozzanak a csúcsok tömbjének elemeire. Ez az index buffer. Minden GPU támogatja.
19 Index buffer-ek Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet s t r u c t t r i a n g l e { unsigned i n t a, b, c ; } ; s t r u c t vec3 { f l o a t x, y, z ; } ; std : : vector <vec3> i n d e x B u f f e r ;
20 Példa Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Vegyünk egy N N db négyzetből álló rácsot! Mérete index buffer nélkül: 4 csúcs/négyzet, N N négyzet: 4N 2. Mérete index buffer-rel: összesen pn 1q pn 1q csúcs: pn 1q 2 N 2 2N 1. 4N 2 vs. N 2 2N 1 4N 2 N 2 2N 1 0 3N 2 2N 1 N 1, ha N P Z
21 Példa Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Vegyünk egy N N db négyzetből álló rácsot! Mérete index buffer nélkül: 4 csúcs/négyzet, N N négyzet: 4N 2. Mérete index buffer-rel: összesen pn 1q pn 1q csúcs: pn 1q 2 N 2 2N 1. 4N 2 vs. N 2 2N 1 4N 2 N 2 2N 1 0 3N 2 2N 1 N 1, ha N P Z
22 Példa Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Vegyünk egy N N db négyzetből álló rácsot! Mérete index buffer nélkül: 4 csúcs/négyzet, N N négyzet: 4N 2. Mérete index buffer-rel: összesen pn 1q pn 1q csúcs: pn 1q 2 N 2 2N 1. 4N 2 vs. N 2 2N 1 4N 2 N 2 2N 1 0 3N 2 2N 1 N 1, ha N P Z
23 Példa Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Vegyünk egy N N db négyzetből álló rácsot! Mérete index buffer nélkül: 4 csúcs/négyzet, N N négyzet: 4N 2. Mérete index buffer-rel: összesen pn 1q pn 1q csúcs: pn 1q 2 N 2 2N 1. 4N 2 vs. N 2 2N 1 4N 2 N 2 2N 1 0 3N 2 2N 1 N 1, ha N P Z
24 Példa folyt. Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Ha több mint egyetlen négyzetünk van, már megéri. Pl. ha N 10 Mérete index buffer nélkül: 400 csúcsot tárolunk és transzformálunk Mérete index buffer-rel: 121 csúcsot tárolunk és transzformálunk
25 Példa folyt. Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Ha több mint egyetlen négyzetünk van, már megéri. Pl. ha N 10 Mérete index buffer nélkül: 400 csúcsot tárolunk és transzformálunk Mérete index buffer-rel: 121 csúcsot tárolunk és transzformálunk
26 Index buffer-ek GPU-n Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Minden videókártya, amit még nem gyűjtenek a múzeumok támogatja az index buffer-eket. A csúcspontok tömbje (vertex buffer) nem csak pozicókat tartalmaz, hanem normálvektorokat, textúra-koordinátákat, és még sok mást. Egy hivatkozás a vertex buffer-ra mindezekre együtt hivatkozik.
27 Index buffer-ek GPU-n Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Minden videókártya, amit még nem gyűjtenek a múzeumok támogatja az index buffer-eket. A csúcspontok tömbje (vertex buffer) nem csak pozicókat tartalmaz, hanem normálvektorokat, textúra-koordinátákat, és még sok mást. Egy hivatkozás a vertex buffer-ra mindezekre együtt hivatkozik.
28 Index buffer-ek GPU-n Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Minden videókártya, amit még nem gyűjtenek a múzeumok támogatja az index buffer-eket. A csúcspontok tömbje (vertex buffer) nem csak pozicókat tartalmaz, hanem normálvektorokat, textúra-koordinátákat, és még sok mást. Egy hivatkozás a vertex buffer-ra mindezekre együtt hivatkozik.
29 Kocka probléma Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Ha egy kockát rakunk össze háromszögekből, akkor egy sarokban lévő csúcs min. három, max. hat háromszögnek a csúcsa. Index buffer-rel elég lenne 8 csúcsot nyílvántartani. Mi lesz a normálisokkal? Hogy éles sarkai legyenek a kockának a normálisoknak merőlegesnek kell lennie a lapokra! Oldalanként külön meg kell adni a csúcsokat: összesen 3 8 csúcs kerül az vertex buffer-ba.
30 Kocka probléma Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Ha egy kockát rakunk össze háromszögekből, akkor egy sarokban lévő csúcs min. három, max. hat háromszögnek a csúcsa. Index buffer-rel elég lenne 8 csúcsot nyílvántartani. Mi lesz a normálisokkal? Hogy éles sarkai legyenek a kockának a normálisoknak merőlegesnek kell lennie a lapokra! Oldalanként külön meg kell adni a csúcsokat: összesen 3 8 csúcs kerül az vertex buffer-ba.
31 Kocka probléma Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Ha egy kockát rakunk össze háromszögekből, akkor egy sarokban lévő csúcs min. három, max. hat háromszögnek a csúcsa. Index buffer-rel elég lenne 8 csúcsot nyílvántartani. Mi lesz a normálisokkal? Hogy éles sarkai legyenek a kockának a normálisoknak merőlegesnek kell lennie a lapokra! Oldalanként külön meg kell adni a csúcsokat: összesen 3 8 csúcs kerül az vertex buffer-ba.
32 Kocka probléma Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Ha egy kockát rakunk össze háromszögekből, akkor egy sarokban lévő csúcs min. három, max. hat háromszögnek a csúcsa. Index buffer-rel elég lenne 8 csúcsot nyílvántartani. Mi lesz a normálisokkal? Hogy éles sarkai legyenek a kockának a normálisoknak merőlegesnek kell lennie a lapokra! Oldalanként külön meg kell adni a csúcsokat: összesen 3 8 csúcs kerül az vertex buffer-ba.
33 Kocka probléma Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet
34 Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Az Index buffer-es tárolás elemzése Tárolás: ált. hatékony. Transzformálás: hatékony. Lekérdezések: közös csúcsokat már tudunk, de igazából még mindig fogalmunk sincs.
35 Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Az Index buffer-es tárolás elemzése Tárolás: ált. hatékony. Transzformálás: hatékony. Lekérdezések: közös csúcsokat már tudunk, de igazából még mindig fogalmunk sincs.
36 Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Az Index buffer-es tárolás elemzése Tárolás: ált. hatékony. Transzformálás: hatékony. Lekérdezések: közös csúcsokat már tudunk, de igazából még mindig fogalmunk sincs.
37 Szomszédsági viszonyok Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Néha kellenek a szomszédok, pl. felület-feolsztásoknál. Ismertek a csúcsok ñ számítható mi, minek a szomszédja. Egy csúcsban tetszőleges számú poligon találkozhat ñ dinamikus adatszerkezet kéne. Jobb megoldás: Szárnyas-él (winged-edge) adatszerkezet!
38 Szomszédsági viszonyok Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Néha kellenek a szomszédok, pl. felület-feolsztásoknál. Ismertek a csúcsok ñ számítható mi, minek a szomszédja. Egy csúcsban tetszőleges számú poligon találkozhat ñ dinamikus adatszerkezet kéne. Jobb megoldás: Szárnyas-él (winged-edge) adatszerkezet!
39 Szomszédsági viszonyok Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Néha kellenek a szomszédok, pl. felület-feolsztásoknál. Ismertek a csúcsok ñ számítható mi, minek a szomszédja. Egy csúcsban tetszőleges számú poligon találkozhat ñ dinamikus adatszerkezet kéne. Jobb megoldás: Szárnyas-él (winged-edge) adatszerkezet!
40 Szomszédsági viszonyok Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Néha kellenek a szomszédok, pl. felület-feolsztásoknál. Ismertek a csúcsok ñ számítható mi, minek a szomszédja. Egy csúcsban tetszőleges számú poligon találkozhat ñ dinamikus adatszerkezet kéne. Jobb megoldás: Szárnyas-él (winged-edge) adatszerkezet!
41 Szárnyas-él adatszerkezet Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Határfelület leíró (B-rep) szerkezet. Az élek szempontjából tároljuk a felületet. Minden élhez fix számú adat tartozik. Segítségével gyorsan körbe lehet járni egy poligon éleit, közben megkapva minden szomszédot.
42 Szárnyas-él adatszerkezet Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Határfelület leíró (B-rep) szerkezet. Az élek szempontjából tároljuk a felületet. Minden élhez fix számú adat tartozik. Segítségével gyorsan körbe lehet járni egy poligon éleit, közben megkapva minden szomszédot.
43 Szárnyas-él adatszerkezet Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Határfelület leíró (B-rep) szerkezet. Az élek szempontjából tároljuk a felületet. Minden élhez fix számú adat tartozik. Segítségével gyorsan körbe lehet járni egy poligon éleit, közben megkapva minden szomszédot.
44 Szárnyas-él adatszerkezet Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Határfelület leíró (B-rep) szerkezet. Az élek szempontjából tároljuk a felületet. Minden élhez fix számú adat tartozik. Segítségével gyorsan körbe lehet járni egy poligon éleit, közben megkapva minden szomszédot.
45 Egyetlen él adatai Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet csúcs lap balra jobbra él start vég bal jobb előző köv. előző köv. a B A 0 1 c b d e
46 Egyéb táblázatok Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Csúcsok táblája csúcs ID csúcsból induló él Lapok táblája lap ID lap egy éle
47 Példa: tetraéder Virtuális világ tárolása Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet Shirley, Fundamentals of Computer Graphics
48 Pl.: Összes szomszéd egy lapra Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet def allneighbours ( face, edges, v e r t i c e s, faces ) : startedge = faces [ face ] edge = startedge i f edges [ startedge ]. f a c e L e f t == face : while edges [ edge ]. succleft!= startedge : p r i n t edges [ edge ]. faceright edge = edges [ edge ]. succleft else : while edges [ edge ]. succright!= startedge : p r i n t edges [ edge ]. f a c e L e f t edge = edges [ edge ]. succright
49 Pl.: Összes lap egy csúcsból Brute force tárolás Index buffer-ek Szárnyas-él adatszerkezet def allfaces ( vertex, edges, v e r t i c e s, faces ) : startedge = v e r t i c e s [ v e r t e x ] edge = startedge done = False while not done : i f edges [ edge ]. v e r t S t a r t == v e rtex : p r i n t edges [ edge ]. f a c e L e f t edge = edges [ edge ]. p r e dleft else : p r i n t edges [ edge ]. faceright edge = edges [ edge ]. predright
50 Tartalom Virtuális világ tárolása Színtérgráf OGRE 1 Virtuális világ tárolása 2 3 Színtérgráf OGRE 4
51 Színtérgráf OGRE Világ, benne Objektumok, ami Primitívekből állnak, amiket Pontok határoznak meg.
52 Színtérgráf OGRE Világ, benne Objektumok, ami Primitívekből állnak, amiket Pontok határoznak meg.
53 Színtérgráf OGRE Világ, benne Objektumok, ami Primitívekből állnak, amiket Pontok határoznak meg.
54 Színtérgráf OGRE Világ, benne Objektumok, ami Primitívekből állnak, amiket Pontok határoznak meg.
55 Színtérgráf OGRE!
56 Színtérgráf OGRE Minden szint a hozzátartozó tulajdonságokat tartja nyílván. Objektum név, modellezési transzformáció, befoglaló doboz, stb. Primitív primitívre jellemző tulajdonságok Pont koordináták
57 Színtérgráf OGRE Minden szint a hozzátartozó tulajdonságokat tartja nyílván. Objektum név, modellezési transzformáció, befoglaló doboz, stb. Primitív primitívre jellemző tulajdonságok Pont koordináták
58 Színtérgráf OGRE Minden szint a hozzátartozó tulajdonságokat tartja nyílván. Objektum név, modellezési transzformáció, befoglaló doboz, stb. Primitív primitívre jellemző tulajdonságok Pont koordináták
59 Színtérgráf OGRE Minden szint a hozzátartozó tulajdonságokat tartja nyílván. Objektum név, modellezési transzformáció, befoglaló doboz, stb. Primitív primitívre jellemző tulajdonságok Pont koordináták
60 Színtérgráf motiváció 1. Színtérgráf OGRE Ahol én vagyok ott van a karom is. (Jobb esetben...) Ha mozgatom a karom, elmozdulnak (világtérben) az ujjaim is. Tudom úgy mozgatni az ujjaimat, hogy közben se a karom, se én nem mozdulok el.
61 Színtérgráf motiváció 1. Színtérgráf OGRE Ahol én vagyok ott van a karom is. (Jobb esetben...) Ha mozgatom a karom, elmozdulnak (világtérben) az ujjaim is. Tudom úgy mozgatni az ujjaimat, hogy közben se a karom, se én nem mozdulok el.
62 Színtérgráf motiváció 1. Színtérgráf OGRE Ahol én vagyok ott van a karom is. (Jobb esetben...) Ha mozgatom a karom, elmozdulnak (világtérben) az ujjaim is. Tudom úgy mozgatni az ujjaimat, hogy közben se a karom, se én nem mozdulok el.
63 Színtérgráf OGRE
64 Színtérgráf motiváció 2. Színtérgráf OGRE Ha mozog egy bicikli, mozognak vele a kerekei meg a kormánya is. A kormányt lehet külön forgatni, és forgatja az első kereket. A két kerék tud forogni a tengelye körül, anélkül hogy a biciklit forgatni kéne.
65 Színtérgráf motiváció 2. Színtérgráf OGRE Ha mozog egy bicikli, mozognak vele a kerekei meg a kormánya is. A kormányt lehet külön forgatni, és forgatja az első kereket. A két kerék tud forogni a tengelye körül, anélkül hogy a biciklit forgatni kéne.
66 Színtérgráf motiváció 2. Színtérgráf OGRE Ha mozog egy bicikli, mozognak vele a kerekei meg a kormánya is. A kormányt lehet külön forgatni, és forgatja az első kereket. A két kerék tud forogni a tengelye körül, anélkül hogy a biciklit forgatni kéne.
67 Színtérgráf OGRE
68 Színtérgráf Virtuális világ tárolása Színtérgráf OGRE Irányított, körmentes gráf (DAG). A színtér ( világ) összes elemét tartalmazza. Az egyes elemek alá-/fölérendeltségi viszonyaik szerint kapcsolódnak egymáshoz. Szülő vagy ős: ahonnan kiindul az él Gyerek: ahova mutat az él A szülő tulajdonságai öröklődnek a gyerekre, amiket a gyerek pontosíthat (pl. transzformációk), vagy felülírhat (pl. színek)
69 Színtérgráf Virtuális világ tárolása Színtérgráf OGRE Irányított, körmentes gráf (DAG). A színtér ( világ) összes elemét tartalmazza. Az egyes elemek alá-/fölérendeltségi viszonyaik szerint kapcsolódnak egymáshoz. Szülő vagy ős: ahonnan kiindul az él Gyerek: ahova mutat az él A szülő tulajdonságai öröklődnek a gyerekre, amiket a gyerek pontosíthat (pl. transzformációk), vagy felülírhat (pl. színek)
70 Színtérgráf Virtuális világ tárolása Színtérgráf OGRE Irányított, körmentes gráf (DAG). A színtér ( világ) összes elemét tartalmazza. Az egyes elemek alá-/fölérendeltségi viszonyaik szerint kapcsolódnak egymáshoz. Szülő vagy ős: ahonnan kiindul az él Gyerek: ahova mutat az él A szülő tulajdonságai öröklődnek a gyerekre, amiket a gyerek pontosíthat (pl. transzformációk), vagy felülírhat (pl. színek)
71 Színtérgráf Virtuális világ tárolása Színtérgráf OGRE Irányított, körmentes gráf (DAG). A színtér ( világ) összes elemét tartalmazza. Az egyes elemek alá-/fölérendeltségi viszonyaik szerint kapcsolódnak egymáshoz. Szülő vagy ős: ahonnan kiindul az él Gyerek: ahova mutat az él A szülő tulajdonságai öröklődnek a gyerekre, amiket a gyerek pontosíthat (pl. transzformációk), vagy felülírhat (pl. színek)
72 Színtérgráf Virtuális világ tárolása Színtérgráf OGRE Irányított, körmentes gráf (DAG). A színtér ( világ) összes elemét tartalmazza. Az egyes elemek alá-/fölérendeltségi viszonyaik szerint kapcsolódnak egymáshoz. Szülő vagy ős: ahonnan kiindul az él Gyerek: ahova mutat az él A szülő tulajdonságai öröklődnek a gyerekre, amiket a gyerek pontosíthat (pl. transzformációk), vagy felülírhat (pl. színek)
73 Színtérgráf Virtuális világ tárolása Színtérgráf OGRE Irányított, körmentes gráf (DAG). A színtér ( világ) összes elemét tartalmazza. Az egyes elemek alá-/fölérendeltségi viszonyaik szerint kapcsolódnak egymáshoz. Szülő vagy ős: ahonnan kiindul az él Gyerek: ahova mutat az él A szülő tulajdonságai öröklődnek a gyerekre, amiket a gyerek pontosíthat (pl. transzformációk), vagy felülírhat (pl. színek)
74 Csomópontok Virtuális világ tárolása Színtérgráf OGRE A gráf egy csomópontja (csúcsa, node-ja) lehet geometria, transzformáció, anyagjellemzők, fényforrás, kamera.
75 Színtérgráf OGRE
76 Csomópontok tulajdonságai Színtérgráf OGRE Geometria A rendszer által támogatott tetszőleges modell leírás. Pl. Mesh. A gráfban levélként szerepel. Transzformáció Gyak. 4 4-es transzformációs mátrix. Az új transzformációs csomópont nem felülírja a megelőzőket, hanem azokkal együtt hat.
77 Csomópontok tulajdonságai Színtérgráf OGRE Geometria A rendszer által támogatott tetszőleges modell leírás. Pl. Mesh. A gráfban levélként szerepel. Transzformáció Gyak. 4 4-es transzformációs mátrix. Az új transzformációs csomópont nem felülírja a megelőzőket, hanem azokkal együtt hat.
78 Csomópontok tulajdonságai Színtérgráf OGRE Anyagjellemzők Színek, optikai tulajdonságok, textúrák, stb. Nyitott kérdés: hogyan ábrázoljuk, ha egy modellünk több textúrát is használ? Fényforrás Kamera Poziciója, iránya, típusa, színe, stb. Levele a gráfnak. Pozíciója, nézeti iránya, látószöge, stb. Levele a gráfnak.
79 Csomópontok tulajdonságai Színtérgráf OGRE Anyagjellemzők Színek, optikai tulajdonságok, textúrák, stb. Nyitott kérdés: hogyan ábrázoljuk, ha egy modellünk több textúrát is használ? Fényforrás Kamera Poziciója, iránya, típusa, színe, stb. Levele a gráfnak. Pozíciója, nézeti iránya, látószöge, stb. Levele a gráfnak.
80 Csomópontok tulajdonságai Színtérgráf OGRE Anyagjellemzők Színek, optikai tulajdonságok, textúrák, stb. Nyitott kérdés: hogyan ábrázoljuk, ha egy modellünk több textúrát is használ? Fényforrás Kamera Poziciója, iránya, típusa, színe, stb. Levele a gráfnak. Pozíciója, nézeti iránya, látószöge, stb. Levele a gráfnak.
81 Színtérgráf a gyakorlatban Színtérgráf OGRE Minden komolyabb 3D alakalmazás használ valamilyen szintérgráfot. Példák: Maya, Java3D OpenSceneGraph OGRE
82 Színtérgráf OGRE-ben Színtérgráf OGRE Ogre::SceneNode: általános osztály, amihez az aktuális elemeket hozzá lehet csatolni az Ogre::MovableObject osztályon keresztül. Tulajdonságai: Bounding box pozíció és összesített pozíció orientációra hasonlóan méretezés tetszőleges felhasználói adat
83 Ogre::MovableObject Színtérgráf OGRE
84 Ogre::MovableObject Színtérgráf OGRE Tulajdonságok: Saját bounding box Rejtett vagy sem? Vethet árnyékot? Milyen fények tartoznak hozzá? Transformációkat nem tartalmaz!
85 Ogre::Entity Virtuális világ tárolása Színtérgráf OGRE Egy kirajzolható objektum! Se nem maga az objektum geometriája, se nem az anyagjellemzői. Ezeket külön objektumok tárolják, ez az osztály csak hivatkozik rájuk. Geometria: Ogre::Mesh Anyagjellemzők: Ogre::Material
86 Színtérgráf OGRE-ben Színtérgráf OGRE...és még sok más objektum. Tanulság: Rengeteg specializált osztály, mindegyik csak a maga feladatával foglalkozik. Amit több helyen is fel lehet használni (Mesh, Material), azt nem kell feleslegesen többször létrehozni. Ahol közös tulajdonságok vannak, azok magasabb szinten vannak összefogva.
87 Színtérgráf összefoglaló Színtérgráf OGRE Valamilyen színtérgráfot érdemes implementálni. Szétválasztja az elhelyezést, a formát és a megjelenést. Lehetővé teszi az egymáshoz képesti relatív elhelyezést. DE, szem előtt kell tartani, hogy milyen szintig érdemes elbonyolítani.
88 Tartalom Virtuális világ tárolása 1 Virtuális világ tárolása 2 3 4
89 CSG modell Virtuális világ tárolása Constructive solid geometry: konstruktív tömör test geometria A modellünket = primitívek + műveletek Primitívek: téglatestek, hasábok, hengerek, gúlák, kúpok, gömbök. Műveletek: boolean műveletek, unió, különbség, metszet.
90 CSG modell Virtuális világ tárolása Constructive solid geometry: konstruktív tömör test geometria A modellünket = primitívek + műveletek Primitívek: téglatestek, hasábok, hengerek, gúlák, kúpok, gömbök. Műveletek: boolean műveletek, unió, különbség, metszet.
91 CSG modell Virtuális világ tárolása Constructive solid geometry: konstruktív tömör test geometria A modellünket = primitívek + műveletek Primitívek: téglatestek, hasábok, hengerek, gúlák, kúpok, gömbök. Műveletek: boolean műveletek, unió, különbség, metszet.
92 CSG modell Virtuális világ tárolása Constructive solid geometry: konstruktív tömör test geometria A modellünket = primitívek + műveletek Primitívek: téglatestek, hasábok, hengerek, gúlák, kúpok, gömbök. Műveletek: boolean műveletek, unió, különbség, metszet.
93 Különbség Metszet Unió Captain Sprite, en.wikipedia Captain Sprite, en.wikipedia Captain Sprite, en.wikipedia
94 CSG fa Virtuális világ tárolása A műveletek eredményein újabb művelet hajtható vége. object = primitive object = object operation object Bináris fával jól leírható! Belső csúcsok: műveletek Levelek: primitívek Gyökér: végleges objektum
95 CSG fa Virtuális világ tárolása A műveletek eredményein újabb művelet hajtható vége. object = primitive object = object operation object Bináris fával jól leírható! Belső csúcsok: műveletek Levelek: primitívek Gyökér: végleges objektum
96 CSG fa Virtuális világ tárolása A műveletek eredményein újabb művelet hajtható vége. object = primitive object = object operation object Bináris fával jól leírható! Belső csúcsok: műveletek Levelek: primitívek Gyökér: végleges objektum
97 CSG fa Virtuális világ tárolása A műveletek eredményein újabb művelet hajtható vége. object = primitive object = object operation object Bináris fával jól leírható! Belső csúcsok: műveletek Levelek: primitívek Gyökér: végleges objektum
98 CSG fa Virtuális világ tárolása A műveletek eredményein újabb művelet hajtható vége. object = primitive object = object operation object Bináris fával jól leírható! Belső csúcsok: műveletek Levelek: primitívek Gyökér: végleges objektum
99 CSG fa Virtuális világ tárolása A műveletek eredményein újabb művelet hajtható vége. object = primitive object = object operation object Bináris fával jól leírható! Belső csúcsok: műveletek Levelek: primitívek Gyökér: végleges objektum
100 CSG fa Virtuális világ tárolása Zottie, wikipedia
101 CSG modellek megjelenítése Inkrementális képszintézis: tesszelálni kell. Sugárkövetés: speciális sugár/model metszéspont számítás Ñ CSG-fa bejárása.
102 CSG modellek megjelenítése Inkrementális képszintézis: tesszelálni kell. Sugárkövetés: speciális sugár/model metszéspont számítás Ñ CSG-fa bejárása.
103 CSG modellek metszése Levél: triv., metszéspontok: p t 1 v és p t 2 v A sugár pp t 1 v, p t 2 vq szakaszon a primitív belsejében halad. Összes levélből: t 1... t n, elég ezeket vizsgálnunk. Szakasz-listákat fogunk nyílvántartani.
104 CSG modellek metszése Levél: triv., metszéspontok: p t 1 v és p t 2 v A sugár pp t 1 v, p t 2 vq szakaszon a primitív belsejében halad. Összes levélből: t 1... t n, elég ezeket vizsgálnunk. Szakasz-listákat fogunk nyílvántartani.
105 CSG modellek metszése Levél: triv., metszéspontok: p t 1 v és p t 2 v A sugár pp t 1 v, p t 2 vq szakaszon a primitív belsejében halad. Összes levélből: t 1... t n, elég ezeket vizsgálnunk. Szakasz-listákat fogunk nyílvántartani.
106 CSG modellek metszése Levél: triv., metszéspontok: p t 1 v és p t 2 v A sugár pp t 1 v, p t 2 vq szakaszon a primitív belsejében halad. Összes levélből: t 1... t n, elég ezeket vizsgálnunk. Szakasz-listákat fogunk nyílvántartani.
107 CSG modellek metszése Belső csúcsok: a gyerekektől származó szakasz-listákra is végrehajtjuk a műveletet Y Összeérő szakaszokat egyesítjük, különben hozzávesszük a listához. X Kiszámítjuk a szakaszok metszeteit. z Kivonjunk a szakaszokat egymásból. Gyökérben: a legkisebb pozitív t értékű pont lesz a szemhez legközelebbi metszés. Ha a metszések száma páros: kívül vagyunk az objektumon, ha páratlan, akkor a belsejében.
108 CSG modellek metszése Belső csúcsok: a gyerekektől származó szakasz-listákra is végrehajtjuk a műveletet Y Összeérő szakaszokat egyesítjük, különben hozzávesszük a listához. X Kiszámítjuk a szakaszok metszeteit. z Kivonjunk a szakaszokat egymásból. Gyökérben: a legkisebb pozitív t értékű pont lesz a szemhez legközelebbi metszés. Ha a metszések száma páros: kívül vagyunk az objektumon, ha páratlan, akkor a belsejében.
109 CSG modellek metszése Belső csúcsok: a gyerekektől származó szakasz-listákra is végrehajtjuk a műveletet Y Összeérő szakaszokat egyesítjük, különben hozzávesszük a listához. X Kiszámítjuk a szakaszok metszeteit. z Kivonjunk a szakaszokat egymásból. Gyökérben: a legkisebb pozitív t értékű pont lesz a szemhez legközelebbi metszés. Ha a metszések száma páros: kívül vagyunk az objektumon, ha páratlan, akkor a belsejében.
110 CSG modellek metszése Belső csúcsok: a gyerekektől származó szakasz-listákra is végrehajtjuk a műveletet Y Összeérő szakaszokat egyesítjük, különben hozzávesszük a listához. X Kiszámítjuk a szakaszok metszeteit. z Kivonjunk a szakaszokat egymásból. Gyökérben: a legkisebb pozitív t értékű pont lesz a szemhez legközelebbi metszés. Ha a metszések száma páros: kívül vagyunk az objektumon, ha páratlan, akkor a belsejében.
111 CSG modellek metszése Belső csúcsok: a gyerekektől származó szakasz-listákra is végrehajtjuk a műveletet Y Összeérő szakaszokat egyesítjük, különben hozzávesszük a listához. X Kiszámítjuk a szakaszok metszeteit. z Kivonjunk a szakaszokat egymásból. Gyökérben: a legkisebb pozitív t értékű pont lesz a szemhez legközelebbi metszés. Ha a metszések száma páros: kívül vagyunk az objektumon, ha páratlan, akkor a belsejében.
Geometria brute force tárolása
 Virtuális világ tárolása - kérdések Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar Hol táruljuk az adatokat? Mem. vagy HDD? Mire optimalizálunk? Rajzolás
Virtuális világ tárolása - kérdések Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar Hol táruljuk az adatokat? Mem. vagy HDD? Mire optimalizálunk? Rajzolás
Valasek Gábor
 Geometria és topológia tárolása Görbék reprezentációja Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2015/2016. őszi félév Geometria és topológia tárolása Görbék reprezentációja
Geometria és topológia tárolása Görbék reprezentációja Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2015/2016. őszi félév Geometria és topológia tárolása Görbék reprezentációja
(Solid modeling, Geometric modeling) Testmodell: egy létező vagy elképzelt objektum digitális reprezentációja.
 Testmodellezés Testmodellezés (Solid modeling, Geometric modeling) Testmodell: egy létező vagy elképzelt objektum digitális reprezentációja. A tervezés (modellezés) során megadjuk a objektum geometria
Testmodellezés Testmodellezés (Solid modeling, Geometric modeling) Testmodell: egy létező vagy elképzelt objektum digitális reprezentációja. A tervezés (modellezés) során megadjuk a objektum geometria
Tartalom. Geometria közvetlen tárolása. Geometria tárolása - brute force. Valasek Gábor valasek@inf.elte.hu. Hermite interpoláció. Subdivision görbék
 Tartalom Számítógépes Grafika Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2015/2016. őszi félév Geometria és topológia tárolása Geometria tárolása Topológia tárolása
Tartalom Számítógépes Grafika Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2015/2016. őszi félév Geometria és topológia tárolása Geometria tárolása Topológia tárolása
Geometriai modellezés. Szécsi László
 Geometriai modellezés Szécsi László Adatáramlás vezérlés Animáció világleírás Modellezés kamera Virtuális világ kép Képszintézis A modellezés részfeladatai Geometria megadása [1. előadás] pont, görbe,
Geometriai modellezés Szécsi László Adatáramlás vezérlés Animáció világleírás Modellezés kamera Virtuális világ kép Képszintézis A modellezés részfeladatai Geometria megadása [1. előadás] pont, görbe,
TÉRINFORMATIKAI ALGORITMUSOK
 Topológiai algoritmusok és adatszerkezetek TÉRINFORMATIKAI ALGORITMUSOK Cserép Máté mcserep@inf.elte.hu 2017. november 22. EÖTVÖS LORÁND TUDOMÁNYEGYETEM INFORMATIKAI KAR BEVEZETŐ Topológia: olyan matematikai
Topológiai algoritmusok és adatszerkezetek TÉRINFORMATIKAI ALGORITMUSOK Cserép Máté mcserep@inf.elte.hu 2017. november 22. EÖTVÖS LORÁND TUDOMÁNYEGYETEM INFORMATIKAI KAR BEVEZETŐ Topológia: olyan matematikai
Termék modell. Definíció:
 Definíció: Termék modell Összetett, többfunkciós, integrált modell (számítógépes reprezentáció) amely leír egy műszaki objektumot annak különböző életfázis szakaszaiban: tervezés, gyártás, szerelés, szervízelés,
Definíció: Termék modell Összetett, többfunkciós, integrált modell (számítógépes reprezentáció) amely leír egy műszaki objektumot annak különböző életfázis szakaszaiban: tervezés, gyártás, szerelés, szervízelés,
TÉRINFORMATIKAI ALGORITMUSOK
 Topológiai algoritmusok és adatszerkezetek TÉRINFORMATIKAI ALGORITMUSOK Cserép Máté mcserep@caesar.elte.hu 2015. november 18. EÖTVÖS LORÁND TUDOMÁNYEGYETEM INFORMATIKAI KAR BEVEZETŐ Topológia: olyan matematikai
Topológiai algoritmusok és adatszerkezetek TÉRINFORMATIKAI ALGORITMUSOK Cserép Máté mcserep@caesar.elte.hu 2015. november 18. EÖTVÖS LORÁND TUDOMÁNYEGYETEM INFORMATIKAI KAR BEVEZETŐ Topológia: olyan matematikai
3D-s számítógépes geometria és alakzatrekonstrukció
 3D-s számítógépes geometria és alakzatrekonstrukció Tesztkörnyezet II http://cg.iit.bme.hu/portal/node/312 https://portal.vik.bme.hu/kepzes/targyak/viiima01 Dr. Várady Tamás, Dr. Salvi Péter BME, Villamosmérnöki
3D-s számítógépes geometria és alakzatrekonstrukció Tesztkörnyezet II http://cg.iit.bme.hu/portal/node/312 https://portal.vik.bme.hu/kepzes/targyak/viiima01 Dr. Várady Tamás, Dr. Salvi Péter BME, Villamosmérnöki
Valasek Gábor tavaszi félév
 Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2016-2017 tavaszi félév Tartalom Test- és felületmodellezés Test- és felületmodellezés Tartalom Test- és felületmodellezés
Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2016-2017 tavaszi félév Tartalom Test- és felületmodellezés Test- és felületmodellezés Tartalom Test- és felületmodellezés
3D számítógépes geometria és alakzatrekonstrukció
 3D számítógépes geometria és alakzatrekonstrukció 12. Tömör testek modellezése http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01 Dr. Várady Tamás, Dr. Salvi Péter BME,
3D számítógépes geometria és alakzatrekonstrukció 12. Tömör testek modellezése http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01 Dr. Várady Tamás, Dr. Salvi Péter BME,
Információ megjelenítés Számítógépes ábrázolás. Dr. Iványi Péter
 Információ megjelenítés Számítógépes ábrázolás Dr. Iványi Péter Raszterizáció OpenGL Mely pixelek vannak a primitíven belül fragment generálása minden ilyen pixelre Attribútumok (pl., szín) hozzárendelése
Információ megjelenítés Számítógépes ábrázolás Dr. Iványi Péter Raszterizáció OpenGL Mely pixelek vannak a primitíven belül fragment generálása minden ilyen pixelre Attribútumok (pl., szín) hozzárendelése
Transzformációk. Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform
 Transzformációk Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform Koordinátarendszerek: modelltér Koordinátarendszerek: világtér Koordinátarendszerek: kameratér up right z eye ahead
Transzformációk Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform Koordinátarendszerek: modelltér Koordinátarendszerek: világtér Koordinátarendszerek: kameratér up right z eye ahead
Valasek Gábor tavaszi félév
 Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2016-2017 tavaszi félév Tartalom Tartalom Áttekintés Tartalom B-reṕ Attekintés Topológiai adatszerkezetek Szárnyas-él adatszerkezet
Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2016-2017 tavaszi félév Tartalom Tartalom Áttekintés Tartalom B-reṕ Attekintés Topológiai adatszerkezetek Szárnyas-él adatszerkezet
Klár Gergely
 Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. őszi félév Tartalom Vágás Szakaszvágás Poligonvágás 1 Vágás Szakaszvágás Poligonvágás 2 Vágás
Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. őszi félév Tartalom Vágás Szakaszvágás Poligonvágás 1 Vágás Szakaszvágás Poligonvágás 2 Vágás
Hajder Levente 2018/2019. II. félév
 Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2018/2019. II. félév Tartalom 1 2 3 4 5 Albrecht Dürer, 1525 Motiváció Tekintsünk minden pixelre úgy, mint egy kis ablakra
Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2018/2019. II. félév Tartalom 1 2 3 4 5 Albrecht Dürer, 1525 Motiváció Tekintsünk minden pixelre úgy, mint egy kis ablakra
Hajder Levente 2014/2015. tavaszi félév
 Hajder Levente hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom 1 2 3 4 5 Albrecht Dürer, 1525 Motiváció Tekintsünk minden pixelre úgy, mint
Hajder Levente hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom 1 2 3 4 5 Albrecht Dürer, 1525 Motiváció Tekintsünk minden pixelre úgy, mint
Feladatok. Tervek alapján látvány terv készítése. Irodai munka Test modellezés. Létező objektum számítógépes modelljének elkészítése
 Virtuális valóság Feladatok Tervek alapján látvány terv készítése Irodai munka Test modellezés Létező objektum számítógépes modelljének elkészítése Geodéziai mérések Fotogrammetriai feldolgozás Egyszerű
Virtuális valóság Feladatok Tervek alapján látvány terv készítése Irodai munka Test modellezés Létező objektum számítógépes modelljének elkészítése Geodéziai mérések Fotogrammetriai feldolgozás Egyszerű
Síklapú testek. Gúlák, hasábok Metszésük egyenessel, síkkal
 Síklapú testek Gúlák, hasábok Metszésük egyenessel, síkkal Az előadás átdolgozott részleteket tartalmaz a következőkből: Gubis Katalin: Ábrázoló geometria Vlasta Szirovicza: Descriptive geometry Síklapú
Síklapú testek Gúlák, hasábok Metszésük egyenessel, síkkal Az előadás átdolgozott részleteket tartalmaz a következőkből: Gubis Katalin: Ábrázoló geometria Vlasta Szirovicza: Descriptive geometry Síklapú
Információ megjelenítés Számítógépes ábrázolás. Dr. Iványi Péter
 Információ megjelenítés Számítógépes ábrázolás Dr. Iványi Péter (adat szerkezet) float x,y,z,w; float r,g,b,a; } vertex; glcolor3f(0, 0.5, 0); glvertex2i(11, 31); glvertex2i(37, 71); glcolor3f(0.5, 0,
Információ megjelenítés Számítógépes ábrázolás Dr. Iványi Péter (adat szerkezet) float x,y,z,w; float r,g,b,a; } vertex; glcolor3f(0, 0.5, 0); glvertex2i(11, 31); glvertex2i(37, 71); glcolor3f(0.5, 0,
Számítógépes Graka - 4. Gyak
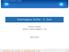 Számítógépes Graka - 4. Gyak Jámbori András andras.jambori@gmail.com 2012.03.01 Jámbori András andras.jambori@gmail.com Számítógépes Graka - 4. Gyak 1/17 Emlékeztet A múlt órákon tárgyaltuk: WinAPI programozás
Számítógépes Graka - 4. Gyak Jámbori András andras.jambori@gmail.com 2012.03.01 Jámbori András andras.jambori@gmail.com Számítógépes Graka - 4. Gyak 1/17 Emlékeztet A múlt órákon tárgyaltuk: WinAPI programozás
Transzformációk. Szécsi László
 Transzformációk Szécsi László A feladat Adott a 3D modell háromszögek csúcspontjai [modellezési koordináták] Háromszögkitöltő algoritmus pixeleket színez be [viewport koordináták] A feladat: számítsuk
Transzformációk Szécsi László A feladat Adott a 3D modell háromszögek csúcspontjai [modellezési koordináták] Háromszögkitöltő algoritmus pixeleket színez be [viewport koordináták] A feladat: számítsuk
Elengedhetetlen a játékokban, mozi produkciós eszközökben Nélküle kvantum hatás lép fel. Az objektumok áthaladnak a többi objektumon
 Bevezetés Ütközés detektálás Elengedhetetlen a játékokban, mozi produkciós eszközökben Nélküle kvantum hatás lép fel Az objektumok áthaladnak a többi objektumon A valósághű megjelenítés része Nem tisztán
Bevezetés Ütközés detektálás Elengedhetetlen a játékokban, mozi produkciós eszközökben Nélküle kvantum hatás lép fel Az objektumok áthaladnak a többi objektumon A valósághű megjelenítés része Nem tisztán
TÉRINFORMATIKAI ÉS TÁVÉRZÉKELÉSI ALKALMAZÁSOK FEJLESZTÉSE
 Topológiai algoritmusok és adatszerkezetek TÉRINFORMATIKAI ÉS TÁVÉRZÉKELÉSI ALKALMAZÁSOK FEJLESZTÉSE Cserép Máté mcserep@caesar.elte.hu 2015. május 5. EÖTVÖS LORÁND TUDOMÁNYEGYETEM INFORMATIKAI KAR BEVEZETŐ
Topológiai algoritmusok és adatszerkezetek TÉRINFORMATIKAI ÉS TÁVÉRZÉKELÉSI ALKALMAZÁSOK FEJLESZTÉSE Cserép Máté mcserep@caesar.elte.hu 2015. május 5. EÖTVÖS LORÁND TUDOMÁNYEGYETEM INFORMATIKAI KAR BEVEZETŐ
Területi primitívek: Zárt görbék által határolt területek (pl. kör, ellipszis, poligon) b) Minden belső pont kirajzolásával (kitöltött)
 Grafikus primitívek kitöltése Téglalap kitöltése Poligon kitöltése Kör, ellipszis kitöltése Kitöltés mintával Grafikus primitívek kitöltése Területi primitívek: Zárt görbék által határolt területek (pl.
Grafikus primitívek kitöltése Téglalap kitöltése Poligon kitöltése Kör, ellipszis kitöltése Kitöltés mintával Grafikus primitívek kitöltése Területi primitívek: Zárt görbék által határolt területek (pl.
Klár Gergely 2010/2011. tavaszi félév
 Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. tavaszi félév Tartalom Pont 1 Pont 2 3 4 5 Tartalom Pont Descartes-koordináták Homogén koordináták
Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. tavaszi félév Tartalom Pont 1 Pont 2 3 4 5 Tartalom Pont Descartes-koordináták Homogén koordináták
GráfRajz fejlesztői dokumentáció
 GráfRajz Követelmények: A GráfRajz gráfokat jelenít meg grafikus eszközökkel. A gráfot többféleképpen lehet a programba betölteni. A program a gráfokat egyedi fájl szerkezetben tárolja. A fájlokból betölthetőek
GráfRajz Követelmények: A GráfRajz gráfokat jelenít meg grafikus eszközökkel. A gráfot többféleképpen lehet a programba betölteni. A program a gráfokat egyedi fájl szerkezetben tárolja. A fájlokból betölthetőek
Számítógépes Grafika mintafeladatok
 Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Plakátok, részecskerendszerek. Szécsi László
 Plakátok, részecskerendszerek Szécsi László Képalapú festés Montázs: képet képekből 2D grafika jellemző eszköze modell: kép [sprite] 3D 2D képével helyettesítsük a komplex geometriát Image-based rendering
Plakátok, részecskerendszerek Szécsi László Képalapú festés Montázs: képet képekből 2D grafika jellemző eszköze modell: kép [sprite] 3D 2D képével helyettesítsük a komplex geometriát Image-based rendering
Adatszerkezetek 2. Dr. Iványi Péter
 Adatszerkezetek 2. Dr. Iványi Péter 1 Fák Fákat akkor használunk, ha az adatok között valamilyen alá- és fölérendeltség van. Pl. könyvtárszerkezet gyökér (root) Nincsennek hurkok!!! 2 Bináris fák Azokat
Adatszerkezetek 2. Dr. Iványi Péter 1 Fák Fákat akkor használunk, ha az adatok között valamilyen alá- és fölérendeltség van. Pl. könyvtárszerkezet gyökér (root) Nincsennek hurkok!!! 2 Bináris fák Azokat
Hajder Levente 2017/2018. II. félév
 Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév Tartalom 1 Sugár és sík metszéspontja Sugár és háromszög metszéspontja Sugár és poligon metszéspontja
Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév Tartalom 1 Sugár és sík metszéspontja Sugár és háromszög metszéspontja Sugár és poligon metszéspontja
Mechatronika segédlet 3. gyakorlat
 Mechatronika segédlet 3. gyakorlat 2017. február 20. Tartalom Vadai Gergely, Faragó Dénes Feladatleírás... 2 Fogaskerék... 2 Nézetváltás 3D modellezéshez... 2 Könnyítés megvalósítása... 2 A fogaskerék
Mechatronika segédlet 3. gyakorlat 2017. február 20. Tartalom Vadai Gergely, Faragó Dénes Feladatleírás... 2 Fogaskerék... 2 Nézetváltás 3D modellezéshez... 2 Könnyítés megvalósítása... 2 A fogaskerék
x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs mátrixa 3D-ben?
 . Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
. Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
Ionogram releváns területeinek meghatározása és elemzésének automatikus megvalósítása
 Ionogram releváns területeinek meghatározása és elemzésének automatikus megvalósítása Előadó: Pieler Gergely, MSc hallgató, Nyugat-magyarországi Egyetem Konzulens: Bencsik Gergely, PhD hallgató, Nyugat-magyarországi
Ionogram releváns területeinek meghatározása és elemzésének automatikus megvalósítása Előadó: Pieler Gergely, MSc hallgató, Nyugat-magyarországi Egyetem Konzulens: Bencsik Gergely, PhD hallgató, Nyugat-magyarországi
Tartalom. Tartalom. Hajder Levente Szakasz raszterizálása. 2017/2018. II. félév. Poligon raszterizáció.
 Tartalom Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév 1 Emlékeztető 2 Vágás 3 Raszterizálás Inkrementális képszintézis Tartalom 1 Emlékeztető Inkrementális
Tartalom Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév 1 Emlékeztető 2 Vágás 3 Raszterizálás Inkrementális képszintézis Tartalom 1 Emlékeztető Inkrementális
2014/2015. tavaszi félév
 Hajder L. és Valasek G. hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom Geometria modellezés 1 Geometria modellezés 2 Geometria modellezés
Hajder L. és Valasek G. hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom Geometria modellezés 1 Geometria modellezés 2 Geometria modellezés
Tartalom. Tartalom. Raycasting. Hajder Levente 2017/2018. II. félév. Raycasting. Raycasting. Sugár és háromszög metszéspontja
 Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév 1 2 1 2 Albrecht Dürer, 1525 Tekintsünk minden pixelre úgy, mint egy kis ablakra a világra Milyen színértéket
Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév 1 2 1 2 Albrecht Dürer, 1525 Tekintsünk minden pixelre úgy, mint egy kis ablakra a világra Milyen színértéket
Láthatósági kérdések
 Láthatósági kérdések Láthatósági algoritmusok Adott térbeli objektum és adott nézőpont esetén el kell döntenünk, hogy mi látható az adott alakzatból a nézőpontból, vagy irányából nézve. Az algoritmusok
Láthatósági kérdések Láthatósági algoritmusok Adott térbeli objektum és adott nézőpont esetén el kell döntenünk, hogy mi látható az adott alakzatból a nézőpontból, vagy irányából nézve. Az algoritmusok
Hajder Levente 2016/2017.
 Hajder Levente hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2016/2017. Tartalom 1 Tartalom Motiváció 2 Grafikus szerelőszalag Áttekintés Modellezési transzformácó Nézeti
Hajder Levente hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2016/2017. Tartalom 1 Tartalom Motiváció 2 Grafikus szerelőszalag Áttekintés Modellezési transzformácó Nézeti
22. GRÁFOK ÁBRÁZOLÁSA
 22. GRÁFOK ÁBRÁZOLÁSA A megoldandó feladatok, problémák modellezése során sokszor gráfokat alkalmazunk. A gráf fogalmát a matematikából ismertnek vehetjük. A modellezés során a gráfok több változata is
22. GRÁFOK ÁBRÁZOLÁSA A megoldandó feladatok, problémák modellezése során sokszor gráfokat alkalmazunk. A gráf fogalmát a matematikából ismertnek vehetjük. A modellezés során a gráfok több változata is
Területi primitívek: Zárt görbék által határolt területek (pl. kör, ellipszis, poligon)
 Grafikus primitívek kitöltése Téglalap kitöltése Poligon kitöltése Kör, ellipszis kitöltése Kitöltés mintával Grafikus primitívek kitöltése Területi primitívek: Zárt görbék által határolt területek (pl.
Grafikus primitívek kitöltése Téglalap kitöltése Poligon kitöltése Kör, ellipszis kitöltése Kitöltés mintával Grafikus primitívek kitöltése Területi primitívek: Zárt görbék által határolt területek (pl.
Területi primitívek: Zárt görbék által határolt területek (pl. kör, ellipszis, poligon)
 Grafikus primitívek kitöltése Téglalap kitöltése Kör, ellipszis kitöltése Kitöltés mintával Grafikus primitívek kitöltése A tertületi primitívek zárt görbével határolt területek, amelyeket megjelníthetünk
Grafikus primitívek kitöltése Téglalap kitöltése Kör, ellipszis kitöltése Kitöltés mintával Grafikus primitívek kitöltése A tertületi primitívek zárt görbével határolt területek, amelyeket megjelníthetünk
Mérnöki létesítmények geodéziája Mérnöki létesítmények valósághű modellezése, modellezési technikák, leíró nyelvek
 Mérnöki létesítmények geodéziája Mérnöki létesítmények valósághű modellezése, modellezési technikák, leíró nyelvek Siki Zoltán siki.zoltan@epito.bme.hu Virtuális valóság Feladat típusok Tervek alapján
Mérnöki létesítmények geodéziája Mérnöki létesítmények valósághű modellezése, modellezési technikák, leíró nyelvek Siki Zoltán siki.zoltan@epito.bme.hu Virtuális valóság Feladat típusok Tervek alapján
A játékfejlesztés több területből áll. A kódolás csupán egy része a munkáknak.
 1 A játékfejlesztés több területből áll. A kódolás csupán egy része a munkáknak. Példák az elvégzendő feladatokra: Tervezés Kódolás Modellezés Textúrázás Pályaszerkesztés Animálás... Többnyire minden terület
1 A játékfejlesztés több területből áll. A kódolás csupán egy része a munkáknak. Példák az elvégzendő feladatokra: Tervezés Kódolás Modellezés Textúrázás Pályaszerkesztés Animálás... Többnyire minden terület
Tartalom. Hajder Levente 2016/2017. I. félév
 Tartalom Hajder Levente hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2016/2017. I. félév 1 Tartalom Motiváció 2 Grafikus szerelőszalag Modellezési transzformácó Nézeti transzformácó
Tartalom Hajder Levente hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2016/2017. I. félév 1 Tartalom Motiváció 2 Grafikus szerelőszalag Modellezési transzformácó Nézeti transzformácó
GPU Lab. 14. fejezet. OpenCL textúra használat. Grafikus Processzorok Tudományos Célú Programozása. Berényi Dániel Nagy-Egri Máté Ferenc
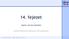 14. fejezet OpenCL textúra használat Grafikus Processzorok Tudományos Célú Programozása Textúrák A textúrák 1, 2, vagy 3D-s tömbök kifejezetten szín információk tárolására Főbb különbségek a bufferekhez
14. fejezet OpenCL textúra használat Grafikus Processzorok Tudományos Célú Programozása Textúrák A textúrák 1, 2, vagy 3D-s tömbök kifejezetten szín információk tárolására Főbb különbségek a bufferekhez
SZE, Doktori Iskola. Számítógépes grafikai algoritmusok. Összeállította: Dr. Gáspár Csaba. Felületmegjelenítés
 Felületmegjelenítés Megjelenítés paramétervonalakkal Drótvázas megjelenítés Megjelenítés takarással Triviális hátsólap eldobás A z-puffer algoritmus Megvilágítás és árnyalás Megjelenítés paramétervonalakkal
Felületmegjelenítés Megjelenítés paramétervonalakkal Drótvázas megjelenítés Megjelenítés takarással Triviális hátsólap eldobás A z-puffer algoritmus Megvilágítás és árnyalás Megjelenítés paramétervonalakkal
Gráfalgoritmusok és hatékony adatszerkezetek szemléltetése
 Gráfalgoritmusok és hatékony adatszerkezetek szemléltetése Készítette: Bognár Gergő Témavezető: Veszprémi Anna Eötvös Loránd Tudományegyetem Informatikai Kar Algoritmusok és Alkalmazásaik Tanszék Budapest,
Gráfalgoritmusok és hatékony adatszerkezetek szemléltetése Készítette: Bognár Gergő Témavezető: Veszprémi Anna Eötvös Loránd Tudományegyetem Informatikai Kar Algoritmusok és Alkalmazásaik Tanszék Budapest,
Klár Gergely Informatikai Kar. 2010/2011. tavaszi félév
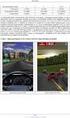 Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. tavaszi félév Tartalom I Sugárkövetés 1 Sugárkövetés 2 3 Tartalom Sugárkövetés Sugarak indítása
Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. tavaszi félév Tartalom I Sugárkövetés 1 Sugárkövetés 2 3 Tartalom Sugárkövetés Sugarak indítása
3D koordináta-rendszerek
 3D koordináta-rendszerek z z y x y x y balkezes bal-sodrású x jobbkezes jobb-sodrású z 3D transzformációk - homogén koordináták (x, y, z) megadása homogén koordinátákkal: (x, y, z, 1) (x, y, z, w) = (x,
3D koordináta-rendszerek z z y x y x y balkezes bal-sodrású x jobbkezes jobb-sodrású z 3D transzformációk - homogén koordináták (x, y, z) megadása homogén koordinátákkal: (x, y, z, 1) (x, y, z, w) = (x,
Struktúra nélküli adatszerkezetek
 Struktúra nélküli adatszerkezetek Homogén adatszerkezetek (minden adatelem azonos típusú) osztályozása Struktúra nélküli (Nincs kapcsolat az adatelemek között.) Halmaz Multihalmaz Asszociatív 20:24 1 A
Struktúra nélküli adatszerkezetek Homogén adatszerkezetek (minden adatelem azonos típusú) osztályozása Struktúra nélküli (Nincs kapcsolat az adatelemek között.) Halmaz Multihalmaz Asszociatív 20:24 1 A
PÉLDATÁR 10. 10. BEGYAKORLÓ FELADAT TÉRBELI FELADAT MEGOLDÁSA VÉGESELEM- MÓDSZERREL
 PÉLDATÁR 10. 10. BEGYAKORLÓ FELADAT TÉRBELI FELADAT MEGOLDÁSA VÉGESELEM- MÓDSZERREL Szerző: Dr. Oldal István 2 Végeselem-módszer 10. TÉRBELI FELADAT MEGOLDÁSA 10.1. Lépcsős tengely vizsgálata Tömör testként,
PÉLDATÁR 10. 10. BEGYAKORLÓ FELADAT TÉRBELI FELADAT MEGOLDÁSA VÉGESELEM- MÓDSZERREL Szerző: Dr. Oldal István 2 Végeselem-módszer 10. TÉRBELI FELADAT MEGOLDÁSA 10.1. Lépcsős tengely vizsgálata Tömör testként,
Robotika. Kinematika. Magyar Attila
 Robotika Kinematika Magyar Attila amagyar@almos.vein.hu Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
Robotika Kinematika Magyar Attila amagyar@almos.vein.hu Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
Ütközések. Szécsi László
 Ütközések Szécsi László Merev testek egymásra hatása két probléma hatnak-e egymásra? összeérnek, ütköznek ütközés-vizsgálat mi a hatás eredménye? erőhatás vagy direkt állapotváltozás ütközés-válasz először
Ütközések Szécsi László Merev testek egymásra hatása két probléma hatnak-e egymásra? összeérnek, ütköznek ütközés-vizsgálat mi a hatás eredménye? erőhatás vagy direkt állapotváltozás ütközés-válasz először
Tartalom. Tartalom. Hajder Levente 2018/2019. I. félév
 Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2018/2019. I. félév Emlékeztető Múlt órán megismerkedtünk a sugárkövetéssel Előnyei: A színtér benépesítésére minden használható,
Hajder Levente hajder@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2018/2019. I. félév Emlékeztető Múlt órán megismerkedtünk a sugárkövetéssel Előnyei: A színtér benépesítésére minden használható,
megjelenítés EDGED FACES átállítjuk a szegmensek számát 5x5x5-re
 Max 4. óra Burkolatok modellezése Az ábrán látható egeret fogjuk elkészíteni. Készítsük el az alaptestet, amiből az egeret fogjuk elkészíteni. Hozzunk létre egy az egér befoglaló méreteinek és arányinak
Max 4. óra Burkolatok modellezése Az ábrán látható egeret fogjuk elkészíteni. Készítsük el az alaptestet, amiből az egeret fogjuk elkészíteni. Hozzunk létre egy az egér befoglaló méreteinek és arányinak
Mesh from file, OrthoCamera, PerspectiveCamera. Szécsi László 3D Grafikus Rendszerek 3. labor
 Mesh from file, OrthoCamera, PerspectiveCamera Szécsi László 3D Grafikus Rendszerek 3. labor OrthoCamera.js const OrthoCamera = function() { this.position = new Vec2(0.5, 0); this.rotation = 0; this.windowsize
Mesh from file, OrthoCamera, PerspectiveCamera Szécsi László 3D Grafikus Rendszerek 3. labor OrthoCamera.js const OrthoCamera = function() { this.position = new Vec2(0.5, 0); this.rotation = 0; this.windowsize
Textúrák. Szécsi László
 Textúrák Szécsi László Textúra interpretációk kép a memóriában ugyanolyan mint a frame buffer pixel helyett texel adatok tömbje 1D, 2D, 3D tömb pl. RGB rekordok függvény diszkrét mintapontjai rácson rekonstrukció:
Textúrák Szécsi László Textúra interpretációk kép a memóriában ugyanolyan mint a frame buffer pixel helyett texel adatok tömbje 1D, 2D, 3D tömb pl. RGB rekordok függvény diszkrét mintapontjai rácson rekonstrukció:
Mechatronika segédlet 1. gyakorlat
 Mechatronika segédlet 1. gyakorlat 2017. február 6. Tartalom Vadai Gergely, Faragó Dénes Indítás, kezelőfelület... 2 Négyzet... 4 Négyzet rajzolásának lépései abszolút koordinátákkal... 4 Kocka, 3D eszközök...
Mechatronika segédlet 1. gyakorlat 2017. február 6. Tartalom Vadai Gergely, Faragó Dénes Indítás, kezelőfelület... 2 Négyzet... 4 Négyzet rajzolásának lépései abszolút koordinátákkal... 4 Kocka, 3D eszközök...
Cohen-Sutherland vágóalgoritmus
 Vágási algoritmusok Alapprobléma Van egy alakzatunk (szakaszokból felépítve) és van egy "ablakunk" (lehet a monitor, vagy egy téglalap alakú tartomány, vagy ennél szabálytalanabb poligon által határolt
Vágási algoritmusok Alapprobléma Van egy alakzatunk (szakaszokból felépítve) és van egy "ablakunk" (lehet a monitor, vagy egy téglalap alakú tartomány, vagy ennél szabálytalanabb poligon által határolt
Síklapú testek. Gúlák, hasábok áthatása. Az előadás átdolgozott részleteket tartalmaz a következőkből: Gubis Katalin: Ábrázoló geometria
 Síklapú testek Gúlák, hasábok áthatása Az előadás átdolgozott részleteket tartalmaz a következőkből: Gubis Katalin: Ábrázoló geometria Áthatás Két test áthatásának nevezzük a testek közös pontjainak összességéből
Síklapú testek Gúlák, hasábok áthatása Az előadás átdolgozott részleteket tartalmaz a következőkből: Gubis Katalin: Ábrázoló geometria Áthatás Két test áthatásának nevezzük a testek közös pontjainak összességéből
Koordináta-geometria feladatgyűjtemény
 Koordináta-geometria feladatgyűjtemény A feladatok megoldásai a dokumentum végén találhatók Vektorok 1. Egy négyzet két szemközti csúcsának koordinátái: A( ; 7) és C(4 ; 1). Határozd meg a másik két csúcs
Koordináta-geometria feladatgyűjtemény A feladatok megoldásai a dokumentum végén találhatók Vektorok 1. Egy négyzet két szemközti csúcsának koordinátái: A( ; 7) és C(4 ; 1). Határozd meg a másik két csúcs
Tanács Attila. Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem
 Tanács Attila Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Direct3D, DirectX o Csak Microsoft platformon OpenGL o Silicon Graphics: IRIS GL (zárt kód) o OpenGL (1992) o Nyílt
Tanács Attila Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Direct3D, DirectX o Csak Microsoft platformon OpenGL o Silicon Graphics: IRIS GL (zárt kód) o OpenGL (1992) o Nyílt
Görbe- és felületmodellezés. Szplájnok Felületmodellezés
 Görbe- és felületmodellezés Szplájnok Felületmodellezés Spline (szplájn) Spline: Szakaszosan, parametrikus polinomokkal leírt görbe A spline nevét arról a rugalmasan hajlítható vonalzóról kapta, melyet
Görbe- és felületmodellezés Szplájnok Felületmodellezés Spline (szplájn) Spline: Szakaszosan, parametrikus polinomokkal leírt görbe A spline nevét arról a rugalmasan hajlítható vonalzóról kapta, melyet
Forgáshenger normálisának és érintősíkjának megszerkesztése II/1
 Forgáshenger normálisának és érintősíkjának megszerkesztése II/1 Adott egy forgáshenger: t főegyenes tengelye két vetületi képével t: 0, 110,170-től jobb felső sarokig egy felületi pontjának második vetületi
Forgáshenger normálisának és érintősíkjának megszerkesztése II/1 Adott egy forgáshenger: t főegyenes tengelye két vetületi képével t: 0, 110,170-től jobb felső sarokig egy felületi pontjának második vetületi
2D képszintézis. Szirmay-Kalos László
 2D képszintézis Szirmay-Kalos László 2D képszintézis Modell szín (200, 200) Kép Kamera ablak (window) viewport Unit=pixel Saját színnel rajzolás Világ koordinátarendszer Pixel vezérelt megközelítés: Tartalmazás
2D képszintézis Szirmay-Kalos László 2D képszintézis Modell szín (200, 200) Kép Kamera ablak (window) viewport Unit=pixel Saját színnel rajzolás Világ koordinátarendszer Pixel vezérelt megközelítés: Tartalmazás
SDL_Universe SDL, C++, 3D szoftver renderelő
 SDL_Universe SDL, C++, 3D szoftver renderelő Boros László, harmadéves mérnökinformatikus I C what you did last summer Programozói Konferencia 2014 iamsemmu@gmail.com http://progkonf.eet.bme.hu SDL_Universe
SDL_Universe SDL, C++, 3D szoftver renderelő Boros László, harmadéves mérnökinformatikus I C what you did last summer Programozói Konferencia 2014 iamsemmu@gmail.com http://progkonf.eet.bme.hu SDL_Universe
Látható felszín algoritmusok
 Látható felszín algoritmusok Látható felszínek Z-buffer algoritmus Festő algoritmus A látható felszín meghatározására szolgáló algoritmusok A tárgyak takarják-e egymást? Mely tárgy látható? Pontokra: P
Látható felszín algoritmusok Látható felszínek Z-buffer algoritmus Festő algoritmus A látható felszín meghatározására szolgáló algoritmusok A tárgyak takarják-e egymást? Mely tárgy látható? Pontokra: P
EGYSZERŰ, NEM IRÁNYÍTOTT (IRÁNYÍTATLAN) GRÁF
 Összefoglaló Gráfok / EGYSZERŰ, NEM IRÁNYÍTOTT (IRÁNYÍTATLAN) GRÁF Adott a G = (V, E) gráf ahol a V a csomópontok, E az élek halmaza E = {(x, y) x, y V, x y (nincs hurokél) és (x, y) = (y, x)) Jelölések:
Összefoglaló Gráfok / EGYSZERŰ, NEM IRÁNYÍTOTT (IRÁNYÍTATLAN) GRÁF Adott a G = (V, E) gráf ahol a V a csomópontok, E az élek halmaza E = {(x, y) x, y V, x y (nincs hurokél) és (x, y) = (y, x)) Jelölések:
Érettségi feladatok: Koordináta-geometria 1/5
 Érettségi feladatok: Koordináta-geometria 1/5 2003. Próba/ 13. Adott egy háromszög három csúcspontja a koordinátáival: A( 4; 4), B(4; 4) és C( 4; 8). Számítsa ki a C csúcsból induló súlyvonal és az A csúcsból
Érettségi feladatok: Koordináta-geometria 1/5 2003. Próba/ 13. Adott egy háromszög három csúcspontja a koordinátáival: A( 4; 4), B(4; 4) és C( 4; 8). Számítsa ki a C csúcsból induló súlyvonal és az A csúcsból
Helyvektorok, műveletek, vektorok a koordináta-rendszerben
 Helyvektorok, műveletek, vektorok a koordináta-rendszerben. Rajzold meg az alábbi helyvektorokat a derékszögű koordináta-rendszerben, majd számítsd ki a hosszúságukat! a) (4 ) b) ( 5 ) c) ( 6 ) d) (4 )
Helyvektorok, műveletek, vektorok a koordináta-rendszerben. Rajzold meg az alábbi helyvektorokat a derékszögű koordináta-rendszerben, majd számítsd ki a hosszúságukat! a) (4 ) b) ( 5 ) c) ( 6 ) d) (4 )
Valasek Gábor
 Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. őszi félév Tartalom 1 Motiváció Görbék Hermite interpoláció Catmull-Rom spline Kochanek-Bartels spline Műveletek
Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. őszi félév Tartalom 1 Motiváció Görbék Hermite interpoláció Catmull-Rom spline Kochanek-Bartels spline Műveletek
CodeCamp Döntő feladat
 CodeCamp Döntő feladat 2014 1 CodeCamp Döntő feladat A feladatban egy játékot kell készíteni, ami az elődöntő feladatán alapul. A feladat az elődöntő során elkészített szimulációs csomagra építve egy két
CodeCamp Döntő feladat 2014 1 CodeCamp Döntő feladat A feladatban egy játékot kell készíteni, ami az elődöntő feladatán alapul. A feladat az elődöntő során elkészített szimulációs csomagra építve egy két
Számítógépes Grafika mintafeladatok
 Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Érettségi feladatok Koordinátageometria_rendszerezve / 5
 Érettségi feladatok Koordinátageometria_rendszerezve 2005-2013 1/ 5 Vektorok 2005. május 28./12. Adottak az a (4; 3) és b ( 2; 1) vektorok. a) Adja meg az a hosszát! b) Számítsa ki az a + b koordinátáit!
Érettségi feladatok Koordinátageometria_rendszerezve 2005-2013 1/ 5 Vektorok 2005. május 28./12. Adottak az a (4; 3) és b ( 2; 1) vektorok. a) Adja meg az a hosszát! b) Számítsa ki az a + b koordinátáit!
1. Munkalap. 1. Fejezze be az előrajzolás szerinti vonalfajták ábrázolását! Ügyeljen a vonalvastagságra!
 1. Munkalap 1. Fejezze be az előrajzolás szerinti vonalfajták ábrázolását! Ügyeljen a vonalvastagságra! 2. Rajzoljon merőleges egyenest az e egyenes P pontjába! e P 3. Ossza fel az AB szakaszt 2:3 arányban!
1. Munkalap 1. Fejezze be az előrajzolás szerinti vonalfajták ábrázolását! Ügyeljen a vonalvastagságra! 2. Rajzoljon merőleges egyenest az e egyenes P pontjába! e P 3. Ossza fel az AB szakaszt 2:3 arányban!
Készítette: niethammer@freemail.hu
 VLogo VRML generáló program Készítette: Niethammer Zoltán niethammer@freemail.hu 2008 Bevezetés A VLogo az általános iskolákban használt Comenius Logo logikájára épülő programozási nyelv. A végeredmény
VLogo VRML generáló program Készítette: Niethammer Zoltán niethammer@freemail.hu 2008 Bevezetés A VLogo az általános iskolákban használt Comenius Logo logikájára épülő programozási nyelv. A végeredmény
Számítógépes grafika
 Számítógépes grafika HEFOP 3.5.1 Korszerű felnőttképzési módszerek kifejlesztése és alkalmazása EMIR azonosító: HEFOP-3.5.1-K-2004-10-0001/2.0 Tananyagfejlesztő: Máté István Lektorálta: Brückler Tamás
Számítógépes grafika HEFOP 3.5.1 Korszerű felnőttképzési módszerek kifejlesztése és alkalmazása EMIR azonosító: HEFOP-3.5.1-K-2004-10-0001/2.0 Tananyagfejlesztő: Máté István Lektorálta: Brückler Tamás
OpenGL és a mátrixok
 OpenGL és a mátrixok Róth Gergő 2013. március 4. Róth Gergő 1/20 A rajzoláskor a videókártya minden csúcson végrehajt egy transzformációt. Mire jó? Kamera helyének beállítása Egy objektum több pozícióra
OpenGL és a mátrixok Róth Gergő 2013. március 4. Róth Gergő 1/20 A rajzoláskor a videókártya minden csúcson végrehajt egy transzformációt. Mire jó? Kamera helyének beállítása Egy objektum több pozícióra
Algoritmusok és adatszerkezetek gyakorlat 07
 Algoritmusok és adatszerkezetek gyakorlat 0 Keresőfák Fák Fa: összefüggő, körmentes gráf, melyre igaz, hogy: - (Általában) egy gyökér csúcsa van, melynek 0 vagy több részfája van - Pontosan egy út vezet
Algoritmusok és adatszerkezetek gyakorlat 0 Keresőfák Fák Fa: összefüggő, körmentes gráf, melyre igaz, hogy: - (Általában) egy gyökér csúcsa van, melynek 0 vagy több részfája van - Pontosan egy út vezet
BASH script programozás II. Vezérlési szerkezetek
 06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
* Az eszköztáron látható menüpontok közül csak a felsoroltak esetén használható a Ctrl.
 Általános fogómód használata Az általános fogómód egy olyan objektum érzékeny kurzor, amely az alább felsorolt szerkesztı mőveleteknél felismeri azt, hogy milyen grafilus elem felett áll, és annak megfelelıen
Általános fogómód használata Az általános fogómód egy olyan objektum érzékeny kurzor, amely az alább felsorolt szerkesztı mőveleteknél felismeri azt, hogy milyen grafilus elem felett áll, és annak megfelelıen
3D számítógépes geometria és alakzatrekonstrukció
 3D számítógépes geometria és alakzatrekonstrukció 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01
3D számítógépes geometria és alakzatrekonstrukció 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01
Bevezetés a CGI-be. 1. Történelem
 Bevezetés a CGI-be 1. Történelem 1.1 Úttörők Euklidész (ie.. 300-250) - A számítógépes grafika geometriai hátterének a megteremtője Bresenham (60 évek) - Első vonalrajzolás raster raster készüléken, később
Bevezetés a CGI-be 1. Történelem 1.1 Úttörők Euklidész (ie.. 300-250) - A számítógépes grafika geometriai hátterének a megteremtője Bresenham (60 évek) - Első vonalrajzolás raster raster készüléken, később
Programozás alapjai II. (7. ea) C++ Speciális adatszerkezetek. Tömbök. Kiegészítő anyag: speciális adatszerkezetek
 Programozás alapjai II. (7. ea) C++ Kiegészítő anyag: speciális adatszerkezetek Szeberényi Imre BME IIT M Ű E G Y E T E M 1 7 8 2 C++ programozási nyelv BME-IIT Sz.I. 2016.04.05. - 1
Programozás alapjai II. (7. ea) C++ Kiegészítő anyag: speciális adatszerkezetek Szeberényi Imre BME IIT M Ű E G Y E T E M 1 7 8 2 C++ programozási nyelv BME-IIT Sz.I. 2016.04.05. - 1
Speciális adatszerkezetek. Programozás alapjai II. (8. ea) C++ Tömbök. Tömbök/2. N dimenziós tömb. Nagyméretű ritka tömbök
 Programozás alapjai II. (8. ea) C++ Kiegészítő anyag: speciális adatszerkezetek Szeberényi Imre BME IIT Speciális adatszerkezetek A helyes adatábrázolás választása, a helyes adatszerkezet
Programozás alapjai II. (8. ea) C++ Kiegészítő anyag: speciális adatszerkezetek Szeberényi Imre BME IIT Speciális adatszerkezetek A helyes adatábrázolás választása, a helyes adatszerkezet
Adatszerkezetek II. 1. előadás
 Adatszerkezetek II. 1. előadás Gráfok A gráf fogalma: Gráf(P,E): P pontok (csúcsok) és E P P élek halmaza Fogalmak: Irányított gráf : (p 1,p 2 ) E-ből nem következik, hogy (p 2,p 1 ) E Irányítatlan gráf
Adatszerkezetek II. 1. előadás Gráfok A gráf fogalma: Gráf(P,E): P pontok (csúcsok) és E P P élek halmaza Fogalmak: Irányított gráf : (p 1,p 2 ) E-ből nem következik, hogy (p 2,p 1 ) E Irányítatlan gráf
openbve objektumkészítés Leírás az objektumkészítéshez használható parancsokról
 Leírás az openbve-vel kompatibilis objektumkészítéshez használható parancsokról 1. oldal openbve objektumkészítés Leírás az objektumkészítéshez használható parancsokról A leírás az openbve-hez készíthető
Leírás az openbve-vel kompatibilis objektumkészítéshez használható parancsokról 1. oldal openbve objektumkészítés Leírás az objektumkészítéshez használható parancsokról A leírás az openbve-hez készíthető
Programozás alapjai II. (7. ea) C++
 Programozás alapjai II. (7. ea) C++ Kiegészítő anyag: speciális adatszerkezetek Szeberényi Imre BME IIT M Ű E G Y E T E M 1 7 8 2 C++ programozási nyelv BME-IIT Sz.I. 2016.04.05. - 1
Programozás alapjai II. (7. ea) C++ Kiegészítő anyag: speciális adatszerkezetek Szeberényi Imre BME IIT M Ű E G Y E T E M 1 7 8 2 C++ programozási nyelv BME-IIT Sz.I. 2016.04.05. - 1
Koordináta-geometria feladatok (középszint)
 Koordináta-geometria feladatok (középszint) 1. (KSZÉV Minta (1) 2004.05/I/4) Adott az A(2; 5) és B(1; 3) pont. Adja meg az AB szakasz felezőpontjának koordinátáit! 2. (KSZÉV Minta (2) 2004.05/I/7) Egy
Koordináta-geometria feladatok (középszint) 1. (KSZÉV Minta (1) 2004.05/I/4) Adott az A(2; 5) és B(1; 3) pont. Adja meg az AB szakasz felezőpontjának koordinátáit! 2. (KSZÉV Minta (2) 2004.05/I/7) Egy
Minimum követelmények matematika tantárgyból 11. évfolyamon
 Minimum követelmények matematika tantárgyból. évfolyamon A hatványozás általánosítása pozitív alap esetén racionális kitevőre. Műveletek hatványokkal. A, a 0 függvény. Az eponenciális függvény. Vizsgálata
Minimum követelmények matematika tantárgyból. évfolyamon A hatványozás általánosítása pozitív alap esetén racionális kitevőre. Műveletek hatványokkal. A, a 0 függvény. Az eponenciális függvény. Vizsgálata
Számítógépes grafika
 Számítógépes grafika XVII. rész A grafikai modellezés A modellezés A generatív számítógépes grafikában és a képfeldolgozás során nem a valódi objektumokat (valóságbeli tárgyakat), hanem azok egy modelljét
Számítógépes grafika XVII. rész A grafikai modellezés A modellezés A generatív számítógépes grafikában és a képfeldolgozás során nem a valódi objektumokat (valóságbeli tárgyakat), hanem azok egy modelljét
Koordinátageometria. M veletek vektorokkal grakusan. Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1
 Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1 Koordinátageometria M veletek vektorokkal grakusan 1. Az ABCD négyzet oldalvektorai közül a = AB és b = BC. Adja meg az AC és BD vektorokat a
Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1 Koordinátageometria M veletek vektorokkal grakusan 1. Az ABCD négyzet oldalvektorai közül a = AB és b = BC. Adja meg az AC és BD vektorokat a
Infobionika ROBOTIKA. X. Előadás. Robot manipulátorok II. Direkt és inverz kinematika. Készült a HEFOP P /1.0 projekt keretében
 Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Direct3D pipeline. Grafikus játékok fejlesztése Szécsi László t03-pipeline
 Direct3D pipeline Grafikus játékok fejlesztése Szécsi László 2013.02.12. t03-pipeline RESOURCES PIPELINE STAGES RENDER STATES Vertex buffer Instance buffer Constant buffers and textures Index buffer Constant
Direct3D pipeline Grafikus játékok fejlesztése Szécsi László 2013.02.12. t03-pipeline RESOURCES PIPELINE STAGES RENDER STATES Vertex buffer Instance buffer Constant buffers and textures Index buffer Constant
Programozási technológia I. 1. beadandó feladatsor
 Programozási technológia I. 1. beadandó feladatsor Közös elvárás a megoldásoknál, hogy gyűjteményben tároljuk az azonos ősosztályból származtatott osztályok objektumait. Az objektumok feldolgozása során
Programozási technológia I. 1. beadandó feladatsor Közös elvárás a megoldásoknál, hogy gyűjteményben tároljuk az azonos ősosztályból származtatott osztályok objektumait. Az objektumok feldolgozása során
7. Koordináta méréstechnika
 7. Koordináta méréstechnika Coordinate Measuring Machine: CMM, 3D-s mérőgép Egyiptomi piramis kövek mérése i.e. 1440 Egyiptomi mérővonalzó, Amenphotep fáraó (i.e. 1550) alkarjának hossza: 524mm A koordináta
7. Koordináta méréstechnika Coordinate Measuring Machine: CMM, 3D-s mérőgép Egyiptomi piramis kövek mérése i.e. 1440 Egyiptomi mérővonalzó, Amenphotep fáraó (i.e. 1550) alkarjának hossza: 524mm A koordináta
A végeselem módszer alapjai. 2. Alapvető elemtípusok
 A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
Összeállította: dr. Leitold Adrien egyetemi docens
 Az R 3 tér geometriája Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. 1 Vektorok Vektor: irányított szakasz Jel.: a, a, a, AB, Jellemzői: irány, hosszúság, (abszolút érték) jel.: a Speciális
Az R 3 tér geometriája Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. 1 Vektorok Vektor: irányított szakasz Jel.: a, a, a, AB, Jellemzői: irány, hosszúság, (abszolút érték) jel.: a Speciális
Diszkrét matematika 2.
 Diszkrét matematika 2. Mérai László előadása alapján Készítette: Nagy Krisztián 4. előadás Eulerséta: Olyan séta, mely a gráf minden élét pontosan egyszer tartalmazza. Tétel: egy összefüggő gráf. Ha minden
Diszkrét matematika 2. Mérai László előadása alapján Készítette: Nagy Krisztián 4. előadás Eulerséta: Olyan séta, mely a gráf minden élét pontosan egyszer tartalmazza. Tétel: egy összefüggő gráf. Ha minden
