Az R&R vizsgálatok tapasztalatai. Minősítése R&R a mindennapokban. Tóth Csaba László fizikus. Tóth László politológus. és benne egy különlegesség
|
|
|
- József Vörös
- 8 évvel ezelőtt
- Látták:
Átírás
1 Az R&R vizsgálatok tapasztalatai és benne egy különlegesség Minősítése R&R a mindennapokban Tóth Csaba László fizikus Tóth László politológus
2 Miért végzünk R&R vizsgálatokat? Szabványkövetelmény A menedzsment mániája Szeretnénk megismerni a folyamatainkat 2
3 Melyik folyamat a jobb? János folyamata Teljes ingadozás (Észlelt ingadozás) Sári folyamata 2 s észlelt (teljes) 3
4 A mérés az adatainkba ingadozást visz be Valódi ingadozás Teljes ingadozás János folyamata 2 s Aktuális 2 s Mérőrendszer + = 2 s Észlelt teljes Sári folyamata Mérés ingadozása 4
5 A mérés eltolhatja a mért értéket Valódi átlag Átl. Észlelt átlag Átl. Átl. A mérés eltolása 5
6 Mi szükséges egy jó R&R vizsgálathoz? Megfelelő szoftver vagy excel tábla Jó mérő emberek és egy mérnök Megfelelő minták (?) Folyamatismerettel rendelkező szakember, aki kellőképpen jártas az MSA tudományában 6
7 Mikor kezdhetünk neki egy R&R vizsgálatnak? Stabilitás Felbontás Eltolódás (kalibráltság) Linearitás 7
8 A modellünk Eltérés a mérési eredményekben Mért termék okozta változás Mérőrendszer okozta változás Ismételhetőség (mérőeszköz) Reprodukálhatóság (operátor-technika) Operátor Operátor - termék kölcsönhatás s 2 total = s 2 termék + s 2 R&R s 2 total = s 2 termék + s 2 ismételhetőség + s 2 reprodukálhatóság s 2 total = s 2 termék + s 2 ism + s 2 operátor +s 2 khatás 8
9 Az operátor-mintadarab kereszthatás Definició: -Az operátorok közti eltérések nem konzisztensek minden darabra. -Az értékelők közötti eltérés attól függ, melyik darabot mérik. Munkadarabok Operátorok Professzor Kigyúrt Kutatóintézet + - Zongora hordár - + Dr. Nagy Attila 9
10 A mérés előkészítése Szükségünk van min két mérő emberre Általában 10 egységet mér Olyan minták használatáról kell gondoskodni, amelyek a teljes, de jellemző folyamatingadozást képviselik. (Ez nem jelenti csak a tűréstartományt, és nem sugallja egy kiveszem, amit akarok mintavételi terv használatát.) 3-3 minta a tűréshatárok közelében, 4 minta a specifikáció középső részéből Mindegyik egységet mindegyik operátor 2-3-szor méri Kritikus a véletlenszerűsítés
11 Terminológia Hozzájárulás-% (%Contribution): Egy összetevő vagy összetevők kombinációja által produkált ingadozás, a teljes észlelt ingadozás százalékában kifejezve. Tűrés-% (% Tolerance): Egy összetevő normális eloszlása 99,73%-ára becsült mérési összetevő által elfogyasztott darab-tűrés százaléka osztva a tűréssel (ismert mint precizitás/tűrés arány (Precision to Tolerance Ratio -P/T Ratio néven is) Diszkriminációs (Discrimination) Index: Az észlelt folyamatingadozás azon tartományainak száma, melyeket a mérőrendszer képes megkülönböztetni
12 A mérőrendszer elfogadhatóságának összegzése Hozzájárulás % Diszkriminációs varianciákra szórásokra index Tűrés % 9% 1% 30% 10% 5 10 X 30% 10% nem függetlenek Mindkét paraméter egyaránt fontos, együttesen figyeljük!
13 Egy R&R vizsgálat eredménye Problémák az ndc számmal ELLENTMONDÁS Feltételes elfogadás Kiváló megfelelés
14 ndc 2 s s 2 R& R % SV % 100 & SV R Part R s s Total 2 %SV ndc %SV ndc Dr. Wheeler (2006): 0,5 282, , , , , , , , , , , , , , , , , , , , , ,60 0 Sajnos, az alapján, amit szerző a gyakorlatban tapasztalt, sem a Discrimination Ratio, sem a Classification Ratio nem alkalmas egyszerű gyakorlati mérőszámnak..egyik sem definiálja a (valódi) megkülönböztethető kategóriák számát.
15 Mérőrendszer "javítás Elkövethetünk-e hibákat az R&R vizsgálatkor? Van egy mérőeszközünk, amely alkalmas 3 különböző méretű krumpli mérésére. Mindegyik méretű krumpliból van db, és van 2 operátorunk is. Mindegyik operátor leméri kétszer a különböző méretű krumplikat. Először a 30-as, utána az 50-es, legvégül a 110-es méretű krumplik mérésére csinálunk GR&R-t. Kérdés: milyen a mérőrendszer?
16 A 30-as méretű krumplik GR&R-ja
17 A 50-es méretű krumplik GR&R-ja
18 A 110-es méretű krumplik GR&R-ja
19 Jó-e a mérőrendszerem? NEM! "Javítsuk" meg a mérőrendszert! Egyesítsük a három mintát!
20 Az összes krumpli GR&R-ja
21 Mi változott meg? Semmi! Tanulság: A mérőrendszer elemzéshez használt minta kiválasztásánál figyelembe kell venni, ha túl nagy a különbség az egyes mintadarabok között, akkor az ugyanazon darab mérései közötti különbséget elmossa a minták mérete közötti különbség!! Volt ugye egy ajánlásunk a 3-3-4!
22 22
23 23
24 Milyen legyen a minta összetétele? Ez függ attól, hogy milyenek a specifikációs határok Egyoldalú határok esetén: Elfogadási tartomány Tűréshatár Elutasítási tartomány 30 % 25 % 25 % 20 % Kétoldalú határok esetén: Elutasítási tartomány TH Elfogadási tartomány Elutasítási tartomány TH 10 % 12,5 % 12,5 % 30 % 12,5 % 12,5 % 10 % 24
25 Biztos, hogy az eszközből jön a változás? Magasságmérés mérőszalaggal Var % Total R&r 1,47 Repeat 1,12 Reprod 0,35 25
26 R&R a mindennapokban Ne feledjük el a követelményeket! Stabilitás (összehasonlíthatóság miatt) Felbontás (differenciált választ tudjunk adni) Eltolódás (nem könnyű eset) Linearitás (a válasz skála lehetőségei) 26
27 Ön hogyan ítéli meg az Etető Kft. Szolgáltatását? Kiváló Elfogadható Elfogadhatatlan 27
28 28
29 29
30 Egy minősítéses adatokra vonatkozó linearitás példa Rögzítve:
31 Lineáris?
32 Ellenőrizze a felbontás és a linearitást! 32
33 33
34 Híres mintavételi hibák 1936: Alf Landon vs F. D. Roosevelt 6 % előnyből 25 % hátrány Literary Digest: 2/10 millió levél gépkocsinyilvántartások, telefonkönyvek George H. Gallup: néhány ezer, szociális momentumok alapján 1948: Thomas Dewey vs Harry Truman Dewey biztos befutó George H. Gallup: néhány ezer, szociális momentumok alapján 1940-es népszámlálás alapján Eredmény: 45,1% vs 49, 6 urbánus (demokrata) népesség megváltozott túlsúlya 34
35 Hogy vezet meg bennünket a média és a közvélemény-kutatók? Szlovák Nemzeti Tanács, 2016 március Probléma: 10 napos közvélemény-kutatási csend kvk1 kvk2 kvk3 exit eredmény kvátlag delta Smer 34,6 38,4 32,5 27,3 28,28 35,17-6,89 0,98 SaS 5,5 5,2 4 13,3 12,1 4,90 7,20-1,20 OL'aNO-NOVA 6,1 6,8 5 11,2 11,02 5,97 5,05-0,18 SNS 8,7 9,1 10,5 8 8,64 9,43-0,79 0,64 Kotleba-L'SNS 2,1 2,5 1,5 6,8 8,04 2,03 6,01 1,24 Sme Rodina 4,2 3,6 4,5 5,9 6,62 4,10 2,52 0,72 Most-Híd 8,2 9,2 7 7,3 6,5 8,13-1,63-0,80 Siet' 14 10,4 14,5 6,7 5,6 12,97-7,37-1,10 KDH 7 6, ,94 7,53-2,59-0,06 SMK-MKP 3, ,6 4,04 4,17-0,13 0,44 SDKÚ-DS 1 1,3 1 0,8 0,26 1,10-0,84-0,54 94,9 97,1 94,5 95,9 96,04 95,5 35
36 Az exit pollnak se hihetünk mindig Románia, elnökválasztás, 2009 december Probléma: az exit pollok csak Románia területén készültek A diaszpóra és a kettős állampolgárok döntöttek! Különbség: 70,048 szavazat, 0,67%!!! A 200,000 moldovai kettős állampolgár 94%-a Basescura szavazott 36
37 Mi a tanulság? A közvélemény-kutatások hasznosak, de tudni kell értelmezni! Nem közvélemény-kutatást kell nyerni, hanem választást! Id.: Kovács László, MSZP elnök, április 7., az urnazárás után Jól mértek, de nem jó következtetéseket vontak le! Gazsó Tibor (Századvég): Utólag vizsgálva, egyértelműen kiderült, hogy jók az adatok A pártválasztásukat eltitkolók is beazonosíthatók 37
38 Hihetünk-e a mandátumbecslésnek? Ismét kétharmadot kapna a Fidesz Honnan tudjuk? Valójában nem tudhatjuk, mert a mandátumok 53%-a egyéni körzetben (SMD) dől el A körzetek egy része erősen megtippelhető (ld. Vörös és Kék államok az Egyesült Államokban) A billegő körzetek dönthetnek jelentős részük háromesélyes A mandátumbecsléseket alapozó közvélemény-kutatások országosan reprezentatívak, ezek alapján lehetetlen a billegő körzetek megtippelése! Ezek a mandátum-becslések szemfényvesztések!!! 38
39 Zárásként egy friss példa: Horvát választások, 2015 november, 2016 szeptember 2015 koal % mandátum DK (HDZ) 33,36 56 HR (SDP) 33,2 56 Most 13,51 19 ZZ 4,24 1 B 365 (k) 3,32 2 IDS (k) 1,83 3 NS-Ref (k) 1,54 1 HDSSB 1,36 2 Σ 140 exit 2015 HR (SDP) 56 DK (HDZ) 57 Most 17 ZZ 3 IDS (k) 3 B 365 (k) 2 HDSSB 2 NS-Ref (k) koal % mandátum HDZ 36,27 59 NK (SDP) 33,82 54 Most 9,91 13 ZZ (k) 6,23 8 B 365 (k) 4,04 2 IDS (k) 2,29 3 PM/ZG (k) 2,06 0 HDSSB (k) 1,25 1 Σ 140 exit 2016 NK (SDP) 57 HDZ 57 Most 12 ZZ (k) 7 IDS (k) 3 B 365 (k) 2 HDSSB 1 PM/ZG (k) 1 Kis pártok mérésének a problémája: A regionális pártot pontosan méri, az országosnál háromszoros eltérés az exit pollnál! Itt sem arról van szó tehát, hogy rosszul mérünk, hanem az interpretációról! 39
40 Köszönöm megtisztelő figyelmüket!
SKIK Thot Quality Management Kaposvár június 8.
 Megtiszteltetés, hogy újra Önök között lehetek Tóth Csaba László Szombathely, 1952 1978. KLTE, Debrecen, (fém)fizikus 1978-1997: Egyesült Izzó, Tungsram, GE Lighting Hajdúböszörmény, Budapest, K+F 1998-2000:
Megtiszteltetés, hogy újra Önök között lehetek Tóth Csaba László Szombathely, 1952 1978. KLTE, Debrecen, (fém)fizikus 1978-1997: Egyesült Izzó, Tungsram, GE Lighting Hajdúböszörmény, Budapest, K+F 1998-2000:
Minőségirányítási rendszerek 9. előadás
 Minőségirányítási rendszerek 9. előadás 013.05.03. MÉRŐESZKÖZÖK MÉRÉSTECHNIKAI TULAJDONSÁGAI Mérőeszköz rendszeres hibája (Systematic Error of Measurement) alatt ugyanannak az értéknek megismételhetőségi
Minőségirányítási rendszerek 9. előadás 013.05.03. MÉRŐESZKÖZÖK MÉRÉSTECHNIKAI TULAJDONSÁGAI Mérőeszköz rendszeres hibája (Systematic Error of Measurement) alatt ugyanannak az értéknek megismételhetőségi
MSA - mérőrendszer elemzés (MSA - measurement systems analysis)
 Mi értünk mérőrendszer alatt? MSA - mérőrendszer elemzés (MSA - measurement systems analysis) Ahhoz, hogy valamilyen termék, folyamatparamétert értékelni, összehasonlítani tudjunk pl.: elvárt értékkel,
Mi értünk mérőrendszer alatt? MSA - mérőrendszer elemzés (MSA - measurement systems analysis) Ahhoz, hogy valamilyen termék, folyamatparamétert értékelni, összehasonlítani tudjunk pl.: elvárt értékkel,
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/54/33134304.jpg) [Biomatematika 2] Orvosi biometria 2016.02.29. A statisztika típusai Leíró jellegű statisztika: összegzi egy adathalmaz jellemzőit. A középértéket jelemzi (medián, módus, átlag) Az adatok változékonyságát
[Biomatematika 2] Orvosi biometria 2016.02.29. A statisztika típusai Leíró jellegű statisztika: összegzi egy adathalmaz jellemzőit. A középértéket jelemzi (medián, módus, átlag) Az adatok változékonyságát
A mérések általános és alapvető metrológiai fogalmai és definíciói. Mérések, mérési eredmények, mérési bizonytalanság. mérés. mérési elv
 Mérések, mérési eredmények, mérési bizonytalanság A mérések általános és alapvető metrológiai fogalmai és definíciói mérés Műveletek összessége, amelyek célja egy mennyiség értékének meghatározása. mérési
Mérések, mérési eredmények, mérési bizonytalanság A mérések általános és alapvető metrológiai fogalmai és definíciói mérés Műveletek összessége, amelyek célja egy mennyiség értékének meghatározása. mérési
MÉRÉSTECHNIKA. Előadások (2.) Galla Jánosné
 1 MÉRÉSTECHNIKA Előadások (2.) 2014 Galla Jánosné 1. A hiba rendűsége Az 2. előadás témái 2. A mérési módszer hibája 3. Műszerhibák 4. A mérési hibák új megközelítése 5. A járműgyártás metrológiai többletkövetelményei
1 MÉRÉSTECHNIKA Előadások (2.) 2014 Galla Jánosné 1. A hiba rendűsége Az 2. előadás témái 2. A mérési módszer hibája 3. Műszerhibák 4. A mérési hibák új megközelítése 5. A járműgyártás metrológiai többletkövetelményei
6. Előadás. Vereb György, DE OEC BSI, október 12.
 6. Előadás Visszatekintés: a normális eloszlás Becslés, mintavételezés Reprezentatív minta A statisztika, mint változó Paraméter és Statisztika Torzítatlan becslés A mintaközép eloszlása - centrális határeloszlás
6. Előadás Visszatekintés: a normális eloszlás Becslés, mintavételezés Reprezentatív minta A statisztika, mint változó Paraméter és Statisztika Torzítatlan becslés A mintaközép eloszlása - centrális határeloszlás
Hipotézis STATISZTIKA. Kétmintás hipotézisek. Munkahipotézis (H a ) Tematika. Tudományos hipotézis. 1. Előadás. Hipotézisvizsgálatok
 STATISZTIKA 1. Előadás Hipotézisvizsgálatok Tematika 1. Hipotézis vizsgálatok 2. t-próbák 3. Variancia-analízis 4. A variancia-analízis validálása, erőfüggvény 5. Korreláció számítás 6. Kétváltozós lineáris
STATISZTIKA 1. Előadás Hipotézisvizsgálatok Tematika 1. Hipotézis vizsgálatok 2. t-próbák 3. Variancia-analízis 4. A variancia-analízis validálása, erőfüggvény 5. Korreláció számítás 6. Kétváltozós lineáris
Gyártástechnológia alapjai Méréstechnika rész. Előadások (2.) 2011.
 Gyártástechnológia alapjai Méréstechnika rész Előadások (2.) 2011. 1 Méréstechnika előadás 2. 1. Mérési hibák 2. A hiba rendszáma 3. A mérési bizonytalanság 2 Mérési folyamat A mérési folyamat négy fő
Gyártástechnológia alapjai Méréstechnika rész Előadások (2.) 2011. 1 Méréstechnika előadás 2. 1. Mérési hibák 2. A hiba rendszáma 3. A mérési bizonytalanság 2 Mérési folyamat A mérési folyamat négy fő
Statisztika - bevezetés Méréselmélet PE MIK MI_BSc VI_BSc 1
 Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Tartalomjegyzék I. RÉSZ: KÍSÉRLETEK MEGTERVEZÉSE
 Tartalomjegyzék 5 Tartalomjegyzék Előszó I. RÉSZ: KÍSÉRLETEK MEGTERVEZÉSE 1. fejezet: Kontrollált kísérletek 21 1. A Salk-oltás kipróbálása 21 2. A porta-cava sönt 25 3. Történeti kontrollok 27 4. Összefoglalás
Tartalomjegyzék 5 Tartalomjegyzék Előszó I. RÉSZ: KÍSÉRLETEK MEGTERVEZÉSE 1. fejezet: Kontrollált kísérletek 21 1. A Salk-oltás kipróbálása 21 2. A porta-cava sönt 25 3. Történeti kontrollok 27 4. Összefoglalás
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011.
 BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
A mintavétel szakszerűtlenségeinek hatása a monitoring-statisztikákra
 A mintavétel szakszerűtlenségeinek hatása a monitoring-statisztikákra Vörös Zsuzsanna NÉBIH RFI tervezési referens 2013. április 17. Egy kis felmérés nem kor Következtetések: 1. a jelenlevők nemi megoszlása:
A mintavétel szakszerűtlenségeinek hatása a monitoring-statisztikákra Vörös Zsuzsanna NÉBIH RFI tervezési referens 2013. április 17. Egy kis felmérés nem kor Következtetések: 1. a jelenlevők nemi megoszlása:
Normális eloszlás tesztje
 Valószínűség, pontbecslés, konfidenciaintervallum Normális eloszlás tesztje Kolmogorov-Szmirnov vagy Wilk-Shapiro próba. R-funkció: shapiro.test(vektor) balra ferde eloszlás jobbra ferde eloszlás balra
Valószínűség, pontbecslés, konfidenciaintervallum Normális eloszlás tesztje Kolmogorov-Szmirnov vagy Wilk-Shapiro próba. R-funkció: shapiro.test(vektor) balra ferde eloszlás jobbra ferde eloszlás balra
Mérési hibák 2006.10.04. 1
 Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
ÚJDONSÁGOK A MINITAB STATISZTIKAI SZOFTVER ÚJ KIADÁSÁNÁL (MINITAB 18)
 ÚJDONSÁGOK A MINITAB STATISZTIKAI SZOFTVER ÚJ KIADÁSÁNÁL (MINITAB 18) Előadó: Lakat Károly, L.K. Quality Bt. 2017 szeptember 27 EOQ MNB Szakbizottsági ülés Minitab 18 újdonságai Session ablak megújítása
ÚJDONSÁGOK A MINITAB STATISZTIKAI SZOFTVER ÚJ KIADÁSÁNÁL (MINITAB 18) Előadó: Lakat Károly, L.K. Quality Bt. 2017 szeptember 27 EOQ MNB Szakbizottsági ülés Minitab 18 újdonságai Session ablak megújítása
Kockázatalapú változó paraméterű szabályozó kártya kidolgozása a mérési bizonytalanság figyelembevételével
 Kockázatalapú változó paraméterű szabályozó kártya kidolgozása a mérési bizonytalanság figyelembevételével Hazai hallgatói, illetve kutatói személyi támogatást biztosító rendszer kidolgozása és működtetése
Kockázatalapú változó paraméterű szabályozó kártya kidolgozása a mérési bizonytalanság figyelembevételével Hazai hallgatói, illetve kutatói személyi támogatást biztosító rendszer kidolgozása és működtetése
Kettőnél több csoport vizsgálata. Makara B. Gábor MTA Kísérleti Orvostudományi Kutatóintézet
 Kettőnél több csoport vizsgálata Makara B. Gábor MTA Kísérleti Orvostudományi Kutatóintézet Gyógytápszerek (kilokalória/adag) Három gyógytápszer A B C 30 5 00 10 05 08 40 45 03 50 35 190 Kérdések: 1. Van-e
Kettőnél több csoport vizsgálata Makara B. Gábor MTA Kísérleti Orvostudományi Kutatóintézet Gyógytápszerek (kilokalória/adag) Három gyógytápszer A B C 30 5 00 10 05 08 40 45 03 50 35 190 Kérdések: 1. Van-e
LINEÁRIS REGRESSZIÓ (I. MODELL) ÉS KORRELÁCIÓ FELADATOK
 LINEÁRIS REGRESSZIÓ (I. MODELL) ÉS KORRELÁCIÓ FELADATOK 2004 november 29. 1.) Lisztbogarak súlyvesztése 9 lisztbogár-csapat súlyát megmérték, (mindegyik 25 bogárból állt, mert egyenként túl kis súlyúak
LINEÁRIS REGRESSZIÓ (I. MODELL) ÉS KORRELÁCIÓ FELADATOK 2004 november 29. 1.) Lisztbogarak súlyvesztése 9 lisztbogár-csapat súlyát megmérték, (mindegyik 25 bogárból állt, mert egyenként túl kis súlyúak
17. Folyamatszabályozás módszerei
 17. Folyamatszabályozás módszerei 200. Egyéb módszerek A folyamatszabályozás alapjai Minőségképesség-elemzés Mérőeszköz-képességelemzés Ellenőrzőkártyák Bedzsula Bálint 249 215. Mérőeszköz-képességelemzés
17. Folyamatszabályozás módszerei 200. Egyéb módszerek A folyamatszabályozás alapjai Minőségképesség-elemzés Mérőeszköz-képességelemzés Ellenőrzőkártyák Bedzsula Bálint 249 215. Mérőeszköz-képességelemzés
STATISZTIKA. Egymintás u-próba. H 0 : Kefir zsírtartalma 3% Próbafüggvény, alfa=0,05. Egymintás u-próba vagy z-próba
 Egymintás u-próba STATISZTIKA 2. Előadás Középérték-összehasonlító tesztek Tesztelhetjük, hogy a valószínűségi változónk értéke megegyezik-e egy konkrét értékkel. Megválaszthatjuk a konfidencia intervallum
Egymintás u-próba STATISZTIKA 2. Előadás Középérték-összehasonlító tesztek Tesztelhetjük, hogy a valószínűségi változónk értéke megegyezik-e egy konkrét értékkel. Megválaszthatjuk a konfidencia intervallum
Mandátumbecslés A REPUBLIKON INTÉZET ELEMZÉSE
 Mandátumbecslés A REPUBLIKON INTÉZET ELEMZÉSE EREDMÉNYEK A Republikon Intézet legfrissebb mandátumbecslése szerint a Fidesz abszolút többségére lehet számítani a vasárnapi választások után. Becslésünk
Mandátumbecslés A REPUBLIKON INTÉZET ELEMZÉSE EREDMÉNYEK A Republikon Intézet legfrissebb mandátumbecslése szerint a Fidesz abszolút többségére lehet számítani a vasárnapi választások után. Becslésünk
Mintavételi eljárások
 Mintavételi eljárások Daróczi Gergely, PPKE BTK 2008. X.6. Óravázlat A mintavétel célja Alapfogalmak Alapsokaság, mintavételi keret, megfigyelési egység, mintavételi egység... Nem valószínűségi mintavételezési
Mintavételi eljárások Daróczi Gergely, PPKE BTK 2008. X.6. Óravázlat A mintavétel célja Alapfogalmak Alapsokaság, mintavételi keret, megfigyelési egység, mintavételi egység... Nem valószínűségi mintavételezési
Biometria az orvosi gyakorlatban. Korrelációszámítás, regresszió
 SZDT-08 p. 1/31 Biometria az orvosi gyakorlatban Korrelációszámítás, regresszió Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Korrelációszámítás
SZDT-08 p. 1/31 Biometria az orvosi gyakorlatban Korrelációszámítás, regresszió Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Korrelációszámítás
Hipotézis, sejtés STATISZTIKA. Kétmintás hipotézisek. Tudományos hipotézis. Munkahipotézis (H a ) Nullhipotézis (H 0 ) 11. Előadás
 STATISZTIKA Hipotézis, sejtés 11. Előadás Hipotézisvizsgálatok, nem paraméteres próbák Tudományos hipotézis Nullhipotézis felállítása (H 0 ): Kétmintás hipotézisek Munkahipotézis (H a ) Nullhipotézis (H
STATISZTIKA Hipotézis, sejtés 11. Előadás Hipotézisvizsgálatok, nem paraméteres próbák Tudományos hipotézis Nullhipotézis felállítása (H 0 ): Kétmintás hipotézisek Munkahipotézis (H a ) Nullhipotézis (H
S atisztika 2. előadás
 Statisztika 2. előadás 4. lépés Terepmunka vagy adatgyűjtés Kutatási módszerek osztályozása Kutatási módszer Feltáró kutatás Következtető kutatás Leíró kutatás Ok-okozati kutatás Keresztmetszeti kutatás
Statisztika 2. előadás 4. lépés Terepmunka vagy adatgyűjtés Kutatási módszerek osztályozása Kutatási módszer Feltáró kutatás Következtető kutatás Leíró kutatás Ok-okozati kutatás Keresztmetszeti kutatás
MINŐSÉGÜGYI STATISZTIKAI MÓDSZEREK. Dr. Drégelyi-Kiss Ágota ÓE BGK
 MINŐSÉGÜGYI STATISZTIKAI MÓDSZEREK Dr. Drégelyi-Kiss Ágota ÓE BGK e-mail: dregelyi.agota@bgk.uni-obuda.hu 1 STATISZTIKA CÉLJA Sokaság Következtetés bizonytalansága Véletlenszerű és reprezentatív mintavétel
MINŐSÉGÜGYI STATISZTIKAI MÓDSZEREK Dr. Drégelyi-Kiss Ágota ÓE BGK e-mail: dregelyi.agota@bgk.uni-obuda.hu 1 STATISZTIKA CÉLJA Sokaság Következtetés bizonytalansága Véletlenszerű és reprezentatív mintavétel
Minőség-képességi index (Process capability)
 Minőség-képességi index (Process capability) Folyamatképesség 68 12. példa Egy gyártási folyamatban a minőségi jellemző becsült várható értéke µ250.727 egység, a variancia négyzetgyökének becslése σ 1.286
Minőség-képességi index (Process capability) Folyamatképesség 68 12. példa Egy gyártási folyamatban a minőségi jellemző becsült várható értéke µ250.727 egység, a variancia négyzetgyökének becslése σ 1.286
biometria II. foglalkozás előadó: Prof. Dr. Rajkó Róbert Matematikai-statisztikai adatfeldolgozás
 Kísérlettervezés - biometria II. foglalkozás előadó: Prof. Dr. Rajkó Róbert Matematikai-statisztikai adatfeldolgozás A matematikai-statisztika feladata tapasztalati adatok feldolgozásával segítséget nyújtani
Kísérlettervezés - biometria II. foglalkozás előadó: Prof. Dr. Rajkó Róbert Matematikai-statisztikai adatfeldolgozás A matematikai-statisztika feladata tapasztalati adatok feldolgozásával segítséget nyújtani
Statisztika I. 8. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 8. előadás Előadó: Dr. Ertsey Imre Minták alapján történő értékelések A statisztika foglalkozik. a tömegjelenségek vizsgálatával Bizonyos esetekben lehetetlen illetve célszerűtlen a teljes
Statisztika I. 8. előadás Előadó: Dr. Ertsey Imre Minták alapján történő értékelések A statisztika foglalkozik. a tömegjelenségek vizsgálatával Bizonyos esetekben lehetetlen illetve célszerűtlen a teljes
Bevezetés a hipotézisvizsgálatokba
 Bevezetés a hipotézisvizsgálatokba Nullhipotézis: pl. az átlag egy adott µ becslése : M ( x -µ ) = 0 Alternatív hipotézis: : M ( x -µ ) 0 Szignifikancia: - teljes bizonyosság csak teljes enumerációra -
Bevezetés a hipotézisvizsgálatokba Nullhipotézis: pl. az átlag egy adott µ becslése : M ( x -µ ) = 0 Alternatív hipotézis: : M ( x -µ ) 0 Szignifikancia: - teljes bizonyosság csak teljes enumerációra -
Populációbecslések és monitoring
 Populációbecslések és monitoring A becslés szerepe az ökológiában és a vadgazdálkodásban. A becslési módszerek csoportosítása. Teljes számlálás. Statisztikai alapfogalmak. Fontos lehet tudnunk, hogy hány
Populációbecslések és monitoring A becslés szerepe az ökológiában és a vadgazdálkodásban. A becslési módszerek csoportosítása. Teljes számlálás. Statisztikai alapfogalmak. Fontos lehet tudnunk, hogy hány
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
Abszorpciós spektroszkópia
 Tartalomjegyzék Abszorpciós spektroszkópia (Nyitrai Miklós; 2011 február 1.) Dolgozat: május 3. 18:00-20:00. Egész éves anyag. Korábbi dolgozatok nem számítanak bele. Felmentés 80% felett. A fény; Elektromágneses
Tartalomjegyzék Abszorpciós spektroszkópia (Nyitrai Miklós; 2011 február 1.) Dolgozat: május 3. 18:00-20:00. Egész éves anyag. Korábbi dolgozatok nem számítanak bele. Felmentés 80% felett. A fény; Elektromágneses
Kockázatkezelés a rezgésdiagnosztikában többváltozós szabályozó kártya segítségével
 Kockázatkezelés a rezgésdiagnosztikában többváltozós szabályozó kártya segítségével Hazai hallgatói, illetve kutatói személyi támogatást biztosító rendszer kidolgozása és működtetése konvergencia program
Kockázatkezelés a rezgésdiagnosztikában többváltozós szabályozó kártya segítségével Hazai hallgatói, illetve kutatói személyi támogatást biztosító rendszer kidolgozása és működtetése konvergencia program
Matematikai statisztika c. tárgy oktatásának célja és tematikája
 Matematikai statisztika c. tárgy oktatásának célja és tematikája 2015 Tematika Matematikai statisztika 1. Időkeret: 12 héten keresztül heti 3x50 perc (előadás és szeminárium) 2. Szükséges előismeretek:
Matematikai statisztika c. tárgy oktatásának célja és tematikája 2015 Tematika Matematikai statisztika 1. Időkeret: 12 héten keresztül heti 3x50 perc (előadás és szeminárium) 2. Szükséges előismeretek:
Anyagvizsgálati módszerek Mérési adatok feldolgozása. Anyagvizsgálati módszerek
 Anyagvizsgálati módszerek Mérési adatok feldolgozása Anyagvizsgálati módszerek Pannon Egyetem Mérnöki Kar Anyagvizsgálati módszerek Statisztika 1/ 22 Mérési eredmények felhasználása Tulajdonságok hierarchikus
Anyagvizsgálati módszerek Mérési adatok feldolgozása Anyagvizsgálati módszerek Pannon Egyetem Mérnöki Kar Anyagvizsgálati módszerek Statisztika 1/ 22 Mérési eredmények felhasználása Tulajdonságok hierarchikus
Hanthy László Tel.: 06 20 9420052
 Hanthy László Tel.: 06 20 9420052 Néhány probléma a gyártási folyamatok statisztikai szabályzásával kapcsolatban Miben kellene segíteni az SPC alkalmazóit? Hanthy László T: 06(20)9420052 Megválaszolandó
Hanthy László Tel.: 06 20 9420052 Néhány probléma a gyártási folyamatok statisztikai szabályzásával kapcsolatban Miben kellene segíteni az SPC alkalmazóit? Hanthy László T: 06(20)9420052 Megválaszolandó
Nagy számok törvényei Statisztikai mintavétel Várható érték becslése. Dr. Berta Miklós Fizika és Kémia Tanszék Széchenyi István Egyetem
 agy számok törvényei Statisztikai mintavétel Várható érték becslése Dr. Berta Miklós Fizika és Kémia Tanszék Széchenyi István Egyetem A mérés mint statisztikai mintavétel A méréssel az eloszlásfüggvénnyel
agy számok törvényei Statisztikai mintavétel Várható érték becslése Dr. Berta Miklós Fizika és Kémia Tanszék Széchenyi István Egyetem A mérés mint statisztikai mintavétel A méréssel az eloszlásfüggvénnyel
Biomatematika 12. Szent István Egyetem Állatorvos-tudományi Kar. Fodor János
 Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
Mintavétel fogalmai STATISZTIKA, BIOMETRIA. Mintavételi hiba. Statisztikai adatgyűjtés. Nem véletlenen alapuló kiválasztás
 STATISZTIKA, BIOMETRIA. Előadás Mintavétel, mintavételi technikák, adatbázis Mintavétel fogalmai A mintavételt meg kell tervezni A sokaság elemei: X, X X N, lehet véges és végtelen Mintaelemek: x, x x
STATISZTIKA, BIOMETRIA. Előadás Mintavétel, mintavételi technikák, adatbázis Mintavétel fogalmai A mintavételt meg kell tervezni A sokaság elemei: X, X X N, lehet véges és végtelen Mintaelemek: x, x x
Véletlen jelenség: okok rendszere hozza létre - nem ismerhetjük mind, ezért sztochasztikus.
 Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Populációbecslések és monitoring
 Populációbecslések és monitoring A becslés szerepe az ökológiában és a vadgazdálkodásban. A becslési módszerek csoportosítása. Teljes számlálás. Statisztikai alapfogalmak. Fontos lehet tudnunk, hogy hány
Populációbecslések és monitoring A becslés szerepe az ökológiában és a vadgazdálkodásban. A becslési módszerek csoportosítása. Teljes számlálás. Statisztikai alapfogalmak. Fontos lehet tudnunk, hogy hány
1. Adatok kiértékelése. 2. A feltételek megvizsgálása. 3. A hipotézis megfogalmazása
 HIPOTÉZIS VIZSGÁLAT A hipotézis feltételezés egy vagy több populációról. (pl. egy gyógyszer az esetek 90%-ában hatásos; egy kezelés jelentősen megnöveli a rákos betegek túlélését). A hipotézis vizsgálat
HIPOTÉZIS VIZSGÁLAT A hipotézis feltételezés egy vagy több populációról. (pl. egy gyógyszer az esetek 90%-ában hatásos; egy kezelés jelentősen megnöveli a rákos betegek túlélését). A hipotézis vizsgálat
Újrarajzolt választókerületi határok: A magyar választási rendszer földrajzi torzulásai 2011 előtt és után
 Újrarajzolt választókerületi határok: A magyar választási rendszer földrajzi torzulásai 2011 előtt és után Vida György egyetemi tanársegéd Szegedi Tudományegyetem Gazdaság- és Társadalomföldrajz Tanszék
Újrarajzolt választókerületi határok: A magyar választási rendszer földrajzi torzulásai 2011 előtt és után Vida György egyetemi tanársegéd Szegedi Tudományegyetem Gazdaság- és Társadalomföldrajz Tanszék
STATISZTIKA. András hármas. Éva ötös. Nóri négyes. 5 4,5 4 3,5 3 2,5 2 1,5 ANNA BÉLA CILI 0,5 MAGY. MAT. TÖRT. KÉM.
 STATISZTIKA 5 4,5 4 3,5 3 2,5 2 1,5 1 0,5 0 MAGY. MAT. TÖRT. KÉM. ANNA BÉLA CILI András hármas. Béla Az átlag 3,5! kettes. Éva ötös. Nóri négyes. 1 mérés: dolgokhoz valamely szabály alapján szám rendelése
STATISZTIKA 5 4,5 4 3,5 3 2,5 2 1,5 1 0,5 0 MAGY. MAT. TÖRT. KÉM. ANNA BÉLA CILI András hármas. Béla Az átlag 3,5! kettes. Éva ötös. Nóri négyes. 1 mérés: dolgokhoz valamely szabály alapján szám rendelése
Kockázatalapú szabályozó kártyák tervezése, kiválasztása és folyamatra illesztése
 Kockázatalapú szabályozó kártyák tervezése, kiválasztása és folyamatra illesztése Hazai hallgatói, illetve kutatói személyi támogatást biztosító rendszer kidolgozása és működtetése konvergencia program
Kockázatalapú szabályozó kártyák tervezése, kiválasztása és folyamatra illesztése Hazai hallgatói, illetve kutatói személyi támogatást biztosító rendszer kidolgozása és működtetése konvergencia program
BIOMETRIA (H 0 ) 5. Előad. zisvizsgálatok. Hipotézisvizsg. Nullhipotézis
 Hipotézis BIOMETRIA 5. Előad adás Hipotézisvizsg zisvizsgálatok Tudományos hipotézis Nullhipotézis feláll llítása (H ): Kétmintás s hipotézisek Munkahipotézis (H a ) Nullhipotézis (H ) > = 1 Statisztikai
Hipotézis BIOMETRIA 5. Előad adás Hipotézisvizsg zisvizsgálatok Tudományos hipotézis Nullhipotézis feláll llítása (H ): Kétmintás s hipotézisek Munkahipotézis (H a ) Nullhipotézis (H ) > = 1 Statisztikai
Félidei eredmények. közvélemény-kutatás a Heti Válasz megbízásából
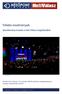 közvélemény-kutatás a Heti Válasz megbízásából Forrás: mti Készült: 2012. február 13-16. között, 1000 fő telefonos megkérdezésével, országos reprezentatív mintán N é z ő p o n t I n t é z e t Z r t., B
közvélemény-kutatás a Heti Válasz megbízásából Forrás: mti Készült: 2012. február 13-16. között, 1000 fő telefonos megkérdezésével, országos reprezentatív mintán N é z ő p o n t I n t é z e t Z r t., B
GVMST22GNC Statisztika II. Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet
 GVMST22GNC Statisztika II. 3. előadás: 8. Hipotézisvizsgálat Kóczy Á. László Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet Hipotézisvizsgálat v becslés Becslés Ismeretlen paraméter Közeĺıtő
GVMST22GNC Statisztika II. 3. előadás: 8. Hipotézisvizsgálat Kóczy Á. László Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet Hipotézisvizsgálat v becslés Becslés Ismeretlen paraméter Közeĺıtő
Statisztika. Politológus képzés. Daróczi Gergely április 17. Politológia Tanszék
 Statisztika Politológus képzés Daróczi Gergely Politológia Tanszék 2012. április 17. Outline 1 Leíró statisztikák 2 Középértékek Példa 3 Szóródási mutatók Példa 4 Néhány megjegyzés a grafikonokról 5 Számítások
Statisztika Politológus képzés Daróczi Gergely Politológia Tanszék 2012. április 17. Outline 1 Leíró statisztikák 2 Középértékek Példa 3 Szóródási mutatók Példa 4 Néhány megjegyzés a grafikonokról 5 Számítások
Kockázatok és mérési bizonytalanság kezelése a termelésmenedzsment területén
 Kockázatok és mérési bizonytalanság kezelése a termelésmenedzsment területén Hazai hallgatói, illetve kutatói személyi támogatást biztosító rendszer kidolgozása és ködtetése konvergencia program Projekt
Kockázatok és mérési bizonytalanság kezelése a termelésmenedzsment területén Hazai hallgatói, illetve kutatói személyi támogatást biztosító rendszer kidolgozása és ködtetése konvergencia program Projekt
Dr. Király István Igazságügyi szakértő Varga Zoltán Igazságügyi szakértő Dr. Marosán Miklós Igazságügyi szakértő
 Dr. Király István Igazságügyi szakértő Varga Zoltán Igazságügyi szakértő Dr. Marosán Miklós Igazságügyi szakértő Mintaterületek kijelölésének javasolt módjai kapás sortávú növényekre Miért is kell mintatér?
Dr. Király István Igazságügyi szakértő Varga Zoltán Igazságügyi szakértő Dr. Marosán Miklós Igazságügyi szakértő Mintaterületek kijelölésének javasolt módjai kapás sortávú növényekre Miért is kell mintatér?
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/47/23623719.jpg) [Biomatematika 2] Orvosi biometria 2016.02.15. Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza) alkotja az eseményteret. Esemény: az eseménytér részhalmazai.
[Biomatematika 2] Orvosi biometria 2016.02.15. Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza) alkotja az eseményteret. Esemény: az eseménytér részhalmazai.
Az antropometria alkalmazásának célja a hatékony, biztonságos és kényelmes tevékenység biztosítása a méretek és elrendezés helyes megválasztásával
 Az antropometria helye TERMÉKFEJLESZTÉS / TERV ERGONÓMIAI FELADATOK ÉS TEVÉKENYSÉGEK ANTROPOMETRIAI ADATOK Az antropometria alkalmazásának célja a hatékony, biztonságos és kényelmes tevékenység biztosítása
Az antropometria helye TERMÉKFEJLESZTÉS / TERV ERGONÓMIAI FELADATOK ÉS TEVÉKENYSÉGEK ANTROPOMETRIAI ADATOK Az antropometria alkalmazásának célja a hatékony, biztonságos és kényelmes tevékenység biztosítása
JÚLIUSI PÁRTPREFERENCIA ADATOK ALAPJÁN
 MANDÁTUMBECSLÉS JÚLIUSI PÁRTPREFERENCIA ADATOK ALAPJÁN A Republikon Intézet által a 2010-es választás előtt készített becslés volt az egyik legpontosabb előrejelzés 1. Noha az új választási törvény számos
MANDÁTUMBECSLÉS JÚLIUSI PÁRTPREFERENCIA ADATOK ALAPJÁN A Republikon Intézet által a 2010-es választás előtt készített becslés volt az egyik legpontosabb előrejelzés 1. Noha az új választási törvény számos
Minőségmenedzsment (módszerek) BEDZSULA BÁLINT
 Minőségmenedzsment (módszerek) BEDZSULA BÁLINT Bedzsula Bálint gyakornok Menedzsment és Vállalatgazdaságtan Tanszék Q. épület A.314. bedzsula@mvt.bme.hu http://doodle.com/bedzsula.mvt Az előző előadás
Minőségmenedzsment (módszerek) BEDZSULA BÁLINT Bedzsula Bálint gyakornok Menedzsment és Vállalatgazdaságtan Tanszék Q. épület A.314. bedzsula@mvt.bme.hu http://doodle.com/bedzsula.mvt Az előző előadás
Matematikai alapok és valószínőségszámítás. Statisztikai becslés Statisztikák eloszlása
 Matematikai alapok és valószínőségszámítás Statisztikai becslés Statisztikák eloszlása Mintavétel A statisztikában a cél, hogy az érdeklõdés tárgyát képezõ populáció bizonyos paramétereit a populációból
Matematikai alapok és valószínőségszámítás Statisztikai becslés Statisztikák eloszlása Mintavétel A statisztikában a cél, hogy az érdeklõdés tárgyát képezõ populáció bizonyos paramétereit a populációból
Hat Szigma Zöldöves Tanfolyam Tematikája
 Hat Szigma Zöldöves Tanfolyam Tematikája Megjegyzések: A tanfolyamon haszáljuk: - Minitab statisztikai (demo) és - Companion by Minitab projektek menedzselésére szolgáló (demo) szoftvert, átadunk: - egy
Hat Szigma Zöldöves Tanfolyam Tematikája Megjegyzések: A tanfolyamon haszáljuk: - Minitab statisztikai (demo) és - Companion by Minitab projektek menedzselésére szolgáló (demo) szoftvert, átadunk: - egy
Biomatematika 2 Orvosi biometria
 Biomatematika 2 Orvosi biometria 2017.02.13. Populáció és minta jellemző adatai Hibaszámítás Valószínűség 1 Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza)
Biomatematika 2 Orvosi biometria 2017.02.13. Populáció és minta jellemző adatai Hibaszámítás Valószínűség 1 Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza)
Kísérlettervezés alapfogalmak
 Kísérlettervezés alapfogalmak Rendszermodellezés Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Kísérlettervezés Cél: a modell paraméterezése a valóság alapján
Kísérlettervezés alapfogalmak Rendszermodellezés Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Kísérlettervezés Cél: a modell paraméterezése a valóság alapján
Elemi statisztika fizikusoknak
 1. oldal Elemi statisztika fizikusoknak Pollner Péter Biológiai Fizika Tanszék pollner@elte.hu Az adatok leírása, megismerése és összehasonlítása 2-1 Áttekintés 2-2 Gyakoriság eloszlások 2-3 Az adatok
1. oldal Elemi statisztika fizikusoknak Pollner Péter Biológiai Fizika Tanszék pollner@elte.hu Az adatok leírása, megismerése és összehasonlítása 2-1 Áttekintés 2-2 Gyakoriság eloszlások 2-3 Az adatok
Több valószínűségi változó együttes eloszlása, korreláció
 Tartalomjegzék Előszó... 6 I. Valószínűségelméleti és matematikai statisztikai alapok... 8 1. A szükséges valószínűségelméleti és matematikai statisztikai alapismeretek összefoglalása... 8 1.1. Alapfogalmak...
Tartalomjegzék Előszó... 6 I. Valószínűségelméleti és matematikai statisztikai alapok... 8 1. A szükséges valószínűségelméleti és matematikai statisztikai alapismeretek összefoglalása... 8 1.1. Alapfogalmak...
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011.
 BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési adatok feldolgozása A mérési eredmény megadása A mérés dokumentálása A vállalati mérőeszközök nyilvántartása 2 A mérés célja: egy
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési adatok feldolgozása A mérési eredmény megadása A mérés dokumentálása A vállalati mérőeszközök nyilvántartása 2 A mérés célja: egy
KÖVETKEZTETŐ STATISZTIKA
 ÁVF GM szak 2010 ősz KÖVETKEZTETŐ STATISZTIKA A MINTAVÉTEL BECSLÉS A sokasági átlag becslése 2010 ősz Utoljára módosítva: 2010-09-07 ÁVF Oktató: Lipécz György 1 A becslés alapfeladata Pl. Hányan láttak
ÁVF GM szak 2010 ősz KÖVETKEZTETŐ STATISZTIKA A MINTAVÉTEL BECSLÉS A sokasági átlag becslése 2010 ősz Utoljára módosítva: 2010-09-07 ÁVF Oktató: Lipécz György 1 A becslés alapfeladata Pl. Hányan láttak
Mangalica specifikus DNS alapú módszer kifejlesztés és validálása a MANGFOOD projekt keretében
 Mangalica specifikus DNS alapú módszer kifejlesztés és validálása a MANGFOOD projekt keretében Szántó-Egész Réka 1, Mohr Anita 1, Sipos Rita 1, Dallmann Klára 1, Ujhelyi Gabriella 2, Koppányné Szabó Erika
Mangalica specifikus DNS alapú módszer kifejlesztés és validálása a MANGFOOD projekt keretében Szántó-Egész Réka 1, Mohr Anita 1, Sipos Rita 1, Dallmann Klára 1, Ujhelyi Gabriella 2, Koppányné Szabó Erika
Gyakorlat 8 1xANOVA. Dr. Nyéki Lajos 2016
 Gyakorlat 8 1xANOVA Dr. Nyéki Lajos 2016 A probléma leírása Azt vizsgáljuk, hogy milyen hatása van a család jövedelmének a tanulók szövegértés teszten elért tanulmányi eredményeire. A minta 59 iskola adatait
Gyakorlat 8 1xANOVA Dr. Nyéki Lajos 2016 A probléma leírása Azt vizsgáljuk, hogy milyen hatása van a család jövedelmének a tanulók szövegértés teszten elért tanulmányi eredményeire. A minta 59 iskola adatait
Kistérségi gazdasági aktivitási adatok
 Kistérségi gazdasági aktivitási adatok 1. A KMSR rendszerben alkalmazott statisztikai módszerek Előadó: Dr. Banai Miklós 2. A KMSR rendszer által szolgáltatott adatok, jelentések Előadó: Kovács Attila
Kistérségi gazdasági aktivitási adatok 1. A KMSR rendszerben alkalmazott statisztikai módszerek Előadó: Dr. Banai Miklós 2. A KMSR rendszer által szolgáltatott adatok, jelentések Előadó: Kovács Attila
Mérés 3 - Ellenörzö mérés - 5. Alakítsunk A-t meg D-t oda-vissza (A/D, D/A átlakító)
 Mérés 3 - Ellenörzö mérés - 5. Alakítsunk A-t meg D-t oda-vissza (A/D, D/A átlakító) 1. A D/A átalakító erısítési hibája és beállása Mérje meg a D/A átalakító erısítési hibáját! A hibát százalékban adja
Mérés 3 - Ellenörzö mérés - 5. Alakítsunk A-t meg D-t oda-vissza (A/D, D/A átlakító) 1. A D/A átalakító erısítési hibája és beállása Mérje meg a D/A átalakító erısítési hibáját! A hibát százalékban adja
Modern műszeres analitika szeminárium Néhány egyszerű statisztikai teszt
 Modern műszeres analitika szeminárium Néhány egyszerű statisztikai teszt Galbács Gábor KIUGRÓ ADATOK KISZŰRÉSE STATISZTIKAI TESZTEKKEL Dixon Q-tesztje Gyakori feladat az analitikai kémiában, hogy kiugrónak
Modern műszeres analitika szeminárium Néhány egyszerű statisztikai teszt Galbács Gábor KIUGRÓ ADATOK KISZŰRÉSE STATISZTIKAI TESZTEKKEL Dixon Q-tesztje Gyakori feladat az analitikai kémiában, hogy kiugrónak
8. A mérıeszközök képességvizsgálata 1
 8. A mérıeszközök képességvizsgálata 1 A vizsgálat célja annak megállapítása, hogy a használt mérıeszköz elég kis hibával használható-e ahhoz, hogy vele a folyamatról információt szerezzünk. Az AIAG (Automotive
8. A mérıeszközök képességvizsgálata 1 A vizsgálat célja annak megállapítása, hogy a használt mérıeszköz elég kis hibával használható-e ahhoz, hogy vele a folyamatról információt szerezzünk. Az AIAG (Automotive
Eloszlás-független módszerek (folytatás) 14. elıadás ( lecke) 27. lecke khí-négyzet eloszlású statisztikák esetszámtáblázatok
 Eloszlás-független módszerek (folytatás) 14. elıadás (7-8. lecke) Illeszkedés-vizsgálat 7. lecke khí-négyzet eloszlású statisztikák esetszámtáblázatok elemzésére Illeszkedés-vizsgálat Gyakorisági sorok
Eloszlás-független módszerek (folytatás) 14. elıadás (7-8. lecke) Illeszkedés-vizsgálat 7. lecke khí-négyzet eloszlású statisztikák esetszámtáblázatok elemzésére Illeszkedés-vizsgálat Gyakorisági sorok
Módszertani Intézeti Tanszéki Osztály. A megoldás részletes mellékszámítások hiányában nem értékelhető!
 BGF KKK Módszertani Intézeti Tanszéki Osztály Budapest, 2012.. Név:... Neptun kód:... Érdemjegy:..... STATISZTIKA II. VIZSGADOLGOZAT Feladatok 1. 2. 3. 4. 5. 6. Összesen Szerezhető pontszám 21 20 7 22
BGF KKK Módszertani Intézeti Tanszéki Osztály Budapest, 2012.. Név:... Neptun kód:... Érdemjegy:..... STATISZTIKA II. VIZSGADOLGOZAT Feladatok 1. 2. 3. 4. 5. 6. Összesen Szerezhető pontszám 21 20 7 22
Energiaaudit szolgáltatások a gyakorlatban. MVM Partner Energiakereskedelmi ZRt. Jakócs Krisztián Termékmenedzser 2012. május 09.
 Energiaaudit szolgáltatások a gyakorlatban MVM Partner Energiakereskedelmi ZRt. Jakócs Krisztián Termékmenedzser 2012. május 09. Az auditról általában Az audit jelentése Az "audit" szó mai jelentése már
Energiaaudit szolgáltatások a gyakorlatban MVM Partner Energiakereskedelmi ZRt. Jakócs Krisztián Termékmenedzser 2012. május 09. Az auditról általában Az audit jelentése Az "audit" szó mai jelentése már
Hat Szigma Testre Szabva (Six Sigma for You 6S4U)
 Hat Szigma Testre Szabva (Six Sigma for You 6S4U) A Six Sigma módszertant az elmúlt 20 évben az igazán nagy vállalatok alkalmazták úgy, hogy minden számba jöhető embert kiképeztek Green Belt-nek. A tapasztalatok
Hat Szigma Testre Szabva (Six Sigma for You 6S4U) A Six Sigma módszertant az elmúlt 20 évben az igazán nagy vállalatok alkalmazták úgy, hogy minden számba jöhető embert kiképeztek Green Belt-nek. A tapasztalatok
Többváltozós lineáris regressziós modell feltételeinek
 Többváltozós lineáris regressziós modell feltételeinek tesztelése I. - A hibatagra vonatkozó feltételek tesztelése - Petrovics Petra Doktorandusz Többváltozós lineáris regressziós modell x 1, x 2,, x p
Többváltozós lineáris regressziós modell feltételeinek tesztelése I. - A hibatagra vonatkozó feltételek tesztelése - Petrovics Petra Doktorandusz Többváltozós lineáris regressziós modell x 1, x 2,, x p
Statisztika. Politológus képzés. Daróczi Gergely április 24. Politológia Tanszék
 Statisztika Politológus képzés Daróczi Gergely Politológia Tanszék 2012. április 24. Outline 1 A mintavételi hiba és konfidencia-intervallum 2 A mintaválasztás A mintaválasztás célja Alapfogalmak A mintaválasztás
Statisztika Politológus képzés Daróczi Gergely Politológia Tanszék 2012. április 24. Outline 1 A mintavételi hiba és konfidencia-intervallum 2 A mintaválasztás A mintaválasztás célja Alapfogalmak A mintaválasztás
Kutatásmódszertan és prezentációkészítés
 Kutatásmódszertan és prezentációkészítés 10. rész: Az adatelemzés alapjai Szerző: Kmetty Zoltán Lektor: Fokasz Nikosz Tizedik rész Az adatelemzés alapjai Tartalomjegyzék Bevezetés Leíró statisztikák I
Kutatásmódszertan és prezentációkészítés 10. rész: Az adatelemzés alapjai Szerző: Kmetty Zoltán Lektor: Fokasz Nikosz Tizedik rész Az adatelemzés alapjai Tartalomjegyzék Bevezetés Leíró statisztikák I
Testméretek, mozgástartományok. Szabó Gyula
 Testméretek, mozgástartományok Szabó Gyula Az antropometria helye TERMÉKFEJLESZTÉS / TERV ERGONÓMIAI FELADATOK ÉS TEVÉKENYSÉGEK ANTROPOMETRIAI ADATOK Az antropometria alkalmazásának célja a hatékony, biztonságos
Testméretek, mozgástartományok Szabó Gyula Az antropometria helye TERMÉKFEJLESZTÉS / TERV ERGONÓMIAI FELADATOK ÉS TEVÉKENYSÉGEK ANTROPOMETRIAI ADATOK Az antropometria alkalmazásának célja a hatékony, biztonságos
Statisztikai következtetések Nemlineáris regresszió Feladatok Vége
 [GVMGS11MNC] Gazdaságstatisztika 10. előadás: 9. Regressziószámítás II. Kóczy Á. László koczy.laszlo@kgk.uni-obuda.hu Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet A standard lineáris modell
[GVMGS11MNC] Gazdaságstatisztika 10. előadás: 9. Regressziószámítás II. Kóczy Á. László koczy.laszlo@kgk.uni-obuda.hu Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet A standard lineáris modell
Kísérlettervezés alapfogalmak
 Kísérlettervezés alapfogalmak Rendszermodellezés Budapest University of Technology and Economics Fault Tolerant Systems Research Group Budapest University of Technology and Economics Department of Measurement
Kísérlettervezés alapfogalmak Rendszermodellezés Budapest University of Technology and Economics Fault Tolerant Systems Research Group Budapest University of Technology and Economics Department of Measurement
A maximum likelihood becslésről
 A maximum likelihood becslésről Definíció Parametrikus becsléssel foglalkozunk. Adott egy modell, mellyel elképzeléseink szerint jól leírható a meghatározni kívánt rendszer. (A modell típusának és rendszámának
A maximum likelihood becslésről Definíció Parametrikus becsléssel foglalkozunk. Adott egy modell, mellyel elképzeléseink szerint jól leírható a meghatározni kívánt rendszer. (A modell típusának és rendszámának
Méréstechnika II. Mérési jegyzőkönyvek FSZ képzésben részt vevők részére. Hosszméréstechnikai és Minőségügyi Labor Mérési jegyzőkönyv
 Méréstechnika II. ek FSZ képzésben részt vevők részére Összeállította: Horváthné Drégelyi-Kiss Ágota Kis Ferenc Lektorálta: Galla Jánosné 009 Tartalomjegyzék. gyakorlat Mérőhasábok, mérési eredmény megadása.
Méréstechnika II. ek FSZ képzésben részt vevők részére Összeállította: Horváthné Drégelyi-Kiss Ágota Kis Ferenc Lektorálta: Galla Jánosné 009 Tartalomjegyzék. gyakorlat Mérőhasábok, mérési eredmény megadása.
A VÁGÁSI KOR, A VÁGÁSI SÚLY ÉS A ROSTÉLYOS KERESZTMETSZET ALAKULÁSA FEHÉR KÉK BELGA ÉS CHAROLAIS KERESZTEZETT HÍZÓBIKÁK ESETÉBEN
 A vágási kor, a vágási súly és a rostélyos keresztmetszet alakulása fehér kék belga és charolais keresztezett hízóbikák esetében 1 () A VÁGÁSI KOR, A VÁGÁSI SÚLY ÉS A ROSTÉLYOS KERESZTMETSZET ALAKULÁSA
A vágási kor, a vágási súly és a rostélyos keresztmetszet alakulása fehér kék belga és charolais keresztezett hízóbikák esetében 1 () A VÁGÁSI KOR, A VÁGÁSI SÚLY ÉS A ROSTÉLYOS KERESZTMETSZET ALAKULÁSA
Varianciaanalízis 4/24/12
 1. Feladat Egy póker kártya keverő gép a kártyákat random módon választja ki. A vizsgálatban 1600 választott kártya színei az alábbi gyakorisággal fordultak elő. Vizsgáljuk meg, hogy a kártyák kiválasztása
1. Feladat Egy póker kártya keverő gép a kártyákat random módon választja ki. A vizsgálatban 1600 választott kártya színei az alábbi gyakorisággal fordultak elő. Vizsgáljuk meg, hogy a kártyák kiválasztása
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/91/106534674.jpg) [Biomatematika 2] Orvosi biometria Bódis Emőke 2016. 04. 25. J J 9 Korrelációanalízis Regresszióanalízis: hogyan változik egy vizsgált változó értéke egy másik változó változásának függvényében. Korrelációs
[Biomatematika 2] Orvosi biometria Bódis Emőke 2016. 04. 25. J J 9 Korrelációanalízis Regresszióanalízis: hogyan változik egy vizsgált változó értéke egy másik változó változásának függvényében. Korrelációs
A társadalomkutatás módszerei I. Outline. A mintavételi hiba és konfidencia-intervallum Elmélet. Szükséges képletek: Tehát:
 A társadalomkutatás módszerei I. 10. hét Daróczi Gergely Budapesti Corvinus Egyetem 2011. november 17. Outline 1 Ismétlés Számítási feladat Egyéb példák 2 A mintavételi hiba dichotóm változók esetében
A társadalomkutatás módszerei I. 10. hét Daróczi Gergely Budapesti Corvinus Egyetem 2011. november 17. Outline 1 Ismétlés Számítási feladat Egyéb példák 2 A mintavételi hiba dichotóm változók esetében
Kontrol kártyák használata a laboratóriumi gyakorlatban
 Kontrol kártyák használata a laboratóriumi gyakorlatban Rikker Tamás tudományos igazgató WESSLING Közhasznú Nonprofit Kft. 2013. január 17. Kis történelem 1920-as években, a Bell Laboratórium telefonjainak
Kontrol kártyák használata a laboratóriumi gyakorlatban Rikker Tamás tudományos igazgató WESSLING Közhasznú Nonprofit Kft. 2013. január 17. Kis történelem 1920-as években, a Bell Laboratórium telefonjainak
Előrehozott parlamenti választások Horvátországban
 Előrehozott parlamenti választások Horvátországban Kolinda Grabar-Kitarović horvát köztársasági elnök 206. szeptember -ére előrehozott parlamenti választásokat írt ki Horvátországban. A Tihomir Orešković
Előrehozott parlamenti választások Horvátországban Kolinda Grabar-Kitarović horvát köztársasági elnök 206. szeptember -ére előrehozott parlamenti választásokat írt ki Horvátországban. A Tihomir Orešković
A PAKSI ATOMERŐMŰ KÖRNYEZETI DÓZISADATAINAK ANALÍZISE
 A PAKSI ATOMERŐMŰ KÖRNYEZETI DÓZISADATAINAK ANALÍZISE Manga László 1, Apáthy István 2, Deme Sándor 2, Hirn Attila 2, Lencsés András 1, Pázmándi Tamás 2 1 MVM Paksi Atomerőmű Zrt. Paks 2 MTA Energiatudományi
A PAKSI ATOMERŐMŰ KÖRNYEZETI DÓZISADATAINAK ANALÍZISE Manga László 1, Apáthy István 2, Deme Sándor 2, Hirn Attila 2, Lencsés András 1, Pázmándi Tamás 2 1 MVM Paksi Atomerőmű Zrt. Paks 2 MTA Energiatudományi
Nyugdíjpénztári rendszerek tapasztalatai Közép-Kelet Európában
 Local knowledge. Global power. Nyugdíjpénztári rendszerek tapasztalatai Közép-Kelet Európában Dr.Kepecs Gábor Hogyan tovább Nyugdíj, Egészségügy, Pénztárkonferencia Budapest 2009. október 14. Local knowledge.
Local knowledge. Global power. Nyugdíjpénztári rendszerek tapasztalatai Közép-Kelet Európában Dr.Kepecs Gábor Hogyan tovább Nyugdíj, Egészségügy, Pénztárkonferencia Budapest 2009. október 14. Local knowledge.
A bergengóc lakosság szemszín szerinti megoszlása a négy tartományban azonos:
 A. Matematikai Statisztika 2.MINTA ZH. 2003 december Név (olvasható) :... A feladatmegoldásnak az alkalmazott matematikai modell valószínűségszámítási ill. statisztikai szóhasználat szerinti megfogalmazását,
A. Matematikai Statisztika 2.MINTA ZH. 2003 december Név (olvasható) :... A feladatmegoldásnak az alkalmazott matematikai modell valószínűségszámítási ill. statisztikai szóhasználat szerinti megfogalmazását,
Kockázatkezelés és biztosítás 1. konzultáció 2. rész
 Kockázatkezelés és biztosítás 1. konzultáció 2. rész Témák 1) A kockázatkezelés eszközei 2) A kockázatkezelés szakmai területei 3) A kockázatelemzés nem holisztikus technikái 4) Kockázatfinanszírozás 5)
Kockázatkezelés és biztosítás 1. konzultáció 2. rész Témák 1) A kockázatkezelés eszközei 2) A kockázatkezelés szakmai területei 3) A kockázatelemzés nem holisztikus technikái 4) Kockázatfinanszírozás 5)
Méréselmélet és mérőrendszerek 2. ELŐADÁS (1. RÉSZ)
 Méréselmélet és mérőrendszerek 2. ELŐADÁS (1. RÉSZ) KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba
Méréselmélet és mérőrendszerek 2. ELŐADÁS (1. RÉSZ) KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba
y ij = µ + α i + e ij
 Elmélet STATISZTIKA 3. Előadás Variancia-analízis Lineáris modellek A magyarázat a függő változó teljes heterogenitásának két részre bontását jelenti. A teljes heterogenitás egyik része az, amelynek okai
Elmélet STATISZTIKA 3. Előadás Variancia-analízis Lineáris modellek A magyarázat a függő változó teljes heterogenitásának két részre bontását jelenti. A teljes heterogenitás egyik része az, amelynek okai
Kettőnél több csoport vizsgálata. Makara B. Gábor
 Kettőnél több csoport vizsgálata Makara B. Gábor Három gyógytápszer elemzéséből az alábbi energia tartalom adatok származtak (kilokalória/adag egységben) Három gyógytápszer elemzésébô A B C 30 5 00 10
Kettőnél több csoport vizsgálata Makara B. Gábor Három gyógytápszer elemzéséből az alábbi energia tartalom adatok származtak (kilokalória/adag egységben) Három gyógytápszer elemzésébô A B C 30 5 00 10
Hipotézis vizsgálatok
 Hipotézis vizsgálatok Hipotézisvizsgálat Hipotézis: az alapsokaság paramétereire vagy az alapsokaság eloszlására vonatkozó feltevés. Hipotézis ellenőrzés: az a statisztikai módszer, amelynek segítségével
Hipotézis vizsgálatok Hipotézisvizsgálat Hipotézis: az alapsokaság paramétereire vagy az alapsokaság eloszlására vonatkozó feltevés. Hipotézis ellenőrzés: az a statisztikai módszer, amelynek segítségével
A mérés. A mérés célja a mérendő mennyiség valódi értékének meghatározása. Ez a valóságban azt jelenti, hogy erre kell
 A mérés A mérés célja a mérendő mennyiség valódi értékének meghatározása. Ez a valóságban azt jelenti, hogy erre kell törekedni, minél közelebb kerülni a mérés során a valós mennyiség megismeréséhez. Mérési
A mérés A mérés célja a mérendő mennyiség valódi értékének meghatározása. Ez a valóságban azt jelenti, hogy erre kell törekedni, minél közelebb kerülni a mérés során a valós mennyiség megismeréséhez. Mérési
Horváth Krisztina Pécsi Tudományegyetem Közgazdaságtudományi Kar Regionális Politika és Gazdaságtan Doktori Iskola, III. évfolyam
 Menedzsment technikák hatása a tudásintenzív és nem tudásintenzív vállalatok produktivitására: magyar kis- és középvállalatok esete Horváth Krisztina Pécsi Tudományegyetem Közgazdaságtudományi Kar Regionális
Menedzsment technikák hatása a tudásintenzív és nem tudásintenzív vállalatok produktivitására: magyar kis- és középvállalatok esete Horváth Krisztina Pécsi Tudományegyetem Közgazdaságtudományi Kar Regionális
