optimalizációs módszerek
|
|
|
- Máté Csonka
- 10 évvel ezelőtt
- Látták:
Átírás
1 optimalizációs módszerek Titkos utazás Réges-régen egy messzi-messzi galaxisban Készítette: Gelencsér Tamás xdthsq
2 1. Bevezetés: Nehéz idők járnak a Lázadókra. Habár a Halálcsillagot elpusztították, a Birodalmi erők kiűzték őket titkos támaszpontjukról és végigüldözték őket a Galaxis-on.A rettegett Birodalmi Csillagflotta elől menekülve a szabadságért küzdők maroknyi csapata, Luke Skywalker vezetésével új, titkos bázist létesített a távoli Hoth jégvilágában. A gonosz Vader nagyúr parancsára, távkutászok ezrei rajzottak ki az űrbe, hogy az ifjú Skywalker nyomára leljenek Menekülés közben, Luke Skywalker egy volt Birodalmi kommandóst (Kyle Katarn) küld a Vjun rendszerbe, Vader nagyúr erődjébe, hogy az ősi jedi holokronok lehetséges lelőhelyéről térképeket és információkat gyűjtsön. A pontosan megtervezett visszaút, nagyban hozzájárul a küldetés sikeréhez 2. Információk az utazásról: A visszaútról a következő ábra áll a rendelkezésre, ahol a piros a birodalmi, a kék a semleges, a zöld pedig a Szövetséges bolygókat jelöli. A nyilak a lehetséges útvonalakat jelölik (fekete-barna között nincs különbség): Továbbá minden bolygóról rendelkezünk egy menetrenddel, ami tartalmazza az utazásidőt és a várakozásidőt is: Honnan Hova: Taris Chazwa Taanab Nar Shaddaa Vjun Honnan Hova: Vortex Carnatos Balmora Manaan Taris N/A Chazwa Taanab N/A Nar Shaddaa N/A 8 9 7
3 Honnan Hova: Galantos Coruscant Corellia Vortex N/A Carnatos Balmora Manaan Honnan Hova: Codian Moon Byss Devaron Tyana Galantos N/A N/A Coruscant N/A Corellia N/A Honnan Hova: Cerea Ghorman Umgul Codian Moon 5 N/A N/A Byss N/A 8 N/A Devaron N/A 10 N/A Tyana N/A 9 12 Honnan Hova Lorta Nkllon Hoth Cerea 8 5 N/A Ghorman 7 5 N/A Umgul N/A N/A 6 Lorta N/A N/A 4 Nkllon N/A N/A 5
4 A rendszer magja felé egyre nagyobb a veszélye a lebukásnak (egyre több az ellenőrző pont), illetve a Birodalmi bolygókon drágábban lehet csak megfelelően biztonságos szállást találni. Ezeket az adatokat az alábbi táblázat foglalja össze: Bolygó neve: Szállás: Ellenőrzőpontok száma: Taris Chazwa Taanab Nar Shaddaa Vortex Carnatos Balmora Manaan Galantos Coruscant Corellia Codian Moon Byss Devaron Tyana Cerea 0 0 Ghorman 0 0 Umgul Lorta Nkllon 0 0 A visszaútra 800 kredit áll rendelkezésre, és az ügynök maximum 15 ellenőrzőponton tud észrevétlenül átjutni. Az indulásig még 3 nap van hátra, így még kaphatunk plusz információkat a Bothán Kémhálózattól, ami megváltoztathatja a visszaút megtervezését.
5 3. A visszaút megtervezése: A csillagtérképet a legegyszerűbb módon egy gráfként tudjuk értelmezni, ahol a bolygók a csúcsok és a lehetséges útvonalak az őket összekötő éleknek felnek meg. Számunkra az utazás a fontos (tehát az élekre koncentrálunk), nem pedig az, hogy melyik bolygókat érintettük, így a bolygókhoz egy sorszámot rendelünk, ezzel leegyszerűsítve a kezelésüket: 1. Vjun 2. Taris 3. Chazwa 4. Taanab 5. Nar Shaddaa 6. Vortex 7. Carnatos 8. Balmora 9. Manaan 10. Galantos 11. Coruscant 12. Corellia 13. Codian Moon 14. Byss 15. Devaron 16. Tyana 17. Cerea 18. Ghorman 19. Umgul 20. Lorta 21. Nkllon 22. Hoth A következő lépésben a fent meghatározott táblázatokból kinyerjük a szükséges információkat és egy mátrixba rendezzük őket (bolygók számozással): Honnan-Hova : út szállás: ellenőrzőpont:
6 Feltételek meghatározása: a.) A legfontosabb feltétel, aminek mindenképpen eleget kell tennünk, hogy utat tervezzünk: tehát, ha egy csúcsba bemegyünk, onnan ki is kell jönnünk. A legegyszerűbb megoldás, ha kezdő ponthoz egy bemenő élt a végponthoz egy kimenő élt rendelünk, így biztos, hogy az algoritmus a két pont között keresi az utat. b.) Továbbá, felső korlátunk van az elkölthető kreditre illetve az ellenőrző pontok maximális számára, amit figyelembe kell vennünk az algoritmus tervezésekor. Ha az előbb említett feltételeknek eleget teszünk, akkor már csak a cél függvényt kell minimalizálni, azaz meg kell keresni a legrövidebb utat. 4. GLPK A feladat megoldását két fájlban oldottam meg (Windows-t használok, így hazi.m.txt illetve hazi.d.txt a kiterjesztés). Hazi.m.txt: param koltseg{(i,j) in HonnanHova}; /*Bolygon tartozkodas koltsege*/ param danger{(i,j) in HonnanHova}; /*Bolygon tartozkodas veszelyessege*/ param start, integer > 0; /*Kezdo bolygo*/ param cel, integer > 0; /*Cel bolygo*/ param penz, integer > 0; /*Rendelkezesre allo kredit*/ param veszely, integer > 0; /*Rejtezkodes*/ var x{(i,j) in HonnanHova}, binary; /*Változó ami az éleket jelöli ki, utaztunk vagy nem*/ s.t. beelkiel{i in 1..Bolygokszama}: sum{(j,i) in HonnanHova} x[j,i] + (if i = start then 1) = sum{(i,j) in HonnanHova} x[i,j] + (if i = cel then 1); /*Azt vizsgaljuk, ha bolygora elmentunk onnan el is kell jonnunk*/ s.t. szallas: sum{(i,j) in HonnanHova} (x[i,j] *koltseg[i,j]) <= penz; /*Szallast kitudjuk-e fizetni*/ s.t. lebukas: sum{(i,j) in HonnanHova} (x[i,j] *danger[i,j]) <= veszely; /*Elkerulheto-e a lebukas*/ minimize utazas: sum{(i,j) in HonnanHova} ut[i,j] * x[i,j];
7 A program megírás közben arra törekedtem, hogy minél kevésbé legyen bedrótozva, ezért amit csak lehetett paraméterként definiáltam: param start, cel, veszely, penz s.t. beelkiel{i in 1..Bolygokszama}: sum{(j,i) in HonnanHova} x[j,i] + (if i = start then 1) = sum{(i,j) in HonnanHova} x[i,j] + (if i = cel then 1); Minden csúcsra ellenőrzi, hogy a belépő élek száma megegyezik-e a kilépő élek számával (esetünkben 1 ki 1 be). s.t. szallas: sum{(i,j) in HonnanHova} (x[i,j] *koltseg[i,j]) <= penz; A kiválasztott élekhez tartozó szállás költség szummája belefér-e a keretbe. s.t. lebukas: sum{(i,j) in HonnanHova} (x[i,j] *danger[i,j]) <= veszely; A kiválasztott élekhez tartozó ellenőrzőpontok száma kisebb-e, mint a megadott összeg. minimize utazas: sum{(i,j) in HonnanHova} ut[i,j] * x[i,j]; A fenti feltételekkel minimalizáljuk a utazás időtartalmát. Az adatokat a Hazi.d.txt fájlba töltöttem fel és futtattam a Hazi.m.txt modellre. A jelenlegi adatokkal a következő megoldást kaptam: , ami azt jelenti, hogy a legrövidebb út: Vjun Nar Shaddaa Balmora Corellia Tyana Ghorman Nkllon Hoth. Idő: 47 nap, Költség: 760 kredit, Ellenőrzőpont: 14. MAY THE Force Be with You!!!
8 Függelék: Hazi.m.txt: param Bolygokszama, integer > 0; /*Grafcsucsai*/ set HonnanHova, within {i in 1..Bolygokszama, j in 1..Bolygokszama}; /*Grafelei*/ param ut{(i,j) in HonnanHova}; /*Grafeleinek a sulya*/ param koltseg{(i,j) in HonnanHova}; /*Bolygon tartozkodas koltsege*/ param danger{(i,j) in HonnanHova}; /*Bolygon tartozkodas veszelyessege*/ param start, integer > 0; /*Kezdo bolygo*/ param cel, integer > 0; /*Cel bolygo*/ param penz, integer > 0; /*Rendelkezesre allo kredit*/ param veszely, integer > 0; /*Rejtezkodes*/ var x{(i,j) in HonnanHova}, binary; /*Változó ami az éleket jelöli ki, utaztunk vagy nem*/ s.t. beelkiel{i in 1..Bolygokszama}: sum{(j,i) in HonnanHova} x[j,i] + (if i = start then 1) = sum{(i,j) in HonnanHova} x[i,j] + (if i = cel then 1); /*Azt vizsgaljuk, ha bolygora elmentunk onnan el is kell jonnunk*/ s.t. szallas: sum{(i,j) in HonnanHova} (x[i,j] *koltseg[i,j]) <= penz; /*Szallast kitudjuk-e fizetni*/ s.t. lebukas: sum{(i,j) in HonnanHova} (x[i,j] *danger[i,j]) <= veszely; /*Elkerulheto-e a lebukas*/ minimize utazas: sum{(i,j) in HonnanHova} ut[i,j] * x[i,j]; /*A fenti feltetelek mellett a legrovidebb utat keressuk*/
9 Data.m.txt: /*Az adott parameterek tarolasara*/ param Bolygokszama:= 22; param start := 1; param cel := 22; param penz := 800; param veszely := 15; param : HonnanHova : ut koltseg danger:= ;
10 Eredmény: Problem: hazi Rows: 25 Columns: 48 (48 integer, 48 binary) Non-zeros: 222 Status: INTEGER OPTIMAL Objective: utazas = 47 (MINimum) No. Row name Activity Lower bound Upper bound beelkiel[1] -1-1 = 2 beelkiel[2] 0-0 = 3 beelkiel[3] 0-0 = 4 beelkiel[4] 0-0 = 5 beelkiel[5] 0-0 = 6 beelkiel[6] 0-0 = 7 beelkiel[7] 0-0 = 8 beelkiel[8] 0-0 = 9 beelkiel[9] 0-0 = 10 beelkiel[10] 0-0 = 11 beelkiel[11] 0-0 = 12 beelkiel[12] 0-0 = 13 beelkiel[13] 0-0 = 14 beelkiel[14] 0-0 = 15 beelkiel[15] 0-0 = 16 beelkiel[16] 0-0 = 17 beelkiel[17] 0-0 = 18 beelkiel[18] 0-0 = 19 beelkiel[19] 0-0 = 20 beelkiel[20] 0-0 = 21 beelkiel[21] 0-0 = 22 beelkiel[22] 1 1 = 23 szallas lebukas utazas 47 No. Column name Activity Lower bound Upper bound x[1,2] * x[1,3] * x[1,4] * x[1,5] * x[2,6] * x[2,7] * x[2,8] * x[3,6] * x[3,7] * x[3,8] * x[3,9] * x[4,7] * x[4,8] * x[4,9] * 0 0 1
11 15 x[5,7] * x[5,8] * x[5,9] * x[6,10] * x[6,11] * x[7,10] * x[7,11] * x[7,12] * x[8,10] * x[8,11] * x[8,12] * x[9,10] * x[9,11] * x[9,12] * x[10,13] * x[10,14] * x[11,14] * x[11,15] * x[11,16] * x[12,14] * x[12,15] * x[12,16] * x[13,17] * x[14,18] * x[15,18] * x[16,18] * x[16,19] * x[17,20] * x[17,21] * x[18,20] * x[18,21] * x[19,22] * x[20,22] * x[21,22] * Integer feasibility conditions: KKT.PE: max.abs.err = 0.00e+000 on row 0 max.rel.err = 0.00e+000 on row 0 High quality KKT.PB: max.abs.err = 0.00e+000 on row 0 max.rel.err = 0.00e+000 on row 0 High quality End of output
Gyártórendszerek modellezése: MILP modell PNS feladatokhoz
 Gyártórendszerek modellezése MILP modell PNS feladatokhoz 1 Pannon Egyetem M szaki Informatikai Kar Számítástudomány Alkalmazása Tanszék Utolsó frissítés: 2008. november 16. 1 hegyhati@dcs.uni-pannon.hu
Gyártórendszerek modellezése MILP modell PNS feladatokhoz 1 Pannon Egyetem M szaki Informatikai Kar Számítástudomány Alkalmazása Tanszék Utolsó frissítés: 2008. november 16. 1 hegyhati@dcs.uni-pannon.hu
Egyszerű példaprogramok gyakorláshoz
 Egyszerű példaprogramok gyakorláshoz Tartalom Feladatok... 2 For ciklus... 2 Szorzótábla... 2 Szorzótábla részlet... 3 Pascal háromszög... 4 Pascal háromszög szebben... 5 DO-LOOP ciklus... 6 Véletlen sorsolás...
Egyszerű példaprogramok gyakorláshoz Tartalom Feladatok... 2 For ciklus... 2 Szorzótábla... 2 Szorzótábla részlet... 3 Pascal háromszög... 4 Pascal háromszög szebben... 5 DO-LOOP ciklus... 6 Véletlen sorsolás...
angolul: greedy algorithms, románul: algoritmi greedy
 Mohó algoritmusok angolul: greedy algorithms, románul: algoritmi greedy 1. feladat. Gazdaságos telefonhálózat építése Bizonyos városok között lehet direkt telefonkapcsolatot kiépíteni, pl. x és y város
Mohó algoritmusok angolul: greedy algorithms, románul: algoritmi greedy 1. feladat. Gazdaságos telefonhálózat építése Bizonyos városok között lehet direkt telefonkapcsolatot kiépíteni, pl. x és y város
11. Előadás. 11. előadás Bevezetés a lineáris programozásba
 11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
Informatikai tehetséggondozás:
 Ég és Föld vonzásában a természet titkai Informatikai tehetséggondozás: Visszalépéses maximumkiválasztás TÁMOP-4.2.3.-12/1/KONV 1. Munkásfelvétel: N állás N jelentkező Egy vállalkozás N különböző állásra
Ég és Föld vonzásában a természet titkai Informatikai tehetséggondozás: Visszalépéses maximumkiválasztás TÁMOP-4.2.3.-12/1/KONV 1. Munkásfelvétel: N állás N jelentkező Egy vállalkozás N különböző állásra
Algoritmusok bonyolultsága
 Algoritmusok bonyolultsága 5. előadás http://www.ms.sapientia.ro/~kasa/komplex.htm 1 / 27 Gazdaságos faváz Kruskal-algoritmus Joseph Kruskal (1928 2010) Legyen V = {v 1, v 2,..., v n }, E = {e 1, e 2,...,
Algoritmusok bonyolultsága 5. előadás http://www.ms.sapientia.ro/~kasa/komplex.htm 1 / 27 Gazdaságos faváz Kruskal-algoritmus Joseph Kruskal (1928 2010) Legyen V = {v 1, v 2,..., v n }, E = {e 1, e 2,...,
Gráfelméleti feladatok. c f
 Gráfelméleti feladatok d e c f a b gráf, csúcsok, élek séta: a, b, c, d, e, c, a, b, f vonal: c, d, e, c, b, a út: f, b, a, e, d (walk, lanţ) (trail, lanţ simplu) (path, lanţ elementar) 1 irányított gráf,
Gráfelméleti feladatok d e c f a b gráf, csúcsok, élek séta: a, b, c, d, e, c, a, b, f vonal: c, d, e, c, b, a út: f, b, a, e, d (walk, lanţ) (trail, lanţ simplu) (path, lanţ elementar) 1 irányított gráf,
Algoritmuselmélet. Legrövidebb utak, Bellmann-Ford, Dijkstra. Katona Gyula Y.
 Algoritmuselmélet Legrövidebb utak, Bellmann-Ford, Dijkstra Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem 3. előadás Katona Gyula Y. (BME
Algoritmuselmélet Legrövidebb utak, Bellmann-Ford, Dijkstra Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem 3. előadás Katona Gyula Y. (BME
Tömbök kezelése. Példa: Vonalkód ellenőrzőjegyének kiszámítása
 Tömbök kezelése Példa: Vonalkód ellenőrzőjegyének kiszámítása A számokkal jellemzett adatok, pl. személyi szám, adószám, taj-szám, vonalkód, bankszámlaszám esetében az elírásból származó hibát ún. ellenőrző
Tömbök kezelése Példa: Vonalkód ellenőrzőjegyének kiszámítása A számokkal jellemzett adatok, pl. személyi szám, adószám, taj-szám, vonalkód, bankszámlaszám esetében az elírásból származó hibát ún. ellenőrző
Bryan Geltfly. A Fekete Lovag. Lélekpárbaj
 Bryan Geltfly A Fekete Lovag Lélekpárbaj Réges-régen, egy messzi, messzi galaxisban Bevezetés Alig fél év telt el azóta, hogy a Szövetségesek elpusztították a rettegett második Halálcsillagot, s ezzel
Bryan Geltfly A Fekete Lovag Lélekpárbaj Réges-régen, egy messzi, messzi galaxisban Bevezetés Alig fél év telt el azóta, hogy a Szövetségesek elpusztították a rettegett második Halálcsillagot, s ezzel
KIEGÉSZÍTŽ FELADATOK. Készlet Bud. Kap. Pápa Sopr. Veszp. Kecsk. 310 4 6 8 10 5 Pécs 260 6 4 5 6 3 Szomb. 280 9 5 4 3 5 Igény 220 200 80 180 160
 KIEGÉSZÍTŽ FELADATOK (Szállítási probléma) Árut kell elszállítani három telephelyr l (Kecskemét, Pécs, Szombathely) öt területi raktárba, melyek Budapesten, Kaposváron, Pápán, Sopronban és Veszprémben
KIEGÉSZÍTŽ FELADATOK (Szállítási probléma) Árut kell elszállítani három telephelyr l (Kecskemét, Pécs, Szombathely) öt területi raktárba, melyek Budapesten, Kaposváron, Pápán, Sopronban és Veszprémben
Előfeltétel: legalább elégséges jegy Diszkrét matematika II. (GEMAK122B) tárgyból
 ÜTEMTERV Programozás-elmélet c. tárgyhoz (GEMAK233B, GEMAK233-B) BSc gazdaságinformatikus, programtervező informatikus alapszakok számára Óraszám: heti 2+0, (aláírás+kollokvium, 3 kredit) 2019/20-es tanév
ÜTEMTERV Programozás-elmélet c. tárgyhoz (GEMAK233B, GEMAK233-B) BSc gazdaságinformatikus, programtervező informatikus alapszakok számára Óraszám: heti 2+0, (aláírás+kollokvium, 3 kredit) 2019/20-es tanév
Gazdasági informatika gyakorlat
 Gazdasági informatika gyakorlat P-Gráfokról röviden Mester Abigél P-Gráf: A P-Gráfok olyan speciális páros gráfok, ahol a csúcsok két halmazba oszthatók: ezek az anyag jellegű csúcsok, valamint a gépek.
Gazdasági informatika gyakorlat P-Gráfokról röviden Mester Abigél P-Gráf: A P-Gráfok olyan speciális páros gráfok, ahol a csúcsok két halmazba oszthatók: ezek az anyag jellegű csúcsok, valamint a gépek.
Gráfok 2. Legrövidebb utak, feszítőfák. Szoftvertervezés és -fejlesztés II. előadás. Szénási Sándor
 Gráfok 2. Legrövidebb utak, feszítőfák előadás http://nik.uni-obuda.hu/sztf2 Szénási Sándor Óbudai Egyetem,Neumann János Informatikai Kar Legrövidebb utak keresése Minimális feszítőfa keresése Gráfok 2
Gráfok 2. Legrövidebb utak, feszítőfák előadás http://nik.uni-obuda.hu/sztf2 Szénási Sándor Óbudai Egyetem,Neumann János Informatikai Kar Legrövidebb utak keresése Minimális feszítőfa keresése Gráfok 2
Statisztikai szoftverek esszé
 Statisztikai szoftverek esszé Csillag Renáta 2011. Helyzetfelmérés Egy internetszolgáltató egy havi adatforgalmát vizsgáltam. A táblázatok az előfizetők letöltési forgalmát tartalmazzák, napi bontásban,
Statisztikai szoftverek esszé Csillag Renáta 2011. Helyzetfelmérés Egy internetszolgáltató egy havi adatforgalmát vizsgáltam. A táblázatok az előfizetők letöltési forgalmát tartalmazzák, napi bontásban,
Útkeresési eljárás a városi közforgalmú közlekedés szimulációjához
 a városi közforgalmú közlekedés szimulációjához Prileszky István prile@sze.hu Pusztai Pál pusztai@sze.hu Bemenő és eredmény adatok Hálózat és menetrend Utazási igények Útkeresési paraméterek Útkeresés
a városi közforgalmú közlekedés szimulációjához Prileszky István prile@sze.hu Pusztai Pál pusztai@sze.hu Bemenő és eredmény adatok Hálózat és menetrend Utazási igények Útkeresési paraméterek Útkeresés
Visszalépéses maximumkiválasztás
 Belépő a tudás közösségébe Informatika szakköri segédanyag Visszalépéses maximumkiválasztás Heizlerné Bakonyi Viktória, Horváth Győző, Menyhárt László, Szlávi Péter, Törley Gábor, Zsakó László Szerkesztő:
Belépő a tudás közösségébe Informatika szakköri segédanyag Visszalépéses maximumkiválasztás Heizlerné Bakonyi Viktória, Horváth Győző, Menyhárt László, Szlávi Péter, Törley Gábor, Zsakó László Szerkesztő:
4. Fejezet : Az egész számok (integer) ábrázolása
 4. Fejezet : Az egész számok (integer) ábrázolása The Architecture of Computer Hardware and Systems Software: An InformationTechnology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson
4. Fejezet : Az egész számok (integer) ábrázolása The Architecture of Computer Hardware and Systems Software: An InformationTechnology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson
DÖNTÉSELMÉLETTEL KAPCSOLATOS FELADATOK
 1.Feladat DÖNTÉSELMÉLETTEL KAPCSOLATOS FELADATOK Egy vállalat egy gázmező kitermelését fontolgatja. A feltárás 10 millió dollárba kerülne,ami tiszta veszteség, ha a feltárás eredménytelen és nem találnak
1.Feladat DÖNTÉSELMÉLETTEL KAPCSOLATOS FELADATOK Egy vállalat egy gázmező kitermelését fontolgatja. A feltárás 10 millió dollárba kerülne,ami tiszta veszteség, ha a feltárás eredménytelen és nem találnak
Algoritmuselmélet. Gráfok megadása, szélességi bejárás, összefüggőség, párosítás. Katona Gyula Y.
 Algoritmuselmélet Gráfok megadása, szélességi bejárás, összefüggőség, párosítás Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem 2. előadás
Algoritmuselmélet Gráfok megadása, szélességi bejárás, összefüggőség, párosítás Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem 2. előadás
ORSZÁGOS KÉKTÚRA APP ANDROIDRA
 ORSZÁGOS KÉKTÚRA APP ANDROIDRA A kéktúra egy szépen kidolgozott és összeszedett útvonal. Az utóbbi időben az Magyar Természetjáró Szövetség komoly energiát fektetett az útvonal fejlesztésébe és reklámozásába.
ORSZÁGOS KÉKTÚRA APP ANDROIDRA A kéktúra egy szépen kidolgozott és összeszedett útvonal. Az utóbbi időben az Magyar Természetjáró Szövetség komoly energiát fektetett az útvonal fejlesztésébe és reklámozásába.
Algoritmuselmélet 7. előadás
 Algoritmuselmélet 7. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu 2002 Március 11. ALGORITMUSELMÉLET 7. ELŐADÁS 1 Múltkori
Algoritmuselmélet 7. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu 2002 Március 11. ALGORITMUSELMÉLET 7. ELŐADÁS 1 Múltkori
Mátrixok és lineáris egyenletrendszerek
 Mátrixok és lineáris egyenletrendszerek A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Mátrixok megadása octave:##> A=[5 7 9-1 3-2] A = 5 7 9-1 3-2 Javasolt kiírni a,-t és ;-t octave:##>
Mátrixok és lineáris egyenletrendszerek A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Mátrixok megadása octave:##> A=[5 7 9-1 3-2] A = 5 7 9-1 3-2 Javasolt kiírni a,-t és ;-t octave:##>
Szimulációs technikák
 SZÉCHENYI ISTVÁN EGYETEM Műszaki Tudományi Kar Informatikai tanszék Szimulációs technikák ( NGB_IN040_1) 2. csapat Comparator - Dokumentáció Mérnök informatikus BSc szak, nappali tagozat 2012/2013 II.
SZÉCHENYI ISTVÁN EGYETEM Műszaki Tudományi Kar Informatikai tanszék Szimulációs technikák ( NGB_IN040_1) 2. csapat Comparator - Dokumentáció Mérnök informatikus BSc szak, nappali tagozat 2012/2013 II.
Gráfelméleti alapfogalmak
 1 Gráfelméleti alapfogalmak Gráf (angol graph= rajz): pontokból és vonalakból álló alakzat. pontok a gráf csúcsai, a vonalak a gráf élei. GRÁ Irányítatlan gráf Vegyes gráf Irányított gráf G H Izolált pont
1 Gráfelméleti alapfogalmak Gráf (angol graph= rajz): pontokból és vonalakból álló alakzat. pontok a gráf csúcsai, a vonalak a gráf élei. GRÁ Irányítatlan gráf Vegyes gráf Irányított gráf G H Izolált pont
Optimumkeresés számítógépen
 C Optimumkeresés számítógépen Az optimumok megtalálása mind a gazdasági életben, mind az élet sok más területén nagy jelentőségű. A matematikában számos módszert dolgoztak ki erre a célra, például a függvények
C Optimumkeresés számítógépen Az optimumok megtalálása mind a gazdasági életben, mind az élet sok más területén nagy jelentőségű. A matematikában számos módszert dolgoztak ki erre a célra, például a függvények
Intelligens Rendszerek Elmélete IRE 4/32/1
 Intelligens Rendszerek Elmélete 4 IRE 4/32/1 Problémamegoldás kereséssel http://nik.uni-obuda.hu/mobil IRE 4/32/2 Egyszerű lények intelligenciája? http://www.youtube.com/watch?v=tlo2n3ymcxw&nr=1 IRE 4/32/3
Intelligens Rendszerek Elmélete 4 IRE 4/32/1 Problémamegoldás kereséssel http://nik.uni-obuda.hu/mobil IRE 4/32/2 Egyszerű lények intelligenciája? http://www.youtube.com/watch?v=tlo2n3ymcxw&nr=1 IRE 4/32/3
Feladatsor 2012/13 2. félév a Programozási alapismeretek tárgyhoz
 Feladatsor 2012/13 2. félév a Programozási alapismeretek tárgyhoz 1. feladat: b) Van-e K másodpercnél hosszabb szám a listán? c) Melyik a leghosszabb dal? d) Melyik előadónak van a legtöbb száma a listán
Feladatsor 2012/13 2. félév a Programozási alapismeretek tárgyhoz 1. feladat: b) Van-e K másodpercnél hosszabb szám a listán? c) Melyik a leghosszabb dal? d) Melyik előadónak van a legtöbb száma a listán
Searching in an Unsorted Database
 Searching in an Unsorted Database "Man - a being in search of meaning." Plato History of data base searching v1 2018.04.20. 2 History of data base searching v2 2018.04.20. 3 History of data base searching
Searching in an Unsorted Database "Man - a being in search of meaning." Plato History of data base searching v1 2018.04.20. 2 History of data base searching v2 2018.04.20. 3 History of data base searching
JEGYZŐKÖNYV. Az ülés határozatképes, az elnökség a napirenden szereplő témákat tárgyalta meg. 1. napirend: Állandó napirendek
 Kékes Turista Egyesület Gyöngyös, Török Ignác út 1. JEGYZŐKÖNYV Készült a KTE elnökségi üléséről, 2014. január 22. az egyesület hivatalos helyiségében. Jelen vannak: Simon Péter elnök, Rajki Sándorné alelnök,
Kékes Turista Egyesület Gyöngyös, Török Ignác út 1. JEGYZŐKÖNYV Készült a KTE elnökségi üléséről, 2014. január 22. az egyesület hivatalos helyiségében. Jelen vannak: Simon Péter elnök, Rajki Sándorné alelnök,
Operációkutatás. Vaik Zsuzsanna. Budapest október 10. First Prev Next Last Go Back Full Screen Close Quit
 Operációkutatás Vaik Zsuzsanna Vaik.Zsuzsanna@ymmfk.szie.hu Budapest 200. október 10. Mit tanulunk ma? Szállítási feladat Megoldása Adott: Egy árucikk, T 1, T 2, T,..., T m termelőhely, melyekben rendre
Operációkutatás Vaik Zsuzsanna Vaik.Zsuzsanna@ymmfk.szie.hu Budapest 200. október 10. Mit tanulunk ma? Szállítási feladat Megoldása Adott: Egy árucikk, T 1, T 2, T,..., T m termelőhely, melyekben rendre
Hasonlósági keresés molekulagráfokon: legnagyobb közös részgráf keresése
 Hasonlósági keresés molekulagráfokon: legnagyobb közös részgráf keresése Kovács Péter ChemAxon Kft., ELTE IK kpeter@inf.elte.hu Budapest, 2018.11.06. Bevezetés Feladat: két molekulagráf legnagyobb közös
Hasonlósági keresés molekulagráfokon: legnagyobb közös részgráf keresése Kovács Péter ChemAxon Kft., ELTE IK kpeter@inf.elte.hu Budapest, 2018.11.06. Bevezetés Feladat: két molekulagráf legnagyobb közös
A lineáris programozás alapfeladata Standard alak Az LP feladat megoldása Az LP megoldása: a szimplex algoritmus 2018/
 Operációkutatás I. 2018/2019-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
Operációkutatás I. 2018/2019-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
IV. Betét kamatok lakosság részére
 IV. Betét kamatok lakosság részére Forint betétek Kamatozó betét Látra szóló 1 évre lekötött 4,50 % 4,50 Takarékszelvény 3 hónapos lekötésű 1-30 nap 1,00 % 31-60 nap 5,00 % 61-90 nap 9,00 % 5,02 ZENGŐ
IV. Betét kamatok lakosság részére Forint betétek Kamatozó betét Látra szóló 1 évre lekötött 4,50 % 4,50 Takarékszelvény 3 hónapos lekötésű 1-30 nap 1,00 % 31-60 nap 5,00 % 61-90 nap 9,00 % 5,02 ZENGŐ
A lineáris programozás alapfeladata Standard alak Az LP feladat megoldása Az LP megoldása: a szimplex algoritmus 2017/
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
2. Milyen értéket határoz meg az alábbi algoritmus, ha A egy vektor?. (2 pont)
 A Név: l 2017.04.06 Neptun kód: Gyakorlat vezet : HG BP l 1. Az A vektor tartalmát az alábbi KUPACOL eljárással rendezzük át maximum kupaccá. A={28, 87, 96, 65, 55, 32, 51, 69} Mi lesz az értéke az A vektor
A Név: l 2017.04.06 Neptun kód: Gyakorlat vezet : HG BP l 1. Az A vektor tartalmát az alábbi KUPACOL eljárással rendezzük át maximum kupaccá. A={28, 87, 96, 65, 55, 32, 51, 69} Mi lesz az értéke az A vektor
Gráfok, definíciók. Gráfok ábrázolása. Az adott probléma megoldásához ténylegesen mely műveletek szükségesek. Ábrázolások. Példa:
 Gráfok, definíciók Irányítatlan gráf: G = (V,E), ahol E rendezetlen (a,b),a,b V párok halmaza. Irányított gráf: G = (V,E) E rendezett (a,b) párok halmaza; E V V. Címkézett (súlyozott) gráf: G = (V,E,C)
Gráfok, definíciók Irányítatlan gráf: G = (V,E), ahol E rendezetlen (a,b),a,b V párok halmaza. Irányított gráf: G = (V,E) E rendezett (a,b) párok halmaza; E V V. Címkézett (súlyozott) gráf: G = (V,E,C)
Algoritmusok. Hogyan csináljam?
 Algoritmusok Hogyan csináljam? 1 Az algoritmus fogalma Algoritmusnak olyan pontos előírást nevezünk, amely megmondja, hogy bizonyos feladat megoldásakor milyen műveleteket milyen meghatározott sorrendben
Algoritmusok Hogyan csináljam? 1 Az algoritmus fogalma Algoritmusnak olyan pontos előírást nevezünk, amely megmondja, hogy bizonyos feladat megoldásakor milyen műveleteket milyen meghatározott sorrendben
Alapfogalmak II. Def.: Egy gráf összefüggő, ha bármely pontjából bármely pontjába eljuthatunk egy úton.
 lapfogalmak II Nézzük meg mégegyszer a königsbergi séták problémáját! város lakói vasárnaponként szerettek sétálni a szigeteken. Felvetődött a kérdés, hogy hogyan lehetne olyan sétát tenni a városban,
lapfogalmak II Nézzük meg mégegyszer a königsbergi séták problémáját! város lakói vasárnaponként szerettek sétálni a szigeteken. Felvetődött a kérdés, hogy hogyan lehetne olyan sétát tenni a városban,
Programozási segédlet
 Programozási segédlet Programozási tételek Az alábbiakban leírtam néhány alap algoritmust, amit ismernie kell annak, aki programozásra adja a fejét. A lista korántsem teljes, ám ennyi elég kell legyen
Programozási segédlet Programozási tételek Az alábbiakban leírtam néhány alap algoritmust, amit ismernie kell annak, aki programozásra adja a fejét. A lista korántsem teljes, ám ennyi elég kell legyen
értékel függvény: rátermettségi függvény (tness function)
 Genetikus algoritmusok globális optimalizálás sok lehetséges megoldás közül keressük a legjobbat értékel függvény: rátermettségi függvény (tness function) populáció kiválasztjuk a legrátermettebb egyedeket
Genetikus algoritmusok globális optimalizálás sok lehetséges megoldás közül keressük a legjobbat értékel függvény: rátermettségi függvény (tness function) populáció kiválasztjuk a legrátermettebb egyedeket
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások. alapfüggvény (ábrán: fekete)
 Megoldások 1. Ábrázold és jellemezd a következő függvényeket! a) f (x) = sin (x π ) + 1 b) f (x) = 3 cos (x) c) f (x) = ctg ( 1 x) 1 a) A kérdéses függvényhez a következő lépésekben juthatunk el: g (x)
Megoldások 1. Ábrázold és jellemezd a következő függvényeket! a) f (x) = sin (x π ) + 1 b) f (x) = 3 cos (x) c) f (x) = ctg ( 1 x) 1 a) A kérdéses függvényhez a következő lépésekben juthatunk el: g (x)
Beszélni akarok a huttal. Szóljon neki!
 Beszélni akarok a huttal. Szóljon neki! * * Hutt nyelvből fordítva. ugh.
Beszélni akarok a huttal. Szóljon neki! * * Hutt nyelvből fordítva. ugh.
Adatbányászati szemelvények MapReduce környezetben
 Adatbányászati szemelvények MapReduce környezetben Salánki Ágnes salanki@mit.bme.hu 2014.11.10. Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Felügyelt
Adatbányászati szemelvények MapReduce környezetben Salánki Ágnes salanki@mit.bme.hu 2014.11.10. Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Felügyelt
EDInet Connector telepítési segédlet
 EDInet Connector telepítési segédlet A cégünk által küldött e-mail-ben található linkre kattintva, a következő weboldal jelenik meg a böngészőben: Az EdinetConnectorInstall szövegre klikkelve(a képen pirossal
EDInet Connector telepítési segédlet A cégünk által küldött e-mail-ben található linkre kattintva, a következő weboldal jelenik meg a böngészőben: Az EdinetConnectorInstall szövegre klikkelve(a képen pirossal
A Markowitz modell: kvadratikus programozás
 A Markowitz modell: kvadratikus programozás Losonczi László Debreceni Egyetem, Közgazdaság- és Gazdaságtudományi Kar Debrecen, 2011/12 tanév, II. félév Losonczi László (DE) A Markowitz modell 2011/12 tanév,
A Markowitz modell: kvadratikus programozás Losonczi László Debreceni Egyetem, Közgazdaság- és Gazdaságtudományi Kar Debrecen, 2011/12 tanév, II. félév Losonczi László (DE) A Markowitz modell 2011/12 tanév,
Simonovits M. Elekes Gyuri és az illeszkedések p. 1
 Elekes Gyuri és az illeszkedések Simonovits M. Elekes Gyuri és az illeszkedések p. 1 On the number of high multiplicity points for 1-parameter families of curves György Elekes, Miklós Simonovits and Endre
Elekes Gyuri és az illeszkedések Simonovits M. Elekes Gyuri és az illeszkedések p. 1 On the number of high multiplicity points for 1-parameter families of curves György Elekes, Miklós Simonovits and Endre
BASH script programozás II. Vezérlési szerkezetek
 06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
Keresési algoritmusok, optimalizáció
 Keresési algoritmusok, optimalizáció Az eddig tanultakból a mostani részben gyakran használt (emiatt szükséges az ismeretük) programozási ismeretek: függvények létrehozása, meghívása (ld. 3. óra anyagában)
Keresési algoritmusok, optimalizáció Az eddig tanultakból a mostani részben gyakran használt (emiatt szükséges az ismeretük) programozási ismeretek: függvények létrehozása, meghívása (ld. 3. óra anyagában)
Diszkrét matematika 2. estis képzés
 Diszkrét matematika 2. estis képzés 2018. tavasz 1. Diszkrét matematika 2. estis képzés 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 2. estis képzés 2018. tavasz 1. Diszkrét matematika 2. estis képzés 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Felvételi vizsga mintatételsor Informatika írásbeli vizsga
 BABEȘ BOLYAI TUDOMÁNYEGYETEM MATEMATIKA ÉS INFORMATIKA KAR A. tételsor (30 pont) Felvételi vizsga mintatételsor Informatika írásbeli vizsga 1. (5p) Egy x biten tárolt egész adattípus (x szigorúan pozitív
BABEȘ BOLYAI TUDOMÁNYEGYETEM MATEMATIKA ÉS INFORMATIKA KAR A. tételsor (30 pont) Felvételi vizsga mintatételsor Informatika írásbeli vizsga 1. (5p) Egy x biten tárolt egész adattípus (x szigorúan pozitív
Összetett programozási tételek Rendezések Keresések PT egymásra építése. 10. előadás. Programozás-elmélet. Programozás-elmélet 10.
 Összetett programozási tételek Sorozathoz sorozatot relő feladatokkal foglalkozunk. A bemenő sorozatot le kell másolni, s közben az elemekre vonatkozó átalakításokat lehet végezni rajta: Input : n N 0,
Összetett programozási tételek Sorozathoz sorozatot relő feladatokkal foglalkozunk. A bemenő sorozatot le kell másolni, s közben az elemekre vonatkozó átalakításokat lehet végezni rajta: Input : n N 0,
Mesterséges Intelligencia MI
 Mesterséges Intelligencia MI Problémamegoldás kereséssel - csak lokális információra alapozva Pataki Béla BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Lokálisan
Mesterséges Intelligencia MI Problémamegoldás kereséssel - csak lokális információra alapozva Pataki Béla BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Lokálisan
Programozási módszertan. Mohó algoritmusok
 PM-08 p. 1/17 Programozási módszertan Mohó algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu PM-08 p. 2/17 Bevezetés Dinamikus programozás
PM-08 p. 1/17 Programozási módszertan Mohó algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu PM-08 p. 2/17 Bevezetés Dinamikus programozás
COBRA MUNKAÜGY ÉS BÉR PROGRAMCSOMAG 2013. ÉVI
 COBRA MUNKAÜGY ÉS BÉR PROGRAMCSOMAG 2013. ÉVI VERZIÓINAK VÁLTOZÁSAI. Tartalomjegyzék: Tartalom MUN v13.0101... 2 MUN v13.0107... 10 MUN v13.0128... 18 MUN v13.0204... 21 MUN v13.0208... 27 MUN v13.0304...
COBRA MUNKAÜGY ÉS BÉR PROGRAMCSOMAG 2013. ÉVI VERZIÓINAK VÁLTOZÁSAI. Tartalomjegyzék: Tartalom MUN v13.0101... 2 MUN v13.0107... 10 MUN v13.0128... 18 MUN v13.0204... 21 MUN v13.0208... 27 MUN v13.0304...
Partíció probléma rekurzíómemorizálással
 Partíció probléma rekurzíómemorizálással A partíciószám rekurzív algoritmusa Ω(2 n ) műveletet végez, pedig a megoldandó részfeladatatok száma sokkal kisebb O(n 2 ). A probléma, hogy bizonyos már megoldott
Partíció probléma rekurzíómemorizálással A partíciószám rekurzív algoritmusa Ω(2 n ) műveletet végez, pedig a megoldandó részfeladatatok száma sokkal kisebb O(n 2 ). A probléma, hogy bizonyos már megoldott
Táblázatos adatok használata
 Táblázatos adatok használata Tartalomjegyzék 1. Az adatok rendezése...2 2. Keresés a táblázatban...2 3. A megjelenő oszlopok kiválasztása...3 4. Az oszlopok sorrendjének meghatározása...4 5. Az oszlopok
Táblázatos adatok használata Tartalomjegyzék 1. Az adatok rendezése...2 2. Keresés a táblázatban...2 3. A megjelenő oszlopok kiválasztása...3 4. Az oszlopok sorrendjének meghatározása...4 5. Az oszlopok
Az optimális megoldást adó algoritmusok
 Az optimális megoldást adó algoritmusok shop ütemezés esetén Ebben a fejezetben olyan modellekkel foglalkozunk, amelyekben a munkák több műveletből állnak. Speciálisan shop ütemezési problémákat vizsgálunk.
Az optimális megoldást adó algoritmusok shop ütemezés esetén Ebben a fejezetben olyan modellekkel foglalkozunk, amelyekben a munkák több műveletből állnak. Speciálisan shop ütemezési problémákat vizsgálunk.
Algoritmuselmélet 1. előadás
 Algoritmuselmélet 1. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu 2002 Február 11. ALGORITMUSELMÉLET 1. ELŐADÁS 1 Források
Algoritmuselmélet 1. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu 2002 Február 11. ALGORITMUSELMÉLET 1. ELŐADÁS 1 Források
Adatbázis Rendszerek II. 5. PLSQL Csomagok 16/1B IT MAN
 Adatbázis Rendszerek II. 5. PLSQL Csomagok 16/1B IT MAN B IT v: 2016.03.03 MAN Csomagok A DBMS csomagok a PL/SQL alkalmazások fejlesztését segítik, bennük tároljuk a létrehozott programok kódjait. A specifikációs
Adatbázis Rendszerek II. 5. PLSQL Csomagok 16/1B IT MAN B IT v: 2016.03.03 MAN Csomagok A DBMS csomagok a PL/SQL alkalmazások fejlesztését segítik, bennük tároljuk a létrehozott programok kódjait. A specifikációs
Számítógépes Hálózatok
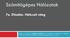 Számítógépes Hálózatok 7a. Előadás: Hálózati réteg ased on slides from Zoltán Ács ELTE and. hoffnes Northeastern U., Philippa Gill from Stonyrook University, Revised Spring 06 by S. Laki Legrövidebb út
Számítógépes Hálózatok 7a. Előadás: Hálózati réteg ased on slides from Zoltán Ács ELTE and. hoffnes Northeastern U., Philippa Gill from Stonyrook University, Revised Spring 06 by S. Laki Legrövidebb út
Novell GroupWise levelező rendszer alapok Kiadványunk célja, hogy a Nemzeti Közszolgálati Egyetemen használt Novell GroupWise (a továbbiakban GW)
 1 Novell GroupWise levelező rendszer alapok Kiadványunk célja, hogy a Nemzeti Közszolgálati Egyetemen használt Novell GroupWise (a továbbiakban GW) levelező rendszer 8. verziójának alap szolgáltatásait
1 Novell GroupWise levelező rendszer alapok Kiadványunk célja, hogy a Nemzeti Közszolgálati Egyetemen használt Novell GroupWise (a továbbiakban GW) levelező rendszer 8. verziójának alap szolgáltatásait
Felfedeztem egy nagyon érdekes és egyszerű internetes pénzkeresési módot, amihez nulla forint befektetés szükséges.
 Kedves Olvasó! Felfedeztem egy nagyon érdekes és egyszerű internetes pénzkeresési módot, amihez nulla forint befektetés szükséges. Eredetileg egy barátomnak akartam segíteni, aki egyik napról a másikra
Kedves Olvasó! Felfedeztem egy nagyon érdekes és egyszerű internetes pénzkeresési módot, amihez nulla forint befektetés szükséges. Eredetileg egy barátomnak akartam segíteni, aki egyik napról a másikra
openbve járműkészítés Leírás az openbve-hez kapcsolódó extensions.cfg fájl elkészítéséhez
 Leírás az openbve-hez kapcsolódó extensions.cfg fájl elkészítéséhez 1. oldal openbve járműkészítés Leírás az openbve-hez kapcsolódó extensions.cfg fájl elkészítéséhez A leírás az openbve-hez készített
Leírás az openbve-hez kapcsolódó extensions.cfg fájl elkészítéséhez 1. oldal openbve járműkészítés Leírás az openbve-hez kapcsolódó extensions.cfg fájl elkészítéséhez A leírás az openbve-hez készített
Gépi tanulás a gyakorlatban. Kiértékelés és Klaszterezés
 Gépi tanulás a gyakorlatban Kiértékelés és Klaszterezés Hogyan alkalmazzuk sikeresen a gépi tanuló módszereket? Hogyan válasszuk az algoritmusokat? Hogyan hangoljuk a paramétereiket? Precízebben: Tegyük
Gépi tanulás a gyakorlatban Kiértékelés és Klaszterezés Hogyan alkalmazzuk sikeresen a gépi tanuló módszereket? Hogyan válasszuk az algoritmusokat? Hogyan hangoljuk a paramétereiket? Precízebben: Tegyük
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 2017. tavasz 1. Diszkrét matematika 2.C szakirány 4. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2017.
Diszkrét matematika 2.C szakirány 2017. tavasz 1. Diszkrét matematika 2.C szakirány 4. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2017.
Algoritmuselmélet. Mélységi keresés és alkalmazásai. Katona Gyula Y.
 Algoritmuselmélet Mélységi keresés és alkalmazásai Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem 9. előadás Katona Gyula Y. (BME SZIT) Algoritmuselmélet
Algoritmuselmélet Mélységi keresés és alkalmazásai Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem 9. előadás Katona Gyula Y. (BME SZIT) Algoritmuselmélet
Minimális feszítőfák Legyen G = (V,E,c), c : E R + egy súlyozott irányítatlan gráf. Terjesszük ki a súlyfüggvényt a T E élhalmazokra:
 Minimális feszítőfák Legyen G = (V,E,c), c : E R + egy súlyozott irányítatlan gráf. Terjesszük ki a súlyfüggvényt a T E élhalmazokra: C(T ) = (u,v) T c(u,v) Az F = (V,T) gráf minimális feszitőfája G-nek,
Minimális feszítőfák Legyen G = (V,E,c), c : E R + egy súlyozott irányítatlan gráf. Terjesszük ki a súlyfüggvényt a T E élhalmazokra: C(T ) = (u,v) T c(u,v) Az F = (V,T) gráf minimális feszitőfája G-nek,
Gyártórendszerek modellezése zh, 2010. december 7.
 Gyártórendszerek modellezése zh, 2010. december 7. A feladatsorban összesen 18 pontnyi feladat van, de a 100%-os ötöshöz elég 15 pontot szerezni. Ponthatárok: 14-15: 5 12-13: 4 10-11: 3 8-9: 2 LP feladatok
Gyártórendszerek modellezése zh, 2010. december 7. A feladatsorban összesen 18 pontnyi feladat van, de a 100%-os ötöshöz elég 15 pontot szerezni. Ponthatárok: 14-15: 5 12-13: 4 10-11: 3 8-9: 2 LP feladatok
A helyhez kötött (vezetékes) internethozzáférési szolgáltatás minőségi célértékei
 Lakossági Általános Szerződési Feltételek 4/c. Melléklet A helyhez kötött (vezetékes) internethozzáférési szolgáltatás minőségi célértékei Tartalomjegyzék 1. Egyéni helyhez kötött (vezetékes) internetszolgáltatás
Lakossági Általános Szerződési Feltételek 4/c. Melléklet A helyhez kötött (vezetékes) internethozzáférési szolgáltatás minőségi célértékei Tartalomjegyzék 1. Egyéni helyhez kötött (vezetékes) internetszolgáltatás
MATEMATIKAI KOMPETENCIATERÜLET A
 MATEMATIKAI KOMPETENCIATERÜLET A Matematika 9. szakiskolai évfolyam 1. félév ESZKÖZÖK Matematika A 9. szakiskolai évfolyam Betűkészlet csoportalakításhoz A D G B E H C F G H I J Matematika A 9. szakiskolai
MATEMATIKAI KOMPETENCIATERÜLET A Matematika 9. szakiskolai évfolyam 1. félév ESZKÖZÖK Matematika A 9. szakiskolai évfolyam Betűkészlet csoportalakításhoz A D G B E H C F G H I J Matematika A 9. szakiskolai
Programozás alapjai C nyelv 8. gyakorlat. Mutatók és címek (ism.) Indirekció (ism)
 Programozás alapjai C nyelv 8. gyakorlat Szeberényi Imre BME IIT Programozás alapjai I. (C nyelv, gyakorlat) BME-IIT Sz.I. 2005.11.07. -1- Mutatók és címek (ism.) Minden változó és függvény
Programozás alapjai C nyelv 8. gyakorlat Szeberényi Imre BME IIT Programozás alapjai I. (C nyelv, gyakorlat) BME-IIT Sz.I. 2005.11.07. -1- Mutatók és címek (ism.) Minden változó és függvény
Mutatók és címek (ism.) Programozás alapjai C nyelv 8. gyakorlat. Indirekció (ism) Néhány dolog érthetőbb (ism.) Változók a memóriában
 Programozás alapjai C nyelv 8. gyakorlat Szeberényi mre BME T Programozás alapjai. (C nyelv, gyakorlat) BME-T Sz.. 2005.11.07. -1- Mutatók és címek (ism.) Minden változó és függvény
Programozás alapjai C nyelv 8. gyakorlat Szeberényi mre BME T Programozás alapjai. (C nyelv, gyakorlat) BME-T Sz.. 2005.11.07. -1- Mutatók és címek (ism.) Minden változó és függvény
1. a. Vegye fel az alábbi táblázatban szereplő adatokat! Ügyeljen a táblázatban szereplő
 1. 1. a. Vegye fel az alábbi táblázatban szereplő adatokat! Ügyeljen a táblázatban szereplő formátumokra is! Sorszám Betét napja Kamatláb Bet. össz. (Ft) Kamat (Ft) Kifiz (Ft) 1. 1997. 08. 14. 12% 100
1. 1. a. Vegye fel az alábbi táblázatban szereplő adatokat! Ügyeljen a táblázatban szereplő formátumokra is! Sorszám Betét napja Kamatláb Bet. össz. (Ft) Kamat (Ft) Kifiz (Ft) 1. 1997. 08. 14. 12% 100
A helyhez kötött (vezetékes) internethozzáférési szolgáltatás minőségi célértékei
 Lakossági Általános Szerződési Feltételek 4/c. Melléklet A helyhez kötött (vezetékes) internethozzáférési szolgáltatás minőségi célértékei Tartalomjegyzék 1. Egyéni helyhez kötött (vezetékes) internetszolgáltatás
Lakossági Általános Szerződési Feltételek 4/c. Melléklet A helyhez kötött (vezetékes) internethozzáférési szolgáltatás minőségi célértékei Tartalomjegyzék 1. Egyéni helyhez kötött (vezetékes) internetszolgáltatás
HU-GO Mobil bemutatása 2014. április 16.
 HU-GO Mobil bemutatása 2014. április 16. A HU-GO Mobil alkalmazás ingyenesen letölthető Android operációs rendszert és ios operációs rendszert használó telefonra. Windows platformra a fejlesztés folyamatban
HU-GO Mobil bemutatása 2014. április 16. A HU-GO Mobil alkalmazás ingyenesen letölthető Android operációs rendszert és ios operációs rendszert használó telefonra. Windows platformra a fejlesztés folyamatban
1.3/C. és 1.3./D. Forgalmi vizsga tesztkérdései F. 1. sz. Jelzési Utasítás
 1.3/C. és 1.3./D. Forgalmi vizsga tesztkérdései F. 1. sz. Jelzési Utasítás 1. Mi a fázishatár? a) A villamos vontatási vonalakon az állomási és a vonali szakaszolók között, illetve transzformátorok felsővezetéki
1.3/C. és 1.3./D. Forgalmi vizsga tesztkérdései F. 1. sz. Jelzési Utasítás 1. Mi a fázishatár? a) A villamos vontatási vonalakon az állomási és a vonali szakaszolók között, illetve transzformátorok felsővezetéki
Operációkutatás vizsga
 Operációkutatás vizsga A csoport Budapesti Corvinus Egyetem 2007. január 16. Egyéb gyakorló és vizsgaanyagok találhatók a honlapon a Letölthető vizsgasorok, segédanyagok menüpont alatt. OPERÁCIÓKUTATÁS,
Operációkutatás vizsga A csoport Budapesti Corvinus Egyetem 2007. január 16. Egyéb gyakorló és vizsgaanyagok találhatók a honlapon a Letölthető vizsgasorok, segédanyagok menüpont alatt. OPERÁCIÓKUTATÁS,
Számítógépes döntéstámogatás. Genetikus algoritmusok
 BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
Hálózati folyamok. A használt fogalmak definiálása
 Hálózati folyamok Hálózat A használt fogalmak definiálása Ez összesen 4 dologból áll: - Egy irányított G gráf - Ennek egy kitüntetett pontja, amit forrásnak hívunk és s-sel jelölünk - A gráf még egy kitüntetett
Hálózati folyamok Hálózat A használt fogalmak definiálása Ez összesen 4 dologból áll: - Egy irányított G gráf - Ennek egy kitüntetett pontja, amit forrásnak hívunk és s-sel jelölünk - A gráf még egy kitüntetett
Adatbázismodellek. 1. ábra Hierarchikus modell
 Eddig az adatbázisokkal általános szempontból foglalkoztunk: mire valók, milyen elemekből épülnek fel. Ennek során tisztáztuk, hogy létezik az adatbázis fogalmi modellje (adatbázisterv), amely az egyedek,
Eddig az adatbázisokkal általános szempontból foglalkoztunk: mire valók, milyen elemekből épülnek fel. Ennek során tisztáztuk, hogy létezik az adatbázis fogalmi modellje (adatbázisterv), amely az egyedek,
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 2017. ősz 1. Diszkrét matematika 2.C szakirány 2. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2017.
Diszkrét matematika 2.C szakirány 2017. ősz 1. Diszkrét matematika 2.C szakirány 2. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2017.
III. osztály 1 Orchidea Iskola IV. Matematika verseny 2011/2012 II. forduló
 III. osztály 1 Orchidea Iskola IV. Matematika verseny 2011/2012 II. forduló 1. Mennyi az eredmény 15+17 15+17 15+17=? A) 28 B) 35 C) 36 D)96 2. Melyik szám van a piramis csúcsán? 42 82 38 A) 168 B) 138
III. osztály 1 Orchidea Iskola IV. Matematika verseny 2011/2012 II. forduló 1. Mennyi az eredmény 15+17 15+17 15+17=? A) 28 B) 35 C) 36 D)96 2. Melyik szám van a piramis csúcsán? 42 82 38 A) 168 B) 138
JÁTÉKSZABÁLY KEZDŐ JÁTSZMA
 Marsha J. Falco JÁTÉKSZABÁLY A játék célja hogy 3 kártyából álló SET-eket találjunk meg az asztalra lehelyezett 12 kártyából. Minden kártyának 4 tulajdonsága van, amik a következők: FORMA: ovális, hullámos,
Marsha J. Falco JÁTÉKSZABÁLY A játék célja hogy 3 kártyából álló SET-eket találjunk meg az asztalra lehelyezett 12 kártyából. Minden kártyának 4 tulajdonsága van, amik a következők: FORMA: ovális, hullámos,
PHP-MySQL. Adatbázisok gyakorlat
 PHP-MySQL Adatbázisok gyakorlat Weboldalak és adatbázisok Az eddigiek során megismertük, hogyan lehet a PHP segítségével dinamikus weblapokat készíteni. A dinamikus weboldalak az esetek többségében valamilyen
PHP-MySQL Adatbázisok gyakorlat Weboldalak és adatbázisok Az eddigiek során megismertük, hogyan lehet a PHP segítségével dinamikus weblapokat készíteni. A dinamikus weboldalak az esetek többségében valamilyen
Ládapakolási játékok
 Ládapakolási játékok 0.1 0.15 Dόsa György Pannon Egyetem Veszprém, Hungary XXXII. MOK, Cegléd, 2017 jun 14 1 A ládapakolási feladat n tárgy Sok láda (1 méretű) Tárgyak méretei: (0,1] Mindegyiket be kell
Ládapakolási játékok 0.1 0.15 Dόsa György Pannon Egyetem Veszprém, Hungary XXXII. MOK, Cegléd, 2017 jun 14 1 A ládapakolási feladat n tárgy Sok láda (1 méretű) Tárgyak méretei: (0,1] Mindegyiket be kell
NULLADIK MATEMATIKA ZÁRTHELYI
 A NULLADIK MATEMATIKA ZÁRTHELYI 20-09-2 Terem: Munkaidő: 0 perc. A dolgozat megírásához íróeszközön kívül semmilyen segédeszköz nem használható! Csak és kizárólag tollal tölthető ki a feladatlap, a ceruzával
A NULLADIK MATEMATIKA ZÁRTHELYI 20-09-2 Terem: Munkaidő: 0 perc. A dolgozat megírásához íróeszközön kívül semmilyen segédeszköz nem használható! Csak és kizárólag tollal tölthető ki a feladatlap, a ceruzával
Delphi programozás I.
 Delphi programozás I. Konzol alkalmazások készítése Delphiben A Delphi konzol alkalmazása (console application) olyan 32 bites program, amely nem grafikus felületen, hanem egy szöveges konzol ablakban
Delphi programozás I. Konzol alkalmazások készítése Delphiben A Delphi konzol alkalmazása (console application) olyan 32 bites program, amely nem grafikus felületen, hanem egy szöveges konzol ablakban
Az emberek jellemzői
 MUNKAESZKÖZÖK Az emberek jellemzői Ők is és családjuk is termékeket használnak. Az emberek szeretnek olyan termékeket bemutatni a környezetüknek, amelyre a másiknak szüksége lehet. Útbaigazítják és motiválják
MUNKAESZKÖZÖK Az emberek jellemzői Ők is és családjuk is termékeket használnak. Az emberek szeretnek olyan termékeket bemutatni a környezetüknek, amelyre a másiknak szüksége lehet. Útbaigazítják és motiválják
PromoCoder_7031/Lx3 rendszer használati utsítás v1.1
 PromoCoder_7031/Lx3 rendszer használati utsítás v1.1 A rendszer leírása a Promociós kódolás MI 7031 lézernyomtatókkal szerelt csomagológépekre című dokumentumban került részletes ismertetésre. Ebben lett
PromoCoder_7031/Lx3 rendszer használati utsítás v1.1 A rendszer leírása a Promociós kódolás MI 7031 lézernyomtatókkal szerelt csomagológépekre című dokumentumban került részletes ismertetésre. Ebben lett
Diszkrét matematika 2.
 Diszkrét matematika 2. Mérai László előadása alapján Készítette: Nagy Krisztián 1. előadás Gráfok halmaza, gráf, ahol a csúcsok halmaza, az élek illesztkedés reláció: illesztkedik az élre, ha ( -él illesztkedik
Diszkrét matematika 2. Mérai László előadása alapján Készítette: Nagy Krisztián 1. előadás Gráfok halmaza, gráf, ahol a csúcsok halmaza, az élek illesztkedés reláció: illesztkedik az élre, ha ( -él illesztkedik
Összefoglalás és gyakorlás
 Összefoglalás és gyakorlás High Speed Networks Laboratory 1 / 28 Hálózatok jellemző paraméterei High Speed Networks Laboratory 2 / 28 Evolúció alkotta adatbázis Önszerveződő adatbázis = (struktúra, lekérdezés)
Összefoglalás és gyakorlás High Speed Networks Laboratory 1 / 28 Hálózatok jellemző paraméterei High Speed Networks Laboratory 2 / 28 Evolúció alkotta adatbázis Önszerveződő adatbázis = (struktúra, lekérdezés)
Ellenőrző kérdések. 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t
 Ellenőrző kérdések 2. Kis dolgozat kérdései 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t 37. Ha t szintű indexet használunk,
Ellenőrző kérdések 2. Kis dolgozat kérdései 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t 37. Ha t szintű indexet használunk,
Java Programozás 9. Gy: Java alapok. Adatkezelő 5.rész
 Java Programozás 9. Gy: Java alapok Adatkezelő 5.rész 15/1 B ITv: MAN 2018.04.22 A Keresés funkció Programlogika: 1. A keresés az etm táblamodellben fog keresni, és a találat rekordokat átmásolja egy másik
Java Programozás 9. Gy: Java alapok Adatkezelő 5.rész 15/1 B ITv: MAN 2018.04.22 A Keresés funkció Programlogika: 1. A keresés az etm táblamodellben fog keresni, és a találat rekordokat átmásolja egy másik
Galaxis Roncsderbi Nagy Kiegészítő kártyasegédlet
 Galaxis Roncsderbi Nagy Kiegészítő kártyasegédlet Rázós Utak Tisztességtelen verseny Az a játékos, aki ki szeretné használni az Elhagyatott Állomást vagy Hajót, először kap egy-egy erős ágyúlövést minden
Galaxis Roncsderbi Nagy Kiegészítő kártyasegédlet Rázós Utak Tisztességtelen verseny Az a játékos, aki ki szeretné használni az Elhagyatott Állomást vagy Hajót, először kap egy-egy erős ágyúlövést minden
Algoritmuselmélet 18. előadás
 Algoritmuselmélet 18. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu 2002 Május 7. ALGORITMUSELMÉLET 18. ELŐADÁS 1 Közelítő algoritmusok
Algoritmuselmélet 18. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu 2002 Május 7. ALGORITMUSELMÉLET 18. ELŐADÁS 1 Közelítő algoritmusok
Adatszerkezetek 7a. Dr. IványiPéter
 Adatszerkezetek 7a. Dr. IványiPéter 1 Fák Fákat akkor használunk, ha az adatok között valamilyen alá- és fölérendeltség van. Pl. könyvtárszerkezet gyökér () Nincsennek hurkok!!! 2 Bináris fák Azokat a
Adatszerkezetek 7a. Dr. IványiPéter 1 Fák Fákat akkor használunk, ha az adatok között valamilyen alá- és fölérendeltség van. Pl. könyvtárszerkezet gyökér () Nincsennek hurkok!!! 2 Bináris fák Azokat a
A 2016/2017 tanévi Országos Középiskolai Tanulmányi Verseny második fordulójának feladatai. INFORMATIKA II. (programozás) kategória
 Oktatási Hivatal A 2016/2017 tanévi Országos özépiskolai Tanulmányi Verseny második fordulójának feladatai INFORMATIA II. (programozás) kategória 1. feladat: Legalább 2 bolygón volt élet (33 pont) Egy
Oktatási Hivatal A 2016/2017 tanévi Országos özépiskolai Tanulmányi Verseny második fordulójának feladatai INFORMATIA II. (programozás) kategória 1. feladat: Legalább 2 bolygón volt élet (33 pont) Egy
9.feladat megoldás. Szigeti Bertalan György január 15.
 9.feladat megoldás Szigeti Bertalan György 2018. január 15. A feladatkiírásnak megfelelően mindkét algoritmust leprogramoztam Matlabban. A forrás kódot kommentált formátumban mellékelem a függelékben.
9.feladat megoldás Szigeti Bertalan György 2018. január 15. A feladatkiírásnak megfelelően mindkét algoritmust leprogramoztam Matlabban. A forrás kódot kommentált formátumban mellékelem a függelékben.
Szerző. Varga Péter ETR azonosító: VAPQAAI.ELTE Email cím: Név: vp.05@hotmail.com Kurzuskód:
 Szerző Név: Varga Péter ETR azonosító: VAPQAAI.ELTE Email cím: vp.05@hotmail.com Kurzuskód: IP-08PAEG/27 Gyakorlatvezető neve: Kőhegyi János Feladatsorszám: 20 1 Tartalom Szerző... 1 Felhasználói dokumentáció...
Szerző Név: Varga Péter ETR azonosító: VAPQAAI.ELTE Email cím: vp.05@hotmail.com Kurzuskód: IP-08PAEG/27 Gyakorlatvezető neve: Kőhegyi János Feladatsorszám: 20 1 Tartalom Szerző... 1 Felhasználói dokumentáció...
