KÖR ÉS GÖMB A MŰVÉSZETEKBEN
|
|
|
- Anna Borbélyné
- 9 évvel ezelőtt
- Látták:
Átírás
1 KÖR ÉS GÖMB A MŰVÉSZETEKBEN Készítették: Kovács Dominika Mezővári Kata Végh Orsolya
2 A GÖMB MATEMATIKAI VONATKOZÁSBAN A gömb egy geometriai alakzat, mely jelenthet egy felületet és egy testet egyaránt. Felület esetén egy adott ponttól a térben egyenlő távolságra lévő pontok halmazát nevezzük így, míg test esetén a legfeljebb adott távolságra lévő pontok halmazát. Az előbbi egy kétdimenziós, az utóbbi egy háromdimenziós alakzat.
3 A KÖR MATEMATIKAI VONATKOZÁSBAN A kör vagy körvonal a geometriában egy sík azon pontjainak halmaza (régies szóhasználattal mértani helye), amelyek a sík egy meghatározott pontjától (középpont) adott távolságra (sugár) vannak. Körlapnak nevezzük azon pontok halmazát, melyekre a távolság kisebb vagy egyenlő a sugárral.
4 A KÖR ÉS A GÖMB, MINT SZIMBÓLUM Nagyon régi ősi szimbólum a kör. Nem véletlen, hogy az első ősi értelmezésekben például éppen a napot, a nap korongját tekintették minden élet forrásának már ők is tudták, hogy fénye nélkül nem létezne maga az ember sem, ezért lett a kör a teremtő erő jelképe, amely egyben teljes és tökéletes, a végtelen egység, a folytonosság szimbóluma. A kör az abszolút jelképe is, mivel mindig saját magába fordul vissza nincs se kezdete, se vége mégis befejezett, tehát tökéletes. Az emberek előszeretettel viselnek például valamilyen karkötőt, gyűrűt végső soron kört. S a karikagyűrű tényleg egyik legkifejezőbb kör, mert a férfi és a nő ezt a szimbólumot a végtelenséget ajándékozza egymásnak szeretetük jeléül. A szimbolikus geometriában a körön keresztül a teljességet és a hatalmat akarják megörökíteni. A kör a misztérium magját, az emberek hitének és életének szent irányelvét határozza meg. A Gömb is hasonló jelentéssel bír, a tökéletességét, teljességet szimbolizálja.
5 Az ember szívesen gondol a gömbre mint a tökéletes testre. Így gondolta ezt már Parminedész is Krisztus előtt a VI. és V. század fordulóján, aki a létezőt, mely örök, nem keletkezett, mentes minden változástól, mozgástól, gömb formájúnak képzelte el. Igaz a gömb nem szerepel a platóni szabályos testek között, hiányzik a tetraéder, hexaéder, oktaéder, dekodaéder és ikozaéder illusztris társaságából.
6 Ha már a tökéletesnél, a szabályosnál tartunk, a NASA, a relativitáselmélet téridővonszolódásának bizonyítására úgynevezett giroszkópakat juttattak el egy szputnyikra. A giroszkóp lelke nem más, mint egy pingponglabda méretű, kvarcból öntött, a tökéleteshez közelítő golyó. Fantasztikusak a paraméterei: felszíne maximum 40 atomrétegnyire tér el a gömbtől, sűrűsége 1:10 millióhoz mértékben egyenletes. Ha a föld is ilyen tökéletes gömb lenne, akkor a Mount Everest csúcsa és a Mariana-árok között mindössze 5 méter szintkülönbség lenne.
7 MŰVÉSZETI VONATKOZÁS NAGY GÁBOR GYÖRGY A gömb szó 'sphaera' egyszerre jelöli a felületet, a középponttól egyenlő távolságban lévő pontok halmazát, és azt a testet, teret, ami e halmaz mögött egzisztál. Nagy Gábor György munkáinak kulcskérdései, a képek jelenleg a Godot Galériában láthatók, megegyeznek a fenti idézet tételeivel. A képek centrumában látható vizuális jelenségek megfogalmazzák a gömbfelület felszínének kalandos optikai világát, de jelzik a csillogó, fénylő felület mögötti test súlyos anyagiságát
8 A művész játszva alkot tökéletesebbet az embernél. Nagy Gábor György például előképeket, mintákat, modelleket sem használ műveihez. Nagy Gábor György az utóbbi években akár digitális, akár klasszikus technikával is dolgozik, igyekszik a témát, a feldolgozásra váró és szánt élményanyagot redukálni. A gúlák, oszlopok, üvegpalackok, üvegburák, hamisgyöngyök után, itt és most a gömbé és a kézművességé a főszerep (olaj/vászon, hidegtű). A képeken látható gömbök egy művészi kísérlet állomásai. Miképp lehet közel kerülni a festőnek a vizuális tények elemi részecskéihez, atommagjaihoz, atomgömbjeihez. Ezzel a kísérlettel Nagy Gábor György látásunk megtisztításához járul hozzá.
9 A KÖR LEONARDO DA VINCI ALKOTÁSÁBAN Matematika, filozófia, építészet, hadászat, festészet, szobrászat, zene, mérnöki és természettudományok ma már szinte elképzelhetetlen, hogy egyetlen ember az előbbi területek mindegyikének mestere legyen. A XV. századi Itáliában azonban még lehetséges volt a kor csaknem összes tudását megszerezni. Ehhez természetesen egy élet munkájára és nem mindennapi képességekre volt szükség.
10 Az elvont tudományok kutatása mellett természetesen nem feledkezett meg tanult szakmájáról sem. A festészetben sok társához hasonlóan a reneszánsz művészetek elsődleges témáját, az ember ábrázolását tekintette fő feladatának. Ehhez az időszámításunk előtti első században élt római tudós, Vitruvius megfigyeléseire támaszkodott. Az emberi test középpontja természetesen a köldök. Ha egy kinyújtott karral és lábbal háton fekvő ember köré egy körzővel a köldökét középpontnak véve kört húzunk, akkor a kéz- és lábujjai érinteni fogják az így megadott kört. [ ] Ha pedig megmérjük a távolságot a talptól a fejtetőig, majd ezt összevetjük a kinyújtott karok hosszával, úgy találjuk, hogy a szélesség megegyezik a magassággal. írta Vitruvius. A tétel igazolását Leonardo egyik legismertebb vázlatán láthatjuk.
Ha a síkot egyenes vagy görbe vonalakkal feldaraboljuk, akkor síkidomokat kapunk.
 Síkidomok Ha a síkot egyenes vagy görbe vonalakkal feldaraboljuk, akkor síkidomokat kapunk. A határoló vonalak által bezárt síkrész a síkidom területe. A síkidomok határoló vonalak szerint lehetnek szabályos
Síkidomok Ha a síkot egyenes vagy görbe vonalakkal feldaraboljuk, akkor síkidomokat kapunk. A határoló vonalak által bezárt síkrész a síkidom területe. A síkidomok határoló vonalak szerint lehetnek szabályos
3. KÖRGEOMETRIA. 3.1. Körrel kapcsolatos alapismeretek
 3. KÖRGEOMETRIA Hajós György: Bevezetés a geometriába, Tankönyvkiadó, Budapest, 89 109. és 121. oldal. Pelle Béla: Geometria, Tankönyvkiadó, Budapest, 86 97. és 117 121. oldal. Kovács Zoltán: Geometria,
3. KÖRGEOMETRIA Hajós György: Bevezetés a geometriába, Tankönyvkiadó, Budapest, 89 109. és 121. oldal. Pelle Béla: Geometria, Tankönyvkiadó, Budapest, 86 97. és 117 121. oldal. Kovács Zoltán: Geometria,
A skatulya-elv alkalmazásai
 1 A skatulya-elv alkalmazásai Számelmélet 1. Az első 4n darab pozitív egész számot beosztjuk n számú halmazba. Igazoljuk, hogy mindig lesz három olyan szám, amelyek ugyanabban a halmazban vannak és valamely
1 A skatulya-elv alkalmazásai Számelmélet 1. Az első 4n darab pozitív egész számot beosztjuk n számú halmazba. Igazoljuk, hogy mindig lesz három olyan szám, amelyek ugyanabban a halmazban vannak és valamely
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Geometria IV.
 Geometria IV. 1. Szerkessz egy adott körhöz egy adott külső ponton átmenő érintőket! Jelöljük az adott kört k val, a kör középpontját O val, az adott külső pontot pedig P vel. A szerkesztéshez azt használjuk
Geometria IV. 1. Szerkessz egy adott körhöz egy adott külső ponton átmenő érintőket! Jelöljük az adott kört k val, a kör középpontját O val, az adott külső pontot pedig P vel. A szerkesztéshez azt használjuk
Térgeometria feladatok. 2. Egy négyzetes oszlop magassága háromszor akkora, mint az alapéle, felszíne 504 cm 2. Mekkora a testátlója és a térfogata?
 Térgeometria feladatok Téglatest 1. Egy téglatest éleinek aránya 2 : 3 : 5, felszíne 992 cm 2. Mekkora a testátlója és a 2. Egy négyzetes oszlop magassága háromszor akkora, mint az alapéle, felszíne 504
Térgeometria feladatok Téglatest 1. Egy téglatest éleinek aránya 2 : 3 : 5, felszíne 992 cm 2. Mekkora a testátlója és a 2. Egy négyzetes oszlop magassága háromszor akkora, mint az alapéle, felszíne 504
Az aktiválódásoknak azonban itt még nincs vége, ugyanis az aktiválódások 30 évenként ismétlődnek!
 1 Mindannyiunk életében előfordulnak jelentős évek, amikor is egy-egy esemény hatására a sorsunk új irányt vesz. Bár ezen események többségének ott és akkor kevésbé tulajdonítunk jelentőséget, csak idővel,
1 Mindannyiunk életében előfordulnak jelentős évek, amikor is egy-egy esemény hatására a sorsunk új irányt vesz. Bár ezen események többségének ott és akkor kevésbé tulajdonítunk jelentőséget, csak idővel,
1. Metrótörténet. A feladat folytatása a következő oldalon található. Informatika emelt szint. m2_blaha.jpg, m3_nagyvaradter.jpg és m4_furopajzs.jpg.
 1. Metrótörténet A fővárosi metróhálózat a tömegközlekedés gerincét adja. A vonalak építésének története egészen a XIX. század végéig nyúlik vissza. Feladata, hogy készítse el a négy metróvonal történetét
1. Metrótörténet A fővárosi metróhálózat a tömegközlekedés gerincét adja. A vonalak építésének története egészen a XIX. század végéig nyúlik vissza. Feladata, hogy készítse el a négy metróvonal történetét
BOLYAI MATEMATIKA CSAPATVERSENY ORSZÁGOS DÖNTŐ SZÓBELI (2012. NOVEMBER 24.) 3. osztály
 3. osztály Két szám összege 33. Mennyi ennek a két számnak a különbsége, ha az egyik kétszerese a másiknak? Hány olyan háromjegyű szám van, amelyben a számjegyek összege legalább 25? 4. osztály A Zimrili
3. osztály Két szám összege 33. Mennyi ennek a két számnak a különbsége, ha az egyik kétszerese a másiknak? Hány olyan háromjegyű szám van, amelyben a számjegyek összege legalább 25? 4. osztály A Zimrili
Földrajzi helymeghatározás
 A mérés megnevezése, célkitűzései: Földrajzi fokhálózat jelentősége és használata a gyakorlatban Eszközszükséglet: Szükséges anyagok: narancs Szükséges eszközök: GPS készülék, földgömb, földrajz atlasz,
A mérés megnevezése, célkitűzései: Földrajzi fokhálózat jelentősége és használata a gyakorlatban Eszközszükséglet: Szükséges anyagok: narancs Szükséges eszközök: GPS készülék, földgömb, földrajz atlasz,
diákmelléklet én ÉS A VILÁG 5. évfolyam 135
 diákmelléklet én ÉS A VILÁG 5. évfolyam 135 D1 1. Kérdőív Válaszolj az alábbi kérdésekre a legjobb tudásod szerint, karikázd be az általad leginkább elfogadott válasz betűjelét! 1. Mit jelent az a szó,
diákmelléklet én ÉS A VILÁG 5. évfolyam 135 D1 1. Kérdőív Válaszolj az alábbi kérdésekre a legjobb tudásod szerint, karikázd be az általad leginkább elfogadott válasz betűjelét! 1. Mit jelent az a szó,
FJÄLLTÅG. Új, limitált kiadású textilkollekció
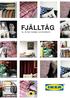 FJÄLLTÅG Új, limitált kiadású textilkollekció Átszövi a történelem A FJÄLLTÅG textilsorozat több különböző történetet mond el. Minden darabnak megvan a maga meséje az elegáns, 20. század eleji hölgynek
FJÄLLTÅG Új, limitált kiadású textilkollekció Átszövi a történelem A FJÄLLTÅG textilsorozat több különböző történetet mond el. Minden darabnak megvan a maga meséje az elegáns, 20. század eleji hölgynek
Koordináta - geometria I.
 Koordináta - geometria I. DEFINÍCIÓ: (Helyvektor) A derékszögű koordináta - rendszerben a pont helyvektora az origóból a pontba mutató vektor. TÉTEL: Ha i az (1; 0) és j a (0; 1) pont helyvektora, akkor
Koordináta - geometria I. DEFINÍCIÓ: (Helyvektor) A derékszögű koordináta - rendszerben a pont helyvektora az origóból a pontba mutató vektor. TÉTEL: Ha i az (1; 0) és j a (0; 1) pont helyvektora, akkor
Épületvillamosság laboratórium. Villámvédelemi felfogó-rendszer hatásosságának vizsgálata
 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék Nagyfeszültségű Technika és Berendezések Csoport Épületvillamosság laboratórium Villámvédelemi felfogó-rendszer hatásosságának
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék Nagyfeszültségű Technika és Berendezések Csoport Épületvillamosság laboratórium Villámvédelemi felfogó-rendszer hatásosságának
Szijártó Éva. Előszó. A tanulás módszere: 1. Megfigyelés 2. Utánozás 3. Gyakorlás 4. Ismétlés
 Előszó A Nail Art a körömdíszítés művészete. Szükség van műveléséhez érzékre, ízlésre. Mesterség is, amely tanulható és tanítható. Könyvünk a tanítás feladatát vállalta magára. A könyv pedagógiája azon
Előszó A Nail Art a körömdíszítés művészete. Szükség van műveléséhez érzékre, ízlésre. Mesterség is, amely tanulható és tanítható. Könyvünk a tanítás feladatát vállalta magára. A könyv pedagógiája azon
Bár a digitális technológia nagyon sokat fejlődött, van még olyan dolog, amit a digitális fényképezőgépek nem tudnak: minden körülmények között
 Dr. Nyári Tibor Bár a digitális technológia nagyon sokat fejlődött, van még olyan dolog, amit a digitális fényképezőgépek nem tudnak: minden körülmények között tökéletes színeket visszaadni. A digitális
Dr. Nyári Tibor Bár a digitális technológia nagyon sokat fejlődött, van még olyan dolog, amit a digitális fényképezőgépek nem tudnak: minden körülmények között tökéletes színeket visszaadni. A digitális
Algebra es sz amelm elet 3 el oad as Rel aci ok Waldhauser Tam as 2014 oszi f el ev
 Algebra és számelmélet 3 előadás Relációk Waldhauser Tamás 2014 őszi félév Relációk reláció lat. 1. kapcsolat, viszony; összefüggés vmivel 2. viszonylat, vonatkozás reláció lat. 3. mat halmazok elemei
Algebra és számelmélet 3 előadás Relációk Waldhauser Tamás 2014 őszi félév Relációk reláció lat. 1. kapcsolat, viszony; összefüggés vmivel 2. viszonylat, vonatkozás reláció lat. 3. mat halmazok elemei
BOLYAI MATEMATIKA CSAPATVERSENY FŐVÁROSI DÖNTŐ SZÓBELI (2005. NOVEMBER 26.) 5. osztály
 5. osztály Írd be az ábrán látható hat üres körbe a 10, 30, 40, 60, 70 és 90 számokat úgy, hogy a háromszög mindhárom oldala mentén a számok összege 200 legyen! 50 20 80 Egy dobozban háromféle színű: piros,
5. osztály Írd be az ábrán látható hat üres körbe a 10, 30, 40, 60, 70 és 90 számokat úgy, hogy a háromszög mindhárom oldala mentén a számok összege 200 legyen! 50 20 80 Egy dobozban háromféle színű: piros,
1. Mintapélda, amikor a fenék lekerekítési sugár (Rb) kicsi
 1 Mélyhúzott edény teríték méretének meghatározása 1. Mintapélda, amikor a fenék lekerekítési sugár (Rb) kicsi A mélyhúzott edény kiindulási teríték átmérőjének meghatározása a térfogat-állandóság alapján
1 Mélyhúzott edény teríték méretének meghatározása 1. Mintapélda, amikor a fenék lekerekítési sugár (Rb) kicsi A mélyhúzott edény kiindulási teríték átmérőjének meghatározása a térfogat-állandóság alapján
Jarabin Kinga LÁBNYOMOK
 Jarabin Kinga LÁBNYOMOK Álmokkal indulunk Már egész kis korban, óvodásként is van arról elképzelésünk, mivel szeretnénk foglalkozni, ha egyszer felnövünk. Álmokkal indulunk az iskolapadba, az iskolapadból
Jarabin Kinga LÁBNYOMOK Álmokkal indulunk Már egész kis korban, óvodásként is van arról elképzelésünk, mivel szeretnénk foglalkozni, ha egyszer felnövünk. Álmokkal indulunk az iskolapadba, az iskolapadból
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Geometria II.
 Geometria II. Síkidomok, testek: A sík feldarabolásával síkidomokat, a tér feldarabolásával testeket kapunk. Törött vonal: A csatlakozó szakaszok törött vonalat alkotnak. DEFNÍCIÓ: (Sokszögvonal) A záródó
Geometria II. Síkidomok, testek: A sík feldarabolásával síkidomokat, a tér feldarabolásával testeket kapunk. Törött vonal: A csatlakozó szakaszok törött vonalat alkotnak. DEFNÍCIÓ: (Sokszögvonal) A záródó
SZÁMÍTÓGÉPES NYELVI ADATBÁZISOK
 SZÁMÍTÓGÉPES NYELVI ADATBÁZISOK A MAGYARÓRÁN Sass Bálint joker@nytud.hu Magyar Tudományos Akadémia Nyelvtudományi Intézet Korpusznyelvészeti Osztály A magyarnyelv-oktatás időszerű kérdései Szlovákiában
SZÁMÍTÓGÉPES NYELVI ADATBÁZISOK A MAGYARÓRÁN Sass Bálint joker@nytud.hu Magyar Tudományos Akadémia Nyelvtudományi Intézet Korpusznyelvészeti Osztály A magyarnyelv-oktatás időszerű kérdései Szlovákiában
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
Az élet színesben Published on www.flagmagazin.hu (http://www.flagmagazin.hu) Még nincs értékelve
 2013 szeptember 04. Flag 0 Értékelés kiválasztása Még nincs értékelve Értéke: 1/5 Értéke: 2/5 Mérték Értéke: 3/5 Értéke: 4/5 Értéke: 5/5 Milyen lehetett az élet színesben? A történelem egyes időszakairól,
2013 szeptember 04. Flag 0 Értékelés kiválasztása Még nincs értékelve Értéke: 1/5 Értéke: 2/5 Mérték Értéke: 3/5 Értéke: 4/5 Értéke: 5/5 Milyen lehetett az élet színesben? A történelem egyes időszakairól,
Shared IMAP beállítása magyar nyelvű webmailes felületen
 Shared IMAP beállítása magyar nyelvű webmailes felületen A következő ismertető segítséget nyújt a szervezeti cím küldőként való beállításában a caesar Webmailes felületén. Ahhoz, hogy a Shared Imaphoz
Shared IMAP beállítása magyar nyelvű webmailes felületen A következő ismertető segítséget nyújt a szervezeti cím küldőként való beállításában a caesar Webmailes felületén. Ahhoz, hogy a Shared Imaphoz
BOLYAI MATEMATIKA CSAPATVERSENY DÖNTŐ 2004. 5. osztály
 5. osztály Ha egy négyzetet az ábrán látható módon feldarabolunk, akkor a tangram nevű ősi kínai játékot kapjuk. Mekkora a nagy négyzet területe, ha a kicsié 8 cm 2? (A kis négyzet egyik csúcsa a nagy
5. osztály Ha egy négyzetet az ábrán látható módon feldarabolunk, akkor a tangram nevű ősi kínai játékot kapjuk. Mekkora a nagy négyzet területe, ha a kicsié 8 cm 2? (A kis négyzet egyik csúcsa a nagy
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI
 SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 12 KRISTÁLYkÉMIA XII. KÖTÉsTÍPUsOK A KRIsTÁLYOKBAN 1. KÉMIAI KÖTÉsEK Valamennyi kötéstípus az atommag és az elektronok, illetve az elektronok egymás közötti
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 12 KRISTÁLYkÉMIA XII. KÖTÉsTÍPUsOK A KRIsTÁLYOKBAN 1. KÉMIAI KÖTÉsEK Valamennyi kötéstípus az atommag és az elektronok, illetve az elektronok egymás közötti
Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Szászné Simon Judit; dátum: 2005. november. I. rész
 Szászné Simon Judit, 005. november Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Szászné Simon Judit; dátum: 005. november. feladat I. rész Oldjuk meg a valós számok halmazán a x 5x
Szászné Simon Judit, 005. november Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Szászné Simon Judit; dátum: 005. november. feladat I. rész Oldjuk meg a valós számok halmazán a x 5x
Vektorok összeadása, kivonása, szorzás számmal, koordináták, lineáris függetlenség
 Vektoralgebra Vektorok összeadása, kivonása, szorzás számmal, koordináták, lineáris függetlenség Feladatok: 1) A koordinátarendszerben úgy helyezzük el az egységkockát, hogy az origó az egyik csúcsba essék,
Vektoralgebra Vektorok összeadása, kivonása, szorzás számmal, koordináták, lineáris függetlenség Feladatok: 1) A koordinátarendszerben úgy helyezzük el az egységkockát, hogy az origó az egyik csúcsba essék,
Vektoralgebrai feladatok
 Vektoralgebrai feladatok 1. Vektorok összeadása és szorzatai, azok alkalmazása 1.1 a) Írja fel a és vektorokat az és átlóvektorok segítségével! b) Milyen hosszú az + ha =1? 1.2 Fejezze ki az alábbi vektorokat
Vektoralgebrai feladatok 1. Vektorok összeadása és szorzatai, azok alkalmazása 1.1 a) Írja fel a és vektorokat az és átlóvektorok segítségével! b) Milyen hosszú az + ha =1? 1.2 Fejezze ki az alábbi vektorokat
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Térgeometria V.
 Térgeometria V. 1. Egy 4, 6 dm átmérőjű, 5 dm magasságú, 7, dm sűrűségű hengerből a lehető legnagyobb szabályos nyolcoldalú oszlopot kell készíteni. Mekkora lesz a tömege? Az oszlop magassága a henger
Térgeometria V. 1. Egy 4, 6 dm átmérőjű, 5 dm magasságú, 7, dm sűrűségű hengerből a lehető legnagyobb szabályos nyolcoldalú oszlopot kell készíteni. Mekkora lesz a tömege? Az oszlop magassága a henger
MBLK12: Relációk és műveletek (levelező) (előadásvázlat) Maróti Miklós, Kátai-Urbán Kamilla
 MBLK12: Relációk és műveletek (levelező) (előadásvázlat) Maróti Miklós, Kátai-Urbán Kamilla Jelölje Z az egész számok halmazát, N a pozitív egészek halmazát, N 0 a nem negatív egészek halmazát, Q a racionális
MBLK12: Relációk és műveletek (levelező) (előadásvázlat) Maróti Miklós, Kátai-Urbán Kamilla Jelölje Z az egész számok halmazát, N a pozitív egészek halmazát, N 0 a nem negatív egészek halmazát, Q a racionális
Országos Középiskolai Tanulmányi Verseny 2011/2012 Matematika I. kategória (SZAKKÖZÉPISKOLA) Döntő. x 3x 2 <
 Oktatási Hivatal Országos Középiskolai Tanulmányi Verseny 011/01 Matematika I. kategória (SZKKÖZÉPISKOL) Döntő 1. Határozza meg az összes olyan egész számot, amely eleget tesz az egyenlőtlenségnek! log
Oktatási Hivatal Országos Középiskolai Tanulmányi Verseny 011/01 Matematika I. kategória (SZKKÖZÉPISKOL) Döntő 1. Határozza meg az összes olyan egész számot, amely eleget tesz az egyenlőtlenségnek! log
Másodrendű felületek
 Azon pontok halmaza a térben, melyek koordinátái kielégítik az egyenletet, ahol feltételezzük, hogy az a, b, c, d, e, f együtthatók egyszerre nem tűnnek el. Minden másodrendű felülethez hozzárendelünk
Azon pontok halmaza a térben, melyek koordinátái kielégítik az egyenletet, ahol feltételezzük, hogy az a, b, c, d, e, f együtthatók egyszerre nem tűnnek el. Minden másodrendű felülethez hozzárendelünk
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló gimnáziuma) Térgeometria III.
 Térgeometria III. 1. Szabályos háromoldalú gúla alapéle 1 cm, oldaléle 1 cm. Milyen magas a gúla? Tekintsük a következő ábrát: Az alaplap szabályos ABC, így a D csúcs merőleges vetülete a háromszög S súlypontja.
Térgeometria III. 1. Szabályos háromoldalú gúla alapéle 1 cm, oldaléle 1 cm. Milyen magas a gúla? Tekintsük a következő ábrát: Az alaplap szabályos ABC, így a D csúcs merőleges vetülete a háromszög S súlypontja.
Egyre nagyobb profitot generálnak a mobiltelefonnal végzett vásárlások, és egyre többet hezitálunk vásárlás előtt
 Egyre nagyobb profitot generálnak a mobiltelefonnal végzett vásárlások, és egyre többet hezitálunk vásárlás előtt 2016 ban még nagyobb hangsúlyt kapnak az e kereskedelmeben az okostelefonok. 2015 ben még
Egyre nagyobb profitot generálnak a mobiltelefonnal végzett vásárlások, és egyre többet hezitálunk vásárlás előtt 2016 ban még nagyobb hangsúlyt kapnak az e kereskedelmeben az okostelefonok. 2015 ben még
Lineáris algebra gyakorlat
 Lineáris algebra gyakorlat 3 gyakorlat Gyakorlatvezet : Bogya Norbert 2012 február 27 Bogya Norbert Lineáris algebra gyakorlat (3 gyakorlat) Tartalom Egyenletrendszerek Cramer-szabály 1 Egyenletrendszerek
Lineáris algebra gyakorlat 3 gyakorlat Gyakorlatvezet : Bogya Norbert 2012 február 27 Bogya Norbert Lineáris algebra gyakorlat (3 gyakorlat) Tartalom Egyenletrendszerek Cramer-szabály 1 Egyenletrendszerek
3. Térvezérlésű tranzisztorok
 1 3. Térvezérlésű tranzisztorok A térvezérlésű tranzisztorok (Field Effect Transistor = FET) működési elve alapjaiban eltér a bipoláris tranzisztoroktól. Az áramvezetés mértéke statikus feszültséggel befolyásolható.
1 3. Térvezérlésű tranzisztorok A térvezérlésű tranzisztorok (Field Effect Transistor = FET) működési elve alapjaiban eltér a bipoláris tranzisztoroktól. Az áramvezetés mértéke statikus feszültséggel befolyásolható.
AUDI A6 4F HANDBUCH DEMONTAGE MITTELKONSOLE UND DEKORLEISTEN
 AUDI A6 4F HANDBUCH DEMONTAGE MITTELKONSOLE UND DEKORLEISTEN AUDI A6 4F 2005-2010 DÍSZÍTŐ ELEMEK SZÉTSZERELÉSE Első körben a középkonzol kerül terítékre. Kezdésképp húzzuk előre a vezető oldali és anyós
AUDI A6 4F HANDBUCH DEMONTAGE MITTELKONSOLE UND DEKORLEISTEN AUDI A6 4F 2005-2010 DÍSZÍTŐ ELEMEK SZÉTSZERELÉSE Első körben a középkonzol kerül terítékre. Kezdésképp húzzuk előre a vezető oldali és anyós
Analízis elo adások. Vajda István. 2012. szeptember 24. Neumann János Informatika Kar Óbudai Egyetem. Vajda István (Óbudai Egyetem)
 Vajda István Neumann János Informatika Kar Óbudai Egyetem 1/8 A halmaz alapfogalom, tehát nem definiáljuk. Jelölés: A halmazokat általában nyomtatott nagybetu vel jelöljük Egy H halmazt akkor tekintünk
Vajda István Neumann János Informatika Kar Óbudai Egyetem 1/8 A halmaz alapfogalom, tehát nem definiáljuk. Jelölés: A halmazokat általában nyomtatott nagybetu vel jelöljük Egy H halmazt akkor tekintünk
Sz ekelyhidi L aszl o Val osz ın us egsz am ıt as es matematikai statisztika *************** Budapest, 1998
 Székelyhidi László Valószínűségszámítás és matematikai statisztika *************** Budapest, 1998 Előszó Ez a jegyzet a valószínűségszámításnak és a matematikai statisztikának azokat a fejezeteit tárgyalja,
Székelyhidi László Valószínűségszámítás és matematikai statisztika *************** Budapest, 1998 Előszó Ez a jegyzet a valószínűségszámításnak és a matematikai statisztikának azokat a fejezeteit tárgyalja,
ORSZÁGOS KÖRNYEZETEGÉSZSÉGÜGYI INTÉZET
 ORSZÁGOS KÖRNYEZETEGÉSZSÉGÜGYI INTÉZET 197 Budapest, Gyáli út 2-6. Levélcím: 1437 Budapest Pf.: 839 Telefon: (6-1) 476-11 Fax: (6-1) 21-148 http://efrirk.antsz.hu/oki/ A PARLAGFŰ POLLENSZÓRÁSÁNAK ALAKULÁSA
ORSZÁGOS KÖRNYEZETEGÉSZSÉGÜGYI INTÉZET 197 Budapest, Gyáli út 2-6. Levélcím: 1437 Budapest Pf.: 839 Telefon: (6-1) 476-11 Fax: (6-1) 21-148 http://efrirk.antsz.hu/oki/ A PARLAGFŰ POLLENSZÓRÁSÁNAK ALAKULÁSA
Adatgyőjtés, mérési alapok, a környezetgazdálkodás fontosabb mőszerei
 GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Adatgyőjtés, mérési
GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Adatgyőjtés, mérési
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
Amit a Hőátbocsátási tényezőről tudni kell
 Amit a Hőátbocsátási tényezőről tudni kell Úton-útfélen mindenki róla beszél, már amikor épületekről van szó. A tervezéskor találkozunk vele először, majd az építkezéstől az épület lakhatási engedélyének
Amit a Hőátbocsátási tényezőről tudni kell Úton-útfélen mindenki róla beszél, már amikor épületekről van szó. A tervezéskor találkozunk vele először, majd az építkezéstől az épület lakhatási engedélyének
Árverés kezelés ECP WEBSHOP BEÉPÜLŐ MODUL ÁRVERÉS KEZELŐ KIEGÉSZÍTÉS. v2.9.28 ECP WEBSHOP V1.8 WEBÁRUHÁZ MODULHOZ
 v2.9.28 Árverés kezelés ECP WEBSHOP BEÉPÜLŐ MODUL ÁRVERÉS KEZELŐ KIEGÉSZÍTÉS ECP WEBSHOP V1.8 WEBÁRUHÁZ MODULHOZ AW STUDIO Nyíregyháza, Luther utca 5. 1/5, info@awstudio.hu Árverés létrehozása Az árverésre
v2.9.28 Árverés kezelés ECP WEBSHOP BEÉPÜLŐ MODUL ÁRVERÉS KEZELŐ KIEGÉSZÍTÉS ECP WEBSHOP V1.8 WEBÁRUHÁZ MODULHOZ AW STUDIO Nyíregyháza, Luther utca 5. 1/5, info@awstudio.hu Árverés létrehozása Az árverésre
Jelölje meg (aláhúzással vagy keretezéssel) Gyakorlatvezetőjét! Györke Gábor Kovács Viktória Barbara Könczöl Sándor. Hőközlés.
 MŰSZAKI HŐTAN II.. ZÁRTHELYI Adja meg az Ön képzési kódját! N Név: Azonosító: Terem Helyszám: K - Jelölje meg (aláhúzással vagy keretezéssel) Gyakorlatvezetőjét! Györke Gábor Kovács Viktória Barbara Könczöl
MŰSZAKI HŐTAN II.. ZÁRTHELYI Adja meg az Ön képzési kódját! N Név: Azonosító: Terem Helyszám: K - Jelölje meg (aláhúzással vagy keretezéssel) Gyakorlatvezetőjét! Györke Gábor Kovács Viktória Barbara Könczöl
Kombinatorika. 9. előadás. Farkas István. DE ATC Gazdaságelemzési és Statisztikai Tanszék. Kombinatorika p. 1/
 Kombinatorika 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Kombinatorika p. 1/ Permutáció Definíció. Adott n különböző elem. Az elemek egy meghatározott sorrendjét az adott
Kombinatorika 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Kombinatorika p. 1/ Permutáció Definíció. Adott n különböző elem. Az elemek egy meghatározott sorrendjét az adott
Oláh Attila. ESRI FlexAPI alapú bevetés irányítási rendszer
 Oláh Attila ESRI FlexAPI alapú bevetés irányítási rendszer A bonyolult helyzetek megkövetelik a modern bevetés irányítást! Ez, pedig ma már szinte elképzelhetetlen az együttműködő szervezetek és azok egységeinek
Oláh Attila ESRI FlexAPI alapú bevetés irányítási rendszer A bonyolult helyzetek megkövetelik a modern bevetés irányítást! Ez, pedig ma már szinte elképzelhetetlen az együttműködő szervezetek és azok egységeinek
Spiel der Türme TORNYOK JÁTÉKA
 Spiel der Türme TORNYOK JÁTÉKA A történet a középkori Tornyok Városával kezdődik. A négy hataloméhes nemesi család mindegyike arra törekszik, hogy megszerezzék a befolyást a legerősebb torony vagy még
Spiel der Türme TORNYOK JÁTÉKA A történet a középkori Tornyok Városával kezdődik. A négy hataloméhes nemesi család mindegyike arra törekszik, hogy megszerezzék a befolyást a legerősebb torony vagy még
avagy, hogyan lehetünk hatékonyabbak (nemcsak) a hivatásunkban
 avagy, hogyan lehetünk hatékonyabbak (nemcsak) a hivatásunkban Rendszerek, amelyekben élünk: Család Munkahely Baráti kör Iskolai közösség stb. - meghatározott rend szerint működnek rend, törv rvények
avagy, hogyan lehetünk hatékonyabbak (nemcsak) a hivatásunkban Rendszerek, amelyekben élünk: Család Munkahely Baráti kör Iskolai közösség stb. - meghatározott rend szerint működnek rend, törv rvények
Koszorúslány katalógus
 Koszorúslány katalógus Egy esküvő a menyasszony legfontosabb napja. Hagyjuk, had gondolják ezt, de mi tudjuk, hogy a koszorúslányok jelentős szerepet vállalnak a lakodalom során. Legfőbb feladatuk a vendégek
Koszorúslány katalógus Egy esküvő a menyasszony legfontosabb napja. Hagyjuk, had gondolják ezt, de mi tudjuk, hogy a koszorúslányok jelentős szerepet vállalnak a lakodalom során. Legfőbb feladatuk a vendégek
Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (13. fejezet)
 Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (3. fejezet). Egy H I = 70 m - 50000 s /m 5 Q jelleggörbéjű szivattyú a H c = 0 m + 0000 s /m 5 Q jelleggörbéjű
Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (3. fejezet). Egy H I = 70 m - 50000 s /m 5 Q jelleggörbéjű szivattyú a H c = 0 m + 0000 s /m 5 Q jelleggörbéjű
Dinamikus geometriai programok
 2011 október 22. Eszköz és médium (fotó: http://sliderulemuseum.com) Enter MTM1007L információ: zeus.nyf.hu/ kovacsz feladatok: moodle.nyf.hu Reform mozgalmak A formális matematikát az életkori sajátosságoknak
2011 október 22. Eszköz és médium (fotó: http://sliderulemuseum.com) Enter MTM1007L információ: zeus.nyf.hu/ kovacsz feladatok: moodle.nyf.hu Reform mozgalmak A formális matematikát az életkori sajátosságoknak
EPER E-KATA integráció
 EPER E-KATA integráció 1. Összhang a Hivatalban A hivatalban használt szoftverek összekapcsolása, integrálása révén az egyes osztályok, nyilvántartások között egyezőség jön létre. Mit is jelent az integráció?
EPER E-KATA integráció 1. Összhang a Hivatalban A hivatalban használt szoftverek összekapcsolása, integrálása révén az egyes osztályok, nyilvántartások között egyezőség jön létre. Mit is jelent az integráció?
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 10 X DETERmINÁNSOk 1 DETERmINÁNS ÉRTELmEZÉSE, TULAJdONSÁGAI A másodrendű determináns értelmezése: A harmadrendű determináns értelmezése és annak első sor szerinti kifejtése: A
KOVÁCS BÉLA, MATEmATIkA I 10 X DETERmINÁNSOk 1 DETERmINÁNS ÉRTELmEZÉSE, TULAJdONSÁGAI A másodrendű determináns értelmezése: A harmadrendű determináns értelmezése és annak első sor szerinti kifejtése: A
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI
 SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 11 KRISTÁLYkÉMIA XI. ATOMOK És IONOK 1. AZ ATOM Az atom az anyag legkisebb olyan része, amely még hordozza a kémiai elem jellegzetességeit. Ezért az ásványtanban
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 11 KRISTÁLYkÉMIA XI. ATOMOK És IONOK 1. AZ ATOM Az atom az anyag legkisebb olyan része, amely még hordozza a kémiai elem jellegzetességeit. Ezért az ásványtanban
ÁR kulcsrakész ÁR lapraszerelt
 Szélesség (cm) 30 Magasság (cm) 85 46 668 Ft 35 395 Ft 49 082 Ft 37 809 Ft 47 769 Ft 36 260 Ft 48 129 Ft 36 620 Ft 48 816 Ft 37 307 Ft 51 070 Ft 39 560 Ft 50 559 Ft 39 050 Ft 51 820 Ft 40 311 Ft 48 989
Szélesség (cm) 30 Magasság (cm) 85 46 668 Ft 35 395 Ft 49 082 Ft 37 809 Ft 47 769 Ft 36 260 Ft 48 129 Ft 36 620 Ft 48 816 Ft 37 307 Ft 51 070 Ft 39 560 Ft 50 559 Ft 39 050 Ft 51 820 Ft 40 311 Ft 48 989
ÁR kulcsrakész ÁR lapraszerelt
 Szélesség (cm) 60 Magasság (cm) 85 44 156 Ft 33 662 Ft 48 153 Ft 37 660 Ft 47 328 Ft 36 363 Ft 48 049 Ft 37 083 Ft 49 423 Ft 38 457 Ft 53 929 Ft 42 964 Ft 52 909 Ft 41 944 Ft 55 430 Ft 44 464 Ft 49 769
Szélesség (cm) 60 Magasság (cm) 85 44 156 Ft 33 662 Ft 48 153 Ft 37 660 Ft 47 328 Ft 36 363 Ft 48 049 Ft 37 083 Ft 49 423 Ft 38 457 Ft 53 929 Ft 42 964 Ft 52 909 Ft 41 944 Ft 55 430 Ft 44 464 Ft 49 769
dr.majoros Mária Kinpán Dániel: Költői művek zeneiségének vizsgálata a hangtan alapján
 dr.majoros Mária Kinpán Dániel: Költői művek zeneiségének vizsgálata a hangtan alapján A kutatásunk arra irányult, hogy megpróbáljunk állítást megfogalmazni azzal kapcsolatban, hogy a hangzás milyen mértékben
dr.majoros Mária Kinpán Dániel: Költői művek zeneiségének vizsgálata a hangtan alapján A kutatásunk arra irányult, hogy megpróbáljunk állítást megfogalmazni azzal kapcsolatban, hogy a hangzás milyen mértékben
O k t a t á si Hivatal
 O k t a t á si Hivatal Kódszám: A 2013/2014. tanévi Országos Középiskolai Tanulmányi Verseny második forduló MŰVÉSZETTÖRTÉNET A FELADATLAP / MŰVÉSZETTÖRTÉNETI TESZT Munkaidő: 120 perc Elérhető pontszám:
O k t a t á si Hivatal Kódszám: A 2013/2014. tanévi Országos Középiskolai Tanulmányi Verseny második forduló MŰVÉSZETTÖRTÉNET A FELADATLAP / MŰVÉSZETTÖRTÉNETI TESZT Munkaidő: 120 perc Elérhető pontszám:
 Októberi fotók Az új nyaralói vasúti megállóhely Szűcs Lajos megyei elnök október 23-i beszéde közben Vermesy Művészeti Napok: a fellépő művészek köszöntése és az iskola kórusa az evangélikus templomban
Októberi fotók Az új nyaralói vasúti megállóhely Szűcs Lajos megyei elnök október 23-i beszéde közben Vermesy Művészeti Napok: a fellépő művészek köszöntése és az iskola kórusa az evangélikus templomban
Reológia 2. Bányai István DE Kolloid- és Környezetkémiai Tanszék
 Reológia 2 Bányai István DE Kolloid- és Környezetkémiai Tanszék Mérése nyomásesés áramlásra p 1 p 2 v=0 folyás csőben z r p 1 p 2 v max I V 1 p p t 8 l 1 2 r 2 x Höppler-típusú viszkoziméter v 2g 9 2 testgömb
Reológia 2 Bányai István DE Kolloid- és Környezetkémiai Tanszék Mérése nyomásesés áramlásra p 1 p 2 v=0 folyás csőben z r p 1 p 2 v max I V 1 p p t 8 l 1 2 r 2 x Höppler-típusú viszkoziméter v 2g 9 2 testgömb
Tolna Megyei Földmérők Napja 2016. Tolna megyei földmérők helyzete a szakmagyakorlási rendelet szerint Németh András TMMK GGT Szakcsoport elnök
 Tolna Megyei Földmérők Napja 2016 Tolna megyei földmérők helyzete a szakmagyakorlási rendelet szerint Németh András TMMK GGT Szakcsoport elnök Földmérők Európai Tanácsa (CLGE) Megyei Földmérő Napok Geodézia
Tolna Megyei Földmérők Napja 2016 Tolna megyei földmérők helyzete a szakmagyakorlási rendelet szerint Németh András TMMK GGT Szakcsoport elnök Földmérők Európai Tanácsa (CLGE) Megyei Földmérő Napok Geodézia
5 pontot, ha az alap-ábrához nem kapcsolódó, azt körülvevő végtag-kezdemények vannak.
 Melléklet Vizuális Narratív Teszt - Értékelési segédlet az 1. sz. itemhez: A figura szerkezete szintek és pontszámok Az értékelés elején keresse meg, hogy a narratív rajzon található emberábrázolások közül
Melléklet Vizuális Narratív Teszt - Értékelési segédlet az 1. sz. itemhez: A figura szerkezete szintek és pontszámok Az értékelés elején keresse meg, hogy a narratív rajzon található emberábrázolások közül
A döntő feladatai. valós számok!
 OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
Számítógépes vírusok
 A vírus fogalma A számítógépes vírus olyan szoftver, mely képes önmaga megsokszorozására és terjesztésére. A vírus célja általában a számítógép rendeltetésszerű működésének megzavarása, esetleg a gép tönkretétele,
A vírus fogalma A számítógépes vírus olyan szoftver, mely képes önmaga megsokszorozására és terjesztésére. A vírus célja általában a számítógép rendeltetésszerű működésének megzavarása, esetleg a gép tönkretétele,
Minta 1. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI FELADATSOR
 1. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI FELADATSOR A feladatok megoldására 240 perc fordítható, az idő leteltével a munkát be kell fejeznie. A feladatok megoldási sorrendje tetszőleges. A II. részben kitűzött
1. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI FELADATSOR A feladatok megoldására 240 perc fordítható, az idő leteltével a munkát be kell fejeznie. A feladatok megoldási sorrendje tetszőleges. A II. részben kitűzött
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria
 005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
118. Szerencsi Többcélú Kistérségi Társulás
 BAZ MTrT TERVEZŐI VÁLASZ 118. Szerencsi Többcélú Kistérségi Társulás 1. Szakmai szempontból elhibázott döntésnek tartjuk a Tokaji Borvidék Világörökségi terület közvetlen környezetében erőmű létesítését.
BAZ MTrT TERVEZŐI VÁLASZ 118. Szerencsi Többcélú Kistérségi Társulás 1. Szakmai szempontból elhibázott döntésnek tartjuk a Tokaji Borvidék Világörökségi terület közvetlen környezetében erőmű létesítését.
Forgómozgás alapjai. Forgómozgás alapjai
 Forgómozgás alapjai Kiterjedt test általános mozgása Kísérlet a forgómozgásra Forgómozgás és haladó mozgás analógiája Merev test általános mozgása Gondolkodtató kérdés Összetett mozgások Egy test általános
Forgómozgás alapjai Kiterjedt test általános mozgása Kísérlet a forgómozgásra Forgómozgás és haladó mozgás analógiája Merev test általános mozgása Gondolkodtató kérdés Összetett mozgások Egy test általános
ÚTMUTATÓ A KONTROLL ADATSZOLGÁLTATÁS ELKÉSZÍTÉSÉHEZ (2012-TŐL)
 ÚTMUTATÓ A KONTROLL ADATSZOLGÁLTATÁS ELKÉSZÍTÉSÉHEZ (2012-TŐL) A 2006-2010. évre vonatkozó, régebbi adatszolgáltatások esetében az adatszolgáltatás menete a mostanitól eltérő, a benyújtáshoz különböző
ÚTMUTATÓ A KONTROLL ADATSZOLGÁLTATÁS ELKÉSZÍTÉSÉHEZ (2012-TŐL) A 2006-2010. évre vonatkozó, régebbi adatszolgáltatások esetében az adatszolgáltatás menete a mostanitól eltérő, a benyújtáshoz különböző
HACK THe PaST! HACKeLD a MÚLTaT! Katharina Roters és Szolnoki József kiállítása
 2016 MÉDIAAJÁNLAT 86 14. évfolyam 2016 / 1 85 1 14. évfolyam 2016 / 2. szám 980 Ft HACK THe PaST! HACKeLD a MÚLTaT! Katharina Roters és Szolnoki József kiállítása Rómer Flóris Muvészeti és Történeti Múzeum,
2016 MÉDIAAJÁNLAT 86 14. évfolyam 2016 / 1 85 1 14. évfolyam 2016 / 2. szám 980 Ft HACK THe PaST! HACKeLD a MÚLTaT! Katharina Roters és Szolnoki József kiállítása Rómer Flóris Muvészeti és Történeti Múzeum,
HWDEV-02A GSM TERMOSZTÁT
 HWDEV-02A GSM TERMOSZTÁT 2010 HASZNÁLATI ÚTMUTATÓ A termosztát egy beépített mobiltelefonnal rendelkezik. Ez fogadja az Ön hívását ha felhívja a termosztát telefonszámát. Érdemes ezt a telefonszámot felírni
HWDEV-02A GSM TERMOSZTÁT 2010 HASZNÁLATI ÚTMUTATÓ A termosztát egy beépített mobiltelefonnal rendelkezik. Ez fogadja az Ön hívását ha felhívja a termosztát telefonszámát. Érdemes ezt a telefonszámot felírni
Pozitron-emissziós tomográf (PET) mire való és hogyan működik?
 Pozitron-emissziós tomográf (PET) mire való és hogyan működik? Major Péter Atomoktól csillagokig, 2011. nov. 10. Vázlat Mi az hogy Tomográf? (fajták, képek) Milyen tomográfok vannak, miért van ennyi? Milyen
Pozitron-emissziós tomográf (PET) mire való és hogyan működik? Major Péter Atomoktól csillagokig, 2011. nov. 10. Vázlat Mi az hogy Tomográf? (fajták, képek) Milyen tomográfok vannak, miért van ennyi? Milyen
Osztályozó és Javító vizsga témakörei matematikából 9. osztály 2. félév
 Osztályozó és Javító vizsga témakörei matematikából 9. osztály 2. félév IV. Háromszögek, négyszögek, sokszögek Pontok, egyenesek, síkok és ezek kölcsönös helyzete Néhány alapvető geometriai fogalom A háromszögekről.
Osztályozó és Javító vizsga témakörei matematikából 9. osztály 2. félév IV. Háromszögek, négyszögek, sokszögek Pontok, egyenesek, síkok és ezek kölcsönös helyzete Néhány alapvető geometriai fogalom A háromszögekről.
Üzembehelyezıi leírás
 Üzembehelyezıi leírás MADE IN ITALY TECHNIKAI ADATOK Falra szerelve Lefedettség 15 m, 90 Mikrohullámú frekvencia 10.525 GHz Jelfeldolgozás DSP(Digital Signal Processing) Érzékelési távolság 3-15 m Érzékelési
Üzembehelyezıi leírás MADE IN ITALY TECHNIKAI ADATOK Falra szerelve Lefedettség 15 m, 90 Mikrohullámú frekvencia 10.525 GHz Jelfeldolgozás DSP(Digital Signal Processing) Érzékelési távolság 3-15 m Érzékelési
MAGYAR NYELV a 4. évfolyamosok számára. MNy2 JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 4. évfolyam MNy2 Javítási-értékelési útmutató MAGYAR NYELV a 4. évfolyamosok számára MNy2 JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A javítási-értékelési útmutatóban feltüntetett válaszokra a megadott pontszámok adhatók.
4. évfolyam MNy2 Javítási-értékelési útmutató MAGYAR NYELV a 4. évfolyamosok számára MNy2 JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A javítási-értékelési útmutatóban feltüntetett válaszokra a megadott pontszámok adhatók.
Pollack Mihály Műszaki és Informatikai Kar. Építészmérnök (BSc) Osztatlan Építész Ipari termék- és formatervező mérnök (BSc) Építőművész (BA)
 Pollack Mihály Műszaki és Informatikai Kar Építészmérnök (BSc) Osztatlan Építész Ipari termék- és formatervező mérnök (BSc) Építőművész (BA) Feladatok: Geometrikus testek ábrázolása Rekonstrukció Beszélgetés
Pollack Mihály Műszaki és Informatikai Kar Építészmérnök (BSc) Osztatlan Építész Ipari termék- és formatervező mérnök (BSc) Építőművész (BA) Feladatok: Geometrikus testek ábrázolása Rekonstrukció Beszélgetés
Azonosító jel: Matematika emelt szint
 I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
IKU WORLD KOCKA Játékszabály. IKU WORLD Gondolkodásfejlesztő Vállalkozás
 NN IKU WORLD KOCKA Játékszabály MAGYAR OLASZ IKU WORLD Gondolkodásfejlesztő Vállalkozás IKU WORLD KOCKA Logikai társasjáték Egy új játék, melyet sokféleképpen lehet használni: kirakójáték, társasjáték,
NN IKU WORLD KOCKA Játékszabály MAGYAR OLASZ IKU WORLD Gondolkodásfejlesztő Vállalkozás IKU WORLD KOCKA Logikai társasjáték Egy új játék, melyet sokféleképpen lehet használni: kirakójáték, társasjáték,
A vizuális képességek rendszere
 A vizuális képességek rendszere Vizuális nevelés tantárgypedagógia Sándor Zsuzsa (animációk nélküli változat a 6-7 éves kisgyerek megdöbbentően jó megfigyelő és emlékező; karakteresen és érzelmi töltettel
A vizuális képességek rendszere Vizuális nevelés tantárgypedagógia Sándor Zsuzsa (animációk nélküli változat a 6-7 éves kisgyerek megdöbbentően jó megfigyelő és emlékező; karakteresen és érzelmi töltettel
Javítóvizsga témakörei matematika tantárgyból
 9.osztály Halmazok: - ismerje és használja a halmazok megadásának különböző módjait, a halmaz elemének fogalmát - halmazműveletek : ismerje és alkalmazza gyakorlati és matematikai feladatokban a következő
9.osztály Halmazok: - ismerje és használja a halmazok megadásának különböző módjait, a halmaz elemének fogalmát - halmazműveletek : ismerje és alkalmazza gyakorlati és matematikai feladatokban a következő
Előre is köszönjük munkádat és izgatottan várjuk válaszaidat! A Helleresek
 A Heller Farkas Szakkollégium 2016-os felvételi kérdőívét tartod a kezedben, amely által megteheted az első lépést a Helleres úton. Az írásbeli kérdőív kitöltése után a felvételi következő lépése egy szóbeli
A Heller Farkas Szakkollégium 2016-os felvételi kérdőívét tartod a kezedben, amely által megteheted az első lépést a Helleres úton. Az írásbeli kérdőív kitöltése után a felvételi következő lépése egy szóbeli
Házi dolgozat. Minta a házi dolgozat formai és tartalmi követelményeihez. Készítette: (név+osztály) Iskola: (az iskola teljes neve)
 Házi dolgozat Minta a házi dolgozat formai és tartalmi követelményeihez Készítette: (név+osztály) Iskola: (az iskola teljes neve) Dátum: (aktuális dátum) Tartalom Itt kezdődik a címbeli anyag érdemi kifejtése...
Házi dolgozat Minta a házi dolgozat formai és tartalmi követelményeihez Készítette: (név+osztály) Iskola: (az iskola teljes neve) Dátum: (aktuális dátum) Tartalom Itt kezdődik a címbeli anyag érdemi kifejtése...
Baka Endre. Szabadka, Jugoszlávia
 ÉRDEKESSÉGEK HÁROMSZÖGEN aka Ende Szabadka, Jugoszlávia LPPONI HÁROMSZÖG Ebben a fejezetben kettő, a talpponti háomszöggel kapsolatos, nem túl ismet tételt szeetnék bemutatni és bizonyítani. De előszö
ÉRDEKESSÉGEK HÁROMSZÖGEN aka Ende Szabadka, Jugoszlávia LPPONI HÁROMSZÖG Ebben a fejezetben kettő, a talpponti háomszöggel kapsolatos, nem túl ismet tételt szeetnék bemutatni és bizonyítani. De előszö
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 12 XII. STATIsZTIKA ellenőrző feladatsorok 1. FELADATsOR Megoldások: láthatók nem láthatók 1. minta: 6.10, 0.01, 6.97, 6.03, 3.85, 1.11,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 12 XII. STATIsZTIKA ellenőrző feladatsorok 1. FELADATsOR Megoldások: láthatók nem láthatók 1. minta: 6.10, 0.01, 6.97, 6.03, 3.85, 1.11,
Analízis elo adások. Vajda István. 2012. október 3. Neumann János Informatika Kar Óbudai Egyetem. Vajda István (Óbudai Egyetem)
 Vajda István Neumann János Informatika Kar Óbudai Egyetem / 40 Fogalmak A függvények értelmezése Definíció: Az (A, B ; R ) bináris relációt függvénynek nevezzük, ha bármely a A -hoz pontosan egy olyan
Vajda István Neumann János Informatika Kar Óbudai Egyetem / 40 Fogalmak A függvények értelmezése Definíció: Az (A, B ; R ) bináris relációt függvénynek nevezzük, ha bármely a A -hoz pontosan egy olyan
MATEMATIKA PRÓBAÉRETTSÉGI MEGOLDÓKULCS EMELT SZINT
 Matematika PRÉ megoldókulcs 0. január. MTEMTIK PRÓBÉRETTSÉGI MEGOLDÓKULCS EMELT SZINT ) dottak a 0; ; ; ; ; ; 5; 7; 7; 8 számjegyek. Hány darab tízjegyű, 5-tel osztható szám készíthető az adott számjegyekből
Matematika PRÉ megoldókulcs 0. január. MTEMTIK PRÓBÉRETTSÉGI MEGOLDÓKULCS EMELT SZINT ) dottak a 0; ; ; ; ; ; 5; 7; 7; 8 számjegyek. Hány darab tízjegyű, 5-tel osztható szám készíthető az adott számjegyekből
Országos kompetenciamérés 2006
 Országos kompetenciamérés 2006 A SULINOVA Kht. jelentései alapján összeállította: Kovács Károly A tesztek alapvetı statisztikai jellemzıi, valamint a tesztfüzetek feladatai és azok jellemzıit bemutató
Országos kompetenciamérés 2006 A SULINOVA Kht. jelentései alapján összeállította: Kovács Károly A tesztek alapvetı statisztikai jellemzıi, valamint a tesztfüzetek feladatai és azok jellemzıit bemutató
Kép részlet kivágás útvonalak létrehozása és szerkesztése útvonalak kijelöléssé alakítása Kijelölés > Lágy szél
 Kép részlet kivágás 2. Az útvonalak létrehozása és szerkesztése eszközzel rajzoljuk körbe a kijelölésre szánt részt 3. Az Útvonalak palettán kattintsunk az útvonalak kijelöléssé alakítása gomra. 4. Most
Kép részlet kivágás 2. Az útvonalak létrehozása és szerkesztése eszközzel rajzoljuk körbe a kijelölésre szánt részt 3. Az Útvonalak palettán kattintsunk az útvonalak kijelöléssé alakítása gomra. 4. Most
Kiskunmajsa Város Önkormányzatának partnertérképe
 Kiskunmajsa Város Önkormányzatának partnertérképe Kiskunmajsa Város Önkormányzatának potenciális partnerei Helyi vállalkozások Kiskunmajsa Város Önkormányzata számára a lehetséges vállalati partnerek feltérképezéséhez
Kiskunmajsa Város Önkormányzatának partnertérképe Kiskunmajsa Város Önkormányzatának potenciális partnerei Helyi vállalkozások Kiskunmajsa Város Önkormányzata számára a lehetséges vállalati partnerek feltérképezéséhez
Bevezetés a lágy számítás módszereibe
 BLSZM-07 p. 1/10 Bevezetés a lágy számítás módszereibe Nem fuzzy halmaz kimenetű fuzzy irányítási rendszerek Egy víztisztító berendezés szabályozását megvalósító modell Viselkedésijósló tervezési példa
BLSZM-07 p. 1/10 Bevezetés a lágy számítás módszereibe Nem fuzzy halmaz kimenetű fuzzy irányítási rendszerek Egy víztisztító berendezés szabályozását megvalósító modell Viselkedésijósló tervezési példa
Trigonometria és koordináta geometria
 Tantárgy neve Trigonometria és koordináta geometria Tantárgy kódja MTB1001 Meghirdetés féléve I. Kreditpont 4k Összóraszám (elm+gyak) 30+30 Számonkérés módja Gyakorlati jegy (2 zárthelyi dolgozat) Előfeltétel
Tantárgy neve Trigonometria és koordináta geometria Tantárgy kódja MTB1001 Meghirdetés féléve I. Kreditpont 4k Összóraszám (elm+gyak) 30+30 Számonkérés módja Gyakorlati jegy (2 zárthelyi dolgozat) Előfeltétel
A történelem viharai a Délvidéken ahogy én megéltem
 A történelem viharai a Délvidéken ahogy én megéltem Dr. Koppány György elıadása A képen elıadónk látható nıvére (és egy nyuszi) társaságában a bajmoki szülıi ház kertjében 1939-ben. 2012. szept. 28. 16.00-17.00
A történelem viharai a Délvidéken ahogy én megéltem Dr. Koppány György elıadása A képen elıadónk látható nıvére (és egy nyuszi) társaságában a bajmoki szülıi ház kertjében 1939-ben. 2012. szept. 28. 16.00-17.00
Lécgerenda. 1. ábra. 2. ábra
 Lécgerenda Egy korábbi dolgozatunkban melynek címe: Karimás csőillesztés már szóltunk arról, hogy a szeezetek számításaiban néha célszerű lehet a diszkrét mennyiségeket folyto - nosan megoszló mennyiségekkel
Lécgerenda Egy korábbi dolgozatunkban melynek címe: Karimás csőillesztés már szóltunk arról, hogy a szeezetek számításaiban néha célszerű lehet a diszkrét mennyiségeket folyto - nosan megoszló mennyiségekkel
tartalmi szabályozók eredményesebb
 Rövid távú, átmeneti intézkedések a tartalmi szabályozók eredményesebb alkalmazására Konkrét javaslatok 1. NAT és a kerettanterv heti összóraszámainak harmonizációja 2. Kerettantervek helyi alkalmazásának
Rövid távú, átmeneti intézkedések a tartalmi szabályozók eredményesebb alkalmazására Konkrét javaslatok 1. NAT és a kerettanterv heti összóraszámainak harmonizációja 2. Kerettantervek helyi alkalmazásának
G Szabályfelismerés 2.2. 2. feladatcsomag
 ÖSSZEFÜÉSEK Szabályfelismerés 2.2 Alapfeladat Szabályfelismerés 2. feladatcsomag összefüggés-felismerő képesség fejlesztése szabályfelismeréssel megkezdett sorozat folytatása a felismert szabály alapján
ÖSSZEFÜÉSEK Szabályfelismerés 2.2 Alapfeladat Szabályfelismerés 2. feladatcsomag összefüggés-felismerő képesség fejlesztése szabályfelismeréssel megkezdett sorozat folytatása a felismert szabály alapján
Kérdések és feladatok
 Kérdések és feladatok 1. A mesében több szám is szerepel. Próbáld meg felidézni ezeket, majd töltsd ki a táblázatot! Ügyelj, hogy a páros és a páratlan számok külön oszlopba kerüljenek! Hány napos volt
Kérdések és feladatok 1. A mesében több szám is szerepel. Próbáld meg felidézni ezeket, majd töltsd ki a táblázatot! Ügyelj, hogy a páros és a páratlan számok külön oszlopba kerüljenek! Hány napos volt
Nagyméretű dokumentumok hivatkozásai
 Nagyméretű dokumentumok hivatkozásai Tartalomjegyzék: Címsorok olyan jegyzéke, melyben a címsorok dokumentumbeli elhelyezkedésük sorrendjében szerepelnek a dokumentumbeli oldalszámukkal együtt, vagy nélkülük.
Nagyméretű dokumentumok hivatkozásai Tartalomjegyzék: Címsorok olyan jegyzéke, melyben a címsorok dokumentumbeli elhelyezkedésük sorrendjében szerepelnek a dokumentumbeli oldalszámukkal együtt, vagy nélkülük.
2011. március 9. Dr. Vincze Szilvia
 . márius 9. Dr. Vinze Szilvia Tartalomjegyzék.) Elemi bázistranszformáió.) Elemi bázistranszformáió alkalmazásai.) Lineáris függőség/függetlenség meghatározása.) Kompatibilitás vizsgálata.) Mátri/vektorrendszer
. márius 9. Dr. Vinze Szilvia Tartalomjegyzék.) Elemi bázistranszformáió.) Elemi bázistranszformáió alkalmazásai.) Lineáris függőség/függetlenség meghatározása.) Kompatibilitás vizsgálata.) Mátri/vektorrendszer
