Hogyan folyik a szemcsés anyag?
|
|
|
- Nóra Gulyás
- 5 évvel ezelőtt
- Látták:
Átírás
1 Hogyan folyik a szemcsés anyag? Börzsönyi Tamás MTA WIGNER FK SZFI, Komplex folyadékok osztály
2 Hogyan folyik a szemcsés anyag? - A szemcsés anyag reológiája - A terhelésnek kitett anyag deformációja (nyírási lokalizáció) - Anizometrikus részecskék nyírási orientációja
3 Szemcsés anyagok reológiája Long range desert group R.A. Bagnold: The physics of blown sand and desert dunes, London, Methuen (1941)
4 Szemcsés anyagok reológiája Long range desert group R.A. Bagnold: The physics of blown sand and desert dunes, London, Methuen (1941) 2 Bagnold (1954): ( ) sebességkülönbség ütközések gyakorisága Folyadékok viszkozitása Nyírási ráta: Viszkozitás: dv x dz F A z 0 dz z x
5 Szemcsés anyagok reológiája Long range desert group R.A. Bagnold: The physics of blown sand and desert dunes, London, Methuen (1941) 2 Bagnold (1954): ( ) 3/ 2 u h
6 Szemcsés anyagok reológiája Long range desert group R.A. Bagnold: The physics of blown sand and desert dunes, London, Methuen (1941) 2 Bagnold (1954): ( ) 3/ 2 u h Flow rule for dense granular flows: u gh h h s Y. Forterre and O. Pouliquen J. Fluid Mech. 486, (2003).
7 Szemcsés anyagok reológiája Long range desert group R.A. Bagnold: The physics of blown sand and desert dunes, London, Methuen (1941) 2 Bagnold (1954): ( ) sand, glass beads, and 4 copper samples Flow rule for dense granular flows: u gh h h s Y. Forterre and O. Pouliquen J. Fluid Mech. 486, (2003). T. Börzsönyi and R.E. Ecke, Flow rule of dense granular flows on a rough incline, Phys. Rev. E (2007)
8 Szemcsés anyagok reológiája Long range desert group R.A. Bagnold: The physics of blown sand and desert dunes, London, Methuen (1941) 2 Bagnold (1954): ( ) Flow rule for dense granular flows: u gh h h s eff P Y. Forterre and O. Pouliquen J. Fluid Mech. 486, (2003). Inerciális szám: (dimenziótlan nyírási ráta)
9 Áramlási instabilitás T. Börzsönyi, R.E. Ecke and J.N. McElwaine, Patterns in flowing sand: understanding the physics of granular flows Phys. Rev. Lett. 103, (2009).
10 Áramlási instabilitás T. Börzsönyi, R.E. Ecke and J.N. McElwaine, Patterns in flowing sand: understanding the physics of granular flows Phys. Rev. Lett. 103, (2009). Magasságprofilok Mintázat átmenő fényben A filmfelvétel itt megtalálható: o 42.6 Felvétel: 4000 f/s Lejátszás: 20 f/s
11 Numerikus szimuláció: Jim McElwaine DAMTP, Cambridge T. Börzsönyi, R.E. Ecke and J.N. McElwaine, Patterns in flowing sand: understanding the physics of granular flows Phys. Rev. Lett. 103, (2009). A filmfelvétel itt megtalálható: o 42.6 Felvétel: 4000 f/s Lejátszás: 20 f/s
12 Numerikus szimuláció: Jim McElwaine DAMTP, Cambridge T. Börzsönyi, R.E. Ecke and J.N. McElwaine, Patterns in flowing sand: understanding the physics of granular flows Phys. Rev. Lett. 103, (2009). A filmfelvétel itt megtalálható: o 42.6 Felvétel: 4000 f/s Lejátszás: 20 f/s eff P
13 Nyírási lokalizáció szemcsés anyagokban
14 Nyírási lokalizáció homogén szemcsés anyagokban A szemcsés anyagot a határoló fal mozgatásával deformáljuk. A deformáció lokalizálódik, így alakul ki a nyírási zóna (piros vonal). felülnézet: (korund mákszemekkel) korund szemcsék
15 Nyírási lokalizáció rétegzett szemcsés anyagokban Homogén anyagban Börzsönyi et al. Phys. Rev. E 2009 Soft Matter 2011 A zóna hamar kimegy a nagy súrlódású részből és a kis súrlódású részben jön a felszínre. Ez az optimális útvonal hasonló elv szerint alakul ki, mint a fénysugár útja inhomogén optikai közegben. eff Pds min. Optika: Fermat elv eff ds min. nds min. eff sin 1 eff sin sin n 2 1 sin n 2 MD szimuláció Unger T., Phys. Rev. Lett kis súrlódás nagy súrlódás
16 Nyírási lokalizáció inhomogén (rétegzett) szemcsés anyagokban Színezett mintát használva a mérés elvégzése után láthatóvá válik a kialakult deformáció. korund színezett üveggolyók színezett korund üveggolyók üveggolyók színezett korund Börzsönyi et al. Phys. Rev. E 2009 Soft Matter 2011 korund színezett üveggolyók
17 A kialakult elmozdulásprofil látható a felszínen Szimuláció Unger Tamás, BME eff P ds min.
18 Teljesül-e az optikából ismert Snellius-Descartes törvény? sin sin eff corundum eff glass Becslés eff corundum eff glass értékére a rézsűszögek mérésével: eff corundum eff glass tanr tan corundum glass r tan 33.2 tan 21.9 o o 1.63 T. Börzsönyi, T. Unger and B. Szabó, Shear zone refraction and deflection in layered granular materials, Phys. Rev. E Rapid Comm. (2009). T. Börzsönyi, B. Szabó, T.Unger, S. Wegner, F. Angenstein and R. Stannarius Reflection and exclusion of shear zones in inhomogeneous granular materials, Soft Matter (2011)
19 Elnyújtott alakú részecskék folyása különböző méretskálákon fatörzsek a folyón mezőgazdaság baktériumok nanorudak, nanohuzalok vírusok nematikus folyadékkristályok MBBA molekula
20 Nematikus folyadékkristályok folyási orientációja Az orientációs szög egy anyagi paraméter, nem függ a nyírási rátától, de szisztematiusan csökken a rendezettség növekedésével. Az anyag viszkozitása jelentősen (~50%) csökken a folyási orientáció következtében
21 Szemcsés anyagok: nyírási orientáció egyenes cellában felülnézet
22 Hengeres elrendezésű nyíró áramlás elnyújtott alakú részecskék Mozi (felülnézet) (rizs: L/D = 3.4) - rizs: L/D = 2.0, 3.4, üveg rudak: L/D = , - fa rudak: L/D = 2.0, 3.3, 5.0 Kísérletek: BT, Törös Gábor, Szabó Balázs
23 Hengeres elrendezésű nyíró áramlás elnyújtott alakú részecskék Mozi (felülnézet) (long grain rice: L/D = 3.4) T. Börzsönyi, B. Szabó, G. Törös, S. Wegner, J. Török, E. Somfai, T. Bien and R. Stannarius, Phys. Rev. Lett. (2012) S. Wegner, T. Börzsönyi, T. Bien, G. Rose and R. Stannarius, Soft Matter (2012) T. Börzsönyi, B. Szabó, S. Wegner, K. Harth, J. Török, E. Somfai, T. Bien and R. Stannarius, Phys. Rev. E (2012) T. Börzsönyi and R. Stannarius, Soft Matter (2013)
24 Átlagos orientáció iránya és a rendezettség mértéke a nyírási ráta függvényében. N n ij n j n i ij l l N T 1 ) ( ) ( ) 3 1 ( 2 3 S = T legnagyobb sajátértéke egytengelyű eset: 3 1 cos S av nem függ a nyírási ráta () értékétől
25 Átlagos orientáció iránya és a rendezettség mértéke a L/d és S függvényében. av nem függ a nyírási ráta () értékétől av csökken L/d növelésével av csökken S növekedésével
26 Átlagos orientáció iránya és a rendezettség mértéke a L/d és S függvényében. av nem függ a nyírási ráta () értékétől av csökken L/d növelésével
27 MD szimlációk Török János (BME)
28 Az egyes részecskék dinamikája Kemény ellipszoid folyadékban Jeffery, 1922 D. Das L/D=3.4
29 Az egyes részecskék dinamikája Kemény ellipszoid folyadékban Jeffery, 1922 D. Das L/D=3.4
30 Mekkorora erő (forgatónyomaték) szükséges a rendszer nyírásához? Hogyan változik a rendszer ellenállása (súrlódása) a rendeződés hatására? M M stat e / T
31 Folyási jelenségek szemcsés anyagokban MTA WIGNER FK SZFI, Komplex reológia, mintázatok Börzsönyi et al. Phys. Rev. Lett Réteges szerkezetű szemcsés anyag deformációja Snellius-Descartes törvény: sin sin eff 1 eff 2 eff P ds min. Börzsönyi et al. Phys. Rev. E 2009 Soft Matter 2011 Elnyújtott részecskék folyási orientációja Börzsönyi et al. Phys. Rev. Lett. 2012, Phys. Rev. E 2012, Börzsönyi & Stannarius. Soft Matter 2013, S. Wegner et al. Soft Matter 2012, 2014 Együttműködők: Szabó Balázs, Törös Gábor, Török János, Somfai Ellák, Unger Tamás Sandra Wegner, Kirsten Harth, Georg Rose, Ralf Stannarius, Jim McElwaine Támogatók: OTKA, MTA (Bolyai Ösztöndíj), MÖB-DAAD
Nyírási lokalizáció és rendeződés szemcsés anyagokban (munkabeszámoló) Szabó Balázs
 Nyírási lokalizáció és rendeződés szemcsés anyagokban (munkabeszámoló) Szabó Balázs fiatal kutató, MTA Wigner FK, SZFI Komplex Folyadékok Osztály, Részben Rendezett Rendszerek Csoport 2010. szeptember
Nyírási lokalizáció és rendeződés szemcsés anyagokban (munkabeszámoló) Szabó Balázs fiatal kutató, MTA Wigner FK, SZFI Komplex Folyadékok Osztály, Részben Rendezett Rendszerek Csoport 2010. szeptember
Nyírási lokalizáció kialakulása szemcsés anyagokban (munkabeszámoló) Szabó Balázs
 Nyírási lokalizáció kialakulása szemcsés anyagokban (munkabeszámoló) Szabó Balázs tudományos segédmunkatárs, MTA Wigner FK, SZFI Komplex Folyadékok Osztály, Részben Rendezett Rendszerek Csoport 2013. júniustól
Nyírási lokalizáció kialakulása szemcsés anyagokban (munkabeszámoló) Szabó Balázs tudományos segédmunkatárs, MTA Wigner FK, SZFI Komplex Folyadékok Osztály, Részben Rendezett Rendszerek Csoport 2013. júniustól
Cím: Szemcsés anyagok dinamikai folyamatainak kísérleti vizsgálata Témavezető: Börzsönyi Tamás
 Zárójelentés OTKA F-060157 sz. kutatási pályázat Cím: Szemcsés anyagok dinamikai folyamatainak kísérleti vizsgálata Témavezető: Börzsönyi Tamás A kutatás célja a szemcsés anyagok dinamikájának jobb megértése
Zárójelentés OTKA F-060157 sz. kutatási pályázat Cím: Szemcsés anyagok dinamikai folyamatainak kísérleti vizsgálata Témavezető: Börzsönyi Tamás A kutatás célja a szemcsés anyagok dinamikájának jobb megértése
Kvázisztatikus határeset Kritikus állapot Couette-teszt
 Wacha András Kvázisztatikus határeset Kritikus állapot Couette-teszt 2006. november 9. Kvázisztatikus határeset GDR_MiDi. On dense granular flows. Eur. Phys. J. E 14. pp 341-365 (2004). Dimenziótlan paraméterek
Wacha András Kvázisztatikus határeset Kritikus állapot Couette-teszt 2006. november 9. Kvázisztatikus határeset GDR_MiDi. On dense granular flows. Eur. Phys. J. E 14. pp 341-365 (2004). Dimenziótlan paraméterek
ELNYÚJTOTT ALAKÚ RÉSZECSKÉK RENDEZÕDÉSE NYÍRÓ ÁRAMLÁSBAN
 nuszt, és rendezik át a bolygó plazmakörnyezetét. Vech és munkatársai [12] szisztematikusan izsgálták a VEX ûrszonda plazma- és mágneses méréseinek segítségéel a CME-k hatását a különbözõ plazmarégiókra.
nuszt, és rendezik át a bolygó plazmakörnyezetét. Vech és munkatársai [12] szisztematikusan izsgálták a VEX ûrszonda plazma- és mágneses méréseinek segítségéel a CME-k hatását a különbözõ plazmarégiókra.
Reológia Mérési technikák
 Reológia Mérési technikák Reológia Testek (és folyadékok) külső erőhatásra bekövetkező deformációját, mozgását írja le. A deformációt irreverzibilisnek nevezzük, ha a az erőhatás megszűnése után a test
Reológia Mérési technikák Reológia Testek (és folyadékok) külső erőhatásra bekövetkező deformációját, mozgását írja le. A deformációt irreverzibilisnek nevezzük, ha a az erőhatás megszűnése után a test
Optika gyakorlat 2. Geometriai optika: planparalel lemez, prizma, hullámvezető
 Optika gyakorlat. Geometriai optika: planparalel lemez, prizma, hullámvezető. példa: Fényterjedés planparalel lemezen keresztül A plánparalel lemezen történő fényterjedés hatására a fénysugár újta távolsággal
Optika gyakorlat. Geometriai optika: planparalel lemez, prizma, hullámvezető. példa: Fényterjedés planparalel lemezen keresztül A plánparalel lemezen történő fényterjedés hatására a fénysugár újta távolsággal
Fogorvosi anyagtan fizikai alapjai 2.
 Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Folyadékok, szilárd anyagok, folyadékkristályok Kiemelt témák: Viszkozitás Víz és nyál Kristályok - apatit Polimorfizmus Kristályhibák
Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Folyadékok, szilárd anyagok, folyadékkristályok Kiemelt témák: Viszkozitás Víz és nyál Kristályok - apatit Polimorfizmus Kristályhibák
Modern Fizika Labor. 17. Folyadékkristályok
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 11. A mérés száma és címe: 17. Folyadékkristályok Értékelés: A beadás dátuma: 2011. okt. 23. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 11. A mérés száma és címe: 17. Folyadékkristályok Értékelés: A beadás dátuma: 2011. okt. 23. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Fázisátalakulások, avagy az anyag ezer arca. Sasvári László ELTE Fizikai Intézet ELTE Bolyai Kollégium
 Fázisátalakulások, avagy az anyag ezer arca Sasvári László ELTE Fizikai Intézet ELTE Bolyai Kollégium Atomoktól a csillagokig, Budapest, 2016. december 8. Fázisátalakulások Csak kondenzált anyag? A kondenzált
Fázisátalakulások, avagy az anyag ezer arca Sasvári László ELTE Fizikai Intézet ELTE Bolyai Kollégium Atomoktól a csillagokig, Budapest, 2016. december 8. Fázisátalakulások Csak kondenzált anyag? A kondenzált
Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Molekulák, folyadékok, szilárd anyagok, folyadékkristályok
 Molekulák energiaállapotai E molekula E elektron E (A tankönyvben nem található téma!) vibráció E rotáció pl. vibráció 1 ev 0,1 ev 0,01 ev Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti
Molekulák energiaállapotai E molekula E elektron E (A tankönyvben nem található téma!) vibráció E rotáció pl. vibráció 1 ev 0,1 ev 0,01 ev Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti
Optika és Relativitáselmélet
 Optika és Relativitáselmélet II. BsC fizikus hallgatóknak 9. Szivárvány, korona és a glória Cserti József, jegyzet, ELTE, 2007. Fı- és mellékszivárvány Fı- és mellékszivárvány Horváth Ákos felvételei Fı-
Optika és Relativitáselmélet II. BsC fizikus hallgatóknak 9. Szivárvány, korona és a glória Cserti József, jegyzet, ELTE, 2007. Fı- és mellékszivárvány Fı- és mellékszivárvány Horváth Ákos felvételei Fı-
Keménységmérés diszkrét elemes (DEM) modellezése
 Szilikátipari Tudományos Egyesület Diplomadíj pályázat Budapest, 2016. május 11. Keménységmérés diszkrét elemes (DEM) modellezése Gyurkó Zoltán BME Építőanyagok és Magasépítés Tanszék Dr. Borosnyói Adorján
Szilikátipari Tudományos Egyesület Diplomadíj pályázat Budapest, 2016. május 11. Keménységmérés diszkrét elemes (DEM) modellezése Gyurkó Zoltán BME Építőanyagok és Magasépítés Tanszék Dr. Borosnyói Adorján
Reológia, a koherens rendszerek tulajdonságai
 Reológia, a koherens rendszerek tulajdonságai Bányai István http://dragon.unideb.hu/~kolloid/ Koherens rendszerek Szubmikroszkópos vagy durva diszkontinuitásokat tartalmazó rendszerek, amelyekben micellák,
Reológia, a koherens rendszerek tulajdonságai Bányai István http://dragon.unideb.hu/~kolloid/ Koherens rendszerek Szubmikroszkópos vagy durva diszkontinuitásokat tartalmazó rendszerek, amelyekben micellák,
OPTIKA. Ma sok mindenre fény derül! /Geometriai optika alapjai/ Dr. Seres István
 Ma sok mindenre fény derül! / alapjai/ Dr. Seres István Legkisebb idő Fermat elve A fény a legrövidebb idejű pályán mozog. I. következmény: A fény a homogén közegben egyenes vonalban terjed t s c minimális,
Ma sok mindenre fény derül! / alapjai/ Dr. Seres István Legkisebb idő Fermat elve A fény a legrövidebb idejű pályán mozog. I. következmény: A fény a homogén közegben egyenes vonalban terjed t s c minimális,
Folyadékok. Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Folyadékok, szilárd anyagok, folyadékkristályok.
 Folyadékok folyékony szilárd Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Folyadékok, szilárd anyagok, folyadékkristályok Kiemelt témák: Viszkozitás Apatit Kristályhibák és
Folyadékok folyékony szilárd Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Folyadékok, szilárd anyagok, folyadékkristályok Kiemelt témák: Viszkozitás Apatit Kristályhibák és
HATÁRRÉTEG ÁRAMLÁS LEJTŐN
 Miskolci Egyetem, Multidiszciplináris tudományok, 1. kötet (011) 1. szám, pp. 111-118. HATÁRRÉTEG ÁRAMLÁS LEJTŐN Vadászné Bognár Gabriella, Hriczó Krisztián egyetemi docens, doktorandusz hallgató Miskolci
Miskolci Egyetem, Multidiszciplináris tudományok, 1. kötet (011) 1. szám, pp. 111-118. HATÁRRÉTEG ÁRAMLÁS LEJTŐN Vadászné Bognár Gabriella, Hriczó Krisztián egyetemi docens, doktorandusz hallgató Miskolci
Molekuláris dinamika I. 10. előadás
 Molekuláris dinamika I. 10. előadás Miről is szól a MD? nagy részecskeszámú rendszerek ismerjük a törvényeket mikroszkópikus szinten minden részecske mozgását szimuláljuk? Hogyan tudjuk megérteni a folyadékok,
Molekuláris dinamika I. 10. előadás Miről is szól a MD? nagy részecskeszámú rendszerek ismerjük a törvényeket mikroszkópikus szinten minden részecske mozgását szimuláljuk? Hogyan tudjuk megérteni a folyadékok,
5. gy. VIZES OLDATOK VISZKOZITÁSÁNAK MÉRÉSE OSTWALD-FENSKE-FÉLE VISZKOZIMÉTERREL
 5. gy. VIZES OLDAOK VISZKOZIÁSÁNAK MÉRÉSE OSWALD-FENSKE-FÉLE VISZKOZIMÉERREL A fluid közegek jellemző anyagi tulajdonsága a viszkozitás, mely erősen befolyásolhatja a bennük lejátszódó reakciók sebességét,
5. gy. VIZES OLDAOK VISZKOZIÁSÁNAK MÉRÉSE OSWALD-FENSKE-FÉLE VISZKOZIMÉERREL A fluid közegek jellemző anyagi tulajdonsága a viszkozitás, mely erősen befolyásolhatja a bennük lejátszódó reakciók sebességét,
Felületi feszültség: cseppfolyós-gáz határfelületen a vonzerő kiegyensúlyozatlan: rugalmas hártyaként viselkedik.
 Felületi feszültség: cseppfolyós-gáz határfelületen a vonzerő kiegyensúlyozatlan: rugalmas hártyaként viselkedik. Mérése: L huzalkeret folyadékhártya mozgatható huzal F F = L σ két oldala van a hártyának
Felületi feszültség: cseppfolyós-gáz határfelületen a vonzerő kiegyensúlyozatlan: rugalmas hártyaként viselkedik. Mérése: L huzalkeret folyadékhártya mozgatható huzal F F = L σ két oldala van a hártyának
Statikus és dinamikus struktúrák jellemzése szemcsés anyagokban
 Statikus és dinamikus struktúrák jellemzése szemcsés anyagokban PhD tézisfüzet Unger Tamás Témavezető: Dr. Kertész János MTA lev. tagja Elméleti Fizika Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem
Statikus és dinamikus struktúrák jellemzése szemcsés anyagokban PhD tézisfüzet Unger Tamás Témavezető: Dr. Kertész János MTA lev. tagja Elméleti Fizika Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem
Folyadékok. Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Folyadékok, szilárd anyagok, folyadékkristályok
 Folyadékok víz Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Folyadékok, szilárd anyagok, folyadékkristályok 1 saját térfogat nincs saját alak/folyékony nincsenek belső nyíróerők
Folyadékok víz Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Folyadékok, szilárd anyagok, folyadékkristályok 1 saját térfogat nincs saját alak/folyékony nincsenek belső nyíróerők
Diplomamunkám felépítése
 Üregek távolhatása gránitos kőzetkörnyezetben Tóth Szilvia Konzulensek: Dr. Török Ákos, BME Építőanyagok és Mérnökgeológia Tanszék Poromb Péter, Mott MacDonald Magyarország Kft. Diplomamunkám felépítése
Üregek távolhatása gránitos kőzetkörnyezetben Tóth Szilvia Konzulensek: Dr. Török Ákos, BME Építőanyagok és Mérnökgeológia Tanszék Poromb Péter, Mott MacDonald Magyarország Kft. Diplomamunkám felépítése
Vázlatos tartalom. Szerkezet jellemzése és vizsgálata Szilárdtestek elektronszerkezete Rácsdinamika Transzportjelenségek Mágneses tulajdonságok
 Szilárdtestfizika Kondenzált Anyagok Fizikája Vázlatos tartalom Szerkezet jellemzése és vizsgálata Szilárdtestek elektronszerkezete Rácsdinamika Transzportjelenségek Mágneses tulajdonságok 2 Szerkezet
Szilárdtestfizika Kondenzált Anyagok Fizikája Vázlatos tartalom Szerkezet jellemzése és vizsgálata Szilárdtestek elektronszerkezete Rácsdinamika Transzportjelenségek Mágneses tulajdonságok 2 Szerkezet
egyetemi tanár Nyugat-Magyarországi Egyetem
 egyetemi tanár Nyugat-Magyarországi Egyetem Folyadékok szerkezeti jellemz i Az el adás témakörei: Mit nevezünk folyadéknak? - részecskék kölcsönhatása, rendezettsége - mechanikai viselkedése alapján A
egyetemi tanár Nyugat-Magyarországi Egyetem Folyadékok szerkezeti jellemz i Az el adás témakörei: Mit nevezünk folyadéknak? - részecskék kölcsönhatása, rendezettsége - mechanikai viselkedése alapján A
V. Moldex3D Szeminárium - econ Felhasználói Találkozó
 V. Moldex3D Szeminárium - econ Felhasználói Találkozó A Moldex3D szerepe a minőségi termékgyártásban Dr. Molnár László econ Engineering Kft 2 econ Engineering Kft. High quality in CAE Cégadatok: Alapítás
V. Moldex3D Szeminárium - econ Felhasználói Találkozó A Moldex3D szerepe a minőségi termékgyártásban Dr. Molnár László econ Engineering Kft 2 econ Engineering Kft. High quality in CAE Cégadatok: Alapítás
Ejtési teszt modellezése a tervezés fázisában
 Antal Dániel, doktorandusz, Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szabó Tamás, egyetemi docens, Ph.D., Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szilágyi Attila, egyetemi adjunktus,
Antal Dániel, doktorandusz, Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szabó Tamás, egyetemi docens, Ph.D., Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szilágyi Attila, egyetemi adjunktus,
Polimerek reológiája
 SZÉCHENYI ISTVÁN EGYETEM ANYAGTUDOMÁNYI ÉS TECHNOLÓGIAI TANSZÉK POLIMERTECHNIKA NGB_AJ050_1 Polimerek reológiája DR Hargitai Hajnalka REOLÓGIA Az anyag deformációjának és folyásának a tudománya. rheo -
SZÉCHENYI ISTVÁN EGYETEM ANYAGTUDOMÁNYI ÉS TECHNOLÓGIAI TANSZÉK POLIMERTECHNIKA NGB_AJ050_1 Polimerek reológiája DR Hargitai Hajnalka REOLÓGIA Az anyag deformációjának és folyásának a tudománya. rheo -
Geometriai és hullámoptika. Utolsó módosítás: május 10..
 Geometriai és hullámoptika Utolsó módosítás: 2016. május 10.. 1 Mi a fény? Részecske vagy hullám? Isaac Newton (1642-1727) Pierre de Fermat (1601-1665) Christiaan Huygens (1629-1695) Thomas Young (1773-1829)
Geometriai és hullámoptika Utolsó módosítás: 2016. május 10.. 1 Mi a fény? Részecske vagy hullám? Isaac Newton (1642-1727) Pierre de Fermat (1601-1665) Christiaan Huygens (1629-1695) Thomas Young (1773-1829)
Szemcsés anyagok részecske
 Szemcsés anyagok részecske alapú szimulációi (PhD tézisfüzet) Fazekas Sándor Témavezető: Dr. Kertész János Budapesti Műszaki és Gazdaságtudományi Egyetem Elméleti Fizika Tanszék (2007) Bevezetés A szemcsés
Szemcsés anyagok részecske alapú szimulációi (PhD tézisfüzet) Fazekas Sándor Témavezető: Dr. Kertész János Budapesti Műszaki és Gazdaságtudományi Egyetem Elméleti Fizika Tanszék (2007) Bevezetés A szemcsés
Folyadékok. Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Folyadékok, szilárd anyagok, folyadékkristályok.
 Folyadékok folyékony nincs saját alakja szilárd van saját alakja (deformálás után úgy marad, nem (deformálás után visszaalakul, mert ébrednek benne visszatérítő nyíróerők) visszatérítő nyíróerők léptek
Folyadékok folyékony nincs saját alakja szilárd van saját alakja (deformálás után úgy marad, nem (deformálás után visszaalakul, mert ébrednek benne visszatérítő nyíróerők) visszatérítő nyíróerők léptek
Mechanika, dinamika. p = m = F t vagy. m t
 Mechanika, dinamika Mozgás, alakváltozás és ennek háttere Newton: a mozgás természetes állapot. A témakör egyik kulcsfontosságú fizikai mennyisége az impulzus (p), vagy lendület, vagy mozgásmennyiség.
Mechanika, dinamika Mozgás, alakváltozás és ennek háttere Newton: a mozgás természetes állapot. A témakör egyik kulcsfontosságú fizikai mennyisége az impulzus (p), vagy lendület, vagy mozgásmennyiség.
MateFIZIKA: Szélsőértékelvek a fizikában
 MateFIZIKA: Szélsőértékelvek a fizikában Tasnádi Tamás 1 2015. április 10.,17. 1 BME, Mat. Int., Analízis Tsz. Tartalom Energiaminimum-elv a mechanikában (ápr. 10.) Okos szappanhártyák (ápr. 10.) Legrövidebb
MateFIZIKA: Szélsőértékelvek a fizikában Tasnádi Tamás 1 2015. április 10.,17. 1 BME, Mat. Int., Analízis Tsz. Tartalom Energiaminimum-elv a mechanikában (ápr. 10.) Okos szappanhártyák (ápr. 10.) Legrövidebb
Optika és Relativitáselmélet II. BsC fizikus hallgatóknak
 Optika és Relativitáselmélet II. BsC fizikus hallgatóknak 2. Fényhullámok tulajdonságai Cserti József, jegyzet, ELTE, 2007. Az elektromágneses spektrum Látható spektrum (erre állt be a szemünk) UV: ultraibolya
Optika és Relativitáselmélet II. BsC fizikus hallgatóknak 2. Fényhullámok tulajdonságai Cserti József, jegyzet, ELTE, 2007. Az elektromágneses spektrum Látható spektrum (erre állt be a szemünk) UV: ultraibolya
BKT fázisátalakulás és a funkcionális renormálási csoport módszer
 BKT fázisátalakulás és a funkcionális renormálási csoport módszer Nándori István MTA-DE Részecskefizikai Kutatócsoport, Debreceni Egyetem MTA-Atomki, Debrecen Wigner FK zilárdtestfizikai és Optikai Intézet,
BKT fázisátalakulás és a funkcionális renormálási csoport módszer Nándori István MTA-DE Részecskefizikai Kutatócsoport, Debreceni Egyetem MTA-Atomki, Debrecen Wigner FK zilárdtestfizikai és Optikai Intézet,
Az Ampère-Maxwell-féle gerjesztési törvény
 Az Ampère-Maxwell-féle gerjesztési törvény Maxwell elméleti meggondolások alapján feltételezte, hogy a változó elektromos tér örvényes mágneses teret kelt (hasonlóan ahhoz ahogy a változó mágneses tér
Az Ampère-Maxwell-féle gerjesztési törvény Maxwell elméleti meggondolások alapján feltételezte, hogy a változó elektromos tér örvényes mágneses teret kelt (hasonlóan ahhoz ahogy a változó mágneses tér
A geometriai optika. Fizika május 25. Rezgések és hullámok. Fizika 11. (Rezgések és hullámok) A geometriai optika május 25.
 A geometriai optika Fizika 11. Rezgések és hullámok 2019. május 25. Fizika 11. (Rezgések és hullámok) A geometriai optika 2019. május 25. 1 / 22 Tartalomjegyzék 1 A fénysebesség meghatározása Olaf Römer
A geometriai optika Fizika 11. Rezgések és hullámok 2019. május 25. Fizika 11. (Rezgések és hullámok) A geometriai optika 2019. május 25. 1 / 22 Tartalomjegyzék 1 A fénysebesség meghatározása Olaf Römer
Evans-Searles fluktuációs tétel Crooks fluktuációs tétel Jarzynski egyenlőség
 Evans-Searles fluktuációs tétel Crooks fluktuációs tétel Jarzynski egyenlőség Osváth Szabolcs Evans-Searles fluktuációs tétel Denis J Evans, Ezechiel DG Cohen, Gary P Morriss (1993) Denis J Evans, Debra
Evans-Searles fluktuációs tétel Crooks fluktuációs tétel Jarzynski egyenlőség Osváth Szabolcs Evans-Searles fluktuációs tétel Denis J Evans, Ezechiel DG Cohen, Gary P Morriss (1993) Denis J Evans, Debra
Folyadékok áramlása Folyadékok. Folyadékok mechanikája. Pascal törvénye
 Folyadékok áramlása Folyadékok Folyékony halmazállapot nyíróerő hatására folytonosan deformálódik (folyik) Folyadék Gáz Plazma Talián Csaba Gábor PTE ÁOK, Biofizikai Intézet 2012.09.12. Folyadék Rövidtávú
Folyadékok áramlása Folyadékok Folyékony halmazállapot nyíróerő hatására folytonosan deformálódik (folyik) Folyadék Gáz Plazma Talián Csaba Gábor PTE ÁOK, Biofizikai Intézet 2012.09.12. Folyadék Rövidtávú
A Standard modellen túli Higgs-bozonok keresése
 A Standard modellen túli Higgs-bozonok keresése Elméleti fizikai iskola, Gyöngyöstarján, 2007. okt. 29. Horváth Dezső MTA KFKI Részecske és Magfizikai Kutatóintézet, Budapest és ATOMKI, Debrecen Horváth
A Standard modellen túli Higgs-bozonok keresése Elméleti fizikai iskola, Gyöngyöstarján, 2007. okt. 29. Horváth Dezső MTA KFKI Részecske és Magfizikai Kutatóintézet, Budapest és ATOMKI, Debrecen Horváth
KALIBRÁCIÓS MÓDSZER SZEMCSÉS HALMAZOK MIKROMECHANIKAI JELLEMZŐINEK MEGHATÁROZÁSÁHOZ
 XX. Fiatal Műszakiak Tudományos Ülésszaka, 2015. Kolozsvár, 271 274. http://hdl.handle.net/10598/28634 Műszaki tudományos közlemények 3. KALIBRÁCIÓS MÓDSZER SZEMCSÉS HALMAZOK MIKROMECHANIKAI JELLEMZŐINEK
XX. Fiatal Műszakiak Tudományos Ülésszaka, 2015. Kolozsvár, 271 274. http://hdl.handle.net/10598/28634 Műszaki tudományos közlemények 3. KALIBRÁCIÓS MÓDSZER SZEMCSÉS HALMAZOK MIKROMECHANIKAI JELLEMZŐINEK
Hidraulika. 1.előadás A hidraulika alapjai. Szilágyi Attila, NYE, 2018.
 Hidraulika 1.előadás A hidraulika alapjai Szilágyi Attila, NYE, 018. Folyadékok mechanikája Ideális folyadék: homogén, súrlódásmentes, kitölti a rendelkezésre álló teret, nincs nyírófeszültség. Folyadékok
Hidraulika 1.előadás A hidraulika alapjai Szilágyi Attila, NYE, 018. Folyadékok mechanikája Ideális folyadék: homogén, súrlódásmentes, kitölti a rendelkezésre álló teret, nincs nyírófeszültség. Folyadékok
Polimerek reológiája
 SZÉCHENYI ISTVÁN EGYETEM ANYAGISMERETI ÉS JÁRMŰGYÁRTÁSI TANSZÉK POLIMERTECHNIKA NGB_AJ050_1 Polimerek reológiája DR Hargitai Hajnalka 2011.09.28. REOLÓGIA Az anyag deformációjának és folyásának a tudománya.
SZÉCHENYI ISTVÁN EGYETEM ANYAGISMERETI ÉS JÁRMŰGYÁRTÁSI TANSZÉK POLIMERTECHNIKA NGB_AJ050_1 Polimerek reológiája DR Hargitai Hajnalka 2011.09.28. REOLÓGIA Az anyag deformációjának és folyásának a tudománya.
Ábragyűjtemény levelező hallgatók számára
 Ábragyűjtemény levelező hallgatók számára Ez a bemutató a tanszéki Fizika jegyzet kiegészítése Mechanika I. félév 1 Stabilitás Az úszás stabilitása indifferens a stabil, b labilis S súlypont Sf a kiszorított
Ábragyűjtemény levelező hallgatók számára Ez a bemutató a tanszéki Fizika jegyzet kiegészítése Mechanika I. félév 1 Stabilitás Az úszás stabilitása indifferens a stabil, b labilis S súlypont Sf a kiszorított
Z bozonok az LHC nehézion programjában
 Z bozonok az LHC nehézion programjában Zsigmond Anna Julia MTA Wigner FK Max Planck Institut für Physik Fizikus Vándorgyűlés Szeged, 2016 augusztus 24-27. Nehézion-ütközések az LHC-nál A-A és p-a ütközések
Z bozonok az LHC nehézion programjában Zsigmond Anna Julia MTA Wigner FK Max Planck Institut für Physik Fizikus Vándorgyűlés Szeged, 2016 augusztus 24-27. Nehézion-ütközések az LHC-nál A-A és p-a ütközések
Kutatási beszámoló. 2015. február. Tangens delta mérésére alkalmas mérési összeállítás elkészítése
 Kutatási beszámoló 2015. február Gyüre Balázs BME Fizika tanszék Dr. Simon Ferenc csoportja Tangens delta mérésére alkalmas mérési összeállítás elkészítése A TKI-Ferrit Fejlsztő és Gyártó Kft.-nek munkája
Kutatási beszámoló 2015. február Gyüre Balázs BME Fizika tanszék Dr. Simon Ferenc csoportja Tangens delta mérésére alkalmas mérési összeállítás elkészítése A TKI-Ferrit Fejlsztő és Gyártó Kft.-nek munkája
2.2.10. VISZKOZITÁS MEGHATÁROZÁSA ROTÁCIÓS VISZKOZIMÉTERREL
 2.2.10. Vszkztás meghatárzása Ph. Hg. VIII. Ph. Eur. 5.3. - 1 01/2006:20210 2.2.10. VISZKOZITÁS MEGHATÁOZÁSA OTÁCIÓS VISZKOZIMÉTEEL A módszer annak az erőnek a mérésén alapul, amely egy flyadékban állandó
2.2.10. Vszkztás meghatárzása Ph. Hg. VIII. Ph. Eur. 5.3. - 1 01/2006:20210 2.2.10. VISZKOZITÁS MEGHATÁOZÁSA OTÁCIÓS VISZKOZIMÉTEEL A módszer annak az erőnek a mérésén alapul, amely egy flyadékban állandó
REPEDÉSEK DINAMIKÁJÁTÓL KATASZTRÓFÁK ELŐREJELZÉSÉIG
 REPEDÉSEK DINAMIKÁJÁTÓL KATASZTRÓFÁK ELŐREJELZÉSÉIG Kun Ferenc Debreceni Egyetem Elméleti Fizikai Tanszék 2018. 12. 12. MTA Székház, Budapest Heterogén anyagok Erős heterogenitás széles méretskálán Beton
REPEDÉSEK DINAMIKÁJÁTÓL KATASZTRÓFÁK ELŐREJELZÉSÉIG Kun Ferenc Debreceni Egyetem Elméleti Fizikai Tanszék 2018. 12. 12. MTA Székház, Budapest Heterogén anyagok Erős heterogenitás széles méretskálán Beton
Molekuláris dinamika. 10. előadás
 Molekuláris dinamika 10. előadás Mirőlis szól a MD? nagy részecskeszámú rendszerek ismerjük a törvényeket mikroszkópikus szinten? Hogyan tudjuk megérteni a folyadékok, gázok, szilárdtestek makroszkópikus
Molekuláris dinamika 10. előadás Mirőlis szól a MD? nagy részecskeszámú rendszerek ismerjük a törvényeket mikroszkópikus szinten? Hogyan tudjuk megérteni a folyadékok, gázok, szilárdtestek makroszkópikus
Optika gyakorlat 1. Fermat-elv, fénytörés, reexió sík és görbült határfelületen. Fermat-elv
 Optika gyakorlat 1. Fermat-elv, fénytörés, reexió sík és görbült határfelületen Kivonat Geometriai optika: közelítés, amely a fényterjedést, közeghatáron való áthaladást geometriai alakzatok görbék segítségével
Optika gyakorlat 1. Fermat-elv, fénytörés, reexió sík és görbült határfelületen Kivonat Geometriai optika: közelítés, amely a fényterjedést, közeghatáron való áthaladást geometriai alakzatok görbék segítségével
7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék)
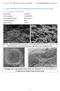 7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék) 7.1.1. SPS: 1150 C; 5 (1312 K1) Mért sűrűség: 3,795 g/cm 3 3,62 0,14 GPa Három pontos törés teszt: 105 4,2 GPa Súrlódási együttható:
7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék) 7.1.1. SPS: 1150 C; 5 (1312 K1) Mért sűrűség: 3,795 g/cm 3 3,62 0,14 GPa Három pontos törés teszt: 105 4,2 GPa Súrlódási együttható:
V e r s e n y f e l h í v á s
 A természettudományos oktatás módszertanának és eszközrendszerének megújítása a Sárospataki Református Kollégium Gimnáziumában TÁMOP-3.1.3-11/2-2012-0021 V e r s e n y f e l h í v á s A Sárospataki Református
A természettudományos oktatás módszertanának és eszközrendszerének megújítása a Sárospataki Református Kollégium Gimnáziumában TÁMOP-3.1.3-11/2-2012-0021 V e r s e n y f e l h í v á s A Sárospataki Református
Fénnyel keltett átorientálások és instabilitások
 Fénnyel keltett átorientálások és instabilitások Bevezetés (fotokróm anyagok & folyadékkristályok); Folyadékkristály cellák fényérzékeny réteggel: - a minták előkészítése; - alapjelenségek megfigyelése:
Fénnyel keltett átorientálások és instabilitások Bevezetés (fotokróm anyagok & folyadékkristályok); Folyadékkristály cellák fényérzékeny réteggel: - a minták előkészítése; - alapjelenségek megfigyelése:
Számítógépes Grafika mintafeladatok
 Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Szilárd testek rugalmas alakváltozásai Nyú y j ú tás y j Hooke törvény, Hooke törvén E E o Y un un modulus a f eszültség ffeszültség
 Kontinuumok mechanikája Szabó Gábor egyetemi tanár SZTE Optikai Tanszék Szilárd testek rugalmas alakváltozásai Nyújtás l l = l E F A Hooke törvény, E Young modulus σ = F A σ a feszültség l l l = σ E Szilárd
Kontinuumok mechanikája Szabó Gábor egyetemi tanár SZTE Optikai Tanszék Szilárd testek rugalmas alakváltozásai Nyújtás l l = l E F A Hooke törvény, E Young modulus σ = F A σ a feszültség l l l = σ E Szilárd
ÉPÍTŐANYAGOK REOLÓGIAI TULAJDONSÁGAINAK VIZSGÁLATA A DE-ATC-MFK MÉLY- ÉS SZERKEZETÉPÍTÉSI TANSZÉKÉN
 ÉPÍTŐANYAGOK REOLÓGIAI TULAJDONSÁGAINAK VIZSGÁLATA A DE-ATC-MK MÉLY- ÉS SZERKEZETÉPÍTÉSI TANSZÉKÉN Dr. Kovács Imre PhD. tanszékvezető főiskolai docens 1 Vizsgálataink szintjei Numerikus szimuláció lineáris,
ÉPÍTŐANYAGOK REOLÓGIAI TULAJDONSÁGAINAK VIZSGÁLATA A DE-ATC-MK MÉLY- ÉS SZERKEZETÉPÍTÉSI TANSZÉKÉN Dr. Kovács Imre PhD. tanszékvezető főiskolai docens 1 Vizsgálataink szintjei Numerikus szimuláció lineáris,
Függőleges és vízszintes vasalás hatása a téglafalazat nyírási ellenállására
 Függőleges és vízszintes vasalás hatása a téglafalazat nyírási ellenállására FÓDI ANITA Témavezető: Dr. Bódi István Budapesti Műszaki és Gazdaságtudományi Egyetem Építőmérnöki kar Hidak és Szerkezetek
Függőleges és vízszintes vasalás hatása a téglafalazat nyírási ellenállására FÓDI ANITA Témavezető: Dr. Bódi István Budapesti Műszaki és Gazdaságtudományi Egyetem Építőmérnöki kar Hidak és Szerkezetek
OPTIKA. Geometriai optika. Snellius Descartes-törvény. www.baranyi.hu 2010. szeptember 19. FIZIKA TÁVOKTATÁS
 OPTIKA Geometriai optika Snellius Descartes-törvény A fényhullám a geometriai optika szempontjából párhuzamos fénysugarakból áll. A vákuumban haladó fénysugár a geometriai egyenes fizikai megfelelője.
OPTIKA Geometriai optika Snellius Descartes-törvény A fényhullám a geometriai optika szempontjából párhuzamos fénysugarakból áll. A vákuumban haladó fénysugár a geometriai egyenes fizikai megfelelője.
Szívókönyökök veszteségeinek és sebességprofiljainak vizsgálata CFD szimuláció segítségével
 GANZ ENGINEERING ÉS ENERGETIKAI GÉPGYÁRTÓ KFT. Szívókönyökök veszteségeinek és sebességprofiljainak vizsgálata CFD szimuláció segítségével Készítette: Bogár Péter Háznagy Gergely Egyed Csaba Zombor Csaba
GANZ ENGINEERING ÉS ENERGETIKAI GÉPGYÁRTÓ KFT. Szívókönyökök veszteségeinek és sebességprofiljainak vizsgálata CFD szimuláció segítségével Készítette: Bogár Péter Háznagy Gergely Egyed Csaba Zombor Csaba
Hogyan kerül a kvarkanyag
 Hogyan kerül a kvarkanyag a Rubik kockára? Csörgő Tamás fizikus, MTA Wigner FK és KRF, Gyöngyös A Rubik (bűvös) kocka feltalálásának 40. évfordulójára Fizikai Szemle 2013/6. sz. 205. o., 2013/7-8. sz.
Hogyan kerül a kvarkanyag a Rubik kockára? Csörgő Tamás fizikus, MTA Wigner FK és KRF, Gyöngyös A Rubik (bűvös) kocka feltalálásának 40. évfordulójára Fizikai Szemle 2013/6. sz. 205. o., 2013/7-8. sz.
SZAKDOLGOZAT VIRÁG DÁVID
 SZAKDOLGOZAT VIRÁG DÁVID 2010 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Áramlástan Tanszék SZÁRNY KÖRÜLI TURBULENS ÁRAMLÁS NUMERIKUS SZIMULÁCIÓJA NYÍLT FORRÁSKÓDÚ SZOFTVERREL VIRÁG
SZAKDOLGOZAT VIRÁG DÁVID 2010 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Áramlástan Tanszék SZÁRNY KÖRÜLI TURBULENS ÁRAMLÁS NUMERIKUS SZIMULÁCIÓJA NYÍLT FORRÁSKÓDÚ SZOFTVERREL VIRÁG
Bevezetés a fúziós plazmafizikába 3.
 Bevezetés a fúziós plazmafizikába 3. Mágneses összetartás konfigurációk Dr. Pokol Gergő BME NTI Bevezetés a fúziós plazmafizikába 2018. szeptember 18. Tematika, időbeosztás Dátum Előadó Cím Szeptember
Bevezetés a fúziós plazmafizikába 3. Mágneses összetartás konfigurációk Dr. Pokol Gergő BME NTI Bevezetés a fúziós plazmafizikába 2018. szeptember 18. Tematika, időbeosztás Dátum Előadó Cím Szeptember
Magasépítési öszvérfödémek numerikus szimuláció alapú méretezése
 BME Hidak és Szerkezetek Tanszéke Magasépítési öszvérfödémek numerikus szimuláció alapú méretezése Seres Noémi DEVSOG Témavezetı: Dr. Dunai László Bevezetés Az elıadás témája öszvérfödémek együttdolgoztató
BME Hidak és Szerkezetek Tanszéke Magasépítési öszvérfödémek numerikus szimuláció alapú méretezése Seres Noémi DEVSOG Témavezetı: Dr. Dunai László Bevezetés Az elıadás témája öszvérfödémek együttdolgoztató
DR. DEMÉNY ANDRÁS-I)R. EROSTYÁK JÁNOS- DR. SZABÓ GÁBOR-DR. TRÓCSÁNYI ZOLTÁN FIZIKA I. Klasszikus mechanika NEMZETI TANKÖNYVKIADÓ, BUDAPEST
 DR. DEMÉNY ANDRÁS-I)R. EROSTYÁK JÁNOS- DR. SZABÓ GÁBOR-DR. TRÓCSÁNYI ZOLTÁN FIZIKA I Klasszikus mechanika NEMZETI TANKÖNYVKIADÓ, BUDAPEST Előszó a Fizika című tankönyvsorozathoz Előszó a Fizika I. (Klasszikus
DR. DEMÉNY ANDRÁS-I)R. EROSTYÁK JÁNOS- DR. SZABÓ GÁBOR-DR. TRÓCSÁNYI ZOLTÁN FIZIKA I Klasszikus mechanika NEMZETI TANKÖNYVKIADÓ, BUDAPEST Előszó a Fizika című tankönyvsorozathoz Előszó a Fizika I. (Klasszikus
Határfelületi reológia vizsgálata cseppalak analízissel
 Határfelületi reológia vizsgálata cseppalak analízissel A reológia alapjai Reológiai folyamatról akkor beszélünk, ha egy anyagra erő hat, mely az anyag (vagy annak egy darabjának) deformációját eredményezi.
Határfelületi reológia vizsgálata cseppalak analízissel A reológia alapjai Reológiai folyamatról akkor beszélünk, ha egy anyagra erő hat, mely az anyag (vagy annak egy darabjának) deformációját eredményezi.
A kísérlet célkitűzései: A fénytani lencsék megismerése, tulajdonságainak kísérleti vizsgálata és felhasználási lehetőségeinek áttekintése.
 A kísérlet célkitűzései: A fénytani lencsék megismerése, tulajdonságainak kísérleti vizsgálata és felhasználási lehetőségeinek áttekintése. Eszközszükséglet: Optika I. tanulói készlet főzőpohár, üvegkád,
A kísérlet célkitűzései: A fénytani lencsék megismerése, tulajdonságainak kísérleti vizsgálata és felhasználási lehetőségeinek áttekintése. Eszközszükséglet: Optika I. tanulói készlet főzőpohár, üvegkád,
Az úszás biomechanikája
 Az úszás biomechanikája Alapvető összetevők Izomerő Kondíció állóképesség Mozgáskoordináció kivitelezés + Nem levegő, mint közeg + Izmok nem gravitációval szembeni mozgása + Levegővétel Az úszóra ható
Az úszás biomechanikája Alapvető összetevők Izomerő Kondíció állóképesség Mozgáskoordináció kivitelezés + Nem levegő, mint közeg + Izmok nem gravitációval szembeni mozgása + Levegővétel Az úszóra ható
Populációdinamika kurzus, projektfeladat. Aszimptotikus viselkedés egy determinisztikus járványterjedési modellben. El adó:
 Populációdinamika kurzus, projektfeladat Aszimptotikus viselkedés egy determinisztikus járványterjedési modellben El adó: Unger Tamás István okleveles villamosmérnök matematika B.Sc. szakos hallgató Szeged
Populációdinamika kurzus, projektfeladat Aszimptotikus viselkedés egy determinisztikus járványterjedési modellben El adó: Unger Tamás István okleveles villamosmérnök matematika B.Sc. szakos hallgató Szeged
RR fa tartók előnyei
 Rétegelt ragasztott fa tartók k vizsgálata Dr. Koris Kálmán, Dr. Bódi István BME Hidak és Szerkezetek Tanszék RR fa tartók előnyei Acélhoz és betonhoz képest kis térfogatsúly Kedvező szilárdsági és merevségi
Rétegelt ragasztott fa tartók k vizsgálata Dr. Koris Kálmán, Dr. Bódi István BME Hidak és Szerkezetek Tanszék RR fa tartók előnyei Acélhoz és betonhoz képest kis térfogatsúly Kedvező szilárdsági és merevségi
Amit a kapacitív gabona nedvességmérésről tudni kell
 Szemestermények korszerű szárítási, tárolási, feldolgozási és mérési technológiái Gödöllő, 2018 Amit a kapacitív gabona nedvességmérésről tudni kell Dr. Gillay Zoltán, adjunktus Szent István Egyetem, Élelmiszertudományi
Szemestermények korszerű szárítási, tárolási, feldolgozási és mérési technológiái Gödöllő, 2018 Amit a kapacitív gabona nedvességmérésről tudni kell Dr. Gillay Zoltán, adjunktus Szent István Egyetem, Élelmiszertudományi
Lineáris algebra zárthelyi dolgozat javítókulcs, Informatika I. 2005.márc.11. A csoport
 Lineáris algebra zárthelyi dolgozat javítókulcs, Informatika I. 2005.márc.11. A csoport 1. Egy egyenesre esnek-e az A (2, 5, 1), B (5, 17, 7) és C (3, 9, 3) pontok? 5 pont Megoldás: Nem, mert AB (3, 12,
Lineáris algebra zárthelyi dolgozat javítókulcs, Informatika I. 2005.márc.11. A csoport 1. Egy egyenesre esnek-e az A (2, 5, 1), B (5, 17, 7) és C (3, 9, 3) pontok? 5 pont Megoldás: Nem, mert AB (3, 12,
Reológia, a koherens (nem-koherens) rendszerek tulajdonságai
 Reológia, a koherens (nem-koherens) rendszerek tulajdonságai Bányai István kolloid.unideb.hu Koherens rendszerek Szubmikroszkópos vagy durva diszkontinuitásokat tartalmazó rendszerek, amelyekben micellák,
Reológia, a koherens (nem-koherens) rendszerek tulajdonságai Bányai István kolloid.unideb.hu Koherens rendszerek Szubmikroszkópos vagy durva diszkontinuitásokat tartalmazó rendszerek, amelyekben micellák,
Perturbációk elméleti és kísérleti vizsgálata a BME Oktatóreaktorán
 Perturbációk elméleti és kísérleti vizsgálata a BME Oktatóreaktorán Horváth András, Kis Dániel Péter, Szatmáry Zoltán XV. Nukleáris Technikai Szimpózium 2016. december 8-9. Paks, Erzsébet Nagyszálloda
Perturbációk elméleti és kísérleti vizsgálata a BME Oktatóreaktorán Horváth András, Kis Dániel Péter, Szatmáry Zoltán XV. Nukleáris Technikai Szimpózium 2016. december 8-9. Paks, Erzsébet Nagyszálloda
TALAJAZONOSÍTÁS Kötött talajok
 2008 PJ-MA SOIL MECHANICS BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GEOTECHNIKAI TANSZÉK TALAJAZONOSÍTÁS Kötött talajok Előadó: Dr. Mahler András mahler@mail.bme.hu Tanszék: K épület, mfsz. 10. &
2008 PJ-MA SOIL MECHANICS BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GEOTECHNIKAI TANSZÉK TALAJAZONOSÍTÁS Kötött talajok Előadó: Dr. Mahler András mahler@mail.bme.hu Tanszék: K épület, mfsz. 10. &
Folyadékkristályok: szépek és hasznosak
 Folyadékkristályok: szépek és hasznosak Dr. Éber Nándor Szilárdtest-fizikai és Optikai Intézet MTA Wigner Fizikai Kutatóközpont Atomoktól a csillagokig, 2012. március 22. Folyadékkristályok mindennapi
Folyadékkristályok: szépek és hasznosak Dr. Éber Nándor Szilárdtest-fizikai és Optikai Intézet MTA Wigner Fizikai Kutatóközpont Atomoktól a csillagokig, 2012. március 22. Folyadékkristályok mindennapi
MŰSZAKI FIZIKA II. Földtudományi mérnöki MSc mesterszak. 2017/18 II. félév TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ
 MŰSZAKI FIZIKA II. Földtudományi mérnöki MSc mesterszak 2017/18 II. félév TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ Miskolci Egyetem Műszaki Földtudományi Kar Geofizikai és Térinformatikai Intézet A tantárgy adatlapja
MŰSZAKI FIZIKA II. Földtudományi mérnöki MSc mesterszak 2017/18 II. félév TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ Miskolci Egyetem Műszaki Földtudományi Kar Geofizikai és Térinformatikai Intézet A tantárgy adatlapja
A gradiens törésmutatójú közeg I.
 10. Előadás A gradiens törésmutatójú közeg I. Az ugrásszerű törésmutató változással szemben a TracePro-ban lehetőség van folytonosan változó törésmutatójú közeg definiálására. Ilyen érdekes típusú közegek
10. Előadás A gradiens törésmutatójú közeg I. Az ugrásszerű törésmutató változással szemben a TracePro-ban lehetőség van folytonosan változó törésmutatójú közeg definiálására. Ilyen érdekes típusú közegek
Speciális fluoreszcencia spektroszkópiai módszerek
 Speciális fluoreszcencia spektroszkópiai módszerek Fluoreszcencia kioltás Fluoreszcencia Rezonancia Energia Transzfer (FRET), Lumineszcencia A molekuláknak azt a fényemisszióját, melyet a valamilyen módon
Speciális fluoreszcencia spektroszkópiai módszerek Fluoreszcencia kioltás Fluoreszcencia Rezonancia Energia Transzfer (FRET), Lumineszcencia A molekuláknak azt a fényemisszióját, melyet a valamilyen módon
Folyadékok és gázok áramlása
 Folyadékok és gázok áramlása Hőkerék készítése házilag Gázok és folyadékok áramlása A meleg fűtőtest vagy rezsó felett a levegő felmelegszik és kitágul, sűrűsége kisebb lesz, mint a környezetéé, ezért
Folyadékok és gázok áramlása Hőkerék készítése házilag Gázok és folyadékok áramlása A meleg fűtőtest vagy rezsó felett a levegő felmelegszik és kitágul, sűrűsége kisebb lesz, mint a környezetéé, ezért
Jahn Teller-effektus Cs 3 C 60 -ban. Pergerné Klupp Gyöngyi. Matus Péter, Kamarás Katalin MTA SZFKI
 Jahn Teller-effektus Cs 3 C 60 -ban Pergerné Klupp Gyöngyi Matus Péter, Kamarás Katalin MTA SZFKI Jahn Teller-effektus Cs 3 C 60 -ban Tartalom 2 Bevezetés az A 3 C 60 (A = K, Rb, Cs) alkálifém-fulleridekről
Jahn Teller-effektus Cs 3 C 60 -ban Pergerné Klupp Gyöngyi Matus Péter, Kamarás Katalin MTA SZFKI Jahn Teller-effektus Cs 3 C 60 -ban Tartalom 2 Bevezetés az A 3 C 60 (A = K, Rb, Cs) alkálifém-fulleridekről
Modern Fizika Labor Fizika BSC
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. április 20. A mérés száma és címe: 20. Folyadékáramlások 2D-ban Értékelés: A beadás dátuma: 2009. április 28. A mérést végezte: Márton Krisztina Zsigmond
Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. április 20. A mérés száma és címe: 20. Folyadékáramlások 2D-ban Értékelés: A beadás dátuma: 2009. április 28. A mérést végezte: Márton Krisztina Zsigmond
F. F, <I> F,, F, <I> F,, F, <J> F F, <I> F,,
 F,=A4>, ahol A arányossági tényező: A= 0.06 ~, oszt as cl> a műszer kitérése. A F, = f(f,,) függvénykapcsolatot felrajzolva (a mérőpontok közé egyenes huzható) az egyenes iránytaogense a mozgó surlódási
F,=A4>, ahol A arányossági tényező: A= 0.06 ~, oszt as cl> a műszer kitérése. A F, = f(f,,) függvénykapcsolatot felrajzolva (a mérőpontok közé egyenes huzható) az egyenes iránytaogense a mozgó surlódási
Az optika tudományterületei
 Az optika tudományterületei Optika FIZIKA BSc, III/1. 1. / 17 Erdei Gábor Elektromágneses spektrum http://infothread.org/science/physics/electromagnetic%20spectrum.jpg Optika FIZIKA BSc, III/1. 2. / 17
Az optika tudományterületei Optika FIZIKA BSc, III/1. 1. / 17 Erdei Gábor Elektromágneses spektrum http://infothread.org/science/physics/electromagnetic%20spectrum.jpg Optika FIZIKA BSc, III/1. 2. / 17
Mágneses erőtér. Ahol az áramtól átjárt vezetőre (vagy mágnestűre) erő hat. A villamos forgógépek mutatós műszerek működésének alapja
 Mágneses erőtér Ahol az áramtól átjárt vezetőre (vagy mágnestűre) erő hat A villamos forgógépek mutatós műszerek működésének alapja Magnetosztatikai mező: nyugvó állandó mágnesek és egyenáramok időben
Mágneses erőtér Ahol az áramtól átjárt vezetőre (vagy mágnestűre) erő hat A villamos forgógépek mutatós műszerek működésének alapja Magnetosztatikai mező: nyugvó állandó mágnesek és egyenáramok időben
Geometriai Optika (sugároptika)
 Geometriai Optika (sugároptika) - Egyszerû optikai eszközök, ahogy már ismerjük õket - Mi van ha egymás után tesszük: leképezések egymásutánja (bonyolult) - Gyakorlatilag fontos eset: paraxiális közelítés
Geometriai Optika (sugároptika) - Egyszerû optikai eszközök, ahogy már ismerjük õket - Mi van ha egymás után tesszük: leképezések egymásutánja (bonyolult) - Gyakorlatilag fontos eset: paraxiális közelítés
ESR-spektrumok különbözı kísérleti körülmények között A számítógépes értékelés alapjai anizotróp kölcsönhatási tenzorok esetén
 ESR-spektrumok különbözı kísérleti körülmények között A számítógépes értékelés alapjai anizotróp kölcsönhatási tenzorok esetén A paraméterek anizotrópiája egykristályok rögzített tengely körüli forgatásakor
ESR-spektrumok különbözı kísérleti körülmények között A számítógépes értékelés alapjai anizotróp kölcsönhatási tenzorok esetén A paraméterek anizotrópiája egykristályok rögzített tengely körüli forgatásakor
Hidrosztatika. Folyadékok fizikai tulajdonságai
 Hidrosztatika A Hidrosztatika a nyugalomban lévő folyadékoknak a szilárd testekre, felületekre gyakorolt hatásával foglalkozik. Tárgyalja a nyugalomban lévő folyadékok nyomásviszonyait, vizsgálja a folyadékba
Hidrosztatika A Hidrosztatika a nyugalomban lévő folyadékoknak a szilárd testekre, felületekre gyakorolt hatásával foglalkozik. Tárgyalja a nyugalomban lévő folyadékok nyomásviszonyait, vizsgálja a folyadékba
Folyami hidrodinamikai modellezés
 Folyami hidrodinamikai modellezés Dr. Krámer Tamás egyetemi docens BME Vízépítési és Vízgazdálkodási Tanszék Numerikus modellezés 0D 1D 2D 3D Alacsony Kézi számítások Részletesség és pontosság Bonyolultság
Folyami hidrodinamikai modellezés Dr. Krámer Tamás egyetemi docens BME Vízépítési és Vízgazdálkodási Tanszék Numerikus modellezés 0D 1D 2D 3D Alacsony Kézi számítások Részletesség és pontosság Bonyolultság
Folyadékkristályok; biológiai és mesterséges membránok
 Folyadékkristályok; biológiai és mesterséges membránok Dr. Voszka István Folyadékkristályok: Átmenet a folyadékok és a kristályos szilárdtestek között (anizotróp folyadékok) Fonal, pálcika, korong alakú
Folyadékkristályok; biológiai és mesterséges membránok Dr. Voszka István Folyadékkristályok: Átmenet a folyadékok és a kristályos szilárdtestek között (anizotróp folyadékok) Fonal, pálcika, korong alakú
A Coulomb-törvény : ahol, = coulomb = 1C. = a vákuum permittivitása (dielektromos álladója) k 9 10 F Q. elektromos térerősség : ponttöltés tere :
 Villamosságtan A Coulomb-tövény : F QQ 4 ahol, Q = coulomb = C = a vákuum pemittivitása (dielektomos álladója) 4 9 k 9 elektomos téeősség : E F Q ponttöltés tee : E Q 4 Az elektosztatika I. alaptövénye
Villamosságtan A Coulomb-tövény : F QQ 4 ahol, Q = coulomb = C = a vákuum pemittivitása (dielektomos álladója) 4 9 k 9 elektomos téeősség : E F Q ponttöltés tee : E Q 4 Az elektosztatika I. alaptövénye
Az áramlási citométer és sejtszorter felépítése és működése, diagnosztikai alkalmazásai
 Az áramlási citométer és sejtszorter felépítése és működése, diagnosztikai alkalmazásai Az áramlási citométer és sejtszorter felépítése és működése Kereskedelmi forgalomban kapható készülékek 1 Fogalmak
Az áramlási citométer és sejtszorter felépítése és működése, diagnosztikai alkalmazásai Az áramlási citométer és sejtszorter felépítése és működése Kereskedelmi forgalomban kapható készülékek 1 Fogalmak
Transzportjelenségek
 Transzportjelenségek Fizikai kémia előadások 8. Turányi Tamás ELTE Kémiai Intézet lamináris (réteges) áramlás: minden réteget a falhoz közelebbi szomszédja fékez, a faltól távolabbi szomszédja gyorsít
Transzportjelenségek Fizikai kémia előadások 8. Turányi Tamás ELTE Kémiai Intézet lamináris (réteges) áramlás: minden réteget a falhoz közelebbi szomszédja fékez, a faltól távolabbi szomszédja gyorsít
Cölöpcsoport ellenőrzése Adatbev.
 Cölöpcsoport ellenőrzése Adatbev. Projekt Leírás Dátu : : Beállítások Pile Group - Exaple 3 28.10.2015 (bevitel az aktuális feladathoz) Anyagok és szabványok Beton szerkezetek : EN 1992-1-1 szerinti tényezők
Cölöpcsoport ellenőrzése Adatbev. Projekt Leírás Dátu : : Beállítások Pile Group - Exaple 3 28.10.2015 (bevitel az aktuális feladathoz) Anyagok és szabványok Beton szerkezetek : EN 1992-1-1 szerinti tényezők
Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások
 Miskolci Egyetem Műszaki Anyagtudományi Kar Anyagtudományi Intézet Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások Dr.Krállics György krallics@eik.bme.hu
Miskolci Egyetem Műszaki Anyagtudományi Kar Anyagtudományi Intézet Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások Dr.Krállics György krallics@eik.bme.hu
Simított részecskedinamika Smoothed Particle Hydrodynamics (SPH)
 Smoothed Particle Hydrodynamics (SPH) Áramlások numerikus modellezése II. Tóth Balázs BME-ÉMK Vízépítési és Vízgazdálkodási Tanszék Numerikus módszerek Osztályozás A numerikus sémák két csoportosítási
Smoothed Particle Hydrodynamics (SPH) Áramlások numerikus modellezése II. Tóth Balázs BME-ÉMK Vízépítési és Vízgazdálkodási Tanszék Numerikus módszerek Osztályozás A numerikus sémák két csoportosítási
Numerikus módszerek 1.
 Numerikus módszerek 1. 9. előadás: Paraméteres iterációk, relaxációs módszerek Lócsi Levente ELTE IK Tartalomjegyzék 1 A Richardson-iteráció 2 Relaxált Jacobi-iteráció 3 Relaxált Gauss Seidel-iteráció
Numerikus módszerek 1. 9. előadás: Paraméteres iterációk, relaxációs módszerek Lócsi Levente ELTE IK Tartalomjegyzék 1 A Richardson-iteráció 2 Relaxált Jacobi-iteráció 3 Relaxált Gauss Seidel-iteráció
Tartalom. Történeti áttekintés A jelenség és mérése Modellek
 Szonolumineszcencia Tartalom Történeti áttekintés A jelenség és mérése Modellek Történeti áttekintés 1917 Lord Rayleigh - kavitáció Történeti áttekintés 1917 Lord Rayleigh - kavitáció 1934-es ultrahang
Szonolumineszcencia Tartalom Történeti áttekintés A jelenség és mérése Modellek Történeti áttekintés 1917 Lord Rayleigh - kavitáció Történeti áttekintés 1917 Lord Rayleigh - kavitáció 1934-es ultrahang
Válasz ÓDOR GÉZANAK. Hőmérsékleti egyensúlytól távoli statisztikus fizikai rendszerek numerikus modellezése. című MTA doktori értekezésem bírálatára
 Válasz ÓDOR GÉZANAK Hőmérsékleti egyensúlytól távoli statisztikus fizikai rendszerek numerikus modellezése című MTA doktori értekezésem bírálatára Mindenek előtt nagyon köszönöm Ódor Gézának az értekezésem
Válasz ÓDOR GÉZANAK Hőmérsékleti egyensúlytól távoli statisztikus fizikai rendszerek numerikus modellezése című MTA doktori értekezésem bírálatára Mindenek előtt nagyon köszönöm Ódor Gézának az értekezésem
Mérés: Millikan olajcsepp-kísérlete
 Mérés: Millikan olajcsepp-kísérlete Mérés célja: 1909-ben ezt a mérést Robert Millikan végezte el először. Mérése során meg tudta határozni az elemi részecskék töltését. Ezért a felfedezéséért Nobel-díjat
Mérés: Millikan olajcsepp-kísérlete Mérés célja: 1909-ben ezt a mérést Robert Millikan végezte el először. Mérése során meg tudta határozni az elemi részecskék töltését. Ezért a felfedezéséért Nobel-díjat

